Prerpints.org logo
Preprint
Article

Optimal Control of Nonlinear, Nonautonomous, Energy Harvesting Systems Applied to Point Absorber Wave Energy Converters

This version is not peer-reviewed.

Submitted:

16 October 2024

Posted:

16 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Pursuing sustainable energy solutions has prompted researchers to focus on optimizing energy extraction from renewable sources. Control laws that optimize energy extraction require accurate modeling, often resulting in time-varying, nonlinear differential equations. An energy-maximizing optimal control law is derived for time-varying, nonlinear, second-order, energy harvesting systems. We demonstrate that sustaining periodic motion under this control law when subjected to periodic disturbances necessitates identifying appropriate initial conditions, inducing the system to follow a limit cycle. The general optimal solution is applied to two point absorber wave energy converter models: a linear model where the analytical derivation of initial conditions suffices and a nonlinear model demanding a numerical approach. A stable limit cycle is obtained for the latter when the initial conditions lie within an ellipse centered at the origin of the phase plane. This work advances energy-maximizing optimal control solutions for nonautonomous nonlinear systems with application to point absorbers. The results also shed light on the significance of initial conditions in achieving physically realizable periodic motion for periodic energy harvesting systems.
Keywords: 
Subject: 
Engineering  -   Control and Systems Engineering

1. Introduction

Optimal control theory provides a powerful framework for determining a dynamic system’s control law that extremizes an objective function [1]. It has been applied in many fields, including engineering, economics, and biology, to name a few. This study focuses on its application to energy maximization for a general class of second-order, nonlinear, time-varying dynamic systems.
A common yet challenging class of optimal control problems are the Linear Optimal Problems (LOPs), also known as singular problems. They occur when the inputs appear linearly in the system’s state equation and cost function, even though the state equations may be nonlinear in the states. This means that the control law cannot be formed directly by applying the stationary condition of optimality [2]. Several researchers have investigated the existence and solution of singular problems in optimal control [3,4,5,6,7]. Scardina [8] investigated the necessary conditions for optimality for singular problems using Pontryagin’s Minimum Principle (PMP). He exploited the fact that the value of the Hamiltonian, the central quantity in PMP that combines the system’s state, control inputs, and co-state variables, should be constant and reach the absolute minimum for an optimal control function while satisfying the system’s dynamics, co-state equations and any induced boundary conditions [6,7] to develop general solutions to singular optimal control problems.
Kelly et al. and Robbins [9,10,11] further explored the optimality conditions and introduced the generalized Legendre-Clebsch condition. It provides additional requirements for optimality, such as when the Hamiltonian is linear in the control input which often leads to a singularity. The generalized Legendre-Clebsch condition has been extensively studied in the context of optimal control, and its application has provided valuable insights into the existence and properties of optimal control solutions [11,12].
Creating an optimal solution for a nonlinear, nonautonomous system often requires finding both the control law and initial conditions such that the system states stay on the optimal path [13,14]. This is the approach taken in this paper. Limit cycles represent bounded periodic motion in a system, and their establishment is crucial for achieving sustained and efficient energy absorption for a point absorber wave energy converter subjected to periodic waves [15]. Due to the complexity of finding an energy-maximizing path of a nonlinear, nonautonomous system, sometimes it is acceptable to linearize the system first [16]. In contrast, the approach below exploits the model’s nonlinear, time-varying nature and applies to a wide range of dynamic systems.
In recent years, optimal control has gained significant attention in energy extraction applications, including designing and controlling wave energy converters (WECs). Wave energy converters are devices that transform water wave energy into valuable forms of energy, such as electricity, through a Power Take-Off system (PTO). The authors in [17] present a review and classification of wave energy converter technologies. This paper focuses on point absorber WECs, which are most commonly modeled using a linear approach based on Cummins equation [18] and are accurate for small motion about an equilibrium. However, energy capture can be increased for large motions where the model contains nonnegligible, nonlinear terms [19]. For heaving point absorbers, an important nonlinearity is the Froude-Krylov (FK) force [20] found by integrating the incident wave pressure over the buoy’s wetted surface area generating both buoyancy and hydrodynamic expressions.
In the pursuit of maximizing the energy output of Wave Energy Converters (WECs), diverse methodologies have been explored. It is widely acknowledged that the shape of a WEC plays a pivotal role in its dynamic response and, consequently, its energy harvesting potential. Therefore, various approaches have incorporated strategies for shape optimization, to increase energy extraction from ocean waves [21,22,23]. In parallel, strategies have focused on optimizing the geometry of WEC arrays [24]. Moreover, a WEC’s performance is highly dependent on the control law used. Thus, significant attention has been directed toward control system development. This domain has witnessed the proposal of diverse control strategies, including sliding mode control [25], numerical model predictive controls [26,27], and latching control techniques [28,29], each offering unique avenues for improving energy conversion efficiency.
Optimal strategies are often proposed with a comprehensive review by Ringwood et al. [30,31]. A well-studied energy-optimal strategy for point absorbers, whose dynamic response can be accurately modeled by a linear differential equation, is called complex conjugate control (CCC) [32]. Its origins date to the 1840s with Moritz von Jacobi’s maximum power transfer law for resistive circuits where the load and source resistance should be equal. This was later expanded to impedance matching, where the load should be equal to the circuit’s Thevinen equivalent source impedance for maximum power transfer [33]. Impedance matching is also used in many engineering fields, including the vibration community, to remove energy from vibrating structures [34,35]. This control strategy results in optimal energy extraction; however, it exaggerates the motion of the device, and it is restricted to linear WEC models. It should be noted that the resulting large motions are inconsistent with the model’s small motion assumption [20]. Therefore, this study develops an energy-maximizing control strategy for nonlinear, nonautonomous second-order periodic systems that applies to nonlinear WEC models as derived in [36].
Establishing limit cycles in WECs ensures the motion remains periodic and bounded, facilitating efficient energy conversion. The derivation of optimal control laws that lead to limit cycles has been investigated in different contexts. Wilson et al. [37] derived feedback linearizing optimal control law for nonlinear WECs, resulting in closed-loop limit cycles. In [38], an optimal control law was obtained by assuming a linear model for WECs exposed to regular waves, where they obtained an explicit expression for the optimal control force maximizing the absorbed energy. The control law was shown to be equivalent to the CCC in this specific linear case. However, they didn’t explore limit cycles to determine the optimal initial condition but instead relied on a switching function to keep the motion bounded.
This article builds upon the existing literature by presenting a general optimal control law for energy maximization in second-order, time-varying, nonlinear periodic dynamic systems. It extends the analysis of singular control problems and explores the existence of limit cycles to find the optimal initial conditions. The approach is applied using linear and nonlinear models motivated by recent WEC applications.
The remainder of the paper is organized as follows. Section 2 shows the derivation of the general optimal control law, while Section 3 applies the control law to both a linear and nonlinear WEC point absorber model. Section 4 provides some conclusions and ideas for further study.

2. General Optimal Control Law

After introducing the form of the second-order dynamic system, the optimal control law is derived, including examining the second-order optimality conditions.

2.1. Control Law Derivation

We consider the general, second-order, time-varying differential equation
M ζ ¨ = F e ( ζ , ζ ˙ , t ) − F c
where (1) is often used to model energy harvesting systems. M is the system’s total mass, ζ is position, and F e is the net external force acting on the system which could be either linear or nonlinear depending on the system explored. F e is exclusive of the externally applied control force, u = F c .
In the remainder, we will develop a control law for u that maximizes energy extraction. For the WEC examples considered later, F e contains time-varying, measurable disturbances due to the waves exploited to extract energy.
A state variable form of (1), x → ˙ = f → ( x → , F e ( x → ) , u ) , is shown below
x ˙ 1 = x 2 x ˙ 2 = F e ( x → ) − u M x ˙ 3 = 1
where the states are defined as x 1 = ζ , x 2 = ζ ˙ and x 3 = t . Time is introduced as a state to manage the nonautonomous nature of (1). It is a classical technique used in control theory to use the mathematical tools developed for autonomous systems to analyze and solve nonautonomous systems [13].
Our optimal problem will be framed in the context of a free end-time problem. For a free end-time problem, the initial state x ( t o ) is given, but the final time t f is not fixed.
The energy E is the integral of power
E = ∫ t o t f u x 2 d t
In (3) we neglect any dissipating electric power terms, concentrating instead on the mechanical energy. This approach is deliberate, as our primary focus is on the mechanical aspects of the system rather than the power electronics. Thus our objective function is framed to maximize the mechanical energy extraction, or conversely, minimize its negative as shown below:
min u ∈ [ t o , t f ] : − E ( x 2 , u ) x → ˙ ( t ) = f → ( x → , F e ( x → ) , u ) x ( t o ) = x o
where
− E ( x 2 , u ) = − ∫ t o t f u x 2 d t = ∫ t o t f ϕ ( x 2 , u ) d t
and ϕ ( x 2 , u ) = − u x 2 .
The Hamiltonian is [1,13]
H ( x → , λ → , F e ( x → ) , u ) = ϕ ( x 2 , u ) + λ → T f → ( x → , F e ( x → ) , u )
where λ → T = [ λ 1 λ 2 λ 3 ] is the adjoint vector also known as co-states.
Substituting (2) and our definition for ϕ ( x 2 , u ) into (5) gives the specific form of the Hamiltonian.
H ( x → , λ → , F e ( x → ) , u ) = − u x 2 + λ 1 x 2 + λ 2 M ( F e ( x → ) − u ) + λ 3
The optimal control, u * , and the resulting optimal trajectory in both states and co-states must certain optimality conditions.
∂ λ H ( x → , λ → , F e ( x → ) , u ) = x → ˙ ∂ x H ( x → , λ → , F e ( x → ) , u ) = − λ → ˙ ∂ u H ( x → , λ → , F e ( x → ) , u ) = 0
The three equations obtained from ∂ λ H ( x → , λ → , F e ( x → ) , u ) = x → ˙ of (7) are a restatement of the system state equations of (2) and the co-state differential equations, obtained from ∂ x H ( x → , λ → , F e ( x → ) , u ) = − λ → ˙ of (7) are known as Euler-Lagrange equations. The expansion of ∂ x H ( x → , λ → , F e ( x → ) , u ) = − λ → ˙ yields
λ ˙ 1 = − λ 2 M ∂ x 1 F e ( x → ) λ ˙ 2 = u − λ 1 − λ 2 M ∂ x 2 F e ( x → ) λ ˙ 3 = − λ 2 M ∂ x 3 F e ( x → )
The stationary condition ∂ u H ( x → , λ → , F e ( x → ) , u ) = 0 of (7) is given as
− x 2 − λ 2 M = 0
One more condition is necessary since a free final time problem is considered. This condition is known as the transversality condition which provide additional boundary conditions at the terminal time t f .
H ( x f → , λ f → , F e ( x → ) , u * ) = 0
Since H is linear in u, (9) does not directly express an optimal u it is called a singular problem which could be challenging to solve analytically. Fortunately, our equations could mathematically be manipulated to derive a closed-form solution for the control force u in terms of the states x → and F e ( x → ) , as shown in the remainder of this section.
The stationary condition of (9) relates x 2 and λ 2
λ 2 = − M x 2
which is differentiated and combined with λ ˙ 2 of (8) to obtain:
M x ˙ 2 = − u + λ 1 + λ 2 M ∂ x 2 F e ( x → )
Substituting x ˙ 2 of (2) and (11) into (12) and simplifying, we obtain the algebraic equation for λ 1 .
λ 1 = F e ( x → ) + x 2 ∂ x 2 F e ( x → )
After obtaining the algebraic expressions of the first two co-states, we can obtain the algebraic expression of the third co-state λ 3 . Although λ 3 is not used explicitly in the optimal control law, it is important to obtain all the co-state expressions to prove optimality later by showing that they are satisfied when applying the assumed optimal u. The value of the Hamiltonian of the optimal control function is constant across time and has the absolute minimum [8]. This could be further seen mathematically by taking the derivative of the Hamiltonian with respect to time. Since we have transformed our nonautonomous system to an autonomous system, time is now treated as a state [13].
d H d t = ∂ x H ∂ t x + ∂ λ H ∂ t λ + ∂ u H ∂ t u
Substituting (7) in (14) yields to d H d t = 0 . Thus, let the Hamiltonian of (6) equal an arbitrary constant H o as shown below
H ( x → , λ → , F e ( x → ) , u * ) = H o
Substituting the algebraic equations of the two other co-states of (11) and (13) into (15), we get (16).
x 2 2 ∂ x 2 F e ( x → ) + λ 3 = H o .
If u * is the optimal control and x → is the vector of corresponding optimal states, then there exists a co-state such that the Hamiltonian H = 0 [7]. Moreover, this satisfies our transversality condition of (10). Thus, imposing H o = 0 , yields the algebraic expression of λ 3 as follows:
λ 3 = − x 2 2 ∂ x 2 F e ( x → )
The algebraic expressions of the first two co-states can now be combined with (2) and (8) to find an algebraic equation for u * , which is the optimal control force. Differentiating (13) with respect to time ( x 3 ), we obtain:
λ ˙ 1 = x ˙ 1 ∂ x 1 F e ( x → ) + 2 x ˙ 2 ∂ x 2 F e ( x → ) + x ˙ 3 ∂ x 3 F e ( x → ) + x 2 x ˙ 1 ∂ x 1 ∂ x 2 F e ( x → ) + x ˙ 2 ∂ x 2 ∂ x 2 F e ( x → ) + x ˙ 3 ∂ x 3 ∂ x 2 F e ( x → )
Substituting λ 1 ˙ of (8) and x ˙ → of (2) in (18) and simplifying, the optimal control force becomes:
u * = F e ( x → ) + M x 2 2 ∂ x 1 ∂ x 2 F e ( x → ) + x 2 ∂ x 3 ∂ x 2 F e ( x → ) + ∂ x 3 F e ( x → ) 2 ∂ x 2 F e ( x → ) + x 2 ∂ x 2 2 F e ( x → )
which can also be written in terms of the state definitions as:
F c * = F e ( ζ , ζ ˙ , t ) + M ζ ˙ 2 ∂ ζ ∂ ζ ˙ F e ( ζ , ζ ˙ , t ) + ζ ˙ ∂ t ∂ ζ ˙ F e ( ζ , ζ ˙ , t ) + ∂ t F e ( ζ , ζ ˙ , t ) 2 ∂ ζ ˙ F e ( ζ , ζ ˙ , t ) + ζ ˙ ∂ ζ ˙ 2 F e ( ζ , ζ ˙ , t )
Interestingly, the control law of (20) still applies for varying mass systems. Consider a system of a varying mass M ( ζ , ζ ˙ , t ) such that its governing equation is:
M ζ ¨ + d M d t ζ ˙ = F e ( ζ , ζ ˙ , t ) − u
Writing (21) in the form of (1), we get
ζ ¨ = F m ( ζ , ζ ˙ , t )
where
F m = F e − d M d t ζ ˙ M
Applying the control law of (20) such that M = 1 and F e = F m , we obtain the optimal control law of a varying mass system as follows:
F c * = F m ( ζ , ζ ˙ , t ) + ζ ˙ 2 ∂ ζ ∂ ζ ˙ F m ( ζ , ζ ˙ , t ) + ζ ˙ ∂ t ∂ ζ ˙ F m ( ζ , ζ ˙ , t ) + ∂ t F m ( ζ , ζ ˙ , t ) 2 ∂ ζ ˙ F m ( ζ , ζ ˙ , t ) + ζ ˙ ∂ ζ ˙ 2 F m ( ζ , ζ ˙ , t )
which has an identical form to (20).

2.2. Second Order Optimality Condition

In addition to satisfying the first-order Euler-Lagrange equations of (7), Kelly et al. and Robbins [9,10,11] showed the existence of another necessary condition known as the generalized Legendre-Clebsch condition when the optimal solution satisfies (25).
( − 1 ) k ∂ u d 2 k d t 2 k ∂ u H ( x → , λ → , u ) ≥ 0 , k = 1 , 2 , 3 …
where k denotes the number of equations used for multiple control inputs. For our single input case, k = 1 . Writing t in its state form, x 3 , (25) can be simplified to (26).
∂ u d 2 d x 3 2 ∂ u H ( x → , λ → , u ) ≤ 0
Applying the test of (26) to the expression of (9) and doing the necessary substitutions and simplifications, yields:
∂ u d 2 d t 2 ∂ u H = 2 ∂ ζ ˙ F e ( x → ) + ζ ˙ ∂ ζ ˙ 2 F e ( x → ) M 2
According to (27), the Legendre-Clebsch condition applies when 2 ∂ ζ ˙ F e ( ζ , ζ ˙ , t ) + ζ ˙ ∂ ζ ˙ 2 F e ( ζ , ζ ˙ , t ) ≤ 0 . The sign of this term depends on the presence of ζ ˙ in F e ( ζ , ζ ˙ , t ) as well as its value and thus on the specifics of the application. For some optimal control problems, the Legendre-Clebsch condition is not satisfied for fixed time intervals. The control law may still be optimal over regions where it applies. Modifying the initial conditions can induce distinct motion patterns within the system, potentially guiding it toward a bounded optimal trajectory. This condition will be explored in detail for the control law derived in Section 3 for point absorber wave energy converters.

3. Application to Point Absorber Wave Energy Converters (WEC)

The control law of (24) is applied to two, time-varying, WEC model cases, one linear and the other nonlinear. Moreover, our solution is assumed periodic since a periodic input disturbance is considered [39], the waves, thus our boundary conditions will be written as follows:
x ( t o ) = x o x ( t f ) = x ( t o + n T )
where x o is to be determined and n is the number of periods.
For the linear case, (24) reduces to a well-known optimal solution along with initial condition requirements. The nonlinear case is more interesting, resulting in a nonlinear, time-varying control law. Initial condition regions that produce the required stable limit cycle motion are also explored. Since the system is time-varying, Poincare maps are used to ensure the motion is quasi-periodic.

3.1. Dynamic Model

Point absorber WECs exhibiting small motions about an equilibrium are often modeled using Cummins equation shown in (29), for the heave-only case [18]
M ζ ¨ + ∫ − ∞ t h r ( t − τ ) ζ ˙ ( τ ) d τ + k ζ = f f
where ζ is the buoy displacement relative to its equilibrium, and the mass M includes physical and added mass components, M = m + m a . The added mass, m a , is due to the water displaced by the oscillating buoy. The convolution term is the radiation damping, where h r is the radiation impulse response function. The linear buoyancy force coefficient is denoted as k, and f f contains all additional external forces acting on the buoy, such as the wave excitation and PTO forces. For regular waves, the convolution term becomes a single, constant coefficient b, and a special case of Cummin’s equation is given in (30).
M ζ ¨ + b ζ ˙ + k ζ = f f
Next, we will generalize (30) to include nonlinear hydrodynamic terms while also showing the PTO force, u, explicitly
M ζ ¨ + b ζ ˙ = F h ( ζ , t ) − F c
where F h ( ζ , t ) can be any continuous nonlinear, time-varying function, for example, due to nonlinear Froude-Krylov force expressions for non-cylindrical buoys undergoing large motions [40]. Comparing (31) to (1) we note that F e ( ζ , ζ ˙ , t ) is
F e ( ζ , ζ ˙ , t ) = F h ( ζ , t ) − b ζ ˙
While we’ve kept the linear damping expression from Cummin’s Equation for regular waves, b ζ ˙ can be replaced by a more general, perhaps nonlinear, damping expression.
When examining simulation results, we’ll use the physical parameters shown in Table 1 from [36] for the linear and nonlinear examples below. Though the optimal control law of (20) applies to any continuous, nonlinear, time-varying second-order model, however, to ease the comparison with previous literature [37], we will restrict our attention to regular waves with elevation
η ( t ) = A sin ( ω t )
where A and ω are the wave amplitude and frequency, respectively.

3.2. Optimal Control Law

Applying the optimal solution of Equation (20) for the F e ( x → ) of Equation (32) gives the optimal control law of Equation (34).
F c * = F h ( ζ , t ) − b ζ ˙ − M 2 b ∂ t F h ( ζ , t )
where the co-states of Equation (13), 11 and 17 become
λ 1 = F h ( ζ , t ) − 2 b ζ ˙ λ 2 = − M ζ ˙ λ 3 = b ζ ˙ 2
The second-order optimality condition, Equation (27), is shown in Equation (36).
2 ∂ ζ ˙ F e ( ζ , ζ ˙ , t ) + ζ ˙ ∂ ζ ˙ 2 F e ( ζ , ζ ˙ , t ) M 2 = − 2 b M 2 ≤ 0
which is always satisfied since both b and M are positive. The optimal state trajectories can now be derived using the control law of Equation (34). Substituting Equation (34) into Equation (31) yields the optimal acceleration
ζ ¨ * = ∂ t F h 2 b
Equation (37) can be integrated in closed form, if F h permits, or numerically to obtain the optimal velocity, displacement, and co-state trajectories by substitution into Equation (35).

3.3. Linear Point Absorber WEC

Consider the model of a linear point absorber below that has been used previously to derive the complex conjugate control (CCC) law [41]
M ζ ¨ + b ζ ˙ + k ζ = F ( t ) − F c
where F ( t ) is the excitation force. To apply the optimal control law of (34), we only need to identify the correct expression for F h , and in this case
F h ( ζ , t ) = F ( t ) − k ζ
which results in
F c * = F ( t ) − b ζ ˙ − k ζ − M 2 b ∂ t F ( t )
This result was previously obtained by Zou et al. using Euler-Lagrange equations applied directly to a linear point absorber model. [38] which was in accordance with the results obtained using CCC [41].
Preprints 121396 g001
Figure 1. Point absorber WEC with a cylindrical shaped buoy.
Figure 1. Point absorber WEC with a cylindrical shaped buoy.
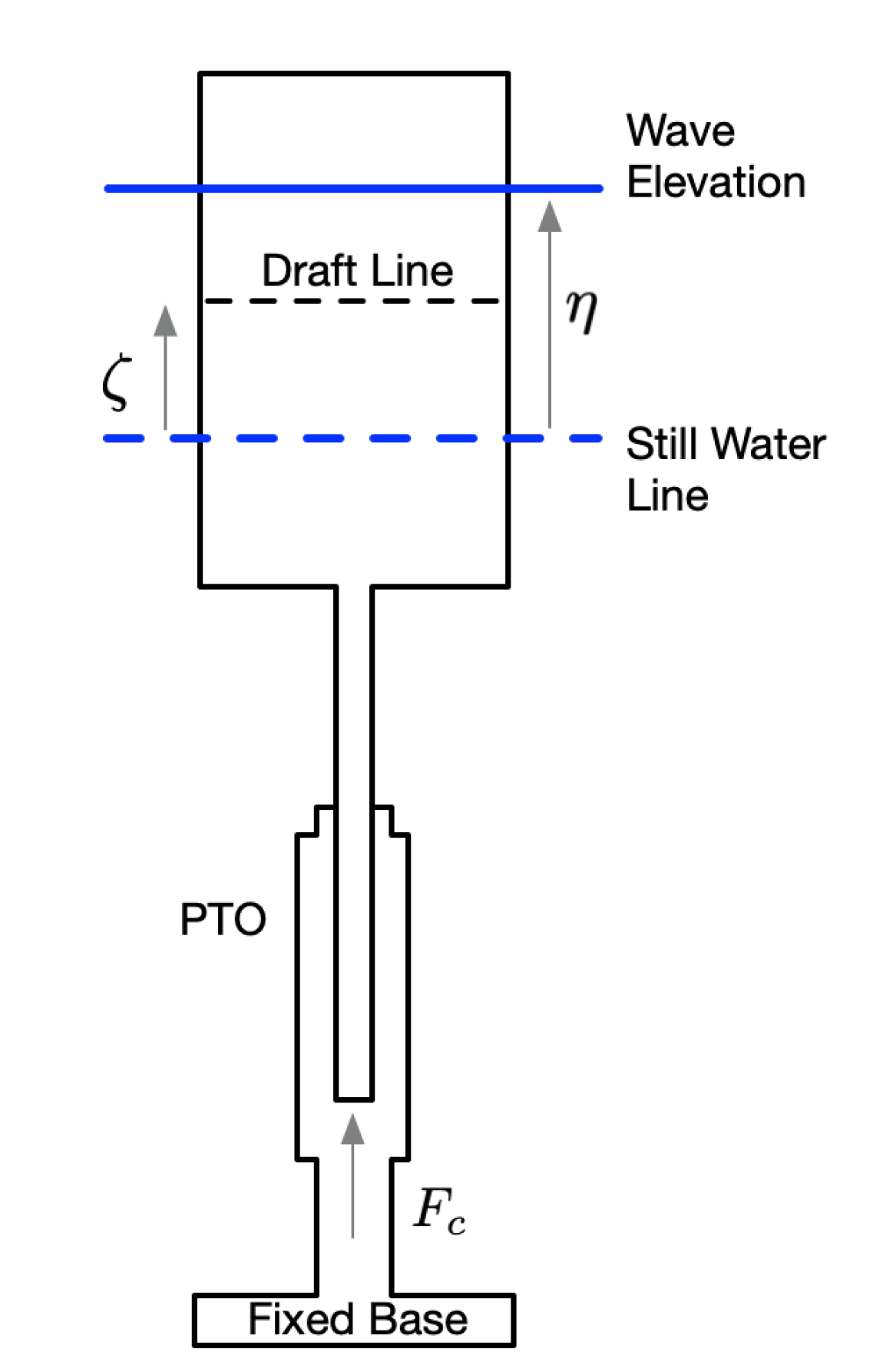
Preprints 121396 g001
However, one often-cited practical limitation of CCC is that the buoy motion becomes larger than the model assumptions used in its derivation [25,31,32,42]. Thus, switching functions were used to keep the linear system bounded. In our work, we have managed to achieve that without the need for a switching function but by obtaining the proper initial condition of (28) to drive our system to a stable limit cycle. To examine this, we will consider the optimality requirement that the buoy’s motion at least resides on a stable limit cycle.
Using (37) the optimal acceleration is
ζ ¨ * = F ˙ ( t ) 2 b
which can be integrated twice to obtain its velocity and position
ζ ˙ * = F ( t ) 2 b + C 1 ζ * = ∫ F ( t ) 2 b d t + C 1 t + C 0
where C 1 and C 0 are integration factors.
To achieve a stable limit cycle, bounded motion, C 1 = 0 , resulting in the optimal buoy velocity of (43), the same result obtained from CCC [19].
ζ ˙ * = F ( t ) 2 b
Achieving C 1 = 0 depends on the excitation force expression, F ( t ) , and the buoy initial conditions defined when the control law is activated. To examine this, consider a particular wave excitation force expression, F ( t ) , used for a cylindrical point absorber buoy in [37].
F ( t ) = k η ( t ) = k A sin ( ω t )
and its corresponding model
M ζ ¨ + b ζ ˙ + k ζ − η ( t ) = − F c
where η ( t ) is the wave elevation.
From (43), at time t o = 0 ,
C 1 = ζ ˙ * ( 0 ) − F ( 0 ) 2 b
To make C 1 = 0 the initial velocity is
ζ ˙ * ( 0 ) = F ( 0 ) 2 b = 0
Thus, for any initial condition of the form [ ζ * ( 0 ) , 0 ] where ζ * ( 0 ) is any convenient initial position, a limit cycle is obtained having bounded periodic motion. However, it is always preferred to have the motion symmetric about ζ = 0 . This requires that C 0 = 0 of (43).
From (43) with C 1 = 0 at t o = 0
C 0 = ζ * ( 0 ) − ∫ F ( t ) 2 b | t = 0
Setting C 0 = 0 , the initial condition of the position ζ * ( 0 ) is
ζ * ( 0 ) = ∫ F ( t ) 2 b | t = 0 = − k A 2 b ω
The optimal, centered, periodic solution of (45), with its required initial condition x o , is
ζ * = ∫ F ( t ) 2 b = − k A 2 b w cos ( ω t ) ζ ˙ * = F ( t ) 2 b = k A 2 b sin ( ω t ) x o = [ ζ * ( 0 ) , ζ ˙ * ( 0 ) ] = − k A 2 b ω , 0
Figure 2 shows simulation results using the model parameters of Table 1 for four different initial conditions indicated by black dots. When the initial condition lacks any initial velocity, [-1.75, 0], [-0.1594, 0], and [1.25, 0], the buoy exhibits bounded, periodic motion indicated by the closed, red contours in the phase space where [-0.1594, 0] produces the desired centered motion. The presence of initial velocity causes a gradual displacement growth over time, as shown by the blue trajectory of Figure 2 for initial conditions of [-1.4, 1]. It’s important to note that the buoy oscillation frequency aligns with the input frequency for linear systems, resulting in the repetition of limit cycles every T seconds.
Figure 3 shows the steady-state simulation results obtained after applying the optimal control law with the centering initial conditions, [-0.1594, 0]. As expected, the periodic motion is bounded and centered about ζ = 0 . Furthermore, the energy extracted has a net positive slope.
In summary, to extract maximum energy using a linear point absorber, it is essential to apply the optimal control law of Equation (40) while ensuring appropriate initial conditions to achieve a bounded periodic motion. Alternatively, a reference tracking controller can be used to follow the bounded analytical periodic optimal states. This can be easily achieved when F ( t ) is analytically integrable.

3.4. Nonlinear Point Absorber WEC

Nonlinear WEC models introduce challenges, such as obtaining analytical solutions to compute initial conditions to achieve limit cycles. This arises when ∂ t F h ( ζ , t ) , used in the optimal acceleration trajectory of (37), is not integrable.
However, not all nonlinear systems exhibit this challenge due to the form of F h . Consider a nonlinear system such that the F h of (31) is
F h ( ζ , t ) = g ( ζ ) + f ( t )
where g ( ζ ) is a nonlinear function and f ( t ) is any integrable function of time. For example, the Duffing Oscillator has this form where the a i are constant coefficients.
ζ ¨ + a 1 ζ ˙ + a 2 ζ + a 3 ζ 3 = a 4 cos ω t − u
Based on (52)
g ( ζ ) = − a 2 ζ − a 3 ζ 3 f ( t ) = a 4 cos ω t
the optimal control law is
u * = g ( ζ ) + f ( t ) − a 1 ζ ˙ − ∂ t f ( t ) 2 a 1
and the rest becomes identical to the linear system of (45).
Unfortunately, this is a special case, and most models of nonlinear WECs possess nonlinearities of the form ∑ a i j f i ( t ) g j ( ζ ) where i and j are integers.
Consider the model of a nonlinear point absorber WEC with an hourglass-shape buoy [37]
M ζ ¨ + b ζ ˙ + k ζ − η ( t ) 3 = − F c
with F h = − k ζ − η ( t ) 3 that is due solely to the buoyancy force. From (34) the optimal control law is (55)
F c * = k η − ζ 3 − b ζ ˙ − 3 M k 2 b η ˙ ( ζ − η ) 2
with an optimal acceleration profile, from (37), of
ζ ¨ * = 3 k 2 b η ˙ ( ζ − η ) 2
Since (57) can not be integrated in closed form, obtaining expressions for the initial conditions that give limit cycle motion is impossible. Thus, we must resort to numerical techniques.
To numerically explore the initial condition space, the system of (55) and the control law of (56) were simulated using a third-order, explicit Runge-Kutta solver with a time step of 0.01 s with the parameters values of Table 1. The results for two different wave amplitude cases are shown in Figure 5, where the simulation duration was 50 s. The left figure is for A = 1.3 m , and on the right, A = 0.65 m .
The blue dashed ellipses indicate the initial conditions resulting in limit cycles. The ellipse corresponding to the higher wave amplitude case has major and minor axes of 0.3 m / s and 0.1 m , respectively, in contrast to the smaller wave amplitude case, whose major and minor axes are 0.5 m / s and 0.3 m . The initial condition region increases with decreasing wave amplitude in these two cases. Other initial conditions may exist outside the ellipses that lead to a limit cycle. However, none were found using an extensive grid search of the phase space.
The red trajectories of Figure 5 show buoy motions when the initial conditions are inside the ellipses, indicated by black dots. While these trajectories provide anecdotal information regarding position and velocity extremums they cannot be used to determine limit cycle existence.
Poincare maps were used to confirm limit cycle behavior with the simulation time increased to 500 seconds. Given an initial condition, it is instructive to view the phase planes of Figure 5 with time being along a third orthogonal axis. The red trajectories then move around the phase plane in the direction of increasing time. Poincare maps were made from sampling points on this three-dimensional trajectory at the excitation period of T = 1 seconds and are shown in Figure 6 for the two initial condition cases of Figure 5. Limit cycle motion is confirmed since the Poincare Maps are closed contours.
Figure 7 shows the dynamics of the nonlinear point absorber for a wave of amplitude A upon the implementation of the optimal control law and choosing proper initial conditions, [0.05, 0.1], within the corresponding blue ellipse of Figure 5. As with the phase plane plots of Figure 7, periodicity is difficult to infer from this relatively short time duration. Once again, the energy time history has a net positive slope.
To further validate the optimality of the control law for both the linear and nonlinear cases, the value of the Hamiltonian is plotted in Figure 8 and is zero for all time. This is a consequence of the PMP and ensures the simulated co-states match the solutions of the co-state differential equations of Equation (35) arising from the Euler-Lagrange equations.
Overall, the presented figures and analyses demonstrate the promising performance of the optimal control approach, providing valuable insights into the dynamic behavior and energy production capabilities of the considered WEC systems.

4. Conclusion and Future Work

Optimal control analysis can be used to maximize the energy of a renewable source even when its second-order model is nonlinear and nonautonomous. To achieve bounded motion the initial condition region resulting in a stable limit cycle should be included in the optimal control analysis. The size and location of the region will, in general, be a function of the wave amplitude and frequency.
A relatively small set of initial conditions was found for the nonlinear hourglass-shaped buoy. It may be possible to find buoy shapes yielding larger initial condition regions extending the practical application of the optimal control law. Consequently, using the control law during shape optimization is one of the next steps to be exploited, finding the form of the nonlinearity that leads to a more extensive set of initial conditions. Finding a more systematic way to obtain initial conditions to drive the system to a limit cycle should also be explored. It should be noted that while the examples presented here used regular waves, the optimal control law form accommodates irregular waves as well.
Initial conditions and wave parameters can result in intriguing limit cycle behavior that could be exploited for operational reasons. One case is illustrated in Figure 9 for A = 0.611 and optimal initial conditions of [0.2, 0]. The buoy response progresses between the five closed contours of the Poincare map. Shaping the location, number, and size of the contours could be used to manage PTO bounds and motion constraints.

5. References

Author Contributions

Conceptualization, H.Y, K.N, G.P, and W.W; methodology H.Y, K.N, G.P, and w.w; software, H.Y and T.D.G; validation, H.Y, G.P and W.W.; formal analysis, H.Y. K.N, G.P; investigation, H.Y, and G.P.; writing—original draft preparation, H.Y T.D.G.; writing—review and editing. H.Y, T.D.G and G.P; visualization, H.Y.; supervision, G.P. W.W; funding acquisition, G.P. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

is work was supported by the John and Cathi Drake Endowed Professorship in Mechanical Engineering.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bryson, A.E. Applied Optimal Control: Optimization, Estimation and Control; CRC Press, 1975.
  2. Johnson, C.; Gibson, J. Singular solutions in problems of optimal control. IEEE Transactions on Automatic Control 1963, 8, 4–15. [Google Scholar] [CrossRef]
  3. Gros, S.; Srinivasan, B.; Chachuat, B.; Bonvin, D. Neighbouring-extremal control for singular dynamic optimisation problems. Part I: Single-input systems. International Journal of Control 2009, 82, 1099–1112. [Google Scholar] [CrossRef]
  4. Willems, J.; Kitapci, A.; Silverman, L. Singular optimal control: a geometric approach. SIAM Journal on Control and Optimization 1986, 24, 323–337. [Google Scholar] [CrossRef]
  5. Lamnabhi-Lagarrigue, F. Singular optimal control problems: on the order of a singular arc. Systems & control letters 1987, 9, 173–182. [Google Scholar]
  6. Pontryagin, L.S. Mathematical theory of optimal processes; Routledge, 2018.
  7. Athans, M.; Falb, P.L. Optimal control: an introduction to the theory and its applications; Courier Corporation, 2013.
  8. Scardina, J.A. An investigation of singular optimal control problems. PhD thesis, Georgia Institute of Technology, 1968.
  9. Kelley, H.J. A second variation test for singular extremals. AIAA Journal 1964, 2, 1380–1382. [Google Scholar] [CrossRef]
  10. Kelley, H.J.; Kopp, R.E.; Moyer, H. Singular extremals, Topics in Optimization, G. Leitmann, ed, 1967.
  11. Robbins, H. A generalized Legendre-Clebsch condition for the singular cases of optimal control. IBM Journal of Research and Development 1967, 11, 361–372. [Google Scholar] [CrossRef]
  12. Bell, D.J.; Jacobson, D.H. Singular optimal control problems; Elsevier, 1975.
  13. Athans, M.; Falb, P.L. Optimal Control: An Introduction to the Theory and Its Applications; Courier Corporation, 2007.
  14. Speyer, J.L.; Jacobson, D.H. Primer on Optimal Control Theory; SIAM, 2010.
  15. Robinett, III, R. D.; Wilson, D.G. What is a limit cycle? International Journal of Control 2008, 81, 1886–1900. [Google Scholar] [CrossRef]
  16. Khalil, H.K. Nonlinear Systems; Prentice Hall, 2002.
  17. Falcão, A.F.d.O. Wave energy utilization: A review of the technologies. Renewable and Sustainable Energy Reviews 2010, 14, 899–918. [Google Scholar] [CrossRef]
  18. Cummins, W. The Impulse Response Function and Ship Motions. Schiffstechnik 1962, 47, 101–109. [Google Scholar]
  19. Falnes, J.; Kurniawan, A. Ocean waves and oscillating systems: linear interactions including wave-energy extraction; Vol. 8, Cambridge university press, 2020.
  20. Giorgi, G.; Penalba, M.; Ringwood, J.V. Nonlinear Hydrodynamic Force Relevance for Heaving Point Absorbers and Oscillating Surge Converters. 2016.
  21. Guo, B.; Ringwood, J.V. Geometric optimisation of wave energy conversion devices: A survey. Applied Energy 2021, 297, 117100. [Google Scholar] [CrossRef]
  22. Garcia-Teruel, A.; DuPont, B.; Forehand, D.I. Hull geometry optimisation of wave energy converters: On the choice of the optimisation algorithm and the geometry definition. Applied Energy 2020, 280, 115952. [Google Scholar] [CrossRef]
  23. Garcia-Teruel, A.; DuPont, B.; Forehand, D.I. Hull geometry optimisation of wave energy converters: On the choice of the objective functions and the optimisation formulation. Applied Energy 2021, 298, 117153. [Google Scholar] [CrossRef]
  24. Shadmani, A.; Nikoo, M.R.; Etri, T.; Gandomi, A.H. A multi-objective approach for location and layout optimization of wave energy converters. Applied Energy 2023, 347, 121397. [Google Scholar] [CrossRef]
  25. Demonte Gonzalez, T.; Parker, G.G.; Anderlini, E.; Weaver, W.W. Sliding mode control of a nonlinear wave energy converter model. Journal of Marine Science and Engineering 2021, 9, 951. [Google Scholar] [CrossRef]
  26. Son, D.; Yeung, R.W. Optimizing ocean-wave energy extraction of a dual coaxial-cylinder WEC using nonlinear model predictive control. Applied energy 2017, 187, 746–757. [Google Scholar] [CrossRef]
  27. Karthikeyan, A.; Previsic, M.; Scruggs, J.; Chertok, A. Non-linear model predictive control of wave energy converters with realistic power take-off configurations and loss model. 2019 IEEE Conference on Control Technology and Applications (CCTA). IEEE, 2019, pp. 270–277.
  28. Babarit, A.; Clément, A.H. Optimal latching control of a wave energy device in regular and irregular waves. Applied Ocean Research 2006, 28, 77–91. [Google Scholar] [CrossRef]
  29. Sheng, W.; Alcorn, R.; Lewis, A. On improving wave energy conversion, part II: Development of latching control technologies. Renewable Energy 2015, 75, 935–944. [Google Scholar] [CrossRef]
  30. Ringwood, J.V.; Bacelli, G.; Fusco, F. Energy-Maximizing Control of Wave-Energy Converters: The Development of Control System Technology to Optimize Their Operation. IEEE Control Systems Magazine 2014, 34, 30–55. [Google Scholar] [CrossRef]
  31. Ringwood, J.V.; Bacelli, G.; Fusco, F. Control, forecasting and optimisation for wave energy conversion. IFAC Proceedings Volumes 2014, 47, 7678–7689. [Google Scholar] [CrossRef]
  32. Salter, S.H. Power conversion systems for ducks. International Conference on Future Energy Concepts, 1979, pp. 100–108.
  33. Karakash, J.J. Transmission Lines and Filter Networks; Macmillan, 1950.
  34. Hartog, J.P.D. Mechanical Vibrations; Courier Corporation, 1985.
  35. Piersol, A.G.; Paez, T.L. Harris’ Shock and Vibration Handbook; McGraw Hill Professional, 2009. “Mechanical Impedance and Mobility,” Chap. 9.
  36. Yassin, H.; Demonte Gonzalez, T.; Parker, G.; Wilson, D. Effect of the Dynamic Froude–Krylov Force on Energy Extraction from a Point Absorber Wave Energy Converter with an Hourglass-Shaped Buoy. Applied Sciences 2023, 13, 4316. [Google Scholar] [CrossRef]
  37. Wilson, D.G.; Robinett III, R.D.; Bacelli, G.; Abdelkhalik, O.; Coe, R.G. Extending complex conjugate control to nonlinear wave energy converters. Journal of Marine Science and Engineering 2020, 8, 84. [Google Scholar] [CrossRef]
  38. Zou, S.; Abdelkhalik, O.; Robinett, R.; Bacelli, G.; Wilson, D. Optimal control of wave energy converters. Renewable energy 2017, 103, 217–225. [Google Scholar] [CrossRef]
  39. Kasturi, P.; Dupont, P. Constrained Optimal Control of Vibration Dampers.
  40. Giorgi, G.; Ringwood, J.V. Computationally efficient nonlinear Froude–Krylov force calculations for heaving axisymmetric wave energy point absorbers. Journal of Ocean Engineering and Marine Energy 2017, 3, 21–33. [Google Scholar] [CrossRef]
  41. Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, 2002. [Google Scholar] [CrossRef]
  42. Nebel, P. Maximizing the efficiency of wave-energy plant using complex-conjugate control. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering 1992, 206, 225–236. [Google Scholar] [CrossRef]
Preprints 121396 g002
Figure 2. Linear point absorber, 50s phase space trajectories using Table 1 model parameters and four different initial conditions, black dots. Two cases are not centered and bounded (red): [-1.75, 0] and [1.25, 0], another is centered and bounded (red): [-0.1594, 0], and one is unbounded (blue) [-1.4, 1].
Figure 2. Linear point absorber, 50s phase space trajectories using Table 1 model parameters and four different initial conditions, black dots. Two cases are not centered and bounded (red): [-1.75, 0] and [1.25, 0], another is centered and bounded (red): [-0.1594, 0], and one is unbounded (blue) [-1.4, 1].
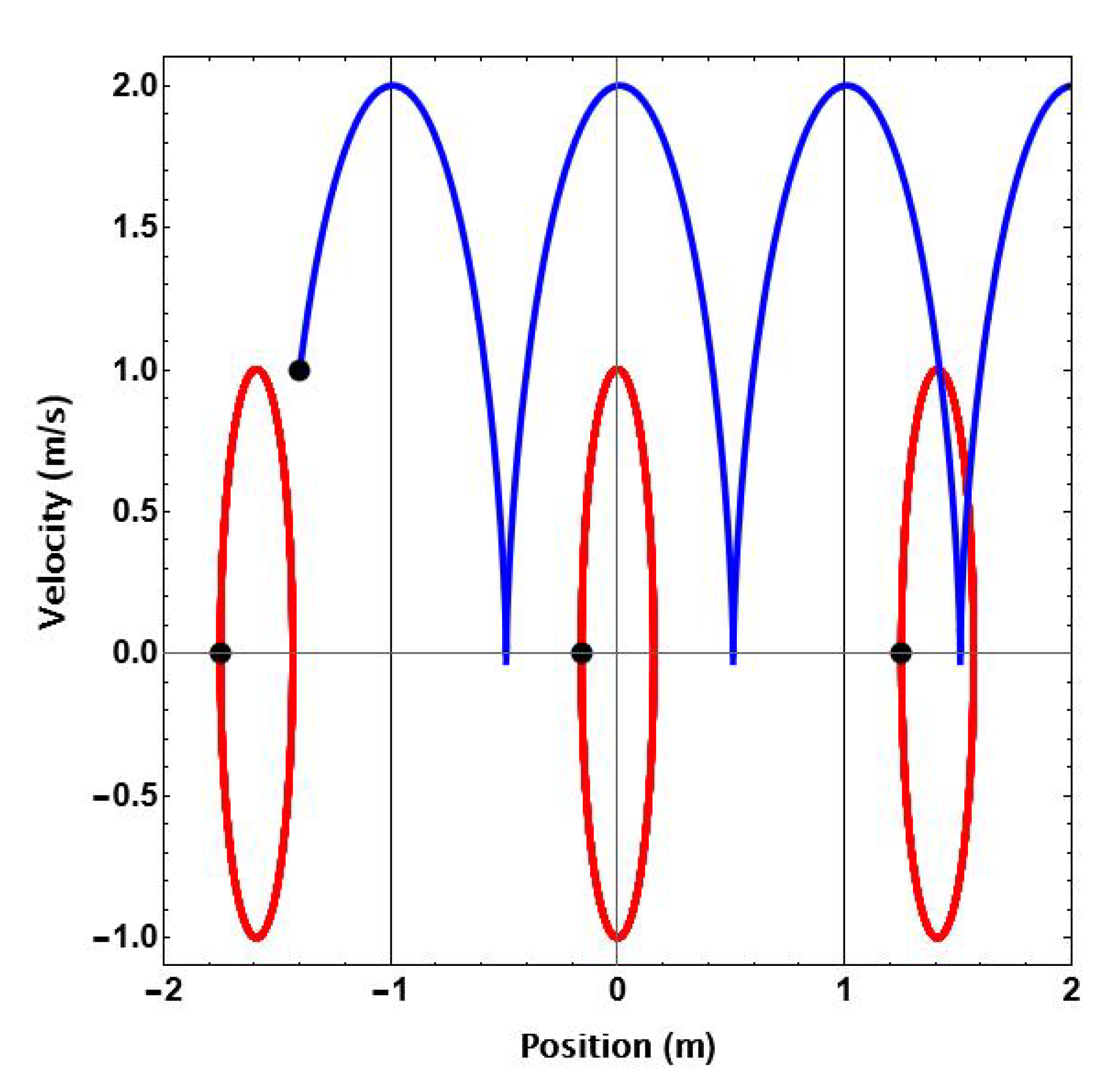
Preprints 121396 g002
Preprints 121396 g003
Figure 3. Simulated response of a linear cylindrical WEC with initial conditions [-0.1594, 0] for the 50s after the initial transient has decayed.
Figure 3. Simulated response of a linear cylindrical WEC with initial conditions [-0.1594, 0] for the 50s after the initial transient has decayed.
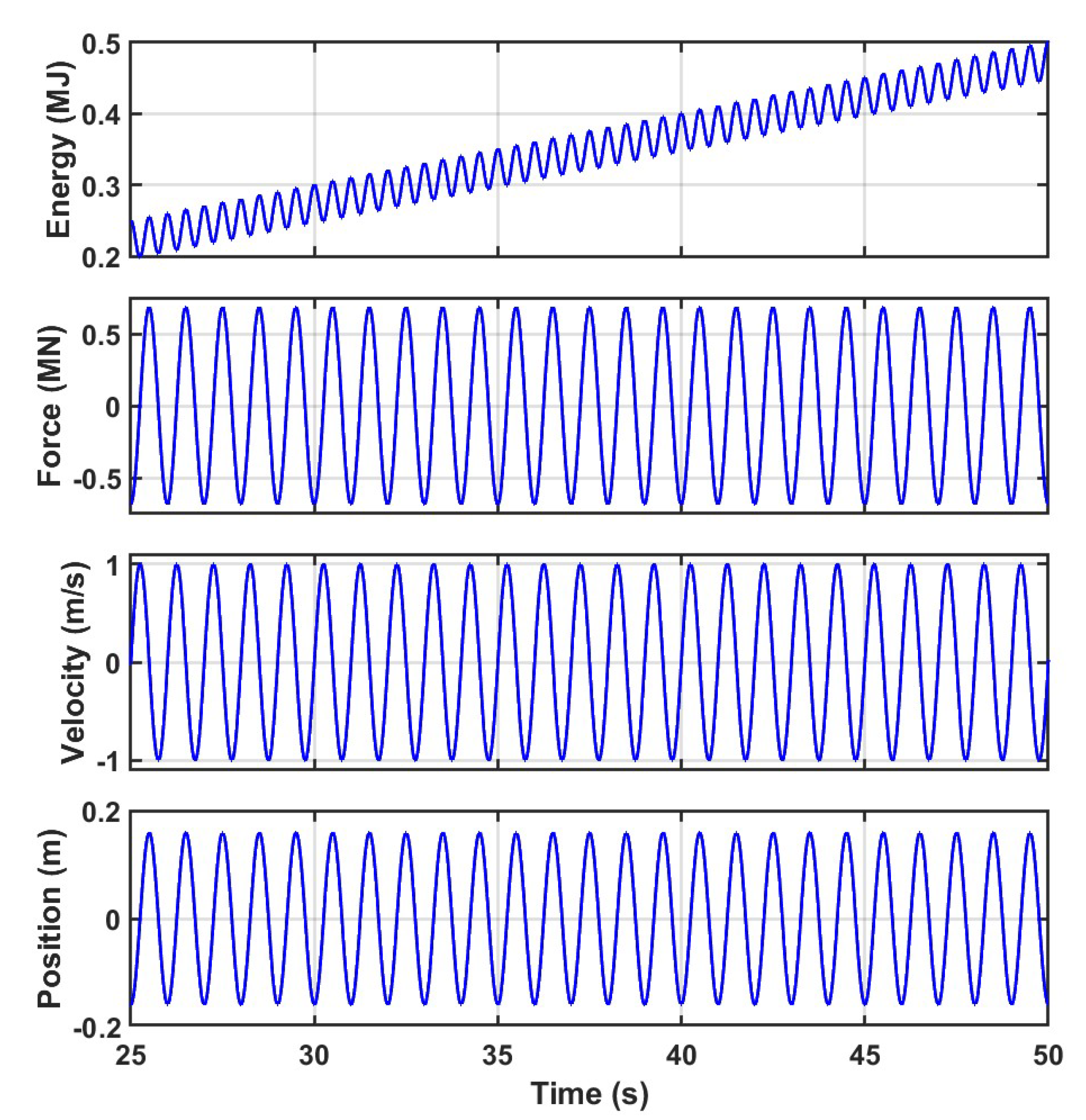
Preprints 121396 g003
Preprints 121396 g004
Figure 4. Point absorber WEC with an hourglass shaped buoy.
Figure 4. Point absorber WEC with an hourglass shaped buoy.
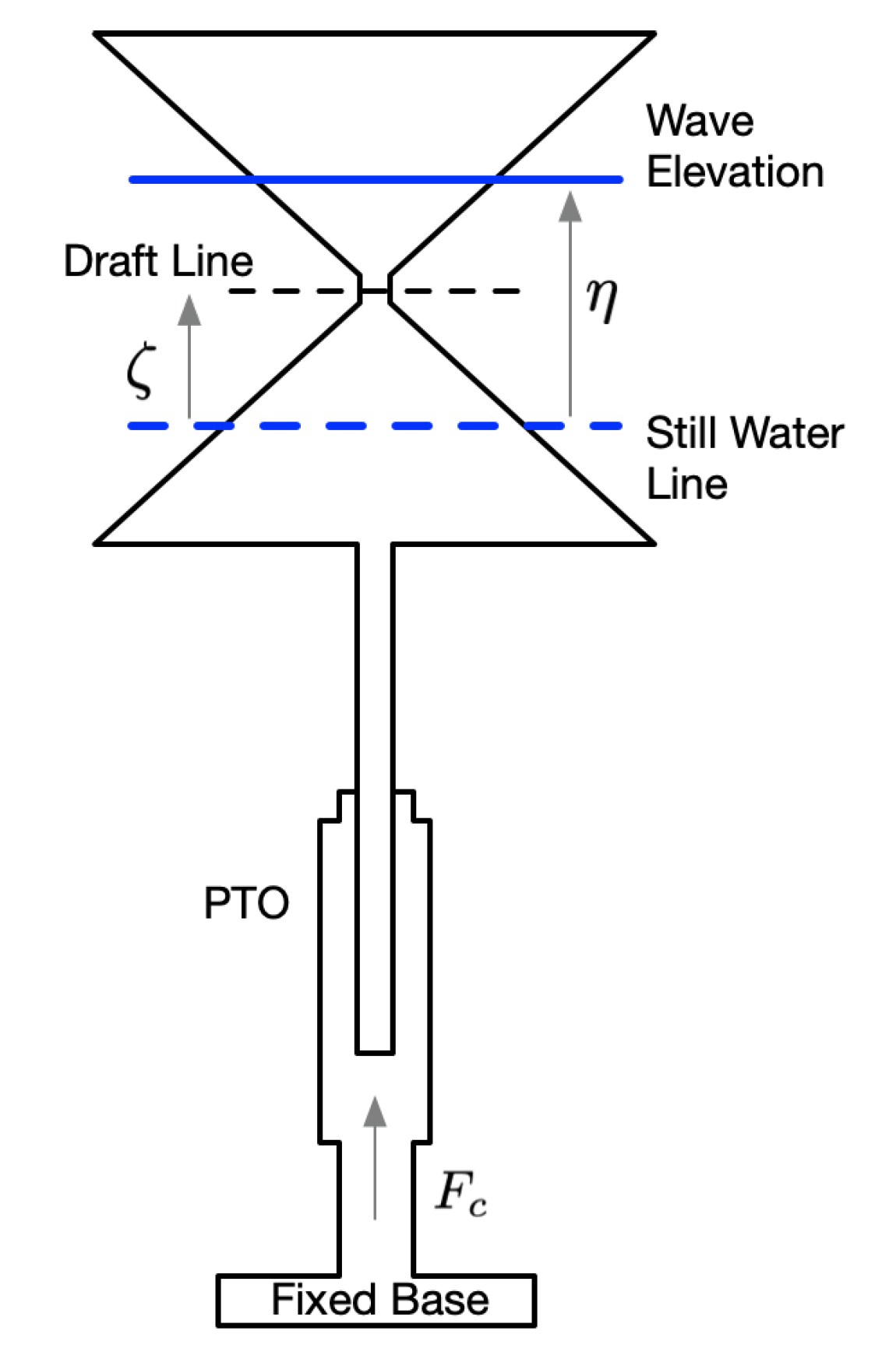
Preprints 121396 g004
Preprints 121396 g005
Figure 5. Phase space of the nonlinear point absorber system, illustrating trajectories for two wave amplitudes over 50 seconds. The left plot shows the trajectory with an amplitude A and initial conditions [0.05,0.1], while the right plot shows the trajectory with an amplitude A 2 and initial conditions [0.15,0.35]. The dashed blue ellipses illustrate the initial conditions space that drives the system to a limit cycle.
Figure 5. Phase space of the nonlinear point absorber system, illustrating trajectories for two wave amplitudes over 50 seconds. The left plot shows the trajectory with an amplitude A and initial conditions [0.05,0.1], while the right plot shows the trajectory with an amplitude A 2 and initial conditions [0.15,0.35]. The dashed blue ellipses illustrate the initial conditions space that drives the system to a limit cycle.
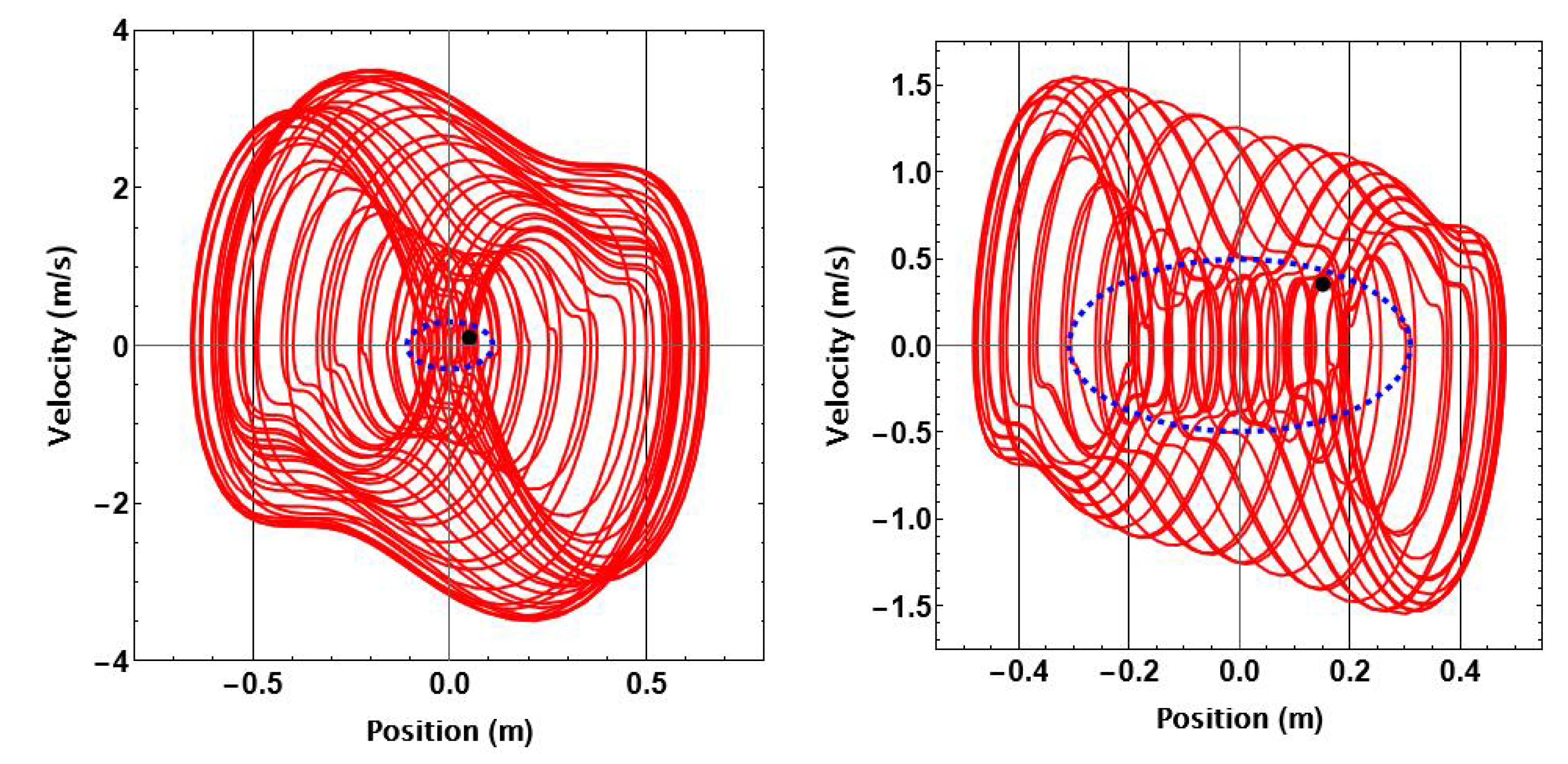
Preprints 121396 g005
Preprints 121396 g006
Figure 6. Poincare maps for the corresponding trajectories of Figure 5 sampled at a period T of the incoming waves for 500s.
Figure 6. Poincare maps for the corresponding trajectories of Figure 5 sampled at a period T of the incoming waves for 500s.
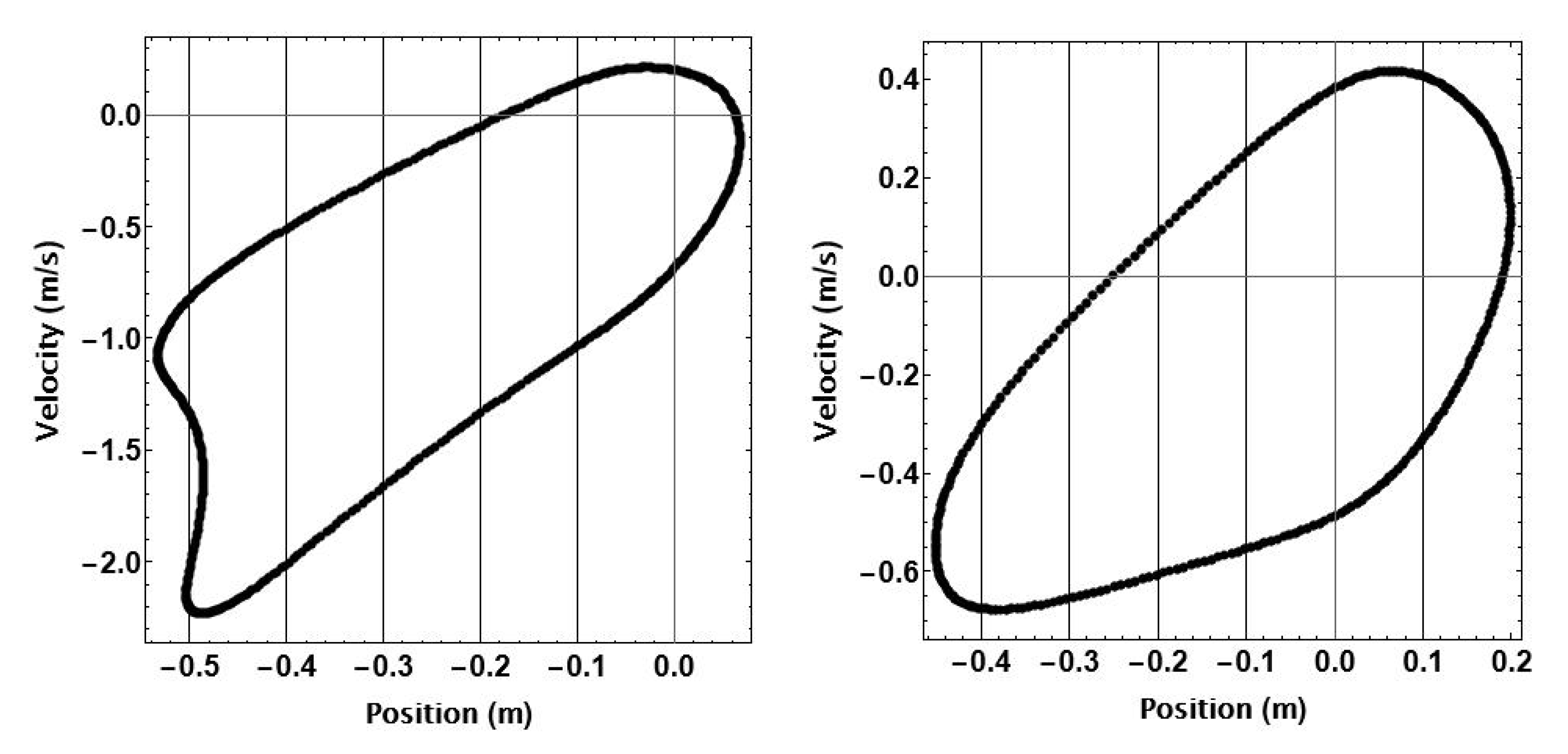
Preprints 121396 g006
Preprints 121396 g007
Figure 7. The dynamics of a nonlinear hourglass-shaped WEC with initial conditions [0.05, 0.1] and wave amplitude A for 50s.
Figure 7. The dynamics of a nonlinear hourglass-shaped WEC with initial conditions [0.05, 0.1] and wave amplitude A for 50s.
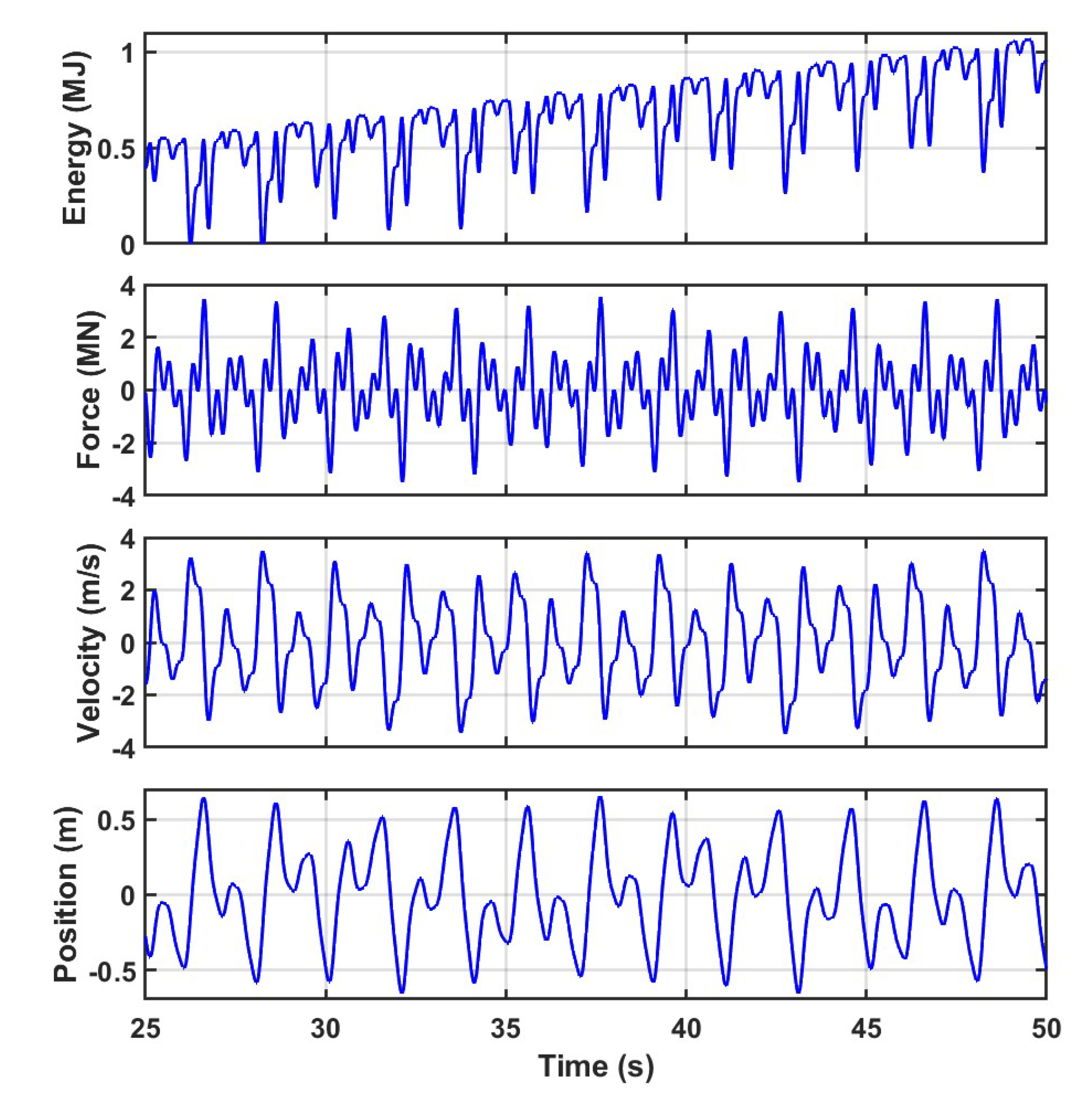
Preprints 121396 g007
Preprints 121396 g008
Figure 8. The conservation of the Hamiltonian over time using the optimal control law for the linear and nonlinear WECs.
Figure 8. The conservation of the Hamiltonian over time using the optimal control law for the linear and nonlinear WECs.
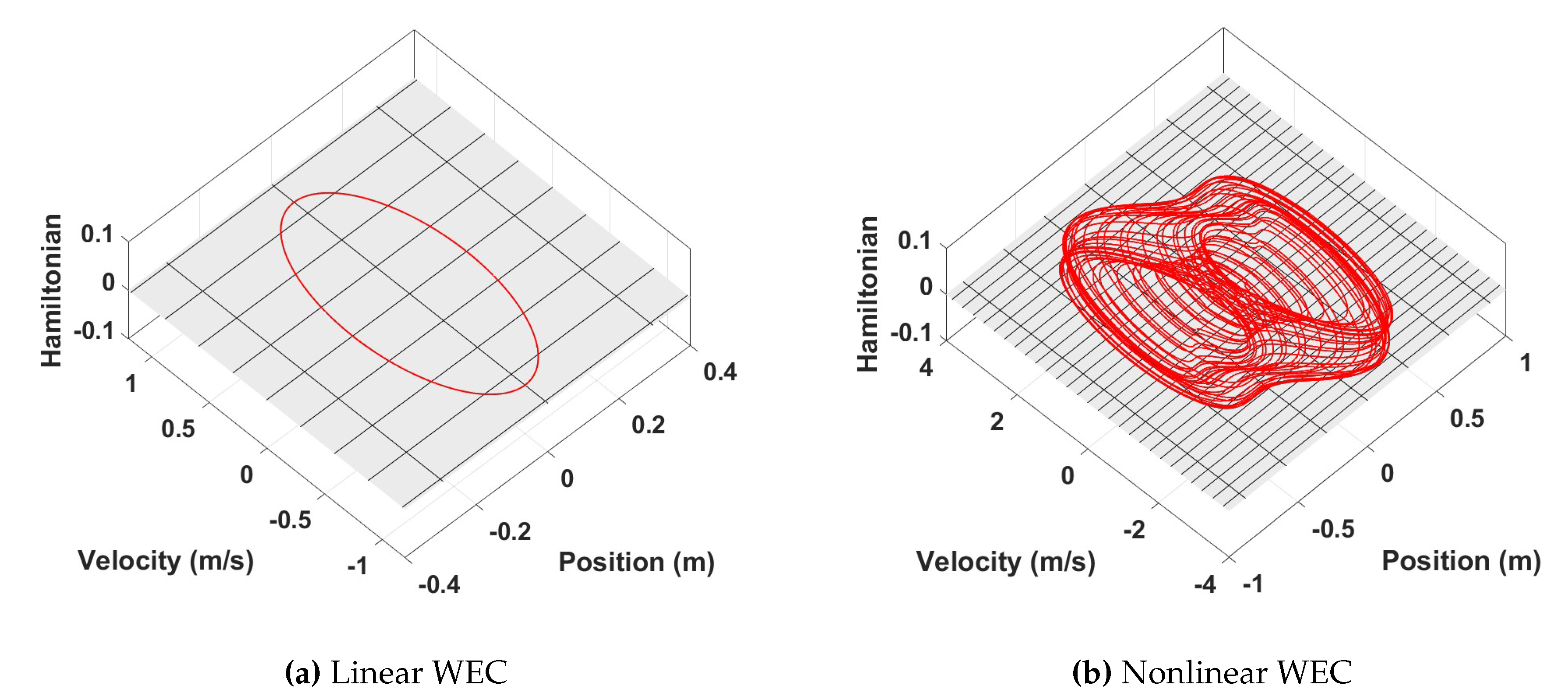
Preprints 121396 g008
Preprints 121396 g009
Figure 9. Multiple contours on Poincare map for an initial conditions of [0.2, 0] and amplitude 0.611 m.
Figure 9. Multiple contours on Poincare map for an initial conditions of [0.2, 0] and amplitude 0.611 m.
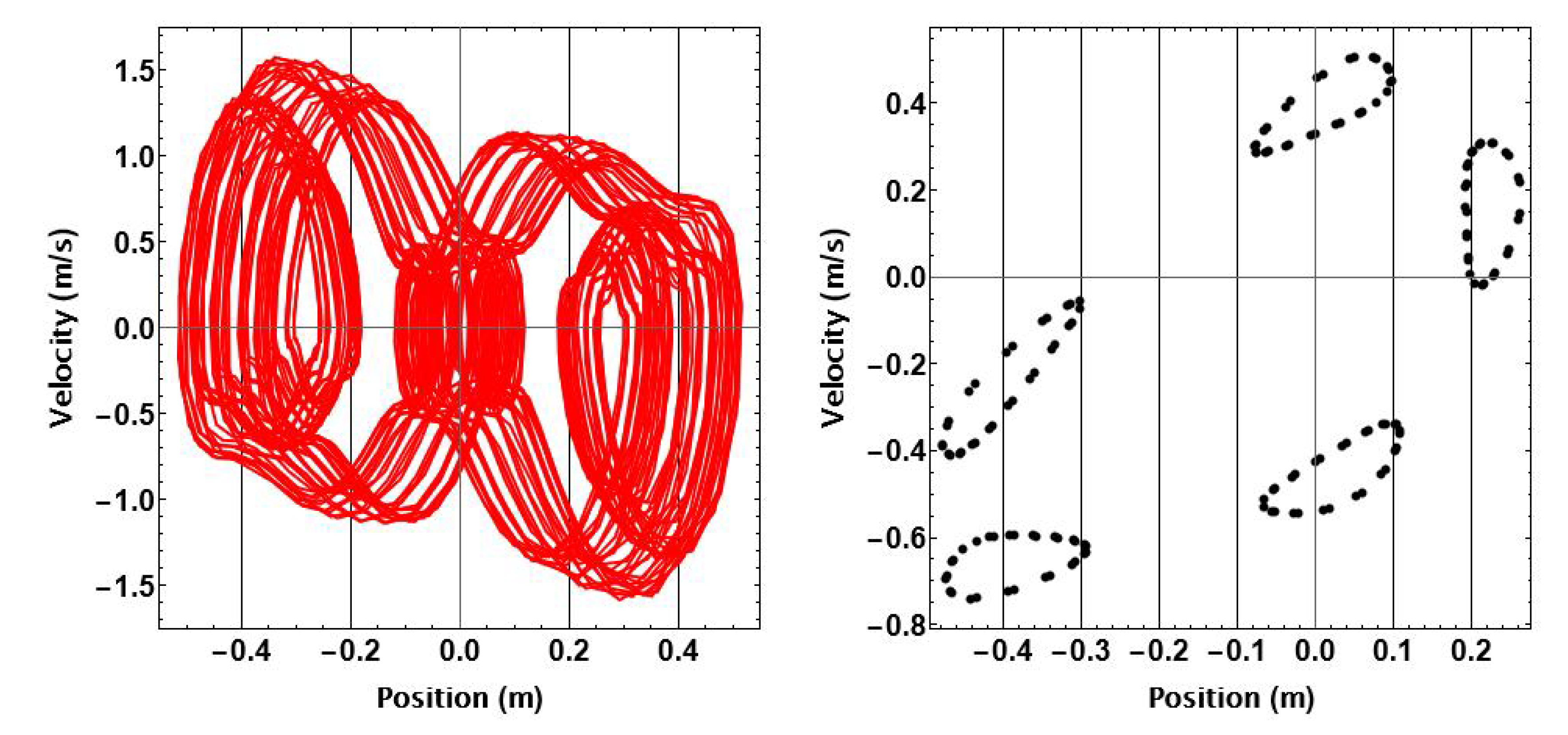
Preprints 121396 g009
Table 1. WEC parameters.
Table 1. WEC parameters.
Feature Symbol Value Units
Mass M 109 , 626 kg
Radiation Damping b 20 , 000 N/(m/s)
Hydrostatic Stiffness k 30 , 819 N/m
Wave Amplitude A 1.3 m
Wave Frequency ω 2 π rad
Wave Period T 1 s
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated