Prerpints.org logo
Preprint
Article

The Impact of the SMOTE Method on Machine Learning and Ensemble Learning Performance Results in Addressing Class Imbalance in Data Used for Predicting Total Testosterone Deficiency in Type 2 Diabetes Patients

This version is not peer-reviewed.

Submitted:

15 October 2024

Posted:

16 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Background and Objective: Diabetes Mellitus is a long-term, multifaceted metabolic condition that necessitates ongoing medical management. Hypogonadism is a syndrome that is a clinical and/or biochemical indicator of testosterone deficiency. Cross-sectional studies have reported that 20-80.4 % of all men with Type 2 diabetes have hypogonadism, and Type 2 diabetes is related with low testosterone. This study presents an analysis of the use of ML and EL classifiers in predicting testosterone deficiency. In our study, we compared optimized traditional ML classifiers and three EL classifiers using grid search and stratified k-fold cross-validation. We used the SMOTE method for the class imbalance problem. Methods: This database contains 3397 patients for the assessment of testosterone deficiency. Among these patients, 1886 patients with type 2 diabetes were included in the study. In the data pre-processing stage, firstly outlier/excessive observation analyses were performed LOF and missing value analyses were performed with random forest. The SMOTE is a method for generating synthetic samples of the minority class. Four basic classifiers, namely MLP, RF, ELM and LR, were used as first level classifiers. Tree ensemble classifiers, namely ADA, AGBoost, and SGB, were used as second level classifiers. Results: After SMOTE, while the diagnostic accuracy decreased in all base classifiers except ELM, sensitivity values increased in all classifiers. Similarly, while the specificity values decreased in all classifiers, F1 score increased. The RF classifier gave more successful results on the base-training dataset. The most successful ensemble classifier in the training dataset was the ADA classifier in the original data and in the after SMOTE data. The testing data, XGBoost is the most suitable model for your intended use in evaluating model performance. XGBoost, which exhibits a balanced performance especially when SMOTE is used, can be preferred to correct class imbalance. Conclusions: SMOTE is used to correct the class imbalance in the original data. However, as seen in this study, when SMOTE was applied, the diagnostic accuracy decreased in some models, but the sensitivity increased significantly. This shows the positive effects of SMOTE to better predict the minority class.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Diabetes Mellitus is a long-term, multifaceted metabolic condition that necessitates ongoing medical management. It is marked by the body's inability to properly process carbohydrates, fats, and proteins, stemming from either a lack of insulin or issues with insulin function [1]. Traditionally, it is mainly categorized into two primary types: Type 1 and Type 2 [2]. Type 2 diabetes constitutes around 90-95% of all diabetes cases. The disease is fundamentally characterized by increasing insulin resistance and gradually decreasing insulin secretion over time, triggered by lifestyle factors in genetically predisposed individuals [3] .
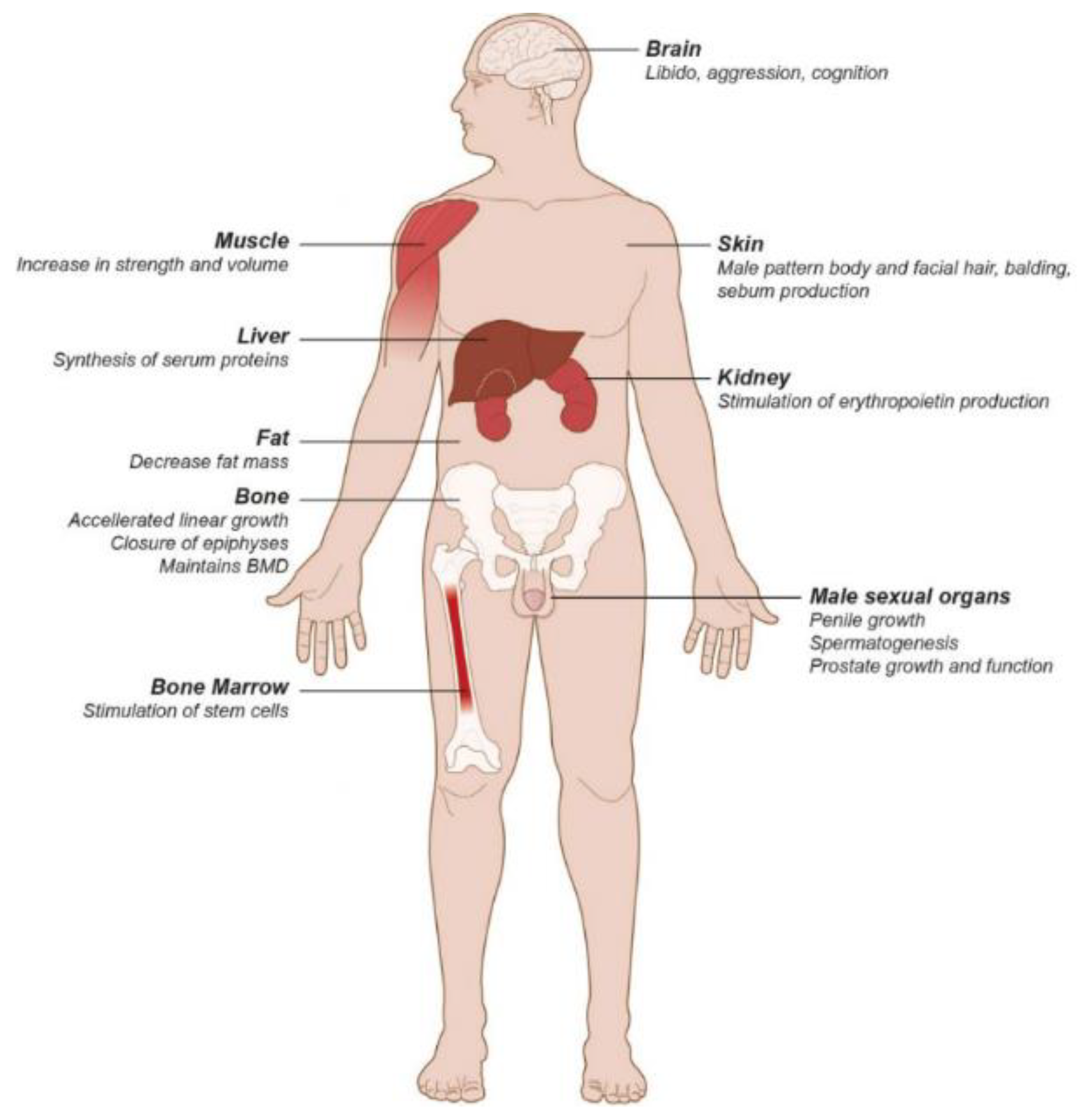
Hypogonadism is a syndrome that is a clinical and/or biochemical indicator of testosterone deficiency [4]. Cross-sectional studies have reported that 20-80.4 % of all men with Type 2 diabetes have hypogonadism, and Type 2 diabetes is related with low testosterone [5]. Some of the clinical features of symptomatic hypogonadism (Figure 1) include erectile dysfunction, loss of libido, depression, irritability, fatigue, anemia, decreased intellectual activity, sleep disturbances, increased abdominal fat, reduced body hair and bone mineral density, and lean body mass [6].
Many studies have shown a relationship between testosterone levels and triglycerides (TG) [8], as well as hypertension (HT) [9,10]. Additionally, low testosterone is strongly associated with Type 2 diabetes (T2D) is associated with secondary hypogonadism, affecting approximately one-third of men with T2D [11]. Low testosterone levels, or hypogonadism, have been reported to be linked with insulin resistance, which is the primary pathogenic mechanism underlying T2D. Long-term testosterone therapy in hypogonadal men has been shown to prevent the progression of prediabetes and induce remission of T2D [12]. These relationships suggest that testosterone plays a role in metabolic syndrome, which encompasses various risk factors, including abdominal obesity, dyslipidemia, hypertension, and insulin resistance [13,14]. As a result, testosterone replacement therapy is sometimes considered an additional treatment option for managing metabolic syndrome [15]. Routine measurement of total testosterone levels can present some challenges and limitations. For instance, testosterone levels can fluctuate even within a single day. Therefore, a single measurement may not provide a complete picture of the actual testosterone level. Due to these reasons, evaluating and interpreting total testosterone levels is complex. Doctors decide to conduct testosterone testing by considering symptoms, the patient's medical history, and other factors. The diagnosis of TD (Testosterone Deficiency) requires evaluation of total testosterone (TT) levels (<300 ng/dl) [16] or free testosterone (FT) levels (<6.5 ng/dl) through blood tests. However, due to high costs, men in the overall population do not routinely monitor their TT and FT levels. This results among a substantial proportion of patients with low testosterone levels who remain undiagnosed and untreated [17].
Artificial Intelligence (AI) algorithms are considerable focus on research in the domain of medical diagnosis [18,19]. Clinical decision support systems calculate risk or probability by aggregating multiple predictors, with each predictor being weighted according to its assigned importance. The likelihood of having a disease can be used for urological referral for further tests focus on the risk of a specific health condition. A literature search related to “testosterone” and “machine learning (ML)” identified many articles [20]. We have evaluated that applying predictive algorithms, such as machine learning and deep learning, to hypogonadism particularly when the condition results from external factors presents significant challenges. However, testosterone deficiency (TD) stemming from secondary causes is frequently linked with comorbidities like obesity, metabolic syndrome, and systemic diseases, offering a wealth of data that can improve the predictive accuracy of machine learning algorithms. Prediction studies utilizing machine learning (ML) and deep learning (DL) methods have demonstrated high performance. However, two factors make traditional ML approaches adequate for many studies [21]. DL performs poorly with limited data and is therefore better suited for large datasets. In this regard, ML methods are more appropriate; however, identifying the optimal machine learning setup for a specific clinical prediction requires testing a series of procedures. For example, this includes different base or ensemble learner (EL) classifiers, strategies to handle imbalanced learning, or the use of various measures for evaluating classification performance. Many studies have used and compared the ML technique [22]. Some challenges are hard to address with a single machine learning classifier, and the best approach is to use an ensemble-based classifier that integrates multiple models to enhance prediction performance [23]. Ensemble-based classifiers have proven effective in many clinical branches such as Alzheimer's diagnosis, breast cancer, and cardiovascular diseases [24]. When applied to small datasets, there are advantages in terms of increased performance and multiple comparison options among methods due to the A tendency to explore various hypotheses in training data prediction and the broad combination of models [25]. In ML methods, data preprocessing is an important step. Depending on the ratio of negative to positive samples, imbalanced data may need to be preprocessed, as traditional algorithms tend to consider minority observations as noise. In this context, imbalanced data can lead to biased results in predictive modeling. Addressing the class imbalance problem at the data level is a crucial step in the preprocessing phase [26].
This study presents an analysis of the use of ML and EL classifiers in predicting testosterone deficiency. In our study, we compared optimized traditional ML classifiers and three EL classifiers using grid search and stratified k-fold cross-validation. We used the SMOTE method for the class imbalance problem. Finally, we compared multiple performance metrics of the base and EL classifiers.

2. Methods

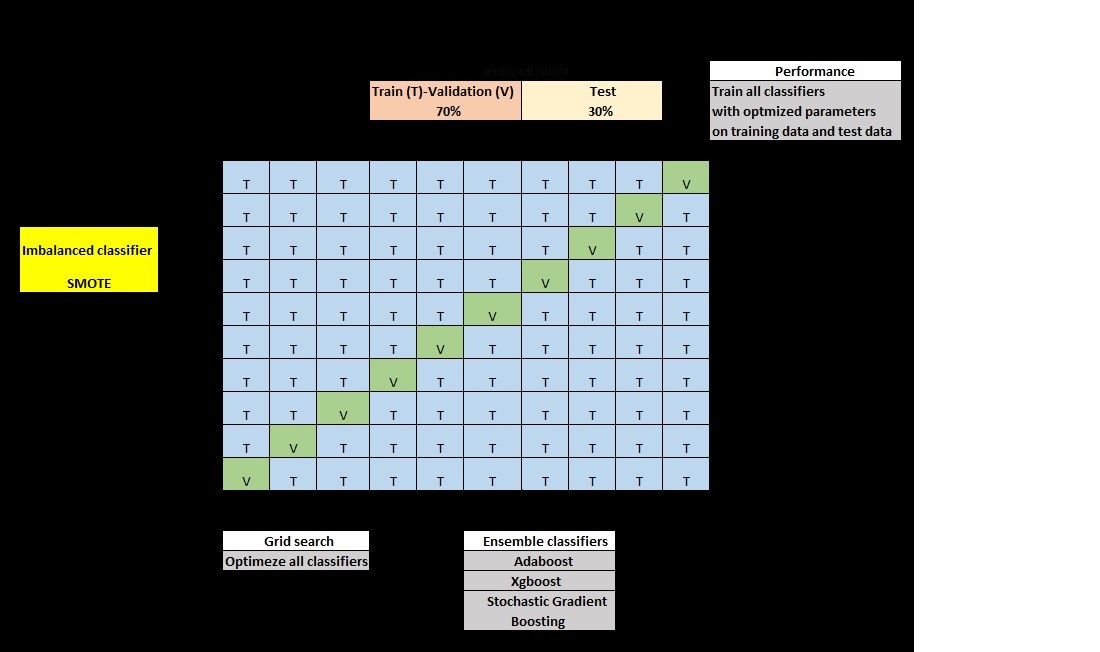
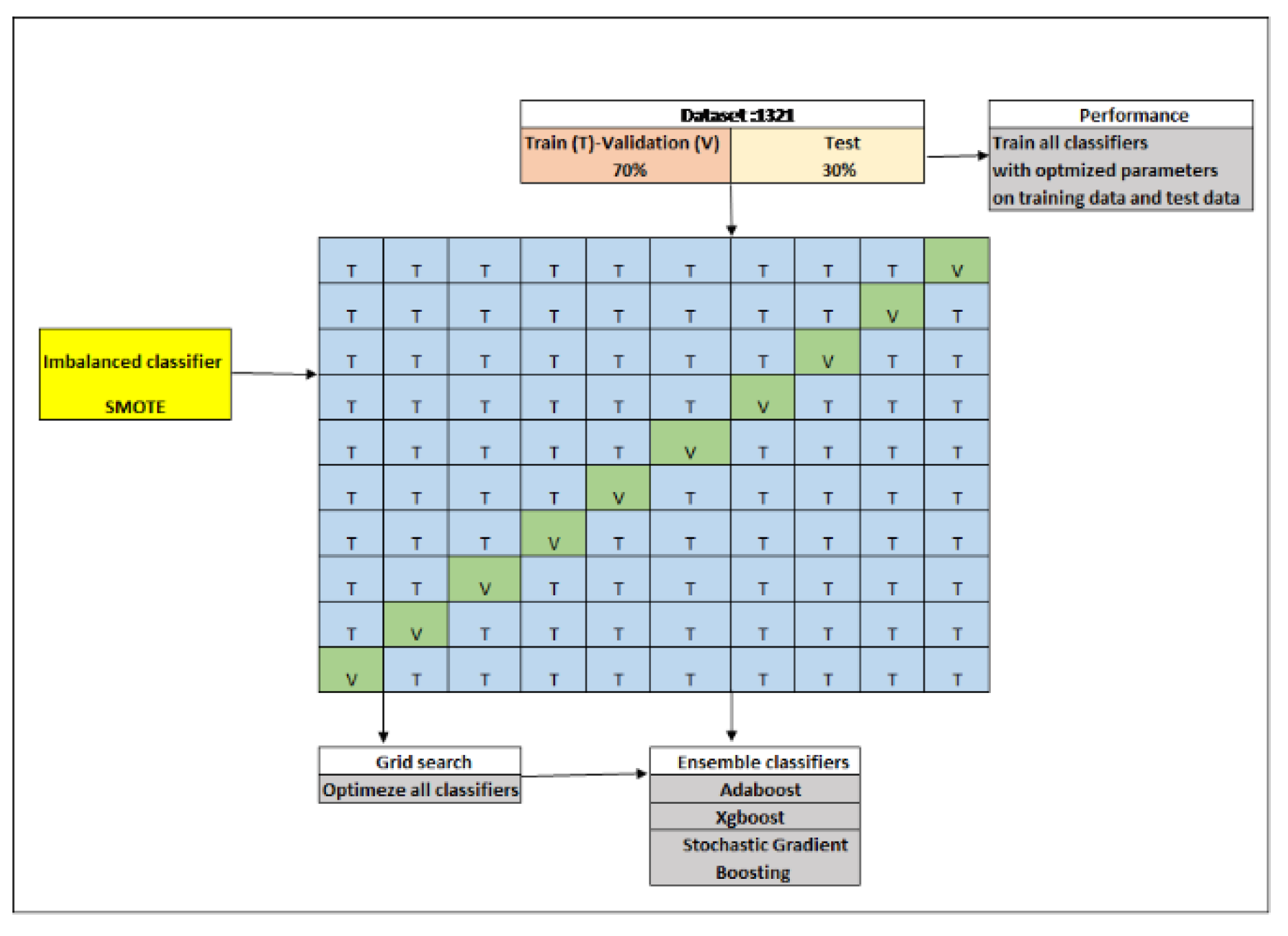
The working steps are given in Figure 2 below. dataset acquisition and splitting, solution of class balance problem (SMOTE), base classifiers, ensemble classifiers (second-level classifiers); stratified k-fold cross-validation, grid search and accuracy analysis.

2.1. Dataset

This database contains 3397 patients for the assessment of testosterone deficiency. Among these patients, 1886 patients with type 2 diabetes were included in the study. The study was granted approval by the Research Ethics Committee of the State University of Feira de Santana in Bahia, Brazil, with the ethical approval code 3.057.301 [27]. The variables used in the study, their roles and definitions are given in Table 1. Participants aged between 45 and 85 years with a mean age of 62.5 were included in the study. The participants' mean TG was 170.0, the mean HDL was 45.4, and the mean AC was 102.0. While 61.9 % of the participants had HT, 38.1 % did not have the disease.
Table 1. The Variables Used In The Study.

2.2. Data Preprocessing

In the data pre-processing stage, firstly outlier/excessive observation analyses were performed with local outlier factor (LOF) (Figure 3) and missing value analyses were performed with random forest. LOF is an unsupervised outlier detection method. This algorithm assesses the uniqueness of each event focus on the distance to its k-nearest neighbors. Because the LOF algorithm does not make any assumptions about data distributions, it can detect outliers independently of the data distribution. The core concept is that the density surrounding an outlier object markedly differs from the density around its neighboring points [28]. Then, the class balance problem was addressed. We divided the testosterone level into two classes: (a) 0 (T < 300 ng/dl) and (b) 1 (T ≥ 300 ng/dl). Regarding data splitting, we allocated 30 % of the data solely for the testing phase and then applied stratified k-fold cross-validation (k=10) on the remaining 70 % of the data. The test set provides independent validation, demonstrating the model's proficiency in handling data it hasn't encountered before. The operations in this process were calculated with the loffactor function in the R program dprep package.

2.2.1. The Problem of Class Imbalance

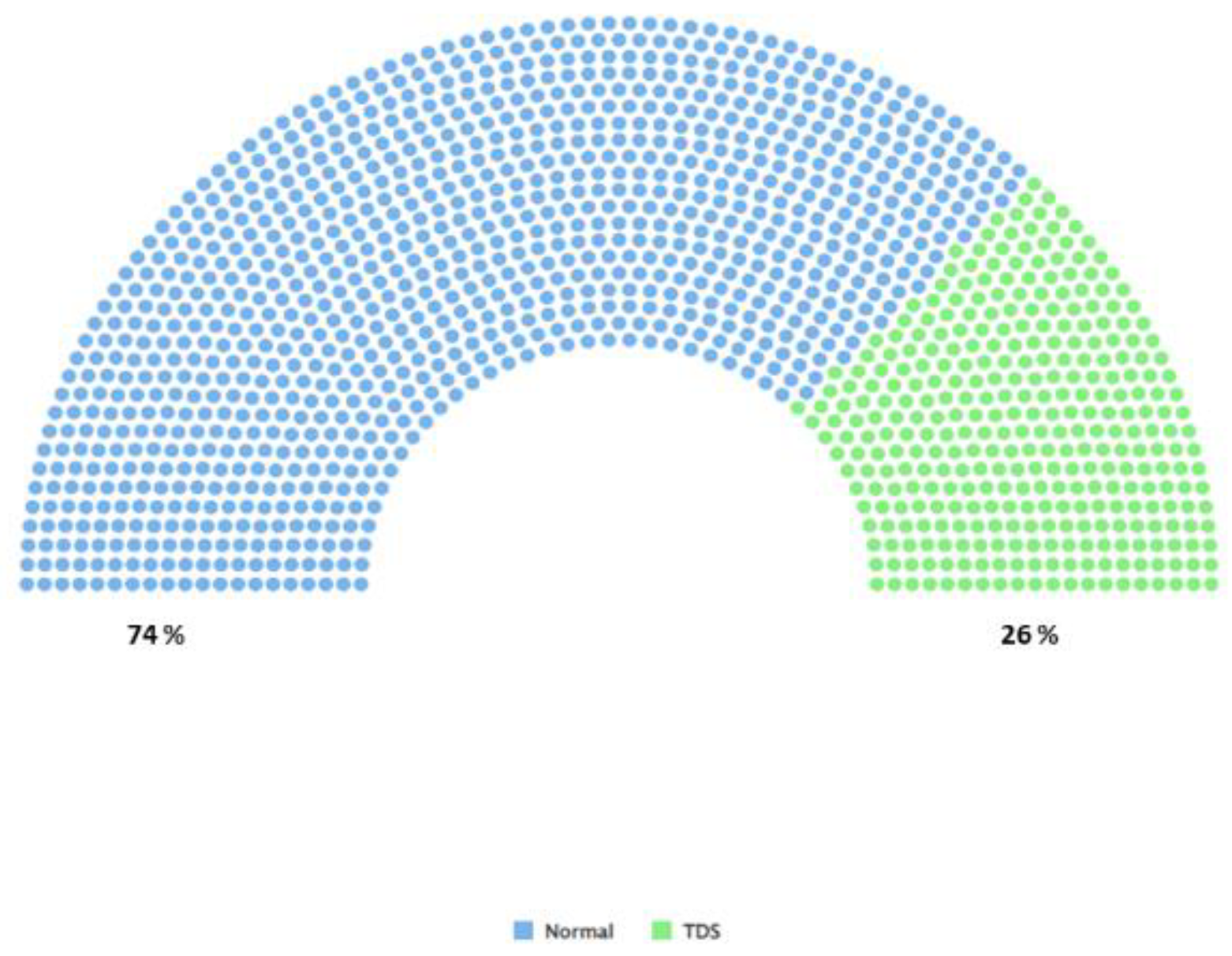
Figure 2 Illustration of class imbalance, green shows patients with testosterone deficiency (TD) (T < 300 ng/dl) and blue shows patients with normal testosterone levels (T ≥ 300 ng/dl). Datasets are imbalanced when the distribution of classes is unequal [29].
Preprints 121327 g004
Figure 4. Illustration of Class Imbalance.
Figure 4. Illustration of Class Imbalance.
Preprints 121327 g004
ML algorithms often yield poor classification results on imbalanced data. There are several ways to address class imbalance [30]. The Synthetic Minority Over-sampling Technique (SMOTE) is a method for generating synthetic samples of the minority class. It typically outperforms simple oversampling and is commonly employed in various applications [31]. The SMOTE method generates a synthetic sample by linearly combining two samples from the minority class (Xi and Xj ) as follows:
Xnew = Xi + (Xj – Xi) * α
For the new artificial instance Xnew​ of the minority class, a sample Xi​ is selected randomly. Then, Xi​ is chosen randomly among the five nearest neighbors of Xi from the minority class based on the euclidean distance [32]. The parameter α takes a random float value in the range (0, 1) [33]. This research used the SMOTE function in the R program open source Smotefamily package.

2.3. Statistical Analysis

Before statistical analysis, normality test (Kolmogorov-Smirnov) was applied to the data set and not all variables met the normality assumption. Descriptive Statistics were given as Mean ± Standard Deviation and Median/(IQR) for continuous data, while they were given as count and percentage for categorical variables. For the significance test of the difference in group categories (testosterone deficiency), the Man-Whitney U Test was used for continuous data and the Chi-Square Test for independent groups was used for categorical data. All statistical analyses were performed with the IBM-SPSS 25.0 program.

2.4. Base Classifiers

In machine learning methods, the use of base classifiers with low correlation with each other enables comprehensive comparisons [34]. Four basic classifiers, namely Multilayer Perceptron Random Forest, Extreme Learning Machine and Logistic regression, were used as first level classifiers.

2.4.1. Multilayer Perceptron (MLP)

The MLP is one of the most widely utilized artificial neural network models. It has been extensively studied, leading to the development of numerous learning algorithms. MLP is a type of forward-feeding network, fully connected neural network that transforms an input dataset into a corresponding output set by fine-tuning the weights between its internal nodes [35]. The input layer contains n input variables X = (x1, x2,…., xn) and output layer contains Y = (y1, y2, ….., ym). The overall count of parameters in an MLP can be determined by [36]
n * h 1 + ∑ k = 1 N h − 1 h k * h k + 1 + h N h * n
where the number of hidden nodes hi in the ith layer is Nh. Longer computational times are required to optimize an MLP when Nh and hk are higher [37].

2.4.2. Random Forest (RF)

RF is an ensemble method that combines multiple decision tree classifiers. It can be seen as an enhanced form of the bagging technique. The RF algorithm works as follows: each decision tree in the forest is created using the bootstrap re-sampling method. This technique allows for the generation of multiple datasets by generating new samples with replacement from the original dataset, regardless of its size. This approach, known as the "Bootstrap Re-sampling Method," enables the extraction of more information from the data. Different samples are then generated by selecting subsets of the data. The RF model aggregates the class predictions from all the decision trees to determine the most accurate class prediction. In RF, a subset of m variables is randomly chosen from the entire set of variables for each tree, and this subset remains constant for each tree. Typically, the number of variables m is chosen as p   (where p is the total number of variables) [38].

2.4.3. Extreme Learning Machine (ELM)

The Extreme Learning Machine (ELM) is a batch regression algorithm designed to train the weights of a Single-Hidden Layer Feedforward Network (SLFN). An SLFN is a type of Artificial Neural Network (ANN) featuring three layers: an input layer, a hidden layer, and an output layer;
x = ∑ e = 1 E w e ɸ ( ∑ d = 1 D v e d x d ) ,
= ∑ e = 1 E w e ɸ z e ,  
whrere ze = ∑ d = 1 D v e d x d ) is the input to the activation function ɸ, which is often chosen to be sigmoid or hyperbolic [39].

2.4.4. Logistic Regression (LR)

Linear models consist of one or more independent variables that establish a relationship with a dependent response variable. In the context of ML, when qualitative or quantitative input features are mapped to a target variable that we aim to predict—such as in financial, biological, or sociological data this approach is called as supervised learning, provided that the labels are known. LR is among the best frequently utilized linear statistical models for discriminant analysis.
y i = β 0 + β 1 X 1 + β 2 X 2 + … + β n X n
yi = dependent variable, β0 = constant, βn = n. beta coefficient and Xn = n.independent variables. In logistic regression, the response variable is quantitative. Specifically, the response variable represents the logarithm of the odds of being classified into the ith group in a binary or multi-class response situation [40].

2.5. Ensemble Classifiers

A boosting algorithm is a method for creating strong classifiers from weak ones with minimal training error. It works by combining a group of weak classifiers using a simple majority vote approach [41].

2.5.1. Adaboost

AdaBoost is among the best widely used algorithms for building a strong classifier by linearly combining individual classifiers. During the training process, the individual classifiers are chosen to minimize errors at each iteration. AdaBoost offers a straightforward and effective way to create ensemble classifiers [42].

2.5.2. XGBoost

XGBoost is fundamentally a decision tree boosting algorithm. Boosting is an ensemble learning technique that involves building multiple models in sequence, with each new model designed to address the shortcomings of the previous one. In tree boosting, every new model added to the ensemble is a decision tree. We will explain how to build a decision tree model and how this process can be extended to generalized gradient boosting using the XGBoost algorithm [43].

2.5.3. Stochastic Gradient Boosting (SGB)

SGB is an ensemble learning algorithm that combines boosting with decision trees. It makes predictions by assigning weights to the ensemble members of all trees in the model [44].

2.6. Parameter Optimization

2.6.1. k-Fold Cross-Validation

k-fold cross-validation splits the dataset into k equally sized folds while preserving the original ratio of positive and negative instances. In each iteration, k-1 folds are used for training while the remaining fold is used for testing. The final result is the average accuracy metric across all testing bins. This method provides more realistic results compared to the standard train/test split, particularly for parameter optimization, as it utilizes multiple aspects of the data and reduces variance [34].

2.6.2. Grid Search

Grid search is a systematic search method for the hyperparameter space, generating all possible combinations regardless of the effects of elements in the optimization process. All parameters have an equal chance of influencing this process (Table 2). While this method provides certain guarantees, it also has significant disadvantages. For instance, in an optimization with many parameters, each having several values, it creates a large variety of combinations, leading to extensive computational effort and time consumption [36]. The R program crosval package was used for k-fold cross-validation and grid search.
Table 2. Grid Search Values for Each Classifier.

2.7. Performance Metrics

Diagnostic accuracy [45] , sensitivity [46], specificity [46], F1 score [47], positive predict value, and negative predict value [48] ​​were used in performance metrics. Detailed information is given in Table 3.
Table 3. Performance Metrics.

3. Results

According to Table 4, the testosterone level group categories showed no statistically significant differences. (Normal and TD) according to the age variable (p= 0.455). There were significant differences in TG, HT, HDL and AC variables according to group categories (p<0.001).
Table 4. Statistical Analysis for Variables.
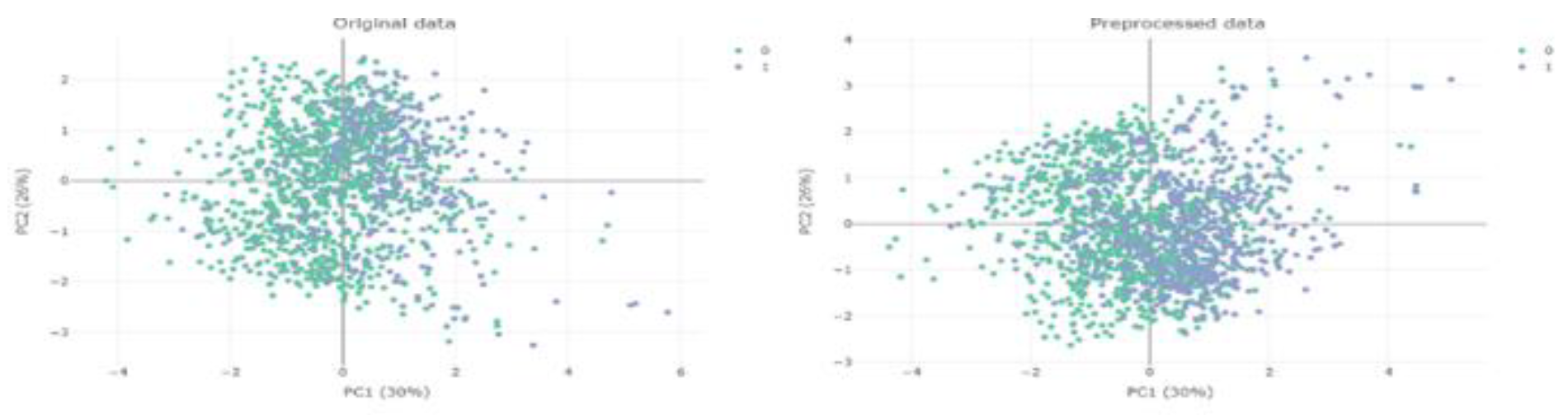
After the SMOTE technique was applied to solve the class balance problem in testosterone levels, the normal (T ≥ 300 ng/dl) and TD (T < 300 ng/dl) category distributions reached a balanced structure (Figure 5).
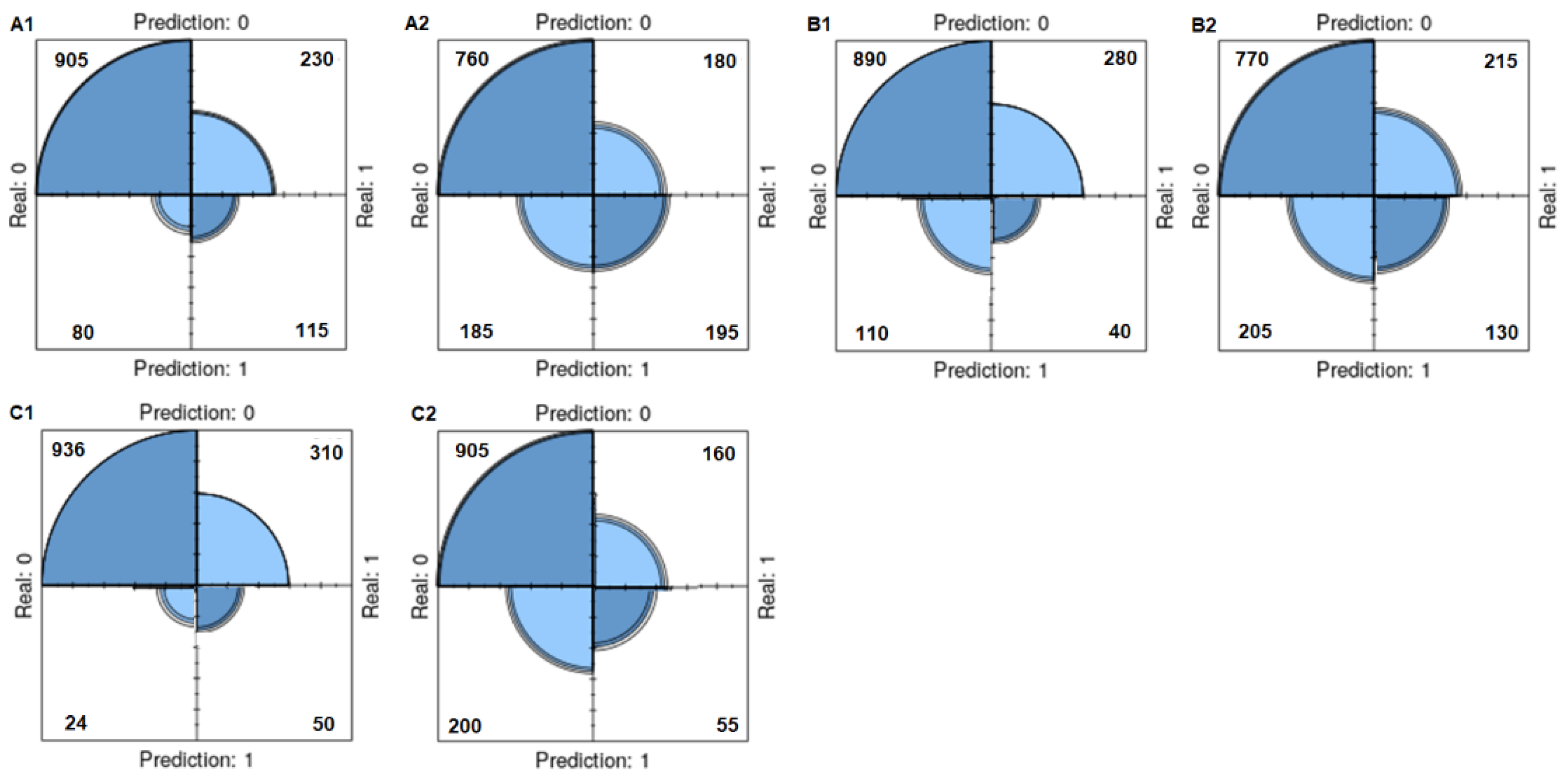
The results in the Table 5 show the performance of the classifiers in a study to predict total testosterone deficiency in patients with type 2 diabetes. The table presents the evaluations performed on original and SMOTE data using four basic classifiers. After SMOTE, while the diagnostic accuracy decreased in all base classifiers except ELM, sensitivity values ​​increased in all classifiers. Similarly, while the specificity values ​​decreased in all classifiers, F1 score increased. In MLP and ELM classifiers, positive predictive value could not be calculated in the original data, but calculations were made after SMOTE. In other classifiers, positive predictive value decreased after SMOTE. The negative predictive value increased after SMOTE in all base classifiers. The classification diagram for the original and smote data using the base classifiers (training data) is presented in Figure 6. The RF classifier gave more successful results on the training dataset.
Table 5. Performance Metrics Original and SMOTE Data for Base Classifiers (Training Data).
Table 6 presents the evaluations performed using three ensemble classifiers on the original and SMOTE data. After SMOTE, the diagnostic accuracy decreased in all ensemble classifiers, while the sensitivity values ​​increased in all classifiers. The specificity values ​​decreased in two classifiers except SGB, but the F1 score increased in the XGBoost classifier. The negative predictive values ​​increased after SMOTE in all ensemble classifiers. The most successful ensemble classifier in the training dataset was the ADA classifier in the original data and in the after SMOTE data. The classification diagram for the original and smote data using the ensemble classifiers (training data) is presented in figure 7.
Table 6. Performance Metrics Original and SMOTE Data for Ensemble Classifiers (Training Data).
According to Table 7 created with testing data, MLP shows high specificity on the original data, but shows an unstable performance as the sensitivity is very low. With SMOTE, the sensitivity increases while the specificity decreases, thus the F1 score becomes calculable. RF provides good stability on the original data. With SMOTE, sensitivity increases, but overall accuracy drops slightly. LR exhibits high specificity in the original data, but low sensitivity. With SMOTE, sensitivity increases, but accuracy and specificity decrease. ELM somewhat reduces the instability by increasing sensitivity with SMOTE, but accuracy and specificity are reduced. ADA shows stable performance on the original data, but improves sensitivity with SMOTE. XGBoost maintains its overall accuracy while improving sensitivity with SMOTE. While SGB shows a balanced performance on the original data, SMOTE provides increased sensitivity but decreased accuracy. As a result of this analysis, we can say that XGBoost is the most suitable model for your intended use in evaluating model performance. XGBoost, which exhibits a balanced performance especially when SMOTE is used, can be preferred to correct class imbalance.
Table 7. Performance Metrics Original and SMOTE Data for Base-Ensemble Classifiers (Testing Data).

4. Discussion

In recent years, the use of machine learning algorithms in the field of medicine has significantly increased [49]. In this study, we aimed to predict total testosterone deficiency in patients with type 2 diabetes by using machine learning and ensemble learning methods on original data with class imbalance and data after SMOTE. LR is a commonly utilized method in medicine and is frequently cited in the literature. For instance, the study by Hastie et al. (2009) reported that while LR achieves high accuracy and specificity, it often shows lower sensitivity, particularly when addressing imbalanced datasets [50]. In this study as well, LR achieved 77 % diagnostic accuracy and 98 % specificity on the original dataset, while its sensitivity remained only 19 %. This indicates that the LR model is limited in detecting the positive class, this observation aligns with findings in the literature concerning imbalanced datasets. RF model is generally known as a robust classifier and performs well on imbalanced datasets. In a study by Liu et al. (2009), it was noted that RF is particularly effective when used in conjunction with techniques like SMOTE to address class imbalance [51]. In this study, the RF model achieved 76 % diagnostic accuracy and 44 % sensitivity on the original dataset, and after applying SMOTE, its sensitivity increased to 58 %. This finding, where SMOTE enhances RF performance, is consistent with the results reported by Liu and colleagues. ELM and MLP are generally reported in the literature to perform well on complex datasets, but their sensitivity may be low on imbalanced datasets. In the study by Huang et al. (2012), it was also noted that ELM is a strong model, particularly for multiclass classification problems, but its performance can decline in situations of data imbalance compared to other methods. In this context, the results presented in the table align with the literature regarding the ELM’s sensitivity to imbalanced datasets [52]. Similarly, in this study, ELM showed 34 % sensitivity on the original dataset, which increased to 49 % with SMOTE. However, the overall diagnostic accuracy dropped from 76 % to 69 % across both datasets, indicating that addressing imbalance with SMOTE does not necessarily improve all metrics. Ensemble learning algorithms such as ADA, XGBoost, and SGB are generally known for their strong performance on imbalanced datasets. Freund and Schapire (1997) demonstrated that AdaBoost improves sensitivity, especially on imbalanced datasets, by iteratively reducing classification errors [53]. In this study as well, AdaBoost increased its sensitivity from 42 % to 61 % when used with SMOTE. However, a decrease in diagnostic accuracy and specificity was observed; this indicates, as noted in the literature, that addressing data imbalance does not always have a positive impact on all metrics. In recent years, XGBoost has emerged in the literature as a model with strong performance on large datasets and imbalanced classes. In their study, Chen and Guestrin (2016) reported that XGBoost is particularly effective in classification problems and achieves successful results when used with SMOTE in situations of data imbalance [54]. In this study, XGBoost achieved 75 % diagnostic accuracy on the original dataset, and with SMOTE, this accuracy changed to 73 %, while sensitivity increased to 52 %. This result is consistent with the findings of Chen and Guestrin, demonstrating that XGBoost can provide balanced performance on imbalanced datasets.

5. Conclusion

SMOTE is used to correct the class imbalance in the original data. However, as seen in this study, when SMOTE was applied, the diagnostic accuracy decreased in some models, but the sensitivity increased significantly. This shows the positive effects of SMOTE to better predict the minority class. RF and ELM models showed higher increase in sensitivity and overall performance after SMOTE application, indicating that these models can be more effective in imbalanced datasets. If total testosterone deficiency is chosen as the reference group (positive class), the choice of meaningful metrics depends on the purpose of the prediction and its clinical significance. Sensitivity, F1 Score, and Positive Predictive Value (PPV) will be the most meaningful metrics when you choose total testosterone deficiency as the reference group because these metrics focus on the importance of correctly identifying individuals with deficiency, which is one of the most critical points for clinical decisions.
In conclusion, this study shows that classifier performance is highly sensitive to data imbalance, and techniques like SMOTE play a crucial role in addressing this imbalance. Specifically, the XGBoost model exhibited the highest performance in sensitivity and diagnostic accuracy when combined with SMOTE. These results are in line with findings from similar studies in the literature. XGBoost, which provides balanced performance especially when SMOTE is used, can be preferred for correcting class imbalance.

References

  1. D.J.D.c. Care, Care in diabetes—2022, 45 (2022) S17.
  2. W.H.O.J.U.o.g.h.i.t.d.i.d. mellitus, Abbreviated report of a WHO consultation, 22 (2011).
  3. Turkish Diabetes Foundation, Diabetes Diagnosis and Treatment Guide (2023).
  4. S. Bhasin, G.R. Cunningham, F.J. Hayes, A.M. Matsumoto, P.J. Snyder, R.S. Swerdloff, V.M.J.T.J.o.C.E. Montori, Metabolism, Testosterone therapy in men with androgen deficiency syndromes: an Endocrine Society clinical practice guideline, 95 (2010) 2536-2559. [CrossRef]
  5. E. Musa, J.M. El-Bashir, F. Sani-Bello, A.G.J.C.D. Bakari, Hypergonadotropic hypogonadism in Nigerian men with type 2 diabetes mellitus, 10 (2021) 129-137.
  6. K. Dhatariya, D. Nagi, T.J.P.D.I. Jones, ABCD position statement on the management of hypogonadal males with type 2 diabetes, 27 (2010) 408-412. [CrossRef]
  7. https://patients.uroweb.org/other-diseases/male-hypogonadism/.
  8. I. Agledahl, P.-A. Skjærpe, J.-B. Hansen, J.J.N. Svartberg, Metabolism, C. Diseases, Low serum testosterone in men is inversely associated with non-fasting serum triglycerides: the Tromsø study, 18 (2008) 256-262. [CrossRef]
  9. Y. Jiang, J. Ye, M. Zhao, A. Tan, H. Zhang, Y. Gao, Z. Lu, C. Wu, Y. Hu, Q.J.C.C.A. Wang, Cross-sectional and longitudinal associations between serum testosterone concentrations and hypertension: Results from the Fangchenggang Area Male Health and Examination Survey in China, 487 (2018) 90-95. [CrossRef]
  10. S. Torkler, H. Wallaschofski, S.E. Baumeister, H. Völzke, M. Dörr, S. Felix, R. Rettig, M. Nauck, R.J.T.a.m. Haring, Inverse association between total testosterone concentrations, incident hypertension and blood pressure, 14 (2011) 176-182. [CrossRef]
  11. G.J.T.w.j.o.m.s.h. Hackett, Type 2 diabetes and testosterone therapy, 37 (2019) 31. [CrossRef]
  12. A. Yassin, A. Haider, K.S. Haider, M. Caliber, G. Doros, F. Saad, W.T.J.D.C. Garvey, Testosterone therapy in men with hypogonadism prevents progression from prediabetes to type 2 diabetes: eight-year data from a registry study, 42 (2019) 1104-1111. [CrossRef]
  13. G. Corona, M. G. Corona, M. Monami, G. Rastrelli, A. Aversa, Y. Tishova, F. Saad, A. Lenzi, G. Forti, E. Mannucci, M.J.T.j.o.s.m. Maggi, Testosterone and metabolic syndrome: A meta-analysis study, 8 (2011) 272-283.
  14. V. Bianchi, V.J.O.R. Locatelli, Testosterone a key factor in gender related metabolic syndrome, 19 (2018) 557-575. [CrossRef]
  15. J. Anaissie, N.H. Roberts, P. Wang, F.A.J.S.m.r. Yafi, Testosterone replacement therapy and components of the metabolic syndrome, 5 (2017) 200-210. [CrossRef]
  16. P.J. Snyder, S. Bhasin, G.R. Cunningham, A.M. Matsumoto, A.J. Stephens-Shields, J.A. Cauley, T.M. Gill, E. Barrett-Connor, R.S. Swerdloff, C.J.N.E.J.o.M. Wang, Effects of testosterone treatment in older men, 374 (2016) 611-624. [CrossRef]
  17. W. Rosner, R.J. Auchus, R. Azziz, P.M. Sluss, H.J.T.J.o.C.E. Raff, Metabolism, Utility, limitations, and pitfalls in measuring testosterone: an Endocrine Society position statement, 92 (2007) 405-413. [CrossRef]
  18. I.J.A.I.i.m. Kononenko, Machine learning for medical diagnosis: history, state of the art and perspective, 23 (2001) 89-109. [CrossRef]
  19. K. Deng, H. Li, Y.J.I. Guan, Treatment stratification of patients with metastatic castration-resistant prostate cancer by machine learning, 23 (2020). [CrossRef]
  20. C.-H. Hsieh, R.-H. Lu, N.-H. Lee, W.-T. Chiu, M.-H. Hsu, Y.-C.J.J.S. Li, Novel solutions for an old disease: diagnosis of acute appendicitis with random forest, support vector machines, and artificial neural networks, 149 (2011) 87-93. [CrossRef]
  21. M.-A. Schulz, B.T. Yeo, J.T. Vogelstein, J. Mourao-Miranada, J.N. Kather, K. Kording, B. Richards, D.J.N.c. Bzdok, Different scaling of linear models and deep learning in UKBiobank brain images versus machine-learning datasets, 11 (2020) 4238. [CrossRef]
  22. E. Christodoulou, J. Ma, G.S. Collins, E.W. Steyerberg, J.Y. Verbakel, B.J.J.o.c.e. Van Calster, A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models, 110 (2019) 12-22. [CrossRef]
  23. L.J.A.i.r. Rokach, Ensemble-based classifiers, 33 (2010) 1-39. [CrossRef]
  24. M. Abdar, M. Zomorodi-Moghadam, X. Zhou, R. Gururajan, X. Tao, P.D. Barua, R.J.P.R.L. Gururajan, A new nested ensemble technique for automated diagnosis of breast cancer, 132 (2020) 123-131. [CrossRef]
  25. A. Jain, S. Ratnoo, D. Kumar, Addressing class imbalance problem in medical diagnosis: A genetic algorithm approach, 2017 international conference on information, communication, instrumentation and control (ICICIC), IEEE, 2017, pp. 1-8.
  26. M. Zhu, J. Xia, X. Jin, M. Yan, G. Cai, J. Yan, G.J.I.A. Ning, Class weights random forest algorithm for processing class imbalanced medical data, 6 (2018) 4641-4652. [CrossRef]
  27. J.P. Mulhall, L.W. Trost, R.E. Brannigan, E.G. Kurtz, J.B. Redmon, K.A. Chiles, D.J. Lightner, M.M. Miner, M.H. Murad, C.J.J.T.J.o.u. Nelson, Evaluation and management of testosterone deficiency: AUA guideline, 200 (2018) 423-432. [CrossRef]
  28. J. Auskalnis, N. Paulauskas, A.J.E.i.E. Baskys, Application of local outlier factor algorithm to detect anomalies in computer network, 24 (2018) 96-99. [CrossRef]
  29. H. He, E.A.J.I.T.o.k. Garcia, d. engineering, Learning from imbalanced data, 21 (2009) 1263-1284. [CrossRef]
  30. J.O. Awoyemi, A.O. Adetunmbi, S.A. Oluwadare, Credit card fraud detection using machine learning techniques: A comparative analysis, 2017 international conference on computing networking and informatics (ICCNI), IEEE, 2017, pp. 1-9.
  31. R. Blagus, L.J.B.b. Lusa, SMOTE for high-dimensional class-imbalanced data, 14 (2013) 1-16. [CrossRef]
  32. D. Elreedy, A.F. Atiya, F.J.M.L. Kamalov, A theoretical distribution analysis of synthetic minority oversampling technique (SMOTE) for imbalanced learning, 113 (2024) 4903-4923. [CrossRef]
  33. A.J. Mohammed, M.M. Hassan, D.H.J.I.J.o.A.T.i.C.S. Kadir, Engineering, Improving classification performance for a novel imbalanced medical dataset using SMOTE method, 9 (2020) 3161-3172. [CrossRef]
  34. D. Berrar, Cross-validation, 2019.
  35. M.J.M.R. Kıvrak, Early Diagnosis of Diabetes Mellitus by Machine Learning Methods According to Plasma Glucose Concentration, Serum Insulin Resistance and Diastolic Blood Pressure Indicators, 4 (2022) 191-195.
  36. D. Marinov, D. Karapetyan, Hyperparameter optimisation with early termination of poor performers, 2019 11th Computer Science and Electronic Engineering (CEEC), IEEE, 2019, pp. 160-163.
  37. K.Y. Chan, B. Abu-Salih, R. Qaddoura, A.-Z. Ala’M, V. Palade, D.-S. Pham, J. Del Ser, K.J.N. Muhammad, Deep neural networks in the cloud: Review, applications, challenges and research directions, 545 (2023) 126327. [CrossRef]
  38. M. Kivrak, E. Guldogan, C.J.C.m. Colak, p.i. biomedicine, Prediction of death status on the course of treatment in SARS-COV-2 patients with deep learning and machine learning methods, 201 (2021) 105951. [CrossRef]
  39. F. Stulp, O.J.N.N. Sigaud, Many regression algorithms, one unified model: A review, 69 (2015) 60-79. [CrossRef]
  40. K. Kirasich, T. Smith, B.J.S.D.S.R. Sadler, Random forest vs logistic regression: binary classification for heterogeneous datasets, 1 (2018) 9.
  41. M. Kıvrak, C. Colak, An investigation of ensemble learning methods in classification problems and an application on non-small-cell lung cancer data, (2022). [CrossRef]
  42. T.-K. An, M.-H. Kim, A new diverse AdaBoost classifier, 2010 International conference on artificial intelligence and computational intelligence, IEEE, 2010, pp. 359-363.
  43. R. Mitchell, E.J.P.C.S. Frank, Accelerating the XGBoost algorithm using GPU computing, 3 (2017) e127.
  44. Y.J.A.i.C.E. Shin, Application of stochastic gradient boosting approach to early prediction of safety accidents at construction site, 2019 (2019) 1574297. [CrossRef]
  45. R. Vinayagamoorthy, T.J.J.o.R.P. Rajmohan, Composites, Machining and its challenges on bio-fibre reinforced plastics: A critical review, 37 (2018) 1037-1050. [CrossRef]
  46. A. Johannes, A. Picon, A. Alvarez-Gila, J. Echazarra, S. Rodriguez-Vaamonde, A.D. Navajas, A.J.C. Ortiz-Barredo, e.i. agriculture, Automatic plant disease diagnosis using mobile capture devices, applied on a wheat use case, 138 (2017) 200-209. [CrossRef]
  47. Kuberski, J. Bialek, N. Perrakis, W. Cools, N. Nuyttens, H. Elakhrass, P.J.M.N.o.t.R.A.S.L. Cunha, Machine-learning classification of astronomical sources: estimating F1-score in the absence of ground truth, 517 (2022) L116-L120.
  48. T.F. Monaghan, S.N. Rahman, C.W. Agudelo, A.J. Wein, J.M. Lazar, K. Everaert, R.R.J.M. Dmochowski, Foundational statistical principles in medical research: sensitivity, specificity, positive predictive value, and negative predictive value, 57 (2021) 503. [CrossRef]
  49. A.L. Beam, I.S.J.J. Kohane, Big data and machine learning in health care, 319 (2018) 1317-1318. [CrossRef]
  50. T. Hastie, The elements of statistical learning: data mining, inference, and prediction, Springer, 2009.
  51. X.-Y. Liu, J. Wu, Z.-H.J.I.T.o.S. Zhou, Man,, P.B. Cybernetics, Exploratory undersampling for class-imbalance learning, 39 (2008) 539-550. [CrossRef]
  52. G. Huang, H. Zhou, X. Ding, R.J.I.T.o.S. Zhang, Man,, P.B. Cybernetics, Extreme Learning Machine for Regression and Multiclass Classification, 42 (2012) 513-529. [CrossRef]
  53. Y. Freund, R.E. Schapire, A desicion-theoretic generalization of on-line learning and an application to boosting, Springer Berlin Heidelberg, Berlin, Heidelberg, 1995, pp. 23-37.
  54. T. Chen, C. Guestrin, XGBoost: A Scalable Tree Boosting System, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, San Francisco, California, USA, 2016, pp. 785–794.
Preprints 121327 g001
Figure 1. Testesterone Target Organs [7].
Figure 1. Testesterone Target Organs [7].
Preprints 121327 g001
Preprints 121327 g002
Figure 2. The Working Step.
Figure 2. The Working Step.
Preprints 121327 g002
Preprints 121327 g003
Figure 3. Outlier/Excessive Observation Analyses With Local Outlier Factor.
Figure 3. Outlier/Excessive Observation Analyses With Local Outlier Factor.
Preprints 121327 g003
Preprints 121327 g005
Figure 5. Original and Preprocessed (SMOTE) Data.
Figure 5. Original and Preprocessed (SMOTE) Data.
Preprints 121327 g005
Preprints 121327 g006
Figure 6. Classification Diagram for Original and Smote Data Using Base Classifiers (Training Data).
Figure 6. Classification Diagram for Original and Smote Data Using Base Classifiers (Training Data).
Preprints 121327 g006
Preprints 121327 g007
Figure 7. Classification Diagram for Original and Smote Data Using Base Classifiers (Training Data).
Figure 7. Classification Diagram for Original and Smote Data Using Base Classifiers (Training Data).
Preprints 121327 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated