Prerpints.org logo
Preprint
Article

Spectral Water Wave Dissipation by Biomimetic Soft Structure

This version is not peer-reviewed.

Submitted:

15 October 2024

Posted:

18 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Coastal protection solutions can be categorized as grey, hybrid, or natural. Grey infrastructure includes artificial structures like dykes. Natural habitats like seagrasses are considered as natural protection infrastructure. Hybrid solutions combine both natural and grey infrastructure. Evidence suggest that grey solutions can negatively impact the environment, while natural habitats prevent flooding without such adverse effects and provide many ecosystem services. New types of protective solutions, called biomimetic solutions, are inspired by natural habitats and reproduce their features using artificial materials. Few studies have been conducted on these new approaches. This study aims to quantify wave dissipation observed in-situ above a biomimetic solution inspired by kelps, known for their wave dampening properties. The solution was deployed in full water column nearby Palavas-les-Flots in southern France. A one-month in-situ experimentation showed that the biomimetic solution dissipates around 10% of total wave energy on average, whatever the meteo-marine conditions. Wave energy dissipation is frequency dependent: short waves are dissipated, while low-frequency energy increased. An anti-dissipative effect occurs for forcing conditions with frequencies close to the eigen mode linked to the biomimetic solution's geometry, suggesting that resonance should be considered in designing future biomimetic protection solutions.
Keywords: 
Subject: 
Engineering  -   Other

1. Introduction

The will to develop coastal defense systems is as old as the desire to secure shorelines for improving mankind safety and developing maritime trade [1,2,3]. Until now, traditional artificial protection solutions, such as dykes and groins, have been largely built throughout the world shorefaces. However, those so-called grey or hard solutions, are currently recognised for their poor longevity in the face of climate change and for their negative impact on the environment like coastal habitat loss or erosion [4,5,6,7].
A first alternative strategy to protect the coast relies on the concept of soft shoreline engineering (SSE) which emerged in the 1990s in the United States and Canada [3]. SSE solutions encompass protective structures that limit their ecological impact without compromising their technical integrity [2,3]. Some SSE solutions are built with artificial materials (concrete, rock) and form artificial reefs that mimic coral or oyster [8,9], and on which life can develop and improve the coastal defence service. The feedback on these solutions is encouraging while their long-term behaviour under global change remains speculative [8]. Within the SSE solutions, engineers have also considered the protection of the coast based on natural habitats (seagrass, mangroves and corals) without any recourse on artificial features [6,7,10,11]. These habitats provide a natural barrier against climatic and coastal events, controlling hydrodynamic conditions and sediment motion [7]. Alongside with their protective hydro-morphodynamic services, natural habitats offer various ecological benefits, including improved water quality and carbon storage [6,10]. As a result, natural habitats are receiving increasing attention of the coastal management community [6]. However their wider adoption in coastal management procedures depends upon more efficient cost-benefice feedback and the development of robust deployment strategies [6,7].
A second alternative strategy for coastal protection is to combine natural habitats and artificial structures in so-called "hybrid" solutions [9]. This approach maximizes the protective capacity of any natural habitat while minimizing their weaknesses [6]. Hybrid solutions offer an interesting compromise, especially in heavily urbanized coastal areas where the deployment of purely natural solutions may be challenging [6]. In this context, some hybrid solutions are called biomimetic because the hydro-morphodynamic services they offer relies on mechanisms inspired by nature (also called bioinspiration) [9,12]. Developing a biomimetic solution starts with a deep understanding of some natural eco-bio-hydro-morphodynamic processes which are then stimulated in the real coastal environment by the deployment of artificial features that mimic its effects. For instance, a biomimetic solution made of a dense network of artificial strips, built by analogy with seagrass meadow, would alter hydrodynamics [11,13] especially wave damping, and can provide a safe place for the seedlings of seagrass [14]. To our knowledge, no field studies have been carried out on the development and deployment of biomimetic solutions mimicking kelps as a protective solution in coastal engineering [9].
The objective of this study is to provide an initial estimate of the spectral dissipative properties of a representative biomimetic protection imitating kelps solution from in-situ measurements in the nearshore zone. First, a state of the art is carried out on wave dissipation by natural habitats. Then, the study area, the features of the biomimetic structure, the experimentation and the methodology for data processing are described. A comprehensive analysis of mean and spectral wave dissipation rates is presented. Observed dissipation is compared with existing literature. Several processes are revealed, and their consequences for the design of biomimetic solution are discussed.

2. Wave Dissipation by Natural Habitats

2.1. State of the Art

The conception of biomimetic solutions relies on the exploration of the impact of coastal natural habitats on hydro-morphodynamics. Indeed, natural habitats drive changes in the fluid velocity profile [15,16,17], inferred turbulence [18,19,20], wave dissipation [21,22,23] or sediment motion [24,25,26,27]. Coral reefs [28,29], salt marshes [30,31,32,33], seagrass/kelp beds [13,21,34,35,36,37,38,39] and mangroves [40,41] dissipate 70%, 72%, 36% and 31% of the waves in average with variations from one study to another [review of 69 projects [10]. Although wave dissipation has been largely investigated in laboratory [23,31,32,34,38,41,42,43,44] and analytically [21,39,43,45,46,47], it has been less studied in the field [13,30,36,37] while few studies have investigated dissipation above giant kelps and none, to our knowledge, have examined biomimetic solutions inspired by kelps. It is difficult to dissociate wave dissipation driven by bottom friction from a kelp effect [48]. Elwany et al. [49] suggest that kelps have practically no effect on wave dissipation with periods of 5-20 s, but they used bottom-mounted pressure sensors, which limit the detection of shorter wave. Rosman et al. [50] quantified wave energy both inside and outside of a giant kelp forest and do not clearly evidence wave dissipation through the forest for a similar wave forcing. Elsmore et al. [51] found that giant kelps dissipate around 7% of the wave energy flux, contrary to a transect without kelps. Lindhart et al. [48] indicated that short wave are more dissipated when kelp surface canopy is high, i.e. in summer. However, the wave dissipation and its frequency-dependence has received very little attention in the literature [48], despite observations which tends to show that kelps have a non-negligible dissipation effect [51].

2.2. Theoretical Formulation of Wave Dissipation

Historically, the theoretical formalization of wave dissipation on soft structures is based on Dalrymple et al. [52] in which dissipation is defined from a wave energy balance equation. Dalrymple et al. [52] hypothesize that vegetation can be represented by rigid vertical cylinders. Assuming that waves propagate along a x-axis, the conservation of wave energy is defined as
∂ E c g ∂ x = − ϵ s .
Here E = 1 8 ρ g H s 2 is the wave energy density of wave given by the linear theory, ρ is the density of water, g is the gravitational acceleration, H s is the significant wave height, c g the wave group velocity and ϵ s is the time-averaged rate of energy dissipation per unit horizontal area driven by the structures opposing the waves:
ϵ s = 1 T ∫ 0 T ∫ z = 0 l s ( F x u + F z w ) d z d t
where l s is the structure length, F x and F z are the horizontal and vertical components of the total force acting on the structure at a given z, and u and w are the horizontal and vertical components of the fluid velocity. The horizontal component F x is considered to be much greater than F z  [34,45]. As the structure is considered rigid no movement occurs along the z-axis. According to Morison’s equations [53], the force F x applied to a rigid structure is
F x = 1 2 ρ S r e f C D | u | u + π 4 N b v 2 ρ C M ∂ u ∂ t
in which S r e f is a surface reference, b v the structure area per unit height, N the density, C D the drag coefficient and C M the inertia coefficient. The reference surface S r e f is the surface perpendicular to the flow per unit volume on which the energy loss is calculated. Its definition varies depending on whether the study is concerned with the spacing between structures s [52], their density N [21] or other geometric characteristics [32,38]. In this study, the form S r e f = N b v defined by Mendez and Losada [21] is used. The first term of Equation (3) represents the drag force F D and the second the inertia force F M . The contribution of the inertia force to wave dissipation is smaller than the drag force and is usually assumed to be zero [21,34,54]. Assuming that the depth is constant along the propagation axis, c g is constant. By combining Equation (1) and (2), the solution to the differential equation is
H s H s 0 = 1 1 + K D H s 0 x .
H s 0 is the significant wave height at the entrance of the transect in deep water. In Dalrymple et al. [52], K D is the dissipation coefficient, defined by
K D = 4 9 π C D k S r e f sinh 3 k l s + 3 sinh k l s sinh k h ( sinh 2 k h + 2 k h )
where S r e f is the variable defined above, k is the wave number and h is the depth. To correctly apply this analytical model, the drag coefficient can be estimated using various strategies [21,23,32,36,38,55].
Kobayashi et al. [34] demonstrate that C D depends on the Reynolds number R e = u c D ν , where D is the diameter of one structure, u c is a characteristic velocity and ν is the kinematic viscosity of water, and express this empirical drag coefficient in the form of a law:
C D = α + β R e γ
where α , β and γ are coefficients determined experimentally. The characteristic velocity u c is defined as the maximum amplitude of the orbital wave motion at the top and in the front side of the structure [22,45,56] and is written as
u c = π H s 0 T m cosh k l s sinh k h
where T m is the mean wave period. The law in Equation (6) has been widely used [22,36,45,57] and reformulated with the Keulegan-Carpenter number K C = u c T m D [21,22,23,39]. The preeminence of K C or R e in the formulation of C D is still under debate [58].
Dalrymple et al. [52] formalism is applied to study wave dissipation either over natural or artificial structures, although they are flexible [21,22,34,56]. Alternative works have tried to include flexibility in the original formalism [32,36,38,45,46,59]. Méndez et al. [45] consider the swaying of the structure thanks to a relative horizontal velocity u r defined as the difference between the velocity of the structure and that of the fluid. This parameter is introduced directly in Equation (3) instead of the horizontal velocity u. Luhar and Nepf [60] employ an effective length l e which represents the length of a rigid structure that generates the same drag force as a flexible structure of length l s . Lei and Nepf [38] applies this length correction directly in Equation (5) from Dalrymple et al. [52] to predict the wave attenuation over a flexible seagrass meadow. In parallel, Dalrymple et al. [52] formalism is improved to take into account irregular waves, using H R M S (root mean squared wave description) instead of H s in the definition of the dissipation [21]. Suzuki et al. [61] adopted this new equation for implementing canopy dissipation in the spectral model SWAN (Simulating Waves Nearshore), adding dependencies to frequency and wave direction. Jacobsen et al. [62] adopts Suzuki’s method to take into account the effect of frequency on the velocity profile inside and outside the canopy and Ascencio et al. [63] applied Jacobsen’s work in laboratory. However, we do not consider those fully spectral/directional developments because (i) this experimentation provides no information about wave direction and (ii) this work is limited to a spectral analysis averaged over frequency bands of physical meaning.

3. Material and Methods

3.1. Study Area

This study was carried out near the outlet of the Lez river and the entrance to the port of Palavas-les-Flots in the south of France (Figure 1a and Figure 1b). The coastline is densely urbanised, with numerous dykes, and attracts a significant number of tourists during the summer season which makes the place strategic for coastal management. A dyke, oriented north-south, is located to the west to delimit the port area. The study area is a microtidal environment of almost constant water depth (3-3.5 m) in the studied area. The sediment is sandy, with some mud in the Lez channel. The beaches of Palavas-les-Flots are subject to different wind regimes throughout the year. Winds come mainly from the north, west and south-east during storms. The orientation of the bay is directly affected by south-east storms. However, the orientation of the breakwater, located at the left side of the experimentation, protects the entrance to the port and the channel from waves from the south or the west. The proximity of the study site to the grey structures was constrained by administrative authorisations. The possible impact of the dykes on the measurements is discussed in Section 5.1.

3.2. The Biomimetic Structure

The biomimetic structures considered in this study were inspired by aquatic vegetation, in particular kelps, especially the Macrocystis Pyrifera. Macrosystis are located essentially over rocky substrate in depth between 5-25 m and occupy the water column, when they are mature, and extend toward the surface [48]. The fronds buoyed by pneumatocysts and are 10 to 40 cm long [51]. The biomimetic structure is designed to attenuate wave height, while providing shaded zones and places sheltered from view that favor the presence of many aquatic species. The structure is made of polypropylene ropes, with a Young modulus of 9.8 MPa. One end of the central rope is secured to a jetting anchor buried in the sand, while the other end is attached to a buoy to keep it upright, as Macrocystis Pyrifera. The structure has a total length l s of 3.5 meters and emerges at the water surface. Fronds are uniformly spaced along the main rope at 10 cm intervals and 40 cm long with a diameter of 1.6 cm. The representative diameter D of a structure is set to 3 cm, which corresponds to the diameter of the central rope without the fronds. The diameter value is discussed in Section 5.2. 16 structures are assembled in modules of 16 m 2 in which they are regularly spaced 1 m apart from each other with respect to their center. Thus the density N of structure per unit area in a module is 1. In the following, the set of modules deployed together is called the biomimetic solution.

3.3. Field Data Collection

A linear transect of 5 pressure sensors R1-R5 (RBR virtuoso 3) was deployed across the biomimetic solution between March and April 2023 (Figure 1c). Pressure time series were collected continuously at a sampling rate of 8 Hz. Initial accuracy of pressure sensor is ± 1.0 cm with a resolution of 2 mm. Each pressure sensor is positioned on a metal structure at an elevation Z m above the seabed. The characteristics of the pressure sensors are given in Table 1. The instrumented transect is oriented 120°/300° very similar to the wave direction during storms. The transect is 47 m long with a flat bottom. An atmospheric pressure sensor B1 (Solinst Barologger) was positioned next to the deployment zone and continuously collected one measurement per minute.
Average wind speed and direction were obtained from the weather station at Montpellier airport, managed by Météo-France located 7 km north of Palavas-les-Flots. These data are averaged over 10 min every hour. Offshore wave forcing is extracted from the Sète wave buoy from the french national coastal wave CANDHIS network managed by Cerema and DREAL Occitanie, in the form of significant wave height, mean period and direction every 30 min.

3.4. Field Data Analysis

The measured pressure data (from R1-R5) was corrected from atmospheric pressure using the measurements of B1. The signal is split into 30 min bursts with a 50% overlap. Wave spectra are calculated over each burst by Fast Fourier Transform. The energy spectral density obtained is depth corrected with the linear theory [64], revealing a cut-off frequency at 0.55 Hz. For each spectrum, wave parameters such as the significant wave height H s and the mean wave period T m are extracted.
To analyse the sensitivity of wave dissipation to wave frequency, the spectrum are divided into 3 frequency bands. The frequency cuts between these bands are defined from the mean of the 2853 elementary spectra (Figure 2). The first band, between 0.004 and 0.04 Hz, is identified as infragravity band (IG) [65]. The second band between 0.04 and 0.114 Hz corresponds to swell (SS) and the last band between 0.114 and 0.55 Hz to wind waves (WW) [66]. The upper limit of the wind wave band is set at the cut-off frequency, beyond which the signal corrected by linear theory diverges with respect to the hydrostatic signal. H s and T m are calculated at each burst for each of these bands.
In the following, H s and T m are named H i , j and T i , j where i refers to the station and j to the frequency band. For example, at R1 station, the significant wave height and the mean period for the IG band are H 1 , I G and T 1 , I G respectively. Wave height and period derived after total spectrum are referred as TOT.

4. Results

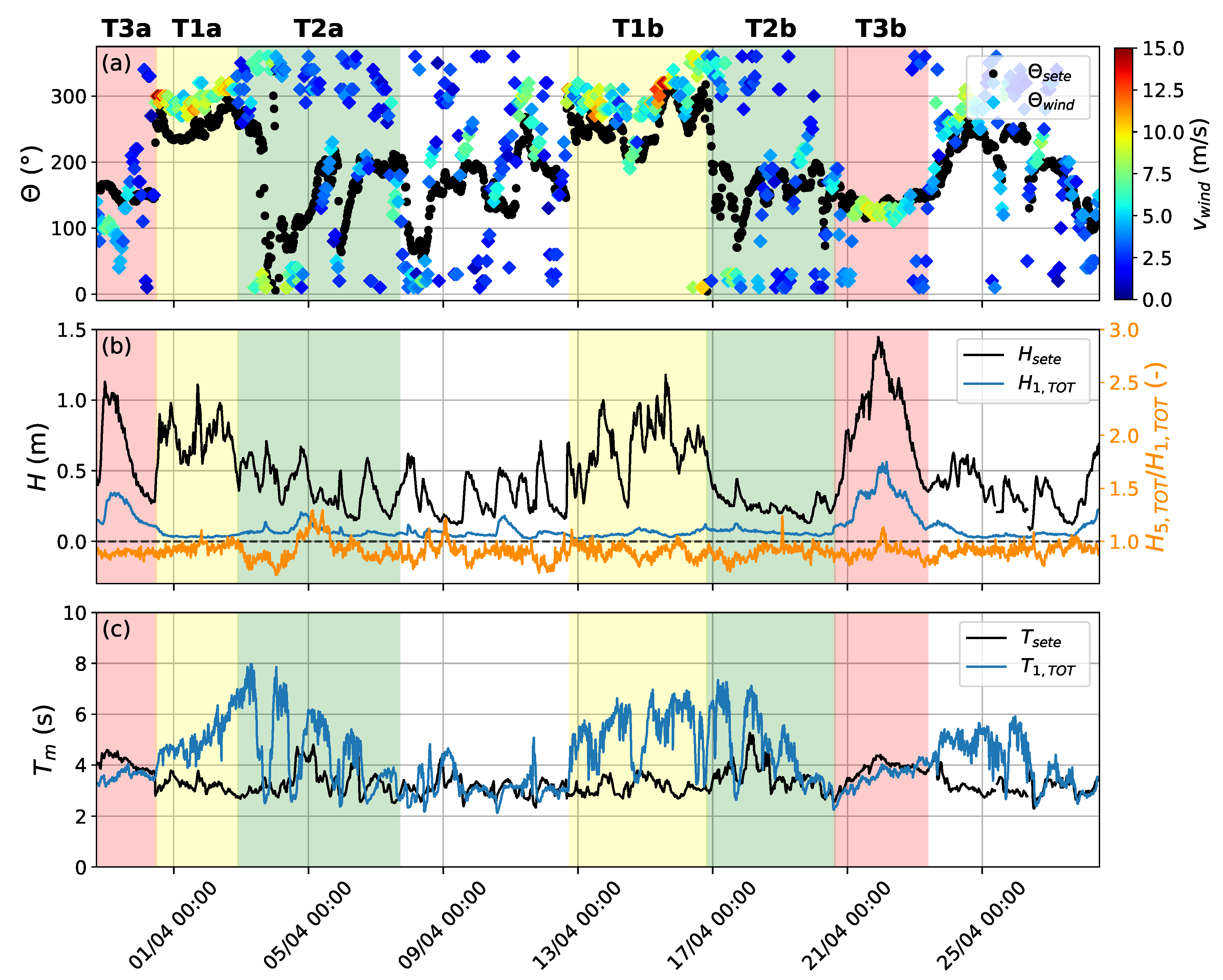
4.1. Forcing Conditions Offshore and at R1 Station

The recorded tidal range did not exceed 0.3 m during the experimentation. The breaking index γ = H / h defined by Munk [67] with a threshold of 0.78 or the more restrictive by Nelson [68] for irregular waves with a threshold of 0.55 are calculated for each burst at all measurement stations. The maximum of γ = H / h obtained during the experimentation is 0.19 at R5 station, so no wave breaking is identified in the studied domain. Relative shallowness k h calculated by linear theory ranged from 0.47 to 3.00, which means that the experimentation occurred in intermediate water depth conditions entirely, far from the dominant breaking zone. The wave nonlinearity is calculated at each burst and each station from Ursell number defined as U r = H i , T O T λ i 2 / h i 3 and ranged from 0.07 to 10.49 (maximum obtained at R5 station). According to Hedges and Ursell [69], the wave nonlinearity threshold is set at U r = 40 , which is larger than the maximum values calculated. The wave steepness defined as H i , T O T / λ i does not exceed 0.034 (maximum value obtained at R3 station), which is below the value defining the Stokes second order domain [69]. So wave nonlinearity is not considered in this study.
Different wind and wave conditions are observed from which 3 types of meteo-marine conditions are identified (Figure 3). Type 1 corresponds to a windy regime, known as "Tramontane" in the south-west of France, that occurred twice between 31 March and 2 April 2023 (T1a) and between 12 and 16 April 2023 (T1b). Forcing parameters during type 1 conditions are: u w i n d , T 1 = 7.9 m/s in average with a westerly to west-northwesterly direction and the range of the other parameters are: H o f f s h o r e , T 1 = 0.24-1.18 m, T o f f s h o r e , T 1 = 2.7-3.78 s, H 1 , T 1 = 0.02-0.12 m and T 1 , T 1 = 3.16-7.0 s, where u w i n d , T i , H o f f s h o r e , T i and T o f f s h o r e , T i refer to measure made offshore and at the airport of Montpellier (see Section 3.3). Type 2 is a thermal northerly/southerly wind regime alternating day and night where H o f f s h o r e , T 2 = 0.13-0.71 m, T o f f s h o r e , T 2 = 2.52-5.26 s, H 1 , T 2 = 0.03-0.2 m and T 1 , T 2 = 2.25-7.96 s. Two type 2 events are recorded between 2 and 7 April 2023 (T2a) and between 16 and 20 April 2023 (T2b). Type 3 conditions are relative to moderate storm and occurred twice during the experimentation, between 29 and 31 March 2023 (T3a) and between 20 and 23 April 2023 (T3b), the first being less energetic than the second. The parameters associated to type 3 conditions are u w i n d , T 3 = 4.94 m/s in average from the south-east direction, H o f f s h o r e , T 3 = 0.27-1.45 m and T o f f s h o r e , T 3 = 2.64-4.31 s, H 1 , T 3 = 0.05-0.56 m and T 1 , T 3 = 2.36-4.31 s.
In the following, the analysis of wave dissipation is realised for the three types of conditions emblematic of the regional meteo-marine regimes. The values of the R e and K C numbers observed under those three types of condition are reported in Figure 7a and Figure 7b.

4.2. Conditions over the First Module of the Biomimetic Solution

The significant wave height averaged over all the bursts increases of 0.9 ± 1.0 cm between R1 and R3 stations (i.e. through the first module), and of 3.0 ± 1.0 cm during type 3 conditions. In the literature, the increase in significant wave height at the front side of a dissipative structure has already been predicted analytically [45] and justified by partial wave reflection against the structure. Such an increase in wave height has also been observed in the field [36]. Alternatively, the biomimetic structure could be blocking the full water column, behaving as a low crested hard structure. In such a case, when waves land on the first module, wave speed would slow down and wave height would increase. To estimate such a shoaling contribution between R1 and R3 stations, a simple shoaling equation can be used [70]. The calculation determines that the mean difference in wave height between R1 and R3 stations driven by shoaling is 0.8 cm. In type 3 conditions, this difference is of 3.0 cm. These values corroborates those observed in the experimentation. Beyond the first module, from R3 to R5 stations, a clear wave decay occurs.

4.3. Mean Wave Dissipation by the Biomimetic Solution

Figure 4a shows the evolution of the energy in each frequency band through the biomimetic solution and for the three types of meteo-marine conditions.
The dissipation of the total wave energy averaged over all bursts is around 10%, with a standard deviation of 7.7%, whatever the meteo-marine conditions (Figure 4a; H 5 , T O T / H 1 , T O T around 0.9), and it decreases linearly after the first module (R3 station). Forth, considering the increase of wave energy between R1 and R3 stations by 5-10% (see previous section), the total wave dissipation after this local shoaling effect is around 15-20% whatever the meteo-marine conditions.
But there is no direct evidence on whether this wave decay is the result of dissipation by bottom friction, breaking waves, energy transfer to currents, or dissipation by the biomimetic solution itself. Bottom friction is assumed negligible, considering that the mean friction factor for this site is around 1.2× 10 − 4 based on the formulation of Phillips [71]. Dissipation by geometric breaking is non-existent as discussed in Section 4.1. Complementary measurements (not shown) of currents made at R1, R3 and R4 stations show that even during the strongest conditions, current measurements do not vary in such a way as to justify wave decay. Thus, the decrease in waves must be attributed mainly to a dissipation process induced by the biomimetic solution.
At R5 station, the energy in the IG band has increased of more than 30% with respect to R1 station and 20% with respect to R3 station (Figure 4a). The SS band energy is mainly dissipated over the second part of the biomimetic solution (after R4 station) and not after the first module (R3 station) although a slight decrease is observed there for type 3 conditions (Figure 4a). In bulk, at R5 station, up to 25% with respect to R1 station (35-40% with respect to R3 station) of the SS band energy is dissipated for type 1 and 2 conditions, compared with 10% with respect to R1 station (20% with respect to R3 station) for type 3 conditions. The energy contained in the WW band globally decreases across the biomimetic solution, although a small increase is observed between R4 and R5 stations for type 1 and 2 conditions. The WW band energy loss represents a total dissipation of 7%, 5% and 10% with respect to R1 station (10%, 10% and 20% with respect to R3 station) for types 1, 2 and 3 respectively (Figure 4a).
To decipher whether the relative evolution of the wave energy by frequency bands at R3, R4 and R5 stations is driven by energy transfer between frequency bands and/ or dissipation, absolute wave energy values by frequency bands are compared at those stations. Table 2 represents the average values of the absolute energy in each frequency band calculated per meteo-marine conditions. In all cases, the spatial variation (from R1 to R5 stations) in absolute energy for each frequency band shows the same trend as that of the normalised energy (Figure 4a). Nevertheless, the ratios of absolute energy between frequency bands are high, with values around 10 between IG and SS bands and 100 between IG and WW bands for type 1 and 2 conditions. For type 3 conditions, IG and SS absolute energies are similar while that of WW band is 100 times that of IG and SS bands. In any case, those ratios are by far too large to justify the wave decay in SS and WW bands by single energy transfers to IG band. So, wave decay most likely results from wave dissipation over the biomimetic solution.

4.4. Variability in Wave Dissipation Driven by Meteo-Marine Conditions

Figure 4a shows the evolution of the mean dissipation at each frequency band and each station calculated over the 624, 822 and 429 bursts contained in types 1, 2 and 3 conditions (Section 4.1). The figure also shows the standard deviation at each frequency band and each station. The standard deviation represents the variability of the dissipation in function of meteo-marine conditions. Taking into account this variability does not change the interpretation of the results presented in Section 4.3. Complementarily, a detailed analysis of the wave dissipation at the scale of the burst provides information on the influence of meteo-marine conditions on the behaviour of the biomimetic solution. Figure 4b shows the relative distribution of the energy at each burst in the different frequency bands between R1 and R5 station see (Figure 1).
Figure 4b shows that the incoming forcing has significantly lower energy in the IG band than the other frequency bands whatever the meteo-marine conditions. For type 1 and 2 conditions, the energy in the SS and WW bands is greater and more spread out, although the energy is greater in the WW band on average. For each burst under type 3 conditions, the energy is condensed in the WW band (more than 90%). Longer incoming waves at R1 station drive higher transfer of energy to IG band for type 1 conditions (Figure 4b). Intermediate and shorter incoming waves transfer more energy to IG band for type 2 conditions. In type 3 conditions the relative energy is mostly contained in the WW band (more than 90%); and whatever the incoming forcing, the amount of energy transmitted to IG band is almost identical between R1 and R5 stations. The impact of the biomimetic solution on wave dissipation is clearly function of the SS and WW signature of the incoming wave conditions.

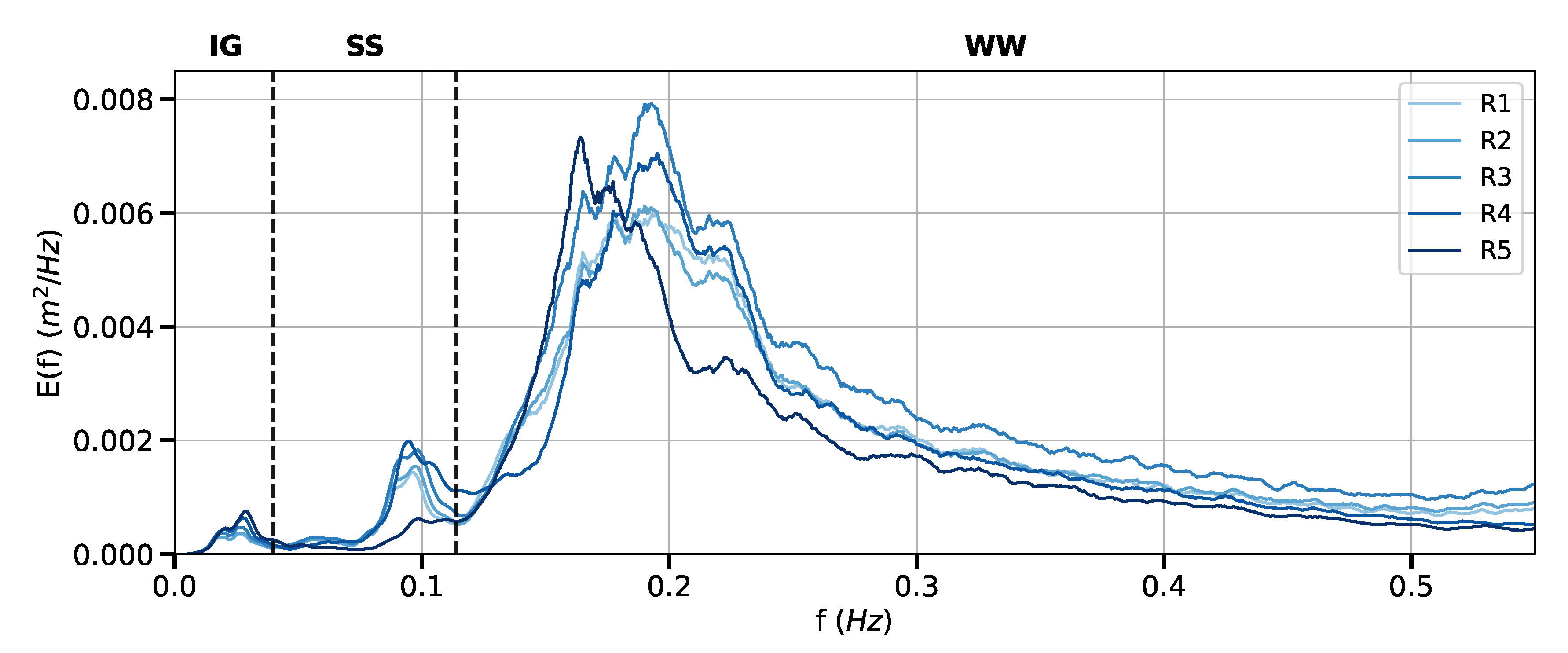
4.5. Spectral Wave Dissipation

Figure 5 shows the average wave spectra for each type of meteo-marine conditions and at each station. For types 1 and 2, the mean wave spectra presents 2 peaks around 0.1 Hz (SS band) and between 0.13-0.14 Hz (WW band) and little amount of energy around 0.025 Hz in IG band. The energy is higher in the WW band than SS band for type 2 conditions, contrary to type 1 conditions. For type 3 conditions, a well marked single energy peak is located in the WW band between 0.16 and 0.25 Hz for all stations.
Whatever the meteo-marine conditions, the energy in IG band increases between R1 and R5 stations. The energy contained in the SS band increases between R1 and R4 stations for type 1 and 2 conditions, then decreases sharply at R5 station, while the amount of energy in the SS band is negligible for type 3 conditions. For type 1 and 2 conditions, the energy in the WW band increases between R1 and R3 station with a slight frequency shift of around 0.05 Hz towards the high frequencies. At R4 station, the energy decreases significantly then increases again to R5 station. For type 3 conditions, the energy increases until R3 station, then decreases until R5 station with a frequency shift of 0.02 Hz towards the low frequency.

5. Discussion

5.1. Control of Stationary Wave Inferred by the Biomimetic Solution on Wave Dissipation

Figure 6 shows the relationship between the dominant wavelength (calculated after peak period) of the wave forcing w.r.t wave dissipation through the full solution ( H 5 , T O T / H 1 , T O T ). An anti-dissipative effect occurs for forcing wavelengths around 37 m corresponding to a peak period of 6.47 s. It appears that, this length corresponds to that of the biomimetic solution projected on a segment between R1 and R5 stations. Forth, the anti-dissipation occurs mainly for intermediate conditions, which are of type 2, possibly type 1 and very rarely for type 3 (see also Figure 3, where H 5 , T O T / H 1 , T O T > 1 ).
Having noticed that a wave characteristic (the peak wavelength) is related to a geometrical property (length of the biomimetic solution), we propose to verify whether the anti-dissipative effect could be linked to a resonance phenomenon. In a closed basin, Rabinovich [73] defines seiche (also called "harbor oscillation" in semi-enclosed basin) as a long stationary wave whose period varies between a few seconds to hours. In such a context, waves coming from the open sea enter into resonance locally or entirely with the basin geometry. The eigen modes of a closed basin oscillation can be calculated from its geometrical features and depth. In the case of a semi-open rectangular basin with constant depth, the period of the eigen modes is:
T n = 4 L ( 2 n + 1 ) g h
where T n is the period of the n-th eigen mode and L the length of the basin. The higher the eigen mode (very large n), the less energetic the resonant wave harmonic. Figure 1 shows the external contour of the biomimetic solution as a rectangular zone which western edge is parallel to the harbour jetty. This domain has a length of 28 m, a width of 25 m and an average depth of 3.3 m. Applying Equation (8), the eigen mode of order 1 has a period of 6.56 s.
Rabinovich [73] also proposes a 2D version of Equation (8) for rectangular basins of length L, width l and constant depth h:
T m n = 2 g h m L 2 + n l 2 − 1 2
where T m n is the period associated with the m,n-th eigen mode. By applying Equation (9) on the external contour defined above, an eigen mode is find for m = 1 and n = 1 associated with a period of 6.55 s.
The similarity between Rabinovitch T 1 and T 11 periods and those observed in the field (Figure 6) suggests that the biomimetic solution may behave like a rectangular semi-enclosed basin open to the south. Such a behaviour would mean that the modules developing throughout the water column act as walls.
However, other features could be at the origin of resonance. First, a resonant basin of 20 m in length could develop between the jetty and the western edge of the biomimetic solution (acting as a wall). For this basin, no eigen mode with a period of the order of 6.5 s is found with Rabinovitch approach. A second resonant basin could extend between the biomimetic solution and the dyke named A on Figure 1 with a length of 176 m. In this case, the ninth eigen mode of period 6.51 s fits the measured period. However, the energy associated to the ninth eigen mode must be negligible in front of the first mode, which in this case shows no energy. Thus, the second resonant basin is not an option. Similar result is obtained with a third basin of length 211 m extending between the biomimetic solution and the beach to the north (point B on Figure 1) for which the eleventh eigen mode has an associated period of 6.44 s.
Rabinovitch formalism shows that the biomimetic solution generates resonant waves for forcings with a wavelength of the same order of magnitude as the length of the solution, independently of the geometry of the jetties surrounding the solution. Resonant waves being known as particularly destructive in harbor contexts, the design of the biomimetic solution should consider integrating a robust control on the development of long wave resonant patterns.

5.2. Defining an Empirical Drag Coefficient for the Biomimetic Solution

Generally, an empirical C D is calculated after measurements carried out in laboratory or in the field. In this section, C D is derived from wave properties and wave dissipation observed during the Palavas-les-Flots experimentation. C D is then expressed as function of Keulegan-Carpenter K C and Reynolds R e numbers and is compared with other analytical expression of C D from the literature.
First, Equation (5) is rewritten to express C D as a function of wave number k, some geometrical properties ( l s , h and S r e f ) and dissipation coefficient K D which is directly calculated with H i , T O T at R1 and R5 stations following Equation (4). Reynolds R e and Keulegan-Carpenter K C numbers are derived after measured orbital velocity (Equation (7)) and wave period. Then, C D is plotted as function of R e (resp. K C ) and two laws in the form of Equation (6) are fitted on the experimental data (Figure 7). The negative values of C D are removed, as they correspond to points with no dissipation (see Section 5.1), i.e. H 5 , T O T / H 1 , T O T > 1 (total of 239 bursts). Calculated C D values range from 0.096 to 188.9, decrease with increasing K C or R e and develop in a range similar to that described in the literature (see Table 3) although fitted C D laws in the case of the biomimetic solution are generally shifted in R e with respect to that already established (Figure 7). The spreading of the values is due to the several meteo-marine conditions measured during experiment as observed by Paul and Amos [37]. The quality of the fit with Equation (6) is relevant when considering all data and for type 3 conditions, but not for type 1 and 2. The correlation coefficient obtained for energetic conditions is better than all data. In such conditions, R e and K C are greater than during fair weather conditions and the values of C D converge rapidly to a constant with limited spreading [30]. Forth, C D calculated over kelp (not extending over the full water column unlike those presented in Table 3) range between 0.2 and 1 for K C values ranging between 5 and 150 [39,74]. Such values are lower than that presented in Figure 7.
In Figure 7c, the position of the experimental curves depends upon the features of the biomimetic structure, in particular the diameter D. The relationships between C D and R e (or K C ) from the literature [30,34,40,56] are plotted for observed R e in a range from 10 2 to 3 × 10 4 corresponding to aquatic vegetation with a representative diameters of the order of a few centimetres. The C D curves for the biomimetic structure (solid red and gray lines in Figure 7c and Figure 7d) fit the extension in R e of those extracted from the literature. They were derived for a representative diameter D = 3 cm not taking into account the fronds around the central main rope. However, the fronds occupy a significant volume in the water column and must contribute to the dissipation. Thus, the effect of fronds on C D is handled redefining D.
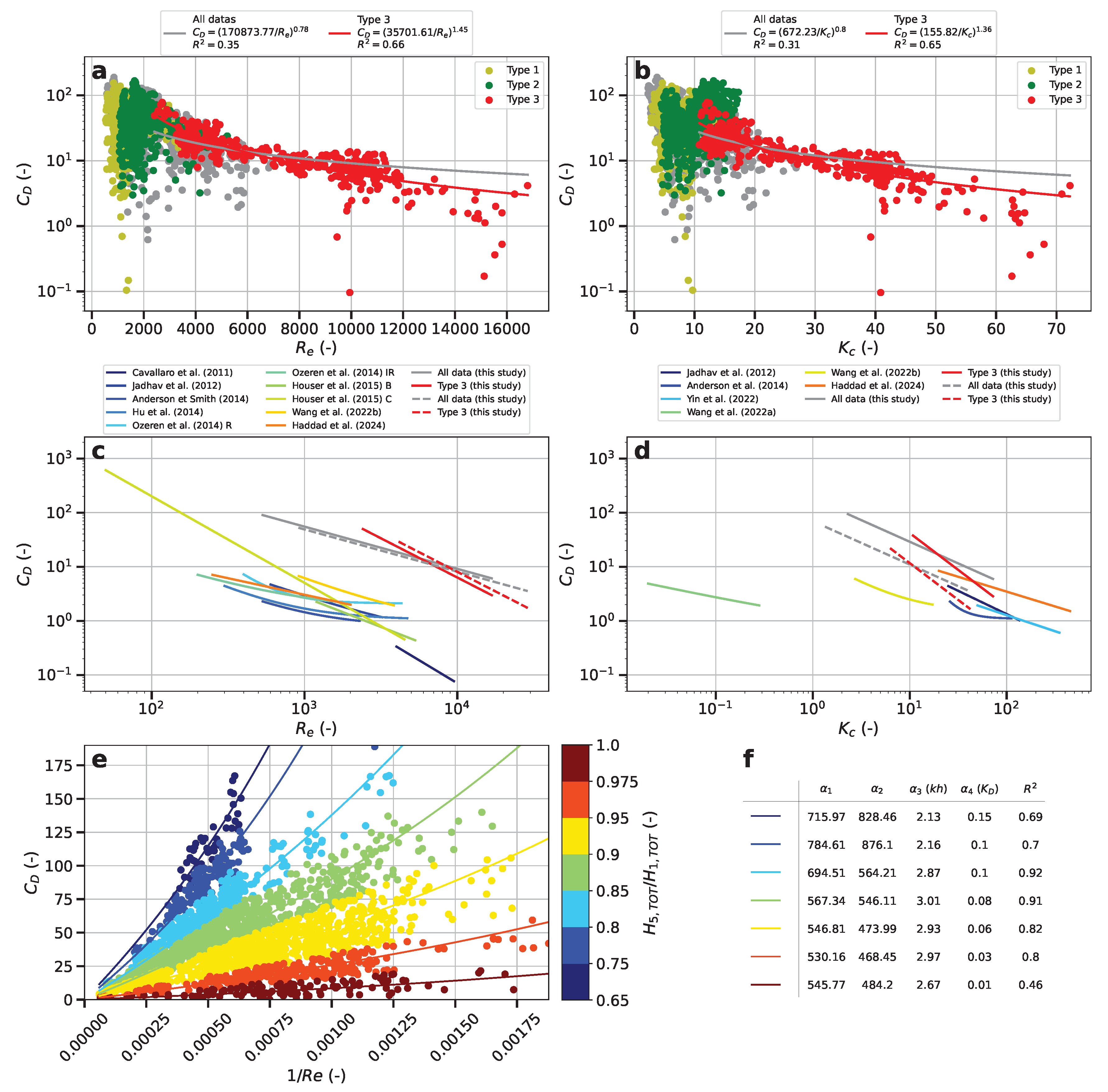
Preprints 121341 g007
Figure 7. Empirical C D represented as a function of the Reynolds R e number (a) and the Keulegan-Carpenter K C number (b) for all bursts. Bursts related to different meteo-marine condition types are represented by different colours. Empirical C D laws in function of (c) R e and (d) K C . Dashed lines represent the new empirical C D laws calculated with the equivalent diameter volume D V . Empirical C D is showed as a function of 1 / R e (e). The colours represent the dissipation intervals over which the new fitted laws are calculated. The optimized parameters associated at each interval is presented in the table next to the plot (f).
Figure 7. Empirical C D represented as a function of the Reynolds R e number (a) and the Keulegan-Carpenter K C number (b) for all bursts. Bursts related to different meteo-marine condition types are represented by different colours. Empirical C D laws in function of (c) R e and (d) K C . Dashed lines represent the new empirical C D laws calculated with the equivalent diameter volume D V . Empirical C D is showed as a function of 1 / R e (e). The colours represent the dissipation intervals over which the new fitted laws are calculated. The optimized parameters associated at each interval is presented in the table next to the plot (f).
Preprints 121341 g007
A new diameter is defined as the volume equivalent diameter D V . Following Dalrymple et al. [52], D V represents the diameter of a vertical rigid cylinder which volume equals that of the solid portions constitutive of a biomimetic structure. D V is calculated digging a 1 m long portion of biomimetic structure in a known quantity of water and measuring the subsequent change in the water volume V. The expression of D V is given by D V = 6 V / π 3 . Following this definition, the D V calculated for a biomimetic structure is 5.15 cm. By applying the same approach explained above, new empirical C D laws are obtained (red and gray dashed dotted lines on Figure 7c and Figure 7d). Introducing D V in the calculation of C D results in a limited change in C D as a function of R e (Figure 7c) and a more significant effect on C D as a function of K C (Figure 7d), and do not improve the correlation coefficients. Last, C D calculated with or without D V are in the range of the values found in the literature.
Alternatively, we investigate how to improve the correlation coefficient R 2 of the empirical C D laws (Figure 7a and Figure 7b) bypassing the existing uncertainties on parameters S r e f , D, l s , K D and h. Doing so, we highlight the parameters that clearly control variations in C D together with R e (resp. K C ) as C D values vary widely. Figure 7e shows C D in function of 1 / R e for different ranges of the total dissipation measured through the biomimetic solution. For a given 1 / R e , C D increases with the total dissipation H 5 , T O T / H 1 , T O T and thus with K D through Equations (4) and (5). From this observation, a new expression for C D is proposed. Equation (5) is rewritten to express C D as a function of K D . The term sinh k h appears and is rewritten in function of Reynolds number R e and orbital velocity thanks to Equation (7), so that:
C D = α 4 α 1 α 2 α 3 R e + α 2 R e 2 α 2 R e 2 + 1
where α 1 = 9 π 2 k S r e f ( sinh k l s 3 + 3 sinh k l s ) , α 2 = π H s 0 D T ν cosh k l s , α 3 = k h and α 4 = K D .
The experimental bursts are classified in seven intervals of H 5 , T O T / H 1 , T O T values. It appears that these intervals follow a clear organisation (Figure 7e) which traduces some control of C D by parameters leading the dissipation. For each dissipation interval, a C D law is calculated following Equation (10). Parameters α 1 to α 4 are set by numerical optimization. Figure 7f shows the optimal parameters and the associated correlation coefficients for the seven C D laws. First, except for extremely low dissipation rates, coefficient correlation R 2 gotten from Equation (10) are clearly better than that from initial formulation. This can be explained by the fact that the formalism of Kobayashi et al. [34] relies mostly on data from flume experimentation where dissipation is explored on a restrictive range and fails to capture the spreading of C D . When field data are available, Equation (10) can be advantageously used to provide a more suitable value of C D .
Defining an experimental C D in function of the wave dissipation, while analytical laws of wave dissipation all rely on the expression of C D , is somewhat paradoxical. However, this paradox can be easily resolved keeping in mind that determining experimental C D and using analytical C D law do not serve the same purpose. Analytical C D laws are essentially used in numerical modelling to reproduce the bottom friction effect, whereas experimental C D are used to characterize the protection solutions resistance against the fluid, in other words the dissipation properties of the solution. For a given solution, experimental C D obtained under various forcing conditions can be resumed by an experimental law. The law proposed in Equation (10) enables C D to be adjusted for the solution studied, whose geometric parameters are already known, as well as the hydrodynamic context in which it is set. In such a context, coastal managers that would plan to deploy the studied solution have the opportunity to estimate C D , without carrying out any experimentation. More generally, the design of an innovative protection solution would be advantageously improved performing a systematic field campaign on wave dissipation over the solution, providing an adapted C D law for this solution.

6. Conclusion and Perspectives

In this paper, a set of pressure time series is used to explore frequency-dependent wave energy dissipation over a biomimetic, soft, artificial solution that emulates natural kelps. The dissipation is calculated from the theory of Dalrymple et al. [52] on a flat bottom under the assumption that the structure studied made of central vertical rope extending from the bottom to the water surface, to which two fronds are regularly tied every 10 cm, although complex and fully flexible, can be represented by a rigid cylinder.
The wave height decay is of 10% whatever the meteo-marine forcing recorded. Such a reduction is attributed to the presence of the biomimetic solution, since it is located far from the breaking zone and bottom friction is negligible. Wave dissipation shows a frequency dependence. Infragravity waves gain up to 35% of energy through the biomimetic solution, unlike swell and shorter waves that are attenuated by up to 25%. Energy variations in each frequency band must be explained by the action of the biomimetic structure and not by frequency band-to-band energy transfer, shoaling or bottom friction. Moreover, stationary waves are trapped within the biomimetic solution and drive an anti-dissipative effect at the lee side of the solution for forcing conditions with frequencies close to the first resonant mode. Last, the biomimetic solution can not be seen as a wall of a semi-enclosed basin extending from the solution toward the beach or toward the dyke.
To handle the complex geometry of a biomimetic structure in the expression of the drag coefficient C D , the concept of volume equivalent diameter D V is defined as the diameter of a vertical rigid cylinder which volume is equal to the volume of the solid portion of the biomimetic structure. However, introducing D V does not change significantly the values of C D with respect to R e or K C and does not improve the correlation. Alternatively, a last type of C D laws is explored, which rely on four parameters (combinations of wave and geometrical properties). For several subsets of C D values for distinct ranges of dissipation ratio, the four parameters are calculated by optimization and define C D laws with correlation coefficient slightly improved with respect to the expression of [34]. Those new C D laws depending upon dissipative properties of the biomimetic solution could be advantageously used when the characterization of a biomimetic solution dissipative properties relies on field observation or improve the C D interval in the design of such a solution.
In the future, the design of biomimetic solution geometry must deal with the increase in both IG and trapped waves. These processes may be explored further with a numerical model to test different conditions such as the placement and density of the modules, with the aim of (i) limiting the increase in long-wave energy and (ii) maximizing wave dissipation.

Author Contributions

Conceptualization, methodology, software, validation, formal analysis, investigation, writing–original draft, writing–review & editing and visualization were contributed by G.M. Conceptualization, validation, resources, writing–review & editing and funding acquisition were contributed by F.B. Conceptualization, validation, investigation and writing–review & editing were contributed by S.M. Writing–review & editing were contributed by R.C. Resources and funding acquisition were contributed by J.-Y.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was conducted as part as the PhD of Ms Marlier funded by P2A Développement and ANRT (CIFRE grant number 2021/1086).

Data Availability Statement

The data used in this article are available upon reasonable request to the corresponding author, until it is deposited in a permanent repository.

Acknowledgments

We would like to thank P2A Développement which allowed us to study their biomimetic structures. We would also like to thank the research group GLADYS (www.gladys-littoral.org) for the equipment provided during the field campaign.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bruun, P. The history and philosophy of coastal protection. In Coastal Engineering 1972; 1972; pp. 33–74. [CrossRef]
  2. Caulk, A.D.; Gannon, J.E.; Shaw, J.R.; Hartig, J.H. Best management practices for soft engineering of shorelines. Greater Detroit American Heritage River Initiative 2000.
  3. Hartig, J.; Zarull, M.; Cook, A. Soft shoreline engineering survey of ecological effectiveness. Ecol. Eng. 2011, 37, 1231–1238. [CrossRef]
  4. Douglass, S.L.; Pickel, B.H. The Tide Doesn’t Go Out Anymore- The Effect of Bulkheads on Urban Bay Shorelines. Shore & Beach 1999, 67, 19–25.
  5. Govarets, A.; Lauwerts, B. Assessment of the impact of coastal defence structures. Biodiversity series: OSPAR Commission 2009.
  6. Sutton-Grier, A.E.; Wowk, K.; Bamford, H. Future of our coasts: The potential for natural and hybrid infrastructure to enhance the resilience of our coastal communities, economies and ecosystems. Environmental Science & Policy 2015, 51, 137–148. [CrossRef]
  7. Morris, R.L.; Konlechner, T.M.; Ghisalberti, M.; Swearer, S.E. From grey to green: Efficacy of eco-engineering solutions for nature-based coastal defence. Glob. Change Biol. 2018, 24, 1827–1842. [CrossRef]
  8. Silva, R.; Mendoza, E.; Mariño-Tapia, I.; Martínez, M.L.; Escalante, E. An artificial reef improves coastal protection and provides a base for coral recovery. J. Coast. Res. 2016, pp. 467–471. Publisher: Coastal Education and Research Foundation.
  9. Perricone, V.; Mutalipassi, M.; Mele, A.; Buono, M.; Vicinanza, D.; Contestabile, P. Nature-based and bioinspired solutions for coastal protection: an overview among key ecosystems and a promising pathway for new functional and sustainable designs. ICES J. Mar. Sci. 2023, p. fsad080. Publisher: Oxford University Press. [CrossRef]
  10. Narayan, S.; Beck, M.W.; Reguero, B.G.; Losada, I.J.; Van Wesenbeeck, B.; Pontee, N.; Sanchirico, J.N.; Ingram, J.C.; Lange, G.M.; Burks-Copes, K.A. The effectiveness, costs and coastal protection benefits of natural and nature-based defences. PloS one 2016, 11, e0154735. Publisher: Public Library of Science San Francisco, CA USA. [CrossRef]
  11. Mullarney, J.C.; Henderson, S.M. Flows within marine vegetation canopies. Advances in coastal hydraulics 2018, pp. 1–46. Publisher: World Scientific Publishing Ltd. Singapore.
  12. Katiyar, N.K.; Goel, G.; Hawi, S.; Goel, S. Nature-inspired materials: Emerging trends and prospects. NPG Asia Mater 2021, 13, 56. [CrossRef]
  13. Nowacki, D.J.; Beudin, A.; Ganju, N.K. Spectral wave dissipation by submerged aquatic vegetation in a back-barrier estuary: Wave dissipation by vegetation. Limnol. Oceanogr. 2017, 62, 736–753. [CrossRef]
  14. Tuya, F.; Vila, F.; Bergasa, O.; Zarranz, M.; Espino, F.; Robaina, R.R. Artificial seagrass leaves shield transplanted seagrass seedlings and increase their survivorship. Aquat. Bot. 2017, 136, 31–34. [CrossRef]
  15. Ghisalberti, M.; Nepf, H.M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res.: Oceans 2002, 107, 3–1. Publisher: Wiley Online Library. [CrossRef]
  16. Luhar, M.; Coutu, S.; Infantes, E.; Fox, S.; Nepf, H. Wave-induced velocities inside a model seagrass bed. J. Geophys. Res.: Oceans 2010, 115. Publisher: Wiley Online Library. [CrossRef]
  17. Tang, C.; Yi, Y.; Zhang, S. Flow and turbulence in unevenly obstructed channels with rigid and flexible vegetation. J. Environ. Manag. 2023, 326, 116736. [CrossRef]
  18. Pujol, D.; Nepf, H. Breaker-generated turbulence in and above a seagrass meadow. Cont. Shelf Res. 2012, 49, 1–9. Publisher: Elsevier. [CrossRef]
  19. Tinoco, R.O.; Coco, G. Turbulence as the Main Driver of Resuspension in Oscillatory Flow Through Vegetation. J. Geophys. Res. Earth Surf. 2018, 123, 891–904. [CrossRef]
  20. Wu, C.; Wu, S.; Wu, X.; Zhang, Y.; Feng, K.; Zhang, W.; Zhao, Y. Hydrodynamics affected by submerged vegetation with different flexibility under unidirectional flow. Front. Mar. Sci. 2023, 9, 1041351. [CrossRef]
  21. Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast Eng. 2004, 51, 103–118. [CrossRef]
  22. Houser, C.; Trimble, S.; Morales, B. Influence of Blade Flexibility on the Drag Coefficient of Aquatic Vegetation. Estuar. Coast 2015, 38, 569–577. [CrossRef]
  23. van Veelen, T.J.; Fairchild, T.P.; Reeve, D.E.; Karunarathna, H. Experimental study on vegetation flexibility as control parameter for wave damping and velocity structure. Coast Eng. 2020, 157, 103648. [CrossRef]
  24. Chen, S.N.; Sanford, L.P.; Koch, E.W.; Shi, F.; North, E.W. A nearshore model to investigate the effects of seagrass bed geometry on wave attenuation and suspended sediment transport. Estuar. Coast 2007, 30, 296–310. Publisher: Springer. [CrossRef]
  25. Hansen, J.C.; Reidenbach, M.A. Wave and tidally driven flows in eelgrass beds and their effect on sediment suspension. Mar. Ecol. Prog. Ser. 2012, 448, 271–287. [CrossRef]
  26. Ganthy, F.; Soissons, L.; Sauriau, P.G.; Verney, R.; Sottolichio, A. Effects of short flexible seagrass Zostera noltei on flow, erosion and deposition processes determined using flume experiments. Sedimentology 2015, 62, 997–1023. Publisher: Wiley Online Library. [CrossRef]
  27. Liu, C.; Shan, Y.; Nepf, H. Impact of Stem Size on Turbulence and Sediment Resuspension Under Unidirectional Flow. Water Resour. Res. 2021, 57. [CrossRef]
  28. Reguero, B.G.; Beck, M.W.; Agostini, V.N.; Kramer, P.; Hancock, B. Coral reefs for coastal protection: A new methodological approach and engineering case study in Grenada. J. Environ. Manag. 2018, 210, 146–161. [CrossRef]
  29. Ghiasian, M.; Carrick, J.; Rhode-Barbarigos, L.; Haus, B.; Baker, A.C.; Lirman, D. Dissipation of wave energy by a hybrid artificial reef in a wave simulator: implications for coastal resilience and shoreline protection. Limnol. Oceanogr. Methods 2021, 19, 1–7. [CrossRef]
  30. Jadhav, R.S.; Chen, Q. Field investigation of wave dissipation over salt marsh vegetation during tropical cyclone. Int. Conf. Coastal. Eng. 2012, 1, 41. [CrossRef]
  31. Anderson, M.; Smith, J. Wave attenuation by flexible, idealized salt marsh vegetation. Coast Eng. 2014, 83, 82–92. [CrossRef]
  32. Zhang, X.; Lin, P.; Nepf, H. A simple-wave damping model for flexible marsh plants. Limnol. Oceanogr. 2021, 66, 4182–4196. Publisher: Wiley Online Library. [CrossRef]
  33. Zhang, X.; Nepf, H. Reconfiguration of and drag on marsh plants in combined waves and current. J. Fluids Struct. 2022, 110, 103539. Publisher: Elsevier. [CrossRef]
  34. Kobayashi, N.; Raichle, A.W.; Asano, T. Wave Attenuation by Vegetation. J. Waterway, Port, Coastal, Ocean Eng. 1993, 119, 30–48. [CrossRef]
  35. Dubi, A.; Tørum, A. Wave damping by kelp vegetation. In Coast Eng. 1994; 1995; pp. 142–156. [CrossRef]
  36. Bradley, K.; Houser, C. Relative velocity of seagrass blades: Implications for wave attenuation in low-energy environments. J. Geophys. Res. 2009, 114, F01004. [CrossRef]
  37. Paul, M.; Amos, C.L. Spatial and seasonal variation in wave attenuation over Zostera noltii. J. Geophys. Res. 2011, 116, C08019. [CrossRef]
  38. Lei, J.; Nepf, H. Wave damping by flexible vegetation: Connecting individual blade dynamics to the meadow scale. Coast Eng. 2019, 147, 138–148. [CrossRef]
  39. Zhu, L.; Huguenard, K.; Fredriksson, D.W.; Lei, J. Wave attenuation by flexible vegetation (and suspended kelp) with blade motion: Analytical solutions. Adv. Water Resour. 2022, 162, 104148. [CrossRef]
  40. Wang, Y.; Yin, Z.; Liu, Y. Experimental investigation of wave attenuation and bulk drag coefficient in mangrove forest with complex root morphology. Appl. Ocean Res. 2022, 118, 102974. [CrossRef]
  41. Wang, Y.; Yin, Z.; Liu, Y. Laboratory study on the drag coefficient for mangrove forests in regular waves. Ocean Eng. 2022, 255, 111522. [CrossRef]
  42. van Veelen, T.J.; Karunarathna, H.; Reeve, D.E. Modelling wave attenuation by quasi-flexible coastal vegetation. Coast Eng. 2021, 164, 103820. [CrossRef]
  43. Yin, K.; Xu, S.; Huang, W.; Liu, S.; Li, M. Numerical investigation of wave attenuation by coupled flexible vegetation dynamic model and XBeach wave model. Ocean Eng. 2021, 235, 109357. [CrossRef]
  44. Beth Schaefer, R.; Nepf, H. Wave damping by seagrass meadows in combined wave-current conditions. Limnol. Oceanogr. 2022, 67, 1554–1565. [CrossRef]
  45. Méndez, F.J.; Losada, I.J.; Losada, M.A. Hydrodynamics induced by wind waves in a vegetation field. J. Geophys. Res. 1999, 104, 18383–18396. [CrossRef]
  46. Maza, M.; Lara, J.L.; Losada, I.J. A coupled model of submerged vegetation under oscillatory flow using Navier–Stokes equations. Coast Eng. 2013, 80, 16–34. [CrossRef]
  47. Henderson, S.M. Motion of buoyant, flexible aquatic vegetation under waves: Simple theoretical models and parameterization of wave dissipation. Coast Eng. 2019, 152, 103497. [CrossRef]
  48. Lindhart, M.; Daly, M.; Walker, H.; Arzeno-Soltero, I.B.; Yin, J.; Bell, T.W.; Monismith, S.G.; Pawlak, G.; Leichter, J. Short wave attenuation by a kelp forest canopy. Limnol. Oceanogr. Letters 2024. Publisher: Wiley Online Library.
  49. Elwany, M.H.S.; O’Reilly, W.C.; Guza, R.T.; Flick, R.E. Effects of Southern California Kelp Beds on Waves. J. Waterway, Port, Coastal, Ocean Eng. 1995, 121, 143–150. [CrossRef]
  50. Rosman, J.H.; Koseff, J.R.; Monismith, S.G.; Grover, J. A field investigation into the effects of a kelp forest (Macrocystis pyrifera) on coastal hydrodynamics and transport. J. Geophys. Res.: Oceans 2007, 112. Publisher: Wiley Online Library.
  51. Elsmore, K.; Nickols, K.J.; Miller, L.P.; Ford, T.; Denny, M.W.; Gaylord, B. Wave damping by giant kelp, Macrocystis pyrifera. Ann. Bot. 2024, 133, 29–40. Publisher: Oxford University Press US.
  52. Dalrymple, R.A.; Kirby, J.T.; Hwang, P.A. Wave Diffraction Due to Areas of Energy Dissipation. J. Waterway, Port, Coastal, Ocean Eng. 1984, 110, 67–79. [CrossRef]
  53. Morison, J.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. Publisher: SPE. [CrossRef]
  54. Luhar, M.; Infantes, E.; Nepf, H. Seagrass blade motion under waves and its impact on wave decay. J. Geophys. Res.: Oceans 2017, 122, 3736–3752. [CrossRef]
  55. Keulegan, G.; Carpenter, L. Forces on cylinders and plates in an oscillating fluid. J. Res. Natl. Bur. Stand. 1958, 60, 423. [CrossRef]
  56. Cavallaro, L.; Re, C.L.; Paratore, G.; Viviano, A.; Foti, E. Response of posidonia oceanica to wave motion in shallow-waters-preliminary experimental results. Coast Eng. Proc. 2011, pp. 49–49.
  57. Cavallaro, L.; Viviano, A.; Paratore, G.; Foti, E. Experiments on Surface Waves Interacting with Flexible Aquatic Vegetation. Ocean Sci. J. 2018, 53, 461–474. [CrossRef]
  58. Haddad, J.; Rosman, J.H.; Luettich, R.A.; Voss, C.M. Canopy drag parameterization from field observations for modeling wave transformation across salt marshes. Coast Eng. 2023, p. 104407. Publisher: Elsevier. [CrossRef]
  59. Luhar, M.; Nepf, H. Wave-induced dynamics of flexible blades. J. Fluids Struct. 2016, 61, 20–41. [CrossRef]
  60. Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [CrossRef]
  61. Suzuki, T.; Zijlema, M.; Burger, B.; Meijer, M.C.; Narayan, S. Wave dissipation by vegetation with layer schematization in SWAN. Coast Eng. 2012, 59, 64–71. [CrossRef]
  62. Jacobsen, N.; McFall, B.; van der A, D. A frequency distributed dissipation model for canopies. Coast Eng. 2019, 150, 135–146. [CrossRef]
  63. Ascencio, J.A.; Jacobsen, N.G.; McFall, B.C.; Groeneweg, J.; Vuik, V.; Reniers, A.J. Evaluation of Implicit and Explicit Wave Dissipation Models for Submerged and Emergent Aquatic Vegetation. J. Coast. Res. 2022, 38. [CrossRef]
  64. Horikawa, K. Nearshore Dynamics and Coastal Processes: Theory. Measurement, and Predictive Models: University of Tokyo Press, Tokyo 1988.
  65. Bertin, X.; de Bakker, A.; Van Dongeren, A.; Coco, G.; André, G.; Ardhuin, F.; Bonneton, P.; Bouchette, F.; Castelle, B.; Crawford, W.C.; others. Infragravity waves: From driving mechanisms to impacts. Earth-Sci. Rev. 2018, 177, 774–799. Publisher: Elsevier.
  66. Massel, S.R. Ocean surface waves: their physics and prediction; Vol. 11, World scientific, 1996.
  67. Munk, W.H. The solitary wave theory and its application to surf problems. Annals of the New York Academy of Sciences 1949, 51, 376–424. Publisher: Wiley Online Library. [CrossRef]
  68. Nelson, R. Height limits in top down and bottom up wave environments. Coast Eng. 1997, 32, 247–254. Publisher: Elsevier. [CrossRef]
  69. Hedges, T.; Ursell. Regions of validity of analytical wave theories. Proceedings of the Institution of Civil Engineers-Water Maritime and Energy 1995, 112, 111–114. Publisher: Thomas Telford-ICE Virtual Library.
  70. Mayençon, R. Météorologie Marine in Ed. Maritimes et d’Outre-Mer 1992.
  71. Phillips, O. The Dynamics of the Upper Ocean. Cambridge monographs on mechanics and applied mathematics 1966, pp. 244–255. Publisher: Cambridge University Press.
  72. Guo, J. Simple and explicit solution of wave dispersion equation. Coast Eng. 2002, 45, 71–74. Publisher: Elsevier. [CrossRef]
  73. Rabinovich, A.B. Seiches and harbor oscillations; World Scientific, 2010. Publication Title: Handbook of coastal and ocean engineering. [CrossRef]
  74. Zhu, L.; Lei, J.; Huguenard, K.; Fredriksson, D.W. Wave attenuation by suspended canopies with cultivated kelp (Saccharina latissima). Coast Eng. 2021, 168, 103947. [CrossRef]
  75. Hu, Z.; Suzuki, T.; Zitman, T.; Uittewaal, W.; Stive, M. Laboratory study on wave dissipation by vegetation in combined current–wave flow. Coast Eng. 2014, 88, 131–142. [CrossRef]
  76. Ozeren, Y.; Wren, D.G.; Wu, W. Experimental Investigation of Wave Attenuation through Model and Live Vegetation. J. Waterway, Port, Coastal, Ocean Eng. 2014, 140, 04014019. [CrossRef]
  77. Yin, K.; Xu, S.; Gong, S.; Chen, J.; Wang, Y.; Li, M. Modeling wave attenuation by submerged flexible vegetation with XBeach phase-averaged model. Ocean Eng. 2022, 257, 111646. [CrossRef]
Preprints 121341 g001
Figure 1. (a) Map of the outlet of the Lez at Palavas-les-Flots. A and B refer to the dyke and the beach in Section 5.1. (b) Map of the position of the devices and the biomimetic structures, composed of ten modules of 4x4 structures. The black dotted lines forming a rectangle delineate the extension of the biomimetic solution and the domain on which Rabinovitch formalism was used (Section 5.1). The colored area represents the bathymetric survey made on July 10th, 2023. (c) The diagram and the photo show one biomimetic structure. (d) Plot of the instrumented transect, where pressure sensors (red diamond) and idealized biomimetic structures are shown. The seabed (black solid line) is placed in function of depth measurement (black dots) made at each devices.
Figure 1. (a) Map of the outlet of the Lez at Palavas-les-Flots. A and B refer to the dyke and the beach in Section 5.1. (b) Map of the position of the devices and the biomimetic structures, composed of ten modules of 4x4 structures. The black dotted lines forming a rectangle delineate the extension of the biomimetic solution and the domain on which Rabinovitch formalism was used (Section 5.1). The colored area represents the bathymetric survey made on July 10th, 2023. (c) The diagram and the photo show one biomimetic structure. (d) Plot of the instrumented transect, where pressure sensors (red diamond) and idealized biomimetic structures are shown. The seabed (black solid line) is placed in function of depth measurement (black dots) made at each devices.
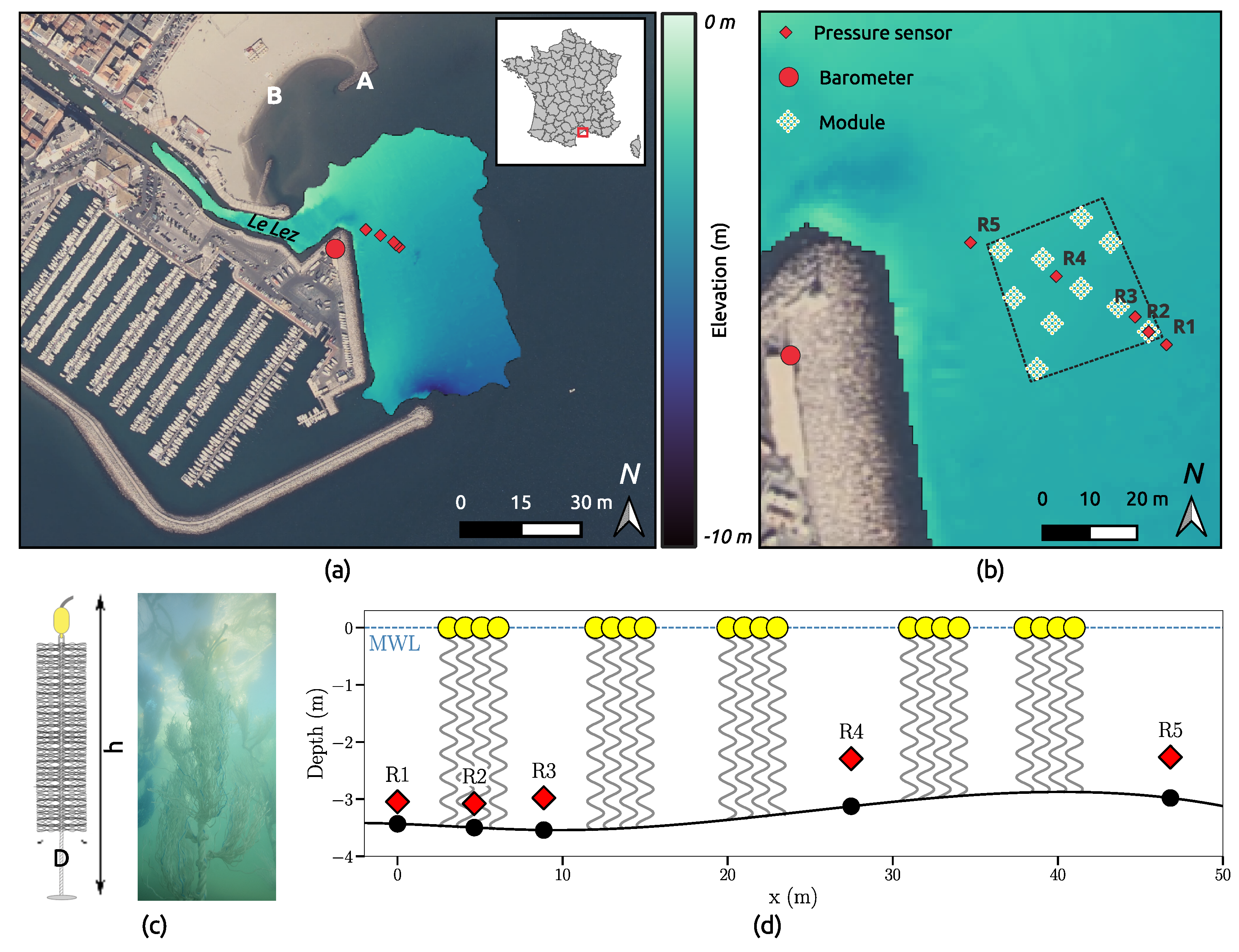
Preprints 121341 g001
Preprints 121341 g002
Figure 2. Energy spectral density spectra calculated at R1 to R5 stations. Each spectrum is calculated averaging all the spectra calculated over the 30 min long bursts. The dotted vertical lines represent the frequency cuts of the infragravity, the swell and the wind waves bands, clearly identified by relative minima on every mean spectrum.
Figure 2. Energy spectral density spectra calculated at R1 to R5 stations. Each spectrum is calculated averaging all the spectra calculated over the 30 min long bursts. The dotted vertical lines represent the frequency cuts of the infragravity, the swell and the wind waves bands, clearly identified by relative minima on every mean spectrum.
Preprints 121341 g002
Preprints 121341 g003
Figure 3. Wind and hydrodynamic forcings during the experimentation. The yellow, green and red boxes represent type 1, 2 and 3 conditions respectively observed at two periods a and b. Periods in white are not used in the analysis. Wave characteristics at Sète are offshore conditions. (a) Wave direction ( θ s e t e ) at Sète, wind direction ( θ w i n d ) and wind speed ( v w i n d ) recorded at the Montpellier airport weather station; (b) Significant wave height measured at Sète ( H s e t e ) and at R1 station, and the ratio H 5 , T O T / H 1 , T O T ; (c) Mean wave period measured at Sète ( T m s e t e ) and at R1 station.
Figure 3. Wind and hydrodynamic forcings during the experimentation. The yellow, green and red boxes represent type 1, 2 and 3 conditions respectively observed at two periods a and b. Periods in white are not used in the analysis. Wave characteristics at Sète are offshore conditions. (a) Wave direction ( θ s e t e ) at Sète, wind direction ( θ w i n d ) and wind speed ( v w i n d ) recorded at the Montpellier airport weather station; (b) Significant wave height measured at Sète ( H s e t e ) and at R1 station, and the ratio H 5 , T O T / H 1 , T O T ; (c) Mean wave period measured at Sète ( T m s e t e ) and at R1 station.
Preprints 121341 g003
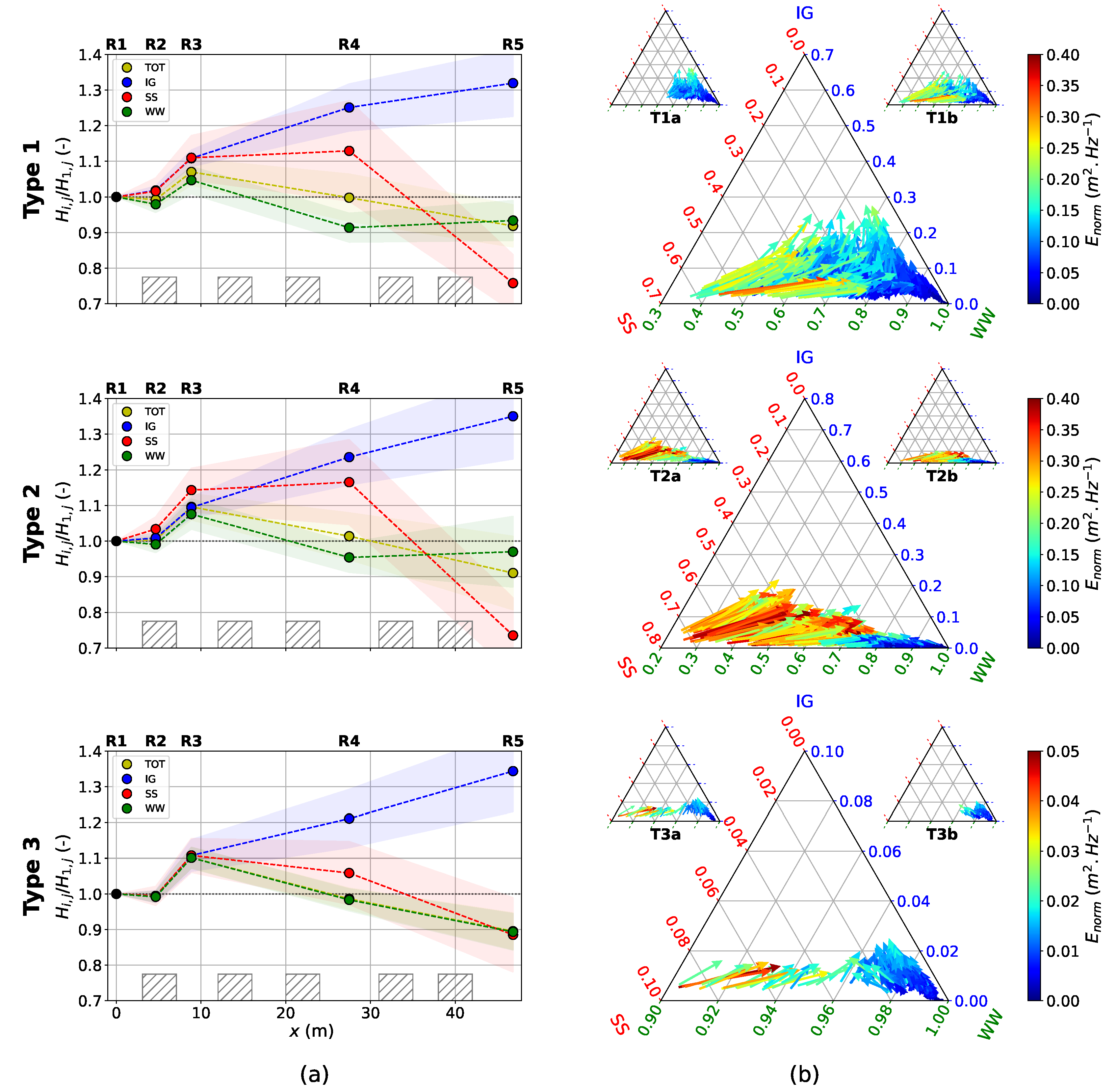
Preprints 121341 g004
Figure 4. (a) Plots of mean wave height reduction for T O T , I G , S S and W W frequency bands from R1 to R5 stations for the three types of meteo-marine conditions, including both periods a and b. The colored envelop represents the standard deviation at each station and for each frequency bands. (b) Ternary diagrams of normalized E I G , E S S and E W W by E T O T for the three types of meteo-marine conditions. The two smaller ternary diagrams represent the same information for periods a and b considered separately. Each arrow represents the evolution of the relative contributions of I G , S S and W W to the energy between R1 and R5 stations for each burst.
Figure 4. (a) Plots of mean wave height reduction for T O T , I G , S S and W W frequency bands from R1 to R5 stations for the three types of meteo-marine conditions, including both periods a and b. The colored envelop represents the standard deviation at each station and for each frequency bands. (b) Ternary diagrams of normalized E I G , E S S and E W W by E T O T for the three types of meteo-marine conditions. The two smaller ternary diagrams represent the same information for periods a and b considered separately. Each arrow represents the evolution of the relative contributions of I G , S S and W W to the energy between R1 and R5 stations for each burst.
Preprints 121341 g004
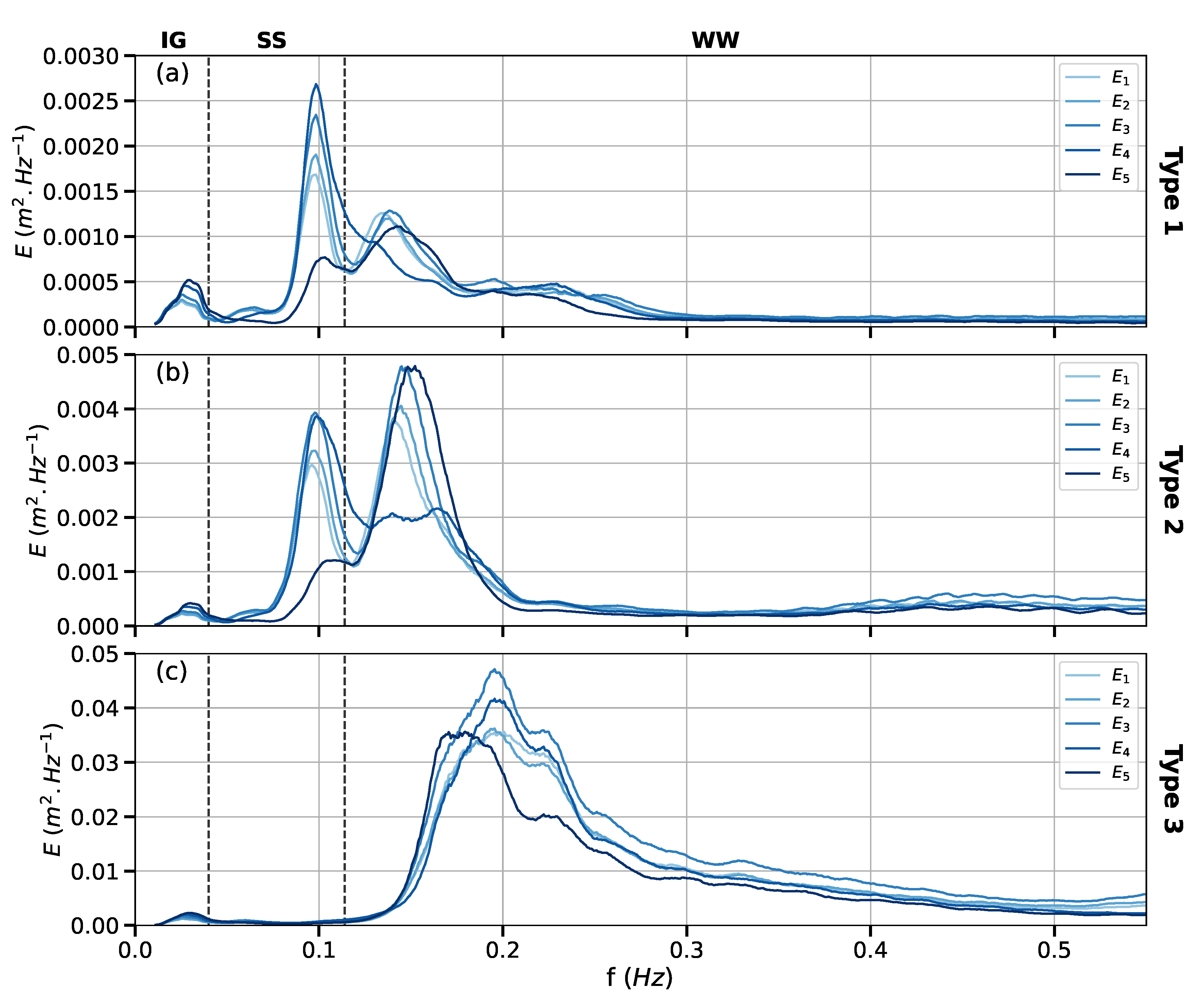
Preprints 121341 g005
Figure 5. Plots of energy density spectrum at R1 to R5 stations for (a) type 1, (b) type 2 and (c) type 3 meteo-marine conditions. Each spectrum is calculated averaging all elementary spectra calculated over 30 min long bursts for each type of meteo-marine conditions.
Figure 5. Plots of energy density spectrum at R1 to R5 stations for (a) type 1, (b) type 2 and (c) type 3 meteo-marine conditions. Each spectrum is calculated averaging all elementary spectra calculated over 30 min long bursts for each type of meteo-marine conditions.
Preprints 121341 g005
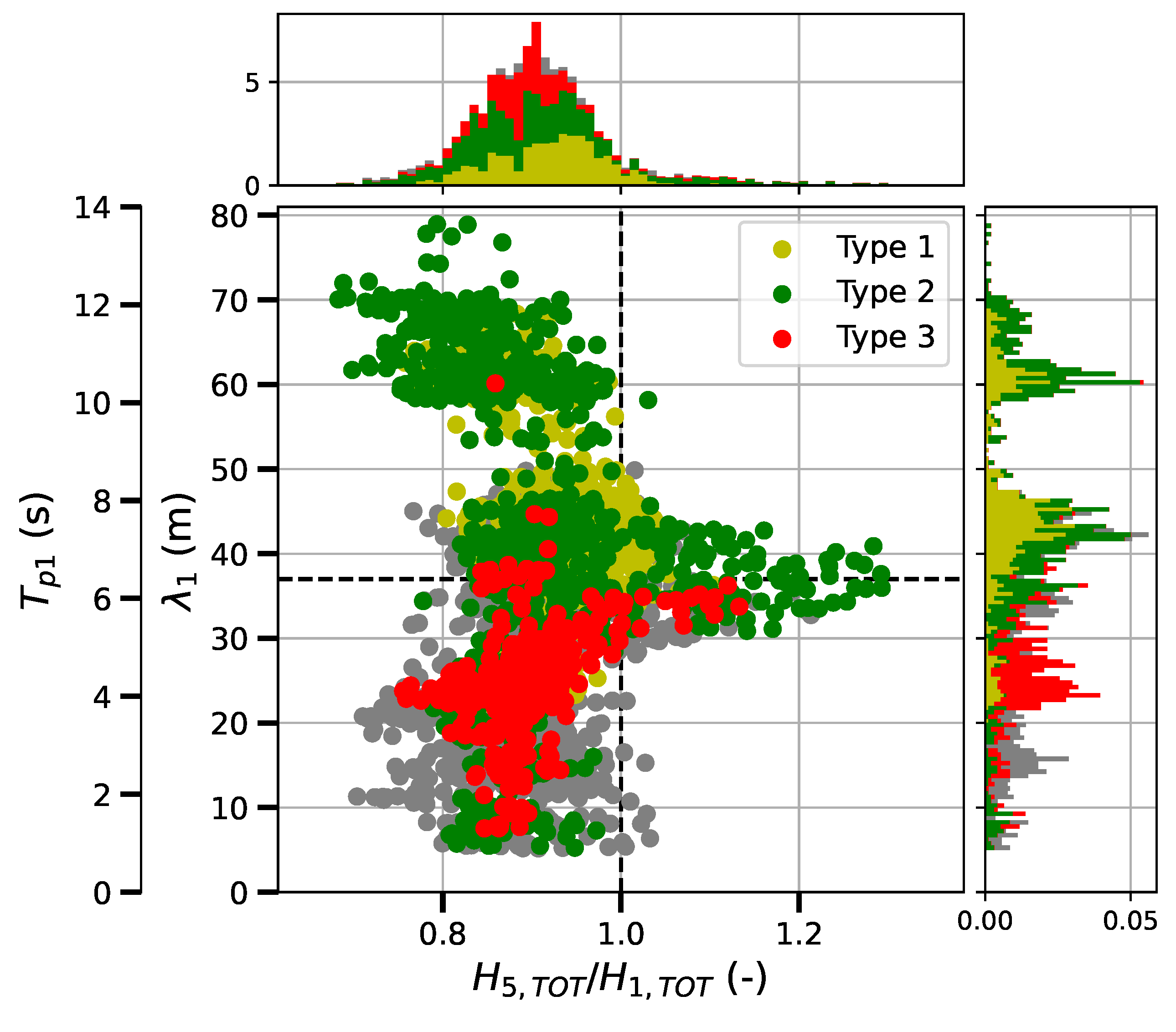
Preprints 121341 g006
Figure 6. Plot of wavelength λ 1 and peak period T p 1 defined at R1 station as a function of H 5 , T O T / H 1 , T O T for each burst. The wavelength is calculated from each frequency peak for each burst with the approximation of Guo [72]. The peak period is calculated from the peak frequency. The vertical dashed line separates dissipative ( H 5 , T O T / H 1 , T O T < 1 ) and anti-dissipative ( H 5 , T O T / H 1 , T O T > 1 ) domains. The horizontal dashed line is placed at λ 1 = 37 m ( T p 1 = 6.47 s) which is roughly equal to the diagonal length of the biomimetic solution.
Figure 6. Plot of wavelength λ 1 and peak period T p 1 defined at R1 station as a function of H 5 , T O T / H 1 , T O T for each burst. The wavelength is calculated from each frequency peak for each burst with the approximation of Guo [72]. The peak period is calculated from the peak frequency. The vertical dashed line separates dissipative ( H 5 , T O T / H 1 , T O T < 1 ) and anti-dissipative ( H 5 , T O T / H 1 , T O T > 1 ) domains. The horizontal dashed line is placed at λ 1 = 37 m ( T p 1 = 6.47 s) which is roughly equal to the diagonal length of the biomimetic solution.
Preprints 121341 g006
Table 1. Characteristics of pressure sensor deployment.
Table 1. Characteristics of pressure sensor deployment.
Station R1 R2 R3 R4 R5
Distance (m) 0 4.65 8.86 27.48 46.82
Depth (m) 2.45 3.07 2.97 2.29 2.26
Z m (m) 0.99 0.42 0.56 0.83 0.71
Table 2. Tables of mean energy E i , j ( m m 2 . H z − 1 ) at each frequency band for R1 to R5 station for type 1, type 2 and type 3 conditions.
Table 2. Tables of mean energy E i , j ( m m 2 . H z − 1 ) at each frequency band for R1 to R5 station for type 1, type 2 and type 3 conditions.
E i , j R1 R2 R3 R4 R5
E i , I G 5.77 5.99 7.10 9.05 10.03
Type 1 E i , S S 42.72 46.05 56.38 63.62 22.39
E i , W W 110.93 106.70 123.54 94.50 94.19
E i , I G 4.81 4.94 5.87 7.40 8.41
Type 2 E i , S S 82.28 88.62 108.45 111.42 36.41
E i , W W 283.36 285.97 344.05 252.35 295.85
E i , I G 26.09 25.78 33.49 40.02 46.80
Type 3 E i , S S 38.68 38.42 49.68 46.70 31.95
E i , W W 4861.36 4832.46 6044.96 4802.65 4153.89
Table 3. List of the relations between C D and R e or K C presented in the literature. Although the literature offers several dozens of reference on the question, only articles performing an analysis on flexible or rigid structures extending over the full water column are considered. Type: L - Laboratory study, I - In-situ deployment, A - Analytical/Numerical modelling. u c : characteristic velocity measured at the B - Bottom, T - Top of the structure. Wave: R - Regular or I - Irregular wave.
Table 3. List of the relations between C D and R e or K C presented in the literature. Although the literature offers several dozens of reference on the question, only articles performing an analysis on flexible or rigid structures extending over the full water column are considered. Type: L - Laboratory study, I - In-situ deployment, A - Analytical/Numerical modelling. u c : characteristic velocity measured at the B - Bottom, T - Top of the structure. Wave: R - Regular or I - Irregular wave.
Reference Type Structure Formulas Ranges u c Wave
Cavallaro et al. [56] L Artificial Posidonia Oceanica C D = ( 2100 / R e ) 1.7 4000 < R e < 9500 T R
Jadhav and Chen [30] I Spartina Alterniflora C D = 2 ( 1300 / R e + 0.18 ) 600 < R e < 3200 B I
C D = 70 K C − 0.86 25 < K C < 135 B I
Anderson and Smith [31] L Artificial Spartina Alterniflora C D = 0.76 + ( 744.2 / R e ) 1.27 533 < R e < 2296 T I
C D = 1.1 + ( 27.4 / K C ) 3.08 26 < K C < 112 T I
Hu et al. [75] L Wooden rods C D = 1.04 + ( 730 / R e ) 1.37 300 < R e < 4700 T R
Ozeren et al. [76] L Birch dowels C D = 2.1 + ( 793 / R e ) 2.39 400 < R e < 4300 T R
C D = 1.5 + ( 1230 / R e ) 0.95 200 < R e < 1600 T I
Houser et al. [22] L Semi-flexible balsa wood C D = 0.001 + ( 2500 / R e ) 1.1 1200 < R e < 5300 T R
Semi-flexible cable tie C D = 0.001 + ( 2750 / R e ) 1.6 50 < R e < 4500 T R
Yin et al. [77] A Polyurethane cylinders C D = ( 150.5 / K C ) 0.5952 50 < K C < 350 T R
Wang et al. [40] L PVC cylinder C D = 0.42 + ( 0.77 / K C ) 0.41 0.02 < K C < 0.28 T R
Wang et al. [41] L PVC cylinder C D = 0.75 + ( 4467.28 / R e ) 1.13 918 < R e < 3839 T R
C D = 1.41 + ( 10.72 / K C ) 1.11 2.74 < K C < 17.14 T R
Haddad et al. [58] I Spartina Alterniflora C D = 207 R e − 0.611 250 < R e < 2000 T I
C D = 43.5 K C − 0.549 20 < K C < 450 T I
Present study I Artificial kelp C D = ( 170873.77 / R e ) 0.78 532 < R e < 16798 T I
C D = ( 35701.61 / R e ) 1.45 2410 < R e < 16798 T I
C D = ( 672.23 / K C ) 0.8 2.3 < K C < 72.2 T I
C D = ( 155.82 / K C ) 1.36 10.8 < K C < 72.2 T I
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated