Overview of Clustering Techniques: From k-Means to Spectral Methods

Preprint

Article

Overview of Clustering Techniques: From k-Means to Spectral Methods

Altmetrics

Downloads

Views

Comments

Richard Murdoch Montgomery^*

This version is not peer-reviewed

This preprints belongs to the Topic

Applications of Machine Learning in Large-Scale Optimization and High-Dimensional Learning

Submitted:

16 October 2024

Posted:

17 October 2024

You are already at the latest version

Alerts

Abstract

This article presents an in-depth overview of clustering techniques, which play a vital role in unsupervised learning by uncovering natural groupings in data. We examine five prominent methods: k-Means, k-Medoids, Kohonen Networks and Self-Organizing Maps (SOMs), Fuzzy C-Means, Hierarchical Clustering, and Spectral Clustering. Each technique is described in detail, including its mathematical foundation, operational mechanism, applications, strengths, and limitations. The goal is to provide a thorough understanding of each approach, helping readers select the most appropriate method for their data analysis needs. Practical examples are also provided, demonstrating the application of these clustering techniques in various real-world contexts such as customer segmentation, image processing, and bioinformatics.

Keywords:

Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity

1. Introduction

Clustering is a fundamental technique in machine learning and data analysis, particularly within the domain of unsupervised learning. It involves dividing a dataset into groups, known as clusters, such that the data points within each cluster share a higher degree of similarity with each other compared to points in different clusters. This property makes clustering a valuable tool for uncovering inherent structures and patterns in data, which can subsequently aid in decision-making, exploratory data analysis, and knowledge discovery (Jain et al., 1999).

The importance of clustering is underscored by its wide range of applications across different fields. In biology, clustering is used for classifying genes with similar expression patterns, enabling researchers to understand complex biological processes (Eisen et al., 1998). In marketing, clustering methods are employed for customer segmentation to create targeted marketing campaigns, resulting in better personalization and improved business outcomes (Wedel & Kamakura, 2000). In healthcare, clustering plays a role in grouping patients based on medical conditions or treatment responses, allowing for more effective healthcare management (Xu & Wunsch, 2005).

Unlike supervised learning, clustering does not require labeled data, which makes it particularly useful in scenarios where obtaining labels is expensive, time-consuming, or impractical. Instead, clustering identifies natural groupings within the data, allowing practitioners to derive meaningful insights without prior knowledge of the data's structure (Hastie, Tibshirani, & Friedman, 2009). For example, clustering techniques have been widely adopted for anomaly detection, customer segmentation, and image compression, among other applications.

This article provides a detailed overview of several well-established clustering techniques, each with unique strengths, limitations, and areas of application. Specifically, we explore the following five clustering methods:

k-Means and k-Medoids: Both are partitioning methods that iteratively divide data into clusters. While k-Means is widely known for its efficiency, k-Medoids offers increased robustness by using actual data points (medoids) as cluster representatives, making it less sensitive to outliers (Kaufman & Rousseeuw, 1990).
Kohonen Networks and Self-Organizing Maps (SOMs): SOMs are neural networks designed for unsupervised learning that map high-dimensional data onto a lower-dimensional grid. These maps preserve the topological relationships of the input data, making them particularly useful for visualization and interpretation of complex datasets (Kohonen, 2001).
Fuzzy C-Means: Fuzzy C-Means (FCM) allows for a point to belong to multiple clusters with varying degrees of membership. This characteristic is especially useful in applications where cluster boundaries are not well-defined, such as in medical image segmentation (Bezdek, 1981).
Hierarchical Clustering: This technique builds a tree-like representation (dendrogram) of the data, which can be interpreted to understand nested relationships among data points. Hierarchical clustering is particularly valuable in bioinformatics, where relationships between genes or proteins are often complex and hierarchical (Murtagh & Contreras, 2012).
Spectral Clustering: Spectral clustering uses graph theory to partition datasets by leveraging the eigenvalues of a similarity matrix. It is well-suited for identifying clusters with non-convex shapes and is often used in image segmentation and social network analysis (Ng, Jordan, & Weiss, 2002).

Each of these methods has its unique advantages and specific challenges. By understanding the mathematical basis and practical applications of each approach, practitioners can make informed decisions when selecting an appropriate clustering technique for their data. This article aims to provide a comprehensive understanding of these methods, their underlying principles, and their practical applicability, thus serving as a valuable resource for both beginners and experts in the field of data science and machine learning.

2. Methodology

In this section, we present a detailed mathematical formulation and explanation of various clustering techniques. We will explore the core equations behind each method, providing a comprehensive understanding of their mathematical foundations.

2.1. Mathematical Background

1. k-Means Clustering

k-Means clustering partitions a dataset into

k

clusters such that the sum of the squared distances from each point to its assigned cluster centroid is minimized. The optimization problem can be expressed as:

J = \sum_{i = 1}^{k} \sum_{x \in C_{i}} {‖x - μ_{i}‖}^{2}

Where:

$J$ is the objective function to be minimized.
$C_{i}$ represents the set of points in cluster $i$ .
$μ_{i}$ is the centroid of cluster $i$ , computed as:

μ_{i} = \frac{1}{|C_{i}|} \sum_{x \in C_{i}} x

The algorithm follows an iterative process:

Initialize $k$ centroids randomly.
Assign each data point $x$ to the nearest centroid based on the Euclidean distance.
Recalculate the centroids $μ_{i}$ as shown in Equation (2).
Repeat steps 2 and 3 until convergence, i.e., when centroids do not change significantly.

k-Medoids Clustering

k-Medoids is a variant of

k

-Means that uses medoids (actual data points) instead of centroids, making it more robust to outliers. The goal is to minimize the sum of dissimilarities between points and their assigned medoid:

J = \sum_{i = 1}^{k} \sum_{x \in C_{i}} d (x, m_{i})

Where:

$m_{i}$ is the medoid of cluster $i$ .
$d (x, m_{i})$ represents the dissimilarity (typically Euclidean distance) between point $x$ and medoid $m_{i}$ .

The algorithm iteratively replaces medoids with non-medoids if doing so reduces the objective function

J

3. Self-Organizing Maps (SOM)

Self-Organizing Maps (SOM) are a type of neural network used for clustering and visualisation by mapping high-dimensional input data onto a lower-dimensional grid. The key mathematical step is identifying the Best Matching Unit (BMU), which minimizes the distance between the input vector

x

and the weight vector

w_{j}

B M U = a r g \underset{j}{m i n} ‖x - w_{j}‖

Once the BMU is identified, the weight vectors are updated using the following rule:

w_{j} (t + 1) = w_{j} (t) + η (t) h (j, B M U, t) (x - w_{j} (t))

Where:

$η (t)$ is the learning rate at time $t$ .
$h (j, B M U, t)$ is the neighbourhood function, which decreases over time and with distance from the BMU.

4. Fuzzy C-Means Clustering

Fuzzy C-Means (FCM) allows each data point to belong to all clusters with a membership value between 0 and 1. The objective function is:

J = \sum_{i = 1}^{k} \sum_{j = 1}^{n} u_{i j}^{m} {‖x_{j} - μ_{i}‖}^{2}

Where:

$u_{i j}$ is the membership of data point $x_{j}$ in cluster $i$ .
$m > 1$ is a parameter that controls the fuzziness of the clusters.
$μ_{i}$ is the centroid of cluster $i$ , calculated as:

$μ_{i} = \frac{\sum_{j = 1}^{n} u_{i j}^{m} x_{j}}{\sum_{j = 1}^{n} u_{i j}^{m}}$

This optimization is subject to the constraint:

\sum_{i = 1}^{k} u_{i j} = 1 \forall j

5. Hierarchical Clustering

Hierarchical clustering builds a tree of clusters (dendrogram) by using a linkage criterion to decide which clusters to merge or split. Common linkage criteria are:

Single Linkage: The distance between two clusters $A$ and $B$ is defined as the shortest distance between points in the two clusters:

$d (A, B) = \underset{x \in A, y \in B}{m i n} d (x, y)$
Complete Linkage: The distance between two clusters is defined as the maximum distance between points in the two clusters:

$d (A, B) = \underset{x \in A, y \in B}{m a x} d (x, y)$
Average Linkage: The distance between two clusters is the average of all pairwise distances between points in the two clusters:

$d (A, B) = \frac{1}{| A | | B |} \sum_{x \in A} \sum_{y \in B} d (x, y)$

6. Spectral Clustering

Spectral clustering uses the graph Laplacian to cluster data. The first step is constructing a similarity graph and computing the Laplacian matrix

L

L = D - A

Where:

$A$ is the adjacency matrix representing the similarity between nodes.
$D$ is the degree matrix, a diagonal matrix where each element $D_{i i}$ represents the sum of similarities for node $i$ .

The normalized Laplacian is given by:

L_{norm} = D^{- \frac{1}{2}} L D^{- \frac{1}{2}}

The next step is to compute the first

k

eigenvectors of

L_{norm}

to form a matrix

X

. Finally, each row of

X

is treated as a point in a lower-dimensional space, and k-Means is applied to cluster these points.

Summary

This methodology section outlines the mathematical formulation of several clustering techniques, providing insight into the internal workings of each algorithm. The equations presented here help build a better understanding of the optimization problems and processes that guide these techniques, making it easier to select the most appropriate method for a given dataset and problem.

2.2 Computational Background in Python

In this section, I explain the code for clustering, step by step, along with the necessary explanations for each part of the process.

Importing Libraries

We begin by importing the essential libraries for numerical operations, data generation, and plotting:

numpy and matplotlib.pyplot: used for numerical operations and plotting, respectively.
sklearn.datasets.make_blobs: generates synthetic datasets for clustering.
sklearn.cluster: provides clustering methods like KMeans, AgglomerativeClustering, and SpectralClustering.
seaborn: sets a consistent plotting style.

Data Generation

The following code generates a synthetic dataset:

makefile

n_samples = 300

n_features = 2

n_clusters = 3

X, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=42)

Explanation:

make_blobs generates a dataset of 300 data points (n_samples) with 2 features (n_features), distributed across 3 clusters (n_clusters).
random_state=42 ensures the results are reproducible.
X contains the generated dataset features, while _ stores the true cluster labels (which are not used in this code).

Plotting Styleuse Seabor

We n to apply a consistent style to our plots:

sns.set(style='whitegrid')

This code applies a clean "whitegrid" style to the visualizations, making the plots easier to interpret.

1. k-Means Clustering

The code for k-Means clustering is as follows:

kmeans = KMeans(n_clusters=n_clusters, random_state=42)

kmeans_labels = kmeans.fit_predict(X)

Explanation:

A KMeans model is created with n_clusters=3.
The fit_predict(X) method trains the model and assigns cluster labels to each data point in X, storing the results in kmeans_labels.

To visualise the k-Means clustering:

plt.figure(figsize=(10, 6))

plt.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='viridis', marker='o', edgecolor='k')

plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', marker='X')

plt.title("k-Means Clustering")

plt.show()

Explanation:

A scatter plot shows the clustering results. Data points are coloured by their predicted clusters (c=kmeans_labels).
Cluster centroids are displayed with red "X" markers.
This plot visualises how well k-Means clusters the synthetic data.

2. Hierarchical Clustering

The code for hierarchical clustering is:

hierarchical = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward')

hierarchical_labels = hierarchical.fit_predict(X)

Explanation:

An AgglomerativeClustering model is created with n_clusters=3 and linkage='ward', which minimizes variance during merging.
The fit_predict(X) method assigns cluster labels to each data point and stores them in hierarchical_labels.

To visualise the hierarchical clustering:

plt.figure(figsize=(10, 6))

plt.scatter(X[:, 0], X[:, 1], c=hierarchical_labels, cmap='viridis', marker='o', edgecolor='k')

plt.title("Hierarchical Clustering")

plt.show()

Explanation:

A scatter plot shows the hierarchical clustering results, with data points coloured according to their predicted clusters.
This plot illustrates how Agglomerative Clustering groups the data hierarchically.

3. Spectral Clustering

The code for spectral clustering is:

spectral = SpectralClustering(n_clusters=n_clusters, affinity='nearest_neighbors', random_state=42)

spectral_labels = spectral.fit_predict(X)

Explanation:

A SpectralClustering model is created with n_clusters=3 and affinity='nearest_neighbors', which computes similarities based on nearest neighbors.
The fit_predict(X) method assigns cluster labels to each data point, storing the results in spectral_labels.

To visualise the spectral clustering:

plt.figure(figsize=(10, 6))

plt.scatter(X[:, 0], X[:, 1], c=spectral_labels, cmap='viridis', marker='o', edgecolor='k')

plt.title("Spectral Clustering")

plt.show()

Explanation:

A scatter plot shows the spectral clustering results, with data points coloured by their predicted clusters.
This plot demonstrates how spectral clustering, which uses graph-based partitioning, performs on the dataset.

Summary

k-Means Clustering: Assigns data points to clusters by minimizing the distance to the centroids.
Hierarchical Clustering: Forms a hierarchical structure, suitable for detecting nested relationships.
Spectral Clustering: Uses graph theory to partition data, ideal for detecting non-convex clusters.

Each clustering method has its own approach to grouping data, and the code provides visual comparisons to assess the effectiveness of each method on a given dataset.

3. Results

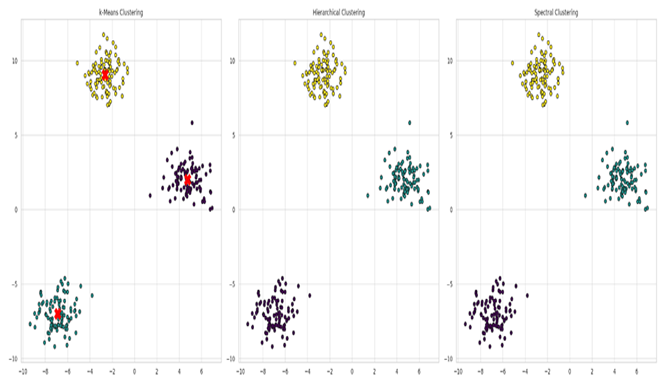Graph 1. K-Means Clustering, Hierarchical Clustering and Spectral Clustering characteristics.

Explanation of the Graphs

1. k-Means Clustering

Graph Description:

o: The k-Means clustering result is displayed with data points assigned to different clusters, each represented by a distinct color. Cluster centroids are marked by red 'X' symbols.
o: The clusters appear roughly circular, as k-Means tends to detect spherical shapes.
o: Data points are grouped based on their proximity to the centroids, which are updated iteratively until an optimal clustering is achieved.

Insights:

o: The three clusters are well-separated and easily distinguishable. Points closer to a centroid are assigned to the respective cluster.
o: This visualization highlights how effectively the k-Means algorithm captures the natural groupings in data when clusters are well-separated and spherical.

2. Hierarchical Clustering

Graph Description:

o: The plot shows the outcome of Agglomerative Hierarchical Clustering, with three clusters, each displayed in a different color.
o: Unlike k-Means, hierarchical clustering doesn’t rely on initialized centroids. Instead, it follows a bottom-up approach, starting with each data point in its own cluster, then successively merging clusters based on similarity.
o: The Ward linkage criterion is used to minimize variance within merged clusters, resulting in compact groupings.

Insights:

o: Data points are effectively grouped into three distinct clusters through hierarchical merging.
o: This method is particularly useful when the number of clusters isn’t known in advance and can handle nested structures within the data.

3. Spectral Clustering

Graph Description:

o: The third graph illustrates the result of Spectral Clustering, an algorithm based on graph theory.
o: Data points are represented as nodes in a graph, with connections determined by similarity. The algorithm then partitions the graph to form clusters, which are visualized in different colors.
o: A warning notes that the graph isn’t fully connected, meaning some data points are not sufficiently linked to others, which may affect the quality of the clustering.

Insights:

o: Spectral Clustering is well-suited for complex, non-convex shapes but can be sensitive to how the graph is constructed.
o: The resulting clusters are clear, though some points may not fit neatly into any cluster due to connectivity issues.
o: This method is particularly useful for datasets with intricate, non-linear structures that other algorithms might struggle to cluster effectively.

General Observations

All three clustering algorithms generate meaningful clusters, but each comes with its own advantages and limitations:

k-Means: Works well for clearly separated, spherical clusters but can be sensitive to initial centroid placement and outliers.
Hierarchical Clustering: Offers flexibility by not requiring the number of clusters in advance and provides a hierarchical view, but it can be computationally intensive for large datasets.
Spectral Clustering: Excels with complex, non-convex clusters but relies heavily on a well-constructed similarity graph and may have issues with loosely connected data points.

These visualizations help demonstrate the different behaviors and outcomes of these clustering algorithms on the same dataset, providing valuable insights into which method may be most suitable based on the dataset’s characteristics.

4. Discussion

4.1. Discussion on Clustering Techniques

Clustering is a core technique in unsupervised learning that helps in understanding the underlying structure of data without any pre-defined labels. In this discussion, we explore the strengths, limitations, and comparative performance of three key clustering methods: k-Means, Hierarchical Clustering, and Spectral Clustering. These methods differ fundamentally in their approach to clustering, which has implications for their use in various types of data and scenarios.

k-Means Clustering

k-Means is perhaps the most well-known clustering algorithm due to its simplicity and efficiency. It operates by partitioning a dataset into clusters, minimizing intra-cluster variance through centroid updates (MacQueen, 1967). As illustrated in the graph generated above, k-Means effectively groups the data into three distinct clusters based on proximity to centroids.

The simplicity of k-Means makes it highly scalable for large datasets. However, this algorithm assumes that clusters are spherical and equally sized, making it less effective when clusters have arbitrary shapes or significantly different sizes (Jain, 2010). Additionally, k-Means is sensitive to the initial placement of centroids, which can lead to local optima rather than the global best solution (Arthur & Vassilvitskii, 2007).

One major drawback of k-Means is its sensitivity to outliers. Outliers can disproportionately influence the position of centroids, resulting in poor clustering quality. For example, the presence of a few extreme data points can skew centroids towards them, thereby misclassifying other points. Strategies such as k-means++ initialization help mitigate this by improving centroid initialization to ensure better convergence (Arthur & Vassilvitskii, 2007).

Hierarchical Clustering

Hierarchical Clustering provides a fundamentally different approach compared to k-Means. Instead of defining the number of clusters in advance, hierarchical clustering creates a tree-like structure called a dendrogram, which allows for exploration of clusters at different levels of granularity (Murtagh & Contreras, 2012). In the agglomerative variant used in the graph, each data point begins as its own cluster, and clusters are successively merged based on the chosen linkage criterion.

The Ward linkage criterion was employed in this analysis, which seeks to minimize variance within clusters during merging, resulting in compact and well-defined clusters. This method is particularly useful in applications where the number of clusters is not known beforehand, such as biological taxonomy and gene expression analysis (Eisen et al., 1998).

However, hierarchical clustering comes with some challenges. Its computational complexity is intense , making it impractical for large datasets (Day & Edelsbrunner, 1984). The method also tends to be sensitive to noise and outliers, as individual noisy points can lead to incorrect early splits or merges, affecting the entire dendrogram structure.

A key advantage of hierarchical clustering is the ability to visualize nested cluster structures through a dendrogram, providing a clear understanding of how clusters are formed and related at different levels. This makes hierarchical clustering particularly attractive for exploratory data analysis when the dataset size is manageable.

Spectral Clustering

Spectral Clustering is a more sophisticated clustering method that is effective in scenarios where clusters are non-convex or connected in complex shapes (Ng, Jordan, & Weiss, 2002). In the graph presented, spectral clustering was applied using a nearest neighbors affinity, which constructs a similarity graph to connect data points based on proximity.

Spectral clustering works by performing dimensionality reduction on the similarity graph using the eigenvectors of the graph Laplacian, and then applying k-Means to cluster the reduced representation. This approach allows spectral clustering to identify clusters that are not necessarily separated by a linear boundary, making it well-suited for data that exhibits more complex, non-spherical relationships (Von Luxburg, 2007).

Despite its strengths, spectral clustering also has limitations. The method is computationally intensive, especially when calculating the similarity graph and eigenvalues for large datasets. Moreover, the clustering result can be sensitive to the parameters used for constructing the similarity graph, such as the number of nearest neighbors or the choice of affinity metric. The warning message observed during the computation suggests that the graph was not fully connected, which may lead to suboptimal clustering results.

Another limitation is that spectral clustering requires knowledge of the number of clusters in advance, similar to k-Means. This constraint can make it challenging to apply in exploratory contexts where the optimal number of clusters is unknown.

4.2. Comparative Analysis

The three clustering methods discussed—k-Means, Hierarchical, and Spectral Clustering—offer distinct approaches to grouping data, each with its strengths and appropriate use cases.

k-Means is well-suited for large datasets where clusters are approximately spherical and balanced. Its efficiency and ease of implementation make it a popular choice in many practical applications, such as customer segmentation and image compression (Jain, 2010), whereas Hierarchical Clustering is preferable for small to medium-sized datasets, where understanding the nested structure of data is important. Its ability to visualize relationships among clusters through a dendrogram is particularly valuable in exploratory analysis, especially in fields like biology and social sciences (Murtagh & Contreras, 2012).

k-Medoids Clustering

k-Medoids, also known as PAM (Partitioning Around Medoids), is a variation of k-Means that seeks to mitigate the impact of outliers by using actual data points (medoids) instead of centroids. It is more robust to outliers and noise compared to k-Means. On the other side, it´scomputationally expensive due to its iterative comparison of data points to determine the best medoid. It´s particularly useful in situations where the data contains outliers or when the underlying distance metric is not Euclidean.

Kohonen Networks and Self-Organizing Maps (SOM)

Kohonen Networks, also known as Self-Organizing Maps (SOMs), are a type of artificial neural network used for clustering and visualizing high-dimensional data. SOMs map the data onto a lower-dimensional grid while preserving the topological structure of the data. It uses competitive learning rather than backpropagation. Neurons compete to represent input vectors, and the winning neuron (Best Matching Unit) and its neighbors are adjusted to better represent the input. SOMs are used for data visualization, dimensionality reduction, and exploratory data analysis. They excel in clustering complex, high-dimensional data such as customer behaviors, speech, and genomic data. SOMs provide an intuitive representation of data and are particularly useful for understanding relationships between clusters. However, training SOMs can be computationally intensive, and interpreting the resulting map can be challenging.

Fuzzy C-Means Clustering

Unlike k-Means, which assigns each point to exactly one cluster, Fuzzy C-Means (FCM) allows data points to belong to multiple clusters with different degrees of membership. This is achieved by using a fuzzy partition matrix that quantifies the likelihood of each point belonging to a cluster. The objective function minimizes a weighted sum of squared distances between each point and the cluster centers, with weights defined by the degree of membership. It´s useful in applications where boundaries between clusters are not well-defined, such as in medical image segmentation, customer segmentation, and pattern recognition.FCM handles data ambiguity well and can represent overlapping clusters effectively. However, it requires more computation due to the need to calculate membership values for each cluster.

Hierarchical Clustering

Hierarchical clustering can be agglomerative (bottom-up) or divisive (top-down). Agglomerative clustering starts with each data point as its own cluster and merges clusters iteratively, while divisive clustering begins with the entire dataset and splits clusters iteratively. Different linkage criteria (single, complete, average) affect how distances between clusters are calculated. The results are represented as a dendrogram, a tree-like diagram that illustrates the nested grouping of data points and the levels at which clusters merge. It is widely used in bioinformatics (e.g., gene expression analysis), document clustering, and social network analysis. Hierarchical clustering is easy to interpret with dendrograms and doesn’t require the number of clusters as an input. However, it is computationally expensive and sensitive to noise and outliers.

Spectral Clustering

Spectral clustering leverages the eigenvalues of a similarity matrix to perform dimensionality reduction before applying a clustering technique like k-Means. It is especially useful for clustering non-convex shapes and discovering clusters in graphs. A graph representation is created from the data, with edges representing the similarity between nodes. The Laplacian matrix is then used to find a lower-dimensional representation of the data. The clustering problem is converted into an eigenvector problem, where the eigenvectors of the Laplacian help identify the cluster structure. Spectral clustering is used in image segmentation, social network analysis, and clustering data with non-linear boundaries. It is very powerful for complex clustering tasks and can handle non-linear boundaries well, but the construction of the similarity matrix can be computationally expensive for large datasets.

5. Conclusions

Each clustering method has its unique strengths and weaknesses, making them suitable for different types of data and use cases. k-Means and k-Medoids are fast and simple but limited to spherical clusters. SOMs offer an intuitive visualization but require significant computational power. Fuzzy C-Means is flexible with overlapping clusters but computationally intensive. Hierarchical clustering provides an interpretable hierarchy but lacks scalability. Finally, Spectral clustering is ideal for complex, non-convex clusters but comes with high computational costs.

Understanding these techniques and their applications is crucial for selecting the best approach for a given problem. The choice of a clustering algorithm depends not only on the structure of the data but also on the specific requirements of the application.

Author Contributions

The Author claims no conflicts of interest.

References

Arthur, D., & Vassilvitskii, S. (2007). k-means++: The Advantages of Careful Seeding. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms.
Bezdek, J. C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. Springer.
Day, W. H., & Edelsbrunner, H. (1984). Efficient algorithms for agglomerative hierarchical clustering methods. Journal of Classification, 1(1), 7-24. [CrossRef]
Eisen, M. B., Spellman, P. T., Brown, P. O., & Botstein, D. (1998). Cluster analysis and display of genome-wide expression patterns. Proceedings of the National Academy of Sciences, 95(25), 14863-14868. [CrossRef]
Fowlkes, C., Belongie, S., Chung, F., & Malik, J. (2004). Spectral grouping using the Nyström method. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26(2), 214-225. [CrossRef]
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer.
Jain, A. K. (2010). Data clustering: 50 years beyond k-means. Pattern Recognition Letters, 31(8), 651-666. [CrossRef]
Kaufman, L., & Rousseeuw, P. J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis. John Wiley & Sons. [CrossRef]
Kohonen, T. (2001). Self-Organizing Maps. Springer.
Kohonen, T. (2013). Essentials of the self-organizing map. Neural Networks, 37, 52-65. [CrossRef]
MacQueen, J. (1967). Some Methods for Classification and Analysis of Multivariate Observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability.
Murtagh, F., & Contreras, P. (2012). Algorithms for hierarchical clustering: an overview. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2(1), 86-97. [CrossRef]
Ng, A. Y., Jordan, M. I., & Weiss, Y. (2002). On Spectral Clustering: Analysis and an Algorithm. Advances in Neural Information Processing Systems.
Pham, D. L. (2001). Fuzzy Clustering for Image Segmentation. Proceedings of the IEEE, 89(9), 1448-1471.
Rokach, L., & Maimon, O. (2005). Clustering Methods. In Data Mining and Knowledge Discovery Handbook (pp. 321-352). Springer.
Shi, J., & Malik, J. (2000). Normalized Cuts and Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905. [CrossRef]
Sneath, P. H. A., & Sokal, R. R. (1973). Numerical Taxonomy. Freeman.
Von Luxburg, U. (2007). A Tutorial on Spectral Clustering. Statistics and Computing, 17(4), 395-416.
Wedel, M., & Kamakura, W. A. (2000). Market Segmentation: Conceptual and Methodological Foundations. Springer.
Xu, R., & Wunsch, D. (2005). Survey of clustering algorithms. IEEE Transactions on Neural Networks, 16(3), 645-678. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Overview of Clustering Techniques: From k-Means to Spectral Methods

Abstract

1. Introduction

2. Methodology

2.1. Mathematical Background

2.2 Computational Background in Python

Data Generation

Summary

3. Results

Explanation of the Graphs

4. Discussion

4.1. Discussion on Clustering Techniques

k-Means Clustering

Hierarchical Clustering

Spectral Clustering

4.2. Comparative Analysis

Kohonen Networks and Self-Organizing Maps (SOM)

Fuzzy C-Means Clustering

Hierarchical Clustering

Spectral Clustering

5. Conclusions

Author Contributions

References

MDPI Initiatives

Important Links

Subscribe