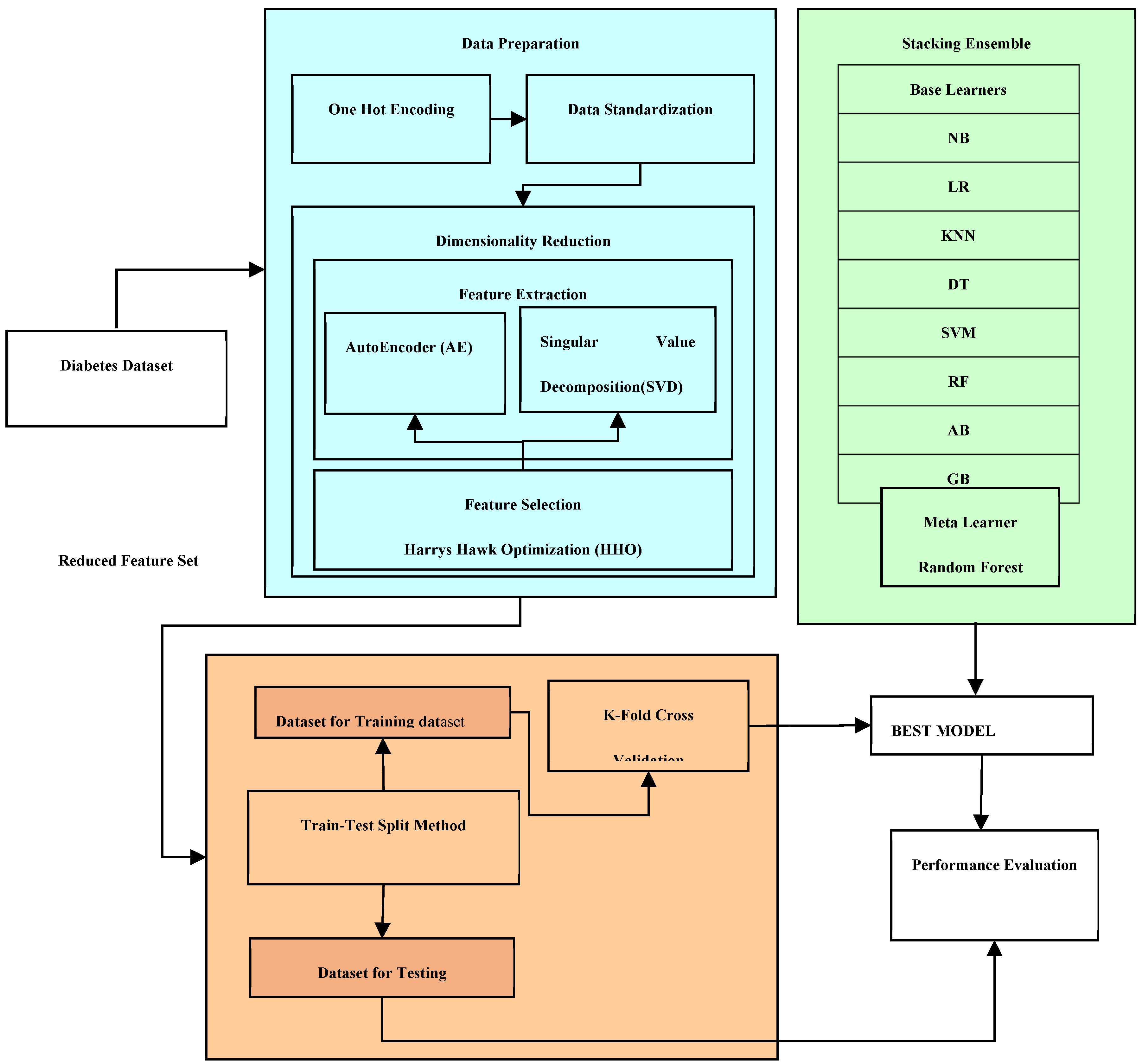
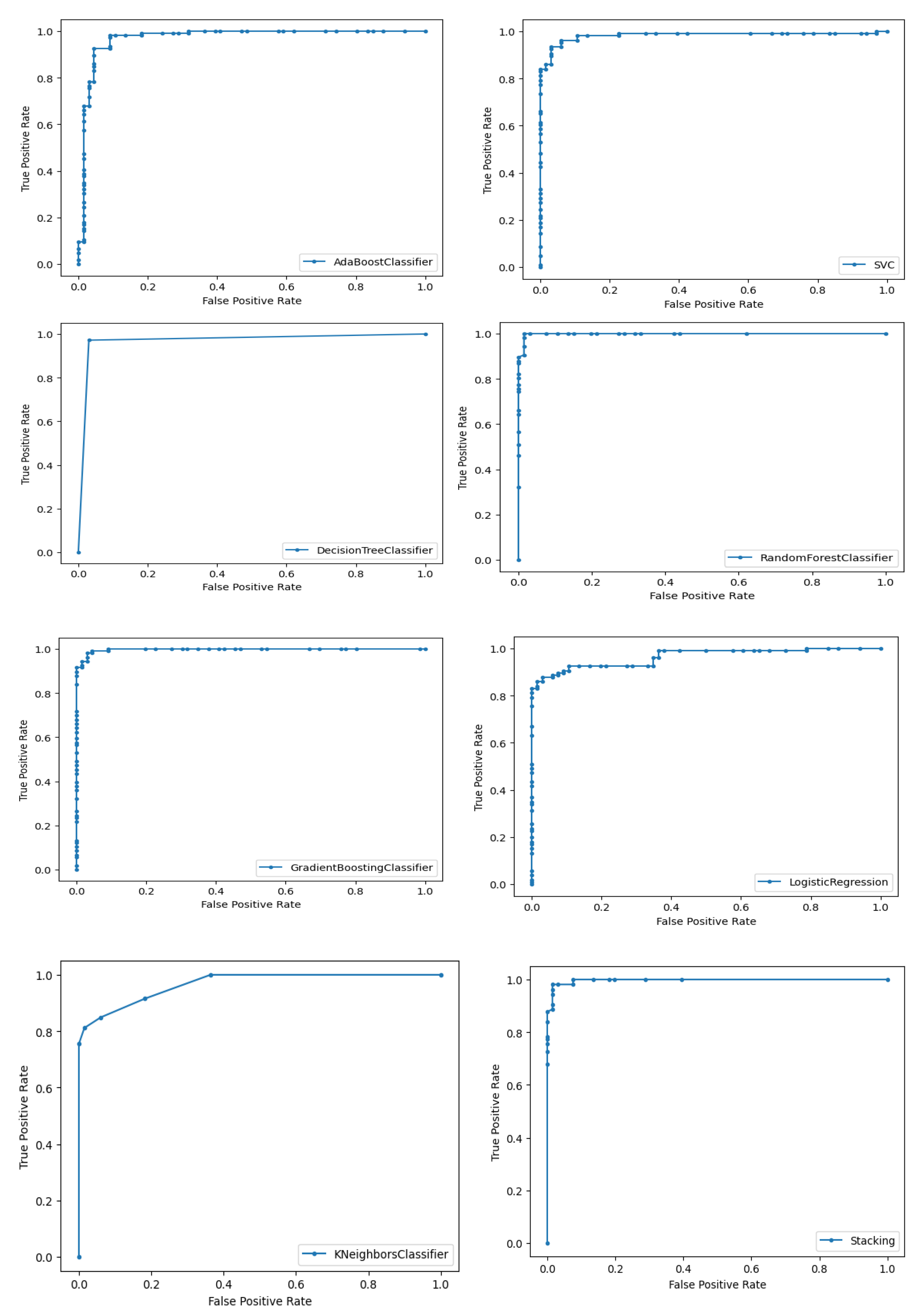
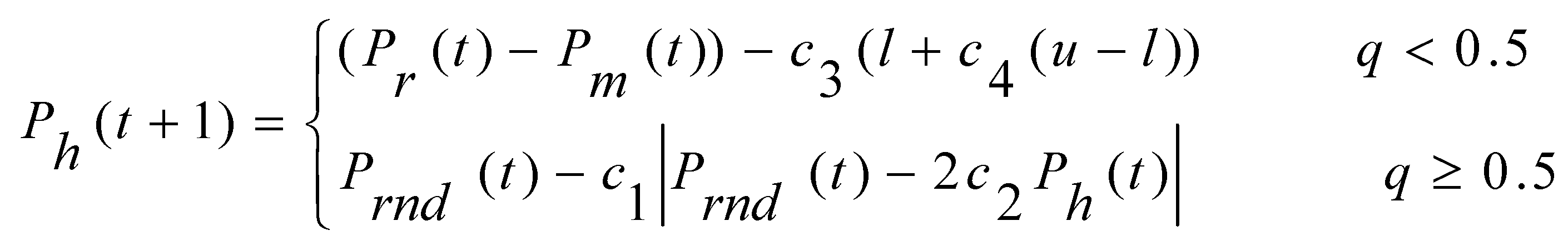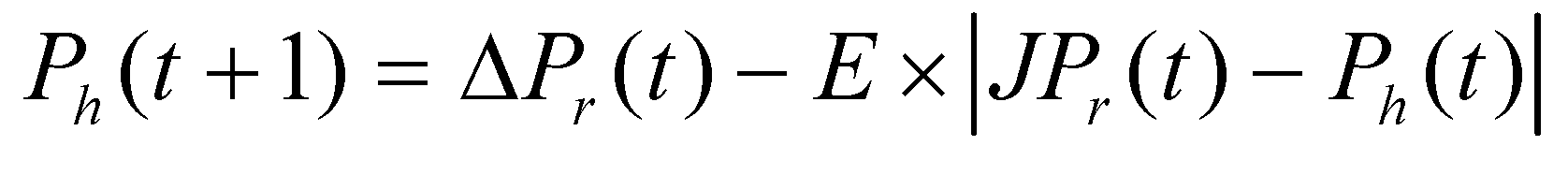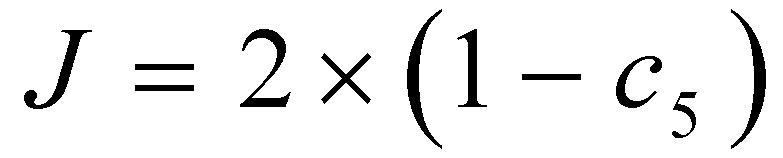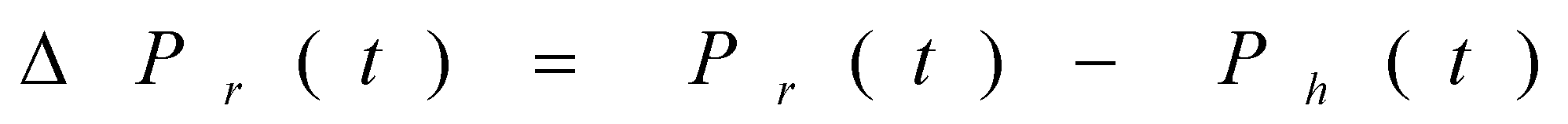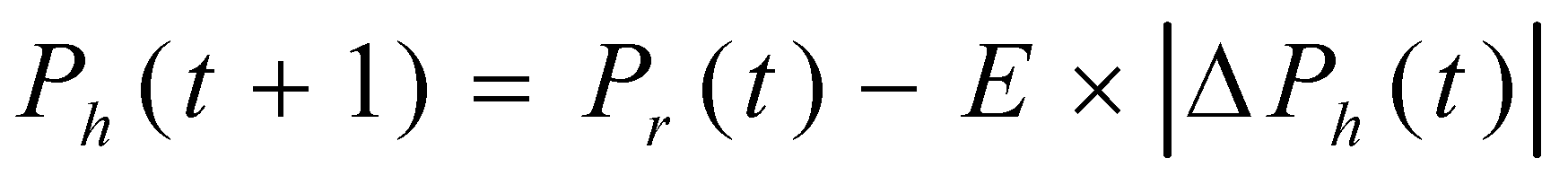Prerpints.org logo
Preprint
Article

Autoencoder and Harris Hawk Optimization Based Timely and Accurate Prediction of Diabetes Using a Minimal-Sized Feature Set

This version is not peer-reviewed.

Submitted:

17 October 2024

Posted:

18 October 2024

You are already at the latest version

Abstract
Timely diagnosis of diabetes helps in avoiding the major risks associated with the disorder. The proposed research involves the prediction of the disorder using a minimal sized and most representative feature set generated using automatic feature extraction through an autoencoder followed by a meta-heuristic feature selection of minimal size using Harris Hawk Optimization that predicts the onset of Diabetes with best accuracy. Specifically, the proposed method uses various classifiers like Support Vector Classifier, Logistic Regression, Decision Trees and Random Forest along with a stacking ensemble classifier upon the new feature set generated by the feature engineering pipeline. The usefulness of the proposed method is evaluated through metrics like accuracy, area under ROC (Receiver Operating Characteristic) curve, precision, recall and F1-score. The predictive ability of the models is affirmed under the presence of any statistical anomalies through the tests for statistical significance.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

One of the most challenging chronic disorders globally ubiquitous has been Diabetes Mellitus. The underlying issue is related to the hormone called insulin secreted by pancreas causing one of the different types of diabetes as Type 1, Type 2 and Gestational diabetes [1]. The first of the types results from the immune system's attack on pancreatic beta cells, leading to insufficient insulin production and the bloodstream’s impairment towards absorbing the glucose. The type-2 diabetes happens when there is failure of the body in insulin production or develops immunity to its impact. Another type of diabetes associated with hormonal changes in pregnancy is termed as Gestational. Diabetes research indicates that it may remain undetected for up to seven years before clinical diagnosis [2].
Severe repercussions are linked to untreated or undetected diabetes including the damage to vital organs. Early intervention soon after the onset of the disease [3] can significantly reduce the severity of these complications.
A survey conducted in 2017 at a global level discovered that 451 million individuals worldwide were diagnosed with diabetes, with projections suggesting an increase to 693 million by 2045 [4]. Additionally, studies have shown a rising prevalence of diabetes among adults in developing countries, with rates escalating from 4.7% to 8.5% between 1980 and 2014 [5]. In Australia, healthcare costs related to undiagnosed Type 2 diabetes amounted to $700 million annually, while in the United States, diagnosed cases incurred costs of $327 billion in 2017 [6]. Significant diabetic-related complications were reported in 9% of China's population, 8% of India's population, and 10% of Bangladesh's population according to a global statistical study in 2011 [7]. Managing these costs poses a substantial challenge for low- and middle-income countries, highlighting the importance of early detection mechanisms for diabetes to prolong life expectancy and reduce national healthcare expenditures.
Traditional diagnostic methods for diabetes, such as the Oral Glucose Tolerance Test and Hemoglobin A1c (HbA1c) test, while recommended by physicians, face practical challenges such as affordability across income groups, time consumption, and potential errors introduced by human technicians. A more cost-effective and accurate approach to diabetes diagnosis involves leveraging machine learning (ML). This method utilizes historical clinical data to build ML models that predict the risk of diabetes in new patients based on their symptoms. For instance, a diabetes dataset [8] comprising 520 instances and 16 attributes, encompassing major symptoms of the disorder, serves as a foundation for such research.
This study's primary contribution lies in developing an optimized machine learning pipeline on the aforementioned diabetes dataset. The pipeline includes comprehensive data preparation and feature engineering techniques aimed at reducing the feature subset while maximizing classification accuracy. Various classifiers are employed, including Naive Bayes (NB), K-Nearest Neighbor (KNN), Logistic Regression (LR), Decision Tree (DT), Support Vector Machine (SVM), Gradient Boost, Adaboost (AB), and Random Forest (RF), alongside a stacking ensemble of classifiers (excluding RF) with RF as a meta-learner for accuracy assessment.
Data preparation involves transforming categorical features into numeric ones via one-hot encoding and standardizing data using a standard scaler. Feature engineering includes techniques such as feature selection and extraction to streamline the feature subset size. The research explores multiple combinations of feature engineering pipelines and classifiers, evaluating their impact on accuracy and efficiency.
The paper is structured as follows: Section 2 presents a comprehensive review of related literature, while Section 3 provides an overview of the dataset and details the proposed predictive model. This section also includes a thorough description of feature selection and extraction techniques, including the application of the Harris Hawk Optimization algorithm and Autoencoders with Singular Value Decomposition. Section 4 delves into performance evaluation metrics, offering a detailed analysis of experimental results that include ROC curves across different predictive models and various classifier configurations. It also includes the tests for statistical significance and sensitivity analysis. Finally, Section 5 concludes the paper and outlines avenues for future research in this domain.

2. Related Work

Recent years have seen extensive research into achieving precise diabetes diagnosis through various machine learning models applied to diverse datasets. These methodologies typically incorporate feature selection methods during data preprocessing to reduce dimensionality, thereby enhancing accuracy and minimizing storage space requirements.
Perveen et al. [9] conducted diabetes prediction using data from the Canadian Primary Care Sentinel Surveillance network. They employed Adaboost and ensemble approach based on bagging with the J48 Decision Tree, and an independent classifier on J48 algorithm. Notably, there was no data preprocessing and it was found that AB's performance was the best.
Maniruzzaman et al. [11] proposed a classification method using Gaussian Process Classification (GPC) on the PID dataset. This approach utilized linear, polynomial, and radial basis kernels to predict diabetes, leveraging GPC's capability to handle non-linearity and correlation in medical datasets. Among various classifiers compared, the radial basis kernel GP achieved the highest accuracy of 81.5%.
Sisodia et al. [12] developed a model using ML techniques with no data preprocessing for diabetes detection through the PID dataset, employing SVM, DT, and NB classifiers. The NB classifier had the best performance with 76.3% accuracy.
Wang et al. [13] also designed a model on ML techniques for diabetes on the PID dataset that addressed missing values and class imbalance using the NB method for data normalization and ADASYN for balancing. Their approach utilized Random Forest (RF) classification, achieving 87.1% accuracy through Cross Validation (CV) using k folds with K=5.
Islam et al. [8] focused on early-stage diabetes risk using a dataset from Sylhet Diabetes Hospital, Bangladesh. Their study employed NB, Logistic Regression (LR), and RF classifiers, achieving the accuracy of 97.4% as best with RF using CV through k folds and the train-test split method giving an accuracy of 99%.
Vaishali et al. [14] aimed to enhance diabetes prediction accuracy using the PID dataset. They applied Goldberg's Genetic algorithm for the selection of features and fuzzy classification with multiple objectives achieving 83% accuracy with a train-test split (70%-30%).
Maniruzzaman et al. [15] proposed a classification framework for diabetes risk stratification, employing various data preprocessing techniques on the PID dataset, such as handling missing values and outliers. Using RF for both feature selection and classification, they achieved the highest accuracy of 92.26%.
Kaur et al. [19] employed the PID dataset for diabetes prediction and data preprocessing through Boruta wrapper feature selection method with the best performance using a linear kernel based SVM achieving the accuracy of 89%.
Li et al. [20] utilized the Coefficient of Variation (CV) for feature selection on the PID dataset, reducing the feature subset to four and achieving 77% accuracy with the Multilayer Perceptron model. Singh et al. [28] employed a stacked ensemble of classifiers for diabetes classification, achieving an accuracy of 83.8%.
Despite these advancements, existing methodologies often reach a maximum accuracy of 95%, predominantly relying on the PID dataset, which has limitations which include the dataset involving only female patients and having a feature set limited to 8 features. The primary challenges include lower prediction accuracy and limited dataset representativeness.
In response to these limitations, the proposed research leverages a dataset for timely diagnosis of diabetes introduced by Islam et al. [8], sourced from the UCI Machine Learning Repository. There are 520 records with a feature set of 16 attributes, significantly improving representativeness. The study achieves higher accuracy by reducing features and employing a diverse array of varying classifiers, individually and in stacking ensembles, to have the highest value for predictive accuracy.
Moreover, recent research (reference [26]) used optimal feature engineering pipelines, featuring the Crow Search optimization algorithm for feature selection and Singular Value Decomposition (SVD) for feature extraction. This approach enhanced accuracy with a reduced feature set, albeit at the cost of increased execution times and diminished interpretability of features.
To address these drawbacks, the current study designs a feature engineering pipeline that first utilizes Autoencoders for efficient feature extraction, followed by the Harris Hawk Optimization algorithm for feature selection, resulting in a reduced feature set of 9 features. This approach aims to balance accuracy and computational efficiency while ensuring a more interpretable feature set crucial for medical decision-making.
For a detailed comparison of methodologies, refer to Table 1, which summarizes feature engineering approaches and classifiers employed across different studies for diabetes prediction.

3. Details of the Dataset Employed

The recent dataset on diabetes from the UCI repository which focused on early detection [8] is used. It includes data from a survey on individuals' physical conditions encompassing 16 distinct attributes. This straightforward dataset, consisting predominantly of binary-valued attributes, proves invaluable for timely identification of diabetes onset.
The dataset comprises symptoms specific to diabetes, gathered from 520 patients categorized into 320 positive cases and 200 negative cases, reflecting a balanced distribution with a ratio of 5:8 between negative and positive cases. This balance informed the selection of performance metrics such as precision, recall, F-Measure, Accuracy, and Area under the ROC Curve, suitable for balanced classification tasks.
Data collection involved administering a survey to individuals recently diagnosed with diabetes or showing symptoms indicative of diabetes but not yet diagnosed, conducted at Sylhet Diabetes Hospital, Bangladesh. The dataset includes features and statistical information related to these symptoms, focusing on predicting early-stage type 2 diabetes likelihood among adults exhibiting traits such as obesity, prediabetes, and general weakness.
Each column in the dataset corresponds to a manifestation associated with the onset of diabetes. One feature (Age) is numeric and the other 15 are categorical. To handle this, one-hot encoding was applied, resulting in the transformation of each categorical feature into two numeric features, thus expanding the feature space to 30 numeric features in total (15 categories × 2 binary values = 30 features).
The feature engineering phase of this study incorporates an amalgamation of feature extraction and feature selection techniques. Harris Hawk Optimization (HHO) algorithm is used for the selection of features, while feature extraction employs AutoEncoder (AE) and Singular Value Decomposition (SVD) techniques. Various experiments explore different combinations of HHO, AE, and SVD in feature engineering pipelines, resulting in reduced feature subsets for each experimental setup.

4. Objectives of the Research and Methodology Employed

The following are the main objectives of the research:
  • Developing an optimized machine learning pipeline to balance accuracy and computational efficiency through an interpretable feature set crucial for medical decision-making.
  • Includes comprehensive data preparation and feature engineering using Autoencoders for efficient feature extraction and Harris Hawk Optimization algorithm for feature selection.
  • Diverse set of classifiers alongside a stacking ensemble with Random Forest as a meta-learner for performance assessment.
Figure 1 showcases the presented predictive model. A critical initial phase involves data preparation, entailing diverse data transformations for generating a minimal-sized and most-representative feature set. Train and test samples are obtained through Repeated stratified K Fold CV. The prediction is done using multiple diverse classifiers, bolstered by their stacking ensemble approach.

4.1. One-Hot Encoding and Standardization

The majority of ML algorithms require the data to be numeric necessitating the conversion of categorical data into a numeric format. When there's no inherent order among categorical data, the most suitable method is one-hot encoding.
In machine learning, the performance of algorithms can suffer if dataset attributes have differing scales. This issue underscores the importance of data standardization. It involves rescaling the value distribution so that the mean becomes zero and the standard deviation becomes one.
In the diabetic dataset utilized in this research, the only numeric attribute is 'age' which has a skewed distribution and the range of values for this attribute have a scale diverse to other attributes produced via one-hot encoding. Therefore, the standard scaler transformation is used as part of the data preparation process.

4.2. Feature Selection

This approach involves reducing the number of features by pinpointing the most significant attributes strongly correlated to the target attribute. It not only results in a lesser cost incurred with storage and computation due to smaller feature set but enhanced performance.
Several advantages accompany the reduction of the feature set. For instance, it aids in diminishing data overfitting by eliminating irrelevant features, thereby reducing noise. Additionally, the accuracy of the model improves as misleading input variables are removed. Moreover, a smaller dataset size translates to reduced time required for constructing and training the model.
In supervised learning, traditional feature selection methods fall into three categories: filter, wrapper, and intrinsic methods. In this current work, we employ a wrapper based feature selection employing a bio-inspired metaheuristic approach termed as Harris Hawk Optimization. Wrapper methods involve utilizing various subsets of the feature set to assess the performance of an ML model for each subset. Each subset is assigned a performance evaluation score, and the one demonstrating the highest score is chosen. The quest for the optimal feature subset can follow methodical or stochastic approaches. The former might employ strategies like best-first search, while the latter could involve algorithms like random hill-climbing.
Feature selection, aimed at maximizing the accuracy of an ML model, can be regarded as an optimization problem, particularly when dealing with a large feature set. The optimization function aims to minimize both the size of the feature subset and the classification error. Assuming there are N features, the total possible subsets amount to 2^N. This exponential increase in search space makes a brute-force approach via exhaustive search impractical. Therefore, meta-heuristics are employed to navigate this extensive search space.
In this context, numerous algorithms have been proposed, including Particle Swarm Optimization [34,35], Artificial Bee Colony [36], Differential Evolution [37], Bat algorithm [38], Moth Flame Optimization [39], Grey Wolf Optimizer [40], Butterfly optimization algorithm [41], Sine Cosine Algorithm [42], CSA and HHO. Among these, HHO stands out as a recently introduced algorithm that has garnered considerable attention within the research community due to its simplicity, ease of implementation, efficiency, and fewer parameters.

4.2.1. Harris Hawk Optimization Algorithm

HHO stands as a well-regarded swarm-based optimization algorithm, characterized by its gradient-free approach and a dynamic interplay between exploration and exploitation phases. First introduced in 2019 within the prestigious Journal of Future Generation Computer Systems (FGCS), this algorithm quickly garnered attention within the research community due to its adaptable structure, remarkable performance, and ability to yield high-quality results. Its fundamental concept draws inspiration from the cooperative behaviors and hunting techniques of Harris' hawks in nature, particularly their "surprise pounce" strategy. In the present day, numerous proposals have emerged aiming to enhance the capabilities of HHO, resulting in several improved versions of the algorithm published in esteemed journals by Elsevier and IEEE.
The genesis of the idea behind HHO is both elegant and straightforward. Harris hawks exhibit a diverse range of team hunting patterns, adapting to the dynamic scenarios and evasion tactics employed by their prey, often involving intricate zig-zag maneuvers. They coordinate their efforts, waiting until the opportune moment to launch a synchronized attack from multiple directions.
From an algorithmic perspective, HHO incorporates several key features contributing to its effectiveness. Notably, the "escaping energy" parameter exhibits a dynamic and randomized time-varying nature, enhancing and harmonizing the exploratory and exploitative behaviors of HHO. This dynamic aspect facilitates a seamless transition between exploration and exploitation phases. HHO employs various exploration mechanisms based on the average location of hawks, bolstering its exploratory tendencies during initial iterations. Additionally, it employs diverse LF-based patterns featuring short-length jumps to enrich its exploitative behaviors when conducting local searches.
A progressive selection scheme empowers search agents to incrementally advance their positions and select only superior ones, elevating solution quality and intensification capabilities throughout the optimization process. HHO employs a range of search strategies before selecting the optimal movement step, further strengthening its exploitation tendencies. The randomized jump strength aids candidate solutions in achieving a balance between exploration and exploitation. Lastly, HHO incorporates adaptive and time-varying components to tackle the challenges posed by complex feature spaces, which may contain local optima, multiple modes, and deceptive optima.
Irrespective of the array of algorithms, they share a common characteristic: their search steps encompass two phases—exploration (diversification) and exploitation (intensification). During the exploration phase, the algorithm aims to extensively traverse various regions and facets of the feature space by leveraging and emphasizing its randomized operators. Consequently, a well-designed optimizer's exploratory behaviors should possess a sufficiently enriched random nature, efficiently distributing randomly-generated solutions across diverse areas of the problem's topography during the initial stages of the search process.
Subsequently, the exploitation phase typically follows the exploration phase. Here, the optimizer directs its attention toward the vicinity of higher-quality solutions situated within the feature space. This phase intensifies the search within a local region rather than encompassing the entire landscape. An adept optimizer should strike a reasonable, delicate balance between the tendencies for exploration and exploitation. Otherwise, there's an increased risk of getting trapped in local optima (LO) and encountering drawbacks related to premature convergence.
Exploration Phase
The HHO introduces an exploration mechanism inspired by the behavior of Harris' hawks. These hawks rely on their keen eyes to track and detect prey, yet sometimes, the prey remains elusive. Consequently, the hawks adopt a strategy of waiting, observing, and monitoring the desert landscape, potentially for several hours, in their pursuit to detect prey. Within the HHO framework, the candidate solutions are likened to the Harris' hawks, with the best candidate solution in each step analogous to the intended prey or a near-optimal solution.
In the HHO context, Harris' hawks symbolize candidate solutions perched randomly at various locations, employing two distinct strategies to detect prey. Under an assumption of equal probability (s) for each perching strategy, these hawks decide their perching location based on two considerations: firstly, positioning themselves close enough to other family members to facilitate coordinated attacks (as detailed in Eq. (1)) when s < 0.5; secondly, perching on random tall trees situated within the group's home range (as described in Eq. (1)) when s ≥ 0.5.
Preprints 121542 i001
In the equation(1) Ph represents the position vector of the hawk, Pr represents the position vector of the rabbit, Pm repreents the average of position vector of all hawks, Prnd represents the random position vector, t represents the time-instant / iteration, t+1 represents the next successive iteration, c1, c2, c3, c4 and q are random numbers in the range (0,1) updated in each iteration, l and b represent the lower and upper bounds of the locations of the hawks.
The HHO algorithm has the ability to transition from exploration to exploitation, and subsequently switch between various exploitative behaviors, all guided by the prey's escaping energy given by the equation (2) below:
Preprints 121542 i002
In the equation (2), E represents the escaping energy of the prey, T is the total number of iterations, t is the current iteration, and E0 represents the initial state of energy ranging and varying between (-1,1) at each iteration.
Exploitation Phase
During the exploitation phase, the HHO algorithm executes a surprise attack by targeting the identified prey encountered in the exploration phase. Based on the escape patterns of the prey and the hunting approaches of Harris' hawks, the HHO suggests four potential strategies to simulate the attack phase. Prey typically aim to flee when faced with danger. If we assume r represents the likelihood of successful (r < 0.5) or unsuccessful (r ≥ 0.5) escape prior to a surprise attack, the hawks react by employing either a hard or soft encirclement tactic to capture the prey. This approach involves surrounding the prey from various directions with differing force levels based on the prey's remaining energy.
To implement this approach and allow the HHO to alternate between soft and hard besiege procedures, the E parameter comes into play. Specifically, when |E| is equal to or greater than 0.5, the gentle besieging occurs, while if |E| is less than 0.5, the intense besieging takes place.
Soft Besiege
The rabbit retains sufficient energy and attempts to evade through random deceptive leaps, yet ultimately fails to escape when the following condition is satisfied: r ≥ 0.5 and |E| ≥ 0.5. Throughout these evasion attempts, the Harris' hawks gently encircle it, leading the rabbit to fatigue further before executing a sudden pounce. This conduct adheres to the subsequent set of rules:
Preprints 121542 i003
Preprints 121542 i004
Preprints 121542 i005
between the position vector of the rabbit and the current location, J stands for the energy of the rabbit for jumping throughout the escaping process. c5 is the random variable between (0, 1).
Hard Besiege
The prey is extremely fatigued with minimal energy for escape when the following condition is satisfied: r ≥ 0.5 and |E| < 0.5. Furthermore, the Harris' hawks barely surround the targeted prey before executing the surprise pounce. In such a scenario, it is termed as hard besiege and below the equation is used to update the current positions.
Preprints 121542 i006

4.3. Feature Extraction

Feature extraction, a fundamental step in machine learning and data analysis, entails the identification and extraction of pertinent features from raw data. These extracted features are subsequently utilized to construct a more informative dataset. Through the process of feature extraction, relevant features are isolated, distinguishing them from the irrelevant ones. This reduction in the number of features simplifies the dataset, leading to enhanced accuracy and efficiency in the analysis.
Autoencoders excel at discerning crucial data features. The essence of the autoencoder concept lies in acquiring knowledge from encoding original datasets to generate novel, more powerful features. This is accomplished by instructing a neural network to replicate its input, compelling it to discern and leverage inherent structures in the data. In this way, autoencoders streamline dimensionality and distill important features from the data, enhancing the effectiveness of machine-learning models.
Due to the presence of 15 one-hot encoded features out of a total of 16, the resulting dataset is sparse. Consequently, the SVD technique from linear algebra is employed to generate a projection of the sparse dataset before fitting the model. This projection involves reducing the dimensions/features of the sparse dataset, allowing the construction of a machine learning model. The approach of projecting for feature reduction ensures a decrease in dimensions while preserving structural relationships among variables in the dataset.
SVD offers a systematic method for determining a low-dimensional approximation to high-dimensional data, focusing on dominant patterns. It is data-driven, meaning patterns are derived solely from the data, without the need for expert knowledge or intuition. SVD is numerically stable and provides a hierarchical representation of data through a new coordinate system defined by dominant correlations. Additionally, SVD is guaranteed to exist for any matrix, unlike eigen decomposition.
The SVD process involves identifying the best approximation of the original matrix with a lower-rank matrix having fewer dimensions. This is achieved by selecting the largest singular values and their corresponding singular vectors from matrices U, S, and V, and multiplying them to create a matrix that retains crucial information while eliminating noise and redundancy. This iterative process can be adjusted with different numbers of singular values and vectors based on the desired level of accuracy and complexity.

4.3.1. Autoencoders Based Feature Extraction

An AutoEncoder represents an unsupervised Artificial Neural Network designed to encode data by compressing it into a lower-dimensional space (commonly referred to as the bottleneck layer or code) and subsequently decoding it to reconstruct the original input. This bottleneck layer serves as the repository for the compressed representation of the input data.
In an AutoEncoder, the number of output units is required to match the number of input units since the goal is to faithfully reconstruct the input data. Typically, AutoEncoders consist of two main components: an encoder and a decoder. The encoder is responsible for compressing the input data into a lower-dimensional space, specifically the size of the bottleneck layer, while the decoder is responsible for decoding the compressed data back into its original form.
The architecture of an AutoEncoder typically involves a progressive reduction in the number of neurons in the encoder layers as you move deeper into the network, and conversely, an increase in the number of neurons in the decoder layers as you progress further. In an example with three layers, the encoder might contain 32, 16, and 7 units in each layer, while the decoder could feature 7, 16, and 32 units in its respective layers. It's essential that the code size, or the number of neurons in the bottleneck layer, is less than the number of features in the input data.
Before inputting data into an AutoEncoder, it is crucial to scale the data within the range of 0 to 1 using a MinMaxScaler. This preprocessing step is necessary because AutoEncoders often employ a sigmoid activation function in the output layer, which produces values between 0 and 1.
When AutoEncoders are employed for dimensionality reduction, the bottleneck layer is extracted and used to reduce the dimensionality of the data. This process effectively acts as a form of feature extraction, allowing for the creation of a lower-dimensional representation of the original data.

4.4. Classifiers Employed

Multiple machine learning models and a stacking ensemble are employed as classifiers. It represents a unique form of ensemble machine learning algorithm that consolidates predictions from diverse models operating at two varying levels. Different models may demonstrate effectiveness in distinct ways for a given dataset and their stacking ensemble aims to merge predictions from typically dissimilar ML models to get an accuracy higher than the individual models.
Usually, bagging and boosting approaches are utilized to create ensembles but stacking stands out by employing various ML models. It utilizes one model termed as the meta model, to interpret the ideal blend of predictions using the base models. It consists of two levels wherein the level 0 involves diverse ML models known as base learners, while level 1 incorporates a single model, the meta learner, responsible for consolidating predictions from the base learners.
The training upon the entire dataset is done for level 0 models and the predictions are utilized to train the level 1 models on out-of-sample data. In essence, the level 0 models are exposed to out-of-training data and their predictions are used with the actual outputs to serve as input and output pairs, respectively, for training the level 1 model. The outputs of level 0 models are either probability values or class labels in classification tasks. The meta model’s training data preparation involves k-fold CV on the base learners and out-of-fold predictions as the meta model's training data. The input fields of the base models' training data can also be included in the meta model's training data, aiding the meta model in learning the optimal way to combine base learners. Stacking is most effective when the prediction errors of different base models are not highly correlated, and selected base learners can be complex and diverse. Models with varying assumptions about predictive modeling and different internal representations, such as trees and samples, tend to perform well. Other ensemble algorithms like Random Forest, Gradient Boosting, and Adaboost can also serve as base learners. Logistic regression is a common choice for the meta model, but the optimal choice depends on the dataset and the statistical relationship between attributes and the target variable.
Although the stacking ensemble aims to enhance accuracy, success is not guaranteed and depends on the dataset's complexity. The representational capability of the training data, facilitating further learning by unifying base learners' predictions, also influences performance. In some cases, base learners may outperform the stacking ensemble, especially when computational complexity is a concern. In the current research, we employed Gradient Boost(GB), AdaBoost(AB), SVC, DT, RF, GB, LR and KNN classifiers as base learners, with the meta learner being an RF Classifier. Base learner selection was empirical, considering the need for a diverse range of models with varying assumptions. Through extensive experimentation, random forests were found to provide the highest accuracy among base learners, leading to the selection of a random forest as the meta learner.

5. Discussion of Results

The results of multiple experiments involving various classifiers and proposed feature engineering pipelines (FEPs) are presented in several subsections. Table 3 displays the results of experiments that employ different FEPs with various classifiers, both independently and as part of a stacking ensemble. In Section 5.1, the rows of Table 6 assess the results obtained through various combinations of the proposed FEPs and the classifiers. We highlight the classifier that achieves the maximum value for accuracy across various FEPs in blue. The columns of Table 6 are used to evaluate each classifier with different FEPs. Subsequently, the FEP giving optimal performance with each classifier is identified in the form of the one which gives highest accuracy with minimal features, which we highlight in orange color.
In Section 5.2, 5.3, 5.4 and 5.5 the following performance metrics are assessed: Precision, Recall, F1 Score, and Area under ROC. The values obtained for each metric are computed through the mean of 20 runs attributed to the stochastic nature of the algorithms.

5.1. Accuracy Metric of Each FEP Across Various Classifiers

Table 3 is used for row-wise analysis and the highest accuracy of 97.10 is found when AutoEncoder is used for feature engineering with AB classifier and a feature subset size of 15 features. With HHO algorithm used for feature engineering, the maximum is 95.93 is achieved with RF classifier and a feature subset size of 14. When a combination of AE + HHO is used as FEP, the maximum is 97.51 is achieved with a stacking classifier and a feature subset of 9 features. With SVD used as FEP, the maximum is 95.93 is achieved with GB classifier and a feature subset of size 15. When a combination of SVD+HHO is used as FEP, the maximum accuracy of 95.74 is obtained with stacking classifier and a feature subset size of 6 features.
With a column-wise analysis of Table 3, it can be seen that the AB classifier has the highest accuracy of 97.10 with a feature set of 15 features using AE as FEP. The SVC has a maximum accuracy of 95.34 with HHO used as FEP and a feature set of 14 features. DT classifier has a maximum accuracy of 94.76 with SVD+HHO used as FEP with 6 features. RF and GB classifiers has a maximum accuracy of 96.51 and 95.93 respectively with AE+HHO used as FEP with 9 features. LR classifier has a maximum accuracy of 93.02 with SVD+HHO used as FEP with 6 feature. KNN and stacking classifiers have maximum accuracy of 95.93 and 97.51 respectively with AE+HHO used as FEP with 9 features.

5.2. Precision Metric of Each FEP Across Various Classifiers

In Table 4, a row-wise analysis shows that when AutoEncoder is used for feature engineering with a feature subset size of 15 features, the highest precision of 99 is achieved with AB classifier for class 0 and for class 1, the highest precision of 98 is achieved through LR classifier. With HHO algorithm used for feature engineering along with 14 features, the highest precision of 97 is achieved with SVC for class 0 as well as class 1.
A FEP with a combination of AE + HHO with a feature set of 9 features gives the highest precision of 98 and 99 for class 0 and class 1 respectively through RF classifier. With SVD used as FEP and feature set of size 15, the highest precision of 98 and 94 is achieved for class 0 and class 1 respectively through RF classifier. When a combination of SVD+HHO is used as FEP along with a feature set of size 6, the highest precision of 98 and 94 is achieved for class 0 and class 1 respectively through RF classifier.
Table 4 has a column-wise analysis which results in the following observations: It can be seen that the AB classifier has the highest precision of 98 for class 0 with a feature set of 6 features using SVD+HHO as FEP; it has a highest precision of 95 for class 1 using AE+HHO as FEP. The SVC has a maximum precision of 97 for class 0 with HHO used as FEP and a feature set of 14 features; it has a precision of 99 for class 1 with AE+HHO as FEP. DT classifier has a maximum precision of 96 and 98 for class 0 and class 1 respectively using AE+HHO as FEP. RF classifier has a maximum precision of 98 and 99 for class 0 and class 1 respectively with AE+HHO used as FEP with 9 features. GB classifier has a maximum precision of 98 for class 0 with AE+HHO as FEP; it has a maximum precision of 98 for class 1using AE as FEP. LR classifier has a maximum precision of 94 with SVD used as FEP with 15 features and for class 1, the highest precision is 98 with AE as FEP . KNN classifier has a highest precision of 93 and 97 with HHO used as FEP; it has a precision highest value of . Stacking classifier has a maximum precision of 99 and 97 for class 0 and class 1 with AE+HHO used as FEP with 9 features.

5.3. Recall Metric of Each FEP Across Various Classifiers

A row-wise analysis of Table 5 shows that AutoEncoder with a feature subset size of 15 features, the highest recall of 99 is achieved with stacking and RF classifiers for class 1, the highest recall of 98 is achieved through RF and SVC classifiers for class 0. With HHO algorithm used for feature engineering along with 14 features, the highest recall of 95 and 98 is achieved with SVC for class 0 and class 1 respectively.
When AE + HHO with a feature set of 9 features is used, the highest recall of 98 is achieved with KNN classifier for class 0 and 99 for class 1 with stacking classifier. With SVD used as FEP and feature set of size 15, the highest recall of 94 is achieved with KNN for class 0 and for class 1, the stacking classifier gives highest recall as 99. When a combination of SVD+HHO is used as FEP along with a feature set of size 6, the highest recall of 92 is achieved for class 0 through DT classifier and 99 is achieved for class 1 with stacking classifier.
With a column-wise analysis of Table 5, it can be seen that the AB classifier has the highest recall of 92 for class 0 with a feature set of 9 features using AE+HH as FEP ; it has a recall with highest value of 99 for class 1 with SVD+HH as FEP with feature set of 6 features. The SVC has a maximum recall of 98 for class 0 with AE as FEP with 15 features; it has a maximum recall of 98 for class 1 with HHO used as FEP and a feature set of 14 features. DT classifier has a maximum recall of 97 for both class 0 and class 1 with AE used as FEP with 15 features. RF classifier has a maximum recall of 98 and 99 for class 0 and class 1 respectively with AE used as FEP with 15 features. GB classifier has a maximum recall of 97 for class 0 with AE as FEP whereas a value of 99 for class 1 with AE +HHO used as FEP. LR classifier has a maximum recall of 97 for class 0 with AE used as FEP; it has a highest value of 96 for class 1 with SVD as FEP. KNN classifier has a maximum recall of 98 with AE+HHO used as FEP with 9 features; it has a highest of 95 with HHO for class 1. Stacking classifier has a maximum recall of 95 and 99 for class 0 and class 1 respectively with AE+HHO used as FEP with 9 features.

5.4. F1-Score Metric of Each FEP Across Various Classifiers

In Table 6, a row-wise analysis shows that AutoEncoder with a feature subset size of 15 features, the highest F1-score of 94 and 97 is achieved with stacking for class 0 and class 1 respectively. With HHO algorithm used for feature engineering along with 14 features, the highest F1-score of 96 and 98 is achieved with SVC for class 0 and class 1 respectively.
When AE + HHO with a feature set of 9 features is used, the highest F1-score of 97 and 98 is achieved with stacking classifier for class 0 and class 1 respectively. With SVD used as FEP and feature set of size 15, the highest F1-score of 95 and 97 is achieved with GB classifier for class 0 and class 1 respectively. When a combination of SVD+HHO is used as FEP along with a feature set of size 6, the highest F1-score of 94 and 96 is achieved for class 0 and class respectively with RF and stacking classifiers.
A column-wise analysis of Table 6 shows that the AB classifier has the highest F1-score of 93 and 96 for class 0 and class 1 respectively with a feature set of 9 features using AE+HH as FEP. The SVC has a maximum F1-score of 96 and 98 for class 0 and class 1 respectively with HHO as FEP with 14 features. DT classifier has a maximum F1-score of 96 and 98 class 0 and class 1 respectively with AE used as FEP with 15 features. RF classifier has a maximum F1-score of 98 and 99 for class 0 and class 1 respectively with AE used as FEP with 15 features. GB classifier has a maximum F1-score of 96 and 98 for class 0 and class 1 respectively with AE+HHO. LR classifier has a maximum F1-score of 91 and 94 for class 0 and class 1 respectively with SVD used as FEP. KNN classifier has a maximum F1-score of 94 and 96 for class 0 and class 1 respectively with HHO used as FEP with 14 features. Stacking classifier has a maximum F1-score of 97 and 98 for class 0 and class 1 respectively with AE+HHO used as FEP with 9 features.
Table 6. F1-Score with Different FEPs and Classifiers.
Table 6. F1-Score with Different FEPs and Classifiers.
Feature Engineering Approach No of Features CLASSIFIERS - F1-SCORE X (0.01)
AB SVC DT RF GB LR KNN Stacking
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
None 31 86 92 93 96 91 95 93 96 93 96 86 92 92 95 94 97
AutoEncoder (AE) 15 90 94 88 91 96 98 98 99 96 97 90 93 86 90 96 98
HarrisHawk (HH) 14 90 94 96 98 94 96 95 97 95 97 90 94 94 96 95 97
AE+HH 9 93 96 93 96 92 95 96 98 96 98 85 91 90 94 97 98
SVD 15 93 96 94 96 92 95 94 96 95 97 91 94 90 93 93 96
SVD + HH 6 92 95 86 91 93 96 94 96 92 95 83 89 88 93 94 96

5.5. ROC AUC Metric of Each FEP Across Various Classifiers

Row-wise analysis of Table 7 shows that when AutoEncoder is used for feature engineering, the highest AUC ROC of 98.66 is achieved with Stacking classifier and a feature subset size of 15 features. With HHO algorithm used for feature engineering, the highest AUC ROC of 98.94 is achieved with Stacking classifier and a feature subset size of 14. When a combination of AE + HHO is used as FEP, the highest AUC ROC of 99.84 is achieved with a RF classifier and a feature subset of 9 features. With SVD used as FEP, the highest AUC ROC of 99.56 is achieved with Stacking classifier and a feature subset of size 15. When a combination of SVD+HHO is used as FEP, the highest AUC ROC of 99.32 is obtained with GB classifier and a feature subset size of 6 features.
With a column-wise analysis of Table 7, it can be seen that the AB classifier has the highest AUC ROC of 98.84 with a feature set of 6 features using SVD+HHO as FEP. The classifiers SVC, DT, RF, and GB have a maximum AUC ROC values of 98.54, 97.06, 99.84 and 99.71 respectively with AE+HHO used as FEP and a feature set of 9 features. LR and KNN classifiers have a maximum AUC ROC values of 98.04 and 98.18 respectively with HHO used as FEP with 14 feature. Stacking classifier has a maximum AUC ROC of 99.70 with AE+HHO used as FEP with 9 features.

5.6. Optimal Combination of the FEP and Classifier

An overall analysis shows that the highest value for accuracy with various classifiers is obtained for highest number of times when AE+HHO is used as FEP in comparison with the remaining FEPs. Figure 2 depicts the ROC curves of each of the classifier with FEP of AE + HHO giving the optimal performance with most of the classifiers with a feature set of 9 features.
Also, the stacking classifier gives the best performance metrics values when AE+HHO is used as FEP concluding that the optimal combination for (FEP, Classifier) is (AE+HHO, Stacking Ensemble). To further affirm the superior performance of the stacking ensemble in comparison with other classifiers, the statistical significance tests are performed as explained in section 5.7

5.7. Tests for Statistical Significance

The selection of ML model is based upon the assessment and comparison of the outcomes of the various ML algorithms. Even though the model with the best performance measure is typically chosen, the statistical anomalies [54] could sometimes lead to inaccurate reflection of genuine superiority. Under these circumstances, a statistical hypothesis test becomes significant.
According to Thomas Dietterich [55], a study on classifier comparison using statistical significance tests, it was found that McNemar's test [56] has to be used when an independent test dataset is employed rather than resampling techniques like K-Fold CV, which involves multiple assessments. It was found that [57] when an independent test dataset is unavailable and resampling methods like cross-validation are used, the instability resulting from training on k-1 subsets of the dataset is directly linked to uncertainty in the model's performance. This uncertainty can be quantified through repeated K-Fold CV followed by a paired t-test.
In K-fold CV, each ML model is assessed on the same splits, and performance scores are computed for each split. As the models are trained using the same data subsets (folds), except in cases where data is held out from the fold, the assumption of model evaluations done independently does not hold good. Consequently, the paired Student’s t-test can exhibit optimistic bias due to this lack of independence.
To mitigate this issue, Thomas Dietterich proposed a mutation to the paired t-test known as 5×2-fold CV. This method is implemented in the MLxtend library through the paired_ttest_5x2cv() function which takes data and models as inputs, calculates the t-statistic and p-value, and compares the p-value to a significance level (typically 0.05, denoted as alpha). In case, p-value turns out to be smaller than or equal to alpha, the null hypothesis suggesting no difference in the average performance between the model is discarded, indicating a likely real difference in performance. In case, the p-value turns out to be greater than alpha, the null hypothesis has to be followed suggesting that any observed performance difference may be due to chance.
The p-values obtained from applying the modified t-test for each classifier compared to a stacking ensemble are presented in Table 8. Four feature engineering pipelines achieved accuracies exceeding 98%. All p-values are below the 0.05 threshold, leading to rejection of the null hypothesis and demonstrating superior performance of the stacking ensemble compared to other classifiers.

5.8. Sensitivity Analysis

We conducted a sensitivity analysis to assess how variations in hyperparameter settings affect performance metrics, aiming to gain insights into the stability of the proposed model. Initially, we selected the feature engineering pipeline that yielded the best performance without considering hyperparameters: AE+HH with 9 features and a Stacking ensemble as the estimator.
Table 9 presents the key performance metrics for various base classifiers and their stacking ensemble. The top three base classifiers, SVC, RF, and GB, which achieved the highest metric values, are highlighted in purple. Given that the stacking ensemble performed best overall, we focused on these three base classifiers and varied their hyperparameters for our sensitivity analysis. Table 9, Table 10 and Table 11 detail the sensitivity analysis conducted through grid searching key hyperparameters for these classifiers, with the optimal hyperparameter settings highlighted in grey.
In Table 10, the focus for the stacking method is on choosing the kernel, which dictates how input variables are transformed. Although there are many options, the most common ones are linear, polynomial, and RBF, with linear and RBF being the most frequently used in practice. Another important consideration is the penalty parameter (C), which varies across a range of values and has a significant impact on the decision boundaries between classes. Starting with a logarithmic scale for this parameter may be a prudent initial strategy. The following list indicates the hyperparameters along with the values employed in the form of key : {values} pairs : { ‘C’: {50,10,1.0,0.1,0.01}, ‘gamma’: {‘scale’}, ‘kernel’:{‘poly’, ‘rbf’, ‘sigmoid’}}. As can be observed, a total of 15 combinations are possible based upon the number of elements in each of the set representing the three hyperparameters.
In Table 11, when using the Gradient Boosting Classifier (GBC), certain parameter combinations require careful attention. The learning_rate and the number of trees in the model indicated by n_estimators are having significance in the predictive performance. Another key combination involves subsample for each tree and the depth of each tree indicated by max_depth. The following list indicates the hyperparameters along with the values employed in the form of key : {values} pairs as follows : {‘learning_rate’: {0.001, 0.01}, ‘max_depth’: {‘3,7,}, ‘n_estimators’:{10,100}, ‘subsample’:{0.5,0.7}}.
In Table 12, when using the Random Forest Classifier (RFC), the key parameter to focus on is the number of random features to sample at each split point (max_features). Additionally, the number of trees in the forest (n_estimators) is also important. This parameter should ideally be increased incrementally until no significant improvement in model performance is noted.
A suitable range of values can be explored on a logarithmic scale from 10 to 1,000. The following list indicates the hyperparameters along with the values employed in the form of key : {values} pairs : {‘max_features’: {‘sqrt’, ‘log2’}, ‘n_estimators’: {10, 100, 1000}}. Table 11, Table 12 and Table 13 show that variations in the hyperparameters do not significantly impact the model's performance, demonstrating the model's stability.

6. Conclusion and Forthcoming Enhancements

In this study, a recent dataset on the diabetes is utilized instead of the conventional PID dataset comprising of only women patients. The adoption of the recent dataset aims to ensure gender-neutral application. The focus is on faster diagnosis, achieved by determining boolean values for various medical parameters indicating the symptoms which happen usually/rarely with the beginning of diabetes.
Diverse FEPs are designed to reduce the dimensions of the feature set and generate a maximum value for accuracy. Leveraging the stacking ensemble's ability to employ the capabilities of diverse ML models to achieve the best performance, it is used to evaluate various FEPs. The FEPs employs various feature selection and extraction approaches employing Harris Hawk Optimization Autoencoders and Singular value decomposition. The research aims to find the optimal combination of FEP and classifier yielding highest accuracy with least number of features.
The maximum value for accuracy reaching 97.51%, involves a combination of AE+HHO as FEP, resulting in 9 features and the classifier employed is a stacking ensemble model. Comparable accuracy of 96.51% is attained with AE used for feature engineering having a feature set size of 15 features.
Future work entails applying the proposed ML pipelines and their variants on other real-world datasets with larger size as well higher-dimensions. Various contexts belonging to healthcare domain might be considered, enabling diagnosis done at an early stage with greater accuracy and minimizing the costs incurred for memory and computations.

Funding

The author would like to thank Deanship of Scientific Research at Majmaah University for supporting this work under Project Number xxxx-xxx.

Data Availability Statement

Dataset available at the following link : https://archive.ics.uci.edu/dataset/529/early+stage+diabetes+risk+prediction+dataset

Acknowledgments

The author would like to thank Deanship of Scientific Research at Majmaah University for supporting this work under Project Number xxxx-xxx.

Conflicts of Interest

The authors declare no conflict of interest

References

  1. The 6 Different Types of Diabetes: (5 Mar 2018). The diabetic journey. https://thediabeticjourney.com/the-6-different-types-of-diabetes.
  2. Failure to detect type 2 diabetes early costing $700 million per year, Diabetes Australia, 8 July 2018.https://www.diabetesaustralia.com.au.
  3. Harris, M.I.; et al. Onset of NIDDM occurs at least 4–7 yr before clinical diagnosis. Diabetes Care 1992, 15, 815–819. [Google Scholar] [CrossRef] [PubMed]
  4. Choac, N.H.; et al. IDF Diabetes Atlas: Global estimates of diabetes prevalence for 2017 and projections for 2045. Diabetes Research and Clinical Practice 2018, 138, 271–281. [Google Scholar]
  5. Sarwar, N.; et al. Diabetes mellitus, fasting blood glucose concentration, and risk of vascular disease: a collaborative meta-analysis of 102 prospective studies. The Lancet 2010, 375, 2215–2222. [Google Scholar]
  6. Statistics About Diabetes: American Diabetes Association, 22 Mar 2018. https://www.diabetes.org.
  7. Akter, S.; et al. Prevalence of diabetes and prediabetes and their risk factors among Bangladeshi adults: a nationwide survey. Bull. World Health Organ 2014, 92, 3204–3213. [Google Scholar] [CrossRef] [PubMed]
  8. Islam, M. M.; Ferdousi, R.; Rahman, S.; Bushra, H. Y. Likelihood prediction of diabetes at early stage using data mining techniques. In Computer Vision and Machine Intelligence in Medical Image Analysis; Springer: Singapore, 2020; pp. 113–125. [Google Scholar]
  9. Perveen, S.; et al. Performance analysis of data mining classification techniques to predict diabetes. Procedia Computer Science 2016, 82, 115–121. [Google Scholar] [CrossRef]
  10. Belhouari, S.B.; Bermak, A. , “Gaussian process for nonstationarytime series prediction. Computational Statistics & Data Analysis 2004, 47, 705–712. [Google Scholar]
  11. Maniruzzaman, M.; et al. Comparative approaches for classification of diabetes mellitus data : Machine learning paradigm. Computer Methods and Programs in Biomedicine 2017, 152, 23–34. [Google Scholar] [CrossRef]
  12. Sisodia, D.; Sisodia, D.S. , “Prediction of diabetes using classification algorithms. Procedia Computer Science 2018, 132, 1578–1585. [Google Scholar] [CrossRef]
  13. Wang, Q.; et al. DMP_MI: An effective diabetes mellitus classification algorithm on imbalanced data with missing values. IEEE Access 2019, 7, 102232–102238. [Google Scholar] [CrossRef]
  14. Vaishali, R.; et al. Genetic algorithm based feature selection and MOE Fuzzy classification algorithm on Pima Indians Diabetes dataset. in Proc. 2017 International Conference on Computing Networking and Informatics (ICCNI), Lagos, 2017, pp. 1–5. [CrossRef]
  15. Maniruzzaman, M.; Rahman, M. J.; Al-MehediHasan, M.; Suri, H. S.; Abedin, M. M.; El-Baz, A.; Suri, J. S. Accurate Diabetes Risk Stratification Using Machine Learning: Role of Missing Value and Outliers. Journal ofMedical Systems 2018, 42. [Google Scholar] [CrossRef]
  16. Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and minredundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
  17. David Howell. Statistical Methods for Psychology. Wadsworth Publishing, June 2001.
  18. Rao, C.R. The use and interpretation of principal component analysis in applied research. Sankhyā: The Indian Journal of Statistics, Series A 1964, 329–358. [Google Scholar]
  19. Kaur, H.; Kumari, V. Predictive modelling and analytics for diabetes using a machine learning approach. Applied Computing and Informatics 2018. [Google Scholar] [CrossRef]
  20. Li, T.; Fong, S. A Fast Feature Selection Method Based on Coefficient of Variation for Diabetics Prediction Using Machine Learning. Inter. Journal of Extreme Automation and Connectivity in Healthcare 2019, 1, 55–65. [Google Scholar] [CrossRef]
  21. Sneha, N.; Gangil, T. Analysis of diabetes mellitus for early prediction using optimal features selection. J Big Data 2019, 6. [Google Scholar] [CrossRef]
  22. Hasan, M.K.; et al. Diabetes Prediction Using Ensembling of Different Machine Learning Classifiers. IEEE Access 2020, 8, 76516–76531. [Google Scholar] [CrossRef]
  23. Hyvärinen, A.; Oja, E. , “Independent Component Analysis: Algorithms and applications. Neural Networks 2000, 13, 411–430. [Google Scholar] [CrossRef]
  24. Han, F.; Liu, H. , “Statistical analysis of latent generalized correlation matrix estimation in transelliptical distribution. Bernoulli: official journal of the Bernoulli Society for Mathematical Statistics and Probability 2017, 23, 23–57. [Google Scholar] [CrossRef]
  25. Chen, T.; Guestrin, C. XGboost: A scalable tree boosting system. in Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2016, pp. 785–794.
  26. Khanam, J.J.; Foo, S.Y. A comparison of machine learning algorithms for diabetes prediction. ICT Express 2021. [Google Scholar] [CrossRef]
  27. Sivaranjani, S.; Ananya, S.; Aravinth, J.; Karthika, R. Diabetes prediction using ma- chine learning algorithms with feature selection and dimensionality reduction, in: 2021 7th International Conference on Advanced Computing and Communi- cation Systems (ICACCS), IEEE, 2021, pp. 141–146. vol. 1.
  28. Singh, N.; Singh, P. , Stacking-based multi-objective evolutionary ensemble framework for prediction of diabetes mellitus, Biocybernetic. Biomed. Eng. 2020, 40, 1–22. [Google Scholar]
  29. Zolghadr-Asli, B.; Bozorg-Haddad, O.; Chu, X. Crow Search Algorithm (CSA). Advanced Optimization by Nature-Inspired Algorithms. Studies in Computational Intelligence 2018, 720, 143–149. [Google Scholar]
  30. Klema, V.; Laub, A. The singular value decomposition: Its computation and some applications. IEEE Transactions on automatic control 1980, 25. [Google Scholar] [CrossRef]
  31. Samreen, S. Memory-Efficient, Accurate and Early Diagnosis of Diabetes Through a Machine Learning Pipeline Employing Crow Search-Based Feature Engineering and a Stacking Ensemble. in IEEE Access 2021, 9, 134335–134354. [Google Scholar] [CrossRef]
  32. AutoEncoders.
  33. Heidari, A. A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future generation computer systems 2019, 97, 849–872. [Google Scholar] [CrossRef]
  34. Chuang, L. Y.; et al. A hybrid feature selection method for DNA microarray data. Computers in Biology and Medicine 2011, 41, 228–237. [Google Scholar] [CrossRef] [PubMed]
  35. Xue, B.; Zhang, M.; Browne, W. N. Particle swarm optimization for feature selection in classification: Novel initialization and updating mechanisms. Applied Soft Computing, Elsevier 2014, 18, 261–276. [Google Scholar] [CrossRef]
  36. Hancer, E.; et al. A binary ABC algorithm based on advanced similarity scheme for feature selection. Applied Soft Computing, Elsevier 2015, 36, 334–348. [Google Scholar] [CrossRef]
  37. Chattopadhyay, S.; Mishra, S.; Goswami, S. Feature selection using differential evolution with binary mutation scheme. in Proc. 2016 Inter conference on microelectronics, computing and comm. (MicroCom), Durgapur, Jan 2016, pp. 1–6. 2016. [Google Scholar]
  38. Nakamura, R.; et al. BBA: A binary bat algorithm for feature selection" in Proc 2012 25th SIBGRAPI conf on graphics, patterns and images, Ouro Preto, Brazil, 2012, pp. 291–297.
  39. Zawbaa, H. M.; Emary, E.; Parv, B.; Sharawi, M. Feature selection approach based on moth-flame optimization algorithm. in Proc.2016 IEEE congress on evolutionary computation (CEC), Vancouver, BC, Canada, July 2016 pp. 4612–4617.
  40. Emary; et al. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
  41. Arora, S.; Anand, P. Binary butterfly optimization approaches for feature selection. Expert Systems with Applications 2019, 116, 47–160. [Google Scholar] [CrossRef]
  42. Abd Elaziz, M.; Oliva, D.; Xiong, S. An improved Opposition-Based Sine Cosine Algorithm for global optimization. Expert Systems with Applications 2017, 90, 484–500. [Google Scholar] [CrossRef]
  43. https://machinelearningmastery.com/mcnemars-test-for-machine-learning/.
  44. Dietterich, T. G. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. Neural Computation 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed]
  45. McNemar and Quinn. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157.
  46. Beleites, C.; Salzer, R. Assessing and improving the stability of chemometric models in small sample size situations. Analytical and Bioanalytical Chemistry 2008, 390, 1261–1271. [Google Scholar] [CrossRef] [PubMed]
Preprints 121542 g001
Figure 1. Proposed ML Pipeline.
Figure 1. Proposed ML Pipeline.
Preprints 121542 g001
Preprints 121542 g002
Figure 2. ROC for different classifiers for the optimal FEP of AE+HHO.
Figure 2. ROC for different classifiers for the optimal FEP of AE+HHO.
Preprints 121542 g002
Table 1. Summarized review of literature.
Table 1. Summarized review of literature.
Authors Year Feature Engg Classifiers Comments
Perveen et al. [20] NIL AB, Bagging ensemble techniques with J48 (C4.5) Decision Tree as a base learner
Maniruzzaman et al. [22] 2017 NIL Gaussian Process(GP), Linear Discriminant Analysis (LDA), Quadratic Discriminant Analysis (QDA), and NB GP has highest accuracy at 81.5%.
Sisodia et al. [25] 2018 NIL SVM, DT, and NB NB achieved highest 76.3% accuracy
Wang et al. [26] 2019 NIL RF Highest accuracy 87.1%
Islam et al. [8] 2020 NIL NB, LR, RF RF with highest accuracy 97.4%
Vaishali et al. [29] 2017 Goldberg's Genetic algorithm for feature selection Fuzzy Classifier Highest accuracy 83%
Maniruzzaman et al. [31] 2018 Mutual Information, ANOVA, PCA LDA, QDA, NB, GPC, SVM, ANN, AB, LR, DT and RF RF highest accuracy 92.26%
Kaur et al. [35] 2018 Boruta algorithm SVM with Linear Kernel and Radial Basis Function kernel, KNN, ANN SVM highest accuracy 89%
Li et al. [36] 2019 Coefficient of Variation (CV) DT and Multilayer Perceptron mlodel Multilayer Perceptron highest accuracy 77%
[37] 2019 correlation-based feature selection method NB, DT, RF, and SVM NB classifier highest accuracy 82.3%.
Hasan et al. [22] 2020 PCA, Independent Component Analysis (ICA), and Correlation-based technique KNN, DT, RF, AB, NB, XGBoost, and Multilayer Perceptron (MLP) Ensemble of AB and XGBoost achieved the highest AUC of 0.95.
[26] 2021 DT, RF, NB, K-NN, and AB AB achieving the best accuracy of 79.42%.
[27] 2021 Step forward and backward fea- ture selection + PCA RF and SVM RF highest accuracy 83%
Singh et al. [28] 2020 NIL Stacking ensemble of Linear and Radial Basis SVM, DT, and K-NN Highest accuracy 83.8%
Table 3. Accuarcy With Different FEPs.
Table 3. Accuarcy With Different FEPs.
Feature Engineering Approach No of Features CLASSIFIERS – ACCURACY
AB SVC DT RF GB LR KNN Stacking
None 31 89.50 94.76 93.60 94.76 94.76 89.53 93.60 95.91
AutoEncoder (AE) 15 97.10 92.44 94.18 95.93 94.76 93.02 87.21 96.51
HarrisHawk (HH) 14 93.02 95.34 94.18 95.93 95.30 91.27 94.18 95.34
AE+HH 9 93.60 94.86 93.60 96.51 95.93 90.69 92.93 97.51
SVD 15 94.76 95.34 93.60 95.35 95.34 93.02 91.86 94.76
SVD + HH 6 95.05 88.95 94.76 95.34 94.18 86.62 91.27 95.74
Table 4. Precision With Different FEPs and Classifiers.
Table 4. Precision With Different FEPs and Classifiers.
Feature Engineering Approach No of Features CLASSIFIERS - PRECISION X (0.01)
AB SVC DT RF GB LR KNN Stacking
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
None 31 88 91 95 94 94 94 95 94 95 94 86 92 88 96 98 95
AE 15 90 94 80 94 92 95 98 96 94 98 83 98 79 96 98 95
HHO 14 92 93 97 97 93 97 95 97 94 97 92 93 93 97 95 97
AE+HHO 9 94 95 95 99 96 98 98 99 98 96 85 91 88 95 99 97
SVD 15 95 94 95 95 92 94 98 94 97 95 94 93 86 96 98 93
SVD + HH 6 98 92 84 92 94 95 98 94 98 92 82 90 92 91 98 94
Table 5. Recall with Different FEPs and Classifiers.
Table 5. Recall with Different FEPs and Classifiers.
Feature Engineering Approach No of Features CLASSIFIERS - RECALL X (0.01)
AB SVC DT RF GB LR KNN Stacking
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
None 31 85 92 91 97 89 96 91 97 91 97 86 92 97 92 91 99
AutoEncoder (AE) 15 91 93 98 95 97 97 98 99 97 96 97 88 95 85 92 99
HarrisHawk (HH) 14 88 95 95 98 95 95 95 97 95 96 88 95 95 95 95 97
AE+HH 9 92 96 91 97 92 95 94 99 94 99 85 91 98 92 95 99
SVD (15) 15 91 97 92 97 91 95 89 99 92 98 88 96 94 91 88 99
SVD + HH 6 86 99 88 90 92 96 89 99 86 99 83 89 85 95 89 99
Table 7. ROC AUC with Different FEPs and Classifiers.
Table 7. ROC AUC with Different FEPs and Classifiers.
Feature Engineering Approach No of Features CLASSIFIERS – ROC AUC x (100)
AB SVC DT RF GB LR KNN Stacking
None 31 98.97 99.62 96.31 99.65 99.78 98.91 98.73 99.85
AutoEncoder (AE) 15 96.54 95.92 90.73 99.07 98.39 96.68 96.40 98.66
HarrisHawk (HH) 14 97.97 97.67 97.79 98.69 98.69 98.04 98.18 98.94
AE+HH 9 97.16 98.54 97.86 99.84 99.71 96.39 96.69 99.70
SVD 15 98.69 98.48 93.09 99.25 99.41 96.98 98.08 99.56
SVD + HH 6 98.84 97.84 96.31 99.71 99.32 95.22 96.97 99.00
Table 8. Modified Paired T-test with different FEPs and Classifiers.
Table 8. Modified Paired T-test with different FEPs and Classifiers.
FEP No of Features Comparison of p-value obtained with each classifier against a Stacking Ensemble
AB SVC DT RF GB LR KNN
AutoEncoder (AE) 15 0.013 0.031 0.011 0.032 0.015 0.022 0.031
HarrisHawk (HH) 14 0.027 0.043 0.041 0.028 0.021 0.046 0.023
AE+HH 9 0.045 0.047 0.036 0.047 0.027 0.027 0.025
SVD 15 0.017 0.023 0.027 0.012 0.029 0.031 0.032
SVD + HH 6 0.019 0.027 0.032 0.018 0.025 0.022 0.019
Table 9. Experimental results for the optimal feature engineering pipeline with different classifiers.
Table 9. Experimental results for the optimal feature engineering pipeline with different classifiers.
AE+HH for Feature Engineering
Classifier Accuracy Precision Recall F1 Score AUC ROC
AB 93.60 94.50 94.00 94.50 97.16
SVC 94.86 97.00 94.00 94.50 98.54
DT 93.60 97.00 93.50 93.50 97.86
RF 96.51 98.50 96.50 97.00 99.84
GB 95.93 97.00 96.50 97.00 99.71
LR 90.69 88.00 88.00 88.00 96.39
KNN 92.93 91.50 95.00 92.00 96.69
Stacking 97.51 98.00 97.00 97.50 99.70
Table 10. Sensitivity analysis with SVC.
Table 10. Sensitivity analysis with SVC.
AE + HH Feature Engineering
Hyperparameters used with SVC Accuracy Precision x 100 Recall x 100 F1 Score x 100 AUC ROC x 100
{50, 'scale', 'poly'} 92.21 96.00 93.00 92.00 97.50
{50, 'scale', 'rbf'} 93.35 95.00 94.00 93.00 97.00
{50, 'scale', 'sigmoid'} 92.56 95.00 93.00 93.00 96.50
{10, 'scale', 'poly'} 94.32 97.00 92.00 93.00 96.50
{10, 'scale', 'rbf'} 93.66 96.00 92.00 92.00 96.00
{10, 'scale', 'sigmoid'} 93.76 97.00 93.00 93.00 98.00
{1.0, 'scale', 'poly'} 94.86 97.00 94.00 94.50 98.54
{1.0, 'scale', 'rbf'} 93.33 96.00 94.00 93.00 97.00
{1.0, 'scale', 'sigmoid'} 92.51 95.00 94.00 93.50 97.50
{0.1, 'scale', 'poly'} 93.88 96.00 93.00 93.00 98.00
{0.1, 'scale', 'rbf'} 92.92 94.00 92.00 92.00 96.50
{0.1, 'scale', 'sigmoid'} 94.27 95.00 93.00 93.00 96.50
{0.01, 'scale', 'poly'} 93.56 96.00 93.00 93.00 96.00
{0.01, 'scale', 'rbf'} 94.27 97.00 93.00 93.00 98.00
{0.01, 'scale', 'sigmoid'} 93.69 96.00 94.00 94.00 96.50
Table 11. Sensitivity analysis with GBC.
Table 11. Sensitivity analysis with GBC.
AE + HH for Feature Engineering
Hyperparameters used with GBC Accuracy Precision x 100 Recall x 100 F1 Score x 100 AUC ROC x 100
{'0.001, 3, 10, 0.5} 94.43 97.00 95.00 96.50 98.00
{ 0.001, 3, 10, 0.7} 94.00 96.50 95.50 96.00 98.50
{ 0.001, 3, 100, 0.5} 93.50 96.50 96.00 97.00 99.00
{0.001, 3, 100, 0.7} 95.00 96.00 96.00 96.00 98.78
{0.001, 7, 10, 0.5} 94.50 97.00 95.50 96.50 98.00
{ 0.001, 7, 10, 0.7} 95.00 96.00 96.00 96.50 99.50
{ 0.001, 7, 100, 0.5} 94.57 96.50 96.50 96.00 98.67
{ 0.001, 7, 100, 0.7} 94.00 97.00 95.00 95.50 99.00
{ 0.01, 3, 10, 0.5} 95.00 96.50 96.00 96.50 98.78
{ 0.01, 3, 10, 0.7} 94.43 96.00 94.50 96.00 98.00
{0.01, 3, 100, 0.5} 94.00 97.00 96.00 97.00 99.50
{0.01, 3, 100, 0.7} 93.50 96.00 96.50 96.50 98.67
{0.01, 7, 10, 0.5} 95.00 96.50 95.00 95.50 99.00
{0.01, 7, 10, 0.7} 94.43 96.50 96.00 96.50 98.78
{0.01, 7, 100, 0.5} 95.93 97.00 96.50 97.00 99.71
{0.01, 7, 100, 0.7} 95.00 96.50 95.50 96.00 98.50
Table 12. Sensitivity analysis with RFC.
Table 12. Sensitivity analysis with RFC.
AE + HH for Feature Engineering
Hyperparameters used with RFC Accuracy Precision x 100 Recall x 100 F1 Score x 100 AUC ROC x 100
{ 'sqrt', 10} 95.55 97.50 96.00 96.50 99.55
{'sqrt', 100} 95.00 98.00 95.50 96.00 98.00
{'sqrt', 1000} 96.00 97.50 95.00 95.55 98.55
{'log2', 10} 95.50 97.00 96.00 96.50 99.00
{'log2', 100} 96.00 97.50 95.55 96.00 99.50
{ 'log2', 1000} 96.51 98.50 96.50 97.00 99.84
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated