Prerpints.org logo
Preprint
Article

Pattani Multi-Dimensional Poverty Classification Analysis: Comparison of Feature Selection Techniques

This version is not peer-reviewed.

Submitted:

18 October 2024

Posted:

21 October 2024

You are already at the latest version

Abstract
Poverty elimination is an essential and unavoidable step in human development. Predicting poverty is the first crucial step in addressing this issue, especially in developing countries where it remains a significant concern. The main objectives of this paper are: (i) to explore and analyze the multidimensional poverty data in Pattani province, and (ii) to apply feature selection techniques (Chi-Square, Mutual Information, and Gini Index) to enhance the prediction process. These techniques help in reducing irrelevant and redundant features, leading to more efficient models and better insights. This paper presents the development of a predictive model aimed at classifying poverty and providing actionable recommendations for policymakers. Machine learning models, including Decision Tree (DT), Random Forest (RF), and Support Vector Machine (SVM), were employed to assess the impact of feature selection methods on model performance. The effectiveness of each model was evaluated through various metrics, including accuracy. The experimental results show that the success of these models in predicting poverty, with DT, RF, and SVM obtaining 93%, 95%, 94% of accuracy, respectively. The findings underline the importance of feature selection in improving the performance of machine learning models.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Poverty is a multidimensional issue that extends beyond mere income levels, encompassing various aspects of human deprivation, such as access to education, healthcare, and living standards. The Oxford Poverty and Human Development Initiative (OPHI) introduce the Multidimensional Poverty Index (MPI) [1], launched a new approach for assessing a critical poverty in developing nations. This index offers a more comprehensive measurement by examining multiple dimensions of deprivation, providing a deeper understanding of poverty beyond income levels alone. This issue stems from the interplay of various political, social, and economic factors that intensify the deprivation experienced by impoverished populations. These complex dynamics collectively contribute to worsening poverty and inequality. Addressing poverty, therefore, requires a holistic approach that considers multiple dimensions beyond income, such as health, education, and living standards. The World Bank’s report on poverty and inequality highlights the ongoing struggle to reduce global poverty, emphasizing that despite numerous efforts, achieving the aim of decreasing poverty rate to below 3% by 2030 is becoming increasingly difficult, especially with global crises impacting economic progress [2]. Achieving this target will be nearly impossible without immediate, bold, and large-scale political interventions that address the underlying factors and accelerate progress towards poverty reduction on a global scale [2]. Over the years, the issue of poverty eradication has evolved into a major international concern, garnering significant attention from governments, organizations, and institutions around the world. This focus has intensified, particularly following the introduction of the Sustainable Development Goals (SDGs) [3], which have set a comprehensive global framework aimed at eliminating poverty in all its forms by addressing its root causes and promoting sustainable development across nations. The SDGs have further solidified poverty eradication as one of the key objectives for ensuring a more equitable and prosperous future for all.
Despite various initiatives aimed at poverty alleviation, a significant portion of the population in one of Thailand's southernmost provinces, Pattani, continues to live below the national poverty line, exemplifying the ongoing challenges of multidimensional poverty in the region. The province's socio-economic landscape is further complicated by political instability and economic inequality. Accurate poverty identification and classification are crucial for effective policymaking and resource allocation. Traditional unidimensional measures, which rely solely on income [4], have proven insufficient in capturing the full spectrum of poverty in Pattani.
Machine learning and data-driven approaches offer promising alternatives for poverty classification and prediction [5]. By leveraging multidimensional data, these techniques can provide more accurate and actionable insights into the factors driving poverty. Feature selection is essential as it identifies the most significant variables from a potentially vast and intricate dataset. By effectively selecting key features, the performance of predictive models can be significantly improved, while also enhancing their interpretability. This, in turn, makes the models more actionable and valuable for policymakers, as they are easier to understand and apply to decision-making processes.
The multidimensional poverty classification analysis in Pattani province, Thailand, aiming to identify the most relevant features influencing poverty levels, is focused on three widely used feature selection techniques: (i) Chi-Square [6], (ii) Mutual Information [7], and (iii)Gini Index [8,9]. Each method has its strengths and weaknesses in handling different types of data and capturing various relationships between variables. By applying these techniques to the multidimensional poverty data from Pattani province, this research aims to identify the key features that influence poverty levels, and to develop robust predictive models for poverty classification.
The structure of the paper is organized as follows: Section 2 presents the related work in relation to feature selection techniques and machine learning models. Section 3 describes the materials and methods used. Section 4 presents the results and Section 5 discusses the results obtained for the methods used. Finally, Section 6 provides the concluding remarks

2. Literature Review

In this section, we examine the significance of machine learning models and feature selection techniques in the context of multi-dimensional poverty classification. Feature selection techniques are crucial for reducing data dimensionality, improving the performance of models, and enhancing interpretability. By focusing on the most relevant features, these techniques help refine the analysis of complex socio-economic datasets.
The use of machine learning models, including Decision Trees, Random Forests, and Support Vector Machines (SVM), has proven highly effective in poverty classification tasks. These models have the capability to manage both linear and non-linear relationships between variables, making them well-suited for multi-dimensional poverty analysis. Decision Trees are known for their simplicity and interpretability [10], while Random Forests, as an ensemble method, reduce the risk of overfitting and improve classification performance [11]. SVMs are especially effective for managing high-dimensional data and detecting intricate relationships within poverty indicators [12].
In multi-dimensional poverty classification, feature selection techniques are essential for identifying the most relevant factors. Techniques such as Chi-Square, Mutual Information, and the Gini Index have been widely used in poverty studies to improve model performance. The Chi-Square test facilitates the identification of the most significant categorical characters in a dataset [13]. Mutual Information measures the dependency between variables and captures both linear and non-linear relationships, making it particularly useful in multi-dimensional poverty studies [14]. The Gini Index, often used in Random Forests, ranks feature importance according to their impact on reducing impurity in the model [15].
Together, these machine learning models and feature selection methods provide powerful tools for categorizing and analyzing multi-dimensional poverty, facilitating more accurate predictions and insights for targeted poverty alleviation interventions. The following subsections outline widely used feature selection techniques and their application in multi-dimensional poverty studies.

2.1. Feature Selection Techniques

2.1.1. Chi-Square

The Chi-square (χ²) test is a statistical technique utilized to evaluate the relationship between variables of categorical to determine if they are independent of each other. In feature selection, it is applied to identify which features show a significant connection with the target variable. In poverty studies, this method is particularly useful for identifying important binary variables, such as whether a household has access to clean drinking water or electricity [13].
In a study by Zhao et al. [16], Chi-square feature selection was applied to classify households' poverty levels in rural China. The analysis found that factors like literacy rates and access to healthcare had significant associations with poverty outcomes.

2.1.2. Mutual Information

Mutual Information (MI) evaluates the dependence between two variables. Mutual Information is especially valuable in multi-dimensional poverty classification, as it detects complex relationships between poverty indicators and outcomes. It is a non-linear method that accounts for both linear and non-linear associations, in contrast to Chi-square, which is confined to categorical data. [17].
For instance, a study by Ahmed et al. [14] used Mutual Information to analyze the dependency between various socio-economic indicators and poverty status in Pakistan. They found that factors such as healthcare accessibility, education, and employment were highly informative in determining poverty.

2.1.3. Gini Index

The Gini Index, originally a measure of inequality, is often applied in decision tree-based algorithms to assess feature importance. The Gini Index evaluates the "purity" of a split by measuring the distribution of classes. Features that lead to more homogenous splits (i.e., with lower Gini Impurity) are considered more important. This method is widely used in classification problems, especially in Random Forest algorithms, where the Gini Index helps in ranking features based on their contribution to reducing impurity [11]. In the context of multi-dimensional poverty classification, Gini Index has been applied to rank the importance of variables such as household income, access to sanitation, and educational attainment. A study by Liang et al. [15] demonstrated that using Gini Index in a Random Forest model improved the accuracy of poverty classification in rural India.

2.2. Machine Learning Models

2.2.1. Decision Tree

Decision Trees are simple yet powerful classification algorithms that split data into subgroups based on certain decision rules. They work by recursively partitioning the dataset and making decisions by focusing on the most important features [10]. Decision Trees have been extensively applied in poverty analysis because of their clarity and capacity to manage both categorical and continuous variables. A study by Jana et al. [18] applied Decision Tree models to a multi-dimensional poverty dataset in India and found that variables like education level, access to healthcare, and household assets were the most critical factors for classifying poverty. The Decision Tree model achieved an accuracy rate of 75% in classifying households into different poverty categories.

2.2.2. Random Forest

Random Forest is an ensemble learning method that builds multiple Decision Trees and aggregates their results to improve classification accuracy. Unlike Decision Trees, Random Forest mitigates the risk of overfitting by combining the predictions from multiple trees, thus improving generalization [11]. For instance, Kalu et al. [19] applied Random Forest models to classify poverty levels in Nigeria, using variables like household income, access to clean water, and healthcare services. The Random Forest model achieved an accuracy rate of 85%, outperforming other models such as Logistic Regression and Decision Trees. In a similar context, applying Random Forest to Pattani's multi-dimensional poverty data could reveal critical variables and ensure more robust poverty classification.
A study by Ahmed et al. [20] further emphasized the strengths of Random Forest in handling imbalanced datasets, which is often a challenge in poverty classification. Their study demonstrated that Random Forest performed well in distinguishing between different levels of poverty by giving appropriate weights to underrepresented classes.

2.2.3. Support Vector Machine (SVM)

Support Vector Machine (SVM) is a supervised learning model used for classification tasks. It works by finding a hyperplane that best separates data into different classes. SVM is particularly useful when dealing with high-dimensional datasets, where it can capture non-linear relationships between variables using kernel functions [12]. A study by Sultana et al. [21] utilized SVM to classify households into poverty categories based on various socio-economic factors in Bangladesh. The SVM model achieved higher accuracy compared to decision trees and logistic regression, notably when utilizing a Radial Basis Function (RBF) kernel [22]. Another study by Sharma et al. [23] demonstrated that SVM performed well in handling noise and outliers in poverty datasets, which is a common issue in real-world data. The authors used a poverty dataset from rural Nepal and found that SVM with a polynomial kernel achieved an accuracy rate of 80%, outperforming traditional models.

2.3. Comparative Analysis of Feature Selection Techniques and machine learning Models

Several studies have compared the effectiveness of different feature selection techniques in the context of poverty classification. For example, Alsharif et al. [24] compared Chi-square, Mutual Information, and Gini Index in a poverty classification model for Egyptian households. Their results indicated that while all methods improved model performance, Mutual Information offered the best balance between capturing non-linear relationships and reducing data dimensionality, while Gini Index performed well in Decision Tree-based models. In another study, Nahakul [25] applied Chi-square, Mutual Information, and Random Forest (using Gini Index) to a dataset of poverty indicators from rural Nepal. They found that Chi-square was most effective for categorical variables, while Mutual Information provided a more holistic understanding of both categorical and continuous data. The Gini Index overtaken the other techniques regarding classification accuracy when combined with tree-based algorithms.
Several studies have compared the effectiveness of Decision Trees, Random Forests, and SVM classifiying poverty. A comparative study by Zhang et al. [26], identified that Random Forest (RF) and Support Vector Machine (SVM) consistently outperformed decision trees in terms of accuracy and generalization. The study applied these models to a multi-dimensional poverty dataset from rural China and reported that Random Forest achieved an accuracy of 87%, while SVM reached 85%. Decision trees, on the other hand, were found to be more interpretable but less accurate, with an accuracy of 72%.
Similarly, Olken et al. [27] compared the three models on a poverty classification task in Indonesia and found that Random Forest and SVM outperformed Decision Trees, particularly in handling non-linear relationships between variables. The study highlighted that while Decision Trees were useful for understanding key poverty indicators, Random Forest and SVM provided better overall classification accuracy.
In Random Forest models, feature importance is determined by measuring how much each variable enhances to the model’s accuracy. For instance, in poverty classification studies, variables like access to education, healthcare, and employment status often rank high in importance [15]. Similarly, SVM models can utilize techniques like Recursive Feature Elimination (RFE) to select the most important features, improving model performance [15].
A study by Silva et al. [28] used RFE in conjunction with SVM to classify poverty levels in Mozambique. The study found that variables such as household income, education, and access to clean water were the most significant predictors of poverty. For Pattani, applying RFE with SVM could help in identifying the key socio-economic factors that contribute to poverty.

3. Materials and Methods

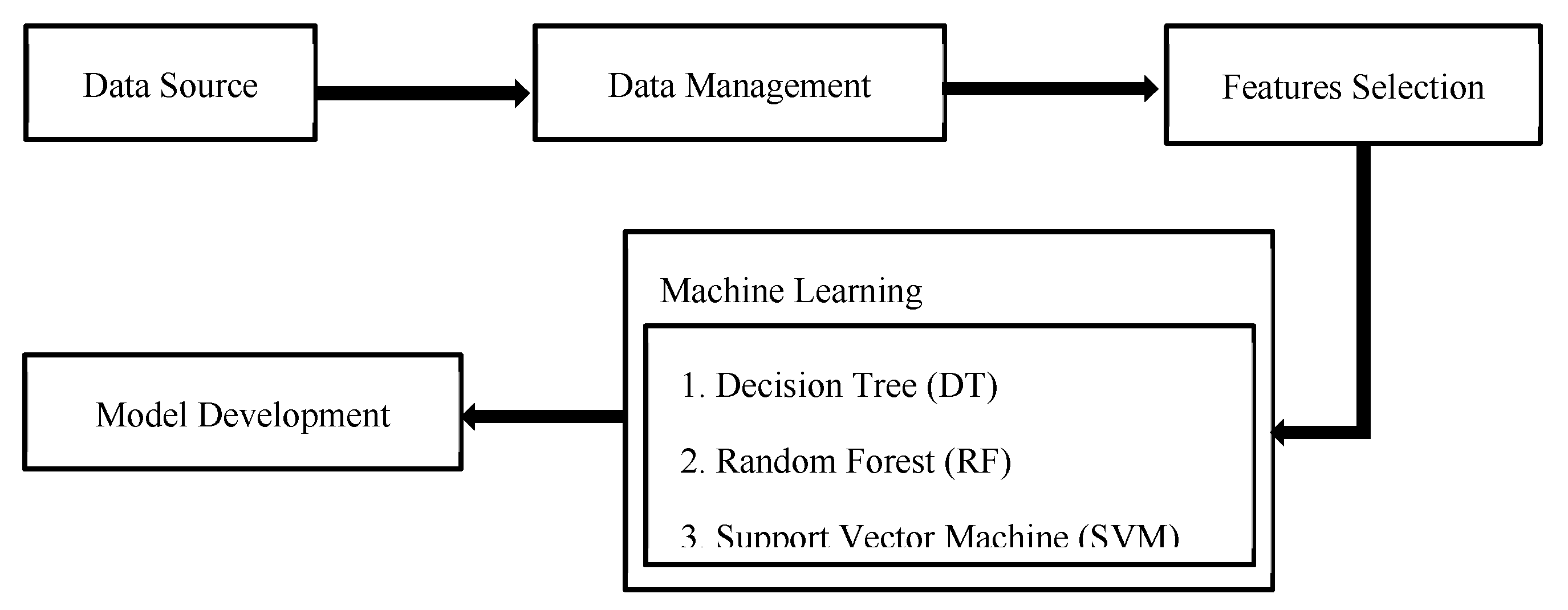
This section provides a detailed description of the comprehensive methodological process undertaken in this study. The entire process is visually represented and explained through Figure 1. The proposed methodology consists of the following stages: (i) data source, (ii) data management, (iii) feature selection, (iv) model development, and (v) model evaluating.
The first stage of this study involves using secondary data, which was provided by the Program Management Unit on Area based development (PMUA) [29]. The second stage consists in managing the obtained data to ensure completeness by extracting input features, which serve as independent variables to represent the five categories of deprivation. In the third stage, feature selection is applied using various descriptive statistics to obtain the important features, and to implement them in the selected model. In the fourth stage, this study proposes the implementation of machine learning models and related algorithms: (i) Decision tree, (ii) Random Forest, and (iii) Support Vector Machine. Finally, the method concludes by evaluating the performances, selecting an appropriate model to be predicted, and categorizing poverty into different classes.

3.1. Data Preparation

In the present study, obtained the data from the Program Management Unit on Area-Based Development (PMUA), which was carried out by the National Higher Education Science Research and Innovation Policy Council (NXPO) [29], were analyzed. The Community Development Department (CDD) classified the households based on the village-accelerated development framework, the analysis was focusing on those with an income below the average of 65,000 THB per person per year, according to fundamental necessities criteria. The original dataset comprised 17,191 impoverished households and 86 variables, with the 12 districts of Pattani province (Khok Pho, Mae Lan, Yaring, Saiburi, Panare, Nong Chik, Muang Pattani, Mayo, Mai Kaen, Kapho, Yarang, and Tung Yang Daeng.). This study aims to view the concept of poverty through the lens of the Sustainable Livelihood Approach, which integrates multiple dimensions of livelihood into the analysis.

3.2. Data Management and Data Exploration

Data preprocessing tasks are often iterative and not necessarily conducted in a predefined order. The preprocessing stage typically consists of two steps: data cleansing and data transformation. Data cleansing involved handling missing data and ensuring data quality. Specifically, this study originally utilized 56 variables across five dimensions (capita) as shown in Table 1.
The data exploration phase was carried out by representing the frequency and percentage distributions for each capita category. During this process, missing values, anomalies, and inconsistencies were identified in the dataset. To address these issues, a manual technique was applied collaboration with the main office responsible for the dataset. This approach was applied to both numerical and categorical datasets, ensuring that any missing, anomalous, or inconsistent data were appropriately managed, thus improving the overall integrity and reliability of the dataset for further analysis [30].
Nonetheless, the missing numerical data included one variable (age), while the missing categorical data included six variables (sex, health status, Thai reading and writing skills, education level, education status, and occupation status), which were addressed manually. Given the richness of the dataset, preprocessing was necessary to eliminate variables that were not relevant to analyse in order to produce a suitable dataset to which to apply feature selection techniques and identify the most important variables for the analysis.

3.3. Feature Selection

Chi-square: The Chi-square method is utilized to analyze and evaluate the relationship between categorical variables within a dataset. Specifically, the Chi-Square test is a statistical technique employed to assess the independence between two categorical variables. It evaluates whether the observed frequency distribution of the data differs from the expected distribution if the variables were independent. This method is particularly useful for feature selection in classification problems involving categorical data [31]. The independent variables in the dataset used in this study consist of 56 variables, while the dependent variables consist of 3 variables (the poverty levels). These dimensions represent five distinct forms of capital that each individual possesses, and feature selection was applied to these dimensions to identify the most relevant variables, as illustrated in Table 1. A total of 56 variables remains after applied each feature selection method.
Mutual Information: The Mutual Information (MI) quantifies the data gained regarding one random variable through the influence of another random variable [32]. It quantifies the dependency between variables and captures both linear and non-linear relationships. Mutual Information is widely used for feature selection in both classification and regression problems.
Gini Index: The Gini Index is a measure of the impurity or purity of a node in a decision tree. It reflects the likelihood of a randomly chosen element being incorrectly classified if it were labelled according to the distribution of labels in the node. The Gini Index is commonly used in decision tree algorithms to select features that best split the data into homogeneous subsets [33].
This process is applied using supervised machine learning algorithms and statistical analysis methods. While Machine Learning algorithms include Random Forests (RF), Decision Trees (DT), and Support Vector Machines (SVM), conventional statistical analysis are analyzed using Multinomial Logistic Regression. The result of the appropriate model is then applied to the poverty dimensions by verifying through model assessment and evaluation. This study also applies several feature selections techniques such as Chi-square, Mutual Information (MI), and Gini Index, while some other methods being applied are Cramer’s V-Test, and Principal Component Analysis (PCA)

3.4. Machine Learning Classification Techniques

Machine Learning (ML) relates to the development and application of models that are generated from data. In other disciplines, this process is often termed predictive modeling or data mining, but in this study, it will be referred to as machine learning. Normally, the objective is to utilize existing data to develop models that can be employed to predict various outcomes for new data. Machine learning is generally divided into three primary types of learning: (i) supervised learning, (ii) unsupervised learning, and (iii) reinforcement learning. In general terms, classification refers to supervised learning, and clustering to unsupervised learning.
Decision Tree (DT) is a structure similar to a flowchart used for decision-making and classification tasks. In this structure, each internal node represents a test or decision on a specific attribute or feature. The branches stemming from each node correspond to the possible outcomes or results of that test, leading to further decisions. The leaf nodes, located at the ends of the branches, represent the final classification outcomes or distributions, indicating the predicted class or value based on the input data. This intuitive model is widely used for both classification and regression tasks due to its simplicity and interpretability [34,35,36].
Random Forest (RF) The algorithm is a bootstrap aggregating ensemble classifier, which combines the predictions of multiple models to improve overall performance. It operates efficiently, processing data quickly, and is recognized for its relatively high accuracy compared to other classification algorithms [37]. This method aids in minimize overfitting and increases the model’s robustness by aggregating the results of several weaker models to make a more reliable final prediction. Random Forests (RF), formally introduced as a bagging method to improve classification accuracy, involve combining multiple models. By using a large number of decision trees, RF can effectively overcome the problem of overfitting, the generalization error approaches a fixed value in accordance with the strong law of large numbers. This method was first developed and introduced by Leo Breiman [11], who aimed to enhance the reliability of classification models [15,16]. The RF algorithm can provide a rank variable base on their importance. To assess the importance of a proposed variable, the average impurity decrease across all trees in the forest is calculated for each node in which the variable is included. The variable that results in the greatest reduction in impurity will be considered the most significant. This process ensures a systematic evaluation of each variable's contribution to the model's predictive accuracy [38].
Support Vector Machine (SVM) is a machine learning technique grounded in statistical learning theory. It identifies an optimal boundary or maximum-margin hyperplane to separate samples from different categories within the training set's sample space. The separation principle aims to maximize the margin [39], ultimately converting the problem into a convex quadratic programming task for solution. SVM model represents data points in space, ensuring categories are separated by a significant ga. As new instances are mapped, they are correctly classified based on their position relative to the gap [40].

3.5. Model Evaluation

The selected Machine Learning models for this study are DT, RF, and SVM, which can have their classification prediction represented as confusion matrix:
Confusion Matrix: shows the number of correct and incorrect classified instances of test data from each class. The confusion matrix presented in Table 2 can be explained as follows:
True Positives (TP): The certain data have been classified as Positive and true data are also Positive. True Negatives (TN): The certain data have been classified as Negative and actual data are also Negative. False Positives (FP): The data are projected to be Positive but actual data are in Negative False Negatives (FN): The data are projected to be Negative but actual data are in Positive.
Accuracy: A critical parameter in measuring the effectiveness of classification models is accuracy, which reflects how often the model correctly predicts the target outcomes. Accuracy is quantified as the fraction of correct predictions to the total the quantity of predictions generated by the classifier. This metric is essential in determining the model's effectiveness in solving classification tasks. It represents the proportion of correctly classified instances over total number of instances, with the result then multiplied by 100 [30,19] and it can be described as:
A c c u r a c y = ( T P + T N ) T P + F P + ( F N + T N ) * 100
Sensitivity (Recall or True positive rate): describes the proportion of actual positive values to be predicted correctly out of the model. (describes the ratio actual positive cases that are suitably predicted by the model). It is useful when false negatives dominate false positives. It is also called Recall (REC) or True Positive Rate (TPR).
Specificity (True Negative Rate): It is computed as the ratio of correct negative predictions to the total number of negatives, also known as the True Negative Rate (TNR).
Precision is a metric that explains how many of the predicted positive values are actually correct. In other words, it accesses the ratio of true positives to the total number of positive predictions generated by the model. This measure is essential in determining the reliability of the model, particularly in scenarios where false positives are more concerning than false negatives [41]. High precision indicates that the model provides more accurate positive predictions, making it useful in cases where minimizing incorrect positive results is a priority.
F-score: In situations where two models exhibit either low precision and high recall or the reverse, it becomes challenging to compare their performance effectively. To resolve this challenge, the F-score metric can be employed. The F-score, which represent the precision and recall are combined using the harmonic mean, provide a comprehensive evaluation of the models. Through the consideration of both precision and recall, enabling a more comprehensive comparison [42]. The F-score represents the precision and recall are combined using the harmonic mean [42]. By calculating F-score, it is possible to simultaneously evaluate both recall and precision, offering a more balanced view of a model's performance.

4. Results

4.1. Data Distribution

The distribution of feature selection of five dimensions is shown in the Table 3 to 7. The first dimension of distribution was Human Capita as shown in Table 3.
Table 3 shows all the 14 independent variables across each of the feature selection methods, (Chi-squared, Mutual Information (MI), and Gini Index (GI)). For instance, when applied with the Chi-squared test, 13 out of the 14 variables were substantial, with a p-value below 0.001, except for education status (0.138), which had a p-value greater than 0.005 indicating its insignificance and potential for omission. In the case of the Mutual Information method, 10 out of the 14 variables were significant. The MI values for variables such as Occupation Status (0.19) and Not Agricultural Income (1.28) are relatively high, indicating that these features have strong relationships with the target variable, and that are likely important for the classification task. On the other hand, variables like Family Member (0.00) and Household Status (0.00) have low MI values, suggesting they do not provide much information and may be less useful for the model. In contrast, when applying the Gini Index Method, 14 variables were significant. The GI values for features such as Not Agricultural Income (0.90), and Occupation Status (0.46) are relatively high, indicating that these features are important for improving the accuracy of the classification model. They help to separate the data into distinct classes more effectively. On the other hand, features like Family Member (0.37) and Household Status (0.37) have lower Gini Index values, suggesting that they are less significant for reducing classification errors. The results of the feature selection methods applied to the Physical Capita variable are shown in Table 4.
Table 4 indicates that all the 13 independent variables were significant when evaluated using the Chi-square and the Gini Index methods. In the Chi-square test, all variables had a p-value of less than 0.001, except for "Alternative energy" with a p-value of 0.039, signifying strong statistical significance for most variables. The Gini Index values were consistently high at 0.89, indicating that all variables contributed substantially to model purity. Results from the Mutual Information (MI) method show that eight variables met the criteria, with MI values greater than 0.001. Among these, House (0.07), House condition (0.04), Get benefit of digit (0.05), and Use digital tech. (0.02) stood out as the most informative variables based on MI values. However, some variables such as Agricultural land, Water source, and Land problem (work) scored 0.00 in MI, suggesting they have little relevance in non-linear relationships. The results of the feature selection methods applied to the Economic Capita variable are presented in Table 5.
Table 5 shows that all the 15 independent variables were significant across the different feature selection methods. The Chi-square test was applied, and all variables had a p-value of less than <0.001, indicating strong statistical significance. For the Mutual Information (MI) and Gini Index (GI) methods, all the 15 variables passed the selection criteria with values greater than > 0.001. In the Mutual Information method, the variables Household income (0.23), Provincial income (0.23), and Agriculture income (0.19) had the highest MI values, showing they provided the most information about the target variable. For the Gini Index, values ranged from (0.59) to (0.68), with Household income and Provincial income having the highest GI values at 0.68, indicating their strong contribution to reducing model impurity. Overall, these results suggest that all variables are important for predicting economic capital outcomes. The application of these feature selection methods reveals that income-related variables, particularly Household income, Provincial income, and Agriculture income, are the most significant indicators of economic capital. The results of the feature selection methods applied to Natural Capita are presented in Table 6.
Table 6 shows that all the 8 independent variables were significant when evaluated using the Chi-square test, with p-values less than <0.001, indicating strong statistical significance. In terms of Mutual Information (MI), six variables passed the criteria with MI values greater than > 0.001. However, two variables (Use natural for living, and Use natural for work) were omitted as their MI values were (0.00), indicating little to no contribution in terms of information gain. The variables Disaster type.W (0.12) and Work in disaster (0.10) had the highest MI values, suggesting they provide the most information regarding natural capital. For the Gini Index (GI), all variables scored between (0.78) and (0.82), with Use natural for work (0.82) and Disaster type.W (0.81) having the highest Gini Index values, indicating their strong contribution to reducing model impurity. These results suggest that natural disaster-related variables, especially Disaster type and Frequency, are the most influential for predicting natural capital outcomes. Results of the feature selection techniques applied to the Social Capita variables are shown in Table 7.
Table 7 shows that all the 7 independent variables were significant when evaluated using the Chi-square test and the Gini Index, with p-values less than <0.001. This indicates that each variable significantly contributes to the classification of Social Capital. For the Mutual Information (MI) method, six variables passed the criteria with MI values greater than >0.001, while one variable (Use Experience) was omitted due to an MI value of 0.00, indicating it provides no information for this classification. Help Problem (0.23) and Participation (0.21) had the highest MI values, suggesting these variables provide the most information regarding social capital. The Gini Index (GI) values range from (0.67) to (0.78), with Help Problem (0.78) having the highest value, reflecting its strong contribution to reducing model impurity, followed by Participation (0.76). Overall, the results highlight that Help Problem, Experience, and Participation are the most important variables for predicting social capital, while Use Experience does not contribute significantly.

4.2. Applying the Machine Learning Models

In modern Machine Learning, the quality and relevance of input data play a critical role in determinant the effectiveness and efficiency of predictive models. When working with high-dimensional datasets, many features can be redundant, irrelevant, or noisy, which can degrade model performance, increase computational costs, and make models more difficult to interpret. Feature selection is a crucial step in mitigating these challenges. By identifying and selecting only the most important features, Machine Learning models can operate more efficiently, leading to better estimates and enhanced insight of the underlying data patterns. This process becomes especially beneficial when applied to models for example Decision Trees (DT), Random Forests (RF), and Support Vector Machines (SVM) [41].
Decision Trees is the first model of study was applied, followed by Random Forest, and finally, the Support Vector Machine model. The dataset comprised 16,373 records and the dataset comprises 56 variables related to poverty in Pattani province, concentrating on five main dimensions of deprivation. The data was split randomly, with 70% (11,461 records) used for training and 30% (4,912 records) used for testing the model. The feature set consisted of various variables: 14 variables representing human and physical capita, 9 variables for economic capita, 8 variables for natural capita, and 7 for social capita. The results of the analysis are shown in Table 8, in which the classification results are compared across three machine learning models: Decision Tree (DT), Random Forest (RF), and Support Vector Machine (SVM) across five capita types: Human, Physical, Economic, Natural, and Social. For each capita type, the models classify individuals or households into three categories: (i) Extreme (ii) (Ext), Moderate (Mod), and (iii) Vulnerable (Vul).
As it can be seen from Table 8, for the Human Capita variable, the number of instances classified under each category is fairly consistent across models, especially in the "Vulnerable" category, where all models show 1,616 records. Random Forest classifies more instances in the "Extreme" category (2,113) compared to Decision Tree (2,015) and SVM (2,036). In the case of the Physical Capita variable, the largest category here is "Moderate," with over 4,700 records across all models. The number of records classified as "Extreme" and "Vulnerable" is significantly smaller in comparison. For the Economic Capita variable, similar trends are observed in the "Moderate" category, where all models classify around 3,490 to 3,625 records. The "Vulnerable" classification shows slight differences across models, with SVM classifying 1,060 records, slightly more than Decision Tree and Random Forest. For the Natural Capita variable, there is a stark difference between the "Extreme" and "Vulnerable" categories. Most records are classified as "Vulnerable" (over 4,600 records) in all models, while "Extreme" classifications are very low (below 31records across models). Finally, in the Social Capita variable, the "Moderate" classification is consistent across all models, with about 4,000 records classified in this group. The "Extreme" classification has fewer records, with Random Forest showing the lowest at 10, while Decision Tree has 82 records and SVM has 39 records. Results of the statistical test are shown in Table 9.
Table 9 provides a comparison of the statistical test results across three machine learning models—Decision Tree (DT), Random Forest (RF), and Support Vector Machine (SVM)—for various classifications (Human Cap, Physical Cap, Economic Cap, Natural Cap, Social Cap). The table presents the accuracy and corresponding confidence intervals for each classification category using the three models. The overall statistical assessment of Decision Tree represented the highest accuracy Natural Capita classification accuracy, followed by Physical Capita, Social Capita, Human Capita and Economic Capita (99%, 94%,94%,93, and 86% respectively). The statistical assessment of Random Forest represented the highest accuracy of Natural Capita classification accuracy, followed by Social Capita, Physical Capita, Human Capita and Economic Capita (98%, 96%,95%,93%, and 87% respectively). Finally, the overall statistical assessment of Support Vector Machine obtained the highest accuracy Natural Capita classification accuracy, followed by Social Capita, Physical Capita, Human Capita, and Economic Capita (98%, 97%,95%,94%, and 86% respectively).

5. Discussion

The feature selection techniques are applied to the five dimensions of poverty—human, physical, economic, natural, and social capital—demonstrated significant variations in the selection of important variables across the Chi-squared test, Mutual Information, and Gini Index methods. Chi-squared test results showed that nearly all variables were significant, while Mutual Information and Gini index omitted some variables in each dimension. This variation highlights the significance of selecting appropriate feature selection techniques based on the dataset and specific requirements of the analysis. The findings show that, for human capita, 15 out of 16 variables were significant using the Chi-squared test, while Mutual Information omitted four variables. Physical, economic, natural, and social capita dimensions followed similar trends, with a substantial number of variables remaining relevant across all feature selection methods. For the Machine Learning models applied (Decision Tree, Random Forest, and Support Vector Machine), the performance was consistent, particularly in terms of accuracy across different poverty classifications. The overall statistical results indicate that all models performed best in classifying natural capita, with accuracy rates reaching up to 99% for Decision Tree, 98% for Random Forest, and 98% for SVM. Social and physical capita classifications also showed high accuracy across models, while human and economic capita classifications were slightly lower, with accuracies ranging from 86% to 94%.

6. Conclusions

In conclusion, the study demonstrates the effectiveness of using feature selection techniques used alongside with Machine Learning models to classify multi-dimensional poverty. Each feature selection method contributed uniquely, and Machine Learning models emerged as the most robust models for accurate poverty classification. The results highlight that feature selection plays an essential role in enhancing the performance of Machine Learning models, particularly in high-dimensional datasets. Chi-square, Mutual Information, and Gini Index each offer unique strengths in identifying key poverty indicators, the integration of these methods can lead to more precise and interpretable models. In the context of Pattani, where poverty is influenced by a range of socio-economic and geographic factors, these techniques provide valuable tools for developing targeted interventions. While the implementation of Machine Learning models such as Decision Trees, Random Forests, and SVM offers promising solutions for multi-dimensional poverty classification in Pattani. These models provide varying strengths in terms of accuracy, interpretability, and the ability to handle complex datasets. Random Forest and SVM generally outperform Decision Trees in terms of accuracy, but Decision Trees remain valuable for their simplicity and ease of interpretation.
To achieve the desired goal of this analysis, it was required to compare different feature selection techniques to determine the most significant variables for multi-dimensional poverty classification. The implementation of the Chi-square, Mutual Information, and Gini Index methods provided a comprehensive assessment of variable importance across different domains of capital. Each method offered unique insights, with Chi-square identifying broad statistical significance, MI highlighting the most informative variables, and Gini Index ranking features based on model performance. Machine Learning models were used in the study conducted to determine their effectiveness (DT, RF, and SVM) in classifying various socio-economic capital types in a multi-dimensional poverty framework. Based on the high accuracy rates across all categories (ranging from 0.86 to 0.99) and the narrow confidence intervals, the models successfully met this goal. Each model demonstrated strengths in specific areas, and SVM and RF, in particular, showed strong performance in most categories. The study offer important insights into the applicability of these models for poverty classification, achieving the intended objective of comparing their effectiveness in this context. Thus, the study confirms that SVM and RF are well-suited for classifying multi-dimensional poverty, with SVM being the most effective overall, and DT excelling in specific simpler contexts like Natural Capita.
Future research may focus on incorporating advanced Machine Learning techniques, liked Deep Learning, which are gradually being applied in feature selection for poverty classification. Techniques like autoencoders, which learn hierarchical features, can automatically identify the most relevant indicators from large datasets [43]. Additionally, there is growing interest in incorporating spatial data into multi-dimensional poverty classification models. Studied by Barham et al. [44] show that integrating geographic data significantly enhances model accuracy, particularly in regions like Pattani where spatial isolation plays a significant role in poverty dynamics. The use of Geography Information System (GIS) data can further improve the precision of poverty classification models. By reducing redundant and irrelevant features, these models not only improve in efficiency but also provide deeper insights into the underlying socio-economic patterns [45]. These findings provide a pathway for further research and implementation in poverty studies, ensuring that data-driven approaches can improve the targeting and effectiveness of poverty reduction strategies. Additionally, they can guide future research and inform policy decisions aimed at addressing poverty in Pattani province and similar regions.

Author Contributions

Conceptualization, M.U., M.G.-C., S.M. and S.C.-A.; methodology, M.U., M.G.-C., S.M. and S.C.-A.; formal analysis M.U., M.G.-C., S.M. and S.C.-A.; writing—original draft preparation, M.U., M.G.-C., and S.M.; writing—review and editing, M.U., M.G.-C., S.M. and S.C.-A.; supervision, S.M. and S.C.-A. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Digital Science for Economy, Society, Human Resources Innovative Development and Environment project funded by Reinventing Universities & Research Institutes under grant no.2046735. Ministry of Higher Education, Science, Research and Innovation, Thailand and the Oversea Thesis Research grant, Graduate School, Prince of Songkla University under grant no. OTR2567-005.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. S. Alkire and J. Foster, “Counting and multidimensional poverty measurement”. Journal of Public Econ., 95(7): pp. 476–487, 2010.
  2. World Bank, Poverty and shared prosperity 2016: Taking on inequality. 2016. [CrossRef]
  3. United Nations, “Sustainable Development Goals,” United Nations, 2015.
  4. S. Alkire, J. S. Alkire, J. Foster, and S. Seth, Multidimensional Poverty Measurement and Analysis: A Counting Approach. Oxford: Oxford University Press, 2015.
  5. W. Zhao, L. W. Zhao, L. Wang, and Y. Liu, “A machine learning approach to multidimensional poverty measurement,” Journal of Big Data, vol. 8, no. 1, pp. 1-18, 2021.
  6. S. Bahassine, A. S. Bahassine, A. Madani, M. Al-Sarem, and M. Kissi, “Feature selection using an improved Chi-square for Arabic text classification,” Journal of King Saud University - Computer and Information Sciences, vol. 32, no. 2, pp. 225-231, 2020.
  7. H. N. Alshaer, M. A. H. N. Alshaer, M. A. Otair, L. Abualigah, M. Alshinwan, and A. M. Khasawneh, “Feature selection method using improved Chi-square on Arabic text classifiers: analysis and application,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 10,373-10,390, 2021.
  8. S. Solorio-Fernández, J. A. S. Solorio-Fernández, J. A. Carrasco-Ochoa, and J. F. Martínez-Trinidad, “A review of unsupervised feature selection methods,” Artificial Intelligence Review, vol. 53, no. 2, pp. 907-948, 2020.
  9. V. Bolón-Canedo, A. V. Bolón-Canedo, A. Alonso-Betanzos, L. Morán-Fernández, and B. Cancela, “Feature selection: From the past to the future,” in Advances in Selected Artificial Intelligence Areas. Learning and Analytics in Intelligent Systems, vol. 24, M. Virvou, G. A. Tsihrintzis, and L. C. Jain, Eds. Springer, Cham, 2022. [CrossRef]
  10. L. Breiman, J. L. Breiman, J. Friedman, C. J. Stone, and R. A. Olshen, Classification and Regression Trees, Wadsworth International Group, 1984.
  11. L. Breiman, "Random forests," Machine Learning, vol. 45, no. 1, pp. 5-32, 2001.
  12. C. Cortes and V. Vapnik, "Support-vector networks," Machine Learning, vol. 20, no. 3, pp. 273-297, 1995.
  13. H. Liu and H. Motoda, Feature Selection for Knowledge Discovery and Data Mining, Springer, 2012.
  14. T. Ahmed, A. T. Ahmed, A. Kumar, and S. Pathak, "Mutual Information and its application in poverty classification," Journal of Data Science, vol. 27, pp. 93-105, 2021.
  15. Y. Liang, L. Y. Liang, L. Chen, and M. Xu, "Application of Gini Index in poverty analysis: A case study from India," Journal of Socio-Economic Development, vol. 44, pp. 112-129, 2022.
  16. M. Zhao, H. M. Zhao, H. Li, and X. Deng, "Poverty classification using Chi-square feature selection," Poverty and Inequality Studies, vol. 18, pp. 110-124, 2020.
  17. B. Ross, "Mutual Information for feature selection: A review," IEEE Transactions on Knowledge and Data Engineering, vol. 26, no. 5, pp. 1000-1015, 2014.
  18. A. Jana, R. A. Jana, R. Biswas, and S. Bhattacharya, "Multi-dimensional poverty classification using decision tree models: A case study from India," Journal of Data Science, vol. 15, pp. 34-49, 2021.
  19. U. Kalu, M. C. U. Kalu, M. C. Nwosu, and J. Okeke, "Multi-dimensional poverty classification using random forests in Nigeria," Poverty Dynamics, vol. 55, pp. 203-218, 2022.
  20. T. Ahmed, A. T. Ahmed, A. Kumar, and S. Pathak, "Handling imbalanced datasets in poverty classification using Random Forest," Journal of Applied Machine Learning, vol. 37, pp. 89-105, 2023.
  21. M. Sultana and A. Hoque, "Classifying poverty using Support Vector Machines: A case study from Bangladesh," Journal of Machine Learning Research, vol. 8, pp. 255-268, 2021.
  22. T. Shen, Z. T. Shen, Z. Zhan, L. Jin, F. Huang, and H. Xu, "Research on Method of Identifying Poor Families Based on Machine Learning," in Proc. 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conf. (IMCEC), Chongqing, China, 2021, pp. -13. [CrossRef]
  23. S. Sharma, R. S. Sharma, R. Gupta, and M. A. Al-Madfai, "Support Vector Machines for poverty classification: A case study from rural Nepal," Journal of Applied Machine Learning, vol. 45, pp. 75-89, 2022.
  24. A. Alsharif, M. A. Alsharif, M. El-Shafei, and R. Abdel-Kader, "Comparing feature selection techniques for poverty classification in Egypt," Journal of Poverty Analysis, vol. 29, pp. 45-63, 2022.
  25. K. C. Nahakul, "Measuring Multi-Dimensional Poverty Analysis in Nepal," Research Nepal Journal of Development Studies (RNJDS), vol. 1, no. 2, pp. 62-83, Nov. 2018.
  26. J. Zhang Y. Li, and Q. Wang, "A comparative study of Random Forest and SVM for poverty classification in rural China," Journal of Machine Learning and Data Science, vol. 17, pp. 101-115, 2022.
  27. B. Olken, A. B. Olken, A. Wong, and F. Adelman, "Evaluating machine learning models for poverty classification in Indonesia: Decision Trees, Random Forests, and SVM," World Development, vol. 114, pp. 103-120, 2022.
  28. P. Silva et al., "Using Recursive Feature Elimination (RFE) with SVM for poverty classification in Mozambique," Journal of Applied Machine Learning, vol. 37, pp. 45-61, 2023.
  29. M. Useng, A. M. Useng, A. Masamae, S. Musikasuwan, and S. Chuai-Aree, "Pattani Poverty Classification Using Decision Tree and Random Forest Techniques," in Proc. 7th Int. Conf. Information Technology & Society (ICITS), Selangor, Malaysia, Oct. 2022, pp. 75-85.
  30. S. A. Zainudin, M. A. S. S. A. Zainudin, M. A. S. Abdullah, and W. M. M. Wan Zaki, “Dealing with missing data: A review of techniques in machine learning,” Journal of Information and Communication Technology, vol. 19, no. 1, pp. 1-23, 2020.
  31. M. Dawas, “Global multidimensional poverty index in Jordan,” International Association of Official Statisticians (IAOS), OECD Headquarters, Paris, France, 2018.
  32. P. Chen, A. P. Chen, A. Wilbik, S. van Loon, A.-K. Boer, and U. Kaymak, "Finding the optimal number of features based on mutual information," in Advances in Fuzzy Logic and Technology 2017 - Proceedings of EUSFLAT-2017 – The 10th Conference of the European Society for Fuzzy Logic and Technology, IWIFSGN’2017 – The 16th International Workshop on Intuitionistic Fuzzy Sets and Generalized Nets, pp. 2018. [Google Scholar] [CrossRef]
  33. S. D. Roy, "Machine Learning Concepts," Medium, Jan. 29, 2020. [Online]. Available: https://medium.com/@shuv.sdr/machine-learning-concepts-d2ddb3aae08. [Accessed: , 2024]. 09 March.
  34. J. A. Talingdan, “Performance Comparison of Different Classification Algorithms for Household Poverty Classification,” 2019 4th International Conference on Information Systems Engineering (ICISE), 2019, pp. -15. [CrossRef]
  35. A. Ashari, I. A. Ashari, I. Paryudi, A. M. Tjoa, “Performance comparison between Naïve Bayes, decision tree and k-nearest neighbor in searching alternative design in an energy simulation tool,” International Journal of Advanced Computer Science and Applications (IJACSA), 4(11) 2013.
  36. A. A. Bakar, R. A. A. Bakar, R. Hamdan and N. S. Sani, “Ensemble learning for multidimensional povert classification,” Sains Malaysiana, vol. 49, no. 2, pp. 447–459, 2020.
  37. R. B: Thoplan, “Random forests for poverty classification,” International Journal of Sciences, 2014; V17.
  38. R. Agrawal, M. R. Agrawal, M. Paprzycki, and N. Gupta, Eds., Big Data, IoT, and Machine Learning: Tools and Applications, 1st ed. Boca Raton, FL, USA: CRC Press, 2020. [CrossRef]
  39. T. Shen, Z. T. Shen, Z. Zhan, L. Jin, F. Huang and H. Xu, "Research on Method of Identifying Poor Families Based on Machine Learning," 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 2021, pp. -13. [CrossRef]
  40. D. Sai, "Gini Index vs Entropy for Decision Trees (Python)," Medium, Aug. 22, 2020. [Online]. Available: https://medium.com/@durgasai2111996/gini-index-vs-entropy-for-decision-trees-python-1a3fdad4ab29. [Accessed: March. 10, 2024].
  41. C. Kamusoko, J. C. Kamusoko, J. Gamba, and H. Murakami, "Mapping woodland cover in the Miombo ecosystem: A comparison of machine learning classifiers," Land, vol. 3, no. 2, pp. 2014. [Google Scholar] [CrossRef]
  42. P. K. Mondal, K. H. P. K. Mondal, K. H. Foysal, B. A. Norman, and L. S. Gittner, "Predicting Childhood Obesity Based on Single and Multiple Well-Child Visit Data Using Machine Learning Classifiers," Sensors, vol. 23, no. 2, p. 2023. [Google Scholar] [CrossRef]
  43. G. Louppe, L. G. Louppe, L. Wehenkel, A. Sutera, P. Geurts, “Understanding variable importances in forests of randomized trees,” Adv. Neural Information Process System, 2013, V26, pp 431–439.
  44. G. Barham, M. G. Barham, M. Smith, and A. Zhao, "Spatial data integration in multi-dimensional poverty analysis," Journal of Geographic Information Science, vol. 29, pp. 75-98, 2022.
  45. P. Silva, A. P. Silva, A. Kumar, and S. Pathak, "Efficient feature selection for poverty classification models using GIS data," Journal of Applied Machine Learning, vol. 37, pp. 89-105, 2023.
Preprints 121652 g001
Figure 1. Methodological process study.
Figure 1. Methodological process study.
Preprints 121652 g001
Table 1. The Multidimensional Poverty Variables are categorized into five types of capita.
Table 1. The Multidimensional Poverty Variables are categorized into five types of capita.
Dimension Variables description
Human capita
(13 variables)		 Member of Family, Status of HH, Highest Education, Health, Occupation Status, State welfare, Write Thai, Read Thai, Study level, not in agricultural income, Get job, Total State welfare, Number of job skill.
Physical capita
(13 variables)		 House, Electricity, Alternative energy, Water source, Agricultural land, Land problem(work), Road to home, Road to work, Comm. Chanel, Chanel job-live, House condition, use digital tech, Get benefit of digital
Economic capita
(15 variables)		 Crop income, Livestock income, Fishery income, Household income, Provincial income, Household expense, Provincial expense, Agricultural, Agricultural income, Child’s income, Expenditure, Savings, Saving Amout, Debt, Assets
Natural capita
(8 variables)		 Disaster type.H, Disaster Freq.H, Disaster type.W, Disaster Freq.W, Use natural live, Use natural work, House in disaster, Work in disaster
Social capita
(7 variables)		 Help Problem, Rules, Follow, Expert, Use Experience, Experience, Participation
Table 2. The Confusion matrix.
Table 2. The Confusion matrix.
True Label
Prediction Label Positive Negative
Positive True Positive (TP) False Negative (FN)
Negative False Positive (FP) True Negative (TN)
Table 3. The comparison of Human Capita.
Table 3. The comparison of Human Capita.
Human Capita in feature selection methods
Variables Chi-squared MI GI
Degree of Freedom Test values p-values
Number of Family 4 75.56 <0.001 0.00 0.37
Status of HH 4 33.76 <0.001 0.00 0.37
Health 6 595.50 <0.001 0.03 0.39
State welfare 10 1,311.89 <0.001 0.06 0.40
State welfare summary 6 1,031.35 <0.001 0.04 0.40
Read Thai 2 1,314.89 <0.001 0.06 0.40
Write Thai 2 1,162.24 <0.001 0.06 0.40
Highest Education 8 1,981.53 <0.001 0.09 0.42
Study level 8 17.80 0.023 0.00 0.37
Education Status 6 9.71 0.138 0.00 0.37
Occupation Status 2 3,636.44 <0.001 0.19 0.46
Number of jobs 4 3993.90 <0.001 0.02 0.38
Number of job skill 4 941.72 <0.001 0.04 0.39
No income in agricultural 4 26,665.31 <0.001 1.28 0.90
Table 4. The comparison of Physical Capita.
Table 4. The comparison of Physical Capita.
Physical Capita in feature selection methods
Variables Chi-square MI GI
Degree of Freedom Test values p-values
House 6 5,978.2 <0.001 0.07 0.89
Electricity 4 279.4 <0.001 0.01 0.89
Alternative energy 2 6.3 0.039 0.00 0.89
Water source 6 105.8 <0.001 0.00 0.89
Agricultural land 12 103.2 <0.001 0.00 0.89
Land problem(work) 2 19.1 <0.001 0.00 0.89
Road to home 6 134.5 <0.001 0.01 0.89
Road to work 4 50.0 <0.001 0.00 0.89
Comm. Chanel 12 296.9 <0.001 0.01 0.89
Chanel job-live 12 265.3 <0.001 0.01 0.89
House condition 4 863.9 <0.001 0.04 0.89
Use digital tech. 2 437.5 <0.001 0.02 0.89
Get benefit of digit 2 1,070.7 <0.001 0.05 0.89
Table 5. The comparison of Economic Capita.
Table 5. The comparison of Economic Capita.
Economic Capita in feature selection methods
Variables Chi-square MI GI
Degree of Freedom Test values p-values
Crop income 6 4,361.69 <0.001 0.17 0.66
Livestock income 4 285.91 <0.001 0.01 0.59
Fishery income 6 120.90 <0.001 0.01 0.59
Household income 6 5,479.97 <0.001 0.23 0.68
Provincial income 6 5,479.97 <0.001 0.23 0.68
Household exp. 6 2,971.11 <0.001 0.13 0.64
Provincial exp 6 2,971.11 <0.001 0.13 0.64
Agriculture 8 3,335.48 <0.001 0.14 0.65
Agriculture income 6 4,706.88 <0.001 0.19 0.67
Child income 6 127.36 <0.001 0.01 0.59
Expense 6 2,807.44 <0.001 0.12 0.63
Saving 2 388.04 <0.001 0.02 0.59
Saving Value 6 402.84 <0.001 0.02 0.59
Debt 2 1,846.15 <0.001 0.09 0.60
Property 2 2,237.04 <0.001 0.11 0.62
Table 6. The comparison of Natural Capita.
Table 6. The comparison of Natural Capita.
Natural Capita in feature selection methods
Variables Chi-square MI GI
Degree of Freedom Test values p-values
Disaster type.H 6 1,906.65 <0.001 0.07 0.79
Disaster Freq.H 8 798.98 <0.001 0.03 0.78
Disaster type.W 6 5,760.95 <0.001 0.12 0.81
Disaster Freq.W 8 2,885.12 <0.001 0.06 0.79
Use natural live 2 19.68 <0.001 0.00 0.80
Use natural work 2 57.73 <0.001 0.00 0.82
House in disaster 2 358.67 <0.001 0.01 0.78
Work in disaster 2 3,930.67 <0.001 0.10 0.80
Table 7. The comparison of Social Capita.
Table 7. The comparison of Social Capita.
Social Capita in feature selection methods
Variables Chi-square MI GI
Degree of Freedom Test values p-values
Help Problem 8 5,865.70 <0.001 0.23 0.78
Rules 4 794.82 <0.001 0.04 0.68
Follow 2 933.97 <0.001 0.03 0.67
Expert 2 712.79 <0.001 0.03 0.68
Use Experience 2 66.77 <0.001 0.00 0.67
Experience 6 4,355.20 <0.001 0.16 0.75
Participation 6 4,929.58 <0.001 0.21 0.76
Table 8. Confusion matrix comparison methods.
Table 8. Confusion matrix comparison methods.
Classification DT RF SVM
Ext Mod Vul Ext Mod Vul Ext Mod Vul
Human Cap 2,015 1,281 1,616 2,113 1,183 1,616 2,036 1,260 1,616
Physical Cap 99 4,727 86 51 4,801 60 58 4,800 54
Economic Cap 386 3,490 1,036 242 3,621 1,049 227 3,625 1,060
Natural Cap 5 238 4,669 31 181 4,700 7 205 4,700
Social Cap 82 4,009 821 10 4,000 902 39 3,958 915
Table 9. Statistical test results.
Table 9. Statistical test results.
Classification Accuracy Confidence Interval
DT RF SVM DT RF SVM
Human Cap 0.93 0.93 0.94 0.93,0.94 0.93,0.94 0.93,0.94
Physical Cap 0.94 0.95 0.95 0.94,0.95 0.94,0.95 0.94,0.95
Economic Cap 0.86 0.87 0.86 0.85,0.87 0.86,0.88 0.85,0.87
Natural Cap 0.99 0.98 0.98 0.99,1.00 0.98,0.99 0.97,0.98
Social Cap 0.94 0.96 0.97 0.93,0.94 0.95,0.96 0.96,0.97
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated