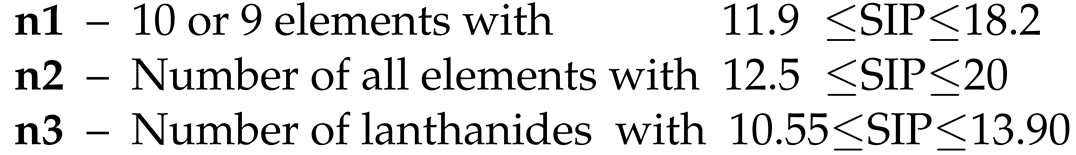Prerpints.org logo
Preprint
Article

The Possible Signs of Accretion from Interstellar Medium in the Atmospheres of G-K-Type Disk and Halo Stars

This version is not peer-reviewed.

Submitted:

20 October 2024

Posted:

21 October 2024

You are already at the latest version

Abstract
The relationships between the relative abundances of chemical elements and their second ionization potentials, as well as their condensation temperatures, were analyzed using four published homogeneous abundance surveys of halo and thin disk stars. We selected 932 stars with effective temperatures ranging from 4900 K to 5900 K and used the abundances of 10 chemical elements common across all surveys: Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, and Ni. The correlation coefficients between the relative abundances of these elements and their second ionization potentials and condensation temperatures were investigated in relation to metallicity and the stars' location in the Galaxy. The observed correlations may result from certain physical processes, such as the accretion of interstellar gas onto stellar atmospheres. We also analyzed the dependencies of relative abundances on second ionization potentials based on published abundance patterns in five halo stars. Evidence of charge-exchange reactions in the atmospheres of these stars was found. For more accurate determination of stellar ages from the abundance ratios of radioactive and stable chemical elements in stellar atmospheres, processes such as charge-exchange reactions and dust-gas separation should be considered in future detailed investigations. Additionally, changes in the chemical abundances in the atmospheres of halo stars after crossing the Galactic plane were found to be possible.
Keywords: 
Subject: 
Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

The main characteristics of stellar abundance patterns were first explained by Burbidge et al. [1] as the result of nuclear reactions occurring in previous generations of stars, as well as in the current generation of evolved stars. However, it was soon recognized that nuclear reactions in stellar interiors alone could not account for the wide variety of stellar chemical compositions. Later, the possibility of accretion from outer space was proposed in many subsequent studies.
For example, Fowler et al. [2] and Proffitt and Michaud [3] proposed that stellar atmospheres could be contaminated by the products of mass transfer from evolved binary companions. Drobyshevski [4] and Cowley [5] explored the possible accretion of asteroids and planets onto stellar atmospheres. In these studies, both mass transfer and accretion were considered short-term processes occurring at specific evolutionary stages.
Another explanation for the variety of stellar chemical compositions was proposed by Michaud [6], who highlighted the significance of radiative diffusion in stellar atmospheres, with a timescale of several million years.
In 1949, Greenstein [7] discovered a decrease in the relative abundances of chemical elements with second ionization potentials (SIP) near the hydrogen ionization potential of 13.6 eV in the atmospheres of metallic line stars. He then proposed charge-exchange reactions between these elements and hydrogen atoms in stellar atmospheres.
Later, Havnes and Conti [8,9] suggested that charge-exchange reactions could result from the accretion of interstellar matter (primarily hydrogen) onto the surfaces of Ap stars with strong magnetic fields. This process was found to not only slow the rotation of these stars but also generate low-energy cosmic rays with energies below 90 MeV/nucleon. While the timescale for this process was comparable to the stars’ lifetimes on the main sequence, more rapid rotational braking (within less than 10 million years) was also deemed possible.
Havnes [10] estimated that magnetic peculiar stars contribute up to 10 percents or less to the cosmic ray flux. North [11] compared Havnes’ work with observations of the rotational periods of Ap stars and demonstrated that at least Si stars do not lose most of their angular momentum during their main-sequence lifetimes, suggesting that the bulk of the loss occurred earlier. North concluded that the contribution of Ap stars to cosmic rays was likely overestimated.
On the other hand, Greenstein [7] and later Böhm-Vitense [12] identified correlations between relative abundances and SIP for stars without strong magnetic fields. The theory explaining this observational effect still needs further development to be applied to stars with weak magnetic fields.
Yushchenko et al. [13] studied the chemical composition of the pulsating variable star HD67523 and found possible signs of accretion from the interstellar (or circumstellar) medium. These features were found not only in the atmosphere of this star but also in B-F type stars, observed by Erspamer and North [14] and Niemczura et al. [15]
Some of these features might be explained by the hypothesis proposed by Greenstein [7] and Havnes [8,9], which suggests that charge-exchange reactions between hydrogen and helium atoms and heavier chemical elements occur in stellar atmospheres. However no definitive conclusion has yet been reached. To confirm or refute this hypothesis, further observational work is needed for various types of stars located in different regions of the Galaxy, with varying densities of interstellar matter. Additionally, Havnes and Conti’s [8,9] numerical results for stars with strong magnetic fields should be extended to include stars with weak magnetic fields.
We have previously investigated possible accretion features in several binary stellar systems [16,17,18,19], in Magellanic Cloud supergiants RM_1-390 and PMMR23 [20,21], in barium stars [22,23], in the supergiant BL138 of the Fornax dwarf spheroidal galaxy [24], in the pulsating variable star V1719 Cyg [25], in F-K giants of the Local region of the Galaxy [26], and in the planetary host halo giant HD47536 [27].
To gain a deeper understanding of charge-exchange reactions in the atmospheres of different stellar types, we analyzed published abundance patterns for G-K type stars with varying metallicities. In particular, we selected four surveys: two for halo stars (Gratton et al. [28] and Roederer et al. [29]) and two for thin disk stars (Adibekyan et al. [30] and Jofre et al. [31]). The analysis of these surveys is presented in the next section, followed by a discussion of the results in the final section.

2. Possible Signs of Accretion in G-K Stars with Different Metallicities

Yushchenko et al. [13,26] discussed possible signs of accretion from the interstellar medium in the atmospheres of B-F type stars and F-K giants in the Local region of the Galaxy. Various correlations have been identified, but no explanations were provided.
In this paper, we aim to identify similar dependencies for cooler stars, specifically G-K stars located in both the halo and disk of the Galaxy. We selected four surveys of chemical composition for these types of stars: two for thin disk stars (Adibekyan et al. and Jofre et al. [30,31]) and two for halo stars (Gratton et al. and Roederer et al. [28,29]).
To compare the results of these studies, we focused on ten chemical elements common to all four cited surveys: Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, and Ni. These elements are indicated with filled symbols in Figure 4 and Figure 5 of Yushchenko et al. [27]. The SIPs of these elements range from 11.9 eV for Ca to 18.2 eV for Ni.
We selected only stars with effective temperatures ranging from 4900 K to 5900 K based on the four surveys mentioned above. Specifically, we included 560 thin disk stars from Adibekyan et al. [30] and 131 from Jofre et al. [31], as well as 93 halo stars from Gratton et al. [28] and 148 from Roederer et al. [29].
It is important to note that the survey by Gratton et al. [28] focuses on objects in the solar vicinity, specifically stars with reliable HIPPARCOS parallaxes. In contrast, the survey by Roederer et al. [29] includes distant halo stars located at significant distances from the Galactic plane.
For all stars included in the surveys, we calculated the correlation coefficients of relative abundances of chemical elements against their second ionization potentials (hereafter CAIP) and the correlation coefficients of the same elements against their condensation temperatures (hereafter CACT).
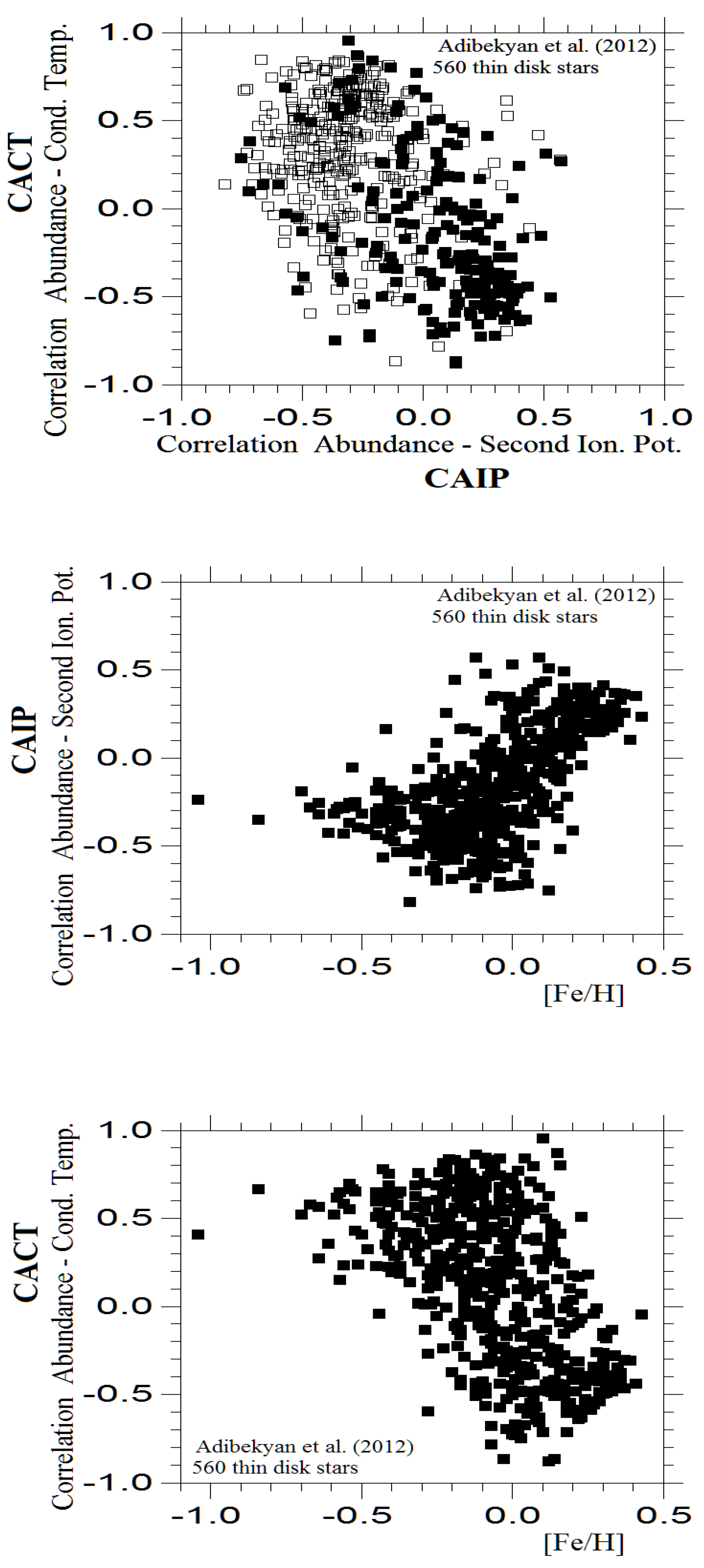
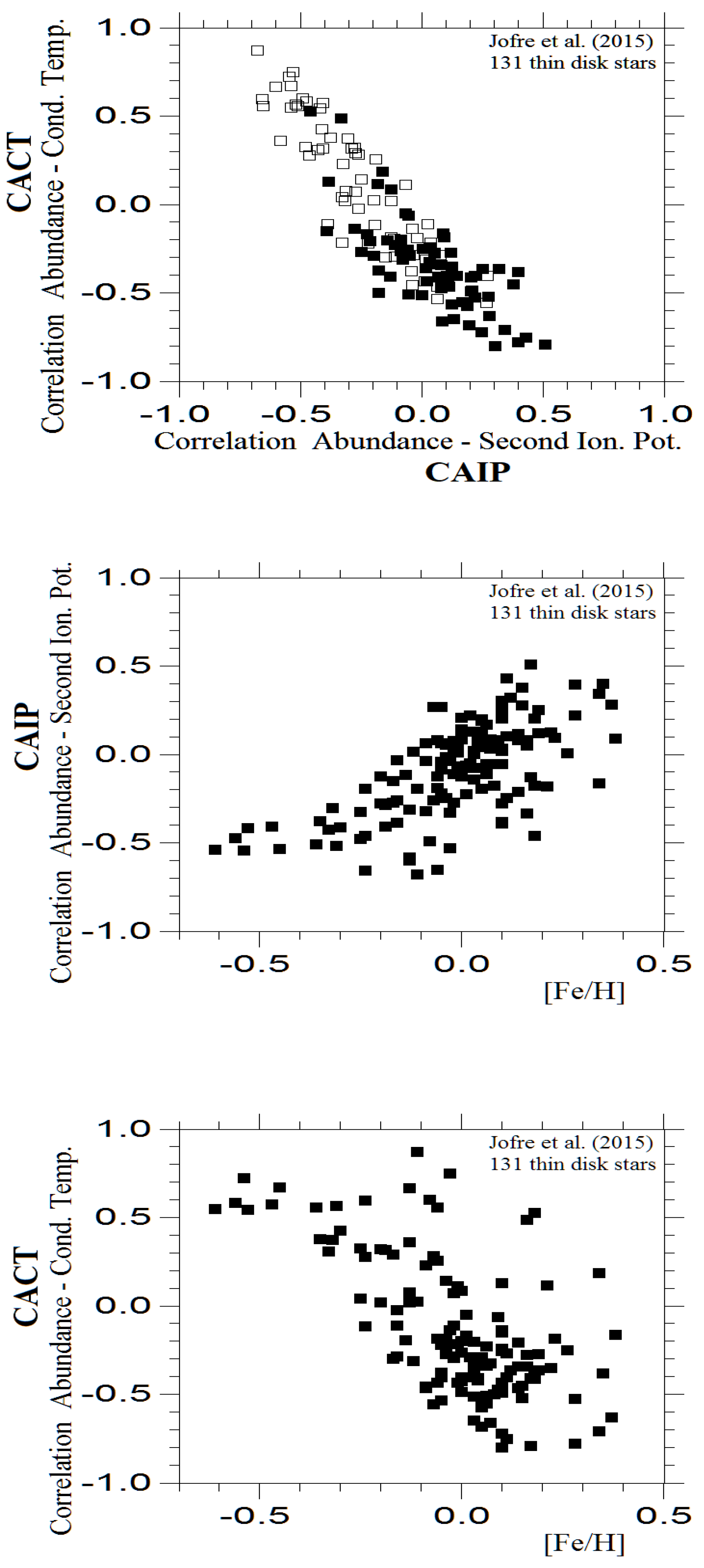
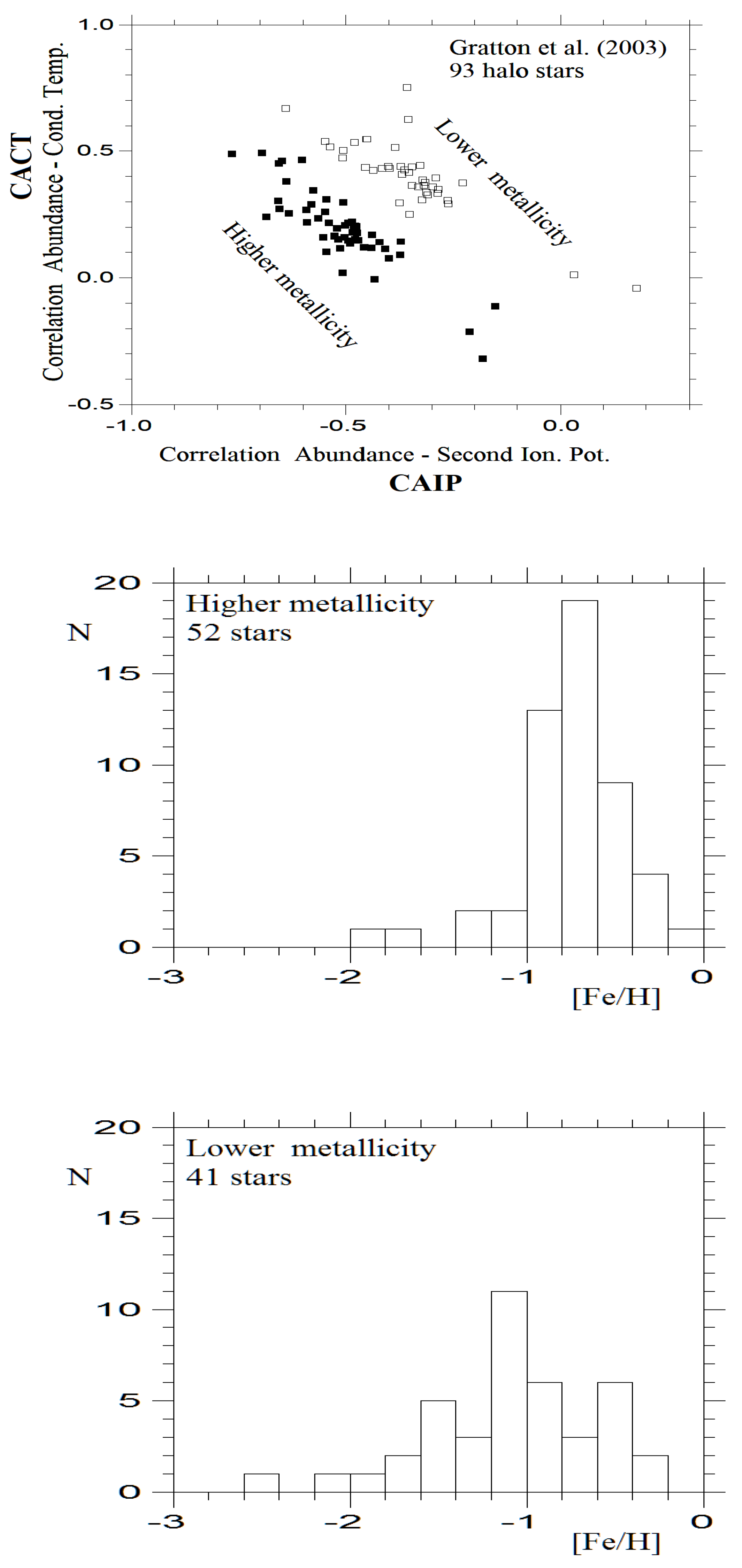
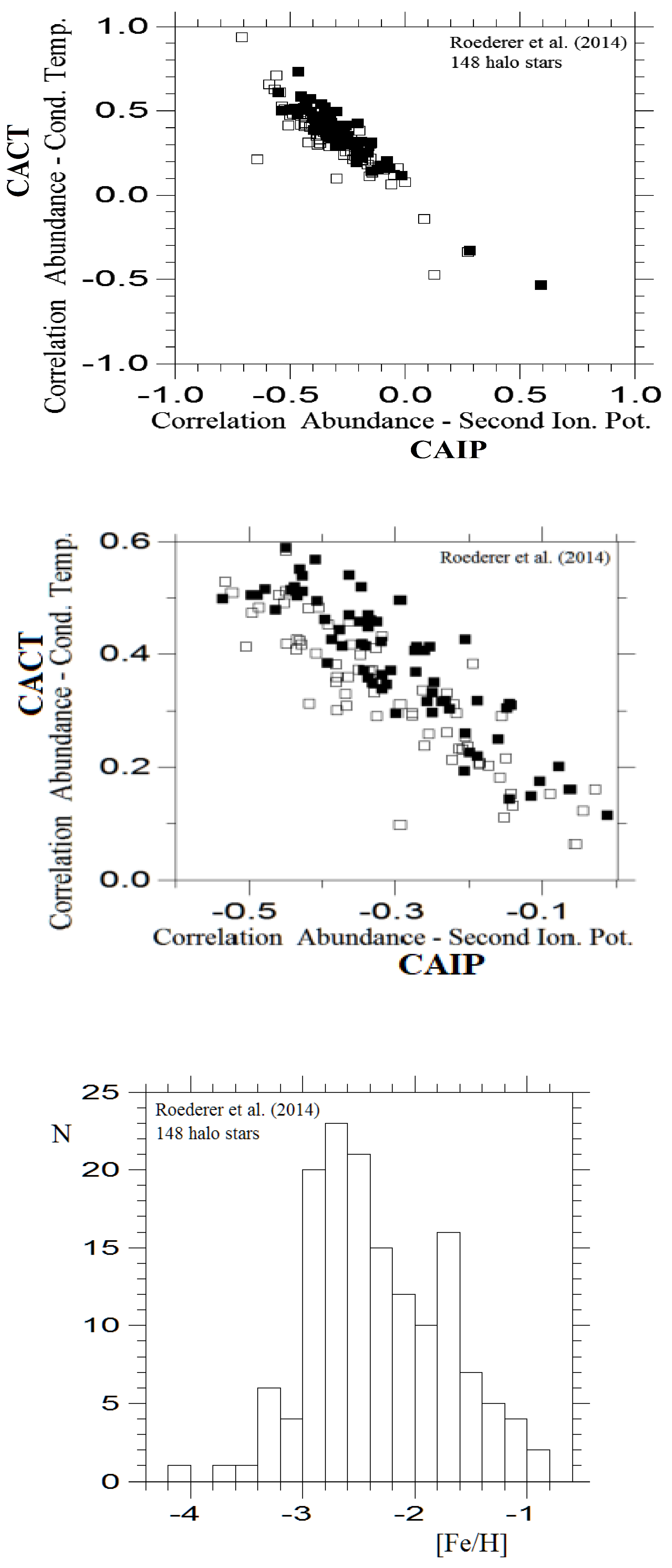
It is worth noting that these two coefficients are correlated with each other; CACT decreases as CAIP increases, as illustrated in the upper panels of Figure 1, Figure 2, Figure 3, Figure 4 for each of the surveys. Stars with varying metallicities are positioned in different parts of these panels, with the highest level of separation observed for stars from Gratton et al. [28].
The middle and bottom panels of Figure 1 and Figure 2 illustrate the dependence of CAIP and CACT on metallicity. The middle and bottom panels of Figure 3 display the metallicity distribution for stellar groups from Gratton et al. survey [28], with higher and lower metallicities indicated by open and filled symbols in the upper panel. The middle panel of Figure 4 provides an enlargement of the most populated region of the upper panel, while the bottom panel shows the metallicity distribution for the stars included in the analysis.
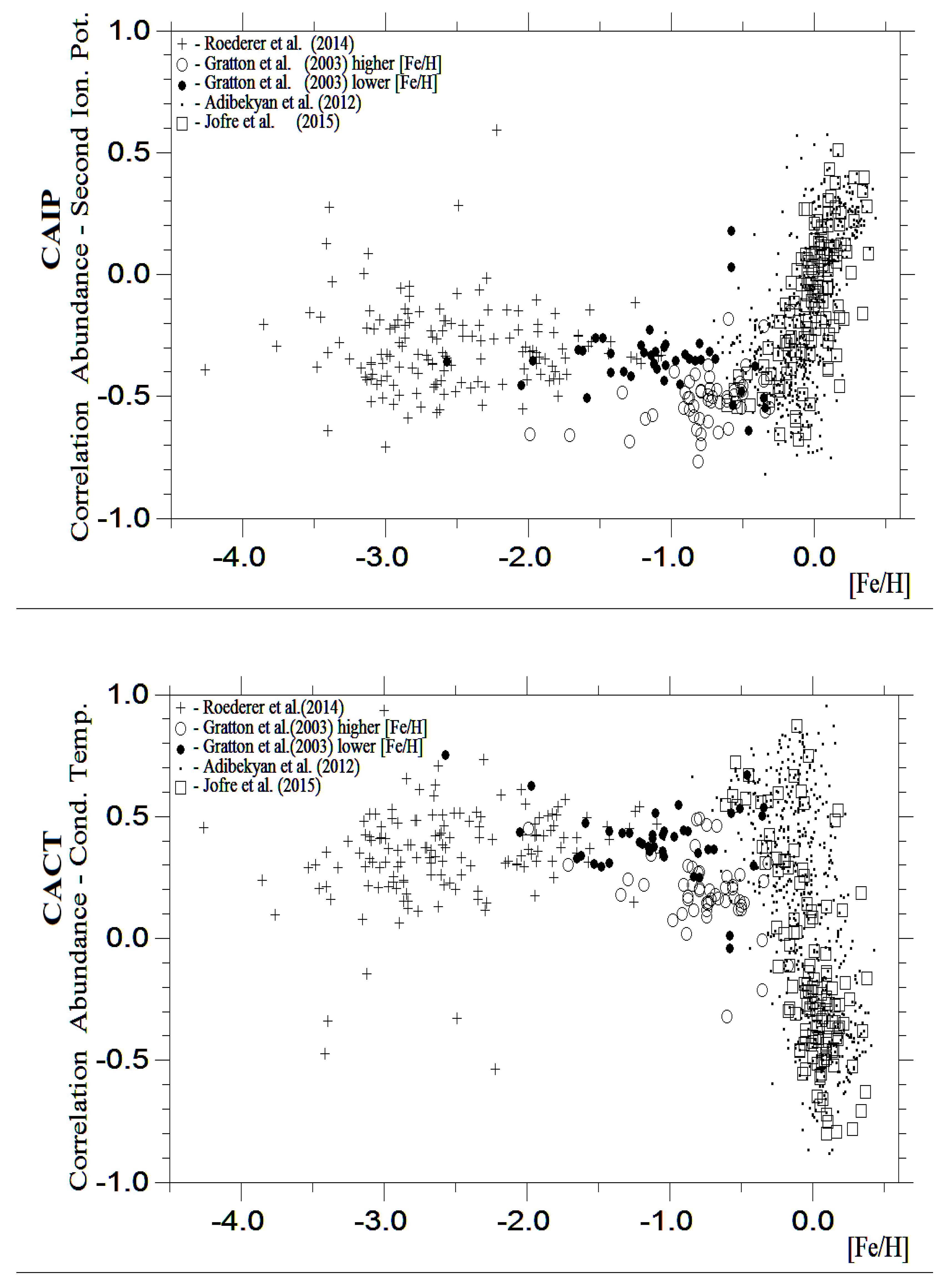
Figure 5 summarizes the previous four plots, illustrating the dependence of CAIP and CACT coefficients on metallicity across all surveys. These coefficients clearly exhibit a dependence on metallicity for thin disk stars, while their dependence remains noticeable for stars from Gratton et al. [28] with metallicities [Fe/H]>-2. However, this correlation practically disappears for stars from Roederer et al. [29] with [Fe/H]<-2.
For halo stars, the CAIP values are predominantly negative, suggesting a possible trend of increasing values as metallicities [Fe/H] decrease from -1 to -4. In contrast, the CACT values for halo stars remain relatively constant, although there may be a slow increasing trend as metallicities [Fe/H] increase from -4 to -1. The next section of this paper provides a more detailed analysis of Figure 1–5.
Preprints 121783 g001
Figure 1. The top panel shows the relationship between two different correlation coefficients calculated for 560 thin disk stars with 5900 K ≥ T eff ≥4900 K taken from Adibekyan et al. (2012) [30]. Solid and open squares mark the stars with positive and negative [Fe/H] values, respectively. The middle and bottom panels show the dependencies of these correlation coefficients on metallicity.
Figure 1. The top panel shows the relationship between two different correlation coefficients calculated for 560 thin disk stars with 5900 K ≥ T eff ≥4900 K taken from Adibekyan et al. (2012) [30]. Solid and open squares mark the stars with positive and negative [Fe/H] values, respectively. The middle and bottom panels show the dependencies of these correlation coefficients on metallicity.
Preprints 121783 g001
Preprints 121783 g002
Figure 2. Similar to previous figure, but for 131 thin disk stars studied by Jofre et al. (2015) [31].
Figure 2. Similar to previous figure, but for 131 thin disk stars studied by Jofre et al. (2015) [31].
Preprints 121783 g002
Preprints 121783 g003
Figure 3. The top panel shows the plot of correlation coefficients of relative abundances versus condensation temperature for ten chemical elements versus the correlation coefficients of the same relative abundances versus a second ionization potential of chemical elements in the atmospheres of 93 halo stars taken from Gratton et al. (2003) [28]. Only these ten chemical elements, namely, Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, and Ni, are shown in Figure 7, 8, 9, and 10. Thin disk stars, as well as stars with an effective temperature higher than 5900 K and lower than 4900 K were not used in this figure. Solid and open squares designate two groups of stars with higher and lower metallicity, respectively. The distribution of [Fe/H] values for these groups are illustrated in middle and bottom panels.
Figure 3. The top panel shows the plot of correlation coefficients of relative abundances versus condensation temperature for ten chemical elements versus the correlation coefficients of the same relative abundances versus a second ionization potential of chemical elements in the atmospheres of 93 halo stars taken from Gratton et al. (2003) [28]. Only these ten chemical elements, namely, Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, and Ni, are shown in Figure 7, 8, 9, and 10. Thin disk stars, as well as stars with an effective temperature higher than 5900 K and lower than 4900 K were not used in this figure. Solid and open squares designate two groups of stars with higher and lower metallicity, respectively. The distribution of [Fe/H] values for these groups are illustrated in middle and bottom panels.
Preprints 121783 g003
Preprints 121783 g004
Figure 4. The top panel, as well as the top panel of the previous figure, illustrates the relationship between correlation coefficients of the relative abundances of ten chemical elements versus a second ionization temperatures and condensation temperatures for 148 halo stars with 5900 K ≥ T eff ≥4900 K taken from Roederer et al. (2014) [29]. The middle panel is an enlarged central part of the top panel. Solid and open squares denote stars with [Fe/H] > − 2.60 and [Fe/H] ≤ − 2.60 , respectively. The distribution of metallicities is shown in the bottom panel.
Figure 4. The top panel, as well as the top panel of the previous figure, illustrates the relationship between correlation coefficients of the relative abundances of ten chemical elements versus a second ionization temperatures and condensation temperatures for 148 halo stars with 5900 K ≥ T eff ≥4900 K taken from Roederer et al. (2014) [29]. The middle panel is an enlarged central part of the top panel. Solid and open squares denote stars with [Fe/H] > − 2.60 and [Fe/H] ≤ − 2.60 , respectively. The distribution of metallicities is shown in the bottom panel.
Preprints 121783 g004
Preprints 121783 g005
Figure 5. The dependencies of correlation coefficients of relative abundances of chemical elements versus the second ionization potentials (top panel) and condensation temperatures (bottom panel) plotted versus metallicity. The stars from Adibekyan et al. (2012) [30], Jofre et al. (2015) [31], Gratton et al. (2003) [28], and Roederer et al. (2014) [29] are marked by different symbols. Only the abundances of common ten chemical elements for the stars with 5900 K ≥ T eff ≥4900 K were selected from mentioned papers. Only thin disk stars were selected from the last two papers. Thick disk stars from the first two papers were not used.
Figure 5. The dependencies of correlation coefficients of relative abundances of chemical elements versus the second ionization potentials (top panel) and condensation temperatures (bottom panel) plotted versus metallicity. The stars from Adibekyan et al. (2012) [30], Jofre et al. (2015) [31], Gratton et al. (2003) [28], and Roederer et al. (2014) [29] are marked by different symbols. Only the abundances of common ten chemical elements for the stars with 5900 K ≥ T eff ≥4900 K were selected from mentioned papers. Only thin disk stars were selected from the last two papers. Thick disk stars from the first two papers were not used.
Preprints 121783 g005

3. Discussion

Yushchenko et al. [13] calculated the correlation coefficients of the relative abundances of chemical elements as a function of second ionization potentials (CAIP) and condensation temperatures (CACT) for several hundred B-F type Galactic stars observed by Erspamer and North [14] and Niemczura et al. [15].
Variations in the relative abundances of chemical elements with respect to their condensation temperatures are generally regarded as a key feature in the abundance patterns of stars with dust and gas envelopes. The dust-gas separation scenario, proposed by Venn and Lambert [32,33] to explain the CACT in lambda Bootis type stars, was utilized by Yushchenko et al. [13] to potentially explain the negative CACT values in hotter stars with effective temperatures as high as 14,000 K,
Yushchenko et al. [26] calculated the same correlation coefficients for F-K giants in the Local region of the Galaxy, using the survey by Luck [34]. It was found that such correlations do indeed exist and depend on the stellar effective temperature. In stars with predominantly radiative energy transfer in their atmospheres, the correlation between relative abundances and SIPs was found to be positive for thirteen chemical elements with SIPs ranging from 12.5 to 20 eV.
Jeong et al. [22] determined the CAIP values for barium stars and suggested that these coefficients might show a correlation with stellar age. Additionally, they found that the CAIP values are sensitive to the selection of chemical elements used in the analysis.
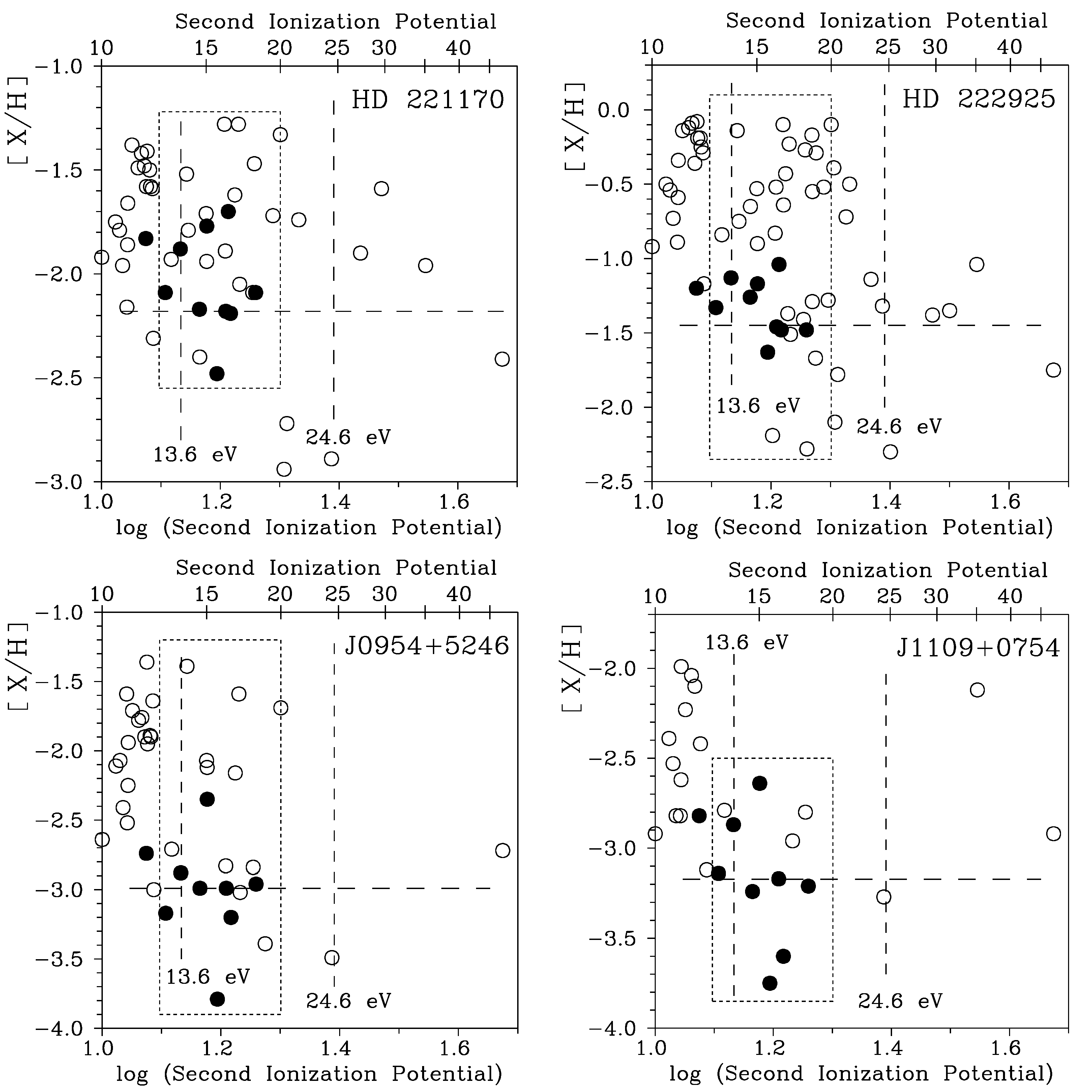
This sensitivity is also illustrated in Figure 6 and Table 1 of the present paper, where we calculated the CAIP in the atmospheres of halo stars HD221170, HD222925, 2MASS J09544277+5246414, and LAMOST J1109+0754 using only ten (or nine) chemical elements. These ten elements are indicated by filled symbols in Figure 6, and the references for the used investigations of these stars are noted in the caption of the figure. The last line of Table 1 presents the results for HD47536 [27].
It is important to note that not all ten chemical elements used in our study were investigated for 2MASS J09544277+5246414 and LAMOST J1109+0754, which results in calculated CAIP values for only nine elements.
Table 1 compares the CAIP coefficients for these ten (or nine) chemical elements with the CAIP calculated for all studied chemical elements having SIPs in the range of 12.5 to 20 eV, as utilized in [13,26].
The CAIP values for only ten or nine chemical elements are negative for all five stars in Table 1, whereas the CAIP values for all investigated chemical elements within the specified SIP range are shifted toward the positive direction, becoming positive for all stars except LAMOST J1109+0754.
Table 1. The CAIP values for five halo stars were calculated using three different methods: with only 9 or 10 chemical elements used in this paper, with all chemical elements having ionization potentials between 12.5 eV and 20 eV studied in the original investigations, and using only the abundances of lanthanides.
Table 1. The CAIP values for five halo stars were calculated using three different methods: with only 9 or 10 chemical elements used in this paper, with all chemical elements having ionization potentials between 12.5 eV and 20 eV studied in the original investigations, and using only the abundances of lanthanides.
Star Ref. n1 CAIP n2 CAIP n3 CAIP
HD221170 [35] 10 −0.27±0.29 24 +0.29±0.19 14 +0.52±0.20
HD222925 [36] 10 −0.42±0.26 35 +0.05±0.17 14 +0.61±0.17
2MASS J09544277+5246414 [37] 9 −0.21±0.32 19 +0.03±0.22 14 +0.78±0.10
LAMOST J1109+0754 [38] 9 −0.48±0.26 11 −0.18±0.29 9 +0.43±0.27
HD47536 [27] 10 −0.17±0.31 17 +0.19±0.23 9 +0.51±0.25
Preprints 121783 i001
For LAMOST J1109+0754, the CAIP value remains negative, but the total number of investigated chemical elements within the specified SIP range is only 11.
Preprints 121783 g006
Figure 6. The plot of relative abundances of chemical elements in halo stars HD221170, HD222925, 2MASS J09544277+5246414, and LAMOST J1109+0754 as a function of second ionization potentials of these elements. The abundances are taken from Ivans et al. (2006) [35], Roederer et al. (2022) [36], Holmbeck et al. (2018) [37], and Mardini et al. (2020) [38] respectively. The positions of the ionizations energies of hydrogen and helium are marked by vertical dotted lines. The horisontal dotted line marks the relative abundance of iron. For HD221170 the abundances of 24 chemical elements with second ionization potentials in the range from 12.5 eV to 20 eV were published. The dotted boxex in all panels show the positions of chemical elements with second ionization potentials from 12.5 to 20 eV. These are 35, 19, and 11 chemical elements for HD222925, 2MASS J09544277+5246414, and LAMOST J1109+0754 respectively. Ten chemical elements discussed in this paper, namely Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, and Ni are marked by filled circles.
Figure 6. The plot of relative abundances of chemical elements in halo stars HD221170, HD222925, 2MASS J09544277+5246414, and LAMOST J1109+0754 as a function of second ionization potentials of these elements. The abundances are taken from Ivans et al. (2006) [35], Roederer et al. (2022) [36], Holmbeck et al. (2018) [37], and Mardini et al. (2020) [38] respectively. The positions of the ionizations energies of hydrogen and helium are marked by vertical dotted lines. The horisontal dotted line marks the relative abundance of iron. For HD221170 the abundances of 24 chemical elements with second ionization potentials in the range from 12.5 eV to 20 eV were published. The dotted boxex in all panels show the positions of chemical elements with second ionization potentials from 12.5 to 20 eV. These are 35, 19, and 11 chemical elements for HD222925, 2MASS J09544277+5246414, and LAMOST J1109+0754 respectively. Ten chemical elements discussed in this paper, namely Mg, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, and Ni are marked by filled circles.
Preprints 121783 g006
We can conclude that the CAIP coefficients for the ten chemical elements used in our study are negative for halo stars. However, as the number of chemical elements included in the calculation increases, the CAIP values are expected to shift in a positive direction. It is important to note that this conclusion is based on the abundance patterns of only five stars.
Figures 3, 4, and 5 of this paper illustrate the negative CAIP values for most of the halo stars analyzed. With a larger number of chemical elements examined, we anticipate that the values of these coefficients will become more positive.
The positive CAIP values within the range of 12.5 to 20 eV may indicate the presence of possible charge-exchange reactions in stellar atmospheres.
Notably, Greenstein [7] observed a decrease in the relative abundances of chemical elements with SIPs near 13.6 eV. Subsequently, both Böhm-Vitense [12] and Yushchenko [13] noted a decrease in the relative abundances of chemical elements not only near 13.6 eV but also near 24.6 eV, the first ionization potential of helium. Figure 6 of Yushchenko [13] displays two cutoffs in the relative abundances near 13.6 eV and 24.6 eV, along with positive correlations between the relative abundances of chemical elements and their SIPs in the intervals between these cutoffs. Positive correlations were also found for chemical elements with SIPs lower than 13.6 eV and higher than 24.6 eV.
The plot of relative abundances versus SIPs resembles a sawtooth wave with two distinct cutoffs. A more detailed examination of the sawtooth pattern in the relative abundances versus SIPs plots for various stars was conducted by Yushchenko et al. [27].
Figure 6 for HD221170 and HD222925 illustrates a sawtooth feature with a cutoff near 12 eV. The last column of Table 4 also presents the CAIP coefficients for five stars calculated specifically for lanthanides. The SIPs for lanthanides range from 10.55 eV for Nd to 12.18 eV for Yb and 13.90 eV for Lu. Notably, the CAIP values for lanthanides are positive for all five stars.
This finding provides additional confirmation of charge-exchange reactions occurring in the atmospheres of these five halo stars. Since the SIP of thorium is 11.9 eV, which is near one of the cutoffs in the relative abundance versus SIP plot, the abundance of thorium also appears to be influenced by these charge-exchange reactions.
Returning to the lanthanide abundances in HD47536 [27], it was noted that the abundances of La, Ce, and Nd decrease relative to the expected s-process enrichment, while the heavier lanthanides align better with potential s-process enrichment, as shown in Figure 3 of [27]. The SIPs for La, Ce, and Nd are 11.06 eV, 10.85 eV, and 10.55 eV, respectively, making them some of the lowest among the lanthanides. This low relative abundance of La, Ce, and Nd likely contributes to the observed positive correlations in the lanthanide relative abundances versus SIPs.
These positive correlations suggest that the abundances of these elements may be influenced by a physical effect identified by Greenstein [7], which could explain the deviation of La, Ce, and Nd abundances from the solar system s-process enrichment trend discussed by Yushchenko et al. [27].
As mentioned earlier, Jeong et al. [22] observed a possible age dependence of the CAIP coefficients in the atmospheres of barium stars. If the abundances of lanthanides and thorium in halo stars are also influenced by charge-exchange reactions, and if this potential age dependence is confirmed, it would complicate the use of the Th to Eu (or other radioactive to stable element) abundance ratio for stellar age determination. This issue requires further investigation.
Is there a way to confirm or refute the possible physical processes involving accretion from the interstellar medium and charge-exchange reactions in the atmospheres of halo stars without additional observations at this time?
If charge-exchange reactions in the atmospheres of halo stars occur due to the accretion of interstellar matter, as proposed by Havnes et al. [8] for magnetic stars, we would expect the CAIP coefficients for halo stars to change when these stars pass through the Galactic plane.
Since the density of interstellar matter in the Galactic plane is higher than in the halo, we anticipate higher values of CAIP coefficients after crossing the Galactic plane. As noted earlier, Gratton et al. [28] investigated some of the nearest halo stars with well-defined HIPPARCOS parallaxes and proper motions, while Roederer et al. [29] analyzed distant halo stars located at significant distances from the Galactic plane.
We calculated the CAIP coefficients for halo stars from the survey by Gratton et al. [28] as a function of time before and after crossing the Galactic plane. The correlation appears to be zero or only slightly positive. Does this indicate that crossing the Galactic plane once is insufficient to change the CAIP coefficients? Not necessarily.
It is important to note that most of the targets from Gratton et al. [28] used in our analysis are stars with surface gravities between log g = 4.0 and log g = 4.6 and effective temperatures ranging from 4900 K to 5900 K. The convection in the atmospheres of these stars likely minimizes any signs of potential accretion and charge-exchange reactions over short time scales. Therefore, it is not surprising that only a small or zero correlation was found.
To confirm or refute changes in CAIP values after crossing the Galactic plane, it is necessary to analyze more luminous halo stars, which primarily exhibit radiative energy transfer in their atmospheres. Such stars are included in the survey by Roederer et al. [29]. Using GAIA DR3 astrometric data collected from the SIMBAD database, we calculated the times before and after crossing the Galactic plane for the stars in Roederer et al. [29] study.
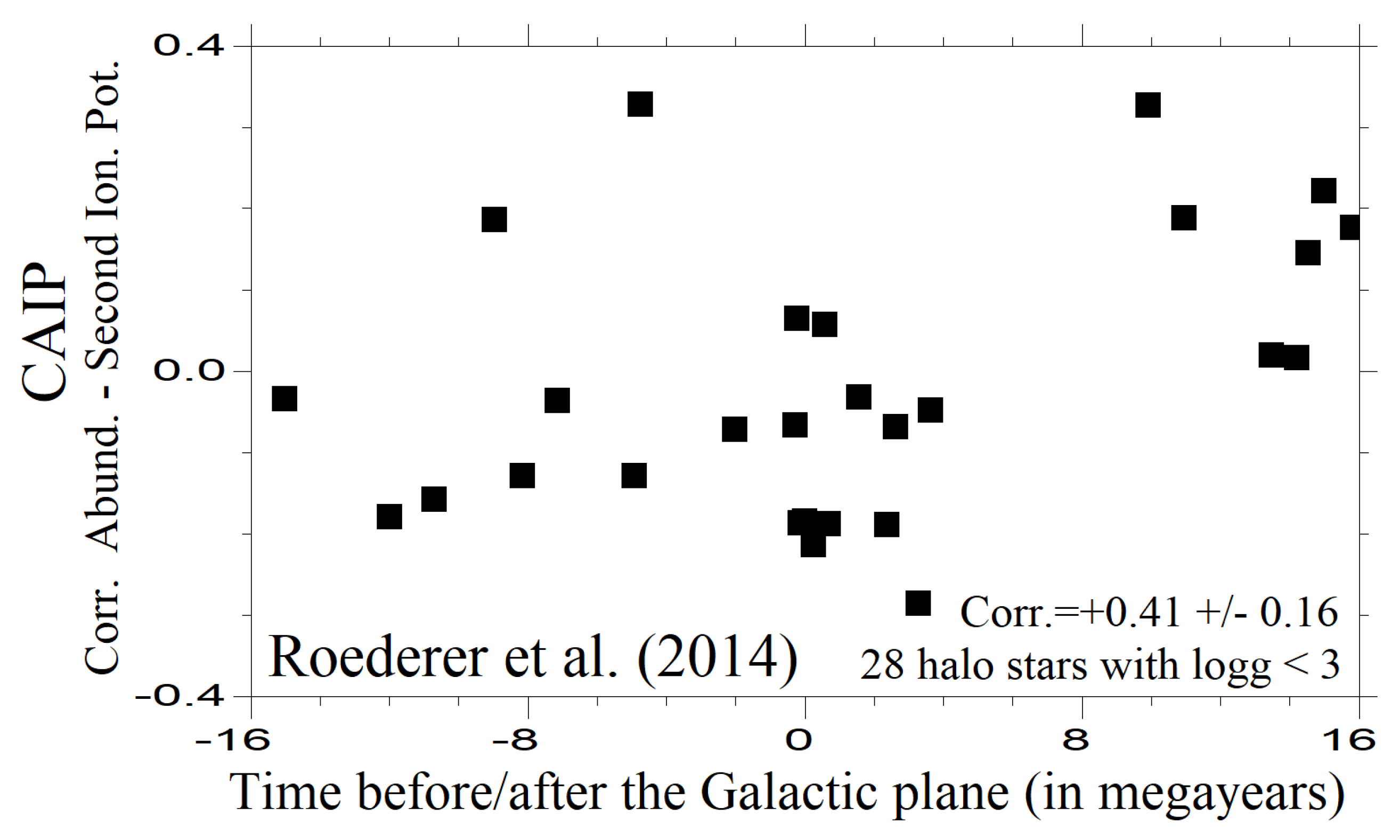
Figure 7 illustrates the dependence of the CAIP coefficients on these times for 28 stars with log g < 3. The correlation coefficient is approximately +0.41±0.16, indicating an increasing trend in CAIP values after crossing the Galactic plane.
Preprints 121783 g007
Figure 7. The vertical axe is the correlation coefficients calculated for relative abundances against second ionization potentials. The abundances are taken from Roederer et al. (2014) [29] paper. The horizontal axe is the times before or after crossing the galactic plane in million years. In this plot only 28 halo stars with effective temperatures 4900 K≤ T eff ≤5900 K and surface gravities log g < 3 are used.
Figure 7. The vertical axe is the correlation coefficients calculated for relative abundances against second ionization potentials. The abundances are taken from Roederer et al. (2014) [29] paper. The horizontal axe is the times before or after crossing the galactic plane in million years. In this plot only 28 halo stars with effective temperatures 4900 K≤ T eff ≤5900 K and surface gravities log g < 3 are used.
Preprints 121783 g007
This correlation trend supports the hypothesis of accretion from interstellar matter into the atmospheres of halo stars. In this context, the observational effect identified by Greenstein et al. [7] could be explained by the hypothesis proposed by Havnes et al. [8] - specifically, the accretion of interstellar matter, primarily in the form of hydrogen, onto stellar atmospheres.
Certainly, the number of stars analyzed is insufficient, and the detected correlation requires further confirmation. It is important to note that any potential changes in chemical abundances after crossing the Galactic plane could complicate the determination of stellar ages based on the ratios of stable to radioactive chemical element abundances in the atmospheres of halo stars. The influence of this effect on age determinations also necessitates additional investigation.
It is also important to note that the potential non-universality of the r-process, as discussed by Yushchenko et al. [39], and a wide scattering of thorium abundances in different stars of up to 4 dex observed by Ren et. al. [40], along with the possible existence of additional nuclear processes [41], suggests that the initial production of heavy elements depends on many variables. The potential variations in stellar abundances over time, as discussed in this paper, cast doubt on the reliability of simple cosmochronological models for determining stellar ages.
Greenstein et al. [7] observed a decrease in relative chemical abundances for elements with second ionization potentials near 13.6 eV as early as the first quantitative measurements of stellar chemical compositions were made. However, the explanation for this observed phenomenon remains largely qualitative.
The correlations between relative chemical abundances and both second ionization potentials and condensation temperatures presented in this paper, along with similar correlations published by Yushchenko et al. [13] for B-F type stars, Jeong et al. [22,23] for barium stars, Yushchenko et al. [26] for F-K type giants, and several other individual stars mentioned earlier, will all be utilized for theoretical explanations of the observed phenomena in future papers.

4. Conclusions

In these paper we investigated the published abundances of chemical elements in the atmospheres of G–K type disk and halo stars. Four different surveys and the abundance patterns of five metal poor stars with detailed abundance patterns were used, the abundances of ten chemical elements common for all surveys were analyzed. The main attention was devoted to correlation of relative ebandances of these elements against its second ionization potentials (CAIP) for stars located in different regions of the Galaxy.
It has been shown that CAIP values differ for stars with varying metallicities. We cannot rule out the possibility that CAIP values for halo stars may change when crossing the galactic plane. These correlations are sensitive to the number of chemical elements used in the calculations, and with an insufficient number of elements, even the sign of the correlations may change.
These conclusions are based on well-defined abundance patterns of just five stars with detailed compositions and on 932 stars where only ten chemical elements were analyzed. Further investigation is needed to confirm these results.

Author Contributions

Conceptualization, A.Y., S.A., methodology, A.Y., A.D., V.G., Y.J., K.S.J., software, A.Y., V.Y., D.D., validation, S.A., Y.J., V.G., N.A., formal analysis, A.Y., S.A., V.Y., D.D., investigation, A.Y., S.A., V.Y., K.S.J., N.A., resources, A.Y., A.D., K.S.J., data curation, A.D., Y.J., D.D., writing—original draft preparation, A.Y., S.A., V.Y., writing—review and editing, A.Y., S.A., Y.J., N.A., visualization, A.D., V.Y., N.A., supervision, A.Y., D.D., V.G., project administration, A.Y., Y.J., funding acquisition, A.D., Y.J., All authors have contributed substantially to the work reported. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

This research is based on a non-standard analysis of previously published abundance patterns for 932 disk and halo stars from four different surveys, as well as the chemical abundances of five stars, also previously published. The numerical data calculated for the plots used in this publication can be requested from the first author or the corresponding authors.

Acknowledgments

This research was funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP14972694).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SIP Second Ionization Potential
CACT Correlation of relative Abundances against Condensation Temperature
CAIP Correlation of relative Abundances against second Ionization Potential

References

  1. Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Review Modern Physics 1957, 29, 547–650. [Google Scholar] [CrossRef]
  2. Fowler, W.A.; Burbidge, E.M.; Burbidge, G.R.; Hoyle, F. The Synthesis and Destruction of Elements in Peculiar Stars of Types A and B. Astrophys. J. 1965, 142, 423–450. [Google Scholar] [CrossRef]
  3. Proffitt, C.R.; Michaud, G. Abundance Anomalies in A and B Stars and the Accretion of Nuclear-processed Material from Supernovae and Evolved Giants Astrophys. J. 1989, 348, 998–1007. [Google Scholar] [CrossRef]
  4. Drobyshevski, E.M. Peculiar A-Stars and Planetary Systems. Astrophysics and Space Sciences 1975, 35, 403–408. [Google Scholar] [CrossRef]
  5. Cowley, C. An examination of the planetesimal impact hypothesis of the formation of CP stars. Astrophysics and Space Sciences 1977, 51, 349–362. [Google Scholar] [CrossRef]
  6. Michaud, G. Diffusion Processes in Peculiar a Stars. Astrophys. J. 1970, 160, 641–658. [Google Scholar] [CrossRef]
  7. Greenstein, J.L. Analysis of the Metallic-Line Stars. II. Astrophys. J. 1949, 109, 121–138. [Google Scholar] [CrossRef]
  8. Havnes, O. Magnetic stars as generators of cosmic rays. Astron. Astrophys. 1971, 13, 52–57. Available online: https://ui.adsabs.harvard.edu/link_gateway/1971A%26A....13...52H/ADS_PDF.
  9. Havnes, O.; Conti, P.S. Magnetic accretion processes in peculiar A stars. Astron. Astrophys. 1971, 14, 1–11. Available online: https://ui.adsabs.harvard.edu/link_gateway/1971A%26A....14....1H/ADS_PDF.
  10. Havnes, O. On Cosmic Rays and Magnetic Stars. Astron. Astrophys. 1973, 24, 435–440. Available online: https://ui.adsabs.harvard.edu/link_gateway/1973A%26A....24..435H/ADS_PDF.
  11. North, P. The rotation of AP stars. Astron. Astrophys. 1984, 141, 328–340. Available online: https://ui.adsabs.harvard.edu/link_gateway/1984A%26A...141..328N/ADS_PDF.
  12. Böhm-Vitense, E. The Puzzle of the Metallic Line Stars Publ. Astron. Soc. Pac. 2006, 118, 419–435. [Google Scholar] [CrossRef]
  13. Yushchenko, A.V.; Gopka, V.F.; Kang, Y.-W.; Kim, C.; Lee, B.-C.; Yushchenko, V.A.; Dorokhova, T.N.; Doikov, D.N.; Pikhitsa, P.V.; Hong, K.; Kim, S.; Lee, J.-W.; Rittipruk, P. The Chemical Composition of rho Puppis and the Signs of Accretion in the Atmospheres of B-F-Type Stars. Astron. J. 2015, 149, A59. [Google Scholar] [CrossRef]
  14. Erspamer, D.; North, P. Automated spectroscopic abundances of A and F-type stars using echelle spectrographs. II. Abundances of 140 A-F stars from ELODIE. Astron. Astrophys. 2003, 398, 1121–1135. [Google Scholar] [CrossRef]
  15. Niemczura, E.; Morel, T.; Aerts, C. Abundance analysis of prime B-type targets for asteroseismology. II. B6-B9.5 stars in the field of view of the CoRoT satellite. Astron. Astrophys. 2009, 506, 213–233. [Google Scholar] [CrossRef]
  16. Yushchenko, A.; Gopka, V.; Khokhlova, V.L.; Lambert, D.L.; Kim, C.; Kang, Y.W. HD 153720 - A SB2 system with twin metallic-line components. Astron. Astrophys. 2004, 425, 171–177. [Google Scholar] [CrossRef]
  17. Kang, Y.-W.; Yushchenko, A.; Hong, K.; Kim, S.; Yushchenko, V. Chemical Composition of the Components of Eclipsing Binary Star ZZ Bootis. Astron. J. 2012, 144, A35. [Google Scholar] [CrossRef]
  18. Kang, Y.-W.; Yushchenko, A.V.; Hong, K.; Guinan, E.F.; Gopka, V.F. Signs of Accretion in the Abundance Patterns of the Components of the RS CVn-type Eclipsing Binary Star LX Persei. Astron. J. 2015, 145, A167. [Google Scholar] [CrossRef]
  19. Jeong, Y.; Yushchenko, A.V.; Doikov, D.N.; Gopka, V.F.; Yushchenko, V.O. Chemical Composition of RR Lyn - an Eclipsing Binary System with Am and lambda Boo Type Components. Journal of Astronomy and Space Sciences 2017, 34, 75–82. [Google Scholar] [CrossRef]
  20. Yushchenko, A.V.; Yeong, Y.P.; Gopka, V.F.; Vasil<sup>′</sup>eva, S.V.; Andrievsky, S.M.; Yushchenko, V.O. Chemical Composition of RM_1-390 - Large Magellanic Cloud Red Supergiant. Journal of Astronomy and Space Sciences 2017, 34, 199–205. [Google Scholar] [CrossRef]
  21. Yushchenko, A.V.; Gopka, V.F.; Shavrina, A.V.; Yushchenko, V.O.; Vasileva, S.V.; Andrievsky, S.M.; Raikov, A.A.; Kim, S.; Rittipruk, P.; Yeong, Y.; Kang, Y.W. The peculiarities of chemical elements abundances in the atmosphere of PMMR23 - red supergiant of Small Magellanic Cloud, as a result of interstellar gas accretion. Kinematics and Physics of Celectial Bodies 2017, 33, 3–26. [Google Scholar] [CrossRef]
  22. Jeong, Y.; Yushchenko, A.V.; Doikov, D.N. The Interaction Between Accretion from the Interstellar Medium and Accretion from the Evolved Binary Component in Barium Stars. Journal of Astronomy and Space Sciences 2018, 35, 1–6. [Google Scholar] [CrossRef]
  23. Jeong, Y.; Yushchenko, A.; Gopka, V.; Yushchenko, V.; Rittitpruk, P.; Jeong, K.S.; Demessinova, A. The Barium Star HD204075: Iron Abundance and the Absence of Evidence for Accretion. Journal of Astronomy and Space Sciences 2019, 36, 105–113. [Google Scholar] [CrossRef]
  24. Gopka, V.F.; Yushchenko, A.V.; Yushchenko, V.A.; Shavrina, A.V.; Andrievsky, S.M.; Jeong, Y.; Shereta, E.P. The abundances of heavy elements in BL138 - red giant of local group fornax dwarf spheroidal galaxy. Physical Sciences and Technology 2018, 5, 70–78. [Google Scholar] [CrossRef]
  25. Yushchenko, A.V.; Kim, C.; Jeong, Y.; Doikov, D.N.; Yushchenko, V.A.; Khrapatyi, S.V.; Demessinova, A. The Chemical Composition of V1719 Cyg: delta Scuti Type Star without the Accretion of Interstellar Matter. Journal of Astronomy and Space Sciences 2020, 37, 157–163. [Google Scholar] [CrossRef]
  26. Yushchenko, A.; Kim, S.; Jeong, Y.; Demessinova, A.; Yushchenko, V.; Doikov, D.; Gopka, V.; Jeong, K.S.; Rittipruk, P. The Possible Signs of Hydrogen and Helium Accretion from Interstellar Medium on the Atmospheres of F-K Giants in the Local Region of the Galaxy. Journal of Astronomy and Space Sciences 2021, 38, 175–183. [Google Scholar] [CrossRef]
  27. Yushchenko, A.; Doikov, D.; Andrievsky, S.; Jeong, Y.; Yushchenko, V.; Rittipruk, P.; Kovtyukh, V.; Demessinova, A.; Gopka, V.; Raikov, A.; Jeong, K.S. The Chemical Composition of HD47536: A Planetary Host Halo Giant with Possible lambda Bootis Features and Signs of Interstellar Matter Accretion. Journal of Astronomy and Space Sciences 2022, 39, 169–180. [Google Scholar] [CrossRef]
  28. Gratton, R.G.; Carretta, E.; Claudi, R.; Lucatello, S.; Barbieri, M. Abundances for metal-poor stars with accurate parallaxes. I. Basic data. Astron. Astrophys. 2003, 404, 187–210. [Google Scholar] [CrossRef]
  29. Roederer, I.U.; Preston, G.W.; Thompson, I.B.; Shectman, S.A.; Sneden, C.; Burley, G.S.; Kelson, D.D. A Search for Stars of Very Low Metal Abundance. VI. Detailed Abundances of 313 Metal-poor Stars. Astron. J. 2014, 147, A136. [Google Scholar] [CrossRef]
  30. Adibekyan, V.Zh.; Sousa1, S.G.; Santos, N.C.; Delgado Mena, E.; González Hernández, J.I.; Israelian, G.; Mayor, M.; Khachatryan, G. Chemical abundances of 1111 FGK stars from the HARPS GTO planet search program. Galactic stellar populations and planets. Astron. Astrophys. 2012, 545, A32. [Google Scholar] [CrossRef]
  31. Jofré, E.; Petrucci, R.; Saffe, C.; Saker, L.; Artur de la Villarmois, E.; Chavero1, C.; Gómez, M.; Mauas, P.J.D. Stellar parameters and chemical abundances of 223 evolved stars with and without planets. Astron. Astrophys. 2015, 574, A50. [Google Scholar] [CrossRef]
  32. Venn, K.A.; Lambert, D.L. The Chemical Composition of Three Lambda Bootis Stars. Astrophys. J. 1990, 363, 234–244. [Google Scholar] [CrossRef]
  33. Venn, K.A.; Lambert, D.L. Could the Ultra-Metal-Poor Stars be Chemically Peculiar and Not Related to the First Stars? Astrophys. J. 2008, 677, 572–580. [Google Scholar] [CrossRef]
  34. Luck, R.E. Abundances in the Local Region. I. G and K Giants. Astron. J. 2015, 150, 88. [Google Scholar] [CrossRef]
  35. Ivans, I.I.; Simmerer, J.; Sneden, C.; Lawler, J.E.; Cowan, J.J.; Gallino, R.; & Bisterzo, S. Near-Ultraviolet Observations of HD 221170: New Insights into the Nature of r-Process-rich Stars. Astrophys. J. 2006, 645, 613–633. [Google Scholar] [CrossRef]
  36. Roederer, I.U.; Lawler, J.E.; Den Hartog, E.A.; Placco, V.M.; et al. The R-process Alliance: A Nearly Complete R-process Abundance Template Derived from Ultraviolet Spectroscopy of the R-process-enhanced Metal-poor Star HD 222925. Astrophys. J. Suppl. 2022, 260, 27. [Google Scholar] [CrossRef]
  37. Holmbeck, E.M.; Beers, T.C.; Roederer I,U. ; Placco, V.M.; Hansen, T.T.; et al. The R-Process Alliance: 2MASS J09544277+5246414, the Most Actinide-enhanced R-II Star Known. Astrophys. J. 2018, 859, L24. [Google Scholar] [CrossRef]
  38. Mardini, K.M.; Placco, V.M.; Meiron, Y.; Ishchenko, M.; Abramov, B.; et al. Cosmological Insights into the Early Accretion of r-process-enhanced Stars. I. A Comprehensive Chemodynamical Analysis of LAMOST J1109+0754. Astrophys. J. 2020, 903, 88. [Google Scholar] [CrossRef]
  39. Yushchenko, A.; Gopka, V.; Goriely, S.; Musaev, F.; Shavrina, A.; Kim, C.; Kang, Y. Woon; Kuznietsova, J.; Yushchenko, V. Thorium-rich halo star HD 221170: Further evidence against the universality of the r-process. Astron. Astrophys. 2005, 430, 255–262. [Google Scholar] [CrossRef]
  40. Ren, J.; Christlieb, N.; Zhao, G. The Hamburg/ESO R-process Enhanced Star survey (HERES). VII. Thorium abundances in metal-poor stars. Astron. Astrophys. 2012, 537, A118–12. [Google Scholar] [CrossRef]
  41. Yushchenko, V.; Gopka, V.; Yushchenko, A.; Demessinova, A.; Jeong, Y.; Pavlenko, Ya.; Shavrina, A.; Musaev, F. ,; Alimgazinova, N. The Radioactive Elements in the Atmosphere of HD25354 - Are They the Result of the Symmetric Decay of the Chemical Elements of the Island of Stability? Galaxies 2024, 12, 57–18. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated