Principles of Market Dynamics: Economic Dynamics and Standard Model (II)

Preprint

Article

Principles of Market Dynamics: Economic Dynamics and Standard Model (II)

Altmetrics

Downloads

105

Views

Comments

Yingrui Yang^*

This version is not peer-reviewed

Submitted:

26 October 2024

Posted:

28 October 2024

You are already at the latest version

Alerts

Abstract

Market dynamics is based on classical electrodynamics and uses quantum electrodynamics as a reference model framework. Its construction is always based on Bourbaki structuralism. Market dynamics studies the interaction between price, demand and supply. Quantum electrodynamics studies the interaction between photons, electrons and positrons. Both belong to the category of single charge dynamics and share a symmetry group. Market dynamics introduces market charge and defines demand and supply respectively. By examining the market hesitation phenomenon, spin is introduced as the intrinsic property of demand and supply. Therefore, demand and supply can be defined by Dirac spinors. By introducing the coin cone and valence shell, virtual prices are defined; demand and supply interact by exchanging virtual prices. These interactions can be described by Feynman diagrams. The cognitive field has the function of polarizing decision-making and is described by the magnetic field. Market dynamics believes that the social economy itself is an experiment and every market participant is an observer. We established the non-commutative relationship of market observation and the market version of the uncertainty principle of observation information, and defined the quantum version of the invisible hand. On the basis of classical electrodynamics, the relationship between price field and Maxwell field is discussed, and the concept of gauge potential is introduced. Market fluctuations (including mesoscopic and quantum fluctuations) caused by high-order cognition (including gaming, decision-making and reasoning). The fluctuation phenomena inherent in various markets are the basis for understanding both the cognition of market participants and the phase transition of the market. Six components of the market wave function are defined, namely the global phase factor, global gauge potential and global gauge field strength, as well as the local phase factor, local gauge potential and local gauge field strength. Gauge transformation is a integral part of quantum electrodynamics and market dynamics. The gauge principle is then given to show that global symmetry is a necessary condition for local symmetry. Four operators are introduced, namely the Newton mean operator, the Einstein cone operator, the Schrödinger evolution operator and the Dirac field theory operator. These four operators are applied to the market wave function respectively, presenting four operator phases of the market wave function. The change of operator state is called the phase transition of the market wave function.

Keywords:

Subject: Social Sciences - Cognitive Science

Preface

This article is the second in a series of articles entitled “Economic Dynamics and Standard Models”. Whenever “previous article” is mentioned in this article, it refers to the first article in this series, “Content, Method and Significance of Economic Dynamics”, see reference [27]. The standard model of economic dynamics includes market dynamics, sub-economic dynamics, economic externality dynamics, and ordinary rationality mechanism. This article focuses on market dynamics. Quantum electrodynamics is recognized as the most mature part of the standard theoretical physics model; market dynamics uses it as a theoretical reference framework for its conceptualization and modeling. This article is divided into seven sections, with the following content titles:

1.Market Hesitation Theory

1.1 Market charge and price, supply, and demand

1.2 Hesitation and Dirac spinors

1.3 Money cone price shell, virtual and real fluctuation.

1.4 Feynman diagrams and interactions

1.5 Cognitive field and decision making

1.6 Price function and selection function

2. Searching the Invisible Hand

2.1 Beliefs and dogmas of market mechanisms

2.2 The quantum version of the invisible hand

3. Price field theory

3.1 The nature of price

3.2 Price fields and classical electrodynamics

3.3 Summary

4. Higher-order cognition and market fluctuations.

4.1 Cognitive magnetism and curl

4.2 Cognitive Field and Samuelson’s Misconception

4.3 Game theory and classical fluctuations

4.4 Decision theory and mesoscopic (semiclassical) fluctuations;

4.5 Reasoning and market quantum fluctuations

4.6 Summary

5. Market wave function with gauge transformation.

5.1 Wave Function Operator and phase space

5.2 Market wave functions and gauge structures

5.3 Gauge symmetry and gauge transformation

5.4 Gauge principle

6. Market Operator phases and phase transitions.

6.1 Newtonian mean value operator state

6.2 Schrödinger evolution operator state

6.3 Einstein's cone operator state

6.4 Dirac field theoretic operator state

6.5 Market Operator phases and phase transitions.

7. General Discussion.

1. Hesitation Theory

Life is full of hesitation; whether it is economic language or daily language, the market is the same. The phenomenon of hesitation carries and bears the largest scale of energy in the market. This is true for both the market as a whole and the market participants. In the language of dynamics, the market potential is like this, and the market kinetic energy is even more so. Fluctuations are natural hesitations. In physics, there is no quantum fluctuation, so why do we need quantum mechanics? Moreover, the closer to the critical point, the more intense the fluctuations. In marketing, the closer to psychology's inherent price, the more hesitation there is. Hesitation is a cautious attitude, a responsible performance, and a great common rationality. If you carefully replay your consumption experience and experience it again without disguising it, what consumes the most energy? It is not driving to the shopping mall or queuing to pay, but hesitation in the face of prices. The energy consumed by each market participant is accommodated in the market, so that hesitation evolves into a natural market nature. Machines search, but humans make choices. Resources are scarce, and facing costs directly, how can people not hesitate? This section discusses some basic concepts shared between market dynamics and quantum electrodynamics from the perspective of hesitation theory.

1.1. Market Charge and Price, Supply and Demand

Market dynamics is an analysis of active dynamics, and the source of this dynamic is market load. The question is, how does this market load appear? To clarify this issue, it is necessary to give appropriate definitions of the two basic economic concepts of demand and supply and write them as follows:

Definition 1. An arbitrary given demand, denoted as D, is a binary tuple:

D = [intention to buy, a certain product].

Definition 2. An arbitrary given supply, denoted as S, is a binary tuple:

S = [intention to sell, a certain product].

In the above two definitions, the expression "an arbitrary given" is a common usage in mathematics, which can refer to the existential quantifier in logic, or to the universal quantifier with the enumerate (each) usage or to the collective (every) usage. All the exchange intentions carry market charge. No matter it is summer or winter, you go to the supermarket to buy groceries and daily necessities; or even drive to a shopping mall farther away to buy electrical appliances, which consumes time and energy. You do this regardless of the weather because you have a need and an intention to buy, which is the mental charge (you are charged.) This charge is called market charge. The same is true for potential buyers and sellers. On a smaller scale, you can go out early in the morning to set up a pancake stand and sell soy milk for breakfast; or open a small shop or a mall restaurant on the street, working hard from morning till night, what do you gain? You have the intention to sell, and you are full of energy. If you have enough money to support your family and lead a comfortable life, or you have the knowledge of getting rich through hard work and the awareness of market exchange, then you have the market value. In a broader sense, if you have the capital to open a store, do international trade, and spend a lot of money on advertising, then you also have the market value. To put it simply, market charge is what people often call business philosophy. To say that someone is full of business philosophy and always thinking about money means that he is sensitive to prices. In the sense of marketing, it is not shameful to satisfy the exchange psychology.

Note that demand in the market sense is different from the "wanting impulse". The former is completely price-sensitive and carries an integer market charge, whereas the latter is not completely price-sensitive and only carries a partial (fractional) market charge. In physics terms, the former speaks at the atomic level, which we will soon see below, while the latter speaks at the subatomic level, which we will elaborate on in another article when introducing sub-economic dynamics [29]. For instance, a child returns home and informs his parents that a classmate has recently transitioned to a new mobile phone, citing its superior features, and expressing his own desire for one. The adult replies, "Child, do you know how expensive that new mobile phone is? Our family's economic conditions cannot be compared with theirs, so we'll think about it later." This is a kind of difference from economic perspectives. The children express their desires and impulses at the sub-economic level and have a vague perception of prices, like a quark, which carries a fractional market charge (electrical charge). Adults, on the other hand, consider issues at the market level, meaning that the right price is completely sensitive and carries integer market charge.

A more typical example is the labor market. A job seeker is interested in an employer, and the employer is also interested in the seeker. The two parties further contact, submit and review application materials, and have interviews and exchanges. These are all interactions at the sub-economic level. However, when the two parties enter the stage of negotiating salary and benefits, each party becomes completely sensitive to labor prices. Job seekers will clearly bid for the labor they are ready to sell, becoming a market supply, and employers will also clearly bid for the labor they are ready to buy. Inquiries for purchasing this person's labor (what are your expectations for salary and benefits?), become a market demand. In other words, both parties’ buying and selling intentions carry market charges.

Market charge can be positive or negative. We agree that the market charge of a demand is negative, denoted by

e^{-}

; on the other hand, the market charge of a supply is positive, denoted by

e^{+}

. Using quantum electrodynamics as the reference framework of modeling, the market charges, demand and supply, are represented by electric charges, namely, electrons and positrons respectively. Speaking in particle language, positron is the antiparticle of electron. By the concept of market dynamics, demand is a unit in the commodity item. Under the same conditions, supply is the inverse of demand, i.e., the anti-unit. The concept of unit is not unfamiliar in neoclassical economics. For example, marginal benefit refers to the benefit obtained by investing one more unit of resources.

As previously mentioned, market dynamics can introduce the three basic concepts of microeconomics—demand, supply, and price—by definition. All three must make an economic and ontological commitment to market charge. However, the existence of market charge is not introduced by definition but rather proposed by experience and observation, and by the exchange characteristic phase in psychological life [25]. Hence, as the first principle, we have:

Principle 1. Market charge is the source of market dynamic analysis. It is a scientific hypothesis derived from experience and observation that has the status of a first principle. It is the ontological reality that market dynamics must commit to. It also necessitates the logical consistency of fundamental elements of market dynamics, such as supply, demand and price.

1.2. Hesitation and Dirac Spinor

As introduced in the preamble of the paper [18,27], the hesitation principle is one of the eight principles of ordinary rationality. Since consumers have limited resources, even if there is demand, they will naturally be sensitive to prices. The market change will inevitably cause hesitation. This creates an internal demand space. Quantum electrodynamics is a single-charge dynamic system that only promises one kind of charge, namely electric charge. Correspondingly, market dynamics is also a single-charge dynamic system that only promises one kind of charge, namely market charge. Therefore, the internal space of demand or supply is one-dimensional. Hesitation causes this one-dimensional internal space to rotate. Hesitation can be strong or weak and can have a fast or slow frequency, which creates the momentum of rotation. In quantum field theory, a particle's spin is defined by the momentum of its internal space rotation. Considering spin from another perspective, a particle with spin -1/2, such as an electron, is considered to have two basic spin directions, called spin up and spin down. It can be said that the spin number is the reciprocal of the number of basic spin directions. In market dynamics, demand or supply also has two basic spin directions: buy and don't buy or selling and not selling, also known as spin-up and spin-down.

Just as hesitation is a psychological phenomenon that is challenging to directly observe, the particle spin also has observable effects but is not directly observable. There are many, or even continuous, intermediate states between the two basic spin directions. These intermediate states are considered to be superposition states of the two basic spin directions. In quantum physics, spin is an intrinsic property of particles and has no corresponding state in Newtonian mechanics. It is not difficult to see that the sum of spin up and spin down is zero, which is unreasonable and violates the law of conservation of energy. Therefore, spin does not satisfy the addition law, but only the superposition law. Now, consider a structure that only involves a pair of particles, their antiparticles, and their two basic spin directions, which we refer to as spin-1/2. This structure can be characterized by the Dirac spinor, which is written as follows:

ψ = (\begin{matrix} \begin{matrix} ψ^{1} (x) \\ ψ^{2} (x) \end{matrix} \\ \begin{matrix} ψ^{3} (x) \\ ψ^{4} (x) \end{matrix} \end{matrix}) = (\begin{matrix} \begin{matrix} u^{1} (x) \\ u^{2} (x) \end{matrix} \\ \begin{matrix} v^{1} (x) \\ v^{2} (x) \end{matrix} \end{matrix}) = (\begin{matrix} u \\ v \end{matrix})

(1.1)

There are some conceptual details here. From the first column of the definition above, we can see that

in quantum mechanics,

ψ

represents a wave function, which we will discuss in detail later. As can be seen from the second column, in quantum field theory, Dirac spinors are processed as a field and characterize spin 1/2 particles. A spinor represents a field, called a spinor field. Finally, from the third column we can see that a field is considered as an operator. It is called second quantization. Since it is an operator, it highlights the category structure applied to different domains. We will see further that Quantum Electrodynamics and Market Dynamics share such a structure. The structure is so perfect that people can't help but applaud, and they are so tight such that they are twins. Now, take a small fragment of each of the two as described above, and apply the Dirac spinor operator to make the following simple category theory description.

Here, category theory expresses a mathematical structure. But neither quantum electrodynamics nor market dynamics are pure mathematics. A mathematical structure, including the Dirac spinor operator, should have a semantic interpretation in the context in which it is applied. Therefore, it is necessary to give out the following semantic graph:

We observed that Figure 2 essentially embodies the meaning of Figure 1 within this particular context. Note that particle nature is a basic concept in physics. Electrons and positrons are both elementary particles. This is common sense. In economics and even in the social sciences, there is no concept of particles. This is also common sense. So, to apply the concept system of physics to the social sciences, the symbols can be retained and shared, but the concepts must not only correspond but also be natural. For instance, introducing the concept of particles into the social sciences may not only seem rigid, but also lead to challenges in academic and cultural acceptance. For this reason, we agree to use quantum electrodynamics as the conceptual framework and units in market dynamics conceptualization. The concept replaces the particle concept. Next, we have:

Proposition 1 states that a demand is a spin-1/2 market unit. A supply is also known as a spin-1/2 market unit. In a pair of demand and supply. When two products are identical, we refer to supply as the inverse unit of demand.

The unit concept is familiar to economics and is used naturally. For example, in economics literature, marginal benefit is defined as the benefit obtained from investing one more unit of resources.

1.3. Money Cone Price Shell, Virtual and Real Fluctuation

In this section, we discuss the interaction between demand and supply. In quantum electrodynamics, the interaction between electrons and positrons is carried out through photons. In market dynamics, prices are characterized by photons. In other words, the interaction between demand and supply is carried out through prices. The complexity lies in that, in addition to photons, there are also virtual photons (virtual photon) It also plays a pivotal role in the interaction between electrons and positrons. That is to say, we need to introduce the concept of virtual pricing accordingly. It can be considered that the hesitation of the market can be understood as the fluctuation of the market. The market's fluctuation is divided into two types: classical fluctuation and quantum fluctuation. The price disturbance market causes classical fluctuation, while the virtual price causes the quantum fluctuation of the market. We can distinguish photons from virtual photons using a concept known as the mass shell. Naturally, the concept of a mass shell pertains to the mass of particles. It is inevitable that the most difficult concept to deal with when applying physical models in the social sciences is mass. Here are two points that need to be explained:

First, the mass problem actually involves a long-standing debate in physics, namely the history of mass. In his book [16], The Lightness of Being, Wilczak specifically discussed the unity of mass, ether, and force. Newtonian mechanics, according to Wilczak, presupposes a zeroth law, which states that mass neither generates nor annihilates. Mass has always been there and will always be there. Of course, Wilczak replaced the concept of ether with the concept of field. Wilczak questioned this Newtonian presupposition. He believed that the concept of energy was more fundamental than the concept of mass, which was a revision of Einstein's mass-energy conversion formula,

E = m c^{2}

, an interpretation of the concept. In quantum physics, the creation and annihilation operators that govern particles are introduced. Therefore, even particles themselves have creation and annihilation, let alone their mass.

Second, the language of gauge field theory, including quantum electrodynamics, describes the standard model of particle physics. There is no mass term in the Lagrange density function in the standard model; that is, all gauge particles are massless, which is a matter of course for gauge symmetry. This is also the reason why the standard model was ignored by many theoretical physicists for quite some time. Later, the Higgs mechanism was proposed, which enabled gauge particles to acquire mass, called spontaneous symmetry breaking. These will be introduced later when discussing ordinary rational mechanisms. There, we will find that mass is also the easiest concept to define in the social sciences.

Now let’s first introduce the concept of mass shell and then construct the price in market dynamics. The following figure is a schematic diagram of a mass shell.

Figure 3. Schematic diagram of four-dimensional momentum and mass-shell hyperbolic surface.

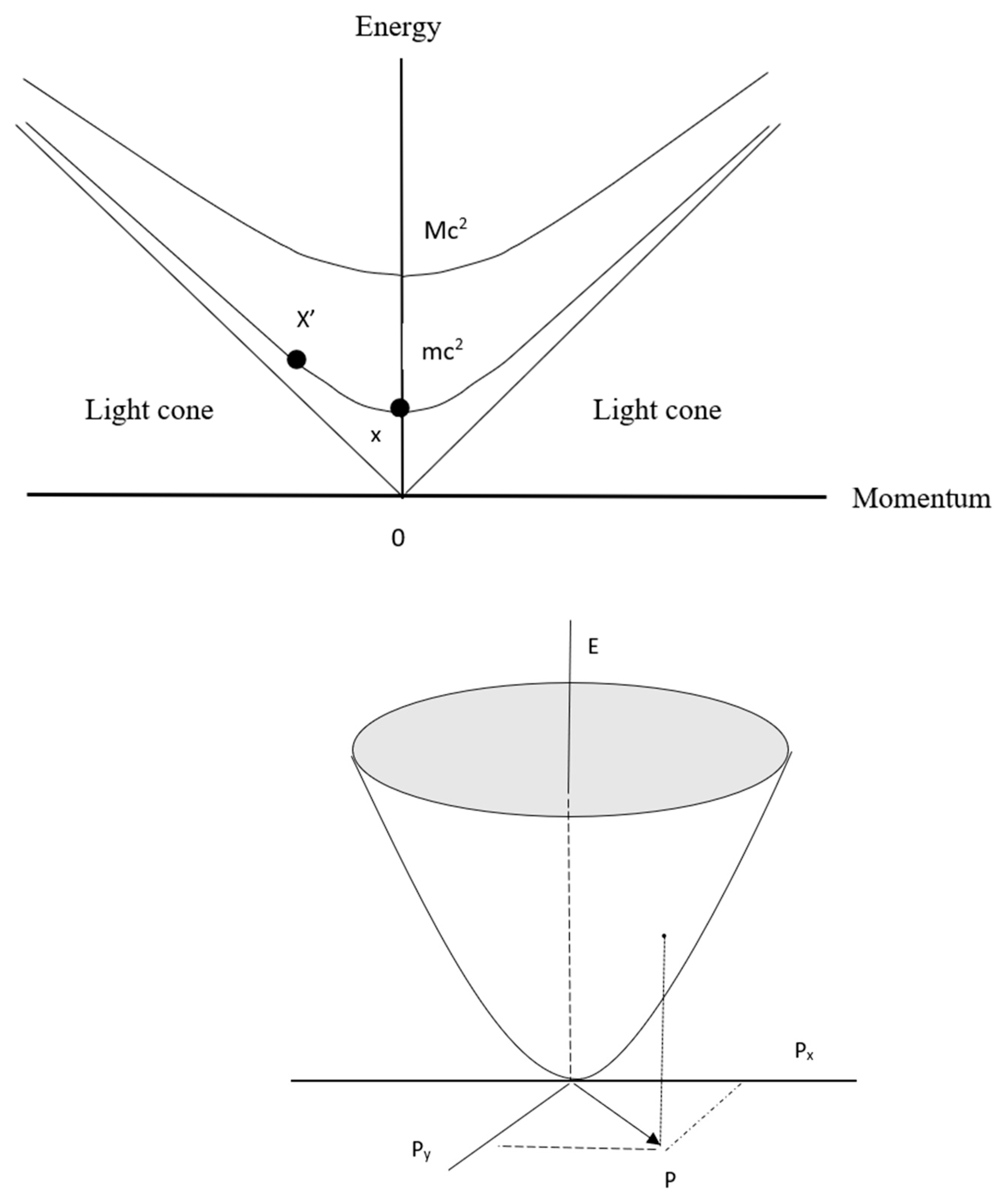
This diagram involves understanding three things. First, Einstein's formula,

E = m c^{2},

for converting mass to energy. The left side of this formula is the energy term, and the right side is the momentum term. Recall that momentum is the product of mass and velocity. The horizontal axis represents the momentum axis, and the vertical axis represents the energy axis, which is the geometric intuition of the mass-energy conversion formula. Second, static photons have no mass, that is, their momentum is zero; therefore, the inverted triangular cone formed by the straight lines in the figure is the light cone introduced earlier, which represents the scattering of photons, and its vertex is connected to the momentum axis. For particles with mass, the greater the mass, the higher the starting position on the energy axis, and the geometric intuition of its scattering is in the shape of a shell, called a mass shell. We note that the mass shell is contained in the light cone, so it represents time-like events. A photon is both in the cone and in the shell, and is called an in-shell particle. A quasi-photon is in the cone but not in the shell, and represents an out-of-shell particle, called a virtual photon. This is a preparation for introducing the concept of virtual price. We also note that for any given mass, a different mass shell is formed in the light cone. The area between the mass shell and the light cone is the home of virtual photons.

In the previous article, we introduced the special relativity model of money (referred to as money). We'll briefly describe it here for the convenience of readers. The mathematical background of special relativity is the four-dimensional Minkowski space, whose metric is agreed to be one positive and three negatives, that is,

g_{μ ν} = (+, -, -, -) .

Each point in this space is called an event. The proximity of events is called the micro-displacement of events, which is defined by the concept of interval and is given again as follows

({∆ S)}^{2} = c^{2} (∆ t)^{2} - ({∆ x)}^{2} - ({∆ y)}^{2} - ({∆ z)}^{2}

(1.2)

The first term on the right side of this formula is positive, which is the speed of light multiplied by the square of the time micro-displacement and is generally regarded as an energy term. The other three terms are negative, namely the space terms (spatial terms). When a light source is excited, it scatters into a cone and diffuses upward and downward, which is called a light cone. We refer to the events within the cone, whose interval exceeds zero, as time-like events; we call the events on the cone surface, whose interval equals zero, as null events; and we call the events outside the cone, with intervals less than zero, as space-like events. The line (straight or curved) that passes through the vertex and crosses the upper and lower cones is called a world line, reflecting local causal relationships. This is Einstein's signature philosophical proposition of the special theory of relativity.

As mentioned above, there is an important concept in the special theory of relativity, called proper time (also known as clock time), which is denoted as

τ_{i}

, where the subscript

i

indicates that the proper time varies from clock to clock, that is, it varies with the running speed of the clock carrier, and can be traversed across all clock carriers. Dividing each term in the interval definition formula by the proper time, the four-dimensional momentum is defined,

u = \frac{{(∆ S)}^{2}}{τ_{i}} = {[c}^{2} (∆ t)^{2}] / τ_{i} - ({∆ x)}^{2} / τ_{i} - ({∆ y)}^{2} / τ_{i} - ({∆ z)}^{2} / τ_{i}

(1.3)

Certainly, this momentum is related to the subscript i. It is the four-momentum. Here, we can make an interesting and instructive comparison. On the left side of Einstein's mass-energy relation is the energy term, and on the right side is the momentum term, which is in the form of

{m c}^{2}

. The first term on the right side of the momentum formula above, that is, the energy term, is in the form of

{[c}^{2} (∆ t)^{2}] / τ_{i}

. It is not difficult to see that on fixing the position of

c^{2}, (∆ t)^{2} / τ_{i}

replaces the position of m. The physical meaning of this interchangeability is for physicists to explain (different interpretations may be given). But at least it gives us a hint that mass is related to the ratio of absolute time to proper time. This coordinate is crucial for further discussion. In market dynamics, this observation can be expressed as a proposition:

Proposition 2. Let P be the absolute market price. For any given market participant

i, τ_{i}

is the proper cost,

m = C ({P / τ}_{i})

, where

m

is called the relativistic market mass and C is a running constant of money.

Next, combining the theoretical preparatory analysis on the nature of money in the previous article [27] and the new clues about the mass shell and virtual photons provided in this article, we will now reveal the emergence of the market dynamics. We aim to explain how prices disrupt the market and fluctuate with demand and supply. The market's hesitant character and behavior reflect the interaction between these three factors.

Absolute time represents the absolute market price, forming a money cone (i.e., analogous of light cone), while intrinsic time represents the intrinsic cost that varies with market participants, forming a momentum cone (poor cone, rich cone) that varies with the amount of capital. Each layer of the intrinsic price shell forms within the money cone. We know that the poorer the individual, the higher the corresponding proper cost (and vice versa), and the smaller the ratio of the absolute market price to the individual proper price. In the previous article, this ratio was referred to as the buying impulse and selling impulse. We can use the mass as a substitute in the mass shell diagram, but the appropriateness of this substitution remains a matter for further study. The gray area between the inherent price shell and the money cone is the fluctuation space of the virtual price outside the shell. The price inside the shell is called the in-shell price. The disturbance of the in-shell price on the market causes classical fluctuations (hesitation), and the disturbance of the virtual price outside the shell on the market causes quantum fluctuations. Quantum fluctuations are limited by Heisenberg's uncertainty principle. Physics tells us that the closer to the price shell, the more turbulent the market fluctuation caused by the virtual price, which is consistent with our market experience.

An example may help to understand the logic in the previous paragraph. Suppose you have $1000. The usual expenses for half a month are $800. When you go to the market to buy vegetables, the price difference is a few cents, a few dimes, or even a few dollars. These can be regarded as shell prices. Although there may be a slight hesitation in your mind, it is just that—a hesitation. The fluctuation is very classic. Suppose your computer has a problem and you want to buy a new one; however, the price of the new computer you like is $600. It feels too expensive. This is the shell price, or virtual price. Although it is affordable, how can you cover your expenses if you buy it? At this time, the hesitation is much deeper and difficult to observe directly. We refer to this as quantum fluctuation. At first, you were considering it, but then the price scared you. The next day, however, the price of the new computer suddenly dropped, approaching your original price range, and your mind became uncertain, fluctuating between choices.

1.4. Feynman Diagrams and Interactions

In quantum electrodynamics, the interaction between electrons and positrons is carried out through interaction with photons. This dynamic process can be described by Feynman diagrams [4]. Feynman diagrams can also be used to describe the interaction between price, demand, and supply in market dynamics. We know that prices are most sensitive to market disturbances, particularly in financial markets. We select several Feynman diagrams (Figure 4, Figure 5 and Figure 6) that represent basic interactions for illustration. In quantum physics, the generation operator (creation operator) and the annihilation operator (annihilation operator) respectively represent the creation and annihilation of a particle.

In Figure 4, the down part of the picture shows that a particular demand releases a price, which is called an inquiry. The up part of the picture shows that a particular supply releases a price, which is called a quote.

In Figure 5, the left picture shows that a pair of demand and supply factors results in a price, called the transaction price, and then both are “annihilated” at the same time in terms of the language of quantum field theory. The right picture demonstrates that a market price then “creates” a new pair of demand and supply factors.

In Figure 6, an ongoing demand “emits” a price, and another ongoing supply “attracts” and considers this price, but no transaction is made for a while; then, this pair of demand and supply continues to move on through negotiations and bargaining, and the previous price is annihilated.

Feynman diagrams have a profound theoretical background that provides rigorous mathematical characterizations, based on the Feynman rule for making and solving diagrams. Feynman diagrams greatly simplify the complicated calculations in quantum field theory and have their own uses in eliminating infinite quantities in the process of renormalization. These are reserved for contents in a quantum electrodynamics or quantum field theory textbook and are beyond the scope of this article. However, the following three points necessary for the presented argument are introduced below.

First, in the Feynman diagram, the junction of the particle line and the photon line is called a vertex. This vertex is not just a point in the graph, but should be considered as a cross section of photon scattering. The size of this cross section is the transition amplitude, that is, it is directly related to the probability of an interaction occurring. If the Feynman diagram is the grammatical structure of particle interactions, then amplitude and probability are its semantics. This photon scattering cross section can be carried over to scattering cross sections of prices in market dynamics, and its meaning is as follows. In Section 1, we introduced a relativistic local running mass, that is, the absolute market price P divided by the proper price

τ_{i}

of each individual market participant. Here, the subscript here i shows that proper price varies from person to person. From Figure 3, as can be seen,

t

he bigger the

τ_{i}

, the smaller the m. Thus, the lower the mass shell, the higher the proper price, and vice versa. From the cone shape of the light cone, it can be seen that the lower the mass shell, the smaller the circular cross section on it becomes. This cross section can be considered the price scattering cross section. The size of this cross section is also related to the probability amplitude of the interaction between price, demand and supply.

Second, both physics and economics are empirical sciences by nature. Quantum electrodynamics (QED) is not only a qualitative but also a quantitative scientific theory. Among its predictions is the measurement of the fine structure constant, that is,

α \approx \frac{1}{137} = \frac{e^{2}}{4 π}

(1.4)

that is,

e = (\sqrt{4 π α}

, which is called the charge coupling constant. The concept of structural constants will be discussed further when introducing the quantum chromodynamics model of sub-economic dynamics [29]. It should be noted here that in market dynamics, the existence of market charge coupling constants is assumed as a working hypothesis; but empirically, the specific structural constants are missing. Despite this, by using QED as a reference modeling framework, it makes us aware of this empirical deficiency limitation of market dynamics, and find the observation point for possible future experiments. As a professionally trained experimental psychologist, I foresee that this gap will be filled in the near future.

Third, here we emphasize the coupling constant, which has another deeper meaning. Dirac proposed that the state of a particle wave function can be represented by its two momenta, denoted as

u (p, s)

. The momentum of an antiparticle is expressed as

u^{-} (p, x)

. When using momentum representation to draw a Feynman diagram, we need to indicate the coupling constant, which is denoted by

g_{e}

. The momentum represents the rotation of particle's internal space, that is, its spin. Spin drives the wave function phase, known as dynamic phase. The particle moves in the background space (parallel transport); its momentum p also corresponds to a kind of phase, which is called the Berry phase [9] or non-integrable phase factor by C. N. Yang [17], referred to a kind of geometric phase. The total phase of a particle's wave function is the dynamical phase combined with the Berry Phase [9]. This will be discussed later in the introduction of the gauge field theoretic model.

1.5. Cognitive Field and Decision Making

In the market dynamics model, the cognitive field is modelled by the magnetic field in electrodynamics. In physics, electric charges in motion generate electric currents, which are always accompanied by magnetic fields. Magnetic fields are vector fields with strength and direction. Magnetic fields are the closure of magnetic lines of force. Magnetic fields are source-free and are always accompanied by two poles, one north and one south, which produce a magnetic moment. Its divergence is null.

The movement of market charge is what causes the market's hesitation in demand. Because of price sensitivity, repeated hesitations display various superposition states between buying and not-buying. At this point, you have two choices: either you firmly resolve to pay for it right away, or you decide not to purchase it. The process of hesitation can be long or short; the frequency can be fast or slow, and the intensity can be large or small. This is called the market current (similar to electric current). A specific market flow must be accompanied by a cognitive field (analogue of magnetic field) with some specific driving factor; otherwise, why hesitate? The cognitive field reflects the factors and intention behind hesitation. For example, “how much budget is left this month”, “do I really need to buy this thing, will I regret after buying it”, or “what will my family say after buying it?”

However, the hesitation process in the market is finite in time. When you are still debating whether to buy a product, and a salesperson walks by to remind you that the business is about to close in 10 minutes, you have two choices: either you resolve to pay for it immediately, or you decide not to purchase it. This is the so-called polarization of market charges. The cognitive field, which encompasses the “thinking lines” surrounding the market flow, plays a crucial role in polarizing market charges, as it possesses a decision-making function. Just as magnetic field performs the function of polarization, pointing either south or north, the cognitive field is responsible for decision-making: either deciding to buy or deciding not to buy. This comparison indicates that the former is suitable as a model of the later. In addition, we have briefly described the cognitive field of buyers, i.e., demanders. We suggest that readers consider the cognitive field of sellers, i.e., suppliers, and its possible influencing factors.

It's important to note that standard quantum electrodynamics only describes electric charge, not magnetic charge. This means that it is a single-charge dynamical system with an one-dimensional internal space that satisfies the U(1) Symmetry. However, string theory has both electric charge and magnetic charge, together they satisfy the strong-weak duality relationship; that is, given a fixed total energy, the stronger the electric charge the weaker the magnetic charge; the same holds vice versa. This is easily accepted in market dynamics. The stronger the market charge, the weaker the cognitive field; to put it bluntly, the stronger the buying and selling intention, the fewer concerns; conversely, the more you think, the greater the concerns, which means the weaker the buying or selling intention.

It is also worth mentioning that in both classical and quantum electrodynamics, not only electromagnetic potential is assumed, but also electric potential and magnetic potential are assumed separately. When calculating the electromagnetic field strength, the electric potential gradient and the magnetic potential curl are taken separately. One of Maxwell's contributions to electrodynamics is that in the fourth equation of the so-called Maxwell equations, the concept of displacement current is derived from the magnetic potential. The Bohm effect also reflects the importance of magnetic potential. All these remind us that the cognitive field and cognitive potential in market dynamics have an indispensable position and role. This reflects the inseparable connection between cognitive science, psychology, and economics. This point will be explained in more detail later in this article, when discussing the gauge field theory model. For example, people usually think that economic rationality and economic rational man are two interchangeable terms. However, in gauge theoretic structure, the global potential of market dynamics, the two must be used differently: economic rationality represents the market potential (electric potential), while economic rational man represents the cognitive potential (magnetic potential).

1.6. Price Function and Selection Function

There is a kind of hesitation, called "Looking for him in the crowd for thousands of times, looking back suddenly, that person is there, in the dim light." Who is that person? In fact, the poet may not be sure, but that person is a psychological existence, a reflection of the ideal, denote it as

x_{0}

. It is recorded as such a person. Where to find him? Of course, you can only look for him in the real crowd, which is actually to select. This kind of selection, like an exam where one out of a hundred is selected, can be described by Dirac

δ_{-} f u n c t i o n

in mathematics and its selectivity.

The reality of this selection process is just described by the integral formula included by Dirac. I say this to realize that the economy is like poetry and the market is like a painting. It is not always a cold face, but it is also engraved with firm and beautiful mathematical lines. This kind of hesitation has many variants. In the vernacular of market consumers, it is shopping. Shopping at second-hand book stalls and antique shops is a typical example; if you find something you like and the price is close to the inherent price of the individual, the shopping is not in vain. It is undeniable that market behavior has a certain degree of randomness. Many consumer behaviors are even quite random. In everyday language, people often say that they go shopping or visit the trading center, which shows the universal existence of this kind of contingency and randomness. Selection is a prominent feature of the market and a normal state of consumption. The following is mathematical expression of Dirac

δ

-function:

δ (x) = \{\begin{matrix} \infty, x = x_{0} \\ 0, x \neq x_{0} \end{matrix}

(1.5)

\int_{- \infty}^{\infty} δ (x) d x = 1

(1.6)

Dirac

δ

function satisfies selectivity, one of its important properties, which is explained by the following formula:

\int_{- \infty}^{\infty} f (x) δ ({x - x}_{0}) d x = f (x_{0})

(1.7))

where

f (x)

is a continuous function. Now, let

f (x)

be a continuous price function. As can be seen from the above equation, the value of the price function at

{x = x}_{0}

is selected. Selectivity has important applications in physics and engineering. Now we show its ability to characterize market dynamics and economics. In the previous article [27] [§3.1.4], we explained its mathematical modeling function in the high disturbance cone, and its role can be seen here. It can be said that in the high disturbance area, Dirac

δ

-function builds a bridge between empirical science (across natural science, engineering and social science) and mathematics. It also has other excellent properties. For example, duality, etc. Through the inverse Fourier transformation, it has a wonderful connection with the imaginary exponent, which is quite inspiring for the application of gauge field theory in social sciences. It can be treated as a single-point process of a series of functions to characterize the cognitive polarization process from hesitation to decision-making.

2. Searching the Invisible Hand

2.1. Beliefs and Dogmas of Market Mechanisms

In the history of modern economic thought, the most mysterious concept is the invisible hand. Adam Smith only mentioned this idea once in his books, Theory of Moral Sentiments and The Wealth of Nations, but it has become so well-known that it has become an eternal legend. Economists have transformed the invisible hand from a metaphor into a concept, and commentators and interpreters have embraced it. It has become the belief of economists, the religion of economic thought, and the totem of the market. The invisible hand not only contains the revelation of chaos but also reveals the pursuit of order. The invisible hand is also a concept with a mixed reputation. When the market is booming, people celebrate and worship it like a river god. When the market is sluggish, people add insults to injury and put all the blame on it. Nobel Prize laurate in economics Krugman once complained: This worldwide financial crisis has lasted for two years. If there is really an invisible hand, why hasn't it come out to save the world? There are individual motivations on the front, social effects on the back, national wealth and security on the left, and moral sentiments on the right. I dare to ask the invisible magic wand: can it tell me which is the cause and which is the result? Since 1840, for nearly three hundred years, the invisible hand, though not seen in textbooks, has been full of vitality in economic thought. Why? What is the basis? The invisible hand symbolizes the scholarly interest in economics to comprehend the workings of the market, and the relentless efforts of economists to decipher this mechanism.

It seems that the invisible hand is almost Market Beliefs, reflecting the persistent pursuit by economists and even ordinary people. It is the mystery of the relationship between the self-interested efforts of individual market participants and the overall growth of the market. When talking about the market, we cannot avoid the concept of the invisible hand. Any economic theory about the market cannot avoid talking about this invisible hand. Because, whether it is the invisible hand mentioned by Adam Smith or the visible hand mentioned by Keynes, they are all discussing the market mechanism. To understand the market, we must not only understand the formation mechanism of the market, but also understand its operation mechanism. People who have studied logic seriously should learn, logic in a broad sense including the theory of concepts. The formation of a concept generally has three cognitive stages. The first stage is just an idea. Ideas can be deep or shallow, and can be clear or vague. The second stage is the primary concept. Primary concepts are generally descriptive and have room for flexibility. The third stage is scientific concepts (notion). Scientific notions need to be defined. Once defined, they can only be tested but cannot be extended. Moreover, the formation of a scientific concept must be a matter of choosing phenomena, called conceptual treatment, and must have a definite scope of application. This is called conceptualization process, which is an important part of creating new knowledge and is also a hard part of doing theorizing.

There are many well-defined scientific and descriptive concepts in contemporary economics. However, there are two most basic concepts that are still at the level of ideas or elementary concepts. The current state of economics is that the model building is magnificent, but it is built on the sand. In the previous article [27], we discussed a concept known as economic rationality. This section aims to define the so-called invisible hand, which refers to the quantum version of the invisible hand. Adam Smith's market analysis is carried out under the framework of Newtonian mechanics. For example, its concept of “center of gravity” was borrowed from Newtonian mechanics. It is a reminder of history, a progress of the past, the frontier of economics in the past, and it is also a historical limitation.

2.2. The Quantum Version of Invisible Hand

Economics is essentially an empirical science. Market dynamics has a pre-set working hypothesis, which is as follows:

Proposition 3: The social economy, including the market, is the largest experiment that our human civilization has ever run. Each and every market participant is an active observer.

This proposition means that every market participant will try to observe the observations made by other participants in order to gain information advantages and profit from them. This is common sense and should be taken for granted in the financial market. Driven by economic rationality, every market participant intends to be the last observer. This tendency is most typical and active in the financial market. Note that what described by this proposition is different from what is currently called experimental economics. The former, in principle, presupposes that each market participant is designing their own experiments and serves as an experimenter, i.e., they are the observers of the market, while the latter assumes that they only serve as subjects who were merely under observation. The two approaches are fundamentally different.

According to Proposition 3, we now consider any two market participants. Let

α_{β}

be the observation

α

of one participant A on the observation

β

of another participant B. Let

β_{α}

be the observation

β

of the participant B on the observation

α

of the participant A. Driven by economic rationality, every market participant wants to be the last observer. So, it is not difficult to understand that the order of appearance of

α_{β}

and

β_{α}

is sensitive to the result. We have

Proposition 4. The market is competitive. The formula for its competitiveness is:

α_{β} \cdot β_{α} - β_{α} \cdot α_{β} \neq 0

(2.1)

Which usually written as

[α_{β}, β_{α}] \neq 0

. This is called a non-commutative relation. In mathematics, a typical non-commutative relation is the matrix multiplication. Heisenberg first discovered that the momentum variation

△ p

and position variation

△ x

of the wave function do not satisfy the commutative relation, his mentor Bohr immediately thought of matrix multiplication. Therefore, the Heisenberg picture of quantum mechanics was first called matrix mechanics.

It should be pointed out immediately that market dynamics is currently a qualitative theory, in the semi-dimensional stage. This reflects its social science characteristics, but does not reduce its significance in terms of conceptualization and structure. The form of Heisenberg's uncertainty principle is,

[△ p

△ x] = i h

, where

h

is a unit of energy, known as Planck's constant. This shows that energy is not continuous but discrete. In other words, energy is calculated in Planck units. In the atomic energy level model, electrons in low-energy polar orbits need enough units of energy to jump to higher-energy orbits. This is a matter of course for market dynamics. Prices have always been discontinuous; a commodity that costs 10 dollars per piece cannot be bought with 9 dollars. Reviewing the definition of interval in the special theory of relativity, the first term on the right is the energy term; in market dynamics, its meaning is the square of the money speed multiplied by the absolute price. As for bargaining, that is another story. As Simmel said in The Philosophy of Money [14], money has evolved into the best unit system. People may easily make mistakes in calculating other things, but rarely make mistakes in calculating money.

When writing academic articles, we always need to give keywords, that is, the key concepts to understand the article. Here, the non-commutative relation is a key concept. The key point is as Wang said in his book, Elementary Quantum Field Theory, that quantization is to find a non-commutative relationship; once a non-commutative relationship is established, the system is quantized [20]. This is from the perspective of market language syntax. In addition, from the above analysis, it is not difficult to see that from the perspective of the semantics of market language, the meaning of

α_{β}

and

β_{α}

is the information obtained by both, and the amount of information is slightly changed to

△ α_{β} a n d △ β_{α}

. From the market competitiveness, we should know that these are two uncertain quantities and they should obey the Heisenberg uncertainty principle. If the accuracy of one of the uncertainties is higher, the accuracy of the other uncertainties will be lower. This is called the market version of the uncertainty principle. So far, we realize that in market dynamics, markets are quantized phenomena. We have

Proposition 5. The invisible hand in the market, also known as the quantum version of the invisible hand, is an interaction of competitive observations that satisfies the non-commutative relationship (Proposition 3) and adheres to the market version of the uncertainty principle.

It is worth emphasizing that the quantum version of the invisible hand defined above meets a key condition: it is invisible to all market participants. Note that in the previous definition, for any given

α_{β}

and

β_{α}

, the non-commutative relationship is satisfied. At the same time, for any information

△ α_{β}

and

△ β_{α}

, the uncertainty principle is satisfied. This implies that for all market participants, they have the same status relative to the quantum version of the invisible hand. This is a kind of symmetry. It is precisely because of this symmetry that the market can become a fair market; and only a market that is fair to every market participant can be conserved and become a sustainable market. Imagine if a financial market participant has a channel to obtain inside information and thus has the opportunity to participate in or even manipulate insider trading, then this guy can use the information advantage to continuously make money from other people's pockets and destroy the symmetry. In this way, after a long time, others can only withdraw from the market, making it difficult for the market to develop sustainably. The quantum version of the invisible hand is equivalent to what is called the non-observables by T. D. Lee [8]. This reflects a famous theorem, known as the Nöether's theorem: non-observables imply symmetry, and symmetry implies conservation. The reason is that symmetry represents a certain invariant, and in this sense, the market can become a conservation system. We can see that Nöether's theorem is not only profound for mathematical physics, but also for market dynamics, economics and even social sciences in large.

Nöether's theorem tells us that if the market is to develop sustainably, symmetry, that is, fairness, must be established among all market participants. To achieve this, we must find something that is superior to any market participant. This is the highest principle of market mechanism design and the meaning of the invisible hand of the market. Note that this article assumes that the market is free, i.e., perfectly competitive. We assume that the perfectly competitive market is a closed, independent system, or a conservative field. As we can see, this conservative field satisfies U (1) symmetry. External forces can, of course, destroy the closedness of this conservative field, leading to spontaneous symmetry breaking. In economics, we collectively refer to the so-called external forces, like economic policies such as monetary policy and fiscal policy, wars, or irresistible natural destruction, are market externalities.

Economic externality dynamics is one of the four models that make up the standard model of economic dynamics. It is characterized by the weak isospin dynamics in theoretical physics and shares the SU (2) symmetry group [28]

3. Price Field Theory

3.1. The Nature of Price

We say that prices move markets. Market dynamics is the study of the interaction between prices and supply and demand, just as quantum electrodynamics is the study of the interaction between photons, electrons, and positrons. In market dynamics, the concept of price is characterized by photons in quantum electrodynamics. Therefore, understanding the concept of photons helps us understand the nature of price. Although photons are a concept in quantum electrodynamics, they are abstracted from Maxwell fields in classical electrodynamics. According to quantum field theory, particles are excited by quantum fields, also known as excited states. Photons are excited states of photon fields. Where there is excitation, there is annihilation, so the creation operator and annihilation operator are introduced in quantum field theory. An electron can release a photon, which is called creation; a photon can also be absorbed by a positron, which is called annihilation. The same is true for prices. A demand, which is an inquiry, can release a price. A supply can also release a price, known as a quotation. The bargaining process is the process by which different intermediate prices are repeatedly created and annihilated. A transaction is completed, starting with the transaction price and ending with the transaction price. Recompleting the transaction initiates a new phase of the price life cycle. Prices excite when they interact with the demand field, the supply field, or both. The price field, also known as the free price, can theoretically independently excite prices, called free price. We know that the market can create wealth. If the market does not produce anything, how can it create wealth? Economics tells us that the market produces prices. Strictly speaking, the market also produces prices in a systematic way, which is called a price system. Let's take an extreme example. Suppose that the price of a piece of clothing is $100. One can't pay $50 to buy half a piece of clothing; that does not conform to the price system.

Maxwell field is also called electromagnetic potential field, denoted by

A_{μ}

. Electromagnetic potential is composed of electric potential and magnetic potential, denoted by

φ

and

A

respectively. Here we have magnetic potential.

A_{μ} = (φ, A)

, where

A

is also called magnetic potential vector. The language of gauge field theory to be introduced later in this article,

A_{μ}

is called gauge field, which is actually gauge potential. We will also see that

A_{μ}

is a component of covariant derivatives, playing a coordinating role for individual differences. The classical electrodynamics says that light is an electromagnetic wave, while quantum electrodynamics says that photon field is the electromagnetic potential vector. Particleization of potential is exactly what is meant by the wave-particle duality of particles. The electromagnetic potential field is called Maxwell field because Maxwell emphasized the electromagnetic potential tribute and expressed it in Maxwell's equations. C. N. Yang [17] particularly discussed the relation of his work on the gauge field theory and the historical origins of Maxwell's electromagnetic potential view. Maxwell's electromagnetic potential, Yang's gauge field theory and Einstein's general relativity are considered to form a landscape of the geometric program of theoretical physics [2]. In economic dynamics, there is such a landscape, called the geometric program of economics [27].

The photon field is also called the Maxwell field. The price field is described by the photon field, so the price field should also be regarded as a Maxwell field, that is,

A_{μ} = (φ, A)

as a combination of market potential

φ

and cognitive potential

A

. In other words, prices carry both electrical (market) and magnetic (cognitive) properties. In this section, we will mainly discuss cognitive potential

A

, or the magnetism of the market. We will argue, this cognitive potential

A

is exactly the decision field in market dynamics. We will also see that at the higher cognitive level, the formation and movement of the decision field are closely related to the game field and the reasoning field. In classical electrodynamics, it was considered just a mathematical trick. But as Feynman said in his famous Lectures on Physics, magnetic potential vector

A

and electromagnetic potential

A_{μ}

are both real physical fields [3,4]. Similarly, as argued in the present paper, the cognitive potential and price potential should be considered as real economic fields.

As introduced in our earlier work [27], dynamics always studies two quantities, Hamiltonian or Lagrangian, both of which involve potential energy and kinetic energy. Electrodynamics, whether classical or quantum, focuses on a pair of things, namely electromagnetic potential and electromagnetic field strength. In the language of gauge field theory, there is a 2 by 2 syntactic structure: at both the global and local levels, the gauge potential and the gauge field strength must be distinguished. The most intuitive understanding of this distinction can be seen through the indefinite integral formula:

\int f (x) d x + C

(2.2)

where the entire indefinite integral is the gauge potential, in which the integrand is the gauge field strength, and the constant C is called the gauge freedom. It is easy to see that finding the gauge field strength from the gauge potential is to apply various differential operations. The differential of the constant is zero, and it is eliminated in the process of finding the field strength. Don't underestimate this gauge freedom. After it is eliminated, it is still hidden in the potential, leaving room for the introduction of various gauge functions. Later, we will see that in market dynamics, this gauge function is the value function, which is of great significance. It can be accumulated into a displacement market flow/current (this can be inferred from the fourth equation in the Maxwell equations). Can any economic theory without value function as a freedom dimension be considered a valuable economic theory? Below, we introduce several basic differential operation formulas commonly used in classical electrodynamics, namely gradient, divergence and curl. This is helpful for understanding the theoretical basis and historical origins of market dynamics.

3.2. Price Field and Classical Electrodynamics

Whether it is Maxwell's classical electrodynamics or Feynman's quantum electrodynamics, they both study one thing, that is, the electromagnetic field strength

F_{μ v}

, also known as curvature. Later, we will introduce the Lagrange density formula, also known as the Lagrange quantity, of which the first term is

{- \frac{1}{4} F}_{μ v}

. To understand this term, we need to understand the following concepts and their formulas. The first concept is the Hamiltonian operator, which is defined as follows:

\nabla = \frac{\partial}{\partial x} i + \frac{\partial}{\partial y} j + \frac{\partial}{\partial z} k

(2.3)

It can be seen that the Hamiltonian operator is the vector sum of three partial derivatives. Hint: Partial derivative is the limit of a certain dimension tending to a point. It is a local concept and speaks in the small neighborhood of this limit point. As the saying goes, Mount Sumeru contains a mustard seed, and a mustard seed contains Mount Sumeru. We will discuss about the function of definite article the in the next section when discussing reasoning and decision-making. For the mental language of each market participant, the definite article, the, is often used as the first-person pronoun my. The I in it is the limit point, sometimes also called the sink or source point. The domain of the independent variable

x

ranges all market participants. For microeconomics, especially consumption theory, the I and the mine of market participants can only and must be the central focus of dynamic analysis, without exception. This should be the presuppositional principle of economic theory regardless of school since Adam Smith. If there is no I, no mine, then what is the use of economics? Economic theory must be localized, which is the great spirit of Einstein. If individual market participants are required to only have long-distance quantum entanglement with social purposes or distant ideals, then it is not economics.

The second concept is the gradient, which is expressed by the following formula:

g r a d s = \nabla s = \frac{\partial s}{\partial x} i + \frac{\partial s}{\partial y} j + \frac{\partial s}{\partial z} k

(2.4)

Generally speaking, gradients are mostly used to calculate sourced fields. From the electric potential or market potential

φ

to calculate the field strength, we calculate the (negative) gradient, which is related to the so-called "electrical properties". Remember, the input of the gradient calculation is a scalar, that is, a number, and its output

E

is a vector. Since the Hamiltonian operator is a vector operator, the gradient of a scalar field is a vector field. Electrostatic fields or static markets are both sourced fields, and this source is the electric charge or market charge. A good salesperson does his homework; for example, the demand is to buy a certain car, which is the market charge. How much do you desire to buy this car? How much do you want to pay for this car? This is your market potential, characterized by a scalar number, which is the strength of your intention to buy this car. Assume that only three indicators of this car are considered, namely, fuel consumption, maintenance convenience, comfort and appearance. The sum of the partial derivatives of your purchase intention in these three indicator dimensions is called the gradient. A good product is something that all market participants want to buy, but the purchase intention of each market participant is different, and the requirements for various indicators of the product are different; in terms of gauge field theory, this is individual difference at the local level. To balance these individual differences and achieve local symmetry, it is necessary to introduce concepts such as covariant derivatives and gauge fields, which are the contents of Section 5. In fact, professional car sellers often calculate the purchasing potential and its negative gradient of a potential customer, and think about the appropriate sales strategy accordingly. This sales strategy is actually a kind of gauge field. As an exercise, readers can think of an example, such as buying and selling a house, and do some dynamic analysis.

The third concept is curl, which is the cross product of the Hamiltonian operator and a vector, expressed by the following formula:

\nabla \times v = (\frac{\partial}{\partial x} i + \frac{\partial}{\partial y} j + \frac{\partial}{\partial z} k) \times (u i + v j + w k)

= (\frac{\partial w}{\partial y} - \frac{\partial v}{\partial z}) i + (\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}) j + (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}) k

(2.5)

Generally speaking, curl is mostly used to calculate fields without source. Calculating the field strength

B

from the magnetic vector potential or cognitive vector potential

A

is calculating its curl, which is related to the so-called "magnetism". We will see later that decision-making is a magnetic mental activity. Remember that the input of curl calculation is a vector, and the output is also a vector. Cognition has a thinking structure. The content and inference of cognition can be right or wrong. Thinking itself is like music, there is no right or wrong. The cognitive structure of thinking can be fine or coarse, wide or narrow, straight or curved, tight or loose; this is what curl means. In other words, thinking has curl. The economy is the support of human survival, and the market is the realm of human civilization. However, cognition is the crystallization of human wisdom. People often say that the market changes rapidly. At this glance, the market is tall and straight, and at another glance, the market is graceful; looking left, the market is standing, looking right, the market is dancing; looking forward, the market is hazy, and looking back, the market is bright. Originally it is a cold market, where money is exchanged and goods are delivered, people's cognition turns it into a kaleidoscope. This is magnetism, the cognitive vector potential. The moment is the limit. The six partial differentials in a curl formula decompose the cognitive vector potential into a linear combination of three vectors and six terms. It can be seen that the cognitive field is a curl field.

In the framework of classical electrodynamics, the price field should also be regarded as a Maxwell field,

A_{μ} = (φ, A),

which is composed of market potential

φ

and cognitive vector potential

A

. We have discussed above how to calculate the gradient from the electric potential (market potential)

φ

, that is, the electric field strength. We also discussed how to calculate the field strength, that is, the curl, from the magnetic vector potential

A

. By combining the two, we can calculate the electromagnetic field strength,

F_{μ v} = \partial_{μ} A_{v} - \partial_{v} A_{μ}

. To expand it, we have

F_{μ v} = (\begin{matrix} 0 E_{x} E_{y} E_{z} \\ - E_{x} 0 - B_{z} B_{y} \\ - E_{y} B_{z} 0 - B_{x} \\ - E_{x} - E_{x} - E_{x} 0 \end{matrix})

(2.6)

This is an antisymmetric matrix with zero diagonal, which is recorded as

T r (F_{μ v}) = 0

. This is an invariant. In the Lagrangian formula introduced later,

F_{μ v}

is called the electromagnetic density term, also known as the curvature term. We can see that the photon field has both electrical and magnetic properties; similarly, the price field has both market and cognitive properties. Its potential is like this, and so is its field strength.

The fourth concept is divergence, which is expressed by the following formula:

d i v v = \nabla \cdot v = \frac{\partial u_{i}}{\partial x_{i}} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}

(2.7)

We observe that when calculating the divergence, the input is a vector and the output is a scalar number. The divergence of the magnetic field is zero; that is,

d i v A = \nabla \cdot A = 0

. Divergence refers to flux. In other words, the magnetic vector potential

A

is a field without source, and the divergence of magnetic flux density is zero, which is a characteristic of magnetism. The magnetic field is a dipole field with north and south poles. The magnetic field is described as an closure of magnetic lines of force. The magnetic lines of force connect the north and south poles without any gaps. It is a closed curve, so it does not form flux on any closed surface, so the divergence is zero. The magnetic field has the function of polarization, which makes the electric charge point to the south or the north in the magnetic field, and it must be one and only one. How is the magnetism of the cognitive field manifested? It is manifested through the decision field. Preference is a binary relationship. In the decision field, any two options are required to have a preference line connecting them, which can be called a decision magnetic line of force, connecting the two poles of "yes or no". It can be seen that the decision field, like the magnetic field, is also a dipole field. When the market charge is placed in the decision field, the market charge will be polarized, either buy or not buy, and one must be chosen. Decision theory requires that preference relations are fully and strictly ordered, so the decision field is a closure of decision magnetic lines of force, such that no flux is formed on any closed surface; that is, the decision field is a field without a source. In the market, no one makes decisions just for the sake of making decisions because making decisions comes at a cost, which is called opportunity cost in economics.

3.3. Summary

In this section, we have discussed that the price field is characterized by the photon field, and the photon field is the quantization of the Maxwell field. So, in classical electrodynamics, the Maxwell field is the essence of the price field. The Maxwell field is an electromagnetic potential field, so the price field is essentially a synthetic field of market potential plus cognitive vector potential, referred to as market-cognitive potential. When calculating the market density from the market potential, its gradient is calculated. The curl is used to calculate the flux density from the cognitive vector potential. The cognitive field, especially the decision field, is a field without source, a non-divergence field, and a dipole field, which has a polarization function for the market charge. The price reflects both the potential of commodity marketization and its market density. At the same time, the price also reflects both market participants' cognitive vector potential as well as their decision density. Such a market dynamics structure will be more completely theoretically processed when the gauge field theoretic model of quantum electrodynamics is introduced in Section 5.

It should be mentioned that in the framework of classical electrodynamics, the laws of electromagnetic motion are fully described by Maxwell's equations. This also applies to market dynamics. However, these are outside the scope of this article. For example, this section discusses the position and role of cognitive vector potential in price structure, but does not delve into the impact of the time-varying magnetic properties of cognitive vector potential on the induced commodity flow and the displacement commodity flow. It should also be mentioned that this section does not discuss the Bohm effect. Starting from the Bohm effect principle, it should be possible to deduce at the basic theoretical level that cognitive vector potential is a market reality [5].

4. Higher-Order Cognition and Market Fluctuation

4.1. Cognitive Field and Samuelson's Misconception

In physics terms, the so-called ever-changing market means that it fluctuates constantly. This section aims to discuss: Section 2 bases the quantization of the market on the inherent quantum fluctuation phenomenon of the market, which stems from the instinctive diversity of reasoning among market participants. Classical economics emphasizes observable market games, and current behavioral economics emphasizes semi-observable market decisions, but both ignore the diversity of mental reasoning of market participants that cannot be directly observed, as well as their observable market effects. This is the fundamental flaw of theoretical economics today; in this regard, Paul Samuelson has a historical responsibility. Around 1938 to 1948, the concept of revealed preference emerged, openly advocating for the removal of economics' last psychological layer to promote its hardline behaviorism in name of making economics a science. [11,12]. On the one hand, it was a bold move to improve the modeling level of economics within the framework of Newtonian mechanics. However, due to its missed opportunity, economics, particularly marketing study, suffered greatly and gradually drifted away from its two natural allies, psychology and theoretical physics. Here, the present author admits that he has worked in the field of logic and psychology of reasoning for many years. [21,22,23,24]. In such an academic background, it is natural to be more sensitive to Samuelson's illusions, and it should be our responsibility to find a more appropriate path for the economic science.

This section mainly deals with the application of higher-order cognition to market dynamics. Higher-order cognition covers a wide range of research, but three subfields have a special status, namely psychology of reasoning, psychology of decision making, and behaviorist game theory. These three subfields are special because they are the few in psychology and even social sciences that have normative formal theories. These fields are logic and psychology of reasoning, modern axiomatic decision theory and psychology of decision making, and game theory and behavioral game theory. Universities have traditionally taught these three sets of six disciplines separately, each possessing unique description languages and conceptual systems. We first developed an integrated theory known as mental decision logic [18].

Decision theory and game theory have long become the common language of economics, especially marketing study. Since Kahneman won the Nobel Prize in Economics in 2002, psychology of decision making and behavioral game theory have even become popular. However, such popular disciplines seem to have rich experimental results but weak theoretical models. The language and concepts employed in behavioral economics demonstrate this. Describing people's various market behaviors as illusions, bias or heuristics is the result of theoretical dependence on classical economics. How can you fly without wings? This section aims to propose a new direction for the development of the integrated theory of classical economics and behavioral economics.

4.2. Game Theory and Classical Fluctuations

This section uses the language of game theory to discuss two things: the pairwise observation problem and classical crossing fluctuations.

In Section 2.2, we demonstrated that market participants observe each other

α_{β}

and

β_{α}

obey non-commutative relations. This is an idealized treatment. We know that in the real market, it is impossible to exhaust the pairwise observations between participants. In fact, in modern markets, especially financial markets, each participant can only observe other participants through market observations and operate indirectly. So, how is this indirect operation implemented? This problem is called the "pairwise puzzle". Let's review the description of Nash equilibrium in non-cooperative game theory.

The basic syntactic structure of non-cooperative games is very simple. Suppose there are n players. Each player

i

has a possible action set

A_{i} = \{a_{i 1,} {\dots, a}_{i m}\} .

Each player must establish his own total order preference relation, denoted by

≻_{i}

. Note that in individual decision theory, the preference relationship of the decision maker is based on his own possible action set. However, in game theory, the preference relationship of any player can only be based on the so-called action scenario set. Consider the possible action sets of all players

A_{i} (i = 1, \dots, n)

, the expression of the Cartesian product is:

X_{1}^{n} = \{(a_{1}, \dots, a_{i}, \dots, a_{n})| {\forall a}_{i} \in A_{i}},

(3.1)

Among them, each n-tuple

(a_{1}, \dots, a_{i}, \dots, a_{n})

is called an action-profile or a scenario. In other words, a game is a set of scenarios, and each player must establish his own total order preference relationship on this set of scenarios, that is, for all players

i

, each must establish their own preference order

≻_{i}

X_{1}^{n} .

Knowing the syntactic structure of non-cooperative games, it is not difficult to understand its meta-properties, namely the well-known Nash equilibrium. Note that the language of Nash equilibrium needs to characterize each player separately, so it is necessary to make some notational rewriting. Consider the n-tuple in

X_{1}^{n}

, we have

(a_{1}, \dots, a_{i}, \dots, a_{n}) = (a_{1}, \dots, a_{i - 1}, a_{i}, a_{i + 1}, \dots {, a}_{n}) = (a_{i} {, a}_{- i})

(3.2)

Here,

a_{- i} = (a_{1}, \dots a_{i - 1}, a_{i + 1},

\dots {, a}_{n}

). Nash equilibrium is a specific scenario

(a_{i}

{, a}_{- i}

)* , i.e.,

(a_{i}^{*}, a_{- i}^{*})

. That is, for each player

i

, and for any

a_{j} \in A_{i}, j \neq i,

it holds

(a_{i}^{*}, a_{- i}^{*}) ≻_{i} {(a}_{j,} a_{- i}^{*})

(3.3)

The meaning of Nash equilibrium requires some speculative mathematical thinking and understanding; roughly speaking, in a non-cooperative game, every player is a loser, but there cannot be a worse loser. We noticed that in the language that describes the definition of Nash equilibrium, the actions of any individual are treated uniformly and separately from the action sets of all other individuals in the same scenario. This is also a typical technique for describing fixed point problems in mathematics.

Now, let's go back to the pairwise observation problem mentioned above. Rewrite

α_{β}

α_{i}^{β_{- i}}

, and rewrite

β_{α}

β_{- i}^{α_{i}}

. It is not difficult to see that,

α_{i}^{β_{- i}} a n d β_{- i}^{α_{i}}

Satisfies the non-commutative relationship, that is,

[α_{i}^{β_{- i}}, β_{- i}^{α_{i}}] \neq 0

. Obviously, in the sense of the information obtained by observation, we should know that

∆ α_{i}^{β_{- i}} a n d ∆ β_{- i}^{α_{i}}

are still two uncertain quantities, which obey the uncertainty principle. In addition, without losing generality, as a special case of

β_{- i}^{α_{i}}

, we can also allow market participants to do self-reflective observation, that is, the observation of participants on their own observations, denoted as

α_{i}^{α_{i}^{'}}

. We regard that

[α_{i}^{β_{- i}}, β_{- i}^{α_{i}}] \neq 0

provides a general solution to the pairwise observation problem.

The Nash framework remains the basic theoretical framework in contemporary game theory. The Nash framework not only clearly differentiates the mathematical structure between non-cooperative and cooperative games, but also establishes the general meta-properties of each, specifically Nash equilibrium and Nash solution. However, a large number of behavioral game theory studies have highlighted a phenomenon in which players go back and forth between non-cooperative games and cooperative games [1], which can be called a cross-fluctuation. For example, the Prisoner's dilemma, which is introduced in almost all game theory textbooks, is originally designed as a non-cooperative game. However, when the game conditions are changed, for instance, the number of years of imprisonment is increased, or repeated games are allowed, the players will change from a non-cooperative state to a cooperative state. This kind of behavioral fluctuation is directly observable, so it can be classified as a classical fluctuation.

In empirical research, the cross-over fluctuations found in behavioral game theory cannot be explained and described within the Nash framework of standard game theory. The root cause and corresponding theoretical explanation behind it can only be found in individual decision-making theory.

4.3. Decision Theory and Mesoscopic (Semiclassical) Fluctuations

To build a unified theory that decomposes a game problem into the decision-making problems of each player, we must first convert the language of game theory into the language of decision theory. This requires some technical treatment. As mentioned earlier, when the language of game theory speaks to a player, a scenario

(a_{1}, \dots, a_{i}, \dots, a_{n})

can be rewritten as

(a_{i} {, a}_{- i}

). Now let's rewrite it further as

a_{i} (a_{- i})

. After rewriting, it looks like a function, which is beyond the language of game theory; but this is a key step in converting the language of game theory to the language of decision theory. We will see why this is the case below.

Savage’s book [10], Foundations of Statistics, is recognized as the pioneering work of contemporary axiomatic decision theory. The following uses Savage language to describe the structure of decision problems. A decision problem is a triple,

< F, S, H >, w h e r e F

is a set of action functions,

S

is a set of states, and H is a set of consequences. For any given action function

f \in F

and environmental status

s \in S

, we have

f (s) = h .

Note that for any given state s, because

f

is a function, the value of

f (s)

is unique; so, without causing confusion, h

can be omitted. For any two action functions,

f_{1} a n d f_{2}

f_{1} ≻ f_{2}

is called a preference relation, that is, prefer

f_{1} t o f_{2}

. Now, compare

a_{i} (a_{- i})

in the previous paragraph with

f_{i} (s)

here, which is really similar in form. Let the former

α_{i}

be the action function

f_{i}

, and

α_{- i} b e

the state variable s, we can transform

α_{i} (α_{- i}) t o f_{i} (s)

Take the prisoner's dilemma as an example. The possible actions of prisoner A are either to confess or not to confess

\{A_{1}, A_{2}\}

. The possible actions of prisoner B are either to confess or not to confess

\{B_{1}, B_{2}\} . L e t \{A_{1}, A_{2}\} = F_{1}, \{B_{1}, B_{2}\} = S_{1}, t h e n < F_{1}, S_{1} >

becomes the individual decision-making problem for prisoner A.

S i m i l a r l y, L e t \{B_{1}, B_{2}\} = F_{2}, \{A_{1}, A_{2}\} = S_{2}, t h e n < F_{2}, S_{2} >

becomes the individual decision problem for prisoner B. In other words, the prisoner's dilemma, as a two-person non-cooperative game, is now decomposed into two individual decision problems. We can see that the transition from game theoretic language to decision theoretic language is only a “three-foot wide river”, which can be crossed with one leap. Note that this language transformation is valid in both directions, and it is only a trivial operation to re-combine the previous individual decision problems into the game theoretic structure of the prisoner's dilemma.

However, when a player changes his role to become an individual decision-maker, he finds that the fluctuations in the decision-making field are not only stronger but also more hidden, and some fluctuations are difficult to observe directly. Savage proposed a decision-theoretic problem in his book, called the "small-grand world problem". We have mentioned this in the previous articles [18] and [27], [§3.2.1]. The three-layer syntactic structure of classical decision theory and its utility semantics are introduced in this section. People usually think that when faced with a given decision problem, the decision maker will immediately calculate the mathematical expectation of each option based on utility semantics and then establish a preference relationship according to the representation theorem to solve the problem. Savage suggested that we should refer to this process as Process 2 [13]. In previous decision-making theories, people have overlooked an early process that should be called Process 1. A given grand world decision problem might not be expressed in a form they are willing to confront. Therefore, there should be an early rewriting process. The so-called grand-small-world puzzle says that when a decision maker faces a given grand-world decision problem, he will consciously edit and rewrite it into a small-world problem. So, how does the decision-maker do this editing and rewriting?

Savage's suggestion is to apply mathematical partitioning [13]. For example, the state set of a decision problem is

S = {s_{1}, s_{2}, s_{3}}

; a possible partition is

S^{*} = \{\{s_{1}\}, \{s_{2}, s_{3}\}\} = {s_{1}^{*}, s_{2}^{*}} .

Note that, there are three elements in

S

but two elements in

S^{*}

, so the former is called the grand world and the latter is called the small world. Also note that, each element in is

S^{*}

is a subset of

S

, which is called a grand-world event. Here, for any

s_{i}^{*}

, it has the double-identity:

s_{i}^{*} \subseteq S b u t s_{i}^{*} \in S^{*}

How does this fluctuation occurs, whether it is significant to the decision maker's mental action, and how does its cognitive process work? These are all challenges of the so-called grand-small world puzzle.

In addition, there are three conditions in the definition of mathematical partition. Condition 1: any elements are mutually exclusive, that is:

s_{i}^{*} \cap s_{j}^{*} = \emptyset

. Condition 2, the union of all elements is collectively exhaustive, that is

: s_{i}^{*} \cap s_{j}^{*} = \emptyset

. Condition 3, it does not include the empty set, that is:

\emptyset \notin S^{*}

. The three conditions are important because they together ensure that the mathematical partition meets the requirements of Boolean algebra. In fact, empirical research in decision psychology tells us that for market participants, these three conditions are too strong. The prospective theory in decision psychology tells us that people have two significant psychological effects in their daily decision-making, namely the editing effect and the framing effect. Note that according to Savage's original intention, a state is a possible description of the world or environment. Two states are considered different states as long as there is at least one detail different in their respective descriptions. It is difficult to imagine that real market participants can refine their descriptions of the market environment to the extent of satisfying Condition 1 when editing. In addition, based on the framing effect, for logically equivalent content, market participants tend to choose the description they prefer and reject the description that makes them uncomfortable, which makes it difficult to meet Condition 2. Furthermore, in the ordinary rationality theory introduced in the previous article [18,27], there is a principle of taking null action. The most common decision people make is to take null actions, which is recorded as

{\emptyset}

. This obviously exceeds the rule of Condition 3.

The above two discussions basically reflect the current academic ecology in the field of decision science. On the one hand, standard decision theory's mathematical model is exquisite and rigorous, and it is clear-headed about the existence of the decision process 1, but the former is far from sufficient for the latter. The reason is that, as Savage claimed, his decision theory model assumes complete rationality. On the other hand, decision psychology has discovered one decision phenomenon after another and named one decision psychological effect after another, but the theoretical modeling is weak. It is obviously a normal manifestation of people's decision-making, but decision psychologists are accustomed to calling it bias, illusions or heuristics, and then push the responsibility to bounded rationality approach, and feel at ease to be a scapegoat for theory and modeling. How can people not feel embarrassed in such a situation? In fact, the true meaning of Savage's grand-small world puzzle is to unify the efforts in the above two aspects.

Savage's theory [13] provides a structure for constructing decision problems, explaining what a decision problem is. Decision psychology investigates how people try to form decision problems that they are willing to face when they are in various situations. Savage believes that in the decision-making process1, there should be a series of different versions of the problem, which is equivalent to what is called fluctuations in physics, called decision-making and mind-action fluctuations. The Savage decision structure is composed of an action function and its environmental state; the action is an observable quantity, and the environmental state is the decision maker's subjective portrayal of the world, which varies from person to person and is difficult to observe directly. Therefore, from the perspective of market fluctuations, decision fluctuations can be viewed as a semi-directly observable fluctuation phenomenon known as mesoscopic fluctuations. The next section will provide a more microscopic exploration of market fluctuations. The “man versus men” dilemma refers to the challenge of integrating economic rationality and bounded rationality within a single theoretical framework. This dilemma is part of the discussion of gauge field theory later in this article.

4.4. Reasoning and Market Quantum Fluctuations

In a strict sense, market quantum fluctuations originate from the reasoning processes of market participants. These reasoning processes are purely mental activities, difficult to observe directly, and are subject to various individual differences. These are all components of mental decision logic. For more details, see Yang [18]. In the following, we will only introduce some selected key points directly related to this article.

First, language transformation and predicate relationship. We have transformed the game theoretic language

(a_{i} {, a}_{- i}

) into decision theoretic language

f_{i} (s)

Next, we need to convert the decision-theoretic language into the reasoning language. The method is to treat the action function as a predicate and the state variable as a logical individual variable:

f (s) \to A (x)

, where

A

is a predicate and

x

is an individual variable in quantified predicate logic. At this step, it is no longer necessary to traverse the subscripts

i

of individual players brought from game theory. Reasoning is a purely mental process, and the mind is embodied in individuals. Predicates can represent some univariate properties, or binary or even multivariate relations. The first advantage of this predicate technology is to edit the option set of a classic decision problem or the action function set of a Savage decision problem. A decision maker may not be interested in a certain option or be unwilling to take a certain action function, which will lead to him giving up this option or action. In other words, the decision maker can establish a predicate relationship between the options he is interested in or the actions he is willing to take. This is the most direct logical step to edit a decision problem, which has psychological and cognitive significance.

Second, intermediate variables and sunk costs. Savage discusses this in his book (p. 8), when discussing the relationship between the grand-world decision problem and the small-world decision problem, a purely mathematical model was presented, introducing three functions. The notation for that model is complex and involves a difficult definition formula. The most embarrassing thing is that the model obscures the significance of psychological and cognitive factors. Here we provide an equivalent logical model [18], To make it easier to discuss the psychological and cognitive significance of the concept of sunk costs in marketing, three individual variables are introduced below:

$x_{i}$ ranging over the large-world state $s$ in $S$
$x^{j}$ ranging over the small-world state $s^{*}$ in $S^{*}$
$x_{i}^{j}$ ranging over the grand world $s_{i}$ in a given small world state $x^{* j}$

The above variables 1 and 2 are easy to understand, but the reason why to introduce variable 3 needs some explanations. Let

\{s_{1}, s_{2}\}

be a given small world state

s^{* j}

\{s_{1}, s_{2}\} \in S^{*}

. At the same time,

\{s_{1}, s_{2}\}

is a grand world event,

\{s_{1}, s_{2}\} \subset S

. Then, the question is how does a grand-world event becomes a small-world state? Note that in

\{s_{1}, s_{2}\}

, both

s_{1}

and

s_{2}

still carry grand-world trace. For example, assume some market participant spent $6000 and bought 300 shares of a stock; the share price is $20. When the stock price drops to $14 per share, according to the advice of financial experts, you should sell to stop loss. If you sell at this time, you will lose $1800. In economic terms, this loss of $1800 is considered as the sunk cost. Economics also warns us that we should never look back on the sunk cost. The difficulty in making decisions for this investor may be based on two considerations.

s_{1}

: this investor didn't tell his family when he bought the stock, but now suddenly lost $1800. How can this investor explain the loss to his family? In addition,

s_{2}

: this investor wanted to make more money with this investment, and he boasted to his friends about it. Now his dream is shattered and his face is gone, what should he do? It can be imagined that to achieve such a small world state

s^{* j}

and treat it as a sunk cost, decision makers must overcome mental pressures, undergo psychological struggle, and make cognitive efforts to erase the traces of the grand-world on

s_{1}

and

s_{2}

. These fluctuations are difficult to observe directly, but they occupy a huge market energy. This step is a typical decision-making process 1. In the process of transitioning from the grand-world decision problem to the small-world decision problem, there are significant psychological and cognitive effects that are difficult to ignore. A variable 3,

x_{i}^{j}

, tells the joys, sorrows, anger and happiness of market participants, and also reveals the uncertain ups and downs of the market. This is a typical quantum fluctuation. Such a lively market life, how can it be represented by a few statistical figures.

Third, definite articles and pronouns. A predicate-variable structure

A (x)

is a free structure without propositional attitude, i.e., it has no logical truth value. To make this free structure acquire truth value, two logical components need to be added: adding quantifiers to the formal syntax and introducing the truth conditions of individual domains for each predicate in the semantic model accordingly. In English syntax, the definite article (the) often plays the role of a quantifier. The definite article can define the scope of the universal quantifier and at the same time reflect the function of the universal quantifier in this scope. The definite article also has a semantic function. Its appearance stipulates that the definition domain of the variable is not empty. In the field of reasoning, psychologists and logicians have many debates; in the field of reasoning psychology, the mental logic school and the mental models school also have a long-standing debate. However, they agree on this point, that is, the definition domain of the variable pointed to by the definite article cannot be an empty set. So why is this so sensitive to understanding market fluctuations? That's because the definite article also has the function of a pronoun. In other words, the definite article indicates to every market participant what is mine and what is not mine. It can be said that the definite article must be served as many times as there are participants in the market; and it must be served carefully because the definite article defines the actual interests of market participants. This is the universal individual difference of participants shown by market psycholinguistics. It is manifested as market quantum fluctuations, which can be called definite article fluctuations.

In standard quantified predicate logic, formal syntax and formal semantics are designed and expressed separately, and then the meta-properties between the two, such as the completeness and coordination of the system, are expressed by the metalanguage. In such a system design,

A (x)

It is a well-formed formula that conforms to the rules of syntactic formation, and its meaning is explained by the truth conditions of the assignment semantics. However, in the theory of mental logic, writing

A (x)

out alone does not meet the syntactic requirements; as long as

A (x)

is written out, it must be followed by its truth conditions

x \in X

. This

X

varies from person to person and from time to time. It is undercurrent and difficult to observe directly, but it has a strong market effect that can be observed indirectly. This

X

is the logical source of market quantum fluctuations.

Fourth, merging-channel fluctuations and quantum computing

It should be acknowledged that the reflection of various market fluctuations in the consciousness of any participant is almost holographic, but some reflections are stronger and some are weaker. Correspondingly, the market participants' cognition of the market is also multi-channel. According to quantum field theory, there are as many cognitive paths as there are cognitive media. This idea inspired the path integral method currently used in quantum field theory. We now go deep into the hinterland of reasoning psychology to observe the so-called cognitive merging-channel fluctuations.

Logic tells us what reasoning is, while reasoning psychology studies how people reason. In the field of reasoning psychology, there are two primary competing schools of thought: the mental logic theory and the mental models theory. The former argues that people reason by applying inference schemas, which is akin to a syntactic approach. The latter argues that people reason by understanding the premise's meaning and constructing mental models, which is considered as a semantic approach. Both approaches of reasoning have significant experimental support, indicating that mental logic and mental models are both effective cognitive channels. However, when we simply combined the two sets of experimental tasks into a new set, the experimental results did not support either the mental logic theory [21] or the mental model theory [22,23,24].

The reason is that solving compound experimental tasks is not like what the theories predict, i.e., taking the mental logic channel at one step and the mental model channel at another step. When switching or merging cognitive channels, cognitive blockage often occurs. This is equivalent to saying that at a merging intersection on the road, there are cars passing by on each side, and they just need to go in order. Some drivers are anxious to cut in, and others drive very fast, resulting in quantum fluctuations. Similarly, in the market, participants sometimes tend to think more and understand the market more, which is equivalent to the semantic channel; sometimes participants tend to act according to the experience mode, which is equivalent to the syntactic channel, according to experts. When the two tendencies are combined among market participants, it will cause quantum fluctuations that are difficult to observe directly.

Incredibly, when the data were calculated using what Feynman called the first formula of quantum mechanics, the results were highly consistent with the statistical results. This calculation method is called the path integral in quantum field theory. It suggests the necessity of applying calculation methods of quantum field theory to economic dynamics.

4.5. Summary

Higher-order cognition has multiple levels of influence on market fluctuations. At the game theory level, it affects the market's classical fluctuations. At the level of decision theory, it affects the mesoscopic (mesoscopic) fluctuations of the market. At the reasoning level, it affects the quantum fluctuations of the market. We introduced the process of converting game theory language into decision theory language, and then further converting decision theory language into inference language. Note that these transformations are bidirectional. In this sense, we proved that it is necessary and inevitable to use quantum electrodynamics as a modeling framework in market dynamics.

5. Market Wave Function and Gauge Transformation

5.1. Wave Function Operator Phase Space

In Section 4, we explained that there are quantum fluctuations in the market. In Section 2, we quantized the market. In this sense, the market is observed through microscopic observation. In our previous work [23], we argued that quantum observation in physics, forward observation in economics, and high-order cognitive observation in psychology all belong to the high disturbance zone of observation. The term "high disturbance zone of observation" refers to a situation where the limitations of observation methods make it difficult to directly observe a phenomenon, which scientists refer to as a quantum phenomenon. So, how do scientists observe quantum phenomena? John Wheeler, a renowned Princeton theoretical physicist, described quantum mechanics as playing a 20-question game with nature, where the wave function serves as the mathematical tool to describe the microscopic observations.

The wave function can be divided into two procedures: The U-procedure and the R-procedure, where U stands for unitary and R stands for reduction [29]. The U-procedure evolves by following the well-known Schrodinger equation. The R-procedure involves the observation, which is the focus here. The wave function is a mathematical language with a syntactic structure and semantics. The syntactic structure of the R-procedure can be expressed in the Dirac bra-ket formalism, its form is as follows:

⟨ψ | A_{i} | φ⟩ .

According to Feynman’s explanation,

| φ ⟩

is called the initial state of the quantum system, and

⟨ ψ |

is the final state of the system, and

| A_{i} |

is the systematic process. I think that a more profound explanation, which is also closer to Dirac's original intention, is the Dirac bra-ket formalism,

⟨ψ | A_{i} | φ⟩,

describes a complete quantization experiment. Let

| φ⟩

represent the quantum phenomenon to be observed; let

⟨ψ |

represent an experiment that attempts to observe this phenomenon. This experiment is similar to a 20-question game, while

A_{i}

is the series of questions, which serves as the experimental stimulus or the set of experimental tasks. When

e x p e r i m e n t ⟨ ψ |

gives a stimulus

A_{i}

, The phenomenon

| φ ⟩

will return a response. So

φ b e c o m e s t h e f u n c t i o n a l o f ψ

, denoted as

φ (ψ)

, called the R-syntax of the wave function [10].

The meaning of wave function, that is, its semantics, is called the amplitude semantics. Given any two experimental stimuli

A_{i}, A_{j}

, we will get two feedbacks

φ (A_{i})

and

φ (A_{j})

and, recorded as

a_{i}, a_{j}

respectively. From this, we can construct a complex number

a_{i} + i a_{j}

. The squared modulus of this complex number,

{| a_{i} + i a_{j} |}^{2}

, is called its amplitude; this amplitude is a real number, and according to the Copenhagen school's interpretation, this real number is a probability. As Dirac once said, the probability is the squared possibility. Imagine that from

φ (A_{i}) t o

φ (A_{j})

is connected by a small line, called a path. This is actually the basic idea of path integral.

The mathematics of quantum mechanics is Hilbert space, and the mathematics of quantum field theory is fiber bundle theory in differential geometry. In quantum mechanics, each state of the wave function is a vector in Hilbert space. A vector has length and direction. As a vector in Hilbert space, its length has no meaning for the state of the wave function. What is meaningful is the direction of the vector, because this direction expresses a phase. In other words, the characterization of a wave function is the corresponding phase space. Even the phase of a single state is meaningless. What is really meaningful is the phase difference between two states. In quantum field theory, each wave function state is a potential point on a fiber, so the wave function is a section on the potential fiber bundle. The symmetry of quantum electrodynamics is represented by the so-called mathematical symmetry group

U (1) = {e^{i θ}}

, where

θ

represents the phase, and its phase space is the unit circle on the complex plane.

It should be added here that the phase space mentioned above, in quantum field theory, refers to the internal space of the particle, called the dynamic phase space. Later, when we introduce the gauge transformation, we will introduce the concept of covariant derivatives. The definition of the covariant derivative contains a factor called the gauge field. The integral of this gauge field is called the non-integrable phase factor introduced by C. N. Yang [17]. The non-integrable phase factor describes the particle's parallel transport in external space. Of course, the non-integrable phase factor also has a phase, called the Berry phase, or geometric phase. The sum of a quantum system's dynamical phase and geometric phase is called the total phase [9].

The symmetry just mentioned is also called gauge symmetry. Symmetry is the research object of mathematical group theory. The definition of a group is very simple. It is a set of elements closed to multiplication, with a unique multiplication identity (that is, 1). Each element has its inverse, and finally it must satisfy the associative law. The definition of a group does not require the commutative law, and the group that also satisfies the commutative law is called a commutative group, also known as an Abelian group. Quantum electrodynamics, and correspondingly, market dynamics, satisfy the

U (1)

symmetry. There is another knowledge point that needs to be mentioned, that is, the wave function was originally a function (functional) in quantum mechanics; in quantum field theory, the wave function is treated as an operator, which is called second quantization.

With the basic concept of wave function, let's construct a market wave function. Since the wave function is an operator in quantum field theory, what we need to do is to give the wave function the meaning of market dynamics according to the syntactic structure of the wave function. Let's make three points first.

First, through the efforts of de Broglie, Planck and others, the wave function was expressed as

ψ (x, t)

. It is obvious that this is a time-dependent expression. The history and philosophy of the formation of wave functions are beyond the scope of this article. Schrödinger constructed the following operator:

i ℏ \frac{\partial}{\partial t} = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V

He applied it to the wave function, discovering the famous Schrödinger equation. We will discuss the Schrödinger equation later. The problem is that in quantum mechanics, observables are treated as operators, while the wave function is not an operator. In other words, the wave function is not observable.

Second, how can we treat the wave function as an operator in the framework of gauge field theory? In our previous work [27], we have introduced that dynamic analysis mainly studies two quantities, the Hamiltonian and the Lagrangian; the two are equivalent but have different uses. In quantum mechanics, the Hamiltonian is studied, and the Schrödinger equation is a kind of Hamiltonian. Its characteristic is that the initial state of the wave function is given, and we see how it evolves with the Hamiltonian equation. In quantum field theory, the focus is on the lagrangian. Its characteristic is that the initial state and final state of the wave function are given, and we pay attention to how to keep the form of the Lagrangian formula describing the density of the system unchanged when the system is perturbated between the initial state and the final state. This requirement is intended to ensure that the Lagrangian density formula can be integrable, and the minimum value of this integral is the minimum action that we are ultimately interested in. Based on this, quantum field theory no longer focuses on whether the phase of a single wave function state is observable. What is important is to abstract out the phase factor, and then introduce covariant derivatives and gauge fields to balance the changes in the phase factor in different states. It is reasonable to assume that this change is indirectly observable, thus creating the conditions for treating the wave function as an operator in quantum field theory.

Third, to construct a wave function operator in the framework of gauge field theory, it must satisfy the gauge structure of its dynamical phase factor. The standard gauge structure of phase factors is two-layers, two-level four-grid framework. First of all, we must distinguish between the local and global levels, and then establish and distinguish the global phase factor and the local phase factor, denoted as

θ = C a n d θ (x)

, where

C

is an arbitrary constant. At the same time and each level, the gauge potential and gauge field strength should be introduced respectively. To obtain the global gauge field strength from the global gauge potential, the standard derivative can be applied. To obtain the local gauge field strength from the local gauge potential, it is necessary to introduce and apply the covariant derivative and gauge field.

5.2. Market Wave Function and Its Gauge Structure

This article, including the previous article [27], a lot of theoretical preparation has been done. This section is the core content of market dynamics, consisting of eight definitions.

Definition 5.1 Let

φ

be a market. Assume

ψ

is an experimental observation of all market participants on market,

α_{i}

ψ

is the observation of an any given individual market participant. Thus, the three form a wave function operator in Dirac bra-ket formalism

⟨ψ | α_{i} | φ⟩

. Let

Δ α_{i}

be the feedback information of the market

φ

to the observation

α_{i}

, then there is a market wave function:

φ (α_{i}) = Δ α_{i}, \forall α_{i} \in ψ

Definition 5.2

L e t Δ α_{k}, Δ α_{j}

be any two pieces of the feedback information introduced by Definition 5.1. We can construct a complex number

(Δ α_{k} + i Δ α_{j})

, called its squared modular

{| Δ α_{k} + i Δ α_{j} |}^{2}

is an amplitude of the market wave function.

According to the Copenhagen school interpretation, the amplitude of the wave function represents probability. As Dirac said, probability is the square of a possibility.

(Δ α_{k} + i Δ α_{j})

is an observation possibility, and its squared modulus is a real number. A market observation experiment is characterized by the market wave function. Its syntactic structure is given by and Definition 5.1, and its semantics is given by Definition 5.2, which is called amplitude semantics, or complex semantics, or phase semantics. The semantics of the wave function is not a single eigenvalue. In Definition 5.2, for any given k and j, there will be an amplitude. Therefore, the semantics of the wave function is an eigenvalue spectrum.

Definition 5.3 The global phase factor of the market wave function is an arbitrary constant, denoted as

θ = C

, which is dictated by the quantum version of the invisible hand of the market.

To review, the quantum version of the invisible hand (see Proposition 5 in Section 2 of this paper) is defined by two overall properties of the market dynamics system. The first property is the non-commutative relationship between market participants’ observations of each other, namely

, [α_{β}, β_{α}] \neq 0 .

The second property is the market version of the uncertainty principle about the information obtained by market participants, that is,

[{∆ α}_{β}, ∆ β_{α}] \neq 0 .

the quantum version of the invisible hand is only related to the "relationship" between individual market participants involving their observations and information obtained, and has nothing to do with the internal space of any individual market participant. Therefore, the quantum version of the invisible hand is a global market hand, and its global phase

θ

can be any given constant

C

This is an appropriate context to emphasize the special significance of the global phase factor of the wave function. Almost all quantum field theory textbooks only briefly mention the global phase factor. It is nothing more than saying that the global phase factor is independent of the particle's internal spatial coordinate system, and its gauge transformation is very simple and can be made conformal using standard derivatives. In addition, the gauge principle will be discussed, and global symmetry is a necessary condition for local symmetry. In fact, after talking about these knowledge points, people often still feel that something is lacking. As a result, it is necessary to include a topic on philosophy of mathematical physics. In physics, water distinguishes between liquid and gaseous states, and this state change is known as a phase transition. The author believes that there are also different states and phase transitions in theoretical models. Different mathematical operators mark different states and phase transitions in theoretical models. In quantum electrodynamics, the wave function operator marks the gauge structure, which has the distinction between global states and local states. From this state to that state, it is a phase transition of a theoretical model. By mathematically trivializing the different states and making them orthogonal to each other, we may have a deeper and more detailed understanding of the gauge structure of the wave function operator. We need to elaborate on this topic in another article.

Definition 5.4 The local phase factor of the market wave function is denoted by

θ (x)

, is a function whose independent variable

x

ranges over all market participants, that is, its syntactic domain is

{α_{i}}

, where each

α_{i}

is the market observation of a market participant

i

; its semantic domain is

{∆ α_{i}}

, where each

{∆ α}_{i}

is the information obtained by the market participant's market observation.

The following we provide four definitions of market gauge structure. For their theoretical preparation and detailed arguments, please refer to the previous work [27].

Definition 5.5 The global gauge potential of the market gauge structure is the economic rationality and economic rational man.

It should be noted that in economics literature, the concepts of economic rationality and economic rational man are generally used interchangeably without distinction. However, in the model structure of market dynamics, it must be distinguished. Because the model background of the global gauge potential is the Maxwell electromagnetic potential, which is the electromagnetic potential

A_{μ} = (φ, A)

, where

φ i s t h e e l e c t r i c p o t e n t i a l a n d A

is the magnetic vector potential. In market dynamics, the economic rationality as the global market potential is characterized by electric potential, and the economic rational man as the global cognitive potential are characterized by magnetic vector potential; the two have different functions and must be distinguished.

Definition 5.6 The global gauge field strength of the market gauge structure characterizes the real market, i.e.

F_{μ υ} = \partial_{μ} A_{υ} - \partial_{υ} A_{μ}

Definition 5.7 The local gauge potential of the market gauge structure characterizes Simon's version of bounded rationality. Its behavioral version is the affordability in Samuelson's revealed preference theory or the so-called budget set.

Definition 5.8 The local gauge field strength of the market gauge structure characterizes the market participants, namely, what Simon called buyers and sellers, or businessmen. Its behavioral version is the consumption set in revealed preference.

Note that in Definition 5.5, The concept of the economic rational man is singular. In Definition 5.8, the expression for buyer and seller is businessmen, which is plural. This distinction [20] is known as the Man vs. Men dilemma. In economic modeling, how to conceptually separate the market from market participants and then put the two back into the same mathematical model framework has always been a difficult problem. As far as the author can see, the only model structure that can properly and successfully do this job is the gauge field theory (and of course the fiber bundle theory behind it).

5.3. Gauge Symmetry and Gauge Transformation

Market dynamics, like quantum electrodynamics, belongs to the category of single charge dynamics. The former only promises market charge, while the latter only promises electric charge. Therefore, its individual internal space is one-dimensional space, its gauge symmetry satisfies the mathematical symmetry group

U (1) = {e^{i θ}}

, and its geometric intuition is the unit circle on the complex plane, in which each unit vector from the origin to the circumference has a phase

θ

. We know that

U (1) = \{e^{i θ}\}

satisfies both the associative law and the commutative law, so it is a commutative group, also known as the Abelian group. The essence of gauge field theory is to study gauge symmetry, and its significance will be more clearly seen through the requirements of gauge transformation.

The gauge transformation at the global level is called the gauge transformation of the first kind. When the global gauge potential of the wave function changes from one state to another, it is written as

φ \to φ^{*} = e^{i θ} φ

(5.1)

Here the global phase factor,

θ = C

, is an arbitrary constant, so

e^{i θ}

is still a constant. Thus, in the corresponding transformation of the global gauge field strength, we have

\partial_{μ} (e^{i θ} φ) = e^{i θ} \partial_{μ} φ

(5.2)

It can be seen that in equation (5.1) and (5.2), the right side

e^{i θ}

is in the same position. Such a transformation is called conformal transformation. However, at the local level, the local phase factor is a function,

θ = θ (x)

, and the local gauge potential is transformed into

φ (x) \to {φ (x)}^{*} = e^{i θ (x)} φ (x)

(5.3)

At this point, the right side of the equation becomes the product of two functions. If the standard derivative is applied, the result is

\partial_{μ} (e^{i θ (x)} φ (x)) = e^{i θ (x)} \partial_{μ} φ (x) + φ (x) e^{i θ (x)} i \partial_{μ} θ (x)

(5.4)

It can be seen that the second term on the right side of the equation breaks the conformality of the transformation. In order to eliminate this redundant term, two new concepts need to be introduced, as follows:

Definition 5.9 Covariant derivatives:

D_{μ} = \partial_{μ} + i q A_{μ}

(5.5)

Definition 5.10 In covariant derivatives, the gauge field:

A_{μ} = A_{μ}^{,} - \frac{1}{q} \partial_{μ} θ (x)

(5.6)

When the gauge potential undergoes a local gauge transformation

φ (x) \to e^{i θ (x)} φ (x)

, by applying covariant derivatives and gauge field, the gauge

U (1)

symmetry can be derived as follows.

D_{μ} {(e}^{i θ (x)} φ (x))

(5.7)

= (\partial_{μ} + i q A_{μ}) e^{i θ (x)} φ (x)

= \partial_{μ} (e^{i θ (x)} φ (x)) + i q A_{μ} e^{i θ (x)} φ (x)

= {φ (x) \partial}_{μ} e^{i θ (x)} + e^{i θ (x)} \partial_{μ} φ (x) + i q (A_{μ}^{,} - \frac{1}{q} \partial_{μ} θ (x)) e^{i θ (x)} φ (x)

= φ (x) i e^{i θ (x)} \partial_{μ} θ (x) + e^{i θ (x)} \partial_{μ} φ (x) + i q A_{μ}^{,} e^{i θ (x)} φ (x) - i \partial_{μ} θ (x) e^{i θ (x)} φ (x)

= e^{i θ (x)} \partial_{μ} φ (x) + i q A_{μ}^{,} e^{i θ (x)} φ (x)

= e^{i θ (x)} (\partial_{μ} + i q A_{μ}^{,}) φ (x)

= e^{i θ (x)} D_{μ} φ (x)

(5.8)

From this derivation we see that by applying covariant derivatives and gauge fields, from (5.7) to (5.8), it realizes the conformal property of the transformation. This is called the gauge transformation of the second kind. Accordingly, the conformal transformation at both the global and local levels achieves the symmetry group,

U (1) = \{e^{i θ (x)}\}

, such that the gauge structure of market dynamics is appropriately characterized.

5.4. Gauge Principles

In the gauge structure, the relationship between global symmetry and local symmetry is governed by the gauge principle. The gauge principle states that if the gauge transformation of the first kind cannot be achieved, then the gauge transformation of the second kind also cannot be achieved. In other words, without global gauge symmetry, there is no local gauge symmetry. For market dynamics, the gauge principle reveals a profound truth. In Definition 5.3, we said that the global phase factor of the market wave function is the quantum version of the invisible hand, which is required to be invisible to all the market participants. If a market participant has the opportunity to obtain inside information, i.e., to peek at the invisible hand in advance, the gauge transformation of the first kind can no longer be realized, thus breaking the global gauge symmetry. For example, if there is inside trading in financial markets, global symmetry is lost. As a consequence, the regulations would lose their power. In such cases, the market could not establish local symmetry between market participants.

Internal transactions in the market, especially in the financial market, will directly cause global symmetry to be trivially broken and produce local infinite quantities, so they cannot be balanced through local gauge transformations and can only be manually resolved using renormalization methods. In the language of logic, internal transactions change the relationship between market participants and the market from a subordinate membership

(\in)

to a containment inclusion (

\subset)

. In this way, there will be one or some individual market participants who lose the conditions to be a limit point and become without a neighborhood, and at the same time lose the meaning of the local frame on their neighborhood. In the words of general relativity, it means losing connections with other individual market participants. By the way, this is also one of the sources for corruption.

6. Market Operator Phases and Phase Transitions

The previous section constructed the market wave function; following the order of constructing a dynamic system, the next step is to establish the dynamic equation. If we remove the wave function from an equation involving a wave function, the remaining mathematical structure transforms into an operator. Operator language not only highlights the structure, but also facilitates the description. This section will take this approach. We know that water has a definite molecular structure. We also understand that water can exist in three distinct states: solid, liquid, and gas, with the transition between these states referred to as a phase change. However, the more advanced form of phase change primarily relates to dynamic fluctuations rather than the physical properties themselves. The following provides an overview of four market phases and their phase changes.

6.1. Newtonian Mean Operator State

Wave functions have statistical characteristics. In essence, physics, economics, and even the general social sciences, are all empirical sciences. Since they are all empirical sciences, they cannot avoid the process of dealing with the original sample data. Statistics is the language of empirical science. In terms of statistical processing, we have two choices. A traditional choice is to take the mean immediately after obtaining the original raw data, which enters the framework of Newtonian mechanics. Because this statistical processing method for raw data is general, in this, and only in this sense, we call it the Newtonian mean operator. The Newtonian mean operator describes the market's macroscopic phenomena and satisfies the so-called large number law. Another option is to carefully protect the original raw data and respect it as a state of the wave function, which enters the quantum physics framework. Where to go depends on the researcher's examination and judgment of the phenomenon to be observed and the means of observation. This issue involves the concept of model appropriateness, which cannot be ignored. For a more detailed explanation of this, please see the previous discussion of scientific observation theory [27].

Newtonian classical mechanics can be regarded as the limiting case of quantum mechanics. Some physicists are accustomed to regarding wave functions as physical reality, and believe that experimental observations cause the collapse of wave functions. This article uses the Dirac bra-ket formalism as the syntactic structure, which regards the wave function itself as an experiment, and believes that the statistical mean can cause the collapse of the wave function. We introduce a Newton mean operator, denoted as

\hat{A}

, and apply it to the market wave function, which destroys the statistical basis of the wave function, so it can and should be regarded as the null state of the market wave function. However, the null state is not meaningless; on the contrary, it’s significance is very important, because the phase state of the market is not a single phase, but a superposition of multiple phases. Taking this factor into account, it is necessary to introduce a function, called the degree of freedom of wave function, to map this null state to an arbitrary constant. We have

\hat{A} φ = 0, f (\hat{A} φ) = f (0) = C

(6.1)

Why do we do this treatment? The wave function itself carries a dynamic phase caused by the internal space spin, which has no comparison in Newtonian mechanics. As mentioned at the beginning of our previous work [23], most of our daily lives rely on Newtonian mechanics. Similarly, as described by classical economics, the market is largely applicable to the Newtonian mean operator. It is then mapped to an arbitrary constant because this is both the most normal state of the market and the most normal state of the psychology of market participants. In physics terms, this is a degenerate state.

6.2. Schrödinger Evolution Operator States

In 5.1, we introduced the Schrödinger operator,

\hat{H}

, which, when applied to the market wave function, gave rise to the famous (market version) Schrödinger equation:

i ℏ \frac{\partial ψ}{\partial t} = \hat{H} ψ = - \frac{ℏ^{2}}{2 m} \nabla^{2} ψ + V_{ψ} = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} ψ}{{\partial x}^{2}} + V_{ψ}

(6.2)

This is the dynamic equation of quantum mechanics. In this way, the market wave function will evolve over time according to the Schrödinger equation, which is called the Schrödinger super-range state of the market. The Schrödinger state of the market wave function has several characteristics.

First, non-relativistic. The Schrödinger state is non-relativistic. In previous work ([27], §3.3) and in the present article (§1.3) , we introduced the special relativity model of monetary property and the price field theory in the previous section. Therefore, a non-relativistic market theory model cannot incorporate these contents, and its limitations are obvious.

Second, quantum entanglement. In our early work [25], we discussed five characteristic periods of psychological life, the second of which is called the contradiction period. The so-called contradiction period refers to the conflict between the psychology of quantum mechanics and the psychology of special relativity. Quantum mechanics promises quantum entanglement at a distance. In market terms, at the global level, the market can be quantum entangled with any distant state, and at the local level, each market participant can be quantum entangled with any dream. Quantum entanglement brings infinite potential and endless energy to the market. It is not difficult to imagine that when the market is in the Schrödinger state, the market as a whole, and market participants as individuals may become active, whether good or bad. On the positive side, the market is full of innovative vitality, reflecting technological progress, knowledge creation, scientific discovery, worldly pursuits, product charm, service taste, and imagination of the future. On the negative side, the market goes crazy without limits and bottom lines, manifested in creating all kinds of unwarranted possibilities and overestimating their probabilities; for example, excessive use of financial leverage, predatory quantitative easing, power rent-seeking, blind speculation, bloody accumulation, fraud and falsification, and even taking unaffordable risks, etc. Therefore, the market needs a boundary. The special theory of relativity emphasizes the local causality; in §6.3, we will explain why this local causality serves as a market boundary.

Third, quantum tunneling. Amplitude semantics refers to the semantics of a wave function, as previously mentioned. The squared modulus of amplitude is probability, so the word "wave" in wave function means probability wave. Since it is a wave, there are fluctuations, ups and downs, and periods. The two wave peak amplitudes form a potential, and the concave shape in the middle is called a potential well. A particle needs enough energy to pass through a potential well; if it fails, it will be refracted, and if it succeeds, it is called scattering. When traveling in a potential well, if the energy of a particle is lower than the potential, it is impossible to pass through the potential well under the concept of Newtonian mechanics; however, under the concept of quantum mechanics, due to the interaction between particle fields, under the condition that the energy of the particle is lower than the potential, the particle may still pass through the potential well, which is called quantum tunneling. Note that what is being said here is all possible! In a sense, quantum mechanics is a scientific theory about possibilities. A possibility is also called a path; the sum of all possible paths is called a path integral. The path integral is now the common language of quantum field theory. We know that in logic, the semantics of modal logic is called possible world semantics; in it, the accessible relationship between possible worlds indicates possible paths. With a little imagination, it is not difficult to understand that the market is actually a collection of possibilities in a certain sense.

The market is volatile; this is common sense. The amplitude of market fluctuations is sometimes high and sometimes low; the potential is uneven; there are potential traps everywhere; and there is always a sense of crisis. The market warriors, as well as those who diligently strive to earn a living, do not consistently attempt to navigate these potential business traps on a daily basis.

There are many competitors in front, and there is a shortage of debts and funds in the back. To overcome the market's potential obstacles, you require energy, which combines capital and opportunities, technology and innovation, willpower and tension, grievances and hard work, brand and reputation, concepts and feelings, and family and friends, all of which are indescribable. Sometimes, you fail and are reflected back. Sometimes, you succeed, and the bitterness is over, and the sweetness comes. When you walk through the tunnel of the market, you feel that you don’t have enough energy. At this time, the voice of Newtonian mechanics warns: This is impossible because you are just a particle, isolated and helpless. At this moment, the voice of quantum mechanics sounds: This is possible because you are still a wave that ripples into a field, and this field interacts with that field to create your opportunity.

I asked the businessman who has survived the market: Friend, when you pass through various market tunnels, do you see light or darkness? Do you feel glorious or miserable? My friend's answer is simple and straightforward: Who cares about these? At that time, I was only thinking about seizing the fleeting opportunity to survive. In physics, quantum tunneling is based on the uncertainty principle and is an instantaneous effect caused by uncertainty.

Fourth, the derivatives are of different orders. In quantum mechanics, the general expression of the wave function is

φ (x, t)

. Note that on the left side of the Schrödinger equation above, the partial differential with respect to the time variable t is of first order, while on the right side the partial differential with respect to the position variable x is of second order. Note that this structure of derivatives of different orders conflicts with the special theory of relativity. In the special theory of relativity, it can be seen from the definition of the concept of interval that the differentials with respect to the time variable and the space variable are of the same order, both of which are of first order. This reflects Einstein's idea of the indivisibility of space and time. We continue to discuss this disagreement in §6.3.

Applying the Schrödinger evolution operator to the market wave function will lead to the phenomenon that market participants may not be willing to do so. People often say that time is life. The time-to-time changes in life status can be described by the first-order derivative. People also often say that only by working hard can you change your position x in the labor market, which is

x

in the Schrödinger operator. So, how hard should market participants work? The Schrödinger operator says, find the second-order derivative, which is acceleration. In other words, with a short life as the opportunity cost, you have to keep accelerating the sale of your labor resources. Is this the market life you are willing to live? Is this a good deal? Are you really willing to be a slave in Schrodinger's manor for your whole life? This is an inquiry of market philosophy, a debate on market life, and a self-reflection of market participants.

6.3. Einstein Cone Operator States

Modern electrodynamics has two versions: classical and quantum. Correspondingly, market dynamics also has two versions: classical and quantum. What is discussed in this section is actually the classical version's content. Classical electrodynamics is non-quantized, and its highest form is Einstein's special theory of relativity. Einstein discovered that space and time are inseparable, called the four-dimensional spacetime, which can be described by mathematical Minkowski space. The Maxwell field is a non-quantized classical field. Einstein realized that there is a certain symmetry implied in Maxwell's equations, and thus discovered the principle of the invariance of the speed of light. In Makowski four-dimensional spacetime, each point is called an event, also known as a permissible observer. Each permitted observer represents a different inertial system. Einstein also understand that the Lorentz transformation, which is a gauge transformation, makes it possible for the observers in different inertial reference frames are covariant to agree on what they are seeing in terms of physical quantities. Einstein's theory of invariance and covariance laid the foundation for the special theory of relativity.

In the previous article [27], we discussed the monetary nature of currencies and its light-like nature, introduced the concept of interval, and characterized the light cone and the money cone. In §1.3 of the present paper, we restated the definition of interval and the characterization of the light and money cones, and we won't repeat them here. In all of these contents involving special relativity, the concept of probability is not included. The semantics of wave function is probability wave; therefore, there seems to be no relationship between special relativity and wave function, and there is no intersection between the two in terms of conceptual system. Quantum electrodynamics is the content of quantum field theory. Quantum field theory is the integrated theory of quantum mechanics and special relativity. Therefore, quantum electrodynamics is relativistic, the same is the quantum version of market dynamics. These are the contents of §6.4.

Here we characterize a hard treatment that establishes a connection between the market wave function and the relativistic money cone; the treatment is similar to that in §1.3. The price shell in the money cone is described in the following section. We introduce a new operator, called the Einstein money cone operator, denoted as

\hat{C}

. Business events that enter the money cone (interval greater than 0, called time-like events) are called money-making events here; business events that fall outside the money cone (interval less than 0, called space-like events) are called money-losing events here; business events attached to the surface of the money cone (interval equal to 0) are called null event, just no loss or gain. Applying this money cone operator to the market wave function,

\hat{C} ψ

, for any business in the market, the wave function will feedback a probability, which is called the degree of chance, predicting whether it will be lucky enough to enter the cone and become a profitable business, or fall outside the cone and become a losing business, or cling tightly to the cone surface, just like many companies and individuals, barely balancing their income and expenditure, eager to make money when entering the cone next year, but also worried about losing money when falling outside the cone. The relativistic money cone and quantum mechanical wave function coexist with certainty and uncertainty, which not only depicts the ups and downs of businessmen, but also lists all kinds of monetary experiences in the business world.

6.4. Dirac Field Operator States

It is quantum field theory that truly integrates special relativity and quantum mechanics, and quantum electrodynamics is the most mature and thorough dynamic system in quantum field theory. Therefore, understanding quantum field theory and its quantum electrodynamics is crucial to constructing market dynamics. One entry point to understanding quantum field theory is the Dirac operator. When applied to the wave function, the resulting Dirac equation describes electrons and positrons, both spin

\frac{1}{2}

. Correspondingly, applying the Dirac operator to the market wave function describes demand and supply. The Dirac operator is given below:

\hat{D} = c \vec{α} \cdot (- i ℏ \nabla) + β m c^{2}

(6.3)

Here we need to make some comments on the Dirac operator. First, the formula is a first-order total differential operator, as follows:

\vec{\nabla} = \frac{\partial}{\partial x_{1}} \hat{e_{1}} + \frac{\partial}{\partial x_{2}} \hat{e_{2}} + \frac{\partial}{\partial x_{3}} \hat{e_{3}}

(6.4)

This total differential operator transforms the position variable to the first order, which is an important change to the second-order position derivative in the Schrödinger operator of quantum mechanics, making the time variable and the position variable differential of the same order, both of which are first order. This solves the first technical difficulty of quantum field theory in relativizing quantum mechanics. According to market dynamics, time is money, and such mathematical treatment believes that the change in capital volume and the change in market behavior should be of the same order in principle. This principle explains, for example, that excessive use of financial leverage will cause excessive tension in market life.

Second, the factor c in the Dirac operator formula represents the speed of light, which shows that the Dirac operator is relativistic. In other words, we are only talking about the situation within the light cone, where electrons and their antiparticles positrons are massive particles, and their speed cannot reach the speed of light; otherwise, Einstein's mass-energy conversion formula would require them to have infinite energy. Similarly, within the money cone, both demand and supply have costs, and their speeds cannot reach a cost-free price relationship. Once a product becomes a market commodity, it becomes a valuable item; or the nature of supply or demand is to be sensitive to price. Without price, how can there be sensitivity? The logical order here is: product (including service) to price, then to commodity, and then to supply and demand. Secondly, in §3.1 of this article, In the we can see that the price shell is built within the money cone. The money cone expresses purchasing power, which requires the price range to fall properly within the money cone. This is common sense in the market and a relativistic requirement.

Third, the Dirac operator is quantized. Applying the Dirac operator to the wave function gives the Dirac equation as follows:

i ℏ \frac{\partial ψ}{\partial t} = [c \vec{α} \cdot (- i ℏ \nabla) + β m c^{2}] ψ

(6.5)

Here,

\vec{α} = α_{1} \hat{e_{1}} + α_{2} \hat{e_{2}} + α_{3} \hat{e_{3}}

represents a three-dimensional vector. Now we introduce the Dirac matrix (also known as gamma matrix) as follows:

γ^{0} = β, γ^{i} = β α_{i}

where

γ_{1} = (\begin{matrix} 0 & σ_{1} \\ - σ_{1} & 0 \end{matrix}), γ_{2} = (\begin{matrix} 0 & σ_{2} \\ {- σ}_{2} & 0 \end{matrix}), γ_{3} = (\begin{matrix} 0 & σ_{3} \\ - σ_{3} & 0 \end{matrix})

where

σ_{1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}), σ_{2} = (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}), σ_{3} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix})

Here

σ_{i}

is called the Pauli matrices. We know that matrix operations generally do not satisfy the commutation rule. Specifically, we have

{{[γ}^{μ}, γ^{υ}] = γ}^{μ} γ^{υ} - γ^{μ} γ^{υ} = 2 g^{μ υ} \neq 0

(6.9)

That is, the Dirac matrix satisfies the non-commutative relation. We also know that the establishment of a non-commutative relationship means quantization. Therefore, the Dirac equation is not only relativistic but also quantized.

Fourth, in §1.2, we directly introduce the Dirac spinor to characterize the spin

\frac{1}{2}

electrons and positrons; i.e., the spin

\frac{1}{2}

demand and supply in our context. The Dirac spinor is the solution to the Dirac equation.

Fifth, in quantum field theory, particles are all described by the concept of field, that is, particles are excited states of field. In this way, the original long-distance entanglement between particles in quantum mechanics is changed to the interaction between particle fields, thus meeting Einstein's requirement for local causality. This eliminates the principle conflict between special relativity and quantum mechanics. For market dynamics, demand and supply both have a certain market background and are excited states of the background field. The emergence of a pair of demand and supply, which are mutually causal, reflects the background field's interaction. Since particles are now regarded as excited states of the field, the creation operator and annihilation operator of particle life are naturally introduced in quantum field theory. In theory, these two operators limit the life of particles, making occasional inexplicable long-distance entanglement less significant even if its local causality remains unexplained. Who hasn't had a dream? When you sell your labor in the human resources market, you have dreams, right? When you act in the financial market, you have dreams, right? This is the excited state allowed by the creation operator. But reality will wake you up, and this is the annihilation operation. When you correct your goals, adjust your mentality, and stimulate the market again, intending to buy and sell, a new creation-annihilation process begins.

Finally, quantum electrodynamics holds that the interaction between electrons and positrons occurs through the exchange of virtual photons. Similarly, in market dynamics, the interaction between demand and supply is carried out through the exchange of virtual prices. So, what is the real price? The transaction price is the true price. The bargaining before the transaction is the exchange of virtual prices between supply and demand. Although a commodity's price is clearly marked in the market, when potential buyers hesitate due to their sensitivity to the market price, there is actually a unilateral bargaining process caused by the individual proper price that is difficult to directly observe. In this sense, the price that the buyer bargains for in his mind is a virtual price. Therefore, hesitation about the market price means exchanging virtual prices between supply and demand. Upon completion of a transaction, the real price becomes the transaction price, simultaneously annihilating the previous demand and supply pair.

We have previously summarized that hesitation carries market energy; now we understand that it is this hesitant energy, also known as fluctuation energy, that stimulates virtual prices. In other words, it is the virtual price that propagating the market, undercurrent surges, and market waves. The transformation of the Maxwell electromagnetic potential field of classical electrodynamics into a photon field is a feature of quantum field theory. In the words of market dynamics, this is the transformation of people's cognition of the monetary nature of currency into the private calculations of individual market participants on prices.

6.5. Operator States of the Market and Their Phase Transitions

In §5.2, we constructed the market wave function. In this section, we constructed four operators that can be applied to the market wave function. The author believes that each time an operator is applied to the market wave function, a phase of the market wave function will be formed, also known as the market phase. The change from one market phase to another is called a market phase transition. This section examines four possible market phases, namely the Newton mean state, the Schrödinger quantum state, the Einstein cone state, and the Dirac field theory state. In physics, the phase of matter and its phase transition are the contents of thermodynamics. The level of energy or temperature correlates with the phase transition. People often say that the market has a temperature; metaphorically, the market is very hot in a bull market and cools down in a bear market. Figuratively speaking, changes in market temperature will cause market phase transitions. Additionally, studying market phase transitions has become an effective market thermometer.

A powerful theoretical framework for studying market phase transitions is Wilson's phase transition theory. Wilson had an important insight. He pointed out that to better understand physical phase transitions, we need to expand the scale and collect more fluctuation information about the system. Physical phase transitions do not depend on physical properties but on system fluctuations. The coexistence of the above-mentioned phase states determines the complexity of market phases. Only by considering the various fluctuations within each phase can we understand market-phase transitions. This is the connection between statistical physics and thermodynamics. An in-depth discussion of the application of Wilson's phase transition theory in market dynamics is beyond the scope of this article.

7. General Discussion

This article covers most of the content of market dynamics, which is also the backbone. Market dynamics is based on classical electrodynamics and uses quantum electrodynamics as the reference model framework to construct the theoretical model of market dynamics in steps. The Bourbaki structuralist school's ideas are always used when developing market dynamics. The method is to decompose the structural components of classical and quantum electrodynamics, embed them into market phenomena one by one, and try to explain their structural components and their market dynamics significance at each step. The following is a brief summary of this article's content.

The first section explains that market dynamics studies the interaction between price, demand and supply. Quantum electrodynamics studies the interaction between photons, electrons and positrons. Both belong to the category of single charge dynamics and share a symmetry group U(1). Based on classical electrodynamics and taking quantum electrodynamics as the reference model framework, this paper constructs a theoretical model of market dynamics in steps. At each step, we try to explain its structural components and its market dynamics significance. Dynamic analysis is an active analysis, and its source is charge, such as electric charge. Market dynamics introduces market charge and defines demand and supply respectively. By examining the market hesitation phenomenon, spin is introduced as an intrinsic property for demand and supply. Therefore, demand and supply can be defined by Dirac spinors. By introducing the coin cone and valence shell, virtual prices are defined; demand and supply interact by exchanging virtual prices. These interactions can be characterized by Feynman diagrams. The cognitive field has the function of polarizing decisions and is characterized by the magnetic field.

In the second section, market dynamics argues that social economy itself is an experiment, and every market participant is an observer. We established the non-commutative relationship between market observations. It characterized the market version of the uncertainty principle of observation information. We then used this to define the quantum version of the invisible hand. In the third section, based on classical electrodynamics, we discussed the relationship between the price field and the Maxwell field and introduced the concept of gauge potential. In the fourth section, we discussed market fluctuations (including mesoscopic and quantum fluctuations) caused by higher-order cognition (including games, decision-making and reasoning). The fluctuation phenomena inherent in various markets serve as the basis for understanding both market participants' cognition and the market's phase transition.

Section 5 begins to introduce the more abstract and mathematical content of quantum electrodynamics. Wave function and gauge field theory are the languages of quantum electrodynamics, and gauge symmetry is the central concept of gauge field theory. The paper defines the six components of the market wave function: the global phase factor, global gauge potential, and global gauge field strength, as well as the local phase factor, local gauge potential, and local gauge field strength. Gauge transformation is an integral part of quantum electrodynamics and market dynamics, and the paper explains it without omission; then the gauge principle is given to explain that global symmetry is a necessary condition for local symmetry.

The narrative style of Section 6 is a new attempt. This paper introduces four operators: The Newton mean operator, the Einstein cone operator, the Schrödinger evolution operator, and the Dirac field theory operator. We apply these four operators to the market wave function, thereby presenting four operator phases of the market wave function. The change in operator state is referred to as the phase transition of the wave function. This treatment is based on three considerations. First, in order to reveal the hierarchy and complex level of market phenomena, multiple operator states should be a natural part of the market wave function. Second, it can avoid redundant theoretical expressions. In addition, the author consciously tries to introduce the concepts of thermodynamics and statistical mechanics in the dynamic analysis.

Finally, this article’s discussion of market dynamics is incomplete; it does not introduce its Lagrangian density function and minimum action. The spontaneous gauge symmetry-breaking mechanism of market dynamics, modeled on the Higgs mechanism, is called the ordinary rationality mechanism [27], which is also not introduced in this article. Lagrangian and ordinary rationality mechanisms are also used in other parts of economic dynamics, such as sub-economic dynamics and economic externality dynamics, which will be introduced in a separate article. As introduced, economic dynamics uses the standard model of theoretical physics as its referential modeling framework. This is a dynamic model that uses gauge field theory as its language, so there is no place for thermodynamics. In physics, Wilson's phase transition theory connects quantum field theory, statistical physics and thermodynamics. Introducing Wilson's theory into the analysis of social science dynamics should be a promising research direction and is exciting.

Acknowledgements

The authors thank Hongbin Wang, Ping Ao, Yi Zhang, Quanhui Liu, and Xiao Xu for their help and discussions. My thanks also go to my students at Rensselaer Polytechnic Institute who did the first-round proofreading of this paper.

References

Camerer, Colin F. (1999/2003). Behavioral Game Theory: Experiments in Strategic Interaction, Princeton University Press. Princeton, New Jersey, USA.
Cao, Tianyu (1997/2019). Conceptual Developments of Twentieth-Century Field Theories. Cambridge University Press, Cambridge, UK.
Feynman, Richard. (1998/2018). Quantum Electrodynamics. Taylor & Francis Group, Boca Raton, FL. USA.
Feynman RP, Leighton RB, and Sand M.L. (1965a) The Feynman Lectures on Physics. Reading, Mass.: Addison-Wesley.
Harley, R. (2007). Gauge What Is Real — The Conceptual Foundations of Contemporary Gauge Theories. Oxford University Press. Oxford, United Kingdom.
Marshall, Alfred. (1890/2010). Principles of Economics, Nabu Press.
Leinster, Tom (2014/2017). Basic Category Theory (Cambridge University Press). Cambridge, UK.
Lee, T. D. (1988). Symmetries, Asymmetries, and the World of Particles, University of Washington Press, USA.
Li, H. Z. (2001). Phase factors in quantum mechanics. Physics, 2001, No.12. China.
Penrose, R. (2004). The Road to Reality – A Complete Guide to the Laws of the Universe. Vintage Books, Random House Inc.
Samuelson, Paul A. (1938). A Note on the Pure Theory of Consumer's Behavior and an Addendum. February 1938, Economica.
Samuelson, Paul A. (1948). Consumption Theory in terms of revealed preference. November 1948, Economica. [CrossRef]
Savage, L. (1954/1972). The Foundations of Statistics. Dover Publications, New York.
Simmel, G. (1900/2004). The Philosophy of Money, Routledge.
Wang, Z. (2008). Elementary Quantum Field Theory. Peking University Press. Beijing.
Wilczek, Frank. (2008). The Lightness of Being: Mass, Ether, and Force Unification. Basic Books. New York, USA.
Yang, C.N. (2014) The conceptual origins of Maxwell's equations and gauge theory. November, Physics Today.
Yang, Y. (2006). Toward a mental decision logic of the small-grand world problem: Its decision structure and arithmetization. In R. Sun and N. Miyake (Eds.), Proceedings of the Twenty-Eighth Annual Conference of the Cognitive Science Society, Mahwah, NJ: Lawrence Erlbaum Associates.
Yang, Y. (2013) Modern Principles of Economic Mechanics — Qualitative initiatives integrating economics, cognitive science, and theoretical physics. Xlibris Publishing House, Bloomington, IN, USA.
Yang, Y. (2015). Gauge field theory of market dynamics: Toward a solution of the “man vs. men” dilemma. MPRA Paper No. 65274. Online at http://mpra.ub.uni-muenchen.de/65274/.
Yang, Y., Brain, M. D. S., and O'Brien, D. (1998). Some empirical justifications of a mental predicate logic. In Braine, Martin DS and O'Brien, David P. Mental Logic, Lawrence Erlbaum Associates. New Jersey, USA.
Yang, Y., and Johnson-Laird, PN (2001). Mental models and logical reasoning problems in the GRE. Journal of Experimental Psychology: Applied, Vol. 7 (4), 308-316.
Yang, Y., and Johnson-Laird, PN (2000). Illusions in quantified reasoning: How to make the impossible seem possible, and vice versa. Memory & Cognition, 28 (3), 452-465. [CrossRef]
Yang, Y., and Johnson-Laird, PN (2000). How to eliminate illusions in quantified reasoning. Memory & Cognition, 28 (6), 1050-1059. [CrossRef]
Yang, Y. (2022). Characteristic Phases of psychological life: Psychological life and theoretical physics (I). Science, Economy and Society, Vol. 40, No. 1. China.
Yang, Y. (2022). The integrated structure of language and language behavior and its psychological path: psychological life and theoretical physics (II). Science, Economy, and Society, Vol. 40, No. 3. China.
Yang, Y. (2022). Content, methods and significance of economic dynamics: Economic dynamics and standard model (I). Science, Economy and Society, Vol. 40, No. 5. China. Yang, Y. Contents, Methods, and Significance of the Economic Dynamics: Economics Dynamics and Standard Model (I). Preprints 2024, 2024080810. [CrossRef]
Yang, Y. (2023). Principles of Econ-Externality Dynamics: Economic dynamics and standard model (III). Science, Economy and Society, Vol. 41, No. 3. China. Yang, Y. Principles of Economic Externality Dynamics Economic Dynamics and the Standard Model (V). Journal of Electrical Electronics Engineering 2024, 3, 01–13, doi:10.33140/jeee.03.04.06.
Yang, Y. (2023). Principles of Sub-Economic Dynamics: Economic dynamics and standard model (V). Science, Economy and Society, Vol. 41, No. 5. China. Yang, Y. Principles of the Sub-Econ Dynamics: The Econ-Dynamics and the Standard Model (III). Preprints 2024, 2024071843. [CrossRef]
Zee, T. (2010). A. Quantum Field Theory in a Nutshell. Princeton University Press, Princeton, New Jersey, USA.

Figure 1

Figure 2. Semantic meaning for Figure 1.

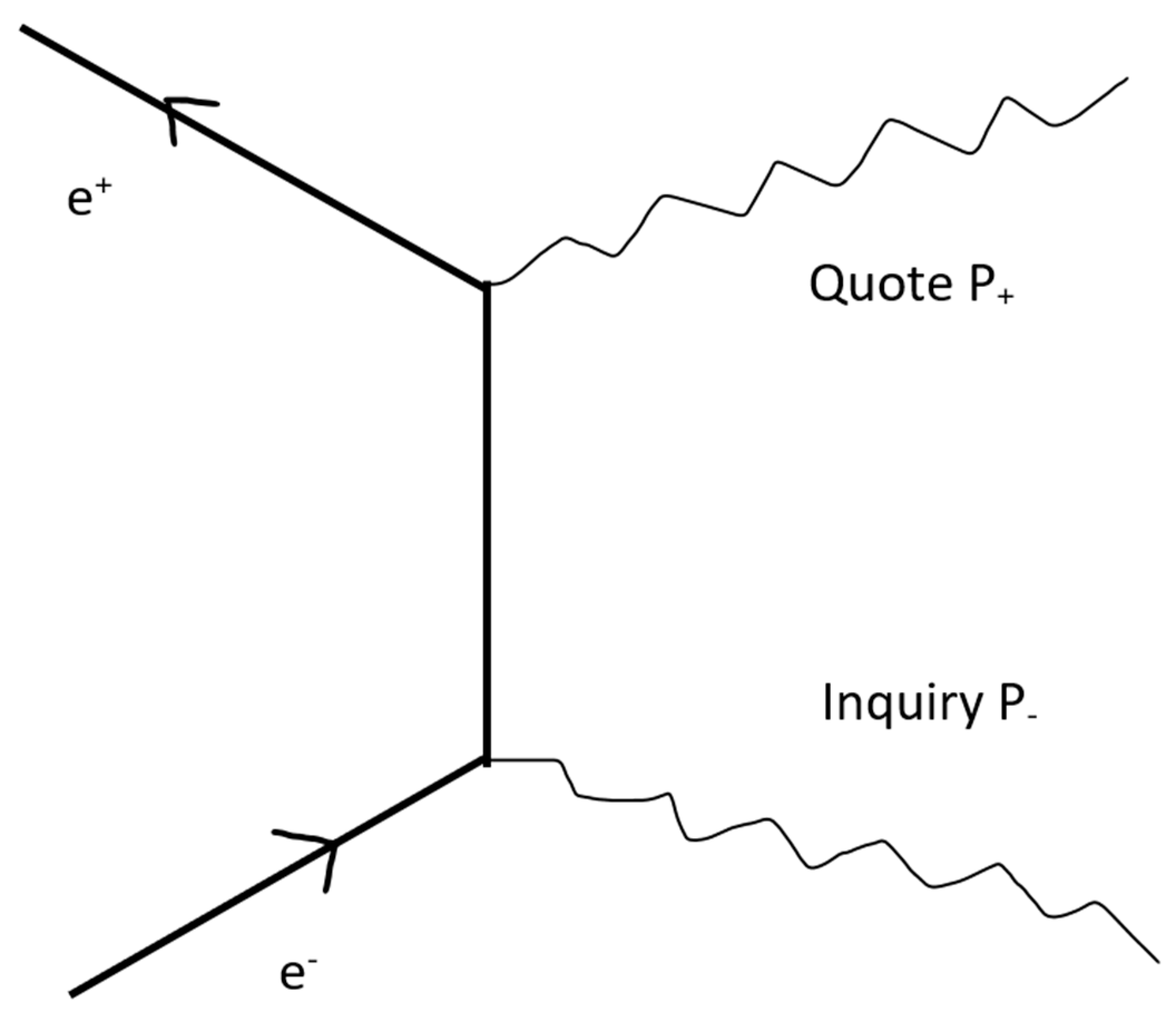
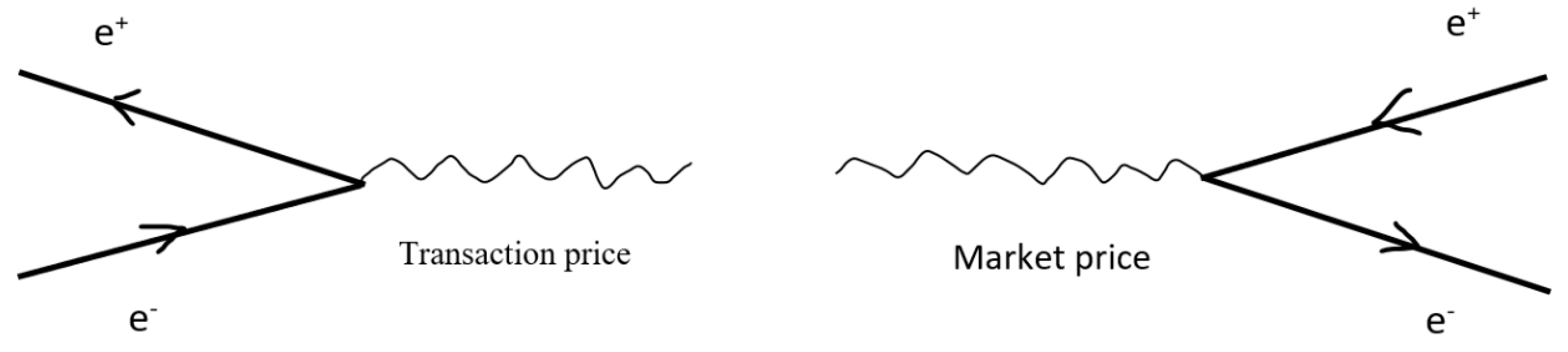
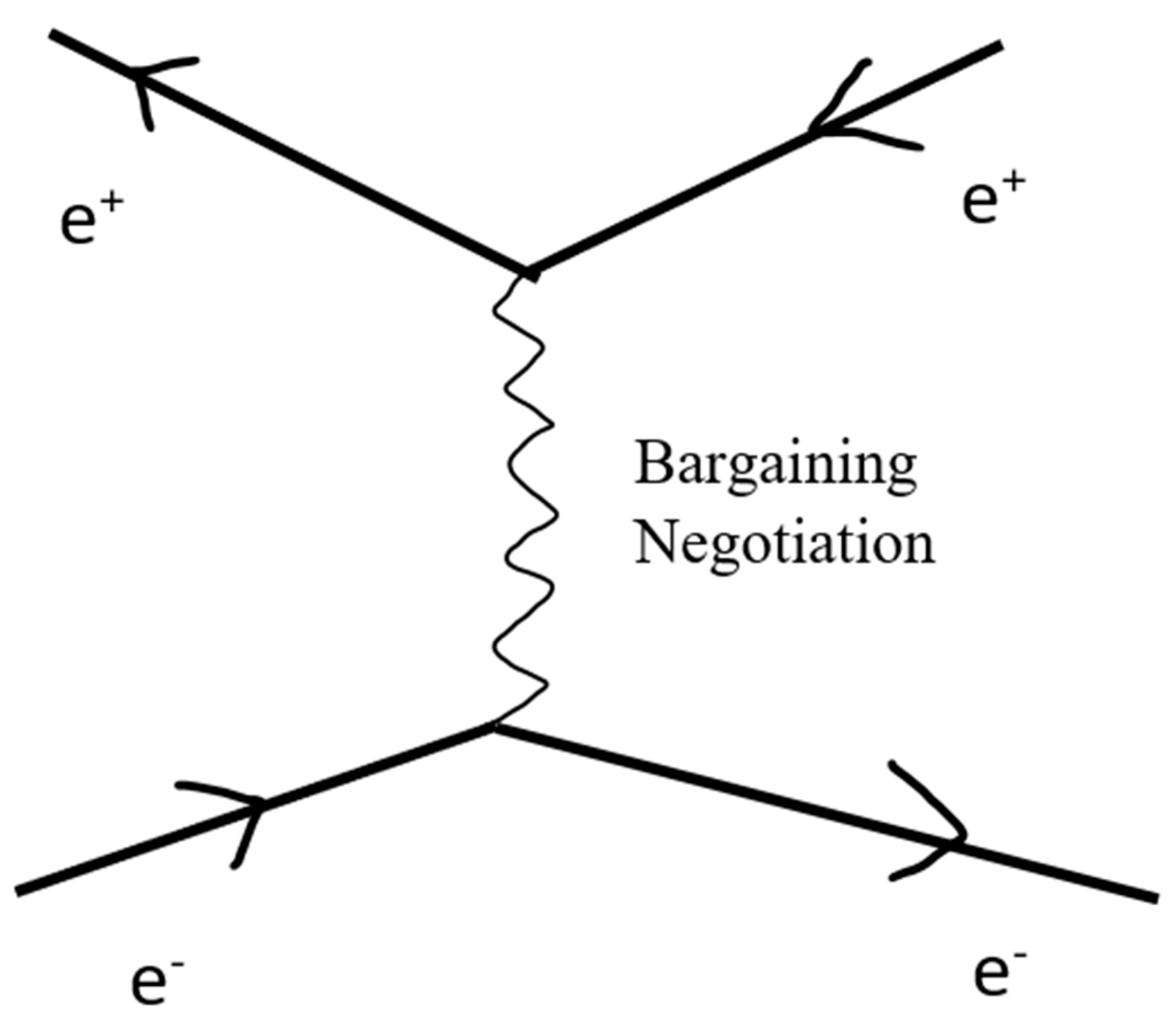
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Principles of Market Dynamics: Economic Dynamics and Standard Model (II)

Abstract

Preface

1. Hesitation Theory

1.1. Market Charge and Price, Supply and Demand

1.2. Hesitation and Dirac Spinor

1.3. Money Cone Price Shell, Virtual and Real Fluctuation

1.4. Feynman Diagrams and Interactions

1.5. Cognitive Field and Decision Making

1.6. Price Function and Selection Function

2. Searching the Invisible Hand

2.1. Beliefs and Dogmas of Market Mechanisms

2.2. The Quantum Version of Invisible Hand

3. Price Field Theory

3.1. The Nature of Price

3.2. Price Field and Classical Electrodynamics

3.3. Summary

4. Higher-Order Cognition and Market Fluctuation

4.1. Cognitive Field and Samuelson's Misconception

4.2. Game Theory and Classical Fluctuations

4.3. Decision Theory and Mesoscopic (Semiclassical) Fluctuations

4.4. Reasoning and Market Quantum Fluctuations

4.5. Summary

5. Market Wave Function and Gauge Transformation

5.1. Wave Function Operator Phase Space

5.2. Market Wave Function and Its Gauge Structure

5.3. Gauge Symmetry and Gauge Transformation

5.4. Gauge Principles

6. Market Operator Phases and Phase Transitions

6.1. Newtonian Mean Operator State

6.2. Schrödinger Evolution Operator States

6.3. Einstein Cone Operator States

6.4. Dirac Field Operator States

6.5. Operator States of the Market and Their Phase Transitions

7. General Discussion

Acknowledgements

References

MDPI Initiatives

Important Links

Subscribe