Integrated Assessment of the Quality of Functioning of Local Electric Energy Systems

Preprint

Review

Integrated Assessment of the Quality of Functioning of Local Electric Energy Systems

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

21 October 2024

Posted:

21 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

The article discusses the formation of local electric energy systems (LEES) based on renewable energy sources (RSE) as balancing groups in the electric power system (EPS). These systems can function autonomously, providing electricity even in extreme conditions. LEES incorporate small hydroelectric, photovoltaic, and wind power plants, whose output is unstable due to varying natural conditions. To address this, energy storage systems are included to ensure stability and balance. LEES may vary significantly in terms of reliability, power losses, and quality, making it essential to choose the optimal configuration. Optimizing power supply by focusing on individual indicators is discouraged, as it may negatively affect others. To evaluate LEES performance, an integral indicator has been developed, combining the theory of Markov processes and similarity. This indicator compares actual performance with an "ideal" standard, simplifying the assessment of complex systems. It allows comparison of different transmission and distribution options without needing to evaluate all technical and economic details. The proposed integral indicator effectively reflects real operating conditions and assesses the efficiency, quality, and optimality of power supply, while remaining adaptable to partial indicators.

Keywords:

Subject:

Engineering - Electrical and Electronic Engineering

1. Introduction

With the development of renewable sources of energy (RSE) in the power grids of electric energy systems (EES) and decentralization of generation, it has become possible to organize local electric energy systems (LEES). LEES can operate in parallel with the EES as a separate balancing group, consuming or generating electricity into the system. Under certain conditions, based on economic interests or due to an extreme situation in the EES, LEES can function autonomously as an isolated intelligent system [1,2,3].

Similar problems and tasks arise in the local electric energy system as in the EES: balancing the mode, regulating frequency and voltage, reducing electricity losses and improving its quality, increasing the reliability of electricity supply, reducing SAIFI and SAIDI. Modern LEES are formed on the basis of renewable energy sources, the vast majority of which are photovoltaic and wind power plants (PVPP and WPP). Since the generation of electricity by PVPP and WPP depends on weather conditions, electricity storage systems are forced to compensate for their unstable generation. In one way or another, all of these factors affect the operation of LEES and the quality of electricity supply to consumers.

The quality of the local electric energy system is characterized by several criteria. The main ones are: quality of electricity, reliability of electricity supply, its cost effectiveness, sustainability and resilience of systems, ability to adapt to changing conditions, and reduction of negative impact on the environment. The process of operation shows the behavior of a local electric energy system in time and can be represented as a sequential change of its states. Therefore, assessing the quality of functioning of a LEES requires information support for, first, retrospective analysis of operation and, second, for operational management of power flows, forecasting of electricity generation and consumption, and diagnostics of electrical equipment.

Assessment of the condition of particular LEES and comparison of their functional availability is relevant in analyzing the quality of functioning and supporting decision-making on the development of distribution power grids in the context of RSE development. The research in this area is carried out in accordance with the requirements in the field of energy efficiency to improve the quality of electricity supply, create a transparent management system to increase investment attractiveness, and intelligence of power grids based on SMART grid technologies.

The search for ways to resolve the contradictions that arise during the assessment of the quality of functioning of LEES is the scientific and practical problem of this study: the need to create a unified theoretical and methodological basis for assessing, providing and maintaining the quality of functioning of LEES by developing optimal strategies for the development of distribution power grids in the context of RSE development.

At the current stage of development of the electric power industry, along with the issues of technology improvement, the issues of rational organization of operation and management of the functioning (behavior) and development of electric power systems are becoming increasingly important. They are caused by the level of power supply to industry and households, which requires increased requirements for the quality of power supply from the electricity industry. the term power supply quality is defined as a characteristic of the level of reliability (continuity) of power supply, commercial quality of services for the transmission, distribution and supply of electricity, as well as the quality of electricity [4].

To assess the quality of electricity supply, it is necessary to analyze a significant number of different indicators: four for reliability of electricity supply; eleven for electricity quality and eight for quality of service. It is not possible to single out the most important indicators from such a large number of indicators, and they depend on the characteristics of consumers. In general, the level of quality of electricity supply can be assessed only by the result for the system as a whole. The solution to this problem in relation to LEES is possible only on the basis of system analysis. System analysis involves considering the object under study as a whole. The requirements for ensuring the quality of power supply largely determine the principles of building power grids. Obviously, the main influence on the level of power supply quality is the quality of functioning of LEES.

The term quality of functioning refers to systems for which it is not possible to formulate an all-or-nothing failure criterion. The electric energy system belongs to such systems. Due to its redundancy, the failure of some (or even many) elements leads to only a partial degradation of the functionality of the LEES. The quality of functioning indicator characterizes the ability of a LEES to perform its main functions with a reduced level of productivity and efficiency. This is reflected in a certain deterioration in the reliability of power supply, an increase in technological losses of electricity and a deterioration in its quality.

The goal of the research is to develop a method and corresponding mathematical models for determining the integral indicator of the quality of functioning and its use in the formation of a local electric energy system with its intelligent control system.

2. Modeling the Operation of Power Grids Using Similarity Theory and Markov Processes

Methods based on the theory of Markov processes make it possible to obtain simple mathematical models. This is achieved due to the basic assumption that a process is Markovian if, for each moment in time, the probability of any state of the system in the future depends only on the state in which the system is now and does not depend on how the system got to that state [5]. The assumptions made when building models do not lead to significant errors, and therefore are acceptable for solving practical problems in such dynamic systems as the electric power industry. Using the methods of the theory of Markov processes, it is possible to model only the period of normal operation of the elements of the electric power grid (section 2 of Figure 1) [6].

The period of normal power grid operation can be divided into separate states. These states are operational, but the system parameters can deteriorate from state to state, approaching complete failure. Stepwise recovery also moves the control system from state to state, but in the opposite direction. Assuming that the change of states follows an exponential distribution law, the main principle of Markovian interest theory is fulfilled - the change of states occurs without an aftereffect. Modern diagnostic systems provide information for determining such states. Determination of intermediate states makes it possible to assess the readiness of power grid elements at any time of its operation. This makes it possible to determine the level of reliability of the power grid and provide recommendations to the maintenance staff to build a strategy for the recovery stages.

Thus, for dynamic systems similar to the electrical system, it is possible to use the theory of Markov processes if we accept the following assumptions: no aftereffect and the choice of states in which the exponential law of distribution of a random variable is fulfilled; failures of system elements are independent; the restored system has the same characteristics as the new one; the intensity of failures and the intensity of restoration is constant [6]. The combination of the principles of Markov process theory and similarity theory will allow us to build mathematical models that combine a probabilistic approach to determining the quality of power grid operation and changes in characteristics during their operation.

To describe the process of distribution grid operation, we use the theory of Markov processes. The fundamental assumption made in the modeling is an exponential distribution law for the occurrence of events related to failures and restoration of power supply system elements. There is research evidence [6,7] that indicates a more complex character of the distribution law of the time of occurrence of failures and recovery time than the exponential one, but the use of the exponential distribution in calculating the probability of failure of these elements can be considered generally accepted. This can be explained by the following:

- there is no consensus on the actual law of distribution of failure and recovery times;

- the use of the exponential law of distribution of time between failures leads to errors in the direction of a certain underestimation of the estimated probability of failure-free operation compared to the actual one, i.e., it cannot be the reason for creating an unreliable system; there are publications, for example [8], which consider systems with elements whose failure and recovery times are a combination of exponential, Weibull, and normal-logarithmic distributions, and which show that for a sufficiently long period of time these systems behave as if all their elements had an exponential distribution of failure and recovery times. The process of functioning can be shown in the form of a graph (Figure 2), which can be used to draw up a system of Kolmogorov differential equations [5,9]. Taking into account the assumption that the dynamics of transients between individual states is not taken into account

(\frac{d p_{i}}{d t} = 0)

, the system of differential equations will have the form:

\begin{array}{l} \sum_{i = 1}^{m + 1} ν_{j i} p_{i} = 0, j = \bar{2, n} \\ \sum_{i = 1}^{m + 1} p_{i} = 1, \end{array}\},

(1)

where

p_{i}

is the vector of probabilities of states of the system under study;

ν_{j i}

– elements of the matrix ν, which is the matrix of intensities of transitions from one state to another;

m + 1

– number of possible states of the system under study; m – number of operating states; n – number of directions of change of states starting from operating state 1 (see Figure 2).

To determine the probabilities of operating states and assess the quality of the system under study, it is necessary to solve the algebraic system of equations (1), which is written in a more general form

ν \cdot p = b .

(2)

In criterion programming, the system of orthogonality and normalization equations can be written as follows [10]:

α \cdot π = b,

(3)

where

α

– the matrix of degree indicators;

π

– the vector of similarity criteria;

b

is the vector of right-hand sides.

If we use an interpolation polynomial [11], then the matrix

α

of the system of orthogonality equations (2) of the criterion programming and the transition matrix ν of the system of equations (3) can be reduced to a matrix polynomial. We will use the exponential function

f (z) = e^{z t}

for this purpose. If the minimal polynomial (in this case, it is a characteristic polynomial

Δ (z)

) consists only of linear factors

(z - z_{k})

, then it is enough to define the function

(z - z_{k})

at the characteristic points

z_{1}, z_{2}, ..., z_{m + 1}

. In this case, the system of equations for the coefficients of the interpolation polynomial is as follows :

f (z_{k}) = a_{0} + a_{1} z_{k} + ... + a_{m} z_{k}^{m},

(4)

or in matrix form

[\begin{array}{l} f (z_{1}) \\ f (z_{2}) \\ ... \\ f (z_{m + 1}) \end{array}] = [\begin{array}{l} 1 z_{1} z_{1}^{2} . . . z_{1}^{m} \\ 1 z_{2} z_{2}^{2} . . . z_{2}^{m} \\ ... ... ... ... ... \\ 1 z_{m + 1} z_{m + 1}^{2} . . . z_{m + 1}^{m} \end{array}] \cdot [\begin{array}{l} a_{0} \\ a_{1} \\ ... \\ a_{m} \end{array}] .

Solving this system relative to

a_{0}, a_{1}, ..., a_{m}

, we obtain

f (A) = \sum_{i = 0}^{m} a_{i} A^{i} .

So, in general, the matrix

α

will have a polynomial of the form:

f (α) = \sum_{i = 0}^{m} a_{i} α^{i} .

(5)

And the matrix ν:

f (ν) = \sum_{i = 0}^{m} a_{i} ν^{i} .

(6)

By performing this transformation, one can use all the properties of scalar polynomials, including the results of the theorems of similarity theory.

It is known [12] that to establish the similarity between the original and the model, instead of the conditions

π_{i} = \frac{a \prod_{j = 1}^{n} u_{j}^{α_{j i}}}{f} = i d e m,

(7)

equivalent expressions can be used

μ_{i} = \frac{μ_{a_{i}} \prod_{j = 1}^{n} μ_{u_{j}}^{a_{j i}}}{μ_{f}} = 1,

(8)

where

π_{i}

– similarity criteria determined by the method of integral analogs;

μ_{i}

– similarity indicators, which are determined by the scale of the relevant coefficients and parameters of the model.

Using these conditions, we can prove the similarity of matrix polynomials and their corresponding matrices. For the matrix polynomials (5) and (6), condition (8) can be written as follows:

\frac{μ_{a_{1}}}{μ_{f}} = 1; \frac{μ_{a_{2}} μ_{a / ν}}{μ_{f}} = 1; \frac{μ_{a_{3}} μ_{a / ν}}{μ_{f}} = 1 ect .

where μ_{a_{i}} = \frac{a_{i a}}{a_{i ν}} μ_{a / ν} = a \cdot ν^{- 1} μ_{f} = \frac{e^{|a| t}}{e^{|ν| t}} .

According to matrix transformations [11], the equivalent transformation can be viewed as transitions to new coordinate bases for the vector

x

and

y

, i.e.,

x^{'} = Q^{- 1} x

and

y^{'} = P y

. That is, the transformation

\tilde{A} = P A Q

corresponds to independent coordinate transformations defined by the matrices

Q^{- 1}

and

P

(non-particular square matrices).

If the vectors

x

and y are transformed to the same coordinate basis, then we can write

P = Q^{- 1}

. That is, we proceed to the similarity transformation

\tilde{A} = Q^{- 1} A Q

. An important property of the similarity transformation is that the determinant of the matrix is invariant with respect to this transformation:

\det \tilde{A} = \det A .

Thus, this transformation does not change the eigenvalues of the matrix, so we can write

\det [z E - \tilde{A}] = \det [z E - A] .

The result of solving the system of equations for matrices

\tilde{A}

and

A

will be the same.

The role

Q

of the transformation matrix is played by the modal matrix

H

, i.e.

H

. It can be defined as a set of columns

h^{(i)}

, which are solutions of homogeneous equations:

(z E - A) h^{(i)} = 0 i = \bar{1, n},

(9)

where n – matrix rank

A

By constructing the matrices α and ν, we can find a matrix

H

that would satisfy the system of homogeneous equations (9). Thus,

μ_{a_{i}} = \frac{a_{i a}}{a_{i ν}}

;

μ_{a / ν} = a \cdot ν^{- 1}

;

μ_{f} = \frac{e^{|a| t}}{e^{|ν| t}}

, and therefore conditions (8) are fulfilled, which confirm the similarity of the orthogonality matrices of the criterion programming and the transitions of the Kolmogorov equations.

The similarity of modeling Markov processes and criterion modeling allows us to apply the principles of criterion programming to the system of equations (2) [10]. As a result, we can obtain a function that is a direct task of criterion programming [7], which can be used to assess the quality of the distribution grid's functioning. In the criterion form, it will have the form [7,13]:

f (x_{*}) = \sum_{i = 1}^{m} p_{i} \prod_{j = 1}^{n} x_{* j}^{ν_{i j}} .

(10)

where

p_{i}

– is the similarity criterion, which in this case is the probability of the system being in the state i;

\prod_{j = 1}^{n} x_{* j}^{ν_{i j}}

– indicator of the quality of the mill's functioning

i

;

x_{* j}

− independent parameters that characterize the basic properties of the system in the corresponding states.

The quality of functioning of an “ideal” power grid, which provides absolutely reliable power supply with maximum power quality and efficiency, is taken as the baseline value. The materials described above make it possible to expand the application of the results of previous research [10] for use in assessing the quality of functioning of power grids. For example, let us consider the case of a two-circuit power line (PL). In Figure 3, (a) shows a graph of its possible states. States 1 - 3 are operating states, state 4 is a complete failure. States 2 and 3 are characterized by a reduced level of functional availability due to the failure of PL1 and PL2 lines, respectively (see Figure 3,(b)).

According to the state graph shown in Figure 3, the matrix of transition intensities will have the form:

ν = |\begin{array}{l} - (λ_{12} + λ_{13}) μ_{21} μ_{31} 0 \\ λ_{12} - (λ_{24} + λ_{21}) 0 μ_{42} \\ λ_{13} 0 - (λ_{34} + λ_{31}) μ_{43} \\ 0 λ_{24} λ_{34} - (μ_{42} + μ_{43}) \end{array}| .

According to the system of equations (1) formed for this matrix, it is possible to find the vector of state probabilities p. In this case, the criterion model (10) will have the form [14]:

\begin{array}{l} f (x) = p_{1} x_{1}^{- (λ_{12} + λ_{13})} x_{2}^{λ_{12}} x_{3}^{λ_{13}} + p_{2} x_{1}^{μ_{21}} x_{2}^{- (λ_{24} + μ_{21})} x_{3}^{0} + \\ + p_{3} x_{1}^{μ_{31}} x_{2}^{0} x_{3}^{- (λ_{34} + μ_{31})} = p_{1} {(\frac{x_{1}}{x_{2}})}^{- λ_{12}} {(\frac{x_{1}}{x_{3}})}^{- λ_{13}} + \\ + p_{2} {(\frac{x_{2}}{x_{1}})}^{- μ_{21}} x_{2}^{- λ_{24}} + p_{3} {(\frac{x_{3}}{x_{1}})}^{- μ_{31}} x_{3}^{- λ_{34}} . \end{array} .

Perform logarithmization and potentiation of the components characterizing each state.

\{\begin{matrix} {(\frac{x_{1}}{x_{2}})}^{- λ_{12}} {(\frac{x_{1}}{x_{2}})}^{- λ_{12}} = e^{- λ_{12} \cdot (\ln (x_{1}) - \ln (x_{2}))} \cdot e^{- λ_{12} \cdot (\ln (x_{1}) - \ln (x_{2}))} \\ {(\frac{x_{2}}{x_{1}})}^{- μ_{12}} {x_{2}}^{- λ_{24}} = e^{- μ_{21} \cdot (\ln (x_{2}) - \ln (x_{1}))} \cdot e^{- λ_{24} \cdot \ln (x_{2})} \\ {(\frac{x_{2}}{x_{1}})}^{- μ_{12}} {x_{3}}^{- λ_{24}} = e^{- μ_{21} \cdot (\ln (x_{2}) - \ln (x_{1}))} \cdot e^{- λ_{24} \cdot \ln (x_{2})} \end{matrix} .

(11)

Based on the fact that the natural logarithm can be regarded as the time required for a variable to reach a certain value [15], rewrite equation (11):

\{\begin{matrix} {(\frac{x_{1}}{x_{2}})}^{- λ_{12}} {(\frac{x_{1}}{x_{2}})}^{- λ_{12}} = e^{- λ_{12} \cdot (\ln (x_{1}) - \ln (x_{2}))} \cdot e^{- λ_{12} \cdot (\ln (x_{1}) - \ln (x_{2}))} \\ {(\frac{x_{2}}{x_{1}})}^{- μ_{12}} {x_{2}}^{- λ_{24}} = e^{- μ_{21} \cdot (\ln (x_{2}) - \ln (x_{1}))} \cdot e^{- λ_{24} \cdot \ln (x_{2})} \\ {(\frac{x_{2}}{x_{1}})}^{- μ_{12}} {x_{3}}^{- λ_{24}} = e^{- μ_{21} \cdot (\ln (x_{2}) - \ln (x_{1}))} \cdot e^{- λ_{24} \cdot \ln (x_{2})} \end{matrix} .

(12)

where

Р

– the probability of achieving the corresponding values of certain parameters of the quality of the power grid functioning.

Taking this into account, the mathematical model of the quality of the power grid functioning will be determined by the expression:

E = p_{1} P_{11} P_{12} + p_{2} P_{21} P_{22} + p_{3} P_{31} P_{32} = \sum_{i = m} p_{i} \prod_{j = n} P_{i j} .

(13)

where

р_{і}

– probability of the operating condition;

Р_{i j}

– is the probability of ensuring the normative value of the parameter j in the state i.

The development of RSE in electric power grids further complicates the task of assessing the quality of functioning and, in particular, the reliability component. Therefore, it is advisable to use Markov models, the main advantage of which is the ability to decompose the problem of assessing the impact of RSE on the reliability of electricity supply [16]. It is possible to consider the process of functioning of the electric power grid as a set of states determined by its structural features. Accordingly, in each state, it is possible to assess the indicators of balance reliability influenced by individual RSE.

Using this approach, it is possible to decompose the problem of assessing the reliability of electric power grid with renewable sources of energy. At the first stage, based on the analysis of the structural reliability of the power grid, it is necessary to build a graph of possible states (see Figure 4) in which the power grid can be located depending on the state of its elements (working/failed). At this stage, the influence of RSE is not taken into account.

The next step is to analyze the balance reliability and other quality components for each operating state. According to the analysis, the quality indicator of the grid functioning in a certain state is determined for each operational state i.

3. Assessment of the Quality of Functioning Components

Efficiency. Level of active power losses. The normal scheme of operation of distribution power grids is an open circuit. However, with the development of distributed sources of energy, power lines with two-way power supply appear in power grids. At the same time, under certain modes of DSE generation, it is possible to achieve a current distribution close to the closed circuit of the grid [17,18]. Such a mode can be considered “ideal”, which corresponds to a minimum level of electricity losses.

The transition from an open circuit to a closed circuit leads to the current distribution, which depends on the parameters of the electrical grid elements and its configuration. Given that the processes associated with the distribution of current in such an electrical grid are subject to the principle of least action [19,20], we can speak of the optimal mode according to the criterion of minimum losses.

In a grid with several power sources, the minimum active power losses for the case when no limits are imposed on the values of nodal currents occur when both the active and reactive components of the currents are distributed in the electrical grid depending only on the active resistances, i.e., according to the substitutional r-grid scheme. This result is consistent with the known conclusions made in [21].

Determining whether the actual mode corresponds to the “ideal” mode can be done by analyzing the statistical data on the condition

P_{D S E i, k =} \sum_{j = 1}^{n} (C_{r k, j} \cdot P_{i, j})

for each I hour of the day and determining the probability based on the analysis.

The probability of ensuring an “ideal” mode is determined by the expression:

P_{Δ P =} \frac{1}{24} \sum_{i = 1}^{24} [Π_{k = 1}^{m} p_{i, k} (P_{D S E i, k} = \sum_{j = 1}^{n} (C_{r k, j} \cdot P_{i, j}))] .

(14)

Expression (14) allows us to assess the correspondence of the actual mode at a certain point in time to the “ideal” one. Given that standard losses are set for each electricity supply company, expression (14) can be used to estimate the probability of ensuring standard losses

\sum_{j = 1}^{n} (C_{r k, j} \cdot P_{i, j}) \geq P_{D S E i, k}

(where

C_{r k, j}

is determined in accordance with the grid configuration and the set value of standard losses) [22]. However, obviously, with such a definition of the efficiency component, it is not possible to compare different power grids.

Ensuring the quality of electricity. Voltage deviations. To determine whether the values of power quality indicators (PQI) meet the requirements of [4], they are measured and statistically processed. For all normalized power quality indicators, the minimum calculation period is 24 hours. The recommended total duration of continuous measurements is 7 days. Assessment of non-normalized PQI (voltage drops, overvoltages, impulses) is based on the results of long-term observations and their registration using specialized measuring instruments.

The statistical processing of the measurement results of normalized PQI consists In the construction of PQI distribution functions. Based on the measurement results, it is possible to determine the frequency of PQI values falling into a certain interval over the entire range of possible values [16].

To estimate the voltage deviation at the consumption nodes, we will use an approach based on the concept of the “ideal” mode. In the “ideal” mode, voltage drops and, as a result, voltage deviations in the grid nodes are smaller. This is confirmed by the modeling results shown in Figure 5, where curve 1 is an arbitrary mode; curve 2 is the “ideal” mode.

By analysis of statistical data, it is possible to determine the probability of condition fulfillment

J_{D S E \min i, k} \leq \sum_{j = 1}^{n} (C_{r k, j} \cdot P_{i, j}) \leq J_{D S E \max i, k}

for each hour of the day i. The voltage quality component in the integral indicator will be determined by the expression:

P_{U =} \frac{1}{24} \sum_{i = 1}^{24} [Π_{k = 1}^{m} р_{i, k} (J_{D S E \min i, k} \leq \sum_{j = 1}^{n} (C_{r k, j} \cdot P_{i, j}) \leq J_{D S E \max i, k})] .

(15)

In accordance with the obtained dependencies (see Figure 5), the limits of permissible DSE generation are determined, and the analysis of the correspondence of voltage deviations at consumption nodes is reduced to analyzing the ratio of generation and consumption currents.

Ensuring balance reliability. The electricity generation schedule of RSE depends on the natural features of the region in which they are located. This feature of RSE introduces certain problems in solving the problem of ensuring reliable and high-quality electricity supply to consumers [23,24].

Developing a method for assessing the component of the mode efficiency and ensuring the quality of electricity is not possible without analyzing the coverage of a given consumption schedule by the potential generation of a solar power plant. To do this, it is necessary to determine the main probabilistic characteristics of the processes of RSE generation and electricity consumption.

Figure 6, as an example, shows the results of the analysis of statistical data on the daily power generation capacity of the PVPP plant and the load power for the Yampil 110/10 kV substation. The analysis was performed in the STATISTICA 10 software environment. The processing of statistical data during the year on the values of the generated power of the PVPP and the electric load makes it possible to determine the law of distribution of these values.

The discrepancy between the schedules of consumption and generation of RSE causes periods when the load power is not provided with the corresponding generation capacity (see Figure 7) [22,26,27].

According to the statistical data (Figure 8), using the mathematical apparatus of Gaussian mixtures, it is possible to estimate the probability of matching generation and consumption

р_{i} = (\sum_{k = 1}^{m} P_{R S E i, k} = \sum_{j = 1}^{n} P_{i, j})

for a certain time of day. Obviously, the analysis consists in comparing the total RSE generation of a feeder with its total load. Since an hourly schedule is considered, the expression for determining the probability of balance will take the form:

P_{b =} \frac{1}{24} \sum_{i = 1}^{24} р_{i} (\sum_{k = 1}^{m} P_{R S E i, k} = \sum_{j = 1}^{n} P_{i, j}) .

(16)

where

m, n

– respectively, the number of sources and consumption nodes.

4. Example. The Impact of Measures on the Value of the Integral Indicator of the Quality of Functioning of Power Grids

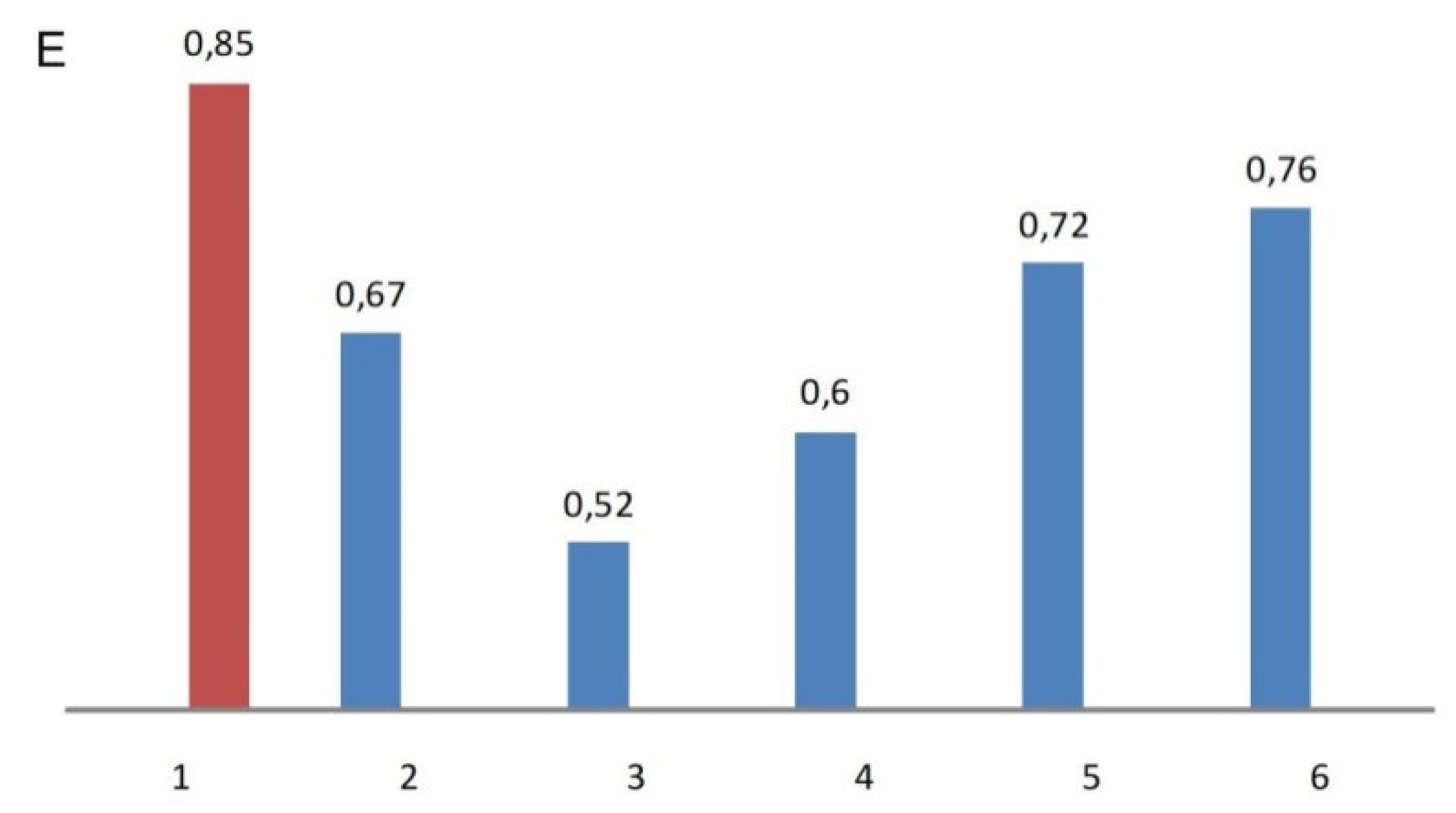
The research analyzes a number of measures to assess the impact on the integral indicator of the quality of the functioning of the power grids of Yampolsky regional power distribution companies (see Figure 9) [25,28,29].

When determining the optimal sectioning of the power grid, the first stage was to analyze the ring configuration of Yampil power distribution companies. For this option, the value of the integral indicator of the quality of functioning was determined to be 0.85. Such a grid configuration is considered “ideal”, which cannot exist under current technical conditions (case 1).

The calculation of the grid circuit scheme allowed us to determine the optimal points of its disconnection. For this configuration, the quality of functioning is 0.67 (case 2). Such a significant decrease is explained by the inconsistency of generation and consumption schedules and a significant discrepancy in power flows compared to the circuit. Since it was not possible to implement the scheme for case 2 due to the lack of switching devices at the relevant points, the best option was determined by the criterion of the quality of functioning from those possible in terms of technical capabilities (case 3).

The use of PVPP as a means of influencing reactive power flows and replacing the most loaded sections of the grid has improved grid efficiency and the quality of electricity. As a result, the integral indicator reached a value of 0.6 (case 4). The coordination of generation and consumption schedules by the method proposed in this research (case 5) and the use of accumulation at PVPP (case 6) allowed to increase the value of the quality of functioning coefficient to 0.72 and 0.76, respectively.

Conclusions

Thanks to the development of renewable sources of energy in electric power systems, in particular in distribution grids, it has become possible to create electricity supply systems for consumers in the form of local electric energy systems based on renewable sources. Beyond the fact that this provides certain advantages in terms of energy efficiency of electricity supply, it is possible to form RSE-based LEES as balancing groups in the electric power system. However, since the generation of photovoltaic and wind power plants depends on weather conditions, they cannot be a guaranteed supplier of electricity without additional means. These can be systems that store (accumulate) electricity when the LEES generate an excess of electricity for its own consumers, and that return electricity to the LEES when there is a shortage. Under such conditions, LEES can remain operational and provide autonomous power supply to consumers.

Since LEES structures can differ significantly in terms of key technical and economic indicators (power supply reliability, power losses, and power quality), it is necessary to choose the optimal one. It is not advisable to optimize the quality of power supply in LEES by individual indicators, since improvement of one indicator may lead to deterioration of another. The functional readiness of a LEES should be assessed by the quality of functioning, which depends on the reliability, efficiency, and quality of electricity. To simplify the task of assessing the quality of functioning, which is vector, a method for determining an integral indicator has been developed, which allows reducing the problem to a scalar one. For this reason, an integral indicator of the functioning of complex systems has been developed based on a combination of the theory of Markov processes and the theory of similarity. The assessment of the integral indicator of the quality of functioning of the electric power grid is carried out by comparing the actual modes with the “ideal” one. This approach allows comparing different variants of electricity transmission and distribution systems without determining technical and economic indicators. The offered integral indicator of the quality of functioning of local electric energy systems with renewable energy sources corresponds to the general requirements for such indicators: it reflects objective reality; allows to assess efficiency, quality and optimality; reflects “extreme” states of the system, taking into account potentially and actually possible ones; can be easily decomposed into partial indicators, etc.

Supplementary Materials

not applicable.

Author Contributions

Conceptualization, W.W., P.L. and V.K.; methodology P.L., V.K., I.H., N.S. and W.W.; software, I.H., N.S., L.Y. and Z.S.; validation, V.K., I.H., N.S., Z.S. and C.K.; formal analysis, W.W., P.L., V.K., I.H. and N.S.; investigation, I.H., N.S., L.Y. and Z.S.; resources, I.H., N.S., Z.S., L.Y. and C.K.; data curation, N.S., I.H., L.Y. and Z.S.; writing—original draft preparation, V.K., I.H., N.S. and Z.S.; writing—review and editing, W.W., P.L. and C.K.; visualization, Z.S. and L.Y.; supervision, W.W. and P.L.; project administration, W.W. and P.L.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Acknowledgments

This paper was supported by 24-PKVV-UM-006 and 24-PKVV-UM-007. We thank Ukrainian Technological Products LLC for all around support.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Denysiuk, S. P.; Derevianko, D. H.; Bielokha, H. S. (2022). Synthesis of models of local power systems with distributed generation sources. Technical Electrodynamics 2022, 4, 48–53, http://jnas.nbuv.gov.ua/article/UJRN-0001341364 [In Ukrainian]. [Google Scholar] [CrossRef]
Formation of local electric energy systems in the composition of the unified energy supply system. Herald of Khmelnytskyi National University. Technical Sciences 2024, 337, 352–356.
Arefifar,A. ;Alam,M.S.;Hamadi,A. A Review on Self-Healing in Modern Power Distribution Systems. Journal of Modern Power Systems and Clean Energy 2023, 11, 1719–1733. [Google Scholar] [CrossRef]
EN 50160:2023 Voltage characteristics of electricity supplied by public electricity networks, 2022.
Boucherie, R.J. (Editor); van Dijk, N.M. (Editor). Markov Decision Processes in Practice. Cham: Springer, 2017. [Google Scholar] [CrossRef]
Kanzariya, B.R.; et al. Review on Reliability Assessment in Power System. In Sustainable Technology and Advanced Computing in Electrical Engineering. Lecture Notes in Electrical Engineering, vol 939, Mahajan, V., Chowdhury, A., Padhy, N.P., Lezama, F.;Eds.; Springer, 2022. [Google Scholar] [CrossRef]
Chen, Z.; Huang, J. Stabilization and Regulation of Nonlinear Systems: A Robust and Adaptive Approach. Springer 2014, p.356.
Ardeshiri, A.; Lotfi, A.; Behkam, R.; Moradzadeh, A.; Barzkar, A. (2021). Introduction and Literature Review of Power System Challenges and Issues. In: Application of Machine Learning and Deep Learning Methods to Power System Problems. Power Systems, Nazari-Heris, M., Asadi, S., Mohammadi-Ivatloo, B., Abdar, M., Jebelli, H., Sadat-Mohammadi, M.,Eds.; Springer, Cham: 2021. [CrossRef]
Komar, V.O.; Pisklyarova, A.V. Formation of the law of management with regard to the quality of system functioning, VPI Bulletin2010, issue 6, pp. 152-156.
Astakhov, Y.N. , Lezhnyuk P.D. Application of criterion method in electric power engineering. UMK VO:Kiev 1989,p. 140.
Fiche, G.;& Hebuterne, G. Mathematics for Engineers. Wiley-ISTE2013,p. 435. ISBN: 978-1-118-62333-6.
Lezhnyuk, P.D.; Sobchuk, N.V. Parametric similarity in the problems of optimization of electrical systems.Monograph. Vinnytsia: Universum-Vinnytsia 2005 p. 100.
Lezhnyuk, P.D.; Komar, V.O. Assessment of the quality of optimal control by the criterion method.Monograph. Vinnytsia: Universum-Vinnytsia 2006 p. 108.
Lezhnyuk, P.D.; Komar, V.O.; Kravtsov, K. Criterion for assessing the quality of distribution grids functioning. Electronic journal “Scientific works of VNTU” 2008. № 3. URL: https://praci.vntu.edu.ua/index.php/praci/article/view/72/71.
Ruiz Florez, H.A.; López, G.P.; Jaramillo-Duque, Á.; López-Lezama, J.M.; Muñoz-Galeano, N. A Mathematical Modeling Approach for Power Flow and State Estimation Analysis in Electric Power Systems through AMPL. Electronics 2022, 11, 3566. [Google Scholar] [CrossRef]
Lezhnyuk, P.D.; Komar, V.O.; Kravchuk, S.; Sobchuk, D. Mathematical modeling of operation quality of electric grid with renewable sources of electric energy (2018) In Proceedings of the International Conference on Modern Electrical and Energy Systems, MEES 2017, January 2018, pp. 324-327. [Google Scholar] [CrossRef]
Lakshmi, G.S.; Rubanenko, O. Hunko, I.. Control of the Sectioned Electrical Network Modes with Renewable Energy Sources. 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 2021, pp. 1-6. [CrossRef]
Samanta, S. Network Optimization of the Electricity Grid to Manage Distributed Energy Resources Using Data and Analytics. In World of Business with Data and Analytics. Studies in Autonomic, Data-driven and Industrial Computing. Sharma, N., Bhatavdekar, M. Eds. Springer, Singapore2022. [CrossRef]
Lezhnyuk,P.D.;Kulyk, V.; Netrebsky, V.; Teptya, V. The principle of least action in electrical engineering and electric energy.Monograph. Vinnytsia: VNTU, 2014. p.212.
Belik, M. Optimisation of energy accumulation for renewable energy sources. Renewable Energy and Power Quality Journal 2021, 19, 205–210. [Google Scholar]
Han, D.; Tong, X.J. Review of Mathematical Methodology for Electric Power Optimization Problems. J. Oper. Res. Soc. China 2020, 8, 295–309. [Google Scholar] [CrossRef]
Lezhniuk, P.; Ngoma, J.P. Rubanenko, O. In Analysis of the Electrical Networks Functioning Quality of with Photovoltaic Power Plants. In Proceedings of the 2021 IEEE 3rd Ukraine Conference on Electrical and Computer Engineering (UKRCON), Lviv, Ukraine; 2021; pp. 305–309. [Google Scholar] [CrossRef]
Kuznietsov, M.; Lysenko, O. Ensuring the energy balance in the local system with renewable generation. Vidnovluvana Energetika 2023, 1, 6–18. [Google Scholar] [CrossRef]
Kudrya, S.; Lezhniuk, P.; Rubanenko, O.; Hunko, I.; Dyachenko, O. (2024). Local Power Systems Based on Renewable Energy Sources. InSystems, Decision and Control in Energy VI. Studies in Systems, Decision and Controlvol 552, Babak, V., Zaporozhets, A.,Eds.; Springer, Cham. [CrossRef]
Lezhniuk, P.; Komar, V.; Belik, M.; Rubanenko, O.; Smaglo, I. Analysis of technical conditions influencing the operation of PV power stations cooperating with controlled power grids, In Preceedings of the 2022 IEEE 4th International Conference on Modern Electrical and Energy System (MEES), Kremenchuk, Ukraine, 2022, pp. 1-6. [CrossRef]
Bisikalo, O.; Kharchenko, V.; Kovtun, V.; Krak, I.; Pavlov, S. Parameterization of the Stochastic Model for Evaluating Variable Small Data in the Shannon Entropy Basis. Entropy 2023, 25, 184. [Google Scholar] [CrossRef] [PubMed]
Kukharchuk, V.V.; Pavlov, S.V.; Holodiuk, V.S.; Kryvonosov, V.E.; Skorupski, K.; Mussabekova, A.; Karnakova, G. Information Conversion in Measuring Channels with Optoelectronic Sensors. Sensors 2022, 22, 271. [Google Scholar] [CrossRef] [PubMed]
Kukharchuk, V.V.; Wójcik, W.; Pavlov, S.V. , et al. Features of the angular speed dynamic measurements with the use of an encoder, Informatyka, Automatyka, Pomiary w Gospodarce i Ochronie Srodowiska 2022, 12, 20–26. [Google Scholar]
Highly linear Microelectronic Sensors Signal Converters Based on Push-Pull Amplifier Circuits edited by Waldemar Wojcik and Sergii Pavlov, Monograph, No. 181, Komitet Inzynierii Srodowiska PAN, 2022, 283 Pages. ISBN 978-83-63714-80-2.

Figure 1. Dependence of the intensity of failures on the operating time.

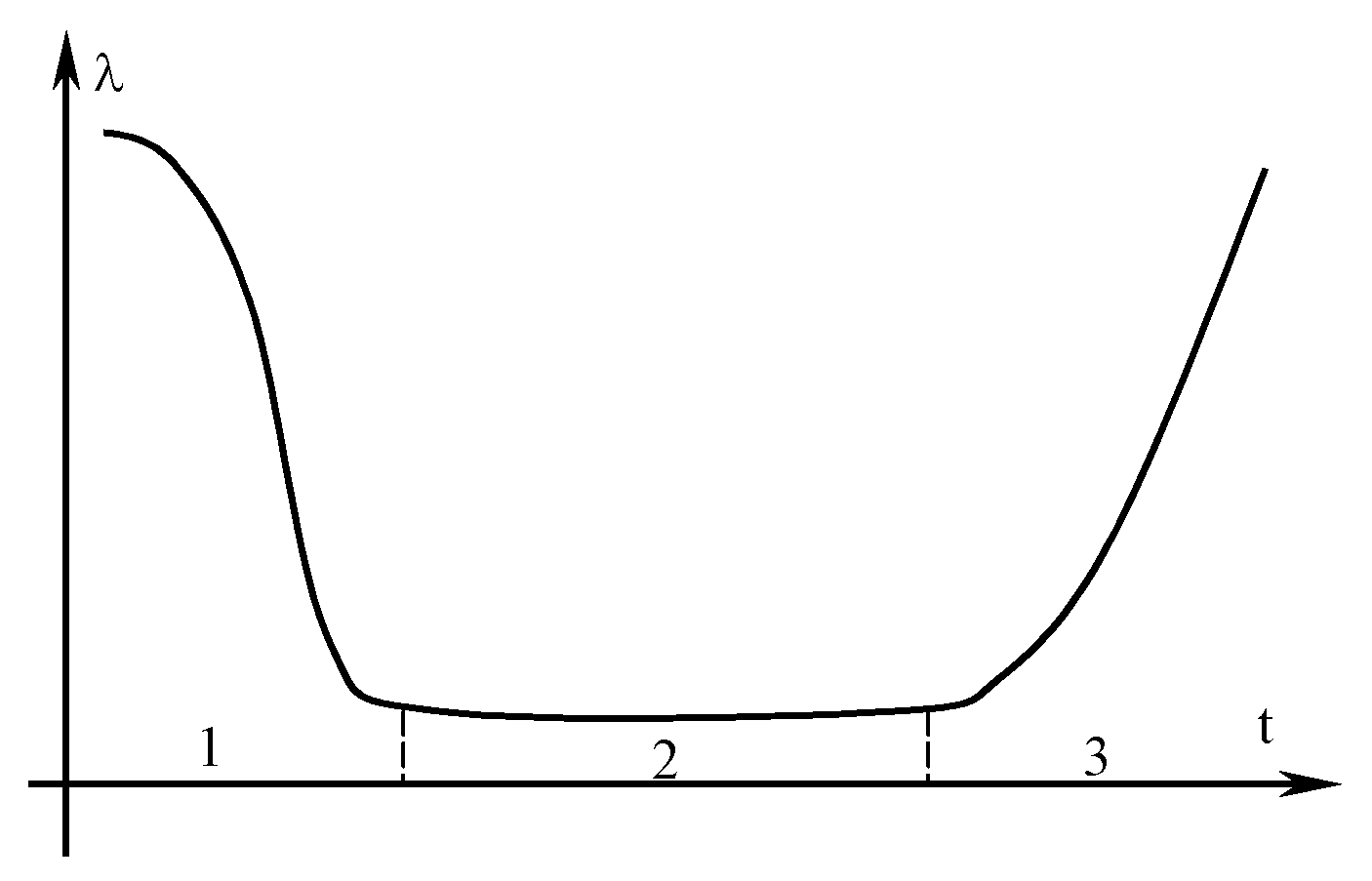
Figure 2. Graph of changes in system states.

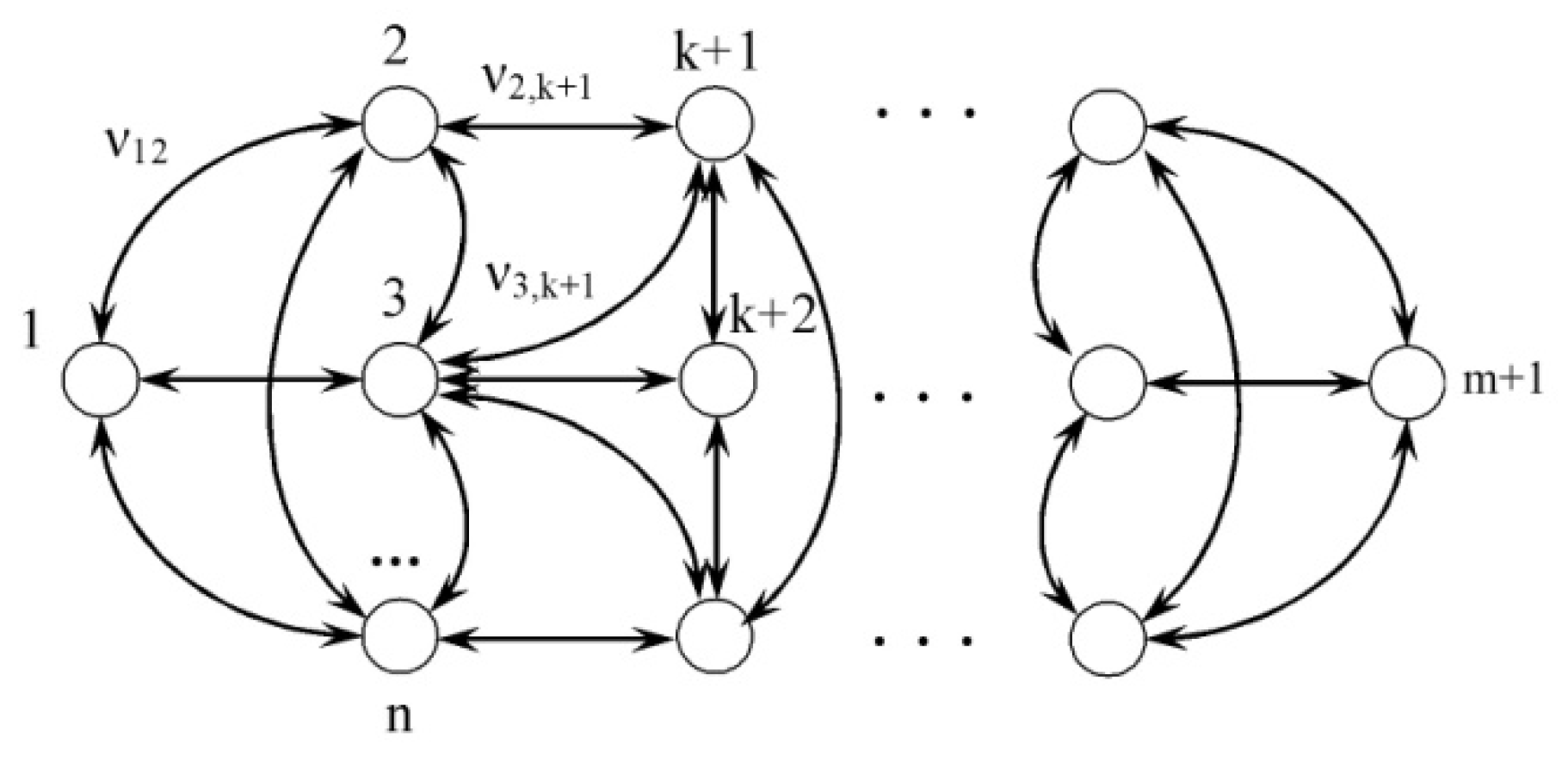
Figure 3. (a) State graph; (b) Two circuit power.

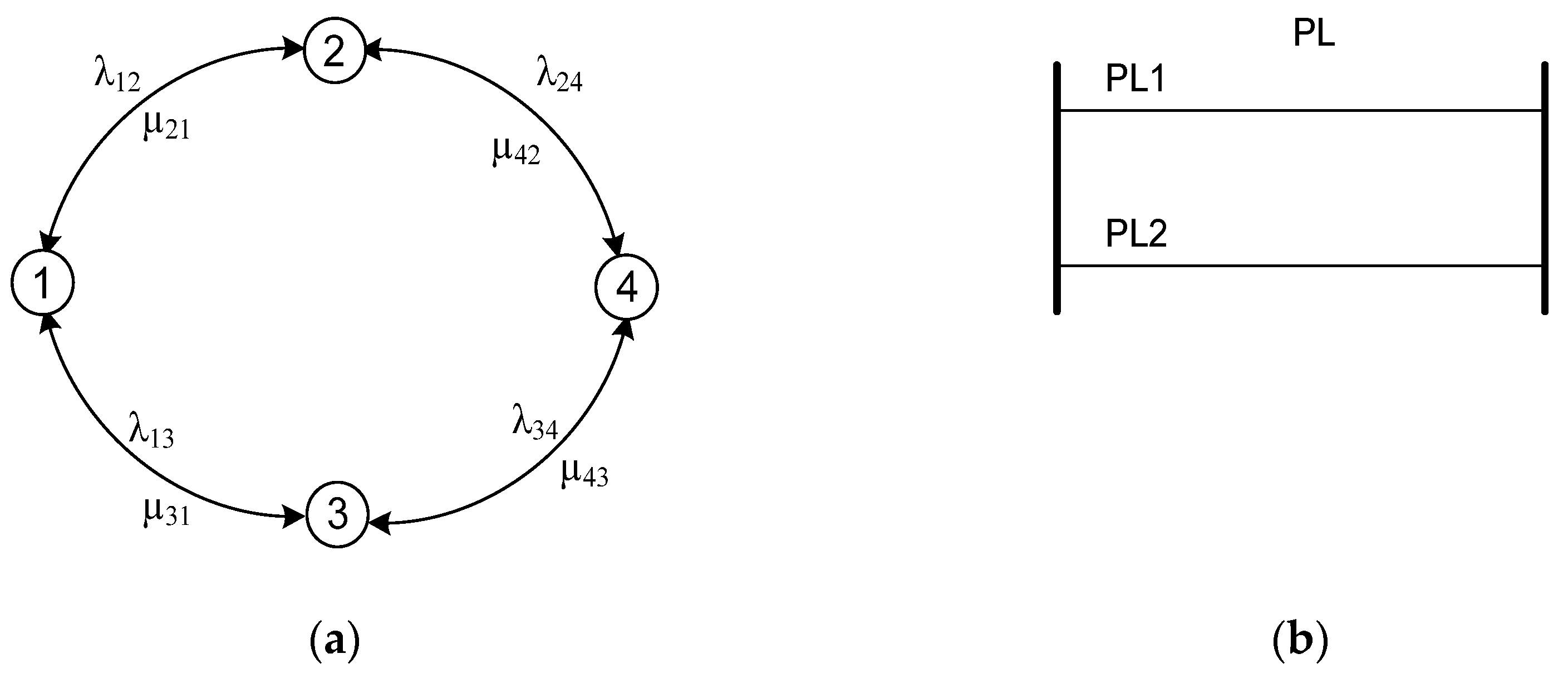
Figure 4. Graphical interpretation of the assessment of the complex indicator of the quality of functioning of the distribution power grid with distributed generation.

Figure 5. Curves

U_{Δ} = f (J_{l})

for a certaingrid.

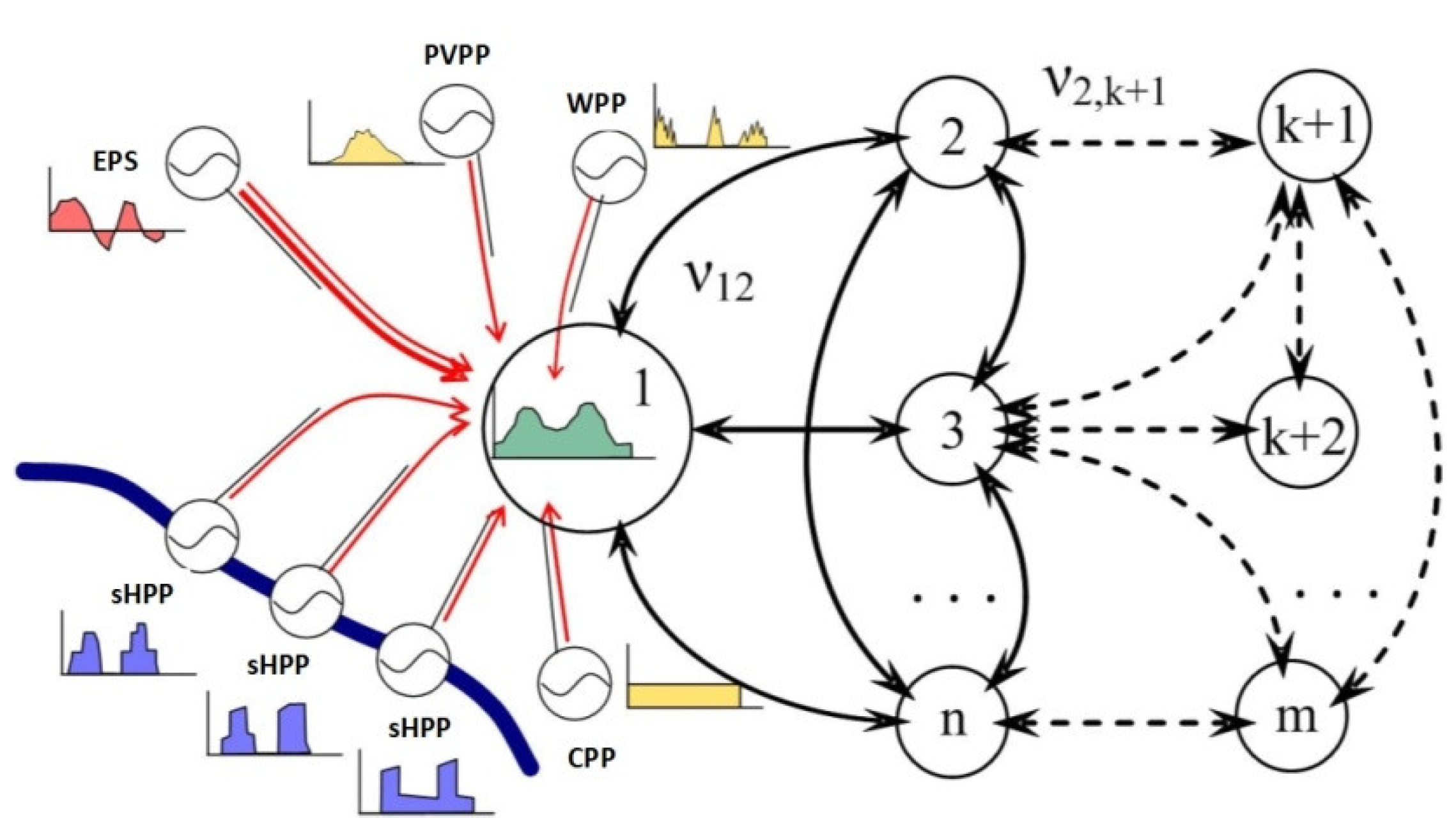
Figure 5. Curves

U_{Δ} = f (J_{l})

for a certaingrid.

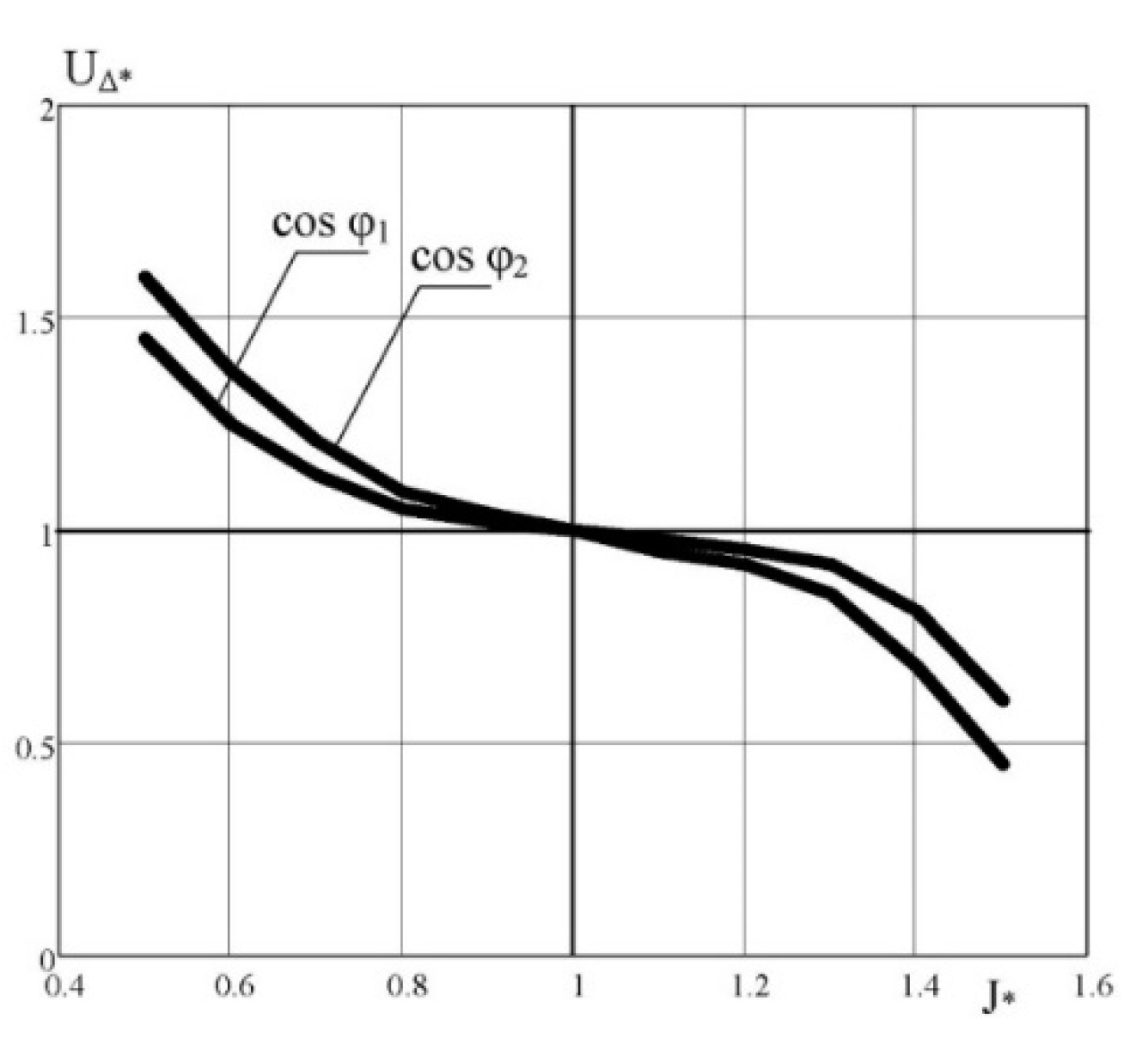
Figure 6. Changes of PVPP generation power (1) and load (2) during the year at a given time of day.

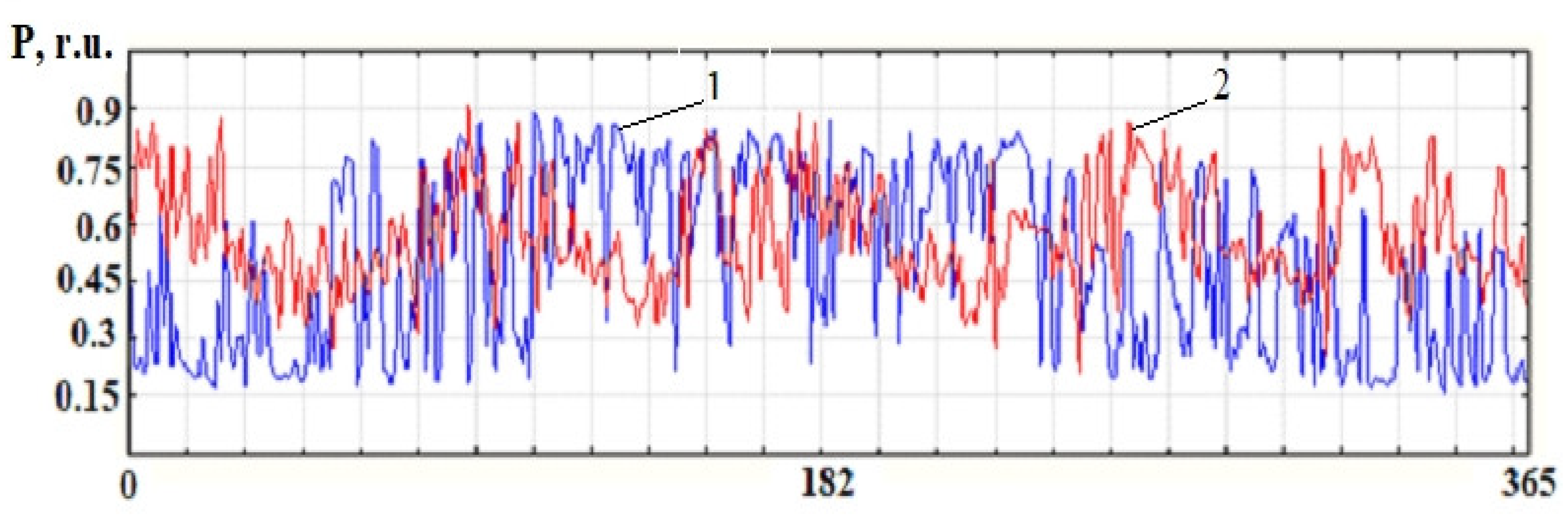
Figure 7. Changes of PVPP generation power (1) and load (2) during the year at a given time of day.

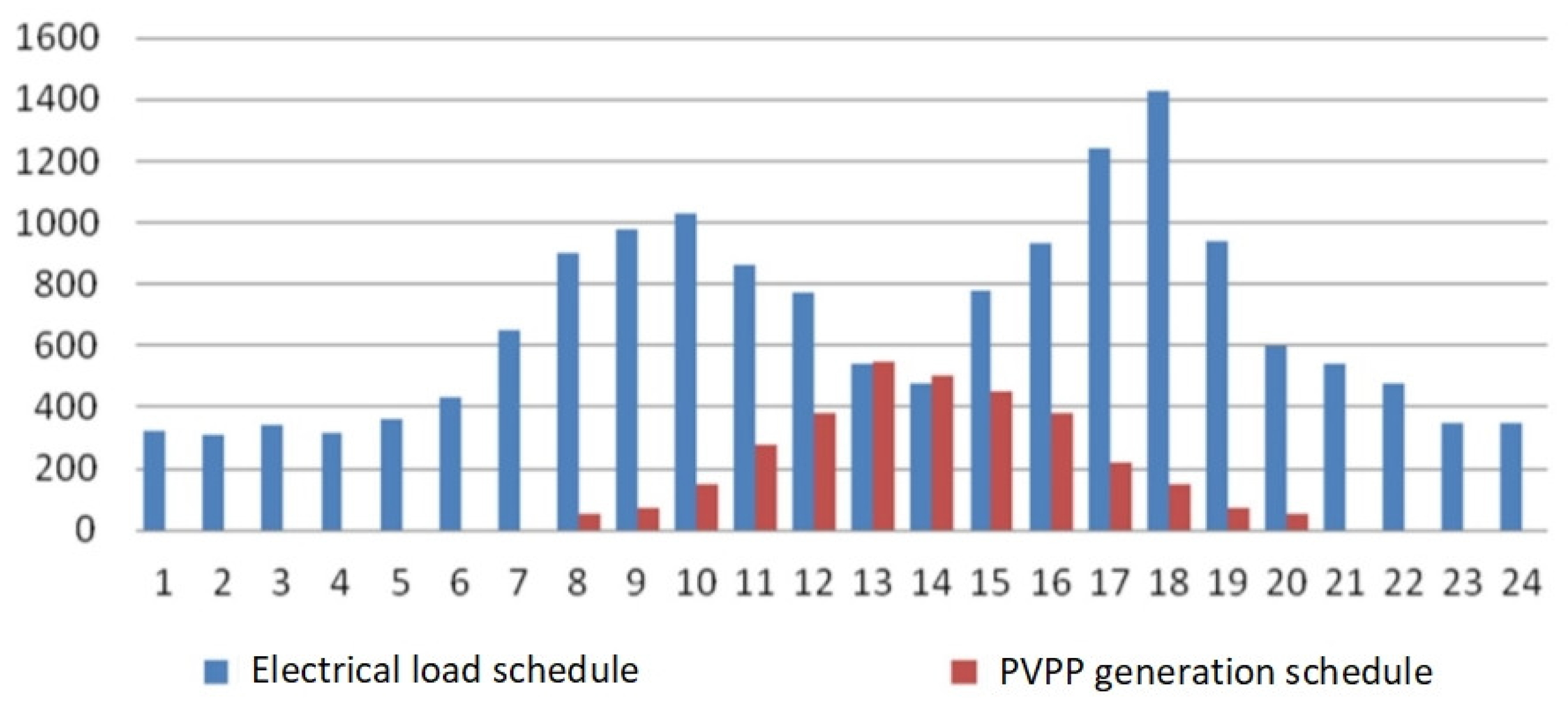
Figure 8. Graphical representation of a set of statistics on generation (a) and consumption (b).

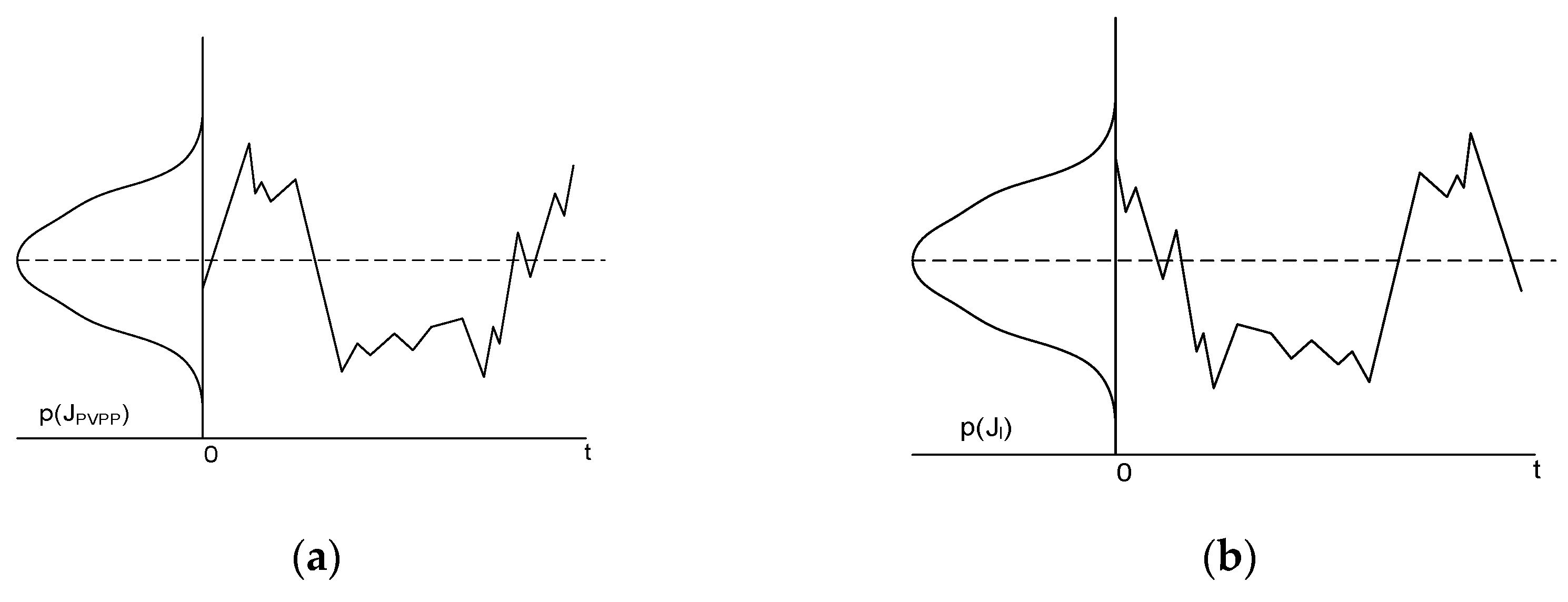
Figure 9. Values of the integral indicator of the quality of functioning for various measures considered in this research.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Integrated Assessment of the Quality of Functioning of Local Electric Energy Systems

Abstract

Keywords:

Subject:

1. Introduction

2. Modeling the Operation of Power Grids Using Similarity Theory and Markov Processes

3. Assessment of the Quality of Functioning Components

4. Example. The Impact of Measures on the Value of the Integral Indicator of the Quality of Functioning of Power Grids

Conclusions

Supplementary Materials

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe