Precision and Characteristics of Satellite Spatial Quality Estimators Measurement using Edge Target imaged with KOMPSAT-3A

After the launch of a high-resolution remote sensing satellite, representative spatial quality estimators (RER, FWHM, MTF50, MTFA) are measured from images taken of ground Edge targets. In this work, the best spatial quality estimator is proposed by quantitatively comparing and analyzing the precision between Relative Edge Response (RER), Full Width at Half Maximum (FWHM), MTF value at Nyquist frequency (MTF50), and MTF Area between 0 and Nyquist frequency (MTFA). While the basic method for the measurement of spatial quality estimators on Edge targets is already well established, this work summarizes and explains the uncertain factors and problems in the measurement procedure that affect the accuracy and precision of spatial quality estimators. It also considers how to improve the precision of spatial quality estimators during the measurement procedure. The contents and results of this work were discussed by various satellite development organizations in the Geo-Spatial Working Group within CEOS WGCV IVOS from 2012 to 2019, and the Edge target Spatial quality Measurement Python code (ESMP) was developed in 2019 to reflect the findings of this workshop. Using 483 Edge targets from worldwide images taken by KOMPSAT-3A, which has been in operation since 2017, the results obtained via ESMP show that the precision of RER, FWHM, and MTFA are approximately three to four times higher than that of MTF50 when comparing the Coefficient of Variance (CV) statistics.

Keywords:

Subject:

Environmental and Earth Sciences - Remote Sensing

1. Introduction

Remote sensing satellites’ spatial quality values play two important roles in the satellite development process. The first involves modulation transfer function (MTF) requirement value, i.e., MTF value at Nyquist frequency (hereinafter MTF50). Using this value, satellite developers can verify that MTF50 requirement is met during satellite design, development, and pre-launch testing. The second role is in measuring the satellite’s MTF50 value in orbit after launch and verifying whether MTF50 requirement is satisfied, which constitutes the calibration and validation phase. This work describes the details of the post-launch on-orbit spatial quality measurement method.

The basic measurement method used to determine the spatial quality (RER, FWHM, MTF50, MTFA) (Figure 1) of an optical remote sensing satellite in orbit after launch has already been proposed and described by several organizations, including ISO12233 [1,2,3,4,5,6,7,8,9,10]. Many other satellite organization and companies have developed and used their own ground reference targets and measurement codes, Maxar (USA), Astrium (France), TELESPAZIO (Italy), I2R Corp. (USA), ESA ESRIN (Italy), CNES (France), ONERA (France), CSIR (South Africa), USGS (USA), NASA (USA), AOE (China), and KARI (Korea) [11,12,13,14]. However, there are many uncertain factors within the procedure for the measurement of spatial quality values [16,17,18]; as a result, even if the same Edge target is used, the resulting values will differ depending on the spatial quality code used [11]. Therefore, the uncertain factors that affect the accuracy and precision of the measured values within the spatial quality measurement procedure have been analyzed with simulated Edge target images [19,20,21,22,23]. However, due to the limitations of simulated Edge target images, it is difficult to identify various problems that exist in real Edge target images.

MTF50 is the most commonly used estimator for satellites’ spatial quality, but the measurement precision of MTF50 is known to be much lower than that of RER, FWHM, and MTFA [25,29]. Therefore, internal calibration and validation (hereinafter Cal/Val) engineers use more precise and intuitive spatial quality estimators, such as RER, FWHM, and MTFA, instead of MTF50 [24,25]. Among these, MTFA is less commonly used. It was first proposed by KARI along with MTF50 as a spatial quality estimator with high precision on the MTF curve [17,24,25]. The precision of each spatial quality estimator in practice has not been quantitatively compared. This study is the first to do so using the Coefficient of Variance (hereinafter CV), which is used to denote the precision of a measurement in statistics [15].

The precision of spatial quality measurement values varies depending on the conditions at the time of imaging, the state of the Edge targets, and the measurement code used, etc. This work compares and summarizes the results of the spatial quality measurement of real Edge targets using KOMPSAT-3A (Ground Sample Distance (GSD), 0.55m; MTF50 > 8%) imagery covering the period of January 29, 2017 to March 16, 2024. Finally, the most reliable estimator in terms of precision is proposed. In addition, as only an MTF50 value of 8% or more is provided as a requirement for KOMPSAT-3A, and RER, FWHM, and MTFA values are not specified, it is difficult to compare the accuracy between these spatial quality estimators. Thus, this work focuses on the analysis and comparison of the precision.

In practical terms, the spatial quality measurement with the Edge target seeks to reflect the state of the satellite and the Edge target as accurately possible at the moment of imaging, while minimizing the influence of factors that could reduce the accuracy and precision of the measurement. Additionally, under the assumption that the satellite is not perfectly manufactured, it is necessary to explain the measurement results using asymmetric Edge Spread Function (ESF) and Line Spread Function (LSF) plots [26].

The Committee on Earth Observation Satellite Working Group on Calibration and Validation, Infrared and Visible Optical Sensors (CEOS WGCV IVOS) [27] has organized the Geo-Spatial Quality Working Group within IVOS since 2012. It seeks to resolve the problems associated with the satellite spatial quality measurement procedure mentioned above, and its findings were summarized and published in 2019 [11,28,29]. The authors of the present work also participated in this working group, which led to the spatial quality measurement code provided by the KARI Cal/Val team and using KOMPSAT-3 (GSD, 0.7m) satellite imagery. They specified the main purpose of this working group as follows: “Get the reasonable quantity of Spatial quality for the remote sensing satellite in the Real conditions” [17]. This work focuses on the findings presented at that time.

Section 2 describes the spatial quality estimators and Edge targets, and Section 3 summarizes the main factors that affect the errors of the measured values within ESMP. Section 4 compares and analyzes the values of the spatial quality estimators measured from the Edge target images taken by KOMPSAT-3A. Section 5 concludes the paper and briefly introduces future directions and topics for future papers.

2. Spatial Quality Measurement Estimators and Edge Targets

2.1. Spatial Quality Measurement Estimators

Figure 1 is a plot showing the procedure of measuring the spatial quality estimators (RER, FWHM, MTF50, MTFA) using the Edge target. We show ESMP output plot, using an edge Region Of Interest (ROI) image from Level 0 (raw image data) in the Across (detector; static) direction, imaged by KOMPSAT-3A on February 26, 2019, at a Roll tilt of 29.31deg, for the Edge target located in Zuunmod, Mongolia. Since KOMPSAT-3A uses a Time Delayed Integration (TDI) CCD, the Along (flight; dynamic) direction has a predicted value known as the line rate and is inaccurate, so only the Across direction’s spatial quality measurement is used.

RER is the slope value at the center inflection point of ESF, and FWHM is LSF width value at a ‘0.5’ normalized Y-axis value in LSF. MTF50 is MTF value at Nyquist frequency of the MTF curve, and MTFA is the area value in the region from ‘0’ to ‘0.5’ (Nyquist frequency). In order to calculate RER in an asymmetric ESF and LSF [24,26], it was suggested by the authors at the Geo-Spatial Working Group to calculate RER as a tangent from the RER center, rather than using the conventional method. This is still under discussion [17] (see Section 3).

2.2. Edge Targets

Figure 2 is a list of Edge targets deployed and in operation around the world that is currently available on the CEOS WGCV IVOS portal webpage [30] and USGS EROS webpage [31]. The Edge target located in Zuunmod, Mongolia was constructed and operated by KARI [32].

3. Factors Affecting Measurement Values in the Spatial Quality Calculation Procedure

This section describes the factors listed in Table 1 that affect the errors of the measured values within ESMP. All factors in Table 1 are implemented in ESMP according to the calculation procedure. The initial values in Column 3 of Table 1 for each factor are obtained according to the statistical InterQuartile Range (IQR) outlier exclusion method (Q1 - IQR * 1.5 to Q3 + IQR * 1.5) using KOMPSAT-3A, which involves a set of 966 Across edge images extracted from Edge targets (Baotou, India, Salon, Zuunmod) imagery acquired from January 2017 to March 2024, and the initial values given in this work are entered in ESMP. The initial values of all factors are not finalized yet.

3.1. ‘1. Asymmetric ESF and LSF’

An asymmetric ESF and LSF are some of the most important factors determining the accuracy and precision of spatial quality measurements [26]. Almost all satellite cameras have asymmetric ESF and LSF characteristics, but to varying degrees. Thus, when fitting ESF, non-parametric fitting should be used. As a result, as shown in Figure 3a, the location of the RER center changes, and the proportional relationship between RER value and FWHM value becomes weaker (Section 4.2).

3.2. ‘2. Straighness of Edge’

‘2. Straightness of Edge’ is a quantitative value used to determine the straightness of the line of edge, which is the most important requirement for the Edge target (Figure 3b). ESMP uses a ‘2. Straightness of Edge’ constraint that excludes edges with a statistical ‘Fitting Error (FitErr)’ greater than ‘0.1’ pixels according to the IQR outlier method using 966 Across edge images acquired by KOMPSAT-3A. ‘FitErr’ is obtained as the standard deviation (StDev) of the edge points over the line of the edge. If ‘4. Straightness of Edge’ value exceeds the constraint value; it directly affects the ESF fitting and reduces the accuracy and precision of the spatial quality measurement.

3.3. ‘3. Noise of Bright and Dark Area on ESF’

‘3. Noise of Bright and Dark area on ESF’ was intended to provide a minimum SNR (Signal-to-Noise Ratio) value to measure the spatial quality, but it is difficult to intuitively provide a minimum SNR value due to the complexity of the factors related to SNR. In the general SNR calculation method [37], the value is proportional to the signal (average DN; Digital Number), so SNR values in bright and dark area are different. Thus, the proposed SNR calculation formula [4], in which it is calculated as the brightness difference between bright and dark area (ΔDN = average bright DN – average dark DN), is incorrect [38]. A lower SNR results in larger noise on ESF, which leads to relatively lower fitting accuracy and precision. ESF fitting accuracy and precision directly depend on noise rather than the signal. Moreover, ‘4. DN difference between Bright and Dark area (ΔDN)’ is somewhat related to the ESF fitting accuracy and precision. The smaller ΔDN, the more sensitive it is to noise. But there is no proportional relationship between SNR and spatial quality results (Figure 6 right).

Increased noise on the ESF can result in poor fitting accuracy and precision in bright and dark area and unreliable MTF curves, as shown in Figure 4. ESMP statistically calculates the standard deviation of each bright and dark area as a noise value and uses it as a constraint. If the ‘noiseBr (noise in bright area)’ is greater than ‘0.05’ and the ‘noiseDa (noise in dark area)’ is greater than ‘0.045’, the result is excluded as a constraint according to the IQR outlier method [36].

3.4. ‘4. DN Difference between Bright and Dark Area (ΔDN)’

‘4. DN difference between Bright and Dark area (ΔDN)’ is the average DN value of the bright area minus the average DN value of the dark area, which indirectly affects spatial quality calculation. Low noise and a high SNR mean that the spatial quality calculation is more accurate and precise. Therefore, it is difficult to use ΔDN alone as a constraint because it must be considered together with ‘3. Noise of Bright and Dark area on ESF’. When ΔDN is small, the spatial quality measurement precision is low, but there is no proportional relationship between ΔDN and the spatial quality result (Figure 6 left).

ΔDN value varies depending on the DN range (radiometric resolution) and SNR of the satellite. KOMPSAT-3A has 14bit radiometric resolution (0~16383 DN) and SNR > 100 at 3000 DN, and constraint values of ΔDN > 1000.

3.5. ‘5. Edge Angle between Line of Edge and Across Direction (EdgeAng)’

‘5. Edge angle between Line of Edge and Across direction (EdgeAng)’ theoretically has no effect on spatial quality calculation. The Edge angle value is reflected in the ESF calculation step as the COS(EdgeAng), and it is found that the spatial quality measurement results of KOMPSAT-3 may not be related to the Edge angle [25]. However, small Edge angle will cause pixel data to clump together on ESF, preventing the use of the Edge angle to ensure that pixel data is uniformly and densely distributed on ESF, resulting in lower ESF fitting accuracy and precision. Thus, a constraint can be used that excludes the Edge angle values less than ‘2.2 deg’ according to the IQR outlier method. It also excludes the Edge angle values greater than ’30 deg’ [36]. In theory, there should be no correlation between the Edge angle and spatial quality values since COS(EdgeAng) is applied, but the spatial quality measurement results of KOMPSAT-3A show that there is a somewhat correlation. (Figure 7).

3.6. ‘6. RER Center’

In general, the ‘0.5’ point of the ESF Y-axis is used as the RER center, but, in practice, the RER center’s location should be determined differently depending on the degree of asymmetry ESF and LSF. ESMP calculates the tangent slope at the RER center, which is the inflection point of the edge region on ESF and the location of the peak on LSF (green line in Figure 3a). There is controversy regarding the definition of the RER center in an asymmetric LSF [17,24]. RER value of the ESMP’s RER center is relatively larger and has higher precision than RER value of the normalized DN = 0.5 center.

3.7. ‘7. Total Trim Width of ESF’

As satellite cameras are not perfectly manufactured, there are two problems: (1) ESF and LSF are asymmetric [26], and (2) the bright and the dark area of ESF are not flat. Therefore, in spatial quality calculation, the edge width of ESF depends on the characteristics of the satellite camera [24]. Due to (2), a large trim width results in a lower spatial quality value, but the result is relatively more reliable. However, it is very difficult to obtain a large edge area with uniform bright and dark area on a ground Edge target, so the total trim width ‘18 pixels’ of KOMPSAT-3A is used in ESMP as a compromise [24].

3.8. ‘8. Fitting Method for ESF’

The fitting method used to measure ESF from the edge pixel data is the factor that has the greatest impact on the results. There are two main types of fitting methods available here: parametric and non-parametric fitting methods. If the satellite camera is symmetrical, a parametric fitting method such as the Fermi–Dirac equation can be used. But most satellite cameras are asymmetrical [26], so a non-parametric fitting method must be used (Figure 3a). As a result, the fitting method used is a critical factor regarding the results of spatial quality measurements. For asymmetric cases, the Savitzky–Golay method is popular, but ESMP uses the Cubic Smoothing Approximation Spline fitting (CSAPS) by default, which has the smallest fitting error though its own testing. CSAPS is sensitive to the number of edge row lines (EdgeLine) and its weight value, so it has the disadvantage that these two must be determined as initial values. However, CSAPS tends to produce better spatial quality values than other fitting methods.

3.9. ‘9. Noise Removal Method for ESF’

The Edge target on the ground is rarely kept perfectly clean, so the final spatial quality value depends on the method applied to remove noise contained in the edge pixel data on ESF. The suitable method depends on the state of the Edge target and how it is coded within ESMP, so the results are different. ESMP uses CSAPS twice to remove noise on the ESF (Figure 4). After the first CSAPS fitting with weight = 0.95 to remove the ESF pixel data as outlier noise over 2σ of noise in the bright and dark area, a second CSAPS fitting with weight = 0.95 is performed. Normalization is performed via the fitted ESF.

3.10. ‘10. Number of Edge Row Lines (EdgeLine)’

‘10. Number of Edge row lines (EdgeLine)’ is directly related to the CSAPS fitting used by ESMP. Due to the nature of CSAPS, ESF is not perfectly fitted, and the fitted ESF is normalized, so there is a proportional relationship between the EdgeLine value and the spatial quality result [24,33]. However, it is assumed that most fitting methods also have the same problem. Statistically, the spatial quality values converge to a certain value when EdgeLine is above 40pixel, but, realistically, it is very difficult to obtain an EdgeLine value above 40pixel on the Edge target. Thus, at present, ESMP has fixed EdgeLine at ‘21’ and continues to conduct further research [33].

4. Results and Discussion

This section presents a comparative analysis of the spatial quality estimators via the spatial quality results obtained using ESMP for 483 Edge target images acquired by KOMPSAT-3A between January 29, 2017, and March 16, 2024. Two Across edges and two Along edges are counted for each Edge target. The Across MTF can be measured in the laboratory before launch, and it is commonly used to represent the spatial quality. Thus, this works describes 840 results obtained with ESMP’s constraint, out of a total of 966 Across edge spatial quality results. Table 2 compares the 966 Across edges and 840 constrained results. After applying the constraint, the average value is slightly improved, and the comparison the Coefficient of Variation (CV; StDev/Average) value, which represents the precision, indicates that the precision is clearly improved.

This section is divided into two main parts: first, it describes the characteristics and biases of the spatial quality measurement results obtained by KOMPSAT-3A; second, it compares and analyzes the representative spatial quality estimators of RER, FWHM, MTF50, and MTFA to highlight the precision of each estimator.

4.1. Characteristics and Biases of Spatial Quality Measurement Results

The characteristics and biases of the spatial quality measurements from 840 Across edge images are plotted and summarized for the following factors:

Julian date (since 20120517 (May 17, 2012), when KOMPSAT-3 was launched);
Roll tilt angle;
ΔDN (bright average DN – dark average DN);
SNR (DN / StDev at DN 3000);
Edge angle;
Edge target (Baotou, India, Salon, Zuunmod).

Figure 5 (left) shows the variation in KOMPSAT-3A’s spatial quality over time with the Julian date. The red number at the top right is CV value. The Y-axis scales for each of RER, FWHM, MTF50, and MTFA are given according to CV value. In Figure 5 (left), we can note the following:

KOMPSAT-3A’s spatial quality is very stable over time and does not show any adverse effect due to aging.

Figure 5 (right) shows the relationship between KOMPSAT-3A’s spatial quality and the roll tilt angle at the moment of imaging. In Figure 5 (right), we can note the following:

There is no proportional relationship between the roll tilt angle and spatial quality.

Figure 6 (left) shows the relation between KOMPSAT-3A’s spatial quality and ΔDN. In Figure 6 (left), we can observe the following:

There is no proportional relationship between ΔDN and the spatial quality.

Figure 6. (left) ΔDN vs. RER, FWHM, MTF50, and MTFA. (right) SNR vs. RER, FWHM, MTF50, and MTFA (upper right in red: CV). Scale of Y-axis was changed to CV value.

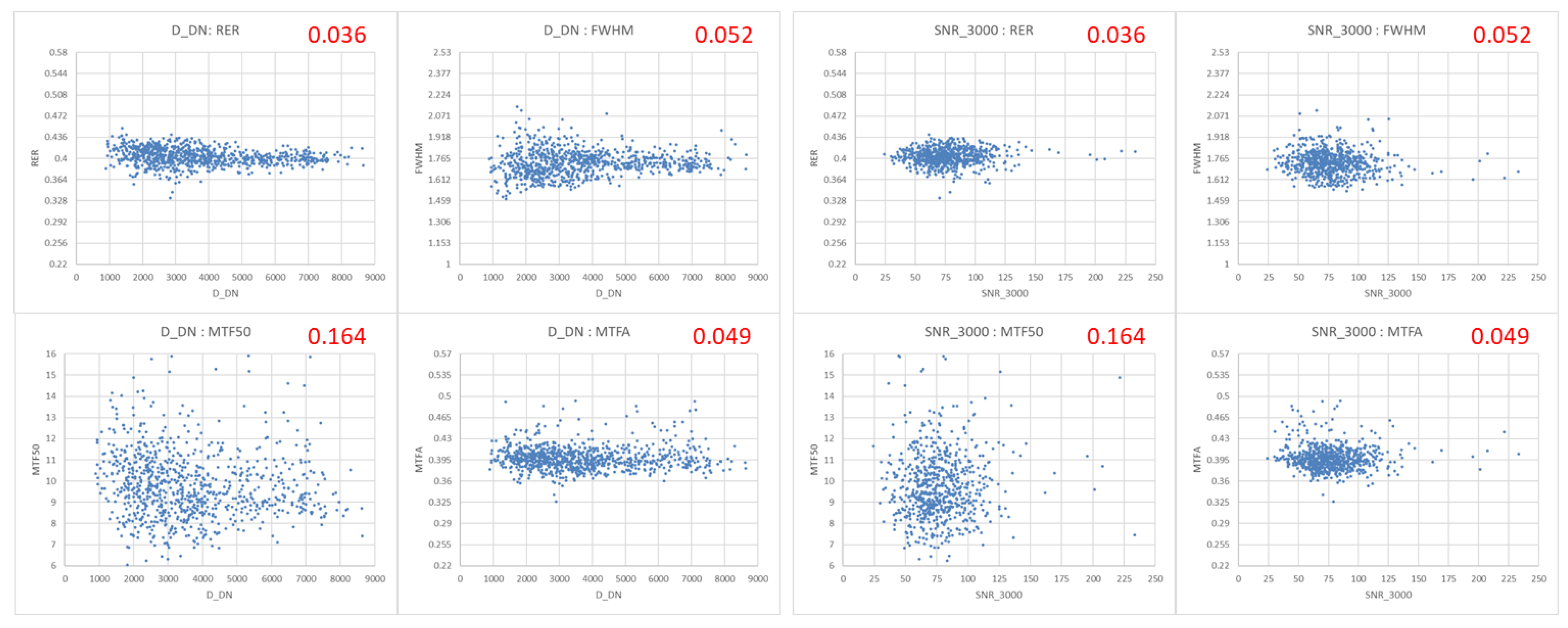
Figure 6 (right) shows the relation between KOMPSAT-3A’s spatial quality and SNR. In Figure 6 (right), we can observe the following:

There is no proportional relationship between SNR and spatial quality.

Figure 7 shows the relationship between the KOMPSAT-3A’s spatial quality and the Edge angle. In Figure 7, we can observe the following:

In Figure 7 (left), there appears to be a correlation between the Edge angle and the spatial quality, and, in Figure 7 (right), this may be due to the difference in state with the Edge target. However, since the Edge angle is different for each Edge target and Baotou's Edge angle is the largest, it is presumed that it is due to the Edge angle.

Figure 7. (left) Edge angle vs. RER, FWHM, MTF50, and MTFA, separated by the Edge target. (right) X-axis for Edge targets in the order of Baotou (blue), India (red), Salon (green), and Zuunmod (purple), separated by imaging order vs. RER, FWHM, MTF50, and MTFA (upper left: average and CV). Scale of Y-axis was changed to CV value.

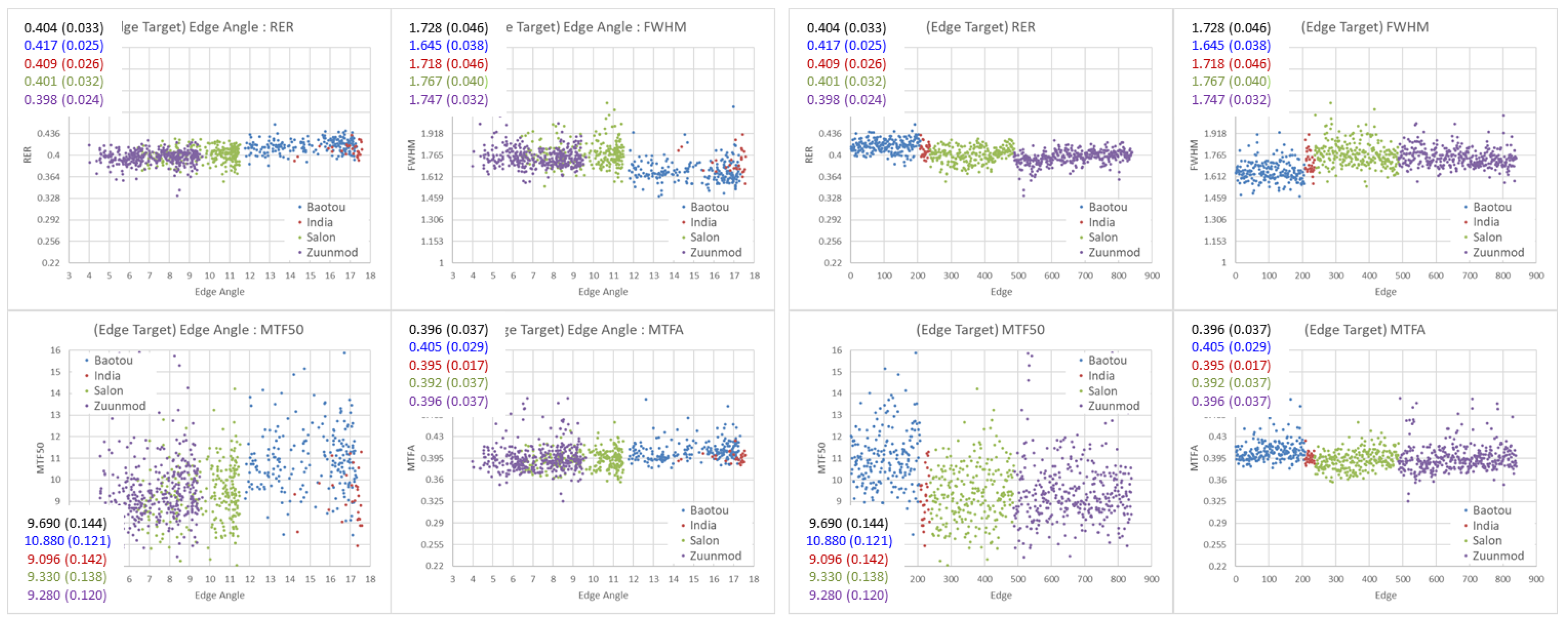
Figure 7 (right) shows the relationship between KOMPSAT-3A’s spatial quality and Edge targets (Baotou, India, Salon, Zuunmod), and Figure 7 (left) shows the Edge angle separated according to the Edge target. The black numbers at the top left of each plot are the overall average and CV values, while the colored numbers are the average and CV values for Baotou, India, Salon, and Zuunmod, respectively. Table 3 shows the average and CV values of the spatial quality according to the Edge target. India has only 29 results, so it is statistically excluded from the comparison. In Figure 7 and Table 3, we observe the following:

The spatial quality values are different for each Edge target. Those of Baotou is the best, while those of Salon and Zuunmod are comparable.
Each Edge target has different CV values, representing the precision. That of Baotou is relatively better than that of Salon and Zunnmod. Baotou is clean and well maintained.

The following two explanations can be given for the correlation between the spatial quality value and the Edge angle:

There is a correlation between the Edge angle and the spatial quality values.
There may be an element of the spatial quality measurement procedure that is missed in the application of the Edge angles.

Looking only at Figure 7 (left), it appears that spatial quality is related to the state of the Edge target. But the spatial quality measurement procedure multiplies COS(EdgeAng) with all pixel data and then the ESF fitting is performed [2,3,6,7], so the possible effects of other factors related to the Edge angle may also need to be considered. If the Edge angle value is large, the Across and the Along boundaries may become unclear, and other factors may be relevant. According to this result, the Edge angle affects both accuracy and precision of the spatial quality measurements of ESMP. Thus, it is necessary to modify and improve ESMP by studying and analyzing the factors that affect the spatial quality measurement via Edge angle. This can be used to draw conclusions through additional research and analysis.

4.2. Comparative Analysis of Spatial Quality Estimators’ Results

We plot and compare the relationships between the spatial quality estimators (RER, FWHM, MTF50, MTFA). In Figure 9, the scale of the plot is changed to a z-distribution (standard normal distribution) because RER, FHWM, MTF50, and MTFA satisfy the conditions of a normal distribution (-0.5 < skew < 0.5). The following formula was used. The red numbers in the top right in Figure 8 is the skew values

z-distribution = (Pixel data – Average) / StDev

Figure 9 and Table 4 demonstrate the relationships among RER vs. FWHM vs. MTF50 vs. MTFA. The first red value at the top right of Figure 9 is Pearson’s correlation coefficient, and the second red value is the Pearson’s value for 766 spatial quality values after excluding outliers using the IQR method. The blue number is CV value in the full case and the IQR. In Figure 9, we observe the following.

RER vs. FWHM in spatial domain and MTF50 vs. MTFA in frequency domain are the best correlations according to Pearson’s correlation coefficient. After excluding outliers with the IQR, the Pearson’s correlation coefficient value for RER vs. FWHM reflects the best correlation, while FWHM vs. MTFA has the worst correlation, and the rest are similar.
It is difficult to identify a strong proportional relationship between the spatial quality estimators other than RER vs. FWHM.

It is necessary to determine the reason that the Pearson’s correlation coefficient values are no greater than ‘0.73’. In particular, the reason for the low value of FWHM vs. MTFA (0.243) should be determined. This is because, if there are any independent characteristics between the spatial quality estimators, it is difficult to represent the spatial quality of a satellite using only one spatial quality estimator. Moreover, it can be assumed that each spatial quality estimator has different spatial quality-related factors involved. It is difficult to say which spatial quality estimator is better based on the results of IQR. It should be noted that only FWHM shows slightly different results from RER and MTFA. This is a subject for further research and analysis.

4.3. Summary

The comparison of CV values confirms that RER is the best spatial quality estimator in terms of precision. RER is more than four times better than MTF50 in terms of precision. In cases where it is difficult to measure RER, FWHM and MTFA are also useful estimators, with more than three times better precision than MTF50.

KOMPSAT-3A’s spatial quality is very stable over time and does not show any adverse effect due to aging.
There is no proportional relationship between the spatial quality and the Roll tilt angle, ΔDN, and SNR.
There appears to be a correlation between the Edge angle and the spatial quality; this may be due to the difference in the Edge angle.
RER vs. FWHM and MTF50 vs. MTFA are the good correlations, and it is difficult to identify any other strong proportional relationship between the spatial quality estimators.

5. Conclusions

By comparing and analyzing the spatial quality measurement results of the 840 edge images of KOMPSAT-3A, it is confirmed that the accuracy and precision of ESMP are sufficient. Of course, the methods used and the initial values of the constraints lead to some statistical values in ESMP, and there is a minor difference in the spatial quality values of the Edge angle and different Edge targets. Thus, further verification of ESMP’s internal algorithms is needed. Nonetheless, in conclusion, all of the presented findings are the result of objective application within the scope of explanation.

As a spatial quality estimator, it is confirmed that RER has the highest precision, and MTF50 has the lowest relative to its reputation. Meanwhile, FWHM and MTFA also exhibit sufficient precision. In addition, it is confirmed that the spatial quality estimators have no correlation with the Roll tilt angle, ΔDN, and SNR, but it is possible that the Edge angle may affect the spatial quality measurement values.

In this work, a comparative analysis was performed using the Edge target images acquired by KOMPSAT-3A with a system MTF50 of ‘> 8%’. This work described the internal structure of ESMP using Edge targets, the initial input conditions, and the factors that affect the results. The following additional research work will do:

Spatial quality measurement with edges of Terrain Feature via statistics [39];
Cause analysis of the differences in the spatial quality measurement with the Edge angle;
Cause analysis results with a Pearson’s correlation coefficient value no greater than ‘0.73’ and a low FWHM and MTFA;
The results and a comparison of the spatial quality measurements of other KARI satellite images, including those of KOMPSAT-3 (GSD, 0.7m; MTF50 > 8%).

Author Contributions

Conceptualization, D.H., D.S. and D.H.Y.; methodology, D.H., D.S. and D.H.Y.; software, D.H., D.S. and D.H.Y.; validation, D.H., D.S. and D.H.Y.; formal analysis, D.H., D.S. and D.H.Y.; investigation, D.H., D.S. and D.H.Y.; resources, D.H.; data curation, D.H.; writing—original draft preparation, D.H.; writing—review and editing, D.H.; visualization, D.H.; supervision, D.H.; project administration, D.H.; funding acquisition, D.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the ‘Development of Calibration and Validation of NeoSat-1 System’ Project of the Korea Aerospace Administration, grant number SR24090.

Data Availability Statement

Not applicable

Acknowledgments

The authors would like to thank Dr. Viallefont-Robinet (ONERA) and Prof. Helder (SDSU) for their experience and technical advice; Dr. Fox (NPL), the CEOS WGCV IVOS leader, for providing us with the opportunity to discuss the content of this paper; and CTO Ryan and CEO Pagnutti (I2R Corp.) for their continued technical advice at JACIE workshop.

Conflicts of Interest

The authors declare no conflicts of interest.

References

ISO12233:2017(E), Photography – Electronic still picture imaging – Resolution and spatial frequency responses, International Organization for Standardization, Geneva, CH, 2017.
Choi, T., IKONOS satellite on orbit modulation transfer function (MTF) measurement using edge and pulse method”, M.S. Thesis, Elect. Eng. Dept., South Dakota State University, 2002.
Helder, D.; Choi, T.; Rangaswamy, M., In-flight characterization of the spatial quality of Remote Sensing imaging systems using point spread function estimation. In Post-Launch Calibration of Satellite Sensors, On-orbit MTF assessment of satellite cameras, Morain & Budge Eds, Taylor and Francis Group 4, 2004, 157-170.
Choi, T.; Helder, D., Generic Sensor Modeling for Modulation Transfer Function (MTF) Estimation, Pecora 16 “Global Priorities in Land Remote Sensing”, Sensor I, 2005.
Pagnutti, S.; Blonski, D.; Cramer, M.; Helder, D.; Holekamp, K.; Honkavaara, E.; Ryan, R., Targets, methods, and sites for assessing the in-flight spatial resolution of electro-optical, Can. J. Remote Sensing, 2010, 36-5, 583–601. [CrossRef]
Blanc, P.; Wald, L, A review of earth-viewing methods for in-flight assessment of modulation transfer function and noise of optical spaceborne sensors, HAL open science, hal-00745076, ESA ESRIN, Italy, 2009.
Blanc, P.; Wald, L., Image Quality – WP224 (ARMINES), TN-WP224-001-ARMINES, Issue 1.0, ESA ESRIN, Italy, 2008.
Viallefont-Robinet, F.; Legar, D., Improvement of the edge method for on-orbit MTF measurement, Optics Express, 2010, 18-4, 3531-3545.
Javan, F.; Samadzadegan, F.; Reinartz, P., Spatial Quality Assessment of Pan-Sharpened High Resolution Satellite Imagery Based on an Automatically Estimated Edge Based Metric, Remote Sensing, 2013, 5-12, 6539-6559. [CrossRef]
Koksal, S.; Canarslan, I.; Coskun, O., Image Quality Characterization of Earth Observation Electro-Optic Imagers through PSF and MTF Analysis, 9th International Conference on Recent Advances in Space Technologies (RAST), 2019, 429-434.
Viallefont-Robinet, F.; Helder, D.; Fraisse, R.; Newbury, A.; van den Bergh, F.; Lee, D.; Saunier, S., Comparison of MTF measurements using edge method: Towards reference data set, Optics Express, 2018, 26-26, 33625–33648. [CrossRef]
Viallefont-Robinet, F.; Helder, D.; Lee, D., Presentations in Geo/Spatial Quality sub-committee”, CEOS WGCV IVOS-29, 2017, https://calvalportal.ceos.org/web/guest/ivos-29.
Zhaocong, W.; Zhipeng, L.; Yi, Z.; Feifei, G.; Lin, H., Image Quality Assessment of High-resolution Satellite Images With MTF-based Fuzzy Comprehensive Evaluation Method, ISPRS TC III Mid-term Symposium, 2018, XLII-3, 1907-1914.
Min, M.; Cao G.; Xu, N.; Bai, Y.; Jiang, S.; Hu, X.; Dong, L.; Guo, J.; Zhang, P., On-Orbit Spatial Quality Evaluation and Image Restoration of FengYun-3C/MERSI, IEEE Transactions on Geoscience and Remote Sensing, 2016, 54-12, 6847-6858. [CrossRef]
Coefficient of Variation (CV), WIKIPEDIA, https://en.wikipedia.org/wiki/Coefficient_of_variation, (accessed on 8 Aug. 2024).
Kim, S.; Youk, Y., Suppressing effects of micro-vibration for MTF measurement of high-resolution electro-optical satellite payload in an optical alignment ground facility, Optics Express, 2023, 31-3, 4942-4953. [CrossRef]
Lee, D.; Helder, D.; Christopherson, J.; Storey, J.; Seo, D.; Stensaas, G., RER, FWHM, MTF Processing Step for Edge target (Draft) & Standard Edge targets by KOMPSAT-3, CEOS WGCV IVOS-26, 2014, https://calvalportal.ceos.org/web/guest/ivos-24.
Park, D.; Lee, D.; Jeong, J.; Seo, D.; Seo, Y., Validation of MTF Measurement method by edge target, CEOS WGCV IVOS-30, 2018, https://calvalportal.ceos.org/web/guest/ivos-30.
Masaoka, K., Accuracy and Precision of Edge-Based Modulation Transfer Function Measurement for Sampled Imaging Systems, IEEE Access, 2018, 6, 41079-41086. [CrossRef]
Masaoka, K., Practical edge-based modulation transfer function measurement, Optics Express, 2019, 27-2, 1345-1352. [CrossRef]
Masaoka, K., Edge-based modulation transfer function measurement method using a variable oversampling ratio, Optics Express, 2021, 29-23, 37628-37638.
Wu, Y.; Xu, W.; Piao, Y.; Yue, W., Analysis of Edge Method Accuracy and Practical Multidirectional Modulation Transfer Function Measurement, Applied Sciences, 2022, 12-24, 12748-12771. [CrossRef]
Zhang, S.; Wang, F.; Wu, X.; Gao, K., MTF Measurement by Slanted-Edge Method Based on Improved Zernike Moments, Sensors, 2023, 23-1, 509-527. [CrossRef]
Lee, D. Park, H. Kim, Y. Seo, J. Jeong and D. Seo, “Analysis on Refinement of On-orbit MTF Measurement using Edge Target”, VH-RODA 2019, ESA ESRIN, Italy, Nov. 2019, https://earth.esa.int/eogateway/events/vh-roda-very-high-resloution-radar-optical-data-assessment-workshop-and-ceos.
Lee, D.; Park, D.; Helder, D.; Jeong, J.; Seo, D., Spatial Quality from Edge target imaged by KOMPSAT-3 (& KARI methodology of MTF Estimation, ver. 2019) (Jan. 2014 ~ July. 2019), JACIE 2019, USGS, USA, 2019, https://usgs.gov/calval/jacie-2019-presentations.
Lee, D.; Yang, J.; Seo, D.; Song, J.; Chung, J.; Lim, H., Image Restoration from Asymmetric Point Spread Function of High Resolution Remote Sensing Satellite with Time Delayed Integration, Advanced in Space Research, 2011, 47-4, 690-701. [CrossRef]
CEOS WGCV IVOS, Committee on Earth Observation Satellite, Working Group on Calibration and Validation, Infrared and Visible Optical Sensors, 2024, https://calvalportal.ceos.org/ceos-wgcv/ivos.
Helder, D.; Viallefont, F., A Frame for Geo/Spatial Quality”, CEOS WGCV IVOS-24, 2012, https://calvalportal.ceos.org/web/guest/ivos-24.
Viallefont, F., Geo Spatial Quality Activity, MTF workshop in CEOS WGCV IVOS-31, 2019, https://calvalportal.ceos.org/web/guest/ivos-31.
CEOS WGCV IVOS, CEOS Cal/Val Portal – Cal/Val Sites, 2024, https://calvalportal.ceos.org/calvalsites.
USGS EROS Cal/Val Center of Excellence (ECCOE), Test Sites Catalog – Spatial Sites Catalog, 2024, https://calval.cr.usgs.gov/apps/spatialsites_catalog.
Lee, D., Edge target in Mongolia, MTF workshop in CEOS WGCV IVOS-30, 2018, https://calvalportal.ceos.org/web/guest/ivos-30.
Lee, D., Reliability Items related within Edge target’s Spatial quality measurement Python code, and Issues of Input number of EdgeWidth(Pixel line) and CSAPS fitting, The Korean Society of Remote Sensing – Fall Conference, South Korea, 2023, https://ksrs.or.kr/Conference.
Yong, S.; Kong, J.; Heo, H.; Kim, Y., Analysis of the MSC(Multi-Spectral Camera) Operational Parameters, Korean Journal on Remote Sensing, 2002, 18-1, 53-59.
Aiazzi, B.; Selva, M.; Arienzo, A.; Baronti, S., Influence of the System MTF on the On-Board Lossless Compression of Hyperspectral Raw Data, remote sensing, 2019, 11-7, 791-805. [CrossRef]
Lee, D.; Yoo, D., Introduction of Improvement of KARI’s MTF measuring Python algorithm, The Korean Society of Remote Sensing – Fall Conference, South Korea, 2022, https://ksrs.or.kr/Conference.
Gao, B., An operational method for estimating signal to noise ratios from data acquired with imaging spectrometers, Remote Sensing of Environment, 1993, 43-1, 23-33. [CrossRef]
Lee, D., Validation of SNR calculation formula in KSPC, KARI Research Note, KARI-SGSRD-ELN-2023-024, KARI, South Korea, Aug. 2023.
Lee, D.; Yoo, D., Python algorithm for measuring the Spatial quality (RER, FWHM, MTF) on the Edge of Terrain feature, 28th ISRS (International Symposium on Remote Sensing), South Korea, 2023, https://isrs.or.kr.

Figure 1. Plot showing the procedure of using the Edge target to measure the spatial quality (RER, FWHM, MTF50, MTFA) using KOMPSAT-3A Level 0 (raw) Across edge image data imaged at Zuunmod with Roll tilt of 29.31deg on Feb. 21, 2019.

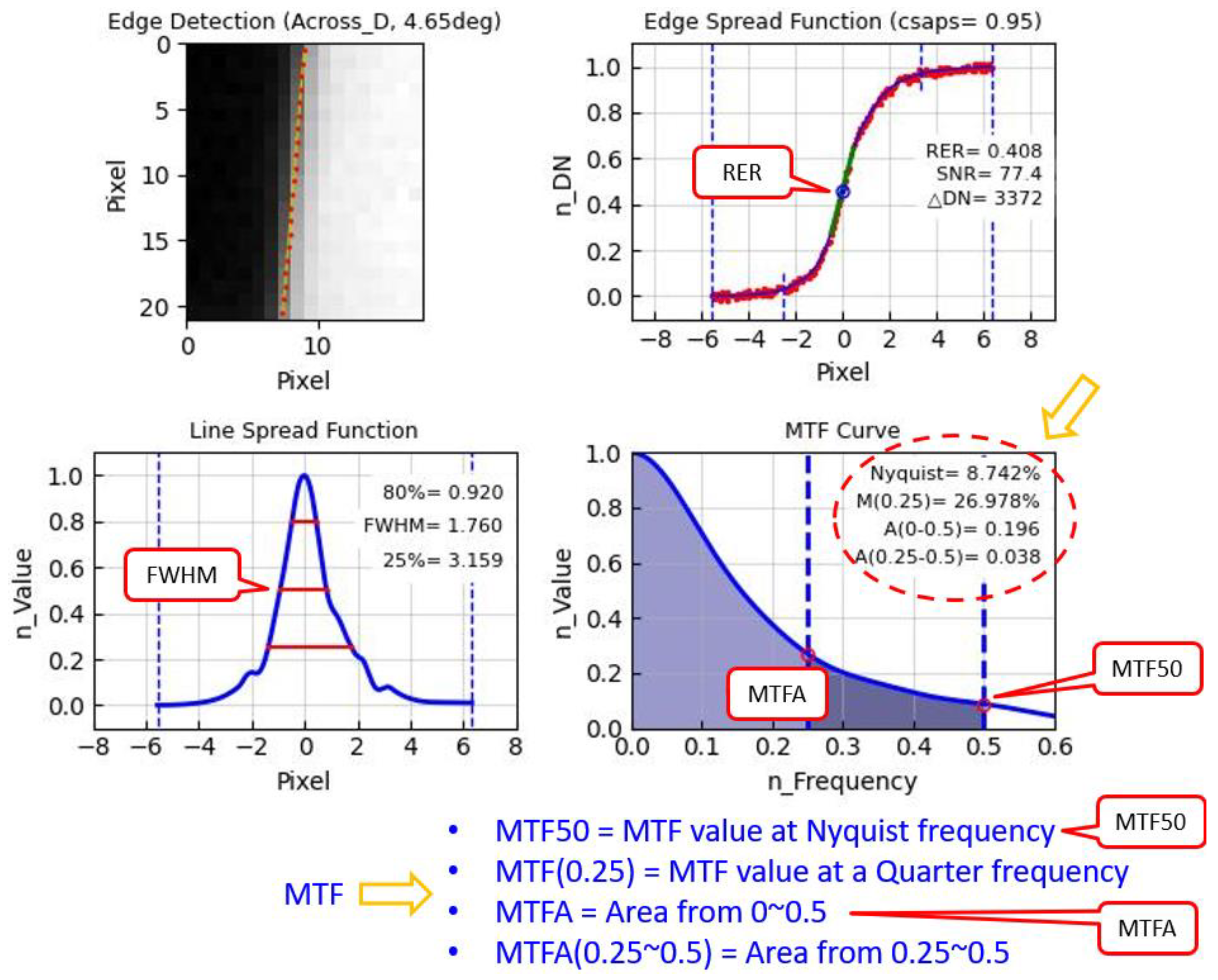
Figure 2. Edge targets in catalog of USGS and CEOS Cal/Val portal site [30,31], imaged by KOMPSAT-3 (GSD, 0.7 m).

Figure 3. (a) RER is slope of edge at -0.5 to 0.5 pixels on ESF (green line); FWHM is width (pixels) of LSF at 0.5 on Y-axis over LSF (blue line); RER and FWHM have different measurement locations and units. (b) Procedure for detection of edge and calculation of the Edge angle and FitErr: obtain line of edge (green line) and calculate the Edge angle and FitErr as standard deviation of edge points (red dot) over line of edge.

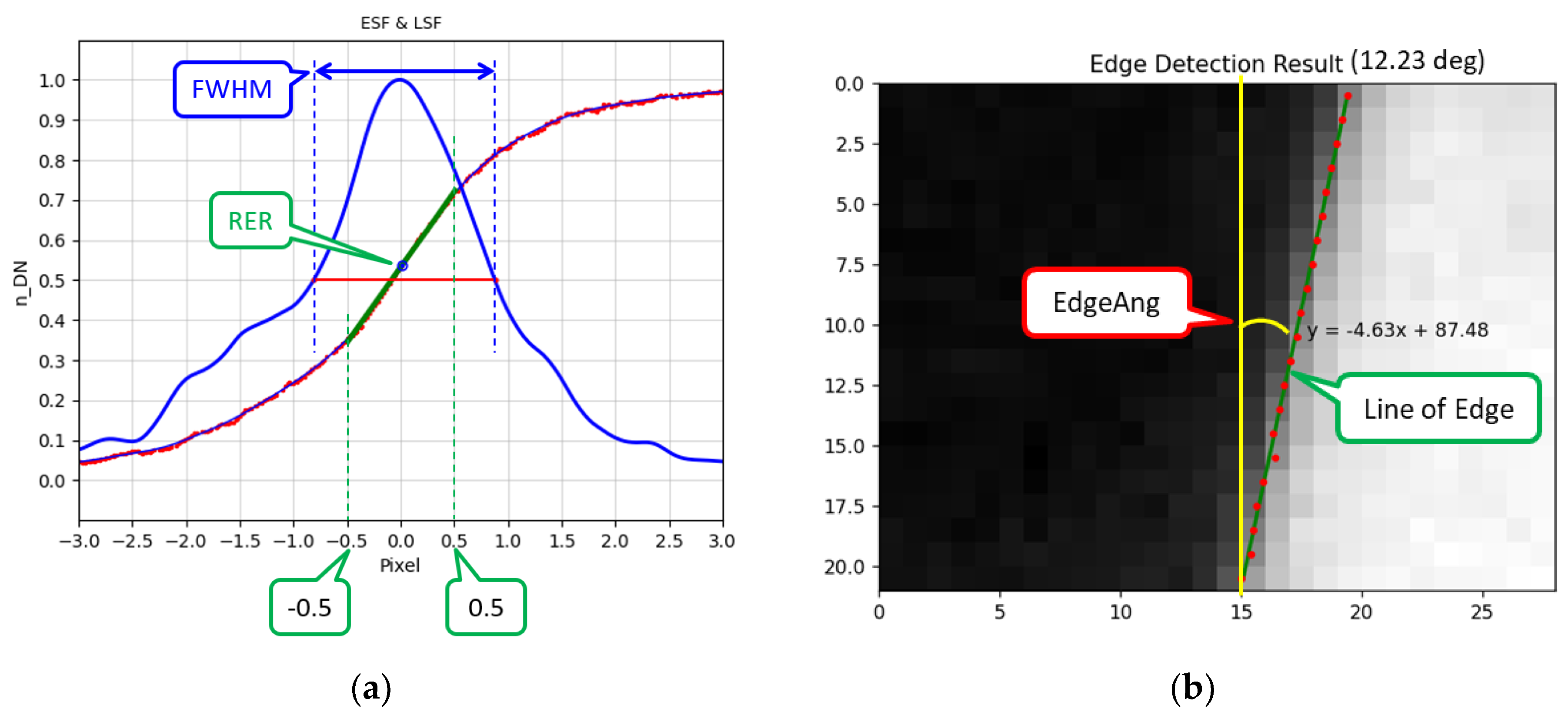
Figure 4. First CSAPS fitting (left) and second CSAPS fitting of ESF after removing outlier noise (right). The measurement result corrupted by noise is restored. Baotou Edge target imaged by KOMPSAT-3A (Jan. 13, 2019).

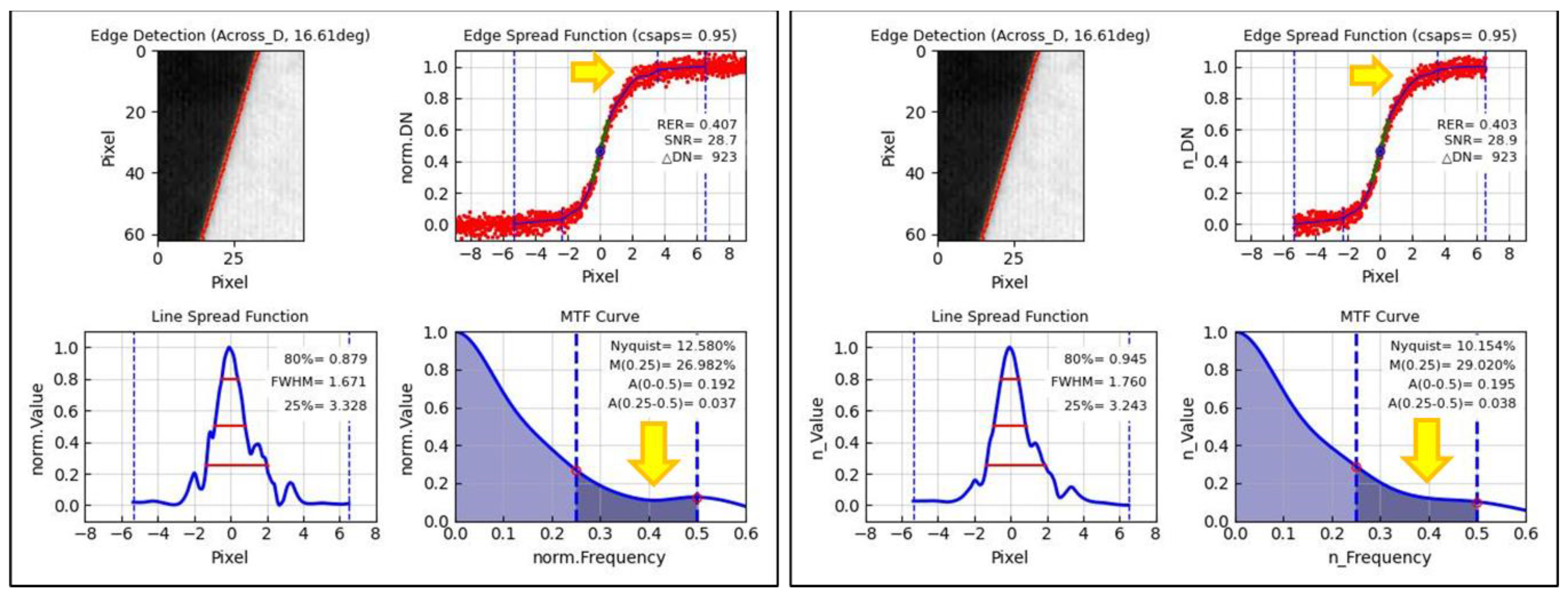
Figure 5. (left) Julian date vs. RER, FWHM, MTF50, and MTFA. (right) Roll tilt angle vs. RER, FWHM, MTF50, and MTFA (upper right in red: CV). Scale of Y-axis was changed to CV value.

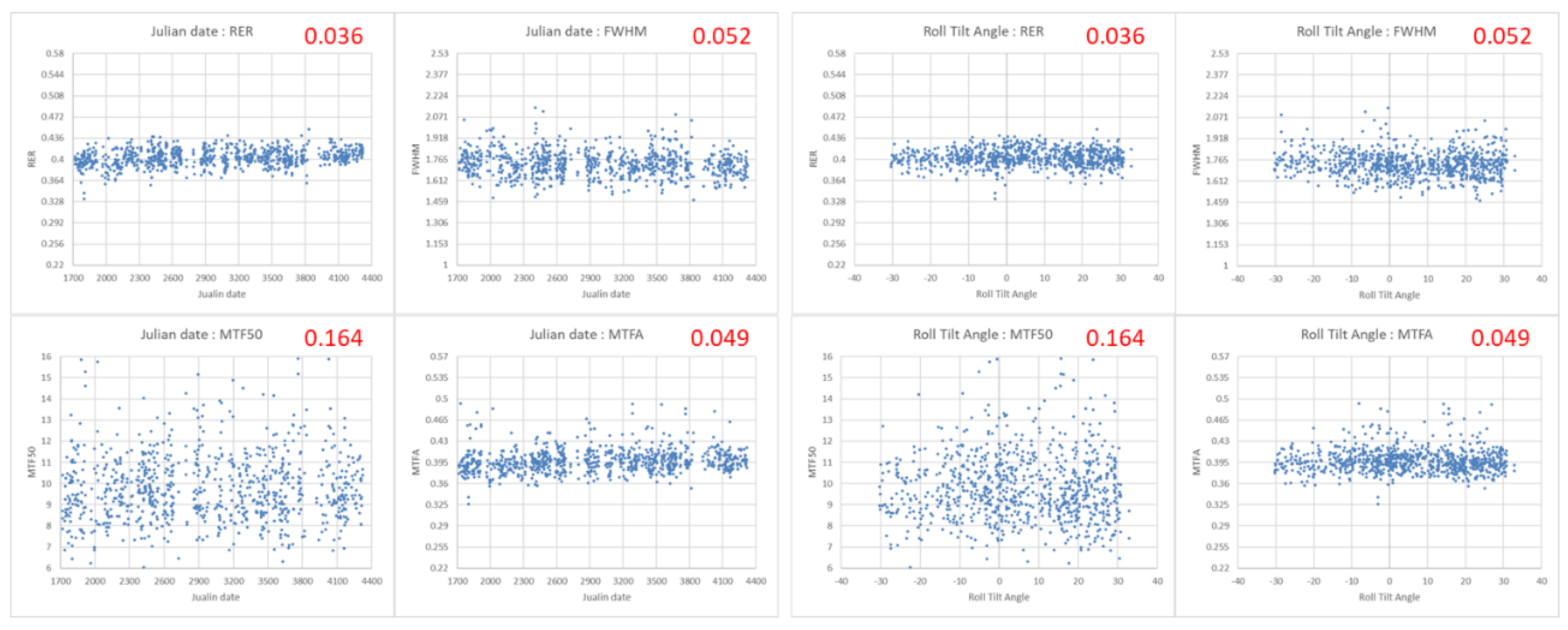
Figure 8. Histograms used to check z-distributions of RER, FWHM, MTF50, and MTFA (upper right: Skew value).

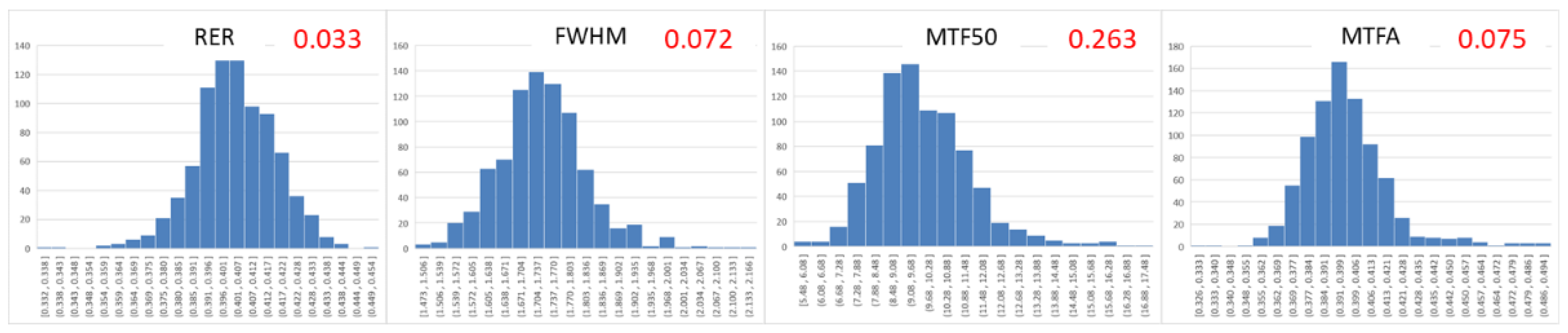
Figure 9. Scatter plot of RER vs. FWHM vs. MTF50 vs. MTFA (upper right: (red) Pearson’s full and IQR and (blue) CV full and IQR). Scale of plot was changed to z-distribution.

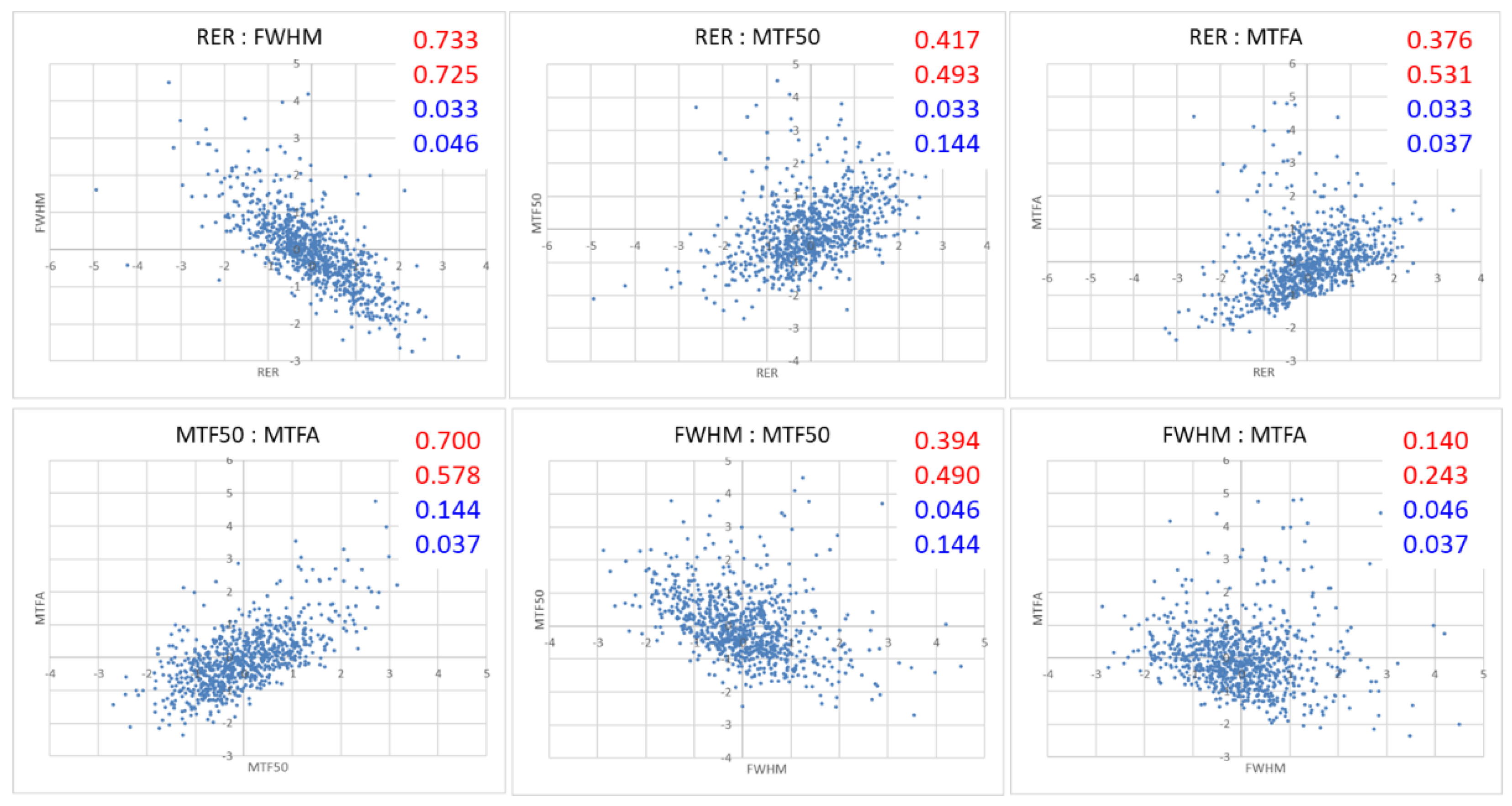
Table 1. Main factors affecting measurement in spatial quality calculation procedure. The constraint values of all factors are not finalized.

Factor		Content and Constraint value
1	Asymmetric ESF and LSF	How to reflect and handle asymmetric ESF and LSF
2	Straightness of Edge	Constraint on straightness of edge (FitErr < 0.1 pixel)
3	Noise of Bright and Dark area on ESF	Noise (StDev) in bright and dark area on normalized ESF
4	DN difference between Bright and Dark area (ΔDN)	Constraint on DN difference between bright and dark area (ΔDN > 1000 of KOMPSAT-3A)
5	Edge angle between Line of Edge and Across direction	Constraint on Edge angle range between line of edge and Across direction (EdgeAng) (2.2 ~ 30 deg)
6	RER center	Center of RER; inflection point (top) on LSF
7	Total trim width of ESF	Total trim width of bright and dark area from edge width on ESF (18 pixels)
8	Fitting method for ESF	Optimal fitting method of ESF for asymmetric ESF and LSF and with noise
9	Noise removal method for ESF	Used to determine and remove noise on ESF
10	Number of Edge row lines (EdgeLine)	Number of edge row lines on edge (dependent on fitting method of ESF) (EdgeLine >= 21 pixels)

Table 2. Results of all Across edges (966) and the constraint (840) using KOMPSAT-3A.

	All (966)				Constraint (840, 87.0%)
	RER	FWHM	MTF50	MTFA	RER	FWHM	MTF50	MTFA
Average	0.403	1.740	9.851	0.398	0.403	1.732	9.805	0.398
StDev	0.017	0.102	1.808	0.022	0.014	0.090	1.604	0.020
CV	0.042	0.059	0.184	0.055	0.036	0.052	0.164	0.049
Max	0.460	2.358	22.704	0.513	0.451	2.138	17.028	0.492
Min	0.311	1.354	4.519	0.326	0.332	1.473	5.482	0.326

Table 3. Spatial quality and CV results for Edge targets obtained with KOMPSAT-3A.

		No.	RER	FWHM	MTF50	MTFA	CV (StDev/Average)
		No.	RER	FWHM	MTF50	MTFA	RER	FWHM	MTF50	MTFA
Edge target	Baotou	207	0.416	1.651	10.944	0.407	0.027	0.048	0.129	0.039
	India	29	0.409	1.718	9.096	0.396	0.026	0.046	0.142	0.021
	Salon	251	0.401	1.775	9.350	0.393	0.032	0.049	0.146	0.040
	Zuunmod	353	0.397	1.750	9.519	0.396	0.030	0.037	0.165	0.057
Average		840	0.403	1.732	9.805	0.398
StDev			0.014	0.090	1.604	0.020
CV (StDev/Average)			0.036	0.052	0.164	0.049
Max			0.451	2.138	17.028	0.492
Min			0.332	1.473	5.482	0.326

Table 4. Pearson’s correlation values of RER vs. FWHM vs. MTF50 vs. MTFA.

Pearson’s	Constraint (840)	IQR (776)
RER vs. FWHM	-0.733	-0.725
RER vs. MTF50	0.417	0.493
RER vs. MTFA	0.376	0.530
MTF50 vs. MTFA	0.700	0.578
FWHM vs. MTF50	-0.394	-0.490
FWHM vs. MTFA	-0.140	-0.243

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer