Explainability is essential for AI models, especially in clinical settings where understanding the model's decisions is crucial. Despite their impressive performance, black-box AI models are unsuitable for clinical use if their operations cannot be explained to clinicians. While deep neural networks (DNNs) represent the forefront of model performance, their explanations are often not easily interpretable by humans. On the other hand, using hand-crafted features extracted to represent different aspects of the input data and traditional machine learning models are generally more understandable. However, they often lack the effectiveness of advanced models due to human limitations in feature design. To address this, we propose ExShall-CNN, a novel explainable shallow convolutional neural network for medical image processing. This model enhances hand-crafted features to maintain human interpretability while achieving performance levels comparable to advanced deep convolutional networks, such as U-Net, for medical image segmentation. ExShall-CNN and its source code are publicly available at: https://github.com/MLBC-lab/ExShall-CNN

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Machine learning models can be simply defined as a mapping from the input data to the output data. This mapping must be usable and robust for unseen samples. Thus, it cannot be a simple tabular mapping. Instead, outputs must be computed from input data. Hence, machine learning models are usually mathematical functions [1].

Two major steps in the development of machine learning models are model selection and training by optimization. The neural networks are a well-known set of models that are shown high capabilities to facilitate both steps [2].

In theory, shallow neural networks, such as two-layer multilayer perceptron (MLP) with activation functions, should be able to approximate any input-output relationship or function if they have enough number of trainable parameters and non-linearity [3].

Deep learning models are shown to need a much smaller number of trainable parameters while preserving similar performance as large shallow networks [4]. A fewer number of parameters means shorter training time and high trainability by finding a better optimum in a fixed running time. Many different architectures and building blocks are deployed for deep learning models, such as convolutional neural networks (CNN) [2], recurrent neural networks (RNN) [5], and transformer neural networks (TNN) [6]. Both CNN and TNN are used in image processing and analysis applications and based on dataset size and model size, one can be preferred over the other. TNNs are usually good for large datasets while CNNs have better performance on small datasets [7,8].

Medical image processing encompasses a wide range of applications and domains, including areas such as radiology and pathology. However, despite the vast potential of this field, only a limited number of these applications have access to large, well-curated datasets [9]. Hence, while transformers are shown slightly better performance on large cohorts, deep CNN are more favorable in medical image processing because they can perform better on smaller cohorts [7,10].

Two well-known deep CNNs for image segmentations are fully convolutional neural networks (FCNN) [11] and U-Nets [12]. However, both FCNN and U-Net are deep neural networks, and their functions cannot be explained clearly [13]. Although many methods are discussed in [14,15,16] can be used for explainability, only a few of them is widely accepted in clinical interpretation since direct visualization of their features is not human-interpretable. This opacity in decision making introduces challenges in clinical setups where the ability to audit a model’s decision-making process are crucial. Explainable models provide transparency by making the model’s reasoning accessible which allows clinicians to validate AI outputs in a manner aligned with their expertise. In the next section, we will elaborate more about human-interpretable and manually engineered features. At the same time, we will develop a theoretical model chronologically from the ground up to include the most essential hand-crafted and machine learning-based features in an explainable shallow convolutional neural network. ExShall-CNN and its source code are publicly available at: https://github.com/MLBC-lab/ExShall-CNN

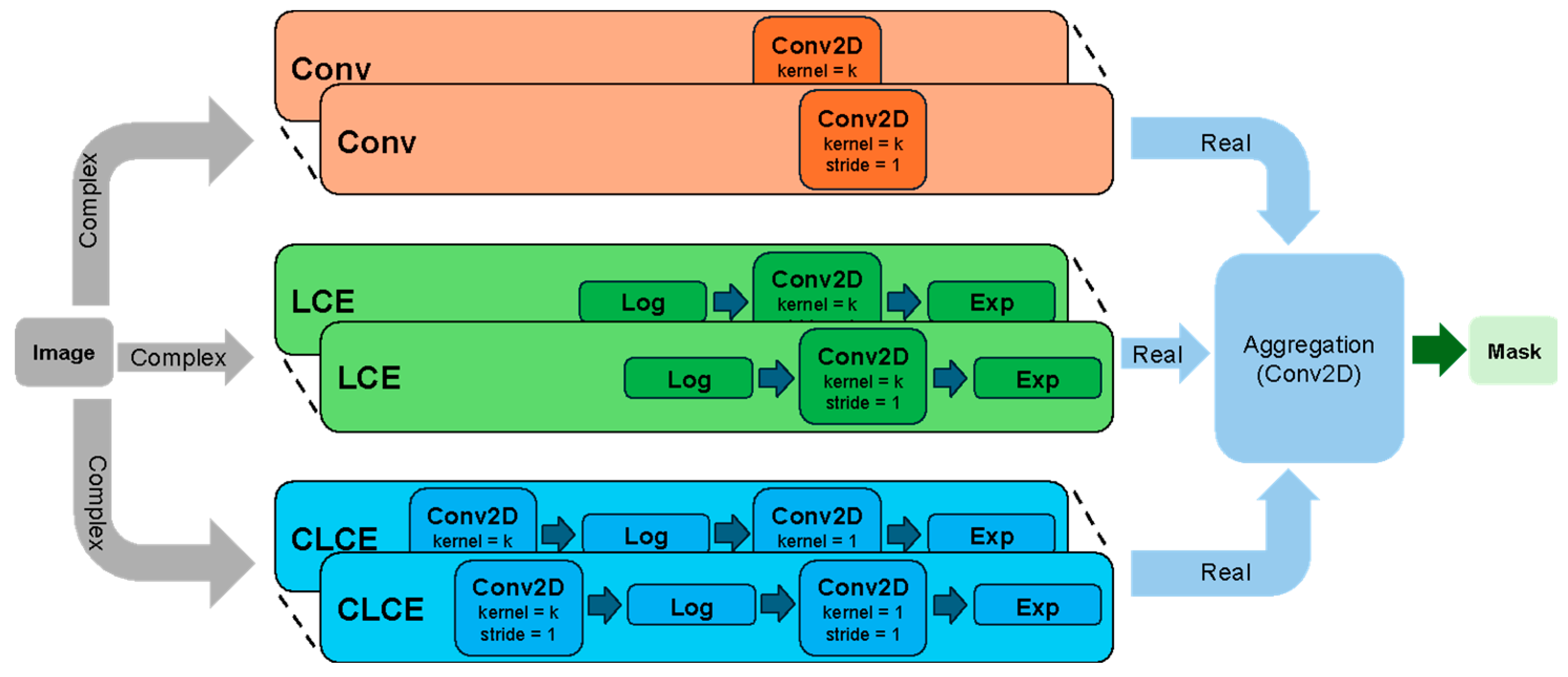
2. Theory and Calculation

Otsu [17] suggested a global thresholding by minimizing the intra-class variance which yields to maximizing inter-class variance for background/foreground segmentation of images.

T_{o t s u} = \arg \arg \begin{matrix} m i n \\ t \end{matrix} \{P (t) (P (L - 1) - P (t)) (\frac{\sum_{i = 0}^{t - 1} i P (i)}{P (t)} - \frac{\sum_{i = t}^{L - 1} i P (i)}{P (L - 1) - P (t)})\}

(1)

where L is the length of the pixels range, e.g. 256 for grayscale images and p and P are probability density and probability cumulative functions, respectively.

This equation is usually solved iteratively, and its computation is often very fast even for very large images since it only needs the frequency of colors or shades of grays to calculate the threshold value. Although this method is highly efficient, it determines a single threshold for the entire image without taking into account the spatial distribution of pixel values. This means it may overlook important variations and contextual information present in different regions of the image, potentially affecting the accuracy of segmentation or analysis. By not considering how pixel values are distributed spatially, the method may not capture the nuances needed for more complex image processing tasks. To address the disparity between local and global pixel value distributions, Sauvola [18] proposed using a local threshold:

T_{s a u v o l a} = μ_{n} (1 + k (\frac{σ_{n}}{r} - 1))

(2)

where n is the local neighborhood diameter, and

µ_{n}

and

σ_{n}

are the mean and standard deviation of local neighborhoods, respectively. k and r are two coefficients that are determined based on application. It is common to select the value of r as half of the pixels’ maximum value. Hence, two values of n and k are needed to be determined to have an acceptable performance. If segmentation labels are available, these two values can be optimized adaptively based on the dataset.

It can be inferred that the mean

µ_{n}

and standard deviation

σ_{n}

serve as local features, with Eq. 2 acting as a classification threshold. Thus, the advantages of the Sauvola method compared to Otsu highlight that local features effectively differentiate between background and foreground in classification tasks. Consequently, a general approach can focus on extracting local features followed by classification. The only raw data available are the pixel values and their spatial arrangement, and all other features must be derived from this foundational information. Mean and standard deviation are examples of features created from this raw data, which can be further expanded.

Raw data comes from two sources: the pixel values themselves and the values of adjacent pixels. Features can be defined as any transformations of these raw values into a new domain that simplifies classification, such as linear mappings. Keeping this in mind, various mappings have been proposed, referred to as kernel methods [19]. Some common kernels are depicted in Table 1 [20].

Kernel methods fully encompass the Otsu and Sauvola methods, as both rely on two key factors: mean and standard deviation. These factors represent linear or second-order combinations of adjacent pixel values. Hence, if a more complicated model can have all the given kernel mappings, it can also cover the Otsu and Sauvola methods. All the kernels contain some fundamental mathematical operations, such as summation, subtraction, multiplying, division, power, and exponent.

Otsu, Sauvola, and kernel methods are notable for their explainability, particularly in visual terms. With these methods, the classifications directly reflect the visual content. Additionally, they are mathematically transparent, illustrating the relationships between neighboring pixels in the classification process.

We will show all the Otsu, Sauvola, and Kernel-based methods can be assimilated in a shallow deep CNN with appropriate activation functions. CNN provides a weighted summation of raw data, and activation can bring the kernel mappings. To assimilate the fundamental operations, i.e., summation/subtraction, multiplication/division, power, and exponent, we propose the following activation functions:

f (x) = e x p (k^{T} x)

(3)

f (x) = l o g (k^{T} x)

(4)

Where x is the input vector and k is the convolution kernel vector. Thus, the length of both vectors is equal to the kernel size. To prove that all basic mathematical operations can be implemented by these activation functions, a simple 2-dimensional input is assumed. More dimension is only an extension of this simplification. The equations presented in Table 2 are implemented in a shallow convolutional neural network.

As it can be seen in Table 2, all required operations are implementable with shallow convolutional neural networks with the given activation functions if there are enough residuals. Residuals that are a well-known contribution to CNNs were first proposed in [21]. Since then, they have been widely used in almost all successful CNNs. It is easy to envision that with the right combinations and configurations of these operations, all the kernels listed in Table 1 can be incorporated, along with many more complex combinations that have yet to be categorized into existing kernel types. An important consideration for these equations (especially taking logarithms) is that negative numbers do not have real-valued logarithms. Hence, we designed complex convolutional neural networks (CCNN) instead of real-valued CNNs.

Moreover, it is known that the receptive fields of CNNs are enlarged through depth [22,23]. Since we are trying to use a shallow CNN for its higher explainability, then we cannot rely on large receptive fields by depth, and we must compensate for it by the size of kernels. In deep CNNs, kernel sizes of 3, 5, and sometimes 7 are the most common. If we assume that the kernel is center aligned, then by a large kernel of size 7, two neighbor pixels in every direction are included in the equation. After many layers in a deep CNN, this receptor field will be significantly increased proportionally to the sizes of kernel, stride, and dilation of hidden layers. In a shallow CNN, there is no depth growth of receptor field, and a wide range of sizes of kernels and dilations take the responsibility to achieve almost similar receptor field sizes in deep CNNs. Larger kernel sizes cause the non-linear equations to converge slowly through backpropagation. Hence, they usually need more time to be trained, while their number of parameters is usually significantly less than the deep CNNs.

3. Material and Methods

In this study, we used the Retina Blood Vessel segmentation dataset as a widely used benchmark for medical image segmentation [24]. This dataset contains 100 color images with their binary mask. The dataset is divided into two subsets: 80 images along with their corresponding masks are designated for training, while the remaining 20 images and their corresponding masks are reserved for testing. This dataset provides a well-curated collection of retinal fundus images, each with precise annotations for blood vessel segmentation. Accurate segmentation of blood vessels is essential in ophthalmology, as it assists in the early diagnosis and treatment of retinal diseases, including diabetic retinopathy and macular degeneration [25].

The structure of our proposed shallow CNN model is shown in Figure 1. As shown in this figure, there are three different modules, namely, Conv, Log-Conv-Exp (LCE), and Conv-Log-Conv-Exp (CLCE), each with different kernel sizes. The Conv layer finds weighted summation and subtraction of juxtaposed pixels and assimilates a linear kernel (Table 2, row 1). The LCE layer calculates multiplications and divisions of neighbor pixels and assimilates cosine, polynomial, and somehow sigmoid kernels (Table 2, rows 2 and 3). Finally, the CLCE layer approximates RBF, Laplacian, and Chi-Squared kernels (Table 2, row 4). Since the weights and biases of convolutional layers can be positive or negative, the expected logarithm values are complex numbers. Hence, the model is totally implemented in the complex numbers set except for the last layer, which aggregates real numbers. Unlike other layers, Conv and Aggregate layers do not have non-linear activation functions. Here we use kernel sizes 1, 3, 5, 9, 13, 17, 21, and 25. As a result, we have 8 * 3 = 24 modules.

We compare our explainable shallow CNN to two well-known models for image segmentation, namely FCNN [11] and U-Net [12]. The former architecture is similar to our proposed model nevertheless much deeper and the latter is the current state-of-the-art in medical image segmentation. Both models have two important differences from our proposed shallow CNN: Both are DNNs with several hidden layers and also use typical ReLU activation functions. All three models are trained and validated on a similar training dataset and evaluated on the testing set.

4. Results and Discussion

4.1. Comparison of Results

Here we use Jaccard similarity, Sørensen–Dice, and F1-Score metrics to evaluate the performance of our models. Since the segmentation is in a binary format (background and foreground), the Dice and F1 scores are expected to be similar. Table 3 shows the performance of the three models. On the training dataset, Shallow-CNN works weaker than both FCNN and U-Net. However, on the test dataset, Shallow-CNN operates better than FCNN while performing worse than U-Net. The superior generalization of Shallow-CNN compared to FCNN is attributed to its smaller parameter space, which reduces the risk of overfitting to the training data. By leveraging hand-crafted features and interpretable transformations, Shallow-CNN achieves a balance between model complexity and effective feature representation, leading to a better performance on unseen data. These findings suggest that although Shallow-CNN does not surpass U-Net in performance, it demonstrates better generalization than FCNN. Additionally, while deep models like FCN and U-Net pose challenges in terms of explainability, the shallow model is more transparent, as will be elaborated in the next section.

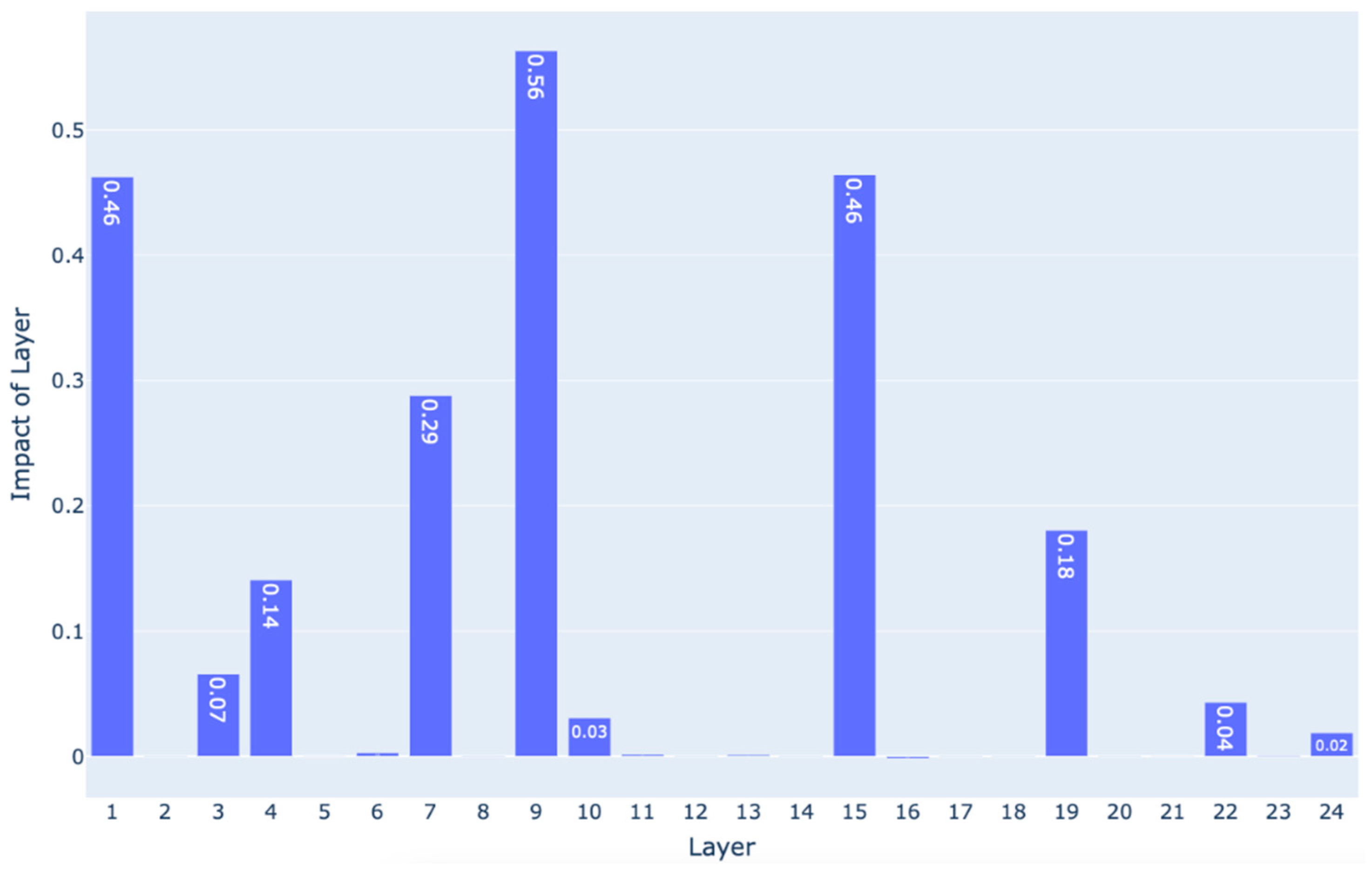
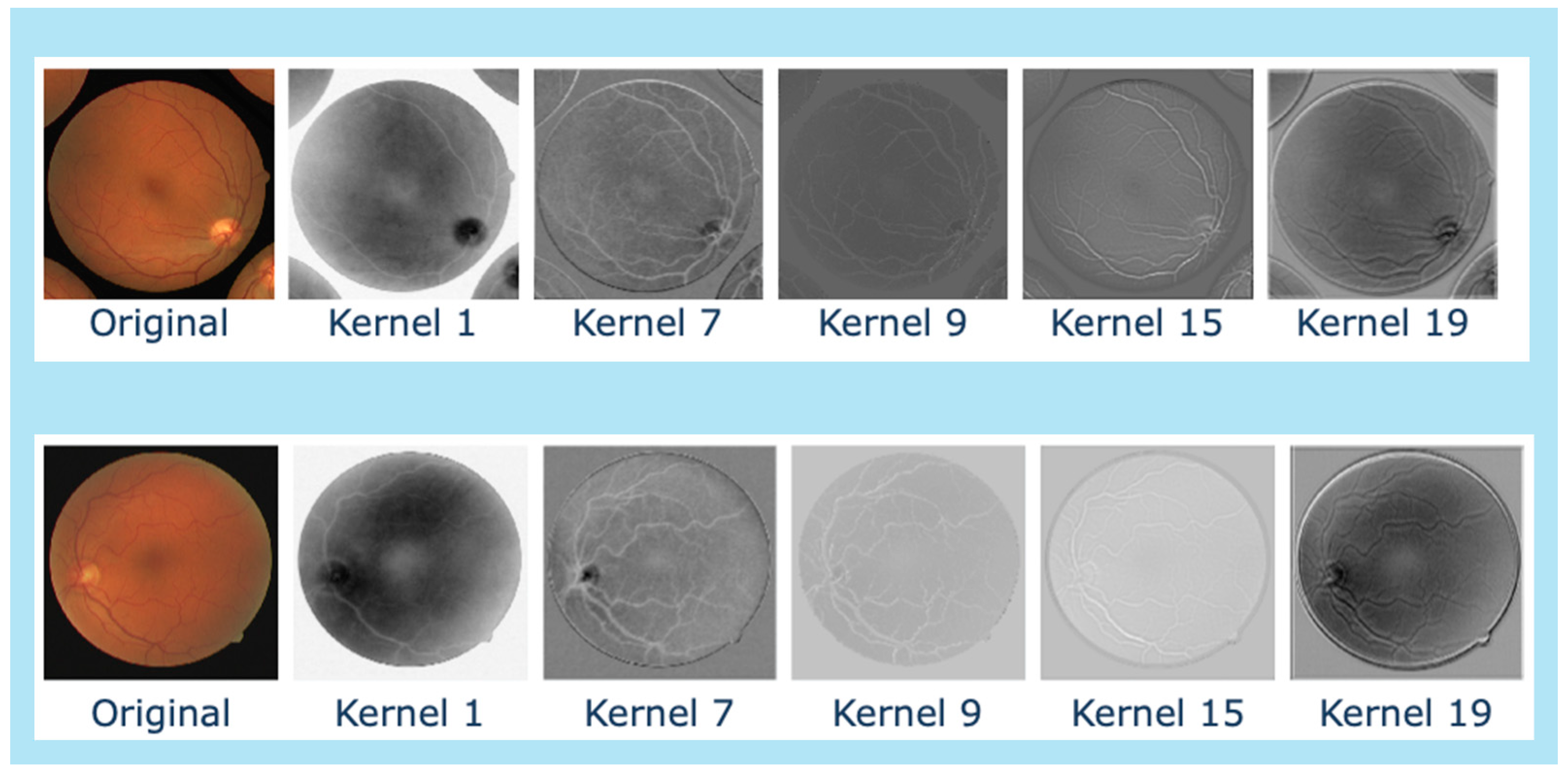
4.2. Explainability

Unlike deep learning models, shallow networks have explainability capabilities [26]. Explainability helps to understand the reason behind the decisions that a model makes which is very important in the clinical reliability of an AI model [16]. The proposed Shallow-CNN is explained by finding the most important modules in Figure 1. Each module is an optimized transformation (kernel) on the training dataset. We used model-based analysis to calculate the impact of each module on the performance of our model [27]. As shown in Figure 1, our model contains 24 modules. In each permutation, we remove that module from the model and try to compute the performance, such as the Dice score. If the module plays an important role, then the score should be drop down significantly. We used the following scoring method to compute the impact of each module:

I {m p a c t}_{i} = \frac{{D I C E}_{m a x} - {D I C E}_{i}}{{D I C E}_{m a x}} = 1 - \frac{{D I C E}_{i}}{{D I C E}_{m a x}}

(5)

Where

{D I C E}_{m a x}

is the maximum score that the model can achieve by including all modules, DICE is the score by removing the module i from the model, and

{I m p a c t}_{i}

is the impact score of module i.

{I m p a c t}_{i}

is a score between 0 and 1, where 0 means no impact and 1 means the highest impact. The impact scores for Shallow-CNN are computed and depicted in Figure 2. As shown in Figure 2, some modules such as 1, 9, and 15 have the highest impact, while others such as 2, 5, and 12 have the lowest impact. This suggests that by retaining the most influential modules and eliminating the least impactful ones, we can attain performance comparable to that of the main Shallow-CNN.

We identify modules with an impact score exceeding 80% of the interquartile range of the total 24 impact scores, selecting modules 1, 7, 9, 15, and 19. The transformations of the selected modules are shown in Figure 3. As Figure 3 shows, while the transformation of kernel 1 is linear, the other kernels have a non-linear response to the input color variation. The comparison of the background and foreground between the original and transformed images supports this observation.

Visualizing transformed images greatly enhances the reliability of black-box AI models in clinical settings. This allows clinicians to understand the basis for decisions, enabling them to assess whether the transformations and resulting inferences are valid.

5. Conclusions

Deploying an AI model in clinical applications requires careful consideration, particularly regarding its explainability. Although deep neural networks have demonstrated exceptional performance in comparison to human diagnosis, they remain black-box models that require transparency. In the traditional machine learning era, human-interpretable features were often developed, making the reasoning behind a model's decisions clear and eliminating the black box nature. However, the performance of these hand-crafted features was inadequate because they did not fully leverage data-driven approaches.

In this study, we explored the evolution of hand-crafted features for image segmentation and demonstrated that a well-designed explainable shallow convolutional neural network (ExShall-CNN) can achieve performance comparable to deep CNN models while offering significantly better explainability. ExShall-CNN is developed as a data-oriented extension of traditional kernel methods, capable of handling complex kernels and incorporating most well-known kernels. In the future, we aim to enhance ExShall-CNN for multi-resolution image analysis to address dimensionality challenges associated with larger kernels. Additionally, we are interested in evaluating its performance on classification tasks. ExShall-CNN and its source code are publicly available at: https://github.com/MLBC-lab/ExShall-CNN

Author Contributions

Conceptualization, Vahid Khalkhali, Sayed Mehedi Azim, and Iman Dehzangi; Methodology, Vahid Khalkhali, and Iman Dehzangi; Software, validation, writing original draft, Vahid Khalkhali; Writing, reviewing, and editing, Sayed Mehedi Azim, and Iman Dehzang. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The source code and data are publicly available at https://github.com/MLBC-lab/ExShall-CNN, and data is publicly available in https://www.kaggle.com/datasets/abdallahwagih/retina-blood-vessel, respectively.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: 2012.
LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural networks 1989, 2, 359–366. [Google Scholar] [CrossRef]
Mhaskar, H.; Liao, Q.; Poggio, T. When and why are deep networks better than shallow ones? In Proceedings of the Proceedings of the AAAI conference on artificial intelligence, 2017.
Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation, parallel distributed processing, explorations in the microstructure of cognition, ed. de rumelhart and j. mcclelland. vol. 1. 1986. Biometrika 1986, 71, 6. [Google Scholar]
Vaswani, A. Attention is all you need. Advances in Neural Information Processing Systems 2017. [Google Scholar]
Murphy, Z.R.; Venkatesh, K.; Sulam, J.; Yi, P.H. Visual transformers and convolutional neural networks for disease classification on radiographs: a comparison of performance, sample efficiency, and hidden stratification. Radiology: Artificial Intelligence 2022, 4, e220012. [Google Scholar] [CrossRef] [PubMed]
Shamshirband, S.; Fathi, M.; Dehzangi, A.; Chronopoulos, A.T.; Alinejad-Rokny, H. A review on deep learning approaches in healthcare systems: Taxonomies, challenges, and open issues. J Biomed Inform 2021, 113, 103627. [Google Scholar] [CrossRef] [PubMed]
Guan, H.; Yap, P.T.; Bozoki, A.; Liu, M. Federated learning for medical image analysis: A survey. Pattern Recognit 2024, 151. [Google Scholar] [CrossRef] [PubMed]
Khan, M.S.I.; Rahman, A.; Debnath, T.; Karim, M.R.; Nasir, M.K.; Band, S.S.; Mosavi, A.; Dehzangi, I. Accurate brain tumor detection using deep convolutional neural network. Comput Struct Biotechnol J 2022, 20, 4733–4745. [Google Scholar] [CrossRef] [PubMed]
Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2015; pp. 3431-3440.
Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18, 2015; pp. 234-241.
Ibrahim, R.; Shafiq, M.O. Explainable Convolutional Neural Networks: A Taxonomy, Review, and Future Directions. ACM Computing Surveys 2023, 55, 1–37. [Google Scholar] [CrossRef]
Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Information fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
S Band, S.; Yarahmadi, A.; Hsu, C.-C.; Biyari, M.; Sookhak, M.; Ameri, R.; Dehzangi, I.; Chronopoulos, A.T.; Liang, H.-W. Application of explainable artificial intelligence in medical health: A systematic review of interpretability methods. Informatics in Medicine Unlocked 2023, 40. [Google Scholar] [CrossRef]
Van der Velden, B.H.; Kuijf, H.J.; Gilhuijs, K.G.; Viergever, M.A. Explainable artificial intelligence (XAI) in deep learning-based medical image analysis. Medical Image Analysis 2022, 79, 102470. [Google Scholar] [CrossRef] [PubMed]
Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
Sauvola, J.; Pietikäinen, M. Adaptive document image binarization. Pattern recognition 2000, 33, 225–236. [Google Scholar] [CrossRef]
Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: 2001.
Zhang, J.; Marszałek, M.; Lazebnik, S.; Schmid, C. Local Features and Kernels for Classification of Texture and Object Categories: A Comprehensive Study. International Journal of Computer Vision 2006, 73, 213–238. [Google Scholar] [CrossRef]
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2016; pp. 770-778.
Araujo, A.; eacute; Norris, W. ; Sim, J. Computing Receptive Fields of Convolutional Neural Networks. Distill 2019, 4. [Google Scholar] [CrossRef]
Luo, W.; Li, Y.; Urtasun, R.; Zemel, R. Understanding the effective receptive field in deep convolutional neural networks. In Proceedings of the Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 2016; pp. 4905–4913.
Retina Blood Vessel. Available online: https://www.kaggle.com/datasets/abdallahwagih/retina-blood-vessel (accessed on July 1).
Cervantes, J.; Cervantes, J.; García-Lamont, F.; Yee-Rendon, A.; Cabrera, J.E.; Jalili, L.D. A comprehensive survey on segmentation techniques for retinal vessel segmentation. Neurocomputing 2023, 556. [Google Scholar] [CrossRef]
Marques dos Santos, J.D.; Marques dos Santos, J.P. Towards XAI: Interpretable Shallow Neural Network Used to Model HCP’s fMRI Motor Paradigm Data. Cham, 2022; pp. 260-274.
Fisher, A.; Rudin, C.; Dominici, F. All models are wrong, but many are useful: Learning a variable's importance by studying an entire class of prediction models simultaneously. Journal of Machine Learning Research 2019, 20, 1–81. [Google Scholar]

Figure 1. Shallow-CNN with 24 parallel complex modules and output real aggregation.

Figure 2. Comparison of layers' impact on the performance of the Shallow-CNN.

Figure 3. Transformations of the most important kernels on the original image.

Table 1. Common kernel mappings.

Kernel Name	Equation
Linear	$x_{1}^{T} x_{2}$
Cosine	$\frac{x_{1} x_{2}^{T}}{\| \|x_{1}\| \| \| \|x_{2}\| \|}$
Polynomial	${(γ x_{1}^{T} x_{2} + c_{0})}^{d}$
Sigmoid	$\tanh t a n h (γ x_{1}^{T} x_{2} + c_{0})$
Radial Basis Function (RBF)	$\exp e x p (- γ {\| \|x_{1} - x_{2}\| \|}^{2})$
Laplacian	$\exp e x p (- γ {\| \|x_{1} - x_{2}\| \|}_{1})$
Chi-Squared	$\exp e x p (- γ \sum_{i} \frac{{(x_{1} [i] - x_{2} [i])}^{2}}{x_{1} [i] + x_{2} [i]})$

Table 2. Feasibility of required operations with proposed activation functions.

Weighted Operation	Induction	Implementation
Summation/Subtraction	$k_{1} x_{1} + k_{2} x_{2}$	$k_{1} x_{1} + k_{2} x_{2}$
Multiplication	$k_{1} x_{1} * k_{2} x_{2}$	$\exp \exp (\log \log (k_{1} x_{1}) + \log l o g (k_{2} x_{2}))$
Division	$k_{1} x_{1} / k_{2} x_{2}$	$\exp \exp (\log \log (k_{1} x_{1}) - \log l o g (k_{2} x_{2}))$
Power	${(k_{1} x_{1})}^{k_{2} x_{2}}$	$\exp (\log \log (k_{1} x_{1}) + \log l o g (\log l o g (k_{2} x_{2})))$

Table 3. Performance of the three models that are compared in this study.

Model	Scores on the training dataset			Scores on the testing dataset
Model	Jaccard (%)	DICE (%)	F1	Jaccard (%)	DICE (%)	F1
Fully CNN	63.3	77.6	0.78	56.8	72.4	0.72
U-Net	63.5	77.7	0.78	65.9	79.0	0.79
Shallow CNN	56.2	72.0	0.72	58.3	73.6	0.73

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.