Prerpints.org logo
Preprint
Article

Cavity Instabilities in a High-Speed Low-Pressure Turbine Stage

Altmetrics

Downloads

59

Views

21

Comments

0

Submitted:

19 October 2024

Posted:

22 October 2024

You are already at the latest version

Alerts
Abstract
This study investigates the time-resolved aerodynamics in the cavity regions of a full-scale, high-speed low-pressure turbine stage representative of geared turbofan engines. The turbine stage is tested in the von Karman Institute’s short-duration rotating facility at different purge rates (PR) injected through the upstream hub cavity. Spectra from the shroud and downstream hub cavity show perturbations linked to blade passing frequency and rotor speed. Asynchronous flow structures associated with ingress/egress mechanisms are observed in the rim seal of the purged cavity. At 0% PR, the ingress region extends to the entire rim seal, and pressure fluctuations are maximized. At 1% PR, the instability is suppressed and the cavity sealed. At 0.5%, the rim-seal instability exhibits multiple peaks in the spectra, each corresponding to a state of the instability. Kelvin-Helmholtz instabilities are identified as trigger mechanisms. A novel technique, based on the properties of the cross-power spectral density, is developed to determine speed and wavelength of the rotating structures, achieving higher precision than the commonly used cross-correlation method. Moreover, unlike the standard methodology, this approach allows to calculate the structure characteristics for all the instability states. Spectral analysis at the turbine outlet shows that rim-seal-induced instabilities propagate into regions occupied by secondary flows. A methodology is proposed to quantify the magnitude of the induced fluctuations, showing that the interaction with secondary flows amplifies the instability at the stage outlet.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

The geared turbofan engine (GTF) is recognized as a key technology for mitigating the environmental impact of modern aviation [1]. The Low-Pressure Turbine (LPT) of geared turbofans operates at higher rotational speeds and expansion ratios compared to LPT modules of conventional direct-drive engines ([2,3]), reaching higher efficiencies while significantly reducing the stage count, weight, and costs.
Despite their key role, the literature suffers from a shortage of experimental studies on high-speed LPT tested under engine-representative conditions, with only a few works addressing this topic. Vazquez and Torre [4] designed and tested a high-speed turbine suitable for a geared LPT. In their work, they evaluated the impact on the stage efficiency of many parameters, such as Mach number [4], surface roughness [5], airfoil thickness [6], and airfoil turning angle [7]. However, none of these studies address the characteristics and intensity of the instabilities developed in the cavity regions of high-speed LPTs.
Many sources of unsteadiness can be recognized within a turbine environment. Typically, a distinction is drawn between unsteady cavity flow and multirow unsteady interactions [8]. Both phenomena are significantly influenced by the conditions of the purge flow, which is responsible for sealing the cavity regions and affects the intensity and characteristics of the secondary flow structures [9,10].
Injection of purge mitigates the metal temperatures and thermal stresses of the engine components in the wheel space. However, it also affects the efficiency of the cycle, stage losses [11], and the onset of rim-seal instabilities [12].
Regina et al. [13] and Jenny et al. [14] detected a decrease in stage efficiency for higher purge flow rates. This was attributed to the strengthening of the secondary flows as a consequence of the additional low-momentum fluid injected into the turbine’s annulus channel. Regina et al. identify an increase in the stochastic component of the pressure field, while Jenny et al. shows that approximately 15 % of the flow in the hub passage vortex originates from the purge. These findings align with earlier studies by Paniagua et al. [15] and Schuepbach et al. [16], emphasizing the impact of purge on secondary flow intensity.
The presence of transient flow structures rotating within the rim-seal or wheel cavity regions has been documented by many authors [12]. These rim-seal instabilities are the manifestation of local ingress/egress mechanisms ([8,17]), and occupy frequency bands distinct from the blade passing or disk frequency. Despite the extensive literature on this topic, the nature of these instabilities is still debated. Typically, three possible triggers mechanisms are considered: Taylor–Couette instability ([18,19]), Kelvin–Helmholtz instability ([20,21]), or inertial waves ([22,23]). Moreover, many authors recognize the impact of rim-seal design [24], operating conditions [25], or both factors combined ([26,27]), on the instabilities that develop. This highlights the need for data collected in engine-representative conditions, particularly for high-speed stages, which suffer the most from the scarcity of data.
Similar unsteady features are found by Perini et al. [28] and Kluge et al. [29], who investigated the unsteady flow developed in the shroud cavity of an LPT. Both works attribute the source of the unsteadiness to shear-layer interactions. Perini et al. demonstrated that the detected lobes’ length scale is compatible with Kelvin-Helmholtz instabilities.
While several studies have focused on the effect of the purge rate on secondary flows and rotating instabilities within cavity areas, the interaction between these two unsteady phenomena remains largely unexplored.
Schädler et al. [8] measured in the stator-rotor interface of a 1.5 axial turbine stage, identifying a penetration of low-frequency pressure fluctuations up to approximately 30% of the span. Under 0.8% purge rate, these effects are recognized on the ensable average phase-locked over the blade position. At high purge conditions (PR = 1. 2%) the fluctuations stabilize and the effect on the ensable average is canceled. Schuepbach et al. [16] measured the time-resolved pressure field developed at the rotor exit of a highly loaded 1.5-stage axial turbine. Under 0.9% purge rate, pressure fluctuations develop at approximately half the rotor blade passing frequency, while at -0.14% the field is dominated by the blade passing fluctuation. The authors associated the fluctuations introduced by purge injection to non-linear interactions with cavity instabilities. However, the absence of time-resolved measurements in the purged cavity prevented them from drawing a definitive conclusion.
The present work aims to describe and quantify the unsteady phenomena manifesting within the cavity regions of a modern high-speed LPT stage. The focus of this analysis is a stage operating under transonic conditions and Reynolds numbers representative of a first LPT stage in a Geared Turbofan (GTF) engine. The article is tested in the von Karman Institute (VKI) short-duration rotating facility [30], highly instrumented with time-resolved pressure transducers to capture the field in the regions of the rim seals and shroud cavity.
The first part of the paper is dedicated to the description of the test article. The following section details the methodologies, providing the mathematical background of the properties exploited during the processing.
In the results section, the nature and intensity of the features that dominate each cavity region are identified through the analysis of the average Power Spectral Density (PSD). The potential constraints related to conducting experiments in short-duration facilities are examined, and a comprehensive framework to perform the analysis of the cavity flow is presented. A new methodology for the analysis of asynchronous modes is introduced and compared against the standard procedure that exploits the properties of cross-correlation ([31]). This new approach, based on the use of the Cross-Power Spectral Density (CPSD), is applied to determine the properties of each state of the rim-seal modes, and to gain deeper insight into their behavior.
In the final section, the spectra collected at the stage outlet are compared to those recorded inside the purge cavity. Moreover, a new methodology is presented to quantify the intensity of the rim-seal-induced fluctuation and to analyze their interactions with the rotor secondary flows.

2. Experimental Setup

The experimental campaign was carried out on the rotating turbine test rig at the von Karman Institute for Fluid Dynamics [30]. The test article examined is a High-Speed LPT stage, which was designed and tested within the framework of the project SPLEEN [32].

2.1. Research Turbine

Figure 1a shows the cross-section of the SPLEEN research turbine. The stage consists of 96 vanes and 96 blades, which are operating in the transonic regime. The vanes are designed to recreate engine-representative wakes and secondary flow structures at the rotor inlet.
The stage includes two hub cavities with engine-realistic angel wing seal designs, which are illustrated in Figure 1b,c. Purge flow is injected into the upstream wheel space through 32 evenly distributed holes, designed with a preinclination to control the rim-seal swirl ratio [32]. No injection occurs in the downstream cavity, which is filled with air from the annulus flow during the early phases of the test, achieving stable flow conditions by the beginning of the useful testing period. The tip of the blade, shown in Figure 1d, features an interlocking light shroud with two inclined forward fins, which delimit the sealing region designed with a single-step labyrinth path. Table 1 summarizes the geometric characteristics of these three regions.

2.2. Operating Conditions

The stage was tested at a rotor speed of 4466 rpm with a total-to-static pressure ratio of 2.052, under various purge conditions. Table 2 presents the stage operating conditions and test-to-test repeatability expressed with a 95% confidence interval.
Table 3 summarizes the flow conditions in the two hub cavities for the tested operating conditions. The downstream cavity, which is not purged, remains consistent at all three operating points, whereas the upstream cavity flow is significantly affected by the purge conditions. For Nominal Purge (NP) and High Purge (HP) conditions, a thorough characterization of the time-averaged and time-resolved stage flow field was conducted, covering the vane periodicity. For Zero Purge condition (ZP), annulus flow measurements were taken only at specific locations, verifying the match of the LPT stage operating point (total-to-static pressure ratio and thermodynamic speed) and ensuring the relevance of the cavity flow analysis. More details on the design, commissioning and operation of the turbine stage can be found in [32].

2.3. Instrumentation

The unsteady field developed within the cavities was monitored through flush-mounted fast-response piezo-resistive absolute pressure transducers (Kulite XCQ-062, 25 psi). The sensors are located at different radial and azimuthal positions. Figure 1b–d show their locations in the meridional plane.
In the upstream cavity, the group of sensors Kh2 is located on the end-wall profile (Hub, Plane 2), while groups KUC01 and KUC12 indicate the transducers at the upper and lower lip of the rim seal. In the downstream cavity the group of sensors Kh3 is located on the end-wall profile (Hub, Plane 3), while the KDC01 and KDC07 groups indicate the transducers in the upper lip and in the buffer cavity of the rim seal. KSC11 and KSC18 indicate the group of sensors located upstream and downstream of the shroud cavity sealing region, which is instrumented with sensors KSC15. The exact locations and number of sensors in each group are detailed in Appendix A in Table A1, Table A2 and Table A3.
The unsteady flow field at the rotor outlet is characterized in Plane 3, located 0.8 C a x , R , M S downstream the trailing edge of the blade rows. Measurements were performed using the four-hole hemispherical fast response probe (FR4H probe) designed by Cernat et al. [33]. The probe was traversed azimuthally to cover a full vane pitch within the quasi-steady testing window, while the radial position of the head was changed from test to test in order to measure the full channel span.
The transfer function of each 4HP pressure tap was experimentally determined by dynamic calibration ([34]). These transfer functions were applied to the signals in the post-processing, increasing the measurement bandwidth. The cutoff frequency, estimated between 30 and 45 kHz for all pressure taps, was determined based on the signal-to-noise ratio of the sensors as described by Paniagua and Dénos [15].
The static calibration of the Kulite sensors was performed in situ, following the method described in [35]. This minimized possible bias due to the temperature effect, as the calibration process was conducted at temperatures and pressures representative of those achieved at nominal test conditions. The uncertainty of the static pressure measurements is estimated at 3 mbar (95% CI) as a result of the calibration and the systematic uncertainty of the transducers. Dynamic compensation is not applied to fixed measurements as the unsteady phenomena in the cavity regions develop within their bandwidths.

2.4. Signal Acquisition

To enhance measurement resolution, the fast-response transducer signals are split into two components: a Low-Frequency (LF) signal and a High-Frequency (HF) signal. Both signals are generated through analog filters with known gain and frequency response, calibrated between 0 Hz and 1 MHz. The LF signal, low-pass filtered at 500 Hz and acquired at 10 kHz with 16-bit resolution, captures lower frequency dynamics. The HF signal, band-pass filtered from 60 Hz to 200 kHz and acquired at 1 MHz with 16-bit resolution, captures high-frequency content. The filter’s transfer function is utilized to demodulate the two signals. The pressure measurement is then reconstructed by merging the average value of the LF signal ( P L F , m e a n ) with the fluctuation of the HF signal ( P H F − P H F , m e a n ).
A period of 200 ms is considered for the analysis of the cavity modes’ characteristics. This ensured the stabilization of steady and unsteady fields in the cavity regions and consistent comparison between a wide range of tests.

3. Methodology

The analysis of the unsteady flow field in the stage cavities is organized into several steps. Initially, the dominant bandwidths of the unsteady field are identified from the average Power-Spectral Density (PSD). The fluctuations associated with the blade passing frequency are quantified through an ensemble averaging procedure. Then, the spatial wavelength and rotating speed of the cavity modes (CMs) are determined through the analysis of the Cross-Power Spectral Density (CPSD) and cross-correlation.

3.1. Spectral Analysis

The PSD distributions are computed via the Welch’s method utilizing the MATLAB function ’pwelch’. Default Hamming windowing is applied with an 80% overlap between windows. A window size of 100k samples, corresponding to a 10 Hz frequency resolution, is chosen to impose a separation of one order of magnitude between the PSD resolution and the distance between consecutive peaks (approximately 70-75 Hz) in the region of the spectra occupied by the CMs.
These settings are applied to each turbine test, and the resulting PSDs are averaged for each sensor. The averaging allows comparisons with studies conducted in continuously running facilities. Such studies often benefit from significantly longer acquisition times, which are subsequently partitioned using Welch’s estimator technique to derive the average distribution (i.e., PSD averaging). Ultimately, the comparison should be based on the total amount of revolutions available. The required number is strongly related to the nature of the instability and the extent of the bandwidth in the frequency domain. Broader bandwidths with multiple peaks will require more samples (i.e., revolutions) to achieve statistical convergence.
The statistical convergence is demonstrated by the asymptotic behavior of the PSD distribution as the number of revolutions increases. Figure 2 shows the impact of tests count and test window duration on the PSD distribution of a rim-seal sensor under NP conditions. Two sets of six tests (blue, ∼90 revolutions) and twelve tests (green, ∼180 revolutions) are randomly selected from all available, considering the nominal 200 ms test duration. These distributions are compared with the averages of all seventeen tests assuming 200 ms (red, ∼250 revolutions) and 150 ms test windows (black, ∼190 revolutions). All distributions, normalized for comparison, consistently capture the main spectral features, with minor deviations in magnitude. Despite the different settings, the deviation between the 180+ revolutions distributions is below 10% in the area highlighted in grey (within the uncertainty range of pressure measurements). This region, dominated by the rim-seal instability, is most sensitive to the number of revolutions. Only the 90-revolutions distribution fails to capture the trend of the PSD peaks intensity. Overall, high agreement and asymptotic behavior are verified for the available number of tests and for 200 ms time windows.
To allow consistent comparisons between tests, the PSD distributions are computed over the normalized pressure fluctuation P ˜ ( t ) and P ¯ ( t ) , defined as ( P ( t ) − P a v g ) / P a v g and ( P ( t ) − P 01 , M S ) / P 01 , M S , respectively. P 01 , M S indicates the inlet total pressure at mid-span.

3.2. Signal Decomposition

The analysis of the unsteady field associated with the blade passing frequency is performed by decomposing the signals into three components. For a generic time-dependent flow field q, these components are defined as:
q ( x , t ) = q a v g ( x ) + 〈 q ( x , t ) 〉 + q ′ ( x , t )
where q a v g is the time-average value, 〈 q 〉 is the deterministic component of the unsteady signal, and q ′ is the stochastic fluctuation. The deterministic component is associated with periodic coherent structures, typically linked to specific bandwidth(s) in the frequency spectrum. Differently, the stochastic component is associated with turbulence and is spread over a wide frequency range [36].
The ensemble average, synchronized with the blade passage, is determined from the pressure data of fixed sensors to measure the intensity of the blade-passing fluctuation. The phase-locked average (PLA) distributions are calculated over the span of 2 rotor revolutions nearest to the nominal rotational speed, encompassing a total of 96x2 blade passing events.

3.3. Cavity Modes Analysis

The analysis of cavity modes typically relies on fast-response pressure measurements, detecting modes as a periodic pressure field rotating at a specific speed v R = 2 π f R . This field consists of periodic fluctuations, where the number of peaks (or lobes) n determines the spatial length scale of the modes β . Figure 3a illustrates a schematic representation of the modes. Typically, their characteristics are determined following a well-established methodology based on the properties of the cross-correlation function, which is extensively described by Beard et al. [31].
The present paper proposes a variation of this method to fit the characteristics of this application. Furthermore, an alternative procedure based on the properties of the CPSD distribution is, to the authors’ knowledge, here introduced for the first time.
The following sections provide a basic description of these two methodologies, analyzing in detail the properties of the CPSD distribution and how to exploit them to gain further insight into the characteristics of the instabilities.

3.3.1. Cross-Correlation Methodology

The standard cross-correlation technique involves the computation of the time delay Δ t α associated with the CM structures traveling between two sensors. The delay is determined through cross-correlation of the pressure signals, which are pass-band filtered to isolate the CMs. By knowing the relative distance between the two sensors α , the frequency of the CMs fluctuation observed by the pressure transducers f P S D , and by assuming that the sensors’ distance is smaller than the wavelength of the rotating structures ( β < α ), velocity and number of lobes are computed from f R = α / ( 2 π Δ t α ) and n = f P S D / f R respectively. To avoid inferring a priori the minimum distance between two consecutive lobes, Beard et al. [31] propose to iterate the time delay computation for various sensor combinations and across multiple time windows (typically of the duration of one rotor revolution). Collecting all the data into Δ t α vs α plots makes it possible to identify n and f R from the linear regression that better fits the measured time lags.
Figure 3b provides an example of an ideal time lag plot where the time delay is normalized through the frequency f P S D . The optimal regression, represented by the red line, is defined by the linear fit that connects the most number of "time delay points".
The effectiveness of this method relies on the availability of multiple sensor measurements, the length of the acquired signals, and is influenced by the nature of the fluctuation itself. Specifically, the signals should be of sufficient duration to ensure an adequate number of revolutions to populate the time-lag plot. As for the PSD distribution, the minimum number of revolutions depends on the specific application and can be determined using a similar procedure. Beard et al. [31] considered a total of 150 revolutions in their analysis.
The requirement on the signal length precludes the use of this method for single short-duration tests, usually characterized by ∼15 revolutions. A possible solution to this problem would be to populate the time lag plot by adding to the measured Δ t α the quantity k i / f P S D , where k i is an integer and 1 / f P S D is the period between two subsequent peaks. This would be equivalent to assuming the presence of k i more lobes between the two sensors, and would provide additional “points” in the Δ t α - α plot, recreating a situation similar to having longer signal acquisitions. This implicitly assumes the predominance of a single harmonic f P S D in the CMs’ band and, consequently, a cross-correlation with a sinusoidal shape at the same frequency f P S D .
This is not the case for the turbine stage analyzed, as the modes develop on a wide range of frequencies and are characterized by the presence of multiple peaks (i.e., f P S D ). Notably, for the same reason, the cross-correlation does not appear regular enough to include additional points in the time lag plot. Therefore, following the same principle of the PSD distribution, the only possible solution is to populate the plots Δ t α - α considering all the available tests.

3.3.2. Frequency-Domain Methodology

An alternative approach to determine the delay between two signals is to move the analysis from the time domain (cross-correlation) to the frequency domain. Specifically, this can be achieved by exploiting the properties of the phase of the CPSD distribution, which is defined as the Fourier transform of the cross-correlation between two signals.
Assuming two generic signals x 1 and x 2 ( t ) = x 1 ( t − Δ t ) , it can be demonstrated that their cross-correlation R 12 ( τ ) is equal to R 11 ( τ − Δ t ) , where R 11 is the auto-correlation of x 1 . This relationship links the first peak of the cross-correlation R 12 ( τ ) to the time delay Δ t , which is the fundamental concept exploited by the cross-correlation method. By computing the Fourier transform of R 12 ( τ ) , it is found that:
G 12 ( f ) = G 11 ( f ) · e − j 2 π f Δ t
where G 11 is equal to the the power spectral density S 11 of x 1 , (i.e. the Fourier transform of R 11 for the Wiener–Khinchin theorem [37]), and G 12 is the cross-power spectral density of the signals x 1 and x 2 . For real functions, the auto-correlation is symmetric and real. Consequently, the same is true for its Fourier transform (i.e., ϕ 11 = 0 ). Equation (2) can be used to demonstrate that the module of G 11 is equivalent to G 12 (as | e − 2 π Δ t | = 1) and that the angular phase of the CPSD distribution must be equal to:
ϕ 12 ( f ) = − 2 π f Δ t
This relation links the time delay Δ t to the phase p = ϕ / 2 π of the CPSD distribution and will be later referred to as the phase law.
Figure 4 and Figure 5 show an application of these properties over two synthetic signals x 1 and x 2 defined as:
x 1 ( t ) = x ( t ) + p ( t ) + w ( t ) , x 2 ( t ) = x ( t − τ ) + w ( t )
The clean periodic signal x ( t ) and spurious fluctuation p ( t ) are defined as:
x ( t ) = s i n ( 2 π f 1 t ) · s i n ( 2 π f 2 t ) · s i n ( 2 π f 3 t ) , p ( t ) = s i n ( 2 π f 4 t )
while w ( t ) is white noise set at 50% of the x ( t ) amplitude. Figure 4a shows a plot of the two signals in the time domain, while Figure 4b displays their cross-correlation. The cross-correlation is computed employing the MATLAB function "xcorr". The figure highlights the position of the first peak in correspondence with the time delay imposed over the "common" component of the signal x ( t ) , proving the effectiveness of the technique even in case of spurious contributions such as p ( t ) , fluctuating at comparable, but distinct, frequencies. Furthermore, since x ( t ) is defined to occupy multiple locations in the frequency spectrum, the cross-correlation plot is not regular after the first peak, showing different spacings between the following peaks, all of lower magnitude.
The four peaks associated with the periodic fluctuation x ( t ) are easily recognizable in both the PSD and CPSD distributions in Figure 5a,b. As expected, the peaks are equal in magnitude (| G 11 | = | G 12 |) and are found in linear combinations of the three frequencies f 1 , f 2 , and f 3 . In contrast, the spurious fluctuation p ( t ) is attenuated by two orders of magnitude in the CPSD distribution, demonstrating the effectiveness of this tool in isolating correlated fluctuations. Moreover, the CPSD modulus exhibits low sensitivity to white noise, whose magnitude is decreased by almost one order compared to the PSD distributions. A similar observation is made by comparing the CPSD modulus with the cross-coherence in Figure 5c, as the latter exhibits a higher sensitivity to noise. This behavior is explained by recalling the definition of the cross-coherence:
C 12 ( f ) = | G 12 ( f ) | 2 S 11 ( f ) · S 22 ( f )
In the region of the spectra that is not occupied by the peaks, both the numerator and the denominator approach zero, magnifying the influence of noise and numerical error.
The phase in Figure 5d shows that Equation (3) is verified in correspondence with the four modulus peaks, which are the zones of the spectra where the signal is well defined. Outside these locations, similarly to the coherence distribution, the module of the CPSD becomes too small, and the effects of numerical error, noise, and frequency resolution become predominant.
From this example, three important conclusions can be drawn:
  • Low-frequency resolution of the CPSD distribution could lead to errors in the determination of the phase, as the effect of the noisy pattern developed outside of the peak’s location could become relevant. For this reason, frequency discretization and intensity of the fluctuations play a relevant role in the phase lag determination process.
  • The CPSD technique does not require any filtering of the signal, as the information is already “stored” in the distribution, and can be extracted for all frequency peaks.
  • If the time delay associated with the CM fluctuations (here depicted by x ( t ) ) is constant, the CPSD phases measured in correspondence of the spectrum peaks will be aligned in the frequency domain, verifying the phase law independently from the complexity of the fluctuation (i.e., the number of f P S D ).
Based on the last observation, if multiple independent coherent structures exist, each with distinct rotational velocities and frequency domain peaks, a unique phase law will emerge for each structure at their respective peaks. Proof of this can be found in the Fourier transform of each structure, which is inherently null outside their harmonic frequencies. Consequently, the superposition of independent signals (i.e., with different harmonics) will not influence the FFT at those locations. In terms of Fourier series decomposition, the signal is decomposed into multiple groups of sinusoids, each associated with a specific coherent structure. Thus, when computing the CPSD, each group will provide a significant contribution only in correspondence with their harmonics, as their cross-correlation with the other sinusoids will be negligible (independent signals).
The characteristics of CMs are determined, similar to the cross-correlation methodology, from the measure of phase lags p i j , defined as Δ t · f P S D , extracted from the CPSD phase as ϕ i j / 2 π . Following the computation of p i j between all available sensors, phase lag plots such as in Figure 6 are generated. Since the value of ϕ i j is confined between -0.5 and 0.5, these plots are “populated” by adding finite integers to the measured Δ p . This is equivalent to adding a finite number of periods to the measured time delays. However, since this step is performed in the phase domain, it is not necessary to select a specific period of fluctuation ( T P S D ) as the phase is already normalized. Once the phase lag plot is completed, the optimum linear regression is searched, and the number and velocity of the rotating structure’s lobes are retrieved.

3.3.3. CPSD Methodology Validation

This methodology was tested and validated on the periodicity induced by the blade passage ( f P S D = B P F ), whose number of lobes is known a priori ( n = N S ), and rotation velocity is measured independently ( f R = Ω / 60 ). The procedure is applied to the pressure measurements on the upper lip of the downstream cavity. These sensors are spaced over a wide sector (135 deg) and detect BPF fluctuations with magnitudes comparable to the CMs instabilities in the upstream cavity, making it an ideal test case.
To minimize the spectral leakage, a Hanning window is applied to the signal to be cross-correlated. Zero-padding is employed to set the frequency resolution to approximately 5 Hz. The CPSD distributions are computed using the Welch’s method via the MATLAB function "cpsd". Figure 6a shows the populated phase lag plot. The optimum linear regression is searched by computing 1 − R 2 for all possible phase lags combinations by identifying which minimizes its value (i.e., the maximum R-square). Each regression differs only in slope, which is related to a specific number of lobes, k, by m = 360 / k , and to f R by f R = B P F / k . Therefore, it is possible to directly relate the number of lobes to the equivalent 1 − R 2 as in Figure 6b and then search for k | m i n = n . In this application, the minimum of 1 − R 2 is detected at k = 96 . 1 , separated by one order of magnitude from the other regressions, and only by an error of 0.1% from the nominal value N S , thus validating the methodology.

4. Results and Discussion

This section investigates the unsteady fields generated within the cavity regions of the turbine stage. Initially, the study focuses on the characteristics and underlying mechanisms of the rotating instabilities present in the upstream purge cavity. Subsequently, the research examines the unsteady phenomena that develop in the downstream cavity and shroud region. Ultimately, the propagation of the cavity instability within the annulus is analyzed at the stage outlet.

4.1. Upstream Cavity

The analysis of the average PSD profiles in the upstream cavity indicates a high degree of uniformity among different sensors at the same radius. Figure 7 illustrates the average distributions derived from the six sensors placed on the upper lip. All major unsteady features are identified by each sensor. The shape and location of these features are consistent across all profiles, with only minor discrepancies in amplitude. The area highlighted in grey is the most affected, with deviations ranging from 10 to 15%. This variation corresponds to pressure fluctuations that are below the uncertainty of the pressure measures, and aligns with the results of the PSD convergence analysis. The exceptions are the sensors KUC01_3 and KUC01_4, which are mounted on the same insert and show an increase in modulus exceeding 20%. This increase is consistent and more pronounced at higher frequencies, suggesting a higher sensitivity to noise.
The same level of agreement is verified at all meridional locations and under all operating conditions. This observation supports the use of single sensors from each group to explore the impact of purge conditions on the unsteady cavity flow field.
Figure 8 shows the averaged PSD distributions measured at the three radial locations. Different colors are used to distinguish the spectra at ZP (black), NP (red), and HP (blue) conditions. Each distribution is normalized, taking as a reference the peak detected at 15 engine orders (EO) in the spectrum of the upper lip sensor for NP conditions.
The analysis of the spectra reveals a bandwidth between 11 and 20 EO strongly affected by both radial location and purge conditions. The strongest pressure fluctuations are detected in the region of the upper lip, suggesting a possible link with the ingress-egress mechanisms developed at the exit of the rim-seal region. Considering the measurements at NP, moving from the upper lip to the lower lip, these fluctuations disappear. In contrast, the hub sensors show an attenuation of the average PSD by a factor of 2.75.
The portion of the spectra associated with the instability is characterized by ten uniformly spaced peaks separated by approximately 1 EO. Each peak, as detailed in the following section, represents a possible state of the rim-seal instability. The locations of the peaks are consistent in the two radial locations where they are observed. This indicates that the sensors detect the same instability (e.g., unsteady ingress-egress mechanism), which is perceived with different strength from the upper lip.
The absence of such peaks at the lower lip implies that the unsteady field within the disk cavity does not exert an influence on the upper lip modes. Notably, the geometry of the lower lip resembles a radial seal with a gap ratio of g / b = 0 . 010 , which Gao et al. [22] describe as less likely to develop unsteady modes. They observe that a small radial gap ( g / b = 0 . 004 in their setup) may prevent the propagation of inertial waves and subsequently the development of these modes. Hence, this could explain the absence of any additional unsteady modes and the decoupling between the dynamics of the disk cavity and the upper lip.
The increase of the purge rate stabilizes the pressure field in the whole cavity region, as the instability within the 10-20 EO band is suppressed. For PR=0.0%, the frequency band occupied by the fluctuations is narrowed and shifted toward higher frequencies. Specifically, the central and stronger peak is moved from 15 to 17.4 EO, and the previously equally spaced ten peaks are now reduced to three in the range from 15 to 20 EO. Similarly to the NP condition, the locations of the peaks are the same for all sensors able to detect the instabilities. This also includes the lower lip region, which is now exposed to the unsteady field. A significant increase in strength is observed throughout the cavity region. Considering the magnitude of the central peak, the instabilities at the hub are amplified by a factor of approximately 5.25 switching from NP to ZP. Meanwhile, the ones at the upper lip are amplified by 7.35. This behavior is consistent with the original hypothesis ascribing the detected fluctuations to unsteady ingress-egress mechanisms. Indeed, for the minimum sealing conditions (no purge rate), the fluctuations exhibit the maximum strength and the maximum penetration in the rim seal.
Peaks at 2 and 4 EO are detected at each meridional location. The magnitude of these peaks is comparable between the measurements at the hub and at the upper lip, while it is sensibly reduced in the region of the lower lip. The opposite is found for the peak at 1 EO, which maintains similar magnitudes in the rim-seal while being halved at the Hub.
The Blade Passing Frequency (BPF) fluctuation ( f / f Ω = 96 ) shows a consistent decrease in magnitude from the Hub sensors to the lower lip in the rim-seal. Moreover, these fluctuations remain one or more orders of magnitude smaller compared to the rim-seal instabilities. As a result, the upstream cavity region is effectively "shielded" from blade passing fluctuations, either by the dominance of the rim-seal modes, or by the purge rate itself when the cavity is sealed.
Table 4 summarizes the information concerning the intensity of the rim-seal instabilities. The Root Mean Square (RMS) of the pass-banded signals is computed for every test (95% CI), providing a precise evaluation of the unsteadiness associated with the entire bandwidth (and not only the central peak). Then, the test-to-test mean is computed and reported in the column "Fluctuation". The data is normalized by the average static pressure measured by the sensor on the upper lip ( P U P ) for the respective operating condition. As expected, the maximum intensity is registered in the upper lip region, where static pressure fluctuations are measured at 1.12% and 0.80% in ZP and NP conditions. The rise in unsteadiness intensity for the ZP condition is less significant compared to the PSD distributions, highlighting the importance of considering the entire bandwidth for an accurate evaluation of the fluctuations.

4.2. Rim-Seal Instability

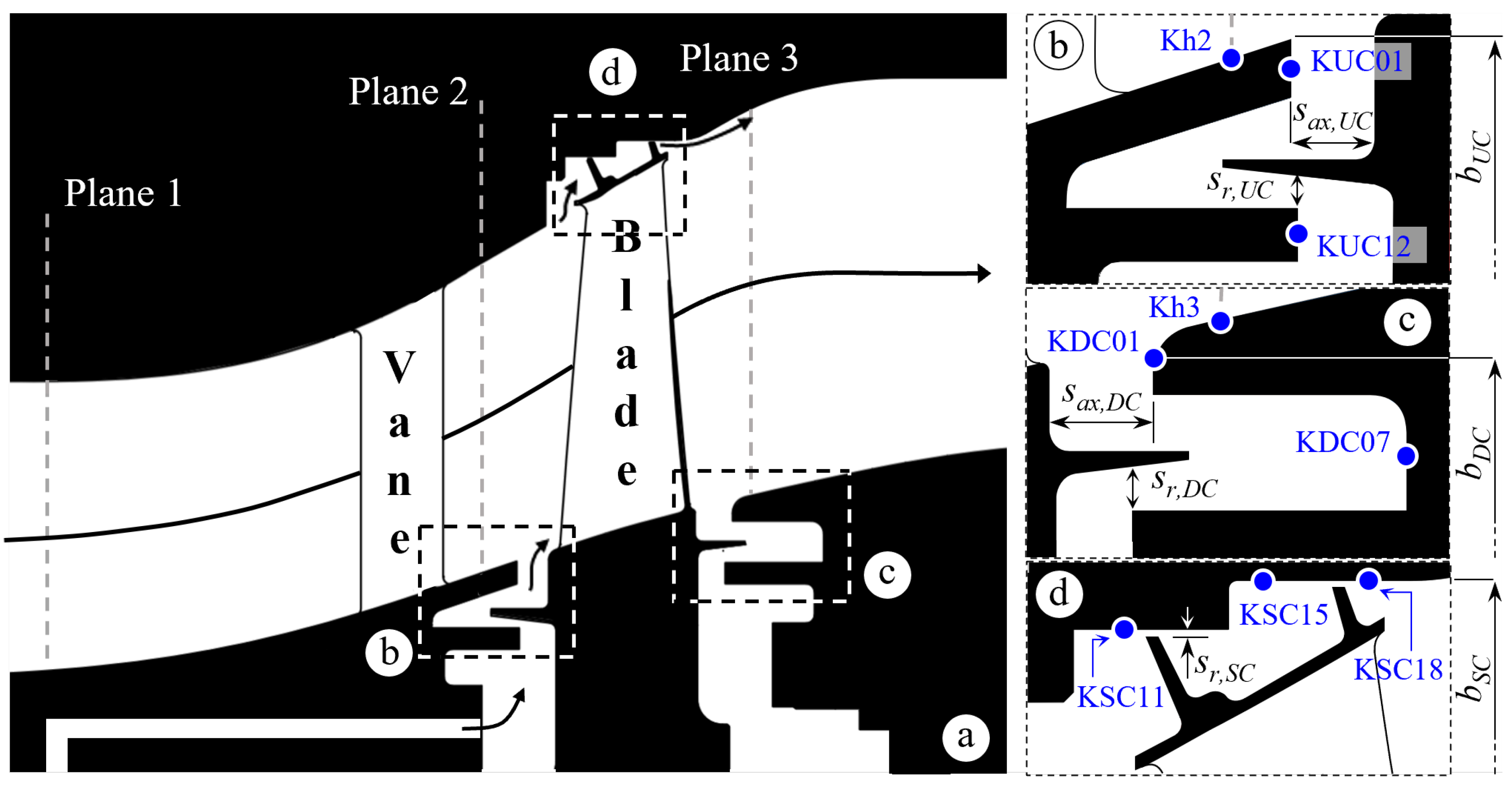
The investigation of rim-seal instabilities is performed at the three measurement locations of the upstream purge cavity. This analysis covers the two purge conditions (NP and ZP) under which these instabilities manifest. The HP case is excluded as it does not exhibit significant rim-seal instabilities. CPSD and cross-correlation methods are applied to the upper lip measurements to determine and compare their accuracy. Concurrently, the behavior of the rim-seal instability is examined, and the insights gained are used to optimize the implementation of both procedures. Finally, the nature of the rim-seal instabilities is discussed in view of existing literature.

4.2.1. Frequency-Domain Analysis

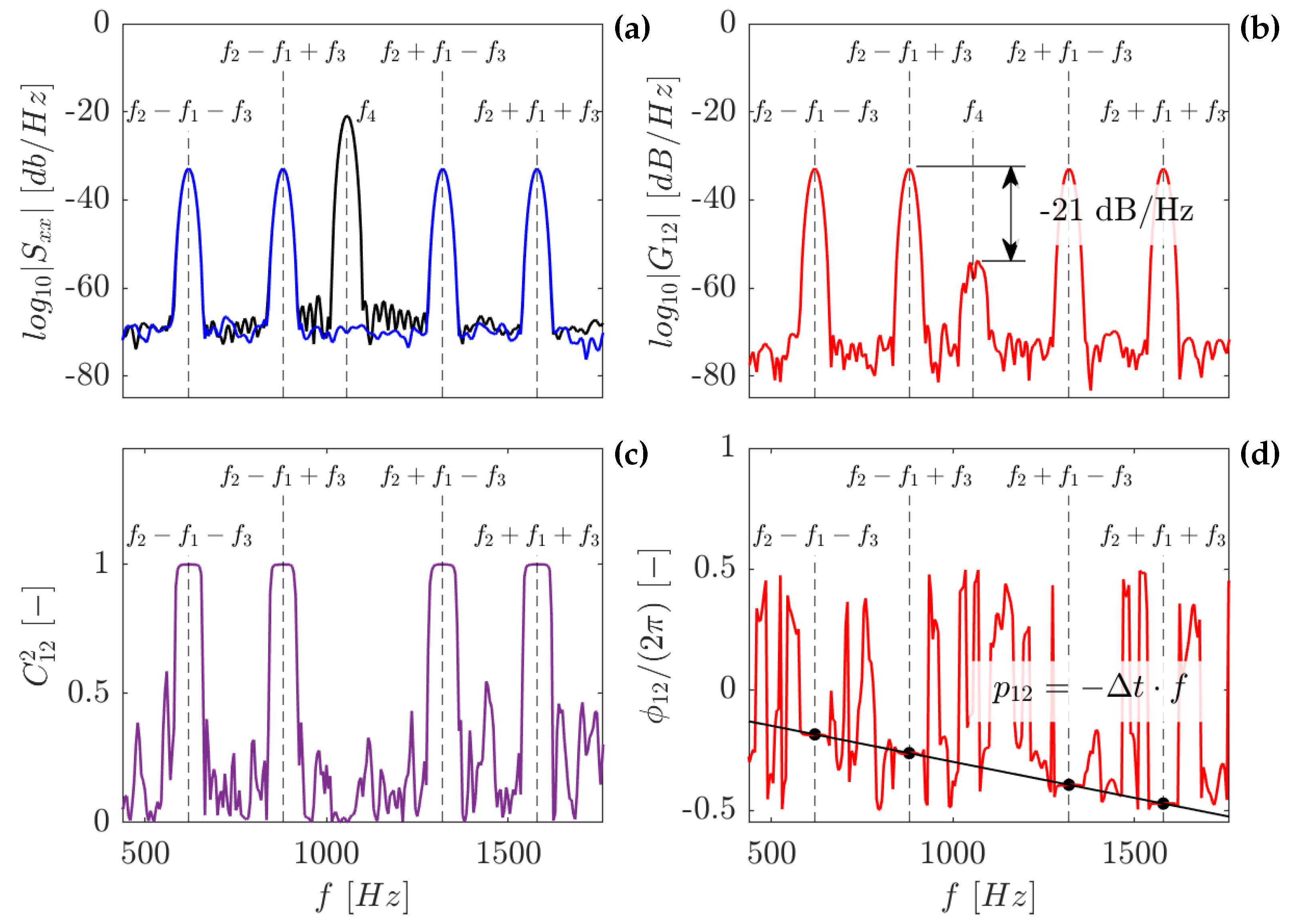
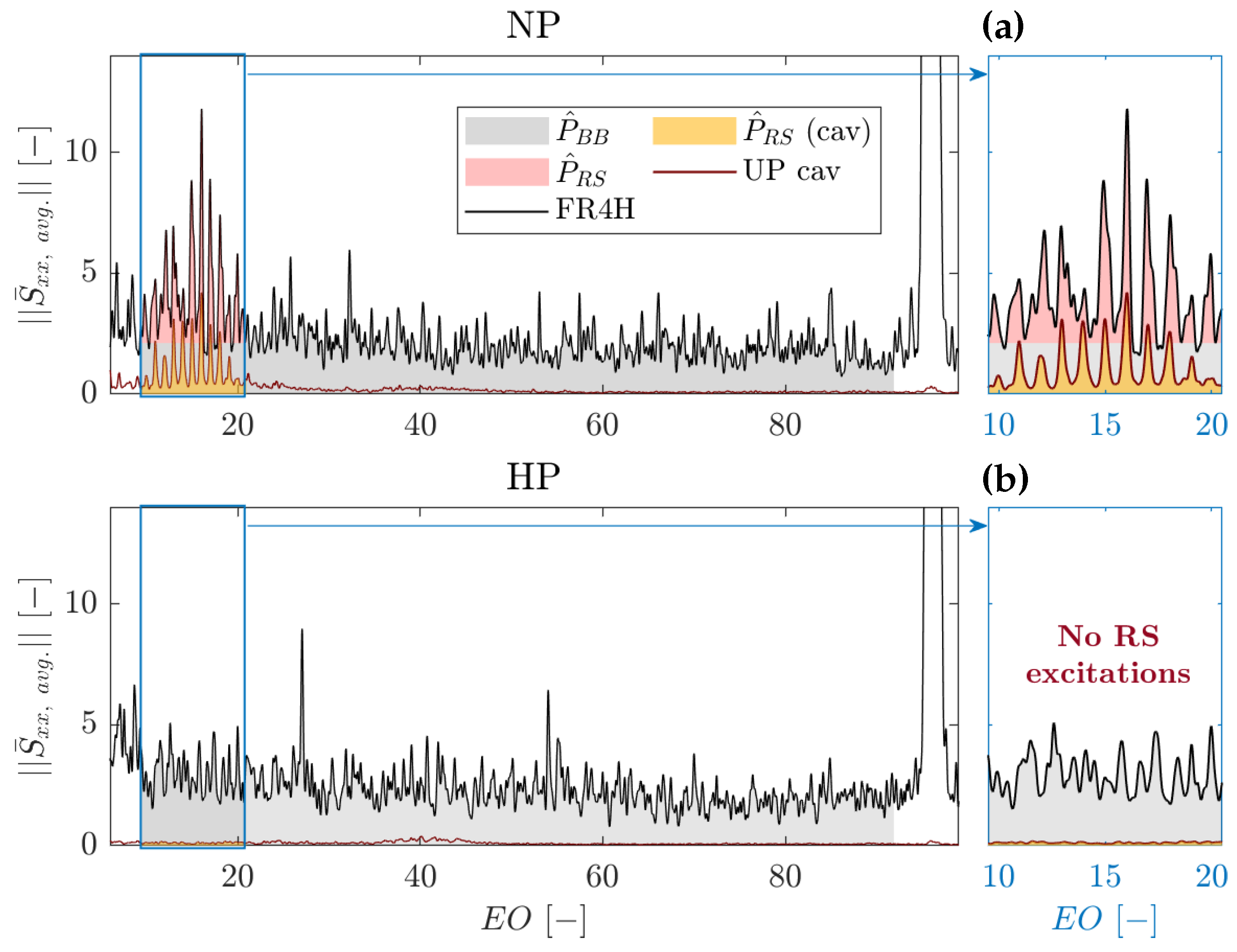
Figure 9 show modulus and phase of the CPSD distribution computed between two sensors on the upper lip for a single turbine test. The CPSD, similarly to the PSD, is highly repeatable between different sensor combinations. This is true for all tests. Therefore, the plots in Figure 9 are representative of a test under nominal purge conditions.
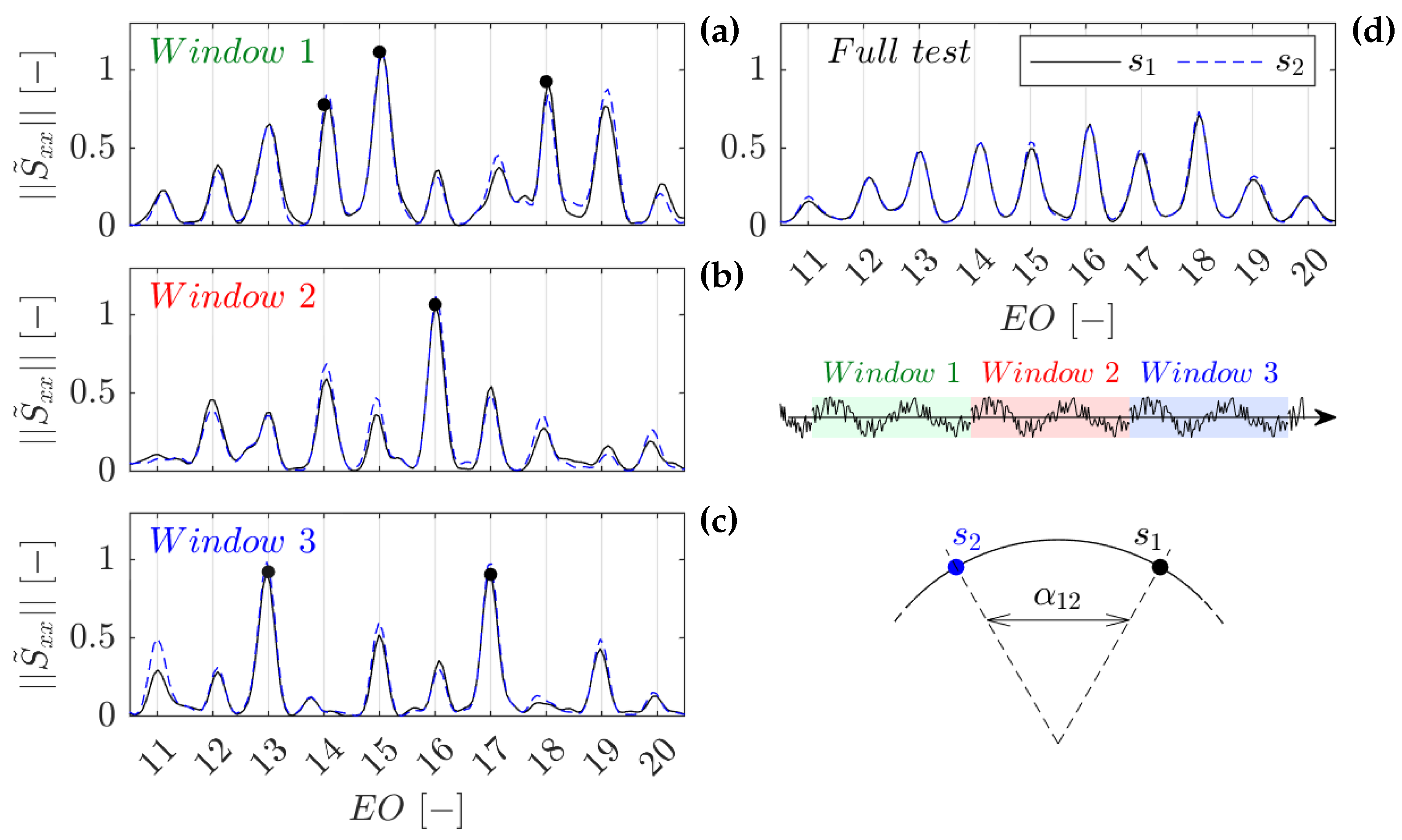
The modulus reveals a reduced number of peaks compared to the average spectra in Figure 8. This observation is confirmed by the PSD distributions of the two sensors, as shown in Figure 10d. When present, the peaks appear at the same locations as in the average PSD distributions in Figure 8, indicating consistency. This explains why the average PSD distribution is influenced by the number of revolutions (i.e., tests) considered.
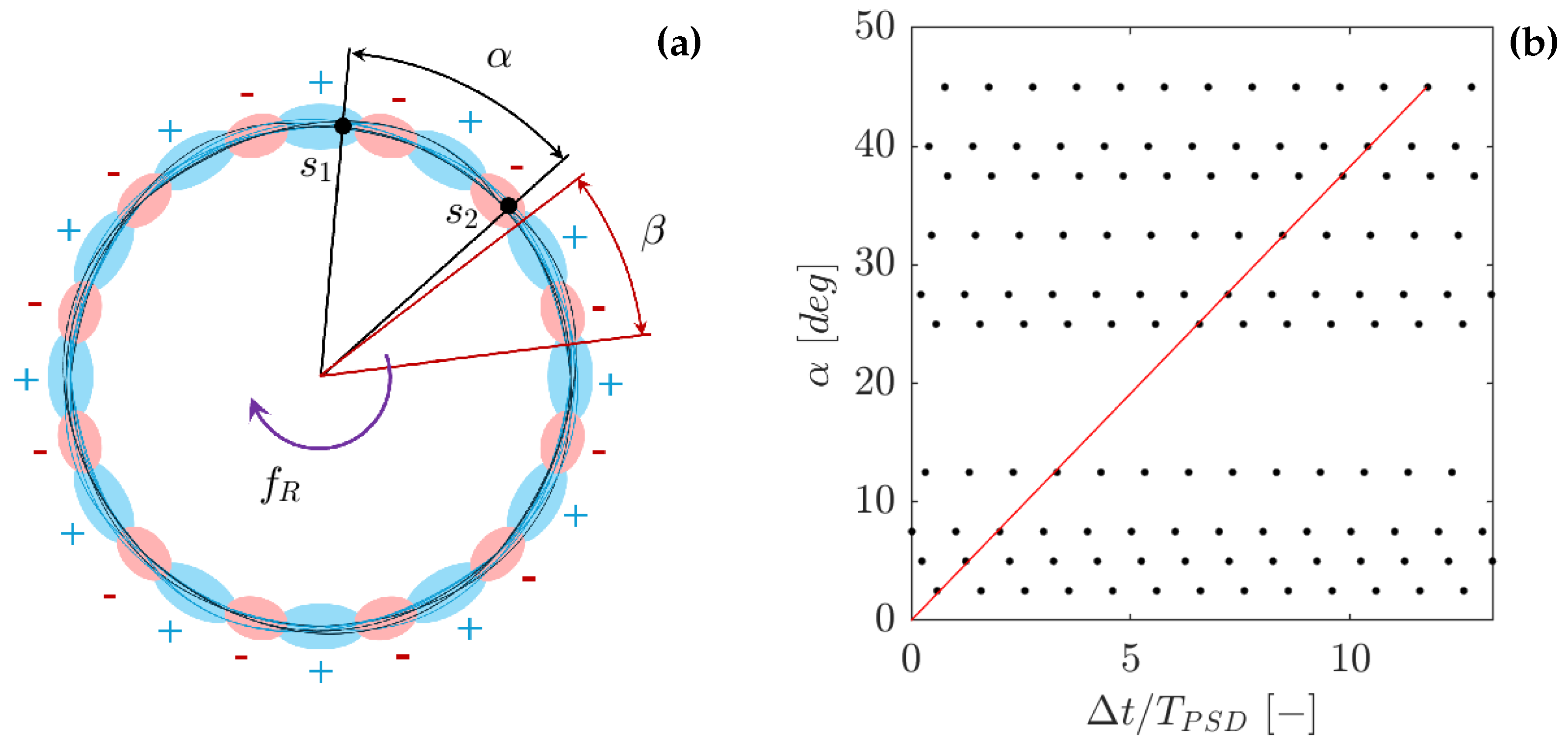
In Figure 9b the phase is aligned at the locations of the strongest peaks (red markers), hinting at a scenario similar to the synthetic example (Figure 5d). This suggests that each state of the unsteady modes is rotating at the same speed, as the pressure fluctuation requires the same time interval ( Δ t 12 ) to travel from position 1 to position 2.
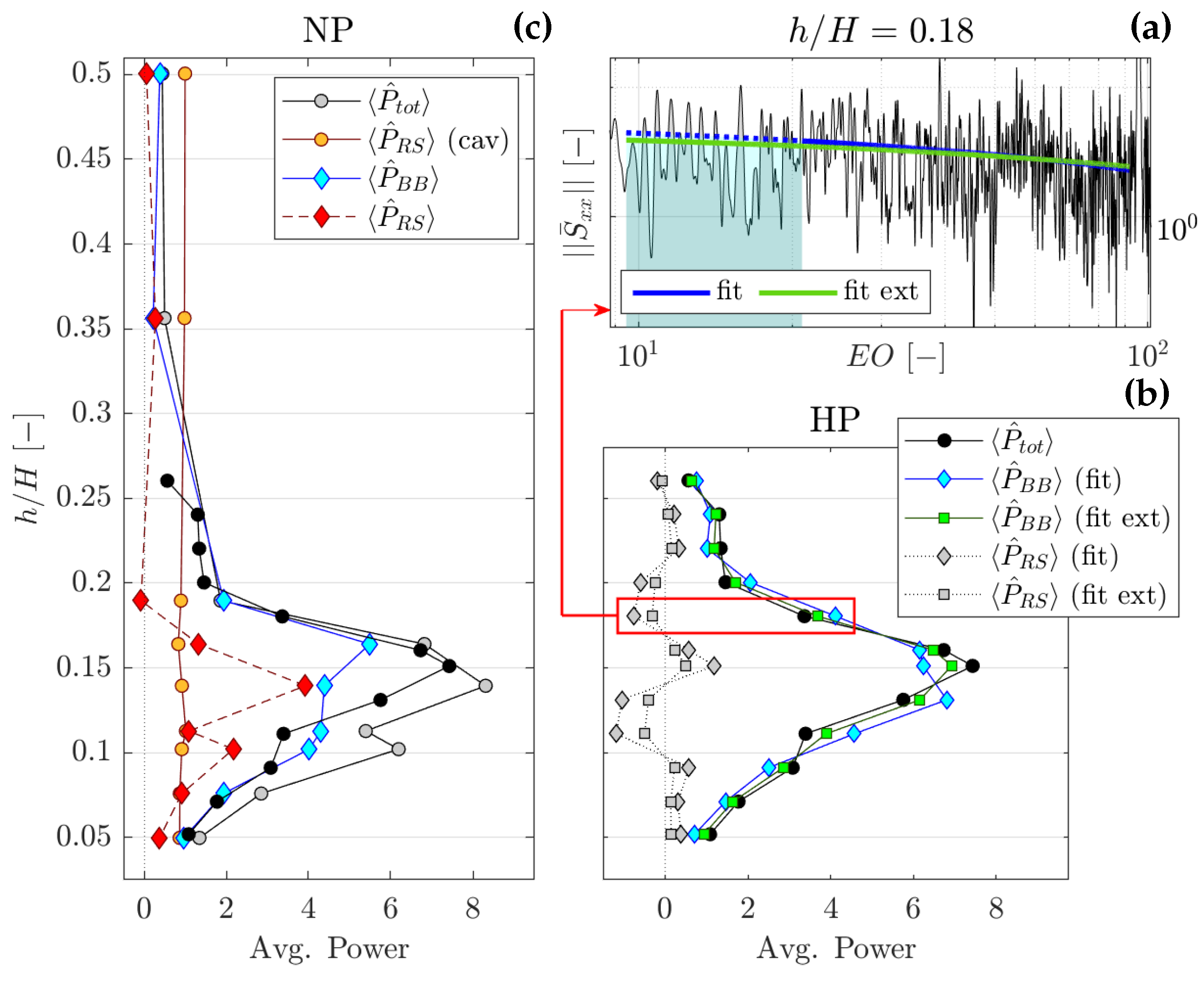
Further insight can be gained by examining the evolution of the PSD distributions in Figure 10a–c, generated by splitting the testing time into three sub-windows. As indicated by the black dots, the number and location of the peaks change, suggesting that the state of the instability is evolving during the test. Despite this, the total power of the structure remains constant for the duration of the test. This quantity can be computed by integrating the PSD over the range of rim-seal instability. An analysis including all available tests (not presented for brevity) shows that most sub-windows remain within ± 15% from the mean for each sensor. This is consistent with the results of the study on the asymptotic behavior of the mean PSD distribution.
This leads to the conclusion that the modes are not solely corotating; instead, they are manifestations of an evolving "structure," transitioning from one state (peak) to another.
Despite the evolution of the flow structure, the effect of sub-window size (i.e., number of revolutions) on the average PSD modulus and CPSD phase is less pronounced. In those cases, the reliability of the average distributions is mainly determined by the number of revolutions included in the averaging process. In fact, although the coherent structure changes over time, it is "stable" when looking at the frequency domain. There, each state (or mode) corresponds to a specific frequency and phase lag, determined by the number of lobes and the angular distance, respectively.
In the PSD, it is the power of the rim-seal instabilities that is maintained across the tests. Hence, the peaks in the average distribution will reflect not only the mode intensity but also its duration. This explain the difference in amplitude between the peaks in Figure 10a–c, and in Figure 10d. Ultimately, the strongest peaks will also be indicative of the most "stable" state of the rim-seal instability.
Differently, the CPSD phase is the result of averaging the signal’s portions where the mode is developed, with others where the mode is not found. In the latter, the phase is highly noisy for the reasons discussed when analyzing Figure 5d, thus affecting the quality of the distribution. The employment of Welch’s estimator allows us to effectively reduce the impact of this source of error. However, a trade-off between frequency resolution and phase accuracy is still required to minimize the dispersion of the data.
This effect is recognizable in Figure 9b, showing points not perfectly aligned with the phase law despite the clear presence of a trend. As a consequence, the reliability of the phase lag plots for each test is not sufficient to compute the modes characteristics with low uncertainty. This precludes the use of the CPSD methodology as presented for the BPF case. Furthermore, not all tests develop all the states of unsteadiness, hence limiting the use of this technique for a comprehensive analysis.
These impediments are overcome by reducing the window considered to detect the single-phase delay, by including all tests available in the computation of the phase law, and by interpolating the phase delay at the frequencies of the peak in the modulus. Reducing the window addresses the "averaging" effect issues, while also increasing the number of phase measurements performed per test. Considering all the tests increases the number of measurements, and reinforces the computation of the phase law by including all the possible states of the instability. Lastly, the definition of an average phase law facilitates the determination of a singular and robust value of the phase lag for each f P S D . This minimizes noise effects, increases the accuracy, and enables the computation of the instability characteristics for each detected state.
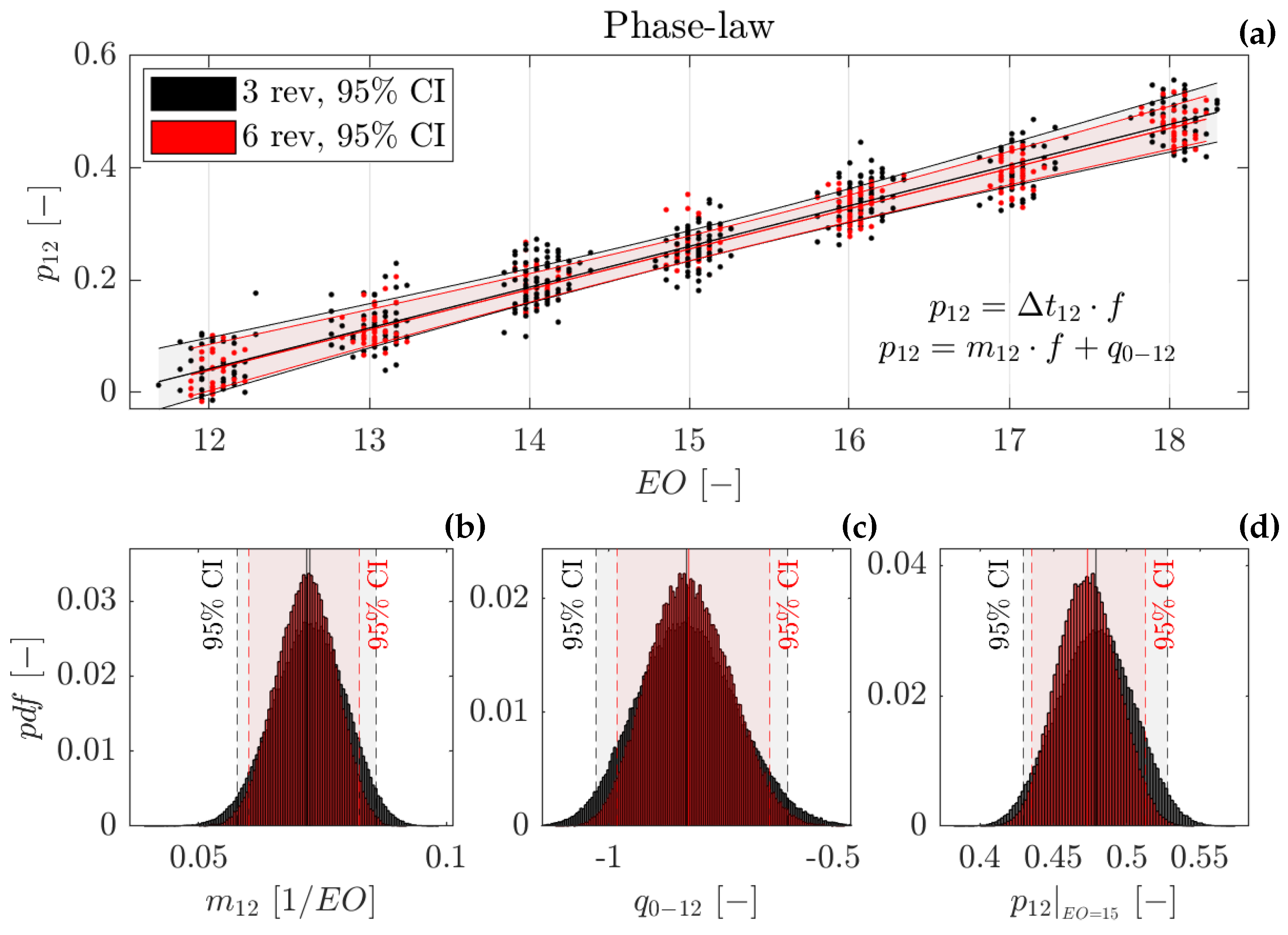
Figure 11a shows an example of the CPSD phase at the location of the modulus peaks, measured between two sensors for all available tests. The figure displays the results when sub-windows long three (black) and six (red) revolutions are considered for the computation of the phase law. The six-revolutions dataset is populated including the first seven most energetic peaks while imposing a minimum cut-off equal to 20% of the maximum peak. The seven peaks are selected considering the characteristics of the average PSD distributions, while the cut-off is applied to maintain only the most energetic peaks and to exclude peaks induced by spectral leakage. Then, the dataset is further filtered to maintain, for each combination of sensors, the most energetic 60 percentile of the peaks. The three-revolutions dataset is generated considering the five most energetic peaks (20% cut-off), also filtered to keep the 60 percentile. These parameters are selected to minimize the uncertainty of the measurements while maintaining a sufficiently representative database.
Figure 11b,c show the probability density function (pdf) of the phase law regression coefficients computed applying a bootstrap technique [38]. The bootstrapping is performed by randomly extracting a single-phase measurement from each of the seven clusters of points. Each cluster is a representation of one state of the instability. All clusters are rotating at the same velocity and are subject to the same phase law, which should be determined to guarantee the alignment at each position. Therefore, a point from each cluster is included to maximize the "information" and reinforce the computation of the best regression. This approach improves the robustness of the regression and minimizes the uncertainty of the phase law for the central (and more stable/energetic) positions of the instability band. This is highlighted in Figure 11a by the 95% CI limits of the phase law. Figure 11d shows the pdf computed using the bootstrap dataset at the most energetic peak (15 EO).
The comparison between the six- and three-revolution datasets shows a higher data dispersion in the latter, translated into a broader probability function distribution of the phase law. This is consistent with the loss of frequency resolution due to the window size reduction. Nevertheless, the effect on the mean value remains negligible, demonstrating the robustness of the methodology. For longer windows, the precision of the measurements does not improve significantly. However, the size of the dataset decreases, affecting the reliability of the bootstrapping technique. Therefore, the six-revolution window was selected for the data analysis.
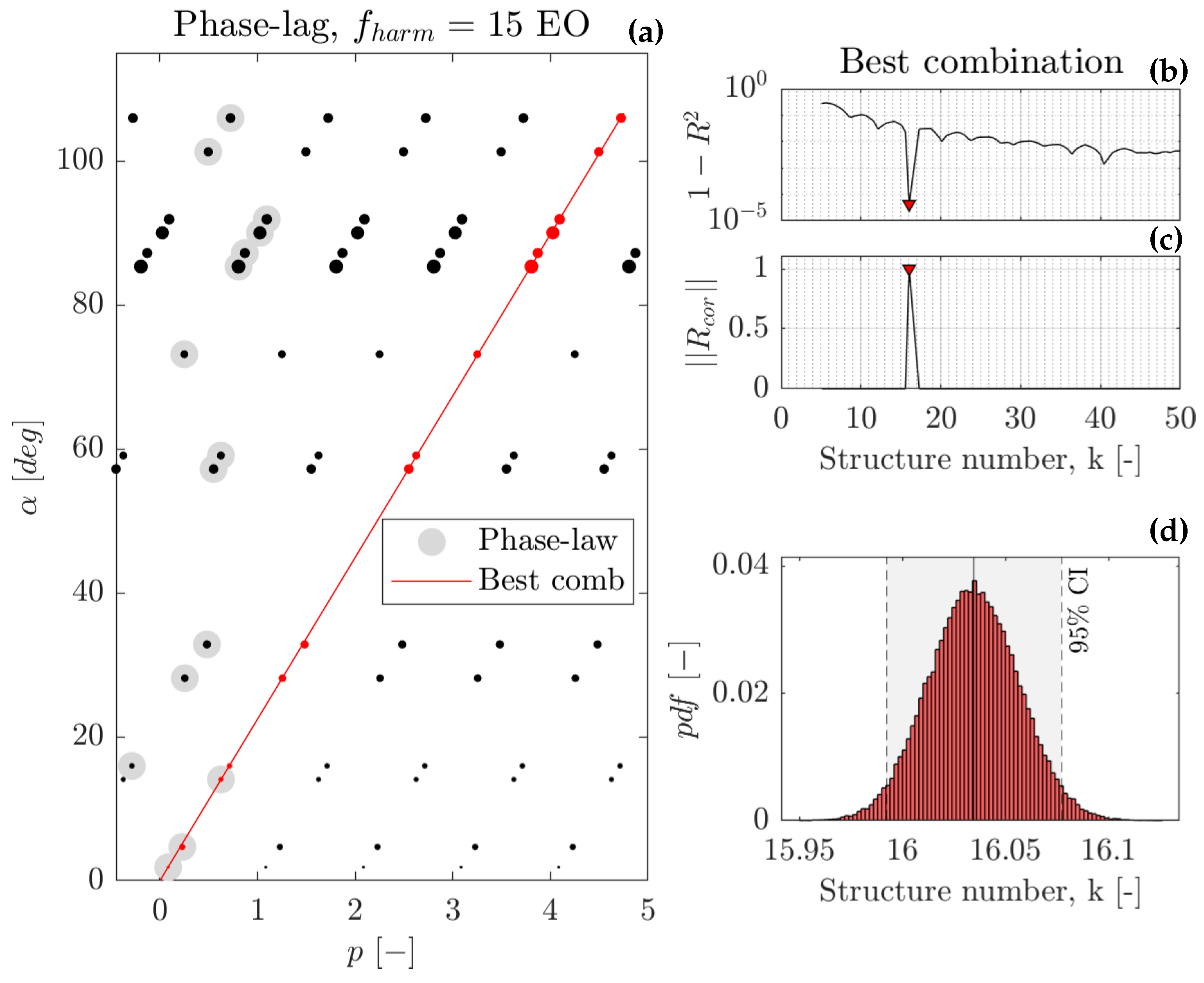
Once the phase law and the phase pdf are determined, the phase lag plot can be populated following the same procedure described for Figure 6a. This is repeated for each state of the instability, and Figure 12a shows the plot for the 15 EO peak. The size of black and red points are representative of the phase lag pdf (95% CI). Notably, the dispersion is not magnified when populating the plot, since each phase delay is, by definition, equally spaced by Δ p = 1 . The original points determined by the phase law are highlighted in grey, while red identifies the combination that minimizes the regression error.
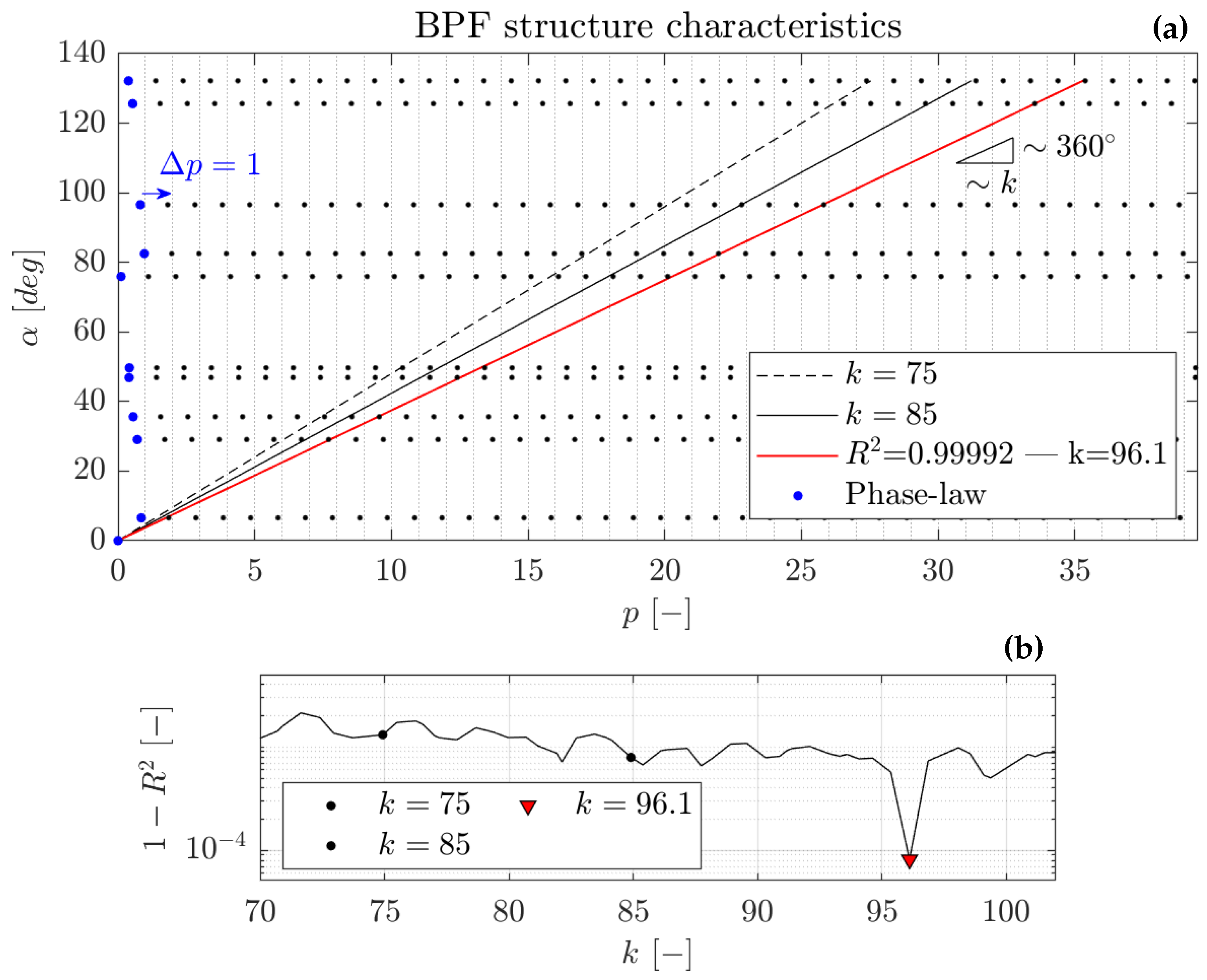
The best combination is determined following the same procedure illustrated for Figure 6. Due to the definition of R 2 , for a dataset in which the angular spacing is not uniform, the search for the best combination leads to favorite lines with lower slopes. This trend is already recognizable in Figure 12b, where 1 − R 2 slowly decreases for higher lobes count (i.e., lower slopes). To solve this issue, the R c o r quantity is defined as it follows:
R c o r = ∑ i = 1 n ( y i − y ¯ ) 2 ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( x i − x ^ i ) 2 ∑ i = 1 n ( x i − x ¯ ) 2
R c o r , differently from R 2 , does not reward combinations spreading over a wide range of phase delay (i.e., low slope’s regressions) and clearly isolate the best combination as displayed in Figure 12c. Ultimately, this definition should be preferred for "extreme" applications where sensors are organized in groups separated by a wide angle.
Once the optimum combination is identified, a new bootstrap procedure is applied to identify the probability density function of the slope. The bootstrap sampling is performed considering the pdf obtained from the phase laws, including one sample for each angular distance since all points should be aligned. Similarly to the phase law, this leads to and increase of the regression robustness and minimizes the uncertainty of the slope measurement.
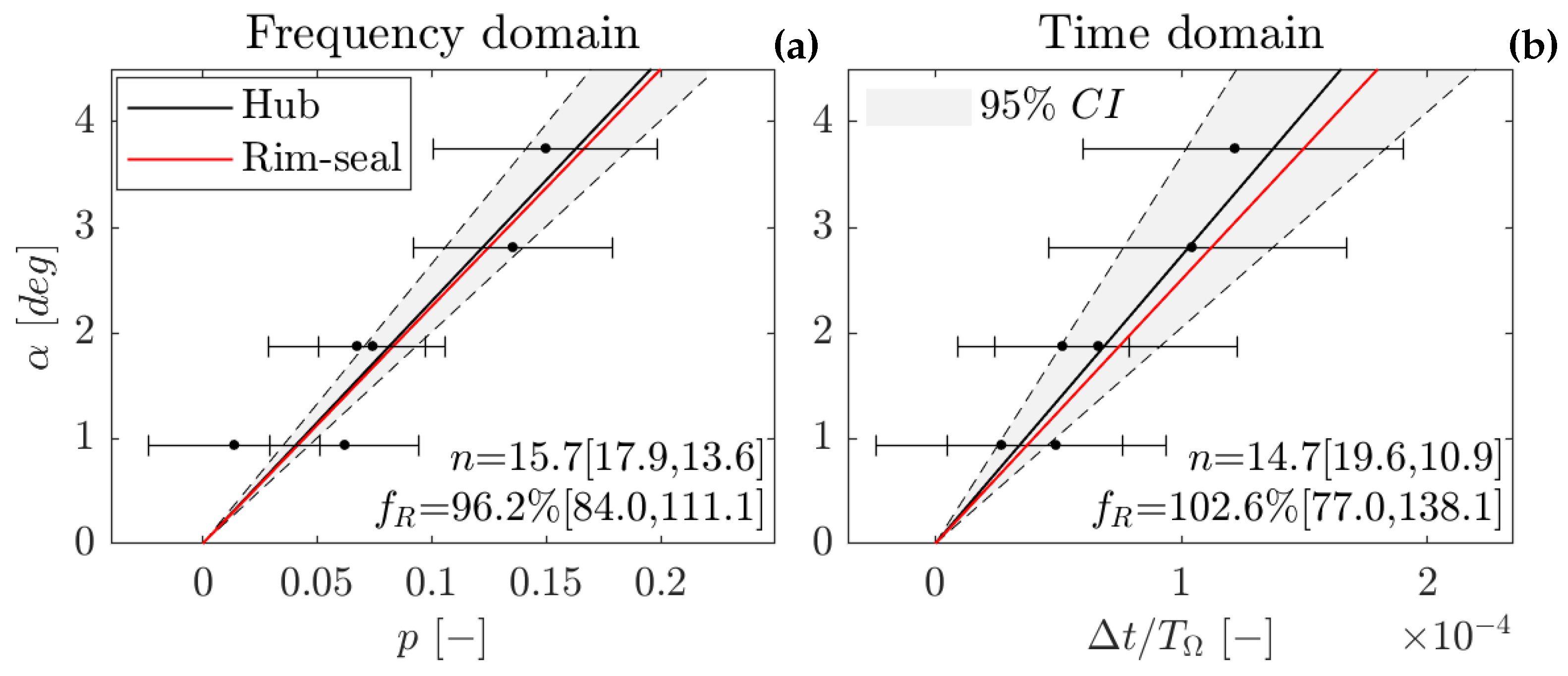
Figure 12d displays the result expressed in terms of lobes count, k = 360 / m . The narrowness of the pdf highlights the precision of the measurement, which identifies 16 lobes rotating at 94% of the rotor speed.

4.2.2. CPSD Method Performance

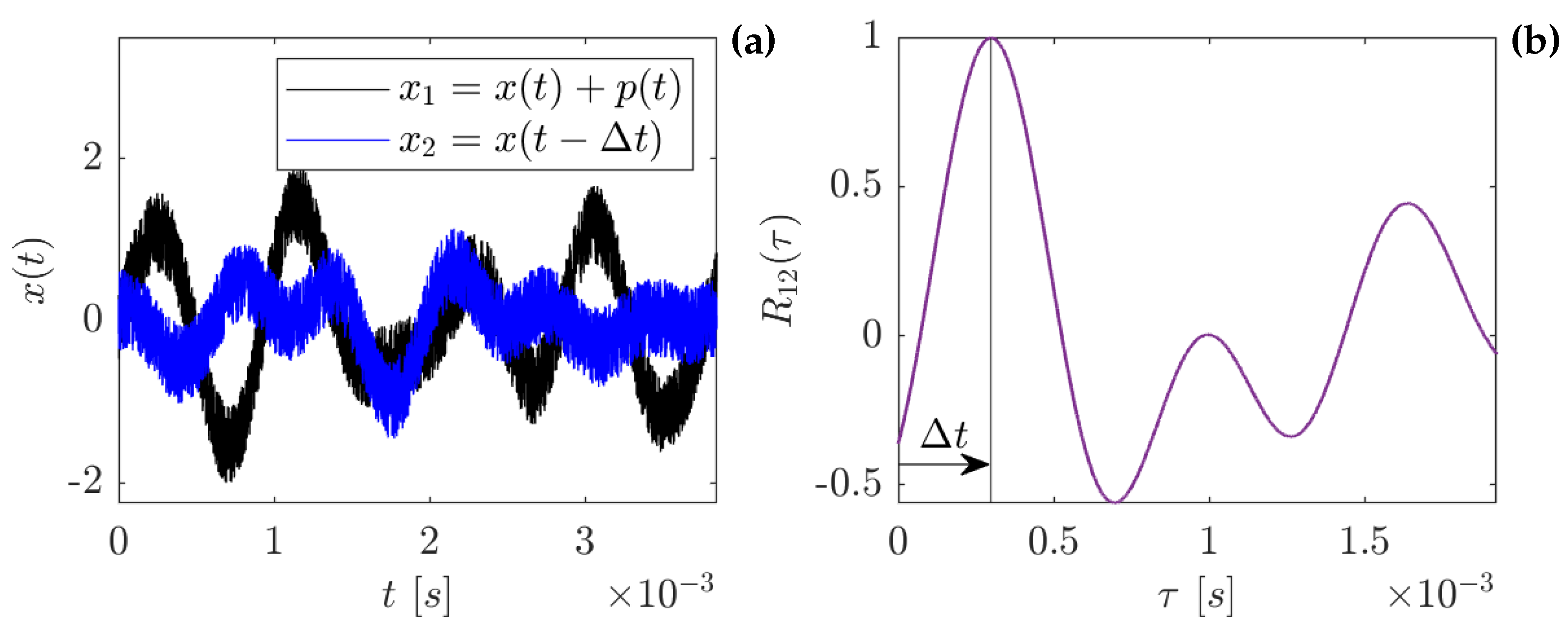
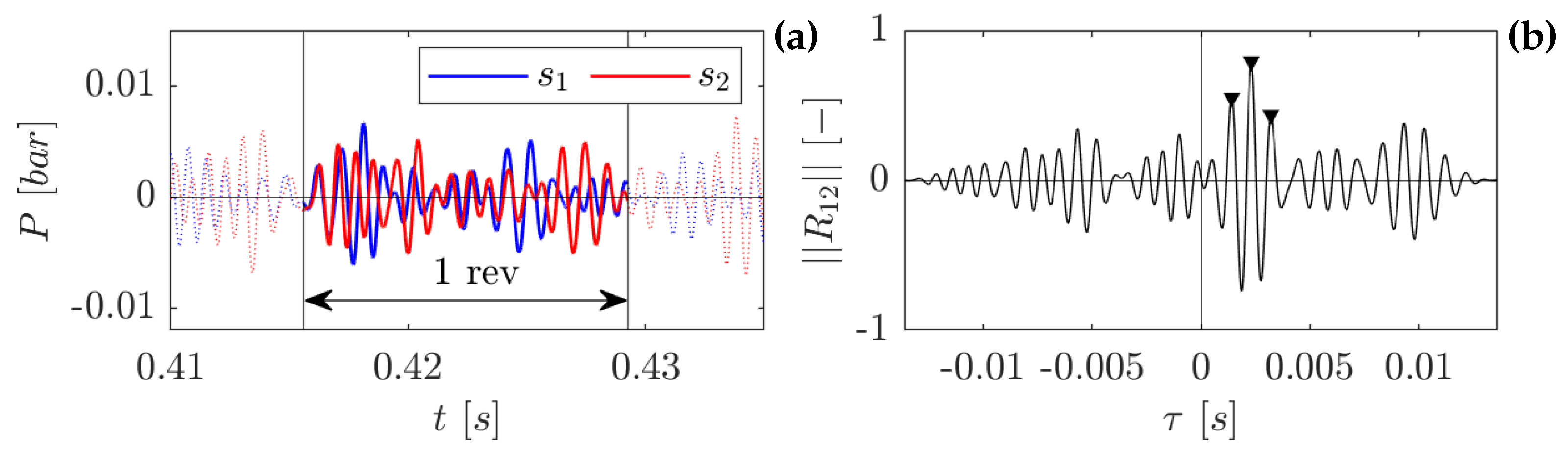
The performance of the CPSD methodology is benchmarked against the cross-correlation method, revised to maximize its accuracy for this application. Figure 13a shows the time history of two sensors (band-pass) filtered to isolate the rim-seal unsteadiness. The plot highlights the portion of the signals equivalent to one full rotor revolution, while Figure 13b displays the result of their cross-correlation.
The evolution of the pressure fluctuation, passing from one state to another while rotating, is easily recognizable in Figure 13a. This translates to a cross-correlation with a complex periodicity and a significant (high-magnitude) isolated peak at the position of the signals’ time delay. This behavior differs from the ideal case of a simple periodic fluctuation (i.e., a single peak in the PSD distribution) in which the most energetic peak must be, by definition, within the first period T P S D . However, this is consistent with the findings of the frequency-domain analysis, as the continuous evolution of the structure characteristics is the cause of the complex periodicity. Intuitively, the evolution of the structures produces time signals with a specific trace producing high values of the cross-correlation only in correspondence with the exact time delay.
Typical applications of the method would require selecting all the peaks of the cross-correlation or, equivalently, the first peak and then assuming a separation of one period ( T P S D = f P S D ). As stated in the methodology section, this is not possible as the rim-seal instabilities occupy a wide range of frequencies. Additionally, the significance of the first peak is not guaranteed, as it could be the result of the complex periodicity. Figure 13b. is an example of this behavior.
Ultimately, the only reliable peaks are the most energetic ones, regardless of their position. Figure 14a,b show the time lag plots populated by the single and two most energetic peaks in the cross-correlations. The figures are generated for rim-seal measurements, computing the cross-correlation over a single revolution, and including all tests available.
In both cases, most points accumulate in clusters that form normal distributions. The most populated clusters fall under the red line that identifies the best combination according to the procedure applied in Figure 12a. Other clusters are also generated in their proximity, separated by one periodicity. Figure 14b shows that when including the second most energetic peak, a series of points not uniformly spaced starts to populate the time lag plot. This is a direct consequence of the evolution of the structures, proving that only the most energetic peaks should be included in the time lag plot, as the others are not representative of any real time delay between the two signals.
Extending the number of peaks considered produces an increase in the dispersion of the clusters determining the best combination. The increase is relatively small, as the points composing these clusters are usually the first or second most energetic peaks. Therefore, the additional time delays, which in theory are less reliable for the reasons above, exert a minimal, yet present, influence on their final probability distribution. Ultimately, the two-peak plots are selected to ensure statistical convergence and precise pdfs.
Once the clusters constituting the best combination are identified, their pdfs are used in the bootstrapping procedure to determine the probability function of the optimum regression. The same procedure described for the CPSD methodology is applied, although in this case the slope is directly linked to the rotating velocity instead of the lobes’ count. Therefore, calculating the number of structures requires inferring f P S D .
Notably, this approach is not capable of discerning the different peaks in the spectrum per se. Typically, the number of lobes is computed assuming f P S D equal to the central frequency. This is valid for applications where the instability is contained in a narrow band with only one predominant state. If this is not verified, this decision comes with the implicit assumption that the instability is rotating at the same speed in all its possible states. This has been proven during the frequency domain analysis, and finds further evidence in the alignment of the clusters of points in Figure 12. Otherwise, spurious peaks would appear aligned with a different regression, superimposed to the first one, as the two states would coexist at the same time. Therefore, its absence is proof that, at least in the region of the pass-band filter, this is not occurring.
Table 5 summarizes the results of the CPSD and cross-correlation methods, applied to the rim-seal measurements (upper lip). Due to the adjustments to their standard implementations, both methods are able to measure the characteristics with high precision. The cross-correlation approach provides a direct link between the best regression slope and the rotating speed, while the cpsd approach links the slope and the number of lobes. Therefore, the comparison of the two methods should focus on these quantities.
Despite the adjustments to the cross-correlation method, the CPSD method demonstrated superior precision under both NP and ZP conditions. For NP, the presence of multiple states becomes an advantage in determining the phase law, as it can rely on more clusters of points. Intuitively, this can be seen as increasing the number of points in a calibration. This advantage is reduced, but still present, for ZP conditions, under which the number of peaks decreases. In contrast, the cross-correlation method cannot make use of this situation, as it is bound only to the central peak of the spectra (15 EO). Due to this limitation, the comparison focuses only on the central and most energetic peak in the average PSD distribution.
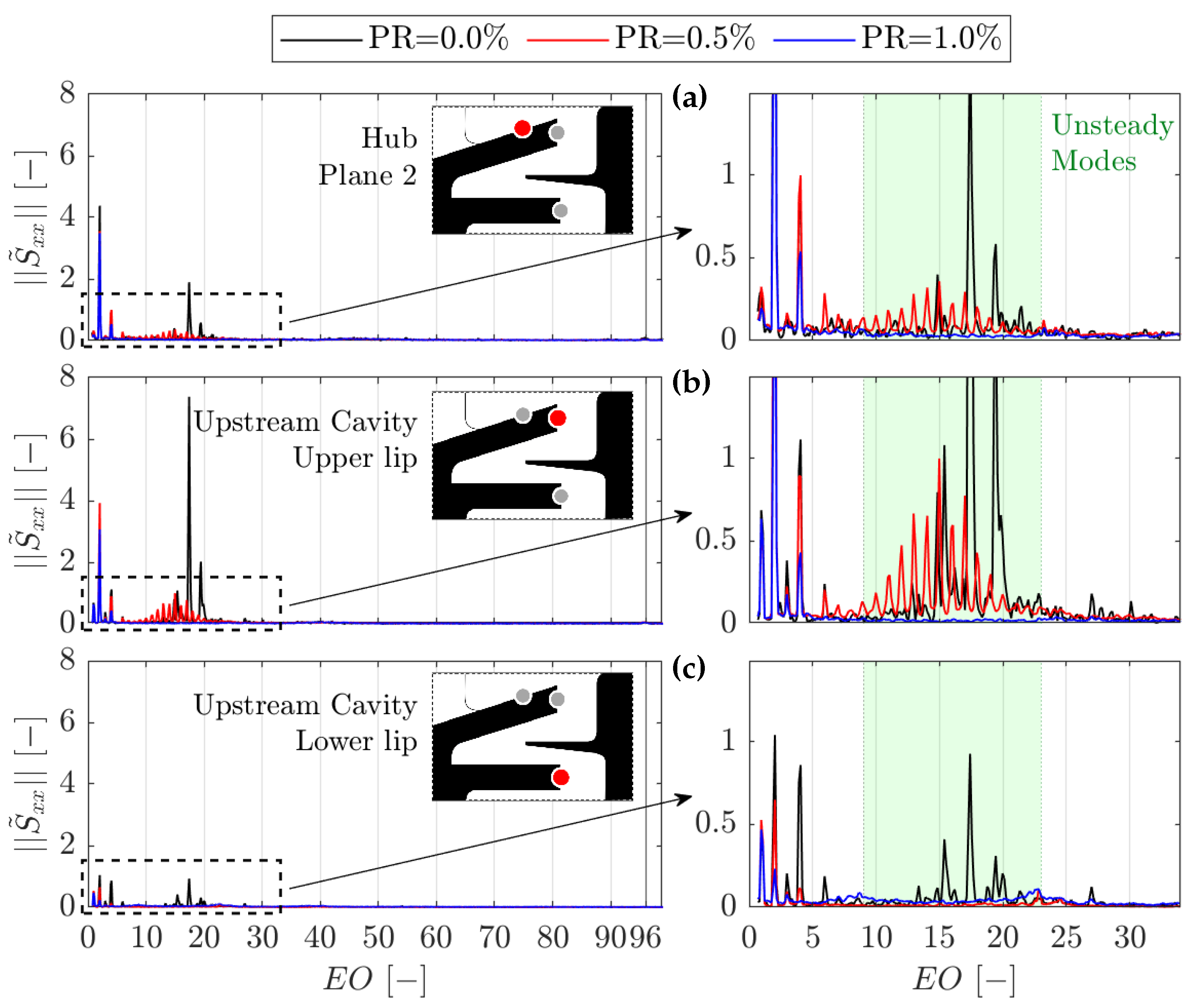
The analysis of the hub measurements under nominal conditions confirms the conclusions of Table 5. Figure 15a,b show, respectively, the results of the frequency and time domain analyzes. Both plots highlight a significant increase in uncertainty in the determination of the slope. The first cause of this behavior is the small spacing between the available sensors, which magnifies the effect of the phase/time lag uncertainty. The second is the lower intensity of the pressure fluctuation, which is translated into larger uncertainties on the lags.
The higher precision of the CPSD method is evident and is projected directly into the confidence interval (in brackets, at 95 %) of the count and velocity of the lobes. Furthermore, the comparison with the rim-seal measurement (red line in the two plots) shows a significant improvement in the measure of both quantities for the CPSD method.

4.2.3. Nature of the Rotating Instability

Table 6 summarizes the characteristics of the rotating instabilities for each operating condition. These values are measured at the upper lip of the rim-seal cavity, where the data is most accurate, and align with the measures at the other meridional positions when the instability is present (e.g., Figure 15a). This result confirms the observations of the spectral analysis and proves that the instability characteristics are maintained across the rim seal.
For NP conditions, the phase law is determined based on the seven most energetic states, and the instability characteristics are delineated for each of these states. For ZP conditions, the phase law includes the two most energetic peaks, but only the most dominant state is analyzed because of its prevalence in the spectra.
The states of the instability, identified from the spectral analysis, are summarized in Table 6. Each of them is associated with a rotating velocity f R , a lobe count n, and their respective uncertainties δ f R and δ n . The term δ n is determined from the pdf of n, while δ f R is calculated from f R = f P S D / n through Taylor expansion [39], assuming for δ f P S D the CPSD discretization error.
For ZP conditions, the lack of tests (only 2) affects the uncertainty of the measurements, causing an increase compared to NP. However, the strength of the peaks and the high signal-to-noise ratio partially compensate for this shortage.
Under NP conditions the minimum variance of the pdfs is recorded at the central peaks. These are the most energetic states and benefit the most from the bootstrapping procedure. In the lateral positions, the number of lobes is no longer an integer, and the rotating frequency diverges from the central value 94%. This trend matches the increase of the measures uncertainty, thereby preserving the nearest integer value of n within its range. The same situation is verified for the values calculated for ZP conditions.
This behavior is the result of a loss of precision of the phase law induced by multiple factors. The accuracy of the CPSD phase and the effect of the CPSD discretization, approximately 6.7% of the EO, affect both the position and the value of the phase in the CPSD plots. The variation of rotor speed within the useful time window, approximately 4.5% of the EO, is also another source of uncertainty. These factors impact the shape of the clusters in the CPSD phase, which ultimately cover a region of ±10-15% EO around the selected peak, as shown in Figure 11a. The area occupied by the clusters has a direct impact on the uncertainty of the phase law, particularly in the lateral positions. Figure 11a provides an example of this behavior. For the central peaks, the pdf of the phase law is lower than the variance of the original cluster. In contrast, the lateral points exhibit similar ranges. This affects every combination of sensors in similar terms, resulting in a wrong estimation of the phase lags and, consequently, of n and f R .
These observations explain the discrepancies between the values in Table 6, the results of the PSD analysis, and the conclusions of the CPSD study, attributing them to the measurement uncertainty. In short, the variance of the cluster of points in the CPSD phase is such that it is impossible to be more precise in the evaluation. However, it is important to emphasize that the CPSD methodology is capable of capturing this "variance", projecting it into the uncertainty of n and f R , thus proving the reliability of the method. Moreover, the precision achieved for each of the possible states is higher than that achieved by the cross-correlation method for the average state of the instability (Table 5).
In conclusion, the values shown in Table 6 represent the average states of the rim-seal instability. The position of f P S D at multiples of the EO suggests a possible link, and potentially the onset of fluid dynamic instabilities due to EO-related perturbations. However, given the uncertainties, this connection cannot be conclusively established. Therefore, a deeper understanding of the developed rim-seal instability requires proper contextualization within the existing literature.
For analogous geometries and flow conditions, the nature of the CMs is typically associated with Kelvin-Helmholtz or Taylor-Couette instabilities. However, this test case exhibits distinctive features that have been proven to influence the development of the modes. This includes the rim-seal design (angel wing seal with double lip), the high number of airfoils (96:96), and engine-representative transonic speed in the mean path.
Looking at the spectral analysis, similar shapes of the spectra can be found in Iranidokht et al. [21], in Horwood et al. [18,20], in Graikos et al. [26], and in Camci et al. [40] which all associate these fluctuations to unsteady ingress-egress mechanisms, and specifically to rotating modes onset by shear layer interactions.
Many authors document the stabilizing effect induced by the purge rate for various sealing geometries and purge flow conditions. Horwood et al. [20] and Graikos et al. [26] confirm this trend for a single lip geometry over a wide range of sealing flow parameters, encompassing the three operating conditions investigated in this work. The effects of disk rotational speed [20], annulus flow coefficient [26], and rotor blades’ presence [26] on the purge rate modulation are also analyzed, concluding that, although the spectral distributions are affected, the stabilizing trend is verified independently from these parameters. Savov et al. [41] describe the modulation of the rim-seal instability as an effect of the purge rate on the size of the Gap Recirculation Zone (GRZ). For high purge rates, it is hypothesized that the GRZ is blown out from the rim seal, explaining the suppression of the unsteady modes.
Horwood et al. [18] also documented the modulation effect by investigating these instabilities on a chute rim-seal geometry. However, contrary to the measurements presented here, the fluctuations were absent at zero purge conditions. This underlines the importance of the rim-seal geometry that is, as extensively documented in the literature review by Chew et al. [12], closely linked to the mechanisms developing at the interface with the annulus flow. Unsteadiness modulation is also detected by Schadler et al. [8] for a rim-seal geometry conceptually similar to the SPLEEN test case. However, the maximum fluctuation intensity was found at a PR of 0.4%.
Despite the significantly different operating conditions and cavity designs, Iranidokht et al. [21] also documented frequency spectra with multiple peaks separated by approximately 1 EO. They identified Kelvin-Helmholtz instabilities as the main drivers of these modes, linking each frequency peak to superimposed structures. Their analysis revealed lobes ranging from 14 to 21, each rotating at about 96% of the disk speed. They observed that the rotational velocity of these lobes increased proportionally with the hub tangential velocity, indicating a dependence on the shear layer gradient. Notably, they were able to predict the location of the most energetic mode (central peak) by employing the results of the velocity profile stability analysis of Michalke et al. [42].
Similar modes characteristics are found by Schadler et al. [8], who detect 22 lobes rotating at 93% of the rotor speed for a rim-seal geometry conceptually similar to the SPLEEN test case. Horwood et al. [20] show evidence of Kelvin-Helmholtz instabilities through the analysis of unsteady RANS simulations for a single lip rim-seal. From the experimental data, they measure 23-26 lobes rotating at 93-103% over a wide range of operating conditions. The relevance of the annulus flow tangential component, and so of the shear layer, is also underlined by Graikos et al. [26], who detect rotating structures composed by 24-32 lobes (depending on the operating condition) and rotating at 85-120% of the disk speed.
Analogous considerations are also made by Savov et al. [27], who analyzed the sealing effectiveness and CMs for two rim-seal geometries with and without rotor blades, identifying Kelvin-Helmholtz instabilities as the main driver of the modes. The dependence on the sealing geometry is also underlined in Town et al. [24], who show how large unobstructed clearances would develop less (in number) but larger (in size) structures and vice versa. These findings align with the results summarized in Table 6, and the conclusions of the spectral analysis in Table 4, which locates the development of the instability at the rim-seal interface and highlights the influence of the shear layer. This constitutes initial evidence of Kelvin-Helmholtz’s instabilities developing under representative engine conditions for a modern high-speed LPT design.
More evidence is provided by applying the results of the stability analysis presented by Michalke et al. [42] to the test case. Michalke et al. identified the wavelength λ of the Kelvin-Helmholtz modes amplified by the velocity profile as λ = 2 π / σ , where σ is related to the thickness of the shear layer, δ 0 , by the relation σ · δ 0 = 0 . 4446 . For the 16-lobe structure, which corresponds to the most dominant (stable) peak of the spectra, δ 0 becomes 8.9 mm. This value is equal to the gap s a x , U C , and falls between the thickness of the upper lip (5.4 mm) and the depth of the sealing region (11.4 mm), the two geometric quantities that affect the most δ 0 . Similar considerations apply to the other states of the instability, for which the equivalent shear layer thicknesses range between 10.1 mm (14-lobes) and 7.9 mm (18-lobes).

4.3. Downstream Cavity Spectra

Figure 16 shows the averaged PSD distributions measured by three fast-response pressure transducers in the downstream cavity region, selected as representative of their location in the meridional plane. The plots are constructed as for Figure 8, normalizing the PSD distributions with the same reference to allow comparisons in terms of relative pressure fluctuations. Similarly to the upstream cavity region, a nearly perfect overlap is found between the average distributions from sensors at the same radial location. For brevity, the plots showing the comparison between different sensors are omitted; nonetheless, the same observations made for the upstream cavity average PSD distributions apply in this case.
The analysis of the spectra shows the absence of frequency bands influenced by the sensor location or the upstream purge condition. Therefore, it is concluded that no cavity instabilities associated with ingress-egress mechanisms are developed. Traces of low-intensity instabilities are found in proximity to the buffer cavity at 40 EO. Interestingly, similar traces are also detected at the lower lip of the upstream cavity, suggesting that this could be related to deep cavity modes. However, this unsteadiness does not seem to interact with the rim-seal region, and its intensity is one order of magnitude smaller than that of the rim-seal modes identified in the upstream cavity region.
Fluctuations are detected at the BPF, which suggests the penetration of the blade potential field into the cavity. The reduction of the fluctuation intensity from the hub to the buffer cavity seems to confirm this behavior. Similar to the upstream cavity, peaks at 2 and 4 EO are detected at the hub but appear to be suppressed inside the cavity region. The magnitude of the fluctuations is maintained under all operating conditions and is comparable to the amplitude of the BPF, hinting to a periodicity associated with the annulus flow.
To quantify the intensity of the BPF perturbation, Table 7 provides the peak-to-peak pressure fluctuations, R 2 , and mean RMS of the ensable average locked at the BPF. The values are determined at each of the three locations for nominal and high purge conditions.

4.4. Shroud Cavity

Figure 17 shows the averaged PSD distributions measured in the shroud cavity region. The spectra are representative of their location in the meridional plane, exhibiting levels of repeatability analogue to the other cavity regions. The averaging process is applied to the PSD of the pressure fluctuations normalized by P 01 , M S . This allows for an easier comparison of the intensity of unsteadiness in all three zones of the shroud cavity, where the static pressure varies significantly. Only one operating condition is considered in Figure 17, as the shroud pressure is not affected by the purge rate (not shown for brevity). Finally, the distributions are normalized to improve the readability of the plots.
The spectrum upstream of the sealing region reveals peaks at 2 and 4 EO, in agreement with the hub measurements shown in the previous sections. A weaker peak (about half the magnitude) is also recognized at approximately 23 EO. Nevertheless, the unsteady field is dominated by the BPF forcing, which is about an order of magnitude more intense than any other instability.
The sealing region exhibits weaker peaks at 2 and 4 EO, with stronger fluctuations at 1 and 3 EO (1 EO peak is about 5 times stronger than the 2 EO peak) dominating the unsteady flow field. The peak of the BPF fluctuation is negligible, reduced by two orders of magnitude compared to the area upstream, showing that this region is isolated from the blade effect.
The spectrum downstream the sealing area is dominated by the BPF. The strength of the fluctuation is 38% stronger compared to the upstream region and is separated by more than one order of magnitude from any other peak in the spectrum. The only exception is the 1 EO peak, which maintains the same intensity registered in the sealed region.
Kluge et al. [29] and Perini et al. [28], detected shear layer instabilities in shroud cavities with comparable magnitudes of BPF and CMs fluctuations. To quantify the intensity of the fluctuations induced by the BPF, Table 8 provides the characteristics of the ensemble average locked at the BPF. Notably, the peak-to-peak variation is 3-to-5 times higher than the rim-seal instability developed in the upstream purge cavity. Therefore, the dominance and the strength of the blade passing periodicity seem to prevent the formation of any type of cavity modes.

4.5. Rotating Instability Propagation

Under NP conditions the spectra of the FR4H probe pressure measurements show traces of the rim-seal instabilities at the outlet of the stage. Figure 18a presents the PSD distributions recorded in Plane 3 by one of the probe pressure transducers at various span locations (y-axis). Figure 18b illustrates the spectra acquired during the same tests by one of the fixed rim seal sensor in the upstream cavity. In Figure 18b, the distributions are displayed at the ordinate of the respective FR4H probe measurement, and each test is identified by a horizontal dotted line. The PSDs are computed applying the same settings on the normalized pressure fluctuation ( P ¯ ). Thereafter, the distributions undergo an additional normalization to facilitate a direct comparison between the spectra.
Rim-seal modes are recognizable in Figure 18a for span positions lower than 50%. Their intensity is seemingly magnified for the measurements in the lower portion of the span. In this area, the PSD distribution rises across a frequency range significantly broader than that associated with rim-seal modes. The cause has been attributed to the amplification of the stochastic component of the field, which is commonly associated with the region of secondary flows [16], precisely where this phenomenon is observed.
The superimposition of these two contributions is depicted in Figure 19, which shows the PSD averages under NP and HP conditions, derived for the tests where the FR4H probe measures in the lower half of the span. Figure 19a reveals a uniform unsteadiness spread across the spectra (grey area), which is not observed in the upper lip measurements. This contribution determines the power of the stochastic events measured in the pressure fields. The band occupied by the rim-seal instability exhibits peaks at the same location as those seen in the upstream cavity (red and ochre areas). The red area appears to be superimposed to the broadband unsteadiness, mirroring the rim-seal measurement trend while also being amplified. These observations are confirmed by the results in Figure 19b, obtained under HP conditions, where rim-seal instabilities are absent and only the broadband contribution is present.
The contemporaneous presence of these two effects precludes a precise evaluation of the intensity of the rim-seal-induced fluctuation. In particular, the RMS method presented in the upstream cavity analysis fails to distinguish the two components. Nonetheless, as a first approximation, the two contributions can be regarded as independent and superimposed, defining the pressure fluctuation P ^ t o t as:
P ^ t o t = P ^ R S + P ^ B B
where P ^ R S represents the contribution of the rim-seal instability, and P ^ B B of the stochastic term. Consequently, the intensity of P ^ R S ( 〈 P ^ R S 〉 ) is determined as the difference between the average powers 〈 P ^ t o t 〉 and 〈 P ^ B B 〉 , both computed over the rim-seal instability band. 〈 P ^ t o t 〉 is obtained from the PSD distribution (integral average), whereas 〈 P ^ B B 〉 must be estimated by extrapolation from the trend of the spectra at higher frequencies. This trend is determined by fitting the PSD distribution over the function y = a · x b + c , which models a "logarithmic decay" of the stochastic component. Among all the functions evaluated, this expression was found to be the most effective in modeling the observed trends.
The influence of the two pressure components is modulated by the secondary flows and, more broadly, by the span location. Consequently, the methodology is applied to each measurement to determine how each contribution is affected by the secondary flows.
Figure 20a illustrates an example of this procedure applied to a test under HP conditions. The solid blue line represents the best fit, whereas the dashed blue line denotes its extrapolation over the rim-seal instability region. The green line represents the best fit calculated over the whole frequency range and serves as a benchmark for the extrapolation procedure. The light blue area corresponds to the region underlying the extrapolated fit, while the grey area identifies the area underlying the actual PSD distribution.
These data are summarized in Figure 20b, which depicts 〈 P ^ t o t 〉 , 〈 P ^ R S 〉 , and 〈 P ^ B B 〉 for all measurements under HP conditions. In the figure, the fluctuation power is normalized by the average rim-seal power, quantified on the upper lip of the upstream cavity under NP conditions. The black-dot profile shows the average power measured within the bandwidth of the rim-seal instabilities, while the green-square and blue-diamond profiles are obtained from the "extended" fit and the fit extrapolation, respectively. As expected, the magnitude of P ^ R S is negligible compared to 〈 P ^ B B 〉 , and both fit effectively capture the correct behavior of the profile, showing consistent estimations of 〈 P ^ B B 〉 . This demonstrates the effectiveness of this approach in providing a first estimate of the strength of P ^ B B and P ^ R S .
The same methodology is applied in Figure 20c for the measurements under NP conditions. The grey-dot profile shows the average PSD intensity, while the black-dot line displays the same quantity computed under HP conditions. The blue and red diamond lines identify the profiles of 〈 P ^ R S 〉 and 〈 P ^ B B 〉 , respectively. The trend of 〈 P ^ B B 〉 follows that obtained under HP conditions, showing a decrease consistent with a reduction in the strength of the secondary flows. This phenomenon is documented in the literature ([9,10]), and is confirmed by the time average measurements in Plane 3 (not shown for brevity). In contrast, the trend of 〈 P ^ R S 〉 exhibits a more uniform contribution in the area of the secondary flows with two peaks in the central region. On average, the intensity of the P ^ R S contribution is comparable to the measurement at the rim seal (ochre-dot line), which remains constant for each test. The fluctuation is amplified at 10% and 14% of the span, where 〈 P ^ R S 〉 is two and four times higher than at the rim seal, and is comparable to the stochastic component. In absolute terms, this is equivalent to 2% and 4% of the total pressure in Plane 3. Outside the region influenced by the secondary flows, the impact of the rim-seal-related instability becomes negligible.
The region of the span affected by the rim-seal-induced instability, along with the amplification of its intensity, indicates that the ingress-egress mechanisms exert an influence on the development of secondary flows. One possible explanation is that the rim-seal instability modifies the rotor inlet flow conditions, thereby affecting the formation of secondary flows. However, the exact nature of this interaction and its contribution to unsteady loss mechanisms remain unclear. Nonetheless, the pronounced rim-seal-induced instability observed in Plane 3 underscores the significant role of ingress-egress mechanisms.
To complete the analysis, it is noted that while all states of the CM’s instabilities manifest at Plane 3, the intensity of the fluctuations is more pronounced at higher EO. This trend is clearly depicted by the spectra in Figure 18b, generated for one of the lateral holes of the FR4H probe (i.e., more sensitive to variations in the yaw angle) and, to a lesser extent, in the average distribution presented in Figure 19 for the central hole. This suggests that the instability states with shorter spatial wavelengths exert a stronger influence on the development of the secondary flows. However, since the nature of this interaction is unclear, the reason behind this behavior remains uncertain.

5. Conclusions

This paper provides a comprehensive analysis of the unsteady phenomena developed in the cavity regions of a modern high-speed LPT stage featuring two hub cavities and an interlocking light shroud. The stage was tested in engine-representative conditions in the short-duration rotating turbine test rig of the von Karman Institute. Different purge rates were investigated to assess the impact of the unsteady flow field.
The analysis of the time-resolved data in the upstream hub-cavity region reveals the generation of cavity modes associated with ingress/egress mechanisms at the rim seal. Their intensity is quantified at 1% of the rim-seal static pressure.
A methodology is presented to compare the spectra of data acquired in short-duration and continuously running facilities. The results show the development of these instabilities in proximity of the rim-seal upper lip. Their intensity is found to be modulated by the purge rate, reaching the maximum intensity for zero purge conditions. Notably, the double lip rim-seal geometry isolates the unsteadiness at the rim-seal interface from the flow dynamics in the inner cavity.
A new technique based on the cross-power spectral density is developed for the determination of the CMs’ rotating speed and lobes’ count. The concept is benchmarked over the BPF fluctuation and applied to determine the rim-seal instabilities. The details of the implementation and the precision of the measurements are provided. Best practices are discussed and the results are compared with the cross-correlation methodology, whose implementation was adapted and made more robust to account for the challenges of this application. The measurement precision is analyzed, developing a standard procedure employing bootstrapping and cross-validation techniques to maximize it. These techniques are integrated into both methodologies, achieving uncertainty levels in the order of 1-2 %. The frequency domain methodology proved to be more precise (~0.5-1%) and capable of measuring the flow characteristics for all the states of the rim-seal instabilities.
The analysis of the cpsd reveals that the different peaks in the spectra distributions correspond to different states of the rim-seal instability, all sharing the same rotating velocity, but differing in lobe count. The alignment of the phase delays and the evolution of the PSD distributions over multiple tests and time windows suggest that the unsteady states do not coexist. Instead, they are the same structure rotating at a fixed velocity, while changing its spatial wavelength.
The rim-seal instabilities rotate at approximately 93-94% of the rotor speed under nominal purge conditions (PR=0.5%). The most energetic states account for 13-19 lobes, and traces of unsteadiness are found in the frequency band between 12 and 18 EO. These instabilities are suppressed under high purge conditions (PR=1.0%) and shifted to a more narrow bandwidth between 15 and 20 EO for zero purge. Under this condition, the structures rotate at about 114% of the rotor speed, and the most energetic and stable state is associated with 15 pressure lobes (17.4 EO peak). These measurements, as for the nominal purge conditions, are verified at each of the three locations monitored in the cavity regions. Ultimately, due to the limited number of tests at zero purge, it is not possible to determine with absolute confidence that the central peak, which is considerably stronger, is the only state of instability. However, the strength of the fluctuations guarantees low-noise cross-correlation and cpsd distributions, allowing an accurate measurement of the instability characteristics at each location.
The shear layer developed at the rim seal is identified as the triggering mechanism for the instabilities. Proof of this is the effect of the purge rate on the intensity and the cavity penetration, which are both maximized for the stronger shear layer. The estimation of the spatial wavelengths of Kelvin-Helmholtz instabilities shows agreement with the measured lobes’ count, confirming the results of the spectral analysis and the role of the shear layer.
The time-resolved measurements in the shroud and the downstream hub cavity show the absence of CMs instabilities for all the tested conditions. This is reconducted to a strong penetration of the blade potential field, which suppresses their development. In the hub cavity, the penetration of the BPF fluctuation suggests that both the upper lip and the buffer cavity are exposed to the field. Similar conclusions apply to the regions upstream and downstream of the sealed region in the shroud cavity.
The spectra measured in Plane 3 under NP conditions highlight the propagation of rim-seal-related instability in the region occupied by the secondary flows. A methodology is proposed to estimate the intensity of these fluctuations and discern them from the stochastic component of the field. The results show a magnification of the instability, reaching the 4% of the total pressure at 14% of the span. The connection between secondary flows and the amplification of the rim-seal instability suggests that by affecting the hub inlet conditions, the ingress-egress mechanisms modulate the generation secondary structures. However, despite being able to measure the intensity of the contribution, the exact nature of this interaction and its effect to unsteady loss mechanisms remain unclear.

Author Contributions

Conceptualization, L.D.V., A.F.M.T., F.M., B.C.C. and S.L.; Methodology, L.D.V., A.F.M.T., F.M., B.C.C. and S.L.; formal analysis, L.D.V., A.F.M.T., F.M., B.C.C. and S.L.; Investigation, L.D.V., A.F.M.T., F.M., B.C.C. and S.L.; Data curation, L.D.V., A.F.M.T., F.M., B.C.C. and S.L.; Writing—original draft preparation, L.D.V., A.F.M.T., F.M., B.C.C. and S.L.; Writing—review and editing, L.D.V., A.F.M.T., F.M., B.C.C. and S.L. All authors have read and agreed to the published version of the manuscript..

Funding

This research was funded by the Clean Sky 2 Joint Undertaking under the EuropeanUnion’s Horizon 2020 research and innovation program under the grant agreement 820883.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The data presented in this study will be openly available in Zenodo.

Acknowledgments

The authors gratefully acknowledge funding of the SPLEEN project by the Clean Sky 2 Joint Undertaking under the European Unions Horizon 2020 research and innovation program under the grant agreement 820883. The authors gratefully acknowledge Safran Aircraft Engines for their support and permission to publish all results. Maxime Hendrix for operating the high-speed turbine rig, and Alexandre Halby and Davide Visconti for their invaluable contribution in the lab. Finally, our thanks go to Terence Boeyen and Oswald Divers for the manufacturing of the high-precision instrumentation.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

Acronyms
LPT Low-Pressure-Turbine
GTF Geared turbofan
HPT High-Pressure Turbine
VKI von Karman Institute for Fluid Dynamics
BPF Bar passing frequency
(U-)RANS (Unsteady) Reynolds-averaged Navier–Stokes
FRSH Fast Response Single Head
FR4HP Fast Response Four Hole Probe
LF Low Frequency
HF High Frequency
PLA Phase-Locked Average
pdf Probability Density Function
GRZ Gas Recirculating Zone
NP Nominal-Purge testing conditions
HP High-Purge testing conditions
ZP Zero-Purge testing conditions
PSD Power Spectral Density
CPSD Cross-Power Spectral Density
CMs Cavity Modes
RMS Root-Mean Square
PR Purge Ratio ( = m ˙ p u r g e / m ˙ )
EO Engine Order ( = f / f Ω )
CI Confidence Interval
Subscripts
0 Total quantities
1, 2, 3 Plane 1. 2, 3
MS Mid-Span position
UC Upstream Cavity
DC Downstream Cavity
SH Shroud Cavity region
Variables
Ω , ω Disk rotation velocity in rpm ( Ω ) and rad/s ( ω )
f Ω Disk rotation velocity (Hz)
N S Number of Stator blades
π t − s , M S Total-to-static pressure ratio at mid-span
U Mean tangential rotation velocity
γ Heat Transfer coefficient
R Air gas-constant
m ˙ Mass-flow
m ˙ p u r g e Purge Mass-flow
Φ Head Coefficient
M Mach number
Re Reynolds number
P R Purge ratio
R e θ Rotational Reynolds
C w 0 Non-dim purge flow rate
U m Mean seal velocity
Φ 0 Sealing flow parameter
λ T Turbulent flow parameter
T 0 , P 0 Total Temperature & Pressure
P 01 , M S Inlet Total Pressure measured at Mid-Span
P ˜ Relative pressure fluctuation
P ¯ Pressure fluctuation normalized by P 01 , M S
D Mean diameter
h/H Normalized Span
b Outer disk radius
s Gap thickness
g/b Seal-to-Gap ratio
n, k Measured and generic number of lobes
v R Lobes’ rotating angular velocity
f R Lobes’ rotating frequency ( = v R / 2 π )
f P S D Lobes’ periodic fluctuation frequency detected by a sensor
T P S D Lobes’ periodic fluctuation period detected by a sensor
( Δ ) α i j Angular distance between two sensors s i and s j
Δ t i j Time delay (or time lag) measured between two sensors s i and s j
R i j Cross-correlation between two signals s i and s j
S i i PSD spectral density of signal s i
G i j CPSD between two signals s i and s j
j Imaginary unit
ϕ i j Angular phase of the CPSD between two signals s i and s j
p i j Phase of the CPSD between two signals s i and s j ( = ϕ i j / 2 π )
R 2 R-square of the linear regression
R c o r Alternative definition of the R-square
λ , Δ β Unsteady structures spatial wave-length
δ 0 Shear layer thickness
m i j , q 0 − i j Phase law slope and intercept (sensors s i and s j )
P ^ t o t Pressure fluctuation (component occupying the instability bandwidth)
P ^ R S Rim-seal induced pressure fluctuation (component occupying the instability bandwidth)
P ^ B B Stochastic component of the pressure fluctuation (occupying the instability bandwidth)
θ V Vane relative phase (normalized by the vane pitch)
g v Vane pitch

Appendix A

This appendix provides the locations of the sensors whose measurements were employed and analyzed in the main text. Table A1, Table A2 and Table A3 include sensor located in the upstream cavity (Figure 1b), in the downstream cavity (Figure 1c), and in the shroud region (Figure 1d), respectively. The angular distance is expressed in terms of vane pitch count ( g = 3.75°C), using different sensors as a reference for each radial position.
Table A1. Upstream purge cavity fast response sensor’s positions.
Table A1. Upstream purge cavity fast response sensor’s positions.
Sensor name Radius [mm] Azimuthal spacing Sensor name Radius [mm] Azimuthal spacing
K2h_1 315.7 - K2h_2 315.7 0.25 g v
K2h_4 315.7 0.50 g v K2h_5 315.7 1.00 g v
KUC01_6 315.6 - KUC01_7 315.6 3.75 g v
KUC01_8 315.6 4.25 g v KUC01_1 315.6 19.50 g v
KUC01_3 315.6 27.00 g v KUC01_4 315.6 28.25 g v
KUC12_5 299.8 - KDC12_6 299.8 1.75 g v
KUC12_7 299.8 4.25 g v KDC12_3 299.8 35.25 g v
Table A2. Downstream purge cavity fast response sensor’s positions.
Table A2. Downstream purge cavity fast response sensor’s positions.
Sensor name Radius [mm] Azimuthal spacing Sensor name Radius [mm] Azimuthal spacing
K3h_1 334.2 - K3h_2 334.2 0.25 g v
K3h_3 334.2 0.50 g v K3h_4 334.2 0.75 g v
K3h_5 334.2 1.00 g v
KDC01_4 329.4 - KDC01_5 329.4 1.50 g v
KDC01_6 329.4 3.25 g v KDC01_8 329.4 11.00 g v
KDC01_2 329.4 23.50 g v KDC01_3 329.4 36.75 g v
KDC07_5 322.7 - KDC07_6 322.7 1.50 g v
KDC07_7 322.7 3.25 g v KDC07_8 322.7 5.75 g v
KDC07_3 322.7 23.50 g v KDC07_4 322.7 36.75 g v
Table A3. Shroud cavity region fast response sensor’s positions.
Table A3. Shroud cavity region fast response sensor’s positions.
Sensor name Radius [mm] Azimuthal spacing Sensor name Radius [mm] Azimuthal spacing
KSC11_1 415.4 -
KSC15_1 419.2 0.00 g v KSC15_2 419.2 0.50 g v
KSC18_1 419.2 0.00 g v KSC18_2 419.2 0.50 g v

References

  1. Kurzke, J. Fundamental Differences Between Conventional and Geared Turbofans. American Society of Mechanical Engineers Digital Collection, pp. 145–153. [CrossRef]
  2. Malzacher, F.J.; Gier, J.; Lippl, F. Aerodesign and Testing of an Aero-Mechanically Highly Loaded LP Turbine. American Society of Mechanical Engineers Digital Collection, pp. 201–209. [CrossRef]
  3. Giovannini, M.; Rubechini, F.; Marconcini, M.; Arnone, A.; Bertini, F. Analysis of a LPT Rotor Blade for a Geared Engine: Part I — Aero-Mechanical Design and Validation. American Society of Mechanical Engineers Digital Collection. [CrossRef]
  4. Vázquez, R.; Torre, D. The Effect of Mach Number on the Loss Generation of LP Turbines. American Society of Mechanical Engineers Digital Collection, pp. 1131–1142. [CrossRef]
  5. Vázquez, R.; Torre, D. The Effect of Surface Roughness on Efficiency of Low Pressure Turbines. 136. [CrossRef]
  6. Torre, D.; Vázquez, R.; Armañanzas, L.; Partida, F.; García-Valdecasas, G. The Effect of Airfoil Thickness on the Efficiency of Low-Pressure Turbines. 136. [CrossRef]
  7. Torre, D.; Garcia-Valdecasas, G.; Cadrecha, D. The Effect of Turning Angle on the Loss Generation of LP Turbines. American Society of Mechanical Engineers Digital Collection. [CrossRef]
  8. Schädler, R.; Kalfas, A.I.; Abhari, R.S.; Schmid, G.; Voelker, S. Modulation and Radial Migration of Turbine Hub Cavity Modes by the Rim Seal Purge Flow. 139. [CrossRef]
  9. Zerobin, S.; Bauinger, S.; Marn, A.; Peters, A.; Heitmeir, F.; Göttlich, E. The Unsteady Flow Field of a Purged High Pressure Turbine Based on Mode Detection. American Society of Mechanical Engineers Digital Collection. [CrossRef]
  10. Zerobin, S.; Peters, A.; Marn, A.; Heitmeir, F.; Göttlich, E. Impact of Purge Flows on the Unsteady HPT Stator-Rotor Interaction.
  11. Scobie, J.A.; Sangan, C.M.; Michael Owen, J.; Lock, G.D. Review of Ingress in Gas Turbines. 138. [CrossRef]
  12. Chew, J.W.; Gao, F.; Palermo, D.M. Flow mechanisms in axial turbine rim sealing. p. 0954406218784612. [CrossRef]
  13. Regina, K.; Kalfas, A.I.; Abhari, R.S. Experimental Investigation of Purge Flow Effects on a High Pressure Turbine Stage. 137. [CrossRef]
  14. Jenny, P.; Abhari, R.S.; Rose, M.G.; Brettschneider, M.; Engel, K.; Gier, J. Unsteady Rotor Hub Passage Vortex Behavior in the Presence of Purge Flow in an Axial Low Pressure Turbine. 135. [CrossRef]
  15. Paniagua, G.; Dénos, R.; Almeida, S. Effect of the Hub Endwall Cavity Flow on the Flow-Field of a Transonic High-Pressure Turbine. 126, 578–586. [CrossRef]
  16. Schuepbach, P.; Abhari, R.S.; Rose, M.G.; Germain, T.; Raab, I.; Gier, J. Effects of Suction and Injection Purge-Flow on the Secondary Flow Structures of a High-Work Turbine. 132. [CrossRef]
  17. Monge-Concepción, I.; Siroka, S.; Berdanier, R.A.; Barringer, M.D.; Thole, K.A.; Robak, C. Influence of Vane Trailing Edge Flow on the Formation of Cavity Cells and Rim Sealing. 144. [CrossRef]
  18. Horwood, J.; Hualca Tigsilema, F.P.; Wilson, M.; Scobie, J.; Sangan, C.; Lock, G.; Dahlqvist, J.; Fridh, J. Flow Instabilities in Gas Turbine Chute Seals. 142. Number: 2. [CrossRef]
  19. Gao, F.; Chew, J.W.; Beard, P.F.; Amirante, D.; Hills, N.J. Large-eddy simulation of unsteady turbine rim sealing flows. 70, 160–170. [CrossRef]
  20. Horwood, J.; Hualca, F.; Scobie, J.; Wilson, M.; Sangan, C.; Lock, G. Experimental and Computational Investigation of Flow Instabilities in Turbine Rim Seals. 141. [CrossRef]
  21. Iranidokht, V.; Kalfas, A.; Abhari, R.; Senoo, S.; Momma, K. Sensitivity Analysis on the Impact of Geometrical and Operational Variations on Turbine Hub Cavity Modes and Practical Methods to Control them. [CrossRef]
  22. Gao, F.; Chew, J.W.; Marxen, O. Inertial waves in turbine rim seal flows. 5, undefined–undefined. Number: 2. [CrossRef]
  23. Bru Revert, A.; Beard, P.F.; Chew, J.W. Measurement of Inertial and Acoustic Waves in a Turbine Chute Rim Seal Cavity. 145. [CrossRef]
  24. Town, J.; Averbach, M.; Camci, C. Experimental and Numerical Investigation of Unsteady Structures Within the Rim Seal Cavity in the Presence of Purge Mass Flow. American Society of Mechanical Engineers Digital Collection. [CrossRef]
  25. Chilla, M.; Hodson, H.; Newman, D. Unsteady Interaction Between Annulus and Turbine Rim Seal Flows. 135. [CrossRef]
  26. Graikos, D.; Carnevale, M.; Sangan, C.M.; Lock, G.D.; Scobie, J.A. Influence of Flow Coefficient on Ingress Through Turbine Rim Seals. 143. [CrossRef]
  27. Savov, S.S.; Atkins, N.R.; Uchida, S. A Comparison of Single and Double Lip Rim Seal Geometries. 139. [CrossRef]
  28. Perini, M.; Binder, N.; Bousquet, Y.; Schwartz, E. Rotating Instabilities in Shrouded Low Pressure Turbine at Design and Off-Design Conditions. 145. [CrossRef]
  29. Kluge, T.; Lettmann, I.; Oettinger, M.; Wein, L.; Seume, J. Unsteady Flow Phenomena in Turbine Shroud Cavities. [CrossRef]
  30. Sieverding, C.H.; Arts, T. The VKI Compression Tube Annular Cascade Facility CT3. American Society of Mechanical Engineers Digital Collection. [CrossRef]
  31. Beard, P.F.; Gao, F.; Chana, K.S.; Chew, J. Unsteady Flow Phenomena in Turbine Rim Seals. 139. [CrossRef]
  32. Torre, A.F.M.; Merli, F.; Valle, L.D.; Patinios, M.; Lavagnoli, S.; Ludovic, P. Adaptation of von Karman Institute for Fluid Dynamics’ Isentropic Compression Tube Facility for High-Speed Low-Pressure Turbines Testing. 146. [CrossRef]
  33. Cernat, B.C.; Pinho, J.; Okada, M.; Lavagnoli, S. Experimental Investigation of a High-Speed Turbine With Rainbow Rotor and Rim Seal Purge Flow. 145. [CrossRef]
  34. Gaetani, P.; Guardone, A.; Persico, G. Shock tube flows past partially opened diaphragms. 602, 267–286. Publisher: Cambridge University Press. [CrossRef]
  35. Dénos, R. Influence of temperature transients and centrifugal force on fast-response pressure transducers. 33, 256–264. [CrossRef]
  36. Sharma, O.P.; Butler, T.L.; Joslyn, H.D.; Dring, R.P. Three-dimensional unsteady flow in an axial flow turbine. 1, 29–38. [CrossRef]
  37. Wiener–Khinchin theorem, Wikipedia, accessed 2024-10-08, https://en.wikipedia.org/w/index.php?title=Wiener%E2%80%93Khinchin_theorem&oldid=1218075429.
  38. Efron, B. Bootstrap Methods: Another Look at the Jackknife. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S.; Johnson, N.L., Eds.; Springer; pp. 569–593. [CrossRef]
  39. Abernethy, R.B.; Benedict, R.P.; Dowdell, R.B. ASME Measurement Uncertainty. 107, 161–164. [CrossRef]
  40. Camci, C.; Averbach, M.; Town, J. Unsteady Flow Structures within a Turbine Rim Seal Cavity in the Presence of Purge Flow—An Experimental and Computational Unsteady Aerodynamics Investigation. 6, 60. Number: 5 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef]
  41. Savov, S.S.; Atkins, N.R. A Rim Seal Ingress Model Based on Turbulent Transport. American Society of Mechanical Engineers Digital Collection. [CrossRef]
  42. Michalke, A. On the inviscid instability of the hyperbolictangent velocity profile. 19, 543–556. Publisher: Cambridge University Press. [CrossRef]
Preprints 121744 g001
Figure 1. Schematic representation of the SPLEEN stage cross-section (a). The right-hand figures show the positions of the fast response pressure transducers in the upstream purge cavity (b), downstream purge cavity (c), and shroud cavity (d).
Figure 1. Schematic representation of the SPLEEN stage cross-section (a). The right-hand figures show the positions of the fast response pressure transducers in the upstream purge cavity (b), downstream purge cavity (c), and shroud cavity (d).
Preprints 121744 g001
Preprints 121744 g002
Figure 2. Effect of the time window on the average PSD distributions.
Figure 2. Effect of the time window on the average PSD distributions.
Preprints 121744 g002
Preprints 121744 g003
Figure 3. (a) shows a schematic representation of the cavity modes, adapted from Beard et al. [31]. (b) shows a synthetic example of an ideal time lag plot.
Figure 3. (a) shows a schematic representation of the cavity modes, adapted from Beard et al. [31]. (b) shows a synthetic example of an ideal time lag plot.
Preprints 121744 g003
Preprints 121744 g004
Figure 4. (a) shows the synthetic signals, x 1 and x 2 , employed in the demonstration of the CPSD properties. (b) shows the cross-correlation computed between the two signals.
Figure 4. (a) shows the synthetic signals, x 1 and x 2 , employed in the demonstration of the CPSD properties. (b) shows the cross-correlation computed between the two signals.
Preprints 121744 g004
Preprints 121744 g005
Figure 5. In the upper row, (a) shows the PSD of the synthetic signals, x 1 and x 2 , while (b) depicts the modulus of their CPSD. In the lower row, (c) shows their coherence, while (d) displays the phase of their CPSD.
Figure 5. In the upper row, (a) shows the PSD of the synthetic signals, x 1 and x 2 , while (b) depicts the modulus of their CPSD. In the lower row, (c) shows their coherence, while (d) displays the phase of their CPSD.
Preprints 121744 g005
Preprints 121744 g006
Figure 6. (a) shows the phase lag plot generated from the analysis of the BPF signal band by applying the CPSD methodology. (b) shows the value of 1 − R 2 computed for possible regression lines.
Figure 6. (a) shows the phase lag plot generated from the analysis of the BPF signal band by applying the CPSD methodology. (b) shows the value of 1 − R 2 computed for possible regression lines.
Preprints 121744 g006
Preprints 121744 g007
Figure 7. Average PSD distributions under NP conditions for different sensors at the same radii.
Figure 7. Average PSD distributions under NP conditions for different sensors at the same radii.
Preprints 121744 g007
Preprints 121744 g008
Figure 8. Average PSD distributions at different purge conditions for fast-response pressure sensors located at different radial positions of the upstream purge cavity region.
Figure 8. Average PSD distributions at different purge conditions for fast-response pressure sensors located at different radial positions of the upstream purge cavity region.
Preprints 121744 g008
Preprints 121744 g009
Figure 9. CPSD distributions of the modulus (a) and phase (b) for a combination of sensors during a single test. The modulus is normalized with respect to the strongest peak, while the phase is normalized by 2 π [i.e. p 12 = ϕ 12 / ( 2 π ) ].
Figure 9. CPSD distributions of the modulus (a) and phase (b) for a combination of sensors during a single test. The modulus is normalized with respect to the strongest peak, while the phase is normalized by 2 π [i.e. p 12 = ϕ 12 / ( 2 π ) ].
Preprints 121744 g009
Preprints 121744 g010
Figure 10. The left-hand figures show the evolution of the PSD distributions during a single test for two sensors s 1 and s 2 separated by an angle of α 12 . On the right, (d) presents the spectra computed over the entire test (covering windows 1 to 3).
Figure 10. The left-hand figures show the evolution of the PSD distributions during a single test for two sensors s 1 and s 2 separated by an angle of α 12 . On the right, (d) presents the spectra computed over the entire test (covering windows 1 to 3).
Preprints 121744 g010
Preprints 121744 g011
Figure 11. (a) shows the CPSD phase collected over multiple tests and sub-windows at the CPSD modulus peaks location. (b) and (c) presents the pdfs computed for the coefficients of the phase law ( m 12 and q 0 − 12 ). (d) show the phase lag pdf, p 12 , computed at the 15 EO peak.
Figure 11. (a) shows the CPSD phase collected over multiple tests and sub-windows at the CPSD modulus peaks location. (b) and (c) presents the pdfs computed for the coefficients of the phase law ( m 12 and q 0 − 12 ). (d) show the phase lag pdf, p 12 , computed at the 15 EO peak.
Preprints 121744 g011
Preprints 121744 g012
Figure 12. (a) shows the phase plot lag for the 15 EO frequency peak. (b) and (c) show the distributions of 1 − R 2 and normalized R c o r r , respectively. (d) shows the pdf of the number of structures.
Figure 12. (a) shows the phase plot lag for the 15 EO frequency peak. (b) and (c) show the distributions of 1 − R 2 and normalized R c o r r , respectively. (d) shows the pdf of the number of structures.
Preprints 121744 g012
Preprints 121744 g013
Figure 13. (a) shows two pressure measurements (1 revolution) pass-band filtered over the rim-seal instability band. (b) shows their cross-correlation and the location of the three most energetic peaks.
Figure 13. (a) shows two pressure measurements (1 revolution) pass-band filtered over the rim-seal instability band. (b) shows their cross-correlation and the location of the three most energetic peaks.
Preprints 121744 g013
Preprints 121744 g014
Figure 14. Time lag plots populated considering the first (a) and the first two (b) strongest peaks of the cross-correlation distribution. Best regression computed considering the centroids of the clusters (no bootstrapping procedure applied yet).
Figure 14. Time lag plots populated considering the first (a) and the first two (b) strongest peaks of the cross-correlation distribution. Best regression computed considering the centroids of the clusters (no bootstrapping procedure applied yet).
Preprints 121744 g014
Preprints 121744 g015
Figure 15. Phase lag (a) and time lag (b) plots obtained at Plane 2 (Hub, f P S D = 15 EO). The uncertainty of phase and time delays are expressed by the horizontal error bars (95% CI).
Figure 15. Phase lag (a) and time lag (b) plots obtained at Plane 2 (Hub, f P S D = 15 EO). The uncertainty of phase and time delays are expressed by the horizontal error bars (95% CI).
Preprints 121744 g015
Preprints 121744 g016
Figure 16. Average PSD distributions at different purge conditions for fast-response pressure sensors located at different radial positions of the downstream purge cavity region.
Figure 16. Average PSD distributions at different purge conditions for fast-response pressure sensors located at different radial positions of the downstream purge cavity region.
Preprints 121744 g016
Preprints 121744 g017
Figure 17. Average PSD distributions at different purge conditions for fast-response pressure sensors located at different radial positions of the shroud cavity region.
Figure 17. Average PSD distributions at different purge conditions for fast-response pressure sensors located at different radial positions of the shroud cavity region.
Preprints 121744 g017
Preprints 121744 g018
Figure 18. PSD distributions measured during the same tests by one of the lateral holes of the FR4H probe in Plane 3 (a), and by a fixed sensor in the upstream purge cavity (b).
Figure 18. PSD distributions measured during the same tests by one of the lateral holes of the FR4H probe in Plane 3 (a), and by a fixed sensor in the upstream purge cavity (b).
Preprints 121744 g018
Preprints 121744 g019
Figure 19. Average PSD distributions measured by a sensor of the FR4H probe (down sensor) and at the upper lip of the upstream purge cavity under NP (a) and HP (b) conditions.
Figure 19. Average PSD distributions measured by a sensor of the FR4H probe (down sensor) and at the upper lip of the upstream purge cavity under NP (a) and HP (b) conditions.
Preprints 121744 g019
Preprints 121744 g020
Figure 20. (a) displays the methodology applied to estimate the contribution of the distributed unsteadiness. (b) and (c) show the contributions of rim-seal instability and distributed unsteadiness to the spectra under HP and NP conditions, respectively.
Figure 20. (a) displays the methodology applied to estimate the contribution of the distributed unsteadiness. (b) and (c) show the contributions of rim-seal instability and distributed unsteadiness to the spectra under HP and NP conditions, respectively.
Preprints 121744 g020
Table 1. Geometry of the SPLEEN stage cavity regions.
Table 1. Geometry of the SPLEEN stage cavity regions.
Parameter value Parameter value
b UC 318.7 mm s ax , UC / b UC 0.028
s r , UC / b UC 0.010
b DC 329.8 mm s ax , DC / b DC 0.022
s r , DC / b DC 0.011
b SC 419.1 mm s r , SC / H 0.004
Table 2. Turbine operating conditions. Repeatability expressed as percentage of mean value (95% CI).
Table 2. Turbine operating conditions. Repeatability expressed as percentage of mean value (95% CI).
Parameter Mean Repeatability (95% CI)
π t − s , M S 2.052 0.56%
U / γ R T 01 0.4806 0.48%
P R = m ˙ p u r g e / m ˙ 0.5%   1.0% 2.0%   2.3%
Φ 2 0.699   0.675 0.59%   0.29%
M 2 0.81   0.80 <0.1%   <0.1%
R e 2 ( · 1000 ) 291.5   289.1 1.01%   1.17%
m ˙ γ R T 01 / ( D 2 P 01 ) 0.0685 0.35%
Table 3. Purge operating conditions.
Table 3. Purge operating conditions.
     Region Parameter Zero Purge (ZP) Nominal Purge (NP) High Purge (HP)
     Upstreamhub cavity P R = m ˙ p u r g e / m ˙ 0.0 % 0.5 % 1.0 %
R e θ = ω b 2 / ν 1.42E+06 1.50E+06 1.53E+06
C w 0 = m ˙ p u r g e / ( b μ ) 0 9881 19711
U m = m ˙ p u r g e / ( ρ · 2 π b s a x ) 0 m/s 5.18 m/s 10.11 m/s
Φ 0 = b / ( ω b ) 0 0.0348 0.0679
λ T = C w 0 / Φ 0 0.8 0 0.1134 0.2222
M 2 , 10 % 0.84 0.84 0.84
     Downstreamhub cavity P R = m ˙ p u r g e / m ˙ - - -
R e θ = ω b 2 / ν 1.25E+06 1.25E+06 1.25E+06
M 3 , 10 % 0.43 0.43 0.43
Table 4. Cavity modes intensity by radial position and purge rate in the upstream cavity region.
Table 4. Cavity modes intensity by radial position and purge rate in the upstream cavity region.
Position PR Bandwidth [ E O ] Fluctuation amplitude ( P f l u c t / P UP )
0.0% 15-20 0.61%
Plane 2, Hub 0.5% 11-19 0.54%
1.0% - -
0.0% 15-20 1.12%
Upper-Lip 0.5% 11-19 0.80%
1.0% - -
0.0% 15-20 0.51%
Lower-Lip 0.5% - -
1.0% - -
Table 5. Cavity instability characteristics measured at the upper lip employing the cross-correlation and CPSD methods for the central peak.
Table 5. Cavity instability characteristics measured at the upper lip employing the cross-correlation and CPSD methods for the central peak.
Method PR f P S D [ E O ] f R / f Ω [ % ] n [ − ]
0.0% 17.45 114.6% ± 2.4% 15.2 ± 2.5%
Time Lag 0.5% 15.0 94.2% ± 1.3% 16.0 ± 1.6%
1.0% - - -
0.0% 17.45 114.5% ± 1.9% 15.2 ± 1.8%
Phase Lag 0.5% 15.0 93.7% ± 1.1% 16.0 ± 0.6%
1.0% - - -
Table 6. Characteristics of the upstream cavity rim-seal instability (most energetic states) and relative uncertainty (95% CI) under different purge conditions.
Table 6. Characteristics of the upstream cavity rim-seal instability (most energetic states) and relative uncertainty (95% CI) under different purge conditions.
PR f P S D [ E O ] f R / f Ω [ % ] n [ − ]
0.0% 17.45 114.5% ± 1.9% 15.2 ± 1.8%
12.0 , 13.0 92.2%  ± 1.7% , 92.8%  ± 1.4% 13.1 ± 1.2% , 14.1 ± 0.9%
0.5% 14.0 , 15.0 93.3%  ± 1.2% , 93.7%  ± 1.1% 15.1 ± 0.7% , 16.0 ± 0.6%
16.0 , 17.0 94.1%  ± 1.1% , 94.5%  ± 1.1% 17.0 ± 0.6% , 18.0 ± 0.7%
18.0 94.8%  ± 1.2% 19.1 ± 0.9%
1.0% - - -
Table 7. BPF fluctuation intensity by radial position and purge rate in the downstream cavity region.
Table 7. BPF fluctuation intensity by radial position and purge rate in the downstream cavity region.
Location Δ P / P 01 , M S [ % ] P R M S / P 01 , M S [ % ] R 2 [ − ]
NP HP NP HP NP HP
Plane 3, Hub 0.62 0.64 0.89 0.91 0.16 0.16
Upper lip 0.66 0.62 1.31 1.05 0.10 0.14
Buffer cavity 0.23 0.27 0.71 0.73 0.05 0.05
Table 8. BPF fluctuation intensity by radial position and purge rate in the shroud cavity region.
Table 8. BPF fluctuation intensity by radial position and purge rate in the shroud cavity region.
Location Δ P / P 01 , M S [ % ] P R M S / P 01 , M S [ % ] R 2 [ − ]
Upstream region 1.37 1.29 0.3730
Sealed region 0.13 0.64 0.0170
Downstream region 2.66 2.28 0.3127
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Numerical and Experimental Study of Flutter in a Realistic Labyrinth Seal

Oscar Bermejo

et al.

,

2023

Assessment of Aerodynamic Plates Subjected to Von Kármán Vortex Street for Enhancing the Wind Energy Generation in Blade-less Devices

John Zuluaga

et al.

,

2023

Application of a Novel WENO Scheme for RANS and RANS/LES Coupled Simulations in Turbomachinery Flows

Hao Wang

et al.

,

2024

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated