Prerpints.org logo
Preprint
Article

State Observer for Time-Delay Systems Applied a Sir Compartmental Epidemiological Model for the COVID-19

This version is not peer-reviewed.

Submitted:

22 October 2024

Posted:

22 October 2024

You are already at the latest version

Abstract
In this paper a Luenberger-type state observer for a class of nonlinear systems with multiple delays is presented. Sufficient conditions are provided to guarantee practical stability of the error dynamics. An exponential decay of the observation error dynamics is assured using Lyapunov-Krasovskii functionals and the feasibility of Linear Matrix Inequalities. Also, a time-delay SIR compartmental epidemiological model is presented. Time delay corresponds to the transition rates between compartments. The model considers that a part of the recovered population becomes susceptible again after a period following recovery. Three time-delays are incorporated due to the exchange of individuals between the population compartments: $\tau_{1,2,3}$, for the dead-times of recovery, immunity loss and incubation, respectively. It is shown that the effective reproduction number of the delay model depends on the rate of the susceptible population which became infected but after a period starts to be infectious and the fraction of the infectious recovered after a time-delay. For the resulting delay model, the problem of state estimation is addressed. To illustrate the efficiency and performance of the proposed observer, we apply the developed results to the COVID-19 pandemic. The observer can estimate the compartmental populations of Susceptible $S(t)$ and Recovered $R(t)$ from only the availability of real data of the Infectious compartmental population $I_r(t)$. The $I_r(t)$ confirmed data used for the state estimation are from a 55-day window with the highest impact on the Mexican population, as reported by the World Health Organization (WHO).
Keywords: 
Subject: 
Computer Science and Mathematics  -   Mathematical and Computational Biology
Preprints on COVID-19 and SARS-CoV-2

1. Introduction

Since its origins, humanity has been immersed in the emergence of infectious diseases and/or its variants, bringing with it a high degree of confusion among the population due to the ignorance of its spread in a susceptible population. The use of epidemiological mathematical models has become a highly recurrent task today for researchers and/or health organizations, since they are a tool that allows describing the dynamics of an infectious disease and knowing some parameters involved in its spread. Among the best-known models for this purpose are the compartmental epidemiological mathematical models which differ according to the number of compartments, populations or subpopulations, considered in each model, as SIS (Susceptible-Infectious), SIR (Susceptible-Infectious-Recovered), and SEIR (Susceptible-Exposed-Infectious-Recovered), to mention a few, [1].
Historically, various infectious diseases have emerged that have seriously affected humanity, such as the so-called spanish flu; black death plague; HIV; among others. Table 1 shows some of the most relevant data on these infectious diseases. In addition to a small compilation of the mathematical models type SIS, SIR and/or SEIR used to study these pandemics.
Through a mathematical model, it is possible to improve the understanding of a disease and lower its prevalence and incidence, and based on the behavior of the model, it is possible to assist in the design of strategies to stabilize the transmission rate of the disease and, if possible, stop the spread of an infectious disease [11]. However, there is not always available information for all the population compartments considered in these models, so it is necessary to use tools of the control theory, such as state observers, to estimate the missing information. It is well known that the main objective of the synthesis of a state observer is the complete reconstruction of the state of the system (mathematical model) using the available information and initial conditions [12], so in the literature it is common to read about the use of this tool for a wide variety of systems.
Throughout history, various preconceptions have been proposed to estimate the state of a system, e.g., [13], but in [14] the term observer is proposed for the first time. This observer is known Luenberger observer. Here it is shown that the state vector of a linear system can be reconstructed by observing the inputs and outputs of the system.
While on observers for time-delay systems, in [15] an extension of the results given in [13] is presented for systems with time delays. A new approach for the construction of a state observer for nonlinear systems when the output measurements are available for computations after a non negligible time delay is proposed in [16]. There, the globally drift-observability is secured by a diffeomorphism using Lie derivatives. In [17] an extension of the observer given in [18] is proposed for a class of nonlinear systems, which present multiple noncommensurate time delays as well as distributed delay terms. In [19] a state observer for drift observable nonlinear systems when output measurements are affected by a known and bounded time varying delay is given. Such observer has a simple structure, it is a generalization of an observer for delay-free systems, the globally drift-observability is secured by a diffeomorphism using Lie derivatives and the convergence of the observation error is based on the Lyapunov–Razumikhin approach. In [20] a combined controller-observer design procedure for a class of time-delay uncertain systems is proposed using matrix’s Singular Value Decomposition (SVD) and Linear Matrix Inequality (LMI) techniques. The stability of the closed-loop systems presented is based on Lyapunov-Krasovskii functionals. In [21] a new method to design observers in a class of nonlinear time-delay systems is suggested. This design procedure of the observer involves two steps: an extension of the pseudo-linearization technique and solving a state-dependent Riccati equation. In [22] is presented a robust observer-based control of nonlinear one-sided Lipschitz systems in the presence of time delay, model uncertainties, and unknown energy-bounded exogenous disturbances. A observer structure requires a predetermined nominal/linear part. The observer-based finite-time robust control problem of a general class of nonlinear time-delay systems via Hamiltonian function method, that proposes some new finite-time robust stabilization results is studied in [23].
Derived from the current health crisis, the scientific community has focused efforts to understand, predict, and mitigate COVID-19. For this, various investigations have been proposed in all areas of science and technology. One of these is the construction of observers for epidemiological models, although this is not new, since in [24] the state estimation for a delay-free SIR model subject to seasonal variations and uncertainties in the transmission rate is considered. Here an asymptotic convergence of the observer is ensured using Lyapunov functions. While in [25] the same approach is presented but now for a nonlinear adaptive observer. The construction of backstepping observers for two linearized Kermack–McKendrick models: a first-order hyperbolic partial differential equation and a SIR model, both delay free models is proposed in [26]. In [27] a SIR model with two time-delays: h 1 in the transmission rate and h 2 in the number of infectious population is considered. Here an observer for the delay-free SIR model which is then uplifted into a predictor to compensate for time delays in the input and output is proposed. In [28] a high-gain observer design for a class of quasi-linear hyperbolic systems is presented. The exponential stability of the observation error is ensured using a Lyapunov-based analysis.
This manuscript presents the design of a Luenberger-type state observer for a class of nonlinear systems with multiple delays to estimate compartmental populations of epidemiological models. As well as an SIR compartmental epidemiological model with three time-delay. The model considers that a part of the recovered population becomes susceptible again after a period of time after its recovery plus three time-delays due to the exchange of individuals between the population compartments: τ 1 , 2 , 3 , for the dead-times of recovery, immunity loss and incubation, respectively. By making a change of variables, this model with three time-delays is transformed into a model with nominal part as a function of the time-delays. The latter allows to design a Luenberger-type state observer for estimation of the compartmental populations of S ( t ) Susceptible and R ( t ) Recovered not reported by the WHO. This only with the availability of real data from the Infectious compartmental population. In addition, using Lyapunov-Krasovskii functionals and the feasibility of Linear Matrix Inequalities, an exponential decay can be ensured on the observation error, thus guaranteeing a convergence between the real data and the estimated. To illustrate the efficiency and performance of the proposed results, without loss of generality real data reported by WHO is used to estimate S ( t ) and R ( t ) in a 55-day time window with the greatest impact on the population of Mexico. The data considered in the present contribution were collected prior to the implementation of the vaccination campaign. This is mainly to the fact that the SIR compartmental epidemiological model under consideration does not include this variable.

2. Problem Statement and Contributions

Next, the statement of the problem and specific contributions are given.

2.1. Problem Statement

Consider the following SIR fundamental model of Kermack and McKendrick (KMK) used in mathematical epidemiology [29]:
d d t S ( t ) = − β S ( t ) I ( t ) , d d t I ( t ) = β S ( t ) I ( t ) − γ I ( t ) , d d t R ( t ) = γ I ( t ) ,
where S ( t ) , I ( t ) and R ( t ) are the populations of Susceptible, Infectious and Recovered, respectively. The total population is denoted as N ( t ) = S ( t ) + I ( t ) + R ( t ) and it is considered constant. Also, β denotes the transmission coefficient or infection rate (recording infectiousness and the probability of contact between people or number of people infected per unit of time) and γ the recovery/death rate in the infected population, this can be estimated as the reciprocal of the average number of days for transition from I ( t ) to R ( t ) , see [30]. In addition, it is considered that if the disease does not induce mortality ( γ is the recovery rate), then the population R ( t ) denotes those who have recovered and are immune to reinfection. On the other hand, if γ records mortality ( γ is the dead rate), then the population R ( t ) records the number of deaths induced by the epidemic, see [31].
Epidemiological models such as SIR can be used to better understand what has happened to the current pandemic, such as rates of infection, recovery or/and spread; estimates of population dynamics, among others, this during short periods/windows of time. However, according to WHO reports and statistics, it is necessary to adapt the fundamental model of KMK to the conditions given by the current pandemic [32], such as:
I. 
Take into account that recovered individuals may again be susceptible to the disease (there is not immunity).
II. 
Consider the dead-times/periods it takes an individual to move from one compartmental population to another.
In addition, the lack of information in the reported data limits the study of this disease and its variants, therefore it is necessary:
III. 
Estimate the dynamics/data of compartmental populations not reported by the authorities responsible for this matter.
Reason why in the present research work, the following is proposed:

2.2. Contributions of this Manuscript

  • A Luenberger-type state observer for a class of nonlinear systems with multiple delays is proposed to estimate the dynamics of compartmental populations not reported by the WHO.
  • A SIR epidemiological model with three time-delays is presented which considers that a part of the recovered population becomes susceptible again after a period of following recovery. Besides, the model consider the dead-times it takes an individual to move from one compartmental population to another, that is:
    -
    τ 1 is the time it takes for an infectious individual to stop being so, in order to recover from the disease and acquire immunity (dead-time by recovery).
    -
    τ 2 is the time it takes for a recovered individual to return to the susceptible population (dead-time by immunity loss).
    -
    τ 3 is the time it takes for a susceptible individual to present symptoms and affect the spread of the disease (dead-time by incubation).
  • To guarantee the estimation of the previous observer, a convergence analysis is presented using Lyapunov-Krasovskii functionals and the feasibility of Linear Matrix Inequalities to ensure that the observation error decreases with an exponential decay σ > 0 .
  • The proposed results are validated through simulations (Simulink-Matlab), and data reported by the WHO for the COVID-19 pandemic in Mexico.
  • The generality of the theoretical results proposed suggest that they can be applied to other types of epidemiological models that meet the conditions stated here; and to other countries (population data).

3. Preliminary Results and Observer Design

Next, some classic results found in the literature regarding time delay systems and state observers are stated; which will serve as the basis for the development of this proposal.

3.1. Systems with Several Delays

Let us consider a general retarded functional differential equations with multiple delays of the form
z ˙ ( t ) = f z ( t ) , z ( t − τ 1 ) , z ( t − τ 2 ) , … , z ( t − τ m ) , y ( t ) = h z ( t ) , z ( t − τ 1 ) , z ( t − τ 2 ) , … , z ( t − τ m , z ( θ ) = ϕ ( θ ) , θ ∈ [ − τ , 0 ] ,
where 0 = τ 0 < τ 1 < ⋯ < τ m = τ are delays and f : R n × ( m + 1 ) → R n is a continuous nonlinear function and satisfies a local Lipschitz condition regarding the elements of the argument and h : R n × ( m + 1 ) → R l is continuously differentiable function with respect to its argument. For t ≥ 0 , y ( t ) ∈ R l is the only measured output of the system, denote by z ( t , ϕ ) ∈ R n the system solution with initial function (condition) ϕ ∈ C , and by C : = C ( [ − τ , 0 ] , R n ) the Banach space with norm ∥ ϕ ∥ τ : = max θ ∈ [ − τ , 0 ] ∥ ϕ ( θ ) ∥ . Here, ∥ · ∥ denotes the euclidean norm. As a natural extension of the initial function, a solution segment of z ( t , ϕ ) in a time interval [ t − τ , t ] is denoted by
z t = z ( t + θ ) ∈ C , θ ∈ [ − τ , 0 ] ;
and called state of the system (2).
Now, let z t ∗ is a non zero constant equilibrium point of (2), namely, f ( z ∗ ( t ) , z ∗ ( t − τ 1 ) , … , z ∗ ( t − τ m ) ) = 0 , for all t > 0 . Using the variable transformation/change
x ( t − τ i ) = z ( t − τ i ) − z ∗ ( t − τ i ) , i = 0 , 1 , … , m ,
the nonlinear system (2) can be rewritten in the form
x ˙ ( t ) = f x t + z t ∗ = L ( x t ) + g ( x t ) , y ( t ) = C ( x t ) ; x ( θ ) = φ ( θ ) = ϕ ( θ ) − z ∗ ( θ ) , θ ∈ [ − τ , 0 ] ,
where f : C → R n , and g : C → R n are nonlinear operators, and C : C → R n and L : C → R n are linear operator, all properly defined. Here, L ( · ) is called the nominal system of the nonlinear system (2) and this is of the form
L ( x t ) = ∑ i = 0 m A i x ( t − τ i ) , and C ( x t ) = ∑ i = 0 m C i x ( t − τ i ) ,
with A i ∈ R n × n and C i ∈ R l × n .
Remark 1. 
It is well-known that just as (2) was taken to (4), (3) can be used to take (4) to (2).
Theorem 1. 
[33] Consider the system given in (2) and let u , v , w : R ¯ + → R ¯ + be continuous nondecreasing functions, where additionally u ( s ) and v ( s ) are positive for s > 0 , and u ( 0 ) = v ( 0 ) = 0 . If there exists a continuous differentiable functional V : R + × C → R such that
  • u ( | | φ ( 0 ) | | ) ≤ V ( t , φ ) ≤ v ( | | φ | | τ ) , and
  • V ˙ ( t , φ ) ≤ − w ( | | φ ( 0 ) | | ) ,
then the trivial solution of (2) is uniformly stable. If w ( s ) > 0 for s > 0 , then it is uniformly asymptotically stable. If, in addition, lim s → ∞ u ( s ) = ∞ , then it is globally uniformly asymptotically stable.
Theorem 2. 
[34] Consider system given in (2), the trivial solution is exponential stable if there exist positive constants α 1 , α 2 and σ; and a functional V ( t , φ ) such that satisfies the following two conditions:
  • α 1 | | φ ( 0 ) | | 2 ≤ V ( t , φ ) ≤ α 2 | | φ | | τ 2 , t ≥ 0 ;
  • V ˙ ( t , x t ) + 2 σ V ( t , x t ) ≤ 0 , t ≥ 0 .

3.2. Luenberger-Type State Observer for Nonlinear Time-Delay Systems

Consider a system of the form (4)-(5):
x ˙ ( t ) = ∑ i = 0 m A i x ( t − τ i ) + g ( x t ) , y ( t ) = ∑ i = 0 m C i x ( t − τ i ) ; x ( θ ) = φ ( θ ) , θ ∈ [ − τ , 0 ] .
Thus, the dynamic Luenberger-type state observer of the system (6) is proposed as
x ^ ˙ ( t ) = ∑ i = 0 m A i x ^ ( t − τ i ) + ∑ i = 0 m L i y ( t ) − y ^ ( t ) + g ( x ^ t ) ,
where L i ∈ R n × l , y ^ ( t ) = ∑ i = 0 m C i x ^ ( t − τ i ) . Defining the observation error by e ( t ) = x ( t ) − x ^ ( t ) and using the equations (6) and (7), the error dynamics can be expressed as
e ˙ ( t ) = ∑ i = 0 m A i − L i C i e ( t − τ i ) + η ( x t , x ^ t ) .
Here η ( x t , x ^ t ) = g ( x t ) − g ( x ^ t ) is such that
| | η ( x t , x ^ t ) | | ≤ M | | e t | | τ , M > 0 .
Remark 2. 
Due to the previous term η ( · ) , the uniformly exponentially convergent of the system response (8) cannot be guaranteed. However, the practical stability is refereed as uniformly exponentially convergent of the system response (8) to a ball B μ with radius μ > 0 [35].
Next, sufficient conditions are proposed to guarantee practical stability on (8).
Proposition 1. 
If there exits 0 < σ ∈ R , R 0 , R i ∈ R n × l , 0 < P , 0 < Q i ∈ R n × n , with i = 1 , … , m ; such that the following linear matrix inequality (LMI)
M ( P , Q 1 , … , Q m , R 0 , … , R m ) + 2 σ N ( P ) < 0 ,
where
N ( P ) = diag P , 0 n , … , 0 n ∈ R n ( m + 1 ) × ( m + 1 ) n , M ( P , Q 1 , … , Q m , R 0 , … , R m ) = diag P + ∑ i = 1 m Q i , − e − 2 σ τ 1 Q 1 , … , − e − 2 σ τ m Q m + P Λ − Γ T Υ + Υ T P Λ − Γ ∈ R n ( m + 1 ) × ( m + 1 ) n .
with Λ = A 0 A 1 … A m ∈ R n × ( m + 1 ) n , Γ = R 0 C 0 R 1 C 1 … R m C m ∈ R n × ( m + 1 ) n , Υ = I n 0 n … 0 n ∈ R n × ( m + 1 ) n , I n ∈ R n × n identity matrix and 0 n ∈ R n × n zero matrix. Then, the solution of the observation error (8) satisfies the following exponential decay
| | e ( t , φ ) | | ≤ α 2 α 1 | | φ | | τ − μ e − σ t + μ , ∀ t ≥ 0 .
Furthermore
| | e ( t , φ ) | | ≤ μ , ∀ t ≥ T ( μ , φ ) ,
where μ = γ α 3 M σ α 1 , with α 3 = | | P | | : = λ m a x ( P ) is the maximum eigenvalue of P, and T ( μ , ϕ ) = 1 σ ln α 2 α 1 | | φ | | τ − μ . The observer gains in (21) are L i = P − 1 R i ∈ R n × l , i = 0 , … , m .
Proof. 
Consider the following candidate Lyapunov-Krasovskii functional [36]:
v ( e t ) = e T ( t ) P e ( t ) + ∑ i = 1 m ∫ − τ i 0 e T ( t + θ ) e 2 σ θ Q i e ( t + θ ) d θ .
Note that
α 1 | | e ( t ) | | 2 ≤ v ( e t ) ≤ α 2 | | e t | | τ 2 ,
where α 1 = λ m i n ( P ) is the minimum eigenvalue of P, and α 2 = λ m a x ( P ) + ∑ i = 1 m τ i λ m a x ( Q i ) . Thus, the time derivative of the functional (12) along the trajectories of system (8) is
d d t v ( e t ) = 2 e T ( t ) P e ˙ ( t ) + ∑ i = 1 m e T ( t ) Q i e ( t ) − ∑ i = 1 m e T ( t − τ i ) e − 2 σ τ i Q i e ( t − τ i ) − 2 σ ∑ i = 1 m ∫ − τ i 0 e T ( t + θ ) e 2 σ θ Q i e ( t + θ ) d θ .
Using (8), notice that
2 e T ( t ) P e ˙ ( t ) = 2 e T ( t ) P ∑ i = 0 m A i − L i C i e ( t − τ i ) + η ( x ( t ) , x ^ t ) = ε m ( t ) P Λ − Γ T Υ + Υ T P Λ − Γ ε m T ( t ) + 2 e T ( t ) P η ( x t , x ^ t ) ,
where ε m ( t ) = [ e ( t ) e ( t − τ 1 ) … e ( t − τ m ) ] and R i = P L i , i = 1 , … , m . Therefore, the observer gain are L i = P − 1 R i , i = 1 , … , m . While, if | | e t | | τ < γ by (9) we get
2 e T ( t ) P η ( x t , x ^ t ) ≤ 2 | | e ( t ) | | | | P | | | | η ( x t , x ^ t ) | | ≤ 2 M | | e ( t ) | | | | P | | | | e t | | τ ≤ 2 γ α 3 M | | e ( t ) | | = O ( | | e ( t ) | | τ ) .
Note that, O ( | | e t | | τ ) | | e t | | τ approaches zero as | | e t | | τ approaches zero. However, using (13) the above equation also satisfies that
O ( | | e ( t ) | | ) = 2 γ α 3 M | | e ( t ) | | ≤ 2 γ α 3 M α 1 v ( e t ) .
Thus, substituting (12), (15) and (16) in (14) we have that
d d t v ( e t ) + 2 σ v ( e t ) − 2 γ α 3 M α 1 v ( e t ) ≤ ε m ( t ) M ( P , Q 1 , … , Q m , R 0 , … , R m ) + 2 σ N ( P ) ε m T ( t ) .
If (10) holds, then
d d t v ( e t ) + 2 σ v ( e t ) − 2 γ α 3 M α 1 v ( e t ) < 0 .
Now, if both sides of the above equation are multiplied by e 2 σ θ , then it can be rewritten as
∂ ∂ θ e 2 σ θ v ( e θ ) ≤ 2 γ α 3 M e σ θ α 1 e 2 σ θ v ( e θ ) .
Thus, integrating from 0 to t gives
∫ 0 t ∂ ∂ θ e 2 σ θ v ( e θ ) e 2 σ θ v ( e θ ) d θ ≤ ∫ 0 t 2 γ α 3 M e σ θ α 1 d θ ⇒ e 2 σ t v ( e t ) − v ( φ ) ≤ 2 γ α 3 M 2 σ α 1 e σ t − 1 .
Therefore
v ( e t ) ≤ γ α 3 M σ α 1 1 − e − σ t + e − σ t v ( φ ) .
Applying the property (13) to the previous inequality we have that
| | e ( t , φ ) | | ≤ v ( e t ) ≤ γ α 3 M σ α 1 1 − e − σ t + e − σ t α 2 α 1 | | φ | | τ ≤ α 2 α 1 | | φ | | τ − γ α 3 M σ α 1 e − σ t + γ α 3 M σ α 1 , ∀ t > 0 .
Further, | | e ( t , φ ) | | converges to the limit μ = γ α 3 M σ α 1 as t tends to infinity. Note that
| | e ( t , φ ) | | ≤ α 2 α 1 | | φ | | τ − μ e − σ t + μ ≤ μ ⟺ t : = T ( μ , φ ) ≥ 1 σ ln α 2 α 1 | | φ | | τ − μ .
□

4. Compartmental Model and Its State Observer

In this section, a SIR epidemiological model with time-delays is proposed for the study of infectious diseases. In addition, because sometimes some population compartments are not available, a state observer is presented for their estimate.
Since March 12, 2020, the World Health Organization (WHO) has declared the infectious disease COVID-19 a pandemic [37]. Because this disease, caused by the SARS-CoV-2 virus, spreads rapidly, it caused severe collapses in various sectors of the population, especially in the hospital, public, and private health sectors. There were effects on the supply of imported inputs as a consequence of the global measures to combat the pandemic [38,39]. This pandemic continues today, in addition to the fact that the SARS-CoV-2 virus is constantly mutating, changing the disease patterns due to new variant strains. The latter present different characteristics, in aspects such as: the prevalence time of the disease in people, the amount of viral load, the effectiveness of the virus to infect cells, the ease of propagation, the efficacy of vaccines, among others, [40]. Therefore, it is important to understand the dynamics of COVID-19 as it evolves.

4.1. SIR Type Compartmental Model with Time-Delays

Model (1) has set the standard for the study of numerous infectious diseases. In order to be used for the COVID-19 pandemic, this section begins with the proposal of a model with time-delays, where it is considered that a part of the recovered population becomes susceptible again after a period of time after their recovery. In addition, three dead-times are incorporated due to the exchange of individuals between the population compartments:
S ˙ ( t ) = − β S ( t ) I t − τ 3 + α R ( t − τ 2 ) , I ˙ ( t ) = β S ( t ) I t − τ 3 − γ I t − τ 1 , R ˙ ( t ) = γ I t − τ 1 − α R ( t − τ 2 ) ,
where α is the rate of loss of immunity and becoming susceptible.
This model is proposed because the current COVID-19 pandemic has shown that individuals who pass from the infected to recovered compartments do not acquire total or permanent immunity, that is, they can be reinfected by another variant of the disease after a time after having recovered. Thus, α R ( t − τ 2 ) represents the individuals that in a dead-time τ 2 lose immunity, so they become susceptible again. While γ I t − τ 1 is the fraction of the infectious that in a dead-time τ 1 cease to be infectious and therefore they will recover. Finally, β S ( t ) I t − τ 3 are all those susceptible individuals who became infected and after a dead-time τ 3 start to become infectious.
On the other hand, the effective reproduction number R e can define the threshold behavior of epidemiological models of the form (17): if R e < 1 the epidemic event will tend to disappear quickly, while if R e > 1 the epidemic event is expected to continue. Here, the higher the value of R e , the more difficult it is to control an epidemic [41]. From model (17), it can be seen that d d t I ( t ) > 0 if and only if β S ( t ) I t − τ 3 − γ I t − τ 1 > 0 , or equivalently if β S ( t ) γ > I t − τ 1 I t − τ 3 , or β S ( t ) γ I t − τ 3 I t − τ 1 > 1 . Therefore, an epidemic/pandemic continues if R e = β S 0 γ I t − τ 3 I t − τ 1 > 1 , where S 0 is the initial condition of the susceptible population. Note that β S 0 γ = R 0 is the basic reproductive number of the classical SIR model (1), which is obtained as follows:
I ˙ ( t ) = ( β S 0 − γ ) I ( t ) ⇒ I ( t ) = I 0 e ( β S 0 − γ ) t = I 0 e γ β S 0 γ − 1 t = I 0 e γ R 0 − 1 t .
Thus, an infectious disease can be classified as an epidemic if R e > 1 , this will be extinguished when R e < 1 and this will remain constant if R e = 1 , see [42].

4.2. Compartmental Model Transformation

Next, a change of variable is proposed to obtain a new model from (17) with a nominal part and a non-linear part which will serve to a large extent for stability analysis.
Let us consider the following change of variable
x 1 ( t ) = S ( t ) − S ∗ , x 2 ( t ) = I ( t ) − I ∗ and x 3 ( t ) = R ( t ) − R ∗ ,
where S ∗ = γ β , I ∗ = α , and R ∗ = γ constitute the equilibrium point of (17). Then, by defining x T ( t ) = x 1 ( t ) x 2 ( t ) x 3 ( t ) model (17) can be rewritten in form (6) as follows
x ˙ ( t ) = ∑ i = 0 3 A i x ( t − τ i ) + g ( x 1 ( t ) , x 2 ( t − τ 3 ) ) ,
where
A 0 = − α β 0 0 α β 0 0 0 0 0 , A 1 = 0 0 0 0 − γ 0 0 γ 0 , A 2 = 0 0 α 0 0 0 0 0 − α , A 3 = 0 − γ 0 0 γ 0 0 0 0 , and g ( x 1 ( t ) , x 2 ( t − τ 3 ) ) = − β x 1 ( t ) x 2 ( t − τ 3 ) β x 1 ( t ) x 2 ( t − τ 3 ) 0 .
Remark 3. 
Since only the infectious population I ( t ) is available as an output from the SIR system, thus y ( t ) = I ( t ) − I ∗ . Note also that the entire history of the population is available, then y ( t ) = I ( t − τ i ) . Considering C i = 0 1 0 , i = 0 , 1 , 2 , 3 , the output vector can be expressed as
y ( t ) = C 0 x ( t ) + C 1 x ( t − τ 1 ) + C 2 x ( t − τ 2 ) + C 3 x ( t − τ 3 ) .

Observer Design and Convergence Analysis

Following (7), the state observer for (19)–(20) is of the form
x ^ ˙ ( t ) = ∑ i = 0 3 A i x ^ ( t − τ i ) + ∑ i = 0 3 L i C i x ( t − τ i ) − C i x ^ ( t − τ i ) + g ( x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) ,
where x ^ T ( t ) = x ^ 1 ( t ) x ^ 2 ( t ) x ^ 3 ( t ) , L i T = L i 1 L i 2 L i 3 and C i = C i 1 C i 2 C i 3 . Thus, by (8) the dynamics of the observation error of (19) and (21) is
e ˙ ( t ) = ∑ i = 0 3 A i − L i C i e ( t − τ i ) + η ( x 1 ( t ) , x 2 ( t − τ 3 ) , x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) ,
with η ( x 1 ( t ) , x 2 ( t − τ 3 ) , x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) = g ( x 1 ( t ) , x 2 ( t − τ 3 ) ) − g ( x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) . Now, by Proposition 1, the observation error (22) satisfies
v ˙ ( e t ) + 2 σ v ( e t ) ≤ ε 3 ( t ) M ( P , Q 1 , Q 2 , Q 3 , R 0 , … , R 3 ) + 2 σ N ( P ) ε 3 T ( t ) + O ( | | e t | | ) ,
where
M ( P , Q 1 , Q 2 , Q 3 , R 0 , … , R 3 ) + 2 σ N ( P ) = Θ 1 , 1 + 2 σ P ( ∗ ) ( ∗ ) ( ∗ ) Θ 2 , 1 Θ 2 , 2 ( ∗ ) ( ∗ ) Θ 3 , 1 0 Θ 3 , 3 ( ∗ ) Θ 4 , 1 0 0 Θ 4 , 4 .
Here, Θ 1 , 1 = P A 0 + A 0 T P − R 0 C 0 − C 0 T R 0 T + Q 1 + Q 2 + Q 3 , Θ 2 , 1 = A 1 T P − C 1 T R 1 T , Θ 3 , 1 = A 2 T P − C 2 T R 2 T , Θ 4 , 1 = A 3 T P − C 3 T R 3 T , Θ 2 , 2 = − e − 2 σ τ 1 Q 1 , Θ 3 , 3 = − e − 2 σ τ 2 Q 2 , Θ 4 , 4 = − e − 2 σ τ 3 Q 3 and ( ∗ ) denote the transpose of the symmetric elements. On the other hand, note that
| | η ( x 1 ( t ) , x 2 ( t − τ 3 ) , x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) | | = | | g ( x 1 ( t ) , x 2 ( t − τ 3 ) ) − g ( x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) | | = 4 β 2 | x 1 ( t ) e 2 ( t − τ 3 ) + x ^ 2 ( t − τ 3 ) e 1 ( t ) | ,
where e 1 ( t ) = x 1 ( t ) − x ^ 1 ( t ) and e 2 ( t − τ 3 ) = x 2 ( t − τ 3 ) − x ^ 2 ( t − τ 3 ) . Now assuming that the populations are bounded, we observe that
| | η ( x 1 ( t ) , x 2 ( t − τ 3 ) , x ^ 1 ( t ) , x ^ 2 ( t − τ 3 ) ) | | ≤ 4 β 2 m | e 2 ( t − τ 3 ) + e 1 ( t ) | ≤ 4 β 2 m | | e t | | = M | | e t | | ,
with m = max { x 1 ( t ) , x ^ 2 ( t − τ 3 ) } , and M = 4 β 2 m . As mentioned above, the total population N ( t ) = S ( t ) + I ( t ) + R ( t ) is considered constant and this is normalized, thus | x i ( t ) | ≤ 1 = m , i = 1 , 2 , 3 , and | | e ( t ) | | < γ = 1 , therefore by (16)
O ( | | e ( t ) | | ) = 2 γ α 3 M α 1 v ( e t ) = 8 α 3 β 2 α 1 v ( e t ) .
Proposition 2. 
If there exist σ ∈ R + , vectors R 0 , R i ∈ R 3 × 1 and positive definite matrices P , Q i > 0 for i = 1 , 2 , 3 ; such that (24) is a negative definite matrix, then the observation error (22) is exponentially convergent to a ball B μ with radius μ > 0 .
Proof. 
The result follows from the Proposition 1. □
Now, we express the equivalent observer in original coordinates, to this end from (21) we have that
x ^ ˙ 1 ( t ) = − α β x ^ 1 ( t ) + α x ^ 3 ( t − τ 2 ) − γ x ^ 2 ( t − τ 3 ) − β x ^ 1 ( t ) x ^ 2 ( t − τ 3 ) + ∑ i = 0 3 ∑ j = 1 3 L i 1 C i j x j ( t − τ i ) − x ^ j ( t − τ i ) , x ^ ˙ 2 ( t ) = α β x ^ 1 ( t ) − γ x ^ 2 ( t − τ 1 ) + γ x ^ 2 ( t − τ 3 ) + β x ^ 1 ( t ) x ^ 2 ( t − τ 3 ) + ∑ i = 0 3 ∑ j = 1 3 L i 2 C i j x j ( t − τ i ) − x ^ j ( t − τ i ) , x ^ ˙ 3 ( t ) = γ x ^ 2 ( t − τ 1 ) − α x ^ 3 ( t − τ 2 ) + ∑ i = 0 3 ∑ j = 1 3 L i 3 C i j x j ( t − τ i ) − x ^ j ( t − τ i ) ,
and following (18) the observer of the model SIR given in (17) takes the form
S ^ ˙ ( t ) = ∑ i = 0 3 L i 1 [ C i 1 S ( t − τ i ) − S ^ ( t − τ i ) + C i 2 I ( t − τ i ) − I ^ ( t − τ i ) + C i 3 R ( t − τ i ) − R ^ ( t − τ i ) ] − β S ^ ( t ) I ^ ( t − τ 3 ) + α R ^ ( t − τ 2 ) ,
I ^ ˙ ( t ) = ∑ i = 0 3 L i 2 [ C i 1 S ( t − τ i ) − S ^ ( t − τ i ) + C i 2 I ( t − τ i ) − I ^ ( t − τ i ) + C i 3 R ( t − τ i ) − R ^ ( t − τ i ) ] + β S ^ ( t ) I ^ ( t − τ 3 ) − γ I ^ ( t − τ 1 ) ,
R ^ ˙ ( t ) = ∑ i = 0 3 L i 3 [ C i 1 S ( t − τ i ) − S ^ ( t − τ i ) + C i 2 I ( t − τ i ) − I ^ ( t − τ i ) + C i 3 R ( t − τ i ) − R ^ ( t − τ i ) ] + γ I ^ t − τ 1 − α R ^ ( t − τ 2 ) .

5. Implementation of Results to the Population of Mexico

In this section, the SIR type compartmental model with time-delays proposed in (17) and the Luenberger-type state observer given in (26)–(28) are used to estimate the compartmental populations of Susceptible  S ( t ) and Recovered R ( t ) not reported by the WHO. Here, the observer only considers data of cases confirmed of Infectious I ( t ) in Mexico, reported by [43]. Matlab® software is used for these simulations.

5.1. Implementation Description

To estimate S ( t ) and R ( t ) the following assumptions are made:
A1. 
Compartmental populations are considered closed and normalized, that is, S ( t ) + R ( t ) + I ( t ) = 1 .
A2. 
Only the population of infectious I ( t ) is available. The real data is denoted by I r ( t ) .
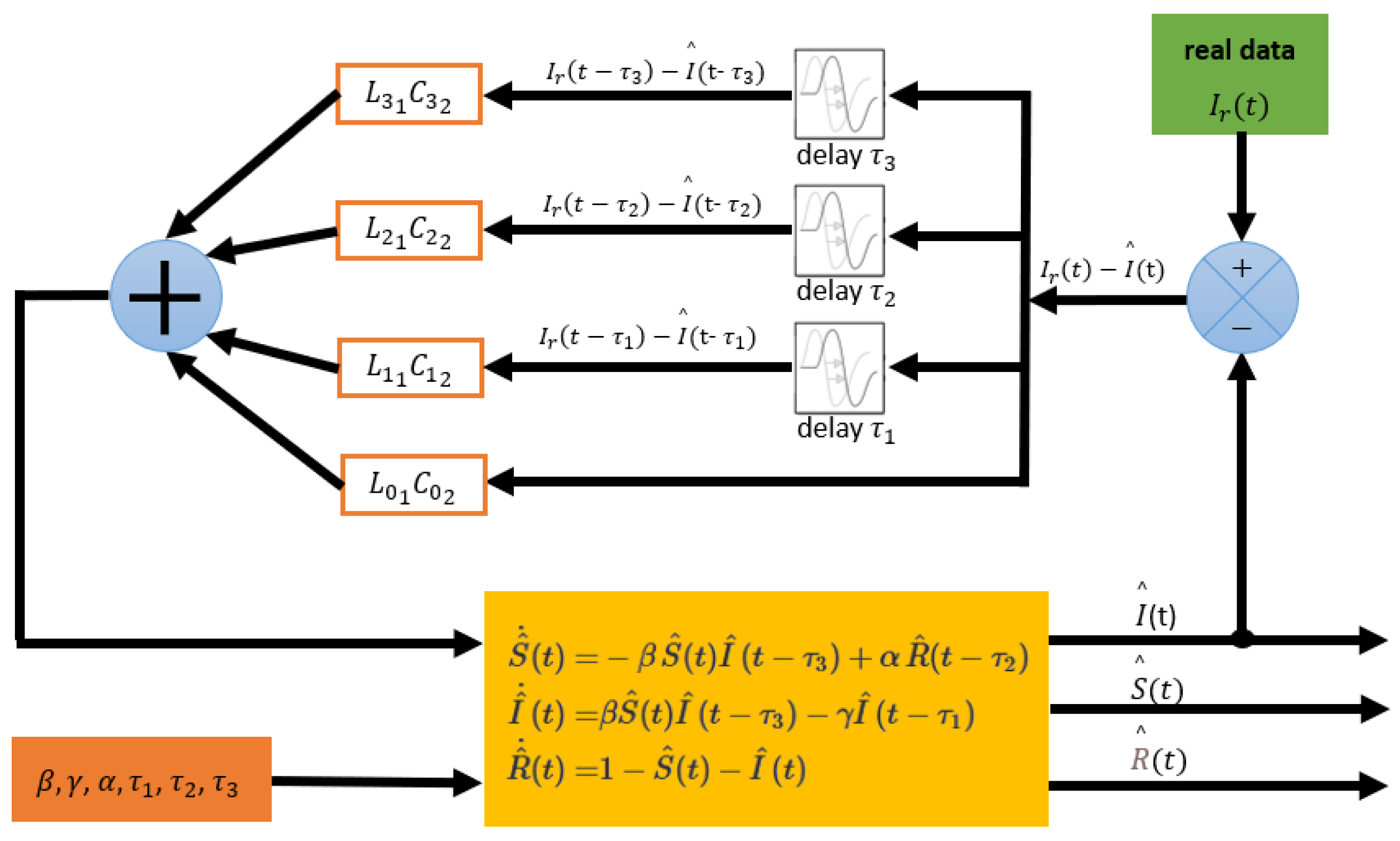
By A2, the state observer (26)–(28) can be rewritten as:
S ^ ˙ ( t ) = − β S ^ ( t ) I ^ ( t − τ 3 ) + α R ^ ( t − τ 2 ) + ∑ i = 0 3 L i 1 C i 2 I ( t − τ i ) − I ^ ( t − τ i ) , I ^ ˙ ( t ) = β S ^ ( t ) I ^ ( t − τ 3 ) − γ I ^ ( t − τ 1 ) + ∑ i = 0 3 L i 2 C i 2 I ( t − τ i ) − I ^ ( t − τ i ) , R ^ ˙ ( t ) = γ I ^ t − τ 1 − α R ^ ( t − τ 2 ) + ∑ i = 0 3 L i 3 C i 2 I ( t − τ i ) − I ^ ( t − τ i ) .
By A1, the third equation of (29) can be replaced by R ( t ) =1- S ^ ( t ) - I ^ ( t ) . Next, the model (17) and the observer (29) are implemented in two processes: tuning of model parameters and of estimation of compartmental populations, which are described below.

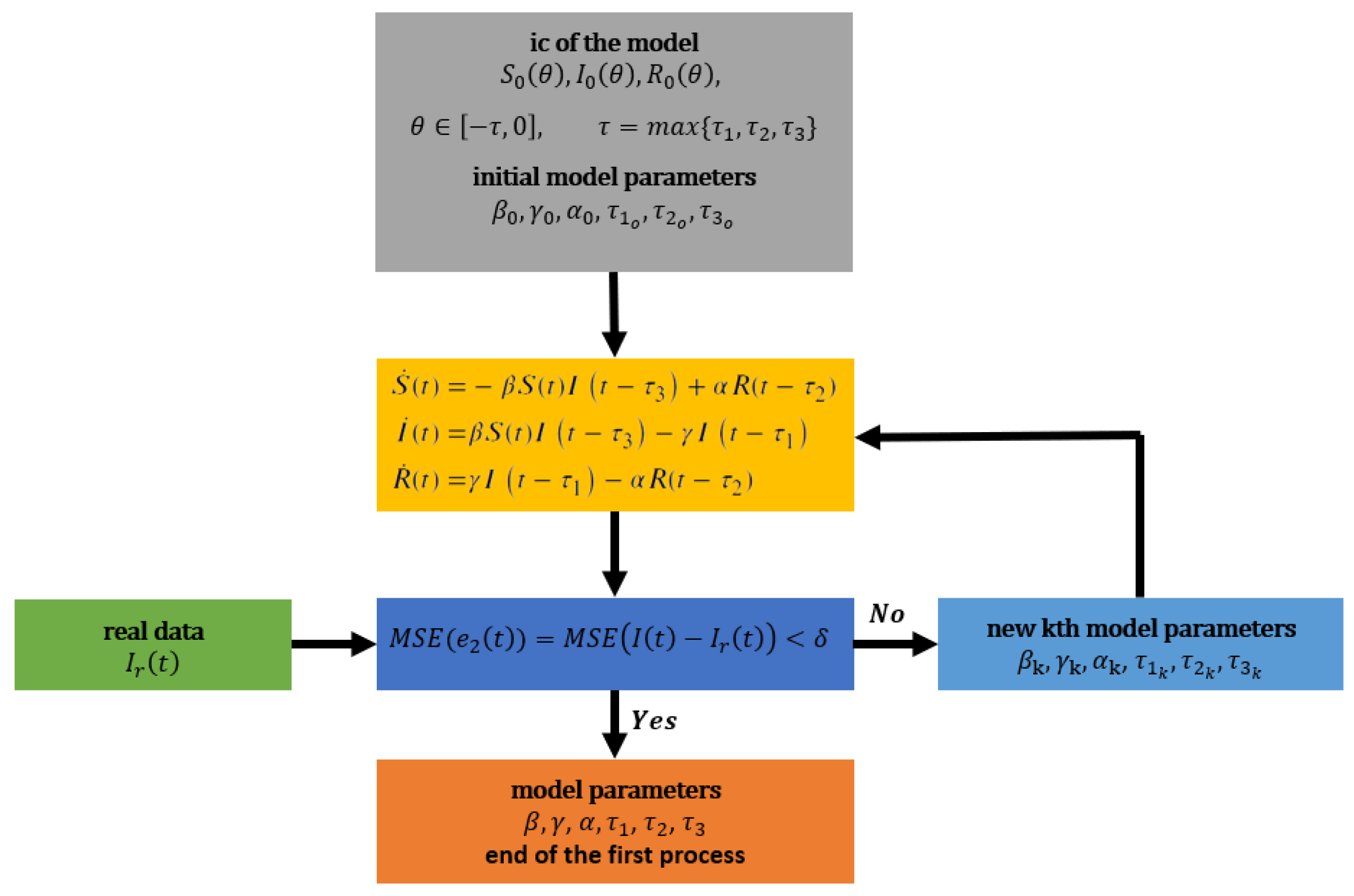
5.1.1. First Process: Tuning of Model Parameters

Assume A1. For given initial conditions α 0 , β 0 , γ 0 , ∈ R + , and S 0 ( θ ) , I 0 ( θ ) , R 0 ( θ ) ∈ C , the epidemiological model (17) is used to tune the parameters α , β , γ , τ 1 , τ 2 , τ 3 ∈ R + that best fit the curve of I r ( t ) reported by the WHO in a 55-day time window which is indeed the real permissible range for each parameter. In this case and without loss of generality, the 55-day time window was selected according to its variability/fruition in the curve/data and the greatest impact it had on the population of Mexico. This is only an illustrative example and can be changed according to the user’s preferences. This process is shown Figure 1 and detailed below:
  • This process begins by proposing initial conditions (ic) for the populations S 0 ( θ ) , R 0 ( θ ) , I 0 ( θ ) ∈ C , with I 0 ( θ ) close to I r ( θ ) . Also, knowing a permissible range of variation of each parameter, an initial tuning of the model parameters α 0 , β 0 , γ 0 , τ 1 o , τ 2 o , τ 3 o ∈ R + is proposed.
  • The response of the model (17) is obtained by using the initial conditions and the model parameters.
  • Given the real data I r ( t ) , the Mean Squared Error (MSE) is calculated between I ( t ) and I r ( t ) , i.e., MSE ( e 2 ) = MSE ( I ( t ) − I r ( t ) ) .
  • Given a δ > 0 , if MSE ( e 2 ) < δ , then the parameters α = α k , β = β k , γ = γ k , τ 1 = τ 1 k , τ 2 = τ 2 k , τ 3 = τ 3 k , for some k = 0 , 1 , … , are used for the second process and the first process ends; otherwise, new k t h model parameters are proposed within the allowed ranges and return to step (2).

5.1.2. Second Process: Estimation of Compartmental Populations

Next, the parameters α , β , γ , τ 1 , τ 2 , τ 3 ∈ R + obtained in the first process are used on the observer given in (29) to estimate the compartmental populations S ( t ) and R ( t ) not reported by the WHO. Here, it is assumed that only I ( t ) is available, that is, y ^ ( t ) = ∑ i = 0 3 C i 2 I ( t − τ i ) . Also the same real data I r ( t ) from the first process is utilized. In Figure 2 this second process is schematized.

5.2. Application of Results via Simulation

In this subsection, what was previously explained on the first and second processes is applied, for which we use the solver Sedumi [44] in Matlab® to determine feasibility of the LMI (24). By this and Proposition 2, it is possible to guarantee an exponential decay in the observation error e ( t ) , in addition to obtaining the observer gains L i , i = 0 , … , 3 . Finally, to corroborate the efficiency of the procedure and the obtained results, a simulation is performed using Simulink in Matlab®.

5.2.1. LMI Feasibility

In the first process, we consider: the rate of immunity loss α = 1 , the infection rate β = 0.0109 , the recovery rate γ = 0.085 , the dead-time by recovery τ 1 = 3 , the dead-time by immunity loss τ 2 = 5 and the dead-time by incubation τ 3 = 6 .
Let C i = 0 1 , i = 0 , 1 , 2 , 3 . Then, the LMI conditions (24), with the appropriate dimensions, is feasible for σ = 0.003 ,
P = 57.7477 − 20.8676 − 20.8676 36.0528 , Q 1 = 0.1890 − 0.0028 − 0.0028 0.2022 , Q 2 = 0.1206 − 0.0028 − 0.0028 0.1170 and Q 3 = 0.1207 − 0.0029 − 0.0029 0.1173 ,
as well as
R 0 = 5.8150 34.8704 , R 1 = 1.7490 − 3.2965 , R 2 = − 0.0198 − 0.2073 and R 3 = − 6.7004 4.6352 .
Thus, by Proposition 2 the variables of the observation error e 2 ( t ) = I r ( t ) − I ^ ( t ) and e 3 ( t ) = R ( t ) − R ^ ( t ) satisfy the exponential decay given in (11), with μ = 0.4771 and T = 770.1474 . Even more, the observer gains obtained are
L 0 = 0.5693 1.2967 , L 1 = − 0.0035 − 0.0935 , L 2 = − 0.0031 − 0.0075 and L 3 = − 0.0880 0.0776 .

5.2.2. Observer Simulation

For simulation purposes, consider that N = 350000 is the total population, of which S 0 = 1 − I 0 − R 0 , where I 0 = 69025 / N and R 0 = 0 are the normalized initial conditions of the model, corresponding to the Susceptible, Infectious and Recovered population, respectively. The initial conditions of the observer are S ^ 0 = 1 − I ^ 0 − R ^ 0 , I ^ 0 = 0.225 and R ^ 0 = 0.05 . Besides the model parameters and the observer gains are given in (30). Next, simulations carried out in Simulink in Matlab® are presented.
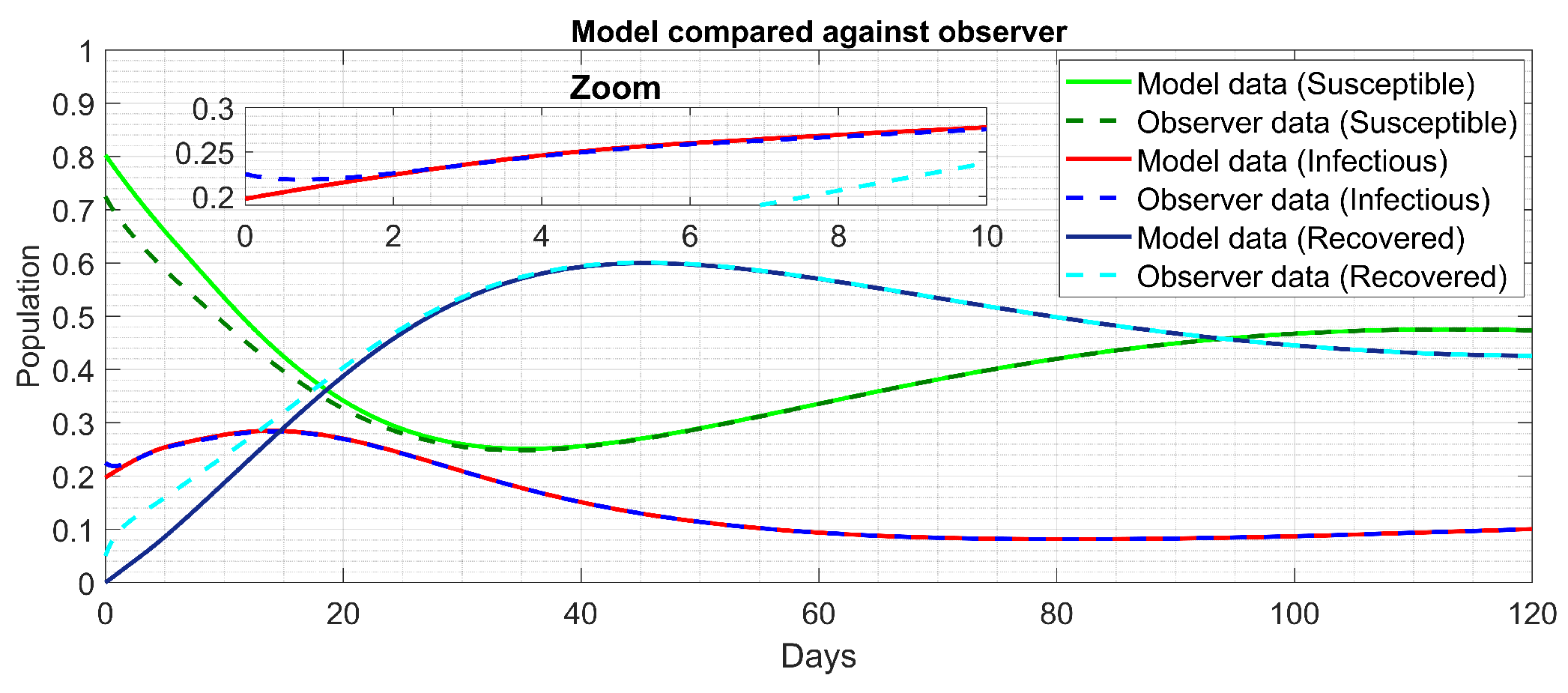
The simulation between the compartmental model (17) and the state observer (29) using a solution step size of t = 0.01 Day is shown in Figure 3. Here, given δ = 0.5 × 10 − 2 , we have that the MSE ( e 1 ( t ) ) = MSE ( S ( t ) − S ^ ( t ) ) = 9.524 × 10 − 2 , MSE ( e 2 ( t ) ) = MSE ( I ( t ) − I ^ ( t ) ) = 0.443 × 10 − 2 and MSE ( e 3 ( t ) ) = MSE ( R ( t ) − R ^ ( t ) ) = 9.601 × 10 − 2 in the observed dynamics of Susceptible, Infectious and Recovered, respectively.
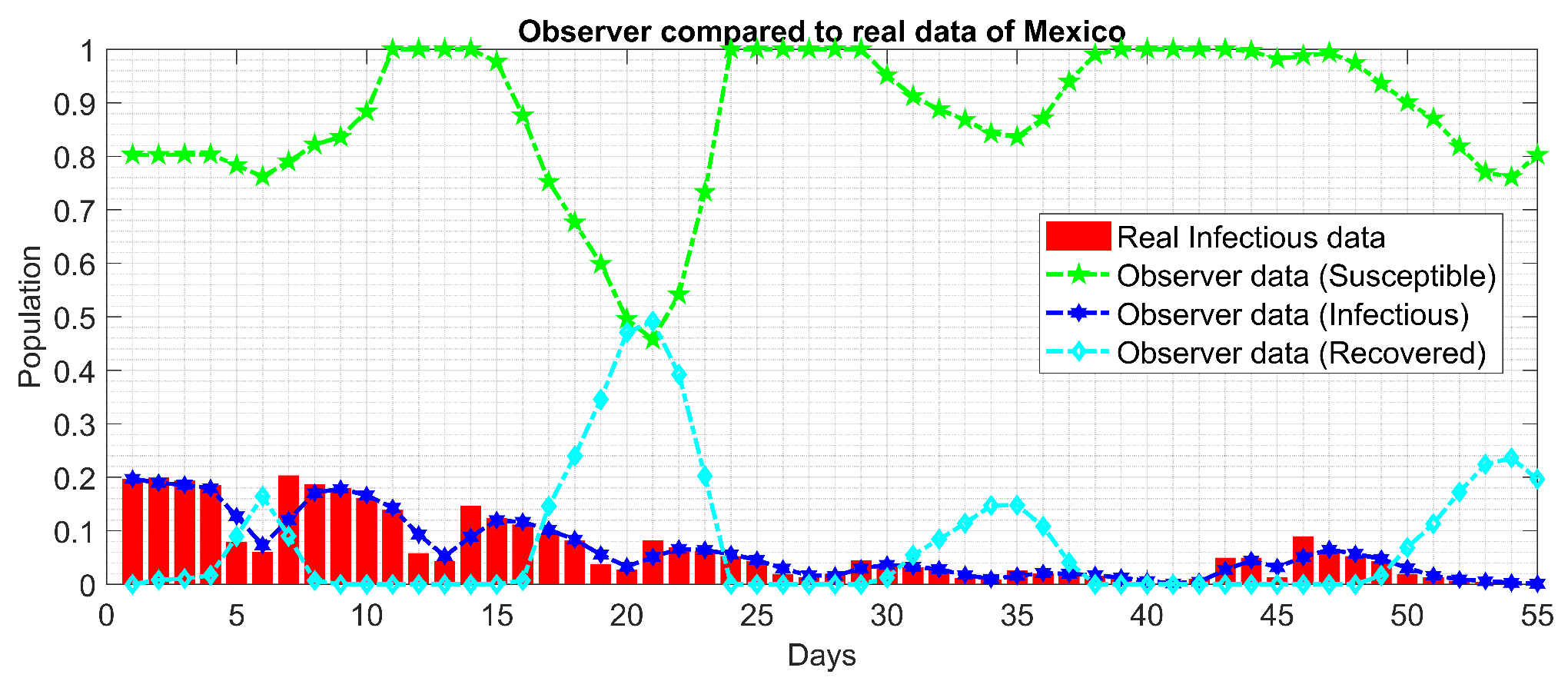
Now, the observer’s behavior is analyzed using real data of the Infectious population I r ( t ) recorded by the WHO of the 13 January to March 8 of 2022 for the COVID-19 pandemic. This period was a time window with the greatest impact on the population of Mexico.
Estimates S ^ ( t ) and R ^ ( t ) of the compartmental populations of Susceptible and Recovered, respectively, not reported by the WHO are presented in Figure 4. Here, the solution step size used is t = 1 Day and we obtain a MSE ( e 2 ( t ) ) = MSE ( I r ( t ) − I ^ ( t ) ) = 1.0203 × 10 − 2 in the dynamic of the Infectious error.
Remark 4. 
Note that the nonlinearity η ( x t , x ^ t ) of the observation error (22) implies that an asymptotic convergence of e ( t ) to zero cannot be guaranteed, but a convergence to a neighborhood μ > 0 at time T can be ensured. Unfortunately this neighborhood μ ∈ [ 0 , 1 ] usually is very conservative and for normalized data this does not seem to make sense. However, although μ = 0.4771 and T = 770.1474 days it seems that these do not affect convergence of the observation error e ( t ) . Since in Figure 4 it can be seen that the variables of I ^ ( t ) converge to the data I r ( t ) , with a MSE ( e 2 ) = 1.0203 × 10 − 2 .

6. Conclusions

In this paper, an epidemiological model of the SIR type and a Luenberger-type observer to estimate compartmental populations not reported by the WHO are presented. The model proposed is a nonlinear system with three time-delays, which considers the dead-times it takes for an individual to move from one compartmental population to another and that recovered individuals may again be susceptible to the disease. This model is used to determine parameters such as the β infection rate, the γ recovery rate and the α rate of immunity loss; and for the design of a Luenberger-type state observer with time-delays. To guarantee the estimation of the observer, a convergence analysis is presented using Lyapunov-Krasovskii functionals to ensure that the observation error decreases with an exponential decay σ > 0 . This observer is employed to estimate the compartmental populations of Susceptible S ( t ) and Recovered R ( t ) from only the availability of the real data I r ( t ) , Infectious compartmental population reported by WHO in a 55-day time window with the highest impact on the population of Mexico. The results shown suggest that the proposed mathematical model and observer are a suggestive alternative to use to estimate missing compartmental populations.

Author Contributions

Conceptualization, R.V.-S. and G.O.-O.; methodology, R.V.-S. and G.O.-O.; software, J.A.H.-A.; validation, M.R.-N.; formal analysis, R.V.-S. and G.O.-O.; investigation, R.V.-S., J.A.H.-A., G.O.-O. and M.R.-N.; resources, M.R.-N.; data curation, J.A.H.-A.; writing—original draft preparation, R.V.-S.; writing—review and editing, R.V.-S.; visualization, G.O.-O.; supervision, R.V.-S., J.A.H.-A., G.O.-O. and M.R.-N.; project administration, M.R.-N.; funding acquisition, M.R.-N. All authors have read and agreed to the published version of the manuscript.

Funding

The authors gratefully acknowledge the financial support from Universidad Iberoamericana Ciudad de Mexico, through the research funds DINVP-025.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

  1. Casals, M.; Guzmán, K.; Caylà, J.A. Modelos matemáticos utilizados en el estudio de las enfermedades transmisibles. Revista española de salud pública 2009, 83, 689–695. [Google Scholar] [CrossRef] [PubMed]
  2. Duncan-Jones, R.P. The impact of the Antonine plague. Journal of Roman Archaeology 1996, 9, 108–136. [Google Scholar] [CrossRef]
  3. Sarris, P. Viewpoint new approaches to the ‘Plague of Justinian’. Past & present 2022, 254, 315–346. [Google Scholar]
  4. Gottfried, R.S. Black death; Simon and Schuster, 2010.
  5. Berche, P. The enigma of the 1889 Russian flu pandemic: A coronavirus? La Presse Médicale 2022, 51, 104111. [Google Scholar] [CrossRef]
  6. Kaur, H.; Garg, S.; Joshi, H.; Ayaz, S.; Sharma, S.; Bhandari, M. A review: Epidemics and pandemics in human history. International Journal of Pharma Research and Health Sciences 2020, 8, 3139–3142. [Google Scholar] [CrossRef]
  7. Trilla, A.; Trilla, G.; Daer, C. The 1918 “spanish flu” in spain. Clinical infectious diseases 2008, 47, 668–673. [Google Scholar] [CrossRef]
  8. Jackson, C. History lessons: the Asian flu pandemic. British journal of general practice 2009, 59, 622–623. [Google Scholar] [CrossRef]
  9. Sharp, P.M.; Hahn, B.H. Origins of HIV and the AIDS pandemic. Cold Spring Harbor Perspectives in Medicine: 2011, 1. [Google Scholar] [CrossRef]
  10. Nations, U. Excess deaths associated with the COVID-19 pandemic in 2020 and 2021, 2022. [Web; accessed on 01-11-2022].
  11. Ávila Pozos, R.; Rangel Zuñiga, D. Historical review on mathematical epidemiology. Pädi Boletín Científico de Ciencias Básicas e Ingenierías del ICBI 2017, 4. [Google Scholar]
  12. Martínez-Guerra, R.; Cruz-Ancona, C.D. Algorithms of estimation for nonlinear systems; Springer, 2017.
  13. Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. Journal of Basic Engineering 1961. [Google Scholar] [CrossRef]
  14. Luenberger, D.G. Observing the state of a linear system. IEEE transactions on military electronics 1964, 8, 74–80. [Google Scholar] [CrossRef]
  15. Kwakernaak, H. Optimal filtering in linear systems with time delays. IEEE Transactions on Automatic Control 1967, 12, 169–173. [Google Scholar] [CrossRef]
  16. Germani, A.; Manes, C.; Pepe, P. A new approach to state observation of nonlinear systems with delayed output. IEEE Transactions on Automatic Control 2002, 47, 96–101. [Google Scholar] [CrossRef]
  17. Germani, A.; Pepe, P. A state observer for a class of nonlinear systems with multiple discrete and distributed time delays. European Journal of Control 2005, 11, 196–205. [Google Scholar] [CrossRef]
  18. Ciccarella, G.; Dalla Mora, M.; Germani, A. A Luenberger-like observer for nonlinear systems. International Journal of Control 1993, 57, 537–556. [Google Scholar] [CrossRef]
  19. Cacace, F.; Germani, A.; Manes, C. An observer for a class of nonlinear systems with time varying observation delay. Systems & Control Letters 2010, 59, 305–312. [Google Scholar]
  20. Lan, Y.H.; Huang, H.X. Observer-based robust control of time-delay uncertain systems with application to engine idle speed control. International Journal of Dynamical Systems and Differential Equations 2012, 4, 274–285. [Google Scholar] [CrossRef]
  21. Batmani, Y.; Khaloozadeh, H. On the design of observer for nonlinear time-delay systems. Asian Journal of Control 2014, 16, 1191–1201. [Google Scholar] [CrossRef]
  22. Gholami, H.; Binazadeh, T. Observer-based H∞ finite-time controller for time-delay nonlinear one-sided Lipschitz systems with exogenous disturbances. Journal of Vibration and Control 2019, 25, 806–819. [Google Scholar] [CrossRef]
  23. Yang, R.; Zhang, G.; Sun, L. Observer-based finite-time robust control of nonlinear time-delay systems via Hamiltonian function method. International Journal of Control 2021, 94, 3533–3550. [Google Scholar] [CrossRef]
  24. Bliman, P.A.; D’Avila Barros, B. Interval observers for SIR epidemic models subject to uncertain seasonality. Positive Systems: Theory and Applications (POSTA 2016) Rome, Italy, September 14-16, 2016 5 2017, pp. 31–39.
  25. Bliman, P.A.; Efimov, D.; Ushirobira, R. A class of nonlinear adaptive observers for SIR epidemic model. 2018 European Control Conference (ECC). IEEE, 2018, pp. 1–6.
  26. Sano, H.; Wakaiki, M.; Maruyama, H. Backstepping observers for two linearized Kermack–McKendrick models. IFAC-PapersOnLine 2018, 51, 456–461. [Google Scholar] [CrossRef]
  27. Castaños, F.; Mondié, S. Observer-based predictor for a susceptible-infectious-recovered model with delays: An optimal-control case study. International Journal of Robust and Nonlinear Control 2021, 31, 5118–5133. [Google Scholar] [CrossRef]
  28. Kitsos, C.; Besancon, G.; Prieur, C. High-Gain Observer Design for a Class of Quasi-Linear Integro-Differential Hyperbolic Systems—Application to an Epidemic Model. IEEE Transactions on Automatic Control 2021, 67, 292–303. [Google Scholar] [CrossRef]
  29. Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character 1927, 115, 700–721. [Google Scholar]
  30. Özdinç, M.; Senel, K.; Ozturkcan, S.; Akgul, A. Predicting the progress of COVID-19: the case for Turkey. Turkiye Klinikleri Journal of Medical Sciences 2020, 40, 117–119. [Google Scholar] [CrossRef]
  31. Anderson, R.M. Discussion: the Kermack-McKendrick epidemic threshold theorem. Bulletin of mathematical biology 1991, 53, 1–32. [Google Scholar] [CrossRef]
  32. Manrique, F.G.; Agudelo, C.A.; González, V.M.; Gutiérrez, O.; Téllez, C.F.; Herrera, G. Modelo SIR de la pandemia de Covid-19 en Colombia. Revista de Salud Pública 2023, 22, 123–131. [Google Scholar] [CrossRef]
  33. Gu, K.; Chen, J.; Kharitonov, V.L. Stability of time-delay systems; Springer Science & Business Media, 2003.
  34. Kharitonov, V. Time-delay systems: Lyapunov functionals and matrices; Springer Science & Business Media, 2012.
  35. Ghanes, M.; De Leon, J.; Barbot, J.P. Observer design for nonlinear systems under unknown time-varying delays. IEEE Transactions on Automatic Control 2012, 58, 1529–1534. [Google Scholar] [CrossRef]
  36. Mondie, S.; Kharitonov, V.L. Exponential estimates for retarded time-delay systems: an LMI approach. IEEE Transactions on Automatic Control 2005, 50, 268–273. [Google Scholar] [CrossRef]
  37. Huamán-Saavedra, J.J. La pandemia del Covid-19. Revista Médica de Trujillo 2020, 15. [Google Scholar] [CrossRef]
  38. Banxico. Impacto de la Pandemia de COVID-19 en la Actividad Económica Sectorial en México y Estados Unidos. https://www.banxico.org.mx/publicaciones-y-prensa/informes-trimestrales/recuadros/%7BDA917798-4324-FE92-BED8-68E8A67CF09D%7D.pdf, 2021. [Online; accessed 04-Mach-2023].
  39. Dávila-Flores, A.; Valdés-Ibarra, M. México. Costos económicos del cierre de las actividades “no esenciales” por la pandemia Covid-19. Análisis multisectorial y regional con modelos SAM. Economía: teoría y práctica 2020, pp. 15–43.
  40. Martínez, J. COVID-19: LA VARIANTE DELTA DEL SARS-COV-2, UN ENEMIGO DE CUIDADO. https://www.anahuac.mx/mexico/noticias/Variante-Delta-del-SARS-Cov-2, 2022. [Web; accedido el 06-03-2022].
  41. Comincini-Cantillo, E.; Wilches Visbal, J.H.; Saraví, F.D. Factores epidemiológicos R0 y Re durante la COVID-19:?` qué son y en qué difieren? rev. cuid.(Bucaramanga. 2010) 2021, pp. e1393–e1393.
  42. Cumsille, P.; Rojas-Díaz, Ó.; de Espanés, P.M.; Verdugo-Hernández, P. Forecasting COVID-19 Chile’second outbreak by a generalized SIR model with constant time delays and a fitted positivity rate. Mathematics and Computers in Simulation 2022, 193, 1–18. [Google Scholar] [CrossRef] [PubMed]
  43. WHO. Tracking SARS-CoV-2 variants. https://www.who.int/es/activities/tracking-SARS-CoV-2-variants/, 2022. [Web; accessed on 03-06-2022].
  44. YALMIP. SEDUMI. https://yalmip.github.io/solver/sedumi/, 2016. [Web; accedido el 11-07-2023].
Preprints 121930 g001
Figure 1. Flowchart of the first process: tuning of model parameters α , β , γ , τ 1 , τ 2 , τ 3 .
Figure 1. Flowchart of the first process: tuning of model parameters α , β , γ , τ 1 , τ 2 , τ 3 .
Preprints 121930 g001
Preprints 121930 g002
Figure 2. Block diagram of the second process: estimation of compartmental populations S ( t ) and R ( t ) .
Figure 2. Block diagram of the second process: estimation of compartmental populations S ( t ) and R ( t ) .
Preprints 121930 g002
Preprints 121930 g003
Figure 3. Simulation employing the state observer (29) and SIR epidemiological model with three time-delays (17) using a solution step size t = 0.01 Day.
Figure 3. Simulation employing the state observer (29) and SIR epidemiological model with three time-delays (17) using a solution step size t = 0.01 Day.
Preprints 121930 g003
Preprints 121930 g004
Figure 4. Simulation employing the state observer (26)-(28) and real data of I r ( t ) Infectious recorded by the WHO using a solution step size t = 1 Day.
Figure 4. Simulation employing the state observer (26)-(28) and real data of I r ( t ) Infectious recorded by the WHO using a solution step size t = 1 Day.
Preprints 121930 g004
Table 1. Main pandemics in the history of humanity and percentages of deaths according to the population in their respective years.
Table 1. Main pandemics in the history of humanity and percentages of deaths according to the population in their respective years.
Pandemic Year Deaths
Antonine Plague [2] 165–180 5 million (7%)
Plague of Justinian[3] 541–542 25 million (25%)
Black Death Plague [4] 1346–1353 75–200 million (50%)
Russian Flu [5] 1889–1890 >1 million (8%)
Sixth Cholera [6] [4] 1899–1923 >1.5 million (5%)
Spanish Flu [7] 1918–1920 50-100 million (10%)
Asian Flu [8] 1957–1958 1.2-2 million (7%)
HIV/AIDS [9] 1960–2005 >39 million (1%)
COVID-19 [10] 2019–2021 >15 million (0.5%)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated