Preprint
Article
Laplacian Spectrum and Vertex Connectivity of the Unit Graph of the Ring Zprqs
This version is not peer-reviewed.
Submitted:
21 October 2024
Posted:
22 October 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
In this paper, we examine the interplay between the structural and spectral properties of the unit graph G(Zn) for n=p1r1p2r2...pkrk, where p1,p2,...,pk are distinct primes and k,r1,r2,...,rk are positive integers such that at least one of the ri must be greater than 1. We first analyze the structure of the unit graph of Zn as a generalized join graph under these conditions. We then determine the Laplacian spectrum of G(Zn) and deduce that it is integral for all n. Consequently, we obtain Laplacian spectral radius and algebraic connectivity of G(Zn). We also prove that the vertex connectivity of G(Zpq) is (p−2)q, where 2≠p<q. We deduce the vertex connectivity of G(Zn) when n=prqs, where 2≠p<q are primes and r,s are positive integers. Finally, we present conjectures about the vertex connectivity of G(Zn) when n=p1p2...pk and n=p1r1p2r2...pkrk, where pi are distinct primes, ri are positive integers, and 1≤i≤k.
Keywords:
Subject:
Computer Science and Mathematics - MathematicsMSC: 05C25; 05C50; 05C75
1. Introduction
For a positive integer n, denotes the ring of integers modulo n. In 1990, the unit graph was first introduced by Grimaldi [1] for the ring as follows: the unit graph is the graph obtained by setting all the elements of to be vertices and defining distinct vertices x and y to be adjacent if and only if . He discussed certain basic properties of the structure of the unit graph and studied the degree of a vertex, covering number, independence number, Hamilton cycles, and chromatic polynomial of the graph . More about the unit graph can be seen in [2,3,4]. Later, Ashrafi et al. [5] generalized the unit graph from to for an arbitrary ring R. They studied the chromatic index, diameter, girth, and planarity of . Some of the work associated with the unit graph on the rings can be found in [6,7,8,9].
In recent years, many researchers have studied the Laplacian spectrum and vertex connectivity of graphs associated with algebraic structures. In 2020, Chattopadhyay et al. [10] studied the Laplacian spectrum of the zero divisor graph of the ring . They discussed the Laplacian integrality, algebraic connectivity, vertex connectivity, and Laplacian spectral radius of . For other related works on the Laplacian spectrum and vertex connectivity of graphs associated to the ring , one may refer to [11,12]. Shen et al. [3] determined the Laplacian spectrum of the unit graphs of the ring for , where p is an odd prime and m is a positive integer. They proved that the algebraic connectivity and vertex connectivity of coincide if and only if .
In this paper, we investigate the structure of . Based on this structure, we study the Laplacian spectrum and vertex connectivity of for various n. The paper is arranged as follows: In Section 2, we provide the preliminary concepts and results that are used throughout the paper. In Section 3, we examine the structure of for , where are distinct primes and are positive integers such that at least one of the must be greater than 1. We prove that the graph is a generalized join of certain complete graphs and null graphs. In Section 4, we study the Laplacian spectrum of , we prove that is Laplacian integral, and we deduce the algebraic connectivity and Laplacian spectral radius of . In Section 5, we investigate the vertex connectivity of and , where are primes and r and s are positive integers, based on their structure and Menger’s theorem. Moreover, we present the following conjectures:
Conjecture I: Let , where are primes. Then, the vertex connectivity of is
Conjecture II: Let , where are primes and are positive integers such that at least one of the must be greater than 1. Then, the vertex connectivity of is
2. Preliminaries
In this section, we will present preliminary definitions and theorems that will be necessary for the following sections. Let G be a graph with vertex set and edge set . For , two vertices and in G are adjacent (or neighbors) in G if and are endpoints of an edge e of G, and we write if is adjacent to in G. For , we denote by the set of all neighbors of v in G. The degree of a vertex v in G, denoted by , is the number of edges incident with it. A path in a graph is a sequence of distinct vertices with the property that each vertex in the sequence is adjacent to the next vertex of it. The graph G is said to be connected if G contains a path between every pair of vertices. A complete graph is a graph in which each pair of distinct vertices is joined by an edge. We denote the complete graph with n vertices by . The complement of is a null graph and is denoted by . A clique of a graph G is a complete subgraph of G. A coclique in a graph G is a set of pairwise nonadjacent vertices. An isomorphism of graphs and , , is a bijection between the vertex sets of and such that for any two vertices x and y of , x and y are adjacent in if and only if and are adjacent in . For two graphs and with disjoint vertex sets, the join of and is the graph obtained from the union of and by adding new edges from each vertex of to every vertex of .
Let R be a ring with unity and be the set of units of R. The unit graph of R is the graph whose vertices are all the elements of R, defining distinct vertices x and y to be adjacent if and only if is a unit in R. Let R be a commutative ring with unity. An element is nilpotent if there exists an integer such that . The nilradical of R, denoted , is the set of all nilpotent elements of R. An ideal in R is a prime ideal if implies that either or for . The nilradical of R is the intersection of prime ideals of R. A maximal ideal of R is an ideal m different from R such that there is no proper ideal I of R properly containing m. The Jacobson radical of R is the intersection of maximal ideals of R. Every maximal ideal in R is a prime ideal. So, . Recall that, the sum of a unit and a nilpotent element is a unit. The following two results give some properties of the unit graph .
Lemma 1.
[5] Let R be a commutative ring and suppose that denotes the Jacobson radical of R. If , then the following statements hold:
- 1.
- If and are adjacent in , then every element of is adjacent to every element of .
- 2.
- If , then is a coclique in .
- 3.
- If , then is a clique in .
Proposition 1.
[5] Let R be a finite ring. Then, the following statements hold for the unit graph of R:
- 1.
- If , then the unit graph is a -regular graph.
- 2.
- If , then for every we have , and for every we have .
For a finite simple undirected graph G, the adjacency matrix is defined as the matrix whose entry is 1 if and 0 otherwise. The Laplacian matrix of G is defined by , where is the diagonal matrix such that are degrees of vertices of G. The matrix is a real, symmetric, and positive semidefinite so that its eigenvalues are real and nonnegative. Since the sum of each row of is zero, the smallest eigenvalue of is 0. The largest eigenvalue of is known as the Laplacian spectral radius of G, and the second smallest eigenvalue of is known as the algebraic connectivity of G and if and only if G is connected. A graph G is called Laplacian integral if all the eigenvalues of are integers. More literature about the Laplacian matrix of graphs can be seen in [13,14].
The spectrum of a square matrix C, denoted by , is the multiset of all the eigenvalues of C. If are distinct eigenvalues of B with respective multiplicities , , then we shall denote the spectrum of C by
For a graph G, the Laplacian spectrum of G is the spectrum of , we write as . For example,
Let G be a graph on k vertices with and let be k pairwise disjoint graphs. The G-generalized join graph of is the graph formed by replacing each vertex of G by the graph and then joining each vertex of to every vertex of whenever in G [15]. The following result is useful in the sequel.
Theorem 1.
[16] Let G be a graph on k vertices with and let be k pairwise disjoint graphs on vertices, respectively. Then, the Laplacian spectrum of is given by
where
and
In (2), means that one copy of the eigenvalue 0 is removed from the multiset , and means that is added to each element of .
Let n be a positive integer. Euler’s totient function, denoted by , is the number of positive integers less than or equal to n that are relatively prime to n. Let and be distinct primes for . Note that, and , so . Fakieh et al. studied the Laplacian spectrum of the unit graphs associated to the ring , where are distinct primes and [4]. This result is the main tool to prove Theorem 4.
Theorem 2.
[4] Let be distinct primes and k be a positive integer, . Then:
- 1.
- If , then the Laplacian spectrum of is
- 2.
- If , then the Laplacian spectrum of is
The vertex connectivity of a graph G is the minimum number of vertices whose removal from G leaves a disconnected or trivial graph. A family of two or more paths in a graph G is said to be internally disjoint if no vertex of G is an internal vertex of more than one path in the family. There is a strong result for the vertex connectivity by Menger’s theorem. Menger’s theorem says that the maximum number of internally disjoint -paths in G is equal to the minimum number of vertices whose deletion destroys all -paths, where u and v are nonadjacent in G [17]. So that
This paper uses Menger’s theorem to examine the vertex connectivity of .
3. as a Generalized Join Graph
For a positive integer n, denotes the ring of integers modulo n. The elements of the ring are referred to as and . A nonzero element is a unit in if x is relatively prime with n, . Through this section, we use as a prime number. Also, an integer n can be written in the form , where are distinct primes and are positive integers such that at least one of the must be greater than 1. In this section, we prove that is a generalized join graph of some complete graphs and null graphs. To this end, first, we study the structure of . Denote the maximal ideal of by , is an ideal generated by the prime divisors of n, that is, . So, . Put , then
Let S be the set of distinct representatives of . For , we denote
Note that the sets form a partition of the vertex set of . Thus,
Let . Then, for
The following result describes the adjacency criterion of vertices in , where is described in Equation (3).
Lemma 2.
For , every vertex of is adjacent to every vertex of in if and only if .
Proof. Clearly.
Suppose that . Let and , which can be written as and , where . Now, . Here is a unit by assumption, and is nilpotent. So, is a unit, and hence every vertex of is adjacent to every vertex of in . □
By using Lemmas 1 [(2),(3)] and 2, the following is evident.
Corollary 1.
The following statements hold:
- 1.
- For , the induced subgraph of on the vertex set is either the complete graph or its complement graph . Indeed, is if and only if .
- 2.
- For with , a vertex of is adjacent to either all or none of the vertices of in .
The above corollary implies that the partition of the vertex set of is an equitable partition in such a way that every vertex of the has equal number of neighbors in for all .
We define by the simple graph whose vertices are the distinct representatives of , that is, the set of vertices is S, and in which two distinct vertices i and j are adjacent if and only if . The graph will play an important role in the rest of the paper.
Lemma 3.
.
Proof.
We define a map such that . Clearly, is well-defined and bijection. From Lemma 2, the adjacency relationships are preserved by . Hence, the result follows. □
The following lemma states that can be expressed as a generalized join of certain complete graphs and null graphs.
Lemma 4.
Let be the induced subgraph of on the vertex set for . Then,
Proof.
Replace the vertex i of by for . Thus, the result follows from Lemma 2 and Corollary 1. □
4. Laplacian Spectrum of
In this section, we investigate the Laplacian spectrum of for , where are primes. For , we give the weight to the vertex i of the graph . Define the integer
for . The vertex weighted Laplacian matrix of defined in Theorem 1 is given by
where
for .
The following remark is an immediate result of Proposition 1.
Remark 1.
The following statements hold:
- 1.
- If , then .
- 2.
- If , then
Lemma 5.
Proof.
The proof is direct from definition of in Equation (4). □
The following theorem describes the Laplacian spectrum of .
Theorem 3.
Let , where are primes, and k are positive integers, and . The Laplacian spectrum of is given by
where and means that is added to each element of the multiset .
Proof.
By Lemma 4, we have
Consequently, the result can be obtained by using Theorem 1 and Lemma 5. □
By Corollary 1, is either or for . By Theorem 3, out of the n number of Laplacian eigenvalues of , of them are known to be nonzero integer values. The remaining Laplacian eigenvalues of will come from the Laplacian eigenvalues of .
Corollary 2.
Let be distinct primes and , , k be positive integers, where . Then, the Laplacian spectrum of is given by
- 1.
- If , then
- 2.
- If , then
Proof.
By the above argument and Remark 1, the result holds. □
The following result gives the Laplacian spectrum of for , where are primes and r, s are positive integers.
Theorem 4.
Let be primes and be positive integers. Then:
- 1.
- If , then the Laplacian spectrum of consists of
- 2.
- If , then the Laplacian spectrum of is
Proof.
1. Let , where are primes and r, s are positive integers. So, the Jacobson radical of is and the set of distinct representatives of is . Thus,
By Corollary 2, the Laplacian spectrum of is given by
By Eq (1), the Laplacian spectrum of and are
Then,
By using Lemma 3, is isomorphic to , and hence . So, by Theorem 2, we have
So,
Hence, the Laplacian spectrum of is as in Eq (5).
2. Let , where is a prime and s are positive integers. Note that, is the vertex set of the graph . Thus,
By Corollary 2, the Laplacian spectrum of is given by
By using Lemma 3, is isomorphic to , and hence . So, by Theorem 2, we have
Hence, the Laplacian spectrum of is
□
Now, we find the Laplacian spectrum of for , where are primes, are positive integers, and . The following theorem can be obtained by arguments similar to those used in the proof of Theorem 4, and therefore the proof is omitted.
Theorem 5.
Let be primes and be positive integers, . Then:
- 1.
- If , then the Laplacian spectrum of consists of
- 2.
- If , then the Laplacian spectrum of consists of
As an immediate consequence of Theorem 5, we have the following results.
Corollary 3.
) is Laplacian integral for all n.
Corollary 4.
The Laplacian spectral radius of is
where are primes, are positive integers, and .
Corollary 5.
The algebraic connectivity of is
where are primes, are positive integers, and .
5. Vertex Connectivity of
In this section, we obtain the vertex connectivity of when and , where are primes and r and s are positive integers. To achieve this goal, we calculate the number of internally disjoint paths between any two nonadjacent vertices in , which allow us to be ready to explore the vertex connectivity of by using Menger’s theorem. We end this section by presenting conjectures about the vertex connectivity of when and , where are distinct primes, are positive integers, and .
5.1. Structure of
The following result will be used in the sequel.
Lemma 6.
[18] Let , where p and q are distinct odd primes. Then the following statements hold:
- 1.
- Let . The induced subgraph of is isomorphic to 1. If , then is .
- 2.
- Let and . If , then every vertex of is adjacent to vertices of .
- 3.
- Let and . If , then every vertex of is nonadjacent to any vertex of .
Now, we study the structure of , where are primes, analogously to Section 3. In this case, we choose the maximal ideal . Let be the set of distinct representatives of . For , we denote
Note that the sets form a partition of the vertex set of . Thus,
This implies that any two vertices x and y that belong to the above union are adjacent if and only if . Let . Then, for .
Note that, Lemma 6 implies that the partition of is an almost equitable partition in such a way that every vertex of has an equal number of neighbors in where and . Also, is isomorphic to and is isomorphic to , where .
Let be defined as the simple graph whose vertices are , where , so that . Two distinct vertices and in are adjacent if and only if , which is equivalent to each vertex in being adjacent to vertices in .
Example 2.
The vertex set of , denoted as , can be expressed as the union , where , , and . From Figure 3 bellow, we observe the following:
- 1.
- is nonadjacent to since .
- 2.
- Each vertex in and is adjacent to 4 vertices in .
- 3.
- is isomorphic to and and are isomorphic to . The red vertices 0, 5, and 10 represent in , , and , respectively. Note that these vertices are multiples of 5.
The following two results determine the neighbors and the number of common neighbors of the vertices in , which help us to calculate the number of internally disjoint paths between any two nonadjacent vertices in .
Lemma 7.
Let . If , then there are neighbors of in . On the other hand, has neighbors in .
Proof.
Let . For , for all except . Consequently, is adjacent to in when . Then, there are neighbors of in . If , then for all . Thus, is adjacent to all vertices in . Therefore, there are neighbors of in . □
Lemma 8.
If , then the following statements hold:
- 1.
- If and are nonadjacent in , then the number of common neighbors between and in is .
- 1.
- If and are adjacent in , where , then the number of common neighbors between and in is .
- 3.
- The number of common neighbors between and in is .
Proof.
Let .
- Let and be nonadjacent in . By Lemma 7, and . Hence, is adjacent to all vertices in except . Similarly, is adjacent to all vertices in except . So, and are adjacent to all vertices in except and . Therefore, there are common neighbors between and in .
-
Let and be adjacent in , where . According to Lemma 7, and are nonadjacent to and in , respectively. So, and are adjacent to all vertices in except and , respectively. Then, the set of common neighbors between and in isThus, there are common neighbors between and in .
-
By Lemma 7, is adjacent to all vertices in . Also, is adjacent to all vertices in except . So, the set of common neighbors between and in isThen, there are common neighbors between and in . □
The following result determines the number of common neighbors between nonadjacent vertices through , where is a neighbor of in .
Lemma 9.
Let be nonadjacent and be a neighbor of in . Then, x and y have common neighbors in .
Proof.
By Part 2 of Lemma 6, both x and y are adjacent to vertices in . Suppose that x and y have the same neighbors in . Then, x and y are adjacent to all vertices in except . This implies that is adjacent to vertices in , a contradiction with Part 2 of Lemma 6. Then, x and y are adjacent to all vertices in except and , respectively. So, the number of common neighbors between x and y in is . □
The following result determines the number of common neighbors between nonadjacent vertices and through , where is a common neighbor between and in .
Lemma 10.
Let and be nonadjacent and be a common neighbor between and in . Then:
- 1.
- If x and y have the same neighbors in , then the number of common neighbors in between x and y is .
- 2.
- If x and y do not have the same neighbors in , then the number of common neighbors in between x and y is .
Proof.
Let and be nonadjacent and be a common neighbor between and in .
- 1.
- The proof is direct from Part 2 of Lemma 6.
- 2.
- Let x and y do not have the same neighbors in . By Part 2 of Lemma 6, both x and y have neighbors in . That is, x and y are adjacent to all vertices in except and , respectively. So, the number of the common neighbors in between x and y is . □
From now to the rest of this section, we denote x, which is a multiple of q in , by (see Example 2). The following proposition characterizes the nonadjacent vertices of for which the relation in Part 1 of Lemma 10 holds when is adjacent to in .
Proposition 2.
Let and be nonadjacent, be adjacent to in , and be a common neighbor between and in . Then, x and y have the same neighbors in if and only if and .
Proof. Suppose that x and y have the same neighbors in . Then, x and y are adjacent to all vertices in except by Part 2 of Lemma 6. We assume that and . Suppose that , , and , where and . Since is adjacent to in and x is nonadjacent to y, then and , this implies that . Similarly, since is adjacent to and in , then and . So,
So, ; this implies that 2 divide , and hence is multiple of q, in this case . But is adjacent to all vertices in and except and , respectively. This is a contradiction with and . So, and .
Assume that and . Then, x is adjacent to vertices of by Part 2 of Lemma 6, that is x is adjacent to all vertices of except , where and . Similarly, y is adjacent to all vertices of except . Then, the result is obtained. □
5.2. Number of Internally Disjoint Paths between Nonadjacent Vertices in
The following two lemmas calculate the number of internally disjoint paths between nonadjacent vertices x and y in .
Lemma 11.
Let be nonadjacent. Then, there are internally disjoint paths of length 2 between x and y.
Proof.
If , then is isomorphic to by Part 1 of Lemma 6. Since represents , then adjacent to all vertices in . Since x is nonadjacent to y, then both x and y are not in . So, there are common neighbors between x and y, and hence there are internally disjoint paths of length 2 between x and y in . Let be a neighbor of in . By Lemma 9, there are common neighbors between x and y in . Hence, there are internally disjoint paths of length 2 through . By Lemma 7, there are neighbors of in , and hence there are internally disjoint paths of length 2 between x and y through all neighbors of in . Thus, the total number of internally disjoint paths of length 2 between x and y is
If , then is isomorphic to , by Part 1 of Lemma 6. So, there is no path between x and y in . By Lemma 9, there are common neighbors between x and y in , where is a neighbor of in . Hence, there are internally disjoint paths of length 2 through . By Lemma 7, there are neighbors of in , and hence there are internally disjoint paths of length 2 between x and y. □
Lemma 12.
Let be nonadjacent. Then:
- 1.
- If , then there are internally disjoint paths of length 4 between x and y.
- 2.
- If , then there are internally disjoint paths of length 4 between x and y.
Proof.
Let be nonadjacent and be a neighbor of in . By proof of Lemma 9, x and y are adjacent to all vertices of except and , respectively.
- Let . By Part 2 of Lemma 6, and in are adjacent to vertices of . Since we investigate the internally disjoint paths between x and y through and , we can choose a vertex w from that is adjacent to both and . This path will be of length 4, as illustrated in Figure 4 (a). Similarly, for each neighbor of in there is one internally disjoint path of length 4 between x and y. By Lemma 7, there are neighbors of in . Therefore, there are internally disjoint paths of length 4 between x and y through all neighbors of .
- Let . By Part 2 of Lemma 6, and in are adjacent to vertices of . Approaching the proof in a similar manner as with Part 1, there is a path of length 4, as shown in Figure 4 (b). By Lemma 7, the number of neighbors of in is . So, there are internally disjoint paths of length 4 between x and y through all neighbors of . □
The following two lemmas determine the number of internally disjoint paths between nonadjacent vertices and , where is nonadjacent to in .
Lemma 13.
Let and be nonadjacent, be nonadjacent to in , and be a common neighbor between and in . Then:
- 1.
- If x and y have the same neighbors in , then there are internally disjoint paths of length 2 between x and y.
- 2.
- If x and y do not have the same neighbors in , then there are internally disjoint paths of length 2 between x and y.
Proof.
Let be nonadjacent to in . By Part 1 of Lemma 8, there are common neighbors between and in . Then:
- If x and y have the same neighbors in , then there are common neighbors between x and y in by Lemma 10. Thus, there are internally disjoint paths of length 2 between x and y through . Hence, there are internally disjoint paths of length 2 between x and y through all common neighbors between and in .
- If x and y do not have the same neighbors in , then there are common neighbors between x and y in by Lemma 10. So, there are internally disjoint paths of length 2 between x and y through . Therefore, there are internally disjoint paths of length 2 between x and y through all common neighbors between and in . □
Lemma 14.
Let and be nonadjacent, be nonadjacent to in , and be a common neighbor between and in . Then:
- 1.
- If x and y have the same neighbors in , then there are internally disjoint paths of length 4 between x and y.
- 2.
- If x and y do not have the same neighbors in , then there are internally disjoint paths of length 3 between x and y.
Proof.
Let be nonadjacent to in . By Part 1 of Lemma 8, there are common neighbors between and in .
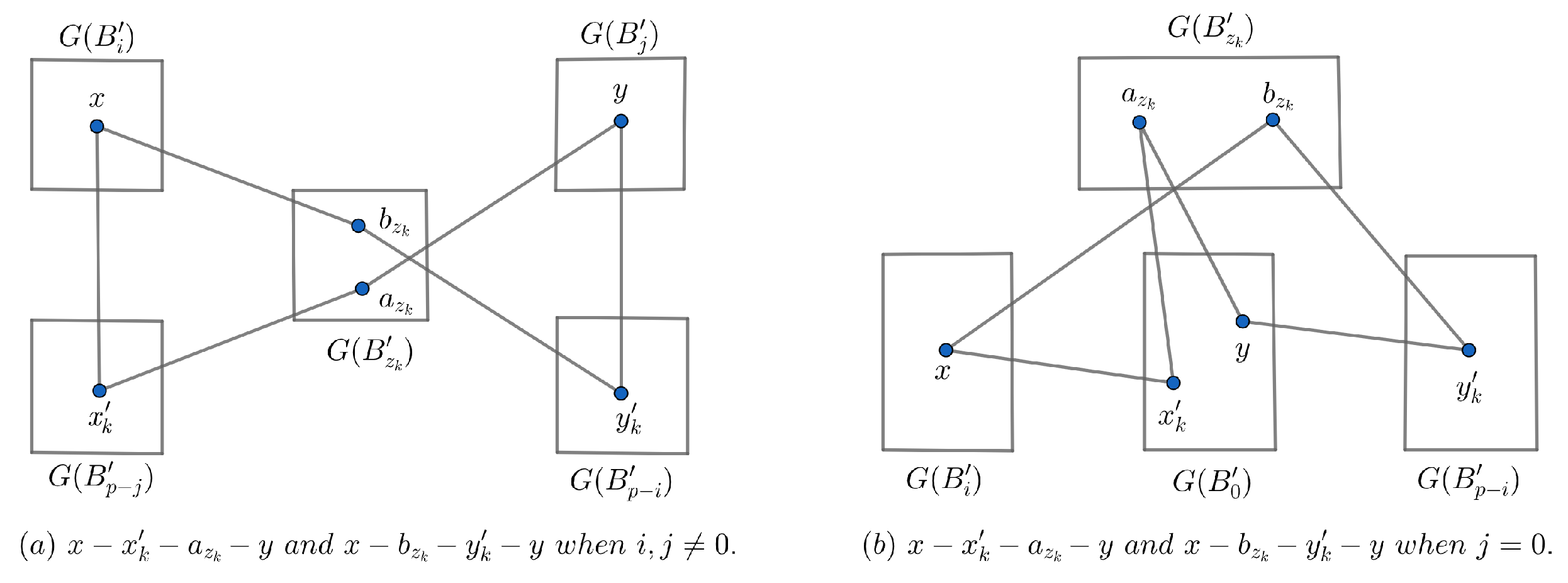
- Let x and y have the same neighbors in . By Lemma 6, has at least neighbors in and each of them is adjacent to vertices of . Then, we can choose a neighbor, say , of x in such that , where is nonadjacent to both x and y. Similarly, we can choose a neighbor of y in such that . Therefore, there exists a path of length 4 of the form , see Figure 5 (a). So, there are internally disjoint paths of length 4 between x and y through all common neighbors between and in .
- Let x and y do not have the same neighbors in . By proof of Lemma 10, x and y are adjacent to all vertices in except and , respectively. Approaching the proof similarly as Part 1, we can choose a neighbor of x in and a neighbor of y in , where and . Since and , two internally disjoint paths of length 3 exist. These paths are described in Figure 5 (b). Hence, there are internally disjoint paths of length 3 between x and y through all common neighbors between and in . □
The following results find the number of internally disjoint paths between nonadjacent vertices and , where is adjacent to in .
Lemma 15.
Let and be nonadjacent and be adjacent to in . One of the following cases holds:
- 1.
- There are internally disjoint paths of length 2 between x and y.
- 2.
- There are internally disjoint paths of length 2 between x and y.
Proof.
By Lemma 8, there are common neighbors between the adjacent vertices and , where , in and there are common neighbors between and in . Let be a common neighbor between and in . Since x and y are nonadjacent, then x and y have the following probabilities:
-
Assume that x and y have the same neighbors in . By Proposition 2 and Lemma 10, and and there are common neighbors between x and y through . So, there are internally disjoint paths of length 2 between x and y through . If , then there are internally disjoint paths of length 2 between x and y through all common neighbors between and in . Further, x (resp. y) is adjacent to all vertices in (resp. ). Also, x (resp. y) is adjacent to all vertices in (resp. ) except y (resp. x). So, the set of common neighbors between x and y in and is union . Thus, there are common neighbors between x and y in and . Consequently, there are internally disjoint paths of length 2 between x and y in and . Therefore, the total number of internally disjoint paths of length 2 between x and y isIf , then there are internally disjoint paths of length 2 between x and y through all common neighbors between and in . Further, x is adjacent to all vertices in and y is nonadjacent to any vertex in . Also, x (resp. y) is adjacent to all vertices in (resp. ) except y (resp. x). So, the set of common neighbors between x and y in and are . Thus, there are common neighbors between x and y in and . Then, there are internally disjoint paths of length 2 between x and y in and . Thus, the total number of internally disjoint paths of length 2 between x and y is
-
Assume that x and y do not have the same neighbors in . By Proposition 2 and Lemma 10, and and there are common neighbors between x and y in . Thus, there are internally disjoint paths of length 2 between x and y through . If , then there are internally disjoint paths of length 2 between x and y through all common neighbors between and in . Furthermore, x (resp. y) is adjacent to all vertices except only one vertex (resp. ) in (resp. ). Also, x (resp. y) is adjacent to all vertices in (resp. ) except y (resp. x). Thus, the set of common neighbors between x and y in and is union . So, there are common neighbors between x and y in and . As a result, there are internally disjoint paths of length 2 between x and y in and . Therefore, the total number of internally disjoint paths of length 2 between x and y isIf , then there are internally disjoint paths of length 2 between x and y through all common neighbors between and in . Further, x is adjacent to all vertices except only one vertex in , and y is nonadjacent to any vertex in . Also, x (resp. y) is adjacent to all vertices in (resp. ) except y (resp. x). Thus, the set of common neighbors between x and y in and is . So, there are common neighbors between x and y in and . Then, there are internally disjoint paths of length 2 between x and y in and . Thus, the total number of internally disjoint paths of length 2 between x and y is
□
Lemma 16.
Let and be nonadjacent, where is adjacent to in . One of the following cases holds:
- 1.
- There are internally disjoint paths of length 3 between x and y.
- 2.
- There are internally disjoint paths of length 3 between x and y.
- 3.
- There are internally disjoint paths of length 3 between x and y.
Proof.
We need to examine whether any -path passes through and because we are sure that (resp. ) is adjacent to (resp. ) and nonadjacent to (resp. ) in . Let be a common neighbor between and in . Since x and y are nonadjacent, then x and y have the following cases:
- Assume that x and y have the same neighbors in . Indeed, and by Proposition 2. If , there are neighbors of x in , denote these neighbors by such that , and each of them is adjacent to vertices of by Part 2 of Lemma 6. Similarly, there are neighbors of y in , and each of them is adjacent to vertices of . To get the internally disjoint paths of length 3 between x and y, we choose one of the neighbors of , say , in such that is a neighbor of y. Indeed, for each in there is one internally disjoint path between x and y through and . Therefore, the total number of internally disjoint paths of length 3 between x and y through and together is equal to the number of neighbors of x in , which is . Now let . There are neighbors of x in and each of them is adjacent to vertices of . Since there are neighbors of y in , so there are more than paths of length 3 between x and y through and together. By applying the same method in the case where , there are internally disjoint paths of length 3 between x and y.
-
Assume that x and y do not have the same neighbors in . So, and by Proposition 2. Suppose that is a common neighbor between and in . By proof of Lemma 10, x and y are adjacent to all vertices in except and , respectively. Let . Since x has neighbors in and each of these neighbors is adjacent to vertices of , then we can choose a neighbor of x in such that . Similarly, we can choose a neighbor of y in such that . Since and , there exist two internally disjoint paths of length 3 between x and y, as illustrated in Figure 6 (a). By Part 2 of Lemma 8, there are common neighbors between and in . Then, there are internally disjoint paths of length 3 between x and y through all common neighbors between and in . After removing all and from and , respectively, then the number of remaining neighbors of x and y in and , respectively, is . So, there are internally disjoint paths length 3 between x and y that pass through the remaining of neighbors of x and y in and , respectively, together. So, the total number of internally disjoint paths of length 3 between x and y isLet . Since x has neighbors in and each of these neighbors is adjacent to vertices of , then we can choose a neighbor of x in such that . Similarly, we can choose a neighbor of y in such that . Since and , there exist two internally disjoint path of length 3 between x and y, as illustrated in Figure 6 (b). By Part 3 of Lemma 8, there are common neighbors between and in . Consequently, there are internally disjoint paths of length 3 between x and y through all common neighbors between and in . After removing all and from and , respectively, then the number of remaining neighbors of x and y in and , respectively, is . So, there are internally disjoint paths length 3 between x and y that pass through the rest of neighbors of x and y in and , respectively, together. So, the total number of internally disjoint paths of length 3 between x and y is
□
5.3. Vertex Connectivity of
The following result is of crucial importance to our study in this section.
Theorem 6.
Let be distinct primes. The vertex connectivity of is
Proof.
Let x and y be nonadjacent in . In this proof, we will calculate the maximum number of internally disjoint paths between any two nonadjacent vertices. There are several cases for x and y, as follows:
Case 1: Let . By Lemma 11, then there are internally disjoint paths of length 2 between x and y. In addition, there are other internally disjoint paths depending on the following cases for i:
- (a)
- Let . By lemma 12, there are internally disjoint paths of length 4 between x and y. So, the maximum number of internally disjoint paths between x and y is
- (b)
- Let . By Lemma 12, there are internally disjoint paths of length 4 between x and y. So, the maximum number of internally disjoint paths between x and y is
Case 2: Let and , where is nonadjacent to in . Let be a common neighbor between and in . The following cases arise for x and y:
- (a)
- If y has the same neighbors as x in , then there are internally disjoint paths of length 2 between x and y by Lemma 13. According to Lemma 14, there are internally disjoint paths of length 4 between x and y. Hence, the maximum number of internally disjoint paths between x and y is
- (b)
- If x and y do not have the same neighbors in , there are internally disjoint paths of length 2 between x and y by Lemma 13. According to Lemma 14, there are internally disjoint paths of length 3 between x and y. Hence, the maximum number of internally disjoint paths between x and y is
Case 3: Let and , where is adjacent to in . Let be a common neighbor between and in . There are the following cases for x and y:
- (a)
- If y has the same neighbors as x in , then there are internally disjoint paths of length 2 between x and y by proof of Lemma 15. According to proof of Lemma 16, there are internally disjoint paths of length 3 between x and y. Hence, the maximum number of internally disjoint paths between x and y is
- (b)
-
If x and y do not have the same neighbors in , then there are internally disjoint paths of length 2 between x and y by proof of Lemma 15. In addition, there are other internally disjoint paths depending on the following cases for i and j:
- (1)
- Let . According to proof of Lemma 16, there are internally disjoint paths of length 3 between x and y. Therefore, the maximum number of internally disjoint paths between x and y is
- (2)
- Let . According to proof of Lemma 16, there are internally disjoint paths of length 3 between x and y. So, the maximum number of internally disjoint paths between x and y is
From the above cases and by Menger’s theorem, we have
□
Now, let us explore the vertex connectivity of if , where are primes and are positive integers such that at least one of must be greater than 1.
Theorem 7.
Let , where are distinct primes, r and s are positive integers. Then, the vertex connectivity of is given by
Proof.
By Lemma 4, the unit graph is
According to Lemma 3, is isomorphic to . Hence, by Theorem 6, we get
Note that, for every vertex i of , we have vertices in . Since for , then the vertex connectivity of is
□
Based on our results for the vertex connectivity of the unit graph, in Theorems 6 and 7, we state the following conjectures:
Conjecture I: Let , where are distinct primes. The vertex connectivity of is
Conjecture II: Let , where are distinct primes, and k are positive integers, and . Then, the vertex connectivity of is given by
6. Conclusions
In this paper, we have investigated the structure of . Based on this structure, the Laplacian spectrum and vertex connectivity of have been determined for various n. First, we study the structure of for , where are distinct primes and are positive integers such that at least one of the must be greater than 1, and we prove that the graph is a generalized join of certain complete graphs and null graphs. Then, we determine the Laplacian spectrum of , we prove that is Laplacian integral, and we deduce the algebraic connectivity and Laplacian spectral radius of . Furthermore, we examine the vertex connectivity of and , where are primes and r and s are positive integers by using their structure and Menger’s theorem. Finally, we present conjectures about the vertex connectivity of when and , where are distinct primes, are positive integers, and . Our results are precise and dependable, as verified by Python programming (see Appendix A).
Author Contributions
Investigation, A. A. and W. F.; Methodology, A. A. and W. F.; Writing—–original draft preparation, A. A., W. F. and H. A.; Writing–—review and editing, A. A., W. F. and H. A; ; supervision, W. F. and H. A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Pranjali et al. [19] provided the generation code of the unit graph of . We utilize this code in Python programming to create the following algorithm that verifies the validity of our results.

References
- Grimaldi, R.P. Graphs from rings. In Proceedings of the 20th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Boca Raton, FL, USA, 20–24 February 1989; Volume 71, pp. 95–103. [Google Scholar]
- Su, H.; Yang, L. Domination number of unit graph of . Discrete Math. Algorithms Appl. 2020, 12, 2050059. [Google Scholar] [CrossRef]
- Shen, S.; Liu, W.; Jin, W. Laplacian eigenvalues of the unit graph of the ring Zn. Appl. Math. Comput. 2023, 459, 128268. [Google Scholar] [CrossRef]
- Fakieh, W.; Alsaluli, A.; Alashwali, H. Laplacian spectrum of the unit graph associated to the ring of integers modulo pq. AIMS Math. 2023, 9, 4098–4108. [Google Scholar] [CrossRef]
- Ashrafi, N.; Maimani, H.R.; Pournaki, M.R.; Yassemi, S. Unit graphs associated with rings. Commun. Algebra 2010, 38, 2851–2871. [Google Scholar] [CrossRef]
- Maimani, H.R.; Pournaki, M.R.; Yassemi, S. Necessary and sufficient conditions for unit graphs to be Hamiltonian. Pacific J. Math. 2011, 249, 419–429. [Google Scholar] [CrossRef]
- Su, H.; Zhou, Y. On the girth of the unit graph of a ring. J. Algebra Appl. 2014, 13, 1350082. [Google Scholar] [CrossRef]
- Akbari, S.; Estaji, E.; Khorsandi, M.R. On the unit graph of a noncommutative ring. Algebra Colloq. 2015, 22, 817–822. [Google Scholar] [CrossRef]
- Abdelkarim, H.A.; Rawshdeh, E.; Rawashdeh, E. The eigensharp property for unit graphs associated with some finite rings. Axioms 2022, 11, 349. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Patra, K.L.; Sahoo, B.K. Laplacian eigenvalues of the zero divisor graph of the ring . Linear Algebra Appl. 2020, 584, 267–286. [Google Scholar] [CrossRef]
- Banerjee, S. Laplacian spectrum of comaximal graph of the ring . Spec. Matrices 2022, 10, 285–298. [Google Scholar] [CrossRef]
- Mathil, P.; Baloda, B.; Kumar, J. On the cozero-divisor graphs associated to rings. AKCE Int. J. of Graphs Comb. 2022, 19, 238–248. [Google Scholar] [CrossRef]
- Cvetković, D.M.; Rowlison, P.; Simić, S. An Introduction to Theory of Graph Spectra; London Math. S. Student Text, 75; Cambridge University Press, Inc.: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Pirzada, S.; Ganie, H.A. On the Laplacian eigenvalues of a graph and Laplacian energy. Linear Algebra Appl. 2015, 486, 454–468. [Google Scholar] [CrossRef]
- Schwenk, A.J. Computing the characteristic polynomial of a graph. In Proceedings of the Capital Conference, Graphs and Combinatorics, Lecture Notes in Mathematics, Springer, Berlin, Heidelberg, 18-22 June 1973; Volume 406, pp. 153–172. [Google Scholar] [CrossRef]
- Cardoso, D.M.; De Freitas, M.A.A.; Martins, E.A.; Robbiano, M. Spectra of graphs obtained by a generalization of the join of graph operation. Discrete Math. 2013, 313, 733–741. [Google Scholar] [CrossRef]
- Balakrishnan, R.; Ranganathan, K. A Textbook of Graph Theory; Springer-Verlag New York, Inc.: New York, 2000. [Google Scholar]
- Alsaluli, A.; Fakieh, W.; Alashwali, H. Laplacian spectrum of the unit graph of the ring . Proceedings of International Conference and Exhibition for Science (ICES 2023), College of Science, King Saud University, Riyadh, Saudi Arabia, February 2023. [Google Scholar]
- Pranjali; Acharya, M. Energy and Wiener index of unit graph. Appl. Math. Inf. Sci. 2015, 9, 1339–1343. [Google Scholar]
| 1 |
is the cocktail party graph, which is obtained from the complete graph , , by deleting a perfect matching, where a perfect matching of graph G is a 1-regular spanning subgraph H of G. |
Figure 1.
The graph ).

Figure 2.
The graph .
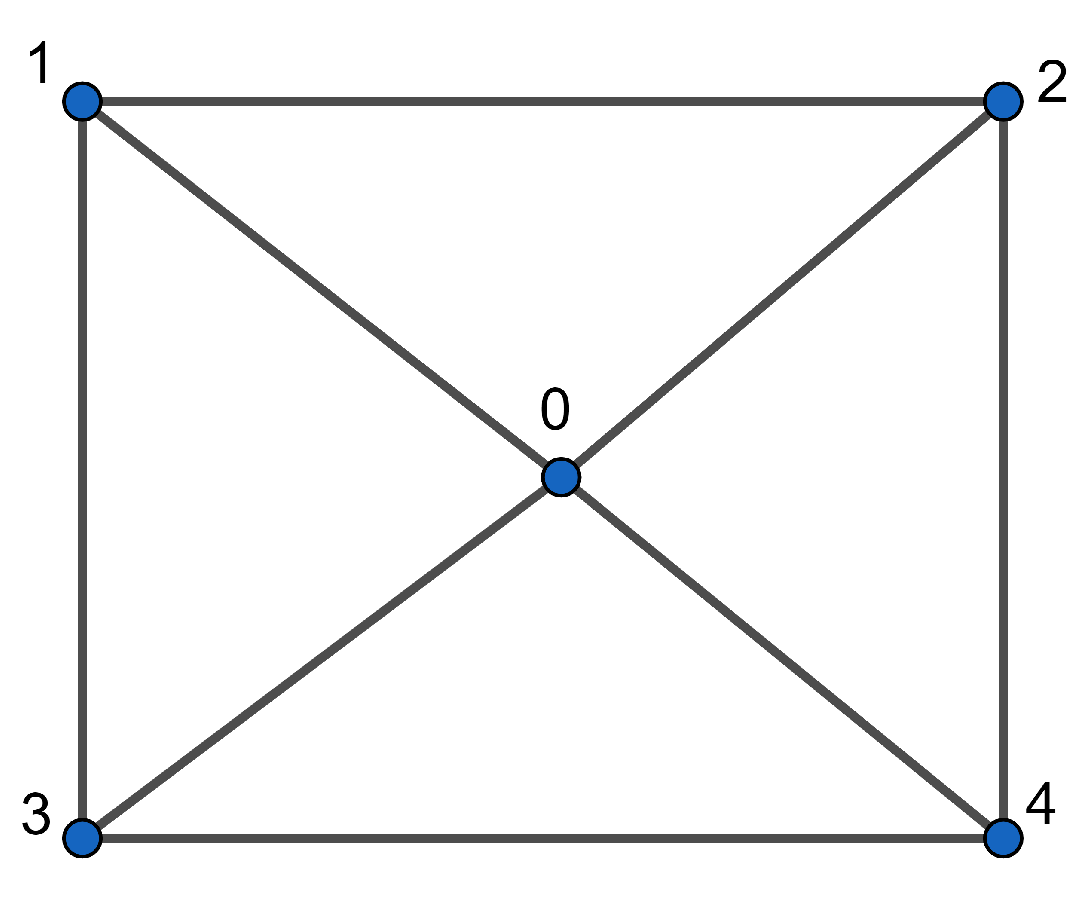
Figure 3.
The graph .
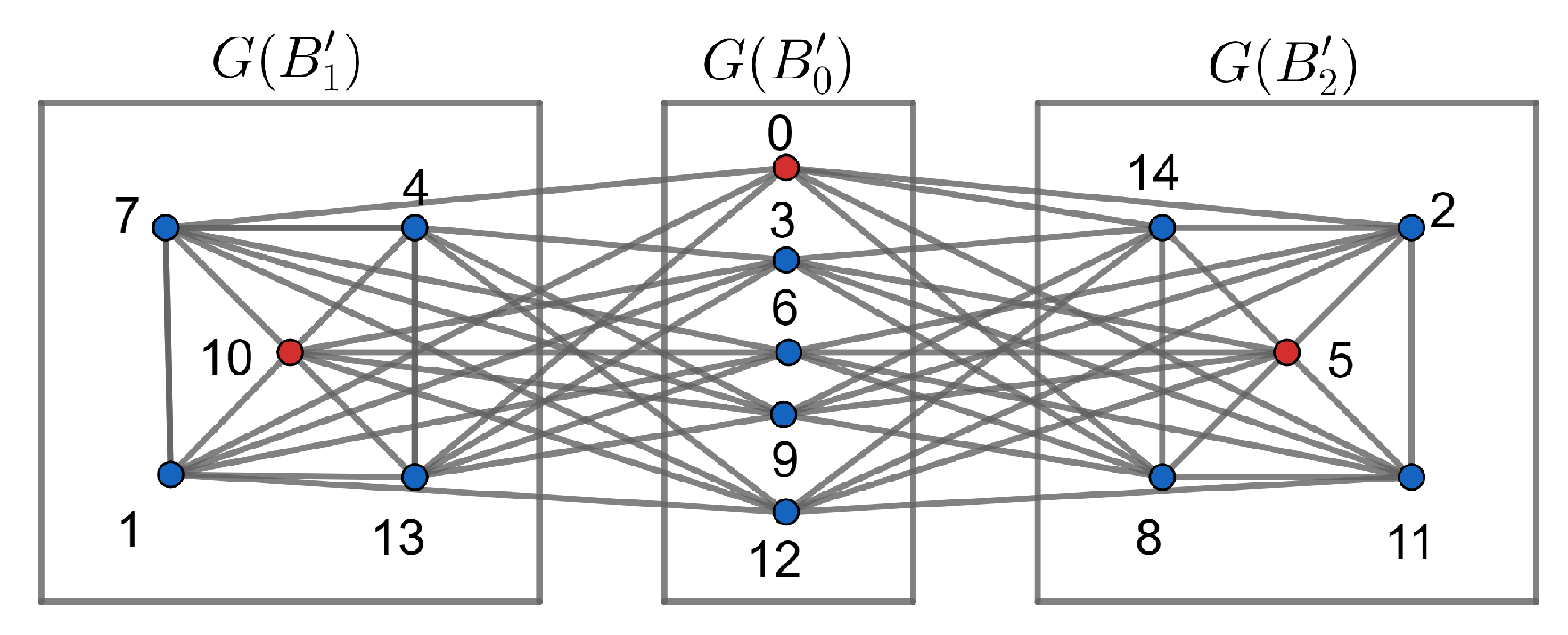
Figure 4.
(a) when . (b) when .
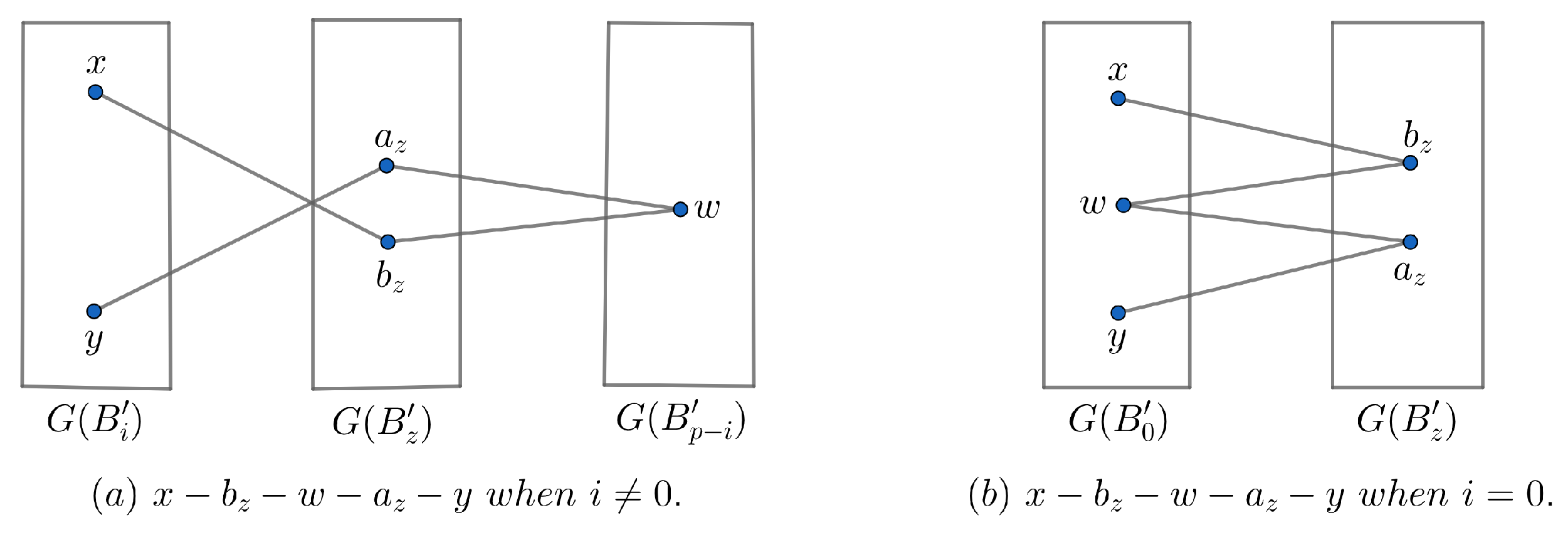
Figure 5.
(a). (b)
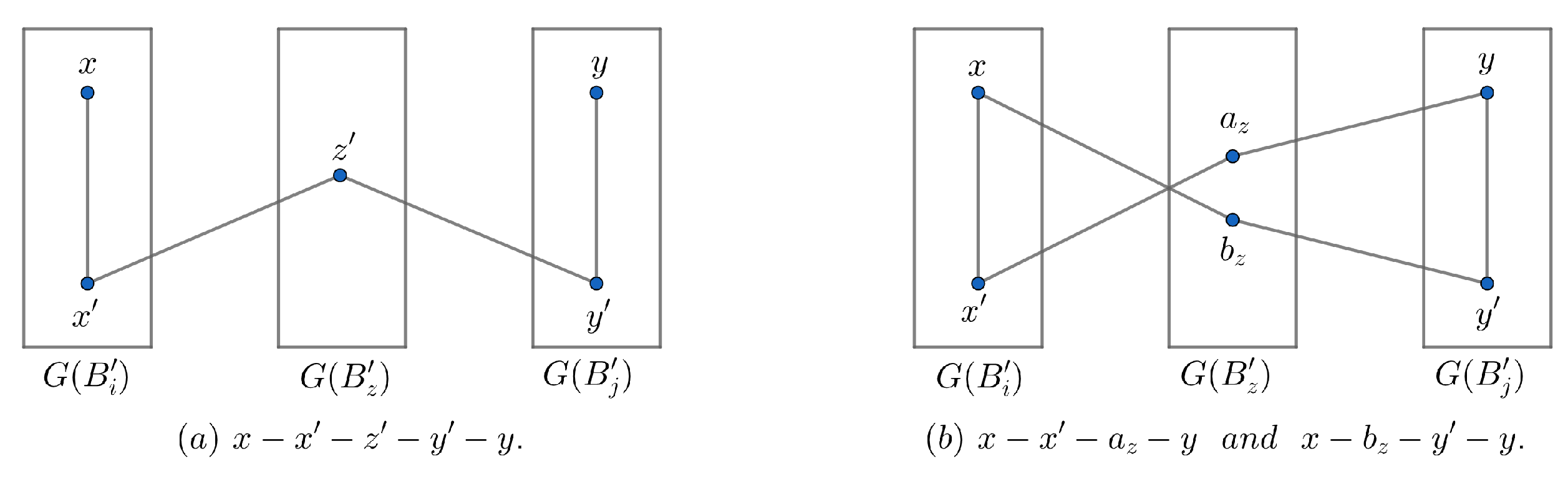
Figure 6.
(a) and when . (b) and when .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated




