Point Cloud as Imaging Effect in Coordinate Optical Measurement—A New Method for Evaluating Measurement Accuracy (OPTI‐U)

Preprint

Article

Point Cloud as Imaging Effect in Coordinate Optical Measurement—A New Method for Evaluating Measurement Accuracy (OPTI‐U)

This version is not peer-reviewed.

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

22 October 2024

Posted:

22 October 2024

You are already at the latest version

Abstract

The article presents extremely current issues concerning imaging and measurements carried out using coordinate optical systems in which the result of scanning spatial objects is a point cloud. What is important, the entire accuracy assessment of the conducted fast, effective coordinate measurement nowadays takes place in the computational area, beyond direct sensory percep-tion, and depends increasingly on its power and the computational algorithms used. Further-more, we are getting closer and closer to recognising virtual standards in coordinate metrology as a direction that allows for an increase in measurement accuracy. Especially in recent years, the importance of the problem has been confirmed by the activities of the most significant scientific and research centres. They focus on improving the accuracy of the data obtained in the form of point clouds, using more precise scanning methods for this purpose, and developing filtering algorithms to remove noise, including methods using artificial intelligence. Based on many years of research, the authors identified a problem regarding the difficulty in developing data obtained from optical systems, such as laser triangulation head systems, systems operating on the principle of structural light, photogrammetric systems, as well as computer tomographs, and the impact of these systems on the assessment of measurement accuracy. Therefore, the optical measurement process was analysed in terms of the quality of the acquired point clouds. The authors presented the division of factors, which, in coordinate optical meas-urements, generate errors in data acquisition and development. The authors also indicated which of these factors generate the most significant errors and, above all, emphasised the impact of the software used, the measurement operator, and the methods of cloud filtration applied by the operator. Therefore, the accuracy assessment of the optical measurement has been noted as a critical problem, and so far, it has not been solved effectively. In the article, as a solution to this problem, the authors proposed the OPTI-U method of estimating uncertainty for optical meas-urements. The method, what is very important, was developed and verified under the conditions of an accredited calibration laboratory. The summary also gives directions for further work on developing and disseminating the developed method, particularly introducing virtual standards.

Keywords:

Subject:

Engineering - Mechanical Engineering

1. Introduction

Coordinate optical systems are a valuable combination of coordinate techniques, enabling any setting of the measured object in the measurement area with a contactless method of imaging and optical measurement, which in turn provides a shortened measurement time. They are also the fastest growing area of spatial measurements, on the example of which breakthroughs in the metrology of spatial measurements of geometric quantities can be seen. It should be noted here that the technique and the idea of measurement are changing, moving from the area of direct sensory cognition of man to the area of computer reality supported by artificial intelligence. Equally crucial in assessing the accuracy of the measurement is the relationship between the value measured and the standard. The question of whether the virtual image of the standard combines all the features of the actual standard with its computer image used to assess the accuracy of the measurement carried out remains more and more relevant. The quality of this connection makes optical coordinate systems an increasingly effective, widely used tool in research, industrial, as well as military units. They are also a response to the requirements of the dynamically developing market in the field of rapid prototyping, reverse engineering, industrial design, material research, biomedical technology, construction, protection of monuments, geodesy, cartography and, above all, media or metrology of the fourth dimension, applicable wherever the digital image of an object is the basis for measuring replication and evaluation.

Numerous key research centres around the world are involved in the development of coordinate optical systems and the improvement of their accuracy, including the National Institute of Standards and Technology (NIST) in the United States, the Physikalisch-Technische Bundesanstalt (PTB) in Germany, the National Physical Laboratory (NPL) in the United Kingdom, the Institut National de la Recherche Scientifique (INRS) in Canada, the National Metrology Institute of Japan (NMIJ) in Japan, the Laboratoire National de Métrologie et d'Essais (LNE) in France, and many others [1,2,3,4,5,6]. This issue is very complex and requires specialist knowledge about the measurement process, factors determining the result, the laws of physics, and statistical issues. Currently observed activities aimed at improving the accuracy of coordinate optical systems are based, among others, on the use of new methods enriched with elements of artificial intelligence enabling machine learning, and deep learning using neural networks. Algorithms are trained to find patterns and correlations in large data sets and to allow the system to make decisions [7,8,9]. Another visible trend is the increasing use of multisensory systems integrated with various measurement systems, such as laser scanners, cameras, and interferometers for measurements in real-time production [10,11].

The common feature of coordinate optical measurements, regardless of the design of the machine used and the measurement method used, is the result in the form of a point cloud. Point clouds coming from structurally and operationally diverse systems (systems operating on the principle of laser triangulation or structural light, photogrammetric systems, and computer tomographs) require performing similar tasks during the analysis. Each cloud should be subjected to "processing". Points resulting from the reflections, including the reflectivity of the measuring table or the fixing devices, should be removed. Appropriate filtration/reduction of points should be carried out, and the points should be adjusted to the basic geometric element. The current work of leading centres on point clouds focuses primarily on improving the quality and accuracy of data. Activities aimed at improving the scanning technology itself can be distinguished in order to obtain more accurate and detailed data, to develop cloud filtering algorithms in order to remove noise, also using innovative methods using deep learning and cloud-merging methods - combining data from various sources, interactive visualisation tools—in order to enable the user to view and analyse data conveniently and efficiently [12,13,14,15].

As a result in the form of a point cloud differs from the result from the contact measurement, the methods used so far to assess the contact measurement based on the comparative method (ISO 15530-3:2011)[16], multi-position (ISO/TS 15530-2 (draft))[17] were considered insufficient for this application and a more adequate method was suggested to take into account the key factors that affect the uncertainty of the optical measurement, which is based on the above, but is supplemented by additional components derived partly from the method known as R&R [18].

The aim of the article is to present the possibility of improving the accuracy of coordinate optical measurement by diagnosing the key factors influencing the measurement result in the form of a point cloud both at the measurement stage, i.e. obtaining data in the form of point clouds, and at the stage of processing, supplemented by presentations of the accuracy assessment method dedicated to coordinate optical measurements using the proprietary OPTI-U method of estimating uncertainty in optical measurements.

The introduction should briefly place the study in a broad context and highlight why it is important. It should define the purpose of the work and its significance. The current state of the research field should be carefully reviewed and key publications cited. Please highlight controversial and diverging hypotheses when necessary. Finally, briefly mention the main aim of the work and highlight the principal conclusions. As far as possible, please keep the introduction comprehensible to scientists outside your particular field of research. References should be numbered in order of appearance and indicated by a numeral or numerals in square brackets—e.g., [1] or [2,3], or [4,5,6]. See the end of the document for further details on references.

2. How to Get "Clean" Point Clouds—Key Error-Generating Factors Based on the Conducted Research

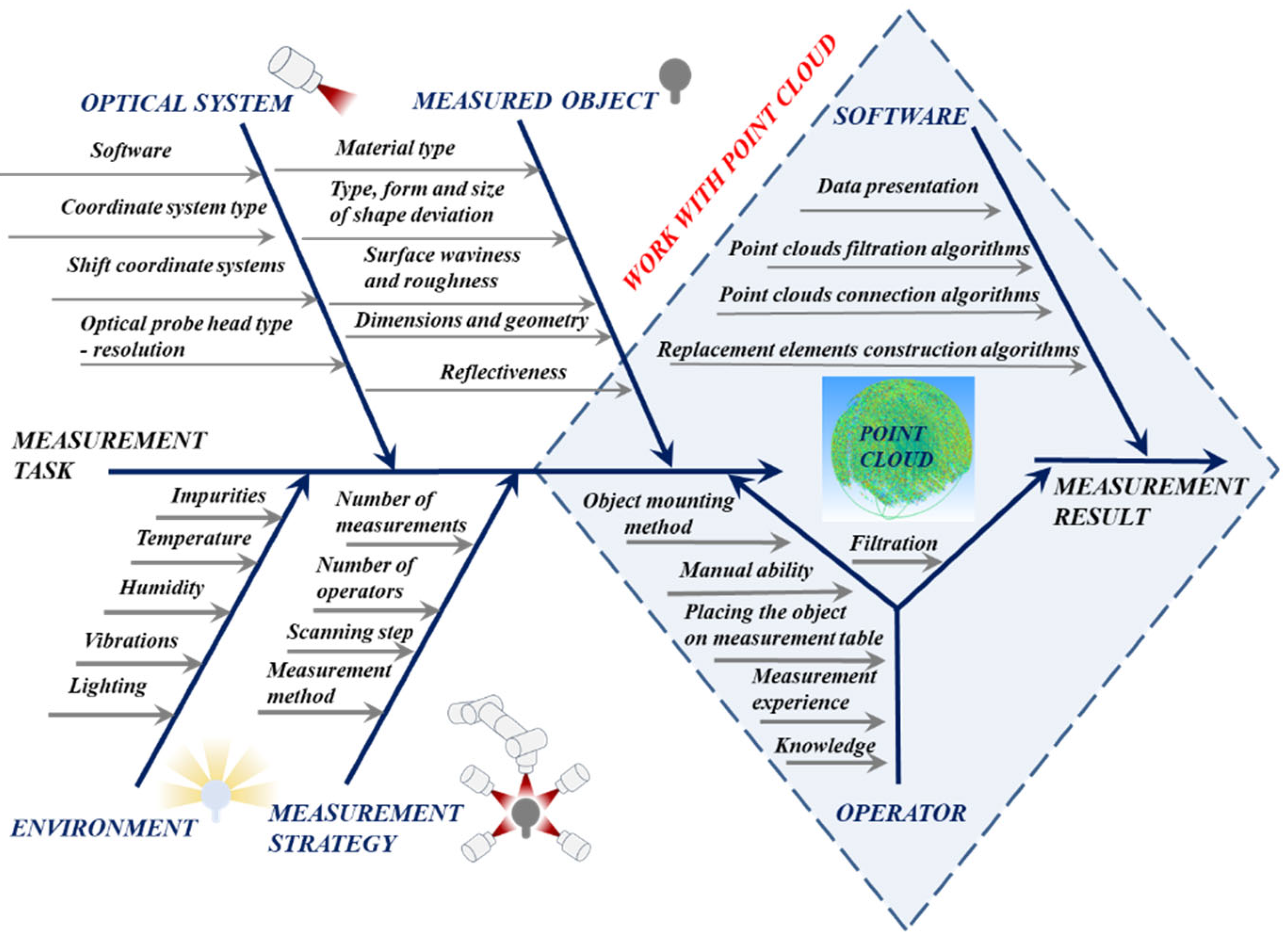
The Laboratory of Coordinate Metrology conducted a series of tests to examine the key factors influencing the result of the measurement using optical systems. A detailed analysis was carried out of those that generate the most significant errors, among others: lighting, resolution, software, operator, and measurement method. The influence of factors on the final measurement result is presented in the Ishikawa diagram (Figure 1). The factors generating errors in coordinate optical measurements were divided into factors occurring at the data acquisition stage (2.1 MEASUREMENT) and factors occurring at the data development stage (2.2 WORK with the POINT CLOUD).

The operator's influence was emphasised in both stages, during the elimination of environmental impacts (e.g. lighting), influences from the measured object (e.g. reflectivity), and also during the development of results from point clouds due to filtration and parameter selection.

Attention was paid to the relationship between individual factors, e.g. the software used. It is both part of the measurement system and a separate part of the diagram (due to the force of interaction). In addition, factors such as reflectivity, lighting, and the type of head used are also strongly related. Therefore the diagram should be treated as a certain representation holistically with the awareness of greater or lesser correlation of individual factors [19,20].

2.1. Measurement—Error-Generating Factors

In Chapter 2.1. selected factors influencing the measurement result in the form of a point cloud at the measurement stage before cloud development were presented. Such factors include factors affecting the quality of the measurement: the measurement method, the operator, the type of surface, the color, the reflective and scattering characteristics, the number of points obtained, and lighting.

Measurement Method

It has been shown that one of the important factors influencing the result is the selected measurement method [19,20]. The measurement strategy is strongly dependent on the method of estimating uncertainty. The Laboratory of Coordinate Metrology uses methods based on the comparative method [16], multi-position [17] and the OPTI-U method developed at the LCM, and dedicated to optical measurements.

In order to check the impact of the measurement method on the result of the optical measurement, measurements of solid elements were carried out using different measurement methods while maintaining the conditions of similarity. The results are given in Table 1. The comparative method for measuring the diameter of the sphere and the deviation of the flatness gave results closer to the nominal. When measuring the distance for this series of measurements, the developed OPTI-U method proved to be more effective. The given measurement method for the established measurement parameters will give results closer/further from the calibrated value.

Number of Points Obtained

Tests were also carried out to check the impact of the number of obtained points on the measurement result. In this case, the number of points obtained is closely related to the scanning speed and the number of collected points of a given area during a single passage of the probe head. The conducted research measured the selected features in the function of changing the number of points due to changing the value of the Stripes Distance parameter Figure 2. As its value decreases, the density of displayed lines increases. Thus, the probe head records a larger number of points.

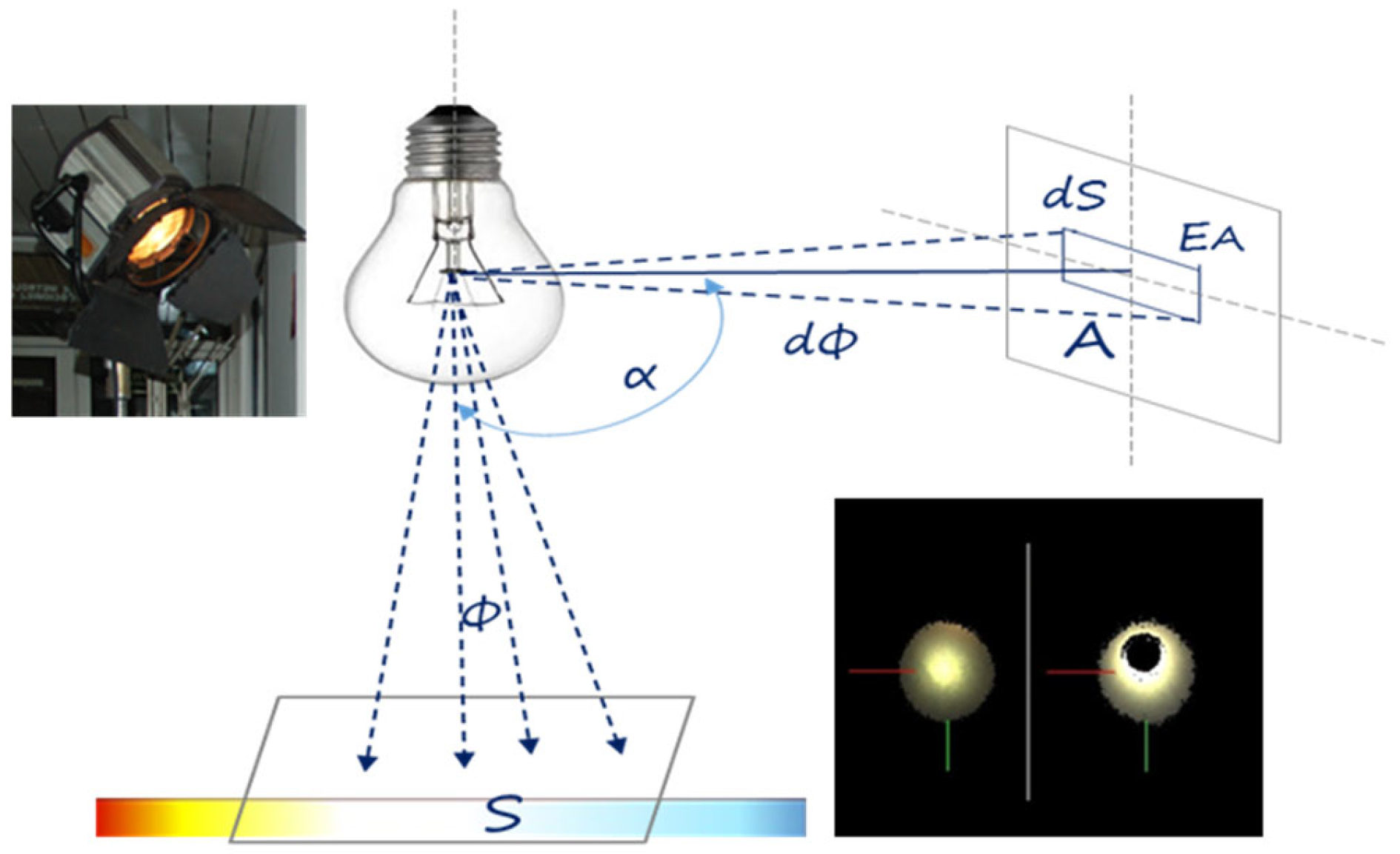
Lighting

In order to study the influence of lighting on the measurement result, measurements of standards were carried out when changing two key parameters of light, i.e. luminous flux intensity, E, lm/m², (ratio of luminous flux density Φ to the surface area S (Figure 3)) and the colour temperature expressed in Kelvin, K, which is a measure of the chromaticity of light radiation compared to the chromaticity of a perfectly black body.

The research used measurement systems: Articulated arm with PC-DMIS Reshaper - Hexagon Metrology software and a 3D Scanner with Mesh 3D software, and two lamps with different colour temperatures. The incandescent lamp emitted warm yellow light with a colour temperature of 3200 K, while the discharge lamp emitted white light (similar to daylight) with a colour temperature of 6000 K. During the measurements, the light intensity was changed in the ranges (0 (without lighting), 120, 2000, 4000 lx), the measurement was performed with a lux meter. The measurements were repeated sequentially six times for each standard, each lamp and each light intensity. During the research, it was observed that as the intensity of external light increases, the number of points obtained decreases (this tendency is more potent for higher colour temperatures), and reflections resulting from its x-ray are formed on the object (Figure 3).

The tests carried out under appropriate measurement conditions, i.e. with the maximum limitation of external light sources, indicate a higher accuracy of measurement using structural light in relation to laser triangulation. However, under variable lighting conditions, the correct results were obtained when scanning using the laser triangulation method, confirming the widespread use of arms equipped with such heads in the production environment. In the context of the significance of the impact of the applied lighting, the conducted research confirms the influence of lighting on the measurement result, especially when using structural light. However, taking into account the lack of significant impact of external light sources on the measurement with the scanning head using laser triangulation, the authors considered this factor to be significant, but not requiring a more comprehensive analysis and separate inclusion in the developed OPTI-U method.

2.2. WORK with POINT CLOUD—Error-Generating Factors

Chapter 2.2. presents selected factors influencing the measurement result in the form of a point cloud at the stage of cloud development. Such factors include the operator, software, and applicable filtration methods.

Overall Operator Impact (R&R Method)

The operator's influence on the measurement result was examined with an articulated arm CMM equipped with a rigid-contact probe head and an integrated laser triangulation head. Three operators with similar experience performed the measurements described in [21]. The subject of the study was a meter ball-bar standard. 10 lengths were measured in three samples under repeatability conditions. The results were developed in metrology software, PC-Dmis, and 3D Reshaper, respectively. The R&R (Repeatability and Reproducibility) method was used to analyse the results, as can be seen in Table 3. The R&R analysis method uses the same mathematical apparatus that Shewhart used to develop his control cards, especially the

\bar{X}

—R card (which is why the R&R methodology is often called the analysis of Averages and Ranges). This method is currently a recognisable and respectable (especially in the automotive industry) tool for identifying and assessing the share of individual components during the monitoring of the production process. The accepted "R&R" analysis procedures were introduced by the so-called "big three" (Ford, Chrysler, General Motors) in cooperation with the Automotive of the American Society for Quality Control (ASQC) and the Automotive Industry Action Group (AIAG) [18]. The R&R method calculates the repeatability of E.V. a component depending on the measurement device, and the reproducibility of A.V. a component depending on the adopted variable conditions (the operator, in this case, is treated as a variable factor).

where:

E . V . % = 100 \cdot \frac{E . V .}{T o l e r a n c e}

(1)

A . V . % = 100 \cdot \frac{A . V .}{T o l e r a n c e}

(2)

and

R & R % = \sqrt{{(A . V . %)}^{2} + {(E . V . %)}^{2}}

(3)

while:

E.V.%—device (repeatability),

A.V.%—operator (reproducibility,

and

R&R%—device and operator together (repeatability and reproducibility).

Regardless of the head used, the operator's influence is decisive in both cases (this is justified because the articulated arm CMMs are manual machines). However, in the light of the conducted considerations, an almost double increase in the error coming from the operator after connecting the optical head (Table 3) is significant.

Operator's Work with the Software

Despite the guidelines in the standards and recommendations for calibration of optical systems regarding the work with the point cloud, e.g. the method of generating geometric elements—the calibration results of the system carried out by several operators differ significantly [21,22]. Furthermore, there is also a lack of official guidance beyond ISO 10360-6:2001 [23] in the context of the comparability of metrology software.

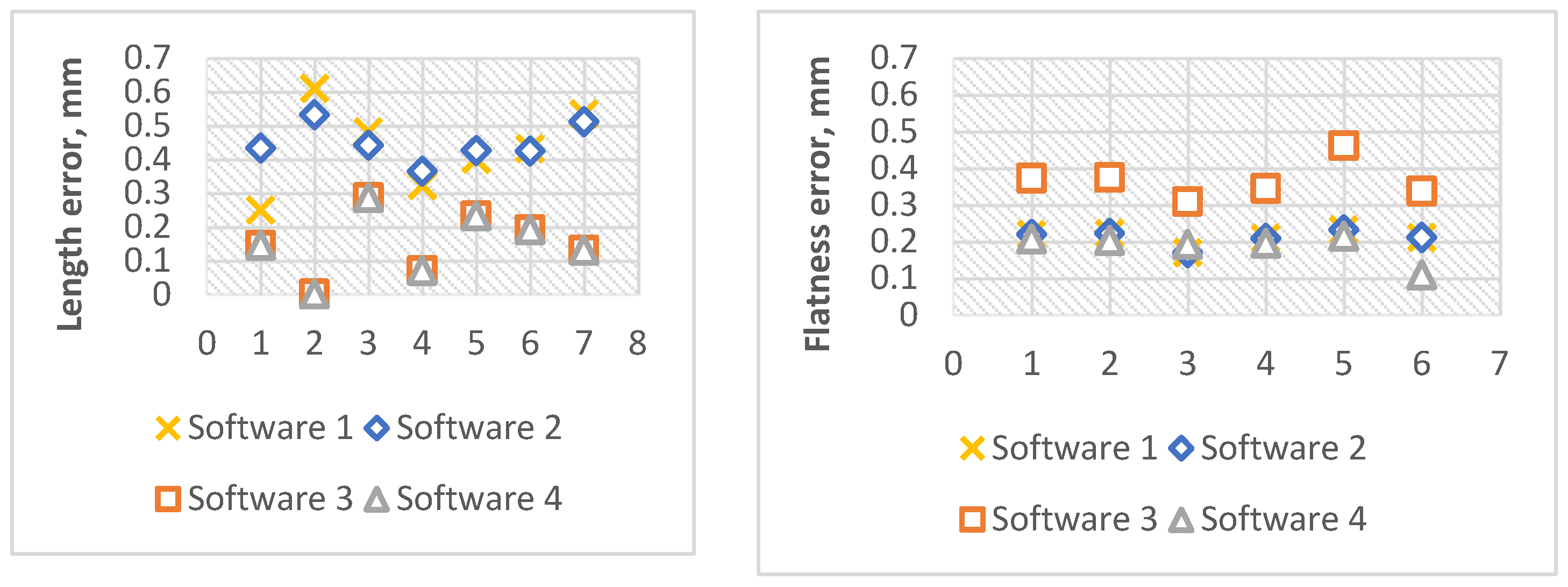
The LCM investigated the impact of algorithms used in four selected leading metrology software for surface analysis to develop measurement results. The measurement was carried out using the articulated arm CMM optical system with an integrated optical head following the VDI/VDE recommendations [24]. First, the test ball was used to determine the error of the head system - it was measured in 10 settings throughout the measurement space. Then the ball-bar standard was measured in 7 settings to determine the indication error on the length and the flatness standard in 6 settings to check the flatness error [22].

The acquired clouds were developed in each of the four software programs with numbers from 1 to 4. The obtained results (Figure 4) indicate an identical and similar algorithm in determining the length for software numbers from 1 to 4. For flatness, however, the results of software 3 clearly differ from the others. The observed differences showed some disturbing influence of the software on the measurement result. They undermined the legitimacy of comparing results in different software due to the significant impact of algorithms allowing for mapping the basic geometric element. In order to improve the quality, it is necessary to carry out the validation of metrological software [19,20]. The authors decided to consider the software's significant impact when estimating uncertainty using the OPTI-U method.

Operator's Work in the Context of Applied Filtration

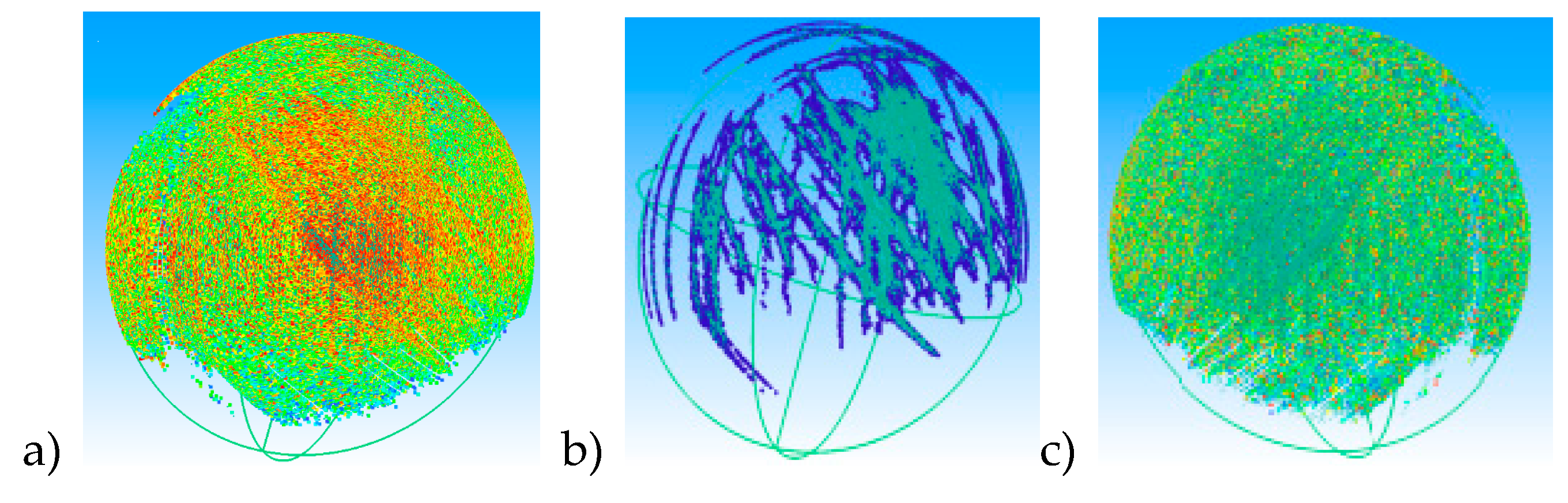
The operator's influence on the measurement result was tested for 3DReshaper and Focus 10 software. Each of the software packages provides the user with a number of possibilities to filter the data in its original form and when using the best-fit tool. These possibilities are based on various criteria for removing points, i.e. the distance between points (explode with distance (Figure 5a), density (points are removed from small clusters—noise reduction) (b), and random reduction (c). It is also possible, for example, to divide the space into small cubes with a side length defined by the operator, leaving a single point in each cube.

The results of simulations taking into account different filtration methods along with the variation in their intensity. It has been shown that filtration strongly changes the nature of the input data without affecting the final measurement result. When conducted by an inexperienced operator, it may result in the loss of information about the actual shapes of the object measured as a result of removing the wrong number of points or improperly distinguishing areas to be removed. Therefore, the authors suggest removing the points with caution and to the best of one's knowledge. During the research, it was observed that the results of system calibration carried out by several operators differ from each other, despite working with the same software and when using the same filtration methods. The authors tend to state that the optical measuring device, operator, and software should be treated together as the entire measurement system during calibration [19,20,21,22].

3. OPTI-U Accuracy Assessment Method for Optical Measurements

The LCM conducted several studies to search for the factors generating the largest errors in optical measurements. The dominant influence of both the operator and the software/program was observed. The research was carried out with different configurations of factors to formulate objective conclusions, considering both different operators and software. Therefore, a method of assessing the accuracy of measurements dedicated to optical measurements was developed, which takes into account the impact of these factors—the OPTI-U method, which is a combination of the comparative, multi-position and R&R method. The OPTI-U method in the context of the measurement procedure is based on the multi-position method [17]—measurement from different directions. Measurement with the OPTI-U method includes a cycle of six repetitions of measurements of a given characteristic (for the standard, these are three repetitions) in three settings. On the other hand, in the context of calculating uncertainty, it is based on the comparative method [16], whereby, unlike the classic method, the standard uncertainty of systematic error was expressed as components of the uncertainty of

u_{A V}

and

u_{E V}

in accordance with (4), which emphasised the clear and systematic influence of the operator and the machine. Thus, the expanded uncertainty in the OPTI-U method is calculated according to the following formula:

U = k \cdot \sqrt{{(u_{c})}^{2} + {(u_{p})}^{2} + {(u_{m})}^{2} + {(u_{A V})}^{2} + {(u_{E V})}^{2}}

(4)

where:

u_{c}

—standard uncertainty of the calibrated object,

u_{p}

—standard uncertainty of the measurement procedure,

u_{m}

—standard uncertainty from the manufacturing process,

u_{A V}

—standard uncertainty of the device operator,

u_{E V}

—standard uncertainty of the machine.

Standard uncertainties

u_{c}

u_{p}

u_{m}

are determined in accordance with similar uncertainties in the standard ISO 15530-3:2011 [16].

Determination of Standard Uncertainty of the Device and Operator: $u_{A V}$ and $u_{E V}$

Uncertainty

u_{A V}

from the operator and

u_{E V}

the machine can be determined with the adaptation of the method mentioned in Chapter 2.2 and known in metrology as the R&R method. In order to determine the components from the operator and the machine, measurements of a given characteristic are made six times in three settings (the first three—operator A, and the next—B). Then the range values (R) for the results from A and B are calculated separately, for each setting, as absolute values from the difference between the maximum value and the minimum value of the measurement results of a given part (5):

R = |P_{M A X} - P_{M I N}|

(5)

where: PMAX—the maximum value of the measurement results, PMIN—the minimum value of the measurement results.

In the next step, the sum of individual ranges (ΣRA, ΣRB) is calculated, and then the average value for the sum of the ranges of individual measurements in one setting made by one operator (6):

R = |P_{M A X} - R_{\bar{A}} = \frac{\sum R_{A}}{L}, R_{\bar{B}} = \frac{\sum R_{B}}{L}|

(6)

where:

R_{A}

– range of measurement results carried out by operator A,

R_{B}

– range of measurement results carried out by operator B, L—number of settings.

Then the value of

R_{B}

is calculated as the sum (

R_{\bar{A}}

R_{\bar{B}}

) divided by the number of operators (7):

\bar{R} = \frac{R_{\bar{A}} {+ R}_{\bar{B}}}{L}

(7)

where:

R_{\bar{A}}

—average value for the sum of the ranges of individual measurements in one setting made by operator A,

R_{\bar{B}}

—average value for the sum of the ranges of individual measurements in one setting made by operator B, L—number of settings.

Then the sum of the individual results in each setting (ΣA₁, ΣA₂, ΣA₃ and (ΣB₁, ΣB₂, ΣB₃) are calculated and added (8) respectively:

\sum X_{A} = \sum A_{1} + \sum A_{2} + \sum A_{3}, \sum X_{B} = \sum B_{1} + \sum B_{2} + \sum B_{3}

(8)

The mean values are calculated as follow:

X_{\bar{A}} = \frac{\sum X_{A}}{3}, X_{\bar{B}} = \frac{\sum X_{B}}{3}

(9)

where:

X_{\bar{A}}

– the average value of the sum of individual results in each setting for operator A,

X_{\bar{B}} —

the average value of the sum of individual results in each setting for operator B.

Finally, we calculate

R \bar{X} = |X_{\bar{A}} - X_{\bar{B}}|

(10)

The uncertainty component derived from the

u_{E V}

(repeatability) can be calculated according to following formula

u_{E V} = \bar{R} \cdot K_{1}

(11)

The values of the K coefficients are read from tables depending on the number of repetitions; for the presented method, they are K1 = 0.00456, K2 = 0.00365 for two repetitions and K1 = 0.00305, K2 = 0.00270 for three repetitions [18], respectively. The uncertainty component from the

u_{A V}

operator (reproducibility) shall be calculated according to following formula

u_{A V} = \sqrt{{(R \bar{X} + K_{2})}^{2} - \frac{{u_{E V}}^{2}}{(n \cdot r)}}

(12)

where: n—number of elements, r—number of repetitions.

Expressing the Measurement Result

With reference to [16], the measurement result should be adjusted by the value of systematic inflows. If this is not possible, the measurement result

\bar{p}

is the average of all the results, including the correction—if the measurement strategy is the same on the item and the standard used, and the standard meets the conditions of similarity (13). Errors inadequate for a given measurement task take the value 0.

W = \bar{p} - (E_{L} + E_{S} + E_{P}) \pm U

(13)

where:

\bar{p}

—the mean value of the results obtained, in accordance with (14), E_L—systematic error of length measurement, E_S—systematic error of measurement of the outer/inner sphere/flat surface, E_P—systematic error of the program used.

\bar{p} = \frac{1}{n_{p} \cdot m_{p}} \sum_{i = 1}^{n_{p}} \sum_{j = 1}^{m_{p}} p_{i j}

(14)

where: n_{p —}number of measurements repeated in one orientation, m_p—number of different orientations, p_ij—the result of the measurement of the determined dimension in the i-th repetition, in the j-th orientation.

Determination of the Systematic Length Measurement Error—E_L

The E_L parameter (15) is determined during length measurements. A length standard designed for calibrating optical systems, appropriately selected for the measured element, is used to determine the parameter. This may be a ball-bar standard (distance from the centre of the sphere to the centre of the sphrere) or a reference plate (plane to plane), depending on the dimensions and shape [19].

E_{L} = \bar{p} \cdot E_{L p}

(15)

where: E_Lp—relative error, determined in accordance with the following formula:

E_{L p} = \frac{1}{n_{w} \cdot m_{w}} \sum_{i = 1}^{n_{w}} \sum_{j = 1}^{m_{w}} \frac{q_{i j} - q_{w}}{q_{w}}

(16)

where: n_{w —}number of measurements repeated in one orientation, m_w—number of different orientations of the length standard, q_w—the reference value of the used standard recorded in its calibration certificate, q_ij—the result of the measurement of the standard in the i-th orientation and in the j-th repetition.

Determination of the Systematic Error of Measurement of the Inner, Outer and Flat Surface—E_S

The E_S error is determined by performing the measurement of selected standards: the E_Sout reference sphere (outer), the concave hemisphere (inner) E_Sin and the E_Sf flatness standard depending on the shape of the measured object and performing calculations in accordance with the relationships (17–19). The E_S error is assumed as the value of the largest error among E_Sout, E_Sin, E_Sf depending on the nature of the variability in the shape of the measured surface—the dominant shape is selected [19].

E_{S o u t} = \frac{1}{n_{w} \cdot m_{w}} \sum_{i = 1}^{n_{w}} \sum_{j = 1}^{m_{w}} (S_{i j} - S_{w})

(17)

and

E_{S i n} = \frac{1}{n_{w} \cdot m_{w}} \sum_{i = 1}^{n_{w}} \sum_{j = 1}^{m_{w}} (s_{i j} - s_{w})

(18)

and

E_{S f} = \frac{1}{n_{w} \cdot m_{w}} \sum_{i = 1}^{n_{w}} \sum_{j = 1}^{m_{w}} (f_{i j} - f_{w})

(19)

where: n_w – number of measurements repeated in one orientation, m_w—number of different orientations of the standard, S_w—reference value of the diameter of the used reference sphere, S_{ij —}measurement result of the diameter of the sphere, s_w—the reference value of the diameter of the used concave hemisphere, s_ij—the result of measuring the diameter of the internal reference sphere, f_{w —}reference value of the flatness of the standard, f_{ij —}the result of measuring the flatness of the standard.

Determination of the Programe Error—E_P

The E_P error (20) is determined using the ball standard, which is measured three times in two settings (measurements from the determination of the E_S component can be used). The diameters of the spheres in the programe used in the measurements are then determined. The situation in which results are developed in more than one programe is relatively rare. However, this parameter is gaining importance due to the increasing use of multisensory systems. The authors mean a situation in which the operator has various tools for a given task and, to obtain the most accurate results possible or for practical reasons, decides to develop fragments of the measured object in various programs. For such situations, it is necessary to determine the uncertainty component of the E_P.

u_{P} = \frac{1}{n_{w} \cdot m_{w}} \sum_{i = 1}^{n_{w}} \sum_{j = 1}^{m_{w}} (P_{i j} - P_{w})

(20)

where: n_w—number of repetitions of measurements in all orientations (2 settings

\times

3 measurements), m_w—the number of program solutions used to obtain the results, P_ij—sphere diameter measurement result, P_w—the nominal value of the sphere diameter.

5. Measurements Carried Out and Validation

The research presented in this article was carried out using the equipment constituting the LCM measurement base, including systems made available to the Laboratory under agreements. The measurements were carried out using the systems presented in Table 4.

The geometric standards that can be compared to the geometric elements of the sphere, plane, and roller type were measured, e.g. a flatness standard with a flatness deviation of 0.0017 ± 0.0006 mm, a reference ball with a diameter of 24.9809 mm ± 0.0006 mm and a shape error of ± 0.0013 mm, a ball-bar with a distance between the centres of the spheres of 99.8773 mm ± 0.0007 mm.

Validation shall be carried out in order to verify and document the fulfilment of the expectations regarding the intended use of the system, method, process, procedure, and device [25]. The validation of the OPTI-U method was carried out in relation to the comparative method, because it is a method commonly used in coordinate measurement techniques based on the PN-EN ISO 15530-3:2011 standard [16].

The tests were carried out on a CMM Nikon LK V-SL10.7.6 equipped with an LC15Dx laser scanner. Three objects were measured, and three standards were specified by determining the diameter of the sphere standard, the deviation of flatness and the distance between the centres of the spheres (Figure 6). The elements were prepared for testing in accordance with the requirements of the standards, so their surfaces were thoroughly cleaned and subjected to temperature stabilisation. The measurements were performed in a sequence corresponding to the specified procedures. The measurement results are presented in Table 5 and in graphs (Figure 7).

The validation of the OPTI-U method was aimed at checking the consistency of the results and obtaining an answer as to whether using the OPTI-U method allows for obtaining results similar to the results obtained using the comparative method, which uses a calibrated object and has been proven and tested for years. The statistical validation parameters determined to verify the usefulness of the OPTI-U method in assessing the accuracy of optical measurements in relation to the method using the calibrated object were determined using a two-way measure of discrepancy with the normal consistency and measures of discrepancies model [25], and based on a statistical test of normal consistency developed by Birge in 1932. When applying a two-way measure of discrepancy, the following conditions shall be met:

The obtained results of measurements xi,..,x_n are random variables, which are determined by the probability density function with expected and unknown values.

The probability distributions of the x_i,..,x_n measurements are normal (Gauss) and independent of each other.

The standard uncertainties of the obtained measurement results u(x_i),..,u(x_n) are standard deviations from the above-mentioned distributions [25].

A bilateral measure of discrepancies T_i-j(x) assumes that the results of x_i and x_j obtained from the two methods of estimating uncertainty are mutually consistent if their differences are small in relation to the difference in their variance (21).

T_{i - j} (x) = (x_{i} - x_{j})

(21)

The predictive value here is p_b given by the following formula

p_{b} = P r {Z \geq \frac{(x_{i} - x_{j})}{\sqrt{u^{2} (x_{i}) + u^{2} (x_{j})}}}

(22)

The results of x_i and x_j are divergent and inconsistent if the probability result is close to 0 or 1, while if the result is in the range from 0.05<Pb<0.95, a convergence and similarity of the results can be found [25]. The validation was carried out in accordance with [25], and its results are presented in Table 5.

The similarity of the results obtained using the OPTI-U method to the results obtained using the reference comparative method is maintained. The probability results for the measured characteristics are in the range from 0.05 to 0.95. Therefore, it is possible to assume a positive result of the OPTI-U method validation for the presented measured values, which confirms the suitability of the OPTI-U method in assessing the accuracy of coordinate optical measurements.

5. Concluding Remarks

Regardless of the type of optical system used, whether it is a system operating on the principle of laser triangulation or structural light, a photogrammetric or a computed tomography system, results that are obtained using it in the form of a point cloud are subject to the same laws. In this article, the key factors determining such a result were indicated both at the measurement stage, i.e. obtaining data in the form of clouds and when already acquired clouds are being developed.

During the first mentioned stage, i.e. conducting a coordinate optical measurement, numerous point clouds are obtained. To improve the accuracy of this stage, the authors recommend the correct tool selection for the intended purpose, ensuring appropriate conditions, including lighting. Limiting light sources is very important when measuring with structural light. The authors also recommend the optimal selection of the parameters of the probe head for the task, resulting in a certain number of points collected from a given area during a single head passage. The right number of points should be collected to get a full picture of the measured object. However, the larger the number of points, the larger errors may occur. With fewer points, the texture of the cloud is simplified, and the measurement is faster and more efficient.

During the second stage, i.e. working with the acquired point cloud, the authors recommend reasonably and consciously using available filtration methods. Current work on point clouds is focused on developing filtration algorithms that allow data to be developed in a more accurate manner. Modern approaches to point cloud filtration take into account the use of artificial intelligence, in particular machine learning, deep learning, enabling automatic detection and reduction of noise and points coming from reflections. The research work also concerns the development of tools for presenting measurement data and making the data available in real time, which is extremely important when using coordinate optical systems in production. The authors draw attention to insufficiently complete top-down guidelines for working with clouds. The available software allows for a lot of freedom in cloud processing, which, in the absence of sufficient operator experience, may result in the loss of information about the actual shapes of the measured objects. As research has shown, filtration changes the nature of the input data. Although the standards and recommendations indicate the number of points that can be removed, the results of work with the same cloud of different operators differ from each other. Therefore, in the process of processing the point cloud, it is recommended to specify the guidelines and impose certain blockages in programs potentially exceeding the permissible threshold. General software validation, taking into account filtration algorithms, and broader inter-laboratory comparisons in this respect would also be advisable.

Bearing in mind the diversity of coordinate optical measurements in terms of contact, not only in terms of the measurement strategy itself, but also the methods of developing the results, the OPTI-U method was developed and presented, taking into account the impact on the accuracy of important factors such as the operator, software. The OPTI-U method has been successfully validated and responds to the need to systematise the evaluation of the accuracy of measurements carried out using coordinate optical systems. In the future, it is planned to further develop the method by further factors affecting the measurement result, such as the type of measured surface in terms of, among others, colour and reflective-dissipating characteristics. It is also planned to examine the degree of correlation of individual components. The question of whether a virtual standard can replace material standards used and measured by optical methods, how to provide a reference and connection with the unit, or whether the nominal value sufficiently represents an error-free reference for the computational algorithm and measurand is becoming increasingly relevant. All these problems are currently the subject of the authors' research.

References

JA Sładek, Coordinate Metrology. Accuracy of Systems and Measurements (2016) Springer Tracts in Mechanical Engineering, Springer-Verlag Berlin Heidelberg.
A Forbes, Approximate models of CMM behaviour and point cloud uncertainties (2021) Measurement. Sensors 18.
J Eastwood, G Gayton, RK Leach, S Piano Improving the localisation of features for the calibration of cameras using EfficientNets (2023) Optics Express 31(5).
M Buhmann, R Roth, T Liebrich, K Frick, E Carelli, M Marxer, New positioning procedure for optical probes integrated on ultra-precision diamond turning machines (2020), CIRP Annals, Manufacturing Technology 69 (1).
A Wozniak, JRR Mayer, Discontinuity check of scanning in coordinate metrology (2015) Measurement 59.
Dewulf, W.; Bosse, H.; Carmignato, S.; Leach, R. Advances in the metrological traceability and performance of X-ray computed tomography. CIRP Ann. 2022, 71, 693–716. [Google Scholar] [CrossRef]
L Rocha, E Savio, M Marxer, F Ferreira Education and training in coordinate metrology for industry towards digital manufacturing (2017) Journal of Physics: Conference Series IMEKO 1044.
I Poroskun, C Rothleitner, D Heißelmann Structure of digital metrological twins as software for uncertainty estimation (2022) J. Sens. Sens. Syst. 11.
S Catalucci, A Thompson, J Eastwood, ZM Zhang, DT Branson III, R Leach, S Piano, Smart optical coordinate and surface metrology (2022) Measurement Science and Technology 34(1).
EK Rafeld, N Koppert, M Franke, F Keller, D Heißelmann., M Stein, K Kniel Recent developments on an interferometric multilateration measurement system for large volume coordinate metrology (2021) Measurement Science and Technology 33(3).
M Wieczorowski, J Trojanowska Towards Metrology 4.0 in Dimensional Measurements (2023) Journal of Machine Engineering 23(1).
N Senin, S Catalucci, M Moretti, RK Leach Statistical point cloud model to investigate measurement uncertainty in coordinate metrology (2021) Precision Engineering 70.
N Covre, A Luchetti, M Lancini, S Pasinetti, E Bertolazzi, M De Cecco Monte Carlo-based 3D surface point cloud volume estimation by exploding local cubes faces (2022) ACTA IMEKO 11(2).
C Berry, MSG Tsuzuki, A Barari Data Analytics for Noise Reduction in Optical Metrology of Reflective Planar Surfaces (2022) Machines 10 (1).
A Forbes Uncertainties associated with position, size and shape for point cloud data (2018) Journal of Physics 1065(14).
ISO/TS 15530-3:2011 Geometrical product specifications (GPS) -- Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement -- Part 3: Use of calibrated workpieces or measurement standards.
ISO/TS 15530-2 (draft) Geometrical Product Specification (GPS). Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement. Part 2: Use of multiple measurements strategies in calibration artefacts.
Measurement Systems Analysis MSA—second edition 1995, Reference manual, AIAG-Work Group, Daimler Chrysler, Corporation, Ford Motor Company, General Motors Corporation.
D Owczarek, Model niepewności we współrzędnościowych pomiarach optycznych, monograph (2017) Cracow University of Technology, Cracow.
D Owczarek, K Ostrowska, JA Sładek Examination of optical coordinate measurement systems in the conditions of their operation (2017) Journal of Machine Construction and Maintenance 4.
K Ostrowska, D Szewczyk, JA Sładek (2013) Determination of operator's impact on the measurement done using coordinate technique, Adv. Sci. Technol. Res. J. 7.
K Ostrowska, D Szewczyk, JA Sładek (2012) Wzorcowanie systemów optycznych zgodnie z normami ISO i zaleceniami VDI/VDE, Technical Transactions.
ISO 10360-6:2001 Geometrical Product Specifications (GPS): Acceptance and reverification tests for coordinate measuring machines (CMM), Part 6: Estimation of errors in computing Gaussian associated features.
VDI-VDE-2634-Systeme-mit-flaechenhafter-Antastung.
Gromczak K Validation Model of coordinate measuring methods (2016) PhD Thesis, Cracow University of Technology, Cracow.

Figure 1. Ishikawa diagram for factors affecting measurement results from optical measurement.

Figure 2. Interpretation of the Stripes Distance parameter.

Figure 3. Schematic diagram of the impact of lighting on the result.

Figure 4. The influence of the used software on the measurement result on the example of length and flatness measurement [19].

Figure 5. Examples of filters a) explode with distance, b) noise reduction, c) random reduction.

Figure 6. Validation of the OPTI-U method—standards (at the top) and objects (at the botton).

Figure 7. Values of measured characteristics together with measurement uncertainties for the OPTI-U method and the comparative method.

Table 1. Methods for assessing the accuracy of optical measurements used in LCM [19]. ¹ O—object, ² S—Standard, ³ SD—parameter value Stripes Distance.

Method	Number of settings		Number of repetitions in a given setting		Orientation of the Object in the measuring space	SD³	Flatness deviation, mm	Diameter of the sphere, mm	Distance between sphere centres, mm
Method	O¹	S²	O	S	Orientation of the Object in the measuring space	SD³	ref. 0.002	ref. 24.980	ref. 99.877
Comparative	1	3	10	10		0.05	0.023	25.020	99.884
						0.125	0.018	25.021	99.886
						0.2	0.022	25.022	99.886
Multi-position	4	4	3	3		0.05	0.028	25.016	99.887
						0.125	0.017	25.027	99.890
						0.2	0.019	25.026	99.890
OPTI-U	3	3	6	3		0.05	0.034	25.022	99.881
						0.125	0.016	25.032	99.884
						0.2	0.021	25.029	99.884

Table 3. Results of the R&R method with interpretation.

R&R method	AA CMM with contact probe, %	AA CMM with optical probe, %	Result	Interpretation of the result
E.V.%	0.0310	0.2110	< 10	Permissible error
A.V.%	13.9950	22.5700	10—30	Permissible error depending on the accuracy of the measurement
R&R%	13.9951	22.5701	> 30	The error is too large, the system should not be used

Table 4. Specification of measurement systems used in the tests.

System	Model	Field of View, mm				MPEP (1σ), µm	Amount of points per 1 sec
System	Model	Width		Depth		MPEP (1σ), µm	Amount of points per 1 sec
Coordinate Measuring Machine Nikon LK V10.7.6 SL + head with laser triangulation	L100	110		60		6.5	200,000
		Measurement scope, mm				Accuracy, µm	Amount of points per 1 sec
		X	Y		Z	Accuracy, µm	Amount of points per 1 sec
Articulated Arm CMM Romer Absolute Arm + head with laser triangulation	7320SI (R2)	2000	2000		2000	± 79	50,000
		Measurement scope, mm² (white or blue light)				Accuracy, µm	Amount of points per 1 sec
Smarttech 3D SCAN3D qualify Optical System 10 Mpi (white light)	3D Qualify	80 x 100 - 1200 x 1600				up to 10	up to 2,000,000

Table 5. Validation of the OPTI-U method.

Measured geometric characteristic	Method for estimating uncertainty	Measured characteristic value, mm	Measurement uncertainty, mm	$\frac{(x_{i} - x_{j})}{\sqrt{u^{2} (x_{i}) + u^{2} (x_{j})}}$	Value Z	Pb	Criterion validation result 0.05<Pb<0.95
Diameter of the sphere	Comparative	24.961	0.028	0.8944	0.9	0.1841	positive
Diameter of the sphere	OPTI-U	24.933	0.014	0.8944	0.9	0.1841	positive
Flatness deviation	Comparative	0.031	0.022	0.9529	0.96	0.1685	positive
Flatness deviation	OPTI-U	0.028	0.016	0.9529	0.96	0.1685	positive
Distance between sphere centres	Comparative	69.151	0.022	0.1103	0.12	0.4522	positive
Distance between sphere centres	OPTI-U	69.129	0.007	0.1103	0.12	0.4522	positive

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Point Cloud as Imaging Effect in Coordinate Optical Measurement—A New Method for Evaluating Measurement Accuracy (OPTI‐U)

Abstract

Keywords:

Subject:

1. Introduction

2. How to Get "Clean" Point Clouds—Key Error-Generating Factors Based on the Conducted Research

2.1. Measurement—Error-Generating Factors

Measurement Method

Number of Points Obtained

Lighting

2.2. WORK with POINT CLOUD—Error-Generating Factors

Overall Operator Impact (R&R Method)

Operator's Work with the Software

Operator's Work in the Context of Applied Filtration

3. OPTI-U Accuracy Assessment Method for Optical Measurements

Determination of Standard Uncertainty of the Device and Operator: u A V and u E V

Expressing the Measurement Result

Determination of the Systematic Length Measurement Error—EL

Determination of the Systematic Error of Measurement of the Inner, Outer and Flat Surface—ES

Determination of the Programe Error—EP

5. Measurements Carried Out and Validation

5. Concluding Remarks

References

MDPI Initiatives

Important Links

Subscribe

Determination of Standard Uncertainty of the Device and Operator: $u_{A V}$ and $u_{E V}$

Determination of the Systematic Length Measurement Error—E_L

Determination of the Systematic Error of Measurement of the Inner, Outer and Flat Surface—E_S

Determination of the Programe Error—E_P