1. Introduction
Public-key cryptography is widely used in areas such as digital signature and mobile communication. However, they have proven to be vulnerable in the future with the advent of quantum computers [
1,
2]. To address this issue, the U.S. National Institute of Standards and Technology (NIST) has been running a Post-Qauntum Cryptography (PQC) competition since 2016, with four final algorithms selected in 2022 and additional algorithm competitions underway. The quantum-resistant ciphers of the future will replace the public-key ciphers we use today, so they need to be tested for security on real devices. Falcon is one of the algorithms selected in the competition. In other words, Falcon [
3] was proposed as an digital signature, and models are needed to evaluate the security of Falcon and its improved crypto algorithms when operating on embedded devices. A cipher that improves on Falcon is proposed as Mitaka [
4], Antrag [
5], and a variation of it is proposed as SOLMAE for 1 round candidate of Korean Post-Qauntum Cryptography (KPQC) [
6]. KPQC is a quantum-resistant cryptography competition held in South Korea.
The core of Falcon and its variants is to generate arrays of random values drawn from a discrete Gaussian distribution table. The generated array performs used with the secret information, which means that if the generated array is known, the secret information can be possibility leaked. Cumulative Distribution Table (CDT) sampling is a method that stores discrete Gaussian probabilities in a table and uses comparisons between the input and stored values to determine output. There is extensive research on side-channel vulnerabilities associated with different implementations of CDT sampling [
7,
8,
9,
10]. CDT sampling based on subtraction operations is vulnerable due to the discrepancy between positive and negative Hamming weights, with successful attacks demonstrated on schemes such as Lizard and FrodoKEM [
11,
12].
However, there is no study of side channel analysis of CDT sampling based on comparison operations used in Falcon-based PQC algorithms. For the first time, we propose a single trace analysis(STA) of CDT sampling based on comparison operations. we presented a single trace analysis for CDT sampling with a non-constant time leakage [
10]. It conducted experiments on a Harvard-based 8-bit AVR microcontroller unit (MCU). A comparison operation-based CDT sampling algorithm that satisfies constant time was proposed as a countermeasure. However, 8-bit AVR MCUs are not realistic enough for Falcon and Mitaka, which deal with 64-bit-sized operators, and to our knowledge, there is no study on the safety of CDT sampling based on comparison operations on MCUs with constant time. This paper extends the work of Choi et al. to study the safety of CDT sampling based on comparison operations in more practical environments.
This paper makes the following significant contributions to the in-depth analysis of the security of comparison operation-based CDT sampling:
A novel single trace analysis for CDT sampling based on comparison operations: We propose a single trace analysis that exploits a novel vulnerability in CDT sampling used by some Falcon-based PQC algorithms. We experimentally investigate the vulnerability in various environments and demonstrate its effectiveness.
Visible vulnerability in 8-bit AVR: This paper proposes a single trace analysis of CDT sampling based on comparison operations occurring in 8-bit AVR. Experiments have shown that 8-bit AVRs are vulnerable to non-constant-time operating of comparison operations on large numbers. We also investigate the cause of the non-constant-time behavior through reverse engineering. We show that the output of CDT sampling can be recovered from a single trace.
Proposing a constant-time CDT based on comparison operations: In this paper, we propose a comparison-based CDT sampling algorithm that eliminates the vulnerability of the comparison operation terminating prematurely and satisfies constant time. It is shown through many power consumption traces that there is no visible non-constant time vulnerability.
Invisible vulnerability in 32-bit Arm Cortex-M4: In this paper, we propose a single trace analysis of CDT sampling in a more realistic environment. In a 32-bit Arm Cortex system, CDT sampling based on comparison operations satisfies constant time. We study the safety of PQC in embedded environments. Therefore, we propose a model to investigate the constant-time vulnerability and study countermeasures. We clarify that the previously proposed countermeasures eliminate non-constant-time vulnerability.
Performance Evaluation and Results: The proposed model achieves a recovery success rate of 99.97% and an F1 score(macro, micro) of 1.0, indicating its effectiveness in recovering the sampled value of constant-time comparison operation-based CDT sampling. These results provide a crucial benchmark for assessing the safety of post-quantum cryptographic algorithms.
CDT sampling and deep learning related copuntermeasure: This study investigates countermeasures for various implementations of CDT sampling that were previously studied and examined in detail the countermeasures related to deep learning. This contributes to the fundamental research for secure PQC in embedded environments.
This thesis is structured as follows:
Section 2 explores the crucial role of CDT sampling in quantum-resistant cryptography and reviews ongoing research on its security.
Section 3 describes the power consumption acquisition environment that occurs when CDT is operating.
Section 4 addresses single trace analysis and countermeasures for visible vulnerabilities in 8-bit AVR microcontrollers.
Section 5 examines single trace analysis and mitigation strategies for invisible vulnerabilities in the 32-bit ARM Cortex-M4. Finally,
Section 6 presents the conclusions and future work.
2. Preliminaries
This section highlights the importance of CDT sampling, a method used to sample values from a discrete Gaussian distribution, and its role in lattice-based cryptosystems. Additionally, it reviews research on side-channel analysis related to CDT sampling, focusing on the limitations of comparison-based CDT sampling in non-constant-time environments. The discussion emphasizes the necessity for further security studies in more generalized environments.
2.1. Lattice-Based Cryptosystems: LWE and NTRU
Definition 1.
Lattice:
Let be a set of linearly independent vectors. The Lattice is defined as the set of all linear combinations of with integer coefficients, that is:
Here, is called the basis of the lattice.
PQC refers to cryptographic algorithms that are secure against quantum computer-based attacks, relying on challenging problems for quantum computers to solve. Currently, many of these problems are classified as NP-hard. The first lattice-based public-key cryptosystem was introduced by Ajtai et al. in 1997, sparking ongoing research aimed at developing efficient cryptographic algorithms [
13]. NTRU, proposed by Hoffstein et al. in 1996, is renowned for its fast encryption process [
14,
15]. Falcon and its variants Mitaka and SOLMAE are examples of quantum-resistant cryptosystems based on NTRU. A common feature among many NTRU-based quantum-resistant ciphers is CDT sampling.
Definition 2.
NTRU
Let q be a positive integer and be a monic polynomial. A set of NTRU secrets consists of four polynomials , and they satisfy the following equation:
And define h as . Then, given h, find f and g.
FrodoKEM, Lizard, and similar quantum-resistant cryptosystems are based on the Learning With Errors (LWE)-problem [
11,
12]. Notably, both FrodoKEM and Lizard employ CDT sampling. LWE-based cryptographic schemes involve adding a small error to the secret information to ensure security. In other words, error
e is a key factor in LWE-based cryptographic algorithms.
Definition 3.
LWE distribution
Let n be a positive integer, q be a prime number, and χ be a probability distribution over the integers. For a secret vector , the LWE distribution over is sampled by choosing a random vector uniformly at random, selecting an error term , and generating the pair:
2.2. Discrete Gaussian Distribution Sampling Using CDT
Many of the lattice-based crypto-systems generate their crucial random values from a discrete Gaussian distribution, a process known as discrete Gaussian sampling.
Definition 4. Discrete Gaussian Distribution over Lattices
For an arbitrary and , the Gaussian function is defined as:
Then, for , , and an n-dimensional lattice , the discrete Gaussian distribution over is defined as:
CDT sampling is an efficient, table-based technique that implements discrete Gaussian sampling. It leverages a Cumulative Distribution Function (CDF) to construct a lookup table. During encryption or signing, random values a random number generator produces serve as inputs to this table. Utilizing the CDF, the table returns the corresponding index for each input value. The CDF of a random variable X is defined as follows.
Definition 5. Cumulative Distribution Function (CDF)
For a given random variable X, the cumulative distribution function is defined as:
In this paper, we conduct a single trace analysis of CDT sampling implemented through comparison operations in Mitaka. We clearly distinguish that CDT sampling is combined with rejection sampling to perform a hybrid form of Gaussian sampling. Mitaka, Antrag, and SOLMAE, a variant of Falcon, also employ CDT sampling using comparison operations.
2.3. Side Channel Analysis on Implementations of CDT Sampling
A substantial body of research on single trace analysis has focused on various implementations of CDT sampling [
7,
8,
9]. CDT sampling operates by generating a random value,
, which is then compared to values in a pre-stored table. The result of these cumulative comparisons is returned as the sampled value. Algorithms 1–3 present different implementation approaches. Algorithm 1 employs a while loop, terminating the comparison operation when
is smaller than a value in the table. In this case, not all values in the table are compared. In other words, Algorithm 1 operates in non-constant time, rendering it vulnerable to timing attacks. Algorithm 2 is a constant-time algorithm in which all elements of the stored table are compared. However, it is also a weak algorithm for single trace analysis. Kim et al. proposed a single trace analysis of Algorithm 2 based on subtraction operations. The power consumption in this method differs depending on whether the resulting value is negative or positive. Zhang et al. further investigated the side-channel vulnerabilities of rejection sampling following CDT sampling in Mitaka.
Algorithm 3 illustrates the comparison operation-based CDT sampling used in Mitaka, with its actual implementation provided in Listing 1. While this approach mitigates vulnerabilities associated with traditional subtraction-based operations. However, it has not been studied whether this is a potential vulnerability.
|
Algorithm 1 The while-loop based CDT sampling |
-
Require:
CDT table , , -
Ensure:
Sampled value S - 1:
uniformly at random - 2:
uniformly at random - 3:
- 4:
while do - 5:
- 6:
end while - 7:
- 8:
return
S
|
|
Algorithm 2 The subtraction operation based CDT sampling |
-
Require:
CDT table of length ℓ, , -
Ensure:
Sampled value S - 1:
uniformly at random - 2:
uniformly at random - 3:
- 4:
for to do - 5:
- 6:
end for - 7:
- 8:
return S
|
|
Algorithm 3 Comparison-based CDT Sampling |
-
Require:
CDT Table , , , and Table length l -
Ensure:
Sampled value S - 1:
uniformly at random - 2:
uniformly at random - 3:
- 4:
for to do - 5:
- 6:
end for - 7:
- 8:
return S
|
|
Listing 1. base_sampler() C code. |
 |
3. Experiments Setup
This paper investigates the vulnerabilities that occur when comparative CDT sampling operates in embedded devices used in the real world. This session describes the power consumption acquisition environment and its two targets. It also describes the main instruction set used in each target.
3.1. Power Consumptions Acquisition
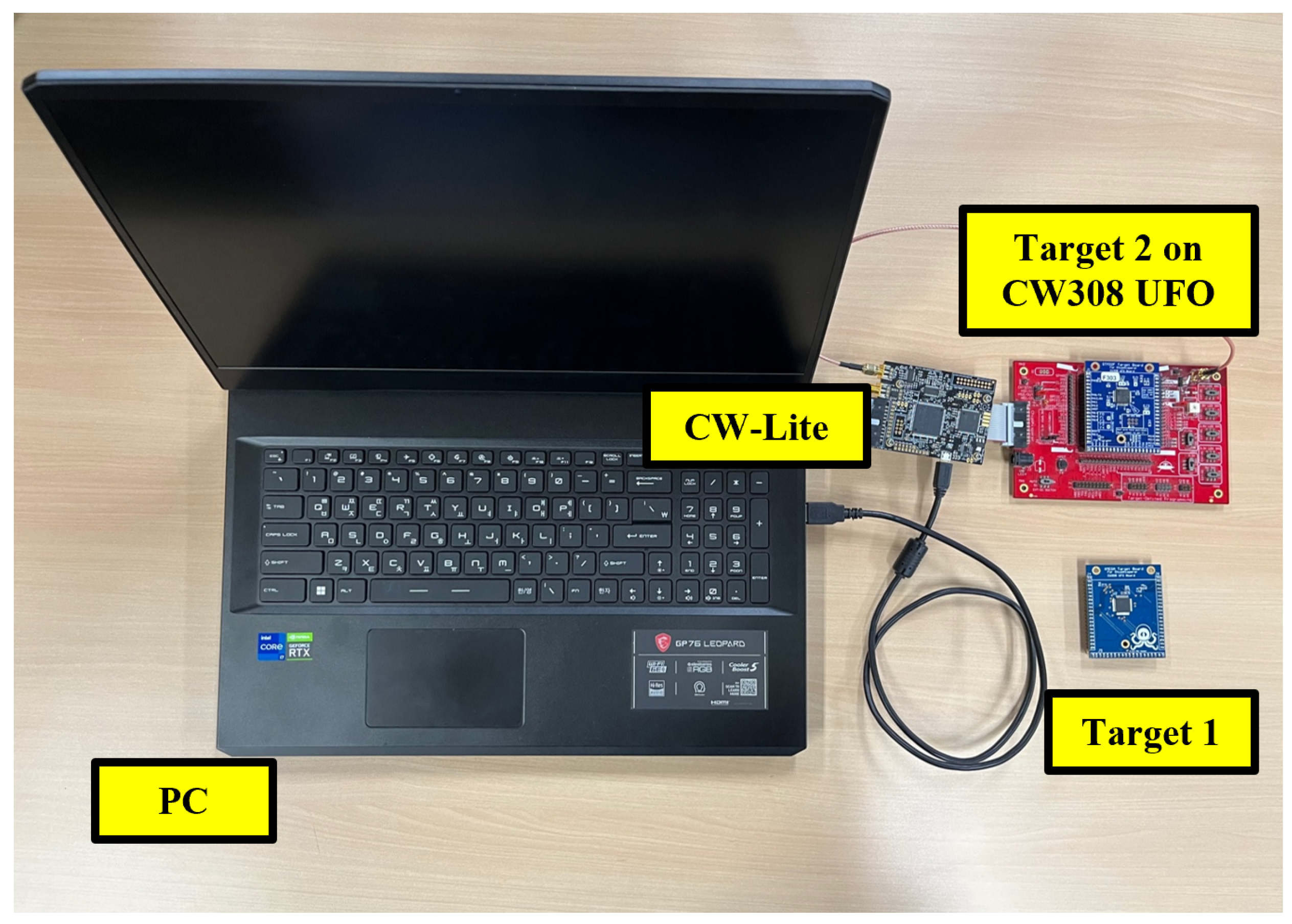
In this paper, we validate CDT sampling operating on two target MCUs. Target 1 is a board with an 8-bit AVR MCU, and Target 2 has a 32-bit Arm Cortex-M4 MCU. In
Figure 1, the Target MCU board was mounted on the ChipWhisperer CW308 UFO board and used in conjunction with the ChipWhisperer Lite (CW-Lite) to measure power consumption traces for the security evaluation of CDT sampling. The ChipWhisperer Lite incorporates an Analog-to-Digital Converter(ADC) that digitizes fluctuations in the applied voltage. The ADC operates at a sampling rate of 4 samples per clock cycle. During the experiment, the CW308 UFO board supplied the voltage across the shunt resistor to the ChipWhisperer Lite via a connecting cable. The resulting digital values from the ChipWhisperer Lite were controlled through the Python API provided by NewAE [
16], enabling data transfer to a PC.
3.2. Instruction Sets of Each Target
The 8-bit AVR MCU and the 32-bit Arm Cortex-M4 used in this thesis use different instruction sets to perform various operations [
17,
18]. The instructions can be categorized according to their role as follows.
Data transfer instructions: instructions used to move and transfer data between registers or between memory and registers.
Arithmetic instructions: instructions for basic operations such as addition and subtraction.
Logical operations instructions: instructions used to perform bitwise logical operations such as AND, OR, and XOR.
Comparison and branch instructions: Instructions that change the flow of the program according to conditions, such as comparing two values and acting differently depending on the result.
Control instructions: Instructions that handle interrupts.
I/O instructions: Instructions that control data transmission to and from external devices.
The number of clocks may vary or be fixed depending on the execution of the instruction. In this paper, we are interested in determining whether the number of clocks in the entire program changes according to the four compare and branch instructions. This is because changing the number of clocks creates a visible vulnerability. This paper’s main compare and branch instructions are ’cp’, ’brcs’, ’brne’, etc. for AVR and ’cmp’ for Arm Cortex-M4.
4. Single Trace Analysis Using Visible Leakage in 8-Bit AVR
To verify the safety of CDT sampling, we gathered the power consumption of CDT sampling operation on an 8-bit AVR.
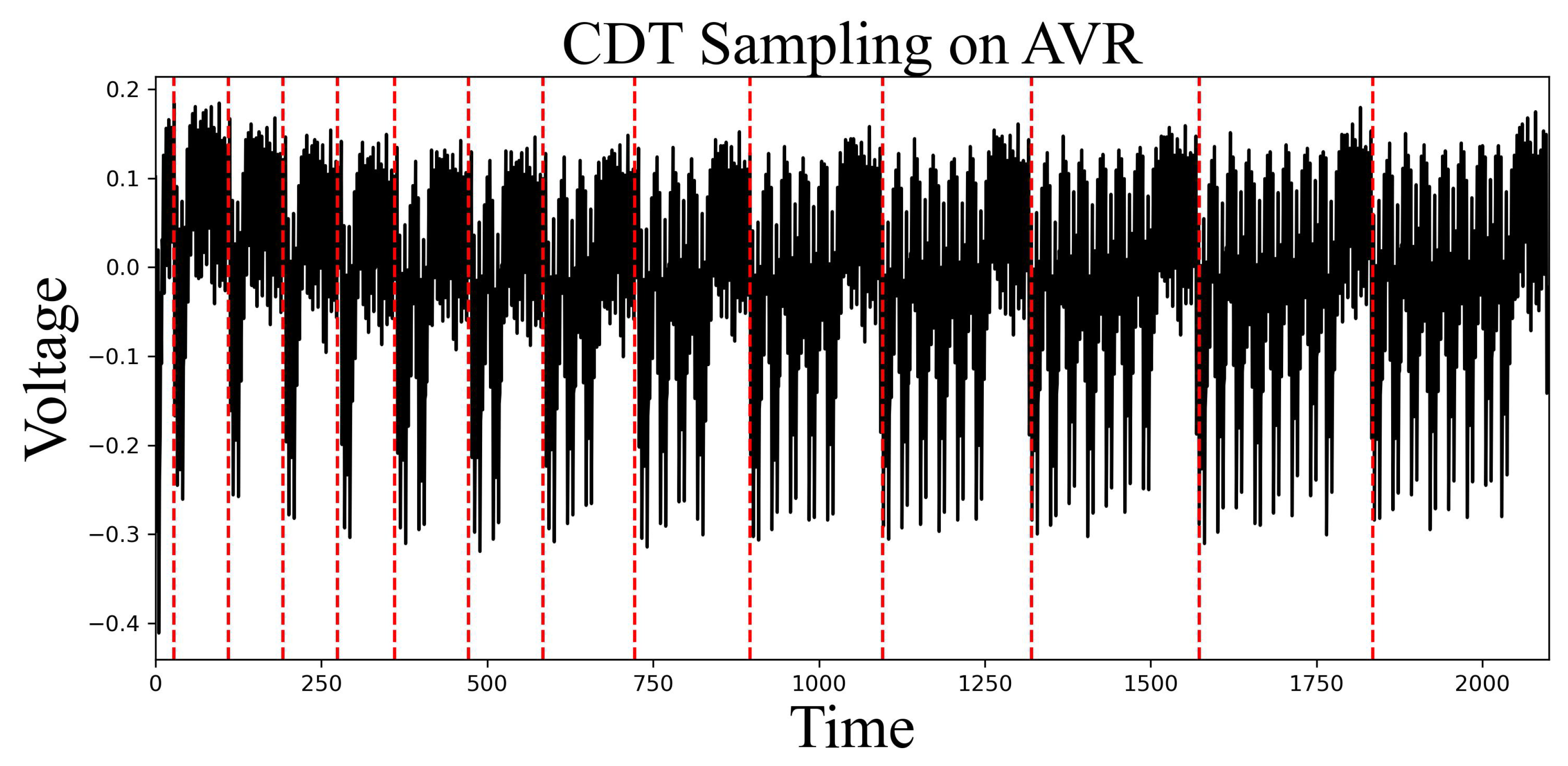
Figure 2 is the power consumption trace gathered when 13 comparison operations of CDT sampling are operated. It can be seen that the time of each comparison operation is different. In other words, CDT operates with non-constant time in 8-bit AVR. Therefore, in this section, we analyze the reasons for this in detail, propose a single trace analysis based on it, and propose and evaluate a comparison operation-based CDT sampling that satisfies the constant time.
4.1. Comparison Operation Based CDT on 8-Bit AVR
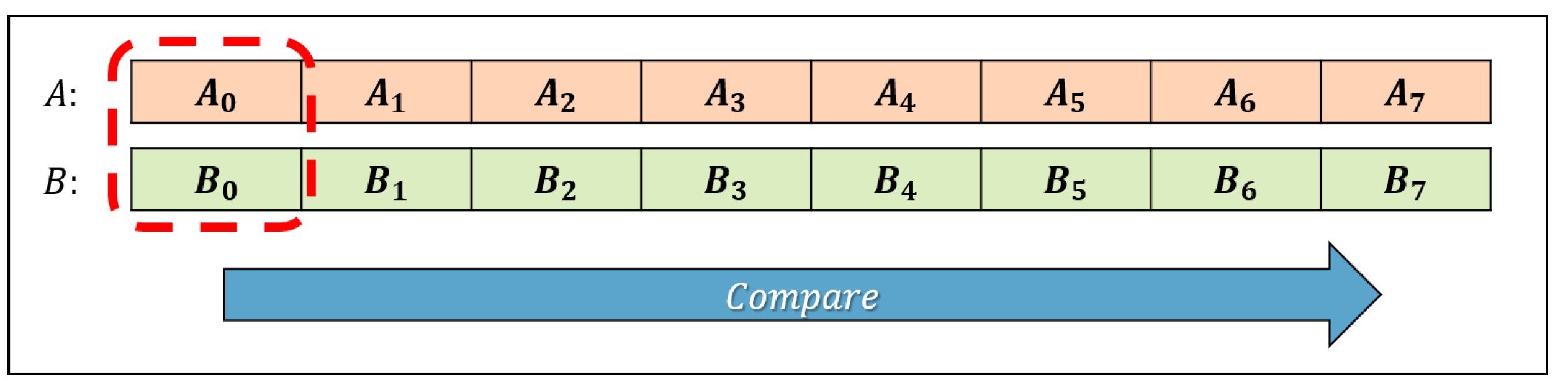
The following is how AVR works in situations where the operands used in comparison operations are larger than 8 bits. In this case, 8 bits refers to the word size of the AVR. Mitaka’s CDT uses 64-bit operands. Therefore, it is stored in eight blocks, as shown in
Figure 3. Assuming a comparison of two numbers, we have
and
, each divided into eight blocks where
i is 0 through 7.
Various methods can be employed to compare these numbers. AVR’s approach is to initiate the comparison with the most significant words. Compare A and B as follows:
Check if is greater than . If so, .
Check if is less than . If true, .
Check if and are equal. If true, continue to compare the next word until the comparison ends.
This implementation is vulnerable to side channel analysis. For instance, let’s consider two scenarios: (1) and (2) . In these situations, the execution time of the comparison operations may differ. As a result, timing vulnerabilities arise, which can be exploited through STA to distinguish between the two scenarios. This paper investigates this process by performing reverse engineering on code that works in a real AVR.
The assembly code depicted in Listing 2 illustrates the part of
function for the optimized s-level. It is evident that the comparisons are performed sequentially, word by word. Notably, vulnerabilities in the word based comparison method are evident. The process of performing comparison operations for each optimization level follows a similar pattern as shown in Listing 2. Subsequent instructions are dependent on the results of the word comparisons, leading to variations in executed operations and resulting in distinct power consumption patterns manifested as differences in power traces.
|
Listing 2. CDT Sampling Assembly Code in 8-bit AVR. |
 |
In more detail, the first word is compared in lines 252, 254, and the next operation varies depending on the result. First, calculate . If a carry occurred, then branch to line 2a0. This indicates that was a greater number than . If no carry has occurred, go to lines 256, 258. Then, calculate . If the values are not the same between and , branch to line 29c. This means that was a greater number than . If the values were the same, compare the next two words by executing the following lines. Repeat this process until the comparison operation is finally completed. In other words, the vulnerability appears in the fact that the processing method in the branch statement varies depending on the result of the comparison operation.
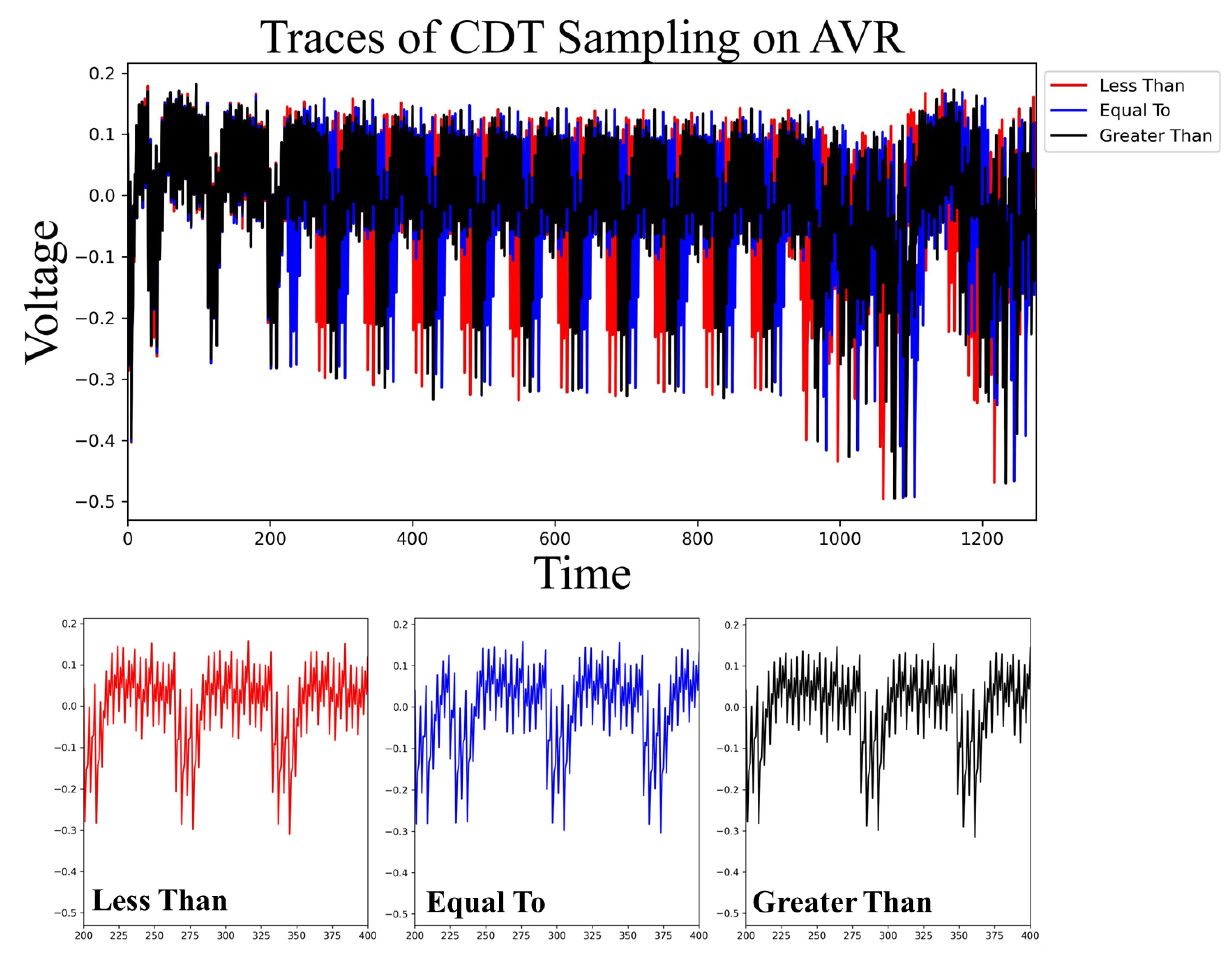
4.2. Analyzing the Security of CDTs
An increment of 1 of the sampling result occurs when
r is greater than or equal to value of table in the comparison between
r and the value of table. Furthermore, the values in the CDT table are arranged in ascending order. Consequently, once
r becomes smaller than a particular value in the CDT table, the resulting value remains unchanged. This implies that if a comparison operation with a CDT table value greater than
r is identified, the output of CDT sampling can be obtained. The power consumption traces of the first word in the comparison operation, as depicted in
Figure 4, exhibit distinct shapes for the scenarios where
r is greater than, equal to, and less than the value in the CDT table, respectively. The visual distinctiveness of these power traces facilitates the acquisition of the CDT sampling value. This vulnerability arises from the inherent characteristics of the weak comparison operation, as discussed earlier.
4.3. Countermeasure
The cause of vulnerability mentioned in this paper was attributed to the varying number of clock cycles depending on the branch statement in the 8-bit AVR environment. Hence, the countermeasure proposed an implementation method that eliminates the number of clock cycles discrepancy. This paper’s proposed secure CDT sampling algorithm is denoted as Algorithm STA-Resistant CDT sampling. The algorithm processes the
r and the CDT table in word-sized blocks, corresponding to the processing units of the processor. The values in
r, CDT table that exceed the word size are divided into
n word blocks. Comparison operations are performed identically for each block. However, if the outcome of a comparison operation is determined in the previous block, subsequent operations are only performed, i.e., it does not affect the result. Due to the inherent nature of comparison operations, methods employing them may result in branching. Branching commands such as ’brne’ and ’brcc’ are commonly used. In AVR instruction sets, ’brne’ and ’brcc’ differ by only 1 concerning true and false conditions, allowing for an equal adjustment in the number of clock cycles for the operation. However, this implementation approach can be considered risky. Therefore, this paper introduces an assembly code that eliminates the need for branch commands while implementing algorithm STA-Resistant CDT sampling.
|
Algorithm 4 Countermeasure for satisfying constant time operating |
-
Require:
- -
Ensure:
Sampled value z - 1:
- 2:
uniformly random with to n - 3:
for to do - 4:
- 5:
for to do - 6:
- 7:
- 8:
end for - 9:
- 10:
end for - 11:
return
z
|
Listing 3 is part of the assembly code, representing the comparison operation in the proposed countermeasure. The blue and red lines in Listing 3 correspond to the comparison operations in Algorithm STA-Resistant CDT sampling. Lines 278 and 288 initialize the value of register r18, where the result of the comparison operation will be stored to zero. Lines 27a and 28a compare registers r22 and r23 using ’cp’ commands, respectively and store the results in the carry flag. Lines 27c and 28c execute an addition operation on the initialized r18 using the ’adc’ (add with carry) instruction. During this operation, the stored carry values are combined, storing the comparison operation’s result within r18. This approach allowed me to eliminate the need for branching instructions, thus removing previously mentioned vulnerabilities.
|
Listing 3. The comparison operation of assembly implementation code of countermeasure. |
 |
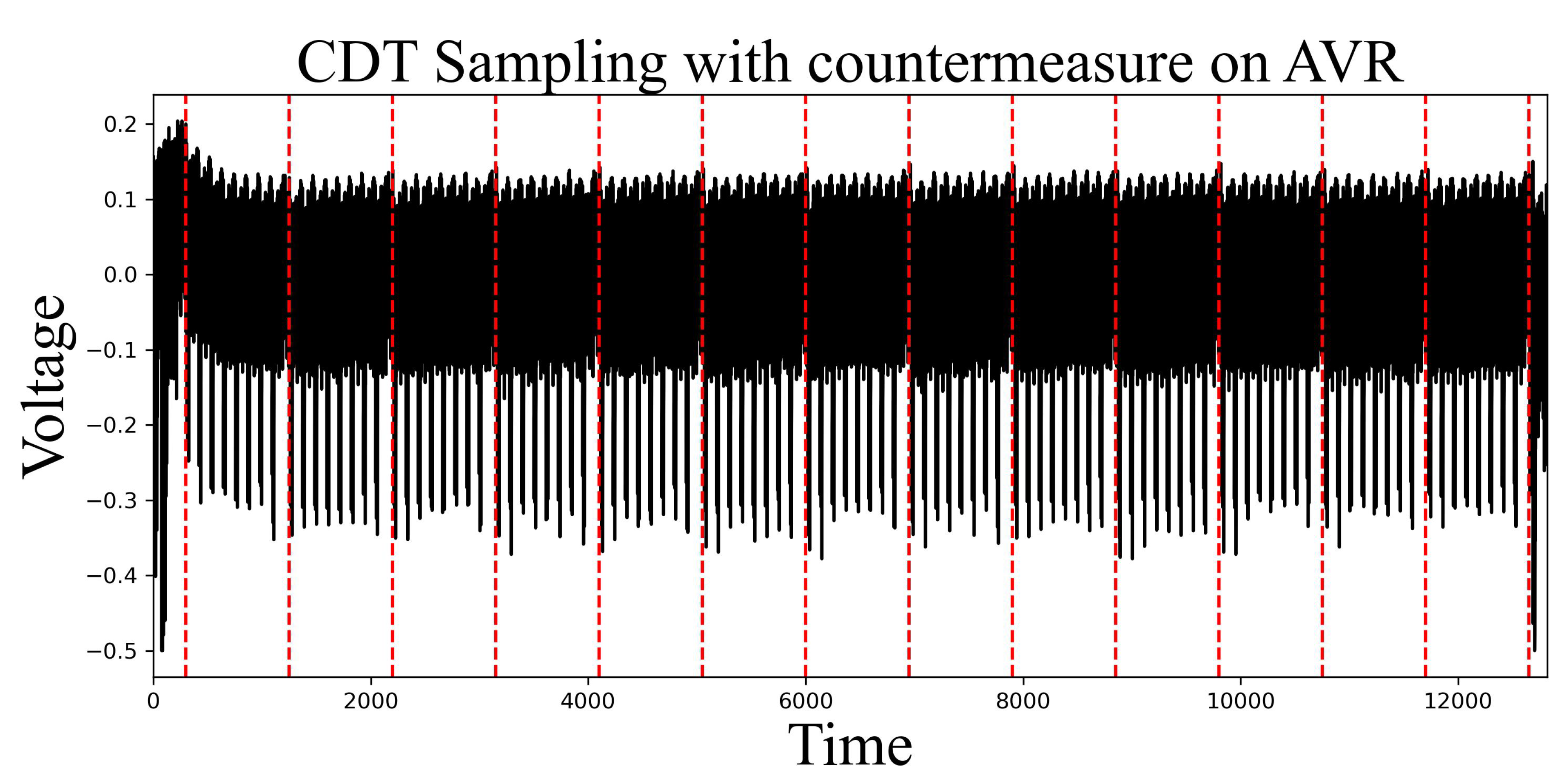
Figure 5 illustrates the power consumption traces of 3 different types of the Listing 3 operating in the 8-bit AVR MCU. This figure is fully examined by overlapping with all results to represent the corresponding power consumption traces. The trace reveals no discernible variations in the comparison time across different values. This serves as compelling evidence that CDT sampling demonstrates resistance against STA.
5. Single Trace Analysis of Invisible Leakage in 32-Bit Arm Cortex-M4
This section demonstrates that CDT sampling based on comparison operations satisfies constant-time execution on an Arm Cortex-M4-based STM32F3 chip. Last section, power consumption traces revealed that compiler-generated branch statements in 8-bit AVR MCU exhibit varying execution times due to differences in clock cycles depending on the result of the comparison operation. In contrast, on the Arm Cortex-M4, although branch statements are present, the clock cycles remain fixed and independent of the comparison result. The
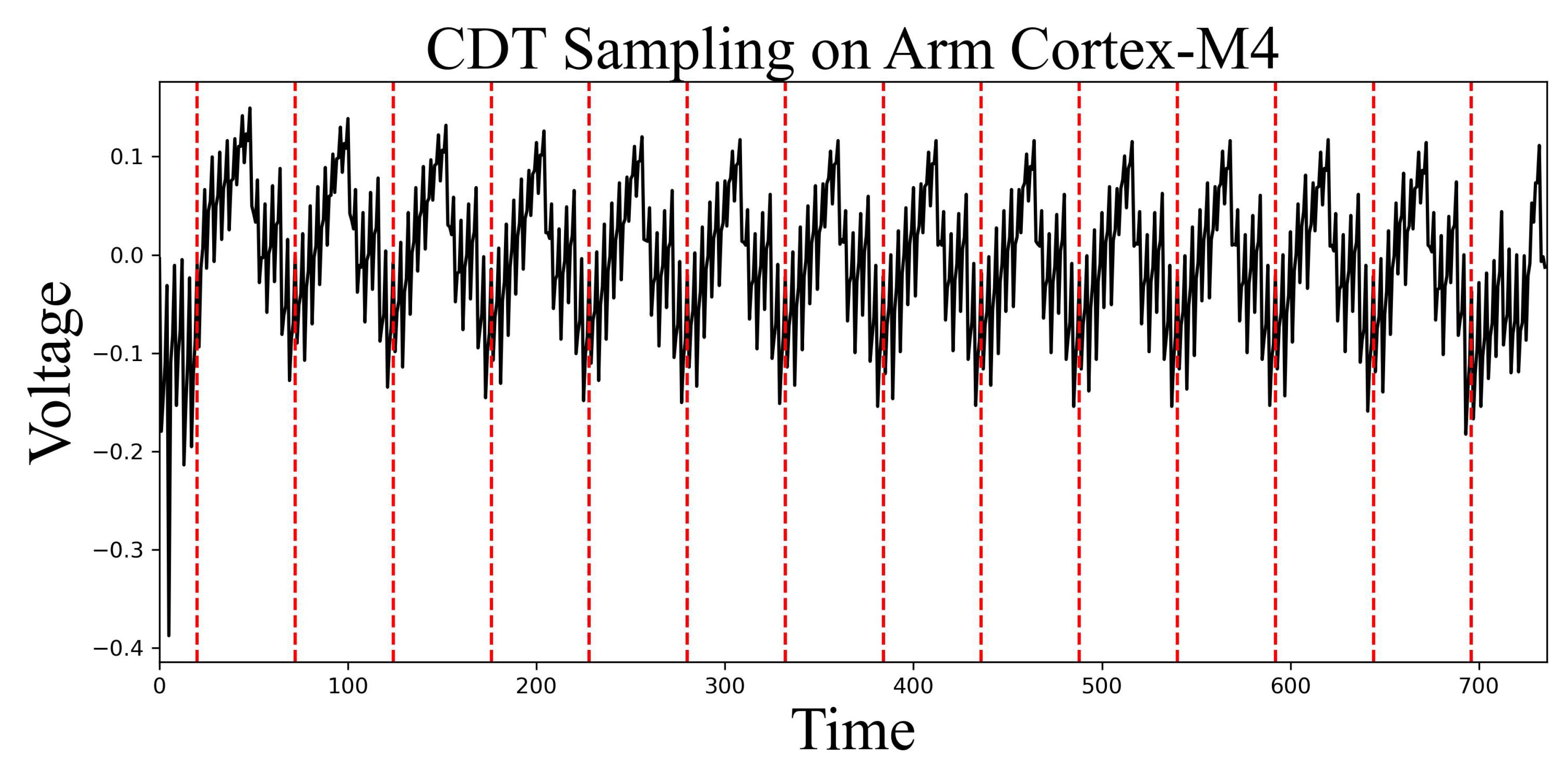
Figure 6 shows the power consumption trace of CDT sampling operating on an Arm Cortex-M4. The x-axis represents time, while the y-axis indicates voltage. It can be seen that all of the comparison operations are of the same time length, which proves that CDT sampling on Arm Cortex-M4 is a constant-time algorithm.
5.1. Comparison Operation Based CDT on 32-Bit Arm Cortex
This study investigates vulnerabilities by analyzing the assembly code. Listing 4 presents the comparison operation section of CDT sampling on the Cortex-M4. The two 32-bit comparisons are performed to handle 64-bit operands, utilizing Z-registers to ensure constant time execution. The operands are stored in registers r7, r6, and CDT in MSB(Most Significant Bit) order, with one table value loaded into registers r1 and r0. The Arm Cortex-M4 stores the result of the operation in its N, Z, C, and V flags. Specifically, Z is set to 1 if the two values are equal, and C is set to 1 if the left-hand side is greater than or equal to the right-hand side. Line 27e checks whether r7 and r1 are equal, executing line 282 if they match and line 284 if not. At this point, the it instruction is folded with the 16-bit Thumb instruction, ensuring that no additional cycles are consumed or, at most, 1 cycle is used [
18]. Consequently, CDT sampling on the Arm Cortex-M4 achieves constant-time execution. However, the values stored in registers r1 and r4, which hold the results of comparison operations on lines 286, 288, and 28c, vary depending on the outcome of the comparison. These variations could potentially expose the results of the comparison operations.
|
Listing 4. base_sampler() assembly code in Arm Cortex-M4. |
 |
5.2. Analyzing the Security of CDTs
Power consumption varies due to differences in Hamming weight [
19]. We employ profiling analysis, a deep learning-based side-channel analysis technique, to evaluate the security of CDT sampling for comparison operations that adhere to constant-time execution. Profiling analysis involves extracting secret information by utilizing a model trained on a profiled device and applying it to data from the attacked device. This method allows for predicting the attack target value from a single power trace.
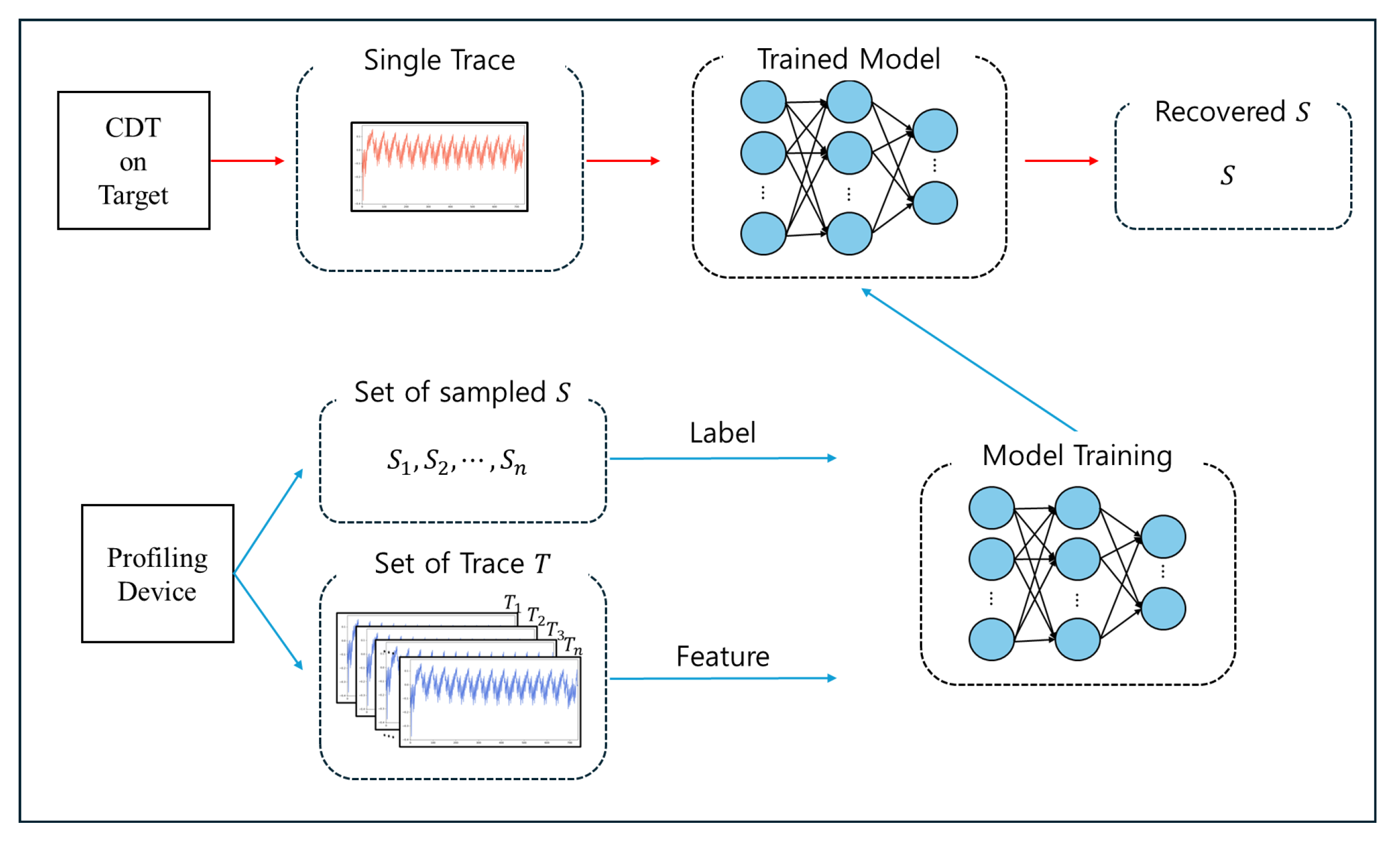
Figure 7 illustrates the procedure for applying profiling analysis to CDT sampling. The proposed model labels 14 distinct CDT result types and learns the corresponding power consumption traces collected from the profiling device. The trained model then analyzes power traces from the device under attack during CDT sampling and predicts the output values.
5.2.1. Attacker Assuming
Adversary Model: The adversary has physical access to the target device and can measure its power consumption. Additionally, the adversary possesses physical access to the same profiling target device as the attacker, with full control over it, including the ability to acquire output values from CDT sampling. This scenario closely mirrors the experimental setup described in
Section 3. The attacker can also measure the power consumption of the base_sampler() function while Mitaka is running. In our experiments, we directly triggered base_sampler(). However, in practical scenarios, it could be collected by activating base_sampler() during Mitaka’s execution or through physical manipulation [
20,
21].
5.2.2. Profiling Phase
The power consumed by the device satisfies the following Equation (
1). Therefore, the power consumption is proportional to the Hamming weight information of the data used in the computation [
19].
is power consumption,
power consumption by operation,
is power consumption based on data, and
refer to the noise inherent in the device and the constant power consumption independent of computation and data, respectively.
This paper analyzes power consumption to recover the values used in CDT sampling. However, signal noise can interfere with the accuracy of the analysis [
8]. For effective evaluation of CDT sampling, it is crucial to distinguish differences in the Hamming weights of operations by a value of 1. Consequently, an analysis method highly sensitive to the data change rate is required. Furthermore, since CDT sampling generates a random value with each execution, the recovery of the sampled value from a single execution’s power consumption should be achievable. To address this, we propose a single-trace analysis using deep learning-based side-channel analysis to assess the security of CDT sampling.
The training data for the profiling analysis consists of power consumption traces obtained by repeatedly executing CDT sampling on random inputs and the corresponding output values for each execution. Specifically, we define a set X of multiple collected power consumption traces and a set Y of sampled values obtained for each run. Each leaks information about its corresponding . Therefore, this study trains a model using pairs , where serves as the input data and serves as the label. 10,000 data sets were collected for each label, with the ratio of training data to validation data at 80:20, resulting in the training set of 112,000 traces and a validation set of 28,000 traces. The test dataset comprises 10,000 pairs generated from random inputs. The model designed to evaluate the security of CDT sampling is a MLP(Multi-Layer Perceptron), with hyperparameters specified in Table 6. The MLP architecture includes an input layer, one hidden layer, and an output layer comprising multiple nodes. The training was conducted with an epoch count of 10 and a batch size of 512, utilizing the ReLU activation function and the Adam optimization algorithm (learning rate = ).
Table 1.
MLP structure.
| Layer Type |
(In, Out) shape |
# Parameters |
| Batch Normalization |
(736, 736) |
2944 |
| Dense |
(736, 512) |
377344 |
| Batch Normalization |
(512, 512) |
2048 |
| Dense |
(512, 256) |
131328 |
| Batch Normalization |
(256, 256) |
1024 |
| Dense |
(256, 14) |
3598 |
5.2.3. Evaluating Model Performance
The training results of the model are presented in
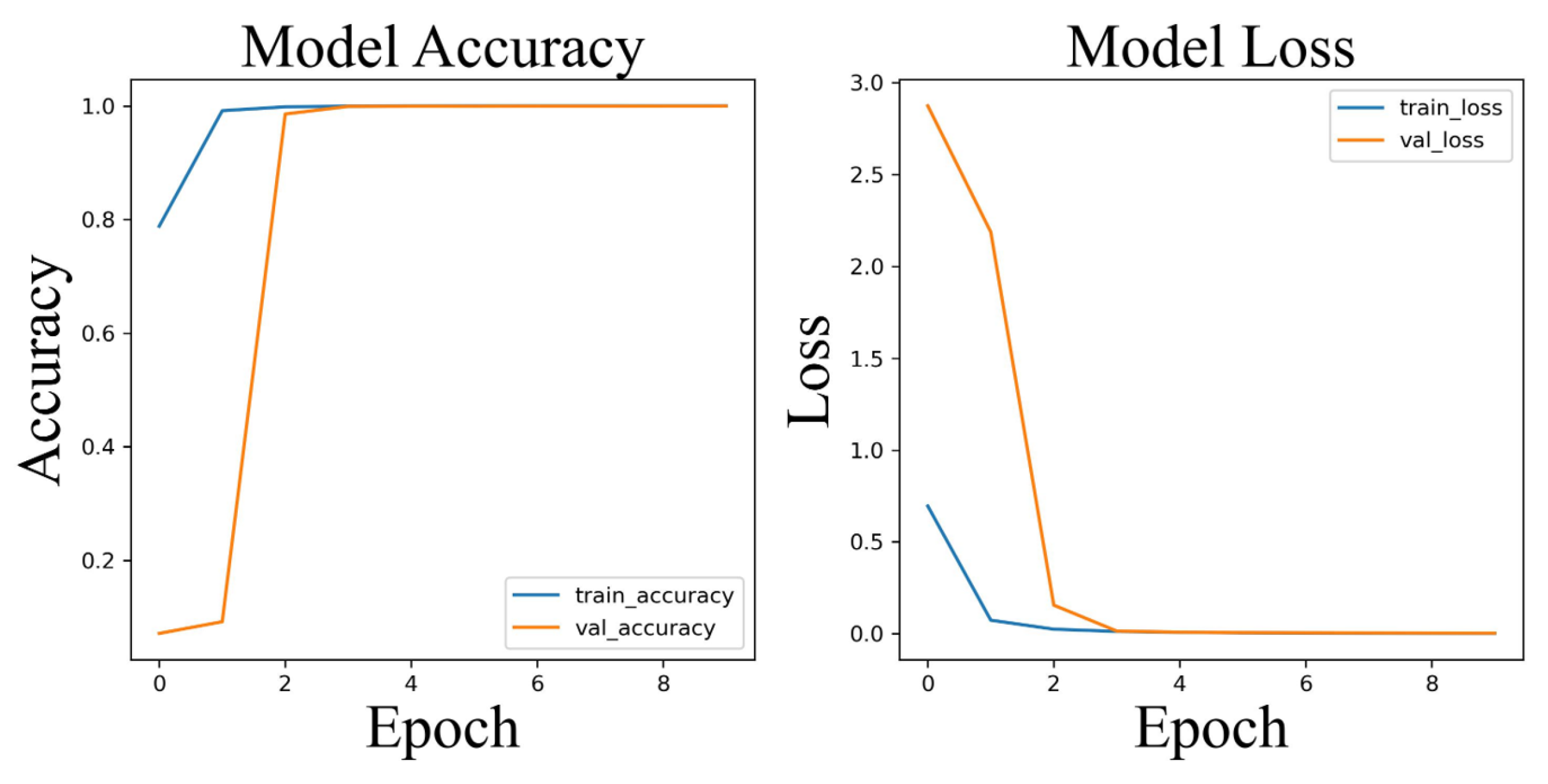
Figure 8. Model Accuracy reflects the accuracy of both the training and validation phases, while Model Loss represents the corresponding loss during these phases. The model converged to 1 for training and validation accuracy and to 0 for both training and validation loss. As shown in
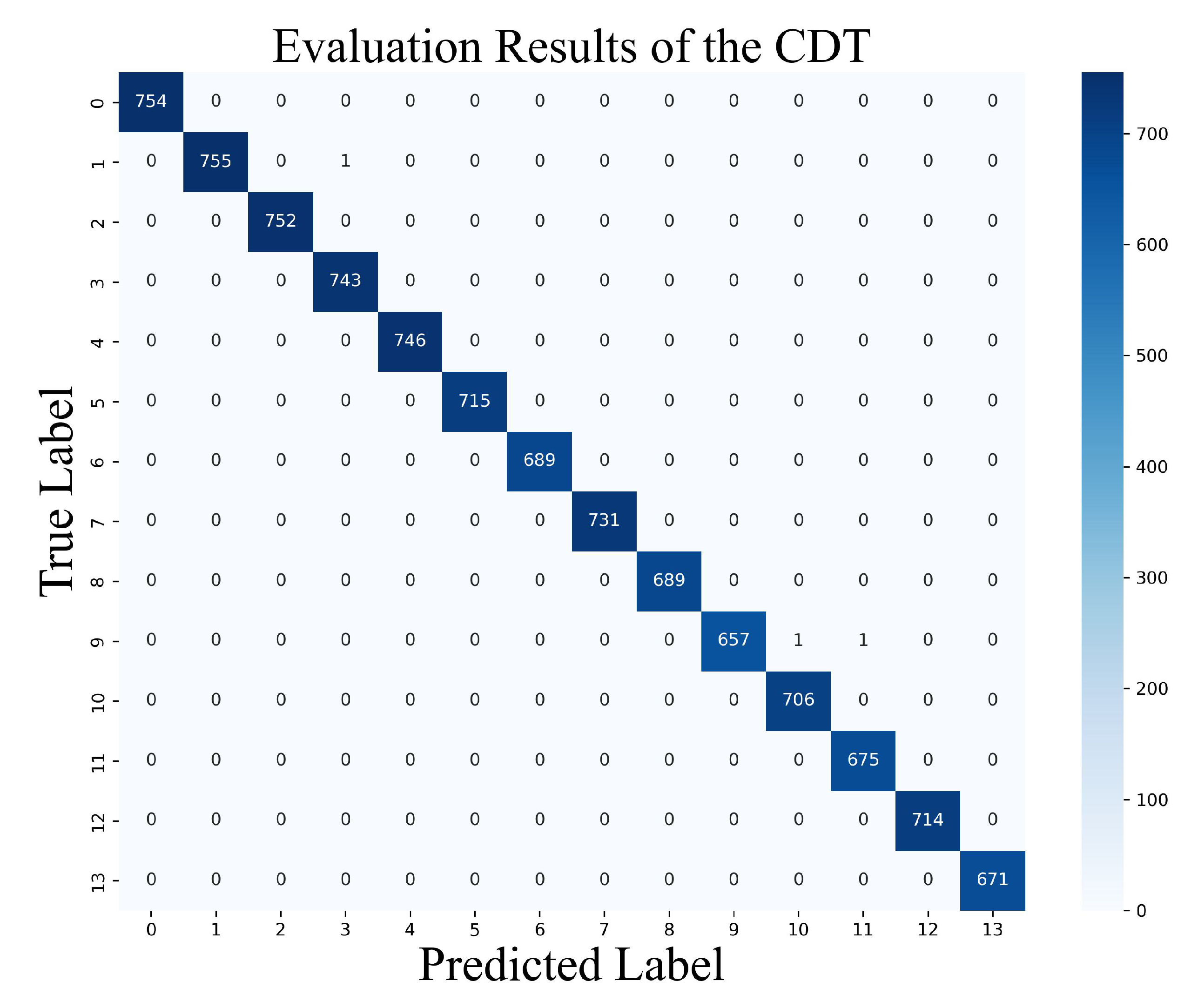
Figure 9, the accuracy on the test dataset is 99.97%. The test dataset consists of 10,000 traces, representing each trace’s classification accuracy. The F1-score for both micro and macro averages is 1.0, indicating that the proposed model can accurately predict the CDT sampling output from a single trace of a comparison operation executed on the Cortex-M4.
5.2.4. Leak Point Analysis Through Weight Analysis
As described in
5.1, the difference in Hamming weights during the CDT sampling process results from comparisons between 32-bit words. By examining the weights of the trained model, it is possible to identify the moments when the model successfully classified the sampled value.
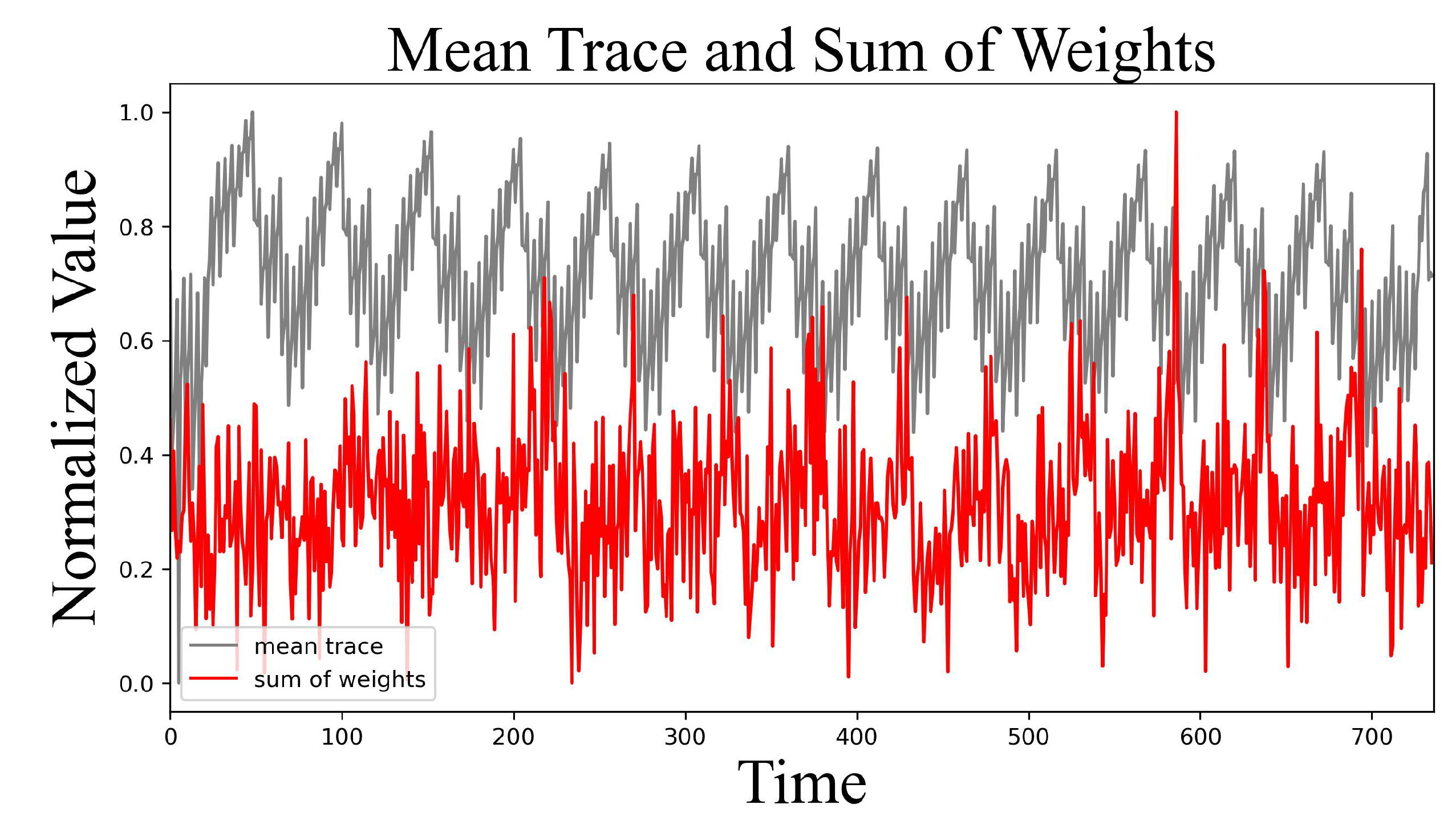
Figure 10 illustrates the sum of the weights for each node in the first layer of the trained model. The red line represents the sum of the weights, while the gray line shows the average across the entire waveform, normalized for visualization purposes. It demonstrates that the model makes its classification decision when comparing random and table values.
5.3. Countermeasure
As research on side-channel analysis continues to expand, there has been increasing focus on developing countermeasure techniques. Traditionally, shuffling and masking have been employed in side-channel analysis [
22,
23], though these methods tend to be computationally slow and memory heavy. Kim et al. proposed a table-based method that requires a minimum-sized table depending on the size of the operands [
7]. But, in the case of Mitaka, which operates with 64-bit data, a byte-sized table is required, demanding significant memory resources. Zhang et al. introduced a correspondence technique utilizing a look-up table with a fixed Hamming weight of 1, offering lower memory and speed overhead than other correspondence methods [
9]. However, this approach is unsuitable for different structures of quantum-resistant ciphers that employ CDT sampling, as it applies to operations performed after CDT sampling. Therefore, ongoing research is necessary to design secure algorithms against deep learning-based side-channel analysis.
6. Conclusion and Future Works
The growing importance of quantum-resistant cryptography has underscored the need for vulnerability verification research in embedded environments. In this paper, we explore the use of CDT sampling in several quantum-resistant cryptosystems, including FALCON and FrodoKEM. Specifically, we conduct a vulnerability analysis of CDT sampling based on comparison operations used in implementations such as Mitaka, Antrag, and SOLMAE.
In this paper, we investigated the visible vulnerabilities in the operation of CDT sampling in 8-bit AVRs and analyzed them in detail through reverse engineering. This paper proposes the first single trace analysis that exploits these vulnerabilities to restore the sampling value. In addition, this paper proposes an algorithm and implementation method that satisfies the constant time and verifies its safety. Furthermore, in this paper, we investigate safety in the more realistic 32-bit Arm Cortex-M4 environment. In 32-bit Arm Cortex-M4, CDT operates in constant time. This study proposes a deep learning-based side-channel analysis model for comparison-based CDT sampling that satisfies constant-time requirements and demonstrates the model’s effectiveness through experimental validation. Our results show that CDT sampling based on comparison operations remains vulnerable, even when constant-time execution is maintained. Additionally, we review existing countermeasures for side-channel analysis and emphasize the need for continued research into secure CDT sampling techniques. Future work will study the direct or potential leakage of secret key information case of the recovered sampled values.
Author Contributions
`Conceptualization, K.-H.C, J. H, D.-G.H; Formal analysis, K.-H.C, J.H., D.-G.H.; Data curation, K.-H.C.; writing—original draft preparation, K.-H.C.; writing—review and editing, J.H, D.-G.H.; All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Mosca, M. Cybersecurity in an era with quantum computers: Will we be ready? IEEE Secur. Priv. 2018, 16, 38–41. [Google Scholar]
- Fouque, P.-A.; Hoffstein, J.; Kirchner, P.; Lyubashevsky, V.; Pornin, T.; Prest, T.; Ricosset, T.; Seiler, G.; Whyte, W.; Zhang, Z. Falcon: Fast-Fourier lattice-based compact signatures over NTRU. Submission to NIST’s Post-Quantum Cryptography Standardization Process 2018, 36, 1–75. [Google Scholar]
- Espitau, T.; Fouque, P.-A.; Gérard, F.; Rossi, M.; Takahashi, A.; Tibouchi, M.; Wallet, A.; Yu, Y. Mitaka: A simpler, parallelizable, maskable variant of Falcon. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2022; pp. 222–253. [Google Scholar]
- Espitau, T.; Nguyen, T.T.Q.; Sun, C.; Tibouchi, M.; Wallet, A. Antrag: Annular NTRU Trapdoor Generation: Making Mitaka as Secure as Falcon. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Yokohama, Japan, 3–6 December 2023; pp. 3–36. [Google Scholar]
- Kim, K.; Tibouchi, M.; Wallet, A.; Espitau, T.; Takahashi, A.; Yu, Y.; Guilley, S.; SOLMAE Algorithm Specifications. KpqC: Korean Post-Quantum Cryptography 2020. Available online: https://kpqc.or.kr/1 (accessed on 16 October 2024).
- Kim, S.; Hong, S. Single trace analysis on constant time CDT sampler and its countermeasure. Appl. Sci. 2018, 8, 1809. [Google Scholar] [CrossRef]
- Marzougui, S.; Kabin, I.; Krämer, J.; Aulbach, T.; Seifert, J.-P. On the feasibility of single-trace attacks on the Gaussian sampler using a CDT. In Proceedings of the International Workshop on Constructive Side-Channel Analysis and Secure Design, Leuven, Belgium, 17–19 April 2023; pp. 149–169. [Google Scholar]
- Zhang, S.; Lin, X.; Yu, Y.; Wang, W. Improved power analysis attacks on Falcon. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2023; pp. 565–595. [Google Scholar]
- Choi, K.-H.; Kim, J.-H.; Han, J.; Huh, J.-W.; Han, D.-G. Single Trace Analysis of Comparison Operation Based Constant-Time CDT Sampling and Its Countermeasure. In Proceedings of the International Conference on Information Security and Cryptology, Seoul, South Korea, 13–15 December 2023; pp. 185–201. [Google Scholar]
- Cheon, J.H.; Kim, D.; Lee, J.; Song, Y. Lizard: Cut off the tail! A practical post-quantum public-key encryption from LWE and LWR. In Proceedings of the International Conference on Security and Cryptography for Networks, Amalfi, Italy, 5–7 September 2018; pp. 160–177. [Google Scholar]
- Bos, J.; Costello, C.; Ducas, L.; Mironov, I.; Naehrig, M.; Nikolaenko, V.; Raghunathan, A.; Stebila, D. Frodo: Take off the ring! Practical, quantum-secure key exchange from LWE. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1006–1018. [Google Scholar]
- Ajtai, M.; Dwork, C. A public-key cryptosystem with worst-case/average-case equivalence. In Proceedings of the Twenty-Ninth Annual ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1997; pp. 284–293. [Google Scholar]
- Hoffstein, J. NTRU: A Ring Based Public Key Cryptosystem. Algorithmic Number Theory (ANTS III) 1998. [Google Scholar]
- Hülsing, A.; Rijneveld, J.; Schanck, J.; Schwabe, P. High-speed key encapsulation from NTRU. In Proceedings of the International Conference on Cryptographic Hardware and Embedded Systems, Taipei, Taiwan, 25–28 September 2017; pp. 232–252. [Google Scholar]
- NewAE Technology Inc. ChipWhisperer API. Available online: https://github.com/newaetech/chipwhisperer (accessed on 16 October 2024).
- Microchip Technology. AVR Instruction Set Manual. Available online: https://ww1.microchip.com/downloads/en/devicedoc/atmel-0856-avr-instruction-set-manual.pdf (accessed on 16 October 2024).
- Arm Developer. Cortex-M4 instructions. Available online: https://developer.arm.com/documentation/ddi0439/b/CHDDIGAC (accessed on 16 October 2024).
- Kocher, P. Differential power analysis. In Proceedings of the Advances in Cryptology (CRYPTO’99), Santa Barbara, CA, USA, 15–19 August 1999. [Google Scholar]
- Inci, M.S.; Gulmezoglu, B.; Irazoqui, G.; Eisenbarth, T.; Sunar, B. Cache attacks enable bulk key recovery on the cloud. In Proceedings of the Cryptographic Hardware and Embedded Systems–CHES 2016, Santa Barbara, CA, USA, 17–19 August 2016; pp. 368–388. [Google Scholar]
- Chen, Z.; Oswald, D. PMFault: Faulting and Bricking Server CPUs through Management Interfaces. arXiv Preprint 2023. Available online: https://arxiv.org/abs/2301.05538. [CrossRef]
- Schneider, T.; Paglialonga, C.; Oder, T.; Güneysu, T. Efficiently masking binomial sampling at arbitrary orders for lattice-based crypto. In Proceedings of the Public-Key Cryptography–PKC 2019, Beijing, China, 14–17 April 2019; pp. 534–564. [Google Scholar]
- Fisher, R.A.; Yates, F. Statistical tables for biological, agricultural and medical research, 6th ed.; Oliver and Boyd: Edinburgh, UK, 1963. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).