Synthetic Jet Actuators for Active Flow Control: A Review

A synthetic jet actuator (SJA) is a fluidic device often consisting of a vibrating diaphragm that alters the volume of a cavity to produce a synthesized jet through an orifice. The cyclic ingestion and expulsion of the working fluid leads to a zero-net mass-flux and the transfer of linear momentum to the working fluid over an actuation cycle, leaving a train of vortex structures propagating away from the orifice. SJAs are a promising technology for flow control applications due to their unique features, such as no external fluid supply or ducting requirements, short response time, low weight, and compactness. Hence, they have been the focus of many research studies over the past few decades. Despite these advantages, implementing an effective control scheme using SJAs is quite challenging due to the large parameter space involving several geometrical and operational variables. This article aims to explain the working mechanism of SJAs and provide a comprehensive review of the effects of SJA design parameters in quiescent conditions and crossflow.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Synthetic jet actuators enhance flow mixing, control turbulence, and manage separation in fluid systems. In aerospace, these devices offer the potential for boundary layer control on aircraft wings, directly impacting flight efficiency and safety [1]. Flow separation can be described as the breakaway or detachment of the boundary layer from its bounding surface, often leading to a significant decline in the efficiency and performance of fluid systems [2]. Flatt [3] defined the term boundary layer control (BLC) as any mechanism or process through which the boundary layer is caused to behave differently than it usually would. However, flow control can generally be described as an attempt to drive the character or disposition of a flow field through flow control devices to a more favorable one [1,4]. To put this definition in context, consider the flow separation phenomenon, commonly regarded as detrimental. Control devices, such as flaps and slats, delay flow separation on a commercial aircraft’s wing, reducing drag and improving lift. However, in some cases, inducing separation can be advantageous, such as when spoilers are used to minimize ground-effect lift during landing [2].

Flow control devices are categorized into two main types: passive and active. Passive devices, such as vortex generators on commercial aircraft wings, function without external energy input by leveraging the flow’s inherent characteristics through geometric modifications. In contrast, active flow control (AFC) devices require energy input, typically adding momentum to the flow [5]. This fundamental distinction in energy requirements defines their operational principles and applications in fluid dynamics. Despite requiring input power, AFC devices may be advantageous as they adapt to off-design flow conditions, do not introduce a drag penalty common with passive control devices, or restore aerodynamic performance when passive devices fail [6,7]. AFC can be used in various applications, such as increasing lift and reducing drag, enhancing mixing for more efficient combustion, aeroacoustic noise attenuation, and vibration reduction [8,9,10]. Traditional active control devices are operated based on the injection or removal of fluid from the control surface. Suction was the first method ever proposed for separation control to deflect the high-momentum freestream flow towards the surface by removing decelerated fluid near it [11]. Alternatively, steady blowing can be employed to add momentum directly to the retarded boundary layer near the surface and delay flow separation [12]. In general, the steady blowing and suction devices increase the mechanical complexity and weight of the system. Therefore, aerodynamic gains made by these techniques may not counterbalance the power required to operate the suction or blowing devices [13]. Instead of a steady momentum addition, modern AFC devices rely on excitation, often regarded as an oscillatory momentum addition. The periodic addition of momentum can achieve the same level of control authority as traditional steady methods with one primary advantage: the momentum input required is lower, ranging from factors to even orders of magnitude [14]. Furthermore, it is feasible for flight vehicles. Recent studies have shown that periodic flow control can be more effective than steady methods for a given momentum input [15,16,17]. Although there have been some attempts to deploy AFC in real-world scale models [18,19,20,21], most applications of AFC remain experimental and confined to laboratory settings, which is also a testament to the challenges involved in designing and implementing AFC systems.

Excitation can be achieved through various means, such as acoustic drivers [22,23,24,25,26,27] or hydrodynamic devices [28,29,30,31]. The present review paper focuses on hydrodynamic excitation, primarily by synthetic jet actuators. A synthetic jet actuator (SJA) is a device often consisting of a vibrating diaphragm or piston that alters the fluid volume within a cavity to eject a quasi-steady jet through an orifice. An actuator is a device, such as a vibrating diaphragm, capable of generating oscillatory momentum. A comprehensive review on actuators has been carried out by Cattafesta and Sheplak [32]. A fluidic jet is a high-momentum stream of fluid ejected from a nozzle, aperture, orifice into the surrounding medium. By definition, a steady jet has negligible temporal variations. A pulsed jet, however, is an unsteady jet that alternates between being fully on or off and can be generated through various methods, such as using a fast-acting solenoid valve or a rotating orifice assembly [31,33]. However, unlike pulsed jets, synthetic jets are formed entirely from the working fluid within the flow system where they are employed. As a result, they can transfer momentum to the flow system without injecting any net mass-flux across the flow boundary [34], and thereby sometimes referred to as zero mass blowing (ZMB) or zero-net mass-flux (ZNMF) jets. SJAs have become more prevalent in the past few decades as a technology for AFC applications as they require no external fluid supply or ducting [34,35,36]. This feature alone significantly reduces the mechanical complexity and weight of the flow control system. Additionally, SJAs are easy to miniaturize through microfabrication [37,38,39], allowing them to be seamlessly integrated into the flow surface.

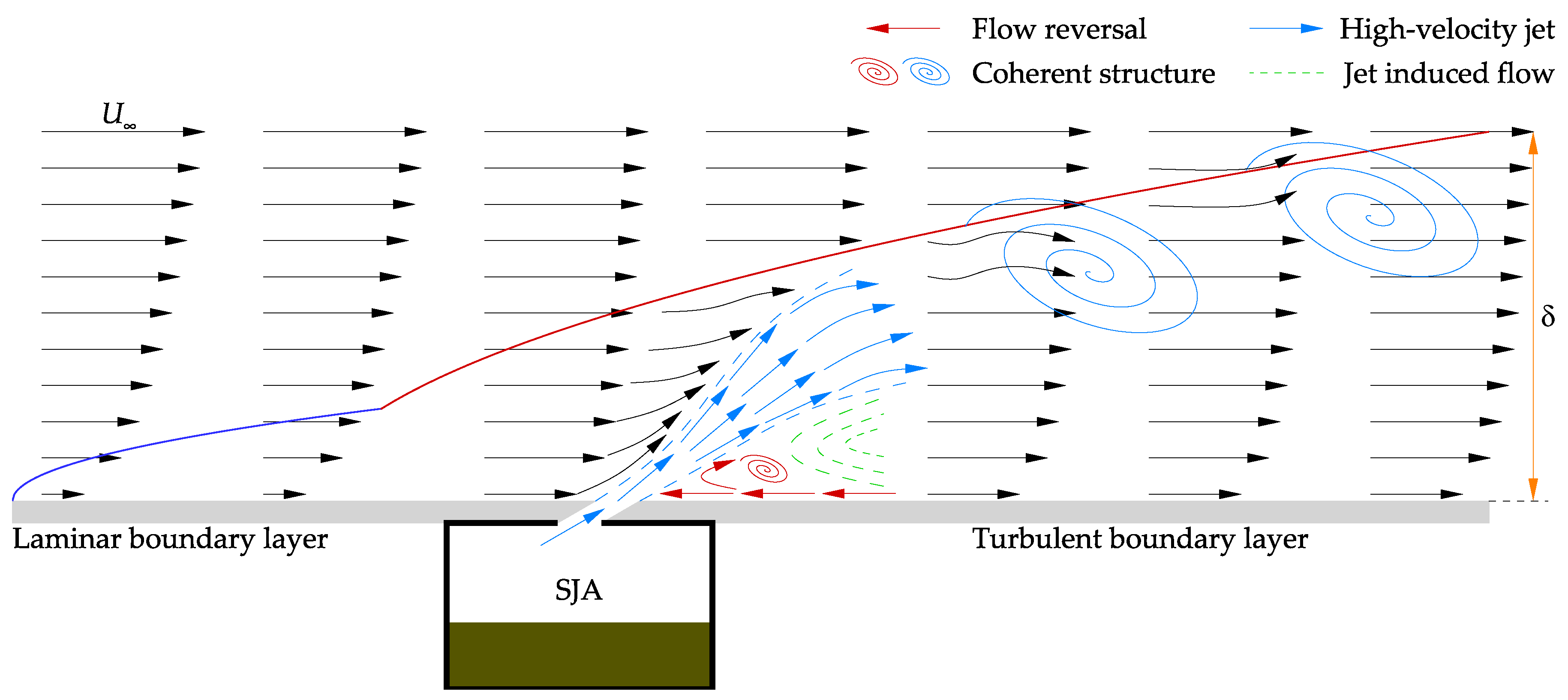
2. SJA Mechanism

A schematic drawing and photograph of an SJA are displayed in Figure 1. Although a variety of devices, such as mechanical pistons [29,40,41,42,43,44] and speakers [45,46,47], have been used as an actuator, the classical SJA comprises a vibrating diaphragm with an amplitude a located at the base of a cavity with a height of

H_{c}

. A neck with height

H_{o}

and diameter d connects the cavity to an exit (either an orifice or a jet slot) on the controlled surface.

The periodic movement of the diaphragm generates a jet cycle, alternating between the ingestion and expulsion cycle of the working fluid as it enters and exits the cavity. The actuation cycle begins with the ingestion cycle (Figure 2a–b), where flow is drawn into the cavity, followed by the expulsion cycle (Figure 2c–d), where the diaphragm forces the increased volume of flow to exit the cavity through the neck and jet slot. Alternating between the ingestion and expulsion cycles, linear momentum is intermittently transferred to the bulk flow. The net momentum arises from the ejection of discrete vortical structures from the slot exit, such as vortex rings for a circular orifice or vortex pairs for a two-dimensional slot.

A traditional circular SJA is typically axisymmetric, but it can be modified to create a slot-based SJA with an aspect ratio at the jet exit. Another method of modifying SJAs involves altering the nozzle geometry and adjusting the lip thickness and profile. The working mechanism of SJAs does not vary significantly when an array of actuators, such as when multiple circular diaphragms placed within the same cavity, is employed to create a slot-based SJA [48]. An example is shown in Figure 3, where an array of actuators are integrated to operate a rectangular SJA. Note how multiple discrete cavities are partially connected near the slot exit.

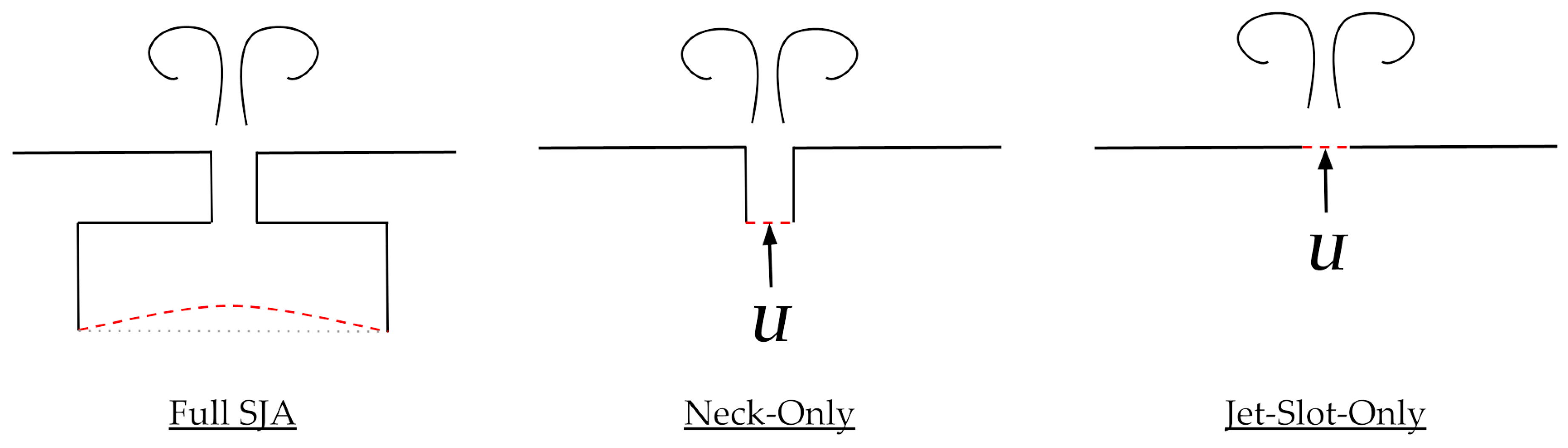
2.1. SJA Modelling Methods

Extensive research has been carried out to characterize and optimize SJAs using both experimental and numerical methods [50,51,52]. One of the main challenges in numerical approaches is accurately modeling the periodic expulsion of synthetic jets to match experimental results. Three primary modeling techniques were used most frequently: full SJA modeling, neck-only, and jet-slot-only method, as shown in Figure 4.

Raju et al. [54] conducted a series of numerical simulations with three different modeling techniques for two-dimensional SJAs in attached grazing flow and canonical separated crossflow. They compared the full SJA method with a radius-based jet profile, applying both a uniform jet

U = f (t)

and a sink-like jet

U, V = f (r, t)

to a neck-only model, as well as a uniform jet to a jet-slot-only model. The study concluded that the sink-like jet profile applied to the neck-only model provided the best agreement with the full SJA method while significantly reducing computational costs. However, although the jet-slot-only model captured the correct trend in separation control, it under-predicted the separation bubble, with the deviation increasing rapidly as the jet Reynolds number was increased. The numerical work by Ho et al. [53] also compared the three methods by applying unsteady Reynolds-averaged Navier-Stokes (URANS) simulations to a three-dimensional circular SJA, with the analytical Womersley solution for the jet profile, previously used by Palumbo et al. [50] in a Direct Numerical Simulation (DNS):

U (r, t) = U_{m} Real [(1 - \frac{J_{o} (i^{\frac{3}{2}} r W o)}{J_{o} (i^{\frac{3}{2}} W o)}) e^{i ω t}]

(1)

where

U_{m}

is the maximum jet centerline velocity,

ω = 2 π f

is the angular actuation frequency,

J_{o}

is the zeroth-order Bessel function, and

W o

is the Womersley number:

W o = d \sqrt{ω / 4 ν}

(2)

It was found that when the modelled neck volume is greater than the total ingested flow volume over the ingestion cycle, the neck-only method can yield comparable results to the full SJA method with a dynamic mesh approach. Meanwhile, the results from insufficient neck volume or the jet-slot-only method might only be accurate further downstream.

3. Synthetic Jet Actuators in Quiescent Flow

SJAs implemented in crossflow control applications are often characterized in quiescent flow conditions prior to deployment. But there are also purely quiescent flow applications, such as cooling applications. This preliminary assessment aims to characterize important input parameters, such as blowing velocity

\bar{U_{j}}

, actuation frequency f, and the peak-to-peak voltage

V_{p p}

applied to the diaphragm [55,56,57]. Smith and Swift [58] proposed that the Reynolds number of the synthetic jet could be determined using the average jet velocity during the expulsion phase, as shown in Equation (3) below:

R e_{d} = \frac{\bar{U_{j}} d}{ν}

(3)

where the average velocity

\bar{U_{j}}

over the expulsion phase, also known as the blowing velocity, is obtained as:

\bar{U_{j}} = \frac{1}{T} \frac{1}{A_{j}} \int_{A_{j}} \int_{0}^{τ} U_{j} d t d A

(4)

In Equation (4),

A_{j}

is the cross-sectional area of the orifice, T is the period of the actuation, and

τ

is the duration of expulsion, typically set to

τ = T / 2

. There are other definition for the average velocity, but for the sake of consistency, only the blowing velocity

\bar{U_{j}}

will be used in this manuscript.

In the remainder of this section, a review of the criteria for synthetic jet formation is presented, followed by an analysis of its development in quiescent conditions, considering the influence of various geometrical and operational parameters on flow evolution. Note that the effects of clustering, concerning an array of multiple SJAs, will not be addressed in this section as it is discussed in detail in Section 4.5.

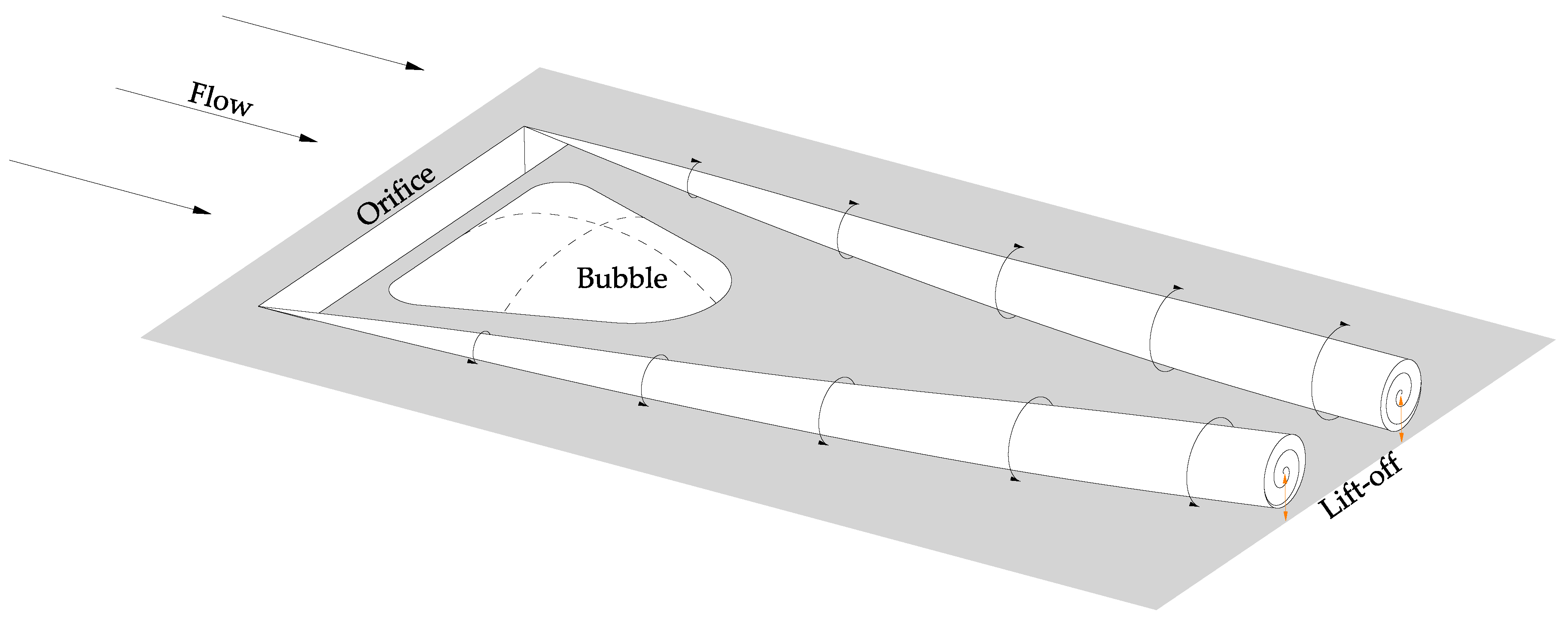
3.1. Synthetic Jet Formation Criterion

The formation and evolution of synthetic jets were studied by Smith and Glezer [57] for a rectangular SJA having an aspect ratio

AR = 150

, by applying the the slug model proposed by Glezer [59] for axisymmetric vortex rings, in which a cylindrical volume of fluid moves at constant velocity

\bar{U_{j}}

for a time T through a circular orifice of d. Hence, the slug length L represents the length of the column (slug) of fluid ejected during the expulsion phase of the cycle and is expressed as:

L = \bar{U_{j}} T \equiv \frac{\bar{U_{j}}}{f}

(5)

Based on the slug model, Smith and Glezer [57] proposed two key dimensionless parameters: the Reynolds number

R e_{d}

and the stroke ratio

L^{+} = L / d

, which can be used to characterize each vortex pair. Jabbal et al. [60] proposed a different variant of the Reynolds number, which was defined based on the stroke length as

R e_{L} = R e_{d} L^{+}

. Further studies by Utturkar et al. [61] and Holman et al. [62] showed that the synthetic jet formation is governed by the jet Strouhal number

S r

or, alternatively, by both Reynolds number

R e_{d}

and Stokes number

S k

\frac{1}{S r} = \frac{R e_{d}}{S k^{2}} > \frac{τ}{T} K

(6)

where K is the formation threshold, and the Strouhal number

S r

and Stokes number

S k

are defined as:

\begin{matrix} S r & = \frac{ω d}{\bar{U_{j}}} \end{matrix}

(7)

\begin{matrix} S k & = \sqrt{ω d^{2} / ν} \end{matrix}

(8)

The formation criterion proposed by Holman et al. [62] outlines the conditions necessary for successful synthetic jet formation, and is related to the stroke ratio according to:

\frac{1}{S r} = \frac{L^{+}}{2 π} > \frac{τ}{T} K

(9)

Note that, for instances where

τ = T / 2

, Equation (9) simply reduces to

L^{+} / π > K

. Generally, a synthetic jet forms when each vortex structure ejected during the blowing stroke propagates downstream at a speed fast enough to escape the influence of the sink-like flow during the suction stroke, which occurs when the stroke ratio

L^{+}

exceeds a certain threshold proportional to K[58,62,63,64]. Dimensional analysis led to the definition of the synthetic jet formation constant K, as follows:

K = \frac{32 C^{2} {(1 + ϵ)}^{p}}{κ π^{2}}

(10)

where the constant C is defined as the ratio of the average velocity, that is

2 \bar{U_{j}}

when

τ = T / 2

, to the centerline velocity

U_{c}

during the peak expulsion phase. The non-dimensional exit radius of curvature

ϵ

is given by

2 r_{l} / d

, where

r_{l}

is the lip radius of curvature and d is the jet orifice diameter or width. The constant

κ

is influenced by the vortex dimensions, while the exponent

p < 1

approximates the flow separation due to the exit curvature. The constant K was proposed for both two-dimensional and axisymmetric synthetic jets, with values of 1 and 0.16 [62], respectively. The former value was derived from computational results, while the latter is empirical. Both values were validated against other experimental studies. For example, Shuster and Smith [63] examined three primary stroke ratios,

L^{+} = 1

, 2, and 3, for a circular SJA across a range of Reynolds numbers, using dye visualization and particle image velocimetry (PIV), observing that the vortex rings could not escape the orifice when

L^{+} < 0.6

, which aligned closely with the criterion

L^{+} > 0.16 \times π \approx 0.5

proposed by Utturkar et al. [61] (see Figures 3 and 6 in Reference [63]). Overall, the synthetic jet formation criterion constant is not universal and is highly dependent on the geometry of the SJA.

3.2. Synthetic Jet Evolution

Once synthetic jets are formed, the flow field in quiescent conditions consists of a train of vortex structures, generally divided into three distinct regions: the near, transitional, and far-field. However, many studies simplify this classification by omitting the transitional region [29,57]. The near-field region is dominated by the time-periodic formation and advection of the vortex structures [56,57]. The coherent vortical structures continue to convect downstream and, in the far-field region, break down into smaller vortical structures, eventually transitioning into a fully turbulent state. For

L^{+} = 1

, 2, and 3, Shuster and Smith [63] reported that vortex ring trajectories scaled exclusively on the stroke ratio

L^{+}

within the near-field, similar to the observations by Smith et al. [65]. Their study demonstrated that the convective velocity of the vortex rings scales, at most, with the slug model velocity

\bar{U_{j}}

(see Figures 3 and 14 in Reference [63]). The study by Jabbal et al. [60] on circular synthetic jets in quiescent conditions revealed that above a threshold value of

L^{+} = 4

, the circulation contained in the primary vortex rings reach a maximum, and secondary eddies are shed as

L^{+}

increases further (see Figures 7 and 8 in Reference [60]).

The similarities and differences between synthetic and conventional steady jets in both near- and far-field regions are intriguing. Cater and Soria [29] examined the evolution of a round SJA, while Smith and Swift [58] studied high-AR rectangular SJAs. Both studies confirmed that the far-field behavior was comparable to steady jets, with time-averaged velocity profiles becoming self-similar. A higher spreading rate and decay constant were observed from synthetic jets, particularly in the near-field region. This was attributed to the increased entrainment caused by the unsteady vortex formation at the synthetic jet origin. The faster-spreading rate accompanied by a more rapid decline in centerline velocity was also confirmed by Shuster and Smith [63]. For a circular SJA, Cater and Soria [29] defined the near-field as extending from the orifice to an axial distance of

30 d

, with the far-field starting beyond this point. Shuster and Smith [63] used the stroke length in their classification, noting that vortex ring dynamics dominated the flow field for distances less than L from the orifice. In contrast, beyond L, the flow entered a short transitional region before resembling a steady round turbulent jet. The transition from vortex rings to a steady jet occurred over a longer streamwise distance when

L^{+} > 3

. Smoke visualization by Smith and Glezer [57] for high-AR rectangular SJAs revealed that, within the transitional region, instabilities caused the formation of rib-like secondary vortical structures wrapped around the cores of the primary vortex pairs, eventually leading to loss of coherence and their breakdown into smaller scales (see Figure 4 in Reference [57]). Cater and Soria [29] described this phenomenon as analogous to the inviscid azimuthal instability responsible for the breakup of vortex rings, as observed by Widnall et al. [66].

3.3. Effects of Orifice Shape

Considerable efforts have been devoted to understanding the effect of jet exit shape on the mixing and turbulent characteristics of SJAs [29,67,68,69,70,71,72]. During the initial expulsion phase, the vortex rings emanating from a slotted orifice have a distorted cross-section that approximates the shape of the orifice. However, as the vortex ring moves downstream, its cross-section expands in the direction of the short axis and contracts in the direction of the long axis, a phenomenon which is referred to as axis switching (see Figure 2 in Reference [73]). Axis switching enhances mixing in both steady and synthetic jets, making non-circular SJAs particularly intriguing for AFC [74,75]. Non-circular SJAs are typically divided into low-AR, finite-span, and high-AR, though there is currently no standardized classification, with various criteria proposed by different researchers [40,76,77].

Lindstrom and Amitay [78] examined three orifice shapes: rectangular, trapezoidal, and triangular, all with the same aspect ratio

AR = 19

and area, at a hydraulic diameter-based Reynolds number

R e_{d} = 7000

using stereoscopic PIV and hot-wire anemometry (HWA). The time-averaged flow fields demonstrated that jet structural vectoring occurred toward the larger cross-sectional areas for the triangular and trapezoidal geometries, which was attributed to asymmetric vortex structures. In contrast, the jet associated with the rectangular orifice was ejected perpendicular to the orifice (see Figures 5 and 6 in Reference [78]). While significant differences were observed in the near-field region among the three orifice shapes, with velocity profiles displaying undulations along the span, all cases eventually attained a bell-shaped velocity profile, as expected in a free jet. Lindstrom and Amitay [78] also proposed a criterion for the location of axis switching, defining it as the point where the averaged wall-normal vorticity exceeds the spanwise vorticity. Garcillan et al. [72] conducted a series of PIV experiments to investigate the effect of aspect ratios

AR = 1

–16 for slotted SJAs while maintaining a constant jet exit area across the different cases. The vortex ring ejected from the slotted SJA initially emerged with a cross-section similar to the shape of the jet exit and appeared two-dimensional. However, as it convected downstream, it underwent axis switching, with this phenomenon becoming more rapid and intense as the aspect ratio of the jet slot increased. It was found that high-AR SJAs generated vortex rings with greater initial jet momentum than circular SJAs. However, the subsequent axis switching led to more rapid structural dissipation and a faster momentum drop-off than circular SJAs. A similar conclusion was reached by Oren et al. [79], who experimentally investigated various nozzle geometries, including triangular, circular, square, and rectangular (

AR = 3.7

) SJA nozzles using PIV.

Several numerical studies have also investigated the effects of SJA orifice shape on determining the optimal configuration for flow control. Lee and Goldstein [80] conducted DNS to examine the effects of SJA neck and lip geometry on flow characteristics in a quiescent environment, focusing on two-dimensional SJAs with flat, round, and cusp lips. It was reported that the flat lip SJA achieved a higher peak streamwise jet velocity. In contrast, the round lip SJA entrained more fluid during the ingestion cycle, increasing spanwise jet velocity. However, this effect was localized near the jet exit and had a limited impact on the external flow. Miró et al. [81] numerically investigated two different SJA configurations using DNS and large eddy simulation (LES) for jet impingement for a two-dimensional slot-based SJA and a circular SJA over a range of

50 < R e_{d} < 500

. The study reported that the circular SJA exhibited greater jet momentum at the center and more coherent structures than the slot-based SJA.

3.4. Effects of Actuation Frequency

The effect of SJA actuation frequency is a critical parameter in flow separation control and has been widely studied in quiescent environments [82,83,84,85]. An essential feature of any SJA is its frequency response, which dictates the output quantities of interest, such as velocity, in relation to the input signal. For an SJA, the frequency response of the jet velocity is influenced by the cavity and orifice geometry, fluid properties, and actuator characteristics [62]. Since an SJA operates similarly to a Helmholtz resonator, the Helmholtz frequency plays a crucial role in its frequency response, which is theoretically given by:

f_{H} = \frac{U_{s}}{2 π} \sqrt{\frac{A_{j}}{H_{n} V_{c}}}

(11)

where

V_{c}

is the cavity volume,

H_{n}

is the effective height of orifice neck (

H_{n} = H_{o}

in case of Figure 1a), and

U_{s}

is the speed of sound. As highlighted by Arafa et al. [86], the Helmholtz frequency, as shown in Equation (11), is formulated for an ideal spherical volume in which sound wave propagation matches the volume boundaries. Gallas et al. [87] implemented a lumped element model for piezoelectric-driven SJAs, observing a good agreement between the analytical and measured frequency responses. The model revealed that a piezoelectric-driven SJA functions as a fourth-order coupled oscillator, with one oscillator being the cavity acting as a Helmholtz resonator and the other being the piezoelectric diaphragm. The system, therefore, may exhibit one or two resonant frequencies, depending on the proximity of the cavity’s Helmholtz frequency to the piezoelectric diaphragm’s natural frequency. It has been shown that an SJA with a high coupling ratio produces a single resonant peak velocity that is greater in magnitude than that of an SJA with a low coupling ratio [87,88,89,90]. The studies mentioned above highlight a significant limitation of piezoelectric actuators: the bandwidth over which acceptable velocity magnitudes can be achieved is often confined to frequencies near resonance. One solution to this limitation is to modulate the input signal, which will be discussed in more detail in Section 4.3.

Mallinson et al. [91] conducted experimental and numerical investigations into the effects of actuation frequency on SJA performance, revealing that operation at the Helmholtz resonance frequency yielded the most significant response, a finding later corroborated by the numerical studies of Lv et al. [92]. Mallinson et al. [91] also proposed that the maximum jet centerline velocity is determined by a balance between the inertia of the membrane forcing and the viscous forces from the jet slot boundary layer. The effect of different modulation signals was investigated by Lu and Wang [93] using URANS, comparing them to a steady jet. The modulation signals included triangular, sinusoidal, trapezoidal, square, bi-frequency, and varying duty cycles. It was reported that the varying duty cycle modulation resulted in significantly stronger jet momentum with proper optimization than conventional sinusoidal modulation.

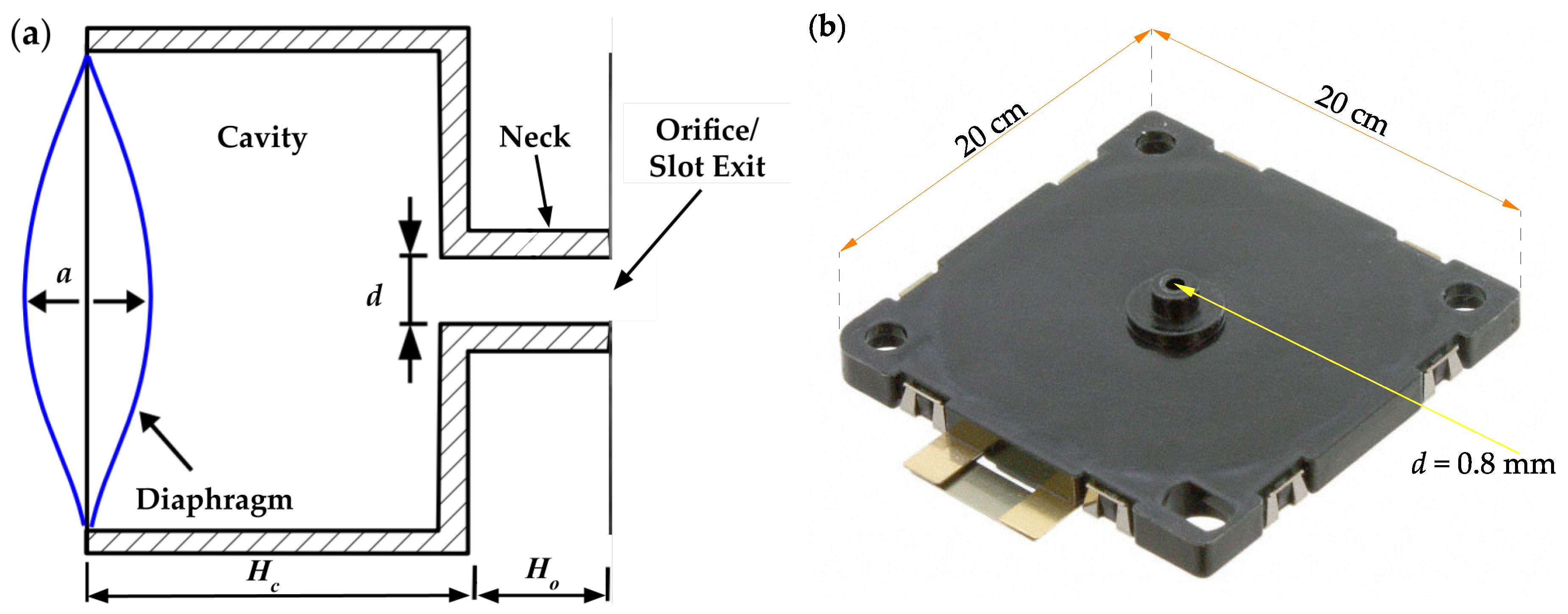
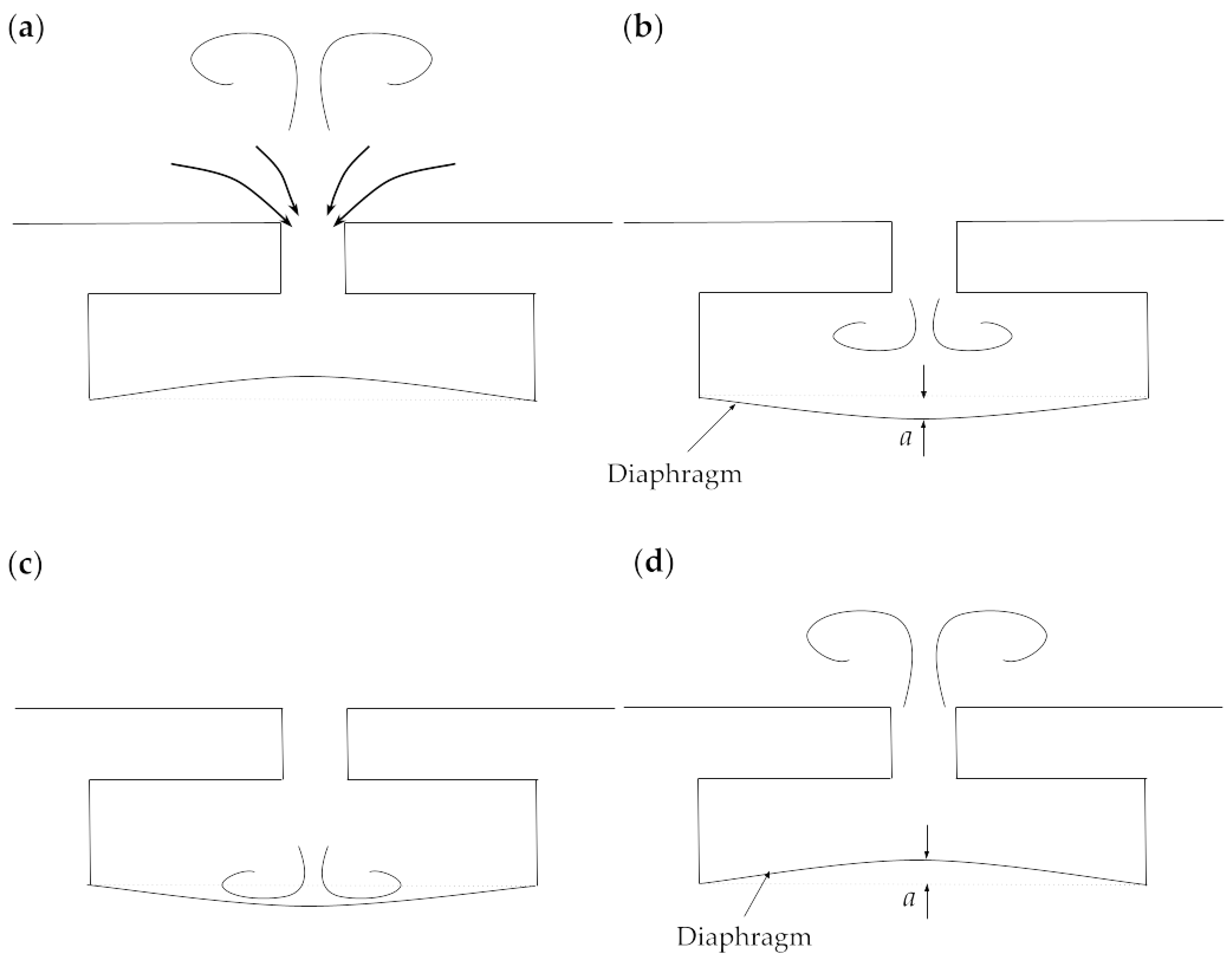
3.5. Effects of Cavity Shape

SJA cavity shape optimization has been studied both experimentally [86,88,94,95,96] and numerically [69,97,98,99]. Feero et al. [100] employed HWA to examine the influence of three cavity shapes, cylindrical, conical, and contracted, on SJAs producing circular synthetic jets in a quiescent flow operated near the Helmholtz frequency. A pressure probe within the cavity was utilized to ensure that the normalized frequency and cavity pressure remained constant across all three cases. Noticeable differences in the radial velocity profile and jet momentum flux were observed across the different cavity shapes. While the jet profile shape was consistent among the three cases, the magnitudes varied. Feero et al. [100] concluded that the basic cylindrical shape maximizes momentum flux. However, they also suggested that the more complex geometry of contracted cavity was able to achieve a lower resonant frequency, and can be used if the goal is to reduce power consumption and enhance efficiency. Ziadé et al. [101] conducted three-dimensional compressible laminar simulations using similar SJA cavities and test conditions as those in Feero et al. [102]. They found that conical and contracted cavities exhibited strong blockage effects, while cylindrical cavities demonstrated more efficient vortex formation.

The experimental work by Jabbal et al. [103] investigated the effect of neck and cavity height on the formation of vortex rings in circular SJAs using PIV. A shorter neck height was observed to result in more rapid vortex circulation when

H_{o} / d < 1

, while

H_{o} / d > 1

yielded consistent results. A compressible numerical model developed by Tang and Zhong [104] was also employed to support this finding. The numerical work by Chiatto et al. [105] investigated the flow inside a three-dimensional double orifice SJA. The study featured a cylindrical cavity, with the two orifices equally spaced from the center of the cavity. By analyzing Q-criterion contours and streamline plots of the flow, it was proposed that the flow within a double orifice SJA behaves like two sub-cavities, provided the jet slots are sufficiently spaced apart. A lumped model for predicting the behavior of a double orifice SJA, validated experimentally, was subsequently proposed, treating the frequency response as a force-damped spring-mass system.

4. Synthetic Jet Actuators in a Crossflow

For effective flow control, it is essential to thoroughly understand the vortical structures formed by the synthetic jet and boundary layer interaction (SJBLI), their effects near the surface, and their overall effectiveness in altering the flow dynamics [106,107]. Several experiments have demonstrated that synthetic jets effectively delay flow separation on aerodynamic bodies of various shapes [108,109,110,111,112,113,114]. The complex SJBLI phenomenon is illustrated schematically in Figure 5. An in-depth understanding of the SJBLI presents several challenges, including accurately characterizing the boundary layer, measuring the high-velocity gradients generated by the synthetic jets, and resolving small-scale rotational coherent structures [115]. In addition to the complex flow physics, ample parameter space must be considered when designing an effective control strategy using SJAs. To establish a systematic approach for characterizing the effects of various geometrical and operational parameters, Jabbal and Zhong [107] applied Buckingham’s

Π

-theorem to an SJA embedded in a crossflow boundary layer. This analysis identified the following dimensionless parameters:

\begin{matrix} π_{1} & = \frac{f d}{U_{\infty}} & π_{2} & = \frac{U_{\infty} δ}{ν} & π_{3} & = \frac{δ}{d} \\ π_{4} & = \frac{τ_{w}}{\frac{1}{2} ρ U_{\infty}^{2}} & π_{5} & = \frac{\bar{U_{j}}}{U_{\infty}} \end{matrix}

(12)

where

π_{1}

represents the Strouhal number

S t

π_{2}

the freestream Reynolds number

R e_{δ}

π_{3}

the ratio of boundary layer thickness to orifice diameter,

π_{4}

the skin friction coefficient

C_{f}

, and

π_{5}

the blowing ratio

C_{b}

(also known as jet-to-freestream velocity ratio VR). The following inter-dependencies exist between these dimensionless groups and the key dimensionless parameters for an SJA in quiescent conditions:

\begin{matrix} S t & = \frac{C_{b}}{L^{+}} \end{matrix}

(13)

\begin{matrix} R e_{L} & = \frac{C_{b} L}{δ} R e_{δ} \end{matrix}

(14)

It is important to note that this parametric study did not include all parameters relevant to flow control applications, essentially neglecting factors such as surface curvature, orifice shape or aspect ratio, and clustering effects [116]. Moreover, quantifying momentum addition as a measure of the overall blowing strength was historically common, rather than using the jet-to-freestream velocity ratio [117]. For a two-dimensional configuration, the momentum coefficient

C_{μ}

may be defined as a ratio of the time-averaged expelled momentum by all the operating SJAs

\bar{I_{j}}

to the momentum of the freestream:

\begin{matrix} C_{μ} & = \frac{\bar{I_{j}}}{\frac{1}{2} ρ_{\infty} U_{\infty}^{2} A_{f}} \end{matrix}

(15a)

\begin{matrix} \bar{I_{j}} & = \frac{1}{T} \int_{A_{j}} \int_{0}^{T} ρ_{j} 〈 U_{j}^{2} 〉 d t d A \end{matrix}

(15b)

where

A_{f}

is a reference area for the body under consideration and T is the actuation period [108,118]. The definition of the momentum coefficient is inconsistent in the literature, with various definitions proposed by different researchers [45,47,76,119,120]. Researchers have often assumed a uniform velocity distribution across the jet exit cross-section or ignored spatial variations by relying solely on the centerline velocity. Furthermore, these definitions often consider only the expelled momentum, integrating over the expulsion phase, which by also assuming a top-hat velocity distribution, leads to the following expression:

\bar{I_{j}} = \frac{1}{τ} ρ_{j} A_{j} \int_{0}^{τ} 〈 U_{j}^{2} 〉 d t

(16)

Also note the denominator in Equation (15b) and compare it with Equation (16). Greenblatt and Wygnanski [120] further simplified Equation (16) by decomposing the jet velocity into mean and oscillatory components as

U_{j} = \bar{U_{j}} + u_{j}

, deriving the following relation for the momentum coefficient:

C_{μ} = \frac{2 A_{j}}{A_{f}} {(\frac{\bar{U_{j}}}{U_{\infty}})}^{2} + \frac{2 A_{j}}{A_{f}} \bar{{(\frac{u_{j}}{U_{\infty}})}^{2}}

(17)

The second term on the right-hand side of Equation (17) may be neglected when it is relatively small compared to the first term. As highlighted by some researchers, the spatial velocity distribution can deviate significantly from the ideal top-hat profile under certain conditions [58,99,100]. Therefore, if the top-hat profile is assumed, the uniformity of the velocity distribution should be validated.

It is interesting to examine how SJA operational and geometric parameters affect their performance in crossflow conditions. The flat plate has been the most commonly used geometrical model in numerous experimental [107,121,122,123,124,125,126,127,128] and numerical [129,130,131] studies, as it eliminates curvature effects, effect of flow separation, and can produce a zero pressure gradient. Consequently, where applicable, discussing these parameters begins with this geometry before considering more complex shapes.

4.1. Effects of Jet Strength

The strength of a synthetic jet relies on both

C_{b}

and

R e_{L}

. As with SJAs in quiescent conditions, a threshold criterion exists for SJAs in crossflow to effectively enhance fluid mixing (see Figure 10 in Reference [124]). Experimental evidence shows that the interaction of the vortices produced by a circular synthetic jet with a boundary layer leads to the formation of streamwise vortical structures, which can delay flow separation by drawing faster-moving fluid from the freestream into the near-wall region [96,132]. As these vortex rings enter the boundary layer, they experience combined effects from shear forces, boundary layer vorticity, and the Magnus force resulted from interactions with the crossflow [112,126,133,134]. These influences cause the vortex rings to tilt and deform at varying degrees, depending on their strength and residence time within the boundary layer, resulting in complex three-dimensional vortical structures.

The dye flow visualization by Zhong et al. [126], with

R e_{L}

ranging from 16 to 245 and

L^{+}

from 0.56 to 1.4, in a laminar boundary layer at blowing ratio

C_{b}

from 0.06 to 0.7, revealed three distinct behaviors:

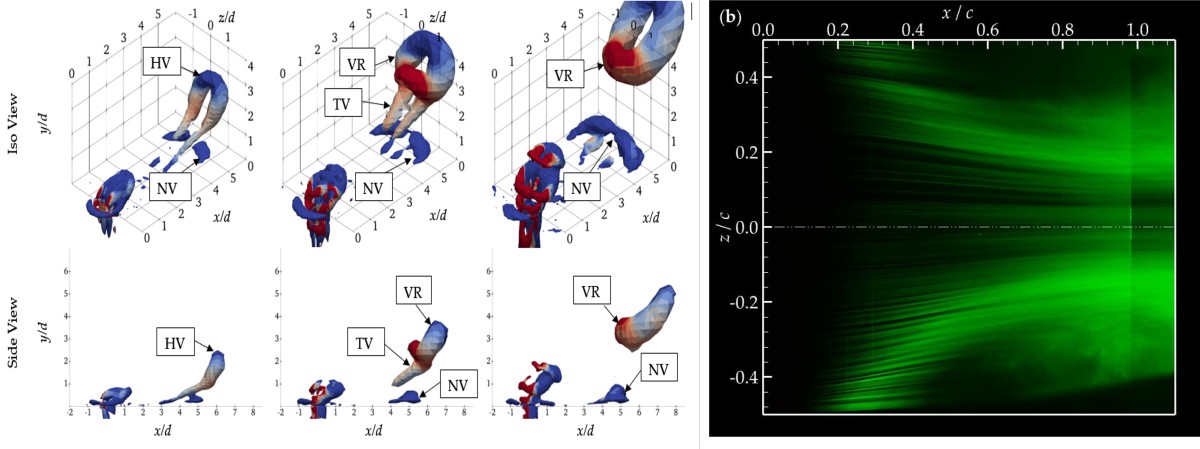
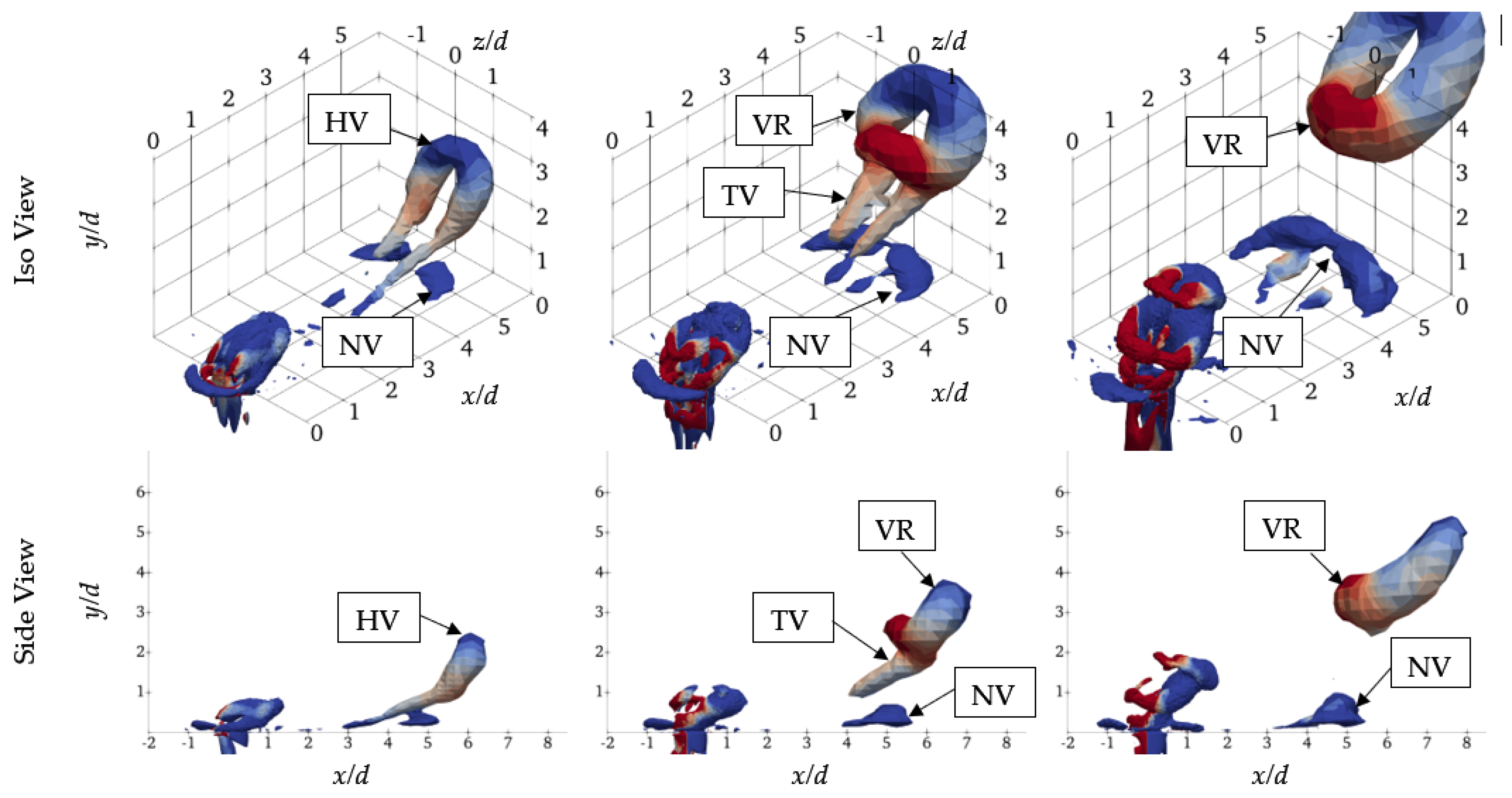
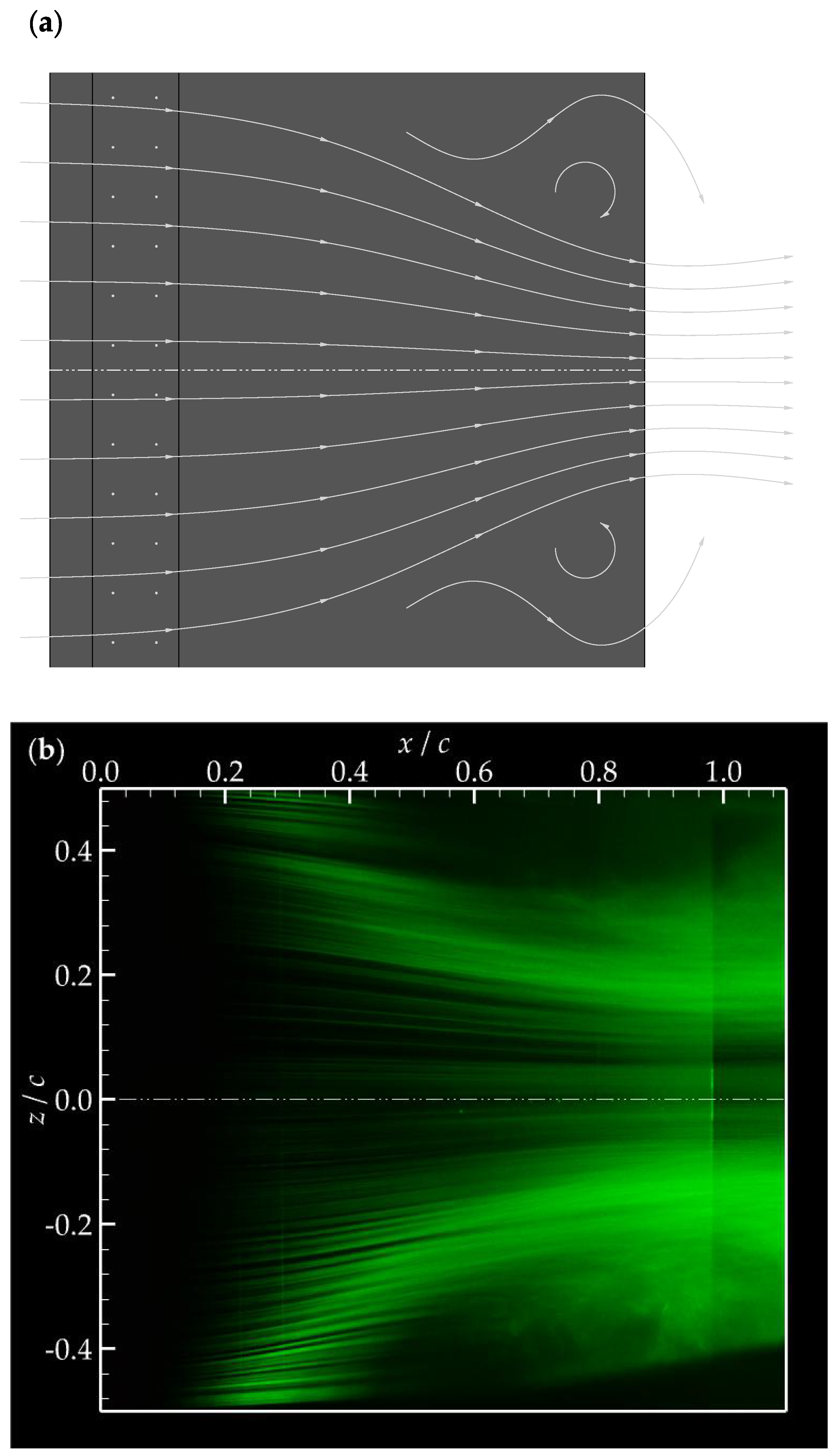
At low blowing ratios $C_{b}$ and jet Reynolds numbers $R e_{L}$ , the vortical structures generated by synthetic jets appeared as hairpin vortices attached to the wall.
At intermediate $C_{b}$ and $R e_{L}$ values, the vortex sheet formed at the orifice rolled up into vortex rings, which experienced significant tilting and stretching as they entered the boundary layer.
At high $C_{b}$ and $R e_{L}$ values, the vortex rings exhibited some tilting but little to no stretching, quickly penetrating the edge of the boundary layer.

Jabbal and Zhong [107] observed the same three types of vortical structures using stereoscopic dye flow visualization. They also performed surface visualization of the vortex footprints by applying a temperature-sensitive liquid crystal (TLC) coating on the test surface. Interestingly, only two distinct types of thermal footprints were observed. Both hairpin vortices and stretched vortex rings produced two streamwise streaks of high heat transfer, corresponding to high-momentum fluid transfer toward the wall outboard of the streamwise counter-rotating legs based on the Reynolds analogy. In contrast, the tilted vortex rings generated only a single streamwise streak of high heat transfer, which was hypothesized to result from an induced vortex adjacent to the wall (see Figure 6 in Reference [107] or Figure 7 in Reference [124]). Q-criterion contours displaying the hairpin vortices, vortex rings, and near-wall vortices are presented in Figure 6.

To understand the underlying flow mechanism, Jabbal and Zhong [107] used two-dimensional PIV to study the flow fields of the three above-mentioned vortical structures. Hairpin vortices (

C_{b} = 0.32

and

L^{+} = 1.6

) and stretched vortex rings (

C_{b} = 0.27

and

L^{+} = 2.7

) exhibited characteristics similar to a streamwise vortex pair with a common upwash. In contrast, tilted vortex rings (

C_{b} = 0.54

and

L^{+} = 2.7

) featuring a common downwash induced a tertiary streamwise vortex pair in the near-wall region. Wall shear stress measurements revealed that stretched vortex rings provided the best performance in terms of higher near-wall fluid mixing, greater persistency, and reduced spatial fluctuations. The numerical work of Ho et al. [131] investigated the effect of varying SJA jet momentum (

0.32 < C_{b} < 1.10

) in a turbulent boundary layer crossflow with three-dimensional URANS. An increase of jet momentum resulted in greater boundary layer penetration under the same actuation frequency. Note that, although in this study the increase of jet momentum resulted in a significant increase of wall shear stress along the streamwise direction, it also reduces the spanwise control authority of the SJA. Classification of structures emerging due to SJBLI is not unique and depends on the considered parameter space. For example, Zhong and Zhang [112] described these vortical structures only based on blowing ratio

C_{b}

given a constant actuation frequency f, first as hairpin-like vortices that are located close to the wall, and then, as

C_{b}

increases, as tilted vortex rings with a pair of trailing legs that penetrate the edge of the boundary layer shortly downstream. The numerical work of Zhou and Zhong [123] of a rounded SJA in a laminar boundary layer provided a similar conclusion. For a constant value of orifice width and wall shear stress, parametric maps are available in the literature that classify synthetic jet or pulsed jet flow behavior based on the blowing ratio

C_{b}

(VR) and the jet Reynolds number

R e_{L}

, or its alternative, the stroke ratio

L^{+}

[121,124,135]. The generated vortex rings will undergo deformation due to the resident shear in the boundary layer for both pulsed and synthetic jets. For a synthetic jet, however, an additional suction effect is expected to be confined to the upstream branch of the vortex, leading to the formation of an asymmetric structure. According to Jabbal and Zhong [124], a hairpin vortex forms as the upstream branch of the vortex ring produced by the synthetic jet is weakened by the suction cycle as it passes over the orifice and is then canceled out by resident vorticity of the opposite sign as it propagates downstream. Supposing the initial strength of the vortex ring at the orifice exit is relatively strong, the vortical structures may first appear as a stretched vortex ring with a weak upstream branch in the near-field before evolving into a hairpin structure further downstream. At higher blowing ratio

C_{b}

and stroke ratio

L^{+}

values, the vortex rings produced by synthetic jets can escape the influence of the suction cycle and the boundary layer’s resident shear, emerging as fully formed rings that appear tilted relative to the wall. Above a threshold stroke ratio

L^{+}

, the vortex rings generated by synthetic jets become increasingly incoherent over time, and secondary vortices can eventually be seen shedding from the primary vortex ring, similar to the observations by Jabbal et al. [60] for SJAs in quiescent condition (see Figure 7 in Reference [124]).

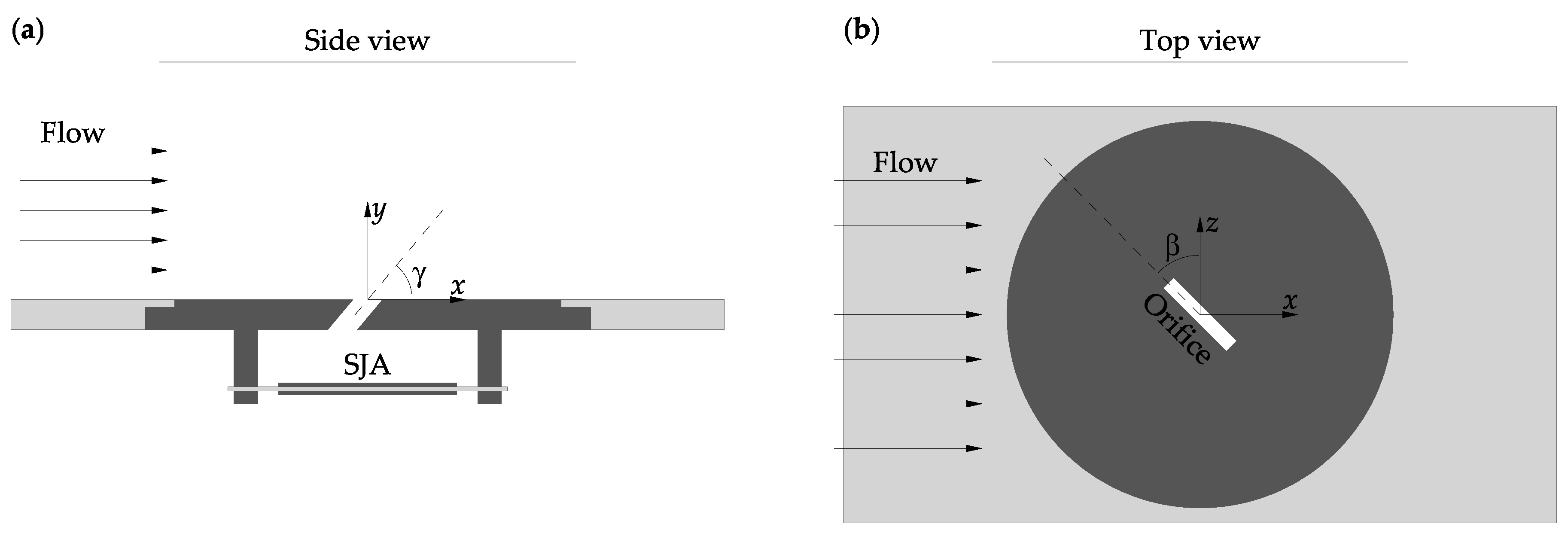
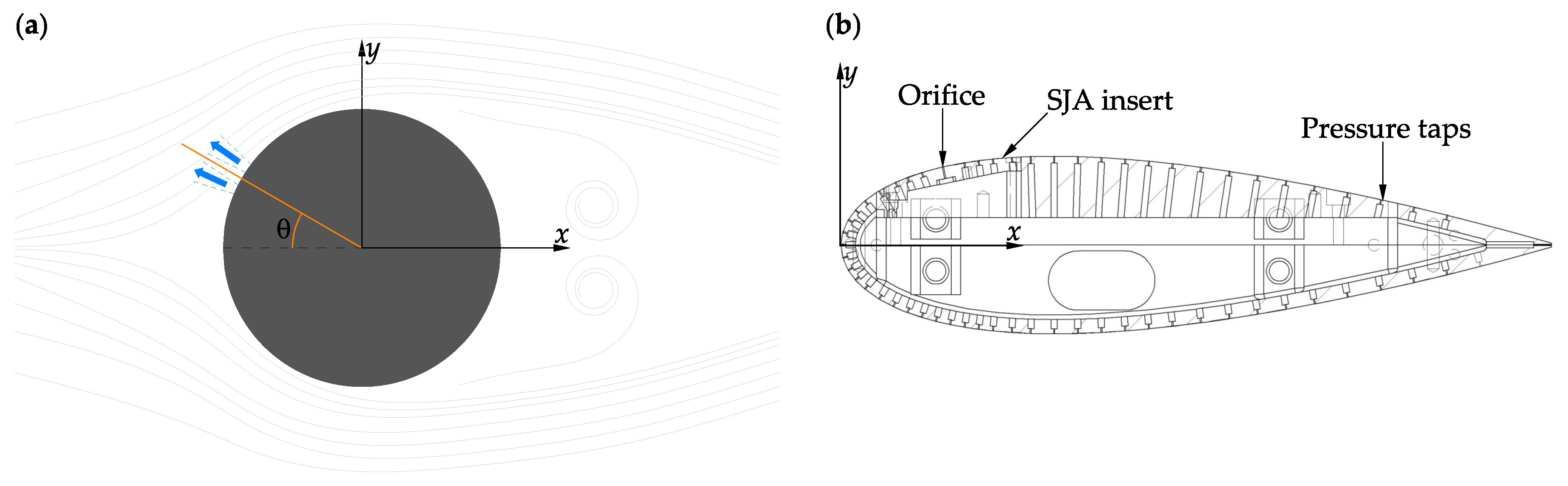
4.2. Effects of Orifice Shape and Orientation

Flow control with synthetic jets from non-circular orifices is of interest because of their enhanced entrainment and mixing capability compared to circular and two-dimensional synthetic jets. A schematic of an SJA with a rectangular orifice in crossflow is shown in Figure 7. In addition to the pitch angle

γ

, for only a non-circular orifice, a skew angle

β

must be defined to fully determine the orientation of the orifice with respect to the crossflow. Shuster et al. [43] examined the orifice pitch angle for perpendicular (

γ = 90

) and inclined (

γ = 60

) circular synthetic jets subjected to a laminar boundary at two stroke ratios,

L^{+} = 1

and 2. At the stroke ratio

L^{+} = 1

, flow structure differences were significant between the perpendicular and inclined orifice orientations. For the perpendicular orifice, the vortex ring that formed at the orifice during the expulsion portion of the actuator cycle did not escape the near vicinity of the orifice and was subsequently ingested during the suction phase of the cycle. The incoming boundary layer diverted over and around this stationary vortex, creating a wake in the boundary layer downstream of the orifice. In contrast, for an inclined orifice at the same stroke length, a train of vortex rings originating from the orifice penetrated the crossflow (see Figures 5 and 8 in Reference [43]). At the stroke ratio

L^{+} = 2

, large discrete vortices were formed at the orifice for both orifice orientations that penetrated deep into the crossflow, well beyond the boundary layer edge. In general, the mean interaction from the perpendicular orifice was shorter in the streamwise direction but extended further into the crossflow, causing a slight deflection of the mean streamlines away from the wall. In contrast, the mean interaction from the inclined orifice extended farther downstream, though it remained confined to a region closer to the wall. Zhao et al. [46] studied the flow over a national advisory committee for aeronautics (NACA) 0021 airfoil, instrumented with circular SJAs, at a maximum Reynolds number of

R e_{c} = 300000

for a range of angle of attacks

- 6 < α < 30

. They observed that, for most configurations, when the momentum coefficient of SJAs was small, a larger pitch angle

γ

was more effective in improving the maximum lift coefficient of the airfoil. Conversely, when the SJAs had a more significant momentum coefficient, a smaller pitch angle

γ

was more effective (see Figure 11, Table 3, and Figure 16 in Reference [46]).

As highlighted by Kim et al. [137], the flow fields generated by circular orifices are significantly different from rectangular orifices, suggesting that their interactions with a boundary layer might also differ. Smith [138] conducted a wind-tunnel experiment for an

AR = 45

rectangular SJA array expelled normally into a turbulent boundary layer at

C_{b} = 1.2

, examining two orifice orientations, with the rectangular long side normal to (

β = 0

) and aligned with the crossflow direction (

β = 90

), respectively. The boundary layer in the former case exhibited a wake-like region due to the blockage effect, while in the latter, evidence suggested the presence of longitudinal vortices embedded in the boundary layer. Van Buren et al. [139] used stereoscopic PIV to study

AR = 6

, 12, and 18 rectangular synthetic jets issued normally into a laminar boundary layer of

R e_{δ} = 2000

C_{b} = 0.5

, 1.0, and 1.5. The flow field was characterized by two salient structures: a recirculation region downstream of the orifice and a steady streamwise vortex pair farther downstream, akin to the findings in Smith [138] and Cui et al. [140]. A conceptual model of these structures is shown in Figure 8. These vortices interact with each other, as well as with the wall [141], to eventually lift off of the surface. The spacing of the edgewise vortices, produced due to the finite span of the orifice, and the virtual blockage of the jet were reduced with the decreased AR.

Van Buren et al. [136] used stereoscopic PIV to study

AR = 18

rectangular synthetic jets issued into a boundary layer of

R e_{δ} = 2000

at three momentum coefficients

C_{μ} = 0.08

, 0.33, and 0.75. The apparatus could accommodate different orifice pitch angles

γ = 20

, 45, 65, and 90 through separate inserts and could also be fixed at skew angles of

β = 0

–90 every 15. It was found that orifice orientation significantly influenced both steady and unsteady flow structures. Different combinations of orifice skew and pitch angles led to the formation of various types of vortical structures downstream, including the absence of coherent vortex structures, a single strong vortex (either positive or negative), or a symmetric vortex pair. The phase-averaged Q-criterion iso-surfaces revealed that orifice pitch angles more aligned with the crossflow produced less coherent vortical structures as they contributed less to generating transverse velocities. In the time-averaged flow field, when the orifice pitch angle was less than 90, the upstream lengthwise vortex dominated the interaction, leading to a single negative vortex downstream. However, when the orifice had a wall-normal pitch, the downstream lengthwise vortex became dominant, as the upstream vortex was constrained by the jet blockage, resulting in a single positive streamwise-oriented vortex downstream (most clearly seen for

β = 45

case, Figure 5 or Figure 6 in Reference [136]). In general, the more wall-normal transverse jets had more blockage, which resulted in a large wake deficit downstream, while the lower-pitch angled jets were more aligned with the flow, generating only regions of higher velocity with no wake. Additionally, the virtual blockage of the jet decreased as the aspect ratio was reduced.

Wang and Feng [40] employed time-resolved tomographic PIV to investigate the three-dimensional flow fields of an

AR = 3

rectangular synthetic jet and its interaction with a laminar boundary layer of

R e_{δ} = 1317

at a fixed blowing ratio

C_{b} = 1

. Two typical orifice orientations, namely spanwise (

β = 0

) and streamwise (

β = 90

) configurations, were examined to analyze the evolution of the vortical structures and the relevant flow physics. The flow field was composed of three major structures: a tilted vortex ring, a secondary trailing vortex, and a tertiary near-wall vortex. This suggested different flow scenarios from those for high-AR cases in Van Buren et al. [139] and Van Buren et al. [136]. Compared with the tilted and distorted vortex rings for circular cases observed by Jabbal and Zhong [107], the legs of the secondary trailing vortex were jointed in the spanwise direction at two different wall-normal heights. In contrast, the tertiary near-wall vortex was a crescent-shaped spanwise vortex instead of a streamwise vortex pair as in Jabbal and Zhong [107] (see Figure 5 in Reference [40]). Additionally, axis switching, a phenomenon typically observed in non-circular vortex rings as described in Section 3.3, was also detected in low-AR rectangular synthetic jets in crossflow. The orientation of the orifice had a direct influence on the timing and location of the axis switching. As for the two different orientations, their observations suggested that the spanwise orientation is more efficient in energizing the boundary layer.

Elimelech et al. [142] and Vasile and Amitay [143] performed stereoscopic PIV to study the interaction of a high-AR rectangular SJA with a three-dimensional boundary layer over a finite 30 swept-back NACA 4421 airfoil at a Reynolds number of

R e_{c} = 100000

and several angles of attack, where the SJA was operated at

C_{b} = 0.8

and 1.2 and several frequencies. High-frequency pairs of spanwise vorticity rollers were generated and shed away from the SJA, while streamwise vortices formed at both edges of the SJA orifice, rotating in opposite directions. The streamwise vortices primarily influenced the time-averaged flow field, as the impact of the spanwise rollers was largely diminished through averaging, with the higher blowing ratio causing deeper penetration into the crossflow (see Figure 10 in Reference [142]). The streamwise structures, along with the three-dimensional boundary layer, disrupt the coherence of the spanwise rollers, causing them to tilt and warp, eventually breaking them down into streamwise vorticity concentrations (see Figure 15 in Reference [142]).

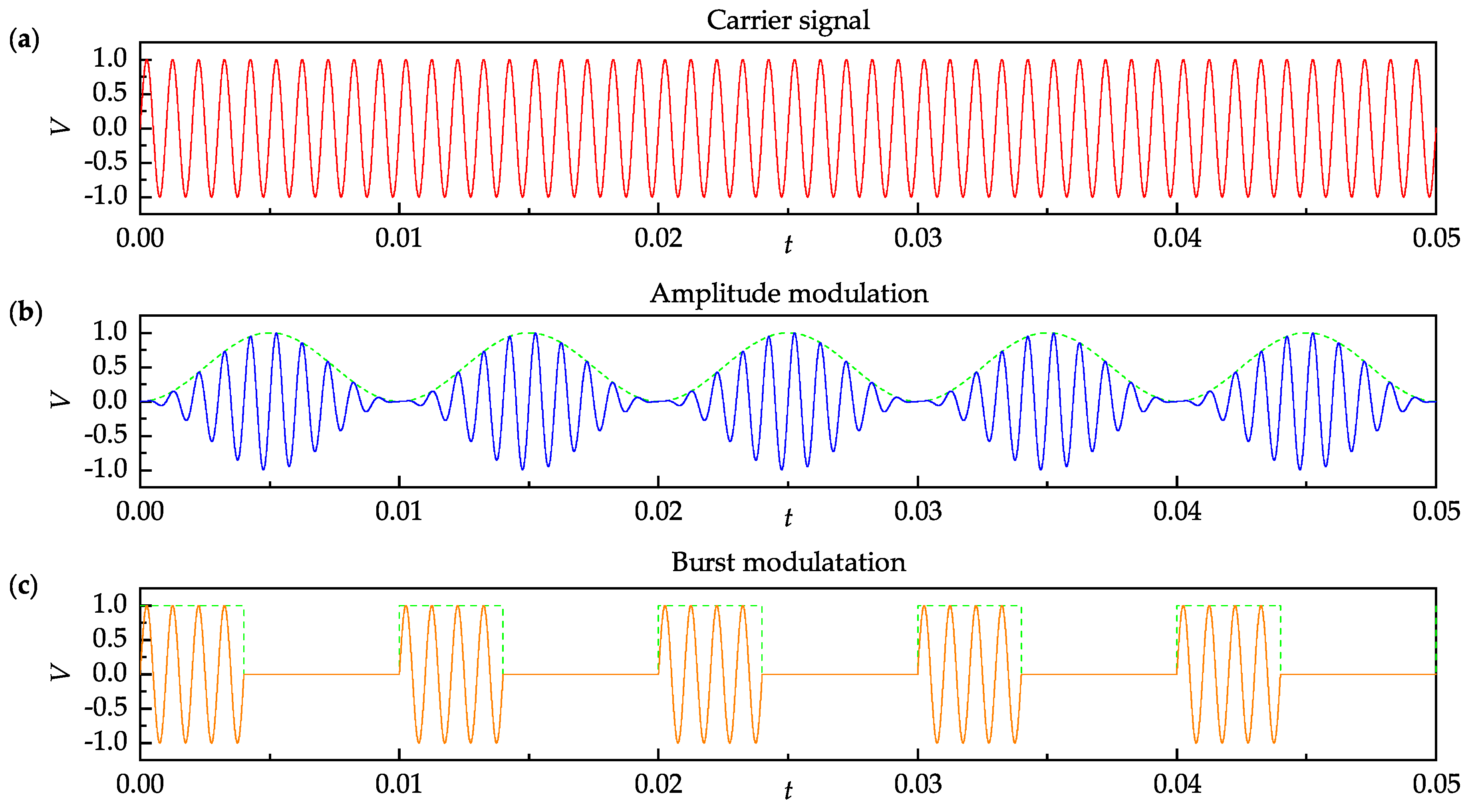
4.3. Effects of Forcing Frequency and Signal Waveform

The prior work indicates that active control schemes may become more effective by targeting the inherent flow instabilities [120,144]. For example, in the case of a flat plate, given that turbulent flow is less susceptible to separation, laminar separation can be delayed by prematurely triggering the transition to turbulence through the excitation of Tollmien-Schlichting waves [145,146]. As illustrated in Figure 9, for separated flow over an airfoil, as the inherently unstable separated shear layer undergoes a laminar-to-turbulent transition, it may or may not reattach to the airfoil surface, leading to two distinct flow regimes [147]. Hence, the post-separated flow is dominated by three instabilities: the global instability for the von Karman-like vortex shedding in the wake, the Kelvin-Helmholtz instability associated with the vortex roll-up in the separated shear layer, and the bubble flapping or shedding frequency in the event that laminar separation bubble (LSB) is present [148,149]. The frequencies of the shear layer and wake instabilities are coupled non-linearly and differ by an order of magnitude, which aligns with traditional scaling arguments as the characteristic length scale of the shear layer is an order of magnitude smaller than that of the wake [150].

SJAs should ideally be operated at their optimal frequency, typically identified under quiescent conditions, to maximize jet velocity and momentum output. In many control scenarios, targeting the natural flow instabilities requires the SJA to operate at a sub-optimal excitation frequency. In such cases, a solution proposed by Amitay and Glezer [151] is to use pulse-modulated actuation. This method allows the SJA to be driven at a carrier frequency that maximizes the jet velocity, while the modulation frequency of the source signal is used to specifically target and trigger the desired flow instabilities. It is noteworthy to mention that, although uncommon for SJAs, it is possible to modulate the carrier signal using non-square pulse envelopes or employ amplitude modulation. Examples of modulation for a sinusoidal carrier wave is shown in Figure 10. Equations (15b) and (16) may also be equivalently applied to modulated SJAs, though in such cases,

τ

should be set to the active duration of the SJA. Typically,

τ

is assigned as

τ = DC \times T

, although an SJA may still generate momentum during the off-phase of the cycle, depending on its response characteristics. Overall, Equation () is more appropriate for burst modulation as Equation (16) does not adequately account for the duty cycle. This can be easily verified by assuming a uniform velocity distribution during the active phase, which is sometimes a reasonable assumption for burst-modulated SJAs (see Figure 4 in Reference [152] or Figure 2 in Reference [153]). It then becomes clear that Equation (16) remains unchanged, whereas Equation (15b) varies linearly with the duty cycle. In any case, the effect of forcing frequency is characterized by the reduced frequency

f^{+}

, defined below:

f^{+} = \frac{f X_{f}}{U_{\infty}}

(18)

where

X_{f}

is an appropriate length scale for the flow under consideration and f is either the excitation, or the modulation frequency if the carrier signal is modulated. As a rule of thumb, an appropriate characteristic length is typically determined by the length scale of flow instabilities [154]. Nevertheless, it is also common to estimate the reduced frequency

f^{+}

using a reference geometrical length, such as the diameter of a cylinder or the chord length of an airfoil.

Goodfellow et al. [155] considered the effects of excitation at

f^{+} = 40

, corresponding to the SJA Helmholtz resonant frequency, on the separated shear layer and wake of a NACA 0025 airfoil at a chord-based Reynolds number of

R e_{c} = 100000

and an angle of attack of

α = 5

. Their results demonstrated that applying excitation above a threshold

C_{μ}

leads to flow reattachment, which in turn significantly alters the wake topology. Although an initial increase in

C_{μ}

above the threshold level resulted in an almost 50 reduction in drag, the positive impact on airfoil performance plateaued at higher

C_{μ}

values, highlighting the limitations of relying solely on

C_{μ}

as a control input. The significance of the forcing frequency and waveform in achieving optimal control becomes evident when comparing the findings of Goodfellow et al. [155] with those of Feero et al. [102], who studied the effects of both the momentum coefficient

C_{μ}

and reduced frequency

f^{+}

of a high-AR rectangular SJA on flow separation over a NACA 0025 airfoil at

R e_{c} = 100000

and

α = 10

. Similar to Goodfellow et al. [155], Feero et al. [102] identified a threshold value for an effective momentum coefficient

C_{μ} = 0.34

at a reduced frequency of

f^{+} = 58

, which corresponded to the SJA resonant peak. For a burst-modulated input at

f^{+} = 0.84

and

DC = 50

, however, flow reattachment occurred at

C_{μ} = 0.12

, which was 63 less than the threshold

C_{μ}

required for high-frequency harmonic excitation at

f^{+} = 58

. Interestingly, as the modulation frequency was increased to

f^{+} = 9.9

, the flow reattached at

C_{μ} = 0.08

, which was an order of magnitude smaller than what was required for high-frequency harmonic excitation. The effectiveness of low- and high-frequency forcing for an airfoil has been studied by several other researchers, in conjunction to different flow conditions, airfoil geometries, and SJA parameters [41,156,157,158,159,160]. Amitay and Glezer [144] conducted wind-tunnel experiments on an unconventional airfoil model at

R e_{c} = 310000

, studying the effects of the reduced frequency ranging from

O (1)

O (10)

on aerodynamic forces. They observed that forcing at

f^{+} \sim O (1)

, corresponding to the wake shedding frequency, leads to the formation of large vortical structures that persist well beyond the trailing edge of the airfoil, resulting in unsteady reattachment and aerodynamic forces. In contrast, actuation at

f^{+} \sim O (10)

, corresponding to the shear layer frequency, led to a complete flow reattachment, marked by the absence of large organized vortical structures. Similar observations were made by Amitay and Glezer [151] and Glezer et al. [119] who investigated the same two ranges of reduced frequency

f^{+}

for the same airfoil model as in Amitay and Glezer [144]. Amitay and Glezer [151] focused on flow transients and observed that the transients following the initiation or termination of pulse-modulated control were quite similar for cases where

f^{+} \sim O (1)

and

f^{+} \sim O (10)

. After the initial transition, the shedding of organized vortical structures gradually diminished for

f^{+} \sim O (10)

case, whereas

f^{+} \sim O (1)

case was characterized by the coherent shedding of a train of large vortices. Similar observations were reported by Amitay and Glezer [161]. For a NACA 0025 airfoil at

R e_{c} = 100000

, both Feero et al. [162] and Xu et al. [163] showed that forcing at the shear layer instability

f^{+} \sim O (10)

maximizes the lift-to-drag ratio, while forcing at the wake instability

f^{+} \sim O (1)

leads to maximum lift increase. Glezer et al. [119] investigated the fundamental differences in the response of separated flow over a two-dimensional circular cylinder at a diameter-based Reynolds number of

R e_{D} = 75500

to both low- and high-frequency actuation. By measuring the changes in circulation around the cylinder, the study confirmed the earlier findings of Amitay and Glezer [144], Amitay and Glezer [151]. Low-frequency actuation at

f^{+} \sim O (0.1)

, coupled with the global shedding frequency of the wake, produced strong oscillations in circulation and, as a result, in the aerodynamic forces. In contrast, under high-frequency actuation at

f^{+} \sim O (1)

, the circulation experienced a brief transient before stabilizing to a quasi-steady state, indicating that the aerodynamic forces became relatively time-invariant. These results underscored the fundamental distinction between low- and high-frequency actuation, that is the latter is decoupled from the unsteady base flow frequencies, leading to aerodynamic forces that are nearly constant and a damping of global flow oscillations.

The second part of the study by Amitay and Glezer [151] focused specifically on the efficiency of SJAs using pulse-modulated forcing at a constant duty cycle

DC = 25

and across a range of reduced frequencies

0.27 < f^{+} < 5

, compared to time-harmonic excitation. A comparison of both methods at

f^{+} = 3.3

, while maintaining the same

C_{μ}

level, revealed that time-harmonic actuation did not produce the same levels of lift coefficient as pulse-modulated excitation. Remarkably, pulse modulation resulted in a 400 increase in the lift coefficient once steady state was achieved, compared to continuous high-frequency

f^{+} \sim O (10)

actuation, while using only 25 of the jet momentum coefficient. Taylor and Amitay [108] investigated the effects of pulse-modulated SJA flow at varying

C_{μ}

and

f^{+}

values on the global forces and moments of a dynamically pitching finite-span national renewable energy laboratory (NREL) S809 blade at

R e_{c} = 220000

. Remarkably, at a reduced modulation frequency of

f^{+} = 1.2

and a duty cycle

DC = 40

, a 50 reduction in lift hysteresis was observed compared with the continuous sinusoidal actuation. Moreover, at a constant

f^{+}

, the reduction in hysteresis was very similar between

DC = 60

and

DC = 100

cases. The effectiveness of pulse-modulated forcing at a constant

C_{μ} = 1.2

and various

f^{+}

values was also confirmed by Rice et al. [153], Rice et al. [164], Rice et al. [165] for an NREL S817 airfoil at

R e_{c} = 375000

. Notably, these studies demonstrated the efficacy of pulse modulation in deep stall conditions, such as at

α = 25

, using a duty cycle of only

DC = 35

, significantly reducing power consumption. All of these works highlight the potential for reducing power requirements for synthetic jets while achieving similar flow reattachment effects or hysteresis reductions through pulse modulation at lower duty cycles.

Margalit et al. [166] conducted a series of tests on a balance-mounted 60 swept-back semi-span delta wing model with a sharp leading edge, and a

5.7

thickness-to-root-chord ratio for a range of Reynolds numbers

117000 < R e_{c} < 350000

and post-stall angles of attack

25 < α < 45

, studying several SJA parameters, including the modulation wave form. Their analyses revealed that the most effective reduced frequencies in improving the normal force were an order of

O (1)

, regardless of the modulation waveform or momentum coefficient

C_{μ}

. Interestingly, high-frequency non-modulated signals resulted in no improvement, or even a slight degradation, of aerodynamic performance (see Figures 4 and 5 in Reference [166]). Furthermore, the square pulse and chainsaw envelopes were somewhat superior to the triangle and sine envelopes in terms of normal force enhancement, for the range of effective frequencies considered (see Figure 6 in Reference [166]). It was found that a square envelope with a duty cycle as low as

DC = 5

was more effective than an amplitude-modulated signal, despite the latter having a larger peak excitation velocity and an order of magnitude greater momentum input. The study by Margalit et al. [166] demonstrates the role of modulation envelope in enhancing the performance of SJAs.

4.4. Effects of Actuator Location

Although not explicitly included in the dimensional analysis presented in Section 4, the location of the SJAs, denoted by

x^{+}

when non-dimensionalized, implicitly influences other parameters, such as the boundary layer thickness

δ

, wall shear stress

τ_{w}

, and the local wall curvature. Amitay et al. [159] investigated the effect of SJA location on the reattached flow over an unconventional airfoil across a range of angles of attack

5 < α < 25

at a Reynolds number of

R e_{c} = 310000

. The results showed that less power was required to reattach the flow as the control was positioned closer to the natural separation point on the unforced airfoil (see Figure 7 in Reference [159]). Surprisingly, reattachment was still achieved in some cases even when the actuators were positioned downstream of the stagnation point on the pressure side of the airfoil. Amitay et al. [159] emphasized that, despite the relatively high levels of

C_{μ}

necessary to affect the flow far upstream of the separation point, the interaction between the jets and the crossflow can yield a higher lift-to-drag ratio that may not be achievable when the jets are closer to the separation point. Zhao et al. [46] considered two chordwise locations

x^{+} = 15

and 40 for a NACA 0021 airfoil. They explained that the rear location was more effective than the front location in increasing the lift coefficient at pre-stall angles of attack

α

as little flow separation occurs near the rear location, allowing the induced jet to directly inject momentum into the separated flow. As

α

increased, the flow separation point moved toward the leading edge of the airfoil and, consequently, the front SJA location proved superior for controlling leading-edge flow separation, resulting in enhanced aerodynamic characteristics of the airfoil (see Figure 12 in Reference [46]). Overall, the upstream location was reported to be more efficient in delaying the stall of airfoil. Tang et al. [167] also studied two chordwise SJA locations

x = 23

and 43 for a national aeronautics and space administration (NASA) straight-wing model at a Reynolds number of

R e_{c} = 120000

and a range of angles of attack

5 < α < 25

, where the SJA was operated at several reduced frequencies

f^{+}

, reporting that the front SJA array was more effective than the rear one (See Figure 7 in Reference [167]).

Amitay et al. [114], Amitay et al. [168] investigated the manipulation of global aerodynamic forces on a two-dimensional circular cylinder model having a pair of surface-mounted SJAs, for a range of Reynolds numbers up to

R e_{D} = 131000

and SJA locations at circumferential angles

0 < θ < 180

. A schematic of their experimental setup is shown in Figure 11a. The smoke visualizations revealed that the interaction between the synthetic jet and the boundary layer led to the formation of closed recirculation regions, which could displace the local streaklines above the cylinder’s top surface, delaying flow separation (see Figures 5 and 7 in Reference [114]). When the SJAs were positioned at

θ = 0

, the circumferential pressure distribution remained nearly unchanged, indicating that the momentum coefficient was too low to affect the flow significantly. As

θ

increased, the effect of the SJAs on the pressure distribution became more pronounced, with a local minimum appearing in the pressure coefficient distribution around the SJAs location compared to the baseline flow (see Figure 2 in Reference [168]). For

θ < 90

, the static pressure between the front stagnation point and the separation point continued to decrease as

θ

increased. Of particular note were the changes in the base pressure of the cylinder between the top and bottom separation points, signifying the effect of actuation on the pressure drag (see Figure 10 in Reference [114]). For

θ > 90

, downstream of the separation point of the baseline flow, the pressure distribution shifted, exhibiting a second local minimum in the static pressure upstream of the separation zone on the unforced lower half of the cylinder. When

θ = 110

, the two minima in the pressure distribution were nearly identical and symmetric, indicating an approximately zero lift force at this angle. For large enough values of

θ

, the pressure distribution near the separation point on the forced side became nearly indistinguishable from that of the baseline flow. The SJAs seemed to influence only the unforced lower half of the cylinder, indicating a reversal in the direction of the lift force (see Figure 11 in Reference [114]). Eventually, for substantially large values of

θ

, when the SJAs were located near the wake, the pressure distributions for both the forced and unforced flows became nearly identical. A remarkable finding from the studies by Amitay et al. [114], Amitay et al. [168] is that the lift force can be entirely nullified or reversed simply by altering the circumferential position of the SJAs. These studies also confirm that when excitation is applied to the stable flow, the disturbances decay before becoming unstable. In contrast, applying excitation near the separation point proves to be an effective control strategy. Tensi et al. [44] studied the flow over a two-dimensional circular cylinder at a Reynolds number of

R e_{D} = 100000

, with two SJAs positioned at

θ = \pm 112.5

, operating at reduced frequencies up to

f^{+} = 0.2

, close to the natural shedding frequency. Surface oil visualizations showed that the separation line shifted downstream. When only one actuator was active, the trends in the pressure distributions were similar to those reported by Amitay et al. [114], Amitay et al. [168]. However, when both SJAs were activated, separation was delayed on both sides of the cylinder, resulting in two distinct local minima in the pressure distribution. These minima were nearly identical and symmetric, indicating an almost zero lift force (see Figures 7 and 11 in Reference [44]).

The study by Feero et al. [162] on a NACA 0025 airfoil, shown in Figure 11b, considered four chordwise SJA locations

x^{+}

around the mean separation point

x_{s}^{+}

, specifically

x^{+} - x_{s}^{+} = - 4.3

- 1.3

1.3

, and

4.3

. The results indicated that once a certain blowing ratio was achieved, the benefits of control saturated for both drag reduction and lift increase. A monotonic decrease in the threshold blowing ratio required to fully reattach the flow, along with an increase in the lift-to-drag ratio, was observed as the slot location moved upstream, with the most upstream location proving to be the most effective, both by requiring the lowest threshold blowing ratio and producing the largest lift-to-drag ratio. Zhao et al. [46] investigated two chordwise SJA locations,

x^{+} = 15

and 40 , for a NACA 0021 airfoil, again concluding that the jet positioned closer to the leading edge of the airfoil was more effective in delaying stall. The analyses by Taylor and Amitay [108] for the pitching NREL S809 blade, with two chordwise SJA locations at

x^{+} = 10

and 20 , revealed that the forward jet location consistently performed better in reducing hysteresis at any given momentum coefficient

C_{μ}

and reduced frequency

f^{+}

(see Figure 8 in Reference [108]). Still, the rear SJA location produced a higher lift coefficient during most of the pitching cycle. Therefore, if the goal is to enhance the lift coefficient, the rear jet location was recommended (see Figure 7 in Reference [108]).

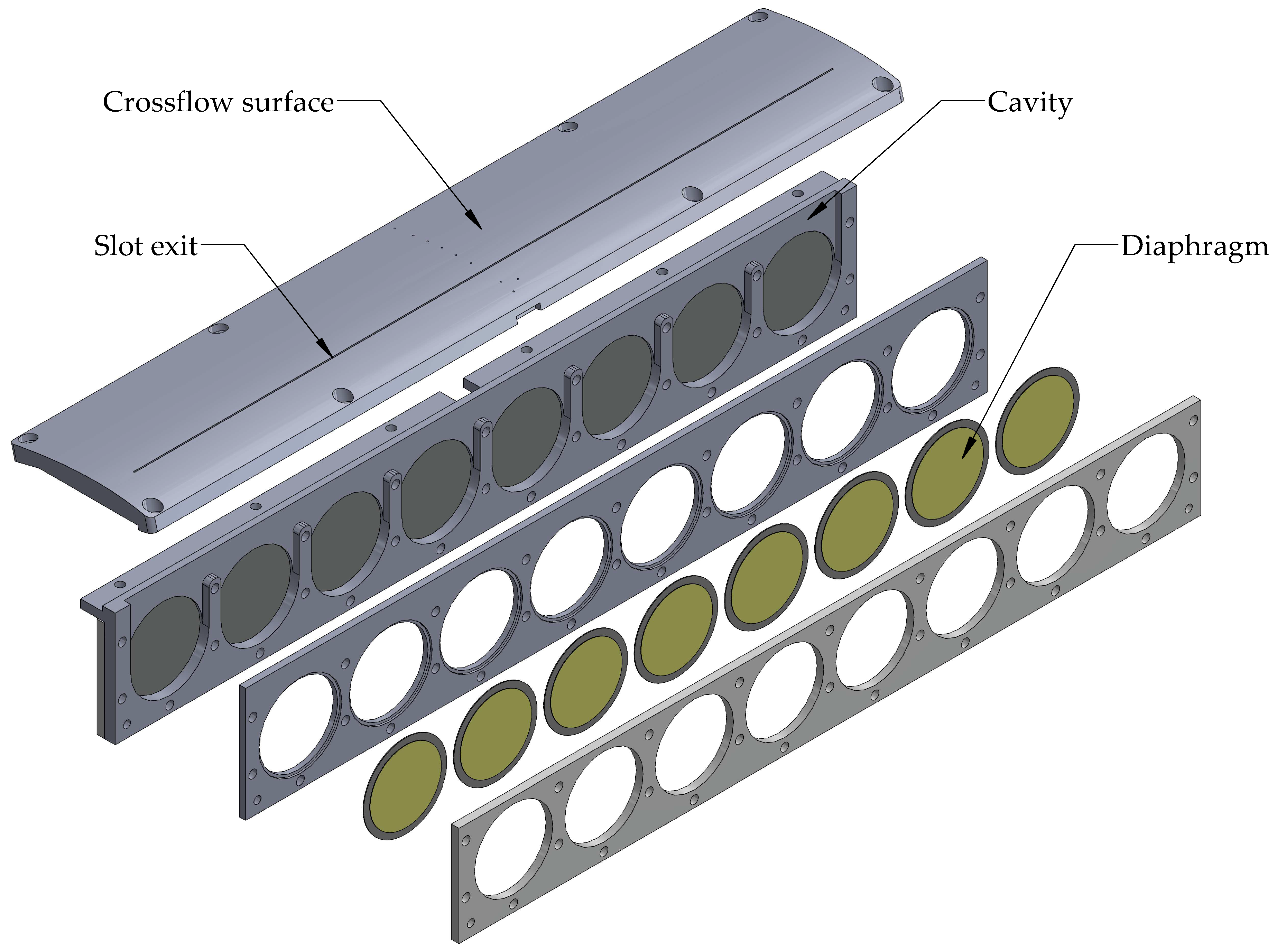
4.5. Effects of Clustering

SJAs are typically smaller than the geometric scales of the body they are intended to control, so they are often arranged in arrays to cover longer spans for more effective flow control [170,171]. For an array of SJAs, the stability of flow structures is crucial for enabling effective mixing of low- and high-momentum fluid across the entire span of the controlled geometry. Feero et al. [169] employed tuft and oil visualizations to examine the shape and spanwise extent of the reattached flow over a NACA 0025 airfoil caused by a high-AR rectangular SJA across a range of reduced excitation frequencies

f^{+}

and blowing ratios

C_{b}

at a constant

α = 12

and

R e_{c} = 125000

. The surface flow visualizations showed that the spanwise extent of the reattached flow narrows toward the trailing edge of the airfoil, a phenomenon described as flow contraction toward the airfoil centerline, which is also illustrated in Figure 12.

In the work of Feero et al. [169], the size and shape of the reattached region remained unchanged with varying

f^{+}

C_{b} = 1

. However, at a constant

f^{+} = 47

, as

C_{b}

increased from 1 to 2.5, the contraction of the attached flow decreased, resulting in a larger spanwise extent of the attached flow. These observations suggest that measurement techniques examining lift and drag improvements solely at the mid-span may fail to capture the full effects occurring across the entire span, which could result in inaccurate assessments of parameters. Also, note that the blowing ratio

C_{b}

was used by Feero et al. [169] as a measure of jet strength instead of the momentum coefficient

C_{μ}

since the SJA was essentially two-dimensional. Machado et al. [49,173] utilized smoke wire visualization to investigate the three-dimensionality of the reattached flow over the same NACA 0025 airfoil model as in Feero et al. [169] at

α = 10

and

R e_{c} = 100000

. The airfoil was equipped with an array of circular SJAs instead, operating at a constant momentum coefficient of

C_{μ} = 0.2

and two burst-modulated reduced frequencies

f^{+} = 1.18

and

f^{+} = 11.76

. Although the contraction phenomenon was observed at both frequencies, in the low-frequency case, the contraction was sharper and occurred at various chordwise locations. In contrast, the high-frequency case resulted in a more gradual contraction along the span. The results indicated that the effective control length is confined to about 40 of the array width, significantly decreasing the sectional lift coefficient as the distance from the mid-span increases.

Clustering SJAs introduces additional parameters, such as phase differences and spacing between individual SJAs, further expanding the complex parameter space. The studies by Liddle et al. [174], Liddle and Wood [175], Wen et al. [176], and Wen and Tang [177] explored the impact of phase differences,

Δ ϕ = 0

–270 in 90 increments, between in-line twin circular SJAs in laminar and turbulent boundary layers over a flat plate. These investigations employed a variety of experimental techniques, including constant temperature anemometry (CTA) [174,175], oil-flow visualization [174], stereoscopic dye visualization [176,177], and PIV [176,177]. In both studies by Liddle et al. [174] and Liddle and Wood [175], power spectral analysis of the downstream velocity time-histories revealed a distinct difference in

Δ ϕ = 270

case, where the prominent peak occurred at twice the actuation frequency, as opposed to the three other instances in which the prominent peak occurred at the actuation frequency. Additionally, the time-averaged streamwise velocity contours for

Δ ϕ = 90

featured more abrupt changes, indicating greater penetration into the boundary layer (see Figure 10 in Reference [174] or Figure 4 in Reference [175]). These findings were confirmed later by Wen et al. [176], Wen and Tang [177]. Both studies identified, three types of vortex structures: one combined vortex at

Δ ϕ = 90

, two completely separated hairpin vortices at

Δ ϕ = 270

, and partially interacting vortex structures at

Δ ϕ = 0

and 180 (see Figure 5 in Reference [176] or Figure 4 in Reference [177]). The strongest structure was the single combined vortex at

Δ ϕ = 90

, which exhibited the greatest penetration into the boundary layer. At

Δ ϕ = 270

, the resulting flow structures resembled a train of completely separated hairpin vortices, effectively doubling the frequency of the hairpin vortices produced by a single SJA. Overall, the results from the above studies indicate the potential for phase angle manipulation to improved flow control. It should be noted that the most effective phase difference between in-line SJAs also depends on the dimensionless jet-to-jet spacing

s^{+}

(usually spacing is normalized by the orifice width). For clarity, consider the study by Zhao et al. [46], where the effects of phase delay and combinations of pitch angles for in-line dual arrays on a NACA 0021 airfoil were investigated. At the angle of attack

α

just after stall, the phase difference of

Δ ϕ = 180

could significantly increase the lift coefficient and help prevent flow separation (see Figure 13 in Reference [46]). On the other hand, the control effects due to combined pitch angles were more complex. However, overall, when the pitch angle of the upstream SJA was lower, the dual jet actuators provided better control over airfoil stall compared to a single actuator (see Figure 16 in Reference [46] for a detailed report on combined pitch angles).

Fewer studies have explored the effects of spacing

s^{+}

and phase difference

Δ ϕ

in the parallel clustering of SJAs within a crossflow. For steady round jets having a parallel twin-jet configuration in a flat plate boundary layer, a detailed investigation was conducted by Zang and New [178], examining various spacing

s^{+}

and velocity ratio values, using laser-induced fluorescence (LIF) and PIV. The study demonstrated that each jet in the cluster achieved greater entrainment and larger jet half-widths compared to a single jet in crossflow. Reducing

s^{+}

caused the twin jets to interact with each other closer to the orifice exit. Similar to the enhancement mechanism in quiescent flow [114], the inner vortices were observed to move toward each other, neutralizing due to their oppositely signed vorticity and merging into a single counter-rotating vortex pair, which prevailed further downstream (see Figures 9 and 10 in Reference [178]). The study by Vasile and Amitay [143] on a 30 swept-back NACA 4421 wing equipped with three parallel rectangular SJAs with a spanwise spacing of

s^{+} = 43

also demonstrated that, when the spanwise spacing between the jets is sufficiently large, there is minimal interaction between the jets. The resulting flow field, formed by the simultaneous activation of all three jets, was essentially a superposition of the flow fields produced when each jet was activated individually. More recently, Jankee and Ganapathisubramani [179] investigated the interaction of parallel

A R = 13

rectangular twin jets with a turbulent boundary layer over a flat plate, for a range of spacing

s^{+}

and phase differences

Δ ϕ

, while keeping all other geometrical and operational parameters constant. A limit in spacing was identified, beyond which any further increase causes the twin jets to behave as two independent synthetic jets, which also aligned with the findings of Watson et al. [180] observed under quiescent conditions. Similar to the observations of Zang and New [178], when the spacing

s^{+}

was sufficiently small, the jets interacted with each other, with the inner vortex of each counter-rotating vortex pair canceling out due to their opposite vorticity signs and the remaining part of the vortices coalescing into a single vortex pair (see Figure 4 in Reference [179]). For the smallest spacing of

s^{+} = 2

with a phase difference

Δ ϕ \neq 0

, the jets exhibited vectoring toward the actuator leading in phase, similar to the behavior observed in quiescent flow conditions [114,181,182] (see Figure 6 in Reference [179]). At a phase difference of

Δ ϕ = 78

, the influence of the crossflow caused the vortical structures from the leading SJA to convect downstream before the lagging SJA reached peak blowing. As a result, the interactions were minimal, and the flow field of the twin jets in this scenario became analogous to that of a single SJA operating at twice the actuation frequency, the doubling effect. The studies mentioned above highlight the potential of clustering parameters

s^{+}

and

Δ ϕ

for enhanced control schemes. A notable example can be found in the work by Amitay et al. [114] on a circular cylinder. When the SJAs were positioned on the downstream edge at

θ = 180

, substantial momentum was necessary to influence the wake. However, with the SJAs operated at

Δ ϕ = 120

, the downward vectoring of the jets caused a downward shift in the entire wake and a simultaneous displacement of the front stagnation point. This led to a decrease in spacing between the streaklines above the cylinder and an increase in spacing below it, indicating a change in circulation and lift generation (see Figures 8 and 9 in Reference [114]).

4.6. Open- and Closed-loop Control

Given the focus on flow control applications, experimental and numerical studies involving airfoils and wing models with open-loop control were reviewed and presented in Table 1 for comparison. In studies employing an open-loop control system, the SJA parameters are preset and performance is evaluated afterward. In many real-world scenarios, the control scheme must be robust to variations in design conditions and, in some cases, even adaptive to ensure optimal performance. Implementing closed-loop systems is an emerging trend in AFC, both in experimental [4,183] and numerical [184,185] works. An effective sensing strategy is essential for expanding open-loop control systems to closed-loop configurations. Researchers have proposed several approaches for this, including visual feedback [4,28,186], pressure sensing [4,183,187,188], and shear sensing [5]. Closed-loop control studies using either model-based or model-free methods hold significant promise for the field. While a detailed examination of these approaches is beyond the scope of this article, readers interested in machine learning approaches for AFC are directed to the recent review by Li et al. [189].

5. Conclusions

SJAs offer significant advantages for flow control due to their ability to inject momentum without an external fluid supply, reducing system complexity, and weight. Technological advancements have made them lightweight, easy to maintain, and highly responsive, spurring increased research and publications on SJAs. This article reviewed SJA working mechanisms and how operational and geometrical factors influence flow fields in quiescent and crossflow conditions. Key studies were summarized, highlighting their contributions.

Author Contributions

Conceptualization, A.S., H.H., E.E., P.E.S.; formal analysis, A.S., H.H.; investigation, A.S., H.H.; resources, E.E., P.E.S.; data curation, A.S., H.H.; writing—original draft preparation, A.S., H.H.; writing—review and editing, A.S., H.H., E.E., P.E.S.; supervision, E.E., P.E.S.; project administration, E.E., P.E.S.; funding acquisition, P.E.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Natural Sciences and Engineering Research Council of Canada (NSERC) grant number RGPIN-2022-03071 and the Digital Research Alliance of Canada (4752).

Data Availability Statement

No new data were created or analyzed in this study.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

AFC	Active Flow Control
AR	Aspect Ratio
BLC	Boundary Layer Control
CTA	Constant Temperature Anemometry
DC	Duty Cycle
DNS	Direct Numerical Simulation
HWA	Hot-Wire Anemometry
LDV	Laser Doppler Velocimetry
LES	Large Eddy Simulation
LIF	Laser-Induced Fluorescence
LSB	Laminar Separation Bubble
NACA	National Advisory Committee for Aeronautics
NASA	National Aeronautics and Space Administration
NREL	National Renewable Energy Laboratory
PIV	Particle Image Velocimetry
SJA	Synthetic Jet Actuator
SJBLI	Synthetic Jet and Boundary Layer Interaction
TLC	Temperature-sensitive Liquid Crystal
URANS	Unsteady Reynolds-Averaged Navier-Stokes
VR	Velocity Ratio
ZMB	Zero Mass Blowing
ZNMF	Zero-Net Mass-Flux

References

Gad-el Hak, M. Flow Control: Passive, Active, and Reactive Flow Management; Cambridge University Press, 2000. [CrossRef]
Gad-el Hak, M.; Bushnell, D.M. Separation control: Review. Journal of Fluids Engineering 1991, 113, 5–30. [CrossRef]
Flatt, J., The history of boundary layer control research in the United States of America. In Boundary Layer and Flow Control: Its Principles and Application; Pergamon, 1961; Vol. 1, pp. 122–143.
Deem, E.A.; Cattafesta, L.N.; Hemati, M.S.; Zhang, H.; Rowley, C.; Mittal, R. Adaptive separation control of a laminar boundary layer using online dynamic mode decomposition. Journal of Fluid Mechanics 2020, 903, A21. [CrossRef]
Debien, A.; Von Krbek, K.A.F.F.; Mazellier, N.; Duriez, T.; Cordier, L.; Noack, B.R.; Abel, M.W.; Kourta, A. Closed-loop separation control over a sharp edge ramp using genetic programming. Experiments in Fluids 2016, 57, 1–19. [CrossRef]
Packard, N.O.; Thake, M.P.; Bonilla, C.H.; Gompertz, K.; Bons, J.P. Active control of flow separation on a laminar airfoil. AIAA Journal 2013, 51, 1032–1041. [CrossRef]
Greenblatt, D.; Wygnanski, I.J. Use of periodic excitation to enhance airfoil performance at low Reynolds numbers. Journal of Aircraft 2001, 38, 190–192. [CrossRef]
Williams, D.R.; Macmynowski, D.G., Brief history of flow control. In Fundamentals and Applications of Modern Flow Control; AIAA, 2009; Vol. 231, pp. 1–20. [CrossRef]
Maldonado, V.; Boucher, M.; Ostman, R.; Amitay, M. Active vibration control of a wind turbine blade using synthetic jets. International Journal of Flow Control 2009, 1. [CrossRef]
Gad-el Hak, M. Flow control: The future. Journal of Aircraft 2001, 38, 402–418. [CrossRef]
Prandtl, L. Über flüssigkeitsbewegung bei sehr kleiner reibung (On the motion of fluid with very small viscosity). Third International Mathematical Congress. Heidelberg, 1904, pp. 484–491.
Carriere, P.; Eichelbrenner, E.A., Theory of flowreattachment by a tangential jet discharging against a strong adverse pressure gradient. In Boundary Layer and Flow Control: Its Principles and Application; Pergamon, 1961; Vol. 1, pp. 209–231.
Betz, A., History of Boundary Layer Control in Germany. In Boundary Layer and Flow Control: Its Principles and Application; Pergamon, 1961; Vol. 1, pp. 1–20.
Wygnanski, I. Boundary layer and flow control by periodic addition of momentum. 4th Shear Flow Control Conference, 1997, p. 2117. [CrossRef]
Eroglu, A.; Breidenthal, R.E. Structure, penetration, and mixing of pulsed jets in crossflow. AIAA Journal 2001, 39, 417–423. [CrossRef]
Seifert, A.; Pack, L.G. Oscillatory control of separation at high Reynolds numbers. AIAA Journal 1999, 37, 1062–1071. [CrossRef]
Wu, J.M.; Vakili, A.D.; Yu, F.M. Investigation of the interacting flow of nonsymmetric jets in crossflow. AIAA Journal 1988, 26, 940–947. [CrossRef]
Lin, J.C.; Whalen, E.A.; Andino, M.Y.; Graff, E.C.; Lacy, D.S.; Washburn, A.E.; Gharib, M.; Wygnanski, I.J. Full-scale testing of active flow control applied to a vertical tail. Journal of Aircraft 2019, 56, 1376–1386. [CrossRef]
Seifert, A.; Shtendel, T.; Dolgopyat, D. From lab to full scale active flow control drag reduction: How to bridge the gap? Journal of Wind Engineering and Industrial Aerodynamics 2015, 147, 262–272. doi:. [CrossRef]
McVeigh, M.A.; Nagib, H.; Wood, T.; Wygnanski, I. Full-scale flight tests of active flow control to reduce tiltrotor aircraft download. Journal of Aircraft 2011, 48, 786–796. [CrossRef]
Shaw, L.; Smith, B.; Saddoughi, S., Full-scale flight demonstration of active control of a pod wake. In 3rd AIAA Flow Control Conference; AIAA, 2006; p. 3185. [CrossRef]
Yarusevych, S.; Sullivan, P.E.; Kawall, J.G. Effect of acoustic excitation amplitude on airfoil boundary layer and wake development. AIAA Journal 2007, 45, 760–771. [CrossRef]
Zaman, K.B.M.Q.; Bar-Sever, A.; Mangalam, S.M. Effect of acoustic excitation on the flow over a low-Re airfoil. Journal of Fluid Mechanics 1987, 182, 127–148. [CrossRef]
Huang, L.; Maestrello, L.; Bryant, T., Separation control over an airfoil at high angles of attack by soundemanating from the surface. In 19th AIAA, Fluid Dynamics, Plasma Dynamics, and Lasers Conference; AIAA, 1987; p. 1261. [CrossRef]
Ahuja, K.K.; Burrin, R.H., Control of flow separation by sound. In 9th Aeroacoustics Conference; AIAA, 1984; p. 2298. [CrossRef]
Hsiao, F.B.; Liu, C.F.; Shyu, J.Y. Control of wall-separated flow by internal acoustic excitation. AIAA Journal 1990, 28, 1440–1446. [CrossRef]
Nishioka, M.; Asai, M.; Yoshida, S. Control of flow separation by acoustic excitation. AIAA Journal 1990, 28, 1909–1915. [CrossRef]
Gautier, N.; Aider, J.L.; Duriez, T.; Noack, B.; Segond, M.; Abel, M. Closed-loop separation control using machine learning. Journal of Fluid Mechanics 2015, 770, 442–457. [CrossRef]
Cater, J.E.; Soria, J. The evolution of round zero-net-mass-flux jets. Journal of Fluid Mechanics 2002, 472, 167–200. [CrossRef]
Gilarranz, J.; Rediniotis, O., Compact, high-power synthetic jet actuators for flow separation control. In 39th Aerospace Sciences Meeting and Exhibit; AIAA, 2001; p. 737. [CrossRef]
McManus, K.; Joshi, P.; Legner, H.; Davis, S., Active control of aerodynamic stall using pulsed jet actuators. In Fluid Dynamics Conference; AIAA, 1995; p. 2187. [CrossRef]
Cattafesta, L.N.; Sheplak, M. Actuators for active flow control. Annual Review of Fluid Mechanics 2011, 43, 247–272. doi:. [CrossRef]
Bons, J.P.; Sondergaard, R.; Rivir, R.B. The fluid dynamics of LPT blade separation control using pulsed jets. Journal of Turbomachinery 2001, 124, 77–85. [CrossRef]
Glezer, A.; Amitay, M. Synthetic jets. Annual Review of Fluid Mechanics 2002, 34, 503–529. doi:. [CrossRef]
Zhong, S.; Jabbal, M.; Tang, H.; Garcillan, L.; Guo, F.; Wood, N.; Warsop, C. Towards the design of synthetic-jet actuators for full-scale flight conditions: Part 1: The fluid mechanics of synthetic-jet actuators. Flow, turbulence and combustion 2007, 78, 283–307. [CrossRef]
Tang, H.; Zhong, S.; Jabbal, M.; Garcillan, L.; Guo, F.; Wood, N.; Warsop, C. Towards the design of synthetic-jet actuators for full-scale flight conditions: Part 2: Low-dimensional performance prediction models and actuator design method. Flow, turbulence and combustion 2007, 78, 309–329.
Ho, C.M.; Tai, Y.C. Review: MEMS and its applications for flow control. Journal of Fluids Engineering 1996, 118, 437–447. [CrossRef]
Gad-el Hak, M. Modern developments in flow control. Applied Mechanics Reviews 1996, 49, 365–379. [CrossRef]
McMichael, J., Progress and prospects for active flow control using microfabricated electromechanical systems (MEMS). In 34th Aerospace Sciences Meeting and Exhibit; AIAA, 1996; p. 306. [CrossRef]
Wang, L.; Feng, L.H. The interactions of rectangular synthetic jets with a laminar cross-flow. Journal of Fluid Mechanics 2020, 899, A32. [CrossRef]
Buchmann, N.; Atkinson, C.; Soria, J. Influence of ZNMF jet flow control on the spatio-temporal flow structure over a NACA-0015 airfoil. Experiments in fluids 2013, 54, 1–14. [CrossRef]
Di Cicca, G.M.; Iuso, G. On the near field of an axisymmetric synthetic jet. Fluid Dynamics Research 2007, 39, 673–693. [CrossRef]
Shuster, J.; Pink, R.; McEligot, D.; Smith, D., The interaction of a circular synthetic jet with a cross-flow boundary layer. In 35th AIAA Fluid Dynamics Conference and Exhibit; AIAA, 2005; p. 4749. [CrossRef]
Tensi, J.; Boué, I.; Paillé, F.; Dury, G. Modification of the wake behind a circular cylinder by using synthetic jets. Journal of visualization 2002, 5, 37–44. [CrossRef]
Jankee, G.K.; Ganapathisubramani, B. Scalings for rectangular synthetic jet trajectory in a turbulent boundary layer. Journal of Fluid Mechanics 2021, 915, A57. [CrossRef]
Zhao, G.; Zhao, Q.; Gu, Y.; Chen, X. Experimental investigations for parametric effects of dual synthetic jets on delaying stall of a thick airfoil. Chinese Journal of Aeronautics 2016, 29, 346–357. doi:. [CrossRef]
McCormick, D., Boundary layer separation control with directed synthetic jets. In 38th Aerospace Sciences Meeting and Exhibit; AIAA, 2000; p. 519. [CrossRef]
Feero, M.A. Investigation of synthetic jet flow control parameters for the mitigation of laminar boundary layer separation. PhD thesis, University of Toronto (Canada), 2018.
Machado, A.; Xu, K.; Sullivan, P.E. Visualizing three-dimensional effects of synthetic jet flow control. Journal of Visualization 2024, pp. 1–10. [CrossRef]
Palumbo, A.; Semeraro, O.; Robinet, J.C.; de Luca, L. Boundary layer transition induced by low-speed synthetic jets. Physics of Fluids 2022, 34, 124113. [CrossRef]
Montazer, E.; Mirzaei, M.; Salami, E.; Ward, T.; Romli, F.; Kazi, S. Optimization of a synthetic jet actuator for flow control around an airfoil. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2016, Vol. 152, p. 012023. [CrossRef]
Ciobaca, V.; Haucke, F.; Rudnik, R.; Nitsche, W. Active flow control on a high-lift airfoil: URANS simulations and comparison with time-accurate measurements. 31st AIAA Applied Aerodynamics Conference 2013, p. 2795. [CrossRef]
Ho, H.H.; Essel, E.E.; Sullivan, P. Improving 3D synthetic jet modeling in a crossflow. Journal of Fluids Engineering 2023, pp. 1–50. [CrossRef]
Raju, R.; Aram, E.; Mittal, R.; Cattafesta, L. Simple models of zero-net mass-flux jets for flow control simulations. International Journal of Flow Control 2009, 1, 179–197. [CrossRef]
Pasa, J.; Panda, S.; Arumuru, V. Focusing of jet from synthetic jet array using non-linear phase delay. Physics of Fluids 2023, 35. [CrossRef]
Smith, B.; Glezer, A.; Smith, B.; Glezer, A., Vectoring and small-scale motions effected in free shear flows using synthetic jet actuators. In 35th Aerospace Sciences Meeting and Exhibit; AIAA, 1997; p. 213. [CrossRef]
Smith, B.L.; Glezer, A. The formation and evolution of synthetic jets. Physics of Fluids 1998, 10, 2281–2297. [CrossRef]
Smith, B.; Swift, G., Synthetic jets at large Reynolds number and comparison to continuous jets. In 15th AIAA Computational Fluid Dynamics Conference; AIAA, 2001; p. 3030. [CrossRef]
Glezer, A. The formation of vortex rings. The Physics of Fluids 1988, 31, 3532–3542. [CrossRef]
Jabbal, M.; Wu, J.; Zhong, S. The performance of round synthetic jets in quiescent flow. The Aeronautical Journal 2006, 110, 385–393. [CrossRef]
Utturkar, Y.; Holman, R.; Mittal, R.; Carroll, B.; Sheplak, M.; Cattafesta, L. A jet formation criterion for synthetic jet actuators. 41st Aerospace Sciences Meeting and Exhibit, 2003, p. 636. [CrossRef]
Holman, R.; Utturkar, Y.; Mittal, R.; Smith, B.L.; Cattafesta, L. Formation criterion for synthetic jets. AIAA Journal 2005, 43, 2110–2116. [CrossRef]
Shuster, J.M.; Smith, D.R. Experimental study of the formation and scaling of a round synthetic jet. Physics of Fluids 2007, 19, 045109. [CrossRef]
Milanovic, I.M.; Zaman, K.B.M.Q. Synthetic jets in cross-flow. AIAA Journal 2005, 43, 929–940. [CrossRef]
Smith, B.; Trautman, M.; Glezer, A., Controlled interactions of adjacent synthetic jets. In 37th Aerospace Sciences Meeting and Exhibit; AIAA, 1999; pp. 11–14. [CrossRef]
Widnall, S.E.; Tsai, C.y.; Stuart, J.T. The instability of the thin vortex ring of constant vorticity. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 1977, 287, 273–305. [CrossRef]
Jankee, G.K.; Ganapathisubramani, B. Influence of internal orifice geometry on synthetic jet performance. Experiments in Fluids 2019, 60, 1–11. [CrossRef]
Nani, D.J.; Smith, B.L. Effect of orifice inner lip radius on synthetic jet efficiency. Physics of Fluids 2012, 24. [CrossRef]
Jain, M.; Puranik, B.; Agrawal, A. A numerical investigation of effects of cavity and orifice parameters on the characteristics of a synthetic jet flow. Sensors and Actuators A: Physical 2011, 165, 351–366. [CrossRef]
Kim, Y.H.; Garry, K., Optimisation of a rectangular orifice synthetic jet generator. In 3rd AIAA Flow Control Conference; AIAA, 2006; p. 2862. [CrossRef]
Fugal, S.R.; Smith, B.L.; Spall, R.E. Displacement amplitude scaling of a two-dimensional synthetic jet. Physics of Fluids 2005, 17, 045103. [CrossRef]
Garcillan, L.; Zhong, S.; Pokusevski, Z.; Wood, N., A PIV study of synthetic jets with different orifice shape and orientation. In 2nd AIAA Flow Control Conference; AIAA, 2004; p. 2213. [CrossRef]
Hong, M.H.; Cheng, S.Y.; Zhong, S. Effect of geometric parameters on synthetic jet: A review. Physics of Fluids 2020, 32, 031301. [CrossRef]
Belanger, R.; Zingg, D.W.; Lavoie, P. Vortex structure of a synthetic jet issuing into a turbulent boundary layer from a finite-span rectangular orifice. AIAA Scitech 2020 Forum, 2020, p. 1815. [CrossRef]
Krishnan, G.; Mohseni, K. An experimental and analytical investigation of rectangular synthetic jets. Journal of Fluids Engineering 2009, 131, 121101. [CrossRef]
Sahni, O.; Wood, J.; Jansen, K.E.; Amitay, M. Three-dimensional interactions between a finite-span synthetic jet and a crossflow. Journal of Fluid Mechanics 2011, 671, 254–287. [CrossRef]
Amitay, M.; Cannelle, F. Evolution of finite span synthetic jets. Physics of Fluids 2006, 18, 054101. [CrossRef]
Lindstrom, A.; Amitay, M. Effect of orifice geometry on synthetic jet evolution. AIAA Journal 2019, 57, 2783–2794. [CrossRef]
Oren, L.; Gutmark, E.; Muragappan, S.; Khosla, S., Flow characteristics of non circular synthetic jets. In 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition; AIAA, 2009; p. 1309. [CrossRef]
Lee, C.Y.; Goldstein, D.B. Two-dimensional synthetic jet simulation. AIAA Journal 2002, 40, 510–516. [CrossRef]
Miró, A.; Soria, M.; Moulinec, C.; Cajas, J.; Fournier, Y.; MFEE, F. Numerical investigations on rectangular and circular synthetic jet impingement. Tenth International Conference on Computational Fluid Dynamics (ICCFD10), 2018, Vol. 18.
Carpy, S.; Manceau, R. Turbulence modelling of statistically periodic flows: Synthetic jet into quiescent air. International Journal of Heat and Fluid Flow 2006, 27, 756–767. [CrossRef]
Cui, J.; Agarwak, R. Three-dimensional computation of a synthetic jet in quiescent air. AIAA Journal 2006, 44, 2857–2865. [CrossRef]
Qayoum, A.; Gupta, V.; Panigrahi, P.; Muralidhar, K. Influence of amplitude and frequency modulation on flow created by a synthetic jet actuator. Sensors and Actuators A: Physical 2010, 162, 36–50. [CrossRef]
Zhang, P.F.; Wang, J.J. Novel signal wave pattern for efficient synthetic jet generation. AIAA Journal 2007, 45, 1058–1065. [CrossRef]
Arafa, N.; Sullivan, P.E.; Ekmekci, A. Jet velocity and acoustic excitation characteristics of a synthetic jet actuator. Fluids 2022, 7, 387. [CrossRef]
Gallas, Q.; Holman, R.; Nishida, T.; Carroll, B.; Sheplak, M.; Cattafesta, L. Lumped element modeling of piezoelectric-driven synthetic jet actuators. AIAA Journal 2003, 41, 240–247. [CrossRef]
Buren, T.V.; Whalen, E.; Amitay, M. Achieving a high-speed and momentum synthetic jet actuator. Journal of Aerospace Engineering 2016, 29, 04015040. [CrossRef]
de Luca, L.; Girfoglio, M.; Coppola, G. Modeling and experimental validation of the frequency response of synthetic jet actuators. AIAA Journal 2014, 52, 1733–1748. [CrossRef]
Gomes, L.; Crowther, W., Towards a practical synthetic jet actuator for industrial scale flow control applications. In IUTAM Symposium on Flow Control and MEMS; Springer Netherlands: Dordrecht, 2008; pp. 111–118. [CrossRef]
Mallinson, S.; Hong, G.; Reizes, J. Some characteristics of synthetic jets. 30th Fluid dynamics conference, 1999, p. 3651. [CrossRef]
Lv, Y.w.; Zhang, J.z.; Shan, Y.; Tan, X.m. Numerical investigation for effects of actuator parameters and excitation frequencies on synthetic jet fluidic characteristics. Sensors and Actuators A: Physical 2014, 219, 100–111. doi:. [CrossRef]
Lu, Y.; Wang, J. Numerical investigation of synthetic jets generated by various signals in quiescent ambient. Physics of Fluids 2023, 35. [CrossRef]
Azzawi, I.D.J. Application of synthetic jet actuators for modification of separated boundary layers. PhD thesis, University of Leeds, 2016.
Tang, H.; Zhong, S. The effect of actuator geometry on the performance of synthetic jets. CEAS/KATnet Conference on Key Aerodynamic Technologies, Bremen, Germany, 2005.
Crook, A.; Wood, N., Measurements and visualisations of synthetic jets. In 39th Aerospace Sciences Meeting and Exhibit; AIAA, 2001; p. 145. [CrossRef]
Utturkar, Y.; Mittal, R.; Rampunggoon, P.; Cattafesta, L., Sensitivity of synthetic jets to the design of the jet cavity. In 40th AIAA Aerospace Sciences Meeting and Exhibit; AIAA, 2002; p. 124. [CrossRef]
Gallas, Q. On the modeling and design of zero-net mass flux actuators. PhD thesis, University of Florida, 2004.
Rizzetta, D.P.; Visbal, M.R.; Stanek, M.J. Numerical investigation of synthetic-jet flowfields. AIAA Journal 1999, 37, 919–927. [CrossRef]
Feero, M.A.; Lavoie, P.; Sullivan, P.E. Influence of cavity shape on synthetic jet performance. Sensors and Actuators A: Physical 2015, 223, 1–10. doi:. [CrossRef]
Ziadé, P.; Feero, M.A.; Sullivan, P.E. A numerical study on the influence of cavity shape on synthetic jet performance. International Journal of Heat and Fluid Flow 2018, 74, 187–197. [CrossRef]
Feero, M.A.; Goodfellow, S.D.; Lavoie, P.; Sullivan, P.E. Flow reattachment using synthetic jet actuation on a low-Reynolds-number airfoil. AIAA Journal 2015, 53, 2005–2014. [CrossRef]
Jabbal, M.; Tang, H.; Zhong, S. The effect of geometry on the performance of synthetic jet actuators. 25th International Congress of the Aeronautical Science (ICAS). Hamburg, Germany. Paper ICAS, 2006, p. P2.
Tang, H.; Zhong, S., Modelling of the characteristics of synthetic jet actuators. In 35th AIAA Fluid Dynamics Conference and Exhibit; AIAA, 2005; p. 4748. [CrossRef]
Chiatto, M.; Capuano, F.; de Luca, L. Numerical and experimental characterization of a double-orifice synthetic jet actuator. Meccanica 2018, 53, 2883–2896. [CrossRef]
Zhang, S.; Zhong, S. Experimental investigation of flow separation control using an array of synthetic jets. AIAA Journal 2010, 48, 611–623. [CrossRef]
Jabbal, M.; Zhong, S. Particle image velocimetry measurements of the interaction of synthetic jets with a zero-pressure gradient laminar boundary layer. Physics of Fluids 2010, 22, 063603. [CrossRef]
Taylor, K.; Amitay, M. Dynamic stall process on a finite span model and its control via synthetic jet actuators. Physics of Fluids 2015, 27, 077104. [CrossRef]
Gul, M.; Uzol, O.; Akmandor, I.S. An experimental study on active flow control using synthetic jet actuators over S809 airfoil. Journal of Physics: Conference Series 2014, 524, 012101. [CrossRef]
Park, H.; Cho, J.H.; Lee, J.; Lee, D.H.; Kim, K.H. Experimental study on synthetic jet array for aerodynamic drag reduction of a simplified car. Journal of Mechanical Science and Technology 2013, 27, 3721–3731. [CrossRef]
Sassoon, A.; Hubbard, J.; Flatau, A.; Hasnain, Z., The flow over a backward facing step subjected to multiple synthetic jet actuators. In 31st AIAA Applied Aerodynamics Conference; AIAA, 2013; p. 3166. [CrossRef]
Zhong, S.; Zhang, S. Further examination of the mechanism of round synthetic jets in delaying turbulent flow separation. Flow, Turbulence and Combustion 2013, 91, 177–208. [CrossRef]
Greenblatt, D.; Paschal, K.B.; Yao, C.S.; Harris, J. Experimental investigation of separation control part 2: Zero mass-flux oscillatory blowing. AIAA Journal 2006, 44, 2831–2845. [CrossRef]
Amitay, M.; Honohan, A.; Trautman, M.; Glezer, A.; Amitay, M.; Honohan, A.; Trautman, M.; Glezer, A., Modification of the aerodynamic characteristics of bluff bodies using fluidic actuators. In 28th Fluid Dynamics Conference; AIAA, 1997; p. 2004. [CrossRef]
Ramasamy, M.; Wilson, J.S.; Martin, P.B. Interaction of synthetic jet with boundary layer using microscopic particle image velocimetry. Journal of Aircraft 2010, 47, 404–422. [CrossRef]
Berk, T.; Gomit, G.; Ganapathisubramani, B. Vectoring of parallel synthetic jets: A parametric study. Journal of Fluid Mechanics 2016, 804, 467–489. [CrossRef]
Poisson-Quinton, P. Recherches thèoriques et expèrimentales sur le contrôl de couche limits. 7th congress of Applied Mechanics, London, 1948.
Steinfurth, B.; Haucke, F. Coherent structures in the actively controlled wake of a high-lift configuration. AIAA Journal 2018, 56, 3848–3856. [CrossRef]
Glezer, A.; Amitay, M.; Honohan, A.M. Aspects of low- and high-frequency actuation for aerodynamic flow control. AIAA Journal 2005, 43, 1501–1511. [CrossRef]
Greenblatt, D.; Wygnanski, I.J. The control of flow separation by periodic excitation. Progress in Aerospace Sciences 2000, 36, 487–545. doi:. [CrossRef]
Chaudhry, I.A.; Zhong, S. A single circular synthetic jet issued into turbulent boundary layer. Journal of Visualization 2014, 17, 101–111. [CrossRef]
Chaudhry, I.A.; Zhong, S. Understanding the interaction of synthetic jet with the flat plate boundary layer. ICARME, Trivandrum, India 2012.
Zhou, J.; Zhong, S. Numerical simulation of the interaction of a circular synthetic jet with a boundary layer. Computers & Fluids 2009, 38, 393–405. [CrossRef]
Jabbal, M.; Zhong, S. The near wall effect of synthetic jets in a boundary layer. International Journal of Heat and Fluid Flow 2008, 29, 119–130. [CrossRef]
Schaeffler, N.W.; Jenkins, L.N. Isolated synthetic jet in crossflow: Experimental protocols for a validation dataset. AIAA Journal 2006, 44, 2846–2856. [CrossRef]
Zhong, S.; Millet, F.; Wood, N.J. The behaviour of circular synthetic jets in a laminar boundary layer. The Aeronautical Journal 2005, 109, 461–470. [CrossRef]
Rathnasingham, R.; Breuer, K.S. Active control of turbulent boundary layers. Journal of Fluid Mechanics 2003, 495, 209–233. [CrossRef]
Savas, Ö.; Coles, D. Coherence measurements in synthetic turbulent boundary layers. Journal of Fluid Mechanics 1985, 160, 421–446. [CrossRef]
Yen, J.; Ahmed, N.A. Synthetic jets as a boundary vorticity flux control tool. AIAA Journal 2013, 51, 510–513. [CrossRef]
Mittal, R.; Rampunggoon, P. On the virtual aeroshaping effect of synthetic jets. Physics of Fluids 2002, 14, 1533–1536. [CrossRef]
Ho, H.H.; Essel, E.E.; Sullivan, P.E. The interactions of a circular synthetic jet with a turbulent crossflow. Physics of Fluids 2022, 34, 075108. [CrossRef]
Crook, A.; Sadri, A.; Wood, N., The development and implementation of synthetic jets for the control of separated flow. In 17th Applied Aerodynamics Conference; AIAA, 1999; p. 3176. [CrossRef]
Iai, T.; Motosuke, M.; Honami, S., Vortex behavior of vertical and inclined synthetic jets in cross flow at low Reynolds number. In 39th AIAA Fluid Dynamics Conference; AIAA, 2009; p. 4178. [CrossRef]
Sauerwein, S.; Vakili, A., An experimental study of zero-mass jets in crossflow. In 37th Aerospace Sciences Meeting and Exhibit; AIAA, 1999; p. 668. [CrossRef]
Sau, R.; Mahesh, K. Dynamics and mixing of vortex rings in crossflow. Journal of Fluid Mechanics 2008, 604, 389–409. [CrossRef]
Van Buren, T.; Leong, C.M.; Whalen, E.; Amitay, M. Impact of orifice orientation on a finite-span synthetic jet interaction with a crossflow. Physics of Fluids 2016, 28, 037106. [CrossRef]
Kim, W.; Kim, C.; Jung, K.J. Separation control characteristics of synthetic jets depending on exit configuration. AIAA Journal 2012, 50, 559–570. [CrossRef]
Smith, D.R. Interaction of a synthetic jet with a crossflow boundary layer. AIAA Journal 2002, 40, 2277–2288. [CrossRef]
Van Buren, T.; Beyar, M.; Leong, C.M.; Amitay, M. Three-dimensional interaction of a finite-span synthetic jet in a crossflow. Physics of Fluids 2016, 28, 037105. [CrossRef]
Cui, J.; Agarwal, R.; Cary, A., Numerical simulation of the interaction of a synthetic jet with a turbulent boundary layer. In 33rd AIAA Fluid Dynamics Conference and Exhibit; AIAA, 2003; pp. 23–26. [CrossRef]
Doligalski, T.L.; Smith, C.R.; Walker, J.D.A. Vortex interactions with walls. Annual Review of Fluid Mechanics 1994, 26, 573–616. doi:. [CrossRef]
Elimelech, Y.; Vasile, J.; Amitay, M. Secondary flow structures due to interaction between a finite-span synthetic jet and a 3-D cross flow. Physics of Fluids 2011, 23, 094104. [CrossRef]
Vasile, J.D.; Amitay, M. Interactions of an array of finite span synthetic jets and a crossflow. AIAA Journal 2013, 51, 2503–2512. [CrossRef]
Amitay, M.; Glezer, A. Role of actuation frequency in controlled flow reattachment over a stalled airfoil. AIAA Journal 2002, 40, 209–216. [CrossRef]
Hong, G. Effectiveness of micro synthetic jet actuator enhanced by flow instability in controlling laminar separation caused by adverse pressure gradient. Sensors and Actuators A: Physical 2006, 132, 607–615. [CrossRef]
Hong, G.; Lee, C.; Ha, Q.P.; Mack, A.; Mallinson, S., Effectiveness of synthetic jets enhanced by instability of Tollmien-Schlichting waves. In 1st Flow Control Conference; AIAA, 2002; p. 2832. [CrossRef]
Yarusevych, S.; Sullivan, P.E.; Kawall, J.G. On vortex shedding from an airfoil in low-Reynolds-number flows. Journal of Fluid Mechanics 2009, 632, 245–271. [CrossRef]
Marxen, O.; Henningson, D.S. The effect of small-amplitude convective disturbances on the size and bursting of a laminar separation bubble. Journal of Fluid Mechanics 2011, 671, 1–33. [CrossRef]
Wu, J.Z.; Lu, X.Y.; Denny, A.G.; Fan, M.; Wu, J.M. Post-stall flow control on an airfoil by local unsteady forcing. Journal of Fluid Mechanics 1998, 371, 21–58. [CrossRef]
Tian, Y.; Cattafesta, L.; Mittal, R., Adaptive control of separated flow. In 44th AIAA Aerospace Sciences Meeting and Exhibit; AIAA, 2006; p. 1401. [CrossRef]
Amitay, M.; Glezer, A. Controlled transients of flow reattachment over stalled airfoils. International Journal of Heat and Fluid Flow 2002, 23, 690–699. doi:. [CrossRef]
Abdolahipour, S.; Mani, M.; Taleghani, A.S. Parametric study of a frequency-modulated pulse jet by measurements of flow characteristics. Physica Scripta 2021, 96, 125012. [CrossRef]
Rice, T.T.; Taylor, K.; Amitay, M. Pulse modulation of synthetic jet actuators for control of separation. Physical Review Fluids 2021, 6, 093902. [CrossRef]
Itsariyapinyo, P.; Sharma, R.N. Experimental study of a NACA0015 circulation control airfoil using synthetic jet actuation. AIAA Journal 2022, 60, 1612–1629. [CrossRef]
Goodfellow, S.D.; Yarusevych, S.; Sullivan, P.E. Momentum coefficient as a parameter for aerodynamic flow control with synthetic jets. AIAA Journal 2013, 51, 623–631. [CrossRef]
Kim, M.; Essel, E.E.; Sullivan, P.E. Effect of varying frequency of a synthetic jet on flow separation over an airfoil. Physics of Fluids 2022, 34, 015122. [CrossRef]
Yang, E.; Ekmekci, A.; Sullivan, P.E. Phase evolution of flow controlled by synthetic jets over NACA 0025 airfoil. Journal of Visualization 2022, 25, 751–765. [CrossRef]
Raju, R.; Mittal, R.; Cattafesta, L. Dynamics of airfoil separation control using zero-net mass-flux forcing. AIAA Journal 2008, 46, 3103–3115. [CrossRef]
Amitay, M.; Smith, D.R.; Kibens, V.; Parekh, D.E.; Glezer, A. Aerodynamic flow control over an unconventional airfoil using synthetic jet actuators. AIAA Journal 2001, 39, 361–370. [CrossRef]
Seifert, A.; Bachar, T.; Koss, D.; Shepshelovich, M.; Wygnanski, I. Oscillatory blowing: A tool to delay boundary-layer separation. AIAA Journal 1993, 31, 2052–2060. [CrossRef]
Amitay, M.; Glezer, A. Flow transients induced on a 2D airfoil by pulse-modulated actuation. Experiments in Fluids 2006, 40, 329–331. [CrossRef]
Feero, M.A.; Lavoie, P.; Sullivan, P.E. Influence of synthetic jet location on active control of an airfoil at low Reynolds number. Experiments in Fluids 2017, 58, 1–12. [CrossRef]
Xu, K.; Lavoie, P.; Sullivan, P. Flow reattachment on a NACA 0025 airfoil using an array of microblowers. AIAA Journal 2023, 61, 2476–2485. [CrossRef]
Rice, T.T.; Taylor, K.; Amitay, M. Quantification of the S817 airfoil aerodynamic properties and their control using synthetic jet actuators. Wind Energy 2018, 21, 823–836. doi:. [CrossRef]
Rice, T.T.; Taylor, K.; Amitay, M. Wind tunnel quantification of dynamic stall on an S817 airfoil and its control using synthetic jet actuators. Wind Energy 2019, 22, 21–33. doi:. [CrossRef]
Margalit, S.; Greenblatt, D.; Seifert, A.; Wygnanski, I. Delta wing stall and roll control using segmented piezoelectric fluidic actuators. Journal of Aircraft 2005, 42, 698–709. [CrossRef]
Tang, H.; Salunkhe, P.; Zheng, Y.; Du, J.; Wu, Y. On the use of synthetic jet actuator arrays for active flow separation control. Experimental Thermal and Fluid Science 2014, 57, 1–10. doi:. [CrossRef]
Amitay, M.; Smith, B.; Glezer, A., Aerodynamic flow control using synthetic jet technology. In 36th AIAA Aerospace Sciences Meeting and Exhibit; AIAA, 1998; p. 208. [CrossRef]
Feero, M.A.; Lavoie, P.; Sullivan, P.E. Three-dimensional span effects of high-aspect ratio synthetic jet forcing for separation control on a low Reynolds number airfoil. Journal of Visualization 2017, 20, 45–51. [CrossRef]
Monastero, M.C.; Lindstrom, A.M.; Amitay, M. Effect of synthetic jets spacing on flow separation over swept, flapped airfoils. AIAA Journal 2019, 57, 4670–4683. [CrossRef]
Jabbal, M.; Liddle, S.; Potts, J.; Crowther, W. Development of design methodology for a synthetic jet actuator array for flow separation control applications. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering 2013, 227, 110–124. [CrossRef]
Ho, H.H.; Machado, A. Computational and experimental study of spanwise synthetic jet flow control. Thirteenth International Symposium on Turbulence and Shear Flow Phenomena (TSFP13), 2024.
Machado, A.; Xu, K.; Sullivan, P.E. Spanwise control authority of synthetic jets on a stalled airfoil. Physics of Fluids 2024, 36, 064113. [CrossRef]
Liddle, S.; Crowther, W.; Wood, N., Investigation of phase and spacing effects in synthetic jet actuator arrays. In 43rd AIAA Aerospace Sciences Meeting and Exhibit; AIAA, 2005; p. 107. [CrossRef]
Liddle, S.C.; Wood, N.J. Investigation into clustering of synthetic jet actuators for flow separation control applications. The Aeronautical Journal 2005, 109, 35–44. [CrossRef]
Wen, X.; Tang, H.; Duan, F. Vortex dynamics of in-line twin synthetic jets in a laminar boundary layer. Physics of Fluids 2015, 27, 083601. [CrossRef]
Wen, X.; Tang, H. Effect of phase difference on the interaction of hairpin vortices induced by in-line twin synthetic jets. Journal of Visualization 2016, 19, 79–87. [CrossRef]
Zang, B.; New, T.H. Near-field dynamics of parallel twin jets in cross-flow. Physics of Fluids 2017, 29, 035103. [CrossRef]
Jankee, G.K.; Ganapathisubramani, B. Interaction and vectoring of parallel rectangular twin jets in a turbulent boundary layer. Physical Review Fluids 2021, 6, 044701. [CrossRef]
Watson, M.; Jaworski, A.J.; Wood, N.J. Contribution to the understanding of flow interactions between multiple synthetic jets. AIAA Journal 2003, 41, 747–749. [CrossRef]
Hasnain, Z.; Flatau, A.; Jr., J.H.; Mulinti, R., Numerical study and experimental validation of the interaction of multiple synthetic jet actuators with cross flow. In 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition; AIAA, 2012; p. 1247. [CrossRef]
Smith, B.L.; Glezer, A. Vectoring of adjacent synthetic jets. AIAA Journal 2005, 43, 2117–2124. [CrossRef]
Shimomura, S.; Sekimoto, S.; Oyama, A.; Fujii, K.; Nishida, H. Closed-loop flow separation control using the deep Q network over airfoil. AIAA Journal 2020, 58, 4260–4270. [CrossRef]
Wang, Y.Z.; Mei, Y.F.; Aubry, N.; Chen, Z.; Wu, P.; Wu, W.T. Deep reinforcement learning based synthetic jet control on disturbed flow over airfoil. Physics of Fluids 2022, 34, 033606. [CrossRef]
Obeid, S.; Ahmadi, G.; Jha, R. NARMAX identification based closed-loop control of flow separation over NACA 0015 airfoil. Fluids 2020, 5, 100. [CrossRef]
Gautier, N.; Aider, J.L. Control of the separated flow downstream of a backward-facing step using visual feedback. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2013, 469, 20130404. [CrossRef]
Shimomura, S.; Ogawa, T.; Sekimoto, S.; Nonomura, T.; Oyama, A.; Fujii, K.; Nishida, H. Experimental analysis of closed-loop flow control around airfoil using DBD plasma actuator. Fluids Engineering Division Summer Meeting. American Society of Mechanical Engineers, 2017, Vol. 58066, p. V01CT22A004. [CrossRef]
Plogmann, B.; Mack, S.; Fasel, H., Experimental investigation of open- and closed-loop control for airfoil under low Reynolds number conditions. In 39th AIAA Fluid Dynamics Conference; AIAA, 2009; p. 4282. [CrossRef]
Li, Y.; Chang, J.; Kong, C.; Bao, W. Recent progress of machine learning in flow modeling and active flow control. Chinese Journal of Aeronautics 2022, 35, 14–44. doi:. [CrossRef]
Salunkhe, P.; Tang, H.; Zheng, Y.; Wu, Y. PIV measurement of mildly controlled flow over a straight-wing model. International Journal of Heat and Fluid Flow 2016, 62, 552–559. doi:. [CrossRef]
Holman, R.; Gallas, Q.; Carroll, B.; Cattafesta, L., Interaction of adjacent synthetic jets in an airfoil separation control application. In 33rd AIAA Fluid Dynamics Conference and Exhibit; AIAA, 2003; p. 3709. [CrossRef]
Yen, J.; Ahmed, N.A. Enhancing vertical axis wind turbine by dynamic stall control using synthetic jets. Journal of Wind Engineering and Industrial Aerodynamics 2013, 114, 12–17. doi:. [CrossRef]
Zhao, Q.; Ma, Y.; Zhao, G. Parametric analyses on dynamic stall control of rotor airfoil via synthetic jet. Chinese Journal of Aeronautics 2017, 30, 1818–1834. doi:. [CrossRef]
Shahrabi, A.F. The control of flow separation: Study of optimal open loop parameters. Physics of Fluids 2019, 31, 035104. [CrossRef]
Tousi, N.; Bergadà, J.; Mellibovsky, F. Large eddy simulation of optimal synthetic jet actuation on a SD7003 airfoil in post-stall conditions. Aerospace Science and Technology 2022, 127, 107679. doi:. [CrossRef]
Li, G.; Yi, S. Large eddy simulation of dynamic stall flow control for wind turbine airfoil using plasma actuator. Energy 2020, 212, 118753. doi:. [CrossRef]
You, D.; Moin, P. Active control of flow separation over an airfoil using synthetic jets. Journal of Fluids and Structures 2008, 24, 1349–1357. doi:. [CrossRef]
Itsariyapinyo, P.; Sharma, R.N. Large eddy simulation of a NACA0015 circulation control airfoil using synthetic jets. Aerospace Science and Technology 2018, 82, 545–556. doi:. [CrossRef]
Kitsios, V.; Cordier, L.; Bonnet, J.P.; Ooi, A.; Soria, J. On the coherent structures and stability properties of a leading-edge separated aerofoil with turbulent recirculation. Journal of Fluid Mechanics 2011, 683, 395–416. [CrossRef]
De Giorgi, M.G.; De Luca, C.G.; Ficarella, A.; Marra, F. Comparison between synthetic jets and continuous jets for active flow control: Application on a NACA 0015 and a compressor stator cascade. Aerospace Science and Technology 2015, 43, 256–280. [CrossRef]
Zhang, W.; Samtaney, R. A direct numerical simulation investigation of the synthetic jet frequency effects on separation control of low-Re flow past an airfoil. Physics of Fluids 2015, 27, 055101. [CrossRef]

Figure 1. (a) A schematic drawing of an SJA in quiescent flow (adapted from Feero [48]) and (b) a Murata MZB1001T02 microblower (adapted from Machado et al. [49]).

Figure 2. Schematic drawing of an SJA in quiescent flow during expulsion and ingestion phase, (a) Initiation of ingestion cycle; (b) Peak ingestion phase ;(c) Initiation of expulsion cycle and (d) Peak expulsion phase.

Figure 3. Schematic drawing of a rectangular SJA having an array of circular actuators (adapted from Feero [48]).

Figure 4. Schematic drawing of different SJA modeling methods, red dotted line indicates where the boundary condition is applied, adapted from Ho et al. [53].

Figure 5. A schematic showcasing the complexities in understanding the interaction between a synthetic jet and a boundary layer (based on Ramasamy et al. [115]).

Figure 6. Q-criterion contours of hairpin vortices and vortex rings as a result of the interaction between a synthetic jet and a boundary layer, showcasing hairpin vortex (HV), vortex ring (VR), trailing vortex pair (TV), and the near-wall vortex (NV) (adapted from Ho et al. [131]).

Figure 7. A schematic illustrating (a) pitch angle

γ

and (b) skew angle

β

for a rectangular SJA in a crossflow (based on Van Buren et al. [136]).

Figure 7. A schematic illustrating (a) pitch angle

γ

and (b) skew angle

β

for a rectangular SJA in a crossflow (based on Van Buren et al. [136]).

Figure 8. A conceptual model of the vortical structures generated by a rectangular synthetic jet within a boundary layer, depicting the recirculation region and the streamwise vortex pair (based on Van Buren et al. [139]).

Figure 9. Separated flow over an airfoil at low Reynolds numbers undergoing (a) shear layer transition without reattachment and (b) flow reattachment and separation bubble formation (based on Yarusevych et al. [147]).

Figure 10. Examples showcasing the modulation of (a) a sinusoidal carrier signal at

f_{c} = 1000 Hz

with (b) a sinusoidal envelope at

f_{m} = 100 Hz

and (c) a square pulse envelope at

f_{m} = 100 Hz

and

DC = 40

, over a duration of

0.05

s

Figure 10. Examples showcasing the modulation of (a) a sinusoidal carrier signal at

f_{c} = 1000 Hz

with (b) a sinusoidal envelope at

f_{m} = 100 Hz

and (c) a square pulse envelope at

f_{m} = 100 Hz

and

DC = 40

, over a duration of

0.05

s

Figure 11. Schematic drawings of SJA location for (a) a two-dimensional circular cylinder, studied by Amitay et al. [114,168] and Glezer et al. [119], and (b) an instrumented NACA 0025 airfoil model used by Feero et al. [169].

Figure 12. Contraction of the controlled flow towards the airfoil centerline showcased by (a) a schematic drawing of the SJA array and the streamlines and (b) a smoke visualization image adapted from Ho and Machado [172].

Table 1. Summary of the test parameters for some studies on flow control over airfoils and wings using SJAs.

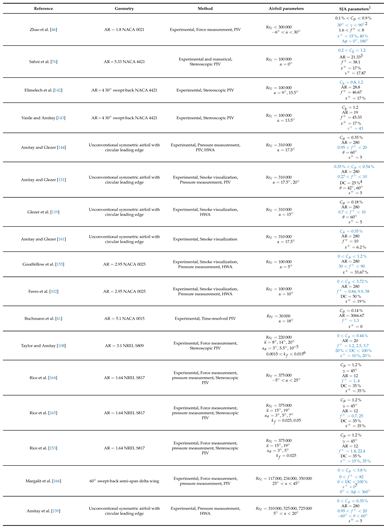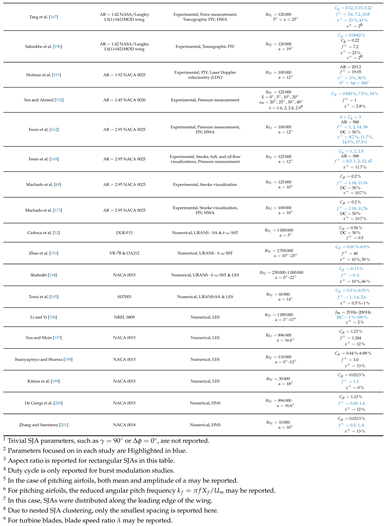Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Synthetic Jet Actuators for Active Flow Control: A Review

Abstract

1. Introduction

2. SJA Mechanism

2.1. SJA Modelling Methods

3. Synthetic Jet Actuators in Quiescent Flow

3.1. Synthetic Jet Formation Criterion

3.2. Synthetic Jet Evolution

3.3. Effects of Orifice Shape

3.4. Effects of Actuation Frequency

3.5. Effects of Cavity Shape

4. Synthetic Jet Actuators in a Crossflow

4.1. Effects of Jet Strength

4.2. Effects of Orifice Shape and Orientation

4.3. Effects of Forcing Frequency and Signal Waveform

4.4. Effects of Actuator Location

4.5. Effects of Clustering

4.6. Open- and Closed-loop Control

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe