Preprint

Article

Increasing the Robustness of Image Quality Assessment Models Through Adversarial Training

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 October 2024

Posted:

24 October 2024

You are already at the latest version

Alerts

Abstract

The adversarial robustness of image quality assessment (IQA) models to adversarial attacks is emerging as a critical issue. Adversarial training has been widely used to improve the robustness of neural networks to adversarial attacks, but little in-depth research has examined adversarial training as a way to improve IQA model robustness. This study introduces an enhanced adversarial training approach tailored to IQA models; it adjusts the perceptual quality scores of adversarial images during training to enhance the correlation between an IQA model’s quality and the subjective quality scores. We also propose a new method for comparing IQA model robustness by measuring the Integral Robustness Score; this method evaluates the IQA model resistance to a set of adversarial perturbations with different magnitudes. We used our adversarial training approach to increase the robustness of five IQA models. Additionally, we tested the robustness of adversarially trained IQA models to 16 adversarial attacks and conducted an empirical probabilistic estimation of this feature. The code is available at https://github.com/wianluna/metrics_at.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Image quality assessment (IQA) is essential to developing image- and video-processing algorithms. These algorithms assess the perceptual quality of processed images and reduce reliance on costly subjective tests. IQA models fall into two main categories, depending on the availability of the original image: full reference (FR), which involves estimating the difference between the original and processed images; reduced reference (RR), which involves calculating the difference between features extracted from the original and processed images; and no reference (NR), which only involves analyzing the distorted image using scene statistics gathered from a large dataset.

In recent years, IQA models have shifted toward deep learning, surpassing traditional approaches in correlation with subjective quality. However, this shift has also introduced new vulnerabilities, as all trainable methods, including IQA models, are susceptible to adversarial attacks. These attacks can occur in many real-life image-quality-measurement scenarios [1,2], such as cheating on benchmarks, manipulating web-search results, increasing the energy consumption and latency of streaming video, and storing unclear video-surveillance footage. Researchers often use IQA models to estimate the perceptual quality of image enhancement algorithms, e.g., underwater image enhancement [3,4], low-light image enhancement [5]. When IQA models are used as the optimization objective to improve the visual quality, unintended attacks may occur, leading to visible image artifacts. Current non-robust learning-based IQA models exhibit low resistance to adversarial attacks, and their use as optimization objectives may lead to visible artifacts.

Recent papers have proposed adversarial attack methods for IQA models [6,7,8,9,10], but only a few of them offer defense methods. Adversarial training is essential to improve neural network resistance to these attacks. Surprisingly, however, little research has considered adversarial training for IQA models. Only in one paper suggesting a new adversarial attack, did the authors try adversarial training for three models [6]. They concluded that adversarial training is a promising defense for deep IQA models and said further research is necessary to investigate more-sophisticated techniques.

The main drawback of applying vanilla adversarial training to increase IQA models’ robustness is a falloff in their correlation with subjective scores, as a previous study has shown [6]. his effect is because these models are more sensitive to image noise than are computer-vision models such as object classification and detection. When attacking the IQA model, the adversarial noise affects the subjective-quality labels. Even an unsuccessful attack that leaves the IQA score unchanged will likely alter an adversarial image’s perceptual quality. Unlike this case, an unsuccessful attack on an image classifier leaves the adversarial image’s target class unchanged. Also, training an IQA model from scratch only on the attacked data generated at each iteration, as in the standard adversarial training approach, may decrease the correlation.

This paper studies adversarial training’s efficiency in improving IQA model robustness to adversarial attacks. We propose a new strategy to adjust perceptual-quality scores for adversarial images during training. Our main contributions are the following:

A new adversarial-training approach with a perceptual-quality-labels penalty. It outperforms standard adversarial training by correlating with subjective quality.
A new method for comparing the robustness of trained IQA models, as well as a new robustness-evaluation metric.
Comprehensive experiments that tested our method’s efficiency on four IQA models: LinearityIQA, KonCept512, HyperIQA, and WSP-IQA.

The paper is organized as follows. Section 2 discusses related work: the task and trends in image quality assessment, the existing adversarial attacks on IQA models, adversarial training as a defense against adversarial attacks, and the existing IQA models designed to be robust to adversarial attacks. In section 3, we describe the proposed method: first, we formulate the problem, and then we describe the main ideas of our adjustments to the vanilla adversarial training procedure. Section 4 describes our experiments’ methodology, including a list of datasets and IQA models, evaluation metrics, and main details of experiment implementation. In section 5, we show the results of the experiments. Section 6 discusses the main findings from the results, and section 7 summarizes the conclusions of this work.

2. Related Work

2.1. Image Quality Assessment

IQA methods aim to make quantitative evaluations that closely approximate human perceptual judgments. NR-IQA models function without an original image or any information about that image; they may serve a broader range of applications than other models, such as controlling video-streaming quality and assessing the quality of text-to-image generation. Initially, the IQA model’s design depended on the task and how its developers understood visual-quality perception by the human eye. Early approaches seldom involved machine learning [11]: examples include error visibility (e.g., PSNR), structural similarity (e.g., SSIM [12]), and information theory (e.g., VIF [13]).

Because subjective quality image and video datasets have proliferated, new IQA methods employ deep learning to model empirical statistics of natural images in the NR case or feature learning in the FR case. The latest comparisons reveal that deep-learning-based IQA outperforms traditional alternatives [14,15]. Image-quality measurement is widening thanks to the appearance of new narrow task-specific models. For example, recognition-aware IQA evaluates image quality as computer vision’s ability to detect or recognize objects, as well as image generation or image super-resolution models. Many IQA models that handle perceptual quality employ CNN-based architectures [16,17,18,19,20], but many also employ ViT [21,22].

2.2. Adversarial Attacks on IQA Models

Adversarial examples are specially crafted inputs that add small imperceptible perturbations to images such that the perturbed input can, with high confidence, mislead an IQA model to yield a false prediction [23]. Depending on the attacker’s knowledge of the victim model, adversarial attacks are either white-box or black-box. In the former case, an attacker has some knowledge about the model, such as its architecture, weights, loss function, or training data. These attacks often use gradients and generate high-confidence adversarial examples that are invisible to the human eye. In the black-box case, an attacker has no direct access to the target model and sometimes only evaluates it on the basis of chosen examples without gradient feedback. Therefore, adversarial examples in this situation are weaker than in the white-box situation. White-box attacks normally have few applications. In the case of IQA models, however, they are practical because IQA model architectures are often available, as with public benchmarks. White-box attacks can obtain gradients to optimize the objective function by taking a single small step (one-step attacks) or multiple small steps (iterative attacks) along the gradient direction in image space.

Several adversarial attacks have targeted IQA models. UAP [8], for example, creates a universal adversarial noise that increases the IQA model score. The generated perturbation is independent of the input image. FACPA [9] is an improved version of this attack; it produces adversarial noise for each input image, increasing success and perceptual quality. The main challenge in attacking IQA models is hiding the perturbations. Korhonen et al. [6] suggested a Sobel filter to hide adversarial distortions in textured regions. An invisible one-iteration (IOI) attack [10] also uses high-frequency filtering to mask perturbations. A subjective comparison proves this attack is invisible, even when applied to videos frame by frame. Zhang et al. [7] used Chebyshev distance, SSIM, LPIPS, DISTS, and other FR metrics to manage visual distortions.

2.3. Adversarial Training

Adversarial training is a popular way to improve the resistance of deep learning models to adversarial attacks. Each training step requires generating a perturbation, thus increasing the computational time. Researchers have used an early version of adversarial training, the Fast Gradient Sign Method (FGSM) [24], to generate perturbed examples. But adversarial training based on noniterative attacks such as FGSM only yields resistance to weak attacks; the model remains vulnerable to stronger iterative attacks. A way to overcome this limitation is adversarial training through multistep Projected Gradient Descent (PGD) [25], which achieves resistance to iterative attacks but can be computationally expensive. Wong et al. designed Fast adversarial training [26], which combines FGSM adversarial training and the random perturbation initialization of PGD attacks to accelerate training. This method is almost as effective as PGD-based training but has a much lower computational cost.

In their recent work, Singh et al. [27] generated adversarial examples using two-step Auto PGD (APGD-2) [28]. This adaptive attack realizes a higher loss than PGD in the same iteration budget, reducing both the number of iterations for adversarial training and the computational cost. For NR-IQA models, Korhonen et al. [6] applied adversarial training to make KonCept512, PHIQNet, and TRIQ more robust. These models exhibited lower correlation with subjective quality than the original ones did.

2.4. Robust IQA Models

Few papers thus far have focused on making particular IQA models more robust. Netflix introduced VMAF NEG (No Enhancement Gain) [29], which is more resistant to contrast enhancement than the original VMAF. VMAF utilizes support-vector regression based on fundamental low- and mid-level frame attributes. The NEG version entails regression over clipped values of base features. In particular, the authors introduced VIF and DLM enhancement-gain limits. These parameters allow limits on the maximum VIF and DLM scores, which are features of the VMAF support-vector regressor. Although this modification increases VMAF’s resistance to attacks [30], limiting base features in a fixed range only protects the model from extreme attacks—for example, increasing scores by 100–200%. An attacker can still increase the VMAF NEG score in its clipped range, however.

Kettunen et al. [31] proposed E-LPIPS, a modification of LPIPS [32]. It applies a series of random transformations to the image before passing the altered image through the neural network. It then calculates the average output over all inputs. This ensemble approach can make manipulating the results more difficult, but it also requires many model runs to generate a single prediction, limiting its real-world applicability. R-LPIPS [33] is another LPIPS variation. The authors left the network architecture unchanged and used adversarial training, during which time they applied adversarial perturbations to just one image in a triplet. They employed cross-entropy loss to generate the adversarial example.

Currently, there are very few studies focusing on improving the stability of NR-IQA models. Recently, Liu et al. [34] proposed Norm regularization Training (NT) method using

l_{1}

-regularization of the gradient norm to enhance the robustness of NR-IQA models against adversarial attacks.

3. Proposed Method

3.1. Problem Setting

Adversarial attacks on IQA models. Our investigation assumes an attacker is trying to increase the IQA model scores by adding small perturbations to images. Recent papers have examined these attacks, which may occur more frequently in the real world than other attacks. Attempts to decrease an image’s estimated quality are all the same up to the attack direction sign. Therefore, this approach avoids violating our study’s generality.

For a given NR-IQA model

f_{θ} : X \to R

parameterized by the vector of weights

θ

, where

X \in {[0, 255]}^{3 \times H \times W}

is a distribution of images, we can mathematically describe an adversarial attack on an input image x with a perturbation

δ

bounded by

ε

with a norm of p as follows:

max_{{∥ δ ∥}_{p} \leq ε} f_{θ} (x + δ) .

(1)

An attack on FR-IQA models can be reformulated as an attack on NR-IQA by manipulating just one of the reference and distorted images. For a given FR-IQA model

f_{θ}

parameterized by

θ

which takes a reference image

\hat{x} \subseteq {[0, 255]}^{3 \times H \times W}

and distorted image

x \subseteq {[0, 255]}^{3 \times H \times W}

as an input, an adversarial attack with a perturbation

δ

bounded by

ε

of norm p is formulated as follows:

max_{{∥ δ ∥}_{p} \leq ε} f_{θ} (\hat{x}, x + δ) .

(2)

Adversarial training for IQA models. Given a NR-IQA or FR-IQA model

f_{θ}

parameterized by

θ

; a distribution of the training data D, where each training sample contains an image

x \subseteq {[0, 255]}^{3 \times H \times W}

and associated quality label

y \in R

; and a loss function

L

of the model

f_{θ}

, vanilla adversarial training is a min-max problem where the inner maximization problem aims to discover strong adversarial examples

x + δ

bounded by the allowable perturbation magnitude

ε

of a norm p. The outer minimization problem fine-tunes the model parameters as follows:

min_{θ} E_{(x, y) \sim D} [max_{{∥ δ ∥}_{p} \leq ε} L (f_{θ} (x + δ), y)]

(3)

As we mentioned in our related work discussion (Section 2), the perceptual quality of perturbed images may change, leading to different quality labels. We therefore add another term to the objective function:

min_{θ} E_{(x, y) \sim D} [max_{{∥ δ ∥}_{p} \leq ε} L (f_{θ} (x), y) + L (f_{θ} (x + δ), y^{'})],

(4)

where y is the original subjective quality score and

y^{'}

is the adjusted subjective quality score.

3.2. Method

We propose the following improvements to the vanilla adversarial training procedure to adapt it for IQA models.

Pre-training and fine-tuning. Many IQA models extract deep features from convolutional neural networks pre-trained on the ImageNet dataset to perform image classification [17,18,19,20,32]. Such transfer learning enables the receipt of more stable features than training on smaller datasets labeled for IQA. Because adversarial training is a nontrivial optimization problem, we propose initializing it from pre-trained standard IQA model weights and then fine-tuning them on clean and perturbed images. Doing so allows us to make the model resistant to adversarial perturbations while keeping a high correlation with subjective quality—a feature we demonstrated in our experiments.

Subjective scores correction. obtaining a subjective quality score for perturbed images during each training epoch would be extremely expensive. Therefore, we propose three strategies to correct the subjective quality scores of clean images after adding adversarial perturbations.

Minimal MOS. The simplest approach to adjusting scores for adversarial images is to set the minimum value for the entire dataset D:

y^{'} = min_{y \sim D} y

(5)

Percentage-based penalty. Another strategy involves penalizing the original subjective evaluation with a constant. During training, adversarial images receive an assigned target value as follows:

y^{'} = y - p \times diam (D),

(6)

where p is 5/100 or 10/100 in our experiments, and

diam (D) = sup_{y, z \in D} {| y - z |}

. This approach’s complexity lies in the emergence of a new hyperparameter, which may be inconvenient in practice.

FR-based penalty. We extended our approach by penalizing subjective quality labels with FR metrics such as SSIM [12], MS-SSIM [35], and PSNR. Also, we incorporated penalties based on the trainable metric LPIPS [32], which emphasizes perceptual similarity. The formula for the target-value assignment then becomes the following:

y^{'} = y - norm (M (x, x + δ), M) * y,

(7)

where

M \in {

SSIM, MS-SSIM, PSNR, LPIPS}. Here, norm denotes a metric-dependent mapping of the original values that transforms the range of M to the closed interval

[0, 1]

norm (x, M) = \{\begin{matrix} 1 - x, if M is SSIM or MS - SSIM, \\ \frac{75 - x}{45}, if M is PSNR, \\ x, if M is LPIPS . \end{matrix}

(8)

Attack methods and magnitudes. The choice of attack for generating adversarial examples during training is crucial to adversarial learning’s effectiveness. Previous research shows that models trained using PGD are resistant to weaker attacks. However, choosing a stronger attack for training may cause the model’s performance to decrease more. Therefore, we applied three attacks previously used for adversarial training of image classifiers [24,26,27]: a one-step FGSM attack [24]; a one-step PGD (PDG-1) attack, which is an FGSM with an initial random perturbation [26]; and an adaptive Auto PGD (APGD-2) attack [28], for which we used two iterations. For FR-IQA models, we propose attacking both distorted images simultaneously for greater strength compared with only one image, as in [33] suggests. Additionally, we examined the impact on model robustness of the adversarial-perturbation magnitude during training. Previous works on adversarial training commonly consider a single value for the perturbation magnitude

ε

. Our study explores different

ε

values from the set {2, 4, 8, 10} / 255.

The complete proposed training procedure is summarized in Algorithm 1 and Figure 1. Our ablation study (Section 5.1) shows the impact of each component of our adversarial training.

Algorithm 1 Proposed adversarial training for T epochs, given attack magnitude

ε

, step size

α

, and dataset D for pre-trained NR-IQA model

f_{θ}

, loss function

L

, and FR metric M.

for

t = 1 \dots T

for

(x_{i}, y_{i}) \in D

// PGD-1 adversarial attack:

δ = U n i f o r m (- ε, ε)

δ = δ + α \cdot s i g n (\nabla_{δ} L (f_{θ} (x_{i} + δ), y_{i}))

δ = max (min (δ, ε), - ε)

// Subjective score correction:

y_{i}^{'} = y_{i} - norm (M (x_{i}, x_{i} + δ), M) * y_{i}

// norm is calculated according to Equation (7)

x_{i} = c o n c a t e n a t e (x_{i}, x_{i}^{'})

y_{i} = c o n c a t e n a t e (y_{i}, y_{i}^{'})

θ = θ - β \cdot \nabla_{θ} l (f_{θ} (x_{i} + δ), y_{i})

// Update model with some optimizer and step size β

end for

4. Materials and Methods

4.1. Experimental Setup

NR-IQA datasets and models. We used KonIQ-10k [17], a popular IQA dataset that commonly serves for training and evaluating IQA models, to perform adversarial training of the NR-IQA model. This dataset comprises 10,073 images paired with subjective quality values based on Mean Opinion Scores (MOSs). To add an extra evaluation layer, we also used the NIPS2017 [36] dataset, which serves in attack development and testing and contains 1,000 images without MOSs. The decision to incorporate the NIPS2017 dataset in our experiments was to validate model robustness across varied datasets, extending beyond the scope of their original training domain.

We evaluated our method using four NR-IQA models originally developed using KonIQ-10k and showed a high correlation with subjective quality in public benchmarks. KonCept512 [17] was the first IQA model trained on the KonIQ-10k dataset. WSP-IQA [19] employs weighted spatial pooling (WSP) instead of global average pooling (GAP) to aggregate spatial information from different-size weight maps. HyperIQA [18] uses a hyper-convolutional network to predict the weights of fully connected layers. LinearityIQA [20] introduces the norm-in-norm loss function, which enables faster convergence than MSE or MAE when serving with the ResNet architecture.

FR-IQA datasets and models. For full-reference assessment we enhanced LPIPS [32]. . Among learning-based FR-IQA models that have proven vulnerable to adversarial attacks, it’s the most widely used option with an open training dataset [31,37]. Training of the original model version used the BAPPS [32] dataset, so our approach involves modifying the training process using this dataset. BAPPS consists of 36,344 image triplets: one image is the reference and the other two are distorted. Each triplet has two alternative forced-choice (2AFC) scores, indicating which of the two distorted images is more similar to the reference image. Additionally, we used the KADID-10k dataset [38], which contains 10,125 distorted images derived from 81 reference images. Each distorted image is associated with a subjective quality score based on MOS.

4.2. Evaluation Metrics

Performance evaluation. We used the Spearman rank order correlation coefficient (SROCC) to measure the correlation of NR-IQA model scores with subjective ratings. For FR-IQA models, we measured two-alternative forced choice (2AFC), which Zhang et al. [32] used.

Robustness evaluation. We applied FGSM and PGD attacks with 10 iterations to test adversarially trained models. Our evaluation of IQA model robustness employed two metrics.

Robustness score (R) [7] is the average ratio of the maximum allowable quality-prediction change to the actual change over all adversarial images in a logarithmic scale:

R = \frac{1}{N} \sum_{i = 1}^{N} log (\frac{max {β_{1} - f (x_{i}), f (x_{i}) - β_{2}}}{| f (x_{i}) - f (x_{i}^{'}) |}),

(9)

where f is an IQA model,

x_{i}

and

x_{i}^{'}

are, respectively, the clean and perturbed versions of

i^{t h}

image from the dataset;

β_{1}

is the maximum MOS value; and

β_{2}

is the minimum MOS value.

Integral Robustness Score (IR-score). We introduce a new method to measure the resistance of adversarially trained models to perturbations of various magnitudes. Unlike R, our integral robustness score (IR-score) accounts for attack success versus perturbation-budget dependency, as Carlini et al. recommended [39].

We generated adversarial examples with different perturbation sizes

ε

from {2, 4, 8, 10} / 255 for each image in the test set and each IQA model. We then obtained the IQA-model scores for images before and after the attack and performed min-max normalization. Our next step was to calculate the minimum and maximum scores for each IQA model using the training dataset. Afterward, we transformed the IQA-model scores into the unified domain using neural optimal transport [40]. This step is necessary because the scores of different IQA models are nonuniformly distributed. We therefore trained a small neural network with four linear layers and one-dimensional input, as in [1]. suggested. Our experiments used LinearityIQA as a unified domain. Next was computing the absolute gain: the score difference for each image pair before and after the attack. We performed the abovementioned procedure for the original and adversarially trained models. The final step was to calculate the IR-score as the difference between two integrals (for the original and adversarially trained models) of absolute gain-

ε

curves averaged over all test-dataset images. Formally, for a given IQA model f parameterized by

θ

and adversarially trained model

f_{A T}

parameterized by

θ_{A T}

, the IR-score for a set of images

{x_{i}}_{i = 1}^{N}

is the following:

\begin{matrix} IR - score = \frac{1}{N} \sum_{i = 1}^{N} \int_{ε} (\hat{f} (x_{i}) - \hat{f} (x_{i} + δ (θ, ε)) - {\hat{f}}_{A T} (x_{i}) + {\hat{f}}_{A T} (x_{i} + δ (θ_{A T}, ε))) d ε, \end{matrix}

(10)

where

δ (θ, ε)

is the attack perturbation with a magnitude of

ε

applied to the model parameterized by

θ

, and

\hat{f} (x_{i})

is a metric score mapped by neural optimal transport (NOT) [40]:

\begin{matrix} \hat{f} (x_{i}) \leftarrow NOT (diam (f_{θ} (x_{i}))) . \end{matrix}

(11)

4.3. Implementation Details

Pretraining of each IQA model employed the settings described in the source articles. Subsequently, we conducted 30 fine-tuning epochs for NR-IQA models, applying our proposed method with the hyperparameters listed in the supplementary materials. LPIPS involved five epochs using the Adam optimizer with a learning rate of

10^{- 4}

as well as five epochs with a linearly decreasing learning rate. To train their LPIPS model, the authors of [41] chose the features of various classification models trained on ImageNet. Following the R-LPIPS researchers [33], we used the AlexNet features.

Selection of the best model first required analysis of the SROCC for WSP-IQA, HyperIQA, and LinearityIQA and of the Pearson linear correlation coefficient (PLCC) for KonCept512, in accordance with the original paper’s recommendation [17]. We measured correlation coefficients on the validation subset after each training epoch and saved the best-performing model. During adversarial retraining, we saved the best model after three epochs, as we expected to obtain a more robust model exhibiting a natural decrease in correlation with subjective scores over more epochs. All our experiments with NR-IQA models were performed using eight Nvidia Tesla A100 80-Gb GPUs, while experiments with FR-IQA models used four NVIDIA RTX A6000 GPUs.

5. Results

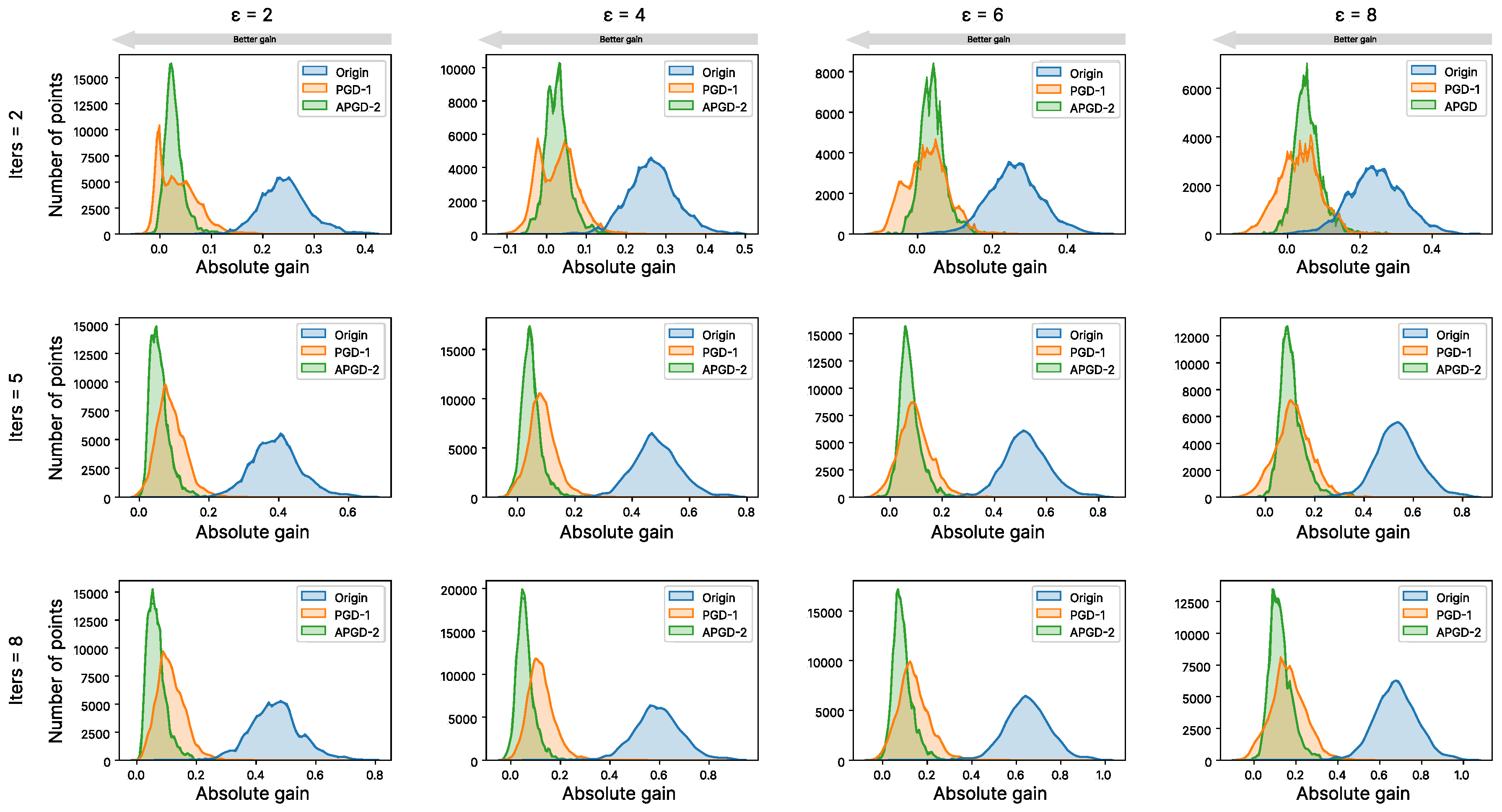
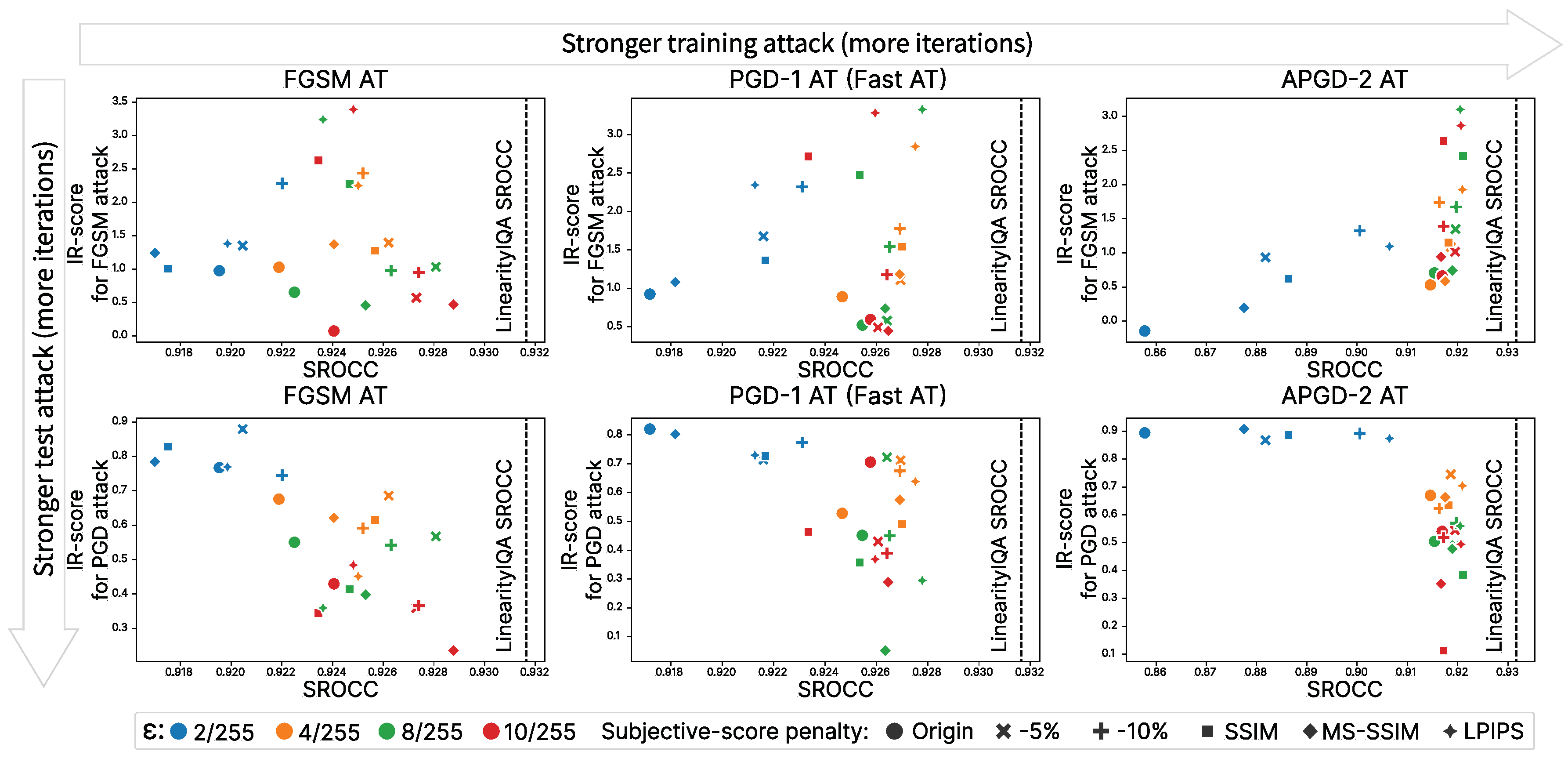
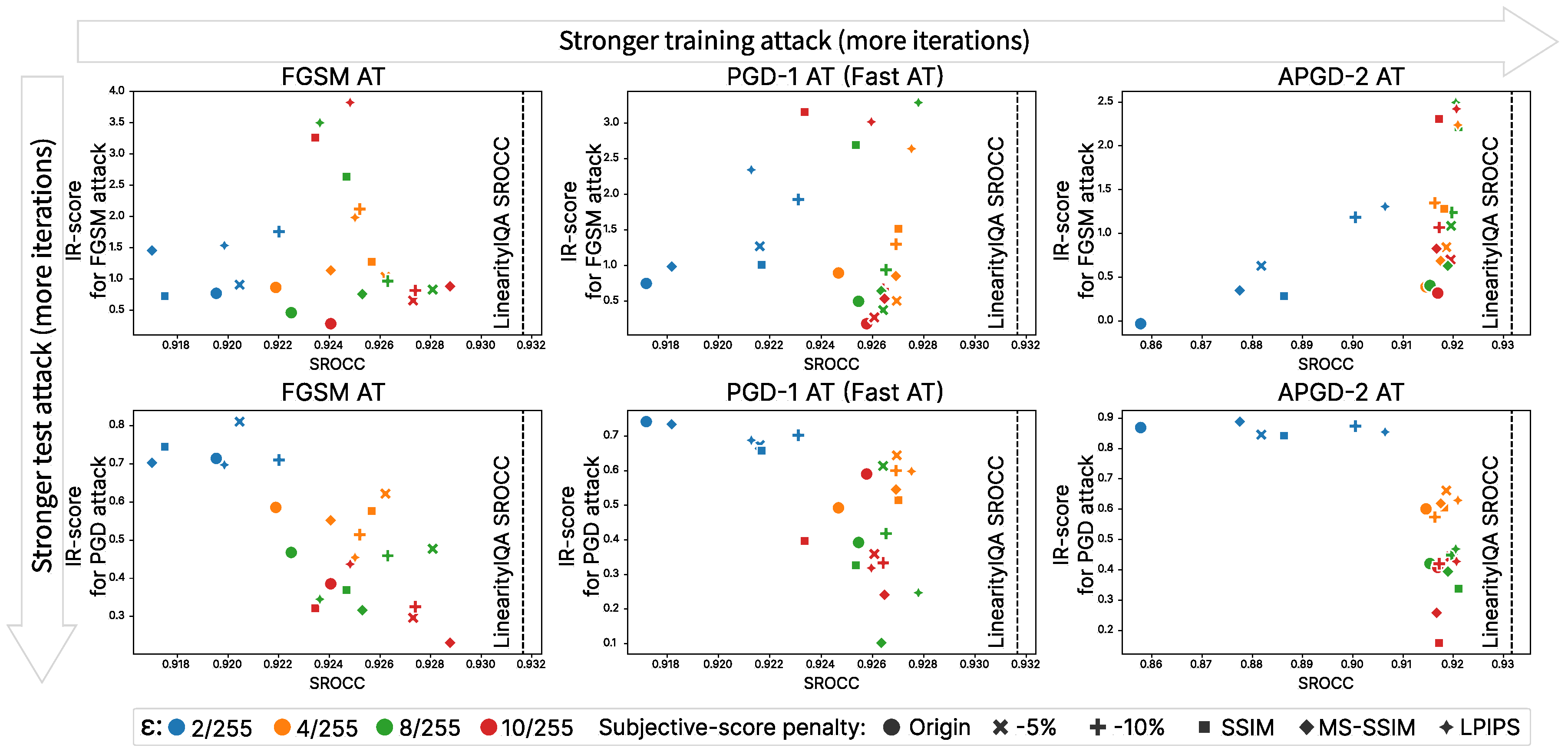
5.1. Ablation Study

Role of pre-training and training data in adversarial robustness. Table 1 shows pre-training’s impact on the performance and robustness of the adversarially trained LinearityIQA as measured by the SROCC and IR-score. Similarly, Table 2 shows the performance and robustness of the adversarially trained FR-IQA model LPIPS. AT means vanilla adversarial training with an FGSM attack, +clean means concatenated batches of clean and adversarial data, +pretr. means pre-training. For training, we set the allowable perturbation magnitude

ε

to 4/255.

Although vanilla adversarial training for classification typically involves training the model solely on perturbed data, our experiments showed this approach is ineffective for IQA models. Adversarial training of these models without pre-training causes the model’s correlation with subjective quality to decline sharply.

Subjective score correction. Table 3 shows that assigning minimal MOS labels and PSNR-based score correction produces a greater decrease in correlation with subjective quality on clean images, a phenomenon we want to avoid. The best correlations are for fixed penalties of 5% and 10%, followed by FR-based penalties on LPIPS and SSIM. A fixed rate, however, will require manual selection of a penalty percentage, that may depend on image content, its corruption level and other properties. In total, LPIPS-based penalty shows better IR-score than fixed rate, keeping high correlation with original quality labels.

Impact of attack type during training. Table 3 shows the correlation between model predictions and subjective-quality scores for the original NR-IQA model LinearityIQA and its adversarially trained versions. The results showed that NR-IQA models trained with a PGD-1 attack correlated better with subjective quality. PGD-1 is a stronger FGSM version requiring one iteration of forward and backward passes. Interestingly, use of a stronger attack during image-classifier training decreases the model’s accuracy on clean images [25,26]. Table 4 presents the results for different versions of the FR-IQA model, LPIPS. More-sophisticated attacks increased robustness and decreased SROCC.

Impact of perturbation magnitude during training. Figure 2 illustrates the impact of the allowable perturbation values on the NR-IQA model’s correlation and robustness. The upper row of plots illustrates the resistance of each model to a simple FGSM attack. The lower row illustrates the same models’ resistance to a stronger PGD attack with 10 iterations. Models trained using a lower

ε

value correlate less well with MOS values, but during evaluation, they become more resistant to a stronger attack. LPIPS exhibits a similar effect, as Table 4: smaller magnitudes are used while adversarial training yields better resistance to PGD.

5.2. Overall Results

Our final adversarial training method employed the best strategies according to our experiment results noted in the ablation study (Section 5.1): we fine-tuned pre-trained IQA models on clean and attacked images using the PGD-1 attack with

ε = 2 / 255

; for NR-IQA models, we computed a penalty for subjective scores using the SSIM metric. Table 5 compares the original NR-IQA models with the robust versions from vanilla adversarial training, Norm regularization Training, and our proposed method. Our adversarially trained models demonstrate better resistance than the base and NT versions. Moreover, the SROCC decrease of models trained with our process is no more than 1.8% — a substantial improvement over vanilla adversarial training.

Table 6 shows the adversarial robustness of the FR-IQA LPIPS model trained with different approaches. Our approach to attacking two images simultaneously demonstrates improved robustness while insignificantly reducing the SROCC compared to vanilla adversarial training used in R-LPIPS.

For each final model, we provide information on training time. Although our method for NR-IQA requires more GPU hours than previous methods, this does not affect inference time.

6. Discussion

Applicability of proposed method to other adversarial attacks. We tested the robustness of the adversarially trained NR-IQA Linearity model to 16 other attacks. Appendix A provides the details about attacks and their hyperparameters. Figure 3 shows the R values for each pair of attack and version of IQA model. The proposed approach improves NR-IQA model resistance to almost every attack, except AdvCF [42]. This is because the training process used the noise attack, and models were therefore intended to be resistant to perturbations rather than color distortion which is how AdvCF works. Also, the SSIM-based label penalty chosen in the ablation study as the best strategy showed the best results in this experiment since it provided the best robustness for 13 of 16 unforeseen attacks.

Performance on clean images. Since vanilla adversarial training decreases model performance on clean data, we tested the performance of our adversarial training method when images did not contain adversarial noise. This property is more pronounced for IQA models because we added adversarial noise to images during training. The proposed approach helped reduce this effect of NR-IQA models: it decreased the correlation by less than 1.8% for four NR-IQA models. For LPIPS, our approach yielded 4.6% lower SROCC compared with the original LPIPS and less than 1% compared with R-LPIPS.

Empirical probabilistic estimation. When comparing the robustness of adversarially trained models, we launched each attach once and varied only the perturbation norm. We conducted an empirical study involving 100 attack launches for each parameter set to show that our adversarially trained models provide statistically significant improvement. Then, we used the Wilcoxon signed-rank test with the alternative hypothesis that the attack gains for the original and adversarially trained models differ. The test yielded a p-value of 0, confirming that adversarial training enhances model resistance to adversarial attacks. Details of the experiment appear in the Appendix B.

7. Conclusions

This paper presents a novel adversarial training method for IQA models. Unlike the vanilla approaches created for computer-vision models, our method is for IQA specifically, a feature that allowed us to create an IQA model that is robust to adversarial attacks without significantly reducing correlation with human image-quality perception. We conducted a comprehensive ablation study to determine the best adversarial training components for IQA. We also introduced a new evaluation strategy for our method and compared the robustness of IQA models. Our results showed that the best approach is to fine-tune IQA models on clean and adversarial images with a low perturbation level (

ε = 2 / 255

in our experiments). In the case of NR-IQA models, the adjusted perceptual-quality scores for perturbed images generated during adversarial training maintain a high correlation with subjective quality. For FR-IQA LPIPS model, our approach of adding perturbations to two images during training improves robustness relative to other methods.

Future work. This study primarily focused on applying attacks during training with a restriction on the

l_{\infty}

norm. An interesting variation would be to explore perceptually constrained attacks for quality metrics.

Author Contributions

Conceptualization, A.A. and S.L.; methodology, A.C. and A.A.; software, A.C. and M.K.; writing—original draft preparation, A.C., A.A. and M.K.; writing—review and editing, S.L.; visualization, A.C.; supervision, A.A., S.L. and K.A.; funding acquisition, D.T. and D.V. All authors have read and agreed to the published version of the manuscript.

Funding

This work received support from a grant for research centers in the field of artificial intelligence, provided by the Analytical Center in accordance with a subsidy agreement (identifier 000000D730321P5Q0002) and an agreement with the Ivannikov Institute for System Programming dated November 2, 2021, No. 70-2021-00142.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The datasets used in our paper are available at https://database.mmsp-kn.de/koniq-10k-database.html and https://www.kaggle.com/datasets/google-brain/nips-2017-adversarial-learning-development-set.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

IQA	Image quality assessment
FR	Full reference
NR	No reference
CNN	Convolutional neural network
ViT	Vision transformer
SROCC	Spearman rank order correlation coefficient
NOT	Neural optimal transport
AT	Adversarial Training
NT	Norm regularization Training

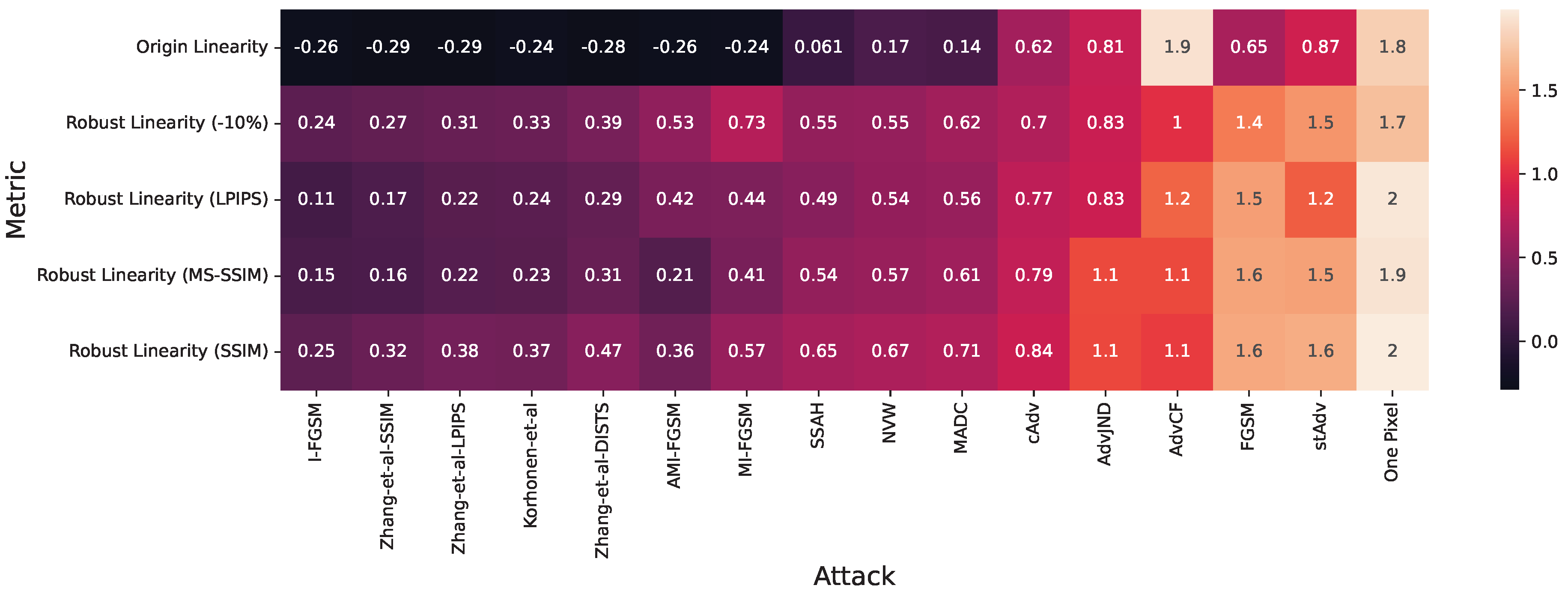
Appendix A. Applicability of Proposed Method to other Adversarial Attacks

To evaluate our defense, we selected four LinearityIQA models [20] trained using our method with PGD-1 (

ε = 2

) and tested them against 16 attacks on the NIPS2017 dataset. The chosen attack methods exploit various aspects of the input data to create adversarial examples, such as basic gradients methods [24,43,44,45], approaches based on image quality models [7,46,47], spatial characteristics [6,48,49] and techniques that manipulate colors [42,50] and pixel arrangements [51,52]. These attacks include methods with different whitebox/blackbox settings and distortion metrics such as

l_{2}

l_{\infty}

, LPIPS, SSIM, and DISTS. Details about attack methods are in Table A1.

Appendix B. Empirical Probabilistic Estimation

We conducted an empirical study to investigate the attack gain distributions. For this purpose, we chose the original LinearityIQA model and two adversarially trained models using our proposed subjective score correction method based on the SSIM metric and attack methods PGD-1 and APGD-2 with

ε = 2

. We used the adaptive APGD attack, which allowed us to obtain more robust adversarial perturbations due to the adaptive step. For the experiment’s randomness, as the adversarial perturbation search’s starting point, we used a uniform noise from the

l_{\infty}

-ball with a radius of the allowable magnitude of the attack

ε

. For each image from the NIPS2017 dataset, we generated 100 adversarial examples with fixed attack parameters: the number of iterations iters and the allowable magnitude of the perturbation

ε

. Therefore, we got 100’000 adversarial data points for each IQA model. Then, we computed the objective scores and plotted the difference in the distribution of the IQA model’s scores before and after the attack. Figure A1 show a significant left shift in distributions for adversarially trained models, indicating the usefulness of adversarial training against adversarial attacks. To test our hypothesis, we used the Wilcoxon signed-rank test with the alternative hypothesis that the original and adversarially trained models’ gains are different. The test resulted in a p-value of 0 for both no-reference and full-reference models, indicating that the difference in medians is statistically significant and confirming that adversarial training enhances models’ robustness against adversarial attacks.

Figure A1. Attack success against original LinearityIQA model and adversarially trained versions under APGD-2 attack with different attack magnitude (

ε

) and iterations (Iters).

Figure A1. Attack success against original LinearityIQA model and adversarially trained versions under APGD-2 attack with different attack magnitude (

ε

) and iterations (Iters).

Appendix C. Comparison with Adversarial Purification Methods

In Table A4, we compare our adversarial training with simple adversarial purification methods, such as image resizing and cropping, for the KonCept512 model. After applying the transformations, the resize factor indicated in brackets was selected such that the SROCC approximately equals the SROCC of a model trained using our method. The results show that our adversarially trained model with PGD-1 is more robust to the simple FGSM attack than purification methods and slightly inferior to the resizing method against a significantly more complex PGD-10 attack. However, it is essential to recognize the limitations of purification techniques. If an attacker is aware of a defense mechanism, they can use an adaptive attack to significantly reduce the effectiveness of these techniques. At the same time, all attacks on models that have been adversarially trained are inherently adaptive to defense methods. It makes adversarial training a more robust defense strategy overall.

Appendix D. Additional Attack Details

To adapt attack methods for the IQA task, we define the loss function for a given IQA metric

f_{θ}

during evaluation as follows:

L (θ, x) = 1 - \frac{f_{θ} (x)}{diam (f_{θ})},

(A1)

where

diam (f_{θ}) = sup_{x, z \in D} {| f_{θ} (x) - f_{θ} (z) |}

represents the range of IQA metric’s values.

To increase the IQA model score we minimize loss by making small steps along the gradient direction in the image space.

In Table A1, Table A2 and Table A3, we provide a list of attack methods with descriptions and parameters that were used for adversarial training and evaluation in our ablation study (Section 5.1) and discussion of the transferability of our approach to other attacks (Section 6).

Appendix E. Ablation Study Results

This part presents the full results of our ablation study.

For NR-IQA models, we show the impact of pre-training and fine-tuning using different score correction strategies (Table A5). We also show the effect of the choice of subjective score correction method, attack type, and attack magnitude on SROCC, our IR-score (Figure A2 and Table A6, Table A7, Table A8, Table A9 and Table A10) and R-score [7] (Table A11, Table A12, Table A13 and Table A14).

Figure A2. Impact of subjective score correction, perturbation magnitude, and attack type during training. Metric: Linearity. Dataset: NIPS2017.

For FR IQA models, we provide SROCC and 2AFC values for different attacks and their magnitudes during training and evaluation (Table A15 and Table A16).

Table A1. Parameters and sources of implemented attacks for evaluation.

Attack	Description	Invisibility Metric	Optimizer	Optimization parameters
FGSM [24]	One-step gradient attack.	$l_{\infty}$ distance $ε = 10 / 255$	Gradient descent	Number of iterations $n = 1$
I-FGSM [43]	Iterative version of FGSM.	$l_{\infty}$ distance $ε = 10 / 255$	Gradient descent	Step size at each iteration $α = 1 / 255$ Number of iterations $n = 10$
MI-FGSM [44]	I-FGSM with momentum.	$l_{\infty}$ distance $ε = 10 / 255$	Gradient descent	Step size at each iteration $α = 1 / 255$ Number of iterations $n = 10$ Decay factor $ν = 1.0$
AMI-FGSM [45]	MI-FGSM with $ε = 1 / N I Q E (x)$ .	$l_{\infty}$ distance $ε = 10 / 255$	Gradient descent	Step size at each iteration $α = 1 / 255$ Number of iterations $n = 10$ Decay factor $ν = 1.0$
Korhonen et al. [6]	Using spatial activity map to concentrate perturbations in textured regions. Spatial activity map is computed using the Sobel filter.	$l_{\infty}$ distance	Adam	Learning rate $l r = 0.005$ Number of iterations $n = 10$
NVW [48]	Using variance map to concentrate perturbations in the high variance areas.	$l_{\infty}$ distance	Adam	Learning rate $l r = 0.001$ Number of iterations $n = 10$
Zhang-SSIM Zhang-LPIPS [7] Zhang-DISTS	Adding a full-reference metric as an additional term of the objective function.	$l_{\infty}$ distance	Adam	Learning rate $l r = 0.005$ Number of iterations $n = 10$
SSAH [49]	Attacking the semantic similarity of the image.	Low-Frequency component distortion	Adam	Learning rate $l r = 0.001$ Number of iterations $n = 10$ Hyperparameter $λ = 0.1$ Wavelet type – haar
AdvJND [46]	Adding the just noticeable difference (JND) coefficients in the constraint to improve the quality of images.	$l_{\infty}$ distance $ε = 10 / 255$	Gradient descent	Number of iterations $n = 1$
MADC [47]	Updating image in the direction of increasing the metric score while keeping MSE fixed.	$l_{\infty}$ distance $ε = 10 / 255$	Gradient descent	Learning rate $l r = 0.001$ Number of iterations $n = 8$
AdvCF [42]	Using gradient information in the parameter space of a simple color filter.	Unrestricted color perturbation	Adam	Learning rate $l r = 0.1$ Number of iterations $n = 10$
cAdv [50]	Adaptive selection of locations in the image to change their colors.	Unrestricted color perturbation	Adam	Learning rate $l r = 0.0005$ Number of iterations $n = 10$
StAdv [51]	Adversarial examples based on spatial transformation.	The sum of spatial movement distance for any two adjacent pixels	L-BFGS-B	Hyperparameter to balance two losses $τ = 1 e - 5$ Number of iterations $n = 3$
One Pixel [52]	Using differential evolution to perturbe several pixels without gradient-based methods.	$l_{0}$ distance Number of perturbed pixels $p = 8$	Differential evolution	Number of iterations $n = 5$ A multiplier for setting the total population size $p o p s i z e = 40$

Table A2. Parameters and sources of implemented attacks during training.

Attack	Description	Perturbation budget $ε$	Number of iterations n	Step size $α$
FGSM [24]	One-step gradient attack.	${2, 4, 8, 10} / 255$	1	$ε$
PGD-1 [26]	FGSM with initial random perturbation.	${2, 4, 8, 10} / 255$	1	$1.25 ε$
APGD-2 [28]	Step size-free variant of PGD.	${2, 4, 8, 10} / 255$	2	Adaptive

Table A3. Parameters and sources of implemented attacks in the ablation study.

Attack	Description	Perturbation budget $ε$	Number of iterations n	Step size $α$
FGSM [24]	One-step gradient attack.	${2, 4, 6, 8, 10} / 255$	1	$ε$
PGD-1 [26]	FGSM with initial random perturbation.	${2, 4, 6, 8, 10} / 255$	1	$1.25 ε$
PGD-10 [25]	Iterative FGSM with initial random perturbation.	${2, 4, 6, 8, 10} / 255$	10	$1 / 255$

Table A4. Comparison of AT with simple defense methods equivalent to AT in reducing SROCC. NR-IQA model: KonCept512. Bold denotes the top 2 values. Dataset: KonIQ-10k.

Defense method	SROCC	R ( $ε = 2$ ) ↑				IR-score ↑
		FGSM	Adaptive FGSM	PGD-10	Adaptive PGD-10	FGSM	Adaptive FGSM	PGD-10	Adaptive PGD-10
w/o	0.925	0.706	-	0.353	-	-	-	-	-
Crop (0.79)	0.909	0.893	0.832	0.552	0.465	0.540	0.443	0.452	0.428
Resize (0.8)	0.910	0.992	0.651	0.833	0.250	0.612	0.019	0.668	0.067
AT	0.913	1.221	1.221	0.587	0.587	1.030	1.030	0.604	0.604
AT+Resize (0.9)	0.911	1.347	1.270	1.002	0.581	1.360	0.967	0.792	0.596
AT+Crop (0.9)	0.913	1.309	1.213	0.901	0.770	1.306	1.203	0.743	0.718

Table A5. Influence of pre-training and fine-tuning for NR-IQA models. Bold denotes the top 2 values for each penalty strategy.

Training strategy	Penalty	SROCC	IR-score↑
			FGSM		PGD-10
			KonIQ-10k	NIPS2017	KonIQ-10k	NIPS2017
Base model	–	0.931	–	–	–	–
adv	–	0.837	1.106	1.366	0.542	0.555
+ pretr.	–	0.848	1.337	1.407	0.445	0.510
+ clean	–	0.920	1.257	1.489	0.569	0.645
+ clean + pretr.	–	0.921	0.865	1.026	0.585	0.675
adv	-5%	0.844	0.993	0.982	0.635	0.686
+ pretr.	-5%	0.841	1.500	1.549	0.648	0.718
+ clean	-5%	0.922	1.482	1.910	0.596	0.602
+ clean + pretr.	-5%	0.926	1.036	1.393	0.621	0.685
adv	LPIPS	0.784	1.001	1.011	0.424	0.323
+ pretr.	LPIPS	0.717	1.554	1.685	0.565	0.603
+ clean	LPIPS	0.924	2.092	2.218	0.516	0.527
+ clean + pretr.	LPIPS	0.925	1.984	2.248	0.454	0.451

Table A6. SROCC↑ of Linearity metric on KonIQ-10k dataset for different MOS penalty strategies, attack types, and epsilon used during adversarial training. SROCC of the original Linearity is 0.931. Bold denotes the top 3 values.

	Trained with	FGSM AT				PGD-1 AT				APGD-2 AT
	Trained with	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.920	0.922	0.922	0.924	0.917	0.925	0.925	0.926	0.858	0.915	0.915	0.917
	Min	0.908	0.917	0.921	0.920	0.911	0.925	0.926	0.926	0.870	0.876	0.847	0.843
	-5%	0.920	0.926	0.928	0.927	0.922	0.927	0.926	0.923	0.882	0.919	0.920	0.919
	-10%	0.922	0.925	0.926	0.927	0.923	0.927	0.927	0.926	0.901	0.916	0.920	0.917
	PSNR	0.906	0.913	0.916	0.917	0.907	0.914	0.923	0.924	0.922	0.912	0.911	0.912
	SSIM	0.917	0.926	0.925	0.923	0.922	0.927	0.925	0.923	0.886	0.918	0.921	0.917
	MS_SSIM	0.917	0.924	0.925	0.928	0.918	0.927	0.926	0.926	0.878	0.918	0.919	0.917
	LPIPS	0.920	0.925	0.924	0.925	0.921	0.928	0.928	0.926	0.906	0.921	0.921	0.921

Table A7. IR-score↑ of Linearity metric measured under FGSM attacks for different MOS penalty strategies, attack types, and epsilon used during adversarial training. Bold denotes the top 3 values in each column. Gray values indicate a failed defense or a significant penalty impact. Dataset: KonIQ-10k.

	Trained with	FGSM AT				PGD-1 AT				APGD-2 AT
	Trained with	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.772	0.866	0.462	0.285	0.749	0.896	0.498	0.184	-0.032	0.390	0.405	0.318
	Min	8.134	7.269	6.539	5.644	8.173	7.051	5.184	4.635	6.716	5.747	4.415	3.416
	-5%	0.908	1.036	0.831	0.656	1.270	0.504	0.375	0.271	0.629	0.842	1.085	0.700
	-10%	1.761	2.119	0.969	0.817	1.927	1.300	0.938	0.664	1.184	1.348	1.240	1.067
	PSNR	7.422	7.712	6.381	5.997	7.114	7.663	5.518	4.827	5.609	7.468	4.196	3.102
	SSIM	0.724	1.278	2.638	3.262	1.010	1.518	2.691	3.153	0.282	1.281	2.210	2.305
	MS_SSIM	1.455	1.138	0.761	0.883	0.986	0.853	0.642	0.534	0.348	0.687	0.629	0.825
	LPIPS	1.537	1.984	3.500	3.825	2.343	2.640	3.288	3.016	1.306	2.238	2.495	2.422

Table A8. IR-score↑ of Linearity metric measured under PGD-10 attacks for different MOS penalty strategies, attack types, and epsilon used during adversarial training. Bold denotes the top 3 values in each column. Bold denotes the top 3 values in each column. Gray values indicate a failed defense. Dataset: KonIQ-10k.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.714	0.586	0.468	0.386	0.742	0.493	0.392	0.590	0.869	0.601	0.421	0.408
	Min	1.777	0.316	0.156	0.174	1.795	0.359	0.260	-0.048	1.528	0.406	0.403	0.110
	-5%	0.810	0.621	0.477	0.297	0.674	0.644	0.614	0.359	0.845	0.662	0.448	0.444
	-10%	0.710	0.514	0.459	0.325	0.702	0.600	0.418	0.334	0.874	0.574	0.449	0.420
	PSNR	1.404	0.637	0.392	0.617	1.333	0.389	0.012	0.089	1.261	1.001	0.113	-0.045
	SSIM	0.744	0.576	0.370	0.322	0.658	0.515	0.326	0.397	0.842	0.606	0.339	0.160
	MS_SSIM	0.702	0.552	0.317	0.231	0.734	0.546	0.103	0.241	0.889	0.619	0.395	0.259
	LPIPS	0.697	0.455	0.345	0.437	0.688	0.598	0.247	0.319	0.854	0.629	0.469	0.428

Table A9. IR-score↑ of Linearity metric measured under FGSM attacks for different MOS penalty strategies, attack types, and epsilon used during adversarial training. Bold denotes the top 3 values in each column. Gray values indicate a failed defense or a significant penalty impact. Dataset: NIPS2017.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.974	1.027	0.651	0.072	0.925	0.891	0.522	0.596	-0.144	0.531	0.708	0.662
	Min	12.589	11.962	10.624	9.024	13.022	11.728	8.580	7.558	10.455	10.206	7.685	6.859
	-5%	1.350	1.394	1.032	0.570	1.678	1.109	0.579	0.493	0.934	1.085	1.348	1.016
	-10%	2.280	2.435	0.976	0.948	2.323	1.775	1.541	1.179	1.324	1.739	1.673	1.388
	PSNR	11.401	12.235	10.438	9.254	10.852	12.372	9.356	8.329	7.008	11.493	6.807	5.043
	SSIM	1.004	1.274	2.272	2.627	1.364	1.542	2.476	2.717	0.619	1.152	2.420	2.636
	MS_SSIM	1.239	1.368	0.457	0.467	1.081	1.184	0.739	0.446	0.194	0.585	0.741	0.941
	LPIPS	1.378	2.249	3.237	3.388	2.346	2.846	3.328	3.283	1.095	1.927	3.101	2.864

Table A10. IR-score↑ of Linearity metric measured under PGD-10 attacks for different MOS penalty strategies, attack types, and epsilon used during adversarial training. Bold denotes the top 3 values in each column. Gray values indicate a failed defense. Dataset: NIPS2017.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.767	0.676	0.550	0.430	0.820	0.528	0.451	0.706	0.894	0.670	0.505	0.541
	Min	1.826	0.447	0.250	0.224	1.846	0.461	0.333	0.000	1.389	0.411	0.521	0.235
	-5%	0.879	0.686	0.567	0.360	0.714	0.712	0.723	0.430	0.867	0.745	0.490	0.545
	-10%	0.745	0.591	0.542	0.366	0.774	0.676	0.450	0.389	0.892	0.623	0.570	0.519
	PSNR	1.445	0.650	0.490	0.735	1.300	0.512	0.037	0.101	1.126	0.775	0.000	-0.118
	SSIM	0.828	0.615	0.414	0.345	0.727	0.491	0.358	0.464	0.886	0.635	0.385	0.113
	MS_SSIM	0.784	0.622	0.398	0.236	0.803	0.575	0.052	0.289	0.908	0.663	0.478	0.352
	LPIPS	0.769	0.452	0.360	0.484	0.730	0.639	0.295	0.369	0.874	0.704	0.560	0.494

Table A11. R↑ of Linearity metric measured under FGSM attacks for different MOS penalty strategies, attack types, and epsilon used during adversarial training. In this evaluation, we applied the attack with the same epsilon we used during training. Bold denotes the top 3 values in each column. Dataset: KonIQ-10k.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	1.431	1.202	1.309	1.032	1.474	1.359	1.278	1.251	1.361	1.472	1.429	1.304
	Min	0.157	0.222	0.175	0.189	0.159	0.199	0.199	0.165	0.345	0.334	0.269	0.261
	-5%	1.418	1.371	1.336	1.346	1.413	1.348	1.253	1.229	1.508	1.534	1.259	1.261
	-10%	1.424	1.420	1.345	1.328	1.359	1.258	1.194	1.160	1.222	1.260	1.084	1.076
	PSNR	0.218	0.176	0.208	0.184	0.240	0.167	0.211	0.142	0.265	0.173	0.192	0.154
	SSIM	1.426	1.312	0.850	0.723	1.332	1.190	0.591	0.431	1.607	1.302	0.623	0.464
	MS_SSIM	1.407	1.179	1.116	1.153	1.435	1.355	1.225	1.107	1.554	1.458	1.235	1.163
	LPIPS	1.218	1.129	0.647	0.497	1.192	0.751	0.508	0.449	1.288	0.899	0.546	0.452

Table A12. R↑ of Linearity metric measured under PGD-10 attacks for different MOS penalty strategies, attack types and epsilon used during adversarial training. In this evaluation, we applied the attack with the same epsilon we used during training. Bold denotes the top 3 values in each column. Gray values indicate a failed defense. Dataset: KonIQ-10k.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.826	0.446	0.277	0.200	0.840	0.337	0.210	0.422	1.313	0.439	0.240	0.228
	Min	0.178	0.212	0.096	0.102	0.164	0.252	0.149	-0.010	0.426	0.242	0.248	0.039
	-5%	1.107	0.520	0.300	0.129	0.759	0.535	0.465	0.205	1.074	0.495	0.273	0.250
	-10%	0.991	0.396	0.290	0.179	0.881	0.462	0.250	0.196	1.336	0.412	0.276	0.245
	PSNR	0.323	0.308	0.252	0.517	0.381	0.247	0.016	0.043	0.447	0.518	0.047	-0.055
	SSIM	0.928	0.445	0.214	0.187	0.731	0.366	0.182	0.231	1.084	0.434	0.177	0.053
	MS_SSIM	0.779	0.441	0.178	0.119	0.842	0.395	0.053	0.080	1.495	0.457	0.208	0.129
	LPIPS	0.854	0.319	0.204	0.279	0.831	0.459	0.133	0.180	1.186	0.485	0.277	0.240

Table A13. R↑ of Linearity metric measured under FGSM attacks for different MOS penalty strategies, attack types and epsilon used during adversarial training. In this evaluation, we applied the attack with the same epsilon we used during training. Bold denotes the top 3 values in each column. Dataset: NIPS2017.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	1.467	1.338	1.459	1.267	1.473	1.391	1.327	1.340	1.488	1.583	1.497	1.461
	Min	0.146	0.151	0.123	0.135	0.147	0.130	0.135	0.114	0.471	0.247	0.262	0.263
	-5%	1.678	1.629	1.441	1.455	1.556	1.613	1.400	1.193	1.495	1.540	1.291	1.282
	-10%	1.382	1.401	1.422	1.284	1.333	1.404	0.979	0.933	1.257	1.243	1.148	1.094
	PSNR	0.183	0.133	0.147	0.136	0.244	0.114	0.138	0.093	0.341	0.143	0.152	0.076
	SSIM	1.639	1.472	1.037	0.964	1.562	1.387	0.795	0.632	1.695	1.440	0.803	0.573
	MS_SSIM	1.567	1.482	1.295	1.308	1.590	1.595	1.193	1.117	1.666	1.538	1.389	1.193
	LPIPS	1.489	1.329	0.837	0.660	1.410	1.018	0.631	0.540	1.514	1.148	0.612	0.517

Table A14. R↑ of Linearity metric measured under PGD-10 attacks for different MOS penalty strategies, attack types, and epsilon used during adversarial training. In this evaluation, we applied the attack with the same epsilon we used during training. Bold denotes the top 3 values in each column. Gray values indicate a failed defense. Dataset: NIPS2017.

		FGSM AT				PGD-1 AT				APGD-2 AT
		$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$	$ε = 2$	$ε = 4$	$ε = 8$	$ε = 10$
Label strategy	Origin	0.997	0.585	0.380	0.269	1.042	0.428	0.286	0.580	1.440	0.585	0.354	0.382
	Min	0.158	0.322	0.187	0.162	0.156	0.349	0.228	0.055	0.463	0.332	0.400	0.216
	-5%	1.334	0.635	0.415	0.212	0.905	0.681	0.618	0.279	1.188	0.687	0.346	0.371
	-10%	1.129	0.507	0.389	0.248	1.115	0.597	0.312	0.265	1.401	0.535	0.417	0.356
	PSNR	0.307	0.413	0.357	0.686	0.434	0.349	0.071	0.096	0.566	0.270	0.034	-0.033
	SSIM	1.170	0.547	0.279	0.227	0.923	0.408	0.238	0.306	1.279	0.540	0.252	0.070
	MS_SSIM	0.992	0.574	0.276	0.163	1.032	0.490	0.078	0.168	1.607	0.571	0.312	0.227
	LPIPS	0.982	0.370	0.246	0.338	0.915	0.552	0.200	0.251	1.265	0.632	0.390	0.325

Table A15. 2AFC↑ score of LPIPS and robust modifications on BAPPS dataset. Bold denotes the best value for each defense type.

			Attack type
Defense type			No attack	FGSM					PGD
			No attack	2	4	6	8	10	2	4	6	8	10
	No defense		0.738	0.327	0.281	0.252	0.227	0.205	0.171	0.053	0.021	0.009	0.005
	R-LPIPS [33]		0.728	0.471	0.445	0.427	0.414	0.405	0.279	0.163	0.114	0.091	0.077
	FGSM	2	0.729	0.501	0.477	0.459	0.444	0.430	0.311	0.193	0.139	0.111	0.094
		4	0.725	0.500	0.476	0.458	0.444	0.430	0.318	0.200	0.147	0.117	0.099
		8	0.726	0.504	0.481	0.464	0.449	0.435	0.318	0.202	0.150	0.120	0.102
		10	0.727	0.505	0.484	0.467	0.451	0.439	0.317	0.203	0.150	0.120	0.103
	PGD-1	2	0.729	0.491	0.466	0.447	0.430	0.415	0.307	0.184	0.129	0.100	0.083
		4	0.727	0.500	0.476	0.459	0.445	0.431	0.317	0.197	0.144	0.114	0.096
		8	0.724	0.516	0.497	0.483	0.472	0.461	0.323	0.210	0.161	0.132	0.115
		10	0.721	0.518	0.499	0.485	0.472	0.463	0.326	0.214	0.164	0.135	0.118
	APGD-2	2	0.733	0.483	0.454	0.435	0.418	0.403	0.297	0.175	0.121	0.094	0.077
		4	0.726	0.498	0.473	0.455	0.442	0.428	0.318	0.202	0.150	0.120	0.103
		8	0.722	0.512	0.490	0.475	0.462	0.449	0.332	0.224	0.175	0.149	0.131
		10	0.722	0.514	0.494	0.479	0.467	0.457	0.332	0.228	0.180	0.154	0.139

Table A16. SROCC↑ of LPIPS and robust modifications on the KADID-10k dataset. Bold denotes the best value for each defense type.

			Attack type
Defense type			No attack	FGSM					PGD
			No attack	2	4	6	8	10	2	4	6	8	10
	No defense		0.887	0.873	0.866	0.849	0.819	0.778	0.625	0.459	0.338	0.245	0.169
	R-LPIPS [33]		0.869	0.865	0.861	0.856	0.828	0.801	0.821	0.771	0.717	0.666	0.608
	FGSM	2	0.802	0.795	0.792	0.782	0.767	0.745	0.679	0.631	0.592	0.548	0.499
		4	0.806	0.799	0.796	0.786	0.771	0.748	0.685	0.636	0.596	0.553	0.503
		8	0.804	0.796	0.793	0.783	0.766	0.743	0.668	0.616	0.575	0.528	0.476
		10	0.805	0.797	0.793	0.783	0.766	0.743	0.659	0.605	0.557	0.507	0.453
	PGD-1	2	0.865	0.862	0.86	0.854	0.84	0.82	0.828	0.8	0.765	0.725	0.685
		4	0.859	0.856	0.854	0.849	0.838	0.822	0.829	0.811	0.787	0.758	0.727
		8	0.852	0.849	0.847	0.842	0.834	0.822	0.828	0.819	0.806	0.788	0.767
		10	0.847	0.844	0.842	0.838	0.83	0.819	0.823	0.815	0.803	0.787	0.769
	APGD-2	2	0.837	0.832	0.829	0.820	0.803	0.780	0.749	0.703	0.658	0.611	0.562
		4	0.830	0.825	0.822	0.814	0.800	0.779	0.752	0.716	0.682	0.645	0.605
		8	0.818	0.813	0.810	0.802	0.787	0.766	0.736	0.701	0.668	0.633	0.595
		10	0.817	0.812	0.808	0.800	0.785	0.764	0.730	0.695	0.660	0.623	0.585

References

Antsiferova, A.; Abud, K.; Gushchin, A.; Shumitskaya, E.; Lavrushkin, S.; Vatolin, D. Comparing the robustness of modern no-reference image-and video-quality metrics to adversarial attacks. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, 2024, Vol. 38, pp. 700–708. [CrossRef]
Meftah, H.F.B.; Fezza, S.A.; Hamidouche, W.; Déforges, O. Evaluating the Vulnerability of Deep Learning-based Image Quality Assessment Methods to Adversarial Attacks. In Proceedings of the 2023 11th European Workshop on Visual Information Processing (EUVIP). IEEE, 2023, pp. 1–6. [CrossRef]
Wang, H.; Zhang, W.; Ren, P. Self-organized underwater image enhancement. ISPRS Journal of Photogrammetry and Remote Sensing 2024, 215, 1–14. [CrossRef]
Zhou, J.; Pang, L.; Zhang, D.; Zhang, W. Underwater image enhancement method via multi-interval subhistogram perspective equalization. IEEE Journal of Oceanic Engineering 2023, 48, 474–488. [CrossRef]
Wu, Y.; Pan, C.; Wang, G.; Yang, Y.; Wei, J.; Li, C.; Shen, H.T. Learning semantic-aware knowledge guidance for low-light image enhancement. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 1662–1671.
Korhonen, J.; You, J. Adversarial attacks against blind image quality assessment models. In Proceedings of the Proceedings of the 2nd Workshop on Quality of Experience in Visual Multimedia Applications, 2022, pp. 3–11. [CrossRef]
Zhang, W.; Li, D.; Min, X.; Zhai, G.; Guo, G.; Yang, X.; Ma, K. Perceptual Attacks of No-Reference Image Quality Models with Human-in-the-Loop. Advances in Neural Information Processing Systems 2022, 35, 2916–2929.
Shumitskaya, E.; Antsiferova, A.; Vatolin, D.S. Universal Perturbation Attack on Differentiable No-Reference Image- and Video-Quality Metrics. In Proceedings of the 33rd British Machine Vision Conference 2022, BMVC 2022, London, UK, November 21-24, 2022. BMVA Press, 2022.
Shumitskaya, E.; Antsiferova, A.; Vatolin, D.S. Fast Adversarial CNN-based Perturbation Attack on No-Reference Image- and Video-Quality Metrics. In Proceedings of the The First Tiny Papers Track at ICLR 2023, Tiny Papers @ ICLR 2023, Kigali, Rwanda, May 5, 2023; Maughan, K.; Liu, R.; Burns, T.F., Eds. OpenReview.net, 2023.
Shumitskaya, E.; Antsiferova, A.; Vatolin, D. IOI: Invisible One-Iteration Adversarial Attack on No-Reference Image-and Video-Quality Metrics. arXiv preprint arXiv:2403.05955 2024.
Duanmu, Z.; Liu, W.; Wang, Z.; Wang, Z. Quantifying visual image quality: A bayesian view. Annual Review of Vision Science 2021, 7, 437–464. [CrossRef]
Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 2004, 13, 600–612. [CrossRef]
Sheikh, H.R.; Bovik, A.C.; De Veciana, G. An information fidelity criterion for image quality assessment using natural scene statistics. IEEE Transactions on image processing 2005, 14, 2117–2128. [CrossRef]
Antsiferova, A.; Lavrushkin, S.; Smirnov, M.; Gushchin, A.; Vatolin, D.; Kulikov, D. Video compression dataset and benchmark of learning-based video-quality metrics. Advances in Neural Information Processing Systems 2022, 35, 13814–13825.
Tu, Z.; Wang, Y.; Birkbeck, N.; Adsumilli, B.; Bovik, A.C. UGC-VQA: Benchmarking blind video quality assessment for user generated content. IEEE Transactions on Image Processing 2021, 30, 4449–4464. [CrossRef]
Zhu, H.; Li, L.; Wu, J.; Dong, W.; Shi, G. MetaIQA: Deep Meta-Learning for No-Reference Image Quality Assessment. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2020, pp. 14143–14152.
Hosu, V.; Lin, H.; Sziranyi, T.; Saupe, D. KonIQ-10k: An Ecologically Valid Database for Deep Learning of Blind Image Quality Assessment. IEEE Transactions on Image Processing 2020, 29, 4041–4056. https://doi.org/10.1109/tip.2020.2967829. [CrossRef]
Su, S.; Yan, Q.; Zhu, Y.; Zhang, C.; Ge, X.; Sun, J.; Zhang, Y. Blindly Assess Image Quality in the Wild Guided by a Self-Adaptive Hyper Network. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2020, pp. 3664–3673.
Su, Y.; Korhonen, J. Blind Natural Image Quality Prediction Using Convolutional Neural Networks And Weighted Spatial Pooling. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), 2020, pp. 191–195. https://doi.org/10.1109/ICIP40778.2020.9190789. [CrossRef]
Li, D.; Jiang, T.; Jiang, M. Norm-in-Norm Loss with Faster Convergence and Better Performance for Image Quality Assessment. In Proceedings of the Proceedings of the 28th ACM International Conference on Multimedia. ACM, 2020, MM ’20. https://doi.org/10.1145/3394171.3413804. [CrossRef]
Ke, J.; Wang, Q.; Wang, Y.; Milanfar, P.; Yang, F. MUSIQ: Multi-Scale Image Quality Transformer. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), October 2021, pp. 5148–5157.
Yang, S.; Wu, T.; Shi, S.; Lao, S.; Gong, Y.; Cao, M.; Wang, J.; Yang, Y. MANIQA: Multi-dimension Attention Network for No-Reference Image Quality Assessment. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 1191–1200.
Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks, 2014, [arXiv:cs.CV/1312.6199].
Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. CoRR 2014, abs/1412.6572.
Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. ArXiv 2017, abs/1706.06083.
Wong, E.; Rice, L.; Kolter, J.Z. Fast is better than free: Revisiting adversarial training. ArXiv 2020, abs/2001.03994.
Singh, N.D.; Croce, F.; Hein, M. Revisiting Adversarial Training for ImageNet: Architectures, Training and Generalization across Threat Models. ArXiv 2023, abs/2303.01870.
Croce, F.; Hein, M. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In Proceedings of the International Conference on Machine Learning, 2020.
Li, Z. On VMAF’s property in the presence of image enhancement operations, 2021.
Siniukov, M.; Antsiferova, A.; Kulikov, D.; Vatolin, D. Hacking VMAF and VMAF NEG: vulnerability to different preprocessing methods. In Proceedings of the 2021 4th Artificial Intelligence and Cloud Computing Conference, 2021, pp. 89–96. [CrossRef]
Kettunen, M.; Härkönen, E.; Lehtinen, J. E-LPIPS: Robust Perceptual Image Similarity via Random Transformation Ensembles, 2019, [arXiv:cs.CV/1906.03973].
Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric, 2018, [arXiv:cs.CV/1801.03924].
Ghazanfari, S.; Garg, S.; Krishnamurthy, P.; Khorrami, F.; Araujo, A. R-LPIPS: An Adversarially Robust Perceptual Similarity Metric, 2023, [arXiv:cs.CV/2307.15157].
Liu, Y.; Yang, C.; Li, D.; Ding, J.; Jiang, T. Defense Against Adversarial Attacks on No-Reference Image Quality Models with Gradient Norm Regularization, 2024, [arXiv:cs.CV/2403.11397].
Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003. Ieee, 2003, Vol. 2, pp. 1398–1402. [CrossRef]
K, A.; Hamner, B.; Goodfellow, I. NIPS 2017: Adversarial Learning Development Set. https://www.kaggle.com/datasets/google-brain/nips2017-adversarial-learning-development-set, 2017.
Siniukov, M.; Kulikov, D.; Vatolin, D. Applicability limitations of differentiable full-reference image-quality metrics. In Proceedings of the 2023 Data Compression Conference (DCC). IEEE, 2023, pp. 1–1. [CrossRef]
Lin, H.; Hosu, V.; Saupe, D. KADID-10k: A Large-scale Artificially Distorted IQA Database. In Proceedings of the 2019 Eleventh International Conference on Quality of Multimedia Experience (QoMEX), 2019, pp. 1–3. https://doi.org/10.1109/QoMEX.2019.8743252. [CrossRef]
Carlini, N.; Athalye, A.; Papernot, N.; Brendel, W.; Rauber, J.; Tsipras, D.; Goodfellow, I.; Madry, A.; Kurakin, A. On evaluating adversarial robustness. arXiv preprint arXiv:1902.06705 2019. [CrossRef]
Korotin, A.; Selikhanovych, D.; Burnaev, E. Neural Optimal Transport. CoRR 2022, abs/2201.12220, [2201.12220]. [CrossRef]
Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE conference on computer vision and pattern recognition. Ieee, 2009, pp. 248–255. [CrossRef]
Zhao, Z.; Liu, Z.; Larson, M. Adversarial Color Enhancement: Generating Unrestricted Adversarial Images by Optimizing a Color Filter, 2020, [arXiv:cs.CV/2002.01008]. [CrossRef]
Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. CoRR 2016, abs/1607.02533, [1607.02533].
Dong, Y.; Liao, F.; Pang, T.; Hu, X.; Zhu, J. Discovering Adversarial Examples with Momentum. CoRR 2017, abs/1710.06081, [1710.06081].
Sang, Q.; Zhang, H.; Liu, L.; Wu, X.; Bovik, A.C. On the generation of adversarial examples for image quality assessment. The Visual Computer 2023, pp. 1–16. [CrossRef]
Zhang, Z.; Qiao, K.; Jiang, L.; Wang, L.; Yan, B. AdvJND: Generating Adversarial Examples with Just Noticeable Difference, 2020, [arXiv:cs.CV/2002.00179]. [CrossRef]
Wang, Z.; Simoncelli, E.P. Maximum differentiation (MAD) competition: a methodology for comparing computational models of perceptual quantities. Journal of vision 2008, 8 12, 8.1–13. [CrossRef]
Karli, B.T.; Sen, D.; Temizel, A. Improving Perceptual Quality of Adversarial Images Using Perceptual Distance Minimization and Normalized Variance Weighting. 2021.
Luo, C.; Lin, Q.; Xie, W.; Wu, B.; Xie, J.; Shen, L. Frequency-Driven Imperceptible Adversarial Attack on Semantic Similarity. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2022, pp. 15315–15324.
Bhattad, A.; Chong, M.J.; Liang, K.; Li, B.; Forsyth, D.A. Unrestricted Adversarial Examples via Semantic Manipulation, 2020, [arXiv:cs.CV/1904.06347].
Xiao, C.; Zhu, J.Y.; Li, B.; He, W.; Liu, M.; Song, D. Spatially Transformed Adversarial Examples, 2018, [arXiv:cs.CR/1801.02612]. [CrossRef]
Su, J.; Vargas, D.V.; Sakurai, K. One Pixel Attack for Fooling Deep Neural Networks. IEEE Transactions on Evolutionary Computation 2019, 23, 828–841. https://doi.org/10.1109/tevc.2019.2890858. [CrossRef]

Figure 1. Procedure for proposed IQA models adversarial training.

Figure 2. Impact of subjective score correction, perturbation magnitude, and attack type during training for the LinearityIQA NR-IQA model and KonIQ-10k dataset.

Figure 3. Adversarial robustness

R ↑

for LinearityIQA. Attack methods appear on the x-axis and LinearityIQA versions on the y-axis. Columns and rows are sorted by mean value.

Figure 3. Adversarial robustness

R ↑

for LinearityIQA. Attack methods appear on the x-axis and LinearityIQA versions on the y-axis. Columns and rows are sorted by mean value.

Table 1. Influence of pre-training and fine-tuning on NR-IQA models. Bold denotes the best value, and underlined denotes the second best.

Training		IR-score↑
strategy	SROCC	FGSM		PGD-10
		KonIQ-10K	NIPS2017	KonIQ-10K	NIPS2017
AT	0.784	1.001	1.011	0.424	0.323
+ pretr.	0.717	1.554	1.685	0.565	0.603
+ clean	0.924	2.092	2.218	0.516	0.527
+ clean, pretr.	0.925	1.984	2.248	0.454	0.451

Table 2. Influence of pre-training and fine-tuning on FR-IQA model LPIPS for KADID-10k dataset. Bold denotes the best value, and underlined denotes the second best.

Training strategy	SROCC	IR-score↑
Training strategy	SROCC	FGSM	PGD-10
AT	0.668	0.665	0.597
+ pretr.	0.817	0.801	0.732
+ clean	0.701	0.696	0.621
+ clean, pretr.	0.832	0.872	0.765

Table 3. SROCC ↑ and IR-score of LinearityIQA model on KonIQ-10k dataset for different MOS-penalty strategies and attack types in our adversarial training. Bold denotes the best value, and underlined denotes the second best. SROCC of the original LinearityIQA is 0.931.

		SROCC (train $ε = 2 / 255$ )			IR-score↑ (trained with PGD-1)
Trained with		FGSM	PGD-1	APGD-2	$ε = 2 / 255$	$ε = 4 / 255$	$ε = 8 / 255$
Label strategy	–	0.920	0.917	0.858	0.848	1.231	1.013
	Min	0.908	0.911	0.870	6.252	5.730	4.253
	-5%	0.920	0.922	0.882	1.331	1.301	0.773
	-10%	0.922	0.923	0.901	1.819	1.637	1.264
	PSNR	0.906	0.907	0.922	5.938	5.872	4.504
	SSIM	0.917	0.922	0.886	1.350	1.905	2.458
	MS-SSIM	0.917	0.918	0.878	1.002	1.384	1.165
	LPIPS	0.920	0.921	0.906	1.857	2.608	2.679
	Avg	0.916	0.918	0.888

Table 4. SROCC and IR-score of LPIPS on KADID-10k for different attack types in our adversarial training. Bold denotes the best value, and underlined denotes the second best. SROCC of the original LPIPS is 0.893.

FR-IQA model	Train $ε$	SROCC	IR-score↑
FR-IQA model	Train $ε$	SROCC	FGSM	PGD-10
R-LPIPS [33]		0.858	0.791	0.777
AT-LPIPS (FGSM)	2 / 255	0.855	0.804	0.782
	4 / 255	0.843	0.811	0.791
	8 / 255	0.845	0.807	0.786
	10 / 255	0.832	0.792	0.775
AT-LPIPS (PGD-1)	2 / 255	0.848	0.817	0.801
	4 / 255	0.837	0.821	0.808
	8 / 255	0.856	0.814	0.799
	10 / 255	0.849	0.802	0.783
AT-LPIPS (APGD-2)	2 / 255	0.841	0.802	0.788
	4 / 255	0.834	0.805	0.791
	8 / 255	0.830	0.799	0.783
	10 / 255	0.835	0.788	0.775

Table 5. SROCC↑ on clean data,

R ↑

and IR-score↑ of different NR-IQA models trained using different techniques. The SROCC value is for KonIQ-10k without attacks. The training time is calculated using an Nvidia Tesla A100 80-Gb GPU. Bold denotes the best value for each model, and underlined denotes the second best.

Table 5. SROCC↑ on clean data,

R ↑

		SROCC	$R ↑$ [7] ( $ε = 2 / 255$ )				IR-score ↑				Train.
NR-IQA model		↑	FGSM		PGD-10		FGSM		PGD-10		time
			KonIQ	NIPS	KonIQ	NIPS	KonIQ	NIPS	KonIQ	NIPS	(min)
LinearityIQA [20]	base	0.931	0.699	0.780	0.182	0.266	-	-	-	-	73
	AT	0.824	1.507	1.628	1.485	1.573	0.162	0.069	0.901	0.918	237
	NT [34]	0.930	0.797	0.844	0.304	0.382	0.029	-0.356	0.239	0.227	79
	AT (ours)	0.922	1.555	1.567	0.731	0.921	1.020	1.366	0.657	0.726	275
KonCept512 [17]	base	0.925	0.706	0.620	0.353	0.033	-	-	-	-	93
	AT	0.868	1.246	1.383	0.873	1.135	0.547	0.850	0.657	0.957	222
	NT [34]	0.822	1.459	1.246	1.096	1.008	0.687	0.784	0.774	0.946	101
	AT (ours)	0.913	1.265	1.416	0.632	0.726	1.044	0.900	0.538	0.831	255
HyperIQA [18]	base	0.894	0.531	0.505	-0.168	-0.090	-	-	-	-	133
	AT	0.778	1.624	1.779	1.376	1.634	0.547	0.682	0.945	0.961	141
	NT [34]	0.846	1.093	1.013	0.742	0.733	0.243	0.043	0.826	0.775	219
	AT (ours)	0.891	0.848	1.625	0.622	1.010	1.385	1.413	0.762	0.911	163
WSP-IQA [19]	base	0.916	0.618	0.711	0.124	0.285	-	-	-	-	68
	AT	0.882	0.948	1.140	0.405	0.609	0.534	0.662	0.459	0.506	76
	NT [34]	0.915	0.644	0.742	0.109	0.280	0.279	0.243	-0.094	-0.109	92
	AT (ours)	0.899	1.135	1.224	0.319	0.461	1.352	1.428	0.355	0.317	117

Table 6. SROCC on clean data, 2AFC ↑,

R ↑

and IR-score↑ of different LPIPS versions. The training time is calculated using an NVIDIA RTX A6000 GPU. Bold denotes the best value, and underlined denotes the second best.

Table 6. SROCC on clean data, 2AFC ↑,

R ↑

and IR-score↑ of different LPIPS versions. The training time is calculated using an NVIDIA RTX A6000 GPU. Bold denotes the best value, and underlined denotes the second best.

LPIPS version	SROCC	2AFC ↑			$R ↑$ [7]		IR-score ↑		Train. time
		No attack	FGSM	PGD-10	FGSM	PGD-10	FGSM	PGD-10	(min)
base LPIPS	0.893	0.742	0.260	0.102	0.525	0.311	-	-	46
R-LPIPS [33]	0.858	0.741	0.487	0.306	0.701	0.658	0.791	0.777	663
AT-LPIPS (ours)	0.852	0.742	0.495	0.440	0.753	0.737	0.817	0.801	101

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Increasing the Robustness of Image Quality Assessment Models Through Adversarial Training

Abstract

1. Introduction

2. Related Work

2.1. Image Quality Assessment

2.2. Adversarial Attacks on IQA Models

2.3. Adversarial Training

2.4. Robust IQA Models

3. Proposed Method

3.1. Problem Setting

3.2. Method

4. Materials and Methods

4.1. Experimental Setup

4.2. Evaluation Metrics

4.3. Implementation Details

5. Results

5.1. Ablation Study

5.2. Overall Results

6. Discussion

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

Appendix A. Applicability of Proposed Method to other Adversarial Attacks

Appendix B. Empirical Probabilistic Estimation

Appendix C. Comparison with Adversarial Purification Methods

Appendix D. Additional Attack Details

Appendix E. Ablation Study Results

References

MDPI Initiatives

Important Links

Subscribe