The objective was to explore the contributions and limitations of structure learning methods within an epidemiological analysis of real-world data. The specific aim was to use these networks to identify determinants of access to healthcare among various social factors. We analyzed data from the 2010 wave of the SIRS cohort, which included a sample of 3,006 adults from the Paris region, France. Healthcare utilization, encompassing both direct and indirect access, was the primary outcome. Candidate determinants included health status, demographic characteristics, and socio-cultural and economic positions. We employed a dual approach: a non-automated epidemiological method (initial expert-knowledge network and logistic regression models) and structure-learning techniques based on several algorithms, with and without knowledge con-straints. We compared the results based on the presence, direction, and strength of specific links within the produced network. Although the interdependencies and relative strengths identified by approaches were similar, the structure-learning algorithms detected fewer associations with the outcome than the non-automated method. Relationships between variables were sometimes incorrectly oriented when using a purely data-driven approach. Structure learning algorithms can be valuable in exploratory stages, helping to generate new hypotheses or mining novel databases. However, results should be validated against prior knowledge and supplemented with additional confirmatory analyses.

Keywords:

Subject: Public Health and Healthcare - Other

1. Introduction

Machine learning (ML) methods, which are computational algorithms designed to optimize and automate modelling, were primarily developed for predictive purposes, making their application to causal inference, especially in epidemiology, less straightforward [1,2]. Causal inference typically relies on prior hypotheses and existing knowledge, which are not inherently derived from data [2,3,4,5]. While ML can enhance effect estimation by optimizing models, it does not inherently address the challenge of identifying confounders, a crucial step for causal inference from observational data [2]. Thus, ML methods are most beneficial for refining effect estimation using more flexible models than traditional regressions—such as VanderLaan’s SuperLearner [6,7]—once causal structures have been established based on prior knowledge. However, these methods remain underutilized in practice: a 2021 review identified only eight studies applying ML to causal inference in social epidemiology [2].

Recently, a field known as ‘automatic discovery of causal structures using Bayesian networks’ (also referred to as ‘causal discovery’) has emerged [8]. These methods, developed as a distinct branch of machine learning [1], aim to automatically identify causal structures with varying levels of constraint from prior knowledge [4,8,9]. However, like other ML methods, they have not been widely adopted in epidemiological practice [8,9,10,11]. Despite numerous algorithms being developed using simulated data, challenges such as model parameterization, result validation, accuracy measurement, and generalizability hinder their application to real-world data [8]. Yet, these methods could be particularly valuable in clinical and epidemiological research, as they facilitate the exploration of complex phenomena in an intuitive manner, integrating both expert knowledge and empirical data [11]. In summary, causal discovery methods could benefit epidemiology by (a) mining large datasets with numerous variables, by enabling the simultaneous assessment of the role of the roles of various variables and their direct or indirect contributions to a given outcome in a holistic and conditional framework; (b) serving as an alternative or complementary approach to traditional statistical inference, utilizing uncertainty quantification and propagation within a Bayesian framework rather than relying solely on frequentist methods; (c) enabling the translation of validated knowledge into actionable insights based on updatable data and observations.

However, the use of structure learning methods in epidemiology still raises several questions. Confidence in the discovered structures, parameter estimates, and probability calculations remains uncertain, as the criteria for assessing reliability, robustness, and accuracy have not yet been established. Additionally, it is unclear whether the identified links are truly causal. These methods may not yet be mature enough for application to real epidemiological data, and the conditions under which they could be effectively used need to be clarified.

The objective of this study was to explore the potential contributions and limitations of structure learning methods in an explanatory epidemiological analysis using real-world data. We compared networks of interdependencies between variables identified by various algorithms to a conceptual model proposed by experts and tested through a non-automated analysis, assessing the presence, direction, and strength of links. Our specific aim was to use these networks to identify the direct determinants of access to care among various social candidate factors.

2. Materials and Methods

2.1. Population

The SIRS cohort (French acronym for Health, Inequality, and Social Disruptions) has been following a representative sample of approximately 3,000 adults from the Paris metropolitan area since 2005, as part of a multidisciplinary research program, designed to study the social and territorial determinants of health and healthcare utilization. In 2005, 50 neighborhoods (50 ‘IRIS’, i.e., census-based units each comprising around 2,300 inhabitants and covering an average area of 0.25 km²) were randomly selected from the 2,595 IRIS in Paris and the nearby departments of Hauts-de-Seine, Seine-Saint-Denis, and Val-de-Marne. Sixty households were then randomly drawn from each IRIS, and one adult per household was selected for interviews at their home. In 2010, 47% of the participants from the initial 2005 survey were successfully re-interviewed (2.6% had died, 1.8% were too ill to participate, 13.9% had moved out of the selected IRIS, 2.7% were unavailable during the survey period, 18.4% declined to participate, and 13.4% could not be contacted). Those who could not be re-interviewed were replaced by new participants selected from the same IRIS. The refusal rate for new participants was 29%, consistent across both 2005 and 2010. This study utilizes data collected in 2010. The final sample of 3,006 French-speaking adults was adjusted to account for the sampling strategy and then stratified by age and gender according to census data. There are no missing data in the dataset used. The detailed methodology of the SIRS study has been described previously [12,13,14].

2.2. Measures

The initial SIRS study focused on three key areas that justified the creation of the cohort: the impact of social ties and integration into various spheres of sociability on health-related behaviors, including the pursuit of curative and preventive care; the health status of immigrants and individuals of immigrant descent; and, finally, the influence of living environments, as captured by a geographic information system that integrates participants’ home addresses and some of their daily destinations [14]. The cohort is well known in the field of access-to-care studies in social epidemiology, having produced numerous publications on this topic [12,13,14,15,16,17,18].

In our study, healthcare utilization was the outcome. Since 2004, the French healthcare system has implemented a ‘soft gate-keeping’ model [19], allowing two types of ambulatory medical care access: (1) access to general practitioners (GPs) as a primary point of care or as an entry to specialists, and direct access to certain specialists (gynecologists, ophthalmologists, pediatricians, or psychiatrists); and (2) access to non-direct-access specialists, which typically requires a referral from a GP or, alternatively, direct consultation at full cost. Our primary outcome was the type of access, measured by the ‘Direct Access to Care’ (DAC) variable, coded as ‘yes’ if the individual had consulted a GP or a direct-access specialist at least once in the past twelve months. In a subsequent analysis, we explored the second type of healthcare utilization, measured by the ‘Indirect Access to Care’ (IAC) variable, coded as ‘yes’ if the individual had consulted a non-direct-access specialist at least once in the past twelve months.

The candidate determinants of healthcare utilization were selected from the available data and based on existing literature, encompassing variables related to health status, demographic characteristics, and socio-cultural and economic position. Health status was assessed using perceived health (categorized as ‘good’ or ‘average/poor’) and the presence of chronic health conditions. Demographic characteristics included age (grouped as ‘18-29,’ ‘30-44,’ ‘45-59,’ ‘60-74,’ and ‘75 or older’) and gender (women or men). Socio-cultural and economic position was measured using several variables: origin (categorized as French born to two French parents, French born to at least one foreign parent, and foreign-born immigrant), education level (none/primary, secondary, tertiary), employment status (employed, unemployed, inactive, or retired), income (total household income divided by the number of consumption units, sorted into quintiles), health insurance status (full coverage by statutory health insurance [SHI] and voluntary health insurance, or SHI coverage only), social integration (frequency of social contacts, categorized into quartiles), and proximity to the medical profession (having or not having a medical professional among close relatives). A detailed description of these variables has been provided previously [14,15,16].

2.3. Statistical analysis

We performed analyses based on the identification of a network of oriented links between the determinants of healthcare utilization, using several approaches. For the principal analysis, we used “direct access to care” as outcome, then we used “indirect access to care”.Considering the following network W→X →Y, where arrows denote oriented links between 3 variables, X is called a “direct determinant” (or “parent”) of Y (“child”) and W, a “indirect determinant” (“grand-parent”) of Y.

We used several approaches: first we used a non-automated approach, then structure-learning approaches, based on several algorithms.

2.3.1. “Non-Automated Approach”

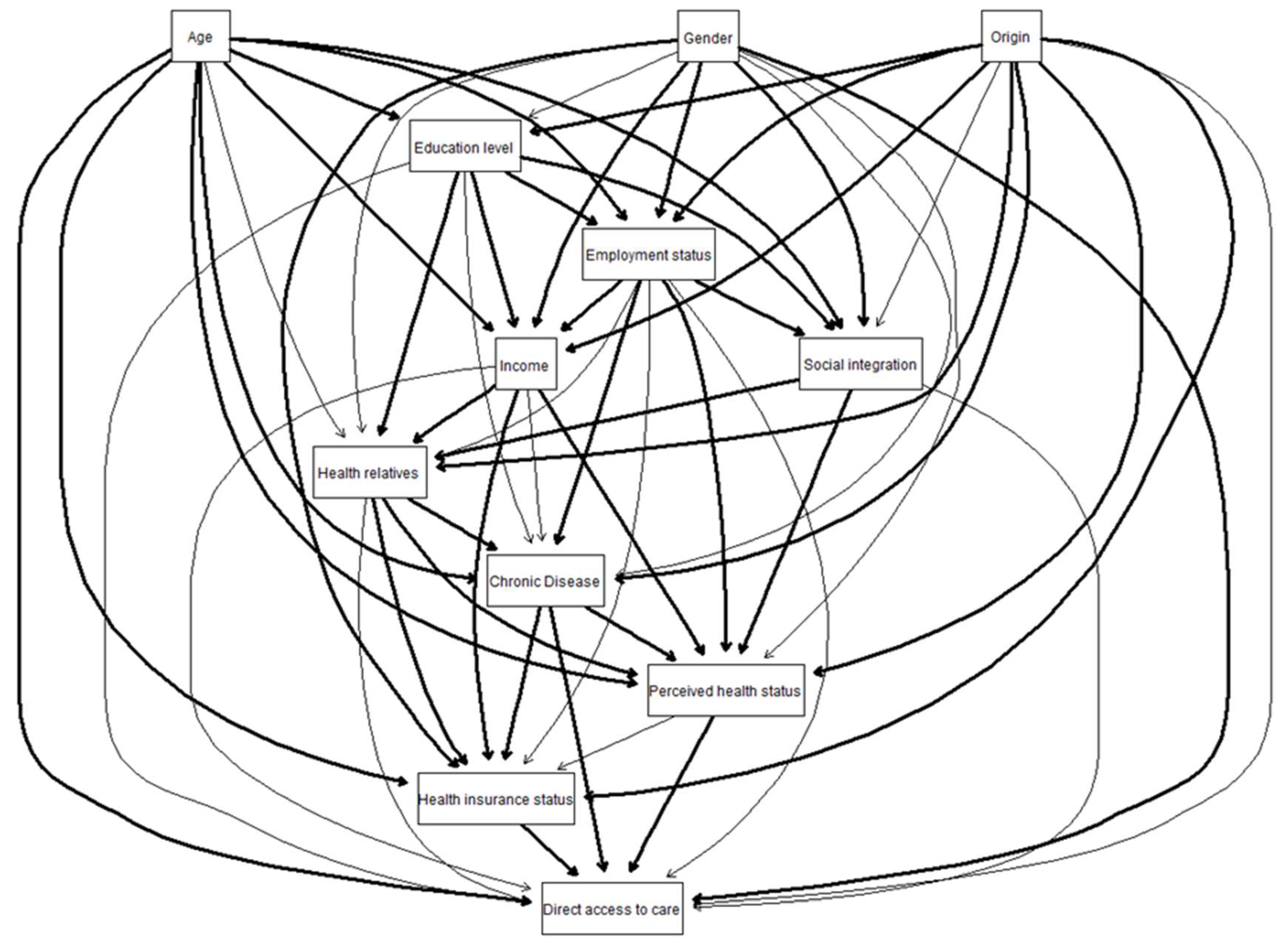
An initial conceptual network was developed by two social epidemiology experts, drawing on existing literature and prior knowledge. Each variable was then modelled by its potential direct determinants using logistic regression. A step-by-step selection process was applied to produce a final network, where all arrows represented significant associations (p < 0.05) between variables, with directions based on the initial expert-defined network. This final network, along with those produced by structure-learning approaches, was visualized using the bnlearn and Rgraphviz packages in R. Links confirmed by the non-automated approach were represented with thick lines, while those proposed by experts but not confirmed were shown with thin lines.

2.3.2. Structure Learning Approaches

We constructed networks using several structure-learning algorithms, which fall into three main categories [20,21]:

Score-based algorithms: These identify the network that maximizes a score function reflecting how well the network fits the data [22]. We used the Hill Climbing algorithm with a BIC score (Bayesian Information Criteria) from this category.
Constraint-based algorithms: These infer conditional dependencies between variables based on the Markov property of Bayesian networks and orient links using d-separation and acyclicity constraints, resulting in partially oriented networks [21,23,24]; We used the Inter-IAMB [25] algorithm.
Pairwise algorithms: These employ an information-theoretic approach to filter out indirect interactions, resulting in non-oriented networks [26]. We used the ARACNE [26] algorithm.

Each algorithm was run 100 times on bootstrap samples, and a link was included in the final network if its frequency in the bootstrap replicates was ≥ 5% (a conservative selection threshold). Initially, the algorithms were applied without constraints (“only data-driven learning”). We then introduced constraints (“constrained learning”) by specifying certain forbidden oriented links: i.e., ‘age,’ ‘gender,’ and ‘origin’ could not have any determinants, and ‘income’ could not be a determinant of ‘educational level’ or ‘employment status.’ Additionally, ‘employment status’ could not influence ‘educational level,’ and ‘health insurance status’ could not be a determinant of ‘income,’ ‘educational level,’ ‘employment status,’ or having a medical professional among relatives.

2.3.3. Comparison of Approaches

To streamline the results, we focus solely on the identified direct links with the outcome—specifically, the connections between ‘access to care’ and other variables identified as direct determinants of ‘access to care’ or as dependent on it. For these links, we compare their presence or absence based on the different approaches used, their direction (whether they are directed toward or away from the outcome), and their strength. In the non-automated approach, strength is represented by the odds ratios in the final multivariate logistic regression. In the ‘structure learning’ approach, strength is measured by the frequency of the link’s selection in bootstrap replications (expressed as a percentage). While these measures of strength are not directly comparable, the ranking of link strength can still provide valuable insights.

Analyses were performed with R 3.6.1 [27] and R studio 1.2.5001. For the structure learning algorithms, we used the “bnlearn” package [21]. Code and data available on demand.

2.4. Ethical Approval

The SIRS cohort received legal authorization from the “Comite consultatif sur le traitement de l’information en matière de recherche dans domaine de la sante” (CCTIRS) and from the “Commission nationale de l’informatique et des libertés” (CNIL). Participants provide their verbal informed consent. For this study, written consent was not necessary according to the French law [14,16].

3. Results

3.1. Description of Population

3006 people were included in the study. Among the cohort, 60.5% were women, slightly over-represented, and 89.2% of the population had at least one direct access to care within the year. The characteristics of the population are detailed in Supplementary Data.

3.2. Non-automated Epidemiological Approach

3.2.1. Direct Access to Care

The final network, identified by the non-automated epidemiological approach from the conceptual network proposed by experts, is given in Figure 1. Concerning the direct links to DAC, the experts first considered that all the candidate determinants of “direct access to care” could potentially be direct determinants of the outcome. After a step-backward selection, 5 variables among the 11 had been identify as direct determinants. The results are synthetized in Table 1.

3.2.2. Indirect Access to Care

After a step-backward approach, 8 variables among the 11 candidate variables had been confirmed as direct determinants: “age”, “gender”, “education level”, “income”, “health relatives”, “health insurance status”, “chronic disease” and “perceived health status”. Detailed results are given in Supplementary Data.

3.3. Structure Learning Approaches

3.3.1. Direct Access to Care

The only data-driven Hill-climbing algorithms identified 4 variables directly linked to “direct access to care”: “gender”, “health insurance status”, “chronic disease” and “perceived health status”. The only data-driven ARACNE algorithms and Interleaved Incremental Association identified links between direct access to care for 3 variables: “gender”, “health insurance status”, “chronic disease”. The relative strengths of the links seemed to follow the same order in each approach: link with “gender” was always the strongest, followed by the presence of a chronic disease. And “perceived health status”, which was retained only by Hill-Climbing approach and with the least strength. “Age”, which was never retained in the structure learning approaches. The links were not always directed to the outcome. For example, the Hill-climbing and Interleaved Incremental Association algorithms identified “gender” as a child of “direct access to care”.

With knowledge constraints

The knowledge-constraints did not change the absence or presence of links, nor their relative strengths. It changed however the direction of several links, particularly with the Hill-climbing models where the 4 links became oriented to the outcome. The final networks of all the approaches are given in Supplementary Data.

3.3.2. Indirect Access to Care

Blind Hill-climbing algorithm identified the same 8 direct determinants than non-automated approach. “Gender” and “education level” was no longer retained when knowledge-constraints were added. Interleaved Incremental Association algorithms identified 6 of the 8 (did not retained “income” and “health insurance status”) but selected one more: “social integration” (with the lowest strength). ARACNE algorithm retained only “age” and “chronic disease”. The strengths of the links seemed to globally follow the same order in all the approaches. The direction of the links was not homogeneous. The addition of constraints changed some directions. Details are given in Supplementary Data.

Table 2. Results of structure learning approach with “direct access to care” (DAC) as outcome.

	Only data-driven learning			Constrained learning
	Link¹	Direction²	Strength³	Link¹	Direction²	Strength³
Hill-climbing
Age	No	-	-	No	-	-
Gender	Yes	From DAC (70%)	100%	Yes	To DAC (100%)	100%
Origin	No	-	-	No	-	-
Education level	No	-	-	No	-	-
Employment status	No	-	-	No	-	-
Income	No	-	-	No	-	-
Health insurance status	Yes	To DAC (86%)	86%	Yes	To DAC (72%)	69%
Health relatives	No	-	-	No	-	-
Social integration	No	-	-	No	-	-
Chronic Disease	Yes	To DAC (98%)	98%	Yes	To DAC (99%)	99%
Perceived health status	Yes	To DAC (88%)	47%	Yes	To DAC (73%)	26%
Interleaved Incremental Association
Age	No	-	-	No	-	-
Gender	Yes	From DAC (74%)	95%	Yes	To DAC (100%)	95%
Origin	No	-	-	No	-	-
Education level	No	-	-	No	-	-
Employment status	No	-	-	No	-	-
Income	No	-	-	No	-	-
Health insurance status	Yes	To DAC (77%)	24%	Yes	To DAC (69%)	24%
Health relatives	No	-	-	No	-	-
Social integration	No	-	-	No	-	-
Chronic Disease	Yes	From DAC (83%)	59%	Yes	From DAC (81%)	59%
Perceived health status	No	-	-	No	-	-
ARACNE
Age	No	-	-
Gender	Yes	-	100%
Origin	No	-	-
Education level	No	-	-
Employment status	No	-	-
Income	No	-	-
Health insurance status	Yes	-	40%
Health relatives	No	-	-
Social integration	No	-	-
Chronic Disease	Yes	-	97%
Perceived health status	No	-	-

¹ relative apparition of the link in the bootstrap replicates ≥ 5%; ²: direction of the link in ≥ 50% of the bootstrap replicates; ³: frequency of the link in the bootstrap replication (given if ≥ 5%).

4. Discussion

We compared a conceptual model developed by experts, based on prior knowledge, and tested using stepwise logistic regression to networks of interdependencies identified by several structural learning algorithms. The comparison focused on the presence or absence of links, as well as their direction and strength. Although the interdependency patterns and relative strengths were generally similar, the algorithms identified fewer links with the outcome compared to the non-automated approach. Additionally, the direction of some links between variables differed across methods. Introducing knowledge constraints results in networks that more closely resembled the non-automated approach.

Currently, most structure-learning (SL) algorithms have been developed and validated using simulated data and are not widely applied to real-world data [8,9,10,11], which tend to be more complex, often contain missing values, and are typically smaller in size [28]. In this paper, we apply three of these algorithms to a real, complex, but well-known dataset to assess their ability to detect links that are well established in the literature. Our findings suggest that, despite their strong performance on simulated data, these methods are still challenging to implement on real-world datasets. This conclusion aligns with similar research comparing multiple algorithms for identifying causal factors of childhood diarrhea [28]. That study showed that results were highly sensitive to the choice of algorithm, handling of missing data, and learning procedure, concluding that these methods are not yet mature enough to achieve reliable results. Over the past 30 years, many ‘causal discovery’ algorithms have been developed [4], primarily falling into two categories: score-based and constraint-based [29]. Kitson et al. provided a comprehensive overview of these algorithms and their evolution [30]. However, there is still a lack of simple, accessible guides to assist epidemiologists in selecting the appropriate algorithm.

The choice of the ‘non-automated’ method is based on a frequent approach in epidemiology, though it is often implicit and also highly debatable. It does not represent a gold standard, and we do not consider its results as the ‘causal truth.’ The goal was here to compare the consistency of results between automated and non-automated within an exploratory perspective, i.e., as a preliminary step before implementing a more in-depth causal analysis. Validation of results has been identified as a significant challenge when applying these methods to real data [8]. Specifically, it is difficult to validate results in real-world scenarios where the ‘true’ structure cannot be observed, making it impossible to measure the distance between the predicted and observed structures [8,31]. Results are often accepted if validated by experts, which may lead to circular reasoning and confirmation bias: the expert adjusts the results based on prior knowledge, and the outcome is interpreted as confirmation of this prior knowledge [8,32,33].

Regarding the automated methods, we chose a representative algorithm from each of the main families and use the bnlearn method. Other types of algorithms and packages, such as pcalg, could have been used. The aim was not to exhaustively evaluate all packages and algorithms but to test a few on real data in a context where recommendations accessible for epidemiologists are lacking. There are no clear guidelines on how to parameterize these algorithms neither [30]. We therefore used standard parameters for all three algorithms and opted for a conservative threshold (links appearing in more than 5% of bootstrap samples) to minimize false negatives in this initial exploration of the data. However, all three algorithms were less sensitive than the non-automated approach, which is consistent with the literature indicating that these methods require large samples to achieve robust results [4,29]. It may be necessary to adapt thresholds based on sample size and algorithm-specific power, making ‘human choices’ unavoidable. Unfortunately, no clear guidelines exist on this issue.

We used a very conservative threshold for selecting links between variables based on their frequency in bootstrap replications. Despite this, and although the interdependence networks and relative strengths were similar, the algorithms identified fewer links with the outcome compared to the non-automated approach. Relationships between variables were sometimes considered misdirected in the purely data-driven approach, whereas the non-automated model appeared more intuitively accurate (e.g., gender → DAC). Adding knowledge constraints adjusted some link directions, making the networks more consistent with the non-automated model when ‘direct access to care’ was the outcome. This was also true for ‘indirect access to care’ when using the Interleaved Incremental Association algorithm. Additionally, none of the algorithms identified a link between age and the outcome, possibly due to the multinomial nature of the age variable. Even though recent algorithmic developments can handle various types of variables, the effectiveness may still depend on the variable’s form. Binary or continuous Gaussian variables are generally easier for these algorithms to process.

Several assumptions are commonly made when interpreting learned networks as causal networks: (1) the Causal Markov condition, which states that all variables are independent of their non-descendants, conditional on their parents (direct causes) [34] ; (2) Faithfulness, which posits that causally connected variables are probabilistically dependent—this assumption may fail if the effects of multiple paths cancel each other out, rendering the cause and effect probabilistically independent [35]; and (3) Causal sufficiency, which assumes no unobserved common causes (confounders) [36]. These assumptions are nearly impossible to satisfy with real data, but the same is true for many assumptions underlying non-automated statistical methods, such as normality. This may explain the misoriented links in our results. Incorporating expert knowledge is essential, at least to exclude impossible directed links (e.g., income → sex) and to correct potential misorientations [28,37]. Selection biases are also challenging to identify and account for, whether the approach is automated or not. For example, an observed link between ‘age’ and ‘origin’ likely results from selection bias (collider bias), but the consequences on the results are complex to assess for both approaches.

Despite these limitations, structure learning holds significant promise for epidemiology. First, these methods are more interpretable than other machine learning models because they use visual representations [28]. The increasing complexity of machine learning models has amplified the ‘black box’ issue, making them difficult to use, evaluate, and interpret, especially for clinical decision-making [38]. In contrast, structure learning relies on graphical Bayesian networks, which can be considered a more ‘explainable’ machine learning method, at least in terms of result interpretation [39]. Second, these methods are specifically designed for identifying causal structures rather than purely predictive goals, which is particularly relevant for epidemiology, where causal inference is central. However, epidemiologists must be fully aware of the type of causality being addressed: the causality considered by data scientists often differs from that sought by epidemiologists. Unless specific assumptions—such as no hidden confounders and normality for all continuous variables—are met, the directed link established by structure learning algorithms is only informational. This means that the direction of a link is determined by how one variable informs about another. For example, age may provide more information about socioeconomic status than vice versa. For an epidemiologist, a causal link between from X to Y refers to the fact that a intervention in X changes Y [40]. Therefore, the chosen direction between two characteristics might differ from that derived from data and related conditional probabilities. Once this distinction is understood, we can use the term ‘causality’ with greater confidence.

5. Conclusions

Our study highlights two important issues. The first pertains to disciplinary differences, not only in terms and concepts but also in applications and objectives. Both epidemiologists and data scientists work with data, but their approaches differ significantly. Epidemiologists rely on statistical methods to compensate for deviations from an experimental and controlled design, reasoning primarily in terms of experiential evidence. Data scientists, on the other hand, often adopt a data-driven approach, treating data as the reality of the field itself, sometimes at the expense of considering the actual context. This can lead to a confusion of territory, where conclusions drawn from data may hold true for one context but not for the other. Consequently, the meaning of directed link diverges: epidemiologists seek to identify mechanisms linking exposure to disease, while data scientists focus on the best representation of the data, in an informational perspective. The second issue relates to the potential of structure learning algorithms. Our study shows that the current diversity of these algorithms, the lack of clear guidelines for parameter selection, and the implications of these choices prevent us from recommending their use without caution. Epidemiologists lacking a solid theoretical background or technical support in this area may find it challenging to use these methods safely and effectively. Given the rapid advancement of these techniques and their adoption across disciplines, it is crucial for epidemiologists to engage with them. This engagement is necessary not only to identify appropriate applications but also to determine what conclusions can be reliably drawn from these methods.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, TL, CDe, PC, BL and HC; methodology, TL, CDe, PC, BL, CDi and HC; formal analysis, CDi and HC; data curation, TL, PC; writing—original draft preparation, HC; writing—review and editing, TL, CDe, PC, BL and HC; supervision, TL, CDe, PC, BL. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Informed Consent Statement

Participants provide their verbal informed consent. For this study, written consent was not necessary according to the French law.

Data Availability Statement

The authors confirm that all data underlying the findings are fully available without restriction. All relevant data have been deposited to Dryad (DOI:10.5061/dryad.9v79s). cf article Plos One healthcare utilization. Requests can be made to the ERES team (UMRS 1136, Pierre Louis Institute of Epidemiology and Public Health, Department of Social Epidemiology, INSERM, Sorbonne University, Paris, France) for access to data.

Acknowledgments

None.

Conflicts of Interest

authors declare no conflicts of interest.

References

Bi, Q.; E Goodman, K.; Kaminsky, J.; Lessler, J. What is Machine Learning? A Primer for the Epidemiologist. Am. J. Epidemiology 2019, 188, 2222–2239. [Google Scholar] [CrossRef] [PubMed]
Kino, S.; Hsu, Y.-T.; Shiba, K.; Chien, Y.-S.; Mita, C.; Kawachi, I.; Daoud, A. A scoping review on the use of machine learning in research on social determinants of health: Trends and research prospects. SSM - Popul. Heal. 2021, 15, 100836. [Google Scholar] [CrossRef]
Hernán, M.A.; Hernández-Díaz, S.; Werler, M.M. Causal Knowledge as a Prerequisite for Confounding Evaluation: An Application to Birth Defects Epidemiology. Am. J. Epidemiology 2002, 155, 176–184. [Google Scholar] [CrossRef] [PubMed]
Glymour, C.; Zhang, K.; Spirtes, P. Review of Causal Discovery Methods Based on Graphical Models. Front. Genet. 2019, 10, 524. [Google Scholar] [CrossRef]
Peters, J.; Janzing, D.; Schölkopf, B. Elements of Causal Inference: Foundations and Learning Algorithms. The MIT Press, 2017. [Google Scholar]
Laan MJ van der, Rose S. Targeted Learning: Causal Inference for Observational and Experimental Data. Springer Science & Business Media; 2011.
Ahern, J.; Karasek, D.; Luedtke, A.R.; Bruckner, T.A.; van der Laan, M.J. Racial/Ethnic Differences in the Role of Childhood Adversities for Mental Disorders Among a Nationally Representative Sample of Adolescents. Epidemiology 2016, 27, 697–704. [Google Scholar] [CrossRef] [PubMed]
Butcher, B.; Huang, V.S.; Robinson, C.; Reffin, J.; Sgaier, S.K.; Charles, G.; Quadrianto, N. Causal Datasheet for Datasets: An Evaluation Guide for Real-World Data Analysis and Data Collection Design Using Bayesian Networks. Front. Artif. Intell. 2021, 4, 612551. [Google Scholar] [CrossRef]
Arora, P.; Boyne, D.; Slater, J.J.; Gupta, A.; Brenner, D.R.; Druzdzel, M.J. Bayesian Networks for Risk Prediction Using Real-World Data: A Tool for Precision Medicine. Value Heal. 2019, 22, 439–445. [Google Scholar] [CrossRef]
Sgaier, S.K.; Huang, V.; Charles, G. The Case for Causal AI. Stanf. Soc. Innov. Rev. 2020, 18, 50–55. [Google Scholar] [CrossRef]
Kyrimi E, McLachlan S, Dube K, Fenton N. Bayesian Networks in Healthcare: the chasm between research enthusiasm and clinical adoption. 2020. [CrossRef]
Martin-Fernandez, J.; Grillo, F.; Parizot, I.; Caillavet, F.; Chauvin, P. Prevalence and socioeconomic and geographical inequalities of household food insecurity in the Paris region, France, 2010. BMC Public Heal. 2013, 13, 486–486. [Google Scholar] [CrossRef]
Vallée, J.; Chauvin, P. Investigating the effects of medical density on health-seeking behaviours using a multiscale approach to residential and activity spaces: Results from a prospective cohort study in the Paris metropolitan area, France. Int. J. Heal. Geogr. 2012, 11, 54–54. [Google Scholar] [CrossRef]
Chauvin P, Parizot I. Les inégalités sociales et territoriales de santé dans l’agglomération parisienne. Une analyse de la cohorte Sirs (2005). Délégation interministérielle à la Ville; 2009.
Vallée, J.; Cadot, E.; Grillo, F.; Parizot, I.; Chauvin, P. The combined effects of activity space and neighbourhood of residence on participation in preventive health-care activities: The case of cervical screening in the Paris metropolitan area (France). Heal. Place 2010, 16, 838–852. [Google Scholar] [CrossRef] [PubMed]
Lefèvre, T.; Rondet, C.; Parizot, I.; Chauvin, P. Applying Multivariate Clustering Techniques to Health Data: The 4 Types of Healthcare Utilization in the Paris Metropolitan Area. PLOS ONE 2014, 9, e115064. [Google Scholar] [CrossRef] [PubMed]
Rondet, C.; Soler, M.; Ringa, V.; Parizot, I.; Chauvin, P. The role of a lack of social integration in never having undergone breast cancer screening: Results from a population-based, representative survey in the Paris metropolitan area in 2010. Prev. Med. 2013, 57, 386–391. [Google Scholar] [CrossRef] [PubMed]
Trohel, G.; Bertaud-Gounot, V.; Soler, M.; Chauvin, P.; Grimaud, O. Socio-Economic Determinants of the Need for Dental Care in Adults. PLoS ONE 2016, 11, e0158842. [Google Scholar] [CrossRef] [PubMed]
Chevreul, K.; Durand-Zaleski, I.; Bahrami, S.B.; Hernández-Quevedo, C.; Mladovsky, P. France: Health system review. Health Syst. Transit. 2010, 12, 1–291, xxi–xxii. [Google Scholar]
Tsamardinos, I.; Brown, L.E.; Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef]
Scutari, M. Learning Bayesian Networks with thebnlearnRPackage. J. Stat. Softw. 2010, 35, 1–22. [Google Scholar] [CrossRef]
Cooper, G.F.; Herskovits, E. A Bayesian method for the induction of probabilistic networks from data. Mach. Learn. 1992, 9, 309–347. [Google Scholar] [CrossRef]
Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search, Second Edition. second edition edition. Cambridge, Mass: A Bradford Book; 2001.
Verma T, Pearl J. Equivalence and synthesis of causal models. UCLA, Computer Science Department; 1991.
Yaramakala, S.; Margaritis, D. Speculative Markov Blanket Discovery for Optimal Feature Selection. Fifth IEEE International Conference on Data Mining (ICDM'05). LOCATION OF CONFERENCE, USADATE OF CONFERENCE; p. 4 pp.
A Margolin, A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinform. 2006, 7, 1–15. [Google Scholar] [CrossRef]
R Development Core Team. R: A language and environment for statistical computing. Vienna, Austria: 2005.
Kitson, N.K.; Constantinou, A.C. Learning Bayesian networks from demographic and health survey data. J. Biomed. Informatics 2020, 113, 103588. [Google Scholar] [CrossRef]
Gemert, S.l.B.-V.; Stolk, R.P.; Heuvel, E.R.v.D.; Fidler, V. Causal inference algorithms can be useful in life course epidemiology. J. Clin. Epidemiology 2014, 67, 190–198. [Google Scholar] [CrossRef] [PubMed]
Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. Artif. Intell. Rev. 2023, 56, 8721–8814. [Google Scholar] [CrossRef]
Constantinou, A.C.; Fenton, N. Things to know about Bayesian Networks: Decisions under Uncertainty, Part 2. Significance 2018, 15, 19–23. [Google Scholar] [CrossRef]
Lewis, F.I.; McCormick, B.J.J. Revealing the Complexity of Health Determinants in Resource-poor Settings. Am. J. Epidemiology 2012, 176, 1051–1059. [Google Scholar] [CrossRef]
Requejo Castro D, Giné Garriga R, Pérez Foguet A. Exploring the interlinkages of water and sanitation across the 2030 Agenda: a Bayesian Network approach. ISDRS 2018 24th Int. Sustain. Dev. Res. Soc. Conf. Messina Italy -15 2018 Book Pap., 2018, p. 121–35. 13 June.
Spirtes, P.; Zhang, K. Causal discovery and inference: concepts and recent methodological advances. Appl. Informatics 2016, 3, 1–28. [Google Scholar] [CrossRef] [PubMed]
Weinberger, N. Faithfulness, Coordination and Causal Coincidences. Erkenntnis 2017, 83, 113–133. [Google Scholar] [CrossRef]
Scheines, R. An Introduction to Causal Inference n.d.
Shen, X.; Ma, S.; Vemuri, P.; Simon, G. Challenges and Opportunities with Causal Discovery Algorithms: Application to Alzheimer’s Pathophysiology. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
Belle, V.; Papantonis, I. Principles and Practice of Explainable Machine Learning. Front. Big Data 2021, 4. [Google Scholar] [CrossRef]
Pearl, J. Causality. Cambridge University Press, 2009. [Google Scholar]

Figure 1. Network identified by a non-automated epidemiological approach. With: solid thick lines for links proposed by experts and confirmed by the non-automated epidemiological approach, thin lines for links considered as potential by experts but not confirmed by the approach. Direction of arrows was defined by expert (totally not data driven). Graph produced by bnlearn and Rgraphiz package in R.

Table 1. Results of non-automated approach with “direct access to care” (DAC) as outcome.

		Link to DAC¹	Direction²	Strength³
Age	18-29	Yes	To DAC	Ref
	30-44			1.39 (0.98 to 1.98)
	45-59			1.20 (0.83 to 1.72)
	60-74			1.72 (1.12 to 2.64)
	75+			2.23 (1.22 to 4.31)
Gender	Men	Yes	To DAC	Ref
	Women			3.13 (2.45 to 4.02)
Origin	French, French parents	No	-	-
	French, foreign parents			-
	Migrant
Education level	Primary or none	No	-
	Secondary			-
	Tertiary			-
Employment status	Employed	No	-
	Unemployed			-
	Inactive			-
Income	1stquintile	No	-
	2ndquintile			-
	3rdquintile			-
	4thquintile			-
	5thquintile			-
Health insurance status	None or SHI only	Yes	To DAC	Ref
	SHI and VHI			2.38 (1.75 to 3.23)
Health relatives	No	No	-
	Yes			-
Social integration	1st quartile	No	-
	2nd quartile			-
	3rd quartile			-
	4th quartile			-
Chronic Disease	No	Yes	To DAC	Ref
	Yes			2.94 (2.12 to 4.16)
Perceived health status	Good	Yes	To DAC	Ref
	Bad-Average			2.16 (1.50 to 3.20)

¹ significant association found in final logistic regression modelling DAC by other variables identified as its potential direct determinants by experts; ² based on the initial network defined by expert; ³ given here by the Odds Ratio and its 95% confidence interval as estimated by the final logistic regression.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Contribution Of Structure Learning Algorithms In Epidemiology: An Application In A Real-World Dataset

Abstract