Josephson Junction Dynamics as a Ride on a Roller Coaster

1. Introduction

Quantum mechanics approach to the development of a new paradigm in computation methods and advanced sensor systems, renewed the interest in the physics of Josephson junctions. The present work, educational in nature, has been written for researcher and students interested in the Josephson junction subject. It presents the classical Josephson junction dynamics from the refreshing perspective of a familiar mechanical analogy: that with a roller coaster cart dynamics.

To introduce undergraduates and beginners to the electrodynamics of a Josephson junction (JJ), the immediate mechanical analogy with a driven-damped physical pendulum is often used [1,2]. This is advantageously done according to the principle that "The same equations have the same solutions", as often quoted from R. Feynman [3]. The analogy between a JJ and a mechanical pendulum was introduced soon after the discovery of the Josephson effect [4] already by Anderson [5].

The dynamical variables obeying identical equations in this comparison, between JJs and a pendulum, are the Josephson phase difference between the two superconducting electrodes, in the case of a JJ and the deviation angle from the vertical in the case of the pendulum (see Appendix A).

In this note we dwell on a variant of this analogy [6]: We point out the connection between the dynamical states of a point-like Josephson junction and the motion of a small (or big) cart driven by a constant force along an arbitrarily long, specially shaped track. In short, a particular winding roller coaster (see Figure 1a,b). As easily shown, the motion of the cart on such type of roller coaster is ruled by the same equation ruling the phase dynamics in a JJ. To illustrate this mechanical analogy and its possible educational use in the context of the Josephson effect (but also in the very context of elementary mechanics), we focus straightforwardly on solving a specific exercise, chosen among those involving the basic evolution possibilities of the cart, and transpose the solution, together with its meaning, into the Josephson effect domain.

The exercise, allows tracing back to a particular, hardly known and seldom discussed process occurring in a JJ: We refer to the possibility of ’dynamical switchings’ of the junction from the zero voltage state to the resistive state. The analogy seems particularly fitting for this case study, as the authors themselves were able to experience.

In a ’dynamical switching’, a JJ undergoes unexpected, spontaneous switchings from the zero voltage state to the resistive state, even in the absence of fluctuations, when solicited by fast signals. In reference [7], the phenomenon is introduced and analyzed from the point of view of the theory. Furthermore, it is rightly put in connection with the observed so called ’punchthrough’ effect (see [8] and references in [7])). Note that ’unexpected’ here means simply ’for a current lower, or much lower, than the maximum critical current $I_{c0}$ of the junction’ (with values, typically, in the range $1÷10\mu A$). The maximum critical current of a Josephson junction can be defined as the maximum Josephson current observed under ideal lab conditions: minimum fluctuations (near zero temperature), quasistatic current variation, perfect magnetic shielding, etc. Given the operation temperature, it is a key quality parameter of the junction.

It is worth to describe more precisely what one really observes in a ’dynamical switching’: Initially we have a junction in the zero voltage state (see Section 5), then the current i is increased from an initial value $i_1$ (may be zero) to a greater value $i_2$, lesser than the critical current $I_{c0}$ (but greater than a threshold $i_c>i_1$), in a very short time $\Delta t$, much shorter than the characteristic time $\tau$, given by $\tau ={(\hslash C/2e{I}_{c0})}^{1/2}$, the inverse of the Josephson plasma frequency (typically, ${10}^{-10}÷{10}^{-9}s$).

Under this condition of fast increment, the new value of current reveals unstable for the zero voltage state. That is, after the current has reached the value $i_2$, the junction switches stably to the finite voltage state (the time it takes, depends sensitively on $i_2$, as estimated in Appendix B). Had the current $i_2$ been reached gradually or more gradually in comparison with $\tau$ ($\Delta t>>\tau$), no such switch would have been observed at the current value $i_2$. The junction would have simply remained on the superconducting current branch, with that new value of the current and zero voltage across the electrodes. This, in practice, constitutes an effective reduction of the junction critical current and, ultimately, an issue to be taken into account at fast signals.

Likewise, in the mechanical analogy here presented, a cart is launched from the bottom of one of the valleys for an indefinite long ride (the equivalent of the finite voltage state in Josephson junction) on the roller coaster of Figure 1. A pushing engine imparts a constant force f on the cart, providing a maximum thrust lesser than the full weight of the cart, but greater than a threshold $f_c$ to be determined in the exercise. The rise time to the maximum thrust level is fixed to be much less than the typical period of oscillation of the cart $\tau$ ($0.5÷3s$, a time interval ranging from a lab model prototype to a hypothetical human scale amusement park roller coaster with the shape of Figure 1).

We remark that the same exercise we discuss hereafter, could have been carried out as well by adopting the classical analogy between a JJ and the winding-oscillating physical pendulum and stress that our emphasis, here, is on introducing a further educational tool to accompany the existing one.

The paper is organized as follows: in Section 2, Section 3,Section 4, we find the equation of motion of the cart on the track and discuss in detail the particular dynamical evolution of the cart, which we are interested in. This mechanical process can be synthesized as ’the launch of the cart on the roller coaster’. In Section 5, the Josephson equations are briefly reviewed, together with the famous CRSJ (Capacitively and Resistively Shunted Junction) model, for convenience of those readers completely unfamiliar with the Josephson effect. Then the ’launch of the cart’ is confronted with the ’dynamical switching of the junction’ to fix the main points of the analogy. In Section 6, we illustrate an extension of the analogy to the case of Josephson interferometers, i.e. to superconducting circuits containing two or more coupled junctions. Then we go to the Conclusions.

2. The Equation of Motion of the Mechanical System

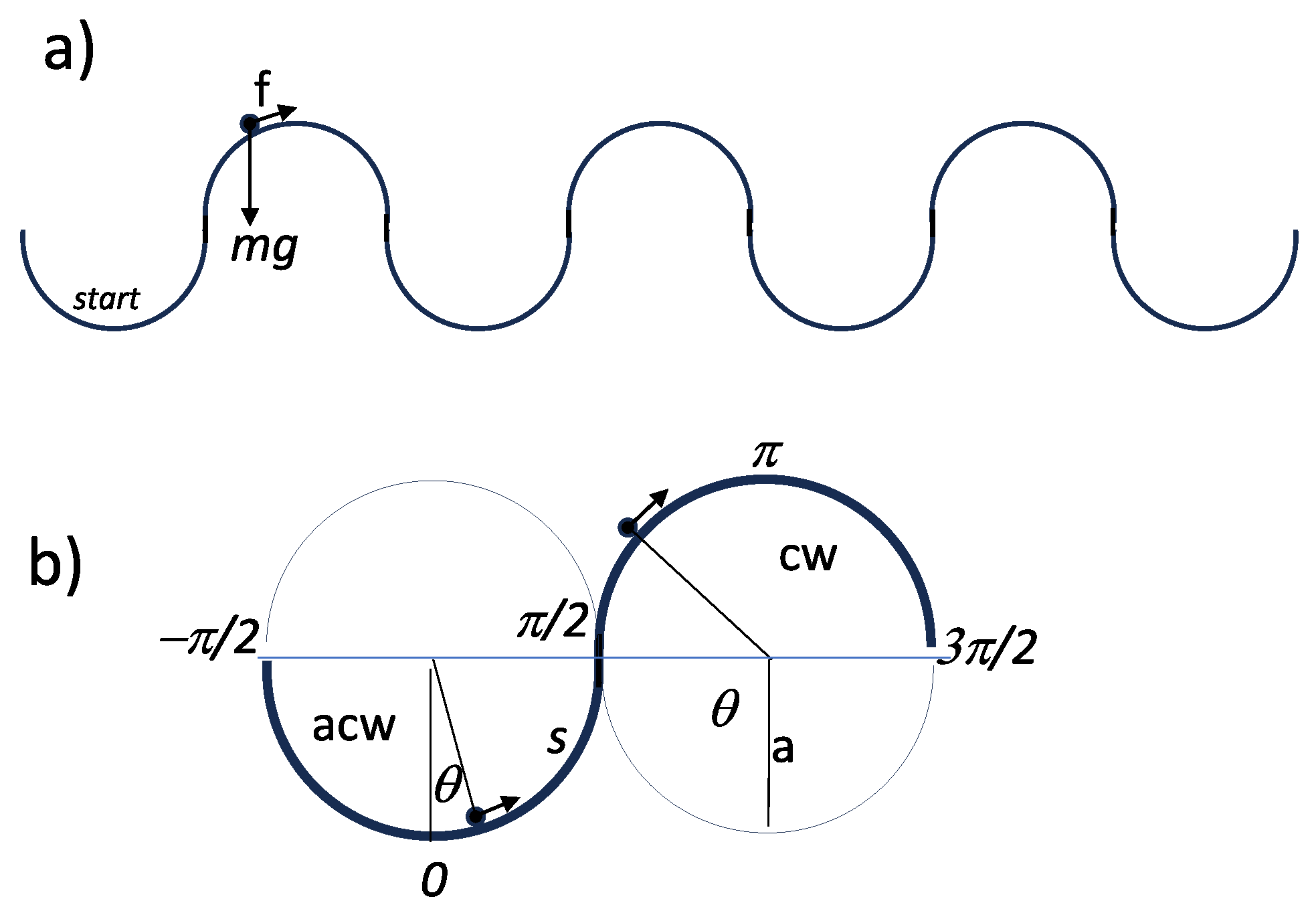
Suppose, as shown in Figure 1, that we have a suspended track and a small cart of mass m, which is constrained to it. The cart can roll on the track with negligible friction. The track itself has a special periodic wavy shape: it is obtained by using an arbitrary number of equal semicircular track segments of the same radius a, alternating valleys and hills.

Three forces act on the cart: a) the weight force ($mg$), b) a constant thrust f pushing the cart ($0\le f\le mg$), c) the reaction force of the track. The component of the weight normal to the track is exactly balanced by the constraint reaction of the track itself. The component of the weight parallel to the track acts upon the cart together with the thrust of the engine and determine, together, the cart acceleration.

Note that an approximately constant thrust parallel to the track can be realized on the human scale in many ways: rocket engines, water jet engines, or linear electric motors, such as in a certain futuristic roller coaster [9], or in a more humble physics lab educational project, by using a small cart driven by a fan engine or a propeller.

We will assume that the thrust f can be turned on instantaneously ($\Delta t<<\tau$), as said, to a certain value and kept constant to that value for an arbitrary time-lapse, or also reduced instantaneously from a high to a lower value, or even stopped. As easily recognized, the thrust on the cart is the equivalent of the current supplied to the junction, so that the assumption of instantaneously thrust turning on is the hypothesis that the current in the junction can be raised instantaneously to a requested value, a condition met when measuring small capacitance, high Josephson critical current junctions.

The position of the cart on the track is our dynamical variable. It is determined in the curvilinear coordinate system $s=a\theta$, $-\infty <\theta <+\infty$, by the difference $s-s_0$, where $s_0$ is the point at the bottom of one of the valleys taken as the origin ($s_0=0)$. In Figure 1 the self-explaining details of the geometry used are illustrated.

The trajectory of the cart is a regular sequence of $\mathit{vertical\; semicircles}$ such that the component of the weight force parallel to the track is given by $-mgsin(s/a)$ at any s, as easily verified, and the acceleration of the cart has the simple form $a(d^2\theta /d{t}^2)$. Under these conditions, the equation of motion, completed by a damping term introduced for future reference ($\mu ds/dt$, with constant coefficient $\mu$), writes

$$m{\displaystyle \frac{d^{2}s}{d{t}^2}}=-mgsin\left({\displaystyle \frac{s}{a}}\right)+f-\mu {\displaystyle \frac{ds}{dt}}$$

(1)

which is the equation of a driven-damped pendulum. Note that the sinusoidal form of the gravity force term in Equation (1) is essential for the analogy with a Josephson junction to apply. In the case at the hands of the roller coaster, the sinusoidal form, is a consequence of the special shape of the track. To avoid scaling effects, we write the above equation in dimensionless form (which we use for the rest of the paper)

$${\displaystyle \frac{d^{2}s}{d{t}^2}}=-sin\left(s\right)+\overline{f}-\beta {\displaystyle \frac{ds}{dt}}$$

(2)

where now lengths are in units of a, time is in units of $\tau ={(a/g)}^{1/2}$, $\overline{f}=f/mg$ and $\beta =(\mu /m){(a/g)}^{1/2}$ is a dimensionless damping coefficient. In these units velocity is in units of ${\left(ga\right)}^{1/2}$, the acceleration in unity of g, energy is in units of $mga$.

Finally, we recall that the conservative force terms on the right-hand side of Equation (2) can be derived from the potential $U\left(s\right)=1-cos\left(s\right)-\overline{f}s$ (an arbitrary constant has been set to 1 such that $U\left(0\right)=0$). This way, the motion of the cart in real space (as well as the dynamics of the junction) could be analyzed, likewise the motion of the pendulum, in terms of a hypothetical particle of the same mass m, falling in the so-called ’washboard’ or ’tilted washboard’ potential, the name by which this potential is known. In this note, however, we choose deliberately to base our analysis directly on the equation of motion in the form of Equation (2) omitting, as much as possible, reference to the washboard potential.

3. An Exercise: Dynamical Condition for the Roller Coaster Ride

Now we pose the following question: Neglecting damping, and in the conditions above described for the engine operation, what is the minimum thrust, ${\overline{f}}_c$, needed to launch the cart in an indefinite duration ride (a ’running state’), assuming that the cart starts at rest (removable wheel chocks can be used to this aim) from the bottom of a valley (i. e. ${s\left(t\right)|}_{t=0}{=ds\left(t\right)/dt|}_{t=0}=0$) ?

3.1. The Statics of the Cart

Preliminarily, we observe that, as easily seen, Equation (2) admits two stationary (no time dependence) solutions corresponding to two positions (depending on $\overline{f}$, with $0\le \overline{f}\le 1)$ on the track given by $s_1={sin}^{-1}\left(\overline{f}\right)$, and $s_2=\pi -{sin}^{-1}\left(\overline{f}\right)$. At these two points, between 0 and $\pi$, the vehicle, placed there, can stand still with the engine running, because the thrust of the engine balances exactly the gravity. However, while the equilibrium in $s_1$ (a point in $[0,\pi /2]$) is a stable one (except possibly for innocuous small oscillations (Appendix C), which we do not discuss here), that in $s_2$ (a point in $[\pi /2,\pi ]$) is critical, or unstable, (as a simple perturbation analysis of Equation (2) shows). This in practice means that placing the cart at the instability point $s_2$ with a positive velocity, even though small, ensures that the cart, after a while, leaves $s_2$ and crosses the top of the hill. As we will show, this is possible, in particular, when the cart starts at rest from the bottom of the track, which will enable us to respond the question asked above (see Section 3.3).

3.2. The Dynamics of the Cart: Integral of Motion

After multiplying by $\dot{s}$ Equation (2) ($\dot{s}$ denoting $ds/dt$), and integrating in time, we find the integral of motion

$${\displaystyle \frac{1}{2}}{\dot{s}}^2-cos\left(s\right)-\overline{f}s=constant$$

(3)

The initial conditions (${s\left(t\right)|}_{t=0}{=ds\left(t\right)/dt|}_{t=0}=0$) fix the constant (and the integral of motion) to $-1$ in our exercise. This equation is nothing else than the kinetic energy theorem applied to the cart driven along the track: In the absence of dissipation, the overall work done by the applied forces, in going from 0 to s, is equal to the variation of kinetic energy of the body (the material point):

$${\displaystyle \frac{1}{2}}{\dot{s}}^2-0={\int }_0^s(-sin\left(z\right)+\overline{f})dz=cos\left(s\right)+\overline{f}s-1$$

(4)

(Incidentally, we note that the integral of motion Equation (3) is the conserved total energy. In fact, write Equation (4) as $(1/2)\dot{s}+1-cos\left(s\right)-\overline{f}s=0$, this last equation, with the identification of the tilted washboard potential, $U\left(s\right)=1-cos\left(s\right)-\overline{f}s$, is in the form of kinetic energy plus the potential energy: $(1/2)\dot{s}+U\left(s\right)=0$. The arbitrary choice $U\left(0\right)=0$ sets at 0 the total energy.)

Equation (4) gives the velocity as a function of the position in the form

$$\dot{s}=\pm \sqrt{2(cos\left(s\right)-1+\overline{fs})}$$

(5)

From Equation (5), by zeroing the velocity, i.e. requiring $cos\left(s\right)+\overline{f}s-1=0$, we obtain the locus of the points in the plane $s-\overline{f}$ where the velocity of the cart is zero (in addition to the starting point in the origin) as

$$\overline{f}={\displaystyle \frac{1-cos\left(s\right)}{s}}$$

(6)

This relationship is represented graphically in Figure 2a, together with three representative lines drawn at constant thrust values. In Figure 2b, the orbits corresponding to these fixed values of the thrust on the cart have been calculated by Equation (5), to give, together with Figure 2a, a qualitative classification of the paths in the phase space.

3.3. The Minimum Thrust to Launch the cart.

Horizontal lines at constant thrust may cross or not the curve predicted by Equation (6) (see Figure 2a) :

a) There can be no intersection at all. The thrust is greater than the highest peak in the curve: the velocity is never zero along the trajectory. This means that, in this case, an open orbit is realized. The cart easily enters the running state starting from $s=0$ (see Figure 2b, the curve with $\overline{f}=0.9$).

b) A single intersection between curves occurs. The thrust corresponding to this point (the top of the first peak in Figure 2a) is the critical thrust value ${\overline{f}}_c$ that fixes the threshold to enter the running state, assuming $\overline{f}>{\overline{f}}_c$ (or not entering the running state, assuming $\overline{f}<{\overline{f}}_c$).

This value, most of all, is the solution to our exercise. In fact,

i) $s_c$, the position of the maximum in the curve of Figure 2a, is a point of the track, reached by the cart thanks to the thrust ${\overline{f}}_c$. At $s_c$the velocity of the cart is zero, since the couple ($s_c$,${\overline{f}}_c$) is a point of the curve representing Equation (6). ii) $s_c$is an instability point because in $s_c$, $d\overline{f}/ds=0$, that is, $ssin\left(s\right)-1+cos\left(s\right)=0$, so that $s_c$ solves also $\overline{f}=sin\left(s\right)$, as easily seen by substitution in Equation (6). Furthermore, $s_c$ cannot be ${sin}^{-1}\left({\overline{f}}_c\right)$ since in ${sin}^{-1}\left({\overline{f}}_c\right)$ the second derivative $d^2\overline{f}/d{s}^2=cos\left(s\right)/s$, is positive (it takes the value $\sqrt{1-({\overline{f}}_c}{)}^2)/{sin}^{-1}\left({\overline{f}}_c\right)$). Thus $s_c$ must be the instability point $\pi -{sin}^{-1}\left({\overline{f}}_c\right)$.

In brief, ${\overline{f}}_c$ is the thrust taking the cart from $s=0$ to the instability point $s_c=\pi -{sin}^{-1}\left({\overline{f}}_c\right)$, where the cart arrives with zero residual velocity. Thus, ${\overline{f}}_c$ is the thrust threshold to launch the cart from $s=0$. To be definite, we find numerically $s_c=2.33112$ for the position, and ${\overline{f}}_c=0.72461$ for the thrust threshold (see Figure 2b, the curve with $\overline{f}=0.7246$). It is interesting to note that, at the top of the track ($s=\pi$), the cart has a velocity $\simeq 0.74$ in units of $\sqrt{ga}$ and that it is not possible to cross this point with a lower velocity. The maximum acceleration at launch is $0.7246g$, and is reached at $s=0$ and $s=\pi$. After crossing the top (actually, even a little before crossing the top, as can be calculated by energetic considerations), the engine could be also safely shut off while the cart continues its ride by inertia (with a constant average velocity). If not, of course, the velocity of the cart in the present approximation of zero damping, would continue to grow indefinitely. In the presence of moderate damping, the launched cart reaches a dynamical state similar to the ’inertial’ one in which the average velocity, after a transient, remains constant and the energy lost by drag is continuously provided by the engine thrust (energy balance state). This is also the essence of the ’running state’ in a Josephson junction where the average velocity is the equivalent of the average voltage across the junction.

c) Two intersections occur at the points $s_I$ and $s_{II}$, (see Figure 2a). In the figure we consider the case $\overline{f}=0.6$ for which $s_I=1.42$ and $s_{II}=3.31$. No running state is entered. The phase path is a closed orbit, indicating that the thrust on the cart is too weak. The cart simply moves back and forth between the origin and the point $s_I$, where the velocity cyclically reverses (see Figure 2b).

As far as the point $s_{II}$ is concerned, this point marks a position where an open orbit can start, as the figure shows. At that point, the velocity is zero, but the position is different from zero, so this solution, although possible, is extraneous to our exercise. The point here is that the integral of motion, Equation (5), does not correspond uniquely to the initial conditions assumed in the exercise. The cart would describe an orbit (an open orbit in the case considered) characterized by the same integral of motion, that is, -1, also when it is set at rest in $s_{II}=3.31$ (shortly after the top) and pushed with the thrust $\overline{f}=0.6$. (The integral of motion is quickly verified to be -1 since $-cos\left(s_{II}\right)+0.6s_{II}=-1$.)

Let us summarize. With a step-like time-rising thrust, corresponding to about the $72\%$ of its weight, $mg$ ($f_c=0.7246$ mg), the cart, in the absence of damping, starting at rest from the bottom of the valley, has enough energy to climb up to the instability point at $\pi -{sin}^{-1}\left(0.7246\right)=2.33$ rad (about $133;30$). A thrust ${\overline{f}}_c+ϵ$ of a small amount $ϵ$ greater than ${\overline{f}}_c$, put the cart in the running state for an indefinite time.

4. Further Considerations About the Launch of the Cart

4.1. Minimum Thrust for More General Initial Conditions

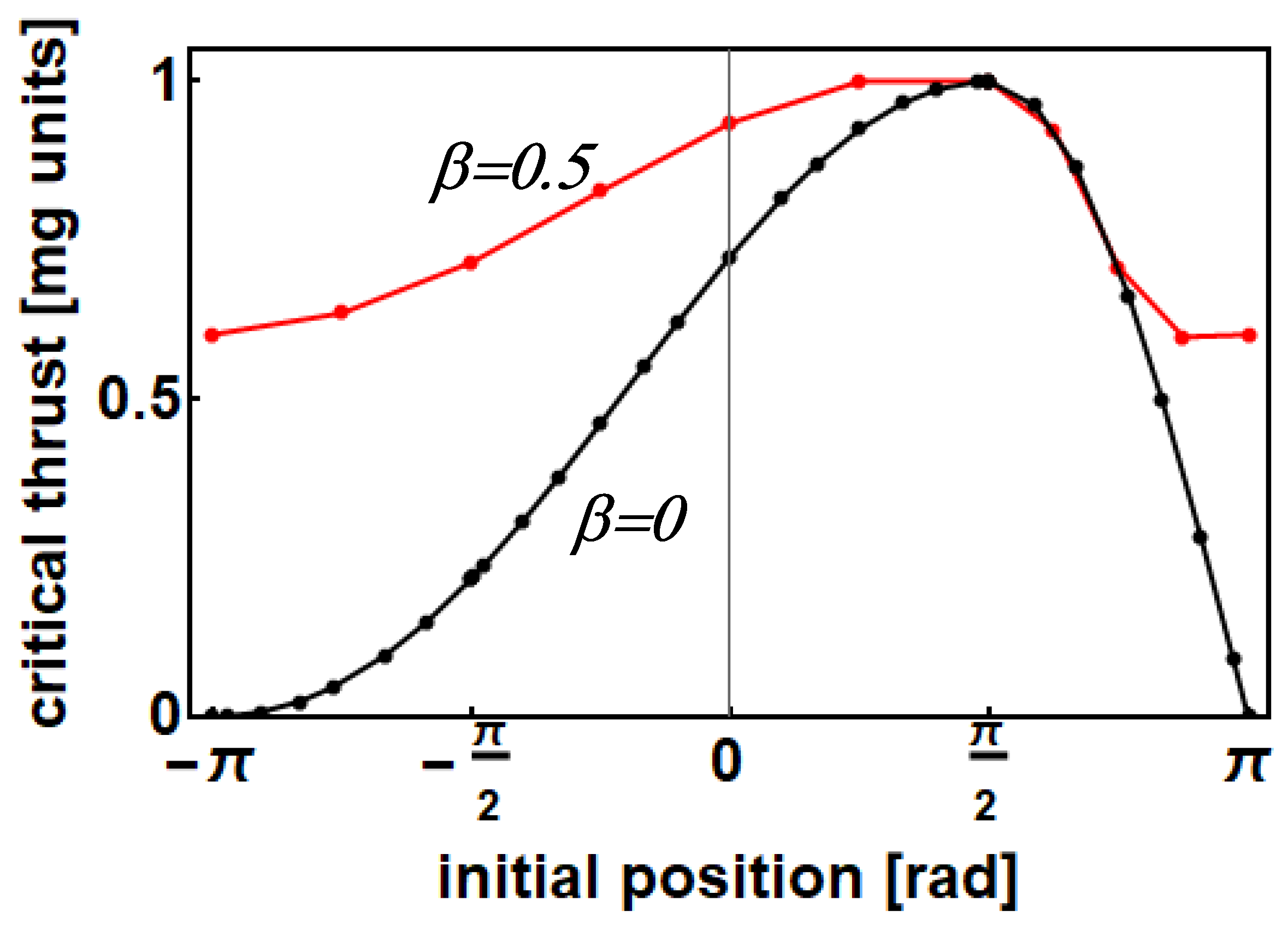
The threshold found for entering the running state, ${\overline{f}}_c=0.7243$, corresponds to the initial conditions ${s\left(t\right)|}_{s=0}{=ds\left(t\right)/dt|}_{s=0}=0$. However, thresholds smaller than ${\overline{f}}_c=0.7243$ can be obtained for more general initial conditions, in the idealistic condition of absence of damping.

Let us suppose, for instance, that the cart oscillates around zero in the first valley of the roller coaster, waiting for the ignition (i.e. with $\overline{f}=0$). The max elongation is $|s_0|$ ($s_0\in [-\pi ,\pi ]$) and let us, for simplicity, assume that at the instant of ignition the position of the cart is the point $s_0$ (at this point, its velocity is also zero, because $s_0$, the maximum elongation, is an inversion point for the velocity). Then, following the same argument as in the previous section (Section 3.3, point b), Equation (6) is generalized as follows:

$$\overline{f}={\displaystyle \frac{cos\left(s_0\right)-cos\left(s\right)}{s-s_0}}.$$

(7)

The integral of motion for the new initial conditions is $-cos{s}_0-\overline{f}{s}_0$. Equation (7) represents the locus of the points in the plane $s-\overline{f}$ where the velocity of the cart is zero (in addition to the starting point at $s_0$). Again the critical thrust is the maximun of the curve of Equation (7) in the interval $[0,\pi ]$. The condition $d\overline{f}/d\theta =0$ gives $coss=cos{s}_0-(s-s_0)sins=0$, this, in turn, gives $\overline{f}=sins$, when used in Equation (7). Then, assigned $s_0$, we can find numerically the root, $s_c$, of $coss=cos{s}_0-(s-s_0)sins$ in the interval$[0,\pi ]$ and we obtain $f_c$ for each $s_0$ (either using Equation (7) or, which is the same, simply as $\overline{f_c}=sin{s}_c$). This curve is reported in Figure 3 (black line).

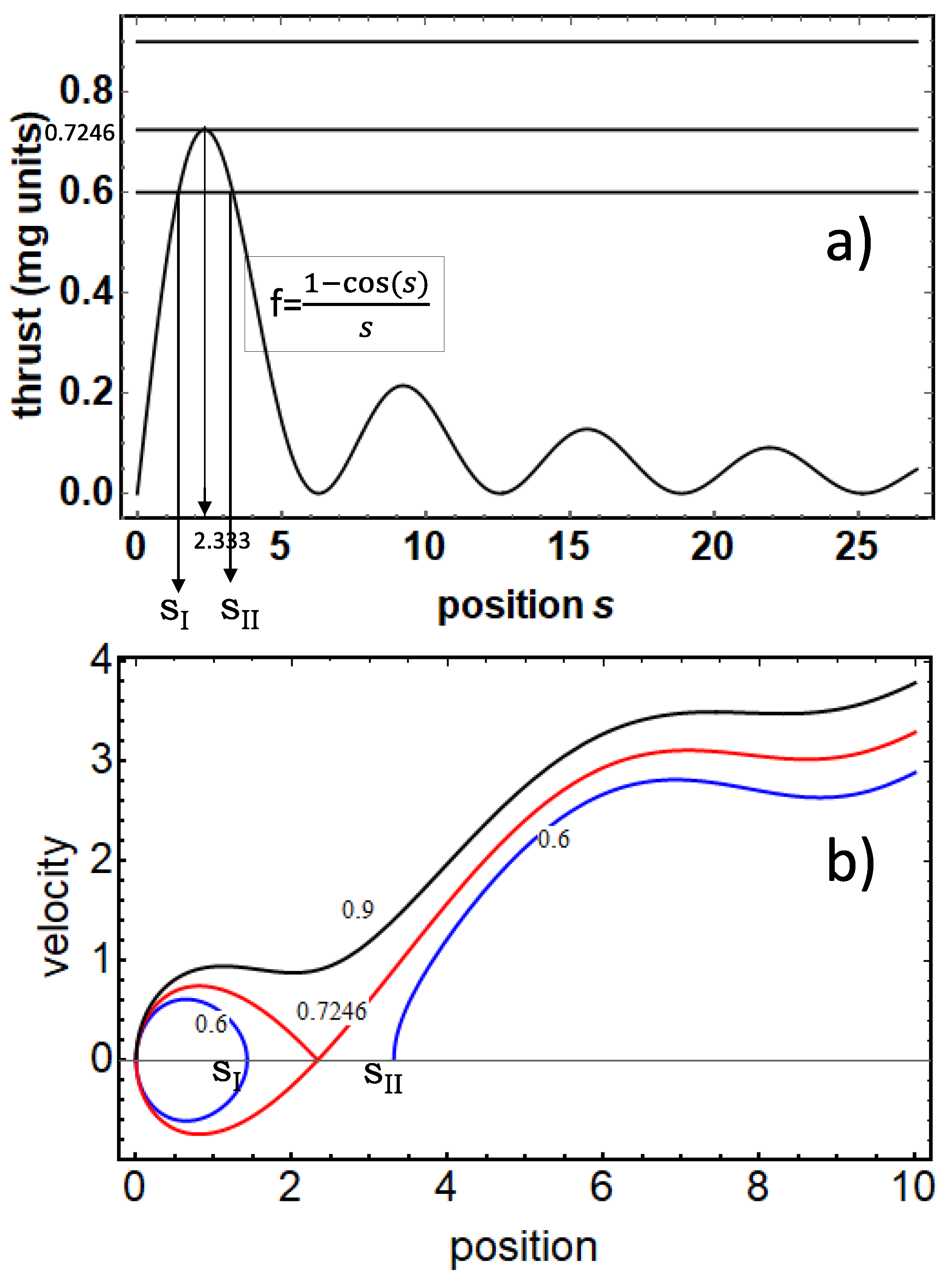
As can be seen, the choice of the initial positions of the cart can strongly lift the requirement for the thrust intensity. For initial positions included between $-\pi$ and $\pi /2$ the minimum thrust needed to reach the instability point $s_2$, and ensure the launching of the cart, decreases monotonically from the maximum intensity ($mg$), reached in correspondence of the point $s=\pi /2$ up to zero intensity as $s_0\to -\pi$.

This behavior can be understood by observing that the weight -$mgsin(s/a)$ term changes sign at $s=0$ so that the launch is gravity-assisted for $s_0\in [-\pi ,0]$ (less thrust is requested as compared to 0.7246 to reach $s_2$), while it is gravity-contrasted for $s_0\in [0,\pi /2]$ (more thrust is requested, up to 1, as compared to $0.7246$, to reach $s_2$).

Above $\pi /2$ the minimum required thrust starts decreasing again (reaching 0 for $s_0=\pi$) because the gravity contrasting term $mgsin(s/a)$ lowers although the motion of the cart is still gravity-contrasted.

4.2. Quasi Static Launch

In contrast with this impulsive thrust mechanism (sudden ignition to a constant thrust level with a consequent dynamical launch of the cart) depicted in Section 3, one can also imagine an ’adiabatic’ or quasi-static launch operation. The thrust on the cart is ramped very slowly, such that the cart moves (starting, at rest, from $s_0=0$) very slowly, i.e. with velocity and acceleration close to zero. The thrust ramps in time between 0 and 1, so that the mass can adjust its position, such as to reside all the time in the equilibrium point $s_1$, or very close to it ($s_1\left(t\right)\approx {sin}^{-1}\left(\overline{f}\left(t\right)\right)$).

When $\overline{f}=1$ the position of the cart is $s_1=s_2=s=\pi /2$, the cart is perfectly vertical, hold up by a thrust equal to its weight in an unstable equilibrium on the track. In this condition it is impossible to increase the thrust, even slightly, without entering the running state of the cart. Of course, this kind of launch operation necessarily requires a thrust equal to the weight of the cart at some point ($s=\pi /2$).

The quasi-static operation just described is close to the experimental protocol typically used to characterize a junction in terms of its maximum Josephson current, except for the fact that, differently from the cart case, any possibility of control of the initial conditions is out of reach in the case of the junction phase difference. The current is increased from zero with a slow sweep rate until a switching from the zero voltage state to a finite voltage state is observed at a certain current $I_c$. It is reasonable to assume that this observed critical current value $I_c$ is the best approximation of the ’ideal’ maximum critical current $I_{c0}$ at the operation temperature of the junction. On the other hand, since the plasma frequency for a Josephson junction is extremely high (THz), it would be difficult to do otherwise, that is, to raise the current on a timescale shorter than the plasma period, except under special equipment lab conditions.

The other important agent affecting the current at which a junction switches to the finite voltage state, is noise, or thermal fluctuations. Even if the temperature were the absolute zero, quantum fluctuations remain, affecting the performance of the junction. The ideal critical current $I_{c0}$ may be defined by the absence of fluctuations and the quasistatic operaton of current control.

Finally note that, more broadly, between a sudden ignition launch and a quasi static launch, one could operate such that the thrust on the cart is linearly ramped to a certain value $\overline{f}$ (${\overline{f}}_c<\overline{f}<1$) with a ramp duration $\Gamma$ ($0<\Gamma <\infty$). In this case, for each different $\Gamma$ value, a different threshold ${\overline{f}}_c$ would be found ($>0.7246$) such that a dynamical launch is possible for values of $\overline{f}$ between the found ${\overline{f}}_c$ and 1 (trapeziodal AC supply current, in the case of a JJ). See $\mathit{mutatis}$$\mathit{mutandis}$ Figure 3 in Darula and Kedro [7].

4.3. Considerations About the Damping

In the presence of damping, the phenomenon described so far is strongly obscured or even absent. Damping mitigates, or also impedes, the possibility of premature switchings in Josephson junctions, as we have described them in this note. Likewise, friction prevents using a thrust less than $mg$ for the ’launching of the cart’.

This point is illustrated schematically in Figure 3. The red curve has been calculated numerically in the presence of damping ($\beta =0.5$). It is clear the mitigation of the possibility of using a diminished thrust with respect to $mg$ for the launch (for instance, starting the launch from zero, one numerically obtains that $f_c$ changes from the value of 0.7246 to 0.7746, 0.9346, 0.9815, for $\beta$ respectively 0.1, 0.5, 0.7). For $\beta$ near 1 yet, the request of thrust is in practice 1, whatever $s_0$. In a Josephson junction, most of the dynamical switchings can be suppressed by using an appropriate shunt resistance thanks to this circumstance.

We explicitly note, however, that it is always possible to launch the cart, even with huge damping, by using a thrust not greater than $mg$ (the minimum thrust needed is always, at most, $mg$). In fact, suppose that $\beta \to \infty$ (worst hypothesis), the equation of motion becomes

$$\beta {\displaystyle \frac{ds}{dt}}=\overline{f}-sin\left(s\right)$$

(8)

The minimum thrust to have the cart riding indefinitely, whatever the initial condition, is ${\overline{f}}_c=1$. De Luca et al recently in ref. [10] studied the case of overdamped junctions, based on Equation (8), with special reference to the pendulum as a mechanical analog.

5. Analogous to What? (Equation of Motion for the Phase in a Josephson Junction)

Next, for the sake of completeness, we retrace the conceptual steps leading to the equation of motion for the phase in a JJ. In the derived equation for the junction, the reader will easily recognize Equation (1) and make the due connections. The two main ingredients for this task are: the Josephson equations and a circuital schematization of a real superconducting junction.

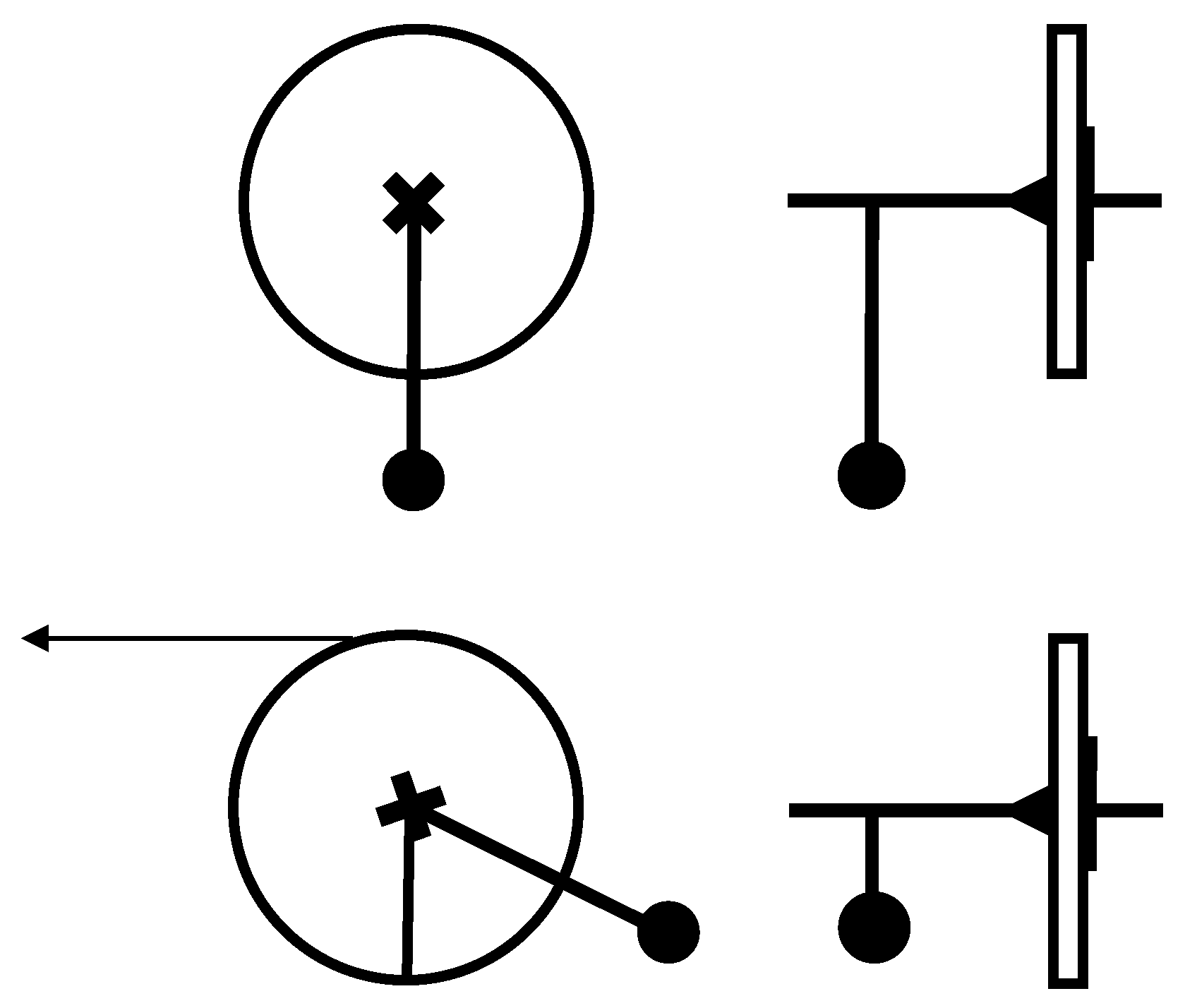
5.1. The Josephson Equations

As first suggested by Josephson [4], when two superconductors are sufficiently close to each other, for instance, separated, over a small contact area, by a thin (few nanometers) insulating oxide layer, and connected to a current source, a dissipationless current, made of coupled electrons (Cooper pairs), can flow by tunneling between the electrodes with no voltage difference. Josephson also predicted successfully [11] that:

a) the supercurrent is a function of the macroscopic quantum phase difference between the two superconductors $\phi \left(t\right)={\theta }_1-{\theta }_2$, given by $I_J\left(t\right)=I_{c0}sin\left(\phi \left(t\right)\right)$ (current phase relation), where $I_{c0}$ is the max critical current, i.e., the maximum supercurrent that the junction can support.

b) when the current changes over time (controlled by a current supply), a voltage difference is generated across the junction, whose instantaneous value is given by $V\left(t\right)=(\hslash /2e)d\phi \left(t\right)/dt$ (voltage phase relation). Note that the proportionality factor ($\hslash /2e$) involves, as few other situations in Physics, only universal constants, that marks the macroscopic quantum nature of the effect.

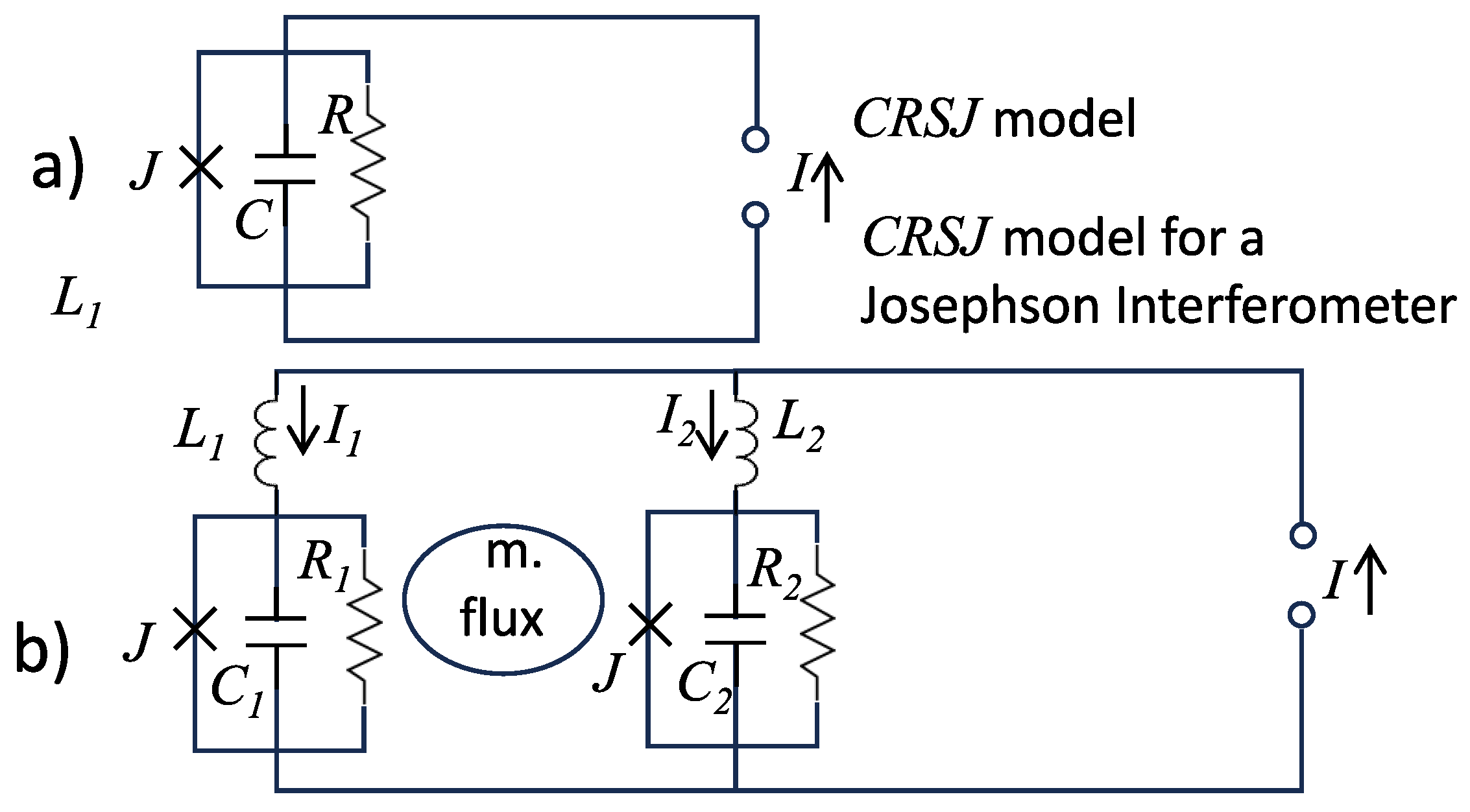
5.2. CRSJ Model

Despite the quantum nature of the phase difference, a real junction may be treated (characterized by measurements of current and voltage) as an ordinary electric element, ruled by ordinary electromagnetism, for most purposes.

In fact, it can be described successfully as the parallel circuit of three single current channels (Figure 4a): capacitive ($CdV/dt$), resistive ($V/R$), superconductive ($I_{c0}sin\left(\phi \right)$). This widely used schematization (resistively and capacitively shunted junction, or CRSJ model) provides, by current balancing, and use of the voltage-phase relation, the following equation for the time evolution of the phase $\phi$, in analogy to Equation (1) for the position of the cart on the track:

$${\displaystyle \frac{\hslash }{2e}}C{\displaystyle \frac{d^2\phi }{d{t}^2}}=-I_{c0}sin\left(\phi \right)+I_{dc}-{\displaystyle \frac{\hslash }{2e}}{\displaystyle \frac{1}{R}}{\displaystyle \frac{d\phi }{dt}}.$$

(9)

Here C is the geometric capacitance between the two electrodes and R the resistance.

Rather counterintuitively, a lower resistance means a higher dissipation (the dissipative term is proportional to $1/R$). This result comes from R being in parallel to the superconducting branch. The lower is the resistance the greater the normal current made by normal electrons, and the higher the dissipation. To obtain an overdamped junction (useful in many applications) one has to use lower R’s.

Equation (9) describes two possible regimes: Below $I_{c0}$, it describes a dynamical state for which the average value of $d\phi /dt$ is zero (the zero voltage state). Beyond $I_{c0}$, the equation describes a dissipative regime (finite voltage state) in which a current of normal electrons (quasiparticle) adds up to that of Cooper pairs and a finite voltage (the average value of the oscillating term $d\phi /dt$) together with a finite resistance appear across the junction. Here, the average is taken as $\langle {\displaystyle \frac{d\phi }{dt}}\rangle ={lim}_{T\to \infty }(1/T){\int }_0^T\left(d\phi /dt\right)dt$.

Equation (9) is written in dimensionless form as

$${\displaystyle \frac{d^2\phi }{d{t}^2}}=-sin\left(\phi \right)+\alpha -{\beta }_J{\displaystyle \frac{d\phi }{dt}}$$

(10)

where time is in units of $\tau ={(\hslash C/2e{I}_{c0})}^{1/2}$, $\alpha =I/I_{c0}$, and ${\beta }_J=\tau /RC$ is a dimensionless damping coefficient (Johnson parameter). In these units, the voltage is in units of ${(\hslash I_{c0}/2eC)}^{1/2}$, and the energy is in units of $\hslash I_{c0}/2e$. In Table 1 the corresponding elements of the CRSJ model (sometimes referred to as the ’electric analog’ of a Josephson junction) and mechanical analog introduced in this note are reported.

5.3. Analogy Highlights

Let us summarize the main points characterizing the analogy between the junction dynamics and that of the cart on the roller coaster:

a)The thrust on the cart corresponds to the bias current in the junction.

b)The ’launch attempts’ (failed attempts) experienced by the cart at the bottom of the first valley of the roller coaster under the action of an insufficient thrust, corresponds to the zero voltage regime of the junction with the phase difference undergoing the same kind of bound oscillations unable to make the junction switch to the finite voltage state.

c)The riding of the cart on the roller coaster corresponds to the finite voltage state of the junction. In this case, both the dynamical variables $s\left(t\right)$, the position of the cart (in units of a) on the track and $\phi \left(t\right)$, the phase difference between the two superconducting electrodes making the junction, grow in time without limits. Both are characterized by a finite average rate of growth, the velocity of the cart in the mechanical analog, and the voltage across the two electrodes in the junction.

d) Translated to the language of the Josephson effect, the exercise proposed in previous sections would have been read: Is it possible for a Josephson junction to switch to the finite voltage state for a current lower than the critical current? A (positive) answer to this question has come out easily, as we have seen, by examining the mechanical analog.

It should be stressed right away at this point that, although analog, the two systems remain much different. Apart from the characteristic times, differing for a factor between ${10}^{10}-{10}^{15}$, there is the important aspect related to the thermal fluctuations. Thermal noise has a critical impact on the performances of a Josephson junctions and is, actually, the real major factor of detriment of the critical current. The Josephson coupling energy $\hslash I_{c0}/2e$ is typically $1.2\times {10}^{-2}$eV ($I_{c0}\sim 1\mu A$) the thermal noise fluctuations typical value is $kT\sim 8.6\times {10}^{-3}$eV (typical noise temperature $\sim 100$K, with standard noise screening conditions), so that the phase difference enters very easily (up to very close 0 K) the domain of a random variable subject to thermal fluctuations.

5.4. Dynamical Switching and ’Punchthrough’ Effect

What remains of the exercise carried out for the roller coaster in the domain of a Josephson junction? As said, the effect we have described in the previous sections (dynamical, or inertial, launch of the cart) corresponds to the possibility of observing in an underdamped Josephson junction a ’dynamical switching’. The underdamped condition being matched in high capacitance-low resistance junctions in agreement with the definition of $\beta$.

The mechanism is completely analogous to the critical dynamical launch of the cart: the current value is raised instantaneously to the critical value of $0.7246I_{c0}$. This is sufficient to make the phase reach the unstable value $\pi -{sin}^{-1}\left(0.7246\right)$, from which an average $\dot{\phi }\ne 0$ (i.e. $V\ne 0$) regime starts.

In certain applications that use Josephson junctions in the latching mode (logic circuits that need to be rapidly reset to the zero voltage state from the finite voltage state), this effect assumes a special form, known as punchthrough’, which can be particularly detrimental. In an emphasized image, the junction ’refuses’ to remain on the dissipassionless Josephson current branch just when you would need it, as first studied by Fulton and Dynes long time ago [8].

That, we stress, occurs because the current feeding the junction is rapidly swept. We notice in passing that high sweep rate signals (’pulsed’ excitation) have been used in the recent past in connection with the CRSJ model, to make emerge interesting unusual non equilibrium phenomena whose features mimick in Josephson junctions macroscopic quantum effects (see ref.[12] and references therein).

Finally, it is useful to remark that while thermal fluctuations cannot be eliminated, dynamical switchings can, in principle. This can be accomplished in those case when it is not an issue to work with an overdamped junction, by shunting the latter with an appropriate resistance so that the damping term in Equation (9) becomes dominant.

6. Two Cart Train Roller Coaster: A Josephson Interferometer

How far the roller coaster analogy with a Josephson junction can be carried on? In this section, we give an indication for its most natural possible generalization: The presence of more than a single Josephson junction. We refer to superconducting circuits containing N coupled junctions in parallel (a discrete version of a so called ’long Josephson junction’).

The mechanical analog for an array of this kind is represented by a roller coaster train made by a line of N elastically coupled carts whose positions $s_1,s_2,...s_N$ represent the values of the N phase differences ${\phi }_1,{\phi }_2,..{\phi }_N$. This identification is reminiscent of the well known extension of the pendulum analogy of a single junction to a parallel array of Josephson junctions, represented by a chain of coupled winding pendula [1,13]. In such a mechanical device, as well as in a train of many carts riding the roller coaster, true waves can propagate (along the train) likewise phase waves (linear and nonlinear) propagate in a long Josephson junction.

We treat hereafter the simplest case of this kind of possible extensions to arrays of junctions: That of a circuit made by two junctions connected in parallel, a noteworthy configuration known as ’Josephson interferometer’ (or dc SQUID, ’Superconducting Quantum Interference Device’) (Figure 4b). In the circuit of Figure 4b) a superconducting current, which splits between the two channels $I_1=I_{c0}sin{\phi }_1$, $I_2=I_{c0}sin{\phi }_2$ with two phase differences ${\phi }_1$,${\phi }_2$, can flow without a voltage develops across the two resistances, until a maximum current is reached, beyond which the circuit starts oscillating.

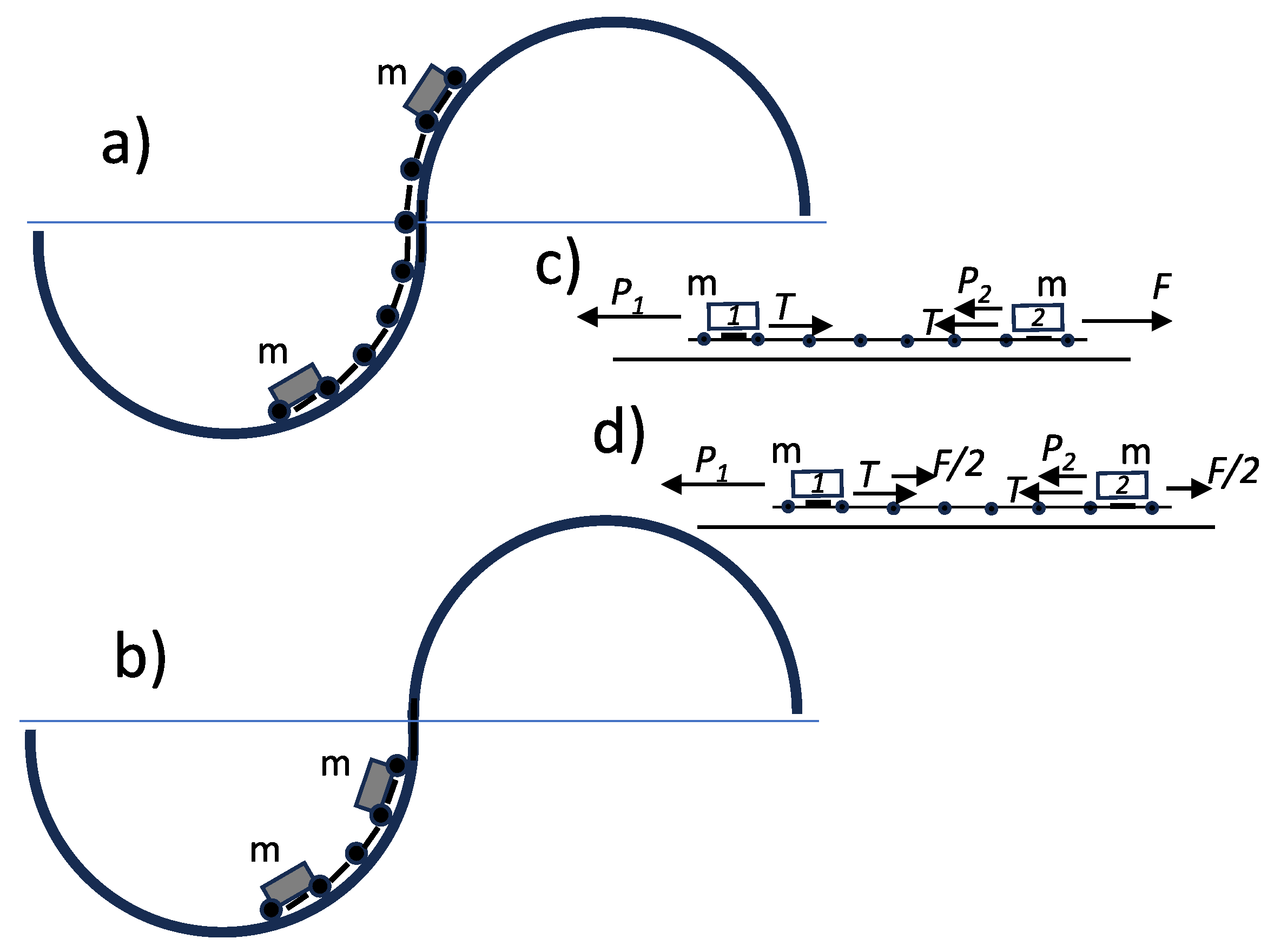
The maximum current (the Maximum Josephson current of the SQUID) is a highly sensitive function of the magnetic field normally applied to the plane of the circuit (a basis for a magnetometer). In this case, the mechanical analogy consists in a roller coaster train, made by two coupled in-line carts, riding the roller coaster track of Figure 1 (see Figure 5).

So let us consider two carts, 1 and 2, of vanishing dimensions and the same mass m, individuated on the track by $s_1$ and $s_2$, respectively (so that the train is long $s_2-s_1$), and tied to each other by an articulated rod (with inserts of elastic material) of negligible weight as compared with the weight of each cart (Figure 5). Let us assume that the rod slides on, and is constrained to the track, like the carts themselves; as said, it is elastically deformable to a certain degree (thanks to the inserts) and similar to a stiff spring with an elastic constant k.

We also assume that a thrust F acts on the cart no. 2 driving the entire train (in the circuit of Figure 4b this corresponds to the asymmetric situation in which one of the two geometrical self-inductances $L_1$, $L_2$, has a value much smaller than the other). Under these conditions the length of the train ($s_2-s_1$), depends on the mechanical tension T to which the rod is subject and the dynamics of the two coupled carts, included the effect of the weight components $P_1=-mgsin{s}_1$ and $P_2=-mgsin{s}_2$ on cart 1 and 2, respectively (see Figure 5a for a sketch of the forces at play), is governed by the equations (again, we neglect the friction):

$$\begin{array}{ccc}& & m{\displaystyle \frac{d^2{s}_2}{d{t}^2}}=F-T-mgsin{s}_2\hfill \end{array}$$

(11)

$$\begin{array}{ccc}& & m{\displaystyle \frac{d^2{s}_1}{d{t}^2}}=T-mgsin{s}_1\hfill \end{array}$$

(12)

where $s_1$ and $s_2$ satisfy also

$$s_2-s_1=H+kT$$

(13)

Here H is the length of unsolicited ($T=0$) train, and $kT$ the change in length of the train, assumed simply proportional to T, through k.

In the dimensionless time and length:

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d^2{s}_2}{d{t}^2}}=\overline{F}-\overline{T}-sin{s}_2\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d^2{s}_1}{d{t}^2}}=\overline{T}-sin{s}_1\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill & & s_2-s_1=H+\kappa \overline{T}\hfill \end{array}$$

(16)

where $\overline{F}$ and $\overline{T}$ are $F/mg$ are $T/mg$, respectively and $\kappa =kmg/a$ is the reduced elastic constant.

6.1. On the Statics and Dynamics of a Two Cart Train of Assigned Length ($\kappa =0$)

Let us write the equation of motion for the relative position $s_d=(s_2-s_1)$ and the center of mass $s_s=(s_1+s_2)/2$. To this end, we add and subtract Equations (14) and () to write

$$\begin{array}{ccc}\hfill & & 2{\displaystyle \frac{d^2{s}_s}{d{t}^2}}=\overline{F}-2sin{s}_{s}cos{\displaystyle \frac{s_d}{2}}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d^2{s}_d}{d{t}^2}}=\overline{F}-2\overline{T}-2cos{s}_{s}sin{\displaystyle \frac{s_d}{2}}\hfill \end{array}$$

(18)

In the simple case of $\kappa =0$ (rigid connection between the two carts), we simply have $s_d=s_2-s_1=H=constant$, and we obtain from Equation (17) (requiring $d^2{s}_s/d{t}^2=0$):

a) The equilibrium points for the center of mass $s_s$, similar to the stationary points $s_1$ and $s_2$ of the single cart,

$$\begin{array}{c}\hfill S_1={sin}^{-1}\left({\displaystyle \frac{\overline{F}}{2cos\frac{H}{2}}}\right),\\ \hfill S_2=\pi -{sin}^{-1}\left({\displaystyle \frac{\overline{F}}{2cos\frac{H}{2}}}\right)\end{array}$$

and,

b) The limits of the static equilibrium for the two rigidly coupled cart train. That is

$$F_c=\underset{s_s\in [0,2\pi ]}{max}\left[2sin{s}_{s}cos{\displaystyle \frac{H}{2}}\right]=2\left|cos{\displaystyle \frac{H}{2}}\right|.$$

(19)

Assigned H, there is a corresponding thrust, $\overline{F}$, and a corresponding position of the center of mass ($S_1$) for which the train can be kept still at $S_1$. However, when the required thrust, for the assigned value of H, overcomes a threshold $F_c$, no static equilibrium is possible any more and the train starts moving. The threshold curve $F_c$ vs H, a periodic function of H, is exactly expressed by Equation (19).

In particular, a train long $H=\pi$ (or $3\pi$, or $5\pi$,...) does not need any force $\overline{F}$ to be kept still on the track, because in this case, Equation (19) gives ${\overline{F}}_c=0$: Whatever its position, the train will remain there in a static indifferent equilibrium under the gravity force and the tension T. To put it in another way, just an infinitesimal thrust $\overline{F}\simeq 0$ is sufficient to make the train long $\pi$ move against gravity along the roller coaster (of course the friction remains to be won, as for a train on a perfectly flat track). Equation (), with $H=\pi$ and $\overline{F}=0$, provides the value of the tension for any position of the center of mass of the train, $s_s$, as $T=-cos{s}_s$.

The resulting Equation (19) is well known in the Josephson effect domain (as well, it is analogous to the form of the two-slit interference pattern of optics). It describes the diffraction pattern displayed by the critical current in a Josephson interferometer in response to an applied magnetic flux and is the basis of a dc SQUID magnetometer. In the analogy the role of the flux is played by the length H of the two cart train.

Furthermore, from Equation (17) we obtain:

c) the critical thrust to launch the train formed by two carts (Dynamical Switching of a SQUID);

We follow here the same line followed in Section 3.2. Equation (17), with the initial conditions ($s_s\left(t\right){{|}_{t=0}=d{s}_s\left(t\right)/dt|}_{t=0}=0$) admits the integral of motion

$${\dot{s_s}}^2-2cos{s}_{s}cos{\displaystyle \frac{H}{2}}-F{s}_s=-2cos{\displaystyle \frac{H}{2}}=constant$$

(20)

Thus the velocity as a function of the position on the track can be obtained as

$${\displaystyle \frac{d{s}_s}{dt}}=\sqrt{\left(\overline{F}{s}_s+2cos{\displaystyle \frac{H}{2}}(cos{s}_s-1)\right)}$$

(21)

From this the condition that it is zero provides the generalization of Equation (6)

$$\overline{F}={\displaystyle \frac{\left(1-cos{s}_s\right)2cos\frac{H}{2}}{s_s}}$$

(22)

The thrust is maximum at $s_s=2.33112$ where takes the value

$$\overline{F_c}=2*0.7246\left|cos{\displaystyle \frac{H}{2}}\right|$$

(23)

6.2. Mechanical Analog of the Self-Flux: Elastically Coupled Carts ($\kappa \ne 0$)

Most interestingly, as noted above, the length of the train H (or the length of the rod, which is the same) plays here the same role that the externally applied magnetic flux plays in a Josephson interferometer.

The analogy extends further: One can distinguish between this component of the flux, identified with the length of the unstrained train ($\kappa =0$), and the self-induced flux component, i.e., that part of flux generated in the interferometer loop by the circulating currents themselves (then $\kappa$ plays the same role of the self-inductance of the loop containing the flux in Figure 4b). This latter is to be identified with the changes of the length of the train when it is solicited and when it is not solicited. In fact, the train stretches or shortens to a certain degree under its own weight ($\kappa \ne 0$). When it stands in a valley, it shortens due to the compressing gravity effect. On the contrary, hanging in equilibrium on a top, it is stretched by the pulling gravity effect.

So one can speak of a ’total length’ of the train, the one corresponding to its length in the absence of stresses (at rest on flat track), plus the contribution due to self-deformation in the presence of stresses. Likewise in a Josephson interferometer one can speak of ’total flux’ and ’external flux’, whose difference is the self-induced flux.

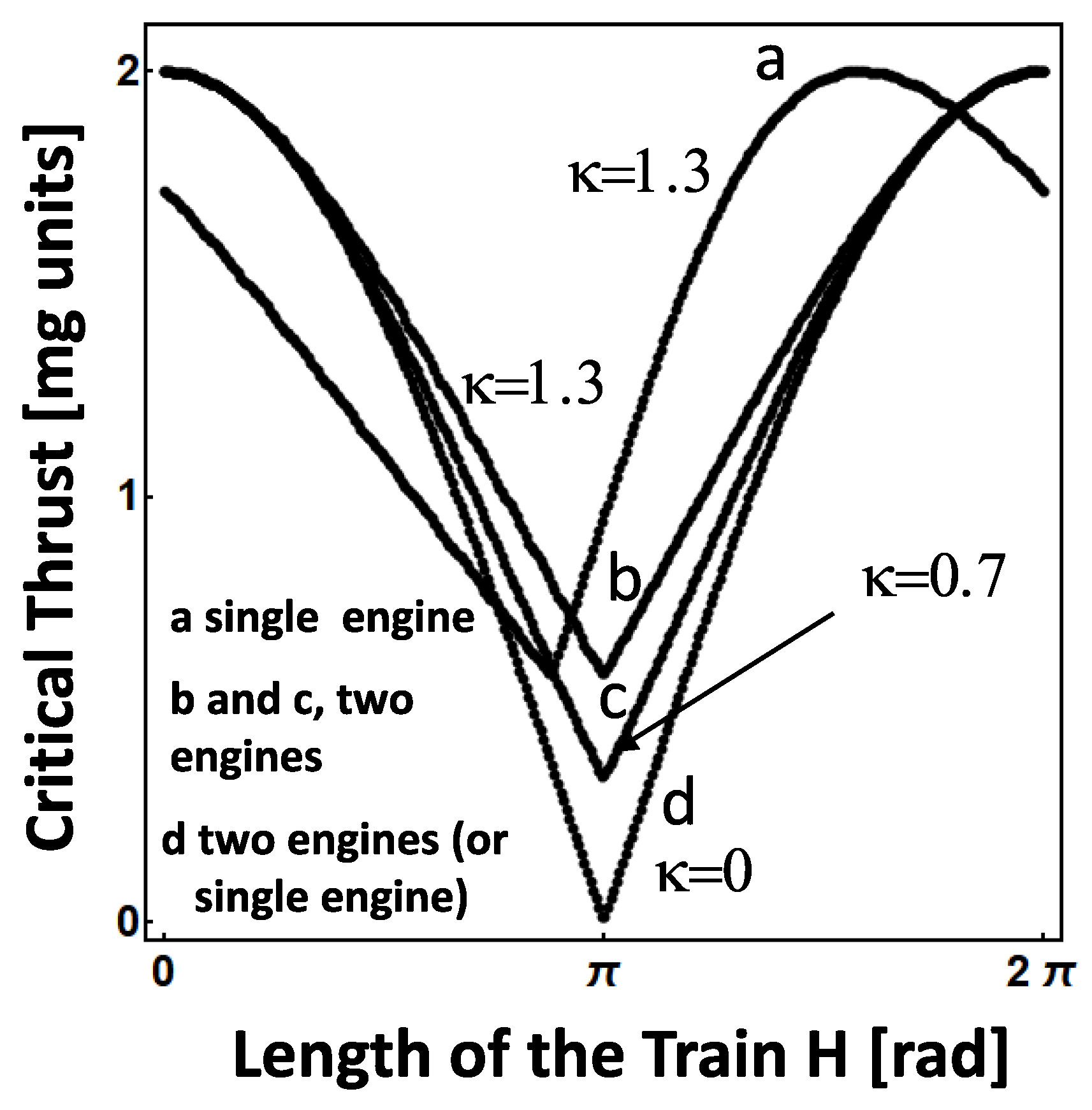
Let us analyze more closely this case ($\kappa \ne 0$). In particular we can evaluate the equivalent of the equilibrium curve ${\overline{F}}_c\left(H\right)$ (Equation (19)) for the case of two elastically coupled carts on the roller coaster (the results are graphically anticipated in Figure 6).

To obtain these results, we go back to Equations (14)–(). The static part reduces to

$$\begin{array}{ccc}\hfill & & \overline{F}=sin{s}_1+sin{s}_2\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill & & \overline{T}={\displaystyle \frac{\overline{F}}{2}}+{\displaystyle \frac{sin{s}_1-sin{s}_2}{2}}\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill & & s_2-s_1=H+\kappa \overline{T}\hfill \end{array}$$

(26)

We can eliminate $s_2$ and obtain for $\overline{F}$ the expression

$$\overline{F}=sin{s}_1+sin\left(s_1+H+\kappa sin{s}_1\right)$$

(27)

which can be (numerically) maximized with respect to $s_1$ (Chose $\kappa$, then for each H, calculate $\overline{F}$ as $s_1$ varies in the range $0,\pi$, take the maximum $\overline{F}$, build $F_c\left(H\right)$)(Figure 6a).

In the same way, we consider the more symmetric case of a train pulled and pushed at the same time, that is we can assume that both carts, one and two, are equipped with an engine producing half of the thrust $\overline{F}$, (see Figure 5d; in Figure 4 this corresponds to having $L_1\eqsim L_2$). It easily shown that the Equation (27) transforms into

$$\overline{F}=sin{s}_1+sin\left[s_1+H+\kappa \left(sin{s}_1-{\displaystyle \frac{\overline{F}}{2}}\right)\right]$$

(28)

This is an implicit equation for F. The procedure to build ${\overline{F}}_c\left(H\right)$ however is the same but for an additional step needed to solve numerically the implicit Equation (Figure 6b,c).

These representative curves, collected in Figure 6 have been calculated through Equation (27) and Equation (28) by using simple MATHEMATICA (Wolfram Research Inc. Champaign (IL, USA)) codes. These curves, too, are well known in the physics of superconducting Josephson interferometer [14] [15].

Along the line sketched in this section, it would be possible to consider the case of a multi-cart elastic train of arbitrary length and number of carts (unpractical for a mechanical prototype as compared with a chain of pendula, we admit). This step would make us to land on the territory of famous Frenkel-Kontorova model [16,17] (and in particular on the sine Gordon equation [18]). The simplest realization of the Frenkel-Kontorova model is in fact a chain of N particles interacting via harmonic springs with elastic coupling and subjected to the action of an external periodic potential. In our case, the tilt washboard potential.

7. Conclusions

In this note, we have illustrated a mechanical analogy for the dynamics of a Josephson junction (in practice an alternative way to realize a tilted washboard potential for a material point). A cart on a vertically winding roller coaster driven by a constant force possesses as a matter of fact, the same dynamics of a JJ. Both systems are ruled by the same equation of motion. To explain the details of the analogy and its use as an educational tool, we have taken a cue from a particular possible evolution of the cart: Its departure for a long ride from a valley of the track when pushed by a step-like thrust, what we have named ’the launch of the cart’. In a Josephson junction this mechanical process has its own equivalent in a premature switching (dynamical switching) of the junction to the finite voltage state, not related to the presence of noise. We have extended furthermore the analogy to the case of two coupled carts (a train) riding over the roller coaster and shown that this extension is a mechanical analog of a Josephson interferometer.