Preprint
Article
Quaternion Spin: From Bell to Baryogenesis
Altmetrics
Downloads
65
Views
28
Comments
0
This version is not peer-reviewed
Submitted:
18 October 2024
Posted:
24 October 2024
You are already at the latest version
Alerts
Abstract
Changing the symmetry of spin from SU(2) to the quaternion group, Q8, introduces Q-spin which has a number of ramifications. We first summarize the properties of Q-spin and then discuss some of those resulting changes. Many are counter to well-established ideas which change our view of the microscopic. Dirac’s matter-antimatter pair is challenged, being replaced by a 2D structured spin. His negative energy issue and the baryon asymmetry problem are resolved; parity is not violated in beta decay, and the existence of neutrinos is questioned. Bell’s theorem is disproven by counter example, restoring Local Realism to Nature. The singlet state is an approximation; teleportation is not feasible, quantum computing must change to remove teleportation and focus on the qubit form of Q-spin which gives deterministic outcomes of ±1. This impinges on the Foundations of Quantum Mechanics, and we discuss the reasons for the failure of Bell’s theorem; the use of Hidden Variables, wave function collapse and explain the violation of Bell’s Inequalities by showing Q-spin is a boson of odd parity in free flight, and a fermion of even parity in a polarizing field. The violation of Bell’s Inequalities is due to an anyon transition between a boson and a fermion, formulating wave-particle duality. These changes are a result of compexifying the Dirac field.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
MSC: 81P40

1. Introduction
In 1925, one hundred years ago, [1] and Heisenberg, [2] formulated quantum mechanics. In 1927, Hendrik Lorentz organized the Solvay conference with the theme of electrons and photons, [3]. He, and many others, wanted to understand the meaning of wave mechanics. Einstein was mostly quiet at this conference, but at the end, he remarked that he supported Louis de Broglie because the idea of a pilot-wave, a hidden variable theory, offered a deterministic interpretation of quantum mechanics. Einstein was uncomfortable with the purely probabilistic nature of quantum mechanics as described by the Copenhagen interpretation, and at that early time, saw de Broglie’s theory as more consistent with his belief in determinism and causality over purely statistical interpretations. The Einstein-Bohr debates began and became focused in 1935 when EPR [4] published their famous paper. The debate continues today and Lorentz’s theme is just as relevant.
The EPR paradox motivated the development of quaternion, or Q-spin, [5]. Rather than accept Bell’s theorem, which asserts non-locality is necessary to account for the violation of Bell’s Inequalities, (BI), we have shown it is due to the coherent property of spin, its helicity, [5,6,7]. A simulation, [7], confirms this and Bell’s Theorem, [8], is disproven by counter example, [6]. Despite defying rational explanation, however, acceptance of Bell’s Theorem has led to the vast field of quantum information theory which rests upon his classical treatment of correlation. Our findings suggest the violation of BI, [9,10,11], is not evidence for non-locality, but rather for local realism! Entanglement cannot extend over spacetime, and quantum teleportation is unfeasible, [12].
There are, however, several other changes that Q-spin reveals and the purpose of this article is to discuss these relative to our appreciation of the microscopic. Critical to this is a clear description of Q-spin, and in the first sections we attempt a pedagogical explanation. Although the full details are given elsewhere, [5,6,7], we review them here so the treatment is more self contained.
Some of the consequences that follow are as controversial as disproving Bell’s Theorem because they question well established results. This motivates re-examination of reasoning that was accepted at the dawn of quantum theory. We explore these, and other ramification of complexifying the Dirac field.
2. Quaternion Spin
Spin is defined as a point particle of intrinsic angular momentum of magnitude , with two polarized states of where is a unit vector on the Bloch sphere. It is a fermion, even to parity, has SU(2) symmetry and is one of the two solutions to the Dirac equation. Call this Dirac spin, [13].
A polarizing field is required to lift the degeneracy in order to form these states, , which are used, for example, to form qubits. In contrast, in the absence of a polarizer, the two states cannot form and they are degenerate. Qubits then don’t exist. We call a spin in the absence of a polarizing field, a free flight spin. Its properties are crucial to resolving the EPR paradox, and several other problems within the foundations of physics, [5,6,7]. In contrast to the standard treatment, we change the symmetry from SU(2) to the quaternion group , and the spin that emerges carries the property of coherence in addition to polarization. We call this quaternion, or Q-spin.
The well known expression for the geometric product of two Pauli spin components is, [14],
The first term is symmetric and leads to the polarized states, , and the second is anti-symmetric, in terms of the Levi-Civita tensor and a bivector, , which leads to the helicity. The two terms in Equation (1) are complementary, by which we mean they are mutually exclusive since i cannot simultaneously be equal and not equal to j.
There is no bivector in the Dirac Equation, and introducing one is the only change made from the usual approach. To do this, one gamma matrix is multiplied by the imaginary number, i, , (subscipt "s" for spin spacetime). This renders the Dirac equation non-Hermitian, and complexifies spin spacetime, [5].
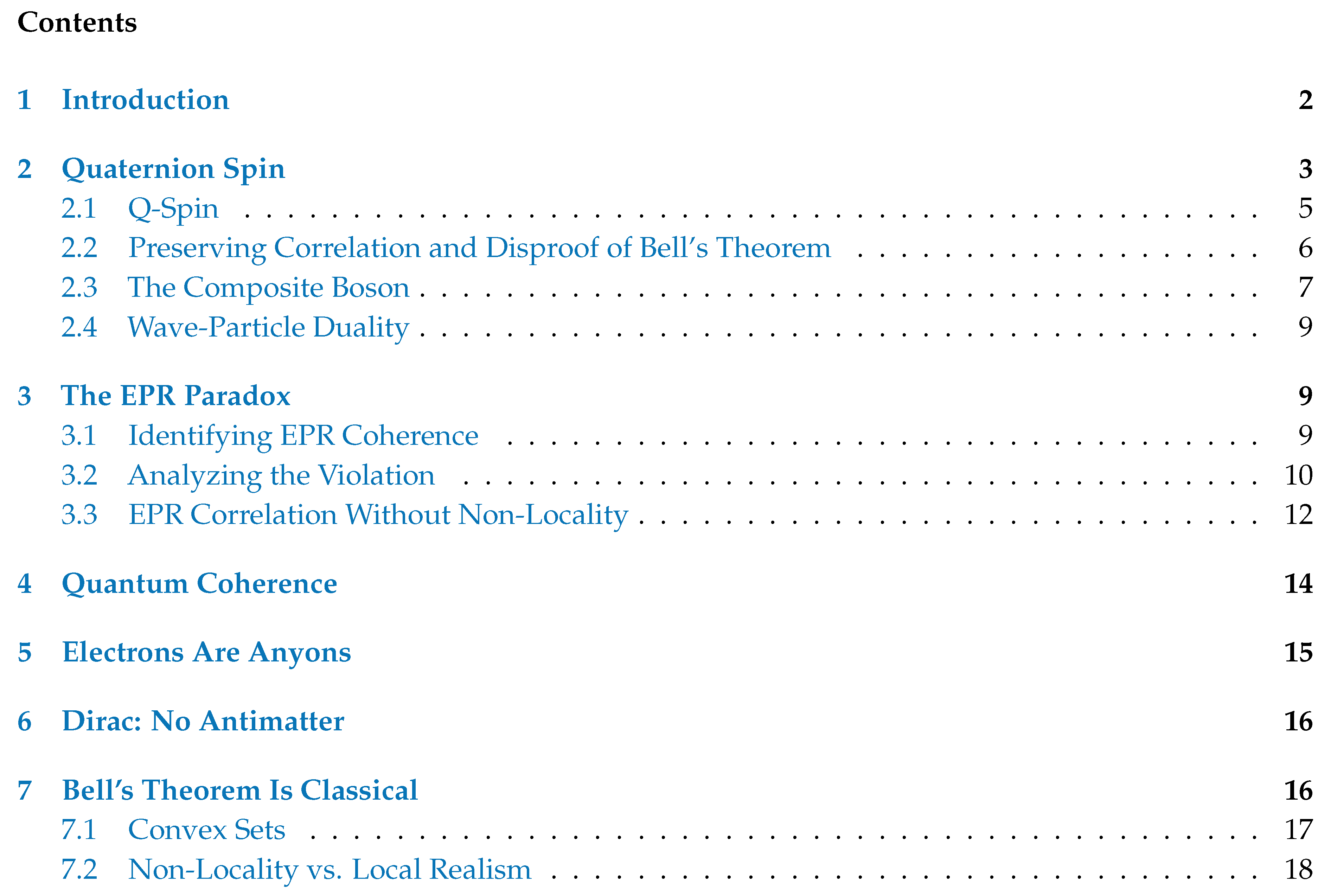
The gamma matrices represent the Dirac field in Minkowski space, which is a four dimensional real manifold where we live and observe. It is our Lab Fixed Frame, LFF, with dimensions of time and three spatial components, . The signature, or Clifford algebra, [15], is . Since Q-spin has structure, each can be oriented differently in Minkowski space. Therefore, each Q-spin has its own Body Fixed Frame, BFF, called spin spacetime denoted by, . It is a boost and rotation away from Minkowski space, Figure 1.
Spin spacetime is governed by a non-Hermitian Dirac equation,
We suppress the subscripts "s" on the derivatives. Due to the bivector, the algebra becomes . The gamma matrices, are changed to in spin spacetime. Notice there are two gamma fields , due to the non-Hermiticity. These are related by complex conjugation.
The two axes are indistinguishable in the isotropy of free flight. Therefore, permutation with the parity operator ,5], does not change the dependence of Equation (2), but the bivector is anti-symmetric to the 13 permutation. Therefore, the above equations provide two solutions in left- and right-handed coordinate frames, which are reflective or mirror states, Figure 2,
Mirror states have been reviewed, [16,17], and are used in areas of particle physics, dark matter, and PC violations. In our use, a reflective states are defined by the above equation. They have no parity, but are related to it, so the two states, , might be called parity-conjugates, see below. Figure 2 shows these states also reflect the imaginary axis which we cannot observe in our spacetime.
The anti-commutation of the matrices ensures energy is conserved and the Klein–Gordon equation is recovered.
Adding and subtracting the two equations in Equation (2), see, Figure 2, leads to their separation into a Hermitian part and an anti-Hermitian part,
where the parity-conjugates combine into states with odd and even parity, , with the definition
The even-parity states describe polarization, and the odd-parity states describe its helicity.
The Hermitian part, Equation (4), is the same as the usual Dirac equation but in two dimensions rather than three. It describes a disk, as visualized in Figure 3. Equation (5) is a massless Weyl equation and the solution is a unit quaternion, [18,19] originating from the bivector. It spins the (2) axis either L or R, Figure 3. Figure 1 shows the three spaces and their relationship. We cannot observe the quaternion on the 3-sphere, but we can observe its effect in spin spacetime, since the spins with its helicity. A quaternion is the engine that drives the axis to spin.
2.1. Q-Spin
The bivector complexifies the Dirac field and extends spin beyond our real LFF space. The underlying motivation behind Twistor Theory, [20,21], is Nature is fundamentally complex and we live in the real part. That is, the real manifold of Minkowski space is replaced with its complex form, , where all parameters are real. Penrose then introduced twistors, which are four-component objects that encode both the spacetime coordinates and spin information in a compact way. The results obtained here support this idea. Indeed the bivector leads directly to the definition of helicity as the complementary attribute of spin. We extend the definition of spin from a Hermitian Pauli spin vector, to a non-Hermitian complex spin operator which is an element of reality:
The geometric helicity is defined by,
This introduces into spin an anti-symmetric, anti-Hermitian second rank tensor. Its fundamental origin is the wedge product in GA, a plane that can rotate either L or R. Whereas is a vector on the Bloch sphere, is a complex vector, a quaternion, spinning on the Bloch sphere. Instead of having the dot product, , we have a quaternion, . Defining spin as a non-Hermitian element of reality extends Nature to the complex domain.
is the spin carried by each Q-spin axis, ( 3,1), with opposite but equal magnetic moments of . The 2D Dirac equation describes these two orthogonal axes on the same particle, as seen in Figure 3. Since Q-spin has structure, it also has internal energy, [5]. The definition of Q-spin, , is a consequence of the geometric product, which is responsible for the complementary nature of: polarization, a vector, ; and coherence, a bivector, . Despite their complementarity, both must be retained in our mathematical description. This underscores that both exist simultaneously, but only one is manifest at any instant.
2.2. Preserving Correlation and Disproof of Bell’s Theorem
With the EPR paradox in mind, we define an EPR pair as two spins of in a singlet state. Contrary to the usual concept that the entanglement in the singlet is maintained after separation, here we assume no connectivity between Alice and Bob.
We define a singlet state as usual, [11]:
State vectors, like Equation (9), do not explicitly display coherence, so taking its outer product gives a matrix, which is the state operator, [22]:
is also called a density operator. However, as discussed later, we deal only with pure states, and so call this a state operator to distinguish from density operators, which include mixed states.
The polarized states are diagonal, , and the coherent states are off-diagonal, . The resulting matrix is the entangled singlet state, , and can be represented as the tensor product between the two identity matrices, , and the scalar product between the two Pauli spin vectors, one for Alice and one for Bob. We always use the operator form in calculations and not the matrix form.
The off-diagonal coherent terms are responsible for the entanglement and preclude the product state. If those two coherent states are dropped, then the singlet state becomes a product state:
According to Bell’s Theorem, [8], product states cannot account for the violation of BI. However, rather than asserting that this means that the violation is due to non-locality, here we find it is due to the dropped coherent terms. The violation of BI is due entirely to the presence of a correlation due to coherence, thereby obviating non-locality.
To show this, consider the correlation from an EPR pair before and after separation, [6],
where . The first line is the definition of correlation where † is the adjoint operator. The trace is over the two spins, 1 and 2, for Alice and Bob. The unit vectors, and denote the filter angles which Alice and Bob randomly dial their filters to.
The second line of Equation (12) gives the usual correlation from a singlet state using QM. The third line drops the entanglement, the off-diagonal element in Equation (10), giving the correlation from that product state. Finally, the last line gives the correlation from helicity, [6].
A product state, devoid of entanglement, is considered unable to account for the violation of BI. Rather, Bell’s Theorem asserts the extra correlation requires that entanglement must persists over spacetime. That is non-locality is a property of Nature. However, the fourth line of Equation (12), [6], gives the contribution from coherence, and this shows helicity accounts for the correlation that leads to the violation of BI. Therefore, when an EPR pair separates, their polarization remains anti-correlated, and their opposite helicities remain in-phase. Both contribute to the total correlation observed,
Correlation is conserved upon separation into a product state. This equation expresses the LHS correlation is from an entangled singlet before separation. The RHS expresses the correlation after separation when entanglement is dropped. The two contributions can also be viewed as the symmetric and anti-symmetric irreducible representations under the rotation group. Correlation is preserved upon separation, [6]. Non-locality is not needed, and Bell’s Theorem, [8], is disproven.
2.3. The Composite Boson
Upon complexifying the Dirac field, the Dirac equation is non-Hermitian, and the two solutions, complex conjugates of each other, are mirror states, [16] and have no parity, . They are reflective twins, and Dirac interpreted them as a matter-antimatter pair, [23], two point-particle spins with two states each. Whereas a Dirac spin has components of a Q-spin has . The former is a point in Minkowski space, the latter has two orthogonal spin axes, and a bivector. This is interpreted as the 2D structure. Q-spin is one particle in a complex Dirac field with four states: two polarized states of up and down, , and two helicity states of L and R.
The two orthogonal axes and are counter rotating, in phase and are coherent vectors needed to maintain their reflective property, Figure (Figure 4), upper middle. These two axes each carry equal and opposite magnetic moments , and constructively interfere, producing resonance, and purely coherent spin, as shown. Such a resonance structure would minimize the energy and stabilize the 2D structure.
A photon has electric and magnetic components orthogonal to the direction of motion that spins with its own helicity. Q-spin is geometrically equivalent to a photon, Figure (Figure 3).
Parity separates spin spacetime into complementary spaces, Equations (4–5). Polarization has two spatial components, (3,1), and coherence lies along the (2) axis. Polarization spacetime now has algebra of a 2D disc, . The unit quaternions are defined in coherent space (not spacetime), on the 3-sphere, , and they spin the axis, , either L or R.
The two point-particle Dirac spins becomes one particle with two orthogonal axes, and , shown in Figure 3. Each is a fermion of spin-, and each carries a magnetic momentum of . Therefore, their sum is defined in a disc,
The two axes, (3,1), carry components of the same operators, , so in the BFF, components lie along axis 3 and along axis 1. That is, the two components, and do not commute. Rather than causing dispersion, they couple to form a composite boson, , which bisects the quadrant. Usually we expect two components of the same spin operator, which do not commute, to disrupt the other. Here we find this does not happen. Rather the two orthogonal spin components constructively interfere to generate the composite boson. The commutation relations of the can be found in [5], Equations (4) and (5), and, due to the bivector, there are two expressions: one gives rotation in the disc and the other has an imaginary component that damps all rotations out of the disc. This supports the idea that Q-spin is a 2D disc.
Despite the boson spin-1, the helicity spins the axis and averages out the polarization. Only the helicity remains. An electron is a boson spin-1, , odd to parity, and spinning with two helicity states of L or R. The magnetic moment of the boson is twice that of each fermion axis, being . We justify calling both and Q-spin since both are quaternions, and the sums of quaternions are also quaternions. Using Faraday’s Law, the spinning dipole momentum productes a time dependent electric field of concentric circles around the y axis, forming the usual spinning cone.
The quaternion is realized in the presence of a polarizing field, , and the two spin axes are no longer indistinguishable. Two general situations arise, Figure (Figure 3): if the field lies close to the boson axis, , it precesses as a vector with Larmor frequency of . If the field lies close to one of the two fermion spin axes, or , each with Larmor frequency of , then the boson decouples and one of the spin axes aligns with the external field: the two axes have opposite magnetic moments, so the decoupling gives a deterministic outcome of either .
These ideas are visualized in Figure 4, L and R panels. If one aligned axis carries state, , then the other carries the state, .
2.4. Wave-Particle Duality
Whether the boson remains intact or decouples, depends upon the orientation of Q-spin in the field, and upon the field strength, relative to the spin-spin coupling within the boson. The EPR paradox is resolved by including the correlation from both polarization and helicity, and the transition between the two.
Q-spin embodies wave-particle duality showing the properties of spin depend upon its environment. The polarization (particle), , and the coherence (wave), , are manifest as complementary attributes such that the polarization exists only in an anisotropic environment as a fermion, whereas the coherence exists only in an isotropic environment as a boson. The experimenter can change the environment to cause a boson-fermion transition, and this observer induced contextuality and expressed as,
Q-spin gives a boson electron of odd parity in free flight and a fermion electron of even parity when measured. This is the wave-particle duality.
When we complexified the Dirac field, we did not expect a 2D spinning disc, a World sheet, [24], nor spin being an anyon, [25]. We did not expect that antimatter production by Dirac’s interpretation would be unnecessary. Our original goal was to find a local way (product state) that accounts for the violation of BI. Once Q-spin was found, not only did it resolve the EPR paradox and disproved Bell’s theorem, but also many other dominos fell.
3. The EPR Paradox
3.1. Identifying EPR Coherence
In reference [7] it is shown the violation of BI is due to the transition from a boson in free flight to a fermion when measured. A simulation confirms this and generates the EPR correlation which is plotted in Figure 5 versus their filter angle difference, . Using the CHSH form of BI, [9], gives the usual value from the singlet state, . If the entanglement is dropped, then so is the coherence. This leaves only a product state displayed as the triangle, with CHSH = 2 which does not violate BI. The difference between the two is the part that violates BI, called the mustache function, with CHSH = 0.828.
The simulation results are also shown on the same figure along with their CHSH values. The classical simulation algorithm, [7] for the vector polarization has one spinning axis, , or 3, and the bivector has two counter spinning axes, , but only one aligns. Concisely, when both Alice and Bob are fermions, the correlation contributes to the triangle. When both are bosons, the correlation contributes to the mustache. When one of Alice or Bob is a boson and the other a fermion, then only polarized correlation is possible, [5].
When doing the classical computer simulation, [7], the Least Action Principle was used to determine alignments. Least action minimizes the Lagrangian so that the axis with the strongest attraction aligns. There are three axes, , and as shown in Figure 4. The simulation algorithm models polarization with a vector, and coherence with a bivector.
3.2. Analyzing the Violation
Consider a correlation experiment with Alice and Bob’s filters set to differ by . Both spins are anti-correlated as they approach their filters, the two space-like separated. Again, Least Action deterministically predicts the outcomes for both. Since the magnetic moment of the boson is twice that of the fermion, the boson attraction is double that of the fermions. We conclude that the boson persists uncoupled over a larger range than do the fermions, and precesses intact until the field is close to either the or axes. The boson then begins to nutate until finally it decouples.
Figure 6 illustrates the four experiments used in the CHSH experiment, with the filter settings for Alice of and , and Bob’s at and . The four S = CHSH experiments give correlation of , , , and . Any orientations of these field vectors can be used, but those shown in Figure 6 have the maximum correlation and violates BI. Using the quantum result, gives the quantum violation,
Whereas each of the filter settings of Alice and Bob are fixed in an experiment, the orientations of Q-spin are not. Rather Q-spin impinges on a filter at random orientations, , determined at the source. Both spins-1 bosons of Alice and Bob are anti-correlated up until they encounter their space-like separated filters. The two bosons have opposite helicity and common phase. Alice, independent of Bob, aligns with her filter. Likewise Bob aligns with his. Each decouples either directly to a fermion, or indirectly as a boson, depending on how far each is from its filter axis.
However, within a wedge, both Alice and Bob are close enough to their filters that their bosons do not decouple. Outside the wedge, a boson starts to decouple into its fermion form, and the coherence becomes polarization. We conclude that in EPR coincidence experiments, Figure 5, as approaches both Alice and Bob’s spins precess with frequency as bosons, giving the mustache function. On either side of , the spins start to decouple into fermions which precess as and give the triangle correlation. The bosons precession is shown in Figure 7. A spin makes an angle of with the field direction. For a spin-, the angle is while a spin-1 has an angle of . The two bosons show more correlation than fermions, thereby supporting the assertion that the boson is precessing in the field before decoupling and is responsible for the violation.
The classical simulation gives more correlation than from QM. CHSH = 2 (2.027) for polarization and 1 (0.968) for the coherence, giving a total of 3 (2.995). Although neither polarization nor coherence violate BI their sum does because EPR coincidence experiments cannot yet distinguish between coincidences that are from polarization and coherence.
The simulated correlation also violates the Tsirel’son bound, [26]. We assert this is because the quantum calculation uses a singlet state. The simulation shows the classical triangle is reproduced. The disagreement is between the simulated and quantum contributions to the coherence. The reason is that the singlet state is an approximation and misses coherent terms. This is shown later in this paper, Section 9.
The simulation demonstrates that persistent, non-local connectivity between separated EPR pairs is not needed to account for the violation. Rather the missing correlation, given by the mustache function, is due to spin coherence. There is no quantum weirdness.
3.3. EPR Correlation Without Non-Locality
Q-spin is defined in Equation (7), and has two orthogonal axes in the 3 and 1 directions in the BBF, Equation (14). Each axis carries a component of its spin , being along the and axes. To compare with experiment, we must calculate the expectation values, , in the LFF. For this we choose the pure state operator, , to be, [7],
Written this way underscores the fact that Q-spin is two components of the same spin operator. The two axes are not distinct spin operators, but two components of the same spin . These are defined in the BFF but easily transform to the LFF.
There are no contributions in the state operator from helicity or its complementary quaternions since we are not observing in the hyperspace. Observation of complementary spaces cannot be simultaneous.
For the two components we find the expectation values are complex,
where . The BFF vectors are then transformed to the LFF. An advantage of Q-spin is the expectation values are all unit quaternions which are easy to use since a product of quaternions is also a quaternion. Consider the correlation between an EPR pair approaching their filters,
The complex conjugation changes helicity from L to R because Alice and Bob’s spins have opposite helicities. The products are of quaternions, one for Alice and one for Bob. Also the correlation must be real, so we take into account the two opposite helicity states by the second term. This is similar to forming polarized light for photons. We obtain the full quantum EPR correlation, , the same as the entangled result, but without any non-local entanglement. The full correlation is obtained from a product state. For this, it is essential that Alice and Bob’s spins both be complex, [20,21], and carry helicity.
The details are elsewhere, [5], but to obtain this equation, add the two terms in Equation (18). Note that Alice and Bob are anti-correlated, so will differ by between them. The result, , is transformed to the LFF, giving a unit quaternion,
After Hamilton’s discovery and formulation of quaternions in 1843, they saw widespread use in physics. Although Maxwell did not employ them, his contemporary, John Tait [27], rewrote Maxwell’s equations using quaternions, demonstrating that they could represent electromagnetism in a compact and convenient form. Despite their advantages, quaternions—defined in four dimensions—are challenging to visualize (see however, [28]). As vector algebra gained popularity, quaternion-based formulations gradually fell out of favor. Vector calculus, which is more intuitive and easier to visualize, was promoted by Heaviside [29] and Gibbs [30] around the turn of the 20th century. Quaternions experienced a resurgence with the advent of computer graphics due to their computational efficiency and their ability to avoid the problem of Gimbal lock [31,32].
Quaternions reappeared in physics during the development of quantum mechanics, as their non-commutative properties and ability to handle rotational symmetries made them useful. They influenced the development of spinor algebras, and were further explored by von Neumann [33]. In modern theoretical frameworks, Hestenes integrated quaternions into his geometric algebra formalism for quantum mechanics and relativity [34]. Doran and Lasenby [18] expanded on this, combining quaternions and geometric algebra to provide both mathematical foundations and practical applications in quantum mechanics.
Given their intrinsic connection to rotational symmetries, it is unsurprising that quaternions naturally describe the rotational properties of spin.
4. Quantum Coherence
Quantum mechanics is also called wave mechanics because states are expressed as waves. As such they can superpose, interfere, have phase relations and decohere. Waves are expressed using complex functions and superposition creates different states. The feasible umbrella motion of can be treated as a double well potential separated by a surmountable barrier. The umbrella motion is an example of quantum coherence.
Generally, coherence is distinguished from polarized states by the latter being diagonal elements of the density matrix, and the former being off-diagonal elements, see, Equation (30). We have shown, [6], that dropping the off-diagonal terms results in a product state devoid of coherence. Without coherence, QM would not violate BI.
Parity arguments, [5], separate spin spacetime into complementary spaces of even and odd parity. The quaternion symmetry renders one of the BFF axes imaginary, . This axis connects spin to the hyperspace of quaternions. Since beyond our spacetime, we assert quaternions are unobservable elements of reality that generate L or R coherent helicity states in spin spacetime. Recall in free flight helicity averages out the polarization. Only helicity remains to give the wave part of the wave-particle duality.
The upper middle panel of Figure 4, depicts the two mirror axes precesings in tandem. They carry the same frequency, but in opposite directions, constructively interfering to produce the boson spin. It has no physical axis; is a pure resonance state, like a tuning folk; and is the manifestation of the bivector, .
A spin-1 boson has no magnetic state. Suppose the precessions as shown in Figure 4 are responsible for the states. Reversing both precessions then gives . They precess in a magnetic field because it exerts a torque on . However, the state has no dipole to align, so no counter-precession occurs between the two axes. We interpret this as precluding the state because it cannot form the mirror symmetry. Neither a photon nor a boson electron has an component.
The correlation between bosons is responsible for the mustache function. Note the coherent correlation, , resembles two opposing sine waves reflected at . The following gives a good fit,
This is plotted in Figure 8 along with the simulated data points which match Equation (21). Also plotted for comparison is the correlation from quantum theory. The simulation gives more correlation, CHSH = 1, than obtained from the singlet state and QM, CHSH = 0.828. We have proposed the difference is due to the singlet state being an approximation.
The doubling of the filter angles, is due to the boson magnetic moment of which gives two periods over . The first period in Figure 5 starts off at where Alice and Bob’s spins remain anti-correlated. As moves to , the anti-correlation means that the bosons’ magnetic quantum numbers, m, must be opposite, making the mustache negative up to . At that point, the two bosons begin to correlate, with equal magnetic quantum numbers, rendering the boson correlation positive.
The second period starts at , but the bosons remain correlated up to , after which they are again anti-correlated. Therefore, the boson correlation in the second period starts off positive. The sign of the boson correlation is in tandem with the sign of the correlation from polarization. We have not discussed here, [7], the small, hardly discernible, residual correlation seen in Figure 5 which lies along the abscissa and originates from the polarization. Its CHSH value is 2.027 - 2,000 = 0.027. The sign of this small residual correlation is also in tandem. Therefore all three contributions add to the correlation and none subtract, as they physically should.
We view the correlations from polarization (pol) and coherencies (coh) as distinct. By dropping the coherent terms, only fermion electrons remain and the correlation is the triangle in Figure 5. Putting back the boson spins gives the mustache function, Equation (21). However, recall that to get correlation from coherence, both Alice and Bob must be bosons, and both in coherent states, coh-coh. There are four types of coincidences between them: pol-pol, pol-coh, coh-pol, and coh-coh. Therefore, only of the coincidences lead to coherence, which is the origin of that factor in Equation (21).
5. Electrons Are Anyons
Although we cannot measure a free flight electron, we can envision one. In our spacetime, it is a charged spinning disc, with no net magnetic polarization. Faraday’s Law tells us a spinning magnetic moment produces an electric field of concentric circles around the Y axis. This field is distinct from its electric charge. Since that is the axis of linear momentum, then the electric field vector, tangential to the circle, traces out a helical path much like a photon. Under quaternion symmetry, we have shown, [5], the complementary properties are respectively a disc, governed by a Hermitian 2D Dirac equation with algebra, ; and a quaternion on , governed by the massless Weyl equation, which spins the disc.
We have proposed the two spatial components are not two point particles, but two axes on the same particle. We permute the indistinguishable axes rather than indistinguishable particles. An electron is an anyon, [25], without being a quasiparticle. Generally any spin is an anyon. One might call the anyon state between the boson and fermion a quasistate since it emerges in the presence of an external field, and is a transition state between the fermion and boson forms,
In a polarizing field, the indistinguishability is lost, the two axes respond differently until one becomes the fermion we measure, and the other randomizes, Figure 4, left and right panels.
We suggest the anyon transition state is the boson decoupling by nutating. One axis rotates about the other, thereby forming braids, [35,36]. The braiding depends upon , with common to both Alice and Bob. The coherent correlation, and violation of BI, can possibly be quantitatively described by this common braiding.
6. Dirac: No Antimatter
Linearizing the Klein-Gordon equation, as Dirac did, led to his four dimensional gamma matrices defined in Minkowski space, . The necessary requirement is they anticommute. From this field the matter-antimatter pair emerged, and spin formalized. In contrast, we use the spin field represented by . Since they too anticommute, they present an alternate and viable linearization of the Klein-Gordon equation.
A perplexing point for Dirac was the twin spins have opposite, or negative, energies from its partner and these went to minus infinity, [23], which is non-physical. Dirac resolved this by proposing a fermionic continuum of negative energy, and added electrons according to the Pauli principle until the continuum was filled. Holes of antimatter positrons are formed as electrons jump to positive energy. Although this structure might exist in solid state physics, with the bound and conduction bands distinguished, for other systems and single particles, hole theory is a rationalization, not satisfying, and is contrived to resolve a problem.
Since Q-spin has two spins that precess oppositely and in phase, Figure 4, the two energies must be equal and opposite. Conservation of energy resolves the negative energy problem Dirac encountered. No sea of electrons is needed.
We do not dispute the existence of antimatter, [37,38], but question the Dirac interpretation of its production. Experimentally, only trace amounts are found in the universe from the decay of unstable nuclei. At higher energies, pair particle production also occurs. It is commonly stated that an asymmetry, [39,40], of 1 in 300 million gave matter the edge over antimatter. If such large-scale matter-antimatter annihilation took place, we should see evidence in the form of intense gamma radiation, annihilation zones, abundant antimatter in cosmic rays, and distortions in the CMB, [41,42]. However, none of these are observed, leading to the conclusion that such widespread annihilation did not occur after the Big Bang.
If Q-spin was formed at the Big Bang, rather than fermion matter-antimatter pairs, the baryon asymmetry problem is resolved .
7. Bell’s Theorem Is Classical
Bell’s Inequalities, [43], show that the correlation between real classical properties is bounded. Noting that QM can violate these inequalities, Bell concluded this can only happen if certain hidden variables (HV), account for the violation, however, these must be non-local. We accept BI, but reject Bell’s Theorem, [8], which states in his own words,
“If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."
A more formal statement is the impossibility that local HV can reproduce the results of quantum mechanics, with the conclusion that non-locality is a property of Nature. Our work shows that a local theory can violate BI, thereby disproving Bell’s theorem by counter example, [6].
Bell only examined classical correlation with BI giving the upper bound. The proof of Bell’s Theorem is also classical. Having proven classical correlation is bounded, he then examined under what conditions those classical variables could violate that bound even though he knew no classical correlation could. He arrive, therefore, at the conclusion that the classical HV must be non-local. Since non-locality makes no sense, Bell’s proof should be considered as ,44]. Attention would logically then shift to finding what is missing that gives the quantum violation of BI. Bell, however, did not take that course. Rather he assumed that quantum variables and classical variables have the same properties.
Classical variables are all real; and they form a single commuting convex set [45]. Pure states are extreme points and mixed states are interior points. Quantum variables, in stark contrast, may not commute; are complex; are complementary; and form two convex sets. All particles are produced in pure states which remain pure until encountering a polarizing field. We discuss this further in Section 12 . On the other hand, Q-spin does not violate BI when viewed as two complementary sources of correlation. That is, polarization and coherence are complementary elements of reality. If experiments could separate the two, then the correlation for these would be CHSH = 2 for polarization and CHSH = 1 for coherence. Neither violates BI and each can be considered a separate experiment.
Bell’s work inspired experiments, [9,10,11], which confirmed QM violates BI. This is regarded as proof that local HV theories must be rejected, and established non-locality as a property of Nature. This conclusion cannot be supported with Q-spin. Although Bell’s work stimulated research into the foundations and philosophy of quantum mechanics, the view of this work is that non-locality has led physics into unfathomable directions which have hindered progress.
7.1. Convex Sets
Unpublished comments erroneously assert the two contributions to the correlation, polarization and coherence, should be averaged and not added as we do in Equation (13). Averaging would disagree with experiment whereas adding agrees. This is seen in Figure 5 showing the triangle and the mustache added to give the total correlation violating BI. Adding is a direct consequence of complemenarity.
We raise this point because it underscores a limitation of Bell’s theorem due to using only classical concepts. As mentioned above, Bell considered only variables with outcomes that lie in a common convex set, S. Suppose two operators, and , commute with measured outcomes of A and B, then the measured combination obeys a lever law,
Since and have compatible eigenvalues, their pure states are extreme points on S with or 1. The interior points are outcomes, Equation (23), from mixed states, . This is the case that Bell treated. Averaging, rather than adding, however, does not take into account that polarization and coherence are complementary.
and are complementary when their outcomes belong to distinct convex sets, say and . This reflects the fact that their outcomes are not jointly measurable, and there is no common eigenbasis between them. This is true for Q-spin, and the Minkowski sum, [46] is the way to combine different convex sets,
which adds them. This is the case we treat, and therefore non-commuting operators justify the sum. Bell’s work does not include different convex sets, and not doing so is the reason for the violation.
Conflicting variables, like position-momentum, , require different experiments to detect them. Pauli stated [47], “Intuitively, observables are complementary if the experimental arrangements allowing their unambiguous definitions are mutually exclusive”. Coincidence EPR experiments are not yet able to distinguish polarization from coherent events. At the source, and separation, the angle is common to Alice and Bob, but whether the outcomes are polarization or coherence is not decided until a spin reaches its filter. This sets and in doing so defines a different experiment each time the setting is changed. Mutually exclusive experiments that Pauli described can occur each time the filter is set by Alice or by Bob. The timings can be set so one particle is measured per setting, and that setting determines which attribute is measured. Equation (24) depicts, say, A clicks and B clicks, and each click belongs to a different convex set, and , and each set acts as a bin where the clicks outcomes are saved. After performing a statistically large number of experiments, the bins are analyzed. This is exactly the way the simulation was done, and describes common experiments.
7.2. Non-Locality vs. Local Realism
An immediate consequence of the inapplicability of Bell’s Theorem is that non-local connectivity is not viable. Out of the myriad descriptions we feel that Wikipedia sums up non-locality the best, [48]:
“The paradox is that a measurement made on either of the particles apparently collapses the state of the entire entangled system—and does so instantaneously, before any information about the measurement result could have been communicated to the other particle ... and hence assured the “proper" outcome of the measurement of the other part of the entangled pair."
Scholarpedia states [49], “Bell’s theorem asserts that if certain predictions of QM are correct then our world is non-local. “Non-local" here means that there exist interactions between events that are too far apart in space and too close together in time for the events to be connected even by signals moving at the speed of light."
Without Bell’s Theorem, these definitions cannot be supported.
The violation of BI now takes on an entirely different meaning. Spin polarization and helicity both simultaneously exist as elements of reality; coincidence experiments are sensitive to both; the experimental violation of Bell’s inequalities confirms helicity is an element of reality, and non-locality is rebuked. This defines local realism. Polarization and helicity are inherent properties of Nature, and ontologically real. Therefore, reality of the microscopic is complex. Quantum weirdness, [50], is explained by complex helicity.
This should help in the philosophy of QM which is generally flummoxed by non-locality, indeterminism, and the death of ontology and free will. It is impossible to reconcile the probabilistic and non-local nature of QM with established notions of reality, causality, and determinism, although they try, [51,52].
The diametrically opposite conclusion is reached in Bell-type experiments of which an enormous literature exists, see “The Big Bell Test" [53]. The paper’s conclusion is incorrect claiming local realism is challenged. Rather their data shows just the opposite: evidence for local realism by the existence of elements of reality that account for the violation.
7.3. Quantum Teleportation Is Unfeasible
Quantum teleportation, [12], depends solely upon long range, non-local, correlation between three entangled particles. The opening paragraph in that paper confirms, “The existence of long range correlations between Einstein-Podolsky-Rosen (EPR) pairs of particles raises the question of their use for information transfer." This statement rests on the now defunct Bell’s Theorem.
Teleportation claims that non-locality is mediated by “Einstein, Podolsky, Rosen Channels", but nowhere are these “channels" formulated and there is no evidence they exist other than Bell’s Theorem. Our work shows they are not needed, and do not exist. In particular the steps up to their Equation (5), which are critical to quantum teleportation, cannot be justified. This requires swapping entanglement over spacetime separations. When Alice’s spin, 1, is far from Bob’s entangled pair, 23, then the following process is applied which is physically unfeasible:
Therefore their Equation (5) is impossible and the notion of quantum teleportation collapses. Recall Longuet-Higgins [54] made the distinction between mathematical operations and feasible operations, like ammonia, , and methyl fluoride, , both have the possibility of umbrella symmetry, but only for ammonia is it feasible.
The concept of quantum teleportation is unfeasible, along with emerging technologies [55,56,57,58], that rely on it.
The question arises about the results from the above experiments which appear to support non-locality. First note the correlation from an entangled singlet is conserved when separated into its complementary pair Equation (12);. For example, quantum cryptography relies on a third party interloper entangling with the communication between Alice and Bob. Using Q-spin, in contrast, any interloper will introduce a local phase change in the helicity, disrupting the transmission, and giving similar outcomes had entanglement persisted. The same approach effects all Bell-type coincidence experiments which rely on non-locality. Examples are entanglement swapping, [59], delayed choice quantum eraser, [60], and loop-hole free Bell tests, [61,62].
7.4. Quantum Computing Changes
The prospects of having large working quantum computers (QC) has not been realized, [63]. Major obstacles have inhibited the engineering development which is motivated by extensive theoretical research showing considerable advantages over classical computation. Major difficulties include error correction, scalability and in writing quantum code. Also extremely low temperatures are needed to reduce noise, and the cost of building QC is high.
The treatment here might help resolve some of these difficulties. Teleportation is unfeasible and should be removed from all code, in favour of controlling . Moreover, the use of entanglement is an approximation and misses coherence, Section 9. As shown there, the singlet is better viewed as a product of non-Hermitian state operators. Another issue is the stability of qubits which decohere. Therefore, much effort is spent on finding suitable two-state quantum systems that are stable.
Presently the use of electrons in circuitry is based upon their charge. If spin can be controlled, then the two spin components, with opposite magnetic moments, might serve as a stable qubit. Electrons and other charged particles cannot be used because the Lorentz force would dominate the magnetic effects, which causes deflection due to their charge rather than just their spin.
Consider the qubit form of Q-spin in the BFF,
The two axes, and have opposite magnetic moments, and these project along the field axis,
By controlling and , the experimenter can determine which axis will align with the field. Spin is a stable property of many particles. That is, spin is a natural qubit. Although the boson state is present, such experiments would focus on the ± outcomes, with causing to align giving say , and causing to align giving .
One can envision microscopic Stern-Gerlach apparati on a chip. Consider a neutron, with a stable spin . By controlling from a previous gate, the system can set the Stern-Gerlach filter giving a deterministic two bit outcome of . In QC, the boson form will likely not be of interest unless some advantage for its persistence can be found. The role of the boson is to transfer the information of spin properties from one gate to the next: carrying energy in its helicity and internal structure, and orientation in the phase of the helicity, .
Stern-Gerlach experiments have already been performed with neutrons, [64]. These confirm the quantum mechanical properties of neutron spin. We note techniques that use NMR are candidates for QC, [65]. NMR spectroscopy routinely transports polarization and coherence between states, [66], performing spin "gymnastics", [67], and producing echos, [68].
An advantage of Q-spin qubits is the algorithms are products of quaternions.
8. Hidden Variables
Bell’s work depends upon the existence of HV theories which are defined in Bell’s paper, [43] and discussed below. HV are supposed to either reproduce QM, or embellish it to give a deeper understanding. Since HV are generally misunderstood, yet figure important in Bell’s work, we review them here. The goal is to question their value and therefore their existence.
Much of the conceptual difficulty with QM is the incompatibility of some observables, like position and momentum, which obey the Heisenberg Uncertainly relations. HV refer to hypothetical parameters that can lead to all observables being dispersion free. Proponents argue that quantum mechanics is incomplete and that an underlying deterministic framework, governed by these HV, could explain the randomness in quantum measurements.
Below we prove Q-spin has no HV local or not, and consequently there can be no loopholes; hidden mechanism to create non-locality; or hidden ways of removing dispersion. The only variable in this work is the angle which orients a spin on the Bloch sphere, is a local variable and which is all that is needed. We see no evidence which are consequences of HV, and if included, it is doubtful things might improve. More to the point, we see nothing missing that HV might fix, and if we did, we would employ the concepts of QM, and discover something. There is no evidence that HV can improve on quantum theory.
Bell’s Theorem is a no-go theorem that posits that local HV cannot describe the quantum results. However, von Neumann had already shown, [33], that HV do not exist if it is assumed that expectations values are linear, . Although he did not discuss contextuality explicitly, he assumed values are assigned independently of other observables. That is, he did not assume measurement contextuality, which occurs when the measurement of B with A gives a different result for A if C is measured with A, particualrly when B and C do not commute. Contrast this with how the apparatus is set up by the experimenter, which is called observer contextuality.
Bell’s HV are a complete set of objectively real numbers, , which are local, deterministic and non-contextual. The outcome is encoded at the source. For Q-spin, since the polarization and helicity are pure states, each is a single extreme point on different convex sets. There can be no compatible states associated with Q-spin that can produce measurement contextuality.
Bell objections to von Neumann’s work, [69], criticizes his linearity assumption when observables do not commute, requiring different experiments. Using Pauli spin components as an example, their expectation values obey von Neumann’s assumption, because the state operator is linear. Bell argued, however, that is too restrictive and those HV, , might exist such that . Linearity, Bell argued, does not extend to different experiments, pointing out that three Stern Gerlach orientations are needed to measure the three expectation values. This may be true, but changing the orientation of a Stern-Gerlach filter defines a new z axis, and gives identical results in all three cases if the source remains random. Bell’s three experiments only rearrange the states in the same vector space common to the Pauli components he used.
Bell did not consider dispersion between complementary variables. His example involves two non-commuting Pauli spin components. They are only incompatible. They do not have complementary or dual vector spaces, like position-momentum, and for spin, polarization-helicity. The dispersion between incompatible spin components is understood, and is due to randomization of the spin states due to precession in the plane which is perpendicular to the field axis along z. Quantum calculations confirm this, [70,71]. No hidden variables are needed to understand the dispersion between spin components. Bell’s critique of von Neumann did not address hidden variables that might resolve dispersion between complementary spin properties.
We do not know, but Bell may have assumed the non-linearity argument also applies to complementary dispersion. It does not for Q-spin. We have already established that Q-spin is measurement non-contextual. Additionally, it is linear, . In addition to the linearity of the density operator, this expression is also a direct result of the geometric product, Equation (1). It is also a consequence of the decomposition of a dyadic under the rotation group into symmetric and asymmetrical irreducible representations. Expectation values that depend upon HV cannot change this to , without violating GA and symmetry. Q-spin is, therefore, consistent with von Neumann’s assumptions and confirms our conclusion that no HV exist for Q-spin, and the dispersion that exists between polarization and coherence is inherent and cannot be removed.
Bell did not consider the natural constraints between complementary spaces which would also constrain any HVs. Such complementary pairs, like position-momentum, must obey, , . Using this, we find the wave-particle duality as related by the Fourier transform between position and momentum wave functions,
It is difficult to envision HV theories that could enhance this relation without disrupting the duality between position and momentum spaces, or well established results, like the uncertainty principle. Bell’s argument might not apply to complementary variables due to other constraints between them. While not a proof, these points suggest that HV may offer little advantage in improving quantum theory and might be better abandoned.
If HV did exist by somehow overcoming the above issues, we must also contend with not knowing how these parameters create non-local connections with no mechanism whatsoever to support it. There are two types of HV theories. Those that provide a different framework from QM and are stand alone. Those that are within the framework and introducing HV aims to extend and improve QM.
8.1. Independent Hidden Variable Theories
de Broglie’s pilot wave was the first HV theory and it provided a different framework from QM, [72]. Bohmian mechanics, [73], followed. There are other such theories we omit, except superdeterminism, [74] which posits that the universe is fully deterministic so everything, including experimental settings and particle behaviors, is predetermined by HV. The main detractors say that this takes away from the free will of the experimentalist.
The success of Bohmian mechanics was held as an example that refuted von Neumann’s conclusion that HV do not exist in QM. Bohmian mechanics, however, is an alternate formulation of QM, and not an additional hidden structure. The particles have definite positions and follow deterministic trajectories, but the momentum of a particle is determined from the gradient of the wave function’s phase: the pilot wave. Bohmian mechanics does not resolve dispersion in the sense of removing it; rather, it provides a different way to understand dispersion. The evolution of the wave function and the associated dispersion are still present, but Bohmian mechanics interprets the outcomes in terms of particles with definite trajectories rather than a probability measure. The dispersion mechanism in Bohmian mechanics relates to how the particle trajectories spread out under the influence of the quantum potential. The wave function still undergoes standard quantum evolution, so the particles spread out or disperse in a way that corresponds to the probabilistic wave distribution, but this process is underpinned by the guiding equations that dictate the precise path of each particle.
Bohmian mechanics is a deterministic theory with hidden variables and leads to the same outcomes as standard QM [73,75]. This is because Bohmian mechanics uses the Born rule for probability distributions, which is empirically indistinguishable from quantum mechanics. However, the “quantum potential” must be non-local. This is the main objection, along with its incompatibility with relativity, [73], that this otherwise successful and alternate formulaton of QM was not pursued.
Bell’s beables, [8], refer to fundamental variables in a HV theory. In contrast to quantum mechanical observables, beables represent quantities that describe the physical state of a system, whether a measurement has been performed or not–so "be-able" to express reality even in the absence of measurement. For example, in Bohmian mechanics, the position of a particle is considered a beable because it exists as a definite property, even when being observed. Bell introduced beables to represent physically real properties, independent of observation. In contrast, quantum observables depend on measurement to have definite values.
We mention them because they form a conceptual framework for local realism in HV theories. Beables are part of a stand-alone realist approach, as they aim to provide a complete and deterministic description of physical reality. They are not meant to enhance quantum mechanics but rather to replace it in hidden variable theories, where objective properties of systems exist independently of measurement. Beyond Bell’s work, [8], the number of papers we found specifically addressing beables is not large, but the topic has garnered attention in discussions of fundamental ontology and interpretations of quantum mechanics, [76].
8.2. Hidden Variables That Improve Quantum Theory
We are interested in HV theories that are within the framework of QM, and attempt to provide the underlying reasons for its probabilistic nature. Bell’s theory can be one, and his aim was to see how HV might improve on quantum mechanics. He found, of course, any viable HV theory must be non-local, although some other mechanism like retrocausality, [77,78], or superdeterminism, [74], may allow non-local correlations between distant particles that explains quantum weirdness. Bell explored whether alternative HV theories could fit the predictions of QM.
The Bell-Kochen-Specker theorem, [8,79], also applies within the framework of QM. It discusses contextuality showing that non-contextual hidden variable theories are incompatible with QM. Although this theorem is insightful, it is not applicable to Q-spin since their conclusions are valid for three dimensions or more, and Q-spin is two dimensional in spin spacetime. This contextual compatibility doesn’t arise in 2D systems because of insufficient surrounding states needed to create different measurement contexts needed for their proof.
8.3. Hidden Variables Do Not Help
Von Neumann’s considered HV that are within the framework of QM. He argued the HV assign definite values to all observables, regardless of the measurement context. However, if the observables don’t commute, no hidden variable theory could consistently assign definite values to all observables. He argued against the existence of HVs in quantum mechanics, claiming any HV theory that could reproduce the predictions of quantum mechanics would be equivalent to it. If HVs existed, there should be observable effects, and QM works very well without them. He concluded that quantum mechanics, as then formulated, is complete and that the randomness observed in quantum phenomena is intrinsic rather than a result of underlying deterministic variables.
Although not a HV theory, the no-cloning theorem, [55], is a well known no-go theorem. It uses linearity, and unitarity of QM to show that the following transformation is impossible, . Although this is a local result, the theorem is universally used in quantum information theory which relies entirely on non-locality and quantum teleportation. As shown in Section 7.3, teleportation is unfeasible. Interestingly, and to be contrary, Bell may have objected to the application of the no-cloning theorem to non-local cases because of his objection to the linearity assumption.
It is also of interest that recent work, [80,81], re-examined von Neumann and noted that the English translation of the German, "prufen" is "check" or "examine" and not "prove". Therefore Bell did not disprove a theorem by von Neumann. Nonetheless, Bell’s work discredited von Neumann’s arguments and opened the door for Bell’s Theorem. Bell needed HV to exist in order to derive his inequalities and theorem, and von Neumann’s "proof" stood in the way. In assessment, HV theories are unnecessary and have led to confusion. QM is better without them. None have improved upon quantum theory.
Macroscopic properties benefit from HV due to the dynamics of many microscopic properties to give a few macroscopic observables. Bell theorem and work on correlation is applicable only to such classical systems.
We do not dispute the mathematical proof of Bell’s theorem. Rather we conclude that it is inapplicable to quantum systems. Q-spin shows that few of Bell’s conclusions about QM are correct, [8]. The purely classical BI are an exception. They quantitatively define the “Infamous Boundary” [82] between the classical and the quantum. For the CHSH form of Bell’s inequalities, the Infamous boundary is 2, [9]. For Q-spin the infamous boundary is the distinction between a Pauli vector and a Pauli bivector.
Parenthetically, we note again in Figure 5, there is a small simulated correlation from the polarizations that violates Bell’s Theorem with a CHSH = 2.027. It is known that classical simulations can violate BI without non-locality, [83,84,85,86]. Despite the wide acceptance of Bell’s theorem, there exist a number of critics who also raise cogent doubts about its applicability and use, see [83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98].
9. The Singlet State Is Approximate
Entanglement, as Schrödinger famously said [99] is difference from classical systems. Without Bell’s theorem, persistence of entanglement between separated pairs is not possible. Therefore we accept entanglement as a useful property of QM but reject that it persists after separation, [6], to non-local situations.
A singlet state is always expressed by opposing polarized states which are anti-symmetrized, , where , ,
We replace the states with Q-spins. Using is an approximation and the reason the Tsirel’son bound, [26], is less than the simulated result of CHSH =3.
We suggest a singlet state of an electron is more realistically expressed as shown in Figure 9 where the two magnetic axes are attracted which are balanced by the repulsion of the charges. The helicity now spins the axis as shown. To show the missing parts of the quantum form of the singlet state, Equation (29), first take its outer product, and then separate the state operator, , into a sum of eight non-Hermitian product states, [100],
The final matrix displays the diagonal polarized states, and the off-diagonal coherent states. This expression leads to the correlation between the two spins, and a CHSH = 2.828. Recall the off-diagonal coherent terms are responsible for entanglement, [6].
The eight product states in Equation (30) are the possible ways an EPR pair can separate. Each EPR pair separates randomly into only one of the eight terms in the above sum which represent states of definite polarization and helicity. One term describe left and the other right helicity for each quadrant. We suggest that after initial separation, each spin settles into a trajectory with the disc of polarization spinning along the axis of linear momentum, see Figure 3, governed by the Intermediate Axis theorem, [101].
Inserting the Pauli spin matrices into Equation (30), and summing the eight terms reproduces the entangled singlet matrix shown in the last line. In the process, coherent terms cancel, and those, we suggest, are responsible for the difference between QM and the classical simulation.
To demonstrate this consider the first quadrant in Equation (30) with , giving the tensor product of two matrices, one for Alice and one for Bob. They have opposite polarization and helicity. Using these non-Hermitian matrices requires tacit acceptance that polarization and coherence simultaneously exist.
Upon separation, either the left or right handed persists. That is, for each quadrant, at separation, the EPR pair is one of the eight products, for example for the first quadrant, ,
The state with opposite helicity is also possible in the first quadrant, and adding the left and right , matrices, Equation (30), leads to a Hermitian matrix for each quadrant,
Permutations of gives similar matrices for the other three quadrants. Finally summing over the quadrants gives the entangled singlet, Equation (30). Comparing this final singlet matrix with Equation (32), shows the outer coherent terms, indicated by bold fonts cancel in the final sum. We suggest these terms are responsible for violating the Tsirel’son bound, [26], which leads to the difference between quantum, CHSH and the simulation, CHSH.
We conclude that use of the singlet state in QM, Equation (29) is an approximation which misses these canceled terms. That is entanglement is a property of QM, but not of Nature. Entanglement simplifies calculation but missing correlation is the price.
10. Black Holes and Wormholes Are Not Entangled
Suggestions by Maldacena and Susskind [24] are expressed by the relationship ER=EPR where ER stands for Einstein-Rosen Bridges, (wormholes), [102], while the EPR [4], refers to QM and entanglement as a way to quantize spacetime [103].
Wormholes are solutions to the Einstein Field Equations [104] and are purely geometric distortions of spacetime, mathematically connecting different spacetime spaces. Maldacena and Susskind suggest that the wormholes are equivalent to, or created by, a pair of entangled black holes, with Alice at one end and Bob at the other performing gedanken experiments with credible outcomes. When two particles are entangled, the "quantum channels", [12], form a kind of wormhole connecting them over spacetime. Therefore, this implies that the fabric of spacetime is underpinned with quantum mechanics, which could lead to a quantum description of gravity. In essence, the conjecture suggests that quantum entanglement is geometrically represented by Einstein-Rosen bridges, which are theoretical solutions to the Einstein field equations, thereby connecting the two.
Although we assert non-local entanglement is not possible, [7], Q-spin presents an alternative that replaces non-locality. We point to [6,18], ,
as perhaps the smallest quantum entity which could be the building blocks of spacetime, with the LHS indicating the smallest component of quantum spin in free flight, and the RHS indicating the connection to geometry,
The following construction is speculative but not unlike the entangled construction: consider Minkowski space as composed of a diffuse gas, a lattice, of particles in free flight with spin . Each particle has a mass of at least a rest mass, and energy of at least a zero point. These particles attract each other according to an inverse power law like Newton’s Law of gravity, but because space is so diffuse and the masses so small, there is little attraction between the particles. We are assuming that throughout the vastness of space, these particles form the microscopic fabric of spacetime.
In regions where the density and mass increase, these particles pull closer and eventually they merge and coalesce. For N coalesced points the structure is now , with Black Holes in the limit that . Examination of n-tuples of spin operators, [105], suggests the first step is to find the irreducible representations under some group. If relativistic effects are important, the Lorentz group is appropriate. Otherwise, the rotation group SO(3) should suffice. In either case, the irreducible representations have geometric structures and relate quantum theory to geometry. We have done that in this paper, using the geometric product, to define Q-spin. The irr. reps. of higher n-tuples, not unlike the parentage scheme depicted in Figure 11, can also be quantized.
We have found Q-spin has a microscopic hyperspace with four spatial dimensions. Quantum gravity is a macroscopic force with a far reach. Gravity is related to the curvature of spacetime with a metric tensor of rank 2, which suggests it to be mediated by a boson with spin-2. Whereas we have found that reality must extend to the fourth dimensional quaternion projective space, the hypersphere, one can only suggest that gravity is more complicated and likely extends to the next credible projective space of octonions in the hypersphere, or beyond. We do not know the nature of matter and energy in the dark regions of these vast hyperspaces beyond our visualization. All we can know are their stereographic projections onto our dimension, and from these observations we must try to visualize what lies beyond our senses.
11. Standard Model
The success of the Standard Model, SU(3)⊗SU(2)⊗U(1), is marred by problems with the Weak Force, [106], with Lepton number [107] and parity violations, [108]. Our work suggests replacing SU(2) with the quaternion group. In this section we explore some consequences of this change on beta decay and parity violation.
11.1. Neutrinos Do Not Exist
Beta decay, [109], can be expressed as a neutron in a nucleus decaying into a proton by emitting a beta particle, a fermion electron, and an anti-neutrino,
The second line gives the total spin magnitudes, each with two magnetic quantum numbers of . These components will always conserve spin angular momentum, . Without the neutrino, a fermion electron alone cannot, .
The issues of conservation of spin angular momentum and energy led Pauli, [47,110] to hypothesize neutrinos to be fermions, with neither mass nor charge, and with the fermion axis colinear to the axis of linear momentum. This immediately reveals that neutrinos have no mirror image and violate parity. Neutrinos are only left handed while antineutrinos are only right handed. They carry no magnetic moment. We consider these properties peculiar.
Moreover, neutrinos have an exceedingly small collision cross section, so they are not significantly removed by reactions. That is, once produced, neutrinos are basically of no use, yet they are postulated to keep on being produced at enormous rates. All particles have a purpose. For neutrinos, once they have balanced energy and spin in nuclear reactions, they have no further use. They are already the most abundant particles in the Universe by far, [111]. Neutrinos have a source but no known sinks. In that case, consider the back-of-an-envelope calculation:
There are about stars in the universe with an average neutrino flux of neutrinos/star/second. Assume that production is constant for the last 14 billion years sec. With no neutrino sinks, neutrinos presently exist in the universe. The value of the average mass of a neutrino is not certain, with most stating one millionth that of an electron, [112]. We used the smallest value we could find, kg, [113] giving the present mass of neutrinos in the Universe of about tons. This is about ten times the estimated visible mass of the Universe. Either neutrinos have sinks, or they do not exist. One might argue that the mass used is still too high, but dropping the mass to kg, still leaves a total neutrino mass of tonnes, equal to that of the universe. This would subsequently compromise the neutrino oscillation theory which requires much higher masses for the three neutrino flavours. Such argument are again speculative and open to criticism, but are intended to underscore non-physical properties of neutrinos.
Boson beta electrons, , in contrast, have a spin of 1 and internal structure. The latter should account for the energy distribution, and therefore not violate the conservation of energy. The spin-1 boson balances the spin without a neutrino,
With almost no detection; strange parity properties; their persistence after production; and now the boson electron obviating the for a fermion electron neutrino, we assert again they do not exist.
This contradicts experimental evidence, [114,115,116,117,118,119,120]. No direct detection has been observed. Detected is based upon collision product using the Standard Model, with the Weak Force of SU(2) symmetry. A great advantage of QFT is the range of processes that can be constructed. Whether real or hypothetical, neutrinos are consistent with a number of processes, such as inverse beta decay; scattering and recoil experiments; nuclear reactions, decaying to ; and Cherenkov radiation, [114], created from neutrino interactions when charged particles move faster than the speed of light in a medium. Today, Cherenkov radiation, [119] and inverse beta decay, [120] are most common.
Nonetheless, using these method, over enormous fluxes of neutrinos, very few such indirect events are recorded. A typical experiment over a year with a calculated flux of, say, neutrinos, only a few hundred are detected. Although steps are taken to avoid them, we suggest these are due to other events, like cosmic rays. They can give false detections of neutrinos because both can produce similar secondary particles like muons from cosmic ray showers, and Cherenkov radiation. However, neutrino detectors use several methods, such as deep placement underground, coincidence rejection, muon veto systems, and directional analysis, to reduce the chances of misidentifying cosmic ray signals as neutrinos. Despite these precautions, cosmic rays still represent a significant challenge, with an extensive literature, [121,122,123,124,125,126,127,128].
We suggest the data be reconsidered in the light of boson beta electrons.
11.2. Parity Is Not Violated
In the 1950’s, Yang and Lee, [129], suggested that the weak force may not obey parity which motivated experiments. The 1956 experiment, conducted by Chien-Shiung Wu and her colleagues, [130], confirmed parity violation which was a crucial yet disrupting contribution to the field, [109]. Parity conservation was a widely accepted principle that stated that the mirror image of a physical process should be indistinguishable from the original process in the real world. Parity violation is as weird as quantum weirdness.
Wu’s experiment focused on the beta decay of cobalt-60 nuclei, emitting a beta electron (), and an electron antineutrino, Equation (35). According to the law of parity conservation, this process should be isotropic in all directions. However, Wu’s team observed a clear asymmetry in the emitted electrons’ distribution. Wu stated, [130],
“If an asymmetry in the distribution between and ... is observed, it provides unequivocal proof that parity is not conserved in beta decay.”
Q-spin suggests an alternate explanation of her data.
Under quaternion symmetry, a beta particle is a boson of odd parity, . As discussed in the last section, this immediately shows that for beta decay, the antineutrino is not needed to balance spin, and the internal structure of Q-spin conserves the energy. Therefore, without neutrinos, we assert the beta decay process for cobalt is given by,
In the experiment, [130], the cobalt sample was placed in a solenoid that produced a polarizing field along the polar axis and which can be reversed. Wu measured the gamma rays, the distribution of which is the same as that for the beta particles. Equatorial counts were used to normalize the polarization. By reversing the current in the solenoids, the experiment detected an asymmetry in the number of counts between the north and south. The mirror symmetry is not faithful and parity is violated.
This is shown in Figure 10. The first column is the real world. The second column depicts the parity transformations, and the last column performs a rotation, needed so the first and third columns are mirror images.
If parity is conserved the expected distribution must be symmetrical, which is shown in the first row,
(a) Since the magnetic field; the cobalt spin; and the fermion electron; are all axial vectors, they are symmetrical under parity. As stated above, Wu expected this result if parity is conserved.
The real world image in the second row,
(b) This is what Wu actually observed, an asymmetrical distribution of beta events. Performing the same transformations as in (a), it is a clear that the mirror reflection is not faithful, showing parity is violated. For this reason it is concluded that parity is violated in Nature.
In contrast, if the beta particle is a boson electron with odd parity, then row
(c) of Figure 10 shows the real world data is faithfully reproduced for any distribution observed. Parity is not violated under the quaternion group.
This result is surprising. At the time, Wu’s experiment was also a surprise. Considerable effort is, and has been, devoted to understanding the implications of parity violation. The 1956 results caused a paradigm shift in physics, and ended the belief that all physical processes are symmetric under mirror reflection. This has consequences. The laws of physics are not completely uniform under all symmetry transformations. Key components in the Standard Model are a direct consequence. Charge violation emerged so that CP is conserved, along with theories of dark matter, baryogenesis and other unexplained phenomena.
If, indeed, parity is not violated, it would cause another paradigm shift back. Although tumultuous, it may simplify our view of Nature.
11.3. Twistor Theory Gives Helicity
At the microscopic level, particles are indistinguishable and described by quantum wave functions, which include complex phases. These phases determine behavior of particles in quantum systems. However, at the macroscopic level, the Random Phase Approximation (RPA) averages out these complex phases. Quantum effects that rely on phase coherence are lost, and physical phenomena appear classical, consistent with our everyday experiences.
A goal of Twistor Theory is to unify quantum mechanics and general relativity by complexifying Minkowski space into a geometric Twistor space, T. As a complex space, it has two projections onto helicity states of + and −, denoted by . The boundary between the two, , is a real space of null vectors, which are light rays from the light cone. From this a number of mathematical developments followed, along with incorporating twistors into string theory [131], and QFT, [132,133]. Complex geometry emerged as an elegant theory and has led to simpler formulation of scattering processes. Feynman diagrams become increasingly complicated as the number of interacting particles rises. Complex geometry reformulates these calculations in terms of algebraic structures in complex space. This leads to a significant reduction in computational complexity and allows for more efficient calculations of multi-particle scattering processes.
We find similar simplification by complexifying the Dirac field. In analogy to Twistor space, denote the complex spin spacetime by a Dirac field, . This leads to two projective helicity states of . Upon measurement, the real part is observed. No additional parameters are introduced, and a non-Hermitian Dirac equation determines the fields. Under parity, this splits further into complementary spaces, and .
The purpose of our complexification is to introduce a bivector into spin, and, again, consistent with Twistor Theory, helicity is formulated. At the microscopic level, neglecting coherence gives incorrect results, leading us to accept Nature is complex.
12. Interpretations of Quantum Mechanics
To arrive at our result, we went outside the usual structure of QM. Much involves Equation (7) which is . Despite being non-Hermitian, and represented by a complex field, we view is an element of reality. The two contributions are complementary, yet both are included simultaneously in the definition of Q-spin. The quaternion that leads to the observed helicity of L or R, is in and is not observable. We observe in our spacetime, hence a state operator is also so restricted. For this reason, we do not call an observable.
Helicity and coherence are manifest as phase. The RPA, [134,135,136] removes the phases by decoherence. To avoid this, we deal with a single particle in a pure state.
Consider a child blows a bubble. The ground state is a sphere, but that bubble undulates reflecting its creation when the child blew. Molecules are similar. Valence Bond theory gives resonance structures; Molecular Orbital theory delocalizes electrons over molecules for stability; bonds vibrate; and angular momenta couple. However, in free flight a molecule is like the bubble, it is a wave which expresses its pure state, so when measured, it is the only state observable. When encountering a field, that dynamic wave rearranges in response as the pure state is measured or interacts. Even if the particle displays undulating resonance motions, like the bubble, it is still in a pure state. We might take that state and decompose it into objects we prefer, like spherical harmonics. No matter what we do, a single particle in free flight is in a pure state, because it cannot be in a mixed one.
However, we might well have difficulty describing the initial pure state. Due to the energy and other parameters involved in the state preparation, a large number of pure states may be possible subject to these constraints. Therefore, we consider a collection of pure states that cover all possible ways a particle can form. Each experimental click is from detecting a single particle in a pure state. After many events are collected, the ensemble average is obtained. The individual particle states that make up these ensembles are pure. Even free evolution that results in the spread of a wave function over time, does not detract from that state remaining pure. Conflicting states only conflict when measured.
These changes are evident in the treatment here:
- Elements of reality can be non-Hermitian, Equation (7).
- Calculate the expectation values using the usual state operator which is Hermitian, positive semi-definite of trace 1, . Equation (17)
- Expectation values of non-Hermitian operators can be complex with two complex conjugate states, Equation (18).
- To avoid decoherence of complex phases, we treat single particles in pure states.
- Take the real part to obtain the measured value , Equation (19).
- When dealing in complex spaces, non-Hermitian operators lead to the separation of entangled states, Equation (30)
QM should be extended to accommodate spaces beyond our LFF. However, state or density operators remain in our LFF from which we observe. The pure state operator is an idempotent projector.
The quaternion field is more fundamental than Dirac’s. The latter leads to the two-spin matter-antimatter pair, two point particles with two states each, while the former leads to one structured particle, Q-spin, with four states: two polarized up or down, the particle, and two coherent with helicity L or R, the wave.
This section argues that Q-spin gives a deeper and more realistic view of spin than Dirac. First, however, Q-spin becomes a particle in a polarizing field, where most interest lies. In that case, the two possible fermions (left and right panels of Figure 4) cannot be distinguished from Dirac spin of up and down. We expect quantum calculations based on Q-spin in a field to be identical to those of Dirac spin, albeit with no antimatter twin.
We know of no experiments other than coincidence EPR types, [9,10,11], which are sensitive to the anyon transition. However, one expects that transition to be ubiquitous in Nature.
Q-spin is also the first building block of a parentage scheme to higher spins, similar to the Clebsch-Gordan series, [137]. The dyadic, Equation (1), stops at the bivector, but higher n-tuples contain trivectors and higher structures which can be decomposed into irreducible components under some group, [138,139,140,141,142]. The usual parentage scheme is based upon the addition of spinors, see Figure 11. Extension to complex Q-spin includes a phase for each spin, and any parentage scheme will likely contain insightful relationships as Q-spin couples to produce quaternion spins of higher weight. The way these couple may be crucial steps to understanding and, like Twistor theory, simplifying some processes. This underscores the assertion we must maintain the phase relations in calculations, and only project into our real space when observation is needed.
12.1. Symmetry Changes Everything
The four elements of Q-spin can be used to represent the discrete quaternion group , which is isomorphic to the group of unit quaternions, , under multiplication. The solutions to the massless Weyl equation [5] are unit quaternions. These form a continuous group of rotations that lie on the surface of the 3-sphere, , and rotate the axis in our three-dimensional space. By changing the symmetry from the continuous group SU(2) to the continuous group of quaternions, and in accordance with Noether’s Theorem [143], the results of this paper naturally follow. Several of these changes are profound, challenging well-established ideas in quantum mechanics. Some paradoxical features of QM are eliminated under the quaternion framework.
Concepts like non-locality, often referred to as "quantum weirdness" [50], defy rational interpretation. Likewise, parity violation contradicts our everyday experience—how can a mirror not reflect an accurate image of the real world? The existence of infinitely deep fermionic continua (as in Dirac seas), teleportation, nondeterminism, wave function collapse, and persistent entanglement have long been considered "spooky" phenomena [144] and, as Isaac Newton famously said, "an absurdity" [44]. The Q-spin framework resolves these issues.
A bosonic electron is odd under parity, while a fermionic electron is even under parity. This significantly alters our understanding of the weak force: a beta particle is a boson, neutrinos are no longer required, and parity is no longer violated. This reinterpretation also changes our view of antimatter production, providing a solution to the baryon asymmetry problem.
Additionally, the framework allows us to define helicity, introduces the complementary spin space associated with coherence, makes intrinsic angular momentum extrinsic, and offers a clear mechanism for the wave-particle duality of spin.
12.2. Non-Hermitian Product States Resolve Entanglement
Non-Hermitian state operators can separate entangled states into products, [100]. We propose non-Hermitian state operators be used to resolve approximations. All 16 components of Equation (30) are non-Hermitian state operators, like each matrix in Equation (31). That is, both polarization, (diagonal element) and coherence (off-diagonal element) are needed to separate the singlet into product states. Once separated, each term can be evaluated and then projected onto our dimensions in the LFF.
Each spin has eight orientations in spin spacetime to form a singlet: four BFF quadrants, and each quadrant has two helicity states. The simulation treats all orientations, [7] whereas the singlet state alone, as we have shown, cancels coherent terms, Equation (32).
All four Bell states can be written as a product of non-Hermitian states, [100], and these, in turn, can be combined to give Hermitian operators,
Each one of the Bell states is an approximation because coherent terms cancel. Non-Hermitian operators resolve entangled states into products, and remove approximations. We suggest that any entangled quantum operator can be expressed as a product state when using non-Hermitian states.
12.3. No Wave Function Collapse
Wave function collapse, [33,145] describes the change in a quantum system when it undergoes a non-deterministic transition from a superposition of states to a single state due to measurement. This concept primarily applies to individual quantum systems, such as particles like electrons or photons, rather than macroscopic objects like liquids or solids. As mentioned above, the quantum effects of macroscopic systems are usually averaged out due to the RPA. The collective behavior of atoms and molecules in liquids and solids generally conforms to classical physics rather than quantum mechanics. Therefore, wave function collapse applies at the quantum level, while its direct application to the bulk properties of liquids and solids is limited.
We restrict the discussion, therefore, to single particle processes, like EPR coincidence experiments, molecular beams, , for simplicity. We ignore particle-particle interactions. Q-spin perhaps provides the simplest system that undergoes wave function collapse that we can follow.
We have shown a boson-fermion transition occurs when the boson encounters its filter. From its source, a boson spin-1 electron carries the two possible outcomes in its helicity state, and not as two fermions states of . Bosons do not describe matter; do not obey Pauli exclusion, and certainly do not describe a particle in two different states (or places) at the same time, as many express to astonish and confuse the layman. When measured, the boson wave "collapses" into a fermion particle, being one of the states , Figure 4, left and right panels. This process is deterministic from the initial orientation to its filtering into the observed state. The outcome is determined at the source, but the information is carried by helicity as a recipe of its orientation. Only when the filter is encountered does the state give an outcome. Therefore, the process is observer contextual.
A single particle pure state is a solution to the Schrödinger equation. When measured, that pure state is the only one detected. That initial state is always pure, and remains pure until encountering a field that induces transitions. Inducing a transition is what measurement does. The interaction, along with the incoming pure state, rearranges that state deterministically, even if we might not follow the details. Much, however, is known as any book on spectroscopy will reveal.
As it leaves the interaction, the rearranged state is released as pure. Quantum mechanics, however, allows us to anticipate the outcome before measurement using the Born rule and a guess at the Hamiltonian. We simply find the normal modes of the system, the eigenvalue problem, and this allows us to know the possible outcomes as a superposition, along with a probability for each. That does not reflect the wave before measurement or in free flight, but rather the possible outcomes if measured over an ensemble of similarly prepared states, [146].
Measurement produces an outcome in the form of a click that depends upon the initial pure state. We add it to a bin, and wait for the next. After statistically adding, we compare with our quantum predictions. Deviations from experimental data motivate refinements to the Hamiltonian.
Although a wave function can be expressed as a superposition of all the states, when measured we observe only the consequence of the initially prepared pure state. Rather than collapse from a general superposed wave function, the observed outcome is predetermined, and the "old One" does not play dice, [147].
12.4. Visualizing the Wave Function
The interpretation of the wave function as a probability amplitude often leads to confusion, especially for those who attempt to visualize it as a physical quantity. It is not. If you can visualize a Gaussian distribution, you can visualize a wave function. We never directly measure a wave function or a probability wave. Instead, we set up experiments to measure specific observables, such as A. That is we probe the state. The outcome of such experiments provide measurable quantities which can be visualized. These are usually given as average values, . Since all measurements carry error, error bars, we can infer the probability of measuring A to be for that specific measurement setup. Classically, we express this as . This is what Bell used, [43]. The QM expectation value is , and is replaced by called the density matrix or density operator. Since is a matrix, it can be written as the outer product of two vectors, , and gives . QM recognizes a state is given by its probability amplitude, the wave vector, , or by the matrix operator, ,33], which express the expectation values obtained from measurement. carries all our knowledge of the state, and measurement reveals that content.
The goal and success of QM is the Schrödinger equation deterministically describes such states and their evolution under interactions from one initial condition to the next. The success is that, once found, that state works consistently for other properties, such as B,C,D... The wave function thus encapsulates the state as a probability distribution for measuring these properties, and extends its utility across other observables. Of course, we can study the density operator and the states, and express them as functions, like various normal modes or harmonics, which give insight, but the only physical manifestations of the state are its expectation values which we can physically visualize, and from these observations, we can construct its state.
However, quantum mechanics introduces a crucial difference from classical physics: certain measurements, such as position and momentum or polarization and coherence, are complementary. This leads to conflicting outcomes when attempting to simultaneously measure these properties of the same system. In such cases, the probability distribution derived from the wave function in one context (e.g., position) does not apply in another (e.g., momentum), reflecting the inherent non-commutative nature of quantum observables. This conflict illustrates that the wave function’s role is tied to specific measurement contexts, making it impossible to generalize a single probability distribution across all observables in the same way we would in classical physics.
When viewed as describing the state of a system, the physical properties are only evident upon measurement. Therefore, all we know about a system are those real parameters we use that describe and define it. An electron has charge, , mass, and a spin . All electrons have the same properties. A photon is a massless particle of spin 1. A system is defined by what we observe. Helicity arose from interpreting experimental data showing the violation of BI. Our above description of an electron is now changed because now we must include helicity as a new property.
We remark that taking the next steps in extending our description of a system are best motivated by experiment. The violation of BI motivated the formulation of helicity. Without the guiding role of measurement, logical directions may be physically unfeasible. Deciding which direction might be viable is a major challenge, and this rests upon the most fundamental property we attach to mother Nature, her symmetry. Get that wrong, and seemingly viable directions will be boondoggles, leaving us with billion dollar investments into detectors with nothing to detect.
12.5. The Quaternion Interpretation
The approach used here is fundamentally different from all other interpretations, and an apt name might be the Twistor, Quaternion or Complex Interpretation. The existence of helicity impacts the Einstein-Bohr debates [3,147,148]. Bohr claimed that contrary to Einstein, only the measured property exists in his philosophy of complementarity [148]. Einstein believed that both elements of reality exist simultaneously. Indeed, both properties of Q-spin exist simultaneously, see Equations (7), (31), supporting Einstein. Only one is manifest at any instant, supporting Bohr.
That HV do not exist for Q-spin does not support the Copenhagen interpretation as usually asserted because with Q-spins, both elements of reality are needed, and both exist simultaneously. The Copenhagen Interpretation asserts the complementary attribute does not exist since QM only formulates its partner. As such Bohr’s approach takes a Positivist position. It avoids the existence of unobservable, complementary, attributes. It focuses only on observable phenomena and measurement outcomes. Physical quantities only appear when measured, and the act of measurement defines them.
All interpretations are concerned with the measurement problem and the meaning of reality. Several rely on non-deterministic wave function collapse which we reject and do not discuss here. Some work involves the human brain in the wave function, which lacks clarity, is ambiguous and subjective. An example is Quantum Bayesianism (QBism), [149] an interpretation of quantum mechanics that views the wave function not as a physical entity, but as a tool representing an observer’s personal beliefs or probabilities about the outcomes of measurements. Other examples are Consciousness Causes Collapse, [33,150], Relational Quantum Mechanics (RQM), [151,152], and The Many-Minds Interpretation, [153,154]. Ballentine, [146], rejects interpretations that give the observer a central role in determining reality, which he calls a move to a solipsistic viewpoint. This applies, more or less, to the above approaches. It is an extreme philosophical position that asserts the only certain existence is one’s own mind.
From our perspective, QM is burdened by such ideas which defy rationality. The measurement problem, wave function collapse, Bell’s Theorem’s spooky action-at-a-distance, nondeterminism, Dirac’s hole theory, point particle spin, parity violation, , we assert, are the reasons for confusion, and lack of clarity in the interpretation of QM. As we already said, philosophers are put in an untenable position of trying to explain the impossible. This has resulted in exhausting semantic debates, too many to reference, most speculative, confusing, unpublished, and mostly irrelevant, which surround all current interpretations: the resolution of which is doubtful under existing concepts. This has resulted in the mantra of "Shut up and calculate", [155], and during his famous 1964 lectures on physics, Richard Feynman said, "I think I can safely say that nobody understands quantum mechanics". Such pithy phrases are intimidating for many, and undermine the tenet of our intelligence. It is unacceptable that we accept phenomena, and do research, in areas based upon revelation. Our confusion is not due to our inability to follow the logic of Nature, but rather our incomplete and incorrect description of the microscopic. One guiding principle should be, "if it doesn’t make sense, it is probably wrong". We should trust our intuition.
Only two interpretations are microscopic: the ensemble, [146] and the de Broglie-Bohm, [73] interpretations, discussed in Section 8.
The Ensemble approach, [146], as we discussed above, is closest to the details of an experiment. It assumes the wave function is an ensemble of similarly prepared systems consistent with the statistical mechanical view. Measurement is ensemble averaging over distinct convex sets, [156]. We believe the Statistical Interpretation provides a realistic and pragmatic approach by focusing on distributions of ensembles to give the statistical nature of quantum predictions. The view discussed here treats each ensemble as expressing all possible pure states available to a single particle within the constraints. If our Hamiltonian is accurate, the experimental results will agree with the calculated probabilities, and given as a superposition of all the pure states. In the bubble analogy, the ensemble describes every possible way the child can blow.
Except for the evidence for neutrinos, this work does not disagree with existing experimental data. We only interpret the data differently under Q-spin. It should be possible to separate coherence from polarization in EPR coincidence experiments. If the two axes of some neutral particle with a spin can serve as a qubit, then outcomes can be deterministically realized.
That Nature exists beyond our ability to measure, we must accept that information is lost upon measurement, [157], like determining which slit a particle passes. That knowledge disrupts the helicity of spin, that is in Equation (13) decoheres, leaving only its particle nature. The epistemological question is to find methods to account for real properties of Nature we cannot observe. This is not easy, as spin taught us, taking almost 100 years to find helicity as the complementary attribute of spin, the cryptic evidence being the violation of BI, [43].
Quantum mechanics gives an incomplete description of Nature. Instead, it is a theory of measurement restricted to our spacetime.
13. Conclusions
The ideas presented here are quantum yet provide an alternate view of the microscopic. Important and satisfying features of the macro classical view carry over to the micro. Both are locally real, albeit reality of the microscopic is complex. Equally satisfying is determinism prevails in all dimensions: you measure only what you prepare. Dispersion between complementary variables is fundamental to Nature, and cannot be removed. Although stand alone HV theories that replace QM are viable, we believe that HV cannot improve upon quantum theory. Von Neumann already proved that linear HV do not exist. We expect that additional constraints will exclude non-linear HV theories, as it does for Q-spin. This does not exclude the future discoveries of elements of reality that can be described within quantum theory without HV. The helicity, , is an expample.
It is of note that our classical simulation relies on Least Action between classical vectors. This gives more correlation than from QM. It underscores that QM results in classical outcome, , which can be modeled classically. Generally, however, the initial conditions are unknown, and the successes of quantum methods are the predictions we rely on.
We do not believe that the identical geometric structure of Q-spin and a photon is a coincidence, but rather shows a continuity of properties between microscopic particles (a massless Q-spin with one magnetic axis changed to an electric one describes a photon). Presently, all particles in the standard model are bosons or fermions, and we suspect those particles should be treated under the quaternion group.
Quaternions, [158], one of the many legacies of Hamilton, [159] are more than mathematical constructs defined on the hypersphere, with four spatial dimensions. Quaternions are elements of reality possessed by spin, complementary to its vector polarizations. Reality extends beyond our three spatial dimensions. The origin of the unit quaternions coincides with the origin of the Bloch sphere and extends it by adding helicity to each Bloch vector, and these spin either L or R with a constant frequency. Spin is not purely a vector quantity but includes the hypersphere of unit quaternions, and only the 2×2 vector part of a spin, , is projected into our spacetime.
Hamilton’s Eureka moment, discovering that rotations in 3D are generated by quaternions in 4D, set the stage for understanding spin. Spin is a quaternion.
References
- Schrödinger, E. (1926). Quantisierung als Eigenwertproblem; von Erwin Schrödinger. Annalen der Physik, 384(4), 361-377.
- Heisenberg, W. (1925). Quantum-theoretical re-interpretation of kinematic and mechanical relations. Z. Phys, 33, 879-893.
- Jammer, M. (1974). Philosophy of Quantum Mechanics. the interpretations of quantum mechanics in historical perspective.
- Einstein, A, Podolsky, rn and Rosen, N, “Can quantum mechanical description of physical reality be considered complete?” Phys Rev 47, 777-780, (1935).
- Sanctuary, B. Quaternion Spin. Mathematics 2024, 12, 1962. [CrossRef]
- Sanctuary, B. Spin Helicity and the Disproof of Bell’s Theorem. Quantum Rep. 2024, 6, 436–441. [CrossRef]
- Sanctuary, B. C., Non-local EPR Correlations using Quaternion Spin. Quantum Rep. 2024, 6(3), 409-425. [CrossRef]
- Bell, J. S. (1987). Speakable and unspeakable in quantum mechanics Cambridge University Press. New York, Bell’s quote is on page 65.
- Clauser, J. F., Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880. [CrossRef]
- Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 14 (8): 1944–1951. [CrossRef]
- Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039.
- Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical review letters, 70(13), 1895.
- Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624.
- Wikipedia contributors. (2024, July 12). Pauli matrices. In Wikipedia, The Free Encyclopedia. Retrieved 12:06, August 15, 2024.
- Hestenes, D., & Sobczyk, G. (2012). Clifford algebra to geometric calculus: a unified language for mathematics and physics (Vol. 5). Springer Science & Business Media.
- Okun, Lev B. “Mirror particles and mirror matter: 50 years of speculation and searching." Physics-Uspekhi 50.4 (2007): 380.
- Zheng, Z.; Yu, Z. Interaction effects on the PT-symmetry-breaking transition in atomic gases. Phys. Rev. 2019, 99, 043412.
- Doran, C., Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
- Peskin, M.; Schroeder, D.V. An Introduction To Quantum Field Theory; Frontiers in Physics: Boulder, CO, USA, 1995.
- Penrose, Roger. "Twistor algebra." Journal of Mathematical Physics 8.2 (1967): 345-366.
- Penrose, Roger. "Solutions of the Zero-Rest-Mass Equations." Journal of Mathematical Physics 10.1 (1969): 38-39.
- Fano, U. Description of states in quantum mechanics by density matrix and operator techniques. Rev. Mod. Phys. 1957, 29, 74. [CrossRef]
- Dirac, P. A. M. (1930). "A Theory of Electrons and Protons". Proc. R. Soc. Lond. A. 126 (801): 360–365. [CrossRef]
- Susskind, Leonard (1970). “Dual-symmetric theory of hadrons, I.". Nuovo Cimento A. 69 (1): 457–496 781-811.
- Wilczek, F. (1982). Quantum mechanics of fractional-spin particles. Physical review letters, 49(14), 957.
- Tsirel’son, B. S. (1987). Quantum analogues of the Bell inequalities. The case of two spatially separated domains. Journal of Soviet Mathematics, 36, 557-570.
- Whittaker, E. (1954). History of the Theories of Aether and Electricity (Vol. 77, No. 5, p. 417). LWW.
- To visualize quaternions, see 3blue1brown: https://www.3blue1brown.com/lessons/quaternions.
- Heaviside, O. (2003). Electromagnetic theory (Vol. 237). American Mathematical Soc..
- Gibbs, J. W. (2022). Classical Vector Analysis. Fundamentals of Partial Differential Equations, 13.
- Goldstein, H. (2011). Classical mechanics. Pearson Education India.
- Kuipers, J. B. (1999). Quaternions and rotation sequences: a primer with applications to orbits, aerospace, and virtual reality. Princeton university press.
- Von Neumann, John. Mathematical foundations of quantum mechanics. Princeton university press, 1955.
- Hestenes, D. (2015). Space-time algebra. Switzerland: Springer International Publishing..
- Freedman, M., Kitaev, A., Larsen, M., and Wang, Z. (2003). Topological quantum computation. Bulletin of the American Mathematical Society, 40(1), 31-38.
- Kauffman, L. H., and Lomonaco, S. J. (2004). Braiding operators are universal quantum gates. New Journal of Physics, 6(1), 134.
- Ahmadi, M.; Alves, B.X.R.; Baker, C.J.; Bertsche, W.; Butler, E.; Capra, A.; Carruth, C.; Cesar, C.L.; Charlton, M.; Cohen, S.; et al. Observation of the 1S–2S transition in trapped antihydrogen. Nature 2017, 541, 506–510. [CrossRef]
- Anderson, E. K., Baker, C. J., Bertsche, W., Bhatt, N. M., Bonomi, G., Capra, A., ... and Wurtele, J. S. (2023). Observation of the effect of gravity on the motion of antimatter. Nature, 621(7980), 716-722.
- Baryon Asymmetry. In Wikipedia. Available online: https://en.wikipedia.org/wiki/Baryon_asymmetry (accessed on 6 April 2024).
- Riotto, A., & Trodden, M. (1999). Recent progress in baryogenesis. Annual Review of Nuclear and Particle Science, 49(1), 35-75.
- Steigman, G. (2007). "Primordial Nucleosynthesis in the Precision Cosmology Era". Annual Review of Nuclear and Particle Science, 57: 463-491. This paper discusses how the baryon asymmetry is connected to both Big Bang nucleosynthesis and CMB data.
- Ade, P. A. R. et al. (Planck Collaboration) (2016). "Planck 2015 results. XIII. Cosmological parameters". Astronomy & Astrophysics, 594, A13. This paper presents data from the Planck satellite, which provides one of the most accurate measurements of the baryon-to-photon ratio, key for understanding baryon asymmetry.
- Bell, John S. "On the Einstein Podolsky Rosen paradox." Physics Physique Fizika 1.3 (1964): 195.
- Original letter from Isaac Newton to Richard Bentley Author: Isaac Newton, Source: 189.R.4.47, ff. 7-8, Trinity College Library, Cambridge, UK: extract:“That gravity should be innate inherent and essential to matter so that one body may act upon another at a distance through a vacuum without the mediation of any thing else by and through which their action or force may be conveyed from one to another is to me so great an absurdity that I believe no man who has in philosophical matters any competent faculty of thinking can ever fall into it.".
- Feynman, R. P. (2018). Statistical mechanics: a set of lectures. CRC press.
- Hadwiger, H. (1950). Minkowskische addition und subtraktion beliebiger punktmengen und die theoreme von erhard schmidt. Mathematische Zeitschrift, 53(3), 210-218. [CrossRef]
- Pauli, W. (1930). Pauli letter collection: letter to Lise Meitner (No. CERN-ARCH-PLC, pp. Letter-2412).
- See “Quantum entanglement" Wikipedia.
- Scholarpedia, see “Bell’s theorem".
- Mullin, W. J. (2017). Quantum weirdness, Oxford University Press.
- Ladyman, J., & Ross, D. (2007). Every thing must go: Metaphysics naturalized. Oxford University Press.
- Tim Maudlin’s Philosophy ofPhysics: Quantum Theory (2019),.
- Big Bell Test Collaboration. “Challenging local realism with human choices." Nature 557.7704 (2018): 212-216.
- Longuet-Higgins, Hugh C. “The symmetry groups of non-rigid molecules." Molecular Physics 6.5 (1963): 445-460.
- Scarani, V., Iblipedir, S., Gisin, N., and Acín, A. (2005). Quantum cloning. Reviews of Modern Physics, 77(4), 1225-1256.
- Bashar, M. A., Chowdhury,M. A., Islam, R., Rahman, M. S., and Das,S. K. , “A Review and Prospects of Quantum Teleportation," 2009 International Conference on Computer and Automation Engineering, 2009, pp. 213-217, doi: 10.1109/ICCAE.2009.77.
- National Academies of Sciences, Engineering, and Medicine. (2019). Quantum computing: progress and prospects.
- Gisin, N., Ribordy, G., Tittel, W., Zbinden, H., Quantum cryptography. Reviews of modern physics, 74(1), 145, 2002.
- Pan, J. W., Bouwmeester, D., Weinfurter, H., and Zeilinger, A. (1998). Experimental entanglement swapping: Entangling photons that never interacted. Physical Review Letters, 80(18), 3891-3894. [CrossRef]
- Kim, Y. H., Yu, R., Kulik, S. P., Shih, Y., and Scully, M. O. (2000). Delayed "choice" quantum eraser. Physical Review Letters, 84(1), 1-5.
- Hensen, B., Bernien, H., Dréau, A. E., Reiserer, A., Kalb, N., Blok, M. S., ... and Hanson, R. (2015). Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometers. Nature, 526(7575), 682-686.
- Giustina, M., Versteegh, M. A., Wengerowsky, S., Handsteiner, J., Hochrainer, A., Phelan, K., ... and Zeilinger, A. (2015). Significant-loophole-free test of Bell’s theorem with entangled photons. Physical Review Letters, 115(25), 250401.
- Brooks, M. (2023). Quantum computers: What are they good for? [CrossRef]
- Gentner, W., & Damburg, R. (1954). "Experiments on the Stern-Gerlach Effect with Neutrons." Physical Review, 94(5), 951-952. DOI: 10.1103/PhysRev.94.951.
- Zhang, Z., Chen, G., Diao, Z., Hemmer, P.R. (2009). NMR Quantum Computing. In: Gao, D., Sherali, H. (eds) Advances in Applied Mathematics and Global Optimization. Advances in Mechanics and Mathematics, vol 17. Springer, Boston, MA.
- Sanctuary, B. C., and Halstead, T. K. (1990). Multipole NMR. In Advances in magnetic and optical resonance (Vol. 15, pp. 79-161). Academic Press.
- Freeman, R., and Kupce, E. (1994). Spin gymnastics with selective radiofrequency pulses.
- Sanctuary, B. C., and Halstead, T. K. (1990). Multipole NMR. In Advances in magnetic and optical resonance (Vol. 15, pp. 79-161). Academic Press.
- Bell, J. S. (1966). "On the problem of HV in quantum mechanics." Reviews of Modern Physics, 38(3), 447-452. [CrossRef]
- Scully, M. O., Lamb Jr, W. E., & Barut, A. (1987). Theory of the Stern-Gerlach apparatus. Found. Phys.;(United States), 17(6).
- Wennerström, H., & Westlund, P. O. (2017). A quantum description of the Stern–Gerlach experiment. Entropy, 19(5), 186.
- De Broglie, L. "La Nouvelle Dynamique des Quanta." Electrons et Photons: Rapports et Discussions du Cinquième Conseil de Physique, Institut International de Physique Solvay. Gauthier-Villars, 1928, pp. 105–132.
- Bohm, D. "A Suggested Interpretation of the Quantum Theory in Terms of ’Hidden’ Variables I and II." Physical Review, vol. 85, no. 2, 1952, pp. 166–193.
- ’t Hooft, G. "Determinism Beneath Quantum Mechanics." Journal of Physics: Conference Series, vol. 67, no. 1, 2007, pp. 012015.).
- Dürr, D., Goldstein, S., & Zanghì, N. (2012). Quantum Physics Without Quantum Philosophy:.
- Oldofredi, A. (2022). Beables, primitive ontology and beyond: how theories meet the world. In Quantum Mechanics and Fundamentality: Naturalizing Quantum Theory between Scientific Realism and Ontological Indeterminacy (pp. 97-111). Cham: Springer International Publishing.
- Price, H. Time’s Arrow and Archimedes’ Point: New Directions for the Physics of Time. Oxford University Press, 1996.
- Wharton, K. B. "Time-Symmetric Quantum Mechanics." Foundations of Physics, vol. 37, 2007, pp. 159–168. [CrossRef]
- Kochen, S., and Specker, E. P. (1990). The problem of HV in quantum mechanics. Ernst Specker Selecta, 235-263.
- Dieks, D. (2017). Von Neumann’s impossibility proof: Mathematics in the service of rhetorics. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 60, 136-148.
- Golub R, Lamoreaux SK. A retrospective review of von Neumann’s analysis of HV in quantum mechanics. Academia Quantum 2024;1. [CrossRef]
- Wick, David. The Infamous Boundary: Seven decades of heresy in quantum physics. Springer Science and Business Media, 2012.
- Annila, A. (2021). Quantum Entanglement: Bell’s Inequality Trivially Violated Also Classically. Available at SSRN 4388586.
- Arto Annila, Marten Wikstrom, 2021, viXra:2112.0118 Quantum Entanglement: Bell’s Inequality Trivially Violated Also Classically. Category: Quantum Physics.
- Geurdes, H. (2023). Requiring Negative Probabilities From’The Thing’Researched, Else That Thing Doesn’t Exist, is Insufficient Ground for Any Conclusion. Else That Thing Doesn’t Exist, is Insufficient Ground for Any Conclusion (August 21, 2023).
- Jakumeit, J., and Hess, K. (2024). Breaking a Combinatorial Symmetry Resolves the Paradox of Einstein-Podolsky-Rosen and Bell. Symmetry, 16(3), 255.
- Nordén, Bengt. “Quantum entanglement: facts and fiction–how wrong was Einstein after all?." Quarterly reviews of biophysics 49 (2016).
- Cetto, A. M., Casado, A., Hess, K., and Valdés-Hernández, A. (2021). “Towards a Local Realist View of the Quantum Phenomenon." in Towards a Local Realist View of the Quantum Phenomenon, 4.
- Hess, Karl, “A critical review of works pertinent to the Einstein-Bohr debate and Bell’s Theorem" pre-print, November 2021.
- Khrennikov, A. (2019). Get rid of nonlocality from quantum physics. Entropy, 21(8), 806. [CrossRef]
- Oaknin, D. H. (2020). The Bell theorem revisited: geometric phases in gauge theories. Frontiers in Physics, 8, 142. [CrossRef]
- De Raedt, H., Jattana, M. S., Willsch, D., Willsch, M., Jin, F., and Michielsen, K. (2020). Discrete-event simulation of an extended Einstein-Podolsky-Rosen-Bohm experiment. Frontiers in physics, 8, 160. [CrossRef]
- Dieks, D. (2002). Inequalities that test locality in quantum mechanics. Physical Review A, 66(6), 062104. [CrossRef]
- Kupczynski, M. (2020). “Is the Moon there if nobody looks: Bell Inequalities and Physical Reality." Frontiers in Physics, 8, 273.
- Christian, J. (2014). Disproof of Bell’s Theorem: Illuminating the Illusion of Entanglement. Universal-Publishers.
- Hooft, Gerard T. “Ontology in quantum mechanics." arXiv (2021). arXiv:2107.14191.
- Hooft, Gerard T. Deterministic quantum mechanics: the mathematical equations. Frontiers in Physics, 8, 253, (2020).
- Santos, E. (2020). “Local realistic interpretation of entangled photon pairs in the Weyl-Wigner formalism. Frontiers in Physics, 8, 191.
- Schrödinger E., “Discussion of probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. 31 (4): 555–563 (1935).
- Sanctuary, B. C. “Separation of Bell states." arXiv preprint arXiv:0705.3657 (2007).
- Poinsot, Louis. New theory of the rotation of bodies extracted from a memoir read at the Academy of Sciences of the Institute, May 19, 1834 by M. Poinsot . Bachelor, 1834.
- Einstein, Albert, and Nathan Rosen. “The particle problem in the general theory of relativity." Physical Review 48.1 (1935): 73.
- Van Raamsdonk, M. (2010). Building up spacetime with quantum entanglement. General Relativity and Gravitation, 42(10), 2323-2329.
- Carroll, S. M. (2019). Spacetime and geometry. Cambridge University Press.
- Sanctuary, B. C. (1976). Multipole operators for an arbitrary number of spins. The Journal of Chemical Physics, 64(11), 4352-4361. [CrossRef]
- Bose, T., Boveia, A., Doglioni, C., Griso, S. P., Hirschauer, J., Lipeles, E., ... and Wang, L. T. (2021). Physics beyond the standard model.
- Fonseca, R. M. (2020, August). Violation of lepton number in 3 units. In Journal of Physics: Conference Series (Vol. 1586, No. 1, p. 012003). IOP Publishing.
- Schwartz, M. D. (2014). Quantum field theory and the standard model. Cambridge University Press.
- Griffiths, David (2009). Introduction to Elementary Particles. pp. 59–60. ISBN 978-3-527-40601-2.
- Fermi, E. (1934). Versuch einer Theorie der β-Strahlen. I. Zeitschrift für Physik, 88(3-4), 161-177.
- Close, F. Particle physicsavery short introduction,Oxford: Oxford University Press(2004).
- Weiler, T. Neutrinos, Einstein, time and paradox: Tom Weiler at TEDxNashville [Presentation],Nashville, TN(2012).
- Immerman, Neil. Sacramento Peak: The Universe. University of Massachusetts Amherst. 21 May 2001.
- Fukuda, S., Fukuda, Y., Hayakawa, T., Ichihara, E., Ishitsuka, M., Itow, Y., ... and Ichikawa, Y. (2003). The super-kamiokande detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 501(2-3), 418-462.
- Abbasi, R., Ackermann, M., Adams, J., Ahlers, M., Ahrens, J., Andeen, K., ... and Madsen, J. (2009). The IceCube data acquisition system: Signal capture, digitization, and timestamping. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 601(3), 294-316.
- Bellerive, A., Klein, J. R., McDonald, A. B., Noble, A. J., and Poon, A. W. (2016). The Sudbury Neutrino Observatory. ArXiv. [CrossRef]
- Waxman, E. (2007). Neutrino astrophysics: A new tool for exploring the universe. Science, 315(5808), 63-65. [CrossRef]
- Mertens, S. (2016, May). Direct neutrino mass experiments. In Journal of Physics: Conference Series (Vol. 718, No. 2, p. 022013). IOP Publishing.
- Abe, S., et al. (2008). "KamLAND Measurement of Reactor Antineutrino Disappearance in the First Phase of the KamLAND Experiment." Physical Review Letters, 100(22), 221803. [CrossRef]
- An, F. P., et al. (2016). "Observation of electron-antineutrino disappearance at Daya Bay." Physical Review Letters, 108(17), 171803. [CrossRef]
- Bellini, G., Benziger, J., Bick, D., Bonfini, G., Bravo, D., Avanzini, M. B., ... & Zuzel, G. (2012). Cosmic-muon flux and annual modulation in Borexino at 3800 m water-equivalent depth. Journal of Cosmology and Astroparticle Physics, 2012(05), 015. [CrossRef]
- Aartsen, M. G., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., Ahrens, M., ... & Kunnen, J. (2014). Observation of high-energy astrophysical neutrinos in three years of IceCube data. Physical review letters, 113(10), 101101. [CrossRef]
- Abe, K., Hayato, Y., Iida, T., Iyogi, K., Kameda, J., Koshio, Y., ... & (Super-Kamiokande Collaboration). (2013). Evidence for the appearance of atmospheric tau neutrinos in Super-Kamiokande. Physical review letters, 110(18), 181802.
- Cowan Jr, C. L., Reines, F., Harrison, F. B., Kruse, H. W., & McGuire, A. D. (1956). Detection of the free neutrino: a confirmation. Science, 124(3212), 103-104.
- Wiebusch, C. H. V. (1995). The detection of faint light in deep underwater neutrino telescopes (Doctoral dissertation, Physikal. Inst., RWTH Aachen).
- Adrián-Martínez, S., Al Samarai, I., Albert, A., André, M., Anghinolfi, M., Anton, G., ... & Wijnker, G. (2012). Search for cosmic neutrino point sources with four years of data from the ANTARES telescope. The Astrophysical Journal, 760(1), 53.
- Gaisser, T. K. (1982). Cosmic rays and particle physics. Comments on Nuclear and Particle Physics, 11(1), 25-39.
- Patrignani, C., Agashe, K., Aielli, G., Amsler, C., Antonelli, M., Asner, D. M., ... & Ringwald, A. (2016). Review of particle physics.
- Lee, T. D., and Yang, C. N. (1956). Question of parity conservation in weak interactions. Physical Review, 104(1), 254. [CrossRef]
- Wu, C. S., Ambler, E., Hayward, R. W., Hoppes, D. D., and Hudson, R. P. (1957). Experimental test of parity conservation in beta decay. Physical review, 105(4), 1413. [CrossRef]
- Witten, E. (2004). "Perturbative Gauge Theory As A String Theory In Twistor Space." Communications in Mathematical Physics, 252, 189-258. [CrossRef]
- Hodges, A. (1990). Twistor diagrams and Feynman diagrams (pp. 339-366). Cambridge Univ. Press, Cambridge.
- Mason, L., and Skinner, D. (2010). Scattering amplitudes and BCFW recursion in twistor space. Journal of High Energy Physics, 2010(1), 1-66. [CrossRef]
- Zurek, W. H. (2003). "Decoherence, einselection, and the quantum origins of the classical." Reviews of Modern Physics, 75(3), 715. [CrossRef]
- Joos, E., Zeh, H. D., Kiefer, C., Giulini, D. J., Kupsch, J., and Stamatescu, I. O. (2003). Decoherence and the Appearance of a Classical World in Quantum Theory. Springer.
- Leggett, A. J. (2002). "Testing the limits of quantum mechanics: motivation, state of play, prospects." Journal of Physics: Condensed Matter, 14(15), R415.
- Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-07912-7.
- Coope, J. A. R., Snider, R. F., and McCourt, F. R. (1965). Irreducible cartesian tensors. The Journal of Chemical Physics, 43(7), 2269-2275.
- Coope, J. A. R., and Snider, R. F. (1970). Irreducible cartesian tensors. II. General formulation. Journal of Mathematical Physics, 11(3), 1003-1017.
- Coope, J. A. R. (1970). Irreducible Cartesian Tensors. III. Clebsch-Gordan Reduction. Journal of Mathematical Physics, 11(5), 1591-1612.
- Coope, J. A. R., Sanctuary, B. C., and Beenakker, J. J. M. (1975). The influence of nuclear spins on the transport properties of molecular gases and application to HD. Physica A: Statistical Mechanics and its Applications, 79(2), 129-170.
- Snider, R. F. (2017). Irreducible Cartesian Tensors (Vol. 43). Walter de Gruyter GmbH and Co KG.
- Emmy Noether. Invariante Variationsprobleme. Gott. Nachr., pages 235–257, 1918.
- Einstein, Albert. Born-Einstein Letters 1916-1955: Friendship, Politics and Physics in Uncertain Times. Palgrave Macmillan, 2014.
- Wave function collapse." Wikipedia, The Free Encyclopedia, 6 Jul. 2024. Web. 10 Aug. 2024.Howard, D. (1985). Einstein on locality and separability. Studies in History and Philosophy of Science Part A, 16(3), 171-201. [CrossRef]
- Ballentine, Leslie E. “The statistical interpretation of quantum mechanics." Reviews of Modern Physics 42.4 (1970): 358. [CrossRef]
- Born, M., Born, H., Born, I., and Einstein, A. (1971). The Born-Einstein letters: correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955. Walker.
- Bohr, Niels. “Can quantum-mechanical description of physical reality be considered complete?." Physical review 48.8 (1935): 696. [CrossRef]
- Fuchs, C. A., & Schack, R. (2013). Quantum-bayesian coherence. Reviews of modern physics, 85(4), 1693-1715. [CrossRef]
- Eugene Wigner: "Remarks on the Mind-Body Question." Symmetries and Reflections: Scientific Essays. Indiana University Press, 1967.
- Carlo Rovelli: "Relational Quantum Mechanics." International Journal of Theoretical Physics, vol. 35, no. 8, 1996, pp. 1637–1678.
- Carlo Rovelli: Helgoland: Making Sense of the Quantum Revolution. Allen Lane, 2021.
- H. Dieter Zeh: "On the Interpretation of Measurement in Quantum Theory." Foundations of Physics, vol. 1, 1970, pp. 69–76. Zeh discusses early ideas related to many-minds interpretations.
- David Albert and Barry Loewer: "Interpreting the Many-Worlds Interpretation." Synthese, vol. 77, 1988, pp. 195–213.
- Mermin, N. D. (2004). Could Feynman have said this?. Physics Today, 57(5), 10-11. [CrossRef]
- Leonard, I. E., and Lewis, J. E. (2015). Geometry of convex sets. John Wiley and Sons.
- Braunstein, Samuel L., and Arun K. Pati. “Quantum information cannot be completely hidden in correlations: implications for the black-hole information paradox." Physical review letters 98.8 (2007): 080502.). [CrossRef]
- Snygg, J. (1997). Clifford Algebra: A Computational Tool for Physicists. Oxford University Press on Demand.
- Gsponer, A., Hurni, J. P. (2002). The physical heritage of Sir WR Hamilton. arXiv preprint math-ph/0201058.
Figure 1.
Spin is oriented in spin spacetime by the BFF basis vectors , which spin about the axis so that in Minkowski space, with the basis vectors , only a smeared-out image of the precessing spin is projected. The lower right insert contrasts Dirac spin and Q-spin, which is displayed as the resonance formed from coupling the N and E axes.
Figure 1.
Spin is oriented in spin spacetime by the BFF basis vectors , which spin about the axis so that in Minkowski space, with the basis vectors , only a smeared-out image of the precessing spin is projected. The lower right insert contrasts Dirac spin and Q-spin, which is displayed as the resonance formed from coupling the N and E axes.
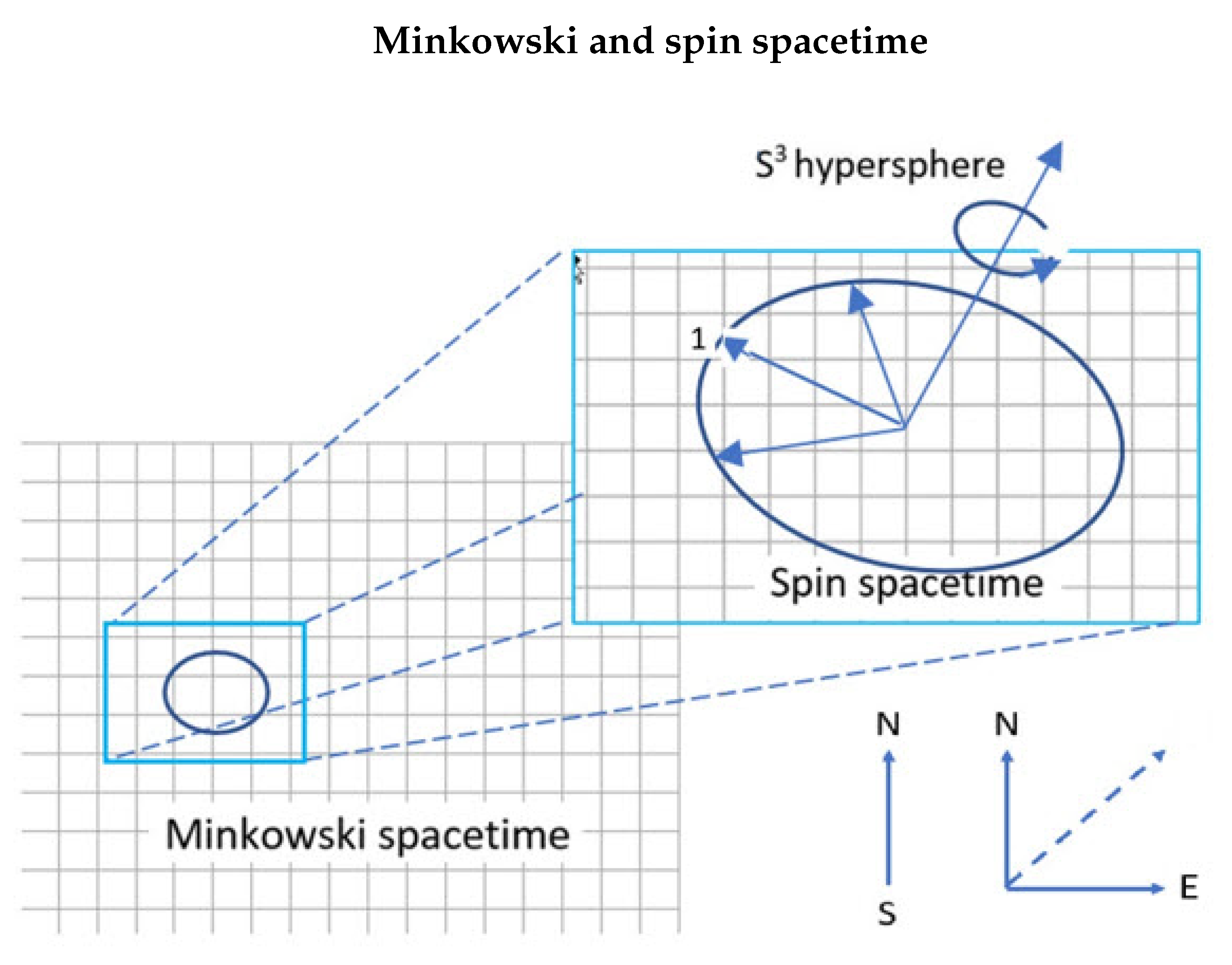
Figure 2.
The mirror states of a Q-spin with on the right and on the left. Note that adding these states is independent of and subtracting them is independent of and .
Figure 2.
The mirror states of a Q-spin with on the right and on the left. Note that adding these states is independent of and subtracting them is independent of and .
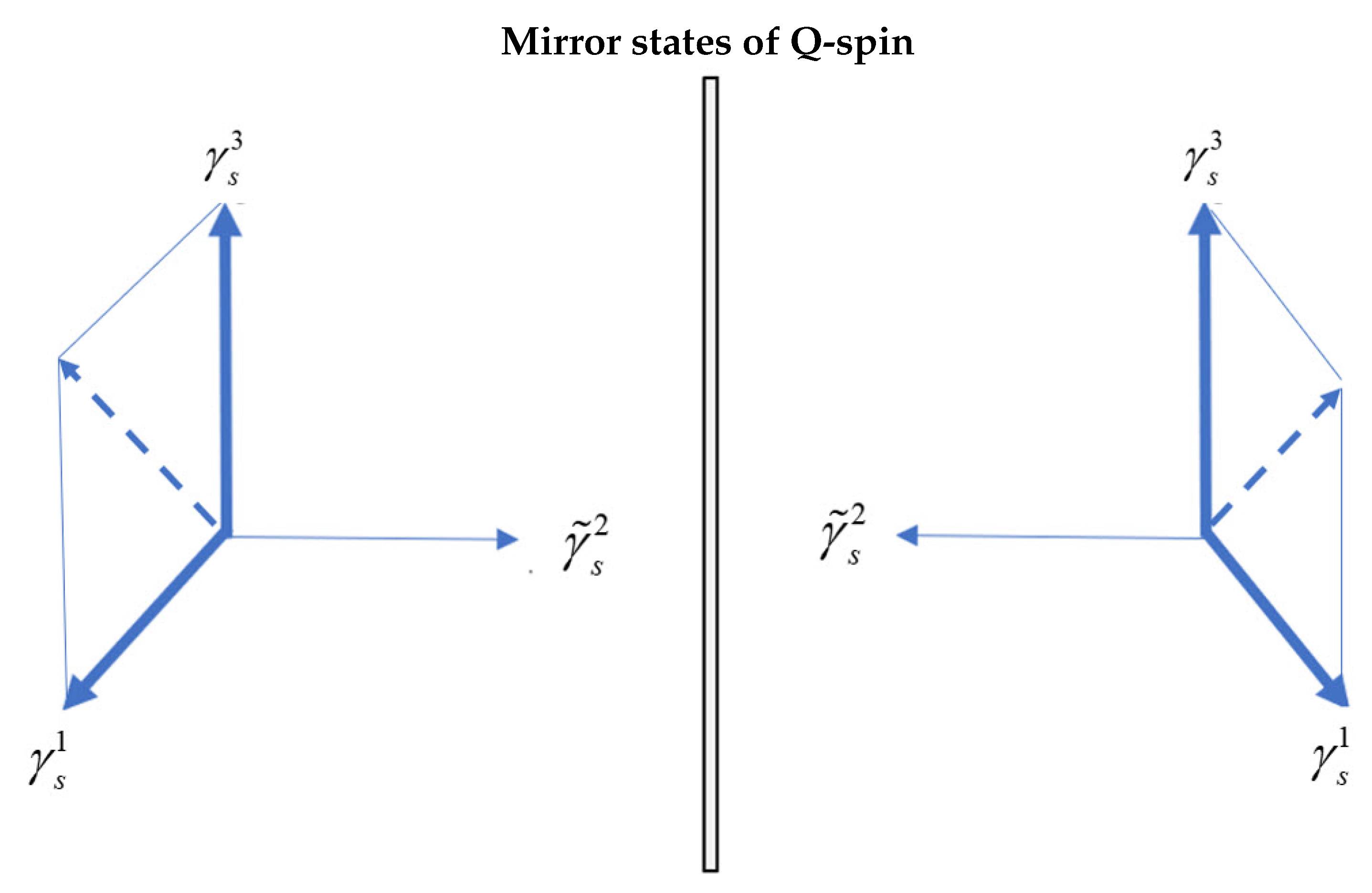
Figure 3.
Two properties of spin: two orthogonal spin- polarization vectors, and , perpendicular to the direction of linear momentum, Y. The helicity is in the direction of propagation, , and spins R or L. The two spin- vectors, and , couple to give a composite boson, , of magnitude 1. These properties show that the spin is geometrically equivalent to a photon.
Figure 3.
Two properties of spin: two orthogonal spin- polarization vectors, and , perpendicular to the direction of linear momentum, Y. The helicity is in the direction of propagation, , and spins R or L. The two spin- vectors, and , couple to give a composite boson, , of magnitude 1. These properties show that the spin is geometrically equivalent to a photon.
Figure 4.
The longer arrow denotes the direction of the polarizing field. Middle top: The two mirror states in free flight, and , couple to give a boson spin-1. Left and right: The fermionic axis closer to the field axis aligns, and the boson decouples. These two panels do not indicate two particles but one Q-spin depicted with one for the other axis aligned with the field. Middle bottom: When the boson spin is close to the field, it initially precesses as a spin-1 without decoupling.
Figure 4.
The longer arrow denotes the direction of the polarizing field. Middle top: The two mirror states in free flight, and , couple to give a boson spin-1. Left and right: The fermionic axis closer to the field axis aligns, and the boson decouples. These two panels do not indicate two particles but one Q-spin depicted with one for the other axis aligned with the field. Middle bottom: When the boson spin is close to the field, it initially precesses as a spin-1 without decoupling.
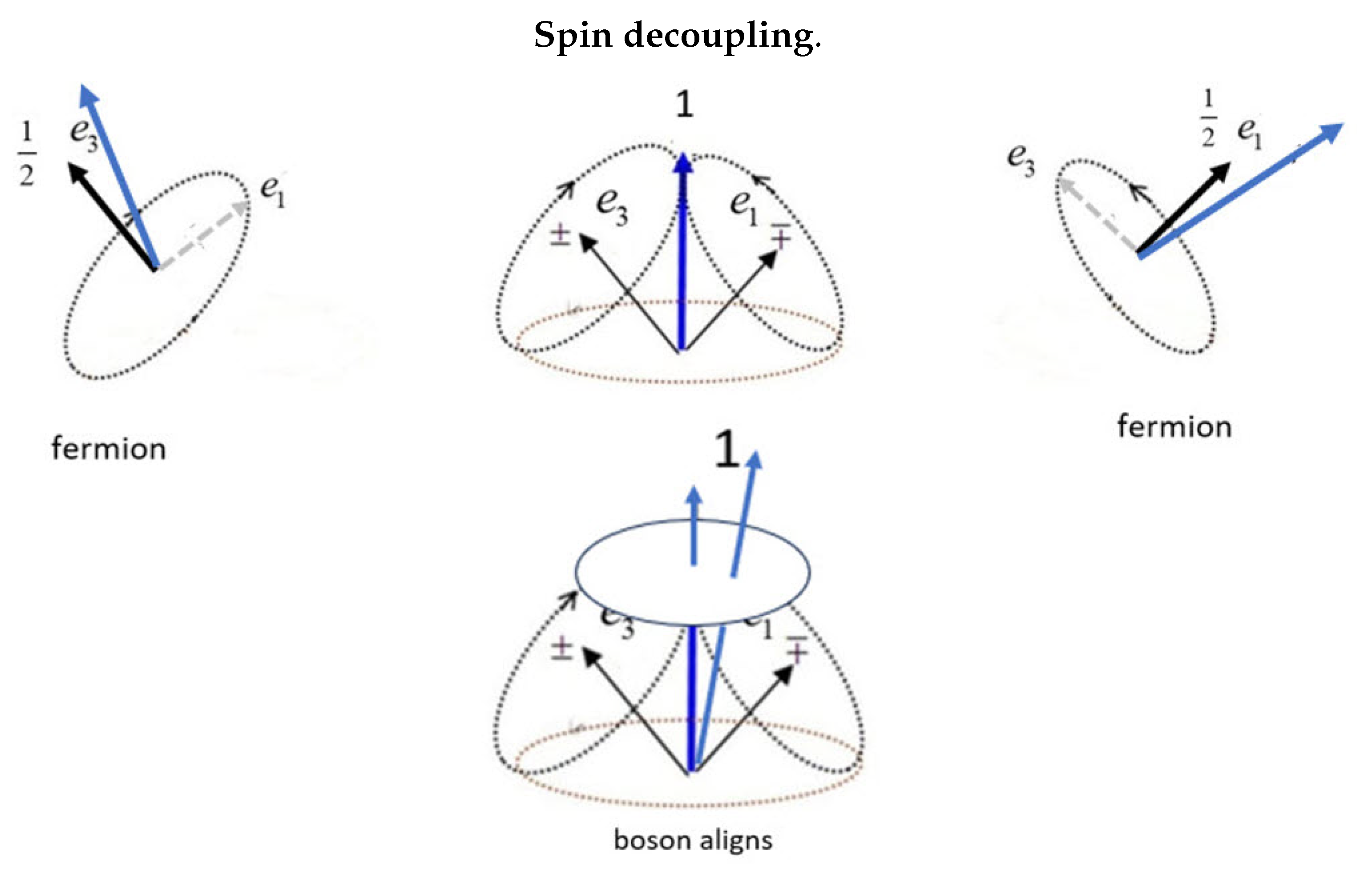
Figure 5.
Plotting EPR correlation versus the angle difference . The blue points give the results of the simulation. The CHSH values are listed and the full correlation is the sum of polarization, the triangle, and coherence, the mustache. Note the, hardly discernible, residual quaternion correlation along the horizontal axis.
Figure 5.
Plotting EPR correlation versus the angle difference . The blue points give the results of the simulation. The CHSH values are listed and the full correlation is the sum of polarization, the triangle, and coherence, the mustache. Note the, hardly discernible, residual quaternion correlation along the horizontal axis.
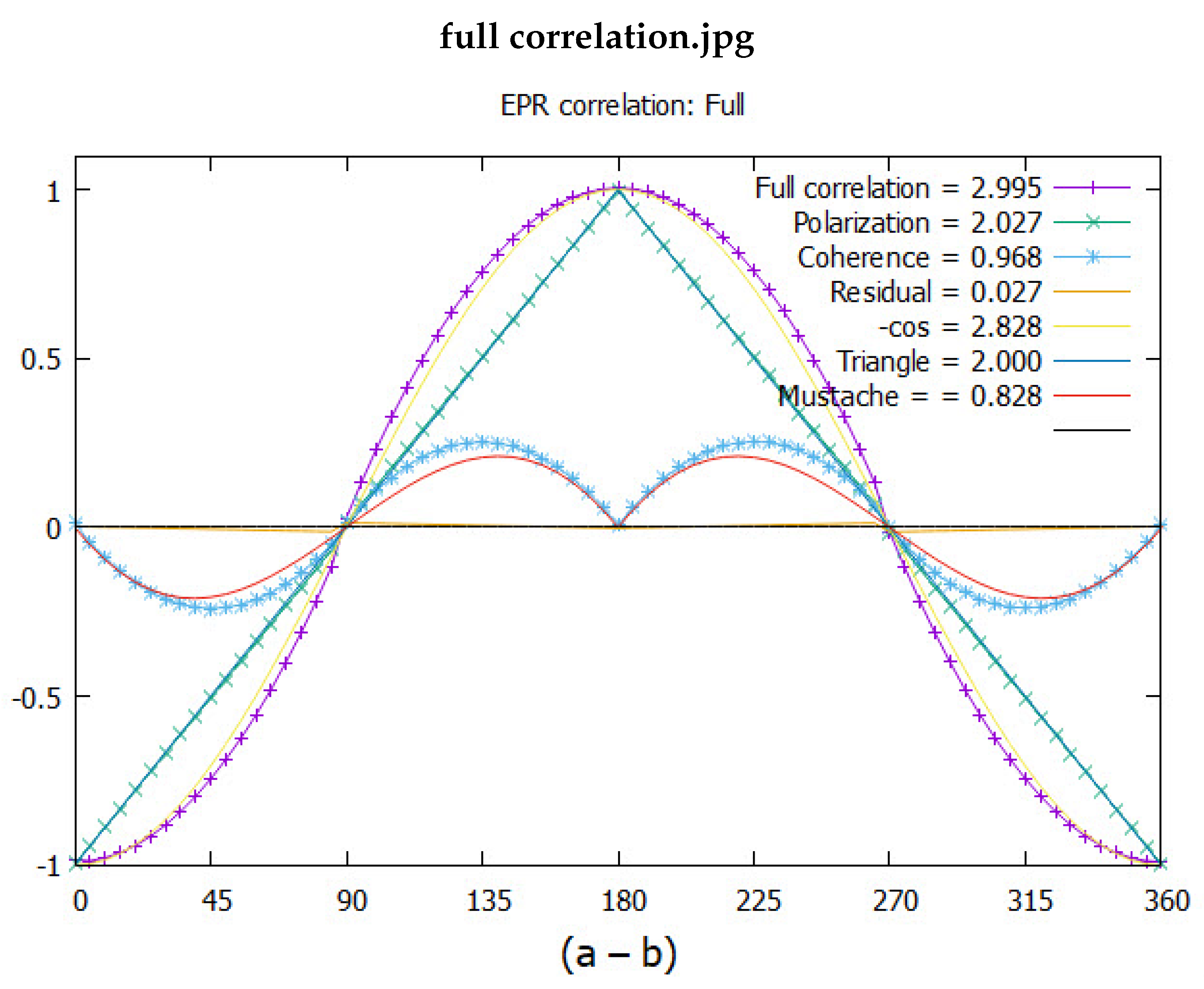
Figure 6.
Showing both Alice and Bob’s spins by looking along the axis of linear momentum, orthogonal to the screen. Within the two wedges both Alice and Bob’s spins are bosons. The heavy lines are possible filter settings, such that if one axis is Alice’s filter setting, the adjacent setting is Bob’s and so on alternating from Alice and Bob.
Figure 6.
Showing both Alice and Bob’s spins by looking along the axis of linear momentum, orthogonal to the screen. Within the two wedges both Alice and Bob’s spins are bosons. The heavy lines are possible filter settings, such that if one axis is Alice’s filter setting, the adjacent setting is Bob’s and so on alternating from Alice and Bob.
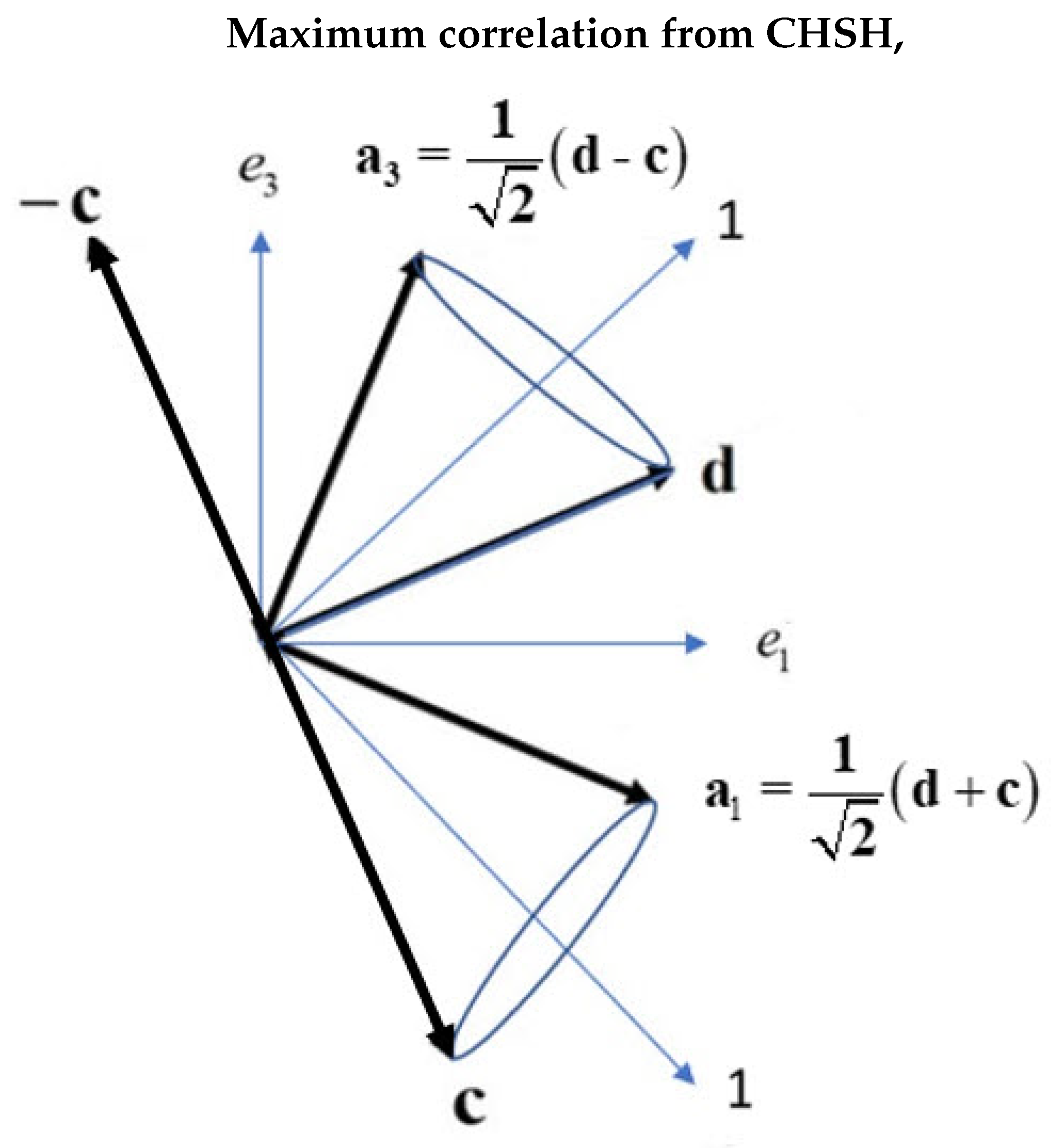
Figure 7.
Displaying the maximum correlation from coherence. Alice sets her filter to and the boson spin-1 aligns. Bob has two settings that will give the maximum violation by applying his filter either along or along at from . Alternately, Alice can set her filter angle to and Bob has two filter settings, and that lead to the maximum correlation. Note that a spin-1 makes an angle of with filter directions.
Figure 7.
Displaying the maximum correlation from coherence. Alice sets her filter to and the boson spin-1 aligns. Bob has two settings that will give the maximum violation by applying his filter either along or along at from . Alternately, Alice can set her filter angle to and Bob has two filter settings, and that lead to the maximum correlation. Note that a spin-1 makes an angle of with filter directions.
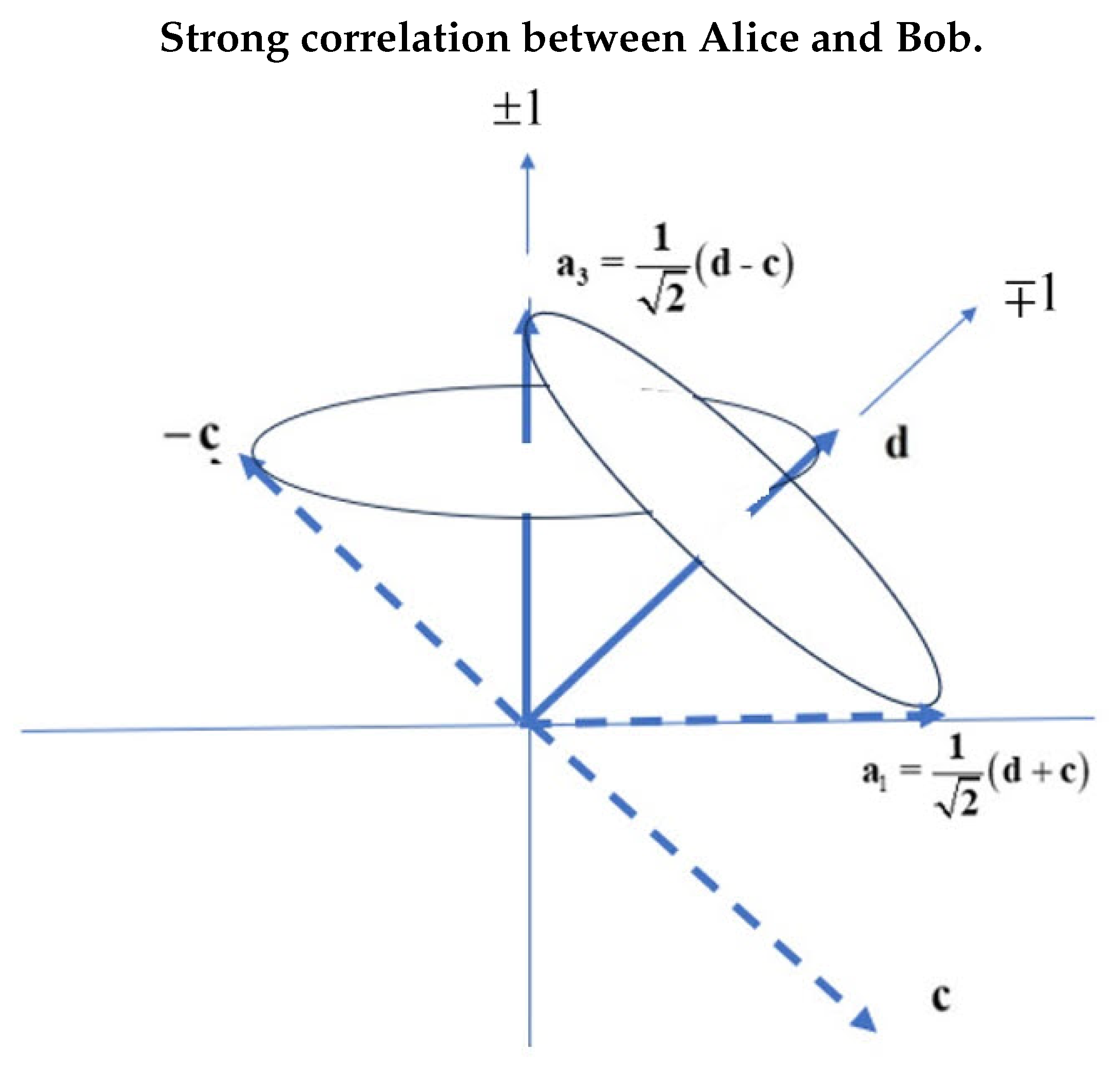
Figure 8.
The function given in Equation (21) compared to the simulation. Also shown is the correlation from QM showing less than the simulation.
Figure 8.
The function given in Equation (21) compared to the simulation. Also shown is the correlation from QM showing less than the simulation.
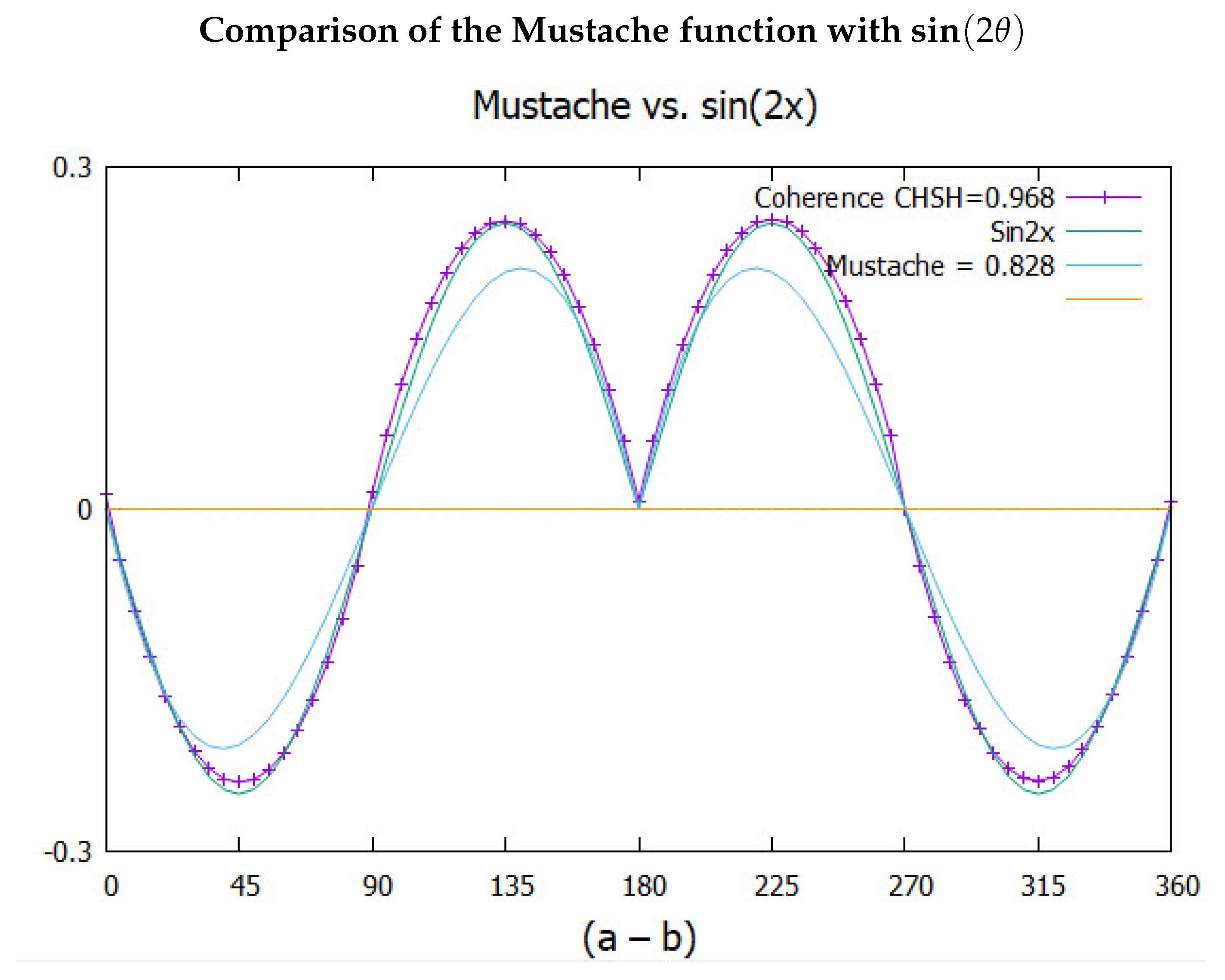
Figure 9.
A possible structure of the singlet with two electrons. While the electric charges repel, the magnetic moments attract. If one spin is in a LH frame, the other is in a RH frame. The helicities are opposite.
Figure 9.
A possible structure of the singlet with two electrons. While the electric charges repel, the magnetic moments attract. If one spin is in a LH frame, the other is in a RH frame. The helicities are opposite.
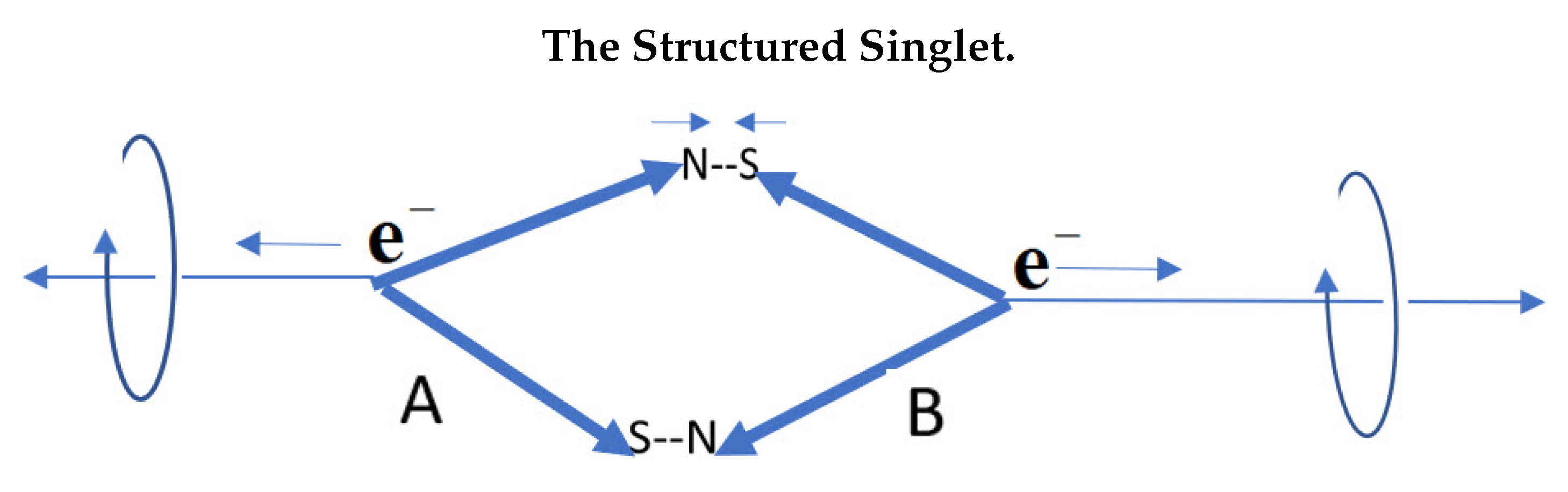
Figure 10.
The cobalt nuclei are the large spheres. The thick arrows are the magnetic fields. The small arrows are beta particles. The first column is the real world and the last is the mirror world. a) For a symmetrical distribution of beta fermion electrons parity is conserved. b) For a asymmetrical distribution of beta fermion electrons parity is not conserved. c) Using boson electrons, parity is conserved for any distribution.
Figure 10.
The cobalt nuclei are the large spheres. The thick arrows are the magnetic fields. The small arrows are beta particles. The first column is the real world and the last is the mirror world. a) For a symmetrical distribution of beta fermion electrons parity is conserved. b) For a asymmetrical distribution of beta fermion electrons parity is not conserved. c) Using boson electrons, parity is conserved for any distribution.
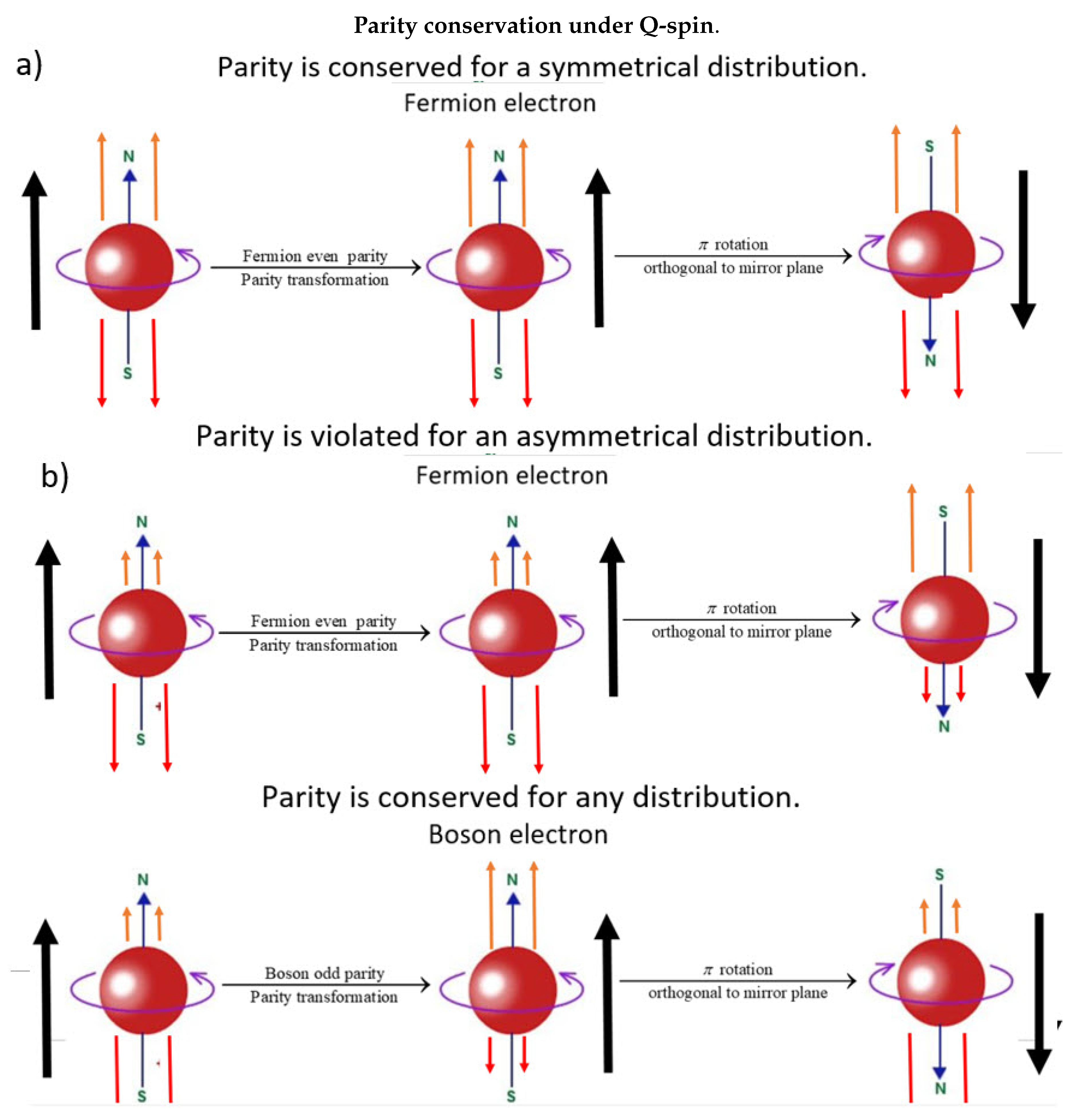
Figure 11.
Parentage Scheme. The number of linearly independent irreducible representations of weight ℓ in a spinor of order p, [142].
Figure 11.
Parentage Scheme. The number of linearly independent irreducible representations of weight ℓ in a spinor of order p, [142].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





