Prerpints.org logo
Preprint
Article

Multimodal Explainability Using Class Activation Maps and Canonical Correlation for MI-EEG Deep Learning Classification

This version is not peer-reviewed.

Submitted:

24 October 2024

Posted:

25 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Brain-Computer Interfaces (BCIs) are essential in advancing medical diagnosis and treatment by providing non-invasive tools to assess neurological states. Among these, Motor Imagery (MI), where patients mentally simulate motor tasks without physical movement, has proven to be an effective paradigm for diagnosing and monitoring neurological conditions. Electroencephalography (EEG) is widely used for MI data collection due to its high temporal resolution, cost-effectiveness, and portability. However, EEG signals can be noisy from a number of sources, including physiological artifacts and electromagnetic interference. They can also vary from person to person, which makes it harder to extract features and understand the signals. Additionally, this variability, influenced by genetic and cognitive factors, presents challenges for developing subject-independent solutions. To address these limitations, this paper presents a Multimodal and Explainable Deep Learning (MEDL) approach for MI-EEG classification and physiological interpretability. Our approach involves: i) evaluating different deep learning (DL) models for subject-dependent MI-EEG discrimination; ii) employing Class Activation Mapping (CAM) to visualize relevant MI-EEG features; and iii) utilizing a Questionnaire-MI Performance Canonical Correlation Analysis (QMIP-CCA) to provide multidomain interpretability. On the GIGAScience MI dataset, experiments show that shallow neural networks are good at classifying MI-EEG data, while the CAM-based method finds spatio-frequency patterns. Moreover, the QMIP-CCA framework successfully correlates physiological data with MI-EEG performance, offering an enhanced, interpretable solution for BCIs.
Keywords: 
Subject: 
Engineering  -   Bioengineering

1. Introduction

The 2021 UNESCO Engineering for Sustainable Development report points out the role the profession has on the 2030 Agenda. The third goal, "ensure healthy lives and promote well-being for all at all ages," highlights the advancements in improving medical diagnosis and care through low-cost tools [1]. The most affordable tool in neuroscience is Electroencephalography (EEG), which is also the most studied thanks to its high temporal resolution and portability. EEG captures subjects’ neural bioelectric activity generated by neuron activation through electrodes placed on the scalp [2]. Techniques like Event-Related Potentials (ERPs) extract representative time-frequency information within the time-series data for understanding the neurological activity of a subject or a group [3]. Also, Brain-Computer Interfaces (BCI) profit from those patterns for controlling external devices, such as prostheses [4]. To learn the brain patterns, a BCI paradigm presents stimuli and asks the subject to perform tasks. For instance, the Motor Imagery (MI) paradigm, which consists of the mental rehearsal of motor tasks without physical movement, has been used to support the diagnosis, treatment, and follow-up of brain diseases [5].
However, EEG is far from the panacea for all neuroimaging needs. Due to its non-invasive nature, superficial EEG sacrifices spatial resolution and becomes highly susceptible to electromagnetic artifacts (e.g., electrical devices) and physiological noise (e.g., eye movement and muscle activity), yielding less useful features [6,7]. Moreover, the volume conduction effect introduces noise or cross-talk between electrodes, hampering the source localization of brain activity and the interpretation of EEG data [8]. Lastly, both between- and within-subject variability challenge the development of a universal MI-EEG algorithm. Differences in genetic, cognitive, and neurodevelopmental factors cause the same task or stimuli to evoke distinct brain patterns across individuals, complicating the creation of subject-independent solutions [9,10]. Additionally, as users become more familiar with the BCI device or task over time, their performance and initial brain patterns evolve, demanding personalized calibration sessions [11].
Traditional MI-EEG algorithms attempt to extract features by analyzing the signal’s power levels. The baseline Common Spatial Patterns (CSP) exploits the power distribution over the scalp to find spatial patterns discriminating two tasks [12]. Variations of CSP include L1-CSP, which regularizes the patterns using the L1-norm; Sparse Filter Band CSP (SFBCSP), which automatically selects useful spectral bands from a precomputed set [13]; and Multi-Kernel Stein Spatial Patterns (MKSSP), which extracts nonlinear patterns in a low-dimensional Riemannian manifold [14]. However, a low signal-to-noise ratio makes CSP and its variants extract features from artifacts rather than the actual EEG [15].
Conversely, machine learning algorithms exploit their ability to automatically learn features from a given training dataset to minimize the prediction error as much as possible [16]. Deep Learning (DL) methods extract nonlinear patterns, dealing with EEG noise and volume conduction effect [17]. Convolutional Neural Networks (CNNs), a DL model, are the most successful EEG feature extraction architectures because they look for space and time patterns [18]. Examples of CNNs for MI-EEG classification are EEGNet, ShallowConvNet, and DeepConvNet, which, like SFBCSP, also extract spatial patterns from certain frequency bands [19]. Unlike SFBCSP, the above architectures unravel nonlinear, deeper, and more complex patterns [20]. Other DL models for EEG applications include Autoencoders that embed EEG signals into a generative noise-reduced feature space [21]; Recurrent Neural Networks (RNNs) that exploit the sequential nature of EEG features [22]; and, more recently, Transformers that use their long-term memory to capture both global and local patterns [23].
However, there are two main concerns about the medical applications of the above DL models. Firstly, they become "black boxes," lacking interpretable information to understand each subject’s neurological abilities [24]. Secondly, they ignore the closed link between neurological, physiological, and personal behaviors [25]. Analyzing how these factors influence the model provides users and scientists with valuable information to improve the results beforehand. Thus, multimodal and multidomain strategies can couple information from patients’ moods and habits to understand their neurophysiological responses and exploit this additional information to improve model performance and interpretability.
This work proposes Multimodal and Explainable Deep Learning (MEDL) as an approach for MI-EEG discrimination and physiological interpretability. Specifically, our proposal is threefold: i) Different DL models are tested for subject-dependent MI-EEG discrimination. ii) A CAM-based approach is used to quantify and visualize relevant MI-EEG features. iii) A Questionnaire-MI Performance Canonical Correlation Analysis (QMIP-CCA) strategy is introduced as a multidomain explainability stage for physiological and MI-EEG discrimination non-linear feature matching. Experiments are carried out with the GIGAScience MI dataset due to its relatively large number of subjects and the additional questionnaire that it offers for physiological subject information [26]. The results obtained demonstrate that shallow networks achieve acceptable MI discrimination results. In addition, our CAM-based method allows us to code MI spatio-frequency group patterns and measure EEG features of the sensorimotor cortex in people who are getting better at MI. Finally, our QMIP-CCA allows quantifying and visualizing relevant physiological questions from tabular data and matching them to MI-EEG performance measures.
The agenda for this paper is as follows. Section 2 summarizes the related work. Section 3 describes the materials and methods. Section 4 describes the experiments and discuss the results. Lastly, Section 5 outlines the conclusions and future work.

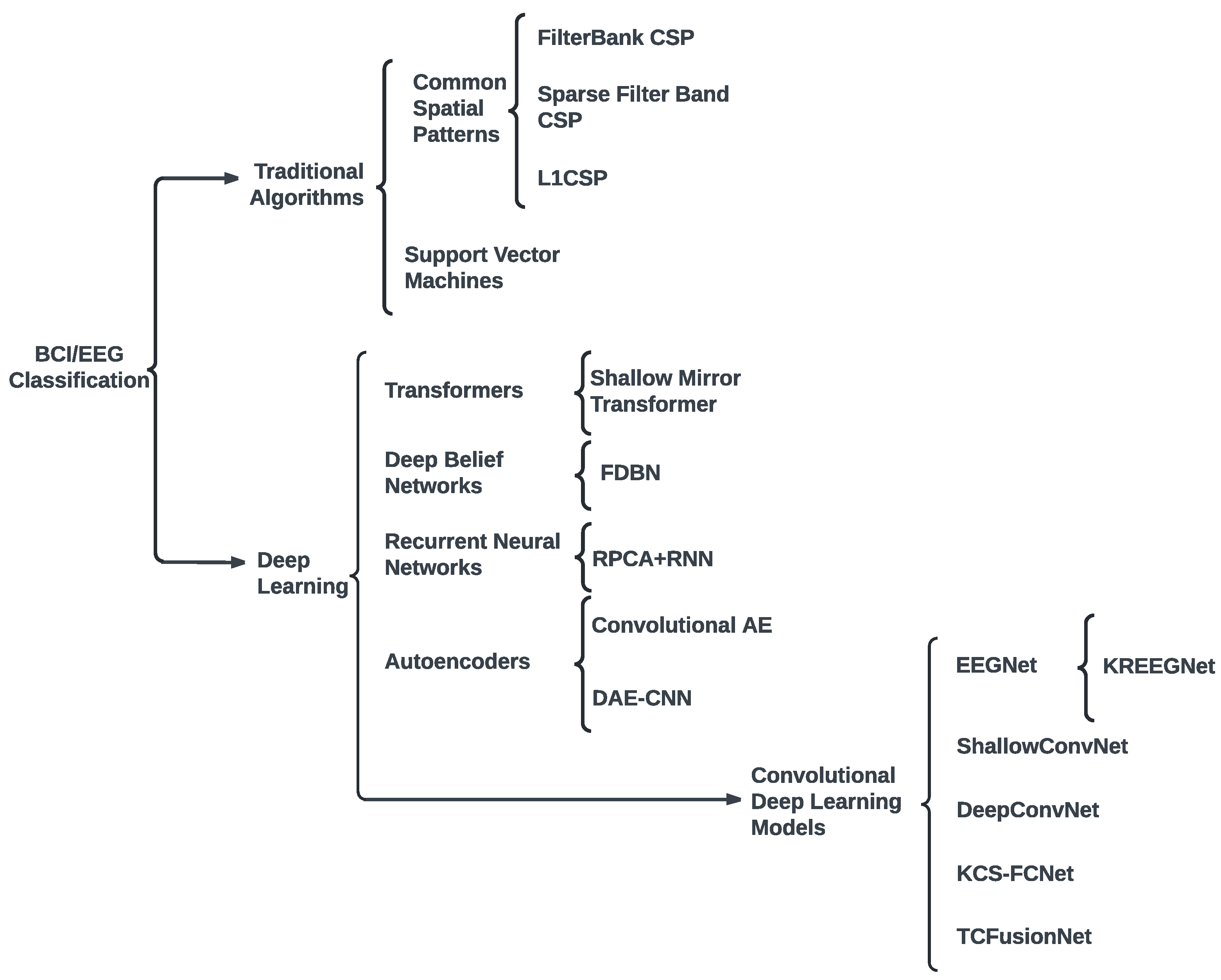
2. Related work

Since Koles et al.’s work in 1990, CSP has been the go-to tool for feature extraction in EEG data [27]. CSP provides spatial filters that maximize the variance ratio of two multivariate signals, enabling the discrimination of two classes for classification purposes. Unfortunately, since the technique depends on the signals’ variance, it becomes sensitive to noise and struggles in small datasets [28]. In turn, variants of CSP have sprung up to enhance the original algorithm. L1CSP redefines the base objective in terms of the L1-norm instead of the usual L2-norm to reduce artifacts’ influence on the signal [29]. In contrast, FBCSP adds a bandpass filtering stage for multiple, manually selected frequency bands before the usual spatial filtering. After that, it uses a mutual information algorithm to select discriminant features [30]. Lastly, SFBCSP selects the bandpass filters semi-automatically, rather than manually like FBCSP, by integrating a sparse regression model to learn the optimal features from each input filter band [31]. However, these models remain power-reliant and, in the case of FBCSP and SFBCSP, require some form of manual input. Once features have been extracted, classification can be performed by various methods. One such technique are Support Vector Machines (SVMs). SVM works by finding the optimal hyperplane for separating classes [32]. However, SVMs fail to classify data when features are too similar between classes [33].
Thanks to their ability to recognize and extract non-linear features from raw EEG data [34], DL models solve many of these traditional algorithms’ shortcomings. CNNs are a family of DL strategies that scan the input signal for representative patterns, starting from simple structures until reaching a more complex combination of these initial features. These algorithms are commonly used for image processing, but by tuning the size and number of filters, it is possible to extract information from the temporal, spatial, and frequency domains, e.g., for MI-EEG classification. Also, unlike CSP, these models automatically fine-tune the best filters for the given task through gradient decent [35]. Some relevant examples of CNNs for MI-EEG include the EEGNet, KREEGNet, ShallowConvNet, DeepConvNet, TCFusionnet, and KCS-FCNet.
In particular, EEGNet gets different features from EEG data in three steps: temporal convolution, depthwise convolution (to find patterns in time and space), and separable convolution (to combine the data from the first two steps) [36]. Variations of this original architecture have since emerged. TCFusionNet, for example, integrates the EEGNet architecture with residual blocks composed of dilated convolutions, which add these residual features to the ones from the separable convolution to increase the size of the receptive field while avoiding the exploding/vanishing gradient problem of deeper models [37]. ShallowConvNet works similarly to EEGNet but skips the separable convolution stage and uses regular convolution for spatial filtering. This reduces the number of parameters requiring training, leading to faster training and better interpretability, but at the cost of some performance. DeepConvNet, on the other hand, goes much further by adding a series of 2D convolutions that get bigger and bigger to pull information from the earlier stages and find complex structures [19]. Regarding Deep Kernel Learning (DKL) methods, KREEGNet computes the functional connectivities from the temporal convolution through a Gaussian similarity, alongside Delta Kernel for label outputs, all to use Central Kernel Alignment (CKA) as a regularizer [38]. Likewise, KCS-FCNet computes the functional connectivities from a temporal convolution through a Gaussian kernel, much like KREEGNet; however, it then relies on the measured connectivities as input for a Fully-Connected block to classify the MI data on a high-dimensional space [39].
Nevertheless, as computational power has increased, more powerful and complex algorithms have been developed to extract more information from EEG signals. Deep Belief Networks (DBNs) stack multiple Restricted Boltzmann Machines (RBMs), which learn to reconstruct a given input through unsupervised training; however, as a result of using RBMs, DBNs require a pre-training stage on a separate dataset, which is a luxury only available on larger databases [40]. Another set of neural networks for EEG data is Autoencoders, which have been used as dynamic Principal Component Analysis (PCAs) to select the most relevant characteristics before classification [41]. Ideally, the model will filter out any kind of noise contaminating the signals, as it acts as redundant information, leaving only features intrinsic to the EEG for classification [42]. Unfortunately, physiological noise is extremely difficult to properly filter, as it is influenced by factors such as stress levels, personal background, and even the testing environment [43]. Alternatively, RNNs are a natural choice for EEG analysis, as their ability to remember previous inputs makes them ideal for time series data, thanks to their strong modeling capabilities, making them useful at leveraging cross-series information, even when handling heterogenous signals [44]. Recently, Transformer networks utilize an Attention Mechanism to capture global information from EEG by encoding information from temporal, frequency, and spatial features, allowing the model to identify relevant sample dependencies while dealing with the low signal-noise ratio problem [45]. Despite these models’ multiple advantages, their use is severely limited in tasks requiring interpretability, as these architectures lack tools to allow users to properly assess the cause for a given output, as it is difficult to assure if their performance is thanks to them extracting meaningful information, or noise [46]. Furthermore, precisely due to their complexity, they are vulnerable to overfitting [47]. EEG-BCI classification methods are summarized in Figure 1.
Now, multiple strategies have emerged to provide interpretable results from DL-based methods. The authors in [48] propose four different types of explanations offered by the many algorithms: Example, Attribution, Hidden Semantics, and Rules. Example algorithms check which inputs are similar to each other according to the model. Attribution looks at which elements of the input had the greatest influence on the given output. Hidden Semantics employs the network’s neurons to explain the output; for instance, when classifying animals, it determines whether the neurons are focusing on the head, legs, or other parts of the creature. Finally, rules explain the output in terms of a series of decisions taken by the model; in their most simple incarnation, these rules take the form "If X is present, then Y." However, when working with EEG data, not every algorithm will provide useful insight. Rules as explanation reduce the model to a Decision Tree algorithm but do not necessarily create explainable rules themselves [49]. This leaves open the other three types of explanations. Hidden Semantics are useful for evaluating the importance of specific features at certain points, but they produce abstract results the deeper the neurons are [50]. For inter-subject analysis, Example algorithms are capable of finding similarities between subjects, providing information as to which patients share similar attributes, but struggle in providing explainability to extracted features as these must already make sense to the BCI professionals beforehand [51]. Next, Attribution possesses the most potential for BCI insight, as these techniques map the importance of the output back to the original input (EEG data). Common attribution algorithms are CAMs, which create a mask that highlights which pixels from the input image supply the most important information for the output. Introduced by [52], CAMs map out the elements within an image most relevant for the CNN. This method involves weighting the activation maps from a given layer and finding the average contribution of each pixel to the model’s decision. Grad-CAM, by [53], generalizes CAMs by redefining the weights in terms of the gradient produced by the model. However, this technique uses a global average for weight calculations, assuming each activation to be equally important. Grad-Cam++ [54] then redefines Grad-Cam to be in terms of a weighted average instead of global. Next, LayerCAM enables the use of CAMs for any convolutional layer [55]. By utilizing the backward class-specific gradients, it is possible to generate a separate weight for each spatial location.
Another strategy to improve EEG classification and interpretability is to incorporate information from different domains into the DL structure. Multi-domain Fusion Deep Graph CNN (MdGCNN) by [56] fuses time-frequency and spatial information through the use of graph convolutions, which learn the discriminant features across the domains, followed by a sort pooling layer to act as a fusion stage to bridge the extracted information to regular convolutions, which then produce the output. Still, this approach does not include information from external sources to the EEG, limiting its interpretability, unlike the authors in [57] who perform emotion recognition through RNNs using visual information from videos in addition to the EEG, fusing into a hierarchical attention mechanism to organize features based on their perceived significance. This method allows the analysis of how physiological and neurological responses relate to each other during classification. Lastly, [58] uses a deep and wide CNN to pull out features and perform an initial classification. Kernel matching via Gaussian embedding is then used to combine data from questionnaires and make the model output more accurate.
Ultimately, it is evident that traditional feature extraction algorithms, like CSP, provide the best interpretability but are also the least powerful for EEG-based classification, primarily due to their need for manual tuning. Complex DL solutions such as Autoencoder, RNNs, and Transformers offer the ability to extract much more information when compared to other solutions, but their results aren’t easily interpretable or require large datasets [59]. This, in turn, leaves CNNs-based EEGNet variants as the best compromise between the two. They work similarly to traditional CSP algorithms, requiring no manual tuning for the filters; can be expanded upon to exploit information present in much deeper structures; and possess extremely useful interpretation tools in the form of CAMs.

3. Materials and Methods

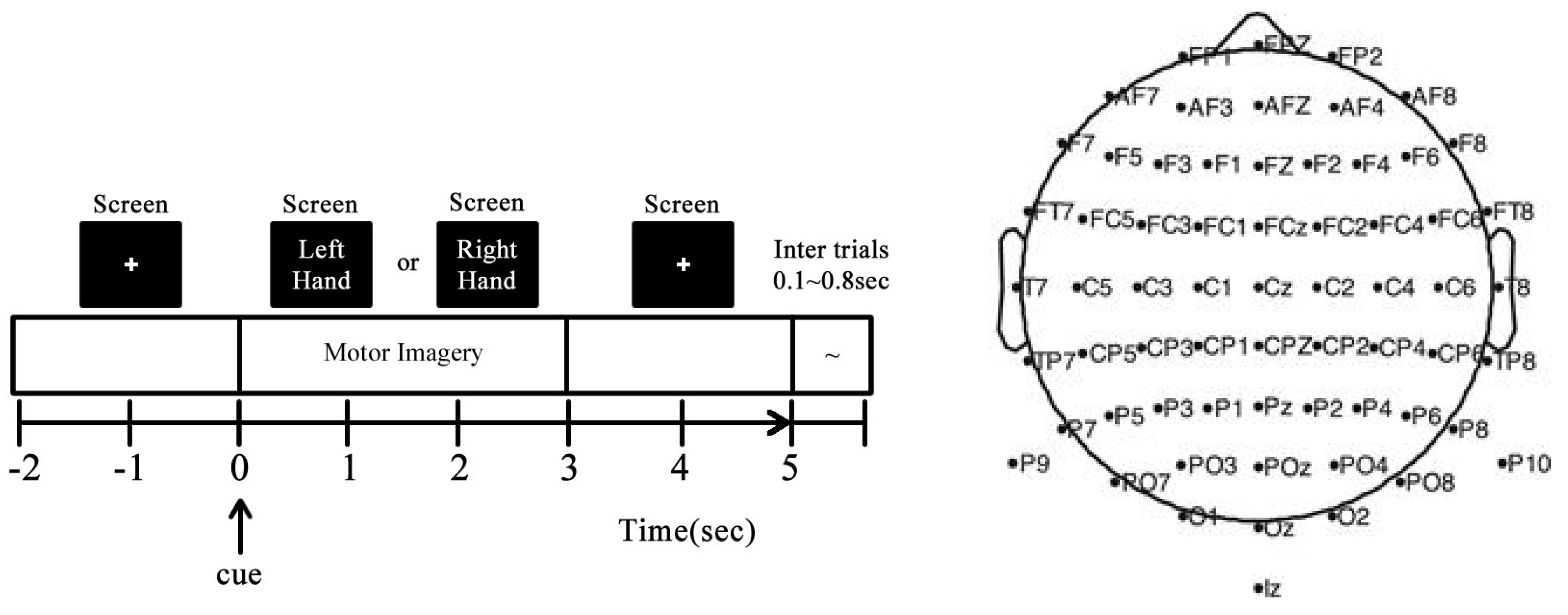
3.1. GIGAScience Dataset for MI-EEG

DB-I - GiGaScience[26] (http://gigadb.org/dataset/100295). It consists of 52 subjects, 50 of which have their EEG data available for evaluation. Each subject is asked to perform a single session of MI, comprised of five to six runs with 100 to 120 trials per class. Each trial lasts seven seconds, starting with a blank screen, followed by a cue within two seconds. When the cue appears on screen, the subject imagines moving their left or right hand. The trial ends with two more seconds of a blank screen and an inter-trial break of 0.1 to 0.8 seconds. The EEG data was collected using 64 electrodes placed according to the international 10-10 system, as seen on Figure 2, sampled at 512 Hz. Actual movement and six types of non-task-related data (blinking eyes, eyeball movement up/down, eyeball movement left/right, head movement, jaw clenching, and resting state) were also collected.
Additionally, subjects were asked to complete a physiological questionnaire during the MI experiment. Before beginning the MI experiment, subjects answered 15 personal questions such as Age, Sex, BCI experience, or any recent consumption of coffee, alcohol, or cigarettes. After every run, subjects answered another ten questions about their mood and expected performance. Finally, after the MI experiment, subjects had to answer four questions regarding their thoughts on the experiment and overall personal performance. In total, each subject answered 69 questions. Questions relating to how the patient felt were answered on a scale from one to five, while open questions such as age or expected performance were answered numerically without decimals. However, not all questions were utilized in this study. Shannon’s entropy, as presented in Equation 1:
H ( ξ q ) = − E log ( p ( ξ r q ) ) : ∀ r ∈ R ,
was measured for each of the Q questions, ξ r q ∈ ξ q , q ∈ Q , correctly encoded and normalized between [ 0 , 1 ] , along the R subjects to find the ones that had the most expected information, with the response’s histogram giving an estimate of p ( ξ r q ) . Figure 3 illustrates a significant decline in entropy following the initial 31 questions, arranged from highest to lowest entropy, indicating that subsequent questions yield considerably less informational value. As a result, only questions with entropy above or equal to the 25th percentile were selected for this study. This then totals 52 out of the 69 available questions (see Table A1).

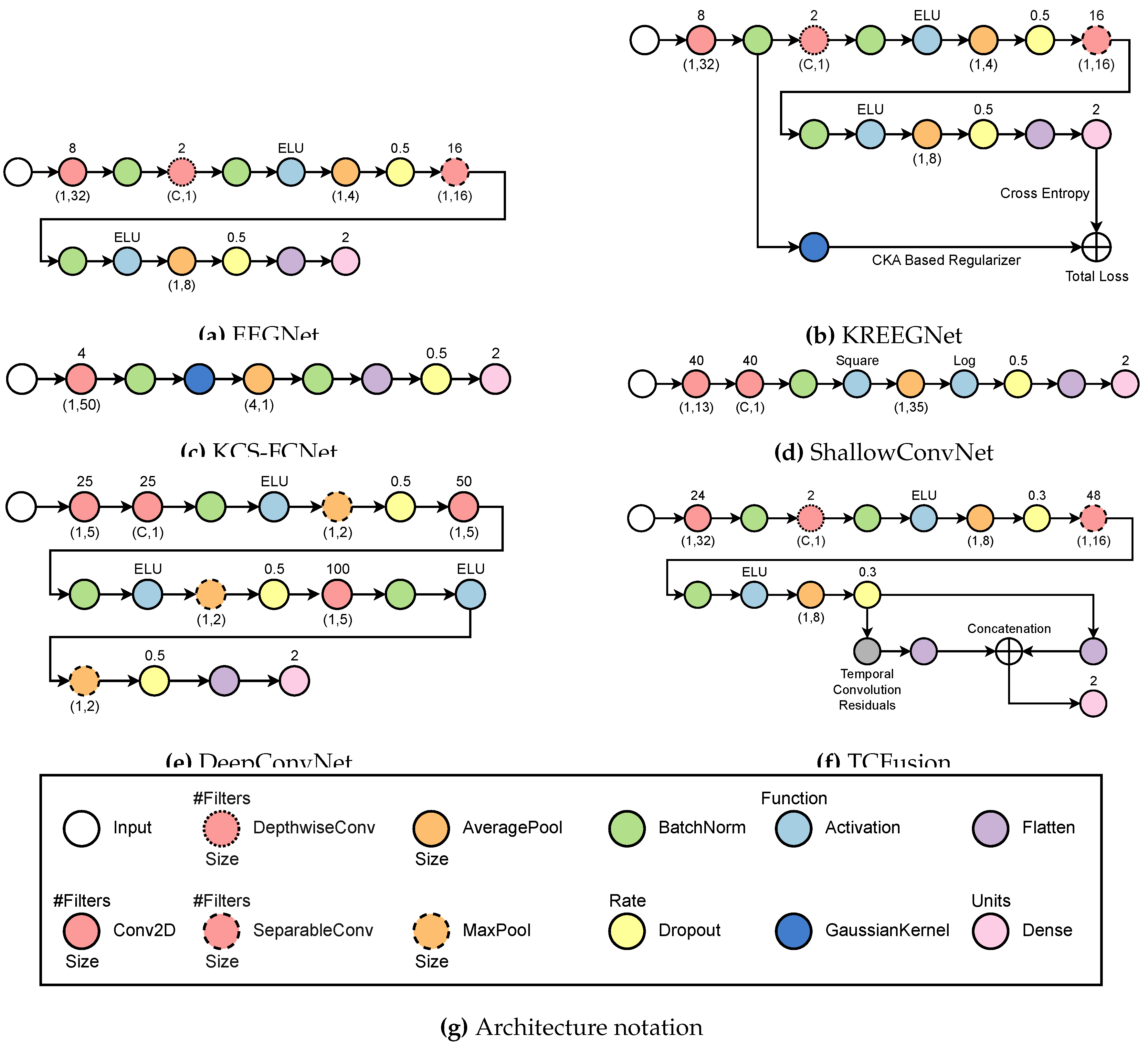
3.2. Subject-Dependent MI-EEG Classification Using Deep Learning

Let D = { X n ∈ R C × τ , y n ∈ { 0 , 1 } K ˜ } n = 1 N be a subject-dependent input-output MI-EEG dataset, gathering N trials, τ time samples, C channels, and K ˜ MI-classes ( K ˜ = 2 for the GIGAScience dataset). To optimize the meaningful EEG spatial-temporal-spectral patterns from a given X ∈ D and diminish noise for enhanced MI class prediction, a DL approach can be employed as follows:
y ^ = f ˜ ( X | θ ) = ( f L ∘ f L − 1 ∘ ⋯ ∘ f 1 ) ( X ) ,
y ^ ∈ [ 0 , 1 ] K , ∑ k = 1 K y ^ k = 1 , L stands for the number of layers, and:
Z l = f l ( Z l − 1 ) = φ ( Z l − 1 ⊗ W l + B l ) ,
where φ ( · ) is a given non-linear activation function, Z l ∈ R C l ′ × τ l ′ × P ˜ l is the l-th feature map; W l and B l hold the weights and bias of proper size, P ˜ l stands for the number of filters, and θ = { W l , b l } l = 1 L collects the network parameters. Furthermore, ⊗ represents the tensor product operator for fully connected, convolutional, or recurrent layers.
Then, an optimization problem can be formulated as:
θ ^ = arg min θ E { L ( y n , f ˜ ( X n | θ ) ) : ∀ n ∈ { 1 , 2 , ⋯ , N } } ,
where L ( · , · ) is a given loss function, i.e., cross-entropy. In addition, a gradient descent-based framework using back-propagation is employed to optimize the parameter set [60]:
θ i = θ i − 1 − η i ∂ ∂ θ i 1 N ∑ n = 1 N L ( y n , f ˜ ( X n | θ i ) ) ,
where a sample mean estimation is used to approximate the expected value, and an autodiff-based approach computes the gradient ( η i ∈ R + is a learning rate).
Here, the following MI-EEG DL networks will be considered:
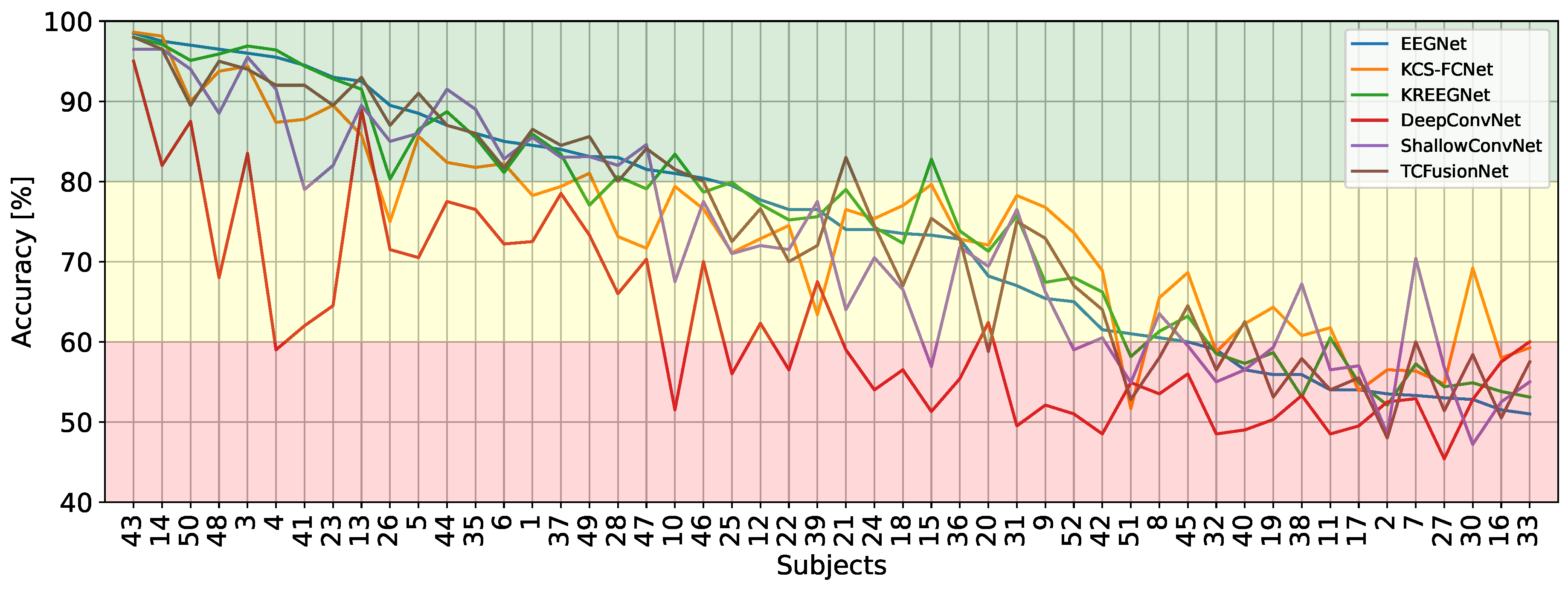
  • EEGNet [36]: The process begins with a temporal convolution, which is followed by a depthwise layer that serves as a spatial representation for each filter produced at the previous stage. Afterward, an exponential linear activation function (ELU) is used before an average pooling and a dropout to help minimize overfitting. Next, it applies a separable convolution, which is followed by another ELU activation and an average pooling. Lastly, a second dropout layer precedes the flattening and classification stages. Batch normalization is always performed immediately after each convolutional layer.
  • KREEGNet [38]: Similar to EEGNet, it uses a Gaussian kernel after batch normalization to extract the connectivity between EEG channels. A delta kernel is implemented on the label data, and a Centered Kernel Alignment (CKA)-based regularization between connectivities and label data is added as a penalty to the straightforward cross-entropy.
  • KCS-FCNet [39]: A single convolutional stage before using a gaussian kernel to measure EEG connectivity is utilized. These are then run through an average pooling layer before batch normalization and classification. Interestingly enough, a dropout step is done between the flatten layer and the dense layer.
  • ShallowConvNet [61]: It performs two consecutive convolutions, then proceeds with batch normalization and square activation. After that, average pooling is done before logarithmic activation and dropout. Finally, a layer of flattening and density is applied for classification.
  • DeepConvNet [19]: The system employs two convolutional layers sequentially, followed by batch normalization and ELU activation. Then, a max pooling and a dropout are employed before another convolutional layer and batch normalization. Another set of ELU activation, max pooling, and dropouts is performed before a final convolution and batch normalization. Finally, another ELU, max pooling, and dropout are performed before classifying.
  • TCFusionNet [37]: Similar to EEGNet, it employs a sequence of residual blocks to gather extra data prior to classification. Each residual block is comprised of a dilated convolution followed by batch normalization, ELU, and dropout twice. In parallel, a 1x1 convolution is done and then concatenated to the output of the residual block. Before flattening and joining the flattened features from the separable convolution stage, multiple residual blocks are put in place in a cascading fashion. Finally, a dense layer is used for classification.
Figure 4 shows a summarized visual guide of the different MI-EEG architectures.

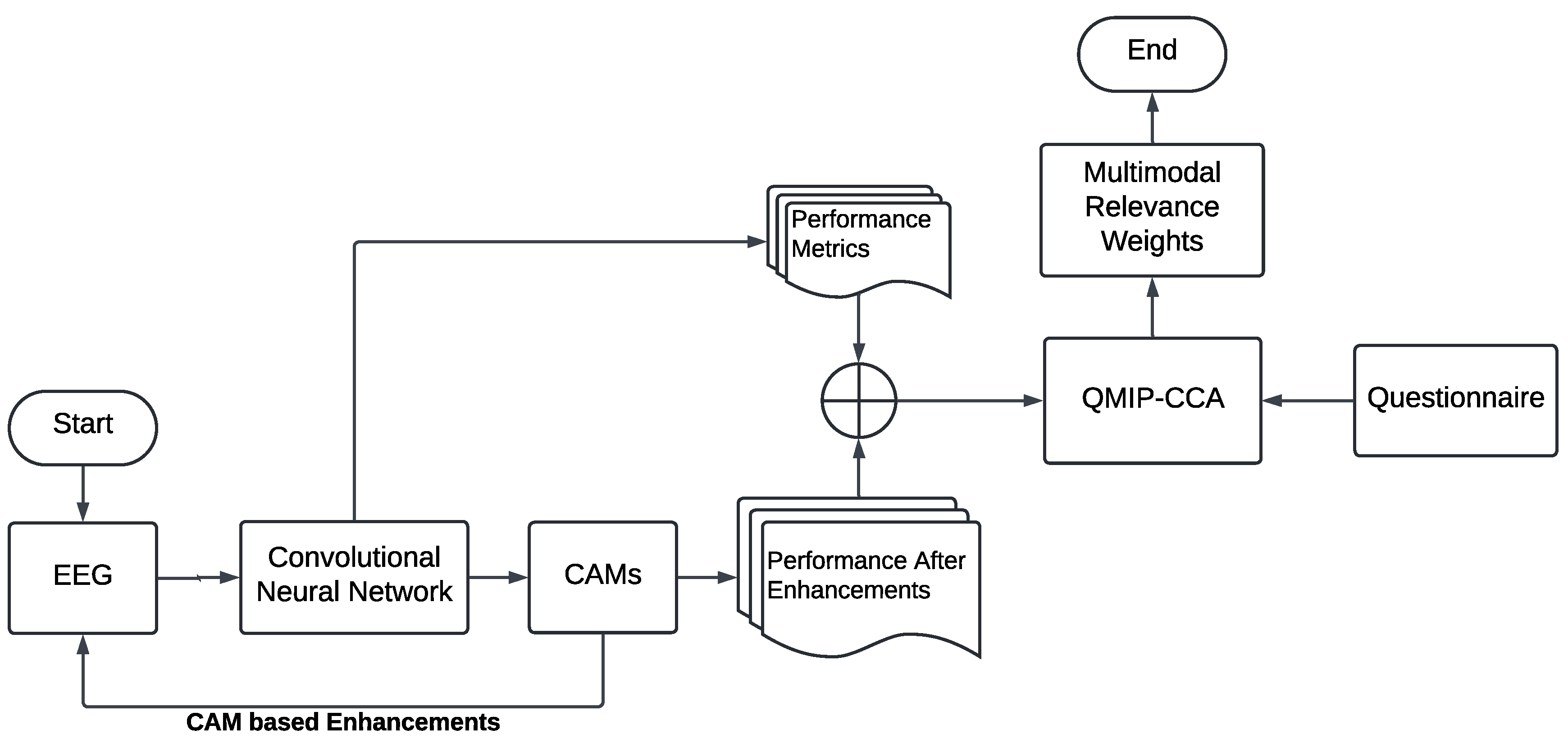
3.3. Layer-Wise Class Activation Maps for Explainable MI-EEG Classification

Layer-wise Class Activation Mapping (Layer-CAM) is a powerful technique for DL interpretability that addresses the need to understand how neural networks make decisions [55]. By generating heatmaps that highlight the most relevant regions in an input image, Layer-CAM allows researchers to visualize the specific features contributing to the network’s predictions at various layers. Unlike traditional CAM methods, Layer-CAM captures class-discriminative regions at intermediate layers, providing a more detailed and multilevel perspective on feature importance. Moreover, it supports model refinement by highlighting misinterpreted regions. Here, we implement Layer-CAM within a MI-EEG framework, by modeling each EEG trial as an image that holds C rows and τ columns. Then, let S l k ( X ) ∈ R C × τ be the upsampled MI-EEG CAM of a given input trial X for the k-th class ( k ∈ K ) in the l-th layer ( l ∈ L ), defined as:
S l k ( X ) = ReLU ζ ∑ p = 1 P ˜ l β l p k ⊙ Z ˜ l p k ,
where ζ ( · ) is an up-sampling function, ReLU ( x ) = max ( 0 , x ) , Z ˜ l p k ∈ R C l ′ × τ l ′ represents the network activation map for the l-th layer regarding the p-th filter and the k-th MI class, and β l p k ∈ R C l ′ × τ l ′ gathers the corresponding CAM weight matrix with respect to the k-th output score. By utilizing the backward class-specific gradients, Layer-CAM computes each β l p k as:
β l p k = ReLU ∂ y ˜ k ∂ Z l p k ,
being y ˜ k ∈ R + the k-th class score holding a linear activation.
To highlight relevant spatial and temporal EEG inputs while avoiding spurious CAM artifacts, we normalize the EEG Layer-CAM as:
S ˜ l k ( X ) = 2 S l k ( X ) max l ′ ∈ L ; k ′ ∈ K S l ′ k ′ ( X ) + 1 C 1 τ ⊤ ,
where 1 is an all-ones column vector of proper size. Afterward, an EEG explanation map X ˜ l k ∈ R C × τ can be computed from trial X as follows:
X ˜ l k = X ⊙ S ˜ l k ( X ) .
Lastly, the Gain measure (see Equation 10) is used to assess the importance of different regions in an input EEG that contribute to the model’s decision for a specific class [62]:
Gain ( X | l , k , θ ^ ) = f ˜ ( X ˜ l k | θ ^ ) − f ˜ ( X | θ ^ ) | f ˜ ( X | θ ^ ) | , ∀ k ∈ { − 1 , + 1 } .

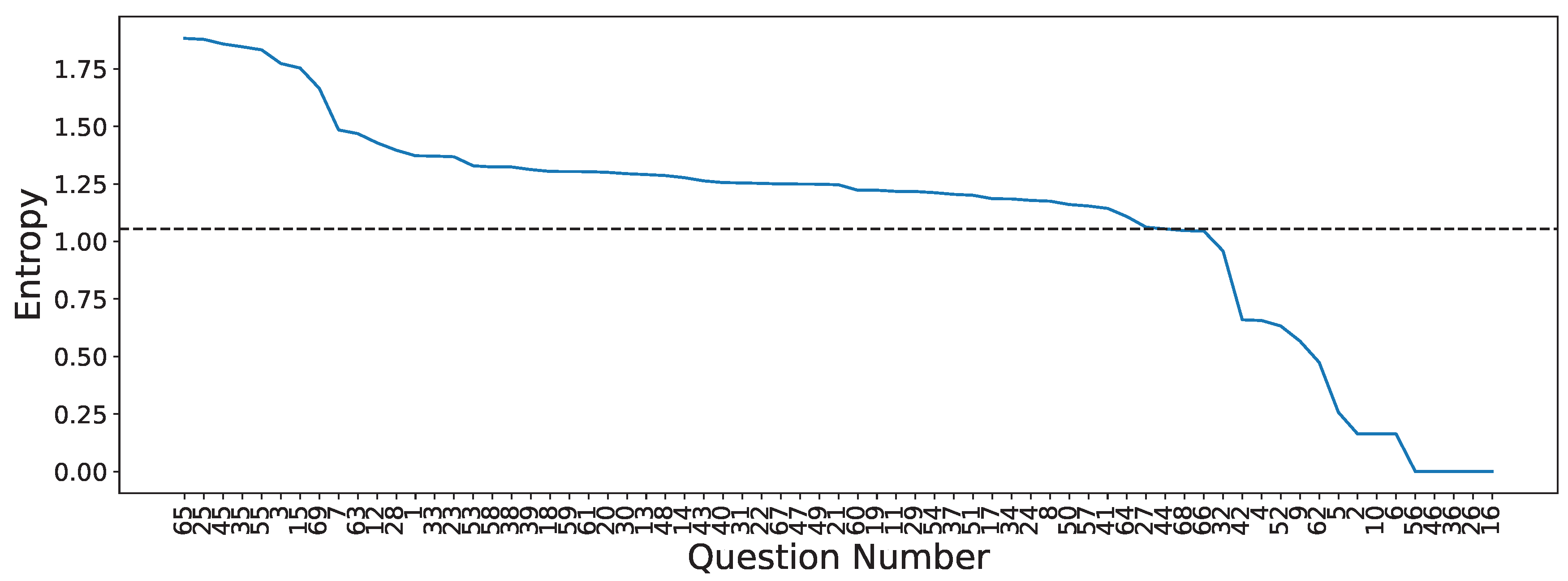
3.4. Questionnaire-MI Performance Canonical Correlation Analysis (QMIP-CCA)

Let us consider the questionnaire matrix Ξ ∈ [ 0 , 1 ] R × Q holding Q informative MI-EEG questions (see Section 3.1) along R subjects. In turn, let Γ ∈ R R × A be an MI-EEG classification performance matrix, holding the following measures:
Accuracy = T P + T N T P + T N + F P + F N
AUC = ∫ 0 1 TP TP + FN d FP FP + TN
Kappa = 2 · ( T P · T N − F P · F N ) ( T P + F P ) · ( F P + T N ) + ( T P + F N ) · ( F N + T N ) ,
where T P , T N , F P , and F N stand for true positive, true negative, false positive, and false negative, respectively. Of note, the Accuracy, Area Under the Curve (AUC), and the Kappa (see Equations 11-13) quantify the DL MI-EEG classification performance [60]. We also compute the aforementioned MI performance measures using, as input, the explanation maps in Equation 9. Consequently, A = 6 for a given DL model.
Next, we propose to compute the questionnaire and MI-performance inter-subject matching matrices, Ξ ˜ ∈ [ 0 , 1 ] R × Q and Γ ˜ ∈ [ 0 , 1 ] R × A , as:
Ξ ˜ r q = 1 R ∑ r ′ = 1 R κ ( ξ r q − ξ r ′ q | σ q 2 ) = 1 R ∑ r ′ = 1 R exp − ∥ ξ r q − ξ r ′ q ∥ 2 2 2 σ q 2
Γ ˜ r a = 1 R ∑ r ′ = 1 R κ ( γ r a − γ r ′ a | σ a 2 ) = 1 R ∑ r ′ = 1 R exp − ∥ γ r a − γ r ′ a ∥ 2 2 2 σ a 2 ,
with ξ r q ∈ Ξ and γ r a ∈ Γ ; r , r ′ ∈ { 1 , 2 , ⋯ , R } , q ∈ { 1 , 2 , ⋯ , Q } , and a ∈ { 1 , 2 , ⋯ , A } . The kernel function κ ( · , σ 2 ) is set as a Gaussian similarity with bandwidth σ 2 ∈ R + , which is found by taking the median of the Euclidean distances between the kernel input samples as: σ q 2 = Median { ∥ ξ r q − ξ r ′ q ∥ 2 : ∀ r , r ′ ∈ R } and σ a 2 = Median { ∥ γ r a − γ r ′ a ∥ 2 : ∀ r , r ′ ∈ R } .
Lastly, to code the questionnaire and MI-performance non-linear matching between subjects by projecting them into a higher-dimensional feature space using κ ( · , σ 2 ) , we employ the following CCA-based optimization [63]:
α ^ m Ξ , α ^ m Γ = arg max α m Ξ , α m Γ ∑ m = 1 M 〈 Ξ ˜ α m Ξ , Γ ˜ α m Γ 〉 s . t . ∥ Ξ ˜ α m Ξ ∥ 2 = 1 ∥ Γ ˜ α m Γ ∥ 2 = 1 , ∀ m ∈ M ; M ≤ min ( A , Q ) .
The constraint optimization problem in Equation 16, with α Γ ∈ R A and α Ξ ∈ R Q , can be solved by the following generalized eigenvalue-based solution:
Γ ˜ ⊤ Γ ˜ − 1 Ξ ˜ ⊤ Γ ˜ Ξ ˜ ⊤ Ξ ˜ − 1 Ξ ˜ ⊤ Γ ˜ α ˜ m Γ = ν m α m Γ ,
Ξ ˜ ⊤ Ξ ˜ − 1 ν m Ξ ˜ ⊤ Γ ˜ α ˜ m Γ = α ˜ m Ξ ; ν m ∈ R .
The weights in α ˜ m Ξ and α ˜ m Γ code the relevance of the Q questions and the A MI performance measures to matching the multimodal feature spaces. Besides, the basis matrices: Λ Ξ = α ˜ 1 Ξ , α ˜ 2 Ξ , ⋯ , α ˜ M Ξ ∈ R Q × M and Λ Γ = α ˜ 1 Γ , α ˜ 2 Γ , ⋯ , α ˜ M Γ ∈ R A × M , allow us to compute the subspaces Ψ Ξ = Ξ ˜ Λ Ξ ∈ R R × M and Ψ Γ = Γ ˜ Λ Γ ∈ R R × M , and the relevance vectors ρ Γ ∈ [ 0 , 1 ] A , ρ Ξ ∈ [ 0 , 1 ] Q , yielding:
ρ ι = softmax Λ ι ( Ψ ι ) ⊤ Ψ ι 1 M , ι ∈ { Ξ , Γ } ;
being softmax ( · ) the softmax function.

3.5. Multimodal and Explainable Deep Learning Implementation Details

Our Multimodal and Explainable Deep Learning (MEDL) pipeline can be summarized as in Figure 5. First, the GiGaScience dataset is used to train a subject-dependent DL classifier based on convolutional networks (see Section 3.2 and Figure 4 for DL architectures). Then, a Layer-CAM-based approach is carried out to visualize and quantify the MI-EEG explainability (see Section 3.3). Lastly, QMIP-CCA approach is used to compute the questionnaire and the MI-EEG performance matching (see Section 3.4).
We trained each model using TensorFlow version 2.17.0 and Keras version 3.2.1. All tests were done in Kaggle notebook environments. These environments provide two Tesla T4 GPUs with 15GB of VRAM, 30GB of RAM, an Intel Xeon CPU @ 2GHz with two threads per core, and two sockets per core. We fixed 500 epochs, terminated it on nan, and reduced the learning rate on plateaus as callbacks. Also, Adam optimizer and the categorical cross-entropy-based loss are fixed. Table 1 summarizes the DL hyperparameters employed. Any values not mentioned are fixed regarding TensorFlow’s default selection. The approaches were trained using stratified cross-validation for five folds, primarily measuring accuracy to determine the best model for each subject. For this research, the best fold was selected for each model and subject to generate the best CAM possible for each subject and network. Additionally, all notebooks and codes are publicly available at https://github.com/Marcos-L/CAMs-Enhancements.

4. Results and Discussion

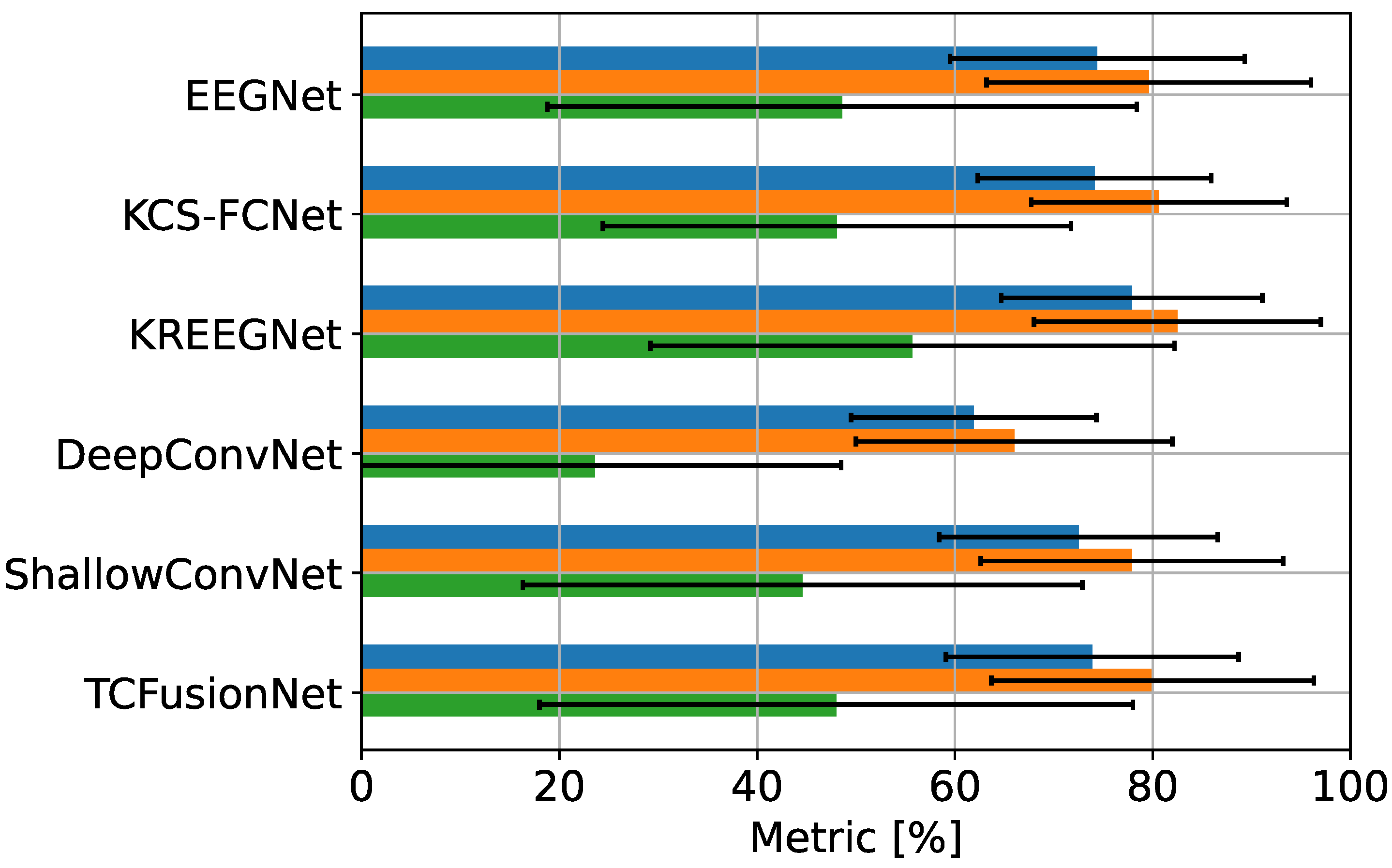
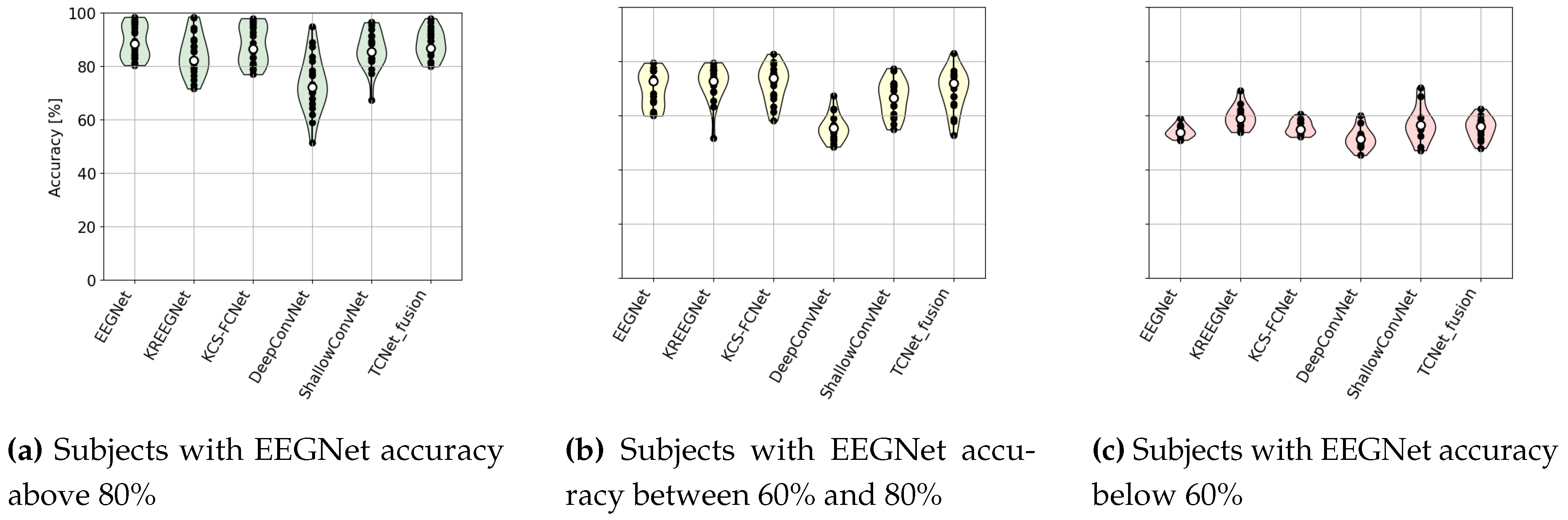
4.1. MI Classification Performance

All six CNN models were trained, evaluated, and contrasted among themselves based on their cross-validation results. Figure 6 shows the different metrics for each model prior to the CAM-based enhancements. KREEGNet shows the best accuracy and AUC score, while DeepConvNet shows the worst. In general, kernel methods improve upon the baseline EEGNet. Despite having fewer feature extraction layers, ShallowConvNet remains comparable, while DeepConvNet, due to its higher parameter count, loses a significant amount of accuracy compared to the other techniques. Moreover, despite its more complex architecture, TCFusion performs almost identically to EEGNet. This shows that simple and shallow models outperform deeper networks, implying that complex strategies may overfit more easily when training subject-specific MI-EEG tasks.
Furthermore, when observing inter-subject accuracy across models, as seen in Figure 7, DeepConvNet’s low performance becomes more apparent. Grouping subjects into three groups based on their classification accuracy on EEGNet (good, mid, and poor), DeepConvNet struggles a lot to properly classify good MI subjects, only ever outperforming EEGNet for the two worst subjects. In contrast, KCS-FCNet, although underperforming for good subjects, remains consistent for mid- and poor subjects. Interestingly, ShallowConvNet performs well in the poor performing group, indicating that the EEG for these subjects is highly contaminated, making fewer features more effective for classification than more.
Figure 8 shows the distribution of subject performance across groups for each model. It is clear that DeepConvNet yields lower results compared to other models such as EEGNet, which are capable of producing comparable results. I This is likely due to DeepConvNet’s greater parameter count and higher number of layers, which cause a slight overfitting problem and result in less refined early feature extraction than could be expected.

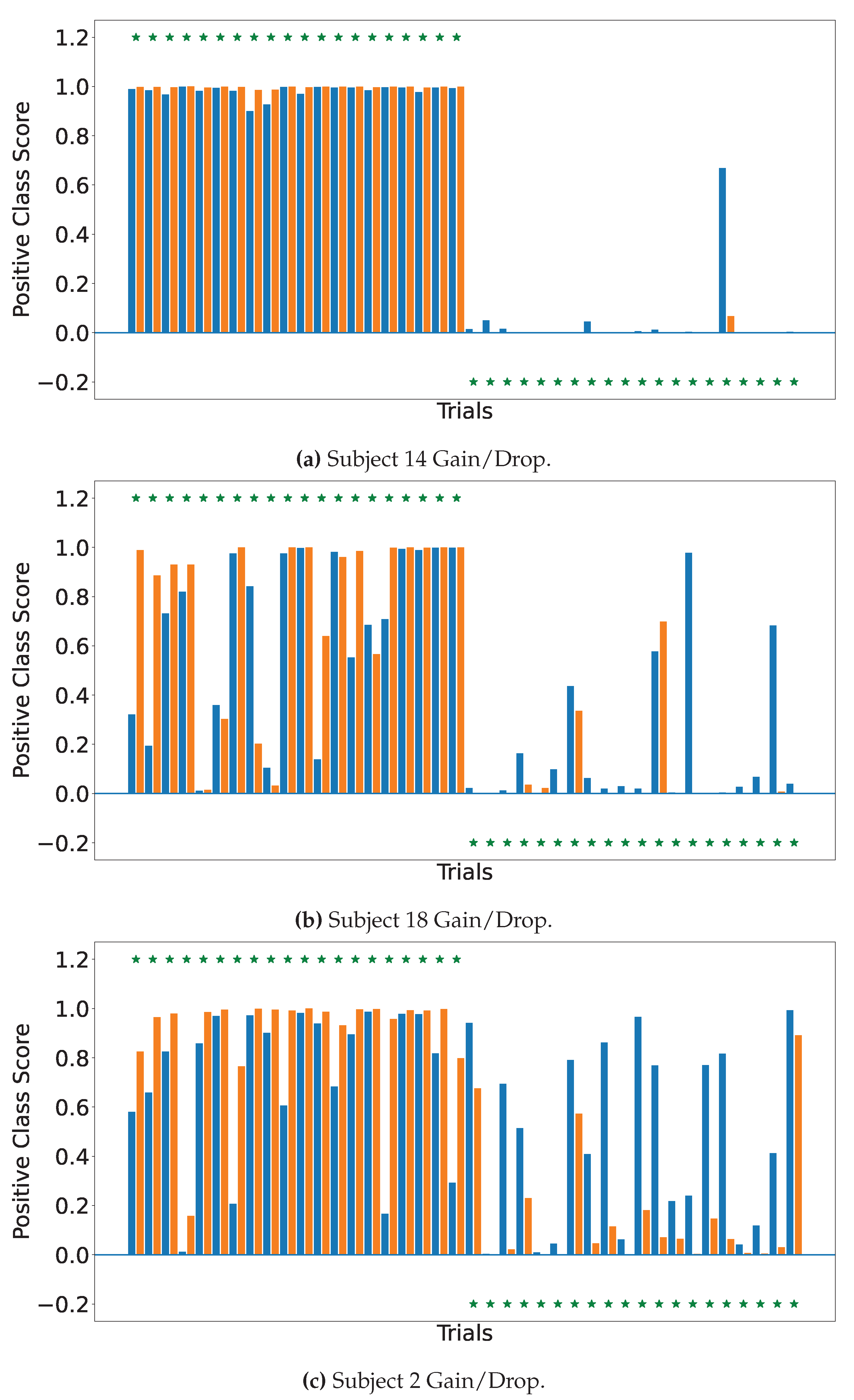
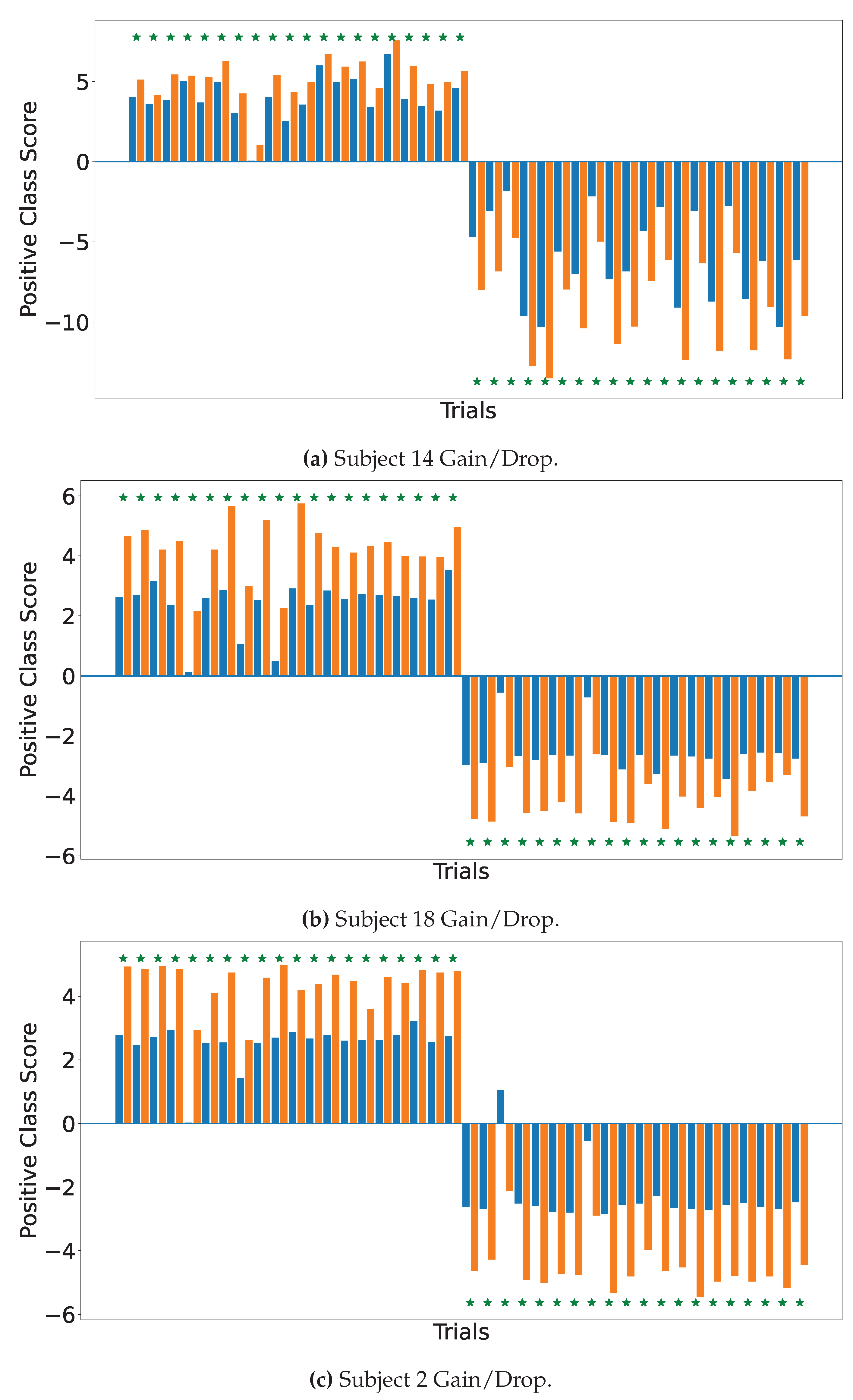
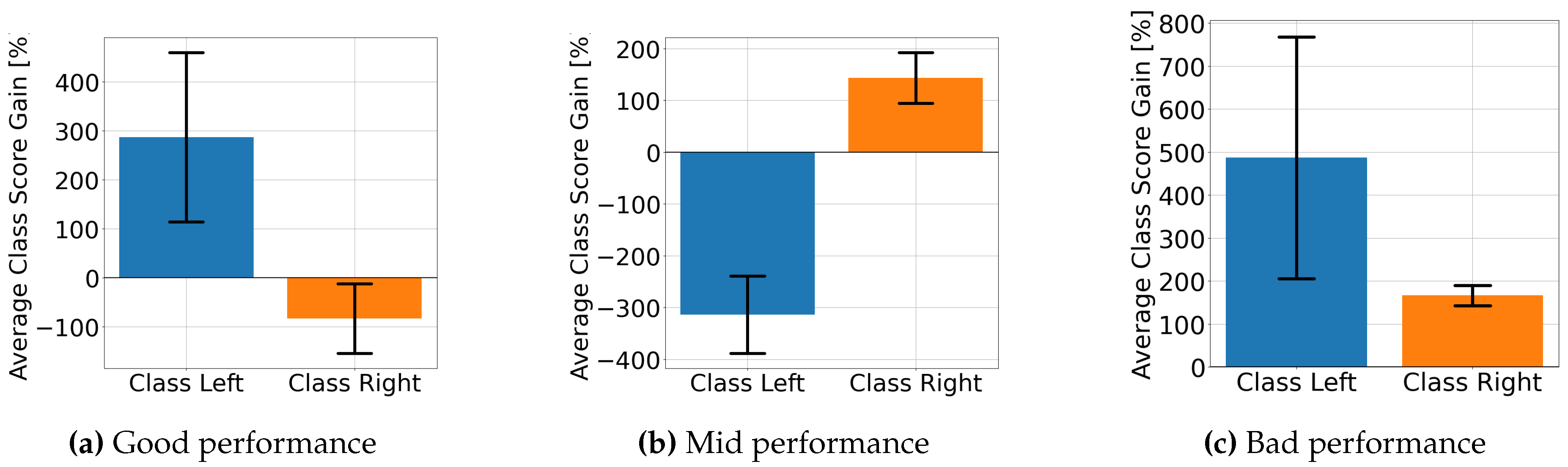
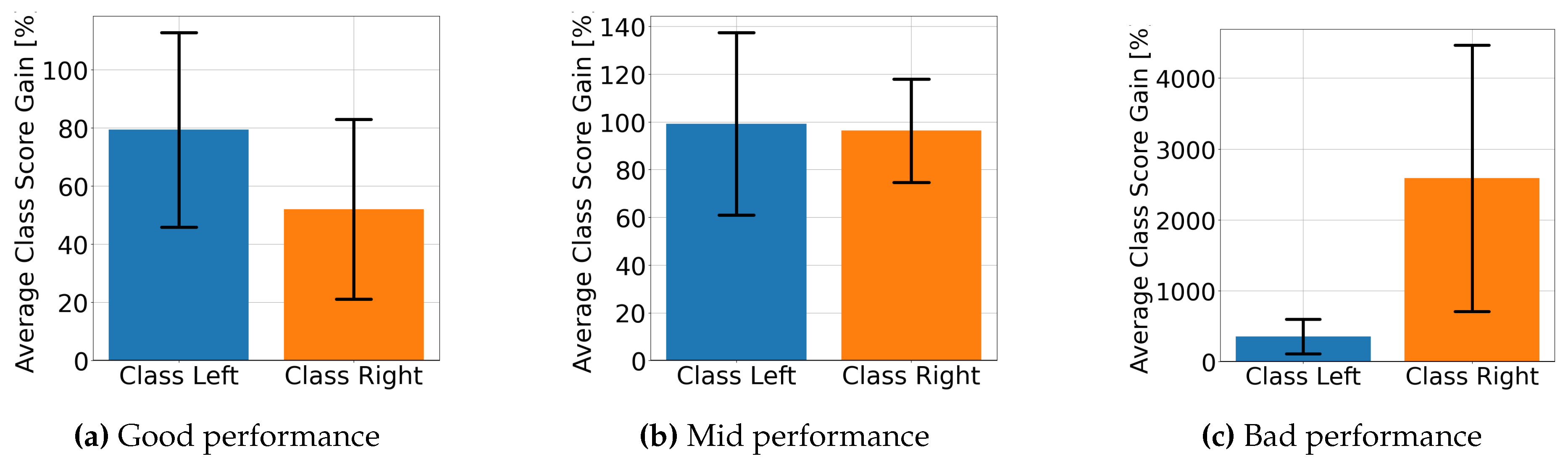
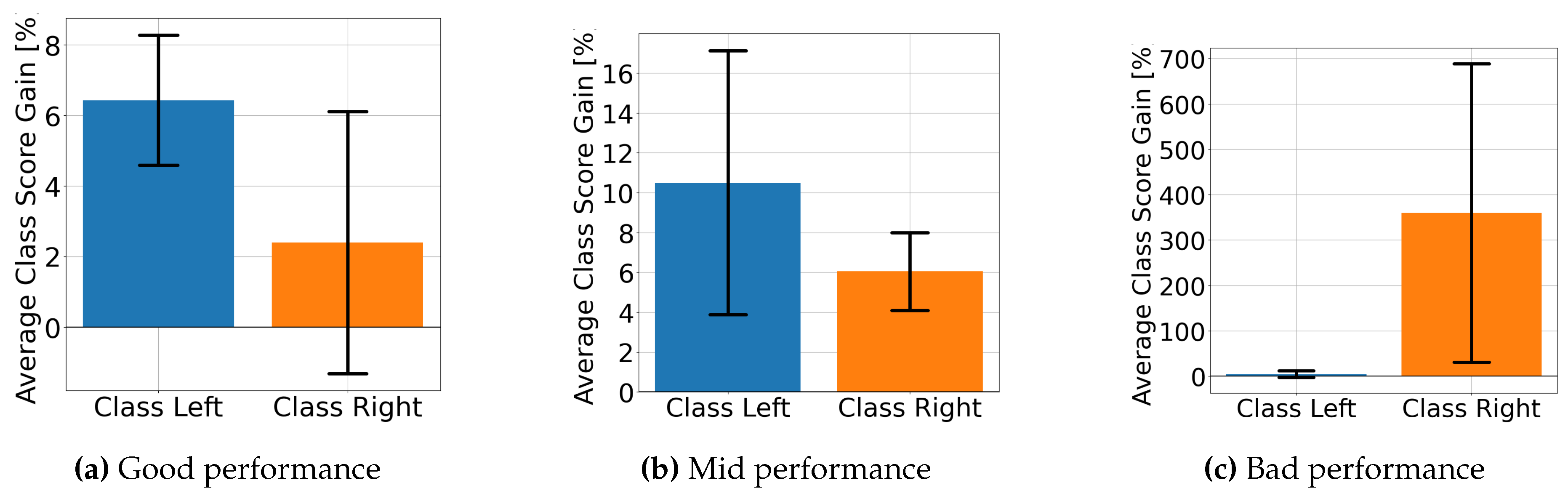
4.2. Explainable MI-EEG Classification Results

Figure 9 displays the average class score percentage gain for EEGNet across performance groups and class labels. This is used to look at how the proposed solution affected the class score. Figure 9a,b show that the good and mid-performing groups are biased towards a specific class, with only the poor performing subjects presenting improvements for both. In contrast, ShallowConvNet’s percentage gains presented in Figure 10 consistently have all groups improve for both classes. On the other hand, TCFusion barely shows any gain at all. Figure 11 shows both good and mid-performing groups only having tiny amounts of improvement when compared to the other two models. The only group to have substantial improvements is the poor performing one, but only for right-hand MI.
When examining the CAMs used per class, it is possible to observe a pattern emerge. Figure 12a,c show the average topomaps for good and poor performing subjects. The good-performing subject has the most important features located in the right sensorimotor area, with no information being highlighted on the left side. Then, the model learns the features related to one class and classifies the other whenever the information in this area is non-conclusive, which explains the bias presented by the percentage gain. In contrast, the poor-performing subject has information highlighted all across the head, with both classes highlighting almost the same regions. However, subjects with average performance, like the one shown in Figure 12b, appear to be a mix of the two. The most important information is found in the sensorimotor area for one side, while the rest of the EEG is messed up by noise. This behavior is consistent between models, except for TCFusion, as presented in Figure 15, which generates spatially noisy CAMs, possibly explaining why the boost-to-class score is minimal when CAM enhancement is applied.
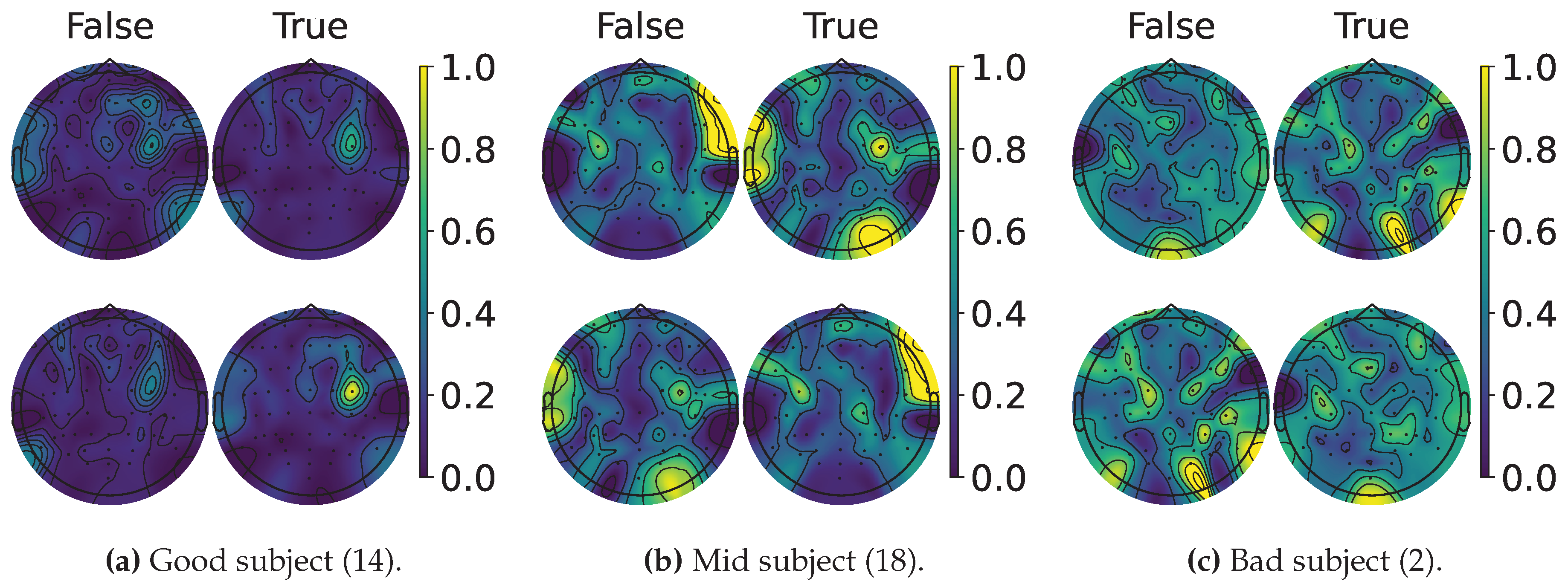
Preprints 137354 g012
Figure 12. Topomaps of EEGNet. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Figure 12. Topomaps of EEGNet. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Preprints 137354 g012
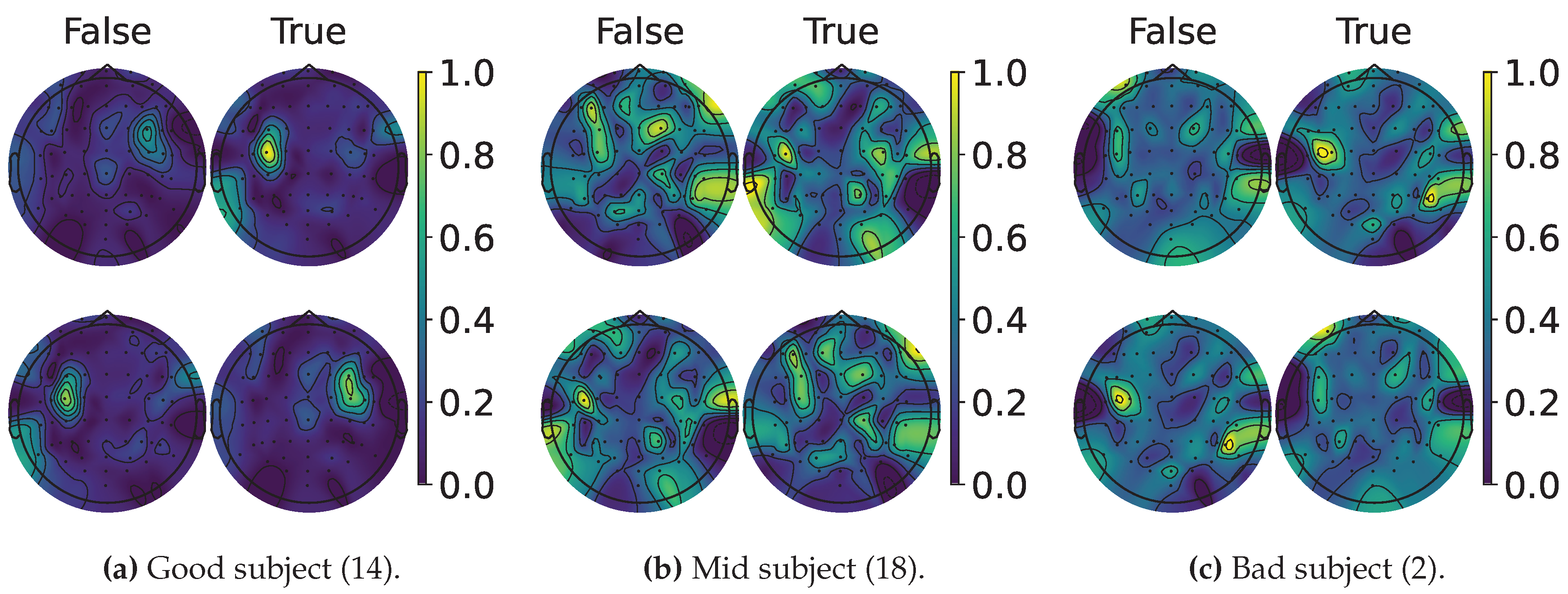
Preprints 137354 g013
Figure 13. Topomaps of KREEGNet. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Figure 13. Topomaps of KREEGNet. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Preprints 137354 g013
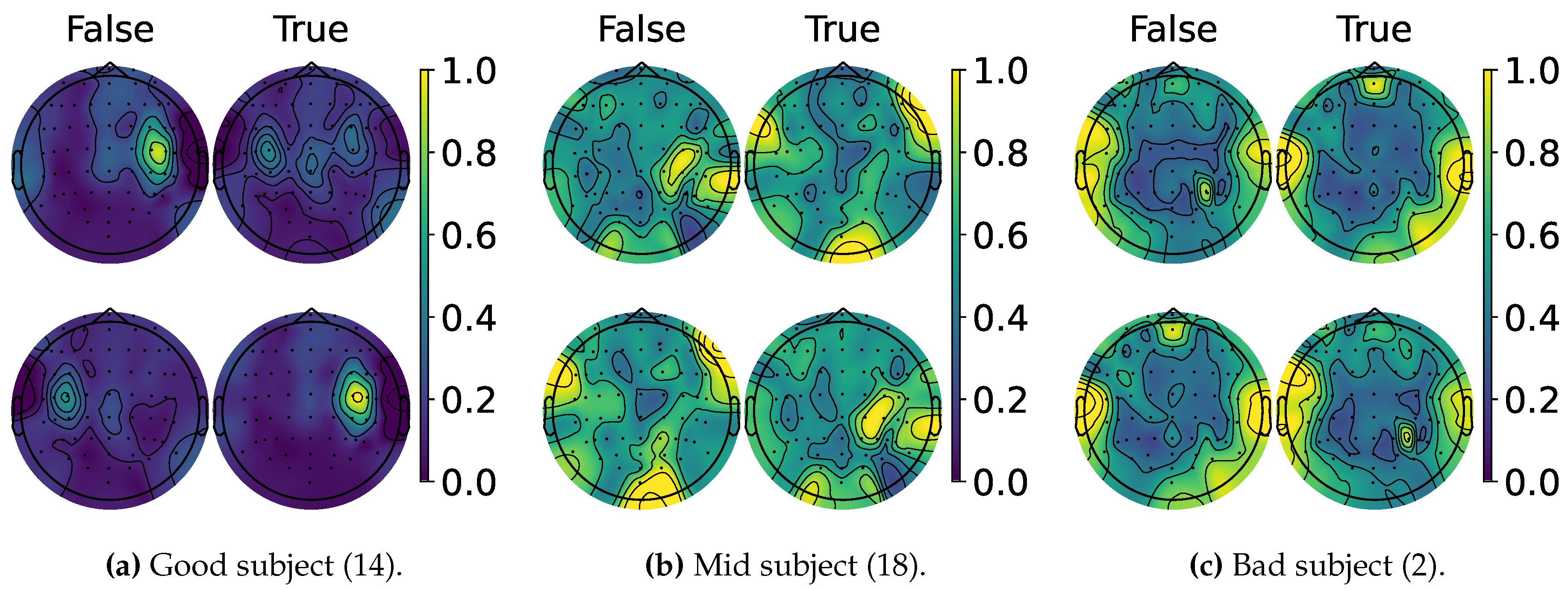
Preprints 137354 g014
Figure 14. Topomaps of ShallowConvNet. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Figure 14. Topomaps of ShallowConvNet. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Preprints 137354 g014
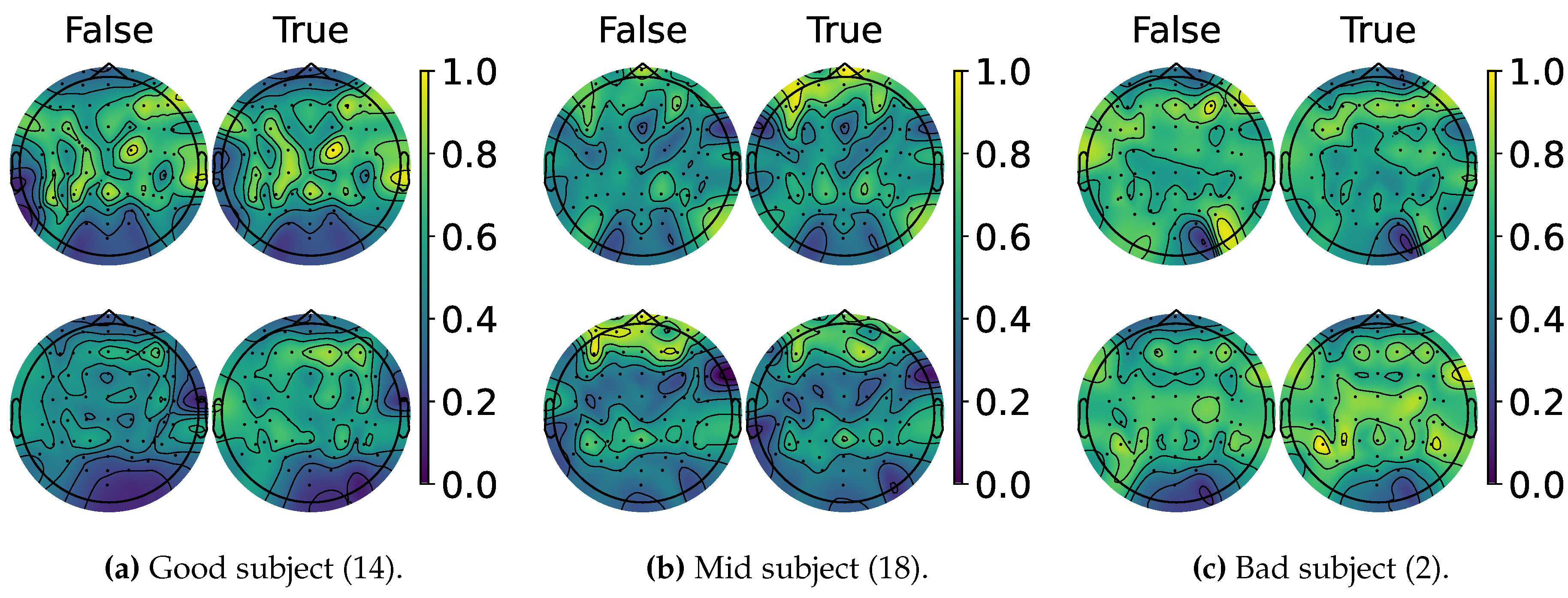
Preprints 137354 g015
Figure 15. Topomaps of TCFusion. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Figure 15. Topomaps of TCFusion. The top row shows the maps for the left-hand class while the bottom row shows the same for the right-hand class. Topomaps are min-max normalized horizontally.
Preprints 137354 g015
Finally, Figure 16 shows the improvement distribution for the different models across all three groups. Noticeably, ShallowConvNet has consistently positive improvements as oppose to other models which have a mix of improvements and losses. However, in general, all models tend to show improvements or at least remain the same with a median improvement close to zero across all three groups, with some edge cases showing massive losses. The only exception to this rule is TCFusion, which consistently loses accuracy across all three groups. This then implies that model improvement is tied to the complexity of the neural network, as shallow architectures either improve or remain consistent.

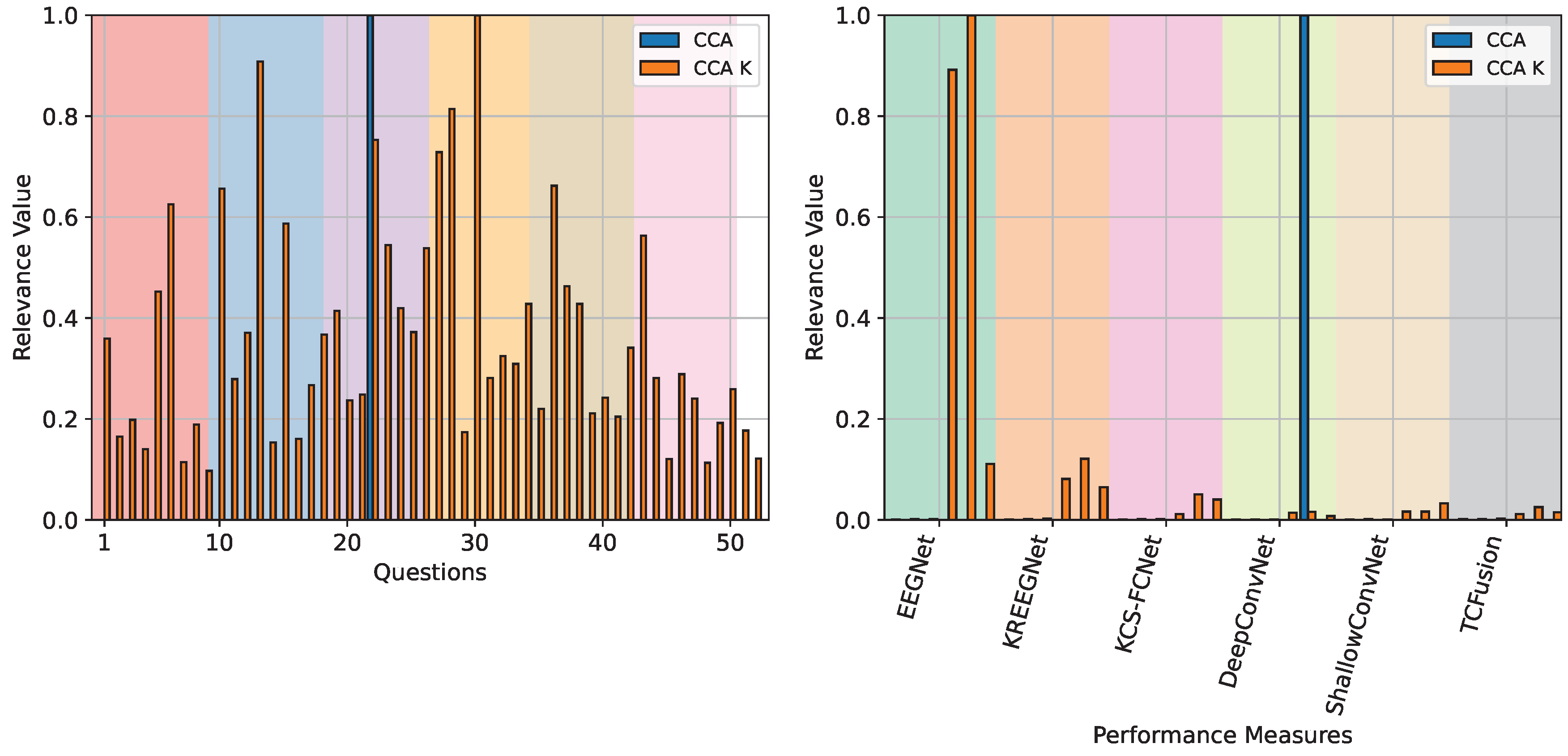
4.3. Questionnaire and MI-EEG Performance Relevance Analysis Results

Figure 17 shows the CCA and our kernel-based CCA variant relevance analysis for the questionnaire data compared to the MI-EEG performance measures. While linear CCA only yields a single correlation for the "How do you feel?" question, which spans from "very good" to "very bad" or "tired," our approach reveals a more diverse range of questions. The questions that have a relevance value greater than or equal to 0.5 pertain to the patient’s overall feelings across various runs, with the exception of a single question with an expected relevance of 0.54. On the other hand, CCA says that DeepConvNet’s kappa after improvements is the most important MI performance. On the other hand, kernel-based CCA says that EEGNet’s accuracy after improvements and kappa after improvements are the most important features. These results suggest how a person feels during the experiment relates to the expected improvements produced by the feedback. As these improvements come from the CAMs, the results imply a connection between the regions observed by the model and how comfortable or relaxed the subject feels. It is also likely that EEGNet is the most important model as it is the basis for the other CNNs, with KREEGNet being the second most important as it is a direct evolution.

5. Conclusions

We present a Multimodal and Explainable Deep Learning (MEDL) framework for MI-EEG classification, combining Class Activation Maps (CAMs) and Canonical Correlation Analysis (CCA) to improve classification accuracy and enhance the interpretability of MI-EEG-based models. The proposed approach involves evaluating various deep learning approaches for MI-EEG classification. Additionally, the use of CAM-based methods successfully highlighted relevant patterns crucial for decision-making in motor imagery classification. Using the Questionnaire-MI Performance Canonical Correlation Analysis (QMIP-CCA) framework gave us a new way to connect subjective questionnaire data with MI-EEG classification performance. This showed us important physiological and cognitive factors that affect how well the models explain things and how accurate the classifications are. ShallowConvNet, in particular, showed the most consistent improvements across different performance groups, proving to be more robust in handling noisy EEG data for poorly performing subjects.
For future work, we aim to extend the multimodal approach by integrating more diverse physiological and environmental data sources to further enhance model accuracy and interpretability. Additionally, exploring more advanced explainability methods, such as Transformer-based networks and more sophisticated attention mechanisms, could improve the robustness of CAMs in capturing relevant EEG features across a wider variety of tasks. Another direction would be the development of subject-independent models to address inter-subject variability, which remains a significant challenge in EEG classification.

Author Contributions

Conceptualization, M.L.-A., A.A.-M. and G.C.-D.; data curation, M.L.-A.; methodology, M.L.-A., A.A.-M., D.C.-P.; project administration, A. A.-M., and A.O.-G.; supervision, A.A.-M., A.O.-G., and G. C.-D.; resources, M.L.-A. and D. C.-P. All authors have read and agreed to the published version of the manuscript..

Funding

Under grants provided by the projects: "Sistema de monitoreo automático para la evaluación clínica de infantes con alteraciones neurológicas motoras mediante el análisis de volumetría cerebral y patrón de marcha" (Code 1110-897-84907 CTO 706-2021, CONV. 897-2021), supported by MINCIENCIAS.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable

Data Availability Statement

The publicly available dataset analyzed in this study can be found at https://github.com/Marcos-L/CAMs-Enhancements (accessed on 22 October 2024).

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Additional Results

Table A1. Questionnaire questions selected with their respective entropy value.
Table A1. Questionnaire questions selected with their respective entropy value.
Set Question Answer Type Entropy
Pre-MI Time slot (1=9:30/2=12:30/3=15:30/4=19:00) 1.373
Age (number) 1.774
How long did you sleep? (1=less than 4h/2=5 6h/3=6 7h/4=7 8/5=more than 8) 1.485
Did you drink coffee within the past 24 hours (0=no, number=hours before) 1.172
How do you feel? Relaxed 1 2 3 4 5 Anxious 1.218
How do you feel? Exciting 1 2 3 4 5 Boring 1.429
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.291
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.277
The BCI performance (accuracy) expected? % 1.754
Run 1 How do you feel? Relaxed 1 2 3 4 5 Anxious 1.186
How do you feel? Exciting 1 2 3 4 5 Boring 1.305
How do you feel? High 1 2 3 4 5 Low 1.223
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.301
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.247
Have you nodded off (slept a while) during this run? (0=no/number = how many times) 1.253
Was it easy to imagine finger movements? Easy 1 2 3 4 5 Difficult 1.368
How many trials you missed? (0=no/number = how many times) 1.179
The BCI performance (accuracy) expected? % 1.879
Run 2 How do you feel? Relaxed 1 2 3 4 5 Anxious 1.062
How do you feel? Exciting 1 2 3 4 5 Boring 1.397
How do you feel? High 1 2 3 4 5 Low 1.217
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.295
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.254
Was it easy to imagine finger movements? Easy 1 2 3 4 5 Difficult 1.371
How many trials you missed? (0=no/number = how many times) 1.185
The BCI performance (accuracy) expected? % 1.846
Run 3 How do you feel? Relaxed 1 2 3 4 5 Anxious 1.205
How do you feel? Exciting 1 2 3 4 5 Boring 1.324
How do you feel? High 1 2 3 4 5 Low 1.313
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.256
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.144
Was it easy to imagine finger movements? Easy 1 2 3 4 5 Difficult 1.263
How many trials you missed? (0=no/number = how many times) 1.055
The BCI performance (accuracy) expected? % 1.859
Run 4 How do you feel? Relaxed 1 2 3 4 5 Anxious 1.250
How do you feel? Exciting 1 2 3 4 5 Boring 1.287
How do you feel? High 1 2 3 4 5 Low 1.249
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.161
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.201
Was it easy to imagine finger movements? Easy 1 2 3 4 5 Difficult 1.329
How many trials you missed? (0=no/number = how many times) 1.212
The BCI performance (accuracy) expected? % 1.833
Run 5 How do you feel? Relaxed 1 2 3 4 5 Anxious 1.154
How do you feel? Exciting 1 2 3 4 5 Boring 1.324
How do you feel? High 1 2 3 4 5 Low 1.304
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.223
How do you feel? Very good 1 2 3 4 5 Very bad or tired 1.304
Was it easy to imagine finger movements? Easy 1 2 3 4 5 Difficult 1.469
How many trials you missed? (0=no/number = how many times) 1.108
The BCI performance (accuracy) expected? % 1.883
Post-MI How was this experiment? Good 1 2 3 4 5 Bad 1.250
The BCI performance (accuracy) of whole data expected? % 1.665
Preprints 137354 g0a1
Figure A1. Sparse output for two subjects of KREEGNet. Blue shows the class score before enhancements, orange shows the class score after, and green stars show the ground truth.
Figure A1. Sparse output for two subjects of KREEGNet. Blue shows the class score before enhancements, orange shows the class score after, and green stars show the ground truth.
Preprints 137354 g0a1
Preprints 137354 g0a2
Figure A2. Sparse output for two subjects of EEGNet. Blue shows the class score before enhancements, orange shows the class score after, and green stars show the ground truth.
Figure A2. Sparse output for two subjects of EEGNet. Blue shows the class score before enhancements, orange shows the class score after, and green stars show the ground truth.
Preprints 137354 g0a2

References

  1. Unesco.; for Engineering Education, U.I.C.; she, Z.y.b.y.c.b. Engineering for sustainable development : delivering on the Sustainable Development Goals; United Nations Educational, Scientific, and Cultural Organization ; International Center for Engineering Education under the auspices of UNESCO : Compilation and Translation Press: Paris, France, Beijing, China, 2021.
  2. Mayo Clinic Editorial Staff. EEG (electroencephalogram). https://www.mayoclinic.org/tests-procedures/eeg/about/pac-20393875, 2024.
  3. Altaheri, H.; Muhammad, G.; Alsulaiman, M.; Amin, S.U.; Altuwaijri, G.A.; Abdul, W.; Bencherif, M.A.; Faisal, M. Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: A review. Neural Computing and Applications 2023, 35, 14681–14722. [Google Scholar] [CrossRef]
  4. Ramadan, R.A.; Altamimi, A.B. Unraveling the potential of brain-computer interface technology in medical diagnostics and rehabilitation: A comprehensive literature review. Health and Technology 2024, 14, 263–276. [Google Scholar] [CrossRef]
  5. Abidi, M.; De Marco, G.; Grami, F.; Termoz, N.; Couillandre, A.; Querin, G.; Bede, P.; Pradat, P.F. Neural correlates of motor imagery of gait in amyotrophic lateral sclerosis. Journal of Magnetic Resonance Imaging 2021, 53, 223–233. [Google Scholar] [CrossRef] [PubMed]
  6. Zhang, H.; Zhao, M.; Wei, C.; Mantini, D.; Li, Z.; Liu, Q. EEGdenoiseNet: a benchmark dataset for deep learning solutions of EEG denoising. Journal of Neural Engineering 2021, 18, 056057. [Google Scholar] [CrossRef] [PubMed]
  7. Saini, M.; Satija, U.; Upadhayay, M.D. Wavelet based waveform distortion measures for assessment of denoised EEG quality with reference to noise-free EEG signal. IEEE Signal Processing Letters 2020, 27, 1260–1264. [Google Scholar] [CrossRef]
  8. Tsuchimoto, S.; Shibusawa, S.; Iwama, S.; Hayashi, M.; Okuyama, K.; Mizuguchi, N.; Kato, K.; Ushiba, J. Use of common average reference and large-Laplacian spatial-filters enhances EEG signal-to-noise ratios in intrinsic sensorimotor activity. Journal of neuroscience methods 2021, 353, 109089. [Google Scholar] [CrossRef] [PubMed]
  9. Croce, P.; Quercia, A.; Costa, S.; Zappasodi, F. EEG microstates associated with intra-and inter-subject alpha variability. Scientific reports 2020, 10, 2469. [Google Scholar] [CrossRef] [PubMed]
  10. Saha, S.; Baumert, M. Intra-and inter-subject variability in EEG-based sensorimotor brain computer interface: a review. Frontiers in computational neuroscience 2020, 13, 87. [Google Scholar] [CrossRef]
  11. Maswanganyi, R.C.; Tu, C.; Owolawi, P.A.; Du, S. Statistical evaluation of factors influencing inter-session and inter-subject variability in eeg-based brain computer interface. IEEE Access 2022, 10, 96821–96839. [Google Scholar] [CrossRef]
  12. Blanco-Diaz, C.F.; Antelis, J.M.; Ruiz-Olaya, A.F. Comparative analysis of spectral and temporal combinations in CSP-based methods for decoding hand motor imagery tasks. Journal of Neuroscience Methods 2022, 371, 109495. [Google Scholar] [CrossRef]
  13. Wang, B.; Wong, C.M.; Kang, Z.; Liu, F.; Shui, C.; Wan, F.; Chen, C.P. Common spatial pattern reformulated for regularizations in brain–computer interfaces. IEEE transactions on cybernetics 2020, 51, 5008–5020. [Google Scholar] [CrossRef]
  14. Galindo-Noreña, S.; Cárdenas-Peña, D.; Orozco-Gutierrez, A. Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks. Applied Sciences 2020, 10. [Google Scholar] [CrossRef]
  15. Geng, X.; Li, D.; Chen, H.; Yu, P.; Yan, H.; Yue, M. An improved feature extraction algorithms of EEG signals based on motor imagery brain-computer interface. Alexandria Engineering Journal 2022, 61, 4807–4820. [Google Scholar] [CrossRef]
  16. Chollet, F. Deep Learning with Python; Manning, 2017.
  17. Collazos-Huertas, D.F.; Álvarez-Meza, A.M.; Castellanos-Dominguez, G. Image-based learning using gradient class activation maps for enhanced physiological interpretability of motor imagery skills. Applied Sciences 2022, 12, 1695. [Google Scholar] [CrossRef]
  18. Rakhmatulin, I.; Dao, M.S.; Nassibi, A.; Mandic, D. Exploring Convolutional Neural Network Architectures for EEG Feature Extraction. Sensors 2024, 24. [Google Scholar] [CrossRef] [PubMed]
  19. Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Human Brain Mapping 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [PubMed]
  20. Li, F.; He, F.; Wang, F.; Zhang, D.; Xia, Y.; Li, X. A novel simplified convolutional neural network classification algorithm of motor imagery EEG signals based on deep learning. Applied Sciences 2020, 10, 1605. [Google Scholar] [CrossRef]
  21. Liu, J.; Wu, G.; Luo, Y.; Qiu, S.; Yang, S.; Li, W.; Bi, Y. EEG-based emotion classification using a deep neural network and sparse autoencoder. Frontiers in Systems Neuroscience 2020, 14, 43. [Google Scholar] [CrossRef] [PubMed]
  22. Chowdary, M.K.; Anitha, J.; Hemanth, D.J. Emotion recognition from EEG signals using recurrent neural networks. Electronics 2022, 11, 2387. [Google Scholar] [CrossRef]
  23. Ma, Y.; Song, Y.; Gao, F. A novel hybrid CNN-transformer model for EEG motor imagery classification. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN); IEEE, 2022; pp. 1–8. [Google Scholar]
  24. Li, X.; Xiong, H.; Li, X.; Wu, X.; Zhang, X.; Liu, J.; Bian, J.; Dou, D. Interpretable deep learning: Interpretation, interpretability, trustworthiness, and beyond. Knowledge and Information Systems 2022, 64, 3197–3234. [Google Scholar] [CrossRef]
  25. Bhardwaj, H.; Tomar, P.; Sakalle, A.; Ibrahim, W. Eeg-based personality prediction using fast fourier transform and deeplstm model. Computational Intelligence and Neuroscience 2021, 2021, 6524858. [Google Scholar] [CrossRef] [PubMed]
  26. Cho, H.; Ahn, M.; Ahn, S.; Kwon, M.; Jun, S.C. EEG datasets for motor imagery brain–computer interface. GigaScience 2017, 6, gix034. [Google Scholar] [CrossRef] [PubMed]
  27. Rahman, A.U.; Tubaishat, A.; Al-Obeidat, F.; Halim, Z.; Tahir, M.; Qayum, F. Extended ICA and M-CSP with BiLSTM towards improved classification of EEG signals. Soft Computing 2022, 26, 10687–10698. [Google Scholar] [CrossRef]
  28. Jin, J.; Xiao, R.; Daly, I.; Miao, Y.; Wang, X.; Cichocki, A. Internal Feature Selection Method of CSP Based on L1-Norm and Dempster–Shafer Theory. IEEE Transactions on Neural Networks and Learning Systems 2021, 32, 4814–4825. [Google Scholar] [CrossRef] [PubMed]
  29. Wang, H.; Tang, Q.; Zheng, W. L1-Norm-Based Common Spatial Patterns. IEEE Transactions on Biomedical Engineering 2012, 59, 653–662. [Google Scholar] [CrossRef] [PubMed]
  30. Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter Bank Common Spatial Pattern (FBCSP) in Brain-Computer Interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence); 2008; pp. 2390–2397. [Google Scholar] [CrossRef]
  31. Zhang, Y.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Optimizing spatial patterns with sparse filter bands for motor-imagery based brain–computer interface. Journal of neuroscience methods 2015, 255, 85–91. [Google Scholar] [CrossRef] [PubMed]
  32. Miao, Y.; Jin, J.; Daly, I.; Zuo, C.; Wang, X.; Cichocki, A.; Jung, T.P. Learning common time-frequency-spatial patterns for motor imagery classification. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2021, 29, 699–707. [Google Scholar] [CrossRef]
  33. Luo, J.; Gao, X.; Zhu, X.; Wang, B.; Lu, N.; Wang, J. Motor imagery EEG classification based on ensemble support vector learning. Computer methods and programs in biomedicine 2020, 193, 105464. [Google Scholar] [CrossRef] [PubMed]
  34. Tibrewal, N.; Leeuwis, N.; Alimardani, M. Classification of motor imagery EEG using deep learning increases performance in inefficient BCI users. Plos one 2022, 17, e0268880. [Google Scholar] [CrossRef]
  35. Lopes, M.; Cassani, R.; Falk, T.H. Using CNN Saliency Maps and EEG Modulation Spectra for Improved and More Interpretable Machine Learning-Based Alzheimer’s Disease Diagnosis. Computational Intelligence and Neuroscience 2023, 2023, 3198066. [Google Scholar] [CrossRef] [PubMed]
  36. Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces. Journal of Neural Engineering 2018, 15, 056013. [Google Scholar] [CrossRef] [PubMed]
  37. Musallam, Y.K.; AlFassam, N.I.; Muhammad, G.; Amin, S.U.; Alsulaiman, M.; Abdul, W.; Altaheri, H.; Bencherif, M.A.; Algabri, M. Electroencephalography-based motor imagery classification using temporal convolutional network fusion. Biomedical Signal Processing and Control 2021, 69, 102826. [Google Scholar] [CrossRef]
  38. Tobón-Henao, M.; Álvarez Meza, A.M.; Castellanos-Dominguez, C.G. Kernel-Based Regularized EEGNet Using Centered Alignment and Gaussian Connectivity for Motor Imagery Discrimination. Computers 2023, 12. [Google Scholar] [CrossRef]
  39. García-Murillo, D.G.; Álvarez Meza, A.M.; Castellanos-Dominguez, C.G. KCS-FCnet: Kernel Cross-Spectral Functional Connectivity Network for EEG-Based Motor Imagery Classification. Diagnostics 2023, 13. [Google Scholar] [CrossRef] [PubMed]
  40. Lu, N.; Li, T.; Ren, X.; Miao, H. A deep learning scheme for motor imagery classification based on restricted Boltzmann machines. IEEE transactions on neural systems and rehabilitation engineering 2016, 25, 566–576. [Google Scholar] [CrossRef]
  41. Mirzaei, S.; Ghasemi, P. EEG motor imagery classification using dynamic connectivity patterns and convolutional autoencoder. Biomedical Signal Processing and Control 2021, 68, 102584. [Google Scholar] [CrossRef]
  42. Hwaidi, J.F.; Chen, T.M. Classification of motor imagery EEG signals based on deep autoencoder and convolutional neural network approach. IEEE access 2022, 10, 48071–48081. [Google Scholar] [CrossRef]
  43. Wei, C.S.; Keller, C.J.; Li, J.; Lin, Y.P.; Nakanishi, M.; Wagner, J.; Wu, W.; Zhang, Y.; Jung, T.P. Inter-and intra-subject variability in brain imaging and decoding, 2021.
  44. Alessandrini, M.; Biagetti, G.; Crippa, P.; Falaschetti, L.; Luzzi, S.; Turchetti, C. Eeg-based alzheimer’s disease recognition using robust-pca and lstm recurrent neural network. Sensors 2022, 22, 3696. [Google Scholar] [CrossRef] [PubMed]
  45. Luo, J.; Wang, Y.; Xia, S.; Lu, N.; Ren, X.; Shi, Z.; Hei, X. A shallow mirror transformer for subject-independent motor imagery BCI. Computers in Biology and Medicine 2023, 164, 107254. [Google Scholar] [CrossRef]
  46. Bang, J.S.; Lee, S.W. Interpretable convolutional neural networks for subject-independent motor imagery classification. In Proceedings of the 2022 10th International Winter Conference on Brain-Computer Interface (BCI); IEEE, 2022; pp. 1–5. [Google Scholar]
  47. Bejani, M.M.; Ghatee, M. A systematic review on overfitting control in shallow and deep neural networks. Artificial Intelligence Review 2021, 54, 6391–6438. [Google Scholar] [CrossRef]
  48. Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A survey on neural network interpretability. IEEE Transactions on Emerging Topics in Computational Intelligence 2021, 5, 726–742. [Google Scholar] [CrossRef]
  49. Onishi, S.; Nishimura, M.; Fujimura, R.; Hayashi, Y. Why Do Tree Ensemble Approximators Not Outperform the Recursive-Rule eXtraction Algorithm? Machine Learning and Knowledge Extraction 2024, 6, 658–678. [Google Scholar] [CrossRef]
  50. Hong, Q.; Wang, Y.; Li, H.; Zhao, Y.; Guo, W.; Wang, X. Probing filters to interpret CNN semantic configurations by occlusion. In Proceedings of the Data Science: 7th International Conference of Pioneering Computer Scientists, Engineers and Educators, ICPCSEE 2021, Taiyuan, China, 2021, ,, September 17–20; Proceedings, Part II 7. Springer, 2021; pp. 103–115. [Google Scholar]
  51. Christoph, M. Interpretable machine learning: A guide for making black box models explainable; Leanpub, 2020.
  52. Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2016; pp. 2921–2929. [Google Scholar] [CrossRef]
  53. Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. International Journal of Computer Vision 2019, 128, 336–359. [Google Scholar] [CrossRef]
  54. Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV); IEEE, 2018. [Google Scholar] [CrossRef]
  55. Jiang, P.T.; Zhang, C.B.; Hou, Q.; Cheng, M.M.; Wei, Y. Layercam: Exploring hierarchical class activation maps for localization. IEEE Transactions on Image Processing 2021, 30, 5875–5888. [Google Scholar] [CrossRef] [PubMed]
  56. Bi, J.; Wang, F.; Yan, X.; Ping, J.; Wen, Y. Multi-domain fusion deep graph convolution neural network for EEG emotion recognition. Neural Computing and Applications 2022, 34, 22241–22255. [Google Scholar] [CrossRef]
  57. Wu, D.; Zhang, J.; Zhao, Q. Multimodal Fused Emotion Recognition About Expression-EEG Interaction and Collaboration Using Deep Learning. IEEE Access 2020, 8, 133180–133189. [Google Scholar] [CrossRef]
  58. Collazos-Huertas, D.F.; Velasquez-Martinez, L.F.; Perez-Nastar, H.D.; Alvarez-Meza, A.M.; Castellanos-Dominguez, G. Deep and wide transfer learning with kernel matching for pooling data from electroencephalography and psychological questionnaires. Sensors 2021, 21, 5105. [Google Scholar] [CrossRef]
  59. Abibullaev, B.; Keutayeva, A.; Zollanvari, A. Deep learning in EEG-based BCIs: a comprehensive review of transformer models, advantages, challenges, and applications. IEEE Access 2023. [Google Scholar] [CrossRef]
  60. Murphy, K.P. Probabilistic machine learning: an introduction; MIT press, 2022.
  61. Kim, S.J.; Lee, D.H.; Lee, S.W. Rethinking CNN Architecture for Enhancing Decoding Performance of Motor Imagery-based EEG Signals. IEEE Access 2022. [Google Scholar] [CrossRef]
  62. Jung, H.; Oh, Y. Towards better explanations of class activation mapping. In Proceedings of the Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 1336–1344.
  63. Fukumizu, K.; Bach, F.R.; Gretton, A. Statistical consistency of kernel canonical correlation analysis. Journal of Machine Learning Research 2007, 8. [Google Scholar]
Preprints 137354 g001
Figure 1. EEG-BCI classification methods. Both traditional and DL approaches are presented.
Figure 1. EEG-BCI classification methods. Both traditional and DL approaches are presented.
Preprints 137354 g001
Preprints 137354 g002
Figure 2. GIGAScience database experiment for MI-EEG classification (left vs right hand). Left: Trial timing: A marker appears onscreen; after two seconds, an instruction is shown to the patient to imagine moving either their left or right hand. The instruction stays onscreen for three seconds before disappearing. Right: Spatial EEG montage: Electrodes are placed starting at the left-frontal nodes and going on a serpent pattern until they reach the back, at which point they go back to the front down the center until they reach the CPZ node (10-10 system).
Figure 2. GIGAScience database experiment for MI-EEG classification (left vs right hand). Left: Trial timing: A marker appears onscreen; after two seconds, an instruction is shown to the patient to imagine moving either their left or right hand. The instruction stays onscreen for three seconds before disappearing. Right: Spatial EEG montage: Electrodes are placed starting at the left-frontal nodes and going on a serpent pattern until they reach the back, at which point they go back to the front down the center until they reach the CPZ node (10-10 system).
Preprints 137354 g002
Preprints 137354 g003
Figure 3. Shannon’s entropy for the GIGAScience database questionnaire answers. Questions were sorted by their entropy value in decreasing order. The dotted line shows the selected threshold (25th percentile) for selecting questions.
Figure 3. Shannon’s entropy for the GIGAScience database questionnaire answers. Questions were sorted by their entropy value in decreasing order. The dotted line shows the selected threshold (25th percentile) for selecting questions.
Preprints 137354 g003
Preprints 137354 g004
Figure 4. MI-EEG classification models based on Deep Learning. A softmax activation is always used after the final dense layer for label prediction.
Figure 4. MI-EEG classification models based on Deep Learning. A softmax activation is always used after the final dense layer for label prediction.
Preprints 137354 g004
Preprints 137354 g005
Figure 5. Experiment’s workflow using MEDL. Each model generates CAMs which are then used to enhance the original EEG input. Model and CAM-based performace measure along with the questionnaire are used to perform multimodal analysis via QMIP-CCA.
Figure 5. Experiment’s workflow using MEDL. Each model generates CAMs which are then used to enhance the original EEG input. Model and CAM-based performace measure along with the questionnaire are used to perform multimodal analysis via QMIP-CCA.
Preprints 137354 g005
Preprints 137354 g006
Figure 6. MI-EEG GiGaScience classification results. Blue: Accuracy; Orange: AUC; Green: Kappa
Figure 6. MI-EEG GiGaScience classification results. Blue: Accuracy; Orange: AUC; Green: Kappa
Preprints 137354 g006
Preprints 137354 g007
Figure 7. Inter-subject accuracies results. Subjects are sorted based on EEGNet performance.
Figure 7. Inter-subject accuracies results. Subjects are sorted based on EEGNet performance.
Preprints 137354 g007
Preprints 137354 g008
Figure 8. Group performing MI-EEG classification results.
Figure 8. Group performing MI-EEG classification results.
Preprints 137354 g008
Preprints 137354 g009
Figure 9. Class score percentage gain per MI class for EEGNet.
Figure 9. Class score percentage gain per MI class for EEGNet.
Preprints 137354 g009
Preprints 137354 g010
Figure 10. Class score percentage gain per MI class for ShallowConvNet.
Figure 10. Class score percentage gain per MI class for ShallowConvNet.
Preprints 137354 g010
Preprints 137354 g011
Figure 11. Class score percentage gain per MI class for TCFusion.
Figure 11. Class score percentage gain per MI class for TCFusion.
Preprints 137354 g011
Preprints 137354 g016
Figure 16. Violin plot of change in accuracy after CAM enhancements for different subject groups across DL models.
Figure 16. Violin plot of change in accuracy after CAM enhancements for different subject groups across DL models.
Preprints 137354 g016
Preprints 137354 g017
Figure 17. The QMIP-CCA relevance analysis results are derived from the multimodal GiGaScience dataset. Questionnaire (left) and MI-EEG classification performance measures (right) are studied. Linear CCA and our kernel-based CA enhancement are presented. Background colors for the questionnaire divide the questions into Pre-MI, Run 1 through 5, and Post-MI. For the MI-EEG classification measures, colors show the corresponding DL model.
Figure 17. The QMIP-CCA relevance analysis results are derived from the multimodal GiGaScience dataset. Questionnaire (left) and MI-EEG classification performance measures (right) are studied. Linear CCA and our kernel-based CA enhancement are presented. Background colors for the questionnaire divide the questions into Pre-MI, Run 1 through 5, and Post-MI. For the MI-EEG classification measures, colors show the corresponding DL model.
Preprints 137354 g017
Table 1. Subject-dependent MI-EEG classification DL hyperparameters.
Table 1. Subject-dependent MI-EEG classification DL hyperparameters.
Training Hyperparameter Argument Value
Monitor Training Loss
Factor 0.1
Reduce learning rate on plateau Patience 30
Min Delta 0.01
Min Learning Rate 0
Adam Learning Rate 0.01
Stratified Shuffle Split Splits 5
Test size 0.2
Table 2. MI-EEG classification performance comparison: ACC vs. CAM-enhanced ACC. Average ACC ± standard deviation.
Table 2. MI-EEG classification performance comparison: ACC vs. CAM-enhanced ACC. Average ACC ± standard deviation.
Model ACC [ % ] CAM-enhanced ACC [ % ] Difference [ % ] .
EEGNet 95.22 ± 7.02 93.44 ± 13.65 − 1.77 ± 11.63
KREEGNet 79.61 ± 13.69 81.82 ± 21.30 2.20 ± 24.09
KCS-FCNet 74.48 ± 13.93 75.65 ± 19.96 1.17 ± 14.55
DeepConvNet 89.59 ± 11.53 94.72 ± 18.70 5.12 ± 19.27
ShallowConvNet 94.93 ± 6.14 99.46 ± 1.29 4.53 ± 5.56
TCFusion 93.11 ± 8.57 91.88 ± 10.39 − 1.23 ± 3.14
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated