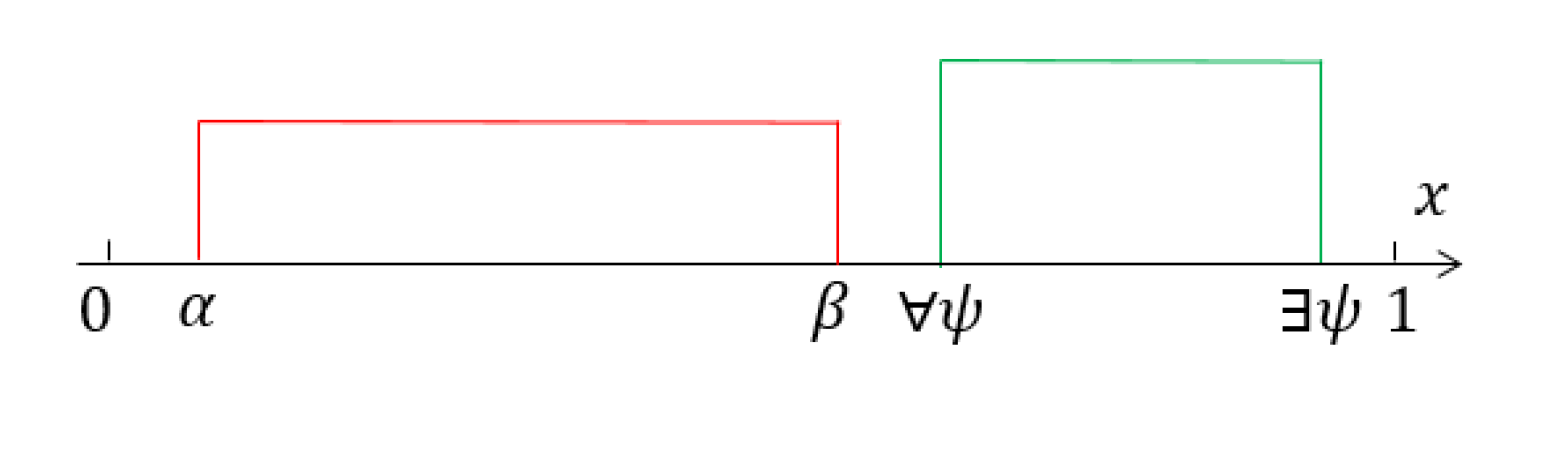1. Introduction
Model checking [
1,
2] is a cornerstone in formal verification, prominently featuring model checking for Linear Temporal Logic (LTL) and Computation Tree Logic (CTL). The automation inherent in model checking has facilitated its widespread adoption in the analysis and validation of software and hardware systems[
3,
4,
5], communication protocols[
6,
7], and security protocols[
8,
9], achieving commendable outcomes. As computer systems grow in scale and complexity, practical systems increasingly exhibit quantitative behavioral attributes. Multi-agent systems [
10,
11,
12,
13], for instance, feature intricate dynamic structures and behavioral patterns that require the integration of quantitative information for an accurate portrayal of their dynamic behavior. In addressing the verification challenges posed by systems endowed with quantitative data, quantitative model checking methodologies have piqued considerable interest from academic and industrial circles alike. Hart et al. [
14,
15] pioneered probabilistic model checking, rooted in probability measures, employing Markov chains or Markov decision processes to model system behaviors and probabilistic computation tree logic or probabilistic linear temporal logic to define system properties. Sultan et al. [
16,
17] extended the probabilistic framework to multi-agent systems, introducing probabilistic multi-agent model checking. Chechik et al. [
18,
19] explored model checking for CTL and LTL on multi-valued Kripke structures, where values reside within a finite De Morgan algebra. Moreover, Li YongMing et al. established the theoretical foundation for possibility temporal logic and its applications in model checking. Literature [
20] proposed Possibility Computation Tree Temporal Logic (PoCTL) and investigated its expressiveness. It was proven that PoCTL, particularly qualitative PoCTL, is more expressive than CTL. Equivalences for expressing fundamental CTL formulas using qualitative PoCTL formulas were provided. Some PoCTL formulas that cannot be expressed by any CTL formula were given. Qualitative properties of repeat accessibility and persistence were represented with PoCTL formulas. A model-checking approach for PoCTL based on fuzzy matrix composite operations and fixed-point techniques was presented, and the time complexity of the algorithm was analyzed. Literature [
21] introduced the theory of generalized possibility measures and Generalized Possibility Kripke Structure (GPKS). Generalized Possibility Computation Tree Temporal Logic(GPoCTL) was proposed, with its syntax and semantics defined. A model-checking method for GPoCTL based on fuzzy matrix composite operations and fixed-point techniques was provided, and the time complexity of the algorithm was analyzed.
Quality constraints serve to delineate specific quality requisites that systems or computation trees must satisfy [
22,
23]. These requisites encompass a spectrum of performance metrics—such as response time and throughput—reliability metrics—such as failure rates—and security metrics. In our pioneering research pursuits, we innovatively amalgamated specific quality functions and predicates into Possibility Linear Temporal Logic (PoLTL), culminating in the proposition of Fuzzy Linear Temporal Logic with Quality Constraints (QFLTL) [
24]. QFLTL empowers the articulation of a system's more intricate temporal attributes. These functions and predicates are meticulously defined based on the system's empirical operational data or projected objectives, yielding fuzzy truth values indicative of quality levels. The introduction of quality constraints significantly bolsters QFLTL's expressive capabilities in several facets: (1) Departing from PoLTL's singular information amalgamation operator, the minimum "
", QFLTL introduces an enhanced repertoire of information aggregation operators, encompassing minimum "
", product "
", and the weighted average operator "
". This innovation effectively mitigates the issue of information erosion. (2) The weighted average operator "
" enables a preference-sensitive integration of path reachability insights and property satisfaction measures or the synthesis of disparate property subformulas, facilitating the delineation of more nuanced temporal properties. (3) The linear differential operators
, coupled with the quality predicate "
", can impose quality constraints on property formulas grounded in anticipated objectives, thereby enriching the portrayal of diverse system quantifiable properties. (4) By recursively defining formula satisfaction values onto path segments that meet property conditions, it ensures the synchronous alignment of path reachability and property satisfaction. These enhancements have been empirically validated in reference [
24].
Building on the robust foundation established by QFLTL research, we introduce quality functions and quality predicates into PoCTL, culminating in the proposition of QFCTL. We delve into its logical characteristics and investigate the model checking theory of QFCTL on Fuzzy Kripke Structure(FKS).
Section 2 delineates the syntax and semantics of QFCTL, illustrating its robust expressive capabilities and practical utility through instructive examples.
Section 3 explores the intricate logical properties of QFCTL, encompassing the equivalence calculation and partial order relations of its formulas, the functional completeness of QFCTL operators, and the fundamental properties and determination of the characteristic predicate operator
, which delineates the fulfillment characteristics of property formulas under the constraint of quality predicate
P on pertinent paths, indicating full, none, or partial satisfaction.
Section 4 focuses on the model checking problem of QFCTL on FKS. By ingeniously reducing the computation of QFCTL formulas from infinite to finite paths, we introduce a model checking algorithm with a time complexity proportional to the product of the QFCTL formula's length and the FKS's scale, and a space complexity equivalent to the FKS's scale. The reasonableness and complexity of the algorithm are rigorously substantiated.
Section 5 builds upon QFCTL by introducing the quantitative characteristic predicate operator
, leading to the proposal of QFCTL*. We investigate the logical properties of QFCTL*, provide a determination theorem for the operator
, which describes the fulfillment status of property formula
under the constraint of quality predicate
on pertinent paths, signifying the ratio of paths satisfying
under
constraint among all paths satisfying
. We prove the well-defined nature of
, delineate the model checking algorithm for QFCTL*, and conduct a thorough analysis of the algorithm's complexity.
Section 6 presents model checking application examples of ten illustrative QFCTL formulas and QFCTL* formulas on the FKS that characterizes the patient treatment process, as outlined in reference [
24]. Through these applications, we vividly demonstrate the robust expressive capabilities and practical applicability of QFCTL and QFCTL*. Simultaneously, the automatic and effective nature of the model checking algorithms for QFCTL and QFCTL* presented in the paper is empirically validated. Conclusively, in
Section 7, we summarize the primary research content of the article and outline some meaningful research directions pertaining to temporal logic with quality constraints and its reasoning problems.
2. The Syntax and Semantics of QFCTL
We introduce these quality functions and quality predicates into PoCTL to propose QFCTL, and present the syntax and semantics of QFCTL.
2.1. The Syntax of QFCTL
In a concerted effort to enhance the paper's reachability and readability, we will first revisit the fuzzy propositional operators delineated in reference [
24].
Definition1(
Fuzzy Operations [
24])
, the fuzzy propositional operators are defined as follows:
;
;
;
.
Adhering to the syntactical blueprints established by CTL, FCTL, and PoCTL, QFCTL's formulaic structure should incorporate basic propositions, logical conjunctions (such as AND, OR, NOT), path quantifiers (including EXISTS, FOR ALL), and a suite of temporal operators (comprising NEXT, GLOBALLY, EVENTUALLY, UNTIL, and the like). Building upon this robust framework, we incorporate the fuzzy propositional operators meticulously explicated in reference [
24]. We augment this foundation with the introduction of the characteristic predicate operator
, a critical quality constraint operator. This operator intricately delineates the fulfillment characteristics of property formulas under the constraint of quality predicate
P on pertinent paths, signifying scenarios encompassing full satisfaction, none satisfaction, or partial satisfaction, thereby significantly amplifying QFCTL's expressive capacity.
The syntactic form of QFCTL is defined as follows.
Definition 2 [Syntax of QFCTL] Letdenote a set of atomic propositions, andrepresent the set of rational numbers. signifies a finite set of fuzzy propositional constants. Univariate fuzzy propositional logic operators are symbolized by, and bivariate fuzzy propositional logic operators by. Temporal logic operators are designated by. The universal path quantifier is denoted bypreceding a path formula, and the existential path quantifier bypreceding a path formula. Quality predicates are represented by, andsignifies the characteristic predicate operator.
QFCTL state formulasare recursively defined overas follows:
An atomic proposition, where, is a QFCTL state formula.
A propositional constant, where, is a QFCTL state formula, with special cases forcorresponding to "False" andto "True".
Formulasare QFCTL state formulas, whereare QFCTL state formulas.
Expressionsare QFCTL state formulas, whereis a QFCTL path formula.
QFCTL path formulasare recursively defined as follows:
A QFCTL state formulais a path formula.
Formulasare QFCTL path formulas, whereare QFCTL state formulas.
To facilitate discussions regarding the complexity of the QFCTL model checking algorithm, the concept of a QFCTL formula's length is defined as follows.
Definition 3 [Length of a QFCTL Formula] Letbe a QFCTL state formula. The length of, denoted as, is defined recursively as follows,
;
;
;
;
;
.
Note 1:The focus on state formulas when defining the length of QFCTL formulas is due to the model checking process which assesses the satisfaction value of formulas in specific states.Path formulas are integral components, nested within state formulas. According to Definition 2, part (4), path formulasare structured as state formulas under the constraints imposed by quantifiers and characteristic predicates.
Example 1.Given an atomic proposition set, consider the QFCTL formula below,
The process for computing the length of formula is as follows,
.
2.2. The Semantics of QFCTL
The semantics of QFCTL is anchored in fuzzy Kripke structures, wherein propositions are mapped onto states via a fuzzy valuation function to determine fuzzy truth values. For a QFCTL formula, its truth value at a particular state is determined by recursively computing the truth values of its constituent subformulas. Let's begin by revisiting the definition of a Fuzzy Kripke Structure (FKS), essential for grounding our understanding of QFCTL's semantic framework.
Definition 4 [Fuzzy Kripke Structures (FKSs)][
24]
.An FKS is a tupl, where,
is a finite set of states;
The fuzzy distributionrepresents the fuzzy set of each state as the initial state;
represents the fuzzy transition relationship between system states;
is a set of finite atomic propositions;
is a state label function that characterizes a set of fuzzy atomic propositions.
Definition 5 [path and path reachability]. Supposeis an FKS, where a pathis a state sequence, andrepresents a set of fuzzy atomic propositions as a fuzzy label function. (whererepresents the set of natural numbers)represents the fuzzy atomic proposition induced by atomic propositionon state.
represents a path starting from state. The recursive definition of path reachability is as follows.
where
represents the reachability of the path fragment
. This reflects the idea of the “barrel principle”, which states that the overall reachability of a path is determined by the minimum reachability of any path fragment. When
represents the reachability of the infinite path
.
is the set of infinite paths in . For every state within , signifies the collection of all infinite paths starting at , whereas designates the ensemble of states that are immediately accessible from state , as defined by the transition function .
For every belonging to the set of natural numbers , determine the fulfillment value of the QFCTL state formula over the path segment denoted by within the infinite sequence of states . This involves synthesizing the path reachability of the path from the initial state up to the current state with the fulfillment value of the formula at state .
Definition 6. [Semantics for QFCTL]Letbe a Fuzzy Kripke Structure (FKS), wheresignifies a quality predicate. Letrepresent a QFCTL state formula anda QFCTL path formula. The semantics of QFCTL can be characterized by a fuzzy function:. Employing an information fusion operator, facilitates the combination of fuzzy truth values. The interpretationis recursively defined as follows,
;
;
;
;
;
;
;
Note 2: (1) If the quality constraint operators , the quality property predicate operator , are removed from QFCTL, and the information fusion operator "" is restricted to "" only; then QFCTL degrades to PoCTL. It is evident that the set of PoCTL formulas constitutes a true subset of the set of QFCTL formulas.
(2) The semantics of QFCTL state formulas, excluding those that contain the quality property predicate operator , are directly defined on the current state without considering path reachability. Essentially, they are interpreted as fuzzy propositional logic.
(3) The semantics for QFCTL formulas are recursively defined over paths, with the fifth clause of Definition 6 serving as a pivotal base case in the recursive definition. Formally, it appears as if the path reachability information is synthesized onto the path segment only when the QFCTL path formula is distilled to its core—a state formula . This information does not seem to feature in other recursive cases. However, the innermost component of any QFCTL formula is invariably a state formula. Consequently, irrespective of the superficial form of the QFCTL formula, the path reachability information will inevitably be synthesized through the process of recursive iteration. To superimpose at each level of the formula would introduce redundancy in reachability information and lead to informational asynchrony, thus compromising the integrity of the recursive structure.
As an example, let us examine the computation of semantics for the "
" operator,
The information fusion operator "" encapsulates the essence of the multiplicative principle. In the quest for the truth value of the QFLTL formula on the path , one initiates the process by computing the path reachability of the prefix path, spanning from to . Subsequently, this value is multiplied by the satisfaction value of the formula at , ensuring a methodical integration of path reachability and formula satisfaction. The information fusion operator "", on the other hand, embodies the philosophy of weighted averages. It calls for the sophisticated amalgamation of path reachability and formula satisfaction values, calibrated according to distinct weights, thereby facilitating a nuanced understanding of formula satisfaction across the path.
2.3. Exemplary Illustrations of QFCTL's Practicality
QFCTL formulas embody a rich expressive capacity. Reflect on the QFCTL formula delineated in Example 1:
.
Upon confining the atomic propositions '' and '' to Boolean values of 0 or 1, elucidates the process's unvarying adherence to the stipulation that, post-request initiation (""), there is a temporal sequence in the future where permission is conferred (" "). Should permission be granted consecutively twice, the satisfaction value materializes as 1; if granted solely once, the satisfaction value is assuredly not less than 1/4. Conversely, should the process abstain from initiating a request, the satisfaction value is no less than 1/5.
When the atomic propositions '' and '' assume values over a more extensive domain, and with due consideration paid to varying degrees of path reachability, furnishes an array of values. These disparate values encapsulate distinct process execution trajectories, manifestly evidencing that QFCTL wields a more copious expressive potential than PoCTL.
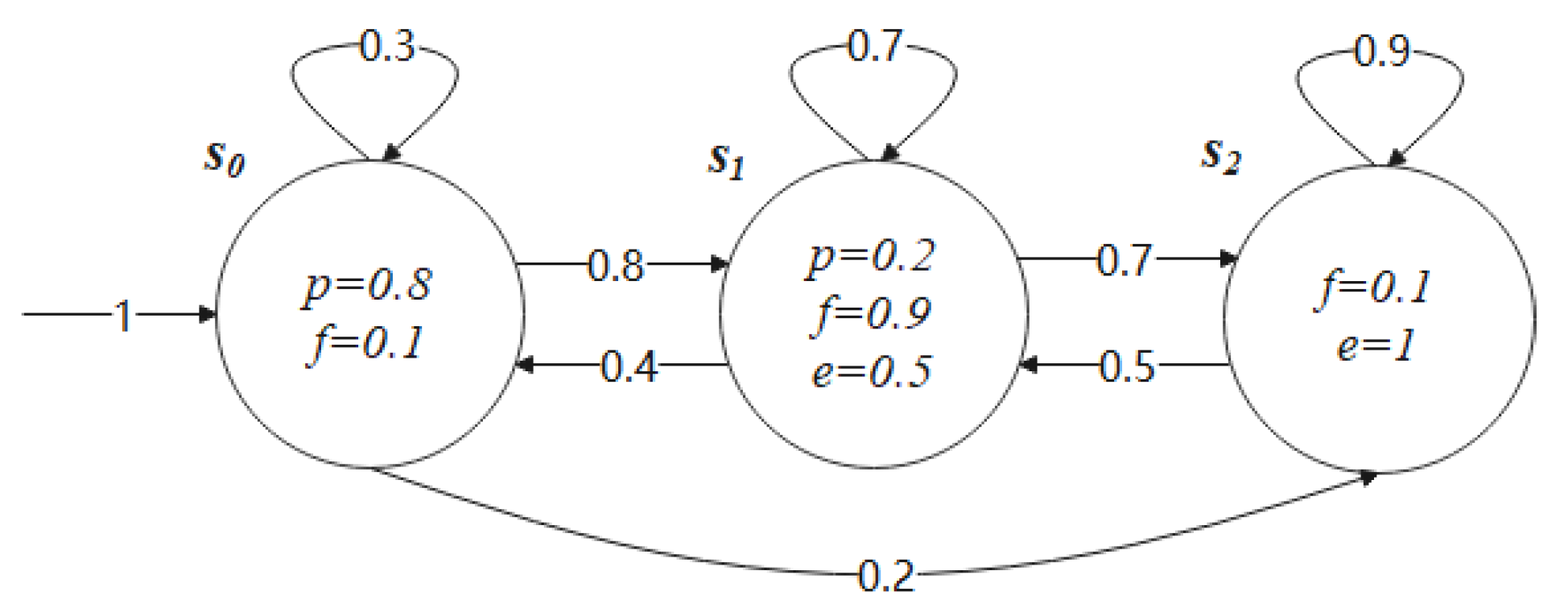
Example 2.Figure 1 illustrates the Fuzzy Kripke Structure (FKS), as delineated in reference [24], which characterizes the evolution of a patient's health condition throughout treatment. The atomic propositions '', '', '' embody the patient's health status, with each state assigning a fuzzy value within the specified interval [0,1] to these propositions, thereby representing a fuzzy proposition. For example, the assignment, signifies that when the patient is in the state, their health status has a 0.5 possibility of being "excellent". The orientation of the directed edges delineates the direction of state transition, and the fuzzy values inscribed upon these edges denote the possibilities of transition between interrelated states. Notably, the sole initial state is identified as.
for the patient's treatment process.
The subsequent QFCTL formulas are presented, accompanied by their detailed semantic interpretations:
delineates the maximal possibility that, among all therapeutic alternatives in the medical treatment course, the patient's ultimate health status will be "excellent" with a possibility of not less than 0.8.
signifies the least possibility that, among all therapeutic alternatives in the medical treatment course, the patient's ultimate health status will be "excellent" with a possibility of not less than 0.8.
encapsulates the highest possibility that, within all therapeutic alternatives, the patient's health status will consistently satisfies the "fine" condition with a 40% weightage, simultaneously alongside the "excellent" condition with a 60% weightage.
illustrates the least possibility that, within all therapeutic alternatives, the patient's health status will persistently adhere to the requirement of being "fine" with a 40% weightage and "excellent" with a 60% weightage.
delineates the maximal possibility that the patient's health status will remain "fine" with a necessity not exceeding 0.5 until it transitions to "excellent."
signifies the least possibility that the patient's health status will remain "fine" with a necessity not exceeding 0.5 until it transitions to "excellent."
delineates the fulfillment condition (whether entirely, partially, or not at all) for the possibility of the patient's health status being "excellent" with a possibility of not more than 0.8, with a likelihood of not less than 0.3 across all therapeutic alternatives.
encapsulates the fulfillment condition for the possibility that the patient's health status will consistently comply with the requirement of being "fine" with a 40% weightage and "excellent" with a 60% weightage, with a likelihood exceeding 0.5 across all therapeutic alternatives.
delineates the fulfillment condition for the possibility that the patient's health status will remain "fine" with a necessity not exceeding 0.5 until it transitions to "excellent," with a likelihood exceeding 0.6 across all therapeutic alternatives.
It is abundantly clear that these temporal properties with quality constraints exceed the expressive capabilities of PoCTL.
3. The Relations and Attributes of QFCTL Formulas.
Initially, we delineate the notion of relationships between QFCTL formulas.
Definition 7 [Relationships Between QFCTL Formulas] Letdenote QFCTL state formulas anddenote QFCTL path formulas.Considerto be a FKS, whereis the set of infinite paths in. Let“” represent a relational operator, which may be selected from the set. The relations among QFCTL formulas are delineated as follows:
(1) If for every state, the evaluation, thenis deemed to be in relation “” with, indicated as.
(2) If for every path, the evaluation, thenis deemed to be in relation “” with, indicated as.
Subsequently, our research expedition advances towards the meticulous examination of the distinctive logical attributes intrinsic to Quantified Fuzzy Computation Tree Logic (QFCTL). As a pivotal pillar within its own theoretical architecture, this in-depth exploration is paramount for enhancing comprehension of the fundamental logical mechanisms that underpin this specialized field.
Theorem 1 [Equivalence Calculus of QFCTL Formulas]Letbe state formulas in QFCTL, andbe an FKS.Then the following conclusions hold:
;
;
;
;
,;
;
;
;
,;
;
;
;
;
;
Proof: The above conclusions can be readily proven through straightforward calculations based on Definition 6. Here, we provide proof examples for (2), (5), (14), (15), and (16) as follows.
Proof of Conclusion (2). For all ,
.
Therefore,. By analogous reasoning, it can be shown that,
.
Proof of Conclusion (5). For all ,
.
Therefore,. By analogous reasoning, it can be shown that,.
Proof of Conclusion (14). For all ,,
.
Conclusion (14) Established.
Proof of Conclusion (15). For all ,
.
Conclusion (15) Established.
The proof for Conclusion (16) is identical to that of Conclusion (15) and will not be repeated here. This completes the proof of Theorem 1. □
Proposition 1. The set constitutes a functionally complete set of operators for QFCTL.
With the functionally complete set of operators for QFCTL, we only need to consider the operators within this set during model checking.
Proposition 2 [Inequality Relations Among QFCTL Formulas]Letbe an FKS,signifies a QFCTL state formula, anddenotes a QFCTL path formula. Then,
(1) , with equality holding if and only if ;
(2) ;
(3) .
The aforementioned conclusions can be readily proven by simple calculations according to Definition 6.
The characteristic predicate operator qualitatively characterizes the relationship between the satisfaction value of a QFCTL formula and a quality predicate . Below are the properties and decision theorems for the characteristic predicate operator.
Theorem 2 [Fundamental Properties and Decisions of the Characteristic Predicate Operator]Letbe an FKS,
denotes a QFCTL path formula. Letbe a quality predicate, where denotes the complement ofin [0,1], andrepresents the set of satisfaction values ofover all paths starting from state. Then,
(1) ;
(2) if and only if or ;
(3) if and only if ;
(4) if and only if or .
Proof: (1) For all , if , then for all ,. Consequently, for all ,, where denotes the complement of . This implies , so we have . Conversely, if , then it follows that , again yielding .
For all , if , then there exist and simultaneously. Consequently,. Therefore,.
This demonstrates that the sum of the predicates is always unity, reflecting the complementary nature of the sets and within the logical framework defined.
For all , if , then for all ,. Consequently, for all ,, which implies . Thus ,. Conversely, if , then , and also .
For all , if , then there exist and . This implies that and . Hence . Therefore, .
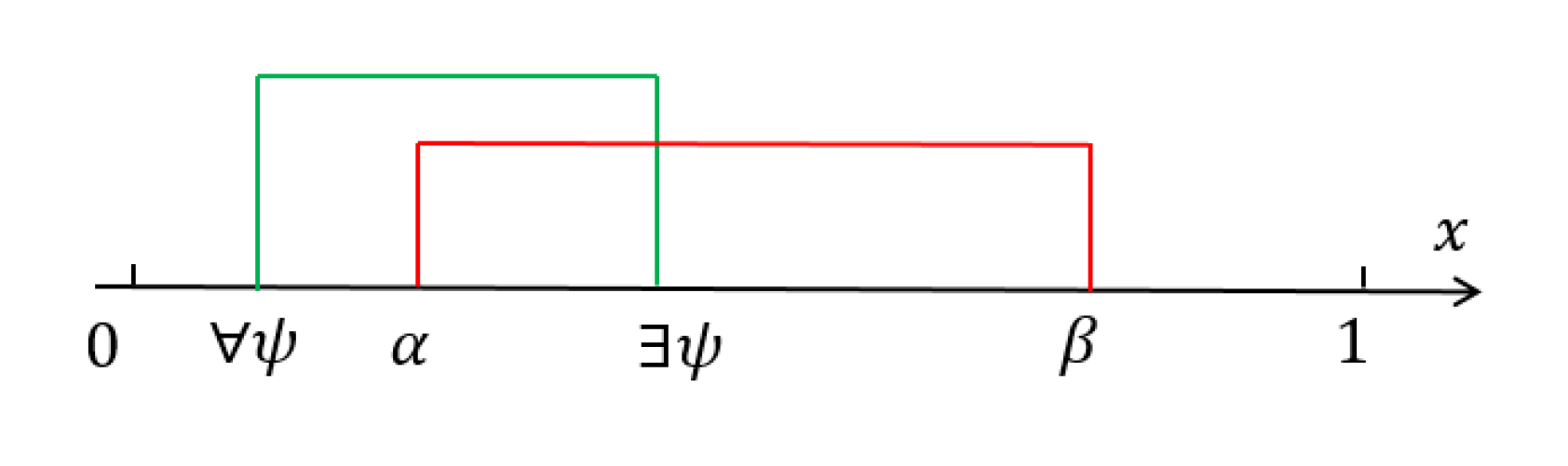
(2) First, prove the sufficiency. When
, for all
, since
, it follows that for all
. Given that
is the upper bound of
, it implies that for all
,
. According to Definition 6, we conclude that
. This intuitive result is illustrated in
Figure 2.
when
When
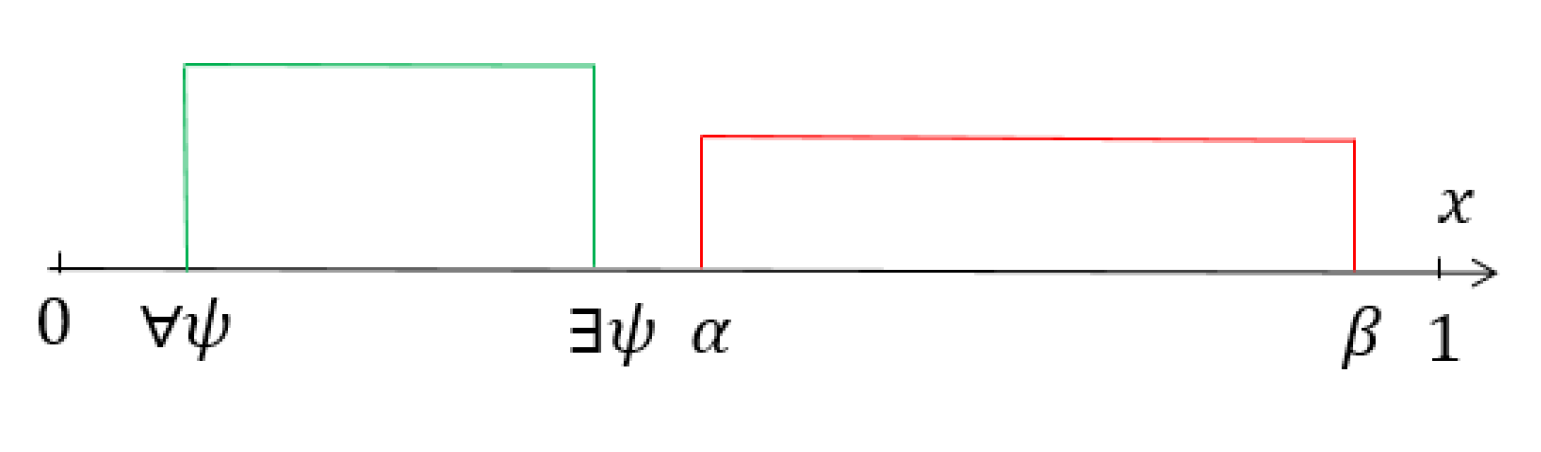
, for all
, since
, it follows that for all
. Given that
is the lower bound of
,, it implies that for all
. According to Definition 6, we conclude that
. This intuitive result is illustrated in
Figure 3.
when
In fact, (2) corresponds to
, which means that
are disjoint. Conversely, when proving the necessity,
corresponds to two scenarios depicted in
Figure 2 and
Figure 3, leading straightforwardly to the conclusion that either
or . Thus, conclusion (2) is proven.
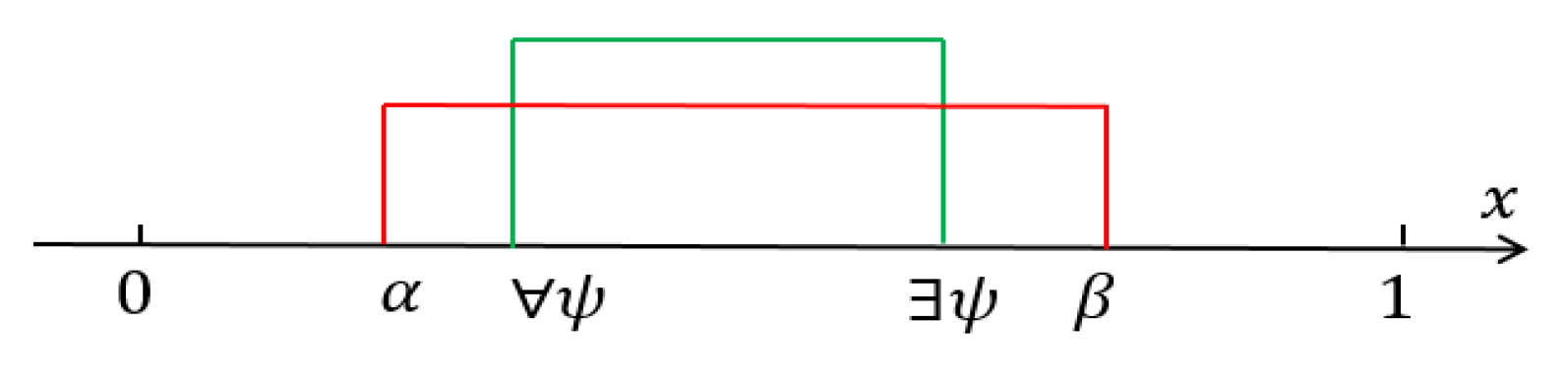
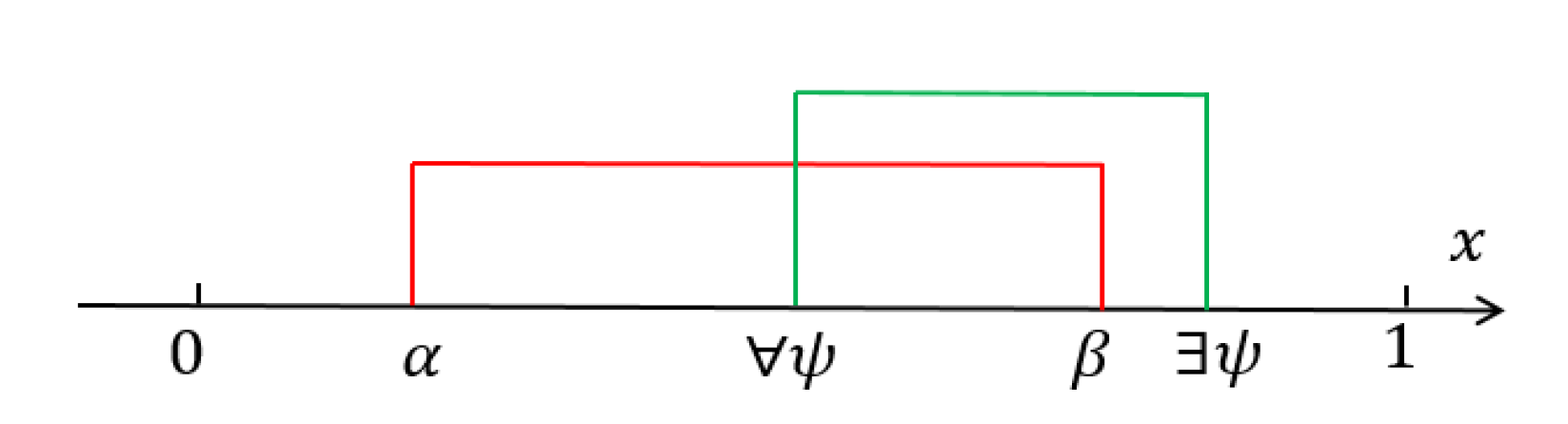
(3) First, prove the sufficiency. When
, for all
, on one hand, we have
, implying that for all
. On the other hand,
, implying that for all
. Consequently, for all
. According to Definition 6, we conclude that
. This intuitive result is illustrated in
Figure 4. In fact, (3) corresponds to
, i.e.,
is contained within
.
when
With reference to
Figure 4, it is straightforward to demonstrate the necessity of conclusion (3). Thus, conclusion (3) is proven.
(4) First, prove the sufficiency. When
, for all
, on one hand,
, which implies that there exists
, so that
. On the other hand, from
, we know that
, which indicates that there exists
, so that
. . Therefore, there exists
, so that
. According to Definition 6, we conclude that
. This intuitive result is illustrated in
Figure 5.
when
When
, similarly, it can be proven that
. This is intuitively illustrated in
Figure 6.
when
In fact, (4) corresponds to the case where
partially intersects with
. With reference to
Figure 5 and
Figure 6, the proof of the necessity of conclusion (4) is also evident.
Proof of Theorem 4 is complete. □
Corollary 1. Letbe an FKS, andbe a QFCTL path formula. When the quality predicateis an open or half-open interval, the conclusion (1) of Theorem 2 holds. The conditions for conclusions (2), (3), and (4) can be slightly modified to yield the following conclusions:
When, we have:
(1) if and only if or ;
(2) if and only if ;
(3) if and only if or .
When, we have:
(4) if and only if or ;
(5) if and only if ;
(6) if and only if or .
When, we have:
(7) if and only if or ;
(8) if and only if ;
(9) if and only if or .
From Theorem 2 and Corollary 1, we know that the values of can be computed first, and then the value of can be derived.
4. Model Checking for QFCTL
The semantics of QFCTL are defined on FKS (Fuzzy Kripke Structures), incorporating quality constraint operators and characteristic predicate operators. Compared to PoCTL model checking, QFCTL poses additional challenges in three key areas. Firstly, when computing the semantics of formulas, it integrates information from both path reachability degrees and satisfaction values of system properties. This integration is not a binary choice but a synthesis based on different preference requirements, undoubtedly increasing computational complexity. Secondly, the integration of these two types of information necessitates constant synchronization, meaning that the satisfaction value of a property on a specific path segment should be combined with the reachability degree of that segment, rather than aggregating the satisfaction value of the property over the entire path and then combining it with the overall reachability degree of the path. This synchronization requirement further elevates computational difficulty. Lastly, quality constraints are applied to subformulas of properties to reflect the importance and preferences of different properties, which also adds to the computational complexity. Therefore, explicit model checking for QFCTL cannot be conducted using fuzzy matrix composition operations[
20,
21], as these operations are incompatible with quality constraint computations. Fortunately, FKS are finite, with limited numbers of atomic propositions, propositional constants, and quality constraint operators. By leveraging ideas from fixed-point theory[
18,
19], we reduce the semantic computation of QFCTL on infinite paths to iterative calculations within a finite number of steps.
4.1. Description of the Model Checking Problem for QFCTL
Analogous to the model checking problem for PoCTL, the model checking problem for QFCTL can be described as follows. Let be a QFCTL state formula, and be an FKS (Fuzzy Kripke Structure). Let denote the quality predicate, and be a finite set of fuzzy constants. The model checking problem for QFCTL involves computing the value of for all such that . For QFCTL, the model checking problem is extended to compute the truth values of formulas that incorporate quality constraint functions and characteristic predicates, thus necessitating a different model checking approach.
From Proposition 1, it is known that constitutes a functionally complete set of operators for QFCTL formulas. According to Definition 6, the operators can be directly evaluated on the current state or the current state along with its immediate successor state to obtain solutions. Therefore, it suffices to provide algorithms for solving QFCTL formulas with the operators . Theorems 2 and Corollary 1 can serve as decision theorems for model checking with the operator . For any path formula and quality predicate , by solving for and for all , we can obtain the value of . Hence, the core problem of QFCTL model checking lies in computing the truth values of QFCTL formulas with the operators and . We reduce the computation of these two operators to finite paths, and the QFCTL model checking problem can be solved through a finite number of iterations.
For all , the semantics of the "bounded until" operator are defined as follows:
.
The following theorem provides the basis for iteratively solving the model checking problem for QFCTL formulas with the operators and within a finite number of steps.
Theorem 3. Letbe QFCTL state formulas, andbe an FKS. Then the following conclusions hold:
(1);
(2);
(3);
(4).
Proof: (1) It is naturally true that . What needs to be proven is that .
We prove that for all
and for all
, it holds that,
It suffices to prove that for all
,
When
, the Inequality (2) obviously holds. When
,
,the Inequality (2) also holds. Now, assume that the Inequality (2) holds when
, i.e.,
We prove that the inequality (2) holds when . The discussion is divided into cases as follows:
If there exists where , then,
.
Therefore, applying the induction hypothesis (Inequality (3)), we have
.
If for all , where , then since there must exist on the path , such that , creating a loop. By removing the path segment we construct a new path . Relabeling in order, we obtain , where , and for all .
.
Since
, it follows that
. According to the induction hypothesis (Inequality (3)), we have,
Combining Inequality (3) and (4), we obtain,
.
Thus, Inequality (2) holds, for all , . Therefore,
.
This completes the proof of Conclusion (1).
The proof of Conclusion (2) is analogous to the proof of (1) and will not be repeated here.
Next, we proceed to prove Conclusion (3). For all ,
(Based on Inequality (2))
. (Based on Conclusion (1))
The proof of Conclusion (4) is similar to the proof of Conclusion (3) and will not be repeated here. This completes the proof of Theorem 3. □
4.2. Solution Algorithms and Complexity Analysis for the Model Checking Problem of QFCTL
Below, we present the solution algorithm for the model checking problem of the QFCTL formula
.
Solution process:
;// Label the current expanded state.
;// Update the reachability of the path.
;// Update the current state.
11 END
12 END
When computing , it suffices to modify the objective function update formula in Step 6 of Algorithm 1 to,
.
To avoid confusion, we will use to denote the computation result of and to denote the computation result of.
Theorem 3 guarantees the correctness of Algorithm 1.
The following delineates an algorithm aimed at addressing the model-checking challenge pertinent to the QFCTL formula, specifically .
Algorithm 2, formulated explicitly in alignment with the stipulations of Definition 6 to directly compute , exhibits a correctness that is patently obvious.
Below is presented an algorithm for solving the model checking problem of QFCTL formula
.
Solution process:
=0;
=0
=1;
7 END
=1
=0.5;
10 BREAK;
11 END
12 END
Solution process:
7 END
12 END
17 END
22 END
23 END
Theorem 2 and Corollary 1 guarantee the correctness of Algorithm 3.
Theorem 4. Letbe a QFCTL state formula,be a FKS, andbe a quality predicate. Then, the time complexity of the model checking problem foronis, and the space complexity is.
Proof: The primary computational time is spent on evaluating and within Algorithm 1. The algorithm consists of two nested loops: the outer loop iterates over , and the inner loop iterates over . Within the inner loop, there is a nested operation of supremum (Step 7 of Algorithm 1). Since , a total of 3 operations are performed (One for each successor state , with three operations each executed once). Steps 8, 9, and 10 of Algorithm 1 execute a total of operations (During Each loop iteration performs one minimum operation and three assignment operations). Therefore, the overall time complexity of Algorithm 1 is. The space overhead is used to store state and transition function values, which can be reused. Hence, the space complexity is . Consequently, the time complexity of the model checking problem for on is , and the space complexity is.□
5. QFCTL* and Its Model Checking
To more precisely characterize the satisfaction of a QFCTL path formula on the set of paths originating from any state , under the constraint of a quality predicate , we introduce a quantifier characteristic predicate operator into QFCTL, resulting in an Enhanced Fuzzy Computation Tree Temporal Logic with Quality Constraints, denoted as QFCTL*. Furthermore, we discuss the logical properties and model checking techniques of QFCTL*.
QFCTL* differs from QFCTL by incorporating an additional quantifier characteristic predicate operator and discuss the associated logical properties and model checking algorithms related to it.
Definition 8 [Semantics of the Operator]
Letbe an FKS (Fuzzy Kripke Structure),be a quality predicate, andbe a QFCTL path formula. For all, the semantics of the operatoris defined as follows:
qualitatively characterizes the satisfaction of the property formula on in terms of three scenarios: fully satisfied, fully unsatisfied, or partially satisfied. provides a more granular characterization of the satisfaction of the property formula on , specifically quantifying the proportion of paths in that satisfy the constraint with respect to .
Example 3 (Continuing from Example 2). The QFCTL* formula represents the proportion of all treatment plans during the course of treatment that maintain the patient's condition with a necessity of at least "fine" (with a threshold of 0.5) until there is a transition to "excellent" with a possibility greater than 0.6. For instance, if , this signifies that 20% of the treatment plans fulfill the criterion where the patient's condition remains with a necessity of at least "fine" (with a threshold of 0.5) throughout the treatment process until there is a transition to "excellent" with a likelihood exceeding 0.6.
The following explains that the sets in both the numerator and the denominator of formula (5) are finite sets, indicating that Definition 8 is well-defined.
For all
,
, denote
as the prefix path of π with length
. We define the semantics of QFCTL path formula
on
as follows:
Lemma 1. Letbe an FKS (Finite Kripke Structure),be a quality constraint predicate, andis a QFCTL path formula. Then, for all,
.
Proof: When is a QFCTL state formula (where a state formula is a special type of path formula with semantics defined at ), the conclusion holds. We consider two cases: and .
When , we have , where depends only on and . Therefore, the conclusion holds.
When
, based on Definition 6 and Formula (6), we derive the following conclusion:
We prove that for all
, there exists a path
such that,
When , taking , Inequality (8) holds.
Assume that Equation (8) holds when
. That is, there exists a path
in
such that:
Then, when , the classification discussion is as follows:
If there exists a such that and , then,
(Inductive Hypothesis (9))
If for all
, we have
, then since
, there must exist
on the path
before the state
, such that
, forming a loop. By removing the path segment
from the path, we construct a new path
as follows:
Numbering sequentially, we obtain:
.
Where , for all , and for all .
(Inductive Hypothesis (9))
In this way, we have proven Inequality (8).
Furthermore, it is evident that for all , . Combining this with Inequality (8), we have:
For all
, there exists a path
, such that ,
Furthermore, combining this with Equation Inequality (7), we obtain:
For all , let us arbitrarily choose any (). For any , construct . It is evident that . Continuing the discussion as follows:
If there exists a such that and .
In this way, we obtain,
. By repeating this process, we can derive that,
Denote the limit as
, and we obtain that,
If for all , it holds that , then there must exist , such that , generating a cycle. After traversing the path segment times, we obtain the path segment:
.
The following conclusion is readily apparent on
.
Denote
. We have proven that,
From Equations (12) and (14), we obtain that,
By synthesizing the conclusions (10) and (15), we can deduce that the conclusion of Lemma 1 holds. □
Theorem 5 [Decision Theorem for the Operator] Letbe an FKS, whereis a quality predicate, andis a QFCTL path formula. For all, it holds that,
Based on Lemma 1 and Definition 8, Theorem 5 is established. Theorem 5 clarifies that the semantic of the operator is well-defined, and it also furnishes a foundation for model checking the operator .
Proposition 3 [The fundamental properties of quantified characteristic predicate operators] Letbe an FKS,be a QFCTL path formula, andbe a quality predicate. Let denotes the complement ofin [0,1]. Then,
(1) ;
(2) if and only if;
(3) if and only if .
The proof of Conclusion (1) of Proposition 3 is similar to the proof of Conclusion (1) of Theorem 2. The proofs of Conclusion (2) and Conclusion (3) of Proposition 3 are evident.
Next, we present the model-checking algorithm for
. We only need to provide the algorithm for the case when
, as other cases are either trivial and can be directly computed based on Definition 6 and Theorem 5, or they can be reduced to the case of
Solution process:
represents the set in the denominator of Equation (16).
onto stack OPEN;
is the root node of TREE.
=0;// Record the number of child nodes of TREE.head.
11 LOOP stack OPEN is not empty.
is popped from stack OPEN.
in table TREE.
;//Update the objective
;// Calculate the path reachability from the root node
in the spanning
tree, is stored in table TREE.
's child nodes is incremented by one.
, in
in TREE.
onto stack OPEN.;
24 END
25 END
// Reach the deepest level of the search.
is found.
29 END
39 END
32 END
Theorem 6Letbe an FKS, whereis a quality predicate, andis a QFCTL path formula. For all,, the output of Algorithm 4 ensures. The time complexity of model checkingis, and the space complexity is.
Proof: Algorithm 4 employs a bounded depth-first search algorithm with a maximum search depth of
. Starting from each initial state
, it produces a specific path that begins at s with
and terminates at a state
with
, as detailed below,
During the iterative search process, the objective function is continuously evaluated (as specified in step 17 of Algorithm 4), making it straightforward to obtain the following results,
.
Step 27: If , then ;
Step 28: If , then .
Consequently, it is straightforward to derive the following:
;
Therefore, . The correctness of Algorithm 4 is thereby established.
During the search process, for each node generated, the seven main computations from Step 17 to Step 23 are executed, and the resulting nodes are continuously stored in the generated tree, TREE. The primary time and space costs associated with generating TREE are both linearly related to the number of nodes in TREE. Specifically, TREE has 1 node at level 0, at most nodes at level 1, at most nodes at level 2, ..., and at most nodes at the deepest level . Therefore, the number of nodes in TREE is given by . The number of elements in the sets and does not exceed the number of leaf nodes in TREE, which is . Consequently, the time complexity for computing and is . Since this search process needs to be repeated for all , the overall time complexity becomes . However, the space occupied by TREE, and can be reused, so the space complexity is determined by the size of TREE, which is. □
Theorem 7 Letbe an FKS,be a QFCTL* state formula, andbe a quality predicate. The time complexity of QFCTL* model checking is, and the space complexity is.
Based on Theorem 6, when considering an arbitrary QFCTL* formula , the complexity of model checking is the product of the length of (denoted as ) and the complexity of Algorithm 4. Therefore, the time complexity of QFCTL* model checking is . The space complexity remains due to the reusable nature of the space.
6. Illustrative Examples
Up to this point, we have expounded on the theoretical underpinnings of QFCTL model checking. In this section, we will elucidate the modeling advantages of QFCTL, and the efficacy of our model checking techniques through a series of illustrative examples. All the model-checking examples provided herein are executed within the FKS depicted in
Figure 1.
First, we present the outcomes of evaluating QFCTL formulas through from Example 2 using Algorithm 1. The information fusion operator "" is instantiated as "".
The computation of requires iterations, where denotes the initial state, and indicates the cardinality of the state space .
The initial value is given by
Furthermore,
Let
; the first iteration proceeds as follows:
The second iteration proceeds as follows:
.
The third iteration proceeds as follows:
.
Ultimately, the evaluation yields,
When computing
, one merely needs to substitute Formula (17) with the following Formula (18).
Following three iterations, the computed value is .
When computing
, where
, one merely needs to substitute Formula (17) with the following Formula (19).
Upon completing another trio of iterations, the calculated outcome is .
In computing
, where
, replace Formula (17) with the following Formula (20).
After undergoing three iterations, the solution obtained is .
Upon completing another trio of iterations, the calculated outcome is .
In computing
, where
, replace Formula (17) with the following Formula (21).
After undergoing three iterations, the solution obtained is .
In computing
, where
, replace Formula (17) with the following Formula (22).
After undergoing three iterations, the solution obtained is .
We tabulate the model checking outcomes for properties to in Model as follow.
0.77
0.3
0.328
0.088
0.685
0.3
In the literature [
20,
21], PoCTL is studied, which solely utilizes the classical max–min operation for information synthesis, excluding quality constraint operators such as
,
, and
. As a result, it cannot express the more nuanced properties like
to
in QFCTL. We have computed the satisfaction values of the PoCTL formulas
,
,
,
,
,
and
, which correspond to these six QFLTL formulas, on the KFS in the example regarding the patient treatment process. The calculation results are presented in
Table 2 to facilitate comparison and analysis between QFCTL and PoCTL.
By conducting a comparative analysis of
Table 1 and
Table 2, we arrive at the following conclusions:
(1) QFCTL demonstrates superior expressivity in comparison to PoCTL. PoCTL is unable to articulate temporal properties that incorporate qualitative constraints, such as to , which specify concrete quality constraints. QFCTL enables a more precise and quantitative portrayal of system attributes, as exemplified by the second row of the two tables, showcasing the diversity of satisfaction values achieved by the corresponding formulas within the system. Evidently, under identical systems, QFCTL formulas differentiate values with greater granularity, whereas PoCTL is relatively coarser.
(2) PoCTL may lead to the loss of information from either side of the path reachability and property formula satisfaction levels. However, QFCTL avoids this deficiency. PoCTL simply employs the "
" operator to amalgamate the values of path reachability and property formulas, ultimately opting for the lesser value as the satisfaction gauge. For instance, in
Table 2, the bold figures represent the path reachability, whereas the non-bold values correspond to property formula values. Conversely, QFCTL in
Table 1 perpetually integrates information from both domains, thereby overcoming the information loss in PoCTL.
(3) PoCTL is incapable of distinguishing between the relative importance of sub-formulas within a property formula, nor does it differentiate between the significance of the property formula itself and path reachability. On the other hand, QFCTL adroitly discriminates between such information types. For example, both the PoCTL formulas and , and the QFCTL formulas and , require simultaneous occurrences of and along the path. However, and select the lesser value of and , whereas and unify and with a weight ratio of 0.4:0.6, signifying the greater importance attributed to . In the fusion of path reachability and property satisfaction, PoCTL solely picks the minimal value, whereas QFCTL formulas can blend the two using the operation, applying a weight ratio of 0.3:0.7, indicating QFCTL places greater emphasis on property formula satisfaction over path reachability.
(4) PoCTL might induce asynchrony between property formula values and path-reachability information, whereas QFCTL invariably ensures these two aspects of information remain synchronized. As seen in
Table 2, the truth values of
and
are always "0," resulting from computations within
where, irrespective of the path taken from
, the value of the property formula
is always "0." Therefore, regardless of the current path reachability level, taking the minimum with the property formula satisfaction value of "0" results in "0." This clearly instigates a mismatch between path reachability and property formula satisfaction values. The valuation processes of QFCTL formulas
and
, as evident from
Table 1 and the examples, illustrate the remediation of information asynchrony in QFCTL.
Proceeding forth, Algorithm 2 will be applied to conduct model checking for temporal logic properties through .
The temporal logic property is articulated as , while the quality predicate is delineated within the interval .
Having previously determined via Algorithm 1 that
and
, it follows that,
Consequently, .
This result elucidates that across all therapeutic pathways, the criterion which stipulates "the patient's physical condition being maximally in an ‘excellent’ state with a possibility of 0.8 occurs with a likelihood of no less than 0.3" is fully satisfied. This affirms that our treatment protocols adhere to the possibility standards for achieving a high level of clinical efficacy.
The temporal logic property , with the quality predicate delineated as .
Owing to the fact that , it logically follows that .
This finding elucidates that across every conceivable therapeutic trajectory, the proposition stating "the patient's health status continuously meets the criteria of being ‘fine’ with a 40% stipulation and ‘excellent’ with a 60% stipulation with a likelihood exceeding 0.5" is not upheld. Consequently, it is affirmed that our current therapeutic paths do not fulfill the possibility threshold for concurrently maintaining these health standards at the specified frequencies.
The temporal logic property , complemented by the quality predicate defined as (0.6,1).
Previously determined, we have and,
.
Given that , it is deduced that .
This reveals that some, but not all, therapeutic courses satisfy the property that "the patient’s health status, being maximally under a necessity of 0.5 to be ‘fine’, until transitioning to ‘excellent’, does so with a possibility greater than 0.6". This indicates a mixed fulfillment of the possibility condition across different treatment pathways.
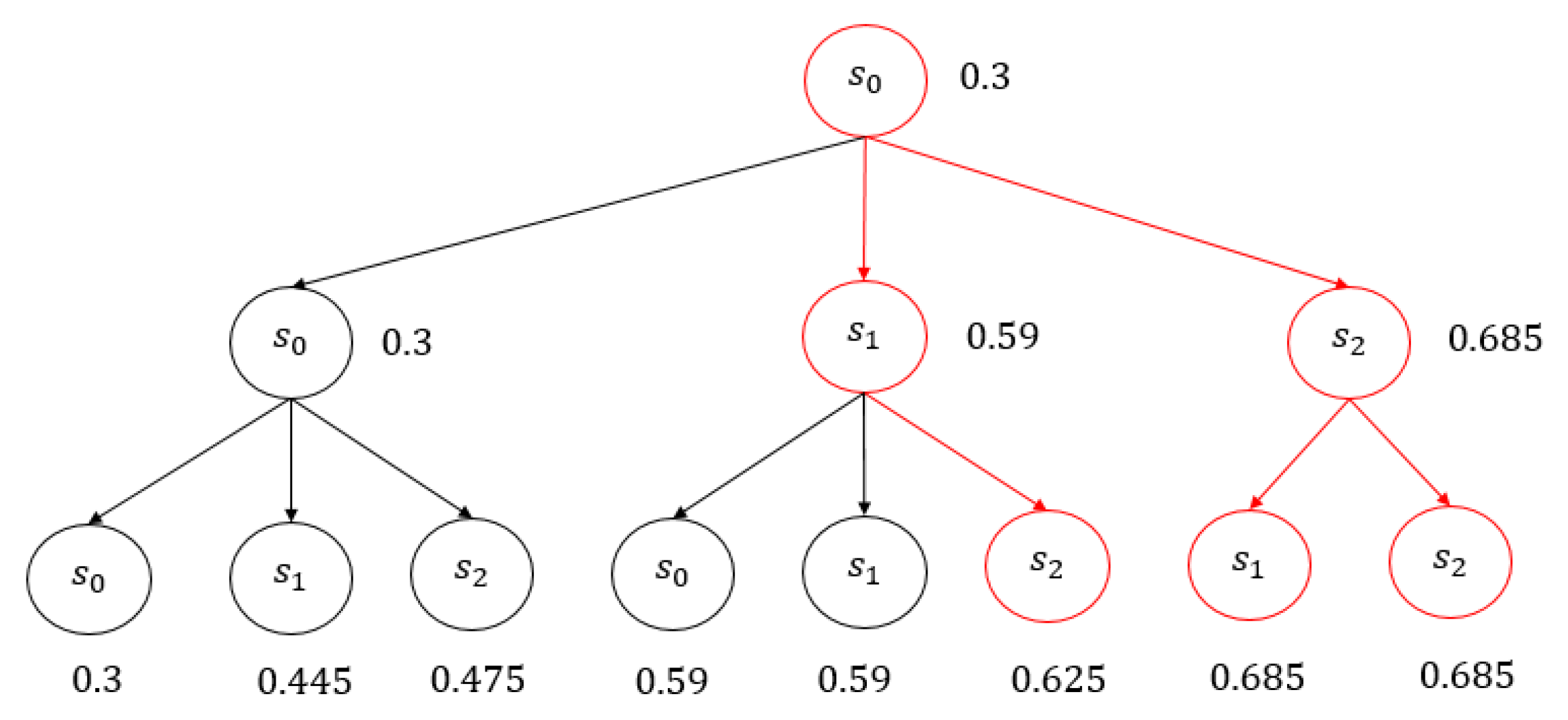
Proceeding with Algorithm 4, we conduct model checking on the QFCTL* formula
. The generation tree TREE, produced by the FKS
with the unique initial state
as the root node, as depicted in
Figure 7 corresponding to what was shown in
Figure 1, illustrates the values calculated for the objective function
upon the creation of node
, which are placed to the right or below each node
in the tree diagram.
In TREE, there exist 8 paths of length , among which 3 highlighted in red satisfy the following conclusions:
;
;
.
.
It indicates that 37.5% of the treatment regimens meet the criterion of the patient's condition being maximally at 'fine' with a necessity of 0.5 throughout the treatment course, until transitioning to 'excellent' with a likelihood greater than 0.6.
These examples illustrate that PoCTL lacks formulas akin to the qualitative QFCTL formulas and , which describe the qualitative fulfillment status of property formulas. Similarly, it does not possess formulas like the quantitative QFCTL* formula , capable of delineating the quantitative satisfaction condition of property formulas. This unequivocally demonstrates that QFCTL and QFCTL* exhibit superior expressive power over PoCTL, enabling a more refined formal description of temporal system properties. This enhanced capability facilitates a deeper analysis and a more detailed modeling of system temporal behaviors.
These model-checking instances, first and foremost, substantiate the rich expressiveness and practical applicability of QFCTL and QFCTL* proposed in the article, capable of elaborately and accurately depicting the temporal properties of uncertain systems. Secondly, these examples affirm the effectiveness of the model-checking algorithm put forward, enabling automated and efficient formal verification of uncertain systems.
7. Conclusions and Future Work
This paper introduces quality constraint functions and quality predicates into Possibility Computation Tree Logic (PoCTL), proposing Fuzzy Computation Tree Logic with quality Constraints (QFCTL). We explore the logical characteristics of QFCTL and present model checking algorithms for QFCTL on Fuzzy Kripke Structure Systems (FKS). Key contributions include:
(1)
Section 2 elaborates on QFCTL syntax in section 2.1, defines its semantics in 2.2, and demonstrates QFCTL's expressive power and practical applicability through illustrative examples in 2.3.
(2) In section 3, we discuss QFCTL's logical features, encompassing equivalences of QFCTL formulas (Theorem 1), partial order relations (Proposition 2), and a complete set of functional operators for QFCTL (Proposition 1). Special focus is given to the basic properties and determination of the Quality Predicate Operator (Theorem 2, Corollary 1), which signifies formula satisfaction under the constraints of predicate on relevant paths, yielding truth values of either "1" for full satisfaction, "0" for none, or "0.5" indicating partial satisfaction.
(3)
Section 4 delineates a model checking algorithm for QFCTL on FKS, reducing the computation of QFCTL formulas from infinite to finite paths. Model-checking algorithms (Algorithm 1, 2, and 3) are provided with a time complexity proportional to the product of the formula's length and the scale of the FKS (
, and space complexity dependent on FKS size (
. Rigorous proofs of the algorithm's validity (Theorem 3) and complexity analysis (Theorem 4 ) are provided.
(4)
Section 5 advances by introducing a quantitative quality predicate operator
(Definition 8), characterizing property formula
satisfaction under predicate
based on the ratio of satisfied paths among those fulfilling
. The well-definedness of operator
is proven (Theorem 5). Logical traits of QFCTL* are explored alongside the relationship between operators
and
(Proposition 3). An algorithm for model checking QFCTL* (Algorithm 4) is presented, accompanied by complexity analysis (Theorem 11).
(5)
Section 6 provides ten exemplary QFCTL and QFCTL* formulas(
) applied in model checking scenarios involving patient treatment processes on FKS, as illustrated in literature [
24]. These cases attest to the robust expressiveness and practical utility of QFCTL and QFCTL*. They also affirm the automation and effectiveness of our proposed model checking algorithms.
Subsequent primary research efforts will encompass:
(1) The complexity of the QFCTL* model checking algorithm is exponential. We anticipate reducing the complexity of the QFCTL* model checking algorithm through formal reduction methods such as possibility bisimulation and partial-order reduction.
(2) Integrating fuzzy temporal constraints [
22,
25], path reachability information, and property satisfaction values in a biased, synchronized manner. We aim to investigate fuzzy temporal logic with dual constraints of fuzzy time and quality attributes, thereby enhancing the completeness and accuracy of information representation.
(3) The search and decision problems within QFCTL based on possible decision processes [
25,
26] remain a domain requiring further exploration. This endeavor will focus on advancing methodologies to address these issues, contributing to the field's mathematical, academic, and readability standards.
These research directions not only aim to tackle existing challenges but also to pave the way for future advancements in the field of fuzzy temporal logic and model checking algorithms.
Author Contributions
X.Y. designed the syntax and semantics of QFCTL, articulated its model checking problem, and provided relevant solution algorithms. S.G. did likewise for QFCTL*, crafting its syntactic and semantic framework, delineating its model checking issue, and offering corresponding algorithmic solutions. Y.L. devoted efforts to investigating the logical properties of both QFLTL and QFCTL. H.L. furnished illustrative examples showcasing QFLTL applications and conducted a meticulous review of the entire paper to guarantee compliance with requisite writing standards, ensuring mathematical rigor, academic integrity, and readability throughout.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No: 12071271,11671244, 12471437), Shaanxi Fundamental Science Research Project for Mathematics and Physics (Grant No: 23JSZ011, 23JSY048), National Key R&Dplan (Grant No: 2020YFC1523305), Key R&Dand transformation plan of Qinghai Province (Grant No: 2022-QY-203), Scientific and Technological Research Fund of Shangluo University (Grant NO. 20SKY021),and Shangluo University Key Disciplines Project, Discipline name:Mathematics.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Baier C, Katoen J P. Principles of Model Checking. Cambridge: MIT Press, 2008.
- Edmund M, Grumberg O, Peled D. Model Checking. Cambridge: MIT Press, 1999.
- P. Camurati and P. Prinetto. Formal verification of hardware correctness: Introduction and survey of current research. Computer, 8: (7).
- Araujo C, Cavalcante E, Batista T, et al. A research landscape on formal verification of software architecture descriptions. IEEE Access, 1: 7, 1717.
- Kern C, Greenstreet M R. Formal verification in hardware design: a survey. ACM Transactions on Design Automation of Electronic Systems (TODAES), 1: 4(2).
- Šimoňák, S. Verification of communication protocols based on formal methods integration. Acta Polytechnica Hungarica, 1: 9(4).
- Boigelot B, Godefroid P. Symbolic verification of communication protocols with infinite state spaces using QDDs. Formal Methods in System Design, 1999, 14: 237-255.
- Avalle M, Pironti A, Sisto R. Formal verification of security protocol implementations: a survey. Formal Aspects of Computing, 9: 26.
- Coffey T, Dojen R, Flanagan T. Formal verification: an imperative step in the design of security protocols. 6: Networks, 2003, 43(5), 2003.
- Zheng Y, Wang L. Consensus of switched multi-agent systems. IEEE Trans Circ Syst II, 3: 63.
- Zheng Y, Wang L. A novel group consensus protocol for heterogeneous multi-agent systems. Int J Contr, 1: 106.
- Li T, Zhang J F. Consensus conditions of multi-agent systems with time-varying topologies and stochastic communication noises. IEEE Trans Automat Contr, 2: 55, 2043.
- Li T, Fu M, Xie L, et al. Distributed consensus with limited communication data rate. IEEE Trans Automat Contr.
- Baier C, Kwiatkowska M. Model checking for a probabilistic branching time logic with fairness. Distrib Comput.
- Hart S, Sharir M. Termination of probabilistic concurrent programs. ACM Trans Prog Lang Syst, 3: 5.
- Sultan K, Bentahar J, Wei W, et al. Modeling and verifying probabilistic multi-agent systems using knowledge andsocial commitments. Expert Syst Appl, 6: 41, 6291.
- Sultan K, Bentahar J, EI-Menshawy M. Model checking probabilistic social commitments for intelligent agent com-munication. Appl Softw Comput, 3: 22.
- Chechik M, Devereux B, Easterbrook S, et al. Multi-valued symbolic model-checking. ACM Trans Softw Eng Method.
- Chechik M, Gurfinkel A, Devereux B, et al. Data structures for symbolic multi-valued model-checking. Formal MethodsSyst Des, 2: 29.
- Li Y M, Li Y N, Ma Z Y. Computation tree logic model checking based on possibility measures. Fuzzy Sets and Systems.
- Li Y M, Ma Z. Quantitative computation tree logic model checking based on generalized possibility measures. IEEE Transactions on Fuzzy Systems, 2034.
- A.Frigeri, L. A.Frigeri, L.Pasquale, P.Spoletini. Fuzzy time in linear temporal logic. ACM Transaction on Computational Logic.
- Almagor S, Boker U, Kupferman O. Formally reasoning about quality. Journal of the ACM, 1: 63(3).
- Yu, X.; Li, Y.; Geng, S. Fuzzy Linear Temporal Logic with Quality Constraints. Mathematics 2024, 12, 3148. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Wang, J.; Yu, X.; Li, C. Model checking of possibilistic linear-time properties based on generalized possibilistic decision processes. IEEE Trans. Fuzzy Syst. 2023, 31, 3495–3506. [Google Scholar] [CrossRef]
- Liu WN, Li Y M. Optimal strategy model checking in possibilistic decision processes. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 6: (53)10, 6620.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).