Submitted:
22 October 2024
Posted:
25 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Force Considerations
3. Retardation Effects
4. Momentum Generated
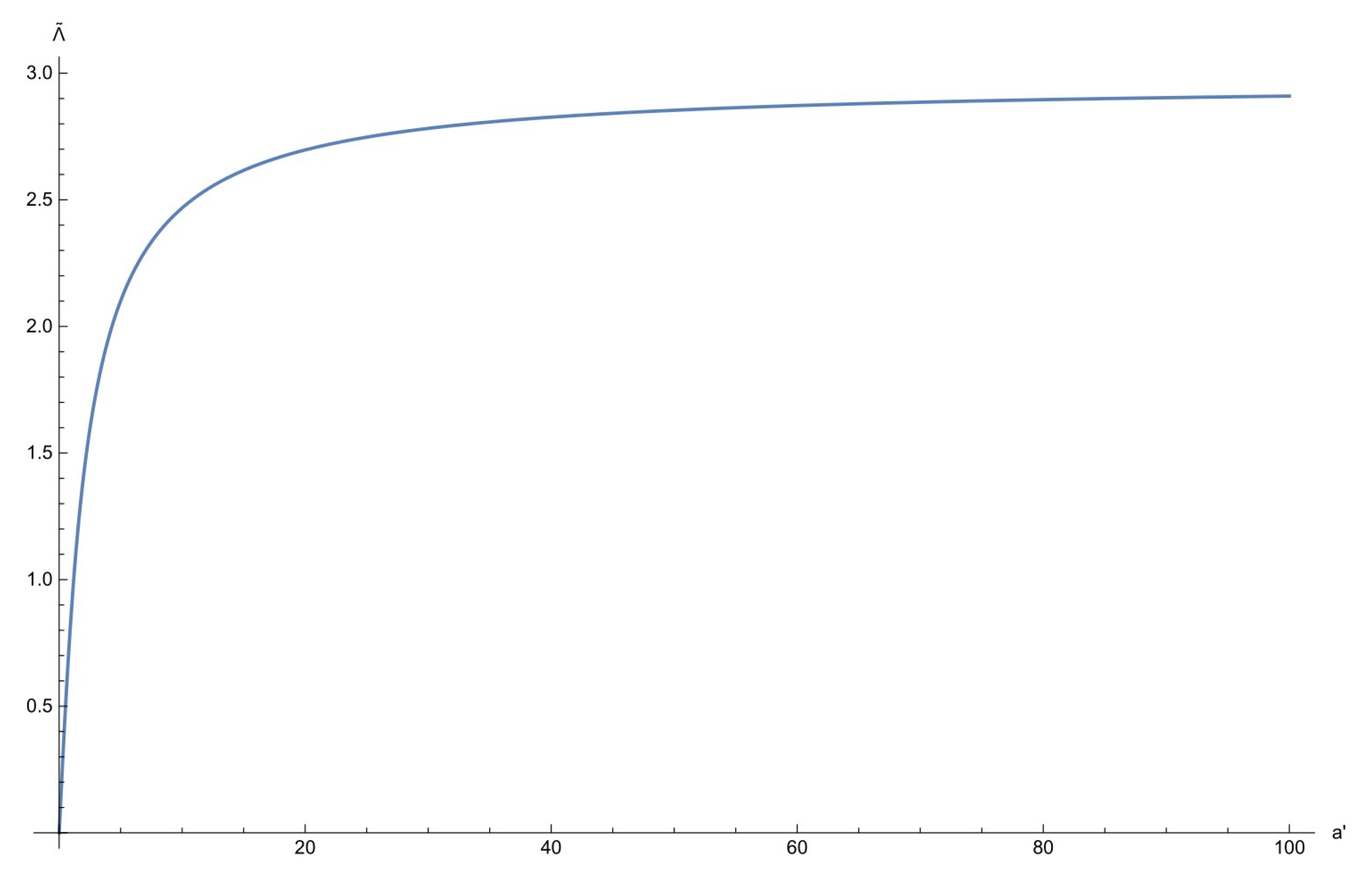
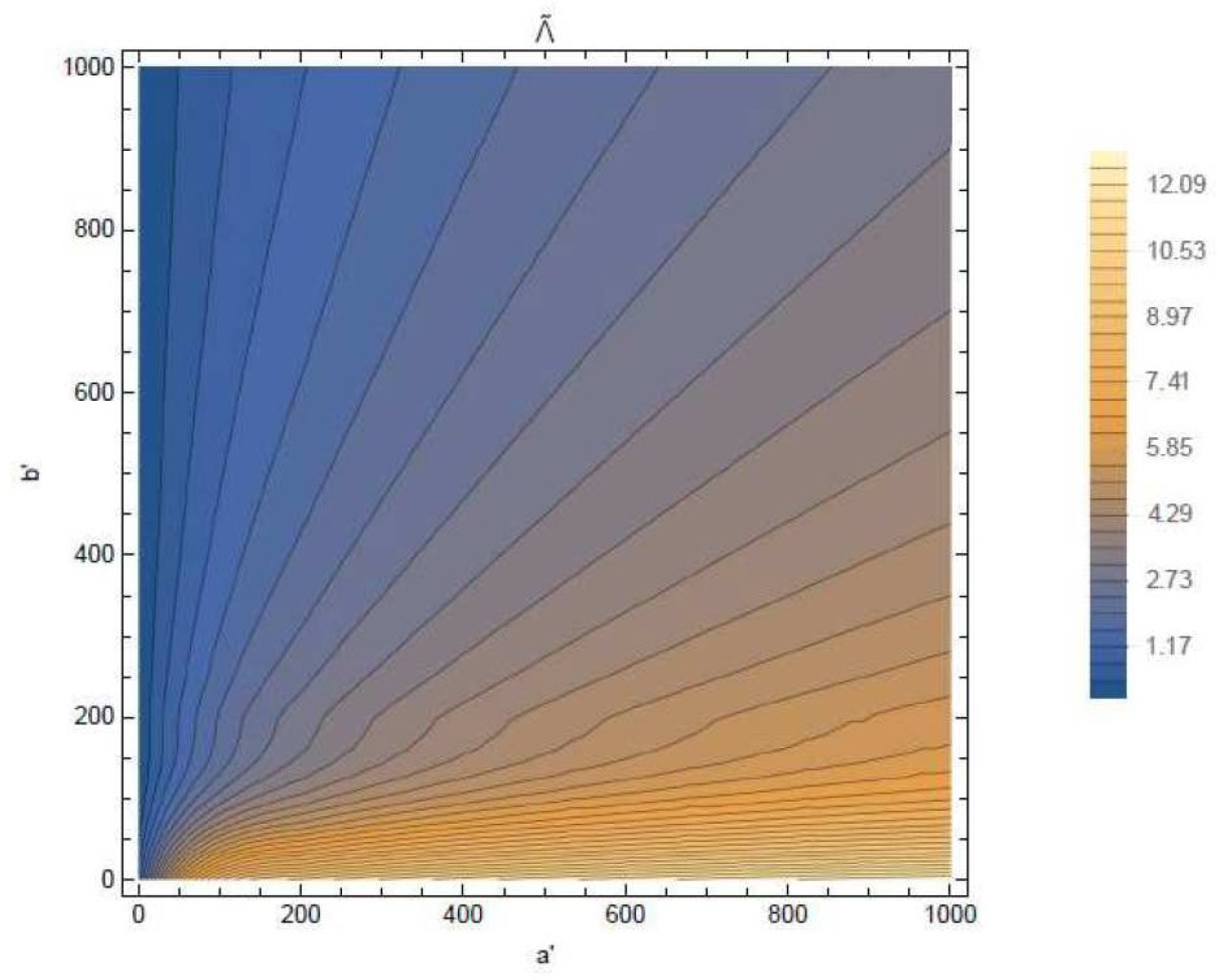
5. Upper bounds
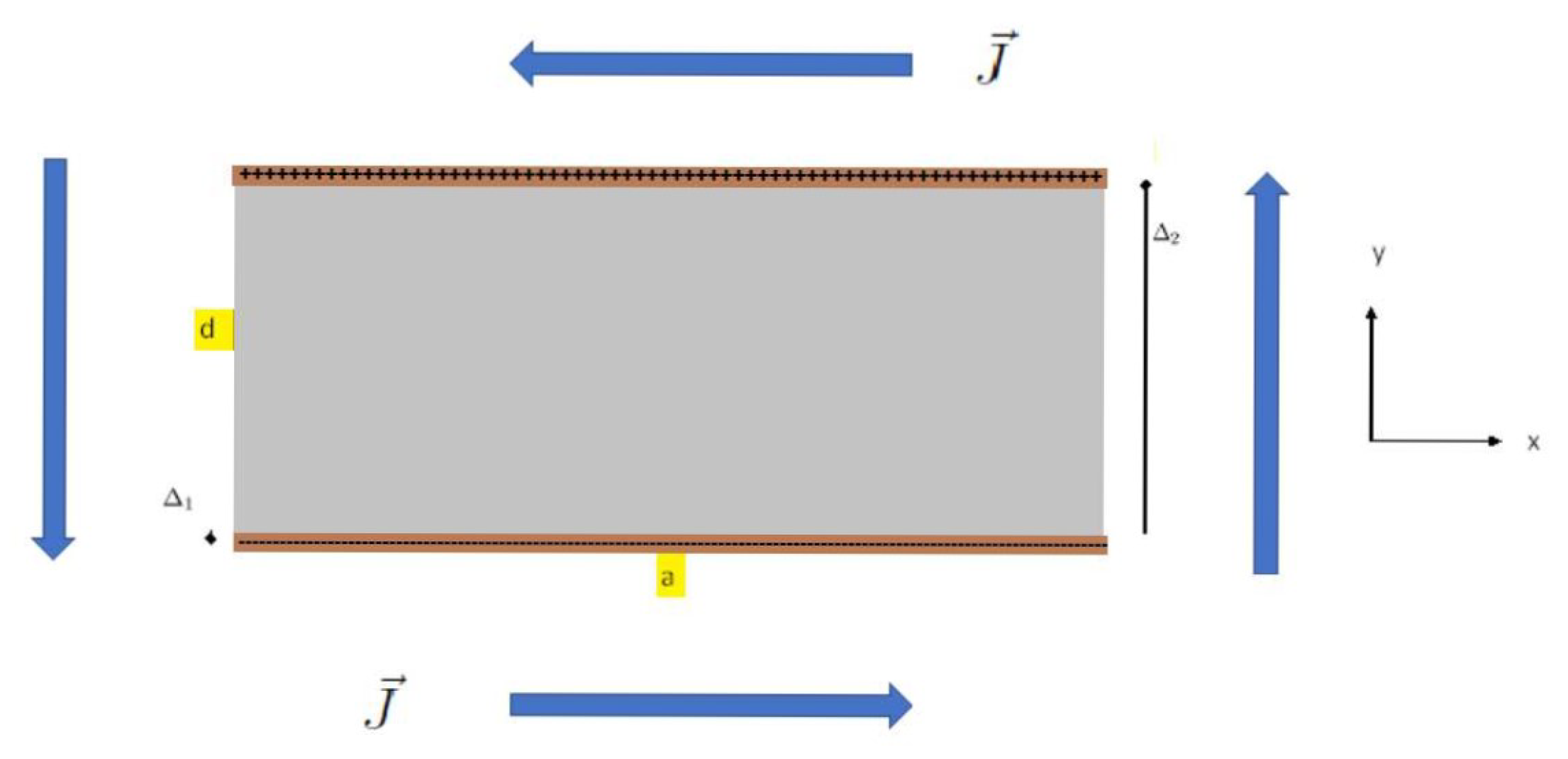
6. Configuration
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- A. Einstein, On the Electrodynamics of Moving Bodies, Annalen der Physik 17 (10): 891-921 (1905).
- J.C. Maxwell, A dynamical theory of the electromagnetic field, Philosophical Transactions of the Royal Society of London 155, 459-512 (1865).
- J. D. Jackson, Classical Electrodynamics, Third Edition. Wiley: New York, 1999.
- R. P. Feynman, R. B. Leighton & M. L. Sands, Feynman Lectures on Physics, Basic Books; revised 50th anniversary edition 2011.
- O. Heaviside, On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric, Philosophical Magazine, (1889).
- I. Newton, Philosophi Naturalis Principia Mathematica, 1687.
- H. Goldstein, C. P. Poole Jr. & J. L. Safko, Classical Mechanics, Pearson; 3rd edition, 2001.
- M. Tuval and A. Yahalom, Momentum Conservation in a Relativistic Engine, Eur. Phys. J. Plus 131, 374 (2016). [CrossRef]
- D. J. Griffiths & M. A. Heald, "Time dependent generalizations of the Biot-Savart andCoulomb laws" American Journal of Physics, 59, 111-117 (1991).
- O. D. Jefimenko, Electricity and Magnetism, Appleton-Century Crofts, New York 1966; 2nd edition, Electret Scientific, Star City, WV 1989.
- Miron Tuval & Asher Yahalom "Newton’s Third Law in the Framework of Special Relativity" Eur. Phys. J. Plus (11 Nov 2014) 129: 240. [CrossRef]
- Miron Tuval and Asher Yahalom "A Permanent Magnet Relativistic Engine" Proceedings of the Ninth International Conference on Materials Technologies and Modeling (MMT-2016) Ariel University, Ariel, Israel, July 25-29, 2016.
- Asher Yahalom "Retardation in Special Relativity and the Design of a Relativistic Motor".Acta Physica Polonica A, Vol. 131 (2017) No. 5, 1285-1288.
- Asher Yahalom "Preliminary Energy Considerations in a Relativistic Engine" Proceedings of the Israeli-Russian Bi-National Workshop "The optimization of composition, structure and properties of metals, oxides, composites, nano - and amorphous materials", page 203-213, 28 - 31 August 2017, Ariel, Israel.
- S. Rajput and A. Yahalom, "Preliminary Magnetic Energy Considerations in a Relativistic Engine: Mutual Inductance vs. Kinetic Terms" 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 2018, pp. 1-5. [CrossRef]
- S. Rajput and A. Yahalom, "Material Engineering and Design of a Relativistic Engine: How to Avoid Radiation Losses". Advanced Engineering Forum ISSN: 2234-991X, Vol. 36, pp 126-131. Submitted: 2019-06-16, Accepted: 2020-05-18, Online: 2020-06-17. ©2020 Trans Tech Publications Ltd, Switzerland.
- Shailendra Rajput, Asher Yahalom & Hong Qin "Lorentz Symmetry Group, Retardation and Energy Transformations in a Relativistic Engine" Symmetry 2021, 13, 420. [CrossRef]
- Rajput, Shailendra, and Asher Yahalom. 2021. "Newton’s Third Law in the Framework of Special Relativity for Charged Bodies" Symmetry 13, no. 7: 1250. [CrossRef]
- Yahalom, Asher. 2022. "Newton’s Third Law in the Framework of Special Relativity for Charged Bodies Part 2: Preliminary Analysis of a Nano Relativistic Motor" Symmetry 14, no. 1: 94.
- Yahalom, Asher. 2023. "Implementing a Relativistic Motor over Atomic Scales" Symmetry 15, no. 8: 1613. [CrossRef]
| 1 | We use the notation . |

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




