Prerpints.org logo
Preprint
Article

Probabilistic Flood Modeling in the Lake Nokoue Basin Using Statistical Models

Altmetrics

Downloads

40

Views

22

Comments

0

Submitted:

27 October 2024

Posted:

28 October 2024

You are already at the latest version

Alerts
Abstract
The evolution and acceleration of the effects of climate change on the water cycle demand adaptation and mitigation plans. Consequently, the implementation of public policies (management, governance, and strategy) regarding flood risk management or prevention (such as levee heights and spillway dimensions of dams) is based on the characterization of flood hazards. This requires understanding extreme climate phenomena and conducting a rigorous probabilistic analysis of hydrometric data. This study aims to estimate the flood quantiles for lake Nokoue. To achieve this, the adopted methodology involved fitting the Generalized Extreme Value (GEV) distribution, the Gumbel distribution, and the Generalized Pareto (GPA) distribution to the annual maximum water levels of lake Nokoue from 2015 to 2022. We estimated experimental probabilities using the Weibull formula. The assessment of the fit quality of the theoretical probability distributions to our data sample indicated that the Gumbel distribution was the most suitable, with a root mean square error (RMSE) of 0.0724, compared to 0.0754 and 0.0761 for the GEV and GPA distributions, respectively. The position and scale parameters (φ; α) of the Gumbel distribution were estimated to be 3.802 and 0.249, respectively. This allows for the calculation of the probability of an extreme water level occurring within a return period in a single day. Thus, the extreme water levels (flood quantiles) associated with return periods of 10, 50, and 100 years, as determined by the Gumbel distribution, are 4.36m, 4.77m, and 4.95m, respectively. These values are of crucial importance for the design of flood prevention structures (infrastructure) intended to mitigate flood risk.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

Floods are currently the most frequent and damaging natural risk in West Africa [1,2,3,4]. They have harmful effects on the activities and populations living along the banks and involve significant security challenges for the most exposed areas. They are natural phenomena that are integral to the natural regime of water bodies (lakes) and watercourses (rivers), and protection against them requires prevention and forecasting [5,6,7]. Unlike the management approaches of the 1960s, current policies tend to better account for the significant role of floods and the means of managing the flood risk of a water body or a watercourse. Flood risk is particularly complex to understand due to its random nature associated with climate change, especially in highly developed and urbanized areas such as urban and peri-urban zones [8,9,10]. This issue is also present in the lake Nokoue basin. The basin is indeed subject to high rainfall intensities that can be potentially devastating due to the rapid urban growth along its banks. Scientific literature has shown that, regardless of the nature of the floods, hydrological studies are often overlooked, and flood prevention structures are poorly designed due to the use of outdated empirical formulas [11,12,13]. Therefore, to reduce anxiety about the threat of flooding from lake Nokoue in Benin, the estimation of extreme water levels is used in the context of public policy implementation for risk prevention or coastal management, particularly through the characterization of flood hazards. The purpose of these estimations is to provide a high level of safety in flood risk prevention. In this study, we apply probabilistic models to estimate extreme water levels up to a 100-year return period for lake Nokoue. The estimates are made using an extreme value statistical analysis method. The choice of a 100-year return period is driven by political rather than scientific reasons. However, the estimation of extreme surcharges (quantiles) for return periods close to 100 years is useful for analyzing rare extreme events. The results of this study could provide valuable insights for evaluating the extreme scenarios referenced by public policies in flood risk prevention for lake Nokoue.

2. Materials and methods

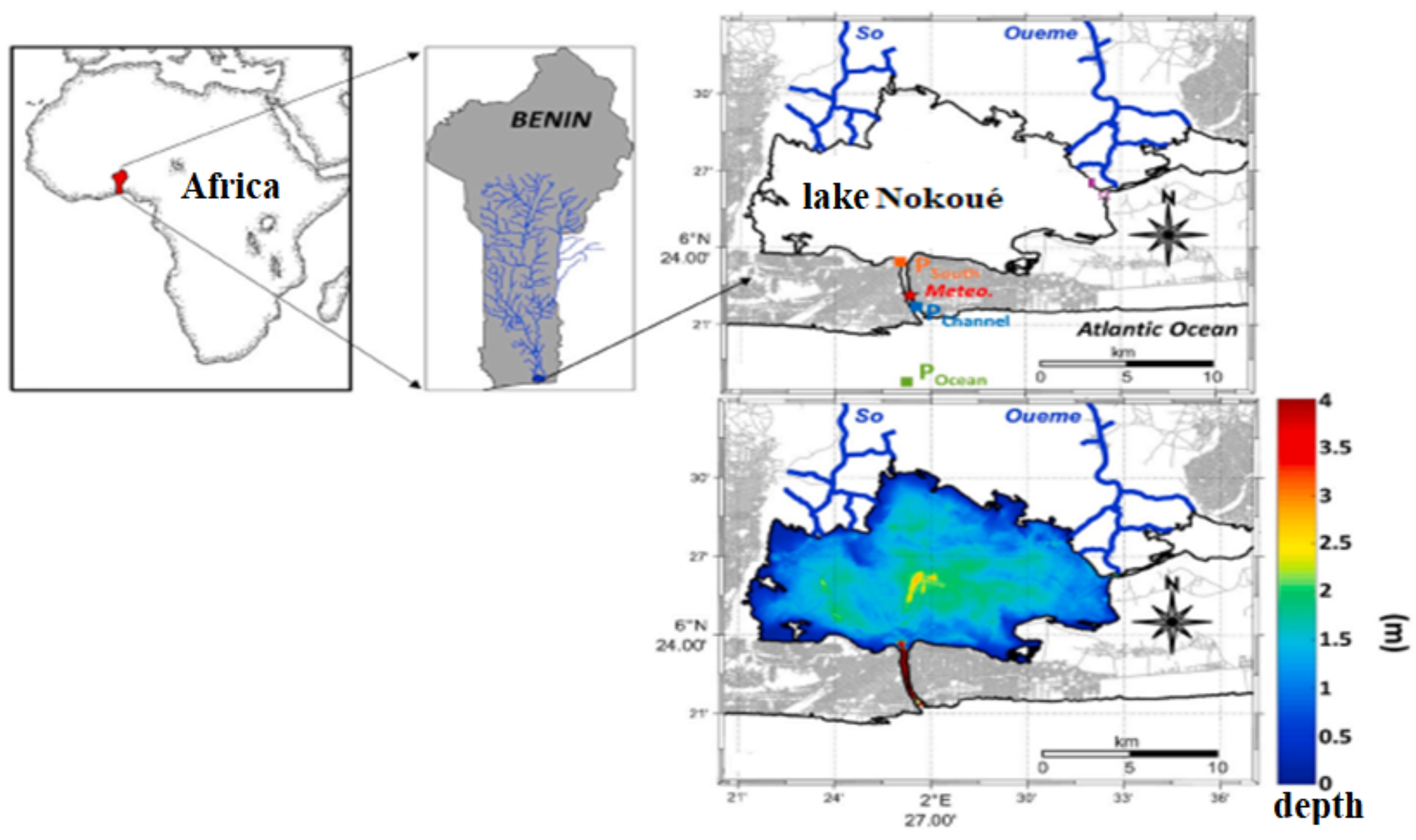
2.1. Study areas

Lake Nokoue is located in southern Benin between 6°38′ and 6°50′ North latitude, and 2°35′ and 2°55′ West longitude. It extends between 150 and 170 km², respectively, during the low water period and the high-water period “Figure 1”.

2.2. Implementation of frequency models

Extreme water levels are estimated using a method of statistical fitting and extrapolation of extremes. Only the main points of the method are outlined here. For more information, please refer to [14]. The calculations were performed using the R environment because it is well known nowadays well.
  • Data on water levels of lake Nokoue
This study focuses on the statistical analysis of extreme water levels of lake Nokoue, sourced from the Institute of Hydrology and Oceanology Research of Benin (IRHOB). An extreme water level is defined as the maximum observed value within a year. These values were extracted from a series spanning from 1997 to 2022.
  • Detection of hydrological flood risk thresholds
The categorization of flood risk hazard thresholds is based on the classification of the standardized water height index. This categorization was made possible through a transposition of daily data used by McKee et al. (2002) [15]. By normalizing the water height series of lake Nokoue, these thresholds were determined (Totin et al., 2016; WMO, 2012) [16,17]. Water height anomaly indices and McKee’s classification were used to characterize flood thresholds. The risk categories (limited, moderate, significant, and critical) are shown in Table 1. The occurrence period of flood water heights associated with flood risk threshold indices is determined using the Gumbel distribution with the method of linear moments.
This table categorizes daily maximum water heights into different flood risk levels (limited, moderate, significant, and critical) based on the standardized water height index.
  • Selection and calculation of empirical probabilities of observations
The experimental probabilities associated with the observations were calculated using formula “(1)” with the Weibull formula, which aims to obtain unbiased exceedance probabilities for all distributions [18].
p x i = i N + 1 e t T x i = 1 1 − p x i
where p is the exceedance probability of the maximum water level, iii is the rank of the height in the series, and N is the size of the series consisting of the annual maximum water levels.
  • Test of stationarity, independence, and homogeneity.
The Mann-Kendall, Wald-Wolfowitz, and Wilcoxon tests were used respectively for stationarity, independence, and homogeneity. The p-value represents the risk of error if we consider that the null hypothesis H 0 (the hypothesis that the sample is stationary, homogeneous, and independent) is not true. The maximum acceptable value for the risk of error is set at 5%. If the p-value is less than 5%, there is less than a one in five chance of being wrong in considering that the series of extreme water levels is not independent, stationary, and homogeneous [19].
  • Parametric fitting and extrapolation
A parametric distribution law is fitted to the extreme water levels. Adopting a distribution law to study and describe maximum water levels is undoubtedly the most critical step, introducing the greatest uncertainties [20,21]. Il est prudent de tester d’autres lois de distribution appartenant au domaine asymptotique des évènements extrêmes. Diverses pistes ont contribué à faciliter ce choix, mais il n’existe malheureusement pas de méthode universelle et infaillible [22]. It is prudent to test other distribution belonging to the asymptotic domain of extreme events. Various approaches can help facilitate this choice, but unfortunately, there is no universal and infallible method. [23]: The Generalized Extreme Value (GEV) distribution, the Gumbel distribution, and the Generalized Pareto (GPA) distribution are all types of generalized extreme value laws that are often used to model extreme events, such as river or lake floods. A comparative study of the performance of these recommended distributions by [24] is the best approach for justifying the choice of a distribution. The linear moments method available in the (lmomco) package, based on negative logarithmic likelihood, was used for parameter estimation. The distribution functions of the three laws used in this article are as follows “(2)” to “(4)”:
Gumbel : F X = e − e − α ( x − x 0 )
where α ( x − x 0 ) for the Gumbel distribution, where α is the scale parameter and x 0 is the location parameter.
GEV   :   F X = e − 1 + k x + x 0 . − 1 k
With k ≠ 0 et k x + x 0 . − 1 k > 0
GPA : Let X be a random variable with distribution function F and u be a threshold value. The random variable Y = X − u pour X > u follows the conditional distribution function:
G y = G x − μ = F x − F ( μ ) 1 − F ( x )
With x > μ
G y = 1 − 1 + k y σ − 1 k
  • Model performance metrics
The quality of the statistical extrapolation of extreme events is assessed using linear moments diagrams, Taylor diagrams, cumulative distribution functions, and the root mean square error (RMSE), as these methods are more practical and powerful compared to the χ² test, Bayesian Information Criterion (BIC), and Akaike Information Criterion (AIC).
  • Linear moments diagram
par la formule de The linear moments diagram (LM) is based on the combination of skewness coefficients ( τ 3 ) and kurtosis coefficients ( τ 4 ) to graphically assess which distribution best fits the sample observations. Constructing the diagram requires knowledge of the function relating τ 3 to τ 4 through the formula of “(6)”:
𝜏 4   = ∑ j = 0 8 a j ( τ 3 2 )
With aj : polynomial approximation coefficient. The L-moments package in the R programming language was used to represent the kurtosis coefficients as a function of skewness coefficients and the experimental characteristic of the sample.
  • Root Mean Square Error criterion
The root mean square error (RMSE) is a method for objectively evaluating the performance of models. It provides a measure of the average magnitude of prediction errors, with lower values indicating better model accuracy. It is formulated as follows “(7)”:
R M S E = 1 N ∑ i = 1 N ( O n − M n ) 2

3. Results

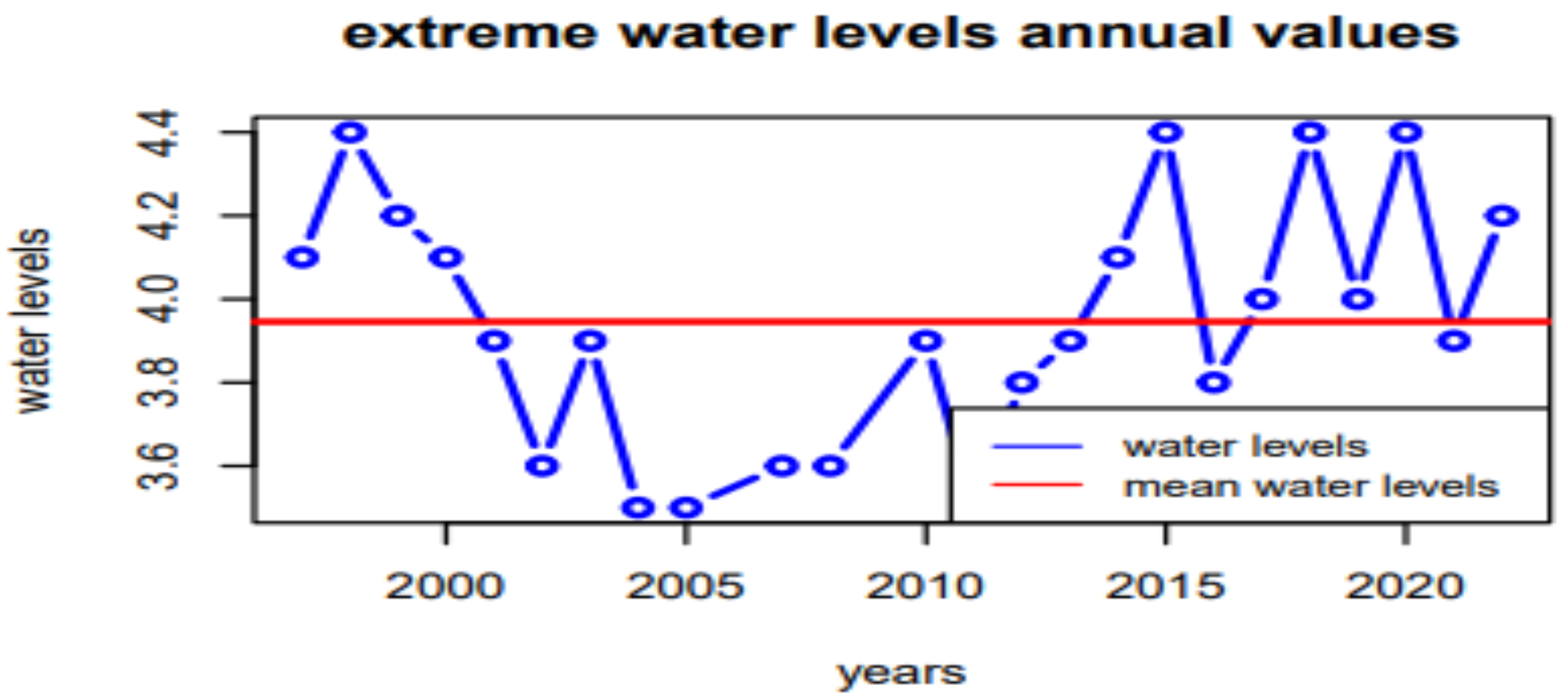
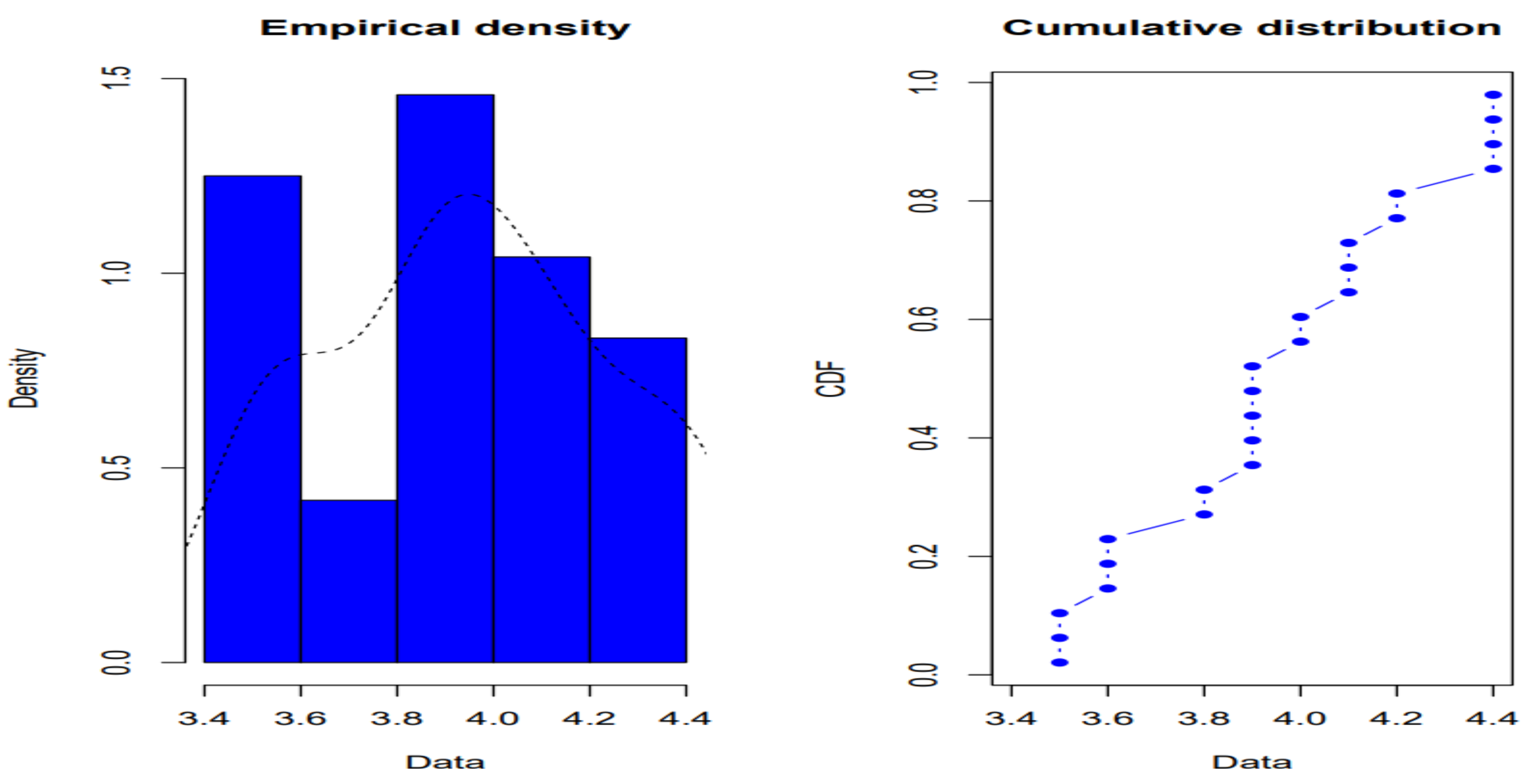
3.1. Description of the data

The statistical examination of the data series indicated that, over an 8-year period, the annual maximum water levels of lake Nokoue ranged from 3.5 to 4.4 meters, observed in 2015 and 2022, respectively, with an average annual maximum of 3.95 meters (see Table 1 and “Figure 2”). The empirical probability density is composed of two phases: a rising phase from 0.3 to 1.2 and a declining phase from 1.25 to 0.5. The extreme water levels with the highest empirical probability densities are between 3.8 meters and 4.0 meters “Figure 3”.
Table 1. Summary statistics of the data.
Table 1. Summary statistics of the data.
min 25% 50% 75% max
3.5 3.75 3.95 4.13 4.4

3.2. Results of hypothesis tests

The various statistical tests yielded the following p-values for the series of annual maximum water levels, as shown in Table 2.
  • The hypothesis that the data series of annual maximum water levels is independent is accepted with a 95% confidence level. There is no correlation between the data in the series.
  • The absolute value of the Mann-Kendall statistic ( | K | ) is evaluated at 0.04. The hypothesis that there is no trend in the 10-minute and 15-minute data series is accepted at a 5% significance level.
  • The absolute value of the Wilcoxon statistic ( | W | ) is evaluated at 0.04. The mean of the two sub-samples (2015-2018 and 2019-2022) is statistically equal, meaning the series is homogeneous. Thus, the null hypothesis H 0 is accepted at a 5% significance level.

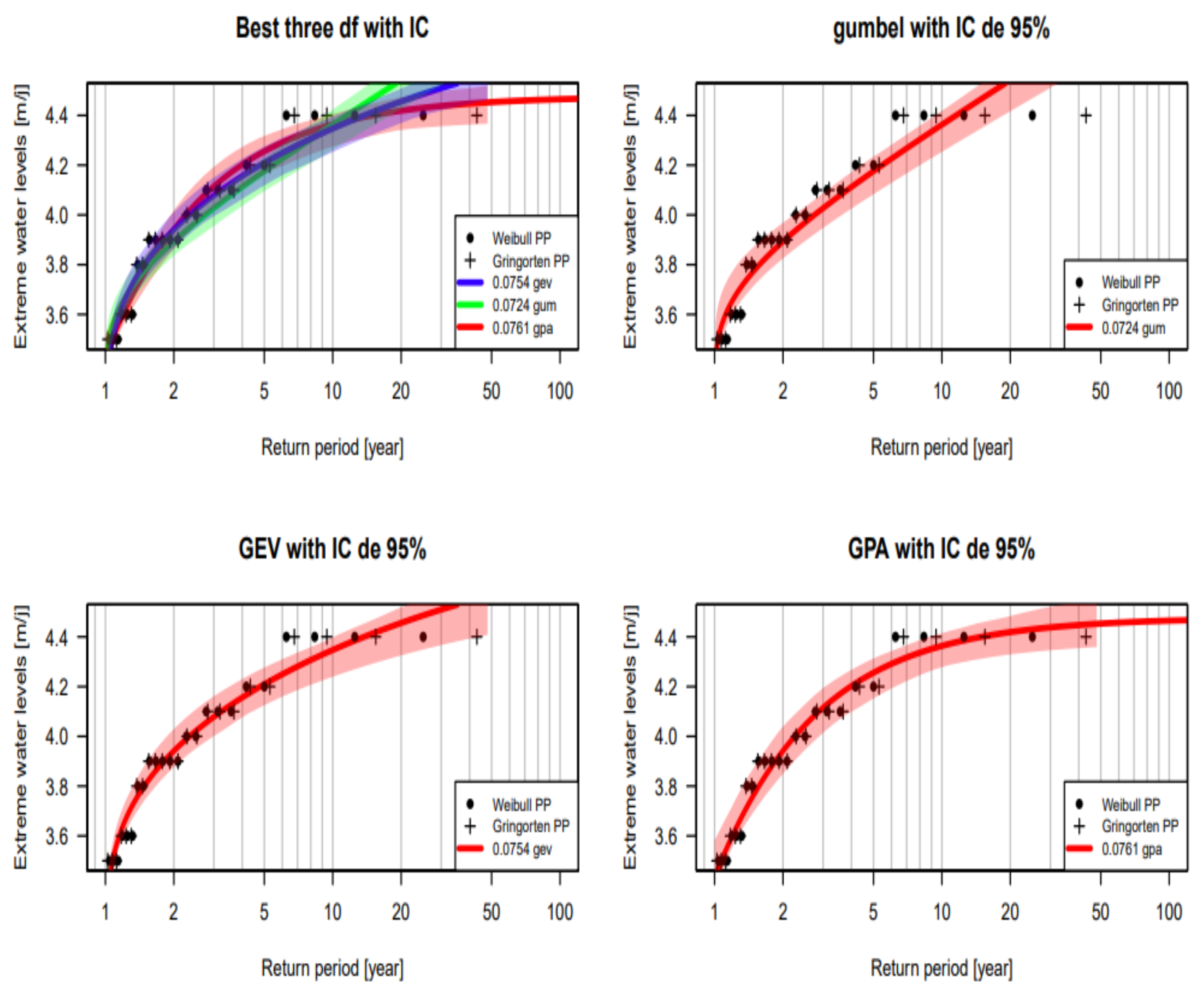
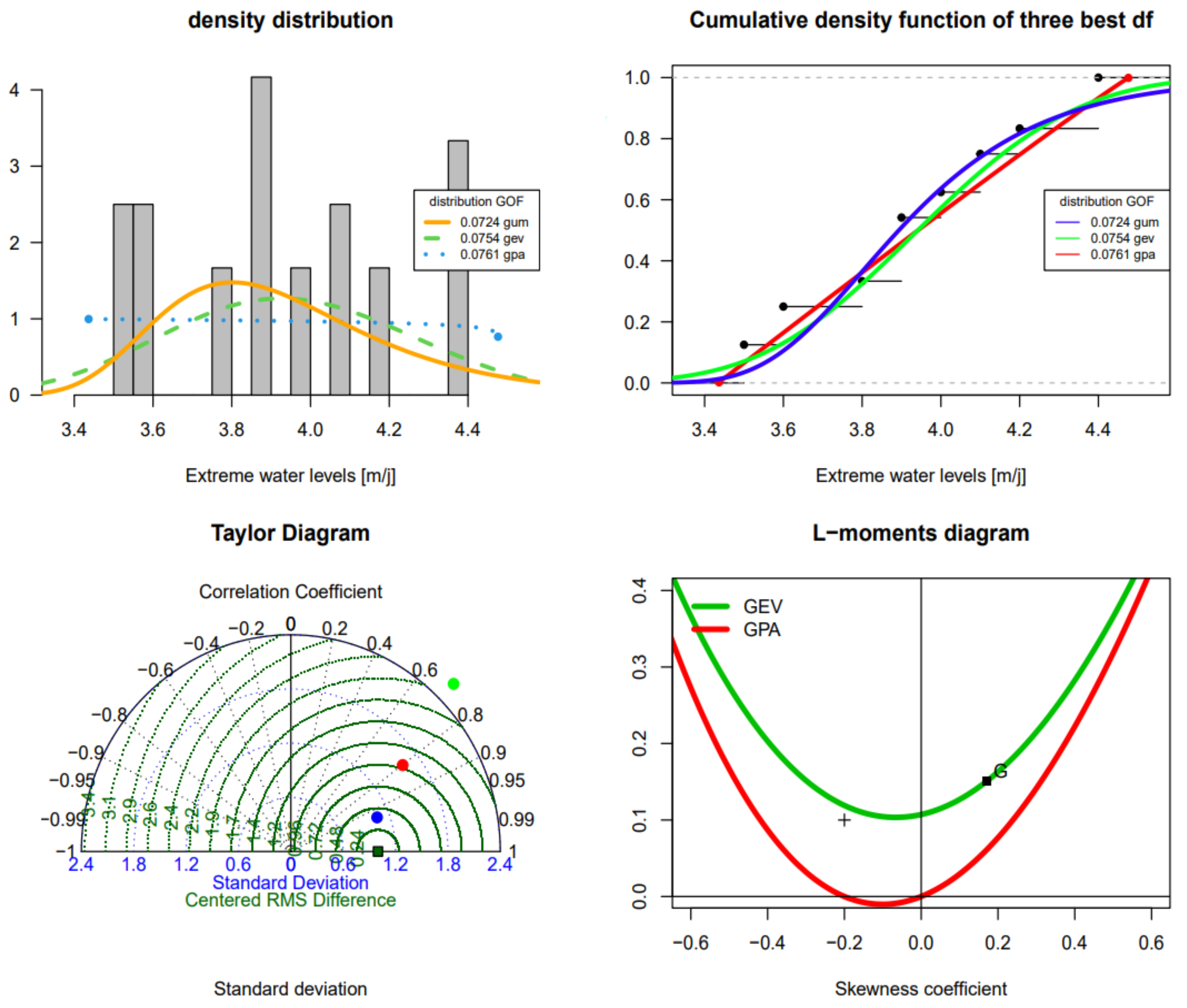
3.3. Results of the fitting to statistical distributions

The parameter values for the Gumbel, GEV, and GPA distributions are recorded in Table 3, and the “Figure 4”–“Figure 7” are presented below.
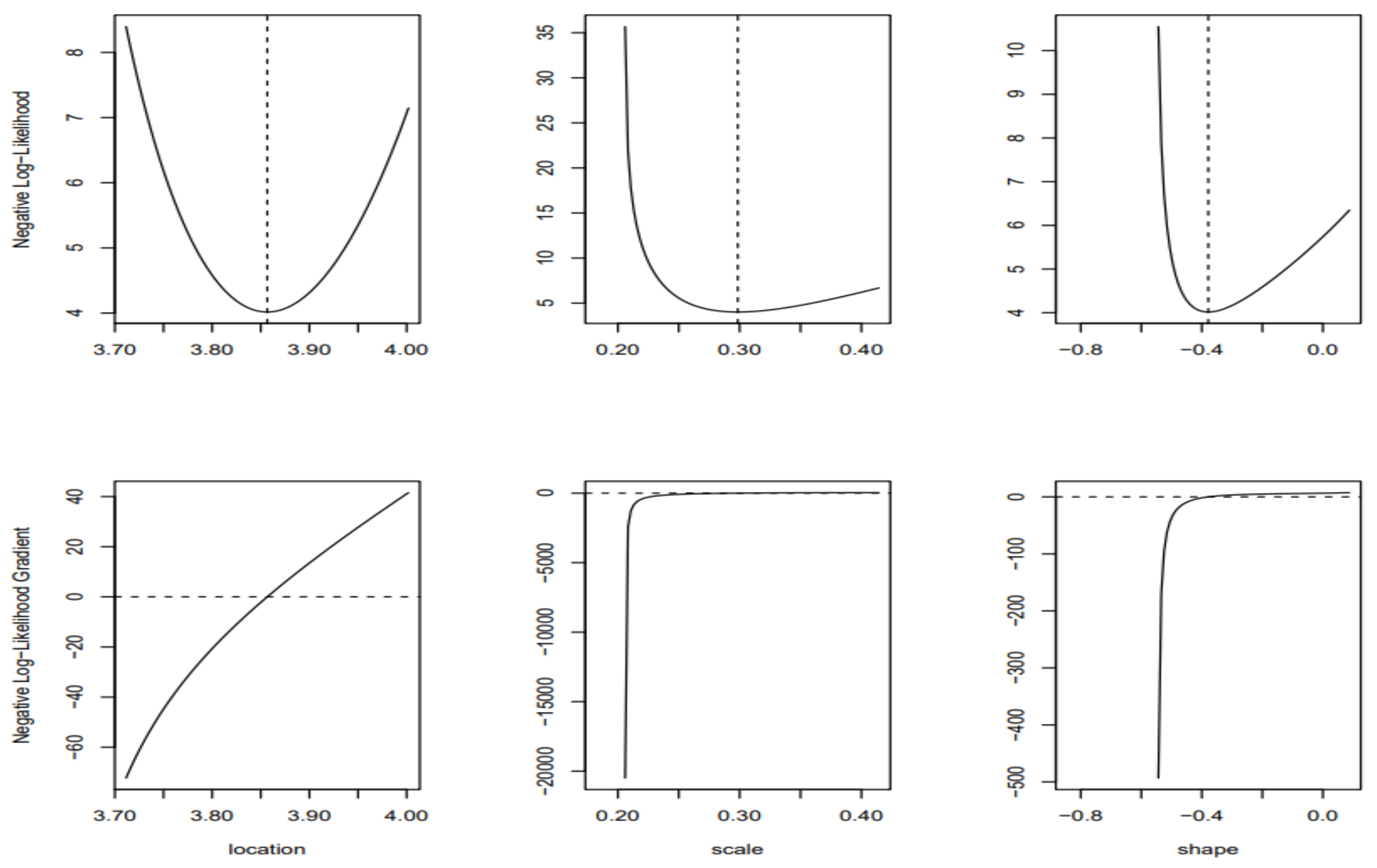
Preprints 137628 g004
Figure 4. Parameters of the Generalized Extreme Value (GEV) distribution.
Figure 4. Parameters of the Generalized Extreme Value (GEV) distribution.
Preprints 137628 g004
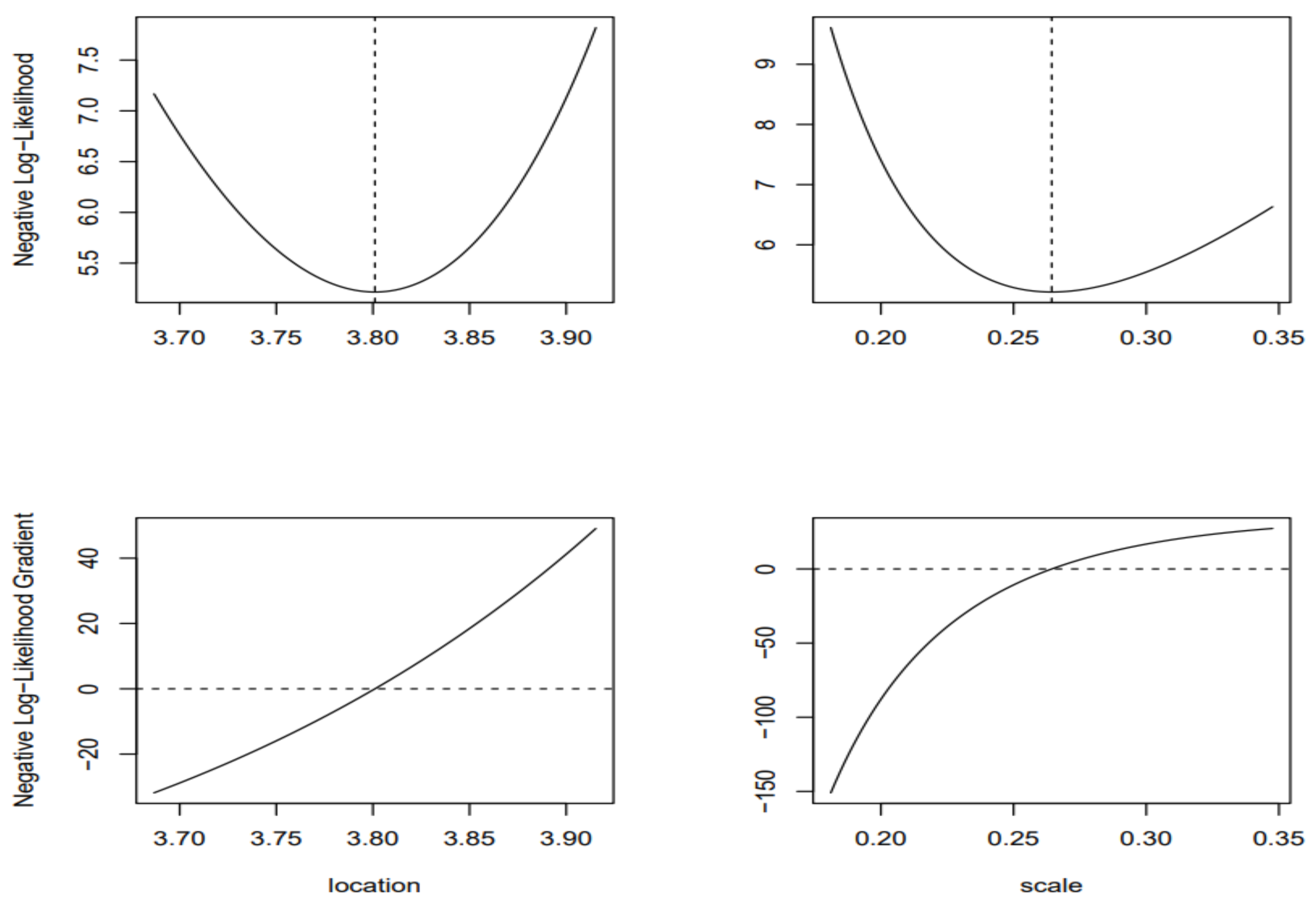
Preprints 137628 g005
Figure 5. Parameters of the Gumbel distribution.
Figure 5. Parameters of the Gumbel distribution.
Preprints 137628 g005
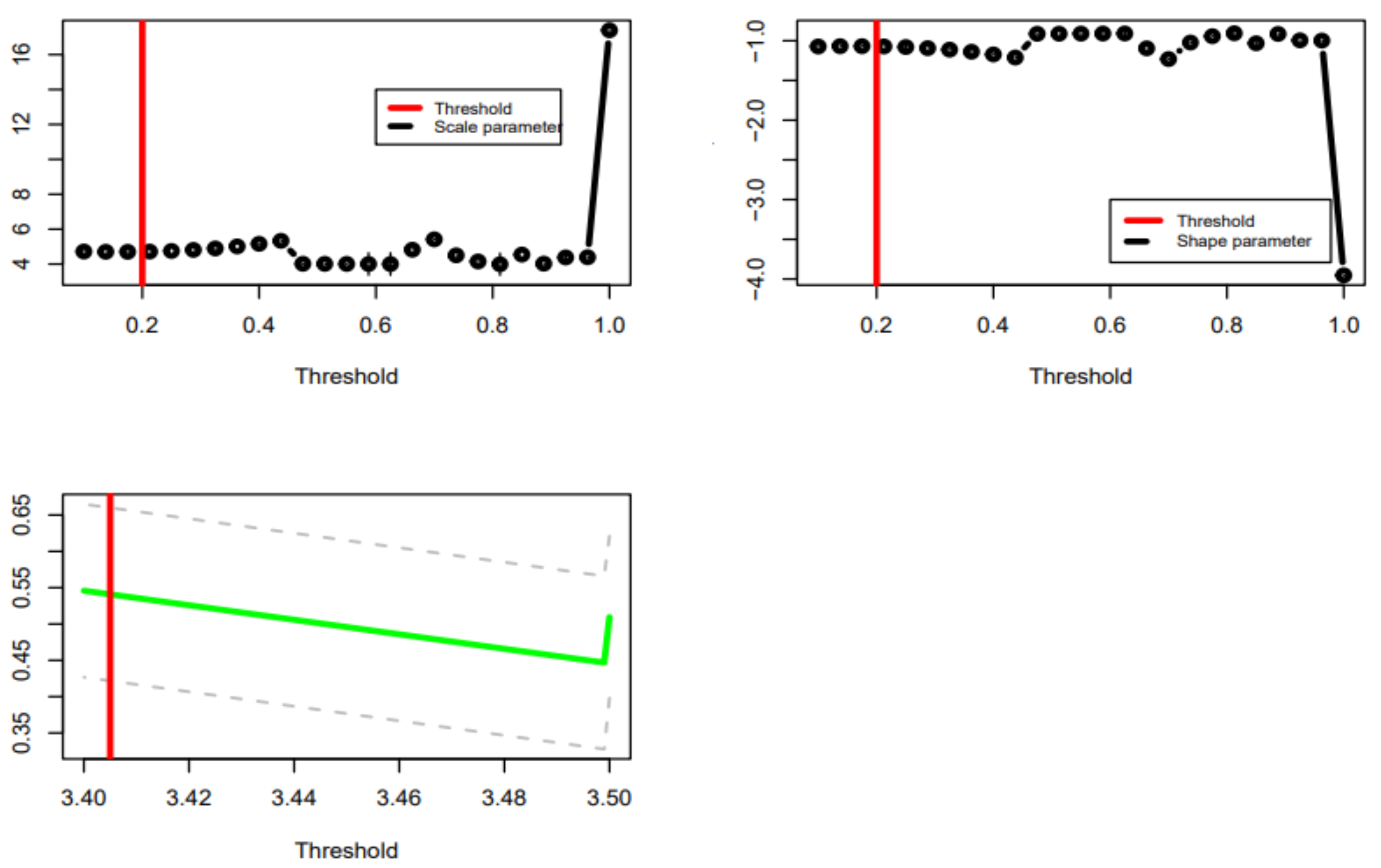
Preprints 137628 g006
Figure 6. Selection of the threshold for extreme water levels of Lake Nokoue.
Figure 6. Selection of the threshold for extreme water levels of Lake Nokoue.
Preprints 137628 g006
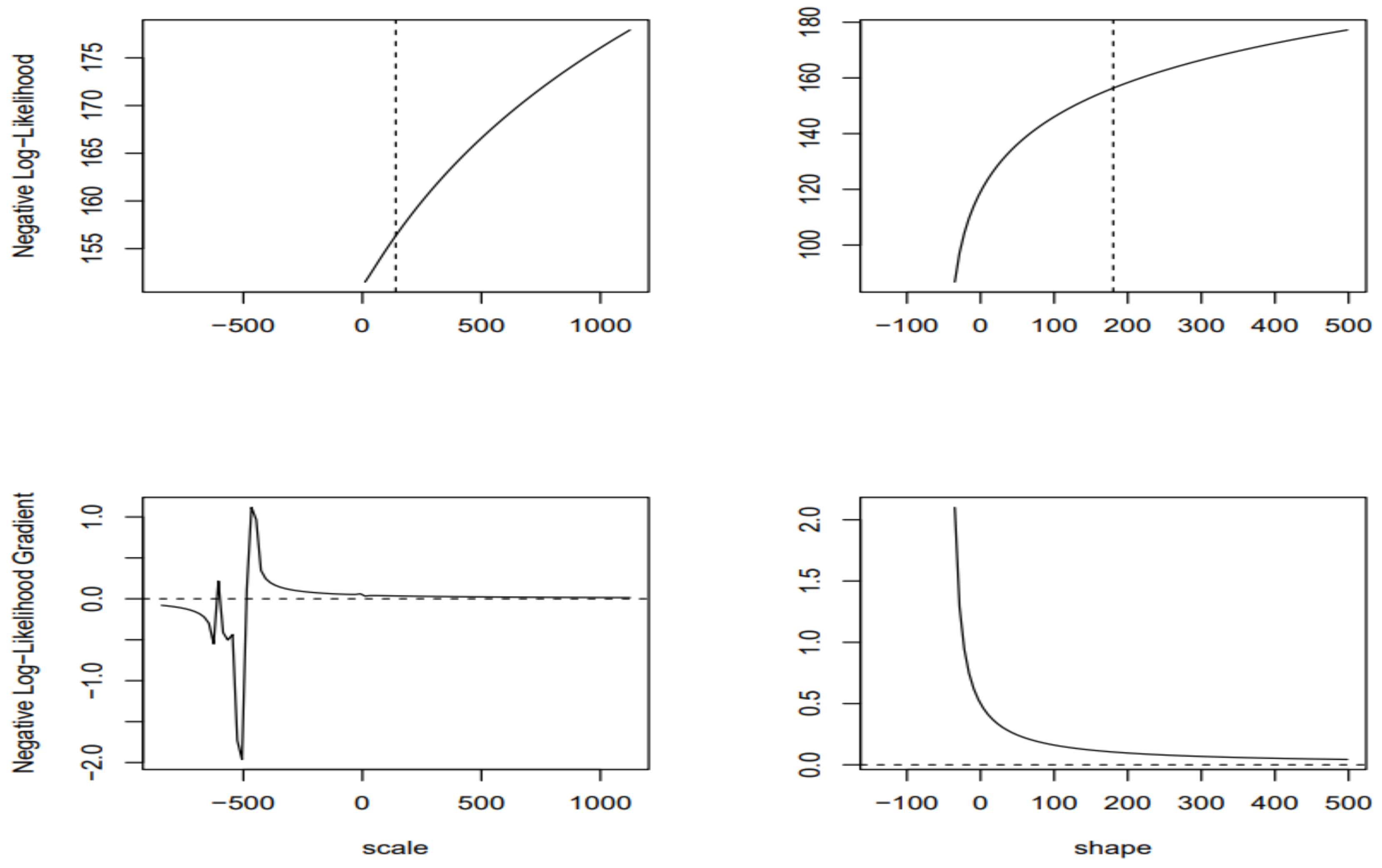
Preprints 137628 g007
Figure 7. Parameters of the Generalized Pareto (GPA) distribution.
Figure 7. Parameters of the Generalized Pareto (GPA) distribution.
Preprints 137628 g007
“Figure 8” below shows the results of the fitting performed for each of the three statistical distributions Gumbel, GEV, and GPA applied to the series of extreme water levels of lake Nokoue. The graphical analysis indicates that the scatter plot is best represented by the Gumbel distribution. The best result in the root mean square error (RMSE) test is for the Gumbel distribution, estimated at 0.0721. Therefore, the Gumbel distribution appropriately fits the extreme water levels of lake Nokoue. The L-moments diagrams and cumulative density curve also confirm the suitability of the Gumbel distribution for predicting the extreme flood water levels of Lake Nokoue, as shown in “Figure 9”.

3.4. Results of the quantile estimates for the Gumbel, GEV, and GPA distributions

The estimates from the Gumbel (G), GEV, and GPA distributions differ. At this stage, there is no criterion that clearly favors one distribution over the others. The Gumbel distribution appears to fit the tail of the distribution better. The estimates obtained with the Gumbel distribution are.
Table 4. valeurs des quantiles associées aux périodes de retour.
Table 4. valeurs des quantiles associées aux périodes de retour.
Période de retour Gumbel GEV GPA

100
50
30
20
15
10
5
3
2
4.95
4.77
4.65
4.54
4.47
4.36
4.18
4.03
3.89
4.64
4.57
4.51
4.46
4.41
4.35
4.21
4.08
3.94
4.47
4.45
4.44
4.42
4.40
4.36
4.25
4.11
3.94

4. Discussion

There are many examples where the Gumbel distribution provides remarkable results, but it seems that, with equal theoretical justifications, in some cases, it would be more beneficial to use the Fréchet distribution, particularly due to the slower decay of the latter [25,26,27,28]. This could be explained by its asymptotic behavior. Reference [29,30,31,32] in its study demonstrated that the GPA distribution was much more suitable for a series composed of values exceeding a threshold. It confirms that the tail of the GPA distribution is thicker as the value of the parameter k increases. Our results corroborate with those of [33,34,35,36,37,38,39]. These authors, in their study, demonstrated that the Gumbel distribution was more efficient than the Weibull and GPA distributions. They recommended that the estimation of parameters using the maximum likelihood method for the generalized extreme value distribution (GEV) and the generalized Pareto distribution (GPA) can be carried out very effectively and accurately using a global optimization tool that can bypass various local optima.”

5. Conclusion

The Gumbel model correctly reproduces the curves of maximum flood water heights for lake Nokoue. The return period of the largest flood experienced by lake Nokoue is 7 years. The Gumbel model will be used for the preliminary determination of the maximum water heights related to floods in the lake Nokoue basin. The main limitation of this work lies in the choice of probability distributions and the method of parameter estimation. Indeed, there is no universal and infallible method for choosing the distributions suited to different situations. However, this case study of the lake Nokoue basin serves as a basis for all flood prevention structures in the lake Nokoue basin and the determination of alert thresholds.

Acknowledgments

This work is supported in part by the world bank and the french development agency through “centre d’excellence pour l’eau et l’assainissement en afrique (c2ea)” of university of abomey-calavi in benin. the authors would like to thank the reviewers for their constructive comments, which have certainly improved the quality and readability of the article.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

References

  1. S. YUE et P. A. PILON. Comparison of the power of the test, Mann–Kendall and bootstrap tests for trend detection. Hydrol. Sci. J. 2004,49, 1, 21–38.
  2. Dabire, N.; Ezin, E.C.;Firmin, A.M. Forecasting Lake Nokoue Water Levels Using Long Short-Term Memory Network. Hydrology journal 2024. [CrossRef]
  3. Namwinwelbere, D., Eugène, E. C., & Firmin, A. M. Current State of Flooding and Water Quality of Nokoue Lake in Benin (Ouest Africa). European Journal of Environment and Earth Sciences 2022, 3(6), 75–81. [CrossRef]
  4. N. Dabire, E.C. Ezin and A.M. Firmin. Water quality index of lake Nokoue prediction using random forest and artificial neural network Int. J. of Adv. Res 2024, 610-624.
  5. N. Dabire, E. C. Ezin and A. M. Firmin, “Water Quality Assessment Using Normalized Difference Index by Applying Remote Sensing Techniques: Case of Lake Nokoue,” 2024 IEEE 15th Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 2024, pp. 1-6. [CrossRef]
  6. Meylan, P. et Musy, A., 1999. Hydrologie fréquentielle. Editions H.G.A Bucarest, p.413.
  7. Paturel J. E. et Servat E. Variabilité du régime pluviométrique de l’Afrique de l’Ouest non sahélienne entre 1950 et 1989 : Hydrological Sciences Journal 1998, 43, 921-935.
  8. Liang Peng and A.H. Welsh. Robust estimation of the generalized pareto distribution. Extremes 2001, 4(1), 53–65. [CrossRef]
  9. Smith R. L 1994. Multivariate Threshold Methods. Kluwer, Dordrecht.
  10. Meylan, P., Favre, A.C, Musy, A. Hydrologie fréquentielle : Une science prédictive. Presses Polytechniques et Universitaires Romandes, 2008, 168. Édition : Édition du millénaire, p.265.
  11. Coles S. An Introduction to Statistical Modelling of Extreme Values. Springers Series in Statistics, 2001, London.
  12. Laborde J.P. Eléments d’hydrologie de surface. L’Université de Nice-Sophia Antipolis, Edition Centre National de la Recherche Scientifique (C.N.R.S), 2000, 8- 137.
  13. Hosking J.R.M. and J.R. Wallis. Parameter and quantile estimation for the generalized pareto distribution. Technometrics 1987, 29(3), 339–349.
  14. Kluppelberg C. and A. Bivariate extreme value distributions based on polynomial dependence ¨ functions. Math Methods Appl Sci, 2006, 29(12),1467–1480. [CrossRef]
  15. B. T. Goula, A. Konan, T. Brou, Y. Issiaka, S. V. Fadika et B Srohourou. Estimation des pluies exceptionnelles journalières en zone tropicale: cas de la Côte d’Ivoire par comparaison des lois log normale et de Gumbel. Hydrological sciences journal, 2007, 52 (1), 49 -67.
  16. Habibi, M. Meddi et A. Boucefiane. Analyse fréquentielle des pluies journalières maximales : Cas du Bassin Chott-Chergui. Nature et Technology 2013, (8), 41.
  17. N. Soro, T. Lasm, B. H. Kouadio, G. Soro, K. E. Ahoussi. Variabilité du régime pluviométrique du Sud de la Côte d’Ivoire et son impact sur l’alimentation de la nappe d’Abidjan. Rev. Sud Sciences et technologies 2006, (14), 30-40.
  18. Mises, R., von. La distribution de la plus grande de n valeurs. Selected papers, 1954,2, 271-294.
  19. Bortot P. and S. Coles. The multivariate gaussian tail model: An application to oceanographic data. Journal of the Royal Statistical Society. Series C: Applied Statistics 2000, 49(1), 31–49. [CrossRef]
  20. Coles, J. Heffernan, and J. Tawn. Dependence measures for extreme value analyses. Extremes 1999, 2(4), 339–365.
  21. Fisher R.A. and L.H. Tippett. Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Proceedings of the Cambridge Philosophical Society 1928, 24, 180–190. [CrossRef]
  22. Fréchet M. Sur la loi de probabilité de l’écart maximum. Annales de la Société polo-naise de Mathématique 1927, 6. Cracovie.
  23. Gumbel É.J. Statistical theory of extreme values and some practical applications. National Bureau of Standards 1954, Washington. [CrossRef]
  24. Jenkinson A. F. The frequency distribution of the annual maximum (or minimum) values of meteorological events. Quaterly Journal of the Royal Meteorological Society 1955, 81,158–172.
  25. Jowitt, P.W. The extreme-value type 1 and the principal of maximums entropy. J. Hydrol 1979, 42, 23-38.
  26. Ju’arez S.F. and W.R. Schucany. Robust and efficient estimation for the generalized pareto distribution. Extremes 2004, 7(3),237–251. [CrossRef]
  27. Pickands J 1981. Multivariate extreme value distributions. In Proceedings 43rd Session International Statistical Institute.
  28. Pickands J. III 1975. Statistical inference using extreme order statistics. Annals of Statistics, 3:119–131.
  29. CIEH. Courbes hauteur de pluie-fréquence Afrique de l‘Ouest et Centrale pour des pluies de durée 5 mn à 24 h. 1984.
  30. Christophe Ancey. Risques hydrologiques et aménagement du territoire. École Polytechnique Fédérale de Lausanne, Ecublens, CH-1015 Lausanne, Suisse 2011.
  31. Cunnane C. Note on the poisson assumption in partial duration series model. Water Resour Res, 1979, 15(2), 489–494. [CrossRef]
  32. Matthew J. Purvis, Paul D. Bates, Christopher M. Hayes. A probabilistic methodology to estimate future coastal flood risk due to sea level rise,Coastal Engineering 2008, 55, 12, 1062-1073. [CrossRef]
  33. Courtney M. Thompson, Tim G. Frazier, Deterministic and probabilistic flood modeling for contemporary and future coastal and inland precipitation inundation, Applied Geography 2014, 50, 1-14. [CrossRef]
  34. Roman Krzysztofowicz. Probabilistic flood forecast: Exact and approximate predictive distributions, Journal of Hydrology 2014, 517, 643-651. [CrossRef]
  35. Pascal Lardet, Charles Obled. Real-time flood forecasting using a stochastic rainfall generator, Journal of Hydrology 1994, 162, 3–4, 391-408. [CrossRef]
  36. Shien-Tsung Chen, Pao-Shan Yu. Real-time probabilistic forecasting of flood stages, Journal of Hydrology 2007, 340, 12, 63-77. [CrossRef]
  37. Roman Krzysztofowicz. The case for probabilistic forecasting in hydrology, Journal of Hydrology 2001, 249, 14, 2-9. [CrossRef]
  38. Kupfer, S., MacPherson, L. R., Hinkel, J., Arns, A., & Vafeidis, A. T. A comprehensive probabilistic flood assessment accounting for hydrograph variability of ESL events. Journal of Geophysical Research: Oceans, 2024 ,129. [CrossRef]
  39. Karl-Erich Lindenschmidt, Prabin Rokaya, Apurba Das, Zhaoqin Li, Dominique Richard.
  40. A novel stochastic modelling approach for operational real-time ice-jam flood forecasting, Journal of Hydrology 2019, 575, 381-394.
Preprints 137628 g001
Figure 1. Location of the study area.
Figure 1. Location of the study area.
Preprints 137628 g001
Preprints 137628 g002
Figure 2. Annual maximum water levels.
Figure 2. Annual maximum water levels.
Preprints 137628 g002
Preprints 137628 g003
Figure 3. Empirical probability density of annual maximum water levels.
Figure 3. Empirical probability density of annual maximum water levels.
Preprints 137628 g003
Preprints 137628 g008
Figure 8. Fitting of the three distributions.
Figure 8. Fitting of the three distributions.
Preprints 137628 g008
Preprints 137628 g009
Figure 9. Performance criteria: Probability density function; Cumulative distribution function; Taylor diagram; and L-moment diagrams..
Figure 9. Performance criteria: Probability density function; Cumulative distribution function; Taylor diagram; and L-moment diagrams..
Preprints 137628 g009
Table 1. Standardized Classification of Water Heights.
Table 1. Standardized Classification of Water Heights.
Risk Level Standardized Water Height Index
Critical Catastrophique Index ≥ 2.0
Significant 1.5 ≤ Index < 1.99
Moderate 1 ≤ Index < 1.49
Limited -∞≤ Index < 0.99
Table 2. Values of the statistical tests.
Table 2. Values of the statistical tests.
Statistical tests p-value
independance 0.2
homogeneity 0.4
stationarity 0.4
Table 3. Results of the parameters for the gumbel, gev, and gpa distributions.
Table 3. Results of the parameters for the gumbel, gev, and gpa distributions.
Statistical distributions Parameters
xi         alpha kappa
lois de Gumbel 3.80         0.25
lois GEV 0.30         0.3 0.27
Lois GPA 3.43        1.003 0.96
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated