Prerpints.org logo
Preprint
Article

Multi-Frequency Microwave Sensing System with Frequency Selection Method for Pulverized Coal Concentration

This version is not peer-reviewed.

Submitted:

28 October 2024

Posted:

28 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Accurate measurement of pulverized coal concentration (PCC) is crucial for optimizing the production efficiency and safety of coal-fired power plants. Traditional microwave attenuation methods typically rely on a single frequency for analysis while neglecting valuable information in the frequency domain, making them susceptible to the varying sensitivity of the signal at different frequencies. To address this issue, we propose an innovative frequency selection method based on principal component analysis (PCA) and orthogonal matching pursuit (OMP) algorithms and implement a multi-frequency microwave sensing system for PCC measurement. This method transcends the constraints of single-frequency analysis by employing a developed hardware system to control multiple working frequencies and signal paths. It measures insertion loss data across the sensor cross-section at various frequencies and utilizes PCA to reduce the dimensionality of the high-dimensional full-path insertion loss data. Subsequently, the OMP algorithm is applied to select the optimal frequency signal combination based on the contribution rates of the eigenvectors, enhancing measurement accuracy through multi-dimensional fusion. Experimental results demonstrate that the multi-frequency microwave sensing system effectively extracts features from high-dimensional PCC samples and selects the optimal frequency combination. Filed experiments conducted on five coal mills show that, within a common PCC range of 0–0.5 kg/kg, the system achieves a minimum mean absolute error (MAE) of 1.41% and a correlation coefficient of 0.85. These results indicate that the system can quantitatively predict PCC and promptly detect PCC fluctuations, highlighting its immediacy and reliability.
Keywords: 
Subject: 
Engineering  -   Electrical and Electronic Engineering

1. Introduction

In coal-fired power plants, the combustion conditions within boilers are intricately linked to the conveying conditions of pulverized coal in each burner. Factors such as the velocity and concentration of pulverized coal, as well as the uniformity of the air-coal mixture in individual burners, directly affect combustion stability and boiler efficiency [1]. Issues such as flame skewing and unstable ignition may lead to significant economic losses and compromise plant safety. Achieving optimal boiler combustion requires meticulous real-time control of pulverized coal parameters, which includes precise measurement of airflow and pulverized coal flow.
In power plants, pulverized coal flow is classified as dilute-phase gas-solid two-phase flow. Influenced by pipeline geometric, air temperature and humidity, and the physical properties of coal particles, the flow exhibits diverse patterns and random distributions, making the process highly complex [2]. Consequently, measuring the parameters of pulverized coal flow presents substantial challenges. Over the years, researchers have made various attempts to address these challenges. Baucum et al. [3] employed Coriolis flow meters in the 1970s to measure dense-phase coal flows. Gu et al. [4] utilized dual-frequency ultrasound for the online detection of coal particle volume fractions and sizes, while Wang et al. [5] applied electrical capacitance tomography (ECT) to mitigate the impact of gas-solid flow patterns and measure pulverized coal concentration (PCC). Cai et al. [6] analyzed particle size, average particle number density, and concentration using light transmission fluctuation. With the advancement of computing techniques, researchers have leveraged advanced algorithms and models to enhance measurement processes [7]. For instance, Wang et al. [8,9] integrated adaptive wavelet and adaptive fuzzy neural networks to enhance electrostatic and capacitive sensors for measuring coal/biomass/air three-phase flows. Jin et al. [10] introduced a digital holographic particle analyzer (DHPA) for the three-dimensional measurement of fuel particles using pulsed digital inline holography.
Microwave technology, successfully applied in various industrial contexts, has also been explored for the measurement of pulverized coal. Methods include transmission methods, resonant cavity methods, microwave tomography methods (MWT), and Doppler methods. Transmission methods [11,12,13] estimate solid particle concentration based on the propagation loss of microwave signal after passing through the space of pulverized coal. Resonant cavity methods [14,15] utilize phase shifts induced by changes in effective permittivity at resonance frequencies to determine solid concentrations. MWT reconstructs spatial distributions of permittivity using multiple transmitting and receiving antennas, initially applied in medical research before being adapted for industrial imaging of oil-gas two-phase flows [16,17]. Doppler methods [18,19] typically detect particle velocities by measuring frequency shifts in reflected microwave signals from solid-gas two-phase flow.
Microwave techniques are non-invasive and can enhance the reliability, stability, and representativeness of PCC measurement. Common microwave measurement methods typically employ single frequency, [14,17,18,19,20]. However, variations in signal sensitivity at different frequencies may affect measurement results. Consequently, microwave characteristics, such as attenuation and phase shift, yield different results at various frequencies, suggesting that multi-frequency measurements can provide more comprehensive information [21], although excessive frequencies may introduce redundancy. Therefore, effective methods for frequency selection are essential. Table 1 summarizes similar efforts made by other researchers.
In this paper, a frequency selection method for the PCC sensing system is presented. By applying dual-dimensionality reduction through principal component analysis(PCA) and orthogonal matching pursuit(OMP), this data-driven method analyzes complex features of extensive frequency signals and evaluates the contribution of each frequency signal to develop a multi-frequency microwave sensing system for optimizing PCC measurement at power plants.

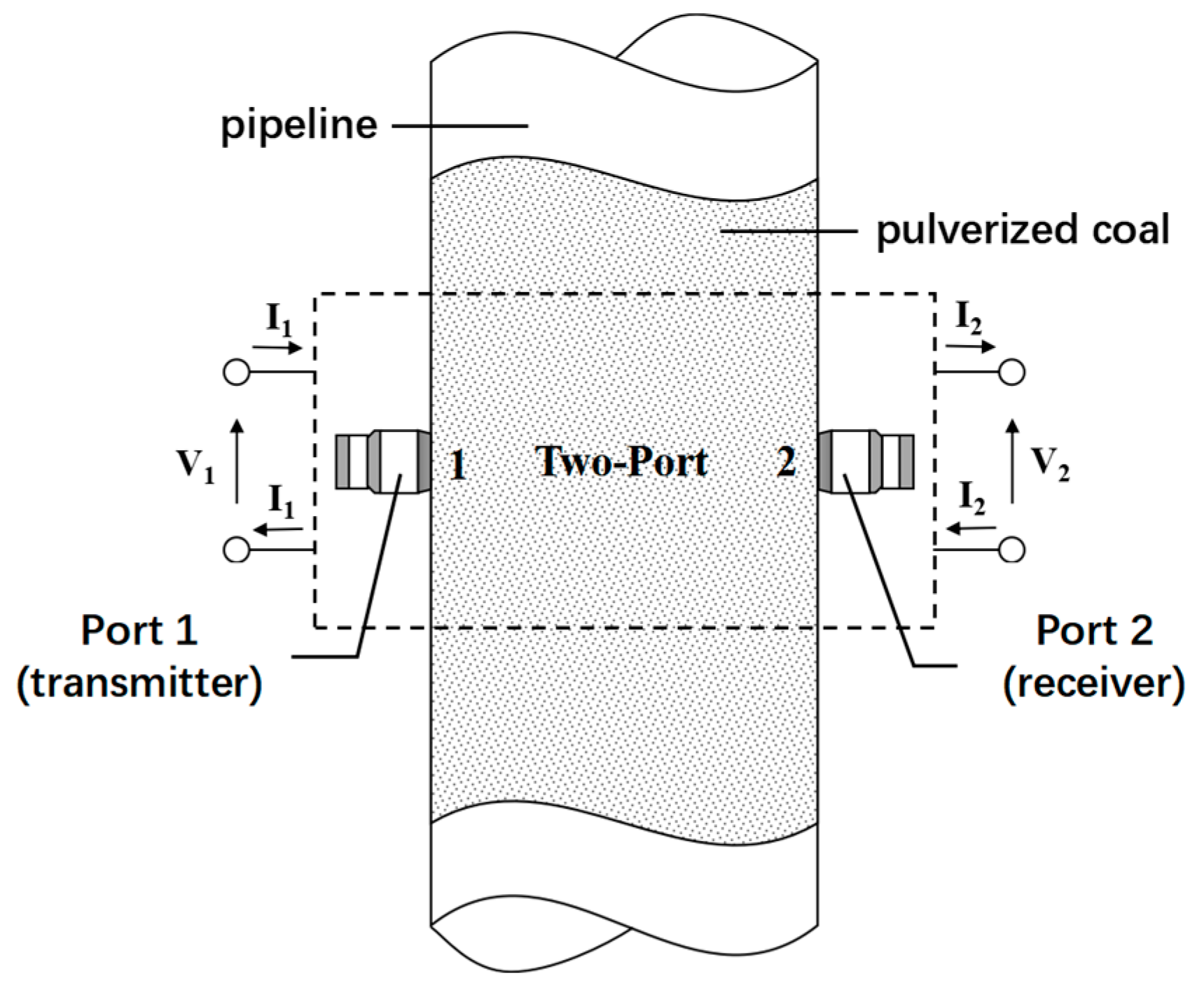
2. PCC-Sensing Mechanism

As illustrated in Figure 1, the coal pipeline for pulverized coal flow can be regarded as a two-port guided wave system. By placing a transmitter (Port 1) on the pipeline, the transmitted wave passes through pulverized coal particles and received by the receiver at Port 2. Due to the lossy property of PCC, the transmitted wave is attenuated and the attenuation is proportional to the concentrations of pulverized coal. Such fact allowes the determination of PCC based on wave attenuation. The attenuation is quantified by the ratio of the receiving power at Port 2 to the emitting power at Port 1, i.e., the insertion loss S21.
Denote the power emitted by the transmitter as P 0 . The received power at distance z from the source can be quantified by
P z = P 0 e − 2 α z
where α is the attenuatioin constant, which depends on the frequency and the electromagnetic parameter (e.g., conductivity) of the medium. The expression for α is:
α = ω c ε r 2 1 + σ ω ε r ε 0 2 − 1
where   ω is the angular frequency, c is the wave speed, ε r is the relative permittivity of the medium, σ is the conductivity of the medium, and ε 0 is the permittivity of free space.
The pneumatic conveying process for pulverized coal is a typical gas-solid two-phase flow, which is inherently complex, making the study of electromagnetic behavior of such multiphase systems challenging. We introduce the macroscopic dielectric constant to analyze the pulverized coal conveying process. The macroscopic dielectric constant incorporates the geometric parameters of the mixture, such as the dielectric constant and volume ratio of material components. The heterogeneous mixture can be electromagnetically equivalent to a homogeneous medium with the dielectric constant for two-phase mixtures [23]:
ε m = 1 − Δ V s ε g + Δ V s ε s
where Δ V s is the volume ratio of solid phase in the mixture ε g is the dielectric constant of the gas phase, and ε s of the solid phase.
Deriving the equation for the volume ratio of the solid phase Δ V s yields the following formula::
ε m ′ = ε s − ε g
Since the dielectric constant of solids is generally higher than that of gases, the dielectric constant of a gas-solid mixture positively correlates with the volume ratio of the solid phase. As the volume ratio of solid phase increases, the macroscopic dielectric constant of the gas-solid mixture increases, resulting in a stronger attenuation effect of the microwave signal as it traverses the solid phase. Moreover, combining Equation (2), the attenuation constant α can be expressed as a function f x related to ε m . Due to the correlation between ε m and Δ V s , a function g ( x ) can be employed to represent the mapping relationship between α and Δ V s , as shown in the following equation:
α = K · f ε m = K · g ( Δ V s )
where K is a characteristic parameter of the PCC sensor, determined by the sensor's dimensions, structure, and other attributes.
Given that the insertion loss S21 is directly linked to the attenuation constant, it indicates an indirect relationship between the insertion loss S21 of the two-port system and the volume ratio of the solid phase. Therefore, by extracting the characteristics of the insertion loss S21, we can analyze sensor data to reveval the abstract relationship. Consequently, this enables the inference of solid phase concentration at the measured cross-section based on the measured S21 data of the two-port system.

3. Materials and Methods

The overall framework of the proposed PCC measurement system is illustrated in Figure 2. The system is composed of three main components: a microwave sensor, a high-speed microwave signal routing module, and a programmable frequency and signal path control module. The microwave sensor is made of 16 electrodes which can emit or collect the electromagnetic waves, while the emitting and collecting function can be altered by a switch matrix. The high-speed microwave signal routing module is responsible for amplification, noise-reduction, filtering, and analogue-to-digital conversion. The programmable frequency and signal path control module communicates bidirectionally with the high-speed microwave signal routing module. It has the function of setting working frequency and signal path.

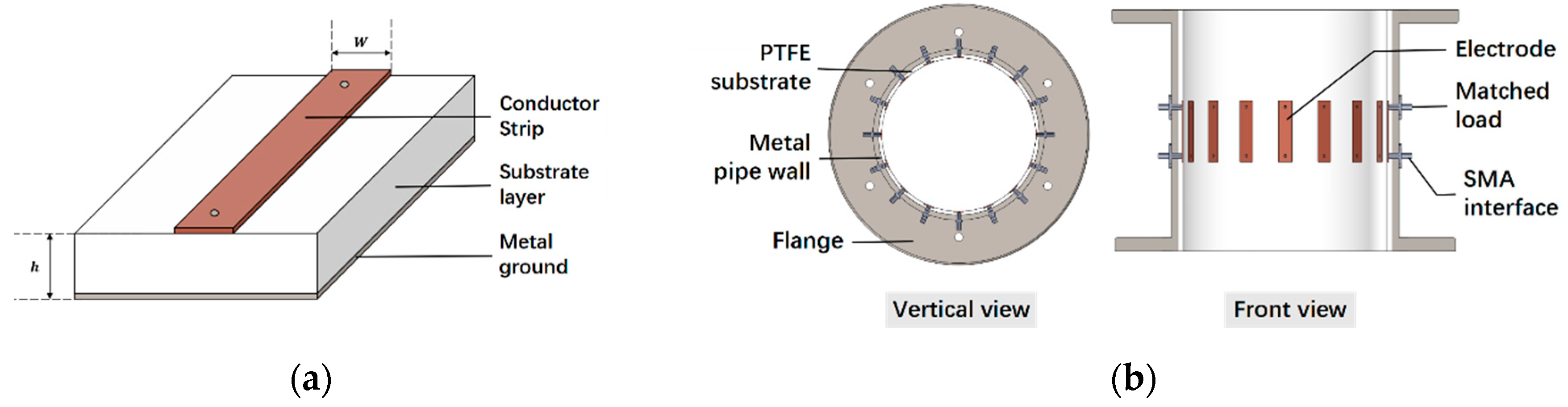
3.1. Design of Microwave Sensor

The metal electrodes constitute the core unit of the sensor, primarily responsible for transmitting and receiving microwave signals to establish a signal path. A polytetrafluoroethylene (PTFE) substrate layer, positioned beneath the electrodes, securely anchors them in place. Each electrode is soldered to two SMA connectors, which connect to the SMA cable and matching load, respectively. In microwave signal transmission lines, impedance matching involves adjusting the load impedance to match the internal impedance of the excitation source, thereby maximizing the device's output power. The dimensions of the electrodes and the PTFE substrate layer are tailored to meet the 50-ohm characteristic impedance requirements, ensuring efficient microwave signal transmission. The microstrip line depicted in Figure 3(a) is a commonly used transmission line, with its characteristic impedance described by the following formula:
ε r e = ε r + 1 2 + ε r − 1 2 1 + 12 h W − 1 2
Z 0 = 120 π ε r e W h + 1.393 + 0.667 ln ⁡ W h + 1.444
where ε r e is the equivalent dielectric constant of the dielectric substrate, ε r and h are the dielectric constant and height of the dielectric substrate, respectively, W is the width of the conductor band, and Z 0 is the characteristic impedance of the microstrip transmission line.
The sensor proposed in this paper, as illustrated in Figure 3(b), is primarily designed for tomography techniques [21,24]. Its ring shape that allows it to directly replace a section of a coal pipeline in practical applications. The sensor consists of metal electrodes, a PTFE substrate layer, SMA connectors, a flange, and a metal outer wall. The metal outer wall, constructed from carbon steel, provides mechanical support and protection while also functioning as a grounding layer for microwave signals, thereby mitigating the effects of external electromagnetic interference. Furthermore, the sensor meets the necessary requirements for wear resistance, heat resistance, and non-intrusiveness.

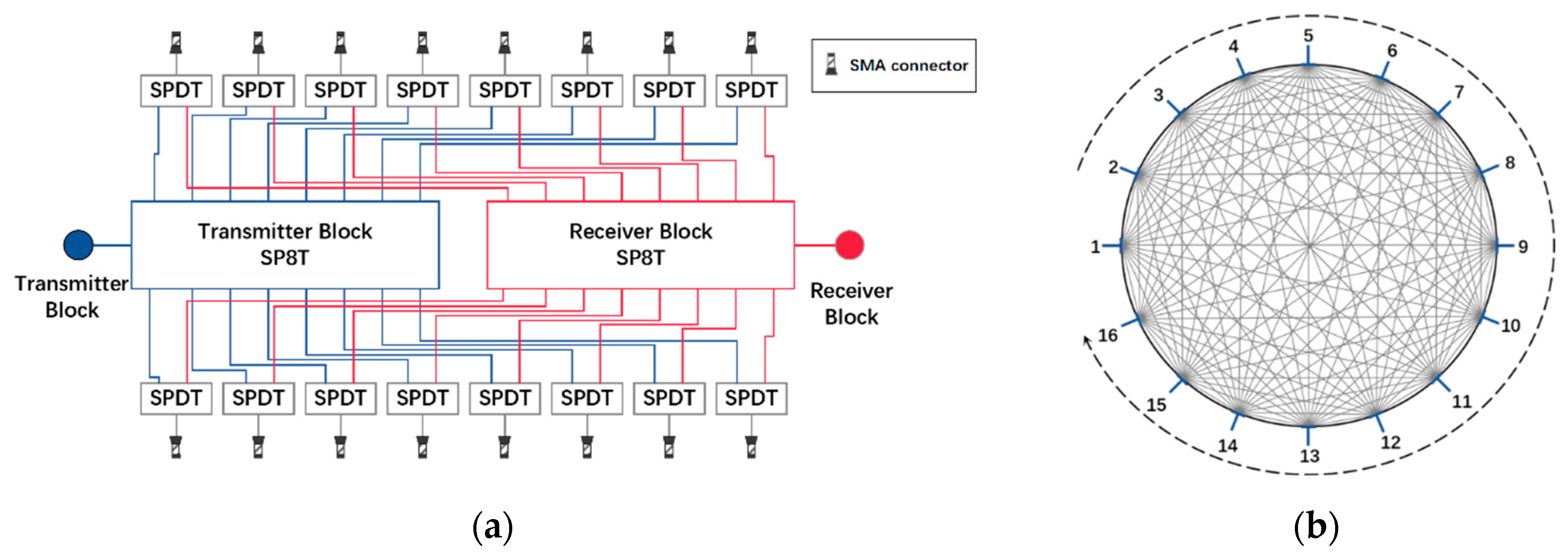
3.2. High-Speed Microwave Signal Routing Module

The high-speed microwave signal routing module comprises a 2-by-16 switch matrix and a microwave signal conditioning module. The 2-by-16 switch matrix interfaces the RF cable with the 16 electrodes of the sensor via SMA connectors, and then adjusts the switching states by controlling the transmission and reception links in the microwave signal conditioning module.
The 2-by-16 switch matrix consists of two 1-by-2 switching circuits and two 2-by-8 switching circuits [25,26]. The 1-by-2 switching circuits connect to either the transmission link or the reception link, while the 2-by-8 switching circuits select specific signal paths and determine the direction of signal flow. Signals are routed through various paths between the electrodes, as illustrated in Figure 4(a).
The SPDT RF switch and the 3-to-8 line decoder demultiplexer used in the circuit are detailed in Table 2. These components exhibit extremely fast switching times of 6 ns and 12 ns, respectively, enabling effective measurement of the rapid flow of pulverized coal.
During system operation, one pair of electrodes is designated as the transmitter and receiver, forming a signal path. By switching the signal propagation path, a total of C 16 2 = 120 electrode pairs can be generated. Considering the hardware asymmetry, it is necessary to alternate the transmitter and receiver, resulting in a total of A 16 2 = 240 distinct electrode pairs and corresponding signal paths, as illustrated in Figure 4(b). The abundance of signal paths allows the measurement area to transition from a linear to a surface format, thereby covering a larger area. This approach effectively mitigates the uneven distribution of pulverized coal and addresses the low sensitivity of the central electric field, leading to more accurate measurements.
The conditioning of microwave signals primarily depends on the transmission and reception links. The transmission link regulates the output frequency and power of the microwave signal through a voltage controlled oscillator (VCO) and an amplifier. Due to the varying sensitivity of signals across different frequency bands, changes in the working environment may lead to fluctuations in measurement performance. Therefore, prior to deployment, it is essential to identify the frequency that best suits the current operating conditions, ensuring effective noise suppression and optimal measurement results. The VCO used is the ROS-2500+, which provides frequency sweeping from 1.2 GHz to 2.5 GHz with a voltage range of 0-11 V. The reception link consists of an attenuator and a power detector, which are primarily used to measure the amplitude of the received signal. The power detector employed is the AD8362 chip, capable of detecting microwave signals with a minimum signal strength of -55 dBm.

3.3. Programmable Frequency and Signal Path Control Module

The module integrates a host computer with a Data Acquisition card (DAQ). To mitigate dust pollution in industrial environments, the host computer employs a specialized industrial computer designed to withstand a wide range of operating temperatures, humidity, vibrations, and dust, ensuring long-term reliable performance. Additionally, a software has been developed to issue hardware control commands, managing the system’s working frequency and signal path while receiving and processing sensor data. It facilitates visual interaction with the user. The DAQ executes commands from the host computer and provides bidirectional communication between the hardware circuits and the host computer. The PCIE-6361 is employed as the DAQ, offering exceptionally high sampling and data transfer rates to meet the system’s high-speed read and write requirements.
The high-dimensional PCC dataset contains full-path data across multiple frequencies, which makes direct computation highly complex and challenging to interpret intuitively. To address this, we implemented a dual-dimensionality reduction approach using PCA and OMP. PCA is used to reduce dimensionality of the full-path data, while OMP selects the optimal frequency.
PCA aims to identify k new variables that capture the primary features of the dataset, effectively compressing the original data matrix and retaining the minimum number of dimensions that represent the most significant characteristics. During PCA, the process involves calculating the covariance matrix and deriving its eigenvalues and corresponding eigenvectors. Each eigenvector corresponds to a principal component, representing the projection of the original data onto the eigenspace. The i-th principal component P C i can be expressed by the following formula:
P C i = ∑ j a i j x j
where a i j is the weight of the i-th principal component on the j-th original dimension, and x j is the j-th dimension of the original data.
The information content of the i-th principal component, i.e., the cumulative explained variance, is calculated as the ratio of its eigenvalue to the sum of all eigenvalues. The number of principal components, k, can be determined based on the desired level of cumulative explained variance.
After applying PCA, a reduced number of principal components is retained for each frequency. However, due to the large number of frequencies, directly using iterative methods to select the optimal frequency combination may still risk computational explosion. OMP is a sparse signal reconstruction algorithm based on a greedy strategy that, constructs a sparse representation of a signal by iteratively selecting the dictionary atoms most relevant to the residuals. In each iteration, OMP updates the residuals and coefficients through orthogonal projections, ensuring orthogonality and stability among the selected atoms. Therefore, OMP can effectively mitigate the risk of computational explosion. For the PCC dataset, the objective is to determine a combination S of frequency signals from a matrix A ∈ R t × v of multiple sets of eigenvectors such that the predicted PCC y ∈ R t closely matches the actual PCC of the coal pipeline. During computation, the eigenvector with the largest inner product with the residual vector is continuously selected and added to the frequency combination S ← S ∪ i . Subsequently, the optimal eigenvector x S = A s T A S − 1 A S T y is computed using the least squares method based on the eigenvectors in the current frequency combination S to make A S x S approximate the actual PCC as closely as possible, where A S is a sub-matrix consisting of the eigenvectors in the combination S .

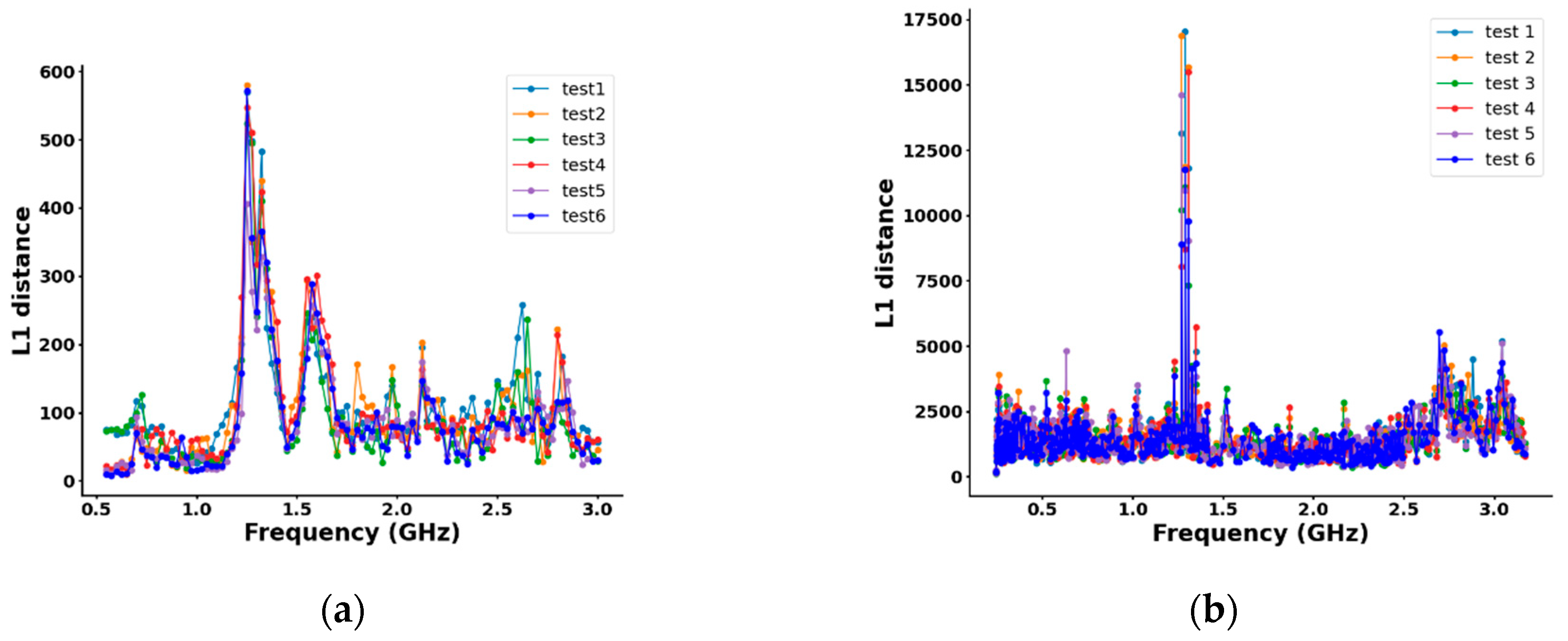
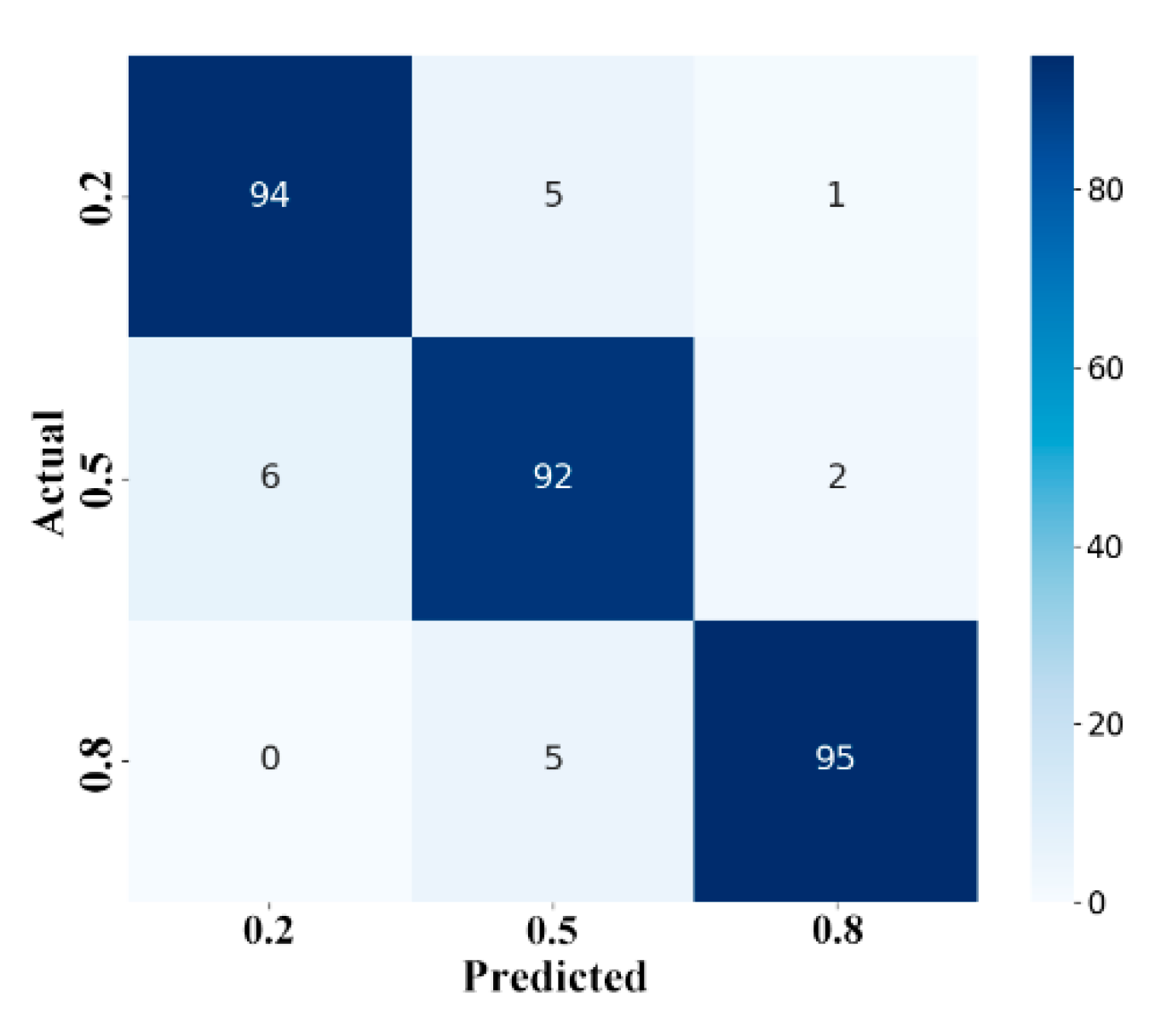
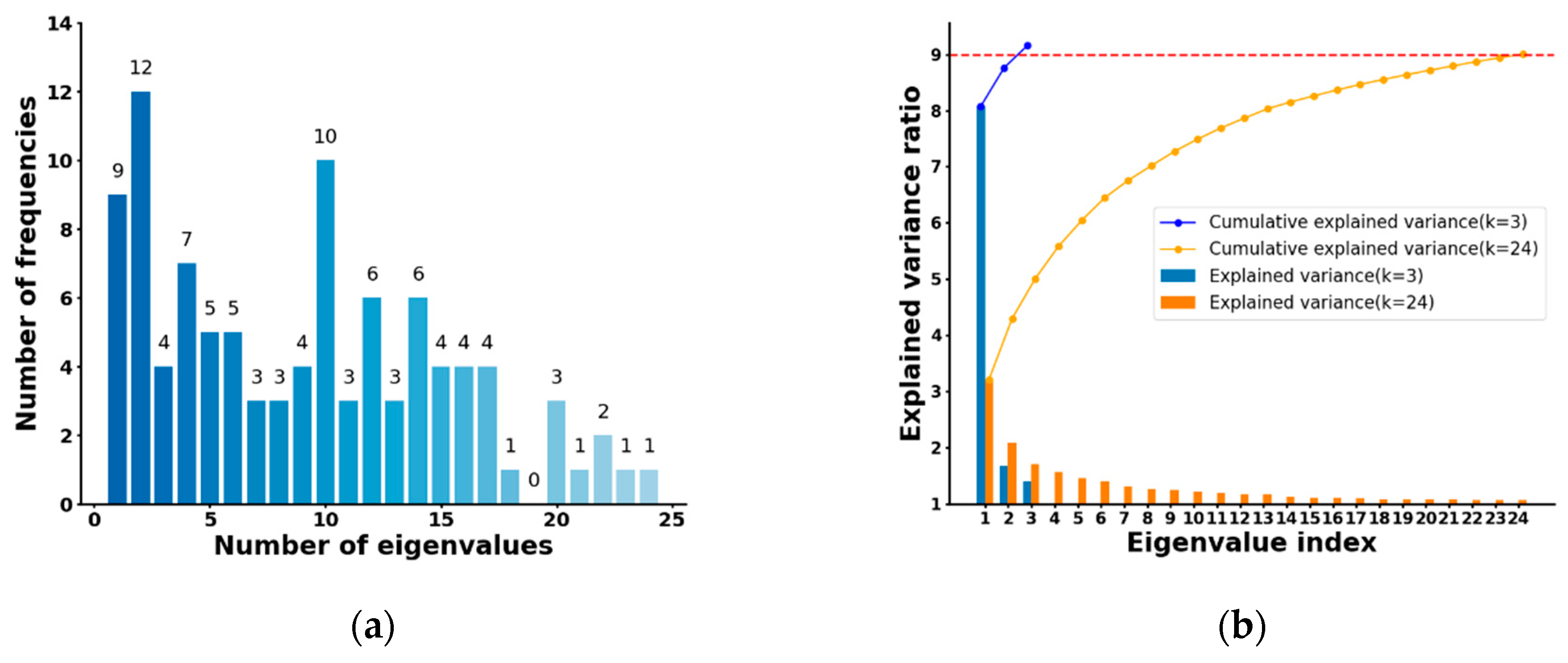
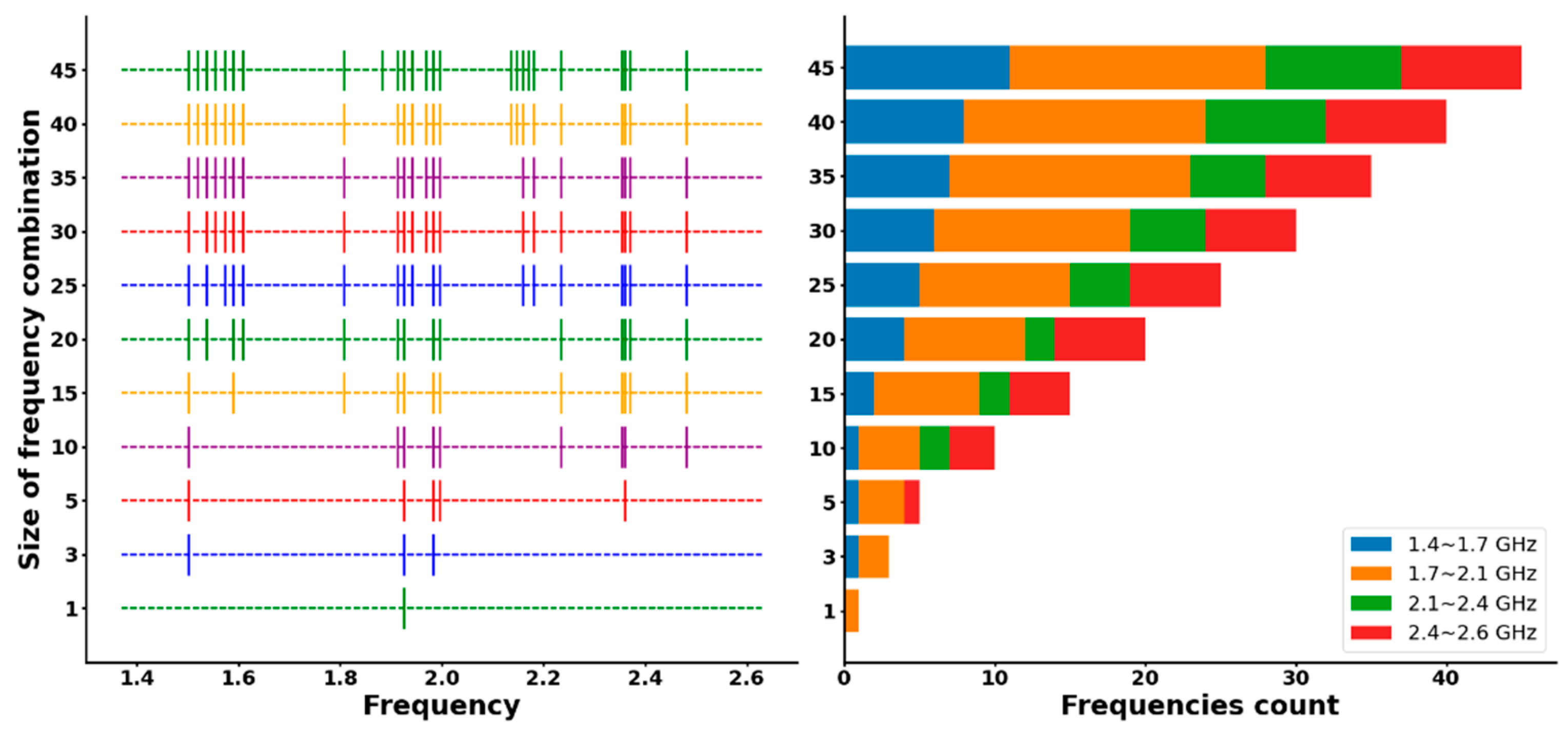
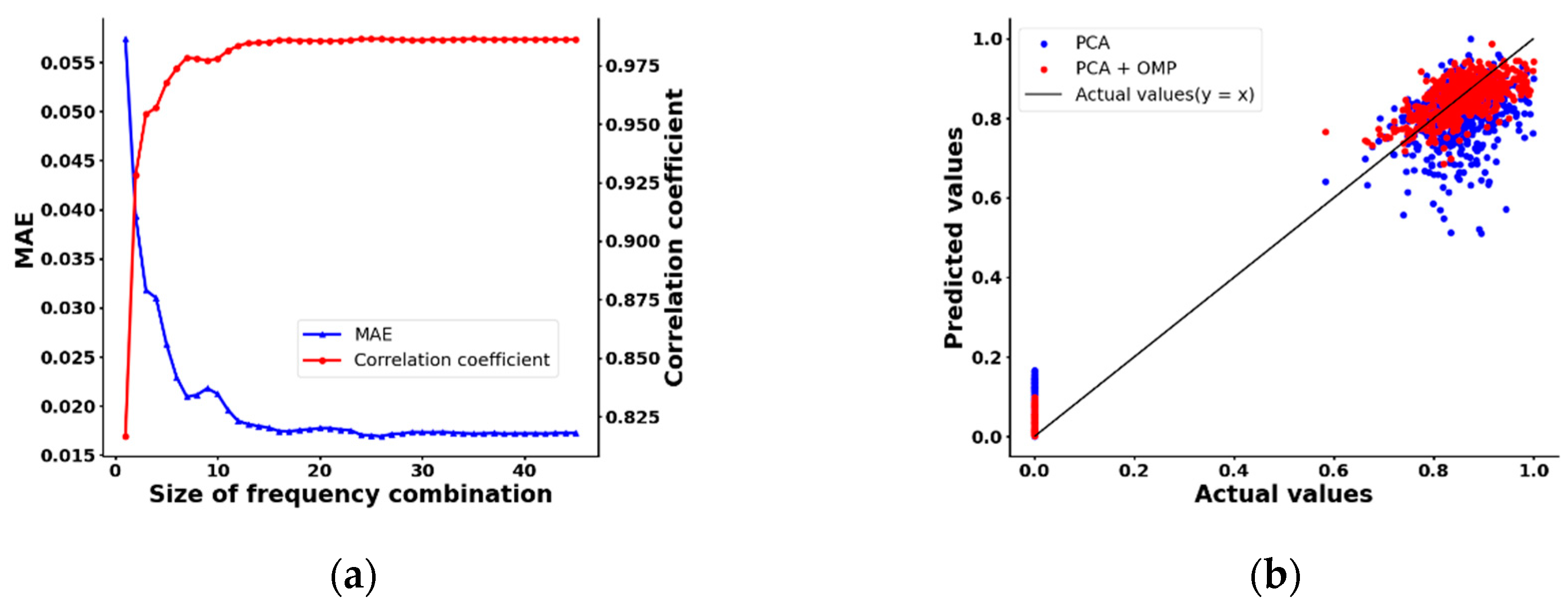
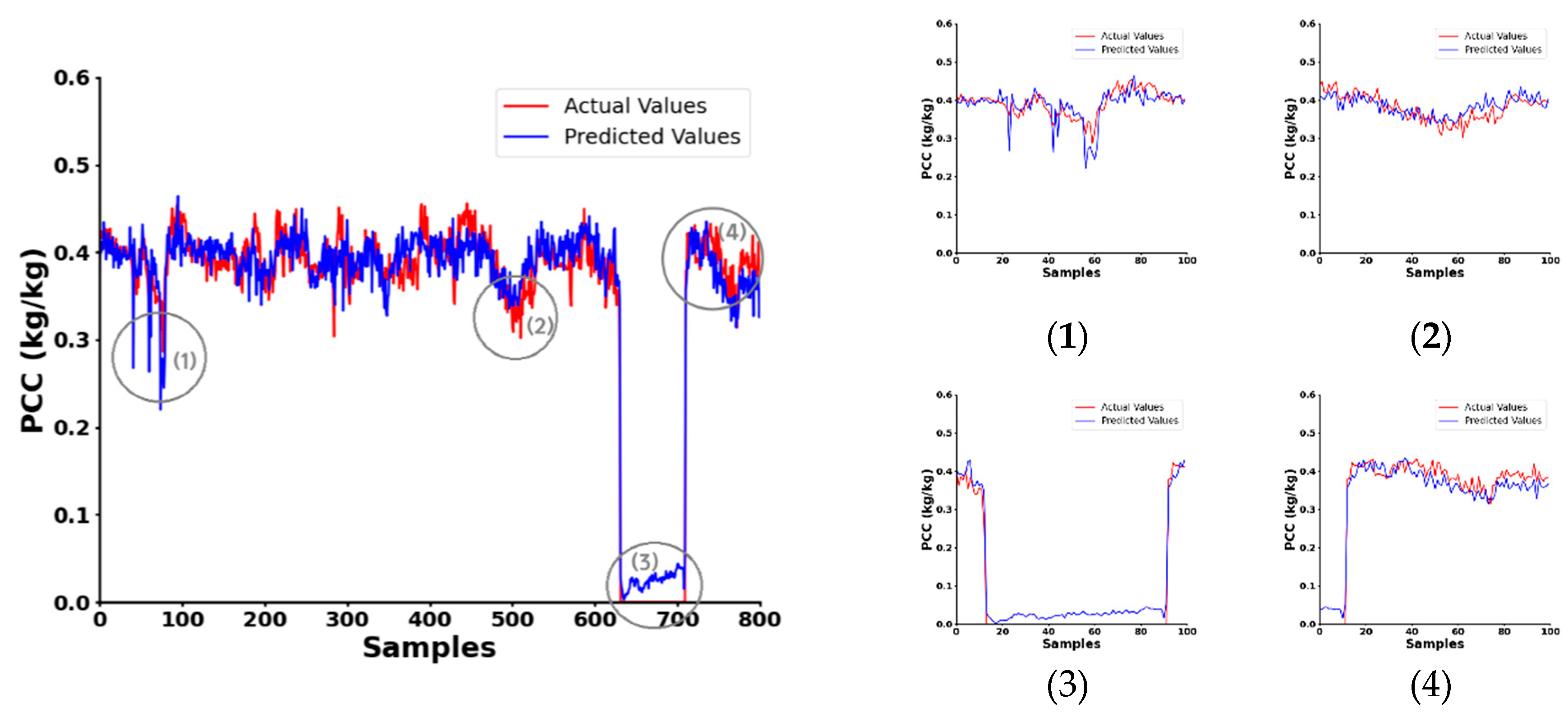
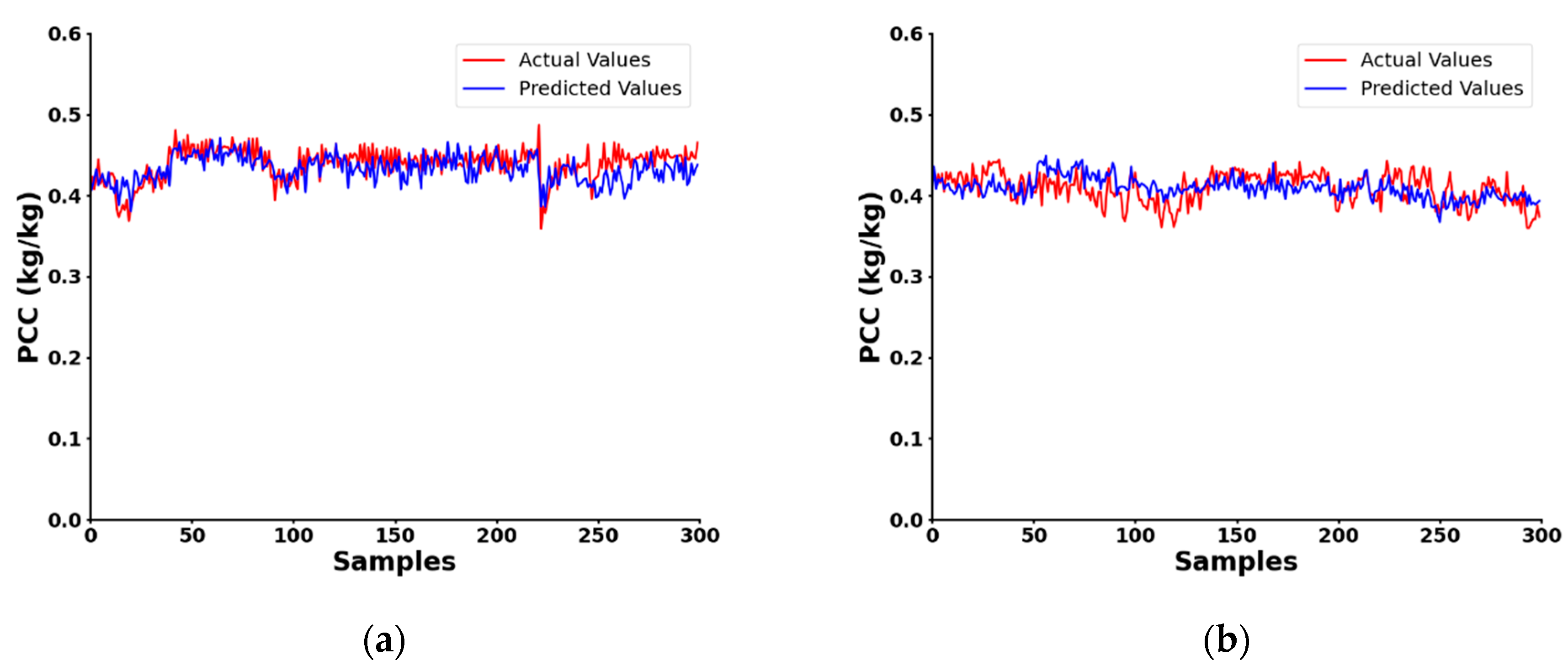
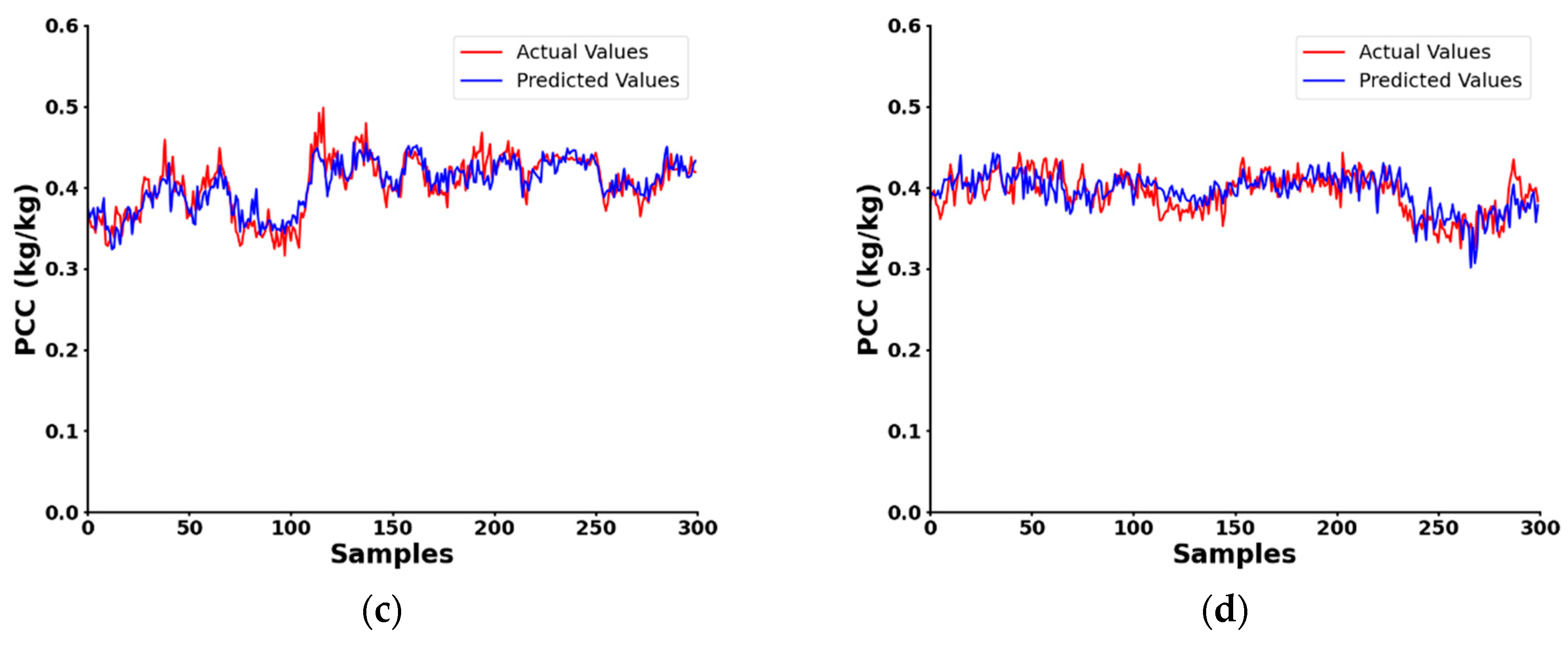
4. Experiments and Results

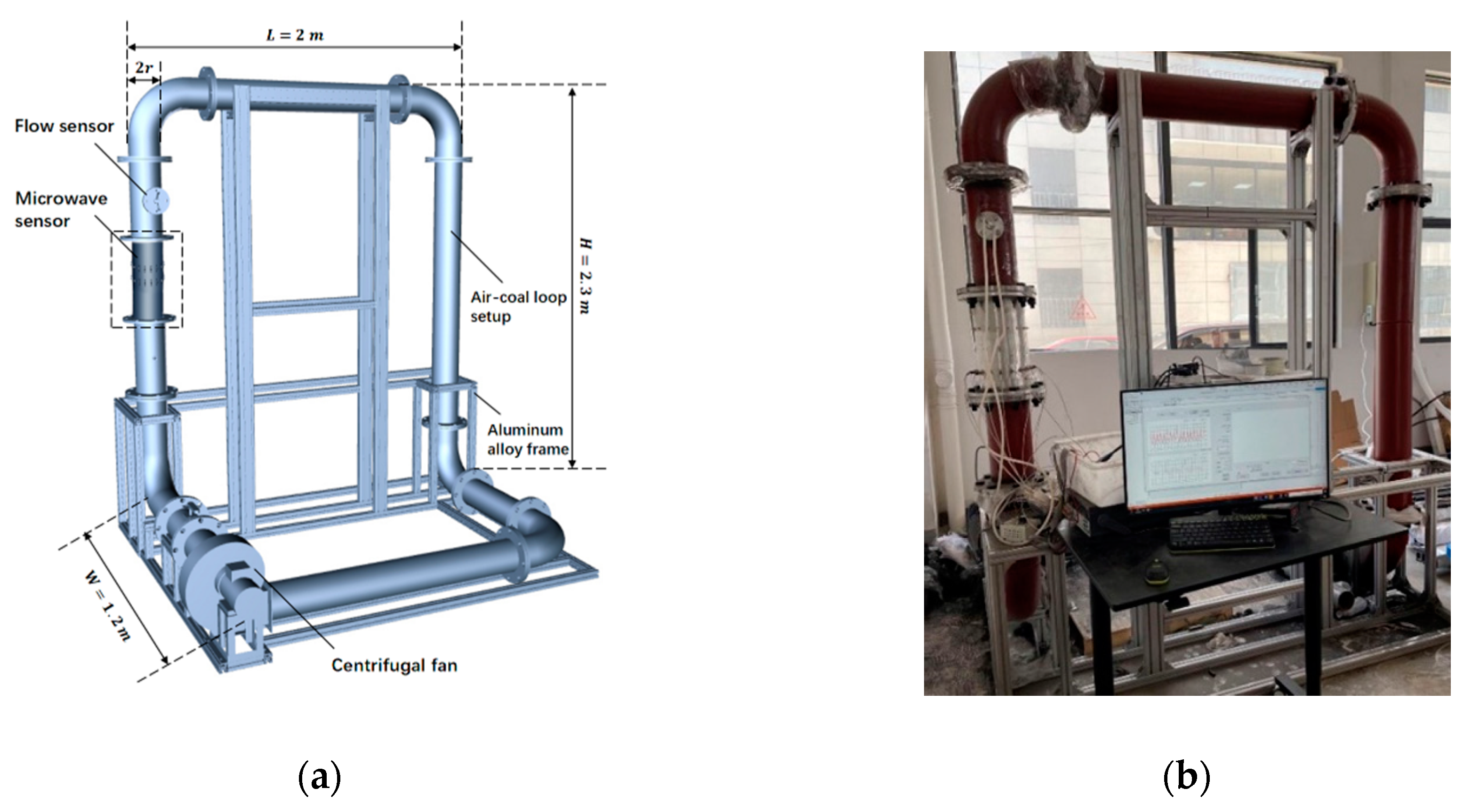
4.1. Prototype Experiments

To simulate the working conditions of pulverized coal flow, we constructed an air-coal loop setup [28]. This setup, depicted in Figure 5, was designed as a prototype system to investigate the interaction between microwave signals and pulverized coal. The setup is supported by an aluminum alloy frame, with the microwave sensor mounted at the center of the left steel pipe via a flange. The air-coal loop setup facilitates the circulation of pulverized coal using an industrial fan. A centrifugal fan with a power rating of 750 W and a nominal flow rate of 1810 m3/h serves as the power source for air circulation. Under this configuration, the internal flow velocity of the setup can reach up to 28.4 m/s, meeting the actual flow velocity requirements of 20-30 m/s.
The microwave signal was swept from 0.55 to 3 GHz in steps of 0.025 GHz. For the full-path S21 data with a PCC of 0.8 kg/kg, the L1 distance metric was utilized for calculation, which can be expressed as follows:
f X = D X , Y = ∑ i = 1 n x i − y i
where x i is the S21 data under pulverized coal-air mixture conditions, y i is the S21 data under pure air conditions, and i is the signal path index.
The results are presented in Figure 6(a). It can be concluded that, under this specific condition, the microwave signal at approximately 1.25 GHz exhibits the peak L1 distance metric, indicating that microwave signals near this frequency band experience the strongest attenuation after passing through the pulverized coal flow. Therefore, with consistent hardware and measurement environments, it is evident that selecting the appropriate working frequency is crucial for obtaining accurate measurement results.
After determining the optimal working frequency, we collected full-path S21 data at PCC of 0.2, 0.5, and 0.8 kg/kg, respectively, and calculated their L1 distances. Using the SVM model, successful classification was achieved. The confusion matrix, presented in Figure 7, demonstrates that the majority of predicted values were accurately classified, thereby validating the effectiveness of the prototype design and methodology for microwave measurement of PCC.

4.2. Field Experiments

The coal-fired unit typically utilizes a direct-firing pulverizing system. Raw coal is transported from the coal bunker to the coal feeder via a conveyor belt. Subsequently, the raw coal is fed into the coal mill in a controlled, continuous, and adjustable manner for pulverization. The pulverized coal is then conveyed to the boiler through the coal pipeline with the aid of heated primary air for combustion.
After preliminary certification of the prototype experiments, we conducted tests directly in the coal-fired units at the power plant to evaluate the system's performance under field conditions. The multi-frequency microwave sensing system was installed on the coal pipelines of several coal mills. As shown in Figure 8, the outcomes of the installation are illustrated.
Currently, there is no consensus on methods for measuring the concentration of gas-solid two-phase flows, which complicates the direct determination of absolute concentrations. Consequently, during the experiments, we monitored both the primary air flow rate of the coal mill and the coal quantity from the coal feeder, as recorded by the DCS system. PCC at each moment was calculated using the following formula:
P C C = M C o a l V a i r ,
V a i r = Q a i r ρ a i r ,
where M C o a l is the coal quantity from the coal feeder, V a i r is the primary air flow volume, and Q a i r is the primary air flow rate.
After integrating the system into the field environment, adjustments were made to factors such as sensor size and fabrication materials to better suit the conditions, as detailed in Table 3. The ability to identify an appropriate working frequency range for the scenario significantly influences the measurement results.
Table 3. Sensor specifications for different experimental scenarios.
Table 3. Sensor specifications for different experimental scenarios.
Experiments Scenario Sensor Diameter(mm) Outer Wall Material Substrate Layer Material
Prototype Experiments 150 Aluminium Epoxy Resin
Field Experiments 508 Carbon Steel PTFE
A frequency sweep was conducted across the range of 0.55 to 3 GHz. The L1 distance metric was used to assess signal attenuation at each frequency through the pulverized coal flow, with the results presented in Figure 6(b). The results clearly indicate that microwave signals experience the greatest attenuation within the frequency range of 1.2 to 1.5 GHz. This suggests higher sensitivity to pulverized coal within this range, which provides a basis for subsequent frequency selection.
To address redundant information in excess frequencies and the non-linear relationship between S21 parameters and solid phase concentration, a frequency selection method based on principal component analysis (PCA) and orthogonal matching pursuit (OMP) [27] was employed. By varying the voltage from 0 to 10 V in increments of 0.1 V using a VCO during each acquisition, extensive frequency domain information was collected. Additionally, signal path switching is managed by a high-speed microwave signal routing module, resulting in a comprehensive 240-dimensional dataset across 101 frequencies, which forms the raw data matrix. Eigenvalue decomposition is performed for each frequency to derive multiple eigenvectors and their explained variances. We ensure that the eigenvectors for each frequency retain more than 80% of the information content from the raw data matrix, i.e., the cumulative explained variance exceeds 80%. As illustrated in Figure 9(a), the number of eigenvectors k is generally below 24 for most frequencies, demonstrating that PCA effectively reduces the dimensionality of high-dimensional full-path data. The cumulative explained variance is plotted for frequencies corresponding to eigenvector counts of k = 3 and k = 23, respectively. As shown in Figure 9(b), when k is smaller, each eigenvector contains more information, allowing for the characterization of the original dataset with less data. This effectively reduces computational requirements.
After applying PCA, 25 frequencies with k≤3 are selected, resulting in a dataset comprising 45 sets of eigenvectors. Subsequently, OMP is used to select the optimal subset of these eigenvectors. The distribution of eigenvectors across various sizes of frequency combinations is illustrated in Figure 10. It is evident that these eigenvectors exhibit clustering in specific frequency bands, suggesting that measurements in these bands more effectively represent the actual value.
The mean absolute error (MAE) and correlation coefficient between the predicted and the actual values for various sizes of frequency combinations are shown in Figure 11(a). As the size of the frequency combination increases, the MAE decreases while the correlation coefficient increases. This trend indicates that incorporating more eigenvectors improves the accuracy of the predictions. However, beyond a certain point, both the MAE and correlation coefficient tend to stabilize, suggesting that some eigenvectors become redundant and have minimal impact on the prediction results.
Based on the results of the OMP calculations, we can determine the optimal size N of the frequency combination S by identifying the point at which both the MAE and the correlation coefficient stabilize. Considering both the OMP results and the efficiency of data collection and processing, we concluded that N=16. Figure 11(b) presents a preliminary comparison of prediction results from two stages of the frequency selection method: using PCA alone versus integrating PCA with OMP. After normalizing these predictions through min-max normalization, we visualized their distances from the actual values. The predictions from PCA combined with OMP are closer to the actual values. Error analysis reveals that the MAE for PCA alone can be as low as 7%, whereas the PCA+OMP method achieves a MAE of 3.8%. This demonstrates that combining PCA with OMP effectively integrates multi-frequency information, thereby improving prediction accuracy.
We conducted on-site monitoring of the C# coal mill, as illustrated in Figure 12, which displays the predicted results from our frequency selection method alongside the actual PCC data. This comparison indicates that the system effectively captures the trend of PCC variations within the 0 to 0.5 kg/kg range. We have highlighted several notable regions with circles and included an enlarged view of these areas. In these marked regions, the slopes of the predicted values closely align with those of the actual measurements. Even when the conveying of pulverized coal ceases and PCC approaches zero, the multi-frequency microwave sensing system continues to detect changes promptly. Error analysis reveals a MAE of 2.1%, demonstrating the system’s effectiveness and reliability.
Identical tests were conducted on various coal mills within the same unit to evaluate the reproducibility of the proposed method. The results, shown in Figure 13, indicate that the system effectively estimates PCC within the typical range of 0.3 to 0.5 kg/kg, which is commonly observed in power plants. A comparison of these estimates with the PCC data provided by the DCS system reveals that the predicted results closely align with the actual values in terms of trends. Furthermore, at points with more pronounced slopes, the predicted and actual values exhibit simultaneous peaks and troughs, further confirming the system's accuracy.
A numerical analysis of the experimental results was conducted, focusing on error and correlation. As shown in Table 3, the MAE for nearly all coal mills did not exceed 2.1%, with the best result reaching 1.41%. This indicates a high level of consistency between predicted and actual values, thereby validating the repeatability and effectiveness of the multi-frequency microwave sensing system. Furthermore, it was observed that the amplitude of changes in PCC is positively correlated with the correlation coefficient. This suggests that when amplitude changes are substantial, measurement errors in the system are negligible, resulting in an increased correlation coefficient. Conversely, when amplitude changes are minor, the relative error increases, and the effects of amplitude changes on the results become less pronounced, leading to a decrease in the correlation coefficient. Thus, the system can achieve higher measurement accuracy under conditions of significant PCC variation, thereby maintaining the accuracy and reliability of predictions in dynamic environments.
Table 3. Numerical analysis of test results on different coal mills.
Table 3. Numerical analysis of test results on different coal mills.
A# B# C# D# E#
Mean Absolute Error(%) 1.46 1.58 2.07 1.41 1.55
Correlation coefficient 0.57 0.31 0.98 0.85 0.66

5. Conclusions

In summary, this study demonstrates the efficient application of a novel non-contact, non-invasive sensing technology for PCC measurement by integrating a frequency selection method with a microwave sensor. First, a hardware system was designed to flexibly control the working frequency and signal path, enabling the measurement of full-path insertion loss S21 across various frequencies, which serves as input for data processing. Second, a frequency selection method was developed based on PCA and OMP algorithms to filter out redundant frequency signals and extract relevant information from the high-dimensional PCC dataset. Experimental results demonstrate that the multi-frequency microwave sensing system effectively utilizes frequency information and employs a multi-frequency strategy to enhance prediction accuracy, validating the feasibility of quantitatively predicting of PCC. Long-term measurements and recordings in coal-fired power plants reveal that the system effectively captures changes in PCC within the range of 0 to 0.5, achieving an optimal MAE of 1.41%. Future work could focus on reducing the system's error rate while also enhancing its adaptive capability, enabling dynamic adjustments to changes in the measurement environment caused by factors such as temperature fluctuations or pulverized coal accumulation.

Author Contributions

Conceptualization, Y.M. and R.Y; Data curation, H.T.; Formal analysis, H.T. and Z.L.; Funding acquisition, Y.M., X.J. and R.Y.; Investigation, H.T. and F.G.; Methodology, H.T., F.G., Z.W. and Z.L.; Project administration, F.G. and Z.W.; Resources, Y.M., X.J., R.Y. and Z.W.; Software, H.T. and Z.L.; Supervision, Z.W. and Z.L.; Validation, H.T.; Visualization, H.T.; Writing – original draft, H.T. and F.G.; Writing – review & editing, H.T., Z.W. and Z.L..

Funding

This research was funded by Zhejiang Provincial Energy Group Company Ltd., grant number ZNKJ-2020-020.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Liakos, H.H.; Theologos, K.N.; Boudouvis, A.G.; Markatos, N.C. Pulverized Coal Char Combustion: The Effect of Particle Size on Burner Performance. Applied Thermal Engineering 1998. [Google Scholar] [CrossRef]
  2. Zheng, Y.; Liu, Q. Review of Certain Key Issues in Indirect Measurements of the Mass Flow Rate of Solids in Pneumatic Conveying Pipelines. Measurement 2010, 43, 727–734. [Google Scholar] [CrossRef]
  3. Baucum, W.E. Evaluation of a Coriolis Mass Flow Meter for Pulverized Coal Flows; 1979; p. DOE/ET/10815-T2, 5228038. [Google Scholar]
  4. Gu, J.; Su, M.; Cai, X. In-Line Measurement of Pulverized Coal Concentration and Size in Pneumatic Pipelines Using Dual-Frequency Ultrasound. Applied Acoustics 2018, 138, 163–170. [Google Scholar] [CrossRef]
  5. Wang, X.X.; Hu, H.L.; Liu, X.; Zhang, Y.Y. Concentration Measurement of Dilute Pulverized Fuel Flow by Electrical Capacitance Tomography. Instrumentation Science & Technology 2015, 43, 89–106. [Google Scholar]
  6. Cai, X.; Li, J.; Ouyang, X.; Zhao, Z.; Su, M. In-Line Measurement of Pneumatically Conveyed Particles by a Light Transmission Fluctuation Method. Flow Measurement and Instrumentation 2005, 16, 315–320. [Google Scholar] [CrossRef]
  7. Yan, Y.; Wang, L.; Wang, T.; Wang, X.; Hu, Y.; Duan, Q. Application of Soft Computing Techniques to Multiphase Flow Measurement: A Review. Flow Measurement and Instrumentation 2018, 60, 30–43. [Google Scholar] [CrossRef]
  8. Wang, X.; Hu, H.; Liu, X. Multisensor Data Fusion Techniques With ELM for Pulverized-Fuel Flow Concentration Measurement in Cofired Power Plant. IEEE Trans. Instrum. Meas. 2015, 64, 2769–2780. [Google Scholar] [CrossRef]
  9. Wang, X.; Hu, H.; Zhang, A. Concentration Measurement of Three-Phase Flow Based on Multi-Sensor Data Fusion Using Adaptive Fuzzy Inference System. Flow Measurement and Instrumentation 2014, 39, 1–8. [Google Scholar] [CrossRef]
  10. Jin, Q.; Zeng, L.; Chen, X.; Li, P.; Fu, H.; Zhou, Y.; Wu, Y.; Wu, X. Portable Digital Holographic Particle Analyzer (DHPA) for Pneumatically Conveyed Fuel Monitoring: Design and Validation. Powder Technology 2023, 430, 119030. [Google Scholar] [CrossRef]
  11. Sheila-Vadde, A.C.; Melapudi, V.; Suma, M.N.; Kumar, K.M.M.; Ward, J. Non-Intrusive Microwave System for Multiphase Flow Metering. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC); IEEE: Houston, TX, 2018; pp. 1–6. [Google Scholar]
  12. Guo, Z.; Zhang, G. Application of a Microwave Mass Flow Meter in a Dense Phase Pneumatic Conveying System of Pulverized Coal. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC); IEEE: Chongqing, 2018; pp. 2547–2551. [Google Scholar]
  13. Cen, K.; Ma, B.; Qiu, K.; Zhou, H. On-Line Electromagnetic Wave Based Coal Concentration Monitoring Technique for Pipe Flow. In Proceedings of the AIP Conference Proceedings; AIP: Macau (China), 2007; Vol. 914, pp. 262–267. [Google Scholar]
  14. Penirschke, A.; Jakoby, R. Microwave Mass Flow Detector for Particulate Solids Based on Spatial Filtering Velocimetry. IEEE Trans. Microwave Theory Techn. 2008, 56, 3193–3199. [Google Scholar] [CrossRef]
  15. Wang, D.; Liu, X.; Wang, Y.; Zhu, Z.; Chen, D.; Xie, Z. Measurement of Solid Concentration in Gas–Solid Flows Using a Microwave Resonant Cavity Sensor. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
  16. Rahiman, M.H.F.; Wan Kiat, T.T.; Ping Jack, S.; Abdul Rahim, R. Microwave Tomography Application and Approaches – A Review. Jurnal Teknologi 2015, 73. [Google Scholar] [CrossRef]
  17. Wu, Z. Developing a Microwave Tomographic System for Multiphase Flow Imaging: Advances and Challenges. Transactions of the Institute of Measurement and Control 2015, 37, 760–768. [Google Scholar] [CrossRef]
  18. Pang, L.; Shao, Y.; Geng, C.; Zhong, W.; Liu, G.; Liu, L.; Tian, W. Measurement of Solid Mass Flow Rate by a Non-Intrusive Microwave Method. Powder Technology 2018, 323, 525–532. [Google Scholar] [CrossRef]
  19. Stuchly, S.S.; Sabir, M.S.; Hamid, A. Advances in Monitoring of Velocities and Densities of Particulates Using Microwave Doppler Effect. IEEE Trans. Instrum. Meas. 1977, 26, 21–24. [Google Scholar] [CrossRef]
  20. Chen, L.; Wang, Y.; Su, C. Simulation Study on Measuring Pulverized Coal Concentration in Power Plant Boiler. Journal of Information Processing Systems 2019, 15, 189–202. [Google Scholar]
  21. Gilmore, C.; Mojabi, P.; Zakaria, A.; Ostadrahimi, M.; Kaye, C.; Noghanian, S.; Shafai, L.; Pistorius, S.; LoVetri, J. A Wideband Microwave Tomography System With a Novel Frequency Selection Procedure. IEEE Trans. Biomed. Eng. 2010, 57, 894–904. [Google Scholar] [CrossRef]
  22. Zhang, J.; Bao, Y.; Du, D.; Wang, J.; Wei, Z. OM2S2: On-Line Moisture-Sensing System Using Multifrequency Microwave Signals Optimized by a Two-Stage Frequency Selection Framework. IEEE Trans. Ind. Electron. 2021, 68, 11501–11510. [Google Scholar] [CrossRef]
  23. Gladstone, J.; Dale, T. Researches on the Refraction, Dispersion, and Sensitiveness of Liquids. Phil. Trans. R. Soc. 1863, 153, 317–343. [Google Scholar]
  24. Huang, S.M.; Plaskowski, A.B.; Xie, C.G.; Beck, M.S. Tomographic Imaging of Two-Component Flow Using Capacitance Sensors. J. Phys. E: Sci. Instrum. 1989, 22, 173–177. [Google Scholar] [CrossRef]
  25. Zaatar, O.; Zakaria, A.; Qaddoumi, N. A Novel Switch for Microwave Imaging Systems. IEEE Access 2024, 12, 26978–26990. [Google Scholar] [CrossRef]
  26. Tong, H.; Gao, F.; Yuan, C.; Jin, Z.; Tian, B.; Tian, H. Experimental Investigation on Microwave Switch Matrix System for Real-Time Microwave Tomography Imaging Applications. In Proceedings of the 2022 IEEE 9th International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications (MAPE); IEEE: Chengdu, China, 2022; pp. 415–418. [Google Scholar]
  27. Cai, T.T.; Wang, L. Orthogonal Matching Pursuit for Sparse Signal Recovery With Noise. IEEE Trans. Inform. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
  28. Tian, H.; Zhong, Y.; Zheng, X.; Gao, F.; Song, G.; Wang, Z. Airflow Concentration Sensing for Pulverized Coal: System Design and Validation. In Proceedings of the 2023 4th International Conference on Computer Engineering and Application (ICCEA); IEEE: Hangzhou, China, 2023; pp. 436–439. [Google Scholar]
Preprints 137639 g001
Figure 1. Two-port waveguide system for coal pipeline.
Figure 1. Two-port waveguide system for coal pipeline.
Preprints 137639 g001
Preprints 137639 g002
Figure 2. Overall framework of the multi-frequency microwave sensing system.
Figure 2. Overall framework of the multi-frequency microwave sensing system.
Preprints 137639 g002
Preprints 137639 g003
Figure 3. Schematic structure: (a) Typical microstrip Line; (b) Microwave sensor.
Figure 3. Schematic structure: (a) Typical microstrip Line; (b) Microwave sensor.
Preprints 137639 g003
Preprints 137639 g004
Figure 4. (a) Schematic diagram of the 2-by-16 switch matrix; (b) Electrode pair combinations at 16 electrodes.
Figure 4. (a) Schematic diagram of the 2-by-16 switch matrix; (b) Electrode pair combinations at 16 electrodes.
Preprints 137639 g004
Preprints 137639 g005
Figure 5. The air-coal loop setup: (a) Simulation model; (b) Actual installation.
Figure 5. The air-coal loop setup: (a) Simulation model; (b) Actual installation.
Preprints 137639 g005
Preprints 137639 g006
Figure 6. Distribution of L1 distance values at each frequency: (a) Prototype experiments; (b) Field experiments.
Figure 6. Distribution of L1 distance values at each frequency: (a) Prototype experiments; (b) Field experiments.
Preprints 137639 g006
Preprints 137639 g007
Figure 7. Confusion matrix using the SVM method.
Figure 7. Confusion matrix using the SVM method.
Preprints 137639 g007
Preprints 137639 g008
Figure 8. Installation outcomes.(a)Overall System Overview; (b)Hardware of the High-speed Microwave Signal Routing Module.
Figure 8. Installation outcomes.(a)Overall System Overview; (b)Hardware of the High-speed Microwave Signal Routing Module.
Preprints 137639 g008
Preprints 137639 g009
Figure 9. (a) Distribution of frequencies by number of eigenvalues; (b) Cumulative explained variance chart for different frequencies.
Figure 9. (a) Distribution of frequencies by number of eigenvalues; (b) Cumulative explained variance chart for different frequencies.
Preprints 137639 g009
Preprints 137639 g010
Figure 10. Eigenvector distribution for frequency combinations.
Figure 10. Eigenvector distribution for frequency combinations.
Preprints 137639 g010
Preprints 137639 g011
Figure 11. (a) Effect of frequency combination size on prediction result; (b) Comparison of prediction results at different stages of frequency selection methods.
Figure 11. (a) Effect of frequency combination size on prediction result; (b) Comparison of prediction results at different stages of frequency selection methods.
Preprints 137639 g011
Preprints 137639 g012
Figure 12. Test results on the C# coal mill
Figure 12. Test results on the C# coal mill
Preprints 137639 g012
Preprints 137639 g013aPreprints 137639 g013b
Figure 13. Test results on other coal mill: (a)A#; (b)B#; (c)D#; (d)E#.
Figure 13. Test results on other coal mill: (a)A#; (b)B#; (c)D#; (d)E#.
Preprints 137639 g013aPreprints 137639 g013b
Table 1. Performance comparison with multi-frequency systems in the literature.
Table 1. Performance comparison with multi-frequency systems in the literature.
Ref. Method Frequency Range (GHz) Selection Method Pros Cons Application
[15] Resonant Cavity Methods 1.5~1.8 Sweep range of Vector Network Analyzer(VNA) -Strong interpretability-Low environmental impact -Calibration required-Narrow bandwidth Industrial: gas-solid two-phase flow
[21] MWT Methods 3~6 Compare single antenna vs. co-located measurements; choose frequency with minimal coupling difference -Strong interpretability-Simple Calibration -Additional measurements required-High hardware requirements Biomedical: dielectric phantoms
[22] Transmission Methods 2~10 Random Forest-Recursive Feature Elimination (RF-RFE) + Majority Voting Method (MVM) -Data-driven -Lack of interpretability-High data dependency Agriculture: corn moisture
This Work Transmission Methods 1.5~2.5 Principal Component Analysis (PCA)+Orthogonal Matching Pursuit (OMP) -Data-driven -High data dependency-Narrow bandwidth Industrial: Pulerized Coal Concentration(PCC)
Table 2. Parameters of the chips used in the switch matrix.
Table 2. Parameters of the chips used in the switch matrix.
Device Type Part # Switching Time(ns)
SPDT RF Switch M3SWA2-63DRC+ 6
3 TO 8 Line Decoder Demultiplexer 74HC138 12
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated