Prerpints.org logo
Preprint
Review

Origin of Life: A Symmetry-Breaking Physical Phase Transition

Altmetrics

Downloads

71

Views

94

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 October 2024

Posted:

28 October 2024

You are already at the latest version

Alerts
Abstract
The origin of life has previously been subject to numerous studies and hypotheses. Typically, related models focus on the emergence of chemical networks such as the RNA world or the Krebs energy cycle. Here, the onset of life is described as a symmetry-breaking kinetic phase transition of the II. kind. The novel symmetry of life is the arbitrariness of code that is fundamental to symbolic information processing, coining all forms of life from the very beginning. Symbols evolved from non-symbolic, structural information of the inanimate physical world. The responsible transition process had been discovered a century ago in behavioural biology, regarded as 'ritualisation'. Physical properties of this transition include neutral Lyapunov stability and critical fluctuations of the associated Goldstone modes. As a conceptual model, a hypothetical simple molecular ritualisation process is suggested, along with the emergent semiotics of symbolic information processing.
Keywords: 
Subject: Biology and Life Sciences  -   Ecology, Evolution, Behavior and Systematics
          Scientists are led into the problems of evolution,
            and, ultimately, of the origin of living matter.
                   Hermann Haken, 1977
  [In] the evolution of biomolecules, … an intimate connection exists
    between dramatic changes on the microscopic, molecular level,
          and changes on the macroscopic, phenotypic level.
                   Hermann Haken, 1982

1. Introduction

“The origin of life is often seen as the mother of all chicken-or-egg problems. Scientists could never figure out which came first, the informational molecule or the functional molecule. … To solve the origin-of-life conundrum, scientists needed somehow to find a molecule that could play both rules – carry the information, the code for life, and reproduce that code all by itself” (Cech 2024: p. 111).
From ancient Greek philosophy to date, under varying perspectives, a wealth of studies has been published about the dualism between physical objects and their symbolic representations, between realities and their shadows (Plato 375 BCE), between sensation and reason (Kant 1787), between deed and name (Feuerbach 1848), between real structures and their mental images (Hertz 1899), between things and signs (Oehler 1990, Coeckelbergh 2020), between body and mind/soul (Sebeok 2001, Mendie and Udofia 2018, Meincke 2023, Clark 2023), between targets and vehicles (Facchin 2024), or, very generally, between physics and semiotics (Pattee 2001) or object and subject (Pattee 1982, 2015). “Physics is about natural laws, while semiotics is about code processes” (Kull 2007: p.167).
Previously, general relations between semiotics and life, especially human life and consciousness, have often been emphasised. “Phenomena and symbols have function and meaning only if they arise in the context of the memory of the individual self. Individual symbols make sense only by virtue of their interpretation that depends on an organism’s genetic and cognitive symbol system” (Pattee 2015). “Humans are instances of physical symbol systems, and, by virtue of this, mind enters into the physical universe” (Newell 1980: p. 136). “There could not have been semiosis prior to the evolution of life” (Sebeok 1997: p. 436). “The world of sign-likes appears as a stage of evolution that was preceded by a world of not yet sign-likes” (Nöth 2000: p. 135). “Sign systems embrace all living systems, and the roots of semiotics lie in biology… Sign science and life science are coextensive” (Kull 2001: p. 1,3). “The origin of life could have been related to a specific aspect of molecular semiotics, especially in the transition from molecules as the physical symbols of material units to molecules as the semiotic signs having the capacity of pointing to something else other than the molecules themselves” (Matsuno 2008: p. 131). “The origin of life cannot even be formulated without a better understanding of how molecules can function symbolically” (Pattee 1969: p.1).
In the context of symbols being a characteristic of life, certain intrinsically associated aspects have only rarely been addressed yet in greater detail, namely,
(i)
the arbitrariness of symbols viewed as a specific kind of physical symmetry,
(ii)
the emergence of symbols as a molecular evolution process, understood as ritualisation, and consequently,
(iii)
the origin of life defined as a kinetic phase transition from “object” to “subject”.
In the literature, the term “model” is differently understood by alternative authors. Here, models are simplified representations of real structures or processes (Stachowiak 1973). “The word ‘model’ … is used … to mean an approximate description of an aspect of reality, with this description being developed for a specific purpose” (Willink 2013: p. 16). Representing something else than themselves, also models are special, typically complex symbols, consisting of structured sets of simpler symbols (Feistel 2023a). Prediction models are indispensable for active living beings; the selective advantage offered by exploiting such models was the actual evolutionary driving force for the emergence of symbols (Feistel 2023b). The very first coded gene, that is, an ordered set of mutually related molecular symbols, is the very first prediction model as a recipe for future survival.
In order to bring together here the fairly distinct topics of the chemical origin of life, behavioural ritualisation, semiotics of symbols and physical phase transitions, in this paper literal quotations and related key properties of tutorial examples are considered. Structural information is distinguished from symbolic information in Section 2. Semiotic arbitrariness, or code symmetry, is introduced in Section 3. Kinetic phase transitions far from thermodynamic equilibrium, in particular those of the second kind, and their symmetry transitions are the topic of Section 4. Far from thermodynamic equilibrium, usual passive physical systems need to become active, self-reproducing, competing individuals as a first step on the way to life, discussed in Section 5. Choosing beneficial such activities requires decisions based on prediction models which exploit symbolic memory. “Records require some form of material symbols that represent the events and an agent that interprets the symbols” (Pattee and Rączaszek-Leonardi 2012: p. 2). The universal phenomenon of the ritualisation transition in evolution processes, responsible for the emergence of symbolic information, is briefly explained in Section 6. All those previous features are joined then in Section 7, suggesting a conceptual stepwise process leading from the chemistry of ribonucleic acid (RNA) to the primordial genetic code, where the phase transition to life is identified with the emergence of the very first symbols. “This largely arbitrary symbol-matter relation first appears with evolvable self-replication, which I define as the origin of life” (Pattee and Rączaszek-Leonardi 2012: p. 2).

2. Information

Communication is transfer of information. This article is about symmetry of communication. “As a physicist, I want to know how to distinguish communication between molecules from the normal physical interactions or forces between molecules which we believe account for all their motions” (Pattee 1969: p. 1). To present an instructive example, in their book about the origin of biological information and order, Haken and Haken-Krell (1989) describe two different situations of information transfer. On the one hand, there is information in the sense of Shannon. “Shannon’s [encoded] information does not possess any semantics. … Information is similarly contained in a scientific publication as in a construction plan of a house. … Information cannot be transferred without information carrier. … Information transfer means elimination of [the receiver’s] uncertainty” (Haken and Haken-Krell 1989: p. 37, 38).
On the other hand, there is also information in the sense of physical interaction of atoms in a laser. “A single, coherent wave … informs the single atoms how they have to oscillate in time with one another. … This coherent wave acts as ‘informator’ for the single atoms. At the same time, in the form of coherent light, it also informs the environment about the internal state of the laser” (Haken and Haken-Krell 1989: p. 55). A similar kind of information is analysed by Hawking (2018).  »Hawking’s information paradox« is a phenomenon that results from the inconsistency between microscopic “conservation of quantum information” (Braunstein and Pati 2007, Roncaglia 2019) and macroscopic irreversibility of black hole growth (Almheiri et al. 2020).
In the following, those two alternative forms of transfer of just “information” will rigorously be distinguished from one another with respect to their carrier properties involved (Ebeling and Feistel 1994, Feistel and Ebeling 2011, Feistel 2017a, 2023b). The first form will be regarded as symbolic information (or free information) for the reason that the related information carrier is in the form of symbols or signs. “All fundamental laws are expressed in mathematical symbols, and the result of measurements is symbolic information. … Symbols are the carriers of communication between individuals and thus decisive for the possibility of objective knowledge” (Pattee 2015).
The second form will be termed structural information (or bound information) because it is transferred by natural physical interaction rather than by any kind of code encrypted by convention between sender and receiver. A text typed by a journalist, distributed in a newspaper and understood by the reader, communicates symbolic information. By contrast, the shaking ground of an earthquake, propagating to a city and damaging houses there, is structural information transmitted by the quake, transferred by the ground and received by the house. The meaning of structural information is objective, independent of any receiver, while the meaning of symbolic information is subjective, depending on the contextual properties of transmitter or receiver.
Several further general properties of structural information may be mentioned (Feistel and Ebeling 2011: p. 370), namely:
(i)
Structural information is inherent to its carrier substance or process. Information cannot loss-free be copied to any other carrier or identically multiplied in the form of additional physical instances. The physical carrier is an integral constituent of the information itself. The state of the physical context of the system is also an integral part of the information.
(ii)
There is no invariance of information with respect to structure transformations. Different structures represent different information.
(iii)
Structural information emerges and exists on its own, without being produced or supported by any kind of separate information source. No coding rules are involved when the structure is formed by natural processes.
(iv)
Over the relaxation time of the carrier structure, structural information degrades systematically as a consequence of the Second Law of thermodynamics, and ultimately disappears when the equilibrium state is approached.
(v)
Internal physical processes or external interference may destroy structural information; it cannot be regenerated or recovered. Periodic processes can rebuild similar structures but never exactly the same, in particular because the surrounding world is not the same again at any later point of time.
(vi)
Structural information is not represented in the form of codes. No particular coding rule or language is required or distinguished to decipher a structure.
(vii)
Structural information is a physical property; it is represented by the spatial and temporal configuration of matter, its governing laws are the laws of physics.
(viii)
Structural information is of physical nature and is independent of life.
(ix)
Structural information is objective and has no purpose.
By contrast, of symbolic information several other general properties may be reported (Feistel and Ebeling 2011: p. 367):
(i)
Symbolic information systems possess a new symmetry, the carrier invariance. Information may loss-free be copied to other carriers or multiplied in the form of an unlimited number of physical instances. The information content is independent of the physical carrier system used.
(ii)
Symbolic information systems possess a new symmetry, the coding invariance. The functionality of the processing system is unaffected by substitution of symbols by other symbols as long as unambiguous bidirectional conversion remains possible. In particular, the stock of symbols can be extended by the addition of new symbols or the differentiation of existing symbols. At higher functional levels, code invariance applies similarly also to the substitution of groups of symbols, synonymous words or of equivalent languages.
(iii)
Within the physical relaxation time of the carrier structure, discrete symbols represent quanta of information that do not degrade and can be refreshed unlimitedly.
(iv)
Imperfect functioning or external interference may destroy symbolic information but only biological processing systems can generate new or recover lost information.
(v)
Symbolic communication systems consist of complementary physical components that are capable of producing the structures of the symbols upon writing, of keeping the structures intact over the duration of transmission or storage, and of detecting each of those structures upon reading the information. If the stock of symbols is subject to evolutionary change, a consistent co-evolution of all those components must occur.
(vi)
Symbolic information is an emergent property; its governing laws are beyond the framework of physics, even though the supporting structures and processes do not violate physical laws.
(vii)
Symbolic information has a meaning or purpose beyond the scope of physics.
(viii)
In their structural information, the constituents of the symbolic information system preserve a frozen history (“fossils”) of their own evolution pathway.
(ix)
Symbolic information processing is an irreversible, non-equilibrium processes that produces entropy and requires free-energy supply.
(x)
Symbolic information is encoded in the form of structural information of its carrier system. Source, transmitter and receiver represent and transform physical structures.
(xi)
Symbolic information exists only in the realm of life.
(xii)
Symbolic information is subjective, depending on the processing context.
“The invariance of free [symbolic] information with respect to the physical nature of the data carrier is not just a marginal property, but from the physical perspective it is its most important one” (Ebeling and Feistel 1994: p. 56). Symbolic information is qualified to be protected against the destructive, degrading impact of physical laws, such as the Second Law of thermodynamics, which inevitably acts on the structural information from which the symbolic information once had originated. Only the symmetry of symbolic arbitrariness empowers living structures to preserve and exploit their information collected and inherited in tiny fragile molecules through billions of years of survival experience.

3. Code Symmetry

Previously, numerous authors have emphasised and described the fundamental arbitrariness of symbols and its relevance for communication processes (Plato 430 BCE, Leibniz 1904, Oehler 1995, Nöth 2000, Coeckelbergh 2020, Çengel 2023). “If the [communication] channel sequences are not already sequences of binary digits, they can be ascribed binary numbers in an arbitrary fashion and the binary code thus translated into signals suitable for the channel” (Shannon and Weaver 1964: p. 60). “The origin of languages and messages is inseparable from the origin of arbitrary rules. It is a general property of languages and symbol systems that their constraints are arbitrary in the sense that the same function can be accomplished by many different physical and logical structures” (Pattee 1969). “We can formulate this as the principle of code plurality - which states that any text, any sign, any semiosis assumes the co-existence of several codes, of many codes” (Kull 2007: p. 174). “As the central dogma of semiotics, it can be stated [that] any property of a physical medium can serve as a sign vehicle of any type referring to any object of reference” (Deacon 2021). With different emphasis on certain aspects, the varying nomenclature of “arbitrariness” may include “conventionality”, “carrier invariance”, “code invariance”, “code symmetry”, “code plurality”, “neutral Lyapunov stability”, “Goldstone mode”, “Goldstone boson”, “indifference”, “criticality” or “degeneracy”. The rule that defines the interpretation of a symbol is sometimes regarded as a “convention”, a “protocol” or a “code”.
In relation to their meaning, symbols may even possess stacked levels of arbitrariness (Lacková et al. 2017). Languages, for example, may vary in their alphabet used, in their wording, in their local dialect or tongue spoken. Genetic codons have a meaning in the amino acid they represent, in the protein they form, in the kind of cell or tissue they belong to, in the traits, the shape and functioning of the organisms, and finally in the selective values of the individual or the species in a “phenotypic” or “fitness landscape” (Wright 1931, Feistel and Ebeling 1982, 1983, Ebeling et al. 1984, Kauffman and Levin 1987), see Section 3. Hierarchically, at the lowest level this arbitrariness may be the irrelevance of the kind of ink used for writing on paper, or of the hardware used to store a computer bit. At advanced levels, arbitrariness is related to the freedom of choosing different models for the simplified representation of the same given object (Feistel 2023a) or to Turing’s computational universality theorem, saying that the algorithm implemented on one digital computer may be performed as well by any other digital computer. “This special property of digital computers, that they can mimic any discrete state machine, is described by saying that they are universal machines” (Turing 1950: p. 441).
A formal example from biology may illustrate genetic arbitrariness of organisms. “Evolution requires the genotype-phenotype distinction … that separates energy-degenerate, rate-independent genetic symbols from the rate-dependent dynamics of construction that they control” (Pattee 2001). Let a set g denote the collection of genetic (say, mRNA) sequences of an organism which control its phenotype. By translation, this genotype is interpreted as a set of enzymes possessing specific quantitative catalytic activities, say, e g . Changes of the genotype g '  are arbitrary at the enzymatic level if e g = e g ' . Such changes may include the replacement of a certain codon by another, redundant one associated with the same amino acid, but as well the replacement of the whole genetic code system by modified or extended one. Via modified tRNA identifiers, such an alternative system may associate other codons to the given set of amino acids.
At another, higher level, the enzymatic properties are responsible for the organism’s set of quantitative phenotypic properties, say, q e . Changes of the genotype g '  are arbitrary at the phenotypic level if q e = q e ' , even if those changes are not necessarily arbitrary at the enzymatic level, e g ≠ e ' g ' . At the top level of this hierarchy, the selective value E q , that is, the net reproduction rate of an individual, depends on the phenotypic traits, q . A mutation q '  is regarded as neutral (Kimura 1983, Muñoz-Gómez et al. 2021), or arbitrary at the selection level, if it does not affect its selective value, E q ' = E q .
The number, n, of different phenotypic properties of an individual is typically large. A given phenotype may be represented by a point q  in an n-dimensional phenotype space (Fisher 1930, Wright 1931, Conrad 1982, Feistel and Ebeling 1982, 1983, 2011, Ebeling et al. 1984, Feistel 1984). Subject to selective pressure, in the course of evolution, the point q  representing the phenotype is driven to move along the gradient of the phenotypic landscape, see Figure 1, to increase its selective value at maximum steepness,
d q d t ~ ∂ E ∂ q
In a high-dimensional phenotype space, the manifold of phenotypes with equal selective values, E q = c o n s t , is a high-dimensional hyperspace just one dimension lower than the phenotype space itself. If random mutations happen at arbitrary directions in the full q-space, almost all of them will point to an adjacent state within that hyperspace. In other words, with respect to a given fitness landscape, the majority of mutations is locally neutral, i.e., arbitrary at the selection level (but not necessarily neutral at the phenotype level). In a feedback process, the evolution of phenotypes is gradually deforming the shape of the landscape E q  so that separate points belonging to the same neutral hypersurface E q = c o n s t  at some point of time may belong to different such spaces at later times.
Note that dynamical equations similar eq. (1) are also valid for the quantum mechanics of electrons in random media such as amorphous solids (Ebeling et al. 1984). In that case, arbitrariness appears in the form of energetic degeneracy of quantum states.

4. Kinetic Phase Transitions

As a kinetic phase transition of the second kind, Haken (1970, 1977) described the change of the functioning of a laser from incoherently emitting light in a “lamp mode” at low excitation rates to coherent light emission in the “laser mode” at strong excitation. This transition is continuous but is breaking the system’s symmetry, in quite a similar manner as such thermodynamic equilibrium phase transitions do (Landau and Lifschitz 1966). “When studying the transition-region lamp laser, we shall find that the laser shows features of a second-order phase transition” (Haken 1977: p. 225). A similar example is the so-called Hopf bifurcation, namely, the spontaneous onset of self-sustained oscillations under supercritical conditions, such as of a bowed violin string (Schelleng 1974). In that case, the continuous time symmetry of the steady state below the threshold is replaced by a finite periodic symmetry of oscillations beyond the threshold.
This second-order transition of the Hopf bifurcation is continuous because the oscillations exhibit zero amplitudes at the critical point (Feistel and Ebeling 1978). In the vicinity of the transition point, otherwise microscopic fluctuations grow to macroscopic amplitudes due to the weakness of restoring forces (mathematically, disappearing real parts of Lyapunov coefficients). This behaviour is universal for transitions of the second kind (Nicolis and Prigogine 1987) and may be studied in detail by investigating stochastic chemical oscillations (Feistel and Ebeling 1978, 1989). “The occurrence of a periodic reaction is a process which is breaking the time symmetry in the same way as ferromagnetism is a process breaking the spatial symmetry” (Prigogine 1977: p. 156).
A tutorial example for a (mathematical) phase transition of the 2nd kind is the percolation transition of random networks (Austin et al. 1959, Erdös and Rényi 1960, Sonntag et al. 1983, Allard et al. 2015). Consider N points (vertices) and K arrows (edges) which are directed from one randomly selected vertex to a different randomly selected vertex. There are N N − 1
 different such vertex pairs in such a random directed graph. Let the ratio
c = K N
be regarded as the graph’s coordination number. A graph is compact (i.e. completely occupied) if c = N − 1 , and weakly coordinated (i.e. sparsely populated) if c ≪ 1 . For a large such graph, a thermodynamic limit may formally be carried out by setting N → ∞ , K → ∞  at fixed finite coordination, c = c o n s t . In weakly coordinated graphs, the probability P c l  to find a directed loop of edges of length l  is approximately
P c l ≈ c l l
which at small values of c  decreases rapidly with the cycle length, l . The chance, P c , to find any cycle in the thermodynamic limit of a weakly coordinated directed random graph is (Figure 2)
P c = 1 − 1 − c exp ⁡ c f o r c ≤ 1 1 f o r c ≥ 1
Below the critical point, c = 1 , the graph consists of finite clusters only. Beyond the transition, the graph includes a “giant” (infinite) component and has a different symmetry therefore. The transition itself is continuous with a discontinuous slope which is smoothed out if the graph is finite or if only finite cycles are considered (Sonntag et al. 1981).
At small c ≪ 1 , the probability P c  is almost completely represented by the chance for binary cycles,
P c 2 = 1 − exp ⁡ − c 2 / 2 ≈ c 2 2
In the “primordial soup” of the young planet Earth, coordination numbers for spontaneous catalytic networks have roughly been guessed to values like c = 10 − 10 … 10 − 20  (Kaplan 1978, Feistel 1979). Under similar conditions, only the shortest self-reproducing catalytic loops may have had a plausible chance to come into function as a spark to life, such as RNA producing its own mirror image (Shelke and Piccirilli 2014, Cech 2024), see Section 7.
Observed historical evolution is a single realisation of a stochastic process. In such a case, as in thermodynamic phase transitions of finite systems (Stanley 1971), or chemical oscillations performed by a small number of molecules (Feistel and Ebeling 1978), transition processes typically appear in softened form with strong fluctuations. Sharp, sudden transitions appear only in theoretical, idealised thermodynamic limits of infinitely large systems. With respect to evolution, such a fictitious limit may be imagined if an infinitely large ensemble of randomly evolving systems under equal conditions is considered.

5. Activity, Prediction and Decision

Multi-particle systems possess large numbers of degrees of freedom, such as three degrees of position and three degrees of velocity per mass point of a perfect gas. At thermodynamic equilibrium, almost all of those are subject to fast thermal motion, except, say, two such degrees of pure fluid, such as temperature and density. The latter quantities are termed “control parameters”, while the others are “slaved variables” whose statistical properties are functions of the control parameters, the latter ones considered as being fixed. At small deviations from equilibrium, additional modes of the system are observed to appear, known as “order parameters” (Haken 1977, Ebeling and Feistel 1982, Nicolis and Prigogine 1987, Feistel and Ebeling 1989, 2011), such as irreversible thermodynamic forces and fluxes. “The concept of order parameters had originally been introduced by Lev Landau” (Haken et al. 2016: p. 50). Governed by the system’s dynamical laws, order parameters vary on time scales of the observer’s interest; they change much slower than those of the slaved variables and much faster than those of the control parameters (Hahn 1974, Battelli and Lazzari 1985).
With increasing distance from equilibrium, with more energy available in excess over the thermal background, the number of excited modes described by order parameters is typically increasing and their dynamics is becoming more and more complex. In particular, in dependence on the control parameters, the order parameters may undergo kinetic phase transitions (bifurcations) at certain critical points where the system may choose between alternative optional dynamical regimes, such as steady states, oscillations or chaotic attractors. Systems under such conditions may be regarded as “active systems” in the sense that their internal state or behaviour is no longer uniquely determined by the boundary conditions currently imposed or historically experienced. “The defining property of an active system is that of the energy input that maintains the system out of equilibrium. … The dynamics of such active entities breaks time-reversal symmetry” (Bowick et al. 2022: p.2).
Active systems can make decisions in response to varying external conditions and may perform transitions even under persistent circumstances. Those decisions or activities do not necessarily serve a certain purpose or aim. Organisms (except perhaps viruses) are always active systems, but not all active systems are definitely alive. However, not-yet-living active systems are plausible candidates for physical structures at the threshold to life.
Of central interest are active systems capable of individual growth and self-reproduction. If autocatalysis is excluded, derived from the mathematical theory of random graphs (Austin et al. 1959, Erdös and Rényi 1960), the most likely catalytic cycles in an under-occupied random chemical network are binary ones (Feistel 1979, Ebeling and Feistel 1979, Sonntag et al. 1981, Feistel and Ebeling 2011), see Section 4. If such a cycle possesses “parasitic” catalytic side chains that form a droplet-like individual, such coacervates may grow at constant composition, and variants thereof may mutually compete with respect to their net growth rate (Feistel et al. 1980, Ratner and Shamin 1983, Feistel 1983, Saakian and Red’ko 2018, 2021). Those conceptual droplets are active in the sense that they can grow, divide, consume energy-rich chemicals and release metabolic residues. Their stoichiometry represents structural information about how to survive by self-reproduction under persistent environmental conditions. Under changing external conditions, their internal reaction dynamics may pass critical points of bifurcation, where the droplet will choose, perhaps randomly, one of several optional branches to proceed. This choice will affect the droplet’s reproduction rate, that is, its selective value in competition with other coacervates.
“For an organism the world must be predictable, otherwise it cannot live therein” (Eibl-Eibesfeld 1998: p. 21). “Anticipatory acts or predictive behavior are prerequisites for living organisms to sustain their survival when escaping from a predator, catching prey, or schooling” (Nomura et al. 2019: p. 267). “The method, though, which we always use for deriving futurity from the past, and therefore to gain the desired foresight, is this: we build for ourselves internal virtual images, or symbols, of the external objects in such a way that the thought-necessary consequences of those images may always be images of the nature-necessary consequences of the external objects previously mapped” (Hertz 1894: p. 1). What Heinrich Hertz described here for human mental prediction is valid in similar form for any prediction models of any organisms, including the very first ones. Beneficial action requires decisions derived from prediction models (Feistel 2023a).
When an organism is passing genetic information to its offspring, it transfers and executes an individual symbolic prediction model. This inherited model represents successful experience from the past and is suggesting to perform the same kind of actions and to make the same decisions as the parent in order to survive again in the future. Such actions may include exploiting the same metabolism chemistry, and such decisions may include a way of avoiding dangerous and preferring helpful external food supply. The emergence of the very first such model, of the first genetic code, of the first symbols, may therefore be regarded as the beginning of life. Active self-reproducing individuals capable of making decisions will systematically gain selective advantage over other competitors if they remember previous decisions and repeat those beneficially in the future under similar circumstances. This faculty constitutes the key evolutionary driving force for the emergence of prediction models (Feistel 2023b). Inheriting previous experience is the key to unlocking the gate to Darwinian evolution. “How strong is the tendency to inheritance; that like produces like” (Darwin 1911: p. 10).
In particular, the ability of mammals to decide about their immediate activity on the basis of predictions of expected future situations is regarded as “deliberation” (LeDoux 2021: §45). “By using cognitive models, animals can predict before they act” (Pattee 2015). “Prediction is also the engine of action. … Action and perception form a single whole, jointly orchestrated by the drive to eliminate errors in prediction” (Clark 2023: p. 70, 71). “The animal is always ‘deciding’ which response to perform” (Williams 1994). “The primary task of all the prediction … is to help us stay alive” (Clark 2023: p. 89).

6. Ritualisation

Originally discovered in behavioural biology a century ago, ritualisation is the general transition process from structural to symbolic information (Feistel 1990, 2017a, 2023b, Feistel and Ebeling 2011), creating an unprecedented kind of symbol. Due to transition continuity in combination with the emergence of a novel symmetry, namely, the arbitrariness of the symbols, ritualisation may be regarded as a kinetic phase transition of the second kind. This process may happen in very similar form in various different fields of self-organisation where symbols and information play a role.
Quite apart from the origin of life, but as a tutorial, conceptual example for a ritualisation transition, the human division of labour may serve here. Long ago, a successful hunter may have had more food available than he could eat himself, but was perhaps lacking a crafted stony hand axe. Such things could be exchanged with mutual benefit for both partners of the deal, value per value, quid pro quo (Smith 1789). With the development of systematic such bargains at markets, universal exchange equivalents were introduced for completing a pending exchange process at a later point of time, or at another place, or with additional persons or goods involved. Those typical universal equivalents in the form of suitable commodities, such as pieces of gold or silver, pearls or feathers, had themselves an exchange value equivalent to that of the things given or taken. The currencies “pound” or “libra/lira” still remind us that weight was a numerical measure of value. „The introduction of coins completed the guarantee of the weight; the number appeared substituting the weight“ (Bloch 1906: p. 96). In advanced societies with centralised power of a king or government, valuable metallic coins could be replaced by fiat money, namely, by relatively worthless paper slips which give a symbolic promise of representing a certain amount of gold or silver, Figure 3, granted by a commonly accepted authority.
Paper money is a carrier of symbolic information about a certain exchange value, while a piece of gold or silver is structural information, representing that value simply by itself. Paper money is arbitrary in the sense that it may be replaced, without affecting its meaning, at any time by a newly printed edition, or manipulated details against criminal fakes, or by entirely different design, shape or material upon decision of the emitter. By contrast, a coin of gold cannot be replaced arbitrarily by something else without losing its meaning. The transition from gold to fiat money, from actual payment of the debt to a symbolic promise to pay that debt in the future, is a ritualisation transition in economy (Feistel 1990, 2017b), establishing a new kind of arbitrary symbol. Arbitrariness, or conventionality, of that money is the new symmetry. Modern symbolic crypto currencies exist as a kind of money only by convention of their users.
Convenience and flexibility of fiat money has finally convinced modern countries to abstain completely from the previous “gold standard” with fixed mutual currency exchange rates. “The prewar gold standard was supported by a particular set of economic and political circumstances specific to that time and place. … By 1990, roughly 15 percent of all countries had moved to floating rates. By 2016, this share had risen to nearly 40 percent” (Eichengreen 2019). To the advantageous novel features and options that become available after a ritualisation transition belongs, for example, the accumulation of money as a fortune or of symbolic information as memory. This way, “a rate-dependent dynamical state is coded into quiescent symbols” (Pattee 2001: p. 5).
Paper money is used to symbolically document debts or assets of persons with respect to not-yet-completed acts of exchange of goods or services. Modern digital money increasingly takes over this function by numerical bookkeeping of individual accounts on central computers of banks. While the physical appearance of banknotes and coins still resembles its origins as weights of valuable metals, the bits in the computer memory are completely arbitrary representations of their meaning.
A ritualisation transition is fully completed only as soon as the original structural information transfer is completely replaced by a symbolic one. Money is received in return for a good or service given to others. Symbolic money represents “exchange value” (or price) but is itself practically without any “use value” (Smith 1789, Marx 1867). It has the only and ultimate purpose of being transformed back into the use value of a good or service provided by others. In similar form, this essence is universal for any symbolic information transfer. Symbolic information is received from structural information by a symbolisation process (such as perception, observation, measurement), is practically useless in its own right but unleashes its importance upon transformation back into structural information in the form of decisions or actions (Feistel 2023b). By the evolutionary ritualisation process, a flexible interface of symbolic information becomes sandwiched into a rigid structural information transfer chain, Figure 4, rendering also this chain flexible with respect to selectively advantageous modifications (Feistel 2017b). At the transition to life, symbol processing is implemented in a feedback loop between perception of the external world and acting on it (Feistel 2023b), see Section 6.
Various ritualisation processes have previously been described in behavioural biology (Huxley 1914, Lorenz 1963, Tembrock 1977, Osche 1983) with extensions to human social, cultural and technical processes (Koenig 1970, Wickler 1970, Klix 1980, Grammer and Eibl-Eibesfeld 1990, Wunn et al. 2015, Feistel 2017a). All these ritualisation processes are immersed in the realm of life with its pre-existing complex information processing facilities.  However, a ritualisation scenario at the beginning of life is in a less comfortable explanation situation in which there is no functioning life present yet when the ritualisation process starts to take place. A conceptual solution to this difficulty at the edge to life is the assumption of self-reproducing active systems, see Section 5. Those are individual entities (doplets, coacervates) containing a self-sustained catalytic loop supplied by energy-rich chemicals provided externally under non-equilibrium conditions.
Julian Huxley’s (1914) original definition of ritualisation was “the gradual change of a useful action into a symbol and then into a ritual; or in other words, the change by which the same act which first subserved a definite purpose directly comes later to subserve it only indirectly (symbolically) and then not at all”. Later, Konrad Lorenz (1970) understood ritualisation as “a process by which behavioural or physical forms, or both, that had originally developed to serve certain different purposes for the species‘ survival, turned into symbols that serve the communication within a population”. By that time, the perhaps most abstract version was due to Günter Tembrock (1977), who declared ritualisation simply to be “the development of signal-activity from use-activity”. In this sense, being suggested here, the most general definition of the ritualisation transition may be the emergence of symbolic from structural information transfer (Feistel and Ebeling 2016).

7. Molecular Ritualisation Scenario

Chemically, ribose is an energy-rich, ring-shaped sugar molecule of five carbon atoms with short side chains. With a phosphate molecule acting as “glue”, stacked ribose rings can form long strings – a scaffold along which different nucleobases such as guanine G, uracil U, adenine A and cytosine C may be attached at each ribose ring. Such a string is termed ribonucleic acid, or RNA for short. RNA is an amazingly versatile structure (Fry 2010, Cech 2024). “RNA is thus the prime candidate for early life’s supermolecule… Able to replicate and mutate, acting as both enzyme and gene, RNA performs operations that form more of itself” (Margulis and Sagan 1995: p. 84). “RNA indeed had information and function in the same molecule" (Cech 2024: p. 114).
A key feature of RNA is its property to fold and cleave to itself, forming enzyme-like catalytic “ribozymes” (Cech 1989). In the “RNA World” model (Gilbert 1986), RNA is a preferred candidate for spontaneously formed molecules at the threshold to life (Müller et al. 2022). However, “the evidence that is currently [1987] available does not support the availability of ribose on the prebiotic earth, except perhaps for brief periods of time, in low concentration as part of a complex mixture, and under conditions unsuitable for nucleoside synthesis” (Shapiro 1988: p. 71). On the other hand, “ribose was found in carbonaceous chondrites. Its exogenous delivery onto the Hadean Earth could be a crucial step toward the emergence of the RNA world” (Paschek et al. 2022), and “a microdroplet environment … [may provide] a possible scenario for the spontaneous production of random ribonucleosides [i.e., ribonucleotides without phosphate group] necessary to generate various types of primitive RNA” (Nam et al. 2017: p. 36). "The reaction conditions needed to make the U and C bricks were quite different from the conditions needed to make A and G bricks, and the two sets of conditions were largely incompatible... [However,] cycling between wet and dry conditions allowed all four nucleotides to accumulate essentially in one pot" (Cech et al. 2024: p. 117).
A chain molecule similar to RNA is desoxyribonucleic acid, DNA, which is chemically more stable and catalytically less active than RNA, and may form very long “rope ladders”. As its name suggests, desoxyribose molecules include one oxygen atom less than the related side chain of ribose. After the discovery of the DNA double helix by Watson and Crick (1953), numerous details of molecular genetics could be revealed, in particular also the table of the genetic code (Nirenberg et al. 1965).
Triplets of the DNA or mRNA chain molecules, the codons, are symbols representing amino acids to be assembled to proteins, following a convention as physically implemented by tRNA molecules (Eigen and Winkler-Oswatitsch 1981, Xie 2021, Cech 2024). Here, messenger RNA (mRNA) means a linear RNA strand, typically copied from a piece of DNA, and transfer RNA (tRNA) denotes a folded RNA whose one side may bind to a specific triplet of mRNA while the other side may bind to a specific amino acid. “Francis Crick raised in 1955 a purely theoretical adaptor hypothesis to explain how sequences of four nucleotides in a nucleic acid template determine sequences of 20 amino acids in proteins” (Fry 2022). “However, solving this secret of DNA would ultimately require DNA’s own daughter – ribonucleic acid, or RNA” (Cech 2024: p. 11). The inherited genetic information of each living being is stored in DNA or RNA strands and is read as symbolic information. 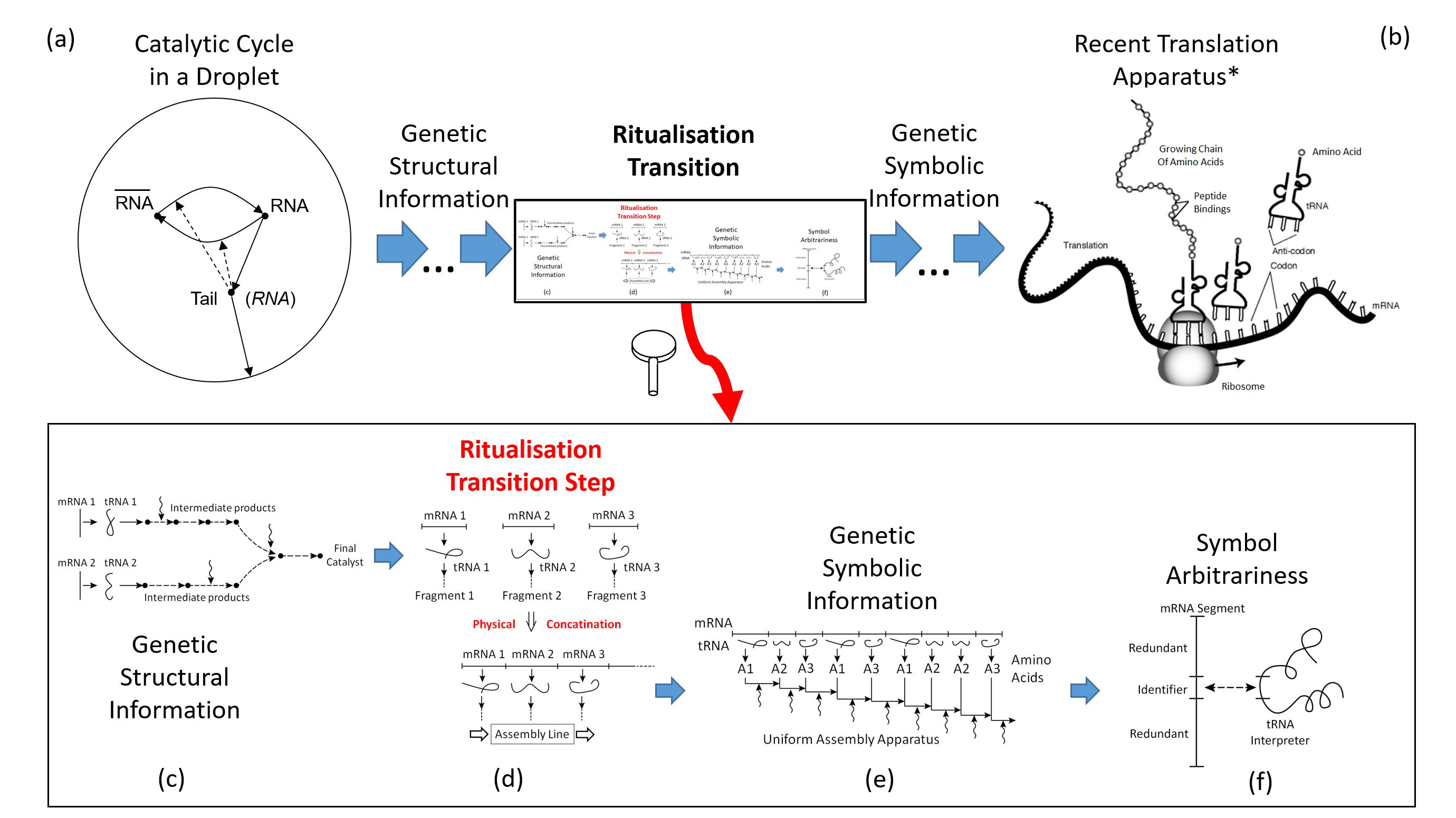This is the current upper end of the genetic evolution process that transformed chemistry into biology, depicted in image (b) of Figure 5.
On the other hand, at the lower end, image (a) of Figure 5, sparking that process, there must have been a beginning of molecular evolution, of merely spontaneous chemical self-reproduction (Eigen 1971). Here, this beginning is assumed to be a binary cross-catalytic loop, such as an RNA strand and its complementary sequence, enclosed in a droplet. If autocatalysis is excluded for its vanishing likeliness, a binary cycle is by far the most probable loop in a sparsely populated random directed graph (Feistel 1979, Ebeling and Feistel 1979, 1982, Sonntag et al. 1981, Feistel and Ebeling 2011, Eigen 2013), see Section 4.
(a)
Likely, molecular evolution had started from a catalytic cycle in a droplet. Catalysts may had been spontaneous random RNA strands and their complements, supporting as “ribozymes” the RNA self-reproduction as well as an enclosing membrane via “parasitic” side chains (Ebeling and Feistel 1979, Feistel et al. 1980, Feistel 1983, Feistel and Ebeling 2011). The linear RNA strand will be denoted here as “mRNA”, the catalytic ribozyme RNA as “tRNA”, for their similar roles in the recent translation process.
(b)
Present-day life utilises a translation apparatus that assembles large proteins from a sequence of amino acids that is controlled by a chain of symbolic codons, with arbitrary mutual assignments via tRNA “clover leafs” (Cech 2024).*Modified public domain image created by the National Human Genome Research Institute, National Institutes of Health (United States Department of Health and Human Services), https://commons.wikimedia.org/w/index.php?curid=13280126
(c)
Right before the ritualisation transition, mutation and selection of the droplet chemistry has resulted in a collection of different separate genetic strands (precursor of mRNA), each of which is translated to (precursor of) tRNA and subsequently, via intermediate catalytic steps, into self-assembled primitive proteins with random sequences of available constituents.
(d)
Separate mRNA strands become concatenated to a sequence of those segments which controls the successive assembly of only one primitive protein out of the many previous, randomly free combinations.
(e)
Identically repeated strands in the mRNA chain are redundant and error-prone; they may be replaced by shorter symbolic strands which no longer provide the full chemical information for the synthesis of the related protein fragment but will still maintain the information on the assembly sequence.
(f)
The post-ritualisation arbitrariness of the symbolic strands permits their “weathering” and gradual reduction to minimum length, in parallel to the tRNA which constitutes the interpreter of conventionally assigned meanings of the symbols.
Such an example could be a "hypothetical RNA self-replication in which small scraps of RNA bind by base-pairing to a preexisting RNA strand … and are then stitched together by a ribozyme... The product is a double-stranded RNA. The energy provided by sunlight then "melts" this double-stranded RNA, separating it into its two strands. The [second] strand folds within itself to form a new ribozyme, while the [first] strand provides a template for another round of replication” (Cech 2024: p. 115).
In homogeneous solution, the nonlinearity of catalytic feedback prevents gradual improvement by mutual competition between different molecules. Importantly, this qualitative selection behaviour is different if those molecules are enclosed in separate droplets which may grow at different speeds and compete by their total reproduction rates, that is, their selective values (Feistel et al. 1980, Feistel 1983, Ratner and Shamin 1983, Fry 2010). "A bunch of molecules in a drop of liquid is ... not an organism... It needs to be encased in some sort of envelop... Envelops facilitate evolution… Protocells can grow and then divide, although not with the regularity with which modern cells undergo cell division” (Cech 2024: p. 122, 123). Assuming that the droplet’s relative stoichiometry, c , does not change during growth and division, then the droplet’s selective value, E , is given by an eigenvalue of the set of involved chemical rate equations, c ˙ = f c , (Feistel et al. 1980, Feistel 1983, Feistel and Ebeling 2011),
E c = f c .
"Yet the simplest definitions of life have just two basic requirements: a living thing must be able to reproduce itself, and it must be able to mutate" (Cech 2024: p. 110). Chemical self-reproduction is transfer of structural information from a parent droplet to an offspring droplet. Prior to the existence of symbols, this information may be denoted here as “genetic structural information”. Somewhere in between the structural information accumulated during the initial chemical evolution on one side, and the symbolic information controlling the later biological evolution on the other side, a transition between the two is to be expected. This critical point may be approached theoretically from both directions in a fictitious conceptual model.
Seen from below, see image (c) of Figure 5, the single initial binary cycle in a droplet may have been quantitatively replaced by a collection of different such cycles with different side chains for catalytic support of various branches of the droplet’s metabolism. It is worth noting that such a network implies natural limitations of structural growth. If we think of n such cycles, each of those giving rise a specialised catalyst through m successive chemical mounting steps, the full support of each such step would require n × m different catalysts while only m of those are available. That is, with increasing complexity of metabolism, the demand for catalysts is growing faster than the enzyme production capabilities of the droplet, so that the efficiency of such a system remains systematically restricted in its evolution.
Seen from above, see image (f) of Figure 5, permitted by the arbitrariness of symbols, the modern triplets of mRNA may represent the final stage of a gradual but systematic shortening of previously longer identifiers, omitting redundant pieces of those. This process may have started from a coding system like that of Crick’s (1966, 1968) wobble hypothesis and subsequently evolving to the recent genetic code. As is generally known from any ritualisation processes, at some later stage the arbitrary code becomes frozen-in for stability and uniqueness of information management, and preserves in its details some residual structural information about its own evolution process.
This process of reduction to short symbols may have commenced at a point where each identifier had provided the full structural information required for addressing a certain amino acid. At this stage, the tRNA sequence was identical with the complementary mRNA coding for that amino acid, image (e) of Figure 5. It is a general characteristic of the ritualisation transition that at this critical point, image (d) of Figure 5, structural and symbolic information are indistinguishable from one another. In this symmetry-breaking step, the formerly disordered set of mutually independent mRNA strands is transformed into an ordered such set so that the mutual sequence of strands becomes a novel symbolic information. The partial strands turn into symbols of themselves in this ritualisation transition step where for the very first time molecules became symbols (Pattee 1969, Feistel 1990, 2023b, Feistel and Ebeling 2011, Deacon 2021). Converting genotypic symbolic information to phenotypic structural information, an organism is a "machinery that transforms the code of life into the stuff of life" (Cech 2024: p. 28). This way, assumingly, it had happened with the first ritualisation process ever. “With biology, the only rule is: whatever works. Once a system, however convoluted it may seem, starts to work well, it gets locked into place by evolution and becomes very hard to change” (Cech 2024: p 20).
Before the ritualisation transition, it is assumed here that simple proteins were produced by random self-assembly from at least two different simple amino acids. Only few of those various sequences may have possessed relevant catalytic properties, so that the efficiency of such a random production method is low. The amino acids, in turn, may be produced by separate catalytic RNA molecules, taking both roles of modern mRNA and tRNA. “RNA can make proteins, in principle, without any DNA” (Margulis and Sagan 1995: p. 83).
In the course of the transition, the separate RNA strands could be concatenated to longer chain molecules which not only identified the necessary amino acids but also the mutual sequence of their successive mounting to more complex catalysts. This transition is the replacement of a “workshop production” by an “assembly line production” of proteins with the related increase in efficiency and accuracy of the translation process. It is important to note here that the concatenation of RNA segments to longer units is the essential step which defines the succession of building blocks and permits the reduction of the full structural information of each segment to a minimum symbolic information to specify the assembly sequence. The assumed transition from many small, independent catalytic clusters to a few large such clusters has similarities with the percolation transition, see Section 4.
The crucial step of this model may be emphasised here once more. Before the transition, a self-replicating droplet contains at least one catalytically active sort of mRNA molecule in numerous instances/copies, as well as other molecules which belong to the same reaction network of that mRNA, likely including also certain of its error copies. This evolution stage is still mere chemistry, performing replication of structural information. As soon as those identical mRNA instances, together with some error copies, stick together and jointly form a longer chain, the relative position of those segments in the chain becomes a novel relevant structural information, instructing the subsequent catalytic assembly network to mount a specific building block. Repeated identical such segments become redundant then and may be reduced to shorter pointers referring to just the one original, complete mRNA segment. These arbitrary pointers, acting like names of procedures to be called, are the first symbols emerging in the ritualisation transition. Names of procedures, such as codons of a genetic prescription sequence, constitute arbitrary symbols for those procedures.

8. Summary

The description of the origin of life as a physical phase transition is a very general approach, independent of the specific terrestrial environmental conditions or of exceptional physical and chemical properties of certain organic molecules. As a ritualisation transition which results in emerging symbols that permit symbolic information processing, memory of past experience, and exploiting prediction models, this abstract description may also apply to processes very far from the terrestrial forms of life that are the only ones we are aware of yet.
The struggle for survival of any living being, subject to Darwinian evolution, is active behaviour of complex, open physical systems far from thermodynamic equilibrium. The nonlinear dynamics of such systems includes bifurcation states at which a system decides between different branches of future states to be occupied. Some of those future states are more beneficial for survival than others, and the ability of systematically choosing the most promising options provides significant selective advantage. Causal prediction models deliver the proper information for such essential decisions. Models, however, are complex symbols, consisting of structured sets of simpler symbols. The emergence of symbols is the central transition to the realm of life.
Sun, moon and stars are carriers of structural information. Observing them may inform us about seasonal changes, tides and interplanetary forces. Books and images are symbolic information carriers; they may tell us anything. To understand the latter ones, knowledge is requisite of a convention about the meaning of letters, words, or screen pixels. Considered as the central dogma of semiotics, the relation between symbol and its meaning is fundamentally arbitrary; this is the new symmetry of symbolic information carriers in distinction to structural information carriers.
Ritualisation is the emergence of symbolic information carriers from structural ones in the course of evolution. Ritualisation has properties of kinetic phase transitions of the 2nd kind, namely, that the transition is continuous and is breaking the symmetry. At the transition point, structural information carriers remain themselves structurally unaltered but take an additional new role of being symbols. The related novel arbitrariness of symbols corresponds to their neutral stability with respect to mutations; subject to fluctuations, symbols may gradually change by weathering, random drift and diversification. Neutral stability with respect to certain fluctuations means the absence of restoring forces which otherwise tend to attenuate those perturbations. However, despite its fragile stability, symbolic information carried by suitable physical structures may losslessly and repeatedly be copied or refreshed to render that information more durable than any structural information limited by its finite decay time. This unique feature enables life to inherit and perpetually exploit previous observations and discoveries made in a very distant past.
Here, it is argued that starting from random chemical catalysts which may spontaneously be formed in aqueous solution, the origin of life on Earth occurred along with the emergence of a symbolic carrier of genetic information. As a recipe for future survival of offspring, this information represents an inherited prediction model. In a conceptual scenario of this ritualisation process it is suggested that in a self-reproducing droplet, it was especially the concatenation of separately available RNA strands that provided an assembly line for proteins and liberated its repeating segments to be arbitrarily modified and reduced to form the very first primitive genetic code.

References

  1. Allard, A. , Hebert-Dufresne, L., Young, J.-G., Dube, L.J. General and exact approach to percolation on random graphs. Phys. Rev. E 2015, 92, 062807. [Google Scholar] [CrossRef] [PubMed]
  2. Almheiri, A. , Hartman, T. , Maldaceda, J., Shagoulian, E., Tajdini, A. Replica wormholes and the entropy of Hawking radiation. JHEP05, 2020, 013. [Google Scholar] [CrossRef]
  3. Austin, T.L. , Fagen, R.E., Penney, W.F., Riordan, J. The Number of Components in Random Linear Graphs. The Annals of Mathematical Statistics 1959, 30, 747–754. [Google Scholar] [CrossRef]
  4. Battelli, F. , Lazzari, C. On the pseudo-steady-state approximation and Tikhonov theorem for general enzyme systems. Mathematical Biosciences 1985, 75, 229–246. [Google Scholar] [CrossRef]
  5. Bloch, L. (1906): Römische Altertumskunde.
  6. Bowick, M.J. , Fakhri, N., Marchetti, M.C., Ramaswamy, S. Symmetry, Thermodynamics, and Topology in Active Matter. Physical Review X 2022, 12, 010501. [Google Scholar] [CrossRef]
  7. Braunstein, S.L. , Pati, A.K. Quantum Information Cannot Be Completely Hidden in Correlations: Implications for the Black-Hole Information Paradox. Physical Review Letters 2007, 98, 080502. [Google Scholar] [CrossRef]
  8. Cech, T.R. Self-Splicing and Enzymatic Activity of an Intervening Sequence RNA from Tetrahymena. Nobel Lecture, December 1989, 8, 1989. [Google Scholar]
  9. Cech, T.R. (2024): The Catalyst: RNA and the Quest to Unlock Life’s Deepest Secrets. W.W. Norton Co., New York.
  10. Çengel, Y.A. A concise account of information as meaning ascribed to symbols and its association with conscious mind. Entropy 2023, 25, 177. [Google Scholar] [CrossRef]
  11. Clark, A. (2023): The Prediction Machine.
  12. Coeckelbergh, M. (2020): Using Words and Things: Language and Philosophy of Technology.
  13. Conrad, M. Natural selection and the evolution of neutralism. Biosystems 1982, 15, 83–85. [Google Scholar] [CrossRef]
  14. Crick, F.H.C. Codon-anticodon pairing: The wobble hypothesis. Journal of Molecular Biology 1966, 19, 548–555. [Google Scholar] [CrossRef]
  15. Crick, F.H.C. The origin of the genetic code. J. Mol. Biol. 1968, 38, 367–379. [Google Scholar] [CrossRef] [PubMed]
  16. Darwin, C. (1911): The Origin of Species by Natural Selection.
  17. Deacon, T.W. How Molecules Became Signs. Biosemiotics 2021, 14, 537–559. [Google Scholar] [CrossRef]
  18. Ebeling, W. , Engel, A., Esser, B., Feistel, R. Diffusion and Reaction in Random Media and Models of Evolution Processes. Journal of Statistical Physics 1984, 37, 269–284. [Google Scholar] [CrossRef]
  19. Ebeling, W. , Feistel, R. On the Evolution of Biological Macromolecules: I. Physico-chemical Self-organization. Studia biophysica 1979, 75, 131–146. [Google Scholar]
  20. Ebeling, W. , Feistel, R. (1982): Physik der Selbstorganisation und Evolution.
  21. Ebeling, W. , Feistel, R. (1994): Chaos und Kosmos. Prinzipien der Evolution.
  22. Eibl-Eibesfeldt, I. (1998): Ernst Haeckel – Der Künstler im Wissenschaftler. In: Haeckel, E. (1904): Kunstformen der Natur. Neudruck.
  23. Eichengreen, B. (2019): Globalizing Capital: A History of the International Monetary System - Third Edition. Princeton University Press, Princeton. [CrossRef]
  24. Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef]
  25. Eigen, M. (2013): From Strange Simplicity to Complex Familiarity. A Treatise on Matter, Information, Life and Thought.
  26. Eigen, M. , Winkler-Oswatitsch, R. Transfer-RNA, an early gene? Die Naturwissenschaften 1981, 68, 282–292. [Google Scholar] [CrossRef]
  27. Erdös, P. , Rényi, A. On the Evolution of Random Graphs. Publication of the Mathematical Institute of the Hungarian Academy of Sciences, 1960, 5, 17–61. [Google Scholar]
  28. Facchin, M. (2024): Maps, Simulations, Spaces and Dynamics: On Distinguishing Types of Structural Representations. [CrossRef]
  29. Feistel, R. (1979): Selektion und nichtlineare Oszillationen in chemischen Modellreaktionen.
  30. Feistel, R. On the Evolution of Biological Macromolecules. IV. Holobiotic Competition. studia biophysica 1983, 93, 121–128. [Google Scholar]
  31. Feistel, R. Species Competition and Phenotypic Change. studia biophysica 1984, 102, 247–254. [Google Scholar]
  32. Feistel, R. (1990): Ritualisation und die Selbstorganisation der Information. In: Niedersen, U., Pohlmann, L. (eds): Selbstorganisation. Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, Band 1. [CrossRef]
  33. Feistel, R. Self-organisation of symbolic information. The European Physical Journal Special Topics 2017, 226, 207–228. [Google Scholar] [CrossRef]
  34. Feistel, R. (2017b): Chapter 4: Emergence of Symbolic Information by the Ritualisation Transition. Information Studies and the Quest for Transdisciplinarity. World Scientific, Singapore, pp. [CrossRef]
  35. Feistel, R. On the Evolution of Symbols and Prediction Models. Biosemiotics 2023, 16, 311–371. [Google Scholar] [CrossRef]
  36. Feistel, R. Self-Organisation of Prediction Models. Entropy 2023, 25, 1596. [Google Scholar] [CrossRef] [PubMed]
  37. Feistel, R. , Ebeling, W. Deterministic and Stochastic Theory of Sustained Oscillations in Autocatalytic Reaction Systems. Physica 1978, 93A, 114–137. [Google Scholar] [CrossRef]
  38. Feistel, R. , Ebeling, W. Models of Darwinian processes and evolutionary principles. BioSystems 1982, 15, 291–299. [Google Scholar] [CrossRef]
  39. Feistel, R. , Ebeling, W. (1983): Stochastic Models of Evolutionary Processes. In: Lamprecht, I., Zotin, A.I. (eds): Thermodynamics and Regulation of Biological Processes. W. de Gruyter, Berlin, pp. [CrossRef]
  40. Feistel, R. , Ebeling, W. (1989): Evolution of Complex Systems.
  41. Feistel, R. , Ebeling, W. (2011): Physics of Self-Organization and Evolution.
  42. Feistel, R. , Ebeling, W. Entropy and the Self-Organization of Information and Value. Entropy 2016, 18, 193. [Google Scholar] [CrossRef]
  43. Feistel, R. , Romanovsky, Yu.M., Vasiliev, V.A. Evolyutsiya Gipertsiklov Eigena, Protekayushchikh v Koatservatakh (Evolution of Eigen's Hypercycles Existing in Coacervates). Biofizika 1980, 25, 882–887. [Google Scholar]
  44. Feuerbach, L. (1848): Darstellung, Entwicklung und Kritik der Leibnitz’schen Philosophie. Ludwig Feuerbach’s sämmtliche Werke, Fünfter Band.
  45. Fisher, R.A. (1930): The Genetical Theory of Natural Selection.
  46. Fry, M. The Role of Natural Selection in the Origin of Life. Orig. Life Evol. Biosph. 2010, 41, 3–16. [Google Scholar] [CrossRef]
  47. Fry, M. (2022): The Adaptor Hypothesis. Reference Module in Life Sciences, Elsevier. [CrossRef]
  48. Gilbert, W. Origin of life: the RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
  49. Grammer, K. and Eibl-Eibesfeldt, I. (1990): The Ritualisation of Laughter. In: Koch, W.A. (ed): Natürlichkeit der Sprache und der Kultur. Acta Colloquii, Brockmeyer, Bochum, pp.
  50. Hahn, H. (1974): Geometrical Aspects of the Pseudo Steady State Hypothesis in Enzyme Reactions. In: Conrad, M., Güttinger, W., Dal Cin, M.: Physics and Mathematics of the Nervous System. 4. [CrossRef]
  51. Haken, H. (1970): Laser Theory.
  52. Haken, H. (1977): Synergetics. An Introduction. Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry and Biology.
  53. Haken, H. , Haken-Krell (1989): Entstehung von biologischer Information und Ordnung.
  54. Haken, H. , Plath, P.J., Ebeling, W., Romanovsky, Yu.M. (2016): Beiträge zur Geschichte der Synergetik.
  55. Hawking, S. (2018): Brief Answers to the Big Questions.
  56. Hertz, H. (1894): Die Prinzipien der Mechanik. Johann Ambrosius Barth, Leipzig. W: Photocopy reprint (1963), 1963. [Google Scholar]
  57. Hertz, H. (1899): The Principles of Mechanics Presented in a New Form. Jones, D.E., Walley, J.T., Translators; foreword by von Helmholtz, H.. MacMillan and Co., Ltd.
  58. Huxley, S.J. The Courtship-habits of the Great Crested Grebe (Podiceps cristatus); with an addition to the Theory of Sexual Selection. Proc. Zool. Soc. Lond. 1914, XXXV, 491–562. [Google Scholar] [CrossRef]
  59. Kant, I. (1787): Kritik der reinen Vernunft. F: Reprint (1956), 1956. [Google Scholar]
  60. Kaplan, R.W. (1978): Der Ursprung des Lebens.
  61. Kauffman, S. , Levin, S. Towards a general theory of adaptive walks on rugged landscapes. Journal of Theoretical Biology 1987, 128, 11–45. [Google Scholar] [CrossRef]
  62. Kimura, M. (1983): The neutral theory of molecular evolution.
  63. Klix, F. (1980): Erwachendes Denken. Eine Entwicklungsgeschichte der menschlichen Intelligenz.
  64. Koenig, O. (1970): Kultur und Verhaltensforschung.
  65. Kull, K. Jakob von Uexküll: An introduction. Semiotica 2001, 134, 1–59. [Google Scholar] [CrossRef]
  66. Kull, K. (2007): Biosemiotics and Biophysics – the Fundamental Approaches to the Study of Life. In: Barbieri, M. (ed.): Introduction to Biosemiotics. Springer, Dordrecht, pp. [CrossRef]
  67. Lacková, L. , Matlach, V., Faltýnek, D. Arbitrariness is not enough: Towards a functional approach to the genetic code. Theory in Biosciences 2017, 136, 187–191. [Google Scholar] [CrossRef] [PubMed]
  68. Landau, L.D. , Lifschitz, E.M. (1966): Lehrbuch der Theoretischen Physik Band V, Statistische Physik.
  69. LeDoux, J. (2021): Bewusstsein. Die ersten vier Milliarden Jahre.
  70. Leibniz, G.W. (1904): Neue Abhandlungen über den menschlichen Verstand.
  71. Lorenz, K. (1963): Das sogenannte Böse.
  72. Lorenz, K. 1970.
  73. Margulis, L. , Sagan, D. (1995): What is life? The Eternal Enigma.
  74. Marx, K. (1867): Das Kapital. Kritik der politischen Oekonomie, Erster Band.
  75. Matsuno, K. Molecular Semiotics toward the Emergence of Life. Biosemiotics 2008, 1, 131–144. [Google Scholar] [CrossRef]
  76. Meincke, A.S. (2023): The Metaphysics of Living Consciousness: Metabolism, Agency and Purposiveness. [CrossRef]
  77. Mendie, J.G. , Udofia, S.N. The Problem of Mind-Body Dichotomy: A Critique of the Cartesian Approach. GNOSI: An Interdisciplinary Journal of Human Theory and Praxis 2018, 1, 45–55. [Google Scholar] [CrossRef]
  78. Müller, F. , Escobar, L., Xu, F., Węgrzyn, E., Nainytė, M., Amatov, T., Chan, C.-Y., Pichler, A., Carell, T. A prebiotically plausible scenario of an RNA–peptide world. Nature 2022, 605, 279–284. [Google Scholar] [CrossRef]
  79. Muñoz-Gómez, S.A. , Bilolikar, G., Wideman, J.G., Geiler-Samerotte, K. Constructive Neutral Evolution 20 Years Later. Journal of Molecular Evolution 2021, 89, 172–182. [Google Scholar] [CrossRef]
  80. Nam, I. , Nam, H.G., Zare, R.N. Abiotic synthesis of purine and pyrimidine ribonucleosides in aqueous microdroplets. PNAS 2017, 115, 36–40. [Google Scholar] [CrossRef]
  81. Newell, A. Physical Symbol Systems. Cognitive Science 1980, 4, 135–183. [Google Scholar] [CrossRef]
  82. Nicolis, G. , Prigogine, I. (1987): Die Erforschung des Komplexen.
  83. Nirenberg, M. , Leder, P., Bernfield, M., Brimacombe, R., Trupin, J., Rottman, F., O'Neal, C. RNA codewords and protein synthesis, VII. On the general nature of the RNA code. Proc. Natl. Acad. Sci. USA 1965, 53, 1161–1168. [Google Scholar] [CrossRef]
  84. Nöth, W. (2000): Handbuch der Semiotik, 2nd edition. J.B.
  85. Nomura, N. , Matsuno, K., Muranaka, T., Tomita, J. How Does Time Flow in Living Systems? Retrocausal Scaffolding and E-series Time. Biosemiotics 2019, 12, 267–287. [Google Scholar] [CrossRef]
  86. Oehler, K. (1995): Sachen und Zeichen. Zur Philosophie des Pragmatismus.
  87. Osche, G. (1983): Zur Evolution optischer Signale bei Pflanze, Tier und Mensch.
  88. Paschek, K. , Kohler, K., Pearce, B.K.D., Lange, K., Henning, T.K., Trapp, O., Pudritz, R.E., Semenov, D.A. Possible Ribose Synthesis in Carbonaceous Planetesimals. Life 2022, 12, 404. [Google Scholar] [CrossRef]
  89. Pattee, H.H. How Does a Molecule Become a Message? Developmental Biology Supplement 1969, 3, 1–16. [Google Scholar] [CrossRef]
  90. Pattee, H.H. Cell Psychology: An Evolutionary Approach To The Symbol-Matter Problem. Cognition and Brain Theory 1982, 5, 325–341. [Google Scholar] [CrossRef]
  91. Pattee, H.H. The Physics of Symbols: Bridging the Epistemic Cut. Biosystems 2001, 60, 5–21. [Google Scholar] [CrossRef] [PubMed]
  92. Pattee, H.H. Cell Phenomenology: The First Phenomenon. Progress in Biophysics and Molecular Biology 2015, 119, 461–468. [Google Scholar] [CrossRef] [PubMed]
  93. Pattee, H.H. , Rączaszek-Leonardi, J. (2012): Historical Introduction to Laws Language and Life. [CrossRef]
  94. Plato (430 BCE): German edition (2013): Sämtliche Werke, Band 3. 37. Auflage.
  95. Plato (375 BCE): The Republic of Plato/Book 7. https://en.wikisource.
  96. Prigogine, I. (1977): Vom Sein zum Werden.
  97. Ratner, V.A. , Shamin, V.V. Modeling of fundamental features of molecular-biological organization. Zhurnal Obshchei Biologii 1983, 44, 51–61. [Google Scholar]
  98. Roncaglia, M. On the Conservation of Information in Quantum Physics. Foundations of Physics 2019, 49, 1278–1286. [Google Scholar] [CrossRef]
  99. Saakian, D.B. , Red’ko, V.G. Sysers: The important model of self-reproducing system. Biologically Inspired Cognitive Architectures 2018, 24, 115–121. [Google Scholar] [CrossRef]
  100. Saakian, D.B. , Red’ko, V.G. The model of a simple self-reproducing system. Cognitive Systems Research 2021, 65, 17–22. [Google Scholar] [CrossRef]
  101. Schelleng, J.C. The Physics of the Bowed String. Scientific American 1974, 230, 87–95. [Google Scholar] [CrossRef]
  102. Sebeok, T.A. The evolution of semiosis. In Posner, R., Robering, K., Seboek, T.A. (eds): Semiotics: A Handbook on the Sign - Theoretic Foundations of Nature and Culture, vol. 1997, 1, 436–446. [Google Scholar]
  103. Sebeok, T.A. (2001): Signs: An Introduction to Semiotics.
  104. Shannon, C.E. , Weaver, W. (1964): The mathematical theory of communication.
  105. Shapiro, R. Prebiotic ribose synthesis: A critical analysis. Origins of Life and Evolution of the Biosphere 1988, 18, 71–85. [Google Scholar] [CrossRef] [PubMed]
  106. Shelke, S.A. , Piccirilli, J.A. Origins of life: RNA made in its own mirror image. Nature 2014, 515, 347–348. [Google Scholar] [CrossRef]
  107. Smith, A. (1789): An Inquiry into the Nature and Causes of the Wealth of Nations. Methuen & Co., London. German edition (2013): Der Wohlstand der Nationen.
  108. Sonntag, I. , Feistel, R., Ebeling, W. Random Networks of Catalytic Biochemical Reactions. Biometrical Journal 1984, 23, 501–515. [Google Scholar] [CrossRef]
  109. Stachowiak, H. (1973): Allgemeine Modelltheorie.
  110. Stanley, H.E. (1971): Introduction to Phase Transitions and Critical Phenomena.
  111. Tembrock, G. (1977): Grundlagen des Tierverhaltens.
  112. Turing, A.M. Computing machinery and intelligence. Mind 1950, 59, 433–460. [Google Scholar] [CrossRef]
  113. Watson, J. , Crick, F. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef]
  114. Wickler, W. (1970): Stammesgeschichte und Ritualisierung.
  115. Williams, B.A. (1994): Reinforcement and choice. In: Mackintosh, N.J. (ed.): Animal Learning and Cognition. San Diego, Academic Press, pp. [CrossRef]
  116. Willink, R. (2013): Measurement Uncertainty and Probability.
  117. Wright, S. Evolution in Mendelian Populations. Genetics 1931, 16, 97–159. [Google Scholar] [CrossRef]
  118. Wunn, I. , Urban, P., Klein, C. (2015): Götter - Gene - Genesis: Die Biologie der Religionsentstehung.
  119. Xie, P. Who is the missing “matchmaker” between proteins and nucleic acids? The Innovation 2021, 2, 100120. [Google Scholar] [CrossRef]
Preprints 137560 g001
Figure 1. In the n-dimensional phenotype space, evolution of a phenotype q  proceeds to higher selective values E q  in direction of the steepest ascent, that is, along the gradient of the fitness landscape, perpendicular to the (n – 1)-dimensional hyperspace E q = c o n s t . Random mutations within that hyperspace are selectively neutral, i.e., arbitrary, even though they may change the genotype or the phenotype.
Figure 1. In the n-dimensional phenotype space, evolution of a phenotype q  proceeds to higher selective values E q  in direction of the steepest ascent, that is, along the gradient of the fitness landscape, perpendicular to the (n – 1)-dimensional hyperspace E q = c o n s t . Random mutations within that hyperspace are selectively neutral, i.e., arbitrary, even though they may change the genotype or the phenotype.
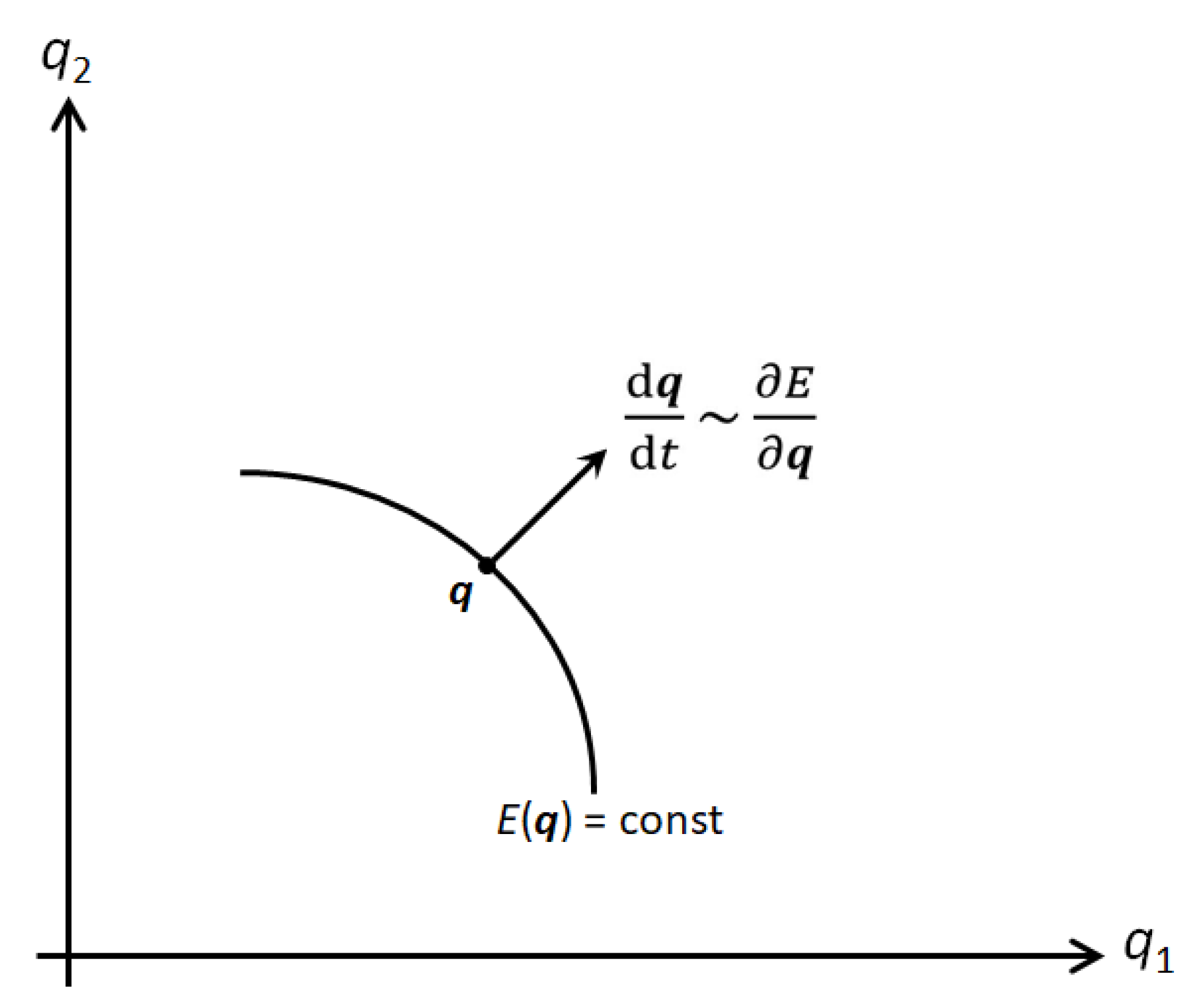
Preprints 137560 g001
Preprints 137560 g002
Figure 2. The probability P c , eq. (4), for a cycle to exist in an infinite random directed graph with coordination number c  exhibits a percolation transition at c = 1 . For weakly coordinated graphs, c ≪ 1 , this probability is dominated by the appearance of binary cycles, P c 2 , eq. (5). Figure from Feistel (1979).
Figure 2. The probability P c , eq. (4), for a cycle to exist in an infinite random directed graph with coordination number c  exhibits a percolation transition at c = 1 . For weakly coordinated graphs, c ≪ 1 , this probability is dominated by the appearance of binary cycles, P c 2 , eq. (5). Figure from Feistel (1979).
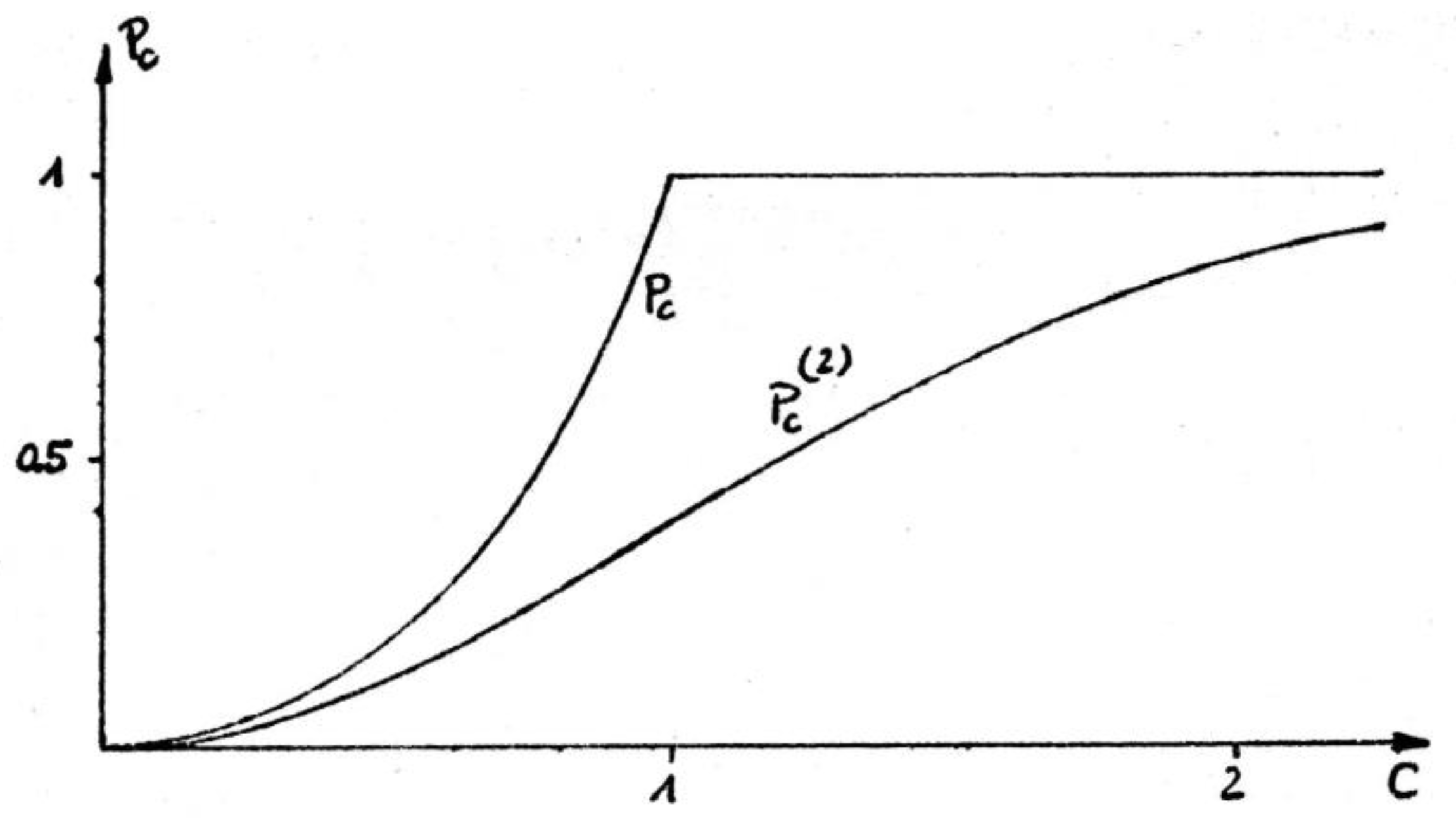
Preprints 137560 g002
Preprints 137560 g003
Figure 3. British 10 ₤ banknote: “Bank of Scotland plc promises to pay the Bearer on demand ten pounds sterling at its registered office, Edinburgh” is printed on top of the note. Photo taken in 2015.
Figure 3. British 10 ₤ banknote: “Bank of Scotland plc promises to pay the Bearer on demand ten pounds sterling at its registered office, Edinburgh” is printed on top of the note. Photo taken in 2015.
Preprints 137560 g003
Preprints 137560 g004
Figure 4. Schematic of the emergence of fiat money in the exchange of goods (upper box) as an example for the evolutionary ritualisation transition, sandwiching symbolic information transfer as a flexible arbitrary interface in between given solid forms of structural information (lower box).
Figure 4. Schematic of the emergence of fiat money in the exchange of goods (upper box) as an example for the evolutionary ritualisation transition, sandwiching symbolic information transfer as a flexible arbitrary interface in between given solid forms of structural information (lower box).
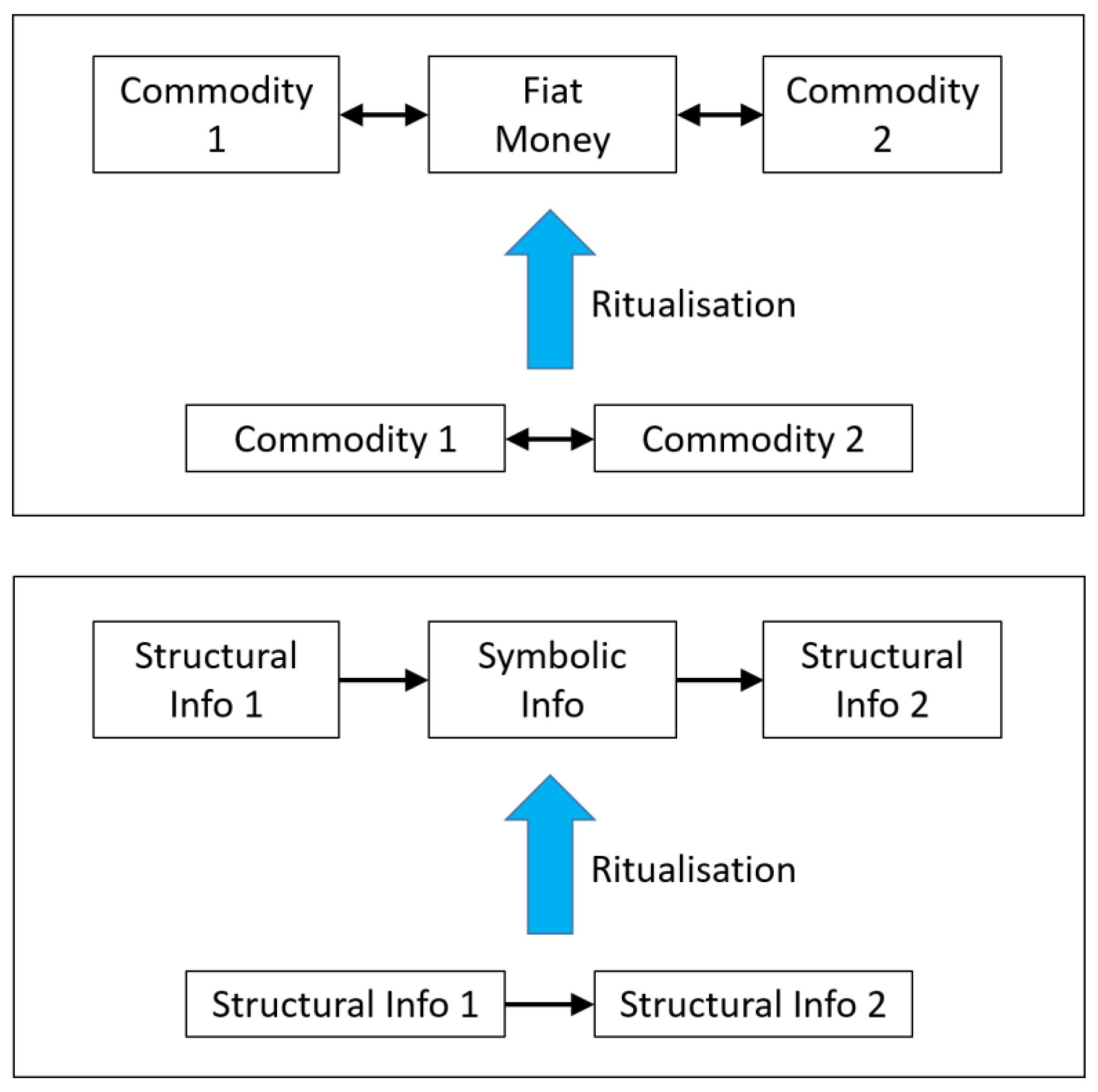
Preprints 137560 g004
Preprints 137560 g005
Figure 5. Schematic of a conceptual ritualisation scenario for the origin of life (Ebeling and Feistel 1982, Feistel 1990). During the evolution from the primordial, structural chemical beginning up to the recent biological, symbolic genetic code there must have been a transition point at which symbols emerged:
Figure 5. Schematic of a conceptual ritualisation scenario for the origin of life (Ebeling and Feistel 1982, Feistel 1990). During the evolution from the primordial, structural chemical beginning up to the recent biological, symbolic genetic code there must have been a transition point at which symbols emerged:
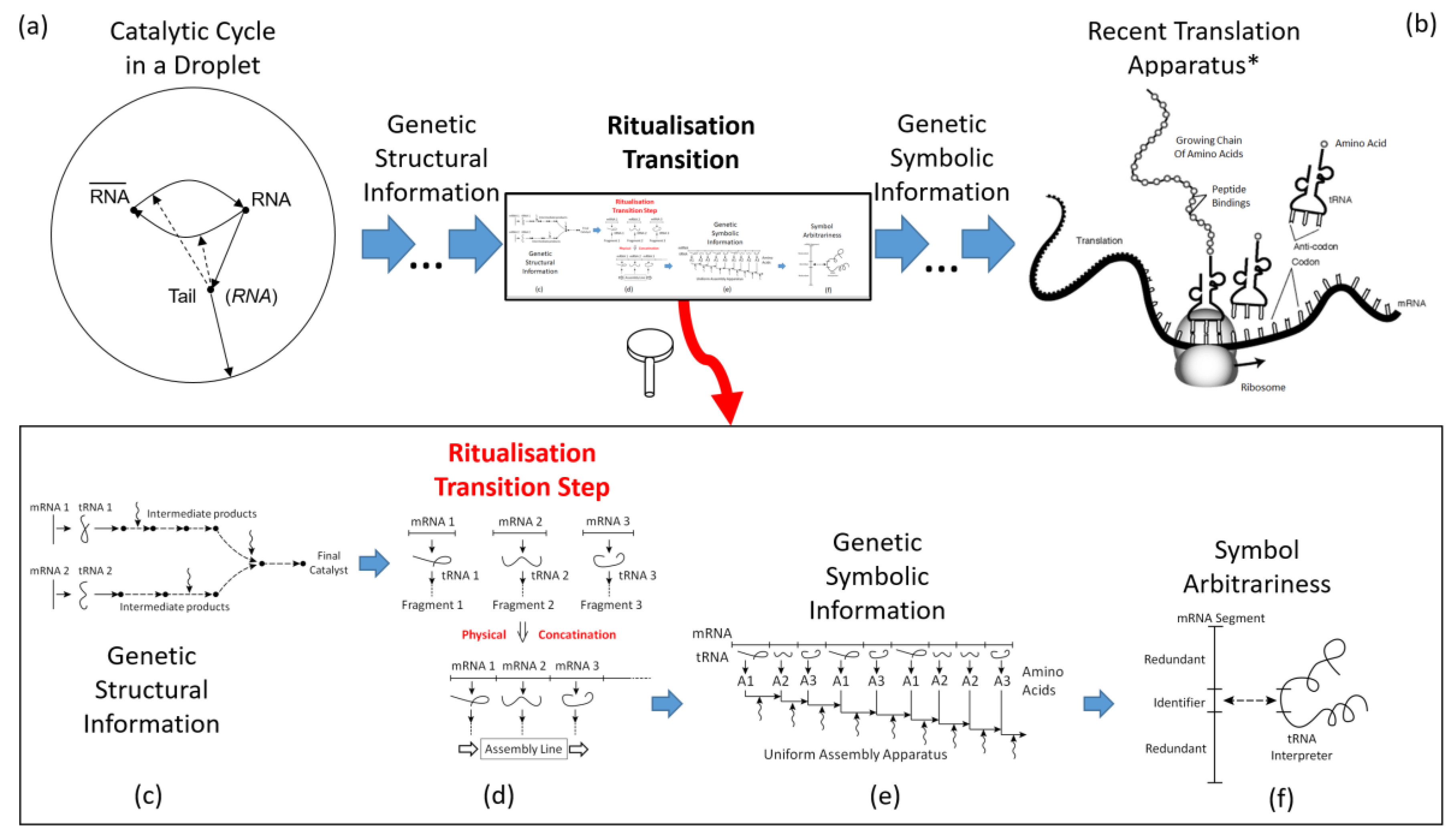
Preprints 137560 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated