FIDO2 Facing Kleptographic Threats by-Design

In this paper, we analyze the FIDO2 authentication scheme from the point of view of its resilience to kleptographic attacks. We show that despite its spartan design and apparent efforts to make it immune to dishonest protocol participants, the unlinkability features of FIDO2 can be effectively broken without a chance to detect it by observing the interactions. Similarly, a malicious authenticator can enable an adversary to seize the authenticator’s private keys and thereby enable impersonating the authenticator’s owner. As a few components of the FIDO 2 protocol are the source of the problem, we indicate that either their implementation details must be scrutinized during a certification process or one can introduce some minor local changes in the FIDO2 protocol that effectively disable attacks of this kind.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

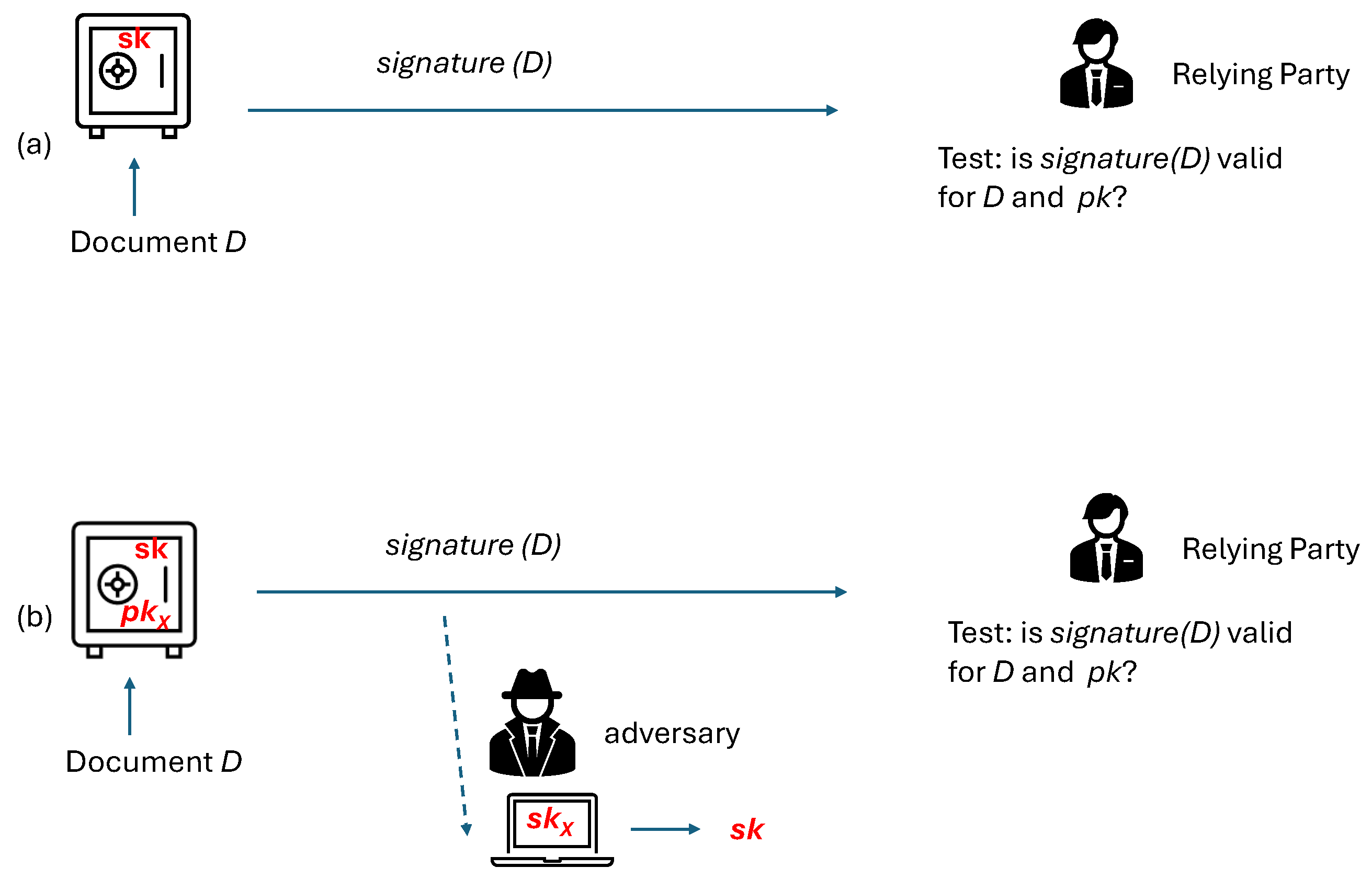
1. Introduction

User authentication is one of the critical elements in IT services. With the growing role of digital processing, secure authentication resilient to impersonation attacks is more important than ever. The old-fashioned solutions based on passwords memorized by human users have reached their limits; the trend is to rely upon digital tokens kept by the users. Such tokens, especially hardware ones, separated from the rest of the user’s devices, may offer high protection while relying on strong cryptographic authentication schemes. Moreover, effective inspection of dedicated authentication tokens with no other functionalities might be feasible, but it is rather hopeless for general-purpose computing devices.

Theoretically, deploying a reliable authentication token is easy today, given the current state of the art. In practice, it is problematic.

Implementing a global authentication system based on identical dedicated devices is virtually impossible for economic, technical, and political reasons. Nevertheless, there are efforts to solve this problem on a wide scale. One approach is to enforce some solution by political decisions in a top-down approach. The European Union’s EIDAS 2.0 regulation goes in this direction. The idea of a European Identity Wallet introduced by EIDAS 2.0 is ambitious and far-reaching, particularly concerning personal data protection issues. However, this endeavor may fail due to its complexity and high expectations.

The second strategy is to use already available resources, both hardware and software products, and attempt to build a flexible ecosystem where different devices may be integrated smoothly. In that case, the time-to-market should be substantially shorter, and the overall costs might be significantly reduced. Also, the risks can be addressed appropriately by using devices with security levels proportional to the particular risks.

Nevertheless, such a spontaneous ecosystem requires a common protocol to be executed by all devices. For this reason, it must not rely on any cryptographic primitive that is not commonly used. Challenge-and-response protocols with responses based on digital signatures are definitely well-suited for such ecosystems.

Legal Requirements

Broad application of an authentication system implies security requirements to be fulfilled. This is due not only to objective necessity but also to the applicable law. Enforcing a proper security level by setting minimal requirements for authentication systems is the current strategy of the European Union. Moreover, the rules are tightened over time. Due to cyberspace globality, these rules have a high impact on other countries, which frequently follow the same concepts.

As authentication concerns an identifiable individual, authentication systems fall into the scope of GDPR regulation [1]. One of the basic principles of GDPR is data minimalization: only those data should be processed, which are necessary for a given purpose. This creates a challenge for authentication schemes: The real user identity of an IT system should be used only if necessary; otherwise, it should be replaced by a pseudonymous identity. Even if the real identity is to be linked with a user account, the link should be concealed in standard processing due to the need to minimize the data leakage risk and implement the privacy-by-design principle: if no real identity is used, then it cannot be leaked. Of course, most systems still do not follow this strategy today, but the emerging FIDO2 authentication discussed in this paper is a good example of automatic pseudonymization.

Another European regulation greatly impacting authentication systems is EIDAS 2.0 [2]. It is explicitly devoted to digital identity and, thereby, authentication processes. The main EIDAS 2.0 concept is the European Identity Wallet, allowing individuals in the EU to authenticate themselves with an attribute and not necessarily with their real identity. What the technical realization of this concept will be is an open question, especially given the member states’ freedom to implement the EIW and vague general rules. Even the European authorities’ mandate to determine wallet standards does not preclude the diversity of low-level details.

EIDAS 2 may influence many security services in an indirect and somewhat unexpected way. It defines trust services and strict obligations for entities providing such services. Note that “the creation of electronic signatures or electronic seals” falls into the category of trust services (Article 3, point 16c). Therefore, any service where electronic signatures are created on behalf of the user falls into this category. This may be interpreted widely, with electronic signatures created by devices provided by the service supplier. Signatures need not serve the classical purpose of signing digital documents; they may relate to any data, in particular to ephemeral challenges during challenge-response authentication processes. From the civil law point of view, such a signature is a declaration of will to log into the system.

Another stepping stone towards security in European cyberspace is the Cybersecurity Act (CSA) [3]. It establishes a European certification framework based on Common Criteria for, among others, ICT products. An ICT product is understood here as an element or a group of elements of a network or information system. Any online authentication system falls clearly into this category. Although CSA introduces a framework of voluntary certification under the auspices of ENISA European authority, it may be expected that once the framework reaches its maturity, there will be a trend to request authentication with certified devices and schemes. To this end, it will be necessary to formulate relevant CC Protection Profile documents dealing with security requirements to be tested. This is a critical stage since omitting some aspects or attack scenarios may result in dangerous products with certificates that give a false sense of security.

FIDO2 Initiative

Given the diversity of authentication schemes and their lack of interoperability it is desirable to create a common framework that would enable usage of authentication tokens of different vendors within a single ecosystem. This necessity gave rise to the establishment of Fast Identity Online (FIDO) Alliance created by a large group of leading tech companies. The Alliance includes, among others, Google, Amazon, Apple, Intel, Microsoft, and Samsung.

The main flagship result of activities of the FIDO Alliance is a set of protocols called FIDO2. The goal was to provide an interoperable and convenient passwordless authentication resistant to man-in-the-middle attacks and phishing, and flexible enough to be implemented on a wide range of user devices offered by different vendors.

From the cryptographic point of view, FIDO2 is based on three fundamental concepts:

creating at random separate authentication keys for each service,
authentication based on a simple challenge-and-response protocol, where the response is signed by the authenticator,
separating the authenticator device from the network.

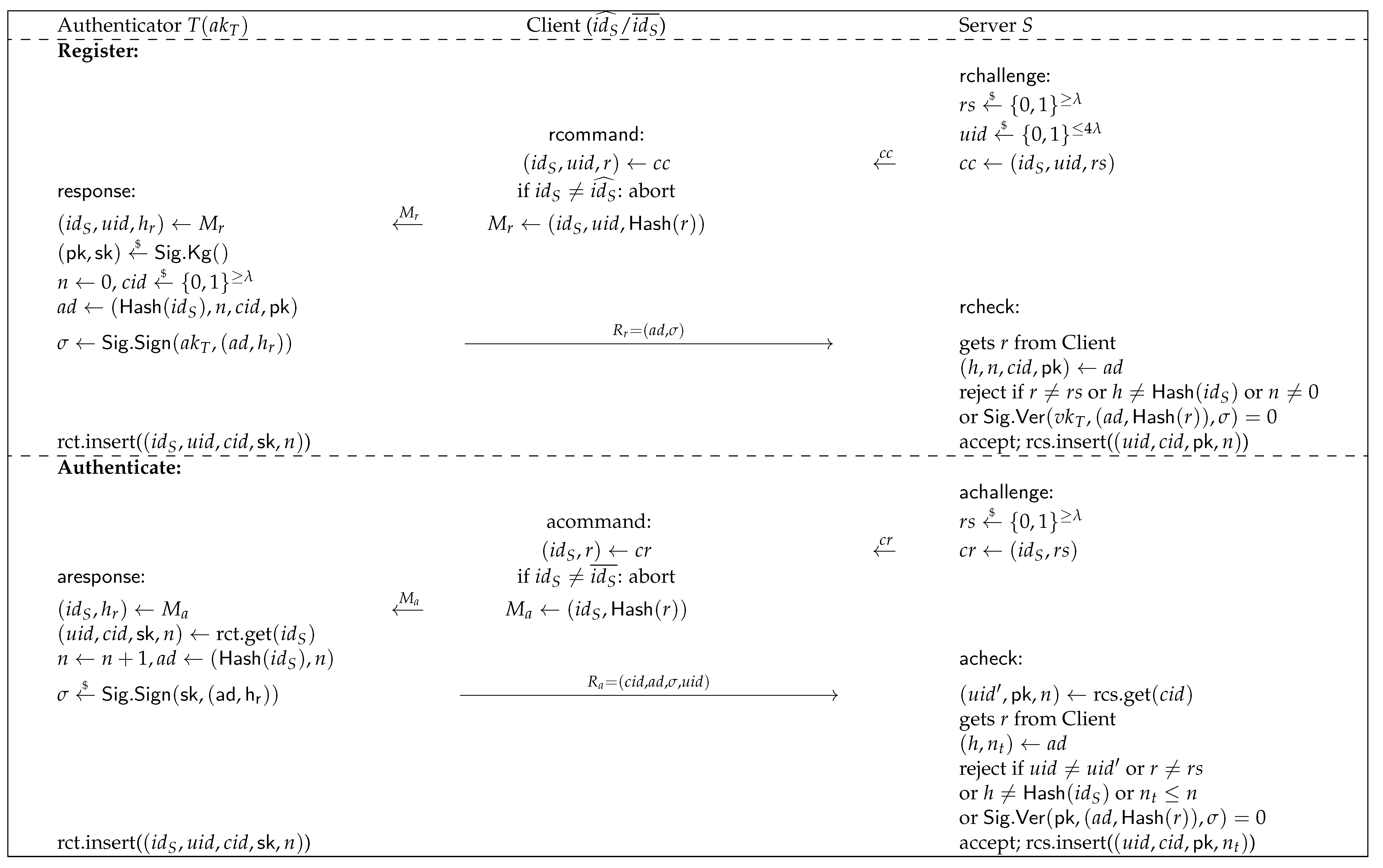
From the user’s point of view, there are three actors:

a remote servers offering services and requesting authentication,
a client - a web browser run on the user’s local computer,
an authenticator - a device like a hardware key in the hands of the user and authenticating with the client.

The interaction between these three actors is sketched on Figure 1. As one can guess from the figure, authentication is based on the secret keys (one per service) stored in the authenticator and the corresponding public keys shared with corresponding servers.

The first step of the user U, when getting in touch with a server S for the first time, is to create a dedicated key pair

({pk}_{U, S}, {sk}_{U, S})

associated with user identifiers

u i d

and

c i d

(see Figure 2).

Once a user has an account in a server S associated with a public key

{pk}_{S}

and user ID

u i d

, the user can authenticate themself by letting the client to interact with the user’s authenticator holding the corresponding key

{sk}_{S}

. Simplifying a little bit, the authentication mechanism is based on signing a hash of a random challenge received from the server (see Figure 3). A full description with all (crucial) details will be given in Figure 5.

FIDO2 is an example of a design that may have a significant impact on security practice: It is simple, it is open, and it is a self-organizing distributed ecosystem. On top of that, FIDO2 addresses nicely privacy protection issues by separating identities and public keys used for authentication in different systems. Last but not least, it is flexible: the key security primitives - hash function and signature scheme - are used as plugins and can be easily exchanged.

1.1. The Damocles Sword of Malicious Cryptography

It is known that cryptographic products might be anamorphic in the sense that they pretend to execute the scheme from their official specification while, in reality, they are running a different one with additional functionalities. In this case, cryptographic technology may provide not only powerful tools for implementing the original schemes but also for hiding additional hidden features in a provably effective way.

The above-mentioned anamorphic techniques may serve both good and bad purposes. One good purpose is implementing a signature creation device so that in a case of forgeries (resulting from breaking the public key by a powerful adversary), it is possible to fish out the signatures created by the legitimate device [4] or to prevent censorship [5]. On the other hand, anamorphic methods may be used on the dark side. A prominent example is kleptography (for an overview see [6]), where an innocently-looking protocol is used for the covert transfer of secret data. Moreover, kleptography is based on the concepts of asymmetric cryptography: Only a designated receiver can take advantage of the channel. Moreover, inspecting the kleptographic code stored in the infected device (including all keys implemented there) does not enable the derivation of the secrets handed to the adversary.

Unfortunately, kleptography can be easily hidden in many standard primitives, such as digital signatures [7]. It may also happen that an evidently kleptographic scheme is adopted as a technical standard (the case of Dual_EC_DRBG standard, cf. [8]).

Kleptography takes advantage of a black-box design: To protect the secret keys, a device implementing the protocol must restrict external access to the device. This is particularly important for electronic signatures and authentication based on asymmetric cryptography, as the whole security concept is based on the possession of the secret key. Consequently, it is typical that one can observe only the messages that should be created according to the protocol’s official description, and it is impossible to see how these messages have been created. In very few cases, the products are based on the end-to-end verifiability concept, where the protocol is resistant to malicious implementation of an arbitrary system component.

A common practice among practitioners is to rely on the most straightforward protocols. In this case, not only is the implementation cost low and the number of possible implementation mistakes reduced but there might also be less room for converting the system to a malicious one. A complicated scheme might have such complex security analysis and/or proof that they are omitted or, if they exist, never seriously checked.

A pragmatic way to improve the reliability of cryptographic products is to deliver well-examined and secure cryptographic primitives. Then, a system designer relying on these primitives can make legitimate assumptions about their properties and deduce the security features of the whole system.

One of the most challenging issues is using randomness in cryptographic protocols. When honestly implemented, randomness supports unpredictability and protects against many kinds of replay attacks. On the other hand, randomness is an anchor point for kleptographic attacks, as random parameters can be replaced by data that looks completely random but carries information for the adversary in an undetectable way.

Eliminating entirely the threat of kleptographic attacks by appropriate design of cryptographic schemes is hard or even impossible. Some attack methods, like rejection sampling [5], are extremely hard to defer in this way. What seems to be plausible is to substantially reduce the bandwidth of such channels and eliminate all kleptography-friendly protocol points.

The threat of kleptography is particularly concerning in the case of basic application tools. Any global system of user authentication is definitely such a critical case.

1.2. Paper Outline and Contribution

The main question considered in this paper is “can we trust FIDO2”? There are some security proofs for the protocol but do we need to trust the authenticators? What can happen if the authenticators (and servers) deviate from the protocol specification unnoticeably?

The situation is, in some sense, typical. On one hand, we have trusted manufacturers, supervised accreditation laboratories, whose evaluation reports are internationally recognized, and there are strong penalties for misbehavior.

On the other hand, there are criminal penalties for those who just want to reverse-engineer the authenticators to check them against malicious content. Last but not least, not all EU member states are guided by the same values, and cases of cybersecurity and privacy misconduct for political gain have been reported. Finally, malicious counterfeit authenticators may appear on the market, and at least some of them may pass the attestation steps of FIDO2. It may endanger the reputation of the manufacturers as well, regardless of their honest behavior. The problems reported here concern not only the FIDO Alliance as the host of FIDO2 but also the general public security, especially if FIDO2 becomes a component of the EU Digital Identity Wallet.

We aim to find what can go wrong, especially when physical protection will hide what is going on inside a device. We focus on threats that may lurk in cryptographic devices.

1.2.1. Paper Organization

The paper is organized as follows:

In Section 2, we recall FIDO2 and WebAuthn protocol. In Section 3, we recall their certification and attestation framework, aiming to show how relevant it is for kleptographic attacks.
Section 4 describes shortly the attack vectors considered in the paper.

In the following sections, we present drafts of kleptographic attacks:

Section 5 describes a series of attacks enabling a malicious authenticator to leak its identity information to the adversary. These attacks apply if FIDO2 authentication is based on discrete logarithm signatures.
Section 6 is devoted to several attacks leaking the private keys of the authenticator. Again, the attacks are initiated by a malicious authenticator and apply for FIDO2 with discrete logarithm signatures.
Section 7 drafts linking and impersonation attacks when the signature used for FIDO2 are RSA.

The rest of the paper explains some technicalities of the above attacks:

Section 8 explains how to use error-correcting codes for hidden messages to increase the leakage speed.
Section 9 explains technical details of embedding a hidden Diffie-Hellman key agreement between a malicious authenticator and a malicious server within FIDO2 communication.
Section 10 shows how a malicious server can uncover its TLS communication with the user’s client. This opens room for those attacks, where the attacker is only observing the messages sent to the server from the authenticator (via the client).

Finally,

In Section 11 we discuss the situation and propose the countermeasures. Apart from the general recommendations, we show which protocol elements might be changed to defer most of the attacks.

1.2.2. Our Contribution

We show that the FIDO2 standard is not resistant to kleptographic setups. The attacks are relatively easy to install and difficult to detect with conventional methods unless the implementation is uncareful.

The previous security analysis for the FIDO2 protocol has silently assumed that the authenticators are honest. In practice, this is hard to guarantee, and definitely, in regular application cases, an authenticator cannot be tested against kleptography by its owner.

2. FIDO2 and WebAuthn Protocol - Detains

FIDO2 consists of two protocols:

WebAuthn:: it takes the form of a web API incorporated into the user’s browser. WebAuthn is executed by the server, the client (that is, the client’s browser), and the user’s authenticator,
CTAP:: Client To Authenticator Protocol is executed locally by the authenticator and the client. CTAP has to guarantee that the client can access the authenticator only with the user’s permission.

Interestingly, although the authenticator is usually a hardware token, it may be implemented in software [9].

In the following, we consider the last two versions of the FIDO2 standard:

FIDO2 with the WebAuthn 1 and CTAP 2.0 protocols,
FIDO2 with the WebAuthn 2 and CTAP 2.1 protocols.

Of course, because of already deployed implementations, both versions must coexist in actual use. Security analysis of FIDO2 versions is given, respectively, in [10] and [11]. Privacy features of FIDO2 are analyzed in [12].

2.1. WebAuthn 1

WebAuthn 1 is depicted on Figure 5. It consists of two main procedures: Registration and Authentication. Recall that the protocol has three actors: the authenticator, the client, and the server. Typically, the connection between the client and the server is over a secure TLS channel. The connection between the client and the authenticator is a local one.

Figure 5. The WebAuthn 1 protocol (its description borrowed from [10])

In the registration protocol, the authenticator may use an attestation protocol – the choice depends on the server’s attestation preferences and the authenticator’s capabilities – see Section 3.2 for more details. Figure 5 is borrowed from [10], where the attestation mode basic is analyzed: the signature

σ

is generated with the attestation (private) key

a k_{T}

, which is expected to be deployed on more than 100000 authenticators (see [Section 3.2][13]).

The parameter

λ

defining the minimal bit length of random elements generated during protocol execution is currently set to 128. Accordingly, the registration procedure is initiated by generating two random strings by the server: at least 128-bit long random string

r s

and 512-bit user id

u i d

. These random values are sent to the client together with the server’s identifier

i d_{S}

(domain name) as a server’s challenge.

The client parses the challenge and aborts if the received identifier

i d_{S}

does not match the intended identifier

\hat{i d_{S}}

. Then the client hashes the last component of the challenge (the random string

r s

); the resulting hash value

M_{r}

is sent to the authenticator.

The authenticator parses

M_{r}

and generates a fresh key pair

(pk, sk)

, which will be used in subsequent authentications to the server

i d_{S}

. Next, the authenticator sets the counter n to zero (the counter shall be incremented at each subsequent authentication session with

i d_{S}

) and generates a random credential

c i d

of bit length at least

λ

. Then the tuple

a d

is assembled by the authenticator, and (depending on the choice of attestation mode) a signature on

a d

and the hash of the random string

h_{r} = Hash (r)

received in

M_{r}

is generated. Finally,

a d

and the generated signature

σ

are sent to the client, and the authenticator updates its registration context by inserting a new record containing the server identifier

i d_{S}

, the user’s identifiers

u i d, c i d

, the private key

sk

, and the counter n.

The client passes

(a d, σ)

to the server; the server executes the procedure

rcheck

on it. If the checked conditions are satisfied, the server also updates its registration context by inserting the corresponding record containing the identifiers

u i d, c i d

, public key

pk

and the counter n.

The authentication procedure starts with choosing by the server a string

r s

of length at least

λ

at random. Next, the server assembles the challenge

c r

consisting of

r s

and the server identifier

i d_{S}

. The challenge is passed to the client. If the client expects an authentication process to be executed by server

i d_{S}

, then, similarly to the registration procedure, the client transforms the challenge by hashing the random string

r s

received. The resulting message

M_{a}

is sent to the authenticator. The authenticator parses

M_{a}

retrieves

i d_{S}

and finds the record corresponding to

i d_{S}

created during the registration procedure. This record contains, among others, the counter and the dedicated signing key

sk

. Then, the counter is incremented, the authenticator creates a signature over

Hash (i d_{S})

, the counter, and the hash of

r s

using the key

sk

. Finally, the authenticator sends the response (including the signature) to the client and updates the stored record.

2.2. WebAuthn 2

This protocol has a richer set of options compared to WebAuthn 1. However, from our point of view, the most interesting features of its predecessor are preserved: both in the registration procedure and the authentication procedure some random bit-strings are generated. Namely,

during the registration procedure, the server generates

-

a challenge randomly chosen from the set ${0, 1}^{\geq λ}$ , and

-

the user identifier randomly chosen from the set ${0, 1}^{\leq 4 λ}$ ,
in the registration procedure, the authenticator generates the credential identifier $c i d$ consisting of at least $λ$ bits.
in the authentication procedure, the server generates the challenge from the set ${0, 1}^{\geq λ}$ ,

We omit further details of WebAuthn 2 as they are less relevant to our work.

2.3. The Client - Server Channel: Cipher Suites

Since the FIDO2 messages between the server and the client are sent over a TLS channel, we need to recall a few details about TLS.

The latest TLS version aims to improve security and offers greater efficiency than its predecessor. In the meantime, it became quite widespread, as according to [14], "62.1% of surveyed websites have adopted TLS 1.3 since its release." For this reason, we concentrate on TLS 1.3.

The following encryption and authentication modes can be used with TLS 1.3 [Appendix B.4][15]: AES GCM, CHACHA20 POLY1305, AES CCM, AES CCM 8 (the difference between CCM and CCM 8 is a reduced, eight-byte long authentication tag in the latter case). All the modes enumerated are Authenticated Encryption with Associated Data (AEAD) modes.

An interesting feature of the modes used by TLS 1.3 is that encryption can be separated in time from computing the authentication tag: encryption can be completed first, and then the authentication tag can be calculated. What is more, if a part of the plaintext is supposed to be random, then we can reverse the order of the computation: first, we can choose certain ciphertext bits and then find the corresponding plaintext by xor-ing with the bit stream produced by the encryption algorithm. Once the plaintext and the ciphertext are determined, one can proceed to calculate the authentication tag.

Note that the AEAD modes can also be negotiated in TLS 1.2, e.g., the cipher suite TLS_ECDHE_ ECDSA_WITH_AES_128_GCM_SHA256.

3. Certification of FIDO2 Authenticators

From the security point of view of the overall FIDO2 framework, it is essential to know how much we can trust the authenticators. The authors of the FIDO2 concept have addressed this question by creating a formalized framework for certifying authenticator devices. Below, we sketch this concept and its practical consequences.

3.1. Certified Authenticator Levels

Authenticators can be implemented in different ways:

as software,
as software run in an Allowed Restricted Operating Environment (AROE),
as secure elements, that is, a software and hardware product protected against remote software and hardware attacks.

Each form should provide some level of protection. The expected protection levels are formalized into Certified Authenticator Levels [9]. They are summarised in Table 1 (we borrow the description from [9]).

3.2. Attestation Modes

During registration, an authenticator generates a pair of asymmetric keys

(s k, p k)

and passes the public key

p k

to the Relying Party server. The Relying Party may want to verify that the public key comes from a genuine source. Therefore, an attestation protocol may be executed during user registration. It is composed of two stages:

The Relying Party sends information about preferred attestation mode. Available options are none, indirect, direct and enterprise. They are summarized in Table 2.
The authenticator responds to the Relying Party’s preferences. The most interesting case is the preference direct. In this case, the WebAuthen protocol allows the following attestation modes: basic, self, AttCA, AnonCA, None. In the WebAuthn 1 protocol, ECDAA mode was allowed but is not present in the current protocol version. See Table 3 for details.

As we can see, by running attestation, the Relying Party does not test the authenticator in the sense of checking its implementation. All the information obtained is a declaration of origin that may come from a trusted party and/or be based on secure architecture mechanisms. In this way, the Relaying Party may effectively ban no-name devices or devices coming from blacklisted sources. However, attestation alone does not eliminate the possibility of a known and accepted vendor installing a trapdoor in an authenticator. This problem has to be addressed by certification of the devices, preferably within some trustworthy certification framework, e.g., within the framework created by CSA regulation [3] or provided by authorities such as NIST.

3.3. Possible Certification Scope

We assume that an auditor might scrutinize a certain sample of authenticators during the certification process. This may happen at different stages of the authenticators’ lifetime (which is not always the case for the Common Criteria evaluation!). Let us summarize the capabilities of the auditor:

The auditor may run the authenticator with an input data of their choice and may confront its output with the collected history of interactions with the device.
The auditor may observe the input and output of the authenticator for real input data coming from the original services during real authentication sessions.

Depending on the implementation security level (see Section 3.1), the auditor may have additional opportunities for testing the authenticator. This may include read access to its selected memory areas, while in principle, the access should be restricted due to confidentiality protection of the signing keys used for authentication. Debuggers and similar tools may endanger these keys for similar reasons, so it is reasonable to block them.

The most challenging task is evaluating the authenticators with the highest security level. Note that during a more general Common Criteria certification process, the evaluator cooperates with the manufacturer, receives extensive documentation, and might request an open sample of the evaluated product (cf. Section 5.3.4 of [23]). A more specific document [24] states that “A side-channel or fault analysis on a TOE using ECC in the context of a higher Evaluation Assurance Level (...) is not a black-box analysis.”

In our case, an auditor examining an authenticator for malicious implementation cannot fully trust the manufacturer. In particular, they cannot always guarantee that the samples received from the manufacturer during the certification process contain precisely the same implementation as all devices delivered to the market. Consequently, to some extent, the auditor needs to use the black box approach, which is less effective.

Conclusions

All we have said so far indicates that a carefully designed trapdoor on the authenticators (especially when implemented so that side-channel analysis does not show any deviation from the original description) as well as malicious execution by the servers may remain unnoticed despite the certification and attestation framework. As we show below, the consequences might be profound taking into account privacy protection issues and even impersonation threats.

4. Attack Modes

In this paper, we consider two attack vectors against FIDO2 that aim to endanger the fundamental targets of the FIDO2 ecosystem:

for each user account, a separate set of unlikable identifiers and dedicated authentication keys should be used,
logging into a service should be possible only with an authenticator held by the account owner, the authenticator should be the same as the one used during registration.

Linking Attacks.

A linking attack aims to break the first property. There are many different scenarios here. For example,

two different servers may wish to learn whether two accounts in their services have been registered with the same authenticator device,
a malicious authenticator may want to pass information about its unique identity to an observer that only monitors encrypted TLS communication.

These scenarios are not the only possible; further options are described in the following sections. The point is that a linking attack does not enable the attacker to do anything other than break (some) privacy protection mechanisms on the level of the FIDO2 protocol.

Impersonation attacks.

An impersonation attack aims to enable to impersonate a user (in fact, their authenticator) against at least one server and thereby get access to the user’s resources on the server. In this paper, we focus on the fundamental impersonation scenario, where a private key

sk

is generated by the authenticator is leaked to an attacker. Consequently, in this case, the attacker can impersonate the user without any constraints.

Again, there are many options concerning the attack scenario and its participants. As we focus on kleptographic threats, the authenticator is a part of the malicious setup. However, there are many options regarding who is the attacker getting the private key

sk

an adversary that only monitors encrypted TLS communication but can derive $sk$ due to a malicious setup of an authenticator. In particular, this attack may be performed by a manufacturer that provides both the authenticator devices and the network equipment,
the target server may need $sk$ to offer it to third parties aiming to access the user account smoothly without any obvious trace,
the user himself, just to create a clone of the authenticator for his own purposes. One potential scenario is that a user and a user’s accomplice share the account and use it as a means of anonymous communication (e.g., for criminal purposes).

5. Linking Attacks with Discrete Logarithm Signatures

This section focuses on malicious authenticators that create signatures based on the discrete logarithm problem during FIDO2 authentication. The other popular option – RSA signatures – will be covered in Section 7.

As there are many attack scenarios concerning, among others, who will receive the linking information, for each attack presented we provide a short sketch of the most important features. To keep the paper as concise as possible, we omit a listing of attack steps in the cases, where it can reconstructed easily from the general description.

The initial description skips some (tedious) technical details, which are treated in more detail in the later sections.

In the subsequent attacks, we need to point out some bits, for example: “set j to a most significant bits of R, let v be a bit of R at position

a + 1

”. In this example, we, in fact, consider a sequence of

a + 1

most significant bits of R, where the bit “at position

a + 1

” is the bit at position

a + 1

in the sequence, counting from the most significant to the least significant bits.

5.1. Attack 1: Signature tagging

Attack prerequisites:

each user U has a unique public identifier ${id}_{U}$ (it might be the personal identity number assigned by a state authority or just a public key from a known certificate),
the authenticator ${Auth}_{U}$ of user U is aware about ${id}_{U}$ ,
${uid}_{U}$ is the ID resulting from registration of ${Auth}_{U}$ with the server S,
${Auth}_{U}$ holds the “public” kleptographic key Y of the attacker,
the attacker $Adv$ knows the private kleptographic key y, where $Y = g^{y}$ ,
$Adv$ knows (at least a fraction) of signatures delivered by ${Auth}_{U}$ while executing FIDO2 with a server S. ( $Adv$ might be the target server S but it is not required).

Attack type and result:

A linking attack in which

Adv

learns

{id}_{U}

of the user hidden behind identifier

{uid}_{U}

Auxiliary techniques:

id expansion: ${id}_{U}$ might be compressed in the sense that its every bit is necessary to identify a user. As we will be running a Coupon Collector process, this is inefficient as to learn n bits, and we have to draw at average $n \cdot H_{n}$ one-bit coupons. ( $H_{n} \cdot n \approx ln (n)$ is the nth harmonic number). The idea is to apply encoding $C ({id}_{U})$ of ${id}_{U}$ such that the Coupon Collection Process can be interrupted, and the missing bits can be found by brute force search. For details, see Section 8.

For the sake of simplicity, we assume that $C ({id}_{U})$ consists of $2^{a}$ bits.
two rabbits trick: this is a trick borrowed from [25]. It enables transmitting a single hidden bit in a signature, avoiding backtracking of the rejection sampling technique.

Algorithm:

The attack reuses the classical kleptographic trick of reusing an ephemeral value

g^{k}

to establish a secret shared by the authenticator and the adversary

Adv

From the point of view of the authenticator, the following changes in FIDO2 execution are introduced when creating a signature. The key moment is the choice of k: Instead of choosing k at random, the following steps are executed:

choose $κ$ at random,
compute $Z = Y^{κ}$ and $Z^{'} = Z^{- 1}$ ,
compute $R = min (Hash (Z), Hash (Z^{'}))$ ,
let $κ^{'} = \pm κ$ be such that $R = Hash (Y^{κ^{'}})$ ,
set j to a most significant bits of R, let v be bit of R at position $a + 1$ ,
let w be the jth bit of $C ({id}_{U})$ ,
set $k = κ^{'}$ if $v = w$ and $k = - κ^{'}$ , otherwise.

From the point of view of

Adv

, each obtained signature indicates one bit of

C ({id}_{U})

. For this purpose,

Adv

executes the following steps:

retrieve $g^{k}$ from the signature (k is unavailable to $Adv$ , but standard signature schemes enable either reconstructing $g^{k}$ , or provide it directly. For example, in the case of ECDSA signatures, the component s of the signature allows to reconstruct the element needed),
calculate $K = {(g^{k})}^{y}$ ,
compute $R = min (Hash (K), Hash (K^{- 1}))$ ,
set j to a most significant bits of R, let v be bit of R at position $a + 1$ ,
if $R = Hash (K)$ , then the jth bit of $C ({id}_{U})$ is v,
if $R \neq Hash (K)$ , then the jth bit of $C ({id}_{U})$ is $1 - v$ .

Given many authentication sessions,

Adv

collects many bits of

C ({id}_{U})

. Some repetitions (leaking the same bit twice) are possible as the address j is selected by a randomized algorithm. In Section 8, we discuss in more detail how many signatures are necessary in average to recover the whole identifier

{id}_{U}

5.2. Attack 2: Identity Sieve via Rejection Sampling

Attack prerequisites:

The same as in Section 5.1, but additionally:

the adversary $Adv$ has a set of potential identities I which may contain ${id}_{U}$ of ${Auth}_{U}$ .

Attack type and result:

This is a linking attack where

Adv

will fish out the identities from I that may correspond to

{Auth}_{U}

or find that none of them corresponds to

{Auth}_{U}

Auxiliary techniques:

long pseudorandom identifier:: instead of a regular identifier, a long pseudorandom identifier $Long ({id}_{U})$ is used. Simply, we may use a cryptographic DRNG (deterministic random number generator, e.g., one of the generators recommended by NIST): $Long ({id}_{U})$ are the first N bits of the output of $DRNG ({id}_{U})$ .
rejection sampling with errors:: we take into account that the authenticator must run the protocol without suspicious delays and failures. So, we use the rejection sampling technique, where the output is taken after a few trials even if it is invalid from the information leakage point of view.
two rabbits trick: may also be used, but we skip it here for clarity of presentation.

Algorithm:

Assume that

Long ({id}_{U})

consists of

2^{L} \cdot b

bits, that is,

2^{L}

blocks of b bits. The parameter L is big enough to avoid collisions, while b is very small, like

b = 3

From the point of view of the authenticator, the following changes in FIDO2 execution are introduced when creating a signature. Instead of choosing k at random, the following steps are executed (rejection sampling with at most

m - 1

backtracking steps):

$i : = 1$ ,
choose k at random,
compute $R = Hash (Y^{k}$ ),
set j to L most significant bits of R, let v be the sequence of b bits of R that starts at position $L + 1$ ,
let w be the sequence of b bits of $Long ({id}_{U})$ that starts at position $j \cdot b + 1$ ,
if $i < m$ and $v \neq w$ , then $i : = i + 1$ and goto 2.

From the point of view of

Adv

, each obtained signature is a witness indicating whether a given

id

may correspond to

{Auth}_{U}

. Due to the bound m on backtracking steps, false witnesses are possible. In each execution of step 6,

v = w

with probability

2^{- b}

. Hence, a signature provides a false witness with probability

p_{f} = {(1 - 2^{- b})}^{m}

. Example parameters are

b = m = 3

, then

p_{f} \approx 0.6699

, we have the probability of a correct witness

1 - p_{f} \approx 0.33

When receiving a signature, the following steps are executed to gather statistics for identities from I. Let S be the table holding the current statistics. Initially,

Adv

sets

S [{id}_{i}] = 0

for each

{id}_{i} \in I

retrieve $g^{k}$ from the signature (k is unavailable to $Adv$ , but standard signature schemes enable either reconstructing $g^{k}$ or provide it directly),
calculate $K = {(g^{k})}^{y}$ ,
compute $R = Hash (K)$ ,
set j to L most significant bits of R,
let v be the b-bit sequence of R starting at position $L + 1$ ,
for every ${id}_{i} \in I$ : if $Long ({id}_{i})$ contains sequence v on positions $j \cdot b + 1$ through $(j + 1) \cdot b$ , then $S [{id}_{i}] : = S [{id}_{i}] + 1$ .

Let us observe that for

{id}_{i} \neq {id}_{U}

, the counter

S [{id}_{i}]

is incremented by analyzing a signature with the probability

2^{- b}

, provided that we treat

Long

as a random function, and the sequences

Long ({id}_{U}

and

{Long}_{(} i d_{i}

are stochastically independent. In turn, if

{id}_{i} = {id}_{U}

, then the counter is incremented with probability

1 - {(1 - 2^{- b})}^{m}

. For example, for

m = b = 3

, we have the probability

0.125

in the first case and the probability

\approx 0.33

in the second case.

5.3. Attack 3: Signature Tagging with Permutation

This attack improves the bandwidth of the attack from Section 5.1 with a technique borrowed from [26].

Attack prerequisites:

the same as in Section 5.1, except for the last condition,
$Adv$ has access to all signatures in a certain fixed interval of interactions between ${Auth}_{U}$ and S,
$Auth$ can create in advance and store t random parameters k used in signatures created in the consecutive steps; t is a parameter - the greater it is, the greater the additional hidden information channel.

Attack type and result:

This is a linking attack where

Adv

learns

{id}_{U}

of the user hidden behind identifier

{uid}_{U}

Auxiliary techniques:

The same as in Section 5.1, plus the following encoding via permutation:

encoding via permutation:: we convert permutations over $S_{t}$ to integers. For this purpose, one can use Algorithm P and the “factorial number system” (see [Section 3.3.2][27]).

Algorithm:

Assume that

C ({id}_{U})

consists of

2^{a}

bits. The attack requires a sequence of t signatures that

{Auth}_{U}

and

Adv

agree upon (e.g., t consecutive signatures after some triggering moment). The parameter t must be chosen so that a permutation over

S_{t}

can be used to encode a b-bit number where

b + t \geq a

. In the procedure presented below, the first t bits of

{id}_{U}

are leaked directly via the two-rabbits trick, while the remaining

a - t

bits are encoded via a permutation

π \in S_{t}

In advance,

{Auth}_{U}

runs the following procedure:

choose $κ_{1}, \dots, κ_{t}$ at random,
for $i = 1$ to t do:

(a)

calculate $Z_{i} = Y^{κ_{i}}$ , $Z_{i}^{'} = Z^{- 1}$ ,

(b)

calculate $R_{i} = min (Hash (Z_{i}), Hash (Z_{i}^{'}))$ ,

(c)

let $κ_{i}^{'} = \pm κ_{i}$ be such that $R_{i} = Hash (Y^{κ_{i}^{'}})$ ,

(d)

sort $R_{1}, \dots, R_{t}$ in ascending order, let the resulting sequence be $R_{ρ (1)}, \dots, R_{ρ (t)}$ (let us remark that $Adv$ will not try to learn $ρ$ , but the ordered sequence will be a reference point for encoding another permutation),

(e)

let $ζ_{i}$ be such that $R_{ρ (i)} = Hash (Y^{ζ_{i}})$ , that is, $ζ_{i} = κ_{ρ (i)}^{'}$ ,

(f)

find a permutation $π$ such that $π$ encodes $a - t$ least significant bits of ${id}_{U}$ ,

(g)

we set $k_{i}$ to $\pm ζ_{π (i)}$ , where $k_{i} = ζ_{π (i)} = κ_{π (ρ (i))}^{'}$ , if the ith most significant bit of ${id}_{u}$ is 0. Otherwise, $k_{i} = - ζ_{π (i)} = - κ_{π (ρ (i))}^{'}$ .

(Note that $Hash (Y^{k_{i}}) = Hash (Y^{κ_{π (ρ (i))}^{'}}) = R_{π (ρ (i))}$ if and only if the ith most significant bit of ${id}_{u}$ is 0).

During the ith execution of FIDO2 devoted to leaking

{id}_{U}

{Auth}_{U}

uses already stored

k_{i}

to create the signature.

Adv

has to analyze all t signatures to derive

{id}_{U}

derive the ordered list $(g^{k_{1}}, \dots, g^{k_{t}})$ by inspecting t consecutive signatures created by ${Auth}_{U}$ in the time when ${id}_{U}$ has to be leaked; that is, consecutive $g^{k_{i}}$ on the list are derived from consecutive signatures,
for $i \leq t$ do

(a)

calculate $K_{i} = {(g^{k_{i}})}^{y}$ , $P_{i} = Hash (K_{i})$ , $P_{i}^{'} = Hash (K_{i}^{- 1})$ ,

(b)

set ${\tilde{R}}_{i} = min (P_{i}, P_{i}^{'})$ ; (note that because the minimum value is taken, ${\tilde{R}}_{i}$ is uniquely determined and equal to the corresponding $R_{π (ρ (i))}$ calculated in step (2b) of the encoding procedure),

(c)

if ${\tilde{R}}_{i} = P_{i}$ , then $j = 0$ , else $j = 1$ ,

(d)

output “j is the ith most significant bit of ${id}_{U}$ ”,
find permutation $θ$ that converts ${\tilde{R}}_{1}, \dots, {\tilde{R}}_{t}$ into an ordered sequence,
calculate $π = θ^{- 1}$ ,
decode $π$ to an integer $\hat{m}$ , derive $(a - t)$ -bit representation m of $\hat{m}$ ,
output “m is the sequence of $a - t$ least significant bits of ${id}_{u}$ ”.

Note that the scheme does not need to use codes C, as we have to assume that all signatures from a given time are received by

Adv

as an ordered sequence. Therefore, the Coupon Collector Problem is irrelevant here. The number of bits that can be transmitted in this way equals

t + ⌊ log (t!) ⌋

. For example, for

t = 40

, one can encode 264 bits in this way, enough to leak a secret key for many standard schemes.

5.4. Attack 4: Signature Tagging with a Proof

Attack prerequisites:

the same as in Section 5.1,
${Auth}_{U}$ does not contain any secret symmetric key $K_{U}$ shared with $Adv$ (the other case will be considered later); however, ${Auth}_{U}$ knows asymmetric kleptographic key Y such that $Y = g^{y}$ , where the exponent y is private and known only to $Adv$ ,
a third party P and the adversary $Adv$ jointly observe interaction between a server and ${Auth}_{U}$ , and P is convinced that the interaction is genuine.

Attack type and result:

This is a linking attack where

Adv

can convince a third party P that

{Auth}_{U}

is leaking the identifier

{id}_{U}

Algorithm:

The adversary executes one of the tagging attacks described above. Additionally,

Adv

creates a proof for the third party P about the validity of leaked bits. Namely, when

Adv

and P observe an interaction where a signature carries an element

g^{k}

, then

$Adv$ computes $K : = {(g^{k})}^{y}$ , creates a noninteractive zero-knowledge proof f about equality of discrete logarithms for pairs $(g, g^{k})$ and $(Y, K)$ , and passes $(K, Y, f)$ to P (it suffices to show Y only once),
P checks f and aborts interaction if it is invalid,
P follows the steps 3-6 of $Adv$ of, respectively, Attack 1 or Attack 2.

There might be a more sophisticated version of this attack, where

Adv

creates a non-interactive zero-knowledge proof without disclosing Y.

5.5. Attack 5: Correlated Secret Keys with a Shared Secret

In this attack,

{Auth}_{U}

creates secret keys

{sk}_{0}

{sk}_{1}

with different services so that

Adv

may detect that the corresponding public keys

{pk}_{0}

{pk}_{1}

originate from the same device. Alternatively,

{sk}_{0}

might be the main secret key assigned to user U with

{pk}_{0} = g^{{sk}_{0}}

known to

Adv

Attack prerequisites:

${Auth}_{U}$ and $Adv$ share a secret $K_{U}$ (this can be achieved on-the-fly as described in Section 9),
$Adv$ has access to public keys created by authenticators in interaction with different servers during the registration procedure of FIDO2.

Attack type and result:

Having a public key

{pk}_{1}

, allegedly created by

{Auth}_{U}

for interaction with server

S_{1}

Adv

may derive the key

{pk}_{2}

that

{Auth}_{U}

would create for interaction with server

S_{2}

. This will fail if

{pk}_{1}

does not originate from

{Auth}_{U}

Algorithm:

The registration procedure is modified on the side of

{Auth}_{U}

. Instead of choosing

{sk}_{2}

at random, the following steps are executed:

calculate $z = DRNG (K_{U}, S_{1}, S_{2})$ ,
set ${sk}_{2} = {sk}_{1} + z (mod error g)$ (addition modulo the order of the generator g).

The public key

{pk}_{2}

is calculated as before:

{pk}_{2} = g^{{sk}_{2}}

Adv

may test whether

{pk}_{1}

and

{pk}_{2}

from services

S_{1}, S_{2}

correspond to

{Auth}_{U}

. The test consists of the following steps:

calculate $z = DRNG (K_{U}, S_{1}, S_{2})$ ,
if ${pk}_{2} = {pk}_{1} \cdot g^{z}$ , then output “ $p k_{1}$ and ${pk}_{2}$ have been created by ${Auth}_{U}$ ”.

Remark 1.

Even if

{sk}_{1}

and

{sk}_{2}

created in this way are correlated in a visible way for the adversary,

Adv

does not get an opportunity to impersonate

{Auth}_{U}

. However, for certain signature schemes,

Adv

would be able to convert a signature over

(a d, h_{r})

verifiable with key

{pk}_{1}

to a signature over the same

(a d, h_{r})

and verifiable with key

{pk}_{2}

. However,

h_{r}

is a random parameter chosen anew during each execution, so it is unlikely that it will be chosen by

S_{2}

. More importantly, the server name

S_{1}

is contained in the parameter

a d

of the first signature, so the signature will be useless for interaction with

S_{2}

5.6. Attack 6: Correlated Secret Keys with a Trigger Signature

In this attack,

{Auth}_{U}

will be able to convince

Adv

that public key

pk

used for authentication with a server S was created by an authenticator holding the master secret key

{sk}_{U}

of user U. Moreover, the proof can be provided at a time freely chosen by

{Auth}_{U}

, particularly when triggered by some event.

Attack prerequisites:

there is a master key pair $({sk}_{U}, {pk}_{U})$ associated with user U, where ${sk}_{U}$ is stored in ${Auth}_{U}$ , while ${pk}_{U}$ is known to $Adv$ ,
${Auth}_{U}$ holds the “public” kleptographic key Y of the attacker,
$Adv$ knows y such that $Y = g^{y}$ ,
${Auth}_{U}$ can store a random parameter k for a future use,
$Adv$ has access to the signatures created by ${Auth}_{U}$ in interaction with server S.

Attack type and result:

This is a linking attack where at a freely chosen time,

{Auth}_{U}

can enable

Adv

to detect that a public key

pk = g^{sk}

used in some service S by

{Auth}_{U}

belongs to U, or more precisely, to an authenticator that holds the master secret key

{sk}_{U}

of user U. The secret key

sk

is not exposed to

Adv

Algorithm:

At the moment of registration with a server S, the procedure of generating the key pair

(sk, pk)

on the side of

{Auth}_{U}

is modified in the following way:

choose $k_{S}$ at random,
calculate $z = Hash (Y^{k_{S}})$ ,
set $sk = {sk}_{U} + z (mod error g)$ , $pk = g^{sk}$ ,
store $k_{S}$ for the future use.

At the moment when the link between U and

pk

has to be revealed to

Adv

{Auth}_{U}

executes FIDO2 with server S in a slightly modified way. Namely, during the signature creation process, instead of choosing k at random,

{Auth}_{U}

takes

k = k_{S}

Adv

that monitors the signatures provided to server S executes the following steps for every signature suspected to link

pk

with the user’s master key:

derive $R = g^{k}$ from the signature,
calculate $z = Hash (R^{y})$ ,
for each known master public key ${pk}_{V}$ , $Adv$ tests whether $pk = {pk}_{V} \cdot g^{z}$ .
if $pk = {pk}_{V} \cdot g^{z}$ for a certain ${pk}_{V}$ , then the test output is “ $pk$ belongs to the owner of ${pk}_{V}$ ”. Otherwise, the output is “ the key $pk$ does not correspond to any ${pk}_{V}$ tested, or the authenticator using $pk$ has not decided yet to reveal the link”.

Remark 2.

The above procedure can be modified slightly, making it even more harmful in practice. That is,

{Auth}_{U}

may reveal the link between

pk

and

{pk}_{U}

when interacting with a server different than S. In this case, exactly the same steps are executed. Mounting such an attack could be easier since the alternative server

S^{'}

may be fully controlled by

Adv

, while for some reason, user U may be forced to register with

S^{'}

and authenticate there. For example,

S^{'}

might be a server provided by a courier company where a customer has to log in to send a package.

6. Impersonation Attacks

The general strategy of the attacks is to enable the adversary to seize the private key used to authenticate. There are two main attack scenarios:

In the first scenario, the adversary transmits a secret K to an authenticator in a hidden channel over FIDO2 execution. Then the authenticator uses K as a seed for an $DRNG$ and derives the secret keys $sk$ from the output of the DRNG in a deterministic way. As the adversary holds K, the secret keys may be calculated on the adversary’s side following the same steps.
In the second scenario, the hidden information flow is reversed: an authenticator transmits a hidden message M to the adversary within a FIDO2 execution. Using M, the adversary can derive the secret key $sk$ used by the authenticator.

Remark 3.

The attack may enable

Adv

to derive all secret keys generated by

{Auth}_{U}

. However, it is easy to confine the scope of the leakage to, say, the secret key used to authenticate with a single server S. In this case, the key derivation procedure may be altered: instead of deriving

sk

from the seed K and the identifier

I_{S}

of S, a new dedicated seed

K_{S} = Hash (K, I_{S})

can be used. Consequently, the leaked information will be

K_{S}

instead of K.

In many cases, the impersonation attacks are variants of the linking attacks. Then, we refer to the linking attacks and describe only the necessary modifications.

6.1. Attack 7

This is a modified version of Attack 1 from Section 5.1.

Attack type and result:

This is an impersonation attack in which

{Auth}_{U}

leaks a DRNG seed K used by

{Auth}_{U}

to generate the FIDO2 private keys.

Adv

(and only

Adv

) can derive K and, thereby, seize the private keys generated by

{Auth}_{U}

during registration.

Algorithm:

This is a slightly modified algorithm from Section 5.1. The crucial difference is that the leaked information is not

C ({id}_{U})

, but

C (K)

Note that now the adversary may stop collecting bits much earlier. Namely,

Adv

can guess some number of missing bits (say 30), recalculate the seed as, say,

K^{'}

, derive a secret key

{sk}^{'}

from

K^{'}

, and finally check whether it matches the public key

pk

used by the authenticator.

On the other hand, the seed is presumably much longer than the identifier

{id}_{U}

6.2. Attack 8

This is a modified version of Attack 3 from Section 5.3.

Attack type and result:

This is an impersonation attack, where the result is the same as in the case of Attack 7.

Algorithm:

It is a slightly modified algorithm from Attack 3. The difference is that the leaked information is not

C ({id}_{U})

, but

C (K)

, and that

Adv

may stop with some bits missing.

6.3. Attack 9

This is a modified version of Attack 5 from Section 5.5.

Attack type and result:

This is an impersonation attack where

Adv

learns the private key

{sk}_{2}

that was generated or would be generated by

{Auth}_{U}

when registering with a server

S_{2}

Algorithm:

It is a modified version of the algorithm from Attack 5: instead of deriving

{sk}_{2} = {sk}_{1} + z

, the authenticator sets

{sk}_{2} = z

. As

Adv

can calculate z in the same way as

{Auth}_{U}

, it can derive

{sk}_{2}

as well. The computation of

{pk}_{2}

is modified to simply

{pk}_{2} = g^{s k_{2}}

, and

{pk}_{2}

can be compared with the keys used in FIDO2 interactions with server

S_{2}

6.4. Attack 10

This is a modified version of Attack 6 from Section 5.6.

Attack type and result:

This is an impersonation attack where

Adv

, who controls a server

S^{'}

, learns the private key

{sk}_{S}

that was generated or would be generated by

{Auth}_{U}

when registering with a server S. The possibility to derive

{sk}_{2}

is triggered by

{Auth}_{U}

at any time by releasing a specially prepared signature within a FIDO2 authentication.

Algorithm:

There are the following modifications:

{Auth}_{U}

generates

{sk}_{S}

for server S as

{sk}_{S} = z = Hash (Y^{k_{S}})

. As

Adv

can recalculate z as for Attack 6,

Adv

seizes

{sk}_{S}

when

{Auth}_{U}

authenticates with FIDO2 against the server

S^{'}

and during this process the signature based on

g^{k_{S}}

is delivered by

{Auth}_{U}

S^{'}

6.5. Attack 11

This is a devastating attack where all private keys created or to be created by

{Auth}_{U}

are leaked to the adversary.

Attack type and result:

This is an impersonation attack, where

Adv

learns the seed used by

{Auth}_{U}

for random number generation, hence

Adv

can recalculate all the private keys generated by

{Auth}_{U}

after the attack. Moreover, if

Adv

has access to the signatures created after the attack then, in the case of standard signatures based on the discrete logarithm problem, can reconstruct private ephemeral values, and thus the signature private keys, even if the private keys were established before the attack.

Attack prerequisites:

${Auth}_{U}$ colludes with a malicious server S,
to keep this attack stealth, the malicious server, with probability very close to $\frac{1}{2}$ , decides to establish a shared key with the authenticator during the registration procedure (the reasons are explained in Section 9.2); when the authenticator learns that the shared key will not be established then it behaves honestly, hence about half of the colluding authenticators will finally be affected by the attack,
for some reason, the user U holding ${Auth}_{U}$ is forced to register with S (in a dictatorship, this could be, for example, the server used by the citizens to fill out a tax return form),
the implementation of ${Auth}_{U}$ supports domain parameters that the server S selects during the attack; on the other hand the server chooses the domain parameters that are supported by the malicious implementation of the authenticators.

Auxiliary techniques

ephemeral-ephemeral Diffie-Hellman key exchange:: to be described in Section 9.2.

Notation:

In FIDO2, all the allowed signature schemes based on the discrete logarithm problem utilize elliptic curves [Section 3.7][28]. To illustrate the attack, we assume that a prime order elliptic curve is used (e.g., the case of ECDSA signatures). Let

p be the prime determining the field over which the curve is defined,
n denotes the number of points of the curve (according to our assumption, n is also prime).

Algorithm:

The first stage of the attack is when

{Auth}_{U}

registers with server S:

S generates $u i d$ at random but in a specific way. First, S tosses an asymmetric coin, where tails appear with probability $\frac{n - 1}{2 p}$ , and heads with probability $1 - \frac{n - 1}{2 p}$ .
If heads are thrown, then S runs steps that will not lead to establishing a shared key with ${Auth}_{U}$ . (This execution path is needed to avoid detection of malicious activity by an auditor.) S picks at random $x \in F_{p}$ such that x is not the x-coordinate of a point of that curve. This means that the x must yield a quadratic non-residue on the right-hand side of the elliptic curve equation (see Section 9.2 for more details). Such x shall be encoded in $u i d$ with the help of the Probabilistic Bias Removal Method (Section 9.3.1).
If tails are thrown by S, then S start a procedure that will result in establishing a shared key with ${Auth}_{U}$ with the help of the ephemeral-ephemeral Diffie-Hellman protocol. To do so, $u i d$ should encode a group element V so that S knows its discrete logarithm v, $V = g^{v}$ (extensive technical details are postponed to Section 9). Note that in both versions of the WebAuthn protocol, the server S may choose $u i d$ long enough1 to encode hidden V.
Apart from sending the group element the server S must indicate which curve has been chosen for the key agreement. The same curve must be chosen by ${Auth}_{U}$ as the domain parameters for the signature scheme. Therefore, a natural and legal place to indicate the curve is the preference list the server sends to the authenticator (for details, see Section 9.4).
$u i d$ , $i d_{S}$ , and the server’s preference list are delivered to the authenticator ${Auth}_{U}$ by the client, unaware of the evil intent of S and ${Auth}_{U}$ . (Note that, unlike other parameters from S, the identifier $u i d$ is not hashed before delivering to the authenticator!)
${Auth}_{U}$ recognizes $i d_{S}$ of the “colluding server” and follows the registration procedure by creating a dedicated key pair $(pk, sk)$ using the curve indicated by the server. The key $sk$ is honestly chosen uniformly at random.
Now ${Auth}_{U}$ checks if $u i d$ encodes the x-coordinate of some point of the curve. If decoded x yields a quadratic non-residue on the right-hand side of the curve’s equation, then ${Auth}_{U}$ stops the attempt to establish a shared key with S.
Otherwise, ${Auth}_{U}$ sets an appropriate flag f that the shared key with S is to be established and prepares in advance an ephemeral key pair $(g^{k}, k)$ , for the first signature to be generated for the service S. Let $r = g^{k}$ .
${Auth}_{U}$ resets its DRNG seed to $T = Hash (x (V^{k}))$ , where $x (V)$ denotes the x-coordinate of the point V (for the sake of simplicity, we have abused notation, the group of points of the elliptic curve is usually treated as an additive group). From now on, all random numbers are generated from the seed T, except the ephemeral exponent k that is temporarily stored for the first authentication against S. The service S does not know T yet.

The second stage of the attack is when

{Auth}_{U}

uses FIDO2 to authenticate against S for the very first time:

If the flag f is not set, ${Auth}_{U}$ generates a signature in a honest way.
Otherwise, the signature created by ${Auth}_{U}$ utilizes the random parameter k stored during the registration procedure. Once the key k has been used up, it is deleted from the authenticator’s internal memory and flag f is also removed.
If the shared key is to be established, S takes the signature obtained during the first authentication and derives the component r of the signature. Then S calculates $T = Hash (x (r^{v}))$ .

From now on, if the shared key T has been established, the authenticator

{Auth}_{U}

creates random values from a DRNG seeded with T, with a mirror DRNG on the side of S. There are two scenarios for the following attack events:

Scenario 1: ${Auth}_{U}$ registers with the service $S^{'}$ after registering with S.

In this case, ${Auth}_{U}$ generates a dedicated key pair $({pk}^{'}, {sk}^{'})$ for interactions with $S^{'}$ . However, for this purpose, ${Auth}_{U}$ has to run a deterministic algorithm making calls to its DRNG. As S has a clone of this DRNG with its internal state, the same key ${sk}^{'}$ can be derived by S.

Afterwards, S will be able to impersonate the victim user against $S^{'}$ . The only trace of this activity might be an activity record of the user associated to $c i d$ maintained by the server $S^{'}$ .
Scenario 2: the authenticator ${Auth}_{U}$ has registered with the service $S^{'}$ before registering with S.

In this case, S cannot derive the key ${sk}^{''}$ for service $S^{'}$ as it has been created before a shared secret between S and ${Auth}_{U}$ has been established. The key ${sk}^{''}$ and its corresponding key ${pk}^{''}$ cannot be changed by S since S would have first to impersonate ${Auth}_{U}$ . As there is no communication channel from ${Auth}_{U}$ to S (maybe, apart from kleptographic channels in the signatures), we may hope to be on the safe side from the point of view of the protocol design.

Unfortunately, ${pk}^{''}$ can be broken by $Adv$ in the standard cases. Namely, most signature schemes based on the discrete logarithm problem used in practice generate a one-time ephemeral value for each signature. Typically, this ephemeral value must not be revealed since, otherwise, the signing key will be leaked. However, S may derive the same ephemeral value using its clone of the DRNG used by ${Auth}_{U}$ . So once S learns a single signature delivered to $S^{''}$ , it can derive ${sk}^{''}$ ! So, the security depends solely on the secrecy of the signature returned by ${Auth}_{U}$ during the authentication procedure.

Remark 4.

Not only the element

u i d

poses a threat. The random

c i d

chosen by

{Auth}_{U}

can be used in a similar way if a public key of the server is somehow available to

{Auth}_{U}

Remark 5.

Note that if the auditor logs the first signature and can recover the secret key

sk

, then they can calculate T. Indeed, for the signature

(r, s)

, where

s = k^{- 1} \cdot (h + r \cdot sk)

, one might define

u_{1} = h \cdot s^{- 1}

u_{2} = r \cdot s^{- 1}

, and then

U^{k} = U^{u_{1}} \cdot {(U^{sk})}^{u_{2}} .

Thus, hiding the ephemeral-ephemeral DH scheme would depend on security mechanisms protecting the confidentiality of key

s k

against the auditor. For tamper-proof authenticator devices, the attack remains undetectable!

7. RSA Signatures

The list of signature algorithms to be used by

{Auth}_{U}

[Section 3.7][28] contains not only signatures based on the discrete logarithm problem but also RSA signatures with RSA PSS and RSA PKCS v1.5 encodings. (Note, however, that a disclaimer present in the abstract of this webpage states that “so the presence or absence of an algorithm in this list does not suggest that this algorithm is or is not allowed within any FIDO protocol”.) Both encodings are standardized in [29]. In [Section 3.7][28], the lengths of the RSA keys are specified as follows:

2048-bit RSA PSS,
$1024 \cdot n$ -bit RSA PKCS v1.5 ( $n = 2, 3, 4$ ).

That is, the RSA key length is at least 2048 bits. In the case of PSS encoding, a

s a l t

field is allowed to be random. This

s a l t

field is recovered by the signature verifier and thus can be used to transmit a covert message (as noted in [29]). In point 4 on page 36 of [29], we read that “Typical salt lengths in octets are

h L e n

(the length of the output of the hash function Hash) and 0”. As a result, this channel may have the capacity of at least 256 bits.

From now on, we assume that a deterministic version of the RSA signatures is utilized (RSA PKCS v1.5 or RSA PSS without random salt). Then, a malicious manufacturer can benefit from the key generation process. The paper [30] presents a kleptographic RSA key generation procedure. That is, only the owner of the master key resulting from the Diffie-Hellman (DH) protocol can factorize the generated key. An accelerated version of the key generation with a backdoor was presented in [31], and it is even faster than the OpenSSL implementation of the honest RSA key generation procedure. The papers [30,31] use the ephemeral-static version of the DH protocol, where the ephemeral part is present in the RSA modulus.

We adapt the idea presented in the mentioned papers to show the feasibility of a linking attack also in the case where

{Auth}_{U}

creates RSA signatures during FIDO2 execution. We also present an impersonation attack in which we point at a capability of the RSA backdoor that, to our knowledge, has not been discussed in the literature so far. That is, we point to the possibility of transmitting a ciphertext in a prime factor of the RSA modulus.

7.1. Diffie-Hellman Protocol in the RSA Modulus

Below we depict a fragment of GetPrimesFast(bits,e,

s_{p u b}

s_{p r i v}

) procedure from [31]. The arguments of the procedure are:

bits – the number of bits of the resulting modulus,
e – the public exponent of the RSA key,
$s_{p u b}$ – the x-coordinate of the elliptic curve point expressed by formula (11), that is the x-coordinate of the ephemeral part of the DH protocol,
$s_{p r i v}$ – the shared secret, that is the x-coordinate of the elliptic curve point $u \cdot Y_{a}$ resulting from the ephemeral-static DH protocol (for details see Section 9.3.2).

The fragment presented below illustrates how

s_{p u b}

is embedded into an upper part of the RSA modulus.

GetPrimesFast(bits,e,

s_{p u b}

s_{p r i v}

Output: a pair of acceptable RSA primes

(p_{1}, q_{1})

$len = bits / 2$
$p_{1} = GenPrimeWithOracleIncr (s_{p r i v}, len, e)$
$μ = bits - (8 + m + 1)$ , where $m + 1$ is the length of $s_{p u b}$
choose $r_{1} \in_{R} {0, 1}^{7}$ and $r_{2} \in_{R} {0, 1}^{μ}$
set $n_{c} = 1 | | r_{1} | | s_{p u b} | | r_{2}$
solve for $(q_{1}, r)$ in $n_{c} = q_{1} p_{1} + r$ , where $r < p_{1}$
...

Let us explain a few details. In line 1, the length of prime numbers is determined. In the next line, the first prime

p_{1}

is generated from the seed

s_{p r i v}

. The exponent e must be co-prime to the order of the multiplicative group; hence, the condition

gcd (p_{1} - 1, e) = 1

is verified when running the GenPrimeWithOracleIncr function. In line 3, the size

μ

of random tail

r_{2}

is set: in [31] the length of

s_{p u b}

is denoted as

m + 1

, and

s_{p u b}

placed in the RSA modulus shall be prefixed with 8 bits,

1 | | r_{1}

, where

r_{1}

is a 7-bit random string. In line 5, the first approximation

n_{c}

of the RSA modulus is found. In the next line, the first approximation of the second prime

q_{1}

is determined; however, the approximation probably is not a prime yet.

The next steps of the procedure, omitted above, consist of setting the least significant bit of

q_{1}

and incrementing

q_{1}

by 2 until a prime number is found. In addition, a sieve has been incorporated here in a very effective way that, before applying the Miller-Rabin test, excludes

q_{1}

p ‘ | q_{1}

or if

p ’ | q_{1} - 1

, where

p^{'}

takes consecutive values from the sequence of the first 2048 odd primes2.

The procedure GetPrimesFast includes loops, and sometimes the execution path returns to line 4, but

p_{1}

and

s_{p u b}

remain unchanged. By the Prime Number Theorem, the number t of increments by 2 of the number

q_{1}

has the expected value

O (ln (q_{1}))

Let

q_{1}^{'}

denote the value of

q_{1}

just after the last execution of line 4 and after setting the least significant bit. Then for the final

q_{1}

we have:

p_{1} \cdot q_{1} \approx p_{1} \cdot (q_{1}^{'} + 2 t) \approx (n_{c} - r) + 2 t \cdot p_{1} = n_{c} + (2 t \cdot p_{1} - r) .

(1)

For a 2048-bit RSA modulus we have

ln (q_{1}) \leq ln (2^{1024} - 1) \approx 710

. For a 4096-bit RSA modulus, the upper bound is around 1420. Therefore, taking into account the carry bits and the variance in the search of prime

q_{1}

, it seems that usually no more than len+64 least significant bits of the

n_{c}

calculated in line 5 will be affected by the component

2 t \cdot p_{1} - r

. Consequently, the value

s_{p u b}

residing in the area of the most significant bits of

n_{c}

is not at risk of being changed by the component

2 t \cdot p_{1} - r

, and it will be available to

Adv

directly from the RSA modulus.

The value

s_{p u b}

has just 257 bits in length: in [31] a pair of twisted elliptic curves over a binary field

F_{2^{m}}

, where

m = 257

, is defined. The element

s_{p u b}

is represented in [31] as a compressed point

(x, y b i t)

: the x-coordinate and one bit of the y-coordinate. That is why

m + 1

is used in line 3 of the procedure GetPrimesFast. However, just the x-coordinate of the point is enough; hence, the expression

m + 1

can be replaced by the value 257.

7.2. Linking Attack

Attack type and result:

This is a linking attack where

Adv

learns

{id}_{U}

. This information is encrypted and hidden in the generated RSA modulus.

Attack prerequisites:

The asymmetric keys of the

Adv

are stored on

{Auth}_{U}

. However,

Adv

does not need to be an active participant of the protocol. It suffices that

Adv

has access to public keys generated by authenticators.

Auxiliary techniques:

embedding a ciphertext into a RSA modulus: consider the smallest size of RSA keys allowed in WebAuthn, which is 2048 bits. Then we may assume that

μ

from line 3 of the GetPrimesFast procedure equals

2048 - (8 + 257) = 1783

. We assumed that the component

2 t \cdot p_{1} - r

from (1) will usually change no more than len

+ 64 = 1024 + 64

tailing bits of

n_{c}

. Therefore in case of

r_{2}

calculated in line 4 of the GetPrimesFast procedure we have

1783 - (1024 + 64) = 695

(2)

leading bits unchanged when we add

2 t \cdot p_{1} - r

n_{c}

. Therefore, the 695 most significant bits of

r_{2}

may carry a ciphertext. Note that when the execution path returns to line 4, then it suffices to re-randomize

r_{1}

and, e.g., 128 least significant bits of

r_{2}

. Consequently, the ciphertext bits of

r_{2}

remain unchanged, and enough entropy is still provided.

In the case of a larger modulus, the space available for the ciphertext is even larger.

Diffie-Hellman key exchange: the ephemeral-static version of the DH protocol should be applied, that is, the technique from [30,31] should be followed. Consequently, the asymmetric keys of

Adv

are stored on

{Auth}_{U}

(see Section 9.3.2 for details). Why the ephemeral-ephemeral DH protocol is excluded is explained in Section 9.2.

Algorithm:

It is a modified version of the attack presented in [30,31].

{Auth}_{U}

generates

pk

during registration so that it passes

{id}_{U}

to S as a ciphertext hidden in

pk

This time, the shared secret established using the DH protocol is not used as a seed to generate the prime

p_{1}

. The factor

p_{1}

shall now be generated at random. In this attack, the shared secret is used to derive a key for encrypting a linking identifier. The ciphertext is directly embedded in the generated modulus. The identifier could be an identifier of the user from some other service or a publicly known identifier if

{Auth}_{U}

has access to it.

7.3. Impersonation Attack

Attack type and result:

This is an impersonation attack where

Adv

can factor the RSA modulus of

pk

generated by

{Auth}_{U}

and thereby derive the corresponding signing key

sk

Additionally, the channel for ciphertexts used in the linking attack becomes widened. This opens doors for further attack options based, e.g., on a covert transmission of the DRNG seed, for example transferred together with short fingerprints of user identifiers on some other services.

Attack prerequisites:

are the same as in the previous attack.

Auxiliary techniques:

embedding two ciphertexts into a RSA modulus: The channel for encryption will be extended in the following way:

The first ciphertext of length expressed by the formula (2) is created as in the case of the linking attack.
The second ciphertext is available to the addressee only after factoring the RSA modulus. In the paper [30], the prime $p_{1}$ is generated in a slightly different manner: only the upper half of the prime is generated from the shared seed $s_{p r i v}$ , the half with least significant bits are allowed to be truly random. The authors of [30] indicate that still the modulus can be efficiently factorized by the adversary: knowledge of $\frac{bits}{4}$ most significant bits of $p_{1}$ allows the adversary to run the Coppersmith’s attack [33] to find $p_{1}$ and $q_{1}$ .

Accordingly, we modify the accelerated attack from [31], where the prime $p_{1}$ is generated in the following way:

-

at first a bit-string of length $len$ is obtained from a DRNG with the seed $s_{p r i v}$ (so the entire number $p_{1}$ is obtained); the two most significant bits and the least significant bit of $p_{1}$ are set to `1’,

-

the next steps of the procedure consist of incrementing $p_{1}$ by 2 until a prime number is found. Like for $q_{1}$ , a sieve has been incorporated here. The sieve forces to skip $p_{1}$ , if $p ‘ | p_{1}$ or if $p ’ | p_{1} - 1$ , where $p^{'}$ takes consecutive values from the sequence of the first odd prime numbers not greater than a threshold configured in the implementation. The procedure includes loops, and sometimes the execution path goes back to generate again the number $p_{1}$ by the DRNG seeded with $s_{p r i v}$ . In such a case, the next block of $len$ pseudorandom bits is taken from the generator, and the two uppermost bits and the least significant bit of $p_{1}$ are again set to `1’. As previously, by the Prime Number Theorem, the expected number $t^{'}$ of increments by 2 of the number $p_{1}$ is $O (ln (p_{1}))$ . Let $p_{1}^{'}$ denote the value of $p_{1}$ immediately after taking it from the generator for the last time and setting the least significant bit and the two uppermost bits to `1’. Then for the final $p_{1}$ we have:

$p_{1} \approx p_{1}^{'} + 2 t^{'} .$

(3)

Let us modify the above procedure. Instead of taking $len$ bits from a generator and assigning them directly to $p_{1}$ (initially, and each time the number $p_{1}$ must be re-generated), we apply the following steps:
- Assign to $α$ the first $len$ bits of the output of the pseudorandom number generator seeded with $s_{p r i v}$ :
  
  $α = DRNG (s_{p r i v}, len)$
  
  (4)
- Split $α$ into three bit-strings:
  
  $α = α_{1} | | α_{2} | | α_{3} .$
  
  where $α_{1}$ , $α_{2}$ , $α_{3}$ consist of $\frac{len}{2}$ , $\frac{len}{2} - 64$ , 64 bits, correspondingly.
- Assign
  
  $p_{1} = α_{1} | | α_{2} xor m | | α_{3},$
  
  where m is $(\frac{len}{2} - 64)$ -bit message to be encrypted. For the value bits $= 2048$ , the message m may have 448 bits.
We expect that the buffer $α_{3}$ is usually large enough to completely absorb all the increments (3). Knowledge of the bit-string $α_{1}$ is sufficient for $Adv$ to factorize RSA modulus with the Coppersmith’s attack. Having the factor $p_{1}$ , the adversary can compare it with the output $α$ of the generator and immediately recovers m.

Diffie-Hellman key exchange: the same technique as in the linking attack should be applied.

Algorithm:

The shared secret established with the help of the DH protocol is used to seed the pseudorandom number generator. The first portion of the output bits from this generator is used to generate the first ciphertext, that is, the one to be embedded in the upper half of the RSA modulus. The next portions are consumed on demand to generate the bit-strings

α

(4).

Remark 6.

A simplified version of the attack can be implemented to make factorization faster for the

Adv

. That is, exactly like in [31], the entire number

p_{1}

is generated from the shared seed

s_{p r i v}

, not just its upper half. However, one ciphertext can still be embedded in the most significant area of the generated modulus, as in the case of the linking attack.

8. Technical Details -Leakage with Error Correcting Codes

In the remaining part of the paper, we explain some technical details and ideas that have already been used but are not discussed in depth.

In this section, we detail how error correction codes are used to encode hidden secrets in binary strings. Specifically, let us consider a secret message consisting of n bits that is leaked one bit at a time at a random position, with possible repetitions. We seek to determine the expected time required to recover the entire secret. This problem is an instance of the Coupon Collector’s Problem. It is known that the expected number of bits that must be leaked to recover all n bits is given by the formula

n \cdot H_{n}

, where

H_{n} = \sum_{k = 1}^{n} \frac{1}{k}

denotes the n-th harmonic number.

If we apply an error-correcting code, let

n^{'}

denote the number of bits in the encoded message. Then, the expected time to leak all

n^{'}

bits that the code can correct even if all missing bits are set in a wrong way is given by the formula

n^{'} \cdot (H_{n^{'}} - H_{t}),

where t is the upper bound on the number of incorrect bits.

Although the method seems to be straightforward, most error correction codes have a fixed block size and can be applied to strings with a length that is a multiple of the block size. If the bit-string length is different, then we get implementation problems.

Typically, an error-correcting code has two parameters: m is a size parameter, and t is the number of errors that can be corrected. Let

n (m, t)

denote the number of bits in the original string and

n^{'} (m, t)

total number of bits of its error-correcting code. To assess whether using an error-correcting code is beneficial, we calculate the ratio:

R (m, t) = \frac{n (m, t) H_{n (m, t)}}{n^{'} (m, t) (H_{n^{'} (m, t)} - H_{t})}

(5)

R (m, t) > 1

, then applying the error correction code speeds up information leakage.

Below, we discuss this problem for concrete examples where the leaked data is a Polish personal identity number (PESEL) or a phone number, both with 11 decimal digits. To encode each digit, we use 4 bits (e.g., 0 is encoded as `0000`, 1 as `0001`, and so on up to 9 as `1001`). This results in a bit-string with 44 bits.

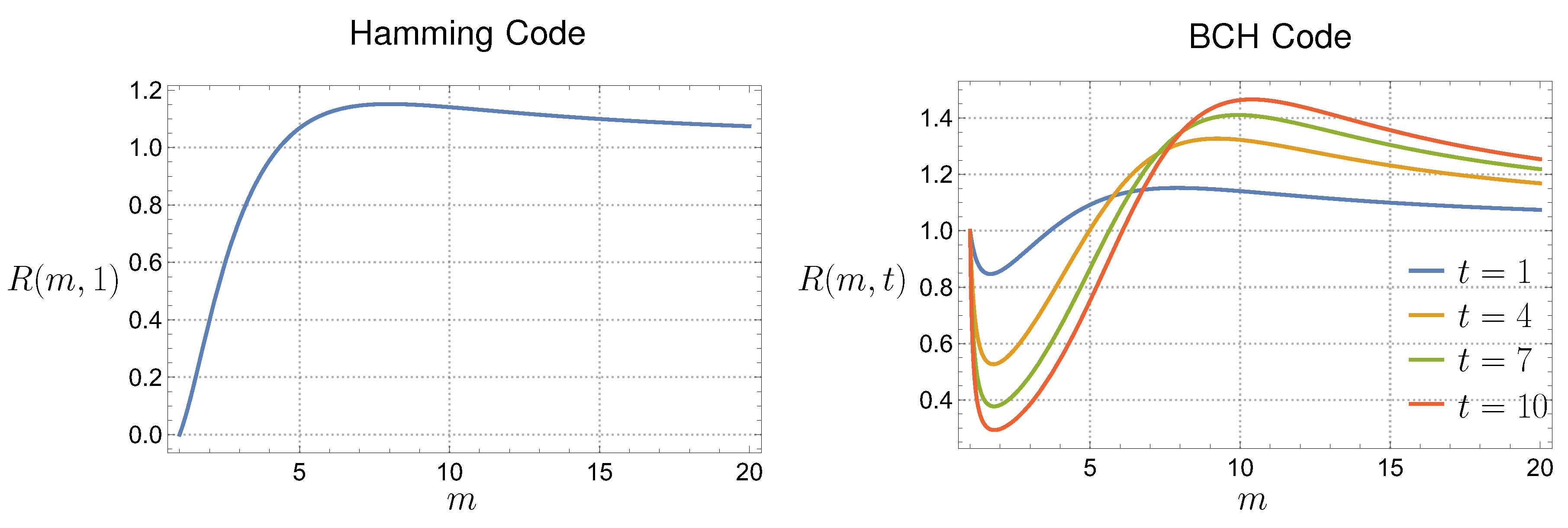
8.1. Hamming Codes

For binary Hamming codes, the code length is typically

n^{'} = 2^{m} - 1

, where m is a positive integer. The message (secret) length to be encoded is given by

n = 2^{m} - m - 1

. Hamming codes can correct up to one error, i.e.,

t = 1

In Figure 6, we see that even a single error correction provided by Hamming codes reduces the expected time to leak a secret. However, it does not mean that we can save time for any length of the leaked string. For example, for

n = 44

, collecting all bits without error correction requires, on average,

44 \cdot H_{44} \approx 192.4

steps. For Hamming codes, we have to take

m = 6

and a Hamming code with

n^{'} = 2^{6} - 1 = 63

bits. Then the expected time to recover the secret is

n^{'} (H_{n^{'}} - H_{t}) = 63 \cdot (H_{63} - H_{1}) \approx 234.88

. In this case, the Hamming codes are useless.

8.2. BCH Codes

Bose-Chaudhuri-Hocquenghem (BCH) codes offer the capability to correct more than one error. According to [34], for code length

n^{'} = 2^{m} - 1

, a BCH code can correct up to t errors, where the input string has length

n = 2^{m} - 1 - r (m, t) \geq 2^{m} - 1 - m t,

where

r (m, t)

is a function of m and t, bounded by

m t

In Figure 6, we provide plots of the ratio

R (m, t)

for different values of t and m. These plots illustrate that the R ratio is above 1 for relatively small values of m, indicating that error correction using BCH codes can be beneficial even with moderate code lengths. For our example, we consider the following configurations of the BCH codes:

For $n^{'} = 63$ , which corresponds to $m = 6$ :

-

when correcting $t = 2$ errors, the number of information bits is $n = 63 - 6 \cdot 2 = 51$ ,

-

when correcting $t = 3$ errors, the number of information bits is $n = 63 - 6 \cdot 3 = 45$ .
For $n^{'} = 127$ , which corresponds to $m = 7$ we can correct 4 errors. Thus $n = 127 - 7 \cdot 4 = 99$ bits.

The expected times to recover the secret with these BCH codes are as follows:

n^′	n	t	nH_n	$(H_{n^{'}} - H_{t})$
63	51	2	230.46	203.38
63	45	3	197.77	182.38
127	99	4	512.56	424.43

The most efficient option for BCH codes in our example of 11-digit secret is a 63-bit code correcting 3 errors, which allows for the transmission of 45 bits of information with an expected leakage time of 182.38, outperforming the 192.40 expected time for transmitting 44 bits without error correction. However, the last code shows that the gain might be quite significant if the information leaked is data like cryptographic keys or seeds to DRNG.

Conclusions

We have shown that:

Even with moderate code lengths, error correcting codes can speed up information leakage.
In practice, the advantage of using error correction when encoding the secret to be leaked is higher with longer secrets.
for a given secret length, a careful choice of the error correction scheme might be necessary to optimize the leakage speed.

In particular, we should not underestimate the capacity of possible covert channels created with the rejection sampling technique by taking the numbers derived for the Coupon Collector Problem.

9. Technical Details - Kleptographic Shared Key Agreement

The kleptographic attacks discussed in the paper are mainly based on the Diffie-Hellman (DH) key agreement protocol. The versions of the DH protocol utilized in the paper fall into two main categories:

Ephemeral-static version, where an authenticator knows the “public” kleptographic key Y of the adversary, such that $Y = g^{y}$ , where g defines a prime order (sub)group, and y is adversary’s (static) private kleptographic key. The ephemeral component is determined by the authenticator: it freshly generates a random exponent k and sends $g^{k}$ to the other side, while privately it computes the master shared key as $K = Y^{k}$ . The adversary, having learned $g^{k}$ calculates K as ${(g^{k})}^{y}$ . The advantage of this version is that only one side needs to send a message, and this can be particularly important in kleptographic applications:

-

it is easier to fit fewer messages into the underlying protocol,

-

the other party of the underlying protocol may be unaware of the malicious functionality and may not cooperate during the execution of the protocol (the adversary may access kleptographic messages at a different stage or as a passive eavesdropper),

On the other hand, there are some key management issues, such as protection of y by the adversary (once y is compromised, the whole malicious framework becomes evident and, therefore, useless to the adversary).
Ephemeral-ephemeral version, where there is no public key known to one side in advance. Both parties send freshly generated components: an authenticator picks random $k_{A}$ and sends $g^{k_{A}}$ , and the server picks random $k_{S}$ and sends $g^{k_{S}}$ . Both parties can compute the master shared key $K = g^{k_{A} \cdot k_{S}}$ . This version is free of the issues related to managing “public” keys but requires kleptographic messages sent by both sides of the protocol.

Obviously, to be undetectable, the kleptographic Diffie-Hellman key agreement must be hidden within the regular (random) messages of the host protocol. Our question is how to hide the kleptographic DH key agreement in the WebAuthn. There are two constructions known in the literature that can be used to encode DH components as uniformly distributed bit-strings:

Probabilistic Bias Removal Method,
Binary Twisted Elliptic Curves.

The first one is very helpful when the inputs to encode are, e.g., residues modulo a prime number. However, an unpleasant property of this method is that encoding may take several iterations (how many is not known in advance). This should not be a problem if the encoding is done on the server side (a separate thread can execute the algorithm). However, in embedded systems, runtime variances can become visible. The second method, based on Binary Twisted Elliptic Curves, is fast but only works on bit-strings, and is therefore not suitable for, for example, converting values from a prime field. We consider two versions of the DH protocol below to analyze which method is better in a given situation.

9.1. Ephemeral-Static DH Protocol

This version is the simpler one when it comes to designing a hidden message flow in the underlying protocol because only one message must be hidden. Moreover, if the signature scheme used by the authenticator is based on the discrete logarithm, then a signature component can be used directly.

Discrete logarithm signatures used for authentication

Typically, an ephemeral public key

g^{k}

is calculated during signature generation. Moreover,

g^{k}

can be retrieved from the signature (for example, in the case of ECDSA signatures, the component s of the signature allows to reconstruct

g^{k}

). If at the same time

{Auth}_{U}

has access to

Y = g^{y}

, then

{Auth}_{U}

may calculate

Y^{k}

as a shared secret. Of course,

Adv

knowing y may reconstruct the shared secret from the signature. Proof of security of this construction is given in [25].

In the WebAuthn protocol,

{Auth}_{U}

should take into account the server preferences (see Section 9.4). Assuming that most of the servers are honest, hence their preferences are unpredictable from the point of view of the

Adv

, the best option is to embed on the

{Auth}_{U}

a separate “public” key Y of the adversary

Adv

for each domain parameters supported by the

{Auth}_{U}

RSA Signatures Used for Authentication

For RSA signatures, the choice of domain parameters for the hidden DH protocol does not depend on the underlying protocol. The primary objective of the choice of the domain parameters should be:

to hide the presence of the kleptographic protocol,
to optimize the efficiency of shared key generation.

Both conditions are met by the construction to be presented in Section 9.3.2. In Section 7, we already demonstrated how the construction is utilized, that is how ephemeral-static DH protocol is embedded in an RSA modulus.

9.2. Ephemeral-Ephemeral DH Protocol

We assume that server S is aware of the hidden functionality implemented on some of the authenticators and colludes with them. The malicious server is recognized by

{Auth}_{U}

by the identifier

i d_{S}

S initiates the execution of the DH protocol by sending a crafted

u i d

during registration. Fortunately,

u i d

can be long enough (

\leq 4 λ

) to accommodate the DH protocol component

g^{k_{S}}

. However,

u i d

encodes uniformly distributed bit-strings; hence, to hide numbers representing residues modulo a prime number (x-coordinate of an elliptic curve point), a protocol from Section 9.3.1 should be utilized. If

{Auth}_{U}

is not contaminated, then it will treat

u i d

as a purely random value, unaware of its hidden meaning.

Discrete Logarithm Signatures Used for Authentication

Apart from sending

g^{k_{S}}

u i d

, the domain parameters corresponding to

g^{k_{S}}

must be somehow agreed upon between the server and the authenticator. For this purpose, the preference list discussed in Section 9.4 can be used. According to [16] “the client makes a best-effort to create the most preferred credential that it can”. Of course, the server chooses the domain parameters that are supported by the malicious authenticators, thus, the first item on the server’s list of preferences is a convenient place to indicate the domain parameters corresponding to

g^{k_{S}}

In response,

{Auth}_{U}

generates signature keys for these domain parameters. Later, when authenticating for the first time to this server, it passes its DH component as the ephemeral key

g^{k}

included in the signature.

While the described procedure enables the colluding server and authenticator to derive a secret shared key, the question is whether the execution of DH protocol can be detected by an auditor. Let us examine this issue for signatures based on elliptic curves. In the above procedure,

g^{k_{S}}

encoded in

u i d

always belongs to the elliptic curve indicated by the first item on the list of server’s preferences. Consequently, the authenticator will use the same curve to generate the keys. This correlation is easy for an auditor to detect.

To be more specific,

u i d

will be generated in such a way that it will appear to have a uniform distribution among bit-strings of the given length. We must assume that the auditor will nevertheless try different ways of examining

u i d

to check that it does not carry hidden information3. Therefore, the auditor may also try to decode

u i d

in the same way as a malicious authenticator would do.

Unfortunately, there is a feature that distinguishes our encoding of elliptic curve points from truly random strings: to test if

u i d

may carry the x-coordinate of a point of a curve, it suffices to substitute the tested value x into the right-hand side of the equation defining the curve (see (6) below). For random values x, we get a quadratic residue on the right-hand side of the equation with probability very close to

\frac{1}{2}

. However, if the auditor analyzes several user registration processes on the same malicious server, they will detect that for every such registration, the tested x yields a quadratic residue on the right-hand side (RHS) of the curve’s equation.

Thus, the above key agreement procedure must be modified to fool the auditor. Now, to make the

u i d

and domain parameter selection appear to be uncorrelated, the server will attempt to establish a shared key with the authenticator not always, but only with a certain probability. How should the probability be determined? To illustrate the idea, we focus on prime-order elliptic curves, a typical case for ECDSA signatures. Let

y^{2} = x^{3} + a x + b

(6)

be an elliptic curve defined over a prime field

F_{p}

. It is usually denoted as

E_{a, b} (F_{p})

. Let the domain parameters chosen by the server utilize the curve

E_{a, b} (F_{p})

Let

d \in F_{p} ∖ {0}

be a quadratic non-residue. Then the curve

d y^{2} = x^{3} + a x + b

(7)

is called a quadratic twist of

E_{a, b} (F_{p})

and is denoted as

E_{a, b}^{d} (F_{p})

. It is known that:

| E_{a, b} (F_{p}) | + | E_{a, b}^{d} (F_{p}) | = 2 p + 2

(8)

We shall consider points that can be represented as a pair

(x, y)

, therefore on each of the curves

E_{a, b} (F_{p})

E_{a, b}^{d} (F_{p})

we exclude a so-called “zero at infinity” point

θ

. Then we have:

| E_{a, b} (F_{p}) ∖ {θ_{a, b}} | + | E_{a, b}^{d} (F_{p}) ∖ {θ_{a, b}^{d}} | = 2 p

Since p is large (so

p > 2

) and the order of

E_{a, b} (F_{p})

is assumed to be prime, there is no point of order 2 on

E_{a, b} (F_{p})

. As a point

(x, 0)

would have order 2, it cannot belong to

E_{a, b} (F_{p})

. Consequently, there is no

x \in F_{p}

yielding 0 on the RHS of (6), and, consequently, on the RHS of (7). Hence, each

x \in F_{p}

gives RHS that is either a quadratic residue (and gives two points on (6)) or is a quadratic non-residue (and gives two points on (7)). The probability that a random x gives two points on (6) is

\frac{| E_{a, b} (F_{p}) | - 1}{2 p}

, which indeed, according to Hasse’s Theorem, is close enough to

\frac{1}{2}

for large prime p.

Therefore, to hide the correlation mentioned above, with probability

\frac{| E_{a, b} (F_{p}) | - 1}{2 p}

, the server will attempt to establish a shared key with the authenticator. In the case of elliptic curves, the shared secret is represented by the x-coordinate of the result of the DH key agreement, and it also suffices to transfer just the x-coordinate of the DH component to uniquely determine the x-coordinate of the resulting shared key.

In conclusion:

with probability $\frac{| E_{a, b} (F_{p}) | - 1}{2 p}$ the server picks random $k_{S}$ , calculates the DH component (denoted in the text as $g^{k_{S}}$ ), takes its x-coordinate, and enters the algorithm explained in Section 9.3.1. The output of the algorithm is uniformly distributed as a bit-string. Thus it can be transferred in $u i d$ ,
with probability $1 - \frac{| E_{a, b} (F_{p}) | - 1}{2 p} = \frac{| E_{a, b}^{d} (F_{p}) | - 1}{2 p}$ the server picks a random x yielding a quadratic non-residue on the RHS of (6) and enters the algorithm from Section 9.3.1. Again, the algorithm’s output has uniform distribution as a bit-string; hence, it can be transferred in $u i d$ .

The use of this key agreement scheme is demonstrated in Section 6.5.

RSA Signatures Used for Authentication

If the twisted elliptic curves discussed in Section 9.3.2 are used for ephemeral-ephemeral DH protocol, then an auditor observing malicious participants will be able to see some correlation. Indeed, the server’s component will utilize one of the twisted curves, and the infected authenticator must follow the server’s choice of the curve – both components will exhibit the same

a \in {0, 1}

(see Section 9.3.2 for details). On the other hand, for truly random choice, the values a tested by the auditor should be statistically independent on both sides.

For the same reason, usage of a single elliptic curve together with the probabilistic bias removal method, would compromise the hidden functionality: both DH components will represent a bit-string yielding a point on that particular curve (in fact, in the case of RSA, usage of a single curve is even more complicated than in the case of discrete logarithm signatures, discussed above, and requires more effort to hide the DH protocol).

We can see that hiding the ephemeral-ephemeral DH protocol when RSA signatures are used is problematic. Therefore, in this case, the ephemeral-static DH protocol seems more advantageous.

9.3. Uniformly Distributed Bitstrings

The underlying group for the hidden DH key exchange must be chosen so that neither the uniformness of the random bit strings in the host protocol is affected nor the keys established in the hidden DH protocol are biased. So, we have to take care of some low-level details necessary for the attack to succeed.

9.3.1. Probabilistic Bias Removal Method (PBRM)

The method proposed in [7] solves the following general problem encountered in subliminal channels and kleptography: assume that a random variable X is uniformly distributed in

{0, 1, \dots, R - 1}

and this random variable is going to be transferred through a channel where it should be perceived as a random variable

X^{'}

uniformly distributed in a different set

{0, 1, \dots, S - 1}

. A typical example is that R is a prime number and

S = 2^{n}

for some n. That is, remainders modulo the prime number R transferred via a kleptographic channel should be perceived by an external observer as uniformly distributed random bit-strings, just as described in the specification of the host protocol.

It is also assumed that

S > R > S / 2

. In the exemplary case, this corresponds to the equality

n = ⌊ {log}_{2} p ⌋ + 1

, so n is the bitlength of p. Of course,

2^{n} > p > 2^{n} / 2 = 2^{n - 1}

. There is also a requirement that for any value

x^{'}

of the random variable

X^{'}

, the corresponding original value x of the random variable X should be easily obtainable.

The method uses a symmetric coin and proceeds as follows:

A random value x of the variable X is chosen with uniform probability distribution.
The coin is tossed.
If $x < S - R$ and we get heads, then return $x^{'} = x$ .
If $x < S - R$ and we get tails, then return $x^{'} = (S - 1) - x$ .
If $x \geq S - R$ and we get heads, then return $x^{'} : = x$ .
If $x \geq S - R$ and we get tails, then go to Step 1 of the procedure.

The authors of [7] show that values

x^{'}

generated according to the above procedure are indeed uniformly distributed in

{0, 1, \dots, S - 1}

. Obviously, x are chosen uniformly at random from

{0, 1, \dots, R - 1}

, therefore a particular x is chosen with probability

1 / R

. Let us consider the intervals to which the produced

x^{'}

belongs:

In Step 3, $x^{'}$ is set to x, hence $x^{'} < S - R$ ,
In Step 4, we have $(S - 1) - x > (S - 1) - (S - R) = R - 1$ . Thus, $R \leq x^{'} \leq S - 1$ .
In Step 5 we obviously have $x < R$ , hence in this step $S - R \leq x^{'} < R$ ,

The Step 6 does not produce an output directly but repeats the whole procedure.

All in all, the interval

[0, S - 1]

has been divided into three sub-intervals:

$[0, S - R)$ , defined by Step 3,
$[S - R, R)$ , defined by Step 5,
$[R, S - 1]$ , defined by Step 4,

and any

x^{'}

belonging to any of the sub-intervals is generated with the same probability (in a single iteration, the probability equals

1 / (2 R)

Note also that x is easy to obtain from

x^{'}

. The only case where

x^{'} \geq R

occurs for Step 4, and then

x = (S - 1) - x^{'}

. In the remaining steps

x^{'} = x

, hence for

x^{'} < R

, one can take

x = x^{'}

Of course, if a bit-string has more than n bits, then the first n bits can be utilized to transfer values modulo p, and the remaining bits can be truly random, or they can be utilized in a different manner.

Suppose that the value x used above is the x-coordinate of an elliptic curve point representing an ephemeral DH component (denoted in the text as

g^{k}

). If a new x must be chosen, a new random k must be picked, and the ephemeral DH component shall be re-calculated.

9.3.2. Binary Twisted Elliptic Curves

Another approach to build a kleptographic channel having available only binary strings expected to be uniformly distributed is to utilize the solution from [36] based on twisted binary elliptic curves ( and re-used in [30]). The original construction uses curves defined over 163-bit binary fields, but there are no constraints to increase the field size. The report [37] suggests that binary curves defined over the 233-bit field provide 112-bit security strength. In contrast, the paper [38] considers, among other sizes, also the binary Edwards curves defined over the 223-bit field. Thus, the binary fields of size ranging from 233 to 256 bits seem to provide a satisfactory security level (in fact, we shall use the fields

F_{2^{m}}

for m being a prime number, thus for the sizes mentioned, we have:

m \in {233, 239, 241, 251}

Let

E_{a, b} (F_{2^{m}})

denote an elliptic curve defined over a binary field

F_{2^{m}}

, given by the equation

y^{2} + x y = x^{3} + a x^{2} + b .

(9)

We shall use a pair of twisted curves

E_{0, b} (F_{2^{m}})

E_{1, b} (F_{2^{m}})

, where m is prime (see [36]). Usage of the twisted curves is necessary to ensure indistinguishability of the ephemeral keys transmitted from truly random bit-strings.

Note that the point

(0, \sqrt{b})

belongs to both curves. At the same time, for each nonzero x, there are two distinct points (

(x, y)

and

(x, x + y) = - (x, y)

) both on exactly one of the curves

E_{0, b} (F_{2^{m}})

E_{1, b} (F_{2^{m}})

. Consequently, each

x \in F_{2^{m}}

occurs twice as an x-coordinate of points in in the set

E_{0, b} (F_{2^{m}}) \cup E_{1, b} (F_{2^{m}})

Of course, in addition to the points

(x, y)

that satisfy the formula (9), also the “zero at infinity”

θ_{a, b}

belongs to the curve

E_{a, b} (F_{2^{m}})

for

a = 0, 1

. Therefore,

2 \cdot 2^{m}

corresponds to the number of points in the set

(E_{0, b} (F_{2^{m}}) ∖ {θ_{0, b}}) \cup (E_{1, b} (F_{2^{m}}) ∖ {θ_{1, b}}) .

According to [36], we can choose the curves

E_{0, b} (F_{2^{m}})

E_{1, b} (F_{2^{m}})

with orders

4 q_{0}

2 q_{1}

, respectively, where

q_{0}

and

q_{1}

are prime. Consequently,

| E_{0, b} (F_{2^{m}}) ∖ {θ_{0, b}} | = 4 q_{0} - 1

| E_{1, b} (F_{2^{m}}) ∖ {θ_{1, b}} | = 2 q_{1} - 1

. Then:

$H_{1} = (0, \sqrt{b})$ is a point of order 2 on $E_{1, b} (F_{2^{m}})$ ,
$H_{0} = (\sqrt[4]{b}, \sqrt{b})$ is a point of order 4 on $E_{0, b} (F_{2^{m}})$ .

We choose points

G_{0}

G_{1}

such that

G_{a} \in E_{a, b} (F_{2^{m}})

and

error G_{a} = q_{a}

, for

a = 0, 1

. Thus, every point

P \in E_{a, b} (F_{2^{m}})

, for

a \in {0, 1}

, can be expressed as a linear combination:

P = u \cdot G_{a} + v \cdot H_{a}

(10)

for unique

u \in {0, 1, \dots, q_{a} - 1}

and

v \in {0, 1, \dots, 2^{2 - a} - 1}

The points

G_{0}

G_{1}

are the base points (generators of subgroups of prime orders); thus, to generate an asymmetric “encoding” key for each of the curves

E_{0, b} (F_{2^{m}})

E_{1, b} (F_{2^{m}})

, the adversary chooses private keys

x_{a} \in {2, \dots, q_{a} - 1}

uniformly at random and calculates

Y_{a} = x_{a} \cdot G_{a}

for

a = 0, 1

. All in all, the definition of

F_{2^{m}}

, value b, and

(G_{0}, G_{1}, Y_{0}, Y_{1})

are kleptographic setup parameters stored in the malicious implementation.

To execute the ephemeral-static DH protocol, the malicious implementation will choose

a = 0

with probability

\frac{4 q_{0} - 1}{2^{m + 1}}

and

a = 1

with probability

\frac{2 q_{1} - 1}{2^{m + 1}}

(we subtract “1” in the numerators because the “zero at infinity” points

θ_{a, b}

should not be generated). The malicious implementation then takes

u \in {2, \dots, q_{a} - 1}

with a uniform probability distribution, calculates

u \cdot G_{a}

u \cdot Y_{a}

, and randomly (and uniformly) chooses

v \in {0, \dots, 2^{2 - a} - 1}

. Then the implementation assigns the following:

P^{'} : = u \cdot G_{a} + v \cdot H_{a} .

(11)

Since we excluded

u \in {0, 1}

, almost all points belonging to

E_{a, b} (F_{2^{m}})

can be generated (only

2 \cdot 2^{2 - a}

points, including

θ_{a, b}

, are excluded). Accordingly, taking into account the formula (10) and both the twisted curves, the x-coordinates

x (P^{'})

of the generated points

P^{'}

from (11) are almost uniformly distributed. That is, there are

2^{m} - 7 - 3

possible results for

x (P^{'})

, and due to the probability of the choices of a, u, v, the bias is negligible.

The value

x (P^{'})

will be sent in plaintext by the malicious implementation. At the same time, the implementation takes the x-coordinate of the point

u \cdot Y_{a}

as a shared secret to be used later (e.g., as a seed for the deterministic random number generator, DRNG).

The adversary who monitors the messages sent by the malicious implementation learns the value of

x (P^{'})

. To learn

u \cdot Y_{a}

, the adversary must first learn the value of a, that is, determine which of the twisted curves was chosen by the device. For that purpose, the trace function is used: note that if

a \in {0, 1}

, then for odd m, we have

a = {T r}_{F_{2^{m}} / F_{2}} (x (P^{'}) + b \cdot {(x (P^{'}))}^{- 2}),

(12)

where

{T r}_{F_{2^{m}} / F_{2}} (α) = α + α^{2} + α^{2^{2}} + \dots + α^{2^{m - 1}} .

The formula (12) follows from (9) and from the properties of the trace function, namely,

{T r}_{F_{2^{m}} / F_{2}} (α + β) = {T r}_{F_{2^{m}} / F_{2}} (α) + {T r}_{F_{2^{m}} / F_{2}} (β)

for any

α, β \in F_{2^{m}}

;

{T r}_{F_{2^{m}} / F_{2}} (α^{2}) = {T r}_{F_{2^{m}} / F_{2}} (α)

and

{T r}_{F_{2^{m}} / F_{2}} (α) \in F_{2}

for any

α \in F_{2^{m}}

. Then, for known a, the adversary can calculate any of the two y-coordinates for

x (P^{'})

. This way, they finds the value of the point

R = \pm P^{'} .

Knowing the value of a, the adversary could also apply to the point R the correct private scalar

x_{a}

and the ECKA method described in [Section 4.3][39]. Namely, the order n of the base point

G_{a}

q_{a}

, the cofactor h is

2^{2 - a}

, so the adversary calculates

ℓ = h^{- 1} mod n

, then computes the point

Z : = h \cdot R .

In this way, the component

v \cdot H_{a}

of (11) is annihilated. Then the point

Y^{'} : = x_{a} \cdot (ℓ \cdot Z)

(13)

is found. Note that

Y^{'} = \pm u \cdot Y_{a}

. Therefore, the x coordinate

x (Y^{'})

of the point

Y^{'}

is exactly the same as the one used by the malicious malicious implementation.

9.4. How the Service Can Indicate the Domain Parameters for Diffie-Hellman

During the registration procedure, server S indicates a list of preferences regarding the algorithms. This functionality is described in [16] Section 5.4. More specifically, during registration, the server sends to the authenticator an object of the type

PublicKeyCredentialCreationOptions, and its field pubKeyCredParams determines the preference list of the server. It contains “information about the desired properties of the credential to be created. The sequence is ordered from most preferred to least preferred. The client makes the best effort to create the most preferred credential that it can.” The properties determine (see [16]) Section 5.3 “the cryptographic signature algorithm with which the newly generated credential will be used, and thus also the type of asymmetric key pair to be generated, e.g., RSA or Elliptic Curve”.

The options described here are required. The first algorithm on the list might determine the type of the hidden DH message sent by the server.

Surprisingly, the list of supported elliptic curves seems very narrow – see [16] Section 5.8.3. For example: “Keys with algorithm ES256 (-7) MUST specify P-256 (1) as the crv parameter and MUST NOT use the compressed point form.” The name ES256 denotes ECDSA with SHA-256, see [Section 8.1][40].

10. Technical Details- Kleptographic Attack on Server Side

Now, we aim to show that a server can run WebAuth protocol so that it creates a kleptographic channel to an adversary observing WebAuth messages secured with TLS encryption.

10.1. Channel Setup

The malicious implementation of the server will always attempt to negotiate the TLS cipher suite with the key agreement protocol based on the (elliptic curve) Diffie-Hellman protocol and the AEAD encryption mode. All cipher suites used by TLS 1.3 meet this condition. We assume that for each setting of the domain parameters used in the DH protocol and supported by the server, the adversary

Adv

has left some “public” key Y, and only

Adv

knows the corresponding private exponent y such that

Y = g^{y}

, where g is a fixed generator specified by the domain parameters.

We assume that the adversary

Adv

can see the whole encrypted traffic between the client and the server protected by TLS. We assume that the shared secret resulting from the TLS handshake executed by the client and the server is established according to ephemeral-ephemeral DH protocol. That is, the client chooses a random exponent

r_{c}

, and the server chooses a random exponent

r_{s}

. The master shared secret for the TLS channel is

g^{r_{c} \cdot r_{s}}

. (Of course, this key is secure from the adversary.)

For the attack, the server creates a secondary key

K = KDF (Y^{r_{s}})

. Note that

Adv

can calculate K as

K = KDF ({(g^{r_{s}})}^{y})

(recall that

g^{r_{S}}

is transmitted in clear!), while the client would have to break the CDH Problem to derive K.

Note that K does not enable to break the TLS channel – it is merely a key automatically shared between the server and the adversary

Adv

. Moreover, nothing can prevent

Adv

and the server from deriving K.

10.2. Second Attack Phase

For the sake of simplicity, first, we describe the general attack idea and disregard some technical TLS issues. In Section 10.3, we explain the attack in the real setting.

During the authentication procedure, the server generates a random string

r s

and sends it in an encrypted form to the client. The malicious implementation on the server’s side changes the procedure in a way so that the first

λ

bits of encrypted data will carry hidden information to the adversary

Adv

generate the TLS bit stream S to be xor-ed with the plaintext to yield the ciphertext portion corresponding to $r s$ within the AEAD cipher,
generate a separate ciphertext $C = {Enc}_{K} (M)$ of length $λ$ encrypted with the key K shared with $Adv$ ; here, M is a secret message to be delivered to $Adv$ ,
if $r s$ is to have length $m > λ$ , then generate a string $C^{'}$ of length $m - λ$ at random,
set $r s = (C | | C^{'}) xor S$ .

Note that in this way the TLS traffic will contain C at a certain position and the adversary

Adv

merely monitoring the messages will be able to derive

M = {Dec}_{K} (C)

. The rest of WebAuthn is executed according to the original specification. Note that the client will get the same

r s

after decrypting the TLS ciphertext and that

r s

looks random (it is the decryption result for a ciphertext of M with a wrong key and possibly a different cipher!).

Note that the adversary does not know (and does not need to know)the content of the TLS payload. It suffices to guess that the TLS traffic follows FIDO2 authentication or registration pattern. If this is correct,

Adv

may also guess the location of C embedded in the TLS traffic and attempt to decrypt it with the key K.

In the case of FIDO2 registration, embedding a hidden message might be similar, but the number of bits to embed the ciphertext to the adversary is even larger: Apart from

r s

(of the length at least

λ

), similarly, one can use the random string

u i d

of length

4 λ

10.3. Low Level Details for TLS 1.3 Ciphertext and Base64url Encoding

According to programming interface documentation of Web Authentication Protocol [16] Section 5, the server communicates with the client’s browser through a JavaScript Application run on the client’s side. The key point is that the objects containing the strings

r s

and

u i d

are encoded as base64url strings. Their position can be calculated and therefore, the problem to solve is how to encode the ciphertext C for the adversary

Adv

in an innocently looking stream ciphertext of the base64url codes of

r s

and

u i d

The base64url encoding maps 64 characters to octets (presented below in binary form). Namely, it maps

A, B, ..., Z to 01000001, 01000010, ..., 01011010,
a, b, ..., z to 01100001, 01100010, ..., 01111010,
0, 1, ..., 9 to 00110000, 00110001, ..., 00111001,
the characters - and _ to 00101101, 01011111.

In this way, only 64 octets out of 256 are utilized as base64url codes.

The encoding creates a challenge for the malicious server: one cannot use the next byte b of a ciphertext C and simply set the next byte of the TLS ciphertext to b. Namely, after decryption with the TLS key (already fixed by the handshake between the server and the client), the resulting octet might be invalid as a base64url code. Moreover, this would occur in

75 %

cases.

Recall also that

Adv

does not know the TLS encryption key, so

Adv

cannot determine the octets that would not lead to an error at a given position. Thus, if the server attempts to transmit a 6-bit number i as a part of C, it cannot send the ciphertext of the ith character from the base64url character set. So, the described naïve method fails, as

Adv

cannot reconstruct i due to the lack of the TLS encryption key.

The embedding of bits of the ciphertext C must be based only on what the adversary

Adv

can see during the TLS transmission. To some extent, this is possible. Below, we sketch a method that embeds one bit per base64url character, however, with a small error probability.

Our method focuses on the least significant bit (lsb) of the base64url codes. One can check that 0 occurs on the lsb position 31 times, while 1 occurs there 33 times. (And for no position of base64url codes there is a perfect balance between the number of zeroes and ones.) Let

B_{0}

denote the set of base64url codes with the least significant bit equal to 0, and let

B_{1}

be the set of the remaining base64url codes.

To encode a bit b, the following steps are executed by the server:

1.

calculate the next octet

κ

of the TLS key stream, let

β

be its least significant bit,

2.

calculate

B^{'} = B_{0} xor κ

B^{''} = B_{1} xor κ

(i.e, apply

xor

with

κ

to every element of, respectively, the sets

B_{0}

and

B_{1}

);

3.

set a bit c so that

c = 1

with probability

p = \frac{31}{32}

, and

c = 0

with probability

\frac{1}{32}

4.

c = 0

, then choose

ζ

uniformly at random from

B^{''}

(so,

ζ

is a ciphertext of randomly chosen base64url code from

B_{1}

, and it does not depend on b),

5.

c = 1

, then do:

if $b = 0$ , then
- choose $ζ$ uniformly at random from $B^{'}$ , if $β = 0$ , or from $B^{''}$ , if $β = 1$ ,
if $b = 1$ , then
- choose $ζ$ uniformly at random from $B^{''}$ , if $β = 0$ , or from $B^{'}$ , if $β = 1$ ,
( Note that the least significant bit of $ζ$ equals b in every case.)

6.

output

ζ

as the next octet of the TLS ciphertext encoding base64url code of 6 bits of

r s

(or

u i d

Remark 7.

The above procedure has the following properties:

The encrypted stream is correct from the client’s point of view: $ζ \in B^{'} \cup B^{''}$ , so it is a ciphertext of abase64urlcode. Therefore, the client will not detect any encoding error.
For eachbase64urlcode ρ, the probability that ζ will be the ciphertext of ρ is $\frac{1}{64}$ . Indeed, if $ρ \in B_{0}$ , then it can be chosen only for $c = 1$ , and then with the conditional probability $\frac{1}{2} \cdot \frac{1}{31}$ . So the overall probability to get ρ equals $p \cdot (\frac{1}{2} \cdot \frac{1}{31}) = \frac{1}{64}$ . If $ρ \in B_{1}$ , then it is chosen with probability $(1 - p) \cdot \frac{1}{33} + p \cdot \frac{1}{2} \cdot \frac{1}{33} = \frac{1}{64}$ . Therefore, the client will detect no irregularity concerning statistics of occurrences of thebase64urlcodes in the plaintext.
If $c = 1$ , then ζ always encodes b from the point of view of the adversary. So, the encoding of b is correct. If $c = 0$ , this is no longer true, as from the adversary’s point of view, the TLS ciphertext always encodes $1 xor β$ . So, with conditional probability $\frac{1}{2}$ , this is incorrect. Hence, the overall probability that b is not encoded correctly is $\frac{1}{32} \cdot \frac{1}{2} = \frac{1}{64}$ . is $n / 32$ , where n is the number of ones in C. If, say, C is a DRNG seed of the length 128, the expected number of errors is 2. There are only $(\binom{128}{2}) = 8128$ options to choose two error positions out of 128.
Eliminating the encoding errors may be dealt with in two ways. The first case is that the adversary gets a key that can be effectively tested. For example, suppose that the plaintext of C is the seed to the generator used by the server to derive the TLS parameter $r_{S}$ . In that case, the adversary may guess the error positions, recalculate $r_{S}$ according to the guess, and test the result against $g^{r_{S}}$ really sent by the server. As the number of possible guesses is small, finding the right $r_{S}$ is relatively easy.

The second option is to insert an error detection code in the plaintext of C. The error detection scheme has to be chosen according to the particular application and the decision about how far we need to reduce the number of false guesses.

Both techniques can be combined. For example, inserting a single parity bit within the plaintext of C would reduce the number of tests of false guesses by half.

10.4. Applications of the Hidden Channel

There are many ways to exploit the hidden channel described above. However, the main one from our point of view is the possibility to deactivate the protection provided by the TLS channel against the adversary: In this case, the message hidden in C is the seed for DRNG used by the server to generate the TLS ephemeral keys

r_{s}

. In this way, the adversary gets access to the content of the TLS channel. Thereby, the whole payload traffic to the webserver will be visible to the adversary – constituting a severe privacy breach even if the users are identified by pseudonyms

pk

. However, we will see that this is not the end of the troubles.

Based on the above mechanism, in later sections, we shall assume that the adversary monitors the whole FIDO2 communication regardless of TLS protection.

10.5. Possible Defense Strategies

The presented attack cannot be prevented as long as the plaintext message sent by WebAuthn contains a freely chosen random string on certain fixed positions, and the encryption method is based on a stream cipher. So, one can attempt to deal with the problem in the following way:

Use a kind of a“verifiable” randomness: for example, the string $r s$ might be a server’s EdDSA signature over $(i d_{S}, T)$ where T is the current time. This approach takes the freedom to arbitrarily set out the bits of $r s$ while the client can check that the server follows the protocol. This seems to be a pragmatic solution since only a change on the server’s side is necessary (the client may perform the check or skip it, unaware of the additional security mechanism).
Instead of sending the random string $r s$ alone, one can transmit $r s$ mixed with $Hash (r s)$ . “Mixed” means here an encoding such that each transmitted bit depends both on $r s$ and $Hash (r s)$ so that no position corresponds solely to the bits of $r s$ . One simple solution of this kind is to use (a few rounds of) a block encryption scheme, where $r s$ and $Hash (r s)$ fit into one block and where the encryption key is a known protocol parameter. The ability to reverse the mixing is crucial for verification of the redundancy $r s ∥ Hash (r s)$ .

11. Final Remarks and Conclusions

FIDO2 is an excellent example of a careful and spartan design of an authentication framework that addresses practical deployment issues remarkably well. FIDO2 has significant advantages concerning its simplicity and flexibility on one side and personal data protection on the other side. Finding a good compromise between usability and personal data protection is frequently challenging, with no good solution. For web authentication, FIDO2 is a candidate for being such a good solution.

At first look, it seems that nothing can go wrong during FIDO2 implementation, even if the party deploying the system is malicious: The authenticators are well separated from the network and the server, and their functionalities are severely restricted, leaving little or no room for an attack. To some extent, the client plays the role of a watchdog, controlling the information flow to the authenticator.

We show that the initial hopes are false. In this paper, we have presented a full range of attacks where malicious servers and authenticators may install kleptographic setups with quite dangerous consequences:

dismounting privacy protection mechanisms by enabling a (third party) adversary to link different public keys generated by an authenticator,
or even worse: enabling an adversary to impersonate the authenticator against a (third party) server.

The attacks are kleptographic: there are no detectable changes in the information flow, and the protocol execution seems to be honest. The kleptographic setup is straightforward and concerns quite minimal changes of protocol execution on the side of a server and/or an authenticator.

The real threat is a false sense of security:

security audits and certification may be waived,
A superficial inspection of system components may fail to detect trapdoors installed for kleptographic purposes.

The threats may propagate, as FIDO2 is only an authentication tool. A designer of a sensitive service may falsely assume that the protection given by FIDO2 is tight, while the attacker may be able to clone the authenticator remotely.

Fortunately, minor changes in the protocol may defer the detected threats. From the practical point of view, the good news is that:

the proposed changes always concern only two-party communication: client-server or client-authenticator,
the new version is backward compatible.

If the changes are not possible anymore (e.g., one cannot change the code inserted in the ROM memory of an authenticator), a deep inspection of the device is necessary during a certification process. In that sense, this paper is a hint what to look for when attempting to detect malicious FIDO2 implementations.

11.1. General Design Rules Proposed

For the design or improvement of protocols such as FIDO2, we propose the following design rules that at least make the kleptographic attacks significantly harder and simplify the audit of the system components:

sending a random string over a channel secured with a stream cipher should be avoided,
the client should randomize every random element transmitted between the server and the authenticator,
while hashing random elements seemingly reduces the applicability of kleptographic channels to rejection sampling techniques, and thereby reduces the bandwidth of kleptographic channels to a few hidden bits per random element, it does not close the channel completely,
the signatures created by an authenticator may serve as a carrier for a relatively wide kleptographic channel. Therefore, whenever possible, randomizing the signatures is necessary.

11.2. Particular Standard Modifications Proposed

With minimal local changes, FIDO2 can become much more resistant to kleptographic protocols. The general idea is to use the client as a kind of watchdog that modifies each random element shared by the authenticator and the server. We deal with these elements one by one:

Element $u i d$

When

u i d

is delivered to the client, it becomes modified in the following way:

the client chooses $Δ_{u i d}$ and assigns $u i d = Hash (u i d, Δ_{u i d})$ (the hash value will be truncated if it is too long),
the (modified) $u i d$ is transmitted to the authenticator; $Δ_{u i d}$ is appended to the next message sent from the client to the server,
the server adjusts $u i d$ in the same way as the client.

Element $c i d$

There are analogous steps as for

u i d

: the client chooses

Δ_{c i d}

at random and

c i d

is updated to

Hash (c i d, Δ_{c i d})

Element $r s$

Although we have not used

r s

in any attack, it may carry a limited kleptographic channel as well (we have not utilized it as

u i d

was so handy to use). The point is that the server can calculate

Hash (r s)

delivered to the authenticator. So, a hidden channel can be created with the rejection sampling technique. Fortunately, the client can destroy this channel as well:

the client chooses $Δ_{r s}$ and assigns $h_{r} = Hash (r s, Δ_{r s})$ instead of $h_{r} = Hash (r s)$ ,
the (modified) $h_{r}$ is transmitted to the authenticator; $Δ_{r s}$ is appended to the next message sent from the client to the server,
the server calculates $h_{r}$ in the same way as the client before checking the signature of the authenticator.

Generating $p k$

In the case of signatures based on the discrete logarithm problem, the client can easily randomize

pk

when the client obtains $pk$ during registration, it chooses $Δ_{pk}$ at random,
the client assigns $pk = pk \cdot g^{Δ_{pk}}$ and forwards the modified $pk$ to the server, following the FIDO2 specification,
the client sends $Δ_{pk}$ to the authenticator,
the authenticator updates the private key: $sk = sk + Δ_{pk}$ (addition modulo the group order).

For RSA signatures, there is no such simple solution.

Generating signatures

Again, the solution is straightforward in the case of standard non-deterministic signatures based on the discrete logarithm problem. Signature creation starts with choosing k at random, and the rest of the algorithm is deterministic. The value

r = g^{k}

will be eventually visible, so it can be transmitted to the client before the signature is finalized. So, we introduce the following steps:

the authenticator sends r to the client,
the client chooses $Δ_{k}$ at random and sends it to the authenticator,
the authenticator updates $k = k + Δ_{k}$ and proceeds the signature creation process,
the authenticator sends the resulting signature to the client,
the client retrieves the value $g^{k}$ for the obtained signature,
the client aborts the protocol if $(g^{k}) \neq r \cdot g^{Δ_{k}}$ , otherwise it proceeds according to the FIDO2 specification.

11.3. Final Note

This paper does not provide any link to a prototype implementation of the attacks. This is intentional: We do not want to facilitate any misuse of the information contained in this paper. The extent of the information provided is limited to what an auditor should look for in the inspected system components as a potentially malicious code.

Notes

1	$u i d$ is also called “user handle”. The specification [16] states in Section 14.6.1 that “It is RECOMMENDED to let the user handle be 64 random bytes, and store this value in the user’s account”.
2	For embedded devices, such as authenticators, the number of small primes used in this procedure could be lower. In [32], the effectiveness of the first-primes-sets of different sizes is analyzed, and satisfactory results are achieved even for $p^{'}$ not greater than the threshold $T = 29$ .
3	Such approach resembles, e.g., searching for irregularities in the randomness of generated RSA moduli in the attack [35].

References

The European Parliament and the Council of the European Union. REGULATION (EU) 2016/679 OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data, and repealing Directive 95/46/EC (General Data Protection Regulation). Official Journal of the European Union 2016, 119.
European Commission. Proposal for a REGULATION OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL amending Regulation (EU) No 910/2014 as regards establishing a framework for a European Digital Identity. https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:52021PC0281, 2021.
The European Parliament and the Council of the European Union. Regulation (EU) No 2019/881 of the European Parliament and of the Council of 17 April 2019 on ENISA (the European Union Agency for Cybersecurity) and on information and communications technology cybersecurity certification and repealing Regulation (EU) No 526/2013 (Cybersecurity Act). Official Journal of the European Union 2019, 151/15.
Kubiak, P.; Kutylowski, M. Supervised Usage of Signature Creation Devices. Information Security and Cryptology - 9th International Conference, Inscrypt 2013, Guangzhou, China, November 27-30, 2013, Revised Selected Papers; Lin, D.; Xu, S.; Yung, M., Eds. Springer, 2013, Vol. 8567, LNCS, pp. 132–149. [CrossRef]
Persiano, G.; Phan, D.H.; Yung, M. Anamorphic Encryption: Private Communication Against a Dictator. Advances in Cryptology - EUROCRYPT 2022 - 41st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, May 30 - June 3, 2022, Proceedings, Part II; Dunkelman, O.; Dziembowski, S., Eds. Springer, 2022, Vol. 13276, LNCS, pp. 34–63. [CrossRef]
Young, A.L.; Yung, M. Malicious cryptography - exposing cryptovirology; Wiley, 2004.
Young, A.L.; Yung, M. Kleptography: Using Cryptography Against Cryptography. Advances in Cryptology - EUROCRYPT ’97, International Conference on the Theory and Application of Cryptographic Techniques, Konstanz, Germany, May 11-15, 1997, Proceeding; Fumy, W., Ed. Springer, 1997, Vol. 1233, LNCS, pp. 62–74. [CrossRef]
Green, M. A Few Thoughts on Cryptographic Engineering: A few more notes on NSA random number generators. https://Blog.cryptographyengineering.com, 2013.
FIDO Alliance. Certified Authenticator Levels. https://fidoalliance.org/certification/authenticator-certification-levels.
Barbosa, M.; Boldyreva, A.; Chen, S.; Warinschi, B. Provable Security Analysis of FIDO2. Advances in Cryptology - CRYPTO 2021 - 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, August 16-20, 2021, Proceedings, Part III; Malkin, T.; Peikert, C., Eds. Springer, 2021, Vol. 12827, LNCS, pp. 125–156. [CrossRef]
Bindel, N.; Cremers, C.; Zhao, M. FIDO2, CTAP 2.1, and WebAuthn 2: Provable Security and Post-Quantum Instantiation. 44th IEEE Symposium on Security and Privacy, SP 2023, San Francisco, CA, USA, May 21-25, 2023. IEEE, 2023, pp. 1471–1490. [CrossRef]
Hanzlik, L.; Loss, J.; Wagner, B. Token meets Wallet: Formalizing Privacy and Revocation for FIDO2. 44th IEEE Symposium on Security and Privacy, SP 2023, San Francisco, CA, USA, May 21-25, 2023. IEEE, 2023, pp. 1491–1508. [CrossRef]
FIDO Alliance. FIDO Attestation: Enhancing Trust, Privacy, and Interoperability in Passwordless Authentication. https://fidoalliance.org/wp-content/uploads/2024/06/EDWG_Attestation-White-Paper_2024-1.pdf, 2024.
SSL Insights. 11+ Latest SSL/TLS Certificates Statistics. https://sslinsights.com/ssl-certificates-statistics/, 2024.
Internet Engineering Task Force (IETF). The Transport Layer Security (TLS) Protocol Version 1.3. Request for Comments: 8446, 2018.
W3C. Web Authentication: An API for accessing Public Key Credentials, Level 2. https://www.w3.org/TR/webauthn-2/, 2021.
Segal, D. Beginner’s Guide to Bypassing Modern Authentication Methods to SSO. RSAConference, 2024. https://www.rsaconference.com/Library/presentation/usa/2024/beginners%20guide%20for%20destroying%20fido2s%20security.
FIDO Alliance. FIDO Authenticator Security Requirements. https://fidoalliance.org/specs/fido-security-requirements-v1.0-fd-20170524/fido-authenticator-security-requirements_20170524.html, 2023.
FIDO Alliance. Authenticator Level 3+. https://fidoalliance.org/certification/authenticator-certification-levels/authenticator-level-3-plus/, accessed: 2024.
Camenisch, J.; Drijvers, M.; Lehmann, A. Universally Composable Direct Anonymous Attestation. Public-Key Cryptography - PKC 2016 - 19th IACR International Conference on Practice and Theory in Public-Key Cryptography, Taipei, Taiwan, March 6-9, 2016, Proceedings, Part II; Cheng, C.; Chung, K.; Persiano, G.; Yang, B., Eds. Springer, 2016, Vol. 9615, LNCS, pp. 234–264. [CrossRef]
W3C. Web Authentication: An API for accessing Public Key Credentials, Level 1. https://www.w3.org/TR/2019/PR-webauthn-20190117/, 2019.
Bindel, N.; Gama, N.; Guasch, S.; Ronen, E. To Attest or Not to Attest, This is the Question - Provable Attestation in FIDO2. Advances in Cryptology - ASIACRYPT 2023 - 29th International Conference on the Theory and Application of Cryptology and Information Security, Guangzhou, China, December 4-8, 2023, Proceedings, Part VI; Guo, J.; Steinfeld, R., Eds. Springer, 2023, Vol. 14443, LNCS, pp. 297–328. [CrossRef]
Bundesamt für Sicherheit in der Informationstechnik. Product certification: IT security certification scheme Common Criteria (CC). https://www.bsi.bund.de/, 2023.
Bundesamt für Sicherheit in der Informationstechnik. Guidelines for Evaluating Side-Channel and Fault Attack Resistance of Elliptic Curve Implementations (Part of AIS 46). https://www.bsi.bund.de/, 2024.
Bojko, D.; Cichoń, J.; Kutyłowski, M.; Sobolewski, O. Rejection Sampling for Covert Information Channel: Symmetric Power-of-2-Choices. In preparation, 2024.
Kubiak, P.; Kutylowski, M.; Zagórski, F. Kleptographic attacks on a cascade of mix servers. Proceedings of the 2007 ACM Symposium on Information, Computer and Communications Security, ASIACCS 2007, Singapore, March 20-22, 2007; Bao, F.; Miller, S., Eds. ACM, 2007, pp. 57–62. [CrossRef]
Knuth, D.E. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, third ed.; Addison-Wesley: Boston, 1997.
FIDO Alliance. FIDO Authenticator Allowed Cryptography List. https://fidoalliance.org/specs/fido-security-requirements-v1.0-fd-20170524/fido-authenticator-allowed-cryptography-list_20170524.html, 2023.
RSA Laboratories. PKCS #1 v2.2 RSA Cryptography Standard. RFC 8017, 2012.
Young, A.L.; Yung, M. A Space Efficient Backdoor in RSA and Its Applications. Selected Areas in Cryptography, 12th International Workshop, SAC 2005, Kingston, ON, Canada, August 11-12, 2005, Revised Selected Papers; Preneel, B.; Tavares, S.E., Eds. Springer, 2005, Vol. 3897, LNCS, pp. 128–143. [CrossRef]
Young, A.L.; Yung, M. A Timing-Resistant Elliptic Curve Backdoor in RSA. Information Security and Cryptology, Third SKLOIS Conference, Inscrypt 2007, Xining, China, August 31 - September 5, 2007, Revised Selected Papers; Pei, D.; Yung, M.; Lin, D.; Wu, C., Eds. Springer, 2007, Vol. 4990, LNCS, pp. 427–441. [CrossRef]
Lu, C.; dos Santos, A.L.M.; Pimentel, F.R. Implementation of fast RSA key generation on smart cards. Proceedings of the 2002 ACM Symposium on Applied Computing (SAC), March 10-14, 2002, Madrid, Spain; Lamont, G.B.; Haddad, H.; Papadopoulos, G.A.; Panda, B., Eds. ACM, 2002, pp. 214–220. [CrossRef]
Coppersmith, D. Finding a Small Root of a Bivariate Integer Equation; Factoring with High Bits Known. Advances in Cryptology - EUROCRYPT ’96, International Conference on the Theory and Application of Cryptographic Techniques, Saragossa, Spain, May 12-16, 1996, Proceeding; Maurer, U.M., Ed. Springer, 1996, Vol. 1070, LNCS, pp. 178–189. [CrossRef]
Bose, R.C.; Ray-Chaudhuri, D.K. On a class of error correcting binary group codes. Information and control 1960, 3, 68–79.
Nemec, M.; Sýs, M.; Svenda, P.; Klinec, D.; Matyas, V. The Return of Coppersmith’s Attack: Practical Factorization of Widely Used RSA Moduli. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, Dallas, TX, USA, October 30 - November 03, 2017; Thuraisingham, B.; Evans, D.; Malkin, T.; Xu, D., Eds. ACM, 2017, pp. 1631–1648. [CrossRef]
Möller, B. A Public-Key Encryption Scheme with Pseudo-random Ciphertexts. Computer Security - ESORICS 2004, 9th European Symposium on Research Computer Security, Sophia Antipolis, France, September 13-15, 2004, Proceedings; Samarati, P.; Ryan, P.Y.A.; Gollmann, D.; Molva, R., Eds. Springer, 2004, Vol. 3193, LNCS, pp. 335–351. [CrossRef]
Chen, L.; Moody, D.; Regenscheid, A.; Robinson, A.; Randall, K. Recommendations for Discrete Logarithm-based Cryptography: Elliptic Curve Domain Parameters. NIST Special Publication NIST SP 800-186, 2023.
Loiseau, A.; Fournier, J.J.A. Binary Edwards Curves for Intrinsically Secure ECC Implementations for the IoT. Proceedings of the 15th International Joint Conference on e-Business and Telecommunications, ICETE 2018 - Volume 2: SECRYPT, Porto, Portugal, July 26-28, 2018; Samarati, P.; Obaidat, M.S., Eds. SciTePress, 2018, pp. 625–631. [CrossRef]
Bundesamt für Sicherheit in der Informationstechnik. Technical Guideline TR-03111 v2.10 – Elliptic Curve Cryptography. Available at BSI webpage, TechnicalGuidelines/TR03111/BSITR03111.html, 2018.
Internet Engineering Task Force (IETF). CBOR Object Signing and Encryption (COSE). Request for Comments: 8152, 2017.

Figure 1. FIDO2 system from the point of view of a user.

Figure 2. FIDO2 registration of a user in a server.

Figure 3. FIDO2 authentication.

Figure 4. A general picture of kleptography: (a) the information flow in the case of an honest setup of a signing device (b) the case of an infected signing device .

Figure 6. The figure show the ratio (Eq. 5) for Hamming Code and BCH Code

Table 1. Certified Authenticator Levels.

Level	HW & SW Requirements	Defend against	Remarks
Level 1	all software and hardware authenticators	the main goals are to protect against phishing attacks and server breaches (asymmetric cryptography is utilized); what is more, the optional `tokenBinding` field in the `CollectedClientData` (see[Section 5.8.1] [16]) protects against Man in the Middle attacks – cf. [17]	in the FIDO Certification for this level, the authenticator must pass Functional Certification; the next step is the Vendor Questionnaire, which must be submitted to the FIDO Security Secretariat for Security Evaluation. The questionnaire must contain a rationale for how security requirements are met. The Security Secretariat reviews the rationale. Level 1 security certification is the minimum requirement for all FIDO authenticators.
Level 1+	similar as above, but the authenticators should be implemented according to the Whitebox cryptography paradigm	same as above	security evaluation is conducted in a FIDO Accredited Security Laboratory and includes penetration testing
Level 2	Device must support AROE (Allowed Restricted Operating Environment); for example, it is a Trusted Execution Environment (TEE) based on ARM TrustZone HW or TEE Based on Intel VT HW. See [Section 3][18] for the list.	same as above plus protection against remote software attacks	Level 2 is not met by authenticators that do not support attestation
Level 3	Device must support AROE and must provide resistance against physical attacks	same as above plus protection against local hardware attacks	authenticator protection is evaluated against enhanced-basic effort software and hardware attacks
Level 3+	same as above	same as above	according to [19]: “Authenticator Certification Level 3+ (L3+) evaluates FIDO Authenticator protection against moderate or high effort software and hardware attacks. The confidence in the Authenticator’s security properties is high, and the risk for having a successful attack is mitigated."

Table 2. Relying Party’s attestation preferences.

Name of preference	Description
none	The server does not require attestation from the authenticator. The client should replace potentially uniquely identifying information with a non-identifying version of that information. For example, if AAGUID (Authenticator Attestation Globally Unique ID – a 128-bit identifier of the authenticator model) is present, it should be replaced with a sequence of 16 zero bytes.
indirect	The Relying Party allows the client to alter the authenticator’s attestation statement with a more privacy-friendly one. For example, the client may employ an Anonymization CA.
direct	The authenticator’s attestation statement is to be forwarded by the client to the server without any changes. However, the authenticator can use any attestation mode, even the mode None.
enterprise	This preference is intended for “controlled deployments within an enterprise” [16]. The Relying Party wants to receive an attestation statement that may uniquely identify the authenticator. The authenticator verifies if the service is allowed to request enterprise attestation – the identifier of the Relying Party is permanently written to the authenticator by its manufacturer, see the "Provisioning" Section in [13].

Table 3. Attestation modes.

Attestation mode	Description
Basic	In the basic attestation, the attestation statement is signed with a key shared by a group of devices. That is, the same key is expected to be embedded by the manufacturer in more than $10^{5}$ devices of the same authenticator’s model (cf. [13]). The manufacturer puts information about devices holding this keypair to the MDS (FIDO Alliance’s Metadata Service). The Relying Party may consult the MDS to learn more about the authenticator model.
Self	In the self attestation, the authenticator does not have specific attestation keys. The attestation statement is signed with the private credential key generated during registration.
AttCA	In the attestation CA mode, the authenticator is based on a Trusted Platform Module. That is, the attestation statement is signed by a TPM attestation key. A trusted authority managing the authenticator signs the attestation key’s certificate. To communicate with the authority, the authenticator utilizes a so-called endorsement key.
AnonCA	In the anonymization CA mode, for each credential, a certificate is dynamically generated by a cloud-operated CA owned by the authenticator’s manufacturer. This mode is similar to the AttCA mode.
None	In this mode, the authenticator does not generate a signature during the registration process.
ECDAA	The Elliptic Curve based Direct Anonymous Attestation [20] was included in the WebAuthn 1 protocol [21], but has been removed from its successor WebAuthn 2. According to [22], the scheme "seemed to offer an interesting compromise between security, privacy, and availability of the CA."

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer