Prerpints.org logo
Preprint
Article

Two-Step Image Registration for Dual-Layer Flat-Panel Detectors

Altmetrics

Downloads

47

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 October 2024

Posted:

29 October 2024

You are already at the latest version

Alerts
Abstract
For a single exposure in radiography, a dual-layer flat-panel detector (DFD) can provide spectral images based on copper filtering or beam hardening, and efficiently utilize the transmitted x-ray photons to improve the detective quantum efficiency (DQE) performance. In this paper, we present a registration method for x-ray images acquired from DFD considering only spatial translations and scale factors. Note that the spatial translation difference between the upper and lower detector layers arises when attaching the layers, and the scale difference arises from the x-ray projection relative to the source and detector distances. The conventional registration methods have inconsistent estimate accuracies depending on the captured object scene even when using entire pixels, and have deteriorated frequency performance due to the interpolation method employed. The proposed method consists of two steps; the first step is conducting a spatial translation according to the Fourier shift theorem with a subpixel registration, and the second step is conducting a scale transformation using cubic interpolation to process the x-ray projections. To estimate the subpixel spatial translation, a maximum-amplitude method using a small portion of the slant-edge phantom is used. The performance of the proposed two-step method is first theoretically analyzed, and then observed by conducting extensive experiments and measuring the noise power spectrum and DQE. An example for registering chest images is also shown. For DFD, it is shown that the proposed method shows a better registration result than the conventional one-step registration.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

Dual-layer flat-panel detectors (DFDs) enable single-exposure spectral imaging based on energy-selective imaging from copper filtering or beam hardening [1,2,3]. This detector has a variety of applications, such as in bone and tissue separations [1], material decomposition [4], and bone mineral density estimation [5]. It can also improve the contrast-to-noise ratio and detective quantum efficiency (DQE) [6,7,8]. Engel et al. [7] showed an increased DQE from DFDs than a case of a single-layer detector having an added thickness of the scintillator layers of DFD. Kim [8] showed that a convex combination of the upper and lower images acquired from DFD yielded the added DQE of their values and decreased the noise power spectrum (NPS) [9]. Su et al. [10] obtained super-resolution images based on DFD. Dual-energy cone-beam computed tomography is a suitable field for the application of DFD [4,5,6].
As shown in Figure 1, the structure of DFD consists of two layers, where the upper and lower detector layers are attached as close as possible [3,8,12]. The lower layer usually absorbs relatively high-energy x-ray photons due to the beam hardening compared to the upper layer case. The intermediate layer between the upper and lower layers can prevent mutual transmission of light photons and can contain a spectral filter for x-rays [1,8,13]. The DFDs introduced in the literatures are summarized in Table 1, where indirect conversion flat-panel detectors with CsI(Tl) scintillator layers and pixel pitches of 0.140 mm and 0.145 mm are used [3,5,6,8,10,11,12].
When stacking the upper and lower detector layers to construct a DFD, the images acquired from the layers should be registered because misalignments occur between the layers. By using a physical positioning device, the rotational deviation between the layers can be controlled to be as small as possible while stacking the layers. However, physically aligning the detector-element positions of the lower thin-film transistor (TFT) layers with respect to those of the upper layer is not easy [8,12]. Hence, geometric translocation of the lower layer exists in both horizontal and vertical directions with respect to the upper layer.
To conduct an image registration, geometric transformations are first estimated between the upper and lower images acquired with an object and then are employed to register the images based on interpolation schemes [14]. Various registration methods have been developed [15,16]. Shi et al. [3] registered the lower image using an affine transform accounting for translation, rotation, and scale based on an interpolation with the IsoCal phantom [17]. Kim [8], and Lee and Kim [11] estimated the translation parameters based on a slant-edge phantom, which is used for measuring the modulation transfer function (MTF), and conducted transforms with those translation parameters. Wang et al. [5] also aligned the lower image based on an interpolation. However, the employed registrations and transforms are usually based on interpolation schemes and thus cause registration errors due to the amplitude and phase distortions of interpolation. Note that the traditional intensity-based and feature-based registration approaches [15,18], which use natural scenes, produce large registration errors and thus are not appropriate for the registration purpose of DFD.
When registering the upper and lower images acquired from DFD, the following two items should be considered.
  • Spatial translation while stacking the layers
  • Scale due to the x-ray projection
The first item is concerned with the registration of the spatial horizontal and vertical translations as shown in Figure 2(a). In DFD, image registration is a simple process of finding the misaligned spatial translations and using these to transform the lower image. Here, a subpixel registration method [19,20,21,22,23,24,25,26,27,28] is required to accurately find the spatial translation. Subpixel registration is not only important for obtaining aligned image pairs, but also for checking the uniform pixel alignment of the stacked detector layers [10]. If the translation parameter of DFD is accurately estimated, then using the parameter the translation of the images acquired from the same DFD can be performed every time to acquire registered image pairs. Hence, there is no need to perform separate image registration in the application of an image processing method. The second item is concerned with a transform of the image scale change due to the x-ray projection as shown in Figure 2(b). Because x-rays generated in the form of a point source in an x-ray tube are projected onto DFD, the x-ray image obtained from the lower layer is more magnified than the image obtained from the upper layer.
In this paper, a two-step image registration method for DFD is introduced. Conventional one-step registration methods have errors depending on objects in the x-ray images acquired from the upper and lower detector layers [15]. The proposed method for high-precision image registration for DFD consists of two steps; the first step is conducting a spatial translation according to the Fourier shift theorem with a subpixel registration, and the second step is conducting a scale transformation using a cubic interpolation to process the x-ray projections. To conduct an accurate subpixel registration, we employed a method based on the notion of maximum amplitude, where a conventional slant-edge phantom is used as a fiducial mark [11,12]. This maximum-amplitude method can provide high-precision spatial translation compared to the methods that use the entire pixels of natural scenes [19,20,22,23,24,25,27,28]. The proposed two-step method can achieve more accurate image registration than the conventional one-step case, especially for the DFD applications.
This paper is organized in the following way. In Section 2, we first describe the registration of images acquired from DFD. We then propose a two-step registration method for DFD. Theoretical analysis on the proposed method is conducted to observe the registration performance in Section 3. To experimentally evaluate the registration accuracies, extensive experiments using x-ray images acquired from DFD are conducted in Section 4 with discussions. The conclusion is then stated in the last section.

2. Two-Step Registration for the Dual-Layer Flat-Panel Detector

In this section, we first comparatively discuss subpixel registration methods for the images acquired from DFD. We then introduce a two-step registration method that takes into account the magnified image due to the x-ray projection.
In order to obtain an aligned image pair from DFD, the lower image acquired from the lower detector layer should be accurately aligned with respect to the upper layer. We first consider the translation of horizontal and vertical directions as shown in Figure 2(a), where the lower detector is translated by (-2.6, 1.8) pixels as an example. We can transform the lower image by using the translation parameter based on the Fourier shift theorem or interpolation schemes, such as the linear and cubic interpolations. Here, the translation parameter can be estimated from a subpixel registration method [19]. Conventional intensity-based subpixel registration algorithms generally use the entirety of pixels of natural scenes and thus are not suitable to find such a fine translation of subpixel resolutions for DFD.
To increase the accuracy of subpixel registration for a given small area, we should design a complicate phantom with special patterns as a fiducial mark. However, designing a phantom with such a special pattern is difficult for radiography detector applications. Instead of using such a special phantom, Kim [8] used the conventional slant-edge phantom and maximized the DQE value to obtain a registered convex combination image. Lee and Kim [11,12] recently conducted a subpixel registration based on a necessary condition on maximizing an amplitude response and extended this notion to developing a high-precision measurement algorithm, where a cyclic-coordinate optimization based on the maximum amplitude is conducted. Note that this method can find local subpixel translations using a small portion of the slant edge as Positions 1, 2, and 3 in Figure 3.
Because the x-ray generated in the form of a point source from the x-ray tube is projected onto DFD, the x-ray image acquired from the lower layer is more enlarged than the image obtained from the upper layer. As shown in Figure 2(b), letting d SID denote the source-to-image distance (SID), a horizontal pixel location of u from the aligned center pixel produces the deviation Δ u : = u d TT / d SID pixels in the lower layer with respect to the upper layer. In other words, the lower image is enlarged by a scale factor of 1 + d TT / d SID compared to the upper image. To minimize the deviation Δ u due to the projection, we need to minimize the distance d TT between the TFT layers of the upper and lower detector layers. Several examples of the distance are shown in Table 1. We can compensate the enlarged lower image using the scale factor and an interpolation scheme to conduct a high-precision image registration considering the projection. We can also experimentally obtain the sale factor by measuring pixel deviations from the three slant-edge phantoms of Figure 3.
By using the estimated translation and scale parameters, we can conduct an image transformation based on an interpolation [14]. However, the employed interpolation usually deteriorates frequency responses of the transformed image. To alleviate the deterioration, we propose a two-step method based on the Fourier shift and scaling with an interpolation. 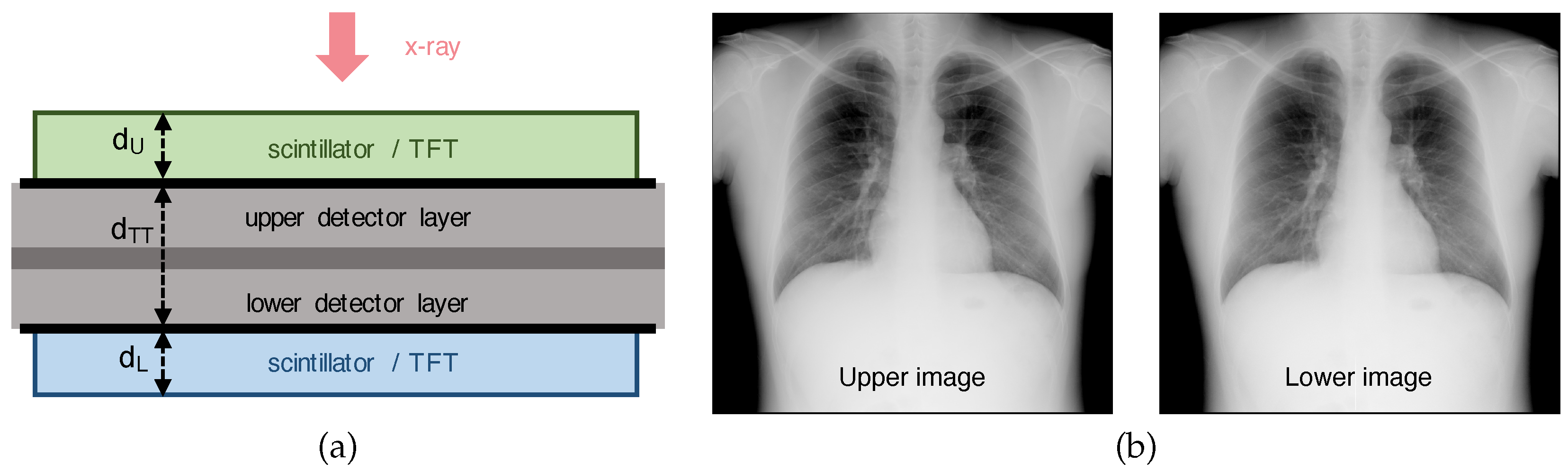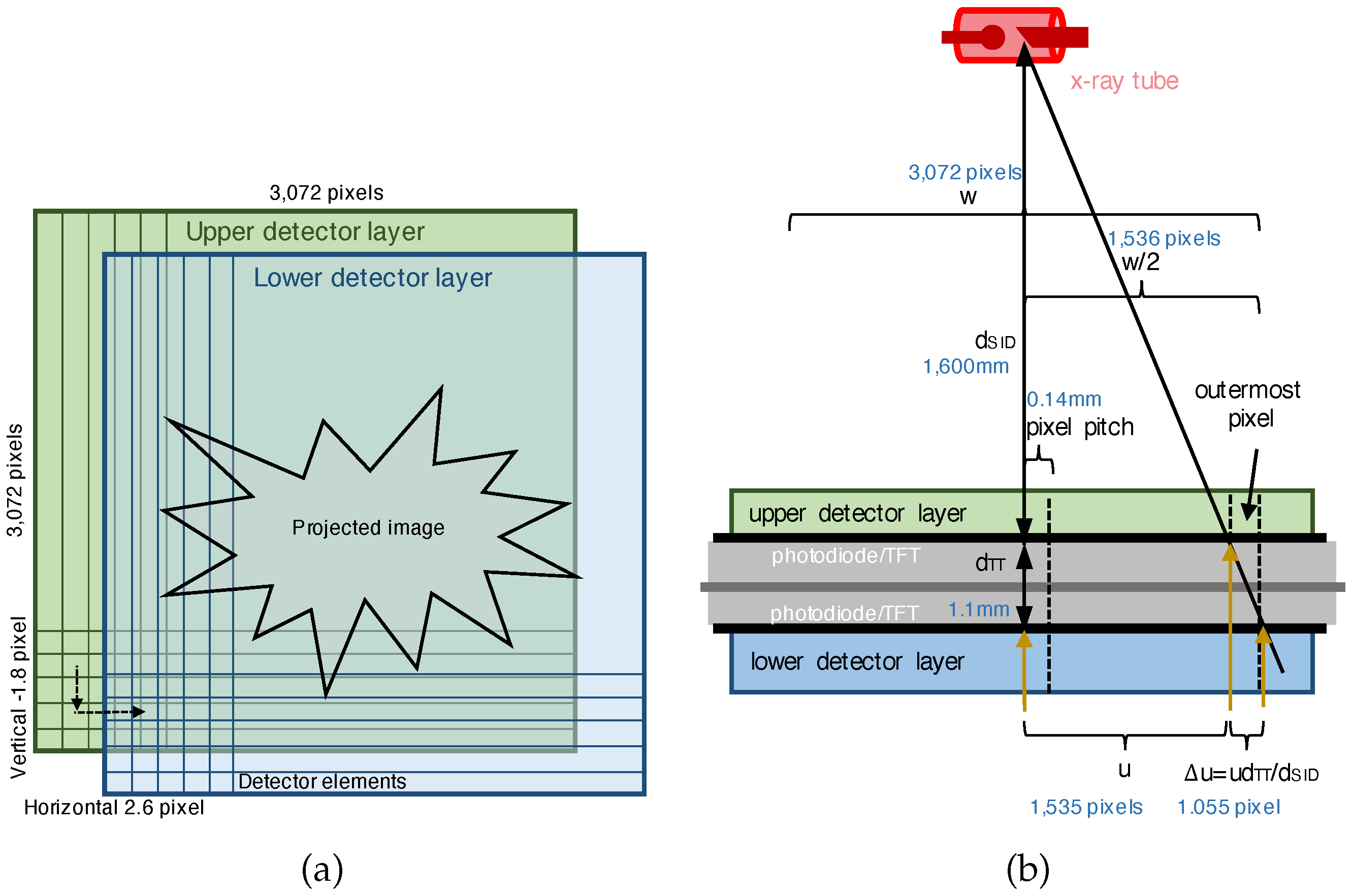The proposed method for DFD is summarized as follows.
Two-Step Registration for the Dual-Layer Flat-Panel Detector:
0)
Find the translation of the lower image based on a subpixel registration; calculate the scale factor for a given SID.
1)
Translate the lower image using the translation estimate based on the Fourier shift theorem.
2)
Transform the lower image using the scale factor based on a cubic interpolation.
Note that the proposed method is composed of two steps: translation based on the Fourier shift theorem and scaling based on a cubic interpolation. Instead of these two steps, we can consider a one-step translation with the translation and scale parameters based on an appropriate interpolation, such as the linear or cubic schemes. However, this single translation can reduce the MTF response and distort the phase response due to the employed interpolation scheme [14]. On the other hand, the proposed two-step method can alleviate the degradation problem from the interpolation-based transformation approach.

3. Theoretical Analysis of the Registration Method

In this section, the performance of the proposed two-step registration method for DFD is theoretically analyzed. We investigate the registration performance by observing the MTF of a convex combination of the upper and registered lower images.

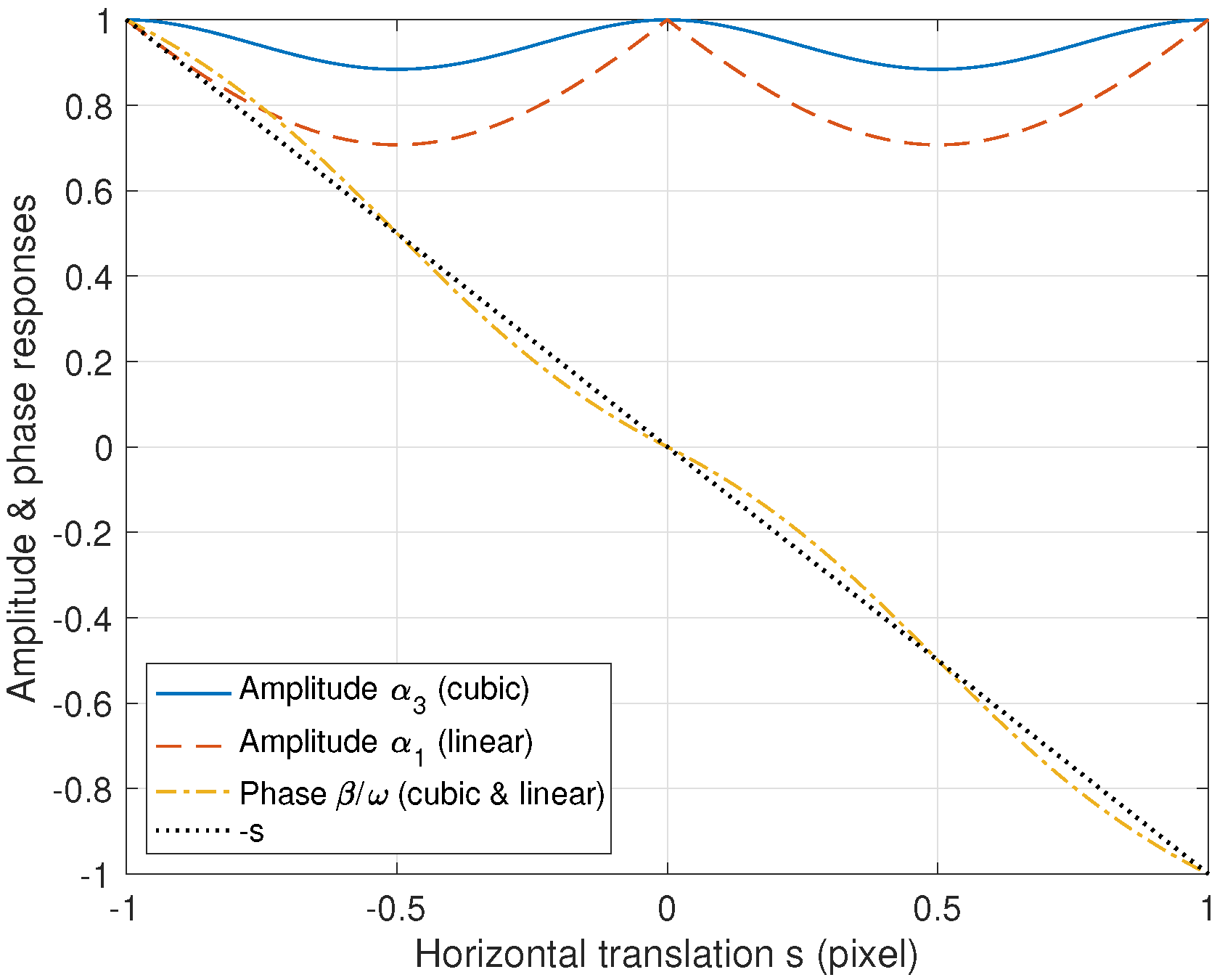
3.1. Modulation Transfer Function of the Convex Combination Image

We analyze the registration performance of the proposed registration method by observing the MTF of a convex combination image.
For a pixel position of u , let p [ u ] denote a convex combination [5,8] of the acquired upper and lower images p U and p L as
p ( u ) : = λ p U ( u ) + ( 1 − λ ) p L ( u ) ,
with a combination coefficient of λ such that 0 ≤ λ ≤ 1 . Here, optimal coefficients of λ can be found in terms of maximizing the NPS or DQE performance [8]. The mean of (1) is given as μ : = λ μ U + ( 1 − λ ) μ L , where μ U and μ L are the means of the upper and lower images, respectively. The frequency performance of imaging systems can be evaluated by measuring the detector MTF, which is the amplitude response acquired from the Fourier transform of the impulse response or the point spread function. We first measure directional MTF curves from the convex combination image p based on a method described in the IEC standard [29]. Here, to avoid overlaps of aliases and increase measurement accuracies [30], the oversampled impulse response is calculated from the derivative of the oversampled step response, which is acquired from upper and lower x-ray images using a tungsten slant-edge phantom.
At Position 1 of Figure 3, a directional translation of s 0 is estimated based on a subpixel registration method. This step is corresponding to Step 0) in preparation for the proposed registration. By multiplying e − j ω s , the lower image is aligned based on the Fourier shift theorem. This step is corresponding to Step 1) of the proposed registration. The directional MTF of the convex combination image, which is denoted as T, then satisfies the following relationship:
T ( ω , s ) : = a 1 ( ω ) cos ω ( s 0 − s ) + a 2 ( ω ) μ ,
where ω is the normalized radian frequency given as ω : = 2 π f / f s and | ω | ≤ π . In (2), a 1 and a 2 are defined as a 1 ( ω ) : = 2 λ ( 1 − λ ) μ U μ L T U ( ω ) T L ( ω ) and a 2 ( ω ) : = λ μ U T U ( ω ) 2 + ( 1 − λ ) μ L T L ( ω ) 2 , respectively, where T U and T L denote the upper and lower MTF curves, respectively [8]. If the estimate s from a subpixel registration method is equal to s = s 0 , then the maximum MTF of (2) can be rewritten as
T ( ω , s 0 ) = λ μ U T U ( ω ) + ( 1 − λ ) μ L T L ( ω ) μ ,
which is a convex combination and thus is between those of the upper and lower layers. Note that a relationship of T ( ω , s ) ≤ T ( ω , s 0 ) holds. Hence, the lower image should be aligned with the true s 0 to maximize the MTF performance.
If we conduct the translation based on an interpolation scheme instead of the Fourier shift theorem, then the MTF of (2) is reduced due to the interpolation. Let Ψ denote such a reduced MTF. The MTF from the interpolation is then given as
Ψ ( ω , s ) : = b 1 ( ω , s ) cos ω s 0 + β ( ω , s ) + b 2 ( ω , s ) μ ,
where the constants b 1 and b 2 are defined as
b 1 ( ω , s ) : = 2 λ ( 1 − λ ) μ U μ L α ( ω , s ) T U ( ω ) T L ( ω )
and
b 2 ( ω , s ) : = λ μ U T U ( ω ) 2 + ( 1 − λ ) μ L α ( ω , s ) T L ( ω ) 2 ,
respectively. In (4)-(6), α and β are the amplitude and phase responses, respectively, from the translation with interpolation.
We now observe the amplitude and phase responses of the interpolation-based translation to observe the reduced MTF of (4). Let α 1 denote the amplitude response of a translation of s to the right direction based on the linear interpolation (B-spline of degree 1 [31]). α 1 is then given as
α 1 ( ω , s ) : = 1 − 2 | s | ( 1 − | s | ) 1 − cos ( ω ) ,
for | s | ≤ 1 , and is periodic with a fundamental period of 1 [12]. Here, the relationship 0 ≤ α 1 ≤ 1 is satisfied. In a similar manner, the amplitude response of the translation α 3 , which is based on a cubic interpolation (Catmull-Rom spline [32]), is given as
α 3 ( ω , s ) : = 1 + | s | ( 1 − | s | ) 1 − cos ( ω ) α 1 ( ω , s ) .
Because a relationship of α 1 ≤ α 3 ≤ 1 holds, we can alleviate the amplitude reduction problem by using the cubic interpolation instead of the linear interpolation. In (5) and (6), α can be α 1 or α 3 for the linear or cubic interpolation, respectively. Furthermore, the phase responses of both linear and cubic interpolations are given as
β ( ω , s ) : = − arctan s sin ( ω ) 1 − | s | 1 − cos ( ω )
for a translation of s [12].
Examples of the amplitude responses on α 1 and α 3 , and phase responses on β are illustrated in Figure 4. When the translation s is an integer, the amplitude response becomes the largest value, 1, and when the remainder divided by an integer is 0.5, it becomes the smallest value. In other words, Ψ ( ω , s ) ≤ T ( ω , s ) is satisfied, where the equality holds when s is an integer. Hence, if the true translation s 0 is not an integer, then Ψ ( ω , s 0 ) < T ( ω , s 0 ) holds. Therefore, even if aligned precisely to the true s 0 , the interpolation-based translation does not guarantee the maximum MTF performance.

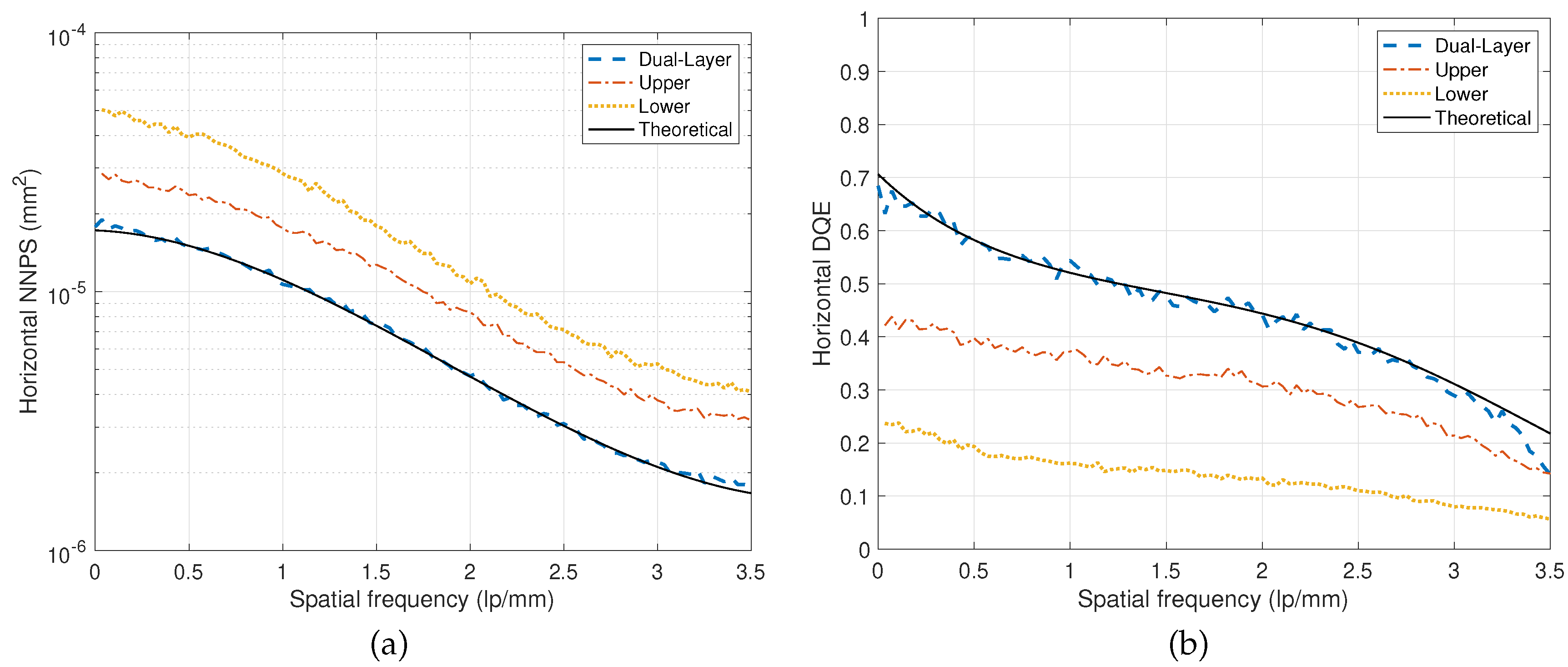
3.2. Noise Power Spectrum and the Detective Quantum Efficiency

We now observe a noise performance of the convex combination. Let P U and P L denote the normalized NPS (NNPS) of the upper and lower layers, respectively [9]. The directional NNPS, which is denoted as P, has an approximate relationship:
min λ P ( ω ) ≈ 1 P U ( ω ) + 1 P L ( ω ) − 1 ,
which is a harmonic mean of the upper and lower NNPS values [8]. For a given ω , an optimal coefficient λ 1 ( ω ) , which yields the relationship (10), can be calculated by using the upper and lower NPS values [8]. From (10), we notice that min λ P ( ω ) is approximately less than both P U ( ω ) and P L ( ω ) . In other words, the NNPS of the convex combination can be improved from those of the upper and lower layers if the images are registered.
We next observe and analyze the DQE performance. The DQE value denoted as Q can be written as Q ( ω ) : = T 2 ( ω ) / Φ P ( ω ) , where Φ is the mean quanta per area. An optimal coefficient of λ , which is denoted as λ 2 ( ω ) , for maximizing Q can be calculated by using the upper and lower NPS and MTF curves for a fixed ω [8]. If λ = λ 2 ( ω ) , then we can asymptotically obtain an algebraic DQE summation:
max λ Q ( ω ) ≈ Q U ( ω ) + Q L ( ω )
for a fixed ω , where Q U and Q L are the upper and lower DQE values, respectively [8]. Hence, we can significantly improve the detector DQE performance from DFD.

3.3. Projection and a Scale Translation with Interpolation

We now analyze the scale translation of Step 2) of the proposed registration. We assume that the lower image is translated based on the Fourier shift theorem and hence the true shift satisfies s 0 = 0 . As shown in Figure 3, the pixel location u from the center produces a projection deviation of Δ u . Due to this projection, the shift between the upper and lower images is given as s = Δ u and decreases the MTF value as T ( ω , s ) of (2) with s 0 = 0 . We can observe from "Fourier shift" in Figure 5 that the MTF value with a misalignment of s is reduced as | s | increases.
To alleviate the deviation problem due to the enlarged lower image, we conduct a transformation with the scale factor to the lower image, which is translated based on the Fourier shift theorem. This step corresponds to Step 2) of the proposed registration. The resultant MTF is given as Ψ ( ω , s ) of (4) with s 0 = s and is shown in Figure 5. For the linear and cubic interpolation cases, α is α 1 and α 3 , respectively. The cubic interpolation "Fourier shift & cubic scale" in Figure 5 shows a better MTF performance than the case without scale translation. In other words, even though the interpolation from the scale translation reduces the MTF value, conducting a scale transformation can improve the MTF performance. Therefore, we notice that the proposed two-step approach can yield a better performance than the conventional case of one-step transforms. In other words, if the incident exposure is uniform for a given SID, nearly uniform MTF and DQE performance can be achieved across all pixels in the image.

4. Numerical Results

In this section, we experimentally observe the registration performance of the proposed high-precision two-step registration method for DFD, which is constructed by stacking upper and lower detector layers as shown in Figure 1 (DRTECH Co. Ltd., South Korea, www.drtech.com) [8]. Each layer has a CsI(Tl)-scintillator layer with 3 , 072 × 3 , 072 photodiode pixels controlled by amorphous indium-gallium-zinc-oxide (a-IGZO) TFT panel. The pixel pitch is 140 μ m yielding a sampling frequency of f s = 7 . 143 lp/mm and the resolution is 16 bits/pixel. The thicknesses of the upper and lower scintillator layers are d U = 0 . 35 mm and d L = 0 . 5 mm, respectively.
For Step 0), several methods are applied to estimate the translation parameters and the results are illustrated in Figure 6. The conventional registration methods using chest images show erroneous deviations compared to the methods that use the slant-edge phantom as a fiducial mark to estimate only two translation parameters. The maximum-amplitude method yields a translation estimate of ( 0 . 9582 , 6 . 8656 ) , which will be shown as an accurate estimate in terms of the MTF and DQE in this section. In Step 1), the lower image is shifted using the translation estimate based on the Fourier shift theorem, and in the following step, Step 2), the shifted image is then transformed by using the scale factor 1 + d TT / d SID = 1 . 0006875 with an interpolation method, where d TT = 1 . 1 mm and d SID = 1 , 600 mm.

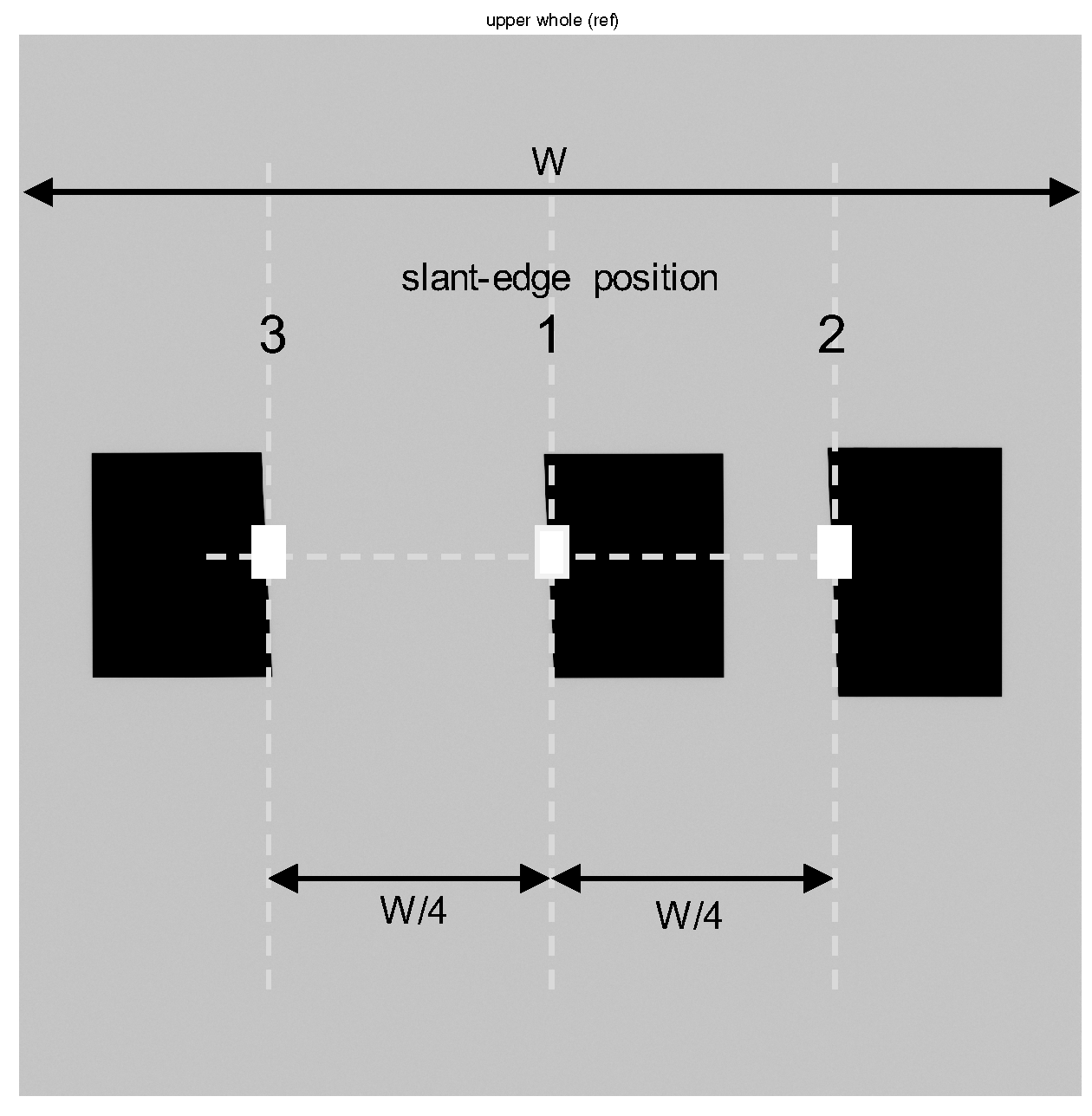
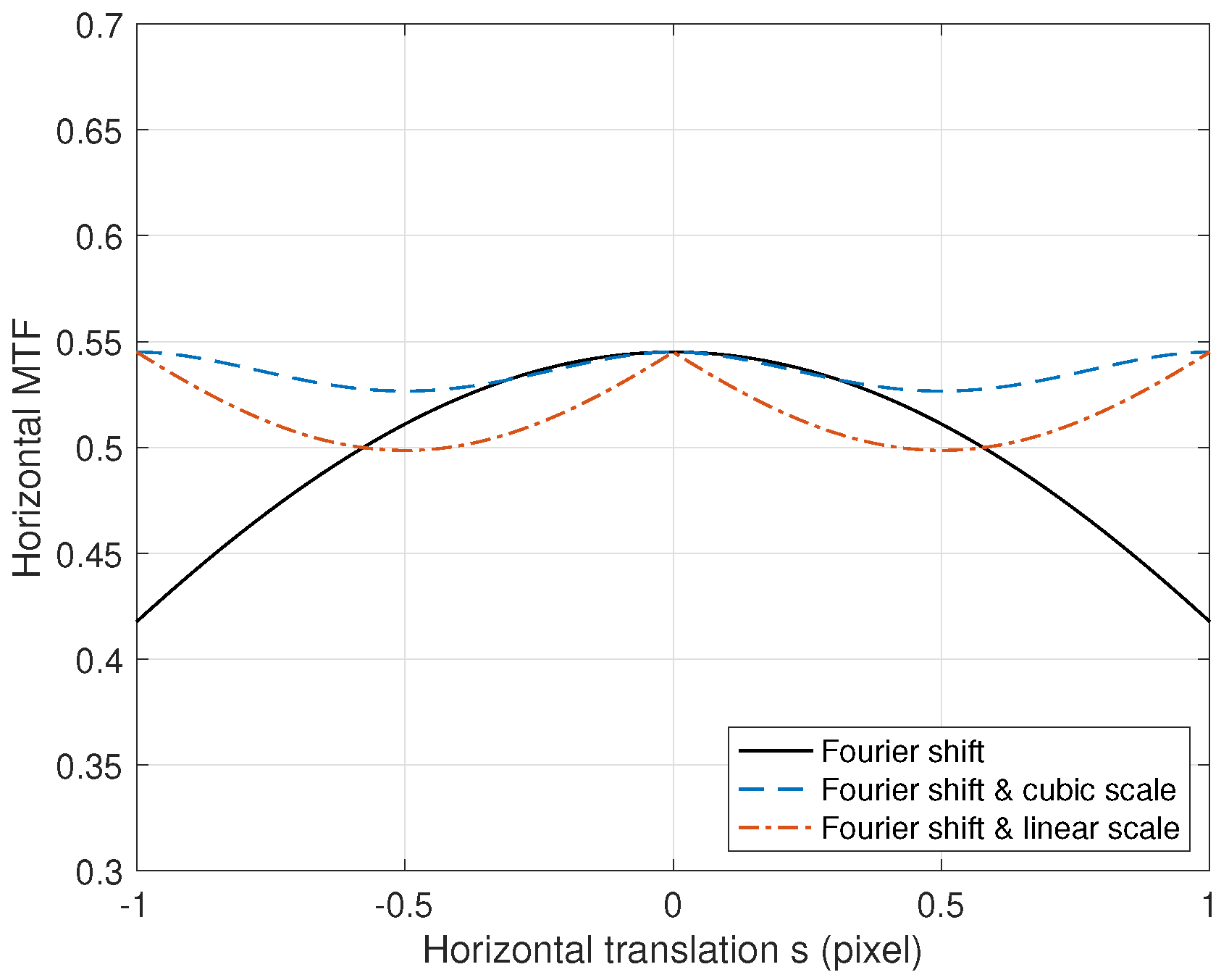
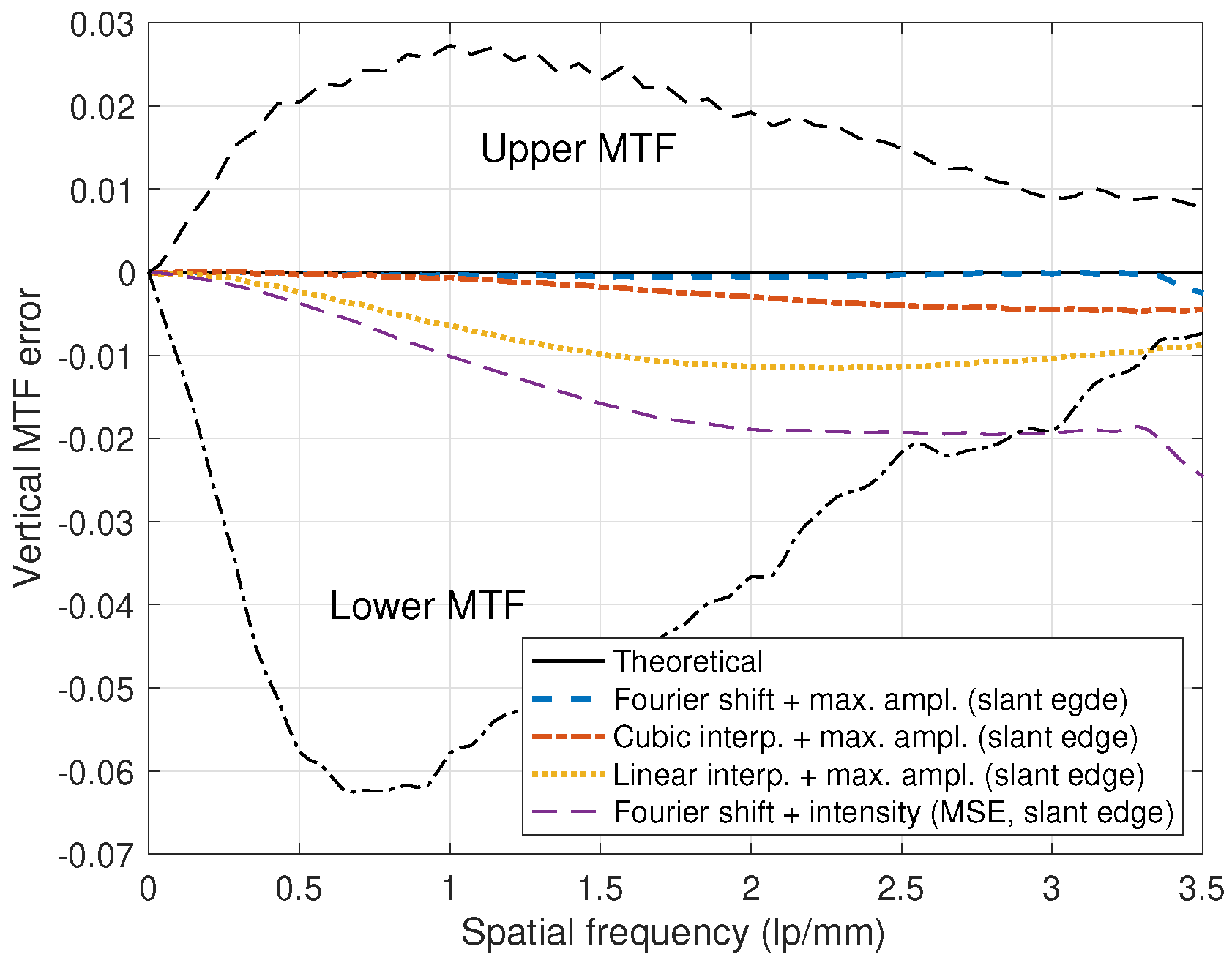
4.1. Numerical Performance Observation

In Figure 7, numerical results on measuring directional MTF values are illustrated for the convex combination of the registered images from the proposed registration method. From "Theoretical" and "Trans. (Fourier shift)" in Figure 7(a), we can observe that the MTF of the convex combination is very close to the theoretical value. As shown in (3), we can observe that the theoretical MTF is between the upper and lower MTF values. If we conduct the translation based on the interpolation scheme, then the MTF is reduced as mentioned in (7) and (8) ("Cubic interp.+max ampl. (slant edge)" and "Linear interp.+max ampl. (slant edge)" in Figure 7).
If the lower image is not aligned, then the MTF values of relatively high frequencies are usually lower than the theoretical ones. Hence, precisely aligning the lower image is important to ensure good MTF performance even at relatively high frequencies. In the intensity-based or feature-based subpixel registration methods, the estimate accuracy depends on the object of the x-ray image and can be degraded as shown in Figure 6. For example in Figure 7, the translation result from the maximum amplitude is close to the theoretical value ("Fourier shift+max ampl. (slant edge)"). However, the shift parameter estimated from an intensity-based subpixel registration method shows lower values than the theoretical case ("Fourier shift+intensity (MSE, slant edge)").
Directional NNPS measurement examples are illustrated in Figure 8(a). Here, we compensated the NNPS values, which were inflated during the gain correction procedure, by considering the number of white images acquired under an incident exposure for the gain map design [9,38]. We can observe that the NNPS value of the upper layer is less or better than that of the lower layer and the NNPS value of the convex combination is less than those of both layers. Hence, to improve the noise performance, we can use the convex combination of the images from both upper and lower layers for an appropriate combination coefficient of λ . In the experiments of Figure 7 and Figure 8(a), optimal values of λ 1 ( 0 ) are used for the combination coefficient.
Under an x-ray beam of RQA 9, DQE experiments are illustrated in Figure 8(b) for an optimum of λ 2 ( 0 ) = 0 . 525 , which is equal to λ 1 ( 0 ) . As observed in this figure, DFD showed improved DQE values closely to the theoretically achievable values, which are derived based on a parametric model [8]. Here, the MTF and NPS curves are modeled by performing third-order polynomial fits. For the experiments of the detector, the optimal curve of λ 2 ( ω ) is approximately constant for all ω [8]. Hence, we can observe from Figure 8(b) that Q ≈ Q U + Q L overall frequencies as shown in (11). For high energy x-ray tube voltages such as in RQA 9 of Figure 8(b), the upper detector layer showed Q U ( 0 ) = 45 . 1 % . The lower detector layer had a lower Q L ( 0 ) = 25 . 5 % than the upper layer case, because the remaining photons were utilized in the lower layer. Using DFD, we can increase the DQE value as Q ( 0 ) = 70 . 6 % at the zero frequency.

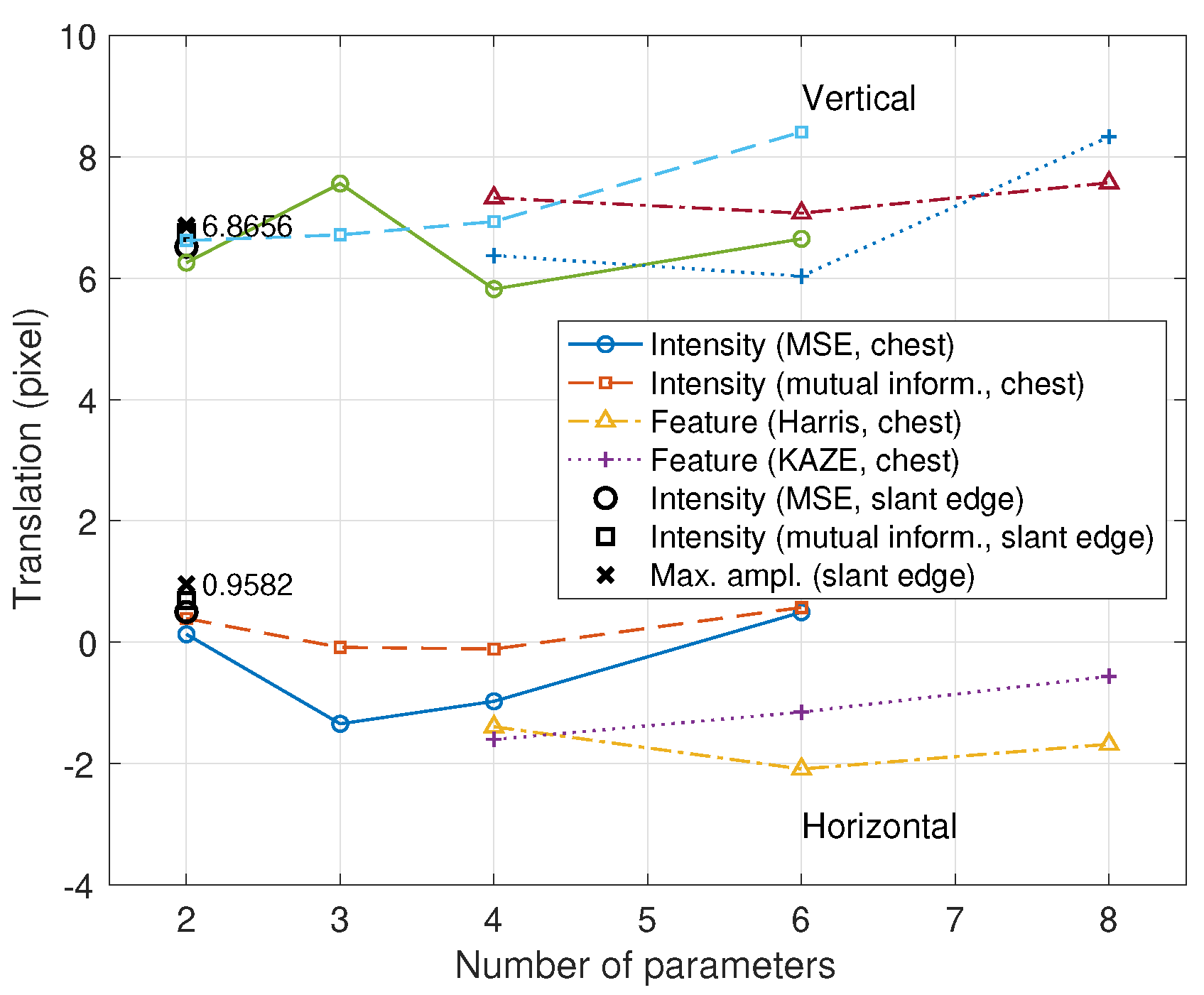
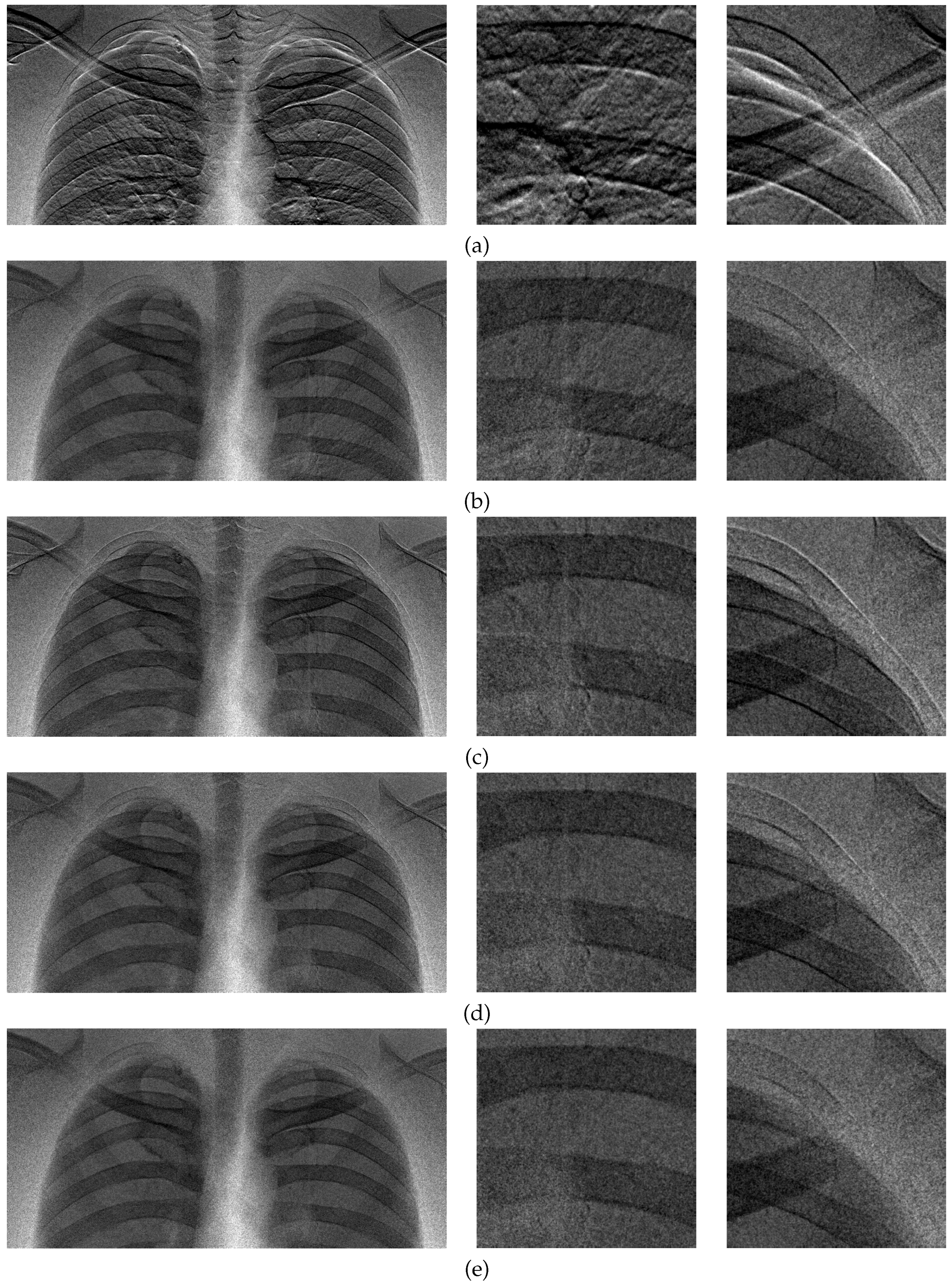
4.2. Registration Example of the Chest X-Ray Images

We now observe a registration example for the chest x-ray images acquired from the upper and lower layers as in Figure 1. To observe misalignments between the images acquired from DFD, we use the ratio of the upper and lower images and show several ratio images in Figure 9. We can observe from Figure 9(a) that the upper and lower images acquired from DFD is severely misaligned. In Figure 9(b) and (c), registration examples from conventional gradient-based and feature-based methods are shown. Here, a one-step transform with the translation and scale was conducted. The bronchioles inside the lung and lines outside of the lung are observed due to misalignment.
Based on the Fourier shift theorem, we can translate the lower image without attenuating its magnitude response. Here, the translation parameter was estimated based on the maximum-amplitude subpixel registration method. The registration result is shown in Figure 9(d). However, due to the enlarged lower image caused by the x-ray projection, the alignment error increases as the pixel positions move further outward from the image. In the proposed registration method, the translated lower image is then scaled based on a cubic interpolation as shown in Figure 9(e). We can observe very low misalignment errors over the entire image area.

5. Conclusion

In this paper, a two-step x-ray image registration method is proposed for DFD. The first step is conducting a spatial translation according to the Fourier shift theorem using a spatial translation parameter estimated from a subpixel registration method based on the maximum amplitude. The second step is conducting a scale transformation using a cubic interpolation to process the x-ray projection. The conventional methods suffer from inconsistent registration accuracies depending on object shapes, pixel intensities, and interpolation methods in conducting a high-precision registration. However, the proposed two-step method showed better registration results than the conventional methods for DFD with a high precision.

Author Contributions

D.S.K formulated the issues in high-precision registration for the dual-layer flat-panel detectors, proposed a two-step registration method, theoretical derivations, and organized the manuscript. D.L. conducted theoretical derivations and analyses, and computer simulations.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grants funded by the Korean government (MISP) (No. RS-2024-00459219) and by the Hankuk University of Foreign Studies Research Fund of 2024.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

DFD Dual-layer flat-panel detector
DQE Detective quantum efficiency
MTF Modulation transfer function
NNPS Normalized noise power spectrum
NPS Noise power spectrum
TFT Thin-film-transistor
SID Source-to-image distance

References

  1. Ishigaki, T.; Sakuma, S.; Horikawa, Y.; Ikeda, M.; Yamaguchi, H. One-shot dual-energy subtraction imaging. Radiology 1986, 161, 271–273. [CrossRef]
  2. McCollough, C.H.; Leng, S.; Yu, L.; Fletcher, J.G. Dual- and multi-energy CT: principles, technical approaches, and clinical applications. Radiology 2015, 276, 637–653. [CrossRef]
  3. Shi, L.; Lu, M.; Bennett, N.R.; Shapiro, E.; Zhang, J.; Colbeth, R.; Star-Lack, J.; Wang, A.S. Characterization and potential applications of a dual-layer flat-panel detector. Med. Phys. 2020, 47, 3332–3343. [CrossRef]
  4. van Hamersvelt, R.; Schilham, A.; Engelke K, den Harder, A.; de Keizer, B.; Verhaar, H.; Leiner, T.; de Jong, P.; Willemink, M. Accuracy of bone mineral density quantification using dual-layer spectral detector CT: a phantom study. Eur Radiol. 2017, 27, 4351–4359. [CrossRef]
  5. Wang, Z.; Zhou, H.; Gu, S.; Xia, Y.; Liao, H.; Deng, Y.; Gao, H. Dual-energy head cone-beam CT using a dual-layer flat-panel detector: Hybrid material decomposition and a feasibility study. Medical Physics 2023, 50, 6762–6778. [CrossRef]
  6. Lu, M.; Wang, A.; Shapiro, E.; Shiroma, A.; Zhang, J.; Steiger, J.; Star-Lack, J. Dual energy imaging with a dual-layer flat panel detector. In Proceedings of the Med. Imag.: Phys. Med. Imag. SPIE, 2019, Vol. 10948, pp. 269 – 278. [CrossRef]
  7. Engel, K.J.; Menser, B.; Rohr, P.; Ruetten, W.; Simon, M.; Thran, A. Dual layer x-ray detector simulation. In Proceedings of the Med. Imag.: Phys. Med. Imag. SPIE, 2020, Vol. 11312, pp. 398 – 409. [CrossRef]
  8. Kim, D.S. Convex combination of images from dual-layer detectors for high detective quantum efficiencies. IEEE Trans. Biomed. Eng. 2023, 70, 1804–1814. [CrossRef]
  9. Kim, D.S. Measurements of the noise power spectrum for digital x-ray imaging devices. Phys. Med. Biol. 2024, 69, 03TR01. [CrossRef]
  10. Su, T.; Zhu, J.; Zhang, X.; Tan, Y.; Cui, H.; Zeng, D.; Guo, J.; Zheng, H.; Ma, J.; Liang, D.; et al. Super resolution dual-energy cone-beam CT imaging with dual-layer flat-panel detector. IEEE Trans. Med. Imag. 2024, 43, 734–744. [CrossRef]
  11. Lee, D.; Kim, D.S. High-precision alignments for dual-layer detectors based on a slant-edge phantom. In Proceedings of the IEEE Int. Symp. Biomed. Imag. (ISBI), 2024, pp. 1–5. [CrossRef]
  12. Lee, D.; Kim, D.S. Subpixel registration for dual-layer detectors based on the amplitude response. IEEE Access 2024, 12, 153019–153029. [CrossRef]
  13. Alvarez, R.E.; Seibert, J.A.; Thompson, S.K. Comparison of dual energy detector system performance. Med. Phys. 2004, 31, 556–565. [CrossRef]
  14. Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd. ed.; Prentice Hall: NY, 2008.
  15. Maintz, J.; Viergever, M.A. A survey of medical image registration. Med. Image Anal. 1998, 2, 1–36. [CrossRef]
  16. Sharma, K.; Goyal, A. Classification based survey of image registration methods. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), 2013, pp. 1–7. [CrossRef]
  17. Du, W.; Gao, S.; Jiang, W.; Kudchadker, R.J. Independent evaluation of the effectiveness of IsoCal in improving image center accuracy on Varian TrueBeam and Clinac machines. Journal of Applied Clinical Medical Physics 2018, 19, 483–490. [CrossRef]
  18. Zitová, B.; Flusser, J. Image registration methods: a survey. Image, Vis., Comput. 2003, 21, 977–1000. [CrossRef]
  19. Tian, Q.; Huhns, M.N. Algorithms for subpixel registration. Comput. Vis., Graph., Image Process. 1986, 35, 220–233. [CrossRef]
  20. Kim, S.; Su, W. Subpixel accuracy image registration by spectrum cancellation. In Proceedings of the IEEE Int. Conf. Acoustics, Speech, Signal Process., 1993, Vol. 5, pp. 153–156 vol.5. [CrossRef]
  21. Efrat, A.; Gotsman, C. Subpixel image registration using circular fiducials. In Proceedings of the 2nd Israel Symp. Theory Comput. Syst., 1993, pp. 49–58. [CrossRef]
  22. Shekarforoush, H.; Berthod, M.; Zerubia, J. Subpixel image registration by estimating the polyphase decomposition of cross power spectrum. In Proceedings of the IEEE Conf. Comput. Vision, Patt. Recog., 1996, pp. 532–537. [CrossRef]
  23. Foroosh, H.; Zerubia, J.; Berthod, M. Extension of phase correlation to subpixel registration. IEEE Trans. Image Process. 2002, 11, 188–200. [CrossRef]
  24. Argyriou, V.; Vlachos, T. Sub-pixel motion estimation using gradient cross-correlation. In Proceedings of the 7th Int. Symp. Signal Process., Its Appls, 2003. Proceedings., 2003, Vol. 2, pp. 215–218. [CrossRef]
  25. Guizar-Sicairos, M.; Thurman, S.T.; Fienup, J.R. Efficient subpixel image registration algorithms. Opt. Lett. 2008, 33, 156–158. [CrossRef]
  26. Rohde, G.K.; Aldroubi, A.; Healy, D.M. Interpolation artifacts in sub-pixel image registration. IEEE Trans. Image Process. 2009, 18, 333–345. [CrossRef]
  27. Tzimiropoulos, G.; Argyriou, V.; Stathaki, T. Subpixel registration with gradient correlation. IEEE Trans. Image Process. 2011, 20, 1761–1767. [CrossRef]
  28. HajiRassouliha, A.; Taberner, A.J.; Nash, M.P.; Nielsen, P.M. Subpixel phase-based image registration using Savitzky–Golay differentiators in gradient-correlation. Comp. Vision, Image Understanding 2018, 170, 28–39. [CrossRef]
  29. International Electrotechnical Commission. Medical Electrical Equipment Characteristics of Digital X-ray Imaging Devices-Part1-1: Determination of the Detective Quantum Efficiency Detectors used in Radiographic Imaging; IEC 62220-1-1: Geneva, Switzerland, 2015.
  30. Fujita, H.; Tsai, D.Y.; Itoh, T.; Doi, K.; Morishita, J.; Ueda, K.; Ohtsuka, A. A simple method for determining the modulation transfer function in digital radiography. IEEE Trans. Med. Imag. 1992, 11, 34–39. [CrossRef]
  31. Unser, M. Splines: a perfect fit for signal and image processing. IEEE Signal Process. Mag. 1999, 16, 22–38. [CrossRef]
  32. Catmull, E.E.; Rom, R. A class of local interpolating splines. Computer Aided Geometric Design 1974, pp. 317–326. [CrossRef]
  33. Lucas, B.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the Imaging Understanding Workshop, 1981, pp. 121–130.
  34. Viola, P.; Wells, W. Alignment by maximization of mutual information. In Proceedings of the IEEE Int. Conf. Comput. Vision, 1995, pp. 16–23. [CrossRef]
  35. Kim, D.S.; Lee, K. Block-coordinate Gauss-Newton optimization and constrained monotone regression for image registration in the presence of outlier objects. IEEE Trans. Image Process. 2008, 17, 798–810. [CrossRef]
  36. Harris, C.G.; Stephens, M.J. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, 1988.
  37. Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE features. In Proceedings of the Computer Vision – ECCV 2012; Springer Berlin Heidelberg: Berlin, Heidelberg, 2012; pp. 214–227.
  38. Kim, D.S. Noise power spectrum measurements in digital imaging with gain nonuniformilty correction. IEEE Trans. Image Process. 2016, 25, 3712–3722. [CrossRef]
Preprints 137716 g001
Figure 1. Structure of the dual-layer flat-panel detector (DFD) and acquired images (DRTECH Co. Ltd., South Korea, www.drtech.com). (a) Two flat-panel detector layers are attached as close as possible. Conventionally, the upper and lower layers can have the same direction to the incident x-ray. In this example, the lower layer is inverted. The upper layer can also be inverted [8]. d TT is the distance between TFT layers, and d U and d L are the thicknesses of the upper and lower scintillator layers, respectively. (b) An example of chest images acquired from a DFD. The pixel pitch is 0.14 mm and the image size is 3 , 072 × 3 , 072 pixels, where d TT = 1 . 1 mm and d U = d L = 0 . 5 mm.
Figure 1. Structure of the dual-layer flat-panel detector (DFD) and acquired images (DRTECH Co. Ltd., South Korea, www.drtech.com). (a) Two flat-panel detector layers are attached as close as possible. Conventionally, the upper and lower layers can have the same direction to the incident x-ray. In this example, the lower layer is inverted. The upper layer can also be inverted [8]. d TT is the distance between TFT layers, and d U and d L are the thicknesses of the upper and lower scintillator layers, respectively. (b) An example of chest images acquired from a DFD. The pixel pitch is 0.14 mm and the image size is 3 , 072 × 3 , 072 pixels, where d TT = 1 . 1 mm and d U = d L = 0 . 5 mm.
Preprints 137716 g001
Preprints 137716 g002
Figure 2. Misalignment example for translation and scale parameters in DFD. (a) Translation misalignment while stacking. The lower layer is translated with respect to the upper layer by (2.6, -1.8) pixels to be registered. We assume that the stacked angle between the layers is approximately zero. (b) Scale misalignment due to x-ray projection. For d SID = 1 , 600 mm and d TT = 1 . 1 mm, the scale factor is 1 . 0006875 and the outermost pixel, which has its start location at u = 1 , 535 pixels from the center, consequently has an image deviation of 1 . 055 pixel.
Figure 2. Misalignment example for translation and scale parameters in DFD. (a) Translation misalignment while stacking. The lower layer is translated with respect to the upper layer by (2.6, -1.8) pixels to be registered. We assume that the stacked angle between the layers is approximately zero. (b) Scale misalignment due to x-ray projection. For d SID = 1 , 600 mm and d TT = 1 . 1 mm, the scale factor is 1 . 0006875 and the outermost pixel, which has its start location at u = 1 , 535 pixels from the center, consequently has an image deviation of 1 . 055 pixel.
Preprints 137716 g002
Preprints 137716 g003
Figure 3. Example images of three slant-edge phantoms for measuring horizontal MTF curves at three different locations.
Figure 3. Example images of three slant-edge phantoms for measuring horizontal MTF curves at three different locations.
Preprints 137716 g003
Preprints 137716 g004
Figure 4. Amplitude and phase responses of the translation with s based on the linear (B-spline of degree 1 [31]) and cubic (Catmull-Rom spline [32]) interpolations, where ω = π / 2 .
Figure 4. Amplitude and phase responses of the translation with s based on the linear (B-spline of degree 1 [31]) and cubic (Catmull-Rom spline [32]) interpolations, where ω = π / 2 .
Preprints 137716 g004
Preprints 137716 g005
Figure 5. MTF comparison with respect to the shift s, where ω = π / 2 . "Fourier shift" implies the MTF with a misalignment of s and given as T ( ω , s ) with s 0 = 0 . "Fourier shift & cubic scale" implies the scale transform with the cubic interpolation and shows better MTF performance than when there is no scale transformation. In this case the MTF value is given as Ψ ( ω , s ) with s 0 = s and α = α 3 . "Fourier shift & linear scale" is the result based on the linear interpolation.
Figure 5. MTF comparison with respect to the shift s, where ω = π / 2 . "Fourier shift" implies the MTF with a misalignment of s and given as T ( ω , s ) with s 0 = 0 . "Fourier shift & cubic scale" implies the scale transform with the cubic interpolation and shows better MTF performance than when there is no scale transformation. In this case the MTF value is given as Ψ ( ω , s ) with s 0 = s and α = α 3 . "Fourier shift & linear scale" is the result based on the linear interpolation.
Preprints 137716 g005
Preprints 137716 g006
Figure 6. Translation estimate comparison from intensity-based and feature-based image registrations using chest image pairs [33,34,35,36,37]. For the number of parameters, "2" implies the horizontal and vertical translations, "3" additionally has the rotation, and "4" additionally has the scale. "6" implies the affine transform and "8" implies the projection transform [14]. "Max. ampl. (slant edge)" has a translation of ( 0 . 9582 , 6 . 8656 ) using the slant-edge phantom.
Figure 6. Translation estimate comparison from intensity-based and feature-based image registrations using chest image pairs [33,34,35,36,37]. For the number of parameters, "2" implies the horizontal and vertical translations, "3" additionally has the rotation, and "4" additionally has the scale. "6" implies the affine transform and "8" implies the projection transform [14]. "Max. ampl. (slant edge)" has a translation of ( 0 . 9582 , 6 . 8656 ) using the slant-edge phantom.
Preprints 137716 g006
Preprints 137716 g007
Figure 7. Measured MTF error comparison (the thicknesses of the upper and lower scintillator layers are d U = d L = 0 . 5 mm, the x-ray tube voltage is 112 kVp under RQA 9, the subpixel translation is ( 0 . 9582 , 6 . 8656 ) based on the maximum amplitude, and the combination coefficient is λ = 0 . 525 ). The empirical MTF based on the Fourier shift theorem is between those of the upper and lower detector layers and is close to the theoretical value. The translations based on the cubic and linear interpolations show lower MTF values than the theoretical case because the amplitude reduction and phase delay arise from interpolation. An intensity-based registration for the translation is erroneous (0.5000,6.5175) as "Intensity (MSE, slant edge)" in Figure 6.
Figure 7. Measured MTF error comparison (the thicknesses of the upper and lower scintillator layers are d U = d L = 0 . 5 mm, the x-ray tube voltage is 112 kVp under RQA 9, the subpixel translation is ( 0 . 9582 , 6 . 8656 ) based on the maximum amplitude, and the combination coefficient is λ = 0 . 525 ). The empirical MTF based on the Fourier shift theorem is between those of the upper and lower detector layers and is close to the theoretical value. The translations based on the cubic and linear interpolations show lower MTF values than the theoretical case because the amplitude reduction and phase delay arise from interpolation. An intensity-based registration for the translation is erroneous (0.5000,6.5175) as "Intensity (MSE, slant edge)" in Figure 6.
Preprints 137716 g007
Preprints 137716 g008
Figure 8. Measured NNPS and DQE of the dual-layer detectors, where d U = 0 . 20 mm and d L = 0 . 5 mm. The x-ray tube voltage is 112 kVp under RQA 9, the incident dose is 2.65 μ Gy, and λ = 0 . 525 . (a) NNPS. (b) DQE.
Figure 8. Measured NNPS and DQE of the dual-layer detectors, where d U = 0 . 20 mm and d L = 0 . 5 mm. The x-ray tube voltage is 112 kVp under RQA 9, the incident dose is 2.65 μ Gy, and λ = 0 . 525 . (a) NNPS. (b) DQE.
Preprints 137716 g008
Preprints 137716 g009
Figure 9. Example of chest-image registrations for DFD. An image ratio of the upper and lower images is used to clearly observe the misalignment artifact. (a) Image ratio without registration. Severe misalignments between the images are observed. (b) Intensity-based registration example from a conventional gradient-based method with least squares. The bronchioles are observed due to misalignment inside the lung. (c) Feature-based registration example (Harris). Misalignment is observed in the scapula area. (d) Image registration with the Fourier shift. A subpixel translation of ( 0 . 9582 , 6 . 8656 ) is estimated from the maximum-amplitude method [12]. Misalignment is observed towards the periphery of the image due to the projection. (e) Image registration from the proposed two-step method (Fourier shift and scale with a cubic interpolation), where the scale factor is 1 . 0006875 .
Figure 9. Example of chest-image registrations for DFD. An image ratio of the upper and lower images is used to clearly observe the misalignment artifact. (a) Image ratio without registration. Severe misalignments between the images are observed. (b) Intensity-based registration example from a conventional gradient-based method with least squares. The bronchioles are observed due to misalignment inside the lung. (c) Feature-based registration example (Harris). Misalignment is observed in the scapula area. (d) Image registration with the Fourier shift. A subpixel translation of ( 0 . 9582 , 6 . 8656 ) is estimated from the maximum-amplitude method [12]. Misalignment is observed towards the periphery of the image due to the projection. (e) Image registration from the proposed two-step method (Fourier shift and scale with a cubic interpolation), where the scale factor is 1 . 0006875 .
Preprints 137716 g009
Table 1. Dual-layer flat-panel detectors (DFDs).
Table 1. Dual-layer flat-panel detectors (DFDs).
Distance CsI(Tl) scintillator Intermediate TFT
Detector d TT d U d L filter Photodiode Stacking Company
Lu et al. [6], 2019 2.5 0.2 0.55 1 Cu a-Si Normal Varex,USA
Shi et al. [3], 2020 2.5 0.2 0.55 1 Cu a-Si Normal Varex,USA
Kim [8], 2023 1.3-2.2 0.5 0.5 No filter,0.5 Cu a-Si/IGZO Normal,inverted upper/lower DRTECH,Korea
Wang et al. [5], 2023 - 0.2-0.55 0.55 No filter,1 Cu a-Si Normal Varex,USA
Su et al. [10], 2024 6.6 0.26 0.55 1 Cu a-Si Normal CareRay,China
Lee & Kim [11,12], 2024 1.1 0.35-0.5 0.5 No filter a-IGZO Inverted lower DRTECH,Korea
The unit of thickness is millimeter (mm)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated