Application of Complex Fuzzy Relational Compositions to Medical Diagnosis

Preprint

Article

Application of Complex Fuzzy Relational Compositions to Medical Diagnosis

This version is not peer-reviewed.

Muhammad Gulzar,

Samina Ashraf,

And Etienne E Kerre^*

Muhammad Gulzar,

Samina Ashraf,

And Etienne E Kerre^*

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

26 October 2024

Posted:

29 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

The capability of the complex fuzzy sets plays a valuable role to resolve many real life problems. In this paper, we present the compositions of complex fuzzy relations by using the idea of implication operators and max-product compositions of complex fuzzy relations and illustrate these compositions with concrete examples. The converse of these newly invented triangular compositions in terms of compositions of the converse relations are also defined. We also study the interactions with union and intersection. The main goal of this article to present a new technique to enhance medical diagnostic model that can assist to increase the features of healthcare systems. We utilize these compositions to determine the diseases of patients on the basis of intensity of symptoms.

Keywords:

Subject:

Computer Science and Mathematics - Applied Mathematics

1. Introduction

Healthcare system has significant sector in developed countries. The rapidly growing fuzzy logic network practices play a key role in health care department and provide easy medical guideline and minimize individual efforts and costs. This logic is used in cloud based setup to pass the key history about patient and disease. Later the health information is compiled through cloud server via systematical networking as it is highly vital to figure out the disease instantly.

Zadeh [1] initiated fuzzy sets where elements have degree of membership instead of strict binary classification. The inherent ambiguity, imprecision, and uncertainty present in real-world data and decision-making processes are crucial to analyze and address by employing fuzzy sets. This adaptability is crucial in domains where clear boundaries may be difficult to establish, such as control systems, artificial intelligence, and decision support systems. Many mathematicians have applied different hybrid models of fuzzy sets to various fields such as topological spaces [2] and decision making [3]. The triangular norm and triangular co-norm first appeared in the framework of probabilistic metric space [4,5]. The concept of triangular norms (T-norms) became a fundamental element in the framework of fuzzy logic and set theory. These norms particular describe the operation of conjunction in fuzzy logic, allowing for the combination of fuzzy set membership values. This laid the groundwork for the enlargement of mathematical operations on fuzzy sets.

Smets and Magrez [6] discussed implication in fuzzy logic. Bandler and Kohout [7] introduced useful local properties and defined the notions of interior and closure of a relation. Mas et al. [8] described the systematic review of fuzzy implication functions. Baczynski and Jayaram [9] gave a review about

(S, N)

-implications and R-implications and presented some new results related to fuzzy negations and

(S, N)

-implications. The in-depth fuzzy implications were investigated by Jayaram and Mesiar [10]. The fuzzy relational compositions were introduced by Bandler and Kohout [11,12]. Beg and Ashraf [13] discussed some properties of fuzzy equivalence relations. Fuzzy relational inference scheme based on the Bandler and Kohout sub-product and super-product were studied in [14,15]. The fuzzy compositions play important role in medical diagnosis [16], and neural networks [17].

The novel extension from fuzzy sets to complex fuzzy sets was initiated by Ramot et al. [18], in which the membership function is enlarge from

[0, 1]

closed interval to unit circle in complex plane. Complex fuzzy sets are significant in various fields due to their ability to model convoluted, uncertain, and non-linear, relationships more accurately as compared to fuzzy sets. T-norm and t-conorm of complex fuzzy sets were initiated by Zhang et al. [19]. The more development about t-norm and t-conorm may be viewed in [20]. Dick [21] gave the conception of complex fuzzy S-implication. The inverse relation, reflexive relation, symmetric relation and anti-symmetric relation of complex fuzzy set were presented in [22]. There are various scientific applications of complex fuzzy set in numerous fields [23,24,25,26,27,28]. De Baets and Kerre [29] extended the definitions of triangular compositions to fuzzy case and discussed their characteristics.

This paper focuses on the compositions of complex fuzzy relations (CFRs) by applying the notions of implication operators defined in [30]. We extend the compositions of De-Baets and Kerre to complex fuzzy compositions. Keeping the advantage of complex fuzzy sets and taking the importance of implication operators, this article presents the more transparent theory of complex fuzzy compositions by using complex fuzzy product operators. Moreover, it is a powerful extension of fuzzy relational compositions. Complex fuzzy relational composition will be utilized in relation based systems to conduct patient info, symptoms data and patients diseases.

The main objectives of this article are:

To allocate a large dataset for numerous diseases and symptoms.
Provide an accommodation to physicians for the diagnosis of different diseases linked with symptoms at any time.
To develop a new health care technique based on complex fuzzy relations and implication operators.

An outline of this article is shaped as: In section 2, we demonstrate primary theory related to complex fuzzy sets and complex fuzzy implication, which are compulsory for our further discussion. Section 3 presents the compositions of complex fuzzy relations by using the idea of implication operators and max-product compositions of complex fuzzy relations and illustrate these compositions with concrete examples. The converse of these newly invented triangular compositions in term of compositions of the converse relations are also defined. We also study the interactions with union and intersection. We also utilize these compositions to determine the diseases of patients on the basis of intensity of symptoms in section 4.

2. Preliminaries

In this section, some basic theory of complex fuzzy sets (CFSs) and complex fuzzy relations (CFRs) are defined, which are essential for advancing discussions about complex fuzzy relational compositions..

Definition 1

([1]). A fuzzy set is a set whose elements have a membership grade in the closed unit interval

[0, 1]

. A fuzzy set F of universal set U is defined as

F = {(α, F (α)) : α \in U}

, where, F is called the membership function which indicates the degree to which an element α is a part of the set U.

Definition 2

([4]). A t-norm is a binary operation defined by the function

T : [0, 1] \times [0, 1] \to [0, 1]

, which is increasing, commutative, associative and 1 working as neutral element.

The most important T-norms are:

$T (α, γ) = min {α, γ}$
$T (α, γ) = α . γ$
$T (α, γ) = max {0, α + γ - 1}$

Definition 3

([6]). A binary operator

I : {[0, 1]}^{2} \to [0, 1]

is said to be a fuzzy implication if it fulfill the following axioms:

$I (α, β) = I (1 - β, 1 - α),$ for all $α, β \in [0, 1]$ , (contra-positive),
$I (α, I (β, γ)) = I (β, I (α, γ))$ , for all $α, β, γ \in [0, 1],$ (exchange principle),
$I (α, .)$ is increasing, for all $α \in [0, 1],$ (hybrid monotonicity),
$I (., β)$ is decreasing, for all $β \in [0, 1],$ (hybrid monotonicity),
$I (1, β) = β$ for all $β \in [0, 1],$ (neutrality principle),
$I (0, 0) = I (1, 1) = I (0, 1) = 1$ and $I (1, 0) = 0,$ (boundary conditions).

Definition 4

([29]). Let U and V be two universal sets. A fuzzy relation R between U and V is a fuzzy set of the form

R = {((α, β), R (α, β)) | α \in U, β \in V}

Definition 5

([29]). Let R be a fuzzy relations from U to V and S be fuzzy relation from V to W. Then the compositions

R ⊲_{k} S, R ⊳_{k} S

, and

R ◊_{k} S

of R and S are fuzzy relations from U to W specified by the mapping

\begin{matrix} R ⊲_{k} S (α, γ) = min [inf_{β \in V} I (R (α, β), S (β, γ)), sup_{β \in V} T (R (α, β), S (β, γ))], \\ R ⊳_{k} S (α, γ) = min [inf_{β \in V} I (S (β, γ), R (α, β)), sup_{β \in V} T (R (α, β), S (β, γ))], \\ R ◊_{k} S (α, γ) = min [R ⊲_{k} S (α, γ), R ⊳_{k} S (α, γ)] . \end{matrix}

Where T and I are t-norm and fuzzy implication respectively.

By using height and plinth operators these formulation can be written as:

\begin{matrix} R ⊲_{k} S (α, γ) & = & min (Plt I (α R, S γ), Hgt T (α R, S γ), \\ R ⊳_{k} S (α, γ) & = & min (Plt I (S γ, α R), Hgt T (α R, S γ)) . \end{matrix}

Definition 6

([18]). A CFS A, on a universe of discourse U, is an object of the form

A = {(α, η_{A} (α)) : α \in U},

where

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}

represents the membership function that assigns a complex-valued grade of membership to the element of

U .

This membership function is defined as

η_{A} (α) : U \to {z \in C : ∣ z ∣ \leq 1},

where C is the set of complex numbers. This membership function

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}

receives all the degrees of membership from unit disc in the complex plane, where

p_{A} (α) \in [0, 1]

and

θ_{A} (α) \in (0, 2 π]

be a real valued function. We shall use

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}, α \in U,

as membership function of CFS.

Definition 7

([30]). Let U and V be two universal sets. A CFR

\tilde{R}

from U to V is a CFS of the form

\tilde{R} = {((α, β), η_{\tilde{R}} (α, β)) | α \in U, β \in V} .

where

η_{\tilde{R}} (α, β)

represents the membership function of CFR and is defined as

η_{\tilde{R}} (α, β) = p_{\tilde{R}} (α, β) e^{i θ_{\tilde{R}} (α, β)}

. Throughout this paper we shall use membership function of CFR

\tilde{R} (α, β)

from U to V in the form

η_{\tilde{R}} (α, β) = p_{\tilde{R}} (α, β) e^{i θ_{\tilde{R}} (α, β)}

, for all

α \in U

and for all

β \in V

Definition 8

([19]). Let M and N be two CFSs of U with the membership functions

η_{M} (α) = p_{M} (α) e^{i θ_{M} (α)}

and

η_{N} (α) = p_{N} (α) e^{i θ_{N} (α)}

, for all

α \in U

. Then the following set theoretic operations of CFS of M and N are defined as:

$η_{M \cup N} (α) = p_{M \cup N} (α) e^{i θ_{M \cup N} (α)},$

$= max {p_{M} (α), p_{N} (α)} e^{i max {θ_{M} (α), θ_{N} (α)}},$ for all $α \in U$

(complex fuzzy union),
$η_{M \cap N} (α) = p_{M \cap N} (α) e^{i θ_{M \cap N} (α)},$

$= min {p_{M} (α), p_{N} (α)} e^{i min {θ_{M} (α), θ_{N} (α)}},$ for all $α \in U,$

(complex fuzzy intersection),
$η_{M \cap_{p} N} (α) = p_{M \cap_{p} N} (α) e^{i θ_{M \cap_{p} N} (α)},$

$= {p_{M} (α) . p_{N} (α)} e^{i 2 π {\frac{θ_{M} (α)}{2 π} . \frac{θ_{N} (α)}{2 π}}},$ for all $α \in U,$

(complex fuzzy bold product),
$M \subseteq N$ if and only if $η_{M} (α) \leq η_{N} (α) \Leftrightarrow p_{M} (α) \leq p_{N} (α)$ and $θ_{M} (α) \leq θ_{N} (α),$ for all $α \in U,$

(complex fuzzy subsethood),
$M = N$ if and only if $η_{M} (α) = η_{N} (α) \Leftrightarrow p_{M} (α) = p_{N} (α)$ and $θ_{M} (α) = θ_{N} (α),$ for all $α \in U,$

(complex fuzzy equality).

3. Algebraic Structure of Complex Fuzzy Relational Compositions

Fuzzy relational compositions are an important abstraction in fuzzy logic, assisting the combination of fuzzy relations to obtain new relations. This section contribute the new notions of complex fuzzy relational compositions. A new type of compositions under the concept of implication operator and max-product of complex fuzzy compositions are defined in this section.

Zhang et al [19] developed a complex fuzzy implication operator whose membership value lies within unit circle of complex plain, and with the membership of phase term from

(0, 2 π] .

Consider the rule: If

α

is A then

β

is B, A and B are two CFSs described in different universe of discourse U and V, where

α, β

are variables taken from the corresponding universe of discourse. The membership function

η_{\tilde{I} (A, B)} (α, β) = I (p_{A} (α), p_{B} (β)) . e^{i \hat{I} (θ_{A} (α), θ_{B} (β))}

of complex fuzzy implication operator represent:

Dienes-Rescher implication operator if

$I (p_{A} (α), p_{B} (β)) = max {1 - p_{A} (α), p_{B} (β)}$ and

$\hat{I} (θ_{A} (α), θ_{B} (β)) = max {2 π - θ_{A} (α), θ_{B} (β)}$
Reichenbach product implication if

$I (p_{A} (α), p_{B} (β)) = 1 - p_{A} (α) + p_{A} (α) . p_{B} (β)$ and

$\hat{I} (θ_{A} (α), θ_{B} (β)) = 2 π - θ_{A} (α) + 2 π \frac{θ_{A} (α)}{2 π} . \frac{θ_{B} (β)}{2 π} .$

Remark 9.

Let

{(A_{j})}_{j}^{n}, j = 1, 2, 3, . . ., n

be a family of CFSs and B be any CFS with membership functions,

η_{A_{j}} (α) = p_{A_{j}} (α) e^{i θ_{A_{j}} (α)}

and

η_{B} (β) = p_{B} (β) e^{i θ_{B} (β)}

, for all

p_{A_{j}} (α), p_{B} (β) \in [0, 1]

and

θ_{A_{j}} (α), θ_{B} (β) \in (0, 2 π]

, where

α \in U

and

β \in V

. Consider a complex fuzzy implication operator characterized by the membership functions

η_{\tilde{I} (A_{j}, B)} = p_{I (A_{j}, B)} (α, β) e^{i θ_{\hat{I} (A_{j}, B)} (α, β)}

and

η_{\tilde{I} (B, A_{j},)} = p_{I (B, A_{j})} (β, α) e^{i θ_{\hat{I} (B, A_{j})} (β, α)}

. Then

1.: $I ({max}_{j = 1}^{n} p_{A_{j}} (α), p_{B} (β)) = {min}_{j = 1}^{n} I (p_{A_{j}} (α), p_{B} (β))$ and

$\hat{I} ({max}_{j = 1}^{n} θ_{A_{j}} (α), θ_{B} (β)) = {min}_{j = 1}^{n} \hat{I} (θ_{A_{j}} (α), θ_{B} (β)),$
2.: $I ({min}_{j = 1}^{n} p_{A_{j}} (α), p_{B} (β)) = {max}_{j = 1}^{n} I (p_{A_{j}} (α), p_{B} (β))$ and

$\hat{I} ({min}_{j = 1}^{n} θ_{A_{j}} (α), θ_{B} (β)) = {max}_{j = 1}^{n} \hat{I} (θ_{A_{j}} (α), θ_{B} (β)),$
3.: $I (p_{B} (β), {max}_{j = 1}^{n} p_{A_{j}} (α)) = {max}_{j = 1}^{n} I (p_{B} (β), p_{A_{j}} (α))$ and

$\hat{I} (θ_{B} (β), {max}_{j = 1}^{n} θ_{A_{j}} (α)) = {max}_{j = 1}^{n} \hat{I} (θ_{B} (β), θ_{A_{j}} (α)),$
4.: $I (p_{B} (β), {min}_{j = 1}^{n} p_{A_{j}} (α)) = {min}_{j = 1}^{n} I (p_{B} (β), p_{A_{j}} (α))$ and

$\hat{I} (θ_{B} (β), {min}_{j = 1}^{n} θ_{A_{j}} (α)) = {min}_{j = 1}^{n} \hat{I} (θ_{B} (β), θ_{A_{j}} (α)) .$

Definition 10.

Let A be a CFS of U with the membership functions

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}

, for all

α \in U

. The height Hgt

(A)

and plinth Plt

(A)

of CFS A in U are specified by the functions:

1.: $Hgt (A) = {sup}_{α \in U} (A (α))$
2.: $Plt (A) = {inf}_{α \in U} (A (α))$

Definition 11.

Let A and B be two CFSs of U with the membership functions

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}

and

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}

for all

α \in U

. The height of A is less than height of B if the following condition hold:

${sup}_{α \in U} p_{A} (α) \leq {sup}_{α \in U} p_{B} (α)$ and ${sup}_{α \in U} θ_{A} (α) \leq {sup}_{α \in U} θ_{B} (α)$

The plinth of A is less than plinth of B if the following condition hold:

${inf}_{α \in U} p_{A} (α) \leq {inf}_{α \in U} p_{B} (α)$ and ${inf}_{α \in U} θ_{A} (α) \leq {inf}_{α \in U} θ_{B} (α)$

Remark 12.

Let A and B be two CFSs of U. Then

height and plinth are increasing:

1.: $A \subseteq B \Rightarrow Hgt (A) \leq Hgt (B)$
2.: $A \subseteq B \Rightarrow Plt (A) \leq Plt (B)$

Theorem 13.

Let A and B be two CFSs in U, the membership functions of A and B are

η_{A} (α) = p_{A} (α) e^{i θ_{A} (α)}

and

η_{B} (α) = p_{B} (α) e^{i θ_{B} (α)}

, respectively. The height and plinth of the intersection and union of two CFSs satisfy the following characterizations,

1.: $H g t {η_{A} \cap η_{B}} \leq min (H g t (η_{A}), H g t (η_{B}))$
2.: $H g t {η_{A} \cup η_{B}} = max (H g t (η_{A}), H g t (η_{B}))$
3.: $P l t {η_{A} \cap η_{B}} = min (P l t (η_{A}), P l t (η_{B}))$
4.: $P l t {η_{A} \cup η_{B}} \geq max (P l t (η_{A}), P l t (η_{B}))$

Proof.

We shall prove the 1 and 4. For any element

α \in U

, the individual degree of memberships values

η_{A} (α) and η_{B} (α)

cannot be less than the minimum value of

η_{A} (α) and η_{B} (α)

. Thus, we can write as

\begin{matrix} m i n (η_{A} (α), η_{B} (α)) & \leq & η_{A} (α) \\ m i n (η_{A} (α), η_{B} (α)) & \leq & η_{B} (α) \\ Taking supremum \\ sup_{α \in U} {m i n (η_{A} (α), η_{B} (α))} & \leq & sup_{α \in U} {η_{A} (α)} \\ sup_{α \in U} {m i n (η_{A} (α), η_{B} (α))} & \leq & sup_{α \in U} {η_{B} (α)} \\ sup_{α \in U} {m i n (η_{A} (α), η_{B} (α))} & \leq & min {sup_{α \in U} {η_{A} (α)}, sup_{α \in U} {η_{B} (α)}} \\ H g t {η_{A} \cap η_{B}} & \leq & min (H g t (η_{A}), H g t (η_{B})) \end{matrix}

For any element

α \in U

, the individual degree of memberships values

η_{A} (α) and η_{B} (α)

cannot exceed the maximum value of

η_{A} (α) and η_{B} (α)

. Thus, we can write as

\begin{matrix} m a x (η_{A} (α), η_{B} (α)) & \geq & η_{A} (α) \\ m a x (η_{A} (α), η_{B} (α)) & \geq & η_{B} (α) \\ Taking infimum \\ inf_{α \in U} {m a x (η_{A} (α), η_{B} (α))} & \geq & inf_{α \in U} {η_{A} (α)} \\ inf_{α \in U} {m a x (η_{A} (α), η_{B} (α))} & \geq & inf_{α \in U} {η_{B} (α)} \\ inf_{α \in U} {m a x (η_{A} (α), η_{B} (α))} & \geq & max {inf_{α \in U} {η_{A} (α)}, inf_{α \in U} {η_{B} (α)}} \\ P l t {η_{A} \cup η_{B}} & \geq & max (P l t (η_{A}), P l t (η_{B})) \end{matrix}

□

Corollary 14.

Let

{(A_{k})}_{k \in K}

be an arbitrary family of CFSs in U, the membership function of each

A_{k}

η_{A_{k}} (α) = p_{A_{k}} (α) e^{i θ_{A_{k}} (α)}

. The height and plinth of the union and intersection of family of CFSs satisfy the following properties,

1.: $Hgt (\cup_{k \in K} A_{k}) = {max}_{k \in K} Hgt (A_{k})$
2.: $Hgt (\cap_{k \in K} A_{k}) \leq {min}_{k \in K} Hgt (A_{k})$
3.: $Plt (\cup_{k \in K} A_{k}) \geq {max}_{k \in K} Plt (A_{k})$
4.: $Plt (\cap_{k \in K} A_{k}) = {min}_{k \in K} Plt (A_{k})$

Definition 15.

Let

\tilde{R}

be a CFR from U to V and

\tilde{S}

be CFR from V to W. Then the composition

\tilde{R} \circ_{p} \tilde{S}

\tilde{R}

and

\tilde{S}

is a CFR from U to W and specified by the mapping:

\begin{matrix} η_{\tilde{R} \circ_{p} \tilde{S}} (α, γ) = p_{\tilde{R} \circ_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} \circ_{p} \tilde{S}} (α, γ)}, \\ = sup_{β \in V} (p_{\tilde{R}} (α, β) \cap_{p} p_{\tilde{S}} (β, γ)) e^{i {sup}_{β \in V} (θ_{\tilde{R}} (α, β) \cap_{p} θ_{\tilde{S}} (β, γ))} . \end{matrix}

Also, this composition can be define as:

\begin{matrix} η_{\tilde{R} \circ_{p} \tilde{S}} (α, γ) & = & Hgt (p_{α R} \circ_{p} p_{S γ}) e^{i Hgt (θ_{α R} \cap_{p} θ_{S γ})}, \\ Here η_{α R} (β) & = & {((α, β), η_{R} (α, β)), for all β \in γ R}, \\ η_{S γ} (β) & = & {((β, γ), η_{S} (β, γ)), for all β \in S γ} . \end{matrix}

Definition 16.

Let

\tilde{R}

be a CFR from U to V and

\tilde{S}

be CFR from V to W. Then the compositions

\tilde{R} ⊲_{p} \tilde{S}, \tilde{R} ⊳_{p} \tilde{S}, and \tilde{R} ◊_{p} \tilde{S}

\tilde{R}

and

\tilde{S}

are a CFR from U to W specified by the mappings:

\begin{matrix} η_{\tilde{R} ⊲_{p} \tilde{S}} (α, γ) & = & p_{\tilde{R} ⊲_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ⊲_{p} \tilde{S}} (α, γ)}, \\ = & [min [inf_{β \in V} I (p_{\tilde{R}} (α, β), p_{\tilde{S}} (β, γ)), sup_{β \in V} (p_{\tilde{R}} (α, β) \cap_{p} p_{\tilde{S}} (β, γ))] \\ \times e^{i min [inf_{β \in V} \hat{I} (θ_{\tilde{R}} (α, β), θ_{\tilde{S}} (β, γ)), sup_{β \in V} (θ_{\tilde{R}} (α, β) \cap_{p} θ_{\tilde{S}} (β, γ))]}] . \\ η_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ) & = & p_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)}, \\ = & [min [inf_{β \in V} I (p_{\tilde{S}} (β, γ), p_{\tilde{R}} (α, β)), sup_{β \in V} (p_{\tilde{R}} (α, β) \cap_{p} p_{\tilde{S}} (β, γ))] \\ \times e^{i min [inf_{β \in V} \hat{I} (θ_{\tilde{S}} (β, γ), θ_{\tilde{R}} (α, β)), sup_{β \in V} (θ_{\tilde{S}} (β, γ) \cap_{p} θ_{\tilde{R}} (α, β))]}] . \\ η_{R ◊_{p} S} (α, γ) & = & p_{\tilde{R} ◊_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ◊_{p} \tilde{S}} (α, γ)}, \\ = & [min [p_{\tilde{R} ⊲_{p} \tilde{S}} (α, β), p_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)] \times e^{i min [θ_{\tilde{R} ⊲_{p} \tilde{S}} (α, β), θ_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)]}] . \end{matrix}

Using plinth and height operators these formulations can be written as:

\begin{matrix} η_{\tilde{R} ⊲_{p} \tilde{S}} (α, γ) & = & p_{\tilde{R} ⊲_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ⊲_{p} \tilde{S}} (α, γ)}, \\ = & [min [Plt I (p_{α \tilde{R}}, p_{\tilde{S} γ}), Hgt (p_{α \tilde{R}} \cap_{p} p_{\tilde{S} γ}))] \times e^{i min [Plt \hat{I} (θ_{α \tilde{R}}, θ_{\tilde{S} γ}), Hgt (θ_{α \tilde{R}} \cap_{p} θ_{\tilde{S} γ}))]}] . \\ η_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ) & = & p_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)}, \\ = & [min [Plt I (p_{γ \tilde{S}}, p_{\tilde{R} α}), Hgt (p_{γ \tilde{S}} \cap_{p} p_{\tilde{R} α}))] \times e^{i min [Plt \hat{I} (θ_{γ \tilde{S}}, θ_{\tilde{R} α}), Hgt (θ_{γ \tilde{S}} \cap_{p} θ_{\tilde{R} α}))]}], \\ η_{R ◊_{p} S} (α, γ) & = & p_{\tilde{R} ◊_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ◊_{p} \tilde{S}} (α, γ)}, \\ = & [min [p_{\tilde{R} ⊲_{p} \tilde{S}} (α, β), p_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)] \times e^{i min [θ_{\tilde{R} ⊲_{p} \tilde{S}} (α, β), θ_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)]}] . \end{matrix}

Example 17.

Consider the Dienes-Rescher implication operator

\tilde{I} (A, B) (α, β) = I (p_{A} (α), p_{B} (β)) . e^{i \hat{I} (θ_{A} (α), θ_{B} (β))},

where

I (p_{A} (α), p_{B} (β)) = max {1 - p_{A} (α), p_{B} (β)}

and

I (θ_{A} (α), θ_{B} (β)) = max {1 - θ_{A} (α), θ_{B} (β)}

Let

\tilde{R} = [\begin{matrix} \tilde{R} & β_{1} & β_{2} & β_{3} \\ a_{1} & 0.2 e^{0.9 π i} & 0.4 e^{π i} & 0.7 e^{1.1 π i} \\ a_{2} & 0.9 e^{1.5 π i} & 0.4 e^{0.5 π i} & 0.5 e^{1.5 π i} \\ a_{3} & 0.1 e^{0.9 π i} & 0.3 e^{1.2 π i} & 0.6 e^{1.3 π i} \end{matrix}]

be a CFR from U to V and

\tilde{S} = [\begin{matrix} \tilde{S} & γ_{1} & γ_{2} & γ_{3} \\ β_{1} & 0.8 e^{1.8 π i} & 0.1 e^{1.3 π i} & 0.9 e^{1.7 π i} \\ β_{2} & 0.7 e^{1.2 π i} & 0.3 e^{0.5 π i} & 0.8 e^{1.8 π i} \\ β_{3} & 0.2 e^{1.2 π i} & 0.5 e^{1.6 π i} & 0.4 e^{1.9 π i} \end{matrix}]

be a CFR from V to

W,

for all

α \in U

β \in V

and

γ \in W .

The different complex fuzzy compositions of CFRs

\tilde{R}

and

\tilde{S}

are given as:

\tilde{R} ⊲_{p} \tilde{S} = [\begin{matrix} \tilde{R} ⊲_{p} \tilde{S} & γ_{1} & γ_{2} & γ_{3} \\ α_{1} & 0.28 e^{0.81 π i} & 0.35 e^{0.88 π i} & 0.32 e^{1.045 π i} \\ α_{2} & 0.5 e^{1.2 π i} & 0.1 e^{1.2 π i} & 0.5 e^{1.425 π i} \\ α_{3} & 0.21 e^{0.81 π i} & 0.3 e^{0.8 π i} & 0.24 e^{1.235 π i} \end{matrix}],

\tilde{R} ⊳_{p} \tilde{S} = [\begin{matrix} \tilde{R} ⊳_{p} \tilde{S} & γ_{1} & γ_{2} & γ_{3} \\ α_{1} & 0.1 e^{0.81 π i} & 0.3 e^{0.7 π i} & 0.32 e^{1.045 π i} \\ α_{2} & 0.2 e^{0.9 π i} & 0.25 e^{0.1 π i} & 0.6 e^{1.1 π i} \\ α_{3} & 0.21 e^{0.81 π i} & 0.3 e^{0.5 π i} & 0.24 e^{1.1 π i} \end{matrix}],

\tilde{R} ◊_{p} \tilde{S} = [\begin{matrix} \tilde{R} ◊_{p} \tilde{S} & γ_{1} & γ_{2} & γ_{3} \\ α_{1} & 0.1 e^{0.81 π i} & 0.3 e^{0.7 π i} & 0.32 e^{1.045 π i} \\ α_{2} & 0.2 e^{0.9 π i} & 0.1 e^{0.1 π i} & 0.5 e^{1.1 π i} \\ α_{3} & 0.21 e^{0.81 π i} & 0.3 e^{0.5 π i} & 0.24 e^{1.1 π i} \end{matrix}] .

Theorem 18.

Let

\tilde{R}

be a CFR from U to V and

\tilde{S}

be CFR from V to W. Then

1.: ${(\tilde{R} ◊_{p} \tilde{S})}^{t} = {\tilde{S}}^{t} ◊_{p} {\tilde{R}}^{t},$
2.: ${(\tilde{R} ⊳_{p} \tilde{S})}^{t} = {\tilde{S}}^{t} ⊲_{p} {\tilde{R}}^{t},$
3.: ${(\tilde{R} ⊲_{p} \tilde{S})}^{t} = {\tilde{S}}^{t} ⊳_{p} {\tilde{R}}^{t} .$

Where t represents the transpose of a relation.

Proof.

We prove the statement (2), for Definition 16. Assume that,

α \in U, and γ \in W,

consider

\begin{matrix} η_{{(\tilde{R} ⊳_{p} \tilde{S})}^{t}} (γ, α) & = & η_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ) \\ = & p_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R} ⊳_{p} \tilde{S}} (α, γ)} \\ = & [min [inf_{β \in V} I (p_{\tilde{R}} (α, β), p_{\tilde{S}} (β, γ)), sup_{β \in V} (p_{\tilde{R}} (α, β) \cap_{p} p_{\tilde{S}} (β, γ))] \\ \times e^{i min [inf_{β \in V} \hat{I} (p_{\tilde{R}} (α, β), p_{\tilde{S}} (β, γ)), sup_{β \in V} (p_{\tilde{R}} (α, β) \cap_{p} p_{\tilde{S}} (β, γ))]}] \\ = & [min [inf_{β \in V} I (p_{{\tilde{R}}^{t}} (β, α), p_{{\tilde{S}}^{t}} (γ, β)), sup_{β \in V} (p_{{\tilde{R}}^{t}} (β, α) \cap_{p} p_{{\tilde{S}}^{t}} (γ, β))] \\ \times e^{i min [inf_{β \in V} \hat{I} (p_{{\tilde{R}}^{t}} (β, α), p_{{\tilde{S}}^{t}} (γ, β)), {sup}_{β \in V} (p_{{\tilde{R}}^{t}} (β, α) \cap_{p} p_{{\tilde{S}}^{t}} (γ, β))]}] \\ = & p_{{\tilde{S}}^{t} ⊲_{p} {\tilde{R}}^{t}} (γ, α) e^{i θ_{{\tilde{S}}^{t} ⊲_{p} {\tilde{R}}^{t}} (γ, α)} \\ = & η_{{\tilde{S}}^{t} ⊲_{p} {\tilde{R}}^{t}} (γ, α) . \end{matrix}

Similarly, we can prove (1) and (3). □

Theorem 19.

Let

\tilde{R}

be a CFR from U to V and

\tilde{S}

be CFR from V to W. Then the following statements hold:

1.: $d o m ({\tilde{R}}_{1}) = d o m ({\tilde{R}}_{2}) \land {\tilde{R}}_{1} \subseteq {\tilde{R}}_{2} \Rightarrow {\tilde{R}}_{2} ⊲_{p} \tilde{S} \subseteq {\tilde{R}}_{1} ⊲_{p} \tilde{S},$
2.: ${\tilde{R}}_{1} \subseteq {\tilde{R}}_{2} \Rightarrow {\tilde{R}}_{1} ⊳_{p} \tilde{S} \subseteq {\tilde{R}}_{2} ⊳_{p} \tilde{S},$
3.: $r n g ({\tilde{S}}_{1}) = r n g (\tilde{S_{2}}) \land {\tilde{S}}_{1} \subseteq {\tilde{S}}_{2} \Rightarrow \tilde{R} ⊳_{p} \tilde{S_{2}} \subseteq \tilde{R} ⊳_{p} \tilde{S_{1}},$
4.: ${\tilde{S}}_{1} \subseteq {\tilde{S}}_{2}) \Rightarrow \tilde{R} ⊲_{p} {\tilde{S}}_{1} \subseteq \tilde{R} ⊲_{p} \tilde{S_{2}} .$

Proof.

We prove the 2nd property for Definition 16.

\begin{matrix} η_{\tilde{R_{2}} ⊲_{p} \tilde{S}} (α, γ) & = & p_{\tilde{R_{2}} ⊲_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R_{2}} ⊲_{p} \tilde{S}} (α, γ)} \\ = & [min [Plt I (p_{α \tilde{R_{2}}}, p_{\tilde{S} γ}), Hgt (p_{α \tilde{R_{2}}} \cap_{p} p_{\tilde{S} γ}))] \\ \times e^{i min [Plt \hat{I} (θ_{α \tilde{R_{2}}}, θ_{\tilde{S} γ}), Hgt (θ_{α \tilde{R_{2}}} \cap_{p} θ_{\tilde{S} γ}))]}] \\ \leq & [min [Plt I (p_{α \tilde{R_{1}}}, p_{\tilde{S} γ}), Hgt (p_{a \tilde{R_{1}}} \cap_{p} p_{\tilde{S} γ}))] \\ \times e^{i min [(Plt \hat{I} (θ_{α \tilde{R_{1}}}, θ_{\tilde{S} γ}), Hgt (θ_{α \tilde{R_{1}}} \cap_{p} θ_{\tilde{S} γ}))]}] \\ = & p_{\tilde{R_{1}} ⊲_{p} \tilde{S}} (α, γ) e^{i θ_{\tilde{R_{1}} ⊲_{p} \tilde{S}} (α, γ)} \\ \Rightarrow & η_{\tilde{R_{2}} ⊲_{p} \tilde{S}} (α, γ) \leq η_{\tilde{R_{1}} ⊲_{p} \tilde{S}} (α, γ) \end{matrix}

Now we prove the fourth property for Definition 16.

\begin{matrix} η_{\tilde{R} ⊲_{p} \tilde{S_{1}}} (α, γ) & = & p_{\tilde{R} ⊲_{p} \tilde{S_{1}}} (α, γ) e^{i θ_{\tilde{R} ⊲_{p} \tilde{S_{1}}} (α, γ)} \\ = & [min [Plt I (p_{α \tilde{R}}, p_{\tilde{S_{1}} γ}), Hgt (p_{α \tilde{R}} \cap_{p} p_{\tilde{S_{1}} γ})] \\ \times e^{i min [(Plt \hat{I} (θ_{α \tilde{R}}, θ_{\tilde{S_{1}} γ}), Hgt (p_{α \tilde{R}} \cap_{p} p_{\tilde{S_{1}} γ}))]}] \end{matrix}

\begin{matrix} \leq & [min [(Plt I (p_{α \tilde{R}}, p_{\tilde{S_{2}} γ}), Hgt (p_{α \tilde{R}} \cap_{p} p_{\tilde{S_{2}} γ}))] \\ \times e^{i min [(Plt \hat{I} (θ_{α \tilde{R}}, θ_{\tilde{S_{2}} γ}), Hgt (p_{α \tilde{R}} \cap_{p} p_{\tilde{S_{2}} γ}))]}] \\ = & p_{\tilde{R} ⊲_{p} \tilde{S_{2}}} (α, γ) e^{i θ_{\tilde{R} ⊲_{p} \tilde{S_{2}}} (α, γ)} \\ \Rightarrow & η_{\tilde{R} ⊲_{p} \tilde{S_{1}}} (α, γ) \leq η_{\tilde{R} ⊲_{p} \tilde{S_{2}}} (α, γ) \end{matrix}

□

Theorem 20.

Let

{({\tilde{R}}_{i})}_{i = 1}^{n}

be a family of CFRs from U to V and

\tilde{S}

be a CFR from V to W. Then

1.: $\cap_{i = 1}^{n} \tilde{R_{i}} ⊲_{p} \tilde{S} \subseteq (\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}) \subseteq \cup_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S}),$
2.: $(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊳_{p} \tilde{S} \supseteq \cup_{i = 1}^{n} (\tilde{R_{i}} ⊳_{p} \tilde{S}) .$

Proof.

We prove the first result for Definition 16.

\begin{matrix} η_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ) & = & p_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ) e^{i θ_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{b} \tilde{S}} (α, γ)} \\ = & [min [Plt I (p_{α (\cup_{i = 1}^{n} \tilde{R_{i}})}, p_{\tilde{S} γ}), Hgt (p_{α (\cup_{i = 1}^{n} \tilde{R_{i}})} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i min [Plt \hat{I} (θ_{α (\cup_{i = 1}^{n} \tilde{R_{i}})}, θ_{\tilde{S} γ}), Hgt (θ_{α (\cup_{i = 1}^{n} \tilde{R_{i}})} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & [min [Plt I (p_{(\cup_{i = 1}^{n} α \tilde{R_{i}})}, p_{\tilde{S} γ}), Hgt (p_{(\cup_{i = 1}^{n} α \tilde{R_{i}})} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i min [Plt \hat{I} (θ_{(\cup_{i = 1}^{n} α \tilde{R_{i}})}, θ_{\tilde{S} γ}), Hgt (θ_{(\cup_{i = 1}^{n} α \tilde{R_{i}})} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & [min [Plt ({min}_{i = 1}^{n} I (p_{α \tilde{R_{i}}}, p_{\tilde{S} γ})), Hgt ({max}_{i = 1}^{n} p_{α \tilde{R_{i}}} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i min [Plt ({min}_{i = 1}^{n} \hat{I} (θ_{α \tilde{R_{i}}}, θ_{\tilde{S} γ}), Hgt ({max}_{i = 1}^{n} θ_{α \tilde{R_{i}}} \cap_{p} θ_{\tilde{S} γ}))]}] \\ = & [min [{min}_{i = 1}^{n} (Plt (I (p_{α \tilde{R_{i}}}, p_{\tilde{S} w}))), {max}_{i = 1}^{n} (Hgt (p_{α \tilde{R_{i}}} \cap_{p} p_{\tilde{S} γ}))] \\ \times e^{i min [{min}_{i = 1}^{n} Plt (\hat{I} (θ_{α \tilde{R_{i}}}, θ_{\tilde{S} γ}), {max}_{i = 1}^{n} (Hgt (θ_{α \tilde{R_{i}}} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & [{min}_{i = 1}^{n} [min (Plt (I (p_{α \tilde{R_{i}}}, p_{\tilde{S} γ}))), {max}_{j = 1}^{n} (Hgt (p_{α \tilde{R_{j}}} \cap_{p} p_{\tilde{S} w}))] \\ \times e^{i {min}_{i = 1}^{n} [min (Plt (\hat{I} (θ_{α \tilde{R_{i}}}, θ_{\tilde{S} γ}), {max}_{j = 1}^{n} (Hgt (θ_{α \tilde{R_{j}}} \cap_{p} θ_{\tilde{S} γ}))]}] \\ \geq & [{min}_{i = 1}^{n} [min (Plt (I (p_{α \tilde{R_{i}}}, p_{\tilde{S} w}))), Hgt (p_{α \tilde{R_{i}}} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i {min}_{i = 1}^{n} [min (Plt (\hat{I} (θ_{α \tilde{R_{i}}}, θ_{\tilde{S} γ}), (Hgt (θ_{α \tilde{R_{i}}} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & {min}_{i = 1}^{n} p_{\tilde{R_{i}} ⊲_{p} \tilde{S}} (α, γ) e^{i {min}_{i = 1}^{n} θ_{\tilde{R_{i}} ⊲_{p} \tilde{S}} (α, γ)} \end{matrix}

\begin{matrix} η_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ) \geq p_{\cap_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S})} (α, γ) e^{i θ_{\cap_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S})} (α, γ)} \\ \Rightarrow \cap_{i = 1}^{n} \tilde{R_{i}} ⊲_{p} \tilde{S} \subseteq (\cup_{i = 1}^{n}) \tilde{R_{i}} ⊲_{p} \tilde{S}) (1) \end{matrix}

\begin{matrix} η_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ) & = & p_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ) e^{i θ_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ)} \\ = & [min [Plt I (p_{α (\cup_{j = 1}^{n} R_{j})}, p_{\tilde{S} γ}), Hgt (p_{α (\cup_{i = 1}^{n} \tilde{R_{i}})} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i min [Plt (\hat{I} (θ_{α (\cup_{j = 1}^{n} \tilde{R_{i}})}, θ_{\tilde{S} w}), Hgt (θ_{α (\cup_{i = 1}^{n} \tilde{R_{i}})} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & [min [Plt I (p_{(\cup_{j = 1}^{n} α \tilde{R_{i}})}, p_{\tilde{S} γ}), Hgt (p_{(\cup_{i = 1}^{n} α \tilde{R_{i}})} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i min [Plt (\hat{I} (θ_{(\cup_{j = 1}^{n} α \tilde{R_{i}})}, θ_{\tilde{S} γ}), Hgt (θ_{(\cup_{i = 1}^{n} α \tilde{R_{i}})} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & [min [Plt ({min}_{j = 1}^{n} I (p_{α \tilde{R_{j}}}, p_{\tilde{S} γ})), Hgt ({max}_{i = 1}^{n} p_{α R_{i}} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i min [Plt ({min}_{j = 1}^{n} \hat{I} (θ_{α \tilde{R_{i}}}, θ_{\tilde{S} γ}), Hgt ({max}_{j = 1}^{n} θ_{α \tilde{R_{j}}} \cap_{p} θ_{\tilde{S} γ})]}] \\ = & [min [{min}_{j = 1}^{n} (Plt (I (p_{α \tilde{R_{j}}}, p_{\tilde{S} w})), {max}_{i = 1}^{n} (Hgt (p_{α \tilde{R_{i}}} \cap_{p} p_{\tilde{S} γ}))] \\ \times e^{i min [{min}_{j = 1}^{n} Plt (\hat{I} (θ_{α \tilde{R} j}, θ_{\tilde{S} γ}), {max}_{i = 1}^{n} (Hgt (θ_{α \tilde{R}} \cap_{p} θ_{\tilde{S} γ}))]}] \\ = & [{max}_{i = 1}^{n} min [{min}_{j = 1}^{n} (Plt (I (p_{α \tilde{R_{j}}}, p_{\tilde{S} γ})), Hgt (p_{α \tilde{R_{i}}} \cap_{p} p_{\tilde{S} γ})] \\ \times e^{i {max}_{i = 1}^{n} [min ({min}_{j = 1}^{n} Plt (\hat{I} (θ_{α {\tilde{R}}_{j}}, θ_{\tilde{S} γ}), (Hgt (θ_{α \tilde{R}} \cap_{p} θ_{\tilde{S} γ})]}] \\ \leq [{max}_{i = 1}^{n} min [(Plt (I (p_{α \tilde{R_{i}}}, p_{\tilde{S} γ})), Hgt (p_{α \tilde{R_{i}}} \cap_{p} p_{\tilde{S} γ}))] \\ \times e^{i {max}_{i = 1}^{n} \min [Plt (\hat{I} (θ_{α \tilde{R_{i}}}, θ_{\tilde{S} γ}), Hgt (θ_{α \tilde{R_{i}}} \cap_{p} θ_{\tilde{S} γ})]}] (2) \end{matrix}

\begin{matrix} = & {max}_{i = 1}^{n} p_{\tilde{R_{i}} ⊲_{p} \tilde{S}} (α, γ) e^{i {max}_{i = 1}^{n} θ_{\tilde{R_{i}} ⊲_{p} \tilde{S}} (α, γ)} \\ η_{(\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}} (α, γ) \leq p_{\cup_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S})} (α, γ) e^{i θ_{\cup_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S})} (α, γ)} \\ \Rightarrow (\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}) \subseteq \cup_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S}), (3) \end{matrix}

From (1) and (3), we get,

\begin{matrix} \cap_{i = 1}^{n} \tilde{R_{i}} ⊲_{p} \tilde{S} \subseteq (\cup_{i = 1}^{n} \tilde{R_{i}}) ⊲_{p} \tilde{S}) \subseteq \cup_{i = 1}^{n} (\tilde{R_{i}} ⊲_{p} \tilde{S}) . \end{matrix}

□

4. Application to Diagnose the Diseases on the Basis of Intensity of Symptoms

Intensity of the symptoms related to diseases means the level of a disease. Symptoms can vary from serious to moderate one basing on one’s health position, kind of disease and other factors as well. Sometimes, severity of symptoms can highlight the seriousness of disorder itself. Like a patient with minor flu can have low level of body aches and flu, while the patient with severe case can experience serious level of temperature, muscle weakness and loads of others symptoms. It is pertinent to mention that intensity of symptoms can substantially be different in case of same ailment.

Treatment approaches are done in accordance with intensity of symptoms including lifestyle changes and medication . Severity of symptoms holds significant role to pinpoint the disorder. This intensity can be used as diagnostic scale for certain ills. In chest pain various factors like severity, location and other characteristics of pain will be of key importance to determine whether it is due to cardiac arrest or some other factors are behind it. In a nutshell, intensity of symptoms is supremely essential to trace the disease and its effective therapy. The idea of a complex fuzzy relation is confined as below. Suppose that

W = {γ_{1}, γ_{2}, . . . γ_{l}}, V = {β_{1}, β_{2}, . . . β_{m}},

and

U = {α_{1}, α_{2}, . . . α_{n}}

represent a set of diseases related symptoms, a set of symptoms, and a set of patients, respectively. Let we have two complex fuzzy relations

R (U \to V)

and

S (V \to γ)

such that

R (α_{i}, β_{j}) = {〈 (α_{i}, β_{j}), p_{R} (α_{i}, β_{j}) e^{i θ_{R} (α_{i}, β_{j})} 〉, (α_{i}, β_{j}) \in U \times V}

and

S (β_{j}, γ_{k}) = {〈 (β_{j}, γ_{k}), p_{R} (β_{j}, γ_{k}) e^{i θ_{R} (β_{j}, γ_{k})} 〉, (β_{j}, γ_{k}) \in V \times W},

Where,

R (α_{i}, β_{j}) =

p_{R} (α_{i}, β_{j}) e^{i θ_{R} (α, β)}

represents the membership degree in complex plane to which the patient,

α_{i}

, represent the symptom

β_{j}

. Similarly,

S (β_{j}, γ_{k}) = p_{S} (β_{j}, γ_{k}) e^{i θ_{S} (β_{j}, γ_{k})}

represents the membership degree in complex plane to which the intensity of symptoms,

β_{j}

, to determine the disease

γ_{k}

. The compositions

R ⊲_{p} S, R ⊳_{p} S, R ⋄_{p} S

of R and S are defined in Definition 16 . The complex fuzzy backward triangular composition means that every symptom of a patient

a_{i}

associated to a disease

γ_{k}

and the complex fuzzy forward triangular composition means that a patient

a_{i}

has every symptom associate to disease

γ_{k} .

The complex fuzzy square composition designs that a patient

α_{i}

has each symptom of the disease

γ_{k}

and each symptom of the patient belong to disease

γ_{k} .

The diagnosis of diseases can be completed if the value of

R ★ S

is established by the following score function

S (R ★ S) = p_{R ★ S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ★ S} (α_{i}, γ_{k}),

where

★ \in {⊲_{p}, ⊳_{p}, ⋄_{p}},

and

S (R ★ S) \in [0, 2] .

The largest value for the patient

α_{i}

for all

γ_{k}

with respect to

β_{j}

is calculated from R and S.

We use a hypothetical scenario with actual data to use this strategy. We have selected five patients from emergence ward of hospital which are suffering in the common symptoms of community acquired pneumonia, COVID-19 and other similar diseases. Suppose that there are five patients Haider, Bilal, Dilshad, Shahbaz, Rafique in a hospital with symptoms Headache (H), Sore throat (ST), Shortness of breathing (SB), Cough (CH), and Fever (T). Let the possible diseases associate to the above symptoms be COVID-19 (C19), Flu (F), Allergy (A), Cold (C), and community acquired pneumonia (CAP). Table 1, explains the link of each patient with the degree of symptoms.

This link is theorized from healthcare professional viewpoints and research works about these disease. Since these variables are linguistic and the doctors who don’t having any friendship with fuzzy logic only can define disease in terms of severity of disease. It is with the researcher to change linguistic variables to numeric quantities within unit circle of complex plane. Table 2, defines the CFR between symptoms and diseases. First of all we use complex fuzzy backward triangular composition method to identify the patient’s diseases on the basis of intensity of symptoms in Table 3. If we fix the Dienes-Rescher implication operator, then the compositions analyze to identify the symptoms profiles that are most commonly associated with specific diseases.

According to the result of score function values of complex fuzzy backward triangular composition defined in Table 4, the diagnostic treatment is representing that the patients Haider and Bilal appear to have higher degree of community acquired pneumonia. Patients Dilshad and Shahbaz have experienced symptoms of community acquired pneumonia and cold and patient Rafique is suffering from community acquired pneumonia and COVID-19.

In Table 5, the forward composition is another way for medical diagnosis to explain the diseases of patients by connecting symptoms-diseases relations.

According to Table 6 the patients Haider Bilal, Dilshad, Shahbaz and Rafique are suffering from community acquired pneumonia and Covid-19 with higher degree but Shahbaz is also suffering in allergy and Rafique is suffering in flu.

The complex fuzzy square composition is a serviceable kit for medical specialist in diagnostic process, as it can assist them to eliminate the suspicion of diseases efficiently and quickly. The complex fuzzy square composition is not a definitive diagnostic kit to monitor diseases. It is used in conjunction with backward triangular composition and forward triangular composition. The results of this composition are summarized in Table 7. By calculating the score values of composition in Table 8 shows that all the patients are suffering from community acquired pneumonia but the Rafique has also high degree symptoms of COVID-19. The flow Chart for the analysis of these compositions is defined in Figure 1

5. Conclusion

The new complex fuzzy relational compositions have been studied in this paper. We have presented the compositions of CFRs by using the implication operators and max-product compositions. The converse of these newly presented triangular compositions in terms of compositions of the converse relations have been defined. We have defined the interactions of newly constructed compositions with union and intersection. We have utilized these compositions to determine the diseases of patients on the basis of intensity of symptoms.

In future, these structures can be extended in numerous ways. To evaluate customer’s behavior and preferences during online shopping. The role of these compositions to determine the behavior of customers in Amazon E-commerce website. Customizing the interactions with customers by using unclear rules that are based on their choices and behavior. To find the application in polymer composite. Polymer composites have significantly different physical and chemical properties. They are considered essential and important high performance material. To cope with the unpredictability of market movements, financial risk, and investment choices. To control the uncertainty connected with supplier efficiency, projection of demand, and inventory management. To develop a model of complex business system feedback loops and relationships in side company structures.

Author Contributions

M. Gulzar, S. Ashraf developed the theory and performed the computations. M. Gulzar, S. Ashraf and E. E. Kerre verified the analytical methods. All authors have read and agreed to the published version of the manuscript.

Funding

No funding.

Data Availability Statement

No real data were used to support this study. The data used in this study are hypothetical and anyone can use them by just citing this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Zadeh, L. ; A Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
Saleh, S.; Al-shami, T. M.; Azzam, A.; Hosny, M. Stronger forms of fuzzy pre-separation and regularity axioms via fuzzy topology. Mathematics 2023, 11, 23, 4801. [Google Scholar] [CrossRef]
Al-shami, T. M.; Ibrahim, H. Z.; Azzam, A.; EL-Maghrabi, A. I. ; Sr-fuzzy sets and their weighted aggregated operators in application to decision-making. Journal of Functions Spaces 2022, 3653225, 1–14. [Google Scholar] [CrossRef]
Menger, K. ; Statistical metrics. Proceeding of National Academy of Sciences of the United of America 1942, 28, 535–537. [Google Scholar] [CrossRef] [PubMed]
Schweizer, B. Sklar, A.; Probabilistic metric spaces. North-Holland, Amsterdam 1983.
Smets, P. Magrez, P.; Implication in fuzzy logic. International journal of approximate Reasoning 1987, 1, 4, 327–347. [Google Scholar] [CrossRef]
Bandler, W. L. Kohout, Special properties, closures and interiors of crisp and fuzzy relations. Fuzzy Sets Systems. 1988, 26, 317–331. [Google Scholar] [CrossRef]
Mas, M. Monserrat, M. Torrens, J. Trillas, E.; A survey on fuzzy implication functions. IEEE Trans. Fuzzy Syst 2007, 15, 6, 1107–1121. [Google Scholar] [CrossRef]
Baczynski, M. Jayaram, B.; (S,N)-and R-implications: A state-of-the art survey. Fuzzy Sets and Systems 2008, 159, 1836–1859. [Google Scholar] [CrossRef]
Jayaram, B. Mesiar, R.; On special fuzzy implications. Fuzzy Sets and Systems 2009, 160, 14, 2063–2085. [Google Scholar] [CrossRef]
Bandler, W. Kohout, L,; Fuzzy relational products as a tool for analysis and synthesis of the behavior of complex natural and artificial systems. in Fuzzy Sets: Theory and Application to Policy Analysis and Information Systems, P. Wang and S. Chang, Eds. New York: Plenum, 1980, 341–367.
Bandler, L. Kohout, W.; Semantics of implication operators and fuzzy relational products. Int. J. Man-Mach.Stud 1980, 12, 89–116. [Google Scholar] [CrossRef]
Beg, I, Ashraf, S. ; Fuzzy equivalence relations. Kuwait Journal of Science and Engineering 2008, 35, 1A, 33–51. [Google Scholar]
Stepnicka, M. Jayaram, B. On the suitability of the bandler–kohout subproduct as an inference mechanism. IEEE Transactions on Fuzzy Systems 2010, 18, 2, 285–298. [Google Scholar] [CrossRef]
Tang, Y. Pedrycz, W.; Oscillation-bound estimation of perturbations under bandler–kohout sub-product. IEEE Transactions on Cybernetics 2022, 52, 7, 6269–6282. [Google Scholar] [CrossRef] [PubMed]
Samuel, A. E.; Balamurugan, M. ; Fuzzy max-min composition technique in medical diagnosis. Applied Mathematical Sciences 2012, 6, 35, 1741–1746. [Google Scholar]
Horikawa, S. Furuhashi, T. Okuma, S.; Uchikawa, Y.; Composition methods of fuzzy neural networks. in [Proceedings] IECON ’90: 16th Annual Conference of IEEE Industrial Electronics Society 1990, 2, 1253–1258.
D. Ramot, R. Milo, M. Friedman, and A. Kandel, Complex fuzzy sets. IEEE Trans. Fuzzy Syst 2002, 10, 171–186.
Zhang, G. Dillon, T. Cai, K. Ma, J Lu, J.; Operation properties and delta-equalities of complex fuzzy sets. Int. J. Approx. Reason 2009, 8, 1227–1249. [Google Scholar] [CrossRef]
Nhung, C. Martin, S.; Compositions of partial fuzzy relations. in International Conference on Information Processing and Management of Uncertainty 2018, 855, 1, 187–198. [Google Scholar]
Dick, S. ; On complex fuzzy S-implications. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 409–415. [Google Scholar] [CrossRef]
Khan, M. Zeeshan, M. Song, S. Z. Iqbal, S.; Types of complex fuzzy relations with applications in future commission market. Journal of Mathematics 2021, 6685977, 14. [Google Scholar]
B. Hu, L. Bi, S. Dai, and S. Li, Distances of complex fuzzy sets and continuity of complex fuzzy operations. J. Intell. Fuzzy Syst. 2018, 35, 2247–2255. [CrossRef]
Hu, B. Bi, L. Dai, S.; Approximate orthogonality of complex fuzzy sets and approximately orthogonality preserving operators. J. Intell. Fuzzy Syst 2019, 37, 5025–5030. [Google Scholar] [CrossRef]
Gulzar, M. Mateen, M. H. Alghazzawi, D. Kausar, N.; A novel application of complex intuitionistic fuzzy sets in group theory. IEEE Access 2020, 8, 196075–196085. [Google Scholar] [CrossRef]
Gulzar, M. Mateen, M. H. Chu, Y. M. Alghazzawi, D. Abbas, G.; Generalized direct product of complex intuitionistic fuzzy subrings. Int. J. Comput. Intell. Syst 2021, 14, 582–593. [Google Scholar] [CrossRef]
Nasir, A. Jan, N. Gumaei, A. Khan, S. U.; Medical diagnosis and life span of sufferer using interval valued complex fuzzy relations. IEEE Access 2021, 9, 93764–93780. [Google Scholar] [CrossRef]
Mahmood, T. Ahmmad, J. Ali, Z. Yang, M. S.; Confidence level aggregation operators based on intuitionistic fuzzy rough sets with application in medical diagnosis. IEEE Access 2023, 11, 8674–8688. [Google Scholar] [CrossRef]
De-Baets, B Kerre, E.; Fuzzy relational compositions. Fuzzy Sets Syst 1993, 60, 1, 109–120.
Zhang, G. Dillon, T. S. Cai, K. Ma, J. Lu, J.; δ-equalities of complex fuzzy relations. in 2010 24th IEEE International Conference on Advanced Information Networking and Applications 2010, pp. 1218–1224.

Figure 1.

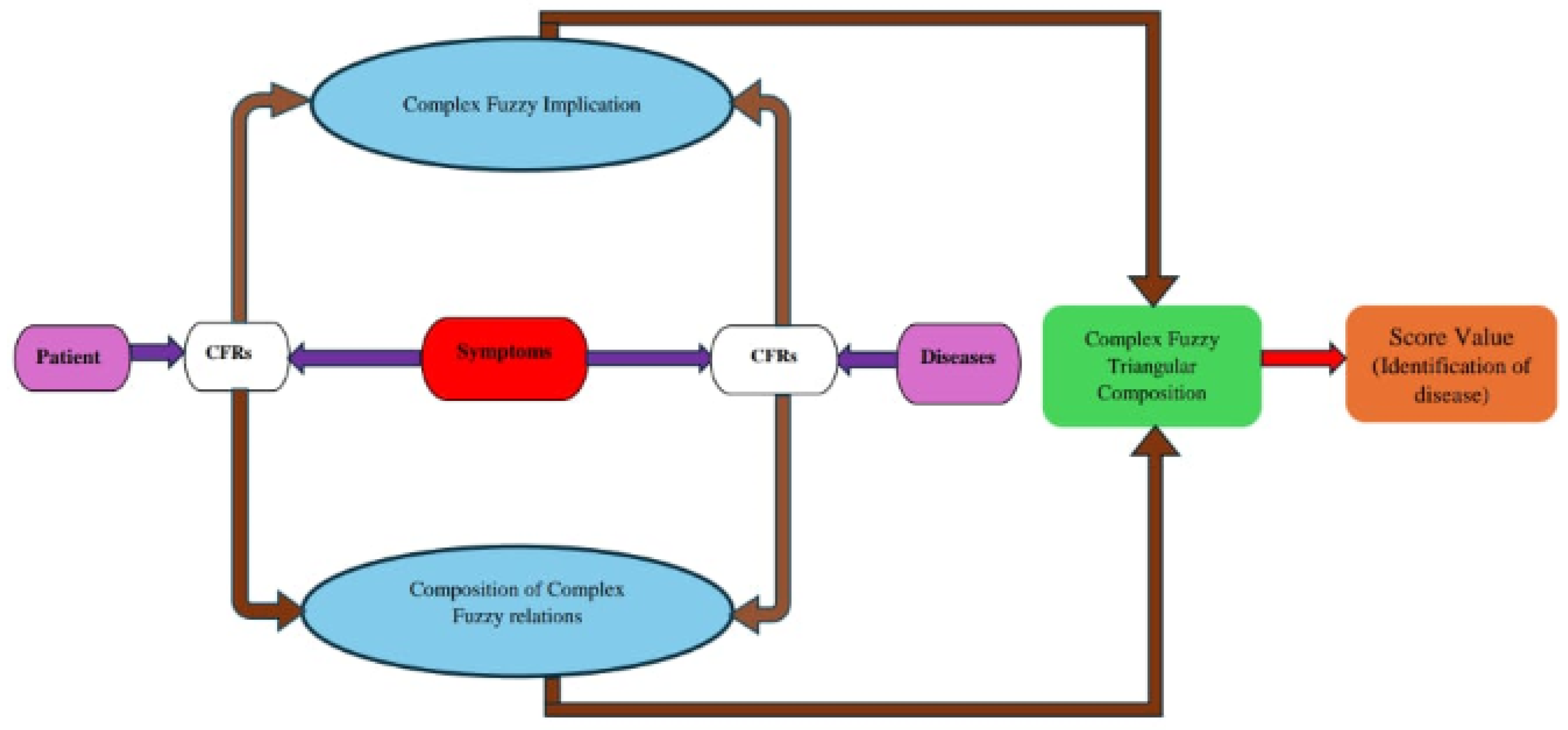
Table 1. Patients-symptoms relation.

Table 2. Symptoms-diseases relation.

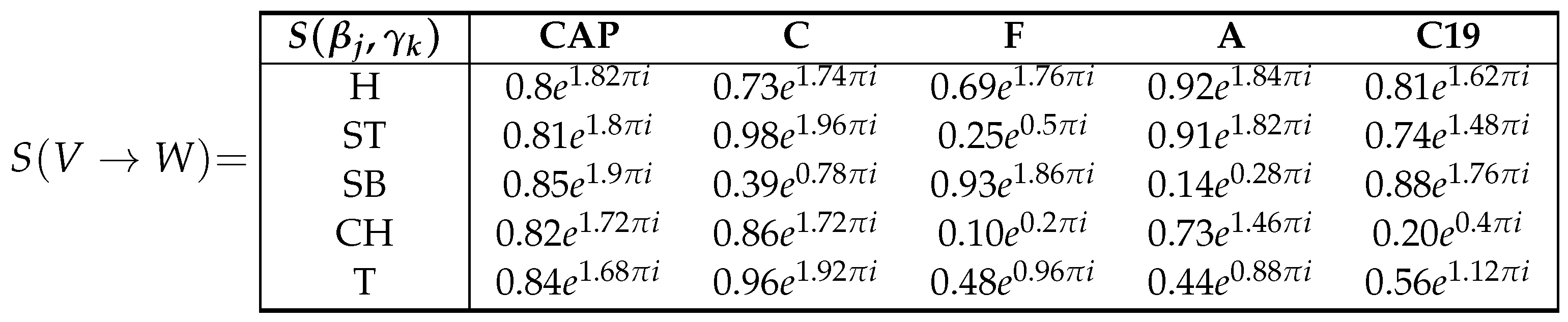
Table 3. Patients-diseases relation.

Table 4.

S (R ⊲_{p} S) = p_{R ⊲_{p} S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ⊲_{p} S} (α_{i}, γ_{k})

Table 4.

S (R ⊲_{p} S) = p_{R ⊲_{p} S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ⊲_{p} S} (α_{i}, γ_{k})

Table 5. Patients-symptoms relation.

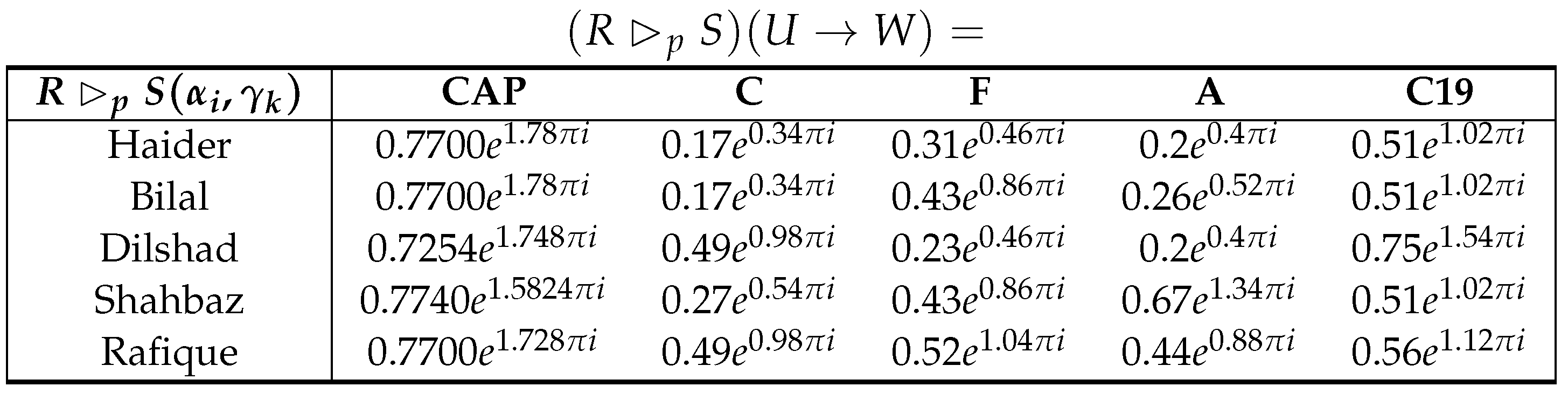
Table 6.

S (R ⊳_{p} S) = p_{R ⊳_{p} S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ⊳_{p} S} (α_{i}, γ_{k})

Table 6.

S (R ⊳_{p} S) = p_{R ⊳_{p} S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ⊳_{p} S} (α_{i}, γ_{k})

Table 7. Patients-symptoms relation.

Table 8.

S (R ⋄_{p} S) = p_{R ⋄_{p} S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ⋄_{p} S} (α_{i}, γ_{k})

Table 8.

S (R ⋄_{p} S) = p_{R ⋄_{p} S} (α_{i}, γ_{k}) + \frac{1}{2 π} θ_{R ⋄_{p} S} (α_{i}, γ_{k})

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Application of Complex Fuzzy Relational Compositions to Medical Diagnosis

Abstract

Keywords:

Subject:

1. Introduction

2. Preliminaries

3. Algebraic Structure of Complex Fuzzy Relational Compositions

4. Application to Diagnose the Diseases on the Basis of Intensity of Symptoms

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe