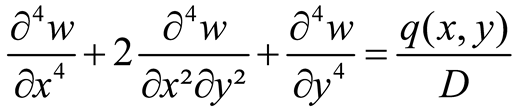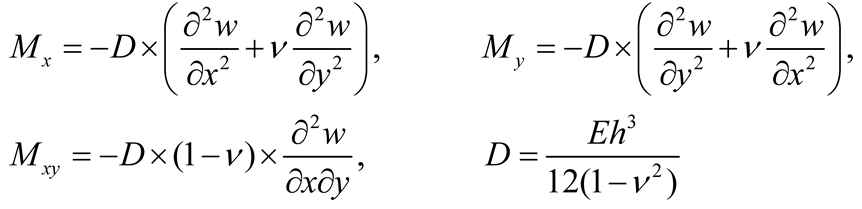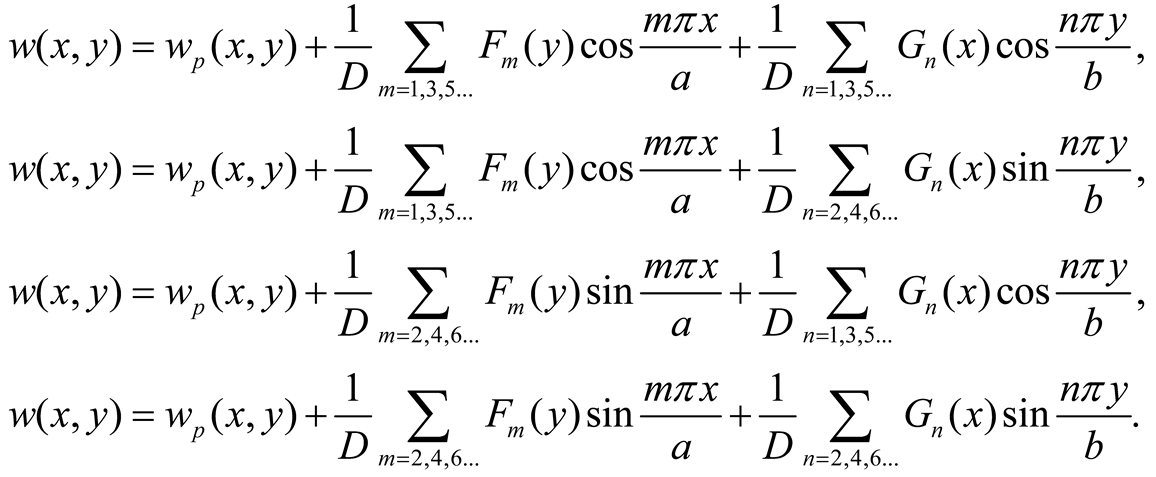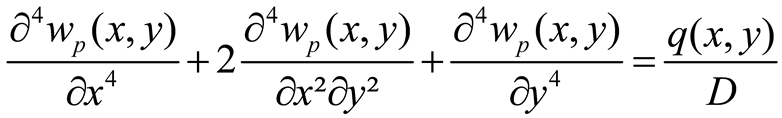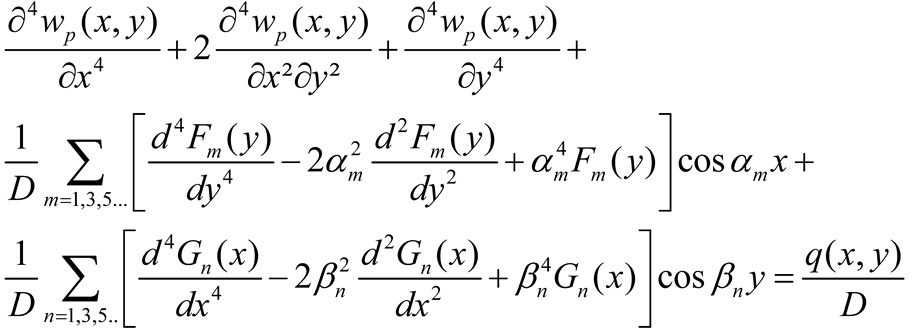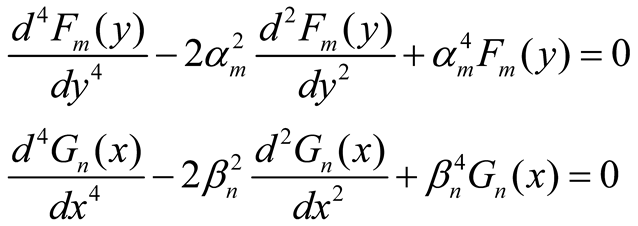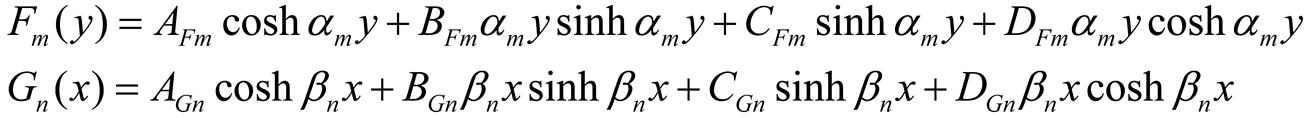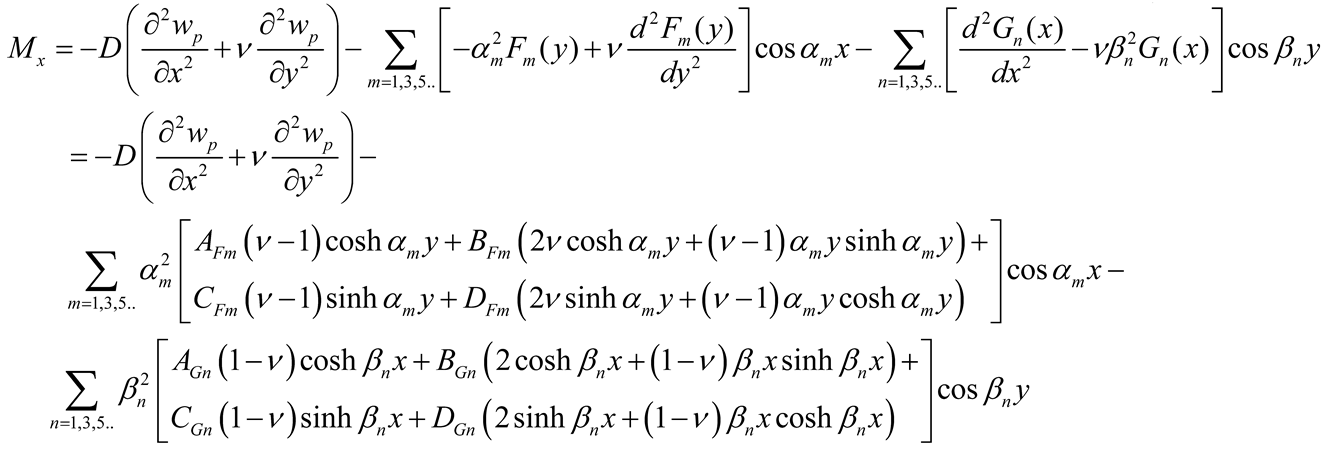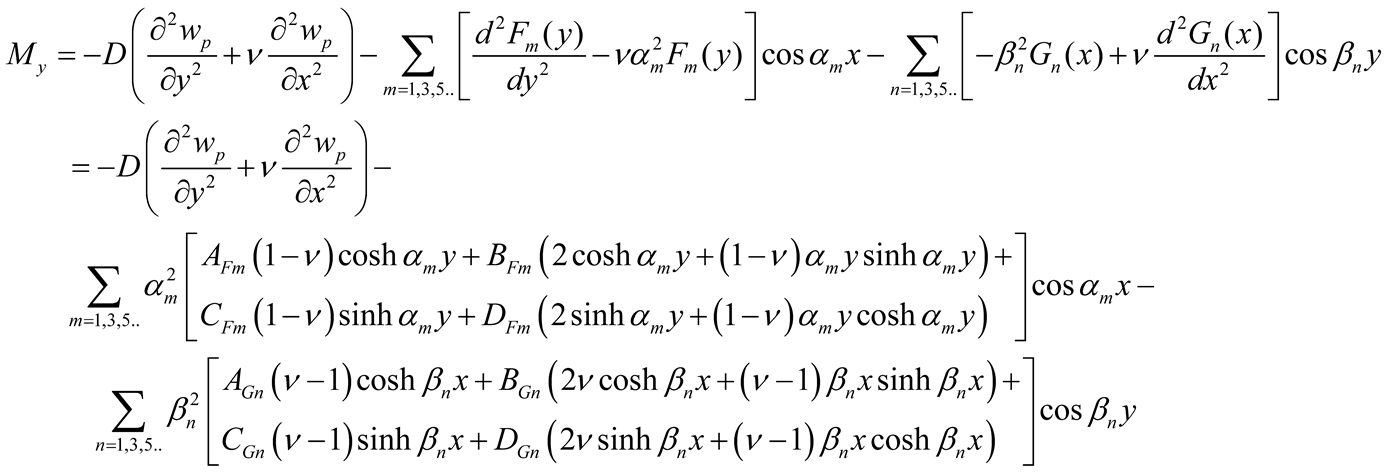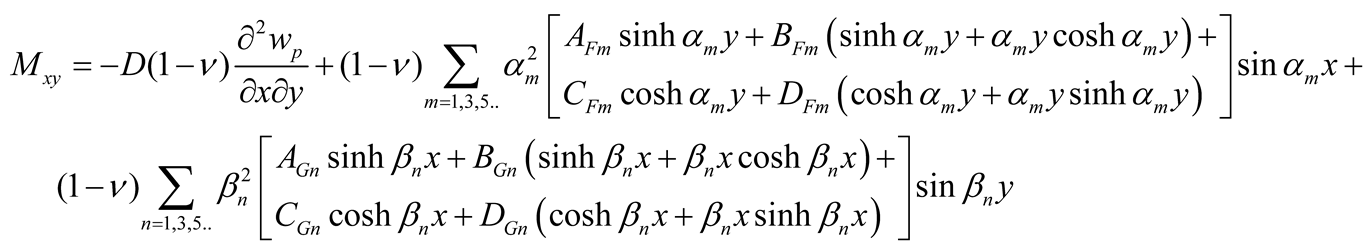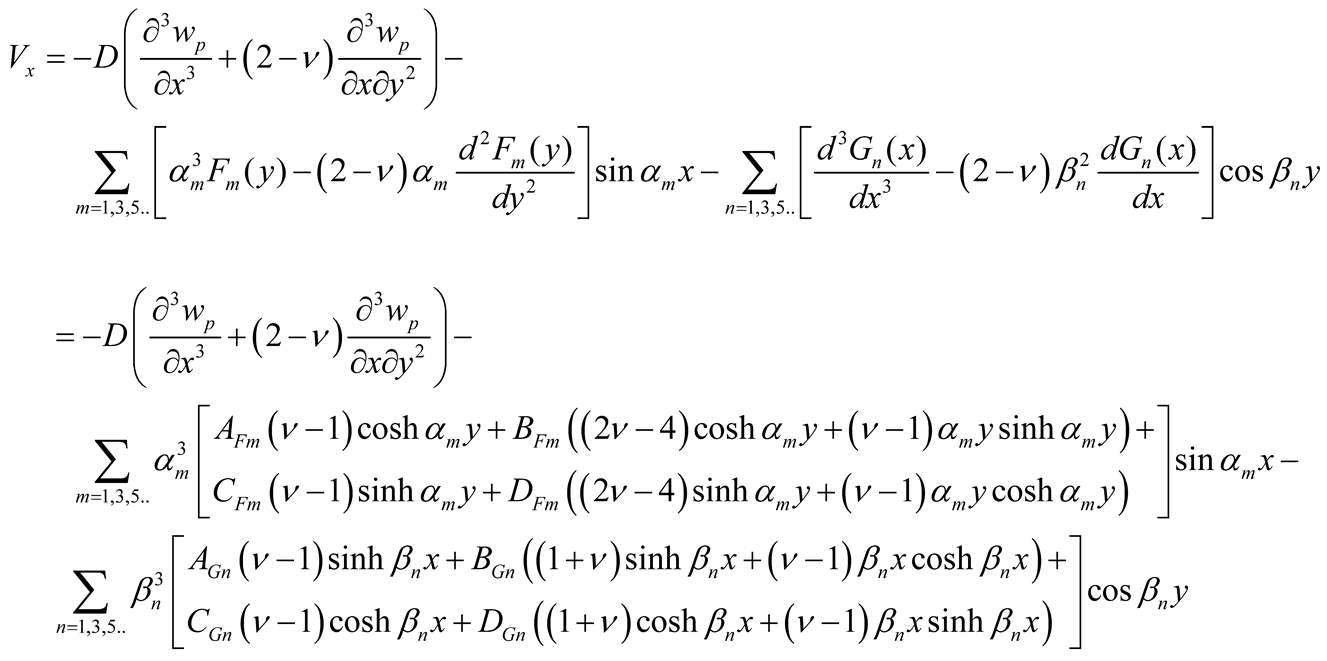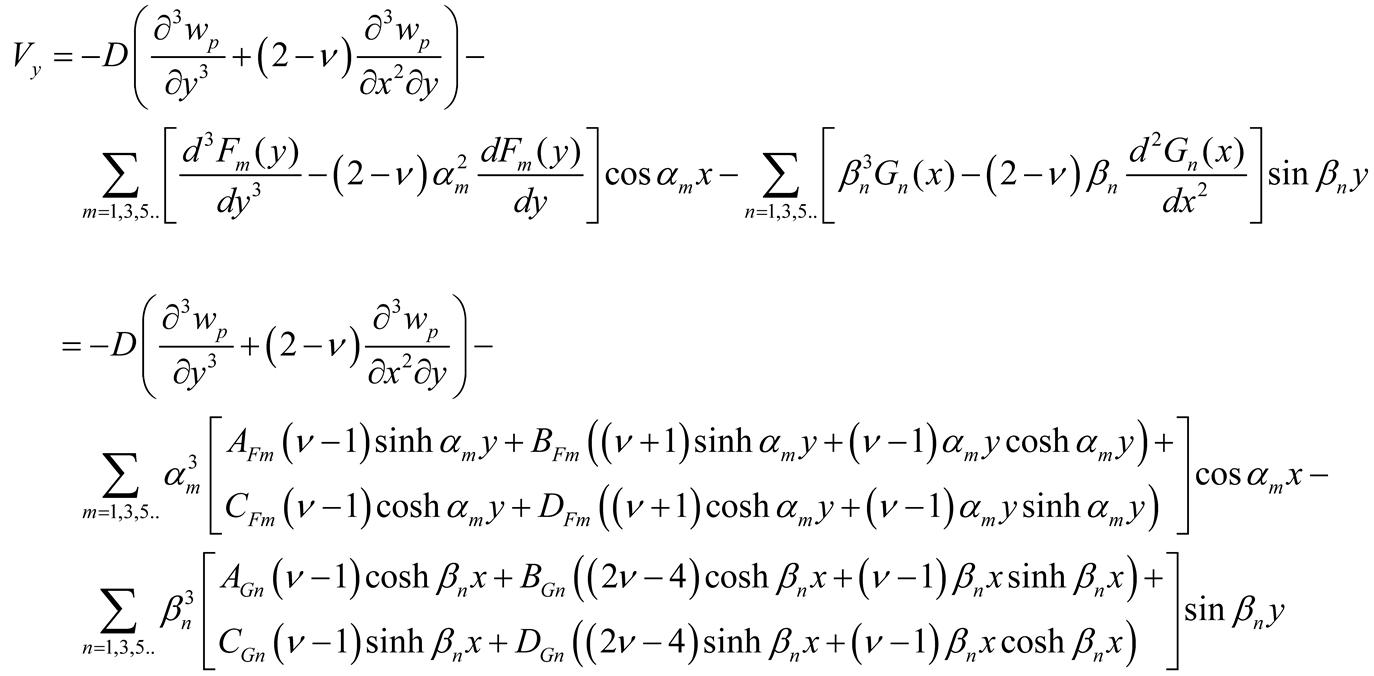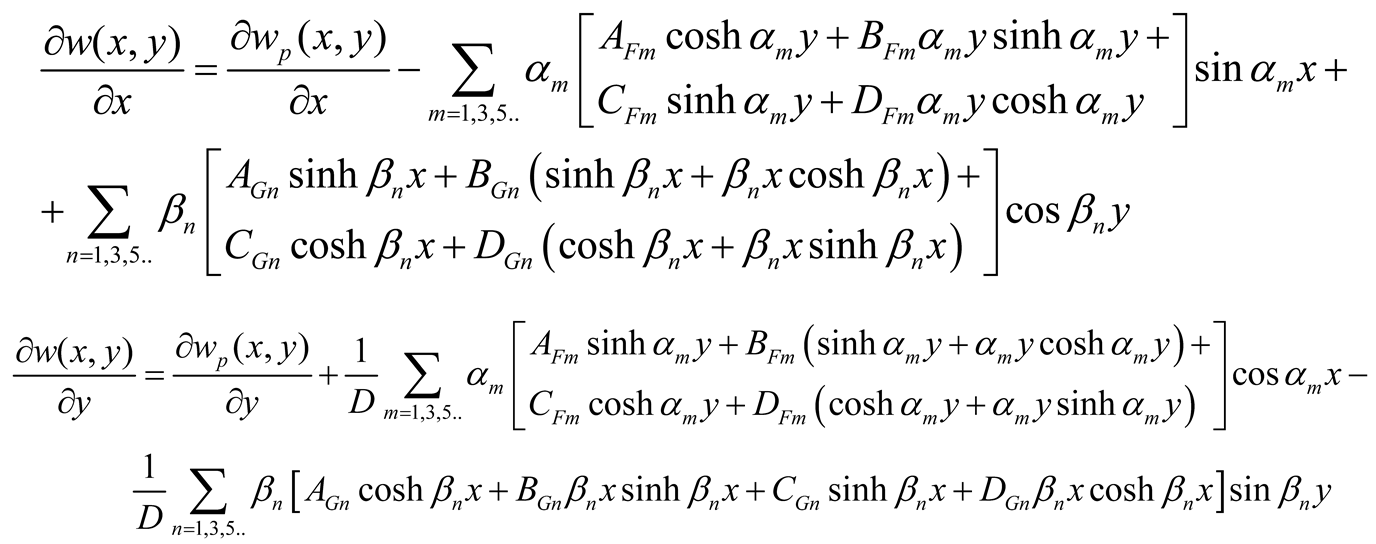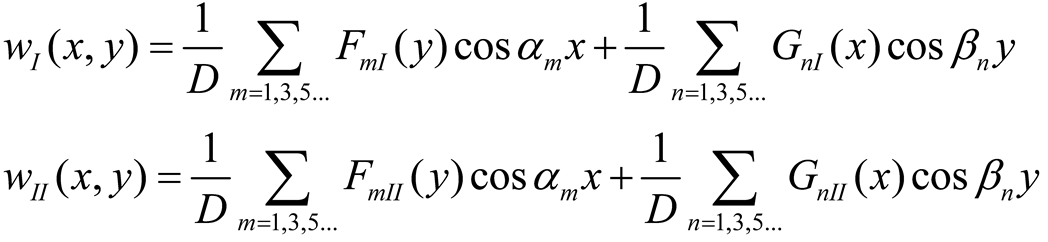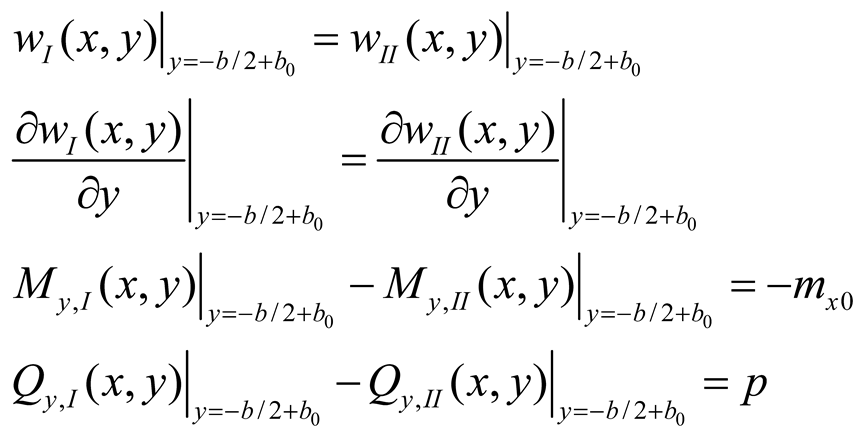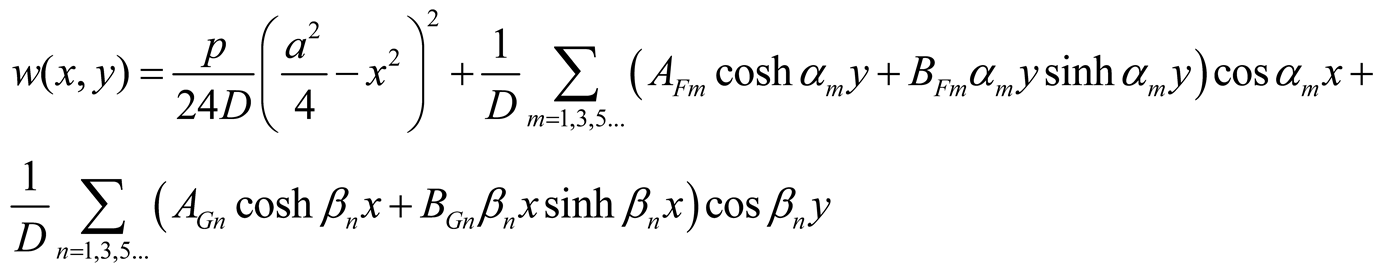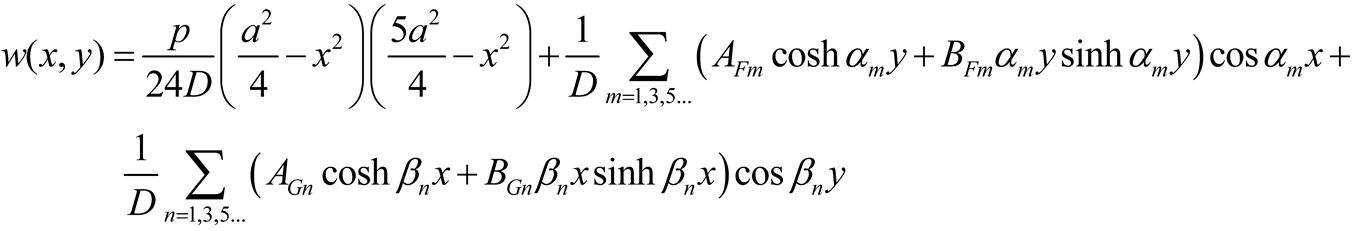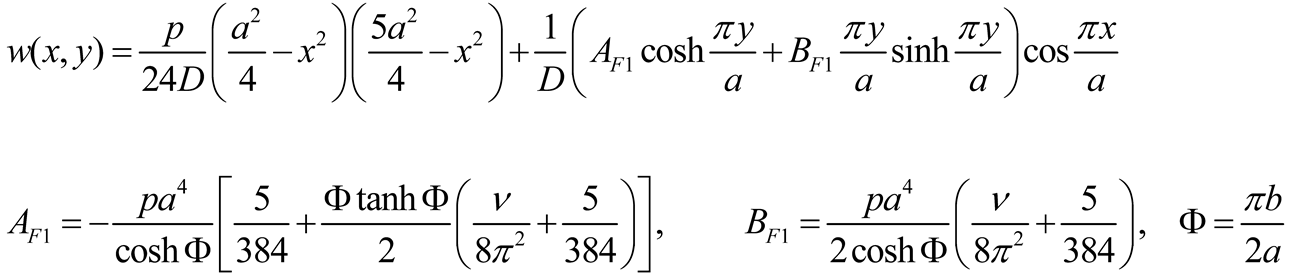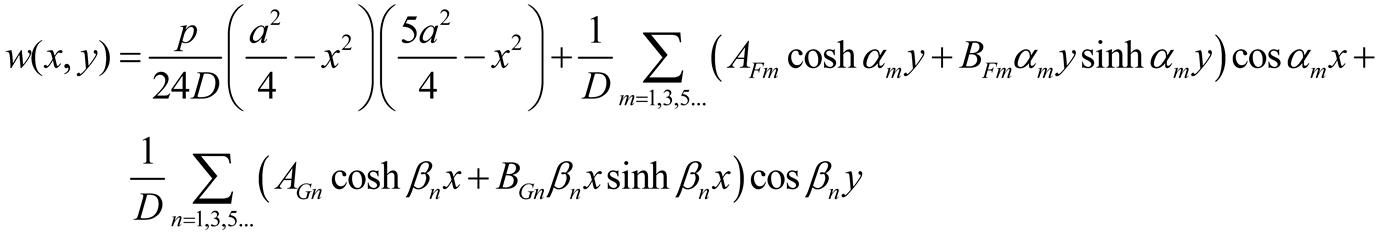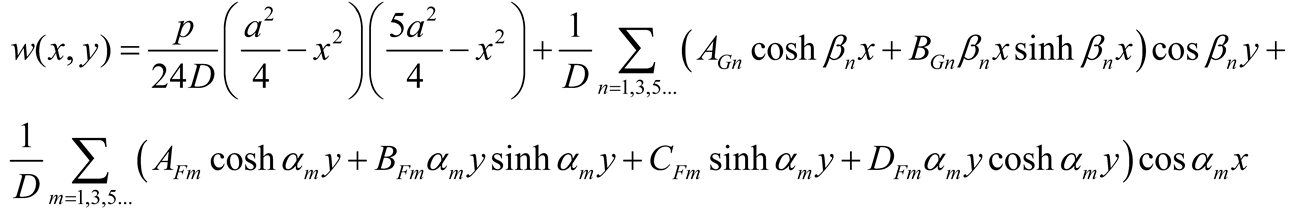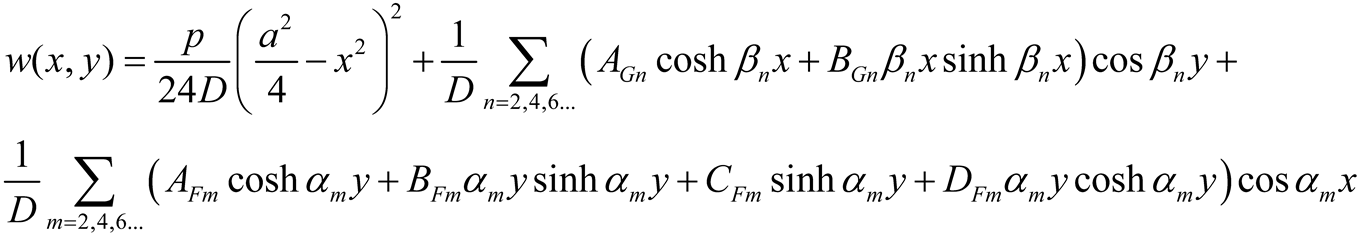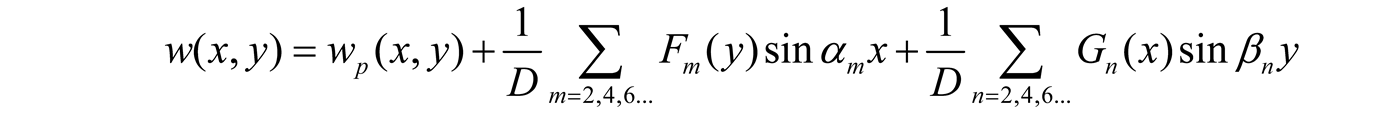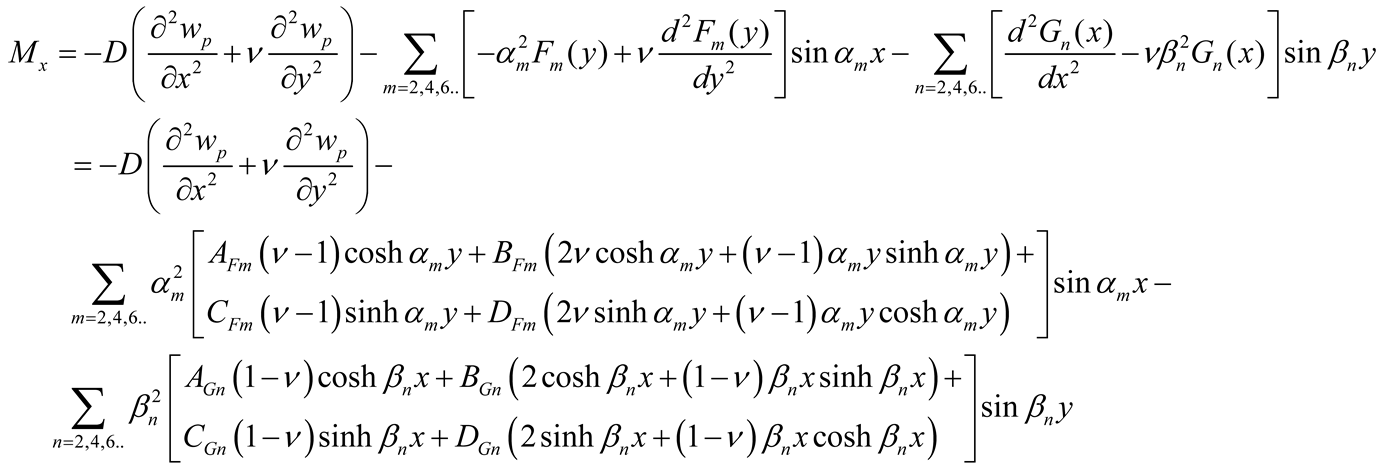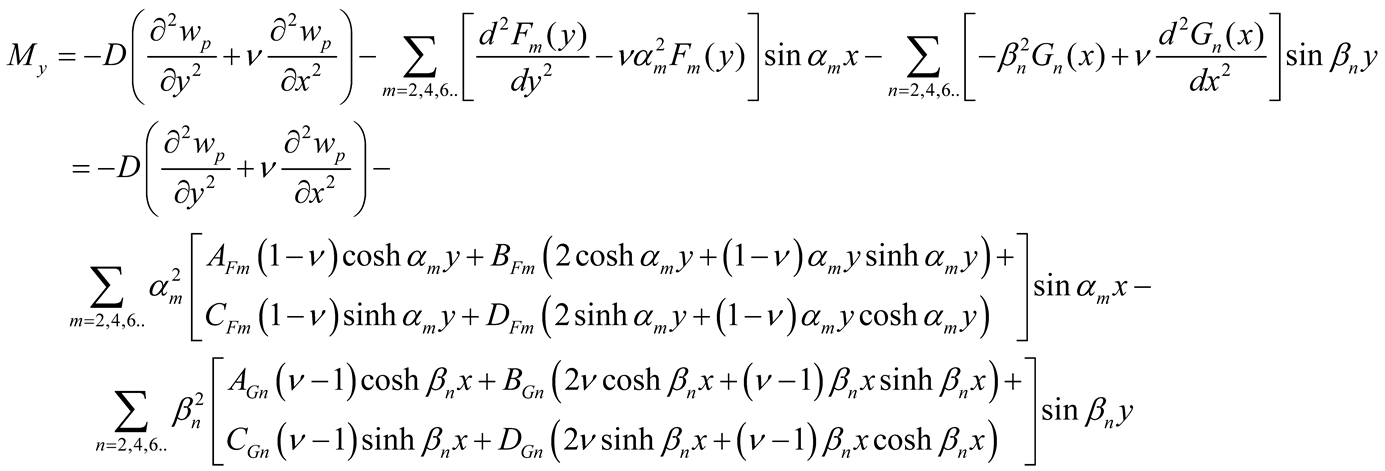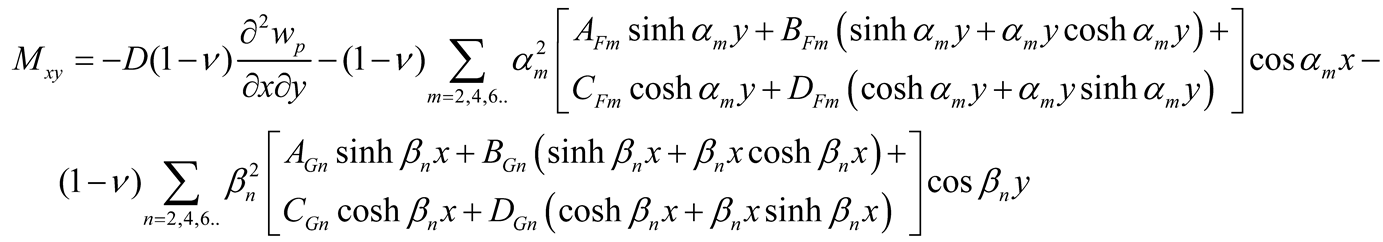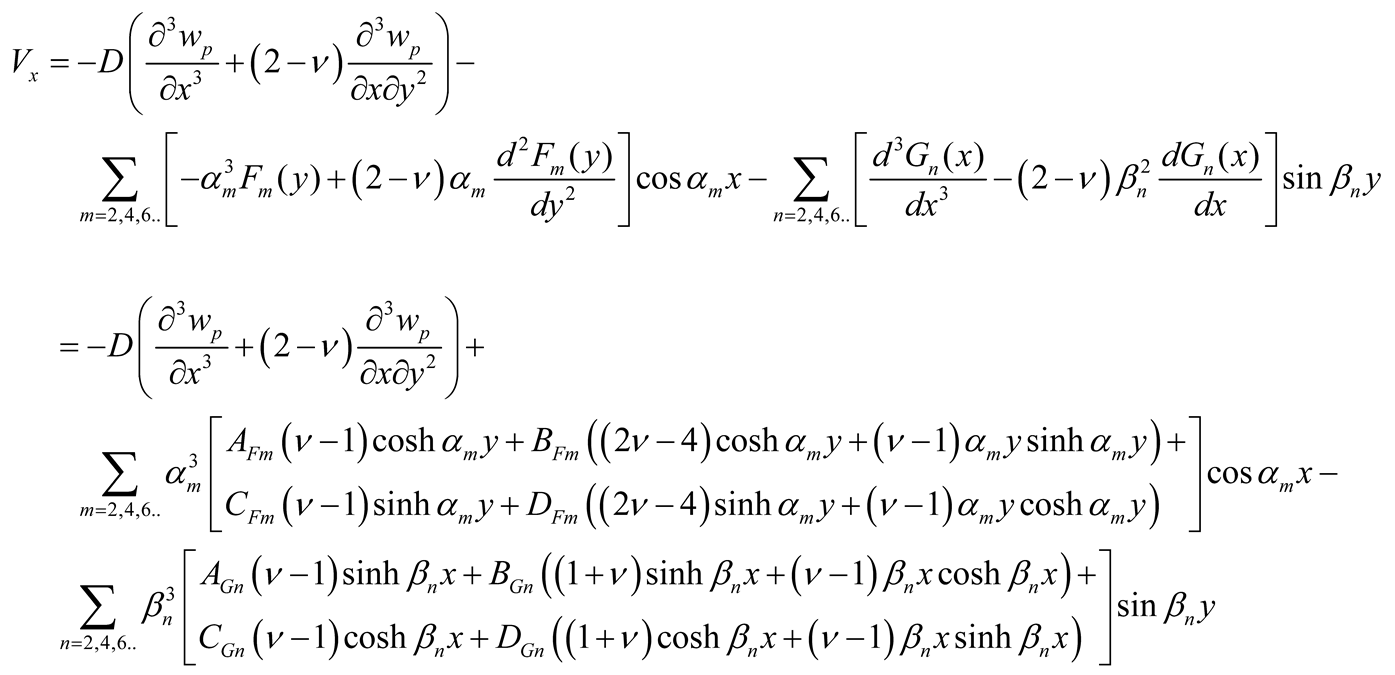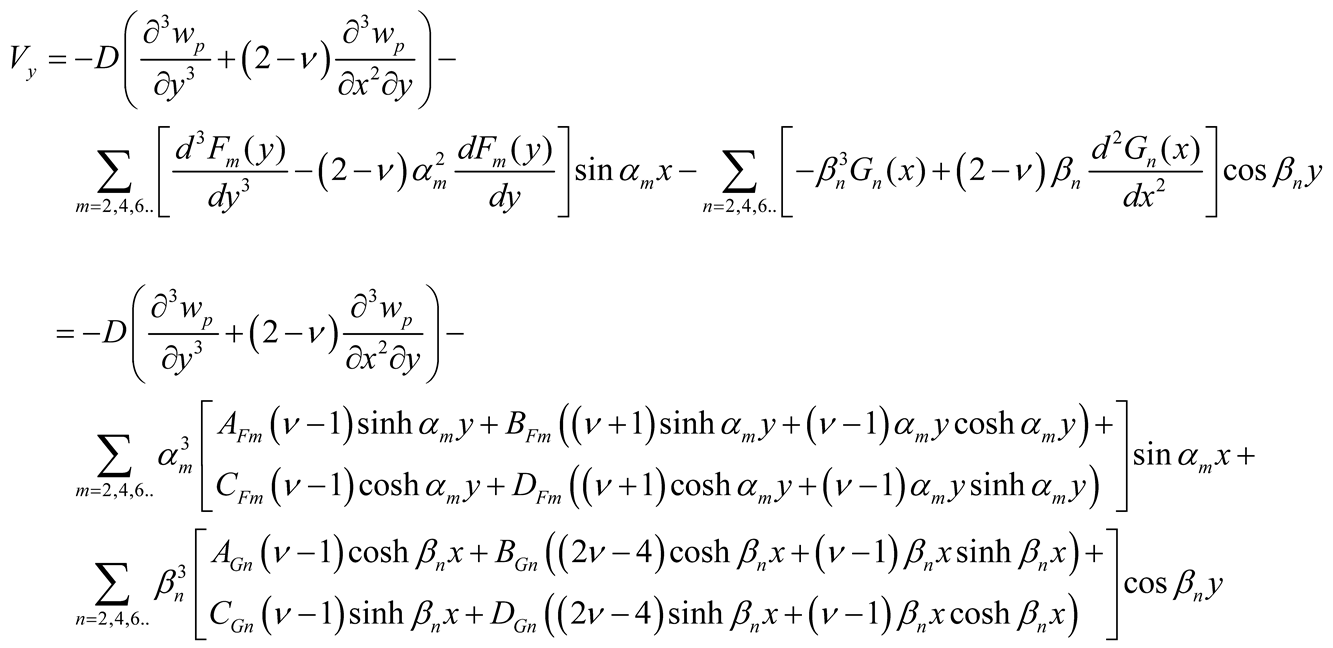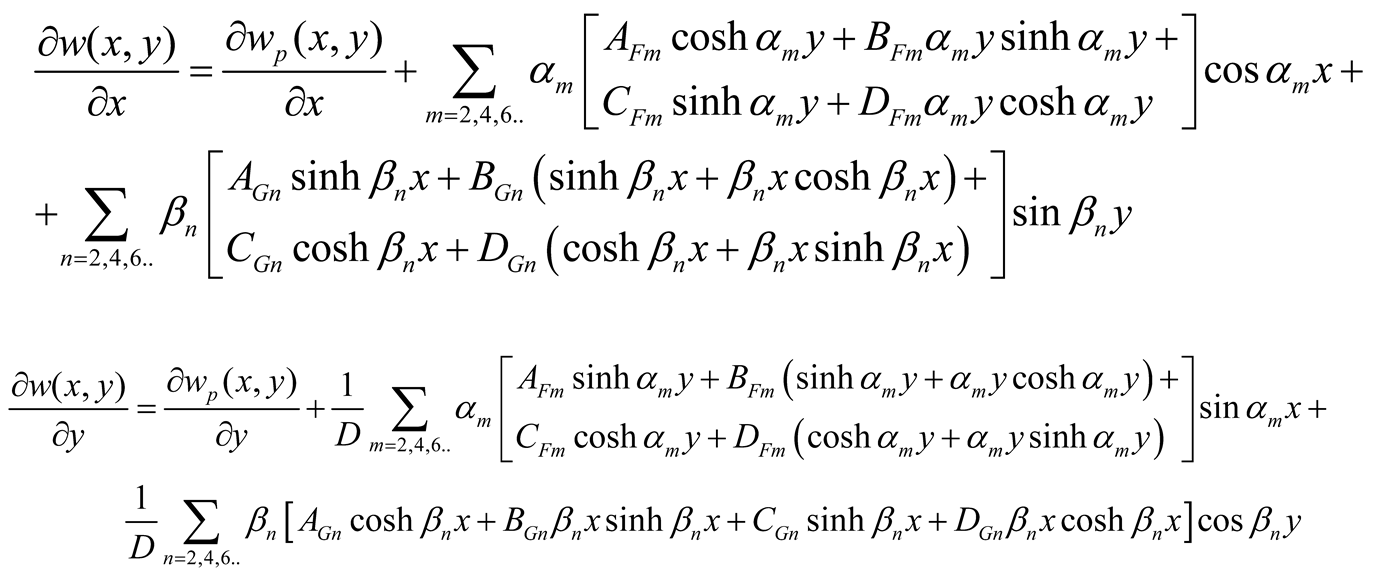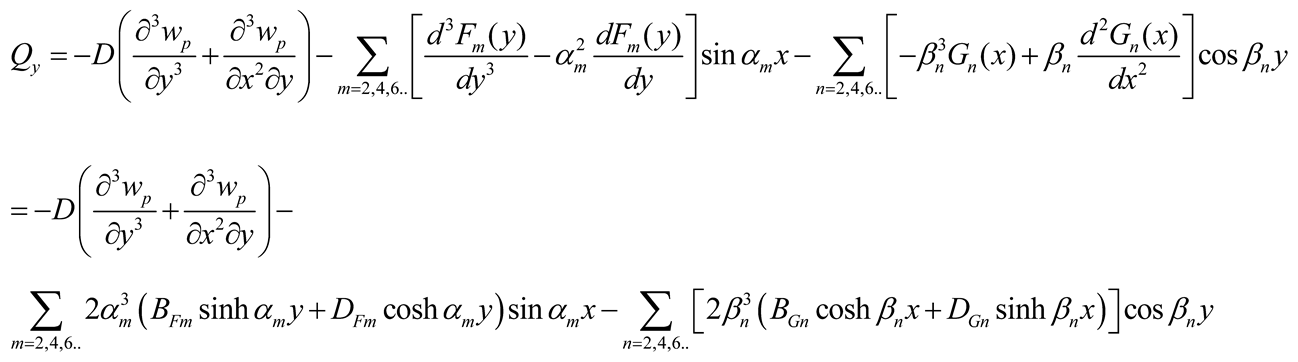An Analytical Solution to Rectangular Kirchhoff Plates Supported at All Corner Points Using Two Single Series and the Boundary Collocation Method

Preprint

Article

An Analytical Solution to Rectangular Kirchhoff Plates Supported at All Corner Points Using Two Single Series and the Boundary Collocation Method

Altmetrics

Downloads

Views

108

Comments

Supplementary Material

supplementary.rar (533.12KB )

Valentin Fogang^*

This version is not peer-reviewed

Submitted:

28 October 2024

Posted:

30 October 2024

You are already at the latest version

Alerts

Abstract

The aim of this paper is the analysis of arbitrarily loaded isotropic rectangular Kirchhoff plates supported at all corner points, whereby the edges are arbitrarily supported (simply supported, clamped, or free). Analytical methods commonly used include the single trigonometric series of Lévy, the double trigonometric series of Navier, the power series expansions, etc. In this paper the deflection surface was approximated with the sum of a particular solution to the governing differential equation (GDE) and two single series. The terms of the single series were the product of an unknown function of an independent variable and a trigonometric function of the other independent variable, whereby the trigonometric functions were chosen to vanish at the corner points. On the one hand the terms of the series were required to satisfy the homogeneous GDE, leading to two uncoupled differential equations, one for each unknown function, and so the approximate solution satisﬁed exactly the GDE. On the other hand the boundary conditions were satisﬁed only at selected collocation points along the boundary, the number of collocation points in each direction corresponding to the number of terms of the associated series. Results for several plates supported at all corner points with arbitrary edge support conditions were presented and showed good agreement with the exact results, the accuracy increasing the more terms of series were considered. Cantilevered plates and plates having two adjacent edges free will be analyzed using this approach in future research.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

The Kirchhoff–Love plate theory (KLPT) was developed in 1888 by Love using assumptions proposed by Kirchhoff [1]. The KLPT is governed by the Germain−Lagrange plate equation; this equation was first derived by Lagrange in 1811 in correcting the work of Germain [2] who provided the basis of the theory. Numerous exact analytical solutions for rectangular isotropic linear elastic thin plates have been developed in the literature; among them the double trigonometric series of Navier [3] for plates simply supported along all edges, the single trigonometric series of Lévy [4] for rectangular plates simply supported along two opposite edges, the power series expansion, etc. Timoshenko [5] presented solutions for several cases where the single trigonometric series of Lévy was mostly considered. In this study the analysis was conducted using the boundary collocation method. This method, also called the generalized Trefftz [6] approach, consists of the use of trial functions which satisfy the governing differential equations of the problem. The unknown coefficients of those functions are determined by the satisfaction of the boundary conditions at collocation points. Many authors worked on collocation techniques. Herrera [7] proposed a precise definition of Trefftz method and, starting with it, explained briefly a general theory. This led to formulating numerical methods from a domain decomposition perspective. Deng et al. [8] presented a theoretical framework for the accuracy analysis of meshfree collocation methods with a particular focus on the effects of boundary conditions. The error of a meshfree collocation formulation is decomposed into three parts, namely, the collocation errors associated with the interior nodes, the Dirichlet boundary nodes and the Neumann boundary nodes, respectively. Borkowska et al. [9] analyzed the generalized collocation Trefftz method which allows to combine the advantages of the T-Trefftz and the method of fundamental solutions. The initial idea of the method is to approximate the solution with a linear combination of many basis functions with many source points. Volkov-Bogorodskiy et al. [10] proposed a Trefftz approximation scheme on the structure of subdomains-blocks for the problems of the gradient elasticity. The scheme was based on the analytical representation for the gradient elasticity solutions of Papkovich–Neuber type. Piltner [11] presented a collection of personal choices to help future developers of numerical methods based on Trefftz trial functions. Hu et al. [12] introduced radial basis functions into the collocation methods and the combined methods for elliptic boundary value problems. Yang et al. [13] discussed Trefftz discretization techniques with a focus on their coupling with shape functions computed by the method of Taylor series. The highlights are the control of ill-conditioning, the solving of large scale problems, and the applications to non-linear Partial Differential Equations.

In this paper two single series were considered due to the possibility to satisfy the boundary conditions along the four edges, inspired from the Lévy solution that involves one single series and the satisfaction of the boundary conditions along two opposite edges (the other edges are simply supported). Moreover the approach can be seen as a mixed analytical-numerical method: analytical since the efforts and deformations are described analytically throughout the plate and numerical since the boundary conditions are only satisfied at collocation points on the boundary.

2. Materials and Methods

2.1. Governing Equations of the Plate

The Kirchhoff–Love plate theory (KLPT) [1] is used for thin plates and shear deformations are not considered. The spatial axis convention (X, Y, Z) is represented in Figure 1 below with the origin of the axes at the plate center.

The equations of the KLPT are recalled in the present section. The governing equation of the isotropic Kirchhoff plate, derived by Lagrange, is given by

(1)

where w(x,y,z) is the mid-plane displacement in z-direction, q(x,y) the transverse distributed load, and D the flexural rigidity of the plate. The bending moments per unit length M_x and M_y, and the twisting moments per unit length M_xy are given by

(2a-d)

The shear forces per unit length are given by

(3a-b)

The Kirchhoff shear forces per unit length used along the free edges combine shear forces and twisting moments, and are expressed as follows:

((4a-b))

In these equations, E is the elastic modulus of the plate material, h is the plate thickness, and ν is the Poisson’s ratio.

2.2. Rectangular Plate Supported at All Corner Points with the Edges Supported or Free

The plate dimensions in x- and y-direction were denoted by a and b, respectively. The rectangular plate was assumed supported at the four corner points whereby the edges had arbitrary support conditions (simply supported, clamped or free). The displacement function was approximated with the sum of a particular solution w_p(x,y) to the governing differential Equation (1) and two single series. The choice of two single series is on the one hand due to the possibility to satisfy the boundary conditions along the four edges, inspired from the Lévy solution that involves one single series and the satisfaction of the boundary conditions along two opposite edges (the other edges are simply supported). On the other hand two single series are “geometrically isotropic,” in that the independent variables x and y are treated in the same fair way in terms of accuracy.

Requiring that the particular solution w_p(x,y) and the single series are zero at the corner points and recalling that the origin of the axes is at the plate center, four possible formulations of the displacement function are as follows

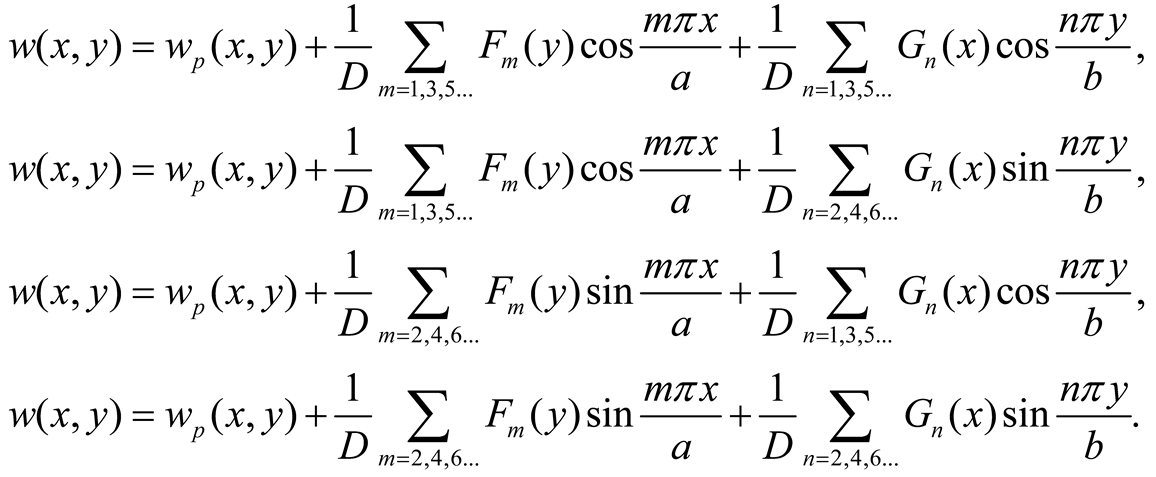(5a-b)

Furthermore the term w_p(x,y) can be taken as the deflection of a plate strip parallel to the x-axis (or the y-axis), supported at both ends and subjected to the load q(x,y).

Each of the formulation of Equations (5a-d) can generally be considered. In the following the formulation of Equation (5a) is considered. The term w_p(x,y) is a particular solution to Equation (1) and consequently

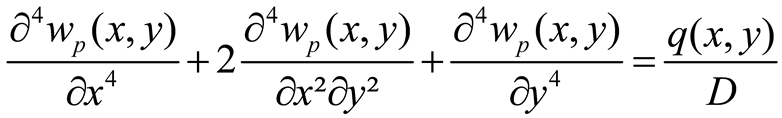(6)

Setting αm = mπ/a and βn = nπ/b and substituting Equation (5a) into (1) yield

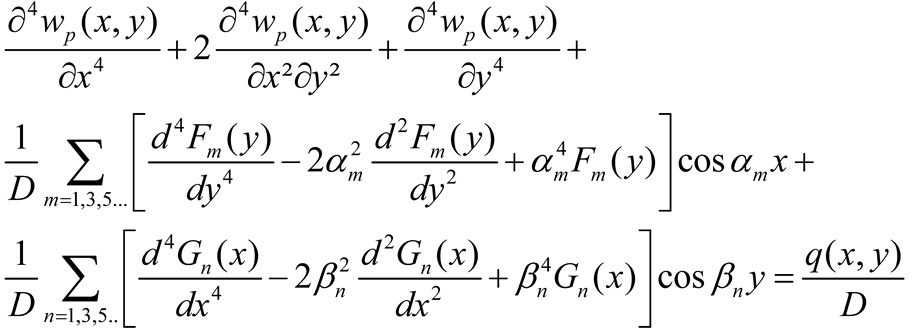(7)

Observing Equation (6) and given that (7) holds for any value of x and y, it results the following differential equations

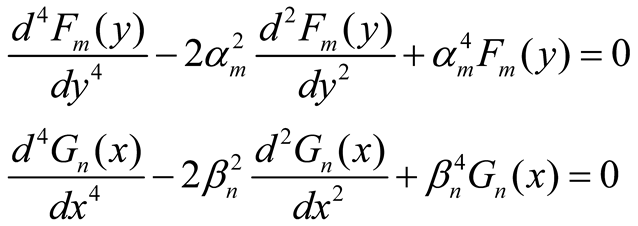(8a,b)

Equations (8a, b) further applied in case of Equations (5b-d) for the displacement function. The solutions are given by

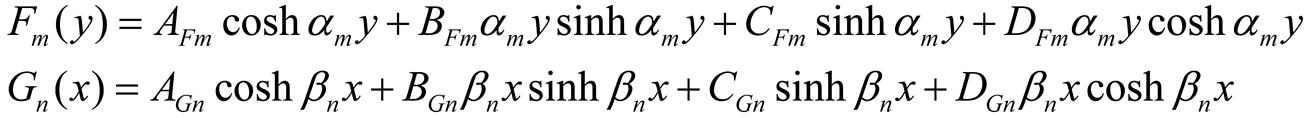(9a,b)

where the coefficients A_Fm, B_Fm, C_Fm, D_Fm, A_Gn, B_Gn, C_Gn, and D_Gn are determined by satisfying the boundary conditions at selected collocation points. The collocation points should be suitably distributed along the edges, and particularly so as to avoid singular matrices. Furthermore, the external running moments and running loads should also be suitably distributed at these points.

It is noted that the collocation points at the edges x = ± a/2 are associated with the series having the function G_n(x) while those at y = ± b/2 are associated with the series having the function F_m(y). Let us consider an approximate solution where the first and second series have M and N terms, respectively. It results in 4M + 4N unknown coefficients. Therefore M collocation points should be considered at each of the edges y = ± b/2 and N collocation points at each of the edges x = ± a/2. Since two boundary conditions are set at each collocation point it results in 4M + 4N equations. So there are as many unknowns as equations.

However in case of symmetry of the structure about an axis and symmetry/anti-symmetry of the loading an appropriate choice can simplify the analysis: here are some useful examples

Symmetrical system about x and y axis and loading symmetrical about x and y axis: Equation (5a) is considered for the displacement whereby only the even parts of F_m(y) and G_n(x) are considered, leading to C_Fm = D_fm = C_Gn = D_Gn = 0. The boundary conditions are then applied at only one fourth of the structure.
Symmetrical system about x and y axis and loading symmetrical about the x axis, i.e., q(x, y) = q(x, -y), and anti-symmetrical about the y axis, i.e., q(x, y) = -q(-x, y): Equation (5c) is considered for the displacement whereby only the odd parts of G_n(x) and the even parts of F_m(y) are considered, leading to A_Gn = B_Gn = C_Fm = D_fm = 0. The boundary conditions are applied at only one fourth of the structure.
Symmetrical system about the x axis and loading symmetrical about the x axis, i.e., q(x, y) = q(x, -y): Equations (5a) or (5c) are considered for the displacement and only the even parts of F_m(y) are considered, leading to C_Fm = D_Fm = 0. The boundary conditions are applied at one half of the structure.
Symmetrical system about the y-axis and loading anti-symmetrical about y-axis, i.e., q(x, y) = -q(-x, y): Equations (5c) or (5d) are considered for the displacement and only the odd parts of G_n(x are considered, leading to A_Gn = B_Gn = 0. The boundary conditions are applied at one half of the structure.

The efforts are expressed using Equations (2a-c), (3a-b), (4a-b), (5a), and (9a-b) as follows

	(10a)
	(10b)
	(10c)
	(11a)
	(11b)

The slopes ∂w/∂x and ∂w/∂y used as boundary conditions are given by

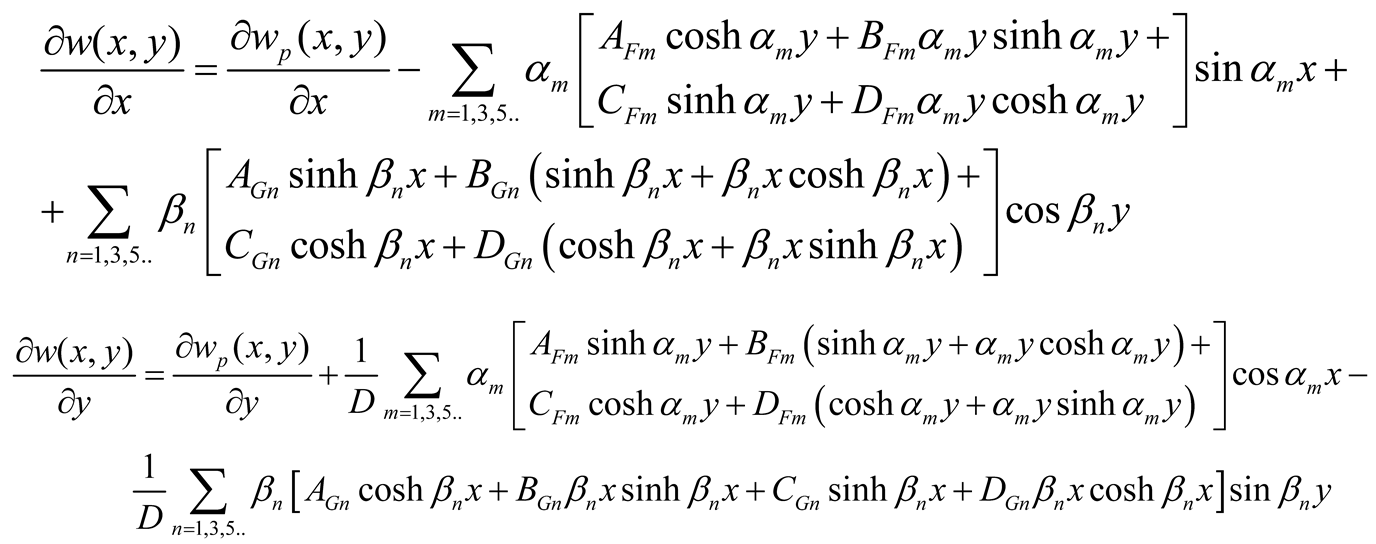(11c-d)

The shear force Q_y used by continuity equations and in case of symmetry are expressed using Equations (3b), (5), and (9a, b), as follows

(11e)

The efforts and deformations above for other formulations of the deflection surface (Equations (5b-d)) are expressed in Appendix A.

With the determination of the coefficients A_Fm, B_Fm, C_Fm, D_Fm, A_Gn, B_Gn, C_Gn, and D_Gn the deflections are calculated using Equations (5) and (9a, b) and the efforts (bending moments M_x, M_y, and twisting moments M_xy , and effective shear forces V_x and V_y) using Equations (10a-c) and (11a-b).

Analysis of special cases

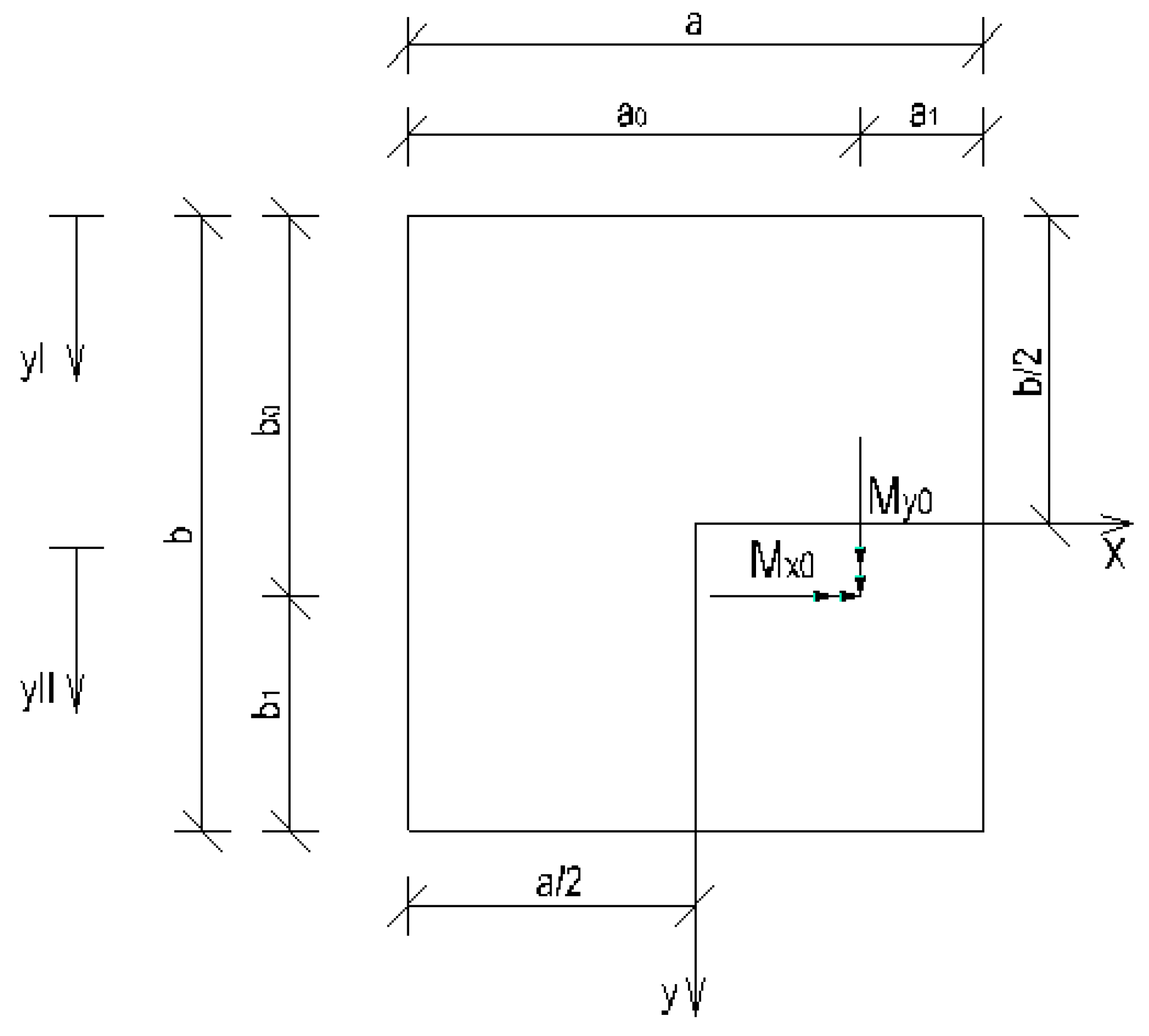
a): Concentrated force and moment applied at the interior of the plate

Let an external force P and external concentrated moments Mx0 and My0 be applied at the position (x₀, y₀) as shown in Figure 2.

Referring to Figure 2, the deflections defined as before (Equations (5)) are represented with the subscripts I and II for the plate zones –b/2 ≤ y ≤ –b/2 + b₀ and –b/2 + b₀ ≤ y ≤ b/2, respectively, as follows

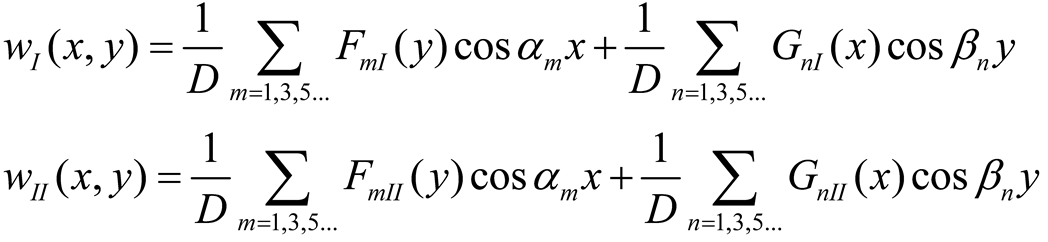(12a-b)

Let the first series of w_I and w_II have each M terms, and the second series have N_I and N_II terms, respectively. Therefore, the lines y = –b/2, y = –b/2 + b₀, and y = b/2 should be discretized with M nodes, and each of the edges x = ± a/2 of the plate zone I and II should be discretized with N_I and N_II nodes, respectively. It results in 4M + 4N_I unknowns in plate zone I and 4M + 4N_II unknowns in plate zone II. The external force P and the moments are distributed to the nodes as follows

If the force P or moment Mx0 is applied at a node the corresponding distributed load p or moment m_x0 is obtained by dividing it with the node spacing; otherwise the force or moment is first distributed to the two neighboring nodes and then divided with the grid spacing to obtain the corresponding distributed loads or moments at the nodes.

The continuity equations along the line y = -b/2 + b₀ express the continuity of the deflection w and slope ∂w/∂y and the equilibrium of bending moment myy and shear force Qy: these equations are given by

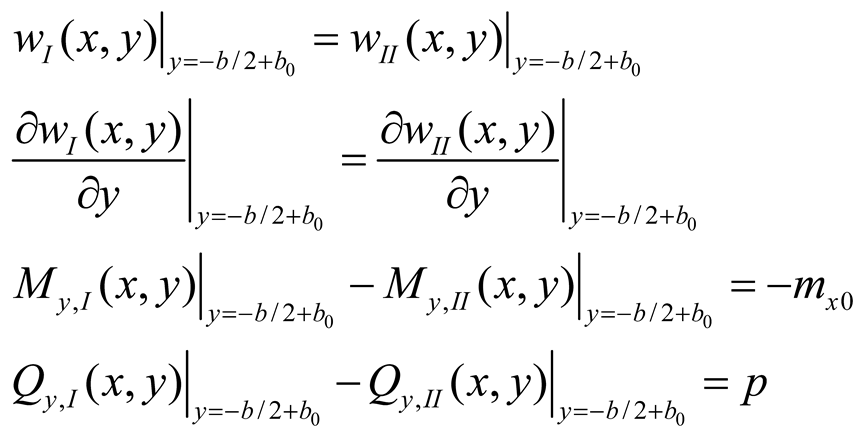(13a-d)

Equations (13a-d) are set at each of the M nodes along the line y = -b/2 + b₀.

Following number of equations are set for boundary conditions an continuity equations

Plate zone I: 2N_I equations at x = -a/2, 2N_I equations at x = a/2, and 2M equations at y = -b/2
Plate zone II: 2N_II equations at x = -a/2, 2N_II equations at x = a/2, and 2M equations at y = b/2
4M continuity equations at y = -b/2 + b₀.

So there are as many unknowns as equations.

In case of an external moment My0, the continuity equations are applied along the line x = x₀.

It is noted that discrete supports can also be modeled. In this case a node is placed at the position of the support and the continuity equation involving the shear force is replaced with a zero deflection equation.

b): Continuous rectangular plates

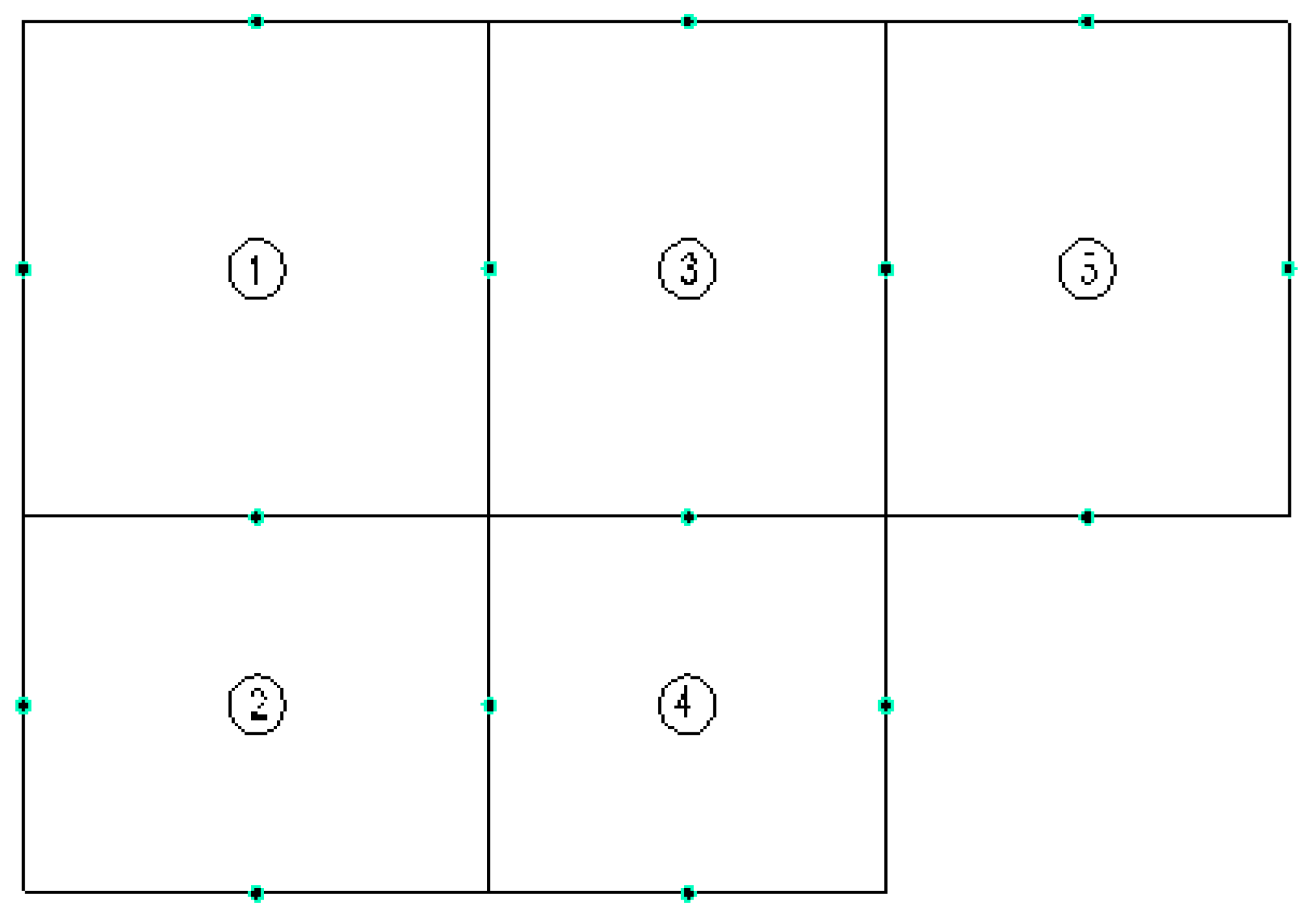
Let us consider the continuous plate represented in Figure 3. The same deflection approximation is taken in each panel of the plate. For simplification purpose in the current example, only one term of each series is considered and consequently only one collocation point along the sides of each panel. This leads to eight unknowns for each panel, hence to forty unknowns for the five panels of our example.

On the one hand two boundary conditions are applied at each collocation point along the boundary of the plate, leading to twenty equations. On the other hand four continuity equations are applied at the collocation points between two panels, leading to twenty equations. So there are as many unknowns as equations.

Generally the panels aligned in x-direction should have the same number of collocation points in the edges parallel to y-axis, and vice versa.

c): Plate having a free edge clamped at its ends

A plate having a free edge that is clamped at one or at both ends was considered. Recalling that the corner points do not deflect due to the single series (the trigonometric functions are so chosen), the free edge clamped moments due to the series are automatically zero. To fix this, the odd an even numbering of the series was inverted: this led to deflections at the corner points of the plate due to the series and the boundary conditions had to be satisfied accordingly. An example was calculated in Results 3.5, but the results were not satisfactorily. Further research is needed to analyze this case.

3. Results and Discussion

3.1. Plate Clamped Along All Edges and Subjected to a Uniformly Distributed Loading P

Taking the particular solution w_p(x,y) as the deflection of a plate strip parallel to x-axis and clamped at both ends, the displacement surface using the symmetry considerations mentioned earlier is given by

(14)

The bending moments per unit length at the plate center, depending on the ratio b/a, are M_x,m = qa²/N_xm, M_y,m = qa²/N_ym and the clamped moments are M_xcl = -qa²/N_xcl, M_ycl = -qa²/N_ycl whereby M and N are the number of terms of the first and second single series, respectively. Details of the analysis and results are presented in the supplementary material “Rectangular plate clamped along all edges” and the collocation points are the following

Case M = 1 N = 1: (a/2, 0) and (0, b/2)
Case M = 2 N = 2: (a/2, 0), (a/2, b/4), and (0, b/2), (a/4, b/2)
Case M = 3 N = 3: (a/2, 0), (a/2, b/6), (a/2, b/3) and (0, b/2), (a/6, b/2), (a/3, b/2)

Table 1 lists the results obtained using the Czerny tables [14] (exact results) and those obtained in the present study.

As Table 1 shows, the results show good agreement with the exact results and the accuracy is increased the more terms of series are considered. It is worth mentioning that Czerny [14] presents the maximal bending moments M_y,max that not necessarily occur at the plate center while the present study presents the value at the plate center.

3.2. Rectangular Plate Simply Supported Along All Edges and Subjected to a Uniform Load

Taking the particular solution w_p(x,y) as the deflection of a plate strip parallel to x-axis and simply supported at both ends, the displacement function using the symmetry considerations mentioned earlier is given by

(15)

The bending moments per unit length at the plate center, depending on the ratio b/a, are M_x,m = qa²N_xm, M_y,m = qa²N_ym whereby M and N are the number of terms of the first and second single series, respectively. Details of the analysis and results are presented in the supplementary material “Rectangular plate simply supported along all edges” whereby the collocation points were (a/2, 0) and (0, b/2). Table 2 lists the results obtained by Courbon [15] using the Fourier analysis (exact results) and those obtained in the present study.

As Table 2 shows, the results are in agreement with the exact results, with only one term of each series. It was observed that the constants of the second single series are zero, which corresponds to a Lévy solution routinely used in case of two opposite edges simply supported. It can be concluded that the Lévy solution is a special case of the solution of the present study. The deflection surface taking only the first term of the series is then

(16)

3.3. Square Plate Resting on Four Corner Points with All Edges Free Subjected to a Uniform Load

The square plate is supported on the four corner points while the edges are free. Taking the particular solution w_p(x,y) as the deflection of a plate strip parallel to x-axis and simply supported at both ends, the displacement function using the symmetry considerations mentioned earlier is given by

(17)

The bending moments per unit length at the plate center are M_x,m = qa²N_xm, M_y,m = qa²N_ym, and at the middle of the free edges M_xfe = qa²N_xfe, M_yfe = qa²N_yfe whereby M and N are the number of terms of the first and second single series, respectively. Table 3 displays the results obtained by Timoshenko [5] taking the Poisson ratio ν = 0.25 and those obtained in the present study. Details of the analysis and results are presented in the supplementary material “Square plate resting on four corner points” whereby the collocation points were the same as those of Results 3.1.

As Table 3 shows, the results show good agreement with the exact results, and the accuracy is increased the more terms are considered.

3.4. Rectangular Plate Simply Supported at Edges x = ± a/2, Clamped at y = b/2, Free at y = -b/2 and Subjected to a Uniformly Distributed Loading p

(18)

The bending moments at the middles of the free and clamped edge, depending on the ratio b/a, are M_xfe = qb²/N_xfe and M_ycl = -qb²/N_ycl, respectively, whereby N and M are the number of terms of the first and second single series, respectively. Details of the analysis and results are presented in the supplementary material “Rectangular plate free, clamped, and simply supported” with the following collocation points

Case M = 1 N = 1: (a/2, 0), (0, b/2), and (0, -b/2)
Case M = 1 N = 2: (a/2, -b/6), and (a/2, b/4), (0, b/2), and (0, -b/2)

Here the collocation points were distributed along the edge x = a/2 so as to avoid a singular matrix. Table 4 lists the results obtained using the Czerny tables [14] (exact results) and those obtained in the present study.

As Table 4 shows, the results are in agreement with the exact results. It was observed that the constants of the first single series (N = 1, N = 2) are zero, which leads to a Lévy solution used in case of two opposite edges simply supported. Therefore in order to increase the accuracy more terms of the second series (M = 2, 3 …) should be considered.

3.5. Rectangular Plate Clamped at Edges x = ± a/2 and y = b/2, Free at y = -b/2 and Subjected to a Uniformly Distributed Loading

This case of a plate having a free edge that is clamped at one or at both ends was analyzed in Materials and Methods Section. Taking the particular solution w_p(x,y) as the deflection of a plate strip parallel to x-axis and clamped at both ends, the displacement function using the symmetry considerations mentioned earlier is given by

(19)

The bending moments at the middles of the free and clamped edge, depending on the ratio b/a, are M_xfe = qb²/N_xfe and M_ycl = -qb²/N_ycl, respectively, whereby N and M are the number of terms of the first and second single series, respectively. Details of the analysis and results are presented in the supplementary material “Rectangular plate free at one edge and clamped along the other edges.” Table 5 lists the results obtained using the Czerny tables [14] (exact results) and those obtained in the present study.

As Table 5 shows, the results are not in agreement with the exact results and no convergence is observed with increasing number of terms. Further research is needed to analyze this case, whereby a powerful tool may be utilized to avoid computing errors. Fogang [16] proposed a solution to this problem using the flexibility method and a Lévy type solution.

4. Conclusion

In this paper, arbitrarily loaded isotropic rectangular Kirchhoff plates supported at all corners, the edges being simply supported, clamped or free, were analyzed. The deflection surface was approximated with the sum of a particular solution to the governing differential equation and two single series: the terms of the series were the product of an unknown function of an independent variable and a trigonometric function of the other independent variable, whereby the trigonometric functions were zero at the corner points. On the one hand the particular solution satisfied the nonhomogeneous differential equation and the single series were chosen so as to satisfy the homogeneous differential equation. On the other hand the boundary conditions were satisfied at selected collocation points along the boundary, the number of collocation points in each direction corresponding to the number of terms of the associated series. Numerical results were presented and showed good agreement with the exact results. In future research cantilevered plates and plates having two adjacent edges free will be analyzed using this approach.

However, the following study limitations were noted: the case of a plate having a free edge clamped at its ends was analyzed but the results were not satisfactorily. This should be investigated in future research.

Supplementary Materials

The following supporting information can be downloaded at: Preprints.Org, The following files were uploaded during submission: “Rectangular plate clamped along all edges” “Rectangular plate simply supported along all edges” “Square plate resting on four corner points,” “Rectangular plate free, clamped, and simply supported,” “Rectangular plate free at one edge and clamped along the other edges.”

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Efforts and Deformations for the Formulation of Equation (5d)

	(A1)
	(A2)
	(A3)
	(A4)
	(A5)
	(A6)

The slopes ∂w/∂x and ∂w/∂y used as boundary conditions are given by

(A7)

The shear force Q_y used by continuity equations and in case of symmetry are expressed using Equations (3b), (5), and (9a, b), as follows

(A8)

The efforts and deformations for formulations of the deflection surface according to Equations (5b-c) will be expressed through a combination of the formulations of (5a, d).

References

Kirchhoff, G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. J. für die Reine und Angew. Math.; vol. 18, no. 40, pp. 51-88, 1850. [CrossRef]
Germain, S. Remarques sur la nature, les bornes et l’étendue de la question des surfaces élastiques et équation générale de ces surfaces. impr. de Huzard-Courcier, paris, 1826.
Navier, C.L. Extrait des recherches sur la flexion des plaques élastiques. Bull. des Sci. Société Philomath, Paris, vol. 10, no. 1, pp. 92–102, 1823.
Lévy, M. Sur l’équilibre élastique d’une plaque rectangulaire. Comptes rendus l’Académie des Sci. Paris, vol. 129, no. 1, pp. 535-539, 1899.
Timoshenko, S., Woinowsky-Krieger, S. Theory of plates and shells. Second ed., McGraw Hill, New York (1959).
Trefftz, E. Ein Gegenstück zum Ritzschen Verfahren (An alternative to the Ritz method). Proceedings, 2nd International Congress of Applied Mechanics, Zurich, pp. 131-137, 1926.
Herrera, I. (2000), Trefftz method: A general theory. Numer. Methods Partial Differential Eq., 16: 561-580. [CrossRef]
Like Deng, Dongdong Wang. An accuracy analysis framework for meshfree collocation methods with particular emphasis on boundary effects. Computer Methods in Applied Mechanics and Engineering, Volume 404. 2023. 115782. [CrossRef]
D. Borkowska, M. Borkowski. A numerical analysis of the generalized collocation Trefftz method for some 2D Laplace problems. Engineering Analysis with Boundary Elements, Volume 152, Pages 608-626. 2023. [CrossRef]
Volkov-Bogorodskiy, D.B., Moiseev, E.I. Generalized Trefftz Method in the Gradient Elasticity Theory. Lobachevskii J Math 42, 1944–1953 (2021). [CrossRef]
R. Piltner. Some remarks on Trefftz type approximations. Engineering Analysis with Boundary Elements, Volume 101, Pages 102-112. 2019. [CrossRef]
Hsin-Yun Hu, Zi-Cai Li, Alexander H.-D. Cheng. Radial basis collocation methods for elliptic boundary value problems. Computers & Mathematics with Applications, Volume 50, Issues 1–2, 2005, Pages 289-320. [CrossRef]
Yang, Jie & Potier-Ferry, Michel & Akpama, Koffi & Hu, Heng & Koutsawa, Yao & Tian, Haitao & Zeze, Djedje. (2019). Trefftz Methods and Taylor Series. Archives of Computational Methods in Engineering. 27. [CrossRef]
Czerny, F. Tafeln für vierseitig und dreiseitig gelagerte Rechteckplatten (Tables for rectangular plates supported along four and along three edges). Beton-Kalender 1982, Teil 1. Verlag Von Wilhelm, Ernst & Sohn Berlin, München S. 397-474. In German.
Courbon, J., Theillout, JN. Formulaire de résistance des matériaux. Techniques de l’Ingénieur, traité Construction. 1987. https://www.techniques-ingenieur.fr/base-documentaire/archives-th12/archives-le-second-oeuvre-et-l-equipement-du-batiment-tiacc/archive-1/resistance-des-materiaux-c2060/.
Fogang, V. Analysis of Arbitrarily Loaded Rectangular Thin Plates with Two Opposite Edges Supported, One or Both of them Clamped, Using the Flexibility Method and a Modified Lévy Solution. Preprints 2023, 2023052121. [CrossRef]

Figure 1. Spatial axis convention X, Y, Z.

Figure 2. Plate subjected to an external force P and external moments Mx0 and My0.

Figure 3. Continuous plate.

Table 1. Coefficients of bending moments.

b/a =	1.00
	N_xm	N_ym	N_xcl	N_ycl	N_xm	N_ym	N_xcl	N_ycl
	Czerny tables [14]
	56.80	56.80	19.40	19.40	29.60	93.50	13.20	17.50
	Present study
M = 1 N = 1	54.50	58.09	29.48	25.62	32.34	83.91	15.93	27.41
M = 2 N = 2	55.85	55.91	17.97	17.88	29.61	94.69	12.67	16.44
M = 3 N = 3	56.62	56.56	19.76	19.93	29.56	99.21	13.36	17.99

Table 2. Coefficients of bending moments at the middle of the plate.

b/a =	1.00		1.25		1.667		2.00
	N_xm	N_ym	N_xm	N_ym	N_xm	N_ym	N_xm	N_ym
	Courbon [15]
	0.0368	0.0368	0.0561	0.0334	0.0820	0.0242	0.0965	0.0174
	Present study
M = 1 N = 1	0.0369	0.0369	0.0562	0.0334	0.0822	0.0242	0.0966	0.0173

Table 3. Coefficients of bending moments.

	N_xm	N_ym	N_xfe	N_yfe
	Timoshenko [5]
	0.1109	0.1109	0.1527	0.1527
	Present study
M = 1 N = 1	0.1048	0.0962	0.1384	0.1302
M = 2 N = 2	0.1082	0.1073	0.1481	0.1475
M = 3 N = 3	0.1094	0.1091	0.1498	0.1496

Table 4. Coefficients of bending moments.

b/a =	0.50		1.00		1.20		1.50
	N_xfe	N_ycl	N_xfe	N_ycl	N_xfe	N_ycl	N_xfe	N_ycl
	Czerny tables [14]
	9.71	3.41	11.37	8.51	14.06	11.79	19.64	18.13
	Present study
M = 1 N = 1	9.71	3.24	11.35	8.25	14.05	11.47	19.62	17.60
M = 1 N = 2	9.71	3.24	11.35	8.25	14.05	11.47	19.62	17.60

Table 5. Coefficients of bending moments.

b/a =		0.50			1.00			1.50
	N_xfem	N_ycl	N_xfecl	N_xfem	N_ycl	N_xfecl	N_xfem	N_ycl	N_xfecl
	Czerny tables [14]
	10.64	4.93	3.43	24.29	17.59	11.59	53.69	39.47	26.73
	Present study
M = 1 N = 1	18.35	2.51	1.43	25.18	9.73	12.02	54.16	21.90	27.03
M = 1 N = 2	21.89	2.61	0.36	25.41	9.65	8.72	53.92	21.61	25.82
M = 2 N = 2	28.53	1.37	0.22	27.52	5.28	7.21	54.73	13.12	25.13
M = 2 N = 3	-10.08	1.54	-0.10	27.22	7.41	-2.82	48.68	18.42	-28.25

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Analytical Solution to Rectangular Kirchhoff Plates Supported at All Corner Points Using Two Single Series and the Boundary Collocation Method

Abstract

1. Introduction

2. Materials and Methods

2.1. Governing Equations of the Plate

2.2. Rectangular Plate Supported at All Corner Points with the Edges Supported or Free

3. Results and Discussion

3.1. Plate Clamped Along All Edges and Subjected to a Uniformly Distributed Loading P

3.2. Rectangular Plate Simply Supported Along All Edges and Subjected to a Uniform Load

3.3. Square Plate Resting on Four Corner Points with All Edges Free Subjected to a Uniform Load

3.4. Rectangular Plate Simply Supported at Edges x = ± a/2, Clamped at y = b/2, Free at y = -b/2 and Subjected to a Uniformly Distributed Loading p

3.5. Rectangular Plate Clamped at Edges x = ± a/2 and y = b/2, Free at y = -b/2 and Subjected to a Uniformly Distributed Loading

4. Conclusion

Supplementary Materials

Conflicts of Interest

Appendix A. Efforts and Deformations for the Formulation of Equation (5d)

References

MDPI Initiatives

Important Links

Subscribe