Physics-Informed Neural Networks for UAV System Estimation

Preprint

Article

Physics-Informed Neural Networks for UAV System Estimation

Altmetrics

Downloads

107

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 October 2024

Posted:

30 October 2024

You are already at the latest version

Alerts

Abstract

The dynamic nature of quadrotor flight introduces significant uncertainty in system parameters, such as thrust and drag factor. Consequently, operators grapple with escalating challenges in implementing real-time control actions. This study delves into an approach for estimating the model of quadrotor Unmanned Aerial Vehicles using Physics-Informed Neural Networks (PINNs) when you have a limited amount of data available. PINNs offer the potential to tackle issues like heightened non-linearities in low-inertia systems, elevated measurement noise, and constraints on data availability. The effectiveness of the estimator is showcased in a simulation environment with real data and juxtaposed with a state-of-the-art technique, such as the Extended Kalman Filter (EKF).

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

One of the main challenges in control theory consists in realizing a dynamic model of the physical system under study to understand and predict its behavior over time. This may lead to a highly complex mathematical description of the considered system, also requiring to yield dedicated experiments to estimate the unknown model parameters [1]. This is particularly true for complex systems, such as, for instance, Unmanned Aerial Vehicle (UAVs), since they are considered unstable multiple-input and multiple-output (MIMO) dynamics systems. When actual real data are not available (e.g., due to the lack of reliable knowledge about the system behavior or the lack of or inaccuracy of measurements), an efficient alternative is the so-called system identification, which relies on obtaining the mathematical models of a dynamic system from measured data of its input and output parameters. Two approaches can be adopted for system identification, namely, grey box model, also known as semi-physical model (i.e., when the constructed model still has a number of unknown free parameters that are estimated through system identification) and black box model (i.e., when no prior model is available) [2]. Regardless of the adopted model, system identification strategies consist in designing and conducting an identification experiment to collect data, selecting the structure of the dynamic system also specifying which parameters are to be identified, and fitting the model parameters to the obtained data; the overall quality of the resulting model is then evaluated through a validation procedure [1].

Research on systems identification has garnered considerable attention in recent decades, starting from 50s, and has become a vital discipline in various applications within the field of automatic control. This includes areas such as robotics, industrial processes, reduced-order modeling, and model testing.

In recent decades, as researchers and engineers have gained access to larger amounts of data, one of the most widely used methods for system identification has been the Least Squares Method. This approach can be considered the foundation of data-driven system modeling.

In [3], a classification of models identification is presented based on the applied methodologies. The classification includes Fuzzy Logic Theory, Genetic Algorithm, Neural Network, Swarm Intelligence Optimization Algorithms, Auxiliary Model Identification Method, Hierarchical Method, and Stochastic Theory [4].

Referring to the last method, in [5] crucial principles of realization theory were introduced, particularly emphasizing controllability and observability concepts. Their focus was on linear systems identification, with a special emphasis on establishing the minimal state-space representation to define the subspace within which the system dynamics evolves. They pioneered the concept of state-variable equations, which facilitates the realization of an external description through an equivalent internal description of a dynamical system. A second algorithm addressing the same problem was simultaneously presented by Kalman (see [6]), utilizing the principles of controllability and observability and necessitating linear algebra-type computations. State-space models are particularly well-suited for this approach as they lend themselves to linear algebra techniques, robust numerical simulation, and modern control design methods. A few years later, Ho and Kalman [5] approached the same problem from a new perspective. They demonstrated that the minimum realization problem is equivalent to a representation problem involving a sequence of real matrices known as Markov parameters (pulse response samples).

During the 90s, expanding upon the foundational work by Gilbert and Kalman, various methods were developed to identify the most observable and controllable subspace of a system based on given input-output (I/O) data. Some years later, at NASA, Juang devised an approach to concurrently ascertain a linear state-space model and the corresponding Kalman filter using noisy input-output measurements (see [7] for details). Referred to as the Observer/Kalman Identification Algorithm (OKID) and exclusively formulated in the time domain, this method computes the Markov parameters of a linear system. Subsequently, both the state-space model and a corresponding observer are determined simultaneously from these parameters. The Kalman Filter was therefore a reference point for identification in the case of linear systems and its parameters. Subsequently, the theory was extended to nonlinear systems through the Extended Kalman Filter (EKF) in various versions (see, e.g., the work in [8] for the polynomial one), starting from a series of measurements subject to noise, and was successful in any application that can be linked to control theory.

In this regard, it is worth noting that, an interesting comparison among modern methods for parameter estimation of aircrafts is presented in [9]. In particular, by using real flight data, the authors find that the performance of Filter Error Methods (FEMs), such as Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF), prevail over Equation Error Methods (EEMs) and Output Error Methods (OEMs), particularly in the presence of turbulence and noise.

More recently, the use of many machine learning tools for control problems is gaining attention. The technology of artificial neural networks has undergone significant development since the late 20th century. Over time, neural networks have found applications in various fields, particularly for cyber-physical systems, with notable contributions in intelligent control, nonlinear optimization, computer vision, biomedical engineering, robotics, and system identification. Neural network identification leverages the structure of a nonlinear system, enabling the simulation of input-output relationships through the network’s ability to approximate any nonlinear mapping. It employs the self-adaptation and self-learning capabilities of neural networks to implement simple learning algorithms in engineering, ultimately achieving the forward or inverse model of the system through training. This method exhibits the following characteristics:

No need to establish the model structure of the actual system, as the neural network itself serves as a model for network identification.
It is capable of identifying any linear or nonlinear model.
The neural network not only serves as a model but is also an actual system achievable through physics.

However, it comes with certain limitations:

Local minimum problem.
Lengthy training time and slow learning speed.
Difficulty in extracting ideal training samples.
Challenges in optimizing the network structure.
Difficulty in completely solving the convergence problem theoretically for the neural network algorithm.

To address these limitations, numerous researchers have proposed improved neural network identification methods, resulting in favorable identification outcomes (see, e.g., [10,11]).

In the above described context, the main contribution of this paper is to exploit the power in the management and use of a limited amount of data available data in Neural Networks with the physical laws of the flight dynamics of a quadcopter. In particular, we use Physics-Informed Neural Networks (PINNs), also known as Theory-Trained Neural Networks, to estimate the drone model. In fact, in the last decade, aerial robots, and particularly small UAVs and drones, have witnessed a continuously increasing use in a wide range of services (see, e.g., [12]). As a consequence, the identification and control (and hence the system parameters estimation) of these systems is of paramount importance from different point of view (see [13,14]).

We conclude this section highlighting that the use of PINNs for system identification is recently reaching relevant interest in the research community. As an example, the work in [15] proposes the use of PINNs for non-linear system identification for power system dynamics. In particular, the final aim of this contribution is to discover the frequency dynamics of future power systems. To assess the performance of the presented model and validate their proposal, the authors compare the estimator against the UKF. PINNS are also used in [16] to discover the ordinary differential equation (ODE) of a rotor system from noise measurements and assess the healthy/faulty machine condition. The validation is performed on a test bench. System identification of structural systems with a multiphysics damping model through PINNs is presented in [17], while in [18] they are adopted to estimate motion and identify system parameters of a moored buoy under different sea states. To the best of authors knowledge, a first attempt in the use of PINNs for quadrotor dynamical modeling is proposed in [19], where a comparison with other existing approaches is performed, showing that PINNs outperform linearized mathematical models and classical black-box approaches based on Deep Neural Networks (DNNs) in terms of test error, while also exhibiting better capability of underlying existing relationships between parameters. In particular, in [19] the orientation estimation of a quadrotor is dealt with, while in the present paper we focus on all the state variables, therefore also the spatial ones.

The reminder of the paper is organized as follows. In Section 2 the drone dynamics model is recalled. Section 3 illustrates the two methodologies chosen to compare system model identification: a quick recall of the Extended Kalman Filter and then the idea on which PINNs are based is described. Section 4 shows the simulation and comparison results between the methods mentioned above. Some final considerations and future research ideas conclude the paper.

2. Mathematical Model of a Quadrotor

The quadrotor analyzed in this study is composed of a rigid structure with four rotors (for more details, refer to [20,21]). The propellers produce a force

F_{i} = b \cdot ω_{p, i}^{2}

, which is proportional to their angular velocity

ω_{p, i}

, for

i = 1, 2, 3, 4

. Propellers 1 and 3 spin counterclockwise, while propellers 2 and 4 spin clockwise. In the following discussion, the quadrotor’s orientation will be described using Euler angles. The frames

R C (O, e_{1}, e_{2}, e_{3})

and

R Γ (Ω, ε_{1}, ε_{2}, ε_{3})

) represent the reference systems fixed to the Earth and the quadrotor, respectively, with

Ω

located at the quadrotor’s center of mass (see Figure 1).

The quadrotor’s position in

R C

is represented by

p = {(x, y, z)}^{T}

, while its orientation is defined by the Euler angles

α = {(ϕ, θ, ψ)}^{T}

, where

ϕ \in [- π / 2, π / 2)

θ \in (- π / 2, π / 2)

, and

ψ \in [- π, π)

correspond to the roll, pitch, and yaw angles, respectively. The 3–2–1 sequence is utilized here, as in [22]. Furthermore,

v = {(v_{x}, v_{y}, v_{z})}^{T}

and

ω = {(ω_{1}, ω_{2}, ω_{3})}^{T}

denote the linear and angular velocities of the quadrotor’s center of mass, expressed in

R C

and

R Γ

, respectively. The quadrotor’s translational dynamics are expressed in

R C

, while its rotational dynamics are expressed in

R Γ

\begin{matrix} \dot{p} & = v \\ \dot{v} & = \frac{1}{m} (f_{p} + f_{g}) \\ \dot{α} & = M (α) ω \\ \dot{ω} & = J^{- 1} (- \tilde{ω} J ω + τ_{p} + τ_{g y}) \end{matrix}

(1)

where m represents the mass of the quadrotor,

f_{p} = R (α) φ_{p}

is the force exerted by the propellers in

R C

(

φ_{p}

is the same force, but expressed in

R Γ

), and J (a positive definite symmetric matrix in

R^{3 \times 3}

, expressed in

R Γ

) is the quadrotor’s inertia matrix, and

\tilde{ω} = (\begin{matrix} 0 & - ω_{3} & ω_{2} \\ ω_{3} & 0 & - ω_{1} \\ - ω_{2} & ω_{1} & 0 \end{matrix})

(2)

is the so-called dyadic representation of

ω

. Furthermore,

φ_{p} = (\begin{matrix} 0 \\ 0 \\ u_{p} \end{matrix}), u_{p} = \sum_{i = 1}^{4} F_{i}, f_{g} = (\begin{matrix} 0 \\ 0 \\ - m g \end{matrix})

(3)

τ_{p} = (\begin{matrix} τ_{1} \\ τ_{2} \\ τ_{3} \end{matrix}) = (\begin{matrix} ℓ b (ω_{p, 2}^{2} - ω_{p, 4}^{2}) \\ ℓ b (ω_{p, 3}^{2} - ω_{p, 1}^{2}) \\ c (ω_{p, 1}^{2} - ω_{p, 2}^{2} - ω_{p, 3}^{2} - ω_{p, 4}^{2}) \end{matrix})

(4)

are the input forces (as shown in 3) and moments (as shown in Section 2) generated by the propellers (expressed in

R Γ

), where ℓ is the distance from the center of mass

C G

to the rotor shaft, and b (with units [b]=

\frac{N, s^{2}}{r a d^{2}}

) and c (with units [c]=

\frac{N, s^{2}, m}{r a d^{2}}

) are the thrust and drag coefficients, respectively. It is evident that:

\begin{matrix} (\begin{matrix} F_{1} \\ F_{2} \\ F_{3} \\ F_{4} \end{matrix}) = {(\begin{matrix} 1 & 1 & 1 & 1 \\ 0 & ℓ & 0 & - ℓ \\ - ℓ & 0 & ℓ & 0 \\ c & - c & c & - c \end{matrix})}^{- 1} (\begin{matrix} u_{p} \\ τ_{1} \\ τ_{2} \\ τ_{3} \end{matrix}), \\ (\begin{matrix} ω_{p, 1}^{2} \\ ω_{p, 2}^{2} \\ ω_{p, 3}^{2} \\ ω_{p, 4}^{2} \end{matrix}) = (\begin{matrix} \frac{1}{4 b} & 0 & \frac{- 1}{2 b ℓ} & \frac{1}{4 c} \\ \frac{1}{4 b} & \frac{1}{2 b ℓ} & 0 & \frac{- 1}{4 c} \\ \frac{1}{4 b} & 0 & \frac{1}{2 b ℓ} & \frac{1}{4 c} \\ \frac{1}{4 b} & \frac{- 1}{2 b ℓ} & 0 & \frac{- 1}{4 c} \end{matrix}) (\begin{matrix} u_{p} \\ τ_{1} \\ τ_{2} \\ τ_{3} \end{matrix}), \\ ω_{p, i} = \sqrt{\frac{F_{i}}{b}}, 0 \leq F_{i} \leq F_{i, m a x}, 0 \leq ω_{p, i} \leq ω_{p, i, m a x} \end{matrix}

(5)

with

i = 1, 2, 3, 4

, where

F_{i, m a x}

and

ω_{p, i, m a x}

represent the maximum forces and angular velocities for each propeller, constrained by physical limitations. Additionally,

f_{g}

in (3) refers to the gravitational force, expressed in

R C

. Vectors expressed in

R Γ

are converted into vectors in

R C

using the rotation matrix

R (α) = (\begin{matrix} c_{θ} c_{ψ} & s_{ϕ} s_{θ} c_{ψ} - c_{ϕ} s_{ψ} & c_{ϕ} s_{θ} c_{ψ} + s_{ϕ} s_{ψ} \\ c_{θ} s_{ψ} & s_{ϕ} s_{θ} s_{ψ} + c_{ϕ} c_{ψ} & c_{ϕ} s_{θ} s_{ψ} - s_{ϕ} c_{ψ} \\ - s_{θ} & s_{ϕ} c_{θ} & c_{ϕ} c_{θ} \end{matrix})

(6)

where

c_{★} = cos (★)

s_{★} = sin (★)

★ = ϕ, θ, ψ

. The angular velocity dynamics are expressed using the following matrix:

M (α) = (\begin{matrix} 1 & s_{ϕ} {tg}_{θ} & c_{ϕ} {tg}_{θ} \\ 0 & c_{ϕ} & - s_{ϕ} \\ 0 & s_{ϕ} {sc}_{θ} & c_{ϕ} {sc}_{θ} \end{matrix})

where

{tg}_{★} = tan (★)

and

{sc}_{★} = sec (★)

with

★ = ϕ, θ, ψ

.Assuming small angles for

ϕ

(roll) and

θ

(pitch), which is reasonable for a quadrotor performing non-aggressive maneuvers, this matrix can be approximated by the identity matrix, i.e.,

M (α) ≃ I_{3 x 3}

[23]. Therolling torque

τ_{1}

is generated by the forces

F_{2}

and

F_{4}

, while the pitching torque

τ_{2}

is generated by the forces

F_{1}

and

F_{3}

. According to Newton’s third law, the propellers exert a yawing torque

τ_{3}

on the quadrotor body in the direction opposite to the propeller rotation. Furthermore, the gyroscopic torque arising from the propeller rotations is given by

τ_{g y} = \sum_{i = 1}^{4} {(- 1)}^{i} J_{p, i} ω_{p, i} \tilde{ω} ϵ_{3}

(7)

where

J_{p, i}

, for

i = 1, 2, 3, 4

, represents the moment of inertia of the

i_{th}

motor and propeller about its axis of rotation. Finally, the gyroscopic torque can also be expressed as

τ_{g y}^{\circ} = \sum_{i = 1}^{4} {(- 1)}^{i} J_{p}^{\circ} ω_{p, i} \tilde{ω} ϵ_{3} = J_{p}^{\circ} ω_{p} (\begin{matrix} ω_{2} \\ - ω_{1} \\ 0 \end{matrix})

(8)

where

ω_{p} = - ω_{p, 1} + ω_{p, 2} - ω_{p, 3} + ω_{p, 4}

is referred to as the rotor relative speed. Given these conditions, the mathematical model (1) of the quadrotor can be rewritten as:

\begin{matrix} \dot{x} (t) & = v_{x} (t), \dot{y} (t) = v_{y} (t), \dot{z} (t) = v_{z} (t) \\ {\dot{v}}_{x} (t) & = (c_{ϕ (t)} s_{θ (t)} c_{ψ (t)} + s_{ϕ (t)} s_{ψ (t)}) \frac{u_{p} (t)}{m} \\ {\dot{v}}_{y} (t) & = (c_{ϕ (t)} s_{θ (t)} s_{ψ (t)} - s_{ϕ (t)} c_{ψ (t)}) \frac{u_{p} (t)}{m} \\ {\dot{v}}_{z} (t) & = - g + c_{ϕ (t)} c_{θ (t)} \frac{u_{p} (t)}{m} \\ \dot{ϕ} (t) & = ω_{1} (t), \dot{θ} (t) = ω_{2} (t), \dot{ψ} (t) = ω_{3} (t) \\ {\dot{ω}}_{1} (t) & = \frac{J_{2} - J_{3}}{J_{1}} ω_{2} (t) ω_{3} (t) + \frac{J_{p}}{J_{1}} ω_{p} (t) ω_{2} (t) + \frac{1}{J_{1}} τ_{1} (t) \\ {\dot{ω}}_{2} (t) & = \frac{J_{3} - J_{1}}{J_{2}} ω_{1} (t) ω_{3} (t) - \frac{J_{p}}{J_{2}} ω_{p} (t) ω_{1} (t) + \frac{1}{J_{2}} τ_{2} (t) \\ {\dot{ω}}_{3} (t) & = \frac{J_{1} - J_{2}}{J_{3}} ω_{1} (t) ω_{2} (t) + \frac{1}{J_{3}} τ_{3} (t) . \end{matrix}

(9)

where the state space vector is

[x y z v_{x} v_{y} v_{z} ϕ θ ψ ω_{1} ω 2 ω_{3}]

, the control input are

[u_{p} τ_{1} τ_{2} τ_{3}]

. Given the aims of the research, it is assumed that we have a limited amount of data available in the form input-output (state). Moreover, the system identification methods that will be presented in Section 3 are in discrete form, Thus, the quadrotor system equations (9) will be implemented in discrete form by keeping the functions constant over each time interval

[t_{i}, t_{i + 1})

, where

t_{i + 1} - t_{i} = Δ t

for

i = 0, \dots, i_{max} - 1

, and

t_{i_{max}} = t_{f}

represents the final mission time. This discrete-time formulation allows for accurate modeling within each interval, enhancing the overall performance of the UAV system. The digitalization is obtained by a first-order discretization.

3. System Identification Methods

3.1. Extended Kalman Filter

The EKF ([24]) is an adaptation of the standard Kalman filter designed for use when the system and/or measurement models are nonlinear. The approach underlying the extended Kalman filter is based on the following procedure. Given the system type:

\begin{matrix} s_{k} = f (s_{k - 1}, μ_{k - 1}) + n_{1, k} \\ z_{k} = h (x_{k}) + n_{2, k} \end{matrix}

(10)

where

s_{k}

is the state space vector,

z_{k}

is the output and

μ_{k - 1}

is the control input, it approximates the nonlinear functions of the system

x_{k}

and

z_{k}

, through a Taylor series expansion stopped at the first order around the current estimate, thus making the system linear. The noise vectors

n_{1, k}

and

n_{2, k}

represent disturbances affecting the state and measurements, respectively, and are assumed to be uncorrelated with each other. Given a random variable s we want to know the probability density of the variable y obtained from the transformation of the variable s. Moments up to first order are studied.

\begin{matrix} s \sim N (\hat{s}, σ_{s}^{2}) = \hat{s} + δ_{s} with δ_{s} \sim N (0, σ_{s}^{2}) \end{matrix}

(11)

\begin{matrix} y = f (s) = f (\hat{s} + δ_{s}) \end{matrix}

(12)

whose development is

y = f (\hat{s}) + λ f δ_{s} + \frac{1}{2} Δ^{2} f δ_{s}^{2}

. Then,

J_{s}^{h} = {[\frac{\partial h}{\partial s}]}_{s = {\hat{s}}_{k | k}}

is defined as the Jacobian matrix of the function h with respect to s and

J_{s}^{f} = {[\frac{\partial f}{\partial s}]}_{s = {\hat{s}}_{k | k}}

is the Jacobian matrix of f respect to s. Moreover, the conditional probability function is assumed to be Gaussian. Using these approximations the system turns out to be linear, so the Kalman filter can be applied, obtaining the following recursive equations (respectively referred to the prediction and the correction):

\begin{matrix} {\hat{s}}_{k | k - 1} = f (s_{k | k - 1}, μ_{k}) \\ P_{k | k - 1} = J_{s}^{f} P_{k - 1 | k - 1} J_{s}^{f^{T}} + Q \end{matrix}

(13)

\begin{matrix} n_{2, k} = z_{k} - h ({\hat{s}}_{k | k - 1}) \\ S_{k} = J_{s}^{h} P_{k | k - 1} J_{s}^{h^{T}} + R_{k} \\ K_{k} = P_{k | k - 1} J_{s}^{h^{T}} S_{k}^{- 1} \\ s_{k | k} = s_{k | k - 1} + K_{k} n_{2, k} \\ P_{k | k} = (I - K_{k} J_{s}^{h}) P_{k | k - 1} \end{matrix}

(14)

where the matrices Q and R have the same properties as in the linear Kalman filter. However, there are no assurances regarding the quality of the estimates produced, and the extended Kalman filter is highly sensitive to the accuracy of the initial estimates (see [24]).

3.2. Physics-Informed Neural Networks

PINNs are introduced to integrate physical laws, typically described by Ordinary Differential Equations (ODEs), into Deep Neural Networks (DNNs) (see [25]). This approach trains DNNs in a supervised fashion to comply with given physical laws, enabling the automatic discovery of data-driven solutions for ODEs, as demonstrated in the application under consideration (Equation (9)). The core idea behind PINNs is to incorporate the differential equation into the loss function, as illustrated in Figure 2, enhancing the network’s robustness and facilitating accurate approximations even in data-scarce scenarios. In this study, we focus on parametrized and nonlinear partial differential equations in the general form:

\partial_{t} \hat{y} + N [\hat{y}; λ] = 0 . t \in [0, T]

(15)

where

\hat{y} (t, x)

represents the latent (hidden) solution or the state of the dynamic system, and

N [\cdot]

denotes a nonlinear differential operator parametrized by

λ

. We define

l (t, x)

as the expression on the left-hand-side of Equation (15), i.e.:

l : = \partial \hat{y} + N [\hat{y}]

(16)

and then, we continue by modeling

\hat{y} (t, x)

using a deep neural network. In this context,

\hat{y}

serves as the output of a layered architecture neural network, denoted by

l_{w} (t)

, where

\hat{y} = l_{w} (t)

, let

l_{w}

denotes the mapping function learned by a deep network with adaptive weights w. In this context, the neural network is expected to learn the solution of a specified ODE as a function of continuous time t.

By using automatic differentiation and the chain rule, we can derive a neural network representing

\hat{y} (t, x)

. Importantly, this network shares the same parameters as the one representing

\hat{y} (t, x)

, but may employ different activation functions due to the influence of the differential operator N. Assuming an autonomous system, we train a neural network

\hat{y} (t)

by optimizing its shared parameters with those of

\hat{y} (t, x)

and

l (t, x)

. Our goal is to minimize a Mean Squared Error (MSE) cost function.

M S E = M S E_{\hat{y}} + γ M S E_{l} .

(17)

where:

M S E_{\hat{y}} = \frac{1}{N_{\hat{y}}} \sum_{i = 1}^{N_{\hat{y}}} \frac{1}{N_{t}} \sum_{j = 1}^{N_{t}} {| {\hat{y}}_{i} (t^{j}) - {\hat{y}}_{i, r e f}^{j} |}^{2}

(18)

M S E_{l} = \frac{1}{N_{\hat{y}}} \sum_{i = 1}^{N_{\hat{y}}} \frac{1}{N_{l}} \sum_{j = 1}^{N_{l}} {| l ({\hat{y}}_{i} (t^{k})) |}^{2}

(19)

being

0 \leq γ \leq 1

a hyper-parameter that should reflect how confident we are in the physical constraints of our system,

N_{t}

represent the total number of training data samples,

N_{l}

the number of collocation points, and

N_{\hat{y}}

the number of outputs produced by the neural network. For each output i, we denote the network’s prediction as

{\hat{y}}_{i} (\cdot)

. Given a data pair

(t^{j}, {\hat{y}}_{i, r e f}^{j})

, where j indexes the pair and

{\hat{y}}_{i, r e f}^{j}

is the desired output, we can compare it to the network’s prediction

{\hat{y}}_{i} (\cdot)

. In particular, the outputs of the system equations (9) in the application considered are enclosed in the following vector

\hat{y} = [x y z ϕ θ ψ]

The initial loss term

M S E_{\hat{y}}

is associated with the conventional regression cost function applied to the acquired training data

{(t^{j}, {\hat{y}}_{i, ref}^{j})}_{j = 1}^{N_{t}}

, typically used to establish the boundary (initial or terminal) conditions of ODEs during their solution. The second loss term,

M S E_{l}

, penalizes deviations in the behavior of

\hat{y} (t)

as measured by

l (\hat{y})

. This ensures that the solution adheres to the required physical properties, as defined by

l (\hat{y})

, at a specific set of randomly chosen collocation points

{t^{k}}_{k = 1}^{N_{l}}

. The experimental findings indicate a substantial reduction in the needed training data size

N_{t}

to learn specific dynamical behaviors. This reduction is attributed to the a priori information incorporated from

M S E_{l}

. Considering the assumed representation of the differential equation of the physical system as

l (\hat{y}) = 0

, the term

M S E_{l}

serves as an indicator of how effectively the PINN conforms to the solution of the physical model. The physics-informed method outlined in this study offers a unified framework that combines a pre-existing theoretical model, potentially approximate, with measured data from processes. This framework is intended to address shortcomings in the theoretical model or increase the effectiveness of sample data in process modeling.

4. Simulation Results

In this part, we execute some computer simulations to validate the proposed approach and theoretical findings.

4.1. PINNs Hyperparameters Tuning

Hyperparameter tuning involves selecting the best values for a neural network’s hyperparameters, which are parameters set before training that significantly impact the model’s performance. This process is crucial for enhancing the accuracy and efficiency of the model, helping to achieve optimal results. For instance, the learning rate controls the speed at which the model learns. If this value is too high or too low, the model may not fit the data effectively. Therefore, finding the right combination of hyperparameters is key to ensuring good model performance.

There are various methods for hyperparameter tuning such as grid search, random search, and Bayesian optimization. Grid search involves defining a range of hyperparameter values and systematically evaluating the model for every possible combination. In contrast, random search selects random combinations of hyperparameter values to evaluate the model, which can be more efficient since it doesn’t require testing all combinations. Bayesian optimization, a more sophisticated approach, uses a probabilistic model that relates hyperparameters to performance metrics, helping to predict which hyperparameter values are likely to improve the model’s performance. A broad review of tuning algorithms is available in [26], which also explores a genetic approach. The fundamental hyperparameters to adjust include the number of layers, the number of neurons per layer, the learning rate, and the batch size for the neural network. For Physics-Informed Neural Networks (PINNs), there is an additional hyperparameter called lambda, which controls the balance between the data and the model. Future research will likely focus on a deeper theoretical investigation of this specific parameter.

In this study, the random search method was employed for hyperparameter tuning.

4.2. Model and Performance Comparison

To assess the effectiveness of the proposed Physics-Informed Neural Networks method and to make a comparison with the Extended Kalman Filter-based model identification approach outlined in Section 3, a simulation of the quadrotor system described in Section 2 was conducted using Simulink from MATLAB^®. We want to underline that we have available measured data in limited quantities that link the input and output (corresponding to the state). This makes the problem difficult and a hybrid approach between the use of neural networks and impositions of physical laws represents an excellent compromise between results obtained and computational load. In Table 1 the values of the known and unknown model parameters are reported.

An important factor to take into account and which is a strong point of PINNs is that for them every system parameter is assumed to be unknown, while for the EKF it is assumed that some trivial parameters, such as the mass and the distance of the motors from the center of mass, are known. Furthermore, at the simulation level, noise is added to all measured available data in order to make the simulation more realistic. The considered network is comprised of four layers, with each hidden layer featuring 80 neurons activated by the hyperbolic tangent function.

To evaluate the performance of two proposed system estimators in some missions, various metrics including Mean Absolute Error (MAE), Mean Square Error (MSE), Integral Squared Error (ISE), Integral Absolute Error (IAE), and Integral Time–weighted Absolute Error (ITAE) have been utilized as comparative indicators for system identification. The performance indices are defined for the output state variables

\hat{y}

(the same reasoning applies to other variables) concerning the reference

y_{r e f}

that needs to be tracked across N sampling instances. They are defined as follows:

M A E = \frac{\sum_{i = 1}^{N} [y_{r e f, i} - y_{i}]}{N}, M S E = \frac{1}{N} \sum_{i = 1}^{N} {(y_{r e f, i} - y_{i})}^{2}

I S E = \int {(y_{r e f} - y)}^{2} d t, I A E = \int ∣ y_{r e f} - y ∣ d t

I T A E = \int (t ∣ y_{r e f} - y ∣) d t

where

y_{r e f, i}

and

y_{i}

respectively are the values of the variables

y_{r e f}

and y at sampling time i, and ISE, IAE, and ITAE integrate over time. Furthermore, the gains in the EKF and the architecture, some parameters of the neural network as well as a weight on the two cost functionals considered to calculate MSE in the PINNs assume an important value for evaluating the results. Some preliminary findings are reported in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, illustrating the disparity between the EKF and PINNs estimators in each performance metric of the monitored variables for the x position (Table 2), y position (Table 3), z position (Table 4),

ϕ

roll angle (Table 5),

θ

pitch angle (Table 6), and

ψ

yaw angle (Table 7).

Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show the trends of the Extended Kalman Filter and PINNs to approximate the real system respectively for position x, yz, and the angles

ϕ

θ

, and

ψ

. Both methods will achieve excellent results considering the type of maneuver presented here, the disturbances present. But it is evident that the PINNs outperform the EKF, with the additional strength of requiring a reduced computational effort, despite they require training prior to their use or during the simulation.

5. Conclusions

In this research work we investigated the praticatability of employing a physics-informed machine learning technique, specifically physics-informed neural networks (PINNs), for nonlinear system model identification in the context of a quadrotor when input-output available real data are limited. Our discussion centered around the potential of PINNs to replace intricate nonlinear dynamics with a more computationally efficient approximation. Leveraging automatic differentiation, PINN approximations enable a cost-effective and straightforward computation of derivatives of the state. The technique is compared on experimental data with the extended Kalman filter, which according to previous literature is the method that has always obtained the best performance. The simulation comparison is performed on both spatial and orientation variables and shows excellent performances from both techniques, but PINNs are better both at the error level with respect to real data and at the computational level, but with a greater preliminary workload, at a higher training level.

Future research extensions will involve analyzing the results concerning a comparative computational analysis and variations in some identification parameters like

γ

to understand the performance moving from an hybrid weighted approach data driven-model based.

Author Contributions

Conceptualization, first author; Methodology, first author; Resources, all authors; Software, first author; Validation, first author; Formal analysis, first and second authors; Investigation, first author and second authors; Data curation, first author; Roles/Writing - original draft, first author; Writing—review and editing, all authors; Visualization, first author; Supervision, first author; Project administration, fourth author; Funding acquisition, fourth author.

Funding

This work is partially supported by the European Project ECSEL – Joint Undertaking RIA–2018 “Comp4Drones” under grant agreement No. 826610, and by MAECI Project 2018–2020 “Coordination of autonomous unmanned vehicles for highly complex performances” PGR01083.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing not applicable.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

References

Wang, J.; Ricardo, A. RM; Jorge, J. L.S.; Introducing system identification strategy into Model Predictive Control, Journal Systems Science Complexity, 2020, 33, pp. 1402–1421. [Google Scholar] [CrossRef]
Forssell, U.; Lindskog, P. ; Combining Semi-Physical and Neural Network modeling: An example of its usefulness, IFAC Proceedings, 1997, 30 (11), pp. [CrossRef]
Fu, L.; Li, P. ; The Research Survey of System Identification Method, In Proceedings of 5th International Conference on Intelligent Human-Machine Systems and Cybernetics, 2013, pp. 397-401. [CrossRef]
Gueho, D.; Singla, P.; Majji, M.; Juang, J.-N. ; Advances in System Identification: Theory and Applications, In Proceedings of 60th IEEE Conference on Decision and Control, 2021, pp. 22-30. [CrossRef]
Ho, B.L.; Kalman, R.E. ; Editorial: Effective construction of linear state-variable models from input/output functions: Die Konstruktion von linearen Modeilen in der Darstellung durch Zustandsvariable aus den Beziehungen für Ein-und Ausgangsgrößen" at - Automatisierungstechnik, 1966, 14 (1-12), pp. [CrossRef]
Kalman, R.E. ; Mathematical Description of Linear Dynamical Systems, Journal of the Society for Industrial and Applied Mathematics, Series A: Control, 1963, 1 (2), pp. 152-192. [CrossRef]
Chen, C.W.; Lee, G.; Juang, J.-N. ; Several recursive techniques for observer/Kalman filter system identification from data, 1992, 92-4386, Hilton Head Island, SC, U.S.A. [CrossRef]
Germani, A.; Manes, C.; Palumbo, P. ; Polynomial extended Kalman filter, IEEE Transaction on Automatic Control, 2005, 50 (12), pp. 2059-2064. [CrossRef]
Peyada, N.K.; Sen, A.; Ghosh, A.K. 2008. [CrossRef]
Bianchi, D.; Borri, A.; Di Benedetto, M.D.; Di Gennaro, S. ; Active Attitude Control of Ground Vehicles with Partially Unknown Model, IFAC-PapersOnLine 2020, 53 (2), pp. 14420-14425, doi.org/10.1016/j.ifacol.2020.12.1440.
Rodrigues, L.; Givigi, S. ; System Identification and Control Using Quadratic Neural Networks, IEEE Control Systems Letters 2023, 7, pp. 2209-2214. [CrossRef]
Cavone, G.; Epicoco, N.; Carli, R.; Del Zotti, A.; Ribeiro Pereira, J.P.; Dotoli, M. ; Parcel delivery with drones: Multi-criteria analysis of trendy system architectures, Proceedings of 29th Mediterranean Conference on Control and Automation 2021, pp. 693-698. [CrossRef]
Carli, R. ; Cavone, G; Epicoco, N., Di Ferdinando, M., Scarabaggio, P., Dotoli, M., Eds.; Consensus-based algorithms for controlling swarms of Unmanned Aerial Vehicles, In: Lecture Notes in Computer Science 2020, 12338; pp. 84–99. [Google Scholar] [CrossRef]
Bianchi, D.; Borri, A.; Di Gennaro, S.; Preziuso, M. ; UAV trajectory control with rule-based minimum-energy reference generation, Proceedings of European Control Conference 2022, London, United Kingdom, pp. 1497-1502. [CrossRef]
Stiasny, J.; Misyris, G.S.; Chatzivasileiadis, S. ; Physics-Informed Neural Networks for Non-linear System Identification for Power System Dynamics, 2021, IEEE Madrid PowerTech. [CrossRef]
Liu, X.; Cheng, W.; Xing, J. ; Physics-informed Neural Network for system identification of rotors, IFAC-PapersOnLine, 2024, 58 (15), pp. 307-312. [CrossRef]
Liu, T.; Meidani, H. ; Physics-Informed Neural Networks for System Identification of Structural Systems with a Multiphysics Damping Model, 2023, Journal of Engineering Mechanics, 149 (10), art. 04023079. [CrossRef]
Li, H.W.X.; Lu, L.; Cao, Q. ; Motion estimation and system identification of a moored buoy via physics-informed neural network, Applied Ocean Research, 2023, 138, art. 10 3677. [CrossRef]
Gu, W.; Primatesta, S.; Rizzo, A. ; Physics-informed Neural Network for Quadrotor Dynamical Modeling, Robotics and Autonomous Systems, 2024, 171. [CrossRef]
Bianchi, D.; Borri, A.; Cappuzzo, F.; Di Gennaro, S. Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator, Drones 2024, 8, 29. [CrossRef]
Bianchi, D.; Di Gennaro, S.; Di Ferdinando, M.; Lua, C.A. ; Robust Control of UAV with Disturbances and Uncertainty Estimation, Machines 2023, 11 (3): 352. [CrossRef]
Hughes, P.C. ; Spacecraft Attitude Dynamics. Dover Publications, Inc.: Mineola, NY, USA, 1986.
Nagaty, A.; Saeedi, S.; Thibault, C.; Seto, M.; Li, H. ; Control and Navigation Framework for Quadrotor Helicopters, Journal of Intelligent and Robotic Systems 2013, 70, pp. 1-12. [CrossRef]
Fujii, K. ; Extended kalman filter, 2013, Refernce Manual.
Raissi, M.; Perdikaris, P.; Karniadakis, G.E. ; Physics-Informed Neural Networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, Journal of Computational Physics 2019, 378, pp. 686-707. [CrossRef]
Kumar, P. ; Batra, S; Raman, B. ; Deep neural network hyper-parameter tuning through twofold genetic approach, Soft Computing 2021, 25, pp. 8747–8771. [Google Scholar] [CrossRef]

Figure 1. Quadrotor orientation using Euler angles.

Figure 2. PINN architecture. It functions by employing its own output prediction as the initial state.

Figure 3. Position x-axis and corresponding error.

Figure 4. Position y-axis and corresponding error.

Figure 5. Position z-axis and corresponding error.

Figure 6. Roll angle

ϕ

and corresponding error.

Figure 6. Roll angle

ϕ

and corresponding error.

Figure 7. Pitch angle

θ

and corresponding error.

Figure 7. Pitch angle

θ

and corresponding error.

Figure 8. Yaw angle

ψ

and corresponding error.

Figure 8. Yaw angle

ψ

and corresponding error.

Table 1. Actual parameter values.

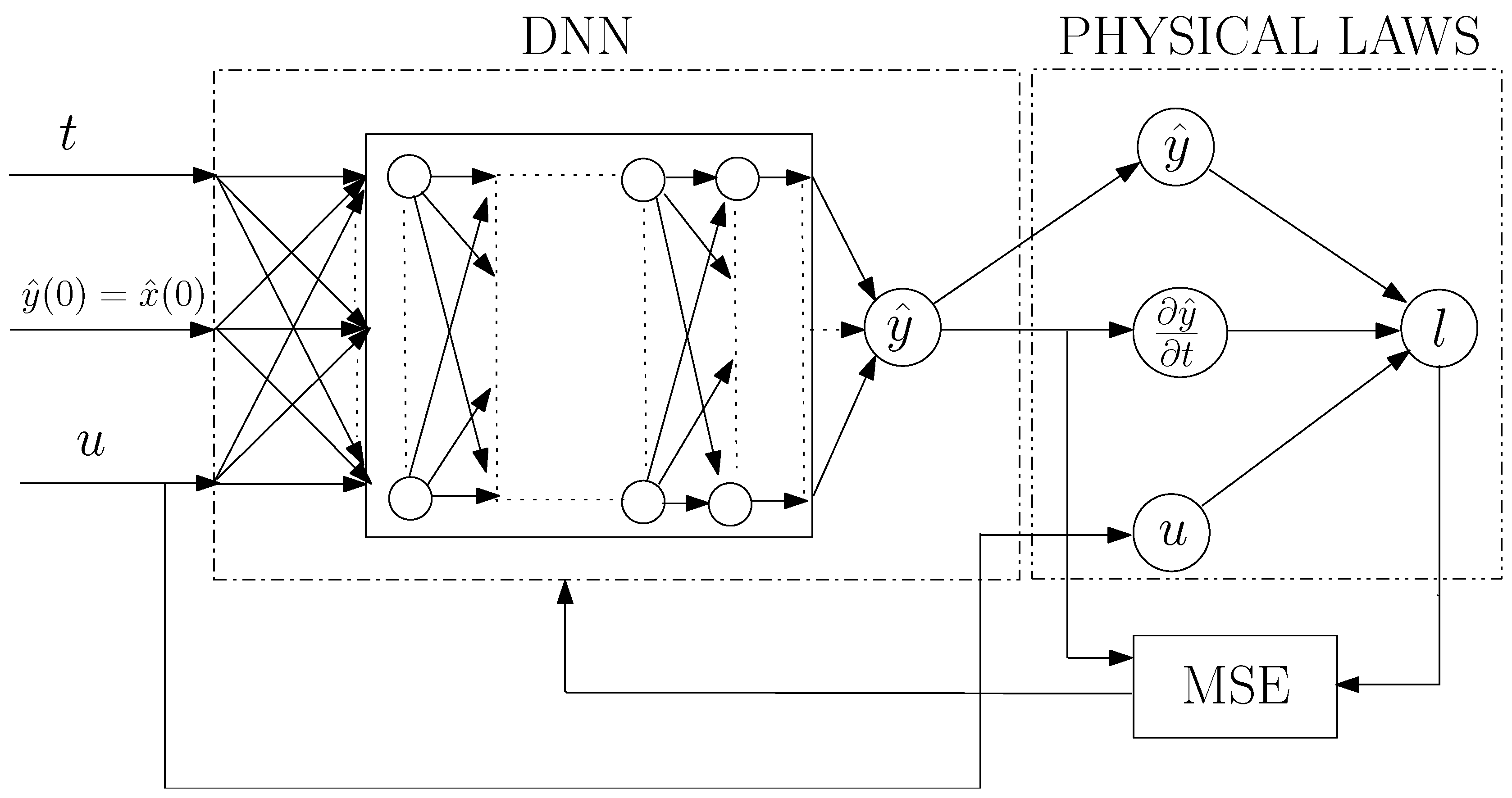
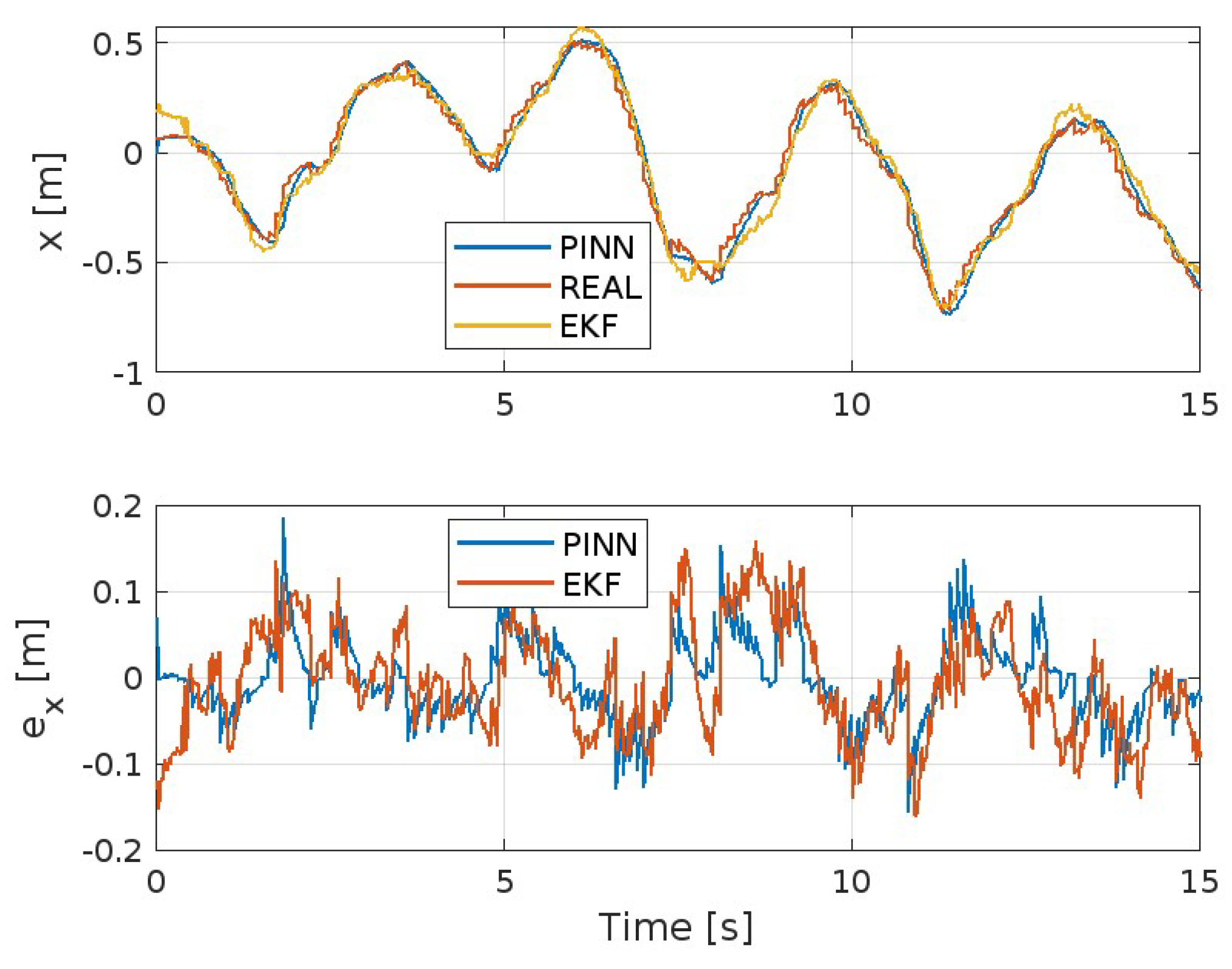
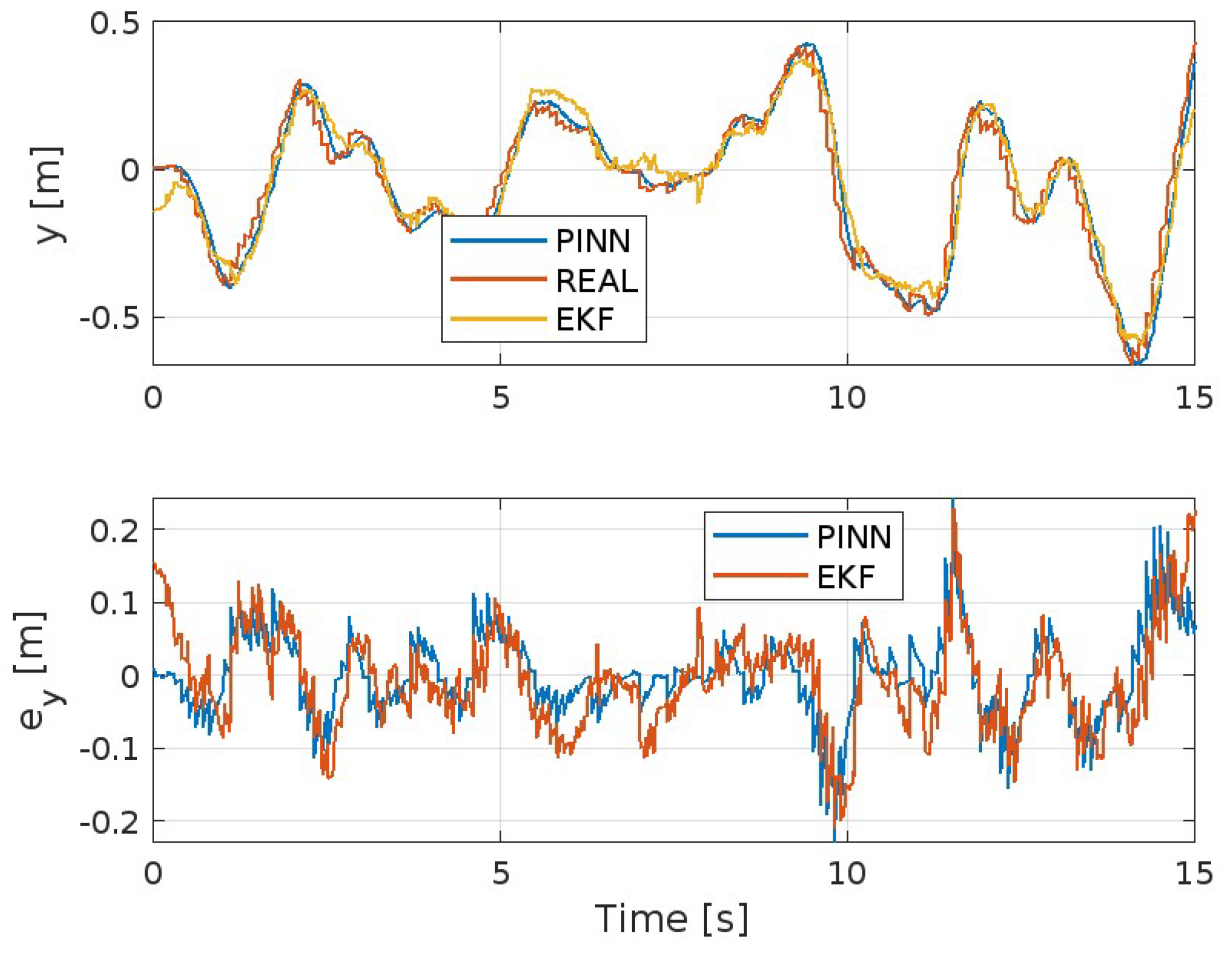
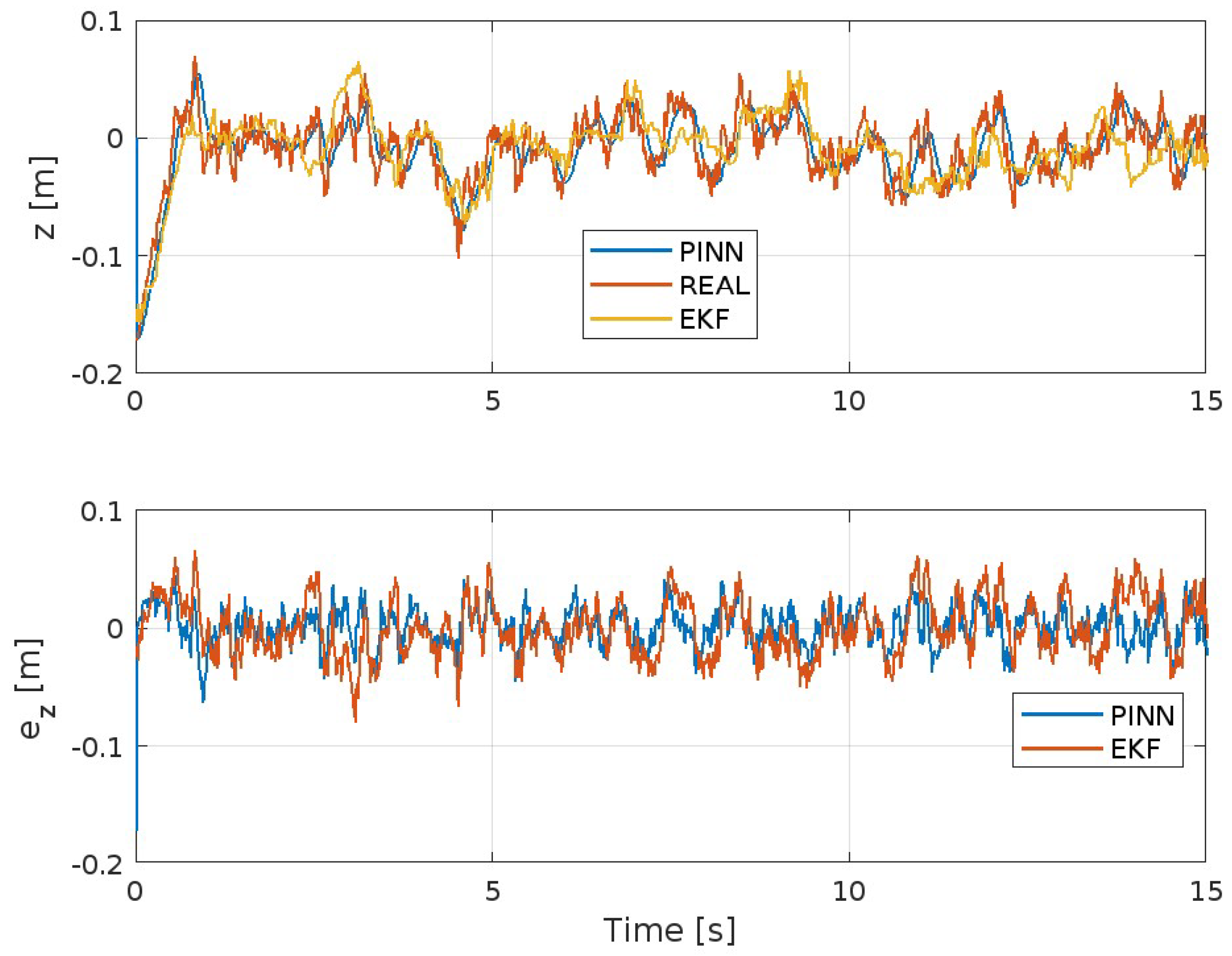
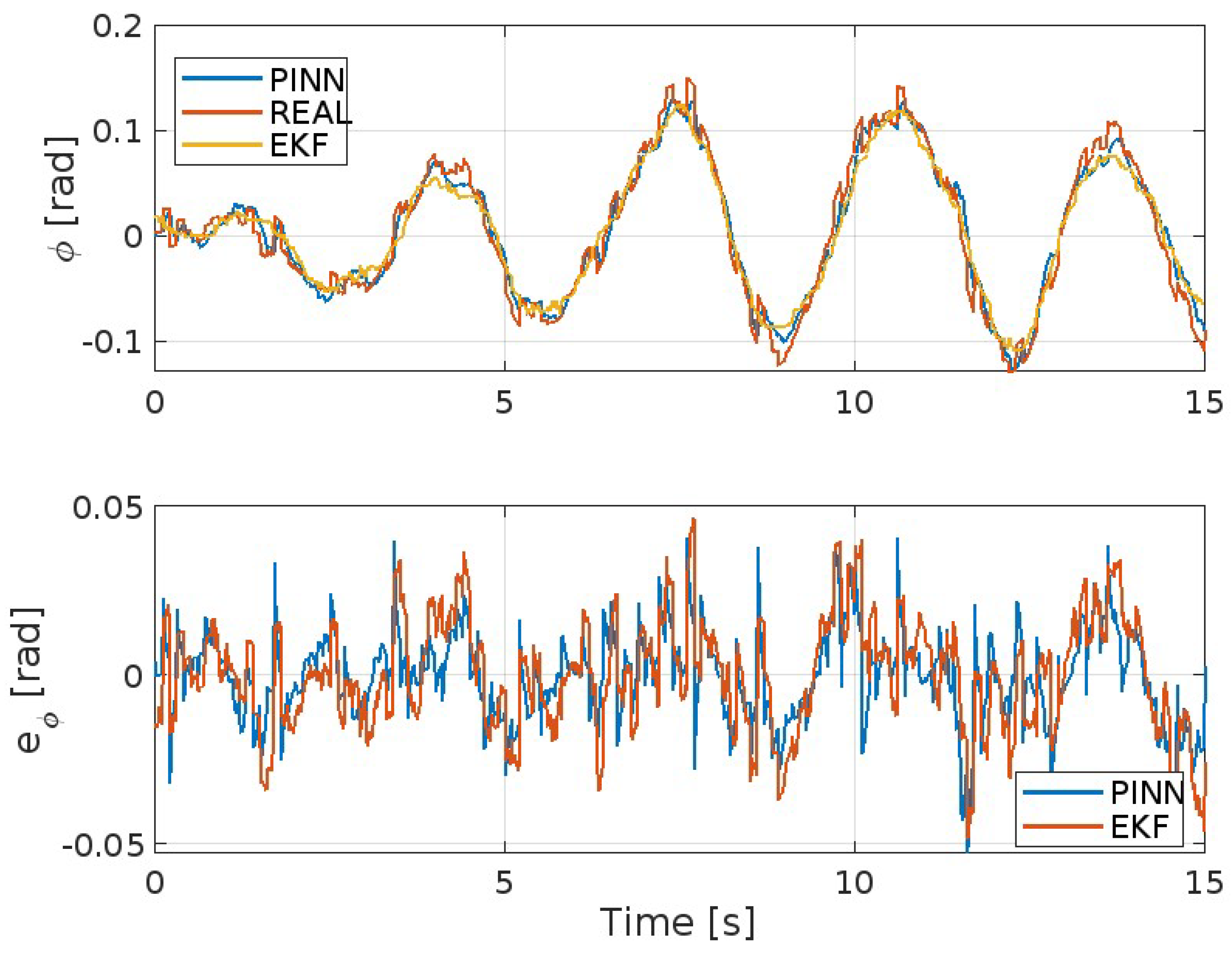
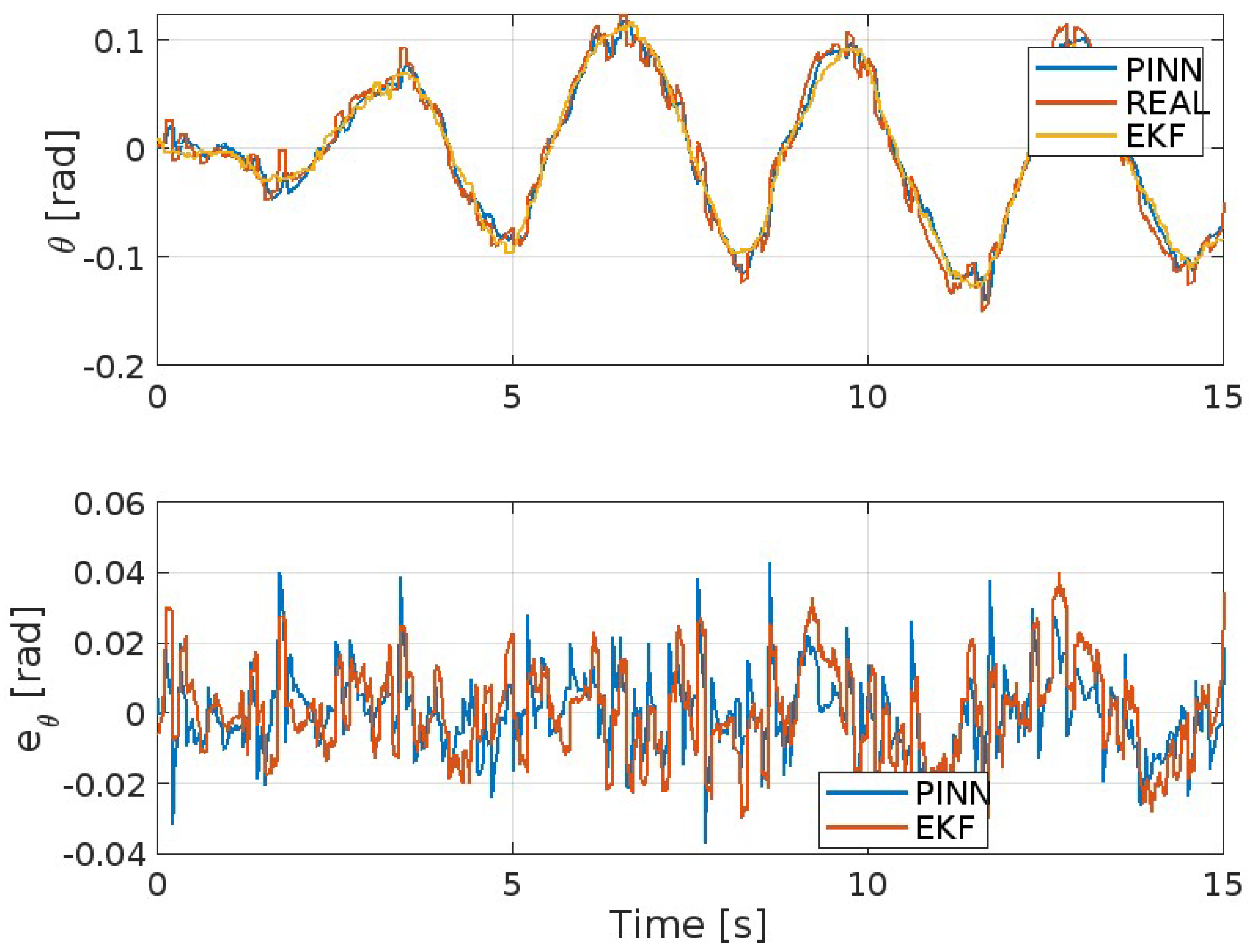
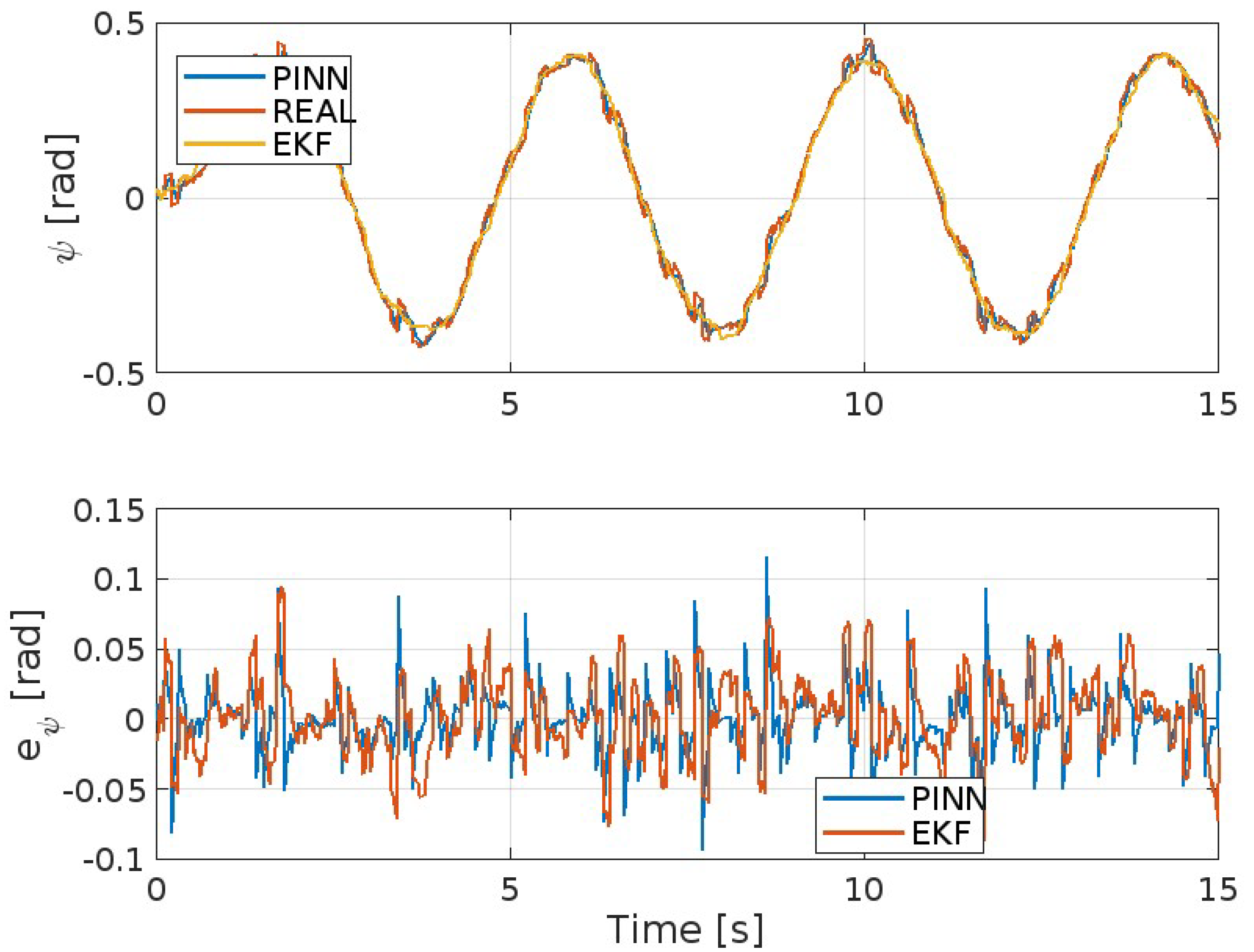
Parameter	Value	Units	Known	Known
			for EKF	for PINNs
m	0.65	kg	YES	NO
d	0.165	m	YES	NO
$J_{x}$	0.03	$k g \cdot m^{2}$	NO	NO
$J_{y}$	0.025	$k g \cdot m^{2}$	NO	NO
$J_{z}$	0.045	$k g \cdot m^{2}$	NO	NO
b	3.50	$N / r a d / s$	NO	NO
k	0.06	$N \cdot m / r a d / s$	NO	NO

Table 2. Performance indices for the x model errors expressed in meters.

	MAE	MSE	ISE	IAE	ITAE
EKF	0.0514	0.0039	5.8711	77.17	599.94
PINNs	0.0367	0.0022	3.3427	55.07	432.52

Table 3. Performance indices for the y model errors expressed in meters.

	MAE	MSE	ISE	IAE	ITAE
EKF	0.0533	0.0047	7.0927	79.96	638.23
PINNs	0.0426	0.0033	4.8822	64	543.46

Table 4. Performance indices for the z model errors expressed in meters.

	MAE	MSE	ISE	IAE	ITAE
EKF	0.0198	5.85e-04	0.8786	29.71	229.05
PINNs	0.0135	2.99e-04	0.4491	20.3	147.99

Table 5. Performance indices for the

ϕ