Prerpints.org logo
Preprint
Article

SIT-Conversion: Transformer Spiking Neural Networks with Spiking-Softmax Function

Altmetrics

Downloads

77

Views

48

Comments

0

This version is not peer-reviewed

Submitted:

28 October 2024

Posted:

30 October 2024

You are already at the latest version

Alerts
Abstract
Studies on integrating Spiking Neural Networks (SNNs) with the Transformer architecture holds promise for enabling models to achieve ultra-low energy consumption while possessing the performance of the Transformer architecture. Currently, studies on ANN-to-SNN conversion of integrating Spiking Neural Networks (SNNs) with the Transformer architecture mainly focuses on simple activation functions in MLPs, and has not yet addressed the mismatch between the Softmax activation function in the self-attention mechanism and the computation rules of SNNs. Consequently, the ANN-to-SNN conversion efforts have consistently failed to make the Transformer architecture directly applicable to SNNs. To address this challenge, we propose the Spiking-Softmax method, which integrates Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm). The Spiking-Softmax method accurately simulates the Softmax activation function with only 12 time steps. Building upon this, we propose the Spike Integrated Transformer conversion (SIT-conversion) method, which enables the conversion of the Transformer architecture to SNNs. The SNNs generated by the SIT-conversion of Transformer models of various sizes achieve accuracy nearly identical to their ANNs counterparts, achieving nearly lossless and ultra-low-latency ANN-to-SNN conversion. This work represents the first implementation of simulating the Softmax activation function and fully converting the Transformer architecture into SNNs through spike firing.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Spiking Neural Networks (SNNs) [1] use discrete spike sequences (0 or 1) for computation and information transmission. They offer promising prospects for brain-like intelligence due to their low power consumption, event-driven characteristics, and biological plausibility [2] compared to Artificial Neural Networks (ANNs). However, the development of SNNs lags far behind that of ANNs, particularly at the level of network architecture [3]. With technological advancements, SNNs can leverage advanced architectures from ANNs to enhance performance, such as ResNet-style SNNs [4,5,6] and Recurrent Neural Networks (RNNs) [7].
However, currently, SNNs cannot effectively harness more complex and powerful ANN frameworks, such as the Transformer architecture [8]. The Transformer architecture is considered one of the most powerful network structures in deep learning [9], flourishing across various computer vision tasks, including image classification [10,11], and object detection [12,13,14], among others. Furthermore, the recently acclaimed ChatGPT [15] is also based on the Transformer architecture. Thus, integrating the Transformer structure into SNNs while retaining its brain-like and low-power advantages is a crucial factor for the current development of SNN algorithms and neuromorphic chips [16].
Currently, there have been some studies devoted to integrating SNNs with the Transformer architecture. These studies could be categorized into two main types: (1) direct training methods [17,18] and (2) the ANN-to-SNN conversion methods for SNNs-Transformer, wherein an ANN Transformer model is trained, and subsequently, the pre-trained ANN parameters are mapped onto an SNN with an identical structure [19,20].
Direct training methods focus on simulating Transformer by designing novel variants of self-attention. The attention maps calculated through spike-form Query and Key [18] possessed natural non-negativity, obviating the necessity for the softmax function to maintain the non-negativity of the attention maps. However, the removal of the crucial Softmax function could make the model difficult to clearly distinguish the importance of relevant features. This makes it challenging for these SNN models to achieve performance comparable to leading ANNs.
SNNs-Transformer models, derived through ANN-to-SNN conversion, have been found to achieve performance comparable to ANNs-Transformer. For example, Z. Wang et al. [20] proposed MST model based on the ANN-to-SNN conversion method, which successfully integrates Transformer into SNNs by pruning the self-attention modules of Transformers and designing new spiking neurons to simulate simple activation functions like ReLU. However, they typically required more time steps to achieve high-level performance [21]. Additionally, they could not simulate the Softmax activation function in Transformers through spiking neurons [22], which significantly impacts the model’s performance and the overall feasibility of SNNs-Transformer.
The Softmax activation function in the Transformer architecture [10] and multi-head self-attention [23] highlights the important features in the attention weight matrix, while suppressing significantly lower values. It’s essential in maintaining the non-negativity of the matrix and holds an irreplaceable position. However, the computational process of the Softmax function involves complex exponentiation and division operations, which are incompatible with the computational rules of SNNs, rendering simulation through spiking neurons challenging [24]. Therefore, implementing this function based on spiking neurons is crucial for fully applying the Transformer architecture to SNNs.
In order to simulate the Softmax function using spiking neurons and realize the full structure conversion model of SNNs-Transformer comparable to ANNs, we propose the Spiking-Softmax method, which includes Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm), filling the gap in Softmax function research in ANN-to-SNN conversion methods. Based on the Spiking-Softmax method, we have implemented the Spike Integrated Transformer conversion (SIT-conversion) method, which yields an SNNs-Transformer model compliant with spiking neuron rules. We evaluated the SIT-conversion on various Transformer models using static datasets, demonstrating the strong applicability of our method to Transformer structures. Our method achieved nearly lossless ANN-to-SNN conversion using a minimal number of time steps. Overall, the contributions of this work can be summarized as follows:
  • We have designed a novel Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm), leveraging the computational rules of spiking neurons to realize the exponential and normalization operations of the Softmax activation function. By integrating SI-exp and SI-norm, we have achieved the Spiking-Softmax method to simulate the Softmax function in SNNs. This marks the first implementation of the Softmax activation function for the self-attention mechanism in SNNs. With these proposed neurons, we have proposed the SIT-conversion method, which fully applied the Transformer into SNNs.
  • We evaluated SIT-conversion on static datasets using various Transformer structures and demonstrated that SNNs generated by SIT-conversion from Transformer models achieved nearly identical accuracy to their ANNs counterparts, thus achieving nearly lossless ANN-to-SNN conversion.

2. Related Works

The Transformer architecture has been proven to significantly enhance model performance in deep learning, and the combination of SNNs and Transformer can fully leverage the advantages of Transformer in performance and SNNs in energy consumption [25]. Some studies have theoretically demonstrated the effectiveness of this combination. The most common techniques for implementing the Transformer architecture in SNNs are (1) direct training methods and (2) ANN-to-SNN conversion methods. Direct training methods often achieve SNNs-compatible Transformer models through structural innovations. To integrate the Transformer structure into SNNs, Zhang et al. [26] proposed the Spiking Transformer Network (STNet), which consists of a Transformer module providing global spatial information and an SNNs module for extracting temporal cues. However, they still use ANNs-Transformer to process spike data and have not fully implemented the Transformer model in SNNs. To accommodate the nature of SNNs, Z. Zhou et al. [18] proposed Spiking Self-Attention (SSA) method, which eliminates the need for Softmax by using sparse spike forms of Query, Key, and Value, thus avoiding multiplication operations. However, removing the pivotal Softmax function in the self-attention mechanism results in an inability to distinctly differentiate the importance of features. Furthermore, SNNs-Transformer models trained using direct training methods typically require longer training times and struggle to achieve performance comparable to leading ANNs on static datasets.
In order to shorten the training time of Transformer models in SNNs and approximate the performance of ANNs-Transformer models, an ANN-to-SNN conversion method for Transformer was provided by Mueller et al. [19], which can convert the Transformer model into SNNs. However, only simple integrate and fire (IF) neurons were used to replace the ReLU activation function after multi-head self-attention to achieve network conversion, without addressing the implementation of self-attention mechanisms in SNNs, thereby deviating from the characteristics of SNNs. In order to overcome this challenge, the MST model proposed by Z. Wang et al. [20] pruned the self-attention modules of Transformers and designed new spiking neurons to simulate activation functions like ReLU, successfully introducing the self-attention mechanism into SNNs, thereby effectively implementing the Transformer architecture in SNNs. However, the converted self-attention mechanism still retains the Softmax function from ANNs, failing to fully convert the entire architecture into SNNs. Although training SNNs-Transformer models through ANN-to-SNN conversion methods can save a significant amount of time compared to direct training, it still requires more time steps to achieve state-of-the-art performance. Moreover, it can only convert simple activation functions such as ReLU and Sigmoid. Complex activation functions such as Softmax in Transformers still cannot be simulated through spiking neurons. Therefore, in the studies mentioned above where Transformer-SNNs models are trained through the ANN-to-SNN conversion method, the converted Transformer model still uses the Softmax activation function of ANNs during the inference process, making it impossible to fully implement the Transformer architecture in SNNs.
To simulate complex activation functions, Stöckl & Maass [27] proposed FS-neuron, utilizing time encoding with spiking patterns to convert more complex activation functions, requiring only a few time steps, which significantly improved latency and throughput. According to their report, it can be applied to almost any activation function, such as SiLU. However, due to the lack of a fixed function curve for the Softmax activation function, trainable FS-neurons cannot simulate it. Therefore, simulating the Softmax activation function through spiking neurons to achieve low-latency ANN-to-SNN conversion for SNNs-Transformer models remains an ongoing challenge. In this study, we decompose the Softmax activation function and leverage the computational characteristics of spiking neurons to separately design different spiking neurons that require only a few time steps to simulate exponential and normalization operations. Ultimately, the integrated collaboration of multiple spiking neurons achieved the Spiking-Softmax method in the self-attention mechanism, thus fully realizing the conversion of the Transformer architecture in SNNs.

3. Methods

3.1. Structure of Spike Integrated Transformer

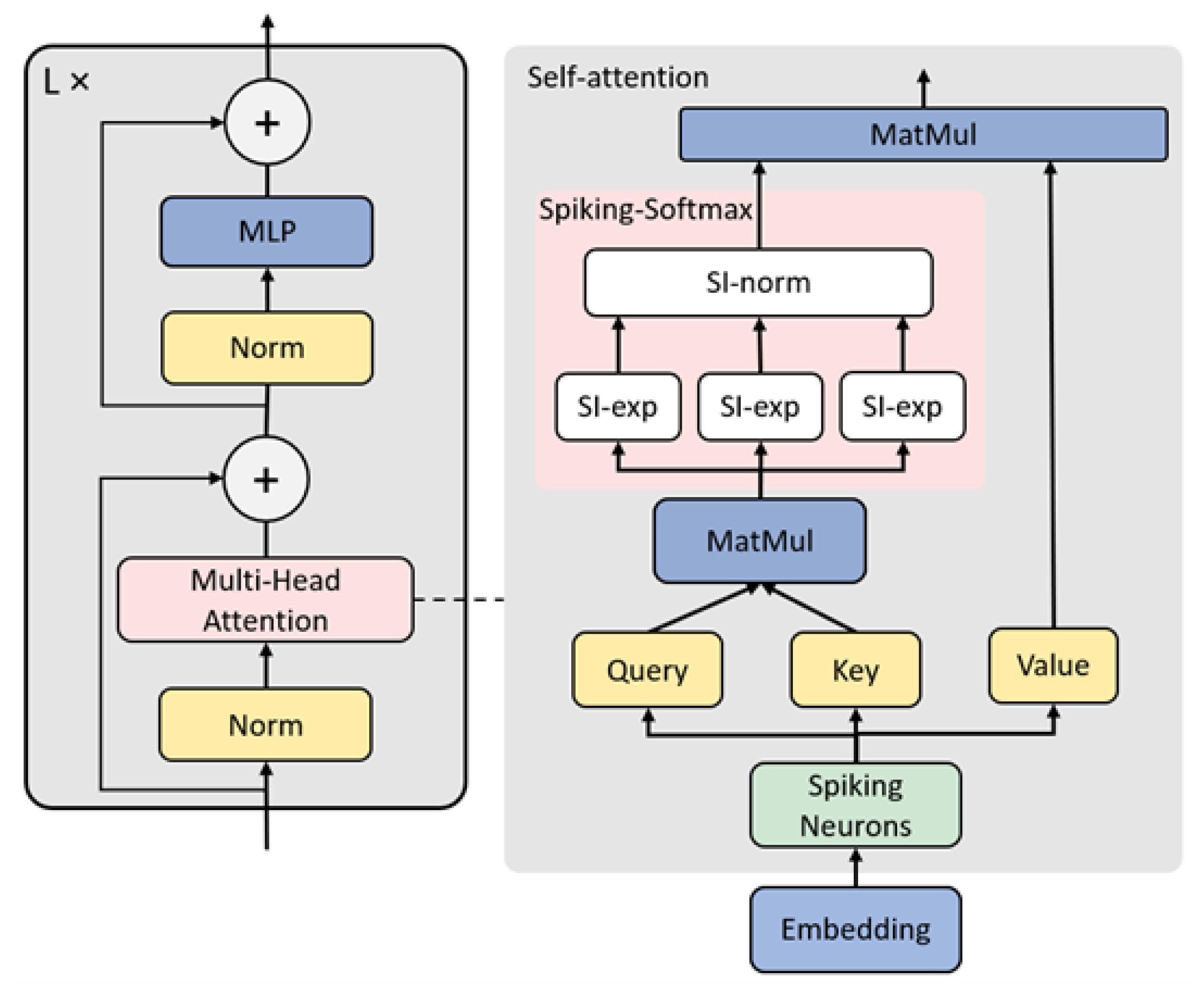
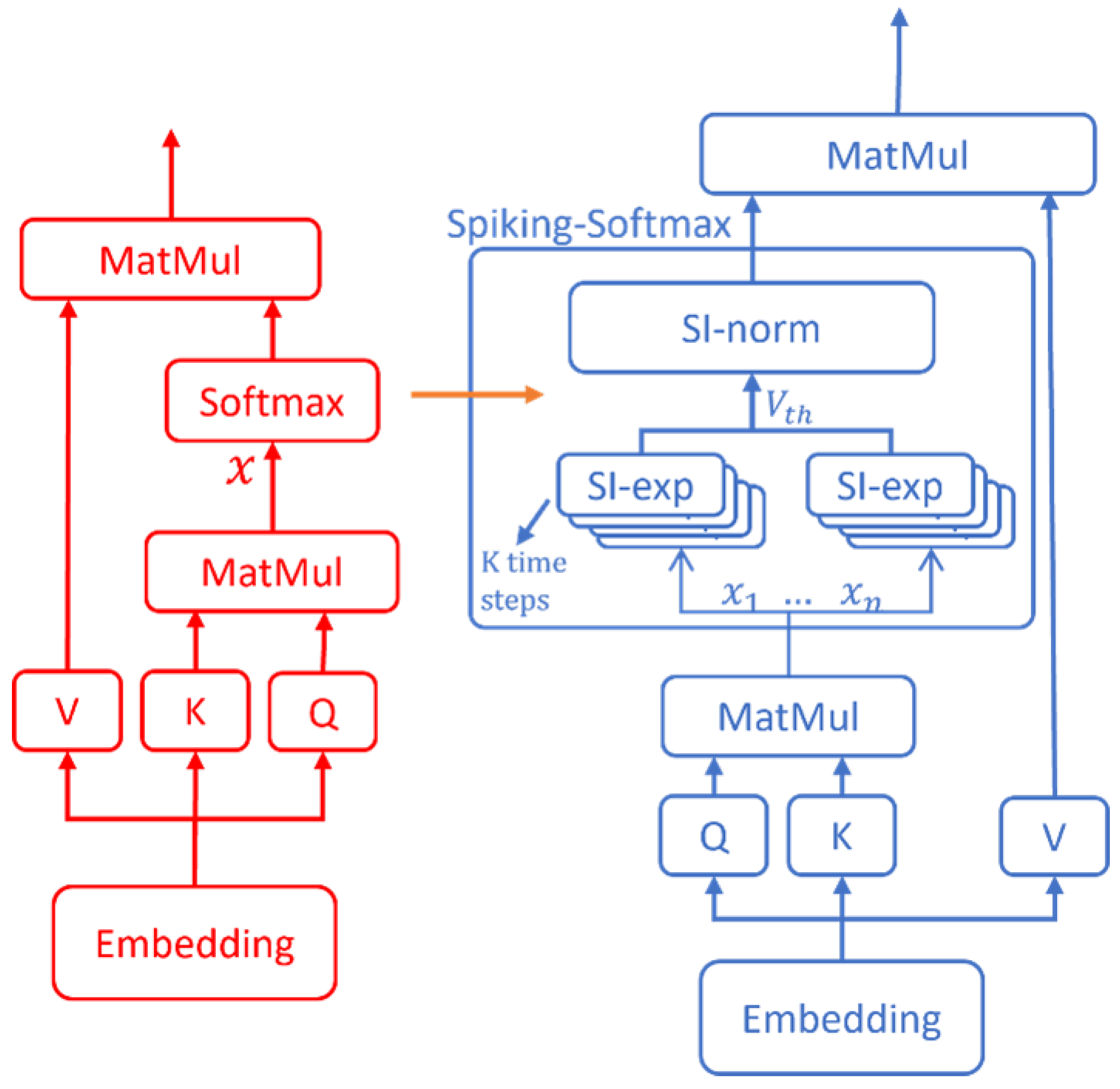
In this study, the Spike Integrated Transformer (SIT) model is proposed, which implements the self-attention mechanism in spiking neural networks (SNNs) through ANN-to-SNN conversion methods, enhancing the learning capability of SNNs. As shown in Figure 1, to convert the original artificial neural network into a fully spiking form, Spiking-Softmax method that includes Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm) is proposed to simulate the Softmax function of the typical self-attention mechanism. The self-attention mechanism of the SIT model computes Query, Key, and Value using Spiking Neurons [20], obtains an attention matrix through Query and Key, and then the Spiking-Softmax method is applied to normalize the attention matrix, thus achieving the complete conversion of the Transformer architecture in SNNs.

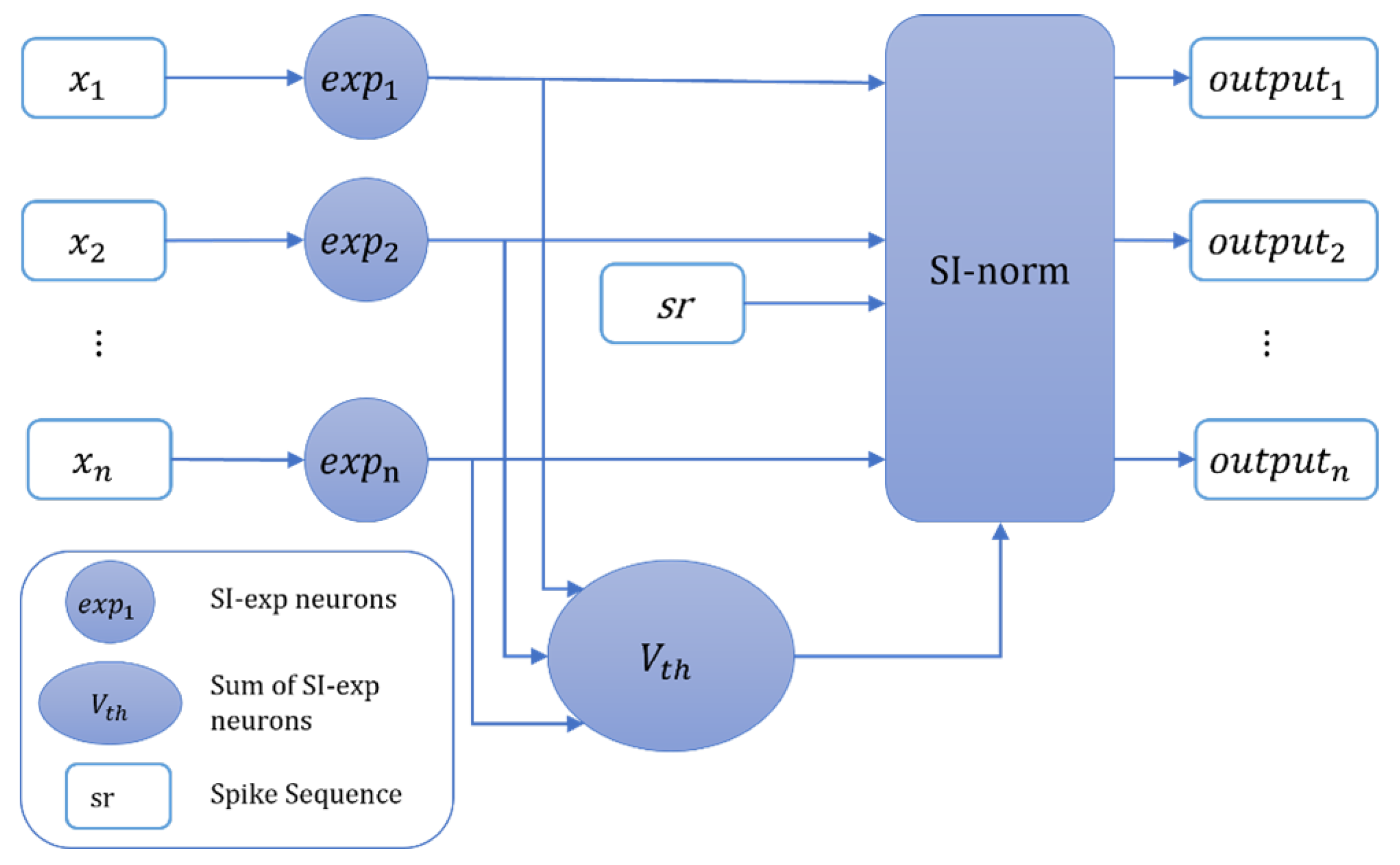
3.2. Spiking-Softmax Method

In this section, we will specifically introduce the method of simulating the Softmax activation function in SNNs. Previous ANN-to-SNN conversion methods mainly focused on converting single-input activation functions, while the Softmax activation function requires processing a set of inputs. Considering this characteristic, we refer to the calculation equation of Softmax and propose the Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm) to simulate the exponentiation and normalization operations in the Softmax function, respectively. Then, we propose the Spiking-Softmax method by integrating SI-exp and SI-norm neurons. As shown in Equation 1, e x p i denotes the i-th SI-exp neuron, and norm denotes the SI-norm neuron.
S p i k i n g _ S o f t m a x ( x ) = e x p i ( x ) n o r m ( ∑ i e x p i ( x ) )
The threshold voltage V t h of the SI-norm neuron is obtained by summing the outputs of all SI-exp neurons, simulating the summation operation of the Softmax function. The SI-norm neuron receives the outputs of SI-exp neurons and the threshold voltage V t h , normalizing the outputs of the SI-exp neurons. Thus, the simulation of the Softmax function have been achieved based on the integrated collaboration of SI-exp neurons and SI-norm neurons, thereby achieving the Spiking-Softmax method, as illustrated in Figure 2.

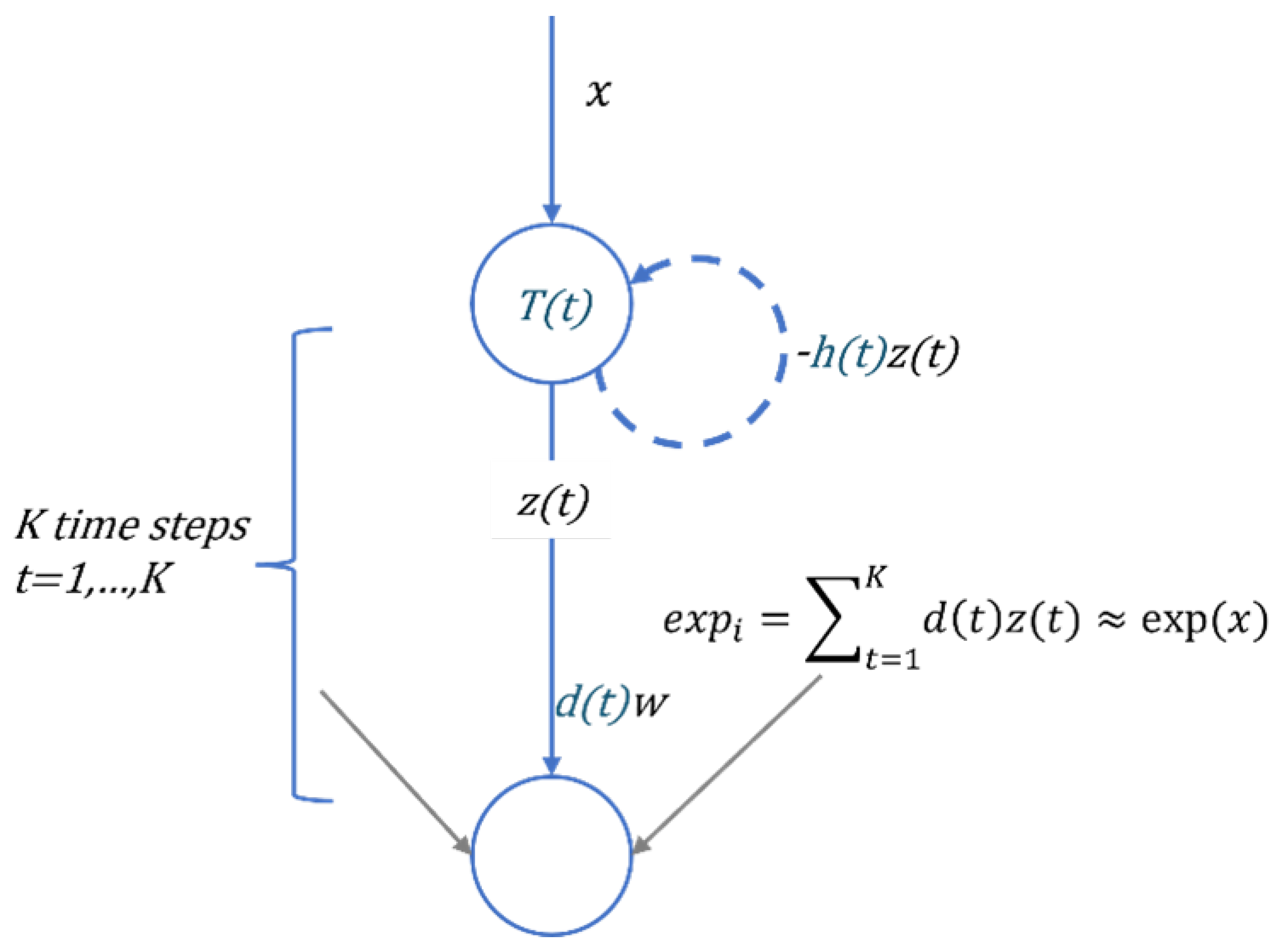
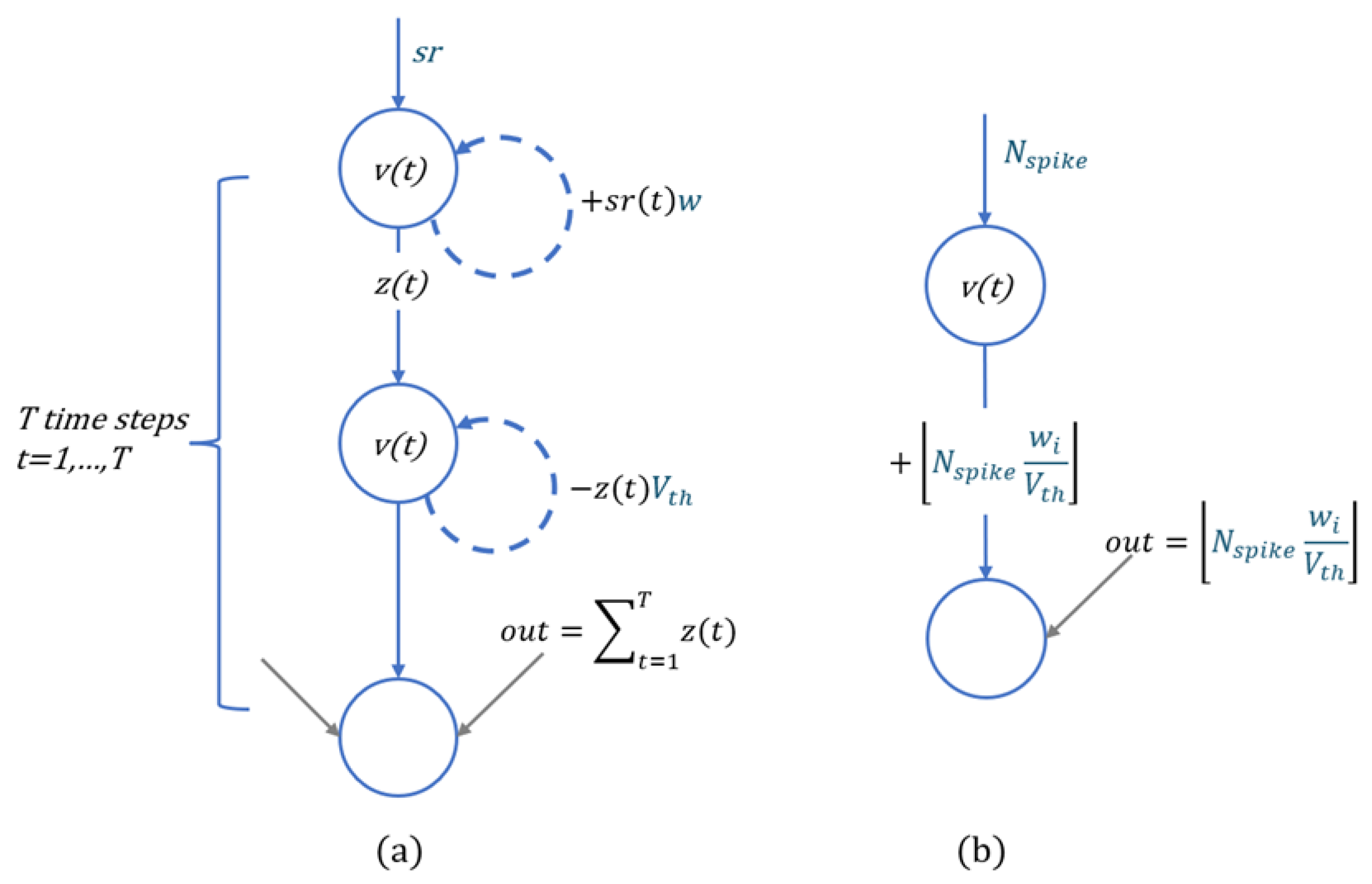
3.3. Spiking Exponential Neuron

Inspired by FS-neuron [27], the Spiking Exponential Neuron (SI-exp) has been improved, allowing it to simulate exponential operations by emitting a few spikes within K time steps. In SI-exp, it is necessary to optimize the internal parameters T(t), h(t), and d(t), where t = 1 , . . . , K . T(t) and d(t) respectively represent the threshold voltage and spike output of the t-th time step, while h(t) is used to control the membrane potential changes at each time step. Through optimization, the exponential operation of a given ANN is simulated by a weighted sum of spikes ∑ t = 1 K d ( t ) z ( t ) , where z(t) denotes the spike train produced by the neuron. Figure 3 illustrates the inference process of the SI-exp neuron.
v ( t + 1 ) = x , t = 0 v ( t ) − h ( t ) z ( t ) , 0 < t < K
x denotes the floating-point input, v(t) denotes the membrane potential of the neuron. If the neuron triggers a spike at time step t, then v(t) must exceed the current discharge threshold T(t), at which point the neuron generates a spike signal z(t)=1; otherwise, z(t)=0. After spiking at time step t, the membrane potential v(t) is reset to v(t)-h(t). The change in membrane potential v(t) over K time steps is represented by Equation 2. The spike signal z(t) of the SI-exp neuron is defined by Equation 3.
z ( t ) = Θ ( v ( t ) − T ( t ) )
Where Θ represents the Heaviside step function. After K time steps of inference, the final output of the SI-exp neuron is as shown in Equation 4. Since the Spiking-Softmax method includes multiple SI-exp neurons, here e x p i is used to represent the output of the i-th SI-exp neuron.
exp i = ∑ t = 1 K d ( t ) z ( t )
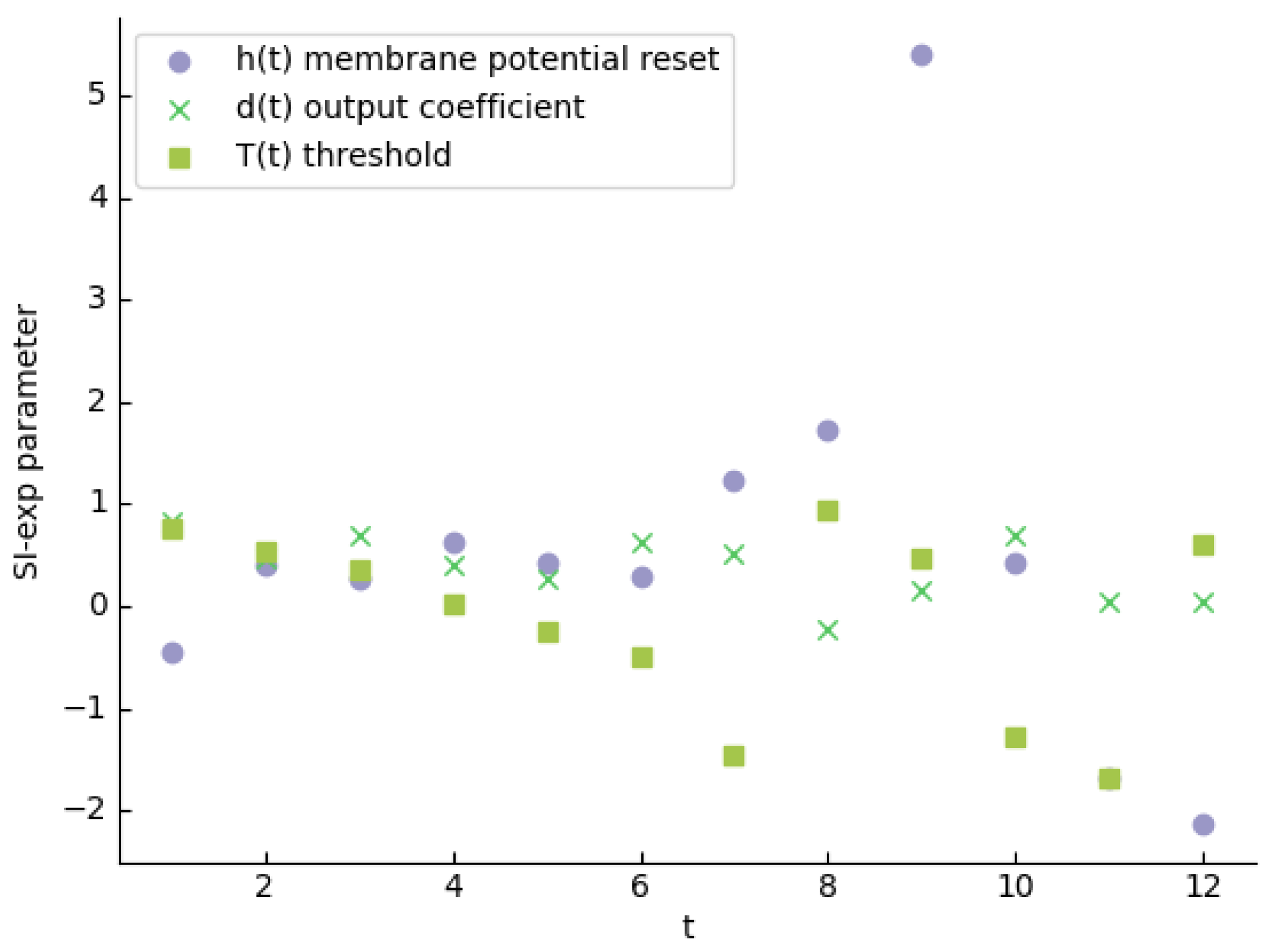
When optimizing the internal parameters h(t), d(t), T(t) of the SI-exp neuron, a selection of 10,000 numbers as independent variables, evenly spaced in the interval [-1, 1], was chosen as training data, with their corresponding exponential values used as training labels. The distribution of the optimized internal parameters T(t), h(t), d(t) is shown in Figure 4. Using the optimized parameters, the output of the SI-exp neuron after K time steps of inference is compared with the exponential function exp(x) of ANNs. The root mean square error is 0.0015413, indicating that the average deviation between the inference of SI-exp and the true values can be negligible.

3.4. Spiking Collaboration Normalized Neuron

The Spiking Collaboration Normalized Neuron (SI-norm) is proposed to simulate the normalization operation of the Softmax function, which includes an input spike sequence ( s r ), a threshold voltage ( V t h ), and weights (w), which can be directly used in the inference process. In the rate encoding method proposed by Zhang & Zhang [28], a floating-point number x is encoded into a spike sequence, with the number of spikes within a period T denoted as N s p i k e . The input of the SI-norm neuron is a regular spike sequence s r obtained by encoding the floating-point number 1.0. The output e x p i of the SI-exp neuron is considered as the weight w of the SI-norm neuron, where i denotes the index of the SI-exp neuron and n denotes the number of SI-exp neurons. The threshold voltage V t h is obtained by summing the outputs e x p i of the SI-exp neurons, as shown in Equation 5.
V t h = ∑ i = 1 n exp i
The membrane potential v(t) changes over T time steps starting from the initial value v(0)=0 as illustrated in Figure 5(a). At each time step t, the spiking neuron first undergoes charging, and the change in membrane potential during charging is given by Equation 6.
v ( t ) = v ( t − 1 ) + sr ( t ) · w
w denotes the weight of the SI-norm neuron, s r t is the value of the regular spiking sequence s r at different time steps, where t = 1 , … , T . If v(t) exceeds the threshold voltage V t h , then the spiking signal of the neuron is z ( t ) = 1 , and the neuron discharges simultaneously; otherwise, z ( t ) = 0 . The change in membrane potential during discharge is given by Equation 7.
v ( t ) = v ( t ) − V t h · z ( t )
Through observation of the charging-discharging activity of the neuron, eventually, the change in the membrane potential of neuron can be given by Equation 8.
v ( t ) = v ( t − 1 ) + sr ( t ) · w − V t h · z ( t )
After T time steps of change, the output of the SI-norm neuron, denoted as out, as shown by Equation 9. If no spikes are emitted, then o u t = 0 .
out = max 0 , ∑ t = 1 T sr ( i ) · w V t h = max 0 , ∑ t = 1 T z ( t )
As shown in Figure 2, the values of V t h and e x p i depend on the inputs x 1 ∼ x n , hence during the ANN-to-SNN conversion process, the weights and threshold voltage of the SI-norm neuron dynamically change. There exists a linear relationship between out and N s p i k e , with the linear factor being w i ⁄ V t h , as shown in Equation 10.
S p i k i n g _ S o f t m a x = out = max 0 , N spike · w V t h
N s p i k e denotes the number of spikes in the spiking sequence s r within the period T. If the threshold voltage V t h is the product of w and N s p i k e , then this voltage accumulates N s p i k e times to generate an output spike. Substituting N s p i k e for the input s r of SI-norm, amplifying the spiking signal, it is possible to save time of charging-discharging activity over T time steps in the inference process, as shown in Figure 5(b).

3.5. ANN-to-SNN Conversion Method

Based on the proposed Spiking-Softmax method, it is possible to achieve the ANN-to-SNN conversion of Transformer into Spike Integrated Transformer (SIT), which we refer to as SIT-conversion. The Spiking-Softmax method we proposed integrates SI-exp and SI-norm neurons, simulating the Softmax activation function in SNNs in the form of spikes, thereby achieving SIT-conversion for the Transformer model. The specific process of SIT-conversion is shown in Figure 6. The red and blue boxes in the middle represent neurons in ANN and SNN, respectively, and the horizontal arrows indicate the corresponding neurons are equivalent.

4. Experiment and Results

4.1. Experiment Setup

4.1.1. Datasets and Parameter Setup

In this section, we evaluated the proposed SIT-conversion on popular image classification datasets CIFAR10 [29], CIFAR100 [30], and ImageNet-1K [31]. The CIFAR10 dataset consists of 60,000 samples, divided into 10 categories, where each sample is a 32×32 pixel RGB image. These 60,000 samples are further split into 50,000 training samples and 10,000 testing samples. The CIFAR100 dataset is similar to CIFAR10, except it has 100 categories, with each category containing 500 training images and 100 testing images. The ImageNet-1K dataset contains 1.2 million training samples, 50,000 validation samples, and is divided into 1000 categories.
To empirically demonstrate the superiority and effectiveness of the proposed method, we optimized the internal parameters of SI-exp neurons by setting different time steps, verifying the approximation quality of the Spiking-Softmax method and the conversion efficiency of SIT-conversion. In addition, we performed SIT-conversion on various Transformer models to verify its effectiveness and robustness across Transformer variants of different sizes, providing comprehensive explanations of the experimental implementation details. Subsequently, we longitudinally compared the performance of SNNs generated by SIT-conversion from different Transformers on CIFAR10, CIFAR100, and ImageNet-1K datasets, discussing the universality of the proposed method, and quantitatively discussing the energy efficiency of the proposed method through calculations. Finally, we compared the effects of SIT-conversion on Transformer models of different sizes with state-of-the-art conversion techniques to validate the superiority of the proposed method.

4.1.2. Calculation of Energy Efficiency

To intuitively compare the energy consumption of ANNs models and SNNs models obtained through SIT-conversion, we used the energy estimation method proposed by [32] to quantitatively calculate energy reduction. First, we quantified the computational complexity of the l layers of both models using floating-point operations (FLOPs).
F L O P s ANN ( l ) = k 2 × c in × c out × w in × h out , Conv layer f in × f out , Linear layer
F L O P s S N N ( l ) = F L O P s A N N ( l ) × S p i k e N u m ( l ) N e u r o n N u m ( l )
Where k denotes the size of the convolutional kernel, c i n and c o u t denote the numbers of input and output channels, w i n and h o u t denote the widths and heights of the output feature maps, and f i n and f o u t are the numbers of input and output features. S p i k e N u m ( l ) and N e u r o n N u m ( l ) denote the total number of spikes and the number of neurons in layer l across all time steps. F L O P s A N N ( l ) and F L O P s S N N ( l ) denote the computational complexity of layer l for ANN and SNN models, respectively.
E A N N = ∑ l F L O P s A N N ( l ) × E M A C
E A N N = ∑ l F L O P s A N N ( l ) × E A C
In ANNs, each operation involves a floating-point multiply-accumulate (MAC) operation, whereas in SNNs, each operation is simply a floating-point addition (AC). In 45 nm CMOS, the energy cost of an ANN MAC operation is 4.6pJ, while the energy cost of an SNN addition operation is only 0.9pJ [33]. Therefore, by considering the FLOPs of the model and the energy cost of operations, we can calculate the energy consumption of SNN and ANN models.

4.2. Loss of the Spiking-Softmax Method in Different Time Steps

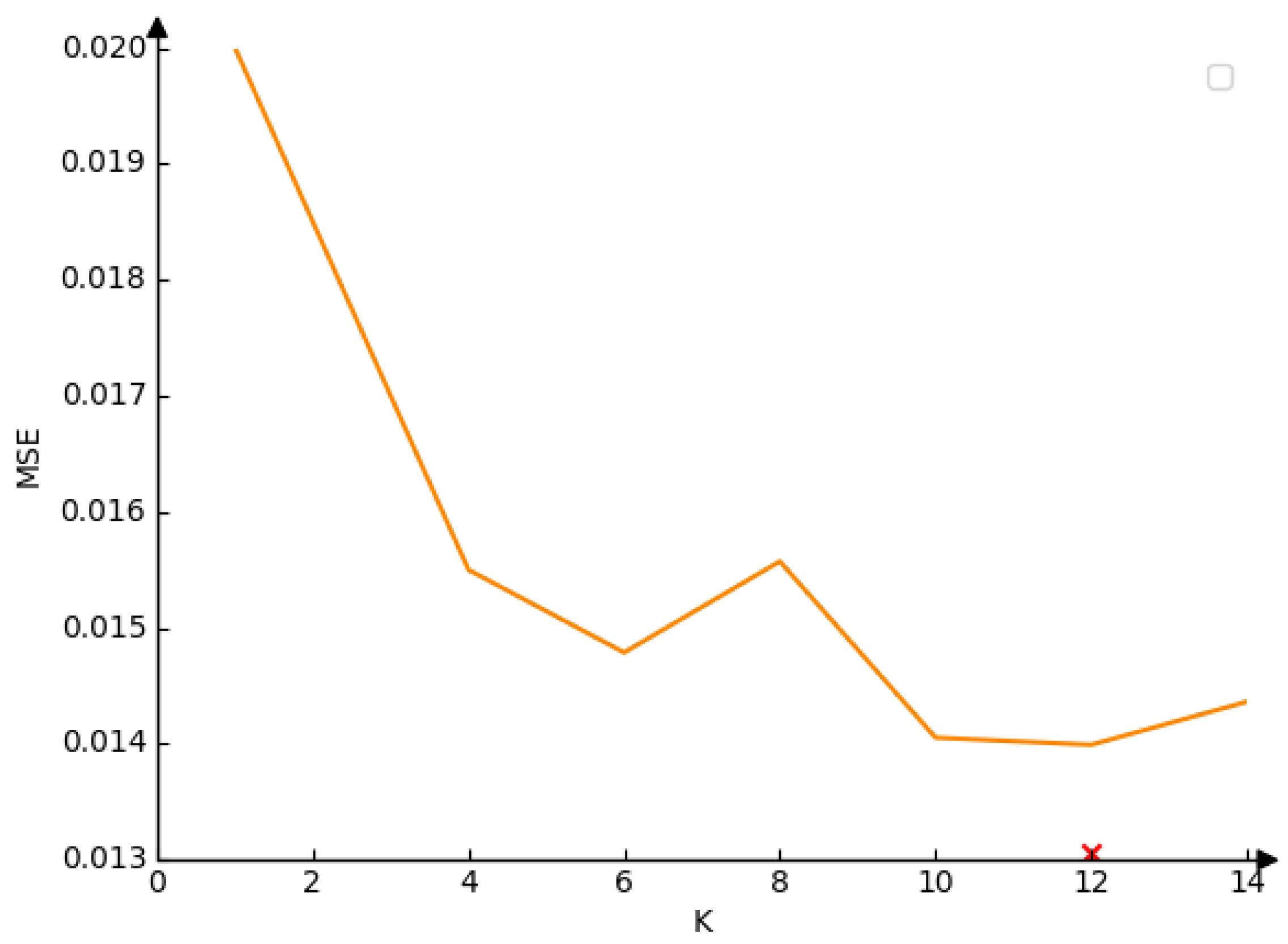
The time step K required by the SI-exp neuron not only affects the inference speed of the Spiking-Softmax method in SNNs but also correlates with the approximation quality of Spiking-Softmax. Since the internal parameters H(t), d(t), T(t) of the SI-exp neuron are related to the time step K and need to be pretrained. Therefore, a selection of 10,000 numbers as independent variables, evenly spaced in the interval [-1, 1], was chosen as training data, with their corresponding exponential values used as training labels. Then, by setting different time steps K, we trained the internal parameters of the SI-exp neuron for different K values, verifying the relationship between the time step K and the approximation quality of Spiking-Softmax.
The essence of the trade-off between the size of K and the approximation quality of Spiking-Softmax is illustrated in Figure 7, with the specific effect reflected in the values of mean square error. Since the training range of the internal parameters of SI-exp neurons is [-1, 1], we computed the mean square error using random values in the range [-1, 1], independent of any specific dataset. Therefore, our Spiking-Softmax method exhibits extremely strong generalization. Typically, rate-based conversions can only simulate simple activation functions, such as ReLU. Additionally, a large number of time steps are usually required to achieve a sufficiently accurate approximation, leading to high power consumption. However, our proposed SIT-conversion based on the Spiking-Softmax method only requires 12 time steps to simulate the Softmax activation function, with an MSE of only 0.013991, making the error almost negligible.

4.3. Performance on Different Transformer Models

To demonstrate the effectiveness and robustness of SIT-conversion across various scales of Transformer variants, three typical CNN-Transformer hybrid architecture models, EdgeNeXt [34], Next-ViT [35], and UniFormer [36], were selected to validate the proposed method on CIFAR10, CIFAR100, and ImageNet-1K datasets. EdgeNeXt and Next-ViT represent relatively shallow Transformer models, whereas UniFormer represents a deeper Transformer model. The models were trained in parallel using two NVIDIA RTX4090 GPUs, and one was employed during the SNN inference phase.
The input size of the model was set to 224×224, with a batch size of 256. All experiments were conducted using the AdamW optimizer [37] with a cosine learning rate schedule, as detailed in Table 1. Pretrained model (EdgeNeXt-S) obtained from the ImageNet-1K dataset was fine-tuned on CIFAR10 and CIFAR100 datasets. By default, the EdgeNeXt model had learning rate and weight decay set to 6e-3 and 0.05, respectively, and was fine-tuned for 100 epochs on both CIFAR10 and CIFAR100. For the Next-ViT model, pretrained model weights (Next-ViT-S) were loaded and fine-tuned on CIFAR10, CIFAR100, and ImageNet-1K datasets. By default, the learning rate and weight decay were set to 5e-6 and 0.1, respectively, with a gradual decay in learning rate. The model was fine-tuned for 20 epochs on the ImageNet-1K dataset with a weight decay of 1e-8. Fine-tuning was performed for 100 epochs on CIFAR10 and CIFAR100 with a learning rate of 5e-4 to achieve better convergence. For the UniFormer model, pretrained model weights (UniFormer_XXS) were loaded and fine-tuned on CIFAR10, CIFAR100, and ImageNet-1K datasets. By default, the learning rate and weight decay were set to 4e-5 and 0.05, respectively, with a gradual decay in learning rate. To prevent overfitting, the model was fine-tuned for 25 epochs on the ImageNet-1K dataset. Fine-tuning was conducted for 100 epochs on CIFAR10 and CIFAR100 with a learning rate of 5e-4. For the fine-tuned ANNs of EdgeNeXt, Next-ViT, and UniFormer models, we employed SIT-conversion to obtain corresponding converted SNNs models, and inference was conducted on different datasets to validate the effectiveness of SIT-conversion.

4.3.1. Performance on EdgeNeXt Model

To validate the effectiveness and efficiency of SIT-conversion for shallow Transformer architecture conversion, we selected the CNN-Transformer architecture image classification model, EdgeNeXt [34], for experimentation. The fine-tuned ANNs EdgeNeXt model demonstrates outstanding image classification performance on CIFAR10 (97.69%), CIFAR100 (85.40%), and ImageNet-1K (79.42%) datasets. The EdgeNeXt model comprises three Vision Transformer encoders, and in the experiment, SIT-conversion was employed to perform ANN-to-SNN conversion of the Transformer blocks within the EdgeNeXt model. To visually demonstrate the advantages of our SIT-conversion in the process of Transformer conversion, we systematically converted the Transformer Blocks within EdgeNeXt layer by layer, while recording the accuracy loss during the ANN-to-SNN conversion process.
The accuracy variations of the EdgeNeXt model during ANN-to-SNN conversion of Transformer blocks via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets are depicted in Table 2. With an increasing number of Transformer blocks converted, the accuracy of the EdgeNeXt model on CIFAR10 ranges from 97.68% to 97.69%, on CIFAR100 ranges from 85.37% to 85.42%, and on ImageNet-1K ranges from 79.18% to 79.30%. Upon conversion of all Transformer blocks in the EdgeNeXt model, the performances of the resulting SNNs generated by EdgeNeXt’s SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets are 97.69%, 85.37%, and 79.18%, respectively. The accuracy losses caused by SIT-conversion on CIFAR10 and CIFAR100 are only 0.01% and 0.03%, respectively, while the maximum loss on the ImageNet-1K dataset is 0.24%. The accuracy loss is negligible, achieving nearly lossless conversion.

4.3.2. Performance on Next-Vit Model

To validate the universality of SIT-conversion for shallow Transformer architecture conversion, the experiment selected the model Next-ViT [35], which adopts the same CNN-Transformer architecture and can be efficiently deployed in real-world industrial scenarios. Due to the majority of inputs to the Softmax function of the Transformer block in the Next-ViT model exceeding the training range of SI-exp neurons, a Sigmoid function was added before the model’s Softmax function. Fine-tuning yields excellent performance of the ANNs-based Next-ViT model on the CIFAR10, CIFAR100, and ImageNet-1K datasets, achieving accuracies of 97.62%, 86.54%, and 81.71% respectively. The Next-ViT model comprises four Transformer blocks. The SIT-conversion was employed in the experiment to achieve ANN-to-SNN conversion of the Transformer blocks within the Next-ViT model.
In order to visually demonstrate the advantages of our SIT-conversion in the process of Transformer blocks conversion, we systematically converted the Transformer blocks in Next-ViT layer by layer, recording the accuracy loss during the ANN-to-SNN conversion process.
The performances of the Next-ViT model when the Transformer blocks are converted layer by layer from ANN to SNN using SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets are shown in Table 3. As the number of converted Transformer blocks increases, the accuracy of Next-ViT varies from 97.61% to 97.62% on CIFAR10, from 86.53% to 86.55% on CIFAR100, and from 81.71% to 81.72% on ImageNet-1K. When all Transformer blocks of the Next-ViT model are converted, the accuracies of the SNNs generated by Next-ViT’s SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets are 97.61%, 86.55%, and 81.71% respectively. The accuracy loss caused by SIT-conversion is maximum on CIFAR10 (-0.01%), which can be neglected, while on CIFAR100 and ImageNet, the accuracies are improved by 0.01% respectively.

4.3.3. Performance on UniFormer Model

In this section, the UniFormer [36] model for efficient visual recognition was employed to verify the effectiveness and efficiency of SIT-conversion on deep Transformer models. Due to the majority of inputs to the Softmax function of the Transformer block in the UniFormer model exceeding the training range of SI-exp neurons, a Sigmoid function was added before the model’s Softmax function. Fine-tuning yields excellent performance of the ANNs-based UniFormer model on the CIFAR10, CIFAR100, and ImageNet-1K datasets, achieving accuracies of 97.46%, 85.70%, and 77.16% respectively. The UniFormer model employs global MHRA in deep layers to learn global token relations, where global MHRA is implemented by stacking Transformer blocks. The global MHRA of the UniFormer_XXS model used in the experiment consists of a total of 10 Transformer blocks. The SIT-conversion was employed to convert the Transformer blocks in UniFormer layer by layer from ANN to SNN, recording the accuracy loss during the transformation process to visually demonstrate the effectiveness of SIT-conversion.
The performances of the UniFormer model when the Transformer blocks are converted layer by layer from ANN to SNN using SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets are shown in Table 4. As the number of converted Transformer blocks increases, the accuracy of UniFormer varies from 97.45% to 97.59% on CIFAR10, from 85.68% to 85.77% on CIFAR100, and from 77.11% to 77.20% on ImageNet-1K. When all Transformer blocks in the UniFormer model are converted, the accuracies of the SNNs generated by UniFormer’s SIT-conversion on CIFAR10, CIFAR100 and ImageNet-1K datasets are 97.59%, 85.77%, and 77.11% respectively. The accuracy loss caused by SIT-conversion reaches a maximum of 0.05% on ImageNet-1K, which can be negligible, achieving almost lossless conversion. Meanwhile, the model accuracies are improved by 0.13% and 0.07% on CIFAR10 and CIFAR100 respectively.

4.3.4. Comparison of Different Transformer Models

In this section, the ANN-to-SNN conversion effects of applying SIT-conversion to the EdgeNeXt, Next-ViT, and UniFormer models were longitudinally compared on the CIFAR10, CIFAR100, and ImageNet-1K datasets.
As shown in Table 5, it can be observed that the SIT-conversion accuracies of the EdgeNeXt, Next-ViT, and UniFormer models on the ImageNet-1K dataset are 79.18%, 81.71%, and 77.11% respectively. As most of the inputs to the Softmax function in the Transformer blocks of the EdgeNeXt model lie within the preset range of SI-exp neurons, we did not add a Sigmoid function before the Softmax function of the EdgeNeXt model to enforce input range restriction, resulting in the maximum accuracy loss of 0.24% compared to its ANN model for the SNN generated by EdgeNeXt’s SIT-conversion on the ImageNet-1K dataset. However, for the UniFormer and Next-ViT models, the input range of the Softmax function was constrained, resulting in negligible accuracy losses of only UniFormer (-0.05%) and Next-ViT (0.00%) respectively. On the CIFAR100 dataset, the SIT-conversion accuracies of the EdgeNeXt, Next-ViT, and UniFormer models are 84.37%, 86.55%, and 85.77% respectively. The maximum accuracy loss of the SNN generated by the SIT-conversion of the EdgeNeXt model reaches 0.03%, while the accuracies after conversion for the Next-ViT and UniFormer models are improved by 0.01% and 0.07% respectively. On the CIFAR10 dataset, the SIT-conversion accuracies of the EdgeNeXt, Next-ViT, and UniFormer models are 97.69%, 97.61%, and 97.59% respectively. The maximum accuracy loss of the SNN generated by the SIT-conversion of the Next-ViT model is 0.01%, while the accuracy improvement after conversion for the UniFormer model is 0.13%. The accuracy of the EdgeNeXt model remains unchanged before and after conversion.
The EdgeNeXt, Next-ViT, and UniFormer models contained different numbers of Transformer blocks, with EdgeNeXt containing 3 Transformer blocks, Next-ViT containing 4 Transformer blocks, and UniFormer containing 10 Transformer blocks. However, the maximum conversion loss generated by SIT-conversion is only 0.24%, which is almost negligible. Furthermore, by using SIT-conversion to convert EdgeNeXt, Next-ViT, and UniFormer models, the energy consumption was significantly reduced. The energy consumption is reduced by 44.44% to 45.13% on the EdgeNeXt model, by 24.75% to 25.08% on the UniFormer model, and by 18.18% to 20.09% on the Next-ViT model, greatly reducing the energy required during the model inference process.
The above results demonstrated that SIT-conversion exhibited excellent performance in the ANN-to-SNN conversion process of various Transformer variants, confirming the universality of the proposed method. Even with 10 Transformer blocks in the UniFormer model, the Spiking-Softmax method could still maintain the accuracy of the attention matrix, without resulting in significant performance loss in the SNNs generated by SIT-conversion, achieving nearly lossless conversion. Simultaneously, it greatly reduced the model’s energy consumption.

4.4. Performance on with SOTA SNN Models

In this section, we compared our ANN-to-SNN framework with several state-of-the-art methods from different technological approaches. Firstly, we presented the comparison results of the proposed Spike-Softmax-based SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets with other advanced ANN-to-SNN methods, including the MST [20] method based on the Transformer architecture, as well as the SNM [38] and QCFS [39] methods based on CNN architecture. Subsequently, we compared the results with some works that directly train SNN-Transformer models, including Spikformer [18] and Spikingformer [17].
The comprehensive comparison results of the SNNs generated by SIT-conversion of EdgeNeXt, Next-ViT, and UniFormer models with other SOTA SNNs models on CIFAR10, CIFAR100, and ImageNet datasets are presented in Table 6. Compared to non-Transformer architecture-based ANN-to-SNN conversion methods, the accuracies of the SNNs generated by SIT-conversion on CIFAR10, CIFAR100, and ImageNet datasets are higher than those of SNM [38] and QCFS [39]. Additionally, our SIT-conversion requires only 12 time steps, significantly fewer than the time steps required by SNM and QCFS. However, due to their non-Transformer architecture, the proposed methods are not directly comparable to SNM and QCFS in terms of conversion loss and model parameter count.
Compared to SNNs based on the Transformer architecture, SNNs generated by the SIT-conversion of EdgeNeXt and Next-ViT models surpass the accuracy of the MST [20] model, which employs ANN-to-SNN conversion approach, on the CIFAR10 and ImageNet-1K datasets. Although the accuracies of SNNs generated by the SIT-conversion of EdgeNeXt, Next-ViT, and UniFormer models on the CIFAR100 dataset is lower than that of the MST model (86.91%) and the accuracy of SNNs generated by the SIT-conversion of the UniFormer model on the ImageNet-1K dataset is lower than that of the MST model (78.51%), the models used in the experiments all adopt a lightweight CNN-Transformer hybrid architecture. Furthermore, the conversion loss of all models on the three datasets is reduced by 1% to 1.89% compared to the MST model. Moreover, the SIT-conversion achieves the conversion of the Transformer core and achieves nearly lossless conversion in only 12 time steps, which is significantly lower than the 256 time steps required by MST.
SNNs generated by the SIT-conversion of EdgeNeXt, Next-ViT, and UniFormer models achieve higher accuracies on the CIFAR10, CIFAR100, and ImageNet-1K datasets compared to directly trained Spikformer [18] and Spikingformer [17]. Furthermore, the ANN-to-SNN conversion method could achieve performance comparable to leading ANNs without requiring prolonged training time.
The results indicate that our proposed SIT-conversion based on the Spiking-Softmax method achieves not only the highest level of SNN inference accuracy but also achieves nearly lossless ANN-to-SNN conversion in the evaluated network architectures and datasets using only 12 time steps, and truly realizes the self-attention mechanism in Transformer models through ANN-to-SNN conversion.

5. Discussion

Currently, studies on ANN-to-SNN conversion of Transformer models achieved energy reduction by converting simple activation functions such as ReLU in MLPs or by pruning the attention maps in the self-attention mechanism. However, the converted SNN-Transformer models still utilized the self-attention mechanism of ANNs. Within the self-attention mechanism lies a complex activation function, Softmax, for which we proposed the Spiking-Softmax method to simulate in SNNs. Based on Spiking-Softmax method, we have proposed the SIT-conversion to achieve energy reduction in Transformer models.
Our proposed Spiking-Softmax method comprises Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm). SI-exp neurons leveraged the use of spike-form-based timing encoding, where spike timing conveys additional information, specifically implemented through their internal parameters T(t), h(t), and d(t). By optimizing these internal parameters, precise simulation of exponential operations could be achieved in SNNs with only a few time steps required for inference. However, due to the simplicity of neuron structure, accurate simulation within a large input range is currently unattainable. Experimental results demonstrate that the current parameter selection method enables iterative processing within the input range of -1 to 1, thus achieving more accurate simulation. SI-norm neurons, receiving outputs from SI-exp neurons, dynamically adjust weights and thresholds to perform normalization operations through spike emission. By integrating SI-exp and SI-norm neurons, complex Softmax activation functions can be simulated with minimal loss.
Our proposed SIT-conversion based on the Spiking-Softmax method achieved the conversion of the core self-attention mechanism of the Transformer model in just 12 time steps. Moreover, SIT-conversion was applicable to Transformer models of various scales, with the UniFormer model tested currently containing up to 10 Transformer blocks. However, because most inputs to the Softmax function of Transformer blocks in the Next-ViT and UniFormer models exceed the training range of SI-exp neurons, we added a Sigmoid layer before them to ensure that the majority of inputs to Spiking-Softmax during inference lie within [-1,1], thus achieving nearly the same accuracy as their corresponding ANNs. Since most inputs to the Softmax function of Transformer blocks in the EdgeNeXt model fall within the training range of SI-exp neurons, we directly performed SIT-conversion on the EdgeNeXt model. The SNNs generated by the SIT-conversion of the EdgeNeXt model exhibit a maximum conversion loss of 0.24%, which is still much lower than previous studies on ANN-to-SNN conversion for Transformer models. Therefore, training the adjusted ANNs-Transformer model directly and then applying the SIT-conversion method can address the aforementioned issue. Additionally, SNNs generated by SIT-conversion significantly reduce energy consumption during inference. For the EdgeNeXt, Next-ViT, and UniFormer models selected in the experiments, the maximum reduction in energy consumption is 45.13% (EdgeNeXt), and the minimum reduction is 18.18% (Next-ViT), greatly reducing the energy required during model inference.
Our method amplified spiking signals through built-in trainable parameters T(t), h(t), and d(t), accurately simulating the Softmax activation function with floating-point outputs, thus achieving nearly lossless ANN-to-SNN conversion. SIT-conversion is applicable to Transformer models of different scales. Despite achieving these exciting results, there is still considerable room for improvement. In the future, we plan to adjust neuron structures, expand the tolerance range of the Spiking-Softmax method, and enhance the usability of SIT-conversion.

6. Conclusions

In this paper, we addressed the inability to convert the self-attention mechanism from ANNs to SNNs in the SNN-Transformer model. We proposed the Spiking-Softmax method, which integrates Spiking Exponential Neuron (SI-exp) and Spiking Collaboration Normalized Neuron (SI-norm), successfully resolving the mismatch between the Softmax activation function in SNN-Transformer and the computation rules of SNNs. Building upon this, we proposed the SIT-conversion method, which enables the conversion of Transformer architectures to SNNs, resolving the limitation of only being able to simulate simple activation functions of Transformer models in SNNs. By optimizing the internal parameters of SI-exp neurons with different time steps, we demonstrated that the Spiking-Softmax method requires only 12 time steps to accurately simulate the Softmax activation function, significantly lower than the current state-of-the-art ANN-to-SNN conversion methods for Transformer models. Furthermore, we performed SIT-conversion on EdgeNeXt, Next-ViT, and UniFormer models and validated the resulting SNNs on the CIFAR10, CIFAR100, and ImageNet-1K datasets. Experimental results demonstrate that SNNs generated by the SIT-conversion of EdgeNeXt, Next-ViT, and UniFormer models achieve nearly identical accuracy to their corresponding ANNs on the CIFAR10, CIFAR100, and ImageNet-1K datasets. Additionally, the conversion loss range of SNNs generated by SIT-conversion is between -0.05 and +0.13, with only the EdgeNeXt model achieving a conversion loss of -0.24 on the ImageNet-1K dataset, demonstrating nearly lossless ANN-to-SNN conversion and validating the effectiveness and generalization capability of the method. Currently, the tested models contain a maximum of 10 layers of Transformer blocks. Furthermore, among the models selected for experimentation, the EdgeNeXt model achieves the highest energy reduction of 44.44% to 45.13%, while the Next-ViT model achieves the least energy reduction of 18.18% to 20.09%, significantly reducing the energy consumption required during model inference. The proposed method represents the first complete conversion of the Softmax activation function and Transformer models in SNNs, which will drive the development of SNN algorithms and reduce the gap between SNN models and ANN models in practical applications.

Author Contributions

Conceptualization, Xuhang Li and Qianzi Shen; methodology, Xuhang Li; software, Haitao Wang; validation, Xuhang Li and Haitao Wang; formal analysis, Haitao Wang; investigation, Qianzi Shen; resources, Xuhang Li; data curation, Qianzi Shen; writing—original draft preparation, Xuhang Li; writing—review and editing, Zijian Wang and Xuhang Li; visualization, Qianzi Shen; supervision, Zijian Wang; project administration, Zijian Wang; funding acquisition, Zijian Wang. All authors have read and agreed to the published version of the manuscript. Xuhang Li and Qianzi Shen contributed equally to this paper

Funding

This research was funded by National Natural Science Foundation of China (No. 62302090 and No. 62272097), Shanghai Sailing Program (No.23YF1401100) and Fundamental Research Funds for the Central Universities (No. 2232021D-26).

Data Availability Statement

The data presented in this study are available in [ImageNet and Cifar] at [https://image-net.org/ and https://www.cs.toronto.edu/~kriz/cifar.html].

Acknowledgments

This research is supported by National Natural Science Foundation of China (No. 62302090 and No. 62272097), Shanghai Sailing Program (No.23YF1401100) and Fundamental Research Funds for the Central Universities (No. 2232021D-26).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Maass, W. Networks of spiking neurons: the third generation of neural network models. Neural networks 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
  2. Roy, K.; Jaiswal, A.; Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 2019, 575, 607–617. [Google Scholar] [CrossRef] [PubMed]
  3. Wang, X.; Lin, X.; Dang, X. Supervised learning in spiking neural networks: A review of algorithms and evaluations. Neural Networks 2020, 125, 258–280. [Google Scholar] [CrossRef] [PubMed]
  4. Fang, W.; Yu, Z.; Chen, Y.; Huang, T.; Masquelier, T.; Tian, Y. Deep residual learning in spiking neural networks. Advances in Neural Information Processing Systems 2021, 34, 21056–21069. [Google Scholar]
  5. Hu, Y.; Tang, H.; Pan, G. Spiking deep residual networks. IEEE Transactions on Neural Networks and Learning Systems 2021, 34, 5200–5205. [Google Scholar] [CrossRef] [PubMed]
  6. Zheng, H.; Wu, Y.; Deng, L.; Hu, Y.; Li, G. Going deeper with directly-trained larger spiking neural networks. Proceedings of the AAAI conference on artificial intelligence, 2021, Vol. 35, pp. 11062–11070.
  7. Lotfi Rezaabad, A.; Vishwanath, S. Long short-term memory spiking networks and their applications. International Conference on Neuromorphic Systems 2020, 2020, pp. 1–9. [Google Scholar]
  8. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser. ; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30. [Google Scholar]
  9. Zhao, W.X.; Zhou, K.; Li, J.; Tang, T.; Wang, X.; Hou, Y.; Min, Y.; Zhang, B.; Zhang, J.; Dong, Z.; others. A survey of large language models. arXiv preprint arXiv:2303.18223 2023.
  10. Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; others. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929 2020.
  11. Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Jiang, Z.H.; Tay, F.E.; Feng, J.; Yan, S. Tokens-to-token vit: Training vision transformers from scratch on imagenet. Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 558–567.
  12. Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. European conference on computer vision. Springer, 2020, pp. 213–229.
  13. Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 10012–10022.
  14. Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable detr: Deformable transformers for end-to-end object detection. arXiv preprint arXiv:2010.04159 2020.
  15. Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; others. Language models are few-shot learners. Advances in neural information processing systems 2020, 33, 1877–1901. [Google Scholar]
  16. Zhou, Z.; Che, K.; Fang, W.; Tian, K.; Zhu, Y.; Yan, S.; Tian, Y.; Yuan, L. Spikformer V2: Join the High Accuracy Club on ImageNet with an SNN Ticket. arXiv preprint arXiv:2401.02020 2024.
  17. Zhou, C.; Yu, L.; Zhou, Z.; Zhang, H.; Ma, Z.; Zhou, H.; Tian, Y. Spikingformer: Spike-driven Residual Learning for Transformer-based Spiking Neural Network. arXiv preprint arXiv:2304.11954 2023.
  18. Zhou, Z.; Zhu, Y.; He, C.; Wang, Y.; Yan, S.; Tian, Y.; Yuan, L. Zhou, Z.; Zhu, Y.; He, C.; Wang, Y.; Yan, S.; Tian, Y.; Yuan, L. Spikformer: When spiking neural network meets transformer. arXiv preprint arXiv:2209.15425 2022.
  19. Mueller, E.; Studenyak, V.; Auge, D.; Knoll, A. Spiking transformer networks: A rate coded approach for processing sequential data. 2021 7th International Conference on Systems and Informatics (ICSAI). IEEE, 2021, pp. 1–5.
  20. Wang, Z.; Fang, Y.; Cao, J.; Zhang, Q.; Wang, Z.; Xu, R. Masked spiking transformer. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023, pp. 1761–1771.
  21. Ho, N.D.; Chang, I.J. TCL: an ANN-to-SNN conversion with trainable clipping layers. 2021 58th ACM/IEEE Design Automation Conference (DAC). IEEE, 2021, pp. 793–798.
  22. Jiang, H.; Anumasa, S.; De Masi, G.; Xiong, H.; Gu, B. A unified optimization framework of ANN-SNN conversion: towards optimal mapping from activation values to firing rates. International Conference on Machine Learning. PMLR, 2023, pp. 14945–14974.
  23. Cordonnier, J.B.; Loukas, A.; Jaggi, M. Cordonnier, J.B.; Loukas, A.; Jaggi, M. On the relationship between self-attention and convolutional layers. arXiv preprint arXiv:1911.03584 2019.
  24. Siddique, A.; Vai, M.I.; Pun, S.H. A low cost neuromorphic learning engine based on a high performance supervised SNN learning algorithm. Scientific Reports 2023, 13, 6280. [Google Scholar] [CrossRef] [PubMed]
  25. Guo, L.; Gao, Z.; Qu, J.; Zheng, S.; Jiang, R.; Lu, Y.; Qiao, H. Transformer-based Spiking Neural Networks for Multimodal Audio-Visual Classification. IEEE Transactions on Cognitive and Developmental Systems 2023. [Google Scholar]
  26. Zhang, J.; Dong, B.; Zhang, H.; Ding, J.; Heide, F.; Yin, B.; Yang, X. Spiking transformers for event-based single object tracking. Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition, 2022, pp. 8801–8810.
  27. Stöckl, C.; Maass, W. Optimized spiking neurons can classify images with high accuracy through temporal coding with two spikes. Nature Machine Intelligence 2021, 3, 230–238. [Google Scholar] [CrossRef]
  28. Zhang, J.; Zhang, L. Spiking Neural Network Implementation on FPGA for Multiclass Classification. 2023 IEEE International Systems Conference (SysCon). IEEE, 2023, pp. 1–8.
  29. LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
  30. Krizhevsky, A.; Hinton, G. ; others. Learning multiple layers of features from tiny images. 2009. [Google Scholar]
  31. Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. 2009 IEEE conference on computer vision and pattern recognition. Ieee, 2009, pp. 248–255.
  32. Rathi, N.; Roy, K. Diet-snn: A low-latency spiking neural network with direct input encoding and leakage and threshold optimization. IEEE Transactions on Neural Networks and Learning Systems 2021, 34, 3174–3182. [Google Scholar] [CrossRef] [PubMed]
  33. Horowitz, M. 1.1 computing’s energy problem (and what we can do about it). 2014 IEEE international solid-state circuits conference digest of technical papers (ISSCC). IEEE, 2014, pp. 10–14.
  34. Maaz, M.; Shaker, A.; Cholakkal, H.; Khan, S.; Zamir, S.W.; Anwer, R.M.; Shahbaz Khan, F. Edgenext: efficiently amalgamated cnn-transformer architecture for mobile vision applications. European Conference on Computer Vision. Springer, 2022, pp. 3–20.
  35. Li, J.; Xia, X.; Li, W.; Li, H.; Wang, X.; Xiao, X.; Wang, R.; Zheng, M.; Pan, X. Next-vit: Next generation vision transformer for efficient deployment in realistic industrial scenarios. arXiv preprint arXiv:2207.05501 2022.
  36. Li, K.; Wang, Y.; Zhang, J.; Gao, P.; Song, G.; Liu, Y.; Li, H.; Qiao, Y. Uniformer: Unifying convolution and self-attention for visual recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 12581–12600. [Google Scholar] [CrossRef] [PubMed]
  37. Loshchilov, I. Loshchilov, I. Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101 2017.
  38. Wang, Y.; Zhang, M.; Chen, Y.; Qu, H. Signed neuron with memory: Towards simple, accurate and high-efficient ann-snn conversion. International Joint Conference on Artificial Intelligence, 2022.
  39. Bu, T.; Fang, W.; Ding, J.; Dai, P.; Yu, Z.; Huang, T. Bu, T.; Fang, W.; Ding, J.; Dai, P.; Yu, Z.; Huang, T. Optimal ANN-SNN conversion for high-accuracy and ultra-low-latency spiking neural networks. arXiv preprint arXiv:2303.04347 2023.
Preprints 137702 g001
Figure 1. Structure of the Spike Integrated Transformer, where the Softmax activation function in the multi-head attention mechanism is replaced by Spiking-Softmax.
Figure 1. Structure of the Spike Integrated Transformer, where the Softmax activation function in the multi-head attention mechanism is replaced by Spiking-Softmax.
Preprints 137702 g001
Preprints 137702 g002
Figure 2. Principle of the Spiking-Softmax method implementation. The e x p i denotes the i-th SI-exp neuron, where i = 1 , 2 , . . . , n . The V t h (the sum of all SI-exp neuron outputs) denotes the threshold voltage of the SI-norm neuron, and the regular spike sequence sr denotes the input to the SI-norm neuron. Simultaneously, the output of the SI-exp neurons serves as the weight w for the SI-norm neuron.
Figure 2. Principle of the Spiking-Softmax method implementation. The e x p i denotes the i-th SI-exp neuron, where i = 1 , 2 , . . . , n . The V t h (the sum of all SI-exp neuron outputs) denotes the threshold voltage of the SI-norm neuron, and the regular spike sequence sr denotes the input to the SI-norm neuron. Simultaneously, the output of the SI-exp neurons serves as the weight w for the SI-norm neuron.
Preprints 137702 g002
Preprints 137702 g003
Figure 3. Inference process of the SI-exp neuron over K time steps. Where x denotes the floating-point input, and the internal parameters h(t), d(t), T(t) are optimized in advance to simulate the charge-discharge activity of the SI-exp neuron. After K time steps of inference, the final output of the SI-exp neuron e x p i is obtained, which approximately equals the result of the exponential operation e x p x in ANNs.
Figure 3. Inference process of the SI-exp neuron over K time steps. Where x denotes the floating-point input, and the internal parameters h(t), d(t), T(t) are optimized in advance to simulate the charge-discharge activity of the SI-exp neuron. After K time steps of inference, the final output of the SI-exp neuron e x p i is obtained, which approximately equals the result of the exponential operation e x p x in ANNs.
Preprints 137702 g003
Preprints 137702 g004
Figure 4. Distribution of optimized internal parameters of the SI-exp neuron. The horizontal axis denotes the time step, and the vertical axis denotes the parameter value.
Figure 4. Distribution of optimized internal parameters of the SI-exp neuron. The horizontal axis denotes the time step, and the vertical axis denotes the parameter value.
Preprints 137702 g004
Preprints 137702 g005
Figure 5. SI-norm neuron. a) A simulation of the SI-norm neuron over T time steps, with the output spike sequence denoted by z(t). b) SI-norm neurons are implemented using N s p i k e rather than s r .
Figure 5. SI-norm neuron. a) A simulation of the SI-norm neuron over T time steps, with the output spike sequence denoted by z(t). b) SI-norm neurons are implemented using N s p i k e rather than s r .
Preprints 137702 g005
Preprints 137702 g006
Figure 6. ANN-to-SNN Conversion Process.
Figure 6. ANN-to-SNN Conversion Process.
Preprints 137702 g006
Preprints 137702 g007
Figure 7. The impact of different time steps on the Spiking-Softmax method’s simulation of the Softmax activation function. K denotes the time step, and MSE is the mean square error of the Spiking-Softmax method’s approximation to the Softmax activation function. The red cross indicates the chosen value of K in the given context, where K=12 achieves the lowest MSE of 0.013991.
Figure 7. The impact of different time steps on the Spiking-Softmax method’s simulation of the Softmax activation function. K denotes the time step, and MSE is the mean square error of the Spiking-Softmax method’s approximation to the Softmax activation function. The red cross indicates the chosen value of K in the given context, where K=12 achieves the lowest MSE of 0.013991.
Preprints 137702 g007
Table 1. Parameter settings of EdgeNeXt, Next-ViT, and UniFormer models trained on CIFAR10, CIFAR100, and ImageNet-1K datasets.
Table 1. Parameter settings of EdgeNeXt, Next-ViT, and UniFormer models trained on CIFAR10, CIFAR100, and ImageNet-1K datasets.
Model Dataset lr weight-decay epoch
EdgeNeXt CIFAR10 6e-3 0.05 100
  CIFAR100 6e-3 0.05 100
  ImageNet-1K / / /
Next-ViT CIFAR10 5e-4 0.1 100
  CIFAR100 5e-4 0.1 100
  ImageNet-1K 5e-6 1e-8 20
UniFormer CIFAR10 5e-4 0.05 100
  CIFAR100 5e-4 0.05 100
  ImageNet-1K 4e-5 0.05 25
Table 2. Accuracy variation of the EdgeNeXt model during layer-by-layer Transformer block conversion via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets, where numbers in parentheses represent conversion losses. Layers represent the number of Transformer blocks converted.
Table 2. Accuracy variation of the EdgeNeXt model during layer-by-layer Transformer block conversion via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets, where numbers in parentheses represent conversion losses. Layers represent the number of Transformer blocks converted.
Layers ImageNet-1K(%) CIFAR100(%) CIFAR10(%)
0 79.42 85.40 97.69
1 79.30(-0.10) 85.37(-0.03) 97.69(0.00)
2 79.30(-0.10) 85.42(+0.02) 97.68(-0.01)
3 79.18(-0.24) 85.37(-0.03) 97.69(0.00)
Table 3. Accuracy variation of the Next-ViT model during layer-by-layer Transformer block conversion via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets, where numbers in parentheses represent conversion losses.
Table 3. Accuracy variation of the Next-ViT model during layer-by-layer Transformer block conversion via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets, where numbers in parentheses represent conversion losses.
Layers ImageNet-1K(%) CIFAR100(%) CIFAR10(%)
0 81.71 86.54 97.62
1 81.71(0.00) 86.55(+0.01) 97.61(-0.01)
2 81.72(+0.01) 86.55(+0.01) 97.61(-0.01)
3 81.72(+0.01) 86.53(-0.01) 97.61(-0.01)
4 81.72(+0.01) 86.55(+0.01) 97.61(-0.01)
Table 4. Accuracy variation of the UniFormer model during layer-by-layer Transformer block conversion via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets, where numbers in parentheses represent conversion losses.
Table 4. Accuracy variation of the UniFormer model during layer-by-layer Transformer block conversion via SIT-conversion on CIFAR10, CIFAR100, and ImageNet-1K datasets, where numbers in parentheses represent conversion losses.
Layers ImageNet-1K(%) CIFAR100(%) CIFAR10(%)
0 77.16 85.70 97.46
1 77.16(0.00) 85.68(-0.02) 97.46(0.00)
2 77.18(+0.02) 85.75(+0.05) 97.45(-0.01)
3 77.18(+0.02) 85.72(+0.02) 97.47(+0.01)
4 77.18(+0.02) 85.68(-0.02) 97.45(-0.01)
5 77.20(+0.04) 85.69(-0.01) 97.45(-0.01)
6 77.19(+0.03) 85.70(0.00) 97.47(+0.01)
7 77.18(+0.02) 85.68(-0.02) 97.46(0.00)
8 77.15(-0.01) 85.72(+0.02) 97.48(+0.02)
9 77.17(+0.01) 85.70(0.00) 97.48(+0.02)
10 77.11(-0.05) 85.77(+0.07) 97.59(+0.13)
Table 5. The accuracy, conversion loss, and theoretical energy consumption per sample during inference (parentheses indicate energy reduction compared to ANN) of SNNs generated by SIT-conversion from three state-of-the-art Transformer models on CIFAR10, CIFAR100, and ImageNet-1K datasets are presented. SNNs generated by Transformer’s SIT-conversion achieve nearly the same accuracy as their ANNs counterparts.
Table 5. The accuracy, conversion loss, and theoretical energy consumption per sample during inference (parentheses indicate energy reduction compared to ANN) of SNNs generated by SIT-conversion from three state-of-the-art Transformer models on CIFAR10, CIFAR100, and ImageNet-1K datasets are presented. SNNs generated by Transformer’s SIT-conversion achieve nearly the same accuracy as their ANNs counterparts.
Model ANN
Acc		 SIT-conversion
Acc		 Conversion
Loss		 Blocks Params FLOPs Energy(mJ)
ImageNet-1K
EdgeNeXt 79.42% 79.18% -0.24% 3 5.59M 1.26G 3.19(-44.96%)
Next-ViT 81.71% 81.71% 0.00% 4 31.76M 5.8G 21.83(-18.18%)
UniFormer 77.16% 77.11% -0.05% 10 10.21M 1.3G 4.49(-24.92%)
CIFAR100
EdgeNeXt 85.40% 85.37% -0.03% 3 5.59M 1.26G 3.22(-44.22%)
Next-ViT 86.54% 86.55% +0.01% 4 31.76M 5.8G 21.32(-20.09%)
UniFormer 85.70% 85.77% +0.07% 10 10.21M 1.3G 4.48(-25.08%)
CIFAR10
EdgeNeXt 97.69% 97.69% 0.00% 3 5.59M 1.26G 3.18(-45.13%)
Next-ViT 97.62% 97.61% -0.01% 4 31.76M 5.8G 21.56(-19.19%)
UniFormer 97.46% 97.59% +0.13% 10 10.21M 1.3G 4.50(-24.75%)
Table 6. Performance comparison of the SNNs generated by SIT-conversion of EdgeNeXt, Next-ViT, and UniFormer models with SOTA SNNs on CIFAR10, CIFAR100, and ImageNet-1K datasets.
Table 6. Performance comparison of the SNNs generated by SIT-conversion of EdgeNeXt, Next-ViT, and UniFormer models with SOTA SNNs on CIFAR10, CIFAR100, and ImageNet-1K datasets.
Model Method Architecture Time Steps ACC(%) Conversion Loss(%)
CIFAR10
Spikformer[18] Direct Training Spikformer-4-384 4 95.19 /
Spikingformer[17] Direct Training Spikingformer-4-384 4 95.61 /
SNM [38] ANN-To-SNN ResNet-18 128 95.19 -0.02
QCFS[39] ANN-To-SNN ResTNet-18 32 96.08 +0.04
MST[20] ANN-To-SNN Swin-T (BN) 256 97.27 -1.01
SIT-EdgeNeXt (ours) ANN-To-SNN EdgeNeXt 12 97.69 0.00
SIT-Next-ViT (ours) ANN-To-SNN Next-ViT 12 97.61 -0.01
SIT-UniFormer (ours) ANN-To-SNN Uniformer 12 97.59 +0.13
CIFAR100
Spikformer[18] Direct Training Spikformer-4-384 4 77.86 /
Spikingformer[17] Direct Training Spikingformer-4-384 4 79.09 /
SNM [38] ANN-To-SNN ResNet-18 128 77.97 -0.29
QCFS[39] ANN-To-SNN RestNet-18 512 79.61 +0.81
MST[20] ANN-To-SNN Swin-T (BN) 256 86.91 -1.81
SIT-EdgeNeXt (ours) ANN-To-SNN EdgeNeXt 12 85.37 -0.03
SIT-Next-ViT (ours) ANN-To-SNN Next-ViT 12 86.55 +0.01
SIT-UniFormer (ours) ANN-To-SNN Uniformer 12 85.77 +0.07
ImageNet-1K
Spikformer[18] Direct Training Spikformer-8-768 4 74.81 /
Spikingformer[17] Direct Training Spikingformer-8-786 4 75.85 /
SNM [38] ANN-To-SNN VGG16 1024 73.16 -0.02
QCFS[39] ANN-To-SNN RestNet-18 1024 74.32 +0.03
MST[20] ANN-To-SNN Swin-T (BN) 512 78.51 -2
SIT-EdgeNeXt (ours) ANN-To-SNN EdgeNeXt 12 79.18 -0.24
SIT-Next-ViT (ours) ANN-To-SNN Next-ViT 12 81.71 0.00
SIT-UniFormer (ours) ANN-To-SNN Uniformer 12 77.11 -0.05
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated