1. Introduction
Currently, it is estimated that nearly 90% of global goods are moved via maritime transport, with around 60% of those being shipped in containers. This highlights the crucial role that container vessels play in both the maritime logistics chain and the global economy. These ships are specifically designed to enhance the efficiency of loading and unloading processes at ports. However, they are particularly vulnerable to bending and torsional stresses. Container vessels feature double bottoms and are framed longitudinally, making this section especially critical when assessing structural integrity [
1]. A key component of the double bottom structure is the transverse elements, often referred to as floors.
Inspection ports, pipe tunnels, weight-reduction cutouts, and apertures that let regular stiffeners from the bottom and double bottom pass through are features that set these constructions apart. Due to the significant concentrations of stress in this location, a mix of these characteristics impacts the structural capability of the floor [
2]. The floor can be treated as reinforced panels or perforated plates for structural analysis, where the buckling strength of the plates is decreased by the cutouts and perforations. The buckling design process needs to take this reduction into consideration. This kind of construction has been extensively studied from a variety of angles. Wang et al. [
3] used both linear and nonlinear FEM models to examine how geometrical parameters affected buckling and ultimate strength. Additionally, they suggested a simplified method that accounts for reduction factors. Liu et al. [
4] provided valuable insights into the effects of small and large apertures on the ultimate strength of longitudinal and transverse girders under lateral and uniaxial stresses on deck panels by experimental and computational study. Apertures’ geometry is crucial for structural assessments. This is illustrated in the study by Saad-Eldeen et al. [
5], which examined how the ultimate strength of steel plates that had undergone compressive testing after being stiffened and unstiffened was affected by variations in opening size, shape, steel composition, and structural configurations. Similarly, Yanli et al. [
6] investigated the effects of size, opening position and form on bending plate buckling strength.
Using a variety of high-strength steels, Saad-Eldeen et al. [
7] extended their research by adding a new variable and examining the effects of various morphologies—circular and elongated circular openings—under uniaxial compression. Given the vulnerability of these structures, adequate reinforcement is essential to maintain structural integrity throughout their service life. As a result, significant research has been directed at this issue. For instance, Kim et al. [
8] developed a formula for this design approach after investigating the best reinforcement strategies to improve perforated plates’ buckling and ultimate strength. Another important consideration when examining these structures is corrosion;
The efficiency of recovering the structural capability of a corroded double bottom side girder plate was examined by Chichi and Garbatov [
9]. This manhole-shaped side girder was subjected to both the irregular, intermittent corrosion-degrading effects and uniaxial compressive loads. Similar to this, Cui and Wang [
10] used both numerical and experimental approaches to examine the ultimate compressive strength of common stiffened plates with perforations, with a focus on the impacts of corrosion phenomenon. Saad-Eldeen et al. [
11] assessed the ultimate strength of steel plates having large, elongated circular holes under uniaxial compressive pressures through experimental testing. They looked at energy dissipation, resilience, toughness, force-displacement, strength-strain, and collapse modes. Other odd geometries have also been studied for their structural implications. For example, the residual structural capability of steel plates having significant centered ellipsoidal holes, both without and with locking cracks, was examined experimentally by Saad-Eldeen et al. [
12].
The behavior of unstiffened plates with rectangular apertures under various variables, such as plate slenderness, opening area ratio, and opening location, was investigated by Yu and Lee [
13]. The collapse behavior and post-peak response of stiffened plates with square holes and angle sections under axial and out-of-plane stresses were investigated by Kumar et al. [
14]. Research on apertures also focuses on other materials. The mechanical properties of typical composite structures with open holes were examined by Li et al. [
15]. Initial defects are an important factor to take into account while assessing a construction. In their assessment of the final compressive strength for similarly stiffened panels made of steel and aluminium, Doan et al. [
16] looked at the effects of the heat-affected zone, early flaws, boundary conditions and the presence of apertures on the web of longitudinal girders.
In structural analysis, defining the boundary conditions is essential. Using finite element (FE) models, Xu et al. [
17] investigated how boundary conditions and model geometry affected the expected collapse response of stiffened panels. The most popular method for evaluating these openings’ performance is finite element analysis (FEA). Through a series of experimental and computational experiments including both mechanical tests and non-linear FEA, Kim et al. [
18] assessed the buckled state and final yield strength of plates and stiffened panels with holes under axial compressive loads. Similarly, using non-linear FEA techniques, Cui and Wang [
19] investigated the ultimate strength of longitudinal girders having apertures in the double bottom region, subjected to longitudinal compression. In order to replicate the major forces resulting from either horizontal or vertical bending moments in vessel hull girders, Paik [
20] examined the ultimate strength properties of steel plates with a single circular hole under axial compressive loads along the short edges. This was achieved by altering the plate’s thickness and aspect ratio as well as the hole size using ANSYS software.
In order to determine the optimal design in terms of fatigue strength, Silva-Campillo et al. [
21] examined the effects of curvature radius in various cut-out shapes in the transverse web frame for longitudinal stiffener transit from the perspective of optimal analysis. Andersen [
22] introduced a novel fatigue-strength cut-out design that uses finite element-based optimization of shapes to lower stress and provide a new ideal cut-out form. In another study, Silva-Campillo et al. [
23] evaluated the impact of all cut-outs placed for the installation of longitudinal stiffeners in the major transverse structure of the torsion box while optimizing the local structural weight using a nonlinear multi-variable optimization tool.
This study examines the structural strength of a perforated plate—which represents the double bottom floor of a container ship—under various combinations of geometric characteristics, stiffening methods, and load conditions. The structure of the paper is as follows: In this study, the structural performance of a perforated plate—which represents the double-bottom floor of a container ship—under various load situations, stiffening techniques, and geometric configurations is assessed. The structure of the paper is as follows: The theoretical underpinnings of linear eigenvalue analysis for buckling are presented in
Section 2. The case study is covered in
Section 3, together with geometric configurations and an explanation of the testing arrangement. The finite element method and the validation procedure, which compares the simulation results to experimental data, are described in
Section 4. Based on the analysis of different geometric characteristics and load scenarios,
Section 5 presents the results pertaining to stress patterns of distribution, buckling strength, and fatigue life. Finally,
Section 6 wraps up the research with conclusions derived from the data.
2. Linear Eigenvalue Analysis for Buckling
According to one definition, linear tensile buckling is an eigenvalue issue, in which the eigenvectors show the associated buckling modes and the eigenvalues reflect the loads that result in buckling [
24].
In the given equation,
[S] symbolizes the stress stiffness matrix,
[K] represents the stiffness matrix and
λi denotes the ith eigenvalue, which is utilized to scale the applied loads. The following formula describes how the plate, both buckling and intact, will react to uniaxial compression [
24].
In the earlier equation,
signifies Poisson’s ratio,
NX refers to the in-plane force,
t represents the thickness of the plate,
E denotes Young’s modulus and
w describes the vertical displacement in the
z-axis of a point positioned on the
(x, y) plane. For a plate that is simply supported along all edges, this displacement can be estimated as [
24]:
In this context, mmm and nnn represent the number of half-waves along the
x and
y axes, where the
x-axis is aligned with the plate’s longer edge and the
y-axis is perpendicular to it. Meanwhile,
a and
b indicate the plate’s dimensions in these respective directions. Based on the boundary conditions, a nontrivial solution is derived [
24]:
where
,
is the stiffness of the plate,
is the factor that accounts for buckling, and
represents the aspect relation. In the case of uniaxial compression, the critical buckling stress under elastic conditions is given by a well-known formula [
25].
The critical buckling strength is assessed using the Johnson-Ostenfeld formula [
25], which incorporates both elastic conditions and a plasticity correction for buckling strength.
Here,
represents the yield stress,
indicates the critical buckling stress, and
is a factor that reflects influence to plasticity phenomenos, generally ranging from 0.5 to 0.6. Shear loads can cause in-plane compressive stress, which can result in buckling. This in-plane compressive stress works at a 45-degree angle to the shear axis in pure shear situations [
26].
The following analytical method is offered to elucidate the elastic buckling behavior of a simply supported plate under different applied stress components [
25].
Here,
,
and
represent the ultimate strengths under axial loads, while
,
and
indicate the axial stresses in the
x-direction,
y-direction and edge shear, respectively. The coefficients
c1,
c2 ,
c3 and
are factors that depend on the load and boundary conditions. For biaxial compressive loading, Equation (8) simplifies to
Paik [
26] offers a different formulation to characterize the biaxial compression of the plate.
4. Methodology
A model of linear elastic material, based on the notion of minor displacement, is assumed for the analysis. Buckling strength is assessed using ANSYS
® Workbench 2024, which provides various 3D solid and tetrahedral finite elements to examine stress distribution across the thickness. The method proposed by Kim et al. [
8] is employed to determine an appropriate fine mesh size, allowing for a seamless transition across different sections of the model. A mesh convergence procedure was implemented by repeatedly adjusting the solution count until the change in von Mises stress between consecutive values was comparable to the finite element reliability criteria mentioned by Patil and Jeyakarthikeyan [
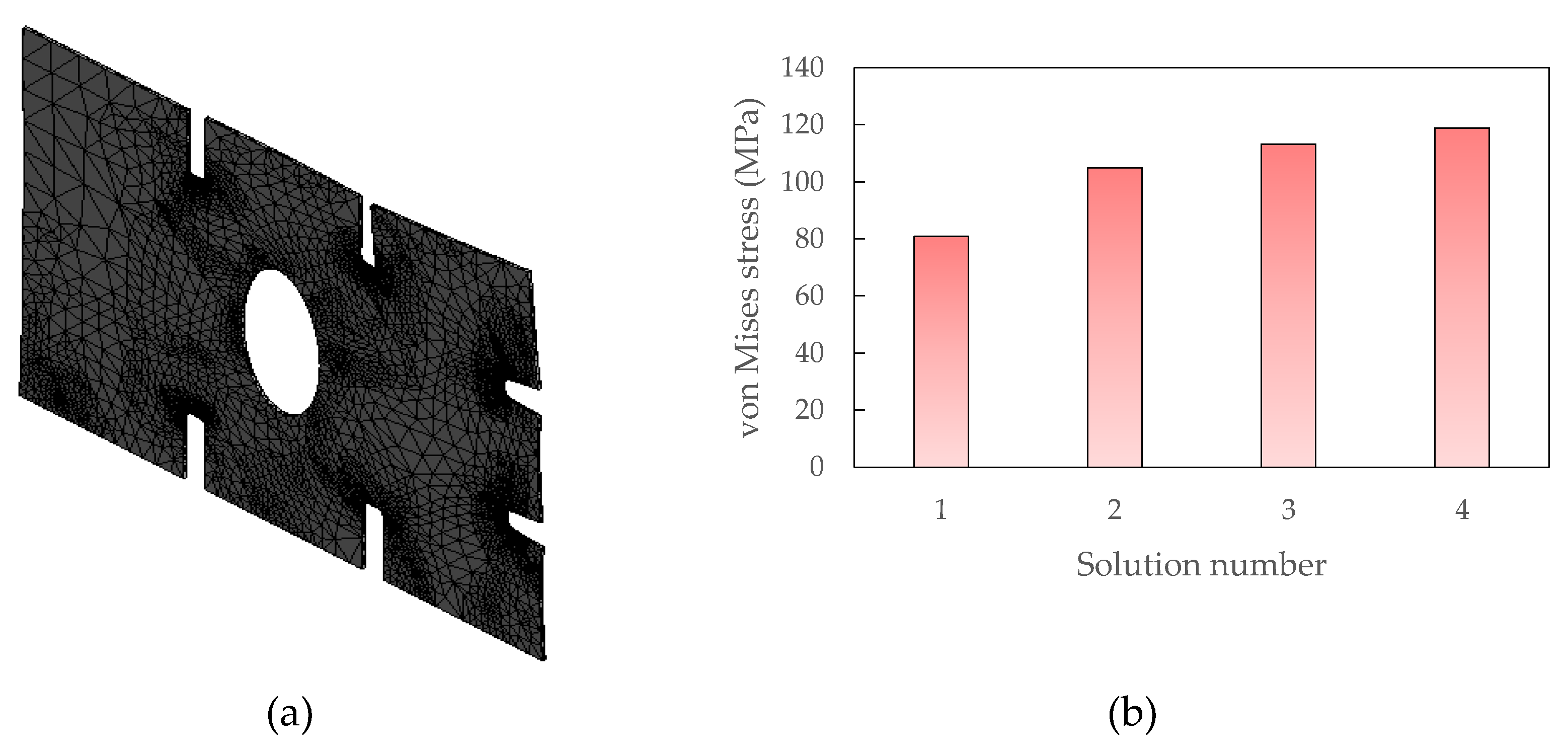
30]. With a typical element edge measurement of 47.765 mm, the mesh speed of convergence as a function of element and node count is shown in
Figure 7 and
Table 3. At lower processing levels, a feasible solution was obtained with 116065 nodes and 74110 elements, yielding a 4.8% deviance.
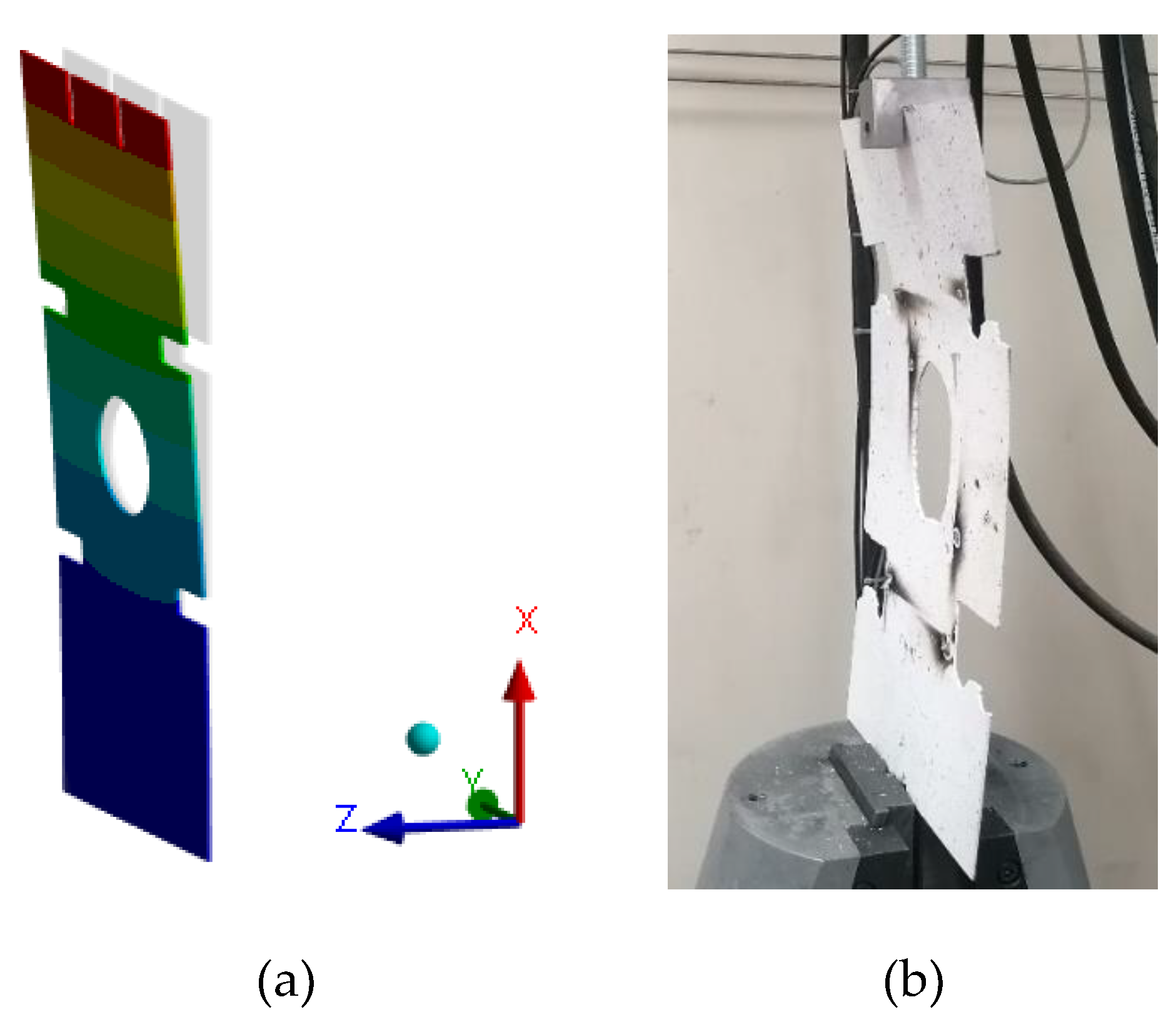
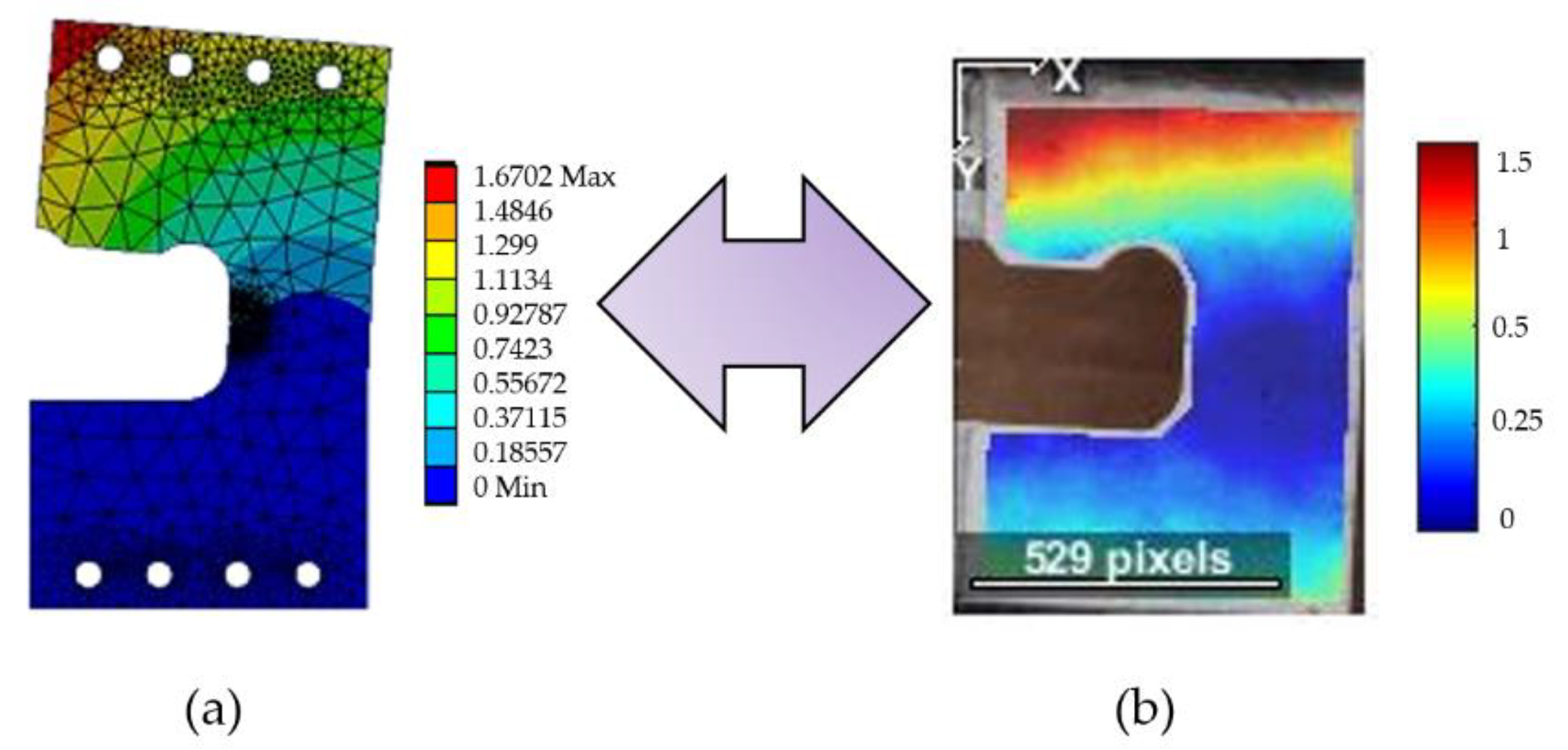
The numerical model is validated in two phases; on the one hand, by a global approach establishing a modification of maximum displacement of 4.2% of the free end of the cantilevered double bottom floor (
Figure 8).
Following the methodology outlined by Kumar et al. [
32], the second stage of validating the numerical model entails comparing numerical (FEM) and experimental results by correlating them using digital image correlation (DIC) with the 2D MATLAB
® software Ncorr
® [
31]. Under the given standard load circumstances, the maximum displacement varies by 7.1% (
Figure 9).
6. Conclusions
This research has advanced the understanding of how geometric discontinuities—such as central openings and cut-outs—affect the structural integrity of perforated plates in the double-bottom floor of Panamax-class container ships. By conducting detailed numerical and experimental analyses, we have achieved a clearer picture of the stress distribution and fatigue behavior of these plates under various load scenarios, addressing the key problem of balancing weight reduction with maintaining structural strength. Our findings offer significant implications for both the design and maintenance of ship structures.
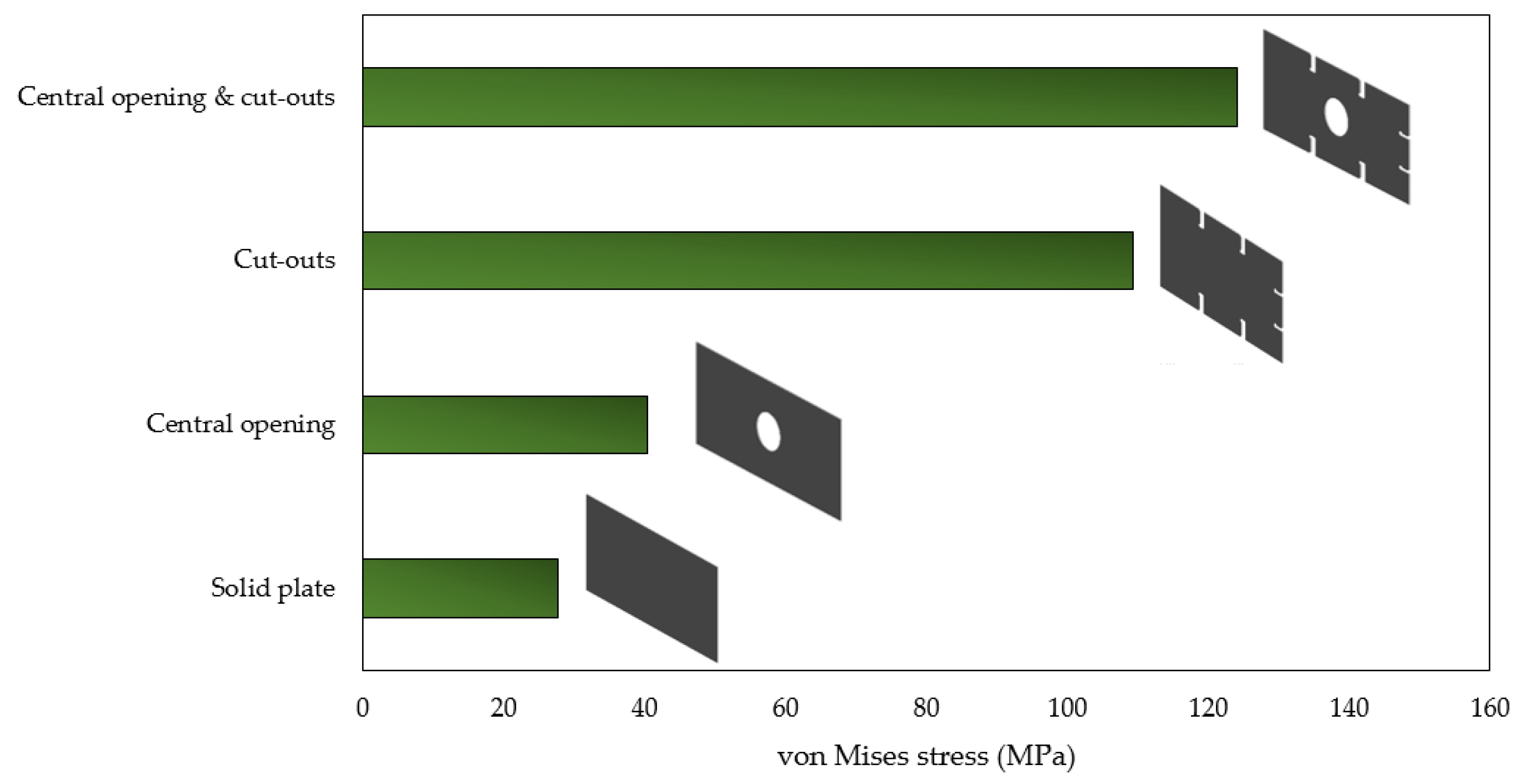
The results highlight the critical role that geometric discontinuities play in weakening the structural strength of the plates, emphasizing the importance of careful design to mitigate stress concentration areas. In particular, it was found that the presence of side cut-outs has a more detrimental effect on stress distribution compared to central openings, a finding that holds under both axial and transverse loading conditions. This emphasizes the need for caution when incorporating these features, as they introduce vulnerabilities that may compromise the structural performance. Furthermore, our fatigue analysis underscores the importance of stiffening configurations, showing that certain stiffening arrangements, especially those with longitudinal stiffeners in the bottom and inner bottom, can significantly enhance the fatigue life of the structure.
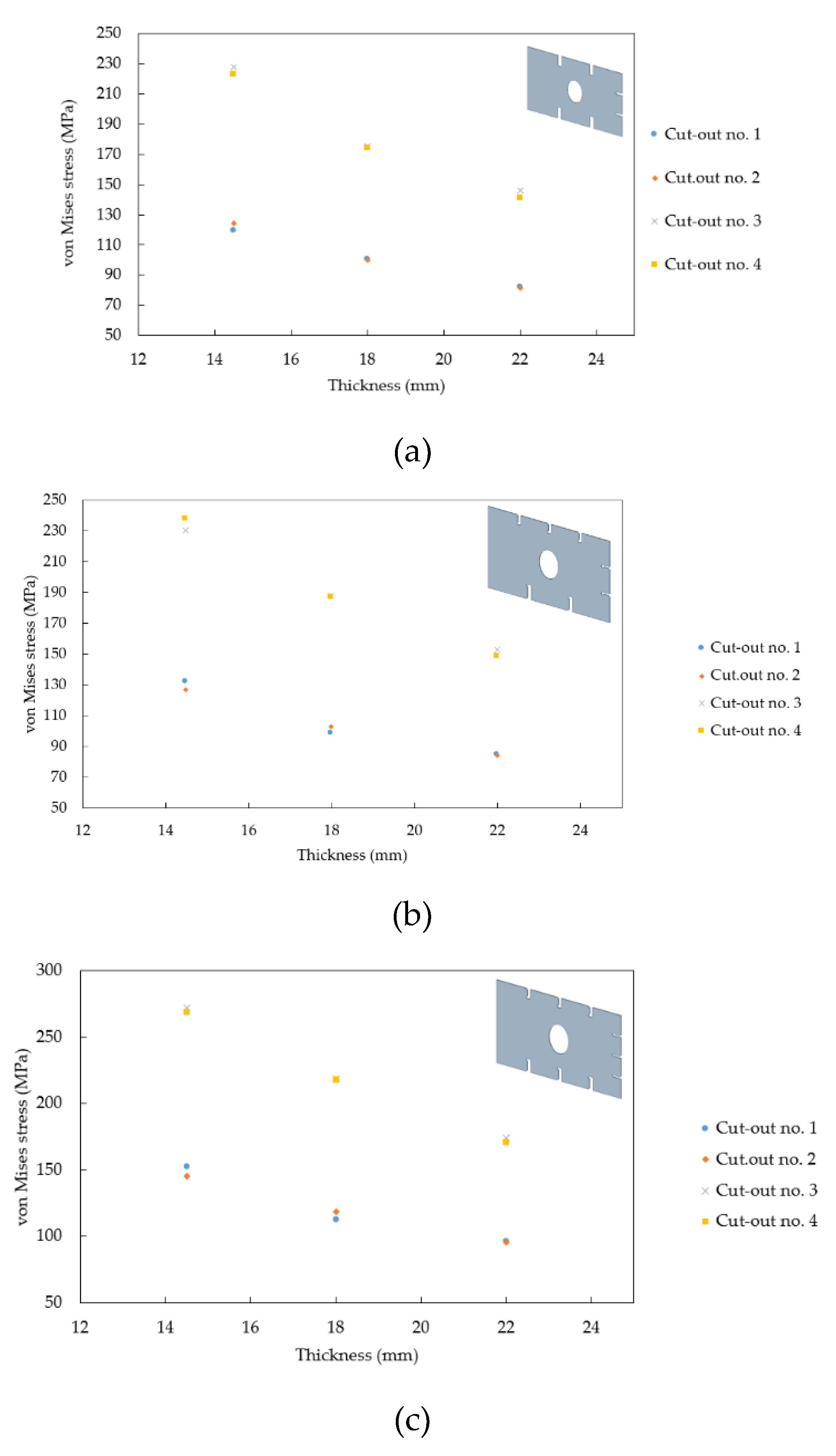
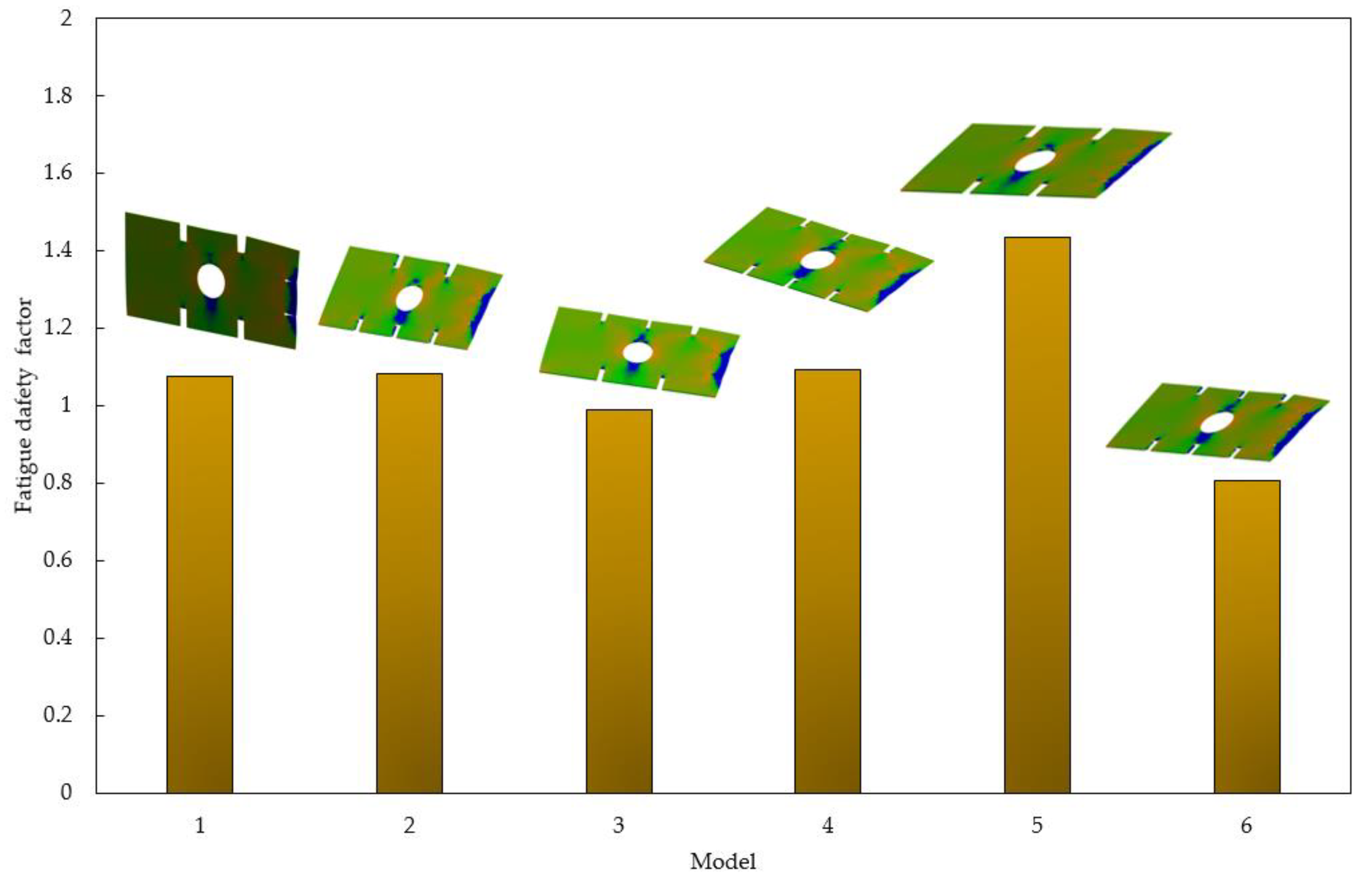
One of the most important outcomes of this study is the identification of stress trends in relation to plate thickness. We observed a consistent reduction in von Mises stress with increased plate thickness across all models and cut-out configurations. This insight provides a clear design strategy for improving the structural resilience of ship floors by adjusting thickness to mitigate stress and prolong fatigue life. Additionally, the study confirms that cut-out geometries no. 1 and no. 2 offer better performance under load, providing a viable alternative to less effective cut-out shapes. The practical implications of these findings are substantial, offering shipbuilders new avenues for optimizing hull designs without compromising safety or performance.
Future research should focus on extending these analyses to more complex loading scenarios, including wave-induced stresses and multi-axial load conditions. Additionally, more detailed studies on fatigue under varying operational conditions could provide further insight into the long-term durability of these design alternatives. Finally, further exploration into the application of topology optimization techniques could lead to even more efficient structural designs that balance weight reduction with enhanced performance. This continued research will be crucial for advancing shipbuilding practices, ensuring safer and more efficient ships in the future. Overall, this study contributes valuable knowledge to the field of naval engineering, offering both immediate practical benefits for ship design and a foundation for future innovations in the structural design of container ships.
Author Contributions
Conceptualization, A.S-C., M.F-M. and M.A.H-S.; methodology, A.S-C. M.F-M.; software, A.S-C; validation, M.A.H-S.; formal analysis, A.S-C., M.F-M. and M.A.H-S.; investigation, A.S-C. and M.F-M.; resources, A.S-C; data curation, M.F-M. and M.A.H-S.; writing—original draft preparation, A.S-C, M.F-M. and M.A.H-S.; writing—review and editing, M.F-M. and M.A.H-S.; visualization, A.S-C.; supervision, M.F-M. and M.A.H-S.; project administration, A.S-C., M.F-M. and M.A.H-S.;
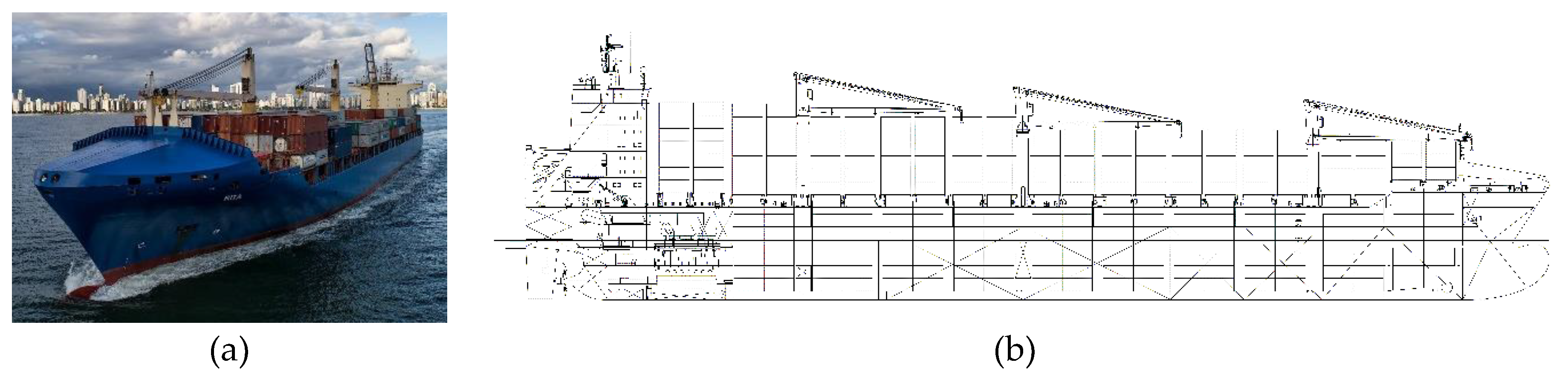
Figure 1.
(a) B-178 vessel [
27], (b) general arrangement.
Figure 1.
(a) B-178 vessel [
27], (b) general arrangement.
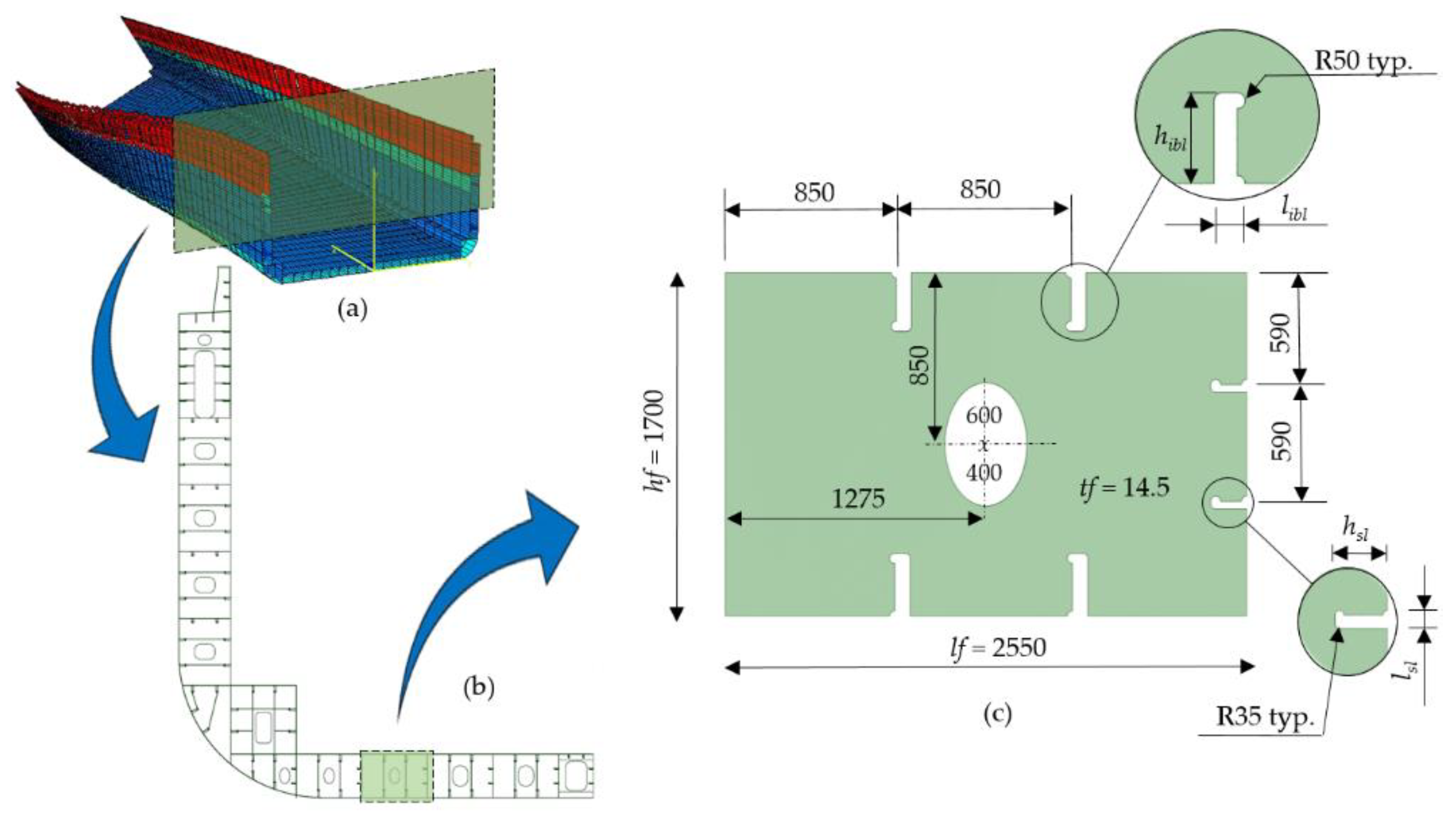
Figure 2.
(a) Container ship torsion model, (b) midship section, (c) double bottom floor (dimensions in mm).
Figure 2.
(a) Container ship torsion model, (b) midship section, (c) double bottom floor (dimensions in mm).
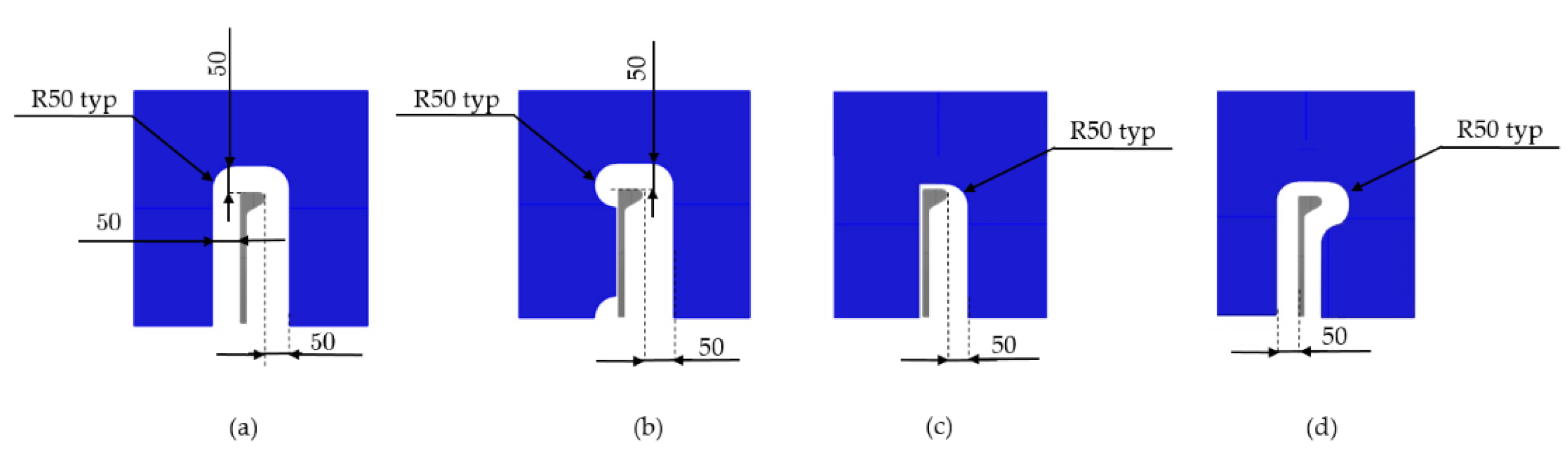
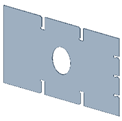
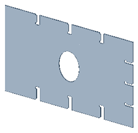
Figure 3.
Geometries for cut-outs (measurements in mm) (a) Cut-out no. 1, (b) cut-out no. 2, (c) cut-out no.3, (d) cut-out no. 4.
Figure 3.
Geometries for cut-outs (measurements in mm) (a) Cut-out no. 1, (b) cut-out no. 2, (c) cut-out no.3, (d) cut-out no. 4.
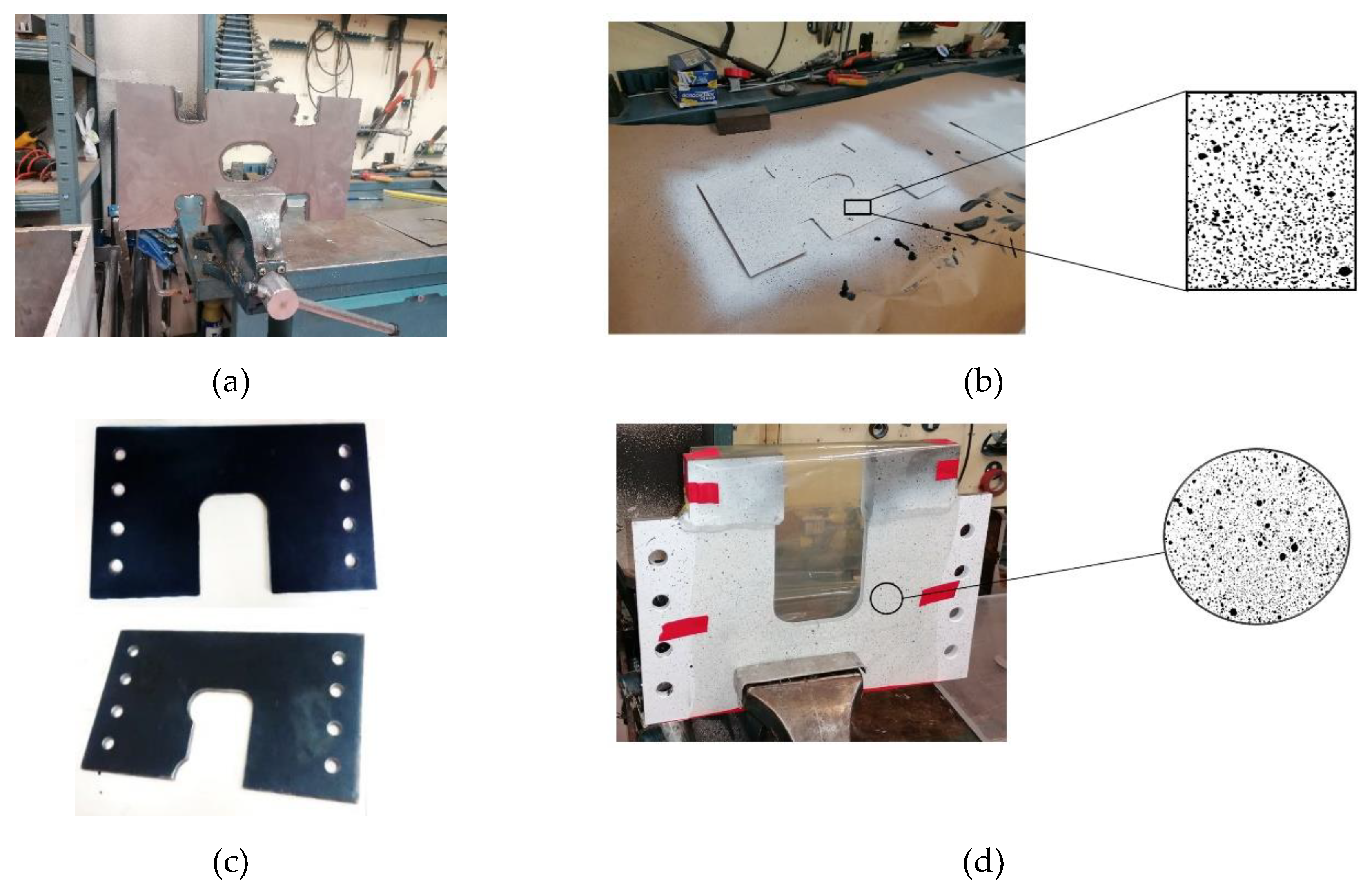
Figure 4.
Getting test specimens ready. (a) Cutting and modeling of the double bottom floor geometry, (b) surface preparation of the double bottom floor, (c) cutting and modeling of the cut-out no. 1 and no. 2 geometry, (d) surface preparation of the cut-out no. 2.
Figure 4.
Getting test specimens ready. (a) Cutting and modeling of the double bottom floor geometry, (b) surface preparation of the double bottom floor, (c) cutting and modeling of the cut-out no. 1 and no. 2 geometry, (d) surface preparation of the cut-out no. 2.
Figure 5.
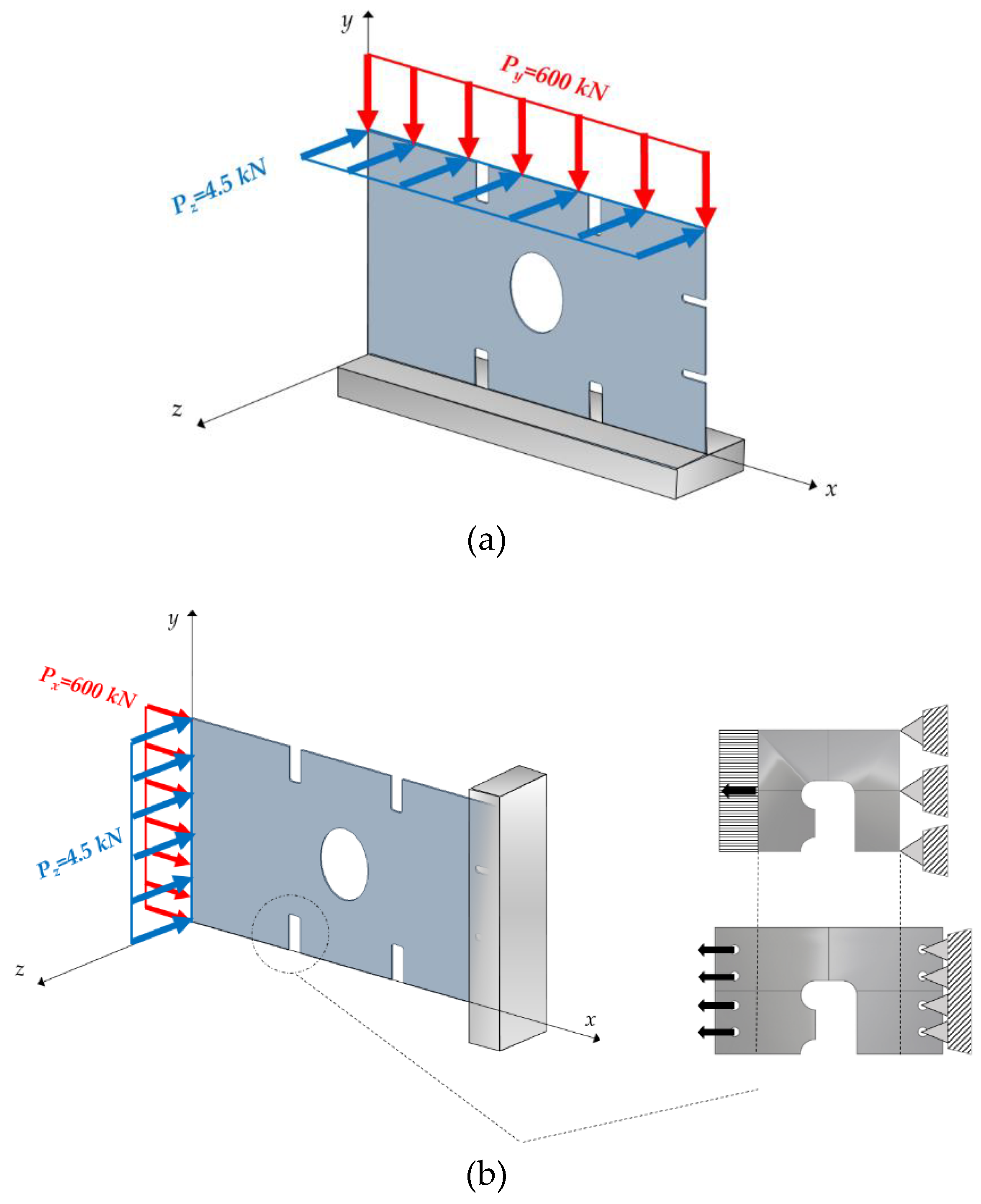
Loading scenarios and boundary conditions. (a) Initial configuration, (b) configuration adapted to the testing machine with isolate model of the cut-out.
Figure 5.
Loading scenarios and boundary conditions. (a) Initial configuration, (b) configuration adapted to the testing machine with isolate model of the cut-out.
Figure 6.
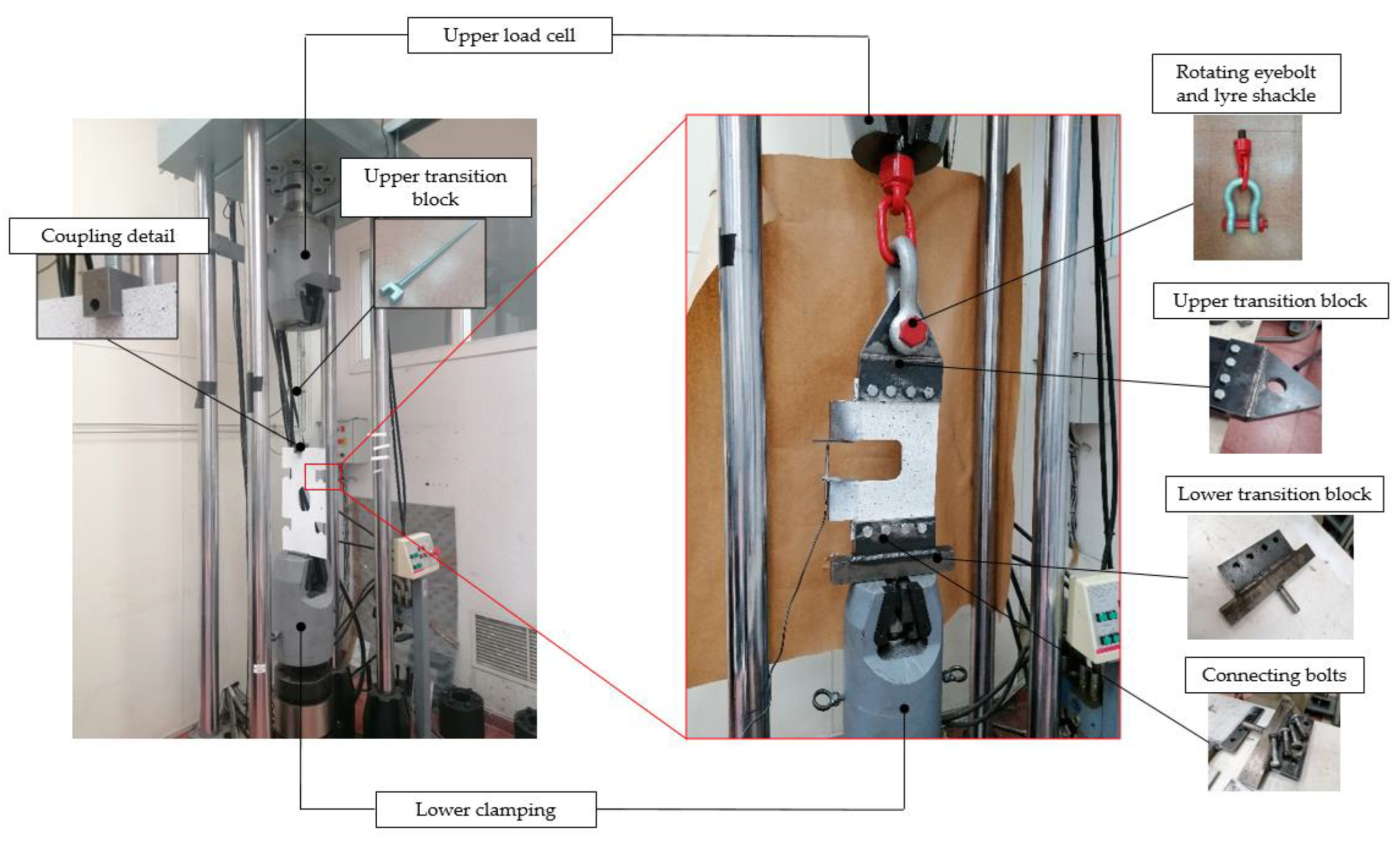
Experimental setup. (a) Double bottom floor, (b) cut-out.
Figure 6.
Experimental setup. (a) Double bottom floor, (b) cut-out.
Figure 7.
(a) Mesh pattern for the solution number four, (b) convergence process.
Figure 7.
(a) Mesh pattern for the solution number four, (b) convergence process.
Figure 8.
Difference between numerical and experimental regime. (a) Finite element analysis, (b) experimental test.
Figure 8.
Difference between numerical and experimental regime. (a) Finite element analysis, (b) experimental test.
Figure 9.
Comparison in maximum displacement (in mm). (a) DIC technique, (b) FEM technique.
Figure 9.
Comparison in maximum displacement (in mm). (a) DIC technique, (b) FEM technique.
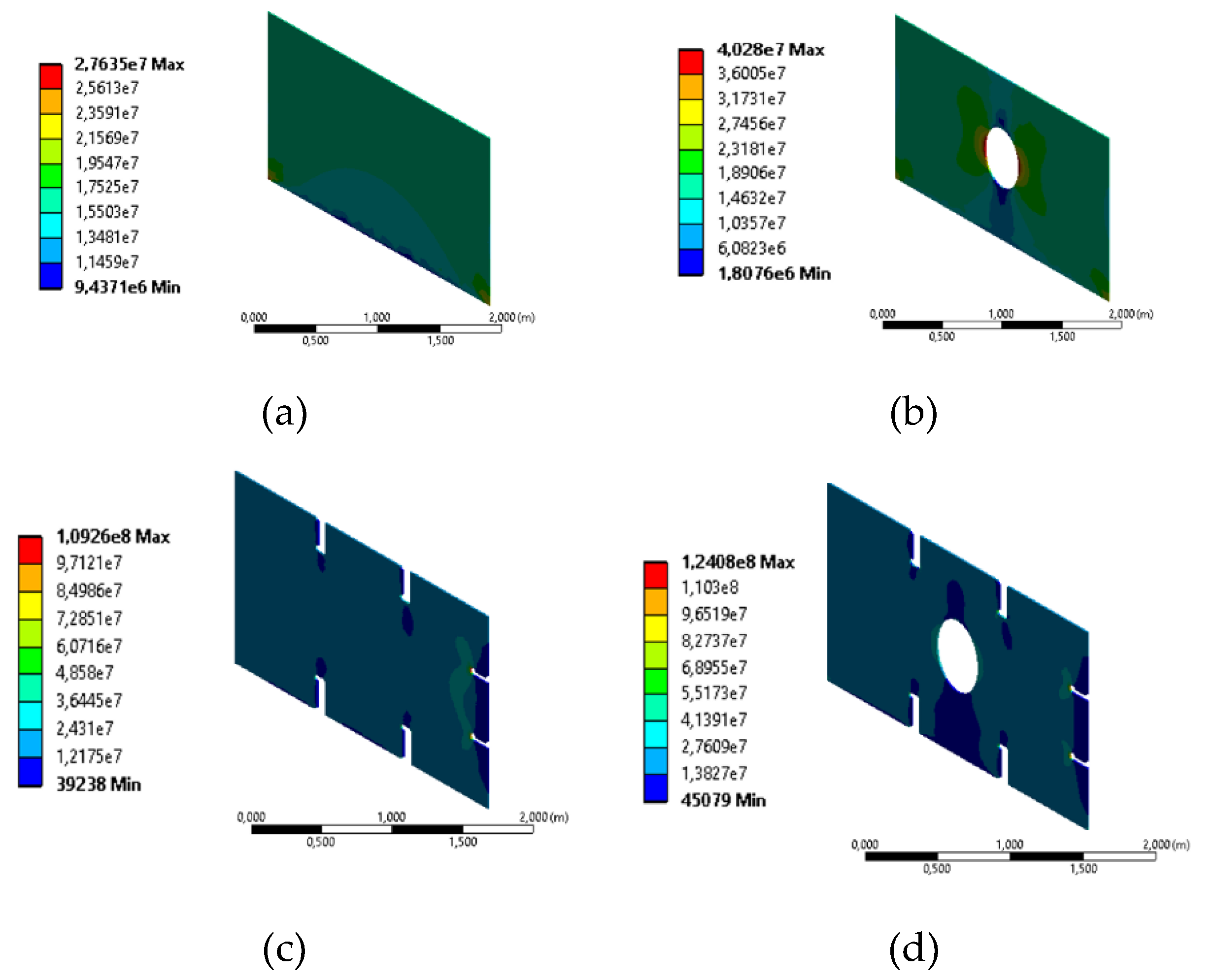
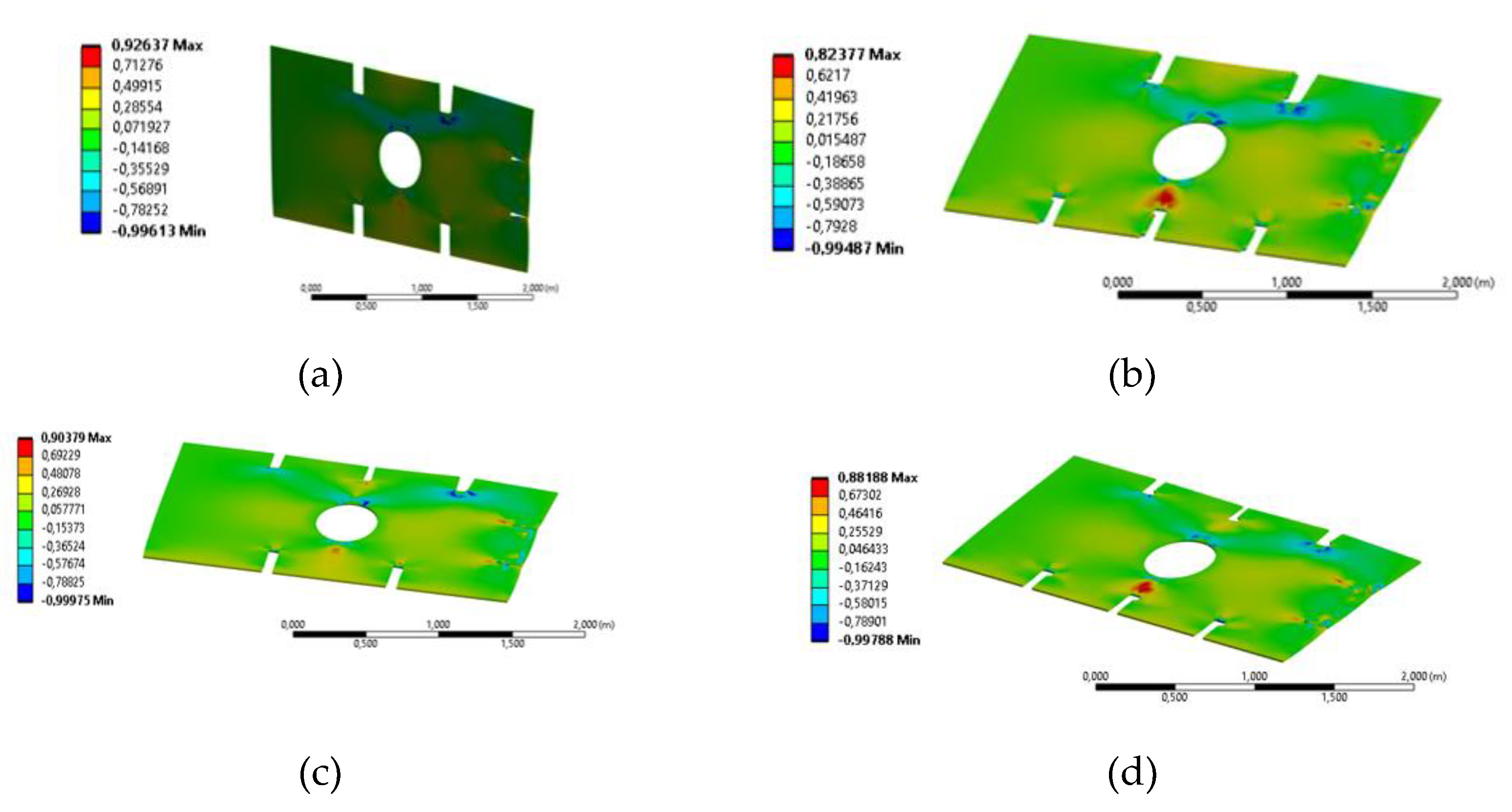
Figure 10.
Von Mises stress distribution (Pa) with 14.5mm thickness and axial load. (a) Solid plate, (b) plate with central opening, (c) plate with cut-outs, (d) plate with central opening and cut-outs.
Figure 10.
Von Mises stress distribution (Pa) with 14.5mm thickness and axial load. (a) Solid plate, (b) plate with central opening, (c) plate with cut-outs, (d) plate with central opening and cut-outs.
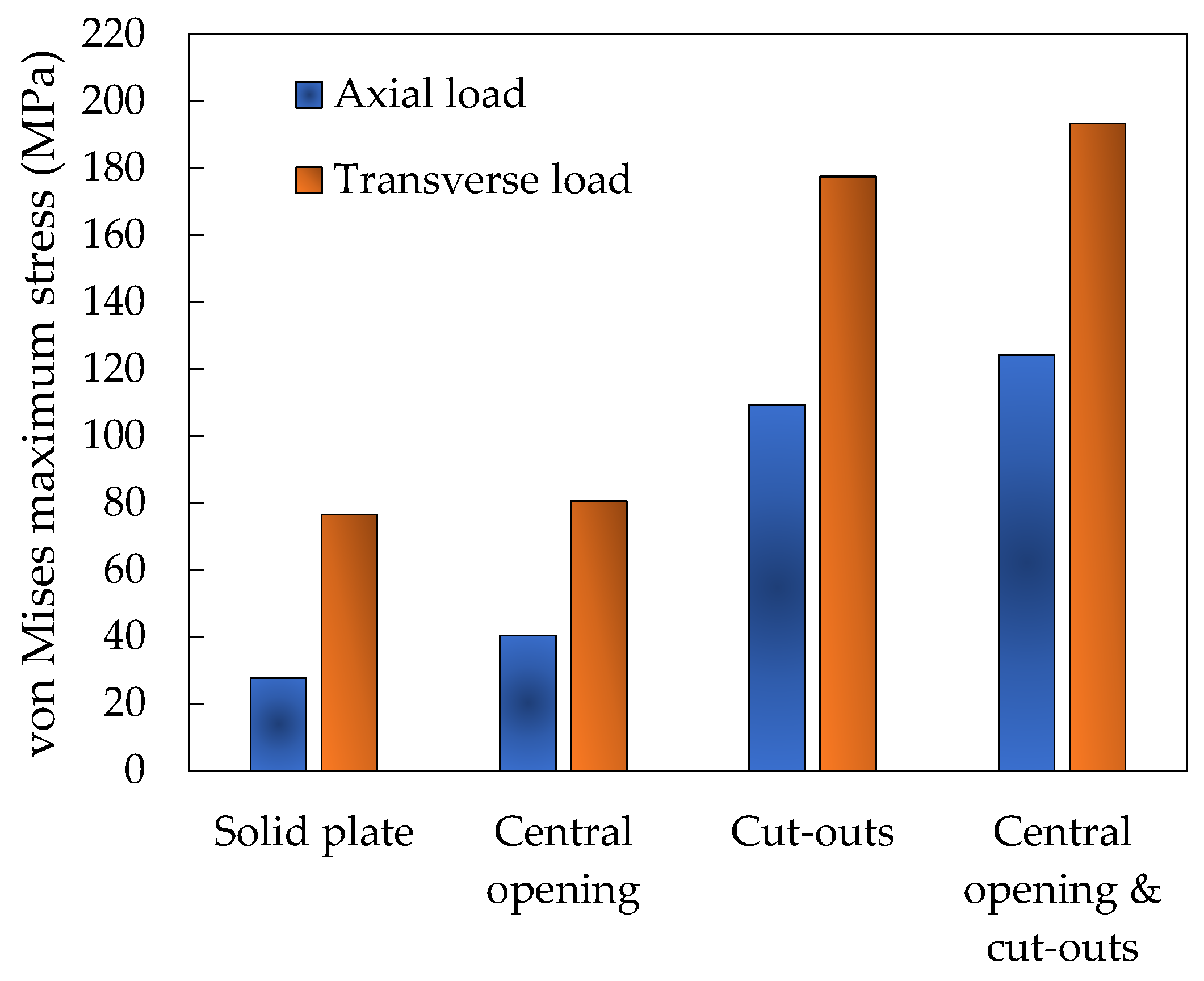
Figure 11.
Difference, in terms of maximum von Mises stress (MPa), between geometrical discontinuities.
Figure 11.
Difference, in terms of maximum von Mises stress (MPa), between geometrical discontinuities.
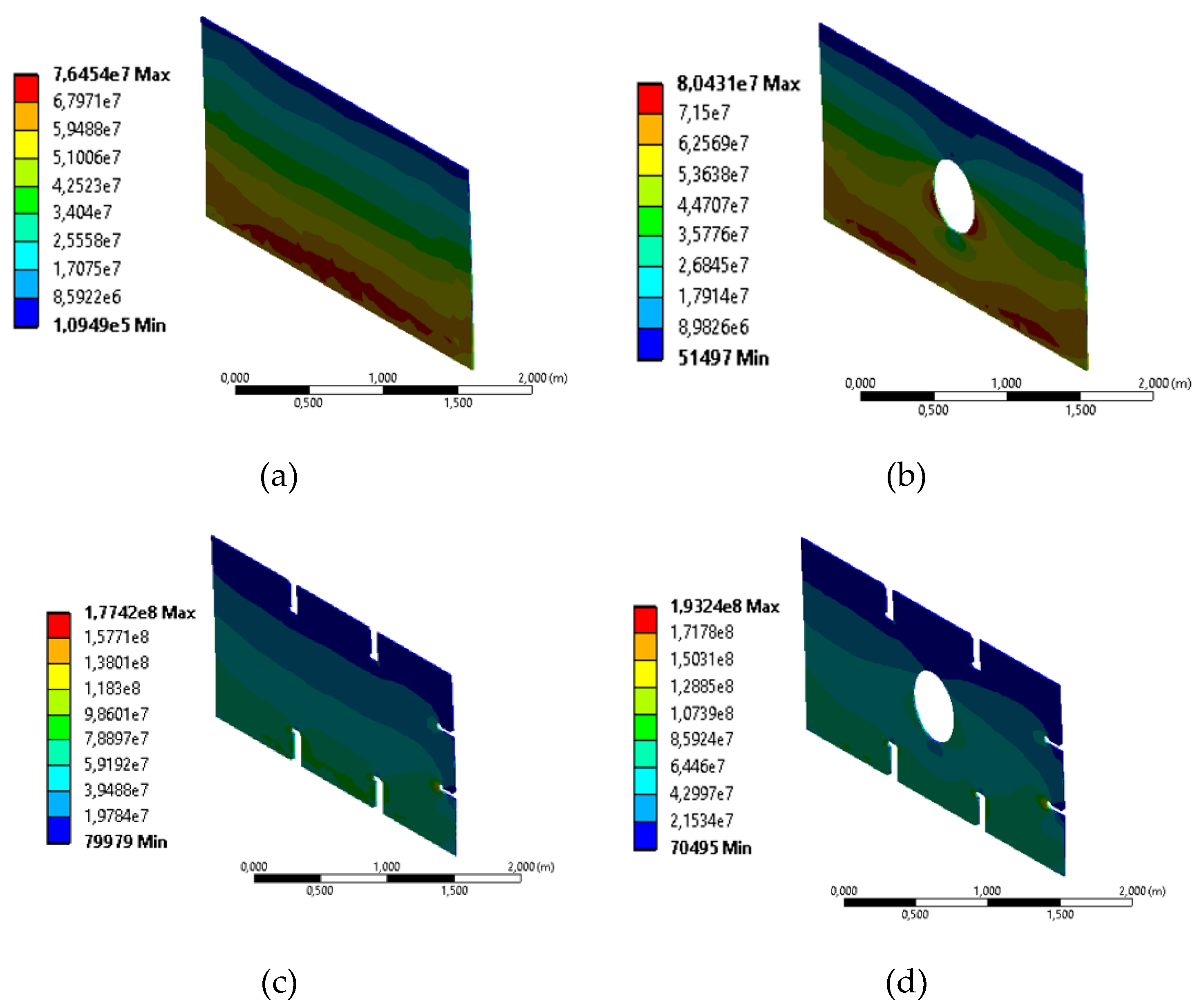
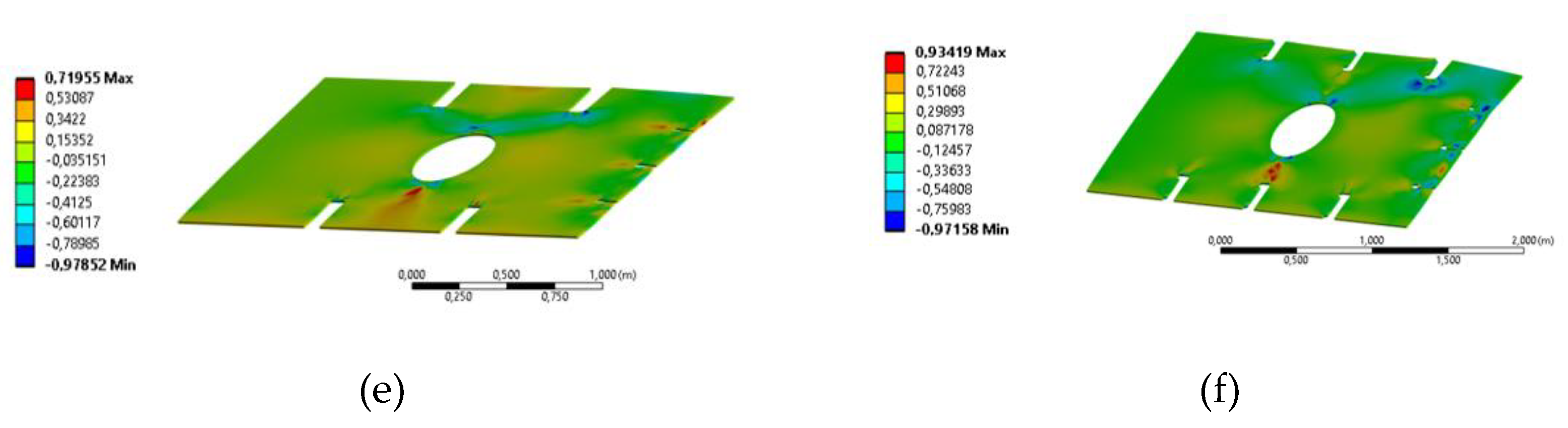
Figure 12.
Von Mises stress distribution (Pa) with 14.5mm thickness and transverse load. (a) Solid plate, (b) plate with central opening, (c) plate with cut-outs, (d) plate with central opening and cut-outs.
Figure 12.
Von Mises stress distribution (Pa) with 14.5mm thickness and transverse load. (a) Solid plate, (b) plate with central opening, (c) plate with cut-outs, (d) plate with central opening and cut-outs.
Figure 13.
Difference of maximum von Mises stress between axial load and transverse load at different geometrical discontinuities.
Figure 13.
Difference of maximum von Mises stress between axial load and transverse load at different geometrical discontinuities.
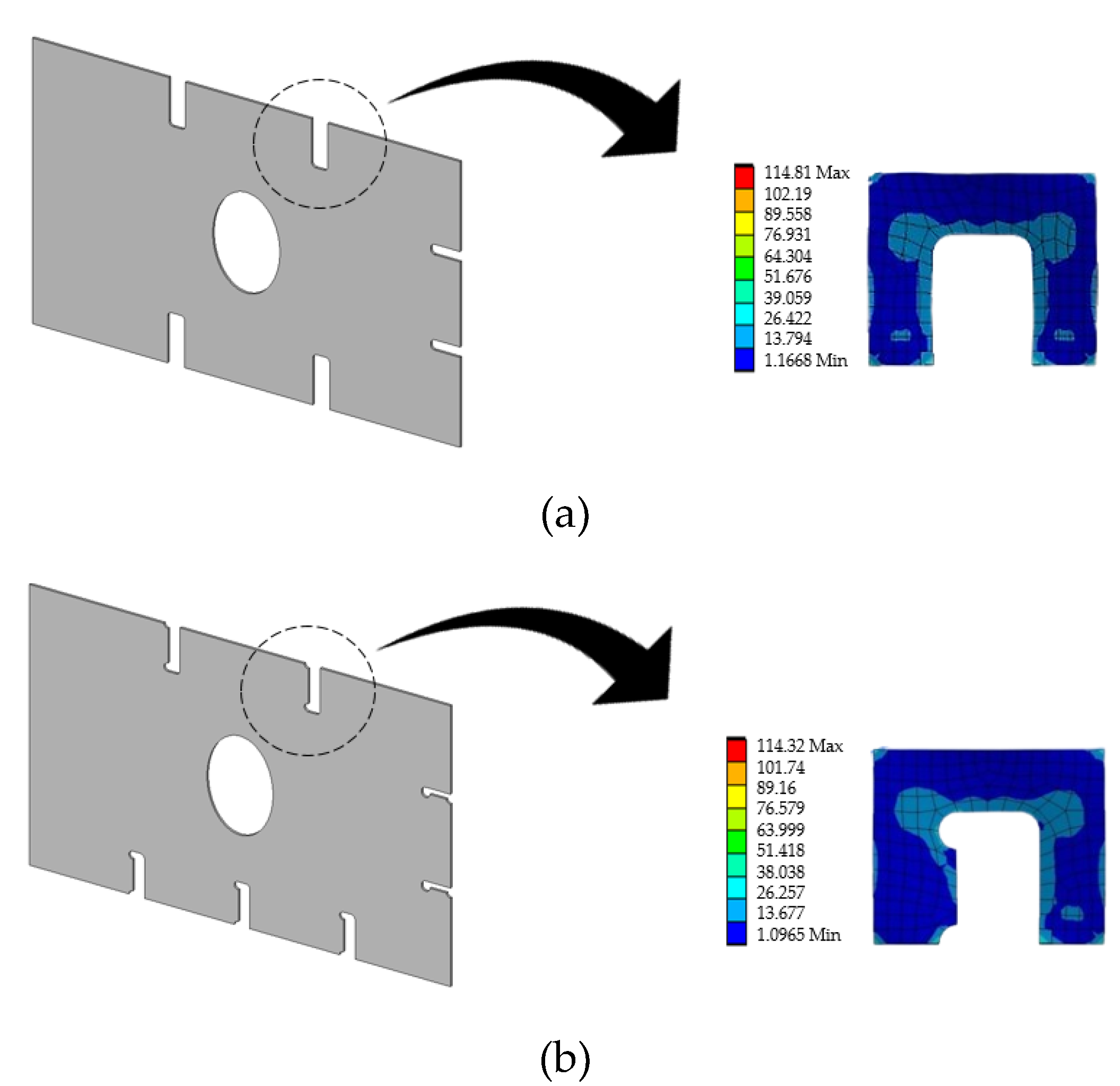
Figure 14.
Distribution of Von Mises stress (MPa). (a) Cut-out no. 1, (b) cut-out no. 2.
Figure 14.
Distribution of Von Mises stress (MPa). (a) Cut-out no. 1, (b) cut-out no. 2.
Figure 15.
Von Mises maximum stress at modification of thickness. (a) Model no. 1, (b) model no. 3, (c) model no. 6.
Figure 15.
Von Mises maximum stress at modification of thickness. (a) Model no. 1, (b) model no. 3, (c) model no. 6.
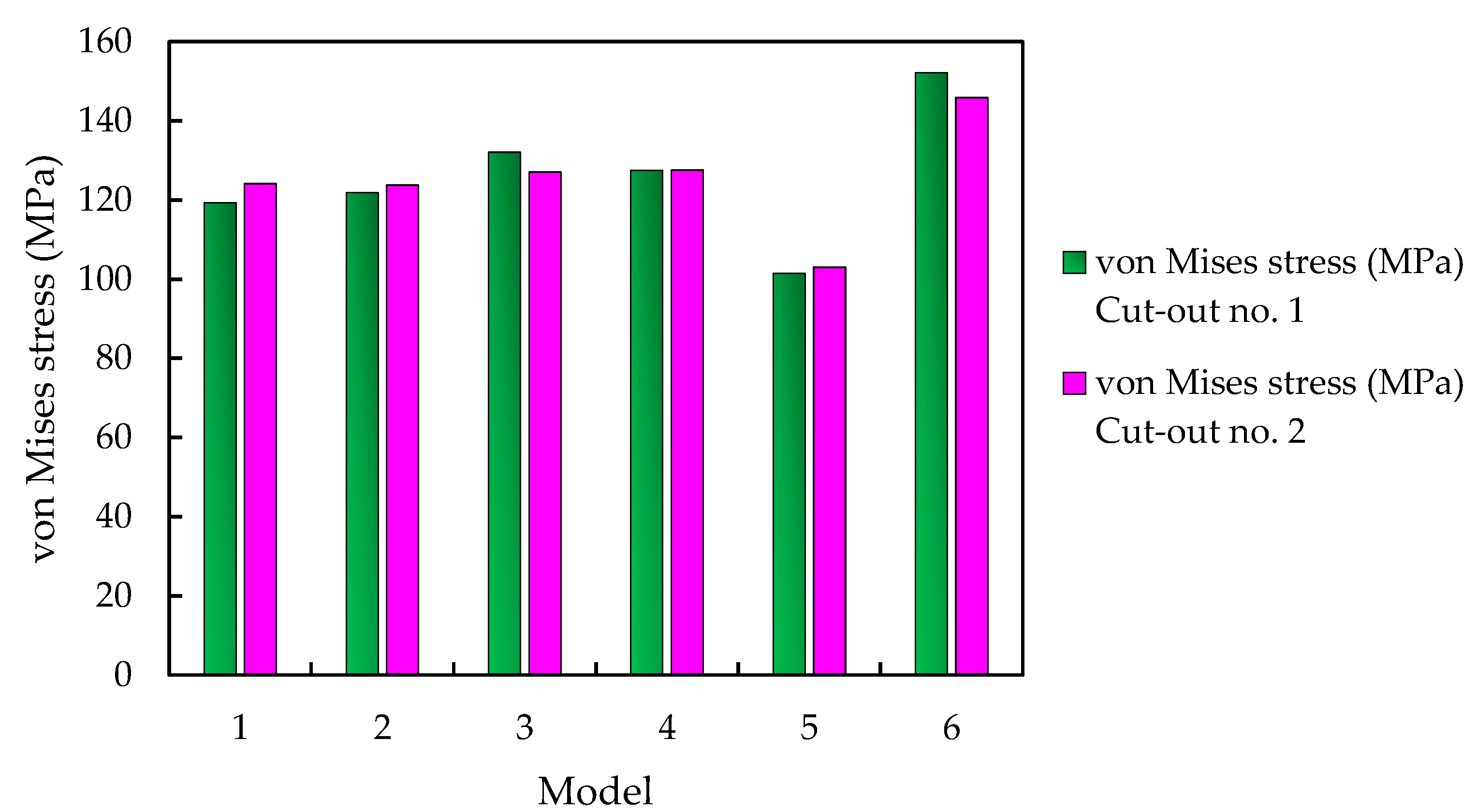
Figure 16.
Von Mises maximum stress of different models at equal thickness (14.5mm) and an axial loading scenario.
Figure 16.
Von Mises maximum stress of different models at equal thickness (14.5mm) and an axial loading scenario.
Figure 17.
Minimun fatigue safety factor FSF. (a) Model no. 1 with cut-out no. 1, (b) model no. 2 with cut-out no. 2, (c) model no. 3 with cut-out no. 3, (d) model no. 4 with cut-out no. 4, (e) model no. 5 with cut-out no. 1, (f) model no. 6 with cut-out no. 2.
Figure 17.
Minimun fatigue safety factor FSF. (a) Model no. 1 with cut-out no. 1, (b) model no. 2 with cut-out no. 2, (c) model no. 3 with cut-out no. 3, (d) model no. 4 with cut-out no. 4, (e) model no. 5 with cut-out no. 1, (f) model no. 6 with cut-out no. 2.
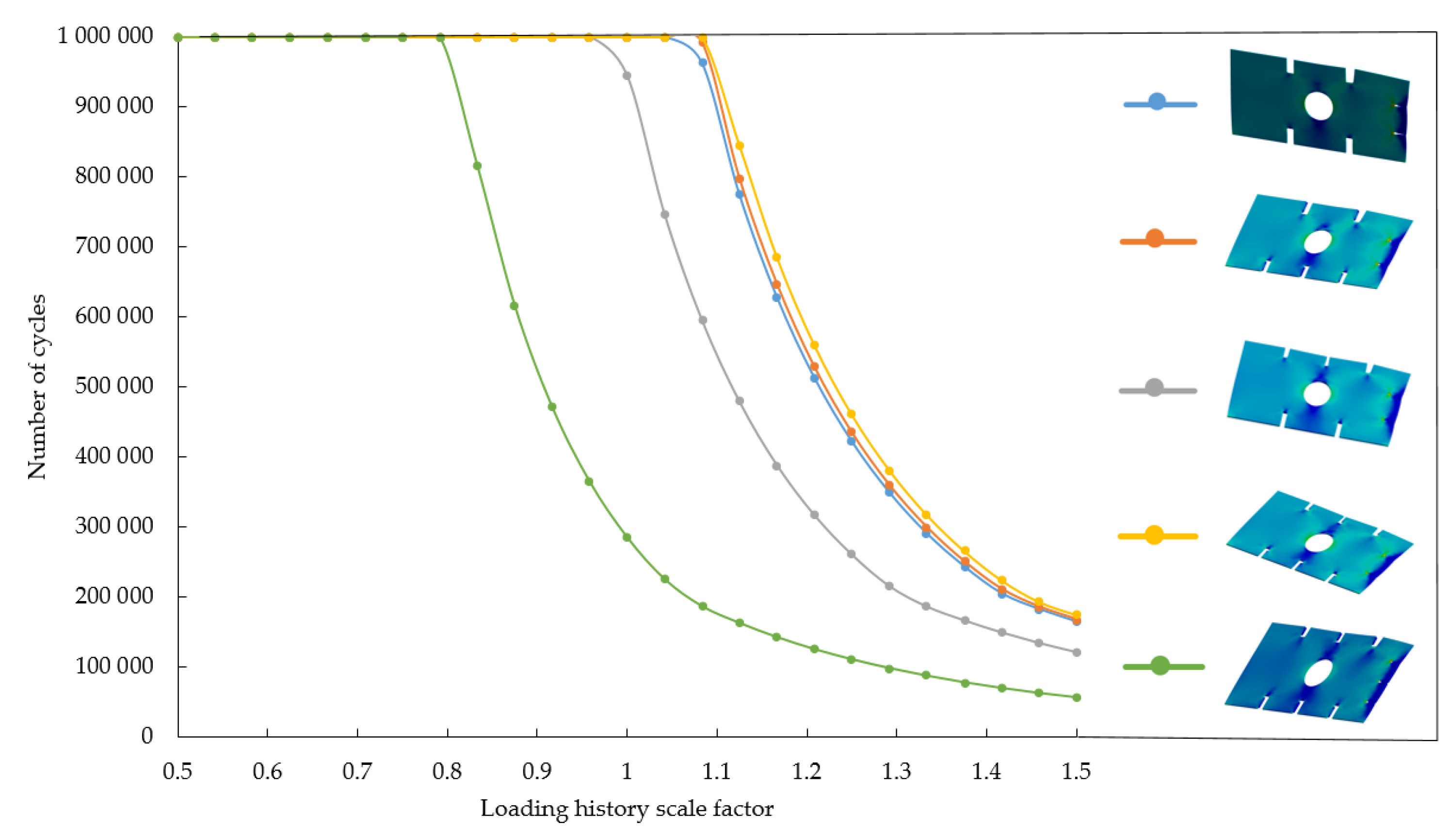
Figure 18.
Fatigue sensitivity curves. Blue line – Model no. 1 with cut-out no. 1, orange line – model no. 2 with cut-out no. 2, grey line – model no. 3 with cut-out no. 3, yellow line – model no. 4 with cut-out no. 4 and green line – model no. 6 with cut-out no. 2.
Figure 18.
Fatigue sensitivity curves. Blue line – Model no. 1 with cut-out no. 1, orange line – model no. 2 with cut-out no. 2, grey line – model no. 3 with cut-out no. 3, yellow line – model no. 4 with cut-out no. 4 and green line – model no. 6 with cut-out no. 2.
Figure 19.
Biaxility indication. (a) Model no. 1 with cut-out no. 1, (b) model no. 2 with cut-out no. 2, (c) model no. 3 with cut-out no. 3, (d) model no. 4 with cut-out no. 4, (e) model no. 5 with cut-out no. 1, (f) model no. 6 with cut-out no. 2.
Figure 19.
Biaxility indication. (a) Model no. 1 with cut-out no. 1, (b) model no. 2 with cut-out no. 2, (c) model no. 3 with cut-out no. 3, (d) model no. 4 with cut-out no. 4, (e) model no. 5 with cut-out no. 1, (f) model no. 6 with cut-out no. 2.
Table 1.
Main particulars.
Table 1.
Main particulars.
| Variables |
Unit |
Value |
| Length between perpendiculars (Lbp) |
m |
169.7 |
| Breadth (B) |
m |
32.24 |
| Depth to main deck (D) |
m |
18.7 |
| Draught (T) |
m |
12.15 |
| Maximum service speed (V) |
kn |
22.5 |
Table 2.
Structural combinations for different cut-out geometries, scantlings and number of longitudinal stiffeners and transverse plate thicknesses (dimensions in mm). (a) Model no. 1, (b) model no. 2, (c) model no. 3, (d) model no. 4, (e) model no. 5 and (f) model no. 6.
Table 3.
Iteration procedure for mesh convergence.
Table 3.
Iteration procedure for mesh convergence.
| |
(MPa) |
Change (%) |
Elements |
Nodes |
|
| 1 |
80.84 |
- |
362 |
2939 |
|
| 2 |
104.98 |
25.9 |
10981 |
19757 |
|
| 3 |
113.16 |
7.5 |
29344 |
48369 |
|
| 4 |
118.83 |
4.8 |
74110 |
116065 |
|