Soret Effect on the Instability of Double-Diffusive Convection in a Saturated Vertical Brinkman Porous Layer of Oldroyd-B Fluid

Preprint

Article

Soret Effect on the Instability of Double-Diffusive Convection in a Saturated Vertical Brinkman Porous Layer of Oldroyd-B Fluid

This is a preprint, it has not been peer-reviewed.

This is a preprint, it has not been peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

30 October 2024

Posted:

31 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

The instability of double-diffusive convection of an Oldroyd-B fluid in a vertical porous layer caused by temperature and solute concentration differences with the Soret effect is studied using a modified Darcy–Brinkman–Oldroyd model. Under the Oberbeck-Boussinesq approximation, the validity of Squire's theorem is demonstrated, allowing for considering only the two-dimensional linear instability. Based upon perturbation theory, an Orr-Sommerfeld eigenvalue problem is derived and numerically simulated using the Chebyshev collocation method. We examine the effects of the relevant dimensionless parameters on the neutral stability curves. It is discovered that PrD and λ1 have dual effects on the instability, respectively. When PrDc1 < PrD < PrDc2, PrD boosts flow stability. The impact of λ1 on fluid stability is influenced by PrD. Furthermore, Le and η have dual effects on the instability. When η< 0.8, it promotes flow instability. Le enhances the flow in-stability when Le < 0.7 and inhibits the instability when Le > 0.7. In addition, the magnitude of Le influences the role of Sr. There exists a critical value for Le. When Le < Lec2, Sr strengthens the in-stability of the flow, and when Le> Lec2, Sr plays an inhibiting role. Finally, the relaxation pa-rameter λ2 promotes flow stability.

Keywords:

1. Introduction

A solid with micropores are called porous media, and these micropores are often interconnected and usually filled with fluid. Porous media encompasses natural substances, such as biological tissues, wood, zeolites, soils, and rocks. Due to its numerous fundamental and industrial applications, double diffusive convection (DDC) in porous media is a phenomenon that occurs in a variety of systems and has attracted a lot of attention in recent decades. These applications include producing high-quality crystals, storing liquid gases, migrating moisture in fiber insulation, transporting contaminants in saturated soils, solidifying molten alloys, and heating lakes and magmas through geothermal processes. Ingham and Pop [1], Nield and Bejan [2], and Vafai [3] have provided comprehensive reviews on this subject.

The stability or instability of fluid flow is a crucial aspect of fluid mechanics in porous media. Research on how buoyancy and shearing forces affect fluid flow stability in a vertical layer of porous media has received significant attention. Gill [4] performed an initial analysis of the stability of natural convection in a vertical porous layer whose boundary is impermeable at different temperatures, using Darcy's law as a framework. He concluded that the system always maintains linear stability. Subsequently, Rees [5] added a temporal derivative of the velocity to the momentum equation and determined that the flow remains linearly stable, which is the same as Gill's conclusion. For porous media with high porosity, Lundgren [6] experimentally confirmed that the extension of Darcy's law by Brinkman is more valid. Shankar et al. [7] investigated the effect of inertial terms on the stability of natural convection in a vertical layer of a porous medium at different temperatures using the Brinkman model. Using the classical linear stability theory, they discovered that instability is caused by the inertia effect.

Viscoelastic fluids naturally exhibit convection when flowing through porous media, which has important implications for reservoir engineering, bioengineering and geophysics. Gözüm and Arpaci [8] initially investigated the stability of natural convection in a vertical layer at various temperatures for a viscoelastic Maxwell fluid. Takashima [9] investigated the same problem with Oldroyd-B fluid. Khuzhayorov et al. [10] proposed a revised Darcy's law for analyzing the viscoelastic properties of saturated porous materials. Using the homogenization method, they discovered a general filtration law that describes the flow of a linear viscoelastic fluid in a porous material. Kim et al. [11] used a modified Darcy model to analyze thermal instability in a horizontal porous layer with saturated Oldroyd-B fluid. The conventional linear stability theory provided the critical conditions for the initiation of convective motion. Using a modified Darcy-Brinkman-Oldroyd model, Zhang et al. [12] investigated the convection of saturated Oldroyd-B fluid in a horizontal porous layer heated from below. They calculated the critical number of stationary and oscillating convection. Sun et al. [13] studied the lower horizontal plate that was heated in a time-periodic pattern. The system changed from a steady convection to a periodic or chaotic state. Barletta and Alves [14] investigated the Gill stability problem for power-law fluids and discovered that Gill's findings are also applicable to the power-law fluid. The Gill problem for Oldroyd-B fluid was addressed by Shankar and Shivakumara [15]. In contrast to the results for Newtonian and power-law fluids, the flow of Oldroyd-B fluid is unstable.

Besides, they [16] considered the situation of local thermal non-equilibrium (LTNE) and instability that existed as well. Then, Shanker and Shivakumara [17] considered the case of a porous layer containing an internal heat source. He established that internal heating and relaxation parameters contribute to system instability. Newtonian fluids flow steady, while Oldroyd-B fluids flow unstable. For double-diffusive convection instead of thermal convection, Wang and Tan [18] used a modified Darcy model to study the stability of Maxwell fluids in porous media with two parallel planes.

Malashetty and Biradar [19] investigated the cross-diffusion effect on DDC. They conducted linear and weakly nonlinear stability analyses using a modified Darcy model with a time derivative term as the momentum equation and found the critical Rayleigh number. Malashetty et al. [20,21] then studied the stability of the Oldroyd-B fluid and the formation of DDC saturated isotropic and anisotropic horizontal porous layers, respectively. As a result, the thermal anisotropy parameter has a dual role in the stability of the flow. Kumar and Bhadauria [22] explored the situation of LTNE, adding a time derivative term to the momentum equation. They discovered that when the interphase heat transfer coefficient was big or small, the system behaved similarly to the local thermal equilibrium (LTE) model. Subsequently, Malashetty et al. [23] investigated the situation of an anisotropic rotating porous layer with LTE and found that the thermal anisotropy parameter has the opposite effect on the onset of convection compared with the no-rotation condition. The onset of DDC in a horizontal porous layer was recently studied by Swamy et al. [24] based on the Darcy-Brinkman-Oldroyd model.

Due to numerous applications in geothermal systems, energy storage devices, thermal insulation, drying technologies, catalytic reactors, and nuclear waste repositories, theoretical and experimental research has focused on heat and mass transmission in porous systems. Density gradients in fluid-saturated media can cause heat and mass transmission to be coupled because of heat and mass inhomogeneities when examining heat and mass transfer processes in porous media channels. The cross-diffusion effect is simultaneously brought on by mass and heat fluxes. The Soret effect transfers mass via a temperature gradient, while the Dufour effect transfers heat via a concentration gradient. The Dufour coefficient has a negligible energy flux in liquids and is an order of magnitude smaller than the Soret coefficient (see Straughan and Hutter [25]). Therefore, while discussing liquid flow, we can ignore the Dufour term. The majority of recent research on DDC in porous layers that takes the Soret effect into account has concentrated on horizontal porous layers. With the Darcy model, Bahloul et al. [26] examined the beginning of natural convection in a horizontal porous layer. They calculated the critical values of finite amplitude, oscillatory, and monotonic convective instability for DDC and Soret convection using linear stability analysis. Subsequently, the case of anisotropic horizontal porous layer based on the previous paper was studied by Gaikwad et al. [27] Using linear and nonlinear stability analysis, they analyzed the critical Rayleigh number, wave number, and oscillation frequency of steady and oscillatory modes. Utilizing linear and weakly nonlinear stability studies, Gaikwad and Dhanraj [28] initially used the Darcy-Brinkman model to study the DDC with the Soret effect in a binary viscoelastic fluid-saturated horizontally porous layer. They discovered that whereas a positive Soret value accelerates the onset of DDC in stationary mode and has the opposite impact in oscillatory and finite amplitude modes, a negative Soret parameter increases system stability. Bouachir et al. [29] investigated DDC flow in a vertical porous chamber filled with a binary mixture exhibiting Soret and Dufour effects. The Darcy-Brinkman model and the Oberbeck-Boussinesq approximation are used to study the impact of the Soret and Dufour effects on convective stability. Overall, the thresholds of oscillatory, overstable, and stationary convection were greatly impacted by the Soret and Dufour effects.

Due to the significant differences in molecular diffusivity, DDC leads to complex flow structures and, consequently, the transport of heat and solute concentrations with different time and length scales. The majority of prior investigations used pure DDC for natural convection in a vertical porous material influenced by horizontal heat and solute concentration differences. Therefore, the Soret effect is introduced in this paper to describe the mass flux induced by the temperature gradient. Until now, there has been no study on the instability of the Soret effect on DDC in a saturated vertical porous layer of Oldroyd-B fluid. Therefore, the present work aims to investigate the linear stability of DDC of Oldroyd-B fluid in a vertical porous layer with the Soret effect. The manuscript is structured as follows. Section 2 presents the mathematical model that outlines the governing equations. The linear stability analysis and numerical procedures are given in Section 3 and Section 4, respectively. In Section 5, we present the results and discussion, while the last section contains the conclusions that we have drawn.

2. Mathematical Model

2.1. Mathematical Description of the Model

Figure 1 depicts an infinitely extended vertical porous layer surrounded by two impermeable plates and saturated with Oldroyd-B fluid in the region −d ≤ x ≤ d, with vertically downward gravity acting on it. The vertical limits of the porous layer are maintained at constant but distinct temperatures T₁ and T₂ (> T₁) and solute concentrations S₁ and S₂ (>S₁). We begin with a Cartesian coordinate frame, in which the z-axis points vertically and the x-axis extends horizontally over the breadth.

Given a temperature T and a solute concentration S, the density ρ of the mixture fluid is expected to change linearly in the following form:

ρ^{*} = ρ_{0} [1 - α (T^{*} - T_{0}) + β (S^{*} - S_{0})],

(1)

The volumetric thermal expansion coefficient α and volumetric solutal expansion coefficient β of the fluid are represented by the variables ρ₀ at T₀=(T₁+T₂)/2 and S₀=(S₁+S₂)/2.

It is assumed that the fluid and medium have constant properties and that few chemical reactions occur in the homogeneous, isotropic media. Furthermore, the porous media exhibits a local thermal equilibrium. After adopting the modified Darcy-Brinkman-Oldroyd model [24], which incorporates the Oberbeck-Boussinesq approximation and a time derivative term, the system governing equations are as follows

\nabla^{*} \cdot u^{*} = 0,

(2)

(1 + λ_{1}^{*} \frac{\partial}{\partial t^{*}}) (\frac{ρ_{0}}{ε} \frac{\partial u^{*}}{\partial t^{*}} + \nabla^{*} p^{*} - ρ^{*} g) = (1 + λ_{2}^{*} \frac{\partial}{\partial t^{*}}) (- \frac{μ}{K} u^{*} + μ_{e} \nabla^{* 2} u^{*}),

(3)

γ \frac{\partial T^{*}}{\partial t^{*}} + (u^{*} \cdot \nabla^{*}) T^{*} = κ_{T} \nabla^{* 2} T^{*},

(4)

ε \frac{\partial S^{*}}{\partial t^{*}} + (u^{*} \cdot \nabla^{*}) S^{*} = κ_{S} \nabla^{* 2} S^{*} + κ_{S T} \nabla^{* 2} T^{*},

(5)

where t^*, p^*, and T^* stand for time, pressure, and temperature in the porous media, respectively, and u^*= (u^*, v^*, w^*) is the velocity vector. The symbols for dynamic viscosity and effective viscosity are μ and μ_e. The medium's porosity and permeability are represented by K and ε. The strain retardation time is represented by λ₂^*, the stress relaxation time by λ₁^*, and the gravity acceleration vector is given by g= (0, 0, -g). κ_ST is the Soret coefficient expressed as a constant, and κ_T and κ_S stand for thermal and solute diffusivity, respectively. The ratio of specific heats is represented by γ=(ρc)_m /(ρc)_f, where (ρc)_f represents the volumetric heat capacity of the fluid and (ρc)_m =ε(ρc)_f + (1-ε)(ρc)_s represents the saturated medium's overall volumetric heat capacity. The subscripts f and s stand for the fluid and solid matrix of the porous medium.

The boundaries are impermeable, and the applicable boundary conditions are

u^{*} = 0, T^{*} = T_{1}, S^{*} = S_{1} at x^{*} = - d,

(6)

u^{*} = 0, T^{*} = T_{2}, S^{*} = S_{2} at x^{*} = d .

(7)

Dimensionless quantities are introduced through the scaling

(x^{*}, y^{*}, z^{*}) = (x, y, z) d t^{*} = (γ d^{2} / κ_{T}) t u^{*} = (κ_{T} / d) u p^{*} = (μ κ_{T} / K) p

(8)

λ_{1}^{*} = (γ d^{2} / κ_{T}) λ_{1} λ_{2}^{*} = (γ d^{2} / κ_{T}) λ_{2} T^{*} - T_{0} = (Δ T) T S^{*} - S_{0} = (Δ S) S

to non-dimensionalize Eqs. (2) -(7) in the form,

\nabla \cdot u = 0,

(9)

(1 + λ_{1} \frac{\partial}{\partial t}) (\frac{1}{P r_{D}} \frac{\partial u}{\partial t} + \nabla p - R a_{T} T {\hat{e}}_{z} + R a_{S} S {\hat{e}}_{z}) = (1 + λ_{2} \frac{\partial}{\partial t}) (- u + D a \nabla^{2} u),

(10)

\frac{\partial T}{\partial t} + (u \cdot \nabla) T = \nabla^{2} T

(11)

η \frac{\partial S}{\partial t} + (u \cdot \nabla) S = \frac{1}{L e} \nabla^{2} S + S_{r} \nabla^{2} T

(12)

here, Pr_D=εγd²v/κ_TK is the Darcy–Prandtl number, Ra_T=αg∆TdK/vκ_T is the Darcy–Rayleigh number, Ra_S=βg∆SdK/vκ_T is solute Rayleigh number, Le=κ_T/κ_S is the Lewis number and η=ε/γ is normalized porosity. Da=μ_eK/μd² is the modified Darcy number. S_r=κ_ST∆T /κ_T∆S is the Soret parameter. There are two possible values for the Soret parameter S_r: positive and negative. The solute diffuses toward the cooler plate when the Soret parameter is positive; the opposite is true when the parameter is negative.

The boundary conditions are

u = 0, at x = \pm 1

(13)

T = \pm \frac{1}{2}, S = \pm \frac{1}{2}, at x = \pm 1

(14)

2.2. Basic Flow

It is assumed that the base flow is stable, unidirectional, and fully developed. In this condition, the physical variables are provided by

u_{b} = (0, 0, w_{b} (x)), T = T_{b} (x), S = S_{b} (x), p = p_{b} (x)

(15)

Applying the preceding assumptions to the governing equations (9)-(14) reduces the system of ordinary differential equations and easily obtains the basic flow equations:

D a D^{2} w_{b} - w_{b} + R a_{T} T_{b} - R a_{S} S_{b} = \frac{\partial p_{b}}{\partial z},

(16)

D^{2} T_{b} = 0,

(17)

\frac{D^{2} S_{b}}{L e} + S_{r} \frac{\partial^{2} T_{b}}{\partial x^{2}} = 0,

(18)

where D=d/dx and the suffix b serves to denote the basic flow. The associated boundary conditions are

w_{b} = 0, at x = \pm 1,

(19)

T_{b} = \pm \frac{1}{2}, S_{b} = \pm \frac{1}{2}, at x = \pm 1 .

(20)

The solution to the basic flow is found to be

w_{b} (x) = \frac{R a_{S} - R a_{T}}{2} [\frac{\sinh (D a^{- \frac{1}{2}} x)}{\sinh D a^{- \frac{1}{2}}} - x], T_{b} = \frac{1}{2} x, S_{b} = \frac{1}{2} x, p_{b} (z) = const .

(21a,b,c,d)

Ra_T, Ra_S, and Da all have an impact on the fundamental velocity profile. When Ra_S →0, it is possible to quickly verify that the basic solution provided by Eqs. (21a, b) coincides with that of Shankar et al. [31]. The base flow velocity profiles are shown in Figure 2(a)–(c). Figure 2(a) shows scaled basic velocity profiles w_b(x) for various Da values. The no-slip condition on the wall and the buoyant term's acceleration of the fluid near the border cause a point of inflection in the velocity profile, as seen in the image. With decreasing Da, it is found that the point of inflection moves closer to the walls. The appearance of an inflection point indicates a potential basis for flow instability. Ra_T and Ra_S have different effects on the base flow, as seen in Figure 2(b) and (c), respectively. As Ra_T or Ra_S rises, the velocity value rises as well. The velocity profiles are significantly asymmetric when compared to the vertical line at x = 0.

3. Linear Stability Analysis

In order to examine linear stability, we must first develop the perturbation equations for the infinitesimal disturbance. Small-amplitude disturbances of the following form are applied to the basic state:

u = u^{'}, v = v^{'}, w = w_{b} + w^{'}, p = p_{b} + p^{'}, T = T_{b} + T^{'}, S = S_{b} + S^{'},

(22)

where the primed amounts denote the perturbations field across the basic state.

The three-dimensional governing linear stability equations are obtained by applying Eq. (22) in Eqs. (9)-(14) and by following the standard process of linear stability theory [30]:

\frac{\partial u^{'}}{\partial x} + \frac{\partial v^{'}}{\partial y} + \frac{\partial w^{'}}{\partial z} = 0,

(23)

(1 + λ_{1} \frac{\partial}{\partial t}) (\frac{1}{P r_{D}} \frac{\partial u^{'}}{\partial t} + \frac{\partial p^{'}}{\partial x}) = (1 + λ_{2} \frac{\partial}{\partial t}) [- u^{'} + D a (\frac{\partial^{2} u^{'}}{\partial x^{2}} + \frac{\partial^{2} u^{'}}{\partial y^{2}} + \frac{\partial^{2} u^{'}}{\partial z^{2}})],

(24)

(1 + λ_{1} \frac{\partial}{\partial t}) (\frac{1}{P r_{D}} \frac{\partial v^{'}}{\partial t} + \frac{\partial p^{'}}{\partial y}) = (1 + λ_{2} \frac{\partial}{\partial t}) [- v^{'} + D a (\frac{\partial^{2} v^{'}}{\partial x^{2}} + \frac{\partial^{2} v^{'}}{\partial y^{2}} + \frac{\partial^{2} v^{'}}{\partial z^{2}})],

(25)

\begin{matrix} (1 + λ_{1} \frac{\partial}{\partial t}) (\frac{1}{P r_{D}} \frac{\partial w^{'}}{\partial t} + \frac{\partial p^{'}}{\partial z} - R a_{T} T^{'} + R a_{S} S^{'}) \\ = (1 + λ_{2} \frac{\partial}{\partial t}) [- w^{'} + D a (\frac{\partial^{2} w^{'}}{\partial x^{2}} + \frac{\partial^{2} w^{'}}{\partial y^{2}} + \frac{\partial^{2} w^{'}}{\partial z^{2}})], \end{matrix}

(26)

\frac{\partial T^{'}}{\partial t} + u^{'} D T_{b} + w_{b} \frac{\partial T^{'}}{\partial z} = \frac{\partial^{2} T^{'}}{\partial x^{2}} + \frac{\partial^{2} T^{'}}{\partial y^{2}} + \frac{\partial^{2} T^{'}}{\partial z^{2}}

(27)

η \frac{\partial S^{'}}{\partial t} + u^{'} D S_{b} + w_{b} \frac{\partial S^{'}}{\partial z} = \frac{1}{L e} (\frac{\partial^{2} S^{'}}{\partial x^{2}} + \frac{\partial^{2} S^{'}}{\partial y^{2}} + \frac{\partial^{2} S^{'}}{\partial z^{2}}) + S_{r} (\frac{\partial^{2} T^{'}}{\partial x^{2}} + \frac{\partial^{2} T^{'}}{\partial y^{2}} + \frac{\partial^{2} T^{'}}{\partial z^{2}})

(28)

The boundary conditions are

u^{'} = v^{'} = w^{'} = T^{'} = S^{'} = 0 x = \pm 1

(29)

To construct linear stability for arbitrary infinitesimal disturbances, superpose normal modes in the following manner:

\{u^{'}, v^{'}, w^{'}, p^{'}, T^{'}, S^{'}\} = \{\overset{⌢}{u}, \overset{⌢}{v}, \overset{⌢}{w}, \overset{⌢}{p}, \overset{⌢}{T}, \overset{⌢}{S}\} (x) e^{i (a z + b y - a c t)}

(30)

where a and b represent the wave numbers in the z and y directions, respectively, and c=c_r+ic_i is the complex parameter whose real part expresses the wave speed and whose imaginary part yields the disturbance growth rate. The basic solution threshold for stability and instability is as follows: if c_i < 0, the system is stable; if c_i > 0, the system is unstable; and if c_i = 0, the system is neutrally stable. When we replace Eq. (30) with Eqs. (23)-(29), we get

D \overset{⌢}{u} + i (b \overset{⌢}{v} + a \overset{⌢}{w}) = 0,

(31)

(1 - a c i λ_{1}) (- \frac{a c i \overset{⌢}{u}}{P r_{D}} + D \overset{⌢}{p}) = (1 - a c i λ_{2}) [D a (D^{2} - a^{2} - b^{2}) - 1] \overset{⌢}{u},

(32)

(1 - a c i λ_{1}) (- \frac{a c i \overset{⌢}{v}}{P r_{D}}) + b (i + a c λ_{1}) \overset{⌢}{p} = (1 - a c i λ_{2}) [D a (D^{2} - a^{2} - b^{2}) - 1] \overset{⌢}{v},

(33)

+ a (i + a c λ_{1}) \overset{⌢}{p} = (1 - a c i λ_{2}) [D a (D^{2} - a^{2} - b^{2}) - 1] \overset{⌢}{w},

(34)

(1 - a c i λ_{1}) (- \frac{a c i \overset{⌢}{w}}{P r_{D}} - R a_{T} \overset{⌢}{T} + R a_{S} \overset{⌢}{S})

i a (w_{b} - c) \overset{⌢}{T} + \overset{⌢}{u} D T_{b} = (D^{2} - a^{2} - b^{2}) \overset{⌢}{T},

(35)

i a (w_{b} - c η) \overset{⌢}{S} + \overset{⌢}{u} D S_{b} = \frac{1}{L e} (D^{2} - a^{2} - b^{2}) \overset{⌢}{S} + S_{r} (D^{2} - a^{2} - b^{2}) \overset{⌢}{T},

(36)

\overset{⌢}{u} = \overset{⌢}{v} = \overset{⌢}{w} = \overset{⌢}{T} = \overset{⌢}{S} = 0, at x = \pm 1 .

(37)

We exclusively examine two-dimensional flows due to the validity of Squire's theorem [31]. Thus, employing Squire's transformation in its extended form

\begin{matrix} \tilde{a} = \sqrt{a^{2} + b^{2}}, \tilde{w} = \frac{a (a \overset{⌢}{w} + b \overset{⌢}{v})}{{\tilde{a}}^{2}}, {\tilde{w}}_{b} = \frac{a}{\tilde{a}} w_{b}, \tilde{c} = \frac{a}{\tilde{a}} c, \tilde{T} = \frac{a}{\tilde{a}} \overset{⌢}{T}, \tilde{S} = \frac{a}{\tilde{a}} \overset{⌢}{S}, \tilde{η} = η, \tilde{L} e = L e, \\ \tilde{p} = \frac{a}{\tilde{a}} \overset{⌢}{p}, \tilde{D} a = D a, \tilde{P} r_{D} = P r_{D}, {\tilde{λ}}_{1} = λ_{1}, {\tilde{λ}}_{2} = λ_{2}, \tilde{R} a_{T} = \frac{a}{\tilde{a}} R a_{T}, \tilde{R} a_{S} = \frac{a}{\tilde{a}} R a_{S} . \end{matrix}

(38)

replacing Eq. (38) into Eqs. (31)-(37) yields:

D \tilde{u} + i \tilde{a} \tilde{w} = 0,

(39)

(1 - i \tilde{a} \tilde{c} {\tilde{λ}}_{1}) (- \frac{i \tilde{a} \tilde{c} \tilde{u}}{\tilde{P} r_{D}} + D \tilde{p}) = (1 - i \tilde{a} \tilde{c} {\tilde{λ}}_{2}) [\tilde{D} a (D^{2} - {\tilde{a}}^{2}) - 1] \tilde{u},

(40)

(1 - i \tilde{a} \tilde{c} {\tilde{λ}}_{1}) (- \frac{i \tilde{a} \tilde{c} \tilde{w}}{\tilde{P} r_{D}} - \tilde{R} a_{T} \tilde{T} + \tilde{R} a_{S} \tilde{S}) + \tilde{a} (i + \tilde{a} \tilde{c} {\tilde{λ}}_{1}) \tilde{p}

= (1 - i \tilde{a} \tilde{c} {\tilde{λ}}_{2}) [\tilde{D} a (D^{2} - {\tilde{a}}^{2}) - 1] \tilde{w},

(41)

i \tilde{a} ({\tilde{w}}_{b} - \tilde{c}) \tilde{T} + \tilde{u} D T_{b} = (D^{2} - {\tilde{a}}^{2}) \tilde{T},

(42)

i \tilde{a} ({\tilde{w}}_{b} - \tilde{c} \tilde{η}) \tilde{S} + \tilde{u} D S_{b} = \frac{1}{\tilde{L} e} (D^{2} - {\tilde{a}}^{2}) \tilde{S} + S_{r} (D^{2} - {\tilde{a}}^{2}) \tilde{T},

(43)

\tilde{u} = \tilde{w} = \tilde{T} = \tilde{S} = 0, at x = \pm 1 .

(44)

Equations (39)-(44) are two-dimensional equations with the same mathematical structure as Eqs. (31)-(37), when v=b=0 (i.e., two-dimensional equations). When b≠0,

\tilde{R} a_{T}

and

\tilde{R} a_{S}

are smaller than Ra_T and Ra_S, respectively. Therefore, it is sufficient to consider only the two-dimensional equations, as two-dimensional perturbations are less favorable for stabilizing the base flow than three-dimensional perturbations. Then, introduce the stream function

\tilde{ψ}

(x, z, t) such that

\tilde{u} = \frac{\partial \tilde{ψ}}{\partial z}, \tilde{w} = - \frac{\partial \tilde{ψ}}{\partial x},

(45)

the following is how the normal mode analysis approach is used:

\{\tilde{ψ}, \tilde{T}, \tilde{S}\} = \{\hat{ψ}, \hat{T}, \hat{S}\} (x) e^{i a (z - c t)},

(46)

eliminating the pressure term by cross differentiation and subtracting the resulting equations, we obtain (on dropping the wave symbols)

\begin{matrix} [D^{2} - a^{2} - D a {(D^{2} - a^{2})}^{2}] \hat{ψ} + R a_{T} D \hat{T} - R a_{S} D \hat{S} \\ + c {[- \frac{i a}{P r_{D}} (D^{2} - a^{2}) + i a λ_{2} D a {(D^{2} - a^{2})}^{2} - i a λ_{2} (D^{2} - a^{2})] \hat{ψ} \\ - i a λ_{1} R a_{T} D \hat{T} + i a λ_{1} R a_{S} D \hat{S}} + c^{2} [- \frac{a^{2} λ_{1}}{P r_{D}} (D^{2} - a^{2}) \hat{ψ}] = 0 \end{matrix}

(47)

\frac{1}{2} i a \hat{ψ} + (i a w_{b} + a^{2} - D^{2}) \hat{T} + c (- i a \hat{T}) = 0

(48)

\frac{1}{2} i a \hat{ψ} + (i a w_{b} + \frac{a^{2}}{L e} - \frac{D^{2}}{L e}) \hat{S} + S_{r} (a^{2} - D^{2}) \hat{T} + c (- i a η \hat{S}) = 0

(49)

The boundary conditions are

\hat{ψ} = D \hat{ψ} = \hat{T} = \hat{S} = 0, at x = \pm 1 .

(50)

4. Numerical Procedure

In general, stability analysis of eigenvalue problems uses numerical methods. Equations (47)-(50) are solved via the Chebyshev collocation method. The following gives the Chebyshev polynomial of k-th order:

ξ_{k} (x) = \cos k θ, θ = \cos^{- 1} x .

(51)

The following gives the Chebyshev collocation points:

x_{j} = \cos (\frac{j π}{N}), j = 0, 1, \dots N,

(52)

where j=0 and j=N represent the left and right wall limits, respectively, and N can be any positive number. The field variables

\hat{ψ}

\hat{T}

, and

\hat{S}

are approximated using Chebyshev polynomials:

\hat{ψ} (x) = \sum_{j = 0}^{N} ψ_{j} ξ_{j} (x), \hat{T} (x) = \sum_{j = 0}^{N} T_{j} ξ_{j} (x), \hat{S} (x) = \sum_{j = 0}^{N} S_{j} ξ_{j} (x),

(53)

The values of ψ_j, T_j, and S_j are constants. Discretizing equations (47)-(50) in terms of Chebyshev polynomials yields:

\begin{matrix} [\sum_{k = 0}^{N} B_{j k} ψ_{k} - a^{2} ψ_{j} - D a (\sum_{k = 0}^{N} E_{j k} ψ_{k} - 2 a^{2} \sum_{k = 0}^{N} B_{j k} ψ_{k} + a^{4} ψ_{j})] + R a_{T} \sum_{k = 0}^{N} A_{j k} T_{j} \\ - R a_{S} \sum_{k = 0}^{N} A_{j k} S_{j} + c [- \frac{i a}{\Pr_{D}} (\sum_{k = 0}^{N} B_{j k} ψ_{k} - a^{2} ψ_{j}) + i a λ_{2} D a (\sum_{k = 0}^{N} E_{j k} ψ_{k} - 2 a^{2} \sum_{k = 0}^{N} B_{j k} ψ_{k} + a^{4} ψ_{j}) \\ - i a λ_{2} (\sum_{k = 0}^{N} B_{j k} ψ_{k} - a^{2} ψ_{j})] - c (i a λ_{1} R a_{T} \sum_{k = 0}^{N} A_{j k} T_{j} + i a λ_{1} R a_{S} \sum_{k = 0}^{N} A_{j k} S_{j}) \\ + c^{2} [- \frac{a^{2} λ_{1}}{\Pr_{D}} (\sum_{k = 0}^{N} B_{j k} ψ_{k} - a^{2} ψ_{j})] = 0, j = 1, \dots, N - 1, \end{matrix}

(54)

\frac{1}{2} i a ψ_{j} + ((i a w_{b} + a^{2}) T_{j} - \sum_{k = 0}^{N} B_{j k} T_{k}) + c (- i a T_{j}) = 0, j = 1, \dots, N - 1,

(55)

\begin{matrix} \frac{1}{2} i a ψ_{j} + ((i a w_{b} + \frac{a^{2}}{L e}) S_{j} - \frac{1}{L e} \sum_{k = 0}^{N} B_{j k} S_{k}) + S_{r} (a^{2} T_{j} - \sum_{k = 0}^{N} B_{j k} T_{k}) \\ + c (- i a η S_{j}) = 0, j = 1, \dots, N - 1, \end{matrix}

(56)

ψ_{0} = ψ_{N} = 0

(57)

\sum_{k = 0}^{N} A_{j k} ψ_{k} = 0 j = 0

(58)

T_{0} = T_{N} = 0

(59)

S_{0} = S_{N} = 0

(60)

Where

A_{j k} = \{\begin{cases} \frac{c_{j} {(- 1)}^{k + j}}{c_{k} (x_{j} - x_{k})} j \neq k, \\ \frac{x_{j}}{2 (1 - x_{j}^{2})} 1 \leq j = k \leq N - 1, \\ \frac{2 N^{2} + 1}{6} j = k = 0, \\ - \frac{2 N^{2} + 1}{6} j = k = N, \end{cases}

(61)

B_{j k} = A_{j m} \cdot A_{m k} and E_{j k} = B_{j m} \cdot B_{m k},

(62)

with

c_{j} = \{\begin{cases} 1 1 \leq j \leq N - 1, \\ 2 j = 0, N . \end{cases}

(63)

A generalized eigenvalue problem can be obtained from the discretization equation:

A_{0} X + c A_{1} X + c^{2} A_{2} X = 0

(1.1)

where A₀, A₁, and A₂ are square matrices, c and X represent the complex eigenvalue and eigenfunction, respectively. The linear stability boundary of the fundamental flow is typically described by the eigenvalue issue. We designate the mode with the biggest imaginary portion c of the eigenvalue as the most growing mode among the eigenvalue and eigenfunction. This mode also happens to be the least decaying. The eigenvalues and eigenfunctions of the generalized eigenvalue problem are found using a QZ method. This algorithm is accessible as a built-in function called polyeig in the MatLab software package.

5. Results and Discussion

With the use of the Chebyshev collocation method, the linear stability of the Soret impact on DDC in a vertical layer of Darcy-Brinkman porous media is numerically explored. The Darcy-Rayleigh number Ra_T, the solute Darcy-Rayleigh number Ra_S, the Lewis number Le, the relaxation parameter λ₁, the retardation parameter λ₂, the Soret parameter S_r, the Darcy-Prandtl number Pr_D, the Darcy number Da, and the normalized porosity of the porous medium η are some of the significant non-dimensional parameters that control the flow.

Firstly, the parameter ranges are discussed based on the works by Shanker et al. [7] and Swamy et al. [24] The value of λ₁ must be greater than that of λ₂ (Bird et al. [32]; Hirata et al. [33]). The range of values for the Soret parameter is −1 < Sr < 1 (Bouachir et al. [29]). In fact, the Darcy-Prandtl number Pr_D can be expressed by Prandtl number, Darcy number, porosity, and specific heat ratio, i.e., Pr_D=γεPr/Da. Pr_D depends on the properties of the fluid and the porous matrix. For a sparse porous media, Da ranges from 0.001 to 1, γ changes from 0 to 1, ε is around 0.5, and the typical Prandtl number for viscoelastic fluids is 10. Therefore, Pr_D varies from 5 to 5000.

Table 1 provides a convergence analysis for numerical calculations by altering the order of the Chebyshev polynomials. Employing 30 to 45 configuration points in Eq. (50), it is found that the value of ac_i is independent of the polynomial order N between 35 and 45 and achieves 4-digit point precision. Therefore, all numerical results given subsequently are obtained by taking N = 40 in the Chebyshev expansion.

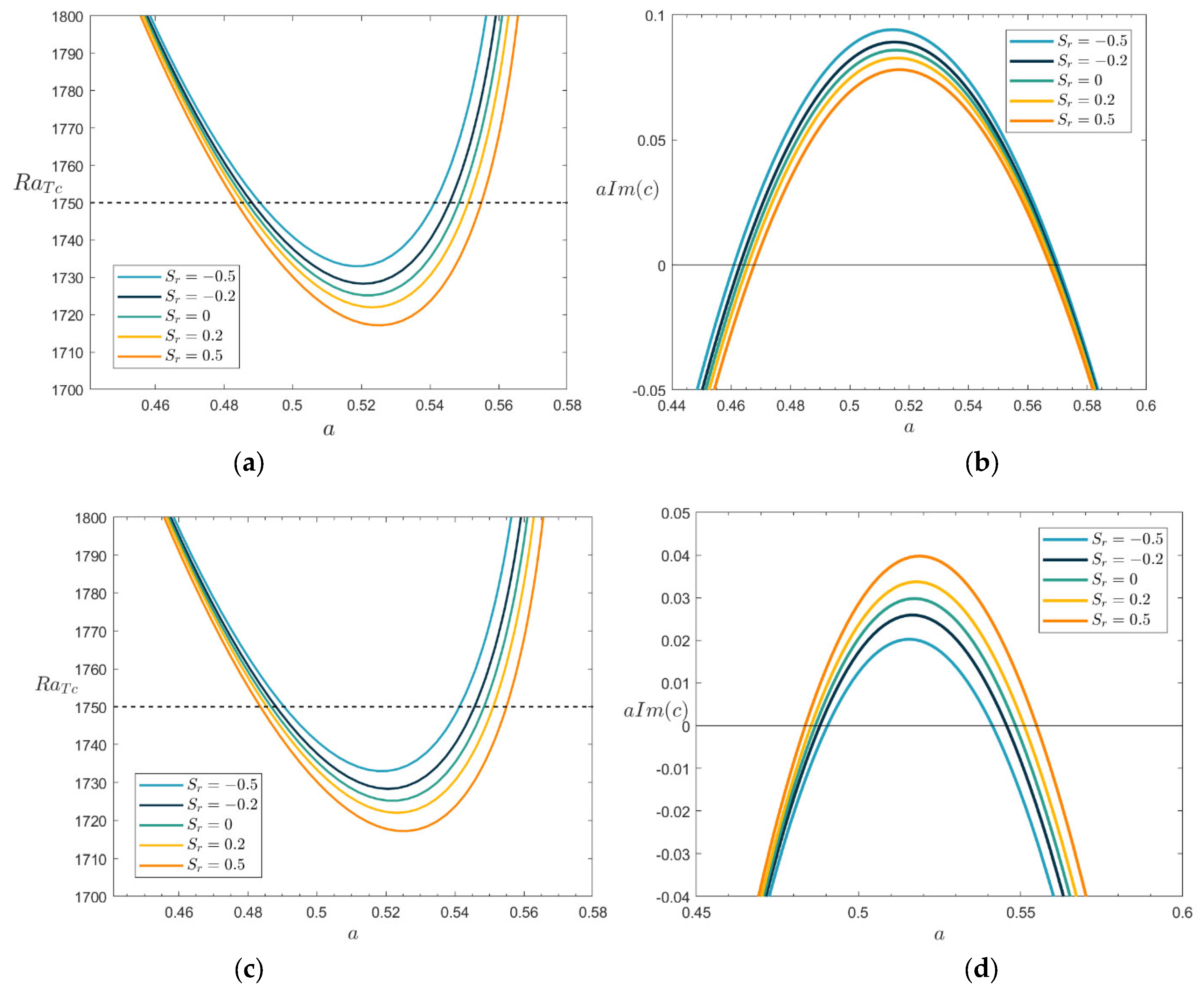
Figure 3(a)–3(d) show the growth rate for the Soret parameter as well as the neutral stability curves. In the neutral stability plot, it is stable outside of the tongue-shaped region and unstable within it. The minimum value of the neutral stability curve indicates the critical condition for the flow changing from a stable to an unstable state. In this paper, the corner symbol c represents the critical value, and the value of Ra_Tc is the critical value of the flow between stable and unstable; when Ra_T> Ra_Tc, it means that the flow is unstable, and when Ra_T < Ra_Tc, it means that the flow is stable. Figure 3(a) depicts the effect of different Soret parameters S_r on the neutral stability curve when Le = 1. When S_r increases, the minimum value of Ra_Tc moves towards the large value of wave number a, indicating that S_r reduces the width of the cell. In addition, S_r =0 denotes the neutral stability curve without the Soret effect. For S_r <0, we find that the minimum value of Ra_Tc decreases with the increase of the negative Soret parameter, which indicates that it weakens the stability of the system. For S_r >0, the minimum value of Ra_Tc increases with the increase of the positive Soret parameter, which indicates that it enhances flow instability. It shows that positive S_r results in a more stable flow, and negative S_r has the opposite effect. Figure 3(b) shows the growth rate curve for Ra_T = 1750, i.e., the growth rate case at the dotted line in Figure 3(a). In Figure 3(b), the growth rate is plotted using the same parameters. The larger the positive S_r is, the smaller the growth rate is, indicating that the positive S_r increases the stability of the system; the more significant the negative S_r is, the larger the growth rate is, indicating that the negative S_r weakens the stability of the system, and the same conclusion as Figure 3(a) is obtained. Figure 3(c) shows the neutral stability curve when Le=2.

We find that for S_r<0, the minimum value of Ra_Tc increases with the increase of the negative Soret parameter, which indicates that it improves stability. For S_r >0, the minimum value of Ra_Tc decreases with the rise of the positive Soret parameter, which suggests that it reduces stability. It shows that the positive S_r parameter has an unstable effect, and the negative S_r parameter has a stabilizing effect. It is opposite to the conclusion for Le =1. Figure 3(d) shows the growth rate curve when Ra_T=1750 and Le=2. The larger the positive S_r is, the bigger the growth rate is; the larger the negative S_r is, the smaller the growth rate is, indicating that the negative S_r enhances the stability, and the same conclusion as that of Figure 3(c) is obtained. In summary, we find that the positive and negative values of S_r have different effects on the instability, and the size of Le affects the impact of S_r on the instability of the flow.

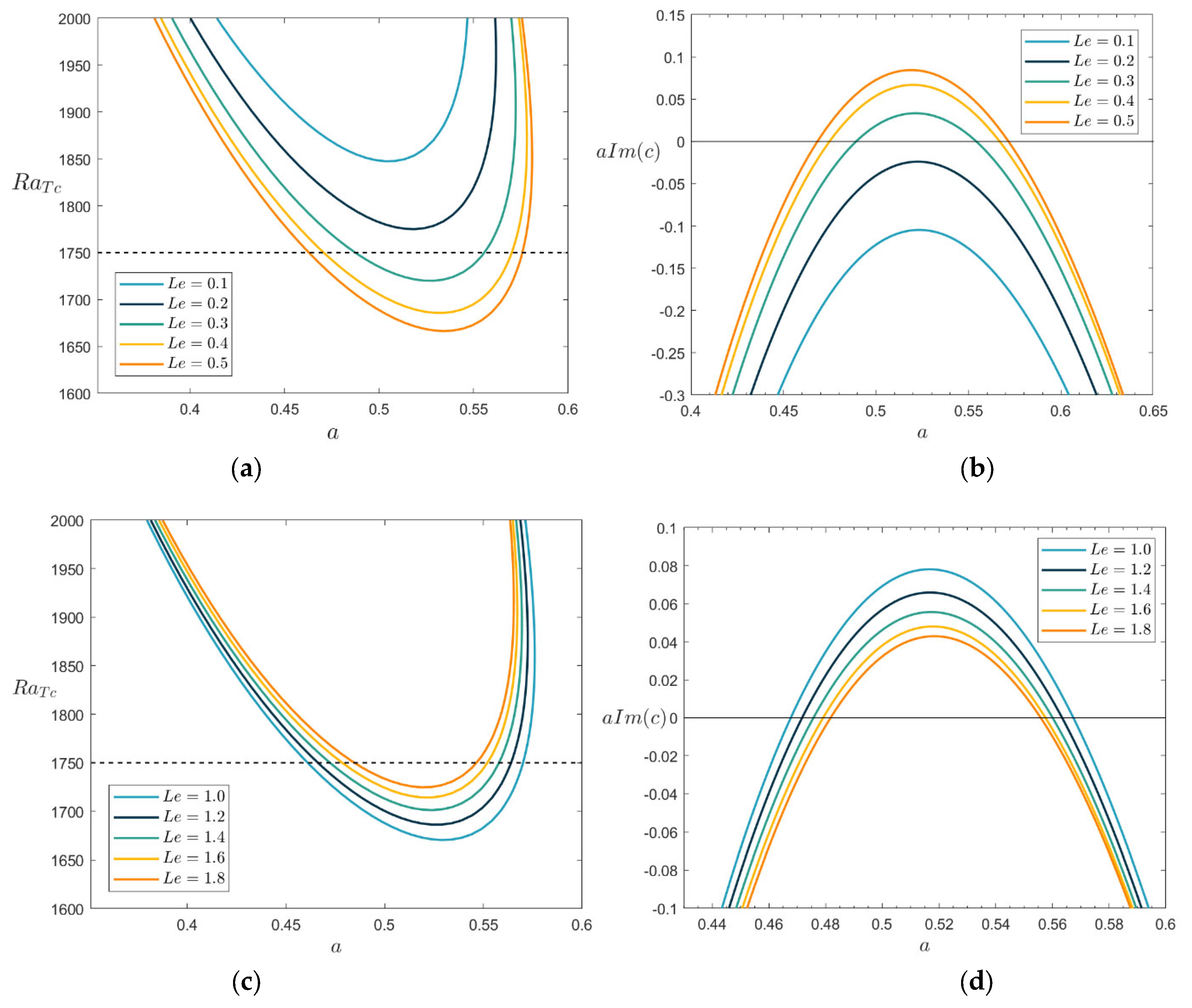
Figure 4(a)-(d) illustrate the neutral stability curves and growth rate curves for different Lewis numbers Le. Figure 4(a) depicts that the minimum value of Ra_Tc decreases with increasing Le for Le <0.5, indicating that Le promotes flow instability at this point. Figure 4(b) shows the growth rate curve when Ra_T = 1750 under the parameters of Figure 4(a). We find that the larger Le is, the larger the growth rate is and the more unstable the flow is. It indicates that Le plays a weakening effect on the stability of the flow when Le <0.5. Figure 4(c) suggests that Le promotes the stability of the flow when Le > 1. Under this parameter, Figure 4(d) depicts the growth rate when Ra_T = 1750, i.e., the growth rate corresponding to the neutral stabilization point intersecting the dashed line in Figure 4(c), and the growth rate is found to decrease with increasing Le. In summary, we find that Le has a dual effect on the instability of the flow.

Table 2 shows the values of Le_c₁ for different S_r. According to the table, Le_c₁ decreases with increasing S_r and remains around 0.7. Therefore, Le enhances the flow instability when Le < 0.7 and inhibits the flow instability when Le > 0.7.

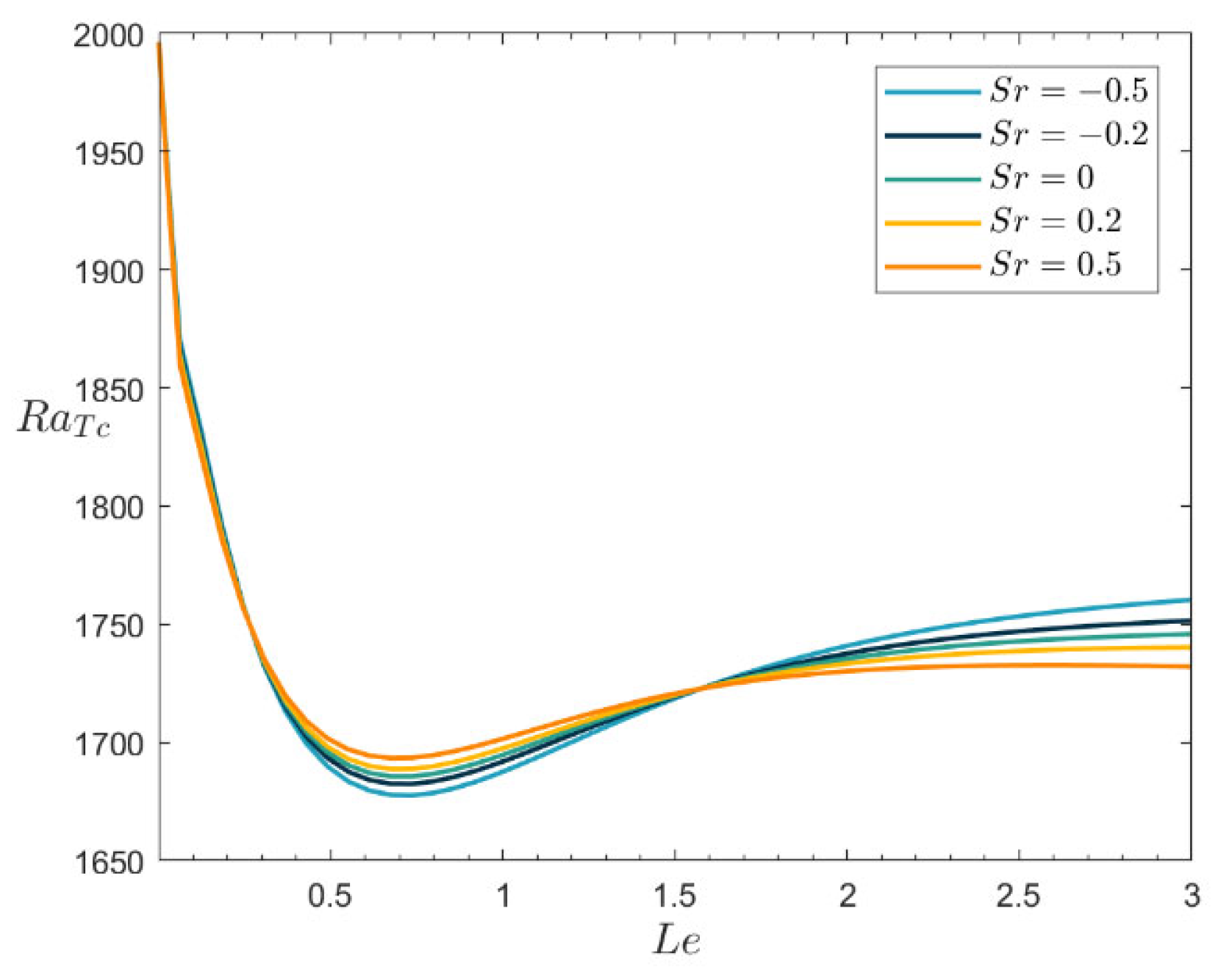
Figure 5 illustrates the neutral stability curves of Ra_Tc as Le varies for different Soret parameters S_r. As Le increases from zero, the value of Ra_Tc first decreases and then increases. This suggests that there is a critical value Le_c₁. This indicates that Le has both promoting and inhibiting effects on the instability of the flow. The minimum value of Ra_Tc corresponds to a critical Le value Le_c1, which promotes the instability of the flow when Le < Le_c1 and inhibits the instability of the flow when Le > Le_c1. According to the graph, it is found that there is also a critical value of Le, Le_c2=1.5735, when Le < Le_c2, S_r contributes to the instability of the flow, and when Le > Le_c2, S_r inhibits the instability of the flow. Thus, we find that Le and S_r have a dual role in the stability of the flow and that the magnitude of Le influences the role of S_r.

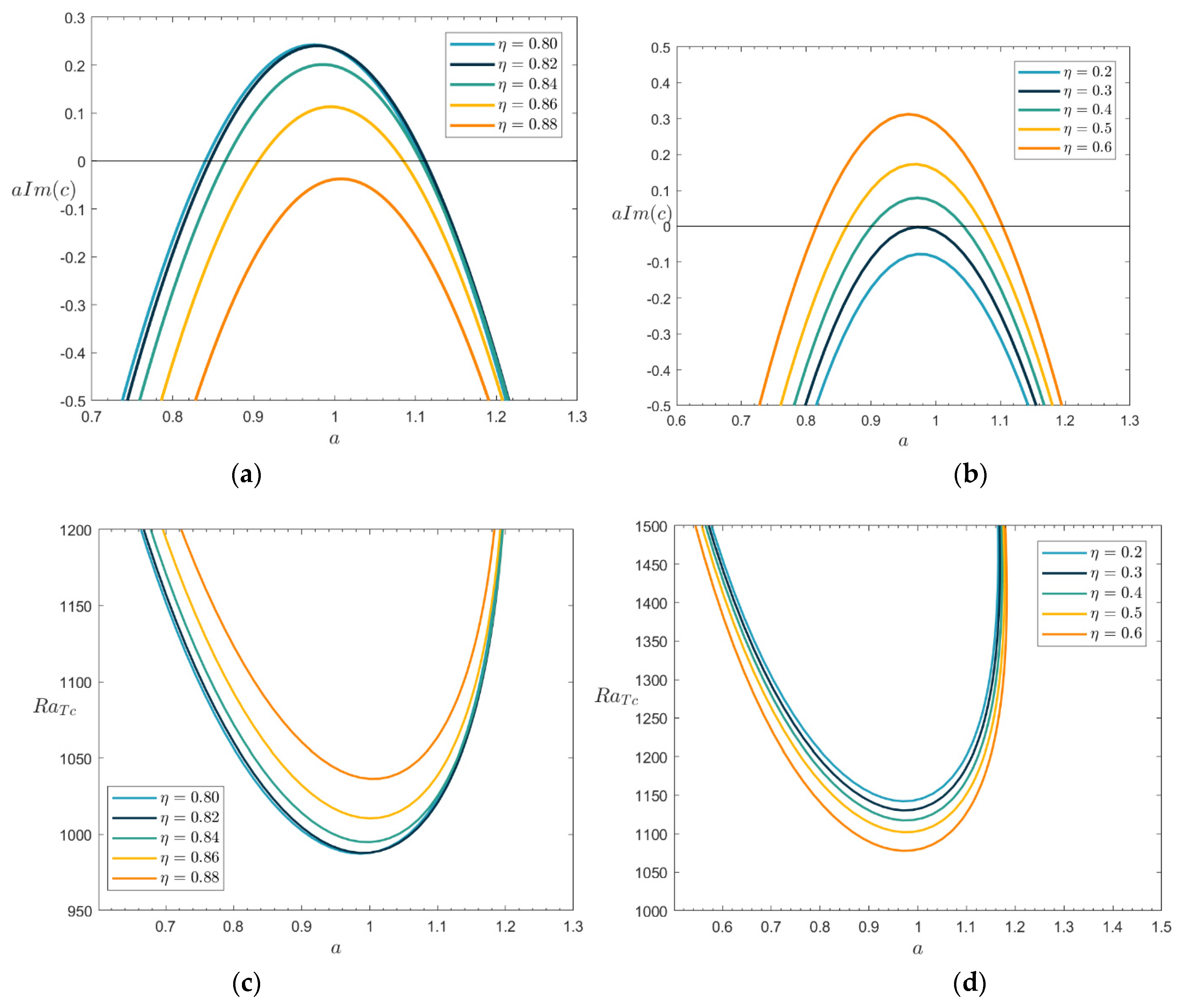
Figure 6(a)-(d) illustrate the neutral stability curves and growth rate curves for different normalized porosity η. Figure 6(a) shows that η promotes flow instability at this point. Figure 6(b) shows the growth rate profile when Ra_T = 1130 under the parameters of Figure 6(a). We find that the larger η is, the larger the growth rate is and the more unstable the flow is. It indicates that η plays a weakening effect on the stability of the flow when 0.2< η < 0.6. Figure 6(c) depicts that the minimum value of Ra_Tc increases with η when 0.8< η < 0.88, indicating that η promotes the stability of the flow. In Figure 6(d), the growth rate decreases with increasing η. In summary, η acts differently on the instability of the flow at different values.

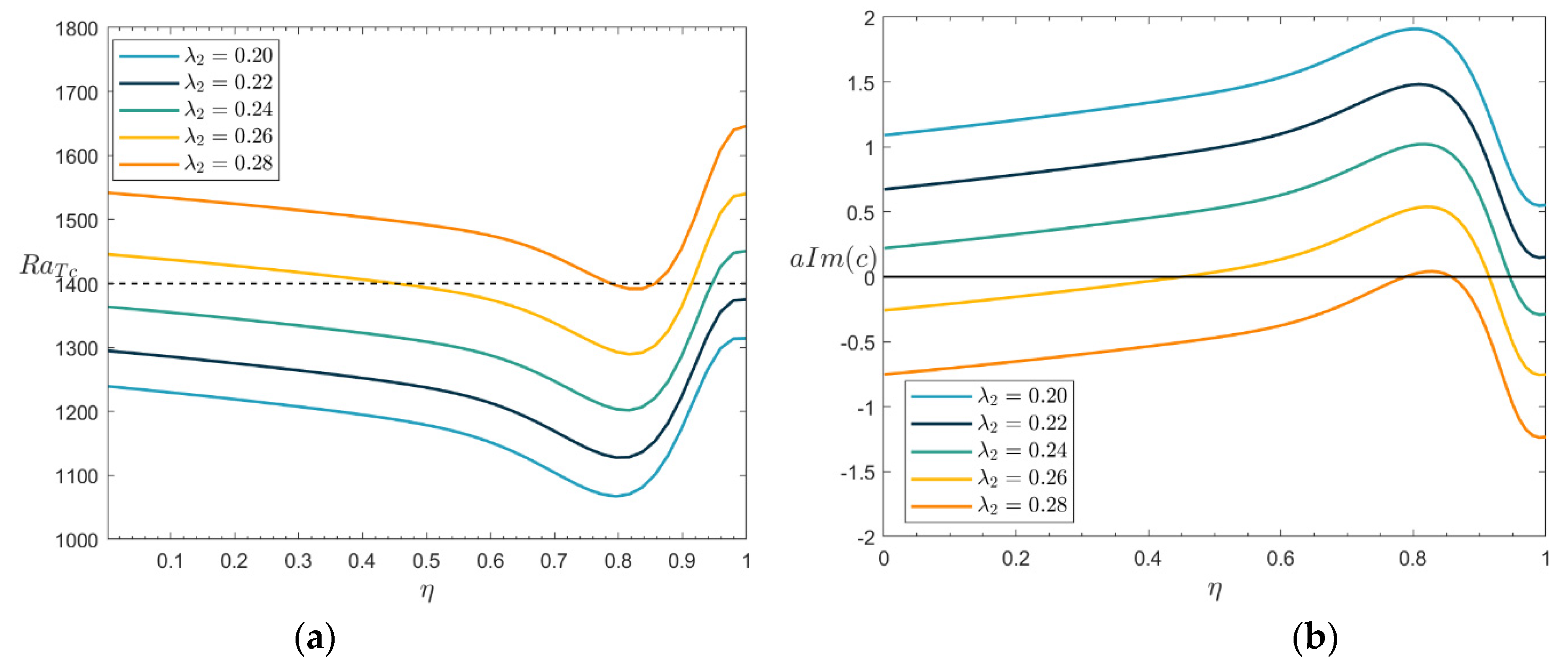
Figure 7(a) demonstrates the neutral stability curve of Ra_Tc as η varies for different relaxation parameters λ₂. As η increases from zero, the value of Ra_Tc decreases and then increases. This suggests that η has a dual effect on the instability. The minimum value of Ra_Tc corresponds to a critical value η_c, which enhances the instability when η < η_c and inhibits the instability when η > η_c. In addition, the minimum value of Ra_Tc increases with λ₂, indicating that λ₂ promotes flow stability. Figure 7(b) shows the growth rate when Ra_T = 1400 for the parameters of Figure 7(a). It shows that when λ₂ increases, the growth rate is smaller, and the flow is more stable.

According to Table 3, η_c increases with increasing λ₂ and stays around 0.8. Thus, we conclude that η enhances the instability of the flow when η<0.8 and suppresses the instability of the flow when η>0.8.

The neutral stability curves for various parameters λ₁ when Pr_D = 50 are shown in Figure 8(a). When λ₁ is larger, the minimum value of Ra_Tc is smaller, showing that the flow is more stable. In Figure 8(b), for Pr_D =200, it is found that the minimum value of Ra_Tc increases for larger λ₁, indicating a more unstable flow. When Pr_D =600, λ₁ promotes the stability of the flow in Figure 8(c). In order to explore the effect of Pr_D on the role of λ₁, the neutral stability curve of (Pr_D, Ra_Tc) is plotted, i.e., Figure 8(d). As Pr_D increases, the value of Ra_Tc decreases, then increases and decreases continuously. This indicates that Pr_D has a dual effect on the stability of the flow. According to the images, we can find the critical values of PrD, PrDc1 and PrDc2. When PrD < PrDc1 or PrD > PrDc2, PrD has an inhibiting effect on the instability, and when PrDc1 < PrD < PrDc2, PrD has a facilitating effect on the instability. According to Figure 8(d), when λ1 = 0.65, the specific critical values PrDc1 is 50.2 and PrDc2 is 398.8. Moreover, the magnitude of PrD affects the stability of λ1. When PrD < 110.8 or PrD > PrDc2, the larger λ1 is, the smaller RaTc is, indicating that λ1 inhibits the stability. Interestingly, when 110.8 < PrD < PrDc2, λ1 suppresses the flow instability. This suggests that λ1 also has a dual effect on the flow stability and is influenced by the size of PrD.

6. Conclusions

The study examines the instability of the Soret Effect on the DDC of an Oldroyd-B fluid in a vertical porous layer. Based on the Darcy-Brinkman-Oldroyd model, an Orr-Sommerfeld eigenvalue problem is obtained using perturbation theory and the Oberbeck-Boussinesq approximation, which is numerically simulated employing the Chebyshev collocation method. Then, the neutral stability curves, as well as growth rates, are obtained. As a result, Pr_D has a dual effect on instability, and it has two critical values, Pr_Dc1 and Pr_Dc₂, which depend on the other parameters. When Pr_Dc₁ < Pr_D < Pr_Dc₂, Pr_D boosts flow stability; when Pr_D < Pr_Dc₁ or Pr_D > Pr_Dc₂, Pr_D enhances the instability. The impact of λ₁ on the instability depends on the value of Pr_D. When 110.8< Pr_D < 398.8, λ₁ suppresses the flow instability. However, when taking other values of Pr_D, λ₁ promotes flow instability. In addition, it is obtained that Le has a dual effect on stability, and a critical value exists for Le. Le enhances the flow instability when Le < 0.7 and inhibits the flow instability when Le > 0.7. At the same time, S_r has a dual role in the stability of the flow. According to the positive and negative values of S_r, S_r has different effects on the instability of the flow. Positive S_r have stable effects and negative S_r parameters have unstable effects. The magnitude of Le influences the role of S_r. When Le < Le_c2, S_r boosts the instability, and when Le> Le_c2, S_r plays an inhibiting role. Furthermore, there is a critical value for η. When η < 0.8, η enhances the instability; when η >0.8, it makes the flow more stable. Finally, the relaxation parameter λ₂ promotes flow stability. In conclusion, Pr_D, λ₁, Le, S_r, and η have a dual impact on the instability.

Author Contributions

Conceptualization, Y.R. and Y.J.; Methodology, Y.R. and Y.J.; Software, Y.R.; Validation, Y.R.; Formal Analysis, Y.R.; Investigation, Y.R.; Resources, Y.R.; Data Curation, Y.R.; Writing – Original Draft Preparation, Y.R.; Writing – Review & Editing, Y.R. and Y.J.; Visualization, Y.R. and Y.J.; Supervision, Y.J.; Project Administration, Y.J.; Funding Acquisition, Y.J. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge financial support provided by the National Natural Science Foundation of China (Grant No.12262026), the Natural Science Foundation of the Inner Mongolia Autonomous Region of China (Grant No. 2021MS01007), the Program for Innovative Research Team in Universities of Inner Mongolia Autonomous Region (Grant No. NMGIRT2323), and the Fundamental Research Funds for the Central Universities (Grant Nos. 2232022G-13, 2232023G-13, 2232024G-13).

Conflicts of Interest

The authors declare no conflicts of interest.

References

Ingham, D.B.; Pop, I. Transport phenomena in porous media; Elsevier: 1998.
Nield, D.A.; Bejan, A. Convection in porous media; Springer: 2006; Vol.3.
Vafai, K. Handbook of porous media; Crc Press: 2015.
Gill, A. A proof that convection in a porous vertical slab is stable. J. Fluid Mech. 1969, 35, 545–547. [Google Scholar] [CrossRef]
Rees, D.A.S. The stability of Prandtl-Darcy convection in a vertical porous layer. Int. J. Heat Mass Transfer 1998, 31, 1529–1534. [Google Scholar] [CrossRef]
Lundgren, T.S. Slow flow through stationary random beds and suspensions of spheres. J. Fluid Mech. 1972, 51, 273–299. [Google Scholar] [CrossRef]
Shankar, B.; Kumar, J.; Shivakumara, I. Stability of natural convection in a vertical layer of Brinkman porous medium. Acta Mech. 2017, 228, 1–19. [Google Scholar] [CrossRef]
Gözüm, D.; Arpaci, V. Natural convection of viscoelastic fluids in a vertical slot. J. Fluid Mech. 1974, 64, 439–448. [Google Scholar] [CrossRef]
Takashima, M. The stability of natural convection in a vertical layer of viscoelastic liquid. Fluid Dyn. Res. 1993, 11, 139. [Google Scholar] [CrossRef]
Khuzhayorov, B.; Auriault, J.L.; Royer, P. Derivation of macroscopic filtration law for transient linear viscoelastic fluid flow in porous media. Int. J. Eng. Sci. 2000, 38, 487–504. [Google Scholar] [CrossRef]
Kim, M.C.; Lee, S.B.; Kim, S.; Chung, B.J. Thermal instability of viscoelastic fluids in porous media. Int. J. Heat Mass Transfer. 2003, 46, 5065–5072. [Google Scholar] [CrossRef]
Zhang, Z.; Fu, C.; Tan, W. Linear and nonlinear stability analyses of thermal convection for Oldroyd-B fluids in porous media heated from below. Phys. Fluids. 2008, 20. [Google Scholar] [CrossRef]
Sun, Q.; Wang, S.; Zhao, M.; Yin, C.; Zhang, Q. Weak nonlinear analysis of Darcy-Brinkman convection in Oldroyd-B fluid saturated porous media under temperature modulation. Int. J. Heat Mass Transfer. 2019, 138, 244–256. [Google Scholar] [CrossRef]
Barletta, A.; Alves, L.B. On Gill’s stability problem for non-Newtonian Darcy’s flow. Int. J. Heat Mass Transfer. 2014, 79, 759–768. [Google Scholar] [CrossRef]
Shankar, B.; Shivakumara, I. On the stability of natural convection in a porous vertical slab saturated with an Oldroyd-B fluid. Theor. Comput. Fluid Dyn. 2017, 31, 221–231. [Google Scholar] [CrossRef]
Shankar, B.; Shivakumara, I. Effect of local thermal nonequilibrium on the stability of natural convection in an Oldroyd-B fluid saturated vertical porous layer. J. Heat Transfer. 2017, 139, 044503. [Google Scholar] [CrossRef]
Shankar, B.; Shivakumara, I. Stability of penetrative natural convection in a non-Newtonian fluid-saturated vertical porous layer. Transp. Porous Med. 2018, 124, 395–411. [Google Scholar] [CrossRef]
Wang, S.; Tan, W. Stability analysis of double-diffusive convection of Maxwell fluid in a porous medium heated from below. Phys. Lett. 2008, 372, 3046–3050. [Google Scholar] [CrossRef]
Malashetty, M.; Biradar, B.S. The onset of double diffusive convection in a binary Maxwell fluid saturated porous layer with cross-diffusion effects. Phys. Fluids. 2011, 23. [Google Scholar] [CrossRef]
Malashetty, M.; Swamy, M.; Heera, R. The onset of convection in a binary viscoelastic fluid saturated porous layer. Z. Angew. Math. Mech. 2009, 89, 356–369. [Google Scholar] [CrossRef]
Malashetty, M.; Tan, W.; Swamy, M. The onset of double diffusive convection in a binary viscoelastic fluid saturated anisotropic porous layer. Phys. Fluids. 2009, 21. [Google Scholar] [CrossRef]
Kumar, A.; Bhadauria, B. Double diffusive convection in a porous layer saturated with viscoelastic fluid using a thermal non-equilibrium model. Phys. Fluids. 2011, 23. [Google Scholar] [CrossRef]
Malashetty, M.; Swamy, M.; Sidram, W. Double diffusive convection in a rotating anisotropic porous layer saturated with viscoelastic fluid. Int. J. Therm Sci. 2011, 50, 1757–1769. [Google Scholar] [CrossRef]
Swamy, M.S.; Naduvinamani, N.; Sidram, W. Onset of Darcy–Brinkman convection in a binary viscoelastic fluid saturated porous layer. Transp. Porous Med. 2012, 94, 339–357. [Google Scholar] [CrossRef]
Straughan, B.; Hutter, K. A priori bounds and structural stability for double-diffusive convection incorporating the Soret effect. Proc. Roy. Soc. A. Phy. 1999, 455, 767–777. [Google Scholar] [CrossRef]
Bahloul, A.; Boutana, N.; Vasseur, P. Double-diffusive and Soret-induced convection in a shallow horizontal porous layer. J. Fluid Mech. 2003, 491, 325–352. [Google Scholar] [CrossRef]
Gaikwad, S.; Malashetty, M.; Prasad, K.R. An analytical study of linear and nonlinear double diffusive convection in a fluid saturated anisotropic porous layer with Soret effect. Appl. Math. Model 2009, 33, 3617–3635. [Google Scholar] [CrossRef]
Gaikwad, S.; Dhanraj, M. Soret effect on Darcy–Brinkman convection in a binary viscoelastic fluid-saturated porous layer. Heat Transf Res. 2014, 43, 297–320. [Google Scholar] [CrossRef]
Bouachir, A.; Mamou, M.; Rebhi, R.; Benissaad, S. Linear and nonlinear stability analyses of double-diffusive convection in a vertical brinkman porous enclosure under soret and dufour effects. Fluids 2021, 6, 292. [Google Scholar] [CrossRef]
Drazin, P.G.; Reid, W.H. Hydrodynamic stability. Cambridge university press: 2004.
Squire, H.B. On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. Roy. Soc. Land. A. 1933, 142, 621–628. [Google Scholar]
Bird, R.B. Transport phenomena. Appl. Mech. Rev. 2002, 55, R1–R4. [Google Scholar] [CrossRef]
Hirata, S.C.; Alves, L.B.; Delenda, N.; Ouarzazi, M. Convective and absolute instabilities in Rayleigh–Bénard–Poiseuille mixed convection for viscoelastic fluids. J. Fluid Mech. 2015, 765, 167–210. [Google Scholar] [CrossRef]

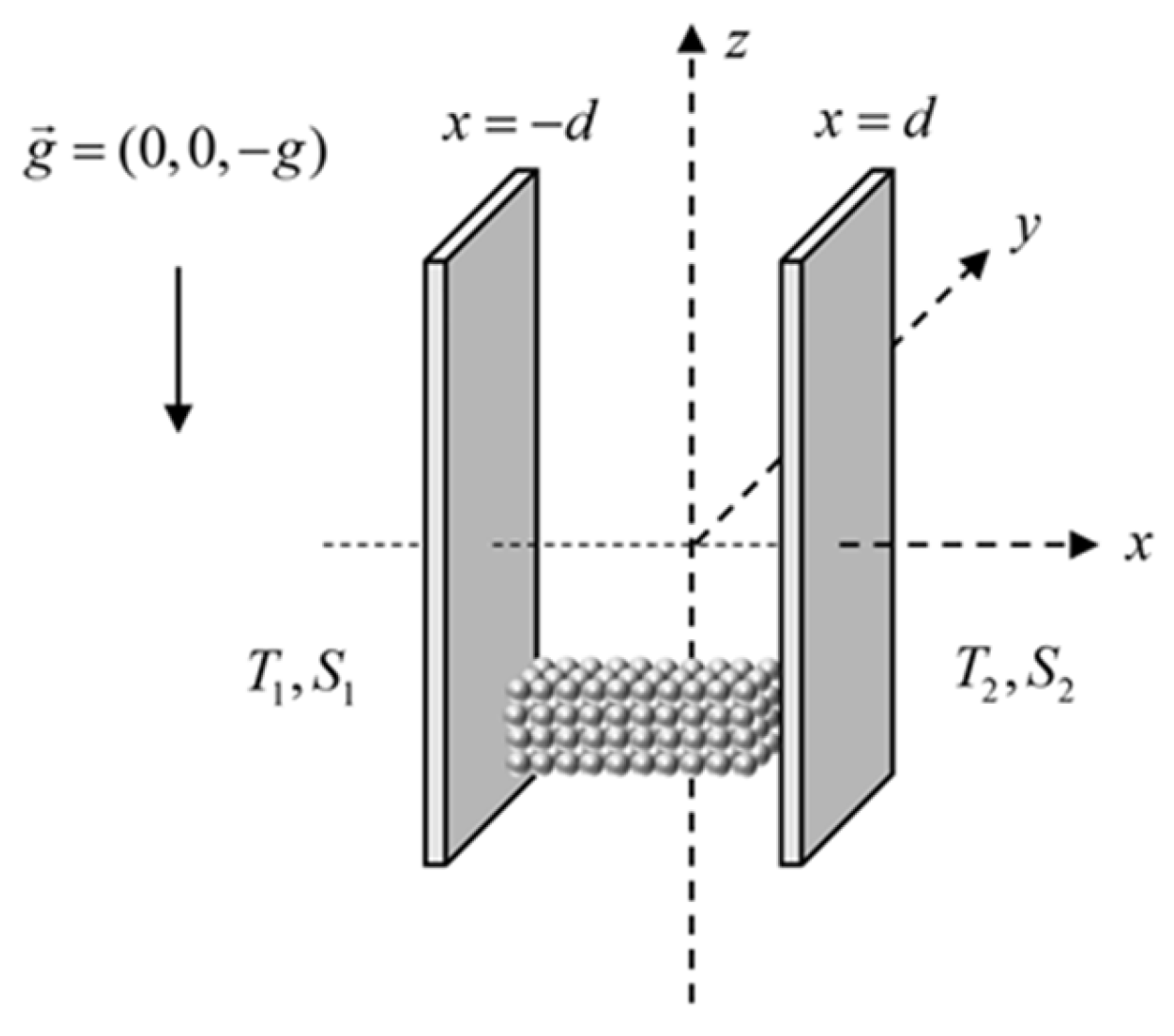
Figure 1. Graphic of the Physical Issue.

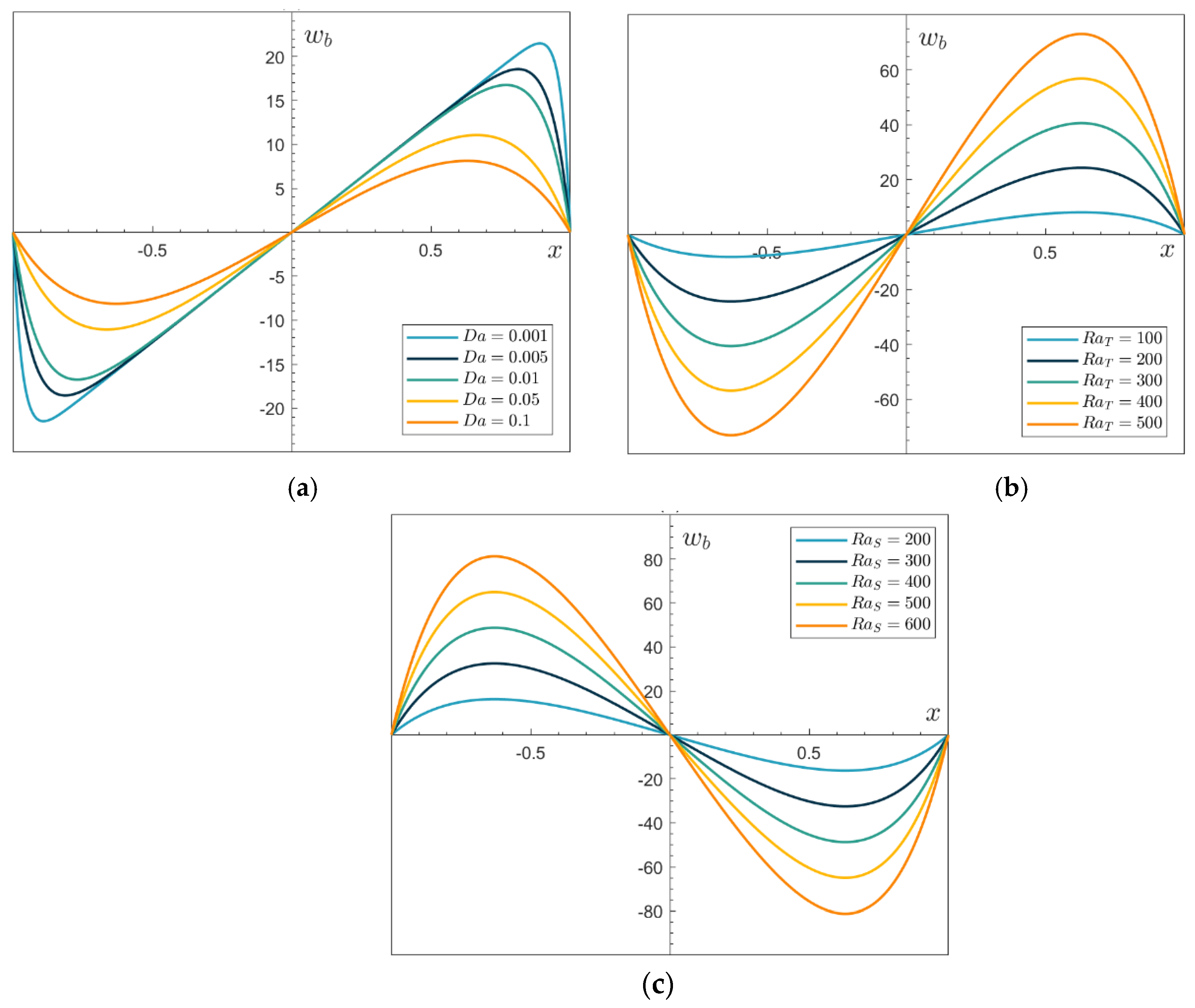
Figure 2. Basic velocity profiles for different values of (a)Ra_T=100, Ra_S=50, (b)Da=0.1, Ra_S=50, (c) Da=0.1.

Figure 3. Plots of the neutral stability curves and the growth rate for various values of (a)Le=1, (b)Le=1, Ra_T=1750, (c)Le=2, (d)Le=2, Ra_T =1750, when Da=0.1, Pr_D=50, λ₁=0.4, λ₂=0.2, Le=2, Ra_S=50, η=0.5.

Figure 4. Plots of the neutral stability curves and the growth rate when Da=0.1, Pr_D=50, λ₁=0.4, λ₂=0.2, Sr=-0.5, Ra_S=50, Ra_T=1750, η=0.5.

Figure 5. Plots of the neutral stability curves when Da=0.1, Pr_D=50, λ₁=0.4, λ₂=0.2, Ra_S=50, η=0.5, a=0.5.

Figure 6. Plots of the neutral stability curves and the growth rate when Da=0.1, Pr_D=100, λ₁=0.4, λ₂=0.2, Ra_S=50, η=0.5, Le=2, (b) Ra_T=1130, (d) Ra_T=1030.

Figure 7. Plots of the neutral stability curves and the growth rate. (a) Da=0.1, Pr_D=100, λ₁=0.4, λ₂=0.2, Ra_S=50, Le=2, Sr=0.5, a=π/4, (b) Da=0.1, Pr_D=100, λ₁=0.4, λ₂=0.2, Ra_S=50, Le=2, Sr=0.5, a=π/4, Ra_T=1400.

Figure 8. Plots of the neutral stability curves and the growth rate for different values of (a) Pr_D=50, (b) Pr_D=200, (c) Pr_D=600, (d)a=π/10, when Da=0.1, Le=2, λ₂=0.2, Ra_S=50, η=0.5, Sr=0.5.

Table 1. The Chebyshev collocation method's convergence process when Da=0.1, λ₁=0.4 λ₂=0.2, Le=2, Pr_D=100, Ra_T=1800, Ra_S=50, η=0.5, S_r=0.5.

	The growth rateac_i
N	a=0.5	a=1	a=1.5
30	1.371890	2.653114	-3.712508
35	1.371895	2.653438	-3.712476
40	1.371895	2.653448	-3.712474
45	1.371895	2.653448	-3.712474

Table 2. Critical values of Lewis number Le_c when Da=0.1, Pr_D=50, λ₁=0.4, λ₂=0.2, Ra_S=50, Ra_T=1750, η=0.5.

S_r	Critical values of Lewis number Le_c₁
S_r	a=0.4	a=0.5
-0.5	0.7578	0.7147
-0.2	0.7525	0.7106
0	0.7485	0.7066
0.2	0.7431	0.7025
0.5	0.7357	0.6944

Table 3. Critical values of normalized porosity η_c when Da=0.1, Pr_D=100, λ₁=0.4, λ₂=0.2, Ra_S=50, η=0.5, Le=2, Sr=0.5.

	Critical values of normalized porosity η_c
λ₂	a=π/6	a=π/5	a=π/4
0.2	0.7895	0.7908	0.7966
0.22	0.7969	0.7990	0.8057
0.24	0.8051	0.8071	0.8118
0.26	0.8112	0.8153	0.8209
0.28	0.8194	0.8215	0.8270

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Soret Effect on the Instability of Double-Diffusive Convection in a Saturated Vertical Brinkman Porous Layer of Oldroyd-B Fluid

Abstract

1. Introduction

2. Mathematical Model

2.1. Mathematical Description of the Model

2.2. Basic Flow

3. Linear Stability Analysis

4. Numerical Procedure

5. Results and Discussion

6. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe