Prerpints.org logo
Preprint
Review

Numerical Simulation of Earthquake Impacts on Marine Structures: A Comprehensive Review

Altmetrics

Downloads

67

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 October 2024

Posted:

31 October 2024

You are already at the latest version

Alerts
Abstract
Earthquakes present a significant risk to marine and underwater structures such as seawalls, piers, dolphins, breakwaters, buried pipelines, and sheet-piled constructions. These structures are particularly susceptible to the destabilizing effects of seismic events, which can result in severe damage. Furthermore, earthquakes can indirectly threaten these installations by destabilizing the underlying soil. Soil liquefaction, induced by seismic shaking, can undermine the stability and integrity of structures. This review discusses advanced simulation programs that have been systematically developed and validated using comparisons with commercial software and existing research . It extensively examines various factors that influence earthquake-induced dynamics in marine environments, including soil conditions, quality of structural components, tunnel length, mooring intervals, seismic wave propagation, and seaquake impacts . Over the past four decades, significant insights have been gained into the seismic design of marine structures, leading to the development of comprehensive guidelines. Recently, the simulation of marine infrastructure—such as breakwaters, platform jackets, and tunnels—has progressed considerably, driven by rapid economic growth and technological advancements in engineering. This review aims to evaluate and categorize recent studies on the numerical simulation of marine structures under seismic forces, with a focus on mitigating earthquake-related damage.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Marine structures are subjected to a variety of dynamic excitations, such as earthquakes, wind forces, traffic loads on bridges, and tsunamis, among others [1]. Over the past decade, several numerical simulations designed specifically for marine structures have emerged, utilizing ocean models of varying complexity. These models often consider the effects of currents, waves, and wind, as well as processes that influence particle interactions during earthquakes, including fragmentation and degradation [2].
Renewable energy, noted for its abundant resources, sustainability, and environmental benefits, has attracted global attention. Earthquakes considerably affect the infrastructure supporting various renewable energy sources in maritime settings. For instance, the seabed composition in Northern Europe is predominantly sandy, while the offshore areas of China feature a mix of sand, silt, and clay—all susceptible to liquefaction. In these regions, earthquakes and liquefaction are crucial factors in ensuring the safety and stability of support structures for offshore wind turbines [3].
The 2011 Tohoku Earthquake revealed the vulnerability of these structures when a wind turbine, mounted on a monopile foundation, tilted because of seabed liquefaction. Earthquake accelerations can have enduring adverse effects on the operational integrity of marine structures, occasionally leading to failures of wind turbines under extreme conditions. With increasing construction in seismically active zones, a comprehensive evaluation of these risks is imperative. Accurate estimation of earthquake-induced hydrodynamic loads, commonly known as seaquakes, is essential. These loads, resulting from the vertical propagation of seismic waves through compressible water, can considerably increase vibrations [4].
In the past two decades, considerable research has been conducted on the dynamic responses of quay walls. For instance, Sumer et al. [5] investigated the displacements of the breakwater at Eregli Fishery port caused by seismic waves during the 1999 Kocaeli earthquake in Turkey, using field-collected data.
Numerical methods based on finite-element analysis have been developed to evaluate the seismic performance of composite breakwaters and their porous seabed foundations under substantial seismic loads [6]. Furthermore, various studies have broadened the scope beyond earthquake loading to include tunnel behavior under various hydrodynamic pressures, such as blast loading and tunnel excavation. These investigations utilized a spring– mass analogy for analyzing tunnels, incorporating insights from the Tokyo Bay tunnel study, and assessed the dynamic response of the Huangpu River crossing tunnel. Sharma et al. developed a coupled model to investigate wave interactions with a submerged floating sea tunnel and a bottom-mounted submerged porous breakwater, aiming to understand the influence of incident waves on the tunnel’s structure [7].
In scientific programming, priorities often extend beyond efficiency to consider critical aspects such as correctness, numerical stability, accurate discretization, and flexibility. However, efficiency remains a crucial constraint for current numerical methods and a primary consideration when developing advanced methods. The governing equations of the marine environment and their interactions with relevant structures are highly complex, necessitating approximations for accurate solutions. Although considerations of computational speed cannot override the meticulous design of optimized algorithms , there are inherent limitations to what can be achieved with sophisticated algorithmic strategies, both in terms of maximum speed and the complexity involved in implementing these algorithms. Enhanced computational speed enables more realistic simulations and analyses, offering the opportunity to investigate more intricate phenomena. In marine engineering, several applications continue to be constrained by numerical efficiency [8].
Structural motions are deduced by numerically integrating a simulation model. For bottom-fixed structures, this typically involves using a finite-element model to capture elastic deformations [9]. In contrast, floating structures are often modeled using a rigid multibody approach to efficiently compute global motions. In preliminary analyses, this may be simplified to a single rigid-body model. However, for an accurate assessment of dynamic loads, a more spatially extended model is essential.
This review paper aims to provide insights into the most suitable methods for simulating marine structures in response to seismic activities. We recommend using numerical models based on the boundary-element method (BEM) for analyzing seismic responses. The paper is structured as follows: Section 2 outlines the theoretical background and models under review, besides it explores the mechanisms of various simulation methods (finite-element method (FEM), computational fluid dynamics (CFD), discrete-element method (DEM), BEM, finite-volume method (FVM), direct numerical simulation (DNS), smoothed-particle hydrodynamics (SPH), lattice Boltzmann method (LBM) ) as applied to recent research on marine structures. Then, Section 3 presents the discussion. Finally, Section 4 concludes with the main findings from this review.

2. Numerical Simulation Methods for Marine Structures

The FEM–SPH adaptive method combines the strengths of both FEM and SPH to efficiently perform impact dynamics calculations. Johnson et al. [10] developed and refined this algorithm, presenting a simplified version of the SPH method integrated into a standard Lagrangian code such as EPIC. Building on these insights, they developed an explicit two-dimensional (2D) Lagrangian algorithm that automatically transforms distorted elements into meshless particles during dynamic deformation. This approach proved effective in various scenarios and was later extended to three-dimensional (3D) contexts, resulting in a 3D explicit Lagrangian algorithm capable of converting distorted tetrahedral elements into meshless particles.
Despite their advantages, both FEM and SPH methods face significant challenges [11]. FEM is recognized for its high efficiency and accuracy but struggles with substantial mesh deformation during simulations, potentially leading to significant errors. Meanwhile, SPH handles large mesh deformations adaptively but suffers from tensile instability, complications in applying boundary conditions, and reduced computational efficiency.
The finite-difference method (FDM) solves governing equations by differentiating directly along each coordinate axis, facilitating rapid execution. In contrast, FEM discretizes the domain into elements of a chosen shape and combines them to form the complete system, typically resulting in slower performance compared to FDM. FDM is predominantly used in fluid mechanics and heat transfer, particularly for problems with fixed boundaries, but is less suitable for scenarios involving significant strain or deformation [12].
FEM excels in addressing large- deformation problems and is versatile enough to handle a wide array of engineering challenges, effectively managing complex geometries and diverse material combinations. CFD has emerged as an essential tool for design and analysis in various industries, including marine structures. The challenges of CFD modeling for naval hydrodynamics include the following [13]:
  • Evaluating forces and addressing hydro-mechanical coupling issues.
  • Generating and propagating surface waves with varying characteristics, such as deterministic single- and multi-frequency wave trains, wave focusing, and statistical modeling of realistic irregular sea states.
  • Modeling both rigid and flexible floating structures.
  • Simulating extreme wave events, such as freak wave impacts .
For analyzing seismic responses, a numerical model utilizing BEM is recommended. This method’s primary advantage is its elimination of the need for artificial domain truncation when modeling an infinite medium. In dynamic scenarios, such truncation can cause artificial wave reflections that lead to numerical inaccuracies. While certain finite-element formulations, such as non-reflecting boundaries and infinite elements, can mitigate these issues, FEM and FDM may introduce other challenges, such as numerical wave dispersion, which require careful management. BEM comprises two main stages [14]:
  • Solving the boundary integral equation to determine displacements and stresses along the domain’s boundary.
  • Conducting further computations for all points within the domain using an integral representation formula .

2.1. FEM Applications in Marine Earthquake Engineering

The finite-element meshing process for a structure involves selecting nodal points where the final solution is required and assigning finite elements to these points. This task demands both expertise and an in-depth understanding of how structures with specific geometries respond to various external actions, including forces, imposed displacements, and temperature changes. The mesh design must consider factors such as geometry, loading methods, constraints, symmetry, proximity to infinite media, and stress concentrations. Depending on the structure’s geometry, elements may be one-dimensional, 2D, or 3D. Given the limited modeling capabilities of most finite-element analysis software, it is advisable to use specialized computer-aided design (CAD) programs for creating geometry. Meshing replaces the infinite degrees of freedom represented by the geometry with a finite network of elements to simulate the shape accurately. The type and application of loading influence the structure’s specific behavior, necessitating a customized meshing approach. Nodes should be placed at locations where external forces are applied, constraints are present, movements are required, and where there are changes in stiffness, characteristics, or material properties.
The density of the nodal network determines the size of the finite elements. Reducing element size and increasing node count generally improve calculation accuracy. However, when establishing the nodal network, it is crucial to consider an optimal balance between desired accuracy, computational efficiency, and analysis costs. Excessively increasing the number of nodes may not be beneficial, as studies suggest that there is a threshold beyond which additional elements do not enhance the solution and may even degrade it [15].
ANSYS software is widely used across various engineering disciplines, including structural, mechanical, electrical, electromagnetic, electronic, thermal, fluid, and biomedical engineering. An analysis with ANSYS typically involves creating a finite-element model, applying geometric and mechanical boundary conditions (loads), obtaining the solution, and interpreting the results. The most time-consuming aspect of this process is developing the finite-element model. The chosen element type influences the degrees of freedom, element shape, and overall analysis scale. Finite-element models can be developed using two approaches : modeling and direct generation. Modeling involves creating a geometry that the software automatically meshes using nodes and elements, allowing users to control the size and shape of the elements. In contrast, direct generation requires users to manually create each node and then define elements based on those nodes. The type of analysis conducted depends on the load conditions and the structure’s response. Once the results are obtained, they can be visualized using a post-processor. In summary, FEM comprises several key steps: meshing the structure into finite elements, selecting shape functions, formulating finite-element equations and their specific matrices, assembling the finite elements while applying boundary conditions, solving the system of equations, and determining the stress and strain states within each finite element [16].
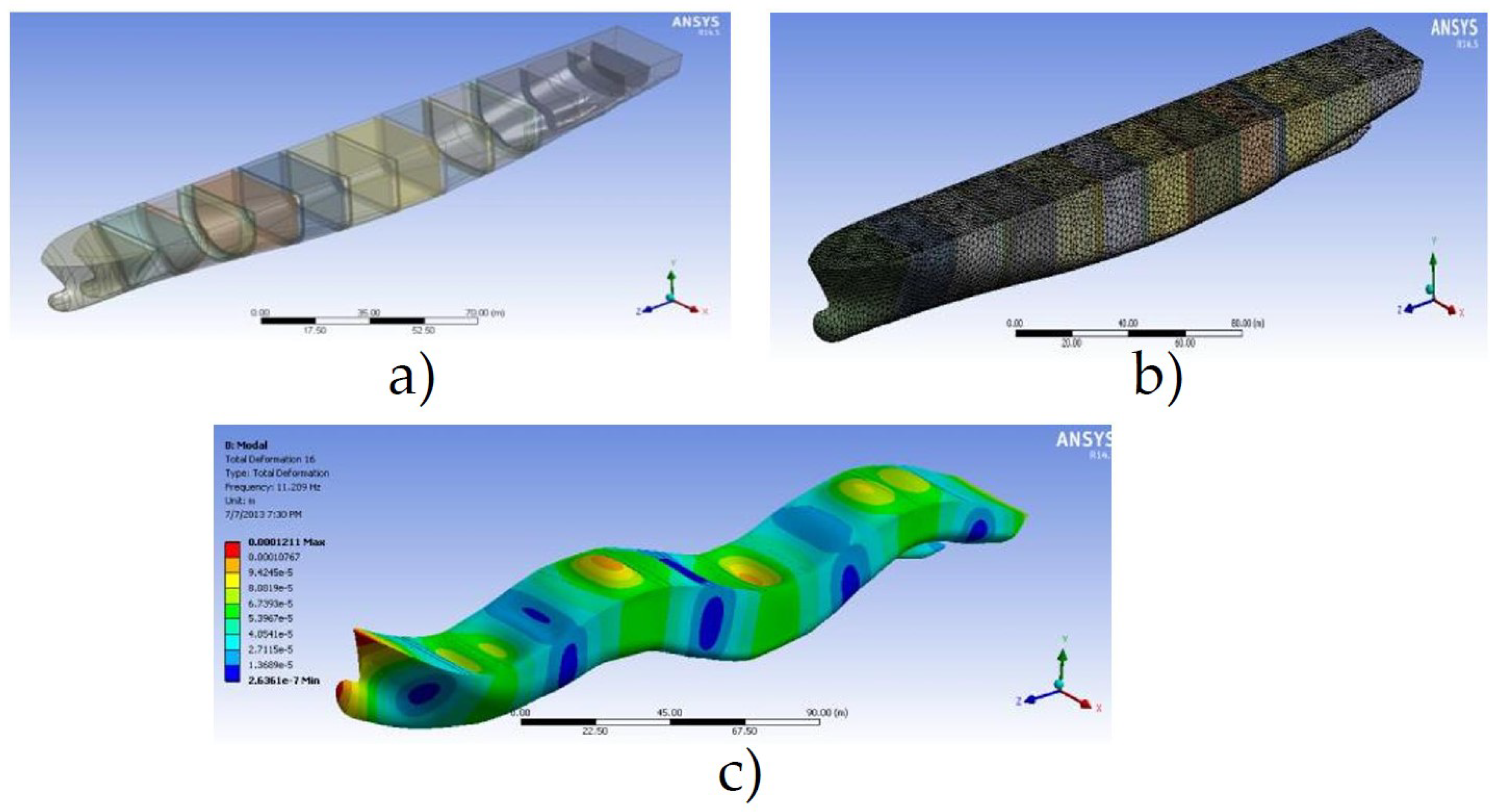
The work of Ion and Ticu [17] shows a modal analysis of a ship’s hull, using a finite-element model based on the study parameters. As the vessel is situated in a continuous medium, no additional boundary conditions are required for this free–free type of modal analysis. Typically, the first six vibration modes represent rigid-body motions, identifiable by their very low frequencies. While the frequencies for rigid-body motions should theoretically be zero, inherent inaccuracies in the solver may result in frequency values, sometimes on the order of MHz. To evaluate the influence of various stiffeners on the frequencies and vibration modes, a previous study examined three variations of hull construction : without stiffeners, with transverse stiffeners, and with both transverse and longitudinal stiffeners. Frequencies and corresponding modes for each construction type were extracted. Although it is not critical to investigate modes with frequencies exceeding 5 Hz for wave action, sound engineering practice suggests extracting between 100 to 200 modes to accommodate the potential variety of excitation sources during a ship’s operation [18]. The Figure 1 shows the mesh preparation and the finite element model for the hull with transverse stiffeners, besides the result of the vibration mode of the hull transversely stiffened at frequency 11.209 Hz is detailed.
The data derived from these analyses are qualitative rather than strictly quantitative. Notably, the visual representations of modal shapes as displacements are conceptual and do not directly represent actual physical displacements. Instead, they depict distinct modes of structural deformation at specific resonance frequencies. A central challenge in this research is accurately estimating the external forces generated by ocean waves and the resultant structural stresses on maritime vessels. Addressing this challenge necessitates a multidisciplinary approach, incorporating expertise from fields such as probability theory, random processes, statistical analysis of extreme values, empirical data analysis, naval hydrodynamics, and numerical modeling. Estimating wave characteristics extends beyond simple metrics such as wave height and frequency. This involves deriving spectral density functions from empirical data, providing a comprehensive depiction of the sea surface. This depiction is crucial for analyzing a vessel’s behavior in real sea conditions and highlights the importance of understanding wave spectra across various scenarios and geographical areas for structural analysis and predicting critical extreme values.
A prior study conducted static analyses on three different structural models of a container port hull: one without stiffeners, one with transverse stiffeners, and one with both transverse and longitudinal stiffeners. These analyses, conducted under various loads resulting from pressure distributions in calm water, aimed to evaluate the effects of stiffeners and loading methods on the hull’s stress state. The implementation of FEM has introduced innovative strategies for addressing complex structural analysis challenges. By utilizing this method, more accurate resistance calculations can be achieved, and criteria for structural failure can assessed precisely. FEM also facilitates the iterative optimization of structural dimensions to ensure compliance with all necessary requirements [19].

2.2. CFD-DEM Simulation of Submarine Landslide

A study simulated a submarine landslide triggered by seismic activity in a region rich in methane hydrates using a coupled computational approach that integrates CFD with DEM [20]. To enhance the accuracy of the simulation for dynamic scenarios, the researchers incorporated dynamic features and considered the Magnus force. They subjected a steep underwater slope containing methane hydrate-bearing sediments, which formed robust inter-layers, to a sinusoidal seismic load. The simulation results indicated a flow-type landslide, leading to a gradual accumulation of debris on a gentler slope. Near the sliding mass, the fluid exhibited an eddy pattern. The findings revealed that the presence of methane hydrate increased sediment strength while reducing its damping properties. At lower methane hydrate saturations (25% and 30% ), the combined effects of seismic loading and particle–fluid interactions led to damage in the methane hydrate-rich layer, resulting in settling behind the slope’s crest and upheaval in front of its toe. However, at higher methane hydrate saturations (40% and 50% ), the sediment exhibited sufficient strength to resist seismic damage. Increased methane hydrate saturation resulted in reduced sediment damping, which facilitated increased energy transfer from the ground base to the potential sliding mass, initiating the sliding process earlier. The implications of these simulation results for assessing submarine hazards induced by earthquakes were discussed.
Zhang and Luan [21] utilized a continuum–discrete approach known as the CFD–DEM coupling scheme. This technique simulates fluid flow by solving the Navier-–Stokes equations within CFD, using coarse-grid local averaging. Concurrently, the motion of individual particles is modeled using Newton’s second law of motion in DEM. The interaction between CFD and DEM is facilitated through the exchange of forces during particle–fluid interactions. The study provided a detailed understanding of this computational scheme. To model submarine landslides triggered by seismic loading in this study, they implemented two significant enhancements to the coupling computation: they expanded the contact model in DEM to include dynamic characteristics and incorporated the Magnus force into fluid–particle interactions. These improvements were briefly outlined in their paper, with more detailed descriptions to be presented in a forthcoming publication. Notably, the DEM simulations followed a 2D approach using disk-shaped particles, while the CFD formulations were primarily 3D; however, the flow velocity in the out-of-plane direction was constrained to zero, effectively treating it as 2D flow. For the purposes of CFD–DEM coupling, the simulation treated these 2D disks as spheres with equivalent diameter and velocity.
Typically, a theoretical arrangement of 3D spheres is used to assess both porosity and particle volume, which are essential for calculating the interaction forces between particles and the surrounding fluid. These forces are then integrated into both the CFD and DEM models to directly influence the calculations of fluid and particle movement. This approach is necessary because the methane hydrate bond contact model is currently available only in a 2D format, while a 3D model remains under development. Although this method may not perfectly replicate physical reality, it effectively captures the general trends in fluid–particle interactions.
In a prior study, to simulate mass flow following slope failure, where finite-element simulations are inadequate, a combination of CFD and DEM (CFD–DEM) was utilized [22]. This integrated approach effectively simulated the initiation, mass transport, and deposition phases of submarine landslides resulting from solid–fluid interactions, as shown in Figure 2 and Figure 3. The study simulated submarine landslides triggered by methane hydrate dissociation, replicating four distinct types of slides—fall, flow, slump–flow, and slump—each varying by the location and extent of methane hydrate dissociation. Given the advantages of the CFD–DEM simulation method in accurately reproducing the entire sliding process, this coupling approach was employed to model seismic loading-induced submarine landslides in methane hydrate-rich regions [23].
The study developed by Jiang et al. [22] simulated a submarine landslide by integrating CFD with DEM. A dynamic contact model was implemented within the discrete-element framework to accurately capture the behavior of sediment containing methane hydrates. The simulations also considered minor fluid compressibility within the CFD component. Additionally, the Magnus force was included in the fluid–particle interactions. The study identified that this force considerably influenced particle trajectories within the typical velocity ranges observed during submarine landslides. Sinusoidal seismic loading was applied to trigger failure in the simulated submarine slope, accounting for varying methane hydrate saturations. The results indicated a flow-type sliding pattern, culminating in a gradual accumulation of debris on a gentler slope. Near the sliding mass, the fluid exhibited an eddy pattern: water flowed upward from the slope’s toe to its crest above the surface while moving in the opposite direction below it. The restoration of slope stability was marked by a circular fluid eddy, approximately the height of the slope, moving away from it [24].

2.3. Marine Turbine Hydrodynamics by a Boundary Element Method

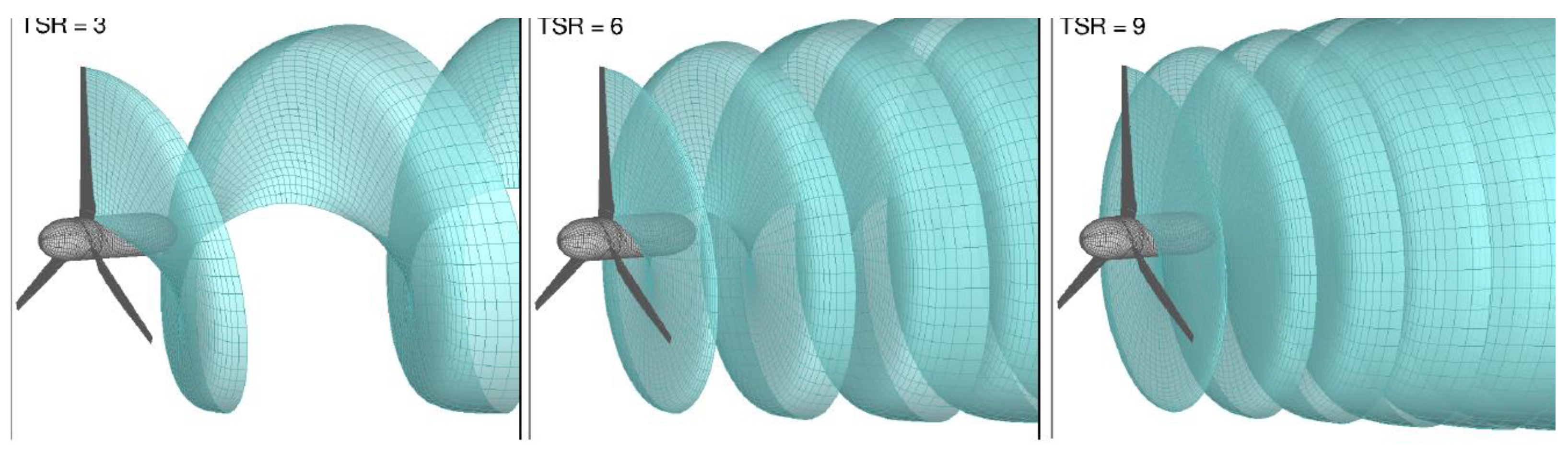
This section discusses a computational method for analyzing the hydrodynamics of horizontal-axis marine current turbines based on the boundary integral equation method (BIEM), originally developed for marine propellers. This method has been adapted to address the unique flow characteristics of hydrokinetic turbines and is enhanced by semi-analytical trailing wake models and corrections for viscous flow effects. Previous studies have validated this methodology by comparing hydrodynamic performance predictions with experimental test cases and results from other numerical models cited in the literature. The ability of this approach to accurately predict turbine thrust and power across a broad range of operating conditions has also been explored. The method accounts for viscous effects related to blade flow separation and stall, with the predicted thrust and power closely aligning with results from the widely used blade-element methods in marine current turbine design, as shown in Figure 3. However, the accuracy of numerical predictions may diminish when turbine blades operate under off-design conditions [25].
Marine or hydrokinetic turbines, used to capture renewable energy from tidal and ocean currents, represent a rapidly advancing technology. Large-scale installations typically consist of horizontal-axis turbines anchored to the seabed or mounted on floating platforms. The swift development of hydrokinetic turbine technology, relative to other ocean energy systems, owes partly to the transfer of knowledge and expertise from the wind energy sector. The design of marine turbine blades closely resembles that of wind rotor blades, albeit with a significantly lower aspect ratio to better withstand the hydrodynamic forces in water. Therefore, blade-element momentum methods, initially devised for wind turbines, are frequently used for the analysis and design of tidal and ocean current turbines [26].
When calibrated properly, the blade-element momentum method provides quick and reliable evaluations of turbine performance, although it requires addressing specific methodological limitations. It calculates blade loading based on defined lift and drag characteristics of 2D profiles. To account for factors such as blade tip interactions, blade/hub dynamics, and the number of blades, semi-empirical adjustments for 3D flow are necessary. In contrast, the hydrodynamic design of marine propellers typically utilizes boundary-element or panel methods. These methods assume inviscid flow and consistently represent 3D flow around rotors in both steady and unsteady states. To distinguish from blade-element (momentum) techniques, this approach is referred to as BIEM. However, the application of BIEMs in hydrokinetic turbine contexts is still limited, with only a few documented examples in the literature. These cases highlight the challenges blade-element momentum methods face in accurately modeling the hydrodynamic performance of turbines designed to capture energy from flowing water. A particular challenge arises when turbine blades operate at high angles of attack, leading to viscosity-induced separation and stall, which negatively impact thrust and power output. To mitigate this, Baltazar and Falcão de Campos proposed models that adjust the inviscid-flow predictions from a BIEM for 3D steady flows. Their approach modified the lift force for each blade section, as calculated by the BIEM, by comparing the lift coefficients of 2D profiles (representing the blade sections) under viscous and inviscid conditions. The drag for the blade sections was derived from 2D polar curves. This methodology utilized the Kutta–Joukowski law to determine the incoming velocity at the blade sections, while XFOIL, a viscous flow simulation tool, was used to generate polar curves. This approach also included an iterative wake alignment model to adjust wake pitch based on local flow conditions, although it did not account for radial expansion [27].
Preprints 138065 g003
Figure 3. Marine current turbine. Wake geometry of BIEM model at different operating conditions. From left to right, TSR = 3, 6, 9. [28].
Figure 3. Marine current turbine. Wake geometry of BIEM model at different operating conditions. From left to right, TSR = 3, 6, 9. [28].
Preprints 138065 g003
A computational approach for analyzing the hydrodynamics of horizontal- axis marine current turbines was introduced, and the findings from a validation study were discussed. This method was based on a BIEM designed for inviscid flows, enhanced by a trailing wake model specifically developed for hydrokinetic turbines. Additionally, a viscous-flow correction model (VFC) was incorporated to account for the effects of blade flow separation and stall on the projected hydrodynamic loads. The VFC used a semi-empirical technique, adjusting the inviscid-flow blade loads calculated through BIEM based on the lift and drag characteristics of 2D profiles that represent blade sections under equivalent 3D flow conditions. To validate the accuracy of numerical predictions obtained through the BIEM–VFC approach, comparisons were made with experimental data and numerical results from the existing literature.
The analysis highlights the effectiveness of the aforementioned methodology in accurately characterizing turbine performance across a diverse range of operational conditions. It provides reliable predictions for turbine thrust, torque, and power in scenarios involving medium to high tip-speed ratios, where blade flow remains largely attached. Additionally, it performs well in conditions involving lower tip-speed ratios, where phenomena such as blade flow separation and stall significantly influence thrust loss and drag. Specifically, this methodology delivers precise predictions for turbine performance when blade pitch settings closely align with design specifications. However, discrepancies arise in off-design conditions, particularly in the accuracy of thrust and torque (power) predictions. In a comparative evaluation with other computational models in the literature, a notable finding is that the accuracy of the proposed approach closely matches that of blade-element methods commonly used in the analysis and design of marine and wind turbines. This is significant because the proposed methodology based on BIEM provides a physically coherent representation of 3D flow around a turbine under varying onset flow conditions. In contrast, blade-element methods often necessitate adjustments for blade tip effects, blade/hub interactions, and the number of blades. Moreover, the well-known limitations of blade-element methods in analyzing nonuniform flow conditions and studying turbine cavitation are effectively addressed by the more comprehensive flow description offered by the BIEM approach.
Future work can focus on enhancing the current VFC scheme to achieve trailing vorticity distributions and induced velocity profiles that fully correspond with the viscosity corrections applied to blade loads. Additional validation studies can aim to assess the generalized BIEM–VFC model’s capability to predict turbine performance at low tip-speed ratios and under off-design operating conditions [29].

2.4. Using Two Different Numerical Models Based on Finite Difference and Finite Volume Methods

The nonlinear forces generated by breaking waves pose a significant challenge in the design of offshore structures. Given the complex nature of wave-breaking phenomena, comprehending their interactions with structures remains a difficult task. Numerical models serve as crucial tools for studying these interactions. There are numerous numerical models that use either FDM or FVM to solve the governing equations involved in wave-breaking research. Various studies have provided credible results using both methods, though comparative analysis of their respective advantages and disadvantages has been limited.
Numerical models that solve the Navier– Stokes equations are widely utilized to simulate breaking waves, employing two primary conventional methods: FDM and FVM. FDM uses Taylor series expansions to approximate the governing differential equations, utilizing a grid of intersecting lines for discretization [30]. In contrast, FVM uses the integral form of the differential equation, ensuring the conservation of the governing quantities within a finite volume.
Both FDM and FVM offer various options for discretizing the terms in the governing equations, impacting the accuracy of each method. The work of Jose et al. [31] presented a comparative analysis of these two approaches in the context of breaking-wave studies. It utilized two distinct 3D Navier–Stokes solvers—2PM3D (FDM) and OpenFOAM (FVM)—to simulate the forces exerted by breaking waves on a monopile structure. The analysis considered two scenarios—one with nonbreaking waves and another with breaking waves—and compared the results against theoretical predictions and existing experimental data. Both numerical models demonstrated strong alignment with experimental measurements in capturing the interactions between breaking waves and the monopile.
In real marine environments, offshore structures are subjected to nonlinear wave interactions, such as wave breaking and green water impacts, which can occasionally result in structural damage. Thus, a thorough understanding of these phenomena is essential for the design of robust offshore structures. The forces generated by breaking waves have long been a major concern for offshore structures in shallow waters and often play a significant role in their overall design [32].
Capturing the physical interactions between breaking waves and structures presents a significant challenge owing to the complex nature of wave-breaking phenomena and the constantly changing shapes of the waves. Conventionally, research on breaking waves has primarily relied on experimental measurements, which are often limited to simpler structures and specific testing conditions. To overcome these limitations, employing rigorously validated numerical models capable of simulating breaking waves offers a promising solution. Advances in computational power and the availability of sophisticated numerical codes have established numerical modeling as a reliable tool for predicting the forces generated by wave breaking on structures. These models evaluate wave forces through direct pressure integration over the structure, reducing reliance on empirical correlations. However, the accuracy and efficiency of such numerical models heavily depend on the choice of numerical methods used.
As mentioned previously, numerical models that solve the Navier– Stokes equations are widely utilized for simulating breaking waves, with two primary classical approaches: FDM and FVM. FDM approximates the governing differential equations using Taylor series expansion and utilizes a grid of intersecting lines for discretization. In contrast, FVM uses the integral form of the differential equations, ensuring the conservation of governing quantities within a finite volume. Both methods offer various options for discretizing the terms in the governing equations, which significantly influences their accuracy [33].
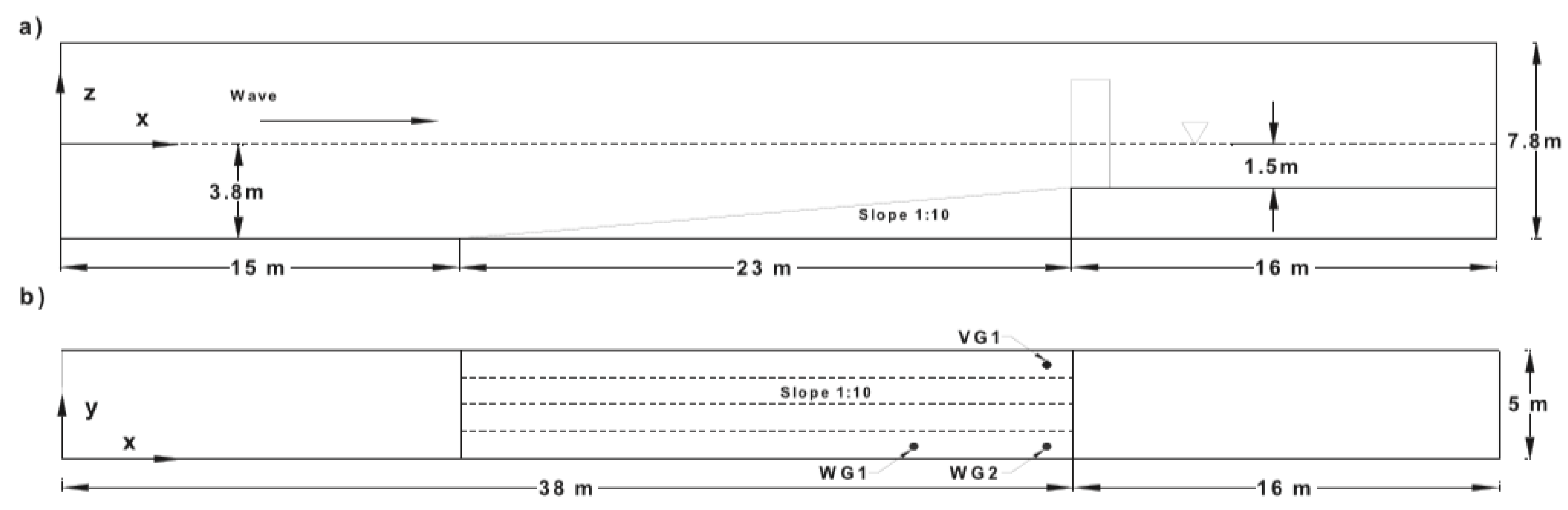
Previous research used experimental data from the study by Irschik et al. [34] to validate the results of the numerical simulations. The numerical models incorporated a numerical wave tank designed to replicate the experimental setup. Figure 4 shows the schematic layout of the numerical wave tank, with a total length of 54 m, not including the inlet and outlet relaxation zones.
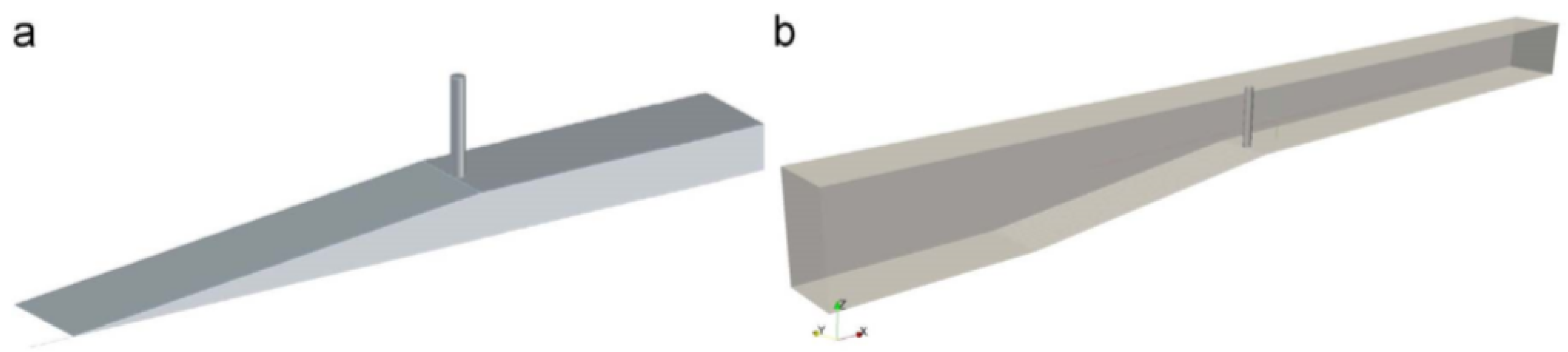
The modeling techniques differ in each numerical model. For instance, 2PM3D uses a separate application called Geometry 3D for pre-processing the geometry. This application computes the fractional volume and area available for fluid flow in the x, y, and z directions, along with the unit normal vectors for each cell within the computational domain. In Figure 5a, the vertical cylinder and the bottom geometry generated by Geometry 3D are shown. Figure 5b shows the intersection of the cell edge with the obstacle (the cylinder) and the point where this edge meets the cell face, with parameters derived for this specific cell also shown. In this case, to minimize wave reflections within the computational domain, numerical dissipation zones were implemented at both the inlet and outlet boundaries. These zones extend a distance of 2L, where L represents the wavelength. The inlet dissipation zone mitigates wave reflections near the boundary where waves are generated, while the outlet dissipation zone prevents reflections at the outlet boundary. An internal wave generator at the end of the inlet dissipation zone produced regular waves within the computational domain. OpenFOAM employs an unstructured mesh and utilizes FVM to solve the governing equations. Its modeling capabilities are highly flexible, allowing for direct import of models from compatible CAD software for simulations. In this case, stereolithography (STL) files for the cylinder and bottom slope were sourced from AutoCAD and integrated into the computational domain using the snappyHexMesh utility [35].
In the aforementioned study , two distinct computational models were utilized to simulate breaking waves within a numerical wave tank. The first model, 2PM3D, utilizes FDM and has undergone prior validation. The second model uses OpenFOAM coupled with the waves2Foam toolbox, based on FVM. Although both models address the same governing equations, their approaches to solving these equations and managing geometric complexities within the computational domain differ significantly. For this research, two numerical models—2PM3D (using FDM) and OpenFOAM with the waves2Foam toolbox (utilizing FVM)—were employed to study the effects of breaking waves on a monopile structure. Validation of both models involved simulating scenarios of nonbreaking and breaking waves and comparing the results with theoretical predictions and experimental data. The simulation results from both models demonstrated strong agreement with the experimental and theoretical findings. Importantly, both models effectively captured the nonlinear characteristics of the waves.
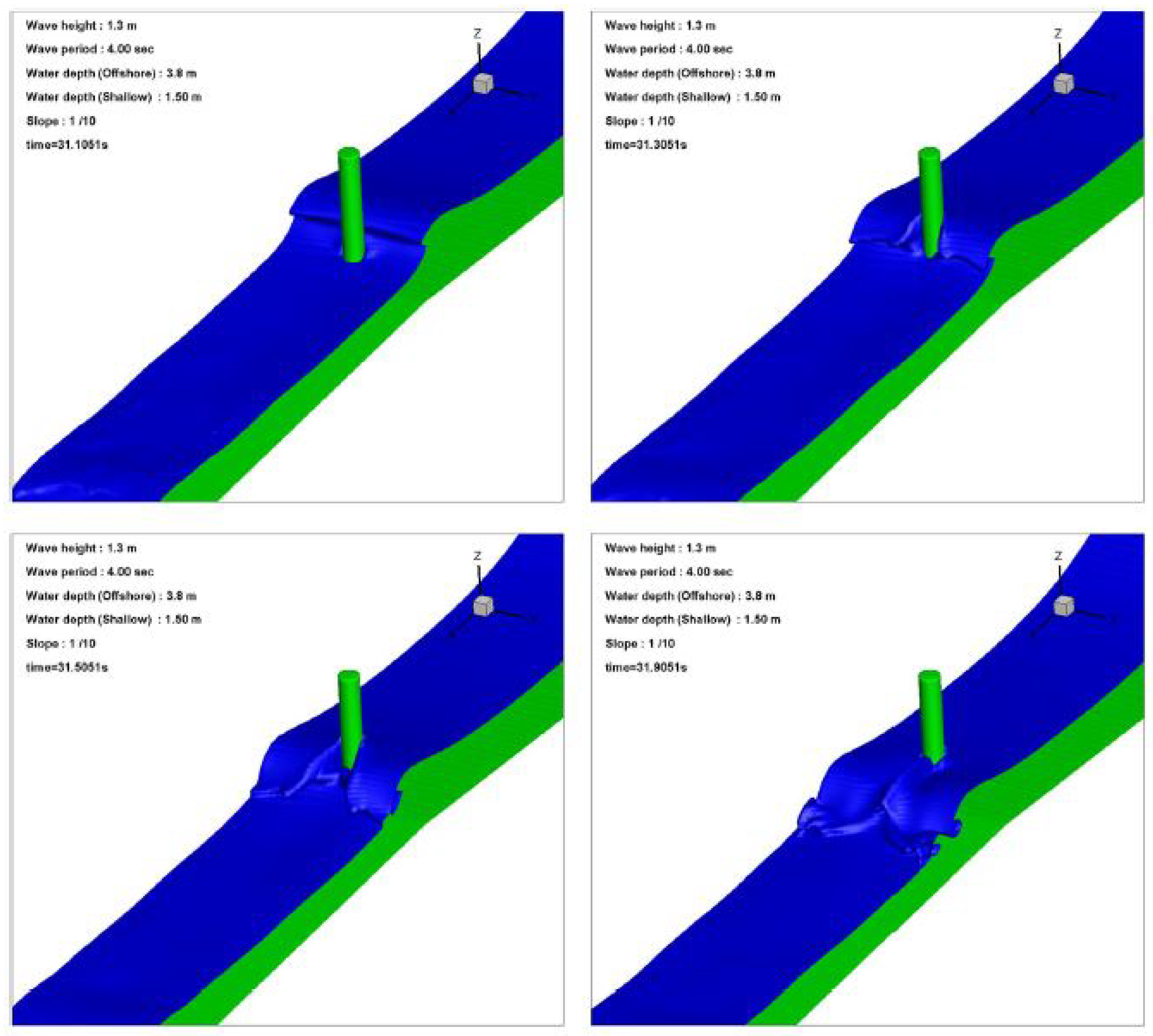
However, both models tended to overestimate the peak total breaking wave forces on the monopile, with an overestimation rate of approximately 7% compared to experimental data. This discrepancy may be attributed to the incompressible flow models used in the simulations, which did not account for the presence of air bubbles in the breaking waves. Additionally, it was observed that the finite-difference model required a greater number of computational cells than the finite-volume model counterpart. Both models successfully calculated the secondary load effects on the structure during wave breaking, though with a minor delay compared to experimental results. This delay can be linked to the incompressible flow model used, resulting in reduced energy dissipation after wave breaking, leading to variations in secondary loads. Further investigation is warranted to estimate cycles of secondary loads through numerical simulation more accurately. Results of waves2Foam simulations in four time steps are showed in Figure 6.
In conclusion, both numerical models effectively simulated wave– structure interactions, demonstrating their capability and reliability in such applications [36]. The comparative analysis confirms their suitability for studying breaking waves.

2.5. DNS of Wind Turbulence Over Breaking Waves

A previous investigation examined wind turbulence over breaking waves using DNS of two-fluid flows. In this DNS approach, air and water were treated as a single system, capturing the interface with a coupled level-set and volume-of-fluid method. Considering that wave breaking is a dynamic process, the study employed ensemble averaging across 100 simulations to establish turbulence statistics. The primary focus was on analyzing the turbulence statistics of airflow over breaking waves, particularly examining the effects of wave age and wave steepness. The findings indicate that turbulence statistics are primarily influenced by wave age prior to wave breaking. Specifically, the vertical gradient of mean streamwise velocity shows a positive trend at small and intermediate wave ages but shifts to negative values near the wave surface as wave age increases, transitioning from drag-dominated to thrust-dominated conditions owing to variations in pressure forces. Additionally, as wave age increases, wave-coherent motions become more significant contributors to momentum flux and kinetic energy flux (KE-F).
During the wave-breaking process, spilling breakers have a minimal impact on the wind field. In contrast, plunging breakers considerably alter the structure of wind turbulence near the wave surface. The DNS results demonstrate that during wave plunging, a high-pressure region forms ahead of the wavefront, further accelerating the wind downstream. Concurrently, a large spanwise vortex is generated, disrupting the surrounding airflow and leading to substantial magnitudes of Reynolds stress and turbulent kinetic energy (TKE) beneath the wave crest. Above the crest, the magnitude of KE-F increases during wave plunging at both small and large wave ages; however, at intermediate wave age, this transient enhancement of KE-F is absent. The impact of wave breaking on KE-F magnitude was also explored through an analysis of KE-F production. This analysis revealed that at small wave ages, the transient enhancement of KE-F results from a local maximum in the total momentum flux profile. Conversely, at large wave ages, it arises from a change in the sign of KE-F production, shifting from negative to positive owing to alterations in the wave-coherent momentum flux. At intermediate wave age, neither of these processes occurs, leading to an absence of transient KE-F growth [37].
The interaction between wind and ocean waves plays a critical role in shaping sea conditions, influencing the marine atmospheric boundary layer, and affecting upper-ocean dynamics. Intense wind forcing often causes wave breaking, which is integral in air–sea interactions [38]. Wave breaking not only restricts the height of surface waves but also generates ocean currents, vorticity, and turbulence, thus facilitating the transfer of mass, momentum, and energy between the ocean and atmosphere. A comprehensive understanding of wind behavior over breaking waves is crucial for enhancing models of ocean–atmosphere interactions. 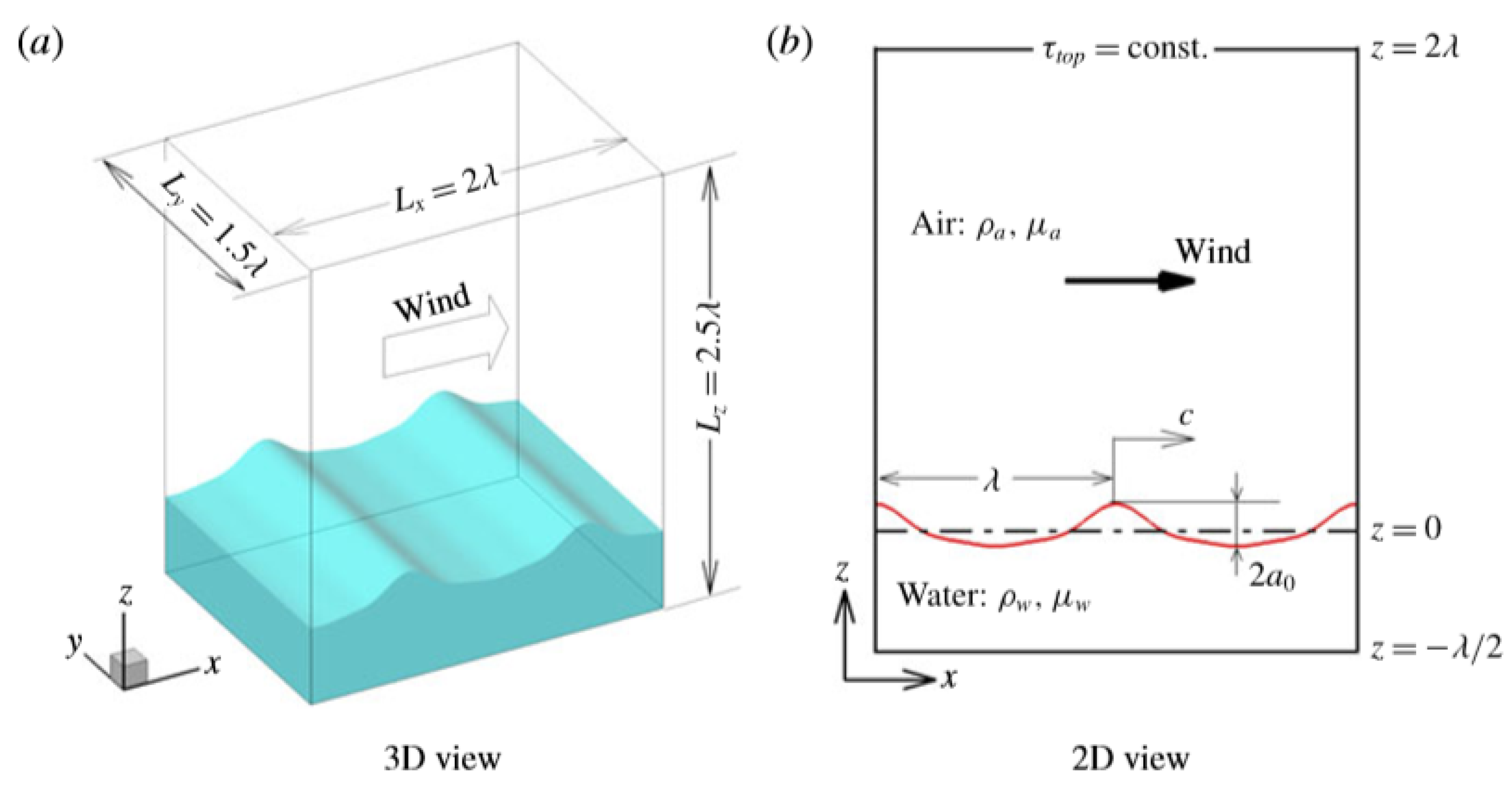Figure 7 shows an example of the computational domain and the coordinate system used in the simulations, where x, y, and z (or x 1 , x 2 , and x 3 ) correspond to the streamwise, spanwise, and vertical directions, respectively. The associated velocity components are denoted by u, v, and w (or u 1 , u 2 , and u 3 ).
In the aforementioned case, air and water were modeled as a coherent system, where density and viscosity vary according to the fluid phase. The behavior of these fluids is governed by continuity and momentum equations [38]:
∂ u ∂ x i = 0
ρ ( ϕ ) ( ∂ u i ∂ t + u j ∂ u i ∂ x j ) = − ∂ p ∂ x i + ∂ ( 2 μ ( ϕ ) S i j ) ∂ x j − ρ ( ϕ ) g δ i 3 + γ κ δ x ( ϕ ) n i
Here, t represents time; ρ and μ denote the fluid’s density and dynamic viscosity, respectively; ϕ is the level-set function defined as the signed distance from the air-–water interface, with positive values in water and negative in air; p represents pressure; g is gravitational acceleration; δ i j is the Kronecker delta; γ denotes the surface tension; κ = ∇ · ∇ ϕ | ∇ ϕ | at ϕ = 0 is the curvature of the air–-water interface; δ s ( ϕ ) is the Dirac delta function at the interface; n = ∇ ϕ | ∇ ϕ | at ϕ = 0 is the normal vector at the interface, pointing from water toward air. Periodic boundary conditions are applied in the x and y directions, and a no-slip boundary condition is imposed at the bottom of the water domain. At the top of the air domain, the wind is driven by a constant shear stress τ top in the streamwise direction.
This DNS study investigated three distinct wave ages and two initial wave steepness values, performing 100 simulations for each scenario to enable robust ensemble averaging. The simulations consistently maintained the initial wind profile and wave configuration, varying only the turbulent fluctuations. The findings indicate that at earlier wave ages, the impact of wave-induced motion on total momentum flux and kinetic energy is minimal, suggesting that wind turbulence predominantly governs airflow dynamics. However, as wave age increases, the influence of wave-induced effects grows more pronounced. While wave spilling has a limited impact on wind turbulence, wave plunging significantly alters turbulence statistics and flow structures near the wave surface [38].
During wave plunging, the dynamic interaction between the overturning jet and the air accelerates the airflow in the streamwise direction. This process is marked by a significant increase in pressure near the jet, leading to a transfer of momentum from water to air—a sharp contrast to the drag conditions dominant before the wave breaks when confronted with steep waves. Consequently, wind speed near the wave surface is significantly enhanced by the breaking process. Concurrently, a counterclockwise rotating spanwise vortex is generated, and its scale expands with the progression of wave age. This large vortex causes considerable disturbances in the surrounding airflow, substantially amplifying both Reynolds shear stress and TKE nearby.
At earlier wave ages, turbulence above the wave crest experiences a transient enhancement during the initial plunging phase, characterized by a temporary increase in KE-F. Detailed analysis indicates that this enhancement originates from a peak in the total momentum flux profile, induced by the disturbances from the plunging wave. As the wave ages further, KE-F above the wave crest continues to rise during plunging phases, owing to a shift from negative to positive in KE-F production. This shift reflects changes in the wave-coherent momentum flux, indicating how different mechanisms influence transient increases in KE-F at varying wave ages. Notably, at intermediate wave ages, these dynamic processes do not occur, resulting in no observed transient growth in KE-F.
In conclusion, the insights obtained from DNSs are useful for delving into the intricate physical processes associated with wind interaction over breaking waves. As computational capabilities advance, there is potential for more detailed, high-resolution simulations of increasingly complex scenarios. For instance, employing the wave-focusing method could simulate breaking waves influenced by wind, capturing the historical effects of wind on wave geometry. Such an approach would necessitate considerably larger computational domains in the streamwise direction. Furthermore, the integration of laboratory and field measurement data into these simulations would significantly enhance their realism [39].

2.6. SPH Simulations of Real Sea Waves Impacting a Large-Scale Structure

The Pont del Petroli, a decommissioned pier located in Badalona, Spain, holds significant historical and social significance. This structure suffered extensive damage during Storm Gloria that struck southeastern Spain in January 2020 [40]. In preparation for the pier’s reconstruction, a detailed evaluation of the wave-induced forces that led to its structural failure is imperative. To support an upcoming experimental campaign concerning this effort, the authors utilized an advanced CFD code. The simulation used the SPH method, specifically configured to replicate the conditions during Storm Gloria. Considering the substantial computational demands of a full 3D simulation, inlet boundary conditions were implemented to generate waves proximate to the pier structure. The numerical analysis revealed that the forces exerted on the pier during the storm surpassed its designed load capacity, accounting for both its self-weight and accidental loads. The findings suggest that a critical factor in the pier’s failure was the inadequacy of lateral soil resistance. This study represents an innovative application of SPH open-boundary conditions in modeling real-world engineering challenges.
The use of CFD to explore fluid– structure interaction (FSI) and wave–structure interaction has a well-established history in the structural analysis of both onshore and offshore facilities. Early methods based on potential flow theory often utilized a velocity potential satisfying a simplified set of governing equations, generally the Euler equations, within the fluid domain. These conventional approaches necessitated assumptions such as irrotational and inviscid fluid flow, adherence to linear or nonlinear wave theories, and considerations of small displacements. However, for scenarios involving severe wave breaking and extreme wave loads, employing the Navier–Stokes equations became standard. This shift necessitated a detailed handling of viscous terms and the complexities of the air–water interface. Generally, these equations are discretized on 2D or 3D grids using FVM or FEM. The advancement of powerful computing hardware, including central processing units (CPUs) and graphics processing units (GPUs), has significantly enhanced the efficiency and feasibility of these methodologies, enabling detailed analyses of real-world problems.
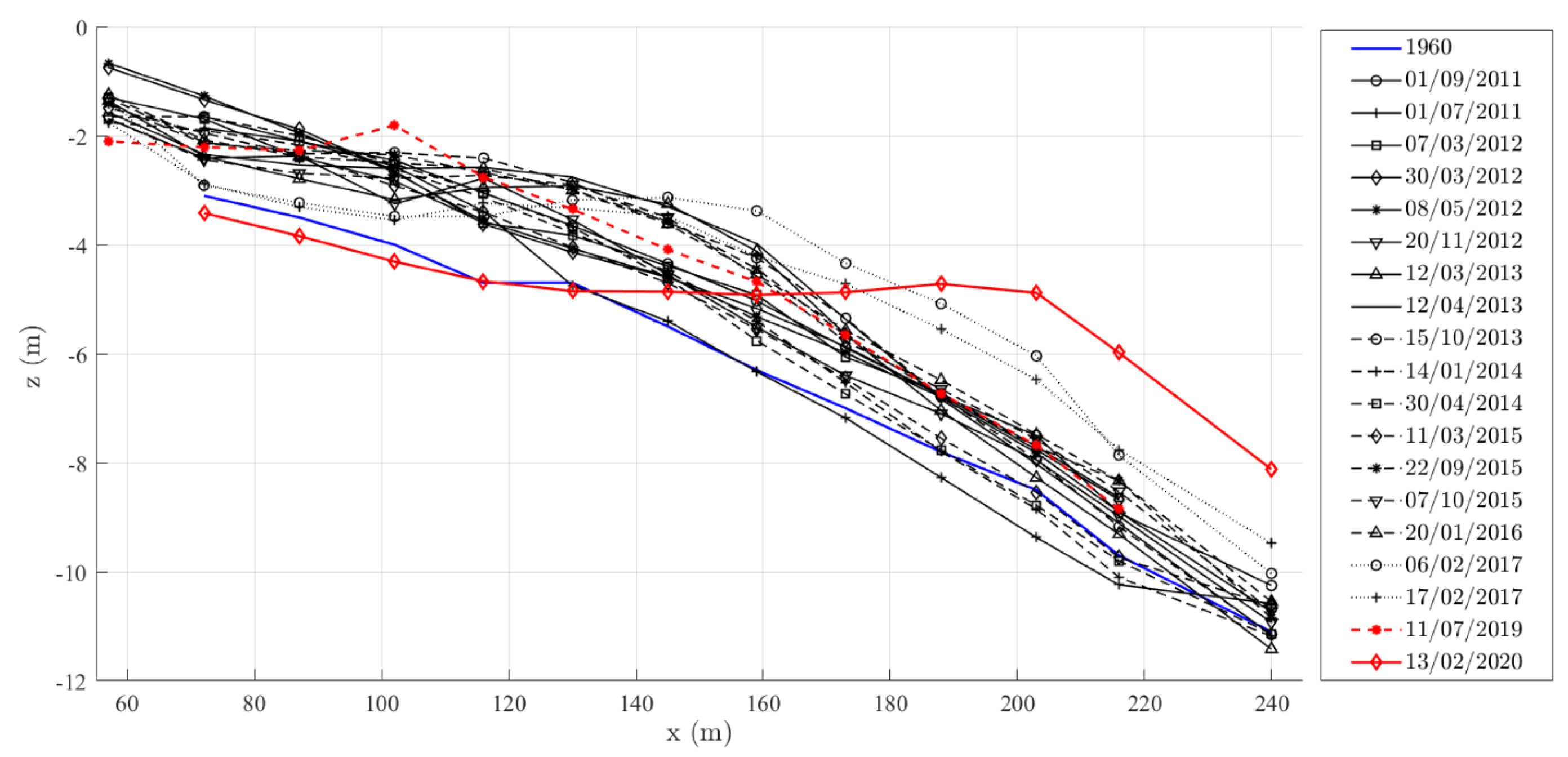
Figure 8 illustrates each structural element. Notably, the piles beneath the pile caps are inclined at an angle of 7.5° from the vertical and are anchored approximately 6 m into the sandy seabed, as detailed in the original design report. All data presented here are sourced from this report and have been reviewed for accuracy. The water depth and beach profile at the Pont del Petroli site have significantly changed since the pier’s initial construction. The pier was originally designed for a maximum water depth of 12 m at the base of the platform; however, both the water depth and seabed slope have undergone considerable modifications. Between 2011 and 2020, LIM/UPC conducted 19 bathymetric surveys to monitor these changes, with the latest survey occurring immediately after Storm Gloria. Figure 9 illustrates these changes, showing the original profile from the design report in blue and the profiles just before and immediately after Storm Gloria in red. The x-coordinate is measured from the landward side, starting at the footbridge’s beginning, with the toe of the platform located at x = 240 m, and the seaward footbridge beam and platform extending from x = 216 m to x = 240 m. The vertical axis indicates distance from the mean water level, with positive values representing an upward direction. The rear section of the pier, from the fourth pile cap to the shoreline, showed minimal changes in bottom slope, generally maintaining an average slope between 1:30 and 1:25. In contrast, the frontmost section, extending from the fourth pile cap to the platform, experienced the most significant alterations, particularly in local water depth. Sand accumulation in this area led to a decrease in water depth from the initial 12 m to nearly 9 m. While a relatively steady linear trend had been observed in previous years, a sudden and marked change was recorded following Storm Gloria in early 2020, with the measured water depth at the platform’s toe dropping to 8 m—a reduction of 4 m from the original design specification [41].
DualSPHysics, an open-source SPH-based software, was used to simulate the interaction between sea waves and the Pont del Petroli pier in Badalona, Spain. This structure suffered significant damage during Storm Gloria in January 2020, which considerably impacted the Spanish coast. The storm led to the loss of one of the footbridge beams and a pile cap, along with considerable damage to several other structural components. The numerical model was developed with two primary objectives: (a) To characterize the wave loads acting on the pier, facilitating the design and preparation for an upcoming experimental campaign in the large-scale wave flume at LIM/UPC. (b) To provide preliminary insights into the primary failure mechanisms that contributed to the damage observed during the storm.
To simulate conditions similar to those experienced during Storm Gloria, and because of the absence of specific local wave data during the storm in Badalona, an initial wave propagation study was conducted using the SWAN model. Visual assessments at the Pont del Petroli indicated wave heights reaching 7–8 m, which exceeded the heights of both the pier platform and footbridge. Following the storm, bathymetric surveys indicated significant changes in the seabed beneath the pier, with sand accumulation leading to an average reduction of 1—2 m in water depth.
Initially, a 2D analysis was conducted under various wave conditions and water depths, with wave heights ranging from 6.1 to 9.0 m and wave periods between 9.6 and 12.7 s. The initial water depths at the pier’s toe varied from 8 to 10 m. The results from the 2D model, which detailed exerted loads and wave-breaking patterns, were then compared to visual observations made during Storm Gloria. Subsequently, two specific wave conditions were selected for more detailed 3D simulations, corresponding to wave heights of 6.5 and 8.0 m, with wave periods of 12.0 and 12.7 s , respectively. The water depth at the pier’s toe for these simulations was aligned with post-Gloria survey data, approximately 8 m in the prototype.
While the 2D discretization closely replicated the layout of the LIM/UPC wave flume and employed the same wave-generation system (a wedge-type wavemaker), an inlet boundary condition was selected for the 3D simulations. Free-surface elevation and velocity data for the inlet area were extrapolated from the 2D results. This strategy improved the efficiency of the 3D model by positioning the inlet near the pier and wave breaking point, thus optimizing computational resources while maintaining high accuracy. Horizontal and vertical forces were measured on three components: the pier head platform, the initial pile cap, and the first seaward π -shaped beam forming the footbridge. Existing formulas for wave loads on exposed jetties could not be directly applied, as they were originally developed for jetties located on a horizontal seabed [42].
In this study, the numerical modeling did not directly simulate the piles themselves. Instead, the forces exerted by the waves on the piles were calculated using Morison’s formula, which accounts for slamming loads from breaking waves. The forces measured on the platform and footbridge beam were then compared to the design loads, which factored in self-weight and accidental loads. For vertical forces, the measured values were found to be comparable to or lower than the design specifications. However, the horizontal forces—especially under the most extreme wave conditions (wave height H = 8.0 m, wave period T = 12.7 s)—exhibited larger values than expected.
These results provided a foundation for specifying the requirements for load cells and pressure sensors for the upcoming experimental campaign at LIM/UPC. Key characteristics considered included nominal force/pressure, breaking load, sensitivity, accuracy, and measuring ranges. Snapshots from the SPH simulations indicated that for waves of this magnitude, the breaking process commenced before reaching the platform. Consequently, the wave, now in a plunging state, impacted the front of the platform, transferring a significant portion of its momentum to the structure. Some energy was also dispersed through overtopping onto the platform deck and footbridge, generating downward-directed vertical forces. In contrast, for waves with H = 6 m and T = 12 s, the waves approached the platform without apparent breaking. While the loads on the platform were lower than under more extreme conditions, the pile cap experienced greater impacts.
The forces acting on the pile cap were used to calculate the axial load transmitted to the two piles beneath it. The horizontal force on the pile cap was then compared to the ultimate lateral resistance of the soil, considering factors such as embedded pile length and eccentricity. This analysis considered both drag and slamming forces on the piles due to wave action. The results indicated that the horizontal force significantly exceeded the lateral soil resistance, although the axial loads on the piles remained within acceptable limits.
The findings from this SPH simulation campaign support the hypothesis presented in the damage report by the Badalona City Council, suggesting that the extensive damage observed after Storm Gloria may have been caused by exceeding lateral soil resistance. The forces acting on the piles and pile cap surpassed this resistance, leading to the overturning of the entire system comprising the piles and pile cap. Consequently, the footbridge beam lost its support and slid into the sea [43].

2.7. 3D Modeling of Fluid-Structure Interaction with External Flow Under Earthquake Using Coupled LBM and FEM

A previous study utilized a 3D FSI approach that integrated LBM for fluid dynamics and FEM for structural behavior. To enhance computational efficiency when simulating external flow around embedded pipes and their interactions with the surrounding environment, the pipes were represented using 3D beam elements instead of shell elements. The study introduced an algorithm that details the coupling process between these 3D beam elements and the lattice Boltzmann grids, facilitating accurate modeling of FSIs at the pipes’ outer surfaces. The developed technique was applied to analyze various numerical examples, enabling an exploration of FSI characteristics. This phenomenon is particularly significant and complex in settings such as power plants and heat exchangers, warranting detailed numerical analysis. Conventionally, structural analysis has predominantly relied on FEM, while flow analysis has often utilized FVM. Consequently, coupling methods have been developed to integrate FEM and FVM, thus effectively resolving FSIs. Furthermore, FEM has been used in multiphysics problems, including FSIs, and has been combined with BEM to address interactions involving structures and shock waves [44].
LBM is a relatively recent technique compared to established methods such as FVM, FEM, and BEM. Developed primarily for fluid flow problems since the 1980s, LBM has proven efficient and effective across various applications, including multiphase, turbulent, and thermal flows. LBM has also been utilized to tackle FSI issues, such as flows around rigid structures in artificial heart valve designs. Although there have been attempts to couple LBM with FDM or FEM for analyzing FSIs involving flexible structures, these earlier techniques were mainly focused on 2D applications. As a result, they face limitations in modeling interactions involving flows around pipes, especially in 3D contexts [45].
LBM has undergone significant advancements over the last two decades since its origins in the 1980s. Initially derived from cellular automata and later integrating concepts from the Boltzmann equation, LBM was developed to overcome the limitations of cellular automata. Cellular automata, first introduced by von Neumann in the late 1940s, serve as a framework for building simple local models that can represent complex global systems through localized rules. Typically, a cellular automaton is structured as a regular lattice of cells, each associated with a set of Boolean variables, with local rules governing how the states of one cell evolve in relation to its neighbors. However, cellular automata face inherent limitations, primarily because of their dependence on Boolean quantities. To overcome this constraint, LBM was developed, employing real-valued quantities instead [46].
This section discusses LBM formulations specifically designed for viscous flow scenarios without considering the deformation of the fluid grid. In modeling the interaction between flexible internal pipes and external fluid flows, pipes can be represented using either shell or beam elements within structural finite-element analysis. Although shell-element models generally yield more accurate results by effectively capturing local deformations and vibrations, such as cross-sectional ovalization or localized wall buckling, they also require significantly higher computational resources, especially when modeling multiple pipes. In contrast, beam-element models, while less detailed, provide a computationally efficient alternative for representing overall pipe deformations and vibrations when local effects are minimal [47,48].
In many practical applications, pipes feature relatively thick walls, rendering local deformations or vibrations less critical. Additionally, given their elongated and slender characteristics, the overall behavior of these pipes often becomes critical in analysis. To address this, a previous study proposed an algorithm that connects lattice Boltzmann fluid grid points with the 3D beam elements modeling the pipes. These beams were assumed to exhibit linear elasticity with small displacements, allowing the deformation in the fluid grid to be disregarded [49].
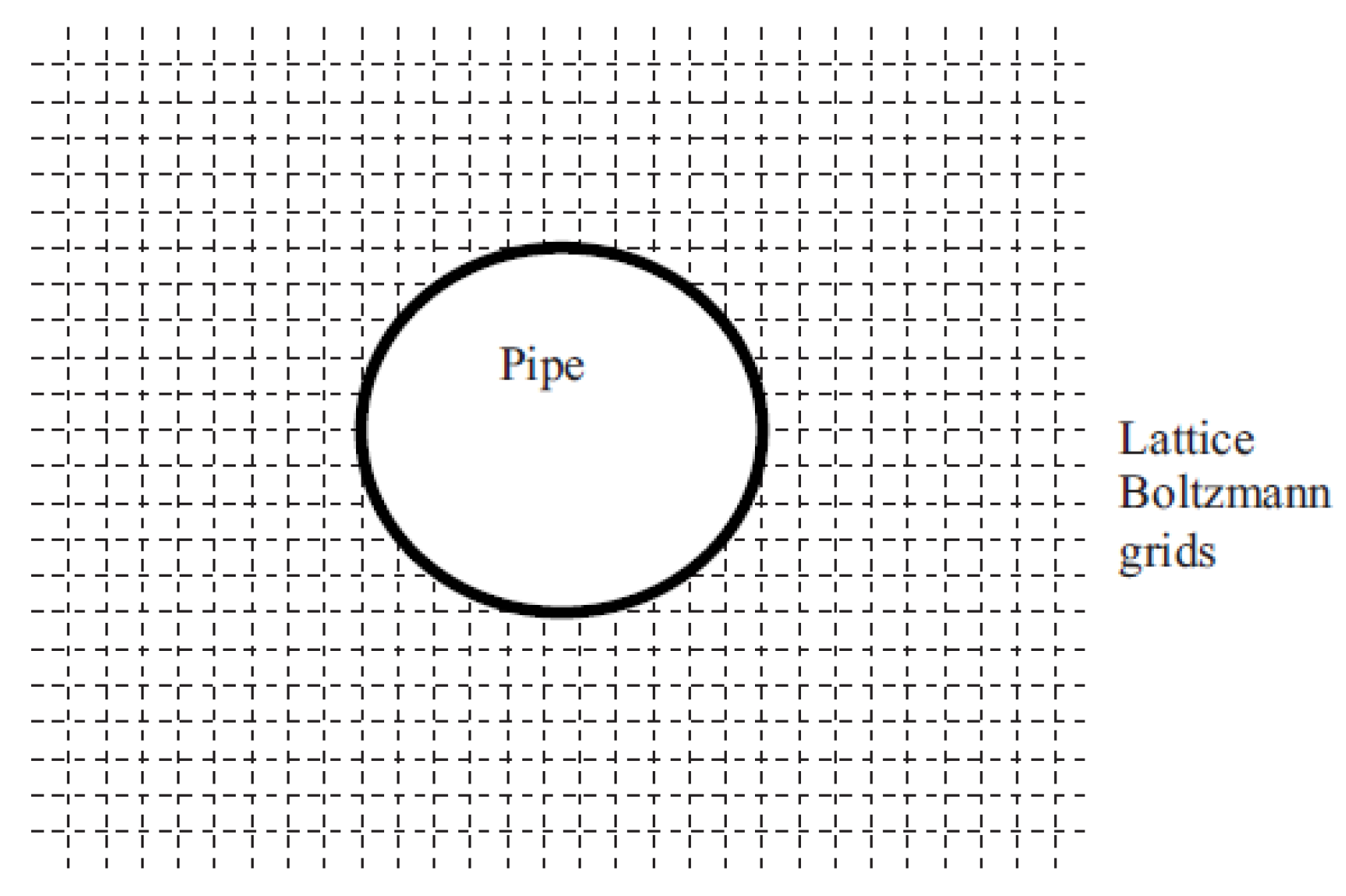
Figure 9 shows a pipe within the fluid grid points from a cross-sectional perspective. Given that 3D beam elements are represented as lines in finite-element analysis, it is crucial to accurately represent the outer surfaces of the pipes within these beam elements to facilitate FSI at those surfaces. During analysis, the outer surface of each 3D beam element is identified, and the fluid grid points contacting this surface are marked for interaction. The steps to achieve FSI using lattice Boltzmann grids and structural 3D beam elements are outlined below, accompanied by detailed algorithms for each step [50].
Preprints 138065 g009
Figure 9. 2D view of a pipe inside the lattice Boltzmann grid points. [51]
Figure 9. 2D view of a pipe inside the lattice Boltzmann grid points. [51]
Preprints 138065 g009
  • Step 1: Identify the fluid grid points that interact with the external surface of the pipe, represented by 3D beam elements.
  • Step 2: Organize the fluid grid points such that each group corresponds to a specific 3D beam element.
  • Step 3: Calculate the representative surface areas for the identified fluid grid points.
  • Step 4: For each beam element, compute the resultant pressure force at each fluid grid point, ensuring the force direction is perpendicular to the beam’s surface. This force is then represented as the equivalent nodal force of the beam element and is calculated for all fluid grid points linked to that element.
  • Step 5: Repeat the calculations from Step 4 for each beam element.
  • Step 6: Perform a transient analysis of the 3D beam structure using the previously computed fluid forces, along with specified boundary conditions and the prior solution state, over a defined time increment.
  • Step 7: Determine the nodal velocities of the beam structures from the structural analysis. Use shape functions to calculate velocities at each fluid grid point in contact with the beam’s surface. Apply these velocities to the fluid grid points through particle-distribution functions. Following this, conduct fluid flow analysis using LBM for the next time increment.
  • Step 8: Continue repeating the aforementioned steps as time progresses [52].
In prior research, a combined approach using both LBM and FEM was developed to address 3D FSI problems, specifically focusing on external flow around pipes. In the structural finite-element model, pipes were modeled as 3D beams instead of shells. This modeling approach simplifies the interaction with the fluid at the outer surfaces, similar to how shell elements function, making the finite-element modeling of the pipes both straightforward and computationally efficient. The D3Q15 lattice was used for LBM in fluid modeling. The fluid and structural domains were solved sequentially, exchanging fluid pressure and structural velocity data between them. Because LBM and FEM use different variables at the grid points, a method was introduced to accurately decompose the structural velocity into the particle-distribution functions within LBM [53,54,55].

3. Discussion

In the field of earthquake engineering, analytical work on civil engineering problems is predominantly conducted through various numerical methods. In this section, these methods are categorized into two tables, summarizing past research on the subject.
The numerical simulation of earthquake impacts on marine structures employs a variety of advanced methods, each suited to capturing different physical phenomena relevant to structural behavior under seismic loads. The finite-element method (FEM) is widely used for structural analysis, offering precise modeling of stress, strain, and deformation within complex geometries. Computational fluid dynamics (CFD) provides insight into fluid-structure interactions, especially when assessing the effect of seismic events on surrounding water. The discrete-element method (DEM) is valuable for simulating granular materials, such as seabeds, and understanding how they respond during seismic disturbances. Blade element momentum (BEM) theory, though primarily used in aerodynamics, can be adapted to evaluate structural components exposed to both fluid and seismic forces. The finite-volume method (FVM) offers an alternative to CFD, ensuring numerical stability when modeling pressure and velocity fields around structures during earthquakes. Direct numerical simulation (DNS) provides detailed flow field solutions but is computationally intensive, making it suitable for small-scale simulations. Smoothed-particle hydrodynamics (SPH) offers a mesh-free alternative, especially useful for modeling large deformations and free surface flows, such as tsunami effects following seismic events. Lastly, the lattice Boltzmann method (LBM) is gaining traction for its efficiency in simulating fluid flows with complex boundaries, particularly in multiphase systems. The combined use of these methods enables a comprehensive understanding of how marine structures respond to earthquakes, accounting for both structural integrity and fluid-structure interactions.
As previously commented, there are different numerical methods for obtaining approximate solutions to a wide variety of engineering problems. In recent decades, a lot of research has been done on the numerical simulation of earthquake effects on marine structures, the main methods identified in this research are presented in the Table 1.
The classification of numerical methods based on their meshing approach, as shown in Table 2, highlights the diversity of strategies employed for simulating complex systems, particularly in the context of marine structures under dynamic conditions. Mesh-based methods, such as Orthogonal Decomposition and Marker-and-Cell techniques, rely on structured grids to accurately capture geometric details and solve governing equations. These methods are well-suited for high-resolution simulations but can be computationally expensive for large, deformable domains. Mesh-free methods, including Smoothed Particle Hydrodynamics (SPH) and the Fast Multipole Method, eliminate the need for predefined grids, making them highly effective for problems involving large deformations, free surfaces, or complex boundary interactions. Their flexibility enables simulations of scenarios such as wave impacts or sediment displacement during earthquakes. Hybrid methods, such as the Particle-in-Cell and Lattice Boltzmann methods, combine the strengths of both mesh-based and mesh-free approaches. These hybrid techniques offer a balance between accuracy and computational efficiency, making them ideal for multiphase and fluid-structure interaction problems. This classification reflects the ongoing advancements in numerical simulation, emphasizing the importance of selecting the appropriate method based on the specific requirements of the marine structure and seismic scenario being studied.

4. Conclusions

This review examined the current state of numerical modeling concerning earthquake impacts within the marine domain. Configurations of CFD, FEM, DEM, FVM, and BEM models provide cost-effective and efficient methodologies for investigating earthquake parameters under real-world environmental conditions. However, their applications within the naval industry encounter limitations related to numerical algorithms and computational resources. This review discussed various numerical models used to simulate marine forces during earthquakes, highlighting a strong correlation between the results from all models and experimental as well as theoretical findings.
Previous numerical models have also assessed the secondary load effects on structures during wave breaking. In the existing models, the secondary load effect was marginally delayed compared to experimental results. This discrepancy may be attributed to the use of an incompressible flow model in the simulations, which restricted energy dissipation after wave breaking and led to variations in secondary loads. Further research is necessary to accurately estimate the cycles of secondary loads through numerical simulation.
Moreover, while the findings suggest that DNS is a useful approach for studying small-scale physical processes related to wind over breaking waves, advancements in computational power are necessary for high-resolution simulations of more complex scenarios. For instance, utilizing the wave-focusing method could simulate breaking waves influenced by wind, enhancing our understanding of how wind impacts wave geometry. This approach would require considerably increased computational resources owing to the need for a larger domain size in the streamwise direction. Additionally, integrating laboratory and field measurement data into the simulations would improve their realism.
Numerical predictions have been validated through comparisons with experimental data and existing numerical results from the literature. This review discussed the effectiveness of the numerical methods in accurately describing the performance of marine structures under various operating conditions. Specifically, reliable predictions of turbine thrust, torque, and power were achieved at medium to high tip-speed ratios, where blade flow remains largely attached. Accurate predictions were also made at relatively low tip-speed ratios, where flow separation and stall significantly impact thrust loss and drag. Reliable predictions of turbine performance were observed for blade pitch settings close to design specifications, although discrepancies in thrust and torque were noted under off-design conditions.
Submarine structures have also been simulated by integrating CFD with DEM. For instance, a dynamic-contact model was used in the discrete-element component to replicate the behavior of methane hydrate-bearing sediments. The fluid dynamics component accounted for the minor compressibility of the fluid, and the Magnus force was included in fluid–particle interactions, significantly affecting particle trajectories within velocities typical for submarine structures.
To improve the accuracy of numerical models capable of directly solving wave pressure, such as 3D models, further advancements are necessary. The parameter settings for earthquake impact modeling remain viable and warrant further exploration. The insights provided will assist in developing numerical simulation tools that can reliably predict the effects of earthquakes and their hydraulic forces on marine structures. Future research can explore numerical simulation techniques for near-field fluctuations of seismoacoustic scattering in marine environments during seismic events. This includes free-field calculations to provide input for scattering problems, a unified computational framework for FSI in internal domains, and the implementation of artificial boundary conditions. Decoupling technology can be advanced through programming. The efficacy of these methods can be validated by comparing them with existing results and confirming continuity conditions at the interface. These methods can utilize concentrated-mass explicit finite elements and local-transmission artificial boundaries, avoiding the need to solve large equations, facilitating parallel computations, and ensuring high efficiency, making them suitable for simulating large-scale marine scattering problems.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, X.X. and Y.Y.; methodology, X.X.; software, X.X.; validation, X.X., Y.Y. and Z.Z.; formal analysis, X.X.; investigation, X.X.; resources, X.X.; data curation, X.X.; writing—original draft preparation, X.X.; writing—review and editing, X.X.; visualization, X.X.; supervision, X.X.; project administration, X.X.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.”, please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

This work has been partially funded by the Spanish Agencia Estatal de Investigación (AEI)—Ministerio de Economía, Industria y Competitividad (MINECO), and the Fondo Europeo de Desarrollo Regional (FEDER) through the research projects PID2021-122132OB-C21, PID2021-126051OB-C44 and TED2021-129512B-I00; and by the Generalitat de Catalunya through the research projects 2021-SGR-01044 and 2021 SGR 01049.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable.

Acknowledgments

This work has been partially funded by the Spanish Agencia Estatal de Investigación (AEI)—Ministerio de Economía, Industria y Competitividad (MINECO), and the Fondo Europeo de Desarrollo Regional (FEDER) through the research projects PID2021-122132OB-C21, PID2021-126051OB-C44 and TED2021-129512B-I00; and by the Generalitat de Catalunya through the research projects 2021-SGR-01044 and 2021 SGR 01049.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CFD Computational fluid dynamics
FEM Finite element method
BEM Boundary element method
DEM Discrete element method
FVM Finite volume method
SPH Smoothed particle hidrodynamics
DNS Direct numerical simulation
LBM Lattice Boltzmann method

References

  1. Shekari, M.R. A coupled numerical approach to simulate the effect of earthquake frequency content on seismic behavior of submarine tunnel. Marine Structures 2021, 75, 102848. [CrossRef]
  2. Han, Q.; Li, M.; Wang, Z.; Sun, J.; Liu, M. Strategy of scaled modeling for underwater shaking table tests on cylindrical marine structures under coupled earthquake and wave–current action: A review. Earthquake Engineering and Resilience 2023, 2, 263–281. [CrossRef]
  3. Lin, J.; Jeng, D.S.; Zhao, H.; Gao, Y.; Liu, J.; Guo, Y. Recent advances of seabed liquefaction around the vicinity of marine structures. Ocean Engineering 2023, 280, 114660. [CrossRef]
  4. Bhattacharya, S.; Goda, K. Use of offshore wind farms to increase seismic resilience of Nuclear Power Plants. Soil Dynamics and Earthquake Engineering 2016, 80, 65–68. [CrossRef]
  5. Sumer, B.M.; Ansal, A.; Cetin, K.O.; Damgaard, J.; Gunbak, A.R.; Hansen, N.E.O.; Sawicki, A.; Synolakis, C.E.; Yalciner, A.C.; Yuksel, Y.; others. Earthquake-induced liquefaction around marine structures. Journal of waterway, port, coastal, and ocean engineering 2007, 133, 55–82. [CrossRef]
  6. Liu, J.; Jia, Y.; Cui, L.; Sun, H.; Lv, X.; Asheghabadi, M.S. Numerical Analysis of Dynamic Response and Liquefaction Phenomena in Sandy Seabed Foundation around a Semi-Circular Breakwater under Wave Loading. Journal of Marine Science and Engineering 2023, 12, 40. [CrossRef]
  7. Sharma, M.; Kaligatla, R.; Sahoo, T. Wave interaction with a submerged floating tunnel in the presence of a bottom mounted submerged porous breakwater. Applied Ocean Research 2020, 96, 102069. [CrossRef]
  8. Zhou, X.; Sutulo, S.; Soares, C.G. A paving algorithm for dynamic generation of quadrilateral meshes for online numerical simulations of ship manoeuvring in shallow water. Ocean Engineering 2016, 122, 10–21. [CrossRef]
  9. Muskulus, M. Efficient numerical simulation of offshore structures and wind turbines on general purpose graphics processing units. International Conference on Computational Methods in Marine Engineering MARINE 2011. CIMNE, 2011, pp. 438–449.
  10. Johnson, G.; Young, A.; Scholes, J.; Horton, P. The dissipation of excess excitation energy in British plant species. Plant, cell & environment 1993, 16, 673–679.
  11. Ubbink, O.; Issa, R. A method for capturing sharp fluid interfaces on arbitrary meshes. Journal of computational physics 1999, 153, 26–50. [CrossRef]
  12. Okamoto, T.; Takenaka, H.; Nakamura, T.; Hara, T. FDM simulation of earthquakes off western Kyushu, Japan, using a land–ocean unified 3D structure model. Earth, Planets and Space 2017, 69, 1–15. [CrossRef]
  13. Mushtaq, M.; Shah, N.; Muhammad, G. A brief description of developments and applications of direct boundary element method for compressible fluid flow problems. Kragujevac Journal of Science 2010, pp. 25–30.
  14. AVRASHI, J.; COOK, R.D. New error estimation for C° eigenproblems in finite element analysis. Engineering computations 1993. [CrossRef]
  15. Chen, X.; Liu, Y. Finite element modeling and simulation with ANSYS Workbench; CRC press, 2018.
  16. Zienkiewicz, O.C.; Taylor, R.L. The finite element method for solid and structural mechanics; Elsevier, 2005.
  17. Ion, A.; Ticu, I. The finite element method for calculating the marine structural design. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2015, Vol. 95, p. 012073.
  18. Bathe, K.J. Finite element procedures; Klaus-Jurgen Bathe, 2006.
  19. Jiang, M.; Liu, J.; Kwok, C.Y.; Shen, Z. Exploring the undrained cyclic behavior of methane-hydrate-bearing sediments using CFD–DEM. Comptes Rendus Mécanique 2018, 346, 815–832. [CrossRef]
  20. Hsu, S.K.; Kuo, J.; Chung-Liang, L.; Ching-Hui, T.; Doo, W.B.; Ku, C.Y.; Sibuet, J.C. Turbidity currents, submarine landslides and the 2006 Pingtung earthquake off SW Taiwan. TAO: Terrestrial, Atmospheric and Oceanic Sciences 2008, 19, 7. [CrossRef]
  21. Zhang, L.; Luan, X. Stability of submarine slopes in the northern South China Sea: a numerical approach. Chinese Journal of Oceanology and Limnology 2013, 31, 146–158. [CrossRef]
  22. Jiang, M.; Shen, Z.; Wu, D. CFD-DEM simulation of submarine landslide triggered by seismic loading in methane hydrate rich zone. Landslides 2018, 15, 2227–2241. [CrossRef]
  23. Thornton, C.; Cummins, S.J.; Cleary, P.W. An investigation of the comparative behaviour of alternative contact force models during inelastic collisions. Powder technology 2013, 233, 30–46. [CrossRef]
  24. Hansen, M.O. Aerodynamics of wind turbines; Routledge, 2015.
  25. Buhl Jr, M.L. New empirical relationship between thrust coefficient and induction factor for the turbulent windmill state. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2005.
  26. He, L.; Kinnas, S.A.; Xu, W. Numerical methods for the prediction of unsteady performance of marine propellers and current turbines. The Twenty-first International Offshore and Polar Engineering Conference. OnePetro, 2011.
  27. Baltazar, J.; Falcao de Campos, J. Unsteady analysis of a horizontal axis marine current turbine in yawed inflow conditions with a panel method. First International Symposium on Marine Propulsors, Trondheim, Norway, 2009.
  28. Salvatore, F.; Sarichloo, Z.; Calcagni, D. Marine turbine hydrodynamics by a boundary element method with viscous flow correction. Journal of Marine Science and Engineering 2018, 6, 53. [CrossRef]
  29. Baltazar, J.; Machado, J.; Falca o de Campos, J. Hydrodynamic design and analysis of horizontal axis marine current turbines with lifting line and panel methods. International Conference on Offshore Mechanics and Arctic Engineering, 2011, Vol. 44373, pp. 453–465.
  30. Wienke, J.; Oumeraci, H. Breaking wave impact force on a vertical and inclined slender pile—theoretical and large-scale model investigations. Coastal engineering 2005, 52, 435–462. [CrossRef]
  31. Jose, J.; Choi, S.J.; Giljarhus, K.E.T.; Gudmestad, O.T. A comparison of numerical simulations of breaking wave forces on a monopile structure using two different numerical models based on finite difference and finite volume methods. Ocean Engineering 2017, 137, 78–88. [CrossRef]
  32. Hull, P.; Müller, G. An investigation of breaker heights, shapes and pressures. Ocean Engineering 2002, 29, 59–79. [CrossRef]
  33. Peiró, J.; Sherwin, S. Finite difference, finite element and finite volume methods for partial differential equations. Handbook of Materials Modeling: Methods 2005, pp. 2415–2446.
  34. Irschik, K.; Sparboom, U.; Oumeraci, H. Breaking wave loads on a slender pile in shallow water. In Coastal Engineering 2004: (In 4 Volumes); World Scientific, 2005; pp. 568–580.
  35. Christensen, E.D.; Bredmose, H.; Hansen, E.A. Extreme wave forces and wave run-up on offshore wind turbine foundations. Proceedings of Copenhagen Offshore Wind 2005, pp. 1–10.
  36. Perlin, M.; Choi, W.; Tian, Z. Breaking waves in deep and intermediate waters. Annual review of fluid mechanics 2013, 45, 115–145. [CrossRef]
  37. Moin, P.; Kim, J. The structure of the vorticity field in turbulent channel flow. Part 1. Analysis of instantaneous fields and statistical correlations. Journal of Fluid Mechanics 1985, 155, 441–464. [CrossRef]
  38. Yang, Z.; Deng, B.Q.; Shen, L. Direct numerical simulation of wind turbulence over breaking waves. Journal of Fluid Mechanics 2018, 850, 120–155. [CrossRef]
  39. Amores, A.; Marcos, M.; Carrió, D.S.; Gómez-Pujol, L. Coastal impacts of Storm Gloria (January 2020) over the north-western Mediterranean. Natural Hazards and Earth System Sciences 2020, 20, 1955–1968. [CrossRef]
  40. Altomare, C.; Tafuni, A.; Domínguez, J.M.; Crespo, A.J.; Gironella, X.; Sospedra, J. SPH simulations of real sea waves impacting a large-scale structure. Journal of Marine Science and Engineering 2020, 8, 826. [CrossRef]
  41. Meyerhof, G. Compaction of sands and bearing capacity of piles. Journal of the Soil Mechanics and Foundations Division, 85.
  42. Beckert, A. Coupling fluid (CFD) and structural (FE) models using finite interpolation elements. Aerospace Science and technology 2000, 4, 13–22. [CrossRef]
  43. Kuntz, M.; Ferreira, J.C.; Menter, F.; Oudendijk, G. Analysis of fluid-structure interaction with an improved coupling strategy. Proceedings of the third international conference on Engineering computational technology, 2002, pp. 85–86.
  44. Zienkiewicz, O. Coupled vibrations of a structure submerged in a compressible fluid. Proc. of Symposium on Finite Element Techniques Held at the University of Stuttgart, 1969.
  45. Cheng, Y.; Oertel, H.; Schenkel, T. Fluid-structure coupled CFD simulation of the left ventricular flow during filling phase. Annals of biomedical engineering 2005, 33, 567–576. [CrossRef]
  46. Bathe, K.; Zhang, H.; Wang, M. Finite element analysis of incompressible and compressible fluid flows with free surfaces and structural interactions. Computers & Structures 1995, 56, 193–213.
  47. Kwon, Y.; McDermott, P. Effects of void growth and nucleation on plastic deformation of plates with fluid-structure interaction. J. Pressure Vessel Technol. 2001, 123, 480–485. [CrossRef]
  48. Newton, R. Finite element study of shock induced cavitation. The finite element method in the 1990’s: A Book Dedicated to OC Zienkiewicz 1991, pp. 389–397.
  49. Zienkiewicz, O.; Paul, D.; Hinton, E. Cavitation in fluid-structure response (with particular reference to dams under earthquake loading). Earthquake Engineering & Structural Dynamics 1983, 11, 463–481.
  50. Bathe, K.; Nitikitpaiboon, C.; Wang, X. A mixed displacement-based finite element formulation for acoustic fluid-structure interaction. Computers & Structures 1995, 56, 225–237.
  51. Kwon, Y.; Jo, J. 3D modeling of fluid-structure interaction with external flow using coupled LBM and FEM 2008.
  52. Kwon, Y.; Cunningham, R. Comparison of USA-DYNA finite element models for a stiffened shell subject to underwater shock. Computers & structures 1998, 66, 127–144.
  53. Cali, A.; Succi, S.; Cancelliere, A.; Benzi, R.; Gramignani, M. Diffusion and hydrodynamic dispersion with the lattice Boltzmann method. Physical Review A 1992, 45, 5771. [CrossRef]
  54. Swift, M.R.; Orlandini, E.; Osborn, W.; Yeomans, J. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Physical Review E 1996, 54, 5041. [CrossRef]
  55. Soe, M.; Vahala, G.; Pavlo, P.; Vahala, L.; Chen, H. Thermal lattice Boltzmann simulations of variable Prandtl number turbulent flows. Physical Review E 1998, 57, 4227. [CrossRef]
  56. Casadei, F.; Halleux, J.; Sala, A.; Chille, F. Transient fluid–structure interaction algorithms for large industrial applications. Computer methods in applied mechanics and engineering 2001, 190, 3081–3110. [CrossRef]
  57. Goda, Y. Wave forces on a vertical circular cylinder: Experiments and a proposed method of wave force computation. Report of the Port and Harbor Research Institute 1964.
  58. Sharma, S.; Kundu, A.; Basu, S.; Shetti, N.P.; Aminabhavi, T.M. Sustainable environmental management and related biofuel technologies. Journal of Environmental Management 2020, 273, 111096. [CrossRef]
  59. Worden, A.Z.; Lee, J.H.; Mock, T.; Rouzé, P.; Simmons, M.P.; Aerts, A.L.; Allen, A.E.; Cuvelier, M.L.; Derelle, E.; Everett, M.V.; others. Green evolution and dynamic adaptations revealed by genomes of the marine picoeukaryotes Micromonas. Science 2009, 324, 268–272. [CrossRef]
  60. Lewis, R.W.; Bettess, P.; Hinton, E. Numerical methods in coupled systems; Vol. 6, John Wiley & Sons Incorporated, 1984.
  61. Verbrugghe, T.; Domínguez, J.M.; Altomare, C.; Tafuni, A.; Vacondio, R.; Troch, P.; Kortenhaus, A. Non-linear wave generation and absorption using open boundaries within DualSPHysics. Computer Physics Communications 2019, 240, 46–59. [CrossRef]
Preprints 138065 g001
Figure 1. (a) Hull with transverse stiffeners CAD detail, (b) Preparation of mesh and for a hull with transverse stiffeners and (c) result of the vibration mode of the hull transversely stiffened at frequency 11.209 Hz [17].
Figure 1. (a) Hull with transverse stiffeners CAD detail, (b) Preparation of mesh and for a hull with transverse stiffeners and (c) result of the vibration mode of the hull transversely stiffened at frequency 11.209 Hz [17].
Preprints 138065 g001
Preprints 138065 g002
Figure 2. CFD-DEM simulation of particle ejection test. (a) setup and (b) Particle motion trajectory with and without Magnus force [22].
Figure 2. CFD-DEM simulation of particle ejection test. (a) setup and (b) Particle motion trajectory with and without Magnus force [22].
Preprints 138065 g002
Preprints 138065 g004
Figure 4. Schematic of numerical wave tank: a) cross section and b) plan view [31].
Figure 4. Schematic of numerical wave tank: a) cross section and b) plan view [31].
Preprints 138065 g004
Preprints 138065 g005
Figure 5. (a) STL files for the bottom geometry and cylinder, and (b) Computational domain with bottom slope and vertical cylinder) Plan view [31].
Figure 5. (a) STL files for the bottom geometry and cylinder, and (b) Computational domain with bottom slope and vertical cylinder) Plan view [31].
Preprints 138065 g005
Preprints 138065 g006
Figure 6. Results of waves2Foam simulations in four time steps from 31.10 s, until 31.90 s [31].
Figure 6. Results of waves2Foam simulations in four time steps from 31.10 s, until 31.90 s [31].
Preprints 138065 g006
Preprints 138065 g007
Figure 7. Computational domain and coordinate system for DNS of wind over steep and breaking waves [38].
Figure 7. Computational domain and coordinate system for DNS of wind over steep and breaking waves [38].
Preprints 138065 g007
Preprints 138065 g008
Figure 8. Beach profiles at Pont del Petroli. The original beach profile from the design report is indicated by a blue line. In red, the two profiles surveyed by LIM/UPC before and after storm Gloria [40].
Figure 8. Beach profiles at Pont del Petroli. The original beach profile from the design report is indicated by a blue line. In red, the two profiles surveyed by LIM/UPC before and after storm Gloria [40].
Preprints 138065 g008
Table 1. Methods for the numerical simulation of earthquake effects on marine structures.
Table 1. Methods for the numerical simulation of earthquake effects on marine structures.
ID References Methods Figures
1 [12,13,14,15] FEM 1
2 [16,17,18,19] CFD-DEM 2,3
3 [20,21,22,23,24] BEM 4
4 [25,26,27,28,29,30] FVM 5
5 [31,32,33] DNS 6,7,8
6 [34,35,36,37,38,39,40] SPH 9,10
7 [40,41,42,43,44,45,46,47,48,49,50,51] LBM-FEM 11
Table 2. Classification of works based on their meshing method.
Table 2. Classification of works based on their meshing method.
Mesh Base Mesh Free Hybrid
simplified Order customizing [22,56] Particle Hydrodynamics [42] Fast liquid Dynamics [57]
correct Orthogonal Decomposition [31] Fast Multipole Method [58,59] Particle in Cell Technique [13]
Single value factorization [23,44] Method of Fundamental Solutions [50] swirl in Cell Technique[53]
Marker&Cell [37] bound Pointset Method [60] Lattice Boltzmann Method [61]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated