Prerpints.org logo
Preprint
Article

A Rolling Window GARCH Analysis to Measure the Change in Efficiency of the Johannesburg Stock Exchange

This version is not peer-reviewed.

Submitted:

31 October 2024

Posted:

01 November 2024

You are already at the latest version

Abstract
The efficiency of a stock exchange has many implications, including the likely effectiveness of active investing and the accurate pricing of assets. The Johannesburg Stock Exchange has been found to be efficient in prior research, but there is recent evidence that its efficiency is declining. The study aimed to determine whether the efficiency of the exchange has declined, as proxied by the speed of mean reversion of returns, and whether any change was specifically driven by smaller stocks as we know that large stocks are efficiently priced on the exchange. A general autoregressive conditional heteroskedasticity (1,1) was applied to the data together with an Augmented Dickey Fuller based test for robustness. The results show a decline in efficiency of the stock exchange as well as for the different sub-indices studied. All sub-indices studied declined in efficiency, but this is not ascribed to smaller listed firms, but rather an overall decline in the efficiency of the stock exchange. A recommendation is made for a future study to consider the speed of reversion of individual stocks which would allow the study of firm characteristics possibly driving the change in efficiency of the exchange.
Keywords: 
Subject: 
Business, Economics and Management  -   Finance

1. Introduction

In the recent past, there has been a decline in the number of listed companies, from over 900 to less than 300, on the Johannesburg Stock Exchange, lower trading volumes and there is evidence of a decline in the efficiency of the exchange (Heymans & Santana, 2018; Kulikova et al, 2024). A significantly large amount of research exists to support the notion of efficiency of the JSE. The exchange is, at the very least, it is weak-form efficient as is the case with many prominent exchanges (Mlambo & Biepke, 2007; Kulikova et al, 2024). Moreover, there is evidence that stocks of higher market capitalization companies on the JSE, likely because of higher levels of analyst coverage, are in specific cases semi-strong form efficient where information is incorporated before being disclosed publicly (Noakes & Rajaratnam, 2016; Kotze, 2023). While there is evidence that the overall the stock exchange is weak- form efficient and that larger companies seem to be priced efficiently, the dearth of listings and the change in composition of the exchange may have affected the efficiency of the exchange.
Prior works have shown thinly traded stocks to be likely less efficiently priced and low volumes are commonly associated with smaller capitalization stocks (see for example: Baily & Gilbert, 2007). On the other hand, large capitalization stocks are more likely to be traded in larger volumes. The change in the composition of the JSE over time has led to it being composed of more higher market capitalization stocks (Nikani & Holland, 2023). Therefore, one could expect that the JSE, being composed of larger companies currently, could have maintained or improved its efficiency over time. Possibly, the negative change in efficiency observed by Kulikova et al (2024), may be driven by a subsection of lesser traded stocks on the exchange. While there is literature supporting the notion that the efficiency of the exchange is not at the same level as in the past, the driving force behind this change has not yet been researched and there is limited research regarding the change in efficiency on the exchange.
Stock exchange efficiency has important academic and practical implications, foremost that the notion that a strongly efficient stock market makes analysis and stock picking essentially moot while any lower form of efficiency points towards the opposite being the case (Fama, 1965). In economic terms, more concentrated stock markets have been shown to have a negative effect on the overall economy of a country, this study adds to our understanding of how such a change affects the JSE specifically and therefore, how it might affect the South African economy in the future (Bae, Bailey & Kang, 2021). Practically, active versus passive investment management choices may be affected by changes in efficiency of the market with lower efficiency markets likely presenting more opportunity for active investment based excess returns as opposed to highly efficient markets pricing in information so efficiently that arbitrage opportunities come by less frequently. In terms of academic importance, knowing whether efficiency changes over time and knowing where such a change emanates from, would add to the current understanding of market related features that influences market efficiency. This study adds to the understanding of how the efficiency of the JSE has changed while adding the puzzle of what is driving the change in efficiency.
There exists significant work detailing the efficiency of the JSE, including over certain notable windows, such as the global financial crisis, but there is little work considering the change in efficiency over time in the whole (Noakes & Rajaratnam, 2016; Kulikova et al, 2024). There is some conflicting research suggesting that other stock exchanges’ efficiency are/ are not declining despite less companies being listed (Koptyug, Persson & Tag, 2020; Arashi & Rounaghi, 2022). While there is some evidence for the NASDAQ specifically indicating that the decline in listings is not affecting efficiency negatively, the differences between the NASDAQ and the JSE makes extrapolation essentially impossible. One may expect the same to hold for the JSE, however, recent studies suggest otherwise for the JSE (Kulikova et al, 2024; Noakes & Rajaratnam, 2016). The JSE is a much smaller exchange, and the NASDAQ remains a very large stock exchange in all respects while also receiving significantly higher trading volume and analyst coverage. In the case of the NASDAQ for example, listings are declining, but the efficiency of the exchange has not. The JSE on the is a much smaller exchange with less large capitalization stocks. These important differences offer us the opportunity to determine whether the efficiency of the exchange has changed due to the composition of the exchange. Such a study would likely be difficult to perform on a high volume, much analyzed exchange because the marginal effect would likely be difficult to discern decisively while on a smaller exchange the effects would be more pronounced. Considering the change in the composition of the JSE being skewed towards larger companies which are often more heavily traded, it may be that the efficiency of the exchange may vary between different subsections of the stock exchange and that efficiency may have increased due to this change in size distribution (Nikani & Holland, 2023; Kotze, 2023). On the other hand, the less efficient trading of smaller firms may be so significant as to affect the overall efficiency of the JSE (Jiang, 2016).
Prior studies have established that less liquid stocks, which are often smaller stocks, are less efficiently priced on the JSE while there is some evidence that larger cap stocks are efficiently priced (Noakes & Rajaratnam, 2016; Kotze, 2023). In the case that the overall efficiency of the exchange is unchanged (or not), it could be that certain sub-sections of the exchange’s efficiency have changed (or not). Recent research has shown that the efficiency of the exchange has declined, which is in stark contrast to the expectations if the exchange is composed of larger capitalization stocks than was the case in the past (Kulikova et al, 2024). To this end, the study explores indices of large, mid and small cap stocks and apply the same rolling window GARCH analysis them to determine whether the efficiency of larger or smaller cap stocks has changed.
Objectives:
  • The objective of the study is to determine if the efficiency of the JSE has changed over time.
  • Determine whether efficiency has changed for large, mid and small cap stocks over time.

2. Research Design

The intuition behind the use of a model such as GARCH, which allows for conditional excess variance, is that shocks are expected in price series and that the model needs to be able to capture such shocks. Fama and French (1988) decomposes these shocks into temporary and permanent shocks as well as noise. Permanent shocks are long term whereas temporary shocks dissipate over the medium term while noise can be attributed to market frictions or essentially irrational investors mispricing, or even over and under reacting (DeBondt and Thaler, 1985). Frequent temporary fluctuations of significant magnitude may be a strong indication of inefficiency (Spierdijk et al, 2012). Having frequent price movements and subsequent reversals away from the mean growth path is likely an indication that the pricing of the stock is somewhat driven by incorrect pricing, a feature of inefficiency. The phenomenon is otherwise known as mean reversion and has been the subject of fervent debate in the literature, however, it has been well established that some degree of mean reversion is present on the JSE (Mangani, 2008).
There are various tests for efficiency, however, not all tests give an indication of the level of efficiency. Mangani (2008) shows that a GARCH (1,1) model fits the return series of the JSE better than more complex alternative specifications of the model, or similar complex models. Fitting a GARCH (1,1) model to the data allows for an estimation of the speed of mean reversion which in turn, provides an indication of the level of efficiency of the stock exchange (Owido et al, 2013; Narayan et al, 2016; Ayadi & Pyun, 1994). The speed of mean reversion is directly related to the efficiency of a stock exchange by the relationship between irrational price changes and the frequency of price fluctuations that deviate from the mean growth path (Spierdijk,et al, 2012). While it is also a measure of volatility, it gives and indication of the efficiency of the price determination. The study employed a rolling window application of a GARCH (1,1) model to determine the efficiency of pricing on the JSE over a twenty-eight year period (1995 to 2024). The daily, weekly and monthly share indices for small, mid and large capitalization stocks as well as the all share index (ALSI) was collected from IRESS which is a private data aggregator of publicly availabe information.
For the main analysis, the collected indices were analyzed with a rolling window application in STATA with one-year windows. To ensure the validity of the main analysis, the data was then also split into various static time windows in such a manner that there are enough observations to perform an analysis, but while providing insights into these distinct time periods to ascertain whether the changes observed in the primary analysis is indeed present in throughout the various sub periods. As measures of robustness, the variance ratio (Lo and MacKinley, 1988), the Augmented Dickey- Fuller (ADF) test and the ARCH effects test (Engel, 2001) were run to ensure that the data are indeed mean reverting. For robustness of the speed of mean reversion analysis the ADF based half-life test, which provides a measure of the speed of mean reversion was calculated to ensure the validity of the primary findings.
The general GARCH(1,1) model is specified as follows:
yt = α0 + πyt−1 + εt
Where a0 is a constant to be estimated,
π is the auto-correlation parameter to be estimated,
yt-1 is one lag length of the dependant variable y and
εt will follow a first order GARCH model.
The error, εt, will follow a random path with decomposing shocks. Specifically, the error term from is defined as follows (Narayan et al, 2016: 124):
εt = ɳt √ht, where ht = x + αε2t-1 + βht-1
Where nt, is an i.i.d. sequence of independent random variables with a mean of zero, zero-unit variance and is stationary. The model is implemented with α0 >0, y> 0 , β > 0 and α + β >= 0 (Engle, 2001).
ht is influenced by past movements of variance and the error and consist of,
x which is an estimated constant in the form of the long run variance of the returns series in this application,
α, which is the coefficient estimated from the past observed squared residuals of the returns, ε2, and
β, is the estimated co-efficient from the past conditional variance of the returns series, h.
Alpha (α), which is the variance of the returns series and beta (β), which is the most recent residual, when summed, gives an indication of the degree and speed of mean reversion present in the series. If summed to less than one, some degree of mean reversion is present and differences in the degree of mean reversion can be explored by interrogating this relationship in a GARCH model. The nearer the summed value is to zero, the quicker mean reversion takes place, conversely, the nearer the summed value is to one, the slower the reversion. The intuition is this study specifically is thus that a factor nearer to one is an indication of efficiency while the opposite being true with regards to lower efficiency.
The Philips- Peron test for autocorrelation with a 15 period lag (10 for monthly data) was fitted to the residuals after the GARCH (1,1) model fitting to ensure that the model captures expected serial correlation in the data adequately. As a further measure of robustnees, the augmented Dicky- Fuller (ADF) test for a unit root was fitted for each series with a similar lag length to that of the main analysis because it allows for a determination of the speed of mean reversion also. The test takes the form:
∆ R t = α − λ R t − 1 + ∑ j = 1 k ϕ j R t − 1 + ω t
Where:
R t is the continuously compounded return on an asset at time t.
α is a constant.
ω t is a stationary shock term with an unconditional mean of zero which may be serially correlated.
∑ j = 1 k ϕ i is a return differential that may use different order lags to remove the serial correlation in ω t + 1 i .
λ measures the speed of mean reversion where values close to one signifies a slow reversion and lower values a higher speed of mean reversion.
A p-value below 0.05 would lead to the rejection of the null hypothesis, that a unit root is present in the series whereas a larger p-value would indicate a random walk. The half-life, a measure of the speed of reversion based on lambda (λ), can be used to verify the findings from the GARCH (1,1) model. The calculation of the speed of reversion is as follows (Shen & Holmes, 2014):
H L = l n ⁡ ( 2 ) λ
A higher value (up to one) indicates a slower speed of reversion and vice versa.
The fitting of the ADF models and the test of the how well the GARCH model accounted for serial correlation was also supplemented by the running of diagnostic statistics to ensure that the data was indeed of the expected form; serially correlated and with ARCH effects. To this end, an OLS model was fitted to the data and the residuals checked for the presence of ARCH effects by applying Engle’s (1982) Lagrange Multiplier test to the residuals where a p-value below 0.05 indicates the presence of ARCH effects.

3. Results

The analysis was conducted on time series data comprised of several time series. The data was saved into full time series and various windows (of which the length differs slightly according to the return horizon to allow for adequate data for each analysis).
A descriptive overview of the data is provided in Table 1.

3.1. Descriptive Statistics and Diagnostics

The index values from 1995 to 2024 were collected with 7200 observations at a daily return horizon, 1500 at a weekly horizon and 350 at a monthly horizon. There are stark differences in the standard deviation of the returns across the different horizons with it being clear that large deviations are more prevalent at daily horizons. Similarly, the standard deviation at a weekly horizon is generally smaller than at the monthly horizon. For the primary, rolling window GARCH (1,1) analysis, the daily returns over the full period were used and one year rolling windows applied with the GARCH analysis applied to the preceding four years of data. For the sake of robustness checks, static windows were also chosen, somewhat at random but covering distinct time periods with similar amounts of observations. The windows compiled at the daily and weekly horizons were as follows: 1995 – 2005; 2006 – 2016; 2014 – 2024. At the monthly horizon, the windows were: 1995 – 2008, 2003 – 2010, 2011 – 2024. This included significant overlap; however, it was the only way to ensure a reasonably sufficient amount of data points to ensure an accurate fit of the model.
An OLS regression was fitted to each index and the residuals tested for the presence of ARCH effects with H0, being ARCH effects not being present, was rejected for all four indices with p-values far below the cut-off of 0.05. For the full indices as well as the static windows compiled from the indices, the Philips Peron and Augmented Dickey- Fuller tests (with 15 lags for daily and weekly horizons and 10 lags for monthly horizons) was tested. In all cases, both tests had p-values below the critical value of 0.05 indicating serial correlation. Further to this, the variance ratio test was done for all indices and windows with all results indicating serial correlation. Hence, in all cases, mean reversion is present across the main index, sub- indices and static windows as indicated by the various diagnostic tests performed.

2.2. Rolling Window Regression Results

The primary analysis that was performed was a rolling window GARCH (1,1) estimation. The results from this estimation is presented in Table 2 below.
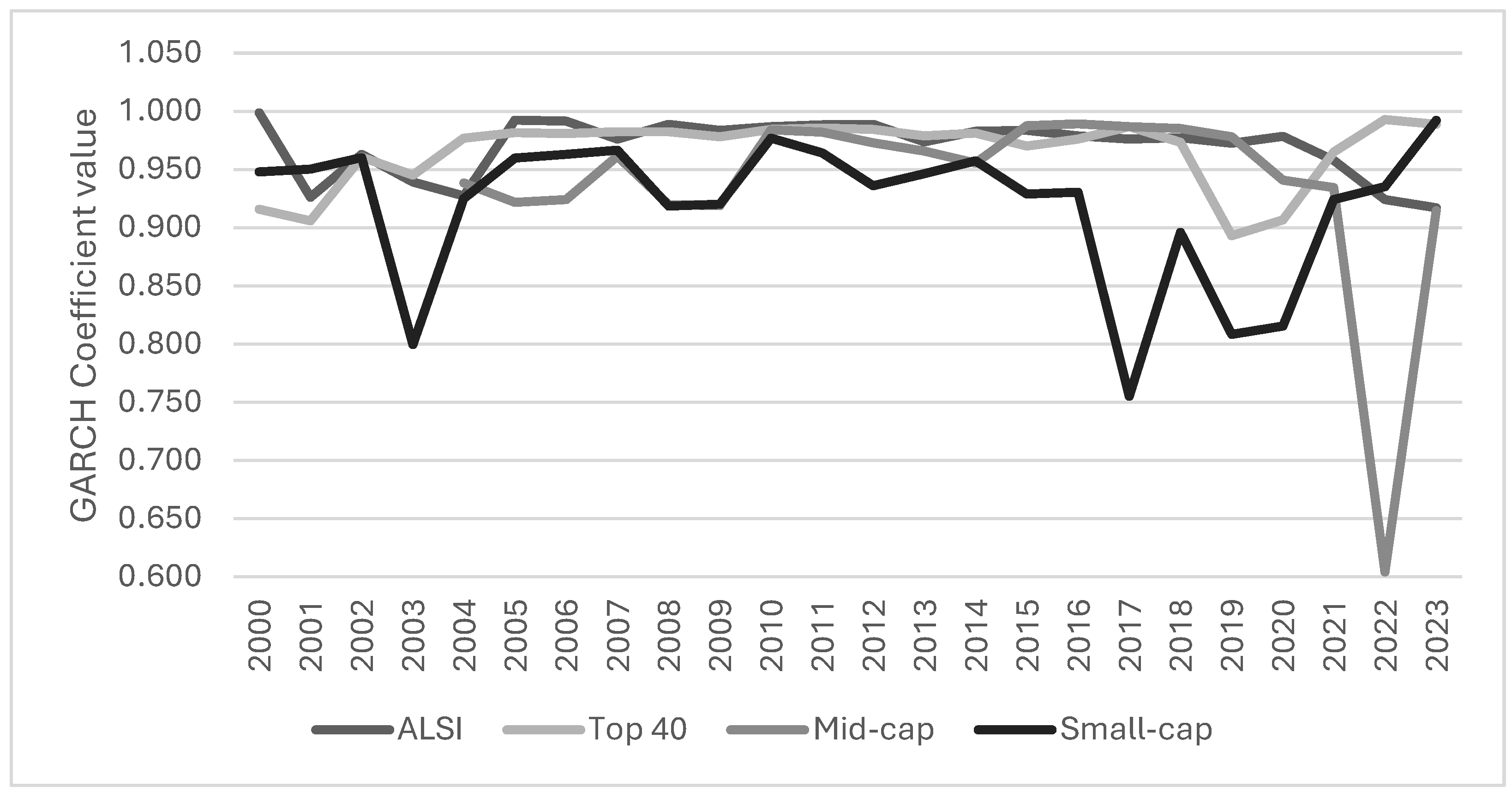
The results of the rolling window analysis based on daily returns with a moving window of one year, but based upon the preceding four years of data, led to the GARCH (1,1) estimation being fitted from 2000 to 2023 despite the sample starting in 1995. The primary concern of this present study was to determine whether the JSE’s efficiency has changed. Based upon the results in the ALSI column of Table 2, where the sum of alpha and beta is presented for each window, the efficiency of the exchange seems to have changed over time. In recent years, the efficiency of the exchange does seem to have decreased somewhat. Throughout much of the sampled time, the coefficient regulating the speed of mean reversion of the exchange is rather close to one or near 0.98 where it clearly drops from 2020 to 2023, leading to an increased speed of reversion and subsequently a decrease in efficiency. Interestingly, the only other time in the sample where the rate dropped as low as it is currently, was in 2001 when the South African economy was severely affected by the recession and the Rand devalued by over 20% in the market. This year however was anomalous, and a repeat was not seen during the 2008 financial crisis. The current trend however seems to start in 2011 and continues to the present, therefore, it likely is not an occurrence tied to a specific event.
The Top 40 index on the other hand seems to exhibit increased efficiency in the recent past and presently. It is however interesting to note the efficiency level being lower than that of the all share index over most years, this may be an indication of co-movement between critically integrated large companies that are listed, whatever the reason may be. The Top 40 is however, as with the ALSI, seemingly close to efficient in terms of not displaying erratic price reversals as indicated by the relatively stable speed of mean reversion. Importantly, both indexes do not exhibit large changes in this speed over time. The mid-cap and small-cap indexes however are not as stable and have some large year on year fluctuations in terms of their speed of mean reversion. The mid-cap index did not have a good fit from 2000 to 2003 for the GARCH(1,1) model and these years were omitted from the analysis. The mid-cap index shows a relatively stable, seemingly slow mean reversion speed indicating relative efficiency but with a trend towards a lower level of efficiency over the past decade with 2022 standing out as an anomalous year on the index. The small cap index showed the most variation in its speed of mean reversion with seemingly, for most years, significantly less stable prices than the other indices. In 2023 however, this is reversed, and the index had an anomalous year with a close to efficient price reversals. It is difficult to draw conclusions directly from the above table, but, given the secondary objective of this study, which was to determine if small companies influenced the efficiency of the JSE, it seems plausible that at least over certain time periods that this could have been the case.
A graphical representation of the results from the rolling window GARCH (1,1) analysis is presented below in Figure 1.
While 2023 in particular seemed to be a good year regarding the efficiency for the small-cap and Top 40 indices, the prior decade seemingly experienced a divergence of efficiency across the different sized stocks on the exchange. The stock exchange overall, proxied for by the ALSI, declined in efficiency estimated in this manner.

2.3. Static Window Regression Results

The results of the rolling window analysis showed the changes in the speed of mean reversion on an annual basis (but based on four years of preceding data). To ensure that the findings are not based on anomalous data or economic events that are difficult to tie directly to the observed changes in efficiency, static windows were also investigated. In this section, the ADF model and the half-life derived from the regression is reported together with the GARCH (1,1) coefficient. In Table 3, the results of the GARCH (1,1) model are shown across indices, windows and return horizons.
The results from the analysis are interesting in that at a daily horizon, the speed of mean reversion is increasing and subsequently, it is likely that the efficiency of the exchange may be inching lower. This is an important finding as it confirms the trend observed in the rolling window analysis and identified in prior research (Kulikova et al, 2024). While arguably marginal, the effect is also present at a daily horizon for the Top 40 index of large companies while it is a similar scenario for the mid-cap and small-cap indices. This is confirmatory evidence for the rolling window analysis. While there is a decrease in efficiency, it is not of an order of magnitude that suggests that the stock exchange has become wholly inefficient. The results merely indicate that there are certainly more frequent price fluctuations that are reversed quickly and while that is of concern, this study does not attempt to delve into the matter of exactly how efficient the market is and what form of efficiency is presently the case. It is also difficult to draw the conclusion that small and medium size stocks are driving the efficiency of the exchange. The Top 40 is marginally more efficient than the other three indices in the third window at a daily horizon, which is expected given the probable higher trading volume and analyst following, amongst other factors, that these stocks attract. Considering the overall picture however, it is evident that for the most part, efficiency has declined across all the indices across all time horizons. The decline for the Top 40 index has been the slightest, however, it has nonetheless been in a decline. At longer return horizons the decline is more evident, although the results from the monthly windows are to be read with caution as there was barely enough data for a wholly reliable estimate. The trend however is similar to that at the weekly horizon, a decline in efficiency for all indices in the third window.
The results for the ADF half-life analysis are presented in Table 4.
The results from the ADF half-life analysis are confirmatory of the results in the rolling window and static window GARCH analysis. The efficiency of the exchange declines from Window 1 to 3 at the daily and monthly horizon. At a weekly horizon, there is a slight decrease in the speed of mean reversion in window 2, but there is still a decline in efficiency from window 1 to 3. The Top 40 index also declines at a daily horizon and at a monthly horizon but shows a slight increase in the third window at a weekly return horizon. The mid-cap index, at a daily horizon, shows a marked increase in efficiency however from the second to third window while the small-cap index shows a marked decline in efficiency. For the most part, despite some contradictions with the GARCH (1,1) model, the ADF half-life analysis paints a similar picture of an increase in the speed of mean reversion and therefore, a probable decline in the efficiency of the exchange.

3. Discussion and Conclusion

Prior studies (Kulikova et al, 2024; Heymans & Santana, 2018; Nkani & Holland, 2023; Kotze, 2023) pointed towards a changing stock exchange and a change in efficiency of the stock exchange. While the stock exchange cannot be said to be perfectly efficient, that was never the case and in most cases stock exchanges are weak form efficient. While the study only attempted to ascertain whether the level of efficiency of the stock exchange has changed over time, the stock exchange is likely still weak form efficient, and the changes observed is not of such a magnitude as to say that the stock exchange is wholly inefficient. It is however clear from the results that there has been a slight decline in the overall efficiency of the JSE over the past decade. This is consistent with the findings of Kulikova et al (2024). The first objective of the study was to determine whether the efficiency of the JSE has changed, and the data certainly points us in this direction. Given that it is difficult to gauge the level of efficiency and the literature is sparse on methods but taking into account the decomposition of returns and in Fama & French (1988) and the features of inefficiency (DeBondt & Thaler, 1985), the results are interpreted within the relationship between the speed of mean reversion and the relationship thereof with efficiency (as in Spierdijk, 2012) to show a clear but small decline in the efficiency of the JSE.
The various sub-indices studied also shows a general decline in efficiency for the most part, especially between 2014 and 2023. There are some exceptions in the rolling window analysis, but, when the static windows were used, these for the most part averaged out. There is thus a definite decline in the efficiency of the JSE over the period under study. It is difficult to point to a particular driver of this decline. The JSE Top 40 showed a decline of a similar magnitude over the study period which contradicts the notion that small and mid-cap stocks are the primary drivers of this decline.
As can be seen in Table 5, there is a decline across all indices from window 2 to window 3. The only instances where was an increase in efficiency, was from window 1 to 2 for the ALSI, mid and small cap indices at a monthly horizon. The subsequent fall from window two to window three however strongly reverses this. From Table 5, one can see that there is no sub-index over the study period that consistently fell at a higher rate than the ALSI did. While not shown here for brevity, an investigation of the rolling window analysis shows that on average, the sub-indices remain at roughly the same level as compared to the ALSI when averaged over the course of the study period. While previous studies have speculated that the large companies on the JSE will be efficiently traded and the changed composition of the exchange may lead to higher efficiency, this does not seem to be the case. Overall, the exchange is slightly less efficient indeed, and this applies across the exchange for the most part, but the efficiency of the sub-indices do not indicate a specific primary sub-index driving this change. Possibly, it may be that there is another, un-investigated, driver of inefficiency, but in this present study, it was not found that inefficiency is driven by smaller companies but rather, that the efficiency of the exchange as a whole is declining. A future study considering individual stocks, their individual characteristics, their change in efficiency over time and their subsequent effect on the exchange overall, would be an important addition to the literature to further our understanding of what drives the observed decline in efficiency.

Funding

This research received no external funding.

Data Availability Statement

The data used is publicly available, however, for this study the data was gathered from a private data provider, namely IRESS, which aggregates the data and allows transformations regarding the share return horizons. The data is therefore only available on request.

Acknowledgments

The author wishes to thank participants at the African Finance Association conference for their helpful inputs to improve the paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Arashi, M. and Rounaghi, M.M. Analysis of market efficiency and fractal feature of NASDAQ stock exchange: Time series modeling and forecasting of stock index using ARMA-GARCH model. Future Business Journal 2022, 8, 14. [Google Scholar] [CrossRef]
  2. Ayadi, O.F. and Pyun, C.S. An application of variance ratio test to the Korean securities market. Journal Of Banking & Finance 1994, 18, 643–658. [Google Scholar]
  3. Bae, K.H. , Bailey, W. and Kang, J. Why is stock market concentration bad for the economy? Journal of Financial Economics 2021, 140, 436–459. [Google Scholar] [CrossRef]
  4. Bailey, G. and Gilbert, E. The impact of liquidity on mean reversion of share returns of the JSE. Investment Analysts Journal 2007, 36, 19–29. [Google Scholar] [CrossRef]
  5. De Bondt, W.F. and Thaler, R. Does the stock market overreact? The Journal of Finance 1985, 40, 793–805. [Google Scholar] [CrossRef]
  6. Engle, R. ARCH/GARCH Models in applied econometrics. The Journal of Economic Perspectives 2001, 15, 157–168. [Google Scholar] [CrossRef]
  7. Engle, R.F. Wald, likelihood ratio, and Lagrange multiplier tests in econometrics. Handbook of Econometrics 1984, 2, 775–826. [Google Scholar]
  8. Fama, E.F. and French, K.R. Permanent and temporary components of stock prices. Journal of Political Economy 1988, 96, 246–273. [Google Scholar] [CrossRef]
  9. Fama, E.F. The behavior of stock-market prices. The Journal of Business 1965, 38, 34–105. [Google Scholar] [CrossRef]
  10. Heymans, A. and Santana, L. How efficient is the Johannesburg Stock Exchange really? South African Journal of Economic and Management Sciences 2018, 21, 1–14. [Google Scholar] [CrossRef]
  11. Jiang, J. Cross-sectional variation of market efficiency. Review of Accounting and Finance 2017, 16, 67–85. [Google Scholar] [CrossRef]
  12. Koptyug, N. , Persson, L and Tåg, J. Should we worry about the decline of the public corporation? A brief survey of the economics and external effects of the stock market. The North American Journal of Economics and Finance 2020, 51, 101061. [Google Scholar] [CrossRef]
  13. Kotze, P.N. Share price reactions to setting the record straight press releases: evidence from the Johannesburg Stock Exchange. Review of Economics and Finance 2023, 21, 1189–1194. [Google Scholar] [CrossRef]
  14. Kulikova, M.V. , Taylor, D.R. and Kulikov, G.Y. Evolving efficiency of the BRICS markets. Economic Systems 2024, 48, 101166. [Google Scholar] [CrossRef]
  15. Lo, A.W. and MacKinlay, A.C. Stock market prices do not follow random walks: Evidence from a simple specification test. The Review of Financial Studies 1988, 1, 41–66. [Google Scholar] [CrossRef]
  16. Mangani, R. Modelling return volatility on the JSE securities exchange of South Africa. African Finance Journal 2008, 10, 55–71. [Google Scholar]
  17. Mlambo, C. and Biekpe, N. The efficient market hypothesis: Evidence from ten African stock markets. Investment Analysts Journal 2007, 36, 5–17. [Google Scholar] [CrossRef]
  18. Narayan, P.K. , Liu, R. and Westerlund, J. A GARCH model for testing market efficiency. Journal of International Financial Markets, Institutions and Money 2016, 41, 121–138. [Google Scholar] [CrossRef]
  19. Nikani, A. and Holland, M., 2022. Why Do Public Companies Go Private? The Case of the Johannesburg Stock Exchange. SSRN (accessed: September 10, 2022).
  20. Noakes, M.A. and Rajaratnam, K. Testing market efficiency on the Johannesburg Stock Exchange using the overlapping serial test. Annals of Operations Research 2016, 243, 273–300. [Google Scholar] [CrossRef]
  21. Spierdijk, L. , Bikker, J.A. and Van den Hoek, P. Mean reversion in international stock markets: An empirical analysis of the 20th century. Journal of International Money and Finance 2012, 31, 228–249. [Google Scholar] [CrossRef]
Preprints 138155 g001
Figure 1. rolling window analysis.
Figure 1. rolling window analysis.
Preprints 138155 g001
Table 1. Descriptive statistics.
Table 1. Descriptive statistics.
Horizon n Mean (ln of return) Standard deviation
All Share index
Daily 7167 0.04% 12.11%
Weekly 1517 0.18% 2.64%
Monthly 349 0.79% 4.40%
Top 40 index
Daily 7214 0.04% 13.16%
Weekly 1519 0.18% 2.87%
Monthly 348 0.79% 5.46%
Mid-cap index
Daily 7169 0.04% 54.81%
Weekly 1519 0.18% 8.54%
Monthly 348 1.07% 7.45%
Small-cap index
Daily 7169 0.04% 0.76%
Weekly 1519 0.17% 1.94%
Monthly 348 0.75% 4.88%
Table 2. Results from the rolling window GARCH (1,1) analysis.
Table 2. Results from the rolling window GARCH (1,1) analysis.
Year ALSI Top 40 Mid-cap Small-cap
2000 0.999 0.916 N/A 0.948
2001 0.926 0.906 N/A 0.950
2002 0.963 0.961 N/A 0.960
2003 0.939 0.945 N/A 0.799
2004 0.927 0.977 0.938 0.925
2005 0.992 0.982 0.922 0.960
2006 0.992 0.981 0.924 0.963
2007 0.976 0.982 0.962 0.966
2008 0.989 0.982 0.920 0.918
2009 0.984 0.978 0.919 0.920
2010 0.987 0.984 0.984 0.977
2011 0.988 0.986 0.982 0.964
2012 0.989 0.985 0.973 0.936
2013 0.974 0.979 0.966 0.946
2014 0.983 0.981 0.955 0.958
2015 0.984 0.970 0.988 0.929
2016 0.979 0.976 0.989 0.931
2017 0.976 0.987 0.987 0.755
2018 0.977 0.973 0.985 0.896
2019 0.972 0.893 0.978 0.808
2020 0.979 0.907 0.941 0.816
2021 0.958 0.965 0.934 0.924
2022 0.924 0.993 0.604 0.935
2023 0.917 0.989 0.915 0.992
Table 3. Results from the static GARCH analysis.
Table 3. Results from the static GARCH analysis.
Daily
ALSI Top 40 Mid-cap Small-cap
Window 1 0.990 0.985 N/a 0.981
Window 2 0.987 0.985 0.983 0.972
Window 3 0.948 0.973 0.965 0.955
Weekly
ALSI Top 40 Mid-cap Small-cap
Window 1 0.999 0.990 N/a 0.982
Window 2 0.974 0.973 0.979 0.929
Window 3 0.722 0.706 0.886 0.925
Monthly
ALSI Top 40 Mid-cap Small-cap
Window 1 0.837 0.986 0.878 0.927
Window 2 0.839 0.920 0.978 0.996
Window 3 0.598 0.580 0.685 0.667
Table 4. Augmented Dickey Fuller half- life results for the static windows analysis.
Table 4. Augmented Dickey Fuller half- life results for the static windows analysis.
Daily
ALSI Top 40 Mid-cap Small-cap
Window 1 0.779 0.715 N/A 0.950
Window 2 0.700 0.666 0.686 0.730
Window 3 0.693 0.654 0.753 0.722
Weekly
ALSI Top 40 Mid-cap Small-cap
Window 1 0.753 0.730 0.686 1.118
Window 2 0.630 0.619 0.730 0.900
Window 3 0.660 0.660 0.648 0.779
Monthly
ALSI Top 40 Mid-cap Small-cap
Window 1 0.963 0.666 0.770 0.950
Window 2 0.924 0.648 0.797 0.950
Window 3 0.707 0.613 0.722 0.835
Table 5. Change in speed of mean reversion (GARCH static window analysis) summary.
Table 5. Change in speed of mean reversion (GARCH static window analysis) summary.
Change between period ALSI Top 40 Mid-cap Small-cap
Daily
Detla 1-2 -0.24% -0.08% N/A -1.02%
Delta 2-3 -3.95% -1.19% -1.81% -1.70%
Weekly
Delta 1-2 -2.43% -1.70% -5.37%
Delta 2-3 -25.95% -27.50% -9.51% -0.46%
Monthly
Delta 1-2 0.27% -6.65% 11.30% 7.39%
Delta 2-3 -28.76% -36.99% -29.96% -32.98%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated