Prerpints.org logo
Preprint
Article

Lunar Calendar Usage to Improve Forecasting Accuracy Rainfall by Machine Learning Methods

Altmetrics

Downloads

52

Views

29

Comments

0

Submitted:

30 October 2024

Posted:

04 November 2024

You are already at the latest version

Alerts
Abstract

The lunar calendar is often overlooked in time series data modelling, despite its importance in understanding seasonal patterns as well as economic, natural phenomena, and consumer behavior. This study aims to investigate the effectiveness of the lunar calendar in modelling and forecasting rainfall levels using various machine learning methods. The methods employed included Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) models to test the accuracy of rainfall forecasts based on the lunar calendar compared to those based on the Gregorian calendar. The results indicated that machine learning models incorporating the lunar calendar generally pro-vided greater accuracy in forecasting for periods of 3, 4, 6, and 12 months compared to models using the Gregorian calendar. These findings contributed to the advancement of forecasting techniques, machine learning, and the adaptation to non-Gregorian calendar systems, while also opening new opportunities for further research into lunar calendar applications across various domains.

Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Forecasting time series data, particularly for monthly predictions, is closely tied to the calendar system used. Adjustments to the number of days in a month, whether in the Gregorian or Lunar calendar, can influence the accuracy of forecast results [1,2]. Therefore, using the appropriate calendar system for forecasting can lead to more accurate seasonal projections and monthly trends [3]. Additionally, precise monthly forecasting aids in planning and decision-making, such as disaster mitigation in cases of extreme rainfall [4,5]. In agriculture, accurate forecasts are especially valuable for the early planning of planting seasons [6,7,8]. In environmental field, accurate forecasting is needed to anticipate disaster such us floods and landslide [9].
The Gregorian calendar and the Lunar calendar are two of the world's most widely used calendar systems. Each provides a unique perspective on timekeeping. Both affect how time series data is analyzed and predicted [10]. The Gregorian calendar, which is based on the solar cycle, enables consistent scheduling in the context of international business [11]. In contrast, the Lunar calendar, which follows the lunar cycle, is often used to plan religious events in Asian and Middle Eastern countries [12,13]. These calendar system differences can affect how we forecast seasonal phenomena, such as rainfall or consumption patterns [14].
The Gregorian calendar is often used to model and forecast rainfall levels in different countries. The use of this calendar as the basis for modeling time series data has been used for various statistical models [15,16]. Time series models, such as ARIMA and Exponential Smoothing, are often applied with data compiled according to the Gregorian calendar [17,18,19]. The forecasting time interval is adjusted to the research needs daily, monthly, and yearly. The performance of the statistical model is evaluated by various measures such as MAPE (Mean Absolute Percentage Error) and MSE (Mean Square Error) [20,21].
Forecasting using the AD calendar often involves machine learning models to improve forecasting accuracy. These machine-learning models can help identify seasonal patterns and trends that may not be obvious [22,23]. Models such as LSTM and Bi-LSTM are used for forecasting according to the AD calendar [24,25,26]. Furthermore, the GRU and Bi-GRU models appear to correct the LSTM model parameters for forecasting [27,28].
However, forecasting using the AD calendar often gives less accurate results because this calendar does not always match specific seasonal patterns. One of the main causes is the incompatibility between the annual cycle of the Gregorian calendar and the natural cycles that may follow different patterns, such as the lunar cycle or the local climate [10]. Additionally, the A.D. calendar may sometimes not reflect significant seasonal fluctuations [29]. Therefore, forecasting models that rely on the AD calendar need to be adjusted or combined with other more suitable calendars to improve the accuracy of prediction results [30].
The lunar calendar can be used for time series data modeling, but its use is still limited among researchers. Many researchers prefer the Gregorian calendar because it is more commonly used and supported by many analysis software [31]. Although the lunar calendar has great potential to capture unique seasonal patterns, few have explored its advantages yet [32]. Further research is needed to develop better methods of using the lunar calendar. Thus, the lunar calendar could become a more popular tool in time series data analysis.
Using lunar calendars in various software such as R is still limited. Currently, there is no custom conversion for the month calendar like the one on the Gregorian calendar [33]. This limitation makes data analysis using a lunar calendar more complicated. Users must perform manual conversions or use additional plans to support monthly calendar-based analysis. The development of the automatic conversion feature of the month calendar in R software is urgently needed to make it easier to forecast time series data.
Machine learning methods for forecasting have not been widely used in the lunar calendar. Most research and machine-learning applications still focus on the Gregorian calendar [34,35,36]. The lack of datasets that support the lunar calendar is one of the main obstacles. In addition, existing machine learning algorithms have not been fully adapted for conversion to the lunar month. Therefore, more research is needed to develop more effective methods in lunar calendar-based forecasting.
The urgency of this research stems from the need to enhance the accuracy of rainfall forecasting, which can serve a wide array of purposes, including flood prediction, disaster mitigation, and more. To address precipitation forecasting while considering the lunar calendar, we propose machine learning-based solutions that integrate historical precipitation data with lunar calendar information to improve forecast accuracy. The goal of this research is to model and predict rainfall rates using various machine learning models based on the lunar calendar, and to compare these results with forecasts generated using the Gregorian calendar.

2. Materials and Methods

The techniques employed for rainfall prediction include Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU). The LSTM and GRU models used in this study include vanilla LSTM and GRU, 2-stacked-LSTM and 2-stacked-GRU, dual-directional LSTM and two-directional GRU, and 2-stacked-biLSTM and 2-stacked-biGRU.
The difference between LSTM and GRU was in the number of gates and memory cells. In LSTM, the number of gates was three, and the number of memory cells was two. On the other hand, GRU had two gates and one memory cell. BiLSTM was similar to LSTM in terms of the number of gates and memory cells, but it had two processes, forward and backward. BiGRU was also similar to GRU, but had two directional processes, forward and backward. Stacked BiLSTM and Stacked BiGRU involved a concatenation process within their architectures.

2.1. Long Short-Term Memory (LSTM)

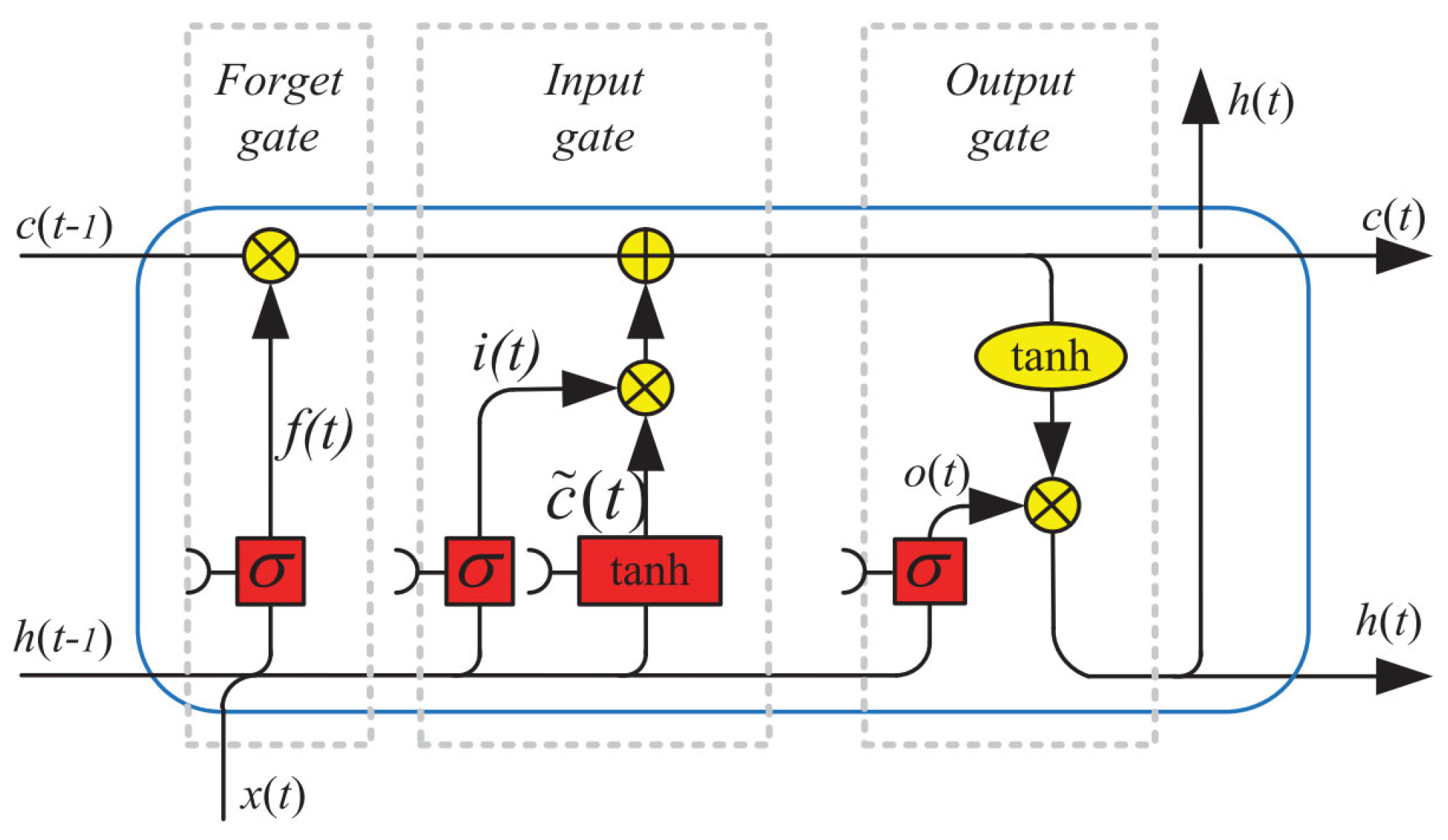
Long Short-Term Memory, or LSTM network was an extension of Recurrent Neural Networks (RNN) originally introduced by [37]. RNNs had a recurrent mechanism that flows through its layers in a recursive way, enabling it to retain information across time steps. This recurrence helps RNNs retain and utilize past information. Nevertheless, it was known that standard RNNs ware difficult to train on tasks with long-term temporal dependencies [38]. This is where LSTM comes to play, as LSTM are designed in such a way that they can keep long term dependencies and efficiently store information in memory [37,38,39]. LSTMs solve the vanishing and exploding gradient problems, making learning in RNN when dealing with long sequences much easier [40,41]. LSTMs were built with a memory cell, containing three key elements: the forget gate, the input gate and the output gate, as illustrated in Figure 1.
  • Forgate Gate
The forget gate equation governs how much of the previous cell state should be discarded:
f t = σ W f . h t − 1 , x ˜ t + b f
Where,
σ : Sigmoid activation function
f t : Forget gate that determines the extent to which previous cell state information should be forgotten,
W s : Weight matrix for the forget gate,
b s : Bias for the forget gate,
h t − 1 : Hidden state from the previous time step,
x ˜ t : Input at time (normalized rainfall data).
2.
Input Gate
The input gate equation determines how much new information should be added to the cell state:
i t = σ W i . h t − 1 , x ˜ t + b i
Where,
i t : Input gate controlling the amount of new information to be stored in the cell state.
W s : Weight matrix for the input gate.
b s : Bias for the input gate.
The new candidate information to be added to the cell state is computed as:
c ˜ t = tanh W c . h t − 1 , x ˜ t + b c
Where,
c ˜ t : Candidate cell state, representing new information to be added to the current cell state
W c : Weight matrix for updating the cell state.
b c : Bias for updating the cell state.
tanh: Hyperbolic tangent activation function.
3.
Cell State
The cell state is updated by combining the information retained by the forget gate and the new information provided by the input gate:
c t = f t . c t − 1 + i t . c ˜ t
Where,
c t − 1 : Previous cell state.
c t : Updated cell state at time
4.
Output gate
The output gate equation determines how much of the updated cell state should contribute to the new hidden state:
o t = σ W o . h t − 1 , x ˜ t + b o
Where,
W o : Weight matrix for the output gate,
b o : Bias for the output gate,
5.
Hidden State.
The hidden state is computed using the output gate and the updated cell state:
h t = o t . tanh c t

2.2. Gated Recurrent Unit (GRU)

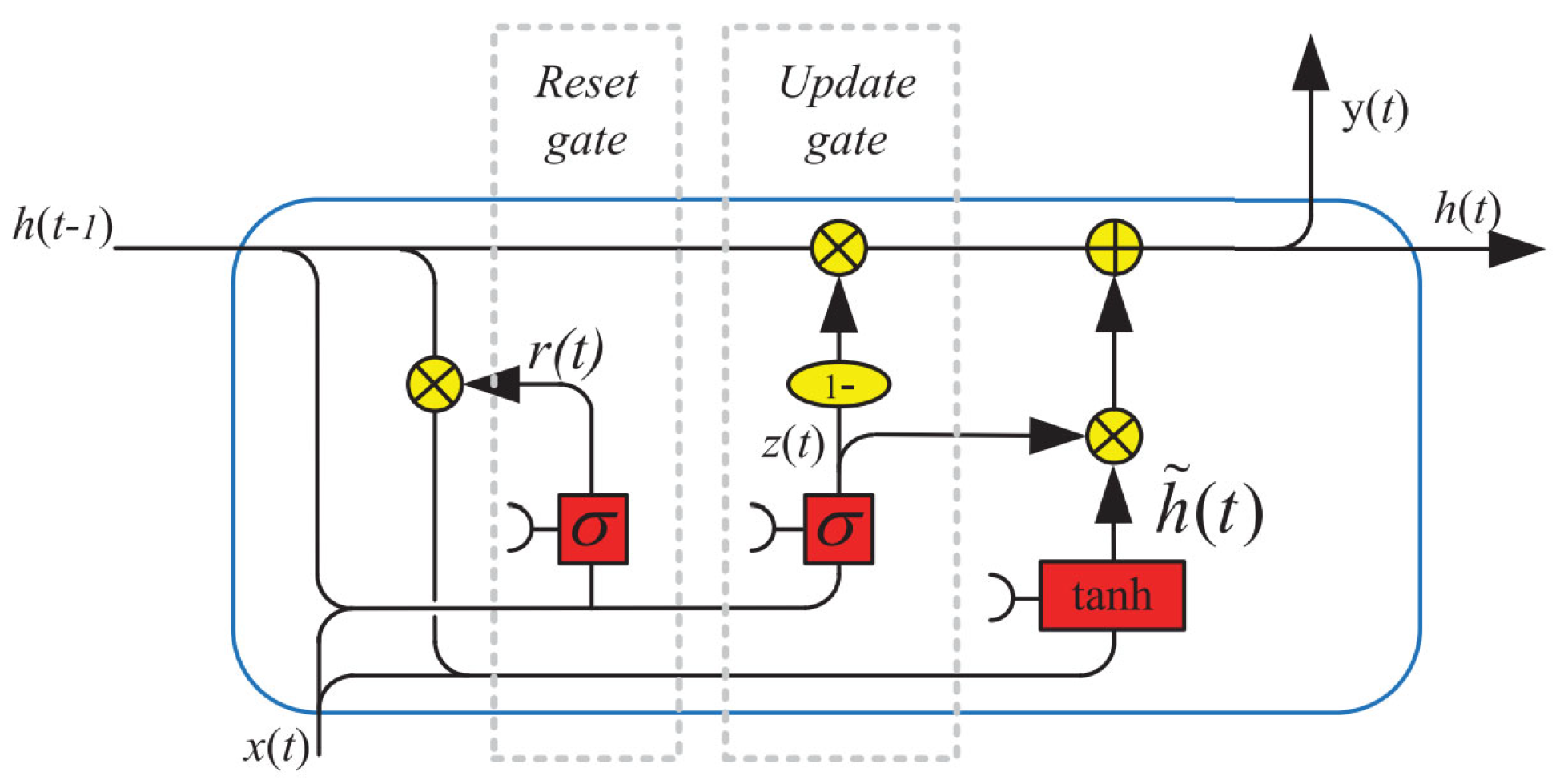
Gated Recurrent Unit, or GRU was a recent development type of RNN architecture, designed to be a more straightforward alternative to the LSTM [42]. GRU also aimed to solve the vanishing gradient problem and handling long-term dependencies in sequential data [43]. Although developed from LSTM, its calculation was considered more efficient because GRU has a simpler structure and fewer parameters [44]. Unlike LSTM which had separate memory cells and gates, GRU integrates the forget and input gate into the update gate, simplifying the architecture to reduce the number of parameters [42,43]. GRU employed only two gates: update gate and reset gate. GRU had a reset gate that determines how much of the hidden state should be considered [45]. This simpler structure enabled GRU to perform well in tasks requiring shorter sequences while remaining robust to longer sequences [46]. Figure 2 depicts the architecture of a GRU, stressing the significant distinctions from LSTM. GRU had been used successfully for machine translation, speech recognition, and other time-series applications [47,48,49].

2.3. Stacked LSTM and GRU

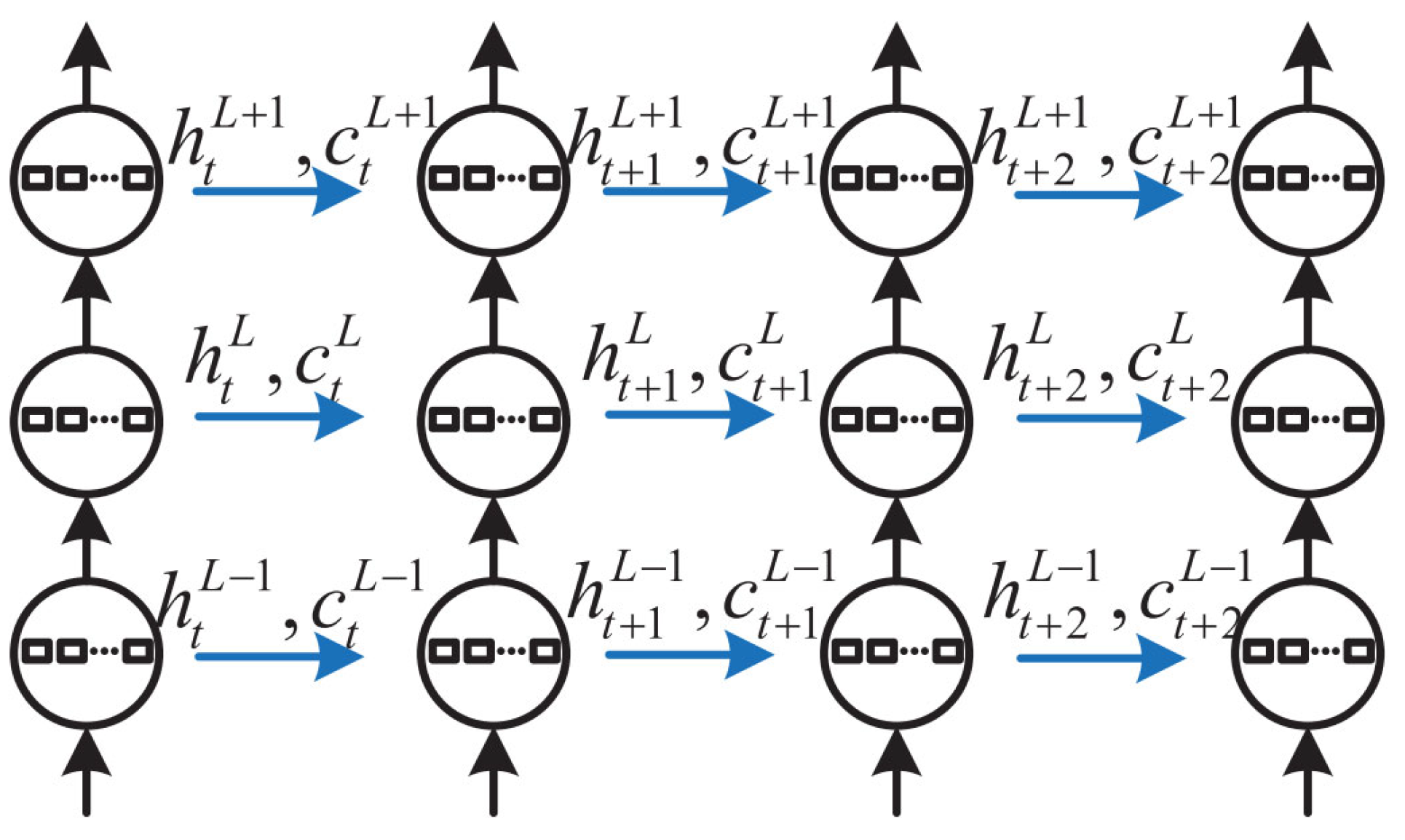
Stacked LSTM and GRU architectures ware more sophisticated variants of the LSTM and GRU architectures, where multiple LSTM or GRU layers ware arranged in sequence to improve the model’s capacity for detecting complex patterns in the data and boosting prediction accuracy [40,50]. The layers integrated the benefits of a single LSTM or GRU layer. In the lower layers, multiple LSTMs or GRUs were stacked to capture short-term dependencies and extract features that reflect the various sources of variance in the input data. These extracted representations were then merged in the higher layers that can capture long-term dependencies [49]. In stacked LSTM and GRU models, the input for the intermediate layer was determined by the computations performed in the preceding layer. Stacking can be accomplished through combining two or more layers. Stacking can be 2-stacked (two levels) or 3-stacked (three levels). Figure 3 displays the structure of stacked LSTM.

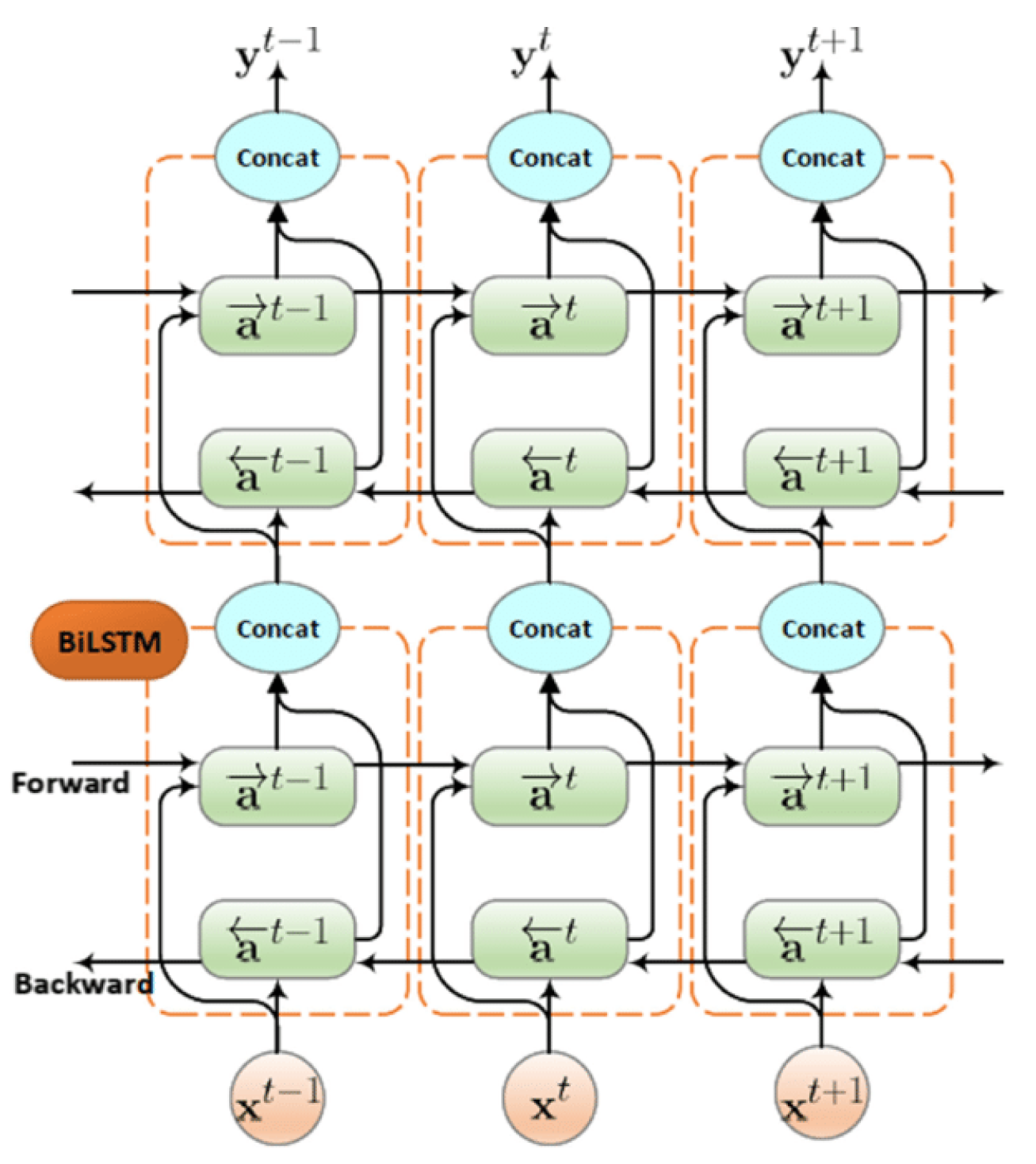
2.4. (Stacked) Bidirectional LSTM and (Stacked) Bidirectional GRU

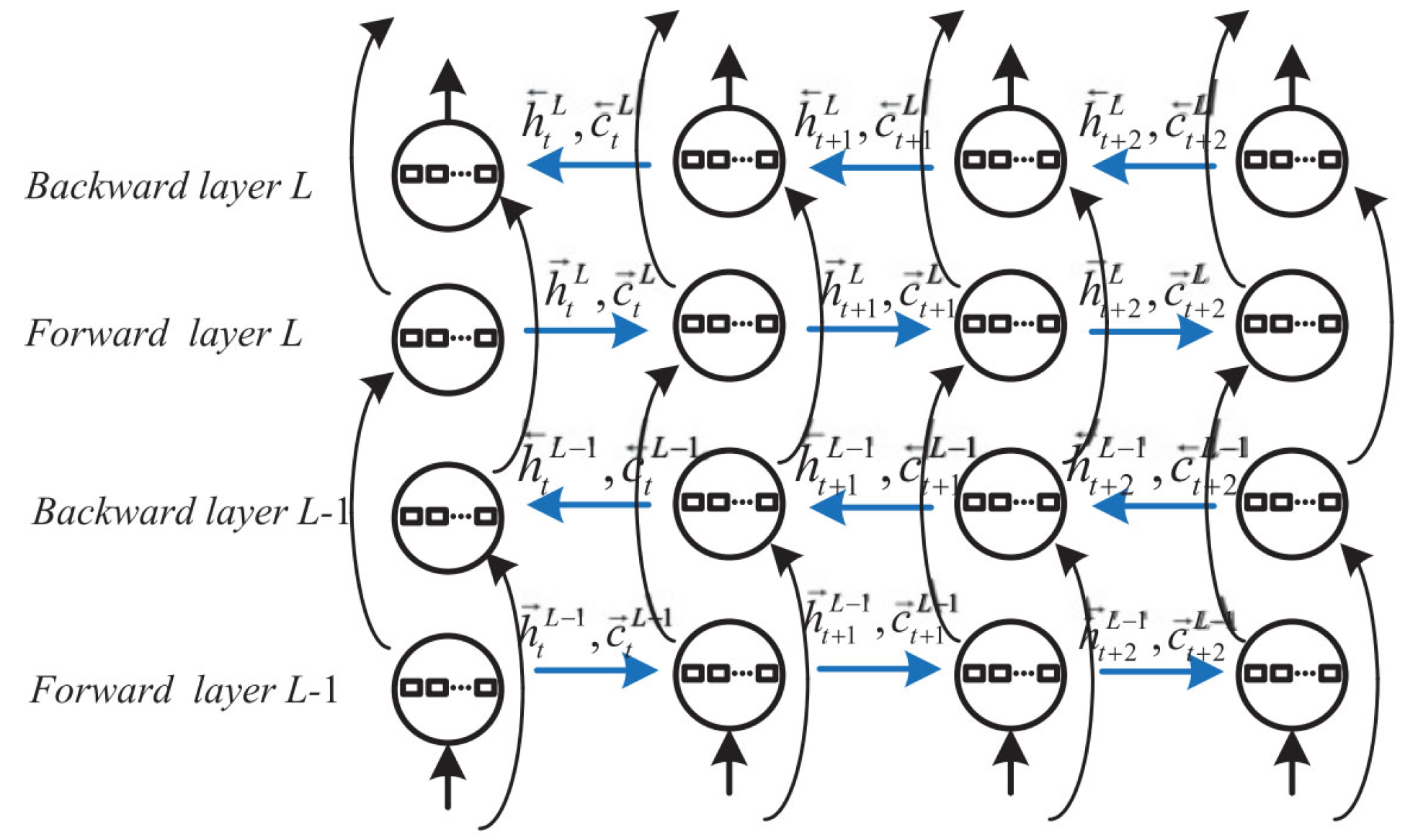
Bidirectional LSTM and Bidirectional GRU network processed the input data in both forward and backward directions by looking at the inputs of future and past context states which offers a more holistic understanding [51,52]. Two separate hidden layers were used in bidirectional models; one was for processing the input forwards, and another one to process it backwards. This method enabled the model to learn dependencies between time steps in both directions. Figure 4 shows the architecture of the BiLSTM network.
During the calculation, bidirectional LSTM and GRU would generate two h t values: ( h t ) → for the forward direction and ( h t ) ← for the backward direction [53]. These two vectors were usually added or concatenated to obtain the final hidden state. To increase their capacity and performance, bidirectional models can also be stacked, as illustrated in Figure 5 showing a stacked bidirectional LSTM network [54,55].

2.5. Preprocessing Data

Data pre-processing was used to improve data processing performance and reduce errors, ensuring high-quality data for the prediction process. The initial step in the data pre-processing procedure was data cleaning, which entails filtering the data to enhance its quality.
In addition, the second procedure involved the sharing or splitting of data by dividing it into training and testing data. Training data was utilized to train models, whilst test data is employed to assess the selection of model architecture with the optimal parameters. The study utilized a total of 286 data points for the lunar calendar and 273 data points for the Gregorian calendar. These data points would be categorized into estimated durations of 3, 6, 12, 18, and 24 months.
The third phase involved normalizing the data through the utilization of a scaling or mapping technique. Min-max normalization was a technique employed in the data normalizing process. The process of data normalization would generate values ranging from 0 to 1. The equations employed in data normalization are as follows:
x ~ n o r m ,   i = x ~ i − x ~ m i n   x ~ m a x − x ~ m i n     ; i = 1 , 2 , 3 , … , t
and data denormalization is
x ~ = x ~ ' x ~ m a x − x ~ m i n + x ~ m i n
where x n o r m , i was the normalized value of ranifall data, x m a x is the maximum value of the entire rainfall data, and x m i n   was the threshold of the entire rainfall data data.

3. Results

3.1. Calendar Conversion Results

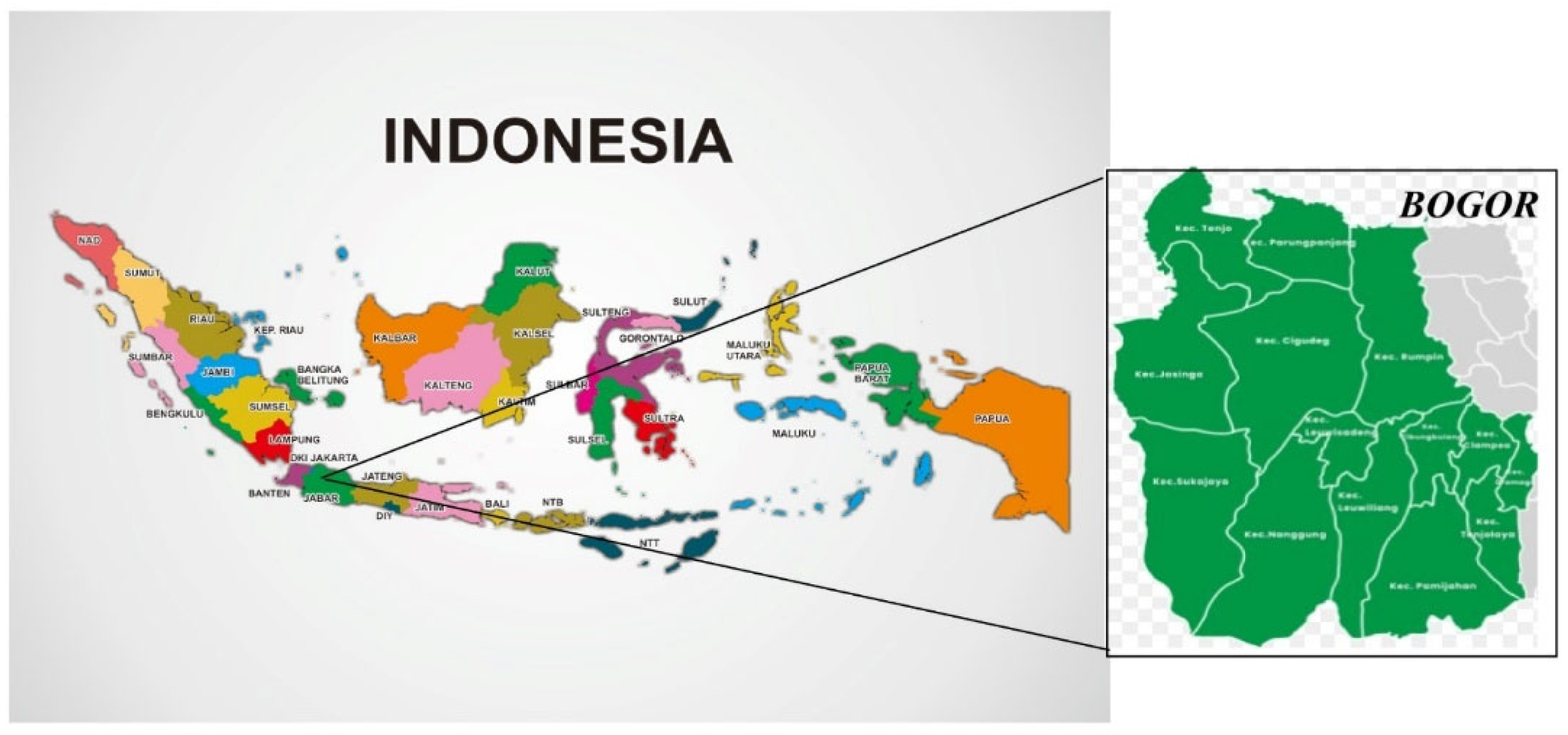
Rainfall data was obtained from Bogor city which was one of the big city of Indonesia. Bogor was selected as place for rainfall data collection because it was called as a rain city. Rainfall in Bogor city can be an indicator of flooding for Indonesia capital city, Jakarta. Figure 6 shows Bogor city which was located in West Java, Indonesia.
The rainfall daily data was collected from Bogor and was converted to monthly data in two types of calendars, Gregorian and Lunar calendar. The daily data was converted to monthly data to catch the seasonal pattern.
Table 1 displayed the outcomes of the conversion from rainfall daily data to the Gregorian calendar to the Lunar calendar. During the 22-year observation period, the Gregorian calendar consists of 273 months, whereas the Lunar calendar consists of 286 months.
After converting daily data to both the Gregorian and Lunar calendars, the time series data from the Lunar calendar was longer than that from the Gregorian calendar. The Gregorian calendar has 365 days, while the Lunar calendar has only 355 days. This difference extends the time series data when using the Lunar calendar.

3.2. Forecasting Result Comparison

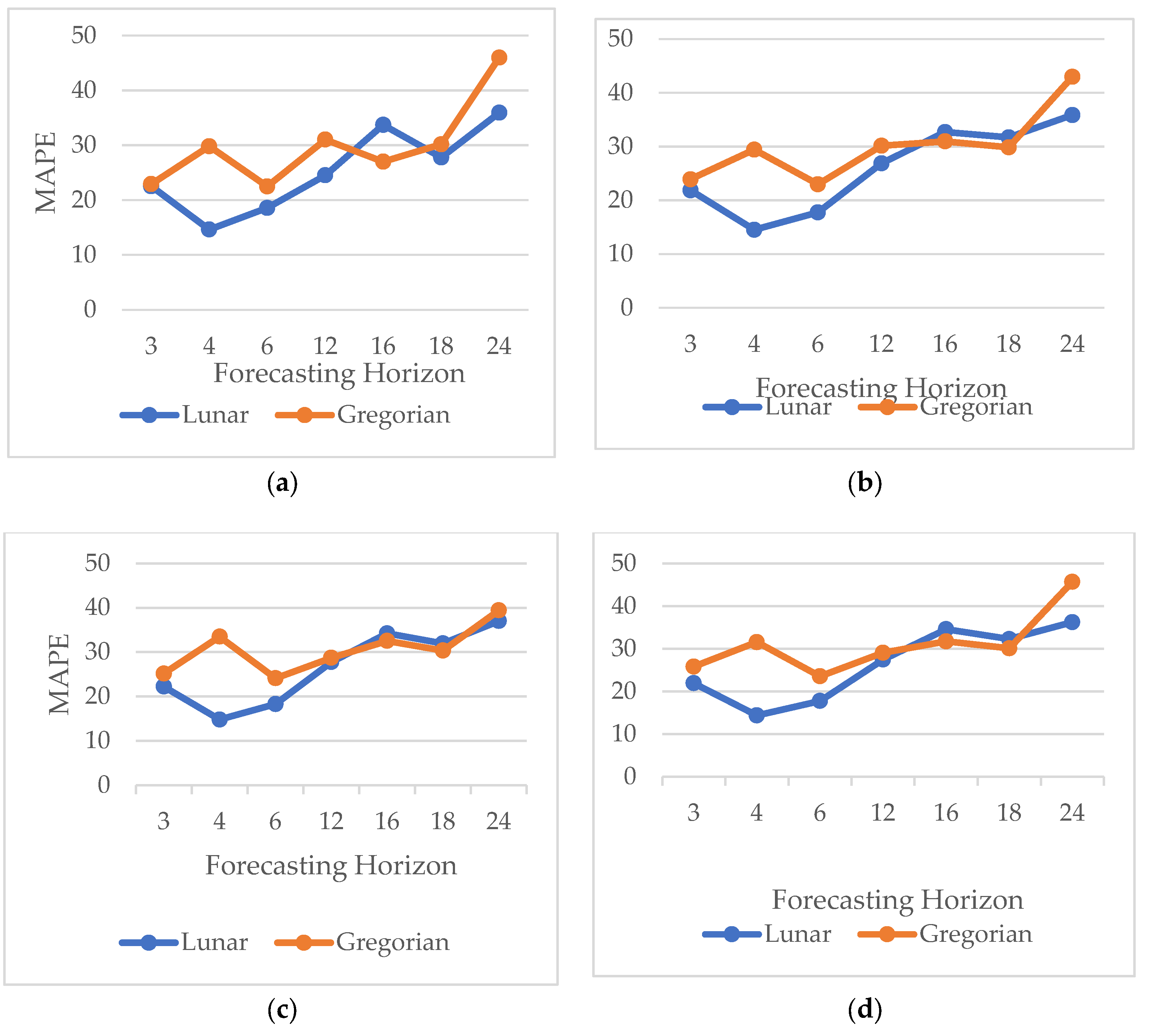
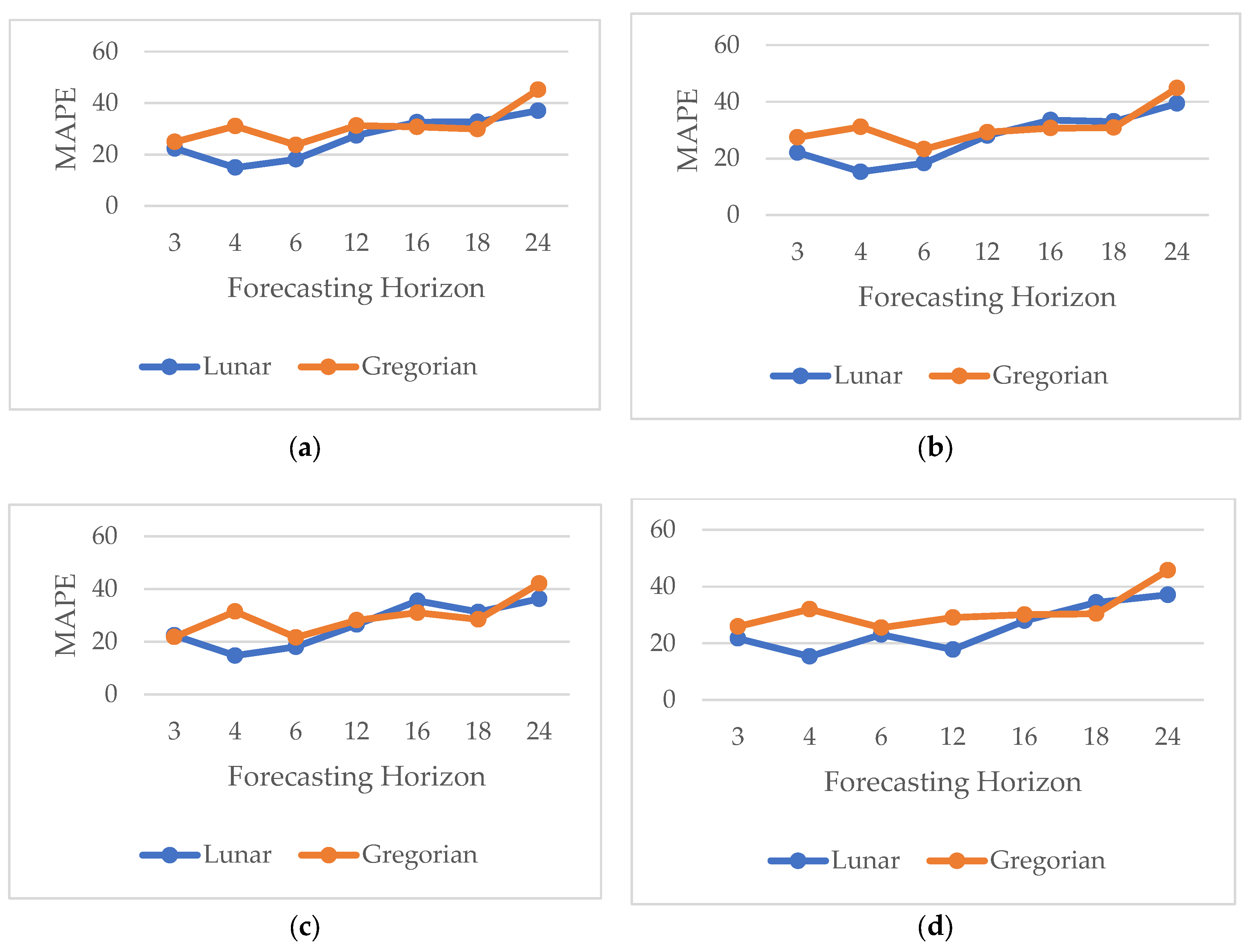
The comparison of forecasting based on two kinds of calendar was presented in Figure 7. Based on Figure 7, the MAPE trend for the four methods across both calendar systems tends to increase as the forecast length increases. Forecasts based on the lunar calendar generally had a lower MAPE than those based on the Gregorian calendar. Specifically, the lunar calendar-based MAPE was lower at forecast lengths of 3, 4, 6, and 12 months for the LSTM, 2-Stacked LSTM, and 2-Stacked BiLSTM methods, as shown in Figure 7a–d.
For the BiLSTM method, at a forecast length of 12 months, the MAPE for both the lunar and Gregorian calendars were almost identical. However, at forecast lengths of 16 and 18 months, the lunar calendar MAPE tended to be higher than that of the Gregorian calendar for the 2-Stacked LSTM, BiLSTM, and 2-Stacked BiLSTM methods. Interestingly, at a forecast length of 24 months, the lunar calendar showed a smaller MAPE.
Figure 8 compares the MAPE for forecasts using two different calendars: (a) the lunar calendar and (b) the Gregorian calendar, across forecast lengths of 3, 4, 6, 12, 16, 18, and 24 months.
In Figure 8a, it was shown that for a forecast length of 4 months, the MAPE produced by all four methods was the smallest compared to other forecast lengths, while a forecast length of 24 months results in the highest MAPE.
On the other hand, for forecasts based on the Gregorian calendar (Figure 8b), the smallest MAPE was observed at a forecast length of 6 months for all methods, with the largest MAPE occurring at 24 months. When comparing the two calendars, the MAPE for the lunar calendar was smaller than that for the Gregorian calendar at forecast lengths of 4 and 6 months.
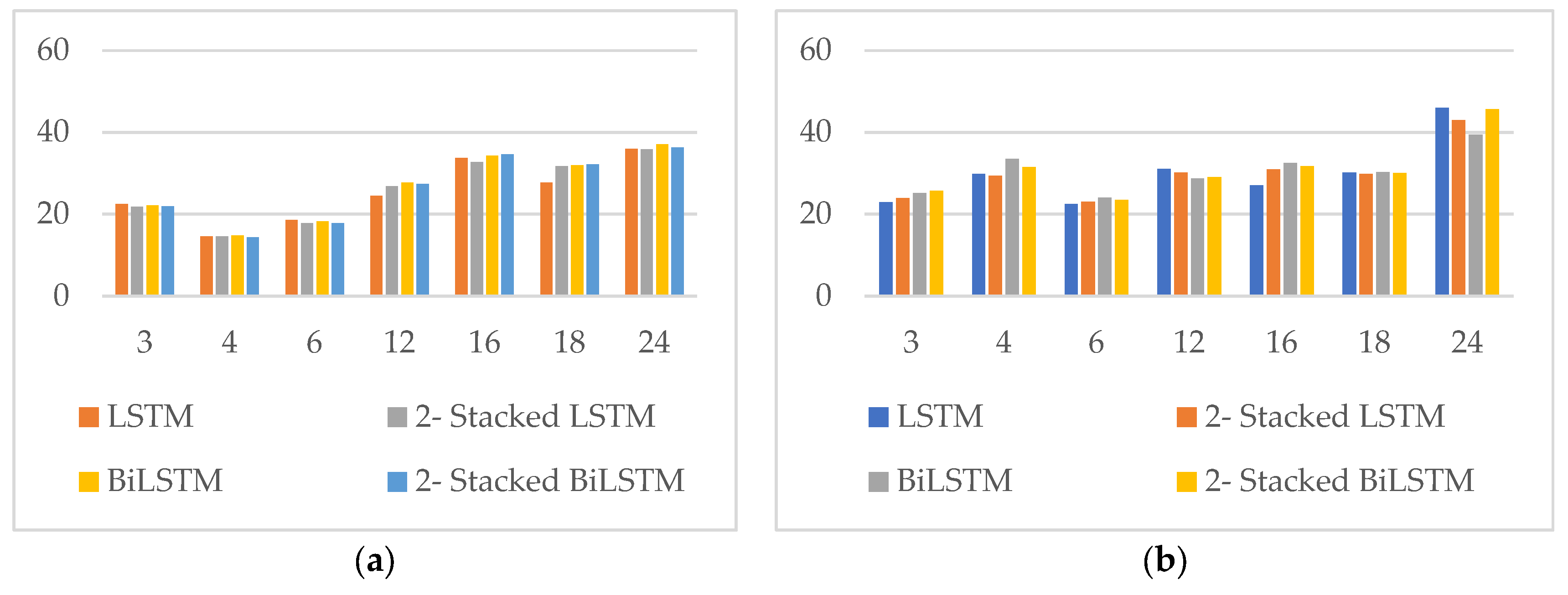
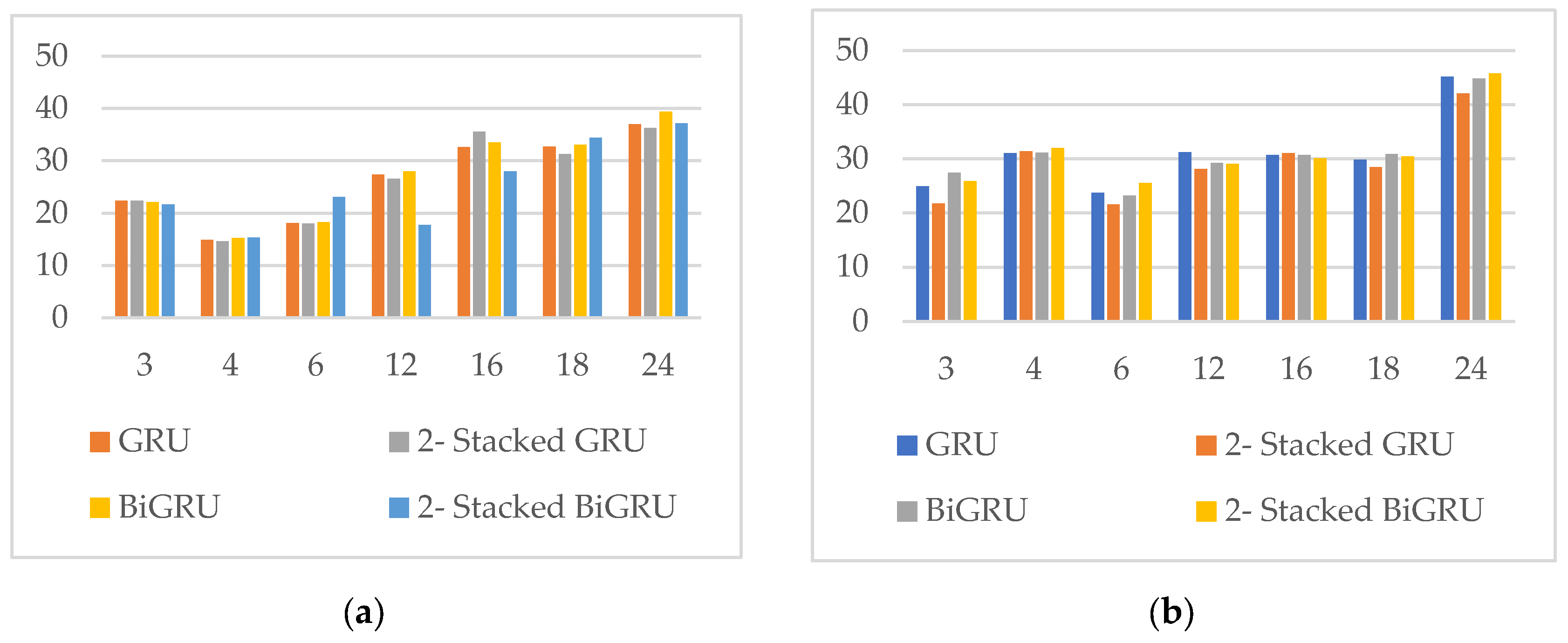
Figure 9 compares the MAPE of different methods: GRU, 2-Stacked GRU, BiGRU, and 2-Stacked BiGRU. Overall, the MAPE for the lunar calendar approach was generally smaller than that for the Gregorian calendar. Specifically, for forecast lengths of 3, 4, and 6 months, all four methods produced a smaller MAPE using the lunar calendar compared to the Gregorian calendar. For the BiGRU and 2-Stacked BiGRU methods, the MAPE at a forecast length of 12 months was similar, typically ranging between 25-30%. However, at forecast lengths of 16 and 18 months, the MAPE for the lunar calendar was larger than that for the Gregorian calendar. Conversely, at a forecast length of 24 months, the MAPE for the Gregorian calendar was greater than that for the lunar calendar.
This comparison examines the MAPE for the lunar and Gregorian calendars across four GRU method types: GRU, BiGRU, 2-Stacked GRU, and 2-Stacked BiGRU. As shown in Figure 10a, the forecast length of 4 months has the smallest MAPE, around 15%, while the forecast length of 24 months produces the highest MAPE, around 35%. In contrast, for the Gregorian calendar (Figure 10b), the smallest MAPE occurs at forecast lengths of 3 and 6 months, approximately 25%, with the largest MAPE at 24 months, exceeding 40%. Generally, the MAPE for the lunar calendar was smaller than that of the Gregorian calendar at forecast lengths of 3, 4, 6, 12, and 24 months. However, at forecast lengths of 16 and 18 months, the MAPE values were relatively similar between the two calendars.

4. Conclusions

The MAPE trend for the four methods and two-based calendars increases with forecast length, with lunar calendar-based forecasting generally showing a lower MAPE than the Gregorian calendar. At a forecast length of 12 months, the BiLSTM method yields a MAPE similar for both the lunar and Gregorian calendars. However, at forecast lengths of 16 and 18 months, the lunar calendar forecasts have a larger MAPE compared to the Gregorian calendar. This study compares MAPE for forecasting using the lunar and Gregorian calendars across various forecast lengths. The smallest MAPE is observed at a forecast length of 4 months, while the highest MAPE occurs at 24 months. For the Gregorian calendar, the smallest MAPE is at 6 months, with the largest at 24 months. Figure 9 compares the MAPE of various methods: GRU, 2-Stacked GRU, BiGRU, and 2-Stacked BiGRU. The lunar calendar approach yields a smaller MAPE than the Gregorian calendar for forecast lengths of 3, 4, and 6 months, while the BiGRU and 2-Stacked BiGRU methods show similar MAPE values for 12-month forecasts. The comparison of MAPE between the lunar and Gregorian calendars across the four GRU methods shows that a forecast length of 4 months has the smallest MAPE at 15%, while a forecast length of 24 months has the highest MAPE at 35%. For the Gregorian calendar, the smallest MAPE occurs at forecast lengths of 3 and 6 months, with the largest at 24 months. As a result, the analysis based on the Lunar calendar can be more accurate. The longer time series data in the Lunar calendar provides more detailed insights. Therefore, using the Lunar calendar may lead to better analysis results than the Gregorian calendar.

Funding

This research was funded by grant number 1652/UN6.3.1/PT.00/2024 and The APC was funded by UNIVERSITAS OF PADJADJARAN.

Institutional Review Board Statement

Not Applicable.

Informed Consent Statement

Not Applicable.

Data Availability Statement

The data presented in this study are available upon request from the
corresponding author.

Acknowledgments

The Author would like to acknowledge to Universitas Padjadjaran for funding this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bartlein, P.J.; Shafer, S.L. Paleo Calendar-Effect Adjustments in Time-Slice and Transient Climate-Model Simulations (PaleoCalAdjust v1.0): Impact and Strategies for Data Analysis. Geosci. Model Dev. 2019, 12, 3889–3913. [Google Scholar] [CrossRef]
  2. Irfan, I. Comparative Study of Fazilet Calendar and Mabims Criteria on Determining Hijri Calendar. Al-Hilal J. Islam. Astron. 2023, 5, 99–116. [Google Scholar] [CrossRef]
  3. Hendikawati, P. ; Subanar; Abdurakhman; Tarno Optimal Adaptive Neuro-Fuzzy Inference System Architecture for Time Series Forecasting with Calendar Effect. Sains Malaysiana 2022, 51, 895–909. [Google Scholar] [CrossRef]
  4. Kumar, D.; Singh, A.; Samui, P.; Jha, R.K. Forecasting Monthly Precipitation Using Sequential Modelling. Hydrol. Sci. J. 2019, 64, 690–700. [Google Scholar] [CrossRef]
  5. Tang, T.; Jiao, D.; Chen, T.; Gui, G. Medium- and Long-Term Precipitation Forecasting Method Based on Data Augmentation and Machine Learning Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1000–1011. [Google Scholar] [CrossRef]
  6. Archontoulis, S. V.; Castellano, M.J.; Licht, M.A.; Nichols, V.; Baum, M.; Huber, I.; Martinez-Feria, R.; Puntel, L.; Ordóñez, R.A.; Iqbal, J.; et al. Predicting Crop Yields and Soil-plant Nitrogen Dynamics in the US Corn Belt. Crop Sci. 2020, 60, 721–738. [Google Scholar] [CrossRef]
  7. Ceglar, A.; Toreti, A. Seasonal Climate Forecast Can Inform the European Agricultural Sector Well in Advance of Harvesting. npj Clim. Atmos. Sci. 2021, 4, 42. [Google Scholar] [CrossRef]
  8. Lala, J.; Tilahun, S.; Block, P. Predicting Rainy Season Onset in the Ethiopian Highlands for Agricultural Planning. J. Hydrometeorol. 2020, 21, 1675–1688. [Google Scholar] [CrossRef]
  9. Sodnik, J.; Mikoš, M.; Bezak, N. Torrential Hazards’ Mitigation Measures in a Typical Alpine Catchment in Slovenia. Appl. Sci. 2023, 13, 11136. [Google Scholar] [CrossRef]
  10. Chambers, L.E.; Plotz, R.D.; Lui, S.; Aiono, F.; Tofaeono, T.; Hiriasia, D.; Tahani, L.; Fa’anunu, ‘Ofa; Finaulahi, S.; Willy, A. Seasonal Calendars Enhance Climate Communication in the Pacific. Weather. Clim. Soc. 2021, 13, 159–172. [CrossRef]
  11. El Mehdi Ferrouhi Omar Kharbouch, S.A.; Naeem, M. Calendar Anomalies in African Stock Markets. Cogent Econ. \& Financ. 2021, 9, 1978639. [Google Scholar] [CrossRef]
  12. Lessan, N.; Ali, T. Energy Metabolism and Intermittent Fasting: The Ramadan Perspective. Nutrients 2019, 11. [Google Scholar] [CrossRef] [PubMed]
  13. Oynotkinova, N.R. Calendar Rites and Holidays of the Altaians and Teleuts: Classification and General Characteristics. Sib. Filol. Zhurnal 2022, 332, 153–165. [Google Scholar] [CrossRef]
  14. Bell, W.R.; Hillmer, S.C. Modeling Time Series with Calendar Variation. J. Am. Stat. Assoc. 1983, 78, 526–534. [Google Scholar] [CrossRef]
  15. Heddam, S.; Ptak, M.; Zhu, S. Modelling of Daily Lake Surface Water Temperature from Air Temperature: Extremely Randomized Trees (ERT) versus Air2Water, MARS, M5Tree, RF and MLPNN. J. Hydrol. 2020, 588, 125130. [Google Scholar] [CrossRef]
  16. Xie, J.; Hong, T. Load Forecasting Using 24 Solar Terms. J. Mod. Power Syst. Clean Energy 2018, 6, 208–214. [Google Scholar] [CrossRef]
  17. Li, G.; Yang, N. A Hybrid SARIMA-LSTM Model for Air Temperature Forecasting. Adv. Theory Simulations 2023, 6. [Google Scholar] [CrossRef]
  18. Sirisha, U.M.; Belavagi, M.C.; Attigeri, G. Profit Prediction Using ARIMA, SARIMA and LSTM Models in Time Series Forecasting: A Comparison. IEEE Access 2022, 10, 124715–124727. [Google Scholar] [CrossRef]
  19. Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
  20. Darmawan, G.; Handoko, B.; Faidah, D.Y.; Islamiaty, D. Improving the Forecasting Accuracy Based on the Lunar Calendar in Modeling Rainfall Levels Using the Bi-LSTM Method through the Grid Search Approach. Sci. World J. 2023, 2023. [Google Scholar] [CrossRef]
  21. Qiu, G.; Gu, Y.; Chen, J. Selective Health Indicator for Bearings Ensemble Remaining Useful Life Prediction with Genetic Algorithm and Weibull Proportional Hazards Model. Meas. J. Int. Meas. Confed. 2020, 150, 107097. [Google Scholar] [CrossRef]
  22. Liu, S.; Ji, H.; Wang, M.C. Nonpooling Convolutional Neural Network Forecasting for Seasonal Time Series with Trends. IEEE Trans. Neural Networks Learn. Syst. 2020, 31, 2879–2888. [Google Scholar] [CrossRef] [PubMed]
  23. Rafael Braga, A.; G. Gomes, D.; M. Freitas, B.; A. Cazier, J. A Cluster-Classification Method for Accurate Mining of Seasonal Honey Bee Patterns. Ecol. Inform. 2020, 59, 101107. [CrossRef]
  24. Karevan, Z.; Suykens, J.A.K. Transductive LSTM for Time-Series Prediction: An Application to Weather Forecasting. Neural Networks 2020, 125, 1–9. [Google Scholar] [CrossRef] [PubMed]
  25. Roy, D.K.; Sarkar, T.K.; Kamar, S.S.A.; Goswami, T.; Muktadir, M.A.; Al-Ghobari, H.M.; Alataway, A.; Dewidar, A.Z.; El-Shafei, A.A.; Mattar, M.A. Daily Prediction and Multi-Step Forward Forecasting of Reference Evapotranspiration Using LSTM and Bi-LSTM Models. Agronomy 2022, 12. [Google Scholar] [CrossRef]
  26. Yin, J.; Deng, Z.; Ines, A.V.M.; Wu, J.; Rasu, E. Forecast of Short-Term Daily Reference Evapotranspiration under Limited Meteorological Variables Using a Hybrid Bi-Directional Long Short-Term Memory Model (Bi-LSTM). Agric. Water Manag. 2020, 242, 106386. [Google Scholar] [CrossRef]
  27. Kong, Z.; Zhang, C.; Lv, H.; Xiong, F.; Fu, Z. Multimodal Feature Extraction and Fusion Deep Neural Networks for Short-Term Load Forecasting. IEEE Access 2020, 8, 185373–185383. [Google Scholar] [CrossRef]
  28. Li, X.; Ma, X.; Xiao, F.; Xiao, C.; Wang, F.; Zhang, S. Time-Series Production Forecasting Method Based on the Integration of Bidirectional Gated Recurrent Unit (Bi-GRU) Network and Sparrow Search Algorithm (SSA). J. Pet. Sci. Eng. 2022, 208, 109309. [Google Scholar] [CrossRef]
  29. Johnson, R.K. Gregorian/Julian Calendar. In The Encyclopedia of Christian Civilization; John Wiley & Sons, Ltd, 2011 ISBN 9780470670606.
  30. Lee, K.W. Analysis of Solar and Lunar Motions in the Seonmyeong Calendar. J. Astron. Sp. Sci. 2019, 36, 87–96. [Google Scholar] [CrossRef]
  31. Gajic, N. The Curious Case of the Milankovitch Calendar. Hist. Geo. Space Sci. 2019, 10, 235–243. [Google Scholar] [CrossRef]
  32. Ando, H.; Shahjahan, M.; Kitahashi, T. Periodic Regulation of Expression of Genes for Kisspeptin, Gonadotropin-Inhibitory Hormone and Their Receptors in the Grass Puffer: Implications in Seasonal, Daily and Lunar Rhythms of Reproduction. Gen. Comp. Endocrinol. 2018, 265, 149–153. [Google Scholar] [CrossRef] [PubMed]
  33. Neri, C.; Schneider, L. Euclidean Affine Functions and Their Application to Calendar Algorithms. Softw. Pract. Exp. 2023, 53, 937–970. [Google Scholar] [CrossRef]
  34. Abdul Majid, A. Forecasting Monthly Wind Energy Using an Alternative Machine Training Method with Curve Fitting and Temporal Error Extraction Algorithm. Energies 2022, 15. [Google Scholar] [CrossRef]
  35. Meng, J.; Dong, Z.; Shao, Y.; Zhu, S.; Wu, S. Monthly Runoff Forecasting Based on Interval Sliding Window and Ensemble Learning. Sustain. 2023, 15. [Google Scholar] [CrossRef]
  36. Zhang, H.; Nguyen, H.; Vu, D.-A.; Bui, X.-N.; Pradhan, B. Forecasting Monthly Copper Price: A Comparative Study of Various Machine Learning-Based Methods. Resour. Policy 2021, 73, 102189. [Google Scholar] [CrossRef]
  37. Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  38. Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient Flow in Recurrent Nets: The Difficulty of Learning Long-Term Dependencies. In A Field Guide to Dynamical Recurrent Neural Networks; Kremer, S.C., Kolen, J.F., Eds.; IEEE Press, 2001.
  39. Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Trans. Neural Networks 1994, 5, 157–166. [Google Scholar] [CrossRef]
  40. Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
  41. Dutta, K.K.; Poornima, S.; Sharma, R.; Nair, D.; Ploeger, P.G. Applications of Recurrent Neural Network: Overview and Case Studies. In Recurrent Neural Networks; CRC press, 2022; pp. 23–41.
  42. Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP); Moschitti, A., Pang, B., Daelemans, W., Eds.; Association for Computational Linguistics: Doha, Qatar, October 2014; pp. 1724–1734. [Google Scholar]
  43. Salem, F.M. Gated RNN. In Recurrent Neural Networks: From Simple to Gated Architectures; Springer International Publishing: Cham, 2022; ISBN 978-3-030-89929-5. [Google Scholar]
  44. Mateus, B.C.; Mendes, M.; Farinha, J.T.; Assis, R.; Cardoso, A.M. Comparing LSTM and GRU Models to Predict the Condition of a Pulp Paper Press. Energies 2021, 14, 6958. [Google Scholar] [CrossRef]
  45. Zhang, W.; Li, H.; Tang, L.; Gu, X.; Wang, L.; Wang, L. Displacement Prediction of Jiuxianping Landslide Using Gated Recurrent Unit (GRU) Networks. Acta Geotech. 2022, 17, 1367–1382. [Google Scholar] [CrossRef]
  46. Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 2014.
  47. Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate 2016.
  48. Boulanger-Lewandowski, N.; Bengio, Y.; Vincent, P. Modeling Temporal Dependencies in High-Dimensional Sequences: Application to Polyphonic Music Generation and Transcription 2012.
  49. Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent Neural Networks: A Comprehensive Review of Architectures, Variants, and Applications. Information 2024, 15. [Google Scholar] [CrossRef]
  50. Sahar, A.; Han, D. An LSTM-Based Indoor Positioning Method Using Wi-Fi Signals.; 2018; pp. 1–5.
  51. Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
  52. Graves, A.; Schmidhuber, J. Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures. Neural Networks 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
  53. Graves, A.; Mohamed, A.-R.; Hinton, G. Speech Recognition with Deep Recurrent Neural Networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing; 2013; pp. 6645–6649.
  54. Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked Bidirectional and Unidirectional LSTM Recurrent Neural Network for Forecasting Network-Wide Traffic State with Missing Values 2020.
  55. Rathore, M.S.; Harsha, S.P. An Attention-Based Stacked BiLSTM Framework for Predicting Remaining Useful Life of Rolling Bearings. Appl. Soft Comput. 2022, 131, 109765. [Google Scholar] [CrossRef]
Preprints 138004 g001
Figure 1. LSTM Structure [40].
Figure 1. LSTM Structure [40].
Preprints 138004 g001
Preprints 138004 g002
Figure 2. GRU Structure [40].
Figure 2. GRU Structure [40].
Preprints 138004 g002
Preprints 138004 g003
Figure 3. Architecture of Stacked LSTM [40].
Figure 3. Architecture of Stacked LSTM [40].
Preprints 138004 g003
Preprints 138004 g004
Figure 4. Architecture of BiLSTM [40].
Figure 4. Architecture of BiLSTM [40].
Preprints 138004 g004
Preprints 138004 g005
Figure 5. Architecture of Stacked BiLSTM.
Figure 5. Architecture of Stacked BiLSTM.
Preprints 138004 g005
Preprints 138004 g006
Figure 6. Bogor maps where the rainfall data was collected.
Figure 6. Bogor maps where the rainfall data was collected.
Preprints 138004 g006
Preprints 138004 g007
Figure 7. Comparison of MAPE for lunar calendar-based forecasting and Gregorian calendar for: (a) LSTM; (b) 2-stacked LSTM; (c) BiLSTM; (d) 2-stacked BiLSTM methods.
Figure 7. Comparison of MAPE for lunar calendar-based forecasting and Gregorian calendar for: (a) LSTM; (b) 2-stacked LSTM; (c) BiLSTM; (d) 2-stacked BiLSTM methods.
Preprints 138004 g007
Preprints 138004 g008
Figure 8. Comparison of MAPE for different forecast lengths for four different LSTM methods for forecasting based on: (a) the Lunar calendar; (b) the Gregorian calendar.
Figure 8. Comparison of MAPE for different forecast lengths for four different LSTM methods for forecasting based on: (a) the Lunar calendar; (b) the Gregorian calendar.
Preprints 138004 g008
Preprints 138004 g009
Figure 9. Comparison of MAPE for lunar calendar-based forecasting and Gregorian calendar for: (a) GRU; (b) 2-stacked GRU; (c) BiGRU; (d) 2-stacked BiGRU methods.
Figure 9. Comparison of MAPE for lunar calendar-based forecasting and Gregorian calendar for: (a) GRU; (b) 2-stacked GRU; (c) BiGRU; (d) 2-stacked BiGRU methods.
Preprints 138004 g009
Preprints 138004 g010
Figure 10. Comparison of MAPE for different forecast lengths for four different GRU methods for forecasting based on: (a) the Lunar calendar; (b) the Gregorian calendar.
Figure 10. Comparison of MAPE for different forecast lengths for four different GRU methods for forecasting based on: (a) the Lunar calendar; (b) the Gregorian calendar.
Preprints 138004 g010
Table 1. Calendar Conversion Results.
Table 1. Calendar Conversion Results.
Month-Year
Gregorian 		Monthly rainfall (mmHg) Month-Year
Lunar 		Monthly rainfall (mmHg)
Apr-00 449 Dhul Hijri 1420 84
May-00 339 Muharram 1420 493
Jun-00 295 Safar 1420 263
Jul-00 376 Rabi Ul-Awal 1420 348
⋯ ⋯ ⋯ ⋯
Sep-22 250.7 Safar 1444 444.7
Oct-22 505.3 Rabi Ul-Awal 1444 334.1
Nov-22 299.2 Rabi Al-Akbar 1444 303.4
Dec-22 428.7 Jumadil Awal 1444 198.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated