Preprint
Article
Hyperspectral Image Segmentation for Optimal Satellite Operations: In-orbit Deployment of 1D-CNN
Submitted:
01 November 2024
Posted:
04 November 2024
You are already at the latest version
Abstract
AI on spaceborne platforms optimizes operations and increases automation, crucial for satellites with limited downlink capacity. It can ensure that only valuable information is transmitted, minimizing resources spent on unnecessary data, which is especially important in hyperspectral Earth Observation missions, producing large data volumes. Our previous work showed that the 1D-CNN, 1D-Justo-LiuNet, outperformed 2D-CNNs and Vision Transformers for hyperspectral segmentation, making our model the best choice for in-orbit deployment. In this work, we mark the first deployment and testing of a 1D-CNN in a satellite. We implement a C version of the 1D-Justo-LiuNet and, after ground validation, we deploy it on the on board the HYPSO-1 satellite. We demonstrate in-flight segmentation of hyperspectral images via the 1D-CNN to classify pixels into sea, land, and cloud categories. We show how in-orbit segmentation improves satellite operations, increases automation, and optimizes downlink. We give examples of how in-orbit segmentation addresses mission challenges in HYPSO-1, such as incomplete data reception, incorrect satellite pointing, and cloud cover, helping decide whether to transmit or discard data on board. An additional CNN autonomously interprets segmented images, enabling on-board decisions on data downlink.
Keywords:
Subject:
Computer Science and Mathematics - Artificial Intelligence and Machine Learning1. Introduction
1.1. Literature Review: Deep Learning for Hyperspectral Imaging Missions
Data science plays a crucial role in the current Big Data era and the AI revolution, where massive volumes of data are continuously generated [1]. It offers data-driven optimization across various industries, such as healthcare, finance, and space. Earth Observation (EO) satellites, which may generate vast amounts of data, can benefit from edge inference. In this context, edge inference refers to Machine Learning models making predictions directly on board the satellite, optimizing operations and automating its decision-making. This is particularly important for satellites equipped with Hypespectral (HS) instruments, generating large data cubes. The interest in HS technology lies in its ability to capture hundreds of wavelengths per image pixel, enabling more detailed target characterization beyond conventional RGB and Multispectral (MS) imagery. Its potential for HS missions was first demonstrated in 2000, when the National Aeronautics and Space Administration (NASA) launched the first HS satellite, Earth Observing-1 (EO-1) [2]. The ongoing significance of HS missions is evident from the numerous current and planned missions. Current HS missions include -sat program from the European Space Agency (ESA) [3], PRecursore IperSpettrale della Missione Applicativa (PRISMA) from the Italian Space Agency (ASI) [4], the Environmental Mapping and Analysis Program (EnMAP) from the German Aerospace Center (DLR) [5], the Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) from NASA [6], and the HYPerspectral small Satellite for Ocean observation (HYPSO) from the Norwegian University of Science and Technology (NTNU) [7], with HYPSO-1 launched in 2022 [8] and HYPSO-2 recently in 2024 [9]. Future HS missions include the Copernicus Hyperspectral Imaging Mission for the Environment (CHIME) from ESA [10], NASA’s Geosynchronous Littoral Imaging and Monitoring Radiometer (GLIMR) [11] and Surface Biology and Geology (SBG) [12]. However, despite the potential and clear interest in this technology, HS imagery has a major drawback: the substantial data volume of each image, leading to considerable processing challenges [13], also affected by the limited computational resources on board satellites [14,15,16,17]. Furthermore, the large data output makes the downlink channel to Earth a critical bottleneck for satellites, as bandwidth is often limited [16,18,19], making efficient resource management essential. To address this, AI deployment on satellites has been explored to autonomously process data and optimize bandwidth by transmitting only essential information, while filtering out cloudy images or pixels [20,21]. In 2021, ESA reached a significant milestone by deploying the first on-board deep neural network for EO, the 2D Convolutional Neural Network (CNN) CloudScout, on the -Sat-1 satellite, to detect clouds [22]. The detection was achieved through semantic segmentation [23], where each image pixel was classified into a binary category for the presence of clouds. Cloud detection is vital for optical remote sensing [24], as cloud cover can obscure target areas [25]. Since then, CloudScout’s performance has been studied and optimized across various hardware platforms, including Field-Programmable Gate Arrays (FPGAs) [26]. CloudScout’s milestone was significant not only because it marked the first deployment of deep learning in space, but also for overcoming the inference challenges induced by the complex physical conditions in space, including noise and diverse atmospheric disturbances [13], making the successful deployment even more remarkable.
1.2. Literature Review: 2D-CNNs
The literature highlights deep learning CNNs as a promising technique for on-board data analysis [13], outperforming Support Vector Machines (SVMs) with linear and radial basis function kernels [27]. CNNs, particularly 2D-CNNs, have been extensively studied and tested on the ground for future deployment on board satellites. Efforts have focused on prototyping 2D-CNN models for applications such as on-board detection of volcanic eruptions in MS imagery [28], real-time change detection in RGB and MS data to improve response times for natural disasters such as floods and earthquakes [19], among other applications where on-board processing is key to accelerate decision-making. The potential of on-board processing is so significant that it may also enable autonomous ground-based responses [29,30]. Furthermore, the use of 2D-CNNs has been wide also in traditional satellite domains using Synthetic Aperture Radar (SAR) imagery. Examples include oil spill detection [31], ship detection [14], and plane detection from space [15], based on lightweight MobileNets [32,33]. 2D-CNNs have also been applied to regular RGB imagery for ship detection, utilizing ResNet architectures [34].
1.3. Literature Review: 1D-CNNs vs 2D-CNNs
2D-CNNs generate predictions by using both spatial and spectral context. While 2D-CNNs dominate the state of the art of HS segmentation, 1D-CNNs have also been explored for HS applications, focusing solely on the spectral domain, similar to time-series classification [35]. Kalomoiris et al. investigated a CNN with approximately 22 million parameters, aiming to reduce computational complexity by using a 1D-CNN for spectroscopic data [18], collected from satellite-based imaging sensors to estimate galaxy redshift [36], while running their experiments on an on-ground FPGA. Nalepa et al. conducted on-ground experiments using 1D-CNN, 2.5D-CNN, and 3D-CNN architectures for segmentation on four conventional HS datasets (Indian Pines, Salinas, Pavia University, and University of Houston) [13]. With limited training data (around 2 million pixels), the authors simulated atmospheric disturbances over Poland to improve model generalization, an important approach for small training sets [37]. Their results showed that the 1D-CNN consistently outperformed 2.5D- and 3D-CNNs for all performance metrics, achieving an average accuracy of 0.69 across datasets [13]. Furthermore, promising results have also been achieved for land cover classification using 1D-CNNs on MS imagery, with a peak accuracy of 0.927, tested on a small set of 50,000 pixels captured by an MS sensor, aimed at future in-orbit deployment [38]. Other authors have proposed networks such as ScannerNet [39] for on-board segmentation, combining 1D-CNN and LSTM architectures. This approach is particularly suited for push-broom sensors, being less computationally intensive and more memory-efficient, while demonstrating competitive accuracy on MS and thermal infrared data from Landsat 8 mission, compared to the most compact versions of 2D-CUNet++ [40]. Subsequent works have tested on ground CHLNET, a model using a 1D-CNN architecture followed by support vector regression (SVR) to predict chlorophyll-A concentration from ocean surface reflectance across a few broad bands [41]. Other works have tested 1D-CNNs for detecting anomalies in one-dimensional satellite telemetry data [42], where the 1D-CNN-based model outperformed transformers, LSTMs, and other deep models. Additionally, further experiments with 1D-CNNs in the HS domain have been conducted in the literature. In our previous work [43], we tested 20 machine learning models, comparing 1D-CNNs against 2D-CNNs and Apple’s 2023 Fast Vision Transformers (FastViTs) for lightweight mobile inference [44]. These tests, conducted on real-world HS data from the HYPSO-1 and EO-1 satellites [43,45], included multiple images across different and diverse geographical locations around the Earth, without needing simulated acquisition conditions. Our proposed network, 1D-Justo-LiuNet, outperformed state-of-the-art 2D-CNN U-Nets [46] and FastViTs [44] in the HS domain. 1D-Justo-LiuNet achieved an average accuracy of 0.93 with just 4,563 parameters, concluding that the model was highly suitable for in-orbit deployment, as also highlighted by recent reviews [47].
1.4. Literature Review: 1D-CNNs for Resource-Limited Platforms
The literature shows that 1D-CNNs have been deployed in, for example, Unmanned Aerial Vehicles (UAVs), such as drones, as 1D-CNNs also suit these resource-limited platforms. In this domain, 1D-CNNs have been widely used for GPS spoofing detection, identifying attacks that emit fake GPS signals to deceive the GPS receiver in UAVs [48,49]. 1D-CNNs have also been explored for predicting droplet deposition during UAV pesticide spraying [50], among other UAV applications. Furthermore, the work of Sung et al. [27] is the first to successfully test 1D-CNNs on board UAVs for GPS spoofing detection in a real drone environment.
1.5. Novelty and Contribution
While many studies have explored the viability and optimization of CNNs in imagery for future in-orbit deployment, especially 2D-CNNs, few have achieved actual deployment - such as ESA’s 2D-CNN CloudScout on the -Sat-1 satellite [22]. To the best of our knowledge, beyond the existing literature on UAVs, no 1D-CNN has been deployed on space satellites at the time of writing. This work is the first to deploy and test a 1D-CNN in a satellite in orbit, marking the novelty of our contribution.
The method followed for this work is part of our scientific contribution, which is also applicable to other on-board processing algorithms. We apply our approach to a 1D-CNN, focusing on minimizing the risk of failure following a gradual development and testing process. Initially, we conduct a detailed study of the 1D-CNN algorithm to understand how the network processes data samples at a granular level, examining sample-by-sample and layer-by-layer behavior. Following this, gradual testing of the C implementation is performed, with results validated against Keras outputs. The network is then moved to a lab-based processing unit for further testing before the final deployment on the operational unit in space. The rigor and detail of this process not only proves essential to the successful deployment of the 1D-CNN but also serves as a recommended framework for future on-board algorithms. Furthermore, we use results on the HYPSO-1 example mission to validate our deployment method. This work demonstrates how in-orbit inference optimizes downlink usage, enhances operations, and increases autonomy, valuable for future operational satellites. Various scenarios are explored, showing how on-board segmentation enables resource-saving decisions and allows for on-ground georeferencing, even without receiving raw HS data.
1.6. Article’s Structure
In Section 2, we present the system architecture of the on-board processing unit, where the 1D-CNN 1D-Justo-LiuNet is integrated for image segmentation in space. Section 3 details our methodology, beginning in Section 3.1 with an overview of the 1D-CNN architecture, including 1D convolutions and pooling layers for feature extraction, followed by a final classification layer. We provide further details on the data flow through the network’s layers in Section 3.2. Section 3.3 to Section 3.7 cover the high-level functionality and implementation details of the network layers, followed by a summary of our testing and verification strategy in Section 3.8. In Section 4.1, we discuss example scenarios, where satellite operations benefit from on-board segmented images. We propose various decision-making approaches to either discard unimportant data or downlink meaningful information. We propose approaches from ground-based segment inspection requiring human intervention (Section 4.2) to fully autonomous on-board interpretation (Section 4.3). The latter includes simple class proportion analysis (Section 4.3.1), and a more advanced method (Section 4.3.2), where a new CNN model is trained and tested to interpret segmented images in space. We provide a case example where the CNN detects satellite mispointing based on the inferred segmented images. In Section 4.4, we discuss data products and compression techniques, such as Compressive Sensing [51], that may benefit from the segmented images. Section 5 presents our results, demonstrating successful segmentation of HS imagery across multiple geographical locations captured from space, and how these results enhance satellite operations. We also show results from the additional CNN trained for autonomous on-board interpretation of segmented images, provide brief Explainable AI insights to explain model predictions, and conduct a timing analysis for future FPGA acceleration. Section 6 concludes our work.
2. System Architecture
Before presenting the implementation of 1D-Justo-LiuNet, we provide an overview of HYPSO-1’s system architecture in flight, where our model is deployed. The satellite’s subsystems are extensively detailed in the current state of the art [7,8,52,53,54]. Thus, we next highlight only the relevant aspects from Langer et al. [55]. We consider that this architecture is representative of current in-orbit processing systems, making our results broadly applicable.
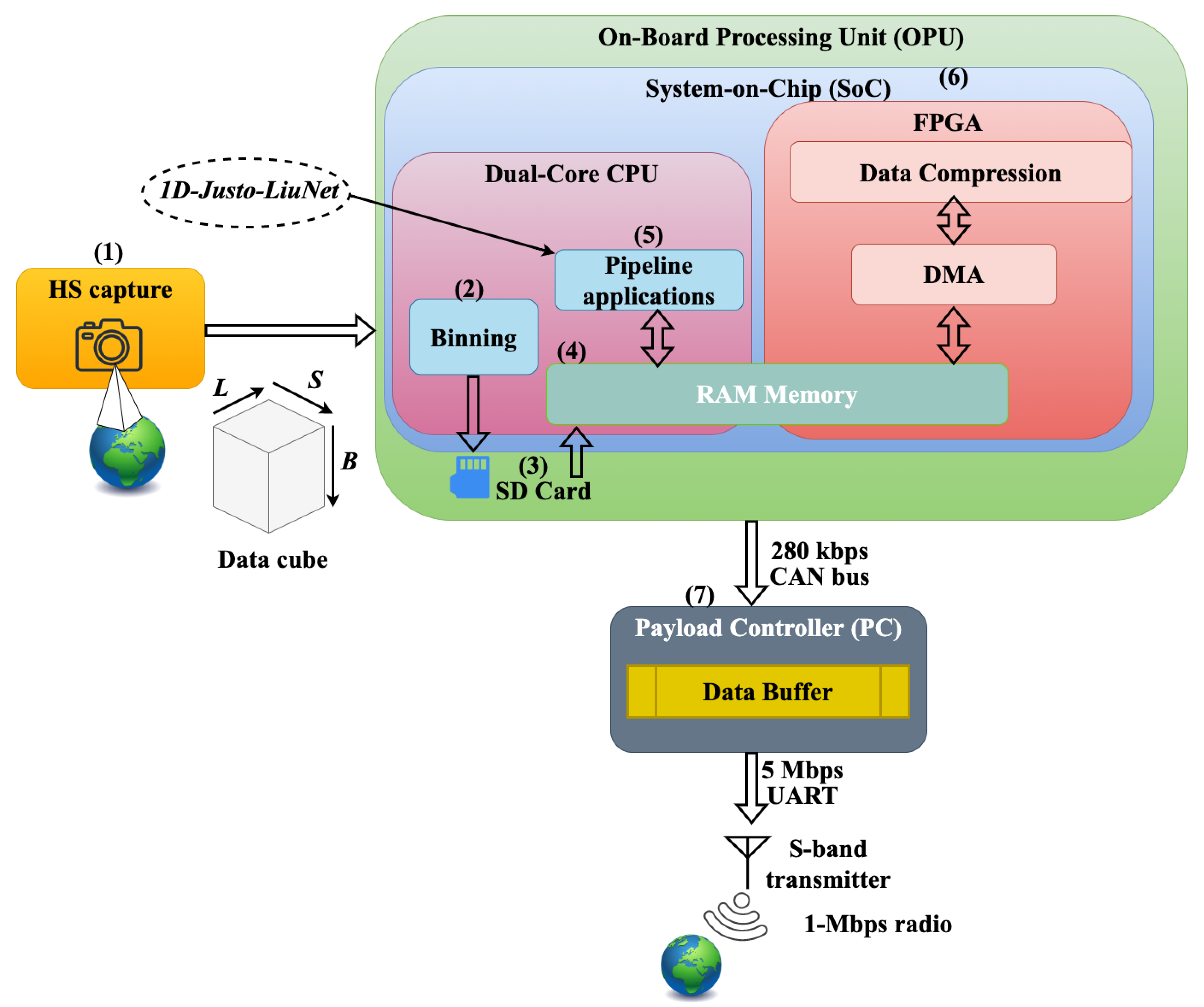
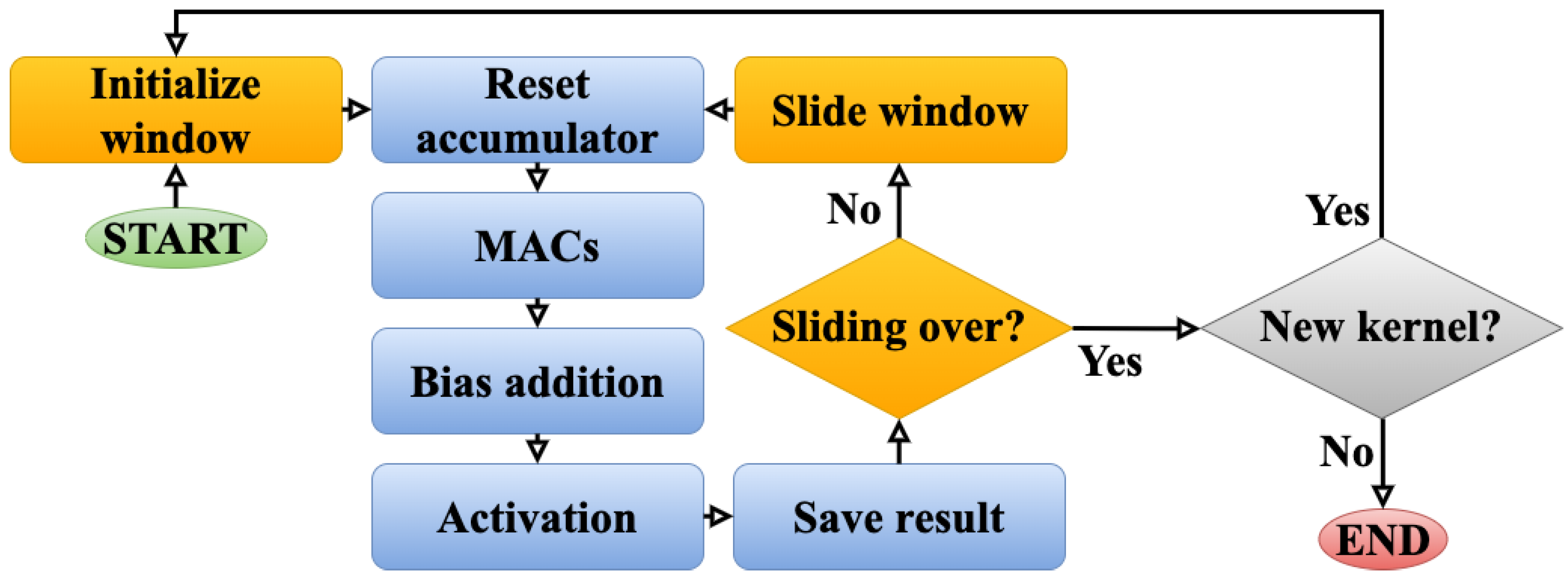
To begin, the processing pipeline includes a hardware stage for data captures, followed by a software for data processing. Langer et al. refers to a Minimal On-Board Image Processing (MOBIP) pipeline for the basic processing steps at launch. Post-launch, this pipeline is updated with additional processing during flight [55]. In Figure 1, we provide an overview of the satellite’s system architecture showing only what is most relevant to this work. Namely, the HS camera captures in (1) an image using a push-broom technique, scanning line frames as the satellite orbits. Subsequent lines form an image with spatial dimensions , each pixel containing B bands, resulting in a 3D data cube with dimensions . The data is serialized as a Band Interleaved by Pixel (BIP) stream and sent to the On-Board Processing Unit (OPU). The OPU, built with Commercial-off-the-Shelf (COTS) components, consists of a Zynq-7030 System-on-Chip (SoC) with a dual-core ARM Cortex-A9 CPU processor and a Kintex-7 FPGA [56]. As seen in Figure 1, after streaming the data, step (2) involves binning it on the CPU, where pixels are grouped into intervals (bins) and replaced by a representative value [55]. While this reduces resolution, Langer et al. note benefits such as compression and improved SNR. Furthermore, in step (3), the binned data cube is stored on a microSD card. In addition, data is loaded in (4) into a RAM memory for CPU processing [53]. In step (5), data processing begins in a submodule named pipeline applications in [55]. This is where we integrate, in this work, 1D-Justo-LiuNet to demonstrate inference at the edge. This will be further described throughout this article. As opposed to the pipeline described by Langer et al., our pipeline implementation has been modified to increase maintainability and ease of use. Instead of a single C program, the pipeline has been split up into individual programs, one for each module, such that they can be executed individually. This reduces time spent in testing and integration. The modules are then run in the pipeline sequence using a Linux shell script.
In addition to 1D-Justo-LiuNet, other modules include smile and keystone HS data cube correction characterized in [57], a linear SVM [58], spatial pixel subsampling [55], and an image composition module from three bands of the data cube [53]. Furthermore, the FPGA in (6) supports additional processing, achieving lower latency and power consumption. Through a Direct Memory Access (DMA) module, the FPGA directly accesses RAM, allowing faster memory reads and writes, bypassing the CPU. This approach enables the FPGA implementation to perform lossless compression CCSDS-123v1 [59]. The compression ratios vary depending on the content, such as cloudy images allowing for more compression [60]. This can reduce the cube size to approximately 40-80 MB. Additionally, near-lossless compression CCSDS-123v2 has been recently tested in [61] for future nominal operations. On the CPU, the segmented images by 1D-Justo-LiuNet are also compressed and packaged together with the data cube into one single file and stored in the SD card. At this stage, the OPU enters an idle state to be powered off and save energy [55]. When the satellite has Line-of-Sight (LoS) with a ground station, the payload is powered to stream the compressed segmented image first, followed by the HS raw data cube, to a Payload Controller’s (PC) buffer in (7) with a limited capacity up to two HS data cubes. Data throughput to the PC is slow (about 280 kbps) via a CAN bus, but the PC sends the buffered data to the S-band radio transmitter at a significantly higher throughput of 5 Mbps using an UART interface, which is higher than the S-band throughput. This is done to ensure we maximize the S-band utilization instead of being limited by the CAN-bus. When the satellite has LoS with a ground station, the data temporarily stored on the PC’s buffer is transmitted to the ground station through the S-band radio at 1 Mbps throughput [9,62].
To integrate 1D-Justo-LiuNet on the OPU, we store the program along with files such as model parameters, all within a single directory. A bash script then triggers the program to process newly acquired images. In our setup, network execution can be toggled on or off from the ground via scheduling software. To prevent interference with other on-board processes, the scheduling software allocates sufficient time for segmentation and related data handling. Once the segmentation is complete, the output image is compressed into a compressed tarball to reduce its size.
3. Methodology
3.1. Deep Learning Model: 1D-Justo-LiuNet
Figure 2 shows the 1D-CNN architecture of the lightweight 1D-Justo-LiuNet trained in our previous work [43], where we increased the kernel size to capture patterns within a larger receptive field, with more spectral bands. Larger kernels allowed us to reduce the total number of kernels, thereby reducing overall model size while preserving accuracy. We demonstrated that 1D-Justo-LiuNet outperformed state-of-the-art 2D-CNNs for on-board segmentation [43]. Furthermore, we also proved that our 1D-CNN outperformed the novel Fast Vision Transformers (FastViT) proposed in 2023 by Apple [44] for computer vision tasks, including image segmentation. In the following sections, we describe how features are automatically extracted from the data for 1D-Justo-LiuNet prior to classification, and detail our implementation of the network using low-level programming in C.
3.1.1. Network Interface
In the CNN architecture in Figure 2, the input is a spectral signature of a single pixel in the HS image, denoted as , where the network outputs class probabilities, , indicating the likelihood of the signature belonging to each class. Following terminology and notation from digital signal processing, we refer to each entry in as a sample and to the entire series as a sequence. We use the same terms for and all sequences in this work.
3.1.2. Overview of Feature Extraction and Classification
The network architecture shown in Figure 2 performs feature extraction followed by feature classification. The first processing stage consists of a 1D convolutional layer to identify basic patterns within the spectral samples in . Unlike 2D convolution, 1D convolution focuses solely on spectral context, reducing the number of model parameters and complexity. The figure shows that the first layer employs six kernels. Each kernel slides over the input sequence to detect a different pattern, producing a characteristic output 1D sequence known as a feature map. The remaining convolutional layers in the figure function similarly, but they gradually add more kernels from 6 to 24, detecting increasingly complex and higher-level abstract patterns. This also results in a greater number of feature maps. To handle this growing complexity, intermediate pooling layers are applied after convolutional layers to reduce the size of the feature maps. In Figure 2, pooling layers consistently halve the length of feature maps with a pooling factor of , by preserving key features while discarding less important ones through max-pooling. This additionally ensures invariant feature representations, less sensitive to minor input changes. Furthermore, Figure 2 shows that the 4th deepest level of feature extraction contains only 24 kernels. This spans a highly compressed 48-dimensional latent space, encoding only the most essential features of the input data in for our sea-land-cloud segmentation task. We will explain later why this feature space is 48-dimensional. Finally, Figure 2 shows that, after extraction, the feature space is flattened and passed through a final dense layer for classification. This output layer estimates the probabilities that the features correspond to one of three classes: sea, land, or clouds, where the class with the highest probability is selected as the final categorical prediction.
3.2. Analysis of Data Sequences and Flow in 1D-Justo-LiuNet
Before detailing the layers, functionality, and implementation, Table 1 first presents the notations for the data sequences at each processing stage of the deep network. The table includes descriptions of the input and output sequences for each layer, its internal weights and biases, and the dimensions of the sequences. Table 2 details the data pipeline within the network by specifying numerical dimensions and showing the layer interconnections that route the data path from the receipt of an input pixel, , to the output class probabilities, . In the following sections, in addition to explaining the numerical dimensions shown in Table 2, we describe our CPU-based implementation of the 1D convolution with single- and multi-component kernels, pooling, flatten, and dense layers.
3.3. Convolution Layer with Single-Component Kernels
3.3.1. High-Level Functionality
Table 2 shows that the sequence is the input to the first convolutional layer. This spectral signature consists of raw sensor data measured across wavelengths. With a spectral resolution of about 5 nm, the signature spans from the Near-Infrared to the visible blue (800–400 nm). Although HYPSO-1’s sensor measures 120 wavelengths [29], we excluded eight wavelengths in our previous work [43], such as those in the oxygen A-band within the NIR, due to significant light absorption [63,64]. Since the input to the convolution is a 1D sequence, and the patterns to be detected also share this dimensionality, the kernel weight parameters must also be 1D. As a result, each convolution kernel has only one component, and with , each kernel contains 6 weight parameters. The detection of each pattern occurs by convolving the input sequence with these weights, sliding the kernel over and scanning small segments (or windows) of the input sequence against the weights. For each window, the operation results in one sample, as follows:
where denotes the windowed samples, the kernel weights, and the kernel bias. The result is then passed through a ReLU activation function, which outputs zero if the result is negative or retains its value if positive. The resulting convolution sample, , where j indexes the window being processed, indicates the strength of the local pattern detected by the kernel at that position in the input sequence. This process is repeated for each window along the sequence , as described by Equation (1).
Figure 3 illustrates how the window slides one sample at a time, with a stride of . The window slides across the entire sequence , ensuring that every sample is processed at least once. However, because 1D-Justo-LiuNet does not employ padding (), the last window does not extend beyond the end of sequence. This slightly reduces computations by avoiding repeating the operations from Equation (1) times, and slightly shortens the convolution sequence. Not extending the window beyond is not critical, as our previous work [43] found that the final samples in for the blue spectrum contain redundant information, while most variance is in the first samples, corresponding to the NIR and visible red [65]. After the window has finally slid over the entire input sequence, the number of samples in produced by the convolution (i.e., the length of the 1D feature map), is calculated as:
where is the length of the input sequence , and represents both the length of the convolution and the number of windows processed. For the first convolution layer, this results in:
indicating that the first convolution layer produces samples per kernel, as also shown in Table 2, reducing the length of the input sequence by samples.
Finally, the same convolution process is applied to the remaining kernels in the layer, but using different weight parameters and bias , as each of the six kernels in the layer is trained to detect a different pattern. The 1D feature map from each kernel is then stacked together at the output, forming the 2D sequence .
3.3.2. Implementation
In Algorithm 1, we present the pseudocode for our implementation in C, with a flow diagram given in Figure 4. The C code for all network layers is also openly available in our GitHub repository at https://github.com/NTNU-SmallSat-Lab/AI_deployment_justoliunet.
Steps (3-5) in Algorithm 1 initialize the window with the first samples from . In steps (6-20), we first process this window. Namely, after initializing an accumulator to 0 in (7), we perform Multiply-Accumulate (MAC) operations between the window samples and weights in (8-10). The bias is added in (11), followed by ReLU activation in (12), and the result is saved in (13) to the output sequence. If more samples remain to be processed in , the window slides by stride in (14-19), where samples are first shifted (15-17), and then a new sample from is introduced in (18). The processing outlined in (6-20) is repeated for all windows, eventually producing a 1D feature map per kernel . As shown in step (2), the processing then restarts for a new kernel to detect a different pattern. A potential minor speed improvement involves initializing the accumulator with in (7), and removing step (11) to reduce the number of addition operations.
| Algorithm 1 Implementation 1 for convolution layer with single-component kernels |
|
To minimize computational resources, we extensively use C pre-compiling directives for all hyper-parameters, such as , , and , among others, substituting their values directly before compilation. This eliminates the overhead of creating and initializing variables at runtime, while also saving memory since no allocation is required for hyper-parameters. However, weights and bias are initialized at runtime and contribute to the program’s memory footprint, along with sequences like input , output , and the internal MAC accumulator. However, the critical aspect in terms of performance is the handling of multi-dimensional sequences in memory since adequate access patterns are crucial for optimizing performance, dependent on memory cache utilization. In our case, the SoC’s dual-core CPU has 32 KB of L1 data cache per core and 512 KB of L2 cache [29,56]. The L1 cache has lower latency due to its proximity to the CPU, while L2 is slower but has larger storage. The caches are handled by the CPU’s cache controller based on data size and access patterns. To this extent, data with adequate spatial and temporal memory locality is more likely to remain in L1 cache for faster access. Spatial locality refers to data being laid out contiguously in memory. For example, when accessing an element in an array, the cache assumes that the contiguous memory addresses will be accessed next and pre-fetches their content for faster access. In our case, for 1D sequences like the spectral signature , window , and bias , samples are stored contiguously in memory, making their access pattern straightforward. However, for multi-dimensional sequences, C uses a row-major order by default, where the columns of each row are stored contiguously in linear memory before the next row. Therefore, to optimize memory access during MAC operations in step (9) in Algorithm 1, we deliberately arrange the K kernel weights in columns within , making it more efficient to access all weights within the same kernel before moving to the next one. We follow this access pattern for most multi-dimensional sequences in this work. In addition, the CPU’s cache controller handles temporal locality by pre-fetching frequently accessed data. Sequences like weight parameters in exhibit strong temporal locality, as they are repeatedly accessed while processing the windows.
Overall, spatial and temporal locality reduce computation time. However, a drawback of our implementation given in Algorithm 1 is the inefficiency caused by the window sliding from the start of for each new kernel. Although we could slide over the input sequence only once, as we propose alternatively in Algorithm 2 and in Figure 5, this implementation would sacrifice row-major memory access. Regardless, we have not implemented this second alternative CPU approach, as the Zynq-7030’s slow dual-core CPU makes FPGA acceleration a more suitable option for faster inference. Therefore, our focus is on creating a C implementation that can be more easily synthesized for the SoC’s FPGA in the future. For example, in our CPU implementation, unlike the linear SVM in [58], we avoid dynamic memory allocation (e.g., malloc), as we verify it cannot be synthesized into Register Transfer Level (RTL) and FPGA logic by High-Level Synthesis (HLS) tools like Xilinx’ Vitis HLS. Using dynamic memory at runtime would prevent the tools from determining the exact memory required, which must be known for placing and routing at design time.
| Algorithm 2 Implementation 2 for convolution layer with single-component kernels |
|
3.4. Pooling Layers
Pooling layers maintain invariant feature representation, prevent convolution layers from escalating further the network’s complexity, and reduce the final latent space dimensionality. Since pooling across 1D-Justo-LiuNet functions similarly, we illustrate our implementation by focusing only on the first pooling layer. It receives input from the first convolution’s output, , consisting of feature maps. While the number of pooled maps remains the same as the input, the length of each is reduced from down to , where also represents the number of pooling operations. The pooling factor, F, determines how much the map’s length is reduced. This length is calculated as . In 1D-Justo-LiuNet, all pooling layers use , halving the length of the feature maps [43]. If is odd, the last sample in - from the blue spectrum - is discarded, given that the network’s pooling layers also do not use padding, requiring the floor operation for odd input lengths.
Algorithm 3 provides the pseudocode for the first pooling layer. Steps (2-6) show that each feature map is pooled individually, following C row-major order. In step (5), the layer compares two consecutive samples and selects the largest one, then moves to the next two samples and repeats the process. The results are stored in . Overall, pooling shows considerably lower complexity than convolutions, as it does not need extensive arithmetic operations with weights and biases. Given that , a potential speed improvement involves replacing the multiplication in step (4) with a left shift operation by one bit, which is typically faster at hardware level than multiplying by 2. This optimization assumes that the iteration in step (4) has been previously initialized to 0, and that j is calculated as the sum of j with F before left shift is applied.
| Algorithm 3 Pooling layer |
|
3.5. Convolution Layer with Multi-Component Kernels
The first convolution layer uses single-component kernels, while the remaining convolution layers utilize multi-component kernels, as illustrated next with an example of the second convolution layer. To begin, while the functionality remains the same as in the first convolution, the kernel weights dimensionality introduces some differences. Unlike the first layer, which processes a 1D input , the pooled features are instead 2D as each position contains components representing the features detected previously. As a result, the kernel weights are also 2D. In short, while the first convolution had coefficients per kernel, the second convolution now includes components for each of the coefficients per kernel. This allows abstract feature extraction combining the simple patterns detected by the previous convolution, yet at the cost of increased complexity. The sliding window also becomes 2D with dimensions (accordingly with ), and following C row-major order, we store the kernel weights as (see notation and description in Table 1). However, the output still remains a 1D feature map per kernel, with all results stacked in .
Algorithm 4 provides the pseudocode for the convolutional layer. Steps (3-7) initialize the 2D window with the first samples from . Following row-major order, columns are accessed first. Then in steps (8-26), we first process this window. The processing is nearly identical to using single-component kernels. Namely, after initializing the accumulator in (9), we perform MAC operations in (10-14) between the window and weights, also following row-major order. The use of multi-component kernels affects only the weights, so the addition of bias and ReLU activation before storing the result, in steps (15-17), remain the same. Finally, the window slides over in (20-22), shifting samples for each separate component and then introducing in (23) a new sample from with all its features. This process is repeated for all windows and restarts for each new kernel. Certainly, the functionality remains the same as for the first convolution layer. However, multiple-component kernels require significantly more operations and parameters, where the number of MAC operations increases critically. Deeper convolution layers also include more kernels, further increasing complexity. In short, convolution layers tend to be considerably more complex than pooling and flatten layers. In this work, we will provide a numerical example to illustrate the growing complexity and explain which convolution layer we propose for future FPGA acceleration.
| Algorithm 4 Implementation 1 for convolution layer with multi-component kernels |
|
3.6. Flatten Layer
In Algorithm 5, we implement the flatten layer. As noted in Table 2, the input to the flatten layer is the sequence from the last pooling layer in the network with dimensions , i.e, 24 feature maps of length 2. The sequence length has reduced across the network from in to 2 due to the repeated pooling operations, ensuring high feature invariance at this stage. The flattening operation now serializes the first column sample with its 24 features, followed by the second sample with its respective 24 features. Because of how Keras implements flattening, this is the only operation in this work where we do not use row-major order. The output is a 1D flattened sequence, , with samples, spanning a 48-dimensional latent space. These feature samples are fully connected to classification neurons in a subsequent dense layer, predicting whether the features correspond to sea, land, or a cloud.
| Algorithm 5 Flatten layer |
|
3.7. Dense Layer
The dense layer classifies the features in into one of the classes: sea, land, or clouds. It calculates one probability per class using neurons. Each neuron is fully connected to the input features in , with synaptic weights stored in with dimensions . The neuron that gets activated the most indicates the most likely class for the spectral signature .
Algorithm 6 follows a similar concept to convolution layers when processing each individual window, yet with some differences due to exponential calculations during activation, unlike simple ReLU functions in convolutions. In steps (2-9), we compute one pre-activation value per neuron, known as logit. Since logits do not represent probabilities, they need to be converted, later in (10-17), into probabilities for easier interpretation. In Algorithm 6, we first reset the accumulator in (3) and perform MAC operations in (4-6) between the input features and the synaptic weights using row-major order, then add the bias in (7) to compute the logit. However, we cannot convert it to a probability yet, as we need the logits from all neurons. Only when all logits are available, we can normalize them into probabilities. Therefore, in (8), we merely store the logit and return to step (2) for computing the next neuron’s logit. Once the process is complete for all neurons, we finally convert the logits in (10-17) into probabilities using the softmax activation, which is standard for multi-class classification. This function scales the logits, representing them as class probabilities as follows:
where is the logit from a given neuron, and the denominator is the normalization factor - summing the exponentials of all logits - ensuring the probabilities add up to 1. In Algorithm 6, steps (10-14) exponentiate each logit and sum the exponentiated values. In (15-17), each exponentiated logit is divided by the normalization factor, yielding the predicted class probabilities in . These values indicate the likelihood and confidence that the spectral sequence belongs to a specific class. The highest probability in gives the final categorical prediction P, i.e., , with an ideally minimal error of . A speed improvement can be achieved by calculating the inverse of the normalization before step (15), so that in step (16) each probability is multiplied by this inverse instead of dividing. This replaces multiple divisions with a single division calculation, making it more scalable as the number of class neurons increases.
| Algorithm 6 Dense layer |
|
3.8. Testing, Verification and Deployment
After completing the C implementation, we first test inference on a general-purpose computer on ground, comparing the results of our implementation with those from a reliable framework like Keras offering higher abstraction. If the results match, it confirms the correctness of our implementation. We perform this evaluation in two steps to facilitate debugging and minimize the risk of failure. Our first step consists of feeding the model’s layers with predefined input stimuli resembling a pixel and manually configuring the layer’s weight and bias parameters using integer values for easier testing. By comparing their outputs to those inferred from the Keras layers with the same weights, biases and input stimuli, we confirm that the outputs are the same, validating our functionality in C. Our second step, after verifying pixel-level functionality, is to test inference at the image level for a complete data cube from HYPSO-1. Our implementation and Keras now utilize the weights and bias parameters obtained during model training for sea-land-cloud segmentation. After this, we confirm that the segmented image by our implementation in C is identical to the one inferred by Keras, further validating the reliability of the segmentation results.
Following this verification, we migrate our implementation in C to a Laboratory Processing Unit (LPU), similar to the method used in the literature for testing deep learning for on ground-based processing units [34]. The LPU replicates on ground the same hardware and configuration flying on board HYPSO-1 with the architecture previously presented in Figure 1. We first confirm that our implementation migrates and runs without issues. We then verify that the segmented images by 1D-Justo-LiuNet in the LPU remain consistent with those inferred by Keras. Additionally, we measure the total time for segmenting each data cube, using available single-core and double-core multi-thread CPU processing. Upon completed verification, our final stage is the deployment of 1D-Justo-LiuNet in space, updating the application pipeline in Figure 1. For the experiments in this work, we modify configuration files to enable this update module and conduct edge inference for each new acquired data cube for sea-land-cloud segmentation.
4. Example Case Scenarios
4.1. Incomplete Downlink of Data Cubes
Satellites may encounter challenges during the radio downlink, leading to incomplete data reception on the ground and requiring re-transmission. We use these challenges to illustrate how in-orbit inference helps optimize the limited downlink resources in this scenario. Furthermore, we will introduce additional case scenarios where edge segmentation enhances satellite operations, such as when the satellite mispoints at space instead of Earth, misses the intended geographical area, or when conditions like high cloud coverage or overexposure make the data cube unusable. We will explain how inferred segments at edge can be interpreted both on ground and autonomously in orbit for more efficient operations.
As an example, in HYPSO-1, the on-board streaming process to the PC and S-band transmitter is generally error-free. Nevertheless, the S-band radio occasionally experiences interruptions due to telecommunication disruptions, which affect the raw data cube more than the segmented images. This occurs because the segmented images are transmitted first, allowing enough time for retransmission of lost packets, while the data cube is more susceptible to disruptions, as it occupies most of the remaining transmission window. For downlink, a radio connection is established during a satellite pass when a ground station has LoS to the satellite. However, the estimated downlink window is sometimes longer than what third-party ground stations can actually provide, which is beyond our control, but may result in the reception of incomplete data cubes [9]. In general terms, other factors can also affect the ground station’s ability to receive sufficient signal strength. Meeting the necessary Signal-to-Noise Ratio (SNR) and Signal-to-Interference Ratio (SIR) thresholds is not always guaranteed [66], which can disrupt the downlink and lead to incomplete data reception. For example, HYPSO-1’s transmitter operates in a congested S-band, where interference from other systems can be expected, even under optimal antenna alignment, polarization, directional pattern with minimal side lobes to minimize interference, and adequate transmission window. In broad terms, while the S-band is also less susceptible to rain fade and other weather-related disruptions compared to higher frequencies, severe weather can still attenuate signals below the levels predicted by Friis’ link nominal budgets, interrupting downlink. In summary, disrupted downlink can occur for various reasons, including ground stations unavailability. In such cases, the data cube received is more likely to be compromised, and when data is missing, the CCSDS-123v1 on-ground decoder cannot recover the lost information, resulting in artifacts being produced to fill the cube’s dimensions (see an example in Figure 6 (c)).
Previously, when receiving incomplete data, we would have generally re-transmitted the entire HS data cube in an attempt to receive it fully. However, with our contribution, the received segmented images allow us to assess first the importance of the missing pixels - whether they correspond e.g. to clouds or irrelevant data. Additionally, it also enables us to perform on-ground georeferencing using the segmented images to align the area with approximate coordinates on the Earth’s surface, although the downlinked HS data cube is incomplete [30]. Furthermore, the images also allow us to make an informed decision from ground on the best course of action: whether to command the satellite to reattempt downlink of the cube or discard it without downlinking and instead command the flight control to revisit the area later. The action taken is important, as revisiting could introduce significant latency, often of least one day for HYPSO-1, compared to reattempting downlink, which can often be performed faster, within an orbital period of 96 minutes, assuming the satellite gets LoS with Svalbard Satellite Station located in the Arctic region. This operational improvement in decision-making would not be possible if segmentation was conducted on ground, where data was missing.
As we will present in the following sections, there are additional use cases where segmented images can enhance and automate future operations. From here on, we will use the terms segmented images and segments interchangeably. In Section 4.2, we present an approach for ground-based segment inspection, while in Section 4.3, we propose on-board automated segment interpretation, eliminating the need for ground-based human inspection. We will present in-orbit automation, from basic techniques, like class proportion analysis, to more advanced segment interpretation using deep learning based on classification of segmented images. This work will demonstrate the latter on ground, by implementing a new CNN to interpret the segments directly during flight.
4.2. Ground-Based Segment Inspection
Instead of blindly streaming captured data cubes into the PC’s buffer for downlink without considering if their content justifies the high transmission cost, we propose buffering all inferred segments first. While the PC’s buffer is limited, this approach is feasible since segments require significantly less space than raw data cubes. When the satellite has LoS with a ground station, numerous segmented images can be downlinked in a single pass, unlike data cubes, which require at least two passes in HYPSO-1. However, several segmented images can be transmitted at once via a radio with an average throughput of 1 Mbps (equivalent to 125 kBps). Since each segmented image is 19 kB in size, downlinking one image takes less than a second using 1-byte encoding.
Once the segmented images are received on ground, a human operator can inspect them to identify any issues with the data cubes on board. Problems that can be detected from the images include the HS camera mistakenly pointing at space, which creates a distinctive striped pattern (e.g., see Figure 9 (b)), or capturing incorrect geographical areas. Other issues, like heavy cloud cover or overexposure, can also be identified. Langer et al. [55] outline parameters the operator must configure on ground for new captures, such as exposure time, gain, and geographic coordinates. We propose that the operator, during this process, also decides whether to buffer the raw data from the SD card to the PC’s buffer or discard it and command flight control to revisit the area. While this process improves operations and bandwidth efficiency, manually inspecting numerous segmented images on ground is time-consuming and depends on human intervention. A more efficient approach would involve using AI algorithms to automate segment interpretation. Ideally, this interpretation should happen in orbit, allowing decisions to downlink or discard data cubes automatically during flight. This is what we address in the following section.
4.3. On-Board Automated Segment Interpretation
Interpreting segmented images in orbit enables actionable intelligence deciding whether to downlink or discard a data cube based on the inference results. In terms of HYPSO-1’s system architecture in Figure 1, we propose that, before streaming data to the PC’s buffer, only the relevant data is buffered for downlink, based on the segments inferred at the pipeline applications. If a HS data cube is flagged as usable, we propose automatically streaming its segments first, followed by the raw HS data cube, to the PC’s buffer for downlink. Streaming segments first maintains maximal optimization in case of downlink disruptions affecting the cube. However, if the HS data cube is flagged as unusable, the system can automatically delete it from the SD card, avoiding unnecessary buffering for downlink, and possibly repeating a new capture over the same coordinates (this demands updating the scheduling software), aiming for a more useful data cube. To track adequate model performance over time, we still recommend downlinking the segmented images, even for the discarded cubes. To flag whether a HS data cube is usable, the inferred segments can be processed, starting with a simple framework of class proportion analysis. However, training deep learning models for classification of the segmented images can provide deeper understanding beyond basic class proportion analysis.
- Class Proportion Analysis: As Langer et al. [55] note, the operator configures various parameters for new captures on the ground. Therefore, we propose using this flexibility by adding class proportion thresholds to the uplink scripts, allowing the OPU to automatically flag captures as usable or not based on the detected class proportions. For example, when planning a capture over an oceanic archipelago of islands where most pixels are expected to be segmented as water, a threshold can be set so that if detected land exceeds an obviously disproportionate high value (e.g., over 90%), it may indicate a pointing error, flagging the capture as not usable. In our previous work [43], 1D-Justo-LiuNet was tested using metrics like Spearman’s correlation and found that it performed well for ranking data cubes to prioritize downlink based on the analysis of sea, land, and cloud coverage proportions, achieving an error-free ranking. We will discuss the strengths and limitations of this method in more detail.
- Segments Classification Analysis: While class proportion analysis is simple and effective, we will show examples where it is insufficient and inadequate for segment interpretation due to the need for spatial context. Therefore, we also test an additional deep model, trained on segmented images inferred in flight, to illustrate how these images can be further interpreted in orbit to enable autonomous decisions on whether to downlink or discard the raw data cubes. We will also discuss the strengths and challenges of this approach.
4.3.1. Class Proportion Analysis
A segment interpreter based on class thresholds can be effective for decision-making in scenarios such as:
- Similar to our previous example, a water scene (e.g., deep ocean, archipelago, coastline) where detected land disproportionately exceeds a threshold.
- A land scene (e.g., inland, coastline, islands) where water pixels unexpectedly surpass a threshold. This also applies to snow or ice scenes (e.g., in Arctic regions) where little to no snow/ice is detected, and water dominates the capture.
- Areas with cloud cover or overexposure exceeding a certain threshold.
In such cases, there is a risk the satellite missed the intended area, possibly making the HS data cube unusable. Segment interpretation based on class thresholds can be suitable for satellites seeking cloud-free scenes, such as ESA’s Phi-Sat-1 mission, which sets cloud cover limits to 70% for acceptable captures [67]. However, this approach has limitations in missions like HYPSO-1, where target areas are often much smaller than the full captured area. Even with high cloud cover percentage, captures may still be useful if the remaining non-cloud pixels cover the small area of interest. Therefore, relying solely on thresholds can be misleading in such cases, although if cloud cover is extremely high (e.g., over 90%), it may suggest the decision to take based on the high risk of relevant target areas being also cloud-affected.
4.3.2. Segment Classification Analysis
Interpretation using AI algorithms or statistical analysis for classification of segmented images is certainly more computationally complex. It demands the OPU’s pipeline applications to run cascaded inference to interpret a segmented image to decide whether to downlink or discard the raw data cube on board. However, this approach is preferred to achieve precise in-orbit automation.
To begin, in computer vision (CV), the term segmentation refers to pixel-level classification (as in 1D-Justo-LiuNet). However, when we next use the term classification from CV, it means labeling the entire segmented image under a single class. In this work, we train and test an additional 2D-CNN model to demonstrate how segmented images can be autonomously interpreted in flight. For illustration, the 2D-CNN is trained to detect the characteristic striped pattern seen in HYPSO-1 data when the satellite mispoints at space instead of Earth (e.g., see Figure 9), allowing the HS data cube to be flagged as unusable and discarded on board. We train the model using 12 segmented images for training (4 with and 8 without mispointing) and 4 for testing (2 with and 2 without mispointing). While more training data could be used, this data split suffices to demonstrate segment interpretation for future in-orbit deployment. Further details on the used data and obtained results will be discussed in Section 5.
Furthermore, given the increased automation level, we consider that it is important to briefly introduce techniques that explain the 2D-CNN model’s final decision on whether a capture is unusable, especially since this decision may lead to irreversibly discarding the data on board. Therefore, to explain the 2D-CNN model’s predictions, we additionally use algorithms from Explainable Artificial Intelligence (XAI) [68], an emerging AI field aimed at revealing how black-box AI models make their decisions. While we emphasize that XAI is not the focus of this work, we deem XAI will most likely play a key role in AI’s future due to ethical and accountability concerns of AI technology. As a result, in this work, we demonstrate XAI on HYPSO-1 using standard methods like model-agnostic SHAP (SHapley Additive exPlanations) and Grad-CAM (Gradient-Weighted Class Activation Mapping). As an example, we apply these algorithms to the 2D-CNN to explain why the model determined whether a capture is usable. SHAP, based on cooperative game theory, assigns an importance score to the individual contribution of each data feature to the model’s final prediction. However, Grad-CAM, more suited for CNNs, uses the gradients of the target class into the last convolution layer to produce a localization map, which highlights the features (in this case, pixels in the segmented image) driving the most the model’s prediction. This localization map is typically displayed as a heatmap, created by combining the last convolution layer’s feature maps with the target class gradients, resulting in a weighted feature map. Results will be discussed in Section 5.
4.4. In-Orbit Data Products and Selective Compressive Sensing
Beyond automated decisions to downlink or discard HS data cubes, the output of 1D-Justo-LiuNet can serve as input for current and future processing modules in the pipeline applications in Figure 1. At the time of writing, these mainly include smile and keystone data cube correction, spatial pixel subsampling, a linear SVM, and an RGB composition module. For example, the linear SVM can detect water colors, with potential for future products such as maps indicating Chlorophyll-A levels for detecting phytoplankton and algae blooms [41,69,70,71,72], which should apply only to pixels segmented as water. For land pixels, indexes like the Normalized Difference Vegetation Index (NDVI) [73] and Enhanced Vegetation Index (EVI) [74] to assess temporal changes in green vegetation can be computed in orbit to monitor crop health and estimate biomass, assisting soil monitoring [75] for food security - one of CHIME’s nominal goals [76]. In addition, if the minimal expected reliability of in-orbit segment interpretation cannot be ensured when flagging data cubes as not usable, we suggest they are marked as potentially unusable instead of being discarded. In this case, rather than downlinking the full data cube, the result from the RGB composition module would be streamed to the ground for operator inspection. The operator can then confirm whether the capture should indeed be discarded. However, this approach would reintroduce human intervention, reducing efficiency.
Moreover, the pipeline applications include a subsampling module. For future implementation, we suggest applying here an informed lossy compression only to certain segmented pixels from 1D-Justo-LiuNet when downlinking usable HS data cubes. Selective compression, proposed e.g. by ESA for missions like CHIME in [25], uses on-board cloud detection to apply higher compression ratios to cloud pixels with different lossy schemes, while non-cloud pixels receive lossless or near-lossless compression. This method was successfully tested on AVIRIS and simulated CHIME data. Additionally, one may also use, for instance, selective Compressive Sensing (CS). Unlike traditional compression methods, CS simplifies on-board compression by subsampling a few random spectral channels for each pixel, transferring computational complexity to ground-based lossy reconstruction. Based on our previous studies [51,77], we recommend using the Generalized Orthogonal Matching Pursuit (GOMP) algorithm [78] due to its faster convergence and acceptable accuracy. For sparse pixel recovery on ground, GOMP can be applied to less relevant pixels, such as clouds, or to other classes - for example, if the target area is water, both land and cloud pixels may undergo in-orbit random subsampling and GOMP reconstruction on ground. However, future efforts are needed to modify the current OPU’s compression capabilities, as the current lossless CCSDS-123v1 implementation in flight [59] only supports compression of entire cubes and does not allow selective lossy compression for selected pixels.
5. Results and Discussion
We will illustrate segmented images inferred in orbit for various examples to demonstrate segmentation performance in the different case scenarios previously described. Most figures will primarily include:
- A Google map image showing the approximate geographical area where it was planned to image with HYPSO-1.
- The segmented image; where blue denotes water, orange indicates land, and gray represents clouds or overexposed pixels.
- An RGB composite created from the raw HS data cube, utilizing bands for the Red, Green, and Blue channels out of the 120 available (at 603, 564, and 497 nm, respectively).
We include various captures, selected to address issues such as incomplete downlink, satellite mispointing, varying levels of cloud cover and thickness, and overexposure. Additionally, the captures cover a broad range of terrain types:
- Arid landscapes and desert regions with different mineral compositions.
- Forested areas and urban environments.
- Lakes, rivers, lagoons and fjords of different sizes.
- Coastlines, islands and oceans.
- Waters with colors ranging from cyan to deep blue.
- Arctic regions with snow and ice.
We will also present results from a 2D-CNN detecting patterns in the segmented images that indicate satellite mispointing at space instead of Earth, enabling autonomous decision-making to discard unusable data cubes on board. Brief results from AI explainers will be included to justify the model’s decision. Finally, we will provide timing results to identify which model layers may benefit the most from FPGA acceleration. In the supplementary material, segmentation results by 1D-Justo-LiuNet for over 300 images processed in orbit are additionally provided.
5.1. Accuracy: Incomplete Downlink of Data Cubes
We assess segmentation accuracy in orbit via visual inspection, as no ground-truth labels are available for comparison. This subjective approach is common in the literature when analyzing segmentation results in unlabeled satellite imagery [79]. However, metrics such as the Davies-Bouldin Index (DBI) and Silhouette Score [80] may be used to evaluate the quality of segmented images without ground truth. These metrics evaluate segment separation (ideally maximized) and distance between data points within clusters (ideally minimized). Nevertheless, objective quality assessments in digital applications are increasingly challenged, as seen in recent standards like ITU/P.910 from the International Telecommunication Union [81]. These standards prioritize subjective quality, as objective metrics, like the ones mentioned, can fail to capture user-perceived quality. In this work, relying on objective metrics can be misleading, as they may not capture mission-critical anomalies, making expert inspection more suitable. Since proposing subjective scores is unnecessary and beyond this work’s scope, the evaluation is based on our own expertise with HYPSO-1. We simply compare the RGB composite from the raw data cube with the inferred segmented image.
5.1.1. Imagery of Venice
We planned a capture of the Venetian Lagoon, shown in Figure 6 (a), where only the water is of interest in this case. Other possible regions captured, like the Northern Italian Alps, are incidental and irrelevant here. When comparing the segments in (b) with the map in (a), we confirm the satellite correctly pointed and captured the intended Earth’s coordinates around the Venetian Lagoon by approximate georeferencing. However, we do not receive the complete HS data cube resulting in the decompression artifacts seen in (c). With the proposed algorithms, in-flight segmentation allows us to decide whether to reattempt downlink or discard the on-board HS data cube and revisit Venice instead. Since the lagoon’s water is segmented as cloud-free, with clouds mainly covering the Alps, we decide to reattempt downlink, thereby optimizing latency over revisiting the area. This informed decision is clearly better than discarding the cube based on the incorrect assumption that cloudy top pixels in (c) indicate the lagoon is also obscured.
After reattempting downlink, we receive the capture in Figure 7 (a) mostly without downlink issues. For easier comparison, the segmented image is overlaid on the RGB composite in (b). We confirm the satellite correctly pointed to Venice’s area and captured the lagoon cloud-free, with only the Alps in the north affected, validating our decision to reattempt downlink. We consider the segmentation accuracy guiding this operation as acceptable for our application, even if some misclassifications occur. Although large water bodies and coastlines are well-detected, cloud shadows are sometimes mistaken for deep water due to their dark color, and lighter-toned river water is confused with clouds. This suggests that improved model training could reduce these errors. However, the focus of this article is on model inference, not on training.
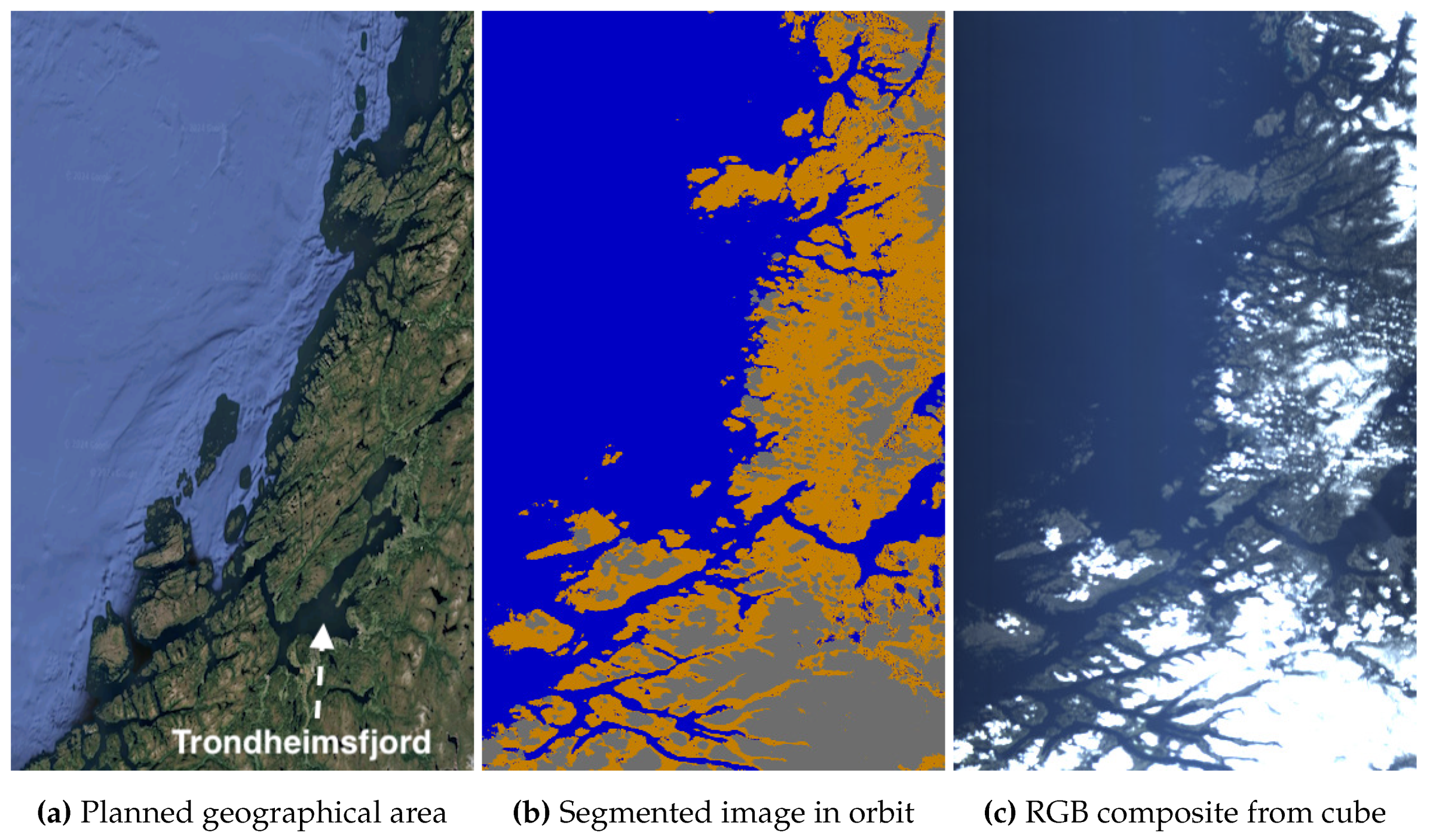
5.1.2. Imagery of Norway
Figure 8 (a) shows our target area around Trondheimsfjord, one of Norway’s longest fjords at over 100 km, surrounded by extensive forests. We aim to capture the fjord and the surrounding forests without significant cloud cover. The segments in (b) confirm that the satellite was correctly oriented toward Trondheim’s area. However, similar to the Venice capture, the data in (c) is affected by artifacts. Despite Norway’s complex and island-dense coastlines, where small islands are often misclassified as water due to stronger ocean reflections overshadowing land scattering, the model still identifies the ocean, land, and clouds at the top of the capture with a precision that meets our operational needs. Although Trondheimsfjord remains cloud-free, substantial cover affects the southern forests. As a result, rather than reattempting downlink, we decide to discard the data cube and plan a revisit for a clearer capture of the southern forests.
5.2. Accuracy: Satellite Mistakenly Pointing at Space
We plan a capture of the Namib desert in Namibia, Africa, shown in Figure 9 (a). The region hosts a station from ESA that is part of RedCalNet (Radiometric Calibration Network), a global network of sites providing publicly available measurements to support data product validation and radiometric calibration. The downlinked segments in (b) exhibit a characteristic stripped pattern, typically inferred when the satellite mistakenly points at space instead of the Earth. The RGB composite in (c) confirms an unusable capture, showing stripes in a mostly gray image. If future operations adopt our Ground-Based Segment Inspection approach (see Section 4.2), operators can manually review the downlinked segments and easily spot the mispointing error solely from the segments in (b). While uplinking parameters for new captures, operators can additionally command the satellite to discard the on-board data cube and revisit the area instead, avoiding the high transmission cost of downlinking this unusable cube.
Alternatively, interpreting segments in orbit offers a more autonomous solution (see Section 4.3). For captures mispointing at space, relying on class proportions alone is insufficient, as it does not account for spatial context. Instead, we propose using a 2D-CNN in flight to detect the striped pattern in the segmented image. The CNN would autonomously decide to discard this unusable data cube without human intervention. This serves as an example of how in-orbit segment interpretation can enable autonomous decision-making.
In our previous work [43], we found that the 1D-CNN model 1D-Justo-LiuNet, which focuses solely on spectral context, outperformed 2D-CNNs and ViTs in the HS domain. However, the resulting segmented images have a single-channel value per pixel: 0 for sea, 1 for land, and 2 for clouds. Therefore, applying a 1D-CNN to each pixel is not viable, and while flattening the image for 1D processing is possible, it would fail to capture the strong spatial patterns in the stripes. Detecting such patterns, with significant global spatial features, is better suited to 2D-CNNs. In Figure 6 (b), we showed a segmented image over the Venice area, which is now part of the test set for validating the 2D-CNN. Manual inspection suggested no mispointing error, but we aim for the satellite to infer this autonomously. The 2D-CNN correctly predicts no mispointing (the Earth was not missed) with 100% confidence, as shown in Table 3. The table shows that the network outputs a probability vector, with the first position representing the likelihood that the segmented image belongs to no mispointing class (1.00 in this case), and the second position indicating the probability of it belonging to the mispointing class (0.00 in this case). Moreover, Figure 9 (b) shows another segmented image, part of the test set, with a striped pattern indicating a pointing error towards space. Table 3 shows the 2D-CNN correctly classifies it as mispointing with 100% confidence. However, future work should focus on optimizing the 2D-CNN into a lightweight version for in-orbit deployment while expanding its capabilities to detect more patterns (e.g., detection of islands, coastlines, etc) to increase automation in flight. If the spatial patterns in the segmented images happen to be more complex than expected, we advise conducting training with more advanced techniques like knowledge distillation, transferring knowledge from a larger teacher model (e.g., ViTs [44,82] based on self-attention mechanisms [83]) into a lighter student model that mimics the teacher’s performance.
Figure 9.
Namib desert close to Gobabeb, Namibia, Africa, on 25 June 2024 at 08:51 UTC. Coordinates: -23.6° latitude and 15.0° longitude. Exposure time: 20 ms.
Figure 9.
Namib desert close to Gobabeb, Namibia, Africa, on 25 June 2024 at 08:51 UTC. Coordinates: -23.6° latitude and 15.0° longitude. Exposure time: 20 ms.
To explain the 2D-CNN model’s predictions, we also use XAI algorithms [68]. In XAI, choosing the adequate explainer is crucial, as some explanations can obscure rather than clarify the reasoning behind a model’s predicted outcome. For our data and 2D-CNN model, initial SHAP tests do not explain the CNN’s predictions intuitively enough, so we focus on Grad-CAM instead, which provides more interpretable explanations in our case and is commonly used for CNNs. Figure 10 (a) shows the segmented image over Venice (rotated in the figure), classified in Table 3 as no mispointing. Figure 10 (b) presents a Grad-CAM heatmap, where lighter colors indicate the pixels that influence the model’s decision the most. Grad-CAM shows that the overexposed cloud pixels, along with the coastline shapes, play the key role in the CNN’s classification as no mispointing, while vegetation and especially water have a minimal impact. Furthermore, Figure 10 (c) shows again the segmented image with a stripped pattern, classified in Table 3 as mispointing. Figure 10 (d) presents the Grad-CAM heatmap. Unlike in (b), the heatmap now lacks clear contributing regions, suggesting the model likely relies on the global striped pattern rather than on local features. We further confirm this with additional SHAP tests, where most Shapley scores are around 0, indicating no significant impact from any local region, unlike in (b), where overexposed cloud pixels and coastlines drive the CNN’s decision the most. This example demonstrates how XAI can be applied to CNNs in HYPSO-1 to gain a better understanding of model predictions.
5.3. Accuracy: Satellite’s Inadequate Pointing at Earth’s Surface (Imagery of Bermuda, Greek and Eritrean Archipelagos)
HYPSO-1’s agile operations allow for flexible changes in the satellite’s orientation. However, this can result in the satellite mispointing at space, as previously mentioned, or, despite pointing at Earth, targeting the wrong geographical area and missing the intended targets. For example, in our planned capture of the Bermuda Archipelago in Figure 11 (a), known for its turquoise waters from shallow depths and coral reefs, the downlinked segments in (b) show mostly water with no land detected, indicating the satellite missed the archipelago. Class proportions reveal 92.03% of pixels are water, 7.93% clouds, and only 0.03% land.
Considering Ground-Based Segment Inspection (Section 4.2), operators would determine the satellite imaged deep Atlantic water and clouds, with no land detected, indicating the archipelago was missed. Consequently, the transmission cost of downlinking the data cube would be unnecessary, leading operators to command the satellite to discard the on-board cube and revisit the area. The composite in (c) confirms that, although some turquoise colors, likely from Bermuda’s coast, appear on the right of the capture, the archipelago was indeed missed. Decompression artifacts from incomplete downlink, visible at the bottom of the capture, have been previously discussed.
For in-flight segment interpretation, we can apply our two approaches for On-Board Automated Segment Interpretation (Section 4.3). In this case, where only 0.03% of pixels are segmented as land, interpretation based on the proportion of detected classes is appropriate. During capture planning, in addition to the setup parameters for new captures, the operator could have also uplinked a rough land threshold (e.g., below 0.5% - at the operator’s choice) for the OPU to flag the capture as not usable due to minimal land detection. In orbit, the 0.03% land proportion would fall below this threshold, making the OPU discard the capture. However, beyond merely evaluating the proportion of segmented land, a deep 2D-CNN could interpret patterns in the segmented image, such as island shapes and their spatial arrangement surrounded by water with sharp land-water transitions. If an island-like scene is not detected, the OPU may discard the cube. While we previously demonstrated the concept with a 2D-CNN trained to detect stripes when the satellite mispoints at space, future training to identify more complex features in flight, like island-shapes and other spatial distributions could be relevant.
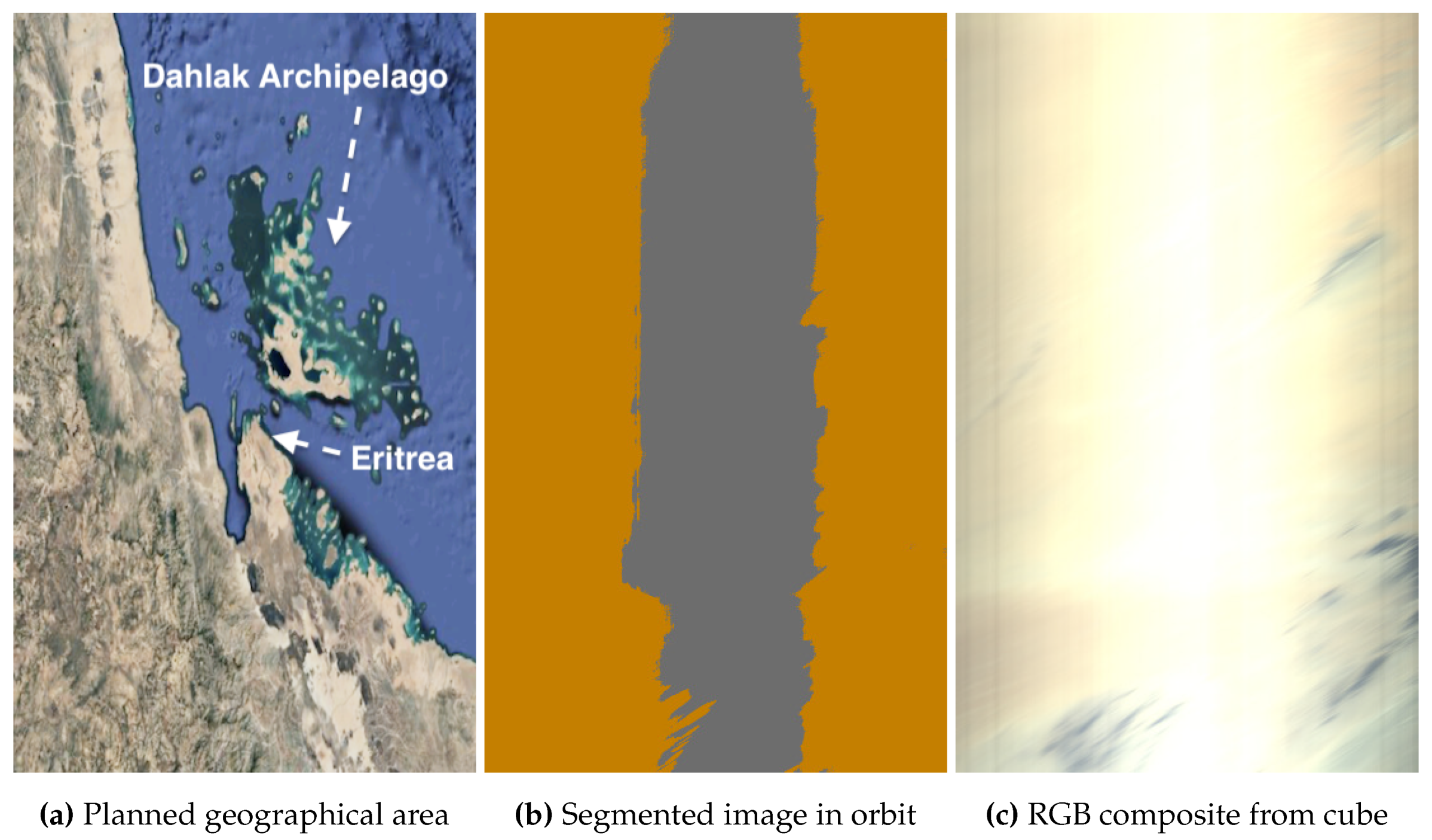
An additional example of satellite mispointing is given in Figure 12 for the Dahlak Archipelago (Eritrea) in the Red Sea. The segmented image indicates no water is detected. The class proportions are: 64.60% land, 35.40% overexposed, and 0.00% water; indicating the satellite did not capture the expected scene of an archipelago surrounded by water. Ground-Based Segment Inspection would reveal the satellite missed the Red Sea around the archipelago, detecting only the arid terrain with high overexposure and no water, leading to operators commanding the satellite to discard the HS data cube and scheduling a revisit. Alternatively, for in-flight segment interpretation, the OPU can easily assess the proportion of detected classes. A minimal water threshold can be set, and if not met, the cube is flagged as unusable. In this case, with 0.00% water pixels, the flagging would be straightforward.
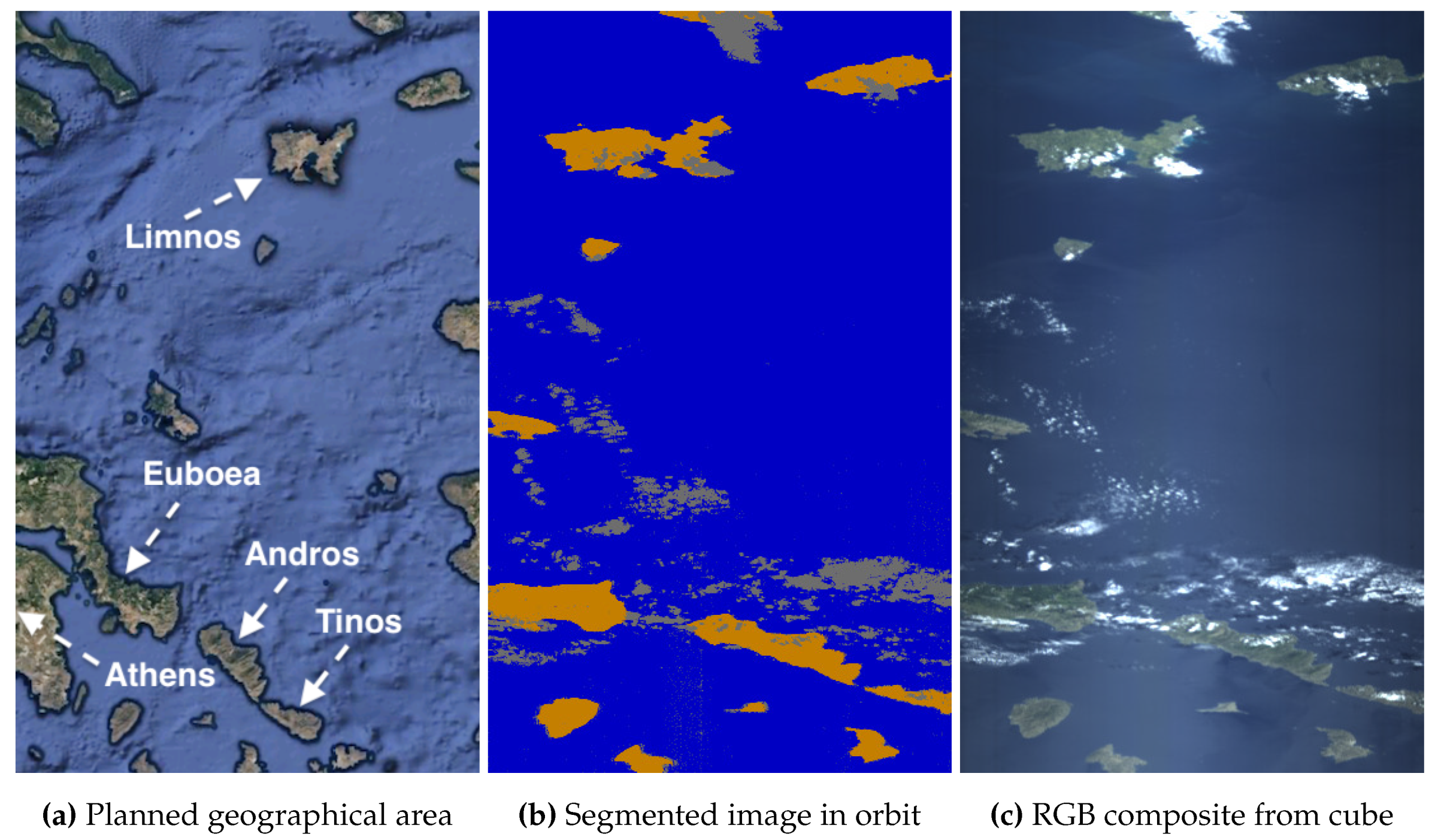
Finally, Figure 13 shows an example of the satellite correctly pointing to the intended area, a Greek Aegean Archipelago near Athens, including islands such as as Andros and Limnos. Ground-Based Segment Inspection would note a more reasonable pattern in (b) for an archipelago, with 87.33% water, 6.80% land, and 5.87% clouds. The class proportions, and especially the segmented image shown in (b), suggest the archipelago was captured correctly. As a result, the operators would command the satellite to downlink the cube, deeming the transmission cost worth, as indeed confirmed by the capture received in (c). For in-flight segment interpretation, the OPU could autonomously check that the class proportions are within certain reasonable thresholds and, using a 2D-CNN, evaluate in orbit if the spatial patterns match an island-like scene.
5.4. Accuracy: Captures of Arid and Desert Regions (Imagery of United Arab Emirates, Namibia and Nevada)
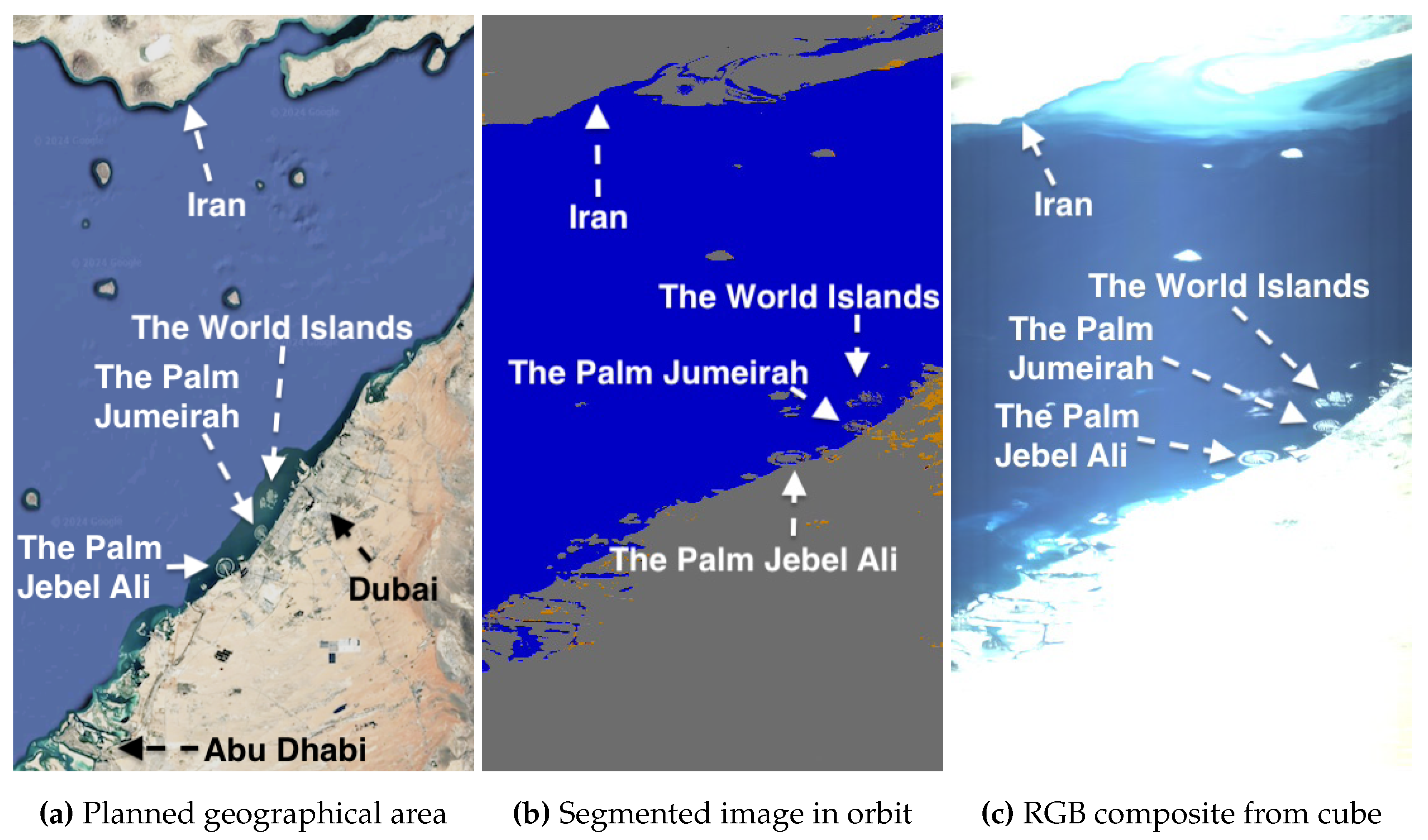
Figure 14 and Figure 15 show captures over the United Arab Emirates (UAE), a region of interest for studying desertification and monitoring aeolian processes resulting in sand movement that could bury roads and threaten urban infrastructure in Abu Dhabi and Dubai. Figure 14 (a) shows that sand near Abu Dhabi has a lighter color, while sand further into the desert takes on a reddish tone. This color variation is due to differences in mineral content: reddish sand has more iron oxide, whereas lighter sand contains more silica and less iron oxide. By monitoring the sand colors over time, the potential aeolian transport of red sand toward Abu Dhabi may indicate the movement of iron oxide-rich sands from the desert dunes into the cities.
Desert regions, especially those with higher silica, are generally more prone to overexposure. Indeed, segments in (b) show most land is detected as overexposed along the UAE’s coast (bottom segments) and extending north to Iran’s coast (top segments). Dubai’s Palm Islands (The Palm Jabel Ali and The Palm Jumeirah) and World Islands, artificial structures built into the sea, are visible on the right. They are highly saturated because the excessive light from the island easily dominates the scattered light from the surrounding water, as confirmed in (c). However, not only is the land overexposed, but some water too. Namely, while the UAE’s coastal water is correctly segmented, the light cyan water along Iran’s coast is overexposed and segmented as such.
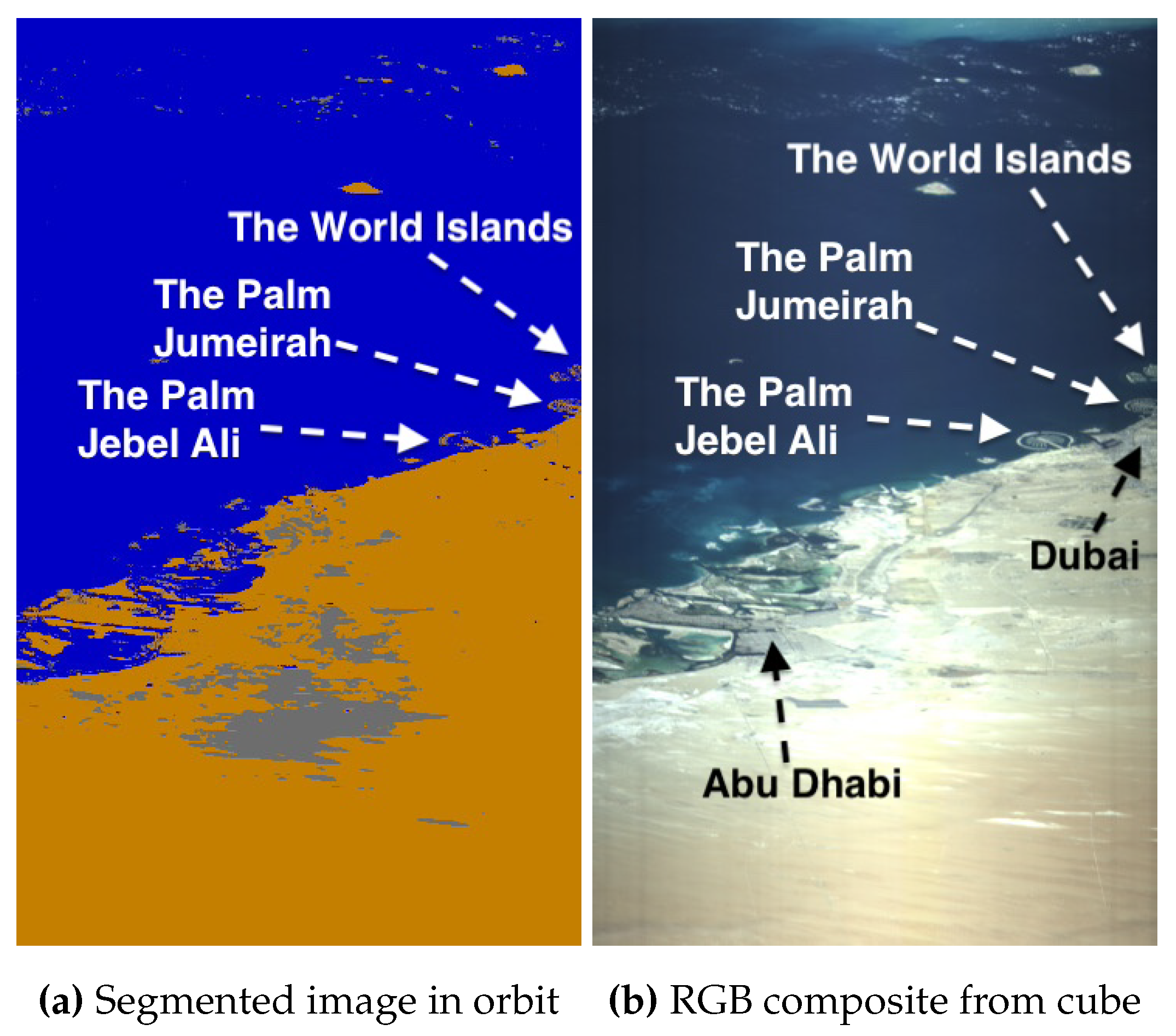
After acquiring a new capture with adjusted exposure settings, the segmented image in Figure 15 (a) shows a significant reduction in overexposure. Only the lighter silica-rich sand near Abu Dhabi is overexposed, while the reddish iron oxide-rich sand deeper in the desert is not. Larger islands are well identified, but the Palms and World Islands are partially misclassified as water due to the now stronger scattering from the surrounding larger water body compared to the thin islands. Despite this, water near Abu Dhabi’s coast, including shallow waters with potential confusion with land, is correctly segmented. The cyan water along Iran’s coast (in the top) is no longer overexposed, being correctly segmented as water.
Ground-Based Segment Inspection can confirm the satellite correctly pointed at the UAE region and assess whether the new cube is worth downlinking. However, the OPU would face challenges to autonomously decide whether to downlink or discard the capture based solely on detected class proportions. In addition, while a 2D-CNN can accurately detect the coastlines, it cannot guarantee with full certainty that the area corresponds to the intended coastline. Therefore, we recommend future work to implement in-orbit georeferencing for better automation in flight. We note that in our upcoming discussion, we will omit the analysis of Ground-Based Segment Inspection and On-Board Automated Segment Interpretation, as several examples have already been discussed.
Finally, to demonstrate segmentation accuracy in other deserts, Figure 16 shows accurate results over iron-rich Namib Desert, hosting ESA’s station part of RedCalNet. Furthermore, Figure 17 captures Mojave Desert in Nevada near Las Vegas, with minor water misclassifications from cloud shadows, which remain acceptable for our application.
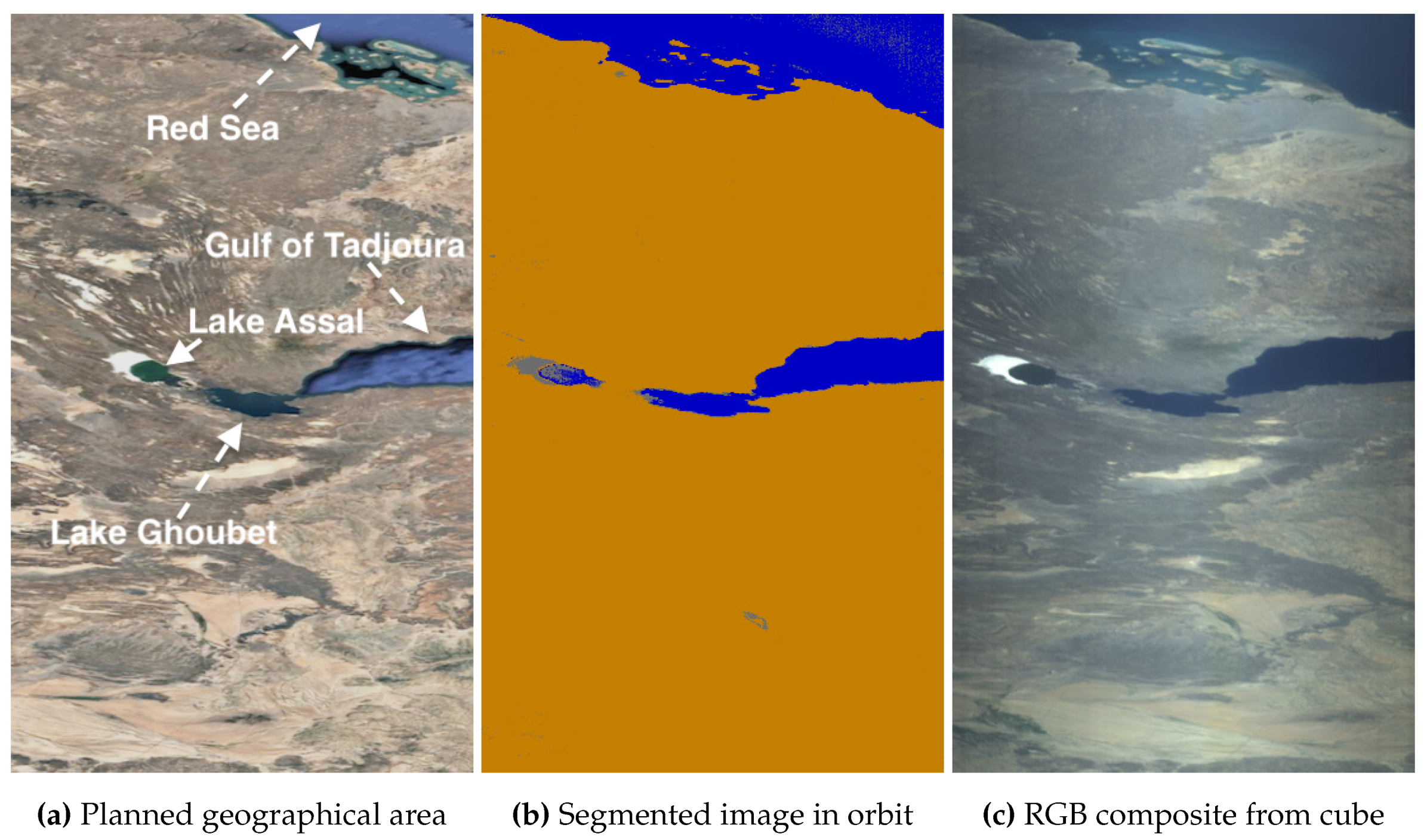
5.5. Accuracy: Captures of Water with Extreme Salinity (Imagery of Lake Assal near the Red Sea)
Given HYPSO’s focus on water observation, Figure 18 captures Lake Assal near the Red Sea, known for its extreme salinity - higher than the ocean and more than the Dead Sea. This volcanic lake, the lowest point in Africa, is surrounded by salt flats. The segments in (b) accurately identify the Gulf of Tadjoura, Lake Ghoubet, and Lake Assal. In Lake Assal, significant overexposure is detected, due to the highly reflective salt flats. The lake’s extreme saline water is also more reflective than typical water systems, resulting in some water pixels being classified as overexposed. The Red Sea, also saline, has similar overexposed pixels in the top segments. The RGB composite in (c) confirms the model accurately segments the salt flats as overexposed. Additionally, although Lake Assal’s water does not appear overexposed in the RGB, segmentation across all HS bands reveals higher reflectance likely due to its extreme salinity.
5.6. Accuracy: Captures of Water Colors (Imagery of South Africa, Vancouver, Caspian Sea and Gulf of Mexico)
Given the importance of water observation and ocean color studies for HYPSO, Figure 19, Figure 20, Figure 21 and Figure 22 present examples of captures with varying water colors, correctly segmented as water. We note that the training set from the HYPSO-1 Sea-Land-Cloud-Labeled Dataset from our previous work [65] does not include subcategories to distinguish water colors due to the lack of ground-truth data to conclude a meaningful and physical interpretation of each color.
Figure 19 images the South African coastline, where darker water colors are correctly segmented due to the extensive dark water annotations in our training set. Furthermore, while thicker clouds are correctly segmented, thinner clouds are misclassified as water, which we will comment later. Additionally, some non-cloud pixels are mistakenly identified as clouds in the top right, suggesting the need for further model training. However, the overall accuracy is still acceptable for our needs. 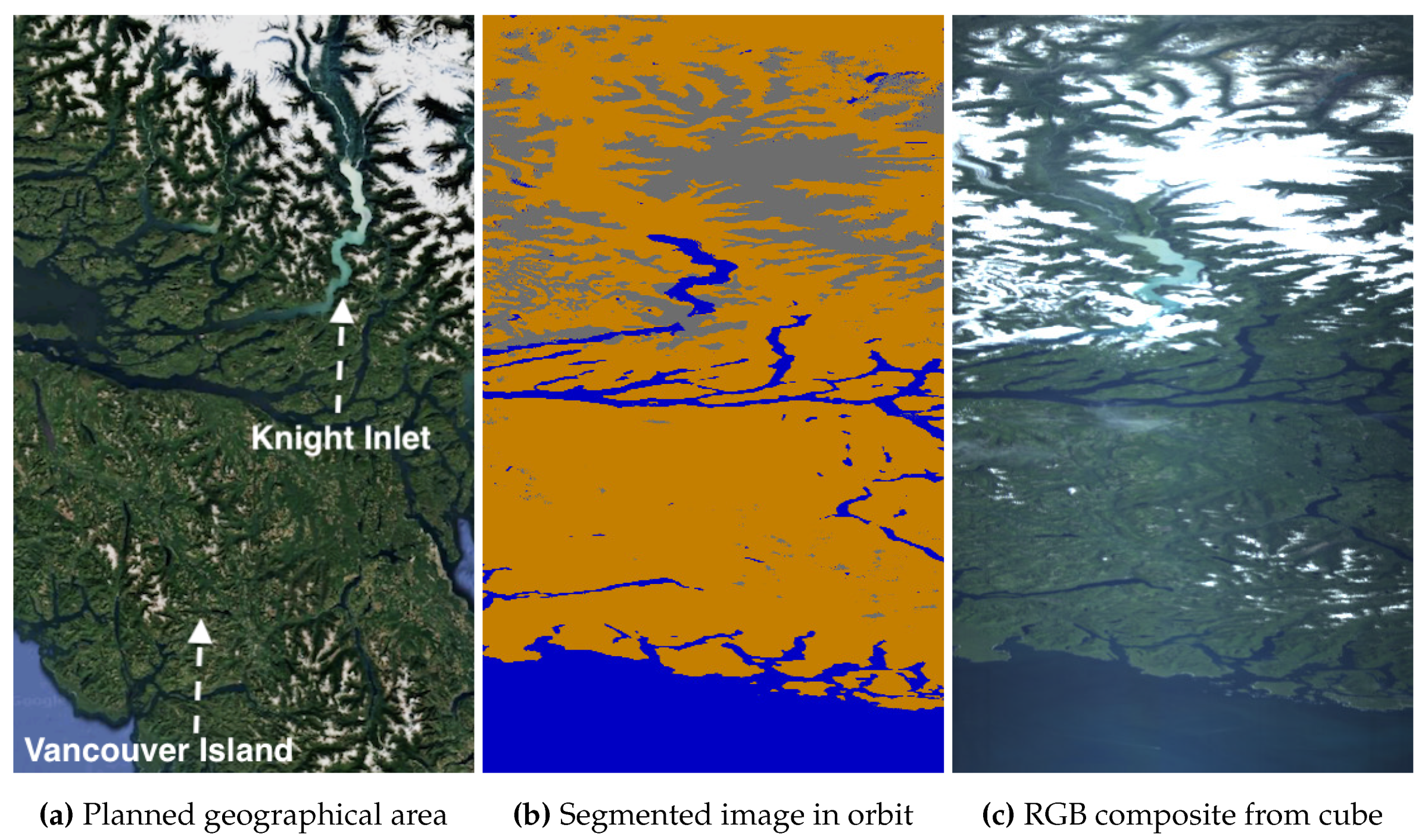Additionally, Figure 20 captures channels near Vancouver Island with clean waters similar to other coastlines, exhibiting cyan colors. The cyan water is correctly segmented. 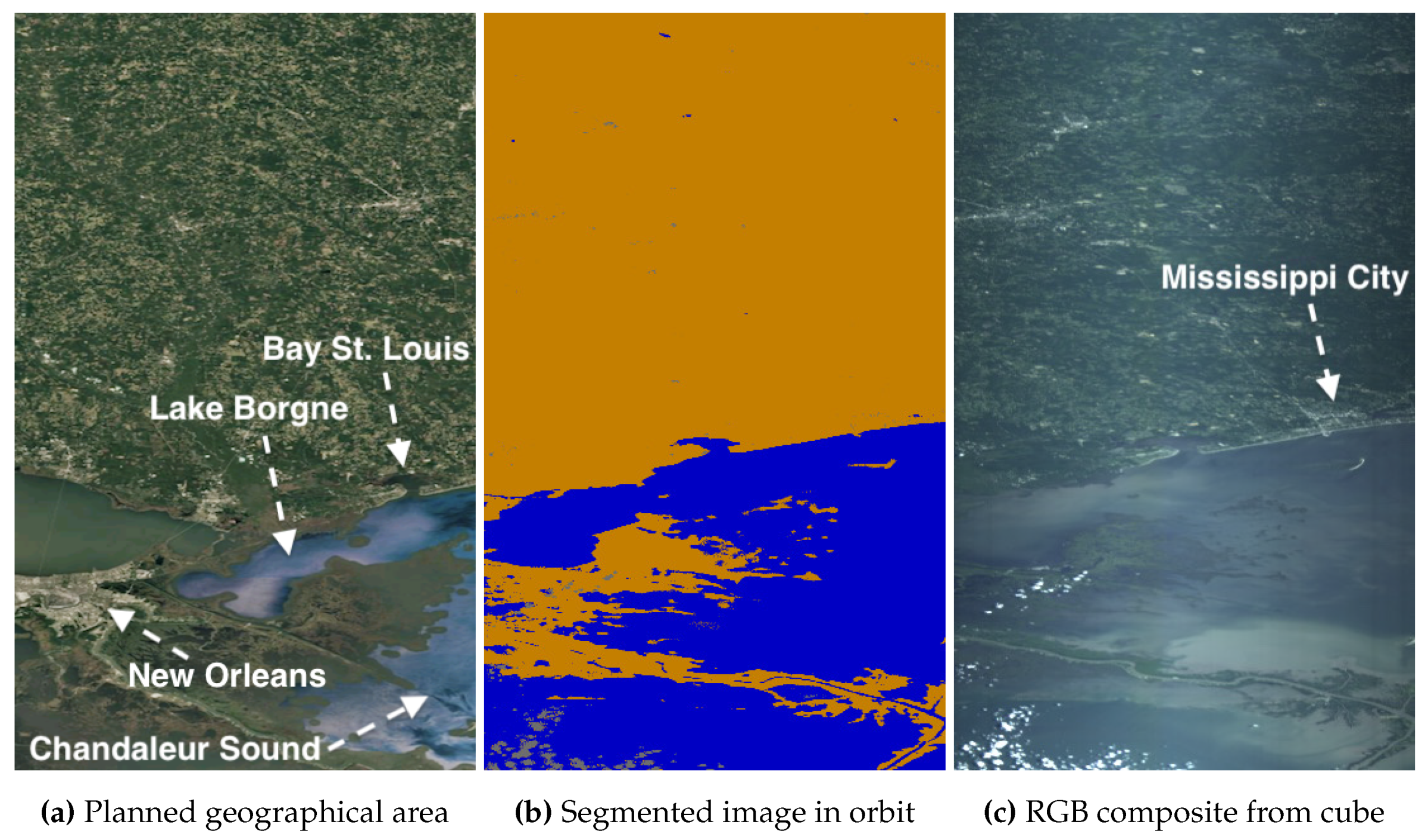Finally, Figure 21 and Figure 22 depict other coastal images from the Caspian Sea and the Gulf of Mexico in New Orleans with light and darker green-blue waters, also accurately segmented.
5.7. Accuracy: Captures with Different Cloud Thickness
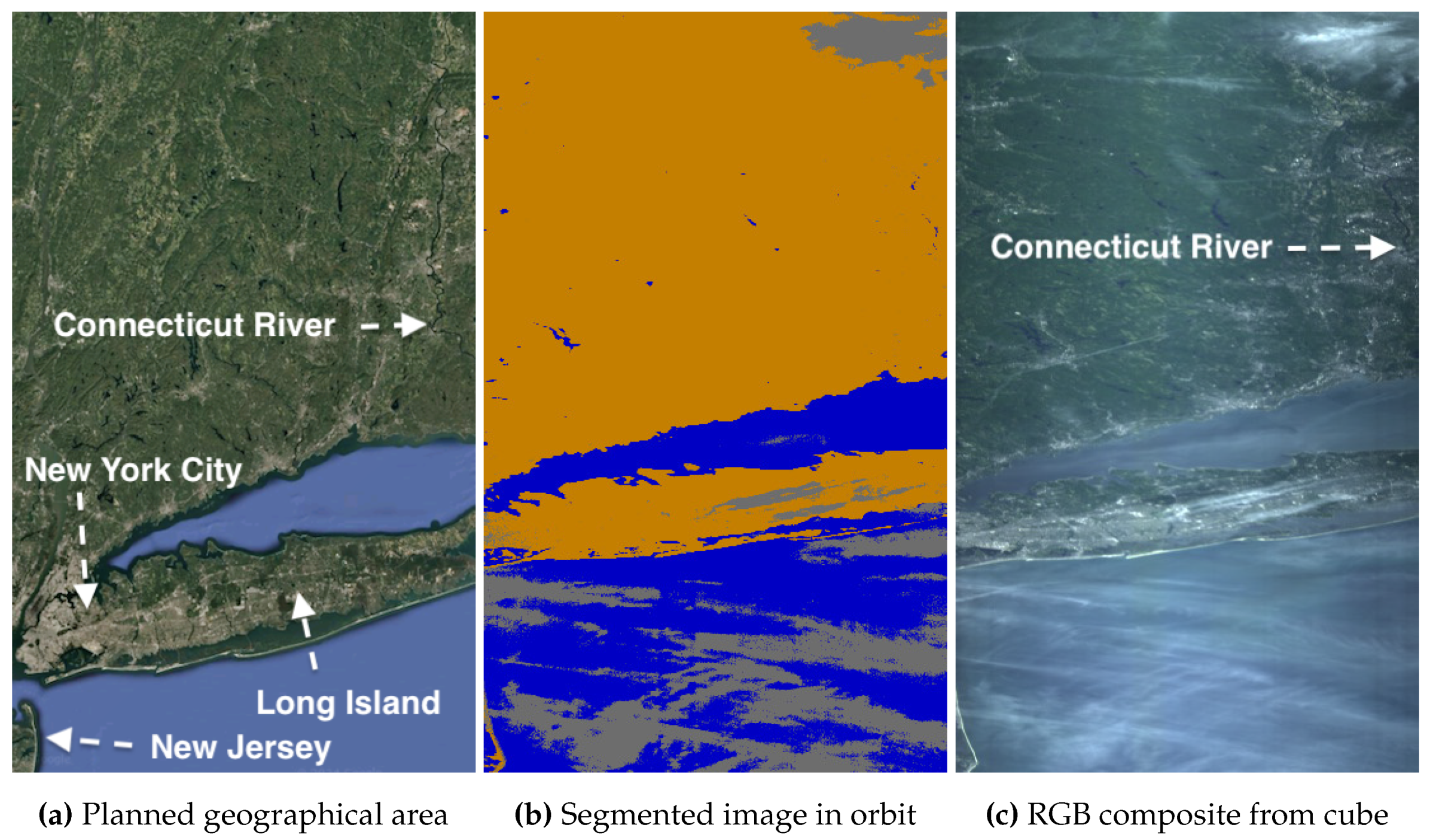
Figure 23 and Figure 24 show varying cloud thickness. Figure 23 captures Trondheimsfjord with thick clouds and acceptable segmentation. Figure 24 over Long Island, New York, shows thinner and more transparent clouds that are harder to segment as light scatters from both the clouds and the background. The segmented image shows cloud cover over the water, and the RGB confirms that, while the clouds are not thick, they obscure enough the water to justify the cloud predictions.
Beyond cloud cover, a few aspects in Figure 24 are worth discussing. Several pixels on the left side of Long Island are segmented as overexposed, likely due to bright urban surfaces in New York City. Light-colored, low iron oxide beaches in New Jersey are also correctly segmented as overexposed. Additionally, the Connecticut River, north of Long Island, is mostly misclassified as land due to strong NIR light scattered from surrounding vegetation, causing the river’s thin water to be misclassified as land.
Regarding cloud cover, detection is heavily influenced by contrast levels. Back to previous Figure 11 of the Bermuda Archipelago, small thin clouds are misclassified as water due to their lower contrast. Only the higher-contrast pixels in the top left are correctly detected as clouds, while the lower-contrast ones are misclassified as water. However, this is still permissible for our application.
5.8. Segmentation in Snow and Ice Conditions
The 1D-Justo-LiuNet model currently operational in orbit was not trained in [43] to reliably segment snow and ice, since the HYPSO-1 Sea-Land-Cloud-Labeled Dataset in [65] excluded these conditions to simplify the time-consuming labeling process. Regardlessly, we attempt to gain any insights from segmenting these scenes. Future training should improve the model’s ability to distinguish between clouds and snow/ice.
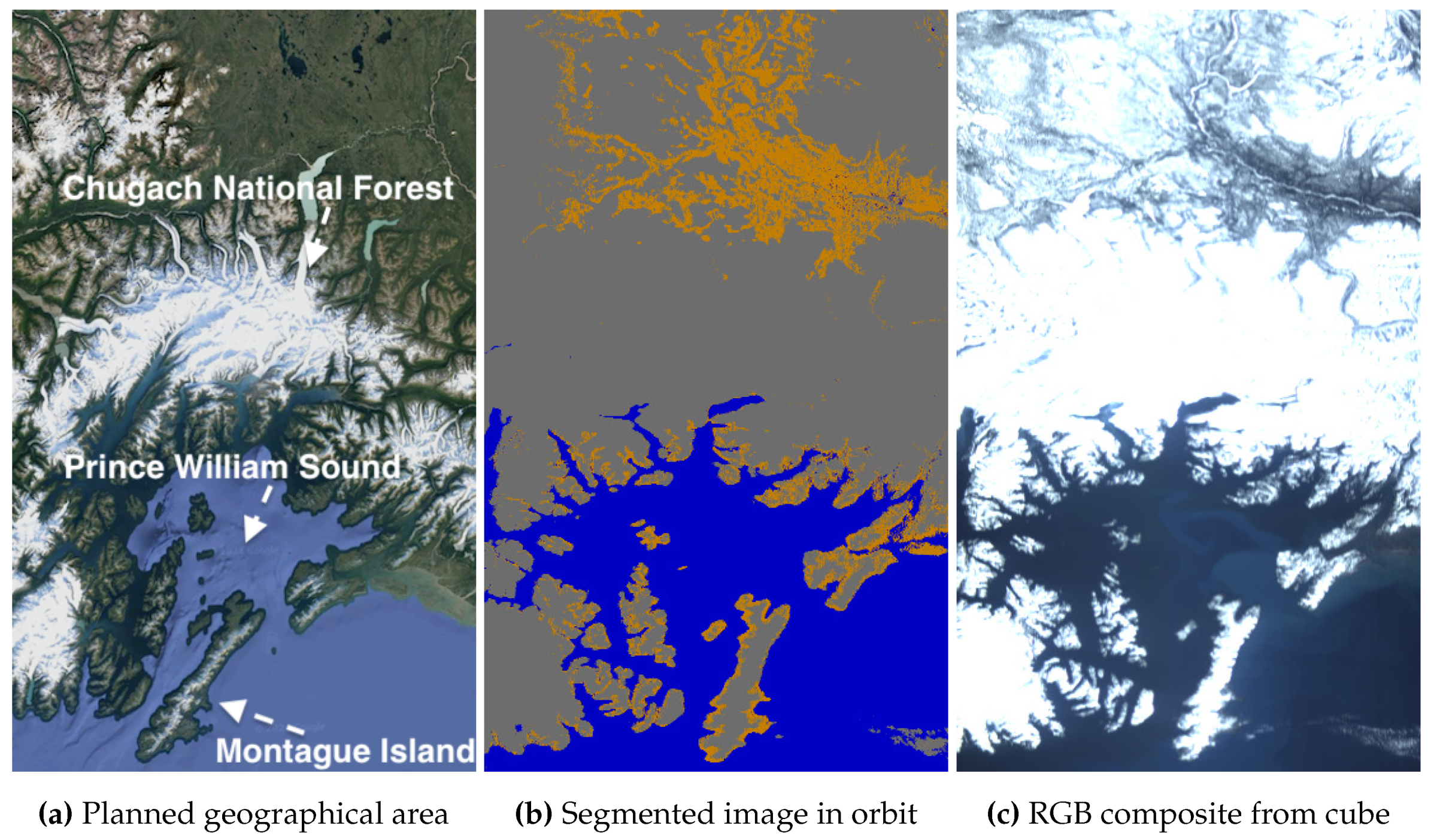
Figure 25 shows Alaska’s Prince William Sound, a water body between the Chugach National Forest and barrier islands, such as Montague Island. If only water was detected in the segments, it would indicate satellite mispointing, as no snow or land would be detected. However, gray segments suggest white pixels that may represent snow. Since the model is not trained to distinguish between clouds and snow, we compare the segmented images with the map for georeferencing. By matching the segment shapes with the map, it seems likely that many of the gray segments represent snow, as they tend to align with the land’s surfaces and contours. Additionally, some pixels also present lower reflectivity, indicating land. While not fully reliable, this method enhances the model’s potential to also segment scenes under snow and ice conditions, as it occurs in the Arctic, where HYPSO-1 often takes captures. 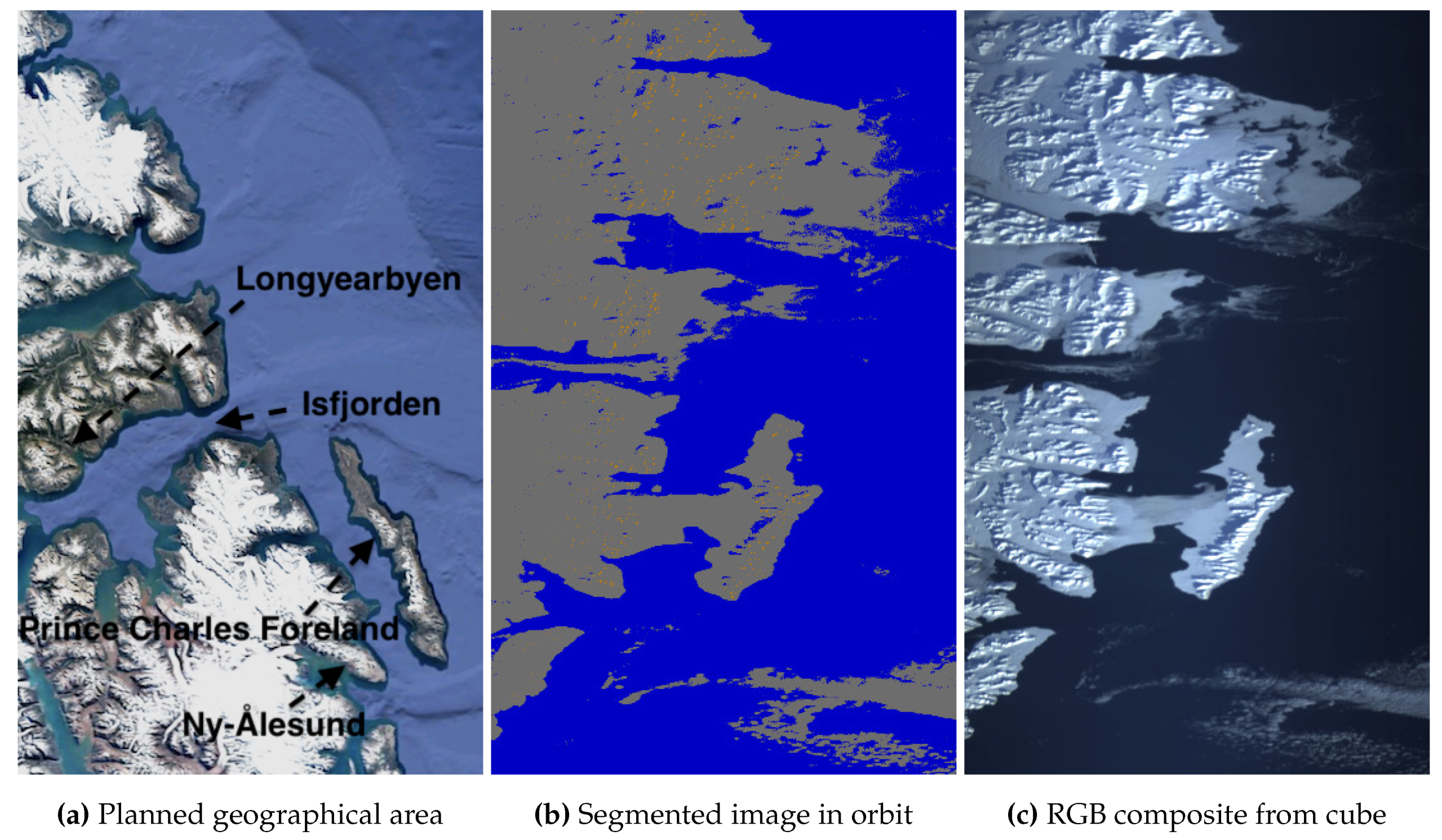For example, Figure 26 captures the Norwegian Archipelago of Svalbard in the Arctic region, crucial for climate change monitoring. Despite the challenges of georeferencing due to ice movement not represented in the available map, we apply the same approach as with Alaska. The snow-covered land (orange dots within gray segments) suggests the satellite correctly pointed and captured the archipelago, despite uncertainties in cloud cover. The composite confirms that the conclusion is correct.
5.9. Accuracy: Relevant Misclassifications (Low-Light Imagery and Florida’s Coast)
Although the 1D-Justo-LiuNet model was not trained to detect snow-covered surfaces, it can still identify them due to extensive training where many white pixels were annotated as clouds or overexposed areas. However, the HYPSO-1 Sea-Land-Cloud-Labeled Dataset lacks nighttime annotations [65], as labeling in such conditions would have been more complex. Consequently, the model performs poorly in low-light conditions, as seen in Figure 27, where a low-light capture from Northern Norway shows significant misclassifications. The segmented image also exhibits a vertical stripe due to the segmentation being applied to uncalibrated sensor data, where sensor stripes have not been corrected. 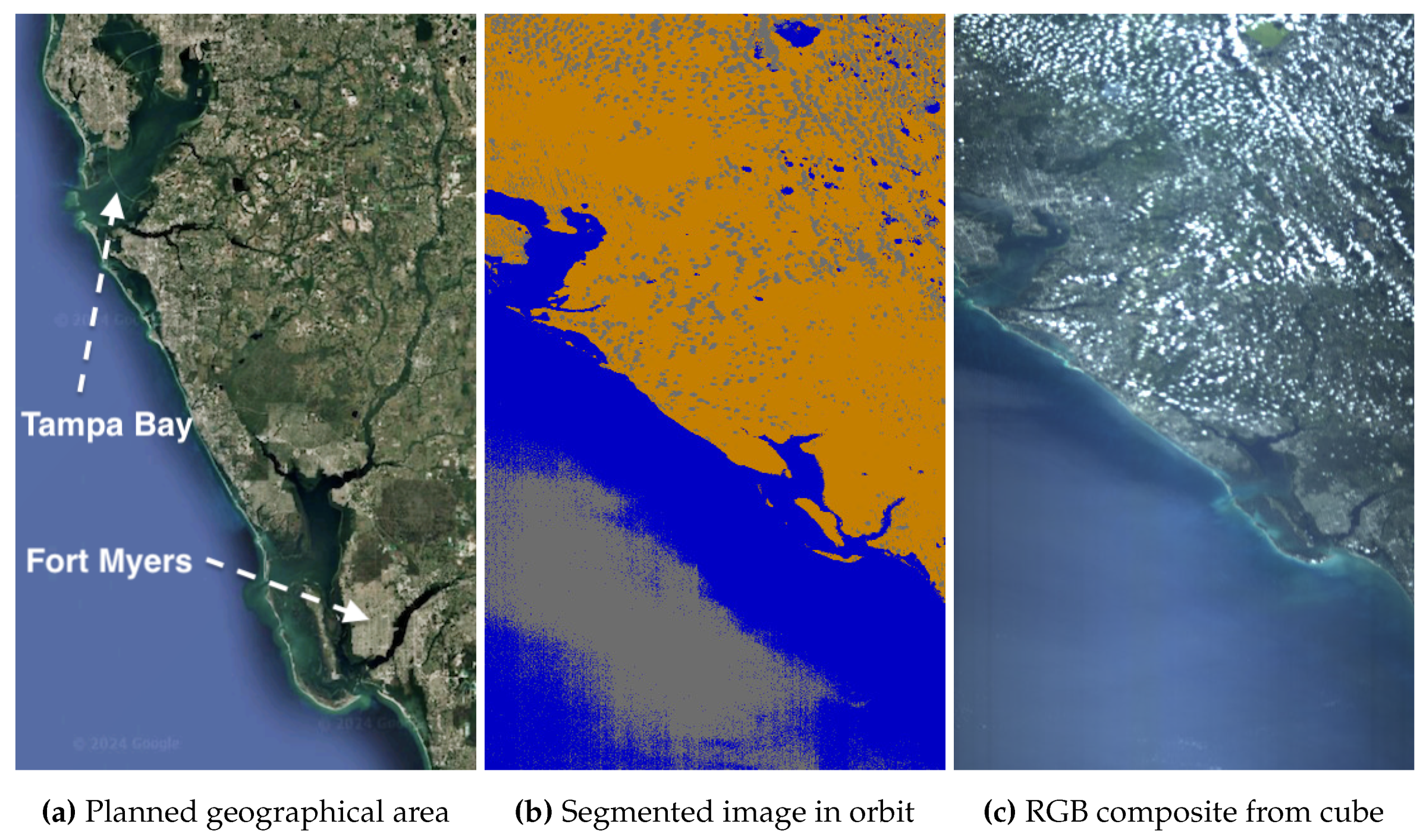Finally, Figure 28 shows misclassified Florida’s coastal waters, where brighter water pixels are mistaken for clouds. This issue, seen across multiple captures in the concrete area off Florida’s coast, suggests the need of further exploration or model training in this region. However, the segmentation of the coastline, land, and clouds remains otherwise acceptable.
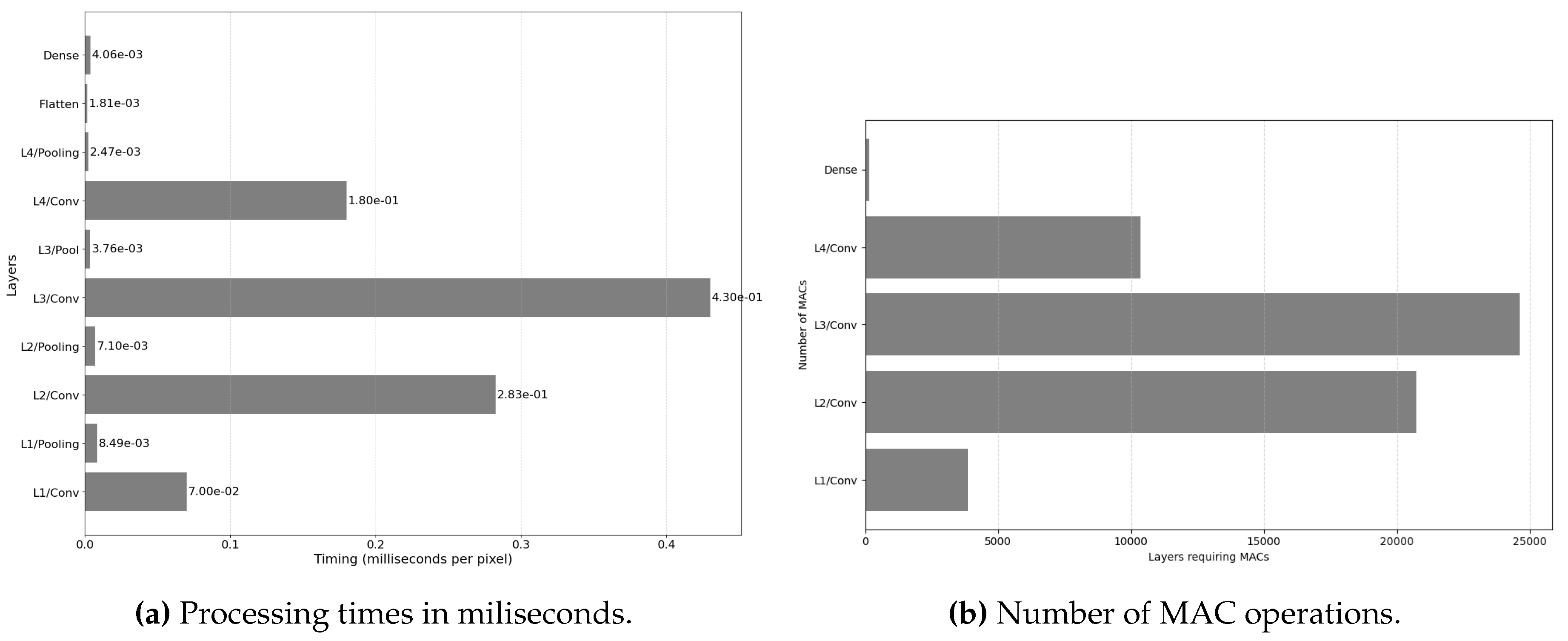
5.10. Inference Time
We continue our discussion by analyzing the processing time of 1D-Justo-LiuNet for segmenting a data cube. While our previous work [43] concluded that the network was one of the fastest lightweight models, the dual-core CPU in the Zynq-7030 remains considerably slow. Although an FPGA implementation is beyond the scope of this work, Appendix A provides an analysis of potential future FPGA acceleration. We conclude that 1D-Justo-LiuNet can benefit significantly from accelerating the MAC operations in the third convolution layer on the FPGA.
6. Conclusions
This work marks the first deployment and testing of a 1D-CNN in a satellite in orbit. We implemented a C version of the lightweight 1D-CNN, 1D-Justo-LiuNet, previously shown to outperform 2D-CNNs and ViTs for semantic segmentation in hyperspectral imagery. The C implementation considered efficient memory access for CPU use, while facilitating future FPGA high-level synthesis. After validating the code on a general-purpose computer against high-level frameworks like Keras, we tested it on lab hardware identical to the hardware flying in space. The implementation was then deployed in space on the HYPSO-1 mission’s On-Board Processing Unit to segment acquired hyperspectral images at pixel-level into sea, land, or cloud categories. We obtained acceptable results in space, meeting our application needs. Additionally, we illustrated case examples demonstrating how the 1D-CNN enhances current and future satellite operations and increases automation. Case scenarios on HYPSO-1 benefiting from in-orbit segmentation included incomplete data downlinks, mispointing to space or incorrect geographic areas, and varying cloud conditions. To this extent, we introduced a framework to decide whether to downlink or discard the data based on the segmented images. Our proposed framework ranged from simple decision-making with human intervention to more autonomous approaches, from basic class proportion-based decisions to more advanced in-orbit automation, by using AI models which can interpret segmented images during flight. We trained a CNN to detect when segmented images indicate mispointing into space, demonstrating how segmentation results can be used in orbit to make autonomous downlink decisions. Finally, based on our acceleration analysis, we recommend implementing multiply-accumulate operations from convolutions on the FPGA, to reduce processing time and accelerate inference. Additionally, training an additional lightweight CNN to interpret more patterns in the segmented images could further enhance satellite autonomy.
Acknowledgments
The authors would like to express their gratitude to the entire HYPSO team for making the HYPSO-1 and HYPSO-2 missions possible, with special thanks to Joseph L. Garrett and Corrado Chiatante for important efforts in satellite operations. We are particularly thankful to Mariana-Iuliana Georgescu for her invaluable support in achieving our milestone of deploying AI for space applications. Our appreciation also goes to Kongsberg NanoAvionics for their assistance with the satellite and to Kongsberg Satellite Services (KSAT) for providing downlink resources via their ground station network. We also extend our thanks to Laurent Despoisse, Nafiseh Ghasemi, and Marco Celesti from ESA’s CHIME team for their valuable insights into the next-generation hyperspectral missions.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Conceptualization, J.A.J., S.B., T.A.J.; state of the art: J.A.J.; methodology, J.A.J.; software, J.A.J.; on-ground testing, J.A.J. and D.D.L.; in-orbit validation: J.A.J., D.D.L., and S.B.; OPU and nominal integration into operations: S.B.; formal analysis, J.A.J.; resources, T.A.J.; data curation, J.A.J.; writing—original draft preparation, J.A.J.; writing—review and editing, D.D.L., S.B., J.N., R.T.I., P.G.K. and T.A.J.; visualization, J.A.J. and D.D.L.; supervision, project administration, and funding acquisition: T.A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Research Council of Norway through NO Grants 2014–2021 under Project ELO-Hyp (Contract No. 24/2020), HYPSCI (Grant No. 325961), Green-Platform (Grant No. 328724), and SoS (Grant No. 337495).
Data Availability Statement
The C implementation of 1D-Justo-LiuNet is openly available at https://github.com/NTNU-SmallSat-Lab/AI_deployment_justoliunet/, which also includes segmented images for approximately 300 hyperspectral data captures. The Keras model for 1D-Justo-LiuNet can be found at the GitHub repository https://github.com/NTNU-SmallSat-Lab/s_l_c_segm_hyp_img/, and The HYPSO-1 Sea-Land-Cloud-Labeled Dataset is available for download at https://ntnu-smallsat-lab.github.io/hypso1_sea_land_clouds_dataset/.
Appendix A. Acceleration Analysis on FPGAs to Reduce Inference Time
When we test 1D-Justo-LiuNet on the Zynq-7030’s CPU, segmenting an entire data cube takes around 10.78 minutes on average. This suggests that the network would benefit from future FPGA acceleration to reduce processing time and power consumption. For this, identifying the most time-consuming operation(s) on the CPU is crucial.
Consistent with the state of the art [17], results in Figure A1 show that most of the runtime is spent on convolution operations, while pooling, flattening, and dense layers require significantly less time. Thus, convolution layers are the primary target for FPGA acceleration. When comparing the time required for each convolution layer, the deeper convolutions take longer, which is expected due to the increasing number of kernels and the use of multi-component kernels. However, in the final convolution, the processing time decreases since the pooled feature maps are smaller, saving time. The processing time of the convolutions correlates with the number of MAC operations, as shown in Figure A1. Therefore, the convolution layer at level 3 is the best candidate for FPGA acceleration. This can be achieved either through a fully FPGA-based design or a software-hardware co-design approach [17], where the CPU handles various operations while the FPGA handles the more time-consuming arithmetic operations.
As future work, we recommend synthesizing our C implementation into Register Transfer Level (RTL) design for the Kintex-7 FPGA within the Zynq-7030 to accelerate the convolutions. Our current C implementation is openly available in our GitHub repository at https://github.com/NTNU-SmallSat-Lab/AI_deployment_justoliunet. The software avoids dynamic memory allocation to make the implementation more easily synthesizable into FPGA logic. Given the promising development of High-Level-Synthesis (HLS) tools for deep learning [84,85,86], we propose using Xilinx’s Vitis HLS. Although a comparison between Vitis AI and Vitis HLS is beyond the scope of this work, we acknowledge the availability of tools like Vitis AI for fast deployment on Xilinx devices [87], offering libraries and compatibility with frameworks like TensorFlow to streamline FPGA design and achieve quick, high-performance results [88]. However, compatibility challenges, such as implementing 1D convolutions in 1D-CNNs, must still be considered. Overall, Vitis HLS offers more hardware control. By applying pragma directives to perform parallel MAC operations [15,18,86,89,90,91], Vitis HLS can significantly reduce the processing time. While MAC operations can be implemented using regular FPGA resources such as Look-Up Tables (LUTs), we highly recommend using the dedicated Digital Signal Processing (DSP) blocks, as the Kintex-7 FPGA incorporates 400 DSP blocks optimized for arithmetic acceleration [56]. These blocks can achieve up to 593 GMACs, allowing many billions of MAC operations per second. In FPGA design, analyzing data inter-dependencies is crucial [17]. Given the absence of dependencies during MAC operations, we recommend using parallel multipliers between windowed samples and kernel weights to achieve an optimal RTL design. These should be followed by an efficient adder configuration such as Carry-lookahead adders [92] with adequate critical path, while maintaining clock frequency and ensuring that MAC computations are completed within a single clock cycle for proper synchronization. Further details on an FPGA implementation are beyond the scope of this work.
Figure A1.
Comparative analysis of timing and MAC operations across 1D-Justo-LiuNet.
References
- Sagiroglu, S.; Sinanc, D. Big data: A review. 2013 international conference on collaboration technologies and systems (CTS). IEEE, 2013, pp. 42–47. [CrossRef]
- Ungar, S.G.; Pearlman, J.S.; Mendenhall, J.A.; Reuter, D. Overview of the earth observing one (EO-1) mission. IEEE Transactions on Geoscience and Remote Sensing 2003, 41, 1149–1159. [CrossRef]
- Pastena, M.; Domínguez, B.C.; Mathieu, P.P.; Regan, A.; Esposito, M.; Conticello, S.; Dijk, C.V.; Vercruyssen, N.; Foglia, P. ESA Earth observation directorate NewSpace initiatives 2019.
- Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G. PRISMA: The Italian hyperspectral mission. IGARSS 2018-2018 IEEE international geoscience and remote sensing symposium. IEEE, 2018, pp. 175–178. [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; others. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sensing 2015, 7, 8830–8857. [CrossRef]
- Gorman, E.T.; Kubalak, D.A.; Patel, D.; Mott, D.B.; Meister, G.; Werdell, P.J.; others. The NASA Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission: an emerging era of global, hyperspectral Earth system remote sensing. Sensors, systems, and next-generation satellites XXIII. SPIE, 2019, Vol. 11151, pp. 78–84.
- Grøtte, M.E.; Birkeland, R.; Honoré-Livermore, E.; Bakken, S.; Garrett, J.L.; Prentice, E.F.; Sigernes, F.; Orlandić, M.; Gravdahl, J.T.; Johansen, T.A. Ocean color hyperspectral remote sensing with high resolution and low latency—The HYPSO-1 CubeSat mission. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–19. [CrossRef]
- Bakken, S.; Henriksen, M.B.; Birkeland, R.; Langer, D.D.; Oudijk, A.E.; Berg, S.; Pursley, Y.; Garrett, J.L.; Gran-Jansen, F.; Honoré-Livermore, E.; others. Hypso-1 cubesat: First images and in-orbit characterization. Remote Sensing 2023, 15, 755. [CrossRef]
- Berg, S.; Bakken, S.; Birkeland, R.; Chiatante, C.; Garrett, J.L.; Johansen, T.A. Ground systems software for automatic operation of the HYPSO-2 hyperspectral imaging satellite. Sensors, Systems, and Next-Generation Satellites XXVII. SPIE, 2023, Vol. 12729, pp. 277–286. [CrossRef]
- Celesti, M.; Rast, M.; Adams, J.; Boccia, V.; Gascon, F.; Isola, C.; Nieke, J. The copernicus hyperspectral imaging mission for the environment (chime): Status and planning. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2022, pp. 5011–5014. [CrossRef]
- Bloomer, J.D.; Puschell, J.J.; Koontz, C.R. Geostationary Littoral Imaging and Monitoring Radiometer (GLIMR) Instrument Capability and Overview. IGARSS 2023-2023 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2023, pp. 4679–4681. [CrossRef]
- Thompson, D.R.; Basilio, R.; Brosnan, I.; Cawse-Nicholson, K.; Chadwick, K.D.; Guild, L.; Gierach, M.; Green, R.O.; Hook, S.; Horner, S.D.; others. Ongoing progress toward NASA’s surface biology and geology mission. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2022, pp. 5007–5010.
- Nalepa, J.; Myller, M.; Cwiek, M.; Zak, L.; Lakota, T.; Tulczyjew, L.; Kawulok, M. Towards on-board hyperspectral satellite image segmentation: Understanding robustness of deep learning through simulating acquisition conditions. Remote sensing 2021, 13, 1532. [CrossRef]
- Yang, G.; Lei, J.; Xie, W.; Fang, Z.; Li, Y.; Wang, J.; Zhang, X. Algorithm/hardware codesign for real-time on-satellite CNN-based ship detection in SAR imagery. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–18. [CrossRef]
- Neris, R.; Rodríguez, A.; Guerra, R.; López, S.; Sarmiento, R. FPGA-Based implementation of a CNN architecture for the on-Board processing of very high-resolution remote sensing images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 3740–3750. [CrossRef]
- Akeboshi, W.W.N.P.; Billones, R.K.; Coching, J.K.; Pe, A.J.L.; Yeung, S.G.D.; Ai, R.J.T.; Sybingco, E.; Dadios, E.P.; Purio, M.A. Evaluation of Quantized CNN Architectures for Land Use Classification for Onboard Cube Satellite Computing. 2024 9th International Conference on Mechatronics Engineering (ICOM). IEEE, 2024, pp. 45–50. [CrossRef]
- Kim, H.; Park, J.; Lee, H.; Won, D.; Han, M. An FPGA-Accelerated CNN with Parallelized Sum Pooling for Onboard Realtime Routing in Dynamic Low-Orbit Satellite Networks. Electronics 2024, 13, 2280. [CrossRef]
- Kalomoiris, I.; Pitsis, G.; Tsagkatakis, G.; Ioannou, A.; Kozanitis, C.; Dollas, A.; Tsakalides, P.; Katevenis, M.G. An experimental analysis of the opportunities to use field programmable gate array multiprocessors for on-board satellite deep learning classification of spectroscopic observations from future ESA space missions. European workshop on on-board data processing (OBDP2019), 2019.
- Serief, C.; Ghelamallah, Y.; Bentoutou, Y. Deep-Learning-Based System for Change Detection Onboard Earth Observation Small Satellites. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2023, 16, 8115–8124. [CrossRef]
- Esposito, M.; Conticello, S.S.; Pastena, M.; Domínguez, B.C. In-orbit demonstration of artificial intelligence applied to hyperspectral and thermal sensing from space. CubeSats and SmallSats for remote sensing III. SPIE, 2019, Vol. 11131, pp. 88–96. [CrossRef]
- Berg, S.; Langer, D.D.; Chiatante, C.; Birkeland, R.; Justo, J.A.; Johansen, T.A. Onboard classification to guide capture downlink using the HYPSO-1 satellite. 75th International Astronautical Congress (IAC); International Astronautical Federation (IAF), , 2024. IAC–24–B.4.3.6.
- Giuffrida, G.; Fanucci, L.; Meoni, G.; Batič, M.; Buckley, L.; Dunne, A.; Van Dijk, C.; Esposito, M.; Hefele, J.; Vercruyssen, N.; others. The Φ-Sat-1 mission: The first on-board deep neural network demonstrator for satellite earth observation. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–14. [CrossRef]
- Yuan, X.; Shi, J.; Gu, L. A review of deep learning methods for semantic segmentation of remote sensing imagery. Expert Systems with Applications 2021, 169, 114417. [CrossRef]
- Koc, Y.E.; Penne, C.L.; Garrett, J.; Orlandić, M. Exploration of Deep Learning for Cloud Segmentation in Multispectral and Hyperspectral Satellite Imagery. 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2023, pp. 1–5. [CrossRef]
- Lebedeff, D.; Foulon, M.; Camarero, R.; Vitulli, R.; Bobichon, Y. On-board cloud detection and selective spatial/spectral compression based on CCSDS 123.0-b-2 for hyperspectral missions. 7th ESA International Worshop on On-Board Payload Data Compression Conference (OBPDC), 2020.
- Pitonak, R.; Mucha, J.; Dobis, L.; Javorka, M.; Marusin, M. Cloudsatnet-1: Fpga-based hardware-accelerated quantized cnn for satellite on-board cloud coverage classification. Remote Sensing 2022, 14, 3180. [CrossRef]
- Sung, Y.H.; Park, S.J.; Kim, D.Y.; Kim, S. GPS spoofing detection method for small UAVs using 1D convolution neural network. Sensors 2022, 22, 9412. [CrossRef]
- Del Rosso, M.P.; Sebastianelli, A.; Spiller, D.; Mathieu, P.P.; Ullo, S.L. On-board volcanic eruption detection through cnns and satellite multispectral imagery. Remote Sensing 2021, 13, 3479. [CrossRef]
- Danielsen, A.S.; Johansen, T.A.; Garrett, J.L. Self-organizing maps for clustering hyperspectral images on-board a cubesat. Remote Sensing 2021, 13, 4174. [CrossRef]
- Chiatante, C.; Langer, D.D.; Garrett, J.L.; Birkeland, R.; Berg, S.; Orlandić, M. Onboard hyperspectral classification enables georeferencing. 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2023, pp. 1–5. [CrossRef]
- Diana, L.; Xu, J.; Fanucci, L. Oil spill identification from SAR images for low power embedded systems using CNN. Remote Sensing 2021, 13, 3606. [CrossRef]
- Howard, A.G. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861 2017.
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 4510–4520. [CrossRef]
- Yao, Y.; Jiang, Z.; Zhang, H.; Zhou, Y. On-board ship detection in micro-nano satellite based on deep learning and COTS component. Remote Sensing 2019, 11, 762. [CrossRef]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: a review. Data mining and knowledge discovery 2019, 33, 917–963. [CrossRef]
- Oschmann Jr, J.M.; Clampin, M.; Fazio, G.G.; MacEwen, H.A. Space telescopes and instrumentation 2014: optical, infrared, and millimeter wave; Vol. 9143, 2014.
- Tulczyjew, L.; Nalepa, J. Investigating the impact of the training set size on deep learning-powered hyperspectral unmixing. 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. IEEE, 2021, pp. 2024–2027. [CrossRef]
- Song, Y.; Zhang, Z.; Baghbaderani, R.K.; Wang, F.; Qu, Y.; Stuttsy, C.; Qi, H. Land cover classification for satellite images through 1D CNN. 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2019, pp. 1–5. [CrossRef]
- Bahl, G.; Lafarge, F. Scanner Neural Network for On-Board Segmentation of Satellite Images. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2022, pp. 3504–3507. [CrossRef]
- Bahl, G.; Daniel, L.; Moretti, M.; Lafarge, F. Low-power neural networks for semantic segmentation of satellite images. Proceedings of the IEEE/CVF international conference on computer vision workshops, 2019, pp. 0–0. [CrossRef]
- Fan, D.; He, H.; Wang, R.; Zeng, Y.; Fu, B.; Xiong, Y.; Liu, L.; Xu, Y.; Gao, E. CHLNET: A novel hybrid 1D CNN-SVR algorithm for estimating ocean surface chlorophyll-a. Frontiers in Marine Science 2022, 9, 934536. [CrossRef]
- Rodriguez, J. Beyond the Horizon: Exploring Anomaly Detection Potentials with Federated Learning and Hybrid Transformers in Spacecraft Telemetry 2024.
- Justo, J.A.; Ghita, A.; Kovac, D.; Garrett, J.L.; Georgescu, M.I.; Gonzalez-Llorente, J.; Ionescu, R.T.; Johansen, T.A. Sea-Land-Cloud Segmentation in Satellite Hyperspectral Imagery by Deep Learning. arXiv preprint arXiv:2310.16210 (accepted for publication in IEEE J-STARS) 2023.
- Vasu, P.K.A.; Gabriel, J.; Zhu, J.; Tuzel, O.; Ranjan, A. FastViT: A fast hybrid vision transformer using structural reparameterization. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023, pp. 5785–5795.
- Kovac, D.; Mucha, J.; Justo, J.A.; Mekyska, J.; Galaz, Z.; Novotny, K.; Pitonak, R.; Knezik, J.; Herec, J.; Johansen, T.A. Deep Learning for In-Orbit Cloud Segmentation and Classification in Hyperspectral Satellite Data. arXiv preprint arXiv:2403.08695 2024. Accepted for publication (IEEE).
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18. Springer, 2015, pp. 234–241.
- Ghasemi, N.; Justo, J.A.; Celesti, M.; Despoisse, L.; Nieke, J. Onboard Processing of Hyperspectral Imagery: Deep Learning Advancements, Methodologies, Challenges, and Emerging Trends. arXiv preprint arXiv:2404.06526 2024.
- Xue, N.; Niu, L.; Hong, X.; Li, Z.; Hoffaeller, L.; Pöpper, C. Deepsim: Gps spoofing detection on uavs using satellite imagery matching. Proceedings of the 36th Annual Computer Security Applications Conference, 2020, pp. 304–319.
- Morales Chacon, C. Design, Optimization, and Hardware Deployment of a Deep Learning Model for GPS Spoofing Detection using GNSS Satellite Receiver Protocol Data 2023.
- Hao, Z.; Li, M.; Yang, W.; Li, X. Evaluation of UAV spraying quality based on 1D-CNN model and wireless multi-sensors system. Information processing in agriculture 2022. [CrossRef]
- Justo, J.A.; Lupu, D.; Orlandić, M.; Necoara, I.; Johansen, T.A. A comparative study of compressive sensing algorithms for hyperspectral imaging reconstruction. 2022 IEEE 14th Image, Video, and Multidimensional Signal Processing Workshop (IVMSP). IEEE, 2022, pp. 1–5.
- Garrett, J.L.; Bakken, S.; Prentice, E.F.; Langer, D.; Leira, F.S.; Honoré-Livermore, E.; Birkeland, R.; Grøtte, M.E.; Johansen, T.A.; Orlandić, M. Hyperspectral image processing pipelines on multiple platforms for coordinated oceanographic observation. 2021 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2021, pp. 1–5.
- Bakken, S.; Danielsen, A.; Døsvik, K.; Garrett, J.; Orlandic, M.; Langer, D.; Johansen, T.A. A modular hyperspectral image processing pipeline for cubesats. 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2022, pp. 1–5.
- Bakken, S.; Honoré-Livermore, E.; Birkeland, R.; Orlandić, M.; Prentice, E.F.; Garrett, J.L.; Langer, D.D.; Haskins, C.; Johansen, T.A. Software development and integration of a hyperspectral imaging payload for hypso-1. 2022 IEEE/SICE International Symposium on System Integration (SII). IEEE, 2022, pp. 183–189.
- Langer, D.D.; Orlandić, M.; Bakken, S.; Birkeland, R.; Garrett, J.L.; Johansen, T.A.; Sørensen, A.J. Robust and reconfigurable on-board processing for a hyperspectral imaging small satellite. Remote Sensing 2023, 15, 3756. [CrossRef]
- Xilinx. Zynq-7000 SoC Data Sheet: Overview. Xilinx, 2018. Product Specification, DS190.
- Henriksen, M.B.; Prentice, E.F.; Johansen, T.A.; Sigernes, F. Pre-launch calibration of the hypso-1 cubesat hyperspectral imager. 2022 IEEE Aerospace Conference (AERO). IEEE, 2022, pp. 1–9.
- Røysland, J.G.; Langer, D.D.; Berg, S.; Orlandić, M.; Garrett, J.L. Hyperspectral classification onboard the hypso-1 cubesat. 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2023, pp. 1–5.
- Orlandić, M.; Fjeldtvedt, J.; Johansen, T.A. A parallel FPGA implementation of the CCSDS-123 compression algorithm. Remote Sensing 2019, 11, 673. [CrossRef]
- Birkeland, R.; Berg, S.; Orlandic, M.; Garrett, J.L. On-board characterization of hyperspectral image exposure and cloud coverage by compression ratio. 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2022, pp. 1–5.
- Vorhaug, D. Hyperspectral Image Compression Accelerator On FPGA Using CCSDS 123.0-B-2. Master’s thesis, NTNU, 2024.
- Prentice, E.F.; Honoré-Livermore, E.; Bakken, S.; Henriksen, M.B.; Birkeland, R.; Hjertenæs, M.; Gjersvik, A.; Johansen, T.A.; Aguado-Agelet, F.; Navarro-Medina, F. Pre-launch assembly, integration, and testing strategy of a hyperspectral imaging CubeSat, HYPSO-1. Remote Sensing 2022, 14, 4584. [CrossRef]
- Wark, D.; Mercer, D. Absorption in the atmosphere by the oxygen “A” band. Applied Optics 1965, 4, 839–845.
- van Diedenhoven, B. Satellite remote sensing of cloud properties in support of tropospheric trace gas retrievals. Phd-thesis - research and graduation internal, Vrije Universiteit Amsterdam, 2007.
- Justo, J.A.; Garrett, J.; Langer, D.D.; Henriksen, M.B.; Ionescu, R.T.; Johansen, T.A. An Open Hyperspectral Dataset with Sea-Land-Cloud Ground-Truth from the Hypso-1 Satellite. 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2023, pp. 1–5. [CrossRef]
- Quintana-Diaz, G.; Ekman, T.; Lago Agra, J.M.; Hurtado de Mendoza, D.; González Muíño, A.; Aguado Agelet, F. In-orbit measurements and analysis of radio interference in the UHF amateur radio band from the LUME-1 satellite. Remote Sensing 2021, 13, 3252. [CrossRef]
- Giuffrida, G.; Diana, L.; de Gioia, F.; Benelli, G.; Meoni, G.; Donati, M.; Fanucci, L. CloudScout: A deep neural network for on-board cloud detection on hyperspectral images. Remote Sensing 2020, 12, 2205. [CrossRef]
- Somani, A.; Horsch, A.; Prasad, D.K. Interpretability in deep learning; Vol. 2, Springer, 2023.
- Blix, K.; Pálffy, K.; R. Tóth, V.; Eltoft, T. Remote sensing of water quality parameters over Lake Balaton by using Sentinel-3 OLCI. Water 2018, 10, 1428. [CrossRef]
- Blix, K.; Li, J.; Massicotte, P.; Matsuoka, A. Developing a new machine-learning algorithm for estimating chlorophyll-a concentration in optically complex waters: A case study for high northern latitude waters by using Sentinel 3 OLCI. Remote Sensing 2019, 11, 2076. [CrossRef]
- Penne, C.; Garrett, J.L.; Johansen, T.A.; Orlandić, M.; Heggebø, R. Independent Component Analysis: A Tool for Algal Bloom Detection. 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2023, pp. 1–5. [CrossRef]
- Flores-Romero, A.; Le Moan, S.; Garrett, J.; Bakken, S. Chlorophyll Estimation on Hypso-1 Using Ensemble Machine Learning. 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2023, pp. 1–5. [CrossRef]
- Pettorelli, N. The normalized difference vegetation index; Oxford University Press, USA, 2013.
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the enhanced vegetation index (EVI) and normalized difference vegetation index (NDVI) to topographic effects: a case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [CrossRef]
- Wijata, A.M.; Lakota, T.; Cwiek, M.; Ruszczak, B.; Gumiela, M.; Tulczyjew, L.; Bartoszek, A.; Longépé, N.; Smykala, K.; Nalepa, J. Intuition-1: Toward In-Orbit Bare Soil Detection Using Spectral Vegetation Indices. IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2024, pp. 1708–1712. [CrossRef]
- Nieke, J.; Despoisse, L.; Gabriele, A.; Weber, H.; Strese, H.; Ghasemi, N.; Gascon, F.; Alonso, K.; Boccia, V.; Tsonevska, B.; others. The copernicus hyperspectral imaging mission for the environment (CHIME): an overview of its mission, system and planning status. Sensors, Systems, and Next-Generation Satellites XXVII 2023, 12729, 21–40. [CrossRef]
- Justo, J.A.; Orlandić, M. Study of the gomp algorithm for recovery of compressed sensed hyperspectral images. 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, 2022, pp. 1–5. [CrossRef]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Transactions on signal processing 2012, 60, 6202–6216. [CrossRef]
- Salazar, C.; Gonzalez-Llorente, J.; Cardenas, L.; Mendez, J.; Rincon, S.; Rodriguez-Ferreira, J.; Acero, I.F. Cloud Detection Autonomous System Based on Machine Learning and COTS Components On-Board Small Satellites. Remote Sensing 2022, 14, 5597. [CrossRef]
- Petrovic, S. A comparison between the silhouette index and the davies-bouldin index in labelling ids clusters. Proceedings of the 11th Nordic workshop of secure IT systems. Citeseer, 2006, Vol. 2006, pp. 53–64.
- International Telecommunication Union. Subjective video quality assessment methods for multimedia applications. Technical Report P.910 (10/23):, International Telecommunication Union, 2023.
- Xu, J.; Xiong, Z.; Bhattacharyya, S.P. PIDNet: A real-time semantic segmentation network inspired by PID controllers. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2023, pp. 19529–19539.
- Vaswani, A. Attention is all you need. Advances in Neural Information Processing Systems 2017.
- Cong, J.; Lau, J.; Liu, G.; Neuendorffer, S.; Pan, P.; Vissers, K.; Zhang, Z. FPGA HLS today: successes, challenges, and opportunities. ACM Transactions on Reconfigurable Technology and Systems (TRETS) 2022, 15, 1–42. [CrossRef]
- Boyle, S.; Gunderson, A.; Orlandić, M. High-level FPGA Design of Deep Learning Hyperspectral Anomaly Detection. 2023 IEEE Nordic Circuits and Systems Conference (NorCAS). IEEE, 2023, pp. 1–5. [CrossRef]
- Gamarra, D.F.; Kjeldsberg, P.G.; Sundbeck, H. Lens Flare Attenuation Accelerator Design with Deep Learning and High-Level Synthesis. 2023 IEEE Nordic Circuits and Systems Conference (NorCAS). IEEE, 2023, pp. 1–7. [CrossRef]
- Xilinx, A. Vitis AI User Guide (UG1414) 2022.
- Ziaja, M.; Bosowski, P.; Myller, M.; Gajoch, G.; Gumiela, M.; Protich, J.; Borda, K.; Jayaraman, D.; Dividino, R.; Nalepa, J. Benchmarking deep learning for on-board space applications. Remote Sensing 2021, 13, 3981. [CrossRef]
- Marwedel, P. Embedded system design: embedded systems foundations of cyber-physical systems, and the internet of things; Springer Nature, 2021.
- Mahendra, H.; Mallikarjunaswamy, S. An efficient classification of hyperspectral remotely sensed data using support vector machine. International Journal of Electronics and Telecommunications 2022, 68. [CrossRef]
- da Costa Azevedo, P.M. Exploring HLS Strategies in Computer Vision Algorithms 2024.
- Preethi, K.; Balasubramanian, P. FPGA implementation of synchronous section-carry based carry look-ahead adders. 2014 2nd International Conference on Devices, Circuits and Systems (ICDCS). IEEE, 2014, pp. 1–4. [CrossRef]
Figure 1.
HYPSO-1 system architecture general pipeline.
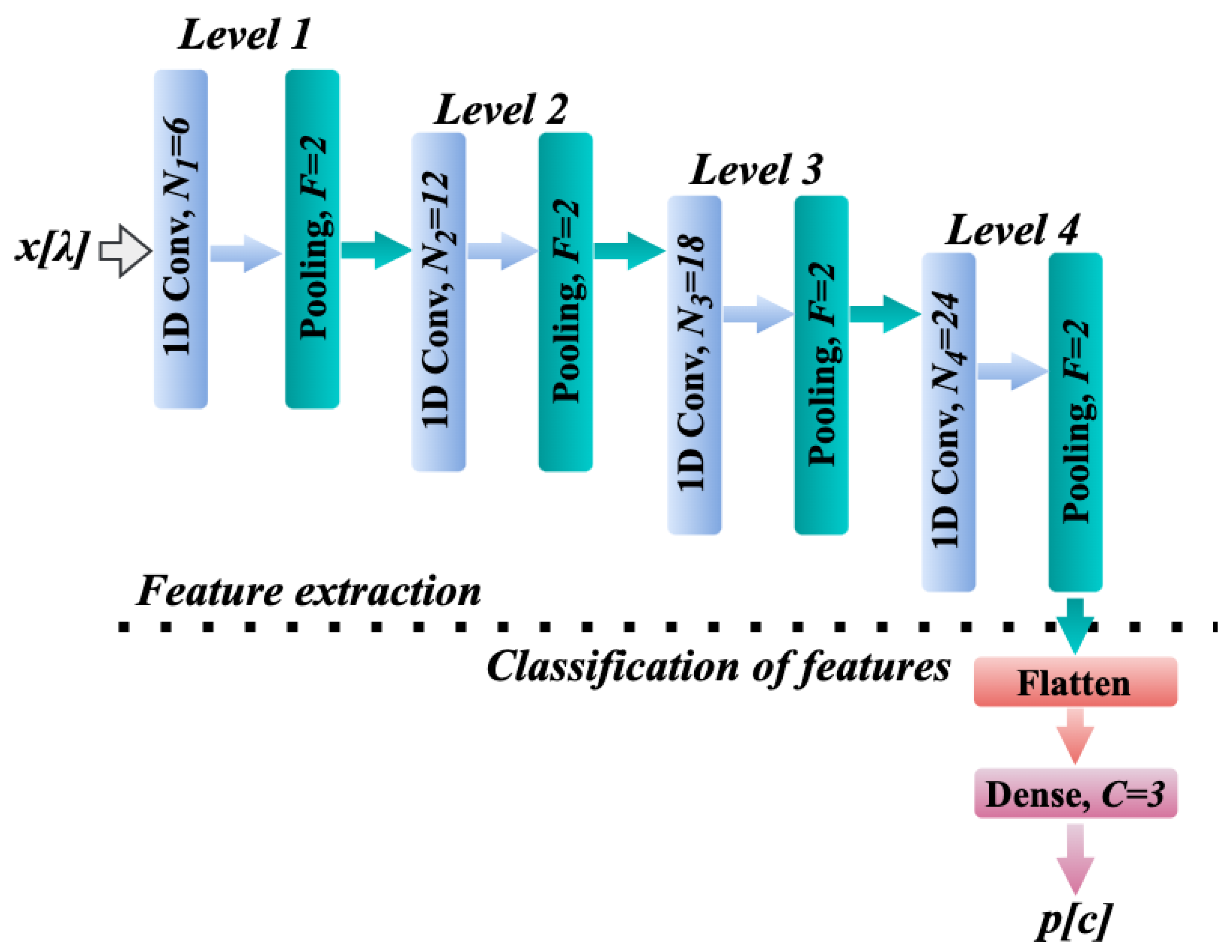
Figure 2.
Architecture of 1D-Justo-LiuNet for feature extraction and classification proposed in our previous work in [43].
Figure 2.
Architecture of 1D-Justo-LiuNet for feature extraction and classification proposed in our previous work in [43].
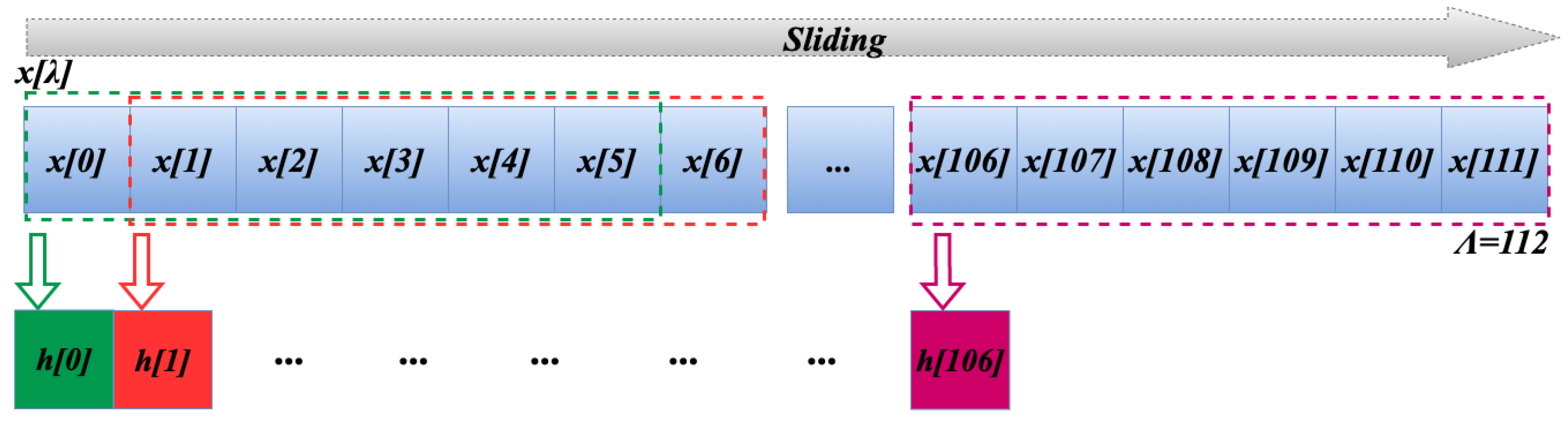
Figure 3.
Sliding process with stride over .
Figure 4.
Flow diagram of operations in the convolution layer (implementation 1).
Figure 5.
Flow diagram of operations in the convolution layer (implementation 2).
Figure 6.
Venice, Italy, Europe, on 22 June 2024 at 09:44 UTC+00. Coordinates: 45.3° latitude and 12.5° longitude. Solar zenith angle: 28.7°, and exposure time: 35 ms.
Figure 6.
Venice, Italy, Europe, on 22 June 2024 at 09:44 UTC+00. Coordinates: 45.3° latitude and 12.5° longitude. Solar zenith angle: 28.7°, and exposure time: 35 ms.
Figure 7.
Venice, Italy, Europe, on 22 June 2024 at 09:44 UTC - retransmitted.
Figure 8.
Trondheim, Norway, Europe, on 17 May 2024 at 10:54 UTC. Coordinates: 63.6° latitude and 9.84° longitude. Solar zenith angle: 44.9°, and exposure time: 50 ms.
Figure 8.
Trondheim, Norway, Europe, on 17 May 2024 at 10:54 UTC. Coordinates: 63.6° latitude and 9.84° longitude. Solar zenith angle: 44.9°, and exposure time: 50 ms.
Figure 10.
Grad-CAM explanations for classification of segmented images.
Figure 11.
Bermuda Archipelago, British Overseas, Atlantic Ocean, on 16 July 2024 at 14:27 UTC. Coordinates: 32.4° latitude and -64.8° longitude. Solar zenith angle: 32.6°, and exposure time: 30 ms.
Figure 11.
Bermuda Archipelago, British Overseas, Atlantic Ocean, on 16 July 2024 at 14:27 UTC. Coordinates: 32.4° latitude and -64.8° longitude. Solar zenith angle: 32.6°, and exposure time: 30 ms.
Figure 12.
Dahlak Archipelago, Eritrea, Africa, on 16 June 2024 at 07:28 UTC. Coordinates: 16.0° latitude and 40.4° longitude. Solar zenith angle: 16.0°, and exposure time: 25 ms.
Figure 12.
Dahlak Archipelago, Eritrea, Africa, on 16 June 2024 at 07:28 UTC. Coordinates: 16.0° latitude and 40.4° longitude. Solar zenith angle: 16.0°, and exposure time: 25 ms.
Figure 13.
Aegean Archipelago, Greece, Europe, on 2 May 2024 at 08:44 UTC. Coordinates: 38.5° latitude and 25.2° longitude. Solar zenith angle: 39.0°, and exposure time: 30 ms.
Figure 13.
Aegean Archipelago, Greece, Europe, on 2 May 2024 at 08:44 UTC. Coordinates: 38.5° latitude and 25.2° longitude. Solar zenith angle: 39.0°, and exposure time: 30 ms.
Figure 14.
Abu Dhabi and Dubai, United Arab Emirates, Asia, on 9 May 2024 at 06:12 UTC. Coordinates: 25.3° latitude and 54.7° longitude. Solar zenith angle: 29.5°, and exposure time: 40 ms.
Figure 14.
Abu Dhabi and Dubai, United Arab Emirates, Asia, on 9 May 2024 at 06:12 UTC. Coordinates: 25.3° latitude and 54.7° longitude. Solar zenith angle: 29.5°, and exposure time: 40 ms.
Figure 15.
Abu Dhabi and Dubai, United Arab Emirates, Asia, on 27 June 2024 at 06:17 UTC. Coordinates: 25.1° latitude and 55.0° longitude. Solar zenith angle: 28.9°, and exposure time: 40 ms.
Figure 15.
Abu Dhabi and Dubai, United Arab Emirates, Asia, on 27 June 2024 at 06:17 UTC. Coordinates: 25.1° latitude and 55.0° longitude. Solar zenith angle: 28.9°, and exposure time: 40 ms.
Figure 16.
Namib desert close to Gobabeb, Namibia, Africa, on 13 June 2024 at 08:49 UTC. Coordinates: -23.6° latitude and 15.0° longitude. Solar zenith angle: 56.8°, and exposure time: 20 ms.
Figure 16.
Namib desert close to Gobabeb, Namibia, Africa, on 13 June 2024 at 08:49 UTC. Coordinates: -23.6° latitude and 15.0° longitude. Solar zenith angle: 56.8°, and exposure time: 20 ms.
Figure 17.
Mojave Desert, USA, North America, on 28 May 2024 at 17:52 UTC. Coordinates: 38.7° latitude and -116.1° longitude. Solar zenith angle: 28.9°, and exposure time: 20 ms.
Figure 17.
Mojave Desert, USA, North America, on 28 May 2024 at 17:52 UTC. Coordinates: 38.7° latitude and -116.1° longitude. Solar zenith angle: 28.9°, and exposure time: 20 ms.
Figure 18.
Lake Assal near Gulf of Tadjoura and the Red Sea, Djibouti, Africa, on 28 May 2024 at 06:57 UTC. Coordinates: 11.6° latitude and 42.8° longitude. Solar zenith angle: 32.6°, and exposure time: 20 ms.
Figure 18.
Lake Assal near Gulf of Tadjoura and the Red Sea, Djibouti, Africa, on 28 May 2024 at 06:57 UTC. Coordinates: 11.6° latitude and 42.8° longitude. Solar zenith angle: 32.6°, and exposure time: 20 ms.
Figure 19.
Cape Town, South Africa, Africa, on 13 April 2024 at 08:06 UTC. Coordinates: -34.3° latitude and 18.2° longitude. Solar zenith angle: 58.1°, and exposure time: 30 ms.
Figure 19.
Cape Town, South Africa, Africa, on 13 April 2024 at 08:06 UTC. Coordinates: -34.3° latitude and 18.2° longitude. Solar zenith angle: 58.1°, and exposure time: 30 ms.
Figure 20.
Vancouver Island, Canada, North America, on 13 July 2024 at 18:43 UTC. Coordinates: 50.4° latitude and -126.0° longitude. Solar zenith angle: 35.2°, and exposure time: 30 ms.
Figure 20.
Vancouver Island, Canada, North America, on 13 July 2024 at 18:43 UTC. Coordinates: 50.4° latitude and -126.0° longitude. Solar zenith angle: 35.2°, and exposure time: 30 ms.
Figure 21.
Caspian Sea, Asia, on 7 July 2024 at 06:58 UTC. Coordinates: 46.2° latitude and 50.4° longitude. Solar zenith angle: 31.4°, and exposure time: 30 ms.
Figure 21.
Caspian Sea, Asia, on 7 July 2024 at 06:58 UTC. Coordinates: 46.2° latitude and 50.4° longitude. Solar zenith angle: 31.4°, and exposure time: 30 ms.
Figure 22.
New Orleans (Gulf of Mexico), USA, North America, on 14 June 2024 at 16:04 UTC. Coordinates: 30.6° latitude and -89.4° longitude. Solar zenith angle: 25.8°, and exposure time: 30 ms.
Figure 22.
New Orleans (Gulf of Mexico), USA, North America, on 14 June 2024 at 16:04 UTC. Coordinates: 30.6° latitude and -89.4° longitude. Solar zenith angle: 25.8°, and exposure time: 30 ms.
Figure 23.
Trondheim, Norway, Europe, on 26 April 2024 at 10:49 UTC. Coordinates: 64.3° latitude and 9.42° longitude. Solar zenith angle: 50.5°, and exposure time: 40 ms.
Figure 23.
Trondheim, Norway, Europe, on 26 April 2024 at 10:49 UTC. Coordinates: 64.3° latitude and 9.42° longitude. Solar zenith angle: 50.5°, and exposure time: 40 ms.
Figure 24.
Long Island - New York, USA, North America, on 16 June 2024 at 15:14 UTC. Coordinates: 41.3° latitude and -73.4° longitude. Solar zenith angle: 27.1°, and exposure time: 35 ms.
Figure 24.
Long Island - New York, USA, North America, on 16 June 2024 at 15:14 UTC. Coordinates: 41.3° latitude and -73.4° longitude. Solar zenith angle: 27.1°, and exposure time: 35 ms.
Figure 25.
Alaska, USA, North America, on 15 April 2024 at 21:08 UTC. Coordinates: 61.3° latitude and -147.1° longitude. Solar zenith angle: 51.1°, and exposure time: 25 ms.
Figure 25.
Alaska, USA, North America, on 15 April 2024 at 21:08 UTC. Coordinates: 61.3° latitude and -147.1° longitude. Solar zenith angle: 51.1°, and exposure time: 25 ms.
Figure 26.
Svalbard, Norway, Europe, on 3 May 2024 at 19:07 UTC. Coordinates: 78.2° latitude and 13.6° longitude. Solar zenith angle: 80.2°, and exposure time: 35 ms.
Figure 26.
Svalbard, Norway, Europe, on 3 May 2024 at 19:07 UTC. Coordinates: 78.2° latitude and 13.6° longitude. Solar zenith angle: 80.2°, and exposure time: 35 ms.
Figure 27.
Finnmark, Norway, Europe, on 21 July 2024 at 18:24 UTC. Coordinates: 70.2° latitude and 22.8° longitude. Solar zenith angle: 79.5°, and exposure time: 35 ms.
Figure 27.
Finnmark, Norway, Europe, on 21 July 2024 at 18:24 UTC. Coordinates: 70.2° latitude and 22.8° longitude. Solar zenith angle: 79.5°, and exposure time: 35 ms.
Figure 28.
Florida, USA, North America, on 21 May 2024 at 15:51 UTC. Coordinates: 27.2° latitude and -82.6° longitude. Solar zenith angle: 22.1°, and exposure time: 30 ms.
Figure 28.
Florida, USA, North America, on 21 May 2024 at 15:51 UTC. Coordinates: 27.2° latitude and -82.6° longitude. Solar zenith angle: 22.1°, and exposure time: 30 ms.
Table 1.
Notation and descriptions of sequences in 1D-Justo-LiuNet.
| NOTATION | DESCRIPTION OF THE SEQUENCE |
|---|---|
| NETWORK’S INPUT | |
| Image pixel to be classified, represented by its spectral signature along wavelengths . In this work, each pixel comprises spectral bands. | |
| CONVOLUTIONS FOR FEATURE EXTRACTION | |
| Weight parameters of the kernels in the convolution layer at level X. Each 2D kernel consists of components across the K dimension. The number of kernel components, , corresponds to the number of kernels used in the convolution at the previous level . Since it is common to use multiple kernels at previous levels, the convolution at level X also demands kernels with multiple components, i.e., . Only at level 1, convolution kernels are, however, single-component (1D) across K as there are no previous convolutions and hence weight parameters are given by . In Table 2, we provide the numerical dimensions for , , and K across 1D-Justo-LiuNet. | |
| Bias parameters of the kernels in the convolution at level X. The sequence is always 1D, regardless of whether the kernel weights are multi-component (2D) or single-component (1D). | |
| Output sequence of the convolution layer at level X, including all one-dimensional feature maps with length produced by the respective kernels. Each feature map is always one-dimensional regardless of whether the kernel weights are multi- or single-component. | |
| POOLING FOR FEATURE REDUCTION | |
| Output sequence of pooling layer at level X with feature maps, where their original length is reduced down to . | |
| CLASSIFICATION OUTPUT | |
| Output sequence of flatten layer representing the I-th highest-level extracted features in the latent space relevant for sea-land-cloud classification. | |
| Weight parameters of the C neurons in the dense layer, where C represents the number of classes to detect. Each neuron is fully connected, with I synapses, to the respective features in to calculate the probability that they belong to the neuron’s respective class. | |
| Bias parameters of the C neurons in the dense layer. | |
| Output sequence of the dense layer (i.e., output of the network), consisting of C class probabilities. | |
Table 2.
Overview of the 1D-CNN 1D-Justo-LiuNet showing sequence dimensions. * N/A: Pooling layers do not contain trainable parameters.
Table 2.
Overview of the 1D-CNN 1D-Justo-LiuNet showing sequence dimensions. * N/A: Pooling layers do not contain trainable parameters.
| INPUT | LAYER PARAMETERS | OUTPUT | |||
|---|---|---|---|---|---|
| SEQUENCE | DIMENSIONS | SEQUENCES | DIMENSIONS | SEQUENCE | DIMENSIONS |
| FEATURE EXTRACTION AND REDUCTION | |||||
| LEVEL 1 | |||||
| CONVOLUTION ( kernels; ) | |||||
| 1 x 112 | 6 x 6 | 6 x 107 | |||
| 3-4[1pt/1pt] | 1 x 6 | ||||
| POOLING | |||||
| 6 x 107 | N/A* | N/A | 6 x 53 | ||
| LEVEL 2 | |||||
| CONVOLUTION ( kernels; ) | |||||
| 6 x 53 | 12 x 6 x 6 | 12 x 48 | |||
| 3-4[1pt/1pt] | 1 x 12 | ||||
| POOLING | |||||
| 12 x 48 | N/A | N/A | 12 x 24 | ||
| LEVEL 3 | |||||
| CONVOLUTION ( kernels; ) | |||||
| 12 x 24 | 18 x 12 x 6 | 18 x 19 | |||
| 3-4[1pt/1pt] | 1 x 18 | ||||
| POOLING | |||||
| 18 x 19 | N/A | N/A | 18 x 9 | ||
| LEVEL 4 | |||||
| CONVOLUTION ( kernels; ) | |||||
| 18 x 9 | 24 x 18 x 6 | 24 x 4 | |||
| 3-4[1pt/1pt] | 1 x 24 | ||||
| POOLING | |||||
| 24 x 4 | N/A | N/A | 24 x 2 | ||
| FLATTENING OF FEATURES | |||||
| 24 x 2 | N/A | N/A | 1 x 48 | ||
| CLASSIFICATION OF FEATURES | |||||
| DENSE ( class neurons to 48-dimensional latent space) | |||||
| 1 x 48 | 3 x 48 | 1 x 3 | |||
| 3-4[1pt/1pt] | 1 x 3 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated