Submitted:
01 November 2024
Posted:
04 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
- 1.
- The proposed algorithm leverages the strengths of EfficientNetB0, MobileNetV2, Logistic Regression, XGBoost, and CatBoost, combining deep learning feature extraction with traditional machine learning classifiers. The multi-branch deep learning architecture enables the extraction of high-level, lesion-specific features, while the attention mechanism enhances the model’s focus on critical regions in medical images. The ensemble outperforms standalone models by integrating both deep and traditional learning approaches, ensuring better generalization and improved class-wise accuracy.
- 2.
- The ensemble model uses PCA for dimensionality reduction and using classifiers for final decision-making; it reduces the risk of overfitting, balances interpretability, and achieves robust performance across different lesion types.
- 3.
- The study aims to examine the impact of different datasets—noisy images in three different solutions, a secondary dataset, and the main study is carried out on denoised images. By applying this proposed model to different secondary datasets and noisy datasets, the research evaluates how dataset variability affects the model’s performance.
- 4.
- The study aims to offer a thorough analysis of existing ensemble and deep learning methodologies to emphasize the advantages and distinctive strengths of the proposed ensemble model. By reviewing similar existing frameworks, it highlights key innovations and performance improvements introduced by the ensemble model.
1.1. Gaps Identified and Corrective Measures Taken
1.2. Organization of the Paper
2. Related Work
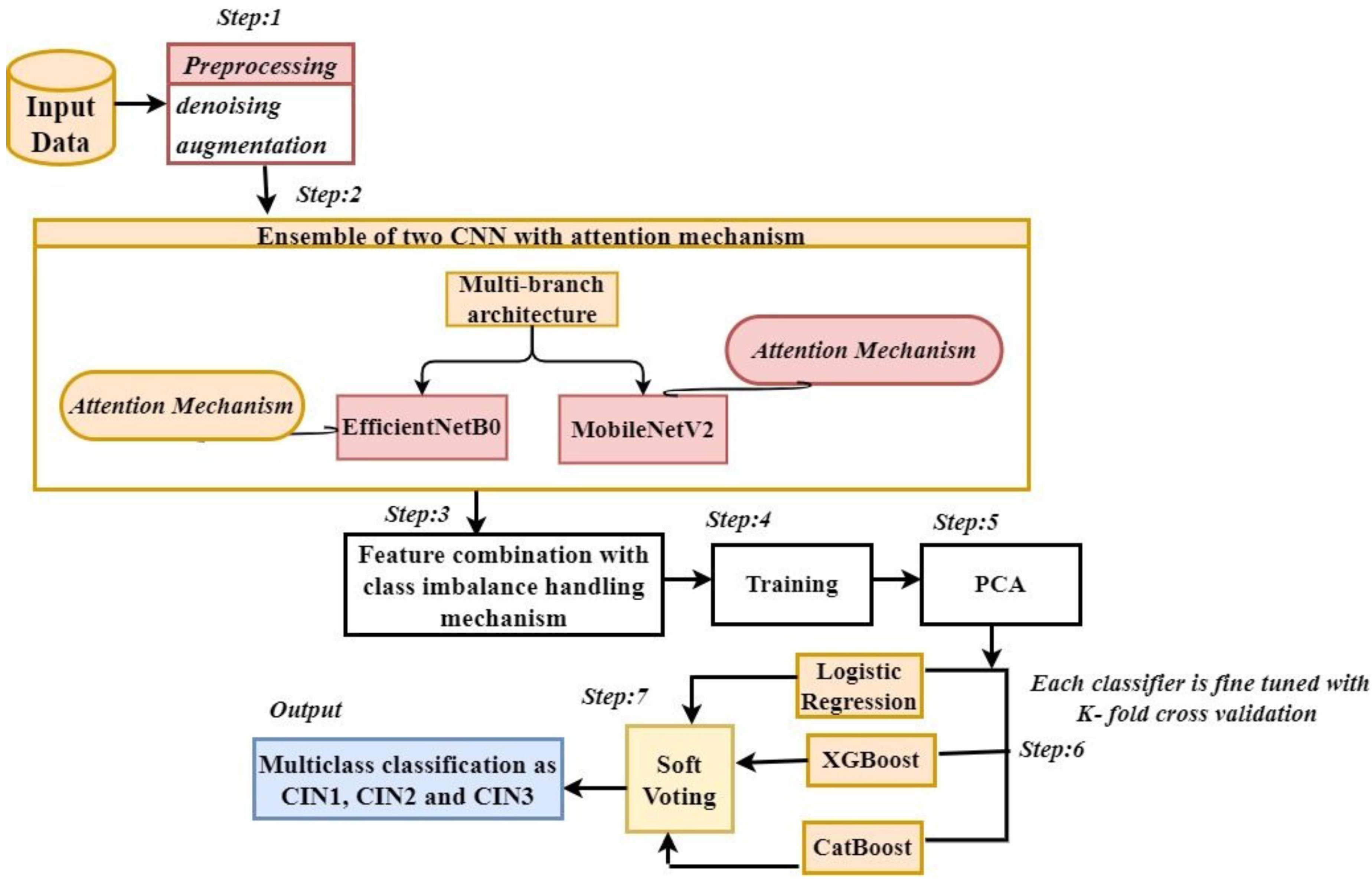
3. Proposed Methodology
3.1. Data Preprocessing
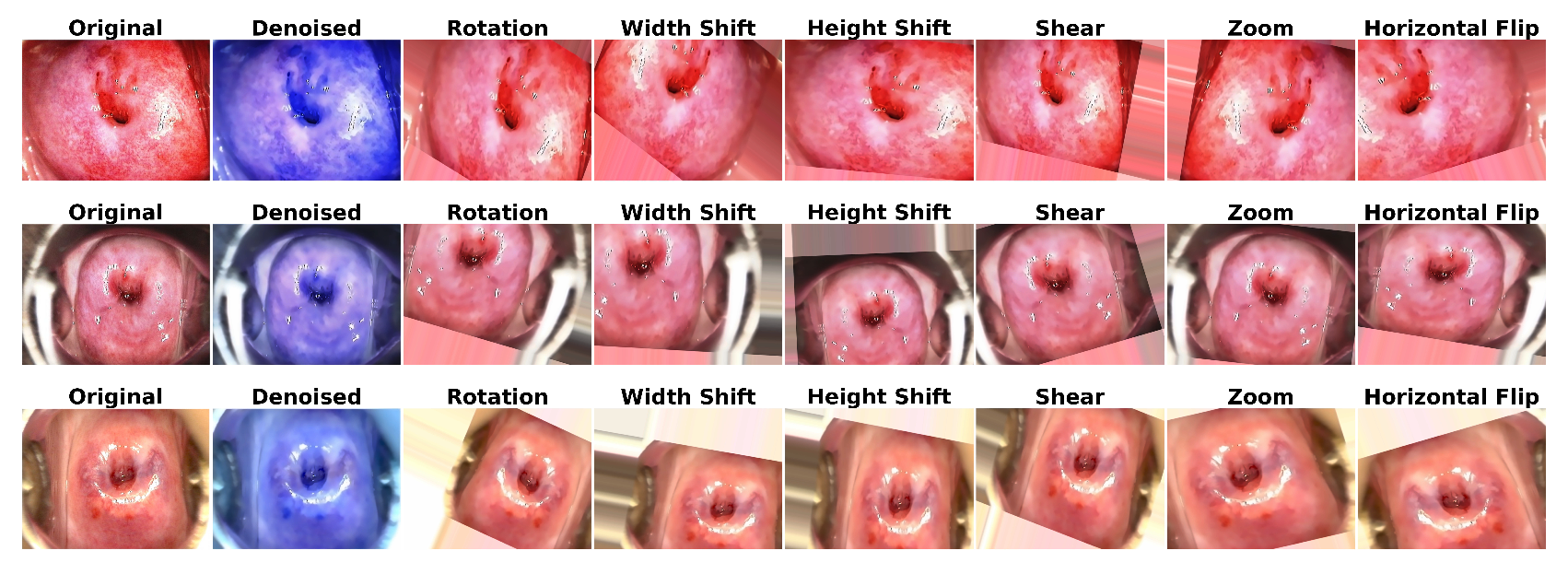
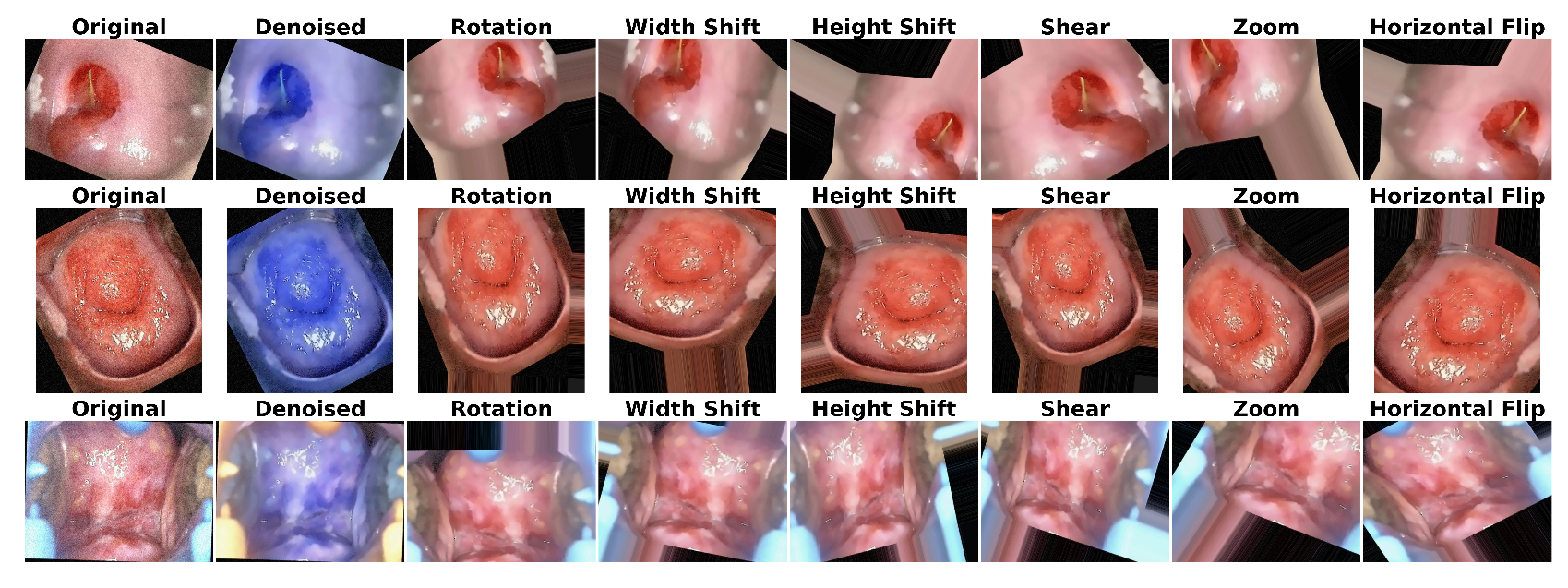
3.1.1. Image Denoising
Mathematical Basis
3.1.2. Data Augmentation
3.2. Ensemble of Two CNNs with Attention Mechanism
Mathematical Basis
3.3. Class Imbalance Handling, Learning Rate Scheduling, Dimensionality Reduction, and Multi Class Classification
Class Weights for Imbalance Handling
Learning Rate Scheduling
PCA for Dimensionality Reduction
Logistic Regression, XGBoost, and CatBoost
Hyperparameter fine tuning and K-Fold cross validation
1. Hyperparameter Tuning with Grid Search
2. Class-wise Evaluation with K-fold Cross-Validation
Soft-Voting Ensemble
4. Algorithm

5. Implementation
5.1. Experimental Setup
5.2. Performance Metrics
5.3. Dataset
5.3.1. Primary Dataset
5.3.2. Distribution of Images of the Primary Dataset in Lugol’s Iodine, Acetic Acid and Normal Saline
5.3.3. Secondary Dataset
6. Results and Discussions
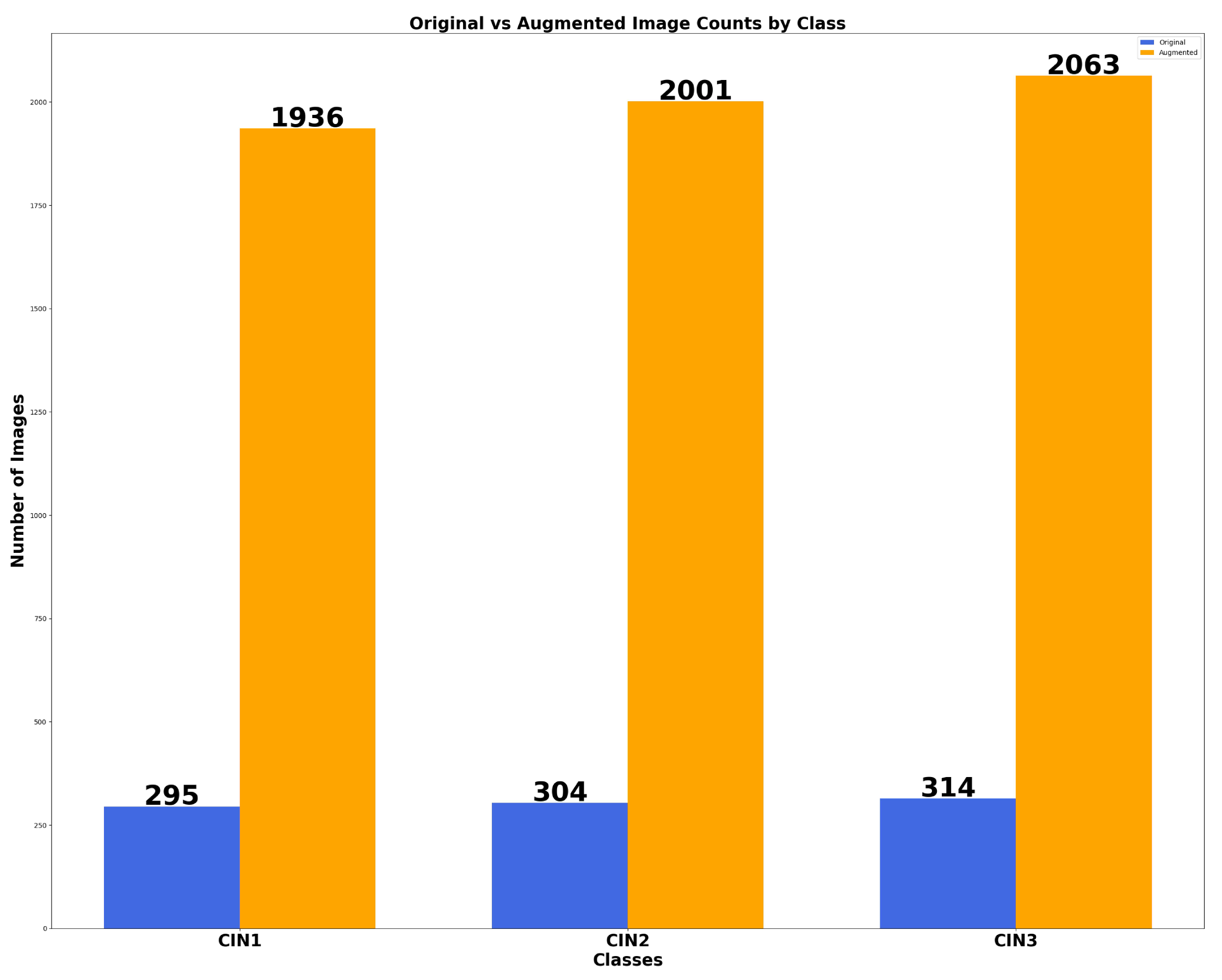
6.1. Results of Data Preprocessing and Image Augmentation
6.2. Results of Model Training on Primary Dataset from IARC
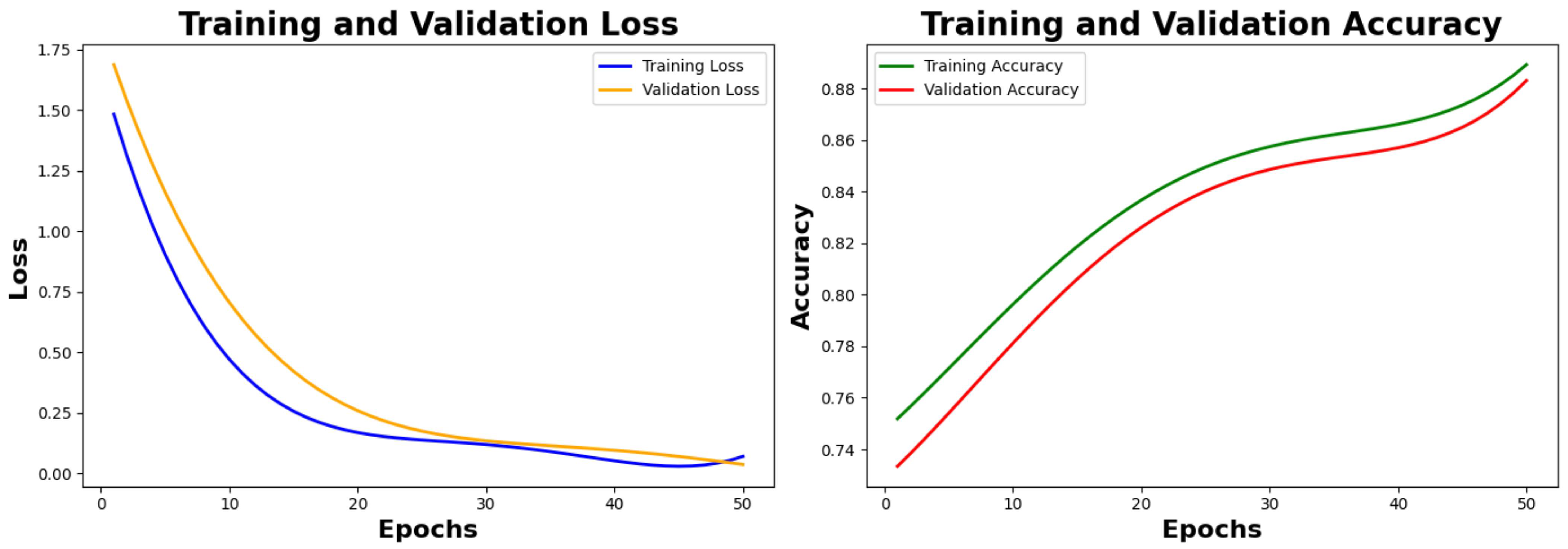
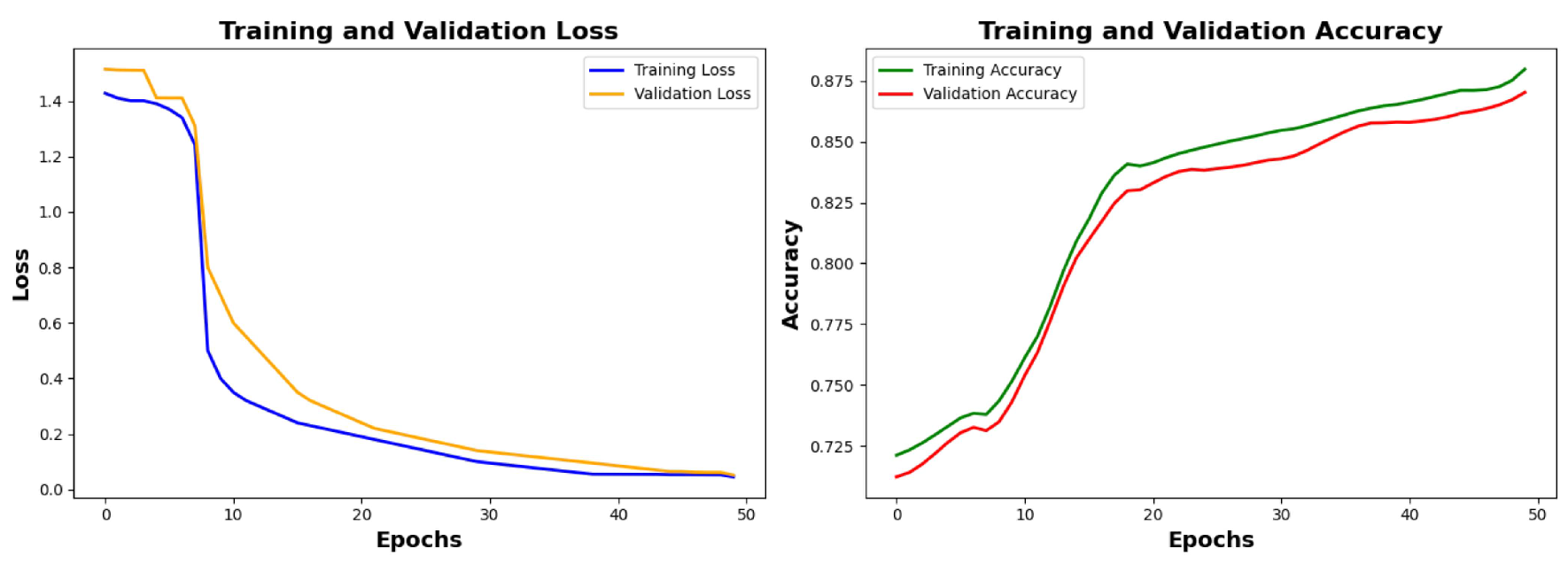
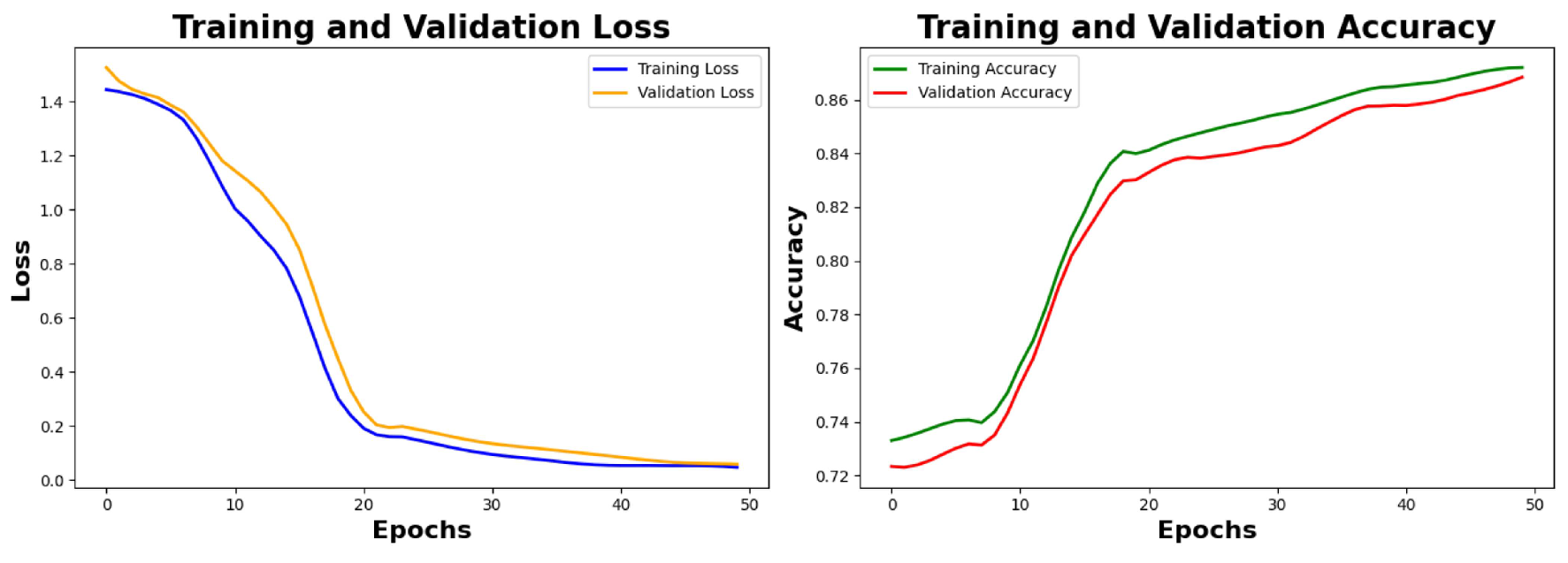
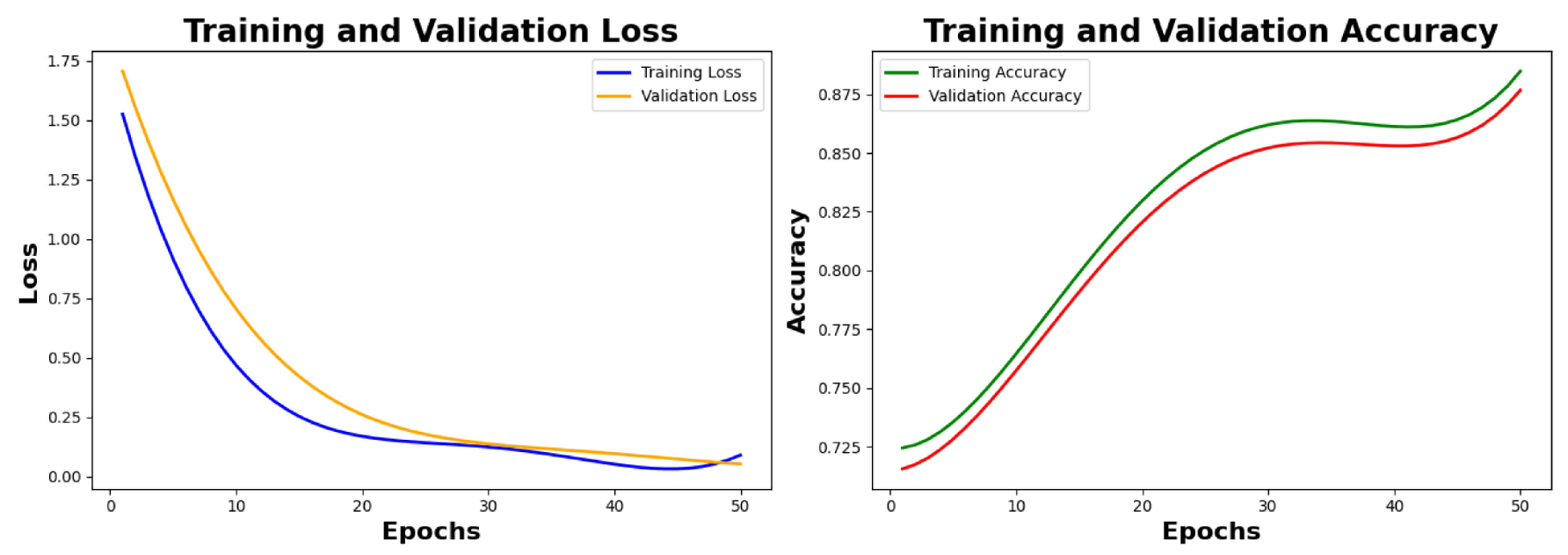
6.2.1. Training Results and Analysis
Analysis
6.2.2. Feature Extraction, PCA, Hyperparameter Fine Tuning and K-Fold Cross Validation Results and Analysis
Analysis
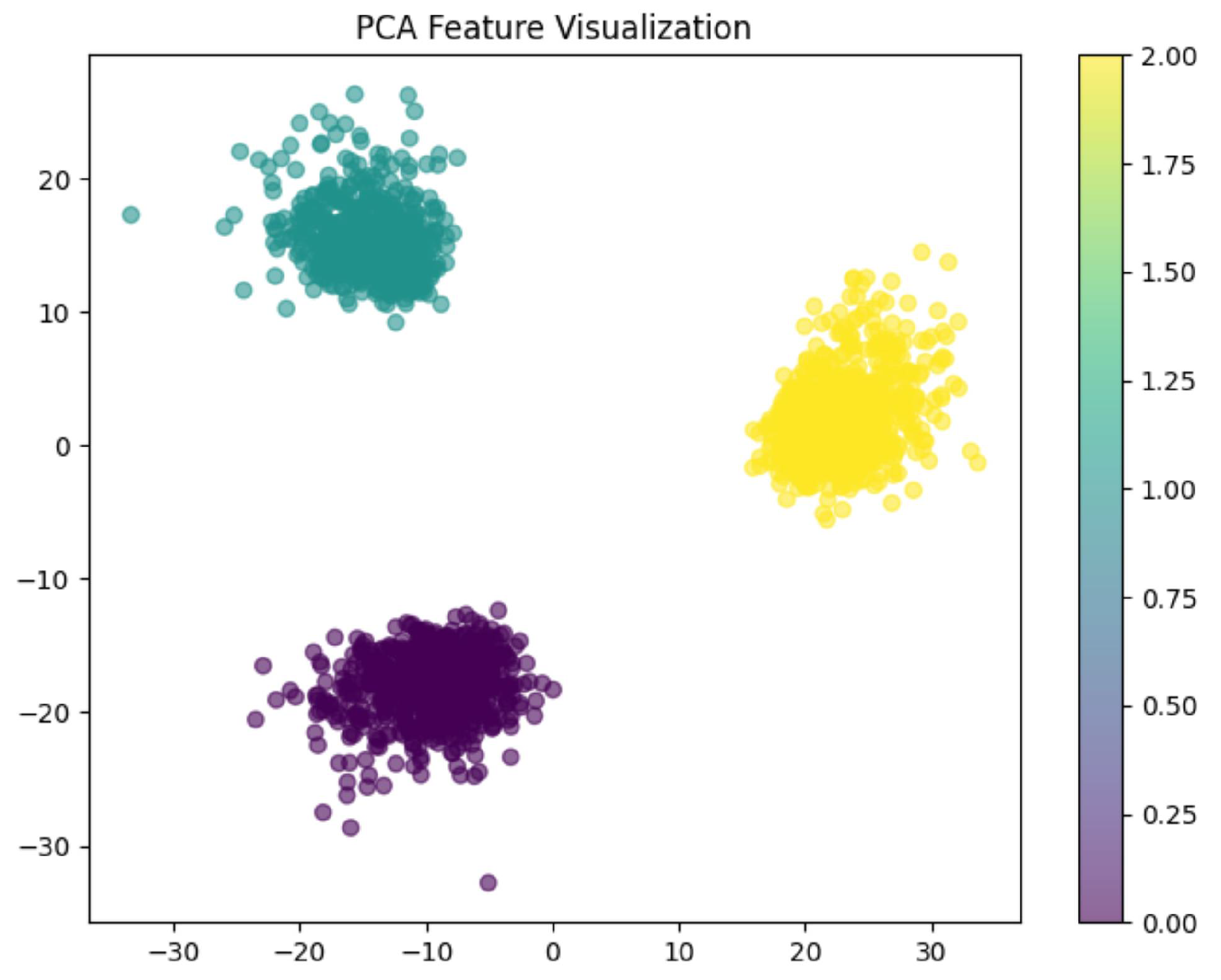
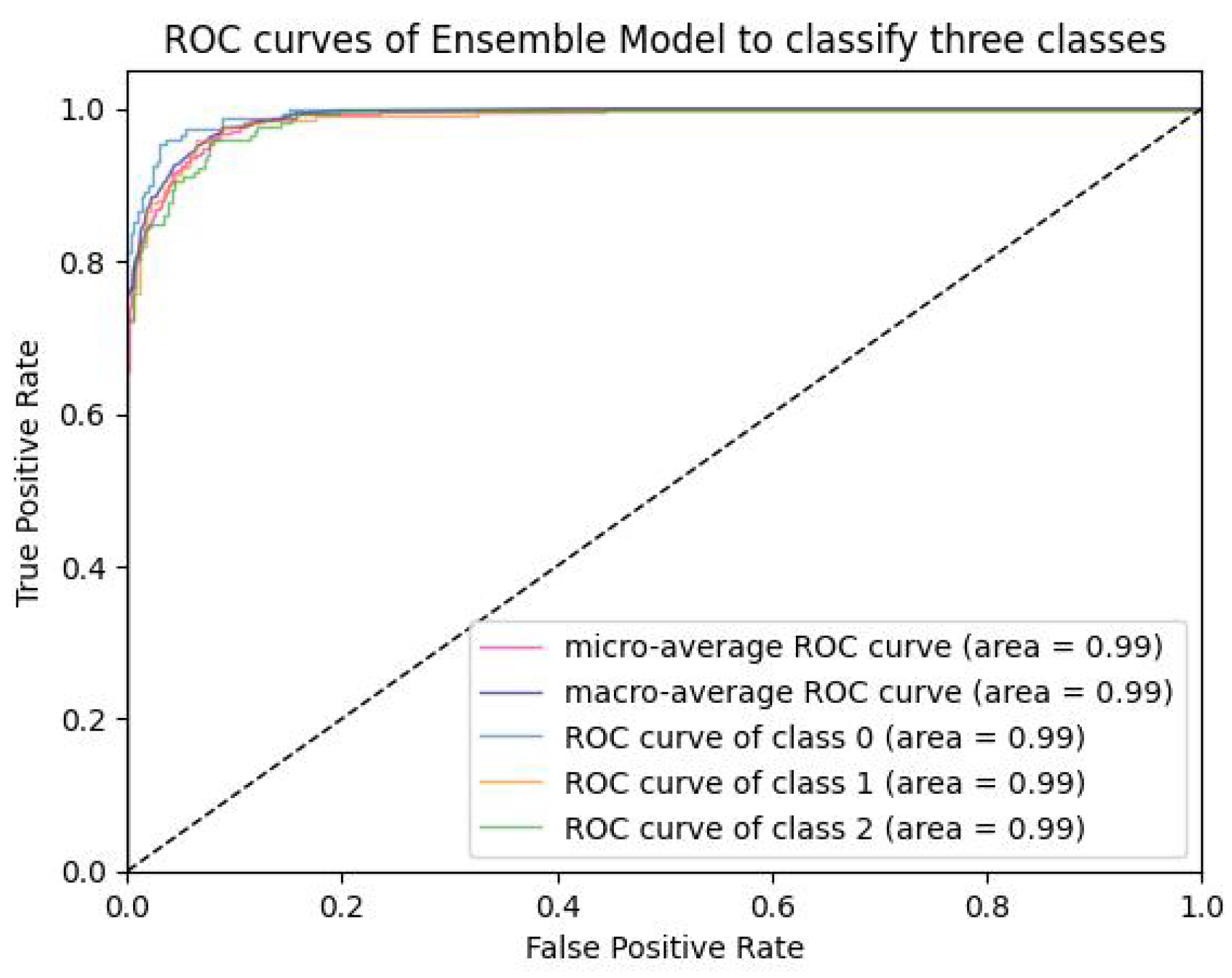
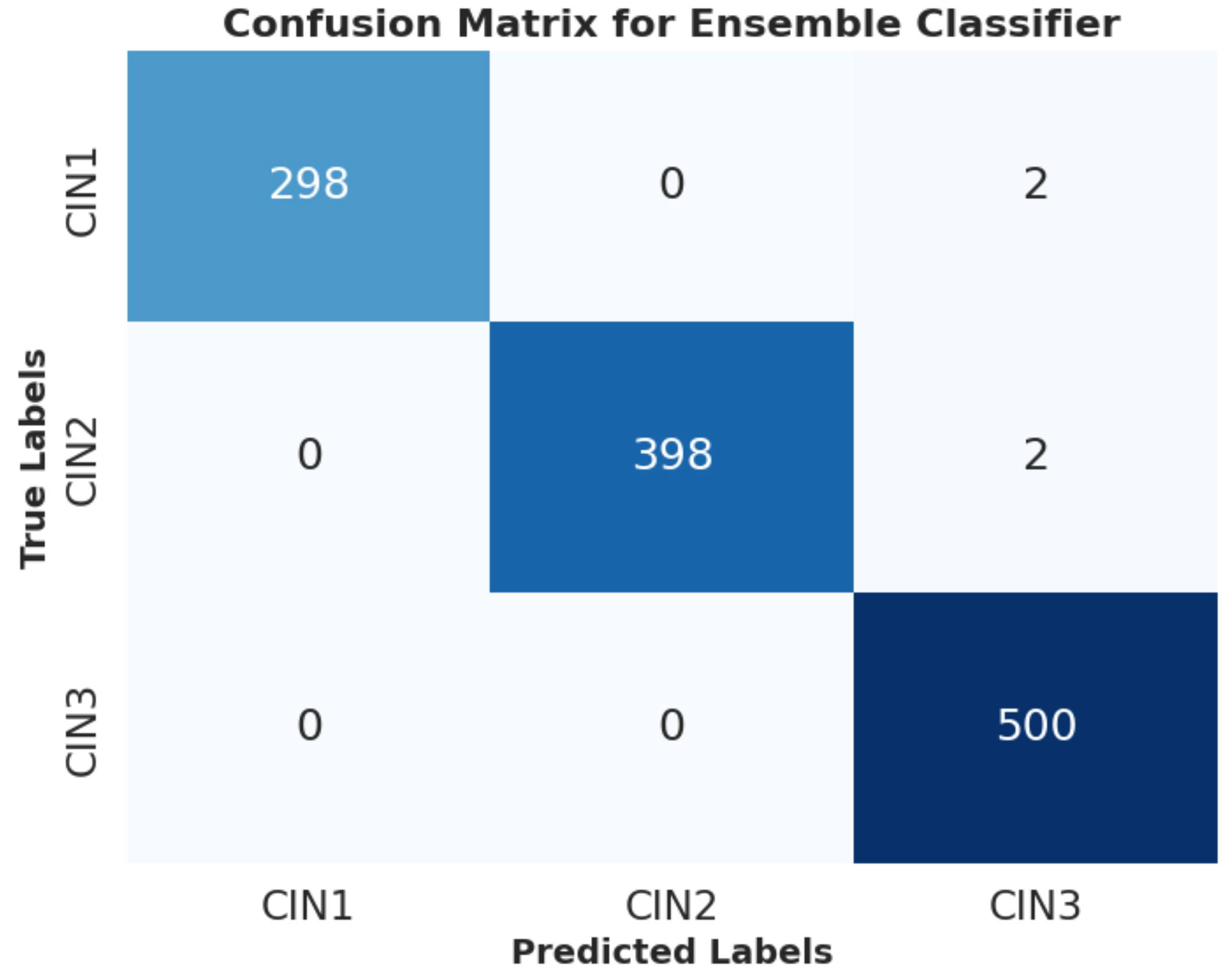
6.2.3. PCA Visualization, AUC Graph and Confusion Matrix Plot
Analysis
6.3. Test Result of the Model on Primary Denoised IARC Dataset
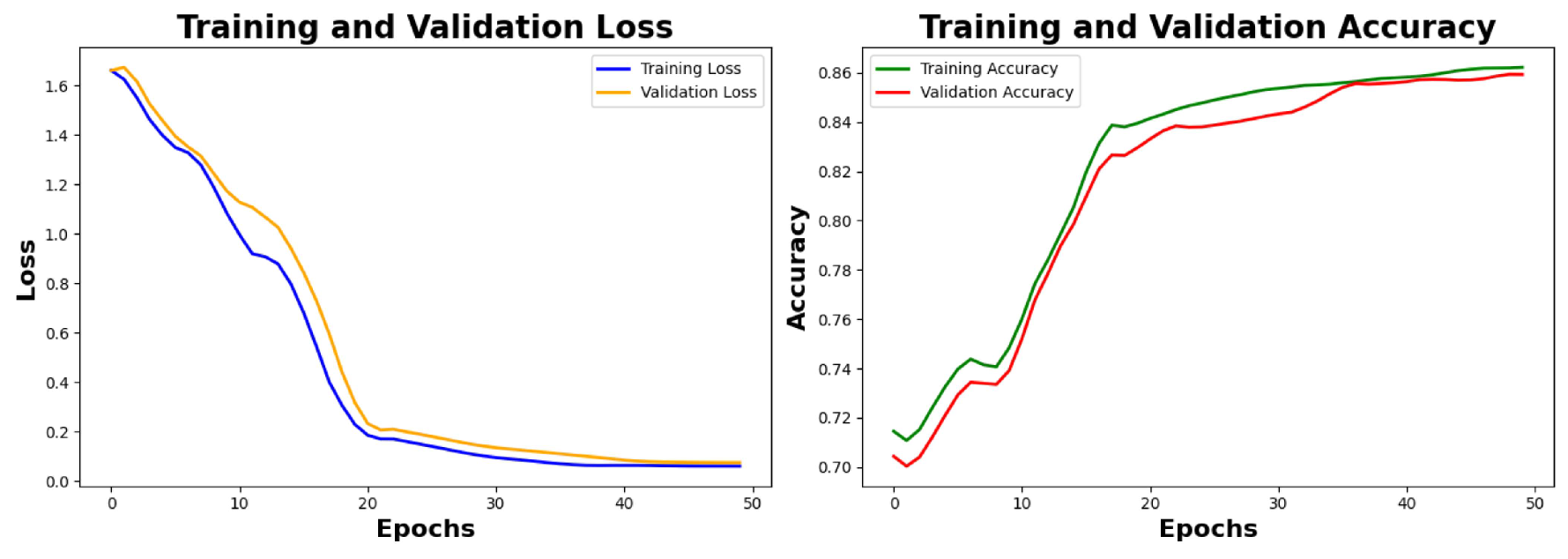
6.4. Result Analysis of the Primary Noisy Dataset Separated by Solutions and Denoised Secondary Dataset
Analysis of Loss graphs and accuracy graphs
Analysis of performance metrics of noisy dataset in three solutions and the secondary dataset
6.5. Result Analysis of Recent Existing Approaches, Baseline Architecture and Variation of the Proposed Model
Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jacot-Guillarmod, M.; Balaya, V.; Mathis, J.; Hübner, M.; Grass, F.; Cavassini, M.; Sempoux, C.; Mathevet, P.; Pache, B. Women with Cervical High-Risk Human Papillomavirus: Be Aware of Your Anus! The ANGY Cross-Sectional Clinical Study. Cancers 2022, 14, 5096. [Google Scholar] [CrossRef] [PubMed]
- Bucchi, L.; Costa, S.; Mancini, S.; Baldacchini, F.; Giuliani, O.; Ravaioli, A.; Vattiato, R.; others. Clinical epidemiology of microinvasive cervical carcinoma in an Italian population targeted by a screening programme. Cancers 2022, 14, 2093. [Google Scholar] [CrossRef]
- Tantari, M.; Bogliolo, S.; Morotti, M.; Balaya, V.; Bouttitie, F.; Buenerd, A.; Magaud, L.; others. Lymph node involvement in early-stage cervical cancer: is lymphangiogenesis a risk factor? Results from the MICROCOL study. Cancers 2022, 14, 212. [Google Scholar] [CrossRef]
- Yao, K.; Huang, K.; Sun, J.; Hussain, A. PointNu-Net: Keypointassisted convolutional neural network for simultaneous multi-tissue histology nuclei segmentation and classification. IEEE Trans. Emerg. Topics Comput. Intell. 2024, 8, 802–813. [Google Scholar] [CrossRef]
- Ramzan, Z.; Hassan, M.A.; Asif, H.M.S.; Farooq, A. A machine learning-based self-risk assessment technique for cervical cancer. Current Bioinformatics 2021, 16, 315–332. [Google Scholar] [CrossRef]
- Parra, S.; Carranza, E.; Coole, J.; Hunt, B.; Smith, C.; Keahey, P.; Maza, M.; Schmeler, K.; Richards-Kortum, R. Development of low-cost point-of-care technologies for cervical cancer prevention based on a single-board computer. IEEE Journal of Translational Engineering in Health and Medicine 2020, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Shah, H.A.; Saeed, F.; Yun, S.; Park, J.H.; Paul, A.; Kang, J.M. A Robust Approach for Brain Tumor Detection in Magnetic Resonance Images Using Finetuned EfficientNet. IEEE Access 2022, 10, 65426–65438. [Google Scholar] [CrossRef]
- Si, L.; others. A Novel Coal-Gangue Recognition Method for Top Coal Caving Face Based on IALO-VMD and Improved MobileNetV2 Network. IEEE Transactions on Instrumentation and Measurement 2023, 72, 1–16, Art no. 2529216. [Google Scholar] [CrossRef]
- Ju, X.; Qian, J.; Chen, Z.; Zhao, C.; Qian, J. Mulr4FL: Effective Fault Localization of Evolution Software Based on Multivariate Logistic Regression Model. IEEE Access 2020, 8, 207858–207870. [Google Scholar] [CrossRef]
- Teng, W.; Wang, N.; Shi, H.; Liu, Y.; Wang, J. Classifier-Constrained Deep Adversarial Domain Adaptation for Cross-Domain Semisupervised Classification in Remote Sensing Images. IEEE Geoscience and Remote Sensing Letters 2020, 17, 789–793. [Google Scholar] [CrossRef]
- Prakash, A.; Thangaraj, J.; Roy, S.; Srivastav, S.; Mishra, J.K. Model-Aware XGBoost Method Towards Optimum Performance of Flexible Distributed Raman Amplifier. IEEE Photonics Journal 2023, 15, 1–10. [Google Scholar] [CrossRef]
- Tammina, S. Transfer learning using VGG-16 with deep convolutional neural network for classifying images. International Journal of Scientific and Research Publications (IJSRP) 2019, 9, 143–150. [Google Scholar] [CrossRef]
- Hasegawa, T.; Kondo, K. Easy Ensemble: Simple Deep Ensemble Learning for Sensor-Based Human Activity Recognition. IEEE Internet of Things Journal 2023, 10, 5506–5518. [Google Scholar] [CrossRef]
- Cui, X.; Wu, S.; Li, Q.; Chan, A.B.; Kuo, T.W.; Xue, C.J. Bits-Ensemble: Toward Light-Weight Robust Deep Ensemble by Bits-Sharing. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2022, 41, 4397–4408. [Google Scholar] [CrossRef]
- Prakash, A.S.J.; Sriramya, P. Accuracy analysis for image classification and identification of nutritional values using convolutional neural networks in comparison with logistic regression model. Journal of Pharmaceutical Negative Results 2022, pp. 606–611.
- Das, P.; Pandey, V. Use of logistic regression in land-cover classification with moderate-resolution multispectral data. Journal of the Indian Society of Remote Sensing 2019, 47, 1443–1454. [Google Scholar] [CrossRef]
- Park, J.; Yang, H.; Roh, H.J.; Jung, W.; Jang, G.J. Encoder-weighted W-Net for unsupervised segmentation of cervix region in colposcopy images. Cancers 2022, 14, 3400. [Google Scholar] [CrossRef]
- Morales-Hernández, A.; Nieuwenhuyse, I.V.; Gonzalez, S.R. A survey on multi-objective hyperparameter optimization algorithms for machine learning. Artificial Intelligence Review 2023, 56, 8043–8093. [Google Scholar] [CrossRef]
- Ahmad, Z.; Li, J.; Mahmood, T. Adaptive hyperparameter fine-tuning for boosting the robustness and quality of the particle swarm optimization algorithm for non-linear RBF neural network modelling and its applications. Mathematics 2023, 11, 242. [Google Scholar] [CrossRef]
- Hua, Q.; Li, Y.; Zhang, J.; others. Convolutional neural networks with attention module and compression strategy based on second-order information. International Journal of Machine Learning and Cybernetics 2024, 15, 2619–2629. [Google Scholar] [CrossRef]
- Jiang, X.; Li, J.; Kan, Y.; Yu, T.; Chang, S.; Sha, X.; Zheng, H. MRI based radiomics approach with deep learning for prediction of vessel invasion in early-stage cervical cancer. IEEE/ACM Trans. Comput. Biol. Bioinf. 2020, 18, 995–1002. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Liu, S. Medical Ultrasound Image Segmentation With Deep Learning Models. IEEE Access 2023, 11, 10158–10168. [Google Scholar] [CrossRef]
- Skouta, A.; Elmoufidi, A.; Jai-Andaloussi, S.; others. Deep learning for diabetic retinopathy assessments: a literature review. Multimedia Tools and Applications 2023, 82, 41701–41766. [Google Scholar] [CrossRef]
- International Agency for Research on Cancer. IARC: International Agency for Research on Cancer 2023.
- Youneszade, N.; Marjani, M.; Ray, S.K. A predictive model to detect cervical diseases using convolutional neural network algorithms and digital colposcopy images. IEEE Access 2023, 11, 59882–59898. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, C.; Chen, F.; Li, M.; Yang, B.; Yan, Z.; Lv, X. Research on application of classification model based on stack generalization in staging of cervical tissue pathological images. IEEE Access 2021, 9, 48980–48991. [Google Scholar] [CrossRef]
- Luo, Y.M.; Zhang, T.; Li, P.; Liu, P.Z.; Sun, P.; Dong, B.; Ruan, G. MDFI: multi-CNN decision feature integration for diagnosis of cervical precancerous lesions. IEEE Access 2020, 8, 29616–29626. [Google Scholar] [CrossRef]
- Chen, P.; Liu, F.; Zhang, J.; Wang, B. MFEM-CIN: A Lightweight Architecture Combining CNN and Transformer for the Classification of Pre-Cancerous Lesions of the Cervix. IEEE Open J. Eng. Med. Biol. 2024, 5, 216–225. [Google Scholar] [CrossRef]
- Mathivanan, S.; Francis, D.; Srinivasan, S.; Khatavkar, V.; P, K.; Shah, M.A. Enhancing cervical cancer detection and robust classification through a fusion of deep learning models. Scientific Reports 2024, 14, 10812. [Google Scholar] [CrossRef]
- He, Y.; Liu, L.; Wang, J.; Zhao, N.; He, H. Colposcopic Image Segmentation Based on Feature Refinement and Attention. IEEE Access 2024, 12, 40856–40870. [Google Scholar] [CrossRef]
- Bappi, J.O.; Rony, M.A.T.; Islam, M.S.; Alshathri, S.; El-Shafai, W. A Novel Deep Learning Approach for Accurate Cancer Type and Subtype Identification. IEEE Access 2024, 12, 94116–94134. [Google Scholar] [CrossRef]
- Kang, J.; Li, N. CerviSegNet-DistillPlus: An Efficient Knowledge Distillation Model for Enhancing Early Detection of Cervical Cancer Pathology. IEEE Access 2024, 12, 85134–85149. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, D.; Kumar, V.; Lee, H.N. MLNet: metaheuristics-based lightweight deep learning network for cervical cancer diagnosis. IEEE Journal of Biomedical and Health Informatics 2022, 27, 5004–5014. [Google Scholar] [CrossRef]
- Sahoo, P.; Saha, S.; Mondal, S.; Seera, M.; Sharma, S.K.; Kumar, M. Enhancing Computer-Aided Cervical Cancer Detection Using a Novel Fuzzy Rank-Based Fusion. IEEE Access 2023, 11, 145281–145294. [Google Scholar] [CrossRef]
- Skerrett, E.; Miao, Z.; Asiedu, M.N.; Richards, M.; Crouch, B.; Sapiro, G.; Qiu, Q.; Ramanujam, N. Multicontrast Pocket Colposcopy Cervical Cancer Diagnostic Algorithm for Referral Populations. BME Frontiers 2022, 2022. [Google Scholar] [CrossRef]
- Devarajan, D.; Alex, D.S.; Mahesh, T.R.; Kumar, V.V.; Aluvalu, R.; Maheswari, V.U.; Shitharth, S. Cervical cancer diagnosis using intelligent living behavior of artificial jellyfish optimized with artificial neural network. IEEE Access 2022, 10, 126957–126968. [Google Scholar] [CrossRef]
- Gaona, Y.J.; Malla, D.C.; Crespo, B.V.; Vicuña, M.J.; Neira, V.A.; Dávila, S.; Verhoeven, V. Radiomics Diagnostic Tool Based on Deep Learning for Colposcopy Image Classification. Diagnostics 2022, 12, 1694. [Google Scholar] [CrossRef]
- Allahqoli, L.; Laganà, A.S.; Mazidimoradi, A.; Salehiniya, H.; Günther, V.; Chiantera, V.; Goghari, S.K.; Ghiasvand, M.M.; Rahmani, A.; Momenimovahed, Z.; Alkatout, I. Diagnosis of Cervical Cancer and Pre-Cancerous Lesions by Artificial Intelligence: A Systematic Review. Diagnostics 2022, 12, 2771. [Google Scholar] [CrossRef]
- Pal, A.; Xue, Z.; Befano, B.; Rodriguez, A.C.; Long, L.R.; Schiffman, M.; Antani, S. Deep metric learning for cervical image classification. IEEE Access 2021, 9, 53266–53275. [Google Scholar] [CrossRef]
- Adweb, K.M.A.; Cavus, N.; Sekeroglu, B. Cervical cancer diagnosis using very deep networks over different activation functions. IEEE Access 2021, 9, 46612–46625. [Google Scholar] [CrossRef]
- Baydoun, A.; Xu, K.E.; Heo, J.U.; Yang, H.; Zhou, F.; Bethell, L.A.; Fredman, E.T.; others. Synthetic CT generation of the pelvis in patients with cervical cancer: a single input approach using generative adversarial network. IEEE Access 2021, 9, 17208–17221. [Google Scholar] [CrossRef]
- Ilyas, Q.M.; Ahmad, M. An enhanced ensemble diagnosis of cervical cancer: a pursuit of machine intelligence towards sustainable health. IEEE Access 2021, 9, 12374–12388. [Google Scholar] [CrossRef]
- Elakkiya, R.; Subramaniyaswamy, V.; Vijayakumar, V.; Mahanti, A. Cervical cancer diagnostics healthcare system using hybrid object detection adversarial networks. IEEE J. Biomed. Health Inform. 2021, 26, 1464–1471. [Google Scholar] [CrossRef]
- Fang, M.; Lei, X.; Liao, B.; Wu, F.X. A Deep Neural Network for Cervical Cell Detection Based on Cytology Images. SSRN 2022, 13, 4231806. [Google Scholar] [CrossRef]
- Jiang, X.; Li, J.; Kan, Y.; Yu, T.; Chang, S.; Sha, X.; Zheng, H.; Luo, Y.; Wang, S. MRI based radiomics approach with deep learning for prediction of vessel invasion in early-stage cervical cancer. IEEE/ACM Transactions on Computational Biology and Bioinformatics 2020, 18, 995–1002. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Xue, P.; Tang, C.; Chang, J.; Chu, C.; Ma, K.; Li, Q.; Zheng, Y.; Qiao, Y. Computer-aided cervical cancer diagnosis using time-lapsed colposcopic images. IEEE Trans. Med. Imaging. 2020, 39, 3403–3415. [Google Scholar] [CrossRef]
- Bai, B.; Du, Y.; Liu, P.; Sun, P.; Li, P.; Lv, Y. Detection of Cervical Lesion Region From Colposcopic Images Based on Feature Reselection. Biomedical Signal Processing and Control 2020, 57. [Google Scholar] [CrossRef]
- Yue, Z.; Ding, S.; Zhao, W.; Wang, H.; Ma, J.; Zhang, Y.; Zhang, Y. Automatic CIN grades prediction of sequential cervigram image using LSTM with multistate CNN features. IEEE J. Biomed. Health Inform. 2019, 24, 844–854. [Google Scholar] [CrossRef]
- Zhang, T.; Luo, Y.M.; Li, P.; Liu, P.Z.; Du, Y.Z.; Sun, P.; Dong, B.; Xue, H. Cervical Precancerous Lesions Classification Using Pre-Trained Densely Connected Convolutional Networks With Colposcopy Images. Biomedical Signal Processing and Control 2020, 55. [Google Scholar] [CrossRef]
- Malhari Colposcopy Dataset original, aug & combined. Malhari Colposcopy Dataset original, aug & combined 2024.
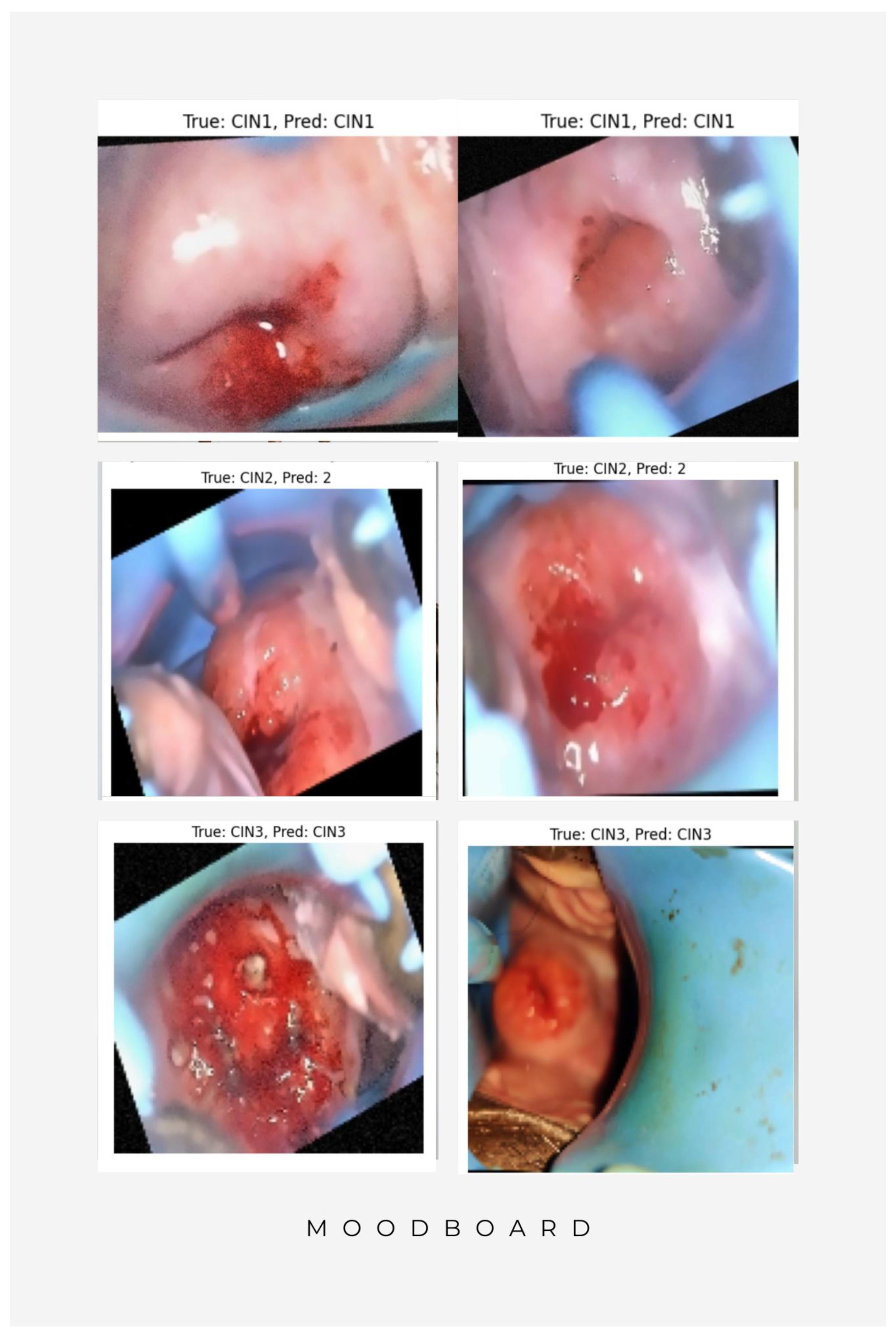
| Research Gap | Description | Corrective Measures |
|---|---|---|
| 1. Flexibility, interpretability , generalizability [25]. | The cited model has limited adaptability to different types of features or data; its dense layers make it harder to interpret the influence of individual features and it may overfit due to its reliance on a single deep network. | Our model has multi-branch that helps to integrate diverse architectures for richer feature extraction. We have used classifiers like Logistic Regression and feature selection (PCA) allows for clearer insight into how decisions are made. With multiple classifiers, it reduces overfitting, improving generalization across diverse lesion types. |
| 2. Feature extraction and attention mechanism [26]. | As per the context of the cited architecture, only ResNet50 is used for feature extraction. While ResNet50 is powerful, it is limited to the feature set learned from a single model. The model does not incorporate an attention mechanism, which is essential in medical imaging to focus on the most critical regions (lesions). | Our multi-branch approach leverages both EfficientNetB0 and MobileNetV2, two different architectures trained on large-scale datasets, enabling a richer and more diverse feature representation that better captures different patterns across lesion types. Our model includes attention layers in both branches, allowing it to prioritize key areas in the medical images, improving the detection of subtle lesions. |
| 3. Limited Model Diversity and class imbalance handling [27]. | The cited algorithm uses two pre-trained CNN models (DenseNet and ResNet), both of which are powerful for image feature extraction. However, they might still provide similar kinds of features as both are deep convolutional architectures. The algorithm does not mention handling class imbalance, which is a common problem in medical datasets. | In our case, the model captures a wider diversity of features, leading to potentially better generalization on medical images with subtle lesion patterns. The algorithm explicitly handles class imbalance by introducing class weights during training, ensuring that all lesion classes (CIN1, CIN2, CIN3) are properly represented and the model doesn’t become biased toward the majority class. |
| 4. Handling lesion cases and dropout [28]. | The cited model focuses on general feature extraction and classification without mentioning specific mechanisms for handling class imbalance or lesion-specific processing. The algorithm uses dropout (0.1 probability) to prevent overfitting. While dropout is effective, it operates by randomly disabling neurons, which can potentially drop important feature representations. | The attention mechanism in our model makes it inherently better at focusing on the critical regions related to lesions, leading to more accurate predictions for different lesion classes. The attention mechanism provides a more targeted approach to overfitting prevention by focusing only on important features. |
| 5. Absence of Class-Specific Fine-Tuning [29]. | The cited algorithm does not mention any fine-tuning or class-specific optimization of the CNN models. It relies on the pre-trained models to extract general features, which may not be tailored to the dataset. | Our approach not only incorporates fine-tuning of EfficientNetB0 and MobileNetV2 but also applies attention mechanisms to focus on the most relevant lesion-specific regions. This helps the network adapt better to the cervical cancer dataset and provide more accurate predictions for CIN1, CIN2, and CIN3.[2] |
| Reference | Dataset | Method | Accuracy | Remarks |
| [30]2024 | Colposcopy | Deep Learning | 94.55% | Has used a hybrid deep neural network for segmentation. |
| [31]2024 | All cancer images | Deep Learning | 99% | Has used a hybrid of pretrained CNN, CNN-LSTM, machine learning and deep neural classifiers. |
| [32]2024 | Pap Smear | Deep Learning | 93% | Has used the CerviSegNet-DistillPlus as a powerful, efficient, and accessible tool for early cervical cancer diagnosis. |
| [33]2023 | Pap Smear | Deep Learning | N/A | Employs a lightweight deep learning network known as MLNet, which is based on metaheuristics. |
| [34]2023 | Pap Smear | Deep Learning | 99.22% | Uses deep learning integrated with MixUp, CutOut, and CutMix. |
| [25]2023 | Colposcopy | Deep Learning | 92% | Uses predictive deep learning model. |
| [35]2022 | Colposcopy | CNN | 87% | Used CNN with weighted loss function. |
| [36]2022 | – | ANN | 98.87% | Applied artificial jellyfish search to ANN. |
| [37]2022 | Colposcopy | CNN,SVM | 80% | ensemble of U-net and SVM. |
| [38]2022 | Colposcopy and histopathological images | AI | N/A | A review on application of AI on cervical cancer screening. |
| [39]2021 | Colposcopy | Deep Learning | 92% | Uses Deep neural techniques for cervical cancer classification. |
| [8]2021 | Colposcopy | Deep Learning | 90% | Using deep neural network generated attention maps for segmentation. |
| [40]2021 | Colposcopy | Residual Learning | 90%, 99% | Employed residual network using Leaky ReLU and PReLU for classification. |
| [41]2021 | MR-CT Images | GAN | N/A | Uses a conditional generative adversarial network (GAN). |
| [42]2021 | Pap Smear | Biosensors | N/A | Uses biosensors for higher accuracy. |
| [43]2021 | Colposcopy | CNN | 99% | Uses Faster Small-Object Detection Neural Networks. |
| [44]2021 | Pap Smear | Deep Convolutional Neural Network | 95.628% | Constructs a CNN called DeepCELL with multiple kernels of varying sizes. |
| [45]2020 | MRI Data of Cervix | Statistical Model | - | A statistical model called LM is used for outlier detection in lognormal distributions. |
| [46]2020 | Colposcopy | CNN | 81.95% | Employs a graph convolutional network with edge features (E-GCN). |
| [47]2020 | Colposcopy | CNN | N/A | The Squeeze-Excitation Convolutional Neural Network (SE-CNN) is utilized to capture depth features across the entire image, leveraging the SE module for targeted feature recalibration. Furthermore, the Region Proposal Network (RPN) produces proposal boxes to pinpoint regions of interest (ROI). |
| [48]2020 | Colposcopy | Pre-trained densenet | 96.13% | Parameters of all layers are fine-tuned with pre-trained DenseNet convolutional neural networks from two datasets (ImageNet and Kaggle). |
| [49]2020 | Colposcopy | CNN | 96.13% | Uses a recurrent convolutional neural network for classification of cervigrams . |
| Metric | Formula | Description |
|---|---|---|
| Recall | The percentage of true positives that are accurately detected | |
| Precision | The percentage of expected positives that turn out to be positive | |
| F1 Score | Harmonic mean of precision and recall | |
| Accuracy | The proportion of correct predictions over all instances |
| CIN Grades | Lugol’s-Iodine | Acetic-Acid | Normal- Saline | |||
|---|---|---|---|---|---|---|
| Ori-ginal | Aug-mented | Ori-ginal | Aug-mented | Ori-ginal | Aug-mented | |
| CIN1 | 114 | 898 | 98 | 691 | 83 | 347 |
| CIN2 | 119 | 945 | 101 | 700 | 84 | 365 |
| CIN3 | 121 | 1005 | 107 | 705 | 86 | 353 |
| CIN1 | CIN2 | CIN3 | |||
|---|---|---|---|---|---|
| Ori-ginal | Aug-mented | Ori-ginal | Aug-mented | Ori-ginal | Aug-mented |
| 900 | 1112 | 930 | 2009 | 960 | 2879 |
| CIN Grades | Precision | Recall | F1-Score |
|---|---|---|---|
| CIN 1 | 0.9733 | 0.9723 | 0.9728 |
| CIN 2 | 0.9740 | 0.9750 | 0.9745 |
| CIN 3 | 0.9769 | 0.9798 | 0.9783 |
| Classifier | Fold | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|---|
| Logistic Regression | Fold 1 | 0.9801 | 0.9800 | 0.9789 | 0.9798 |
| Fold 2 | 0.9804 | 0.9801 | 0.9799 | 0.9798 | |
| Fold 3 | 0.9810 | 0.9804 | 0.9801 | 0.9800 | |
| Fold 4 | 0.9806 | 0.9800 | 0.9798 | 0.9799 | |
| Fold 5 | 0.9803 | 0.9801 | 0.9801 | 0.9805 | |
| XGBoost | Fold 1 | 0.9903 | 0.9843 | 0.9844 | 0.9843 |
| Fold 2 | 0.9910 | 0.9903 | 0.9900 | 0.9906 | |
| Fold 3 | 0.9904 | 0.9900 | 0.9901 | 0.9902 | |
| Fold 4 | 0.9901 | 0.9902 | 0.9900 | 0.9905 | |
| Fold 5 | 0.9906 | 0.9900 | 0.9901 | 0.9903 | |
| CatBoost | Fold 1 | 0.9904 | 0.9901 | 0.9900 | 0.9902 |
| Fold 2 | 0.9901 | 0.9904 | 0.9901 | 0.9902 | |
| Fold 3 | 0.9908 | 0.9905 | 0.9903 | 0.9903 | |
| Fold 4 | 0.9906 | 0.9902 | 0.9901 | 0.9902 | |
| Fold 5 | 0.9905 | 0.9903 | 0.9901 | 0.9902 |
| Class-ifier | Vali-dation Accuracy | CIN1 | CIN2 | CIN3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pre-cision | Rec-all | F1-Score | Pre-cision | Rec-all | F1-Score | Pre-cision | Rec-all | F1-Score | ||
| LR | 0.9823 | 0.9815 | 0.9811 | 0.9814 | 0.9902 | 0.9900 | 0.9901 | 0.9904 | 0.9903 | 0.9902 |
| XGBoost | 0.9905 | 0.9899 | 0.9901 | 0.9901 | 0.9904 | 0.9903 | 0.9904 | 0.9907 | 0.9904 | 0.9904 |
| CatBoost | 0.9909 | 0.9901 | 0.9900 | 0.9901 | 0.9905 | 0.9903 | 0.9904 | 0.9908 | 0.9906 | 0.9905 |
| Ensemble | 0.9985 | 0.9995 | 0.9994 | 0.9993 | 0.9996 | 0.9994 | 0.9998 | 0.9998 | 0.9997 | 0.9996 |
| CIN-Grades | Lugol’s Iodine | Acetic Acid | Normal Saline | Malhari | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prec. | Recall | F1 | Prec. | Recall | F1 | Prec. | Recall | F1 | Prec. | Recall | F1 | |
| CIN1 | 0.97 | 0.97 | 0.97 | 0.96 | 0.95 | 0.96 | 0.95 | 0.95 | 0.95 | 0.98 | 0.98 | 0.98 |
| CIN2 | 0.97 | 0.97 | 0.97 | 0.96 | 0.97 | 0.97 | 0.95 | 0.94 | 0.95 | 0.98 | 0.98 | 0.98 |
| CIN3 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.97 | 0.96 | 0.95 | 0.96 | 0.98 | 0.98 | 0.98 |
| Existing Models | Val Acc. | CIN1 | CIN2 | CIN3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Prec. | Recall | F1 | Prec. | Recall | F1 | Prec. | Recall | F1 | ||
| [25] | 0.97 | 0.95 | 0.94 | 0.95 | 0.96 | 0.96 | 0.95 | 0.97 | 0.96 | 0.96 |
| [26] | 0.96 | 0.94 | 0.92 | 0.93 | 0.94 | 0.93 | 0.93 | 0.95 | 0.94 | 0.94 |
| [27] | 0.95 | 0.91 | 0.90 | 0.91 | 0.92 | 0.91 | 0.91 | 0.93 | 0.92 | 0.92 |
| ResNet50 (baseline) | 0.92 | 0.90 | 0.89 | 0.90 | 0.91 | 0.90 | 0.91 | 0.91 | 0.90 | 0.91 |
| DenseNet-121 (baseline) | 0.93 | 0.91 | 0.90 | 0.91 | 0.91 | 0.91 | 0.91 | 0.92 | 0.91 | 0.92 |
| EffB0 | 0.92 | 0.90 | 0.89 | 0.90 | 0.91 | 0.89 | 0.90 | 0.91 | 0.90 | 0.91 |
| MobV2 | 0.91 | 0.90 | 0.88 | 0.89 | 0.90 | 0.89 | 0.90 | 0.90 | 0.90 | 0.90 |
| EffB0 + MobV2 | 0.94 | 0.91 | 0.90 | 0.91 | 0.92 | 0.91 | 0.92 | 0.93 | 0.91 | 0.92 |
| EffB0 + MobV2 (with attention) | 0.95 | 0.93 | 0.92 | 0.92 | 0.93 | 0.92 | 0.92 | 0.94 | 0.93 | 0.94 |
| Proposed approach | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





