Prerpints.org logo
Preprint
Review

State-of-the-art of Electricity Load and Price Forecasting for the Modern Wholesale Electricity Market

This version is not peer-reviewed.

Submitted:

03 November 2024

Posted:

04 November 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
In modern and dynamic electricity market, ensuring reliable, sustainable and efficient electricity distribution are pillars of primary importance for grid operation. The high penetration of renewable energy sources and the formation of competitive prices for utility, play a critical role in the wider economic development. Electricity load and price forecasting has been a key focus of researchers in the last decade due to the substantial economic implications for both producers, aggregators and end consumers. Many forecasting techniques and methods have emerged during this period. This paper conducts a extensive and analytical review of the prevailing load and electricity price forecasting methods in the context of the modern wholesale electricity market. The study is separated into three main sections. First, the first section delves into the workings of the electricity market, providing a detailed analysis of the three markets that have evolved, their functions and the key factors influencing overall market dynamics. The second section offers a comprehensive review of the existing literature focusing on load forecasting, highlighting various methodologies, models and their applications in load demand forecasting. This section emphasizes the advances that have been made in all categories of forecasting models and their practical application in different market scenarios. The third section focuses on electricity price forecasting methods, summarizing important research papers investigating various modeling approaches to price forecasting. By examining both traditional and cutting-edge forecasting methods, this review identifies key trends, challenges, and future directions in the field. Overall, this paper provides an in-depth analysis leading to the understanding of the state-of-the-art models in load and price forecasting, being an important resource for researchers and professionals in the energy industry.
Keywords: 
Subject: 
Engineering  -   Electrical and Electronic Engineering

1. Introduction

The modern energy market faces several issues and challenges, due to facts such as the dynamic market regulations, the new policies established for environmental protection and the high penetration of renewable energy sources (RES). RES such as wind and solar energy, despite their environmental benefits, cause variability and unpredictability into the operation of the power system. This variability complicates the balance of supply and demand side, making it harder to maintain grid stability. Additionally, the transition to decentralized energy networks, where lagre and small-scale consumers generate their own electricity, creates additional difficulties in managing the system. As a result, energy providers and regulators must constantly adjust to these conditions to meet demand and incorporate these new, variable energy sources.
Accurate forecasting is a key pillar for the optimal operation of the energy market. Accurate prediction of electricity helps grid operators to manage periods of peak and non-peak demand, ensuring the power balance in transmission and distribution network. Simultaneously, electricity price forecasting helps energy companies and large-scale consumers decide the best times to buy or sell energy. This capability is crucial in a market with high price variability, where poor predictions can lead to significant financial losses, creating high risks for all parts of the system. In addition to helping with operational decisions, accurate forecasts also support strategic planning, investment in infrastructure, and the integration of RES. By providing a clearer picture of future conditions, forecasting helps stabilize the market and ensures a reliable energy supply.
Electricity Load (ELF) and Price Forecasting (EPF) are crucial elements for the efficient operation of modern wholesale electricity markets. The integration of RES, particularly wind power, presents new challenges and opportunities in these domains. This paper offers a comprehensive review of recent advancements in ELF and EPF methodologies. We explore state-of-the-art studies, emphasizing the importance of accurate forecasts for maintaining the stability and optimizing market operations, highlighting the interplay and differences between load and price forecasting. The contribution and key areas of our research include:
  • Short-term forecasting approaches for electricity load and prices, underscoring the need for precise predictions of demand fluctuations and price volatility.
  • An in-depth mathematical analysis of various forecasting models, including statistical, machine and deep learning, and ensemble approaches.
  • The application of statistical methods, artificial intelligence, and hybrid models in the time series analysis of load data, crucial for enhancing forecast accuracy.
  • An extended review of evolving trends in ELF and EPF, incorporating economic and engineering perspectives that drive these trends.
  • Case studies from different countries, providing practical examples of electricity market operations and the management of renewable energy integration in forecasting models.
By addressing these areas, the paper aims to deepen the understanding of ELF and EPF methodologies. It also seeks to identify new avenues for research, promoting further innovation in electricity load and price forecasting for the modern wholesale market.
Regarding the structure of the paper: In section 2, the electricity market working mechanism is analyzed in detail. Then, in section 3, the most prevalent models used for load and price forecasting are presented in detail. Following that, in section 4, the most comprehensive papers dealing with ELF are analyzed. Additionally, section 5 presents the corresponding papers in the area of price forecasting. In section 6, a discussion and comparison between load and price forecasting approaches is made. Finally, useful conclusions and future study proposals are discussed.

2. Electricity Market Working Mechanisms

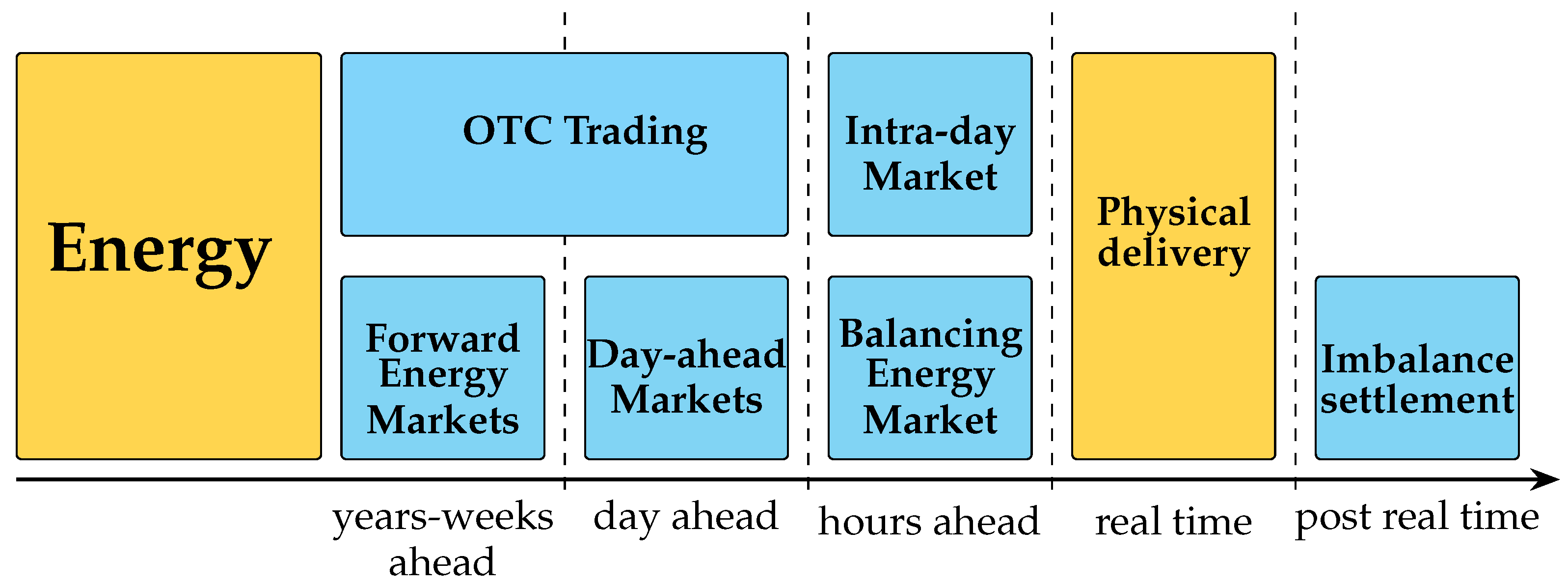
The modern wholesale electricity market is a dynamic and complex system where electricity is bought and sold primarily through competitive bidding processes. It comprises various participants, including generators, retailers, and large consumers, who interact in day-ahead, intraday, and real-time markets to ensure an efficient and reliable supply of electricity. Market operators and power exchanges facilitate these transactions, ensuring transparency and fair pricing. The market incorporates advanced technologies and algorithms for demand forecasting, price setting, and grid management, while also integrating RES to promote sustainability. Regulatory frameworks vary by region but aim to balance competition, reliability, and environmental goals.
Bilateral contracts affect electricity markets by providing stability and predictability in pricing for both buyers and sellers, reducing market volatility. They facilitate long-term planning and investment in energy infrastructure, and can help hedge against price fluctuations in the spot market [1]. The general idea about Electricity Market working sequenceis presented in Figure 1.

2.1. Day-Ahead Market

Day-ahead Market (DAM) involves buying and selling electricity one day before it is generated and delivered. It occurs either on the spot market of a power exchange, or through direct agreements between two parties, typically power trading companies, in over-the-counter (OTC) deals. The main functions of day-ahead markets are:
  • Balancing Supply and Demand: Ensuring that the anticipated electricity supply matches the expected demand for the following day.
  • Market Equilibrium: Creating a fair and competitive environment by matching bids and offers through a transparent auction process.
  • Resource Optimization: Facilitating the efficient use of generation resources by signaling which plants should be operational based on forecasted prices.
The day-ahead market aligns electricity supply and demand before production and delivery by gathering bids from producers and consumers to set hourly prices, ensuring market equilibrium. Market Pools or Power Exchanges publish these hourly prices for the following day. This information helps synchronize the anticipated electricity supply with expected customer usage. In the bidding process, participants indicate the volume of electricity they are able to purchase or supply each hour, along with the corresponding price levels in EUR/MWh (or USD/MWh).
The regulations for day-ahead trading can differ greatly between national markets. These differences include lead times, trading periods, smallest tradable amounts of electricity, various pricing methods, gate closure times, and other specific details.
In DAM, the bidding time period typically refers to the timeframe during which market participants submit their bids and offers for the next operating day. The general timelines and processes involved in the DAM, including the bid submission deadline and the delivery period are the followings:
  • Bid Submission Deadline: 12:00 PM (noon) on day D-1.
  • Market Clearing and Results Publication: Usually by early evening on day D-1.
  • Operating Day (Day D): The delivery period typically starts at 12:00 AM (midnight) and covers the full 24 hours of day D.
From the bid submission deadline to the start of the delivery period, there are typically approximately 12 hours. Different cases of how DAM operates in different markets follow: In the PJM Interconnection market, participants must submit their bids by 12:00 PM Eastern Time on the day before the delivery of the electricity, named as day D-1. The market results are typically published by the early evening of the same day. The delivery period for the transactions occurs from 12:00 AM to 11:59 PM on day D. For the NYISO (New York Independent System Operator), the bid submission deadline is set at 5:00 AM Eastern Time on day D-1. The market results are made available by 10:00 AM on the same day. Similar to PJM Interconnection, the delivery period lasts from 12:00 AM to 11:59 PM on day D.
Additionally, in the EPEX SPOT market, bids must be submitted by 12:00 PM (noon) Central European Time (CET) on day D-1. The market results are published shortly after, by 12:42 PM CET on day D-1. The delivery period for these transactions covers 12:00 AM (midnight) to 11:59 PM on day D. Finally, for the Nord Pool market, the bid submission deadline is also 12:00 PM (noon) Central European Time on day D-1. The market results are similarly published by 12:42 PM CET on the same day. As with the other markets, the delivery period runs from 12:00 AM (midnight) to 11:59 PM on day D [2].

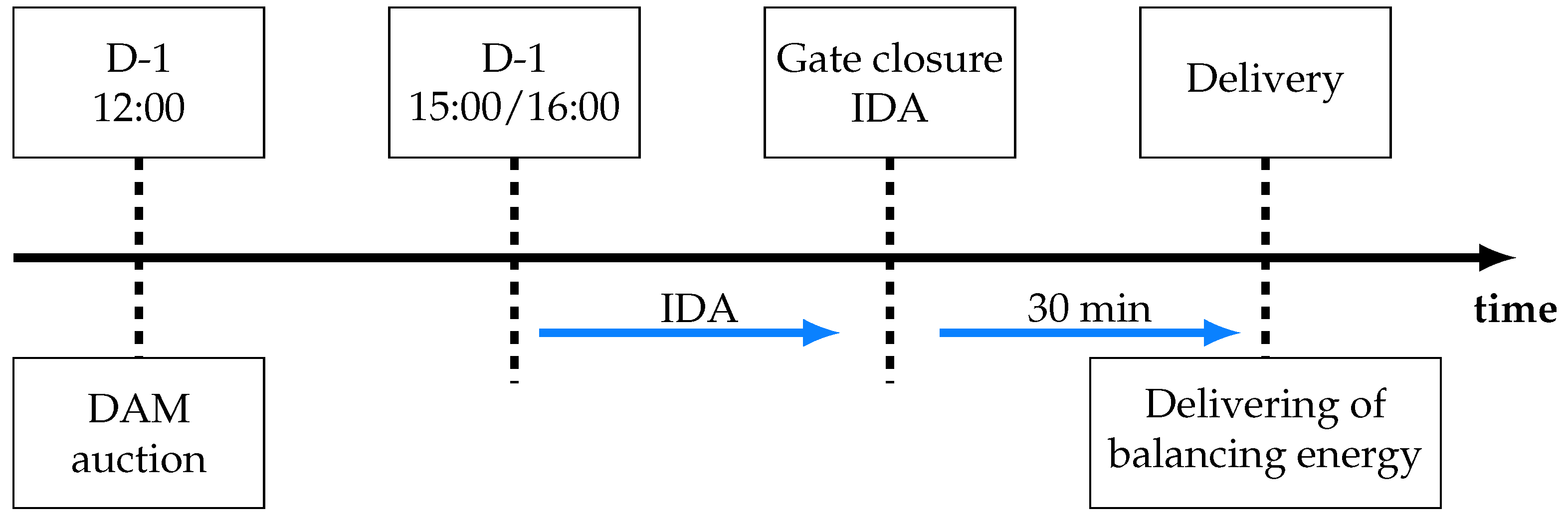
2.2. Intra-Day Market

In Intraday Market (IDA) the energy is traded on the same day it is delivered and is executed in power exchange markets or through direct agreements between buyers and sellers, like DAM. The main functions of IDA are managing imbalances by allowing market participants to handle deviations from their scheduled energy deliveries in DAM. This helps in reducing penalties and associated costs. IDA offers opportunities for market participants to optimize their positions and mitigate important financial risks, helping fulfill balancing group commitments and minimizing potential imbalance costs. As power assets become more flexible, it allows for rapid power generation adjustments, optimizing profitability and maintaining system stability.
The increasing penetration of intermittent RES has heightened interest in IDAs, as market participants face greater challenges in maintaining balance after the DAM closes. The IDA allows for adjustments to be made closer to the actual delivery time, accommodating changes in demand forecasts and generation availability. Here are the general timelines:
  • Continuous Trading: IDA often operate on a continuous trading basis, allowing participants to trade up until a few hours before delivery.
  • Gate Closure Times: These vary by market but are typically set a few hours before the delivery period starts. For example, gate closure might occur 1 to 2 hours before the delivery period.
  • Delivery Period: IDA covers the hours remaining in the operating day (day D).
Cases of how IDA operates in different markets are: In the EPEX SPOT (European Power Exchange) market, continuous trading is available up to 5 minutes before the delivery period in certain regions. The gate typically closes between 30 minutes to 1 hour before delivery in most regions. The delivery period covers the remaining hours of the operating day. For Nord Pool, the trading is available up to 1 hour before the delivery period. The gate closes 1 hour prior to the start of the delivery period. As with EPEX SPOT, the delivery period includes the remaining hours of the operating day [2]. DAM and IDA operation hours are included in Figure 2.

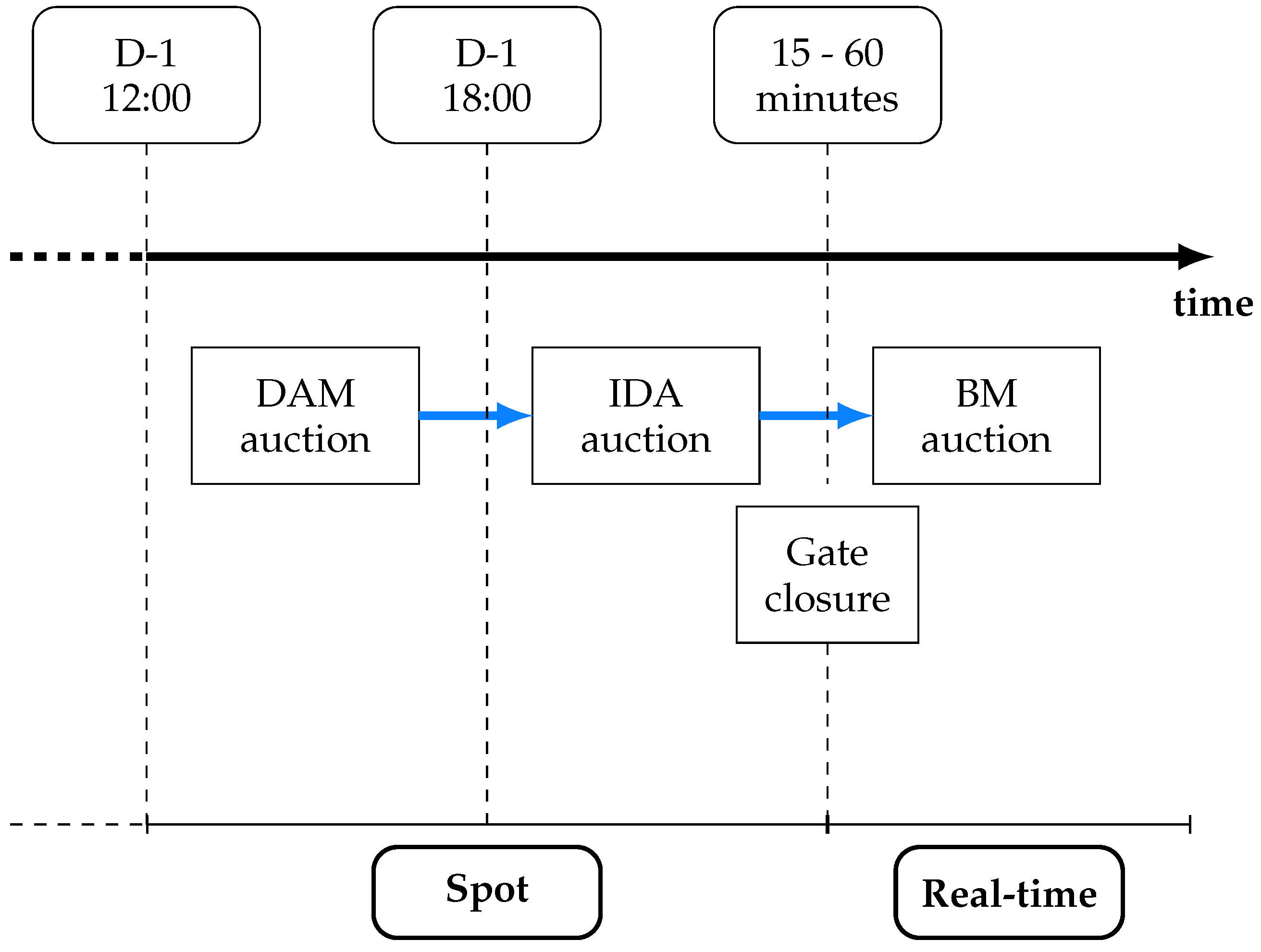
2.3. Balancing Market

The Balancing Market (BM), which is presented in Figure 3, is a critical component of modern electricity markets, ensuring immediate equilibrium between electricity supply and demand in real-time operations. In contrast to the DAM, which plans energy transactions for the next day, the BM responds swiftly to unforeseen fluctuations in supply and demand. Participants such as generators and consumers submit bids to adjust electricity production or consumption at short notice. These bids are managed by the system operator, typically an Independent System Operator (ISO) or Regional Transmission Organization (RTO), which monitors grid conditions continuously. When discrepancies arise between predicted and actual grid conditions, the system operator activates these bids to maintain grid stability, ensuring a consistent match between electricity supply and demand.
The BM involves the activation of reserves to handle unforeseen imbalances. The general timelines are:
  • Real-Time Operation: The Balancing Market operates in real-time, with continuous adjustments being made to balance supply and demand.
  • Activation of Reserves: Reserve power is activated as needed to address imbalances. This can occur at any time during the operating day.
  • Settlement: Imbalances are settled after the operating day, based on the actual deviations from scheduled supply and demand.
The pricing in the BM reflects the real-time cost of adjusting electricity supply or demand, often resulting in higher prices compared to the DAM due to the immediate nature of the required actions. The costs in the BM are usually covered by imbalance charges on market participants whose differences from their planned positions required balancing actions. This mechanism encourages market participants to keep closely to their planned commitments, which improves the performance and sustainability of the power system. Additionally, this market mechanism plays a vital role in integrating RES, which are often variable and less predictable, providing flexible platforms for managing the increased penetration of RES into the grid [2].

3. Forecasting Methodologies for Load and Price

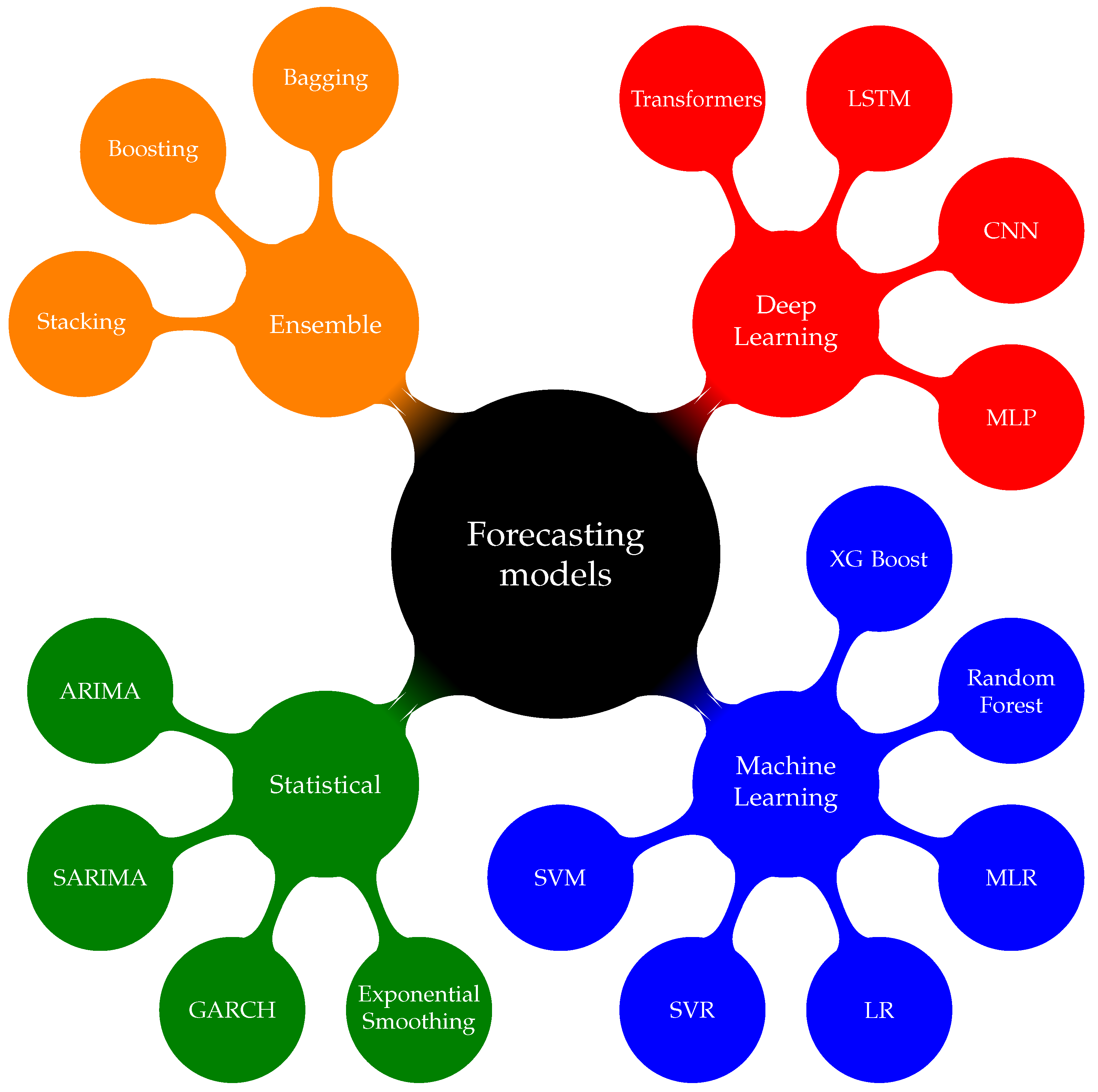
The methodologies used for ELF and EPF have been enhanced and progressed in high level the last five to ten years. Starting from traditional methods, there will be an extensive mathematical presentation of the most fundamental models, both statistical and those involving machine, deep, and ensemble learning methods. This section provides a detailed overview of the most common models used for these purposes. Initially, the statistical methods are presented, followed by the machine (ML) and deep learning (DL) methods, and finally, the ensemble methods are analyzed. For a better understanding of the categories and the variety of the models, Figure 4 graphically presents the aforementioned.

3.1. Statistical Methods

Statistical methods are essential in ELF and EPF, providing robust frameworks for understanding and predicting trends in time series data. Among the most prevalent methods are AutoRegressive Integrated Moving Average (ARIMA) models, which combine autoregression, differencing, and moving averages to model temporal dependencies and achieve stationarity. Seasonal ARIMA (SARIMA) models manage seasonal changes effectively by using seasonal differencing and seasonal autoregressive and moving average parts. Exponential Smoothing methods, like Holt-Winters, are popular for being simple and effective in dealing with seasonality and trends in time series. GARCH models are used to capture and predict volatility patterns, mainly in financial data. State Space Models and Kalman Filters offer a flexible way to model dynamic systems, especially for time-varying processes. These methods are important in the energy sector and are presented in detail below.

3.1.1. AutoRegressive Integrated Moving Average

AutoRegressive Integrated Moving Average (ARIMA) analyzes time series data and predicts future trends based on historical values. This model is characterized by three main parameters: p, d, and q. The first parameter p is the number of lag observations of the model, which constitutes the autoregressive part (AR). The second parameter d is the number of times the raw observations are differenced to achieve stationarity, which is the integrated part (I). The third parameter q refers to the size of the moving average window, which is the moving average part of the model (MA) [4].
The basic equations of this model can be expressed as follows:
y t = c + ∑ i = 1 p ϕ i y t − i + ∑ j = 1 q θ j ϵ t − j + ϵ t
where, y t is the value at time t, c is a constant, ϕ i are the coefficients for the autoregressive parameters (AR), θ i are the coefficients for the moving average parameters (MA), and ϵ t is the error term at time t. The autoregressive (AR) part of the model means that the output is directly influenced by its past values and can be written as:
y t = c + ∑ i = 1 p ϕ i y t − i + ϵ t
The integrated (I) part of the model is used for differencing the raw observations, in order to make the data more stationary. It can be expressed as:
y t ′ = y t − y t − 1
Finally, the MA part represents the dependency between an observation and a residual error. It can be written as:
y t = c + ϵ t + ∑ j = 1 q θ j ϵ t − j

3.1.2. Seasonal AutoRegressive Integrated Moving Average

Seasonal AutoRegressive Integrated Moving Average (SARIMA), is an extension of the ARIMA model, because its capability to handle seasonality in time series. The model integrates both non-seasonal and seasonal components. Three parameters p , d , q are represent the seasonal part and four parameters P , D , Q , s are for the non-seasonal part. p is the number of non-seasonal autoregressive terms, d is the number of non-seasonal differences, and q is the number of non-seasonal moving average terms. For the seasonal components, P indicates the number of seasonal autoregressive terms, D represents the number of seasonal differences, and Q represents the number of seasonal moving average terms. Finally, the parameter s is the length of the seasonal cycle [5].
The general form of a SARIMA model can be expressed with the following equation [5]:
y t = c + ∑ i = 1 p ϕ i y t − i + ∑ j = 1 q θ j ϵ t − j + ∑ k = 1 P Φ k Y t − k s + ∑ l = 1 Q Θ l ϵ t − l s + ϵ t
where, ϕ i are the coefficients for the non-seasonal AR terms, θ i are the coefficients for the non-seasonal MA terms, Φ k are the coefficients for the seasonal AR terms, Θ i are the coefficients for the seasonal MA terms, s is the seasonal period, and ϵ t is the error term at time t.

Non-Seasonal and Seasonal Parts

The non-seasonal part is similar to the ARIMA model and can be written as the Equation (1). The seasonal part operates for the seasonal fluctuations and can be written as:
Y t = ∑ k = 1 P Φ k Y t − k s + ∑ l = 1 Q Θ l ϵ t − l s
where, Y t represents the seasonal component of y t .

Differencing

The seasonal and non-seasonal differencing part can be expressed as follows: The non-seasonal differencing can be expressed as the Equation (3), while the seasonal differencing can be written as:
Y t ′ = Y t − Y t − s

3.1.3. Exponential Smoothing

Exponential Smoothing (ES) method is suitable and effective in dealing with univariate datasets. It gives more importance to recent data values by applying weights that reduced in exponential way from the recent to the older data, so recent observations influence the forecast more than older ones.
There are three main exponential smoothing methods:
  • Single Exponential Smoothing (SES): This method is suitable for time series without trend or seasonality.
  • Double Exponential Smoothing (DES): Proper for data with a trend.
  • Triple Exponential Smoothing (TES): Or Holt-Winters, which is suitable for data with both trend and seasonality patterns.

Single Exponential Smoothing (SES)

The main equation for SES is:
y ^ t + 1 = α y t + ( 1 − α ) y ^ t
where, y ^ t + 1 is the prediction for the time t + 1 , α is the smoothing parameter with 0 < α < 1 , y t is the actual value at time t, and y ^ t is the forecasted value at time t.

Double Exponential Smoothing (DES)

DES introduces a second equation to account for trends:
y ^ t + 1 = l t + b t
l t = α y t + ( 1 − α ) ( l t − 1 + b t − 1 )
b t = β ( l t − l t − 1 ) + ( 1 − β ) b t − 1
where, l t is the level component at time t, b t is the trend component at time t, and α and β are smoothing parameters, with 0 < α , β < 1 .

Triple Exponential Smoothing (TES) - Holt-Winters

TES or Holt-Winters method, adds a seasonal component, as follows:
y ^ t + m = l t + b t m + s t + m − s
l t = α y t s t − s + ( 1 − α ) ( l t − 1 + b t − 1 )
b t = β ( l t − l t − 1 ) + ( 1 − β ) b t − 1
s t = γ y t l t + ( 1 − γ ) s t − s
where, l t is the level component at time t, b t is the trend component at time t, s t is the seasonal component at time t, s is the length of the seasonal cycle, α , β , and γ are smoothing parameters, with 0 < α , β , γ < 1 , and m is the number of periods ahead to be forecasted [6].

3.1.4. Generalized Autoregressive Conditional Heteroskedasticity

The Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model is a statistical model used to forecast the future fluctuations of time series. It is mainly useful in financial applications, where GARCH predicts the volatility of financial markets. This model utilizes lagged terms of both the error and its variance and can be expressed through the mean and variance equations, as follows [7]:
The mean equation:
y t = μ + ϵ t
where, y t is the time series value at time t, μ is the mean, and ϵ t is the error term.
The variance equation:
σ t 2 = α 0 + ∑ i = 1 q α i ϵ t − i 2 + ∑ j = 1 p β j σ t − j 2
where, σ t 2 is the conditional variance at time t, α 0 is a constant term, α i are the coefficients for the lagged squared residuals ( ϵ t − i 2 ), β j are the coefficients for the lagged variances ( σ t − j 2 ), p is the order of the GARCH terms (lagged variances), and q is the order of the ARCH terms (lagged squared residuals). Finally, the error term ϵ t is typically modeled as:
ϵ t = σ t z t
where, z t is a white noise process with zero mean and unit variance.

3.2. Machine Learning Methods

Machine Learning (ML) models are effective in ELF and EPF tasks, and are capable of dealing with complex and nonlinear datasets that contain fluctuations and volatility. They are used for both regression and classification tasks and the most commonly models are presented below.

3.2.1. Support Vector Machine

Support Vector Machine (SVM) is a supervised learning model, of which the basic working mechanism is to find the hyperplane that best separates the data into two different groups, maximizing the margin among them. Given a set of training data { ( x i , y i ) } i = 1 n , where x i is the feature vector and y i is the label, the alrorithm aims to find the optimal hyperplane w · x + b = 0 that separates the data points. There are two categories, the linear and non-linear approach [8].

Linear SVM

For linear SVM, the working function is given by:
f ( x ) = w · x + b
where, w is the weight vector, and b is the bias term.
The optimization problem of finding the optimal hyperplane can be formulated as:
min w , b 1 2 ∥ w ∥ 2
subject to the constraints:
y i ( w · x i + b ) ≥ 1 for all i = 1 , 2 , ⋯ , n

Non-Linear SVM

For non-linearly separable data, SVM can be extended using the kernel trick. The function becomes as follows:
f ( x ) = ∑ i = 1 n α i y i K ( x i , x ) + b
where, α i are the Lagrange multipliers, and K ( x i , x ) is the kernel function, which computes the inner product between two feature vectors in a high-dimensional space.

3.2.2. Support Vector Regression

Support Vector Regression (SVR) is an extension of SVM model used for regression tasks. It aims to find a function that approximates the relationship between input features and continuous output values with minimal error, while maintaining model simplicity.
The objective of the model is to find a function f ( x ) = w · x + b that approximates the target values y i within a margin of ϵ , while keeping the model complexity as low as possible. The SVR optimization problem is expressed as:
min w , b , ξ i , ξ i ∗ 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ( ξ i + ξ i ∗ )
Subject to the constraints:
y i − ( w · x i + b ) ≤ ϵ + ξ i ( w · x i + b ) − y i ≤ ϵ + ξ i ∗ ξ i , ξ i ∗ ≥ 0
where, w is the weight vector, b is the bias term, ξ i and ξ i ∗ are slack variables for points outside the margin, C is the regularization parameter, and n is the number of training samples [8].

3.2.3. Linear Regression

Linear Regression (LR) is a machine learning method, which assumes a linear relationship between an input variable x and the target variable y. The model can be represented as [9]:
y = β 0 + β 1 x + ϵ
where, y is the target variable, β 0 is the intercept, β 1 is the slope (coefficient) of the input variable x, and ϵ is the error term.
The objective is to find the values of β 0 and β 1 that minimize the sum of squared residuals (the difference between the observed and predicted values):
min β 0 , β 1 ∑ i = 1 n ( y i − ( β 0 + β 1 x i ) ) 2
where, n is the number of observations.

3.2.4. Multilinear Regression

Multilinear Regression (MLR) extends Linear Regression by modeling the relationship between a continuous target variable and multiple input features. It assumes a linear relationship between the target variable y and multiple input variables x = ( x 1 , x 2 , … , x p ) . Similarly with Linear Regression, this model can be represented as [9]:
y = β 0 + … + β p x p + ϵ
where, y is the target variable, β 0 is the intercept, β i are the coefficients of the input variables x i , ϵ is the error term.
The objective is to find the values of β 0 , β 1 , … , β p that minimize the sum of squared residuals:
min β 0 , β 1 , … , β p ∑ i = 1 n ( y i − ( β 0 + ∑ j = 1 p β j x i j ) ) 2
where, n is the number of observations, and p is the number of input variables.

3.2.5. Extreme Gradient Boosting

Extreme Gradient Boosting (XGBoost) is a very effective and scalable algorithm used for supervised learning tasks. It belongs to the ensemble learning family and is based on the gradient boosting framework. XGBoost combines the outputs of several models, typically decision trees. It trains each tree sequentially, with each tree correcting the errors made by the previous trees.
The objective function in XGBoost includes two parts: the loss function, which measures the difference between predicted and true values, and a regularization term, which manages model complexity to reduce overfitting.
Obj ( Θ ) = ∑ i = 1 n L ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k )
where, Θ represents the model parameters, L ( y i , y ^ i ) is the loss function measuring the difference between the true label y i and the predicted label y ^ i , and Ω ( f k ) is the regularization term for the k-th tree f k .
About the Loss Function, XGBoost typically uses the mean squared error (MSE):
L ( y i , y ^ i ) = ( y i − y ^ i ) 2
where, y ^ i is the predicted probability of class 1.
Finally, in order the models to avoid overfitting, the regularization term, consists of two parts: tree complexity term and leaf weight regularization term. It can be writtern as:
Ω ( f k ) = γ T + 1 2 λ ∥ w ∥ 2 2
where, T is the number of leaves in the tree f k , and w are the weights associated with the leaf nodes [10].

3.2.6. Random Forest

Random Forest (RF) is an ensemble learning algorithm, which is a combination of multiple decision trees. This model creates a collection of decision trees during training and outputting the mode of the mean prediction of the individual trees. In this model, each decision tree is trained on a random subset of the training data, and at each split in a tree, a random subset of features is considered. This randomness helps in making the model robust and reducing variance.
Mathematically, the prediction y ^ of a Random Forest model is given by [11]:
y ^ = 1 T ∑ t = 1 T f t ( x )
where, T is the number of trees in the forest, f t ( x ) is the prediction of the t-th tree for the input x. For classification, the mode of the class labels predicted by each tree is taken, while for regression, the average of all tree predictions is used.

3.3. Deep Learning Methods

Similar to ML algorithms, the most commonly used DL models are the presented below.

3.3.1. Multilayer Perceptron

The Multilayer Perceptron (MLP) is a simple feedforward neural network (FNN) model that consists of one input layer of nodes, hidden layers, and one output layer, which creates the final prediction. Each node in each layer is connected to every node in the previous and next layer, through neurons, in which correspond synaptic weights, which are used for the transmission of information across the model. An activation function, such as the rectified linear unit (ReLU) is used in order to calculate the output of each node.
Given an input vector x, the output of a node j in the hidden layer h can be calculated as follows:
z j h = ∑ i = 1 n input w i j h x i + b j h
a j h = f ( z j h )
where, n input is the number of nodes in the input layer, w i j h is the weight of the connection between the i-th node in the input layer and the j-th node in the hidden layer, b j h is the bias of the j-th node in the hidden layer, and f is the activation function.
Similarly, the output of a node k in the output layer can be computed as:
z k output = ∑ j = 1 n hidden w j k output a j h + b k output
a k output = f ( z k output )
About the training of MLP model, it is carried out through backpropagation method, in which the error between actual and forecasting values is minimized by adjusting the weights and biases using gradient descent. The loss function used is based on each different task. Usually, mean squared error is used for time series forecasting and cross-entropy loss for classification tasks [12].

3.3.2. Long Short-Term Memory

Long Short-Term Memory (LSTM) is a type of recurrent neural network (RNN) architecture, more suitable to manage sequential data, like energy consumption, and capture long-term dependencies between them. LSTM networks, unlike regular RNNs, are capable of maintaining information for extended periods, which helps solve the vanishing gradient problem that often occurs in simple RNNs.
LSTM networks are composed of LSTM cells, each of which has three main gates:
  • Forget Gate: Determines what information to discard from the cell state.
  • Input Gate: Selects which new information to store in the cell state.
  • Output Gate: Chooses what part of the cell state is proceed to the output.
The equations for the LSTM cell are as follows:

Forget Gate

f t = σ ( W f · [ h t − 1 , x t ] + b f )

Input Gate

i t = σ ( W i · [ h t − 1 , x t ] + b i )
C ˜ t = tanh ( W C · [ h t − 1 , x t ] + b C )

Cell State Update

C t = f t · C t − 1 + i t · C ˜ t

Output Gate

o t = σ ( W o · [ h t − 1 , x t ] + b o )
h t = o t · tanh ( C t )
where, x t is the input at time step t, h t − 1 is the hidden state from the previous time step, C t − 1 is the cell state from the previous time step, f t is the forget gate activation, i t is the input gate activation, C ˜ t is the candidate cell state, C t is the updated cell state, o t is the output gate activation, h t is the hidden state at time step t, W f , W i , W C , W o are the weight matrices, b f , b i , b C , b o are the bias vectors, σ is the sigmoid activation function, and tanh is the hyperbolic tangent activation function [13].

3.3.3. Convolutional Neural Network

A Convolutional Neural Network (CNN) includes convolutional layers, pooling layers, and fully connected layers. More specifically, its structure includes the following:

Convolutional Layer

This layer applies convolution operations to the input data using a set of learnable filters (kernels). Each filter convolves across the input to produce a feature map. The convolution operation is defined as:
( f ∗ x ) ( i , j ) = ∑ m ∑ n x ( i + m , j + n ) · f ( m , n )
where, x is the input, f is the filter, and * denotes convolution.

Pooling Layer

This layer reduces the spatial dimensions (height and width) of the feature maps, which helps in reducing the number of parameters and computation in the network. A common pooling operation is Max Pooling, defined as:
y ( i , j ) = max m , n x ( i + m , j + n )
where, x is the input and y is the pooled output.

Final Fully Connected Layer

After convolutional and pooling layers, the final output is created via a fully connected layer. Each neuron in a fully connected layer is connected to every neuron in the previous layer. The output is computed as:
y = W · x + b
where, W is the weight matrix, x is the input vector, and b is the bias vector [13].

3.3.4. Transformer Models

Transformer models have revolutionized time series forecasting with their ability to handle complex dependencies through self-attention mechanisms. They use an encoder-decoder architecture to capture relationships in sequential data effectively.
The Basic Transformer architecture includes the following components [13]:
- Encoder: Processes input sequences. - Decoder: Generates output sequences from encoded representations.
The core component is the Self-Attention Mechanism, which computes the attention scores using the following equations:

Scaled Dot-Product Attention:

Attention ( Q , K , V ) = softmax Q K T d k V
where, Q is the query matrix, K is the key matrix, V is the value matrix, and d k is the dimension of the key vectors.

Multi-Head Attention:

MultiHead ( Q , K , V ) = Concat head 1 , head 2 , … , head h W O
where, each head is computed as:
head i = Attention ( Q W i Q , K W i K , V W i V )
and W i Q , W i K , W i V are parameter matrices for the i-th attention head, and W O is the output matrix.

3.4. Ensemble Methods

The primary concept underlying ensemble models is to capitalize on the advantages of different algorithms and combine their ultimate predictions, resulting in enhanced accuracy and robustness. These models can be applied to a variety of tasks, including statistical, as well as ML and DL models for classification, regression, and clustering tasks.
A key benefit of these algorithms is their capacity to decrease overfitting, which leads to bad forecasting performance and variance, which represents the level of fluctuation in predictions across different models within the ensemble, respectively. By combining the forecasts of several models, ensemble methods help minimize variance and produce more reliable predictions.
About the disadvantages, they are typically more complicated to implement and interpret compared to individual models, and in most cases they require significantly more computational power. Their performance is highly dependent on the combination of models used, which makes identifying the best set of models a difficult task. Additionally, the ensemble’s model quality is pivotal, due to the fact that poorly performing models can negatively affect the ensemble final prediction, leading to issues such as overfitting or underfitting..
The most common techniques used to create ensemble models are bagging, boosting, and stacking, which are analyzed below [14].

3.4.1. Bagging

Bagging consists of training each model individually and then combining their predictions using a weighted average. This approach can be used with any type of model and is effective at reducing variance and preventing overfitting. Initially, several iterations of the dataset are executed, each containing distinct subsets of the initial data. After, these subsets are used to train models separately, and finally their predictions are integrated to produce the final output. By merging predictions from different models in a weighted average process, bagging improves both the accuracy and reliability of the final predictions [13,14].

3.4.2. Boosting

Boosting is a technique where each model is trained to correct the errors in predictive data analysis. Models are trained using labeled data to make predictions about unlabeled data. This method improves the accuracy of the final predictions, but is more vulnerable to overfitting, in comparison to bagging method. Boosting begins with a simple model and fradually adds more complex models, each focusing on the data points that were wrongly labeled by previous models. Each of the different forecasts is merged using a weighted combination based on their final accuracy [13].

3.4.3. Stacking

Stacking, also called stacked generalization, involves combining the predictions from various base models—sometimes known as first-level models or base learners—to produce a conclusive prediction. This approach entails training multiple base models on an identical dataset and utilizing their output as input for a higher-level model, termed a meta-model or second-level model., to produce the final outcome. The fundamental concept is to improve predictive accuracy by combining the outputs of various base models, rather than depending on a single model. [13].

3.5. Most Commonly Used Evaluation Metrics

For related work, the most commonly prediction metrics used are the following:
Mean Absolute Error (MAE): Computes the mean value of the absolute differences between the predicted values and the actual values.
Mean Absolute Percentage Error (MAPE): Calculates the average of the absolute percentage deviations between the predicted and actual values.
Mean Squared Error (MSE): Measures the average squared difference between the predicted values and the actual values.
Root Mean Squared Error (RMSE): Calculates the square root of the mean of the squared differences between the forecasted and actual values.
R-squared ( R 2 ): This statistical measure evaluates the proportion of variance in the dependent variable that is explained by the independent variable(s) in a forecasting model, with values spanning from 0 to 1. A value of 1 indicates an excellent fit, whereas a value of 0 signifies no relationship between the variables.
The above metrics are defined with the following equations:
M A E = ∑ i = 1 n | y i − x i | n
M A P E = 100 n ∑ i = 1 n y i − x i x i
M S E = ∑ i = 1 n ( y i − x i ) 2 n
R M S E = ∑ i = 1 n ( y i − x i ) 2 n
R 2 = 1 − ∑ i = 1 n ( y i − x ^ i ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
where, x i , y i , x ^ i , and y ¯ are the forecasting values, the actual values, the mean of the forecasting values, and the mean of the actual values, respectively.
Apart from the above metrics, it is observed that some papers additionally use the following: Mean Arctangent Absolute Percentage Error (MAAPE), Mean Percentage Error (MPE), Error Sum of Squares (SSE), Sum of Squares (SSE), Mean of Mean Squared Error (FMSE), Symmetric Mean Absolute Percentage Error (sMAPE), Median Absolute Error (MedAE), Matthews Correlation Coefficient (MCC), Relative Root Mean Square (rRMSE), Normalized Root Mean Square Error (NRMSE), Coefficient of Variation (CV) and Accuracy, which is measured by the proportion of correct predictions out of the total number of predictions.

4. Challenges and Solutions on Electricity Load Forecasting

In this section, important studies that have significantly contributed to the field of load forecasting are extensively analyzed. Initially, statistical methods are presented, followed by papers focusing on ML and DL, and finally, emphasis is given to Ensemble Methods. Because most studies typically present models from both the ML and DL categories, it was chosen to present them in a common subsection, for a more substantial presentation of the related works.

4.1. Statistical Methods

In the field of ELF, several methodologies and techniques have been investigated. These can be separated into two basic groups, the statistical and the modern methods. Statistical methods include models like AR, ARMA, ARIMA,model s with exogenous features, like ARMAX and ARIMAX, grey (GM) and ES. In tis way, Sethi et al. in [15] compares ARIMA method with other ML models for load prediction. Evaluation is done using RMSE and Mean Bias Error (MBE) and as case study is used a commercial building (amusement park) in San Diego. Chou et al. in [16] conduct a comparative analysis, using SARIMA model. The study use real-time consumption data from a smart grid network installed in a three-floor building in Xindian District, New Taipei City, Taiwan. Several metrics including R-squared, Maximum Absolute Error (MaxAE), RMSE, MAE and MAPE are used for the evaluation process. Hadri et al. in [17] conduct a comprehensive research employing ARIMA, SARIMA, XGBoost, Random Forest (RF), and LSTM. For the evaluation period, Mean Percentage Error (MPE), MAPE, MAE, and RMSE are utilized. Simultaneously, Vrablecová et al. in [18] apply ARIMA models in order to create short-term forecasts on public Irish CER dataset.
Some papers conduct comprehensive analysis of various statistical models used for ELF in different European Countries. Following the above, Pelka et al. in [19] investigate the performance of different statistical models, including ARIMA, ETS, and Prophet model. The target is to forecast monthly power demand, which estimates the correlation between past and future demand trends. As case study, electricity time series data for 35 European countries in a monthly resolution are used. In addition, Elamin et al. in [20] introduce a forecasting approach, utilizing a SARIMA model, incorporating both exogenous and interaction variables, to predict hourly load electricity demand. Finally, Mado et al. in [21] smooth the training and testing datasets of Java-Madura-Bali interconnection, Indonesia and propose a SARIMA model for short-term ELF, which considers double seasonal patterns in electricity consumption. The achieve MAPE equal to 1.56%.

4.2. Machine and Deep Learning Methods

The ELF sector has undergone high transition towards the use of ML and DL models, which offer superior accuracy and adaptability compared to traditional statistical methods. ML models are capable of handling with complex non-linear relationships in electricity consumption data. Meanwhile, DL models, including RNNs, LSTMs, and CNNs, excel in handling large volumes of data and uncovering intricate temporal patterns. These advancements play a critical role for improving the performance and sustainability of modern electricity systems, enabling better demand management, grid stability, and integration of RES. According to the above, Abumohsen et al. in [22] utilize several DL models, such as RNN, GRU and LSTM, in order to predict electricity consumption based on current measurements data. Forecasting models are crucial for reducing costs, optimizing resources, and improving load distribution for electric companies. Among the models tested, GRU exhibited superior performance, with MSE equal to 0.00215, MAE of 0.03266 and R-squared equal to 90.228%. Li et al. in [23] introduce a model named TS2ARCformer. This model utilizes multi-dimensional, demonstrating significant forecasting performance, in comparison with to benchmark models, like LSTM and GRU The results show reductions of 43.2% and 37.8% in the aspect of MAPE.
Additionally, the model proposed in [13] utilizes neural network techniques enhanced with PSO to assess the Iranian power system. This approach, based on neural networks, showed lower prediction errors by effectively adapting to the underlying patterns of the consumption load. The evaluation was done using the MAPE metric, which was equal to 0.0338, and the MAE, which was 0.02191. In studies [24,25], empirical modal decomposition (EMD) was used in order to break down the original electricity consumption time series data into various intrinsic mode functions (IMFs) with different frequencies and amplitudes.
Also, in another study a hybrid prediction model is proposed. This model combines a temporal convolutional network (TCN) with variational mode decomposition (VMD). For better accuracy an error correction process is followed. The weighted permutation entropy process is followed, in order to determine the optimal decomposition number and penalty factor for VMD. The accuracy and performance of the proposed model are demonstrated using the Global Energy Competition 2014 dataset [26].
In the same way, Javed et al. in [27] research the short-term load forecasting problem, comparing eight state-of-the-art linear and non-linear models, which are ARX, KNN, ARMAX, Bagged Trees, SVM, OE, NN–PSO, and a single hidden dense layer ANN–LM and a two hidden dense layer ANN–LM, on real-time demand time series. Simultaneously, He et al. in [28], compare individual and decomposition-based forecasting methods. About the the individual methods, these include LSTM, SVR, MLP, LR, and Random Forest Regressor. The decomposition-based methods include Empirical Mode Decomposition-LSTM (EMD-LSTM) and ensemble EEMD-LSTM models.
Additionally to the above, He et al. in [29] introduce a novel DNN architecture for short-term load forecasting. The model integrates various types parameters as input by employing appropriate NN elements designed to process each feature effectively. CNN components are used to extract features and patterns from the historical load time series, while RNN components are used to model the implicit dynamics. Additionally, Dense layers are employed to transform other types of features, improving the generalization of the models in understanding complex trends and patterns. Shi et al. in [30] suggest a model to tackle the unpredictability in electrical load patterns by applying DL and ML techniques to forecast household energy use in Ireland. This research introduces an innovative pooling-based deep RNN (PDRNN), which combines various load curves of consumers into a comprehensive set of inputs. The performance of the PDRNN is compared with ARIMA, SVR, and RNN models. The results demonstrate that the PDRNN method outperforms the other models, with RMSE values (in kWh) of 0.4505 for PDRNN, compared to 0.5593 for ARIMA, 0.518 for SVR, and 0.528 for RNN. Amarasinghe et al. in [31] suggested a framework to forecast short-term electricity consumption in residences by utilizing smart meter data from various properties. Following, Wand et al. in [32] propose an optimized SVM model using genetic algorithm (GA-SVM) in order to predict the hourly electricity demand of a commercial center located in Xin town, China.
Residential forecasting is an area that gathers a lot of scientific interest. Bessani et al. in [33] study the short-term residential forecasting task across multiple households employing Bayesian multivariate networks. This algorithm predicts the forthcoming household demand by analyzing historical consumption patterns, temperature, humidity, socioeconomic variables, and energy use. The assessment utilized actual data sourced from the Irish Intelligent Meter Project. According to the results, the proposed technique provides a robust single forecast model, which is capable of accommodating hundreds of households with various consumption patterns. The reported metrics include an MAE of 1.0085 kWh and a Mean Arctangent Absolute Percentage Error (MAAPE) of 0.5035, highlighting its effectiveness in accurate load forecasting.
Regarding RNN-based approaches, Caicedo-Vivas et al. in [34] analyze the issue of short-term load prediction by employing dataset from a Colombian grid operator. The proposed DL model utilizes a LSTM to predict load across a seven-day time horizon (168 hours ahead). It combines historical data from a specific region in Colombia with calendar attributes like holidays and the month’s index relevant to the forecasting week. Unlike traditional LSTM approaches, this model enables LSTM cells to process multiple load measurements concurrently, with supplementary information (holidays and current month) appended to the LSTM output. This methodology improves the model’s ability to capture and utilize temporal and contextual factors for more accurate load forecasts. Also, Kong et al. in [35] conduct a comparative study between the LSTM model and the extreme learning machine (ELM), back-propagation NN (BPNN), and KNN. They demonstrated significant reduction in prediction errors by employing the LSTM structure. The aggregated average MAPE for their forecasts was 8.18%, while the average MAPE for individual forecasts was 44.39%. This study underscores therich performance of LSTM models in short-term residential forecasting.
Following the above, Gao et al. in [24] investigate the impact of decomposition methods. For this reason, the authors propose an EMD Gated Recurrent Unit with feature selection (EMD-GRU-FS) for short-term electricity forecasting, using Pearson correlation to identify the relationship between subseries and the original series. Experimental results indicated that this method achieved average prediction accuracies of 96.9%, 95.31%, 95.72%, and 97.17% across four datasets. Additionally, Yuan et al. in [25] present an enhanced model combining integrated EMD and LSTM for short-term load forecasting, where the recurrent model is used for feature extraction and creating load predictions. For the final consumers, short-term electricity consumption predictions were obtained by aggregating multiple target prediction results. The results show that the proposed model performs achieving MAPE 2.6249% in winter and 2.3047% in summer, respectively.
Additionally, Hadri et al. in [17] developed load forecasting techniques that can be integrated with occupancy predictions and context-aware control of building appliances. The researchers investigated the accuracy of multiple methods for predicting energy consumption. They deployed an IoT and Big Data-based platform to collect real-time electricity values. The acquired data was used to build predictive models using XGBoost, RF, ARIMA, SARIMA and LSTM. The models’ evaluation was done using metrics such as RMSE, MAE, MAPE, R and maximum absolute error (MaxAE). Similarly, in another study the authors conduct a comparative study between ARIMA and SARIMA, as well as RF, XGBoost, and LSTM models using MAPE, MAPE, Mean Percentage Error (MPE), and RMSE [17]. Li et al. in [36] developed a novel short-term forecasting model based on a modified LSTM model and an autoregressive, which is used for feature selection. The aim is to create forecasts for household electricity consumption. Finally, Fekri et al. in [37] introduced an online adaptive RNN, which is capable of continuous learning from recently acquired data and adaptation to various patterns.
About CNN-based algorithms, Andriopoulos et al. in [38] introduce an advanced CNN model that is concentrating on mathematical analysis of statistical data and advanced preprocessing of time series data for short-term load forecasting. This approach converts the data into a 2-D image format to leverage CNN-based models, which excel in handling stationarity and temporal volatility. The proposed model is compared with LSTM, considered the state-of-the-art solution for load forecasting. Following CNN models, Alanazi et al. in [39] present a novel approach, combining a residual CNN model and a layered Echo State Network (ESN), in order to handle efficiently both spatial and temporal patterns. Residential datasets from the Individual-Household-Electric-Power-Consumption (IHEPC) from Sceaux, Paris, and the Pennsylvania–New Jersey–Maryland (PJM) region are used. The developed model achieves MSE, MAE, and RMSE equal to 0.0713, 0.1978, and 0.2670 MW, respectively. Also, Jalali et al. in [40] study and propose a novel approach for short-term ELF using a deep neuroevolution algorithm, in order to develop a CNN model in automatic way, using an enhanced grey wolf optimizer (EGWO) as a modified advanced algorithm. Finally, Chitalia et al.in [41] present a strong forecasting framework in order to accommodate fluctuations in building operations across different types and locations of commercial buildings.
Finally, in many researches, weather data like temperature and humidity play o crucial role in ELF. In this way, Liao et al. in [42] propose the utilization of XGBoost model, using weekly historical data from a power plant in hourly resolution, incorporating weather factors such as temperature and humidity. The work additionally addresses the computational challenges, due to the complexity of the XGBoost hyperparameter optimization process.

4.3. Ensemble Methods

Ensemble models have gained interest because they improve predictive performance by combining multiple algorithms and minimize individual models’ disadvantages. These models improve forecasting accuracy and generalization, making them effective for complex datasets, reducing overfitting and variance. Advances in computational power and accessible tools have made implementing ensemble methods easier, boosting their popularity.
Advanced combinations of different models is followed in Ensemble Learning methods. In this way, Guo et al. in [43] propose a novel approach to forecasting wind speed using a modified EMD-based Feed-Forward Neural Network (FNN). The model addresses the nonlinear and non-stationary nature of wind speed data by decomposing the time series into multiple components and a residual series, using the EMD technique. The data used are from Zhangye, China. Alobaidi et al. in [44] propose the implementation of an ensemble learning framework to tackle the issue of forecasting the daily mean demand on an individual household level for the day-ahead market. The proposed model incorporates a regression network, making the final model performing with very high accuracy on a dataset from France. Du et al. in [45] introduce an advanced hybrid algorithm that effectively retrieves accurate wind speed series using singular spectrum analysis. This algorithm demonstrates superior adaptive search and optimization capabilities compared to other methods, offering faster performance, fewer parameters, and lower computational cost. As case study, this work applies the model to wind speed data in 10 minutes resolution, from three wind farms located in Shandong Province, eastern China.
Simultaneously and following fuzzy logic, Ma et al. in [46] combines a denoising technique with a dynamic fuzzy neural network to meet the challenges in wind speed forecasting tasks. The raw data is smoothed using singular spectrum analysis, optimized by brain storm optimization, to produce a cleaner dataset. A generalized dynamic fuzzy neural network is then used for forecasting. The model’s simpler and more compact neural network structure allows for faster learning and accurate predictions. Experimental results on wind speed data at 10-minute, 30-minute, and 60-minute intervals show that the model effectively approximates actual values and can serve as a reliable tool for smart grid planning. Also, Sadaei et al. in [47] combine fuzzy time series (FTS) and CNN models for short-term ELF. Multivariate consumption data, temperature and fuzzified version of load time series in hourly resolution, was converted into multi-channel images, in order to be used as input in the proposed model.
At the same way, Rafi et al. in [48] combine CNN and LSTM networks. As case study, the proposed method is applied to data from Bangladesh electricity network, in order to provide short-term forecasting. Finally, Wang et al. in [49] incorporate Q-learning with reinforcement learning. The aim for the final ensemble model is the creation of optimal ensemble weights, achieving predictions with the highest accuracy. As case study, various datasets of 25 households in the Austin area of the United States are used. The evaluation metrics show that the ensemble model surpass three single models in the testing period.

4.4. Aggregated Studies for Electricity Load Forecasting

In order to present the studies analyzed above in a consolidated manner, Table 1 is provided.

5. Challenges and Solutions on Electricity Price Forecasting

Similar to ELF methods, in this section, studies that have significantly contributed to the field of price forecasting are extensively analyzed. Initially, statistical methods are presented, followed by papers focusing on ML and DL, and finally, emphasis is given to Ensemble Methods. Similar to ELF, for a more substantial presentation of the related works, the related studies utilize ML and DL models are presented together.

5.1. Statistical Methods

Similar to ELF methods, the statistical models used to predict electricity prices rely on similar algorithms. Initially, traditional time series forecasting methods, like simple regression techniques, moving averages and smoothing methods were employed. Then, more complex and advanced models like dynamic regression, models, Box-Jenkins, and hybrid statistical models [53] to detect trends and seasonality in electricity price time series data were investigated. Various works, including [54,55,56,57], have explored ELF using the above methods. These foundational models paved the way for the creation of more powerful forecasting techniques. Skopal et al. in [54] propose a hybrid combination of ARIMA and a MLP model. The statistical model identified the linear trends, while the neural network handled the modeling of the nonlinear residuals. This approach leaded in lower forecast metrics, measured by the MAPE and mean absolute deviation (MAD), in comparison to the single models. Similarly, other stydies including [55,56], propose multiple autoregressive models, like SARIMA and GARCH, as weel as more advanced hybrid algorithms to predict electricity prices, evaluating their performance through statistical metrics like R² and MAPE. Their results highlight the effectiveness of these hybrid models. Additionally, a hybrid model combining ARIMA and multivariate linear regression and Holt-Winters is developed in [57]. For the evaluation process, datasets from the Iberian electricity market are used and MAPE is used. The results show that the combined model achieves satisfactory performance compared to other benchmark models. Marcjazz et al. in [58] focuses on the selection of optimal calibration windows for day-ahead EPF. The research utilizes six years of data from three major power markets and involves fitting four autoregressive expert models to both raw and transformed price time series. Also, Sanchez et al. in [59] investigate an ARIMA model using multiple input data for the Pennsylvania-New Jersey-Maryland (PJM) and Spanish electricity market, in order to generate 24 hours ahead forecasts.
Other studies [60,61,62] have focused on comparing different time series analysis methods for EPF. Abunofal et al. in [60] conduct a comparative analysis between different autoregressive models, like ARIMA, SARIMA and SARIMAX, which utilizes exogenous features as input. The aim is to create forecasts for the German DAM. Between the models, the SARIMAX, achieved the highest forecast accuracy. Also, Banitalebi et al. in [61] compare DES and TES for EPF from variability, utilizing elastic net regularization. The forecasted results show that TES provides exceptional performance, and regularization helps minimize the MSE. These outcomes aid in making well-informed decisions for power generation planning within the market. Additionally, various autoregressive statistical models and their derivatives have produced accurate forecasting results, as discussed in [62]. The study provides detailed computational procedures, in detail results, and evaluation metrics, like MAPE, highlighting promising outcomes and areas for further consideration.
Khairuddin et al. in [63] explores the Imbalance Cost Pass-Through (ICPT) within Malaysia’s incentive-based regulation (IBR), emphasizing its role in enabling power producers to adjust tariffs in response to changing fuel prices, thereby strengthening economic resilience in electricity generation. The Energy Commission’s biannual reviews of generation costs lead to either rebates or surcharges for customers. The study proposes forecasting ICPT prices to aid stakeholders in Peninsular Malaysia, utilizing three methods and evaluating performance via the MAPE. Findings indicate that ARIMA is the most accurate forecasting method in comparison to MA and LSSVM, with minimal price differences observed. The forecasted ICPT prices align closely with actual tariffs, suggesting a potential price drop in the upcoming announcement. This research could positively impact Malaysia’s energy sector sustainability.
About GARCH approaches, Entezari et al. in [64] examine methods to quantify risk and forecast the bias of electricity prices to revert to their historical average in Portugal’s energy market. The data were used are from January 2016 to December 2021. They apply both symmetric and asymmetric GARCH models to mitigate data fluctuation peaks, with the asymmetric model capturing the distinct effects of positive and negative shocks. The MSGARCH model, estimated with two distinct states, successfully captures the shifts between low and high volatility periods, as well as the prolonged impact of shocks during high volatility. This method helps power producers predict price movements and adjust their operations accordingly, leading to improved market stability and efficiency. Finally, authors in [65] research the financial impact and sustainability of a RES. More specifically, they use a PV plant with nominal power equal to 5 MWs, which is located in Montenegro. This PV plant has direct market access instead of a long-term Power Purchase Agreement (PPA). Using ARIMA for price forecasting, it finds that this riskier strategy is more profitable and offers a shorter payback period. The study concludes that direct market access is a better option to enhance project returns and support energy transformation in developing countries.

5.2. Machine and Deep Learning Methods

The integration of ML and DL models into wholesale EPF problems has been gaining increasing application in recent years. Gonzalez et al. in [66] examine the effectiveness of two advanced and hybrid models for forecasting next-day spot electricity prices on the APX-UK power exchange. The first model combines a fundamental supply stack model with an econometric model incorporating price driver data. The second model extends this approach by including logistic smooth transition regression (LSTR) to handle regime changes during structural shifts. The evaluation results in the test set from both hybrid models, particularly the hybrid-LSTR, perform better than those from non-hybrid SARMA, SARMAX, and LSTR models. The models’ prediction intervals (PIs) are assessed by comparing nominal to actual coverage, though no formal tests are conducted. The LSTR model achieves the best results, followed by the hybrid-ARX and SARMAX models. However, the hybrid-LSTR model tends to produce too many exceeding prices due to overly narrow PIs.
At the same time, open-source platforms provide great flexibility for such problems. Medina et al. in [67] investigate the application of advanced GPT tools, such as OpenAI’s ChatGPT, to improve electricity price prediction in Spain’s complex energy market. By analyzing energy news and expert reports, they generate supplementary variables that enhance predictive models. Their research includes two methodologies: employing in-context example prompts and fine-tuning GPT models. The results show that insights derived from GPT models closely match post-publication price changes, indicating that these methods can significantly boost prediction accuracy and aid market stakeholders and companies in making informed decisions amidst electricity price volatility. Simultaneously, [52] investigates the problem of short-term ELF using PSO methodologies in order to optimize back propagation feedforward networks. The results comparison is based on MAE and MSE, achieving 8.69% and 1.62%, respectively.
Some works carry out extensive comparisons between ML and DL models. Conte et al. in [68] explore forecasting techniques to enhance sustainable electricity management in Brazil by predicting critical variables such as the price of differences settlement (PLD) and wind speed. They employ two approaches: the first combines deep neural networks (LSTM and MLP) optimized with a canonical genetic algorithm (GA), and the second uses machine committees. One committee includes MLP, decision tree, linear regression, and SVM, while the other consists of MLP, LSTM, SVM, and ARIMA. Their findings indicate that the hybrid GA + LSTM algorithm performs exceptionally well in PLD prediction, achieving a mean square error (MSE) of 4.68, and in wind speed forecasting, with an MSE of 1.26. These methodologies aim to enhance decision-making in Brazil’s electricity market.
Transformer models are gaining more and more interest in EPF sector. Laitsos et al. in [69] utilize advanced DL algorithms, implementing four novel models: a CNN incorporating an attention mechanism, a hybrid CNN-GRU with attention, a soft voting ensemble, and a stacking ensemble model were implemented. Additionally, they developed an optimized transformer model known as the Multi-Head Attention model and the Perceptron model is selected as benchmark. The results reveal substantial predictive accuracy, particularly with the hybrid CNN-GRU model, which achieved a MAPE of 6.333%. The soft voting ensemble and Multi-Head Attention models also demonstrated strong performance, with MAPEs of 6.125% and 6.889%, respectively. These findings underscore the potential of transformer models and attention mechanisms in EPF, suggesting promising directions for future research.
Additionally, the influence of conventional energy forms plays a significant role in shaping the final hourly price. Jin et al. in [70] aim to enhance electricity market price forecasting by accounting for the discrete influences of fuel costs, large-scale generator costs, and demand. They introduce two innovative techniques: one focuses on feature generation and forecasting transformed variables based on fuel cost per unit and the maximum of the Probability Density Function (PDF) derived from Kernel Density Estimation (KDE). The second technique involves demand decomposition followed by feature selection, verified by gain or SHapley Additive exPlanations (SHAP) values. In their case study in the Korean Electricity Market, they observed improvements across all indicators. Feature generation using fuel cost per unit improved forecasting accuracy by reducing monthly volatility and error, achieving a MAPE of 3.83%. The KDE-based method achieved a MAPE of 3.82%. Combining both techniques resulted in the highest accuracy with a MAPE of 3.49%, while using decomposed data alone had a MAPE of 4.41%.
Baskan et al. in [71] explore the use of ML and DL methods to predict day-ahead electricity prices over a 7-day horizon in the German spot market, focusing on the challenge of increasing price volatility. The study underscores the potential of ML models to deliver reliable predictions in volatile and unpredictable market conditions, presenting a compelling alternative to traditional methods that rely heavily on human modeling and assumptions. Through both qualitative and quantitative analysis, the research evaluates model performance based on forecast horizon and robustness determined by hyperparameters. Three distinct test scenarios are manually selected for evaluation. Various models are trained, optimized, and compared using standard performance metrics. The results show that DL models outperform tree-based and statistical models, demonstrating superior effectiveness in managing volatile energy prices.
Other studies address the complexity of data that includes numerous block bids and offers per hour. Pinhão et al. in [72] present an innovative methodology for EPF by predicting the underlying dynamics of supply and demand curves derived from market auctions. The proposed models integrate several seasonal effects and key market variables such as wind generation and load. The evaluation metrics show the superior performance compared to benchmark methods, emphasizing the importance of integrating market bids in EPF.
Additionally, Duo et al. in [73] introduce a day-ahead forecasting method for China’s Shanxi electricity market prices, using a hybrid extreme learning machine (ELM). Initially, they preprocess trading data by eliminating weakly correlated features using the Spearman correlation coefficient. Next, they develop a day-screening model based on grey correlation theory to filter out irrelevant samples. In order to improve the accuracy, they optimize the parameters of the regularized ELM (RELM) using the Marine Predators Algorithm (MPA). The proposed model demonstrates superior performance compared to other existing models, helping to develop strong quotation strategies.
Finally, Saglam et al. in [74] investigate the influence of exogenous independent variables on peak load forecasting by employing multiple combinations of multilinear regression (MLR) models. Data from 1980 to 2020 are used, incorporating factors such as import/export figures, population, and gross domestic product (GDP) to predict instantaneous electricity peak load. The performance of these techniques is evaluated throurg MAE, MSE, MAPE, RMSE, and R-squared. The results show that the ANN and GRO models achieve the highest forecasting accuracy.

5.3. Ensemble Methods

Ensemble models various advantages, as they leverage the capabilities of both statistical algorithms and machine and deep learning. Kushagra Bhatia et al. in [75] investigate the influence the impact of RES on price forecasts, using them in in the training process of the models. The study proposes a bootstrap aggregated-stack generalized architecture for very short-term EPF, aimed at helping market participants develop real-time strategies. Guo et al. in [76] introduce an advanced ensemble model, which is called BND-FOA-LSSVM, by combining three district algorithms. These are Beveridge-Nelson decomposition (BND), fruit fly optimization algorithm (FOA), and least square support vector machine (LSSVM). The results show that the proposed model achieves a MAPE of 3.48%, a RMSE of 11.18 Yuan/MWh, and a MAE of 9.95 Yuan/MWh. These metrics are significantly smaller compared to those of the ARIMA, LSSVM, BND-LSSVM, FOA-LSSVM, and EMD-FOA-LSSVM models.
Yang et al. in [77] research and create a data-driven ensemble DL model (GHTnet) to capture the temporal variation of real-time electricity price values. For this reason, an advanced CNN module based on inception architecture is developed, which is called GoogLeNet. The advantage of this model is the capability of capturing the high-frequency features of data used, while the inclusion of time series summary statistics has been shown to enhance the forecasting of volatile price spikes. Datasets from 49 generators from the NYISO are used for the evaluation of the performance of the models. The final results show that the psoposed model achieves significant improvements over that of state-of-the-art benchmark methods, improving the MAPE by 17.34% approximately.
Also, Jahangir et al. in [78] propose a novel method for EPF by using Grey correlation analysis to select important parameters, denoising data with deep neural networks, implementing dimension reduction, and utilizing rough ANNs. Additionally, Khajeh et al. in [79] focuses on using ANNs with an improved iterative training algorithm for EPF in such markets. This paper introduces a novel forecasting approach for short-term electricity price prediction, addressing the inherent complexity, nonlinearity, volatility, and time-dependent nature of electricity prices. The proposed strategy incorporates two key innovations: a two-stage feature selection algorithm and an iterative training algorithm, both designed to enhance the accuracy and reliability of the proposed model.
Following the above, Zhang et al. in [80] introduce a novel hybrid model based on wavelet transform (WT), ARIMA and least squares SVM (LSSVM). The hyperparameters of the model are optimized by PSO algorithm, making it capable of achieving high performance in EPF tasks. The proposed method is tested using data from New South Wales (NSW) in Australia’s national electricity market. The result show that this method gives more accurate and effective results compared to other EPF methods.
Finally, Jaime et al. in [81] propose a hybrid EPF algorithm that utilizes a two-dimensional approach. In the vertical dimension, the final forecasts were generated by combining the outputs of XGBoost and LSTM models in a stacked array. In the horizontal dimension, the model leveraged available market data at the time of forecasting to create price predictions ranging from 1 hour to 96 hours ahead. Additionally, a new input feature, derived from the slope of thermal power generation output, significantly improved the accuracy of the model.

5.4. Aggregated Studies for Electricity Price Forecasting

In order to present the studies analyzed above in a consolidated manner, Table 2 follows.

6. Discussion and Comparison Between Load and Price forecasting

The comparison between ELF and EPF models does not reveal significant differences in their complexity and application. Load forecasting models primarily focus on predicting the demand for electricity, utilizing historical consumption data, weather conditions, and demographic factors. These models often employ statistical methods and ML techniques to achieve high accuracy. On the other hand, price forecasting models aim to predict the wholesale electricity market prices, which are influenced by a broader range of variables, including supply-demand dynamics, fuel prices, regulatory changes, and the behavior of market participants. Price forecasting models frequently integrate advanced ML and DL algorithms to manage the complexity and volatility of price data. Ensemble models, which combine multiple forecasting methods, have shown considerable promise in both load and price forecasting by capitalizing on the strengths of different approaches. Despite their differences, both types of models are crucial for optimizing the electricity market and ensuring a reliable and cost-effective power supply.
  • Observing the ELF papers we have selected, we see that 26 are from 2019 onwards, and 12 are from before 2019. This observation indicates that significant progress has been made in the last five years in the development of models aimed at load forecasting.
  • Regarding the EPF works, we see that 20 are from 2019 onwards, and 7 are from before 2019. This observation indicates that significant progress has been made in the last five years in the development of models aimed at price forecasting.
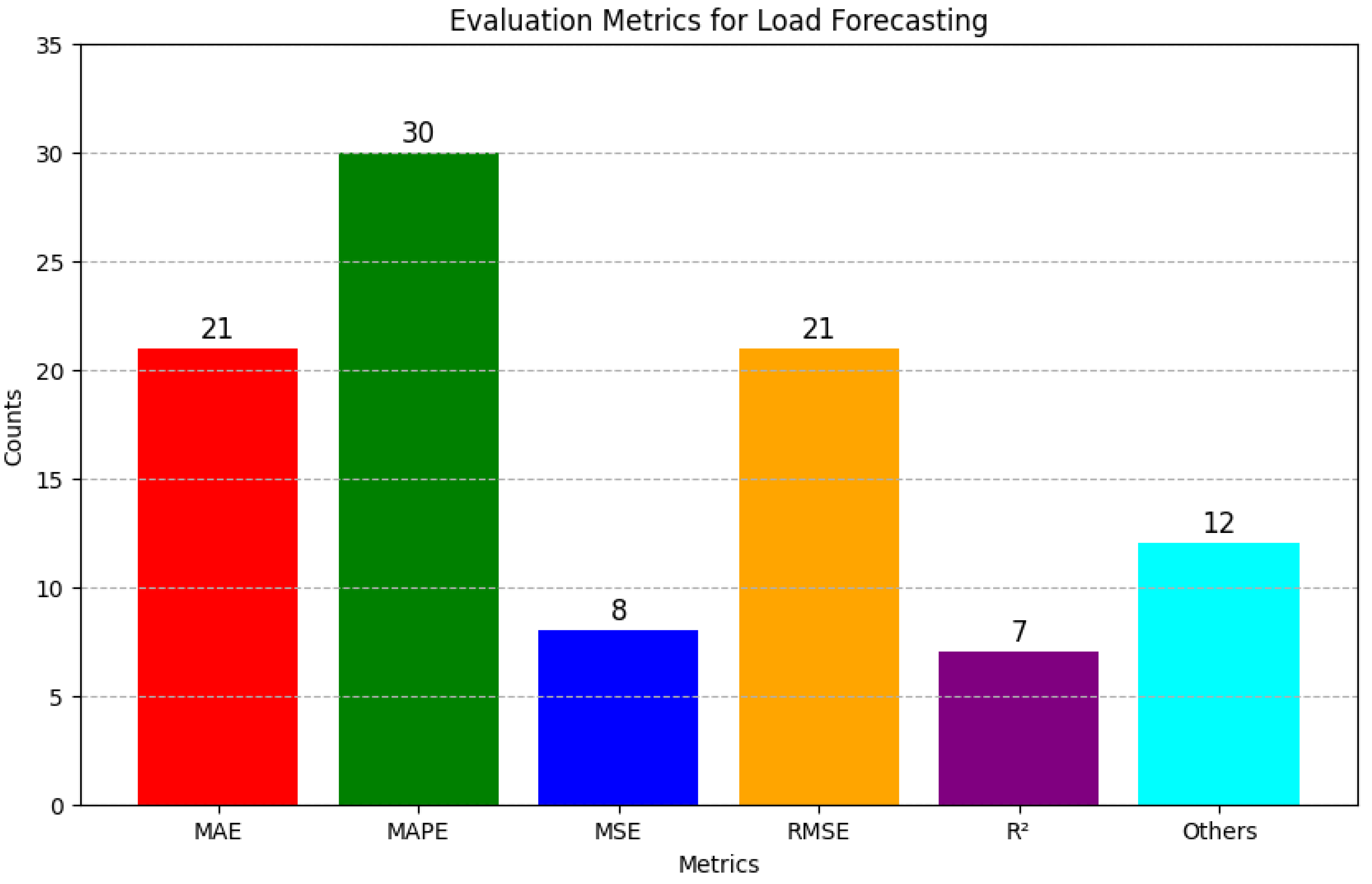
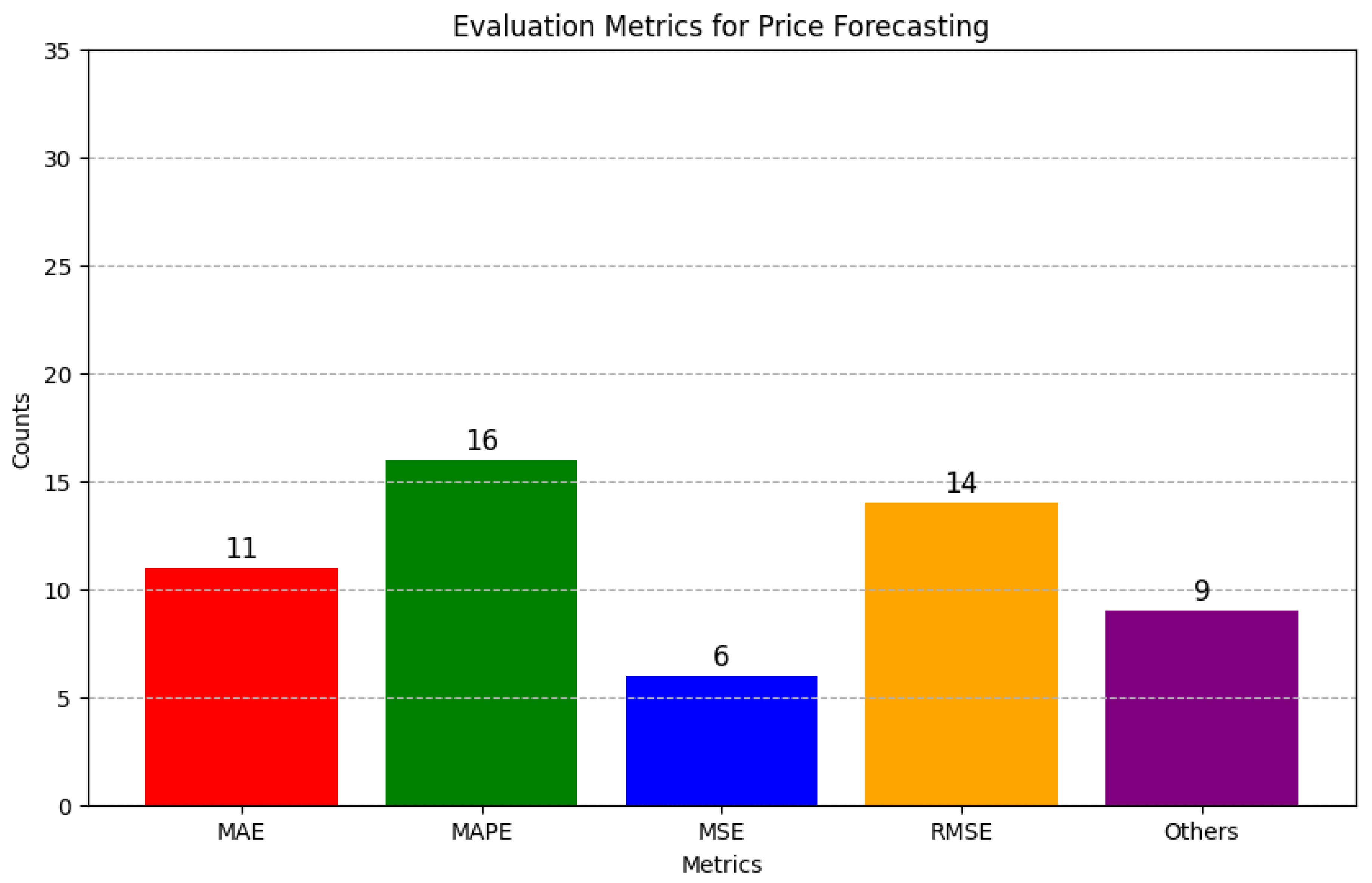
Also, regarding Figure 5 and Figure 6, which present the total number of related papers analyzed for each metric for both ELF and EPF, the following can be noticed:
  • Regarding the related studies of ELF, it is observed that most of them use MAPE and MAE, followed by RMSE, with percentages 78%, 55% and 55%, respectively.
  • Regarding the works of EPF, and similarly to ELF, most of them employ MAPE, MAE and RMSE, with values 57%, 39% and 50%, respectively.
  • Regarding EPF works, it is noted that none of the works use R², indicating the instability of this metric to provide reliable conclusions, due to the greater fluctuations observed in the price time series compared to the load.

7. Conclusion and Future Study Proposals

In this comprehensive review, we have systematically examined the methodologies, challenges, and advancements in electricity load and price forecasting for the modern wholesale electricity market. Our analysis covers a broad spectrum of forecasting techniques, from traditional statistical methods to contemporary ML and artificial intelligence approaches. The dynamic and complex nature of electricity markets necessitates accurate and reliable forecasting to ensure operational efficiency, cost-effectiveness, and grid stability.
The review highlights the diverse range of methodologies employed in load and price forecasting. Traditional methods like ARIMA and SARIMA remain foundational, while ML and DL techniques such as ANN, SVR, and ensemble methods have demonstrated significant improvements in predictive accuracy and adaptability. Accurate performance evaluation is crucial for forecasting models, and metrics such as MAE, MSE, and MAPE are commonly used. However, the selection of appropriate metrics is context-dependent, influenced by the specific needs of market participants and regulatory bodies.
The integration of diverse data sources, including historical load and price data, weather conditions, and economic indicators, enhances the robustness of forecasting models. Advanced data pre-processing techniques and the use of high-frequency data are pivotal in capturing market volatility and trends. The review identifies several challenges, including data scarcity, market volatility, and the non-linear nature of electricity prices. Innovative solutions, such as hybrid models combining multiple forecasting techniques and real-time data analytics, show promise in addressing these issues. The future of load and price forecasting lies in the continued evolution of artificial intelligence and ML. The adoption of DL, real-time analytics, and the Internet of Things (IoT) offers new opportunities for enhancing forecasting accuracy and responsiveness. Furthermore, collaboration between academia, industry, and regulatory bodies is essential for the development of standardized frameworks and best practices.
In conclusion, effective load and price forecasting are integral to the success of modern wholesale electricity markets. The advancements in forecasting techniques hold great potential to improve market operation and sustainability, reduce costs, and enhance the reliability of electricity supply. Ongoing research and innovation, supported by robust data infrastructures and collaborative efforts, will be key to addressing existing challenges and harnessing new opportunities in this dynamic field.
In terms of future study proposals, managing with non-stationary and nonlinear load data is a challenge, as conventional STLF models typically assume that load data remains stationary and linear. Nonetheless, load data can exhibit non-stationarity and nonlinearity as a result of shifts in consumer behavior, the emergence of new technologies, and various other factors. Future investigations might focus on devising STLF models capable of managing non-stationary and nonlinear load data, potentially utilizing advanced ML methods or more adaptable statistical frameworks.
Also, the incorporation of online learning is another avenue for improvement. Online learning, a branch of ML, adapts to real-time changes in the energy system. These algorithms continuously update their learning based on new data, allowing them to refine forecasts in real-time. Future studies could aim to develop STLF models that leverage online learning algorithms, thereby improving the accuracy and timeliness of forecasts.
Finally, the creation of models for Distributed Energy Resources (DERs) is becoming increasingly important with the rise of technologies like solar photovoltaic panels on rooftops and integrated energy storage devices. These developments present new challenges for STLF models. Future studies might aim to develop STLF models that incorporate distributed energy resources, either by projecting renewable energy generation or by estimating the influence of these resources on electricity demand.

Author Contributions

Conceptualization, V.L. and G.V.; methodology, V.L.; software, V.L. and G.V.; validation, V.L., G.V., P.P., E.T., D.B. and L.H.T.; formal analysis, V.L. and G.V.; investigation, V.L. and G.V.; resources, V.L. and G.V.; data curation, V.L. and G.V.; writing—original draft preparation, V.L. and G.V.; writing—review and editing, V.L., G.V., P.P., E.T., D.B. and L.H.T.; visualization, V.L. and G.V.; supervision, D.B. and L.H.T.; project administration, D.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

This study did not utilize any dataset.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ARIMA Autoregressive Integrated Moving Average
SVM Support Vector Machine
TL Transfer Learning
SARIMA Seasonal Autoregressive Integrated Moving Average
MLP Multilayer Perceptron
GARCH Generalized Autoregressive Conditional Heteroskedasticity
ELF Electricity Load Forecasting
EPF Electricity Price Forecasting
ANN Artificial Neural Network
RNN Recurrent Neural Network
LSTM Long Short-Term Memory
CNN Convolutional Neural Network
ESN Echo State Network
GRU Gated Recurrent Unit
LR Linear Regression
MAE Mean Absolute Error
MSE Mean Squared Error
RMSE Root Mean Squared Error
PJM Pennsylvania–New Jersey–Maryland Interconnection
IHEPC Individual-Household-Electric-Power-Consumption
NARX Nonlinear Autoregressive Exogenous Model
DNN Deep Neural Network
XGBoost Extreme Gradient Boosting
RF Random Forest
SVR Support Vector Regression
KNN K-Nearest Neighbors
BPNN Backpropagation Neural Network
DAM Day-Ahead Market
IDA Intraday Market
BM Balancing Market
ES Exponential Smoothing
DES Double Exponential Smoothing
TES Triple Exponential Smoothing
EMD Empirical Mode Decomposition
ELM Extreme Learning Machine
NYISO New York Independent System Operator
DER Distributed Energy Resources

References

  1. Dagoumas, A. Impact of Bilateral Contracts on Wholesale Electricity Markets: In a Case Where a Market Participant Has Dominant Position. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]
  2. Makrygiorgou, J.J.; Karavas, C.S.; Dikaiakos, C.; Moraitis, I.P. The Electricity Market in Greece: Current Status, Identified Challenges, and Arranged Reforms. Sustainability 2023, 15. [Google Scholar] [CrossRef]
  3. What is spot power trading? https://doi.org/https://www.kyos.com/faq/what-is-spot-power-trading/.
  4. Ospina, R.; Gondim, J.A.M.; Leiva, V.; Castro, C. An Overview of Forecast Analysis with ARIMA Models during the COVID-19 Pandemic: Methodology and Case Study in Brazil. Mathematics 2023, 11. [Google Scholar] [CrossRef]
  5. Noor, T.H.; Almars, A.M.; Alwateer, M.; Almaliki, M.; Gad, I.; Atlam, E.S. SARIMA: A Seasonal Autoregressive Integrated Moving Average Model for Crime Analysis in Saudi Arabia. Electronics 2022, 11. [Google Scholar] [CrossRef]
  6. Jónsson, T.; Pinson, P.; Nielsen, H.A.; Madsen, H. Exponential Smoothing Approaches for Prediction in Real-Time Electricity Markets. Energies 2014, 7, 3710–3732. [Google Scholar] [CrossRef]
  7. Queiroz, R.G.S.; David, S.A. Performance of the Realized-GARCH Model against Other GARCH Types in Predicting Cryptocurrency Volatility. Risks 2023, 11. [Google Scholar] [CrossRef]
  8. Guido, R.; Ferrisi, S.; Lofaro, D.; Conforti, D. An Overview on the Advancements of Support Vector Machine Models in Healthcare Applications: A Review. Information 2024, 15. [Google Scholar] [CrossRef]
  9. Kim, S.J.; Bae, S.J.; Jang, M.W. Linear Regression Machine Learning Algorithms for Estimating Reference Evapotranspiration Using Limited Climate Data. Sustainability 2022, 14. [Google Scholar] [CrossRef]
  10. Zhang, J.; Wang, R.; Jia, A.; Feng, N. Optimization and Application of XGBoost Logging Prediction Model for Porosity and Permeability Based on K-means Method. Applied Sciences 2024, 14. [Google Scholar] [CrossRef]
  11. Nadkarni, S.B.; Vijay, G.S.; Kamath, R.C. Comparative Study of Random Forest and Gradient Boosting Algorithms to Predict Airfoil Self-Noise. Engineering Proceedings 2023, 59. [Google Scholar] [CrossRef]
  12. Lazcano, A.; Jaramillo-Morán, M.A.; Sandubete, J.E. Back to Basics: The Power of the Multilayer Perceptron in Financial Time Series Forecasting. Mathematics 2024, 12. [Google Scholar] [CrossRef]
  13. Laitsos, V.; Vontzos, G.; Bargiotas, D.; Daskalopulu, A.; Tsoukalas, L.H. Enhanced Automated Deep Learning Application for Short-Term Load Forecasting. Mathematics 2023, 11, 2912. [Google Scholar] [CrossRef]
  14. Huang, D.; Liu, Z.; Wu, D. Research on Ensemble Learning-Based Feature Selection Method for Time-Series Prediction. Applied Sciences 2024, 14. [Google Scholar] [CrossRef]
  15. Sethi, R.; Kleissl, J. Comparison of short-term load forecasting techniques. In Proceedings of the 2020 IEEE Conference on Technologies for Sustainability (SusTech). IEEE, 2020, pp. 1–6.
  16. Chou, J.S.; Tran, D.S. Forecasting energy consumption time series using machine learning techniques based on usage patterns of residential householders. Energy 2018, 165, 709–726. [Google Scholar] [CrossRef]
  17. Hadri, S.; Naitmalek, Y.; Najib, M.; Bakhouya, M.; Fakhri, Y.; Elaroussi, M. A Comparative Study of Predictive Approaches for Load Forecasting in Smart Buildings. Procedia Computer Science 2019, 160, 173–180, The 10th International Conference on Emerging Ubiquitous Systems and Pervasive Networks (EUSPN-2019) / The 9th International Conference on Currentand Future Trends of Information and Communication Technologies in Healthcare (ICTH-2019) / Affiliated Workshops. [Google Scholar] [CrossRef]
  18. Vrablecová, P.; Bou Ezzeddine, A.; Rozinajová, V.; Šárik, S.; Sangaiah, A.K. Smart grid load forecasting using online support vector regression. Computers & Electrical Engineering 2018, 65, 102–117. [Google Scholar] [CrossRef]
  19. Pełka, P. Analysis and Forecasting of Monthly Electricity Demand Time Series Using Pattern-Based Statistical Methods. Energies 2023, 16. [Google Scholar] [CrossRef]
  20. Elamin, N.; Fukushige, M. Modeling and forecasting hourly electricity demand by SARIMAX with interactions. Energy 2018, 165, 257–268. [Google Scholar] [CrossRef]
  21. Mado, I.; Rajagukguk, A.; Triwiyatno, A.; Fadllullah, A. Short-Term Electricity Load Forecasting Model Based DSARIMA. International Journal of Electrical, Energy and Power System Engineering 2022, 5, 6–11. [Google Scholar] [CrossRef]
  22. Abumohsen, M.; Owda, A.Y.; Owda, M. Electrical Load Forecasting Using LSTM, GRU, and RNN Algorithms. Energies 2023, 16. [Google Scholar] [CrossRef]
  23. Li, S.; Zhang, W.; Wang, P. TS2ARCformer: A Multi-Dimensional Time Series Forecasting Framework for Short-Term Load Prediction. Energies 2023, 16. [Google Scholar] [CrossRef]
  24. Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-Term Electricity Load Forecasting Model Based on EMD-GRU with Feature Selection. Energies 2019, 12. [Google Scholar] [CrossRef]
  25. Yuan, B.; He, B.; Yan, J.; Jiang, J.; Wei, Z.; Shen, X. Short-term electricity consumption forecasting method based on empirical mode decomposition of long-short term memory network. IOP Conference Series: Earth and Environmental Science 2022, 983, 012004. [Google Scholar] [CrossRef]
  26. Zhou, F.; Zhou, H.; Li, Z.; Zhao, K. Multi-Step Ahead Short-Term Electricity Load Forecasting Using VMD-TCN and Error Correction Strategy. Energies 2022, 15. [Google Scholar] [CrossRef]
  27. Javed, U.; Ijaz, K.; Jawad, M.; Ansari, E.A.; Shabbir, N.; Kütt, L.; Husev, O. Exploratory Data Analysis Based Short-Term Electrical Load Forecasting: A Comprehensive Analysis. Energies 2021, 14. [Google Scholar] [CrossRef]
  28. He, F.; Zhou, J.; kai Feng, Z.; Liu, G.; Yang, Y. A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm. Applied Energy 2019, 237, 103–116. [Google Scholar] [CrossRef]
  29. He, W. Load Forecasting via Deep Neural Networks. Procedia Computer Science 2017, 122, 308–314, 5th International Conference on Information Technology and Quantitative Management, ITQM 2017. [Google Scholar] [CrossRef]
  30. Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN. IEEE Transactions on Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
  31. Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE). 2017; pp. 1483–1488. [Google Scholar] [CrossRef]
  32. Wang, M.; Yu, J.; Zhou, M.; Quan, W.; Cheng, R. Joint Forecasting Model for the Hourly Cooling Load and Fluctuation Range of a Large Public Building Based on GA-SVM and IG-SVM. Sustainability 2023, 15. [Google Scholar] [CrossRef]
  33. Bessani, M.; Massignan, J.A.; Santos, T.M.; London, J.B.; Maciel, C.D. Multiple households very short-term load forecasting using bayesian networks. Electric Power Systems Research 2020, 189, 106733. [Google Scholar] [CrossRef]
  34. Caicedo-Vivas, J.S.; Alfonso-Morales, W. Short-Term Load Forecasting Using an LSTM Neural Network for a Grid Operator. Energies 2023, 16. [Google Scholar] [CrossRef]
  35. Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Transactions on Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
  36. Li, L.; Meinrenken, C.J.; Modi, V.; Culligan, P.J. Short-term apartment-level load forecasting using a modified neural network with selected auto-regressive features. Applied Energy 2021, 287, 116509. [Google Scholar] [CrossRef]
  37. Fekri, M.N.; Patel, H.; Grolinger, K.; Sharma, V. Deep learning for load forecasting with smart meter data: Online Adaptive Recurrent Neural Network. Applied Energy 2021, 282, 116177. [Google Scholar] [CrossRef]
  38. Andriopoulos, N.; Magklaras, A.; Birbas, A.; Papalexopoulos, A.; Valouxis, C.; Daskalaki, S.; Birbas, M.; Housos, E.; Papaioannou, G.P. Short Term Electric Load Forecasting Based on Data Transformation and Statistical Machine Learning. Applied Sciences 2021, 11. [Google Scholar] [CrossRef]
  39. Alanazi, M.D.; Saeed, A.; Islam, M.; Habib, S.; Sherazi, H.I.; Khan, S.; Shees, M.M. Enhancing Short-Term Electrical Load Forecasting for Sustainable Energy Management in Low-Carbon Buildings. Sustainability 2023, 15. [Google Scholar] [CrossRef]
  40. Jalali, S.M.J.; Ahmadian, S.; Khosravi, A.; Shafie-khah, M.; Nahavandi, S.; Catalão, J.P.S. A Novel Evolutionary-Based Deep Convolutional Neural Network Model for Intelligent Load Forecasting. IEEE Transactions on Industrial Informatics 2021, 17, 8243–8253. [Google Scholar] [CrossRef]
  41. Chitalia, G.; Pipattanasomporn, M.; Garg, V.; Rahman, S. Robust short-term electrical load forecasting framework for commercial buildings using deep recurrent neural networks. Applied Energy 2020, 278, 115410. [Google Scholar] [CrossRef]
  42. Liao, X.; Cao, N.; Li, M.; Kang, X. Research on Short-Term Load Forecasting Using XGBoost Based on Similar Days. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS); 2019; pp. 675–678. [Google Scholar] [CrossRef]
  43. Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renewable Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
  44. Alobaidi, M.H.; Chebana, F.; Meguid, M.A. Robust ensemble learning framework for day-ahead forecasting of household based energy consumption. Applied Energy 2018, 212, 997–1012. [Google Scholar] [CrossRef]
  45. Du, P.; Jin, Y.; Zhang, K. A Hybrid Multi-Step Rolling Forecasting Model Based on SSA and Simulated Annealing—Adaptive Particle Swarm Optimization for Wind Speed. Sustainability 2016, 8. [Google Scholar] [CrossRef]
  46. Ma, X.; Jin, Y.; Dong, Q. A generalized dynamic fuzzy neural network based on singular spectrum analysis optimized by brain storm optimization for short-term wind speed forecasting. Applied Soft Computing 2017, 54, 296–312. [Google Scholar] [CrossRef]
  47. Sadaei, H.J.; de Lima e Silva, P.C.; Guimarães, F.G.; Lee, M.H. Short-term load forecasting by using a combined method of convolutional neural networks and fuzzy time series. Energy 2019, 175, 365–377. [Google Scholar] [CrossRef]
  48. Rafi, S.H.; Masood, N.-A.; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
  49. Wang, J.; Liu, H.; Zheng, G.; Li, Y.; Yin, S. Short-Term Load Forecasting Based on Outlier Correction, Decomposition, and Ensemble Reinforcement Learning. Energies 2023, 16. [Google Scholar] [CrossRef]
  50. Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and Models for Electric Load Forecasting: A Comprehensive Review. Logistics, Supply Chain, Sustainability and Global Challenges 2020, 11, 51–76. [Google Scholar] [CrossRef]
  51. Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. International Journal of Forecasting 2016, 32, 914–938. [Google Scholar] [CrossRef]
  52. Ozerdem, O.C.; Olaniyi, E.O.; Oyedotun, O.K. Short term load forecasting using particle swarm optimization neural network. Procedia Computer Science 2017, 120, 382–393, 9th International Conference on Theory and Application of Soft Computing, Computing with Words and Perception, ICSCCW 2017, 22-23 August 2017, Budapest, Hungary. [Google Scholar] [CrossRef]
  53. Hyndman, R.J.; Athanasopoulos, G. Forecasting: principles and practice; OTexts, 2018.
  54. Skopal, R. Short-term hourly price forward curve prediction using neural network and hybrid ARIMA-NN model. 2015 International Conference on Information and Digital Technologies, 2015; 335–338. [Google Scholar]
  55. Liu, H.; Shi, J. Applying ARMA–GARCH approaches to forecasting short-term electricity prices. Energy Economics 2013, 37, 152–166. [Google Scholar] [CrossRef]
  56. Rajan, P.; Chandrakala, K.V. Statistical Model Approach of Electricity Price Forecasting for Indian Electricity Market. In Proceedings of the 2021 IEEE Madras Section Conference (MASCON); 2021; pp. 1–5. [Google Scholar] [CrossRef]
  57. Bissing, D.; Klein, M.T.; Chinnathambi, R.A.; Selvaraj, D.F.; Ranganathan, P. A Hybrid Regression Model for Day-Ahead Energy Price Forecasting. IEEE Access 2019, 7, 36833–36842. [Google Scholar] [CrossRef]
  58. Marcjasz, G.; Serafin, T.; Weron, R. Selection of Calibration Windows for Day-Ahead Electricity Price Forecasting. Energies 2018, 11. [Google Scholar] [CrossRef]
  59. Sánchez de la Nieta, A.A.; González, V.; Contreras, J. Portfolio Decision of Short-Term Electricity Forecasted Prices through Stochastic Programming. Energies 2016, 9. [Google Scholar] [CrossRef]
  60. Abunofal, M.; Poshiya, N.; Qussous, R.; Weidlich, A. Comparative Analysis of Electricity Market Prices Based on Different Forecasting Methods. In Proceedings of the 2021 IEEE Madrid PowerTech; 2021; pp. 1–6. [Google Scholar] [CrossRef]
  61. Banitalebi, B.; Hoque, M.E.; Appadoo, S.S.; Thavaneswaran, A. Regularized Probabilistic Forecasting of Electricity Wholesale Price and Demand. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI); 2020; pp. 28–35. [Google Scholar] [CrossRef]
  62. Shikhina, A.; Kochengin, A.; Chrysostomou, G.; Shikhin, V. Investigation of autoregressive forecasting models for market electricity price. In Proceedings of the 2020 IEEE 20th Mediterranean Electrotechnical Conference ( MELECON); 2020; pp. 570–575. [Google Scholar] [CrossRef]
  63. Khairuddin, F.K.; Zaini, F.A.; Sulaima, M.F.; Shamsudin, N.H.; Abu Hanifah, M.S. A Single-Buyer Model of Imbalance Cost Pass-Through Pricing Forecasting in the Malaysian Electricity Supply Industry. Electricity 2024, 5, 295–312. [Google Scholar] [CrossRef]
  64. Entezari, N.; Fuinhas, J.A. Quantifying the Impact of Risk on Market Volatility and Price: Evidence from the Wholesale Electricity Market in Portugal. Sustainability 2024, 16. [Google Scholar] [CrossRef]
  65. Mišnić, N.; Pejović, B.; Jovović, J.; Rogić, S.; Đurišić, V. The Economic Viability of PV Power Plant Based on a Neural Network Model of Electricity Prices Forecast: A Case of a Developing Market. Energies 2022, 15. [Google Scholar] [CrossRef]
  66. Gonzalez, V.; Contreras, J.; Bunn, D.W. Forecasting Power Prices Using a Hybrid Fundamental-Econometric Model. IEEE Transactions on Power Systems 2012, 27, 363–372. [Google Scholar] [CrossRef]
  67. Menéndez Medina, A.; Heredia Álvaro, J.A. Using Generative Pre-Trained Transformers (GPT) for Electricity Price Trend Forecasting in the Spanish Market. Energies 2024, 17. [Google Scholar] [CrossRef]
  68. Conte, T.; Oliveira, R. Comparative Analysis between Intelligent Machine Committees and Hybrid Deep Learning with Genetic Algorithms in Energy Sector Forecasting: A Case Study on Electricity Price and Wind Speed in the Brazilian Market. Energies 2024, 17. [Google Scholar] [CrossRef]
  69. Laitsos, V.; Vontzos, G.; Bargiotas, D.; Daskalopulu, A.; Tsoukalas, L.H. Data-Driven Techniques for Short-Term Electricity Price Forecasting through Novel Deep Learning Approaches with Attention Mechanisms. Energies 2024, 17. [Google Scholar] [CrossRef]
  70. Jin, A.; Lee, D.; Park, J.B.; Roh, J.H. Day-Ahead Electricity Market Price Forecasting Considering the Components of the Electricity Market Price; Using Demand Decomposition, Fuel Cost, and the Kernel Density Estimation. Energies 2023, 16. [Google Scholar] [CrossRef]
  71. Baskan, D.E.; Meyer, D.; Mieck, S.; Faubel, L.; Klöpper, B.; Strem, N.; Wagner, J.A.; Koltermann, J.J. A Scenario-Based Model Comparison for Short-Term Day-Ahead Electricity Prices in Times of Economic and Political Tension. Algorithms 2023, 16. [Google Scholar] [CrossRef]
  72. Pinhão, M.; Fonseca, M.; Covas, R. Electricity Spot Price Forecast by Modelling Supply and Demand Curve. Mathematics 2022, 10. [Google Scholar] [CrossRef]
  73. Dong, J.; Dou, X.; Bao, A.; Zhang, Y.; Liu, D. Day-Ahead Spot Market Price Forecast Based on a Hybrid Extreme Learning Machine Technique: A Case Study in China. Sustainability 2022, 14. [Google Scholar] [CrossRef]
  74. Saglam, M.; Lv, X.; Spataru, C.; Karaman, O.A. Instantaneous Electricity Peak Load Forecasting Using Optimization and Machine Learning. Energies 2024, 17. [Google Scholar] [CrossRef]
  75. Bhatia, K.; Mittal, R.; Varanasi, J.; Tripathi, M. An ensemble approach for electricity price forecasting in markets with renewable energy resources. Utilities Policy 2021, 70, 101185. [Google Scholar] [CrossRef]
  76. Guo, W.; Zhao, Z. A Novel Hybrid BND-FOA-LSSVM Model for Electricity Price Forecasting. Information 2017, 8. [Google Scholar] [CrossRef]
  77. Yang, H.; Schell, K.R. GHTnet: Tri-Branch deep learning network for real-time electricity price forecasting. Energy 2022, 238, 122052. [Google Scholar] [CrossRef]
  78. Jahangir, H.; Tayarani, H.; Baghali, S.; Ahmadian, A.; Elkamel, A.; Golkar, M.A.; Castilla, M. A Novel Electricity Price Forecasting Approach Based on Dimension Reduction Strategy and Rough Artificial Neural Networks. IEEE Transactions on Industrial Informatics 2020, 16, 2369–2381. [Google Scholar] [CrossRef]
  79. Khajeh, M.G.; Maleki, A.; Rosen, M.A.; Ahmadi, M.H. Electricity price forecasting using neural networks with an improved iterative training algorithm. International Journal of Ambient Energy 2018, 39, 147–158. [Google Scholar] [CrossRef]
  80. Zhang, J.; Tan, Z.; Yang, S. Day-ahead electricity price forecasting by a new hybrid method. Computers & Industrial Engineering 2012, 63, 695–701, Energy Management and Economics. [Google Scholar] [CrossRef]
  81. Manfre Jaimes, D.; Zamudio López, M.; Zareipour, H.; Quashie, M. A Hybrid Model for Multi-Day-Ahead Electricity Price Forecasting considering Price Spikes. Forecasting 2023, 5, 499–521. [Google Scholar] [CrossRef]
Preprints 138427 g001
Figure 1. Energy Market Sequence [2].
Figure 1. Energy Market Sequence [2].
Preprints 138427 g001
Preprints 138427 g002
Figure 2. Day-Ahead and Intraday Market.
Figure 2. Day-Ahead and Intraday Market.
Preprints 138427 g002
Preprints 138427 g003
Figure 3. Balancing Market [3]
Figure 3. Balancing Market [3]
Preprints 138427 g003
Preprints 138427 g004
Figure 4. Forecasting models overview.
Figure 4. Forecasting models overview.
Preprints 138427 g004
Preprints 138427 g005
Figure 5. Total number of ELF studies per metric.
Figure 5. Total number of ELF studies per metric.
Preprints 138427 g005
Preprints 138427 g006
Figure 6. Total number of EPF studies per metric.
Figure 6. Total number of EPF studies per metric.
Preprints 138427 g006
Table 1. Aggregated Table with resent publications for load forecasting.
Table 1. Aggregated Table with resent publications for load forecasting.
Ref. Year Models Metrics Dataset Origin
[15] 2020 ARIMA, MLR, RPART, CTREE, BAGGING, RF MAPE, R2 Electricity load data of a residential area
[16] 2018 ANN, SVM, RL, CR Tree, Voting, Bagging, SARIMA-MetaFA-LSSVR, SARIMA-PDO-LSSVR R2, RMSE, MAPE, MaxAE Real-time data collected from a smart grid installed in an experimental building
[17] 2019 ARIMA, SARIMA, XGBoost, Random Forest (RF), Long Short-Term Memory (LSTM) sMAPE, MAPE, MAE, RMSE N/A
[18] 2018 Online SVR, MLP, ARIMA MAPE Public Irish CER dataset
[19] 2023 ARIMA, ETS, Prophet MAPE ENTSOE
[20] 2018 SARIMAX RMSE, MAE, MAPE Tokyo Electric Power Company (TEPCO)
[50] 2020 ARIMA, ARMA, SARIMAX MSE, MAPE, MAE Various datasets
[51] 2016 ANN. LR, MLR, Fuzzy Regression, ARIMA, ARMA, GARCH Various Metrics US utility
[21] 2022 DSARIMA MAPE Java-Madura-Bali interconnection, Indonesia
[22] 2023 LSTM, GRU, RNN R-squared, MSE, MAE Tubas Electricity Company, Palestine
[52] 2017 DNN, PSO MAE, MSE North Cyprus based energy company, Cyprus Turkish Electricity Authority (Kib-Tek)
[24] 2019 GRU, SVR, RF, EMD-GRU, EMD-SVR, EMD-RF MAPE, RMSE U.S. Public Utilities Data Set, Region in Northwest China
[25] 2022 RNN, EMD, LSTM, EMD-LSTM MAPE, RMSE Region in Guangdong Province, China
[28] 2019 LSTM, SVR, MLPR, LR, RFR, EMD-LSTM, EEMD-LSTM RMSE, MAE, MAPE (%), R2 Hubei Province, China
[26] 2022 TCN, VMD, LSTM, GRU, VMD-LSTM, VMD-GRU, VMD-TCN RMSE, MAPE, R2 Global Energy Competition 2014 dataset
[29] 2017 LR, SVR, DNN, CNN MAPE, MAE Hourly loads of a North China city
[30] 2018 ARIMA, SVR, RNN, DRNN, PDRNN RMSE, MAE, NRMSE 920 smart metered customers from Ireland
[31] 2017 CNN, LSTM, SVM, ANN RMSE Benchmark dataset of electricity consumption for a single residential customer
[33] 2020 Bayesian networks NRMSE, MAE, MedAE, MAAPE Real data from the Irish smart meter project
[35] 2019 LSTM, BPNN, KNN, ELM MAPE Real residential smart meter data
[34] 2023 LSTM, XGBOOST MAPE Historical load values from a region in Colombia
[27] 2021 OE, ARX, ARMAX, SVM, ANN–PSO, KNN, ANN–LM RMSE, MAPE, MAE Real-time electrical load and meteorological data of the city of Lahore in Pakistan
[38] 2021 CNN, LSTM, MLP, ANN MAE, RMSE Three open-source, publicly available datasets
[42] 2019 XGBOOST, LSTM MSE, RMSE, MAPE State Grid Corporation
[36] 2021 Persistence, SW-ARIMA, SW-ETS, SW-SVR, ConvLSTM, CLSAF Accuracy Manhattan, New York, residential building
[37] 2021 MLP, KNN, RNN MSE, MAE Five residential consumers provided by London Hydro
[40] 2021 CNN, EGWO, LSTM, SVR, MLP RMSE, MAE, MAPE Australian Energy Market Operator
[41] 2020 LSTM, BiLSTM RMSE, MAPE, CV Bangkok, Thailand; Hyderabad, India; Virginia, USA; New York, USA; and Massachusetts, USA
[23] 2023 LSTM, GRU, TS2ARCformer, TCN MAPE, MSE, MAE National College Student Mathematical Contest in Electrical Engineering
[43] 2012 EMD-FNN MSE, MAE, MAPE Zhangye, China
[44] 2018 IANN, Bagging Ensemble Model RMSE, MAPE, rRMSE Individual household energy consumption
[45] 2016 XNN, GRNN, BPNN, PSO-BP, APSOSA-BP AE, MAE, MAPE, RMSE Wind farms in Shandong Province, eastern China
[46] 2017 FNN, SSA-GDFNN, BSO-SSA-GDFNN FE, MAPE, MAE, RMSE Historical short-term wind speed data collected from Shandong Peninsula of China
[47] 2019 A hybrid model of CNN and FTS MAPE N/A
[48] 2021 CNN, LSTM, CNN-LSTM, XGBOOST, RBFN MAE, RMSE, MAPE Bangladesh power system
[49] 2023 HI-TCN, HI-ELM, HI-GRU, HI-BPNN MAE, MAPE, RMSE Pecan Street datasets contain the load power data of 25 households in the Austin area of the United States
[39] 2023 CNN, CNN-LSTM, CNN-GRU, ESN MSE, MAE, RMSE, MAPE, NRMSE Individual-Household-Electric-Power-Consumption (IHEPC) dataset from residential houses in Sceaux, Paris, and Pennsylvania–New Jersey–Maryland (PJM)
[32] 2023 SVM, GA-SVM MAPE, CV-RMSE, R2 data of a large public building in Xi town, China
Table 2. Aggregated Table with resent publications for price forecasting.
Table 2. Aggregated Table with resent publications for price forecasting.
Ref. Year Models Metrics Dataset Origin
[54] 2015 DNN, ARIMA MAPE, MAD, MFE Czech electricity spot prices
[55] 2013 ARMA, GARCH RMSE, MAPE Electricity prices in the electricity market of New England
[56] 2021 SARIMA, GARCH MAPE, RMSE Indian Energy Exchange (IEX)
[57] 2019 ARIMA, Holt-Winters, MLR MAPE Iberian electricity market
[60] 2021 ARIMA, SARIMA, SARIMAX MAE, RMSE EEX (European Energy Exchange)
[61] 2021 Exponential Smoothing MSE Ontario, Canada
[62] 2020 ARIMA, ARIMAX MAPE Belgorod region in European part of Russian coincides
[63] 2024 ARIMA, MA, LSSVM MAPE Malaysia, the Energy Commission
[66] 2012 NAIVE, SARMA, SARMAX, LSTR MAPE APX power exchange for Great Britain
[67] 2024 Generative pre-trained transformers (GPT) MCC Electricity Spanish market
[69] 2024 CNN Attention, Multi-Head Attention, CNN-GRU Attention, Stacking Ensemble, Soft Voting Ensemble, Perceptron MSE, RMSE, MAPE HEDNO (Hellenic Electricity Distribution Network Operator)
[64] 2024 GARCH, MSGARCH Coefficient, Standard Error, t-Value, p-Value Portugal’s energy market
[68] 2024 MLP, LSTM, SVM, ARIMA, GA, PLD MSE National electric system of Brazil
[70] 2023 XGBoost and Decomposition Techniques MAPE, RMSE, MDE Korean power system
[71] 2023 LSTM, CNN-LSTM, ARIMA, Random Forests, Gradient Boosted Trees, Naive, SVM, KNN, Decision Trees MAE, RMSE German spot market
[72] 2022 XGBOOST, Market Curves, XGBOOST-Market Curves MAE, WMAE OMIE (Electricity Market Operator, Spain)
[74] 2024 ANN, SVR, MLR, PSO, DO, GRO MAE, MSE, MAPE, RMSE Turkish Statistical Institute (TSI), World Bank Open Database
[73] 2022 CRITIC-GRAMPA-RELM, MPA-RELM, GA-ELM, GA-SVM, ELM, SVM SSE, MSE, RMSE, MAE Shanxi spot market
[65] 2022 NNAR, ARIMA ME, RMSE, MAE, MPE, MAPE Hungarian Power Exchang
[75] 2021 LASO, ANN, RANDOM FOREST, RVM, XGBOOST-RVM MAAPE, RMSE, MAE ENTSO-E Transparency Platform
[77] 2022 ARIMA, Lasso, CNN, ANN, GRU, LSTNet, HFnet, Uber, W-GRU, W-HFnet, GHTnet (5,9) MAPE, MAE New York Independent System Operator (NYISO)
[78] 2019 DR-R-SDAE, LSTM, R-DAE, SDAE, CNN, SVM RMSE, MAE, MAPE Ontario, Canada
[79] 2017 RNN, PCA with CNN, MLP with LM, CA with CNN, SVC-RFE with CNN MAPE Pennsylvania–New Jersey–Maryland (PJM) electricity markets
[80] 2012 ANN, ANN-ARIMA MAPE, MAE, RMSE Australian national electricity market
[81] 2023 DTR, LSTM, XGBOOST, Hybrid MAE, RMSE Several market players in the Alberta electricity market
[58] 2018 Several AR models MAE Nord Pool (NP; Northern Europe), PJM Interconnection (Northeastern United States), EPEX Germany and Austria (Central Europe)
[76] 2017 f LSSVM, BND-LSSVM, FOA-LSSVM MAPE, MAE, RMSE The daily electricity price in the northeast power grid of China
[59] 2016 several types of ARIMA FMSE Spanish electricity market
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated