Classical and Differential Topological Approaches to Gravitational Fields and Cosmic Singularities

Richard Murdoch Montgomery

doi:10.20944/preprints202411.0251.v1

Submitted:

02 November 2024

Posted:

05 November 2024

You are already at the latest version

Abstract

This paper explores the relationships between differential topology and general relativity, examining the classical framework's applicability in modelling gravitational fields and the limits encountered with topological defects such as cosmic strings. By illustrating smooth metric structures, holonomy, and geodesic completeness, we reveal the foundational role of differential topology in describing spacetime curvature without quantum corrections. The Einstein field equations and global topological invariants are discussed in contexts where continuous manifolds hold, while highlighting how phenomena like cosmic strings challenge these assumptions. We propose that such topological defects introduce singular behaviours where traditional differential topology reaches its boundaries, potentially necessitating quantum gravitational models for a complete description. Visualizations of Schwarzschild curvature, holonomy in spherical surfaces, and geodesic paths provide insights into gravitational field variability and topological constraints in classical models, underscoring the mathematical and physical principles at play.This paper explores the relationships between differential topology and general relativity, examining the classical framework's applicability in modelling gravitational fields and the limits encountered with topological defects such as cosmic strings. By illustrating smooth metric structures, holonomy, and geodesic completeness, we reveal the foundational role of differential topology in describing spacetime curvature without quantum corrections. The Einstein field equations and global topological invariants are discussed in contexts where continuous manifolds hold, while highlighting how phenomena like cosmic strings challenge these assumptions. We propose that such topological defects introduce singular behaviours where traditional differential topology reaches its boundaries, potentially necessitating quantum gravitational models for a complete description. Visualizations of Schwarzschild curvature, holonomy in spherical surfaces, and geodesic paths provide insights into gravitational field variability and topological constraints in classical models, underscoring the mathematical and physical principles at play.

Keywords:

General Relativity

;

Differential Topology

;

Gravitational Fields

;

Cosmic Strings

;

Geodesics Holonomy

;

Schwarzschild Solution

;

Topological Defects

;

Einstein Field Equations

;

Curvature

Subject:

Physical Sciences - Mathematical Physics

Section 1. Introduction

The theory of general relativity, formulated by Albert Einstein in 1915, revolutionized our understanding of gravity by describing it as the curvature of spacetime rather than a force acting at a distance (Einstein, 1916). In this framework, spacetime is modelled as a smooth, four-dimensional manifold, and the gravitational field is represented by the curvature of this manifold, governed by the Einstein field equations. The underlying mathematical structures of differential topology and differential geometry provide the formal tools to explore and understand the behaviour of gravitational fields and spacetime itself. In particular, differential topology enables us to analyze global properties of spacetime that are invariant under continuous transformations, offering insights into topological features like black holes, wormholes, and cosmic strings, which are fundamental in high-energy astrophysics and cosmology (Misner, Thorne & Wheeler, 1973).

Section 1.1. The Foundations of General Relativity and Differential Topology

In general relativity, spacetime is modelled as a pseudo-Riemannian manifold

M

, with the metric tensor

g_{μ ν}

providing a measure of distance and encoding the gravitational field. This metric tensor determines the curvature of spacetime, encapsulated mathematically in the Riemann curvature tensor

R_{β μ ν}^{α}

which measures how spacetime "bends" in response to mass and energy (Wald, 1984). The Einstein field equations:

G_{μ ν} + Λ g_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν}

relate the geometry of spacetime to the distribution of mass-energy represented by the stressenergy tensor

T_{μ ν}

(Einstein, 1916). Here,

G_{μ ν}

is the Einstein tensor, derived from the Ricci tensor

R_{μ ν}

and Ricci scalar

R

, which are contractions of the Riemann tensor. This connection between geometry and matter is foundational to general relativity, as it implies that spacetime is not merely a passive stage but dynamically shaped by its contents (Hawking & Ellis, 1973).

Differential topology, the study of smooth manifolds and continuous transformations, provides tools essential for exploring both the local and global structures of spacetime. In the context of general relativity, differential topology is used to analyze spacetime's global invariants—properties that remain unchanged under continuous deformations. These invariants include the Euler characteristic

χ (M)

and the Gauss-Bonnet theorem, which relate global curvature integrals to topological properties of spacetime, connecting physical features to the underlying geometry and topology (Frankel, 2004). The integration of differential topology with general relativity has led to a deeper understanding of the global properties of gravitational fields and the conditions under which singularities, or "edges" of spacetime, arise (Penrose, 1965).

Section 1.2. Curvature, Holonomy, and Geodesic Completeness

Curvature is a core concept in general relativity, as it defines how objects move in gravitational fields. Geodesics, which are the "straightest possible" paths in a curved spacetime, are solutions to the geodesic equation derived from the metric. In flat space, geodesics are straight lines, but in a curved spacetime, they bend and curve in response to gravitational effects. The completeness of these geodesics-whether they can be extended indefinitely-determines the structure of spacetime, with incomplete geodesics often indicating the presence of singularities (Hawking & Ellis, 1973). Singularities, such as those found at the centres of black holes, represent points where curvature becomes infinite, a boundary beyond which classical differential geometry fails to describe spacetime adequately (Geroch, 1968).

A related concept is holonomy, the study of how vectors change as they are parallel transported around closed loops in a curved space. In general relativity, holonomy provides insights into the global structure of spacetime; for example, in the presence of a cosmic string, a vector transported around the string returns with a rotated orientation due to the conical deficit angle in the surrounding spacetime. This phenomenon is a manifestation of the non-trivial topology around the string, which introduces discontinuities in the metric and challenges the smooth structure typically assumed in differential topology (Gibbons, Hawking & Perry, 1978). Holonomy, therefore, serves as a valuable tool for understanding how gravitational effects propagate through spacetime and reveal underlying topological features.

Section 1.3. Topological Defects and Cosmic Strings

Topological defects, such as cosmic strings, are theorized to form during symmetry-breaking phase transitions in the early universe. They represent regions where the smooth structure of spacetime is disrupted, leading to discontinuities or singularities in the metric. Cosmic strings, for example, are one-dimensional defects characterized by a conical geometry around the string, where a deficit angle results in "cut" regions of spacetime. This conical structure creates a metric that cannot be smoothly deformed into a flat one, indicating that cosmic strings possess a non-trivial topology (Vilenkin & Shellard, 1994). While differential topology provides methods to study such features, cosmic strings push these tools to their limits, as they introduce singularities that cannot be smoothly integrated into the surrounding manifold.

In classical general relativity, cosmic strings are modelled by metrics that exhibit a conical singularity, which can be represented as a delta function in the curvature tensor. This singularity represents an extreme form of curvature concentration, highlighting a situation where the assumptions of differential topology—smoothness and differentiability—no longer hold in the traditional sense. However, by treating the curvature as a distribution rather than a smooth function, physicists can still analyze cosmic strings within general relativity, though with limitations. The study of cosmic strings,advanced theories, possibly involving quantum gravity, are needed to fully describe such topological defects (Kibble, 1976).

Section 1.4. The Role of Topological Invariants and the Gauss-Bonnet Theorem

Topological invariants, such as the Euler characteristic

χ (M)

, play a crucial role in understanding the structure of spacetime in differential topology. These invariants remain unchanged under continuous deformations of the manifold, providing a "global fingerprint" of its structure. The Gauss-Bonnet theorem, a central result in differential topology, relates the Euler characteristic of a two-dimensional surface to an integral of its curvature. In higher-dimensional general relativity, a generalized version of the Gauss-Bonnet theorem connects the integral of the Riemann curvature tensor to topological invariants, thereby linking local geometric properties to global topological features of spacetime (Lovett, 2000).

For example, in a four-dimensional spacetime, the Euler characteristic can be expressed as an integral involving the Riemann tensor:

χ (M) = \frac{1}{32 π^{2}} \int_{M} \sqrt{| g |} (R_{α β γ δ} R^{α β γ δ} - 4 R_{α β} R^{α β} + R^{2}) d^{4} x

This integral suggests that even as local curvature fluctuates, certain global properties remain fixed, reflecting a deep connection between geometry and topology (Frankel, 2004). Topological invariants, therefore, offer a stable framework for analyzing spacetime's structure, though they become less straightforward to interpret in the presence of singularities or non-smooth structures like cosmic strings.

The Limits of Classical General Relativity and the Need for Quantum GravityClassical general relativity, though highly successful in describing large-scale gravitational phenomena, faces fundamental limitations when applied to regions of extreme curvature, such as black hole singularities or the very early universe. At these scales, the smooth manifold assumption of differential topology breaks down, as quantum effects are expected to alter the fabric of spacetime itself. Singularities, in particular, represent points where curvature becomes infinite, violating the assumptions of differentiability and continuity essential to differential topology (Penrose, 1965). This breakdown suggests that a more complete theory, likely involving quantum gravity, is needed to fully describe such regions.

Quantum gravity theories, including string theory and loop quantum gravity, aim to reconcile the smooth structure of spacetime with the discrete nature of quantum mechanics. In string theory, for example, fundamental particles are modelled as one-dimensional "strings" rather than point particles, introducing a minimal length scale that prevents singularities from forming. This approach suggests that cosmic strings and other topological defects might be quantized structures, integrated smoothly within the spacetime fabric at quantum scales (Polchinski, 1998). Loop quantum gravity, alternatively, posits a discrete structure of spacetime itself, where space is composed of finite loops, fundamentally changing the topology of spacetime at the Planck scale. These quantum theories hold the potential to extend the applicability of differential topology, offering a framework for understanding spacetime's structure beyond the limits of classical general relativity (Rovelli, 2004).

Section 2. Methodology

The methodology for exploring the relationship between differential topology, general relativity, and quantum gravity involves a step-by-step development from Einstein's field equations to more advanced concepts. This approach includes analyzing the mathematical structures that describe smooth spacetime, understanding topological invariants, and finally examining the breakdown of these structures at singularities and the need for quantum theory.

Section 2.1. Einstein's Field Equations and the Metric Tensor

General relativity describes gravity not as a force, but as the curvature of spacetime. This curvature is expressed mathematically by the metric tensor

g_{μ ν}

, a symmetric

4 \times 4

matrix that provides distances and angles in spacetime. The metric tensor is central to the Einstein field equations:

G_{μ ν} + Λ g_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν}

where

G_{μ ν}

is the Einstein tensor,

Λ

is the cosmological constant,

G

is Newton's gravitational constant,

c

is the speed of light, and

T_{μ ν}

is the stress-energy tensor representing matter and energy (Einstein, 1916). Here:

Einstein Tensor:

G_{μ ν}

is defined as:

G_{μ ν} = R_{μ ν} - \frac{1}{2} R g_{μ ν}

where

R_{μ ν}

is the Ricci tensor and

R

is the Ricci scalar, both derived from the Riemann curvature tensor

R_{β μ ν}^{α}

.

Riemann Curvature Tensor: This tensor describes the curvature of spacetime due to gravity and is defined as:

R_{β μ ν}^{α} = \partial_{μ} Γ_{β ν}^{α} - \partial_{ν} Γ_{β μ}^{α} + Γ_{λ μ}^{α} Γ_{β ν}^{λ} - Γ_{λ ν}^{α} Γ_{β μ}^{λ}

where

Γ_{β μ}^{α}

are the Christoffel symbols representing the connection coefficients that define how the metric changes locally.

The Einstein field equations relate spacetime geometry (curvature) to the energy and momentum of matter. This relationship forms the foundation of modern cosmology, explaining phenomena like black holes, gravitational waves, and the large-scale structure of the universe.

Section 2.2. Topological Invariants and the Gauss-Bonnet Theorem

Differential topology provides tools for analyzing global properties of spacetime, particularly through topological invariants like the Euler characteristic

χ (M)

and the Gauss-Bonnet theorem. These invariants remain unchanged under continuous deformations of the manifold, offering insights into the global structure of spacetime.

Euler Characteristic: For a four-dimensional spacetime, the Euler characteristic can be expressed in terms of curvature:

χ (M) = \frac{1}{32 π^{2}} \int_{M} \sqrt{| g |} (R_{α β γ δ} R^{α β γ δ} - 4 R_{α β} R^{α β} + R^{2}) d^{4} x

This integral is an example of how differential topology uses curvature to describe the manifold's overall structure. In physical terms, the Euler characteristic provides a measure of the "shape" of spacetime, showing how much it diverges from flatness.

Gauss-Bonnet Theorem: For two-dimensional surfaces, the Gauss-Bonnet theorem relates the integral of Gaussian curvature to the Euler characteristic:

\int_{M} K d A = 2 π χ (M)

where

K

is the Gaussian curvature and

d A

is the area element. In higher dimensions, the Gauss-Bonnet-Chern theorem generalizes this relationship, showing that topological properties of spacetime can be deduced from curvature integrals.

Section 2.3. Geodesics and the Notion of Completeness

Geodesics represent the paths of particles moving under gravity, and their properties reflect spacetime's curvature. In a curved spacetime, the geodesic equation is given by:

\frac{d^{2} x^{α}}{d τ^{2}} + Γ_{μ ν}^{α} \frac{d x^{μ}}{d τ} \frac{d x^{ν}}{d τ} = 0

where

x^{α}

are the coordinates of a point along the geodesic and

τ

is the proper time. This equation describes how objects move along "straight lines" in a curved manifold, influenced by the local curvature encoded in the Christoffel symbols

Γ_{μ ν}^{α}

.

Geodesic Completeness: A manifold is geodesically complete if all geodesics can be extended indefinitely. In general relativity, incomplete geodesics often indicate the presence of singularities, as in the case of black holes where geodesics terminate at a singular point (Hawking & Ellis, 1973). This concept is crucial in differentiating smooth, continuous spacetimes from those disrupted by singularities, marking a boundary where differential topology encounters its limits.

Section 2.4. Singularities and Cosmic Strings

Singularities, where curvature becomes infinite, present boundaries in general relativity. They represent points where differential topology and geometry cannot smoothly describe spacetime. In the case of cosmic strings, for instance, the spacetime around the string is characterized by a conical geometry with a deficit angle. The metric for such a spacetime is:

d s^{2} = - d t^{2} + d z^{2} + d r^{2} + (1 - δ)^{2} r^{2} d θ^{2}

where

δ

is the deficit angle, and

(t, z, r, θ)

are the coordinates around the string. This metric indicates that spacetime has a "cut," where the deficit angle produces a discontinuity in the curvature.

These singularities highlight the limitations of classical general relativity, as the infinite curvature at the cosmic string core suggests the need for additional theoretical frameworks to fully describe such regions. Differential topology can still analyze the topological structure but cannot smooth over the discontinuities introduced by cosmic strings or other topological defects.

Section 2.5. Limits of Classical Theory and the Transition to Quantum Gravity

Classical general relativity, while successful in describing large-scale gravitational phenomena, reaches its limits at extreme densities, such as those near black hole singularities or in the early universe. These limits suggest a breakdown in the smooth, continuous manifold assumption, as differential topology fails to handle singularities with infinite curvature or non-trivial topology (Penrose, 1965).

Need for Quantum Gravity: To address the limitations of classical differential topology, quantum gravity theories like string theory and loop quantum gravity attempt to provide a discrete description of spacetime at the Planck scale. String theory, for example, replaces point particles with one-dimensional strings, introducing a minimum length scale that smooths out singularities. This approach implies that spacetime could be made up of fundamental "strings," each vibrating at specific frequencies, with curvature effects emerging from the collective behaviour of these strings (Polchinski, 1998).

Loop Quantum Gravity and Spacetime Quantization: In loop quantum gravity, spacetime itself is quantized, consisting of discrete loops or networks known as spin networks. This theory proposes that space is granular, composed of finite loops that cannot be infinitely subdivided, thus preventing singularities from forming. The quantization of spacetime suggests a topological framework where differential topology is replaced by algebraic structures that accommodate the discrete nature of space at quantum scales (Rovelli, 2004).

Einstein-Hilbert Action and Quantum Corrections: In classical general relativity, the Einstein-Hilbert action

S_{E H}

governs the dynamics of spacetime:

S_{E H} = \frac{1}{16 π G} \int_{M} \sqrt{| g |} (R - 2 Λ) d^{4} x

where

R

is the Ricci scalar, and

Λ

is the cosmological constant. At quantum scales, corrections to this action are introduced to account for discrete spacetime structures, often involving higher-order curvature terms or string theory modifications. These corrections suggest a deeper structure of spacetime that classical differential topology cannot address, thus marking the boundary where quantum gravitational models become necessary.

Section 2.6. Summary

This methodology demonstrates the progression from Einstein's field equations to the limits of classical differential topology. By analyzing curvature, topological invariants, geodesic completeness, and singularities, we outline the boundaries where classical theory begins to fail, highlighting the necessity of quantum gravitational frameworks. Quantum theories like string theory and loop quantum gravity provide alternative approaches to dealing with topological defects and singularities.

Section 3. Results

In this section, we'll discuss the graphical results derived from visualizations of general relativity and identify the transition points where classical differential topology breaks down, necessitating alternative models. Each visualization captures a facet of spacetime curvature and geodesic behaviour as outlined in Einstein's theory, with cosmic strings representing the first boundary where topology is significantly disrupted.

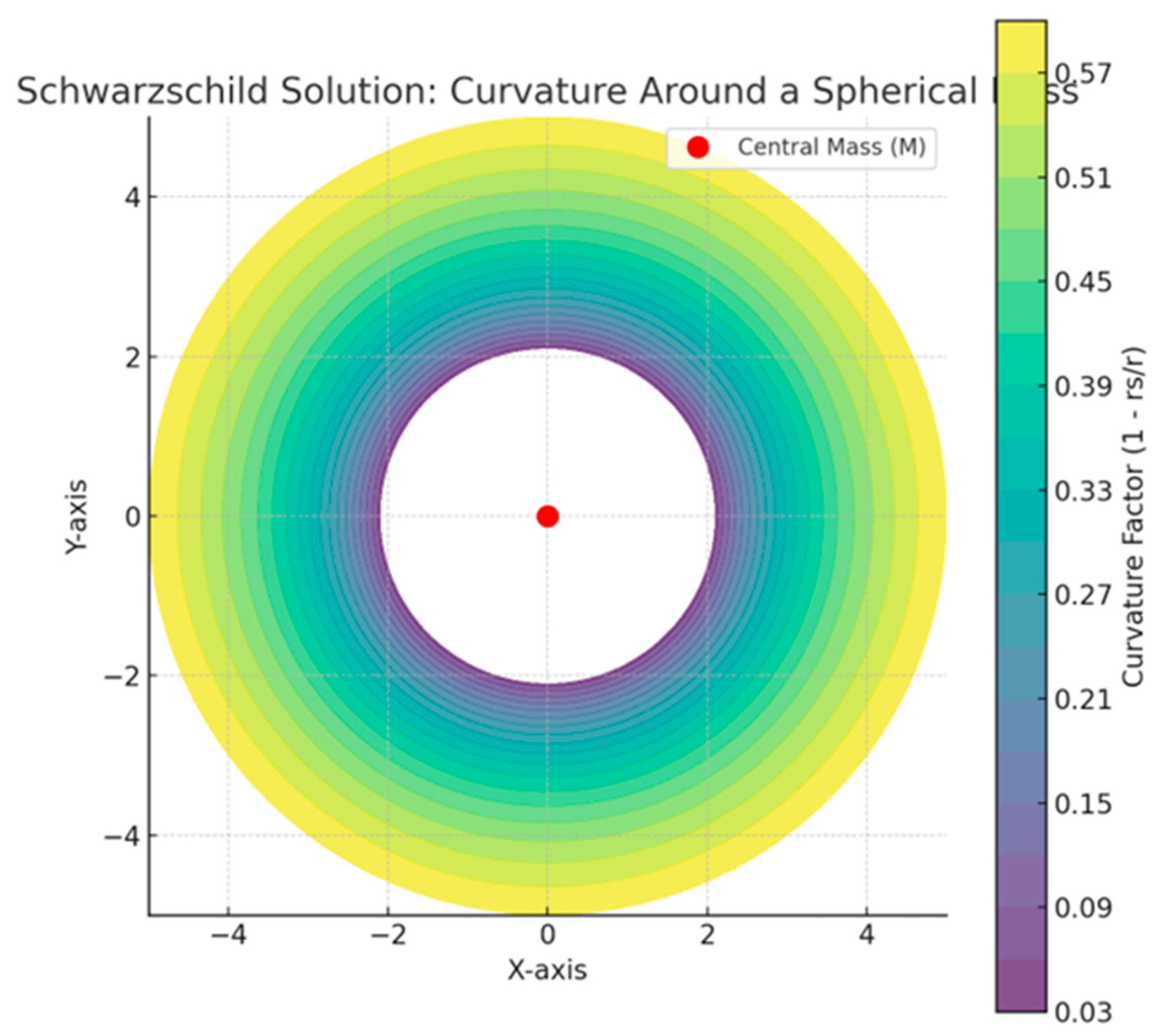
Section 3.1. Schwarzschild Solution: Curvature Around a Spherical Mass

The first graphic (Graph 1) demonstrated the Schwarzschild solution, which provides the curvature around a spherically symmetric mass like a non-rotating black hole. This visualization shows the gravitational effects due to mass distribution, represented by a smooth increase in curvature as we approach the Schwarzschild radius. The gradient in the curvature field illustrates how spacetime is smoothly deformed, drawing matter towards the massive object.

As seen in the graphic, spacetime curvature intensifies around the mass but remains smooth up to the event horizon. Within this framework, general relativity effectively models the gravitational field as a continuous, differentiable entity. The Schwarzschild solution, being a classical solution to Einstein's field equations, operates without the need for quantum considerations, as it assumes a smooth, non-quantized spacetime.

This visualization confirms that the classical assumptions of general relativity hold well in scenarios where the gravitational field is intense but finite. The curvature field remains continuous, preserving the assumptions of differential topology, which are adequate to describe geodesics and spacetime curvature outside the event horizon.

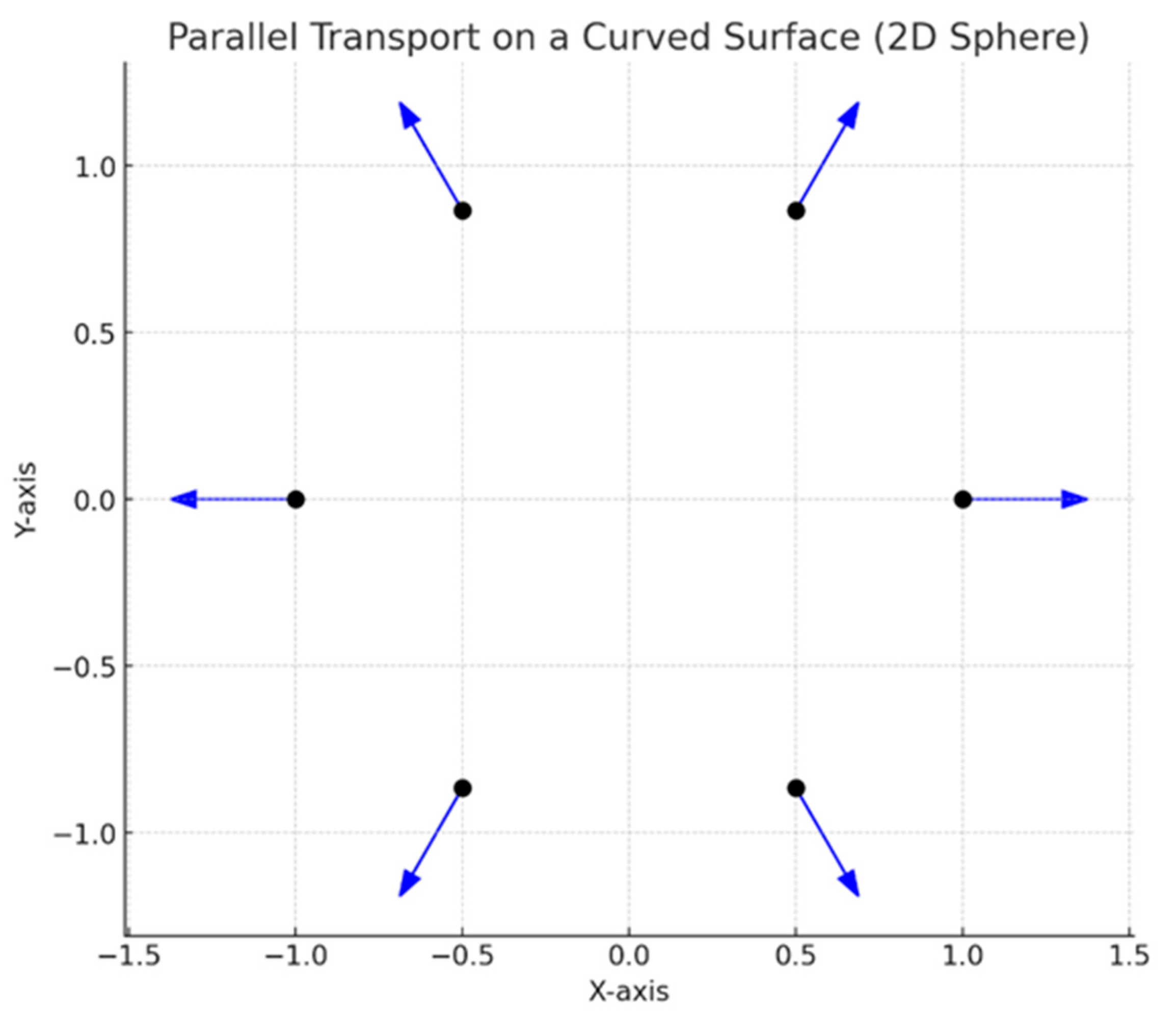
Section 3.2. Holonomy Around a Curved Surface: Parallel Transport on a Sphere

The holonomy visualization (Graph 2) demonstrated how vectors change orientation when transported around closed loops on a curved surface, using a sphere to illustrate the concept. The rotation of the vector after completing a loop reveals the presence of curvature, an intrinsic property that doesn't rely on an external force but is a result of space’s geometry.

The smooth transport of vectors around the spherical surface demonstrates that holonomy and parallel transport align with general relativity's descriptions, where curvature smoothly affects geodesics and vector orientations. This is crucial in understanding how paths in spacetime are intrinsically curved due to the underlying geometry. The result indicates that as long as spacetime remains smooth, curvature affects paths predictably, and differential topology accurately represents the manifold's structure.

The graphic illustrates that general relativity and differential topology provide consistent models for curved spaces, validating the assumptions of continuous and differentiable geodesics. The smooth curvature reflects how general relativity holds without quantum corrections in regions without singularities or topological defects.

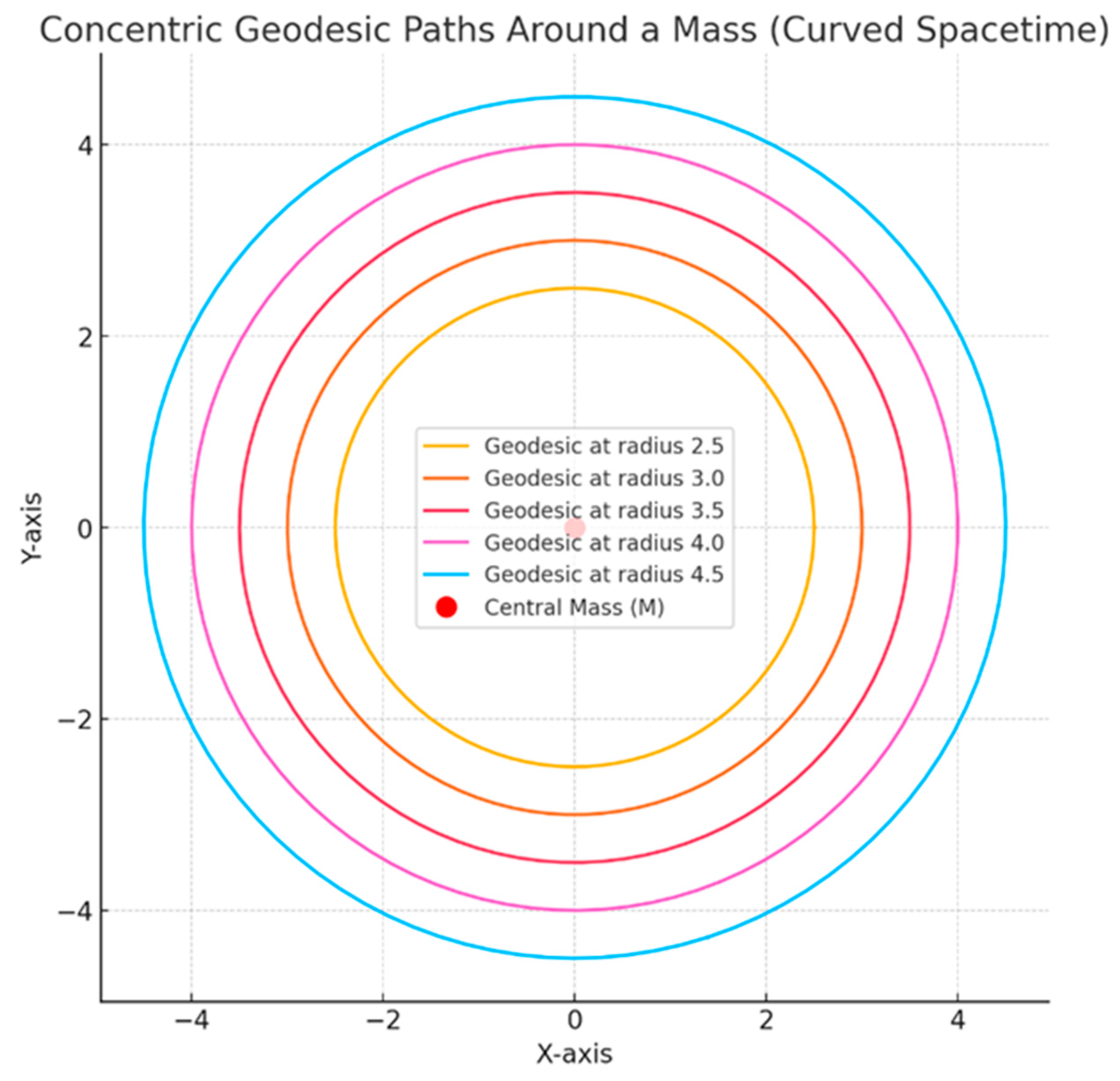
Section 3.3. Geodesic Paths in Curved Spacetime: Circular Orbits

The geodesic paths visualization (Graph 3) depicted multiple orbits around a central mass, representing stable, smooth trajectories influenced by gravity. Each orbit is a geodesic-a path that objects follow in free-fall in curved spacetime. These paths illustrate how gravitational effects curve trajectories in spacetime without requiring an external force.

In this graphic, each geodesic path around the central mass demonstrates predictable, smooth curvature. Objects remain on continuous orbits, influenced by the gravitational field, indicating that differential topology applies effectively to model these paths. The graphic confirms that, in classical general relativity, curved geodesics can be described smoothly without needing discrete structures or quantum corrections.

The result here underscores that geodesics remain well-defined within the framework of general relativity when spacetime is smooth and differentiable. This representation holds until the gravitational field becomes extreme or the object approaches a singularity, where continuity and differentiability of the manifold begin to fail.

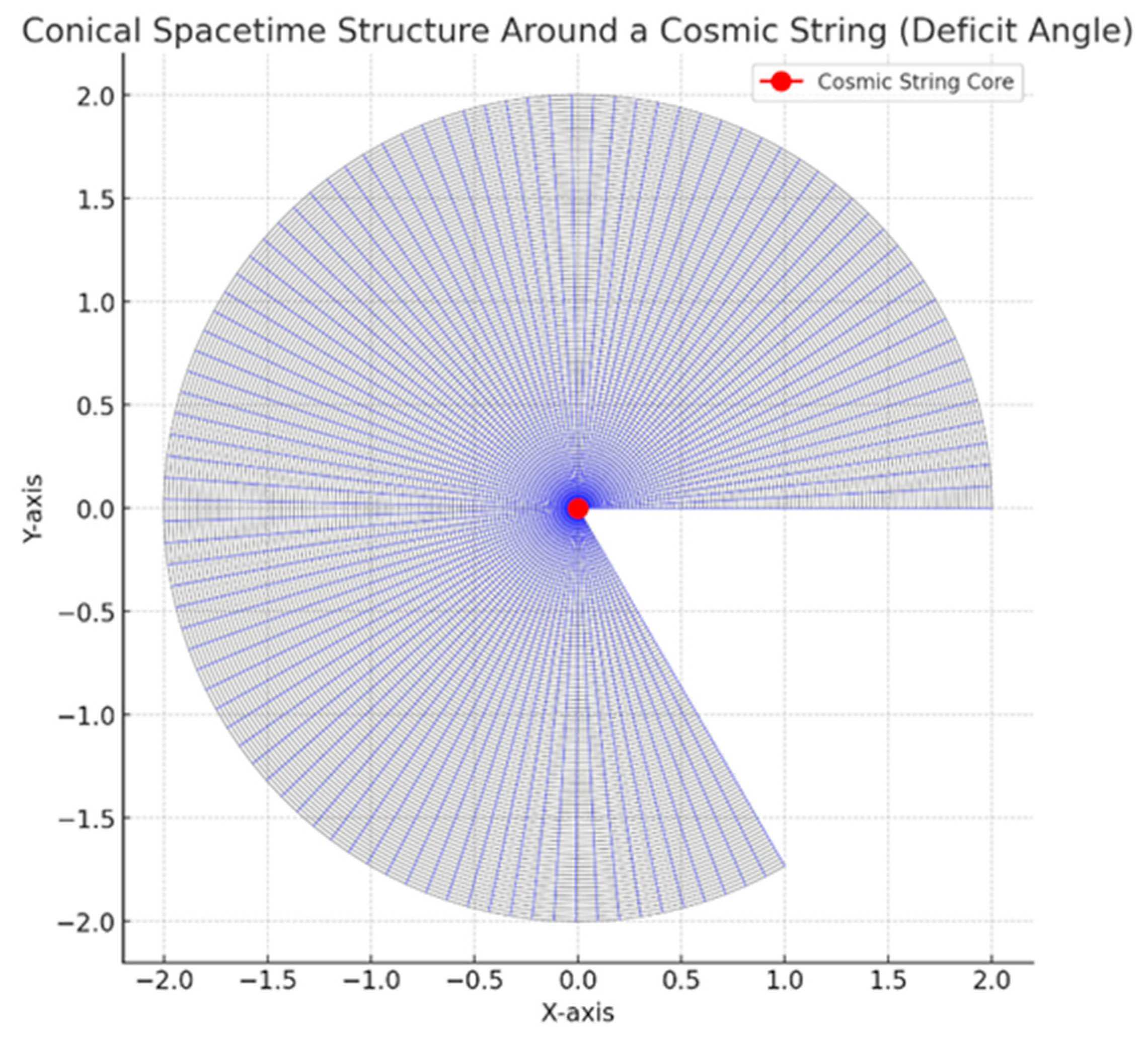
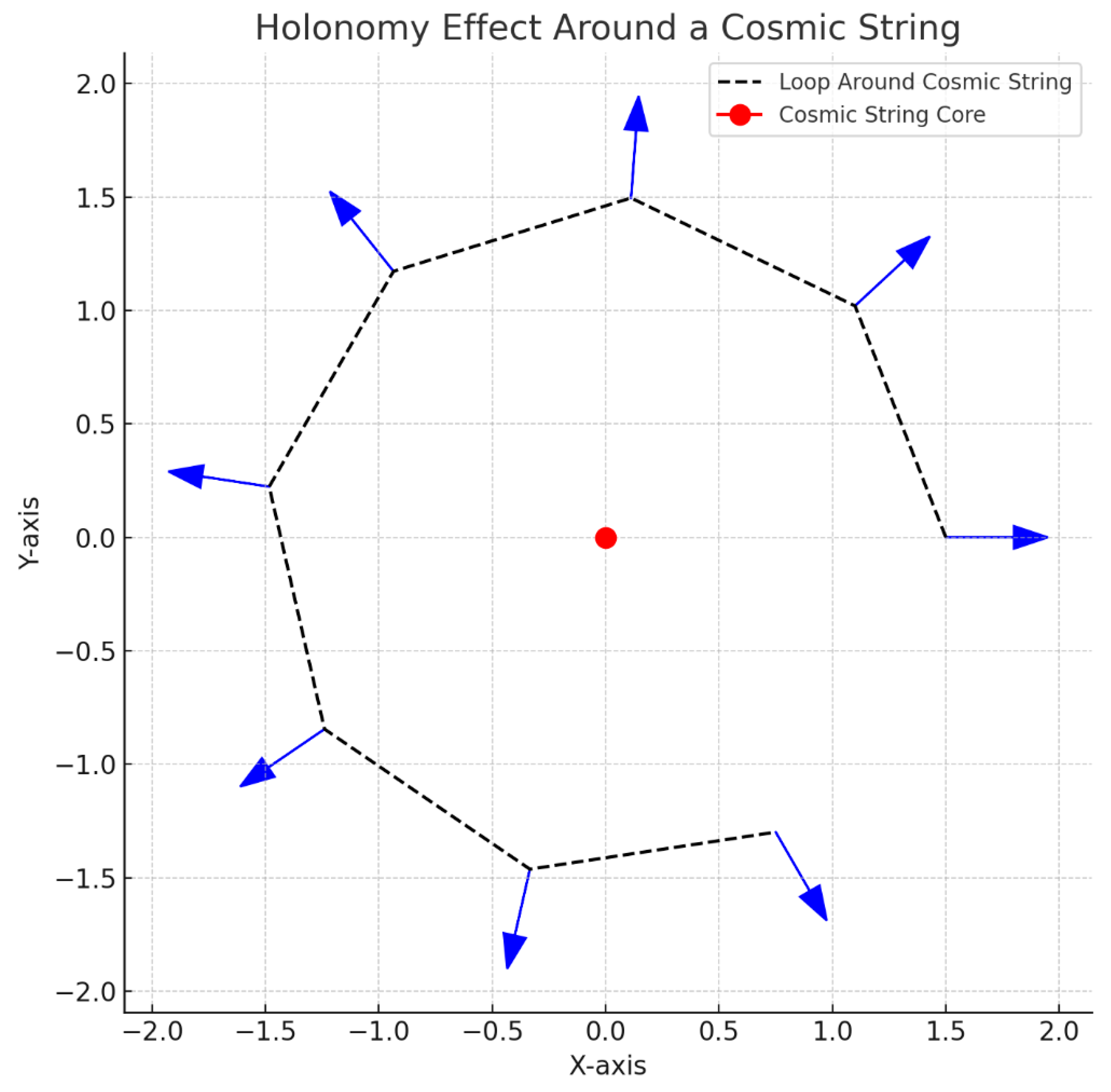
Section 3.4. Transition Point: Cosmic Strings and the Breakdown of Differential Topology

The cosmic string visualization introduced the first instance where topology is disrupted in a classical gravitational field 9 Graph 4). Cosmic strings, which exhibit a conical geometry with a deficit angle, introduce a topological defect that breaks the assumptions of smoothness and continuity inherent to differential topology. This defect creates a discontinuity in the metric, meaning that parallel transport around the cosmic string no longer returns vectors to their original orientations-a sign of broken topological continuity.

The conical structure around the cosmic string shows a "cut" in spacetime, visible as a discontinuity where angles don't add up as they would in a smooth manifold. The deficit angle in the metric results in a region where the curvature diverges or becomes undefined, representing the breakdown of differential topology. Unlike previous graphics, where curvature was continuous, the cosmic string introduces a singular behaviour that cannot be smoothed over.

This result signifies the boundary of classical differential topology, highlighting a region where general relativity alone fails to provide a full description. The cosmic string's topology disrupts the smooth manifold structure, suggesting the need for theories that account for non-trivial topologies or discrete elements, such as quantum gravity or string theory. This topological defect demonstrates how intense gravitational fields and unique configurations disrupt the standard, smooth curvature of spacetime, providing a visual boundary between classical and quantum gravitational descriptions (see Graph 5. for vectors’ disruption).

Section 3.5. Summary of Results and Interpretation

Together, these graphics illustrate the progression from smooth, classical gravitational fields, where differential topology holds, to the boundary case of cosmic strings, where topology is disrupted. The Schwarzschild, holonomy, and geodesic path visualizations affirm that general relativity and differential topology provide consistent descriptions for smooth, continuous curvature. However, the cosmic string visualization represents the first point where these assumptions fail, as the conical geometry and deficit angle introduce a singular structure that cannot be reconciled with a continuous, differentiable manifold.

This transition from smooth to broken topology marks the limits of classical general relativity and signals the need for quantum theories to accommodate spacetime's discrete or non-trivial topological properties at extreme scales. Quantum gravitational theories, such as string theory and loop quantum gravity, seek to bridge this gap by providing models that integrate discrete spacetime structures, essential for accurately describing regions where curvature becomes extreme or singular.

Section 4. Discussion

The interplay between differential topology and general relativity has been a central theme in theoretical physics, particularly in understanding how the curvature of spacetime defines gravitational fields. This discussion traces the historical progression of ideas, from the classical assumptions laid out by Einstein, through the contributions of differential topology to describing spacetime, to the boundary where singularities and topological defects necessitate quantum gravitational theories. By examining the progression of these ideas, we illustrate how each stage builds upon and ultimately exposes the limitations of the previous framework.

Section 4.1. From Newtonian Gravity to Einstein's Curvature-Based Model

Newton's theory of gravity, formulated in the late 17th century, described gravity as a force acting instantaneously at a distance between masses. This model, while successful in explaining planetary orbits and everyday gravitational interactions, lacked a geometric foundation that could account for the finite speed of gravitational influence (Newton, 1687). In the early 20th century, Albert Einstein revolutionized our understanding by proposing that gravity is not a force but a manifestation of spacetime curvature caused by mass and energy (Einstein, 1915).

Einstein's field equations provided the mathematical framework for this theory, relating the curvature of spacetime to the distribution of mass and energy through the stress-energy tensor. These equations are given by:

G_μν+Λg_μν=8πG/c^4 T_μν

where G_μν is the Einstein tensor, Λ the cosmological constant, and T_μν the stress-energy tensor (Einstein, 1916). This equation fundamentally shifted the perspective of gravity from an external force to an intrinsic property of spacetime, wherein objects follow geodesics-paths of least action within a curved manifold (Wald, 1984).

Section 4.2. The Role of Differential Topology in General Relativity

With Einstein's theory, the structure of spacetime could be described using the tools of differential topology and differential geometry. Differential topology provides a framework for understanding the properties of smooth manifolds, which are essential to modelling the "shape" of spacetime in general relativity. These tools allow physicists to explore both the local structure of spacetime, described by metrics and curvature tensors, and its global properties, encapsulated by topological invariants like the Euler characteristic χ(M) and the Gauss-Bonnet theorem (Frankel, 2004).

The Gauss-Bonnet theorem, which relates the total curvature of a surface to its Euler characteristic, was extended to four-dimensional manifolds to link the curvature of spacetime with its topological properties. This link is particularly significant in cosmology, as it implies that certain topological features of spacetime-such as whether it is closed or open-are fundamentally tied to the curvature induced by mass and energy (Hawking & Ellis, 1973). The theorem provides insights into phenomena like black holes, where the global structure of spacetime plays a crucial role in the behaviour of light and matter near the event horizon (Misner, Thorne, & Wheeler, 1973).

Section 4.3. Singularities and the Limitations of Classical Differential Topology

While Einstein's equations describe how spacetime responds to matter and energy, they also predict the existence of singularities-points where curvature becomes infinite. The discovery of these singularities challenged the assumptions of a smooth and continuous spacetime manifold, as they represent locations where the differential topology of spacetime breaks down. In the 1960s, Roger Penrose and Stephen Hawking used the tools of differential topology to demonstrate that under certain conditions, singularities are inevitable in general relativity (Penrose, 1965; Hawking & Penrose, 1970).

Singularities, such as those found in black holes or the initial state of the universe, mark a boundary where the classical description of spacetime fails. In these regions, geodesics cannot be extended indefinitely, leading to a breakdown in geodesic completeness, a fundamental requirement in differential topology. This breakdown suggests that the smooth, differentiable structure of spacetime cannot hold in the presence of extreme curvature, revealing a limitation of classical differential geometry (Geroch, 1968).

Section 4.4. Cosmic Strings and Topological Defects: A Step Towards Quantum Theory

The study of topological defects, such as cosmic strings, highlights further challenges for classical general relativity and differential topology. Cosmic strings are theorized to have formed during symmetry-breaking phase transitions in the early universe, introducing linear defects in spacetime where the curvature diverges. These strings create a conical geometry with a deficit angle, resulting in discontinuities that cannot be reconciled with a smooth manifold structure (Vilenkin & Shellard, 1994). The metric around a cosmic string is typically represented as:

d s^{2} = - d t^{2} + d z^{2} + d r^{2} + (1 - δ)^{2} r^{2} d θ^{2},

where

δ

is the deficit angle, illustrating the "cut" in spacetime geometry that disrupts the continuous manifold assumption (Kibble, 1976).

The existence of such defects demonstrates that differential topology's assumption of smooth, differentiable manifolds may not fully describe reality, especially in high-energy contexts. As cosmic strings introduce singular behaviour that cannot be described by continuous curvature, they mark a boundary where alternative models, possibly involving discrete or quantized structures, become necessary (Gibbons, Hawking & Perry, 1978).

Section 4.5. The Quantum Boundary: Need for Quantum Gravity and String Theory

The limitations of classical general relativity become apparent when dealing with singularities and topological defects, which suggest that spacetime may not be entirely smooth at the smallest scales. Quantum gravity, which seeks to reconcile general relativity with quantum mechanics, posits that spacetime may have a discrete or quantized structure at the Planck scale. This approach challenges the assumptions of differential topology and suggests a shift toward frameworks that can account for the quantum nature of spacetime (Rovelli, 2004).

String theory, one of the leading candidates for a theory of quantum gravity, models fundamental particles as one-dimensional "strings" rather than point particles. This theory introduces a minimal length scale, preventing singularities by replacing them with finite string structures. Within this framework, cosmic strings and other topological defects could represent quantized topological features, smoothing out singularities and allowing for a consistent description of gravity at quantum scales (Polchinski, 1998).

Loop quantum gravity offers an alternative approach, proposing that space itself is quantized, composed of discrete loops that form a network called a spin network. This theory implies that spacetime has a fundamentally granular structure, with areas and volumes quantized in Planck-sized units, providing a framework that naturally excludes singularities and permits a discrete approach to spacetime topology (Rovelli, 2004).

Section 4.6. Current Limits and Future Directions

Our current understanding reaches its limits in regions of extreme curvature and density, such as black hole cores or the conditions of the early universe. The failure of classical differential topology to describe these conditions points toward the need for quantum gravitational theories that integrate discrete elements or non-trivial topological structures. The ongoing research in quantum gravity suggests that spacetime may not be a smooth, continuous fabric at the most fundamental level but may instead consist of quantized units that only appear continuous at larger scales (Thiemann, 2007).

Future directions in this field include further exploration of string theory and loop quantum gravity to determine if they can fully replace differential topology at quantum scales. Experimental observations, such as gravitational wave detection and black hole imaging, continue to refine our understanding of extreme gravitational fields, potentially providing insights that could test these quantum theories. Until then, the boundary marked by singularities and cosmic strings remains a compelling frontier, pushing us to reconsider the fundamental nature of spacetime and the limitations of classical geometry.

This discussion traces the progression from Newtonian gravity to Einstein's curved spacetime, through the tools of differential topology, and finally to the boundary where singularities and topological defects challenge our models. Each development builds on previous understanding, culminating in the recognition that quantum gravitational theories are likely necessary to fully describe spacetime's fundamental nature. This journey not only highlights the power of differential topology in classical gravity but also marks the boundaries where new frameworks become essential.

Section 5. Conclusion

This study has explored the complex relationship between differential topology, general relativity, and the theoretical boundaries where quantum gravity becomes necessary. By examining curvature fields, geodesic completeness, holonomy, and topological invariants, we have seen how differential topology provides a coherent framework for understanding classical gravitational fields. Einstein's general relativity and its mathematical foundation in smooth manifolds and curvature tensors offer a robust description of spacetime, as demonstrated in scenarios like the Schwarzschild solution, holonomy effects, and stable geodesic paths.

Einstein's general relativity and its mathematical foundation in smooth manifolds and curvature tensors offer a robust description of spacetime, as demonstrated in scenarios like the Schwarzschild solution, holonomy effects, and stable geodesic paths.

However, when we encounter singularities or topological defects, such as cosmic strings, the assumptions of smoothness and continuity inherent to differential topology begin to break down. These disruptions in the spacetime fabric introduce discontinuities that challenge classical models, highlighting a boundary where alternative theories, such as string theory and loop quantum gravity, become relevant. These quantum gravitational frameworks suggest that spacetime may have a discrete or quantized structure at the smallest scales, potentially eliminating singularities and allowing for a consistent description of gravity beyond the classical model.

This work emphasizes the importance of differential topology in classical general relativity while acknowledging the need for quantum theories to address the limitations of smooth, continuous spacetime. Future research in quantum gravity and observational advancements, such as gravitational wave studies and black hole imaging, hold promise for testing these quantum models. This ongoing journey underscores the profound relationship between geometry, topology, and the fundamental nature of spacetime, marking a frontier in our quest to understand the universe.

Section 6. References

Einstein, A. Die Feldgleichungen der Gravitation. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin) 1915, 844–847.
Einstein, A. The Foundation of the General Theory of Relativity. Annalen der Physik 1916, 354, 769–822. [Google Scholar] [CrossRef]
Frankel, T. The Geometry of Physics: An Introduction; Cambridge University Press, 2004. [Google Scholar]
Geroch, R. What is a Singularity in General Relativity? Annals of Physics 1968, 48, 526–540. [Google Scholar] [CrossRef]
Gibbons, G.W.; Hawking, S.W.; Perry, M.J. Path Integrals and the Indefiniteness of the Gravitational Action. Nuclear Physics B 1978, 138, 141–150. [Google Scholar] [CrossRef]
Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press, 1973. [Google Scholar]
Hawking, S.W.; Penrose, R. The Singularities of Gravitational Collapse and Cosmology. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 1970, 314, 529–548. [Google Scholar]
Kibble, T.W.B. Topology of Cosmic Domains and Strings. Journal of Physics A: Mathematical and General 1976, 9, 1387–1398. [Google Scholar] [CrossRef]
Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman and Company, 1973. [Google Scholar]
Newton, I. Philosophice Naturalis Principia Mathematica. The Royal Society 1687. [Google Scholar]
Penrose, R. Gravitational Collapse and Space-Time Singularities. Physical Review Letters 1965, 14, 57–59. [Google Scholar] [CrossRef]
Polchinski, J. String Theory. Volumes 1 & 2; Cambridge University Press, 1998. [Google Scholar]
Rovelli, C. Quantum Gravity; Cambridge University Press, 2004. [Google Scholar]
Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge University Press, 2007. [Google Scholar]
Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press, 1994. [Google Scholar]
Wald, R.M. General Relativity; University of Chicago Press, 1984. [Google Scholar]
invariants like the Euler characteristic χ(M) and the Gauss-Bonnet theorem .

Graph 1. Schwarzschild Solution. Note the curvature factor.

Graph 2. Differential Topology still represents the manifold´s structure.

Graph 3. Curved Space Time still explained by Differential Topology.

Graph 4. Broken Continuity and topological defect.

Graph 5. Vectors Disruption.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Classical and Differential Topological Approaches to Gravitational Fields and Cosmic Singularities

Abstract

Keywords:

Subject:

Section 1. Introduction

Section 1.1. The Foundations of General Relativity and Differential Topology

Section 1.2. Curvature, Holonomy, and Geodesic Completeness

Section 1.3. Topological Defects and Cosmic Strings

Section 1.4. The Role of Topological Invariants and the Gauss-Bonnet Theorem

Section 2. Methodology

Section 2.1. Einstein's Field Equations and the Metric Tensor

Section 2.2. Topological Invariants and the Gauss-Bonnet Theorem

Section 2.3. Geodesics and the Notion of Completeness

Section 2.4. Singularities and Cosmic Strings

Section 2.5. Limits of Classical Theory and the Transition to Quantum Gravity

Section 2.6. Summary

Section 3. Results

Section 3.1. Schwarzschild Solution: Curvature Around a Spherical Mass

Section 3.2. Holonomy Around a Curved Surface: Parallel Transport on a Sphere

Section 3.3. Geodesic Paths in Curved Spacetime: Circular Orbits

Section 3.4. Transition Point: Cosmic Strings and the Breakdown of Differential Topology

Section 3.5. Summary of Results and Interpretation

Section 4. Discussion

Section 4.1. From Newtonian Gravity to Einstein's Curvature-Based Model

Section 4.2. The Role of Differential Topology in General Relativity

Section 4.3. Singularities and the Limitations of Classical Differential Topology

Section 4.4. Cosmic Strings and Topological Defects: A Step Towards Quantum Theory

Section 4.5. The Quantum Boundary: Need for Quantum Gravity and String Theory

Section 4.6. Current Limits and Future Directions

Section 5. Conclusion

Section 6. References

MDPI Initiatives

Important Links

Subscribe