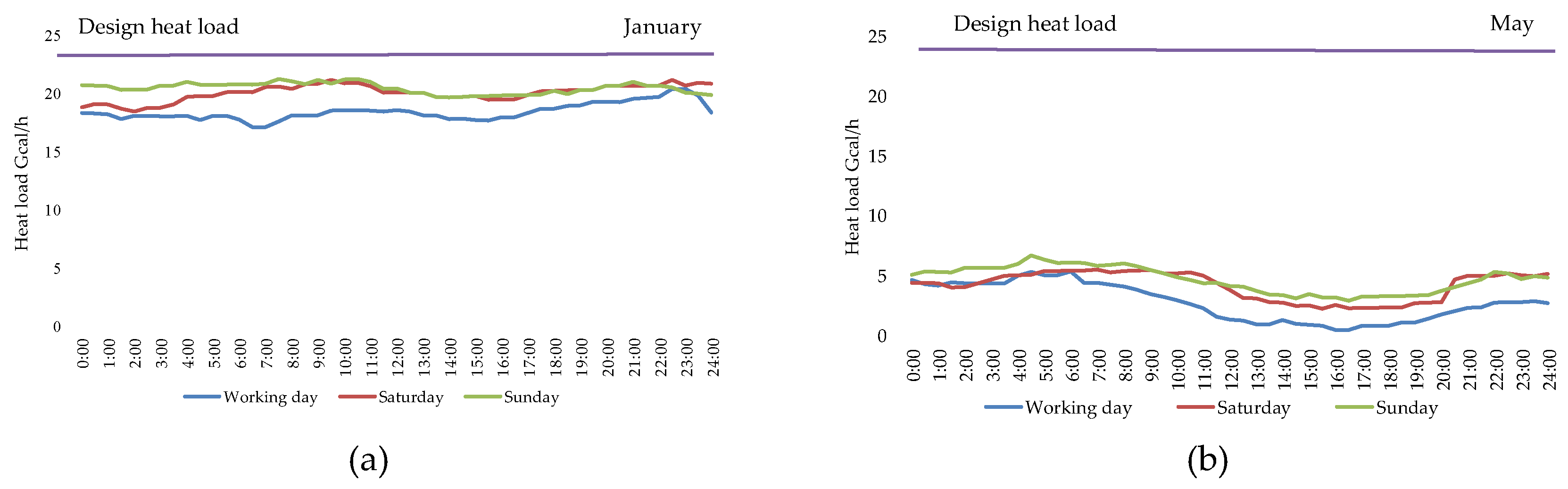Scientific Workflow-Based Synthesis of Microgrids

1. Introduction

In the 21st century, the development of a reliable, sustainable, environmentally friendly, and cost-effective energy supply is of great importance. However, the inefficient use of fossil fuels has resulted in significant environmental pollution. In addition, the disparate planning and operation of different energy sources has resulted in significant energy waste. The advent of new conversion technologies and several generations of more environmentally friendly energy sources has prompted a re-evaluation of the role of Multi-Energy Systems (MESs) in energy production, transmission, and consumption [1].

A microgrid is a small-scale MES that includes a variety of elements, including combined heat and power (CHP) generators and various types of energy storage systems, as well as distribution networks to deliver heat and electricity to isolated communities [2]. In light of these considerations, it is imperative to synthesize the most effective microgrids.

There are three key terms that are commonly used in the context of microgrid synthesis: optimization model, modeling environment, and configuration.

Optimization models are concrete representations of real microgrids with specific levels of detail of modeling aspects [3], including spatial, temporal, technological, economic, and other dimensions. Such representations may include multiple hard- or soft-linked submodels to enhance understanding of technical, environmental, and policy issues. Models are constructed from model generators that generate them based on a specific analytical and mathematical methodology (e.g., by using a predefined set of equations representing different energy technologies). For example, a methodology might minimize the annualized investment and operating costs of the microgrid while improving the environment by reducing fossil fuel consumption.

A modeling environment can be defined as a structured software toolbox that includes a set of specialized tools, model generators, and specific models (renewable energy models) [3]. It allows us to explore optimal microgrid alternatives from a variety of perspectives.

A microgrid configuration describes the potential infrastructure, which includes energy facilities and associated data on natural, climatic, social, economic, and other factors. For example, renewable energy modeling requires the input of a variety of meteorological data sets, including but not limited to the air temperature, atmospheric pressure, humidity, density, solar radiation, wind speed, and direction.

One of the major problems associated with microgrid optimization models is their inherent computational complexity, which is mainly influenced by the level of detail of different modeling dimensions [4]. The microgrid models are designed to provide a comprehensive system-wide perspective and sufficient levels of detail for effective decision making. In addition, any increase in the level of detail of any of the dimensions leads to an exponential increase in computational time. As a result, computationally tractable microgrid models are characterized by either a narrow perspective with a high level of detail or a broad scope with minimal detail. Such simplifications do not guarantee the establishment of the intended microgrid synthesis, especially with respect to the sustainability of the energy supply. This problem arises from the discrepancies in the level of detail of different dimensions, which in turn affects the practical applicability of microgrid optimization results.

To overcome the discrepancies in the level of detail, a number of strategies have been developed with the goal of reducing the amount of computational resources required. These strategies can be classified as either model-based or solver-based [5]. While each model-based technique implies modifications of a model with respect to the conceptual layer and thus is based on the same solution algorithm, solver-based strategies concern all techniques that can be applied in a solver package. However, they are specific implementations of the same solution algorithms or their adaptation by appropriate parameterization.

Recent microgrid synthesis approaches [6] facilitate the construction of optimization models with different modeling environments, such as ETHOS.FINE [7], which integrate the model-based techniques to reduce the spatial or temporal level of detail. However, these approaches still lack capabilities for intelligent management of available computational resources, and comprehensive testing of model-based and solver-based strategies to strike a balance between model computational complexity and acceptable solution time with little loss of modeling accuracy. For example, one of the main results of testing model-based acceleration strategies in the BEAM-ME project [5] is that the computational time of large models can be reduced by a factor of up to 10 by applying model reduction heuristics. A drawback is the reasonable limitation in accuracy. The next result is related to the development of the solver PIPS-IPM++, which allows the parallel solution of linear optimization problems on High-Performance Computing (HPC) architectures. The progress made in testing HPC solver-based acceleration strategies allows to reduce the solution time of large models by a factor of up to 26 without affecting the accuracy [5].

However, the above and other well-known approaches to the multi-energy system synthesis do not address all existing challenges. In this context, we propose a Subject-Oriented Environment (SOE) for solving a multi-energy microgrid optimization problem. The SOE consists of a service-oriented application for solving the aforementioned problem using the resources of a Heterogeneous Distributed Computing Environment (HDCE) and specialized testbeds for software testing and verification, data validation, and optimization algorithm selection in the context of a specific microgrid model. Problem-solving is based on the design and execution of a scientific workflow that determines a sequence of operations for optimizing a multi-energy microgrid. The operations are implemented as services.

2. Related Work

2.1. Energy System Synthesis

We consider the microgrid synthesis as structural and parametric optimization of local MESs. The objective of such optimization is to select the optimal types of energy equipment and determine their optimal locations for installation. In general, it is formulated as a parametric optimization problem. Accordingly, structural and parametric optimization is a more complicated problem from a mathematical and computational point of view compared to parametric optimization. The objective of MES synthesis is to identify an optimal system configuration. Such a configuration represents the optimal combination of disparate energy technologies with the most appropriate equipment unit sizes for the optimal operation of the selected equipment.

The conventional methodology for MES synthesis involves the manual creation of numerous system configurations that are significantly different from each other. The primary disadvantage of this methodology is the significant subjectivity inherent in the decision-making process, which depends on the expertise and experience of the MES configuration designer.

The two-stage decision-making process inherent in the synthesis problem provides the basis for implementing a two-level methodology to address complex, large-scale problems [8]. The high-level methods determine the investments, placements, and dimensions of the equipment, while the low-level methods are responsible for making decisions about the operation of the equipment units. Optimization of high-level decisions requires the simultaneous consideration of low-level decisions. Accordingly, the computational complexity increases hierarchically from the lowest to the highest level of a methodology.

In the literature, two methodologies are highlighted with respect to automating the MES synthesis problem. These methodologies are based on superstructure-based and superstructure-free synthesis, respectively.

The superstructure-based synthesis includes the following main sequential stages [9]:

• Development of a superstructure containing all feasible alternative energy process structures;
• Implementation of the superstructure for a mathematical programming solver;
• Optimization of a system configuration using the solver.

Unlike to superstructure-based synthesis, superstructure-free synthesis does not use the combinatorial search space to obtain alternative energy process structures. The method dynamically generates these structures and then evaluates them using an Energy System Optimization Model (ESOM). The main advantage of the superstructure-based methodology is the use of rigorous optimization techniques at all stages of synthesis. However, this methodology often results in large, non-convex mathematical problems that are difficult to solve [10]. In many cases, the superstructure-free methodology uses meta-heuristic techniques at the highest level of synthesis. It should be noted that meta-heuristic techniques do not guarantee the optimality of the solution obtained. Nevertheless, these techniques are capable of identifying a highly satisfactory solution in a relatively short time [11].

In contrast to the traditional approach, both types of automated synthesis have the potential to yield a large number of MES configurations. This is a significant advantage in the context of decision support. Decision-makers typically seek to obtain several promising MES configurations of high quality, which can then be further evaluated in light of additional information that may emerge in practice. Accordingly, an optimal but singular MES configuration is typically insufficient.

2.2. The Concept of the Energy Hub

The increasing number of interconnections between microgrids, a consequence of their development, gave rise to the concept of the energy hub [12]. An energy hub is defined as an aggregation of production facilities for multiple energy resources, including conversion and accumulation. An energy hub serves as a conduit between microgrids and consumers, ensuring that the latter receive energy resources of the required quality [13].

The energy hub concept is an effective tool for modeling and analyzing the physical interconnections within microgrids. This is due to the fact that the energy hub concept places a primary emphasis on the detailed study of the energy conversion processes that occur between different energy resource types.

Energy hub modeling is based on optimizing the distribution of energy resource flows, originating at the hub's inputs and terminating at its outputs. The inputs and outputs of the energy hub are connected to the corresponding nodes of the distribution networks. Accordingly, a microgrid can be considered as an energy hub network [14].

3. Microgrid Model

Let the time interval under consideration be composed of $T$ periods of the duration $\Delta t$. The energy resources are represented by a set $K$, and the energy infrastructure is represented by a network of $H$ interconnected hubs.

3.1. Input and Output Flows

Each hub $h=\left\{1,\dots ,H\right\}$ is equipped with the set $M_h\subseteq K$ of inputs, the set $N_h\subseteq K$ of outputs, the set $I_h^{in}\subseteq K$ of input storages, and the set $I_h^{out}\subseteq K$ of output storages. Additionally, the hub $h$ has $J_h$converters.

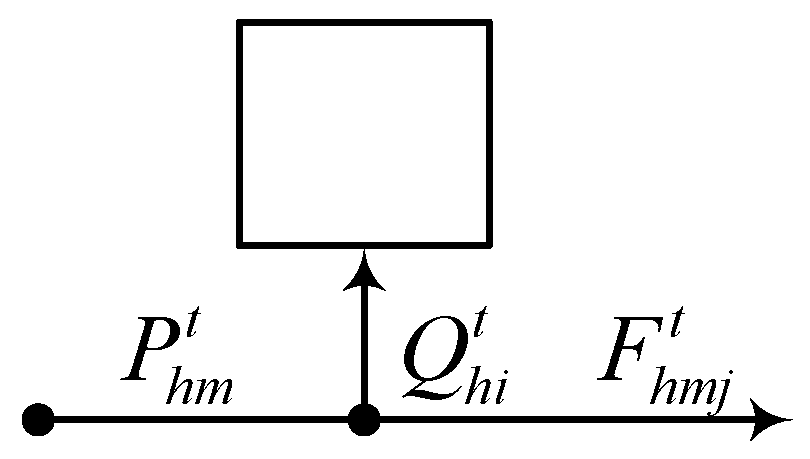
As shown in Figure 1, at the hub $h=\left\{1,\dots ,H\right\}$ in the period $t=\left\{1,\dots ,T\right\}$, the energy flow $P_{hm}^t$ at the input $m\in M_h$ is divided into the flow $Q_{hi}^t$of the input energy storage $i\in I_h^{in}$ and the flows $F_{hmj}^t$ to the converters $j=\left\{1,\dots ,J_h\right\}$ associated with the input $m\in M_h$

$$P_{hm}^t={{\displaystyle \sum }}_{j\in {\Theta }_h\left(m\right)}{F}_{hmj}^t+Q_{hi}^t,$$

(1)

$$F_{hmj}^t\le w_h{\overline{F}}_{hmj},$$

(2)

$$w_h\in \left\{0,1\right\},$$

(3)

where ${\overline{F}}_{hmj}^t$is a throughput of the converter $j$ to the input $m$ of the hub $h$, ${\Theta }_h\left(m\right)$ is a set comprising the converter of the hub $h$ connected to the input $m$, $w_h$ is a binary variable that specifies the hub $h$ status.

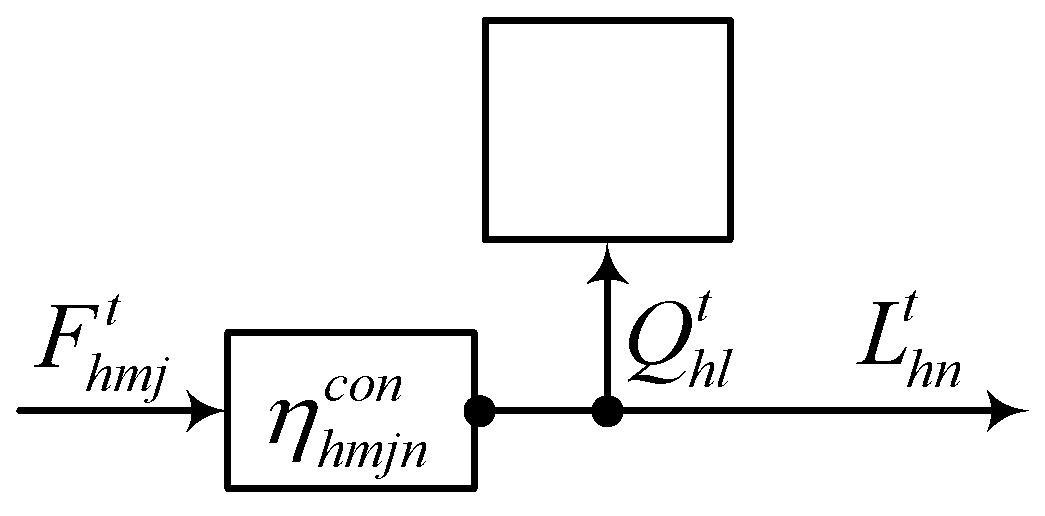
The formation of the energy resource flow $L_{hn}$ at the output $n\in N_h$ of the hub $h=\left\{1,\dots ,H\right\}$is shown in Figure 2. During the time interval $t=\left\{1,\dots ,T\right\}$ the energy converter $=\left\{1,\dots ,J_h\right\}$ of the hub $h$ converts the flow $F_{hmj}^t$with a conversion factor of ${\eta }_{hmjn}^{con}$ and directs it to the output $n$. Given the flow $Q_{hi}^t$ of the output drive $i\in I_h^{out}$, the flow $L_{hn}^t$ at the output $n\in N_h$ is defined as

$$L_{hn}^t={{\displaystyle \sum }}_{m\in M_h}{{\displaystyle \sum }}_{j\in {\Theta }_h\left(m,n\right)}{\eta }_{hmjn}^{con}{F}_{hmj}^t-Q_{hi}^t,$$

(4)

$$L_{hn}^t\le w_h{\overline{L}}_{hn}^t,$$

(5)

where ${\Theta }_h\left(m,n\right)$ is a set consisting of converters connecting the input $m\in M_h$ to the output $n$ of the hub $h$.

3.2. Energy Storage Devices

In formulas (3) and (6), the flow $Q_{hi}^t$ of the storage $i\in I_h^{in}\cup I_h^{out}$ of the hub $h=\left\{1,\dots ,H\right\}$ is formed by the flows of charge $Q_{hi}^{chg,t}$ and the discharge $Q_{hi}^{dis,t}$ in the period $t=\left\{1,\dots ,T\right\}$:

$$L_{hn}^t={{\displaystyle \sum }}_{m\in M_h}{{\displaystyle \sum }}_{j\in {\Theta }_h\left(m,n\right)}{\eta }_{hmjn}^{con}{F}_{hmj}^t-Q_{hi}^t,$$

(6)

The energy level $E_{hi}^t$, stored in $i\in I_h^{in}\cup I_h^{out}$ of the hub $h=\left\{1,\dots ,H\right\}$ at the end of the period $t=\left\{1,\dots ,T\right\}$, depends on its capacity ${\overline{E}}_{hi}$, the level $E_{hi}^{t-1}$ at the end of the previous period $t-1$, the charge flows $Q_{hi}^{chg,t ,}$, and the discharge flows $Q_{hi}^{dis,t}$ in the period $t$:

$$E_{hi}^t=E_{hi}^{t-1}+\left({\eta }_{hi}^{chg}{Q}_{hi}^{chg,t}-{\displaystyle \frac{1}{{\eta }_{hi}^{dis}}}{Q}_{hi}^{dis,t}\right)\Delta t,$$

(7)

$$0\le E_{hi}^t\le {\overline{E}}_{hi},$$

(8)

$$E_{hi}^0={\overline{E}}_{hi},$$

(9)

$$0\le Q_{hi}^{dis,t}\le w_h{\overline{Q}}_{hi}^{dis},$$

(10)

$$0\le Q_{hi}^{chg,t}\le w_h{\overline{Q}}_{hi}^{chg},$$

(11)

where ${\eta }_{hi}^{chg}$is a charge efficiency factor of the storage $i$ of the hub $h$, ${\eta }_{hi}^{dis } is$a discharge efficiency factor of the storage $i$ of the hub $h$, ${\overline{Q}}_{hi}^{dis }$is the maximum possible discharge flow value of the storage $i$ of the hub h, ${\overline{Q}}_{hi}^{chg}$is the maximum possible charge flow value of the storage $i$ of the hub $h$. Equation (11) assumes that before the start of the operation $(t=0$) all the storages contain full charge.

Equations (8), (10), and (11) specify technical constraints on the operation of the storage unit $i$ in the period $t$.

3.3. Energy Transportation Networks

Energy hubs are connected to each other and to consumers through energy distribution networks, as shown in Figure 4. Each network is represented as a graph, denoted by $G_k=\left(V_k,E_k\right)$, where $V_k$ is a set of nodes, $E_k$is a set of oriented arcs, and $k$ is an energy resource drawn from the set $K$. Additional constraints may be imposed on the graph $G_k$due to the physical laws of distribution of the energy resource $k$.

The network $G_k$ may contain the set $V_k^g\subset V_k$ of nodes representing the isolated sources of the energy resources $k\in K$ that do not belong to any of $H$ hubs. For example, $V_k^g$may be associated with fuel sources that are represented by rectangles in Figure 4.

Let $V_k^d\subset V_k$denote a set of nodes consuming the energy resource $k\in K$. The remaining nodes from the set $V_k^o=V_k\backslash \left(V_k^g\cup V_k^d\right)$ are called as the intermediate nodes. These nodes facilitate the interconnection of energy flows within the distribution network. Each node $v$ of the network $G_k$must satisfy one of the conditions for the balance of the energy flows $k\in K$ at the time $t=\left\{1,\dots ,T\right\}$

$$g_v^t+{\displaystyle \sum }_{\left(q,v\right)\in {\Psi }_k\left(v\right)}{a}_{qv}{f}_{qv}^t-{\displaystyle \sum }_{\left(v,q\right)\in {\Omega }_k\left(v\right)}{f}_{vq}^t=0,v\in V_k^g$$

(12)

$${\displaystyle \sum }_{\left(q,v\right)\in {\Psi }_k\left(v\right)}{a}_{qv}{f}_{qv}^t-{\displaystyle \sum }_{\left(v,q\right)\in {\Omega }_k\left(v\right)}{f}_{vq}^t+u_v^t={\overline{d}}_v^t,v\in V_k^d$$

(13)

$${\displaystyle \sum }_{\left(q,v\right)\in {\Psi }_k\left(v\right)}{a}_{qv}{f}_{qv}^t-{\displaystyle \sum }_{\left(v,q\right)\in {\Omega }_k\left(v\right)}{f}_{vq}^t=0,v\in V_k^o$$

(14)

$$0\le u_v^t\le {\overline{u}}_v^t, v\in V_k^d,$$

(15)

$$0\le f_{vq}^t\le w_{vq}{\overline{f}}_{kvq}, \left(v,q\right)\in E_k,$$

(16)

$$0\le g_v^t\le w_v{\overline{g}}_v^t, v\in V_k^g,$$

(17)

$$w_{vq}\in \left\{0,1\right\}, \left(v,q\right)\in E_k,$$

(18)

$$w_v\in \left\{0,1\right\}, v\in V_k^g,$$

(19)

where ${\Psi }_k\left(v\right)\subseteq E_k$ is a set of arcs entering the node $v$, and ${\Omega }_k\left(v\right)\subseteq E_k$ is a set of arcs leaving the node $v$, $f_{qv}^t$is a flow of the energy resource $k$ along the arc $\left(q,v\right)\in E_k$ at the period $t$, $g_v^t$ represents the production of the energy resource $k$ at the node $v\in V_k^g$ at the period $t$, while ${\overline{u}}_v^t$ denotes the demand of the node $v\in V_k^d$ for the energy resource $k$ at the period $t$. $u_v^t$represents the shortage of the energy resource $k$ to the node $v\in V_k^d$in the period $t$. The term $a_{qv}$denotes a coefficient that characterizes the losses incurred during the transportation of the energy resource $k$ along the arc $\left(q,v\right)\in E_k$. The throughput of the arc $\left(q,v\right)\in E_k$ is represented by ${\overline{f}}_{vq},\left(v,q\right)$, whereas the binary variable $w_{vq}$defines the status of the arc $\left(v,q\right)$, the binary variable $w_v$in turn, defines the status of the source node $v$.

If we consider the energy hubs connected to $G_k$at the node $v$, then equations (12)-(14) for the period $t=\left\{1,\dots ,T\right\}$are written as

$$g_v^t+{\displaystyle \sum }_{\left(q,v\right)\in {\Psi }_k\left(v\right)}{a}_{qv}{f}_{qv}^t+{\displaystyle \sum }_{h\in {\Lambda }_k^g\left(v\right)}{L}_{hn}^t-{\displaystyle \sum }_{h\in {\Lambda }_k^d\left(v\right)}{P}_{hm}^t-{\displaystyle \sum }_{\left(v,q\right)\in {\Omega }_k\left(v\right)}{f}_{vq}^t=0,v\in V_k^g,$$

(20)

$${\displaystyle \sum }_{\left(q,v\right)\in {\Psi }_k\left(v\right)}{a}_{qv}{f}_{qv}^t+{\displaystyle \sum }_{h\in {\Lambda }_k^g\left(v\right)}{L}_{hn}^t-{\displaystyle \sum }_{h\in {\Lambda }_k^d\left(v\right)}{P}_{hm}^t-{\displaystyle \sum }_{\left(v,q\right)\in {\Omega }_k\left(v\right)}{f}_{vq}^t+u_v^t={\overline{u}}_v^t,v\in V_k^d,$$

(21)

$${\displaystyle \sum }_{\left(q,v\right)\in {\Psi }_k\left(v\right)}{a}_{qv}{f}_{qv}^t+{\displaystyle \sum }_{h\in {\Lambda }_k^g\left(v\right)}{L}_{hn}^t-{\displaystyle \sum }_{h\in {\Lambda }_k^d\left(v\right)}{P}_{hm}^t-{\displaystyle \sum }_{\left(v,q\right)\in {\Omega }_k\left(v\right)}{f}_{vq}^t=0,v\in V_k^o,$$

(22)

where ${\Lambda }_k^d\left(v\right)$ is a set of hubs whose inputs are connected to the network $G_k$at the node $v$, $P_{hk}^t$is a flow of the energy resource $k\in K$ arriving at the input $m\in M_h$of the hub $h\in {\Lambda }_k^d\left(v\right)$ at the period $t$, ${\Lambda }_k^g\left(v\right)$is a set of hubs whose outputs are connected to the network $G_k$ at the node $v$, $L_{hn}^t$ is a flow of the energy resource $k\in K$ arriving at the output $n\in N_h$ of the hub $h\in {\Lambda }_k^g\left(v\right)$ at the period $t$.

3.4. Environmental Constraints

In the event that constraints on the emission of harmful substances from the plurality $L$ are necessary, they may be imposed on the production of the energy resource $k\in K$. Examples of such substances include particulate the matter, sulfur oxide, nitrogen oxide, carbon dioxide, and benz(a)pyrene.

For the source node $v\in V_k^g$, the emission $e_{lv}^t$ of a harmful substance $l\in L$ at the period $t=\left\{1,\dots ,T\right\}$ is calculated and constrained as follows:

$$e_{lv}^t={\lambda }_{lv}^t{g}_v^t,$$

(23)

$$e_{lv}^t\le {\overline{e}}_{lv}^t,$$

(24)

where ${\lambda }_{lv}^t$ represents the specific emission of the given harmful substance $l$, as associated with the production of the given energy resource $k$ by the source $v$. Meanwhile, ${\overline{e}}_{lv}^t$ denotes the emission limit of the aforementioned harmful substance $l$ for the source $v$.

For the hub $h=\left\{1,\dots ,H\right\}$ the emission $E_{hmjl}^t$of the pollutant $l$ at the time $t$ is tied to the flow $F_{hmj}^t$ of the converter $j=\left\{1,\dots ,J_h\right\}$ consuming the energy resource $m\in M_h$

$$E_{hmjl}^t={\lambda }_{hmjl}^t{F}_{hmj}^t,$$

(25)

$$E_{hmjl}^t\le {\overline{E}}_{hmjl}^t,$$

(26)

where ${\lambda }_{hmjl}^t$ represents the specific emission of a harmful substance $l$ by transducer $j$, while ${\overline{E}}_{hmjl}^t$ denotes the emission limit of the aforementioned substance $l$ for the transducer $j$.

3.5. Objective Function

The objective of optimizing the functionality of interconnected hubs is to achieve the most comprehensive satisfaction of energy resource needs with the least investment on hubs and distribution networks, while minimizing the operational costs of these systems over the specified period $t=\left\{1,\dots ,T\right\}$

$${\displaystyle \sum }_{h=1}^H{Z}_h+{\displaystyle \sum }_{k\in K}{Z}_k+{\displaystyle \sum }_{t=1}^T\left[{\displaystyle \sum }_{h=1}^H{F}_h^t+{\displaystyle \sum }_{k\in K}{F}_k^t+{\displaystyle \sum }_{l\in L}{E}_l^t\right]\to min$$

(27)

$$Z_h=b_h{w}_h,$$

(28)

$$Z_k={\displaystyle \sum }_{v\in V_k^g}{b}_v{w}_v+{\displaystyle \sum }_{\left(v,q\right)\in E_k}{b}_{vq}{w}_{vq}$$

(29)

$$F_h^t={\displaystyle \sum }_{m\in M_h}{C}_{hm}^t{P}_{hm}^t+{\displaystyle \sum }_{n\in N_h}{C}_{hn}^t{L}_{hn}^t+{\displaystyle \sum }_{i\in I_h^{in}\cup I_h^{out}}\left(C_{hi}^{chg,t}{Q}_{hi}^{chg,t}+C_{hi}^{dis,t}{Q}_{hi}^{dis,t}\right)$$

(30)

$$F_k^t={\displaystyle \sum }_{v\in V_k^g}{c}_v^t{g}_v^t+{\displaystyle \sum }_{v\in V_k^d}{y}_v^t{u}_v^t+{\displaystyle \sum }_{\left(v,q\right)\in E_k}{c}_{vq}^t{f}_{vq}^t,$$

(31)

$$E_l^t={\displaystyle \sum }_{h=1}^H{\displaystyle \sum }_{m\in M_h}{\displaystyle \sum }_{j\in {\Theta }_h\left(m\right)}{y}_{hmjl}^t{E}_{hmjl}^t+{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{v\in V_k^g}{y}_{lv}^t{e}_{lv}^t$$

(32)

where $b_h$represents the investment in the hub $h=\left\{1,\dots ,H\right\}$, $b_v$ represents the investments in the source $v\in V_k^g$, $b_{vq}$ is the investment in the arc $\left(v,q\right)\in E_k$, $C_{hm}^t$ is the cost of transferring of the flow $P_{hm}^t$, $C_{hn}^t$ is the cost of transferring of the flow $L_{hn}^t$, $C_{hi}^{chg,t}$ is the cost of transferring of the flow $Q_{hi}^{chg,t}$, $C_{hi}^{dis,t}$ is the cost of transferring of the flow $Q_{hi}^{dis,t}, y_v^t$is the cost of the shortage $u_v^t$, $c_{vq}^t$ is the cost of transferring of the flow $f_{qv}^t,$ $c_v^t$ is the cost of the energy generation $g_v^t, y_{lv}^t$ is the cost of the emission $e_{lv}^t$, $y_{hmjl}^t$ is the cost of the emission $E_{hmjl}^t$.

The objective function (27) has five components. The initial component of (28) determines the investments of the hubs. The second component of (29) is responsible for determining the investments of distribution networks. The third component (30) defines the expenses associated with operating the hubs. The fourth component (31) delineates the financial implications associated with the operation of distribution networks, including penalties for shortage of energy resources. The last component (32) defines the penalties for air pollution by harmful substances. The constraints for the objective function (27) are derived from equations (1) to (11) and from (15) to (26).

4. Application

Formulations (1)-(12), (15)-(32) provide a set of elements that form the microgrid configuration. This set includes main nodes of distribution networks (energy sources and energy resources consumers), intermediate nodes, network arcs, and energy converters and storages.

The description of the microgrid configuration, defined by a set of $H$ interacting energy hubs, consists of two parts. The first part of the description concerns the infrastructure for transporting energy resources, represented by the sets $V_k$ of nodes and $E_k$ of arcs of the distribution network $G_k$. The second part of the description provides information about the infrastructure for generating, converting, and accumulating energy resources. It represents data about the inputs, input drives, converters, output drives, and outputs of all energy hubs. As a whole, this description is sufficient to specify any configuration of autonomous microgrids.

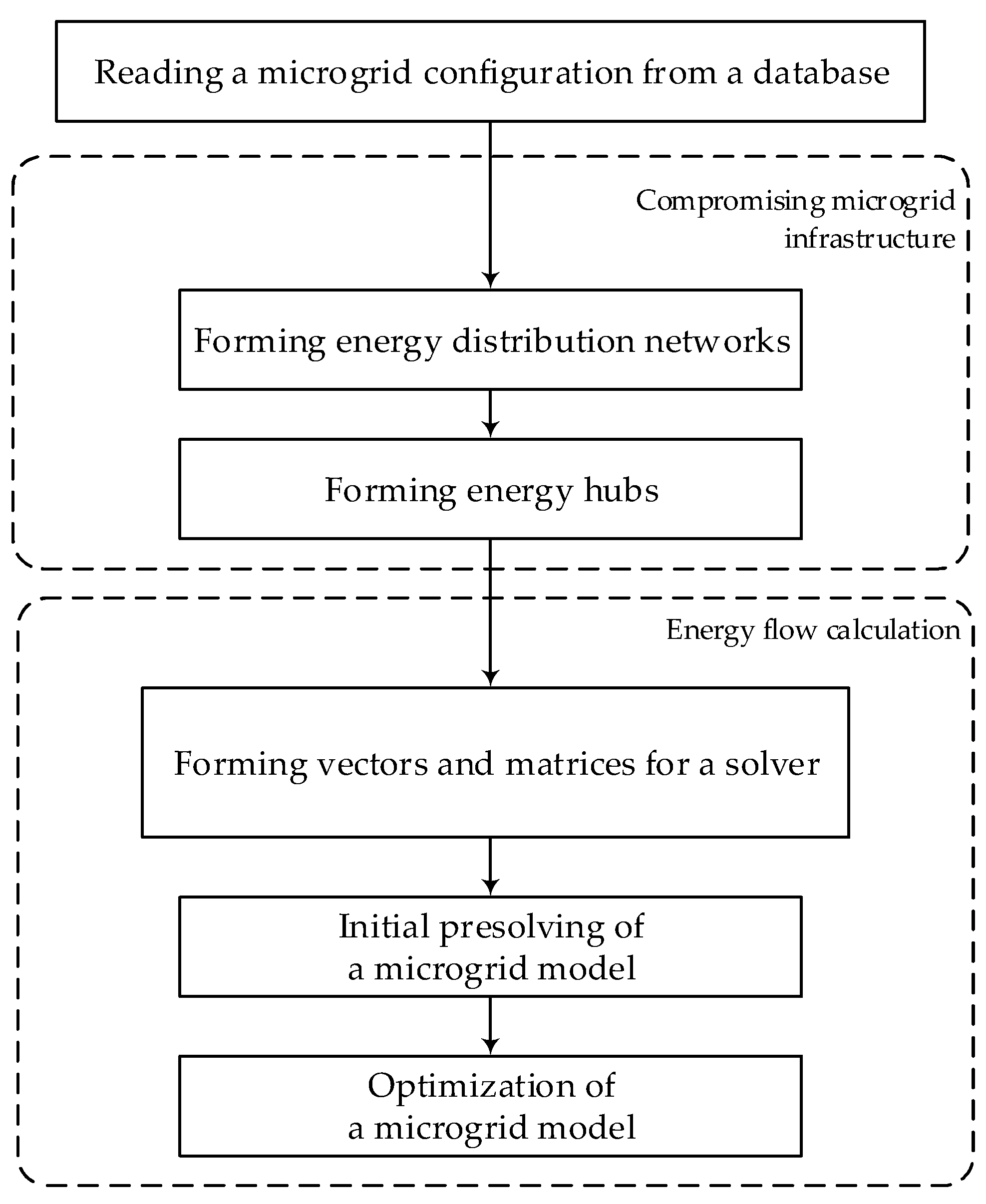
The description of a microgrid configuration is read from the database and transformed into vectors and matrices according to the formulations (1)-(12), (15)-(32). This step is easily automated because each configuration element is characterized by a unique set of equations describing its operational behavior. Next, the vectors and matrices are populated with data characterizing the microgrid operation over T periods. Then, the flow distribution of $K$ energy resources in the microgrid is calculated. This step consists of two distinct stages: the initial presolving and the subsequent optimization of the microgrid model. The above steps are implemented as a software module (Figure 3) using the optimization solvers GLPK, Clp, Cbc, CPLEX, and SCIP. Some of them, such as CPLEX and Cbc, are designed for parallel and distributed computing.

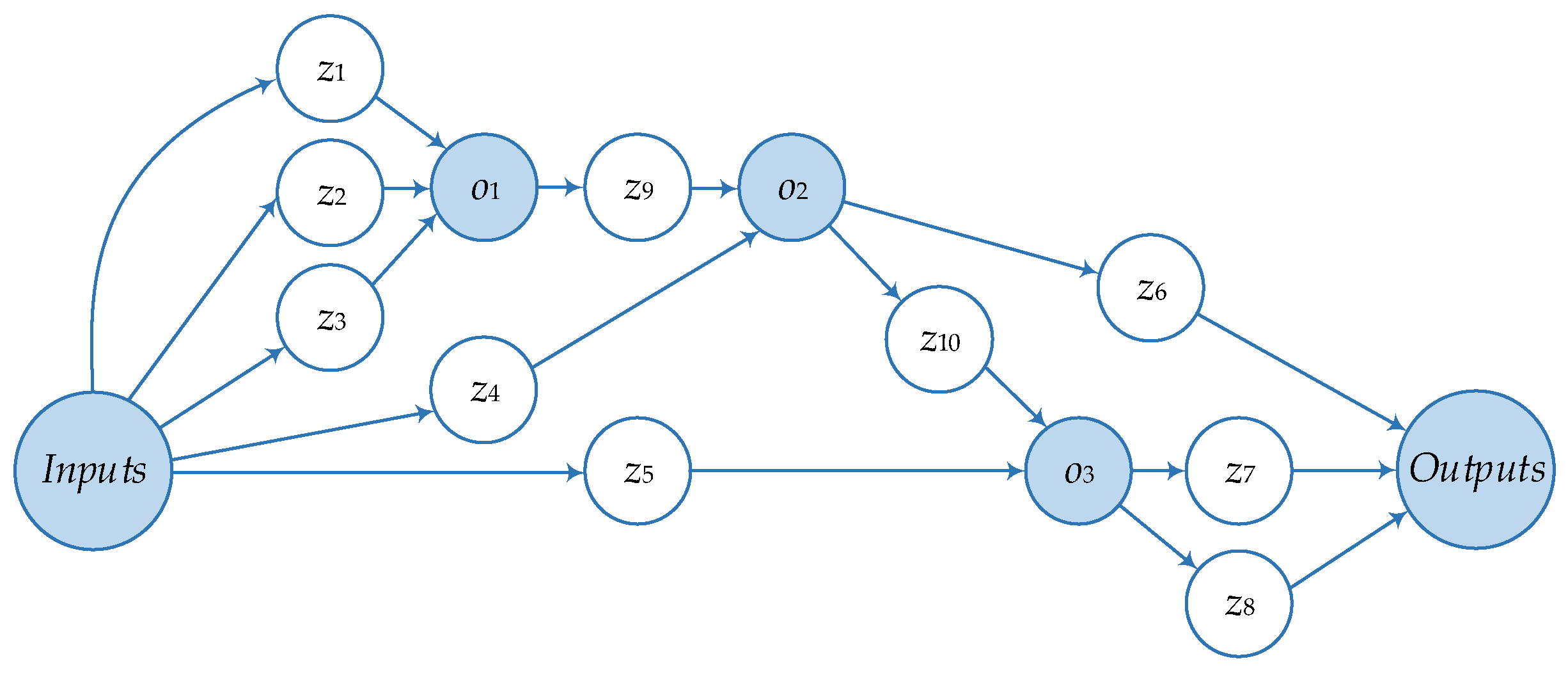
The above model for structural and parametric optimization of a microgrid is implemented within a service-oriented application. A scientific workflow for structural and parametric optimization of a microgrid is represented by a composition of operations implemented by services (Figure 4).

Figure 4. Scientific workflow of structural and parametric optimization.

Figure 4. Scientific workflow of structural and parametric optimization.

Operation $o_1$ implements structural and parametric optimization of a microgrid using the previously selected optimization algorithm Non-dominated Sorting GA II from the PaGMO library [15]. The algorithm pre-selection has been made based on the testing of optimization methods for MESs on different levels of their territorial-industrial hierarchy using the specialized testbed of the application [16]. Within the testing, we used four computational nodes functioning under Ubuntu 22.04.1 LTS OS. Each of the nodes has the following characteristics: CPU AMD Ryzen 9 5950X, 128 GB of RAM, and 2 TB of disk storage.

Next, the operation $o_2$ processes the optimization results.

Finely, operation $o_3$ creates a report the preferred microgrid infrastructure. This infrastructure is defined by the types of equipment, their composition, characteristics, and locations.

The operation uses the following parameters:

• $z_1$ is a file containing optimization algorithm settings,
• $z_2$ is an input database containing a microgrid model,
• $z_3$ is an initial database for storing the microgrid optimization results,
• $z_4$ is the SQL script for processing optimization results,
• $z_5$ is the SQL script for creating reports,
• $z_6$ is the result of the execution of the operation $o_2$,
• $z_7$ is the result of the execution of the operation $o_3$;
• $z_8$ is a report about the preferred types of equipment, their composition, characteristics, and locations,
• $z_9$ is a database with the optimization results,
• $z_{10}$ is a database with the processed and aggregated optimization results for creating $z_8$.

The Framework for Development and Execution of Scientific WorkFlows (FDE-SWFs) [17] was used to develop and execute the considered application in SOE using the resources of HDCE. FDE-SWFs supports the development and execution of scientific workflows based on the distributed service-oriented application paradigm. It is a workflow management system [18]. The usability of such systems largely depends on the availability and ease of use of the necessary set of tools for workflow development and execution. In FDE-SWFs, usability and ease of use of the above tools is achieved by automating their basic system operations. In addition, data and control integration with workflows developed in other systems within the same or similar research also helps to achieve the considered qualities of these tools [19].

FDE-SWFs inherits the architecture and functionality of Orlando Tools (OT) [20]. At the same time, it evolves and extends the architecture and functionality of OT in the following directions:

• Service-oriented application creation and execution in HDCE;
• Containerization of application and system software;
• Development and use of specialized testbeds for software testing and verification and data validation;
• Standardization of workflow specifications;
• Program generation in general-purpose programming languages for workflows to ensure their autonomous execution.

FDE-SWFs supports the entire cycle of preparing and executing computational experiments from configuring the developed application and designing its computational model to visualizing and analyzing the computation results. Its architecture is shown in Figure 5 and its main components are briefly discussed below.

The user interface provides various categories of specialists (developers, administrators, and end users) of FDE-SWFs with access to its components and components of applications being developed. The interface is implemented on the basis of modern web technologies, methods, and tools for organizing service-oriented applications, their execution, and visualization of workflows and data.

The configuration subsystem provides the application developer with the ability to perform the following activities:

• Set up system components, software repositories, and databases;
• Define the structures of computational models, problem formulations, and workflows;
• Deploy and utilize applied and system modules;
• Integrate with the required information and computation resources and systems.
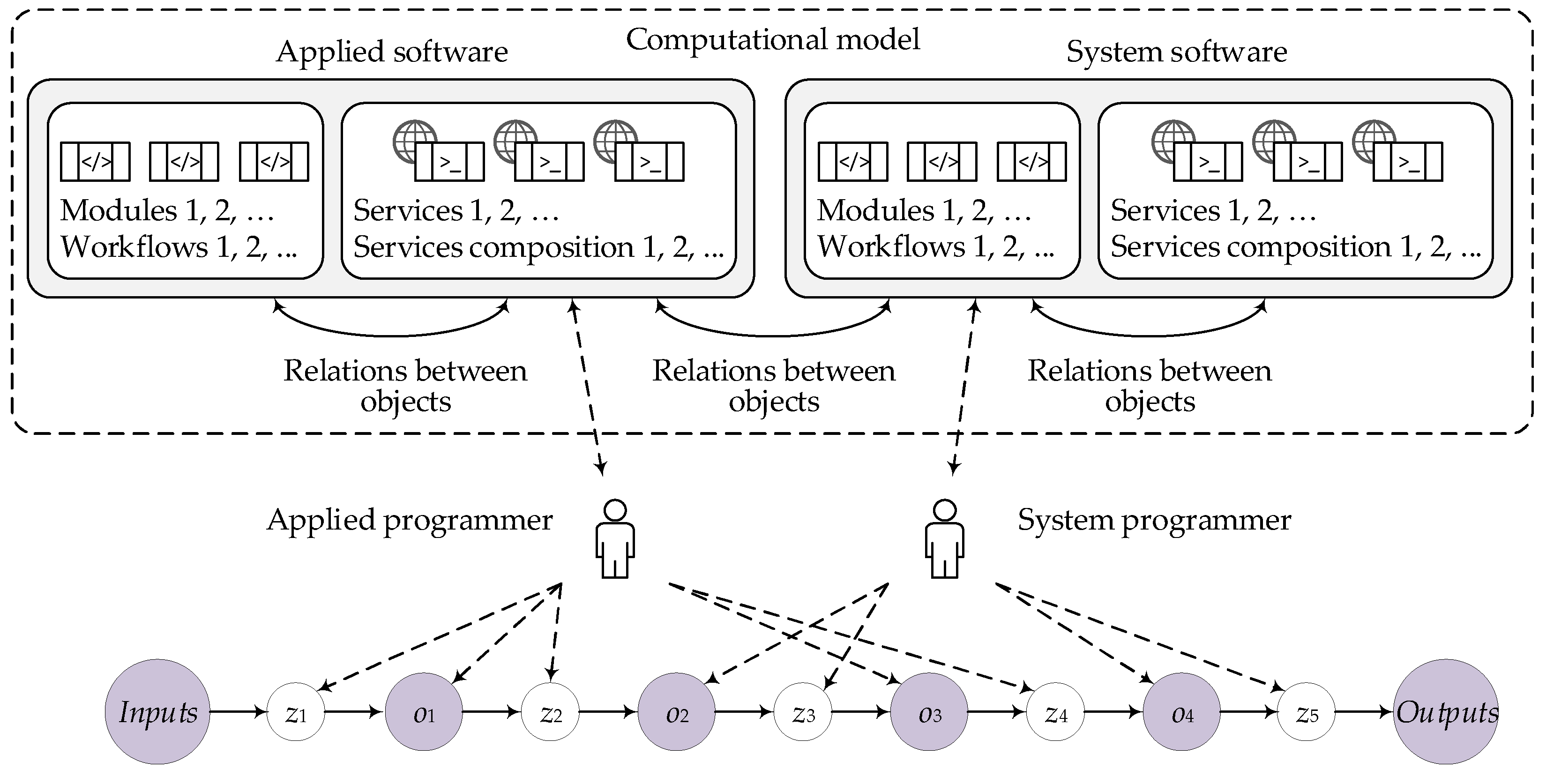
• A computational model of an application is a kind of semantic network that reflects the knowledge about the possibility of computing values of variables on the basis of relations between them. The designer supports the description of the computational model (application subject domain) in the form of a set of abstract parameters (variables), operations (partial relations) defined over the set of parameters, program modules and services implementing the operations, workflows representing compositions of modules or services for problem-solving, and relations between the listed objects. The knowledge base stores application settings, specifications of computational model objects (parameters, operations, modules, workflows, generated services and programs, etc.), and templates for generating services and programs.

This model can be supplemented with system objects intended for realization of interaction of workflows with information and computation resources, management systems, and databases. System objects can be used when designing workflows. In general, the development of the computational model involves applied programmers (specialists in the subject domain, who implement models and algorithms for problem-solving) and system programmers (specialists in working with computational resources of HDCE (Figure 6).

A unique feature of FDE-SWFs compared to other workflow management systems is the support for both procedural and non-procedural problem formulation. In the first case, the developer constructs a workflow as an abstract program with operation calls, cycles, and branches in graphical form by dragging and dropping appropriate elements. In the second case, the developer specifies the initial (inputs) and target (outputs) parameters of the workflow. Then, the computation scheduling subsystem constructs a partially ordered composition of operations in the form of a bipartite directed acyclic graph based on the relations between parameters and operations represented in the computational model.

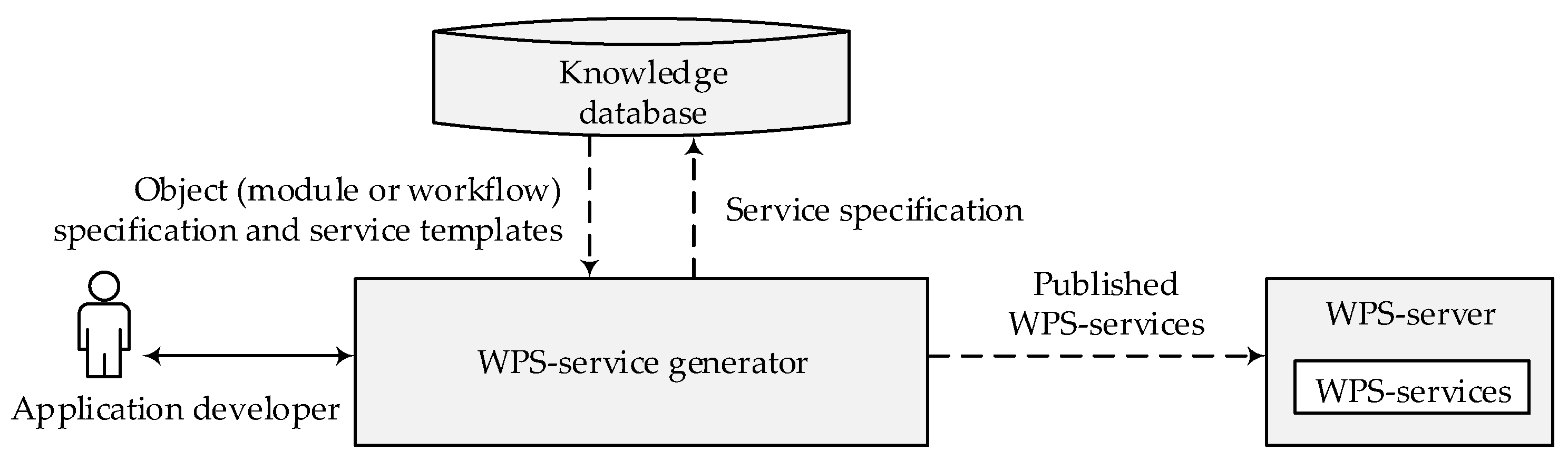
FDE-SWFs supports the conversion of workflows to the Business Process Execution Language (BPEL) [21] to ensure their executability in other workflow management systems based on this language standard. In addition, a program in general-purpose programming language (currently Python is used in the workflow designer) can be generated for the workflow to enable the workflow to be executed independently of the FDE-SWFs environment. In addition, the WPS service generator supports the automatic deployment of applied modules and workflows as new services. It incorporates the description of the newly created services into the computational model (Figure 7).

The workflow schedular is an executive subsystem of FDE-SWFs. It is responsible for executing workflows in the HDCE. With its help, the application end-user can launch workflows and monitor the computation process. The scheduler interacts with meta-schedulers and local resource managers of HDCE to allocate computational resources for the workflow execution. In particular, it generates computational jobs for the workflow module executions in the formats required by meta-schedulers and local resource managers.

The scheduler also provides access to the computation database, from which it is possible to download and visualize the results of previously performed experiments and to prepare initial data for new experiments. For each experiment, the database stores the problem formulation, workflow, input, output, and necessary intermediate data, as well as system information about the progress of the computation process in the form of log files.

The interpreter of workflows implements operators for executing operations implemented by services. These operators ensure the execution of any web service on WSDL implementing the computational process or the process of obtaining and processing data. In particular, work with WPS services for collecting, processing, and analyzing spatiotemporal data is supported. The designer of the computational model controls the strict correspondence of the parameters of operations to the messages of services when defining these objects.

5. Computational Experiment

The class of energy system design problems is based on structural and parametric optimization and consists in determining the structure of the energy sources (types, locations, and composition of equipment). These are closely related to the distribution network scheme and parameters, as the composition of energy sources, their capacities, and connections with consumers determine the amount of energy carriers transferred through the distribution network. The aforementioned problems are solved by the above presented application.

The design of energy source structures is a multi-step process. This study assumes that construction sites are identified by heat network optimization and are located in areas with high heat loads. The next step is to determine the types and sizes of energy source equipment. The type of energy source is determined based on the ability to supply different types of fuels. In addition, the need for heat and power cogeneration is investigated.

The design heat load determines the installed heat capacity of the energy sources. In this case, representative days make it possible to check whether such a calculated load is justified. At the same time, it allows us to plan the management of the current operating modes of the equipment more effectively. In general, representative days for heat loads are chosen from a series of years, in which extreme temperatures are observed or the loads have a specific, irregular character during the day (usually working days and weekends).

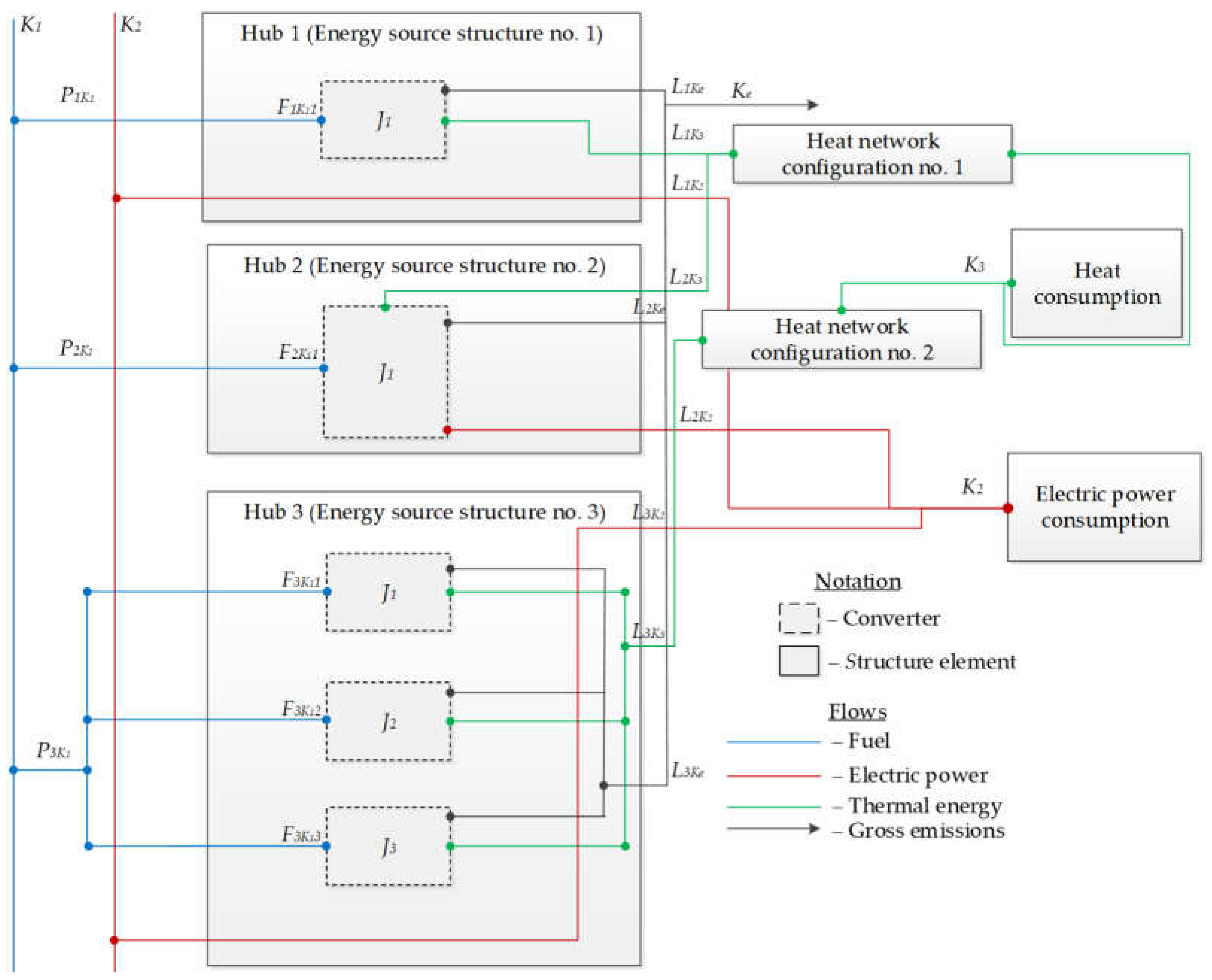
A redundant heat supply system can be visualized as a redundant structure of energy sources and heat network configurations associated with heat and electricity consumers (Figure 8). The resources, respectively, are fuel, electricity, heat, and emissions: $K\in \left\{K_{1 }, K_2, K_3, K_e\right\}$. The energy flow $P_{hm}^t\in \left\{P_{1k_1}, P_{2k_1}, P_{3k_1}\right\}$ represents the fuel burned at energy sources, the redundant structure of which is represented by three hubs $h\in \left\{h_1, h_2,h_3\right\}$. The converters $j\in \left\{J_1, J_2, J_3\right\}$ are situated inside the hubs. For instance, a volume of fuel equal to $F_{1k_{1}1}$ is fed to the input of the hub converter $h_1$. The outputs are the volumes of thermal energy $L_{1k_3}$, electricity $L_{1k_2}$, and emissions $L_{1k_{1e}}$.

Let us demonstrate an example of the development of energy supply systems for a small village (population 6 000 people) in the eastern part of Siberia (Russia), located in the atmospheric influence zone of the Baikal natural territory. The planned prospective heat load of the settlement will amount to 23.19 Gcal/h, electric load – 102.91 thousand MWh per year due to the prospective construction (increase in heat load is 13%) and the need to reconstruct electrical power supply facilities. Currently, the settlement has one Central Boiler House using lignite coal (energy source no. 1). 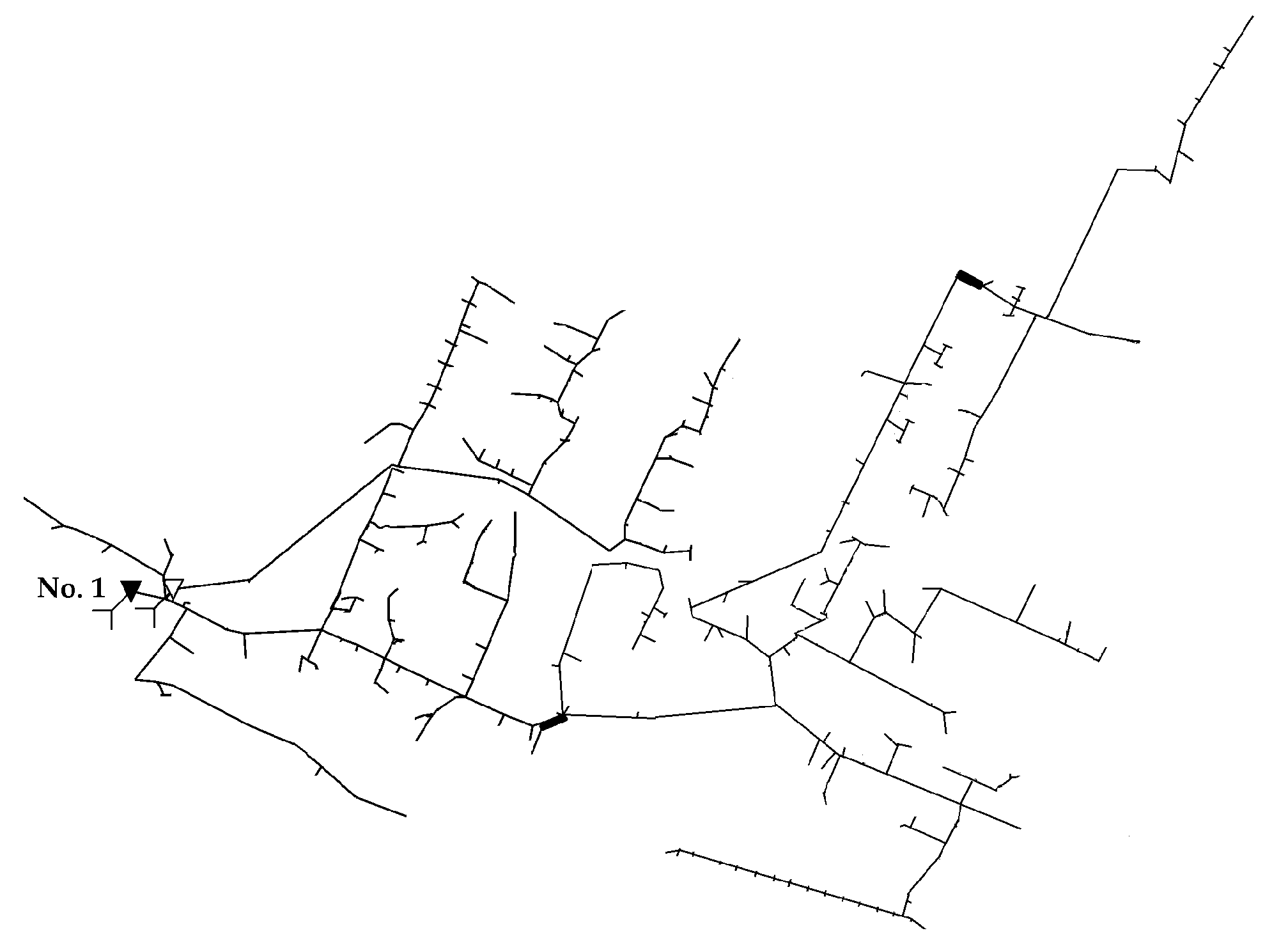Figure 9 shows the heat network configuration with one energy source for a settlement.

When forming technological options of energy sources, two fuel supply options were considered: gas supply for heating purposes (within the gasification program planned to be implemented in the region) and the use of wood chips as fuel (close location of a wood processing plant for the production of dry sawn timber).

Each variant of the energy source structure is specified and characterized by the type of installation, installation size, number of installations, and variant of a heat network configuration. The introduction of 4 types of energy sources was considered: boiler house and mini CHP. Both of them burn gas and wood chips. When the boiler houses are commissioned, the electricity for the settlement is purchased from the external electrical grid. Its cost is included in the operating costs. In a mini CHP case, the equipment size options were selected taking into account the full electricity supply of the settlement. The surplus electricity was set as a profit from its sale to the external energy system. The cost of gas in the technological variants of energy sources was taken as $84/cubic meter. The cost of wood chips was set as $14/ton of oil equivalent.

The capital and operating costs of the heat network are taken as a discounted cost criterion. The discounted costs of the heat network and energy sources represent the full cost of the settlement's energy supply system [22]. Emissions of harmful substances (particulate matter, sulfur oxide, nitrogen oxide, carbon dioxide, benz(a)pyrene) were calculated for each energy source structure taking into account all technical and economic characteristics of equipment sizes and physical and chemical composition of fuel. The equipment of the energy source no. 1 (Table 1) was selected taking into account the design heat load. The structure of the energy source no. 1 can include only one of the four main alternative components: mini gas-turbine cogeneration plant, hot water boiler plant using woodchips, ORC (Organic Rankine Cycle) module and hot water boiler plant using woodchips, and hot water boiler plant using gas. The woodchip plants АС-1000, С-0.15, and С-50 are equipped with a dryer. Reconstruction of 62 sections of the heat network and construction of a pump station are planned.

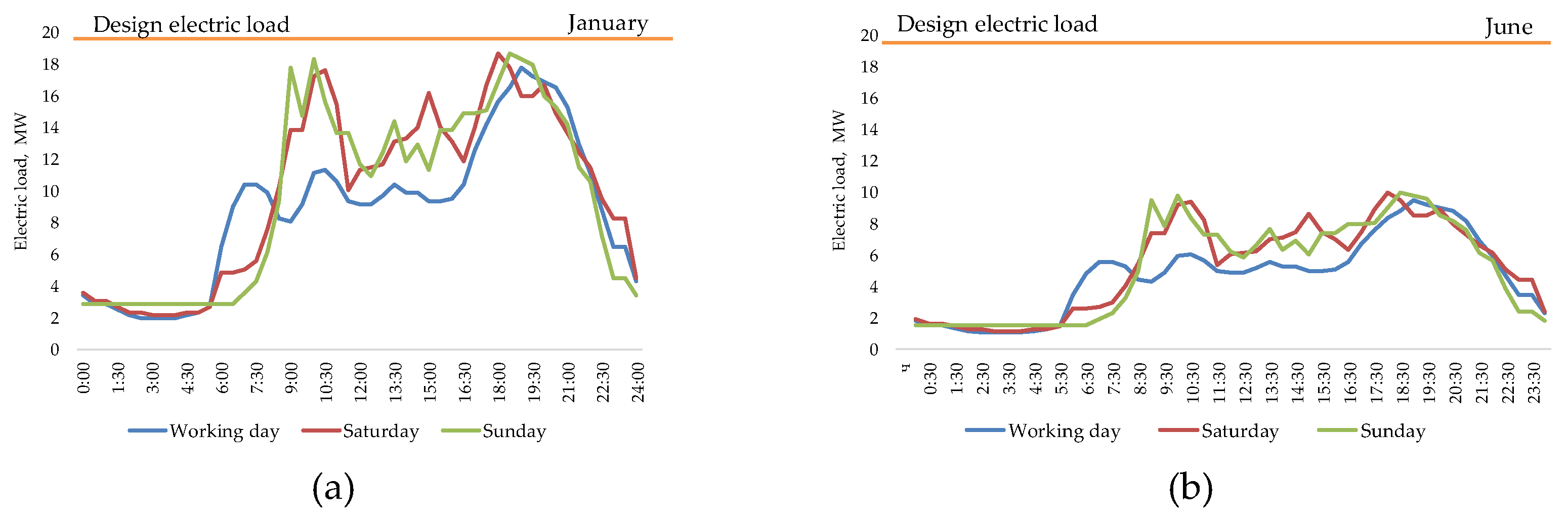
Next, the selected equipment was tested against the current hourly heat (Figure 10) and electrical load (Figure 11) of the selected representative days. These loads were calculated based on natural-climatic data for a period of 10 years.

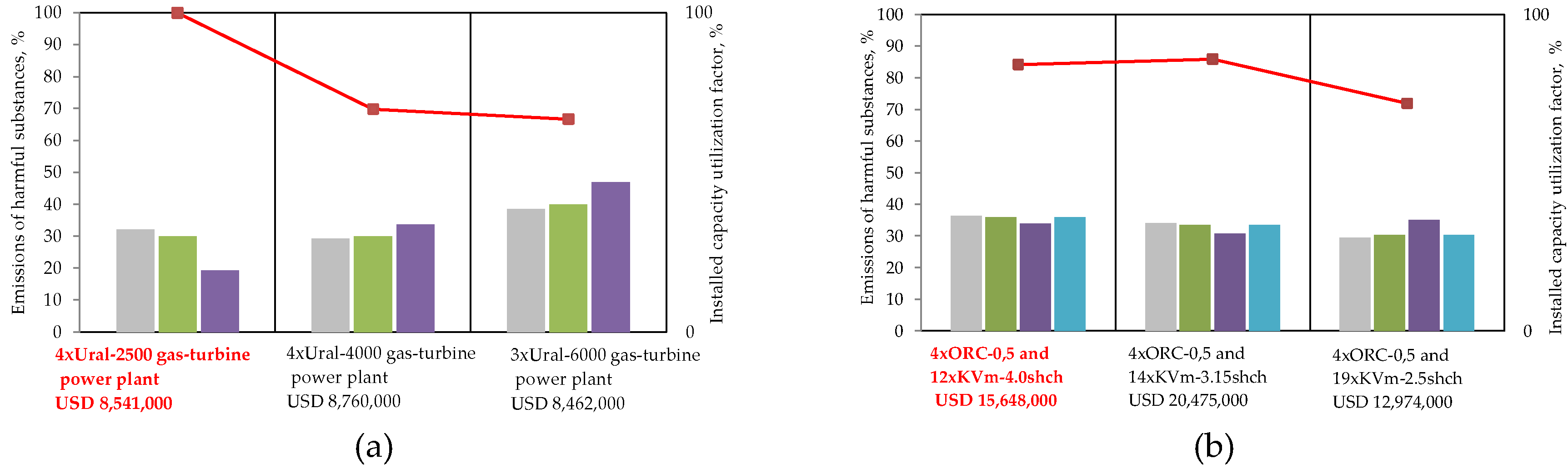
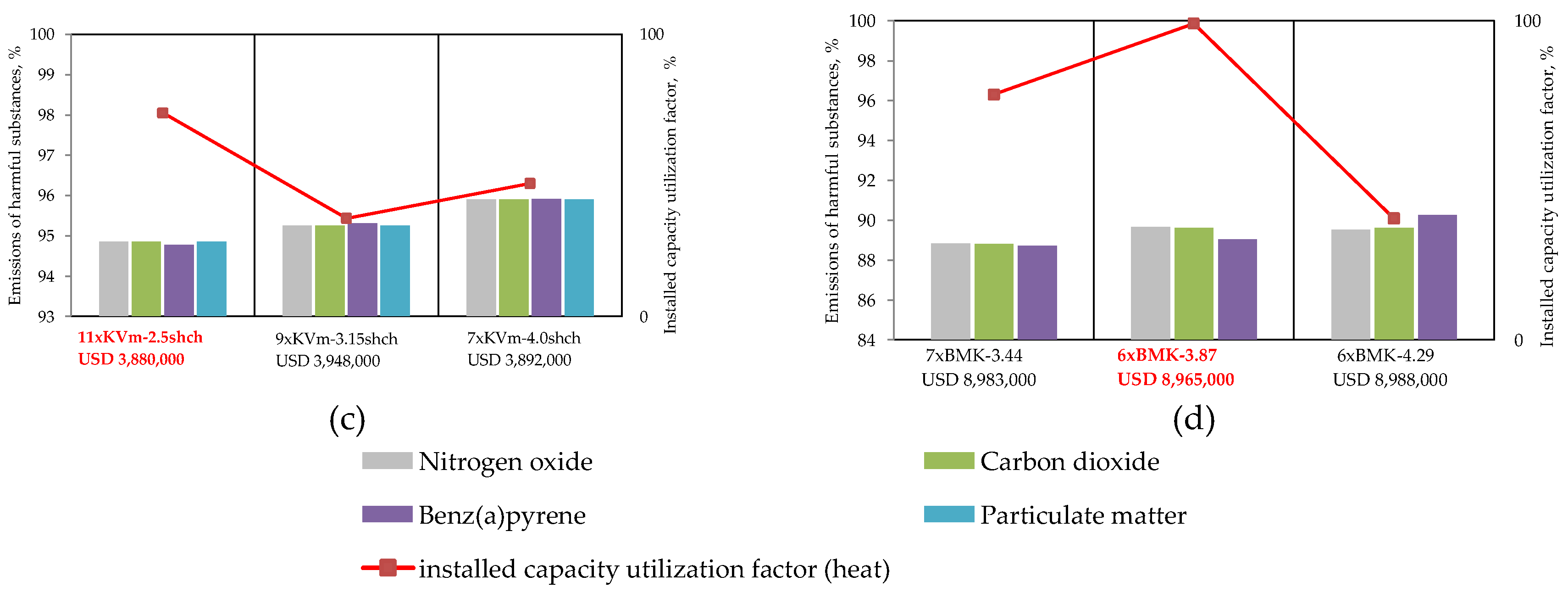
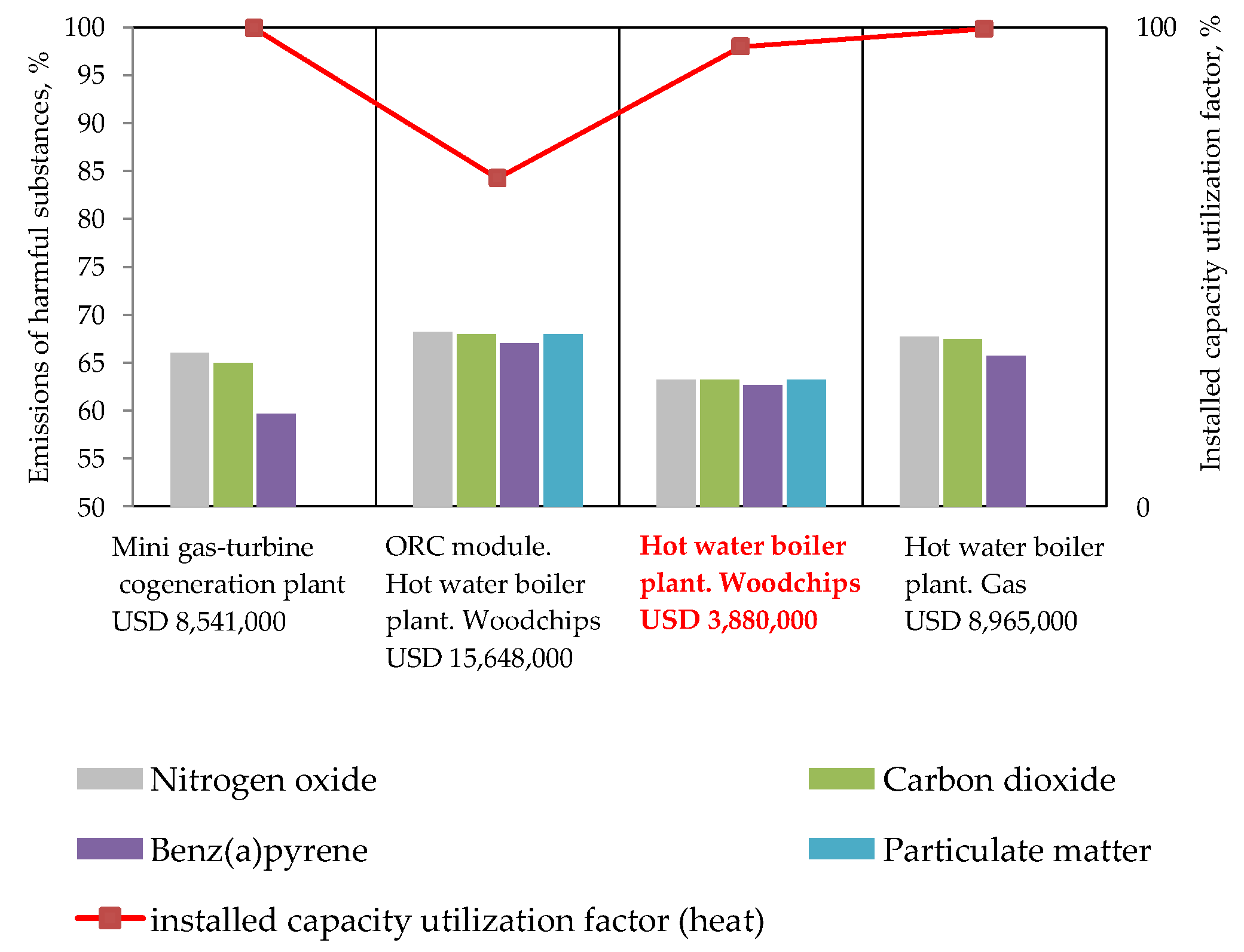
Structural and parametric optimization of the energy source no. 1 was carried out for four alternative components (Figure 12). Each of the components included three sizes of its main equipment. In Figure 12, the optimal options are highlighted in red font. If we compare them (Figure 13), we can emphasize the high degree of technical efficiency and the relatively inexpensive cost of the chip-fired boiler house option with the purchase of electricity from the external energy system.

In terms of efficiency, the option of cogeneration of heat and electricity generation using gas deserves further consideration. Although it is more expensive in terms of cost, it offers high energy efficiency in terms of the coefficient of use of installed thermal energy and reduction of gross emissions. The option of a mini CHP with ORC is not a viable alternative. This is due to the growth in the capacity of energy sources for electricity generation, the raise in gross emissions of harmful substances, and the increase in costs. In addition, the study of the utilization factor of the installed thermal energy shows that the selected standard size of the equipment for mini CHP with ORC does not ensure optimal loading and efficient operation of the equipment on an annual basis.

Within the computational experiment, we have performed the synthesis of the microgrid using the preselected optimization algorithm Non-dominated Sorting GA II for an acceptable time in less than 1 hour.

6. Discussion

The proposed approach to solving the problems of designing energy supply systems has several advantages compared to known approaches. In particular, it provides a joint solution to the structural and parametric optimization problems of energy sources and heating networks. In addition, it allows us for the maximum reduction of atmospheric pollution. At the same time, the principle of simultaneous synthesis is applied at the design and operation levels.

The proposed approach implies a constant interaction and mutual influence between promising development tasks and the current functioning of the energy supply system. So far, the authors have formulated the problem, developed a mathematical model, developed a software tool, and conducted a case study of a small energy supply system with a single energy source. In the future, we plan to increase in the number of competing energy sources and thermal network configurations and to consider additional environmental factors, such as waste water and solid waste. It is assumed that the dispersion will be constructed in conjunction with the gross emissions currently considered in this study. The concentration fields of emissions of harmful substances will allow us to more accurately determine the foci of severe pollution. In addition, they will facilitate the tracing of the sum of pollution in the case of overlapping concentration fields of several energy sources in space.

One promising avenue of investigation is to compare the structures of energy sources using to the life-cycle method, from mining to waste disposal. In addition, it may be beneficial to improve the parameters used to compare the structures of energy sources from the standpoint of reliability and survivability of the energy system. Furthermore, given the inherent uncertainty of energy prices, it is expected that the formulation of the problem of optimizing energy source structures will expand in the future to include the full range of probable prices and the application of robust optimization.

7. Conclusions

In the paper, we propose SOE for the multi-energy system synthesis in a reasonable time considering the available computational resources of HDCE. Our contribution is multifold. We have applied a new framework FDE-SWFs for the automation of structural and parametric optimization within the multi-energy system synthesis. Based on the use of FDE-SWFs, we have developed the workflow-based service-oriented application for modeling and optimizing a microgrid (a special case of MES). For this application, we have designed a modular, flexible architecture to enhance interoperability and facilitate the integration of specialized optimization tools within application workflows. Next, we have provided the case study on the synthesis of the microgrid for acceptable time. Preliminarily, we have selected the required optimization tools and validated the subject data on the specially developed testbeds, taking into account the level of model detail of the system under study.

The results of the study showed that the proposed SOE supports the multiplicity of both the number of options and the composition of the equipment, which could significantly increase the number of redundant circuits of the heat supply system and complicate its topology. At the same time, this allows us to significantly expand the range of considered solutions and in many respects increases the probability of not overlooking possible groups of options for the development of future heat supply systems, which are close in efficiency.

We hope that the proposed SOE can be used in practice to develop in the future heat supply schemes for cities and settlements for the period of planning their sustainable development for 5-15 years. This will make it possible to increase the efficiency of heat supply systems, to meet the requirements of consumers for increased thermal loads and the quality of heat supply, and to reduce the environmental pollution.