Prerpints.org logo
Preprint
Article

Chebyshev Polynomials in the Physics of the One-Dimensional Finite-Size Ising Model: An Alternative View and Some New Results

Altmetrics

Downloads

49

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 November 2024

Posted:

05 November 2024

You are already at the latest version

Alerts
Abstract
For studying of the finite-size behavior of the Ising model under different boundary conditions we propose an alternative to the standard transfer matrix technique approach based on Abel\`{e}s theorem and Chebyshev polynomials. Using it we easily reproduce the known for periodic boundary conditions results for Lee-Yang zeros, the exact position space renormalization group transformation, etc., and extend them deriving new results for antiperiodic boundary conditions. Note that in the latter case one has a nontrivial order-parameter profile, which we also calculate, where the average value of a given spin depends on the distance from the seam with opposite bond in the system. It is interesting to stress that under both boundary conditions, the one-dimensional case exhibits Schottky anomaly.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

The one-dimensional Ising model is one of the simplest and most studied statistical mechanical systems in the last 100 years. However, there are challenged problems which is still meaningful and new results have been obtained. Among them we will note the boundary effects in the context of different canonical Gibbs ensembles, the presence of impurities or other competitive interactions, which have been the subject of intensive research in recent few years [1,2,3,4]. Note in particular that the one-dimensional Ising model always been a field of illustration of various principles [5,6,7], phenomena [1,8,9,10,11,12,13,14,15], and methods of mathematical physics [2,5,7,8,16,17,18] that are effectively used in statistical physics. Quite recently, for example, was also realized that the Chebyshev polynomials are one of the effective tools in the mathematical analysis of the finite-size one-dimensional Ising model [12,13,14,15]. An unified method based on Chebyshev polynomials is, which we now aim to provide. There are an ultimate connection between the algebra of the 2 × 2 transfer matrices of the model and the Chebyshev polynomials that are to explore providing an alternative proof of known results. This imply a simplification of the mathematical treatment that is to explore providing new results especially in the case finite geometry. The benefit result of our present work is the presentation of an unified and at the same time relatively simple method for calculating finite-size quantities in the one-dimensional Ising chain in the case of different boundary conditions. We will note that this is particularly useful in the modelling the thermodynamic behavior of small systems [3,19,20].
The development we present is based on a theorem from the algebra of two dimensional matrix due to Abeles [21]. This route makes the calculations much easier to understand and are more complete, in particular, due to the very well knowledge of the algebra of the Chebyshev polynomials. We discovered that exact and compact results can be obtained even in a much more complicated situation we have chosen to give a thorough treatment of thermodynamic of the model in finite-size geometry in periodic and anti-periodic boundary conditions (PBC’s and ABC’s) — Section 2 and Section 3, and Lee-Yang theorem Section 4, well controlled position space renormalization group and its relation with logistic maps — Section 5 and the finite-size behavior of the specific heat, i.e., of Schottky anomaly, in Section 6. In order to make the presentation self-contained all the used information about the Chebyshev polynomials is shown in the Appendix A. Furthermore, aiming to make the text more easier for reader some longer calculations are separated in the Appendix B.
The article closes with the discussion and concluding remarks section given in Section 7.

2. The Partition Function in the Case of PBC’s and ABC’s

We consider one-dimension Ising model defined on a ring of N spins σ i = ± 1 with imposed PBC’s or ABC’s. The Hamiltonian of the model is given by
H = − J ∑ i = 1 N − 1 σ i σ i + 1 − J B C σ N σ 1 + h ∑ i = 1 N σ i ,
where J B C = J , a n d − J for PBC’s and ABC’s boundary conditions, respectively.
The well-known solution to the model proceeds by expressing the partition function Z N ( ζ ) ( K , h ) in terms of the so called transfer matrix T defined as
T = e K + h e − K e − K e K − h ,
which has two eigenvalues of the form
λ ± = e K cosh ( h ) ± e 2 K sinh 2 ( h ) + e − 2 K , w h e r e K ≡ β J .
Here β = 1 / ( k B T ) is proportional to inverse temperature, the coupling constant J > 0 and h is the dimensionless magnetic field.
Let us introduce an “edge” K * , which obeys the equation
sinh ( h ) = ( i e − 2 K * ) → h = i sin − 1 ( e − 2 K * )
at which the argument of the square root in Eq.(3) vanishes and eigenvalues λ ± become degenerate. In the high-temperature region 0 < K < K * the eigenvalues are reals λ + and λ − , while in the low-temperature region ∞ > K > K * they are complex conjugates.
The well known result for the partition function of the model in the case of PBC’s is determined by the eigenvalues of the transfer matrix and is given as follows
Z N ( per ) ( K , h ) = λ + N + λ − N .
while for the partition function in the case of ABC’s the corresponding result reads
Z N ( anti ) ( K , h ) = cosh ( h ) e 4 K sinh 2 ( h ) + 1 ( λ + N − λ − N ) ,
respectively.
Now we will present our based on the algebra of Chebyshev polynomials approach to the problem. Let us note in advance that the key role of the scaling variable:
x ( K , h ) = e K cosh ( h ) 2 sinh ( 2 K ) ≡ a ,
which encodes a large amount of information about Z N ( per ) ( K , h ) and Z N ( anti ) ( K , h ) . In the remainder of the text, in order to simplify the notations in long expressions, we will use a instead of x ( K , h ) .
Obviously, for the partition functions Z N ( per ) ( K , h ) and Z N ( anti ) ( K , h ) in terms of the transfer matrices one has
Z N ( per ) ( K , h ) = T r ( T N ) ,
and
Z N ( anti ) ( K , h ) = Tr ( T N − 1 · T A ) = Tr ( T A · T N − 1 ) ,
where we have taken into account that the transfer matrix T A , appropriate to an antiferromagnetic bond, is
T A = e − K + h e K e K e − K − h .

2.1. The Case of the PBC’s

Let us introduce the notation
r = 2 sinh ( 2 K ) = det T
and define the unimodular matrix T ˜ (i.e. with det T ˜ = 1 )
T ˜ = e K + h r e − K r e − K r e K − h r , det T ˜ = 1 ,
where the evident relation takes place
T N = [ r ] N T ˜ N ,
Using a result of Abelès [21], see also ([22], pp. 55 and 67) from the theory of matrices, the n − t h power of unimodular matrix T ˜ may be presented in the form [21]:
T ˜ N = e K + h r U N − 1 ( a ) − U N − 2 ( a ) e − K r U N − 1 ( a ) e − K r U N − 1 ( a ) e K − h r U N − 1 ( a ) − U N − 2 ( a ) ,
where U N ( a ) are Chebyshev polynomials of the second kind [23] (for a definition and some properties of the Chebyshev polynomials to be used in the text see Appendix A). We note that, there are several elegant proofs of the result of Abelès about the N-th power of an unimodular 2 × 2 matrix, see e.g. [24] and refs. therein.
So, we have
T r ( T ˜ N ) = 2 x ( K , h ) U N − 1 ( x ( K , h ) ) − U N − 2 ( x ( K , h ) ) = 2 T N ( x ( K , h ) ) ,
where the last equation follows from Eq. (A7).
Using Eq.(13) we get
T r ( T N ) = 2 2 sinh ( 2 K ) N T N ( x ( K , h ) ) ,
and for the partition function we obtain the result:
Z N ( per ) ( K , h ) = 2 sinh ( 2 K ) N Tr ( T ˜ N ) = 2 2 sinh ( 2 K ) N T N ( x ( K , h ) ) ,
in a full agreement with Eq. (2.7) in [12] where this equation has been reported initially but derived in a different way. Note that exactly the explicit dependence on x ( K , h ) is convenient for the further consideration.

2.2. The Case of the ABC’s

Following the idea of the previous sub-section in order to calculate Eq. (9) in an explicit form we will use the following result for T A T ˜ N − 1
T A T ˜ N − 1 = e 2 h + 1 r U N − 2 ( a ) − e − K + h U N − 3 ( a ) 1 r e 2 K − h + e − 2 K + h U N − 2 ( a ) − e K U N − 3 ( a ) 1 r e 2 K + h + e − 2 K − h U N − 2 ( a ) − e K U N − 3 ( a ) e − 2 h + 1 r U N − 2 ( a ) − e − K − h U N − 3 ( a ) .
It is thus found that
T r T A T ˜ N − 1 = e h e − K 2 a U N − 2 ( a ) − U N − 3 ( a ) + e − h e − K 2 a U N − 2 ( a ) − U N − 3 ( a ) = 2 cosh ( h ) e − K U N − 1 ( a ) ,
where the first recurrence equation Eq. (A7) has been already used. Now, after setting in Eq. (A9) from the Appendix A the above expression, we arrive at the relation with the unumodular matrix T ˜ (see Eq.(13)). Performing some simple algebra, we derive the final result
Z N ( anti ) ( K , h ) = 2 e − 2 K 2 sinh ( 2 K ) N x ( K , h ) U N − 1 ( x ( K , h ) ) .
One of the advantages of the proposed approach is that from the many well known mutual recurrence equations for the Chebyshev polynomials, see e.g. Appendixes A and D in Ref. [13], it immediately follows different mutual recurrence relations for the partition functions, e.g., like this one [25]
Z 2 N ( per ) ( K , h ) = [ Z N ( per ) ( K , h ) ] 2 − 2 2 sinh ( 2 K ) 2 N .
Additionally, from Eq. (A8) and Eq. (A10) from Appendix A, one obtains [17]
Z N ( per ) ( K , h ) = 2 e K cosh ( h ) Z N − 1 p e r ( K , h ) − 2 sinh ( 2 K ) Z N − 2 ( K , h ) .

3. Finite-Size Magnetization in the Case of PBC’s and ABC’s

3.1. Finite-Size Magnetization (PBC)

To calculate the average of the spin at site n, i.e., the local magnetization, let us look at
〈 σ 1 ( per ) 〉 : = 1 Z N ( per ) ( K , h ) ∑ σ 1 , . . . , σ N σ 1 T ( σ 1 , σ 2 ) T ( σ 2 , σ 3 ) . . . T ( σ N , σ 1 ) ,
where { T ( σ m , σ n ) } are elements of the transfer matrix T .
So, in terms of the unimodular matrix T ˜ we may also write (using Eq.(13))
〈 σ 1 ( per ) 〉 = r N Z N ( per ) ( K , h ) T r σ 1 · T ˜ N .
Using Eq.(14) the quantity ( σ 1 T ˜ N ) may be presented as 2 × 2 matrix with entries:
σ 1 T ˜ N = e K + h r U N − 1 ( a ) − U N − 2 ( a ) e − K r U N − 1 ( a ) − e − K r U N − 1 ( a ) − e K − h r U N − 1 ( a ) + U N − 2 ( a ) , .
This logic also extends to the magnetization at any other site. Thus we have
〈 σ n ( per ) 〉 = [ 2 sinh ( 2 K ) ] N Z N ( per ) ( K , h ) T r σ z T ˜ N ,
where σ z is the usual third 2 × 2 Pauli matrix.
The standard way to evaluate the expression in (26) is to rotate to a basis where the matrix T is diagonal. Note that under this transformation the Pauli matrix σ z is rotated into σ x . (see, e.g.,[ p.102, Kardar ]) . Instead, directly we will use our Eq.(25). After a simple algebra we get the finite-size-result in a compact form:
〈 σ n ( per ) 〉 = tanh ( h ) ( x ( K , h ) U N − 1 ( x ( K , h ) ) T N ( x ( K , h ) ) , x ( K , h ) = cosh ( h ) 1 − e − 4 K .

3.2. Finite-Size Magnetization (ABC)

In accord with Eq. (1), the − J bond connects the spins σ 1 and σ N . Then, in order to evaluate the average of the spin at site p (the local magnetization), we observe that it may be written in the form
〈 σ p ( anti ) 〉 : = 1 Z N ( anti ) ( K , h ) × ∑ σ 1 , . . . , σ N T ( σ 1 , σ 2 ) T ( σ 2 , σ 3 ) . . . . . . T ( σ p − 1 σ p ) σ p T ( σ p , σ p + 1 ) , T ( σ p + 1 , σ p + 2 ) . . . T ( σ p + N − p − 1 , σ N ) T A ( σ N , σ 1 )
and so
〈 σ p ( anti ) 〉 : = 1 Z N ( anti ) ( K , h ) Tr T p − 1 · σ p T N − p · T A = 1 Z N ( anti ) ( K , h ) Tr T A T p − 1 · σ p · T N − p = r N − 1 Z N ( anti ) ( K , h ) Tr ( A · B )
The matrices in question in the rhs of Eq. (29) are
A = T A · T ˜ p − 1 ≡ A 11 ( h ) A 12 ( h ) A 21 ( h ) A 22 ( h ) a n d B = σ p · T ˜ N − p ≡ B 11 ( h ) B 12 ( h ) B 21 ( h ) B 22 ( h )
and are calculated in the same way as in the previous subsection. It may be convenient to separate the technical details in the special Appendix B. The final result is:
Tr ( A · B ) = 2 sinh ( h ) e − K 1 ( a 2 − 1 ) a T N ( a ) − T | 2 p − N − 1 | ( a ) .
From Eq. (29) and Eq. (31) one obtains
〈 σ p ( anti ) 〉 = tanh ( h ) T | N − 2 p + 1 | ( a ) − a T N ( a ) 1 − a 2 U N − 1 ( a ) ,
which, with the help of Eq. (A7) from Appendix A, easily may be rederived in a more instructive form
〈 σ p ( anti ) 〉 = tanh ( h ) 1 + T | N − 2 p + 1 | ( a ) − T N − 1 ( a ) 1 − a 2 U N − 1 ( a ) .
From the last equation at once follows the remarkably simple result σ 1 = σ N = tanh ( h ) . The behavior of the order-parameter profile is shown in Figure 1.

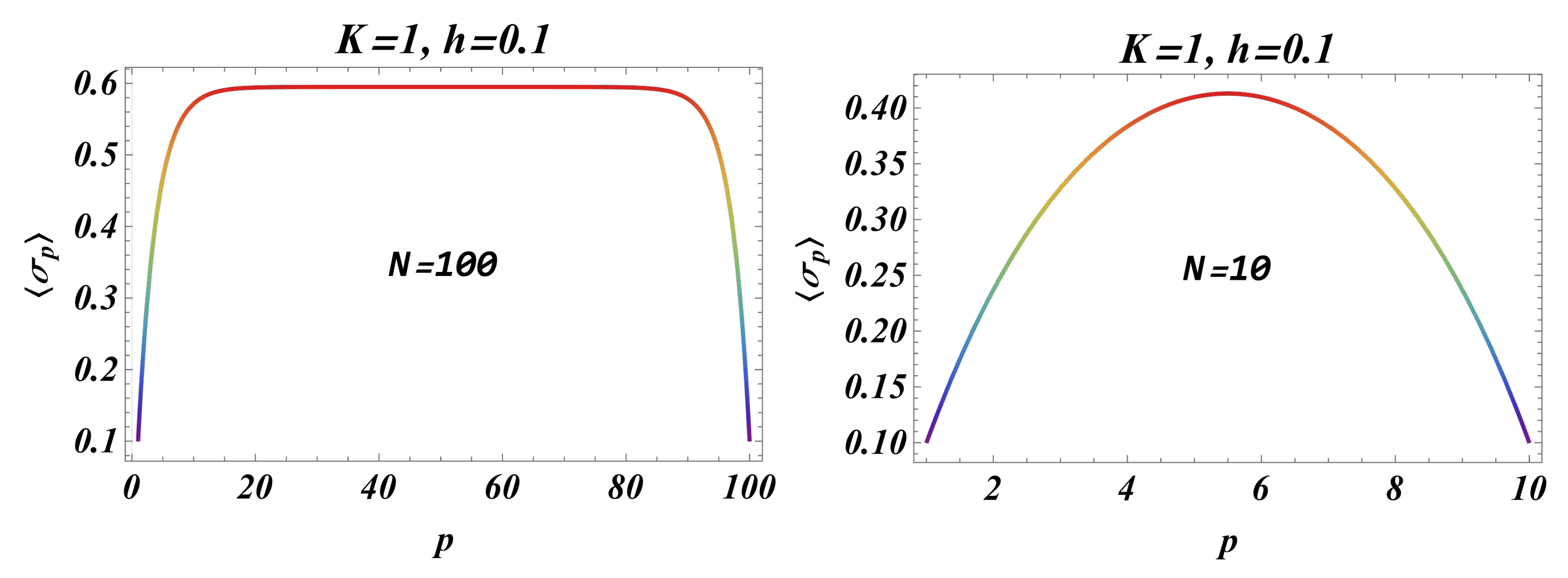
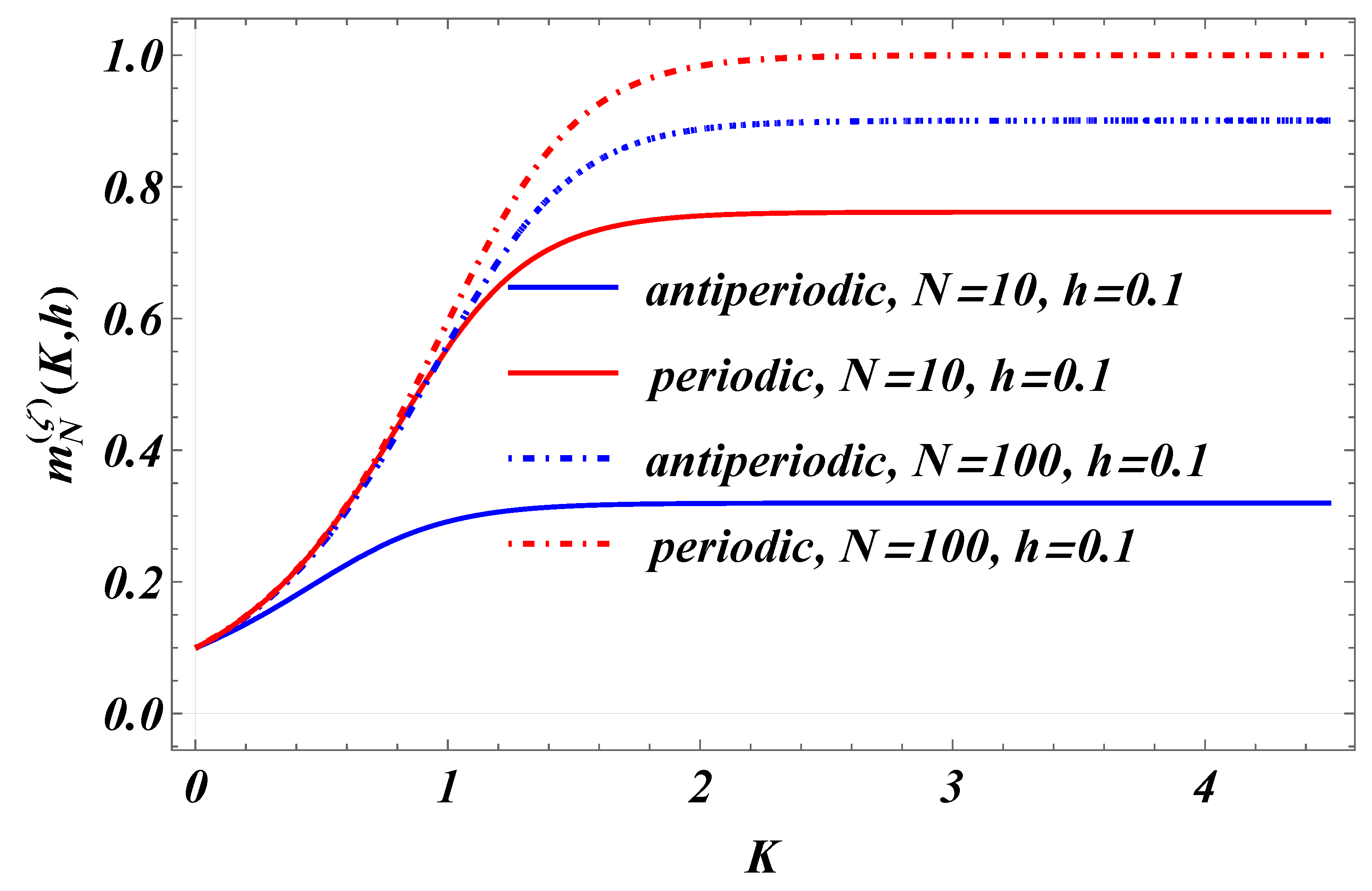
3.3. The Behavior of the Average Finite-Size Magnetization per Site m N ( ζ ) ( K , h ) for PBC’s and ABC’s

In the case of ABC the average magnetization per spin, using the definition
m N ( a n t i ) ( K , h ) = ∑ i = 1 N 〈 σ i 〉 N = − ∂ h f N ( anti ) ( K , h ) ,
where f N ( a n t i ) ( K , h ) is the Gibbs free energy density, leads to
β ∂ h f N ( anti ) ( K , h ) = − 1 N sinh ( h ) 1 − e − 4 K ∂ a U N − 1 ( a ) U N − 1 ( a ) + 1 a .
Using Eq. (A14) from the Appendix A we obtain
∂ a U N − 1 ( a ) U N − 1 ( a ) = N x 2 − 1 T N ( a ) U N − 1 ( a ) − a N .
Thus, the final result is
m N ( a n t i ) ( K , h ) = 1 N ∂ a U N − 1 ( x ) U N − 1 ( a ) + 1 / x ∂ h a = 1 N sinh ( h ) 1 − e − 4 K N a 2 − 1 T N ( a ) U N − 1 ( a ) − a N + 1 a .
It will be instructive to obtain the bulk result from Eq.(37). We have
lim N → ∞ 1 N ∂ a U N − 1 ( a ) U N − 1 ( a ) = 1 a 2 − 1
and since
sinh ( h ) 1 − e − 4 K 1 a 2 − 1 = e K sinh ( h ) [ e K cosh ( h ) ] 2 − 2 sinh ( 2 K )
we obtain the well known bulk result [26]
m ∞ ( K , h ) = e K sinh ( h ) [ e K cosh ( h ) ] 2 − 2 sinh ( 2 K ) .
Therefore, Eq.(37) may be rewritten in the form
m N ( a n t i ) = m ∞ 1 a 2 − 1 T N ( a ) U N − 1 ( a ) − 1 a N ,
The calculation for PBC proceeds exactly as in the previous case except that the derivative of U N ( a ) is replaced throughout by the derivative of T N ( a ) . In this case the corresponding final result is:
m N ( p e r ) = m ∞ a 2 − 1 U N − 1 ( a ) T N ( a ) .
The behavior of the average magnetization for both PBC and ABC is visualized in Figure 2 for N = 100 and N = 10 . We observe that for N = 10 the average magnetization is strongly suppressed being much smaller than the one for periodic boundary conditions. The situation changes when N grows - for N = 100 they are already close to each other. Note that the finite-size corrections in Eqs. (41) and (42).

4. Yang-Lee Zeros

Lee and Yang [27,28] circle theorem states that the grand canonical partition function Lee-Yang’s zeros of the Ising ferromagnet lie on the unit circle in the complex magnetic-field ( e h ) plane. We will demonstrate this statement on the example of 1-d Ising model under PBC and ABC using the presentation of the partition function in terms of Chebyshev polynomials.

4.1. The Case of PBC

As one can see from Eq. (17), the partition function zeros correspond precisely to the zeros of the Chebyshev polynomials of the first kind which enters in Eq,(17). Since T N ( ζ ) is a polynomial of order N the fundamental theorem of algebra asserts that it has N roots. Recall that all zeros ζ k of T N ( ζ ) i.e., defined by
T N ( ζ k ) = 0 , ( k = 1 , 2 , . . . , N ) .
are real, simple, lie in the open interval ( − 1 , 1 ) , moreover the set { ζ k n : 1 ≤ k ≤ n , n = 1 , 2 , . . . } is dense in [ − 1 , 1 ] . The zeros are located at
ζ k = cos ( θ k )
where
θ k = ( k − 1 / 2 ) π N , ( k = 1 , 2 , . . . , N ) .
Since T N ( ζ ) is a polynomial and we know all its zeros, we may write
T N ( ζ ) = γ ∏ k = 1 N ( ζ − ζ k ) ,
where the constant γ = 2 N − 1 .
So the problem of the Lee-Yang zeros by transitivity is easily transforms on the language of the zeros of Chebyshev polynomials. Thus, it will appear that it is necessary to assume
T N x ( K , h ) = 0 .
Here a problem arises, since for all real h and K, by definition x ( K , h ) > 1 , (see Eq. (7)), and thus the Eqs. (43) and (47) obviously failed to determine compatible conditions for common roots. The situation is changed if we introduce into consideration a complex field h with a complex variable (fugacity) z = e h , which can be parametrized by the trigonometric angle α on the unit circle in the complex plane z.
Now, from Eqs (43) and (47) follows a relation which connects the angular variables α and θ . It defines the location of the zeros in the complex z- plane determined by the solution (with respect to z = e h ) of the key equation
e K cosh ( h ) 2 sinh ( 2 K ) = cos ( k − 1 / 2 ) π N .
Indeed, its solutions depends on k and N. Then, setting Eq.(44) in the above equation and using the notation cos ( x 0 ) = 1 − e − 4 K , we obtain
( z + 1 / z ) = 2 cos ( x 0 ) ζ k ( N ) , w h e r e ζ k ( N ) : = cos ( k − 1 / 2 ) π N ,
with solutions
z k 1 , 2 = [ cos ( x 0 ) ζ k ( N ) ± i [ 1 − [ cos ( x 0 ) ζ k ( N ) ] 2 ] .
We see that, | z k | = 1 , and all the zeros lie on the unite circle in the complex z- plane. the zeros lie exactly on the unit circle as proved by Lee - Yang theorem.
The argument α k of the complex z k is given by
A r g ( z k ) : = α k = tan − 1 1 − [ cos ( x 0 ) ζ k ( N ) ] 2 cos ( x 0 ) ζ k ( N )
Using the formula
tan − 1 ± 1 − [ cos ( x 0 ) ζ k ( N ) ] 2 cos ( x 0 ) ζ k ( N ) = cos − 1 cos ( x 0 ) ζ k ( N ) ,
we get
α k = cos − 1 cos ( x 0 ) cos ( k − 1 / 2 ) π N .
If N is finite and at high temperature K → 0 , we have cos ( θ 0 ) = 1 − e − 4 K = 0 and
lim K → 0 θ k = cos − 1 ( 0 ) = π 2 , ( k = 1 , 2 , . . . , N ) ,
i.e. all zeroes cluster around θ = π / 2 , while at low temperatures K → ∞
lim K → ∞ α k = ( k − 1 / 2 ) π N , ( k = 1 , 2 , . . . , N ) ,
and they are uniformly spaced over the unit circle. The points which lies closest to the positive real axis is referred to as the “Yang-Lee edge singularity”.
In the thermodynamic limit
lim N → ∞ ζ k = lim N → ∞ cos ( k − 1 / 2 ) π N = 1 , ( k = 1 , 2 , . . . , N ) .
and the edge singularity is given by
α k = cos − 1 ( cos ( θ 0 ) ) ≡ cos − 1 1 − e 4 K = sin − 1 ( e − 2 K ) ≠ 0 , i f T > 0 .
From here we conclude that it lies outside the real axis and no transition occurs for any T > 0 .

4.2. The Case of ABC

The process of reasoning already employed leads us to consider the key equation
e K cosh ( h ) 2 sinh ( 2 K ) = cos k π N .
instead of the Eq.(48), where
ζ k = cos ( θ k ) = cos k π N , k = 1 , 2 , . . . N
are the roots of the Chebyshev polynomial of the second kind U N − 1 ( ζ ) which in the case is a constituent part of the partition function Z N ( anti ) ( K , h ) , see Eq. (20). For the argument of the complex fugacity we get
α k = cos − 1 cos ( x 0 ) cos k π N .
Further consideration is performed in a standard way on the line of previous case of PBC.

5. Chebyshev Recursion Relations and Exact RG Transformation

From the RG-point of view the study of the one-dimensional Ising model can be considered almost closed. However, from parallels with theory of route to chaos there are important shares to be clarified. It was shown that the exact renormalization transformations (RG) for the one-dimensional Ising model in a field can be cast in the form of a logistic map [29]. It is instructive to re-derive this result in a strait way in terms of Chebyshev polynomials.

5.1. Periodic Boundary Conditions

Our starting point is the partition function of the one dimensional Ising model under periodic boundary conditions Z N ( per ) ( K , h ) (see Eq.(17)) The RG approach is based on the (decimation) procedure known as the Kadanoff construction. It can be performed by a summing the configurations of every alternate spin variable in the chain and thus calculating of the partition function Z N / 2 ( per ) ( K ′ , h ′ ) . In this way one obtains a renormalized chain with only the half of number of the original N spins (N is supposed even). The essence of the RG approach is to obtain from the solution of the equation
Z N ( per ) ( K , h ) = A N ( K , h ) Z N / 2 ( per ) ( K ′ , h ′ ) ,
new couplings K ′ and h ′ such that Eq.(61) should take place.The normalized factor A ( K , h ) is the contribution (per site) from the "decimated" spins. Unfortunately the Kadanoff procedure can be performed exactly only in the one-dimensional case [30].
We will present a straightforward way of solving this problem using the recurrent equations of the Chebyshev polynomials.
First, we make use the substitution
x ( K , h ) = cosh ( Θ )
in the Chebyshev polynomials which is a constituent of the partition function Z N ( per ) ( K , h ) in Eq.(17) (and the physics of the system). Then we get
T N x ( K , h ) = cosh N / 2 ( 2 Θ ) = T N / 2 cosh ( 2 Θ ) = T N / 2 2 cosh ( Θ ) − 1 = T N / 2 2 x 2 ( K , h ) − 1 ,
Note that this is a particular realization of semigroup functional equation (A11). In the case these analytic property the Chebyshev polynomials is intimately related to the physical notion of decimation procedure. Our aim is to clarify this connection. If N is even,Eq.(63) maps the Lee-Yang zeros for a system of size N to the zeros of size N / 2 .
Let us introduce the partition function for the systems with N and constant ( K , h ) ,
Z N ( per ) ( K , h ) = 2 2 sinh ( 2 K ) N T N ( u ) , u = x ( K , h )
and for the partition function obtained from the partial trace by summing over every second spin variable along the chain with new length N / 2 and and ( K ′ , h ′ )
Z N / 2 ( per ) ( K ′ , h ′ ) = 2 2 sinh ( 2 K ′ ) N / 2 T N / 2 ( u ′ ) , u ′ = x ( K ′ , h ′ ) . ,
respectively
Let us note that:
1.) The gist of of the proposed decimation transformation is to use the recursive relation between Chebyshev polynomials T N and T N / 2 with imposed of a "linkage relation" of both arguments.
2.) Indeed, this transformation is such that it does not change the partition function.
So, if we suppose in the partition function Z N / 2 ( per ) ( K ′ , h ′ ) for N / 2 spin-system the pull-back relation
u ′ = 2 u 2 − 1 .
due to Eq. (63) it follows that
Z N / 2 ( per ) ( K ′ , h ′ ) = A − N Z N ( per ) ( K , h ) ,
where A is a normalization factor. The normalization factor A will not be further considered because it cancels in all thermodynamic averages.
The above equation in conjunction with Eq. (63) suggested that one can find new couplings K ′ and h ′ (as a function of K and h, ). In other words the recursive RG transformation for the 1D Ising could takes place, by demanding
x ( K ′ , h ′ ) = 2 x 2 ( K , h ) − 1 ,
which is nothing but of one-dimensional quadratic maps.
Since the quadratic map
y ′ = 4 y ( 4 − 1 ) ,
also referred to as the logistic map, appears frequently in the literature we write down the corresponding transformation between both forms:
x = 1 − 2 y .
A curious fact is that if require the condition Eq. (68) which is coupling with decimation this make an other conjugated form of quadratic map, e.g. Eq. (69) (as stated first in [29]) relevant to the problem.
So we obtain exactly the result of [29] in a different presentation as we will show below. In Ref. [31] shows that the logistic map f ( x ) : T 2 ( x ) = 2 x 2 − 1 on [ − 1 , 1 ] is linearly conjugate to the map g ( x ) = 4 x ( 1 − x ) on [ 0 , 1 ] . Since both maps are "topologically conjugate" i.e. equivalent as far as their dynamics are concerned, one can use any of them to study the other. In particular conjugacy preserves chaos, see. [31].
Now we will give a more friendly (without using special terminology) deduction of the above statement. Eq.(68) in explicit form is
cosh ( h ′ ) 1 − e − 4 K ′ = 2 cosh 2 ( h ) 1 − e − 4 K − 1
It may be rewritten in the form
1 + m ′ e 4 K ′ − 1 = 1 + 2 m e 4 K − 1 ,
where
m = 1 + e 4 K sinh 2 ( h )
is known as a renormalisation transformation invariant, i.e. m ′ = m , but here the last property is not essential to our consideration. It can be checked that for h = 0 , follows m = 1 , and Eq.(72) imply the well known RG-recursion relation for K, see e.g. [Kardar Eq.(6.38) p.106]
4 K ′ = 2 ln [ cosh ( 2 K ) ] .
Finally introducing the new variables [29]
x : = − m e 4 K − 1 = − m e − 4 K 1 − e − 4 K , a n d x ′ = − m ′ e 4 K ′ − 1
instead of K ′ s in Eq.(72), one gets
1 − x ′ = 1 − 2 x
which is exactly the logistic map defined:
x ′ = 4 x ( 1 − x ) , ∀ x ∈ [ 0 , 1 ] .
The condition x ∈ [ 0 , 1 ] is equivalent to
0 ≥ m ≥ e 4 K − 1 .
Thus lhs gets
1 + e 4 K sinh 2 ( h ) ≤ 0 .
These constraints define the external magnetic field to lie at the imaginary axis of h, i.e. on the unit circle of z = e i θ , with
sin 2 ( θ ) > e − 4 K .
This makes a connection to Yang-Lee circle theorem, since it is valid also if h = i θ is an imaginary field.
Here a small comment is in place. If we introduce y = 1 − x in Eq.(76) we get
1 − x ′ = 2 ( 1 − x ) − 1 , → 2 y 2 − 1 = y ′
we have the logistic map in the other form
y ′ = 2 y 2 − 1 , y ∈ [ − 1 , 0 ] .
Both expressions appear equal frequently in the literature, see 1.) in Ref. [32] and 2.) Ref. [33]. Indeed, a linear transformation x = ( 1 / 2 ) ( y + 1 ) and x ′ = ( 1 / 2 ) ( y ′ + 1 ) brings one to the other. A point x * is said to be a fixed point of the map f ( x ) if f ( x * ) = x * . So, Eq. (76) has two fixed point 0 * = 0 and x * = 3 / 4 . Eq. (82) has two fixed points y * = 1 / 2 and y * = − 1 .
We have thus seen that exploiting a decimation-type renormalization transformation based on the Chebyshev polynomials, Eq. (63), gives rise to a recursion relation that in turn be mapped on to the logistic equation. This result is not new (see Doland Dolan and Johnston), but it is obtained in a way that reveals the potential of Chebychev recursion relations.
This will exhibit chaos for almost all 0 < x < 1 , i.e. 1 − e 4 K < m < 0 . The first inequality implies h to be imaginary, i.e. h = i θ (see eq. (4)). The second one implies sin 2 ( θ ) > e − 4 K , see [29,34].

5.2. Antiperiodic boundary conditions

The partition function of the one dimensional Ising model under anti-periodic boundary conditions is given in the form [12]:
Z N ( anti ) ( K , h ) = 2 e − 2 K 2 sinh ( 2 K ) N x ( K , h ) U N − 1 x ( K , h ) ,
In order to obtain the analog of Eq. (67) we make use the identity (valid for every N, K and h):
Z 2 ( N + 1 ) ( anti ) ( K , x ) = 2 e K 2 sinh ( 2 K ) N / 2 cosh ( h ) Z N + 1 ( anti ) ( K , 2 x 2 − 1 ) ,
which results from the following relation for the Chebyshev polynomials of the second kind
U 2 N + 1 ( x ) = 2 x U N ( 2 x 2 − 1 ) .
The realization of the Kadanoff procedure (which in this case is modified since we exclude the inverted spin) is given by
Z N / 2 + 1 ( anti ) ( K ′ , h ′ ) = B − N Z N + 1 ( anti ) ( K , h ) ,
where B is a normalization factor. Eq.(86) holds only if
x ( K ′ , h ′ ) = 2 x 2 ( K , h ) − 1 .
Indeed, in the case of anti-periodic boundary conditions we obtain the same recursion relation as in the periodic case, as it must be.
At the end let us note that it is well known that the logistic map of Eq. (69) is topologically conjugate to a Chebyshev map y = T 2 ( x ) = 2 x − 1 [35].

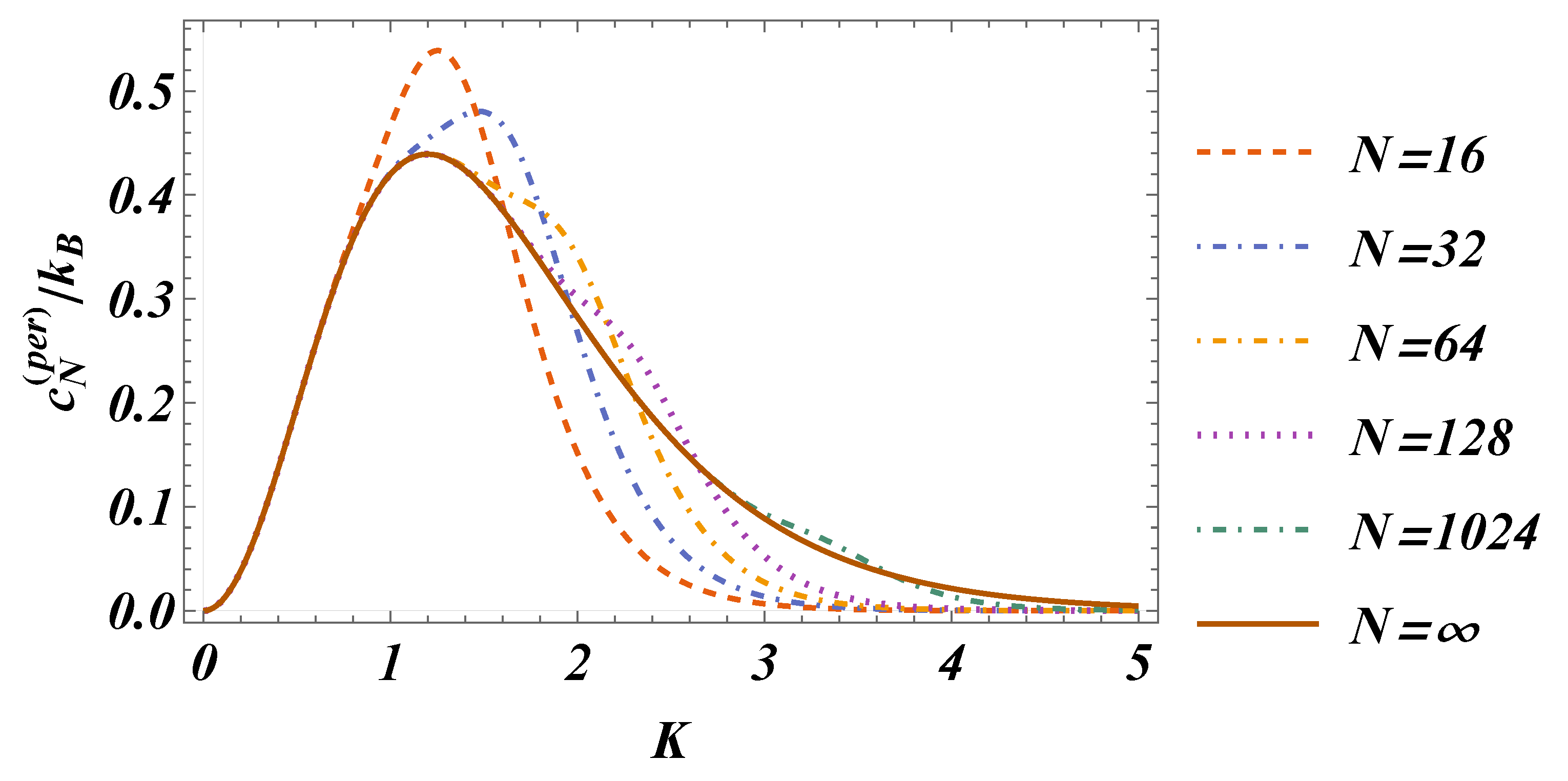
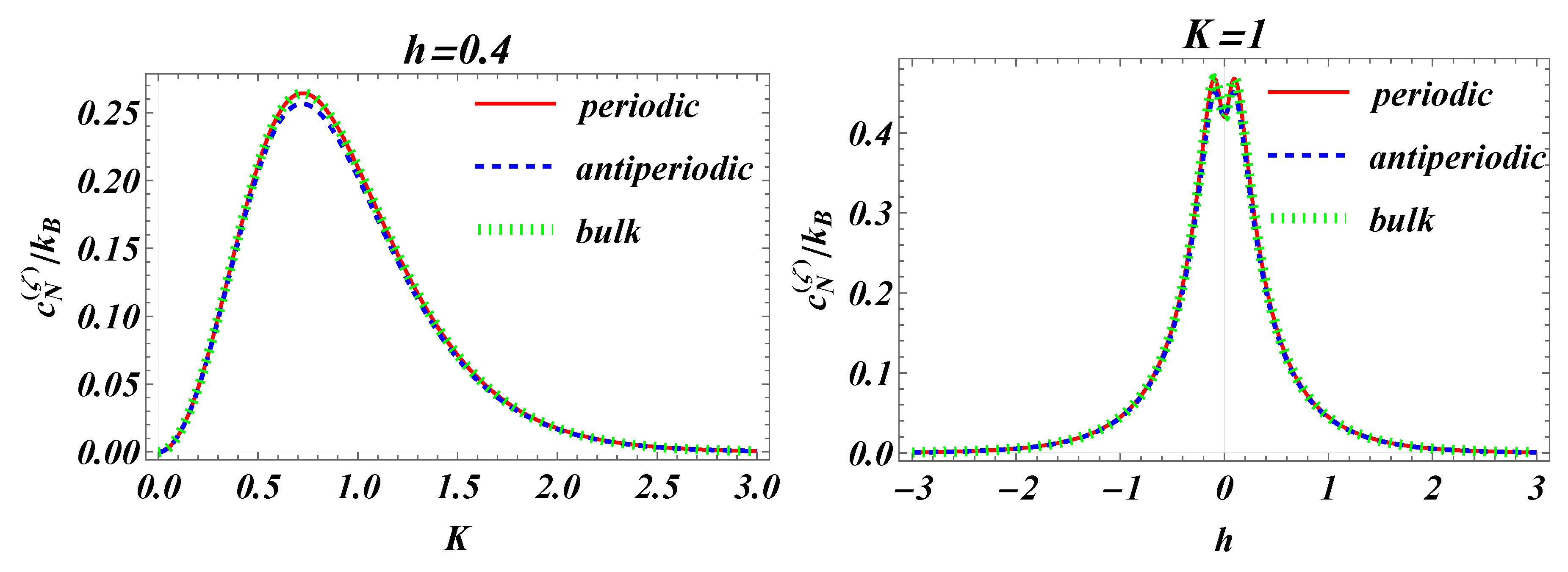
6. Schottky Anomaly

The Schottky anomaly is a phenomenon observed in the specific heat of certain materials at low temperatures that possess a finite number of discrete energy levels in the system. It is named after the German physicist Walter H. Schottky. It is usually observed in systems that have an excitation gap above its ground state [36]. The Schottky anomaly occurs because, at low temperatures, the thermal energy is comparable to the energy differences between these discrete levels. As the temperature increases, more energy levels become accessible and occupied, leading to an increase in specific heat. Once most of the levels are excited, the specific heat decreases again, creating a peak.
It is well know that in the bulk Ising model the heat capacity c N ( K , h ) does not exhibit a singularity, but demonstrates a peak near J ≃ k B T , which is a demonstration of the Schottky anomaly [37]. The behavior of the specific heat in a finite chain under boundary conditions ( ζ ) , i.e., of c N ( ζ ) ( K , h ) is shown in Figure 3 and Figure 4.
Figure 3 shows, in a full agreement with Fig. 1 in [1] that for smaller N the specific heat decreases faster to zero with increase of K (see also Fig. 6 in [38]). The Schottky anomaly is clearly visible.
In Figure 4 we observe that Schottky anomaly is preserved also for the finite Ising chains with both periodic and antiperiodic boundary conditions.
It is interesting to note that for moderate values of K, the maximum of c N ( K , h ) is at nonzero value of h. The maximum shifts to h = 0 , as it is to be expected, with increase of K.
The above results immediately do follow from Eq. (17) and Eq. (20), and the standard relation
c N ( ζ ) ( K , h ) = K 2 ∂ 2 ln Z N ( ζ ) ( K , h ) ∂ K 2 ,
with c N ( ζ ) ( K , h ) measured in terms of k B . The result for the infinite system with h = 0 is well known [1]
c ∞ ( K , h = 0 ) = K 2 sec h 2 ( K ) .
For h ≠ 0 one has
c ∞ ( K , h ) = 4 e − 6 K K 2 sinh 2 ( h ) + e − 4 K λ + ( K , h ) e − K 2 e 4 K sinh 2 ( h ) + 1 sinh 2 ( h ) + e − 4 K − 1 λ + ( K , h ) .

7. Discussion and Concluding Remarks

In the present study, all the results for the case of PBC have been obtained before, but in a different form. The results for the ABC case are new. In both cases, a new approach based on the algebra of Chebyshev’s polynomials was demonstrated.
It is worth noting that to use a special function in the theory of one-dimensional Ising model is not a new attempt, since a relation between the finite-size partition function and the generalized Lucas polynomials is found in Ref. [17], or an approach based on the Bell polynomial for studying one-dimensional lattice gas (equivalent to the Ising model) is demonstrated in Ref. [10]. The resulting formulas, even for such a simple model, are sufficiently complex due to the accounting for of finite-size effects.
In the current article we show the existence of another polynomial form of the solution for the Ising model chain, expressed in terms of Chebyshev polynomials. Thanks to the existence of the scaling variable a, see Eq.(7), there is an isomorphism between the partition function of the model and Chebyshev polynomials having its as argument. It is noteworthy that the index N of the polynomials takes into account the number of spins in the chain, while the type of boundary conditions is directly related to the kind of polynomials: T N ( a ) for the PBC (see Eq. (17)) and U N ( a ) for ABC (see Eq. (20)). These properties make formulas more compact and therefore easier to comprehension, despite complex functional dependencies of K , h and N. An additional advantage is the presence of different recurrence relations between Chebyshev polynomials (see Appendix A) which imply a straightforward calculation. A typical example of this are the expressions Eq. (32), or , for local magnetization in the case of APC, which cannot be obtained by direct differentiation of free energy due to violation of the translation invariance. The corresponding profile is shown in Figure 1.
The requirement of the relationship of the roots of Chebyshev’s polynomials to the scaling variable a (see Eq. (17)) and (20)) elegantly verifies the Lee-Young circle theorem in both cases of PBC and ABC.
An interesting fact is that the functional relations of Chebyshev’s polynomials, Eq. (63) and Eq. (85) have encoded Kadanoff’s procedure, which in this case can lead to chaotic behavior. In particular, the recursive RG transformation for the 1D Ising could takes place, by demanding to validity of Eq. (68) which is nothing but of one-dimensional quadratic map.
A productive use of the proposed approach is related to the calculation of the specific heat capacity associated with the so-called Schottky effect, as the numerical results are presented in Figure 3 and Figure 4, for both cases of boundary conditions.
In a summary, one can conclude that the key point of the calculations procedure based on Chebyshev polynomials is the one during which the degrees of transfer matrix T N , N ∈ N + , are expressed in terms of the Chebyshev polynomials of second kind. Naturally, this method is complementary to the classical approach based on standard way of using a transfer matrix and, of course, it can be used in conjunction to it. The advantages of the method based on the Chebyshev polynomials are expected to be mainly when it is used to calculate object like the multispin correlations [4], however in chains with violation of translation invariance — either due to the the boundary conditions or to site-dependence of an external field applied on the system, say to study systems, e.g. for the periodic Ising chain with length N = n × p (here p defines the period of the chain) with partition function Z N = T r [ ( T p ) n ] , where T p = T 1 · T 2 ⋯ T p [9]. We hope to return to these problems in the future.

Author Contributions

Conceptualization, N. T. and D.D.; methodology, N. T. and D.D.; software, D. D.; validation, N. T. and D.D.; formal analysis, N. T. and D.D.; writing—original draft preparation, N. T. and D.D.; writing—review and editing, N. T. and D.D.; visualization, D.D.; All authors have read and agreed to the published version of the manuscript.

Funding

Partial financial support via Grant No KP-06-H72/5 of the Bulgarian National Science Fund is gratefully acknowledged.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

There are no data related to the study reported in the current article.

Acknowledgments

Partial financial support via Grant No KP-06-H72/5 of the Bulgarian NSF is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest.The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
PBC Periodic Boundary Conditions
ABC Antiperiodic Boundary Conditions
RG Renormalization Group

Appendix A. Chebyshev Polynomials

There are several ways to introduce the Chebyshev polynomials of first and second kind commonly denoted by T N ( x ) and U N ( x ) . An endless variety between Chebishev polynomials may be derived. In this Appendix the reader will find these formulas which are exploiting in the main text. The Chebyshev polynomials in terms of algebraic functions are defined as follows:
T n ( x ) = 1 2 ( x + x 2 − 1 ) n + ( x − x 2 − 1 ) n
and
U n − 1 ( x ) = 1 2 x 2 − 1 ( x + x 2 − 1 ) n − ( x − x 2 − 1 ) n
upon setting x = cos ( θ ) in the above equations after applying De Moivre’s theorem one obtains the results
T n ( cos ( θ ) ) = cos ( n θ ) a n d U n − 1 ( x ) = sin ( n θ ) sin ( θ )
In therms of variable x the defining for these function become
T n ( x ) = cos ( n c o s − 1 ( x ) ) a n d U n ( x ) = sin ( n c o s − 1 ( x ) ) 1 − x 2
Since these two polynomial presentations agree for | x | ≤ 1 , so they must agree for all real or complex x.
For a non-negative integer n ≥ 2 , the Chebyshev polynomials can be defined recursively as follows:
U n ( x ) = 2 x U n − 1 ( x ) − U n − 2 ( x ) , U 0 ( x ) = 1 , U 1 ( x ) = 2 x .
and for T n ( x )
T n ( x ) = 2 x T n − 1 ( x ) − T n − 2 ( x ) , T 0 ( x ) = 1 , T 1 ( x ) = x .
Eq. (A5) is basically used several times in the main text. The Chebyshev polynomials satisfy the following formulas [39]:
a.) the recurrence relations
T n ( x ) = x U n − 1 ( x ) − U n ( x ) ,
and
2 a T n ( x ) = T n + 1 ( x ) + T n − 1 ( x )
b.) the multiplication formulas
U m − 1 ( x ) U n − 1 ( x ) = 1 2 ( 1 − a 2 ) T m − n ( x ) − T m + n ( x )
and
2 T m ( x ) T n ( x ) = T m + n ( x ) + T m − n ( x )
c.) the functional equations
T m ( T n ( x ) ) = T n ( T m ( x ) ) = T m n ( x ) .
and
2 x U n − 1 ( T 2 ( x ) ) = U 2 n − 1 ( x ) , T 2 ( x ) = 2 x − 1 .
It is interesting to note that if one requires T n ( x ) to be a polynomial of degree n, Eq.(A11) uniquely determines Chebishev polynomials [39].
d.) the derivative of T n ( x ) and U n ( x ) are [see Eqs.(3.2-1) and 3.2-2 in M. A. Snyder]
∂ T N ( x ) ∂ x = n U n − 1 ( x )
and
∂ U n − 1 ( x ) ∂ x = N T n ( x ) − x U n − 1 ( x ) x 2 − 1 .

Appendix B

Here we present some of the calculations leading to obtaining the results reported in the main text concerning the behavior of the local order parameter profile in Ising chain with antiperiodic boundary conditions.
The product of the matrices A = T A · T ˜ p − 1 ( a ) has the following explicit form:
A = e − K + h e K e K e − K − h · e K + h r U p − 2 ( a ) − U p − 3 ( a ) e − K r U p − 2 ( a ) e − K r U p − 2 ( a ) e K − h r U p − 2 ( a ) − U p − 3 ( a ) , ≡ A 11 ( h ) A 12 ( h ) A 21 ( h ) A 22 ( h ) ,
and, correspondingly, the other product B = σ p · T ˜ N − p may be written in a similar way as:
B = 1 0 0 − 1 · e K + h r U N − p − 1 ( a ) − U N − p − 2 ( a ) e − K r U N − p − 1 ( a ) e − K r U N − p − 1 ( a ) e K − h r U N − p − 1 ( a ) − U N − p − 2 ( a ) ≡ B 11 ( h ) B 12 ( h ) B 21 ( h ) B ( h ) 22 ,
where
a = 1 2 e K + h r + e K − h r ≡ x ( K , h ) = cosh ( h ) 1 − e − 4 K .
The entries of A and B can be easily obtained as follows:
A 11 ( h ) = e 2 h + 1 r U p − 2 ( a ) − e − K + h U p − 3 ( a ) , A 12 ( h ) = e − 2 K + h r U p − 2 + e 2 K − h r U p − 2 ( a ) − e K U p − 3 ( a )
A 21 ( h ) = A 12 ( − h ) , A 22 ( h ) = A 11 ( − h ) ,
and
B 11 ( h ) = e K + h r U N − p − 1 ( a ) − U N − p − 2 ( a ) , B 12 ( h ) = e − K r U N − p − 1 ( a )
B 21 ( − h ) = − B 12 ( h ) , B 22 ( − h ) = B 11 ( − h ) .
Multiplying the matrices A and B after some simple, but a little bit tedious algebra, we obtain for
Tr ( A · B ) = A 11 B 11 + A 21 B 12 + A 12 B 21 + A 22 B 22
the result
T r ( A · B ) = 2 sinh ( h ) e − K U p − 2 ( a ) U N − p − 1 ( a ) + U p − 1 ( a ) U N − p ( a ) .
It is worth noting that recurrence relation (A5) from the Appendix A is used in order to obtain the Eq. (A23) in a such simplified and compact form. Some time it is useful to have the "p" dependence in a only one of the Chebyshev polynomials. To this aim one can use the recurrence relations Eqs. (A8) and (A9) from the Appendix A. Let us briefly sketch the idea of computations. They are performed in two steps:
A. first if we take the case: p < N + 1 2
From Eq.(A9) (with m = N − p , n = p − 1 ) for the first term in the rectangular brackets in Eq. (A23) we have
U p − 2 ( a ) U N − p − 1 ( a ) = 1 2 ( 1 − a 2 ) [ T N − 2 p + 1 ( a ) − T N − 1 ( a ) ] ,
and from Eq. (A9) (with m = N − p + 1 , n = p ) for the second term in the rectangular brackets in Eq. (A23) we have
U p − 1 ( a ) U N − p ( a ) = 1 2 ( 1 − a 2 ) [ T N − 2 p + 1 ( a ) − T N + 1 ( a ) ]
Thus
U p − 2 ( a ) U N − p − 1 ( a ) + U p − 1 ( a ) U N − p ( a ) = 1 2 ( a 2 − 1 ) − 2 T N − 2 p + 1 ( a ) + T N + 1 ( a ) + T N − 1 ( a ) = 1 ( a 2 − 1 ) a T N ( a ) − T N − 2 p + 1 ( a ) , i f 2 p < N + 1 ,
where recurrence relation Eq. (A8) is used.
B. and in the opposite case: p > N + 1 2
From Eq. (A9) (with n = N − p , m = p − 1 , ) we have
U p − 2 ( a ) U N − p − 1 ( a ) = 1 2 ( 1 − a 2 ) [ T − N + 2 p − 1 ( a ) − T N − 1 ( a ) ]
and from Eq.(A9) (with n = N − p + 1 , m = p ) we have
U p − 1 ( a ) U N − p ( a ) = 1 2 ( 1 − a 2 ) [ T − N + 2 p − 1 ( a ) − T N + 1 ( a ) ]
Thus
U p − 2 ( a ) U N − p − 1 ( a ) + U p − 1 ( a ) U N − p ( a ) = 1 2 ( a 2 − 1 ) − 2 T − N + 2 p − 1 ( a ) + T N + 1 ( a ) + T N − 1 ( a ) = 1 ( a 2 − 1 ) [ a T N ( a ) − T − N + 2 p − 1 ( a ) ] i f 2 p > N + 1 ,
where the relation Eq. (A8) is used. The final result in a unified form is
U p − 2 ( a ) U N − p − 1 ( a ) + U p − 1 ( a ) U N − p ( a ) = 1 ( a 2 − 1 ) a T N ( a ) − T | 2 p − N − 1 | ( a ) , ∀ p , 1 ≤ p ≤ N
and hence for Eq.(A23) we obtain
Tr ( A · B ) = 2 sinh ( h ) e − K 1 ( a 2 − 1 ) a T N ( a ) − T | 2 p − N − 1 | ( a ) .
The above result is easily summable over the index " p " , in comparison with the one given in Eq. (A23).

References

  1. Sitarachu, K.; Zia, R.K.P.; Bachmann, M. Exact microcanonical statistical analysis of transition behavior in Ising chains and strips. J. Stat. Mech: Theory Exp. 2020, 2020, 073204.
  2. Magare, S.; Roy, A.K.; Srivastava, V. 1D Ising model using the Kronecker sum and Kronecker product. Eur. J. Phys. 2022, 43, 035102.
  3. Stepanyan, V.; Tzortzakakis, A.F.; Petrosyan, D.; Allahverdyan, A.E. Thermal transitions in a one-dimensional, finite-size Ising model. J. Stat. Mech: Theory Exp. 2024, 2024, 033202. [CrossRef]
  4. Balcerzak, T. Application of the integral operator method for multispin correlation function calculations in the one-dimensional Ising model. Phys. Rev. E 2024, 109, 024133. [CrossRef]
  5. Yessen, W.N. Properties of 1D Classical and Quantum Ising Models: Rigorous Results. Annales Henri Poincaré 2013, 15, 793–828. [CrossRef]
  6. Fierro, A.; Coniglio, A.; Zannetti, M. Condensation of fluctuations in the Ising model: A transition without spontaneous symmetry breaking. Phys. Rev. E 2019, 99, 042122. [CrossRef]
  7. Bena, I.; Droz, M.; Lipowski, A. Statistical mechanics of equilibrium and nonequilibrium phase transitions: the Yang–lee formalism. Int. J. Mod. Phys. B 2005, 19, 4269–4329. [CrossRef]
  8. Lee, J. Low-temperature behavior of the finite-size one-dimensional Ising model and the partition function zeros 2014. 65, 676683.
  9. Barata, J.C.A.; Goldbaum, P.S. On the Distribution and Gap Structure of Lee–Yang Zeros for the Ising Model: Periodic and Aperiodic Couplings. 103, 857–891. [CrossRef]
  10. Fronczak, A. Cluster properties of the one-dimensional lattice gas: The microscopic meaning of grand potential. Phys. Rev. E 2013, 87, 022131. [CrossRef]
  11. Dantchev, D.; Rudnick, J. Exact expressions for the partition function of the one-dimensional Ising model in the fixed-M ensemble. Phys. Rev. E 2022, 106, L042103. [CrossRef]
  12. Dantchev, D.M.; Tonchev, N.S.; Rudnick, J. Casimir versus Helmholtz forces: Exact results. Annals of Physics 2023, 459, 169533. [CrossRef]
  13. Dantchev, D.M.; Tonchev, N.S.; Rudnick, J. Casimir and Helmholtz forces in one-dimensional Ising model with Dirichlet (free) boundary conditions. Ann. Phys., 464, 169647. [CrossRef]
  14. Dantchev, D. On Casimir and Helmholtz Fluctuation-Induced Forces in Micro- and Nano-Systems: Survey of Some Basic Results. Entropy 2024, 26, 499. [CrossRef]
  15. Dantchev, D.; Tonchev, N. A Brief Survey of Fluctuation-induced Interactions in Micro- and Nano-systems and One Exactly Solvable Model as Example 2024. [2403.17109]. [CrossRef]
  16. Baake, M.; Grimm, U.; Joseph, D. Trace Maps, Invariants, and Some of Their Applications. Int. J. Mod. Phys. B 1993, 07, 1527–1550. [CrossRef]
  17. da Conceição, C.M.S.; Maia, R.N.P. Recurrence relations in one-dimensional Ising models. Phys. Rev. E 2017, 96, 032121. [CrossRef]
  18. Seth, S. Combinatorial approach to exactly solve the 1D Ising model. Eur. J. Phys. 2016, 38, 015104. [CrossRef]
  19. Maniwa, Y.; Kataura, H.; Matsuda, K.; Okabe, Y. A one-dimensional Ising model for C70molecular ordering in C70-peapods. New J. Phys. 2003-10, 5, 127–127. [CrossRef]
  20. Taherkhani, F.; Daryaei, E.; Parsafar, G.; Fortunelli, A. Investigation of size effects on the physical properties of one-dimensional Ising models in nanosystems. Mol. Phys. 2011, 109, 385–395. [CrossRef]
  21. Abelès, F. Sur l’itération des matrices carrées a quatre éléments. Ann. de Physique 1950, 5, 777–782.
  22. Born, M.; Wolf, E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light; Pergamon Press, New York, 1980.
  23. Gradshteyn, I.S.; Ryzhik, I.H. Table of Integrals, Series, and Products; Academic, New York, 2007.
  24. Griffiths, D.J.; Steinke, C.A. Waves in locally periodic media. American Journal of Physics 2001, 69, 137–154.
  25. Nandhini, G.; Sangaranarayanan, M.V. Partition function of nearest neighbour Ising models: Some new insights. J. Chem. Sci. 2009, 121, 595–599. [CrossRef]
  26. Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic, London, 1982.
  27. Yang, C.N.; Lee, T.D. Statistical theory of equations of state and phase transitions. I. Theory of condensation. Physical Review 1952, 87, 404.
  28. Lee, T.D.; Yang, C.N. Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model. Physical Review 1952, 87, 410.
  29. Dolan, B.P. Chaotic behavior of renormalization flow in a complex magnetic field. Physical Review E 1995, 52, 4512.
  30. Kardar, M. Statistical Physics of Fields; Cambridge University Press, Cambridge, 2007.
  31. Elaydi, S.N. Discrete chaos: with applications in science and engineering; CRC press, 2007.
  32. Hao, B.; Zheng, W. Applied symbolic dynamics and chaos, second ed.; World Scientific, 2018.
  33. Strogatz, S.H. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering; CRC press, 2018.
  34. Dolan, B.P.; Johnston, D. One-dimensional Potts model, Lee-Yang edges, and chaos. Physical Review E 2002, 65, 057103.
  35. Geisel, T.; Fairen, V. Statistical properties of chaos in Chebyshev maps. Phys. Lett. A 1984, 105, 263–266. [CrossRef]
  36. Pathria, R.K.; Beale, P.D. Statistical Mechanics, third ed.; Elsevier, Amsterdam, 2011.
  37. Goldenfeld, N. Frontiers in Physics. In Lecture on phase transitions and the renormalization group; Pines, D., Ed.; Frontiers in Physics, Addison-Wesley, New York, 1992.
  38. Ferreira, L.S.; Plascak, J.A. Finite-Size Effects of the One-Dimensional Ising Model. Braz. J. Phys. 2023, 53, 77. [CrossRef]
  39. Snyder, M.A. Chebyshov Methods in Numerical Approximations; Prentice-Hall Inc., Englewood Cliffs N.J., 1966; chapter 2.
Preprints 138376 g001
Figure 1. On the left panel: The behavior of the local magnetization 〈 σ p ( anti ) 〉 for N = 100 , h = 0 . 1 and K = 1 . On the right panel: The behavior of 〈 σ p ( anti ) 〉 with N = 10 , h = 0 . 1 and K = 1 . The profiles visualize Eq. (32) or, equivalently, Eq. (33).
Figure 1. On the left panel: The behavior of the local magnetization 〈 σ p ( anti ) 〉 for N = 100 , h = 0 . 1 and K = 1 . On the right panel: The behavior of 〈 σ p ( anti ) 〉 with N = 10 , h = 0 . 1 and K = 1 . The profiles visualize Eq. (32) or, equivalently, Eq. (33).
Preprints 138376 g001
Preprints 138376 g002
Figure 2. The behavior of the magnetization m N ( ζ ) ( K , h ) as a function of K for N = 100 and N = 10 , for h = 0 . 1 for periodic boundary conditions - see Eq. (42), and Eq. (41) for antiperiodic boundary conditions.
Figure 2. The behavior of the magnetization m N ( ζ ) ( K , h ) as a function of K for N = 100 and N = 10 , for h = 0 . 1 for periodic boundary conditions - see Eq. (42), and Eq. (41) for antiperiodic boundary conditions.
Preprints 138376 g002
Preprints 138376 g003
Figure 3. The behavior of c N ( ζ ) ( K , h = 0 ) for different values of N. This plot is to be compared wth Fig. 1 in [1]. We observe that with smaller N the specific heat drops faster to zero with increasing K.
Figure 3. The behavior of c N ( ζ ) ( K , h = 0 ) for different values of N. This plot is to be compared wth Fig. 1 in [1]. We observe that with smaller N the specific heat drops faster to zero with increasing K.
Preprints 138376 g003
Preprints 138376 g004
Figure 4. On the left panel: The behavior of the specific heat c N ( ζ ) ( K , h ) for N = 100 and h = 0 . 4 as a function of K. On the right panel: The behavior of c N ( ζ ) ( K , h ) with N = 100 and K = 1 as a function of h. Due to the ± h symmetry the two branches are symmetric with respect to h = 0 . The results for the infinite system practically coincide with those for the periodic boundary conditions with N = 100 .
Figure 4. On the left panel: The behavior of the specific heat c N ( ζ ) ( K , h ) for N = 100 and h = 0 . 4 as a function of K. On the right panel: The behavior of c N ( ζ ) ( K , h ) with N = 100 and K = 1 as a function of h. Due to the ± h symmetry the two branches are symmetric with respect to h = 0 . The results for the infinite system practically coincide with those for the periodic boundary conditions with N = 100 .
Preprints 138376 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated