Study on Optimal Charging Current Protocol with Multi-Stage Constant Current Using Dandelion Optimizer for Time- Domain Modeled Lithium-Ion Batteries

Preprint

Article

Study on Optimal Charging Current Protocol with Multi-Stage Constant Current Using Dandelion Optimizer for Time- Domain Modeled Lithium-Ion Batteries

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Seongik Han^*

This version is not peer-reviewed

Submitted:

05 November 2024

Posted:

05 November 2024

You are already at the latest version

Alerts

Abstract

This study utilized a multi-stage constant current (MSCC) charge protocol to identify the optimal current pattern (OCP) for effectively charging lithium-ion batteries (LiBs) using a Dandelion optimizer (DO). A Thevenin equivalent circuit model (ECM) was implemented to simulate an actual LiB with the ECM parameters estimated from offline time response data obtained through a hybrid pulse power characterization (HPPC) test. For the first time, DO was applied to me-taheuristic optimization algorithms (MOAs) to determine the OCP within the MSCC protocol. A composite objective function that incorporates both charging time and charging temperature was constructed to facilitate the use of DO in obtaining the OCP. To verify the performance of the proposed method, various algorithms, including the constant current-constant voltage (CC-CV) technique, formula method (FM), particle swarm optimization (PSO), war strategy op-timization (WSO), jellyfish search algorithm (JSA), grey wolf optimization (GWO), beluga whale optimization (BWO), levy flight distribution algorithm (LFDA), and African gorilla troops op-timizer (AGTO), were introduced. Based on the OCP extracted from simulations using these MOAs for the specified ECM model, a charging experiment was conducted on the Panasonic NCR18650PF LiB to evaluated the charging performance in terms of charging time, temperature, and efficiency. The results demonstrate that the proposed DO technique offers superior charging performance compared to other charging methods.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Recently, climate problem has emerged as a significant issue, primarily, caused by the greenhouse effect stemming from the mass consumption of fossil fuels. In response, renewable energy sectors such as wind and solar energy have been developed to replace fossil fuels. Addtionaly, electric vehicles are being promoted as alternative to fossil fuel-based internal combustion engines along with advancements in energy storage devices designed to store renewable energy. Lithium-ion batteries (LiBs) are widely utilized in energy storage systems and electric vehicles due to their compact size, high energy density, long lifespan, low self-discharge rate, high discharge current tolerance, and absence of memory effect. However, LiBs are sensitive to overcharging, over-discharging, and ambient temperature, and variations, leading to issues such as rapid increases in charging temperature, low charging efficiency (CE), and reduced lifespan. Consequently, ongoing research aims to address these challenges. Generally, battery performance is determined primarily by the selection of battery materials and manufacturing process technology. Once the battery is manufactured, its performance is influence by the effectiveness of the battery management system (BMS) and the operating conditions determined by the user. Among these factors, the most critical aspect of the BMS is that battery charging technology significantly impacts overall battery performance. Efficient charging technology is essential for sevral performance factors, including fast charging speed, lower charging temperature, extended battery life, and improved CE.

By utilizing an effective battery charging algorithm, charging times can be reduced. Elevated charging temperature can induce thermal stress within the battery, which is linked to safety concerns such as rapid performance degradation, battery expansion, and fire hazards. Implmenting appropriate charging technology can alleviate the increase in charging temperature. An improved battery charging technology can mitigate temperature increases during charning. Enhanced battery charging technology can also prolong lifespan by alleviating the decline in state of health (SOH) associated with the number of charge/discharge cycles. Furthermore, increased energy loss during the charging process can diminish CE, thereby reducing overall energy transfer efficicency. Therefore, optimal charging technology can significantly enhance the performances of lithium-ion batteries when integrated with BMS.

The constant current-constant voltage (CC-CV) charging method [1,2] is a commonly used technique that initially charges the battery using constant current (CC), gradually increasing the battery voltage until it reaches the upper limit of 4.2V. At this point, the charging method switches to constant voltage (CV), and the charging curent begins to decrease until it reaches the minimum set value. The CC-CV method combines the advantages of both CC and CV methods and is relatively simple and easy to implement, making it the most widely used charging technology to date. However, the CV charging stage requires a lengthy charging time, which extends the overall charging duration. Addtionally, it does not allow for direct control of the increase in charging temperature, leading to reductions in battery life and charging efficiency (CE). To address these issues, there has been significant in improving chraing time and CE while managing charging temperature. On such advancement, the modified CC-CV method known as the boost charging (BC) CC-CV method, which enhances charging speed compared to the traditional CC-CV approach [3,4]. The BC method differentiats itself from the standard CC-CV by incorporating a high CC or a constant power cycle during the charging process. In this approach, a current pump is utilized in the CC mode, while a pulse current is applied in the CV mode. Experimental results indicate that the BC method achieves a higher and CE while maintaining a total charging time similar to that of the traditional CC-CV method.

The pulse charging technique has been proposed by various researchers to reduce charging time, temperature rise, and extend the lifespan of lithium-ion batteries (LiBs) [5-8]. There are several types of current pulses, characterized by their frequency, amplitude, and duty cycle. Numerous pulse-charging patterns have been suggested in the literature as alternatives to the traditional CC-CV charging method. Pulse charging relies on periodic variations in current pulses with adjustable current speeds and directions. During the charging process, the charging current can be paused, increased, decreased, or replaced with short discharge pulses for a specific duration. This technique can significantly enhance the charging performance when appropriate parameters settings and operating conditions are applied; however, it often requires complex controllers and incurs high implementation costs.

Finally, the multistage constant current (MSCC) charging method offers the advantages such as easy implementation, low temperature rise, and high CE compared to conventional CC-CV-based charging and pulse charging methods. Unlike traditional methods, the MSCC charging approach does not include a CV mode, which imposes constant stress on the battery, thereby helping to extend battery life. Instead of using the CV mode, MSCC employes multiple CC stages with varying current values. In this method, the charging current profile consists of multiple CC stages with different current amplitudes, where the current at each stage is applied to the battery until a specific criterion is met. The stage transition points in the MSCC charging method can be determined using the state of charge (SOC) or cut-off battery terminal voltage. An SOC-based MSCC charging strategy was proposed in [9-13]. In this approach, the SOC value facilitaes the transition from one constant current stage to another. The number of stages can be uniformly divided into ten stages [11] or three stages [12] or optimized to four stages [13], which is applied to LiBs to evalute the charge time, charge efficiency, charge and discharge capacities, and temperature rise during charging. The SOC-based MSCC method can reduce charge time, improve charge efficiency, enhance charge/discharge capacities, reduce temperature rise, and extend the life of LiBs compared to the CC-CV method. However, because the SOC value, which is crucial for intermediate current transfer at each stage, cannot be directly measured, various methods such as Coulomb counting [14], Kalman filtering [15], Extended Kalman filtering [16], and Unscented Kalman filtering [17] have been utilized. Despite these techniques, SOC estimation remains challengng due to significant variations in battery parameters such as voltage, current, and operating temperature. Errors can arise from aging and nonlinear behavior during the battery’s operation life. Moreover, the SOC-based step transition method incurs computational costs and complexity due to the numerous parameters involved in LiB operation. Consequently, applying SOC-based transitions in practical applications can be challenging, as they rely on SOC parameters that are difficult to measure directly.

Therefore, in this study, the cut-off voltage was utilized as the transition criterion or the CC charging technology. This approach simplies the implementation of the MSCC charging method, as the cut-off voltage can be easily measured during the charging process. The cut-off voltage-based is the most commonly used criterion for transitioning from one stage to the next and is typically determined in advance by the battery manufacturer. For cobalt-based LiBs, this is generally set at 4.2V. In this method, when the cut-off voltage is reached during charging, the current is reduced, and the charging continues until the cut-off voltage is reached again. This process is repeated until a predefined number of stages is completed, making the implementation straightforward. Each CC stage can beexecuted in various configurations, including four stages [18-20], five stages [21-29], and ten stages [30], to evaluate the life and performance of the LiB. However, dividing the charging process into five stages has been reported to be optimal in terms of computational efficiency and performance [23]. The MSCC charging strategy has been shown to improve CE, shorten charging time, enhance charge and discharge capacities, reduce temperature rise, and extend the lifespan of LiBs compared to the traditional CC-CV method. Additionally, the cut-off voltage-based criterion is simpler and easier to implement than other SOC-based methods.

The performance indicators of the MSCC charging method, including total charging capacity, charging time, and CE, depend on the selection of current values for each stage. Thus, it is crucial to adopt an efficient method to determine the optimal charging pattern (OCP) to enhance the performance of the MSCC charging method. While mathematical techniques such as the Taguchi method [21,24] and Bayesian optimization [26] have been employed to identify the optimal OCP, these methods necessitate experimental verification of candidate charging patterns, which can be time-consuming and significantly increase the time and cost associated with finding the optimal solution. In [21], a Thevenin equivalent circuit model (ECM) was implemented, which does not require extensive experiments and time costs for lithium-ion batteries. In this study, the OCP was derived by differentiating a charging time equation consisting of mathematically derived current and voltage variables. This approach allows for easy implementation without using the CV mode to charge the battery to its maximum capacity. However, it is important to note that this method primarily optimized, neglecting various performance indicators, such as temperature rise and charging loss.

Metaheuristic optimization algorithms (MOAs) simulate the movements of plants and animals in search of food or survival, as well as the physical chaos phenomena of nature. They have been widely applied to optimization problems due to their advantages, including few parameters, ease to implementation, and the ability to achieve a balance between exploration and exploitation during optimization process. To explore the OCP in the MSCC method, the particle swarm optimization (PSO) algorithm [31] was utilized in [18,23,28], grey wolf optimization (GWO) algorithm [32] was employed in [27], and jellyfish search algorithm (JSA) [33] was applied in [28]. Furthemore, charging time (CT) and charging loss were selected as objective functions for each optimization of the performance indicators of the MSCC charging method [27,28]. However, CT, which is key objective of OCP, and charging loss indicator have an indirect relationship, complicating the optimization process. Additionally, calculating chraging loss during the optimization is complex.

To implement an accurate ECM, electrochemical impedance spectroscopy (EIS) is conducted to derive the internal resistance, polarization resistance, polarization capacity, and time constant values of the model. Since the cycler experimental equipment for battery charging and discharging only measures charging voltage, current, and temperature, a separate and costly potentiostat equipment is required to perform EIS analysis on LiBs.

Based on aforementioned background, this study adopted the ECM of lithium-ion batteries and the Dandelion optimizer (DO) algorithm [34], a type of MOA. The OCP of the MSCC charging method simultaneously considers the performance indices of charging time and charging temperature. Unlike previous research methods, this study first esimated the ECM model parameters, such as internal resistance, polarization resistance, polarization capacity, and time constant, offline based on voltage measurement obtained using the hybrid pulse power characterization (HPPC) test [35-37] in the time domain. In this test, pulse charge/discharge current is applied, and only the output voltage is measured, allowing for a simpler and more cost-effective implementation of the ECM model compared to the EIS method. Second, charging time and temperature were selected as the objective functions for optimizing the performance indices of the MSCC charging method. Consequenlty, the charging temperature and the optimization objective function are direclty related, simplifying cacluation process since the charging temperature is measured diectly during optimization. Third, among the recently strudied metaheuristic algorithms, including PSO, GWO, and JSA, we selected other algorithms such as the war strategy optimization (WSO) algorithm [38], beluga whale optimization (BWO) algorithm [39], levy flight distribution algorithm (LFDA) [40], and African gorilla troops optimizer (AGTO) algorithm [41], which have been relatively frequently cited. We compared these with the DO algorithm applied in this study and evasluated their charging performance indices. By utilizing the DO, the OCP search can be conducted rapidly through application to the ECM-based platform without requiring nemerous lengthy experimental processes.

The remainder of this paper is organized as follows. Section 2 provides a detailed description of the basic concepts of the proposed charging technique, including the construction of the battery ECM, estimation of ECM parameters using the HPPC in the time domain, derivation of the mathematical relations for the proposed MSCC charging method, formulation of the optimization problem, and definition of the objective function. Section 3 describes the DO algorithm. Comparative simulations and experimental results against several existing methods are presented in Section 4, demonstrating that the proposed method is more valid and effective than the current alternatives. Finally, Section 5 concludes the study.

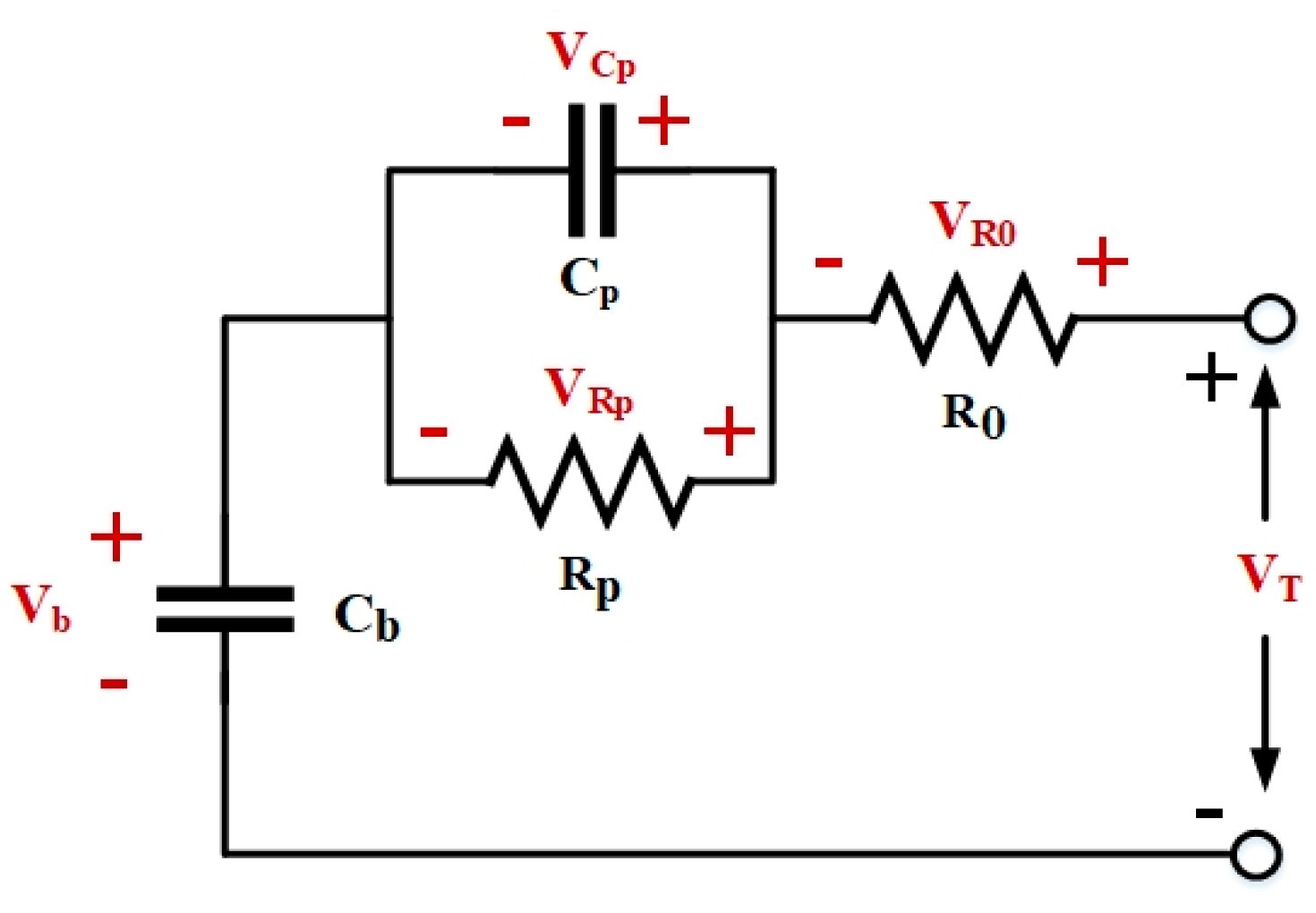
2. Equivalent Circuit Modeling of Lithium-Ion Batteries

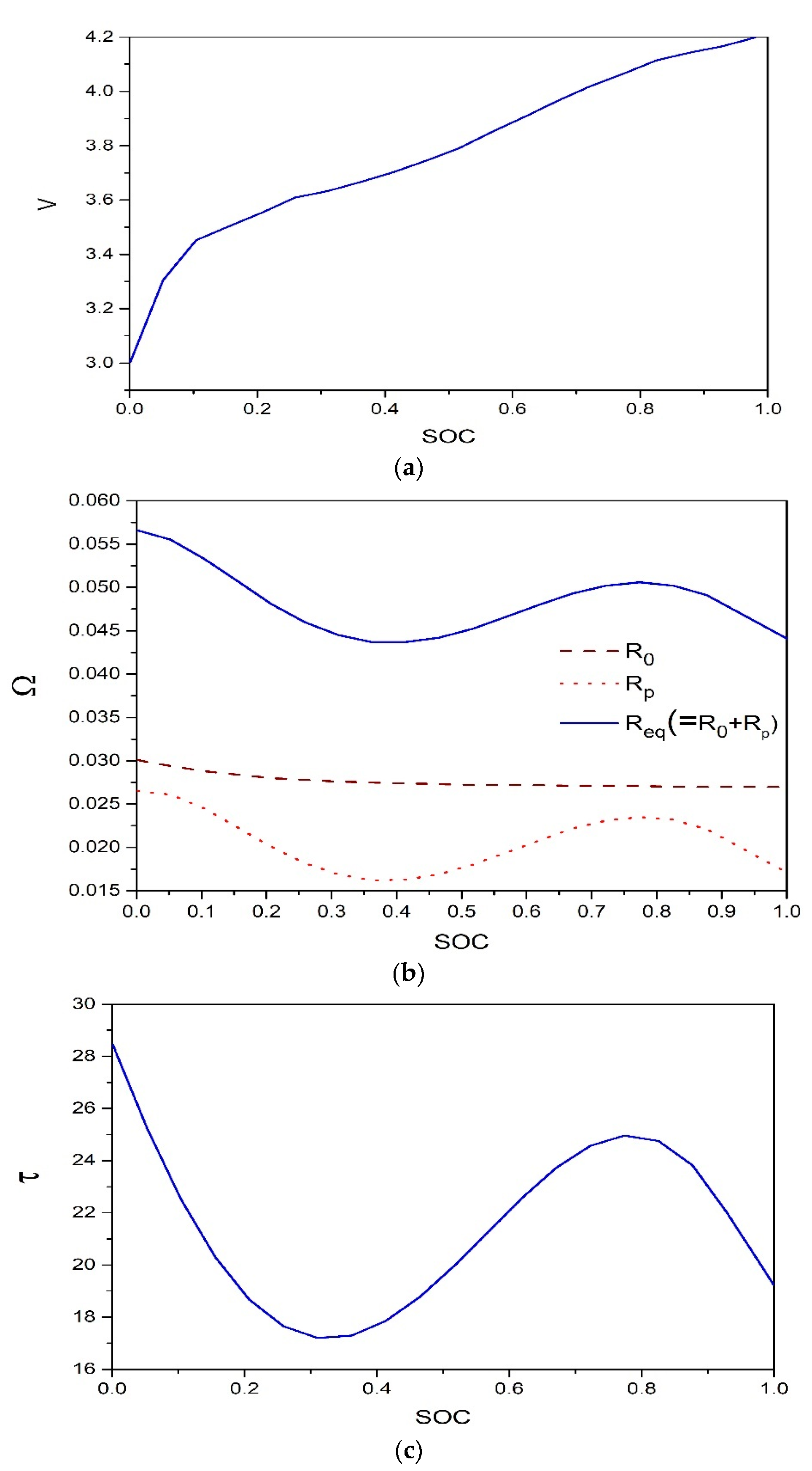
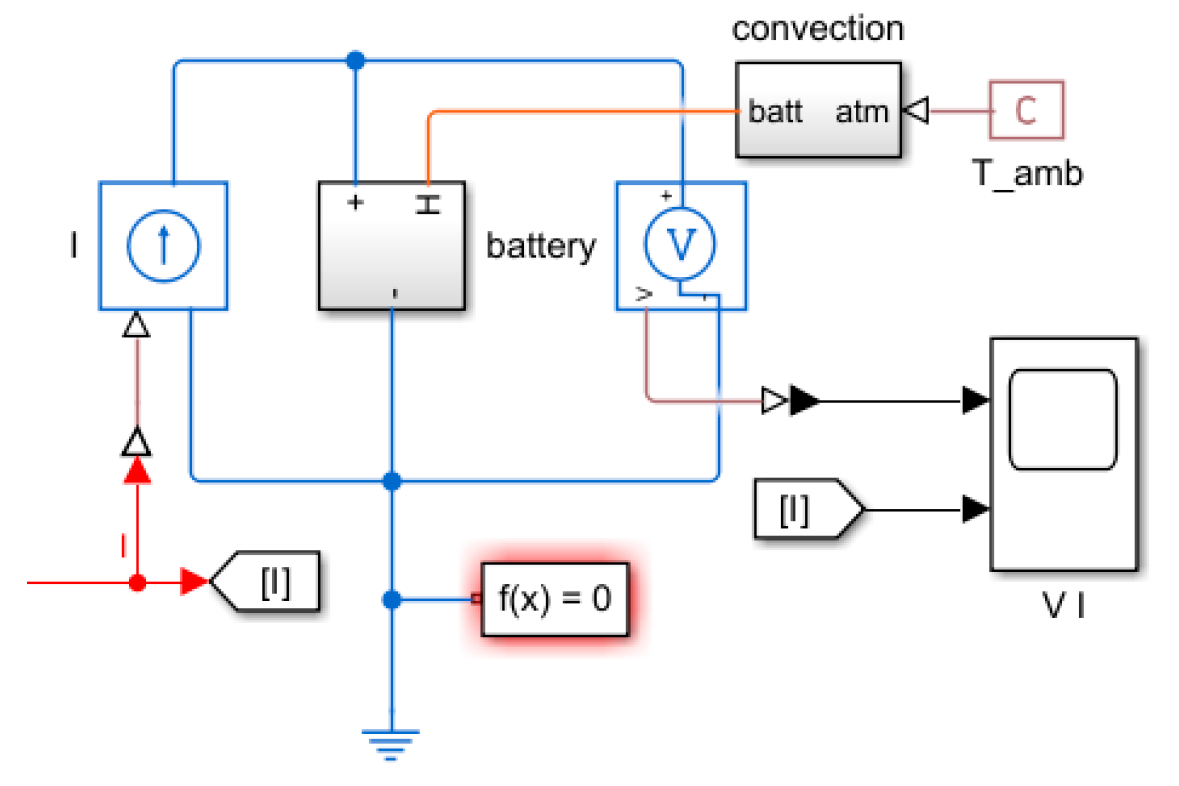
2.1. Modeling of the Equivalent Circuit Model and Parameter Identificaiton of the Lithium-Ion Battery

In general, the Thevenin ECM parameters of LiBs are identified through EIS analysis and time-domain extraction using the HPPC test. The impedance Thevenin ECM is obtained by applying a small-amplitude sine waveform of AC voltage and current to the electrodes. In the AC impedance method, the impedance parameters are identified by generating Nyquist plots based on EIS data measured with a potentiostat. However, this method necessitates additional equipment, specifically a potentiostat, alongside a charge-discharge cycler. In contrast, the time-domain-based Thevenin ECM method utilizes voltage and current time-series data. This approach is advantageous because it eliminates the need for costly impedance measurements using a ptentiostat. Furthermore, battery cells, packs, and modules can be characterized and modeled directly based on data collected solely with batter charge-dischafge cycler equipment. The Thevenin ECM is illustrated in Figure 1.

where

R_{0}

denotes the internal resistance,

R_{p}

and

C_{p}

represent the polarization resistance and capacitance, respectively, which characterize the rapid electrode reaction to the battery, and

C_{b}

indicates the battery capacitance. The equivalent internal resistance is defiend by

R_{e q} = R_{0} + R_{p}

. In this study, the utilized LiB is the Panasonic NCR18650PF LiB with specificaitions listed in Table 1.

The experimental battery charging/discharging cycler system is shown in Figure 2. The WBCS3000S battery cycler and its operating software were manufactured by WonATech Corp. The charging temperatures of the battery were measured using thermocouples attached to the battery, which was fixed in low-temperature chamber. The desired charging and discharging conditions were regulated by smart interface software installed on a desktop computer. The measured voltage, current, and temperature of the battery were transferred to the desktop via the battery cycler.

The single HPPC test involved a cycle 1C discharge/charge current held for 20s, followed by a 3C discharge current held for 60s. Ten cycles were spaced at 1.0, 0.9, 0.8, …, 0.2, and 0.1 of SOC, as depicted in Figure 3.

The corresponding curve of the HPPC experimental voltage variation for the current pulse input variation is shown in Figure 4. Ten open-circuit voltage values corresponding to the SOC values from 1.0 to 0.1 can be obtained directly, as illustrated in Figure 4 (a). The analysis in Figure 4 (b) provides the following four features: (1) As the discharge starts at

t_{1}

, the terminal voltage of the battery drops suddenly from

V_{1}

V_{2}

because of the voltage change caused by the resistance of the battery. (2) From

t_{2}

t_{3}

, the terminal voltage of the battery decreases slowly from

V_{2}

V_{3}

due to the battery’s polarization effect. (3) From

t_{3}

t_{4}

, the terminal voltage of the battery rises suddenly from

V_{3}

V_{4}

because of the voltage changes caused by the internal resistance of the battery. (4) The terminal voltage of the battery increases slowly from

V_{4}

V_{5}

for

t_{4}

t_{5}

, which represents the discharge process of the polarization capacitance through the polarization resistance. To obtain the internal resistance, the sudden change in the battery terminal voltage at the time points of discharge and cessation must be analyzed, both of which are caused by the internal resistance. The internal resistance value can be calculated as

R_{0} = (|V_{1} - V_{2}| + |V_{4} - V_{3}|) / 2 I .

(1)

The time constant is obtained as follows:

τ = - (t_{5} - t_{4}) / \ln (\frac{V_{1} - V_{5}}{V_{1} - V_{4}}) .

(2)

After obtaining the time constant

τ

, the polarization resistance

R_{p}

can be calculated as follows:

R_{p} = (V_{2} - V_{3}) / [I (1 - e^{- (t_{3} - t_{2}) / τ})] .

(3)

The polarization constant

C_{p}

can be obtained using the following relationship:

τ = R_{p} C_{p} .

(4)

The parameter identification results are presented in Figure 5. The simulation model for the Thevenin ECM was constructed using the Simscape and Simulink packages of MATLAB software. The thermal model is constructed as follows:

Q = C_{T} A Δ T,

(4)

where

Q

denotes the convective heat,

C_{T}

represents the heat transfer coefficient, A indicates the cell area, and

Δ T

refers to the temperature increase. The charging temperature was set to 25 °C. The CC-CV charging results at 1C for the Panasonic NCR18650PF LiB based on the identified parameters are shown in Figure 5.

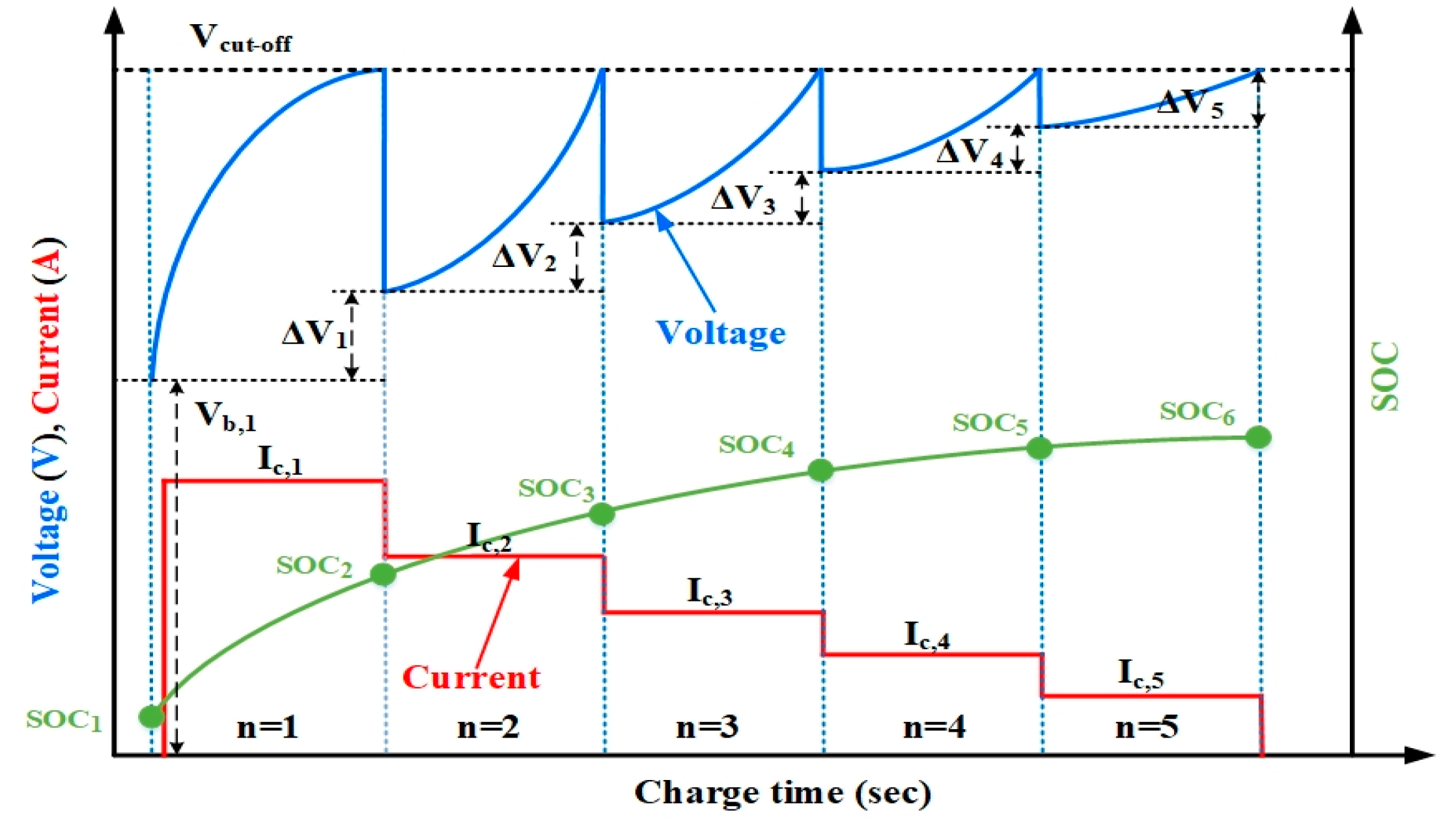
2.2. Mathematical Description of the MSCC Charging Method

The charging time, charging cost, and charging capacity of the MSCC charging method for the Thevenin ECM of the LiB were derived by analyzing the electrical relationships. Based on Kirchhoff’s voltage law for the circuit shown in Figure 1, the terminal voltage can be expressed as

V_{T} = V_{R_{0}} + V_{R_{p}} + V_{b},

(5)

where

V_{C p} = V_{R_{p}}

. Figure 6 illustrates a conceptual diagram of the MSCC method, showing the typical battery charging voltage and current shapes corresponding to varying SOC. A previous work [23] demonstrated that a five-stage CC approach is efficient. Although increasing the number of current stages can reduce charging time, it also increases complexity and implementation costs. From Figure 5, the charged battery capacity of each state is given by

Δ Q_{n} = \int I_{n - 1} d t = I_{n - 1} Δ t_{n} = C_{b} Δ V_{n},

(6)

where

I_{n - 1}

denotes the charging current of the previous stage and

Δ V_{n}

represents the increased OCV of each state compared to the OCV of the previous stage. From (6), the charging time required in the charging stage can be calculated as follows:

Δ t_{n} = \frac{C_{b} Δ V_{n}}{I_{n - 1}} .

(7)

The OCV

V_{C b, n}

in stage s, can be expressed as

V_{b, s} = V_{c u t - o f f} - I_{c, n - 1} R_{e q} (S O C_{n}),

(8)

where

V_{c u t - o f f}

denotes the cut-off voltage of each current transition point and

I_{c, n - 1}

represents the charging current of each stage.

Based on (4), the voltage drop at each stage can be expressed as

Δ V_{1} = V_{c u t - o f f} - I_{c, 1} R_{e q} (S O C_{2}) - V_{b, 1},

(9)

Δ V_{n} = I_{c, n - 1} R_{e q} (S O C_{n}) - I_{c, n} R_{e q} (S O C_{n + 1}),

(10)

Δ V_{5} = V_{c u t - o f f} - I_{c, 5} R_{e q} (S O C_{6}),

(11)

where

I_{c, n}

denotes the charging current of stage. The current amplitude of the final stage was calculated to charge the battery to 100% capacity as follows:

I_{c, 5} = \frac{V_{c u t - o f f} - V_{b, 5}}{R_{e q} (S O C_{6})} .

(12)

Therefore, the total charging time can be obtained by summing the times of the MSCC charging stage as follows:

C T_{t} = \sum_{n = 1}^{5} Δ t_{n} = \sum_{n = 1}^{5} \frac{C_{b} Δ t_{n}}{I_{c, n}} .

(13)

The energy loss (EL) was calculated by integrating the ohmic loss of each CC stage as follows:

L_{t o t} = \sum_{n = 1}^{5} Δ L_{n} .

(14)

2.3. Objective Function Formulation for OCP

Defining and designing the objective function is essential for applying an optimization algorithm before utilizing a metaheuristic optimization approach. The fitness values of each particle were calculated by minimizing the value of the objective functions through the iterative process with random initial conditions for each particle. In previous studies [27,28], charging time and energy loss were selected as the physical quantities of the objective function to achieve the dual benefits of reducing both charging time and temperature rise. While the charge time is closely related to the charging current at each stage, the direct relationship between charge temperature and energy loss, as expressed by (14), remains unclear. The energy loss function is primarily linked to the charging current, which may not directly correspond to variations in charging temperature. Thus, in this study, we consider the charge temperature parameter instead of energy loss as the objective function. This approach allows for a direct optimization of charge temperature. To construct the fitness value function, the maximum and minimum values of charge time and charge temperature were determined using the CC-CV charging method. A charging current range of 0.5C to 2C was applied within the Thevenin ECM developed Simulink and Simscape platforms of MATLAB software. The values obtained are summarized in Table 2.

The objective function

J

in this study is proposed as follows:

J = \sqrt{γ {(\frac{t_{c} ({\bar{I}}_{c, n}) - t_{c, \min}}{t_{c, \max} - t_{c, \min}})}^{2} + (1 - γ) {(\frac{T_{c} ({\bar{I}}_{c, n}) - T_{c, \min}}{T_{c, \max} - T_{c, \min}})}^{2}},

(15)

where

t_{c} ({\bar{I}}_{c, n})

and

T_{c} ({\bar{I}}_{c, n})

denote the charge time and charge temperature, respectively,

{\bar{I}}_{c, n} = [I_{c, 1}, I_{c, 2}, I_{c, 3}, I_{c, 4}, I_{c, 5}]

represent the charging current values, and

γ

indicates the weighting index between the charge time and charge temperature. The optimization problem for obtaining the optimal charge currents in each charge state can be formulated as follows:

M i n i m i z e ​ ​ ​ J, {\bar{I}}_{c, n} \in F C S u b j e c t ​ ​ t o ​ ​ t_{c, \min} \leq t_{c} ({\bar{I}}_{c, n}) \leq t_{c, \max} a n d T_{c, \min} \leq T_{c} ({\bar{I}}_{c, n}) \leq T_{c, \max}, I_{c, n} \leq I_{c, n + 1}, 0 \leq I_{c, n} \leq I_{c, \max}, and V_{c, n} \leq V_{c, \max}, n = 1, 2, 3, 4,

(16)

where

F C

denotes the set of all feasible charging patterns,

I_{c, \max}

and

V_{c, \max}

represent the allowable maximum charging current and voltage values. These parameters are set as

5.8 A

and

4.2 V

, respectively.

3. Metaheuristic Optimization Algorithm for OCP Searching Protocol

3.1. Inspiration for MOA

Searching for the optimal charge current in the MSCC process is challenging when emplying a trial-and-error approach that solves evaluating every possible combination of charging values. This method can be both time comsuming and costly. To address these issues, MOAs have demonstrated significant effectiveness in various studies and applications. In this study, MOAs are emplyed to optimnize the charging current values for the ECM dedrived from the time-domain identification process. The objective function is designed to minimize the charging time and temperature of the selected LiB cell. The ECM constrcuted using the measured battery parameters, is synthesized with the Simscape utility in MATLAB. Owing to limitations of current cycler equipment, it is impratical to construct online experiments for direclty identifying the OCP on a real LiB cell. Therefore, the MOA is applied to the synthesized ECM platform instead. This approach allows for an extensive seach for the OCP within a virtual ECM framework, enabling effective exploration of a wide range of potential charging patterns while ensuring that the optimization process is both efficient and reliable.

3.2. Overview of the Dandelion Optimization Algorithm

3.2.1. Inspiration

The dandelion shown in Figure 7 [42], an herbaceous perennial in the Asteraceae family, reaches heights of over 20 cm and is distinguished by its wind-pollinated seeds. Dandelion is a typical wind-pollinated plant. These seeds are dispersed by wind, aided by a crown of hair that allows them to float for extended durations and travel over vast distances, often covering tens of kilometers under optimal conditions. The seeds fall slowly due to two symmetrical vortices created overhead stabilized by the crown’s porous structure. The seeds’ travel behavior changes based on wind velocity and weather conditions, unfolding in three main stages. In the rising stage, a vortex appears above the seeds, significanly increasing drag under sunny and windy conditions, while rain prevents vortex formation. During the descending phase, the seeds gradually descend after reaching a certain height. Finally, in the landing stage, the seeds disperse randomly depending on local wind and weather conditions, where they may establish new plants.

3.2.2. Mathematical Model

The mathematical model of the DO can be segmented into three primary stages: the rising or exploration stage, the descending or exploitation stage, and the landing stage [34].

Rising Stage

During the rising stage, dandelion seeds must reach a certain height to separate from their parent plant. Weather conditions influence how many seeds rise, with wind speed and humidity acting to increase the number of seeds. For simlicity, weather conditions can be divided into two categories:

Case 1 (clear day): Wind speeds on clear days have a lognormal distribution

\ln Y : N (μ, σ^{2})

along Y-axis, resulting in a greater spread of random numbers, which increases the chance for dandelion seeds to travel distances. As a result, the chance for dandelion seeds are randomly scattered across various locations based on wind conditions within the search space. The wind speed determines the height which a seed can rise; higher wind speeds lead to increase flight height and wider disperation of seeds. The wind also constantly modulates the vortices above the seeds, allowing them to ascend in a spiral motion. The seeds’ motion is expressed as follows:

X_{t + 1} = X_{t} + α υ_{x} υ_{y} \ln Y (X_{s} - X_{t}) .

(17)

In (17),

X_{t}

denotes the position of the dandelion seeds at iteration index t, and

X_{s}

represents the randomly selected position in the search space at iteration index t,

υ_{x} = e^{- θ} \cos θ

and

υ_{y} = e^{- θ} \sin θ

, where

θ \in [- π, π]

is a random number, denote the lift component coefficients of a dandelion caused by the separated eddy action,

Y

denotes a lognormal distribution subject to the mean

μ = 0

, and the variance

σ^{2} = 1

, which is expressed as

\ln Y = \{\begin{matrix} \frac{1}{y \sqrt{2 π}} \exp [- \frac{1}{2 σ^{2}} (\ln y)] y \geq 0 \\ 0 y < 0 \end{matrix},

(18)

where

y

denotes the standard normal distribution, and

α \in [0, 1]

is an adaptive random perturbation, which is expressed as

α = r a n d () \times (\frac{1}{T^{2}} t^{2} - \frac{2}{T} t + 1),

(19)

and

α

eventually approaches 0 with increase in iteration.

α

enables the algorithm to concenturate on global search during the early stages and then trasition to local search in the later stages after completing a full-stage search.

Case 2 (rainy day): Air resistance, humidity, and other environmental factors prevent dandelion seeds from rising, leading them to remain within local neighborhoods. This localized exploitation is described by the following expression:

X_{t + 1} = X_{t} \times κ,

(20)

where

κ \in [0, 1]

is a parameter used to regulate the local search domain of a dandelion expressed by

κ = 1 - r a n d () \times (\frac{1}{T^{2} - 2 T + 1} t^{2} - \frac{2}{T^{2} - 2 T + 1} t + \frac{1}{T^{2} - 2 T + 1}) .

(21)

It exhibits a downwards convex fluctuation. As the number of iteration increases, the value of

κ

gradually approaches 1, ensuring that the population eventually converges to the optimal search agent.

Descending Stage

In this stage, exploration is emphasized in this stage as the dandelion seeds steadily descend to a specific height. Brownian motion is employed to simulate the movement behavior of the dandelions. The normal distribution of Brownian motion enables individuals to traverse multiple search communities during the iterative update process. Average position information is utilized to reflect the stability of the dandelion descent, allowing the population to develop as a cohesive unit within promising communities. This behavior is expressed as follows:

X_{t + 1} = X_{t} - α β_{t} ({\bar{X}}_{t} - α β_{t} X_{t}),

(22)

where

β_{t}

denotes a random number of standard Brownian motions and

{\bar{X}}_{t}

represents the average position of the population in the

t

th iteration. The information regarding the average population position directly influences the evolutionary direction of individuals through iterative updates. The irregular Brownian movement, driven by a global search, increases the likegood of the search agent escaping local extrema and compels the population to seek areas near the global optimum.

Landing Stage

Exploitation is emphasized at this stage. The dandelion seeds are randomly selected landing sites based on information from the previous stages. As the iterations progress, the DO algorithm converges to the global optimal solution. Consequenlty, the optimal solution is considered as the approximated best position where the dandelion seeds can be thrive. To achieve accurate convergence to the global position, search agents leverage information about the current elite for exploitation within their local neighborhoods. As the pollution evolves throughout the iteration process, the global optimal solution can be attained from the behavior expressed as follows:

X_{t + 1} = X_{e l i t e} + L e v y (λ) α (X_{e l i t e} - X_{t} δ),

(23)

where

X_{e l i t e}

denotes the optimal position of the dandelion seed in the tth iteration,

L e v y (λ)

represents the Levy flight function, and

δ \in [0, 2]

indicates a linearly increasing function. To prevent excessive exploitation, a linearly increasing function was applied to individuals. The Levy flight coefficient was utilized to simulate the movement step size of agents, enabling them to make significant strides to other positions with a high probability under a Gaussian distribution. This approach effectively generates more local search areas while requiring fewer iterations.

4. Simulation and Experiment Results and Discussions

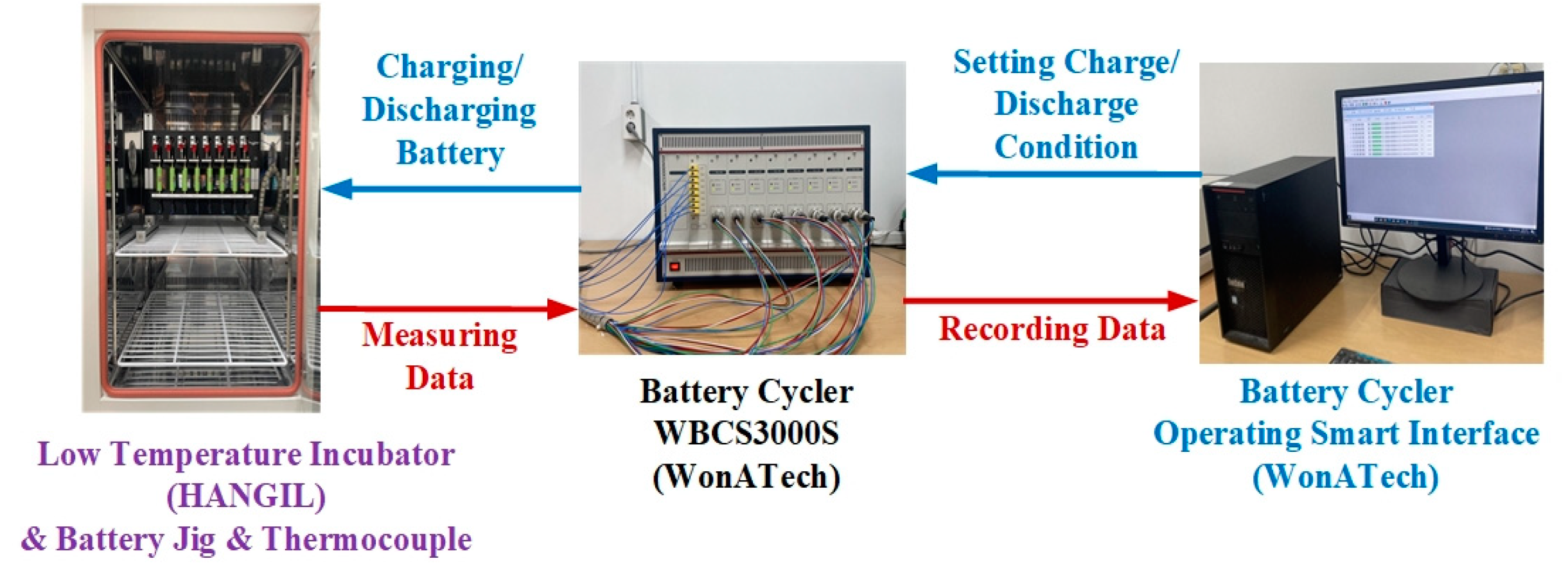
4.1. Computing Parameter Setting

The LiB parameters and maximum and minimum values of the charge time and temperature required for the fitness value function are listed in Table 1 and Table 2, respectively. The weighting index

γ

in (15) was set to 0.5, indicating an equivalent significance in FC assigned to both the charge time and charge temperature. Each current (

I_{c 1} ~ I_{c 5}

) set between

0 C

and

1 C

affects the charging time and temperature. The cuf-off voltage (

V_{c u t - o f f}

), set as

4.2 V

, determines the transition threshold. The ranges of the five objective current parameter values are listed in Table 3. To verify the efficacy and feasibility of the various MOAs, eight MOA methods were considered, in addition to the formula method: PSO, WSO, JSA, GWO, BWO, LFDA, and AGTO. The key considerations for selecting these MOAs include their up-to-date versions, high citation indices among various MOAs, and their applications in other MSCC studies. Most of the chosen MOAs are recent developments. The simulation parameters for each MOA are provided in Table 4.

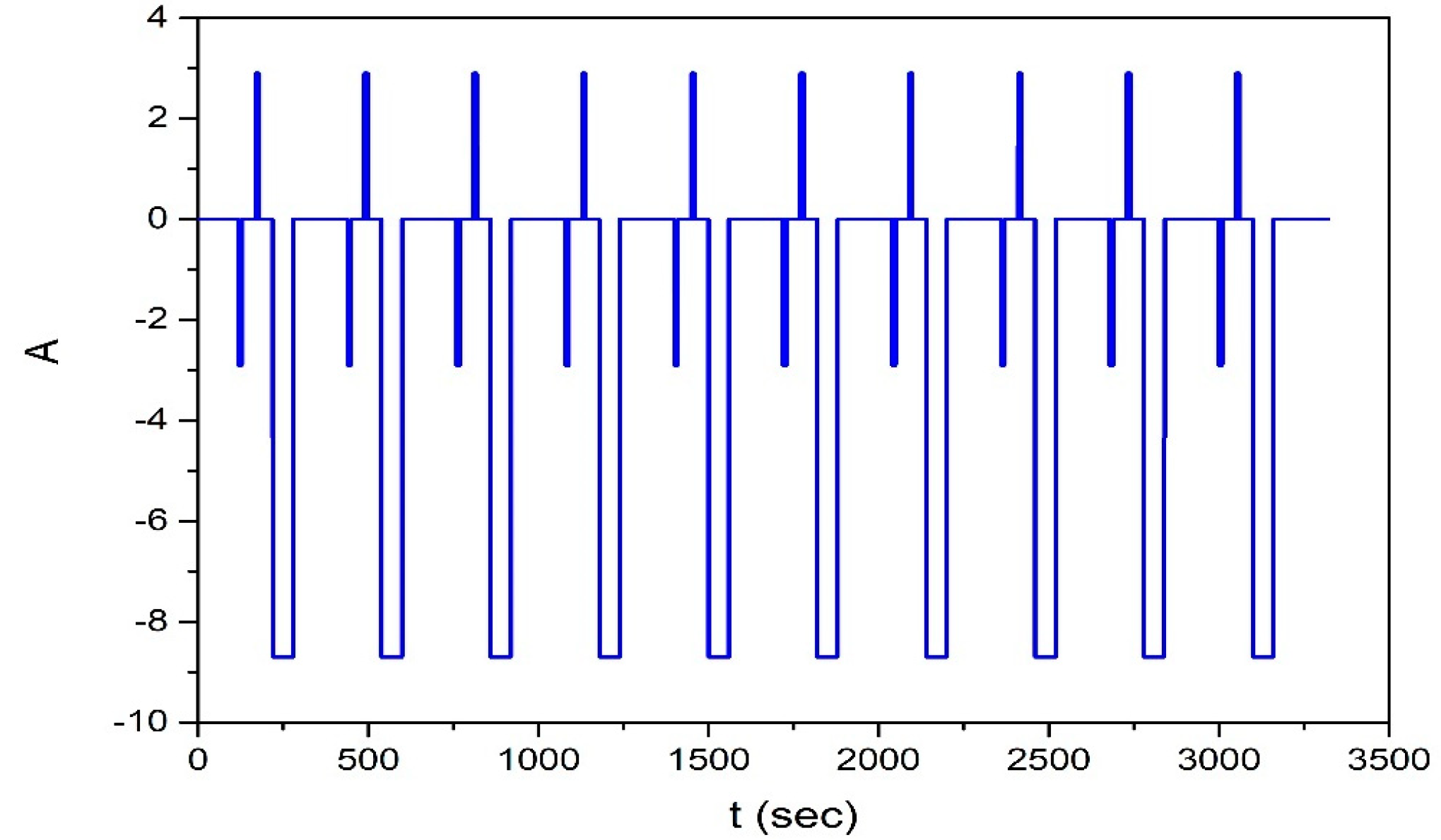
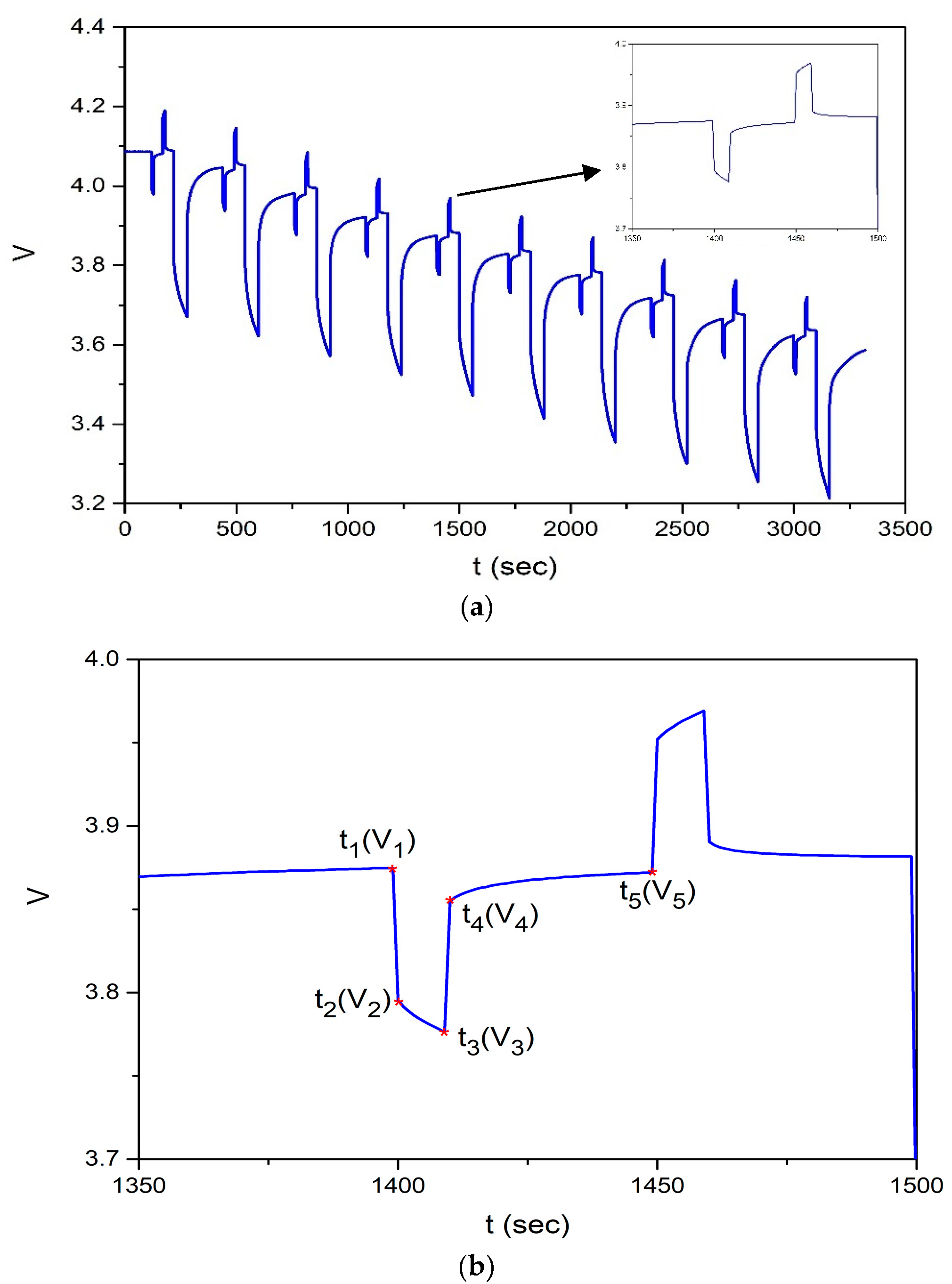
4.2. Simulation Results

The ECM was constructed using the Simscape Battery and Simulink toolboxes within MATLAB package, as illustrated in Figure 8. In the MOAsm the current values began at random starting points to prevent the solutions from getting trapped in local optima. This randomness contributed to variations in the best solutions due to the random fluctuations in the parameters. Consequently, the average MSCC values for each MOA were computed ten times over 100 iterations. The conventional CC-CV method was also included for comparison with the MSCC results obtained through the MOA protocols.

The simulation results are presented in terms of four charging performance evaluation indicators (CPEIs): the best FC (FC_best), chage time (CT), maximum charge temperature (MCT), and EL. The results are summarized in Table 5 and Table 6. Accdoring to the CPEI results in Table 5, the FC value is the highest for the CC-CV method and the lowest for the DO method. Regarding CT, the FM produced the smallest value; however, due to FM’s inablility to manage temperature increases, its CT value was relatively high. Although the CT value for DO was higher than that of FM, it remained the smallest compared to the other MOAs. Furthermore, the MCT value of DO was the lowest, and the EL value for DO was also the lowest, indicating that it was the most efficient method. Selected MSCC values are presented in Table 6.

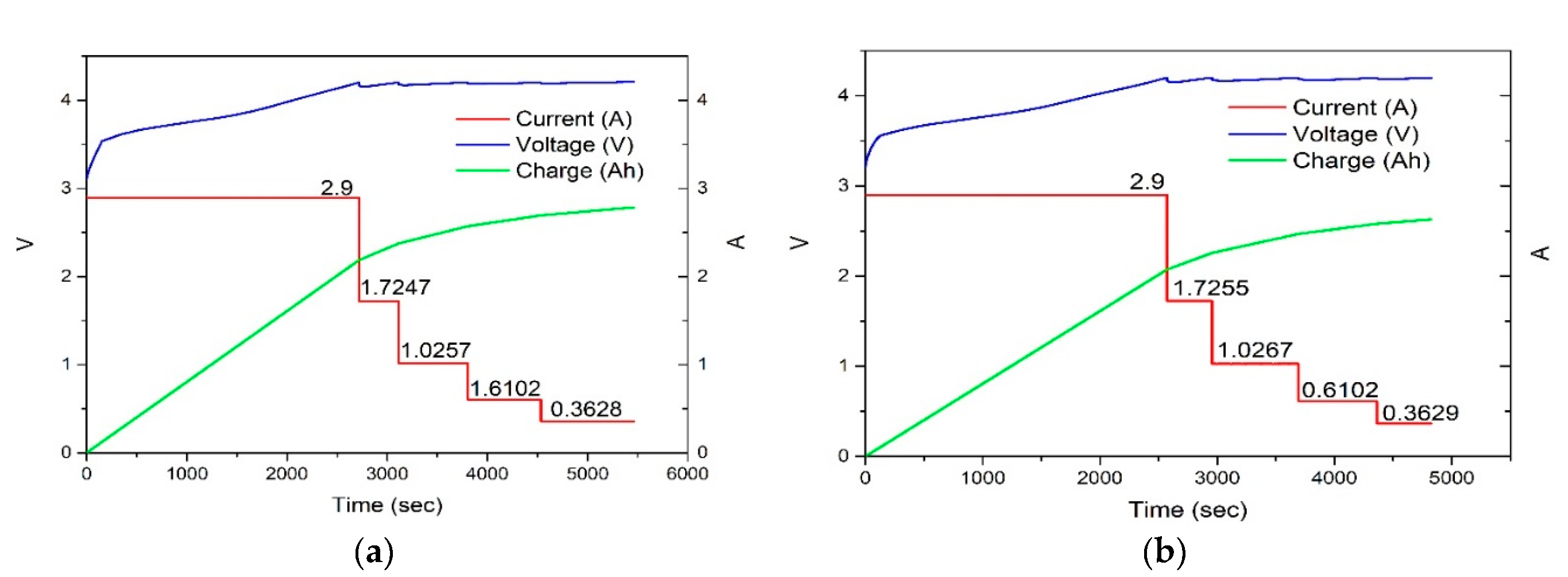
4.2. Experimental Results

The MSCC experiments were conducted using the experimental setup depicted in Figure 2. Both the simulation and the experiment were conducted based on the five-step current values selected through the simulation, as detailed in Table 6. The results for voltage, current, and charge capacity obtained using the CC-CV method and each algorithm are illustrated in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. For the current, the simulation and experimental values were found to be similar. The voltage waveform also showed a close resemblance between the simulation and experimental results. The experimental results for charge temperature are presented in Figure 18, indicating the FM, WSO, and CC-CV methods exhibited the highest maximum charge temperatures, while the DO method result in the lowest maximum charge temperature.

The experimentally obtained CPEIs are summarized in Table 7. The FC value is largest for the CC-CV method and smallest for DO, consistent with simulation results, showing a reduction of 27% compared to the CC-CV method. The CT value was the smallest for FM, followed by DO, while the CC-CV method had the largest CT value. Regarding MCT, DO exhibited the lowest temperature and FM showed the highest temperature value, mirroring the simulation results. The EL value, which indicates the charging efficiency, revealed the largest loss for the CC-CV method and the smallest for DO, reflecting an 18% reduction compared to the CC-CV method. Table 8 lists the MSCC values obtained from the experiments, which closely align with the simulation results. Table 9 displays the normalized CPEI values presented in Table 7, including the results for each normalized CPEI. In Table 9, the normalized CE values are derived from the reciprocal of the EL value, as all values were normalized against the EL value of DO. Higher normalized CE values signify lower EL. The individual values and the total sum of the normalized CPEI values are illustrated in Figure 19. In Figure 19, excluding the CT value, where DO tanked second, DO achieved the highest values among the three indices. The results for the overall performance sums are shown in Figure 19 (e). As depicted in Figure 19 (e), the CC-CV method produced the lowest performance score, while the PSO, JSA, GWO, BWO, and LFDA algorithms exhibited similar performance levels. In contrast, the performance score for FM and WSO were relatively low. Notably, DO achieved the highest overall score compared to the other methods, with an 18% higher score than that of the CC-CV method.

7. Conclusions

This study investigated the charging performance by applying the DO algorithm for the first time to obtain the OCP for MSCC charging of LiBs. The ECM was configured for the NCR18650PF LiB, and a HPPC test was conducted to generate the time-domain data and estimate the model parameters. To optimize using the DO algorithm, an objective function was constructed that considered both charging time and charging temperature was constructed. Several recently studied MOA techniques were introduced to validate the charging performance of the proposed DO approach. The OCPs were obtained by conducting simulations that applied the CC-CV method, various MOA techniques, and the proposed DO to the implemented ECM. These OCPs were subsequently utilized in charging experiments on actual LiBs to compare charging time, charging temperature, and charging efficiency. Analysis of the results from these comparative charging experiments demonstrated that the proposed DO method exhibits the most efficient charging performance when compared to other comparative methods.

Author Contributions

All works for this study are provided by Author S. Han.

Funding

This research was funded by the National Research Foundation of Korea (NRF) funded by the Korea government (MSIT)(NRF-2022R1A2C1003137).

Acknowledgments

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Korea government (MSIT) (NRF- 2022R1A2C1003137).

Conflicts of Interest

The author declares no conflict of interest.

References

Fleury,X ; Noh, M.H.; Geniès, S.; Thivel, P.X.; Lefrou, C.; Bultel, Y.; Fast-charging of lithium iron phosphate battery with ohmic-drop compensation method: Ageing study, J. Energy Storage, 2018, 16, 21–36, https://doi.org/10.1016/j.est.2017.12.015.
Wassiliadis, N.; Schneider, J.; Frank, A.; Lin, X. ; Jossen, A; Lienkamp, M ; Review of fast charging strategies for lithium-ion battery systems and their applicability for battery electric vehicles, J. of Energy Storage, 2021, 44, 103306, https://doi.org/10.1016/j.est.2021.103306. [Google Scholar]
Notten, P.H.; Op Het Veld, J.H.G.; van Beek, J.R.G. ; Bosstcharging Li-ion Batteries: A challenging new charging concept. J. of Power Sources, 2005, 145, 89–94. [Google Scholar] [CrossRef]
Keil, P.; Jossen, A. ; Charging protocols for lithium-ion batteries and their impact on cycle life-an experimental study with different 18650 high-power cells, J. of Energy Storage, 2016, 6, 125–141. [Google Scholar] [CrossRef]
Amanor-Boadu, J.M.; Guiseppi-Elie, A.; Sanchez-Siencio, E. ; The impact of pulse charging parameters on the life cycle of Lithium-ion ploymer batteries. Energies 2018, 11, 2162. [Google Scholar] [CrossRef]
Fang, H.; Depcik, C.; Lvovich, V. ; Optimal pulse-modulated lithium-ion battery charging algorithm, J. of Energy Storage, 2018, 15, 359–367. [Google Scholar] [CrossRef]
Gao, Y.; Zhang, X.; Cheng, Q.; Guo, B.; Yang, J. ; Classification and review of the charging strategies for commercial Lithium-ion batteries. IEEE Access 2020, 7, 43511–43524. [Google Scholar] [CrossRef]
Kannan, D.R.R.; Weatherspoon, M.H. ; The effect of pulse charging on commercial lithium nickel cobalt oxide (NMC) cathode lithium-ion batteries, J. of Power Sources, 2020, 479, 229085. [Google Scholar] [CrossRef]
Vo, T.T.; Chen, X.; Shen, W.; Kapoor, A. ; New charing stragegy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation, J. of Power Sources, 2015, 273, 413–422. [Google Scholar] [CrossRef]
Lee, A.H.; Chen, M.Y.; Hsu, C.H. , Jiang, J. A.; Implementation of a SOC based four stage constant current charger for Li-ion batteries, J. Energy Storage, 2016, 18, 528–537. [Google Scholar]
Zhang, Y.; Xu, S.; Wu, T. Multi-stage constant current charging strategy considering SOC intervals and voltage thresholds. Global Energy Interconnection 2022, 2, 143–163. [Google Scholar] [CrossRef]
Lee, C. H. , Wang, X. J., Lin, K. Y.; Jiang, J.A.; Experiment-based determination of the optimized current level to achieve multiple constant current charging for Lithium-ion batteries, IEEE Trans. Aserosp. Electron Syst., 2023, 59, 2648–2657, https://doi.org/10.1109/taes.2022.3217426. [Google Scholar]
Huang, Q.Y.; Liu, Y.J.; Chen, G. J.; Luo, Y.F.; Liu, C.L. ; Optimization of the SOC-based multi-stage current constant current charging strategy using coyote optimization algorithm, J. of Energy Storage, 2024, 77, 109867. [Google Scholar] [CrossRef]
Zhao, L.; Lin, M.; Chen, Y. ; Least-squares based Coulomb counting method and its application for state-of-charge (SOC) estimation in eletric vehicles, Inter. J. of Energy Research, 2016, 40, 1389–1399. [Google Scholar] [CrossRef]
Li, Y.; Wang, C. , Gong, J. ; A combination Kalman filter approach for state of charge estimation of lithium-ion battery considering model uncertainlty, Energy, 2016, 109, 933–946. [Google Scholar]
Yong, S.; Zilin, M.; Gongyou, T.; Zheng, C.; Nong, Z. ; Estimatoin method of state-of-charge for lithium-ion battery used in hybrid electric vehicles based on variable structure extended Kalman filter, Chinese J. of Mechanical Eng., 2016, 29, 717–726. [Google Scholar]
He, Z.; Chen, D.; Pan, C.; Chen, L.; Wang, S. ; State of charge estimation of power Li-ion batteries using a hybrid estimation algorithm based on UKF, Electrochima Acta, 2016, 211, 101–109.
Lee, C.H.; Chang, T.W.; Hsu, S.H.; Jiang, J.A. ; Taguchi-based PSO for searching an optimal four-stage charge pattern of Li-ion battries, J. of Eenergy Storage, 2019, 21, 301–309. [Google Scholar] [CrossRef]
Li, Y.; Li, K.; Xie, Y.; Liu, B.; Liu, J.; Zheng, J.; Li, W. ; Optimization of charging strategy for lithium-ion batery packs based on complete battery pack model, J. of Energy Storage, 2021, 37, 102466. [Google Scholar] [CrossRef]
Li, Y.; Li, K.; Xie, Y.; Liu, J.; Fu, C.; Liu, B. ; Optimized charging of lithium-ion battery for electric vehicles: Adaptive multistage constant current-constant voltage charging strategy, Renewable Energy, 2020, 46, 2688–2699. https://doi.org/10.1016/j.renene.2019.08.077.
Liu, Y.H.; Luo, Y.F. ; Search for an Optimal rapid-charging pattern for Li-ion batteries using the Taguchi approach, IEEE Trans. on Industrial Electr., 2010, 57, 3963–3971. [Google Scholar] [CrossRef]
Khan, A.B.; Choi, W. ; Optimal charge pattern for high-performance multistage constant current charge method for the Li-ion batteries, IEEE Trans. on Energy Conversion, 2018, 33, 1132–1140. [Google Scholar] [CrossRef]
Wang, S.C.; Liu, Y.H. ; A PSO-based fuzzy-controlled searching for the optimal charge pattern of Li-ion batteries, IEEE Trans. on Industrial Electr., 2015, 62, 2983–2993. [Google Scholar] [CrossRef]
Jiang, L.; Li, Y.; Huang, Y.; Huang, Y.; Yu, J.; Qiao, X.; Wang, Y.; Huang, C. ; Optimization of multi-stage constant current charging pattern based on Taguchi method for Li-ion battery, Applied Energy, 2020, 259, 114148. https://doi.org/10.1016/j.apenergy.2019.114148.
Alhaider, M.M.; Ahmed, E.M.; Aly, M.; Serhan, H.A.; Mohamed, E.A.; Ali, Z.M. ; New temperature-compensated multi-step constant-current charging method for reliable operation of battery energy storage systems, IEEE Access, 2020, 8, pp 27961-27972. https://doi.org/10.1109/access.2020.2972391.
Atta, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.H.; Chen, M.H. , Cheong, B.; Perkins, N.; Yang, Z.; Herring, P.K.; Aykol, M.; Harris, S.J.; Braatz, R.D.; Ermon, S.; Chueh,W.C.; Closed-loop optimization of fast-charging protocols for batteries with machine learning, Nature, 2020, 578, 392–402. https://doi.org/10.1038/s41586-020-1994-5.
Chen, G.J.; Liu, Y.H.; Wang, S.C.; Luo, Y.F.; Yang, Z.Z. ; Searching for the optimal current pattern based on grey wolf optimizer and equivalent circuit model of Li-ion batteries, J. of Energy Storage, 2021, 33, 101933. [Google Scholar] [CrossRef]
Wang, S.C.; Zhang, Z.Y. ; Research on optimum charging current profile with multi-stage constant current based on bio-inspired optimization algorithms for Lithium-ion batteries, Energies, 2023, 16, 7641. https://doi.org/10.3390/en16227641.
Kumar, K.; Pareek, K. ; Fast charging of lithium-ion battery using multistage charging and optimization with Grey relational analysis, J. of Energy Storage, 2023, 68, 107704. [Google Scholar] [CrossRef]
Mathieu, R.; Briat, O.; Gyan, P.; Vinassa, J.M. ; Fast charging for electric vehicles applications: Numerical optimization of a multi-stage charging protocol for lithium-ion battery and impack on cycle life, J. of Energy Storage, 2021, 40, 102756. [Google Scholar] [CrossRef]
Mirjahili, S.; Lewis, A.; Sadiq, A.S. ; Automous particles groups for particle swam optimization, Arabian J. for Science and Eng., 2015, 39, 4683–4697. [Google Scholar]
Mirjalili, S.; Mirjalili, S.M.; Lewis, A. ; Grey wolf optimizer, Advances in Engineering Software, 2014, 69, 46–61.
Chou, J.S.; Truong, D.N. ; A novel metaheuristic optimizer inspired by behaviior of jellyfish in ocean, Appllied Mathematics and Comp. , 2021, 389, 125535. [Google Scholar]
Zhao, S.; Zhang, T.; Ma, S.; Chen, M. ; Dandelion optimizer: A nature-inspired methaheuristic algorithm for engineering applications, Engineering Applications of Artificial Intell. , 2022, 114, 105075. [Google Scholar]
Hentunen, A.; Lehmuspelto, T.; Suomela, J. ; Time-domain parameter extraction method for Thevenin-equivalent circuit battery models, IEEE Trans. on Energy Conversion, 2014, 29, 558–56. https://doi.org/10.1109/tec.2014.2318205.
Takyi-Aninakwa, P.; Wang, S.; Zhang, H.; Appiah, E.; Bobobee, E.D.; Fernadez, C. ; A strong tracking adaptive fading-extended Kalman filter for the state of charge estimation of lithium-ion batteries, Eneregy Research, 2022, 46, 16427–16444. https://doi.org/10.1002/er.8307.
Yuthanava, T.; Khomfoi, S.; Phophongviwat, T. ; Modeling Li-ion battery using measurement data, Third Inter. Symposium on Instrumen. Control Artificial Intell. and Robotics, Thailand, 2023, 131-134.
Ayyarao, T.S.L.V.; Ramakrishna, N.S.S.; Elavarasan, R.M.; Polumanthi, N.; Rambabu, M.; Saini, G.; Khan, B.; Alatas, A.B. ; War strategy optimization algorithm: A new effective metheuristic algorithm for global optimization, IEEE Access, 2022, 10, 25073–252105.
Zhong, C.; Li, G.; Meng, Z. ; Beluga whale optimization: A novel nature-inspired methaheuristic algorithm, Knowdge-Based Systems, 2022, 251, 109215.
Houssein, E.; Saad, M.R.; Hashim, F.; Shalban, H.; Hassaballah, M. ; Levy flight distribution: A new metaheuristic algorithm for solving engineering optimization problems, Engineering Applications of Artificial Intell. , 2020, 94, 103731, https://doi.org/10.1016/j.engappai.2020.103731. [Google Scholar]
Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. ; African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimizaion problems, Computer & Industrial Eng. , 2021, 158, 107408. [Google Scholar]
https://gardenerspath.com, https://treehugger.com.

Figure 1. Thevenin equivalent circuit model.

Figure 2. Experimental battery platform.

Figure 3. Current pulse charge/discharge variations.

Figure 4. HPPC experimental voltage curves. (a) Pulse power tests. (b) Single pulse-power test.

Figure 4. Identified characteristic curves. (a) OCV versus SOC. (b)

R_{0}, R_{p}

, and

R_{e q}

vs. SOC. (c)

τ

vs. SOC.

Figure 4. Identified characteristic curves. (a) OCV versus SOC. (b)

R_{0}, R_{p}

, and

R_{e q}

vs. SOC. (c)

τ

vs. SOC.

Figure 5. CC-CV charging curves. (a) Charging voltage (b) Charging current. (c) Charging temperature.

Figure 6. Conceptual diagram of the MSCC charging method.

Figure 7. Dandelions in nature. (a) Dandelions growth. (b) Dandelion floating in wind.

Figure 8. ECM model for simulation.

Figure 9. Charging configuration of FM . (a) Simulation. (b) Experiement.

Figure 10. Charging configuration of PSO. (a) Simulation. (b) Experiement.

Figure 11. Charging configuration of WSO. (a) Simulation. (b) Experiement.

Figure 12. Charging configuration of JSA. (a) Simulation. (b) Experiement.

Figure 13. Charging configuration of GWO. (a) Simulation. (b) Experiement.

Figure 14. Charging configuration of BWO. (a) Simulation. (b) Experiement.

Figure 15. Charging configuration of LFDA. (a) Simulation. (b) Experiement.

Figure 16. Charging configuration of AGTO. (a) Simulation. (b) Experiement.

Figure 17. Charging configuration of DO. (a) Simulation. (b) Experiement.

Figure 18. Experimental result for charging temperature.

Figure 19. Bar chart of performance indicator. (a) FC. (b) CT. (c) MCT. (d) EL. (e) Total score.

Table 1. Specification of Panasonic NCR18650PF LiB.

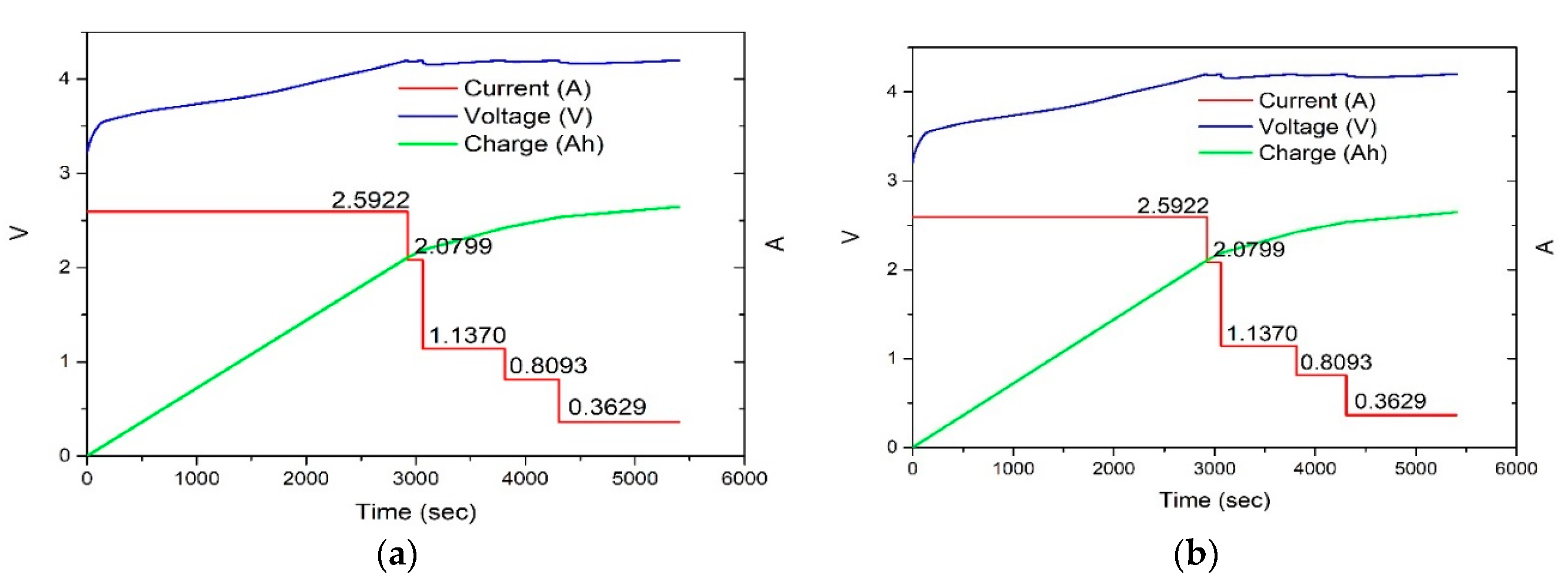
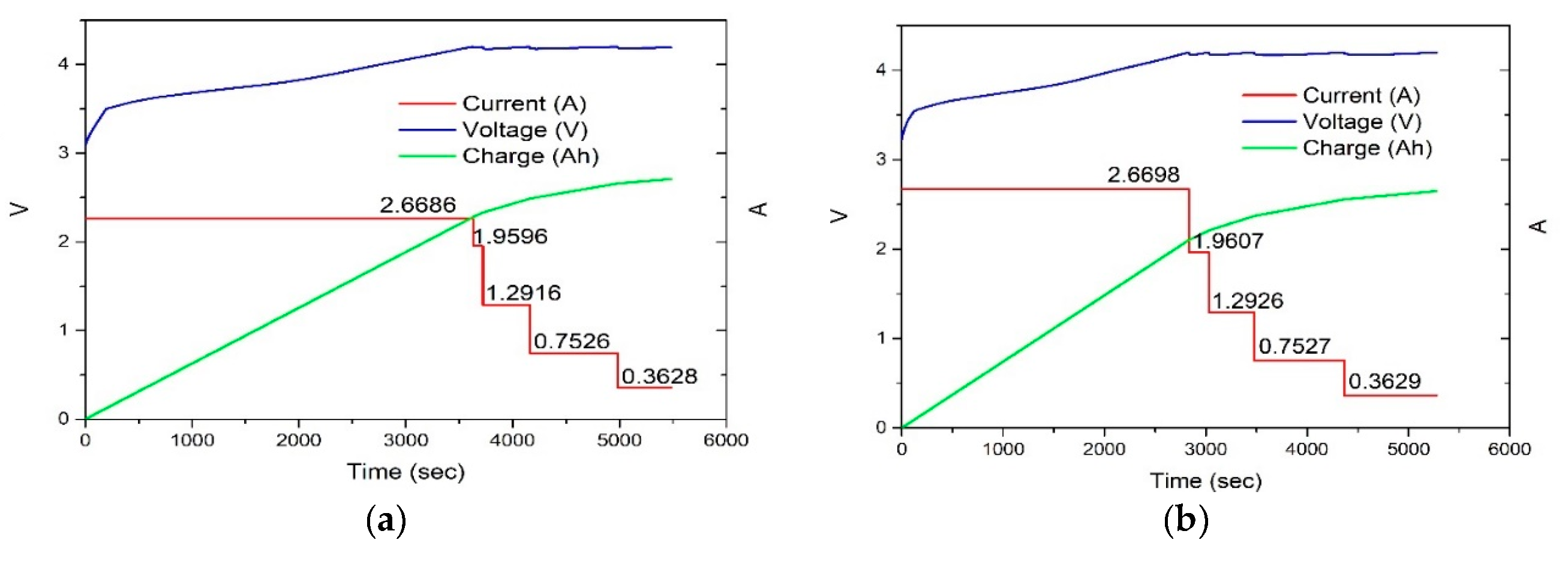
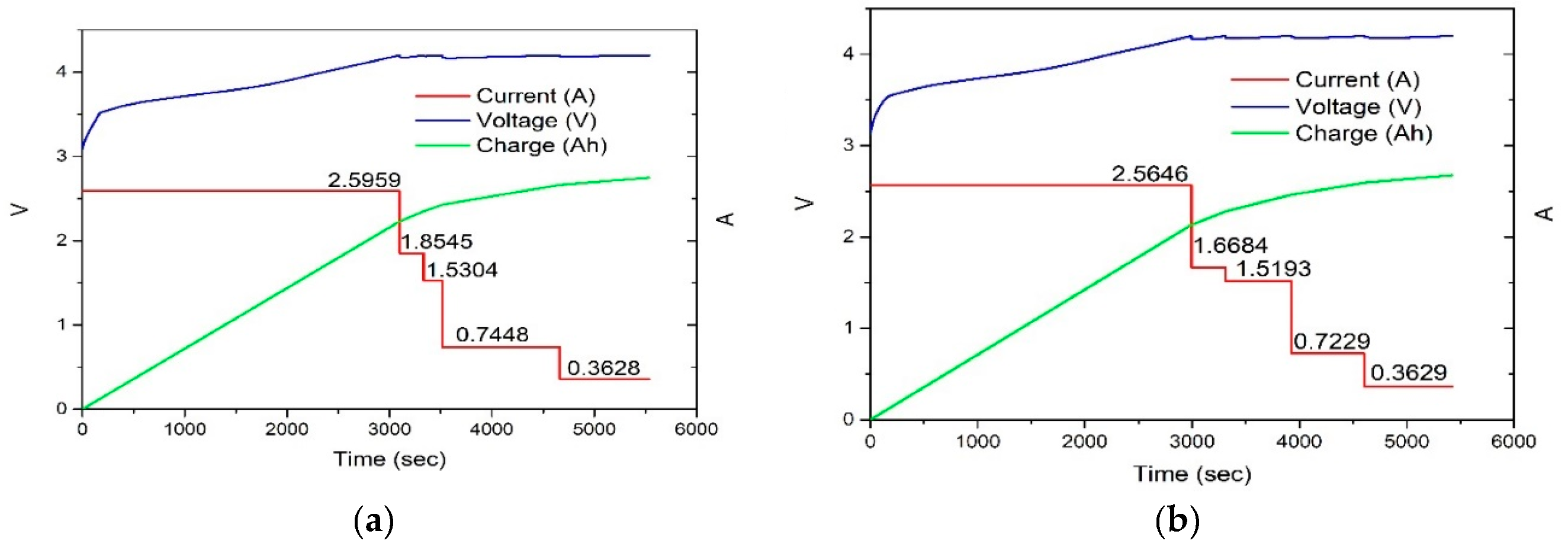
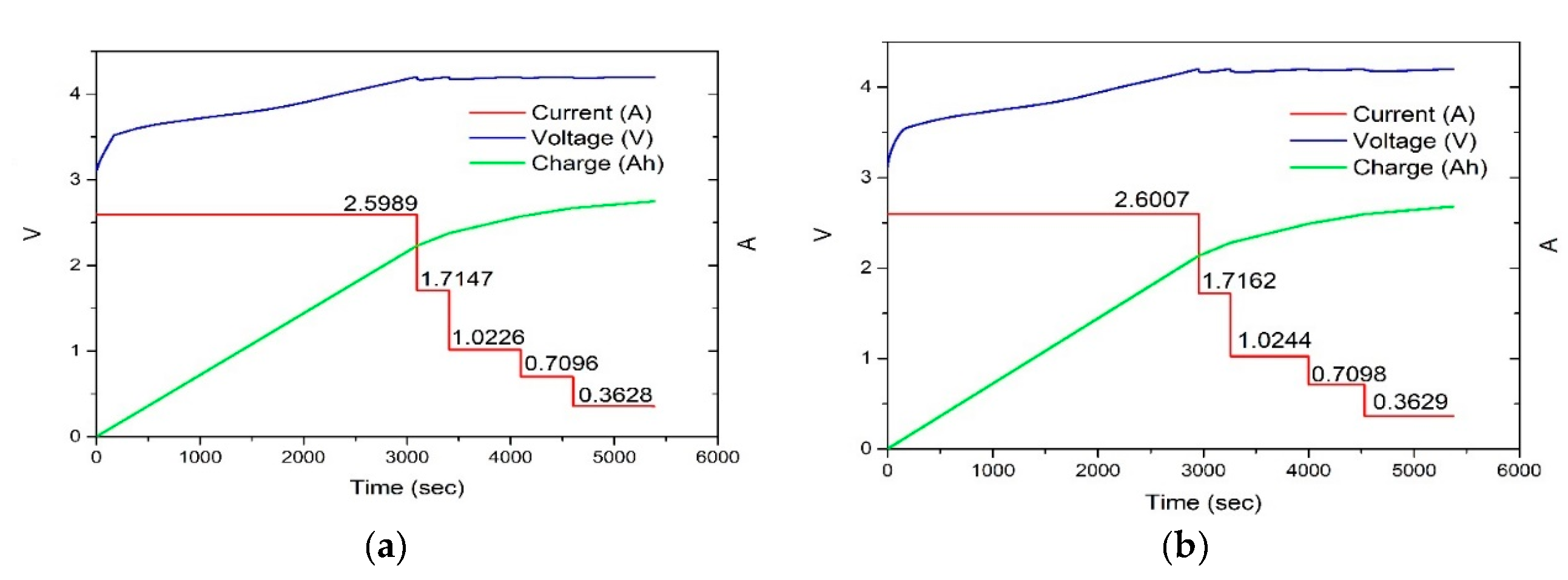
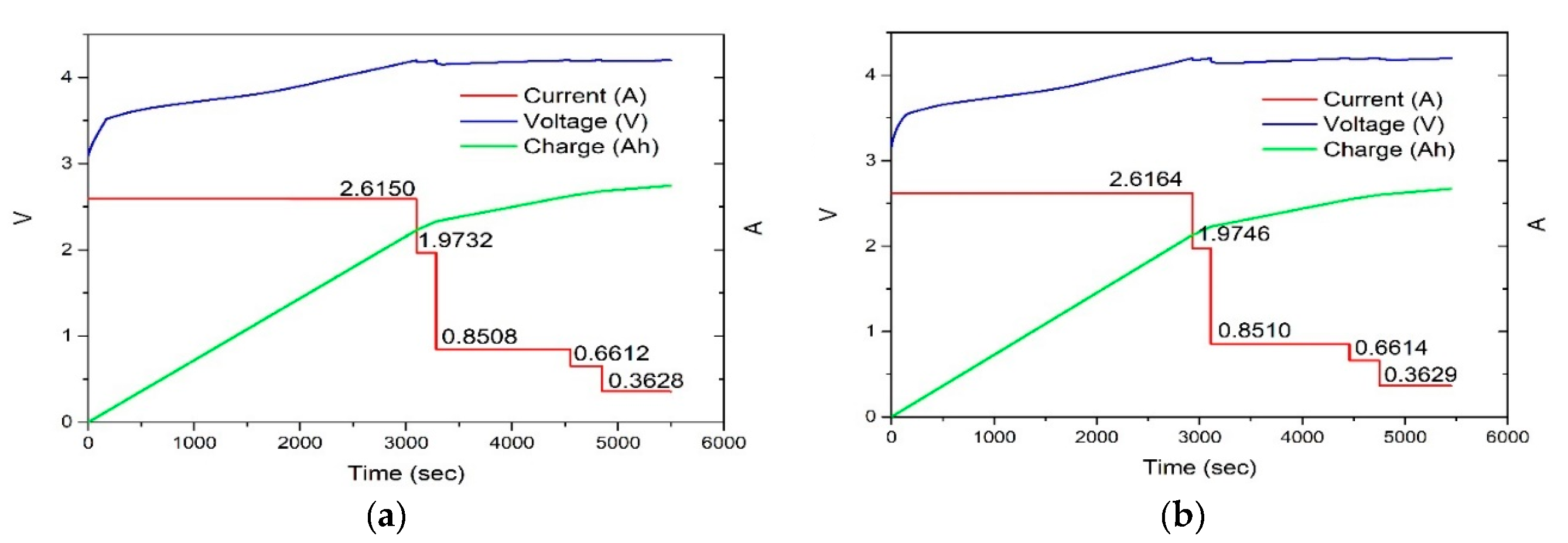
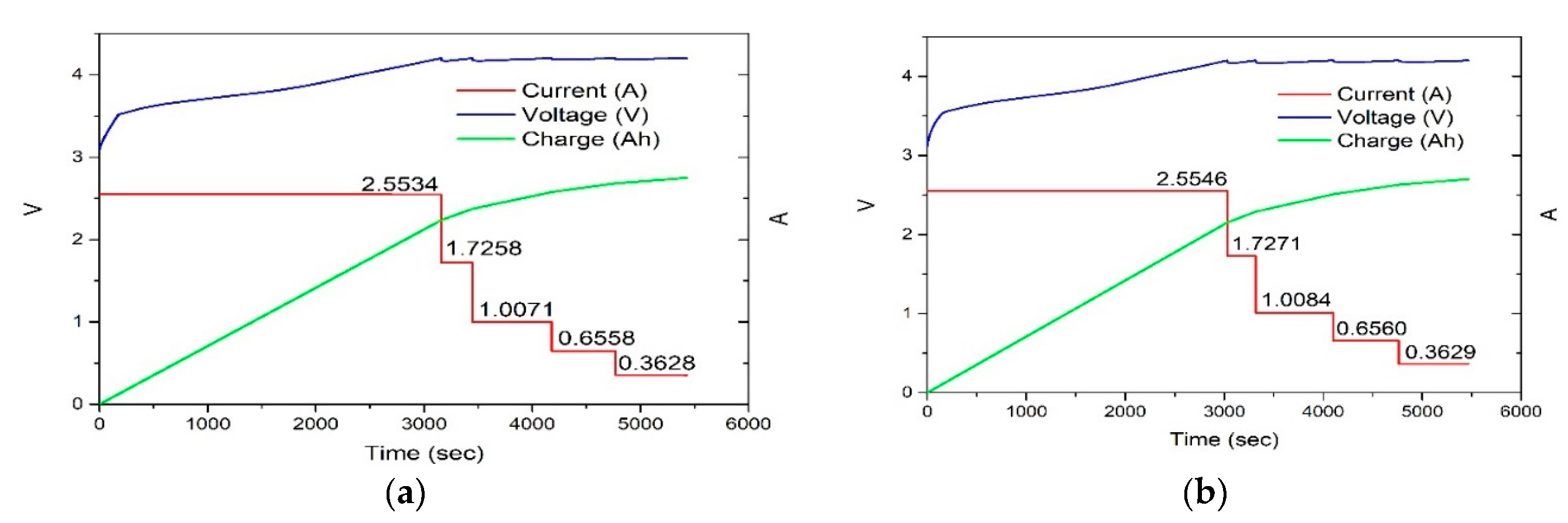
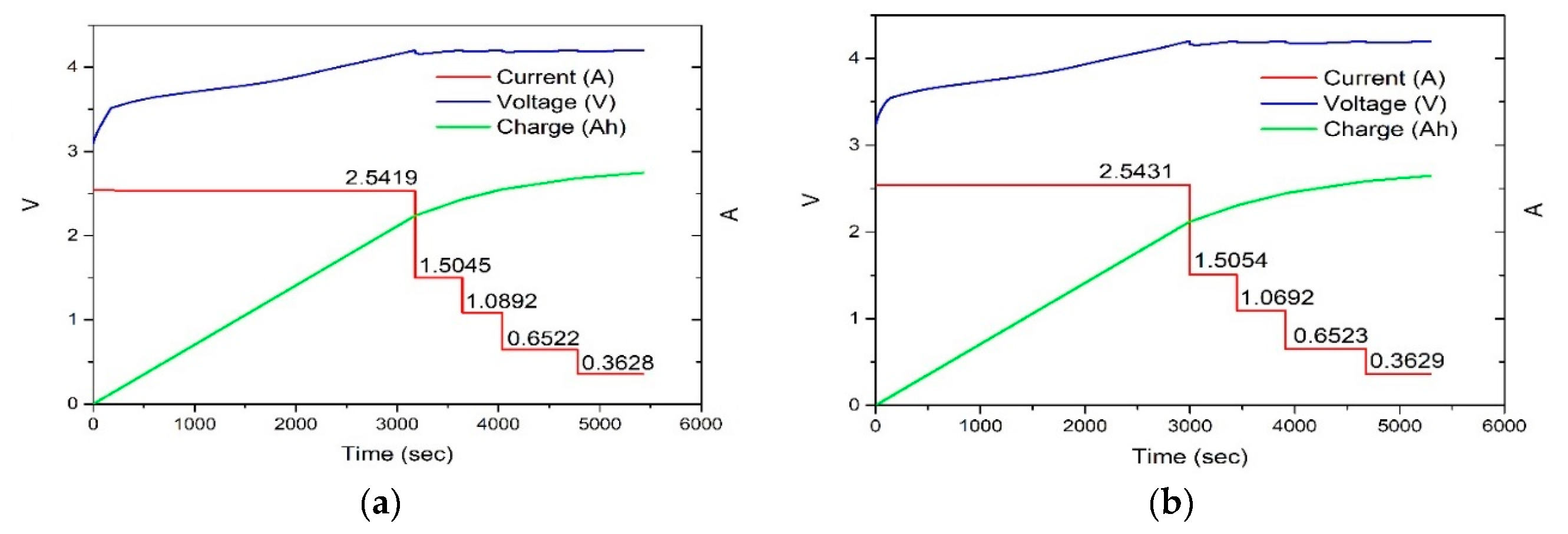
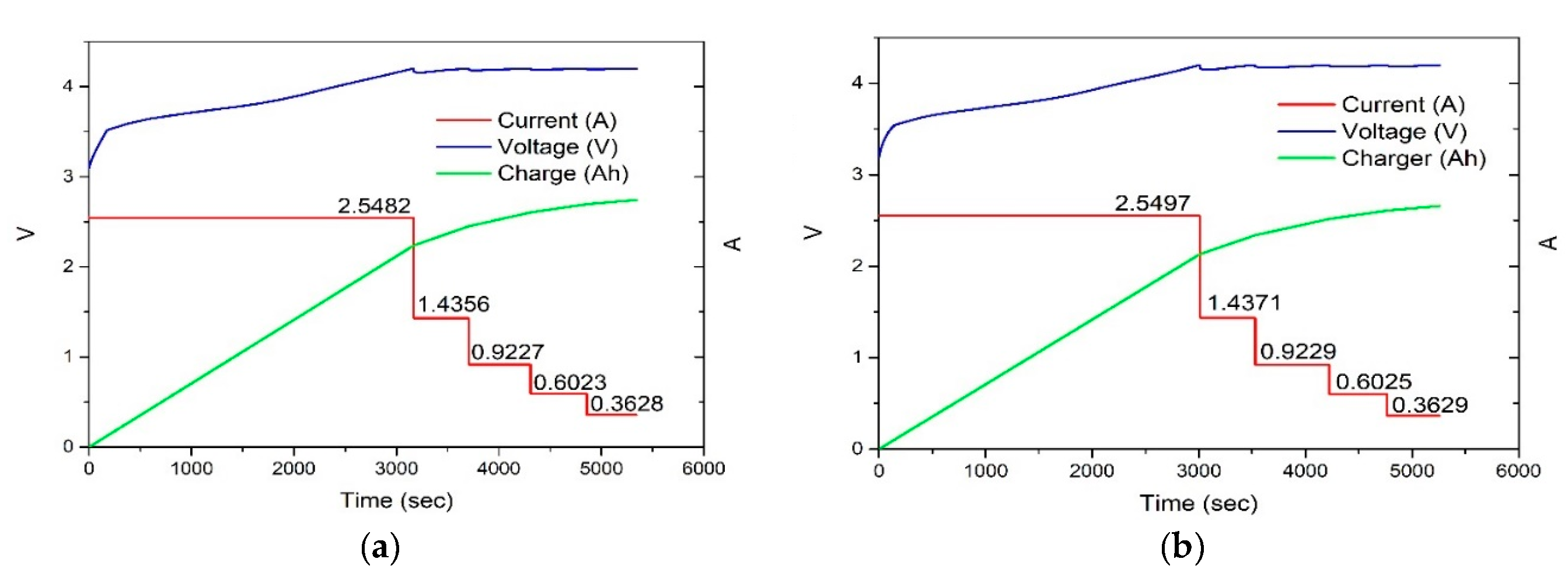
Parameter	Value
Nominal Capacity	$2900 m A h$
Nominal Voltage Cut-off Voltage	$3.6 V$ $2.5 V$
Standard Charge	$C C - C V, 1375 m A, 4.2 V, 4.0 h r s$
Dimensions	$18.5 m m (d i a m e t e r), 65.3 m m (h e i g h t)$
Temparature	$\begin{array}{l} C h a g e : 0 t o + 45^{°} C \\ D i s c h a r g e : - 20 t o + 60^{°} C \\ S t o r a g e : - 20 t o + 50^{°} C \end{array}$

Table 2. Data obtained by CC-CV charge method.

C-rate	Charge Time (sec)	Temperature (°C)
0.5	9910 (T_c,_max)	26 (t_c,_max)
2	4250 (T_c,_min)	42 (t_c,max)

Table 3. Range setting of the objective current parameter.

I_{c 1} (A)

I_{c 2} (A)

I_{c 3} (A)

I_{c 4} (A)

I_{c 5} (A)

0 ~ 2.9

0 ~ 2.9

0 ~ 2.9

0 ~ 2.9

\frac{V_{c u t - o f f} - 4.18}{R_{e q} (S O C)}

Table 4. Selected parameter values of the applied MOAs.

Algorithm	Particle No. Iteration No. Tuning parameter
PSO	$30$ $100$ $c_{1} = 1.2, c_{2} = 0.15, ω \in [0.4, 0.9]$
WSO JSA	$30$ $100$ N/A $30$ $100$ $β = 3, γ = 0.1$
GWO BWO LFDA AGTO	$30$ $100$ N/A $30$ $100$ N/A $30$ $100$ N/A $30$ $100$ $p = 0.3, β = 3, w = 0.8$
DO	$30$ $100$ $α \in [0, 1], κ \in [0, 1]$

Table 5. Simulation CPEI results.

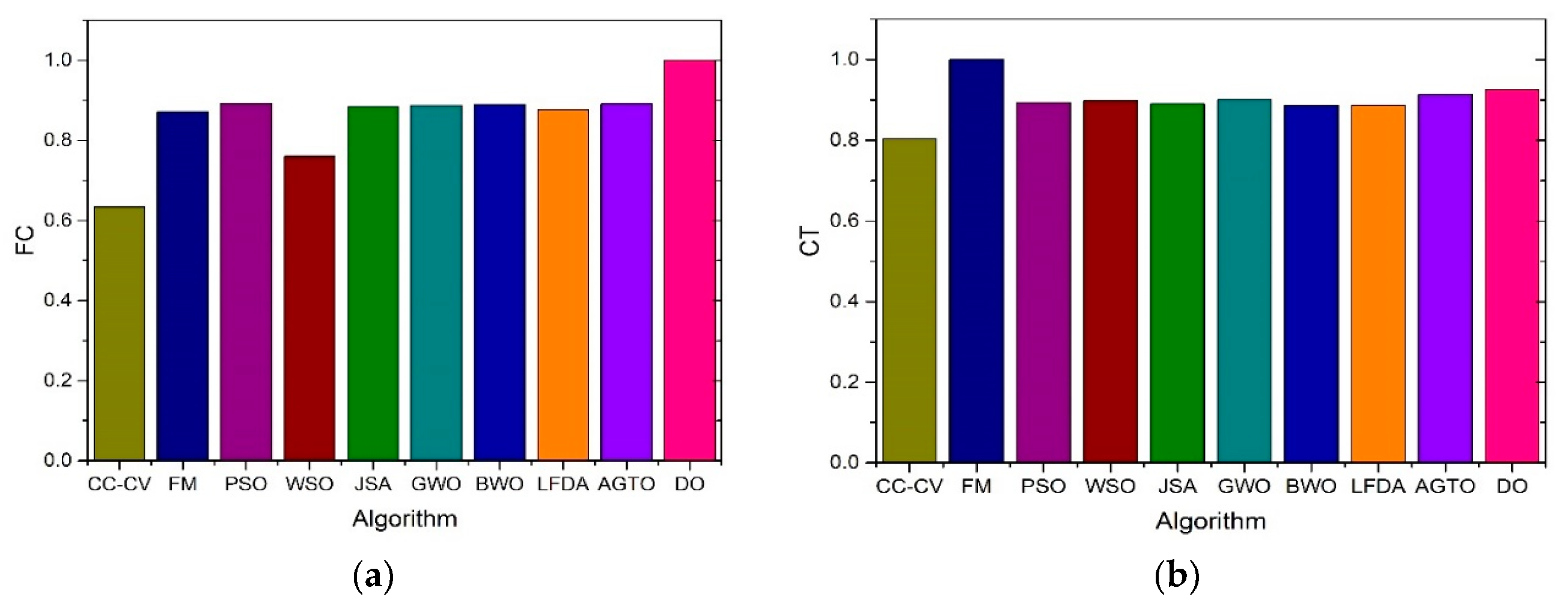
Algorithm	FC CT(sec) MCT(deg) EL(J)
1C CC-CV	$0.2961$ $6127$ $30.2$ $2172$
FM	$0.2126$ $5101$ $30.19$ $2115$
PSO	$0.2159$ $5513$ $29.18$ $1923$
WSO JSA	$0.2154$ $5367$ $29.43$ $1977$ $0.2121$ $5535$ $29.2$ $1925$
GWO BWO LFDA AGTO	$0.2119$ $5388$ $29.21$ $1928$ $0.2103$ $5499$ $29.26$ $2023$ $0.2091$ $5426$ $29.06$ $1898$ $0.1970$ $5435$ $29.03$ $1891$
DO	$0.1934$ $5342$ $29.01$ $1884$

Table 6. Simulation OCC results.

Algorithm	$I_{c 1} (A)$ $I_{c 2} (A)$ $I_{c 3} (A)$ $I_{c 4} (A)$ $I_{c 5} (A)$
1C CC-CV FM	$2.9$ - - - - $2.9$ $1.7247$ $1.0257$ $0.6102$ $0.3628$
PSO	$2.5913$ $2.0793$ $1.1363$ $0.8092$ $0.3628$
WSO JSA	$2.2686$ $1.9596$ $1.2916$ $0.7526$ $0.3628$ $2.5959$ $1.8545$ $1.5304$ $0.7448$ $0.3628$
GWO BWO LFDA AGTO	$2.5989$ $1.7147$ $1.0226$ $0.7096$ $0.3628$ $2.5959$ $1.9732$ $0.8508$ $0.6612$ $0.3628$ $2.5534$ $1.7258$ $1.0071$ $0.6558$ $0.3628$ $2.5419$ $1.5045$ $1.0892$ $0.6522$ $0.3628$
DO	$2.5482$ $1.4356$ $0.9227$ $0.6023$ $0.3628$

Table 7. Experimental CPEI results.

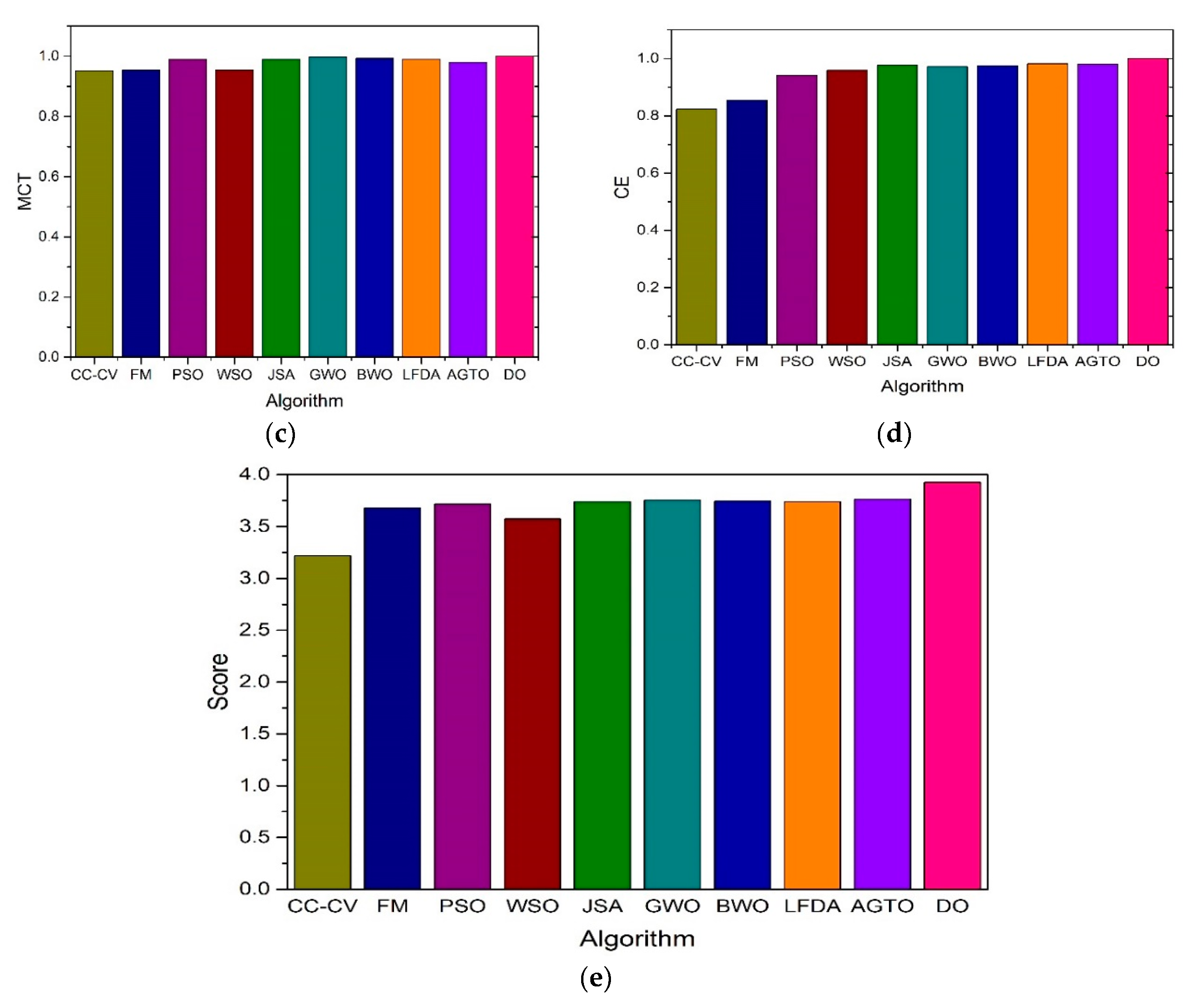
Algorithm	FC CT(sec) MCT(°C) EL(J)
1C CC-CV	$0.2862$ $6016$ $30.25$ $2173$
FM	$0.2082$ $4828$ $30.41$ $2109$
PSO	$0.2034$ $5404$ $29.3$ $1915$
WSO JSA	$0.2389$ $5379$ $30.4$ $1880$ $0.2052$ $5425$ $29.3$ $1843$
GWO BWO LFDA AGTO	$0.2046$ $5364$ $29.1$ $1855$ $0.2041$ $5448$ $29.2$ $1848$ $0.2071$ $5447$ $29.3$ $1836$ $0.2037$ $5285$ $29.6$ $1837$
DO	$0.1815$ $5213$ $29$ $1801$

Table 8. Obtained Experiment OCC values.

Algorithm	$I_{c 1} (A)$ $I_{c 2} (A)$ $I_{c 3} (A)$ $I_{c 4} (A)$ $I_{c 5} (A)$
1C CC-CV FM	$2.9$ - - - - $2.9$ $1.7255$ $1.0267$ $0.6102$ $0.3629$
PSO	$2.5922$ $2.0799$ $1.1370$ $0.8093$ $0.3629$
WSO JSA	$2.2698$ $1.9607$ $1.2926$ $0.7527$ $0.3629$ $2.5646$ $1.66854$ $1.5193$ $0.7229$ $0.3629$
GWO BWO LFDA AGTO	$2.6007$ $1.7162$ $1.0244$ $0.7098$ $0.3629$ $2.6164$ $1.9746$ $0.8510$ $0.6614$ $0.3629$ $2.5546$ $1.7271$ $1.0084$ $0.6560$ $0.3629$ $2.5431$ $1.5054$ $1.0692$ $0.6523$ $0.3629$
DO	$2.5497$ $1.4371$ $0.9229$ $0.6025$ $0.3629$

Table 9. Normalized score of the charging performance for each method.

Algorithm	FC CT MCT CE Total Score
1C CC-CV	$0.6342$ $0.8025$ $0.9587$ $0.8228$ $3.2182$
FM	$0.8718$ $1.0000$ $0.9536$ $0.8540$ $3.6794$
PSO	$0.8923$ $0.8934$ $0.9898$ $0.9405$ $3.7160$
WSO JSA	$0.7597$ $0.8976$ $0.9539$ $0.9580$ $3.5740$ $0.8845$ $0.8900$ $0.9898$ $0.9772$ $3.7415$ ab
GWO BWO LFDA AGTO	$0.8871$ $0.9000$ $0.9966$ $0.9709$ $3.7546$ $0.8893$ $0.8862$ $0.9932$ $0.9746$ $3.7433$ $0.8764$ $0.8864$ $0.9898$ $0.9809$ $3.7375$ $0.8910$ $0.9135$ $0.9797$ $0.9804$ $3.7646$
DO	$1.0000$ $0.9261$ $1.0000$ $1.0000$ $3.9261$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Study on Optimal Charging Current Protocol with Multi-Stage Constant Current Using Dandelion Optimizer for Time- Domain Modeled Lithium-Ion Batteries

Abstract

1. Introduction

2. Equivalent Circuit Modeling of Lithium-Ion Batteries

2.1. Modeling of the Equivalent Circuit Model and Parameter Identificaiton of the Lithium-Ion Battery

2.2. Mathematical Description of the MSCC Charging Method

2.3. Objective Function Formulation for OCP

3. Metaheuristic Optimization Algorithm for OCP Searching Protocol

3.1. Inspiration for MOA

3.2. Overview of the Dandelion Optimization Algorithm

3.2.1. Inspiration

3.2.2. Mathematical Model

Rising Stage

Descending Stage

Landing Stage

4. Simulation and Experiment Results and Discussions

4.1. Computing Parameter Setting

4.2. Simulation Results

4.2. Experimental Results

7. Conclusions

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe