Prerpints.org logo
Preprint
Article

Encapsulating Spatially Varying Relationships with a Generalized Additive Model

Altmetrics

Downloads

91

Views

67

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 November 2024

Posted:

06 November 2024

You are already at the latest version

Alerts
Abstract

This paper describes the specification of spatially varying coefficient (SVC) regression models using Generalized Additive Models (GAMs). The GAMs include Gaussian Process (GP) splines (smooths) for each covariate parameterised with observation location and generate SVC estimates that capture spatially varying relationships. The ability of the proposed GAM approach to estimate true spatially varying coefficients was compared with that of Multiscale Geographically Weighted Regression (MGWR) using simulated data with complex spatial heterogeneities. The geographical GP GAM (GGP-GAM) was found to out-perform MGWR across a range of fit metrics and resulted in more accurate coefficient estimates and lower residual errors. The model for one of simulated datasets was investigated in detail to illustrate GAM diagnostics, model checks, spline / smooth convergence and basis evaluations, and tuning via the number knots. A larger simulated case study was investigated to explore the trade-offs between GGP-GAM complexity, performance and computation. Finally the GGP-GAM and MGWR approaches were applied to an empirical case study. The resulting models had very similar accuracies and fits, and generated subtly different spatially varying coefficient estimates. A number of areas of further work are identified.

Keywords: 
Subject: Computer Science and Mathematics  -   Probability and Statistics

1. Introduction

In regression, the relationship between response and predictor variables may vary with observation location. This may be due to a poor conceptual model, poor measurements with regional biases, omitted local factors, or it may be due to the presence of process spatial heterogeneity, also known as process spatial non-stationarity. In such cases, spatially varying coefficient (SVC) models provide an alternative to global or whole map regressions in which the relationships between response and predictor variables are assumed to be constant across space. SVCs relax the assumption of relationship spatial stationarity [1]. SVC models allow relationships to vary with observation location and generate spatially distributed or local coefficient estimates which can be mapped to indicate how and where statistical relationships vary. They provide a methods for quantifying process spatial non-stationarity or spatial heterogeneity - a key and increasingly common task in spatial data analysis. Importantly SVCs can provide insights by informing on the spatially varying nature of drivers of a response, or may guide further investigations.
The SVC brand leader is Geographically Weighted Regression (GWR) [2]. This uses a single moving window or kernel, whose size is optimised and determines the scale of spatial heterogeneity in the resultant outputs. GWR has been extended to a multiscale approach (MGWR) [3,4] in which multiple kernels are fitted, one for each predictor variable, thereby capturing multiple scales of spatially varying relationship. MGWR is considered by some to be the default GWR model [5]. However, there are a number of limitations associated with MGWR approaches, the main ones being that they cannot predict out of sample and that only approaches for Gaussian and Poisson responses have been developed [6].
This paper addresses these critical gaps and describes the construction of a novel SVC modelling approach that uses Generalized Additive Models (GAMs) [7,8] with Gaussian Process (GP) smooths to capture process spatial non-stationarity. GAM smooths are commonly used to accommodate varying relationships between predictor and response variables in attribute space. But if they are parameterised with observation location, then the result is an SVC as the coefficient estimates vary over geographic space. The GAM-based SVC approach proposed in this paper - the Geographical Gaussian Process GAM (GGP-GAM) - is evaluated through two simulation experiments. The first compares it with MGWR using simulated data with complex and highly localised degrees of spatial heterogeneity. Both models are fully tuned. The second investigates the ability of the GGP-GAM to handle larger datasets. Specifically, it examines whether performance is affected as the number of knots required by the GAM increases and as the number of observations and regression terms increases. Finally, an empirical case study of the UK referendum to leave the European Union in 2016 (Brexit) is used illustrate and compare MGWR and GAM-based approaches.

2. Literature Review

2.1. SVC Models

Spatially varying coefficient regression models seek to capture spatial dependencies in the relationships between target and predictor variables. Their outputs provide explicit indications of the scales of any spatial dependencies and the spatial variations in the predictor-to-response relationships. A widely used SVC model is Geographically Weighted Regression (GWR) [2]. GWR has been extended to Multiscale GWR (MGWR) [3,4] in which the spatial dependency between each predictor variable and the target variable is individually quantified. In a MGWR / GWR a series of local models are created using data subsets extracted using a moving window or kernel. For each local model the subsetted data are weighted by their distance to the location under consideration, resulting local, spatially distributed coefficient estimates. The kernel size is determined using a weighted least squares algorithm in a standard GWR and an iterative back-fitting algorithm in MGWR. Besides GWR/MGWR, other widely utilized multiscale SVC models include Bayesian Gaussian Process (GP) models that employ co-kriging via a Linear Model of Co-regionalisation (LMC) (Bayes-GP) [9,10,11,12], and Eigenvector Spatial Filtering (ESF) with Moran coefficients (ESF-MC) [13,14,15]. The ESF-MC enhances the deterministic ESF model [16] by incorporating random effects to capture stochastic spatial processes. These SVC models are directly interrelated [15], and comparative analyses indicate that no single multiscale SVC model significantly surpasses the others. Recently, other multiscale SVC models have emerged, such as a triangulation model utilizing bivariate spline estimators [17], a GP-based model adopting a frequentist approach with ML estimation [18], and a GLM-based model incorporating a reduced-rank spline [19]. However, these SVC models have not been widely adopted by the research community and the use of GWR approaches has increased rapidly [20]. There are a number of theoretical limitation with GWR approaches (including MGWR): they generate a collection of local models rather than a single one while Bayes-GP, ESF-MC, and GGP-GAM each offer a single non-stationary model formulation (e.g. [10,21]), they use the same observations multiply in different local models and MGWR approaches cannot predict out of sample. As a result it has been argued that GWR / MGWR are essentially exploratory approaches [18,22].

2.2. GAM Based SVC Models

GAMs produce multiple model terms that are additively combined, and can accommodate different types of response variables [7,8,23]. In this way they intuitively model and capture complex data relationships and interactions, including non-linearities between predictor and response variables [24]. GAMs provide a framework for making predictions from complex systems, for quantifying variable relationships, and for making inferences about these relationships [7,8]. They perform as well as many machine learning models in terms of prediction accuracy and computational speed [25], and critically, in the context of varying coefficient modeling, GAMs combine this inferential power with transparency and process understanding. They have been described as providing "intrinsically understandable white-box machine learning models that provide a technically equivalent, but ethically more acceptable alternative to [machine learning] black-box models" ([26] p.2).
GAMs can incorporate smooths or splines to model nonlinear relationships, whose forms can vary depending on the problem and / or the data [8]. Smooths are composed of combinations of basis functions which can be single or multi-dimensional in terms of predictor variables. Consequently, a GAM with smooths is composed of sums of multi-dimensional basis functions that enable complex relationships to be modelled. As a result of these properties a number varying coefficient and Bayesian regression models using GAMs have been proposed [27,28,29,30]. These make few assumptions about the response variable distribution, which may be skewed, kurtotic or discrete, and their varying coefficient aspects relate to target variable properties of location, scale and shape. In these ’location’ refers to target variable central tendencies, ’scale’ to measures of spread such as standard deviation in normal distributions or parameters of a gamma distribution, and ’shape’ refers to the nature of the skew and kurtosis present in the distribution. In this way a typical GAM-based varying coefficient model approach can accommodate spatial effects, but not within in an explicitly geographic framework way with respect to location. Some recent work has proposed an SVC GLM regression model using GAMs [19] with reduced-rank thin-plate smooths, however an alternative approach for modelling predictor-to-response relationship, is to consider as a Gaussian Process (GP) over space. Rather than use a thin-plate approach to spatially varying relationships, a GP captures relationships that decay over distance, reflecting Tobler’s First Law of Geography [31]. As GPs have been found to be effective in handling spatial autocorrelation [32], the approach proposed in this paper uses decomposed or low-rank GP smooths parameterised with observation location for each covariate. It extends initial investigations of GAMs in SVC modelling using the Geographical Gaussian Process GAM (GGP-GAM) [33] by exploring GAM tuning with more complex spatial problems.

3. Methodology

The analyses described below first compared SVC models using GGP-GAM and MGWR approaches through with analyses of 100 simulated each with 625 observations using 3 predictor variables (i.e. x 1 , x 2 , x 3 ). The accuracy in estimating the true coefficient surfaces and in predicting the true values of y was investigated. A second tranche of analyses investigated the ability of GAM based SVC models to handle larger datasets in this case with 250,000 observations) and specifically to investigate model tuning via the knots parameter, k in order to identify possible trade-offs between model performance and computation overheads. This section describes the data, the formulation of the Geographical Gaussian Process GAM (GGP-GAM), the analyses comparing GGP-GAM with GWR, an investigation of GGP-GAM tuning with a larger dataset and an empirical case study.

3.1. Data

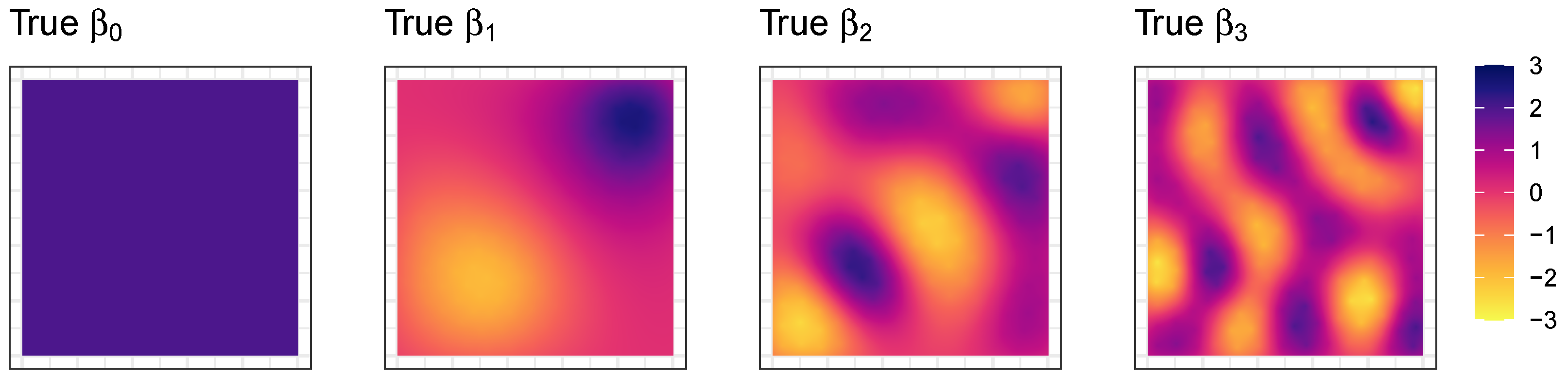
For the first analyses to compare the proposed GGP-GAM and MGWR SVC models, a simulated spatially varying coefficient dataset was created, with three coefficients each having different degrees of spatial heterogeneity. The simulated coefficient dataset was created by extracting Moran eigenvectors [13] generated using the spmoran R package [34]. Here the 1st, 10th and 25th surfaces were selected from the matrix of the first L eigenvectors, for a 25 by 25 grid (625 observations). Each coefficient surface, termed β 1 , β 2 , β 3 has a normal distribution and was rescaled to have a mean of 0 and standard deviation of 1. An intercept surface, β 0 with a constant value of 2 was also defined. These represent the true regression coefficients and are shown in Figure 1.
The values for 100 sets of simulated predictors x 1 , x 2 and x 3 were calculated from a random normal distribution and were rescaled to have a range of [0, 1] and the values for the error term ϵ from a random normal distribution rescaled to range have a of [0, 0.25]. One hundred simulated datasets were created. The simulated response y was calculated directly from these and the coefficients in Figure 1.
For the second analyses, simulated data were again created from Moran eigenvectors [13] but now over a 500 by 500 grid and the 1st, 10th and 25th surfaces were extracted to create 3 true coefficients, over 250,000 observations. The coefficients have different spatial heterogeneities to those in Figure 1. Values for x 1 , x 2 , x 3 , ϵ and y were generated in the same way as for the smaller simulated study. The true coefficients are shown in Figure 2. Note that the range of the true coefficients is slightly larger than those in Figure 1 and their spatial variations are different.

3.2. GAM-Based SVC Models

The standard form for an OLS regression is:
y i = β 0 + ∑ j = 1 m β j x i j + ϵ i
where for observations indexed by i = 1 ⋯ n , y i is the response variable, x i j is the value of the j-th predictor variable, m is the number of predictor variables, β 0 is the intercept term, β j is the regression coefficient for the j-th predictor variable and ϵ i is the random error term. This can be extended to define a SVC regression model:
y i = β 0 ( u i , v i ) + ∑ j = 1 m β j ( u i , v i ) x i j + ϵ i
where now ( u i , v i ) are the spatial coordinates of the observations i and β j ( u i , v i ) are the coefficients estimated at those locations.
GAMs can also calibrate regression models in which the functions of the predictor variables are unknown and these take the following form:
y = α + f 1 ( z 1 ) + f 2 ( z 2 ) + ⋯ + f j ( z j ) + ϵ
where α is the intercept ( β 0 in Equations 1 and 2) and the j-th predictor z j can be a scalar or a vector.
These can be extended so that each f j ( z j ) becomes a linear regression coefficient on another scalar predictor is a linear regression x j :
y = α + f 0 ( z 0 ) + x 1 f 1 ( z 1 ) + x 2 f 2 ( z 2 ) + ⋯ + x m f m ( z m ) + ϵ
And, if z 0 = z 1 = ⋯ z m = z for example, and z is a vector of locations or coordinates (similar to ( u , v ) in Equations 1 and 2) then a spatially varying coefficient model is specified:
y = α + f 0 ( z ) + x 1 f 1 ( z ) + x 2 f 2 ( z ) + ⋯ + x m f m ( z ) + ϵ
where f j ( z ) represents the j-th SVC.
One approach to specify α ( z ) ⋯ f m ( z ) is to generate each function from a GP smooth defined as follows:
f j ( z ) = ∑ p = 1 P κ p ( z ) γ j , p γ j , p ∼ N ( 0 , s j 2 )
where κ p ( z ) represents a basis function, γ j , p is the corresponding coefficient and s j 2 is the smoothing parameter. The SVC f j ( z ) exhibits high spatial variation if s j 2 is large, and remains constant if s j 2 = 0 . In this way the smoothing parameter determines the wiggliness of the SVC, that is how quickly the function varies across its range.
The basis function κ p ( z ) is specified such that f j ( z ) has a spatially smooth pattern, in this case driven by the following covariance function:
Cov ( f m ( z ) , f j ( z ′ ) = s j 2 c ( d z , z ′ )
where d z , z ′ represents the distance between locations z and z ′ and the covariance function c ( d z , z ′ ) decreases with increases in d z , z ′ . This is similar to kriging and MGWR. Kriging uses covariance functions via the semi-variogram and a covariance function is calibrated individually for each f j ( z ) in the same way as bandwidths are optimised in MGWR. Thus a key task in using GAMs to model SVCs is to estimate the smoothness parameters s j 2 and thereby f j ( z ) .
A GAM employs smooth functions of the predictor variables, assuming that the values of the explained variable y follow a some kind of exponential distribution:
f ( y | θ ) = h ( y ) exp ν ( θ ) T ( x ) − A ( θ )
where h ( . ) , ν ( . ) , T ( . ) and A ( . ) are known functions, and θ is a vector of parameters. This has a flexible form and is thus able to handle a wide range of distributions including Gaussian, Poisson, Gamma, or Binomial ones.
In summary, GAMs can estimate SVCs by modelling non-linear relationships as spatially non-stationary ones using GP splines over geographical as well as attribute space: a GP spline with spatial location is defined for each predictor variable j. Additionally an offset α j is added to account for the GP’s zero mean, thereby creating the SVCs β j ( z ) . In the standard 2D case, z i = ( u i , v i ) , defining the Geographical Gaussian Process GAM (GGP-GAM).

3.3. Analysis I: Comparing GGP-GAM and MGWR

Gaussian Process splines can be incorporated within GAM models and here this was done using the gam function in the mgcv R package [35]. The observation spatial locations z were extracted and used to parameterise the splines with a GP smooth. The GPs constructed in this manner have a mean of zero; therefore, an additional fixed offset term is included for each covariate alongside the spatially smoothed terms.
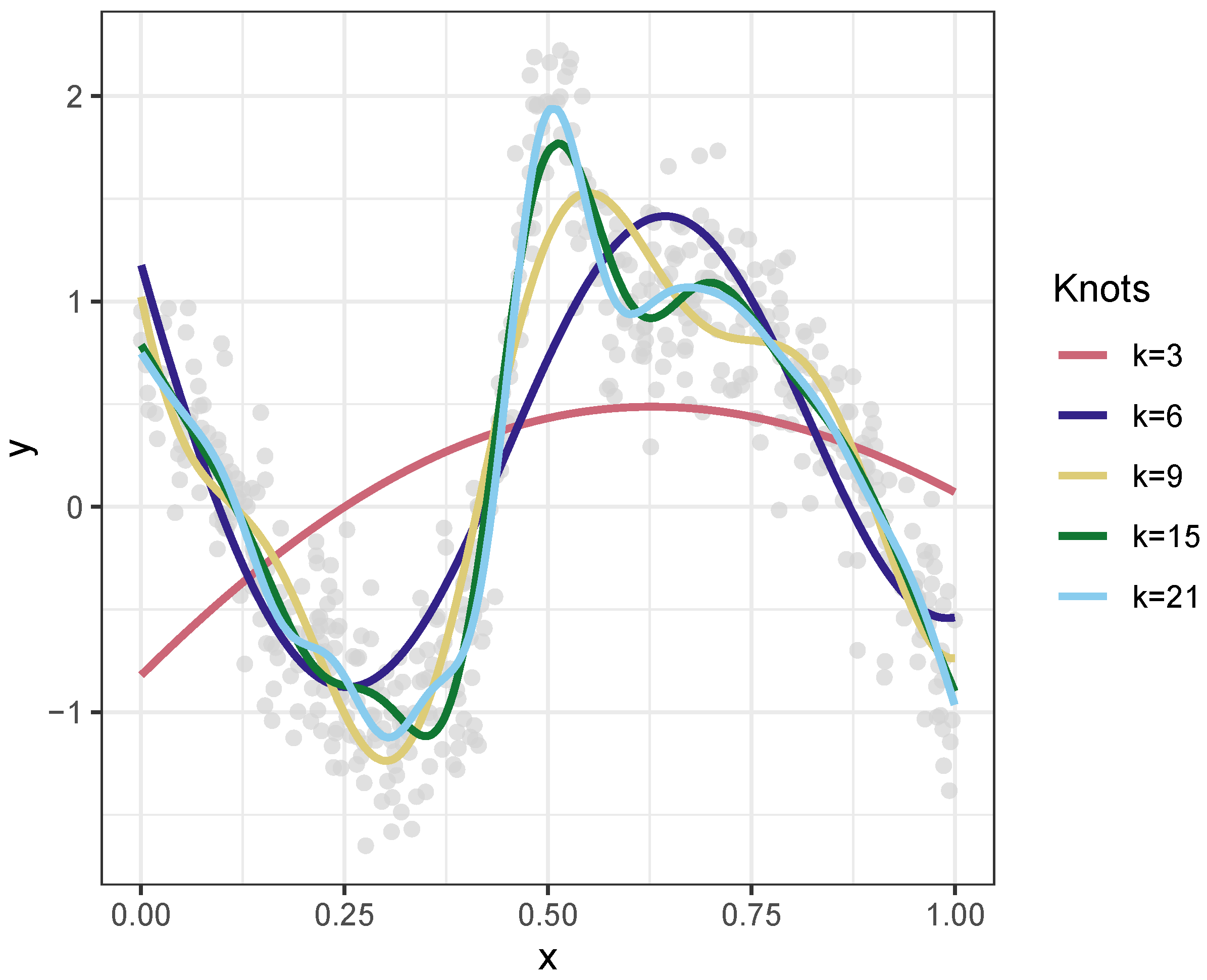
There are some important tuning considerations in fitting GAMs with mgcv including the specification of spline smoothing parameters and the number of knots. These parameters influence the nature of the varying coefficients and the characterization of response-to-predictor relationships across space. The smoothing parameter regulates the degree of data smoothing through a correlation function, and the GAM function in the mgcv package optimizes this using an estimation method. In this case, REML was specified for optimization instead of a cross-validation estimator. The number of knots, k, determines the basis dimensions, the maximum number of base functions, used in the smooth and thus the degree of sensitivity in fitting the model to the data. For example, consider the models predicting y specified with different numbers of knots in Figure 3. Together with the smoothing parameter, determines the degree of relationship non-linearity in the smooth. These are heuristically optimised by most GAM implementations in order to balance over-fitting with capturing relationship complexity. In the approach suggested by Wood [35], k can be manually and iteratively determined: an initial value is set and the resultant splines are examined to determine whether the smoothing optimization has converged and whether the basis dimensions defined by k are adequate. If they not, they are increased. For the analyses comparing GGP-GAM and MGWR, k = 155 was specified after investigation.
The GWmodel R package [36,37] was used to construct the MGWR models and were specified with an adaptive bisquare kernel. Note that fixed kernels were also investigated and the comparisons with the GGP-GAM results reported below were found to be similar. MGWR can accommodate and quantify varying degrees of spatial heterogeneity in the predictor-to-response relationships by determining a kernel bandwidth for each covariate. This requires a series of optimisation problems to be solved and the implementation of MGWR uses a back-fitting algorithm to do this, as does all implementations of MGWR [37,38,39]. Here, the convergence of the back-fitting procedure was evaluated through cross validation of the residual sum of squares and the threshold for convergence was set at 10 − 5 or 2000 convergence iterations.
In the first analyses, the GGP-GAM and MGWR models were fitted to the 100 simulations over the 625 surface points. The SVC estimates were extracted for each model, along with predictions for y (i.e. y ^ ) for each simulation. These were used to calculate measures of coefficient fit by comparing the model coefficient estimates with the true ones in Figure 1, including R2 for β 1 , β 2 and β 2 ( β 0 is stationary), and RMSE and MAE for β 0 , β 1 , β 2 and β 3 . Model fit diagnostics of AIC, R2, RMSE and MAE were also found. Finally, the model residuals ( y − y ^ ) were also extracted to compare the spatial autocorrelation in the residuals arising from the models. To ensure consistency, for AIC, MAE, RMSE and R2, were coded and applied to each GAM and MGWR model, rather than using the values generated by the outputs of the mgcv and the GWmodel packages.

3.4. Analysis II: GGP-GAM Tuning with a Larger Dataset

A second set of analyses investigated the impact of increased observation number on tuning via the knots parameter k in order to identify any trade-offs between performance and computation. To do this seven GGP-GAMs were specified each with an increasing number knots. The effects of the increasing k were evaluated through computation time, coefficient accuracy and predictive performance. Again these were implemented in the mgcv package but using the bam function with parallel processing. Each model had the same input data but with the k parameter varying.

3.5. Empirical Example: Brexit Vote

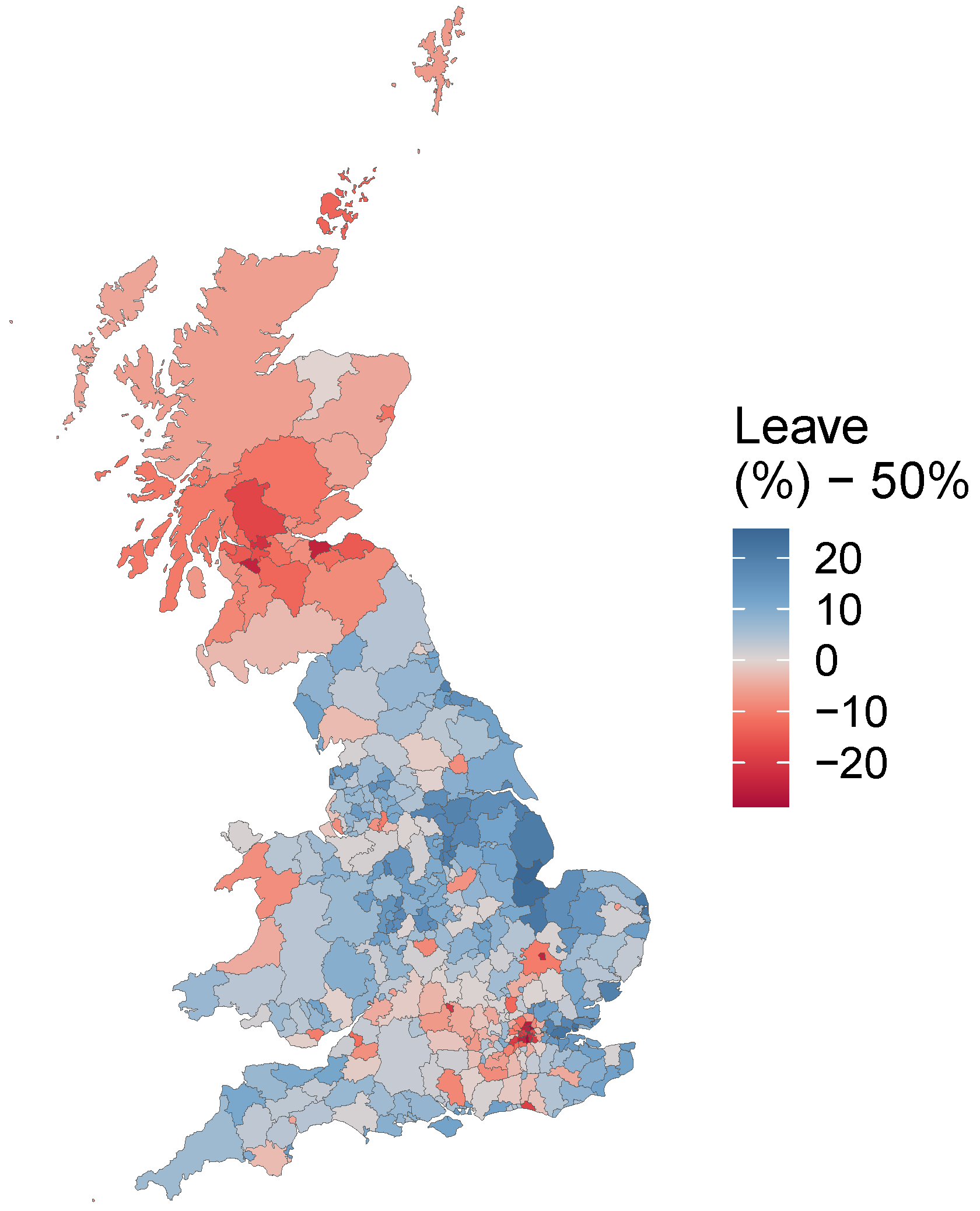
A final analysis to illustrate the approach constructed a GGP-GAM SVC model of the 2016 UK referendum on leaving the EU (the Brexit vote) in England, Wales and Scotland (the Brexit vote) [40]. The spatial distribution of the Leave vote share over 380 Local Authority Districts is shown in Figure 4. This suggests that the overall outcome of a 51.9% majority in favour of ’Leave’ conceals notable regional patterns. A spatially varying coefficient model identifies where the drivers of the outcome vary geographically. For this example, the independent variables from the 2011 UK Census were: Christian the proportion stating their religion as Christian, Degree the proportion with a bachelors degree, No Car the proportion who do not own a car or van, and Younger the proportion of the electorate between the ages of 20 and 44 years old. Each of the dependent variables could influence the Leave vote proportion in a spatially heterogeneous way, in a spatially homogeneous way or not at all. The variables were not rescaled.

4. Results

4.1. Comparing GPP-GAM and MGWR

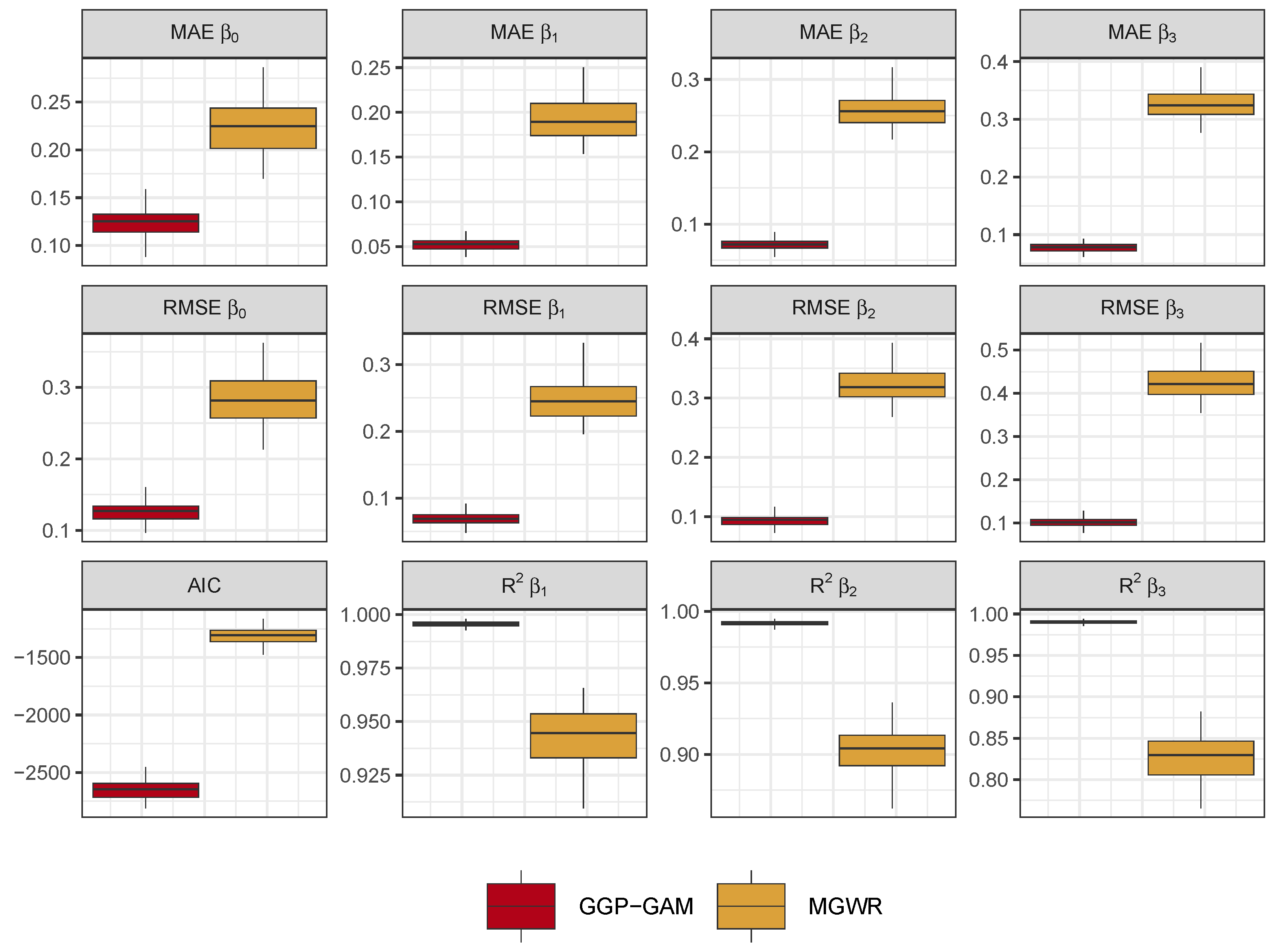
The comparisons of the estimated coefficients with the true coefficients arising from the 100 GGP-GAM and MGWR models are shown in Figure 5. The boxplots have the outliers removed to emphasise the differences between the median values in the fit measures. For each fit measure (RMSE, MAE, R2), the GPP-GAM provides more accurate estimates of the true coefficients than MGWR, with the accuracy difference increasing with the degree of spatial heterogeneity (i.e. from β 1 to β 3 ).
The distributions of model fit indicated by AIC show that the GGP-GAMs consistently have lower AIC values compared to the MGWR models. Investigations of the large differences in AIC values revealed them to be driven by differences in the residuals, rather than the number of model parameters. These are summarised in Table 1.
The spatial variation in the residuals was also compared. A Moran’s I statistic was generated for the residuals arising from each GGP-GAM and MGWR model. Their distributions are summarised in Table 2. The MGWR residuals have higher positive values indicating stronger positive spatial autocorrelation (i.e. clustering), while the GGP-GAM residuals have more negative values indicating stronger negative spatial autocorrelation (i.e. dispersion).
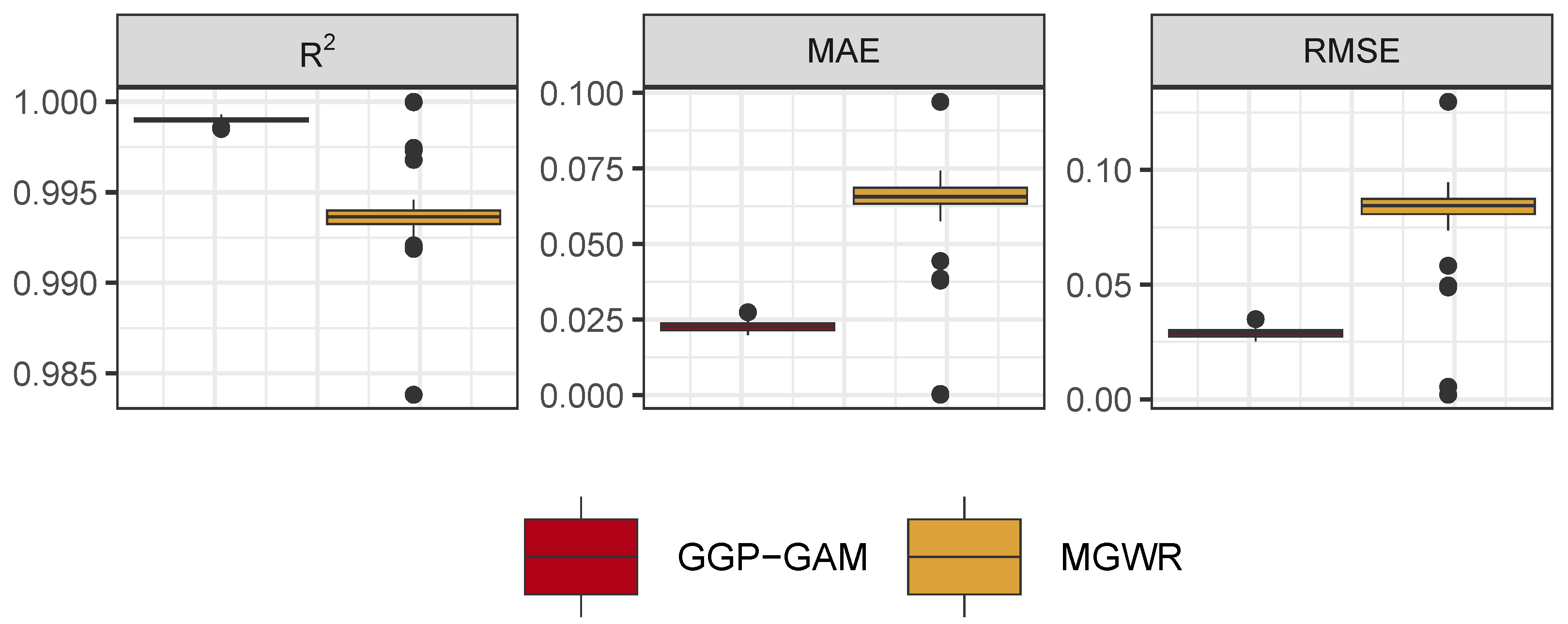
The accuracy of the predicted measures of y (i.e.  y ^ ) arising from the two models are compared in Figure 6, using RMSE, MAE and R2. The GGP-GAMs generate more accurate predictions, reflecting their better of estimation of the true coefficients.
Model calibration can be investigated. The GGP-GAM spline smoothing parameters are part of a covariance function that penalizes model complexity, while the covariate-specific bandwidths in MGWR describe the scale of each predictor-to-response relationship, thereby reflecting the scale of process spatial heterogeneity. These are summarised in Table 3. The homogeneity of these, as indicated by the inter-quartile ranges, reflect the convergence of the bandwidth optimisation in the MGWR models and the optimisation of the spline smoothing parameters in the GGP-GAM models.

4.2. A Single GGP-GAM in Detail

It is instructive to examine the nature of a GGP-GAM and its coefficients in detail. The 51st model was randomly selected and its properties examined. Diagnostics summaries of the model SVCs are shown in Table 4. These are generated by the gam.check function in the mgcv package, summarise the results of the model optimisation procedures and allow the basis dimensions defined by k to be evaluated. Wood [24] notes that a “low p-value and a k-index of < 1 ) may indicate that k is too low, especially if effective degrees of freedom (EDF) are close to k”. Similar results were found for other models that were investigated. It is evident that for these models, a k value of 155 is adequate: the EDFs are lower than k and all the p-values are high.
It is also possible to examine the fixed (parametric) coefficient estimates. These can be considered as the linear model terms, similar to the outputs of a standard OLS regression and are shown in Table 5. The effect of the large k is evident: the Intercept has a significant global effect and the global relationships between the response and the covariates are reduced to zero.
Table 6 summarises the smooth terms, the geographic GP splines (for each SVC). The full set of coefficients are not printed because there many coefficients for each spline, one for each basis function. The edf (effective degrees of freedom) indicates the spline complexity, with higher edf values indicating increasing non-linearity in the predictor-to-response relationship. For example, an edf of 1 suggests a linear relationship, an edf of 2 a quadratic one, etc. In this context, these values apply to each covariate across a 2-dimensional space defined by ( X , Y ) , and the p-values indicate the significance of any spatial variation in the coefficient estimates - i.e. whether they vary significantly over space. In this case the SVCs for β 1 , β 2 and β 3 are locally significant but the Intercept ( β 0 ) is not.
It also is possible to examine whether and how the relationships between y and the covariates vary spatially - i.e. the SVCs. Table 7 summarises these for the single GGP-GAM model. These reflect the relatively low spatial variation in the Intercept and its globally significant effect, and the relatively high spatial variation in the coefficient estimates for x 1 , x 2 and x 3 .
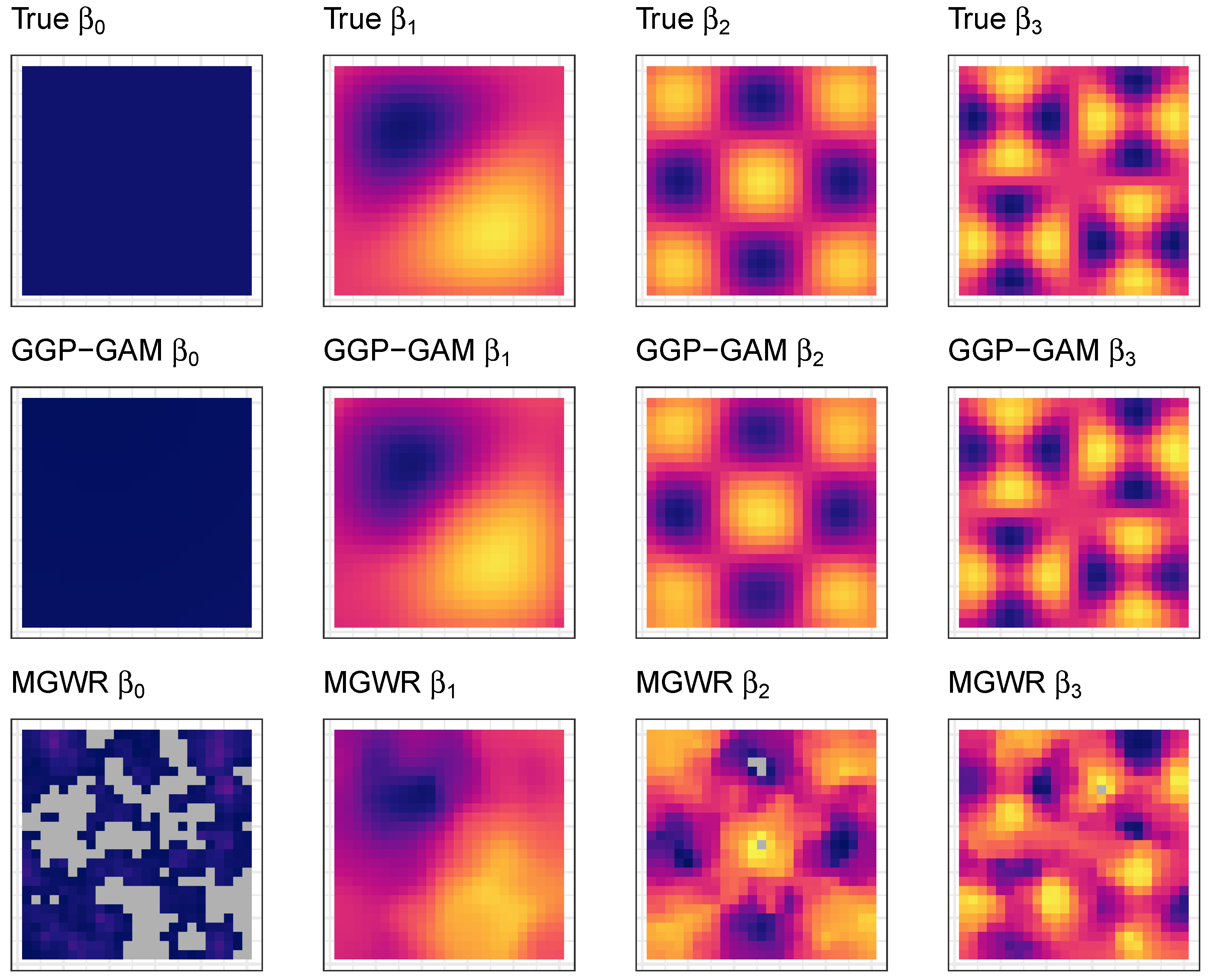
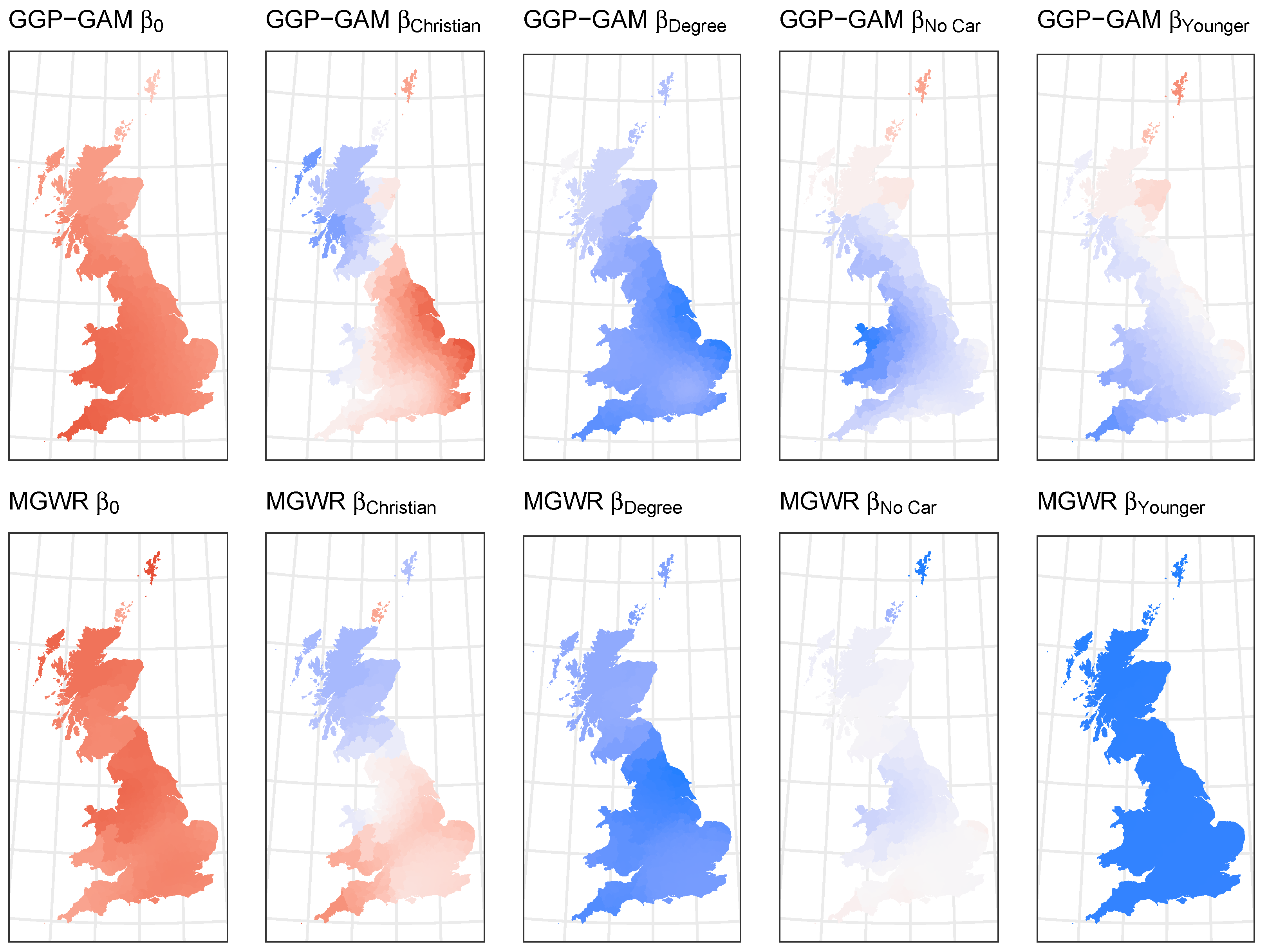
A final investigation maps the estimated GGP-GAM and MGWR SVCs. These are shown for the 51st GGP-GAM and MGWR models in Figure 7 alongside the true coefficients. The GGP-GAM and MGWR coefficients are estimated from the same input data, and the shading range was intentionally set to the same as Figure 1. The estimated coefficient surfaces for β 0 , β 1 , β 2 and β 3 indicate better performance the GAM based approach over MGWR. The grey areas in the MGWR coefficient estimates indicate predicted values outside of range of -2.2 to +2.2.

4.3. GGP-GAM Tuning with a Larger Dataset

A second set of analyses investigated the impact of increased observation number and tuning via the knots parameter for 250,000 observations over a 500 by 500 grid (Figure 2. A single set of simulated predictors x 1 , x 2 and x 3 were again calculated from random normal distributions rescaled to have a range of [0, 1] with a random normally distributed error term ϵ rescaled to [0, 0.25]. The response variable y was calculated directly from these and the coefficients in Figure 2. Seven GGP-GAM models were constructed but specified with different vales of k: 100, 250, 500, 750, 1000, 1500 and 2000. The evaluations included computation time, coefficient accuracy and predictive performance.
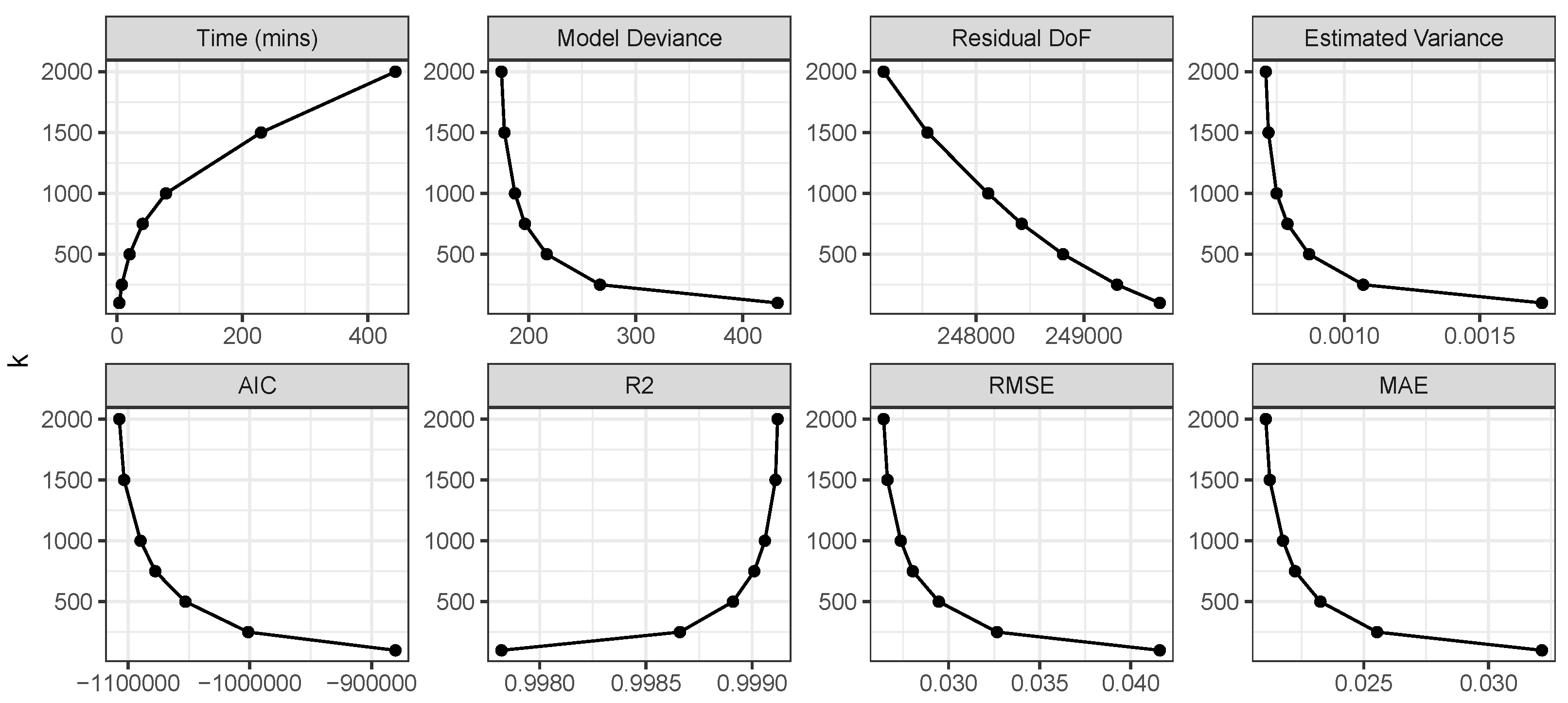
Model characteristics and model fits are shown in Figure 6. Model deviance (unpenalized), the effective model residual degrees of freedom and the estimated variance parameter all decrease with increased k as might be expected. The model fits also increase with as the degree of tuning increases with k. There is a distinct elbow to many of these trends suggesting suggests that a trade-off is possible between more complex models and increased computation times with higher values of k.
Preprints 138530 g008
Figure 8. The GGP-GAM model metrics and fits with increasing number of knots k.
Figure 8. The GGP-GAM model metrics and fits with increasing number of knots k.
Preprints 138530 g008
Table 8 summarises the residuals arising from the different GGP-GAMs. They have similar central tendencies and the inter-quartile ranges indicates that although the models with higher values of k have a lower variation, the differences are not dramatic. Again this reinforces the possibility of a model complexity trade-off with accuracy.
The fixed parametric coefficient estimates of the seven different models were investigated to examine the degree to which the effects observed in Table 5 for the small single GGP-GAM model are also found (i.e. a significant intercept and insignificant covariates whose coefficients were zero). These are shown for models constructed from the larger dataset in Table 9. Whilst the intercept ( β 0 ) has a similar value for each model and is always significant, the trend in the other covariates is more variable, especially at lower values of k. However, they are not significant for the models when k ≥ 1000 .
Table 10 summarises the smooth terms for the seven models, the geographic GP splines. Recall that the effective degrees of freedom (edf) summarises the complexity of the spline smooths and that p-values indicate whether the coefficients are locally significant and whether their respective covariate relationship with the target variable y varies locally. In the model constructed for the single smaller dataset summarised in Table 6, the spatially varying intercept was not significant locally, but all the other covariates were. The same pattern is found with the larger data, but notice how the effective degrees of freedom increases with k.
The GGP-GAM spline smoothing parameters from the different models were examined. Recall that the homogeneity of these indicate the convergence of the models as determined by k which define the spline basis dimensions. These are summarised in Table 11 for the different models. Two trends are evident in the smoothing parameter values across all values of k: the heterogeneity of the Intercept across the different values of k, reflecting its global significance and and local in-significance, in Table 9 and Table 10 respectively, and the homogeneity within each covariate, with values of the same order of magnitude across values of k.
In summary, series of GGP-GAMs were constructed using a larger simulated dataset, with different values of k. As k increases the number of spline bases increase and the models take longer to fit, indicating the trade-off between model complexity and computation time. A distinct elbow was found with increasing k in model deviance, residual degrees of freedom, and estimated variance as well as in the model fit measures (AIC, R2, RMSE, MAE) suggesting possible trade-offs at around k = 500 to k = 750 (Figure 6). The residuals of this model were found to be similar to those of the models with high values of k (Table 8), where greater tuning might be expected to result in stronger model performance. Except for the Intercept, the global parametric coefficients flatten out or are insignificant at all values of k (Table 9) and all the covariates are locally significant at all values of k (Table 10), supporting trade-offs at values of k between 500 and 750 in this case.

4.4. Empirical Example: Brexit Vote

A final empirical analysis compared GGP-GAM and MGWR SVC models of the 2016 UK referendum on leaving the EU in England, Wales and Scotland (Figure 4). The model summaries are shown in Table 12 and in this case both models perform well in terms of fit metrics (R2, AIC, MAE, RMSE) with the MGWR model marginally out-performing the GGP-GAM model, and the GGP-GAM model running more efficiently. However perhaps of greater interest are the minor differences in coefficient estimates as summarised in Table 13 and Table 14 and mapped in Figure 9. The tables include diagnostic metrics of the significance of the GGP-GAM local coefficients and the MGWR bandwidths whose size indicate the degree of localness (their theoretical maximum is 1198 km).
Overall, when the central tendencies and inter-quartile ranges are examined, both sets of coefficient estimates have similar values and ranges. Considering each in turn, a number of observations can be made:
  • Intercept ( β 0 ): This is not locally significant in the GGP-GAM model but is in its parametric form (not shown). The MGWR model indicates that it has a highly localised (i.e. spatially varying) relationship with a relatively small bandwidth. Both sets of coefficient estimates are positive and have similar values and ranges.
  • Christian: Both sets of coefficient estimates indicate a negative association with the Leave vote in Scotland and parts of North Wales and a positive one in England. It is locally significant in the GGP-GAM model and exhibits moderate local variation in the MGWR model, with a bandwidth of 159 km.
  • Degree: This is locally significant in the GGP-GAM model and is negatively associated with the Leave vote throughout the study area in both models. It indicates moderate local variation in the MGWR bandwidth (204 km).
  • No Car: This is locally significant in the GGP-GAM model. It is mostly negatively associated with the Leave vote share in both models and indicates similar areas of positive association with the Leave vote share in the North. The MGWR bandwidth indicates moderate local variation (172 km).
  • Younger: This is not locally significant in the GGP-GAM model In the MGWR, its bandwidth (1196 km) indicates that it is globally (evenly) associated with the Leave vote share.
In summary the two models have similarly high fit and accuracy metrics but they suggest subtly different process spatial heterogeneities and non-stationarities in the relationships between the Brexit Leave vote share as the target variable and the different predictor variables. These are more apparent in the extremes of the study area, potentially reflecting the mechanics of the moving window approach in GWR-based models.

5. Discussion

There is increasing interest in SVC models because of their ability to accommodate, capture and describe process spatial non-stationarity via regression coefficient estimates that are allowed to vary over space. Data are increasingly spatial (i.e. the location of observation is included in some form) and consequently more researchers are working with spatial data. SVC models are attractive because they provide an indication of how and where statistical relationships vary over space and the results can be mapped, providing insights about the spatial heterogeneity of the process being examined.
Some initial work has proposed SVC models using GAMs with Gaussian Process smooths that include observation location - a Geographical GP GAM (GGP-GAM) - and a comparative study with MGWR was undertaken [33]. This used a different, less spatially complex, set of simulated data to those presented here and accepted the default settings for GAMs in the mgcv package [35]. In this study, GGP-GAM and MGWR were applied to a more spatially complex set of simulated data (i.e. with much greater spatial heterogeneity) and the GGP-GAMs were tuned by specifying a sufficiently large number of knots such that the properties of the smooths converged. This was because the number of knots defines the basis dimension in the GP splines and the high value ensured sufficient degrees of freedom. in each of the smooths. MGWR tuning was undertaking through bandwidth optimisation.
For the first part of this study the GGP-GAMs performed better than MGWR across a range of fit measures, although a higher degree of variation was found in the GGP-GAM smoothing parameters than in the MGWR bandwidths (Table 3). The GGP-GAM generated more accurate coefficient estimates than MGWR, a finding that was confirmed when the MGWR analyses were re-run with fixed distance bandwidths rather than the adaptive ones. On investigation, the difference in performance was found to be due to the relatively higher residuals arising from the MGWR models, although objectively both models performed well. This resulted in the MGWR model struggling to estimate the known, true coefficients (Figure 7) and suggests that MGWR models (and potentially other geographically weighted approaches) may struggle with more complex, highly localised spatial heterogeneities, due to their rudimentary kernel / moving window based formulation. Further investigation is required to confirm this assertion.
The GGP-GAM was applied to a larger simulated dataset and a series of models were constructed with varying values of k, defining the number of knots. The results indicate excellent measures of fit at all values of k, and a degree stability in the GGP spline smooths was found for k ≥ 750 , suggesting that acceptable degrees of trade-off are possible between model complexity, computation times and GGP-GAM stability. Identifying the value of k at which model performance stabilises has operational benefits: the value of k determines the upper limit on the effective degrees of freedom linked to spline smoothness and, consequently, the spline bases. Increasing k also prolongs computation time. However, determining the optimal k algorithmically for a given case study is challenging. A common approach is to explore various k values and increasing and decreasing them as necessary. Here it was shown that the gains at values of k ≥ 750 resulted in marginal performance gains at the cost of increases in computation time (a few minutes vs. a few hours).
The final analysis constructed and compared GGP-GAM and MGWR SVC models of the UK’s Brexit referendum vote to Leave the European Union in 2016 with a small number of socio-economic variables. Both approaches generated similarly accurate models in terms of the ability to model the Leave vote share. The spatially varying coefficient estimates they generated indicated minor differences locally, with perhaps the greatest differences evident in the extremes of the study area. Consider, for example, the coefficients for Christian and No Car in the Shetland Islands in Figure 9: these are positive in the GGP-GAM model and negative in the MGWR model, reflecting the smoothing effect of the moving window approach and potentially the adaptive distance kernel. There were also difference in the predictor variables that were found to have a local effect on the target variable. In sum, the MGWR and GGP-GAM approaches generated similar understandings of the process in this empirical case study but with differences in the geographical extremes. This may be due to the way that GWR based approaches capture spatial non-stationarity: they move a weighted window across observations and estimate coefficients at each location rather than quantifying local variation in ’data’ space [22]. Further work will seek to unpick these inferential differences in the face of each model’s predictive power.
Other of areas of work are suggested by the findings of this study. Future work will explore how the GGP-GAM approach may be further calibrated through out of sample predictions, over randomly selected spatial data subsets. MGWR approaches are unable to do this because of their iterative back-fitting approach to model calibration. As a consequence they cannot be applied to ’new’ data. It will also continue to extend the stgam R package [41]. Initial work on spatially varying coefficient modelling using GGP-GAMs simply coded the analysis in R. But as the analysis progressed, the stgam package was developed to contain contains tools to create varying coefficient models based on GAM GP smooths. The functionality of this toolkit will continue to be expanded. One area of development includes explicit metrics of the scale of spatial dependencies in the coefficient estimates. In MGWR this is provided by the kernel bandwidth and in GGP-GAMs a similar indication of scale could be to determine the variogram range for each spatially varying coefficient. Additionally, the opportunities arising from the core GAM functionality of the proposed approach [7,8,35] will be explored. GGP-GAMs are more flexible than GWR based approaches. They are inherently multiscale through their specification, they are able to handle different responses as well as having options for handling collinearity, outliers, heteroskedastic and autocorrelated error terms (options that are not readily available for MGWR, aside from recent work on MGWR with autocorrelated errors [42] and Poisson responses [6]. Finally, extensions into space-time will be explored to investigate how to model space-time dependencies [43], potentially using model averaging [44] to determine optimal space-time model form. The ability to construct coefficient models in which the coefficients are allows to vary over space and / or time is key in, for example, analysis of resilience to climate change where the aim is to determine the varying effects drivers of changes in resilience and to predict tipping points.

6. Conclusion

This study describes spatially varying coefficient modelling using GAMs with Gaussian Process splines parameterised with observation location, referred to as the Geographical Gaussian Process GAM (GGP-GAM). In a series of analyses, the GGP-GAM was applied to simulated data with known spatial heterogeneities and found to performed better than MGWR, the SVC brand leader. This raised questions about the ability of kernel based approaches like GWR to handle highly localised process. The GGP-GAM was then applied to a larger datasets to investigate model tuning. Processes for determining acceptable trade-offs between model complexity, computational efficiency and stability were identified, with respect to the number of knots used in the GP smooths. Finally, the GGP-GAM and MGWR were applied to en empirical case study of the 2016 UK Brexit referendum vote. Both models performed well in terms of fit metrics with the MGWR model marginally out-performing the GGP-GAM model. The coefficient estimates generated by the two approaches for each covariate were broadly similar in terms of their sign (positive / negative), their mapped spatial distributions, and the degree of local heterogeneity they suggested, However, differences were found in the geographical extremes likely due to the mechanics and smoothing effect of the moving window approach in GWR based models. Further will continue to the develop the GGP-GAM approach, including the R package that has been created out of this work [41], handling responses with non-Gaussian distributions, and the extension into the temporal domain to generate spatially and temporally varying coefficient models.

Author Contributions

Conceptualization, A.C., P.H., D.M. and C.B.; methodology, A.C., P.H., D.M. and C.B; code A.C; validation,A.C, P.H., D.M., T.N., N.T., T.Y. and C.B.; formal analysis, A.C., P.H., D.M. and C.B.; investigation, A.C., P.H., D.M. and C.B.; writing—original draft preparation, A.C.; writing—review and editing, A.C, P.H., D.M., T.N., N.T., T.Y. and C.B.. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by The Japan Society for the Promotion of Science BRIDGE fellowship No. 220305, initial ideas were developed under research supported by NERC (NE/S009124/1) and BBSRC (BB/X010961/1, BBS/E/C/000J0100).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data and code used to undertake the full GGP-GAM and MGWR analyses and to generate the results presented in this paper can be found at https://figshare.com/s/2038debc91a82986c503 and if acepted for publication will be at https://github.com/xxxxxx/xxx.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Openshaw, S. Developing GIS-relevant zone-based spatial analysis methods. Spatial analysis: modelling in a GIS environment 1996, pp. 55–73.
  2. Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: a method for exploring spatial nonstationarity. Geographical Analysis 1996, 28, 281–298. [Google Scholar] [CrossRef]
  3. Yang, W. An extension of geographically weighted regression with flexible bandwidths. PhD thesis, University of St Andrews, 2014.
  4. Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Annals of the American Association of Geographers 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
  5. Comber, A.; Brunsdon, C.; Charlton, M.; Dong, G.; Harris, R.; Lu, B.; Lü, Y.; Murakami, D.; Nakaya, T.; Wang, Y.; others. A route map for successful applications of geographically weighted regression. Geographical Analysis 2023, 55, 155–178. [Google Scholar] [CrossRef]
  6. Sachdeva, M.; Fotheringham, A.S.; Li, Z.; Yu, H. On the local modeling of count data: multiscale geographically weighted Poisson regression. International Journal of Geographical Information Science 2023, 37, 2238–2261. [Google Scholar] [CrossRef]
  7. Hastie, T.; Tibshirani, R. Generalized Additive Models. Statistical Science 1986, 1, 297–310. [Google Scholar]
  8. Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman and Hall / CRC Press, 1990.
  9. Gelfand, A.E.; Kim, H.J.; Sirmans, C.; Banerjee, S. Spatial modeling with spatially varying coefficient processes. Journal of the American Statistical Association 2003, 98, 387–396. [Google Scholar] [CrossRef]
  10. Finley, A.O. Comparing spatially-varying coefficients models for analysis of ecological data with non-stationary and anisotropic residual dependence. Methods in Ecology and Evolution 2011, 2, 143–154. [Google Scholar] [CrossRef]
  11. Kim, H.; Lee, J. Hierarchical spatially varying coefficient process model. Technometrics 2017, 59, 521–527. [Google Scholar] [CrossRef]
  12. Finley, A.O.; Banerjee, S. Bayesian spatially varying coefficient models in the spBayes R package. Environmental Modelling & Software 2020, 125, 104608. [Google Scholar]
  13. Murakami, D.; Griffith, D.A. Random effects specifications in eigenvector spatial filtering: a simulation study. Journal of Geographical Systems 2015, 17, 311–331. [Google Scholar] [CrossRef]
  14. Murakami, D.; Griffith, D.A. Balancing Spatial and Non-Spatial Variation in Varying Coefficient Modeling: A Remedy for Spurious Correlation. Geographical Analysis 2023, 55, 31–55. [Google Scholar] [CrossRef]
  15. Murakami, D.; Yoshida, T.; Seya, H.; Griffith, D.A.; Yamagata, Y. A Moran coefficient-based mixed effects approach to investigate spatially varying relationships. Spatial Statistics 2017, 19, 68–89. [Google Scholar] [CrossRef]
  16. Griffith, D.A. Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR). Environment and Planning A 2008, 40, 2751–2769. [Google Scholar] [CrossRef]
  17. Mu, J.; Wang, G.; Wang, L. Estimation and inference in spatially varying coefficient models. Environmetrics 2018, 29, e2485. [Google Scholar] [CrossRef]
  18. Dambon, J.A.; Sigrist, F.; Furrer, R. Maximum likelihood estimation of spatially varying coefficient models for large data with an application to real estate price prediction. Spatial Statistics 2021, 41, 100470. [Google Scholar] [CrossRef]
  19. Fan, Y.T.; Huang, H.C. Spatially varying coefficient models using reduced-rank thin-plate splines. Spatial Statistics 2022, 51, 100654. [Google Scholar] [CrossRef]
  20. Comber, A.; Brunsdon, C.; Charlton, C.; Harris, P.; Harris, Lu, B.; Malleson, N. gwverse: a template for a new generic Geographically Weighted R package. arXiv preprint arXiv:2109.14542 2021. [Google Scholar] [CrossRef]
  21. Wolf, L.J.; Oshan, T.M.; Fotheringham, A.S. Single and multiscale models of process spatial heterogeneity. Geographical Analysis 2018, 50, 223–246. [Google Scholar] [CrossRef]
  22. Bivand, R.S.; Pebesma, E.J.; Gómez-Rubio, V.; Pebesma, E.J. Applied spatial data analysis with R; Vol. 74724 8717, Springer, 2008. [Google Scholar]
  23. Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B.D. Regression models. In Regression; Springer, 2021; pp. 23–84.
  24. Wood, S.N. Generalized additive models: an introduction with R; CRC press, 2017.
  25. Friedman, J.H. Greedy function approximation: a gradient boosting machine. Annals of statistics 2001, pp. 1189–1232.
  26. Zschech, P.; Weinzierl, S.; Hambauer, N.; Zilker, S.; Kraus, M. GAM (e) changer or not? An evaluation of interpretable machine learning models based on additive model constraints. arXiv preprint arXiv:2204.09123 2022. [Google Scholar]
  27. Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. Journal of Statistical Software 2008, 23, 1–46. [Google Scholar]
  28. Stasinopoulos, M.D.; Rigby, R.A.; Heller, G.Z.; Voudouris, V.; De Bastiani, F. Flexible regression and smoothing: using GAMLSS in R; CRC Press, 2017.
  29. Umlauf, N.; Adler, D.; Kneib, T.; Lang, S.; Zeileis, A. Structured additive regression models: An R interface to BayesX 2015.
  30. Umlauf, N.; Klein, N.; Zeileis, A. BAMLSS: Bayesian additive models for location, scale, and shape (and beyond). Journal of Computational and Graphical Statistics 2018, 27, 612–627. [Google Scholar] [CrossRef]
  31. Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Economic geography 1970, 46, 234–240. [Google Scholar] [CrossRef]
  32. Williams, C.K.; Rasmussen, C.E. Gaussian processes for machine learning; Vol. 2, MIT press Cambridge, MA, 2006.
  33. Comber, A.; Harris, P.; Brunsdon, C. Multiscale spatially varying coefficient modelling using a Geographical Gaussian Process GAM. International Journal of Geographical Information Science 2024, 38, 27–47. [Google Scholar] [CrossRef]
  34. Murakami, D. spmoran: An R package for Moran’s eigenvector-based spatial regression analysis. arXiv preprint arXiv:1703.04467, 2017. [Google Scholar]
  35. Wood, S.; Wood, M.S. Package `mgcv’. R package version 2015, 1, 729. [Google Scholar]
  36. Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C. The GWmodel R package: further topics for exploring spatial heterogeneity using geographically weighted models. Geo-spatial Information Science 2014, 17, 85–101. [Google Scholar] [CrossRef]
  37. Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P.; others. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. Journal of Statistical Software 2015, 63. [Google Scholar] [CrossRef]
  38. Lu, B.; Hu, Y.; Yang, D.; Liu, Y.; Liao, L.; Yin, Z.; Xia, T.; Dong, Z.; Harris, P.; Brunsdon, C.; others. GWmodelS: A software for geographically weighted models. SoftwareX 2023, 21, 101291. [Google Scholar] [CrossRef]
  39. Oshan, T.M.; Li, Z.; Kang, W.; Wolf, L.J.; Fotheringham, A.S. mgwr: A Python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale. ISPRS International Journal of Geo-Information 2019, 8, 269. [Google Scholar] [CrossRef]
  40. Beecham, R.; Slingsby, A.; Brunsdon, C. Locally-varying explanations behind the United Kingdom’s vote to leave the European Union. Journal of Spatial Information Science 2018, 16, 117–136. [Google Scholar] [CrossRef]
  41. Comber, L.; Harris, P.; Brunsdon, C. stgam: Spatially and Temporally Varying Coefficient Models Using Generalized Additive Models, 2024. R package version 0.0.1.0.
  42. Geniaux, G.; Martinetti, D. A new method for dealing simultaneously with spatial autocorrelation and spatial heterogeneity in regression models. Regional Science and Urban Economics 2018, 72, 74–85. [Google Scholar] [CrossRef]
  43. Comber, A.; Harris, P.; Brunsdon, C. Multiscale Spatially and Temporally Varying Coefficient Modelling Using a Geographic and Temporal Gaussian Process GAM (GTGP-GAM)(Short Paper). 12th International Conference on Geographic Information Science (GIScience 2023). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2023.
  44. Brunsdon, C.; Harris, P.; Comber, A. Smarter Than Your Average Model-Bayesian Model Averaging as a Spatial Analysis Tool (Short Paper). Proceedings of 12th International Conference on Geographic Information Science (GIScience 2023). Schloss Dagstuhl–Leibniz-Zentrum für Informatik, 2023, Vol. 277, p. 17.
Preprints 138530 g001
Figure 1. Four simulated surfaces with varying degrees and forms of spatial heterogeneity, that serve as the true spatially varying coefficients (n = 625).
Figure 1. Four simulated surfaces with varying degrees and forms of spatial heterogeneity, that serve as the true spatially varying coefficients (n = 625).
Preprints 138530 g001
Preprints 138530 g002
Figure 2. The true regression coefficient surfaces, with varying degrees of spatial heterogeneity, for a larger dataset (n = 250,000).
Figure 2. The true regression coefficient surfaces, with varying degrees of spatial heterogeneity, for a larger dataset (n = 250,000).
Preprints 138530 g002
Preprints 138530 g003
Figure 3. The effect on model accuracy of increasing the knots specified in a GAM smooth.
Figure 3. The effect on model accuracy of increasing the knots specified in a GAM smooth.
Preprints 138530 g003
Preprints 138530 g004
Figure 4. The ’Leave’ vote share of the 2016 UK referendum on leaving the EU over Local Authority Districts (England, Wales and Scotland).
Figure 4. The ’Leave’ vote share of the 2016 UK referendum on leaving the EU over Local Authority Districts (England, Wales and Scotland).
Preprints 138530 g004
Preprints 138530 g005
Figure 5. Assessment of the accuracy of GGP-GAM and MGWR regression coefficient estimates when compared to the true coefficients, along with the distribution of model AIC values.
Figure 5. Assessment of the accuracy of GGP-GAM and MGWR regression coefficient estimates when compared to the true coefficients, along with the distribution of model AIC values.
Preprints 138530 g005
Preprints 138530 g006
Figure 6. The GGP-GAM and MGWR model fits.
Figure 6. The GGP-GAM and MGWR model fits.
Preprints 138530 g006
Preprints 138530 g007
Figure 7. The true coefficients with the GGP-GAM and MGWR estimated spatially varying coefficient surfaces modeled from a single simulated dataset.
Figure 7. The true coefficients with the GGP-GAM and MGWR estimated spatially varying coefficient surfaces modeled from a single simulated dataset.
Preprints 138530 g007
Preprints 138530 g009
Figure 9. The GGP-GAM and MGWR regression coefficient estimates, shaded using diverging palette to indicate negative (blue) and positive (red) values.
Figure 9. The GGP-GAM and MGWR regression coefficient estimates, shaded using diverging palette to indicate negative (blue) and positive (red) values.
Preprints 138530 g009
Table 1. Summaries of the residuals of the 100 GGP-GAM and MGWR models.
Table 1. Summaries of the residuals of the 100 GGP-GAM and MGWR models.
Min. 1st Qu. Median Mean 3rd Qu. Max.
GGP-GAM -0.130 -0.019 0.000 0.000 0.019 0.133
MGWR -0.520 -0.052 0.000 0.001 0.052 0.600
Table 2. Summaries of the Moran’s I of the residuals of the 100 GGP-GAM and MGWR models.
Table 2. Summaries of the Moran’s I of the residuals of the 100 GGP-GAM and MGWR models.
Min. 1st Qu. Median Mean 3rd Qu. Max.
GGP-GAM -0.199 -0.155 -0.002 -0.054 0.000 0.000
MGWR -0.002 -0.002 0.000 0.109 0.313 0.413
Table 3. The distributions of MGWR bandwidths (BW) and GGP-GAM spline smoothing parameters (SP).
Table 3. The distributions of MGWR bandwidths (BW) and GGP-GAM spline smoothing parameters (SP).
Min. 1st Qu. Median 3rd Qu. Max.
GGP-GAM SP β 0 9.5e-04 1.5e-02 8.7e+00 2.5e+01 4.5e+01
GGP-GAM SP β 1 4.7e-06 7.1e-06 7.9e-06 8.6e-06 1.2e-05
GGP-GAM SP β 2 7.0e-07 8.0e-07 8.8e-07 9.7e-07 1.2e-06
GGP-GAM SP β 3 1.5e-07 1.8e-07 1.9e-07 2.1e-07 2.8e-07
MGWR BW β 0 8 10 10 10 12
MGWR BW β 1 22 30 34 42 73
MGWR BW β 2 17 24.75 30 34 42
MGWR BW β 3 4 17 17 21 598
Table 4. Diagnostics of the GGP-GAM smoothing optimisation for the SVCs of a single GGP-GAM model.
Table 4. Diagnostics of the GGP-GAM smoothing optimisation for the SVCs of a single GGP-GAM model.
k’ edf k-index p-value
s(X,Y): β 0 154 2.748 1.192 1
s(X,Y): β 1 155 47.469 1.192 1
s(X,Y): β 2 155 93.353 1.192 1
s(X,Y): β 3 155 136.112 1.192 1
Table 5. The fixed (parametric) coefficients for a single GGP-GAM.
Table 5. The fixed (parametric) coefficients for a single GGP-GAM.
Estimate Std. Error t value Pr(>|t|)
β 0 2.136 0.012 180.69 0
β 1 0.000 0.000 NaN NaN
β 2 0.000 0.000 NaN NaN
β 3 0.000 0.000 NaN NaN
Table 6. The spline smooth terms for a single model.
Table 6. The spline smooth terms for a single model.
edf Ref.df F p-value
s(X,Y): β 0 2.748 3.307 0.638 0.596
s(X,Y): β 1 47.469 60.164 121.679 0.000
s(X,Y): β 2 93.353 110.613 77.813 0.000
s(X,Y): β 3 136.112 142.870 80.537 0.000
Table 7. Summaries of the spatially varying coefficients for a single GGP-GAM model.
Table 7. Summaries of the spatially varying coefficients for a single GGP-GAM model.
Min. 1st Qu. Median Mean 3rd Qu. Max.
β 0 2.091 2.123 2.137 2.136 2.149 2.164
β 1 -1.942 -0.711 0.010 0.010 0.744 1.929
β 2 -1.919 -0.893 0.024 -0.005 0.833 1.924
β 3 -2.121 -0.695 -0.013 -0.020 0.666 1.995
Table 8. Summaries of the GGP-GAM residuals with increasing values of k.
Table 8. Summaries of the GGP-GAM residuals with increasing values of k.
k Min. 1st Qu. Median Mean 3rd Qu. Max.
100 -0.3007 -0.0257 4e-04 0 0.0263 0.2395
250 -0.2508 -0.0209 1e-04 0 0.0212 0.2003
500 -0.2069 -0.0194 0e+00 0 0.0194 0.1828
750 -0.1748 -0.0186 0e+00 0 0.0187 0.1476
1000 -0.1510 -0.0182 0e+00 0 0.0183 0.1357
1500 -0.1284 -0.0179 -1e-04 0 0.0179 0.1278
2000 -0.1208 -0.0177 -1e-04 0 0.0178 0.1256
Table 9. Summaries of the GGP-GAM fixed parametric coefficients with increasing values of k.
Table 9. Summaries of the GGP-GAM fixed parametric coefficients with increasing values of k.
k x 0 p − val x 0 x 1 p − val x 1 x 2 p − val x 2 x 3 p − val x 3
100 2.119 0.000 0.000 NaN 62.613 0.000 0.000 NaN
250 2.119 0.000 0.826 0.789 24.283 0.010 130.407 0.000
500 2.119 0.000 -0.567 0.847 0.000 NaN 5.441 0.784
750 2.120 0.000 0.228 0.938 0.000 NaN 87.764 0.000
1000 2.120 0.000 0.000 NaN 0.000 NaN 0.000 NaN
1500 2.120 0.000 -0.617 0.831 5.618 0.547 -5.470 0.818
2000 2.120 0.000 -0.830 0.775 0.000 NaN -20.802 0.381
Table 10. The effective degrees of freedom of the GGP spline smooth terms and their local significance (p-val) with increasing values of k.
Table 10. The effective degrees of freedom of the GGP spline smooth terms and their local significance (p-val) with increasing values of k.
k x 0 p − val x 0 x 1 p − val x 1 x 2 p − val x 2 x 3 p − val x 3
100 2.011 0.521 95.002 0.000 97.872 0.000 99.889 0.000
250 4.512 0.594 196.866 0.000 239.852 0.000 247.733 0.000
500 3.983 0.705 266.541 0.000 429.945 0.000 490.232 0.000
750 2.006 0.636 294.026 0.000 553.743 0.000 724.258 0.000
1000 2.022 0.643 309.444 0.000 636.787 0.000 938.711 0.000
1500 2.012 0.807 329.487 0.000 771.339 0.000 1344.097 0.000
2000 2.017 0.718 338.441 0.000 839.436 0.000 1674.279 0.000
Table 11. The GGP spline smoothing parameters with increasing k.
Table 11. The GGP spline smoothing parameters with increasing k.
k s(X,Y): x 0 s(X,Y): x 1 s(X,Y): x 2 s(X,Y): x 3
100 15.8204 4.86e-07 3.01e-08 2.95e-09
250 0.0403 5.07e-07 4.93e-08 5.49e-09
500 0.0577 4.57e-07 5.05e-08 5.51e-09
750 32.2305 4.20e-07 4.19e-08 4.46e-09
1000 8.0443 4.06e-07 3.88e-08 4.48e-09
1500 15.3684 3.89e-07 3.69e-08 5.28e-09
2000 10.4797 3.83e-07 3.66e-08 5.29e-09
Table 12. Fit measures from the GGP-GAM and MGWR models of Brexit vote.
Table 12. Fit measures from the GGP-GAM and MGWR models of Brexit vote.
Model R2 MAE RMSE AIC
MGWR 0.940 0.017 0.025 -1701.7
GGP-GAM 0.938 0.018 0.026 -1685.1
Table 13. Summaries of the SVCs for the Brexit GGP-GAM model.
Table 13. Summaries of the SVCs for the Brexit GGP-GAM model.
Min. 1st Qu. Median Mean 3rd Qu. Max. Smooth p-values
β 0 0.346 0.778 0.826 0.829 0.886 1.143 0.617
β C h r i s t i a n -0.326 0.082 0.146 0.137 0.217 0.429 0.001
β D e g r e e -1.532 -1.193 -1.088 -1.084 -0.958 -0.029 0.000
β N o C a r -0.497 -0.229 -0.122 -0.154 -0.078 0.254 0.001
β Y o u n g e r -0.597 -0.181 -0.130 -0.138 -0.083 0.385 0.102
Table 14. Summaries of the SVCs for the Brexit MGWR model.
Table 14. Summaries of the SVCs for the Brexit MGWR model.
Min. 1st Qu. Median Mean 3rd Qu. Max. Bandwidth (km)
β 0 0.421 0.807 0.841 0.850 0.903 1.196 68.8
β C h r i s t i a n -0.403 0.092 0.133 0.118 0.189 0.805 158.5
β D e g r e e -1.275 -1.121 -0.995 -1.027 -0.951 -0.766 204.0
β N o C a r -1.510 -0.156 -0.028 -0.092 -0.009 0.113 171.8
β Y o u n g e r -0.250 -0.244 -0.243 -0.244 -0.243 -0.243 1196.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated