Submitted:
05 November 2024
Posted:
06 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
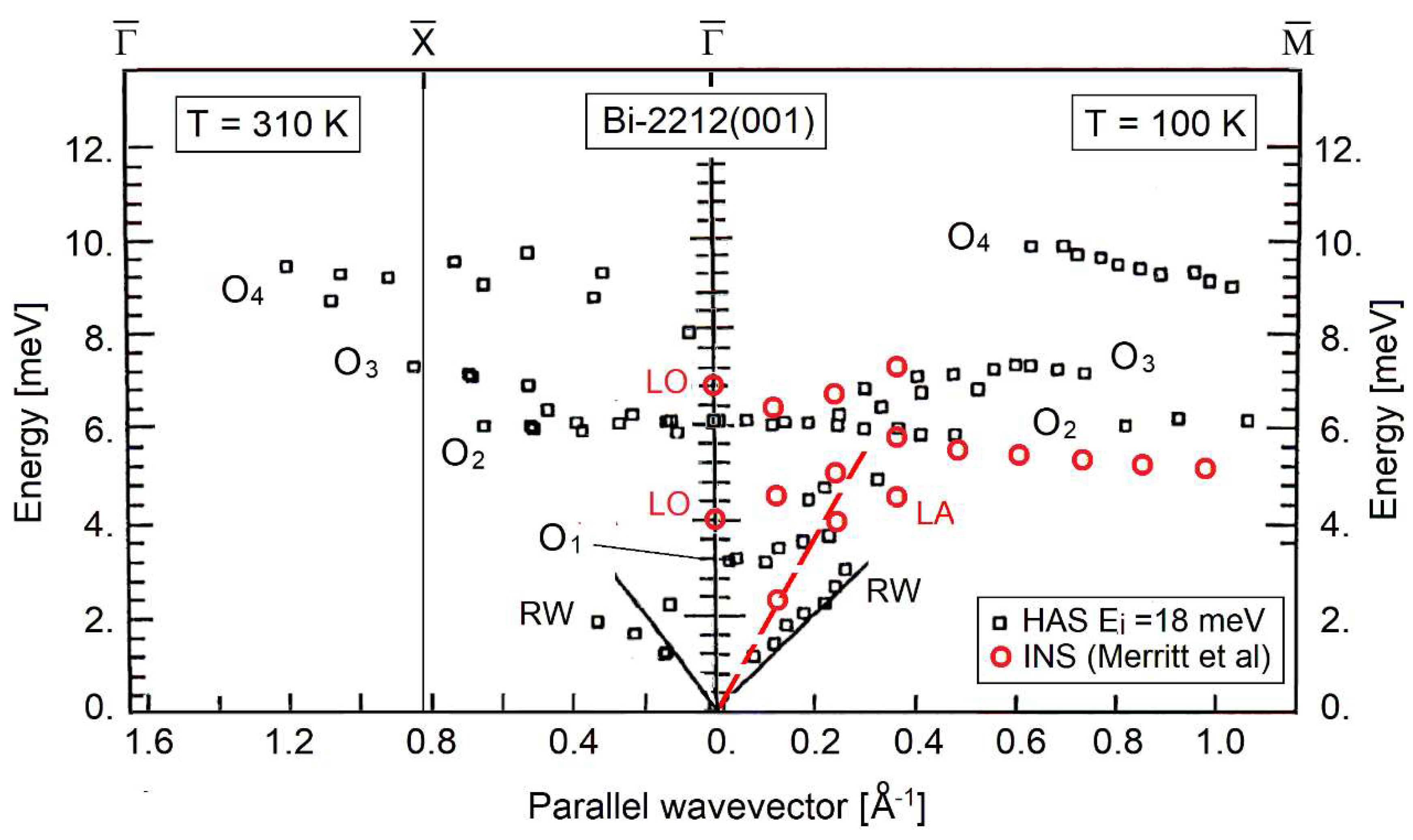
2. He-Atom Scattering Time-of-Flight Data
3. Electron-Phonon Interaction from the Temperature Dependence of the Diffuse Elastic Peak
4. Conclusions
Acknowledgments
References
- D F. Jean, G. Collin, M. Andrieux, N. Blanchard, and J.-F. Marucco, Oxygen nonstoichiometry, point defects and critical temperature in superconducting oxide Bi2Sr2CaCu2O8+, Physica C 2000, 339, 269.
- K. Drozdov, I. Pletikosić, C.-K. Kim, K. Fujita, G. D. Gu, J. C. Séamus Davis, P. D. Johnson, I. Božović, and T. Valla, Phase diagram of Bi2Sr2CaCu2O8+ revisited, Nature comm. 2018, 9, 5210. [CrossRef]
- Y He , T S Nunner, P J Hirschfeld, H-P Cheng, Local electronic structure of near oxygen dopants: a window on the high-Tc pairing mechanism, Phys Rev Lett. 2006, 9,197002.
- Lanzara, P.V. Bogdanov, X.J. Zhou, S.A. Kellar, D.L. Feng, E.D. Lu, T. Yoshida, H. Eisaki, A. Fujimori, K. Kishio, J.-I. Shimoyama, T. Nodak, S. Uchidak, Z. Hussain, and Z.-X. Shen, Evidence for ubiquitous strong electron–phonon coupling in high-temperature superconductors, Nature 2001, 412, 510. [CrossRef]
- Z. X. Shen, A. Lanzara, S. Ishihara, and N. Nagaosa, Role of the electron-phonon interaction in the strongly correlated cuprate superconductors, Phil. Mag. B 2002, 82, 1349.
- S. M. O'Mahony, W. Ren, W. Chen, Y. X. Chong, X. Liu, H. Eisaki, S. Uchida, M.H. Hamidian, J.C. Séamus Davis, On the electron pairing mechanism of copper-oxide high temperature superconductivity, PNAS 2022, 119:37 e2207449119.
- P. W. Anderson, Antiferromagnetism. Theory of superexchange interaction, Phys. Rev. 1950, 79, 350. [CrossRef]
- J. R. Manson, G. Benedek, S. Miret-Artés, Atom scattering as a probe of the surface electron-phonon interaction at conducting surfaces, Surface Science Reports 2022, 77,100552. [CrossRef]
- G. Benedek, J. R. Manson, S. Miret-Artés, A. Ruckhofer, W. E. Ernst, A. Tamtögl, and J. P. Toennies, Measuring the Electron-Phonon Interaction in Two-Dimensional Superconductors with He Atom Scattering, Condens. Matter 2020, 5,79 ; corr: Condens. Matter 2021, 6, 54. [CrossRef]
- G. Benedek and J.P. Toennies, Atomic-Scale Dynamics at Surfaces - Theory and Experimental Studies with Helium Atom Scattering, (Springer-Nature, 2018).
- Y. Yu, L. Ma, P. Cai, R. Zhong, C. Ye, J. Shen, G. D. Gu, X. H. Chen, and Y. Zhang, High-temperature superconductivity in monolayer Bi2Sr2CaCu2O8+, Nature 575, 156-163 (2019). [CrossRef]
- D. Schmicker, Zur Untersuchung der Oberflaechen unterschiedlicher Supraleiter mit der Helium-Atom-Streuung (Study of the surfaces of various superconductors by helium-atom scattering), Dissertation, University of Göttingen, 1993; Max-Planck-Institut für Strömungsforschung, Bericht 6/1993; ISSN 0436-1199.
- U. Paltzer, D. Schmicker, F. W. de Wette, U. Schröder, and J. P. Toennies, Effects of an anisotropic superstructure on surface phonons: The Bi-O surface of Bi2Sr2CaCu2O8 Phys. Rev. B 1996, 54, 11989.
- Zeljkovic, Z. Xu, J. Wen, G. Gu, R. S. Markievicz, and J. E. Hoffmann, Imaging the Impact of Single Oxygen Atoms on Superconducting Bi2Sr2CaCu2O8+x, Science 2021, 337, 320.
- S. Zhou, H. Ding, and Z. Wang, Correlating Off-Stoichiometric Doping and Nanoscale Electronic Inhomogeneity in the High-Tc Superconductor Bi2Sr2CaCu2O8+Phys. Rev. Lett. 2007, 98, 076401.
- U. Paltzer, F. W. de Wette, U. Schröder, E. Rampf, Surface dynamics of Bi2Sr2CaCu2O8, Physica C 1998, 301, 55.
- D. Shimadam N. Tsuda, U. Paltzer, F. W. de Wette, Tunneling phonon structures and the calculated phonon density of states for Bi2Sr2CaCu2O8, Physica C 1998, 298, 195. [CrossRef]
- M. Merritt, J.-P. Castellan, T. Keller, S. R. Park, J. A. Fernandez-Baca, G. D. Gu, and D. Reznik, Low-energy phonons in Bi2Sr2CaCu2O8+ and their possible interaction with electrons measured by inelastic neutron scattering, Phys. Rev. B 2019, 100, 144502.
- S. Saito, T. Sutou, Y. Norimitsu, N. Yajima, Y. Uhara, T. Uenosono, T. Soumura, T. Tani, Temperature dependence of the work function of Bi2Sr2CaCu2O8 single crystal cleaved at low temperature, Appl. Surf. Sci. 2005, 252, 379. [CrossRef]
- E. E. M. Chia, D. Springer, S. K. Nair, X. Q. Zou, S. A. Cheong. C. Panagopoulos, T. Tamegai, H. Eisaki. S. Ishida, S. Uchida, A. J. Taylor. and J-X Zhu, Doping dependence of the electron–phonon and electron–spin fluctuation interactions in the high-Tc superconductor Bi2Sr2CaCu2O8+ , New J. Phys. 2013, 15, 1030.
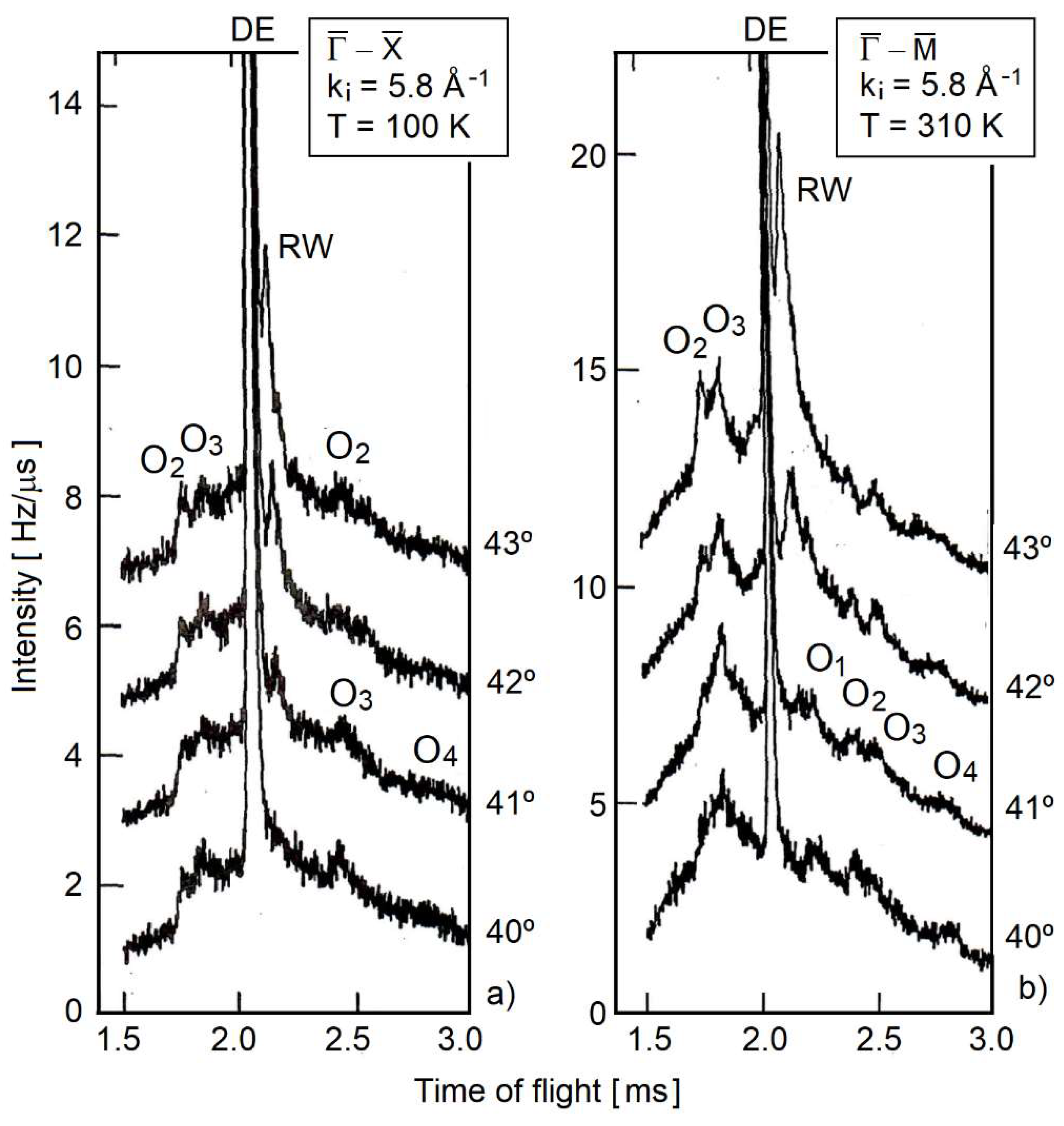

| i [degrees] |
IDE(100 K) [Hz/ s] |
IDE(310 K) [Hz/ s] |
ln[IDE(T)] |
| 43º | 83.3 | 49.5 | 0.52 |
| 42º | 68.8 | 15.0 | 1.52 |
| 41º | 58.3 | 20.0 | 1.07 |
| 40º | 54.5 | 15.5 | 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





