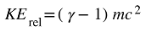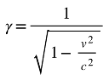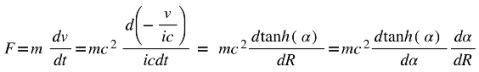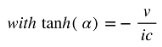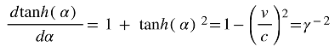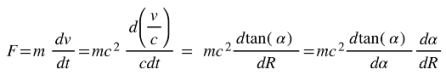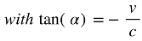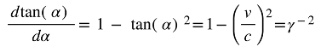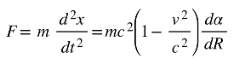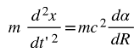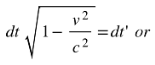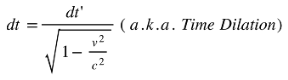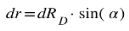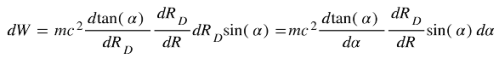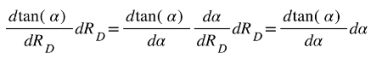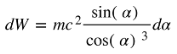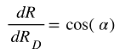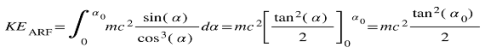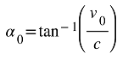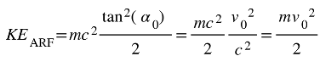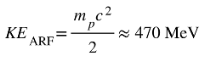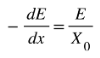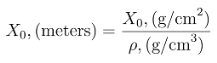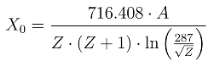Prerpints.org logo
Preprint
Article

The Kinetic Energy of Relativistic Particles

Altmetrics

Downloads

20

Views

29

Comments

0

supplementary.pdf (26.73KB )

This version is not peer-reviewed

Innovation and Inventions in Aerospace and UAV Applications

Submitted:

06 November 2024

Posted:

07 November 2024

You are already at the latest version

Alerts
Abstract
This paper presents a novel approach to relativistic kinetic energy through the lens of the Hypergeometrical Universe (HU) Theory, introducing an Absolute Reference Frame (ARF) that fundamentally reinterprets the Lorentz transformation. HU suggests that the physics underlying Lorentz transformations is not an intrinsic time dilation or relativistic mass increase but rather an Absolute-Velocity-Dependent Force. This force diminishes at high velocities, effectively tapering off particle interactions and yielding a bounded kinetic energy that matches classical expectations at the speed of light: KE = mc**2 /2. This model contrasts sharply with conventional relativity, which predicts unbounded kinetic energy as velocity approaches c. This theoretical divergence finds a compelling empirical anchor in the unusual case of Soviet scientist Anatoli Bugorski, who survived exposure to a high-energy proton beam. While relativistic models would predict an energy deposition near 4.6 kJ, likely resulting in fatal damage, Bugorski’s injuries aligned closely with HU’s prediction of a capped energy deposition, around 0.285 J. The HU model explains this outcome as a natural consequence of diminished force interactions at relativistic speeds, leading to reduced energy transfer upon impact. This reframing has significant implications for high-energy physics and particle penetration in solid materials. According to HU, reduced force efficiency at high velocities leads to phenomena traditionally interpreted as time dilation and relativistic mass. For example, at near-light speeds, particles encounter lower interaction cross-sections, resulting in greater penetration, not because of a true mass increase but due to a physical tapering of the HU force. The paper proposes calorimetric experiments in particle accelerators to empirically differentiate between HU and relativistic predictions. By measuring thermal energy deposition instead of relying on penetration depth, these experiments could directly observe the Absolute-Velocity-Dependent Force in action. This approach could profoundly impact our understanding of high-energy dynamics, particularly in applications like spacecraft shielding. This work invites experimental physicists and theorists to explore HU’s framework through accessible computational models and experimental designs provided in accompanying GitHub repositories. This innovative model challenges the established foundations of relativity and offers a new perspective on high-velocity particle interactions, making it a pivotal contribution to modern physics and potential aerospace applications.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

In conventional relativity, the kinetic energy KErel of a particle with mass m moving at velocity v is given by:
Preprints 138817 i001
where the Lorentz factor γ is:
Preprints 138817 i002
This relativistic formulation has been experimentally confirmed across various high-energy physics applications, as discussed in foundational texts like Jackson's Classical Electrodynamics [1]. However, the ARF hypothesis proposes that kinetic energy may reach a mass-dependent limiting cap at Absolute Velocity c, suggesting a fundamental deviation in energy deposition at high velocities. This implies that kinetic energy might have a different formulation within the Absolute Reference Frame (ARF), where interactions are moderated by an intrinsic absolute velocity cap [1,2].

2. Theory and Derivations:

  • Derivation of Kinetic Energy in an Absolute Reference Frame (ARF)
Notice that ARF is only introduced because I successfully defended the assumption that there is an extra spatial dimension and that our universe is a Lightspeed Expanding Hyperspherical Hypersurface.
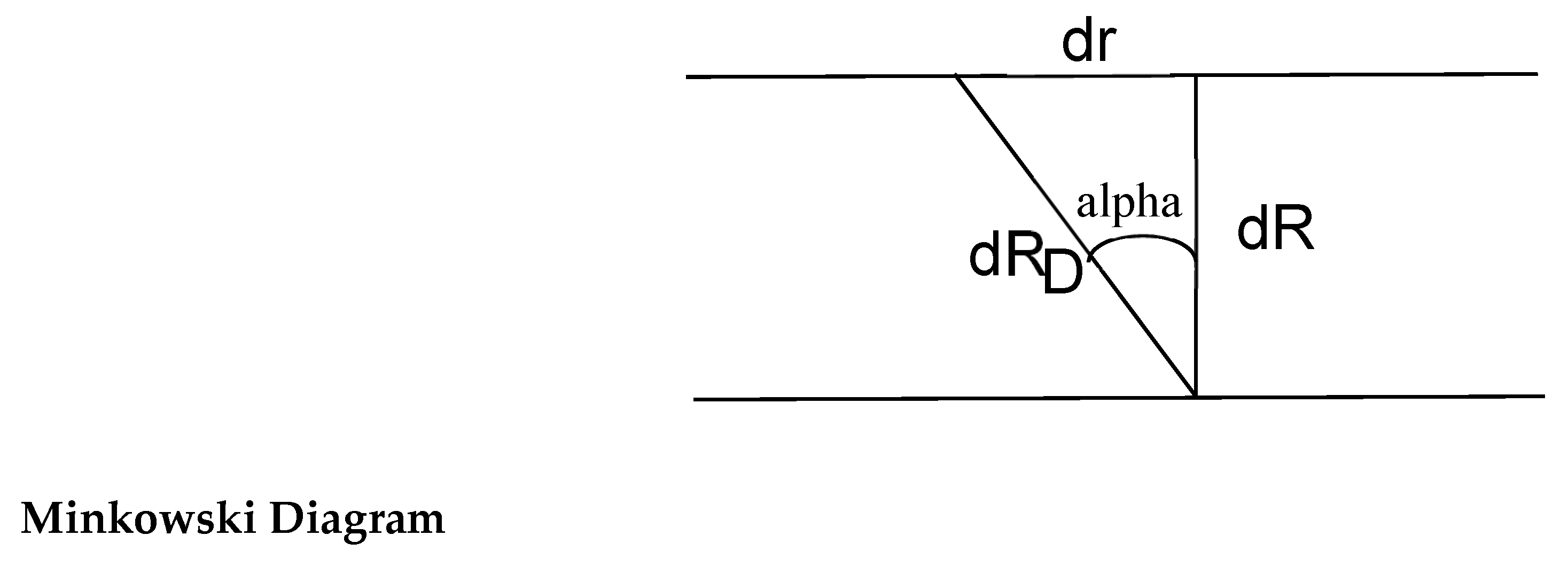
Preprints 138817 g001
Figure 2.1. The derivation of the Kinetic Energy is based on this diagram, and thus, it is relativistic despite using an absolute reference frame (ARF). The ARF comprises the perpendicular axis R and any perpendicular vector within the 3D hyperplane, represented by a horizontal line. The diagram embodies Minkowski's interpretation of Lorentz transformations as rotations of the 4D metric [5]. You can see the angle of rotation as alpha. I am using hyperbolic functions in this derivation. That said, that is irrelevant, and using trigonometric functions would produce the same final conclusion.
Figure 2.1. The derivation of the Kinetic Energy is based on this diagram, and thus, it is relativistic despite using an absolute reference frame (ARF). The ARF comprises the perpendicular axis R and any perpendicular vector within the 3D hyperplane, represented by a horizontal line. The diagram embodies Minkowski's interpretation of Lorentz transformations as rotations of the 4D metric [5]. You can see the angle of rotation as alpha. I am using hyperbolic functions in this derivation. That said, that is irrelevant, and using trigonometric functions would produce the same final conclusion.
Preprints 138817 g001
Minkowski Spacetime reflects what is happening in the actual 4D Spatial Manifold. Minkowski's spatial coordinates describe a hyperplane traveling at the speed of light in some undefined direction. HU shows that this is the local linearization of the hyperspherical hypersurface (for short distances, the hyperspherical hypersurface can be approximated to a hyperplane). The vector perpendicular to the hyperplane is the same as the radial direction on the hyperspherical hypersurface. In other words, there is no sense in speaking about a direction of propagation in time. Once you add one extra spatial dimension, it makes all sense to talk of a perpendicular direction in a 4D Spatial Manifold.
That is why I mentioned ARF. If one just stays in the 4D Spacetime, my argument survives. The only difference is that the perpendicular vector in spacetime becomes an arbitrary inertial framework. The argument remains the same since this reference frame maps to the lab frame.
To derive the kinetic energy, we calculate the work dW done to accelerate the particle from rest ( v = 0 ) to a final velocity of v0 in the ARF. We’ll show that either hyperbolic or trigonometric transformations yield the same force, thus indicating that Lorentz transformation is an artifact of a force that is Absolute-Velocity-Dependent.
  • Definition of Force and Displacement
Force: We define force F as acting in the direction of motion. In the ARF, the force remains aligned with the changes in the particle’s velocity, and we express it as:
Using time as an imaginary quantity
Preprints 138817 i003
Preprints 138817 i004
Preprints 138817 i005
Using time as a real quantity
Preprints 138817 i006
Preprints 138817 i007
Preprints 138817 i008
This means that it is irrelevant if we have time as an imaginary quantity or not. The Physics it describes is in the absolute-velocity dependent force shown below:
Preprints 138817 i009
This means that it is irrelevant if we have time as an imaginary quantity or not. The Physics it describes is in the absolute-velocity dependent force shown below:
From there you can go to:
Preprints 138817 i010
Preprints 138817 i011
Preprints 138817 i012
Preprints 138817 i013
  • Displacement dr:
Displacement dr is defined along a vector within the hyperplane in Minkowski space.
Preprints 138817 i014
  • Energy Integral
To find the kinetic energy, we calculate the work done from v = 0 to v = v0 by integrating the expression for dW = F.dr :
Preprints 138817 i015
  • Change of Variable and Integral Setup: To integrate, we change the variable to α using the following relationship:
Preprints 138817 i016
Resulting:
Preprints 138817 i017
Since:
Preprints 138817 i018
  • Integral in Terms of α: Using the expressions for dRD and substituting into the work integral, we obtain:
Preprints 138817 i019
Here, α0 is the hyperbolic angle corresponding to the final velocity v0 , where:
Preprints 138817 i020
  • Solving the Integral: Integration gives us:
Preprints 138817 i021
This result resembles the classical form for kinetic energy and highlights a cap on kinetic energy when using the ARF, which differs from the prediction of relativity[1].

3. Proposed Experimental Test in Calorimetry

To test the ARF model, we propose measuring the energy deposition of high-velocity protons, like those accelerated in the Large Hadron Collider (LHC). Conventional relativity predicts that a proton with 6.5 TeV energy should deposit all of this energy in a calorimeter. However, according to the ARF model, the energy deposition is capped at approximately 470 MeV:
Preprints 138817 i022
  • Discrepancy in Calorimetric Measurements
In high-energy physics, calorimeters are often calibrated based on penetration depth, an indicator of how deeply particles penetrate the detector material before depositing their energy. Typically, calibration begins with velocity calculations derived from synchronization parameters, which then translate into energy estimates using relativistic formulas. This energy is then correlated with penetration depth, assuming that deeper penetration indicates higher energy deposition.
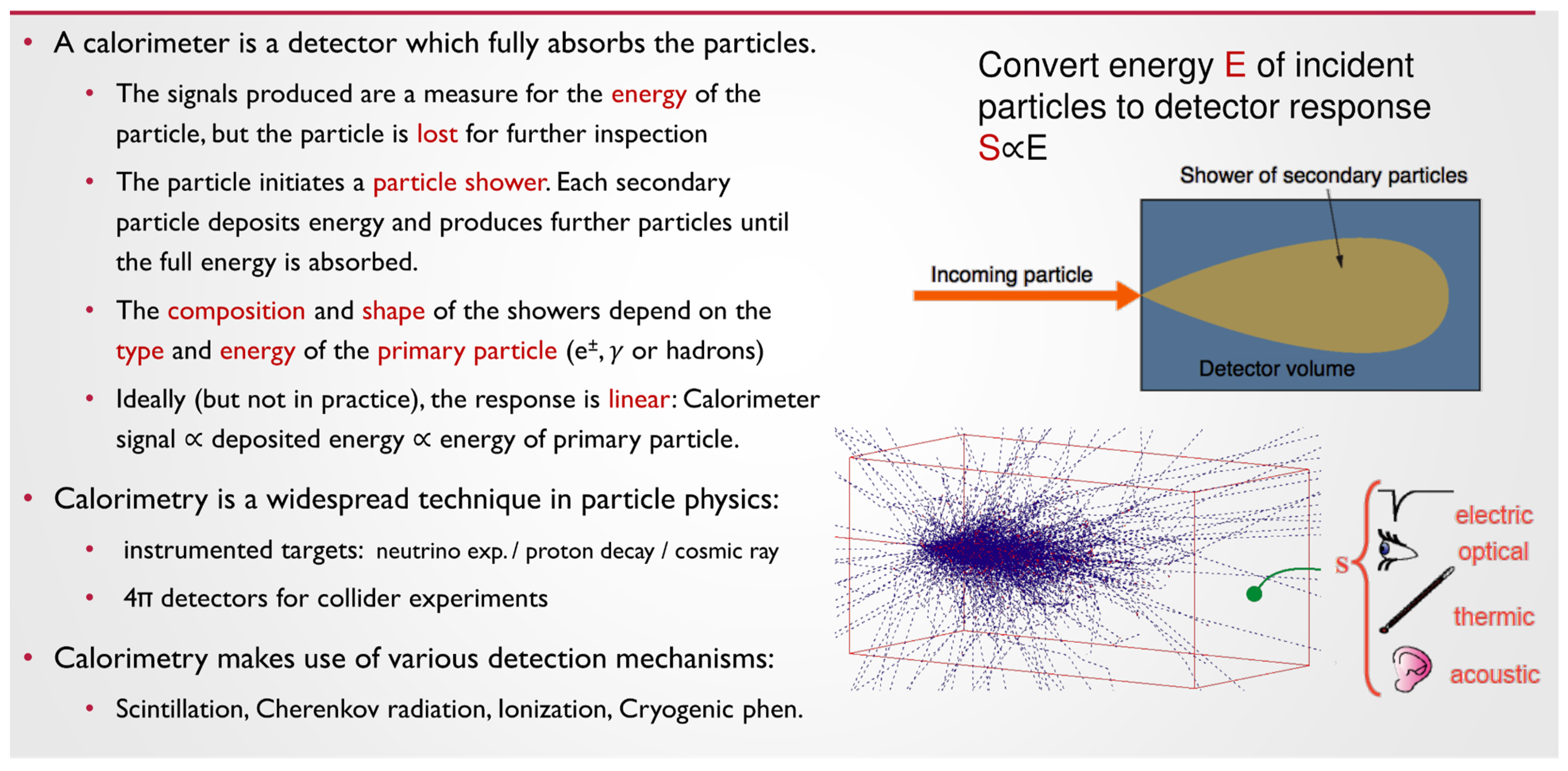
Preprints 138817 g002
Figure 3.1. This figure shows how particles interact with the calorimeter components. The incoming particle creates a show of secondary particles. For speed's sake, the measurement is not done thermally (it takes time for thermal equilibrium), Instead, the detector measures penetration. In other words, one can measure the effect of the particle shower on the different layers of the detector and use that to create a penetration profile. This penetration profile is modeled using Relativity, which creates a biased measurement.
Figure 3.1. This figure shows how particles interact with the calorimeter components. The incoming particle creates a show of secondary particles. For speed's sake, the measurement is not done thermally (it takes time for thermal equilibrium), Instead, the detector measures penetration. In other words, one can measure the effect of the particle shower on the different layers of the detector and use that to create a penetration profile. This penetration profile is modeled using Relativity, which creates a biased measurement.
Preprints 138817 g002
However, under the Absolute Reference Frame (ARF) model, penetration depth could increase without a disproportional increase in energy. This discrepancy arises because particle interactions diminish as velocity approaches the absolute limit ccc, reducing the rate of energy transfer to the detector material. In this scenario, particles could penetrate deeper into the detector with only minimal additional energy since the interaction cross-section decreases significantly at high speeds. This phenomenon challenges the assumption that penetration depth directly correlates with energy, as is typical in relativistic calibrations.
To detect the predictions of the ARF model accurately, calorimeters would need to measure energy deposition as thermal changes rather than relying solely on penetration depth, which may obscure the lower energy transfer rates predicted by the ARF hypothesis [2,3,4].
In Appendices A and B, we present the Russian Scientist Anatoli Bogorski’s event and numerical simulation based on Relativity and the Hypergeometrical Universe Theory

4. Practical Implications: Shielding for Spacecraft

The ARF hypothesis derives a force that is dependent upon the Absolute Velocity. That force diminishes as the Absolute Velocity increases towards lightspeed c. At c, the force goes to zero. This would explain the higher penetration observed in high-energy physics experiments.
This implies a shielding effect for particles approaching the speed of light relative to the ARF. This effect may aid in developing spacecraft shielding technologies, allowing high-speed travel without excessive particle interactions. Notice that this is exactly the opposite of what Relativity predicts, and it would make a good test case.
  • Gaps in Experimental Verification
Many experiments in high-energy physics implicitly assume relativistic models. Calorimeters are designed to measure penetration and shower length, which may mask discrepancies predicted by the ARF model. An unbiased test requires calorimeters that directly measure energy deposition as thermal changes.
  • Temperature-Based Calorimetric Test
A temperature-sensitive calorimeter could directly measure deposited energy without the influence of relativistic assumptions. Such a device could provide empirical evidence to support or challenge the ARF model.

5. The Anatoli Bugorski Event:

Here’s an overview of Anatoli Bugorski's incident, his injuries, and the details surrounding the U-70 Synchrotron accelerator.
The Incident: Anatoli Bugorski’s Accident
-
Date: July 13, 1978.
-
Location: Institute for High Energy Physics in Protvino, Russia.
-
Accelerator: The U-70 Synchrotron was the particle accelerator involved in the accident.
Anatoli Bugorski, a Russian scientist and researcher, was performing maintenance on the U-70 Synchrotron, which was the largest particle accelerator in the Soviet Union at the time. During his work, a malfunction led to an unexpected event where Bugorski accidentally placed his head in the path of a proton beam.
  • Details of the U-70 Synchrotron
-
Type: Proton synchrotron.
-
Operational Energy: The U-70 Synchrotron was capable of accelerating protons to 76 GeV (76 billion electron volts), significantly lower than modern accelerators like the Large Hadron Collider (6.5 TeV per proton).
-
Circumference: Approximately 1,500 meters.
The U-70 was built in the late 1960s and became operational in 1967. It was primarily used for high-energy physics experiments and was a significant achievement in Soviet particle physics.
  • Nature of the Exposure
-
Proton Beam Energy: The beam that struck Bugorski was at the full energy of the U-70’s capability, 76 GeV per proton.
-
Exposure Path: The proton beam entered the back of Bugorski’s head, passed through his skull, and exited near his nose.
-
Duration: Although not precisely measured, the exposure likely lasted several seconds because human can only move slowly and there was no pain. Bugorski was exposed long enough to absorb a large dose of energy. Unlike the Large Hadron Collider, a Synchrotron produces a continuous beam, so the exposure depends only upon the exposure time.
  • Immediate Effects
-
Visual Phenomenon: Bugorski reportedly saw a flash "brighter than a thousand suns" but did not feel any pain.
-
Severe Radiation Dose: He received a localized radiation dose estimated between 200,000 to 300,000 rads (2,000 to 3,000 Gy) to the tissue along the beam path, far beyond a lethal dose for whole-body exposure. However, because the beam was highly localized, the damage was confined to the area it traversed.
  • Medical and Long-Term Effects
  • Initial Injury: The beam severely burned a narrow path of tissue in his head. It destroyed tissue, bone, and nerves along the way, and Bugorski’s face swelled up beyond recognition within days.
  • Partial Paralysis: The right side of his face was paralyzed, and he lost hearing in his left ear. Bugorski also experienced severe seizures in the years following the accident, likely due to damage to brain tissue.
  • Cognitive Effects: Despite the extensive injury, Bugorski’s cognitive functions remained intact, and he was able to continue his work as a scientist after the accident.
  • Long-Term Survival: Bugorski survived against all odds, making his case one of the most unusual in radiation injury history. He continued to live a relatively normal life, albeit with ongoing health issues related to the accident.
  • Legacy and Scientific Interest
Bugorski’s case remains a unique study of the effects of high-energy proton beams on biological tissue and a testament to human resilience. It is still referenced in studies related to radiation injuries, particle beam therapy, and the biological effects of localized high-dose radiation.
The incident underscores both the risks of working with particle accelerators and the unpredictable nature of radiation injuries, especially when dealing with high-energy particles like protons.
  • Energy Deposition Numerical Analysis
Here’s a more detailed explanation with the relevant formulas for dE/dx due to ionization losses, especially as they apply to the 76-GeV proton beam that struck Anatoli Bugorski.
Is the dE/dx in the Code Due to Ionization? Yes, the dE/dx we used in the code to estimate the energy loss of a 76-GeV proton beam passing through tissue or water primarily represents ionization losses.
  • Why Ionization Dominates for Protons at 76 GeV
For high-energy protons like the 76 GeV beam from the U-70 Synchrotron:
Ionization is the dominant mechanism of energy loss when a proton passes through matter, including tissue. This is because ionization losses are significant for heavy charged particles (like protons) over a wide range of energies.
Bremsstrahlung (radiative losses), which becomes significant for lighter particles like electrons, is negligible for protons. This is because Bremsstrahlung losses are inversely proportional to the square of the particle's mass. The proton’s mass is about 1,836 times the electron's, making Bremsstrahlung insignificant even at high energies.
  • Why We Used This Simplified dE/dx in the Code
In our code, we used to approximate the average rate of energy deposition for a proton traveling through 10 cm of material.
Ionization Dominates for Protons: At 76 GeV, a proton's primary energy loss mechanism in tissue is ionization, not Bremsstrahlung. By approximating the rate as a constant over the 10 cm path, we avoid complex particle-by-particle tracking.
  • Relativistic and Classical Calorimetric Analysis
The proton energy decays as it interacts with the medium according to:
Preprints 138817 i023
The formula for the radiation length X0 is empirically determined.
For a given material, the radiation length X0 in units of g/cm2 is given by[4]:
Preprints 138817 i024
This empirical formula (eq. 5.2) was used to calculate the radiation length X0 for water in our code for both relativistic and classical analyses, where we substituted values specific to water:
-
Zeff = 7.42: effective atomic number of water.
-
Aeff = 18.015, g/mol: molar mass of water.
-
ρwater = 1, g/cm3: density of water.
-
The constant 716.408 is an empirical factor (in units of g cm−2).
To obtain X0 in meters, this value must be divided by the density ρ of the material:
Preprints 138817 i025
Python Notebook is available in the GitHub repository[8].

6. Discussion

The Force Absolute-Velocity-dependency implies an innovative method for high-speed shielding, particularly relevant to spacecraft design. By minimizing the interaction rate as the velocity approaches the light speed limit, this ARF property could revolutionize spacecraft shielding, suggesting decreased particle collision rates at high speeds—directly opposing traditional relativity predictions.
The use of temperature-sensitive calorimeters is uniquely positioned to reveal thermal dissipation rates, which relativistic frameworks may not fully capture. This distinction between thermal and penetration depth provides a critical testing ground for verifying the ARF model.
According to traditional relativistic predictions, the energy deposition from a high-energy proton beam would have been significantly higher, around 46 kJ, which would be expected to cause catastrophic tissue damage beyond survival limits. However, the Hypergeometrical Universe (HU) Theory, with its Absolute Reference Frame (ARF) model, predicts a much lower energy deposition cap, closer to 0.285 J. This result aligns with Anatoli Bugorski’s survival, who endured severe but localized injuries after exposure to a high-energy proton beam. The HU model’s absolute energy cap suggests that as particles approach light speed, their interactions with matter diminish, resulting in significantly reduced energy deposition.
The survival of Bugorski presents empirical evidence that challenges the conventional relativistic framework, highlighting the potential validity of the HU model’s predictions. By implementing experiments focused on thermal energy deposition using calorimetry, we could effectively test the ARF model’s predictions against those of relativity-based calibrations, which typically emphasize penetration depth.

7. Conclusions

The Absolute Reference Frame (ARF) model presents an alternative view of kinetic energy that deviates observably from relativistic expectations while recovering the Classical Mechanics definition of kinetic energy. Testing this hypothesis requires calorimetric techniques that measure pure thermal energy independent of the assumptions tied to relativistic calibration. If confirmed, the ARF model could fundamentally shift our understanding of particle dynamics, opening up new possibilities for aerospace applications.
The ARF model is integral to the Hypergeometrical Universe Theory (HU) [6,7]. Validating the ARF model would also validate HU, posing a direct challenge to General Relativity and established physics. Since Relativity is foundational to our current understanding of the Universe, confirmation of the ARF model would require a reevaluation of the principles that underlie modern physics.
The Anatoli Bugorski’s incident supports the Absolute Reference Frame (ARF) or HU model.
-
Relativity Prediction: Under traditional relativistic mechanics, the proton beam's energy deposition would be high enough to be lethal. You noted that relativity predicts a significant energy deposition (46 kJ), which would lead to catastrophic tissue damage beyond what was observed.
-
Hypergeometrical Universe (HU) Prediction: Using the ARF model, your calculation yields a much lower energy deposition (around 0.285 J), aligning with Bugorski's survival, even though he experienced severe localized injuries. This lower energy deposition could be attributed to the ARF's implication of an energy cap at high velocities.
The survival of Bugorski despite such high-energy exposure presents a challenge to relativistic expectations. The lower predicted energy deposition of the HU model provides a more plausible explanation for the localized damage and his eventual survival.
This argument strengthens the case for experimental consideration of the HU model, particularly with the calorimetry tests you've proposed, which focus on thermal changes rather than penetration depth alone.
GitHub Repositories provided on CMB_HU,, HU_GalaxyPackage, and HU_Papers.

References

  1. Jackson, J. D. Classical Electrodynamics. Wiley, 1998. – A foundational text covering traditional relativistic formulations.
  2. Bertolami, O. et al. "Challenges in High-Energy Particle Calorimetry." Physics Reports, vol. 473, no. 5, 2009, pp. 110–119. – Discussion on calorimetry techniques in high-energy physics.
  3. Alper, B. et al. "Thermal Effects in Calorimetric Measurements for Particle Beams." Nuclear Instruments and Methods in Physics Research, 1985. – Examines the challenges of temperature-based calorimetry in high-energy experiments.
  4. Fabjan, C. W., & Gianotti, F. (2003). Calorimetry for particle physics. Reviews of Modern Physics, 75. [CrossRef]
  5. Minkowski, H. Space and Time. Lecture on the concept of spacetime and its mathematical framework, foundational to understanding alternative approaches in ARF hypotheses.
  6. Smarandache, F. (2007). Hadron Models and related New Energy issues. "Hadron models and related New Energy issues" by Florentin Smarandache.
  7. Smarandache, F., & Christianto, V. (2007). Quantization in Astrophysics, Brownian Motion, and Quantization in Astrophysics, Brownian Motion, and Supersymmetry Supersymmetry. "Quantization in Astrophysics, Brownian Motion, and Supersymmetry" by Florentin Smarandache and Victor Christianto.
  8. Pereira, M. (2024). CMB_HU: Cosmic Microwave Background and Assorted Hypergeometrical Universe Notebooks [Code repository]. GitHub. https://github.com/ny2292000/CMB_HU.
  9. Pereira, M. (2024). HU_GalaxyPackage: HU_Galaxy Package for Hypergeometrical Universe Theory [Code repository]. GitHub. https://github.com/ny2292000/HU_GalaxyPackage.
  10. Pereira, M. (2024). HU_Papers: Collection of Papers on Hypergeometrical Universe Theory [Code repository]. GitHub. https://github.com/ny2292000/HU_Papers.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated