The Code Underneath

1. Introduction

After Simon Newcomb’s public note [1] and Benford’s statement [2] that small things are more numerous than large things, and there is a tendency for the step between sizes to be equal to a fixed fraction of the last preceding phenomenon or event, many scientists [3] tried to explicate the strange high frequency of the micro in nature, the rarity of the macro, and the ebbing progression of the gaps in between.

Nature pivots on exponential powers. Benford underlined that the geometric series has long been recognized as a common phenomenon in factual literature and in the ordinary affairs of life. Nevertheless, human functions are often arithmetic-centric. Will there be a natural coding system to convert these realms into one another, the observable into our inner world’s models, and vice versa? In other words, does nature count on a conformal transformation mechanism [4]?

In modern terms, Newcomb-Benford law (NBL) states that the first digits of randomly chosen original data typically outline a logarithmic curve in an impressive diversity of fields regardless of their physical units. Equivalently, the law remarks that raw natural data usually belong to nearly scale-invariant geometric series. Among its manifestations, it is fascinating that linear coefficients represented by mathematical and physical constants [5] (e.g., proportionality parameters or scalar potentials) adhere to the law.

Although this scenario suggests that NBL might account for an elementary principle, we have yet to clarify its origin, realize a theoretical basis, or encounter a convincing reason [6]. Berger [7] laments that There is no known back-of-the-envelope argument, not even a heuristic one, that explains the appearance of Benford’s law across the board in data that is pure or mixed, deterministic or stochastic, discrete or continuous-time, real-valued or multidimensional.

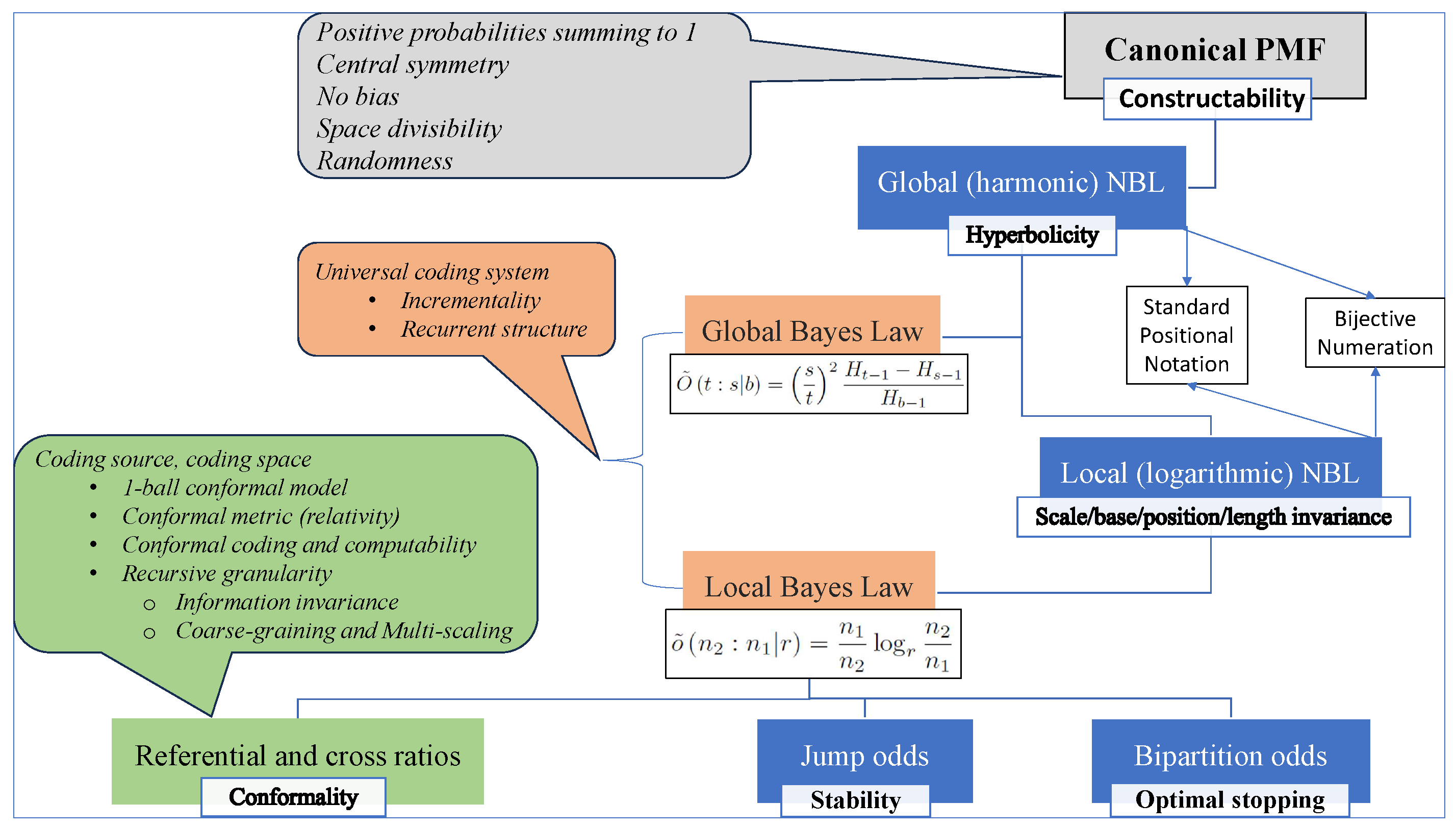
We claim a primordial probability inverse-square law (ISL) is at NBL’s root. This canonical probability mass function (PMF) has a double fundamental effect, namely the NBL for the discrete (global and harmonic) and continuous (local and logarithmic) domains. We prefer to anticipate these three laws’ properties and affiliated terminology in Table 1, indicating their scope and character, baseline set, physical incarnation, scale, formula, information function, cardinality, and how we will denominate the corresponding item, an item list, and an item range.

Are these laws naturally predetermined probability distributions? We champion the view that the canonical PMF is a brute fact and, consequently, the global and local versions of NBL are inescapable. For one thing, their mode is one. This number is the base case for almost all proofs by mathematical induction, statistically the most probable cardinal of a natural set (e.g., one cosmos, one black hole at the center of a galaxy, one star ruling an orbital planetary system, one heart pumping a body’s blood, one nucleus regulating the cellular activity, et cetera), and seed in the majority of recursive computational processes. We read in [8] that numbers close to the multiplicative unit are not preferably rooted in mathematics, but a simple glance at the Table of Constants in [9] points in the opposite direction. Small leading digits and, in general, small significands (mantissae) of coefficients and magnitudes are the most common in sciences, albeit, of course, we can find cardinalities of all sizes.

That the universe is prone to favor slightness is particularly blatant in physics and chemistry. For instance, following the standard cosmological model [10], the abundance of hydrogen and helium is roughly $\left[75\right]\%$ and $\left[23\right]\%$ of all baryonic matter, respectively [11]. Higher atomic numbers than 26 (iron) are progressively more and more infrequent. Nevertheless, the universe’s heaviest elements can comparatively produce the most remarkable galactic phenomena despite their shortage [12] (e.g., the necessary metals to form the Milky Way represent only about $\left[2\right]\%$ of the galaxy’s disk mass). Why do accessibility and reactivity maintain a hyperbolic relationship?

Notwithstanding that NBL assumes standard positional notation (PN) in its fiducial form, our logic also permits obtaining the formulae for non-standard place-value numeral systems. In particular, every NBL’s PMF for standard PN has a bijective numeration [13] peer. For example, the standard and bijective decimal system global and local laws are similar but different. These results show that the precision of NBL is nonessential, while the support positional scale is what matters.

This article’s field of study is mathematical and computational physics, delving into philosophy, theoretical physics, information theory, probability theory, and number theory. We have organized it as follows. We first examine the challenges researchers historically faced in deducing NBL and the state of the art in this field. Afterward, we present a one-parameter inverse-square PMF for the natural numbers with positive probabilities summing to one, extensible to the integers, and diverging mean (no bias). Next, we deduce the fiducial NBL passing through the global NBL; this two-phase derivation clarifies why the tendency for the minor numbers revealed by the natural sciences can be regular only if we assume that an all-encompassing base exists. To support this view, we substantiate that the set of Kempner’s curious series conforms to the global NBL for bijective numeration. Further, we surmise a PN resolution, i.e., the prospect of a natural position threshold ascribed to a place-value number system.

Information theory [14] comes into play when we discover that information is prior to probability in the context of NBL. Likewise, a unit fraction is the harmonic likelihood of an elemental quantum gap, and a digit of a numeral written in PN is a bin that covers a proportion of the available logarithmic likelihood.

The odds between two events is a correlation measure whose entropic contribution to a positional scale ushers in Bayes’ rule [15], namely the product of two factors, a rational prior and a rational likelihood, precisely the NBL probability of the numeric range involved. This structure is recurrent under arithmetic operations and gives place to the algebraic field of referential ratios, the ground for Lorentz covariance, and the cross-ratio, a central instrument of conformality. Then, we determine the conformal metric and iterative coding functions that preserve the local Bayesian information and are compatible with a multiscale complex system [16]. Finally, we resolve the canonical PMF’s parameter, the proportionality constant that ensures the divisibility of the probability mass for naturals and integers. In the epilogue, we comment on the results and conjecture some ideas that open the door to future research.

The primary motivation of this work is seeking a reason for NBL rather than describing how it works [17] or elucidating its pervasiveness. Although Newcomb was an astronomer and Benford was an electrical engineer and physicist, basic research on NBL has usually been the territory of mathematicians; physics must reconsider NBL. Finding a rational version of the law was also a goal of our investigation, given that real numbers are physically unfeasible, mere mathematical abstractions. $\mathbb{Q}$ fits in a relational world ruled by proportions and approximations, contrasting with the continuum’s absolute density and the ultra-accuracy of $\mathbb{R}$. Another motivation is disclosing how a coding source manipulates information in PN. NBL says nothing about the coding process that leads to a digit’s probability of occurrence.

What falls outside our purview? Applications of NBL (e.g., financial) that are irrelevant to computation, information theory, or physics. Neither are we interested in particular virtues of NBL, e.g., the exactness of the law (uncanny, to tell the truth [18]), because they deviate our attention from the critical topics to tackle, to wit, what makes the minor numbers mostly probable, the link to Bayes’ rule, and the efficacy and universality of the conformal coding spaces (see Figure 1). Despite the title, this essay is not about cryptographic protocols or codes enabling source compression and decompression or error detection and correction for data storage or transmission across noisy channels; it is about a source’s system of rules for converting global information into local information.

How did this research develop? Our original rationale was acknowledging that a connection between an NBL and an ISL exists. The rate of change of a significand’s probability drops quadratically, i.e.,

$${\left[P\left(n\right)\right]}^{\prime }\propto {\left[ln\left(1+{\displaystyle \frac{1}{n}}\right)\right]}^{\prime }=-{\displaystyle \frac{1}{n\left(n+1\right)}}$$

According to this expression, a numeral’s occurrence differential is inversely proportional to the square of its distance (plus its distance) from the coding source. Therefore, we could expect this spatial arrangement around the origin based on an ISL for the natural numbers. If a genuine inverse-square PMF exists, we should arrive at it from just a few essentials. We confirmed that three preconditions, namely positive probabilities summing to one, no bias, and central symmetry, unambiguously define a PMF, except for a proportionality constant. Moreover, requiring probability mass compartmentalization fixes such a constant and completely specifies the canonical PMF for the natural and integer numbers. Because the resulting probability for counting numbers is a unit fraction, a rational version of NBL should accompany the logarithmic counterpart. We ultimately gleaned how to calculate the probability of a quantum in a given base as a value in $\mathbb{Q}$.

We have encountered that information has a relational character primally conveyed by the likelihood concept, either harmonic ($\mathcal{L}\left(\left[s,t\right)\right)=[H_{t-1}-H_{s-1}]harmt$, i.e., harmonic units of information) or logarithmic ($\ell \left(\left[i,j\right)\right)=[lnji]nat$). Likelihood is not the information obtained by picking an item from a range but the space allocated to encode an item between the range’s ends. An NBL probability is a proportion of the information total (likelihood density), and an NBL entropy is the weighted mean of the information total (average likelihood). Moreso, odds, referential ratios, and cross-ratios measure likelihood correlations. Because algebra grows on these rational data, geometry embodies algebraic structures, and physics reflects geometrical rules, information turns out to be physical.

Another high-level achievement was finding a hidden connection between NBL and Bayes’ law. This rudimentary rule codes the strength of the relationship between a pair of items normalized in a particular base b or radix r. The global Bayes’ rule, in odds form and b-ary harmonic information units, is the product of a prior, the ratio between the probability of two numbers t and s according to the canonical PMF, by a likelihood factor, the global NBL probability of the bucket $\left[s,t\right)$ in base b. The local Bayes’ rule, in odds form and r-ary logarithmic information units, is the product of the prior, a ratio between the global NBL probability of two quanta j and i on b’s harmonic scale, by a likelihood factor, the local NBL probability of the bin $\left[i,j\right)$ in radix r. Further, Bayesian data conformally encoded constitute normalized likelihood information. Bayes’ rule also recodes information after a change of base or radix, a foundation for incremental computation. Lastly, we learned how a source recursively encodes the observable as Bayesian data and decodes these back into the information of the external world. This Bayesian outlook unifies the frequentist, subjective, likelihoodist, and information-theory interpretations.

We have verified that likelihood, probability masses, entropy, and odds are measurable information, the common factor for the universality of the harmonic and logarithmic patterns appearing in real-life raw numerical series. We have even inferred that information divergence is impossible. In the first place, the entropy of the canonical PMF for the natural and integer numbers converges. Likewise, we have defined global and local Bayesian data supported by confined harmonic and logarithmic scales. The jump odds between consecutive quanta or numerals are also delimited. Physically, the entropic cost of crossing entirely the universe or its local copy agrees with the Bekenstein bound [19].

Effectively, information occupies finite space. This essay introduces various examples of how a law, PMF, concept, or formula supports our theory that the cosmos is a hyperbolic, thrifty, and relational information system at a fundamental level. The notion of conformality implemented into a source’s coding space subsumes these hallmarks. It employs the NBL invariance of scale, base, length, and position in the Bayes’ rule to calculate the entropic contribution of a range of items. This synergy reinforces the thesis that mathematics begets physics and that information is a form of energy. The universe is a natural positional system that rules how a body’s local quantum-mechanical degrees of freedom carve the information of its consubstantial properties, backing the Computable Universe Hypothesis [20].

2. Results

We enumerate the research’s concrete results and answer what this study adds to human knowledge.

2.1. Specific Achivements

We have found a roundabout but intuitive argument to explain the appearance of NBL in the vast array of contexts in which its effect manifests; NBL issues from an ISL of probability.

When choosing a natural number at random, nature follows a particular PMF where zero is possible and interpretable as indeterminate, e.g., not-a-number or inaction. We require zero’s probability to be $1-ϵS$, where $ϵ$ is a proportionality constant, and $ϵS$ is the probability of picking a counting number, i.e., $\left\{1,2,3,\cdots \right\}$. We also need this one-parameter PMF to have no bias so that no number is prominent (up to its probability), i.e., any number can appear. Moreover, the mass of a counting number N is necessarily $ϵN^2$ if we want the probability function extensible to integer numbers, i.e., a number with the same probability regardless of the sign. Thus, the universe weighs the cost of choosing $\pm N$ as growing quadratically with N.

We have obtained the global and local NBL from this predetermined PMF. Under its tail, the probability that a natural number exceeds N is proportional to the trigamma function at N. Likewise, the probability of a natural variable’s second-order cumulative function falling into $\left[s,t\right)$ is a harmonic likelihood ratio that cancels out the constant $ϵ$, namely the bucket’s width $\psi \left(t\right)-\psi \left(s\right)=H_{t-1}-H_{s-1}$ relative to the base’s support width $\psi \left(b\right)-\psi \left(1\right)=H_{b-1}$, where $1\le s<t<b$ and $\left\{s,t,b\right\}\in {\mathbb{N}}^{+}$. The base b is a global referent that changes the status of a number to a computable elemental entity we call a quantum. When the bucket is $\left[q,q+1\right)$, we obtain the global NBL of a generic quantum q, $Pr\left(b,q\right)={\displaystyle \frac{1}{q{H}_{b-1}}}$, an exact and separable function where $q,b\in \mathbb{N}$, $1\le q<b$, and $H_n$ is the nth harmonic number. The global NBL represents in information theory the likelihood q encloses concerning the likelihood total, geometrically a share of the surface area swept by q, and physically a scalar potential harmonically diminishing as q moves away from the origin. The odds-version of this PMF (21), also exact and separable, defines the stability of a quantum jump.

We can handle quanta as real variable values when the global base b is giant. Because a coding source does not know the value of b, it must establish a local referent $r\ll b$ to normalize its information separated from the surrounding environment, changing the status of a quantum to a locally computable elemental entity we call a digit. This scenario involves the canonical PMF’s third-order cumulative distribution; the probability of a quantum falling into $\left[i,j\right)$ is a logarithmic likelihood ratio that cancels out $H_{b-1}$, precisely the bin’s width $lnji$ relative to the radix support’s width $lnr$. When the bin is $\left[d,d+1\right)$, we arrive at the fiducial NBL, i.e., ${log}_r\left(1+1d\right)$, where $d\in \mathbb{N}$ is a digit such that $1\le d<r$. This PMF represents in information theory the likelihood d encloses regarding the likelihood r embraces. It is geometrically a hyperbolic sector equivalent to the surface area swept by d relative to that swept by r and physically a scalar potential r-logarithmically diminishing as d moves away from the origin.

In general, NBL probabilities consider the cutoffs PN imposes as a proportion of the total information. The global and local versions of NBL for standard PN give probability masses similar to a degree. For comparison purposes, 1 in standard ternary occupies $2/3\approx \left[66.7\right]\%$ ($\mathbb{Q}$) and $ln2/ln3\approx \left[63.1\right]\%$ ($\mathbb{R}$), while 2 occupies $1/3\approx \left[33.3\right]\%$ and $ln1.5ln3\approx \left[36.9\right]\%$, respectively. Likewise, 1 in standard decimal occupies $\left[35.3\right]\%$ ($\mathbb{Q}$) and $\left[30.1\right]\%$ ($\mathbb{R}$), while 9 occupies $\left[3.9\right]\%$ and $\left[4.6\right]\%$, respectively.

Furthermore, we provide NBL for bijective numeration to reinforce the thesis that this law is comprehensively universal. All the formulas of standard PN are translatable to bijective numeration. The NBL with standard radix $r+1$ corresponds to the NBL with bijective radix $\underline{r}$, which is length- and position-invariant in addition to other well-known invariances. Regardless of the numeral system, we must conceive of positional scales as hyperbolic spaces in a broad sense, harmonic in the first place, and logarithmic in the second place.

The sums of Kempner’s curious harmonic series [21] echo the bijective harmonic scale traced by the global NBL. This outcome is absolute because every Kempner series is infinite, and the calculations consider every possible numerical chain; extended numerals are increasingly unimportant. For example, in decimal, while removing the terms including less than $\left[10\right]\%$ of 5’s in the denominator makes a harmonic series converge, missing the terms including $[\ge 10]\%$ of 5’s does not impede the divergence of the depleted harmonic series. We also figure that the natural span of a positional system in base b is $b^b$, a measure of the physical quantity of numerals PN can inherently manage. Beyond this computational resolution, quanta or digits could be haphazard for practical purposes.

NBL, a synonym of PN, a subsidiary of the canonical PMF, describes an information field where probability correlates with accessibility, whence, with concentration and durability. Smaller significands occupy more room and enclose less information than greater significands. In other words, the space is denser and more stable near the coding source, while numerals dilute the space and become more reactive as we move away from the origin.

The analysis of NBL from the odds angle drives us to a rudimentary Bayesian framework. The Bayesian view of objectivistic or subjectivistic probability allegedly requires a reasoner to admit ignorance and imperfection expressed by a prior and its likelihood, respectively. The reasoner also accounts for counterhypotheses by considering the product of the prior and its likelihood in the posterior calculation. Natural Bayesianism works similarly but merely involves a coding source supporting PN.

Bayesian encoding, recoding, and decoding are elemental computing routines that handle odds. The Bayesian encoding of the relation between two numbers is the entropic allocation of their correlation for a harmonic scale, i.e., their ratio squared multiplied by the probability of the associated interval in the chosen base. The Bayesian encoding of the relation between two quanta is the entropic contribution of their correlation for a logarithmic scale, i.e., their ratio multiplied by the probability of the associated bucket in the chosen radix. Therefore, we can interpret a Bayesian rule as the formula to encode the rational point $n/d$ or the corresponding range $\left[n,d\right)$ of integers; this duality principle asserting that points and lines are interchangeable is endemic to the cosmos.

The global Bayes’ law bridges numbers with information. We measure global Bayesian data in harmonic units of information that depend on the base. The natural harmonic scale uses bucket $\left[1,2\right)$ as a reference. We measure local global Bayesian data in logarithmic units of information that depend on the radix. The natural logarithmic scale uses bin $\left[1,e\right)$ as a reference, where e is Euler’s number. However, the arithmetic of Bayesian data generally does not refer to the global base or the local radix; it works on natural scales.

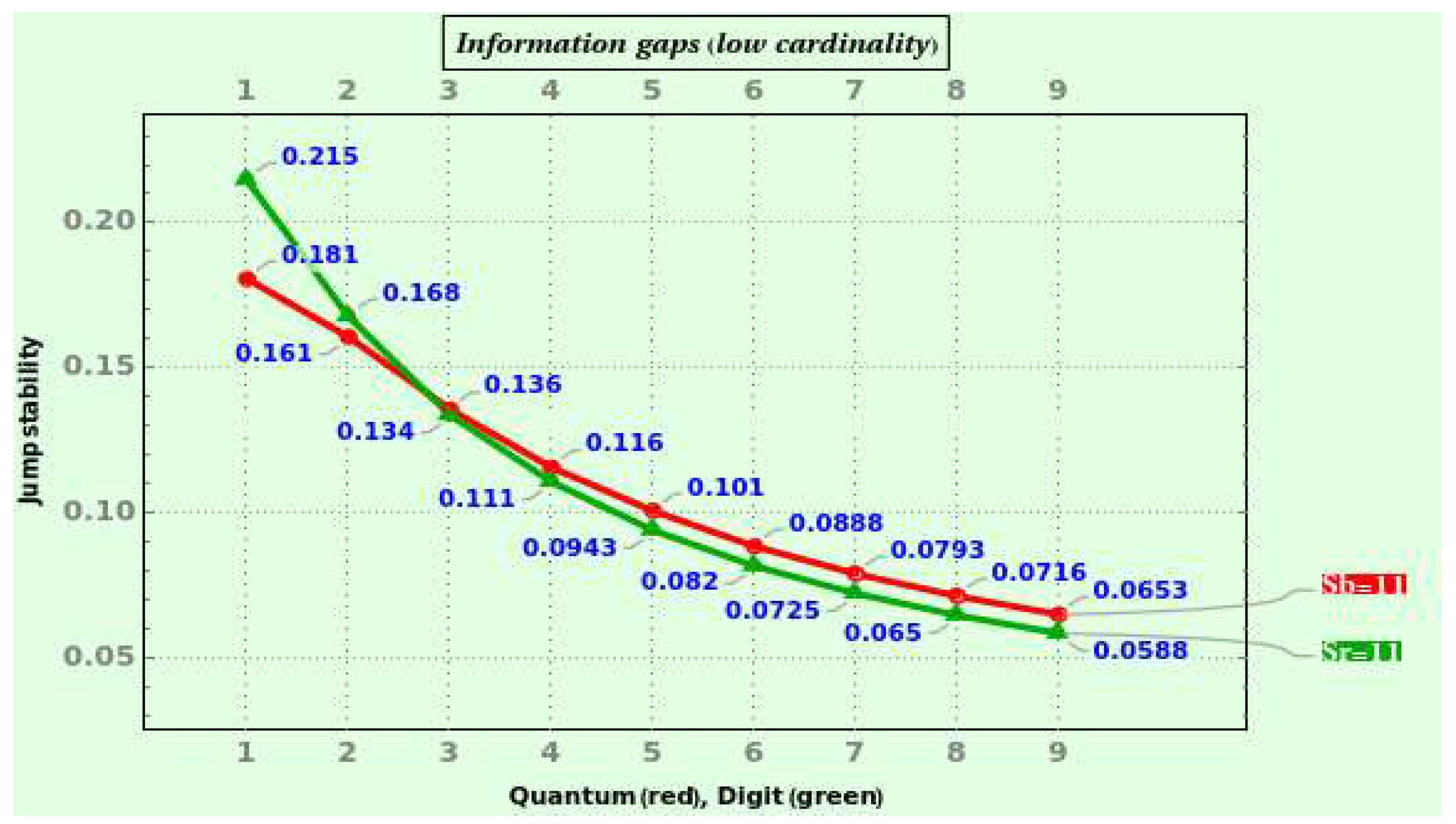
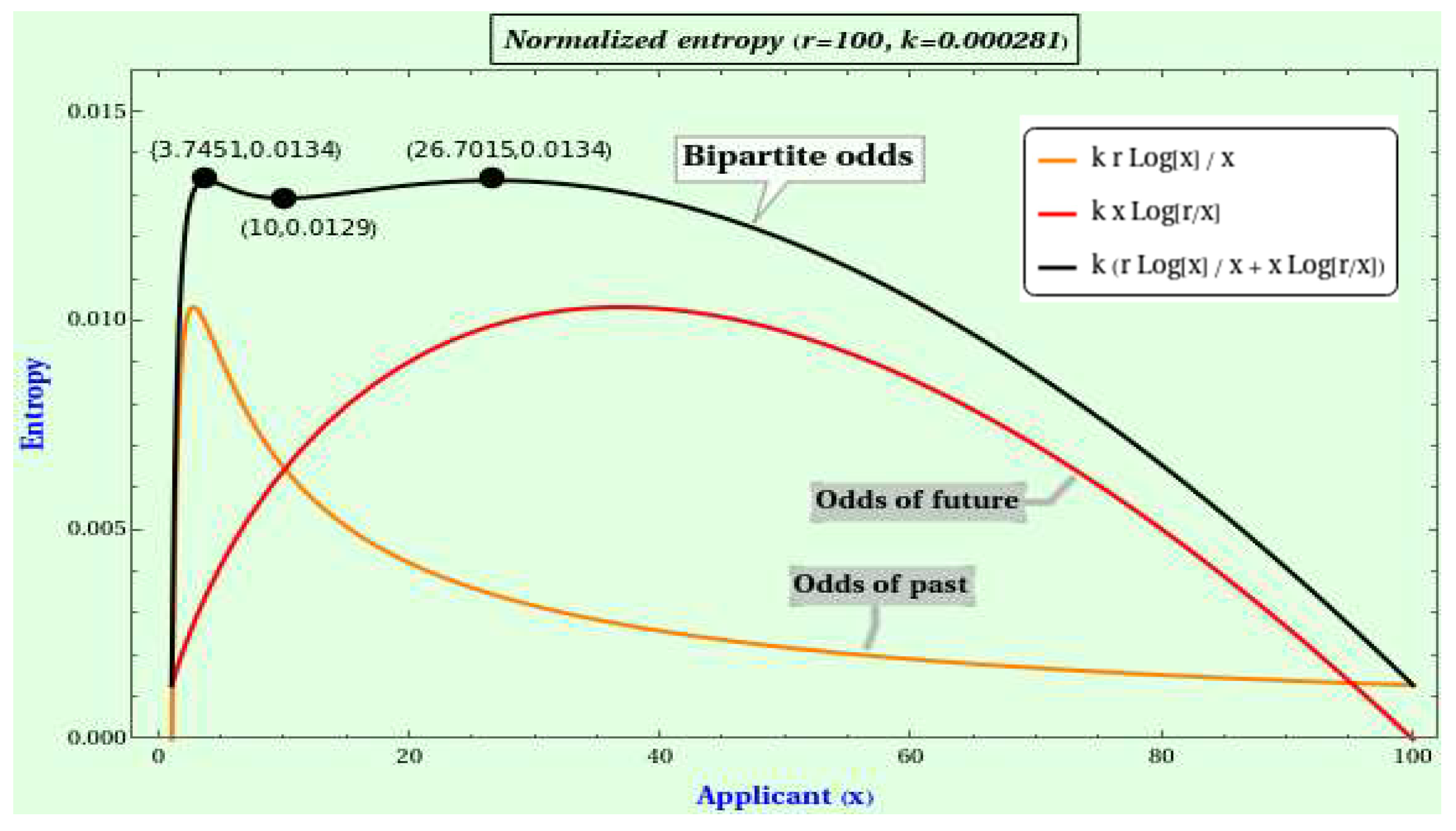
The global Bayesian rule allows for calculating a quantum jump probability, with masses decaying similarly to the global NBL as we move away from the source. Likewise, the local version of Bayesian coding drives us to the PMF of a domain’s bipartition, an information function applicable to stopping problems. Specifically, we deduce the information gained from splitting a radix’s digit set. If we take these digits as generic elements to be processed sequentially, our bipartite odds formula reaches a pair of information maxima involving e. The square root of the radix gives a minimum between the two maxima. We fix ideas by focussing on a variation of the secretary problem pursuing a good instead of the optimal solution. This problem’s representativeness joins the overwhelming evidence supporting the overarching character of the NBL.

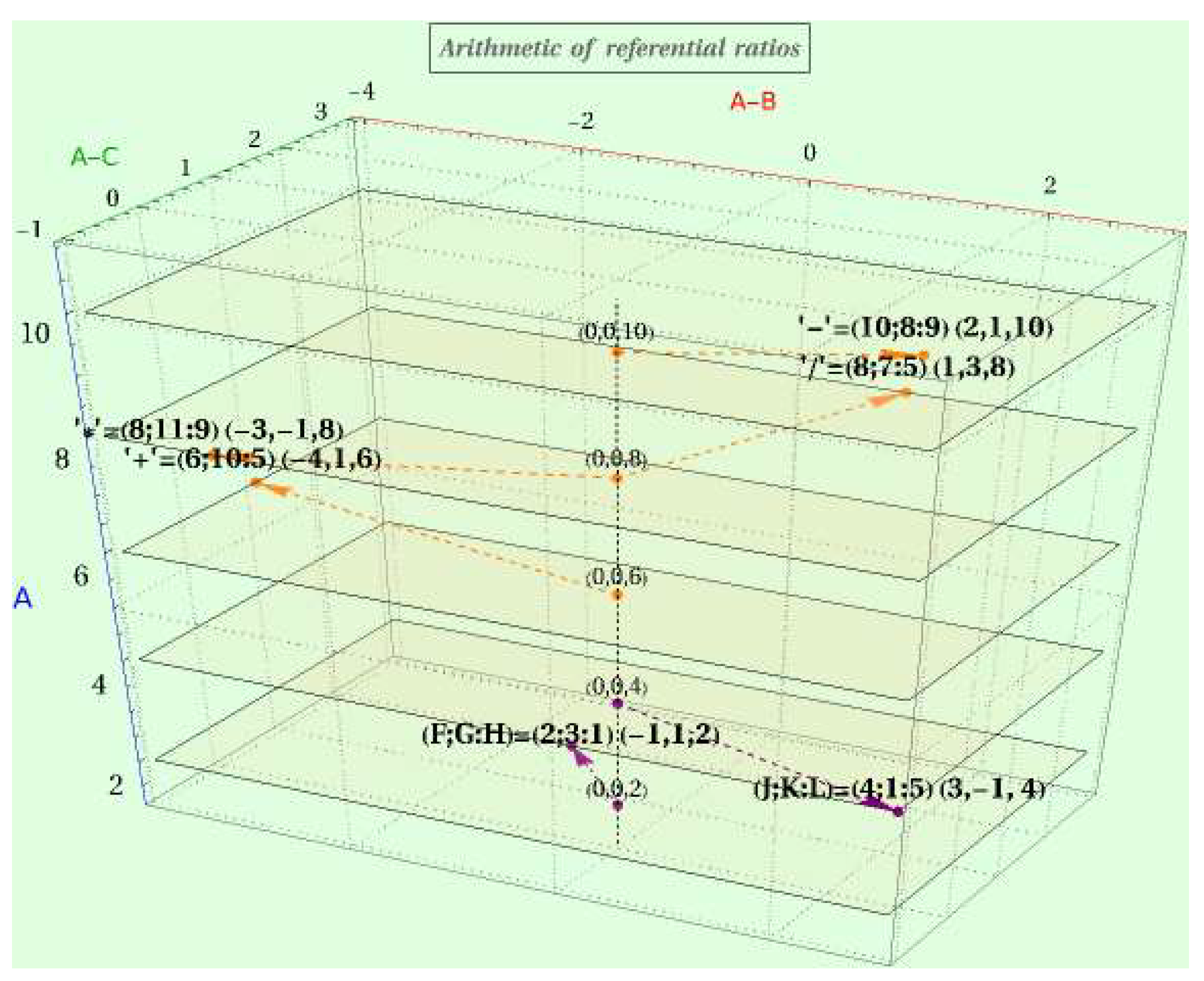
A kicky discovery is that the structure of Bayesian data whose prior factor is the unit is recurrent under arithmetic operations, giving rise to the algebraic field of referential ratios ${\displaystyle \frac{A-B}{A-C}}$. Moreover, a ratio of referential ratios is a cross-ratio, and the logarithm of a cross-ratio locally provides us with the metric of a conformal space reflecting the observable world and consolidating the universal proclivity towards littleness, lightness, brevity, or shortness.

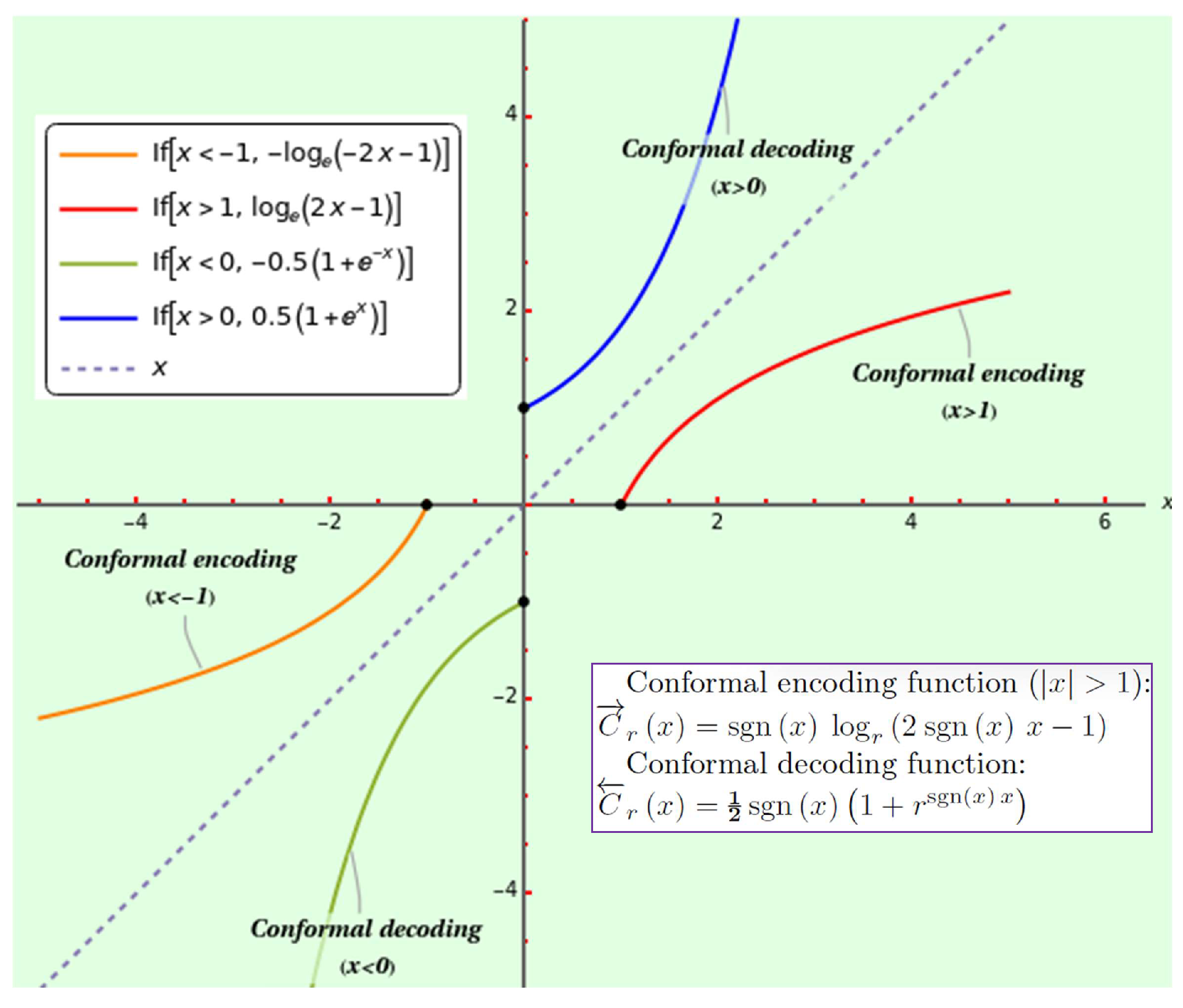
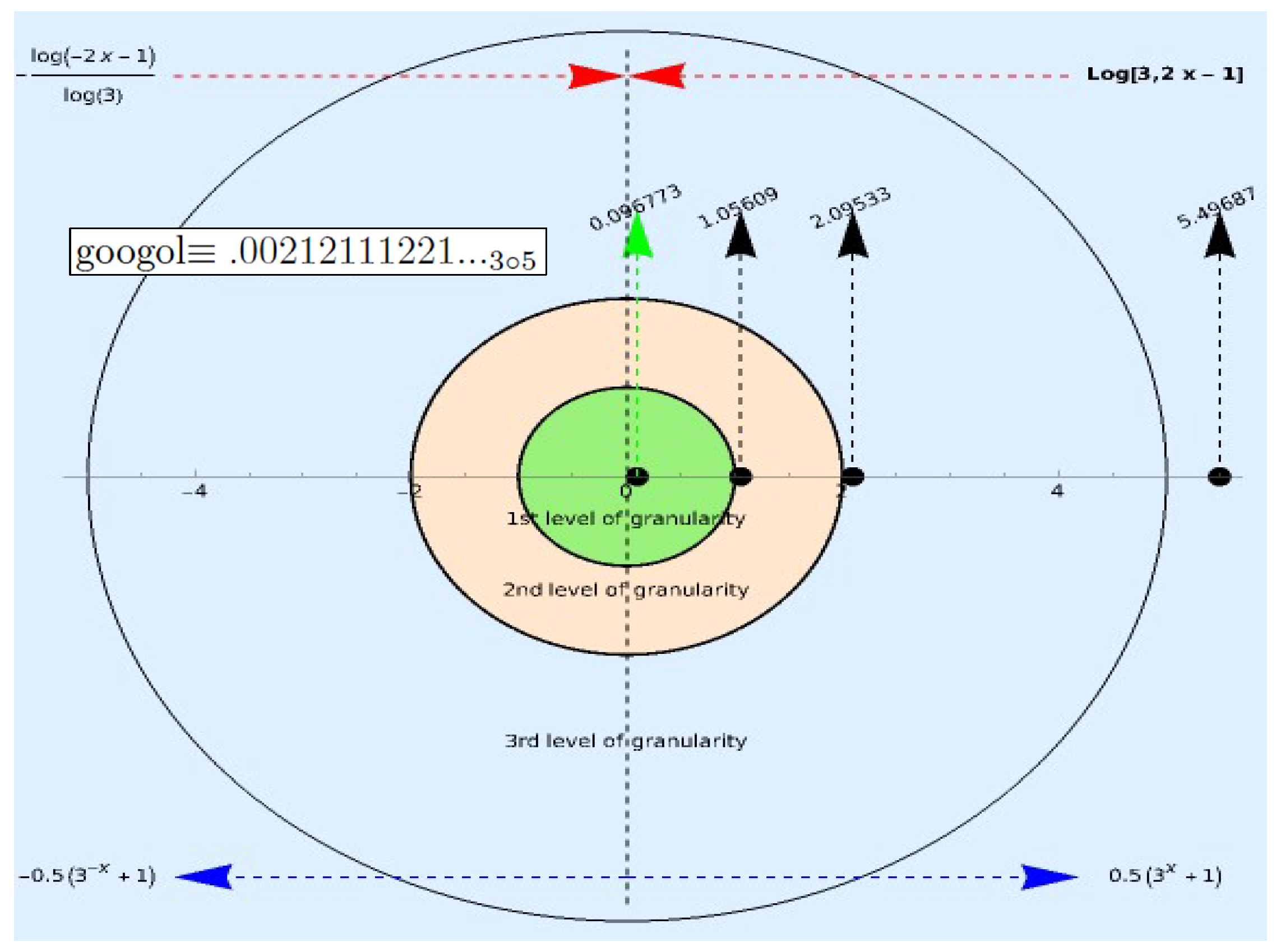
The coding source calculates the conformal distance from the origin as $2\mathrm{artanh}\left(Q\right)lnr$, where $\mathrm{artanh}\left(Q\right)={\sum }_{i=1}^{\infty }{\displaystyle \frac{Q^{2i-1}}{2i-1}}$, $Q=\mathrm{sgn}\left(P\right)-1P$, $\mathrm{sgn}$ is the sign function, and P is the observed Euclidean distance to the point where an external object is. The coding space is the ball $\left\{Q\in \mathbb{Q}|\left|Q\right|<1-1b\right\}$, with constant curvature of $-lnr$, where r is the radix used to normalize the information; the harmonic (outside) and logarithmic (inside) scales have a common origin and are separated by the boundary $\pm 1$ when $b\to \infty$. The conformal encoding function using the logarithm is $C=\mathrm{sgn}\left(P\right){log}_r\left(2\mathrm{sgn}\left(P\right)P-1\right)$, with inverse conformal decoding function $\text{½}\mathrm{sgn}\left(C\right)\left(1+r^{\mathrm{sgn}\left(C\right)C}\right)$. Since the metric ranges between $-\infty$ and ∞, the source can repeat the encoding process inwards until the external object’s hyperbolic distance falls within the local coding space, halting the recursion. Likewise, every 1-ball with a radius given by the iterated decoding of $C=0$ outwards corresponds to a granularity level.

The results of this research stem all from the canonical PMF for the integer numbers, whose characteristics are fundamental and generative, imaging the essence of the cosmos. Physically, positive probabilities summing to one translates into unitarity, central reflection symmetry into parity invariance, fair mean and variance into uncertainty, holistic rationality into discreteness and relationalism, and utmost randomness in picking the number one into the principle of maximum entropy. Likewise, the global NBL (hence Zipf’s law [22] with exponent 1), as well as the local NBL (supported by the logarithmic scale), are arguably physical. More generally, our descriptions and derivations introduce diverse instances of how mathematical functions, rules, or algebraic structures emerge as observable dynamics.

2.2. Hyperbolic World

Hyperbolic geometry is non-Euclidean in that it accepts the first four axioms of Euclidean geometry but not the fifth postulate. The n-dimensional hyperbolic space ${\mathsf{H}}^n$ is the unique, simply-connected, and complete Riemannian manifold of constant sectional curvature (equal to $-1$ [23]). For instance, saddle surfaces resemble the hyperbolic plane ${\mathsf{H}}^2$ in a neighborhood of a (saddle) point. These are typical ways to introduce the notion of hyperbolicity.

Instead, we prefer to identify a hyperbolic space with a domain whose geometry pivots on the hyperbola, contrasting with flat and elliptic spaces, which are parabola-based and circle-based, respectively. Harmonic scales are part of this world because a logarithmic scale results from summing over a harmonic series with vanishing steps between the values of a rational variable. The computational implementation of this hyperbolic world is PN, i.e., representing numeric entities on a positional scale, either harmonic or logarithmic.

Various combinations of exponential forms define the hyperbolic functions, so logarithms characterize the corresponding inverse (or area) hyperbolic functions. In geometry, the extent of the hyperbolic angle about the origin between the rays to $\left(1,1\right)$ and $\left(x,1x\right)$, where $x>1$, is the sector $lnx$. The natural logarithmic scale, factually ${\mathsf{H}}^1$, rules the cosmos to a great degree, developing systems whose properties echo a scale-invariant and base-invariant frequency.

Physics ties an ISL with a geometric dilution corresponding to point-source radiation into three-dimensional space [24]. Math shapes an ISL within a two-dimensional setting [25]. Nonetheless, our brute ISL of probability drives us to various versions of NBL all in one dimension, from which nature can expand the logarithmic scale upon hyperbolic spaces of all ranks to avoid the curse of dimensionality [26]. Remarkably, forming a hyperbolic triangle is more than four times as probable as a non-hyperbolic one. We daresay that hyperbolic geometry beats at the universe’s core.

In information theory, we consider that a hyperbolic space is a coding space within which likelihoodepitomize the physicality of the positional number system. A global NBL probability is a harmonic likelihood ratio, and a local NBL probability is a logarithmic likelihood ratio. A ratio of NBL probabilities determines the relative odds between two buckets of quanta globally or between two bins of digits locally. Typically, a coding source calculates the odds between two numeric events considering the information of the range they embrace regarding the entire informational support provided by the global base or the local radix. These normalized odds are likelihood ratios.

Decoded (prior) odds between two events are correlations that a coding source translates to a positional scale multiplied by a likelihood ratio. This product is Bayes’ rule to encode and transform the information. The shock is that first, addition, subtraction, multiplication, and division reproduce this coding pattern, and second, under certain conditions, it collapses into the algebraic field of referential ratios ${\displaystyle \frac{A-B}{A-C}}$. A quotient of referential ratios is a cross-ratio, the linear fractional transformation’s invariant over rings via the action of the modular group upon the real projective plane [27]. Restricted to one dimension, the cross-ratio’s logarithm in radix r determines the coding space’s metric with curvature $-lnr$. The canonical encoding function $y={log}_r\left(2x-1\right)$ and the canonical decoding function $x=\text{½}\left(1+r^y\right)$ are the unique conformal transformations (i.e., preserving orientation and angles) that, if applied iteratively, map $x>0$ to the coding space’s positive side in accord with the minimal information principle. For the same reason, the hyperbolic distance $d_r\left(A,B\right)=2lnr\left(\mathrm{artanh}\left(B\right)-\mathrm{artanh}\left(A\right)\right)$ between points A and B inside the local coding space is also unique. We conclude that Poincar invariance ultimately stems from the algebraic field of referential ratios.

2.3. Thrifty World

To improve tractability, one can feel tempted to cut the unit uniformly into equal parts. A constant probability distribution assigns the same expected frequency to all the domain values. However, whereas the uniform distribution of probabilities is, in principle, fair and provides maximum entropy, it does not fit well into an open (infinite) outcome space.

Contrariwise, it is noteworthy that [28] the frequency with which objects occur in ’nature’ is an inverse function of their size, indicating that oddity and magnitude usually correlate and conform to a Benford distribution. NBL says the cosmos displays a progressive aversion to larger and larger numbers, somewhat implementing the parsimonae lex [29], a principle of frugality [30] that stimulates economy and effectiveness as universal prime movers, drivers of nascent physics, particularly the spacetime geometry.

The canonical PMF exhibits nature’s bet on the shortest numbers, but NBL provides further precision, pointing to a conservative policy of significands. For instance, the law favors $123.4$ against $12.345$ because 12345 is less probable than 1234. For the same reason, the law favors $0.234$ against those. The last digits might provide negligible, even arbitrary, information [31]. This innate tendency amounts to restricting the resolution of the representational system to preclude unnecessary precision. Carrying long tails of digits from operation to operation is neither intelligent nor evolutionary. Information is gold, much like energy.

Interestingly, the probability that a randomly chosen natural number between 1 and N is prime is inversely proportional to N’s number of digits, whence to the length of its significand [32], i.e., to its logarithm or equivalently its likelihood. Therefore, primality and information are nearly interrelated. Why is finding a big prime so tricky [33]? Because it demands logarithmically growing energy.

NBL denotes productivity. Radix economy $\mathring{E}\left(N,r\right)\approx r{log}_{r}N$ measures the price of a numeral N using radix r as a parameter. Cost-saving number systems will employ an efficient coding radix; the optimal radix economy corresponds to Euler’s number e, another sign of the preeminence of small numbers. The wider the gap between the economy of consecutive numbers relative to the radix, the higher the expected frequency. Thrifty numbers making a difference are winning, meaning that the probability of a number coded with radix r showing up is the rate of change, or derivative, of its economy concerning the radix, specifically

$$P\left(N,r\right)={\displaystyle \frac{\mathring{E}\left(N+1,r\right)-\mathring{E}\left(N,r\right)}{r}}\approx {log}_r\left(N+1\right)-{log}_{r}N={log}_r\left(1+{\displaystyle \frac{1}{N}}\right)$$

This expression indicates the occurrence probability of the numeral N, not necessarily a digit, with radix r. For example, ${log}_{10}\left(1+1/22\right)$ is the probability of running into a decimal number starting with 22, such as $2.29$ or 2237. The logarithmic scale knits the linear space toward the coding source; the closer, the higher the spatial density. A large numeral is less likely due to its representational magnitude, so its space is less contracted than that occupied by a numeral with more probability mass. NBL reflects how PN encodes numbers in agreement with this economic criterium.

Therefore, the radix economy establishes a scalar field where the gap between the potential energies [34] of two objects only depends on their position as perceived from the source. Thus, the canonical PMF and NBL subsidiaries are fundamentally efficient, balancing probability mass against notation size. Minor numbers are accessible at a lower cost, while spatial dilution and the prospect of likelihood increase, although deceleratingly, as we climb to infinity.

NBL maps (the minor numbers of) the linear frequency onto (the least costly digits) of the logarithmic frequency through the harmonic frequency. How does a harmonic scale exhibit its austere nature? The study of constrained harmonic series mainly teaches us that the specific digits involved in the restraining chain do not matter, whereas its length does. Long chains or high densities of quanta are rare and deliver slender harmonic terms that hardly occupy space. In contrast, short chains or low quantum densities are regular and cheap, producing heavy harmonic terms that occupy much space, leading to convergence of the series if eliminated. In other words, only usual and economic constraints can impede the divergence of a harmonic series. More generally, increasingly bigger numbers on a linear scale require hyperbolically less and less attention in accord with the room they take up. Nature builds physics upon proximity because almost all large numbers are expensive and indiscernible [35].

Our theory also associates efficiency with entropy. We can interpret NBL probabilities as degrees of stability or coherence. The lowest digits maintain distinctness from the surroundings thanks to their solid entropic support. The more significant digits are vulnerable and give rise to more transitions, physically translating into higher reactivity or less resistance to integration with the environment.

Parsimonious management of computational resources is crucial, as optimal stopping problems reveal. In the secretary problem, selecting the best applicant is pragmatically less sensible than simply a good one, which requires maximizing the bipartite entropy. The past partition emphasizes the information gathered, while the future partition deals with the information we can obtain from forthcoming aspirants. As the number of examined applicants grows, the past information increases, but the future information decreases. In contrast, the probability of taking advantage of both types of information decreases and increases, respectively. The best applicant implies exclusively focusing on the future partition, but a balanced decision also implies contemplating the past.

Information economy enables cosmological evolution. That the universe optimizes computability follows from NBL embracing several invariances. Base invariance ensures even interaction with the environment because changes in the radix value will imply only incremental updates (recoding), keeping the internal metric up to the curvature. Scale invariance provides the means to recursively perform geometric calculations on nested levels of domain granularity, like a fractal. Rescaling implies only obtaining the powers of any radix using straightforward Moessner’s construction [36]. Length and position invariance ensure fault tolerance. Ultimately, PN is effective because it makes the most expected data readily accessible for iterative coding functions.

Because a thrifty world refuses the continuum, computing hyperbolic spaces requires rationality to be feasible.

2.4. Relational World

Real numbers are unattainable mathematical objects [37], artificial, mere abstractions; hence, $\mathbb{R}$-oriented physical laws and principles are suspicious. In contrast, relative odds, i.e., proportions between two numbers, quanta, or digits, are tractable. Rational numbers are the fitting choice in an inaccurate and defective [38] world, where relations are as important as individual entities [39] and comparative quantities predominate over absolute values. A universe built upon the rational setting facilitates divisibility, discreteness, and operability. Calculus of rational information relies on a harmonic scale and uses harmonic numbers. Regardless, we need rational models of reality to prove that the $\mathbb{Q}$ underpins the universe’s computational machinery.

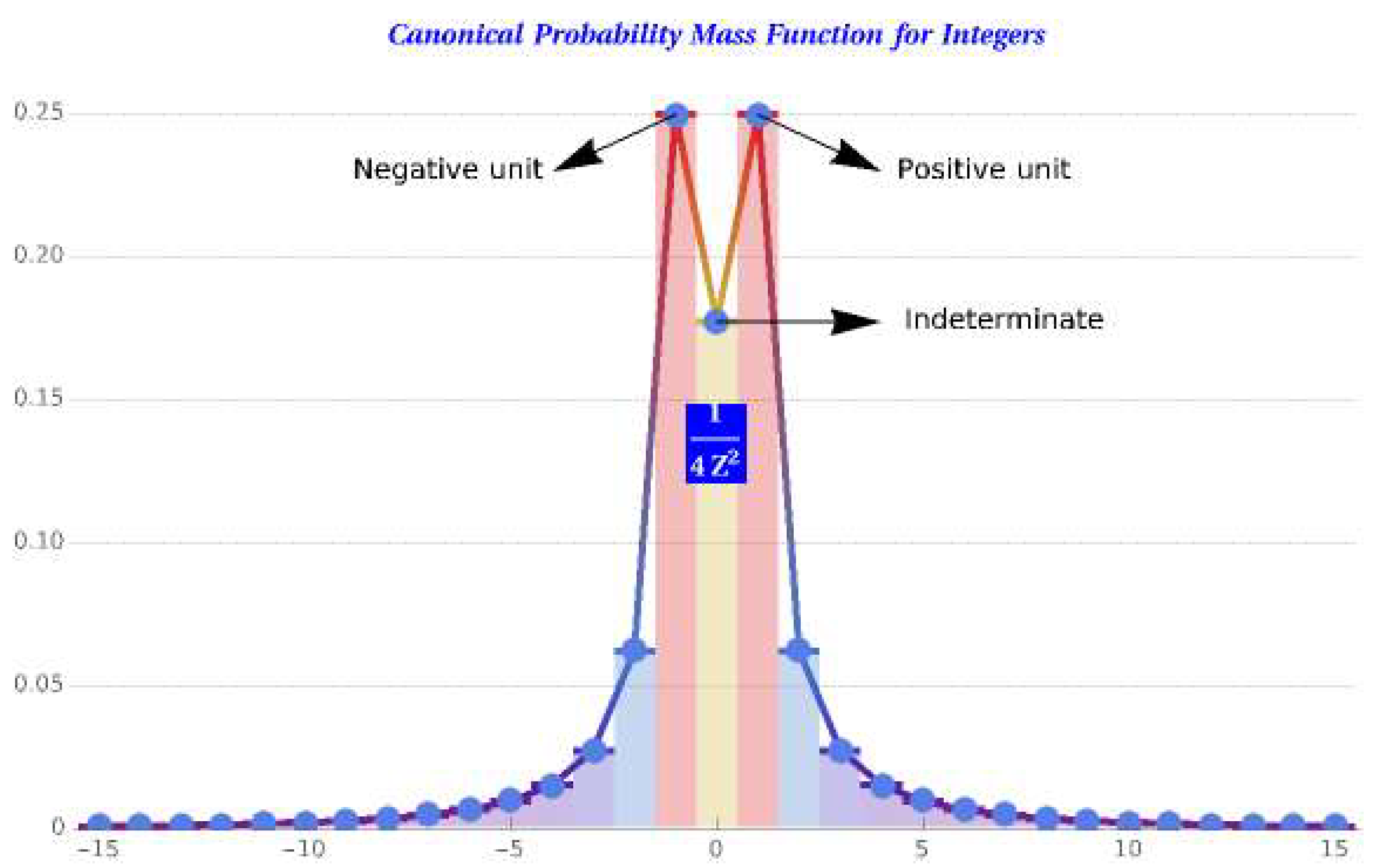
Presuming the minimal information principle, we require a fundamental PMF with positive probabilities summing to one, no bias, and central symmetry. To ensure divisibility of the probability space, which enables the operability of the information, the mass distribution we obtain for the natural numbers must be $\text{½}{N}^{-2}$ if N is nonzero and $1-\text{½}\zeta \left(2\right)$ otherwise. Next, we calculate from this PMF the probability of a natural number being odd or even and prime or composite. We also calculate the probability of getting an elliptic, parabolic, or hyperbolic two-dimensional tiling by examining the triangle group. Similarly, the occurrence probability for a nonzero integer Z is $1/{\left(2Z\right)}^2$. Despite being excluded from the scope of this essay, we can even extend the canonical PMF to rational and algebraic numbers, the computable version of complex numbers. All these laws are rational and inverse square, fulfilling identical requirements.

We underline that the probability mass of a nonzero integer is a unit fraction. Real numbers only appear (in terms of the Riemann zeta function at 2) when the probability of occurrence involves zero or infinity, a sign that these limiting values are virtual. From the canonical PMF, we derive a discrete (global) counterpart of the continuous (local) NBL, where the probability of a significand in a given base is rational. The continuous (local) NBL emanates precisely from the rational (global) NBL by compartmentalizing a one-dimensional hyperbolic space of colossal extent. More generally, whereas the universe originates globally from $\mathbb{Q}$, it is perceived locally as $\mathbb{R}$.

The concept of information is fundamentally rational. Harmonic likelihood is global information defined as ${\left[\mathcal{L}\left(q\right)\right]}_s^t\equiv \left[{\left[\psi \left(q\right)\right]}_s^t{\left[\psi \left(q\right)\right]}_1^2\right]\mathrm{harmt}$, whereas logarithmic likelihood is local information defined as ${\left[\ell \left(d\right)\right]}_i^j\equiv \left[{\left[lnd\right]}_i^j{\left[lnd\right]}_1^e\right]\mathrm{nat}$. A harmt is the global (harmonic) unit of information, peering the local (logarithmic) unit of information, the nat. Likewise, NBL PMFs represent normalized information regarding the global base b, $Pr\left(b,\left[s,t\right)\right)\equiv {\left[\mathcal{L}\left(q\right)\right]}_s^t{\left[\mathcal{L}\left(q\right)\right]}_1^b$, or the local radix locally, $Pr\left(r,\left[i,j\right)\right)\equiv {\left[\ell \left(d\right)\right]}_i^j{\left[\ell \left(d\right)\right]}_1^r$. Likelihood is space on a harmonic (global) or logarithmic (local) scale; for example, if we assume that the bit ($2^1$ possible states) is the minimal (unit) length [40], one byte ($2^8$ possible states) has length eight. If our world is positional, likelihood and entropy would have metric units of length for all practical purposes, meaning that information is a physical and manageable resource.

Rationality in its purest form appears as the NBL probability of a quantum ${\displaystyle \frac{1}{H_{b-1}}}{\displaystyle \frac{1}{q}}$ or a jump ${\displaystyle \frac{1}{H_{b-1}-H_{b-1,2}}}{\displaystyle \frac{q}{{\left(q+1\right)}^2}}$, with masses separable as the product of a function of b and a function of q. However, the relational character of the universal rational setting pops up in all its splendor when we address probability ratios. The odds value between between a pair of numbers, quanta, or numerals is the quotient of their picking probabilities, quantifying the strength of their association. Assuming $a<b$, $Pr\left(a\right)Pr\left(b\right)>1$ estimates how uncorrelated a and b are; if $Pr\left(a\right)Pr\left(b\right)\approx 1$, both events are mutually dependent.

Then, a source encodes, recodes, and decodes odds using Bayes’ law, reminding us that ratios are the atoms of a coding process. The global Bayes’ rule says that the odds of quantum s against t in base b are the odds of the number s versus t times the probability of the bucket $\left[s,t\right)$ in base b. The local Bayes’ rule says that the odds of digit i against j with radix r are the global odds of the quantum i versus j times the probability of the bin $\left[i,j\right)$ with radix r. Both represent the entropic contribution of the items in a range to a positional scale, confirming that information is relational.

Exceptional cases of Bayesian data are the cross-ratio, a conformality invariant, and the referential ratios ${\displaystyle \frac{A-B}{A-C}}$, the basis for relativity. Despite the conformal coding functions using the logarithm and the exponential function, power (infinite) series by definition, the coding source adds or multiplies incrementally a finite series of referential ratio powers to throw a rational result at any time, bettering the approximation with the number of iterates. Rationality is intricately intertwined with decidability in polynomial time and interruptible algorithms in evolving scenarios [41].

Numeric values do not contain information per se, while a common property makes two entities commensurable, with the global base and the local radix as main referents. We can take global Bayesian data as rational quanta, computable numbers, and local Bayesian data as observable correlations of numerals. In the end, mathematics is $\mathbb{Q}$-based, and physics is relational.

3. The Whole Story of NBL

We comment on the aspects of the academic story of the fiducial NBL most relevant to our essay and then traverse the deductive road to it. We have discovered many findings on the run related to the nature of the information at a fundamental level.

First, we introduce an inverse-square law as the origin of NBL. This PMF subsumes a probability law of rational masses, giving place to a normalized universal PN system to manage a hyperbolic, thrifty, and relational world. This harmonic scale system employs a global base as a fundamental referent. When the global base is immense, the scale’s rational setting approaches a domain of real variables and functions ruled by small radices in local settings. In other words, we prove that the local NBL, as everybody knows it, assumes that a prior all-encompassing base exists. Eventually, the interplay between the global base and the local radix will enable us to determine the canonical metric ascribed to a coding source’s conformal space containing an image of the world.

3.1. The Tortuous Road to NBL

The first digits of the numerals found in data series of the most varied sources of natural phenomena [42] do not display a uniform distribution but rather exhibit that the minor ones are the more likely (see [43] for a detailed bibliography and [44,45] for a general overview). Specifically, this law of anomalous numbers claims that the universe obeys an exponential distribution to a greater or lesser extent.

Newcomb’s insight was, The law of probability of the occurrence of numbers is such that all mantissae of their logarithms are equally probable. (What Newcomb refers to as mantissa is what we will call significand.) More than half a century later, Benford defined the exact formula of every random variable satisfying the first-digit (and other digits) law [2]. He could not derive it formally, although seeded a line of research asserting that The basic operation $F=\int {\displaystyle \frac{\mathrm{d}\mathrm{X}}{\mathrm{X}}}$ or $F=\sum {\displaystyle \frac{\Delta \mathrm{X}}{\mathrm{X}}}$ in converting from the linear frequency of the natural numbers to the logarithmic frequency of natural phenomena and human events can be interpreted as meaning that, on the average, these things proceed on a logarithmic or geometric scale.

However, this transition from $\mathbb{N}$ to $log\mathbb{N}$, when the baseline set is unlimited, implies tackling the problem of picking an integer at random [46], and then mathematical difficulties arise. To commence, numerals beginning with a specific digit do not have a natural density. The decimal sequence $\left\{1,11,12,13,\dots ,100,101,102,103\dots \right\}$ that groups the first digits does not converge (e.g., oscillates). Moreover, suppose each natural occurs with equal probability. In that case, the whole space must have probability 0 or ∞, violating countable additivity (by which the measure of a set must be nonzero, finite, and equal to the sum of the measures of the disjoint subsets); hence, we cannot construct a viable discrete probability distribution. The attempt to choose $P\left(N\right)=1N$ fails because it diverges in the limit; it is not countably additive. Furthermore, a universal law such as NBL is supposed to be scale-invariant. However, there are no scale-invariant probability distributions on the Borel (measurable) subsets of the positive reals because the probability of the sets $\left[0,1\right]$ and $\left[0,s\right]$ would be equal for every scale $0\le s\le 1$, disobeying once more countable additivity [47].

Hill [48] resumed Newcomb’s idea; logarithm’s significands of sequences conformant to NBL trace a uniform distribution. He identified an appropriate domain for the natural probability space and, based on the decimal mantissa ςv-algebra (where countable unions and intersections of subsets can be assigned a gauge), formally deduced the law for the first digit and joint distribution of the leading digits. He also provided a new statistical log-limit central-limit-like significant-digit law theorem that stated the scale-invariance, base-invariance, sum-invariance, and uniqueness of NBL. The cumulative distribution function is $Pr\left(r,d\le m\right)={log}_r\left(1+m\right)$, where $d,m\in \left[1..r\right)$ and r is the radix.

Since Hill’s publication in 1995, more derivations have come to light, one of the subtlest appearing in [49] (section $14.2$). Nonetheless, they all ignore foundational causes.

3.2. Properties of the Distribution

A vehicle of NBL is how different measurement records spread and repositories aggregate data. For one thing, the significant-digit frequencies of random samples from random distributions converge to conform to NBL, even though some of the individual distributions selected may not [50]. Besides, many real-world examples of NBL arise from multiplicative fluctuations [51]. What happens is that the absorptive property, exclusive of the fiducial NBL, kicks in [52]; if X obeys Benford’s law, and Y is any positive statistic independent of X, then the product XY also obeys Benford’s law – even if Y did not obey this law. To boot, variable multipliers (or variable growth rates) not only preserve Benford’s law but stabilize it by averaging out the errors.

Which standard probability distributions obey NBL? Rarely does a distribution of distributions disagree with NBL [53]. The ratio distribution of two uniform, two exponential, and two half-normal distributions approximately stick to NBL. The Pareto distribution enjoys the scale-invariance property as long as we move from discrete to continuous variables, and Zipf’s law ($\propto 1z^{\alpha }$ with $\alpha \approx 1$) satisfies the abovementioned absorptive property if one stays over the median number of digits [52]. More generally, right-tailed distributions putting most mass on small values of the random variable (i.e., survival or monotonically decreasing like the log-logistic distribution) are just about compliant with NBL [28] (e.g., the tail of the Yule–Simon distribution [54]). The Log-normal distribution fits NBL, and the Weibull and Inverse Gamma distributions are close to NBL under certain conditions [55]. In short, NBL embraces an ample range of statistical models and mixtures of probability distributions.

Empirical testing of random numerals generated according to the exponential and the generalized normal distributions reveals adherence to NBL [56]. More precisely, almost every exponentially increasing positive sequence is Benford (e.g., sequences of power $a^n$, where $a>1$), and every super-exponentially increasing or decreasing positive sequence (e.g., the factorial) is Benford for almost every starting point [57]. Further, an NBL-compliant data series is inherently sturdy because of its invariance to changes concerning sign, base, and scale [58]; for instance, mining data about the lifetime of mesons or antimesons in microseconds in decimal or seconds in binary results in strict observance of the law.

All these mathematical circumstances we have summarized about NBL explain why it is so widespread but not its reason. Failure to comprehend this distinction has generated confusion and is a typical scientific misunderstanding [59]. In other cases, authors have deemed specific remarks about NBL its cause when they are indeed consequences [60].

We will explain why discrete distributions decaying as $\propto 1z^{\alpha }$ with $\alpha \in {\mathbb{Q}}^{\left(1,2\right]}$ are indirectly NBL-compliant. The common factor of all the quasi-NBL distributions is that proportional data intervals approximately fit their heavy tail (the fatter, the better). Notably, this work does not deal with the NBL invariances as presumed properties but derives them from basic requirements demanded from the canonical PMF, producing a subsidiary global NBL and, thereon, the fiducial NBL. The appearance of NBL in power sequences indeed concerns how PN codes probability ratios (odds), where the logarithm and the exponential constitute a fundamental functional duality. The intricate and critical linkage of the law with the rational numbers jumps out.

3.3. A Fundamental Probability Law

We seek a well-defined PMF, i.e., positive probabilities summing to 1. Not all Zipfian distributions [61] can do the job, for $Pr\left(N\right)\propto N^{-a}$ eludes divergence only if $a>1$. In particular, linear forms for the denominator of a natural’s probability cannot fulfill countable additivity.

We assume that $\mathbb{N}$ is an inductively constructible set from which all physical phenomena can crop up from the source outward, a basis of reductionism and weak emergency [62]. By including nil, we also ponder infinity as its reciprocal. However, both projective concepts are only potential and limiting numbers in the offing; employing the successor and predecessor as symmetric constructors, we must be able to choose any number strictly between 0 and ∞ so that no counting number is extraordinary. Again, many Zipfian distributions cannot do the job, for $Pr\left(N\right)\propto N^{-a}$ has a diverging mean only if $a\le 2$. For instance, cubic or higher polynomials lead to convergent expected values.

Additionally, we require a sound and dependable extension to the integers. Zipfian distributions where a is an even natural do the job, but in the range $a\in \left(1,2\right]$ defined by the two previous requirements, $a=2$ is the fitting choice, the only value assuring central reflection symmetry. To cap it all, $Pr\left(N\right)\propto N^{-2}$ agrees with the minimal information principle [63]; considering other quadratic polynomials for the denominator of a natural’s probability does not yield a better law because it would introduce unwarranted assumptions in vain. For instance, the Zipf–Mandelbrot law [64] $Pr\left(N\right)=1\left(N^2-5N+7\right)$ deals with unexplained coefficients and is not centrally symmetric.

Therefore, the PMF of a random variable X taking natural numbers is

$$Pr\left(X=N\in \mathbb{N}\right)=\left\{\begin{array}{cc}N\in \mathbb{N}-\left\{0\right\}:\hfill & {\displaystyle \frac{ϵ}{N^2}}\hfill \\ else:\hfill & 1-ϵ\zeta \left(2\right)\hfill \end{array}\right.$$

(1)

We will suppose the proportionality parameter $ϵ\in {\mathbb{Q}}^{+}$ to comply again with the minimal information principle. $\zeta \left(2\right)={\pi }^{2}6$ is the value of the Riemann zeta function at 2, brewing gently as a factor of endless aggregation of occurrence probabilities. Because the else (null) case is possible, this PMF is not a pure zeta distribution [65].

Countable additivity holds; the probabilities sum to 1 owing to

$$\sum _{N=1}^{\infty }{\displaystyle \frac{ϵ}{N^2}}=ϵ\zeta \left(2\right)$$

The picking event X is fair owing to the indeterminacy of the expected value of a natural number, i.e.,

$$\widehat{E}\left(X\right)=0\left(1-ϵ\zeta \left(s\right)\right)+\sum _{N=1}^{\infty }N{\displaystyle \frac{ϵ}{N^2}}=ϵ\sum _{N=1}^{\infty }{\displaystyle \frac{1}{N}}=\infty$$

Indeed, the nth-order moment diverges for all nonzero $n\in \mathbb{N}$.

This PMF does not assume the law of large numbers or the law of rare events. On the contrary, it works under the statistical assumption of independence of occurrences and no bias. Outcomes of the picking event are unpredictable, even considering an indefinite trail of repetitions. No predetermined constant mean exists in space or time, nor is there an absolute measure of rarity; the relative frequency between two events solely depends on their probability mass. We can regard it as a brute law.

Let us leave the rational $ϵ$ unfixed for the time being, given that it is unimportant for the derivation of NBL. Remember that $ϵ\in \left(0,6{\pi }^2\right)$ holds the constraint $Pr\left(N\in \mathbb{N}\right)>0$ (i.e., $ϵN^2>0$ and $ϵ\zeta \left(2\right)<1$), and we will return to it in subSection 7.1.

3.4. The Rational (Global) Version of NBL

In analytic number theory, the mesmerizing Euler-Mascheroni constant $\gamma$ ([66], section $1.5$) is the limiting difference between the harmonic series and the logarithm, i.e.,

$$\underset{N\to \infty }{lim}{H}_N-lnN\sim \gamma$$

where $H_N\equiv {\sum }_{k=1}^N{\displaystyle \frac{1}{k}}$ is the Nth harmonic number. If our universe is as harmonic as logarithmic [49], the discrete version of the NBL must exist connected to but separated from the continuous (fiducial) one.

The cumulative distribution function of a random variable X obeying (1) is

$$Pr\left(1\le X<N\right)=ϵ\sum _{k=1}^{N-1}{\displaystyle \frac{1}{k^2}}$$

which tells us how often the random variable X is below N. We call its complementary function natural exceedance probability, quantifying how often X is on level N or above. This dwindling distribution function is

$$Pr\left(X\ge N\right)=Pr\left(X\ge 1\right)-Pr\left(1\le X<N\right)=ϵ\left(\zeta \left(2\right)-H_{N-1,2}\right)$$

where $H_{N,2}\equiv {\sum }_{k=1}^{N}1k^2$ is the generalized Nth harmonic number in power 2.

We can express this probability in terms of the second derivative of the gamma function $\Gamma \left(x\right)$’s logarithm, i.e., the digamma function’s first normal derivative, defined as

$${\psi }^{\prime }\left(x\right)={\left[{\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}ln\left(\Gamma \left(x\right)\right)\right]}^{\prime }={\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}{\displaystyle \frac{{\Gamma }^{\prime }\left(x\right)}{\Gamma \left(x\right)}}$$

Since $\zeta \left(2\right)={\psi }^{\prime }\left(1\right)$ and ${\psi }^{\prime }\left(N+1\right)={\psi }^{\prime }\left(N\right)-1N^2={\psi }^{\prime }\left(1\right)-{\sum }_{k=1}^{N}1k^2$, the natural exceedance of N is

$$Pr\left(X\ge N\right)=ϵ{\psi }^{\prime }\left(N\right)$$

Numbers lack physicality. If numbers were frequencies, the trigamma function would represent a probability fractal signal such that the occurrence probability density (i.e., per frequency range) decays proportionally with the signal’s frequency.

Regardless of the scale, let us divide the natural line into concatenated strings of numbers of the same length, which we name quanta. Then, the second-order cumulative function arrives on the scene for global computability. The plot of $ϵ\psi \left(q\right)+constant$, the natural exceedance’s antiderivative, has an informational flavor. A significant value of the quantum q is more unpredictable and influential than a minor one; this harmonic surprise needs a medium to reify the event occurrence, and the extent of the resulting log note $\psi \left(q\right)$ is its only measure.

So, how likely is the event $X=q$ to fall into bucket $\left[s,t\right)$, assuming a harmonic scale underneath? The natural harmonic likelihood $\mathcal{L}$ depends on the bucket’s extent, namely

$${\left[{\mathcal{L}}_X\left(q\right)\right]}_s^t\equiv {\displaystyle \frac{{\left[ϵ\psi \left(q\right)+constant\right]}_s^t}{{\left[ϵ\psi \left(q\right)+constant\right]}_1^2}}={\displaystyle \frac{{\left[\psi \left(q\right)\right]}_s^t}{{\left[\psi \left(q\right)\right]}_1^2}}=H_{t-1}-H_{s-1}=\mathcal{L}\left(\left[s,t\right)\right)\in \mathbb{Q}$$

(2)

in natural harmonic units of (global) information, where we have considered the generalized recurrence relation $\psi \left(t+1\right)-\psi \left(s+1\right)=H_t-H_s$. Note that (2) is a proportion, canceling the constant $ϵ$.

The natural harmonic likelihood is neither the probability of a quantum falling into $\left[s,t\right)$ nor the probability that $\left[s,t\right)$ is the truth given the observation $X=q$. It is the information obtained by picking a quantum from the bucket $\left[s,t\right)$ or the information that $X=q$ gives when $s\le q<t$, i.e., the space allocated to encode a quantum between the bucket’s ends, which is why it does not refer to q.

The harmonic number function (interpolated to cope with rational arguments) parallels the continuous world’s logarithmic function in information theory, like in analytic number theory. $\mathcal{L}\left(\left[1,2\right)\right)\equiv H_1-H_0=1$ represents the harmt (a portmanteau of harmonic unit), just as the natural local information unit, the nat, corresponds to $\left[1,e\right)$ by ${\left[lnx\right]}_1^e=1$. Thus, natural harmonic and logarithmic likelihoods are analogous, as we will explain in Section 3.6. In particular, $\mathcal{L}\left[q,q+1\right)=\psi \left(q+1\right)-\psi \left(q\right)=H_q-H_{q-1}=1q$ implies that q’s reciprocal denotes information, precisely the natural likelihood of an elemental quantum gap.

A global base b marks the boundary between the mathematical and physical world. We define the probability mass of bucket $\left[s,t\right)$ regarding b’s support as the harmonic likelihood ratio

$$Pr\left(b,\left[s,t\right)\right)={\displaystyle \frac{\mathcal{L}\left(\left[s,t\right)\right)}{\mathcal{L}\left(\left[1,b\right)\right)}}={\displaystyle \frac{H_{t-1}-H_{s-1}}{H_{b-1}}}\in \mathbb{Q}$$

(3)

where $1\le s<t<b$ and $s,t,b\in \mathbb{N}$. This probability is separable as a product of $\left[s,t\right)$’s and b’s functions, expressing a part of the information total that is the b-normalized rational quantum $ts$’s length or bucket $\left[s,t\right)$’s width.

The reader can object that the concept of likelihood is unnecessary to define (3) since we can directly define the probability of a bucket as ${\left[\psi \left(q\right)\right]}_s^t{\left[\psi \left(q\right)\right]}_1^b$. However, we aim to stress that we get information regardless of the base, only relative to the natural harmonic bucket ${\left[\psi \left(q\right)\right]}_1^2$. Because $\left[1,b\right)$ gives the maximum likelihood estimate, $Pr\left(b,\left[s,t\right)\right)$ is the relative likelihood function [67] of the bucket $\left[s,t\right)$ given $1\le s<t<b$.

When $s=q$ and $t=q+1$, we obtain

$$Pr\left(b,q\right)={\displaystyle \frac{\mathcal{L}\left(\left[q,q+1\right)\right)}{\mathcal{L}\left(\left[1,b\right)\right)}}={\displaystyle \frac{H_q-H_{q-1}}{H_{b-1}}}=\left({\displaystyle \frac{1}{H_{b-1}}}\right)\left({\displaystyle \frac{1}{q}}\right)\in \mathbb{Q}\left(1\le q<b\right)$$

(4)

We measure this PMF in b-ary harmonic information units. It is the simplest case of Zipf’s law, geometrically an embryonic form of progressive one-dimensional circle inversion. Further, if q represented a frequency, we could understand the probability of a quantum with a given base as a (physical) potential diminishing hyperbolically with the distance from the source, i.e., a flicker [68] or pink [69] noise.

We have described how the harmonic series bridges equations (1) and (4). Both laws point to minor numbers as the most frequent significands, amassing more probability around the source to increase accessibility. However, we find three main differences between them:

• (1)’s probability masses are rational numbers. Instead, a quantum’s probability represents an area ratio measured through the digamma function; hence, a quantum’s probability is a quota of information.
• The global NBL outlines a hyperbola instead of an ISL. Thus, while the probability of a number is inversely proportional to its norm (the number’s square), the probability assigned to a quantum is inversely proportional to its modulus (the quantum’s absolute value).
• (4) gives us the thing-as-it-appears (perceived potential) stemming from the thing-in-itself (field per se) [70] expressed by (1), two sides of the same property or object, the dual essence of the world.

3.5. Analysis of the Global NBL

The global ($\mathbb{Q}$-based) NBL’s average probability for the decimal system is $1/9{\sum }_{q=1}^{q=9}{\left(q{H}_{10-1}\right)}^{-1}=1/9=.\overline{1}\approx \left[11\right]\%$, which is equal to the local ($\mathbb{R}$-based) NBL’s average probability (due to ${\sum }_{d=1}^{d=9}log\left(1+1d\right)=1$). The mean value for the quanta 1 to 9 following the global NBL is $q\approx 3.18$ (from $Pr\left(10,q\right)=1/9$), whereas it is $d\approx 3.43$ (from $log\left(1+1d\right)=1/9$) for the local NBL. The harmonic mean value for the quanta 1 to 9 following the global NBL is $q=\left(9+1\right)2=5$.

As expected, Equation (4) brings $Pr\left(2,1\right)=1$, i.e., 1 occupies $100\%$ of the space in binary. In base 3, the appearance probabilities of 1 and 2 as the first quantum are $Pr\left(3,1\right)=2/3$ and $Pr\left(3,2\right)=1/3$, respectively, a 2/1 sharing out. We deem this Pareto rule so rudimentary that it might be fundamental in physics. The corresponding Pareto rule is 6337 if we utilize the local NBL. Quantum 1 in decimal occupies $Pr\left(10,1\right)=2520/7129\approx 35.3\%$, while it is $30.1\%$ using the local NBL. 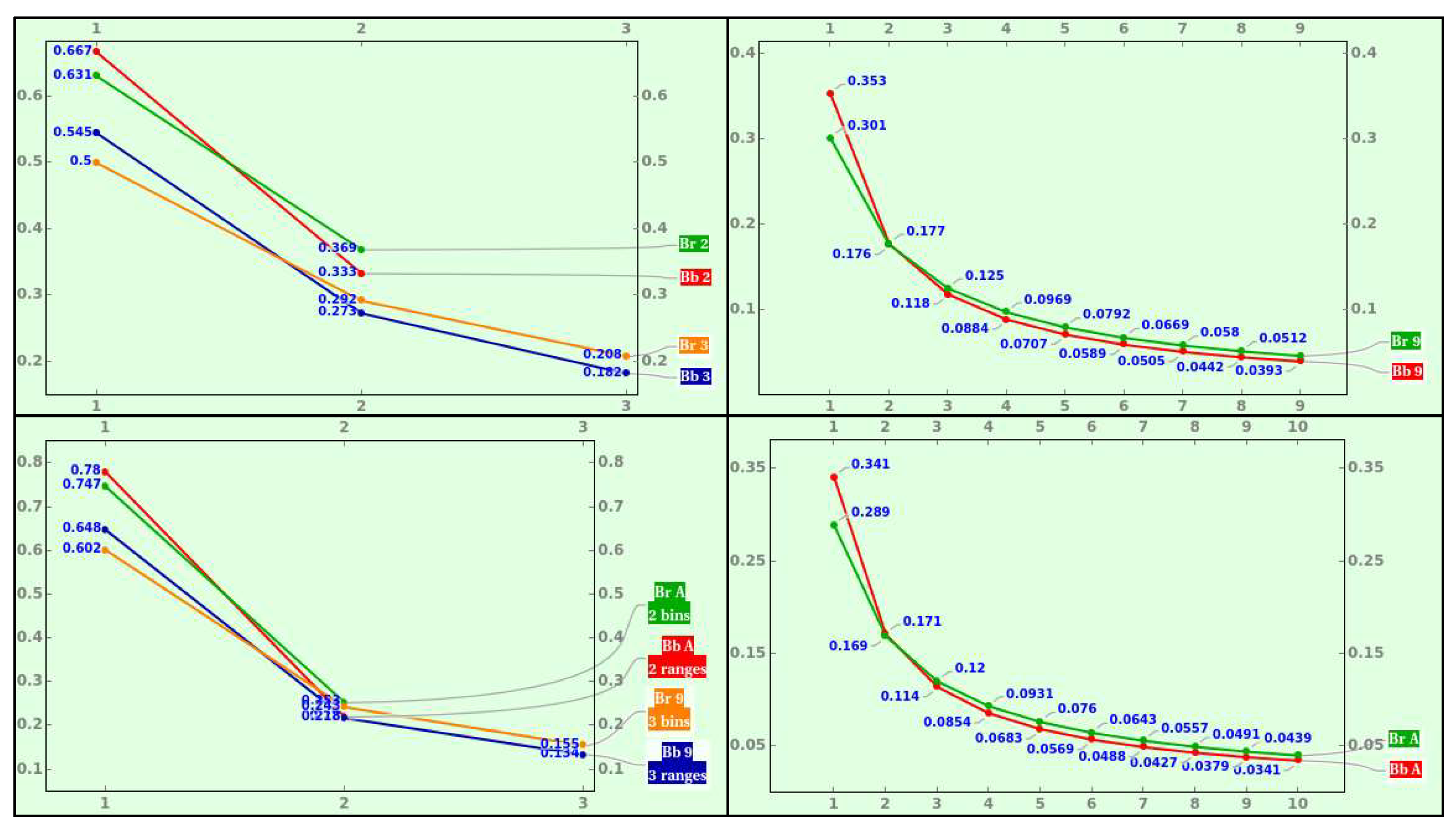Figure 2 compares the probability of a decimal datum’s first position value between the global, discrete, rational, countable, harmonic NBL and the local, continuous, real, uncountable, logarithmic one. Regardless of the cardinality, the former is always steeper.

The unit bucket a quantum represents can be of any size, so we can recursively perform the integration and normalization process that gave rise to (4) within every quantum attributed to base b, obtaining a chain of nested quanta. The probability of getting the leading chain c of quanta with any length in b-ary is simply

$$Pr\left(b,c\right)={\displaystyle \frac{H_c}{H_{b-1}}}-{\displaystyle \frac{H_{c-1}}{H_{b-1}}}={\displaystyle \frac{1}{c{H}_{b-1}}}\in \mathbb{Q}$$

It represents c’s likelihood in b-ary harmonic units and becomes (4) when c is a base’s quantum. For example, the probability masses that a decimal chain starts with 10 (e.g., $0.1071$) and 99 (e.g., 992) are $Pr\left(10,10\right)={\left(10H_9\right)}^{-1}\approx 0.03535$ and $Pr\left(10,99\right)={\left(99H_9\right)}^{-1}\approx 0.00357$.

3.6. The Fiducial (Local) NBL

The global NBL furnishes the frame for constructing a sheer logarithmic system that conserves base and scale. To achieve such a pursuit, we must turn to the local context of a coding source and analyze how it represents a numeral in PN.

We call a bin of digits to a bucket of quanta in the source’s proximity. The third-order cumulative function of (1) arrives on the scene to facilitate local computability. When the base b is enormous, we can handle digits like real values to calculate the antiderivative of (4), $lnd{H}_{b-1}+constant$, which outlines how unexpected and momentous digit d is. Large values locally transmit more information than small ones; for whom? Logarithmic surprise needs an observer to reify the event occurrence. The harmonic information perceived by a receiving system, a coding source, becomes local information with extension $lnd$. Consequently, broad bins are more likely than narrow ones as supporting evidence.

Assuming a logarithmic scale underneath, we define the natural logarithmic likelihood ${\ell }_Y$ of the event $Y=d<b$ to fall into bin $\left[i,j\right)$ as the ratio

$${\left[{\ell }_Y\left(d\right)\right]}_i^j\equiv {\displaystyle \frac{{\left[\frac{lnd}{H_{b-1}}+constant\right]}_i^j}{{\left[\frac{lnd}{H_{b-1}}+constant\right]}_1^e}}={\displaystyle \frac{{\left[lnd\right]}_i^j}{{\left[lnd\right]}_1^e}}=ln{\displaystyle \frac{j}{i}}=\ell \left(\left[i,j\right)\right)\in \mathbb{R}$$

(5)

Note that this proportion no longer refers to base b; a coding source is unaware of the global setting for calculation purposes.

The natural logarithmic likelihood is neither the probability of a digit falling into $\left[i,j\right)$ nor the probability that $\left[i,j\right)$ is the truth given the observation $Y=d$. It is the information obtained by picking a digit from the bin $\left[i,j\right)$ or the information that $Y=d$ gives when $i\le d<j$, i.e., the space allocated to encode a digit between the bin’s ends, which is why it does not refer to d. However, it has nothing to do with surprisal [71]; ℓ denotes informative space rather than information content. Indeed, we can take it as the natural positional length of $ji$ or the natural width of $\left[i,j\right)$. We can also take (5) as the differential entropy of the uniform probability density function $Pr\left(x\right)=ij\forall x<ji$.

We measure the natural logarithmic likelihood in natural units (nats) because of ${\left[lnd\right]}_1^e=1$. It is manifestly scale-invariant; since the area of a hyperbolic sector (in standard position) from $\left(1,1\right)$ to $\left(x,1x\right)$ is $lnx$, another way to define invariance of scale is that a squeeze (geometrical) mapping boosts the logarithmic likelihood up or down arithmetically (see [49] chapter I).

The domain of a digit d spans from the unit to $r-1$, where $r\ll b$ is the cardinality of the local coding space, precisely the source’s radix. We define the r-ary probability mass of bin $\left[d_1,d_2\right)$ relative to the radix’s support as the logarithmic likelihood ratio

$$Pr\left(r,\left[d_1,d_2\right)\right)={\displaystyle \frac{\ell \left(\left[d_1,d_2\right)\right)}{\ell \left(\left[1,r\right)\right)}}={\displaystyle \frac{ln\frac{d_2}{d_1}}{lnr}}={log}_r{\displaystyle \frac{d_2}{d_1}}\in \mathbb{R}\left(1\le d_1<d_2<r\right)$$

(6)

with $d_1,d_2,r\in \mathbb{N}$. We can take it as the representation length of $d_2{d}_1$ or the width of $\left[d_1,d_2\right)$ in r-ary logarithmic information units, in correspondence with equation (3), reckoning the probability of a bucket as a normalized harmonic likelihood. Therefore, in PN, the probability is a quota of the available space, a view we will develop in subSection 5.1 and Section 5.2.

Geometrically, the probability of event $d_1\le d<d_2$ conditioned to r is the ratio between the areas under the hyperbola delimited by bins $\left[d_1,d_2\right)$ and $\left[1,r\right)$, equivalent to the area enclosed by the rays $1d_1$ and $1d_2$ relative to the span of the hyperbolic angle r. Because the hyperbola preserves scale changes, the logarithm uniformly distributes the significant digits of a geometrical sequence, as Newcomb underlined in his note; $klnx=ln{x}^k$ implies that, for example, x must drop to $\sqrt[3]{x}$ to divide the natural likelihood by three ($k=1/3$).

By setting in (6) $d_1=d$ and $d_2=d+1$ , we fit the Y’s occurrences into the digits of a standard PN system with radix r, obtaining

$$Pr\left(r,d\right)={log}_r\left(1+{\displaystyle \frac{1}{d}}\right)\in \mathbb{R}$$

(7)

The original natural random variable $Y\in \mathbb{N}$ and the underlying global base b are absent. This expression is the local (fiducial) NBL, which tells us the PMF of a r-ary numeral’s first digit.

A coding system (observer or source) that uses standard PN handles the unit range as a concatenation of the sub-bins $\left[{log}_{r}1,{log}_{r}2\right)=\left[0,{log}_{r}2\right)$, $\left[{log}_{r}2,{log}_{r}3\right)$, ... $\left[{log}_r\left(r-1\right),{log}_{r}r\right)=\left[{log}_r\left(r-1\right),1\right)$, covering intervals of ${log}_{r}2/1$, ${log}_{r}3/2$, ... ${log}_{r}r\left(r-1\right)$ units of space, and corresponding to the symbols 1, 2, ... and $r-1$, respectively; the addition of these areas is the unit.

More fundamentally, common digits are near the coding source, i.e., the probability of a digit correlates with its accessibility and declines logarithmically. If we liken probability mass to space, smaller digits induce more density than significant digits. In other words, accessibility concentrated around the origin progressively dilutes as we move away, contrasting with the linear scale that distributes the space evenly.

We can generalize (6) to cope with bins outside the radix. The resulting expression is not generally a probability anymore, given that we can have bins of any size, but it is again an r-normalized likelihood that retains the geometric interpretation. In other words,

$$\ell \left(\left[n_1,n_2\right)|r\right)={\displaystyle \frac{\ell \left(\left[n_1,n_2\right)\right)}{\ell \left(\left[1,r\right)\right)}}={log}_r{\displaystyle \frac{n_2}{n_1}}\in \mathbb{R}\left(1\le n_1<n_2\right)$$

(8)

is the r-normalized $n_2{n}_1$’s length or $\left[n_1,n_2\right)$’s width. We can regard it as a fractal dimension where r is the scaling factor, $n_2$ is the number of measurement units, and $n_1$ is the number of fractal copies. For instance, (8) might explain the Weber-Fechner law [72] in psychophysics, where $\ell \left(\left[n_1,n_2\right)|r\right)$ is the intensity of human sensation, $1lnr$ is a perception- and stimulus-dependent proportionality constant, $n_2$ is the strength of the stimulus, and $n_1$ is the zeroing strength threshold.

When $n_1=n$ and $n_2=n+1$, we can again interpret this likelihood as the probability of getting a leading r-ary numeral $n\in {\mathbb{N}}^{+}$ of any length, i.e.,

$$Pr\left(r,n\right)=\ell \left(\left[n,n+1\right)|r\right)={log}_r\left(n+1\right)-{log}_{r}n={log}_r\left(1+{\displaystyle \frac{1}{n}}\right)\in \mathbb{R}$$

The efficiency of a r-ary numeral system worsens as $r\to 1^{+}$ or $r\to b\to \infty$[73] because r diverges from the optimal radix economy, namely Euler’s number e, destroying the information. In the former case, we encounter the unary system, which boils down to a linear frequency. In the latter case, the numerals $n<r$ that only use the first position increase limitlessly. Both are no-coding cases.

4. A Curious Effect

We prove that the Kempner distribution reflects the rational version of NBL for bijective numeration, allows figuring a natural resolution in PN, and confirms a global tendency towards smallness.

Watch the notation; we display the base and the radix underlined to denote bijective numeration rather than standard notation.

4.1. NBL for Bijective Numeration

Suspicion about the authenticity of the number cero [74] suggests that bijective PN is likely more natural than standard PN, the number system we use daily. Various curious series we will analyze in the following subsection, specifically the Kempner distribution, append additional evidence that NBL for bijective numeration [75] is foundational and universal.

Every formula about the NBL for standard PN has a bijective peer. Following the same plot thread we developed in Section 3.4, a sample of chains encoded using bijective $\underline{b}$-ary satisfies the global NBL if the leading quantum falls in bucket $\left[s,t\right)$ relative to the area swept by base $\underline{b}$ with probability

$$Pr\left(\underline{b},\left[s,t\right)\right)={\displaystyle \frac{H_{t-1}-H_{s-1}}{H_{\underline{b}}}}\in \mathbb{Q}$$

where $1\le s<t\le \underline{b}$ and $s,t,\underline{b}\in \mathbb{N}$. When $s=q$ and $t=q+1$ we obtain the probability with base $\underline{b}$ of leading quantum q,

$$Pr\left(\underline{b},q\right)={\displaystyle \frac{1}{q{H}_{\underline{b}}}}\in \mathbb{Q}\left(1\le q\le \underline{b},\left\{q,\underline{b}\right\}\in \mathbb{N}\right)$$

(9)

Thus, NBL for the standard PN in base $b+1$ corresponds to NBL for bijective $\underline{b}$-ary numeration. For example, we obtain $Pr\left(\underline{1},1\right)=\left[100\right]\%$, $Pr\left(\underline{3},1\right)=6/11\approx \left[54.5\right]\%$, $Pr\left(\underline{3},2\right)=3/11\approx \left[27.3\right]\%$, $Pr\left(\underline{3},3\right)=2/11\approx \left[18.2\right]\%$, $Pr\left(\underline{\mathrm{A}},1\right)=0.34142$, and $Pr\left(\underline{\mathrm{A}},\mathrm{A}\right)=0.03414$, where $\underline{\mathrm{A}}$ symbolizes the bijective decimal base. Owing to $Pr\left(\underline{2},1\right)=2/3$ and $Pr\left(\underline{2},2\right)=1/3$, the odds $o\left(2:1|\underline{2}\right)=Pr\left(\underline{2},2\right)Pr\left(\underline{2},1\right)=\text{½}$ constitute an essential sharing out.

The entropy of PMF (9), $\tilde{E}\left(\underline{b}\right)$, is the expected value (weighted arithmetic mean) of the harmonic likelihood function ($\psi \left(x\right)-\psi \left(1\right)=H_{x-1}$) evaluated at the probability mass reciprocal, i.e.,

$$\tilde{E}\left(\underline{b}\right)=\widehat{E}\left(Pr\left(\underline{b},q\right)\right)=\left[\sum _{q=1}^{q=\underline{b}}{\displaystyle \frac{H_{q{H}_{\underline{b}}-1}}{q{H}_{\underline{b}}}}\right]harmt$$

For example, $\tilde{E}\left(\underline{1}\right)=0$, $\tilde{E}\left(\underline{2}\right)=0.90914$, $\tilde{E}\left(\underline{3}\right)=1.35432$, $\tilde{E}\left(\underline{10}\right)=2.47676$, and $\tilde{E}\left(\underline{100}\right)=4.2269$. When $\underline{b}$ acquires a gargantuan value, we can take the summation as an integral and the harmonic number function as the natural logarithm, so that the differential entropy [76] of the global NBL approximately tends to

$${\int }_1^{\underline{b}}{\displaystyle \frac{ln\left(qln\underline{b}\right)}{qln\underline{b}}}\mathrm{d}q=\text{½}ln\underline{b}+ln\left(ln\underline{b}\right)$$

Thus, the global entropy is finite, which agrees with the Bekenstein bound in physics.

The probability of picking a chain of any length starting with c is the likelihood gap it induces on the $\underline{b}$-ary harmonic scale, i.e.,

$$Pr\left(\underline{b},c\right)={\displaystyle \frac{H_c}{H_{\underline{b}}}}-{\displaystyle \frac{H_{c-1}}{H_{\underline{b}}}}={\displaystyle \frac{1}{c{H}_{\underline{b}}}}\in \mathbb{Q}$$

which becomes (9) when c is a base’s quantum. For example, the probability that a bijective decimal chain starts with 11 (e.g., $.111$) and $\mathrm{A}\mathrm{A}$ (e.g., $\mathrm{A}\mathrm{A}\mathrm{A}\mathrm{A}$) is $Pr\left(\underline{\mathrm{A}},11\right)=1\left(11H_{10}\right)\approx 0.03104$ and $Pr\left(\underline{\mathrm{A}},\mathrm{A}\mathrm{A}\right)=1\left(110H_{10}\right)\approx 0.003104$, respectively.

This result allows us to derive the probability of picking a length-l bijective $\underline{b}$-ary chain starting with the quantum q,

$$Pr\left(\underline{b},l,q\right)={\displaystyle \frac{{\sum }_{k=q{\underline{b}}^{l-1}+\frac{{\underline{b}}^{l-1}-1}{\underline{b}-1}}^{k=\left(q+1\right){\underline{b}}^{l-1}+\frac{{\underline{b}}^{l-1}-1}{\underline{b}-1}-1}\frac{1}{k}}{H_{\frac{{\underline{b}}^{l+1}-1}{\underline{b}-1}-1}-H_{\frac{{\underline{b}}^l-1}{\underline{b}-1}-1}}}\in \mathbb{Q}$$

where $1\le q\le \underline{b}$, $\underline{b}>1$, and $\left\{\underline{b},l,q\right\}\in {\mathbb{N}}^{+}$. For instance, the probability of running into 1 to 3 as the first quantum of a bijective ternary chain with length 5 is $\left\{0.46565,0.30602,0.22833\right\}$, and the chances of choosing 1 to $\mathrm{A}$ as the first quantum of a bijective decimal chain with length 2 is $\left\{0.2842,0.1688,0.1205,0.09377,0.07677,0.065,0.05637,0.04976,0.04454,0.04031\right\}$. Watch that this equation boils down to (9) if $l=1$.

Too, the probability that we run into q as the p-th quantum of a bijective $\underline{b}$-ary chain is

$$Pr\left(\underline{b},q,p\right)={\displaystyle \frac{{\sum }_{k=\frac{{\underline{b}}^{p-1}-1}{\underline{b}-1}}^{k=\frac{{\underline{b}}^p-1}{\underline{b}-1}-1}\frac{1}{\underline{b}k+q}}{H_{\frac{{\underline{b}}^{p+1}-1}{\underline{b}-1}-1}-H_{\frac{{\underline{b}}^p-1}{\underline{b}-1}-1}}}\in \mathbb{Q}$$

(10)

where $1\le q\le \underline{b}$, $\underline{b}>1$, and $\left\{\underline{b},q,p\right\}\in {\mathbb{N}}^{+}$. For instance, the probability of getting 1 to 3 as the fifth quantum of a bijective ternary chain is $\left\{0.335011,0.333327,0.331662\right\}$, and the chances of encountering 1 to $\mathrm{A}$ as the second quantum of a bijective decimal chain is $\left\{0.1183,0.113,0.1083,0.1041,0.1004,0.09694,0.09381,0.09094,0.08829,0.08583\right\}$. Watch that this equation reduces to (9) if $p=1$. Figure 3 shows the PMF of various bijective bases for consecutive positions and the hyperbolic progression of the bijective ternary digits as the position increases.

Following the plot thread we developed in Section 3.6, the ratio between the area under the hyperbola delimited by the bin $\left[d_1,d_2\right)$ and the radix support $\left[1,\underline{r}\ll \underline{b}\right)$ is

$$Pr\left(\underline{r},\left[d_1,d_2\right)\right)={log}_{\underline{r}+1}{\displaystyle \frac{d_2}{d_1}}\in \mathbb{R}\left(1\le d_1<d_2\le \underline{r},\left\{d_1,d_2,\underline{r}\right\}\in {\mathbb{N}}^{+}\right)$$

We arrive at the NBL for bijective notation by putting $d_1=d$ and $d_2=d+1$. A sample of numerals expressed in bijective $\underline{r}$-ary PN satisfies the local NBL if the leading digit d occurs with probability

$$Pr\left(\underline{r},d\right)={log}_{\underline{r}+1}\left(1+{\displaystyle \frac{1}{d}}\right)\in \mathbb{R}\left(1\le d\le \underline{r}\right)$$

(11)

The NBL with radix $r+1$ corresponds to the bijective $\underline{r}$-ary numeration’s NBL; for example, the standard ternary system assigns to 1 and 2 the probabilities $\left[63\right]\%$ and $\left[37\right]\%$, which is the PMF of bijective binary numeration. In the usual case where the radix is $r=10$, the standard decimal system assigns to digits 1 and 9 probabilities of $\left[30.1\right]\%$ and $\left[4.6\right]\%$. In contrast, the bijective decimal numeration assigns to digits 1 and $\mathrm{A}\equiv 10$ probabilities of $\left[28.9\right]\%$ and $\left[4.0\right]\%$. Likewise, the local bijective ternary numeration assigns to 1, 2, and 3 the probabilities $\left[50\right]\%$, $\left[29\right]\%$, and $\left[21\right]\%$, contrasting with the percentages $\left[54.5\right]\%$, $\left[27.3\right]\%$, and $\left[18.2\right]\%$ the global bijective ternary numeration assigns.

The entropy of PMF (11) for radix $\underline{r}$, $\tilde{e}\left(\underline{r}\right)$, is the expected value (weighted arithmetic mean) of the likelihood function ($ln\left(x\right)$) evaluated at the probability mass reciprocal, i.e.,

$$\tilde{e}\left(\underline{r}\right)=[\widehat{E}\left(Pr\left(\underline{r},d\right)\right)=\sum _{d=1}^{d=\underline{r}}{log}_{\underline{r}+1}\left(1+{\displaystyle \frac{1}{d}}\right)ln\left({\displaystyle \frac{1}{{log}_{\underline{r}+1}\left(1+\frac{1}{d}\right)}}\right)]nat$$

For example, $\tilde{e}\left(\underline{1}\right)=0$, $\tilde{e}\left(\underline{2}\right)=0.65846$, $\tilde{e}\left(\underline{3}\right)=1.03247$, $\tilde{e}\left(\underline{10}\right)=2.08134$, and $\tilde{e}\left(\underline{100}\right)=3.84099$. Because $\underline{r}<\underline{b}$ and we assume that $\underline{b}$ is a positive natural number, the local entropy is finite, in agreement with the Bekenstein bound.

Note that $\left(\right)$ is also valid for the unitary system ($\underline{r}=1$), unlike (7) in standard PN; bijective unary assigns the probability of $\left[100\right]\%$ to 1. A system encoding data in bijective unary has no curvature and keeps a linear scale. In bijective numeration, (re)coding from unary into $\underline{r}$-ary means summing the number of ones and executing an iterative procedure based on Euclidean division. 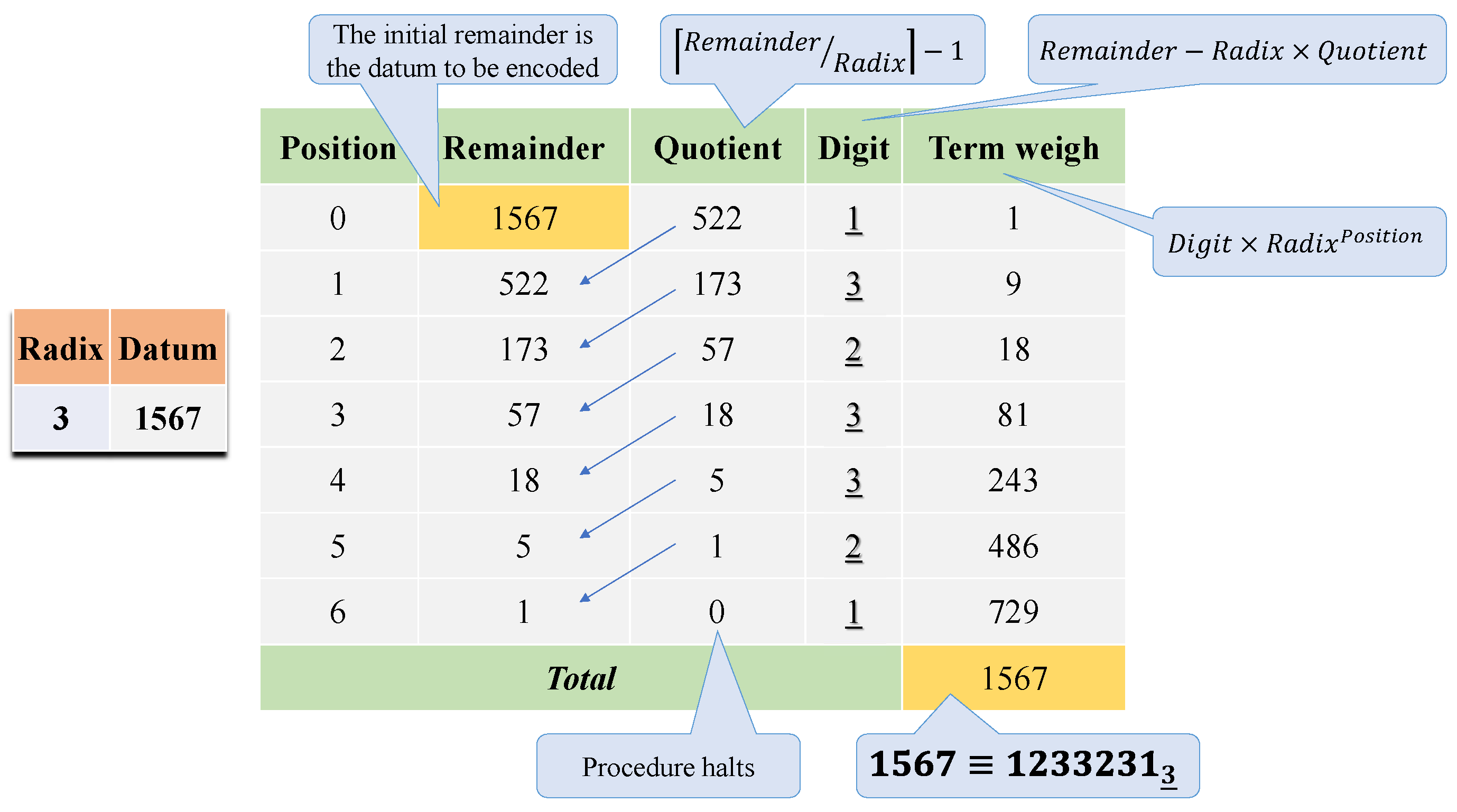Figure 4 describes the encoding algorithm; e.g., it converts the representation of 1567 into ${1233231}_{\underline{3}}$.

We can generalize the PMF given by (11) to the probability of getting a leading $\underline{r}$-ary numeral $n\in {\mathbb{N}}^{+}$ of any length. It is the likelihood gap it induces on the logarithmic scale, i.e.,

$$Pr\left(\underline{r},n\right)={log}_{\underline{r}+1}\left(n+1\right)-{log}_{\underline{r}+1}n={log}_{\underline{r}+1}\left(1+{\displaystyle \frac{1}{n}}\right)\in \mathbb{R}$$

(12)

For example, the probability that a bijective decimal numeral starts with $2\mathrm{A}1$, say $2.\mathrm{A}{1}_{\underline{10}}$ or $2\mathrm{A}{17}_{\underline{10}}$, is $[{log}_{11}\left(1+{\displaystyle \frac{1}{301}}\right)=0.13832]\%$.

This result allows us to derive the probability of picking a bijective $\underline{r}$-ary numeral with length l starting with the digit d,

$$Pr\left(\underline{r},l,d\right)=\sum _{k=d{\underline{r}}^{l-1}+{\displaystyle \frac{{\underline{r}}^{l-1}-1}{\underline{r}-1}}}^{k=\left(d+1\right){\underline{r}}^{l-1}+{\displaystyle \frac{{\underline{r}}^{l-1}-1}{\underline{r}-1}}-1}{log}_{{\displaystyle \frac{{\underline{r}}^{l+1}-1}{{\underline{r}}^l-1}}}\left(1+{\displaystyle \frac{1}{k}}\right)\in \mathbb{R}$$

where $1\le d\le \underline{r}$, $\underline{r}>1$, and $\left\{\underline{r},l,d\right\}\in {\mathbb{N}}^{+}$. For instance, the probability of picking 1 to 3 as the first digit of a bijective ternary numeral with length 5 is $\left\{0.465312,0.306147,0.228541\right\}$, and the probability of choosing 1 to $\mathrm{A}$ as the first digit of a bijective decimal numeral with length 2 is $\left\{0.2797,0.1685,0.1209,0.09442,0.07746,0.06567,0.057,0.05036,0.0451,0.04084\right\}$. Owing to this equation boils down to (11) if $l=1$, the local NBL is length-invariant! Figure 5 shows the PMF of various bijective radices for consecutive lengths and the hyperbolic progression of the bijective ternary digits as the numeral’s length expands.

Likewise, Equation (12) allows us to derive the law for digits beyond the first; the probability of getting a $\underline{r}$-ary digit d at position p is

$$Pr\left(\underline{r},d,p\right)=\sum _{k={\displaystyle \frac{{\underline{r}}^{p-1}-1}{\underline{r}-1}}}^{k={\displaystyle \frac{{\underline{r}}^p-1}{\underline{r}-1}}-1}{log}_{{\displaystyle \frac{{\underline{r}}^{p+1}-1}{{\underline{r}}^p-1}}}\left(1+{\displaystyle \frac{1}{\underline{r}k+d}}\right)\in \mathbb{R}$$

where $1\le d\le \underline{r}$, $\underline{r}>1$, and $\left\{\underline{r},d,p\right\}\in {\mathbb{N}}^{+}$. Because this equation reduces to (11) if $p=1$, the local NBL is position-invariant! For instance, the chance of picking 1 to 3 as the fifth digit of a bijective ternary numeral is $\left\{0.335006,0.333327,0.331667\right\}$, and the probability of choosing 1 to $\mathrm{A}$ as the second digit of a bijective decimal numeral is $\left\{0.1177,0.1126,0.1081,0.1041,0.1004,0.09707,0.09402,0.09121,0.08862,0.0862\right\}$.

4.2. Depleted and Constrained Harmonic Series

The global NBL for bijective numeration suddenly appears in the set of Kempner’s curious series. We say a series is curious when the infinite summation of a harmonic series, divergent, is depleted by constraining its terms to satisfy specific convergence conditions. For example, consider the harmonic series missing the terms where 66 appears in their denominator. Most researchers in this fieldwork use decimal representation, but we can generalize the results to any base. Although their terminology refers to the items of a unit fraction’s denominator as digits, for us, these are quanta of a chain because we are handling terms of a harmonic series.

The point is that most depletions result in an absolute mass because a harmonic series is on the verge of divergence. In particular, a harmonic series becomes convergent by omitting a single quantum. For example, the shrunk harmonic series without the terms in which 4 appears anywhere in the decimal representation of the denominator is $K_4$ of the Kempner series. Offhand, convergence comes up because we withdraw most of the terms; 110 of the terms contain a 4 if the random variable ranges from 0 to 9, $20\%$ have at least one 4 if the random variable ranges from 0 to 99, and eventually, most of the terms of any random chain with 100 quanta will contain at least one 4 and will not sum. However, this explanation needs to be corrected.

A $K_N$ series converges slowly [77]. We will reason that this property is due to large numerical chains’ relative and geometrically short contribution to the total. Table 2 summarizes the outcomes of approximated calculations from 1 ($K_1$) to $\mathrm{A}\equiv 10$ ($K_{\mathrm{A}}$). Nonetheless, the most stunning feature of the Kempner summations (third column) is that they outline a curve that decreases harmonically.

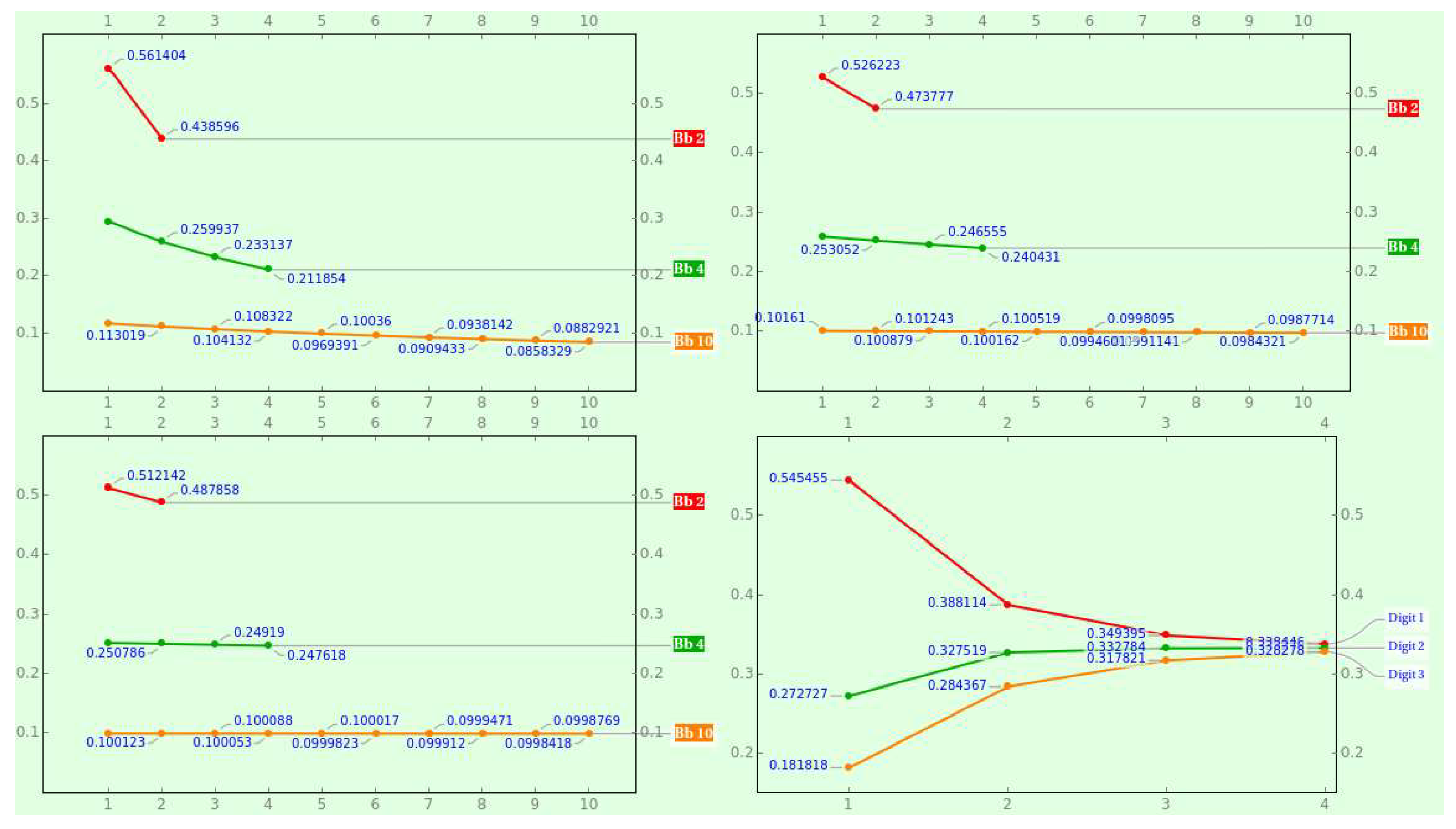
Every quantum eliminates the same number of terms. $K_1<K_2<\cdots <K_A$ means not that 1 is in more terms than 2 or 3 but a heavier mass attributed to the terms with the minor quanta; if we take out 11, the resulting summation is smaller than when we take out 12 or 13, and $\mathrm{A}$ is the quantum that contributes less to the total. (Although $\mathrm{A}$ is taken as 0 for calculation purposes, the value of $K_A$ proves that bijective numeration is underneath.) Considering that a Kempner series is infinite and the set of Kempner series embraces all quanta q represented in bijective decimal, how could we find a better proof that a default probability potential outlines a hyperbolically decreasing function of q?

Since a curious series converges by default of unit fraction terms, the mass share of a quantum globally depends on the reciprocals of the Kempner summations; the third column of the table includes $K_q$’s reciprocals normalized to $\left[100\right]\%$ (e.g., $K_1$’s relative mass is $M_1={\left(K_1{\sum }_{q=1}^{A}1K_q\right)}^{-1}\approx 13\%$). We must underline the relevance of these summations and percentages, reflecting the mass of every quantum irrespective of where it is, in contrast with the global NBL, which indicates the probability mass of a quantum at a given position in a given base.

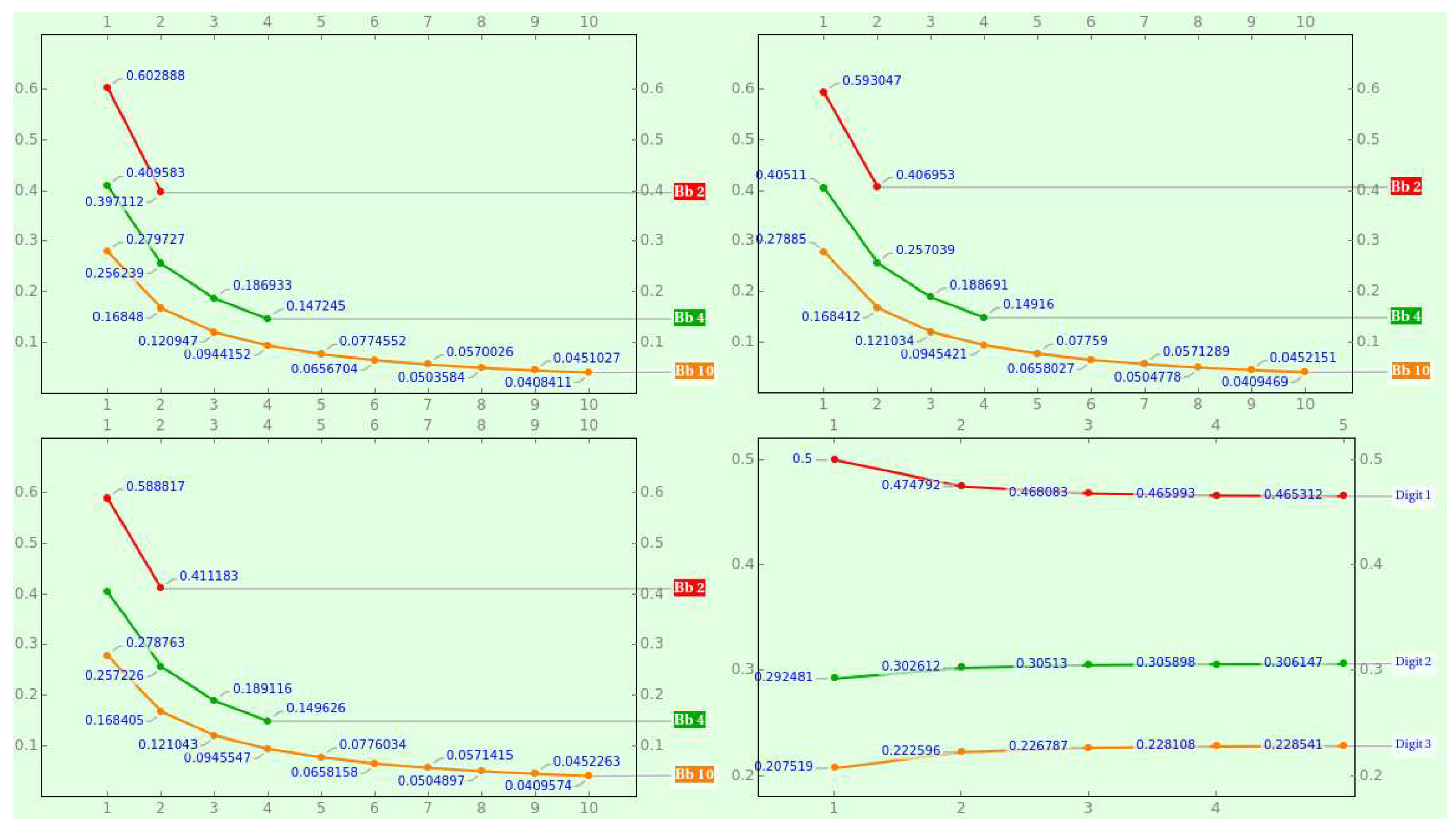
We introduce two caveats to analyze the NBL weights (fourth column). First, the Kempner distribution conforms with NBL via the average of NBL distributions for different positions, which is NBL, too. For instance, $W_1$ is, in principle, the average of quantum 1’s probabilities at first ($34.14\%$), second ($11.89\%$), third ($10.18\%$), fourth ($10.01\%$), et cetera position according to (10). Second, because the distribution of the nth quantum quickly tends to be uniform ($10\%$ for each of the ten quanta from the fifth position), we must suspect that there exists a threshold position above which the contributions to the quantum’s weight do not count; otherwise, the resulting mean distribution will end up reaching uniformity despite the differences that the Benford distribution makes at the first positions. Consequently, the last column calculates $W_q$ as the NBL frequency averaged only over the first nine positions. Averaging ten positions also gives an excellent approximation (with a mean error of $[.091]\%$) to the distribution of Kempner masses, but nine positions deliver the minimal total mean error of $[.024]\%$.

Can we extrapolate this result in $\underline{b}=\underline{\mathrm{A}}$ to any value of $\underline{b}$? If affirmative, PN would ignore a natural significand’s quanta from the $\underline{b}$th place, agreeing with claims often made by mathematicians [78], physicists [79,80], and engineers [81] about the illogicality of a PN system carrying excessive digits in calculations of any type, regardless of the discipline.

We surmise that a bijective b-ary chain c that fulfills ${log}_{\underline{b}}c>\underline{b}$ is physically elusive. The universe in base $\underline{b}$ would cope with at most $\underline{b}$ nesting levels, each distinguishing between b possible quanta. The physical resolution

$$\mathring{R}\left(\underline{b}\right)={\underline{b}}^{\underline{b}}$$

would estimate the scope of quanta a computational system like the cosmos can naturally operate, much as a native resolution describes the number of pixels a screen can display.

In [82], the author contrives an efficient algorithm for summing a series of harmonic numbers whose denominator contains no occurrences of a particular numerical chain. As a result of the calculations, a harmonic series in base b omitting a chain of length n (regardless of its specific quanta) might converge approximately to

$b^{n}lnb$.

This conjecture means that the contribution of linearly more extended chains to an endless series is geometrically lesser. For instance, the harmonic series where we impede the occurrence of the decimal numeral 314159 is about $2302582.334$, whereas the same sum omitting only 3 is $22.921$, ${10}^5$ times as low. Thus, large numerical chains would be exponentially inconsequential.

More general constraints allow several occurrences of a given quantum to calculate summations positively. Let $S\left(n,q,b\right)$ be the sums of the b-base reciprocals of naturals that have precisely n instances of the quantum q. For example, omitting the terms whose denominator in decimal representation contains one or more 6 is the particular case $S\left(0,6,10\right)$. The sequence of values S decreases and tends to

$$\underset{n\to \infty }{lim}S\left(n,q,b\right)=blnb\approx ln\mathring{R}\left(b\right)$$

regardless of q [83].

Except for the gap from $n=0$ to $n=1$, where the total increases, the summation falls as we raise the constraining quantity of quanta. What is the reason? It is not that we get more terms with nqs than terms containing $n+1$qs, but that the longer the chain, the lighter the contribution. Furthermore, when $n\gg 1$, $S\left(n,q,b\right)\gtrsim S\left(n+1,q,b\right)$, whereas if $n\gtrsim 1$, $S\left(n,q,b\right)\gg S\left(n+1,q,b\right)$, i.e., increments of n near the origin produce significant drops and vice versa, increments of n far from the origin produce negligible drops. Although we have not statistically tested the number of quanta for compliance with NBL, we can again conclude that while small is a synonym for solid and discernible, huge numerical chains are fragile and hardly convey differences.

Instead of imposing absolute constraints, we can allow in a term arbitrarily many quanta q irrespective of the position and number so long as the proportion of qs remains below a fixed parameter $\lambda \in \left[0..1\right]$. In [84], the authors prove that the series converges if and only if $\lambda <1b$. In decimal, while Kempner’s original series implies $\lambda =0$, where no term containing a given quantum contributes to the summation, the complete harmonic series means $\lambda =1$, where any density is allowed, i.e., we keep all the reciprocals.

For instance, if we consider the constraint allow a rate of $\lambda =\left[5\right]\%$ of 7s at most, the term 198765432109876543210 disappears ($\left[10\right]\%$ of 7s), but neither 198654321098 (no 7s) nor 198865432109876543210 ($\left[5\right]\%$ of 7s) does. While the series converges in $\lambda \in \left[0..1/10\right)$, it no longer converges above the threshold $\lambda =1/10$. Note that the archetype of the Pareto law appears naturally; on average, $90\%$ of the unit fractions, those with the highest quantum density, offset the remaining $10\%$. Moreover, this result engages with our surmise concerning the physical resolution $\mathring{R}\left(b\right)$ of a universal computational system. Again, densities of b quanta or more are intractable. A PN system must restrict itself to chains with less than b quanta to guarantee the operability of coded data and avoid overflow conditions.

5. Odds

Although odds typically appear in gambling and statistics, this section illustrates how they are central to the computational processes of a coding source, including an application to physics and another to decision theory.

We usually define the odds of an outcome as the ratio of the number of events that generate that particular result to those that do not. In this sense, odds constitute another measure of the chance of a result. Likewise, the ratio between the probabilities of two events determines their relative odds; the higher the odds of an outcome compared with another, the more informative the latter’s occurrence is.

Indeed, odds highlight the rational character of a probability. For instance, we can interpret the one-parameter PMF (1) in terms of odds. Since the odds O of picking a nonzero natural N against piking $N^2$ are precisely $N^2$, we can establish $Pr\left(N\right)=ϵO\left(N^2:N\right)$.

The encoded odds between a pair of events are the product of their probability ratio and likelihood factor. The coding rule agrees with Bayes’ law. Odds between propensities or degrees of belief become information correlations representing entropic contributions in Bayesian coding. Thus, we attribute a metric sense to this theorem, embracing the objectivistic [85] and subjectivistic [86] interpretations.

Our description will exclusively focus on standard PN, omitting the corresponding bijective numeration’s derivations and formulas for conciseness.

5.1. Global Bayesian Coding

The probability ratio between two events diverges from the unit as their correlation weakens. A PN system must multiply this value by a coding factor to fit into the base’s harmonic scale. This operation is rigorously Bayes’ theorem. Specifically, global Bayesian coding employs the formula

$$\tilde{O}\left(t:s|X=b\right)=\tilde{O}\left(t:s\right){\mathrm{\Lambda }}_{\tilde{O}}\left(t:s|X=b\right)\in \mathbb{Q}\left(1\le s<t<b\right)$$

(13)

to encode the odds between two numbers.

• $\tilde{O}\left(t:s|X=b\right)$ represents the global (encoded or posterior) odds of getting quantum t against s in base b. We can consider it the rational quantum $st$ on a b-ary harmonic scale.
• $\tilde{O}\left(t:s\right)$is the ratio between the probabilities of the two events according to (1), namely

$$\tilde{O}\left(t:s\right)=\tilde{O}\left(t:s|1\right)={\displaystyle \frac{Pr\left(t\right)}{Pr\left(s\right)}}={\left({\displaystyle \frac{s}{t}}\right)}^2$$

straightforwardly measuring the (decoded or prior) odds of picking the number t against s on a linear scale. If we fix the center of the range, the narrower the interval, the higher the odds, whereas if we fix the interval width, the minor s (or t), the lower the odds. Note that the odds of two concatenated intervals calculated separately are the product of the interval’s odds,

$$\tilde{O}\left(z:x|1\right)={\left({\displaystyle \frac{x}{y}}\right)}^2{\left({\displaystyle \frac{y}{z}}\right)}^2={\left({\displaystyle \frac{x}{z}}\right)}^2$$

• ${\mathrm{\Lambda }}_{\tilde{O}}\left(t:s|X=b\right)$ is the global coding (Bayes) factor, which measures the degree to which the outcome b of the random variable X supports hypothesist against s, assuming both are independent numbers. Because interval $\left[s,t\right)$ is not yet encoded, the coding law establishes a likelihood difference instead of a likelihood ratio, namely

$${\mathrm{\Lambda }}_{\tilde{O}}\left(t:s|X=b\right)=\mathcal{L}\left(t|X=b\right)-\mathcal{L}\left(s|X=b\right)={\displaystyle \frac{H_{t-1}-H_{s-1}}{H_{b-1}}}=Pr\left(b,\left[s,t\right)\right)$$

where

$$\mathcal{L}\left(q|X=b\right)={\displaystyle \frac{H_{q-1}}{H_{b-1}}}$$

(14)

is the likelihood function of q with b fixed; since $\mathcal{L}\left(1|X=b\right)$ vanishes and $\mathcal{L}\left(b|X=b\right)=1$, we can understand this function as a measure of the nearness between q and $b>1$ normalized to one. The coding factor is precisely Equation (3), measured in b-ary harmonic information units.

Compiling, PN calculates (13) as

$$\tilde{O}\left(t:s|b\right)={\left({\displaystyle \frac{s}{t}}\right)}^2{\displaystyle \frac{H_{t-1}-H_{s-1}}{H_{b-1}}}\in \mathbb{Q}\left(1\le s<t<b\right)$$

(15)

It is the cost of computing the bucket’s harmonic width, i.e., the entropic contribution of bucket $\left[s,t\right)$ to b’s harmonic scale. Because $\tilde{O}\left(2:1|b\right)$ is maximally informative irrespective of the base, the global information unit corresponds to the natural harmonic bucket ${\left[\psi \left(q\right)\right]}_1^2$ we use in (2). The global odds of a quantum against itself vanish, having no representation on a harmonic scale. The reciprocal

$$\tilde{O}\left(s:t|b\right)={\displaystyle \frac{1}{\tilde{O}\left(t:s|b\right)}}={\left({\displaystyle \frac{t}{s}}\right)}^2{\displaystyle \frac{H_{b-1}}{H_{t-1}-H_{s-1}}}\in \mathbb{Q}\left(1\le s<t<b\right)$$

measures the odds of quantum s against t, with a maximum approaching $b^2$ as b climbs to infinity.

A PN system must employ (13)’s variation

$$\tilde{O}\left(t:s|b^{\prime }\right)=\tilde{O}\left(t:s|b\right){\mathrm{\Lambda }}_{\tilde{O}}\left(b^{\prime }:b|q\in \left[s,t\right)\right)\in \mathbb{Q}$$

to recode globally, where $1\le s\le q<t<b$ and $t<b^{\prime }$. The coding (Bayes) factor is a likelihood ratio when it deals with previously encoded data, as usual in statistics; using (14),

$${\mathrm{\Lambda }}_{\tilde{O}}\left(b^{\prime }:b|q\in \left[s,t\right)\right)={\displaystyle \frac{\mathcal{L}\left(b|q\right)}{\mathcal{L}\left(b^{\prime }|q\right)}}={\displaystyle \frac{H_{b-1}{H}_{q-1}}{H_{b^{\prime }-1}{H}_{q-1}}}={\displaystyle \frac{H_{b-1}}{H_{b^{\prime }-1}}}$$

measures the degree to which a given quantum supports hypothesis $b^{\prime }$ against b, assuming both are independent quanta. Hence, the PN system can change to base $b^{\prime }$ utilizing the rule

$$\tilde{O}\left(t:s|b^{\prime }\right)=\tilde{O}\left(t:s|b\right){\displaystyle \frac{H_{b-1}}{H_{b^{\prime }-1}}}\in \mathbb{Q}$$

(16)

which coincides with the odds of $\left[s,t\right)$ in base $b^{\prime }$ for the first time because of

$$\tilde{O}\left(t:s|b^{\prime }\right)=\left({\left({\displaystyle \frac{s}{t}}\right)}^2\left({\displaystyle \frac{H_{t-1}-H_{s-1}}{H_{b-1}}}\right)\right){\displaystyle \frac{H_{b-1}}{H_{b^{\prime }-1}}}={\left({\displaystyle \frac{s}{t}}\right)}^{2}Pr\left(b^{\prime },\left[s,t\right)\right)$$

Equation (16)’ Bayes factor $H_{b-1}{H}_{b^{\prime }-1}$ is the classical Bayes factor replacing probabilities by global likelihoods. Thus, the transformation $b\to b^{\prime }$ constitutes a primal memory (incremental) process that decreases the global odds if $b<b^{\prime }$, and vice versa, increases the global odds if $b>b^{\prime }$. For instance, an asymmetry such that b grows every tic of a global clock would mean an unstoppable progressive information loss for a fixed universe region; this connection between time and entropy is crucial to theoretical physics and cosmology [87].

For example, the PN system encodes bucket $\left[4,13\right)$ to base $b=100$ as

$$\tilde{O}\left(13:4|100\right)={\left({\displaystyle \frac{4}{13}}\right)}^2{\displaystyle \frac{H_{13-1}-H_{4-1}}{H_{100-1}}}\approx 0.0232$$

This value is the entropic contribution of bucket $\left[4,13\right)$ to 100’s harmonic scale. When the PN system changes the base to $b^{\prime }=110$, using (16), it delivers

$$\tilde{O}\left(13:4|110\right)=\tilde{O}\left(13:4|100\right){\displaystyle \frac{H_{100-1}}{H_{110-1}}}\approx 0.0228$$

meaning that the bucket’s entropic contribution decreases. Then, changing to base $b^{\prime }=90$ yields

$$\tilde{O}\left(13:4|90\right)=\tilde{O}\left(13:4|110\right){\displaystyle \frac{H_{110-1}}{H_{90-1}}}\approx 0.0237$$

i.e., the bucket’s entropic contribution increases. Finally, the PN system decodes the odds with base 90 by solving the prior from (15), i.e.,

$$\tilde{O}\left(13:4\right)={\displaystyle \frac{\tilde{O}\left(13:4|90\right)}{Pr\left(90,\left[4,13\right)\right)}}=\tilde{O}\left(13:4|90\right){\displaystyle \frac{H_{90-1}}{H_{13-1}-H_{4-1}}}={\left({\displaystyle \frac{4}{13}}\right)}^2$$

5.2. Local Bayesian Coding

Local Bayesian coding assumes that (13), the global Bayesian law, governs the universe’s information. We express the informational correlation between two numerals by multiplying their harmonic correlation by a coding factor, obtaining a point on a logarithmic scale. This operation is rigorously the Bayes’ theorem that settles down the basis of a conformal metric space. Specifically, local Bayesian coding employs the formula

$$\tilde{o}\left(n_2:n_1|Y=r\right)=\tilde{o}\left(n_2:n_1|b\right){\mathrm{\Lambda }}_{\tilde{o}}\left(n_2:n_1|Y=r\right)\in \mathbb{R}$$

(17)

to encode the probability ratio between $n_1$ and $n_2$, where $\left(1\le n_1<n_2<b\right)\wedge \left(r<b\right)$.

• $\tilde{o}\left(n_2:n_1|Y=r\right)$ represents the local (encoded or posterior) odds of getting $n_2$ against $n_1$ with radix r.
• $\tilde{o}\left(n_2:n_1|b\right)$is the (prior) probability ratio between the two events only assuming that a global base exists; using (4),

$$\tilde{o}\left(n_2:n_1|b\right)={\displaystyle \frac{Pr\left(b,n_2\right)}{Pr\left(b,n_1\right)}}={\displaystyle \frac{\frac{1}{n_2{H}_{b-1}}}{\frac{1}{n_1{H}_{b-1}}}}={\displaystyle \frac{n_1}{n_2}}$$

It measures the strength of the association between $n_1$ and $n_2$ on the harmonic scale provided by b.

• ${\mathrm{\Lambda }}_{\tilde{o}}\left(n_2:n_1|Y=r\right)$ is the local coding (Bayes) factor, which measures the degree to which the outcome r of the random variable Y supports hypothesis$n_2$ against $n_1$, assuming both are independent. Because the bucket $\left[n_1,n_2\right)$ is not locally encoded yet, the coding law establishes a likelihood difference instead of a likelihood ratio, namely

$${\mathrm{\Lambda }}_{\tilde{o}}\left(n_2:n_1|Y=r\right)=\ell \left(n_2|Y=r\right)-\ell \left(n_1|Y=r\right)$$

where $\ell \left(n|Y=r\right)={log}_{r}n$ quantifies the likelihood of n when the actual value r occurs. In short, the local coding factor is the log-odds of $n_2$ relative to $n_1$, equivalent to the support of $\left[n_1,n_2\right)$ with radix r according to (8), i.e.,

$${\mathrm{\Lambda }}_{\tilde{o}}\left(n_2:n_1|Y=r\right)={log}_r{n}_2-{log}_r{n}_1={log}_r{\displaystyle \frac{n_2}{n_1}}=\ell \left(\left[n_1,n_2\right)|r\right)$$

(18)

Compiling, the PN system calculates (17) as

$$\tilde{o}\left(n_2:n_1|r\right)={\displaystyle \frac{n_1}{n_2}}{log}_r{\displaystyle \frac{n_2}{n_1}}\left(1\le n_1<n_2\right)$$

(19)

Note that the local odds of a numeral against itself vanish, having no representation on a logarithmic scale. Consequently, the local Bayes’ rule measures the entropic contribution of bin $\left[n_1,n_2\right)$ on r’s logarithmic scale, with a minimum approaching $\tilde{o}\left(r:1|r\right)=1r$ as r climbs to infinity. Euler’s number has an extraordinary meaning in this setting; a Bayesian datum in this form is maximally informative irrespective of the radix when $n_2{n}_1=e=2.718\dots$, an ideal proportion that induces the local information unit associated with the natural logarithmic bin ${\left[lnn\right]}_1^e$ we use in (5).

A PN system must employ (17)’s variation

$$\tilde{o}\left(n_2:n_1|r^{\prime }\right)=\tilde{o}\left(n_2:n_1|r\right){\mathrm{\Lambda }}_{\tilde{o}}\left(r^{\prime }:r|n\in \left[n_1,n_2\right)\right)\in \mathbb{R}$$

$$\forall \left\{n_1,n,n_2,r,r^{\prime }\right\}\in \mathbb{N}|\left(1\le n_1\le n\le n_2\right)$$

to recode locally. When it deals with previously encoded data, the local Bayes factor is a likelihood ratio, as usual in statistics,

$${\mathrm{\Lambda }}_{\tilde{o}}\left(r^{\prime }:r|n\in \left[n_1,n_2\right)\right)={\displaystyle \frac{\ell \left(r|n\right)}{\ell \left(r^{\prime }|n\right)}}={\displaystyle \frac{{log}_{n}r}{{log}_n{r}^{\prime }}}={\displaystyle \frac{lnr}{ln{r}^{\prime }}}$$

Thus, the degree to which the outcome $n\in \left[n_1,n_2\right)$ of the random variable Y supports hypothesis $r^{\prime }$ against r is independent of n. Then, a coding source can change to standard radix $r^{\prime }$ utilizing

$$\tilde{o}\left(n_2:n_1|r^{\prime }\right)=\tilde{o}\left(n_2:n_1|r\right){\displaystyle \frac{lnr}{ln{r}^{\prime }}}$$

(20)

which coincides with the odds of $n_2$ against $n_1$ with radix $r^{\prime }$ for the first time

$$\tilde{o}\left(n_2:n_1|r\right){\displaystyle \frac{lnr}{ln{r}^{\prime }}}=\left({\displaystyle \frac{n_1}{n_2}}{log}_r{\displaystyle \frac{n_2}{n_1}}\right){\displaystyle \frac{lnr}{ln{r}^{\prime }}}={\displaystyle \frac{n_1}{n_2}}{log}_{r^{\prime }}{\displaystyle \frac{n_2}{n_1}}$$

Equation (20)’ Bayes factor $lnrln{r}^{\prime }$ is the classical Bayes factor replacing probabilities by local likelihoods. Note that the transformation $r\to r^{\prime }$ increases the odds if $r>r^{\prime }$, and vice versa, decreases the odds if $r<r^{\prime }$.

For example, a coding source locally encodes the bin $\left[4,13\right)$ using radix $r=100$ as

$$\tilde{o}\left(13:4|100\right)={\displaystyle \frac{4}{13}}{log}_{100}{\displaystyle \frac{13}{4}}\approx 0.07875$$

This value measures the entropic contribution of bin $\left[4,13\right)$ to standard radix 100. When the coding source changes the radix to $r^{\prime }=110$, it delivers using (20)

$$\tilde{o}\left(13:4|110\right)=\tilde{o}\left(13:4|100\right){\displaystyle \frac{ln100}{ln110}}\approx 0.07715$$

Then, changing the radix to $r^{\prime }=90$ yields

$$\tilde{o}\left(13:4|90\right)=\tilde{o}\left(13:4|110\right){\displaystyle \frac{ln110}{ln90}}\approx 0.0806$$

Finally, the coding source decodes the odds with radix 90 by solving the prior from (19), i.e.,

$$\tilde{o}\left(13:4\right)={\displaystyle \frac{\tilde{o}\left(13:4|90\right)}{Pr\left(90,\left[4,13\right)\right)}}={\displaystyle \frac{0.0806}{{log}_{90}\frac{13}{4}}}\approx 0.30769\approx {\displaystyle \frac{4}{13}}$$

Remember that local Bayesian coding copes not only with ratios of digits but with ratios of numerals in general. For example, the rational 95971 (bin $\left[95,971\right)$) encoded with radix 4 is

$$\tilde{o}\left(971:95|4\right)={\displaystyle \frac{{1133}_4}{{33023}_4}}{log}_4{\displaystyle \frac{{33023}_4}{{1133}_4}}\approx 0.{02213333}_4$$

If environmental conditions cast a change to radix 3, the coding source would decode the datum

$$\tilde{o}\left(971:95|3\right)=0.{02213333}_4{\displaystyle \frac{ln4}{ln3}}\approx {0.01212022}_3$$

as

$$\tilde{o}\left(971:95\right)={\displaystyle \frac{\tilde{o}\left(971:95|3\right)}{\ell \left(\left[95,971\right)|3\right)}}\approx {\displaystyle \frac{0.{01212022}_3}{{log}_3\frac{{1022222}_3}{{10112}_3}}}\approx {\displaystyle \frac{95}{971}}$$

5.3. Elemental Jumps

Using odds instead of probabilities is especially powerful when we measure the gap between successive quanta or digits.

The odds (15) between consecutive quanta

$$\tilde{O}\left(q+1:q|b\right)={\left({\displaystyle \frac{q}{q+1}}\right)}^{2}Pr\left(b,\left[q,q+1\right)\right)={\left({\displaystyle \frac{q}{q+1}}\right)}^2{\displaystyle \frac{1}{q{H}_{b-1}}}={\displaystyle \frac{q}{{\left(q+1\right)}^2{H}_{b-1}}}$$

measure the associated harmonic likelihood gap in a given base b, where we have used equations (3) and (4). b-normalized quantum jumps define the PMF

$${\text{Ç}}_b={\displaystyle \frac{1}{H_{b-1}-H_{b-1,2}}}$$

$${Pr}_{\tilde{O}}\left(b,q\right)={\text{Ç}}_b{\displaystyle \frac{q}{{\left(q+1\right)}^2}}\in \mathbb{Q}$$

(21)

an exact and multiplicatively separable function where $H_{N,2}\equiv {\sum }_{k=1}^{N}1k^2$ is the generalized Nth harmonic number in power two and $1\le q<b-1$. Note that the summation only goes until the penultimate quantum $q=b-2$ because $q=b-1$ cannot jump to b.

PMF (21) is well-defined because of

$$\sum _{q=1}^{b-2}{Pr}_{\tilde{O}}\left(b,q\right)=1$$

so we can take as the odds version of PMF (4). For example, ${\text{Ç}}_4=36/17,$${Pr}_{\tilde{O}}\left(4,1\right)={\text{Ç}}_{4}1/4=9/17$, and ${Pr}_{\tilde{O}}\left(4,2\right)={\text{Ç}}_{4}2/9=8/17$. With $b=7$, we get ${Pr}_{\tilde{O}}\left(7,1\right)=900/3451\approx 0.261$, ${Pr}_{\tilde{O}}\left(7,2\right)=800/3451\approx 0.232$, ${Pr}_{\tilde{O}}\left(7,3\right)=675/3451\approx 0.196$, ${Pr}_{\tilde{O}}\left(7,4\right)=576/3451\approx 0.167$, and ${Pr}_{\tilde{O}}\left(7,5\right)=500/3451\approx 0.145$. Fig. Figure 6 outlines in red the PMF corresponding to standard undecimal in a global setting. The information gap decays harmonically from the second quantum so that transiting from the greatest quanta is easier than from the minor ones. Indeed, only the first few quanta remain stable.

Developing similar reasoning in a local setting, using equations (6), (7), and (19) ($d_1=d$ and $d_2=d+1$), the odds between consecutive digits

$$\tilde{o}\left(d+1:d|r\right)={\displaystyle \frac{d}{d+1}}{log}_r\left(1+{\displaystyle \frac{1}{d}}\right)$$

(22)

measure the associated likelihood gap in radix r. Then, we can calculate the PMF that normalizes these digit gaps in a given radix; the larger the digit, the lesser the information differential. For example, the PMF corresponding to standard quaternary is $\left\{0.561814,0.438186\right\}$. With radix $r=7$, we get ${Pr}_{\tilde{o}}\left(7,1\right)\approx \left[29.8\right]\%$, ${Pr}_{\tilde{o}}\left(7,2\right)\approx \left[23.24\right]\%$, ${Pr}_{\tilde{o}}\left(7,3\right)\approx \left[18.55\right]\%$, ${Pr}_{\tilde{o}}\left(7,4\right)\approx \left[15.35\right]\%$, and ${Pr}_{\tilde{o}}\left(7,5\right)\approx \left[13.06\right]\%$.

Figure 6 outlines in green the logarithmic PMF of standard undecimal, measuring the improbability of a random local jump through its contribution to the coding source’s entropy. The lowest digits maintain discernibility from the environment, while the decreasing entropic support of the more significant digits makes them more vulnerable.

Although the fiducial NBL is steeper than the corresponding ${Pr}_{\tilde{o}}$ regardless of the radix, and this is steeper than ${Pr}_{\tilde{O}}$ irrespective of the base, these three plots are hardly distinguishable for large cardinalities (see Figure 7), meaning that an NBL probability is synonym with stability. A transition from the greatest quanta or digits is generally much more frequent than a transition from the minor ones. This condition resembles the reactivity of the chemical elements periodic table concerning the electron shell (i.e., principal quantum number). More generally, ascending order (of numbers, quanta, digits, or shells) correlates with unsteadiness, which explains why closeness prevails over farness.

5.4. Optimal Stopping

A PN system assigns an information value to the concepts of likelihood, probability, and odds. In subSection 5.1 and Section 5.2, we argue that Bayes’ rule is the entropic contribution of a bucket to a harmonic scale or a bin to a logarithmic scale. In particular, eq. (19) allows us to calculate the information we can extract from a bipartition by nailing the first and last domain digits. Assuming $1\ll r<b$, the local odds of getting digit x against 1 and r against x estimate the information aggregate of the two parts. Inherent to the X’s dichotomy $\left\{\left[1,x\right),\left[x,r\right)\right\}$,

$$\begin{array}{ccc}{\ddot{o}}_r\left(x\right)& =& \ddot{o}\left(\left\{\left[1,x\right),\left[x,r\right)\right\}\right)\\ & =& \tilde{o}\left(x:1|r\right)+\tilde{o}\left(r:x|r\right)\\ & =& {\displaystyle \frac{1}{x}}{log}_{r}x+{\displaystyle \frac{x}{r}}{log}_r{\displaystyle \frac{r}{x}}\end{array}$$

gives the bipartite odds in logarithmic r-ary units of information, where $1<x<r$.

We obtain additive countability by making ${\kappa }_1^r{\ddot{o}}_r\left(x\right)\mathrm{d}x=1$. The entropy (local likelihood) distribution function

$$\kappa ={\displaystyle \frac{4}{r^2+4\left(rlnr-1\right)ln\sqrt{r}-1}}$$

$${\overleftarrow{o}}_r\left(x\right)=\kappa {\displaystyle \frac{r}{x}}lnx$$

$${\overrightarrow{o}}_r\left(x\right)=\kappa xln{\displaystyle \frac{r}{x}}$$

$${\overleftrightarrow{o}}_r\left(x\right)={\overleftarrow{o}}_r\left(x\right)+{\overrightarrow{o}}_r\left(x\right)$$

(23)

gives the normalized bipartite odds so that ${\overleftrightarrow{o}}_r\left(x\right)=\kappa {\ddot{o}}_r\left(x\right)$ acquires a value between 0 and 1.

For ${\overleftrightarrow{o}}_r\left(1\right)={\overleftrightarrow{o}}_r\left(r\right)=\kappa lnr$, both ${\overleftrightarrow{o}}_r\left(1\right)$ and ${\overleftrightarrow{o}}_r\left(r\right)$ tend to vanish in the limit $r\to b\to \infty$. Where does (23) become stationary? When $r\ge 55$, the normalized bipartite odds produce two maxima corresponding to ${\overleftarrow{o}}_r\left(x\right)$ and ${\overrightarrow{o}}_r\left(x\right)$; as $r\to b\to \infty$, the first maximum tends to $x=e$ and the second to $x=r/e$. These maxima optimize the total information transmission of the system. We find at $x=\sqrt{r}$, between the two maxima, a digit that minimizes the distinguishability between the two partitions, which is the analog of the middle point of a segment on the linear scale.

For example, with radix $r=10000$, the bipartitions are maximally entropic about $\left\{\left[1,2.7329\right),\left[2.7329,10000\right)\right\}$ and $\left\{\left[1,3659.1\right),\left[3659.1,10000\right)\right\}$, and ${\overleftrightarrow{o}}_r\left(100\right)$ is the minimum. Figure 8 repeats this exercise and shows the results with $r=100$ applicants.

Supposing that $1x$ and $xr$ are probabilities, Equation (23) is the addition of the corresponding entropies. Both maxima separate a stage of retention from a decision stage. Retention implies input processing, which raises entropy, whereas decision involves output processing, which lowers entropy. Maximum entropy indicates the best resource efficiency between the ascent and descent sections. Overall, the plot of ${\overleftrightarrow{o}}_r\left(x\right)$ reflects a natural entropic imbalance toward the small values; ${\overleftarrow{o}}_r\left(x\right)$ dominates in the short term, whereas ${\overrightarrow{o}}_r\left(x\right)$ dominates in the middle and long term. Computationally, it induces the bulk of processing far before reaching $x=r2$, while physically, it implies a bias of space or time.

The bipartite odds function can have interesting consequences in computational physics, especially in sequential decision-making to solve optimal stopping (or planning) problems with solutions such as the odds algorithm [88]. Specifically, the secretary problem [89] is a mathematical trope to grasp how computation closely ties with incremental (Bayesian) inference, hence with the asymmetric management of fundamental resources. Shortly, one of $r-1$ sequentially interviewed applicants must be nominated, with the proviso that they will be either chosen or rejected just after being examined; past the first $⌊x⌋$ applicants (typically a secretary, but also a lead actor or actress or a car), the judges select the next one that is better than any of the previous ones. Well, $x\approx r/e$ maximizes ${\overrightarrow{o}}_r\left(x\right)$, i.e., the probability of success in choosing the best applicant.

Instead, ${\overleftrightarrow{o}}_r\left(x\right)$ answers a different question. What is the optimal size $⌈x⌉$ of examined applicants to maximize the odds of choosing a good one? This nuance implies a crucial difference in approaching a solution; in this case, we must consider both terms of (23). We define a good prospect as a candidate in terms of the classic secretary problem, i.e., a seeker (or contender, or claimant) better than the previously examined applicants.

Considering that x is the current applicant, the bipartition separates the past from the future because ${\overleftarrow{o}}_r\left(x\right)$ and ${\overrightarrow{o}}_r\left(x\right)$ focus on the expected benefit before and after x and the practicality of preceding against succeeding data.

Regarding the past term, $lnx$ is the amount of information ascribed to examined applicants, and $1x$ is the probability of using such information. As $x\to 1$, we take advantage of less and less gathered information, albeit more likely, whereas if $x\to r$, we can leverage more and more references, albeit less likely. There is a compromise between choosing the first applicant (i.e., utterly uninformed decision-making) and selecting the last applicant (i.e., assuring to miss all the acquired information). We obtain the maximum of ${\overleftarrow{o}}_r\left(x\right)$ at $x\to \mathrm{e}$ as $r\to b\to \infty$.

Regarding the future term, $lnrx$ is the information we can obtain from forthcoming applicants, and $xr$ is the probability of using such information. As $x\to 1$, we will surely miss the most suitable prospects; if $x\to r$, we will hardly find a suitable applicant. There is a compromise between choosing the first applicant (i.e., ignoring the information the remaining applicants can provide) and selecting the last applicant (i.e., information exhausted). We obtain the maximum of ${\overrightarrow{o}}_r\left(x\right)$ at $x\to r/e$ as $r\to b\to \infty$.

Summing both terms implies balancing the partition behind against the partition ahead. If x is too low ($x\gtrsim 1$), you have the most information ahead for an acceptable selection, and if x is too high ($x\lesssim r$), you have many references for a good choice. Unfortunately, if x is too low ($x\gtrsim 1$), you have less probability of making an acceptable selection, and if x is too high ($x\lesssim r$), you have probably missed the finest choices. While bipartition $\left\{\left[1,r/\mathrm{e}\right),\left[r/\mathrm{e},r\right)\right\}$ implies a probability of $[1/\mathrm{e}]\%$ of skipping and selecting the best alternative, bipartition $\left\{\left[1,\mathrm{e}\right),\left[\mathrm{e},r\right)\right\}$ reduces this percentage significantly. Thus, ${\overleftarrow{o}}_r\left(x\right)$ enables promptness and ${\overrightarrow{o}}_r\left(x\right)$ quality.

The entropy distribution function of a bipartiton rises to the first maximum, falls and rises again to reach the second maximum, and decays until it almost vanishes. The right holistic strategy is to wait for the information to stop rising so that $\partial {\overleftrightarrow{o}}_r\left(x\right)\partial x$ vanishes and ${\partial }^2{\overleftrightarrow{o}}_r\left(x\right)\partial x^2$ decreases, i.e., in agreement with the maximum entropy principle for isolated systems (and the minimum energy principle for closed systems) in thermodynamics.

Exclusively concentrating on the past term also makes sense. The idea is to assess the general level after examining only a few applicants. Assuming that ours behaves as a linear time-invariant system, deviations decay as ${\mathrm{e}}^{-x}$, so the probability that the mean of the three first interviewed applicants is close to the pool mean is $1-{\mathrm{e}}^{-3}\approx \left[95\right]\%$. Since a threesome reasonably represents the whole set of applicants, we can confidently pick a forthcoming candidate. ${\overleftarrow{o}}_r\left(x\right)$ considers the cost of the processing; it is a precursor of human intuition and opens the door to computational methods of solution refinement. For instance, assuming that we can retain a (preliminary) solution, we can progressively renew candidates between the two maxima. If the selection process continues after the second maximum, we are in the same scenario as the classic secretary problem.

Deciding near $x=\sqrt{r}$, between the maxima, is questionable because having already spent substantial resources on getting information, the probability of picking the best applicant still needs to reach the optimum. Nonetheless, it is a separator of the two partitions that a living being, for instance, can seek on purpose to maximize internal order or coherence.

5.5. Bayesian Recurrence

PN coding is fundamentally relational. It compares pairs of buckets by figuring out probability double ratios. Using (15), we define

$$\tilde{O}\left(j:i|h:g\right)={\displaystyle \frac{\tilde{O}\left(j:i|b\right)}{\tilde{O}\left(h:g|b\right)}}={\displaystyle \frac{{\left(\frac{i}{j}\right)}^{2}Pr\left(b,\left[i,j\right)\right)}{{\left(\frac{g}{h}\right)}^{2}Pr\left(b,\left[g,h\right)\right)}}={\left({\displaystyle \frac{hi}{gj}}\right)}^2\left({\displaystyle \frac{H_{j-1}-H_{i-1}}{H_{h-1}-H_{g-1}}}\right)\in \mathbb{Q}$$

where $\left(1\le g<h\right)\wedge \left(1\le i<j\right)$. The first factor is the prior (decoded) ratio $\tilde{O}\left(hi:gj|r=1\right)$, and the second is the likelihood ratio measuring the strength of the correlation between the information that the buckets $\left[i,j\right)$ and $\left[g,h\right)$ keep. Note that the formula does not refer to the global base anymore.

This structure is repetitive; a generic probability quadruple ratio is the rational

$${\displaystyle \frac{\tilde{O}\left(j:i|h:g\right)}{\tilde{O}\left(n:m|l:k\right)}}=\tilde{O}\left(j:i|h:g|n:m|l:k\right)=$$

$$={\left({\displaystyle \frac{\frac{hi}{gj}}{\frac{lm}{kn}}}\right)}^2\left({\displaystyle \frac{\left(H_{l-1}-H_{k-1}\right)\left(H_{j-1}-H_{i-1}\right)}{\left(H_{n-1}-H_{m-1}\right)\left(H_{h-1}-H_{g-1}\right)}}\right)=$$

$$={\left({\displaystyle \frac{hikn}{gjlm}}\right)}^2\left({\displaystyle \frac{\left(H_{j-1}{H}_{l-1}+H_{i-1}{H}_{k-1}\right)-\left(H_{j-1}{H}_{k-1}+H_{i-1}{H}_{l-1}\right)}{\left(H_{g-1}{H}_{m-1}+H_{h-1}{H}_{n-1}\right)-\left(H_{g-1}{H}_{n-1}+H_{h-1}{H}_{m-1}\right)}}\right)$$

Thus, we can formulate a probability ratio of order $2^n$ as coded odds, i.e., the product of a rational squared and a likelihood ratio between two rational differences. Moreover, the product of probability ratios also fits Bayes’ coding pattern because of

$$\tilde{O}\left(j:i|h:g\right)\tilde{O}\left(n:m|l:k\right)=\tilde{O}\left(j:i|h:g|l:k|n:m\right)=$$

$$={\left({\displaystyle \frac{hilm}{gjkn}}\right)}^2\left({\displaystyle \frac{\left(H_{j-1}{H}_{n-1}+H_{i-1}{H}_{m-1}\right)-\left(H_{j-1}{H}_{m-1}+H_{i-1}{H}_{n-1}\right)}{\left(H_{g-1}{H}_{k-1}+H_{h-1}{H}_{l-1}\right)-\left(H_{g-1}{H}_{l-1}+H_{h-1}{H}_{k-1}\right)}}\right)$$

It is paramount to highlight that PN coding also copes with probability double ratios in a local setting, with no extra apparatus. A coding source uses the rule

$$\tilde{o}\left(j:i|h:g\right)={\displaystyle \frac{\tilde{o}\left(j:i|r\right)}{\tilde{o}\left(h:g|r\right)}}={\displaystyle \frac{\frac{i}{j}{log}_r\frac{j}{i}}{\frac{g}{h}{log}_r\frac{h}{g}}}=\left({\displaystyle \frac{hi}{gj}}\right)\left({\displaystyle \frac{lnj-lni}{lnh-lng}}\right)\in \mathbb{Q}$$

where $\left(1\le g<h\right)\wedge \left(1\le i<j\right)$, to compare a pair of odds. The first factor is the prior (locally decoded) ratio $\tilde{o}\left(hi:gj|r=1\right)$, and the second is the likelihood ratio (Bayes factor), which measures the strength of the informational correlation between bins $\left[g,h\right)$ and $\left[i,j\right)$ and obliterates the local radix.

In the particular case where the bins have a joint event, either initial or final, we obtain

$$\tilde{o}\left(j:g|h:g\right)=\left({\displaystyle \frac{h}{j}}\right)\left({\displaystyle \frac{lnj-lng}{lnh-lng}}\right)\in \mathbb{Q}$$

If the joint event is the unit, we obtain the subjective ratio

$$\left(j;h\right)=\tilde{o}\left(j:1|h:1\right)=\left({\displaystyle \frac{h}{j}}\right)\left({\displaystyle \frac{lnj}{lnh}}\right)={\displaystyle \frac{ln{j}^h}{ln{h}^j}}\in \mathbb{Q}$$

(24)

where $1<h<j$; e.g., $\left({10}^2;10\right)=1/5$, $\left({10}^{10};{10}^9\right)=1/9$, $\left({10}^3;10\right)=3/100$, $\left({10}^4;10\right)=1/250$, $\left({10}^5;10\right)=1/2000$, and $\left({10}^8;10\right)=1/1250000$. It is the relative mutual likelihood between a pair of numerals regarded from the source, satisfying $\left(j;h\right)=1\left(h;j\right)$; for example, $\left({10}^5;{10}^4\right)=1/8$ and $\left({10}^4;{10}^5\right)=8$.

The structure of a Bayesian datum $\left(AD\right)\left(B-CE-F\right)$ is locally repetitive, like in global coding. The original posterior odds $\tilde{o}\left(j:i|r\right)={\displaystyle \frac{i}{j}}{log}_r{\displaystyle \frac{j}{i}}$ imply $AD=ij$, $B=lnj$, $C=lni$, $E=lnr$, and $F=ln1$, the original prior odds ${\displaystyle \frac{i}{j}}$ imply $AD=ij$ and $B-C=E-F$, and the odds arithmetic always yields the same format; an essential operation * invariably results in the product of a probability ratio (the prior factor) and a likelihood ratio of differences (the Bayes factor). Let

$$\left({\displaystyle \frac{G}{K}}\right)\left({\displaystyle \frac{H-J}{L-M}}\right)*\left({\displaystyle \frac{N}{R}}\right)\left({\displaystyle \frac{P-Q}{S-T}}\right)=\left({\displaystyle \frac{A}{D}}\right)\left({\displaystyle \frac{B-C}{E-F}}\right)$$

then,

$$*\equiv "+"\Rightarrow \left\{\begin{array}{cc}AD=\hfill & 1KR\hfill \\ B=\hfill & GHRS+GJRT+KLNP+KMNQ\hfill \\ C=\hfill & GHRT+GJRS+KLNQ+KMNP\hfill \\ E=\hfill & LS+MT\hfill \\ F=\hfill & MS+LT\hfill \end{array}\right.$$

$$*\equiv "-"\Rightarrow \left\{\begin{array}{cc}AD=\hfill & 1KR\hfill \\ B=\hfill & GHRS+GJRT+KMNP+KLNQ\hfill \\ C=\hfill & GJRS+GHRT+KLNP+KMNQ\hfill \\ E=\hfill & LS+MT\hfill \\ F=\hfill & MS+LT\hfill \end{array}\right.$$

$$*\equiv "\times "\Rightarrow \left\{\begin{array}{cc}AD=\hfill & GNKR\hfill \\ B=\hfill & HP+JQ\hfill \\ C=\hfill & JP+HQ\hfill \\ E=\hfill & LS+MT\hfill \\ F=\hfill & MS+LT\hfill \end{array}\right.$$

$$*\equiv "÷"\Rightarrow \left\{\begin{array}{cc}AD=\hfill & GRKN\hfill \\ B=\hfill & HS+JT\hfill \\ C=\hfill & JS+HT\hfill \\ E=\hfill & LP+MQ\hfill \\ F=\hfill & MP+LQ\hfill \end{array}\right.$$

For instance, the arithmetic of a probability quadruple ratio

$$\tilde{o}\left(n:p|r:s\right)*\tilde{o}\left(v:w|y:z\right)=\left({\displaystyle \frac{A}{D}}\right)\left({\displaystyle \frac{B-C}{E-F}}\right)$$

determines

$$*\equiv "+"\Rightarrow \left\{\begin{array}{cc}AD=\hfill & 1nsvz\hfill \\ B=\hfill & prvz\left(lnnlny+lnplnz\right)+nswy\left(lnrlnv+lnslnw\right)\hfill \\ C=\hfill & prvz\left(lnnlnz+lnplny\right)+nswy\left(lnrlnw+lnslnv\right)\hfill \\ E=\hfill & lnrlny+lnslnz\hfill \\ F=\hfill & lnrlnz+lnslny\hfill \end{array}\right.$$

$$*\equiv "-"\Rightarrow \left\{\begin{array}{cc}AD=\hfill & 1nsvz\hfill \\ B=\hfill & prvz\left(lnnlny+lnplnz\right)+nswy\left(lnrlnw+lnslnv\right)\hfill \\ C=\hfill & prvz\left(lnnlnz+lnplny\right)+nswy\left(lnrlnv+lnslnw\right)\hfill \\ E=\hfill & lnrlny+lnslnz\hfill \\ F=\hfill & lnrlnz+lnslny\hfill \end{array}\right.$$

$$*\equiv "\times "\Rightarrow \left\{\begin{array}{cc}AD=\hfill & prwynsvz\hfill \\ B=\hfill & lnnlnv+lnplnw\hfill \\ C=\hfill & lnnlnw+lnplnv\hfill \\ E=\hfill & lnrlny+lnslnz\hfill \\ F=\hfill & lnrlnz+lnslny\hfill \end{array}\right.$$

$$*\equiv "÷"\Rightarrow \left\{\begin{array}{cc}AD=\hfill & prvznswy\hfill \\ B=\hfill & lnnlny+lnplnz\hfill \\ C=\hfill & lnnlnz+lnplny\hfill \\ E=\hfill & lnrlnv+lnslnw\hfill \\ F=\hfill & lnrlnw+lnslnv\hfill \end{array}\right.$$

As an example, we can express the original local odds (19) as an arithmetic combination of quadruple ratios, namely

$$\tilde{o}\left(j:i|r\right)={\displaystyle \frac{\tilde{o}\left(j:i|r:1\right)}{\tilde{o}\left(r:1|r^2:1\right)+\tilde{o}\left(r:1|r^2:1\right)}}={\displaystyle \frac{\frac{ri}{j}{log}_r\frac{j}{i}}{2\frac{r^2}{r}\frac{lnr}{ln{r}^2}}}={\displaystyle \frac{i}{j}}{log}_r{\displaystyle \frac{j}{i}}$$

This property reinforces a PN system’s recoding process, which takes advantage of the most recent information. Note that one thing is that Bayesian odds boost incremental computing, and a horse of another color is that the structure of Bayesian data is recurrent under arithmetic operations. By exploiting the same representational pattern for all its calculation methods, a coding source can accumulate experience.

5.6. Referential Ratio and Cross-Ratio

The probability quadruple ratio

$${\displaystyle \frac{\tilde{O}\left(j:i|j:g\right)}{\tilde{O}\left(n:i|n:g\right)}}={\left({\displaystyle \frac{\frac{ji}{gj}}{\frac{ni}{gn}}}\right)}^2\left({\displaystyle \frac{\left(H_{n-1}-H_{g-1}\right)\left(H_{j-1}-H_{i-1}\right)}{\left(H_{n-1}-H_{i-1}\right)\left(H_{j-1}-H_{g-1}\right)}}\right)$$

is of foremost interest. Since the prior is the unit, it is a sheer likelihood ratio, i.e., a genuine proportion of information we can rewrite as

$${\displaystyle \frac{\tilde{O}\left(j:i|j:g\right)}{\tilde{O}\left(n:i|n:g\right)}}={\displaystyle \frac{\frac{H_{j-1}-H_{i-1}}{H_{j-1}-H_{g-1}}}{\frac{H_{n-1}-H_{i-1}}{H_{n-1}-H_{g-1}}}}$$

(25)

When $n\to b\to \infty$, the denominator drops from the formula. Using the change of variables $A=H_{j-1}$, $B=H_{i-1}$, and $C=H_{g-1}$, this singular Bayes factor tends to the referential ratio

$$\left(A;B:C\right)\equiv {\displaystyle \frac{A-B}{A-C}}$$

(26)

which is a ratio between the likelihood of two buckets with a joint referent.

Locally, the probability quadruple ratio

$${\displaystyle \frac{\tilde{o}\left(r^A:r^C|r^A:r^B\right)}{\tilde{o}\left(r^D:r^C|r^D:r^B\right)}}={\displaystyle \frac{\tilde{o}\left({\mathrm{e}}^A:{\mathrm{e}}^C|{\mathrm{e}}^A:{\mathrm{e}}^B\right)}{\tilde{o}\left({\mathrm{e}}^D:{\mathrm{e}}^C|{\mathrm{e}}^D:{\mathrm{e}}^B\right)}}$$

also leads to (26) when $r^D\to b\to \infty$, e.g.,

$${\displaystyle \frac{ln{\mathrm{e}}^3{\mathrm{e}}^5}{ln{\mathrm{e}}^3{\mathrm{e}}^7}}=\left(3;5:7\right)=\text{½}$$

and

$${\displaystyle \frac{ln2.51634.5091}{ln2.51636.5065}}\approx \left(0.9228;1.5061:1.8728\right)\approx {\displaystyle \frac{35}{57}}={\displaystyle \frac{H_2-H_4}{H_2-H_6}}$$

Note that the product, quotient, sum, and difference of two referential ratios are referential ratios. In other words, the set of referential ratios, which we will represent by $\tilde{\mathbb{Q}}$, is an ordered algebraic field (of characteristic zero) where

$$\left(F;G:H\right)+\left(J;K:L\right)={\displaystyle \frac{\left(FL+HJ-FJ\right)-\left(FJ+GL+HK-FK-GJ\right)}{\left(FL+HJ-FJ\right)-\left(HL\right)}}$$

$$\left(F;G:H\right)-\left(J;K:L\right)={\displaystyle \frac{\left(FL\right)-\left(FK+GL+HJ-GJ-HK\right)}{\left(FL\right)-\left(FJ+HL-HJ\right)}}$$

$$\left(F;G:H\right)\times \left(J;K:L\right)={\displaystyle \frac{\left(FJ\right)-\left(FK+GJ-GK\right)}{\left(FJ\right)-\left(FL+HJ-HL\right)}}$$

$$\left(F;G:H\right)÷\left(J;K:L\right)={\displaystyle \frac{\left(FJ\right)-\left(FL+GJ-GL\right)}{\left(FJ\right)-\left(FK+HJ-HK\right)}}$$

We can represent a referential ratio $\left(A;B:C\right)$ as the point $\left(A-B,A-C,A\right)$ on a three-dimensional grid where the x component is the numerator, the y component is the denominator, and the z component is the reference. Figure 9 displays the referential ratios $\left(F;G:H\right)=\left(2;3:1\right)$ and $\left(J;K:L\right)=\left(4;1:5\right)$ and the result of the basic operations between them, i.e., addition, subtraction, multiplication, and division.

We can formally define referential ratios as equivalence classes (symbol ∼) of integer triplets where $\left(A;B:C\right)\sim \left(A;D:E\right)⟺BE=CD$. Mind that $\mathbb{Q}\subset \tilde{\mathbb{Q}}$ due to

$${\displaystyle \frac{N}{D}}=\left(;N:D\right)$$

This view lets us comprehend a referential ratio as a dislocated or transported rational number; (26) is $BC$ observed from A. So, $\tilde{\mathbb{Q}}$ is an extension field of $\mathbb{Q}$ such that the latter’s operations are those of the former by restricting the referent to the origin. Specifically, the multiplicative units of the field are $\left(;\pm 1:1\right)$. Besides, $\left(A;B:B\right)=\left(1;:\right)=1$, $\left(A;B:A-1\right)=A-B$, $\left(A;B:C\right)=\left(-A;-B:-C\right)$, and $\left(A;B:C\right)={\left(A;C:B\right)}^{-1}$.

Since a detailed algebraic analysis of this field, its meaning, representation, and potential applications would need a specific article, we will focus herein only on a couple of manifestations.

In physics, we must generically understand the concept of correlation as a ratio between magnitudes of the same physical unit. The most straightforward embodiment of the referential ratio gives the Doppler effect’s relationship between the frequency perceived by the receiver $f_r$ and emitted frequency $f_s$, i.e.,

$${\displaystyle \frac{f_r}{f_s}}=\left(s_w;s_r:-s_s\right)$$

where $s_w$ is the propagation speed of waves in the medium, $s_r<s_w$ is the speed of the receiver relative to the medium, and $s_s<s_w$ is the speed of the source relative to the medium, assuming that they are getting away from each other [90]. Likewise, the formula of the relativistic Doppler effect of the source’s frequency relative to the receiver’s frequency moving away at speed v is [91]

$${\left({\displaystyle \frac{f_s}{f_r}}\right)}^2=\left(1;\left(;-v:c\right):\left(;v:c\right)\right)=\left(1;-vc:vc\right)={\displaystyle \frac{1+vc}{1-vc}}$$

(27)

A referential ratio also appears subsumed into the cross-ratio of four distinct points [92]

$$\left(A,B;C,D\right)={\displaystyle \frac{\frac{A-C}{A-D}}{\frac{B-C}{B-D}}}={\displaystyle \frac{\left(A;C:D\right)}{\left(B;C:D\right)}}=\left(AB+CD;AD+BC:AC+BD\right)$$

(28)

where the alphabetical order indicates that A, B, C, and D are consecutive on the rational projective line, and $A-B$ and $C-D$ have the same sign. This likelihood ratio is the central tool that characterizes the projective line’s geometry. The cross-ratio calculates how much the quadruple’s crossing symmetries deviate from the ideal proportion 1, precisely the extent to which the ratio of how C divides $\left[A,B\right)$ is proportional to how D divides $\left[A,B\right)$. For example, the substitutions $\left\{A=H_{j-1},B=H_{n-1},C=H_{i-1},D=H_{g-1}\right\}$ produce the cross-ratio defined by (25).

6. Conformality

Departing from an inverse-square PMF for the naturals, we gleaned the global and local NBL, implying that a double scale is necessary to support a universal place-value system. A global base specifies the harmonic scale, while a local radix fixes the logarithmic scale that a coding source uses to represent numerals in PN.

In the previous section, we managed odds as probability ratios, i.e., information double ratios. Bayes-compliant information $2^n$-ratios are closed under division. An exceptional case of these is the referential ratio. A ratio of referential ratios is precisely a cross-ratio whose logarithm determines the conformal metric of a local coding space.

Conformal maps preserve angles, hence the shape of the figures, which also implies scale invariance. These properties are critical to translating the elements of a global harmonic space into a local logarithmic subspace, the latter reflecting the state of the former. Conformality is a requirement for coding information that drives complexity; there is a shared very particular characteristic of all complex systems. And that is they internally encode the world in which they live [93].

6.1. the Conformal 1-Annulus Model

The cross-ratio paves the way to conformality because it is invariant under linear fractional transformations over rings [94]. Noteworthy, the group of linear fractional transformations $\left(Az+B\right)\left(Cz+D\right)$, where $\left\{A,B,C,D\right\}\in \mathbb{Z}$, called the modular group (a subset of the M bius group), acts transitively on the points of the grid ${\mathbb{Z}}^2$ visible from the origin, i.e., the irreducible fractions [95], so preserving the form of polygonal shapes through the cross-ratio. A modular map also conserves the referential ratio given by (28).

Because the harmonic and logarithmic scales handle the concept of cross-ratio, we can find a modular transformation between four specific points in a global space S and four points in a given S’s subspace, the coding space where the source makes a local model.

The most powerful application of the cross-ratio is the Poincar disk (The Non-Euclidean World in [96]), a conformal model of hyperbolic geometry that projects the whole ${\mathsf{H}}^2$ in the unit disk. Circle-preserving M bius transformations are the isometries of the complex plane. Assuming that the disk center is at the plane’s origin, points $z_2$ and $z_3$ within the disk connected by the arc of a geodesic circle perpendicularly intersecting the disk’s boundary at $z_1$ and $z_4$ are at a hyperbolic distance of $ln\left(z_1,z_2;z_3,z_4\right)$ [97]. This measure is invariant under the subset of M bius maps acting transitively on the unit disk, the space of the coding source.

In one dimension, the complex plane augmented by the point at infinity can be considered the real projective line [98], and the disk becomes the unit 1-ball. More specifically, the set of irreducible fractions augmented by the point at infinity is the rational projective line; hence the unit 1-ball becomes the rational open unit interval.

While $\left(-1,1\right)$ is the mathematical domain where the modular group acts, we are interested in the global computational space where Bayesian processes and transformative calculation methods occur. We assume that global Bayesian data, i.e., rational quanta, populate a cosmos of information a source perceives and codes to create a continuous world model. Outside a coding source, the information resides on a harmonic scale, whereas inside, a logarithmic scale lodges local Bayesian data.

Suppose that an object is at position P outside $\left(-1,1\right)$. We are ignorant of the actual computation of P, but we know that it is a rational number resulting from applying the rule (15). Be that as it may, we can use Equation (19) to locally figure the odds of $P-1$ against $P+1$ in radix r, whose Bayes factor is the logarithm in r-ary units of a cross-ratio where $z_1=-1$, $z_2=1$, $z_3=P$, and $z_4=\infty$, i.e.,

$${log}_r\left(-1,1;P,\infty \right)\equiv {log}_r\left(P;-1:1\right)={log}_r{\displaystyle \frac{P+1}{P-1}}$$

In information theory, this expression is the representational length in radix r of the rational number $P+1P-1$ and, according to NBL (8), the r-normalized width of bin $\left[P-1,P+1\right)$. We can unite these outlooks by interpreting this Bayes factor as the hyperbolic distance from P to $b\to \infty$, i.e.,

$$d_r\left(P,\infty \right)\equiv {log}_r\left(-1,1;P,\infty \right)={\displaystyle \frac{2}{lnr}}\mathrm{arcoth}\left(P\right)$$

where $\mathrm{arcoth}$ is the inverse function of the hyperbolic cotangent.

A neat inversion conformally maps the outside of the coding source to its inside,

$$\left(-1,1;P,\infty \right)\underset{z\mapsto 1z}{⟶}\left(-1,1;D,0\right)$$

(29)

conserving the cross-ratio. (Other inversions $z\mapsto \propto 1z$ also serve but violate the minimal information principle.) For example, if $P=2$, $\left(-1,1;P,\infty \right)={\displaystyle \frac{-1-2}{1-2}}=3$$={\displaystyle \frac{1+\frac{1}{2}}{1-\frac{1}{2}}}=\left(-1,1;D,0\right)$. Therefore, the r-normalized hyperbolic distance between the origin and $\left|D\right|=\left|1P\right|<1$ is

$$d_r\left(0,D\right)\equiv {log}_r\left(-1,1;D,0\right)\equiv {log}_r\left(0,D;1,-1\right)\equiv$$

$$\equiv {log}_r{\displaystyle \frac{1+D}{1-D}}\equiv {log}_r\left(1;-D:D\right)\equiv {\displaystyle \frac{2}{lnr}}\mathrm{artanh}\left(D\right)$$

where $\mathrm{artanh}$ is the inverse function of the hyperbolic tangent, and $lnr$ is the (constant) curvature’s absolute value of the source’s coding space.

The inverse function of $d_r\left(0,1P\right)$ is $P=coth\left(\left(\text{½}lnr\right)d_r\left(0,1P\right)\right)$. For example, an object at a Euclidean distance $P={10}^6$ from the origin is at a natural hyperbolic distance of $d_r\left(P,\infty \right)=2\mathrm{arcoth}\left({10}^6\right)\approx 2\times {10}^{-6}$ from $b\to \infty$. The coding source positions the object at $D=1P={10}^{-6}$, at a natural hyperbolic distance of $d_e\left(0,D\right)=2\mathrm{artanh}\left({10}^{-6}\right)=2\mathrm{arcoth}\left({10}^6\right)$ from the origin, and decodes it as $P=coth\mathrm{artanh}\left({10}^{-6}\right)={10}^6$.

Mind that the local coding space is the 1-annulus

$${\mathring{\mathrm{a}}}^{-}\equiv \left\{D\in \mathbb{Q}|-1<D<-1b\right\}$$

$${\mathring{\mathrm{a}}}^{+}\equiv \left\{D\in \mathbb{Q}|1b<D<1\right\}$$

$$\mathring{\mathrm{a}}\equiv {\mathring{\mathrm{a}}}^{-}\cup {\mathring{\mathrm{a}}}^{+}\equiv \left\{D\in \mathbb{Q}|1b<\left|D\right|<1\right\}$$

reflecting what the source observes in the 1-annulus

$${\mathring{\mathrm{A}}}^{-}\equiv \left\{P\in \mathbb{Q}|-b<P\le -1\right\}$$

$${\mathring{\mathrm{A}}}^{+}\equiv \left\{P\in \mathbb{Q}|1\le P<b\right\}$$

$$\mathring{\mathrm{A}}\equiv {\mathring{\mathrm{A}}}^{-}\cup {\mathring{\mathrm{A}}}^{+}\equiv \left\{P\in \mathbb{Q}|1\le \left|P\right|<b\right\}$$

(30)

For instance, if $D\in {\mathring{\mathrm{a}}}^{+}$, $d_r\left(0,D\right)$ vanishes if $P\to b\to \infty$, is $>1$ if P is at a Euclidean distance closer than $cothlnr2$ from the origin, and diverges if $P\to 1^{+}$.

6.2. The Conformal 1-Ball Model

The r-normalized hyperbolic distance between two points A and B in $\mathring{\mathrm{a}}$ is $d_r\left(0,Q_B\right)-d_r\left(0,Q_A\right)$, i.e.,

$$d_r\left(Q_A,Q_B\right)={\displaystyle \frac{2}{lnr}}\left(\mathrm{artanh}\left(Q_B\right)-\mathrm{artanh}\left(Q_A\right)\right)$$

where $Q_A$ and $Q_B$ result from the conformal transformation (29), i.e., $P\mapsto 1Q$, which mirrors the external world concerning $\mathring{\mathrm{a}}$’s outward boundary, to wit $\pm 1$. Thus,

$$d_r\left(Q\right)=d_r\left(0,Q\right)={\displaystyle \frac{2}{lnr}}\mathrm{artanh}\left(Q\right)$$

(31)

reflects how far an object at Q is from infinity, situated at the origin.

Nonetheless, we want the origins of the coding source and $\mathring{\mathrm{A}}$ to coincide and $\pm 1$ to be the infinite points of the local model. This requirement implies calculating Q’s complement to one, a logical negation that varies on the left and the right. Recall that all negations are derivations of the canonical one [99], so we will use $Q\to -1-Q$ on the left and $Q\to 1-Q$ on the right to satisfy the minimal information principle. The coding space is now the open 1-ball

$$\text{Ç}\equiv \left\{Q\in \mathbb{Q}|\left|Q\right|<1-1b\right\}$$

(32)

reflecting what the source observes in the 1-annulus $\mathring{\mathrm{A}}$.

An object at $P\in {\mathring{\mathrm{A}}}^{+}$ will be in $d^{+}$ at a Euclidean distance of

$$Q=\left(P;1:\right)=1-{\displaystyle \frac{1}{P}}$$

from the origin and hence at a hyperbolic distance of

$$d_r^{+}\left(Q\right)={\displaystyle \frac{2}{lnr}}\mathrm{artanh}\left(Q\right)={log}_r\left(2P-1\right)={log}_r\left(P;1-P:P-1\right)$$

(33)

with inverse (decoding) function $P=\text{½}\left(1+r^{d_r^{+}\left(Q\right)}\right)$.

Similarly, an object at $P\in {\mathring{\mathrm{A}}}^{-}$ will be in $d^{-}$ at a Euclidean distance of

$$Q=\left(;P+1:-P\right)=-1-{\displaystyle \frac{1}{P}}$$

from the origin and hence at a hyperbolic distance of

$$d_r^{-}\left(Q\right)={\displaystyle \frac{2}{lnr}}\mathrm{artanh}\left(Q\right)=-{log}_r\left(-\left(2P+1\right)\right)={log}_r\left(P;P+1:-P-1\right)$$

(34)

with inverse (decoding) function $P=-\text{½}\left(1+r^{-d_r^{-}\left(Q\right)}\right)$.

For example, a coding source places an object observed at a Euclidean distance of $P=\pm {10}^6$ at $Q=\pm .999999$ in Ç at a natural hyperbolic distance $d_e\left(Q\right)=2\mathrm{artanh}\left(\pm .999999\right)=\pm ln\left(\pm 2\times {10}^6-1\right)=\pm 14.50866$ from the origin, and $P=\pm \text{½}\left(1+e^{14.50866}\right)=\pm {10}^6$. On the positive side, the odds are $\tilde{o}\left(2P-1:1|e\right)={\displaystyle \frac{ln\left(2P-1\right)}{2P-1}}={\displaystyle \frac{ln1999999}{1999999}}\approx 7.254332\times {10}^{-6}$. Suppose that, later, the coding source calculates this value as $7.254265\times {10}^{-6}$, meaning that either the object has moved to $P\approx \pm 1000010$ (because $\tilde{o}\left(2P-1:1|e\right)={\displaystyle \frac{ln2000019}{2000019}}\approx 7.254265\times {10}^{-6}$) or the radix has changed to $r\approx 2.71831$ (because $\tilde{o}\left(2\times {10}^6-1:1|r\right)={\displaystyle \frac{ln1999999}{1999999ln2.718307}}\approx 7.254265\times {10}^{-6}$). Even a combination of these two cases could produce the same odds value.

Note that functions in the form $|{\theta }_1|exp\left(|{\theta }_{2}Q|\right){\mathrm{artanh}}^{{\theta }_3}\left(|{\theta }_4|Q\right)$, where $\left\{{\theta }_1,{\theta }_2,{\theta }_4\in \mathbb{Q}\right\}$ and ${\theta }_3$ is an odd power, e.g., $2exp\left(3Q\right){\mathrm{artanh}}^5\left(7Q\right)$, also give rise to an odd hyperbolic distance that complies with boundary conditions $d_r\left(\pm 1\right)=\pm \infty$ and a vanishing distance when Q vanishes ($\left|P\right|\to 1$). However, they would introduce new factors and parameters we cannot explain; $\mathrm{artanh}\left(Q\right)$ is the only conformal function that retains the origin and conforms with the minimal information principle. Besides, it agrees with the canonical PMF (the first power is the most probable) and satisfies the additional condition of having a non-vanishing derivative at the origin, i.e., the origin is not stationary so that the function can keep its increasing tendency from left to right.

The effect of the radix on (31) is to adjust the point of maximum curvature. If $r\to 1^{+}$ (physically, at very low energies), such a point’s curvature vanishes as $Q\to \pm {\text{½}}^{\pm }$; if $r\to b\to \infty$ (physically, at very high energies), it diverges as $Q\to \pm 1^{\mp }$. As we mentioned in Section 3.6, these extreme values convey no-coding cases. When $r=e=2.718\dots$, i.e., when Ç’s curvature radius is $1lne=1$, the coding source is maximally efficient, and the maximum curvature approximately corresponds to a hyperbolic distance of $d_e\left(0.72543\right)=2\mathrm{artanh}\left(0.72543\right)=1.83803$.

6.3. Conformal Relativity

We must take the hyperbolic distance (31) as an abstract concept that does not have to be a physical length.

Imagine that the global base b physically represents the speed of light. On the right hand, $P=\left(b;:v\right)=b\left(b-v\right)\equiv 1\left(1-vc\right)$ produces $Q=1-1P=vb\equiv vc$; if an object’s speed is $v\to b\equiv c$, then $P\to {\infty }^{+}$ and $Q\to 1^{-}$, and if $v\to 0^{+}$, we get $P\to 1^{+}$ and $Q\to 0^{+}$. On the left hand, $P=\left(;b:-\left(b+v\right)\right)=-b\left(b+v\right)\equiv -1\left(1+vc\right)$ produces $Q=-1-1P=vb\equiv vc$; if an object’s speed is $v\to -b\equiv -c$, then $P\to {\infty }^{-}$ and $Q\to -1^{+}$, and if $v\to 0^{-}$, we get $P\to -1^{-}$ and $Q\to 0^{-}$. In either case, $Q=vb$, and we can write the relativistic Doppler effect (27) in the form

$${\displaystyle \frac{f_s}{f_r}}=e^{\mathrm{artanh}\left(vb\right)}=e^{\mathrm{artanh}\left(Q\right)}$$

Since the rapidity corresponding to velocity v is, by definition,

$$\nu \equiv \mathrm{artanh}\left(vb\right)$$

(35)

the Special Relativity’s Lorentz factor is $\gamma \equiv cosh\nu$ [100]. Thus, the coding source resolves the composition of Doppler shifts as the exponential of the addition of hyperbolic distances, i.e.,

$${\displaystyle \frac{f_s}{f_m}}{\displaystyle \frac{f_m}{f_r}}=e^{{\nu }_{ms}+{\nu }_{rm}}$$

where $f_m$ is the frequency perceived by the first receiver, ${\nu }_{ms}$ the rapidity of the first receiver relative to the source, and ${\nu }_{rm}$ the rapidity of the second receiver relative to the first one.

The special relativity theory is only conformal in terms of rapidity. Visualize two inertial frames, A and B, cruising at relativistic speed ratios of $P_A=3$ and $P_B=18$ about the origin of the coding source. These correspond in Ç at ratios $Q_A=1-1/3=2/3$ and $Q_B=1-1/18=17/18$ of the speed v to $b\equiv c$, defining rapidities ${\nu }_A=\mathrm{artanh}\left(2/3\right)$ and ${\nu }_B=\mathrm{artanh}\left(17/18\right)$, and encoded in ternary as hyperbolic (relativistic) speeds $d_3\left(Q_A\right)=2{\nu }_{A}ln3=1.465$ and $d_3\left(Q_B\right)=2{\nu }_{B}ln3=3.2362$. The difference in hyperbolic speeds is linear in $e$, i.e., $d_3\left(Q_A,Q_B\right)=d_3\left(Q_B\right)-d_3\left(Q_A\right)=1.7712$. Within $\mathring{\mathrm{A}}$ (30), the difference in (Euclidean) velocities is $18-3=15$, but the difference in hyperbolic speeds is

$$\text{½}\left(1+3^{{\displaystyle \frac{2}{ln3}}\left({\nu }_B-{\nu }_A\right)}\right)=\text{½}\left(1+3^{1.7712}\right)=4$$

Rapidity arithmetic is more straightforward than calculating Einstein’s subtraction formula of (Euclidean) velocities, which calculates ${\nu }_B-{\nu }_A$ as $\mathrm{artanh}\left({\displaystyle \frac{1-\left(1718\right)\left(23\right)}{\left(1718\right)-\left(23\right)}}\right)$.

Another way to obtain the same result is directly using the cross-ratio, i.e.,

$$\text{½}\left(1+3^{{log}_3{\displaystyle \frac{\frac{2/3-1}{2/3+1}}{\frac{17/18-1}{17/18+1}}}}\right)=\text{½}\left(1+3^{{log}_{3}7}\right)=4$$

These results mean the weave of Lorentz invariance, and more generally, Poincar invariance, is the algebraic field of referential ratios. Lorentz symmetry [101] locally preserves central reflections and boosts, the latter maintaining constant the speed of light (the global base) when transforming to a reference frame with a different velocity. Poincar symmetry, the entire symmetry group of any relativistic field theory, additionally preserves the laws of physics for inertial coding sources situated at different quantum positions.

6.4. Conformal Coding and Computability

$\mathrm{artanh}$ has a protagonist role in a conformal space not only due to its manifestations in physics, mainly the metric (31), but also because its Taylor series allows calculating iteratively the natural logarithm itself based on the odd powers of the referential ratio ${\displaystyle \frac{x-1}{x+1}}$ ([102], $4.1.27$), i.e.,

$$lnx=2{\displaystyle \sum _{i=1}^{\infty }\frac{{\left(x;1:-1\right)}^{2i-1}}{2i-1}}$$

(36)

It is valid for any $x\in {\mathbb{R}}^{+}$, especially when $x\approx 1$. For example, let us calculate the ternary logarithm of $P={10}^6$. Since ${10}^6={1212210202001}_3$, a numeral with 13 digits, its logarithm’s characteristic is 12. Then, the coding source calculates the logarithm’s mantissa from (36), where $x=P-3^{12}=1.88168$; after five iterations, the mantissa’s error is less than one millionth. So, we calculate ${log}_{3}P=12+{\displaystyle \frac{2}{ln3}}{\sum }_{i=1}^5{\displaystyle \frac{{\left(1.88168;1:-1\right)}^{2i-1}}{2i-1}}=12.57541925$ against the real value of $12.57541965$.

Because the coding source can calculate the logarithm in its coding space (32), $e$’s curvature $-lnr$ is a built-in value. Likewise, $e$’s Euler characteristic $\chi ={\int }_0^{1}lnx\mathrm{d}x=-1$, a topological invariant [103] corresponding to no vertices, one edge, and no faces, is a built-in value. Moreover, the coding source is aware of the PMF (1) through the digamma function $\psi \left(x\right)={\Gamma }^{\prime }\left(x\right)\Gamma \left(x\right)$ (see Section 3.4) because the gamma function results from integrating the powers of $e$’s curvature over the unit segment, namely $\Gamma \left(n+1\right)={\int }_0^1{\left(-lnx\right)}^n\mathrm{d}x$.

Let us denominate the r-normalize hyperbolic distance (equations 33 and 34) in logarithmic terms the conformal encoding function of $P\in \mathring{\mathrm{A}}$, namely

$${\overrightarrow{C}}_r\left(P\right)\equiv \mathrm{sgn}\left(P\right){log}_r\left(2\mathrm{sgn}\left(P\right)P-1\right)$$

(37)

with inverse conformal decoding function

$${\overleftarrow{C}}_r\left(C\right)\equiv \text{½}\mathrm{sgn}\left(C\right)\left(1+r^{\mathrm{sgn}\left(C\right){\overrightarrow{C}}_r\left(P\right)}\right)$$

(38)

where $\mathrm{sgn}$ is the signum function (see Figure 10).

Because the source places an object observed at a Euclidean distance $P\in \mathring{\mathrm{A}}$ at a Euclidean distance

$$Q=\mathrm{sgn}\left(P\right)-{\displaystyle \frac{1}{P}}=\mathrm{sgn}\left(P\right)\left(\left|P\right|;1:\right)$$

from the origin, we can calculate the conformal encoding function using (36) as the infinite summation

$${\overrightarrow{C}}_r\left(Q\right)={\displaystyle \frac{2}{lnr}}{\displaystyle \sum _{i=1}^{\infty }\frac{Q^{2i-1}}{2i-1}}$$

Consequently, the coding source can calculate the conformal decoding function as the infinite product

$${\overleftarrow{C}}_r\left(Q\right)=\text{½}\mathrm{sgn}\left(Q\right)\left(1+r^{\mathrm{sgn}\left(Q\right){\overrightarrow{C}}_r\left(Q\right)}\right)=\text{½}\mathrm{sgn}\left(Q\right)\left(1+\prod _{i=1}^{\infty }{e}^{2\mathrm{sgn}\left(Q\right){\displaystyle \frac{Q^{2i-1}}{2i-1}}}\right)$$

which does not depend on r.

Therefore, Euclidean distances measured in $e$ (32) are the only inputs necessary to compute the coding functions.

Furthermore, a coding source can calculate its first digit probability as

$$Pr\left(r,1\right)={log}_r\left(1+{\displaystyle \frac{1}{1}}\right)={\displaystyle \frac{{\int }_0^1\mathrm{artanh}\left(Q\right)\mathrm{d}Q}{ln\left(r\right)}}=\text{½}{\int }_0^1{\overrightarrow{C}}_r\left(Q\right)\mathrm{d}Q$$

6.5. Local Bayesian Entropy

The conformal encoding function (37) represents the likelihood of the local Bayesian odds, namely

$$\tilde{o}\left(2\mathrm{sgn}\left(P\right)P-1:1|r\right)={\displaystyle \frac{{log}_r\left(2\mathrm{sgn}\left(P\right)P-1\right)}{2\mathrm{sgn}\left(P\right)P-1}}={\displaystyle \frac{{log}_r\left(2\left|P\right|-1\right)}{2\left|P\right|-1}}$$

which expresses the entropic contribution of bin $\left[1,2\left|P\right|-1\right)$, hence of P, to $\mathring{\mathrm{A}}$’s information total, where (30) defines $\mathring{\mathrm{A}}$. Because a cross-ratio is invariant under a conformal transformation, so is the Bayesian information defined by the local odds. The transformed Bayesian datum is

$$\tilde{o}\left(1+\mathrm{sgn}\left(Q\right)Q:1-\mathrm{sgn}\left(Q\right)Q|r\right)={\displaystyle \frac{1-\mathrm{sgn}\left(Q\right)Q}{1+\mathrm{sgn}\left(Q\right)Q}}{log}_r\left({\displaystyle \frac{1+\mathrm{sgn}\left(Q\right)Q}{1-\mathrm{sgn}\left(Q\right)Q}}\right)$$

which expresses the entropic contribution of bin $\left[1-\left|Q\right|,1+\left|Q\right|\right)$, hence of Q, to Ç’s information total, where (32) defines . Moreover, because the mapping is bijective, $\mathring{\mathrm{A}}$ and Ç contain the same absolute likelihood information; therefore, reflects exactly the Bayesian entropy of $\mathring{\mathrm{A}}$.

The limiting function of the rationals in $\mathring{\mathrm{A}}$ to approximate a piece of real average information would require an analysis analogous to [104] (chapter $4b$), which pivots on the differential entropy [76]. Assuming $b\to \infty$, such a differential Bayesian entropy measures the continuous weighted likelihood from the coding source boundary to a point P; it is precisely the integral

$${\tilde{e}}_{{\mathring{\mathrm{A}}}^{+}}\left(P\right){=}_1^P{\displaystyle \frac{{log}_r\left(2x-1\right)}{2x-1}}\mathrm{d}x={\displaystyle \frac{1}{lnr}}{\left({\displaystyle \frac{ln\left(2P-1\right)}{2}}\right)}^2$$

on the right and

$${\tilde{e}}_{{\mathring{\mathrm{A}}}^{-}}\left(P\right){=}_P^{-1}{\displaystyle \frac{{log}_r\left(-2x-1\right)}{\left(-2x-1\right)}}\mathrm{d}x={\displaystyle \frac{1}{lnr}}{\left({\displaystyle \frac{ln\left(-2P-1\right)}{2}}\right)}^2$$

on the left.

Then, $\mathrm{artanh}$ comes up again to estimate the coding source’s entropy ${\tilde{e}}_{\text{Ç}}$. Using (33) and (34),

$$[{\tilde{e}}_e\left(Q\right)={\tilde{e}}_{\mathring{\mathrm{A}}}\left(P\right)={\displaystyle \frac{{\mathrm{artanh}}^2\left(Q\right)}{lnr}}]nat$$

(39)

would dominate the coding source’s Bayesian entropy from the origin to infinite points ($Q\to 1$). In the special theory of relativity, this result means that the entropy grows quadratically with the rapidity (35) when $v\to b\equiv c$. Using (31),

$$[{\tilde{e}}_e\left(Q\right)=lnr{\left(d_r\left(Q\right)2\right)}^2]nat$$

in terms of distance; note that this expression peers Bekenstein-Hawking’s formula of black hole entropy in quantum gravity [105]. Since entropy measures confusion, this result means that objects in remarkably curved coding spaces or at huge distances are indiscernible.

6.6. Conformal Iterated Coding

Because of the hyperbolic distance (equations 31 or 37) and the rapidity range between $-\infty$ and ∞, we can presume the coding source’s logarithmic scale is a (new) whole external world, defined by Euclidean distances, and repeat the encoding process.

If we apply the conformal encoding function on the right recursively

$${log}_r\left(2{log}_r\left(2{log}_r\left(2\dots -1\right)-1\right)-1\right)$$

the source encodes an external object’s position sooner or later in ${\text{Ç}}^{+}$, and the recursion halts. For example, if $r=3$, we can map an object observed at a Euclidean distance of googol from the origin, after five nested conformal transformations, onto a point in ${\text{Ç}}^{+}$ at an approximated hyperbolic distance of $0.096773$ from the origin.

Repeatedly applying the encoding function (37) or the decoding function (38) is information-preserving iterated coding. We will use the notation $r\circ n$ to express the nth iterate ($n\ge 1$) of the encoding function ${\overrightarrow{C}}_r\left(P\right)$ so that ${\overrightarrow{C}}_{r\circ 1}\left(P\right)\equiv {\overrightarrow{C}}_r\left(P\right)$ and

$${\overrightarrow{C}}_{r\circ \left(n+1\right)}\left(P\right)\equiv {\overrightarrow{C}}_r\left(P\right)\circ {\overrightarrow{C}}_{r\circ n}\left(P\right)$$

where ∘ denotes function composition holding the properties

$${\overrightarrow{C}}_{r\circ \left(m+n\right)}\left(P\right)\equiv {\overrightarrow{C}}_{r\circ n}\left(P\right)\circ {\overrightarrow{C}}_{r\circ m}\left(P\right)$$

and

$${\overrightarrow{C}}_{r\circ mn}\left(P\right)\equiv {\overrightarrow{C}}_{r\circ n}\left({\overrightarrow{C}}_{r\circ m}\left(P\right)\right)$$

Note that the limits of the coding space remain unaltered irrespective of the iteration because ${\overrightarrow{C}}_{r\circ n}\left(\pm 1\right)$ vanishes for all n.

The iterated logarithm of $N\in {\mathbb{N}}^{+}$, written ${log}_{*}N$, is the number of times the natural logarithm function must be recursively applied before the result is less than or equal to the unit. Similarly,

$${\overrightarrow{C}}_{r*}\left(P\right)$$

is the number of times we must iteratively apply (37) until the absolute value of the result is less than one.

We call the sequence of values ${\overrightarrow{C}}_{r\circ n}\left(P\right)$, where $1\le n\le {\overrightarrow{C}}_{r*}\left(P\right)$, the conformal orbit of P, which outlines a tetrational plot [106]. For example, the orbit with radix $r=3$ of the quantum minus googol is $\left\{-{10}^{100},-210.221,-5.49687,-2.09533,-1.05609,-0.096773\right\}$. No value of the orbit can be identically 1 because $\pm 1$ represents $\pm \infty$, while the global base b is our universe’s maximum. Indeed, ${\overrightarrow{C}}_{e*}\left(b\right)$ gives us the universe’s maximum natural depth.

We recover the original point by applying (38) iterated the same number of times, i.e.,

$${\overleftarrow{C}}_{r\circ {\overrightarrow{C}}_{r*}\left(P\right)}\left({\overrightarrow{C}}_{r\circ {\overrightarrow{C}}_{r*}\left(P\right)}\left(P\right)\right)$$

where ${\overleftarrow{C}}_{r\circ 1}\left(H\right)\equiv {\overleftarrow{C}}_r\left(H\right)$ and ${\overleftarrow{C}}_{r\circ \left(n+1\right)}\left(H\right)\equiv {\overleftarrow{C}}_r\left(H\right)\circ {\overleftarrow{C}}_{r\circ n}\left(H\right)$.

Every 1-ball of radius ${\overleftarrow{C}}_{r\circ n}\left(0\right)$ might correspond to a granularity level [107], a local setting belonging to the nested information of a (global) complex system such as the universe. Considering that ${\overrightarrow{C}}_{r*}\left(P\right)$ grows with P exceptionally slowly, the natural granularity levels are likely few; the ternary granularity depth for the currently estimated universe size in Planck units would be ${\overrightarrow{C}}_{3*}\left({10}^{61}\right)=5$, and the binary granularity depth for the currently estimated number of atoms in the known universe would be ${\overrightarrow{C}}_{2*}\left({10}^{88}\right)=8$.

Granularity and primality might be related. A PN system encodes a number as a polynomial in a single (integer) variable [108], the base or radix, where the coefficients are the possible outcomes of the variable, either quanta or digits. Imagine now that $b=r^k$, where r is a prime, and $k={\overrightarrow{C}}_{r*}\left(b\right)$ is a nonzero natural that indicates the r-ary depth of the universe. Then, the universe could be a finite (or Galois) field [109] of order b and characteristic r (addition of r copies of any quantum vanishes) where the operations of multiplication, addition, subtraction, and division are well-defined, and equation ${\left(q_1+q_2\right)}^r=q_1^r+q_2^r$ holds. A granularity tier would constitute a prime field of order r represented by its digits $1\le d<r$ (roots of the polynomial $X^{r-1}-1$), and b’s quanta would correspond to the factors of $X^{b-1}-1$ over r’s field.

Because every iteration conserves the local likelihood information, a granularity realm has an identical copy of the Bayesian data that matches its range of distances in the external world. Nevertheless, it is autonomous in creating new information elements, such as those resulting from clustering points or lumping together states of similar behavior, defining emerging organizational layers. We can even take this combination of iterated coding with coarse-grained modeling [110] as a principle of multiscale modeling [111].

From a computational point of view, conformal coding might use a representation similar to the level-index number system [112]. The quantum $P\in {\mathring{\mathrm{A}}}^{+}$ encoded as the (true normalized form of the) significand $0<s<1$ after $n={\overrightarrow{C}}_{r*}\left(P\right)\ge 1$ iterations would be represented as $s_{r\circ n}$ so that

$$P\approx {\overleftarrow{C}}_{r\circ n}\left(s\right)=\text{½}\left(1+r^{\text{½}\left(1+r^{\text{½}\left(1+r^{{\cdots }^{\text{½}\left(1+r^s\right)}}\right)}\right)}\right)$$

where the order (height) of the power tower is n.

For example, a conformal representation of the number googol is $.00212111221..{.}_{3\circ 5}$ (see Figure 11) owing to $.00212111221..{.}_3\equiv .096773\dots$ and

$${10}^{100}={\overleftarrow{C}}_{3\circ 5}\left(.096773\dots \right)=\text{½}\left(1+3^{\text{½}\left(1+3^{\text{½}\left(1+3^{\text{½}\left(1+3^{\text{½}\left(1+3^{.096773\dots }\right)}\right)}\right)}\right)}\right)$$

We similarly obtain that ${10}^{88}={\overleftarrow{C}}_{2\circ 8}\left(.805897\dots \right)\equiv .1100111001{\dots }_{2\circ 8}$.

7. Primordial Distributions

We construct the one-parameter canonical PMF from binomial generators. Then, we fix the parameter of the canonical PMF for the natural and integer numbers by introducing a requirement for the divisibility of the probability mass. This provision is equivalent to making the event picking the number one a Bernoulli process.

The resulting PMF for the natural numbers allows calculating the probability and entropy of dichotomies like odd-even and prime-composite and trichotomies such as negative-zero-positive and elliptic-Euclidean-hyperbolic. The canonical PMF for the integer numbers could be the germ of a fundamentally unitary, parity-invariant, uncertain, discrete, and maximally entropic universal field.

7.1. Ensuring Constructability, Rationality, and Randomness

We can not irrefutably prove that the probability ISL (1) is a foremost PMF beating at the core of the cosmos, but NBL emanating from it is at least evidence supporting that possibility. Because NBL is pervasive and reflects the properties of PN, efficiency must be a rudimentary feature of nature. Following this trend of thought, we will describe how to grow this one-parameter PMF from elemental geometric distributions, guaranteeing universal constructability. We will also tune the PMF’s parameter to achieve the expected divisibility of $\mathbb{N}$’s probability mass and cast probability values as unit fractions, which backs the idea that nature has a prominent rational character.

Euler product formula for the zeta function (equations $1.6$ and $1.13$ in [113]) allows us to define PMF (1)’s primordial random variable $X\in {\mathbb{N}}^{+}$ as the infinite product

$$X=\prod _{p\in \mathbb{P}}{p}^{X\left(1p^2\right)}$$

of independent identically distributed random variables of parameter $1p^2$ with a geometric sequence of probabilities $Pr\left(\underset{p\in \mathbb{P}}{X}\left(1p^2\right)=k\right)={\left(1p^2\right)}^k\left(1-1p^2\right)$ [65], corresponding to the PMF of k failures before the first success, each binomial trial (see below) with failure probability $1p^2$. This construction means that the canonical PMF (up to $ϵ$) consists of geometric distributions that, in turn, are memoryless [114] and infinitely divisible [115]. Of course, this infinitude is theoretical because there must be a maximum prime.

Once we have constructed the one-parameter canonical PMF from elemental generators, which constitutes a rudimentary notion of emergence, we can improve its computability by digging into rationality and making the probability mass of the natural numbers divisible on average to ensure its compartmentalization.

At the end of Section 3.3, we determined that $ϵ\in \left(0,6{\pi }^2\right)$ by merely demanding $Pr\left(N\in \mathbb{N}\right)>0$, i.e., $\left(1-ϵ\zeta \left(2\right)\right)=\left(1-ϵ{\pi }^{2}6\right)>0$. Given that the fraction of square grid ${\mathbb{Z}}^2$’s points visible from the origin is precisely $6{\pi }^2$ [116], our requirement is equivalent to setting $ϵ$ as a rational equal to the size of a subset of them.

We now introduce a new vital constraint on the number of divisors of a natural number intended to narrow the range of possible values of $ϵ$. The rationale is that divisibility, as a dual concept of primality, is paramount to understanding our universe.

Remember that a nonzero natural’s number of divisors $d$ includes one and the number itself; for instance, $d\left(1^2\right)=1$, $d\left(2^2\right)=3$ (1, 2, and 4), $d\left(3^2\right)=3$ (1, 3, and 9), and $d\left(4^2\right)=5$ (1, 2, 4, 8, and 16). Notwithstanding that the distribution $Pr\left(d\left(N^2\right)\right)$ is unknown, we can calculate the mean of divisors of counting numbers squared employing the general law of the expected values (or unconscious statistician) [117]. We require such an expected value to be at least two to guarantee that the divisibility of the entire probability room defined by (1) takes place non-trivial and naturally, for if $N^2$ splits into $d\left(N^2\right)\ge 2$ parts, so can $Pr\left(N\right)$, i.e.,

$$2\le \widehat{E}\left(d\left(N^2\right)\right)=ϵ\sum _{N=1}^{\infty }{\displaystyle \frac{d\left(N^2\right)}{N^2}}=ϵ{\displaystyle \frac{{\zeta }^3\left(2\right)}{\zeta \left(4\right)}}=ϵ{\displaystyle \frac{{\left({\pi }^{2}6\right)}^3}{{\pi }^{4}90}}=ϵ{\displaystyle \frac{5}{12}}{\pi }^2$$

where the summation agrees the equation $3.41$ of [118]. Considering the high probability of picking the unit, this constraint is more rigid than it might seem at first sight.

Let us recap. We are imposing only a pair of constraints to provide $ϵ$ with an accurate value; first, the probability of a natural to be nonzero, and second, the expected probability mass of the set of natural numbers to be splittable. Thus,

$$\left(0<ϵ<6{\pi }^2\right)\wedge \left(ϵ{\displaystyle \frac{5}{12}}{\pi }^2\ge 2\right)$$

constricts the possible values of $ϵ$ to the narrow range

$$ϵ\in {\displaystyle \frac{1}{{\pi }^2}}\left[{\displaystyle \frac{24}{5}},6\right)\approx \left(.4863417,.6079271\right)$$

We aim to define NBL in a strict rational setting to increase operability through multiplication and division (see subSection 3.4 and Section 5.1). Although rationals such as 49100 or 610 satisfy this constraint, the most probable numerator and denominator in agreement with (1) are precisely 1 and 2, so

$$ϵ=\text{½}$$

(40)

In passing, this value assures that the probability mass of a nonzero natural number is splittable. Moreover, it is a unit fraction.

What does (40) mean from the information theory perspective? It means converting the event picking the unit into a Bernoulli (binomial) experiment equivalent to flipping a coin. A sequence of these independent identically distributed picks is a Bernoulli process, unique and universal in that it is the single most random non-mixing process possible [119].

More generally, the corresponding variable that considers obtaining exactly k ones in an experiment with N trials, each with a probability of success $ϵ$, follows the binomial distribution [120]

$$\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k}}\right)={\displaystyle \frac{N!}{k!\left(N-k\right)!}}$$

$$Pr\left(k,N,ϵ\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k}}\right){ϵ}^k{\left(1-ϵ\right)}^{\left(N-k\right)}$$

(41)

isomorphic to exactly k tosses out of $N\ge k$ tosses resulting in a head. The logarithmic scale awesomely comes up when we calculate the entropy of this distribution, which tends to $\text{½}ln\left(2\pi eNϵ\left(1-ϵ\right)\right)$ as N approaches infinity.

Well, the binary entropy function of picking the number one (and the complementary event picking a number with splittable probability) attains its maximum when (40) holds, like a fair coin, where the odds for and against are 1 (heads or tails) by definition. For the same reason, ½ maximizes the entropy of the binomial distribution (41), too.

In summary, (40) ensures five conditions, to wit, positive rational probabilities congruent with the PMF itself, divisibility of $\mathbb{N}$’s probability mass, maximum number of naturals with splittable occurrence probability, counting numbers with unit fraction probability masses, and maximum universal randomness.

7.2. Canonical PMF for the Natural and Integer Numbers

Assuming (40), we can establish that

$$Pr\left(X=N\right)=\left\{\begin{array}{cc}N\in \mathbb{N}-\left\{0\right\}:\hfill & {\displaystyle \frac{1}{2N^2}}\hfill \\ else:\hfill & 1-\text{½}\zeta \left(2\right)\hfill \end{array}\right.$$

(42)

is the canonical PMF for a random variable X that takes natural values. Its mode is one, with undefined mean and variance, and entropy requiring 3 bits because of

$$-\left(1-\text{½}\zeta \left(2\right)\right){log}_2\left(1-\text{½}\zeta \left(2\right)\right)-\text{½}\sum _{N=1}^{\infty }{\displaystyle \frac{{log}_2\left(\text{½}{N}^{-2}\right)}{N^2}}=\left[2.6178\right]bit$$

As required, the expected divisibility value of the global probability mass surpasses two, namely

$$\widehat{E}\left(d\left(N^2\right)\right)=\text{½}{\displaystyle \frac{{\zeta }^3\left(2\right)}{\zeta \left(4\right)}}\approx 2.05617$$

Indeterminacy has chances every tick of the clock because of $1-\text{½}\zeta \left(2\right)\approx 17.75\%$. Therefore, the probability of a counting number coming out is

$$\text{½}\sum _{N=1}^{\infty }{\displaystyle \frac{1}{N^2}}={\displaystyle \frac{\zeta \left(2\right)}{2}}={\displaystyle \frac{{\pi }^2}{12}}\approx 82.25\%$$

The probability of a string of numbers is the product of the indiviual probabiliies; for example, the probability of picking s and t in a row is $Pr\left(<s,t>\right)=Pr\left(<t,s>\right)=Pr\left(s\right)Pr\left(t\right)$. The probability of a choice between a set of numbers is the sum of the indiviual probabiliies; in particular, the probabilty of picking a number in the interval $\left[s..t\right)$ is the sum of $Pr\left(s\right)+Pr\left(s+1\right)+\cdots +Pr\left(t-1\right)$.

The probabilities of a natural number being odd and even are $\left(3/4\right)\left(\zeta \left(2\right)2\right)={\left(\pi 4\right)}^2\approx 5/8$ and $\left(14\right)\left(\zeta \left(2\right)2\right)={\pi }^{2}48\approx 5/24$, respectively (see equation $1.12$ in [121]). So, getting an odd natural number is ${\displaystyle \frac{3/4}{1/4}}=3$ times as probable as picking an even, in sharp contrast with the intuitive ½ size in [48].

The probability of the event picking a natural number greater than 1, i.e., a number with splittable probability, is the unit minus the probabilities of indeterminate and one, namely

$$Pr\left(X\ge 2\right)=1-\left(1-\text{½}\zeta \left(2\right)+\text{½}\right)=\text{½}\left(\zeta \left(2\right)-1\right)\approx 0.32247$$

The probability of the event picking a prime is half the sum of the reciprocals of prime numbers $\mathbb{P}$ squared, i.e.,

$$Pr\left(X=N\in \mathbb{P}\right)=\sum _{N\in \mathbb{P}}{\displaystyle \frac{1}{2N^2}}=\text{½}{P}_{\zeta }\left(2\right)\approx 0.22612$$

where $P_{\zeta }\left(·\right)$ is the prime zeta function. Thus, picking a composite number has a probability of

$$Pr\left(X\ge 2\wedge X\notin \mathbb{P}\right)=\text{½}\left(\zeta \left(2\right)-1-P_{\zeta }\left(2\right)\right)\approx 0.09634$$

and the probability that $N\in \mathbb{P}$, conditioned to be greater than 1, exceeds $70\%$ due to

$$Pr\left(X=N\in \mathbb{P}|X\ge 2\right)={\displaystyle \frac{Pr\left(X=N\in \mathbb{P}\right)}{Pr\left(X\ge 2\right)}}={\displaystyle \frac{P_{\zeta }\left(2\right)}{\zeta \left(2\right)-1}}\approx {\displaystyle \frac{0.22612}{0.32247}}\approx 0.70123$$

Therefore, observing primes in nature is expected; regarding number theory, the odds of prime versus composite are 7030.

On the other hand, the canonical PMF (42) straightforwardly explains the proclaimed supremacy of the hyperbolic configurations concerning the two-dimensional tilings algebraically associated with the finite reflection groups [122].

The probability of a natural number greater than one occurring thrice is

$${\left(Pr\left(X\ge 2\right)\right)}^3={\left(\text{½}\left(\zeta \left(2\right)-1\right)\right)}^3\approx 0.033532$$

In other words, this value is the probability of producing three naturals to form a triangle.

The probability of picking three naturals forming a Euclidean triangle (i.e., $1l+1m+1n=1$) is the probability of picking $\left\{2,3,6\right\}$, $\left\{2,4,4\right\}$, or $\left\{3,3,3\right\}$, namely

$${\left(\text{½}\right)}^3\left({\displaystyle \frac{1}{2^2{3}^2{6}^2}}+{\displaystyle \frac{1}{2^2{4}^2{4}^2}}+{\displaystyle \frac{1}{3^2{3}^2{3}^2}}\right)\approx 0.000390$$

The probability of picking three naturals forming a spherical triangle (i.e., $1l+1m+1n>1$) is

$${\left(\text{½}\right)}^3\left({\displaystyle \frac{\zeta \left(2\right)-1}{2^2{2}^2}}+{\displaystyle \frac{1}{2^2{3}^2{3}^2}}+{\displaystyle \frac{1}{2^2{3}^2{4}^2}}+{\displaystyle \frac{1}{2^2{3}^2{5}^2}}\right)\approx 0.005780$$

where the first term is the probability of a triplet of two 2s and any natural greater than one.

The probability of picking three naturals forming a hyperbolic triangle ($1l+1m+1n<1$) equals the occurrence probability of a triangle that is neither Euclidean nor spherical,

$$0.033532-0.000390-0.005780\approx 0.0273615$$

So, the odds of hyperbolic cases against non-hyperbolic cases point to the former’s predominance, specifically

$${\displaystyle \frac{0.0273615}{0.000390+0.005780}}\approx 4.434429$$

In summary, two-dimensional tilings are usually hyperbolic. Remember that a star of the triangle group [123] is the set of all rotational triangle subgroups $\mathrm{D}\left(2,3,n\right)$ ($1/2+1/3+1n<1$), isomorphic to the modular group we broached at the end of Section 5.6. This group is a subset of the almighty M bius group, which permeates through many fields of geometry, number theory, and significant areas of physics.

In particular, $\mathrm{D}\left(2,3,7\right)$ is the triangle subgroup most probable in the hyperbolic class. It is algebraically the quotient of the group of unit quaternions by its center $\pm 1$ and topologically the cover for all Hurwitz surfaces. The Hurwitz group of a Hurwitz surface maximizes the order of the automorphism group for a given genus through orientation, scale, and angle-preserving transformations, i.e., conformal mappings, with grand importance in Quantum Field Theory, gravitation, and cosmology. The Hurwitz surface of the minor genus (three) is the Klein quartic [124,125] with automorphism group the self-dual Fano plane, closely related to the octonions [126], both appearing in game theory and fundamental physics. Moreover, the mysterious Monster group can grow from $\mathrm{D}\left(2,3,7\right)$ [127].

These facts indicate again that inversive and conformal geometry might be at the world’s heart, built from the simplest simplices (generalizations of a triangle to any dimension).

Finally, we can extend (42) to the set of integer numbers to establish

$$Pr\left(Z\right)=\left\{\begin{array}{cc}Z\in \mathbb{Z}-\left\{0\right\}:\hfill & {\displaystyle \frac{1}{{\left(2Z\right)}^2}}\hfill \\ else:\hfill & 1-\text{½}\zeta \left(2\right)\hfill \end{array}\right.$$

(43)

The canonical PMF for the integers, illustrated in Figure 12, has mode $\pm 1$, with entropy

$$-\left(1-\text{½}\zeta \left(2\right)\right){log}_2\left(1-\text{½}\zeta \left(2\right)\right)-2\sum _{Z=1}^{\infty }{\displaystyle \frac{{log}_2\left({\left(2Z\right)}^{-2}\right)}{{\left(2Z\right)}^2}}=\left[3.44027\right]bit$$

For nonzero integers x and y, it is the solution to the functional equation

$$Pr\left(x\right)Pr\left(y\right)={\left(xyPr\left(xy\right)\right)}^2$$

satisfying the condition $Pr\left(\pm 1\right)={\text{½}}^2$.

This PMF, which accounts for the weight of the ISL in physics [128], cannot be more buildable; take every second integer from the coding source point of view, i.e., $\{\cdots ,-8,-6,-4,-2,,2,4,6,8,\cdots \}$, then their reciprocals squared, obtaining $\{\cdots ,1/64,1/36,1/16,1/4,,1/4,1/16,1/36,1/64,\cdots \}$, which coincides with (43). It satisfies positive probability masses summing to one, central reflection symmetry, fair (i.e., undefined) mean and variance, holistic rationality, and randomness. Unitarity, parity invariance, indeterminism, discreteness, and the principle of maximum entropy are the physical reflections of these properties, which are all fundamental. Besides, the square root of the probability mass (physically, the probability amplitude) of a nonzero integer is precisely half its reciprocal.

Again, the resulting NBL is valid irrespective of the proportionality constant $ϵ$ following Section 3.6, namely

$$Pr\left(r,d\right)={log}_r\left(1+{\displaystyle \frac{1}{\left|d\right|}}\right)$$

where $1\le \left|d\right|<r$, $r\in \mathbb{N}\ge 2$, and $d\in \mathbb{Z}$.

8. Epilogue

Our research shows how discreteness and the continuum interact under the shelter of (1). A complex system and its environment embody the continuous local and discrete global. The NBL probability’s derivative of the local takes us to the global, and vice versa; the global’s integral situates us in a local setting of likelihood-based probability. A harmonic scale of rational numbers supports the global realm, while a logarithmic scale of real values supports the local realm. The harmonic scale’s base is a universal reference that establishes the concept of likelihood-based information, and a logarithmic scale’s radix is an exponentiation constant that normalizes the system’s conformal space of local information coded in PN.

We assume the system is a coding source that observes the outside, operates internally the gathered information, and takes action on the environment. More precisely, a coding source uses the synergy between Benford’s and Bayes’s laws to reflect (encode) the external world, process (recode or arithmetically transform) the information, and return (decode) the results to its immediate surroundings. These laws connect mathematics with physics.

8.1. Canonical PMF

NBL bets on smallness; little objects are more numerous than extensive ones. Why? The fact that many probability distributions partially adhere to NBL does not reveal its root. Nor can we glean its origin from the fact that merging methods via sampling or multiplication of real-world data series produces adherence to NBL. Mathematics alone cannot justify a first-digit law, wrote Raimi. Given that the effects of NBL are well-known in physics, we need to be aware of its fundamental character and ultimate cause.

NBL is not so mysterious if we concede that it originates from an ISL of probability. Whenever the canonical PMF governs a system behavior, we can infer its properties are data spaces that record information on a positional scale. This constructible primordial PMF states an absolute hyperbolic relation between the square of a nonzero number $N\in \mathbb{N}$ and its probability mass $Pr\left(N\right)$, specifically that $N^{2}Pr\left(N\right)$ is constant. We stress that the phenomenology of the canonical PMF and NBL run in parallel, to the point that we aver that ours is an inverse-square world for the most part, much as Havil affirms that It’s a Harmonic World and It’s a Logarithmic World.

If we assume the minimal information principle, PMF (43) is the only way to satisfy that the probabilities are positive summing to 1, guarantee that our random variable’s average value is not finite if we repeat the experiment often enough, ensure mass divisibility, and cope with the extension to all the integers, hence to the rational and algebraic numbers. These requirements’ logic, sturdiness, and feasibility suggest a full-fledged tenet at the heart of mathematics, physics, and higher integrative levels. Besides, this PMF implements the Axiom of Induction; at least one inductive set does exist determined uniquely by its members that has a substrative probability distribution.

Although the canonical PMF consists of Bernoulli generators, we introduce (43) as a brute fact deprived of tangible information. Notwithstanding, this probability ISL could be the embryo for crucial experimental laws of physics, such as Newton’s Universal Gravitation and Coulomb’s Electrostatic Force. Understood as an improbability field, it could even give place to the energy density of space characterized by a sombrero potential with an unstable center and a nonzero vacuum expectation value.

The canonical PMF indicates a manner of arranging availability versus transcendence. Occasional numbers are more startling and influential than abundant ones. While frequent numbers provide resilience, infrequent numbers have the capacity for transformation. Therefore, the universal equilibrium is not enforced via uniformity but achieved by hyperbolically balancing accessibility or stability (position) against magnitude or reactivity (momentum); does not it sound to the Uncertainty Principle?

In particular, our study of depleted harmonic series teaches us that the specific digits involved in a constraining numeral do not matter. In contrast, the length of such a numeral does. Short numerals or low digit densities are accessible and cheap, producing heavy terms that condense the space. In contrast, long numerals or high densities of digits are rare and deliver slender harmonic terms. In other words, increasingly bigger numbers on a linear scale have less and less weight on a positional scale. Moreover, almost all large numbers have a high cost of accessibility and are indistinguishable except for their order of magnitude.

The canonical PMF naturally copes with indeterminacy by introducing the indeterminate value (interpreted as inaction or not-a-number and symbolized by zero) and dodging a finite expected value. Additionally, uncertainty appears with a less metaphysical flavor and a quantum touch. A number’s value and probability represent a foundational (position-momentum) inaccuracy,

$$N·Pr\left(N\right)={\displaystyle \frac{1}{2N}}\le \text{½}$$

Assuming that induction is a rudiment of our cosmos, this inequality is a sort of certainty principle, i.e., a clue that uncertainty is finite.

The canonical PMF defines a large number by its probabilities, proportional to the chance of fitting its tail and inversely proportional to its opportunity, i.e.,

$$N\sim {\displaystyle \frac{ϵ{\psi }^{\prime }\left(N\right)}{\frac{ϵ}{N^2}}}={\displaystyle \frac{Pr\left(\ge N\right)}{Pr\left(N\right)}}$$

Equality exclusively occurs in the infinite limit when the trigamma function approaches a hyperbola asymptotically (see Section 3.4). Alternatively, for ${Pr}^{\prime }\left(\ge N\right)\sim -Pr\left(N\right)$, $\underset{N\to \infty }{lim}Pr\left(\ge N\right)+N{Pr}^{\prime }\left(\ge N\right)$ vanishes. In principle, scale invariance is unreachable because the exact solution $Pr\left(\ge N\right)=ϵN$ exists only in the offing.

Nevertheless, summing from the unit to base b, say the superlative natural number, immediately drives us to the global NBL. b confines the physical framework where numbers become quanta. The trigamma function measures a number’s probability exceedance, i.e., its cumulative distribution function’s upper tail. When normalizing the trigamma function relative to the base’s support, we obtain the probability of quantum q in base b, which is the product’s reciprocal of q and the harmonic number $b-1$. We can interpret $Pr\left(r,q\right)=1q{H}_{b-1}$ as measuring cruising speed because $1q$ and $H_{b-1}$ estimate a quantum’s span (space) and a base’s scope (time); minor quanta or bases raise promptness, while high quanta or bases yield delay.

Pure conformality is only possible within a finite global scope; b ultimately enables implementing a PN-based coding space where the accessibility potential

$$Pr\left(b,q\right)+q{\displaystyle \frac{\partial Pr\left(b,q\right)}{\partial q}}$$

vanishes for all quanta q and the logarithm can germinate.

8.2. the Logarithm Measures Local Information

Integrating under the global NBL’s hyperbola and normalizing concerning a local radix $r\ll b$ immediately drives us to the fiducial, $\mathbb{R}$-based, logarithmic form of NBL.

The logarithm and its inverse (the exponential) are fundamental functions because they appear everywhere in mathematics and physics, to wit generalized means, primes, fractals, solutions to many differential equations, power laws, information transmission, von Neumann entropy, et cetera. This plenty demonstrates that hyperbolic spaces proliferate. Indeed, we prove that the canonical PMF leads to such dominance in Section 7.2. Within the scope of this essay, not only does the logarithm measure the local natural likelihood (5) and probability of a bin (equations 6 and 7), but the local Bayes factor (18), the elemental jumps (22), the entropy distribution function of a bipartition (23), the subjective ratio (24), the hyperbolic distance (31), the rapidity (35), the canonical coding (37) and decoding (38) functions, the differential Bayesian entropy (39), and the repetition of the Bernoulli event picking the unit (41) also involve it.

In geometry, the logarithm gives the normalized area under the hyperbola. The logarithm bridges information and physics, especially thermodynamics, via the Gibbs entropy formula in statistical mechanics and the Bekenstein-Hawking formula in quantum gravity. In information theory, the logarithm mainly estimates the representational extent of a given numeral written in PN. Further, our essay proves that the logarithm resolves the metric of a conformal space by recasting correlations into distances or rapidities, as Section 6.2 describes. This conversion is critical in iterated coding, especially in coarse-grained and multiscale modeling. The radix’s logarithm is precisely the (absolute value of the) coding space’s curvature. In particular, radix $r=e$ defines the natural logarithmic scale, i.e., the standard one-dimensional hyperbolic space.

The logarithm is central to comprehending how profoundly NBL connects with recurrence and incrementality. A coding source implements Bayes’ rule by multiplying the prior odds between two quanta by a likelihood factor represented by a local NBL probability, precisely the logarithm of their ratio’s reciprocal. We say a local datum is Bayesian if it admits this structure, which is recurrent under iterative processes of encoding, recoding, arithmetic operations, and decoding. A local Bayesian datum represents likelihood information, e.g., the encoded odds of an elemental gap or a stopping choice.

Assuming that a digit is an orbit and the radix is the number of orbits, e.g., of an atom, a jump between consecutive orbits introduces significant entropy differences only in the origin’s immediacy. Lower orbits have more difficulty achieving a transition, whereas the reactivity associated with the farthest orbits is logarithmically more probable. This behavior resembles the chemical elements’ periodic table concerning the electron shells.

Assuming that a digit is an item and the radix r is the number of items in a pool, Bayesian coding solves a version of the secretary problem that considers the strategy to select a good item rather than the best one. It belongs to a class called last-success problems with universal scope. Its objective is to determine the last item x on the fly that maximizes the probability of success in accomplishing the stopping rule, i.e., rejecting the first x items and stopping afterward at the next that is better than the preceding ones. We approach the solution by aggregating the odds $\tilde{o}\left(x:1|r\right)\propto {\displaystyle \frac{r}{x}}lnx$ and $\tilde{o}\left(r:x|r\right)\propto xln{\displaystyle \frac{r}{x}}$. We feature a pair of characteristic properties of all these good-choice (best-choice included) and optimal-stopping problems; first, they require a phase for incremental information gathering to deliver a preliminary proper output only refined if there is time left, and second, the solution x generates asymmetry by making the past partition (bin $\left[1,x\right)$) smaller than the future partition (bin $\left[x,r\right)$). Is this procedure not primary management of memory in real-time?

8.3. Conjectures

On the one hand, the canonical PMF and its NBL subsidiaries explain why proximity or slightness provides more stability than distance or heftiness. Occurrence probability attracts information toward a central source; apart from the second thermodynamical law, no other law allows inferring such a fundamental imbalance. However, the entropic leaks from the most outlying digits offset this mass accumulation in the source’s proximity. Therefore, data encoded in PN would induce alternating uphill and downhill flows, reflecting a brute fluctuation between the dual elementary concepts of concentration and dispersion.

On the other hand, Newcomb-Benford and Bayesian laws regulate the implementation of a conformal space through tractable hyperbolic functions. An NBL probability is a likelihood, i.e., a Bayes factor. A referential ratio is a particular case of Bayesian datum with a unit prior (i.e., a sheer Bayes factor) and a point at infinity. A cross-ratio is a quotient of referential ratios, and the logarithm of a cross-ratio yields a conformal metric. The canonical coding functions define how a complex system, say a coding source, creates an image of the world, which can render crucial consequences in physics, principally enabling scalability and boosting efficiency as leitmotifs and chief drivers of cosmological development.

The universal hyperbolicity that the inverse-square, Newcomb-Benford, and Bayesian laws steer can illuminate the measurement problem. If the integer line $\mathbb{Z}$ were the position space of a generic object, the canonical PMF for the integers (43) would match with a default wave function with one degree of freedom expressible as a linear combination of the position eigenstates $|Z\rangle$, namely

$$\Psi =\cdots +1/4|-2\rangle +1/2|-1\rangle +\sqrt{1-\text{½}\zeta \left(2\right)}|0\rangle +1/2|+1\rangle +1/4|+2\rangle +1/6|+3\rangle +\cdots$$

A nonzero integer $Z\in \mathbb{Z}$ represents an actual eigenvalue corresponding to the eigenstate with rational amplitude ${\left(2Z\right)}^{-1}$, and the origin is the idle or vacuum (beable) state with quantum amplitude $\sqrt{1-\text{½}\zeta \left(2\right)}$. By the Born rule, the quantum-mechanical probability of being at place Z is the square modulus of its rational amplitude, precisely its canonical probability mass. From a complementary point of view, the canonical PMF tells us the probability $Pr\left(Z\right)={\left(4E|Z\rangle \right)}^{-1}$ of having energy $E|Z\rangle =Z^2$, corresponding to a wave function’s rational amplitude ${\left(2\sqrt{E|Z\rangle }\right)}^{-1}$ in the momentum space. Thus, the physical existence of the canonical PMF would imply a default wave function and vice versa.

A system object of observation and the measurement entity (e.g., an instrument, an experimenter, or the environment) interact, entangling into a mixture of states represented by their joint wave function. Suppose the observed object is a test particle, and the observing entity is a measurement device whose wave function corresponds to our universally binding canonical PMF. The joint wave function is untestable, but the coding device can measure the particle’s position up to inherent uncertainty.

We assume particles materialize as wave packets with arbitrary widths rather than points. During measurement, a particle in the observation field progressively decoheres, losing its pure quantum nature and dynamics while transferring the information into the coding source, which recursively assigns the particle’s state to nested bins forming a numeral. For example, suppose that a particle has triangular wave function $\text{½}|-1\rangle$+$1\sqrt{2}|0\rangle$+$\text{½}|+1\rangle$ with center of masses objectively at position 200 (and triangular momentum compatible with the uncertainty principle). We can locate the particle’s wave function projected onto a bin of digits at any time. The odds of registering 2 to 1 are $\left(\left({\left(1\sqrt{2}\right)}^2+{\left(12\right)}^2\right){log}_{10}\left(1+12\right)\left({\left(12\right)}^2{log}_{10}\left(1+11\right)\right)\right)=1.755$, the odds of registering 20 to 19 are $\left(\left({\left(1\sqrt{2}\right)}^2+{\left(12\right)}^2\right){log}_{10}\left(1+120\right)\left({\left(12\right)}^2{log}_{10}\left(1+119\right)\right)\right)=2.854$, and the odds of registering 200 to 199 are $\left({\left(1\sqrt{2}\right)}^2{log}_{10}\left(1+1200\right)\left({\left(12\right)}^2{log}_{10}\left(1+1199\right)\right)\right)=1.99$. Note that position data are biased towards the source regarding the expected genuine odds, to wit $3=\left({\left(1\sqrt{2}\right)}^2+{\left(12\right)}^2\right){\left(12\right)}^2$, 3, and $2={\left(1\sqrt{2}\right)}^2{\left(12\right)}^2$; objects would be farther than they appear! After measurement, we have no more coherent position state but a position datum; the particle’s information now lies in the measurement numeral.

8.4. Some Metaphysics

Literature about NBL overlooks its rational aspect. Ours is primarily a harmonic world, where rational numbers guarantee calculability. PMF (42) and PMF (43) tell us that the probabilities of natural and integer numbers are unit fractions. The global NBL, stemming from (1), means that quantum frequencies are unit fractions, too. Besides, although the fiducial NBL appears to be an absolute law that assigns a probability to every digit separately, a digit acquires its informational meaning only compared with another, i.e., in odds form. Contrary to the Special Relativity premises, we take the global base manifesting as the speed of light as proof of the universe’s rational rather than real essence (see Section 6.2).

More fundamentally, holistic rationality implies relationalism (i.e., reciprocity) and operability (i.e., arithmetical tractability), basic properties of a physical transformation. Rationality is budding relativity. Indeed, the quotidian continuum we perceive from our local outlook approximates the discrete reality; the continuum emerges from the rational instead of vice versa. We conclude that $\mathbb{Q}$ is the universal number system at the heart of computability, contrasting with the contrived real numbers.

Infinity has no place in the algebraic field of rational numbers. Further, we have endorsed the universe’s finiteness in many other ways. To begin with, we feature a global base closely related to the maximum natural (or prime) number. Raw data statistics of natural phenomena indicate that no counting system can avoid this universal tendency towards littleness. Perceivable things in the cosmos are typically small but always rationally commensurable from some standpoint; otherwise, they would be incomparable, whence indiscernible. An infinite host universe reduces all its finite guests to zero, an unobservable number. PN ignores numeral positions surpassing a certain threshold. Because a (quantum) measurement obliterates the least significant digits, the models a coding source supports necessarily give rise to non-deterministic mechanics, such as Gisin’s proposal, which is empirically equivalent to classical mechanics but uses only finite-information numbers. A transfinite universe prone to productivity is counterintuitive. The universe is an economic system precisely owing to its limited scope and resources.

This essay generally points to mathematics having a physical status. We have put laws midway between mathematics and physics on the table. The canonical PMF for integer numbers defines a pervasive numeric field of stability that is the germ of a constitutively unitary, parity-invariant, uncertain, discrete, and maximally random universe. The linkage between probability space and physical space, especially within a coding space, is so intricate that we hardly find discrepancies. Further, because the notion of logarithmic likelihood results from comparing two logarithmic sectors (5) and a local NBL probability mass is a ratio of logarithmic likelihoods (6), stating that information is physical means probability is physical.

We have told a hegira from information coding to physics, presuming the Galilean idea that nature is mathematical per se. William K. Clifford (1976, On the Bending of Space, https://doi.org/10.1007/978-94-010-1727-5_49) underlined that we might be treating merely as physical variations effects which are really due to changes in the curvature of our space, although Whether one associates ’geometric’ ideas with a theory is [illegible] a private matter, stated Einstein in a letter written to Reichenbach (Google translation from Doc. AEA 20-117 of the Albert Einstein Archive, 8 April 1926). Our partway philosophical worldview supports the theory that every mathematical concept has a physical peer because physics emerges from algebra via geometry, supported by hyperbolicity, economy, and relationalism. The embodiment of these pillars makes Tegmark’s hypothesis that the observable reality is a mathematical structure defined by computable functions plausible. We must add that such a structure consists of conformal spaces and transformations.