Scaling of Rotational Constants

Preprint

Article

Scaling of Rotational Constants

This version is not peer-reviewed.

Altmetrics

Downloads

Views

129

Comments

Submitted:

07 November 2024

Posted:

08 November 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

This manuscript introduces the concept of scaling factors for rotational constants. These factors are designed to bring computed equilibrium rotational constants closer to experimentally-fitted ground-state-averaged rotational constants. The parameterization of the scaling factors was performed for several levels of theory, namely DF-Dn/def2-mVP (DF=B3LYP,PBE0, n=3(BJ),4, m=S,TZ), PBEh-3c, and r2SCAN-3c. The obtained scaling factors systematically improve the consistency between theoretical and experimental rotational constants.

Keywords:

Subject:

Chemistry and Materials Science - Theoretical Chemistry

Supplementary Material

supplementary.xlsx (542.75KB )

1. Introduction

Rotational spectroscopy, consisting of microwave (MW),[1,2] millimeter wave (MMW),[3] and terahertz (THz)[4,5,6] spectroscopies, is a powerful high-resolution experimental technique that provides unprecedented structural sensitivity for the different structural (including conformational) and constitutional isomerisms of molecules,[7,8,9] as well as for isotopic substitutions and various large-amplitude vibrational motions,[10] such as proton transfer,[11] internal rotation,[12] inversion,[13] and even movements of an entire molecule across another molecule’s surface.[9] This kind of spectroscopic technique can be used in various applications, from monitoring the chemical composition of mixtures[14] and reactions[3,15] to detecting atmospheric[16,17] and interstellar molecular species.[8,18]

In the zeroth approximation, the rotational spectrum of a molecule is given by the rigid rotor approximation, which in the case of non-linear molecules is parametrized using three rotational constants, which are denoted as A, B, and C or, equivalently, as

B_{a}

B_{b}

, and

B_{c}

, respectively.[19,20,21] These constants, usually expressed in MHz, are related to the moments of inertia

I_{α}

along the given

α

-th principal axis of the molecule through the following expression:[19,20]

B_{α} = \frac{ℏ}{4 π I_{α}},

(1)

where

α = a, b, c

is the given principal axis,

ℏ = 1.05 \times 10^{- 34}

J·s is the reduced Planck constant, and the moment of inertia is given as

I_{α} = \sum_{n = 1}^{N} m_{n} \cdot r_{α n}^{2},

(2)

where n enumerates the atoms in the molecule, N is the overall number of atoms in the molecule,

m_{n}

is the mass of the n-th atom, and

r_{α n}

is the distance of the n-th atom to the

α

-th principal axis. In the experiment, the so-called vibrationally averaged rotational constants are obtained, usually in the ground vibrational state, and they are commonly denoted as

A_{0}

B_{0}

, and

C_{0}

.[21]

The initial structural assignment of the spectroscopically observed species is usually done based on quantum-chemical (QC) calculations. The candidate structures are optimized at a chosen level of theory, usually with a dispersion-corrected density functional theory (DFT) calculation, and then the theoretical rotational constants are compared with the experimentally determined ones.[22] However, such a comparison does not always yield an unambiguous assignment of the molecular structures, and the reason is two-fold. First of all, the optimized structure corresponds to the so-called equilibrium geometry with corresponding equilibrium rotational constants

A_{e}

B_{e}

, and

C_{e}

, in which all vibrational effects are absent.[21,23] Therefore, the experimental

A_{0}

B_{0}

C_{0}

values and theoretical

A_{e}

B_{e}

C_{e}

are not equal due to the vibrational anharmonic shifts, which usually expands the molecular size, thus increasing the moments of inertia (Equation 2) and consequently decreasing the corresponding rotational constant (Equation 1).[24] In other words, it is generally expected that

B_{0, α} \leq B_{e, α}

. The second reason is the quality of the QC approximation, which can distort the equilibrium structure due to complicated underestimation and/or overestimation of various intra- and intermolecular chemical bonds and non-covalent interactions. This systematic error does not have a preferred shift of the rotational constant values with respect to their experimental counterparts and thus can be of any type.[21]

In this work, we propose to systematically improve the inconsistency between experimental ground-state averaged rotational constants (

A_{0}

B_{0}

C_{0}

) and their theoretical equilibrium counterparts (

A_{e}

B_{e}

C_{e}

) by applying tabulated scaling factors. Such an approach, where the band shifts due to anharmonic effects and QC approximation failure, was demonstrated to be fruitful in the case of vibrational (e.g., infrared) spectroscopy.[25,26,27,28,29,30,31,32] Therefore, it is interesting to investigate whether a similar systematic improvement for the lower-frequency spectral range can be achieved as well. First, we will introduce the procedure of the scaling, the fitting model, and the training dataset, then we will provide the scaling factors, and in the end, we will give an application example using a few recently studied systems with the usage of the PBE0-D3(BJ)/def2-TZVP level of theory.

2. Scaling Procedure

We propose to perform the scaling of the theoretical equilibrium constants obtained from QC calculations (

A_{e}^{QC}

B_{e}^{QC}

C_{e}^{QC}

) with a single global scaling factor s for a given QC approximation, such that the adjusted constants

A_{s}

B_{s}

, and

C_{s}

are defined as

\{\begin{matrix} A_{s} = s \cdot A_{e}^{QC}, \\ B_{s} = s \cdot B_{e}^{QC}, \\ C_{s} = s \cdot C_{e}^{QC} . \end{matrix}

(3)

Since the rotational constants are inversely proportional to the moments of inertia (see Equations 1 and 2), such scaling procedure is effectively equivalent to a global scaling of the atomic coordinates as

r_{s, n} = \frac{r_{e, n}}{\sqrt{s}},

(4)

where

r_{e, n}

and

r_{s, n}

are the equilibrium and scaled positions of the n-th atom in the molecule (see Equation 2).

To tabulate the scaling factors s for given QC approximations, we need a benchmark dataset. In this case, we chose the set of molecules used for obtaining the scaling factors for harmonic frequencies from Ref. [33]. From the set of 441 neutral singlet molecules, 174 non-linear molecules up to 17 atoms with experimentally available

A_{0}

B_{0}

, and

C_{0}

values were selected. Only the relatively high-quality QC approximations were considered here, namely DF-Dn/def2-mVP (

DF = B 3 LYP, PBE 0

n = 3 (BJ), 4

m = S, TZ

),[34,35,36,37,38,39,40] PBEh-3c,[41] and

r^{2}

SCAN-3c[42] levels of theory. This was done since rotational spectroscopy, as a high-resolution technique, generally requires more high-quality data for comparison than rotationally unresolved infrared spectroscopy. Besides, MW spectroscopy, as the lowest frequency gas-phase spectroscopic technique to this date, is practically limited by the size of the systems that can be brought into the gas phase in sufficient amounts and by the spectral resolution, as for large systems the spectra will become dense and uninterpretable, despite of the experimental resolution being of the order of

Δ ν / ∋ \sim 10^{- 6} - 10^{- 7}

in the standard arrangement.[43]

As the values of the rotational constants

A \geq B \geq C

can differ by orders of magnitude, the metrics that use the absolute deviations between the experimental and theoretical rotational constants are essentially useless, as they will mostly fit the A-rotational constants for the small-size molecules. Therefore, an advantageous approach is switching to relative values fitting, which was introduced in Ref. [33]. In the application to rotational constants, the least-squares problem can be written in the following way:

{rRSMD}^{2} (s) = \sum_{k = 1}^{N_{mol}} ({(s \cdot \frac{A_{e, k}^{QC}}{A_{0, k}^{\exp}} - 1)}^{2} + {(s \cdot \frac{B_{e, k}^{QC}}{B_{0, k}^{\exp}} - 1)}^{2} + {(s \cdot \frac{C_{e, k}^{QC}}{C_{0, k}^{\exp}} - 1)}^{2}) \to min,

(5)

where rRMSD denotes the relative root-mean-square deviation (rRMSD) of the rotational constants, k enumerates the molecules in the dataset, and

N_{mol}

is the total number of molecules in the dataset. The optimal scaling factors are thus given via equation[33]

s_{opt} = \underset{s}{argmin} ({rRSMD}^{2} (s)) = \frac{\sum_{k = 1}^{N_{mol}} (\frac{A_{e, k}^{QC}}{A_{0, k}^{\exp}} + \frac{B_{e, k}^{QC}}{B_{0, k}^{\exp}} + \frac{C_{e, k}^{QC}}{C_{0, k}^{\exp}})}{\sum_{k = 1}^{N_{mol}} ({(\frac{A_{e, k}^{QC}}{A_{0, k}^{\exp}})}^{2} + {(\frac{B_{e, k}^{QC}}{B_{0, k}^{\exp}})}^{2} + {(\frac{C_{e, k}^{QC}}{C_{0, k}^{\exp}})}^{2})},

(6)

where argmin denotes the minimal value of s, which minimizes the corresponding function value. The fitting uncertainty of this value is given by the equation

σ_{opt} = \frac{rRSMD (s_{opt})}{\sqrt{\sum_{k = 1}^{N_{mol}} ({(\frac{A_{e, k}^{QC}}{A_{0, k}^{\exp}})}^{2} + {(\frac{B_{e, k}^{QC}}{B_{0, k}^{\exp}})}^{2} + {(\frac{C_{e, k}^{QC}}{C_{0, k}^{\exp}})}^{2})}},

(7)

where

rRSMD (s_{opt})

is the value of rRMSD (Equation 5) with the optimal scaling factor given in Equation 6. Note that we do not use weighting with the standard deviations of the experimental fits here because the theoretical calculations have much larger systematic uncertainties that we cannot account for.

3. Resulting Scaling Factors

The resulting scaling factors for various levels of theory, as well as the rRMSD values (Equation 5) for the unscaled and optimally scaled theoretical rotational constants, are given in Table 1. Several trends can be observed from these results. First, the scaling improves the match between theory and experiment in most cases, except for B3LYP-Dn/def2-TZVP (

n = 3

(BJ), 4), which we will discuss later. We also see that the increase of the basis set quality from def2-SVP to def2-TZVP improves the agreement between experiment and theory in both scaled and unscaled cases. Applying either the D3(BJ) or D4 dispersion correction leads to the same scaling factors, which probably points to the equal performance of these corrections. A similar trend was observed for the harmonic frequency scaling factors in Ref. [33]. However, the most unexpected yet predictable result is that the optimal scaling factors for the B3LYP-Dn/def2-TZVP levels of theory are equal to one within the margins of error. This means that the scaling does not significantly improve the predicted rotational constant at this approximation. At the same time, the rRMSD values at B3LYP-Dn/def2-TZVP levels are amongst the best in the dataset. Such behavior matches the popularity of these levels of theory for quantum-chemical computations among the rotational spectroscopy community.

4. Illustrative Cases

The simplest way to illustrate the robustness and generality of the scaling procedure is to apply this procedure to cases outside the training dataset. For this, we demonstrate the applicability of the obtained scaling factors for a popular quantum-chemical approximation, namely PBE0-D3(BJ)/def2-TZVP.[37,38,39] The geometries of the molecules discussed here were optimized at this level of theory using the ORCA 5[44,45] software, and then their rotational constants were taken from the calculations. In the case of isotopic substitutions, the rotational constants of the isotopologues were re-computed from the optimized geometries using the UNEX 1.6 software.[46] To demonstrate the numerical performance of the scaling factor, we compared the rRMSD (Equation 5) and mean absolute deviations (MAD) of the rotational constants from the experimentally determined values for the given molecules in the case of scaled and unscaled theoretical equilibrium rotational constants. The MAD values were calculated according to the expression

MAD (s) = \sum_{k = 1}^{N_{mol}} (|s \cdot A_{e, k}^{QC} - A_{0, k}^{\exp}| + |s \cdot B_{e, k}^{QC} - B_{0, k}^{\exp}| + |s \cdot C_{e, k}^{QC} - C_{0, k}^{\exp}|) .

(8)

The first illustrative set of molecules included 15 linear top molecules from di- to pentatomic molecules. Since linear molecules have only one rotational constant, they were excluded from the training set, and the scaling effect on these systems will be the most clearly visible. The calculation of rRMSD and MAD values (Equations 5 and 8) for linear molecules, thus, included only the B rotational constant. The second illustrative set was the case of isotopologues, which, for simplicity of the analysis, were not included in the training dataset. We chose single-substituted isotopologues of imidazole (

C_{3} H_{4} N_{2}

), which had rotational constants of three singly substituted ¹³C and two singly substituted ¹⁵N isotopologues available from the literature.[47] The last example was a set of non-covalently bound molecular systems, namely, water – hydrochloric acid clusters

HCl {(H_{2} O)}_{n} (n = 2 - 5, 7)

, which are examples of hydrogen bond network structures. The rotational constants for these species were taken from Refs. [48] and [49].

We can first take a look at a few exemplary cases of molecular systems from our test dataset, two linear molecules (HCN and HCCCN), one imidazole ¹⁵N-substituted isotopologue, namely

{imidazole-}^{15}

N(1) (nomenclature adapted from Ref. [47]) and also at the largest of our hydrochloric acid clusters,

HCl {(H_{2} O)}_{7}

. The structures of these molecules and their rotational constants are given in Figure 1 and Table 2. As one can see, B3LYP-D3(BJ)/def2-TZVP provides a reasonable estimation of the rotational constants, closer to the experimental values than unscaled constants at the PBE0-D3(BJ)/def2-TZVP level of theory. However, PBE0-D3(BJ)/def2-TZVP after scaling becomes as accurate or even more accurate than the B3LYP-D3(BJ)/def2-TZVP-based results. This can be seen by comparing the deviations within the datasets. By looking at the rRMSD and MAD values for the scaled and unscaled rotational constants of these systems at the PBE0-D3(BJ)/def2-TZVP level of theory (Table 3), we observe that the scaling indeed improves the agreement of the theoretical and experimental values.

5. Conclusions

In this work, we introduced the concept of scaling factors for rotational constants. Applying a single tabulated scaling factor for all rotational constants is effectively equivalent to scaling the molecular size to account for systematic errors in the equilibrium structure due to the quantum-chemical approximation and for absent anharmonic effects. The set of scaling factors for ten different DFT approximations, namely DF-Dn/def2-mVP (

DF = B 3 LYP, PBE 0

n = 3 (BJ), 4

m = S, TZ

) and PBEh-3c and

r^{2}

SCAN-3c, were produced from the database of 174 non-linear molecules. The applicability of these scaling factors was illustrated for the PBE0-D3(BJ)/def2-TZVP level of theory in the case of linear molecules, isotopologues, and non-covalently bonded systems. Thus, the application of such scaling factors can be recommended for the more accurate identification of species in rotational spectra and to support the assignment of specific molecular species in complicated broadband rotational spectra.

Author Contributions

Conceptualization, D.S.T. and M.S.; methodology, D.S.T.; validation, D.S.T.; formal analysis, D.S.T., C.J.S., W.S., F.X., M.K., E.G., J.L., F.B., L.R., H.S, C.M.T.; investigation, D.S.T., C.J.S., W.S., F.X., M.K., E.G., J.L., F.B., L.R., H.S, C.M.T.; resources, M.S.; data curation, M.S.; writing—original draft preparation, D.S.T.; writing—review and editing, M.S.; supervision, M.S.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.

Funding

C.J.S. acknowledges Charles Hamilton Houston Internship Program at Amherst College that sponsored his internship at Deutsches Elektronen-Synchrotron DESY.

Data Availability Statement

The Excel sheet containing the data and computations for obtaining the scaling factors is provided in the electronic supporting information.

Acknowledgments

All authors acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF. In particular, D.S.T.’s calculations were enabled through the Maxwell computational resources operated at DESY.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

MW	microwave
MMW	millimeter wave
THZ	terahertz
QC	quantum-chemical
DFT	density functional theory
rRMSD	relative root-mean-square deviation
MAD	mean absolute deviation

References

Morino, Y.; Hirota, E. Microwave Spectroscopy. Annual Review of Physical Chemistry 1969, 20, 139–166. [Google Scholar] [CrossRef]
Park, G.B.; Field, R.W. Perspective: The first ten years of broadband chirped pulse Fourier transform microwave spectroscopy. The Journal of Chemical Physics 2016, 144, 200901. [Google Scholar] [CrossRef] [PubMed]
Prozument, K.; Barratt Park, G.; Shaver, R.G.; Vasiliou, A.K.; Oldham, J.M.; David, D.E.; Muenter, J.S.; Stanton, J.F.; Suits, A.G.; Barney Ellison, G.; Field, R.W. Chirped-pulse millimeter-wave spectroscopy for dynamics and kinetics studies of pyrolysis reactions. Phys. Chem. Chem. Phys. 2014, 16, 15739–15751. [Google Scholar] [CrossRef] [PubMed]
Cuisset, A.; Hindle, F.; Mouret, G.; Bocquet, R.; Bruckhuisen, J.; Decker, J.; Pienkina, A.; Bray, C.; Fertein, E.; Boudon, V. Terahertz Rotational Spectroscopy of Greenhouse Gases Using Long Interaction Path-Lengths. Applied Sciences 2021, 11. [Google Scholar] [CrossRef]
Swearer, D.F.; Gottheim, S.; Simmons, J.G.; Phillips, D.J.; Kale, M.J.; McClain, M.J.; Christopher, P.; Halas, N.J.; Everitt, H.O. Monitoring Chemical Reactions with Terahertz Rotational Spectroscopy. ACS Photonics 2018, 5, 3097–3106. [Google Scholar] [CrossRef]
Giesen, T.; Brünken, S.; Caris, M.; Neubauer-Guenther, P.; Fuchs, U.; Lewen, F. Terahertz Rotational Spectroscopy. 2005, Vol. 231, pp. 87–96. [CrossRef]
Pinacho, P.; Quesada-Moreno, M.M.; Schnell, M. Conformations of borneol and isoborneol in the gas phase: Their monomers and microsolvation clusters. The Journal of Chemical Physics 2023, 159, 194305. [Google Scholar] [CrossRef]
Loru, Donatella.; Cabezas, Carlos.; Cernicharo, José.; Schnell, Melanie.; Steber, Amanda L.. Detection of ethynylbenzene in TMC-1 and the interstellar search for 1,2-diethynylbenzene. A&A 2023, 677, A166. [CrossRef]
Xie, F.; Sun, W.; Hartwig, B.; Obenchain, D.A.; Schnell, M. Hydrogen-Atom Tunneling in a Homochiral Environment. Angewandte Chemie International Edition 2023, 62, e202308273. [Google Scholar] [CrossRef]
Loru, D.; Steber, A.L.; Pérez, C.; Obenchain, D.A.; Temelso, B.; López, J.C.; Schnell, M. Quantum Tunneling Facilitates Water Motion across the Surface of Phenanthrene. Journal of the American Chemical Society 2023, 145, 17201–17210. [Google Scholar] [CrossRef] [PubMed]
Li, W.; Tikhonov, D.S.; Schnell, M. Double Proton Transfer Across a Table: The Formic Acid Dimer–Fluorobenzene Complex. Angewandte Chemie International Edition 2021, 60, 25674–25679. [Google Scholar] [CrossRef]
Nguyen, H.V.L.; Caminati, W.; Grabow, J.U. The LAM of the Rings: Large Amplitude Motions in Aromatic Molecules Studied by Microwave Spectroscopy. Molecules 2022, 27. [Google Scholar] [CrossRef] [PubMed]
Carlotti, M.; Trombetti, A.; Velino, B.; Vrbancich, J. The rotation-inversion spectrum of 15NH3. Journal of Molecular Spectroscopy 1980, 83, 401–407. [Google Scholar] [CrossRef]
Krin, A.; Quesada Moreno, M.M.; Pérez, C.; Schnell, M. A Scent of Peppermint—A Microwave Spectroscopy Analysis on the Composition of Peppermint Oil. Symmetry 2022, 14. [Google Scholar] [CrossRef]
Sun, W.; Pinacho, P.; Obenchain, D.A.; Schnell, M. Gas-Phase Characterization of Adipic Acid, 6-Hydroxycaproic Acid, and Their Thermal Decomposition Products by Rotational Spectroscopy. The Journal of Physical Chemistry Letters 2024, 15, 817–825. [Google Scholar] [CrossRef] [PubMed]
Tretyakov, M. Spectroscopy underlying microwave remote sensing of atmospheric water vapor. Journal of Molecular Spectroscopy 2016, 328, 7–26. [Google Scholar] [CrossRef]
Muhleman, D.O.; Clancy, R.T. Microwave spectroscopy of the Mars atmosphere. Appl. Opt. 1995, 34, 6067–6080. [Google Scholar] [CrossRef]
Guélin, M.; Cernicharo, J. Organic Molecules in Interstellar Space: Latest Advances. Frontiers in Astronomy and Space Sciences 2022, 9. [Google Scholar] [CrossRef]
Gordy, W.; Cook, R. Microwave molecular spectra, 3rd ed. ed.; Wiley New York, 1984.
Atkins, P.; Friedman, R. Molecular Quantum Mechanics; OUP Oxford, 2011.
Cristina Puzzarini, J.F.S.; Gauss, J. Quantum-chemical calculation of spectroscopic parameters for rotational spectroscopy. International Reviews in Physical Chemistry 2010, 29, 273–367. [Google Scholar] [CrossRef]
Gottschalk, H.C.; Poblotzki, A.; Fatima, M.; Obenchain, D.A.; Pérez, C.; Antony, J.; Auer, A.A.; Baptista, L.; Benoit, D.M.; Bistoni, G.; Bohle, F.; Dahmani, R.; Firaha, D.; Grimme, S.; Hansen, A.; Harding, M.E.; Hochlaf, M.; Holzer, C.; Jansen, G.; Klopper, W.; Kopp, W.A.; Krasowska, M.; Kröger, L.C.; Leonhard, K.; Mogren Al-Mogren, M.; Mouhib, H.; Neese, F.; Pereira, M.N.; Prakash, M.; Ulusoy, I.S.; Mata, R.A.; Suhm, M.A.; Schnell, M. The first microsolvation step for furans: New experiments and benchmarking strategies. The Journal of Chemical Physics 2020, 152, 164303. [CrossRef]
Tikhonov, D.S.; Vishnevskiy, Y.V. Describing nuclear quantum effects in vibrational properties using molecular dynamics with Wigner sampling. Phys. Chem. Chem. Phys. 2023, 25, 18406–18423. [Google Scholar] [CrossRef]
Mata, R.A.; Suhm, M.A. Benchmarking Quantum Chemical Methods: Are We Heading in the Right Direction? Angewandte Chemie International Edition 2017, 56, 11011–11018. [Google Scholar] [CrossRef] [PubMed]
Pulay, P.; Fogarasi, G.; Pongor, G.; Boggs, J.E.; Vargha, A. Combination of theoretical ab initio and experimental information to obtain reliable harmonic force constants. Scaled quantum mechanical (QM) force fields for glyoxal, acrolein, butadiene, formaldehyde, and ethylene. Journal of the American Chemical Society 1983, 105, 7037–7047. [Google Scholar] [CrossRef]
Irikura, K.K.; Johnson, R.D.; Kacker, R.N. Uncertainties in Scaling Factors for ab Initio Vibrational Frequencies. The Journal of Physical Chemistry A 2005, 109, 8430–8437. [Google Scholar] [CrossRef] [PubMed]
Kesharwani, M.K.; Brauer, B.; Martin, J.M.L. Frequency and Zero-Point Vibrational Energy Scale Factors for Double-Hybrid Density Functionals (and Other Selected Methods): Can Anharmonic Force Fields Be Avoided? The Journal of Physical Chemistry A 2015, 119, 1701–1714. [Google Scholar] [CrossRef] [PubMed]
Alecu, I.M.; Zheng, J.; Zhao, Y.; Truhlar, D.G. Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries. Journal of Chemical Theory and Computation 2010, 6, 2872–2887. [Google Scholar] [CrossRef] [PubMed]
Laury, M.L.; Carlson, M.J.; Wilson, A.K. Vibrational frequency scale factors for density functional theory and the polarization consistent basis sets. Journal of Computational Chemistry 2012, 33, 2380–2387. [Google Scholar] [CrossRef]
Merrick, J.P.; Moran, D.; Radom, L. An Evaluation of Harmonic Vibrational Frequency Scale Factors. The Journal of Physical Chemistry A 2007, 111, 11683–11700. [Google Scholar] [CrossRef] [PubMed]
Pople, J.A.; Scott, A.P.; Wong, M.W.; Radom, L. Scaling Factors for Obtaining Fundamental Vibrational Frequencies and Zero-Point Energies from HF/6–31G* and MP2/6–31G* Harmonic Frequencies. Israel Journal of Chemistry 1993, 33, 345–350. [Google Scholar] [CrossRef]
Khaikin, L.S.; Grikina, O.E.; Vogt, N.; Stepanov, N.F. Interpreting the vibrational spectra of uracil molecules and their deuterated isotopomers using a scaled quantum-chemical quadratic force field. Russian Journal of Physical Chemistry A 2012, 86, 1855–1861. [Google Scholar] [CrossRef]
Tikhonov, D.S.; Gordiy, I.; Iakovlev, D.A.; Gorislav, A.A.; Kalinin, M.A.; Nikolenko, S.A.; Malaskeevich, K.M.; Yureva, K.; Matsokin, N.A.; Schnell, M. Harmonic scale factors of fundamental transitions for dispersion-corrected quantum chemical methods. ChemPhysChem, n/a, e202400547, [https://chemistry-europe.onlinelibrary.wiley.com/doi/pdf/10.1002/cphc.202400547]. [CrossRef]
Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. The Journal of Chemical Physics 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Physical Review A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Physical Review B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. The Journal of Chemical Physics 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. Journal of Computational Chemistry 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. The Journal of Chemical Physics 2019, 150, 154122. [Google Scholar] [CrossRef]
Grimme, S.; Brandenburg, J.G.; Bannwarth, C.; Hansen, A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. The Journal of Chemical Physics 2015, 143, 054107. [Google Scholar] [CrossRef]
Grimme, S.; Hansen, A.; Ehlert, S.; Mewes, J.M. r2SCAN-3c: A “Swiss army knife” composite electronic-structure method. The Journal of Chemical Physics 2021, 154, 064103. [Google Scholar] [CrossRef]
Fokin, A.A.; Zhuk, T.S.; Blomeyer, S.; Pérez, C.; Chernish, L.V.; Pashenko, A.E.; Antony, J.; Vishnevskiy, Y.V.; Berger, R.J.F.; Grimme, S.; Logemann, C.; Schnell, M.; Mitzel, N.W.; Schreiner, P.R. Intramolecular London Dispersion Interaction Effects on Gas-Phase and Solid-State Structures of Diamondoid Dimers. Journal of the American Chemical Society 2017, 139, 16696–16707. [Google Scholar] [CrossRef] [PubMed]
Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. The Journal of Chemical Physics 2020, 152, 224108. [Google Scholar] [CrossRef]
Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Computational Molecular Science 2022, 12, e1606. [Google Scholar] [CrossRef]
Vishnevskiy, Y.V. UNEX version 1.6, https://unex.vishnevskiy.group (accessed Fri Oct 13, 2023).
Arenas, B.E.; Batra, G.; Steber, A.L.; Bizzocchi, L.; Pietropolli Charmet, A.; Giuliano, B.M.; Caselli, P.; Harris, B.J.; Pate, B.H.; Guillemin, J.C.; Schnell, M. Rotational spectroscopy of imidazole: Accurate spectroscopic information for three vibrationally excited states and the heavy-atom isotopologues up to 295 GHz. Journal of Molecular Spectroscopy 2021, 378, 111452. [Google Scholar] [CrossRef]
Kisiel, Z.; Białkowska-Jaworska, E.; Pszczółkowski, L.; Milet, A.; Struniewicz, C.; Moszynski, R.; Sadlej, J. Structure and properties of the weakly bound trimer (H2O)2HCl observed by rotational spectroscopy. The Journal of Chemical Physics 2000, 112, 5767–5776. [Google Scholar] [CrossRef]
Xie, F.; Tikhonov, D.S.; Schnell, M. Electric nuclear quadrupole coupling reveals dissociation of HCl with a few water molecules. Science 2024, 384, 1435–1440. [Google Scholar] [CrossRef]
Winnewisser, G.; Maki, A.G.; Johnson, D.R. Rotational constants for HCN and DCN. Journal of Molecular Spectroscopy 1971, 39, 149–158. [Google Scholar] [CrossRef]
Creswell, R.; Winnewisser, G.; Gerry, M. Rotational spectra of the 13C and 15N isotopic species of cyanoacetylene. Journal of Molecular Spectroscopy 1977, 65, 420–429. [Google Scholar] [CrossRef]

Figure 1. Examplary molecular systems to demonstrate the effect of scaling factors (see main text for details). The atomic color scheme is the following: hydrogen – white, carbon – gray, nitrogen – blue, oxygen – red, and chlorine – green. The position of isotopic substitution in imidazole is shown with a yellow halo around the atom.

Table 1. Optimal scaling factors for rotational constants (

s_{opt}

) and their uncertainties (

σ_{opt}

) were determined for the listed quantum-chemical approximations with Equations 6 and 7, respectively. rRMSD denotes the values of the relative root-mean-square deviation (Equation 5) computed for the training dataset without scaling (

s = 1

) and with optimized scaling factor (

s = s_{opt}

Table 1. Optimal scaling factors for rotational constants (

s_{opt}

) and their uncertainties (

σ_{opt}

s = 1

) and with optimized scaling factor (

s = s_{opt}

Method			$s_{opt} \pm σ_{opt}$	rRMSD(s) $\times 100 %$
DF	Dn	Basis	$s_{opt} \pm σ_{opt}$	$s = 1$	$s = s_{opt}$
	D3(BJ)	def2-SVP	$1.008 \pm 0.001$	2.748	2.645
		def2-TZVP	$1.000 \pm 0.001$	2.225	2.225
	D4	def2-SVP	$1.008 \pm 0.001$	2.765	2.656
B3LYP		def2-TZVP	$1.000 \pm 0.001$	2.244	2.244
	D3(BJ)	def2-SVP	$0.995 \pm 0.001$	2.633	2.579
		def2-TZVP	$0.988 \pm 0.001$	2.530	2.202
	D4	def2-SVP	$0.995 \pm 0.001$	2.637	2.583
PBE0		def2-TZVP	$0.988 \pm 0.001$	2.535	2.206
PBEh-3c			$0.987 \pm 0.001$	3.092	2.778
$r^{2}$ SCAN-3c			$1.008 \pm 0.001$	2.689	2.577

Table 2. Comparison of experimental and theoretical rotational constants for a few examples of molecular systems: HCN and HCCCN,

{imidazole-}^{15}

N(1) isotopologue, and HCl(

H_{2}

O)₇ cluster (see Figure 1). “B3LYP” denotes results at the B3LYP-D3(BJ)/def2-TZVP level of theory, and PBE0 denotes results at the PBE0-D3(BJ)/def2-TZVP level of theory. Comparison for all other molecular systems can be found in an Excel spreadsheet in the Supporting Information.

Table 2. Comparison of experimental and theoretical rotational constants for a few examples of molecular systems: HCN and HCCCN,

{imidazole-}^{15}

N(1) isotopologue, and HCl(

H_{2}

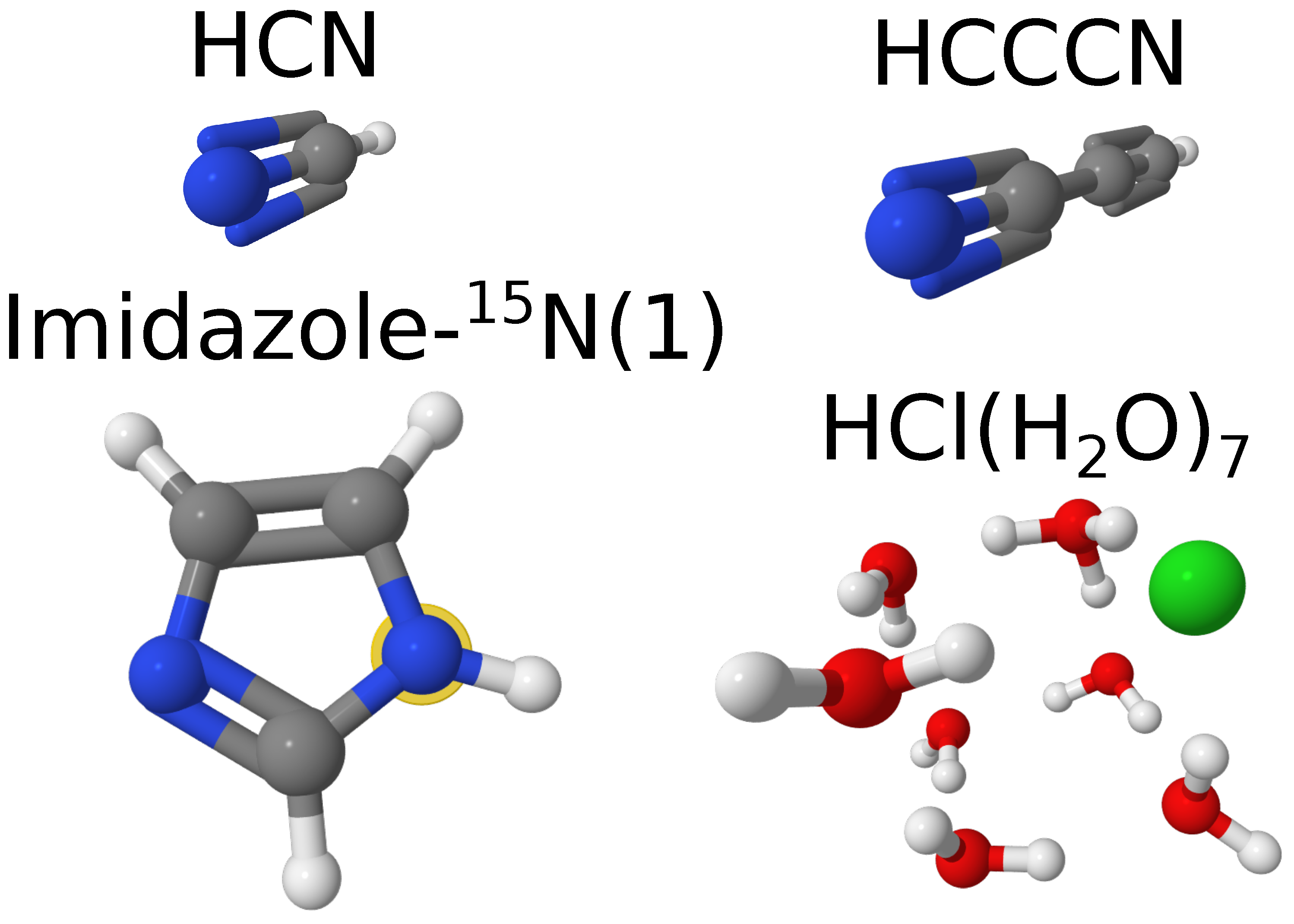
Molecular system	$A / B / C$	Rotational constant value [MHz]
		Experimental	Theoretical
			B3LYP	PBE0
			$s = 1$	$s = 1$	$s = 0.988$
HCN [50]	B	44316	44941	44969	44415
HCCCN [51]	B	4549	4591	4593	4537
${Imidazole-}^{15}$ N(1) [47]	A	9695	9756	9850	9729
	B	9188	9218	9271	9157
	C	4716	4740	4776	4717
HCl( $H_{2}$ O)₇ [49]	A	914	935	947	935
	B	737	739	750	740
	C	689	709	720	711

Table 3. Relative root-mean-square deviation (rRMSD, Equation 5) and mean absolute deviation (MAD, Equation 8) values for rotational constants from three illustrative test sets of molecular systems using the PBE0-D3(BJ)/def2-TZVP level of theory. The optimal scaling factor for this method (

s_{opt} = 0.988

) is taken from Table 1.

s_{opt} = 0.988

) is taken from Table 1.

Dataset	rRMSD(s) $\times 100 %$		MAD(s) [MHz]
Dataset	$s = 1$	$s = 0.988$	$s = 1$	$s = 0.988$
Linear molecules	1.0	0.3	33	16
Isotopologues	1.4	0.4	110	26
HCl( $H_{2}$ O)_n	7.9	6.8	132	115

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Scaling of Rotational Constants

Abstract

Keywords:

Subject:

1. Introduction

2. Scaling Procedure

3. Resulting Scaling Factors

4. Illustrative Cases

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe